3.6 Análise de Capacidade do Processo Multivariado
Em geral, a qualidade dos processos é avaliada por sua família de características da qualidade e não por apenas uma característica. Na maioria das situações, estas características estão correlacionadas, o que impossibilita sua análise individual. Além disso, também temos a situação em que a mesma característica é medida em diversos pontos de uma mesma peça. Por exemplo, em uma engrenagem do câmbio automotivo medimos seu diâmetro em diversos pontos e, como a engrenagem foi usinada no mesmo processo, estas medidas estão correlacionadas.
O uso de técnicas multivariadas tem se tornado cada vez mais necessárias. Iniciado com Hotelling em 1947, vários outros estudos sobre métodos de controle multivariados foram desenvolvidos. Destes, destacamos Croisser (1988), Lowry, Woodall, Champ e Rigdon (1992), Lowry e Montgomery (1995) e Mason e Young (1999).
Em um procedimento de análise da performance de processos multivariados, temos várias características da qualidade, em que cada uma tem seus limites de especificação. Devido ao efeito da correlação entre as características, surgiu a necessidade de desenvolver métodos para analisar a performance conjunta. Com isso, vários índices multivariados foram desenvolvidos.
Neste módulo vamos apresentar o procedimento utilizado para calcular os índices de performance para processos multivariados.
6.1 - Índices de performance do processo
Como objeto de estudo, vamos utilizar o índice proposto por Shahriari, Hubele e Lawrence (1995). Na verdade, eles propõem um vetor composto por três componentes. A primeira, chamada $C_{PM}$, mede a razão de áreas ou volumes (depende da dimensão), esta componente é análoga ao índice $C_{p}$ univariado que mede a razão entre o comprimento de variação dos limites de especificação e o comprimento de variação do processo. A segunda componente, chamada PV, está baseada na suposição de que o centro da região de tolerância é considerado como a média verdadeira da região do processo. A terceira componente do vetor, chamada LI, avalia a locação da região do processo (modificado) e da região de tolerância.
Primeira componente - ${C_{PM}}$
A primeira componente é definida por
$$C_{PM} = \left[\dfrac{\hbox{Volume da região de tolerância}}{\hbox{Volume da região modificada do processo}}\right]^{\frac{1}{\nu}}$$
em que $\nu$ representa o número de características.
Figura 3.6.1: Processo Multivariado.
Os limites do retângulo da região modificada do processo da Figura 3.6.1 ($LIP_{1}$, $LIP_{2}$, $LSP_{1}$ e $LSP_{2}$) são obtidos resolvendo o sistema de equações das primeiras derivadas da forma quadrática com respeito a cada característica (Nickerson (1994))
$$\left(\mathbf{X} - \mathbf{\mu}\right)^{\prime}~\mathbf{\Sigma}^{-1}~\left(\mathbf{X} - \mathbf{\mu}\right) = \chi^2_{(\nu,~\alpha)}$$
Assim,
$$LSP_i = \mu_i+ \sqrt{\dfrac{\chi^2_{(\nu,~\alpha)}~det\left(\mathbf{\Sigma}_i^{-1}\right)}{det\left(\mathbf{\Sigma}^{-1}\right)}}$$
$$LIP_i = \mu_i- \sqrt{\dfrac{\chi^2_{(\nu,~\alpha)}~det\left(\mathbf{\Sigma}_i^{-1}\right)}{det\left(\mathbf{\Sigma}^{-1}\right)}}$$
para $i = 1, \ldots, \nu$ sendo
-
$\mathbf{X}$: vetor aleatório em que $\mathbf{X}\sim N_\nu(\mu, \mathbf{\Sigma});$
-
$\mu$: vetor de médias do processo;
-
$\mu_i$: média do processo para a característica $i;$
-
$\mathbf{\Sigma}$: matriz de variância e covariância;
-
$\chi^2_{(\nu,~\alpha)}$: quantil da distribuição $\chi^2$ com $\nu$ graus de liberdade e nível de confiança $\alpha;$
-
$det\left(\mathbf{\Sigma}_i^{-1}\right)$: determinante da matriz obtida de $\mathbf{\Sigma}^{-1}$, desconsiderando a i-ésima linha e coluna.
Com isso, temos a primeira componente $C_{PM}$
$$C_{PM} = \left[\dfrac{\prod^{\nu}_{i=1}(LSE_i - LIE_i)}{\prod^{\nu}_{i=1}(LSP_i - LIP_i)}\right]^{\frac{1}{\nu}}$$
Segunda componente - PV:
Nesta componente, estamos interessados em avaliar a suposição de que o processo está centrado no alvo especificado. Aqui, adotaremos uma estratégia baseada no p-valor inerente da estatística de Hotelling para o teste:
$$\begin{cases} H_0: \mu = \mu_0 \hbox{ (Processo centrado);} \cr H_1: \mu \ne \mu_0 \hbox{ (Processo não centrado).} \end{cases}$$
em que
-
$\mu_0$: vetor de médias da região de tolerância (Target);
-
$\mu$: vetor de médias do processo.
Para o teste definido acima, utilizamos a estatística propostota por Hotelling (1947), definida como
$$T^2 = n~\left(\overline{\mathbf{X}} - \mu_0\right)^{\prime}~\mathbf{S}^{-1}~\left(\overline{\mathbf{X}} - \mu_0\right)$$
em que
-
$n$: tamanho de cada amostra;
-
$\overline{\mathbf{X}}$: vetor de médias amostrais do processo;
-
$S^{-1}$: inversa da matriz de variância e covariância amostral do processo.
Além disso, sob $H_0$,
$$\frac{n-\nu }{(n-1)\nu }T^2\sim F_{\nu,n-\nu}$$
em que $F_{\nu,n-\nu}$ representa a distribuição $F$ com $\nu$ graus de liberdade no numerador e $n-\nu$ no denominador.
Rejeitamos $H_0$ a um nível de significância $\alpha$ se $T^2_{obs} \geq \frac{(n-1)\nu}{n-\nu}F_{\alpha,\nu,n-\nu}$, em que $F_{\alpha,\nu,n-\nu}$ é o quantil de $\alpha %$ da distribuição $F_{\nu,n-\nu}$. Dessa maneira, podemos calcular o p-valor associado ao teste utilizando a seguinte estratégia:
$$\text{p-valor}=\mathbb{P}\left( T^2 \geq T_{obs} \left| \right. H_0\right)=\mathbb{P}\left( \frac{n-\nu}{(n-1)\nu}T^2 \geq \frac{n-\nu}{(n-1)\nu}T_{obs} \left| \right. H_0\right) =\mathbb{P}\left(F_{\nu,n-\nu} \geq \frac{n-\nu}{(n-1)\nu}T_{obs}\right).$$
Finalmente, definimos a segunda componente como:
$$PV=\text{p-valor}=\mathbb{P}\left(F_{\nu,n-\nu} \geq \frac{n-\nu}{(n-1)\nu}T_{obs}\right).$$
Note que $0 \leq PV \leq 1$, além disso, observamos que valores de PV próximos de zero indicam que o centro do processo está distante do valor do Target.
Terceira componente - $LI$:
A terceira componente é uma função indicadora, ou seja, assume valor 1 se a região modificada do processo está toda dentro da região de tolerância e, assume valor 0 caso contrário. Sendo assim,
$$LI = \begin{cases} 1, \hbox{ se a região modificada do processo está toda dentro da região de tolerância;} \cr 0, \hbox{ caso contrário.} \end{cases}$$
Dependendo do nível de confiança escolhido para construir a região de contorno do processo, a terceira componente, definida acima, pode indicar a quantidade de itens fora de especificação.
Para ilustrar o que foi discutido acima, consideremos o seguinte exemplo:
Exemplo 6.1.1
Consideremos os dados de um sistema de areia, dispostos na Tabela 3.6.1, em que as variáveis de interesse (características) são Compactabilidade e Plasticidade.
| Corrida | Compactabilidade | Plasticidade |
|---|---|---|
| E188 | 11,22 | 21,3 |
| E188 | 11,35 | 21,82 |
| E188 | 10,46 | 20,7 |
| E188 | 10,39 | 20,81 |
| E188 | 9,94 | 19,24 |
| E189 | 9,62 | 20,3 |
| E189 | 10,19 | 19,37 |
| E189 | 9,14 | 20,86 |
| E189 | 10,51 | 21,61 |
| E189 | 9,4 | 17,58 |
| E190 | 10,14 | 18,38 |
| E190 | 9,29 | 20,5 |
| E190 | 9,33 | 19,77 |
| E190 | 8,97 | 19,23 |
| E190 | 10,2 | 20,04 |
| E191 | 8,12 | 17,08 |
| E191 | 10,69 | 21,64 |
| E191 | 10,51 | 20,82 |
| E191 | 8,31 | 18,02 |
| E191 | 9,35 | 19,24 |
| E192 | 10,82 | 20,97 |
| E192 | 11,1 | 21,3 |
| E192 | 10,18 | 19,41 |
| E192 | 9,99 | 20,45 |
| E192 | 9,57 | 19,06 |
| E193 | 9,37 | 17,23 |
| E193 | 9,58 | 20,18 |
| E193 | 10,21 | 19,84 |
| E193 | 10,51 | 20,9 |
| E193 | 10,18 | 20,37 |
| E194 | 9,2 | 19,19 |
| E194 | 9,6 | 18,64 |
| E194 | 9,52 | 19,44 |
| E194 | 11,01 | 21,5 |
| E194 | 10,49 | 19,64 |
| E195 | 8,97 | 15,54 |
| E195 | 10,6 | 20,37 |
| E195 | 10,9 | 22,21 |
| E195 | 9,64 | 18,07 |
| E195 | 9,71 | 20,89 |
| E196 | 10,02 | 18,81 |
| E196 | 9,65 | 18,78 |
| E196 | 8,74 | 18,83 |
| E196 | 9,63 | 18,81 |
| E196 | 10,22 | 19,62 |
| E197 | 9,22 | 18,5 |
| E197 | 10,18 | 18,45 |
| E197 | 10,48 | 21,25 |
| E197 | 10,15 | 19,22 |
| E197 | 8,73 | 19,99 |
| E198 | 11,06 | 23,17 |
| E198 | 10,99 | 19,6 |
| E198 | 11,75 | 22,63 |
| E198 | 10,69 | 20,33 |
| E198 | 9,95 | 19,36 |
| E199 | 8,93 | 17,5 |
| E199 | 8,42 | 17,76 |
| E199 | 10,8 | 19,31 |
| E199 | 9,78 | 18,06 |
| E199 | 9,85 | 21,42 |
| E200 | 10,16 | 17,77 |
| E200 | 10,25 | 20,11 |
| E200 | 9,77 | 18,64 |
| E200 | 9,62 | 20,41 |
| E200 | 9,41 | 18,7 |
| E201 | 9,68 | 18,19 |
| E201 | 8,13 | 15,87 |
| E201 | 10,81 | 22,11 |
| E201 | 10,19 | 19,4 |
| E201 | 10,62 | 18,9 |
| E202 | 11,08 | 21,1 |
| E202 | 10,16 | 20,82 |
| E202 | 9,55 | 21,27 |
| E202 | 9,57 | 19,05 |
| E202 | 11,26 | 20,52 |
Tabela 3.6.1: Dados de um sistema de areia.
Para esses dados temos as seguintes especificações:
| Limites de Especificação | |||
|---|---|---|---|
| LIE | LSE | Alvo | |
| Compactabilidade | 7 | 12 | 9,9704 |
| Plasticidade | 16 | 24 | 19,7035 |
Tabela 3.6.2: Limites de Especificação
| Limites do Processo | ||
|---|---|---|
| LIP | LSP | |
| Compactabilidade | 8,05 | 11,88 |
| Plasticidade | 16,05 | 23,35 |
Tabela 3.6.3: LImite do Processo
Antes de fazer a análise de capacidade do processo precisamos saber se as variáveis de interesse são correlacionadas. Para obter a correlação entre essas variáveis podemos utilizar a ferramenta Matriz de Correlação do Software Action. Dessa forma, temos
| Compactabilidade | Plasticidade | |
|---|---|---|
| Compactabilidade | 1 | 0.6974 |
| Plasticidade | 0.6974 | 1 |
Tabela 3.6.4: Matriz de Correlação
Podemos ver que a correlação positiva (0,7) entre as variáveis Compactabilidade e Plasticidade é significativa. Portanto, concluímos que ambas as variáveis influenciam conjuntamente o processo.
Dessa forma, após algumas manipulações algébricas obtemos as componentes do vetor que representa o estudo de capacidade multivariada. Ou seja, a primeira componente é dada por
$$C_{PM} = \left[\dfrac{(12-7) \ast (24-16)}{(11,88-8,05) \ast (23,35-16,05)}\right]^{\frac{1}{2}} = 1,196$$
O valor do $C_{PM}$ encontrado indica que a região modificada do processo é menor do que a região de tolerância.
A segunda componente é dada por
$$PV = P\left(T^2~>~\dfrac{2 \ast (5-1)}{5-2}F_{(2,~3)}\right) = 1$$
sendo $n = 5$ o tamanho de cada amostra e $\nu = 2$ o número de características.
O p-valor igual a 1 significa que o processo está conseguindo manter a média próximo do valor central dos limites de especificação.
Por fim, temos a terceira componente, isto é
$$LI = 1$$
indicando que a elipse está toda dentro dos limites de especificação.
A seguir temos os resultados obtidos pelo Software Action para esse exemplo.
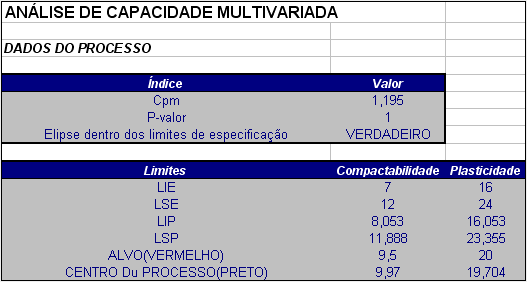
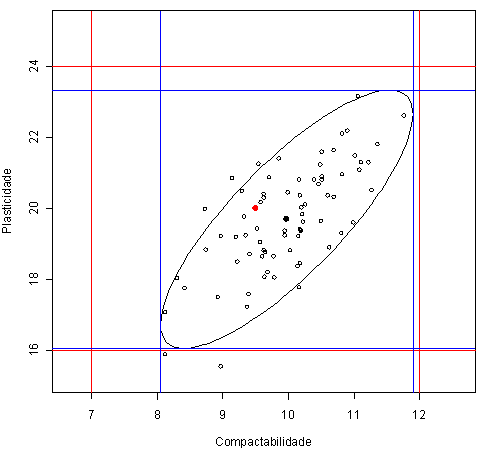
Figura 3.6.2: Gráfico da análise de capacidade do processo multivariado.
A Figura 3.6.2 apresenta o gráfico bivariado (Compactabilidade versus Plasticidade), em que os limites de especificação correspondem às linhas vermelhas e os limites da região modificada do processo às linhas azuis.
Exemplo 6.1.2
Consideremos os dados referentes às características da areia utilizada na fabricação do molde do platô de embragem.
| CORRIDA | COMPACTABILIDADE | RCV.1 | PLASTICIDADE |
|---|---|---|---|
| E188 | 36,5 | 22,026 | 28,87 |
| E188 | 36,5 | 22,026 | 28,87 |
| E188 | 36,75 | 22,3 | 28,572 |
| E188 | 36,75 | 22,3 | 28,572 |
| E188 | 36,571 | 21,12 | 29,924 |
| E189 | 36,571 | 21,12 | 29,924 |
| E189 | 36,571 | 21,12 | 29,924 |
| E189 | 36,571 | 21,12 | 29,924 |
| E189 | 37 | 20,33 | 29,88 |
| E189 | 37 | 20,33 | 29,88 |
| E190 | 37 | 20,33 | 29,88 |
| E190 | 36,167 | 21,182 | 29,368 |
| E190 | 36,167 | 21,182 | 29,368 |
| E190 | 37,625 | 20,423 | 30,047 |
| E190 | 37,625 | 20,423 | 30,047 |
| E191 | 36,5 | 22,134 | 29,822 |
| E191 | 36,5 | 22,134 | 29,822 |
| E191 | 36,5 | 22,134 | 29,822 |
| E191 | 36,833 | 22,402 | 29,178 |
| E191 | 36,833 | 22,402 | 29,178 |
| E192 | 38 | 21,788 | 29,625 |
| E192 | 38 | 21,788 | 29,625 |
| E192 | 38 | 21,788 | 29,625 |
| E192 | 38 | 21,788 | 29,625 |
| E192 | 37,4 | 21,93 | 28,774 |
| E193 | 39 | 21,98 | 28,72 |
| E193 | 39 | 21,98 | 28,72 |
| E193 | 37,333 | 21,507 | 28,812 |
| E193 | 38,667 | 20,39 | 26,397 |
| E193 | 37,167 | 23,132 | 29 |
| E194 | 37,167 | 23,132 | 29 |
| E194 | 37,167 | 23,132 | 29 |
| E194 | 37,167 | 23,132 | 29 |
| E194 | 36,667 | 20,86 | 29,24 |
| E194 | 36,667 | 20,86 | 29,24 |
| E195 | 37,167 | 20,835 | 28,33 |
| E195 | 37,167 | 20,835 | 28,33 |
| E195 | 38 | 19,653 | 30,885 |
| E195 | 38 | 19,653 | 30,885 |
| E195 | 38 | 19,653 | 30,885 |
| E196 | 38 | 19,653 | 30,885 |
| E196 | 38 | 19,867 | 28,543 |
| E196 | 38 | 19,867 | 28,543 |
| E196 | 38 | 19,867 | 28,543 |
| E196 | 38 | 19,867 | 28,543 |
| E197 | 39,75 | 20,05 | 30,255 |
| E197 | 36,5 | 20,993 | 30,568 |
| E197 | 36,5 | 20,993 | 30,568 |
| E197 | 36,5 | 20,993 | 30,568 |
| E197 | 38,25 | 20,733 | 28,84 |
| E198 | 38,25 | 20,733 | 28,84 |
| E198 | 38,25 | 20,733 | 28,84 |
| E198 | 38,25 | 20,733 | 28,84 |
| E198 | 37,25 | 19,48 | 29,225 |
| E198 | 37,25 | 19,48 | 29,225 |
| E199 | 37,643 | 19,513 | 28,818 |
| E199 | 37,643 | 19,513 | 28,818 |
| E199 | 37,643 | 19,513 | 28,818 |
| E199 | 37,667 | 20,613 | 29,035 |
| E199 | 37,667 | 20,613 | 29,035 |
| E200 | 37,667 | 20,613 | 29,035 |
| E200 | 37,667 | 20,613 | 29,035 |
| E200 | 37,714 | 20,333 | 28,415 |
| E200 | 38,5 | 21,722 | 28,695 |
| E200 | 38,5 | 21,722 | 28,695 |
| E201 | 36,833 | 22,423 | 26,685 |
| E201 | 36,833 | 22,423 | 26,685 |
| E201 | 36,833 | 22,423 | 26,685 |
| E201 | 37 | 21,323 | 29,592 |
| E201 | 37,333 | 20,29 | 28,74 |
| E202 | 37,333 | 20,29 | 28,527 |
| E202 | 37,333 | 20,29 | 28,527 |
| E202 | 37,333 | 20,29 | 28,527 |
| E202 | 37 | 20,995 | 28,527 |
| E202 | 35 | 22,78 | 28,655 |
| E203 | 35 | 22,78 | 26,24 |
| E203 | 37,167 | 21,083 | 26,24 |
| E203 | 37,333 | 20,68 | 29,663 |
| E203 | 36 | 18,645 | 28,027 |
| E203 | 36 | 19,523 | 26,93 |
| E204 | 36 | 19,523 | 27,907 |
| E204 | 36 | 19,523 | 27,907 |
| E204 | 36 | 19,523 | 27,907 |
| E204 | 38 | 20,363 | 27,907 |
| E204 | 38 | 20,363 | 29,843 |
| E205 | 38 | 20,363 | 29,843 |
| E205 | 37,5 | 20,62 | 29,843 |
| E205 | 37,5 | 20,62 | 29,037 |
| E205 | 37,667 | 21,147 | 29,037 |
| E205 | 37,667 | 21,147 | 29,273 |
| E206 | 37,667 | 21,147 | 29,273 |
| E206 | 37,667 | 21,147 | 29,273 |
| E206 | 38 | 21,407 | 29,273 |
| E206 | 38 | 21,407 | 29,067 |
| E206 | 37,667 | 20,753 | 29,067 |
| E207 | 37,667 | 20,753 | 28,393 |
| E207 | 38,333 | 19,89 | 28,393 |
| E207 | 36,333 | 21,923 | 27,45 |
| E207 | 36 | 22,89 | 27,753 |
| E207 | 38 | 22,603 | 28,357 |
| E208 | 37 | 21,19 | 29,79 |
| E208 | 37 | 21,19 | 28,523 |
| E208 | 39 | 20,24 | 29,57 |
| E208 | 39 | 20,24 | 29,57 |
| E208 | 39 | 20,24 | 27,557 |
| E209 | 37,333 | 19,75 | 27,557 |
| E209 | 36,333 | 19,9 | 27,557 |
| E209 | 36,333 | 19,9 | 27,89 |
| E209 | 36,333 | 19,9 | 27,633 |
| E209 | 39 | 20,29 | 27,633 |
| E210 | 37,667 | 20,937 | 27,633 |
| E210 | 37,667 | 20,937 | 27,5 |
| E210 | 37,667 | 20,5 | 27,84 |
| E210 | 38 | 19,547 | 27,84 |
| E210 | 38,5 | 21,5 | 28,377 |
| E211 | 39 | 20,24 | 27,557 |
| E211 | 37,333 | 19,75 | 27,89 |
| E211 | 36,333 | 19,9 | 27,633 |
| E211 | 36,333 | 19,9 | 27,633 |
| E211 | 36,333 | 19,9 | 27,633 |
| E212 | 39 | 20,29 | 27,5 |
| E212 | 37,667 | 20,937 | 27,84 |
| E212 | 37,667 | 20,937 | 27,84 |
| E212 | 37,667 | 20,5 | 28,377 |
| E212 | 38 | 19,547 | 27,53 |
Tabela 3.6.5: Dados.
Para esses dados temos as seguintes especificações:
| Limites de Especificação | |||
|---|---|---|---|
| LIE | LSE | Alvo | |
| Compactabilidade | 35 | 38 | 37 |
| RCV.1 | 20 | 22 | 21 |
| Plasticidade | 27 | 30 | 29 |
Tabela 3.6.6: Limites de Especificação
| Limites do Processo | ||
|---|---|---|
| LIP | LSP | |
| Compactabilidade | 34,97 | 39,79 |
| RCV.1 | 18,09 | 23,65 |
| Plasticidade | 25,96 | 31,59 |
Tabela 3.6.7: Limites do Processo
Antes de fazer a análise de capacidade do processo precisamos saber quais variáveis são correlacionadas, com isso podemos trabalhar apenas com aquelas características que conjuntamente influenciam o processo. Para obter a correlação entre as variáveis podemos utilizar a ferramenta Matriz de Correlação disponibilizada pelo Software Action.
Neste exemplo vamos considerar que todas as variáveis são correlacionadas para mostrarmos os cálculos quando temos mais de duas características.
Cuidado!
A correlação deve sempre ser analisada no caso multivariado.
Dessa forma, após algumas manipulações algébricas obtemos as componentes do vetor que representa o estudo de capacidade multivariada. Assim, a primeira componente é dada por
$$C_{PM} = \left[\dfrac{(38-35) \ast (22-20) \ast (30-27)}{(39,79-34,97) \ast (23,65-18,09) \ast (31,59-25,96)}\right]^{\frac{1}{3}} = 0,492$$
O valor do $C_{PM}$ encontrado indica que a região modificada do processo é maior do que a região de tolerância.
A segunda componente é dada por
$$PV = P\left(T^2~>~\dfrac{3 \ast (5-1)}{5-3}F_{(3,~2)}\right) = 1$$
sendo $n = 5$ o tamanho de cada amostra e $\nu = 3$ o número de características.
O p-valor igual a 1 significa que o processo está conseguindo manter a média próximo do valor central dos limites de especificação.
Por fim, temos a terceira componente, isto é
$$LI = 0$$
indicando que a região modificada do processo não está toda contida na região de tolerância e, consequentemente, produzindo peças fora dos limites de especificação.
A seguir temos os resultados obtidos pelo Software Action para esse exemplo.
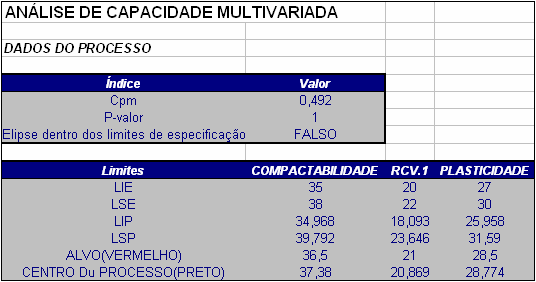
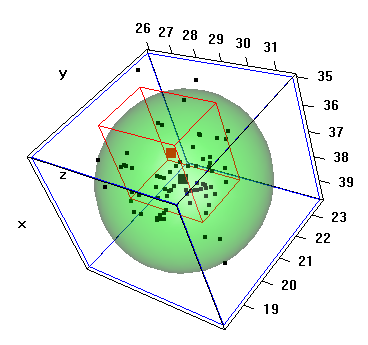
Figura 3.6.3: Gráfico da análise de capacidade do processo multivariado.
