10. Aprendizado de Máquina

O termo aprendizado de máquina refere-se a detecção automática de padrões de comportamento presentes em conjuntos de dados. Em função da complexidade dos problemas envolvidos com dados, programas de computadores usuais não conseguem extrair detalhes sobre o comportamento dos dados. Ao tomarmos como exemplo o comportamento humano, sabemos que muito do nosso comportamento é aprendido e aprimorado com base em nossa experiência. O aprendizado de máquina está relacionado com o desenvolvimento de algoritmos que tem a habilidade de “aprender'' e se “adaptar'' com a experiência que adquirimos ao longo do tempo. Neste trabalho, vamos tratar de forma simples e rigorosa os principais termos relacionados com o aprendizado de máquina:

• O que é aprendizado;
• O que significa uma máquina aprender;
• Como quantificar a quantidade de informação necessária para aprender um conceito;
• É sempre possível aprender?
• Como saber que um processo de aprendizado é “falha'' ou “sucesso''?

O principal objeto deste texto é o aprendizado de máquina supervionado. Isto significa que queremos desenvolver algoritmos capazes de “aprender'' com dados o comportamento de um processo, conforme Figura 1. De forma geral, aprendizado é o processo de transformar a experiência em conhecimento. A entrada de um algoritmo de aprendizado são os dados de treinamento, que representam a experiência, e a saída nos fornece o conhecimento. Em geral, o conhecimento também toma a forma de um algoritmo que pode ser utilizado para compreender o comportamento do processo.

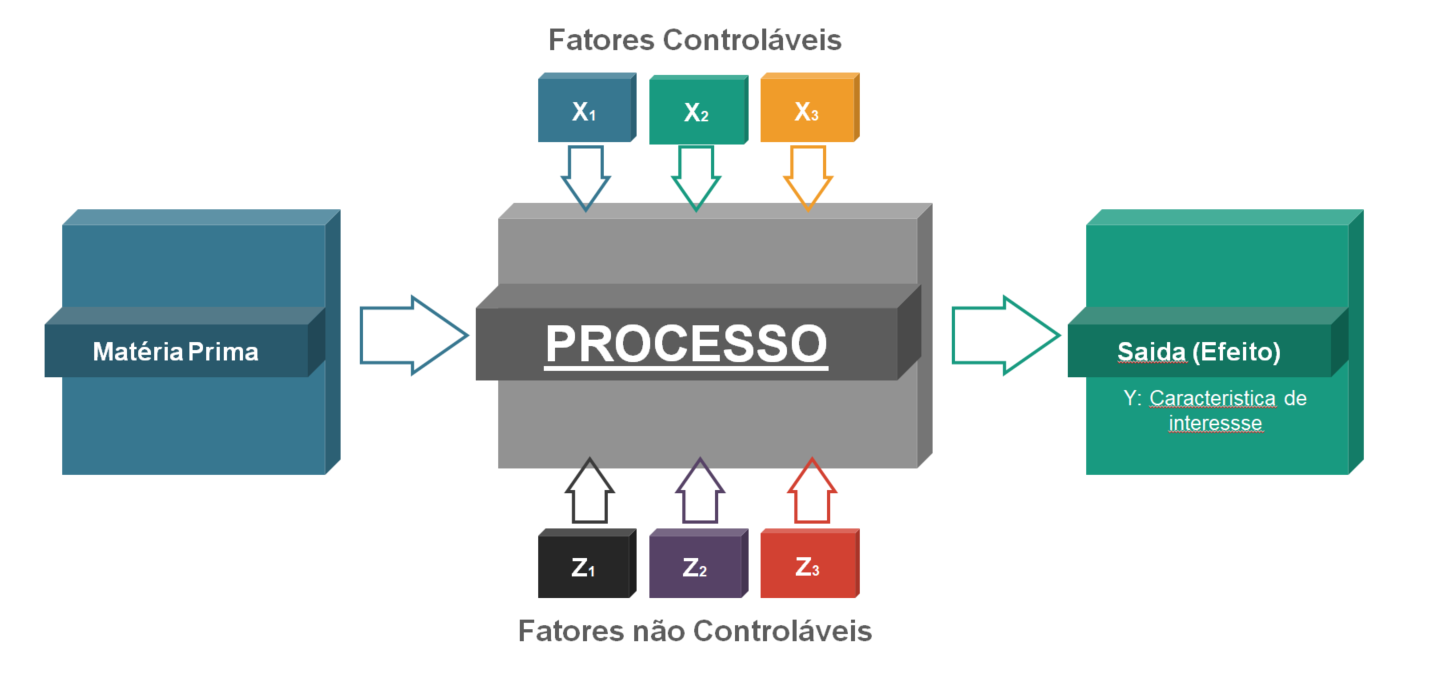
Figura 1: Aprendizado de Máquina Supervionado

No aprendizado de máquina supervionado queremos entender a relação entre a entrada e a saída de um processo. Para isto, temos um conjunto de dados rotulados com informação sobre a saída (Y)

e a respectiva entrada (X), conforme descrito na Figura 1. A partir disto, queremos desenvolver um algoritmo que relaciona os dados com um preditor. Dado a entrada do processo X, queremos prever a saída Y. Os fatores não controlados Z

correspondem a ruído no processo e não são observados, fato que nos leva a propor um modelo de probabilídade para tratar o problema de aprendizado de máquina. Ao considerarmos um modelo de probabilidade, a maneira pela qual os dados são gerados é crucial para o desenvolvimento de algoritmos. A forma mais usual consiste em supor que os dados são gerados de forma independente e identicamente distribuiídos (iid). Com estas hipóteses são estudados os principais algoritmos de aprendizado de máquina como, redes neurais, máquina de vetores de suporte (Support Vector Machine - SVM), árovre binomial, floresta aleatória, entre outros.

Como extensão da hipótese de geração dos dados de forma iid, também trataremos o caso de aprendizado de máquina sequencial ou online. Neste caso, admitimos uma estrutura qualquer de dependência entre os dados. Por exemplo, a maioria dos processos industriais são observados ao longo do tempo, no qual admitimos uma dependência temporal entre os dados. Neste contexto, vamos apresentar o problema de aprendizado de máquina como um problema de jogos soma zero e com isso, derivar os principais algortimos de aprendizado de máquina sequencial como, Exponencial Ponderado (EWA), Having, Winnow, Seguindo o Lider Perturbado e algoritmos desenvolvidos pelos autores do texto.

No aprendizado de máquina supervionado e no aprendizado de máquina sequencial, o aprendiz não interage ou intervém no processo. Em muitos casos, queremos intervir no processo de forma a “otimizar” a performance do processo. Como consequência, queremos “controlar” a entrada X

de tal forma a “otimizar” um funcional da saída Y

do processo correspondente a sua performance. Neste contexto, vamos introduzir o conceito de aprendizado com reforço. Aqui, vamos apresentar a pesquisa desenvolvida pelos autores que utiliza o princípio da programação dinâmica como estratégia para derivar algoritmos para tratar o problema de aprendizado com reforço. O texto apresentado é baseado nos seguinte trabalhos:

1. N. Cesa-Bianchi and G. Lugosi. Prediction, Learning, and Games. Cambridge University Press, 2006.

2. O. Bousquet, S. Boucheron, and G. Lugosi. (2004) - Introduction to Statistical Learning Theory. Advanced Lectures in Machine Learning, pages 169–207. springer.

3. S. Boucheron , O. Bousquet 2 and G Lugosi (2005) - THEORY OF CLASSIFICATION: A SURVEY OF SOME RECENT ADVANCES.

4. D. Blackwell and Meyer A. Girshick. Theory of games and statistical decisions. Wiley publications in statistics. Dover Publications, 1979.

5. D. Leão, J. B. R. do Val, M. Fragoso (2000) - Nonstationary Zero Sum Stochastic Games with Incomplete Observation. In 39 IEEE Conference on Decision and Control, Sidnei.

6. D. Leão, A. Ohashi, A. Simas (2018) - . Weak differentiability of Wiener functionals and occupation times. BULLETIN DES SCIENCES MATHEMATIQUES, v. 149, p. 23-65.

7. D. Leão, A. Ohashi, A. Simas (2018) - A weak version of path-dependent functional Itô calculus. ANNALS OF PROBABILITY, v. 46, p. 3399-3441.

8. D. Leão, A. Ohashi, F. Russo (2019) - Discrete-type approximations for non-Markovian optimal stopping problems. Journal of applied probability, vol. 56, pp. 981-1005.

9. D. Leão, A. Ohashi e F. Souza (2020) - Solving non-Markovian Stochastic Control Problems driven by Wiener Functionals, ArXiv. https://arxiv.org/abs/2003.06981.

10. E. Rosalino, A. da Silva, J. Baczynski e D. Leão (2018) - Pricing and hedging barrier options. APPLIED STOCHASTIC MODELS IN BUSINESS AND INDUSTRY, v. 34, p. 499-512,

11. L. G. Valiant. A theory of learnable. Proc. of the 1984 STOC, pages 436–445, 1984.

12. V. N. Vapnik. Statistical learning theory. J. Wiley, 1998.

13. A. Wald. Statistical decision functions. John Wiley and Sons, 1950.

Aprendizado

Para ilustramos o conceito de aprendizado, vamos refletir sobre o processo de aprendizado de animais domésticos. Sabemos que diversos ratos aprendem a evitar comida envenenada. Quando ratos encontram uma comida com aparência e cheiro novos, eles comem pequenas quantidades e esperam para avaliar as consequências. Caso a comida tenha sabor adequado e não cause consequência fisiológica negativa, eles a utilizam para alimentação. Se a comida produzir efeito fisiológico ruim, a nova comida será relacionada com efeito negativo, e consequentemente, os ratos não a comerão. Neste caso, temos um algoritmo de aprendizado em ação, o animal utiliza experiência passada para desenhar um algoritmo de detecção de veneno em alimentos. Se a experiência passada com o alimento for negativa, o animal prevê que este alimento terá efeito negativo quando encontrado no futuro.

Inspirado no exemplo dos ratos, suponha que queremos prever se um processo terá rendimento acima de 90%

. Suponha que queremos programar uma máquina para aprender a prever o comportamento deste processo. Uma solução simples é dada pelo algoritmo de aprendizado dos ratos. A máquina acompanha o processo durante um período de tempo e memoriza todos os ajustes de processo que levaram a um rendimento superior a 90%. Em uma nova situação do processo, a máquina procura por um ajuste igual no passado nos quais tivemos rendimento superior a 90%. Baseado nesta experiência passada, ela sugere o comportamento do processo para a atual situação. Caso tenhamos a mesma situação no passado memorizada pela máquina, o rendimento será acima de 90%. Caso contrário, o rendimento será abaixo de de 90%. Este processo de aprendizado é denominado ``aprendizado por memorização''.

Este tipo de aprendizado apresenta alguns problemas. Primeiro, a habilidade de tratar com situações diferentes das encontradas no passado. Um bom algoritmo de aprendizado tem que ser capaz de evoluir de exemplos simples para situações mais gerais, denominada inferência indutiva. No exemplo dos ratos, quando estes encontram um novo tipo de comida, eles aplicam seu algoritmo (medem) de detecção de veneno para avaliar e classificar (efeito positivo ou efeito negativo) a nova comida. Da mesma forma, devemos medir características do processo que fornecem informação sobre o comportamento do mesmo. Assim, quando uma nova situação surgir, a máquina pode prever o comportamento do processo para a atual situação, com confiança apropriada.

De forma geral, aprendizado corresponde ao processo de ganhar conhecimento da estrutura de dependência entre as observações de entrada e saída de um processo e/ou produto baseado em dados. A seguir, vamos estabelecer uma definição formal (matemática) para cada um dos termos envolvidos com o processo de aprendizado.

Introdução ao Aprendizado de Máquina Estatístico

Nesta seção, vamos definir os componentes do modelo de aprendizado estatístico. Considere um processo de fermentação do caldo (vinho) proveniente da cana de açúcar. O rendimento do processo de fermentação é definido como a porcentagem de açúcar do caldo que é transformada em álcool. Neste caso, podemos medir diversas características do caldo para melhorar o algoritmo de aprendizado. Suponha que medimos o teor de açúcar e o pH do caldo da cana de açúcar na entrada do processo de fermentação. Ao observarmos o processo, registramos a terna $z_1, z_2, y$ no qual $z_1$ corresponde ao teor de açúcar do caldo, $z_2$ corresponde ao pH do caldo e $y$ é o rótulo (sucesso ou fracasso) relacionado com as variáveis de entrada $x=(z_1, z_2)$.

Na sequência, introduzimos parte da notação que será utilizada neste trabalho. Seja $E$ um espaço métrico completo e separável equipado com a $\sigma$-álgebra de Borel $\beta(E)$. Dado um subconjunto $G \in \beta(E)$, a $\sigma$ álgebra traço de $G$ é definida por $\beta(G) = (G \cap A: A \in \beta(E) )$. Neste caso, dizemos que $G$ é um espaço de Borel equipado com a $\sigma$-álgebra traço $\beta(G))$. Denotamos por $\mathbb{R}$ o conjunto dos números reais com a respectiva $\sigma$-álgebra de Borel $\beta (\mathbb{R})$. Para qualquer espaço mensurável $(Y, \beta (Y))$, denotamos por $Y^n$ para $n=1,2, \cdots, \infty$ o produto Cartesiano de Y com ele mesmo $n$-vezes e por $(\beta(Y) )^n$ a $\sigma$-álgebra dos cilindros mensuráveis de $Y^n$ com base em $(1, \cdots , n)$ (a $\sigma$-álgebra produto). Além disso, sabemos que $(\beta(Y))^n = \beta(Y^n)$ para todo $n=1,2, \cdots, \infty$. Para os leitores não familiarizados com a terminologia de espaços de Borel, considere o espaço de Borel como um subconjunto do espaço Euclidiano $\mathbb{R}^d$, para algum $d=1,2,3, \cdots, \infty$. Os elementos de $Y^n$ são denotados por ${\bf y}_n= (y_1, y_2 , \cdots , y_n)$. De forma geral, a entrada do processo de aprendizado é composto por três elementos: espaço domínio, espaço de rótulos e o conjunto de dados.

1. Espaço domínio: Considere $(\chi, \beta(\chi))$ um espaço de Borel correspondente ao espaço domínio, no qual $\beta(\chi)$ corresponde a $\sigma$-álgebra de Borel dos subconjuntos de $\chi$. Em muitos exemplos, tomamos $\chi$ um subconjunto do $\mathbb{R}^d$ com $d=1,2,3, \ldots$ . Os elementos $x \in \chi$ são as entradas aleatórias com distribuição de probabilidade $\mathbb{P_{\chi}}$ definida sobre $(\chi, \beta(\chi))$. Em geral, não conhecemos a probabilidade $\mathbb{P_\chi}$. No exemplo do processo de fermentação, temos que $\chi = (x=(z_1, z_2) : 0 < z_1 < 1, ~ z_2 > 0 ) \subset \mathbb{R}^2$;

2. Espaço de Rótulos: Considere $(\mathcal{Y}, \beta(\mathcal{Y}))$ um espaço de Borel correspondente ao espaço de rótulos. Para cada $x \in \chi$ associamos um rótulo $y \in \mathcal{Y}$ correspondente a saída do processo. Por exemplo, no processo de fermentação, temos que $\mathcal{Y}=(0,1)$, no qual $1$ representa um processo de fermentação com rendimento acima de $90(porcentagem)$ (sucesso) e $0$ o contrário (fracasso).

3. Conjunto de dados de treinamento: Denotamos por ${\bf o_n} = ((x_1,y_1) , \cdots , (x_n , y_n))$ a sequência de pontos rotulados correspondente aos dados de treinamento. Esta é a entrada que temos disponível para conduzir o processo de aprendizado. Por exemplo, ao acompanharmos o processo de fermentação observamos ${\bf o_n} = (((z_{11},z_{21}),y_1), \ldots , ((z_{1n},z_{2n}),y_n)).$ Para uma amostra de tamanho $n$, denotamos por $\mathbb{O}^n = (\chi \times \mathcal{Y})^n$ o espaço nos quais os dados tomam valores, que será equipado com $\sigma$-álgebra de Borel $\beta(\mathbb{O}^n)$, para todo $n=1,2, \ldots$. Como $\mathbb{O}=\chi \times \mathcal{Y}$ é um espaço de Borel, sabemos que $\mathbb{O}^n$ também é um espaço de Borel, para todo $n=1,2, \ldots , \infty$. O espaço de todos os conjuntos de dados é denotado por $\mathbb{O}^\infty$ e equipado com a $\sigma$-álgebra de Borel $\beta(\mathbb{O}^\infty)$. De forma geral, qualquer conjunto de dados ${\bf o_n}$ de tamanho $n$ pode ser definido como um elemento de $\mathbb{O}^\infty$ através da projeção coordenada $\pi^n: \mathbb{O}^\infty \rightarrow \mathbb{O}^n$, que carrega as sequências $(o_1, o_2 , \ldots) \in \mathbb{O}^\infty$ nas primeiras $n$-coordenadas $(o_1, \ldots , o_n) \in \mathbb{O}^n$.

O problema de aprendizado de máquina consiste desenvolver uma regra de aprendizado (algoritmo) capaz de prever o rótulo futuro do processo $y \in \mathcal{Y}$ baseado nos dados de entrada $x \in \chi$. Tal regra é dada por uma função $h : \chi \rightarrow \mathcal{Y}$. Esta função é denominada um preditor ou uma hipótese ou um classificador. O preditor será utilizado para prever novos rótulos baseados nos pontos de entrada $(x \in \chi)$. No exemplo, esta regra $h$ será utilizada para prever o comportamento do processo (sucesso ou fracasso) baseado nas variáveis de entrada (teor de açúcar e o pH). Denotamos por $\bar{\mathcal{H}} := ( h: \chi \rightarrow \mathcal{Y}, ~ \text{Borel mensurável})$ a classe de preditores possíveis e $\mathcal{H} \subset \bar{\mathcal{H}}$ uma subclasse de preditores admissíveis. Vamos supor que $\mathcal{H}$ também é um espaço de Borel equipado com a $\sigma$-álgebra $\beta(\mathcal{H})$. Um algoritmo de aprendizagem é uma função Borel mensurável $A: \mathbb{O}^n \rightarrow \mathcal{H}$, tal que para cada amostra ${\bf o}_n \in \mathbb{O}^n$ associa um preditor $A({\bf o}_n) = h({\bf o}_n , \cdot) \in \mathcal{H}$ na classe de preditores admissíveis, para todo $n \geq 1$.

O processo de geração dos dados é crítico para o entendimento da estrutura de aprendizado. Assumimos que existe uma probabilidade $\mathbb{P_\chi}$ definida sobre $(\chi , \beta(\chi))$. É importante comentarmos que não temos qualquer conhecimento sobre esta distribuição de probabilidade $\mathbb{P}_\chi$. Com respeito aos rótulos, admitimos que existe uma probabilidade de transição $\nu(\cdot \mid \cdot): \beta(\mathcal{Y}) \times \chi \rightarrow [0,1]$, que relaciona a entrada $x \in \chi$ do processo com o rótulo $y \in \mathcal{Y}$ correspondente à saída do processo. Obviamente, que a probabilidade de transição $\nu$ também é desconhecida. A partir destes componentes, admitimos que cada elemento $ (x,y) \in \mathbb{O}$ é amostrado de uma distribuição de probabilidade conjunta dada por

$$\mathbb{P} (A \times B)= \int_B \nu (A \mid x) \mathbb{P}_{\chi} (dx), \quad A\in \beta(\mathcal{Y}) , B \in \beta(\chi),$$

definida sobre $(\chi \times \mathcal{Y} , \beta(\chi) \times \beta(\mathcal{Y}))$. O ponto crítico é que não conhecemos a probabilidade conjunta $\mathbb{P}$. A única informação que temos sobre a probabilidade $\mathbb{P}$ está nos dados de treinamento. Uma forma simples de chegarmos a probabilidade de transição $\nu$ consiste em admitirmos que existe uma função $f: \chi \rightarrow \mathcal{Y}$ Borel mensurável que corresponde à “verdadeira” função geradora de rótulos. Neste caso, para cada $x \in \chi$ existe um único rótulo $y=f(x)$. Assim, temos que

A partir destes elementos do sistema de aprendizado, precisamos desenvolver uma estratégia para escolher preditores na classe $\mathcal{H}$ de preditores admissíveis. Neste sentido, necessitamos de uma função que avalia a performance dos preditores. Uma função Borel mensurável e limitada $\ell : \mathbb{O} \times \mathcal{H} \rightarrow [0, \bar{a}]$ é denominada função perda, no qual $\bar{a}$ é uma constante positiva. A função risco é dada pelo valor esperado da função perda relacionada com um preditor $h \in \mathcal{H}$ e com uma distribuição de probabilidade $\mathbb{P}$ sobre $(\mathbb{O} , \beta(\mathbb{O}))$, na qual

$$L(\mathbb{P} , h) = \mathbb{E}_{\mathbb{P}} \left[ \ell (\cdot , h) \right], \quad \mathbb{P} \in \mathcal{P}(\mathbb{O}), ~ ~ h \in \mathcal{H},$$

$\mathcal{P}(\mathbb{O})$ corresponde ao espaço de todas as probabilidade definidas sobre $(\mathbb{O} , \beta (\mathbb{O}))$ e $\mathbb{E}_{\mathbb{P}}$ é a esperança tomada com respeito a probabilidade $\mathbb{P}$. Formalmente, queremos encontrar um preditor $h^\star \in \mathcal{H}$ que minimize a função risco $L(\mathbb{P}, \cdot)$,

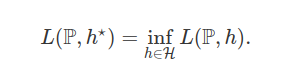
Desde que $(\mathbb{O} , \beta(\mathbb{O}))$ é um espaço de Borel, sabemos que $\mathcal{P}(\mathbb{O})$ também é um espaço de Borel equipado com a topologia da convergência fraca. Além disso, se a função risco $L: \mathcal{P}(\mathbb{O}) \times \mathcal{H}$ for semicontínua inferiormente e o espaço de preditores admissíveis $\mathcal{H}$ for compacto, existe uma função $\Phi: \mathcal{P}(\mathbb{O}) \rightarrow \mathcal{H}$ que é Borel mensurável tal que

$$L(\mathbb{P}, \Phi(\mathbb{P})) = \inf_{h\in \mathcal{H}} L(\mathbb{P} , h).$$

Com isso, basta tomarmos $h^\star = \Phi(\mathbb{P})$. Agora, observe que $h^\star$ é uma função da probabilidade $\mathbb{P}$, que é desconhecida. Portanto, não temos como utilizar $h^\star$ na prática.

Para ilustrarmos a abrangência da formulação do problema de aprendizado de máquina proposto acima, consideramos os seguintes exemplos.

1. Regressão: Tomamos $\chi$ e $\mathcal{Y}$ como um subconjunto do $\mathbb{R}^d$ e $\mathbb{R}$, respectivamente. A classe de preditores admissíveis $\mathcal{H}$ corresponde ao conjunto de funções $h:\chi \rightarrow \mathbb{R}$ Borel mensuráveis e limitadas. Neste caso, a função perda é dada por $\ell ((x,y),h) = (y - h(x))^2$.

No exemplo de rendimento do processo temos o par $(X,Y)$, no qual o domínio é dado por $X=(Z_1 , Z_2)$ com $Z_1$ o teor de açúcar e $Z_2$ o pH do caldo. Neste caso, o espaço de rótulos é binário $\mathcal{Y}= (0,1)$. Dado uma probabilidade $\mathbb{P} \in \mathcal{P}(\mathbb{O})$ e um preditor $h \in \bar{\mathcal{H}}$ quaisquer, a função de risco é dada pela a probabilidade de erro de classificação na forma

Se a distribuição de probabilidade $\mathbb{P}$ é conhecida, o classificador de Bayes $h^{\star}$ é o que apresenta menor erro de classificação. Na prática, temos acesso apenas ao conjunto de dados de treinamento ${\bf o}_n=((x_i , y_i) : i=1, \cdots , n)$ que são amostrados da distribuição de probabilidade $\mathbb{P}$ desconhecida. Portanto, não temos como utilizar o classificador de Bayes na prática. Na sequência, vamos introduzir o primeiro princípio básico da teoria de aprendizado de máquina.

Minimização do Risco Empírico

O algoritmo de aprendizado de máquina $A: \mathbb{O}^n \rightarrow \mathcal{H}$ tem como entrada (domínio) um conjunto de dados rotulados ${\bf o_n}$ amostrado de uma distribuição de probabilidade desconhecida $\mathbb{P}$ definida sobre $(\mathbb{O} , \beta(\mathbb{O}))$. A partir dos dados de treinamento on∈On, o algoritmo de aprendizado nos fornece como saída um preditor $h({\bf o_n} , \cdot) \in \mathcal{H}$. O objetivo do algoritmo é fornecer um preditor que minimiza a função risco com respeito a probabilidade $\mathbb{P}$ desconhecida.

Desde que não conhecemos a probabilidade $\mathbb{P}$, a função risco não pode ser diretamente acessada. Uma forma de contornar este problema consiste em utilizar a função de risco empírica. Para toda amostra de dados ${\bf o}_n = ((x_1,y_1) , \ldots , (x_n , y_n)) \in \mathbb{O}^n$, a função de risco empírica é definida por:

$$L_E({\bf o_n} , h) := \frac{1}{n} \sum_{i=1}^n \ell \left( (x_i , y_i) , h \right), \quad n \geq 1.$$

Como a amostra rotulada ${\bf o_n}$ está disponível e representa o processo em estudo, faz sentido buscarmos uma solução que se ajuste bem aos dados de treinamento. Assim, introduzimos o seguinte princípio de aprendizado de máquina “Minimização do Risco Empírico'' (MRE). O algoritmo de aprendizado dado pelo princípio da MRE nos fornece um preditor $h_E({\bf o}_n , \cdot)$ que minimiza a função de risco empírica, isto é,

$$L_E({\bf o_n} , h_E({\bf o_n})) = \inf_{h \in \mathcal{H}} L_E({\bf o_n} , h), \quad {\bf o_n} \in \mathbb{O}^n.$$

Para o problema de classificação binária, a função de risco empírica corresponde ao erro de classificação do preditor. Neste caso, dado uma amostra de treinamento ${\bf o}_n = ((x_i , y_i): i=1, \ldots , n)$ e um preditor $h \in \mathcal{H}$, temos que

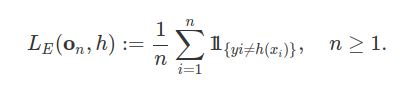
Um ponto importante relacionado com a função de risco empírica é que ela depende apenas dos dados on e do preditor admissível $h$.

Sobreajuste - Overfitting

Apesar do princípio da MRE ser uma regra bem natural, sem o devido cuidado, este método pode facilmente falhar. Para demonstrarmos tal falha, vamos retornar ao problema de classificação das bateladas do processo de fermentação. Considere uma amostra ${\bf o}_n=((x_1,y_1), \cdots , (x_n,y_n))$ distribuída uniformemente no quadrado cinza conforme a figura 1.

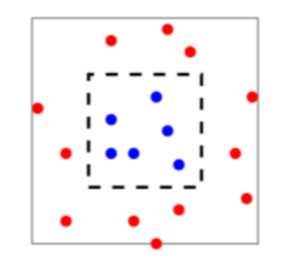
Figura 1: Amostra Rotulada

Assumimos que a probabilidade $\mathbb{P}_{\chi}$ tem distribuição uniforme sobre o quadrado cinza. Na figura 1, suponha que a área do quadrado cinza é igual a 2 e a área do quadrado preto (tracejado) é igual a 1. Também admitimos a existência de uma função $ f: \chi \rightarrow (0,1) $ que determina os rótulos na forma: $ f(x):=1 $ se x pertence ao quadrado preto e $ f(x):=0 $ caso contrário. Considere o seguinte preditor

Com isso, obtemos que $ L_E({\bf o}_n,h_E({\bf o}_n, x))=0 $ para toda amostra $ {\bf o}_n \in \mathbb{O}^n $ e, consequentemente, este preditor minimiza a função de risco empírica. Com isso, dizemos que $ h_E({\bf o}_n, \cdot) $ satisfaz ao princípio da MRE para todo $ n=1,2, \ldots $.

Como a distribuição de probabilidade $ \mathbb{P_\chi} $ é uniforme no quadrado cinza, sabemos que um preditor que assume 1 em um número finito de pontos e zero no restante, é igual a zero $\mathbb{P_\chi}$-quase certamente. Assim, obtemos que

$$L(\mathbb{P} , h_E({\bf o_n}))= \mathbb{E_{\mathbb{P}}} [\ell (\cdot , h_E({\bf o_n})) ] = \mathbb{E_{\mathbb{P}}} [\ell(\cdot , 0) ] = \frac{1}{2}.$$

Portanto, encontramos um preditor $h_E({\bf o_n})$ que tem um desempenho muito bom com os dados, mas seu desempenho prático é ruim. Este fenômeno é conhecido como sobreajuste (overfitting). Intuitivamente, este fenômeno ocorre quando o preditor se ajuste muito bem aos dados de treinamento.

Algoritmo de Aprendizado PAC

Acabamos de mostrar que o princípio da MRE pode nos levar ao problema de sobreajuste. Apesar deste problema, a ideia não é abandonarmos este princípio, mas propormos formas de resolver o problema do sobreajuste. A partir desta seção, vamos propor condições para que o princípio da MRE não nos leve ao sobreajuste. Neste sentido, queremos condições para que se um preditor tenha boa performance para o risco empírico, então este preditor também tenha boa performance para função de risco com probabilidade arbitrária $\mathbb{P} \in \mathcal{P}(\mathbb{O})$.

Uma solução comum consiste em restringirmos a classe de preditores admissíveis $\mathcal{H}$ para aplicarmos o princípio da MRE. Formalmente, escolhemos uma classe apropriada de preditores $\mathcal{H}$ que depende do processo e das características que estudamos. Dado uma classe de preditores admissíveis $\mathcal{H} \subset \bar{\mathcal{H}}$ e um conjunto de dados de treinamento ${\bf o_n} \in \mathbb{O}^n$, queremos um preditor $h_E({\bf o_n})$ que minimiza a função de risco empírica restrita a classe $\mathcal{H}$,

$$L_E ({\bf o_n} , h_E({\bf o_n})) = \inf_{h \in \mathcal{H}} L_E ({\bf o_n} , h), \quad n \geq 1.$$

Observe que o preditor $h_E({\bf o_n} , \cdot)$ que minimiza a função de risco empírica não depende da probabilidade P, ele depende do conjunto de dados de treinamento ${\bf o_n} \in \mathbb{O}^n$ e da classe de controles admissíveis $\mathcal{H}$. O algoritmo de aprendizado definido pelo princípio da MRE é denotado por $A_E$. Neste caso, temos que $A_E({\bf o_n}) = h_E({\bf o_n} , \cdot)$.

Ao restringirmos a classe de preditores admissíveis, introduzimos um vício ao princípio da MRE, que é denominado vício indutivo. Com isso, uma questão fundamental à teoria de aprendizado de máquina consiste em escolher a classe de preditores admissíveis $\mathcal{H}$

no qual o princípio da MRE não nos leva a um problema de sobreajuste. Intuitivamente, quando mais restrita for a classe de preditores admissíveis menor a possibilidade de sobreajuste, porém maior o vício indutivo.

Obviamente que a questão de existência de um preditor que minimiza a função de risco empírica deve ser avaliada. Suponha que a função de perda $\ell: \mathbb{O} \times \mathcal{H} \rightarrow [0,\bar{a}]$ seja semicontínua inferior e H seja um espaço compacto separável. Então, temos que $L_E: \mathbb{O}^n \times \mathcal{H} \rightarrow [0,\bar{a}]$ também é uma função semicontínua. Assim, segue do teorema de seleção Borel mensurável que existe uma função $h_E : \mathbb{O}^n \rightarrow \mathcal{H}$ que é Borel mensurável e satisfaz o princípio da minimização do risco empírico.

No caso do problema de classificação, provamos que o preditor de Bayes apresenta o menor risco na classe de todos os preditores possíveis $(\bar{\mathcal{H}})$. Porém, o fato de desconhecermos a probabilidade $\mathbb{P}$ inviabiliza a aplicação do preditor de Bayes. Para contornarmos esta situação, vamos relaxar a hipótese de que o preditor proposto pelo algoritmo de aprendizado minimize a função de risco. Neste sentido, queremos que nosso algoritmo de aprendizado encontre um preditor admissível cuja função de risco não seja muito maior que a função de risco de algum preditor referência, como o preditor de Bayes. A diferença máxima de performance corresponde ao parâmetro de vício do algoritmo de aprendizado.

Para continuarmos com esta seção, vamos fazer uma hipótese sobre a geração dos dados. Admitimos que as amostras são retiradas de forma independente e identicamente distribuídas (iid) a partir da probabilidade $\mathbb{P}$. Assim, para um conjunto de dados de tamanho $n\geq 1$, a probabilidade conjunta é determinada pela probabilidade produto e denotada por $\mathbb{P}^n$.

Seja $A: \mathbb{O}^n \rightarrow \mathcal{H}$ um algoritmo de aprendizado e $\mathbb{P} \in \mathcal{P}(\mathbb{O})$. Desde que a função de risco $L(\mathbb{P} , A({\bf o_n}))$ depende do conjunto de dados de treinamento on e este conjunto de dados é uma amostra aleatória simples (iid) da probabilidade $\mathbb{P}$, concluímos que o preditor A(on) é um elemento aleatório e, consequentemente, a função de risco $L(\mathbb{P} , A({\bf o_n}))$ é uma variável aleatória. Interpretamos a variável aleatória $L(\mathbb{P} , A({\bf o_n}))$

como a esperança condicional

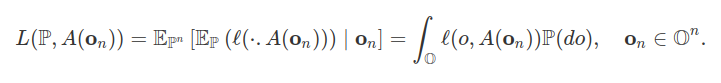
Do ponto de vista probabilístico não temos certeza de que o conjunto de dados de treinamento ${\bf o_n}$ é representativo da probabilidade $\mathbb{P}$. Se voltarmos ao exemplo do rendimento do processo, temos (mesmo que pequena) a possibilidade de que todas as observações selecionadas resultem em rendimento acima de 90% (sucesso). Neste caso, o princípio da MRE nos leva a um preditor constante no qual todos os rendimentos são “sucesso''. Como consequência, precisamos administrar a probabilidade de obtermos uma amostra que não seja representativa.

Para isto, propomos que a probabilidade de selecionarmos um conjunto de dados de treinamento ${\bf o_n}$ para o qual $L(\mathbb{P} , A({\bf o_n}))$ não é muito grande seja controlada. Em geral, denotamos por δ a probabilidade de obtermos uma amostra não representativa e, por (1−δ) o parâmetro de confiança. Por outro lado, não necessariamente atingimos a performance do preditor referência, pois não conhecemos a probabilidade $\mathbb{P} \in \mathcal{P}(\mathbb{O})$. Assim, introduzimos um parâmetro de vício $\epsilon \in (0,1)$, que corresponde a diferença máxima de performance entre o preditor proposto e o preditor referência. Para isto, admitimos que $(\mathcal{H} , \beta(\mathcal{H}))$ seja um espaço de Borel e que o algoritmo de aprendizado $A: \mathbb{O}^n \rightarrow \mathcal{H}$ seja uma função Borel mensurável para todo $n \geq 1$. Assim, temos que $L(\mathbb{P}, A(\cdot)): \mathbb{O} \rightarrow [0,\bar{a}]$ é uma variável aleatória.

Aprendizado PAC: Uma classe de preditores $\mathcal{H}$ tem a propriedade PAC (Provavelmente Aproximadamente Correto) se existe uma função $m_{\mathcal{H}} : (0,1)^2 \rightarrow \mathbb{N}$ e um algoritmo de aprendizado A com a seguinte propriedade: Para todo $\epsilon , \delta \in (0,1)$ e toda a probabilidade $\mathbb{P} \in \mathcal{P}(\mathbb{O})$, o algoritmo de aprendizado A retorna um preditor tal que,

$$\mathbb{P}^n \left[ {\bf o_n} \in \mathbb{O}^n : L(\mathbb{P} , A({\bf o_n})) \leq \inf_{h \in \mathcal{H}} L(\mathbb{P} , h) + \epsilon \right] \geq 1- \delta , \quad \forall ~ n \geq m_{\mathcal{H}}(\epsilon , \delta).$$

Dizemos que $1-\delta \in(0,1)$ corresponde ao parâmetro de confiança da previsão, enquanto que $\epsilon$ corresponde ao parâmetro de vício. A função $m_{\mathcal{H}}$ é denominada complexidade PAC da classe de preditores admissíveis $\mathcal{H}$.

Com a definição de aprendizado PAC, o preditor proposto pelo algoritmo de aprendizado é ótimo se o seu risco não é muito maior que o menor risco entre todos os preditores admissíveis em $\mathcal{H} \subset \bar{\mathcal{H}}$. Também exigimos que o preditor seja admissível $(h \in \mathcal{H})$, o que nos leva ao conceito de aprendizado próprio.

Convergência Uniforme

A ideia da estratégia de aprendizado descrita neste texto é bem simples. Primeiro, restringimos a classe de preditores admissíveis $\mathcal{H} \subset \bar{\mathcal{H}}$ para evitar o sobreajuste. Na sequência, aplicamos o princípio da MRE restrito a subclasse $\mathcal{H}$. A partir de um conjunto de dados de treinamento ${\bf o}_n \in \mathbb{O}^n$, a ideia do princípio da MRE consiste em avaliarmos o risco empírico de todos os preditores admissíveis $(h \in \mathcal{H})$ e, escolher o preditor $h_E \in \mathcal{H}$ que apresenta o menor risco empírico.

Com o princípio da MRE, esperamos que o preditor $h_E \in \mathcal{H}$ tenha função de risco próxima ao mínimo da função da risco com respeito a classe de preditores admissíveis. Em outras palavras, queremos que a classe de preditores admissíveis $\mathcal{H}$ admita a propriedade PAC com algoritmo de aprendizado $A_E$ dado pelo princípio da MRE. Para isto, devemos assegurar que a função de risco empírico de todos os membros de $\mathcal{H}$ são boas aproximações para a função de risco do respectivo membro.

Conjunto de dados $\epsilon$-representativo: Considere $\epsilon \in (0,1)$. Um conjunto de dados de treinamento ${\bf o}_n \in \mathbb{O}^n$ é denominado $\epsilon$-representativo, com respeito ao espaço de observações $\mathbb{O}$, a classe de preditores admissíveis $\mathcal{H}$, a função perda $\ell$ e a probabilidade $\mathbb{P}$ se,

$$\sup_{h \in \mathcal{H}} ~ \big| L_E ({\bf o}_n , h) - L(\mathbb{P} , h) \big| \leq \epsilon .$$

Na sequência, mostramos que se um conjunto de dados de treinamento é $\epsilon/2$-representativo, o algoritmo de aprendizado $A_E$ obtido pelo princípio da MRE tem um bom retorno.

Lema 1: Assumimos que o conjunto de dados de treinamento ${\bf o}_n$ é $\epsilon/2$-representativo. Então, qualquer saída do algoritmo de aprendizado $A_E ({\bf o}_n)$ obtido pelo princípio da MRE satisfaz

$$L(\mathbb{P} , A_E ({\bf o_n})) - \inf_{h \in \mathcal{H}} L(\mathbb{P} , h) \leq \epsilon.$$

Prova:

Para todo $h \in \mathcal{H}$, temos que

$$L(\mathbb{P} , A_E ({\bf o_n}));\leq; L_E ({\bf o_n} , A_E ({\bf o_n})) + \frac{\epsilon}{2} \leq L_E ({\bf o_n} , h) + \frac{\epsilon}{2} \leq ;L(\mathbb{P} , h) + \frac{\epsilon}{2} + \frac{\epsilon}{2} = L(\mathbb{P} , h) + \epsilon$$

nos quais a primeira e a terceira desigualdade são consequências da definição de de conjunto de dados $\epsilon$-representativo e a segunda desigualdade é consequência do princípio da MRE.

O lema 1 nos diz que um algoritmo $A_E$ dado pelo princípio da MRE é um aprendizado PAC se, com probabilidade pelo menos $1- \delta$, podemos escolher um conjunto de dados $\epsilon$-representativo. A seguinte condição de convergência uniforme formaliza este requerimento.

Definição de Convergência Uniforme: Dizemos que uma classe de preditores admissíveis $\mathcal{H} \subset \bar{\mathcal{H}}$ tem a propriedade de convergência uniforme se, existe uma função $m_{\mathcal{H}}^{UC} : (0,1)^2 \rightarrow \mathbb{N}$ tal que:

$$\sup_{\mathbb{P} \in \mathcal{P}(\mathbb{O})} ~\mathbb{P}^n \left[ {\bf o}_n \in \mathbb{O}^n : \sup_{h \in \mathcal{H}} \big| L_E ({\bf o}_n , h) - L(\mathbb{P} , h) \big| \leq \epsilon \right] \geq 1- \delta , \quad n \geq m_{\mathcal{H}}^{UC}(\epsilon , \delta),$$

para todo $\epsilon , \delta \in (0,1)$.

O termo uniforme se refere ao fato de que a função de complexidade $m_{\mathcal{H}}^{UC}$ define um tamanho de amostra independente do preditor admissível $(h \in \mathcal{H})$ e da probabilidade $\mathbb{P} \in \mathcal{P}(\mathbb{O})$. Similar a definição da complexidade para um aprendizado PAC $(m_{\mathcal{H}})$, a função $m_{\mathcal{H}}^{UC}$ estabelece a menor complexidade de uma amostra para obtermos a convergência uniforme. Neste caso, definimos o tamanho mínimo do conjunto de dados ($m_{\mathcal{H}}^{UC}$) que garante com probabilidade pelo menos $1-\delta$ que o conjunto de dados de treinamento será $\epsilon$-representativo. Dados $\epsilon , \delta \in (0,1)$ e $n \geq m_{\mathcal{H}}^{UC} (\epsilon , \delta)$, a propriedade da convergência uniforme nos diz que

$$\mathbb{P}^n \left[ {\bf o_n} \in \mathbb{O}^n : \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq \epsilon \right] \geq 1- \delta,$$

para todo probabilidade $\mathbb{P} \in \mathcal{P}(\mathbb{O})$. Como consequência do lema 1, obtemos que

$$({\bf o_n} \in \mathbb{O}^n: \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq \frac{\epsilon}{2} ) \subset ( {\bf o_n} \in \mathbb{O}^n: L(\mathbb{P} , h_E({\bf o_n})) - \inf_{h \in \mathcal{H}} L(\mathbb{P} , h) \leq \epsilon )$$

Assim, derivamos o seguinte Teorema.

Teorema 1: Se uma classe $\mathcal{H}$ tem a propriedade de convergência uniforme com função de complexidade $m_{\mathcal{H}}^{UC}$, então esta classe também tem a propriedade de aprendizado PAC com $m_{\mathcal{H}} (\epsilon , \delta) \leq m_{\mathcal{H}}^{UC} (\epsilon/2 , \delta)$. Além disso, o princípio da MRE nos fornece um algoritmo de aprendizado PAC com a classe $\mathcal{H}$.

Prova:

Como consequência da propriedade de convergência uniforme, temos que

$$\mathbb{P}^n ({\bf o_n} \in \mathbb{O}^n: L(\mathbb{P} , h_E({\bf o_n})) - \inf_{h \in \mathcal{H}} L(\mathbb{P} , h) \leq \epsilon ) \geq \mathbb{P}^n ( {\bf o_n} \in \mathbb{O}^n: \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq \frac{\epsilon}{2} ) \geq 1-\delta,$$

para todo $n \geq m_{\mathcal{H}}^{UC} (\frac{\epsilon}{2} , \delta)$

A partir do Teorema 1 concluímos que a propriedade de convergência uniforme é suficiente para mostrarmos que uma determinada classe $\mathcal{H}$ de preditores admissíveis tenha a propriedade PAC. Ao tomarmos o complementar em relação a propriedade de convergência uniforme, obtemos que

$$\mathbb{P}^n [ {\bf o_n} \in \mathbb{O}^n : \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \geq \epsilon ] \leq \delta.$$

Pelo teorema de extensão de Kolmogorov, sabemos que existe uma única probabilidade $\mathbb{P}^\infty$ definida sobre $(\mathbb{O}^\infty , \beta (\mathbb{O}^\infty))$ tal que a projeção em $(\mathbb{O}^n , \beta (\mathbb{O}^n))$ coincide com $\mathbb{P}^n$, para todo $n \geq 1$. Com isso, obtemos que

$$\sup_{\mathbb{P}^\infty \in \mathcal{P}(\mathbb{O}^\infty)} \mathbb{P}^\infty \left[ {\bf o} \in \mathbb{O}^\infty : \sup_{h \in \mathcal{H}} \big| L_E (\pi_n ({\bf o}) , h) - L(\mathbb{P} , h) \big| \geq \epsilon \right] \leq \delta, \quad n \geq m_{\mathcal{H}}^{UC} (\epsilon , \delta),$$

no qual $\pi_n : \mathbb{O}^\infty \rightarrow \mathbb{O}^n $denota a projeção coordenada para todo $n \geq 1$. Como consequência, obtemos que $L_E (\pi_n ({\bf o}) , h)$ converge uniformemente em probabilidade para $L(\mathbb{P} , h)$.

Classes de Preditores Finitos

Como consequência do Teorema PAC para convergência uniforme (Teorema 1), para mostrarmos que toda classe finita é um aprendizado PAC basta provarmos que a propriedade de convergência uniforme é válida. Fixado $\epsilon , \delta \in (0,1)$, precisamos encontrar um tamanho amostral $m (\epsilon, \delta)$ tal que para toda probabilidade $\mathbb{P}$, temos que

$$\mathbb{P}^n \left( {\bf o_n} \in \mathbb{O}^n : \sup_{h \in \mathcal{H}} \big|L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq \epsilon, ~ \forall ~ h \in \mathcal{H} \right) \geq 1- \delta , \quad n \geq m (\epsilon, \delta).$$

Ao tomarmos o complementar, obtemos que

$$\mathbb{P}^n \left( {\bf o_n} \in \mathbb{O}^n : \sup_{h \in \mathcal{H}} \big|L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| > \epsilon \right) < \delta .$$

Desde que $\mathcal{H} = (h_1, h_2, \cdots , h_N)$ é um conjunto finito $(N\in \mathbb{N})$, obtemos que

$$( {\bf o_n} \in \mathbb{O}^n : \sup_{h \in \mathcal{H}} \big|L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| > \epsilon ) = \bigcup_{h \in \mathcal{H}} ( {\bf o_n} \in \mathbb{O}^n : \big|L_E ({\bf o_n}, h) - L(\mathbb{P} , h) \big| > \epsilon ) \in \beta(\mathbb{O}^n)$$

e, consequentemente

$$ \mathbb{P}^n \left( {\bf o_n} \in \mathbb{O}^n : \sup_{h \in \mathcal{H}} \big|L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| > \epsilon \right) \leq \sum_{h \in \mathcal{H}} \mathbb{P}^n \left({\bf o_n} \in \mathbb{O}^n : \big|L_E ({\bf o_n}, h) - L(\mathbb{P} , h) \big| > \epsilon \right). $$

Na sequência, vamos mostrar que cada componente da soma na equação acima é suficientemente pequeno para um determinado tamanho do conjunto de dados. Sabemos que

$$ L(\mathbb{P} , h ) = \mathbb{E_{\mathbb{P}}} \left(\ell (\cdot , h) \right) \quad \text{e} \quad L_E ({\bf o_n} , h) = \frac{1}{n} \sum_{i=1}^n \ell ((x_i , y_i) , h). $$

Desde que ${\bf o_n}$ é uma amostra aleatória simples (iid), concluímos que

$$ \mathbb{E_{\mathbb{P}}} \left[ L_E ({\bf o_n} , h) \right] = \left[ \frac{1}{n} \sum_{i=1}^n \ell (\cdot , h) \right] = \mathbb{E_{\mathbb{P}}} \left[ \ell (\cdot , h) \right] = L(\mathbb{P} , h ) . $$ Portanto, a quantidade $\mid L_E (\mathbb{S} , h) - L(\mathbb{P} , h) \mid$ expressa o desvio da variável aleatória $L_E ({\bf o_n} , h)$ em torno do seu valor esperado $L(\mathbb{P} , h )$. Desde que ${\bf o_n}$ é uma amostra aleatória simples, a lei dos grande números nos garante que a variável aleatória $L_E ({\bf o_n} , h)$ converge em probabilidade para o seu valor esperado $L(\mathbb{P} , h )$, para todo $h \in \mathcal{H}$. Porém, a lei dos grande números não nos fornece uma taxa de convergência. Para isto, vamos utilizar a desigualdade de Hoeffding que quantifica a diferença entre médias empíricas e o seu valor esperado.

Lema 1: Desigualdade de Hoeffding

Considere $(\Omega , \mathcal{F}, \mu)$ um espaço de probabilidade. Seja $Z_1 , Z_2 , \cdots$ uma sequência de variáveis aleatórias iid definidas sobre $\Omega , \mathcal{F}, \mu$ com $\mathbb{E} (Z_i)=\theta$ e $\mu \left(a \leq Z_i \leq b \right)=1$. Então, para todo $\epsilon > 0$, temos que

$$ \mu \left[ \left| \frac{1}{n} \sum_{i=1}^n Z_i - \theta \right| > \epsilon \right] \leq 2 \exp \left(\frac{-2 n \epsilon^2}{(b-a)^2}\right). $$

Desde que a função perda $\ell$ é não negativa e limitada por $\bar{a}$ e o conjunto de dados ${\bf o_n}$ é uma amostra aleatória simples, segue da desigualdade de Hoeffding que

$$\mathbb{P}^n \left( {\bf o_n} \in \mathbb{O}^n : \big|L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| > \epsilon \right) \leq 2 \exp \left(\frac{-2 n \epsilon^2}{(\bar{a})^2}\right).$$

A partir destas equações, concluímos que

$$ \mathbb{P}^n \left( {\bf o_n} \in \mathbb{O}^n : \sup_{h \in \mathcal{H}} \big|L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| > \epsilon \right) \leq \sum_{h \in \mathcal{H}} 2 \exp \left(\frac{-2 n \epsilon^2}{(\bar{a})^2}\right) = 2 Card \left( \mathcal{H} \right) \exp \left(\frac{-2 n \epsilon^2}{(\bar{a})^2}\right) , $$ no qual $ Card (\cdot)$ representa a cardinalidade do conjunto. Ao escolhermos,

$$ n \geq \bar{a}^2 \frac{Ln(2 Card (\mathcal{H})/\delta)}{2 \epsilon^2 }, $$ obtemos que

$$ \mathbb{P}^n \left( {\bf o_n} \in \mathbb{O}^n : \sup_{h \in \mathcal{H}} \big|L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| > \epsilon \right) \leq \delta . $$

Teorema 1: Classes Finitas

Seja $\mathcal{H}$ uma classe finita de preditores admissíveis e $\ell : \mathbb{O} \times \mathcal{H} \rightarrow [0, \bar{a}]$ a função perda. Então, a classe $\mathcal{H}$ satisfaz a propriedade de convergência uniforme com função de complexidade

$$ m_{\mathcal{H}}^{UC} (\epsilon , \delta) \leq \bar{a}^2 \frac{Ln(2 Card (\mathcal{H})/\delta)}{2 \epsilon^2 }. $$ Em particular, temos que a classe $\mathcal{H}$ também satisfaz a propriedade PAC com função de complexidade

$$ m_{\mathcal{H}} (\epsilon , \delta) \leq m_{\mathcal{H}}^{UC} (\epsilon , \delta) \leq \bar{a}^2 \frac{Ln(2 Card (\mathcal{H})/\delta)}{2 \epsilon^2 }. $$

A partir do Teorema 1, concluímos que o aprendizado PAC depende da cardinalidade da classe de preditores admissíveis $\mathcal{H}$.

Decomposição do Risco

Dado um conjunto de dados de treinamento ${\bf o}_n$ e um algoritmo de aprendizado $A_E({\bf o}_n)$ obtido via o princípio da MRE, podemos decompor a função de risco na forma:

$$ L(\mathbb{P} ,A_E({\bf o_n})) = \epsilon_{app} + \epsilon_{est}, \quad \text{nos quais} \quad \epsilon_{app} := \inf_{h \in \mathcal{H}} L(\mathbb{P} , h), \quad \epsilon_{est} := L(\mathbb{P} , A_E({\bf o_n})) - \inf_{h \in \mathcal{H}} L(\mathbb{P} , h). $$

O erro de aproximação $(\epsilon_{app})$ é o menor risco atingido por um preditor na classe $\mathcal{H}$ de preditores admissíveis. Este termo mede o risco em restringirmos a classe de preditores e, é denominado vício indutivo. O erro de aproximação não depende do tamanho da amostra, sendo determinado pela classe $\mathcal{H}$. Quanto mais abrangente for a classe de preditores admissíveis $\mathcal{H}$, menor será o erro de aproximação. Mesmo sem impor restrições na classe de preditores admissíveis, o erro de aproximação não necessariamente será nulo. Por exemplo no caso de classificação binária, sempre teremos o erro do preditor de Bayes.

O erro de estimação $(\epsilon_{est})$ corresponde a diferença entre o erro de aproximação e o erro obtido pelo algoritmo de aprendizado derivado do princípio da MRE. O erro de estimação é consequência do fato de que o risco empírico é uma estimativa da função risco. Desta forma, o preditor que minimiza o risco empírico também é uma estimativa do preditor que minimiza a função de risco. A qualidade de estimação depende do tamanho da amostra e da complexidade (tamanho) da classe de preditores admissíveis. Como mostramos na seção Classes de Preditores Finitos, se a classe de preditores admissíveis $\mathcal{H}$ for finita, o erro de estimação $(\epsilon_{est})$ é diretamente proporcional a cardinalidade da classe $\mathcal{H}$ e inversamente proporcional ao tamanho da amostra. Assim, podemos interpretar a cardinalidade da classe de preditores admissíveis como uma medida de complexidade.

De forma geral, nosso principal objetivo consiste em minimizar a função de risco. Em face disto, lidamos com o paradigma do vício indutivo e da complexidade da classe de preditores admissíveis. Por um lado, se escolhemos a classe $\mathcal{H}$ muito rica (complexa) diminuímos o erro de aproximação, mas aumentamos o erro de estimação, o que pode nos levar ao problema de sobreajuste (overfitting). Por outro lado, se escolhemos $\mathcal{H}$ pouco rica (menos complexa) podemos reduzir o erro de estimação, mas aumentamos o erro de aproximação, o que nos leva ao problema de ajuste pobre (underfitting).

O erro de aproximação depende do conhecimento prévio que temos da classe de preditores admissíveis e da probabilidade desconhecida $\mathbb{P}$. Além disso, o aprendizado PAC requer que o erro de estimação seja uniformemente limitado em relação ao conjunto de todas as probabilidades $\mathbb{P} \in \mathcal{P}(\mathbb{O})$. Nosso objetivo consiste em caracterizar que classes de preditores admissíveis $\mathcal{H}$ tem a propriedade PAC e consequentemente, determinar a complexidade amostral $(m_{\mathcal{H}})$ para aplicarmos o algoritmo de aprendizado dado pelo princípio da MRE.

Classificação Binária

Na seção Classe de Preditores Finitos, mostramos que qualquer classe de preditores admissíveis finita é um aprendizado PAC. Todavia, muitas classes interessantes não são finitas. No caso de classes de preditores finitas, a complexidade do aprendizado PAC é determinada pela cardinalidade (complexidade) da classe. Então, para ampliar nossa classe de preditores admissíveis, precisamos encontrar uma forma melhor de medir a complexidade de uma classe de funções. Para isto, vamos introduzir a complexidade de Rademacher e então, utilizá-la para deduzir a dimensão de Vapnik–Chervonenkis (VC) aplicada ao problema de classificação binária. De forma geral, a medida de complexidade da classe de preditores admissíveis defini quantas rotulagens diferentes podemos produzir para uma amostra finita. A partir da dimensão VC, vamos estabelecer condições necessárias e suficientes para o aprendizado PAC. Neste capítulo, vamos tratar a questão do aprendizado PAC no contexto de classificadores binários.

Lema 1: Classificador de Bayes

Para qualquer preditor possível $h \in \bar{\mathcal{H}}$, temos que

como consequência da definição do preditor de Bayes $h^\star$. Ao integrarmos em relação a $\mathbb{P}_{\chi}$ concluímos o lema.

Como consequência do lema 1, temos que

Lema 2: Classe de Preditores com valor de corte (threshold)

Assim, uma condição suficiente para que $L(\mathbb{P}, h_E) \leq \epsilon$ é que $b_0 ({\bf o_n}) \geq a_0$ e $b_1 ({\bf o_n}) \leq a_1$. Com isso, obtemos que

$$ \mathbb{P}^n \left[ {\bf o_n} \in \mathbb{O}^n : L\left(\mathbb{P} , h_E ({\bf o_n}) \right) > \epsilon \right] \leq $$

$$ \mathbb{P}^n \left[ ( {\bf o}_n \in \mathbb{O}^n: b_0 ({\bf o}_n) < a_0) \cup ( {\bf o}_n \in \mathbb{O}^n: b_1 ({\bf o}_n) > a_1) \right] \leq $$

$$ \mathbb{P}^n \left[ ( {\bf o_n} \in \mathbb{O}^n: b_0 ({\bf o_n}) < a_0) \right] + \mathbb{P}^n \left[ ( {\bf o_n} \in \mathbb{O}^n: b_1 ({\bf o_n}) > a_1) \right]. $$

O evento $( {\bf o}_n \in \mathbb{O}^n: b_0 ({\bf o}_n) < a_0)$ ocorre se, e só se, todas as observações do conjunto de dados ${\bf o}_n$ não estão no intervalo $(a_0 , a^\star)$. Desta forma, temos que

$$ \mathbb{P}^n \left[ ( {\bf o_n} \in \mathbb{O}^n: b_0 ({\bf o_n}) < a_0) \right] = \mathbb{P}^n \left[{\bf o_n} \in \mathbb{O}^n : x_i \not \in (a_0,a^\star) \right] = (1-\epsilon)^n \leq \exp^{-\epsilon n} . $$ Como consequência das equações acima, concluímos que

$$ \mathbb{P}^n \left[ {\bf o_n} \in \mathbb{O}^n : L\left(\mathbb{P} , h_E ({\bf o_n}) \right) > \epsilon \right] \leq \exp^{-\epsilon n} + \exp^{-\epsilon n} = 2 \exp^{-\epsilon n}. $$ Ao tomarmos $n > \frac{Ln(2/\delta)}{\epsilon}$, obtemos que

$$ \mathbb{P}^n \left[ {\bf o_n} \in \mathbb{O}^n : L\left(\mathbb{P} , h_E ({\bf o_n}) \right) > \epsilon \right] < \delta. $$ Segue o lema.

Com este lema, mostramos que a propriedade de aprendizado PAC não está restrita a classes finitas de preditores admissíves. Neste módulo, vamos estabelecer condições necessárias e suficientes para que uma classe de preditores admissíveis $\mathcal{H}$ seja PAC para um problema de classificação binária.

Complexidade de Rademacher

No modelo estatístico de aprendizado de máquina temos um conjunto de dados $ {\bf o}_n = ((x_1,y_1), \cdots (x_n , y_n))$, no qual admitimos ser uma amostra aleatória simples (iid) da probabilidade $\mathbb{P}$. Uma estratégia é uma função $A$ definida sobre o espaço de dados $\mathbb{O}^n$ a valores no espaço de preditores admissíveis $\mathcal{H}$ que é Borel mensurável. A performance de uma estratégia $A$ é medida pela probabilidade condicional do erro de classificação dado a amostra, isto é

$$L(\mathbb{P} , A({\bf o}_n )) = \mathbb{P} \left[(x,y) \in \mathbb{O}: y \neq A({\bf o}_n , x) \right], ~ {\bf o}_n \in \mathbb{O}^n.$$

Para mantermos a máxima generalidade possível, vamos tratar durante este módulo com uma função de risco mais abrangente. Considere $\ell: \mathbb{O} \times \mathcal{H} \rightarrow [0,1]$ uma função Borel mensurável qualquer. O objetivo da teoria de classificação binária consiste em encontrar preditores cuja função risco esperado seja o mais próximo possível do risco do preditor de Bayes. Como não temos acesso a probabilidade $\mathbb{P}$, uma estratégia simples e natural é dado pelo princípio da minimização do risco empírico. Considere $\mathcal{H}$ uma subclasse de preditores admissíveis, denotamos por $A_E$ a estratégia que minimiza o risco empírico

$$ L_E ({\bf o_n} , A_E({\bf o_n})) = \inf_{h \in \mathcal{H}}\frac{1}{n} \sum_{i=1}^n \ell (o_i , h) , ~ {\bf o_n} \in \mathbb{O}^n. $$ O risco esperado da estratégia $A_E$ que minimiza o risco empírico satisfaz

$$ L(\mathbb{P}, A_E({\bf o_n})) - \inf_{h \in \mathcal{H}} L(\mathbb{P} , h) = $$ $$ L(\mathbb{P}, A_E({\bf o_n})) - L_E ({\bf o_n} , h^\star) + L_E ({\bf o_n} , h^\star) - L(\mathbb{P} , h^\star) \leq $$ $$ L(\mathbb{P}, A_E({\bf o_n})) - L_E ({\bf o_n} , A_E({\bf o_n})) + L_E ({\bf o_n} , h^\star) - L(\mathbb{P} , h^\star) \leq $$ $$ 2 \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big|, ~ ~ (\text{Desigualdade 1}), $$ no qual $h^\star$ é o classificador de Bayes. Além disso, temos que

$$ \mid L(\mathbb{P}, A_E({\bf o_n})) - L_E ({\bf o_n}, A_E({\bf o_n})) \mid ~ \leq ~ \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big|, ~ ~ (\text{Desigualdade 2}), $$ para todo ${\bf o_n} \in \mathbb{O}^n$ e $\mathbb{P} \in \mathcal{P}(\mathbb{O})$. A partir das desigualdades 1 e 2, concluímos que se tivermos estimativas para a probabilidade da diferença uniforme

$$\sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| = \sup_{h \in \mathcal{H}} \big| \frac{1}{n} \sum_{i=1}^n \ell (o_i , h) - \mathbb{E_{\mathbb{P}}} \ell (\cdot , h) \big| $$ suficientemente baixa, garantimos que a probabilidade de erro (risco esperado) da estratégia $A_E$ não é muito maior que a probabilidade de erro do estimador de Bayes na classe $\mathcal{H}$. Além disso, a estimativa empírica $L_E (\cdot, A_E(\cdot))$ também é uma boa aproximação para $\inf_{h \in \mathcal{H}} L(\mathbb{P} , h)$.

Para todo preditor admissível $h \in \mathcal{H}$, a função $\ell (\cdot , h): \mathbb{O} \rightarrow [0,1]$ Borel mensurável. Desta forma, definimos a seguinte classe de funções $\mathcal{W} = (\ell (\cdot,h) : h \in \mathcal{H} )$ como uma composição da função de risco $\ell$ com a classe de preditores admissíveis $\mathcal{H}$. Ao tomarmos $f \in \mathcal{W}$, $\mathbb{P}(f) = \mathbb{E_{\mathbb{P}}} f((X,Y))$ e $\mathbb{P}_n f= \frac{1}{n} \sum_{i=1}^n f(X_i,Y_i)$, concluímos que a diferença uniforme é dada por

$$\sup_{h \in \mathcal{H}} \big| L_E ({\bf o}_n , h) - L(\mathbb{P} , h) \big| = \sup_{f \in \mathcal{W}} \left| \mathbb{P}_n (f) -\mathbb{P}(f) \right| .$$

Como consequência da definição, para todo $h \in \mathcal{H}$, temos que $L_E(\cdot , h)$ é uma variável aleatória com média $L(\mathbb{P},h)$. Portanto, temos que avaliar a diferença uniforme entre uma variável aleatória com valores no intervalo $[0,1]$ e sua média. No caso particular do risco dado pelo erro de classificação, temos que $nL_E(\cdot , h)$ tem distribuição binomial com parâmetros $n$ e $L(\mathbb{P},h)$. Neste caso, temos que estudar a diferença uniforme entre a distribuição Bernoulli e sua média.

Na sequência, vamos apresentar algumas propriedades relacionadas com o supremo que serão utilizadas durante esta seção. Sejam $f_1 , f_2 : \mathbb{O} \rightarrow \mathbb{R}$ duas funções satisfazendo $- \infty < \sup_x f_i(x) < \infty$ para $i=1,2$. Então temos que

$$ \sup_x f_1(x) - \sup_x f_2 (x) \leq \sup_x (f_1(x) - f_2 (x)), ~ ~ (\text{Desigualdade 3}). $$

De fato, para todo $\epsilon > 0$ existe $x_\epsilon \in \mathbb{O}$ tal que $f_1(x_\epsilon) \geq \sup_x f_1 (x) - \epsilon$. Então, temos que

$$ \sup_x f_1(x) - \sup_x f_2 (x) \leq \sup_x f_1(x) - f_2 (x_\epsilon) \leq f_1 (x_\epsilon) - f_2 (x_\epsilon) + \epsilon $$ $$ \leq \sup_x \left( f_1(x) - f_2 (x) \right) + \epsilon. $$

Como $\epsilon > 0$ é arbitrário, obtemos a desigualdade 3. Por outro lado, temos que

$$\sup_x \left(f_1(x) + f_2 (x) \right) \leq \sup_x f_1 (x) + \sup_x f_2 (x) ~ ~ (\text{Desigualdade 4}).$$

Como consequência da desigualdade 4, concluímos que o supremo é uma função convexa. Considere $(a_i : i \in I)$ e $(a_i^\prime : i \in I)$ duas família de elementos de $\mathbb{R}$ indexadas por $I$. Então, temos que

$$\sup_{i \in I} \left( \lambda a_i + (1-\lambda)a^\prime_i \right) \leq \lambda \sup_{i \in I} a_i + (1-\lambda) \sup_{i \in I} a^\prime_i , ~ ~ (\text{Desigualdade 5}),$$

para todo $0 \leq \lambda \leq 1 $.

As desigualdades relacionadas com concentração estão entre as principais ferramentas utilizadas para estudar a diferença uniforme apresentada nas desigualdade 1 e 2 . A mais simples e extremamente útil é denominada desigualdade das diferenças finitas (bounded differences inequality)

Lema 1: Bounded Differences Inequality - BDI

Seja $g: \mathbb{O}^n \rightarrow \mathbb{R}$ uma função Borel mensurável de $n$ variáveis tal que existem constantes não negativas satisfazendo,

$$\sup_{(x_1 , \cdots , x_n) \in \mathbb{O}^n } ~ \sup_{x^\prime_i \in \mathbb{O} }\big| g(x_1, \cdots , x_n) - g(x_1, \cdots , x_{i-1}, x^\prime_i , x_{i+1} , \cdots , x_n) \big| \leq c_i, $$

para todo $i=1,2, \cdots , n$. Considere $W_1, W_2 , \cdots , W_n$ variáveis aleatórias independentes. Então a variável aleatória $Z=g(W_1, \cdots , W_n)$ satisfaz

$$\mathbb{P}^n \left[ \big| Z - \mathbb{E} Z \big| > t \right] \leq 2 e^{-2t^2 / C},$$

no qual $C = \sum_{i=1}^n c_i^2$.

A hipótese de diferenças limitadas relacionada com a função $g$ nos diz que se alterarmos a i-ésima coordenada e mantermos as demais fixas, o valor da função $g$ não se altera mais que $c_i$. O exemplo de interesse é dado por

$$ Z= \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| = \sup_{f \in \mathcal{W}} \left| \mathbb{P}_n (f) - \mathbb{P}(f) \right|. $$ Como a função $\ell$ assume valores em $[0,1]$, obtemos que $Z$ satisfaz a hipótese de diferenças limitadas com $c_i=1/n$. De fato, considere ${\bf o_n}=(o_1, \cdots , o_n)$ e ${\bf o_n}^\prime = (o_1 , \cdots , o_{i-1}, o^{\prime}_i , o_{i+1} , \cdots , o_n)$. Como consequência da desigualdade 3, temos que

$$ \left| \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| - \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n}^\prime , h) - L(\mathbb{P} , h) \big| \right| \leq $$

$$ \sup_{h \in \mathcal{H}} \left| ~ \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| - \big| L_E ({\bf o_n}^\prime , h) - L(\mathbb{P} , h) \big| ~ \right| = $$

$$ \sup_{h \in \mathcal{H}} \left| ~ \left| \frac{1}{n} \left( \sum_{j\neq i} \ell (o_j , h) - L(\mathbb{P} , h) \right) + \frac{1}{n} \ell (o_i , h) \right| \right. - $$

$$ \left. \left| \frac{1}{n} \left( \sum_{j\neq i} \ell (o_j , h) - L(\mathbb{P} , h) \right) + \frac{1}{n} \ell (o_i^\prime , h) \right| ~ \right| \leq \frac{1}{n}. $$

Como consequência do lema BDI, para todo $0 < \delta < 1/2$, obtemos que

$$ \mathbb{P}^n \left[ ( Z - \mathbb{E_{\mathbb{P}^n }} Z ) > \sqrt{\frac{\ln (1/ \delta)}{2n}} \right] \leq \mathbb{P}^n \left[ \mid Z - \mathbb{E_{\mathbb{P}^n }} Z \mid > \sqrt{\frac{-\ln (\delta)}{2n}} \right] $$

$$\leq \mathbb{P}^n \left[ \mid Z - \mathbb{E_{\mathbb{P}^n }} Z \mid > \sqrt{\frac{-\ln (2 / \delta )}{2n}} \right] $$

$$\leq 2 e^{-2n \ln(2/ \delta) \frac{1}{2n} } = \delta .$$

Portanto, existe um conjunto $G \in \beta (\mathbb{O}^n)$ com probabilidade $\mathbb{P}^n (G) \geq 1-\delta$, tal que

$$ \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq \mathbb{E_{\mathbb{P}^n }} \sup_{h \in \mathcal{H}} \big| L_E (\cdot , h) - L(\mathbb{P} , h) \big| + \sqrt{\frac{\ln (1/ \delta)}{2n}} ~ ~ (\text{Desigualdade 6}), $$ para todo ${\bf o_n} \in G$. Como consequência deste resultado, podemos nos concentrar no valor esperado $EZ$, que pode ser limitado por uma estratégia de simetrização. Introduzimos uma ``amostra fantasma'' $({\bf X}^\prime , {\bf Y}^\prime) = ((X_1^\prime, Y_1^\prime), \cdots , (X_n^\prime, Y_n^\prime) )$ iid com distribuição de probabilidade $\mathbb{P}$ e independente da amostra original $ ({\bf X} , {\bf Y}) = ((X_1 , Y_1), \cdots , (X_n, Y_n) )$. Dado que o vetor aleatório $( ({\bf X} , {\bf Y}) , ({\bf X}^\prime , {\bf Y}^\prime) )$ está definido no espaço de probabilidade produto $(\mathbb{O}^{2n} , \beta (\mathbb{O}^{2n}), \mathbb{P}^{2n})$, segue do fato da função supremo ser convexa (ver desigualdade 5) e da desigualdade de Jensen, que

$$ \mathbb{E_{\mathbb{P}^n }} \sup_{h \in \mathcal{H}} \big| L_E (({\bf X} , {\bf Y}) , h) - L(\mathbb{P} , h) \big| = \mathbb{E_{\mathbb{P}^{2n} }} \sup_{h \in \mathcal{H}} \big| L_E (({\bf X} , {\bf Y}) , h) - L(\mathbb{P} , h) \big| $$ $$= \mathbb{E_{\mathbb{P}^{2n} }} \sup_{h \in \mathcal{H}} \big| L_E (({\bf X} , {\bf Y}) , h) - \mathbb{E_{\mathbb{P}^{2n} }} \left[ L_E (({\bf X}^\prime , {\bf Y}^\prime) , h) \mid ({\bf X} , {\bf Y}) \right] \big| = $$ $$ \mathbb{E_{\mathbb{P}^{2n} }} \sup_{h \in \mathcal{H}} \big| \mathbb{E_{\mathbb{P}^{2n} }} \left[ L_E (({\bf X} , {\bf Y}) , h) - L_E (({\bf X}^\prime , {\bf Y}^\prime) , h) \mid ({\bf X} , {\bf Y}) \right] \big| \leq $$ $$ \mathbb{E_{\mathbb{P}^{2n} }} \sup_{h \in \mathcal{H}} \big| L_E (({\bf X} , {\bf Y}) , h) - L_E (({\bf X}^\prime , {\bf Y}^\prime) , h) \big| ~ ~ (\text{Desigualdade 7}). $$

Considere $\sigma = (\sigma_1, \cdots , \sigma_n)$ variáveis aleatórias independentes e identicamente distribuídas tal que $\mu [\sigma_i= 1 ] = \mu [\sigma_i= -1 ] = 1/2$. Assim, ao tomarmos o espaço de probabilidade produto $ (\mathbb{O}^{2n} \times (1 , -1)^n , \beta (\mathbb{O}^{2n} \times (1 , -1)^n ) , \mathbb{P}^{2n} \times \mu^n)$, concluímos que os vetores aleatórios $(\sigma, ( ({\bf X} , {\bf Y}) , ({\bf X}^\prime , {\bf Y}^\prime) ))$ definidos sobre este espaço de probabilidade são independentes. Desde que a distribuição de probabilidade das variáveis aleatórias $ L_E (({\bf X} , {\bf Y}) , h) - L_E (({\bf X}^\prime , {\bf Y}^\prime) , h)$ e $ L_E (({\bf X}^\prime , {\bf Y}^\prime) , h)- L_E (({\bf X} , {\bf Y}) , h) $ são idênticas e $\sigma$ tem distribuição simétrica, concluímos que

$$ \mathbb{E_{\mathbb{P}^{2n} }} \sup_{h \in \mathcal{H}} \big| L_E (({\bf X} , {\bf Y}) , h) - L_E (({\bf X}^\prime , {\bf Y}^\prime) , h) \big| = \mathbb{E_{\mathbb{P}^{2n} }} \sup_{h \in \mathcal{H}} \frac{1}{n} \left| \sum_{i=1}^n \left( \ell ((X_i , Y_i) , h) - \ell ((X_i^\prime , Y_i^\prime) , h) \right) \right| = $$ $$ \mathbb{E}_{\mathbb{P}^{2n} \times \mu^n } \sup_{h \in \mathcal{H}} \frac{1}{n} \left| \sum_{i=1}^n \sigma_i \left( \ell ((X_i , Y_i) , h) - \ell ((X_i^\prime , Y_i^\prime) , h) \right) \right| \leq $$ $$ \mathbb{E}_{\mathbb{P}^{2n} \times \mu^n } \sup_{h \in \mathcal{H}} \frac{1}{n} \left| \sum_{i=1}^n \sigma_i \left( \ell ((X_i , Y_i) , h) \right) \right| + \mathbb{E}_{\mathbb{P}^{2n} \times \mu^n } \sup_{h \in \mathcal{H}} \frac{1}{n} \left| \sum_{i=1}^n \sigma_i \left( - \ell ((X_i^\prime , Y_i^\prime) , h) \right) \right| = $$ $$ 2 \mathbb{E}_{\mathbb{P}^{n} \times \mu^n } \sup_{h \in \mathcal{H}} \frac{1}{n} \left| \sum_{i=1}^n \sigma_i \ell ((X_i , Y_i) , h) ) \right|~ ~ (\text{Desigualdade 8}). $$ A complexidade empírica de Rademacher da classe $\mathcal{H}$ é dada por

$$ \hat{\mathcal{R_n}} ( {\bf o_n} , \mathcal{H} ) := \mathbb{E_{\mu^n }} \sup_{h \in \mathcal{H}} \frac{1}{n} \left| \sum_{i=1}^n \sigma_i \ell (o_i , h) ) \right|, ~ {\bf o_n} = (o_1, \cdots , o_n)\in \mathbb{O}^n . $$

A nomenclatura vem do fato de que $(\sigma_1 , \cdots , \sigma_n)$ são denominadas variáveis aleatórias de Rademacher. Por outro lado, a complexidade de Rademacher (também conhecida como Rademacher Average) é dada por

$$ \mathcal{R_n} ( \mathcal{H} ) := \mathbb{E}_{\mathbb{P}^{n} } \hat{\mathcal{R_n}} (\cdot , \mathcal{H} ). $$

A seguir, apresentamos o teorema da complexidade de Rademacher.

Teorema 1: Complexidade de Rademacher

Para todo $0 < \delta < 1$, existe um conjunto $G \in \beta (\mathbb{O}^n)$ com $\mathbb{P}(G) \geq 1 - \delta$, tal que $$ \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq 2 \mathcal{R}_n ( \mathcal{H} ) + \sqrt{\frac{\ln (1/ \delta)}{2n}}, ~ {\bf o_n} \in G ~ ~ (\text{Desigualdade 10}). $$ Para todo $0 < \delta < 1/2$, existe um conjunto $\hat{G} \in \beta (\mathbb{O}^n)$ com $\mathbb{P}^n(\hat{G}) \geq 1 - \delta$, tal que $$ \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq 2 \hat{\mathcal{R_n}} ({\bf o_n} , \mathcal{H} ) + 3 \sqrt{\frac{\ln (2/ \delta)}{2n}}, ~ {\bf o_n} \in \hat{G} ~ ~ (\text{Desigualdade 11}). $$

Prova

A desigualdade 10 é consequência das desigualdades 7, 8 e 9. Para demonstrarmos a desigualdade 11, vamos aplicar novamente o lema 1 com $g ({\bf o_n}) = \hat{\mathcal{R_n}} ({\bf o_n} , \mathcal{H} )$ para todo ${\bf o_n} \in \mathbb{O}^n$. Considere ${\bf o_n}=(o_1, \cdots , o_n)$ e ${\bf o_n}^\prime = (o_1 , \cdots , o_{i-1}, o^{\prime}_i , o_{i+1} , \cdots , o_n)$. Como consequência da desigualdade 3, obtemos que

$$g ({\bf o_n}) - g ({\bf o_n}^\prime) = \hat{\mathcal{R_n}} ({\bf o_n} , \mathcal{H} ) - \hat{\mathcal{R_n}} ({\bf o_n}^\prime , \mathcal{H} ) =$$

$$\mathbb{E_{\mu^n}} \left[ \sup_{h \in \mathcal{H}} \frac{1}{n} \left| \sum_{j \neq i } \sigma_j \ell (o_j , h) ) + \sigma_i \ell (o_i , h) \right| - \sup_{h \in \mathcal{H}} \frac{1}{n} \left| \sum_{j \neq i} \sigma_j \ell (o_j , h) ) + \sigma_i \ell (o^\prime_i , h) \right| \right] \leq$$

$$\mathbb{E_{\mu^n}} \left[ \sup_{h \in \mathcal{H}} \left( \frac{1}{n} \left| \sum_{j \neq i } \sigma_j \ell (o_j , h) ) + \sigma_i \ell (o_i , h) \right| - \frac{1}{n} \left| \sum_{j \neq i} \sigma_j \ell (o_j , h) ) + \sigma_i \ell (o^\prime_i , h) \right| \right) \right] \leq$$

$$\sup_{h \in \mathcal{H}} \frac{1}{n} \left|\ell (o_i , h) - \ell (o^\prime_i , h) \right| \leq \frac{1}{n} .$$

De forma similar podemos mostrar que $ g ({\bf o_n}^\prime) - g ({\bf o_n}) \leq 1/n$ e portanto, temos que $\mid g ({\bf o_n}^\prime) - g ({\bf o_n}) \mid \leq 1/n $. Ao aplicarmos o lema 1, obtemos a existência de um conjunto $G_1 \in \beta(\mathbb{O}^n)$ com $\mathbb{P}^n (G_1) \geq 1 - \delta/2$ tal que

$$\left| \hat{\mathcal{R_n}} ( {\bf o_n} , \mathcal{H} ) - \mathcal{R}_n ( \mathcal{H} ) \right| \leq \sqrt{\frac{\ln (2/ \delta)}{2n}}, ~ {\bf o_n} \in G_1 ~ ~ (\text{Desigualdade 12}).$$

Nas desigualdades 10 e 12 tomamos $G$ e $G_1$ com probabilidade de ocorrência maior que $1- \delta/2$. Assim, existe $\hat{G} = G \cap G_1$ satisfazendo

$$\sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq 2 \mathcal{R}_n ( \mathcal{H} ) + \sqrt{\frac{\ln (1/ \delta)}{2n}} = $$

$$2 \left( \mathcal{R}_n ( \mathcal{H} ) - \hat{\mathcal{R_n}} ({\bf o_n} , \mathcal{H} ) \right) + 2 \hat{\mathcal{R_n}} ({\bf o_n} , \mathcal{H} ) + \sqrt{\frac{\ln (2/ \delta)}{2n}} \leq$$

$$ 2 \sqrt{\frac{\ln (2/ \delta)}{2n}} + 2 \hat{\mathcal{R_n}} ({\bf o_n} , \mathcal{H} ) + \sqrt{\frac{\ln (2/ \delta)}{2n}} \leq 2 \hat{\mathcal{R_n}} ({\bf o_n} , \mathcal{H} ) + 3 \sqrt{\frac{\ln (2/ \delta)}{2n}} . $$

Segue o teorema.

A desigualdade 11 é um limitante que depende dos dados, pois envolve a complexidade de Rademacher no ponto ${\bf o_n} \in \mathbb{O}^n$. Condicionada aos dados, a complexidade $\hat{\mathcal{R_n}} ( {\bf o_n} , \mathcal{H} )$ pode ser calculada, por exemplo, por simulação Monte Carlo. A complexidade de Rademacher $\hat{\mathcal{R_n}} ( \cdot , \mathcal{H} )$ depende da função risco relacionado com o problema de classificação binária. Considere a projeção $\mathcal{W} ({\bf o_n} )= ((\ell (o_1 , h) , \cdots , \ell (o_n , h)) : h \in \mathcal{H}) \subset [0,1]^n$ da classe de preditores admissíveis com respeito ao conjunto de dados ${\bf o_n}$. Desta forma, dado uma amostra fixa ${\bf o_n} \in \mathbb{O}^n$, podemos tratar a complexidade de Rademacher como uma função sobre a família de subconjuntos do espaço $(0,1)^n$. Dado um subconjunto $A \subset [0,1]^n$ com vetores ${\bf a}=(a_1 , \cdots , a_n)$, introduzimos a seguinte quantidade

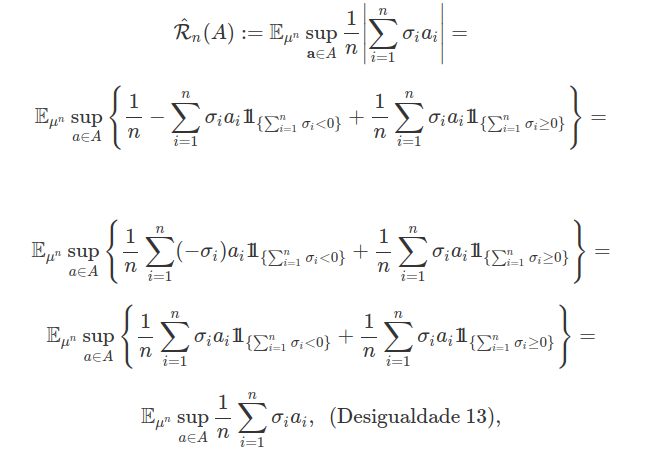
pois as variáveis aleatórias $(\sigma_1, \cdots , \sigma_n)$ são iid e tem distribuição simétrica. A função $\hat{\mathcal{R_n}} (A)$ corresponde a complexidade de Rademacher relacionada com o conjunto $A$. Por definição temos que $\hat{\mathcal{R_n}} (\mathcal{W} ({\bf o_n} ))= \hat{\mathcal{R_n}} ({\bf o_n} , \mathcal{H} )$ para todo ${\bf o_n} \in \mathbb{O}^n$. Com isso, a desigualdade 11 pode escrita na forma

$$\sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq 2 \hat{\mathcal{R_n}} (\mathcal{W} ({\bf o_n} ) ) + 3 \sqrt{\frac{\ln (2/ \delta)}{2n}}, ~ {\bf o_n} \in \hat{G}, ~ ~ (\text{Desigualdade 14}),$$

com $\mathbb{P}^n(\hat{G}) \geq 1 - \delta$ e $0 < \delta < 1/2$. A seguir, apresentamos a desigualdade de Massart para a complexidade de Rademacher.

Teorema 2: Propriedade da Complexidade de Rademacher

Sejam $A$ e $B$ subconjuntos de Borel do espaço $[0,1]^n$. Então, temos que

• $\hat{\mathcal{R_n}} (A \cup B) \leq \hat{\mathcal{R_n}} (A ) + \hat{\mathcal{R_n}} ( B)$
• A desigualdade de Massart é válida:

$$\hat{\mathcal{R_n}} (A) \leq r \frac{\sqrt{2 Ln (Card(A))}}{n}, ~ ~ (\text{Desigualdade 15}),$$

no qual $r^2 = \max_{a \in A} \sum_{i=1}^n a_i$ representa a norma do conjunto $A$ e $Card(A)$ sua respectiva cardinalidade.

• Princípio da contração de Ledoux e Talagrand: Seja $\Phi: \mathbb{R} \rightarrow \mathbb{R}$ uma função Lipschitz com constante $C>0$ (isto é, $\mid \Phi(a) - \Phi(b)\mid \leq C \mid a - b \mid$ para todo $a,b \in \mathbb{R}$). Então, temos que

$$ \hat{\mathcal{R_n}} (\Phi \circ A) \leq C ~ \hat{\mathcal{R_n}} (A) ,$$ no qual $\Phi \circ A = ( (\Phi(a_1) , \cdots , \Phi(a_n)) : (a_1 , \cdots , a_n) \in A ) $.

Prova

A primeira propriedade da complexidade de Rademacher é consequência da desigualdade 4. Na sequência, vamos derivar a desigualdade 15 a partir da desigualdade de Hoeffding. Seja $Z$ uma variável aleatória com valor esperado nulo e limitada no intervalo $[a,b]$. Então, para todo $s>0$, temos que

$$\mathbb{E} \exp (sZ) \leq \exp\left(s^2 \frac{(b-a)^2}{8} \right).$$

Como consequência da desigualdade de Hoeffding e do fato de que as variáveis aleatórias $(\sigma_1, \cdots , \sigma_n)$ são iid e tem distribuição simétrica, temos que

$$\exp^{s \mathbb{E_{\sigma}} \sup_{a \in A} \sum_{i=1}^n \sigma_i a_i } \leq \mathbb{E_{\sigma}} \left[ \exp^{\sup_{a \in A} \sum_{i=1}^n \sigma_i a_i } \right] = \mathbb{E_{\sigma}} \sup_{a \in A} \exp^{ \sum_{i=1}^n \sigma_i a_i } \leq$$

$$\sum_{a \in A} \mathbb{E_{\sigma}} \exp^{ \sum_{i=1}^n \sigma_i a_i } = \sum_{a \in A} \prod_{i=1}^n \mathbb{E_{\sigma}} \exp^{ \sigma_i a_i } \leq \sum_{a \in A} \prod_{i=1}^n \exp^{\frac{s^2 a_i}{2}} \leq$$

$$\sum_{a \in A} \exp^{\frac{s^2}{2} \max_{a \in A} \sum_{i=1}^n a_i } = \sum_{a \in A} \exp^{\frac{s^2}{2} r^2 } = Card(A) \exp^{\frac{s^2}{2} r^2 }.$$

Com isso, obtemos que

$$\mathbb{E_{\sigma}} \sup_{a \in A} \sum_{i=1}^n \sigma_i a_i \leq \frac{1}{s} \ln(Card(A)) + \frac{s}{2} r^2.$$

Ao tomarmos $s= \frac{\sqrt{2 \ln (Card(A))}}{r}$ deduzimos a desigualdade de Massart,

$$\frac{1}{n} \mathbb{E_{\mu^n}} \sup_{a \in A} \sum_{i=1}^n \sigma_i a_i \leq r \frac{\sqrt{2 \ln (Card(A))}}{n}.$$

Na sequência, vamos demonstrar o princípio da contração de Ledoux e Talagrand. A complexidade empírica de Rademacher pode ser escrita na forma

$$\hat{\mathcal{R_n}} (\Phi \circ A) = \mathbb{E_{\mu^n}} \sup_{a \in A} \frac{1}{n} \sum_{i=1}^n \sigma_i \Phi(a_i) = \mathbb{E}_{\mu^{n-1}} \mathbb{E}_{\mu}\sup_{a \in A} \left[ \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) + \sigma_n \Phi(a_n) \right].$$

Assuma que o supremo existe (caso contrario, utilizamos solução $\epsilon$-ótima). Assim, existe $c^\star , d^\star \in A$ tais que

$$ \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(c_i^\star) + \Phi(c_n^\star) = \sup_{a \in A} \left[ \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) + \Phi(a_n) \right] $$ e $$ \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(d_i^\star) - \Phi(d_n^\star) = \sup_{a \in A} \left[ \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) - \Phi(a_n) \right] .$$

Desde que $\sigma_n$ tem distribuição simétrica no conjunto $(-1 , 1)$, concluímos que

$$ \mathbb{E_{\mu}}\sup_{a \in A} \left[ \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) + \sigma_n \Phi(a_n) \right] = \frac{1}{2} \sup_{a \in A} \left[ \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) + \Phi(a_n) \right] + \frac{1}{2} \sup_{a \in A} \left[ \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) - \Phi(a_n) \right] = $$

$$ \frac{1}{2} \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(c_i^\star) + \Phi(c_n^\star) + \frac{1}{2} \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(d_i^\star) - \Phi(d_n^\star) = \frac{1}{2n} \left[ \sum_{i=1}^{n-1} \sigma_i \Phi(c_i^\star) + \sum_{i=1}^{n-1} \sigma_i \Phi(d_i^\star) + \Phi(c_n^\star) - \Phi(d_n^\star) \right] . $$ Na sequência, tomamos $s=sgn(c_n^\star - d_n^\star )$ no qual $sgn$ representa a função sinal. Com isso, temos que

$$ \mathbb{E_{\mu}}\sup_{a \in A} \left[ \frac{1}{n} \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) + \sigma_n \Phi(a_n) \right] \leq \frac{1}{2n} \left[ \sum_{i=1}^{n-1} \sigma_i \Phi(c_i^\star) + \sum_{i=1}^{n-1} \sigma_i \Phi(d_i^\star) + \mid \Phi(c_n^\star) - \Phi(d_n^\star) \mid \right] \leq $$

$$ \frac{1}{2n} \left[ \sum_{i=1}^{n-1} \sigma_i \Phi(c_i^\star) + \sum_{i=1}^{n-1} \sigma_i \Phi(d_i^\star) + C \mid c_n^\star - d_n^\star \mid \right] = \frac{1}{2n} \left[ \sum_{i=1}^{n-1} \sigma_i \Phi(c_i^\star) + \sum_{i=1}^{n-1} \sigma_i \Phi(d_i^\star) + s C \left( c_n^\star - d_n^\star \right) \right] =$$

$$ \frac{1}{2n} \left[ \sum_{i=1}^{n-1} \sigma_i \Phi(c_i^\star) + s C c_n^\star \right] + \frac{1}{2n} \left[ \sum_{i=1}^{n-1} \sigma_i \Phi(d_i^\star) - s C d_n^\star \right] \leq $$

$$\frac{1}{n} \left( \frac{1}{2} \sup_{a \in A} \left[ \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) + s C a_n \right] + \frac{1}{2} \sup_{a \in A} \left[ \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) - s C a_n \right]\right) = $$

$$ \mathbb{E_{\mu}} \sup_{a \in A} \left[ \sum_{i=1}^{n-1} \sigma_i \Phi(a_i) + C \sigma_n a_n \right] ,$$

no qual $C$ é a constante de Lipschitz da função $\Phi$. Procedendo da mesma forma para todo $i <m$, obtemos o princípio da contração de Ledoux e Talagrand.

Este resultado é crucial para que possamos conectar a complexidade de Rademacher com dimensão de Vapnik e Chervonenkis.

Dimensão de Vapnik e Chervonenkis

No problema de classificação binária avaliado na seção Complexidade de Rademacher, toda função $f \in \mathcal{W}$ é a indicadora de algum conjunto na forma $( (x,y) \in \mathbb{O}: y \neq h(x))$ com $h\in \mathcal{H}$. A projeção da classe $\mathcal{W}$ no ponto ${\bf o}_n$ é dada por

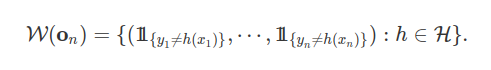
A partir da desigualdade de Massart, obtemos que

$$ \hat{\mathcal{R_n}} (\mathcal{W} ({\bf o_n} ) ) = \mathbb{E_{\sigma}} \sup_{a \in \mathcal{W} ({\bf o_n} )} \frac{1}{n} \sum_{i=1}^n \sigma_i a_i \leq \sqrt{ \frac{2 \ln (Card(\mathcal{W} ({\bf o_n} )))}{n}}, ~ {\bf o_n} \in \mathbb{O}^n, $$

pois $r \leq \sqrt{n}$. Portanto, precisamos estudar a Cardinalidade do conjunto $\mathcal{W} ({\bf o_n} )$. Agora, o conjunto $\mathcal{W} ({\bf o_n} )$ depende da função de risco $\ell$, da entrada do processo $X$ e da saída $Y$. No caso de classificação binária, no qual utilizamos como função de risco a probabilidade de erro de classificação, temos a seguinte simplificação

$$ \hat{\mathcal{R_n}} (\mathcal{W} ({\bf o_n} ) ) = \hat{\mathcal{R_n}} ( {\bf o_n} , \mathcal{H} ) = \mathbb{E_{\mu^n }} \sup_{h \in \mathcal{H}} \frac{1}{n} \sum_{i=1}^n \sigma_i \ell (o_i , h) ) = $$

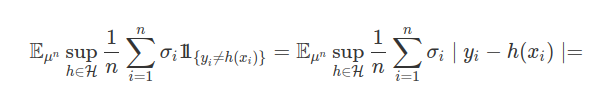
$$ \mathbb{E_{\mu^n }} \sup_{h \in \mathcal{H}} \frac{1}{n} \sum_{i=1}^n \sigma_i \mid h(x_i) - y_i\mid = \mathbb{E_{\mu^n }} \sup_{h \in \mathcal{H}} \frac{1}{n} \sum_{i=1}^n \sigma_i \left( h(x_i) (1-2y_i) + y_i \right) = $$

$$ \mathbb{E_{\mu^n }} \sup_{h \in \mathcal{H}} \frac{1}{n} \sum_{i=1}^n \sigma_i h(x_i)) , $$

para todo $ {\bf o_n} = (o_1, \cdots , o_n)\in \mathbb{O}^n$, pois sabemos que $\mid a - b \mid = a(1-2b) + b $ para todo $a,b \in (0,1)$, $(1-2y_i)\sigma_i$ também tem distribuição de Rademacher e $\sigma_i y_i$ tem valor esperado nulo. Com isto, mostramos que a complexidade de Rademacher depende apenas da entrada do processo ${\bf x}_n=(x_1, \cdots , x_n)$ composta com o preditor admissível $h$ .

$$\mathcal{H} ({\bf x_n}):=( (h(x_1), \cdots , h(x_n)), h \in \mathcal{H} ) \quad \text{e} \quad \hat{\mathcal{R_n}} (\mathcal{H} ({\bf x_n}) ) := \mathbb{E_{\sigma}} \sup_{a \in \mathcal{H} ({\bf x_n})} \frac{1}{n} \sum_{i=1}^n \sigma_i a_i.$$

Assim, ao aplicarmos a desigualdade Massart, concluímos que

$$ \hat{\mathcal{R_n}} (\mathcal{W} ({\bf o_n} ) ) = \hat{\mathcal{R_n}} (\mathcal{H} ({\bf x}_n) ) \leq \sqrt{ \frac{2 \ln (Card(\mathcal{H} ({\bf x}_n)))}{n}}, ~ {\bf o_n} \in \mathbb{O}^n, ~ ~ (\text{Desigualdade 1}) $$

Desta forma, a partir da desigualdade 14 na seção “Complexidade de Rademacher” e da desgualdade 1, obtemos que

$$ \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq 2 \sqrt{ \frac{2 \ln (Card(\mathcal{H} ({\bf x}_n )))}{n}} + 3 \sqrt{\frac{\ln (2/ \delta)}{2n}}, ~ {\bf o_n} \in \hat{G}, ~ ~ (\text{Desigualdade 2}). $$ Com a complexidade de Rademacher, resumimos o problema de aprendizado PAC na questão de avaliar a como a dimensão da classe de preditores composta com os dados de entrada aumenta em função do tamanh da amostra. Dizemos que o subconjunto ${\bf x}_n =(x_1, \cdots , x_n) \subset \chi$ é particionado por $\mathcal{H}$ se a cardinalidade de $\mathcal{H} ({\bf x}_n)$ for igual a $2^{n}$. Nesta condição, temos que $\mathcal{H} ({\bf x}_n) = (0,1)^n$. Obviamente que se ${\bf x}_n$ é particionado por $\mathcal{H}$, então qualquer subconjunto de ${\bf x}_n$ também é particionado.

Definição 1: Dimensão de Vapnik e Chervonenkis

Seja $\mathcal{H}$ uma classe de preditores admissíveis. A VC-dim da classe $\mathcal{H}$ de preditores admissíveis é dada por

$$VC-dim (\mathcal{H}) = max (n : {\bf x}_n ~ \text{é particionado por} ~ \mathcal{H}, ~ \text{para todo} ~ {\bf x}_n \subset \chi^n).$$

Para ilustrar, calculamos a dimensão de Vapnik–Chervonenkis para algumas classes usuais de preditores admissíveis.

Exemplo 1

Exemplo 2

Lema 1: Lema de Vapnik - Chervonenkis - Sauer - Shelah

Seja $\mathcal{H}$ uma classe de preditores com $VC-dim(\mathcal{H})=d<\infty$. Então para todo $n$, $\tau_\mathcal{H}(n)\leq \sum_{i=0}^d\binom{n}{i} = (n+1)^d$. Em particular, se $n>d$ então $\tau_{\mathcal{H}}(n)\leq \left(\frac{en}{d}\right)^d$

Prova

Para $n\leq d$, segue trivialmente que $\tau_\mathcal{H}(n)\leq \sum_{i=0}^d\binom{n}{i}$ uma vez que, neste caso $\sum_{i=0}^d\binom{n}{i}=2^n$. Com $n> d$ e o conjunto $S=(x_1,\dots,x_n)\subset \chi$ fixo, definimos $$\mathcal{B}=\left((x_i\in S:f(x_i)=1), ~i=1, \cdots n :f\in \mathcal{H}\right).$$ Assim, temos que $Card(\mathcal{B})\leq \sum_{i=0}^d\binom{n}{i}$, uma vez que $VC-dim(\mathcal{H})=d$. Agora, como $S$ é arbitrário, temos que

$$\tau_\mathcal{H}(n) \leq Card(\mathcal{B})\leq \sum_{i=0}^d\binom{n}{i} .$$

Agora, note que para $0\leq i\leq d$ e $n\geq d$, temos que

$$\frac{(n/d)^d}{(d/n)^i}\geq 1$$

Portanto,

$$\sum_{i=0}^d\binom{n}{i}\leq (n/d)^d\sum_{i=0}^d\binom{n}{i}(d/n)^i$$

$$\leq (n/d)^d(1+(d/n))^n$$

$$\leq \left(\frac{ e n}{d}\right)^d$$

no qual a última desigualdade decorre da desigualdade de Euler. Segue o lema.

Esse resultado nos mostra que o número de rotulagens induzido por uma amostra cresce de forma polinomial em $n$, caso a dimensão de Vapnik e Chervonenkis da classe de preditores admissíveis seja finita. A partir do Lema 1, concluímos que

$$ \ln ( Card(\mathcal{H} ({\bf x}_n))) \leq d \ln(n+1), $$ no qual $VC-dim(\mathcal{H})=d<\infty$. Assim, como consequência da desigualdade 2, obtemos que

$$ \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq \sqrt{ \frac{16 d \ln(n+1) }{2n}} + \sqrt{\frac{9 \ln (2/ \delta)}{2n}}, ~ {\bf o_n} \in \hat{G}, ~ ~ (\text{Desigualdade 3}), $$ no qual $\mathbb{P}^n (\hat{G}) \geq 1 - \delta$ com $0 \leq \delta \leq 1/2$. Sabemos que para $a,b$ constantes não negativas $\sqrt{a} + \sqrt{b} \leq 2 \sqrt{a+b} $. Com isso, temos que

$$ \sup_{h \in \mathcal{H}} \big| L_E ({\bf o_n} , h) - L(\mathbb{P} , h) \big| \leq 2 \sqrt{\frac{16 d \ln(n+1) + 9 \ln (2/ \delta )}{2n}}, ~ {\bf o_n} \in \hat{G}. $$ Com isso, obtemos o teorema de Vapnik e Chervonenkis.

Teorema 1: Teorema de Vapnik e Chervonenkis

Corolário 1

Suponha que a classe de preditores admissíveis $\mathcal{H}$ satisfaça $VC-dim(\mathcal{H})=d<\infty$. Então, a estratégia $A_E$ obtida pelo princípio da minimização do risco empírico é PAC.

Teorema 2

Seja $V$ um subespaço vetorial do espaço $\mathbb{R}^\chi$ de todas as funções reais sobre o domínio $\chi$. A $VC-dim$ da classe de preditores $\mathcal{H}$ tal que $h_f\in \mathcal{H}$ tal que

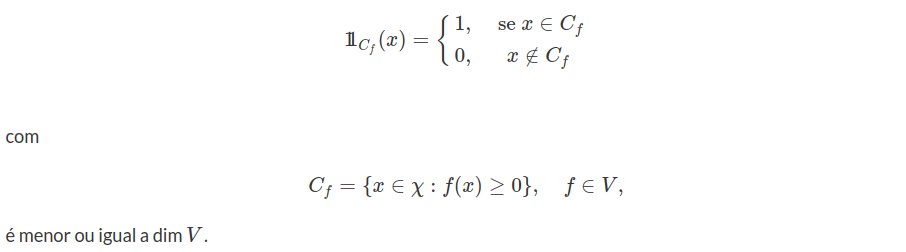
Prova

Algoritmos baseados em função Custo

A partir do Teorema de Vapnik e Chervonenkis temos que minimizar a função de risco empírica com respeito a uma classe $\mathcal{H}$ de preditores admissíveis com dimensão VC bem menor que o tamanho da amostra. Ao requerermos dimensão VC baixa, impomos sérias limitações com respeito a propriedade de aproximação da classe de preditores admissíveis. Além disso, também temos um problema numérico. No problema de classificação binária queremos minimizar o erro de classificação empírico, que geralmente é bem complicado do ponto de vista computacional. Mesmo em casos bem simples o problema pode ter dificuldade NP.

Uma das formas de contornar estes dois problemas consiste em modificar a função de risco empírica ao introduzirmos uma função custo. Considere os preditores admissíveis na forma

$$ L(\mathbb{P} , h_f) \leq C(f, \mathbb{P}) = C(f, \mathbb{P}) + C_E ({\bf o}_n , f) - C_E ({\bf o}_n , f) \leq $$

$$ C_E ({\bf o_n} , f) + \sup_{f \in \mathcal{F}} \mid C(f, \mathbb{P}) - C_E ({\bf o_n} , f) \mid ~ ~ (\text{Desigualdade 1}) .$$

Para todo conjunto de dados ${\bf o_n} =((x_1, y_1) , \cdots (x_n , y_n)) \in \mathbb{O}^n$, denotamos por

$$\mathcal{C_{\mathcal{F}}}({\bf o_n}) := ( (-(2y_1 - 1) f(x_1) , \cdots , -(2y_n - 1)f(x_n)) : f \in \mathcal{F} ).$$

A complexidade de Rademacher relacionada com a classe $\mathcal{H_{\mathcal{F}}}({\bf o_n})$ é dada por

$$ \hat{\mathcal{R_n}} (\psi \circ \mathcal{C_{\mathcal{F}}}({\bf o_n})) = \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^n \sigma_i \psi(-(2y_n - 1)f(x_n)) = \mathbb{E_{\mu^n}} \sup_{a \in \psi \circ \mathcal{C_{\mathcal{F}}}({\bf o_n})} \frac{1}{n} \sum_{i=1}^n \sigma_i a_i ,$$

no qual $\psi \circ \mathcal{C_{\mathcal{F}}}({\bf o_n}) = ( (\psi(a_1), \cdots , \psi(a_n)): (a_1, \cdots , a_n) \in \mathcal{C_{\mathcal{F}}}({\bf o_n}) ) $ . Para todo $0 \leq \delta \leq 1/2$, obtemos do teorema da complexidade de Rademacher que existe um conjunto $\hat{G} \in \beta(\mathbb{O}^n)$ com $\mathbb{P}(\hat{G}) > 1-\delta$ satifazendo

$$ \sup_{f \in \mathcal{F}} \mid C(f, \mathbb{P}) - C_E ({\bf o_n} , f) \mid \leq 2 \hat{\mathcal{R_n}} (\psi \circ \mathcal{C_{\mathcal{F}}}({\bf o_n})) + 3 B \sqrt{\frac{\ln(2/\delta)}{2n} }, \quad {\bf o_n} \in \hat{G} ~ ~ (\text{Desigualdade 2}),$$

no qual assumimos que $$\sup_{ ( (x,y) \in \mathbb{O}) } \psi(-(2y - 1) f(x)) \leq B, $$ com $B$ uma constante positiva .

Teorema 1

Considere $\psi$ uma função Lipschitz com constante $L_{\psi}$. Então, temos que $$L(\mathbb{P} , h_f) \leq C_E({\bf o_n} , f ) + 2L_{\psi} \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^n \sigma_if(x_i) + 3 B \sqrt{\frac{\ln(2/\delta)}{2n} }, \quad {\bf o_n} \in \hat{G}.$$

Prova

Como consequência das desigualdades (1) e (2) e do teorema da contração de Ledoux e Talagrand, obtemos que $$ L(\mathbb{P} , h_f) \leq C_E({\bf o_n} , f ) + 2L_{\psi} \hat{\mathcal{R_n}} (\mathcal{C_{\mathcal{F}}}({\bf o_n})) + 3 B \sqrt{\frac{\ln(2/\delta)}{2n} }. $$ Agora, a complexidade de Rademacher é dada por

$$ \hat{\mathcal{R_n}} (\mathcal{C_{\mathcal{F}}}({\bf o_n})) = \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^n \sigma_i \left( -(2y_n - 1)f(x_i) \right) = \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^n (-\sigma_i) (2y_n - 1)f(x_i) = $$

$$ \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^n \sigma_i (2y_n - 1)f(x_i) = \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^n \sigma_if(x_i), $$

pois a distribuição de $\sigma_i$ é simétrica no conjunto $(-1,1)$. Segue o teorema.

A partir do Teorema 1, sabemos que a complexidade de Rademacher de uma classe de funções reais $\mathcal{F}$ limita a performance dos preditores admissíveis $\mathcal{H_{\mathcal{F}}}$.

Classes de Preditores Lineares

Neste módulo, vamos tratar o caso de preditores lineares em problemas de classificação binária. Considere os preditores admissíveis na forma

A partir do teorema da complexidade de Rademacher (Teorema 1), sabemos que

$$L(\mathbb{P} , h_f) \leq C_E({\bf o_n} , f ) + 2L_{\psi} \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^n \sigma_if(x_i) + 3 B \sqrt{\frac{\ln(2/\delta)}{2n} }, \quad {\bf o_n} \in \hat{G}$$

no qual $\hat{G} \in \beta (\mathbb{O}^n)$ com $\mathbb{P}^n(\hat{G}) \geq 1 - \delta$. Assim, limitamos o comportamento dos preditores admissíveis pela complexidade de Rademacher de uma classe de funções $\mathcal{F}$. Na sequência, vamos estudar a complexidade de Rademacher da classe de funções lineares. Iniciamente, vamos estudar o caso finito dimensional. Para todo $p \geq 1$, definimos

$$B^d_p = ( a \in \mathbb{R}^d : \parallel a \parallel_p \leq 1 ),$$

a bola unitária em $\mathbb{R}^d$ com respeito a norma de ordem $p$. Sabemos que para dois pares $1 \leq p,q \leq \infty$ conjugados $\frac{1}{p} + \frac{1}{q}=1$, temos que

$$ \parallel a \parallel_p = \sup_{b \in B^d_q} \mid \langle a , b \rangle \mid . $$ Como consequência da desigualdade de Holder, temos que

$$ \langle a , b \rangle \leq \parallel a \parallel_p ~ \parallel b \parallel_q , ~ ~ a \in B^d_p , ~ ~ b \in B^d_q. $$

Considere $\chi = B^d_2$ a bola unitária com produto interno $ \langle \cdot , \cdot \rangle_{\chi}$. Dizemos que uma função é linear se $f(x)$ for linear em $x$. A classe $\mathcal{F}$ consiste em todas as funções lineares sobre $\chi$ com valores $\mathbb{R}$. No caso finito dimensional, também podemos interpretar $f$ como um vetor em $B^d_2$ de tal forma que $f(x)=\langle f , x \rangle_{\chi}$. Assim, para qualquer dado de entrada ${\bf x}_n \in \chi^n$, temos que

$$\mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{t=1}^n \sigma_t f(x_t) = \mathbb{E_{\mu^\infty}} \sup_{f \in \mathcal{F}} \left[ \frac{1}{n} \sum_{t=1}^n \sigma_t \langle f , x_t \rangle_\chi \right] = \mathbb{E_{\mu^\infty}} \sup_{f \in \mathcal{F}} \langle f , \frac{1}{n} \sum_{t=1}^n \sigma_t x_t) \rangle_\chi = \mathbb{E_{\mu^\infty}} \parallel \frac{1}{n} \sum_{t=1}^n \sigma_t x_t \parallel_2, $$

pois $f \in \mathcal{F}$ é uma função linear. Assim, podemos interpretar a complexidade de Rademacher como a norma em $B^d_2$ do andar aleatório definido por $\sigma_t x_t$ normalizado por $n$. Como consequência, obtemos a desigualdade de Kahane e Khintchine

$$ \mathbb{E_{\mu^\infty}} \parallel \sum_{t=1}^n \sigma_t a_t \parallel_2 \leq \left( \mathbb{E_{\mu^\infty}} \parallel \sum_{t=1}^n \sigma_t x_t \parallel_2^2 \right)^{1/2} = $$

$$ \left( \mathbb{E_{\mu^\infty}} \sum_{t,s=1}^n \langle \sigma_t x_t , \sigma_s x_s \rangle \right)^{1/2} = \left( \sum_{t=1}^n \mathbb{E_{\mu^\infty}} \parallel x_t \parallel_2^2 \right)^{1/2} \leq \sqrt{n} . $$

Assim, obtemos que

$$\mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{t=1}^n \sigma_t f(x_t) \leq \frac{1}{\sqrt{n}}. $$

Ao utilizarmos a desigualdade de Kahane e Khintchine também podemos obter um limitante inferior, na forma

$$\mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{t=1}^n \sigma_t f(x_t) \geq \frac{1}{2 \sqrt{n}}. $$

De forma similar podemos estender esta propriedade para espaços de Hilbert. Seja $\chi$ um espaço de Hilbert separável com produto interno $\langle \cdot , \cdot \rangle_\chi$. Denotamos por $\chi^\star$ o espaço de todos os funcionais lineares sobre $\chi$ (dual topológico). Pelo teorema da representação de Riesz sabemos que para todo $f \in \chi^\star$ existe $x^f \in \chi$ tal que

$$f(x) = \langle x , x^f \rangle_\chi , \quad x \in \chi.$$

Desta forma, identificamos o dual topológico do espaço de Hilbert $\chi$ com o próprio espaço de Hilbert via o produto interno. De forma usual, a norma dual é dada por

$$ \parallel f \parallel_{\chi^\star} = \sup_{x \in \chi} \mid f(x) \mid = \sup_{x \in \chi} \mid \langle x , x^f \rangle_\chi \mid, \quad f \in \chi^\star .$$

Aqui, tomamos a classe de funções $\mathcal{F} = \chi^\star$. Ao aplicarmos os mesmos argumentos da Bola unitária $B^d_2$, concluímos que

$$ \frac{1}{2 \sqrt{n}} \leq \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{t=1}^n \sigma_t f(x_t) \leq \frac{1}{\sqrt{n}}. $$

Na sequência, vamos estender a teoria de classes de preditores lineares para espaços de Banach. Aqui, vamos utilizar resultados sobre análise convexa em espaços de Banach apresentados no livro:

• J. Peypouquet (2014) - Convex Optimization in Normed Spaces. Springer.

Considere $\chi$ a bola unitária em um espaço de Banach separável e reflexivo com norma $\parallel \cdot \parallel$. O dual topológico do espaço de Banach $\chi$, definido como o espaço dos funcionais lineares sobre $\chi$, será denotado por $\chi^\star$ com norma dual

$$ \parallel f \parallel_{\star} =\sup_{x \in \chi} \mid \langle f , x \rangle \mid,$$

no qual $\langle \cdot , \cdot \rangle : \chi^\star \times \chi \rightarrow \mathbb{R}$ uma função bilinear tal que $\langle f , x \rangle = f(x)$ para todo funcional linear $f \in \chi^\star$ e todo ponto $x \in \chi$. Seja $\Psi^\star$ uma função fortemente $\theta$-convexa com respeito a norma $\parallel \cdot \parallel_{\star}$, isto é, para todos funcionais lineares $f,g \in \chi^\star$ temos que

$$ \Psi^\star(f) \geq \Psi^\star(g) + \langle f-g , \nabla \Psi^\star (g) \rangle + \frac{\theta}{2} \parallel f-g \parallel_{\star}^2 ,$$

no qual $\theta$ é uma constante positiva e $\nabla : \chi^{\star \star} \rightarrow \mathbb{R}$ é o funcional linear dado pela derivada de Gâteaux, no qual $\chi^{\star \star} $ é o dual topológico de $\chi^\star$ (ver, Peypouquet (2014), Teorema 3.12, pg 39). Como $\chi$ é reflexivo, sabemos que $\chi^{\star \star} = \chi$.Por outro lado, o conjugado convexo de Fenchel da função $\Psi^\star$ é dado por

$$ \Psi(x) = \sup_{f \in \mathcal{F}} \left( \langle f , x \rangle - \Psi^\star (h) \right), $$

que satisfaz a propriedade conjugada. Para todo $x , x^\prime \in \chi$, temos que

$$ \Psi(x) \leq \Psi(x^\prime) + \langle \nabla \Psi (x^\prime) , x - x^\prime \rangle + \frac{1}{2 \theta} \parallel x - x^\prime \parallel ^2 ~ ~ (\text{Desigualdade 1}) .$$

Seja $M^2 = \sup_{h \in \mathcal{H}} \Psi^\star (h)$. Através da definição de convexo conjugado acima, obtemos que para todo $\lambda > 0$,

$$ \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{t=1}^n \sigma_t f(x_t) = \frac{\lambda}{\lambda} \mathbb{E_{\mu^\infty}} \sup_{f \in \mathcal{F}} \left[ \frac{1}{n} \sum_{t=1}^n \sigma_t \langle f , x_t \rangle \right] = \frac{1}{\lambda} \mathbb{E_{\mu^\infty}} \sup_{f \in \mathcal{F}} \langle f , \frac{\lambda}{n} \sum_{t=1}^n \sigma_t x_t) \rangle \leq $$

$$ \frac{1}{\lambda} \left[ \sup_{f \in \mathcal{F}} \Psi^\star (f) + \mathbb{E_{\mu^\infty}} \Psi \left( \frac{\lambda}{n} \sum_{t=1}^n \sigma_t x_t \right) \right]. $$

Ao denotarmos por

$$Z_k = \frac{\lambda}{n} \sum_{t=1}^k \sigma_t x_t , \quad k=1, \cdots , n,$$

concluímos da desigualdade 1 que valor esperado da expressão acima é dado por

$$ \mathbb{E_{\mu^\infty}} \Psi \left( Z_n \right) \leq \mathbb{E_{\mu^\infty}} \left[ \Psi \left( Z_{n-1} \right) + \langle \nabla \Psi (Z_{n-1}) , \frac{\lambda}{n} \sigma_n x_n \rangle + \frac{1}{2 \theta} \parallel \frac{\lambda}{n} x_n \parallel^2 \right]. $$

Agora, temos que

$$ \mathbb{E_{\mu^\infty}} \langle \nabla \Psi (Z_{n-1}) , \frac{\lambda}{n} \sigma_n x_n \rangle = 0 \quad \text{e} \quad \mathbb{E_{\mu^\infty}} \frac{1}{2 \theta} \parallel \frac{\lambda}{n} x_n \parallel^2 \leq \frac{\lambda^2}{2 \theta n^2} ,$$

pois $x_n$ pertence a bola unitária de um espaço de Banach $(\chi)$. Desta forma, concluímos que

$$\mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{t=1}^n \sigma_t f(x_t) \leq \frac{M^2}{\lambda} + \frac{\lambda}{2 \theta n} = M \sqrt{\frac{2}{\theta n}}, $$

no qual $\lambda = M \sqrt{2 \theta n}$.

Método de Núcleo - SVM

A classe de preditores lineares são atrativos tanto do ponto de vista de algoritmos quanto do ponto de vista teórico. Porém, o fato dos preditores serem lineares pode gerar alguma desconfiança quanto a representativade da classe. A técnica de núcleo tem como objetivo aliviar este problema. A ideia consiste em transportar os dados de entrada para um espaço de dimensão maior ou infinita denominado “feature space” e então, utilizar preditores lineares. Para ilustrar, considere o problema bidimensional tratado na Figura 1.

Figura 1:

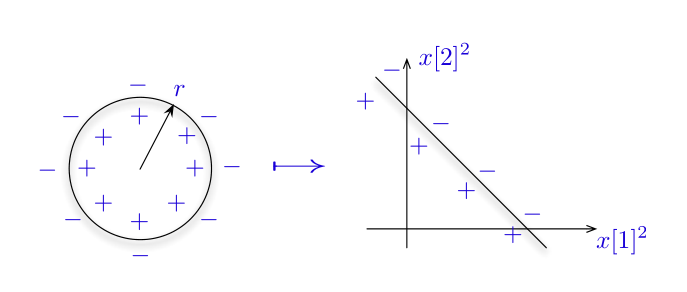
Como dissemos, a vantagem de utilizarmos núcleo como medida de similaridade é que podemos utilizar preditores lineares em espaços de Hilbert infinito dimensional. Como exemplo, considere o seguinte algoritmo. A ideia consite em calcularmos as médias das duas classes no “feature space” $D$, $$c^{+} = \frac{1}{n^+} \sum_{( i: y_i=1 )} \phi(x_i) \quad \text{e} \quad c^{n} = \frac{1}{n^-} \sum_{( i: y_i=0 )} \phi(x_i),$$ no qual $n^+$ é o total de dados com rótulos positivos e $n^-$ é o total de dados com rótulos negativos. Para um novo ponto $x \in \chi$, escolhemos o rótulo cuja média está “mais próxima” de $\phi(x)$, o que nos leva ao preditor

no qual

$$ b = \frac{1}{2} \left(\frac{1}{(n^-)^2} \sum_{{i:y_i=0 }} \langle \phi(x) , \phi(x_i) \rangle_D - \frac{1}{(n^+)^2} \sum_{{i:y_i=1 }} \langle \phi(x) , \phi(x_i) \rangle_D \right)$$

$$ = \frac{1}{2} \left(\frac{1}{(n^-)^2} \sum_{{i:y_i=0 }} \mathcal{K}(x , x_i) - \frac{1}{(n^+)^2} \sum_{{i:y_i=1 }} \mathcal{K}(x , x_i) \right) . $$

Na sequência, vamos utilizar o processo de contrução do RKHS apresentado no módulo Construção do RKHS. Considere uma função núcleo $\mathcal{K} : \chi \times \chi \rightarrow \mathbb{R}$, isto é, uma função simétrica satisfazendo

$$ \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j \mathcal{K} (x_i , x_j) \geq 0 , $$

para qualquer escolha de $n \geq 1$, $\alpha_1 , \cdots \alpha_n \in \mathbb{R}$ e $x_1, \cdots , x_n \in \chi$. A função de similaridade $\mathcal{K}$ naturalmente nos fornece um espaço de funções na forma

$$ \mathcal{F} = \left( f(\cdot) = \sum_{i=1}^n \alpha_i \mathcal{K} (x_i , \cdot): ~ \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j \mathcal{K} (x_i , x_j) \leq M^2, ~ n \in \mathbb{N}, ~ \alpha_i \in \mathbb{R}, ~ x_i \in \chi \right). $$

De forma simples, definimos o seguinte produto interno sobre a classe de funções lineares $\mathcal{F}$, $$ \langle \sum_{i=1}^n \alpha_i \mathcal{K} (x_i , \cdot) , \sum_{j=1}^m \beta_j \mathcal{K} (x_j , \cdot) \rangle = \sum_{i=1}^n \alpha_i \beta_j \mathcal{K} (x_i , x_j) .$$ A partir do produto interno $\langle \cdot , \cdot \rangle$ podemos completar $\mathcal{F}$ para obtermos um espaço de Hilbert $\bar{\mathcal{F}}$, que é denominado **Reproducing Kernel Hilbert Space** (RKHS). Uma propriedade importante do RKHS é que para toda função $f \in \bar{\mathcal{F}}$ temos que

$$f(x) = \langle f , \mathcal{K} (\cdot , x) \rangle_{\bar{\mathcal{F}}}, \quad x \in \chi .$$

Uma questão importante nos algoritmos relacionados com núcleo é a introdução de uma função que mede a complexidade da função $f \in \bar{\mathcal{F}}$. De forma geral, regularizar a norma de $f$ é útil para contornarmos problemas computacionais. Neste sentido, introduzimos o seguinte problema de otimização $$ \min_{f \in \bar{\mathcal{F}}} \left( C_E({\bf o_n} , f ) + R(\parallel f \parallel) \right) ~ ~ ( \text{Equação 1}),$$ no qual $R: [0, \infty) \rightarrow \mathbb{R}$ é uma função não decrescente. Típica escolha para $R$ é dada por $R(a) = \lambda a^2$ com $\lambda$ uma constante positiva. O teorema seguinte nos garante que a solução ao problema de Minimização acima (Equação 1) pertence ao span do conjunto $(\mathcal{K}(\cdot , x_1) , \cdots , \mathcal{K}( \cdot , x_n) )$.

Teorema 1: Teorema da Representação

Suponha que existe solução ao problema de minimização apresentado na equação 1. Então, existe um vetor $(\alpha_1^\star, \cdots , \alpha_n^\star) \in \mathbb{R}^n$ tal que $$f^\star (\cdot) = \sum_{i=1}^n \alpha_i^\star \mathcal{K}(\cdot , x_i) $$ é uma solução ótima ao problema de minimização apresentado na Equação 1.

Prova

Seja $g^\star$ uma soluçao ao problema de minimização dado na equação 1. Como $g^\star$ pertence ao espaço de Hilbert $\bar{\mathcal{F}}$, podemos escrever $g^\star$ na forma $$g^\star (\cdot)= \sum_{i=1}^n \alpha_i^\star \mathcal{K}(\cdot , x_i) + g (\cdot),$$ no qual $\langle g , \mathcal{K}(\cdot , x_i) \rangle = 0$ para todo $i=1, \cdots , n$. Seja $f^\star=g^\star - g$. Obviamente, temos que $\parallel g^\star \parallel^2 = \parallel g \parallel^2 + \parallel f^\star \parallel^2$. Portanto, concluímos que $\parallel f^\star \parallel \leq \parallel g^\star \parallel $. Desde que $R$ é uma função não decrescente, obtemos que $R(\parallel f^\star \parallel) \leq R (\parallel g^\star \parallel)$. Além disso, para todo $i=1, \cdots , n$, temos que

$$ \langle f^\star , \mathcal{K}(\cdot , x_i) \rangle = \langle g^\star - g , \mathcal{K}(\cdot , x_i) \rangle = \langle g^\star , \mathcal{K}(\cdot , x_i) \rangle .$$

Desta forma, concluímos que

$$C_E ({\bf o_n} , f^\star) = \frac{1}{n} \sum_{i=1}^n \psi(- \langle f^\star , \mathcal{K} (\cdot , x_i) \rangle (2y_i-1)) = \frac{1}{n} \sum_{i=1}^n \psi(- \langle g^\star , \mathcal{K} (\cdot , x_i) \rangle (2y_i-1)) = C_E ({\bf o_n} , g^\star) .$$

Com isso, concluímos que a função objetivo da equação 1 no ponto $f^\star$ não pode ser maior que a função objetivo no ponto $g^\star$ e portanto $f^\star$ também é uma solução ótima. Segue o teorema da representação.

A partir do teorema da representação, sabemos que

$$\inf_{f \in \bar{\mathcal{F}}} \left( C_E({\bf o_n} , f ) + R(\parallel f \parallel) \right) = \inf_{f \in \mathcal{F}} \left( C_E({\bf o_n} , f ) + R(\parallel f \parallel) \right) .$$

Assim, podemos nos concentrar na classe $\mathcal{F}$ de funcionais lineares, nos quais

$$L(\mathbb{P} , h_f) \leq C_E({\bf o_n} , f ) + 2L_{\psi} \mathbb{E_{\mu^n}} \sup_{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^n \sigma_if(x_i) + 3 B \sqrt{\frac{\ln(2/\delta)}{2n} }, \quad {\bf o_n} \in \hat{G},$$

Teorema 2

Temos que

$$L(\mathbb{P} , A_C ({\bf o_n})) \leq C_E({\bf o_n} , f_C ({\bf o_n} ) + 2L_{\psi} \frac{M}{n} \sqrt{ \sum_{i=1}^n \mathcal{K}(x_i , x_i) } + 3 B \sqrt{\frac{\ln(2/\delta)}{2n} }, \quad {\bf o_n} \in \hat{G},$$

no qual $\mathbb{P}(\hat{G}) > 1 - \delta$ com $0 < \delta < 1/2$.

O problema de minimização proposto na equação 2 pode ser escrito na seguinte forma

$$ \min_{ ( (\alpha_1 , \cdots , \alpha_n) \in \mathbb{R}^n )} \left( \frac{1}{n} \sum_{i=1}^n \psi(- \langle \sum_{j=1}^n \alpha_j \mathcal{K}(x_j , \cdot) , \mathcal{K} (\cdot , x_i) \rangle (2y_i-1)) + R \left( \sqrt{ \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j \mathcal{K} (x_i , x_j)} \right) \right) =$$

$$ \min_{ ( (\alpha_1 , \cdots , \alpha_n) \in \mathbb{R}^n )} \left( \frac{1}{n} \sum_{i=1}^n \psi(- (2y_i-1) \sum_{j=1}^n \alpha_j \mathcal{K}(x_j , x_i) ) + R \left( \sqrt{ \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j \mathcal{K} (x_i , x_j)} \right) \right) ~ ~ (\text{Equação 3}) .$$

Para resolver o problema de minimização proposto na equação 3, não precisamos acessar diretamente os elementos no “Feature Space”. A única coisa que precisamos calcular são os produtos internos no Feature space, o que pode ser calculado através da função núcleo. Assim, para resolver a equação 3 precisamos conhecer a matrix Gram $G$ nos quais os elementos são dados por $G(i,j) = \mathcal{K} (x_i , x_j)$. Uma vez que aprendemos os coeficientes $(\alpha_1^\star, \cdots , \alpha_n^\star)$ com a equação 3, podemos calcular a previsão de uma nova entrada por

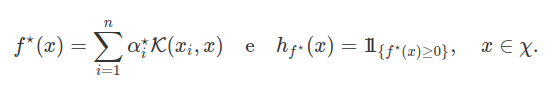
Exemplo 1: Núcleo Polinomial

O núcleo polinomial de ordem $k$ é dado por

$$ \mathcal{K}(x , x^\prime) := \left( 1 + \langle x , x^\prime \rangle \right)^k .$$

A seguir, vamos checar que $\mathcal{K}$ é realmente um núcleo. Para isto, vamos mostrar que existe ma função $\phi$ no espaço domínio tal que $\mathcal{K}(x , x^\prime) = \langle \phi(x) , \phi(x^\prime) \rangle$. Por simplicidade, denotamos $x_0 = x^\prime_0 =1$. Então, temos que

$$\mathcal{K} (x , x^\prime) = \left( 1 + \langle x , x^\prime \rangle \right) \cdots \left( 1 + \langle x , x^\prime \rangle \right) = \left( \sum_{j=0}^n x_j x_j^\prime \right) \cdots \left( \sum_{j=0}^n x_j x_j^\prime \right) =$$

$$ \sum_{J \in (0,1,2 \cdots )^k} \prod_{i=1}^k x_{J_i} x_{J_i}^\prime = \sum_{J \in (0,1,2 \cdots )^k} \prod_{i=1}^k x_{J_i} \prod_{i=1}^k x_{J_i}^\prime .$$

Com isso, definimos uma função $\phi: \mathbb{R} \rightarrow \mathbb{R}^{(n+1)^k}$ tal que para todo $J \in (0,1, 2, \cdots n)^k$ existe um elemento de $\phi(x)$ que é igual a $\prod_{i=1}^k x_{J_i}$. Desta forma, obtemos que

$$ \mathcal{K}(x , x^\prime) = \left( 1 + \langle x , x^\prime \rangle \right)^k = \langle \phi(x) , \phi(x^\prime) \rangle .$$

Exemplo 2: Núcleo Gaussiano

Inicialmente, suponha que o espaço domínio seja dado pela reta $\mathbb{R}$. Considere a função

$$\phi(x) := \frac{x^n}{\sqrt{n !}} e^{- \frac{x^2}{2} } , \quad x \in \mathbb{R}. $$

Desta forma, tomamos

$$\langle \phi(x) , \phi(x^\prime) \rangle = \sum_{n=1}^\infty \frac{x^n}{\sqrt{n !}} e^{- \frac{x^2}{2} } \frac{(x^\prime)^n}{\sqrt{n !}} e^{- \frac{(x^\prime)^2}{2} } = e^{\frac{x^2 + (x^\prime)^2}{2}} \sum_{n=1}^\infty \left( \frac{(x x^\prime)^n}{n!} \right) = e^{-\frac{\parallel x - x^\prime \parallel }{2}} .$$

Aqui, o feature space tem dimensão infinita, enquanto que calcular o núcleo é bem simples. De forma geral, dado um escalar $\sigma > 0$, o núcleo Gaussiano é definido por

$$ \mathcal{K}(x , x^\prime) := e^{-\frac{\parallel x - x^\prime \parallel }{2 \sigma}}, \quad x , x^\prime \in \mathbb{R}^d.$$

Support Vector Machine

Neste módulo, vamos apresentar uma das mais importantes ferramenta de aprendizado de máquina, o support vector machine . O algoritmo de SVM trata o desafio da complexidade da amostra através de um separador com “alta margem” (“large margin”). De forma intuítiva, um hiperplano separa o conjunto de dados de treinamento com “alta margem” se todos os exemplos estão do lado correto do hiperplano e o mais distantes possível dos dados. Restringir o algortimo para fornecer o hiperplano com maior margem diminui a complexidade mesmo com grandes volumes de dados e alta dimensão.

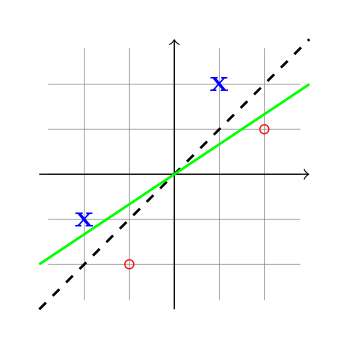
Figura 1: Conjunto de dados de treinameno separável

Enquanto ambos hiperplanos (preto e verde) separam os quatro exemplos, nossa intuição provavelmente escolheria o hiperplano preto ao invés do hiperplano verde. Um forma de formalizarmos nossa intuição consiste no conceito de margem. A margem de um hiperplano com respeito ao conjunto de dados de treinamento é definido com a menor distância entre um ponto no conjunto de dados de treinamento e o hiperplano. Se o hiperplano tem alta margem, então deve separar os dados no conjunto de treinamento mesmo que os dados sejam perturbados em cada exemplo. Support Vector Machine (SVM) é um algoritmo que retorna uma hiperplano que satisfaz o princípio da MRE com maior margem possível. No módulo Método de Núcleo, deduzimos a seguinte equção de otimização ao problema de classificação binária com núcleo.

$$ \min_{ ( (\alpha_1 , \cdots , \alpha_n) \in \mathbb{R}^n )} \left( \frac{1}{n} \sum_{i=1}^n \psi(- (2y_i-1) \sum_{j=1}^n \alpha_j \mathcal{K}(x_j , x_i) ) + R \left( \sqrt{ \sum_{i=1}^n \sum_{j=1}^n \alpha_i \alpha_j \mathcal{K} (x_i , x_j)} \right) \right) ~ ~ (\text{Equação 1}) .$$

Uma vez que aprendemos os coeficientes $(\alpha_1^\star, \cdots , \alpha_n^\star)$ com a equação 1, podemos calcular a previsão de uma nova entrada por

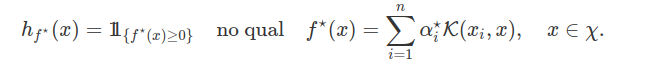
$$\alpha^\star = (\alpha^\star_1 , \cdots , \alpha^\star_n) = arg \min_{ ( \alpha= (\alpha_1 , \cdots , \alpha_n) \in \mathbb{R}^n )} \left( \frac{1}{n} \sum_{i=1}^n \left( \max( 0, 1- (2y_i -1) [G\alpha]_{i}) \right) + \lambda \alpha^T G \alpha \right) ~ ~ (\text {Equação 2}).$$

Para tornar este problema de otimização suave, tomamos a seguinte variável $\xi_i = \max( 0, 1- (2y_i -1) [G\alpha]_{i})$ e reescrevemos o problema de otimização na forma

$$ (\alpha^\star , \xi^\star) = arg \min_{ \alpha , ~ \xi \in \mathbb{R}^n ~ ~ \text{tal que} \ \xi_i \geq 1- (2y_i -1) [G\alpha]_{i} \ \xi \geq 0 } \left( \frac{1}{n} \sum_{i=1}^n \xi_i + \lambda \alpha^T G \alpha \right).$$

Este problema de otimização é suave e convexo. Portanto satisfaz as condições de Karush-Khun-Tucker para o problema dual Lagrangeano no qual

$$ (\alpha^\star , \xi^\star) = arg \min_{ \alpha , ~ \xi \in \mathbb{R}^n ~ ~ \text{tal que} \ \xi_i \geq 1- (2y_i -1) [G\alpha]_{i} \ \xi \geq 0 } \left( \frac{1}{n} \sum_{i=1}^n \xi_i + \lambda \alpha^T G \alpha - \sum_{i=1}^n \left( \eta_i (\xi_i - 1- (2y_i -1) [G\alpha]_{i}) + \theta_i \xi_i \right) \right).$$

A partir das condições de primeira ordem nos dizem que $\alpha^\star_i = \eta_i (2y_i-1) / (2 \lambda)$. Desde que $f^\star (x_i) = [G \alpha^\star]_i$, a primeira condição de negligência nos reforça que $\alpha_i^\star = 0$ se $(2y_i-1) f^\star(x_i) > 1$. A segunda condição de negligência com a segunda condição de primeira ordem nos dizem que $\alpha^\star_i = (2y_i -1) / (2 \lambda n)$ se $\xi^\star_i > 0$ e $0 \leq (2y_i -1) \alpha_i^\star \leq 1 / (2 \lambda n) $ caso contrário. Desta forma, temos que se $\xi^\star > 0$ então $\alpha^\star_i$ e $\eta_i$ são diferentes de zero e, protanto, concluímos que $(2y_i-1) f^\star(x_i) = 1- \xi^\star_i < 1$ de acorodo com a condição de negligência. Com isso, chegamos ao seguinte teorema.

Teorema 1: Support Vector Machine

A solução da equação 2 é dada na forma $f^\star (x) = \sum_{i=1}^n \alpha^\star_i \mathcal{K}(x_i , x) $ para $x \in \mathbb{R}^d$, nos quais

• $\alpha_i^\star = 0$ se $(2y_i -1) f^\star (x_i) > 1$
• $\alpha_i^\star = (2y_i-1) / (2 \lambda n)$ se $(2y_i -1) f^\star (x_i) < 1$
• $0 \leq (2y_i - 1) \alpha^\star_i \leq 1/(2 \lambda n)$ se $(2y_i -1) f^\star (x_i) < 1$

Os vetores de dados $x_i \in \mathbb{R}^d$ com índice $i$ tal que $\alpha^\star_i \neq 0$ são denominados vetores de suporte.

A seguir, vamos apresentar uma interpretação geométrica para o algoritmo SVM. Inicialmente, tomamos a função núcleo $\mathcal{K}(x , x^\prime) = \langle x , x^\prime \rangle$ para todo $x , x^\prime \in \mathbb{R}^d$. O RKHS relacionado é dado pelo espaço das formas lineares $\mathcal{F} = ( \langle x , \cdot \rangle: x \in \mathbb{R}^d )$. Neste caso, temos que $$f^\star (x) = \sum_{i=1}^n \alpha_i^\star \langle x_i , x \rangle = \langle \omega^\star , x \rangle \quad \text{com} \quad \omega^\star = \sum_{i=1}^n \alpha_i^\star x_i .$$

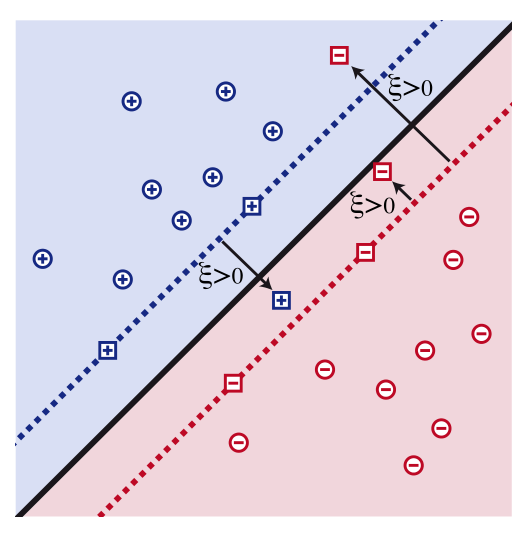
Figura 2: Classificação Binária com SVM linear.

Na figura 2, o hiperplano que separa pontos $(x \in \mathbb{R}^d: \langle \omega^\star , x \rangle=0 )$ é representado pela linha preta. Por outro lado os hiperplanos margem $(x \in \mathbb{R}^d: \langle \omega^\star , x \rangle=1 )$ e $(x \in \mathbb{R}^d: \langle \omega^\star , x \rangle=-1 )$ são representados pelas linhas tracejadas em azul e vermelho, respectivamente. Além disso, os vetores de suporte são representados por quadrados. Com isso, deduzimos a seguinte propriedade do algoritmo SVM. Se adicionarmos um ponto $x_{n+1}$ ao conjunto de dados de treinamento para o qual $(2y_{n+1} -1) \langle \omega^\star , x \rangle> 1$, o vetor $\omega^\star$ e o preditor $h^\star$ não se alteram. Em outras palavras, somente dados que são classificados errados ou classificados com baixa margem (isto é, $(2y_{n+1} -1) \langle \omega^\star , x \rangle \geq 1$) influenciam o hiperplano separador $(x \in \mathbb{R}^d: \langle \omega^\star , x \rangle=0 )$.

Reproducing Kernel Hilbert Space

Neste módulo, vamos definir de forma geral o termo “Reproducing Kernel Hilbert Space” (RKHS) e núcleo (Kernel) relacionado. Seja $D$ um espaço de Hilbert de funções $h: \chi \rightarrow \mathbb{R}$. Um das mais importantes propriedades de um RKHS é que duas funções $h$ e $g$ estão próximas na norma de $D$, então $f(x)$ e $g(x)$ também estão próximos para todo $x \in \chi$. Escrevemos o produto interno em $D$ na forma $\langle f , g \rangle_D$ e a norma é dada por $ \parallel f \parallel_D = \sqrt{\langle f , f \rangle_D}$. Desde que $D$ é um espaço de funções, temos um funcional que relaciona cada função $f \in D$ com seu valor em $x \in \chi$. Para cada $x \in \chi$, a função $\delta_x : D \rightarrow \mathbb{R}$ definida por $\delta_x (f) = f(x)$ é denominada funcional de Dirac.

O Funcional de Dirac é linear. Na realidade, se tomarmos $f,g \in D$ e $c_1 ,c_2 \in \mathbb{R}$, temos que $\delta_x (c_1 f + c_2 g)= (c_1 f + c_2 g)(x) = c_1 f (x) + c_2 g(x) = c_1 \delta_x (f) + c_2 \delta_x (g) $. Naturalmente, a questão é se o funcional de Dirac é contínuo. Esta questão nos leva a definição do RKHS.

Definição 1: Reproducing Kernel Hilbert Space

Um espaço de Hilbert composto por funções $f: \chi \rightarrow \mathbb{R}$ é um RKHS se o funcional de Dirac $\delta_x$ é contínuo para todo $x \in \chi$.

A seguir, apresentamos um resultado relacionado com o comportamento de um RKHS em relação a estrutura de convergência.

Lema 1: Convergência em norma implica em convergência pontual

Seja $D$ um RKHS. Suponha que a sequência $(f_n)$ converge em $D$ para $f$ $(\parallel f_n - f \parallel_D \rightarrow 0)$, então obtemos que $f_n(x) \rightarrow f(x)$ para todo $x \in \chi$.

Prova

Para todo $x \in \chi$, temos que $$ \mid f_n (x) - f(x) \mid = \mid \delta_x (f_n) - \delta_x (f) \mid \leq \parallel \delta_x \parallel_{D^\star} ~ \parallel f_n - f \parallel_D \rightarrow 0 ,$$ no qual $\parallel \delta_x \parallel_{D^\star} $ é a norma dual do funcional linear de Dirac, que é limitada pelo fato de que $D$ é um RKHS. Segue o lema.

De forma geral, a noção de núcleo não aparece diretamente na deinição do RKHS. Na sequência, vamos definir núclo e estabelecr sua relação RKHS.

Definição 2: Núcleo Reprodutivo

Seja $D$ um espaço de Hilbert composto por funções $f: \chi \rightarrow \mathbb{R}$. Uma função $\mathcal{K}: \chi \times \chi \rightarrow \mathbb{R}$ é denominada núcleo reprodutivo se:

1. Para todo $x \in D$, temos que $\mathcal{K}( \cdot , x) \in D$;

2. Para todo $x \in \chi$ e $f \in D$, temos que $$\langle f , \mathcal{K}(\cdot , x) \rangle_D = f(x) ~~(\text{propriedade reprodutiva}). $$

Em particular, para todo $x , x^\prime \in \chi$, temos que $$ \mathcal{K}( x , x^\prime) = \langle \mathcal{K}(\cdot , x^\prime) . \mathcal{K}(x , \cdot ) \rangle_D.$$ A partir desta definição, formulamos diversas questões. Qual a relação entre o núcleo reprodutivo e o RKHS? Tal tipo de núcleo realmente existe? Se existe, é único? Na sequência, vamos avaliar a unicidade do núcleo reprodutivo.

Lema 2: Unicidade do Núcleo reprodutivo

Suponha que existe um núcleo reprodutivo $\mathcal{K}$ no espaço de Hilbert $D$. Então, este núcleo reprodutivo é único.

Prova

Assumimos que $D$ admite dois núcleos reprodutíveis $\mathcal{K}_1$ e $\mathcal{K}_2$. Então, para todo$x \in \chi$ e $f \in D$, temos que $$ \langle f , \mathcal{K}_1 (\cdot , x) - \mathcal{K}_2 (\cdot , x) \rangle_D = f(x) - f(x) =0.$$ Em particular, se tomarmos $f = \mathcal{K}_1 (\cdot , x) - \mathcal{K}_2 (\cdot , x)$, obtemos que $\parallel \mathcal{K}_1 (\cdot , x) - \mathcal{K}_2 (\cdot , x) \parallel_D = 0$ para todo $x \in \chi$. Desta forma, concluímos que $\mathcal{K}_1 = \mathcal{K}_2 $.

Para mostrarmos a existência do núcleo reprodutivo em um RKHS vamos utilizar o Teorema da representação de Riesz, que nos diz todo funcional linear pode ser representado através do produto interno.

Teorema 1: Existência do Núcleo Repredutivo

Um espaço de Hilbert $D$ é um RKHS se, e só se, $D$ admite um núcleo reprodutivo.

Prova

Considere $D$ um espaço de Hilbert com com úcleo reprodutivo $\mathcal{K}$ . Como consequência da desigualdade de Cauchy-Schwarz, obtemos que $$\mid \delta_x (f) \mid = \mid f(x) \mid = \mid \langle f , \mathcal{K}(\cdot , x) \rangle_D \mid \leq \parallel \mathcal{K} (\cdot , x) \parallel_D \parallel f \parallel_D = \langle \mathcal{K} (\cdot , x) , \mathcal{K} (\cdot , x) \rangle_{D}^{1/2} \parallel f \parallel_D = \mathcal{K} (x , x)^{1/2} \parallel f \parallel_D.$$ Assim, concluímos que o funcional linear de Dirac é limitado e consequentemente, $\delta_x$ é contínuo. Portanto, temos que $D$ é um RKHS.

Por outro lado, tomamos $D$ um RKHS, no qual o funcional linear de Dirac $\delta_x$ é contínuo. Pelo teorema da representação de Riesz existe um elemento $f_{\delta_x} \in D$ tal que $$\delta_x (f) = \langle f , f_{\delta_x} \rangle_D, \quad f \in D.$$ Com isso, definimos $\mathcal{K} (x^\prime , x) = f_{\delta_x} (x^\prime)$ para todo $x , x^\prime \in \chi$. Então, obtemos que $\mathcal{K} (\cdot , x) = f_{\delta_x}$ e $\langle f , \mathcal{K} (\cdot , x) = f_{\delta_x} = f(x)$. Portanto $\mathcal{K}$ é um núcleo reprodutivo.

Na sequência, vamos estudar algumas propriedades relacionadas com o núcleo reprodutivo.

Definição 3: Função Positiva Definida

Uma função simétrica $g: \chi \times \chi \rightarrow \mathbb{R}$ é positiva definida s para todo $n \geq 1$, $(a_1 , \cdots , a_n) \in \mathbb{R}^n$, $(x_1, x_2 , \cdots , x_n) \in \chi^n$, temos que $$\sum_{i=1}^n \sum_{j=1}^n a_i a_j g(x_i , x_j) \geq 0. $$ A função $g$ é estritamente positiva definida se para $x_i$ distintos, a igualdade é válida somente quando os valores $a_i$ forem nulos.

Todos produto interno é um função positiva definida. De forma geral, temos o sguinte lema.

Lema 2

Seja $F$ um espaço de Hilbert (não necessariamente um RKHS) com produto interno $\langle \cdot , \cdot \rangle_F$. Seja $\chi$ um espaço de Borel e $\phi: \chi \rightarrow F$ uma função Borel mensurável. Então, temos que a função $h(x^\prime , x) := \langle \phi(x^\prime , \phi(x) \rangle_F$ é uma função positiva definida

Prova

Temos que $$\sum_{i=1}^n \sum_{j=1}^n a_i a_j g(x_i , x_j) = \sum_{i=1}^n \sum_{j=1}^n \langle a_i \phi(x_i , a_j \phi(x_j) \rangle_F = \langle \sum_{i=1}^n a_i \phi(x_i ), \sum_{j=1}^n a_j \phi(x_j) \rangle_F = \parallel \sum_{i=1}^n a_i \phi(x_i) \parallel_F^2 \geq 0 .$$

Com isso, temos os elementos para demonstrar o próximo lema.

Lema 3

Todo núcleo reprodutivo é positivo definido.

Prova

Para todo núcleo reprodutivo $\mathcal{K}$ é um RKHS $D$ satisfaz $\mathcal{K}(x^\prime , x) = \langle \mathcal{K}(\cdot , x^\prime) , \mathcal{K}(\cdot , x) \rangle_D$. Desta forma, é suficiente tomarmos $\phi : \chi \rightarrow D$ na forma $\phi(x) = \mathcal{K}(\cdot , x)$ para todo $x \in \chi$.

O Próximo lema vai na direção contrária do lema 3. Como consequência da desigualdade de Cauchy-Schwarz, mostraremos que todoa função está relacionada com o produto interno no “feature space”.

Lema 4

Se $g$ é uma função positiva definida, então $\mid h(x , x^\prime) \mid ^2 \leq \mid h(x , x) \mid ~ \mid h(x^\prime , x^\prime) \mid$.

Prova

Se $g(x , x^\prime)=0$, a desigualdade é óbvia. Por outro lado, tomamos $a_1 = a$ e $a_2 = g(x , x^\prime)$. Temos que $q(a) = a^2 g(x , x) + 2a \mid g(x , x^\prime) \mid^2 + \mid g(x , x^\prime) \mid^2 g(x^\prime , x^\prime) \geq 0$. Desde que $q$ é uma função quadrática de $a$ a desigualdade é válida para todo $a$, concluímos que $$ \mid h(x , x^\prime) \mid ^4 \leq \mid h(x , x^\prime) \mid ^2 h(x , x) h(x^\prime , x^\prime),$$ o que prova o lema.

Assim, chegamos a seguinte definição de núcleo.

Definição 4: Núcleo

Seja $\chi$ um espaço de Borel. A função $\mathcal{K} : \chi \times \chi \rightarrow \mathbb{R}$ é denominada núcleo se existe um espaço de Hilbert $F$ e um função $\phi: \chi \rightarrow F$ Borel mensurável tal que $$\mathcal{K} (x, x^\prime) = \langle \phi(x) , \phi(x^\prime) \rangle_F, \quad x , x^\prime \in \chi .$$ A função $\phi: \chi \rightarrow F$ é denominada “feature function” e $F$ é denominado “feature space” .

Para um mesmo núcleo, pode existir mais de uma " feature function” como apresentado no exemplo a seguir.

Exemplo 1

Considere $\chi = \mathbb{R}$ e $$ \mathcal{K} (x , x^\prime) = x x^\prime = \left(\frac{x}{\sqrt{2}} , \frac{x}{\sqrt{2}} \right) \left(\frac{x^\prime}{\sqrt{2}} , \frac{x^\prime}{\sqrt{2}} \right)^T,$$ no qual definimos as seguinte “feature functions” $\phi(x) = x$ e $\bar{\phi}(x) = \left(\frac{x}{\sqrt{2}} , \frac{x}{\sqrt{2}} \right)$ com $D = \mathbb{R}$ e $\bar{D} = \mathbb{R}^2$.

Denotamos por $\ell^2$ o espaço de todos as sequência em $\mathbb{R}$ que são quadrado somáveis, isto é, o espaço das sequências $(a_n : n \geq 1)$ tal que $$\sum_{i=1}^\infty a_i^2 < \infty. $$ Sabemos que $\ell^2$ é um espaço de Hilbert com o produto interno $$\langle \bar{a} , \bar{b} \rangle = \sum_{i=1}^\infty a_i b_i , \quad \bar{a} = (a_i : i \geq 1) \in \ell^2 ~ ~ \text{e} ~ ~ \bar{b} = (b_i : i \geq 1 ) \in \ell^2.$$

Lema 5

Para todo $x \in \chi$, assumimos que a sequência $(f_n(x) : n \geq 1) \in \ell^2$, no qual $f_n : \chi \rightarrow \mathbb{R}$ é uma função Borel mensurável para todo $n \geq 1$. Então, temos $$\mathcal{K} (x , x^\prime) := \sum_{i=1}^\infty f_n(x) f_n (x^\prime) $$ é um núcleo.

Prova

A partir da desigualdade de Holder, temos que $$ \sum_{i=1} \mid f_n(x) f_n (x^\prime) \mid \leq \parallel f_n(x) \parallel_{\ell^2} \parallel f_n(x^\prime) \parallel_{\ell^2}.$$ Assim, a série que define $\mathcal{K}$ é absolutamente convergente. Ao definirmos $D:=\ell^2$ e $\phi (x):= (f_n(x) : n \geq 1)$, segue o lema.

Construção do RKHS: Moore - Aronszajn

A partir de um RKHS $D$, obtemos um único núcleo reprodutivo relacionado com $D$ que é positivo definido. Neste módulo vamos estabelecer a relação inversa, para toda função positiva definida $\mathcal{K}$ existe um único RKHS $D$ para o qual $\mathcal{K}$ é um núcleo reprodutivo. Seja $\mathcal{K}: \chi \times \chi \rightarrow \mathbb{R}$ uma função positiva definida. Com isso, vamos construir um pré-RKHS $D_0$, que deve satisfazer duas propriedades básicas:

1. O funcional de Dirac $\delta_x$ é contínuo em $D_0$;

2. Qualquer sequência de Cauchy $(f_n : n \geq 1)$ em $D_0$ que converge pontualmente para $0$ também converge na norma em $D_0$ para zero.

Como consequência da propriedade (2), para qualquer sequência de Cauchy $(f_n : n \geq 1)$ em $D_0$ que converge pontualmente para $f_0 \in D_0$ também converge para $f$ na norma $\parallel \cdot \parallel_{D_0}$. Na realidade, basta observarmos que $f_n - f_0$ converge pontualmente para zero para aplicarmos a propriedade (2). Na sequência, aplicamos a técnica de Moore e Aronszajn para contrução do pré-RKHS. Seja $\mathcal{K}$ uma função positiva definida, tomamos $D_0$ a classe de todas as combinações lineares da classe de funções $( \mathcal{K}(\cdot , x): x \in \chi)$. Assim, toda função $f \in D_0$ é escrita na forma $f = \sum_{i=1}^n a_i \mathcal{K} (\cdot , x_i)$ no qual $(a_1, \cdots , a_n) \in \mathbb{R}^n$ e $n \geq 1$. O produto interno em $D_0$ é definido por

$$ \langle f , g \rangle_{D_0} := \sum_{i=1}^n \sum_{j=1}^m a_i b_j \mathcal{K}(x_i , x_j^\prime), $$

nos quais $f = \sum_{i=1}^n a_i \mathcal{K} (\cdot , x_i)$ no qual $(a_1, \cdots , a_n) \in \mathbb{R}^n$ e $g = \sum_{j=1}^m b_i \mathcal{K} (\cdot , x_j^\prime)$ no qual $(b_1, \cdots , b_m) \in \mathbb{R}^m$.

Inicialmente, precisamos mostrar que este é um produto interno válido. Neste caso, precisamos mostrar que o candidato a produto interno é independente da representação das funções $f,g \in D_0$. Desde que

$$\langle f , g \rangle_{D_0} = \sum_{i=1}^n \sum_{j=1}^m a_i b_j \mathcal{K}(x_i , x_j^\prime) = \sum_{i=1}^n a_i g(x_i) = \sum_{j=1}^m b_j f(x^\prime_j) ,$$

concluímos que o candidato a produto interno é independente da representação. Como consequência deste fato, obtemos a propriedade reprodutiva sobre $D_0$. Ao tomarmos $g=\mathcal{K}(\cdot , x)$, temos que

$$ \langle f , g \rangle_{D_0} = \sum_{i=1}^n a_i g(x_i) = \sum_{i=1}^n a_i \mathcal{K}(x_i , x) = f(x). $$

Na sequência, mostraremos que $\langle f , f \rangle_{D_0} = 0 $ implica que $f=0$. Considere $f = \sum_{i=1}^n a_i \mathcal{K} (\cdot , x_i)$ no qual $(a_1, \cdots , a_n) \in \mathbb{R}^n$. Fixamos $x \in \chi$ e tomamos $c_i= c a_i $ para todo $i=1, \cdots , n$, $c_{n+1} = f(x)$ e $x_{n+1}=x$. Como $\mathcal{K}$ é uma função positiva definida, obtemos que

$$0 \leq \sum_{i=1}^{n+1} \sum_{j=1}^{n+1} c_i c_j \mathcal{K}(x_i , x_j) = c^2 \langle f , f \rangle_{D_0} + 2c \mid f(x) \mid^2 + \mid a f(x) \mid \mathcal{K}(x,x), $$

o que nos leva a concluir que

$$\mid f(x) \mid^4 \leq \mid f(x) \mid^2 \mathcal{K}(x,x) \langle f , f \rangle_{D_0}.$$

Assim, o fato de $\langle f , f \rangle_{D_0} = 0$ implica que $f=0$. Portanto, temos que $D_0$ é um espaço de funções com produto interno $\langle \cdot , \cdot \rangle_{D_0}$ gerado a partir do núcleo reprodutivo $\mathcal{K}$. A seguir, vamos mostrar que $D_0$ satisfaz as propriedades (1) e (2). Considere $x \in \chi$ e $f = \sum_{i=1}^n a_i \mathcal{K} (\cdot , x_i)$, então

$$\langle f , \mathcal{K}(\cdot , x) \rangle_{D_0} = \sum_{i=1}^n a_i \mathcal{K}(x,x_i) = f(x).$$

Como consequência, obtemos que

$$\mid \delta_x(f) - \delta_x(g) \mid =\langle f -g, \mathcal{K}(\cdot , x) \rangle_{D_0} \leq \left( \mathcal{K}(x,x) \right)^{1/2} \parallel f - g \parallel_{D_0} ,$$

o que implic que $\delta_x$ é contínuo em $D_0$. Assim, a primeira propriedade de um pré-RKHS é válida.

A seguir, vamos mostrar que a propriedade (2) é válida para $D_0$ cm o produto interno definido pela função positiva definida $\mathcal{K}$. Considere $\epsilon > 0$ e $(f_n: n \geq 1 )$ uma sequência de Cauchy em $D_0$ que converge pontualmente para zero. Desde que toda sequência de Cauchy é limitada, podemos encontrar $M>0$ tal que $\parallel f_n \parallel_{D_0} < M$ para todo $n \geq 1$. Além disso, existe $n_1 \geq 1$ tal que

$$\parallel f_n - f_m \parallel_{D_0} < \frac{\epsilon}{2M}, \quad n , m \geq n_1.$$

Tomamos $f_{n_1} =\sum_{j=1}^r a_j \mathcal{K}(\cdot , x_i)$ para algum $(a_1, \cdots , a_r) \in \mathbb{R}^r$ e $r \in \mathbb{N}$. Considere $n_2 \geq 1$ tal que $\mid f(x_i) \mid \frac{\epsilon}{2 r \mid a_i \mid}$ para todo $i=1, \cdots , r$. Desta forma, para todo $n \geq \max(n_1 , n_2 )$, obtemos que

$$ \parallel f_n \parallel_{D_0}^2 \leq \big| \langle f_n - f_{n_1} , f_n \rangle_{D_0} \big| + \big| \langle f_{n_1} , f_n \rangle_{D_0} \big| $$

$$ \leq \parallel f_n - f_{n_1} \parallel_{D_0} + \sum_{i=1}^r \mid a_i f_n (x_i) \mid < \epsilon, $$

e consequentemente, temos que $f_n$ converge para zero na norma em$D_0$. Portanto, as propriedades (1) e (2) são válidas para $D_0$.

Definimos $D$ como o conjunto de todas as funções $f : \chi \rightarrow \mathbb{R}$ para o qual existe um sequência $( f_n : n \geq 1 ) \subset D_0$ que é Cauchy em $D_0$ e converge pontualmente para $f$. Assim, definimos $D$ como o completamento topológico de $D_0$ em relação ao produto interno derivado da função positiva definida $\mathcal{R}$. Dado duas funções $f,g \in D$, definimos o produo interno por

$$\langle f , g \rangle_D : = \lim_{n \rightarrow \infty} \lim_{m \rightarrow \infty} \langle f_n , g_m \rangle_{D_0}.$$

A seguir, vamos mostrar que $D$ é um RKHS com núcleo reprodutivo $\mathcal{K}$. Para mostrar que $\mathcal{K}$ é um núcleo reprodutivo sobre $D$, tomamos $f \in D$ e uma sequência $(f_n : n \geq 1 ) \subset D_0$que converge pontualmente para $f$. Assi, temos que

$$\langle f , \mathcal{K} (\cdot , x) \rangle_{D} = \lim_{n \rightarrow \infty} \langle f_n , \mathcal{K} (\cdot , x) \rangle_{D_0} = \lim_{n \rightarrow \infty} f_n(x) = f(x).$$