2.7 Gráficos de Controle Multivariados
Um gráfico de controle multivariado mostra como as variáveis conjuntamente influenciam o processo. São utilizados quando há correlação nas variáveis em estudo.
Uma desvantagem deste tipo de gráfico refere-se a uma dificuldade maior quanto à sua interpretação, uma vez que os pontos fora de controle não revelam especificamente qual ou quais variáveis, ou a combinação delas, causam o problema.
Então, para analisar dados multivariados um procedimento que pode ser utilizado é verificar a correlação entre eles e então trabalhar apenas com aquelas variáveis que são correlacionadas. Com isso, podemos plotar em um gráfico de controle com os valores da estatística T² de Hotelling e da variância generalizada para essas variáveis. Esse procedimento é definido adiante.
A seguir vamos discutir a construção dos gráficos de controle multivariados.
Para a construção desses gráficos vamos considerar dois casos: um caso em que temos observações individuais (não se tem réplicas) e outro caso em que temos réplicas para cada observação.
a) 7.1 - Gráficos de controle multivariados para observações individuais
A seguir vamos apresentar a construção dos gráficos de controle multivariados para observações individuais, ou seja, para as observações que não possuem réplicas.
Para introduzir e ilustrar esse conceito vamos considerar dados dispostos de maneira geral como na Tabela 2.7.1.
| Variáveis | ||||
|---|---|---|---|---|
| Amostra | $ X_1 $ | $ X_2 $ | $ \cdots $ | $ X_p $ |
| 1 | 1 | 2 | 3 | 4 |
| 2 | 1 | 2 | 3 | 4 |
| 3 | 1 | 2 | 3 | 4 |
| $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ |
| m | $ X_{1m} $ | $ X_{2m} $ | $ \cdots $ | $ X_{pm} $ |
| Média | $ \overline{X}_1 $ | $ \overline{X}_2 $ | $ \cdots $ | $ \overline{X}_p $ |
| Desvio padrão amostral | $ s_1 $ | $ s_2 $ | $ \cdots $ | $ s_p $ |
Tabela 2.7.1: Entrada de dados
Gráfico de controle T² de Hotelling
Para o cálculo da estatística T² de Hotelling devemos seguir os passos abaixo.
- Calcular a média para cada variável
$$\overline{X}_1, \overline{X}_2, \ldots, \overline{X}_p$$
- Calcular as variâncias e covariâncias amostrais
$$S_1^2, \ldots, S_ik, \ldots, S_p^2$$
- Calcular a estatística T² para cada amostra
$$T^2 = (X_i - \overline{X})^{\prime} S^{-1}(X_i - \overline{X})$$
em que
- p é o número de variáveis
- m é o número de amostras
- S é a matriz de covariância amostral
- $ S ^ {-1} $ é a matriz inversa de covariância amostral
Assim, os limites de controle são dados por
$$LIC = \dfrac{(m-1)^2}{m}B_{\left(\frac{\alpha}{2};~\frac{p}{2};~\frac{(m-p-1)}{2}\right)}$$
$$LSC = \dfrac{(m-1)^2}{m}B_{\left(1-\frac{\alpha}{2};~\frac{p}{2};~\frac{(m-p-1)}{2}\right)}$$
em que
$$B_{\left(\frac{\alpha}{2};~\frac{p}{2};~\frac{(m-p-1)}{2}\right)} \qquad \hbox{e} \qquad B_{\left(1-\frac{\alpha}{2};~\frac{p}{2};~\frac{(m-p-1)}{2}\right)}$$
indicam os quantis correspondentes à distribuição Beta.
A linha central do gráfico de controle é definido utilizando-se a mediana (isto é, o quantil de 50%) da distribuição Beta correspondente, indicado por
$$LC = B_{\left(0,50;~\frac{p}{2};~\frac{(m-p-1)}{2}\right)}$$
Gráfico de controle para a variância generalizada
O procedimento utilizado para construir os gráficos de controle para a variância generalizada é padronizar os dados utilizando o vetor de médias e a matriz de covariâncias amostrais. A padronização é feita da seguinte forma $$Z_{ij} = \dfrac{ X_{ij} - \overline{X}_i}{S_i}$$
Desta forma, teremos uma matriz conforme apresentado no quadro a seguir
| Variáveis | |||||
|---|---|---|---|---|---|
| Amostra | $ Z_1 $ | $ Z_2 $ | $ \cdots $ | $ Z_p $ | Desvio padrão amostral |
| 1 | $ Z_{11} $ | $ Z_{21} $ | $ \cdots $ | $ Z_{p1} $ | $ s_1 $ |
| 2 | $ Z_{12} $ | $ Z_{22} $ | $ \cdots $ | $ Z_{p2} $ | $ s_2 $ |
| 3 | $ Z_{13} $ | $ Z_{23} $ | $ \cdots $ | $ Z_{p3} $ | $ s_3 $ |
| $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ |
| m | $ Z_{1m} $ | $ Z_{2m} $ | $ \cdots $ | $ Z_{pm} $ | $ s_m $ |
Tabela 2.7.2: Matriz para padronização
Com os dados normalizados podemos construir um gráfico de controle utilizando o mesmo procedimento usado na construção do gráfico de controle usual do desvio padrão $ S $.
Dessa froma, os limites de controle são dados por
- Limite superior de controle:
$$LSC = B_4 \ast \overline{S}$$
- Linha Central:
$$LC = \overline{S}$$
- Limite inferior de controle:
$$LIC = B_3 \ast \overline{S}$$
Exemplo 7.1.1:
Temos um molde de areia onde peças de ferro são moldadas. Neste caso, nossas variáveis de interesse são a compatibilidade, o coeficiente de RCV1 e a plasticidade. Os dados são apresentados na tabela a seguir.
| Corrida | Peça | Qtde Prod | Qtde Refugo | Compactabilidade | RCV1 | Plasticidade |
|---|---|---|---|---|---|---|
| E188 | M20700300 | 6288 | 182 | 36,5 | 22,026 | 28,87 |
| E189 | M20900200 | 655 | 128 | 36,571 | 21,12 | 29,924 |
| E190 | M20701400 | 1290 | 33 | 36,167 | 21,182 | 29,368 |
| E191 | M20600400 | 3176 | 316 | 36,5 | 22,134 | 29,822 |
| E192 | M20900900 | 8052 | 129 | 37,4 | 21,93 | 28,774 |
| E193 | M20900900 | 4436 | 49 | 37,333 | 21,507 | 28,812 |
| E194 | M20701201 | 6424 | 245 | 37,167 | 23,132 | 29 |
| E195 | M20700300 | 6000 | 79 | 38 | 19,653 | 30,885 |
| E196 | M20900900 | 7986 | 183 | 38 | 19,653 | 30,885 |
| E197 | M20701500 | 9024 | 108 | 36,5 | 20,993 | 30,568 |
| E198 | M20700600 | 1680 | 41 | 38,25 | 20,733 | 28,84 |
| E199 | M20701301 | 4248 | 48 | 37,643 | 19,513 | 28,818 |
| E200 | M20900200 | 1190 | 32 | 37,667 | 20,613 | 29,035 |
| E201 | M20404400 | 2400 | 8 | 36,833 | 22,423 | 26,685 |
| E202 | M20701500 | 4752 | 126 | 37,333 | 20,29 | 28,527 |
| E203 | M20900900 | 3072 | 43 | 37,167 | 21,083 | 26,24 |
| E204 | M20701500 | 564 | 19 | 38 | 20,363 | 29,843 |
| E205 | M20701201 | 1192 | 28 | 37,667 | 21,147 | 29,273 |
| E206 | M20900200 | 1275 | 25 | 37,667 | 21,147 | 29,273 |
| E207 | M20600400 | 2056 | 537 | 36 | 22,89 | 27,753 |
| E208 | M20700300 | 7816 | 85 | 39 | 20,24 | 29,57 |
| E209 | M20900200 | 1040 | 44 | 36,333 | 19,9 | 27,89 |
| E210 | M20900900 | 1968 | 16 | 38 | 19,547 | 27,84 |
| E211 | M20701201 | 5016 | 52 | 36,333 | 19,9 | 27,633 |
| E212 | M20600400 | 1656 | 524 | 37,667 | 20,937 | 27,84 |
Tabela 2.7.3: Variáveis de Areia sem réplicas.
Para construir os gráficos de controle multivariados precisamos primeiramente saber quais variáveis são correlacionadas, com isso podemos trabalhar apenas com aquelas variáveis que conjuntamente influenciam o processo. Para obter a correlação entre as variáveis podemos utilizar a ferramenta Matriz de Correlação disponibilizada pelo Software Action.
Neste exemplo vamos considerar que as 3 variáveis estão correlacionadas para mostrar os cálculos com detalhes.
Cuidado!
A correlação deve sempre ser analisada no caso multivariado para que os resultados não sejam mascarados.
A seguir apresentamos os passos para a construção dos gráficos de controle multivariados (T² e Variância generalizada).
As médias das variáveis Compactabilidade, RCV1 e Plasticidade são, respectivamente, $37,267$ ; $20,962$ e $28,878$. A matriz de covariâncias ($S$) e a matriz inversa ($ S ^ {-1} $) são dadas por
$$S = \begin{bmatrix} 0,5810 \qquad -0,3629 \qquad 0,2243 \cr -0,3629 \qquad 1,0728 \qquad -0,2576 \cr 0,2243 \qquad -0,2576 \qquad 1,3649 \end{bmatrix} \qquad \hbox{e} \qquad S^{-1} = \begin{bmatrix} 2,2533 \qquad 0,7053 \qquad 0,2371 \cr 0,7053 \qquad 1,1971 \qquad 0,1101 \cr -0,2371 \qquad 0,1101 \qquad 0,7924 \end{bmatrix}$$
Cálculo dos limites de controle para T² de Hotelling
O cálculo de T² para a primeira corrida (E188) é dado por
$$T^2 = (X_i - \overline{X})S^{-1}(X_i - \overline{X})$$
$$ = [-0,767 \quad 1,063 \quad -0,0087] \ast \begin{bmatrix} 2,2533 \quad 0,7053 \quad -0,2371 \cr 0,7053 \quad 1,1971 \quad 0,1101 \cr -0,2371 \quad 0,1101 \quad 0,7924 \end{bmatrix} \ast \begin{bmatrix} -0,767 \cr 1,063 \cr -0,0087 \end{bmatrix} = 1,5259$$
Para as outras amostras (corridas E189 a E212) o procedimento é análogo.
Os valores de T² para todas as amostras estão dispostos no quadro abaixo.
| Corrida | T² |
|---|---|
| E188 | 152,595 |
| E189 | 221,678 |
| E190 | 291,648 |
| E191 | 299,512 |
| E192 | 133,373 |
| E193 | 0,4124 |
| E194 | 542,531 |
| E195 | 382,223 |
| E196 | 382,223 |
| E197 | 418,464 |
| E198 | 193,979 |
| E199 | 209,762 |
| E200 | 0,28603 |
| E201 | 473,986 |
| E202 | 0,64975 |
| E203 | 534,417 |
| E204 | 129,344 |
| E205 | 0,56833 |
| E206 | 0,56833 |
| E207 | 447,276 |
| E208 | 532,076 |
| E209 | 528,861 |
| E210 | 368,312 |
| E211 | 568,977 |
| E212 | 140,279 |
Tabela 2.7.4: Cálculo dos valores de T²
Os limites de controle com um nível de confiança de 3σ = 99,73% são dados por
$$LIC = \dfrac{(m-1)^2}{m}B_{\left(\frac{\alpha}{2};~\frac{p}{2};~\frac{(m-p-1)}{2}\right)}~=~\dfrac{(25-1)^2}{25}B_{\left(0,00135;~\frac{3}{2};~\frac{(25-3-1)}{2}\right)}~=~0,03183$$
$$LC = \dfrac{(25-1)^2}{25}B_{\left(0,50;~\frac{3}{2};~\frac{(25-3-1)}{2}\right)}~=~2,402$$
$$LSC = \dfrac{(m-1)^2}{m}B_{\left(1-\frac{\alpha}{2};~\frac{p}{2};~\frac{(m-p-1)}{2}\right)}~=~\dfrac{(25-1)^2}{25}B_{\left(0,99865;~\frac{3}{2};~\frac{(25-3-1)}{2}\right)}~=~11,918$$
sendo
- $m$ = número de amostras = 25
- $p$ = número de variáveis correlacionadas = 3
Cálculo dos limites de controle para a variância generalizada
Vamos agora construir os limites de controle para a variância generalizada. Primeiramente calculamos a média e variância, daí procedemos a padronização de cada variável. Assim temos
Para Compactabilidade (X1)
$$\overline{X}_1 = \dfrac{36,5 + 36,571 + \ldots + 36,333 + 37,667}{25} = 37,267$$
$$S_1^2 = \dfrac{(36,5 - 37,267)^2 + \ldots + (37,667 - 37,267)^2}{24} = 0,581$$
Padronização:
$$\dfrac{(36,5 - 37,267)}{\sqrt{0,581}} = -1,00746$$
Para RCV1 (X2)
$$\overline{X}_2 = \dfrac{22,026 + 21,12 + \ldots + 19,9 + 20,937}{25} = 20,962$$
$$S_2^2 = \dfrac{(22,026 - 20,962)^2 + \ldots + (20,937 - 20,962)^2}{24} = 1,072$$
Padronização:
$$\dfrac{(22,026 - 20,962)}{\sqrt{1,072}} = 1,027$$
Para Plasticidade (X3)
$$\overline{X}_3=\dfrac{28,87+29,924+\ldots+27,633+27,84}{25}=28,878$$
$$S_3^2=\dfrac{(28,87-28,878)^2+\ldots+(27,84-28,878)^2}{24}=1,364$$
Padronização:
$$\dfrac{(28,87-28,878)}{\sqrt{1,364}}=-0,00746$$
As variáveis padronizadas para todas as amostras são dadas na Tabela 2.7.5.
| Compactabilidade | RCV1 | Plasticidade | Desvios Padrão |
|---|---|---|---|
| -100,746 | 1,027 | -0,00746 | 101,728 |
| -0,91431 | 0,15231 | 0,89471 | 0,90934 |
| -144,433 | 0,21217 | 0,4188 | 102,127 |
| -100,746 | 113,127 | 0,8074 | 115,273 |
| 0,17328 | 0,93432 | -0,08964 | 0,53179 |
| 0,08538 | 0,52594 | -0,05711 | 0,30396 |
| -0,1324 | 209,478 | 0,10381 | 122,339 |
| 0,96044 | -1,264 | 171,728 | 154,967 |
| 0,96044 | -1,264 | 171,728 | 154,967 |
| -100,746 | 0,0297 | 144,594 | 123,157 |
| 128,842 | -0,22132 | -0,03314 | 0,82272 |
| 0,49208 | -139,916 | -0,05197 | 0,97363 |
| 0,52356 | -0,33717 | 0,13377 | 0,43101 |
| -0,57058 | 141,028 | -187,772 | 165,546 |
| 0,08538 | -0,64901 | -0,30106 | 0,36736 |
| -0,1324 | 0,11659 | -225,862 | 13,054 |
| 0,96044 | -0,57853 | 0,82538 | 0,85222 |
| 0,52356 | 0,17838 | 0,33748 | 0,17277 |
| 0,52356 | 0,17838 | 0,33748 | 0,17277 |
| -166,342 | 186,115 | -0,96356 | 186,598 |
| 227,236 | -0,69728 | 0,5917 | 148,912 |
| -122,655 | -102,553 | -0,8463 | 0,19023 |
| 0,96044 | -136,634 | -0,88909 | 122,898 |
| -122,655 | -102,553 | -106,628 | 0,10626 |
| 0,52356 | -0,02437 | -0,88909 | 0,71222 |
Tabela 2.7.5: Variáveis padronizadas.
A última coluna da Tabela 2.7.5 é o desvio-padrão das variáveis padronizadas em relação a X1, X2 e X3, ou seja,
$$S = \sqrt{\dfrac{\sum_{1}^{p}X_i^{2} - p \ast \overline{X}^2}{p-1}}$$
Para a primeira linha, o valor 1,01728 é obtido através do cálculo de S, dado por
$$S = \sqrt{\dfrac{(2,06976) - 3 \ast (0,00403)^2}{2}} = 1,01728$$
Precisamos ainda calcular $ \overline{S}, $ dado por
$$\overline{S} = \dfrac{\hbox{Soma dos desvios padrão amostrais}}{\hbox{número de amostras}} = \dfrac{\hbox{soma das }S_i}{m}$$
ou seja,
$$\overline{S} = \dfrac{1,01728 + \ldots + 0,71222}{25} = \dfrac{22,8368}{25} = 0,913472$$
Assim a linha central do gráfico de controle é dado pela média dos desvios padrão, ou seja, para este exemplo é a média da última coluna da Tabela 7.1.3, obtendo assim o valor 0,913472. Com isso, o gráfico da variância generalizada com observações individuais segue o mesmo raciocínio do gráfico $ S $ usual.
Aplicando as fórmulas e utilizando o Apêndice para obter os valores de B3 = 0 e B4 = 2,266 (para n = 4) encontramos os limites de controle, que são dados por
$$LSC = B_4 \ast \overline{S} = 2,266 \ast 0,913472 = 2,0699$$
$$LC = \overline{S} = 0,913472$$
$$LIC = B_3 \ast \overline{S} = 0 \ast 0,913472 = 0$$
A seguir temos os resultados obtidos pelo Software Action para esse exemplo.
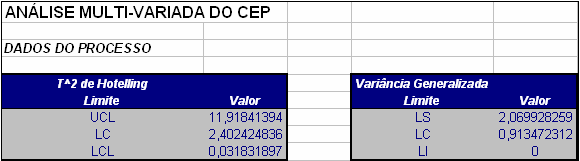
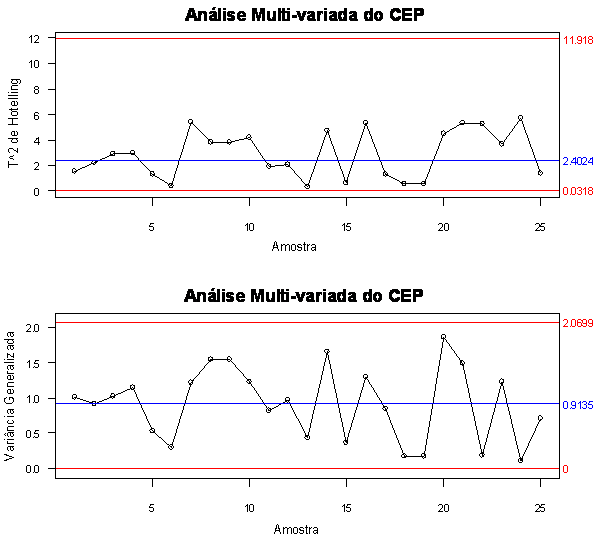
Figura 2.7.1: Gráficos T² de Hotelling e Variância Generalizada.
Observando a Figura 2.7.1 percebemos que nenhum ponto está fora dos limites de controle e a variância permanece estável ao longo do período observado.
Para entender como executar essa função do Software Action, você pode consultar o manual do usuário.
Exemplo 7.1.2:
A Tabela 2.7.6 apresenta dados da área industrial referentes à espessura de engrenagens de câmbio automotivo. A Figura 2.7.2 ilustra o formato da engrenagem.

Figura 2.7.2: Detalhe da engrenagem do câmbio.
| Posição1 | Posição2 | Posição3 |
|---|---|---|
| 98,208 | 98,209 | 21,996 |
| 98,209 | 98,220 | 22,002 |
| 98,206 | 98,204 | 21,999 |
| 98,206 | 98,206 | 21,998 |
| 98,204 | 98,214 | 21,998 |
| 98,209 | 98,203 | 21,983 |
| 98,202 | 98,212 | 21,981 |
| 98,196 | 98,221 | 21,980 |
| 98,215 | 98,201 | 21,986 |
| 98,194 | 98,227 | 21,993 |
| 98,200 | 98,210 | 21,981 |
| 98,206 | 98,207 | 21,983 |
| 98,212 | 98,200 | 22,004 |
| 98,211 | 98,200 | 22,009 |
| 98,212 | 98,199 | 22,008 |
| 98,191 | 98,166 | 22,008 |
| 98,206 | 98,205 | 22,009 |
| 98,192 | 98,207 | 21,982 |
| 98,203 | 98,202 | 21,993 |
| 98,195 | 98,206 | 21,990 |
| 98,207 | 98,204 | 21,999 |
| 98,188 | 98,199 | 21,989 |
| 98,219 | 98,222 | 21,997 |
| 98,196 | 98,205 | 21,998 |
| 98,220 | 98,227 | 22,001 |
| 98,193 | 98,213 | 21,985 |
| 98,194 | 98,217 | 21,988 |
| 98,200 | 98,200 | 21,983 |
| 98,199 | 98,199 | 21,980 |
| 98,199 | 98,197 | 21,985 |
| 98,199 | 98,198 | 21,984 |
| 98,196 | 98,206 | 21,982 |
| 98,203 | 98,207 | 21,984 |
| 98,201 | 98,206 | 21,986 |
| 98,197 | 98,161 | 21,989 |
| 98,192 | 98,205 | 21,984 |
| 98,208 | 98,172 | 22,011 |
| 98,175 | 98,195 | 21,983 |
| 98,176 | 98,196 | 21,983 |
| 98,172 | 98,195 | 21,983 |
| 98,197 | 98,201 | 21,999 |
| 98,195 | 98,211 | 21,993 |
| 98,196 | 98,206 | 21,993 |
| 98,201 | 98,219 | 21,989 |
Tabela 2.7.6: Dados referentes à espessura de engrenagens.
Primeiramente vamos verificar se as variáveis Posição1, Posição2 e Posição3 são correlacionadas. Para obter a correlação entre elas vamos utilizar a ferramenta Matriz de Correlação do Software Action. Dessa forma, temos
| Posicao1 | Posicao2 | Posicao3 | |
|---|---|---|---|
| Posicao1 | 1 | 0.2439 | 0.4712 |
| Posicao2 | 0.2439 | 1 | -0.1661 |
| Posicao3 | 0.4712 | -0.1661 | 1 |
Tabela 2.7.7: Matriz de correlação
| Posicao1 | Posicao2 | Posicao3 | |
|---|---|---|---|
| Posicao1 | 1 | 0.1106 | 0.0012 |
| Posicao2 | 0.1106 | 1 | 0.2811 |
| Posicao3 | 0.0012 | 0.2811 | 1 |
Tabela 2.7.8: Matriz de P-Valores
Podemos ver que a correlação positiva (0,471) entre a Posição 1 e a Posição 3 é significativa, comprovada pelo p-valor de 0,001 que é menor do que o nível de significância adotado de 5%. Portanto, podemos concluir que apenas as variáveis Posição1 e Posição3 influenciam conjuntamente no processo, com isso vamos construir os gráficos de controle multivariados considerando apenas essas duas variáveis.
A seguir apresentamos os passos para a construção dos gráficos de controle multivariados (T² de Hotelling e Variância generalizada).
As médias das variáveis Posição1 e Posição3 são, respectivamente, 98,2 e 21,992.
A matriz de covariâncias ($S$) e a matriz inversa ($ S ^ {-1} $) são dadas por
$$S = \begin{bmatrix} 0,000105 \qquad ~~~38,3226 \cr 38,3226 \qquad ~~~0,000086 \end{bmatrix} ~ \qquad \hbox{e} \qquad ~ S^{-1} = \begin{bmatrix}-0,00000006 \qquad \qquad ~~~0,0261 \qquad \cr \qquad 0,0261 \qquad ~~~-0,000000071 \end{bmatrix}$$
Cálculo dos limites de controle para T² de Hotelling
O cálculo de T² para a primeira linha do conjunto de dados, considerando agora apenas as variáveis correlacionadas (Posição1 e Posição3), é da seguinte forma
$$T^2 = (X_i - \overline{X})S^{-1}(X_i - \overline{X})$$
$$ = [0,008 \qquad ~0,004] \ast \begin{bmatrix} -0,00000006 \qquad \qquad ~~~0,0261 \qquad \cr \qquad 0,0261 \qquad ~~~-0,000000071 \cr \end{bmatrix} \ast \begin{bmatrix} 0,008 \cr 0,004 \end{bmatrix} = 0,0000017$$
Para as outras linhas o procedimento para o cáculo da estatística T² é análogo.
Portanto, os limites de controle com um nível de confiança de 3σ = 99,73% são dados por
$$LIC = \dfrac{(m-1)^2}{m}B_{\left(\frac{\alpha}{2};~\frac{p}{2};~\frac{(m-p-1)}{2}\right)}~=~\dfrac{(44-1)^2}{44}B_{\left(0,00135;~\frac{2}{2};~\frac{(44-2-1)}{2}\right)}~=~0,0028$$
$$LC = \dfrac{(44-1)^2}{44}B_{\left(0,50;~\frac{2}{2};~\frac{(44-2-1)}{2}\right)}~=~1,3971$$
$$LSC = \dfrac{(m-1)^2}{m}B_{\left(1-\frac{\alpha}{2};~\frac{p}{2};~\frac{(m-p-1)}{2}\right)}~=~\dfrac{(44-1)^2}{44}B_{\left(0,99865;~\frac{2}{2};~\frac{(44-2-1)}{2}\right)}~=~11,578$$
sendo
- $m$ = número de amostras = 44
- $p$ = número de variáveis correlacionadas = 2
Cálculo dos limites de controle para a variância generalizada
Vamos agora construir os limites de controle para a variância generalizada. Primeiramente calculamos a média e variância, daí procedemos a padronização de cada variável. Assim temos
Para Posição1 (X1)
$$\overline{X}_1 = \dfrac{98,208 + 98,209 + \ldots + 98,196 + 98,201}{44} = 98,2$$
$$S_1^2 = \dfrac{(98,208 - 98,2)^2 + \ldots + (98,201 - 98,2)^2}{43} = 0,000105$$
Padronização para o primeiro valor da variável Posição1:
$$\dfrac{(98,208 - 98,2)}{\sqrt{0,000105}} = 0,7843$$
Para Posição3 (X2)
$$\overline{X}_2 = \dfrac{21,996 + 22,002 + \ldots + 21,993 + 21,989}{44} = 21,992$$
$$S_2^2 = \dfrac{(21,996 - 21,992)^2 + \ldots + (21,989 - 21,992)^2}{43} = 0,0000861$$
Padronização para o primeiro valor da variável Posição3:
$$\dfrac{(21,996 - 21,992)}{\sqrt{0,0000861}} = 0,431$$
O procedimento para a padronização dos outros valores das variáveis Posição1 e Posição3 é análogo.
O desvio-padrão das variáveis padronizadas em relação a X1 e X2 é dado por
$$S = \sqrt{\dfrac{\sum_{1}^{p}X_i^{2} - p \ast \overline{X}^2}{p-1}}$$
Logo, para a primeira linha o valor de S é obtido da seguinte forma
$$S = \sqrt{\dfrac{(0,8) - 2 \ast (0,608)^2}{1}} = 0,1564$$
Para as outras linhas do conjunto o cálculo é análogo.
Precisamos ainda calcular $ \overline{S}, $ dado por
$$\overline{S} = \dfrac{\hbox{Soma dos desvios padrão amostrais}}{\hbox{número de amostras}} = \dfrac{\hbox{soma das }S_i}{m}$$
ou seja,
$$\overline{S} = 0,5785$$
Assim a linha central do gráfico de controle é dado pela média dos desvios padrão. Com isso, o gráfico da variância generalizada com observações individuais segue o mesmo raciocínio do gráfico $ S $ usual.
Aplicando as fórmulas e utilizando o Apêndice para obter os valores de B3 = 0 e B4 = 2,568 (para n = 3) encontramos os limites de controle, que são dados por
$$LSC = B_4 \ast \overline{S} = 2,568 \ast 0,5785 = 1,4856$$
$$LC = \overline{S} = 0,5785$$
$$LIC = B_3 \ast \overline{S} = 0 \ast 0,5785 = 0$$
A seguir temos os resultados obtidos pelo Software Action para esse exemplo.
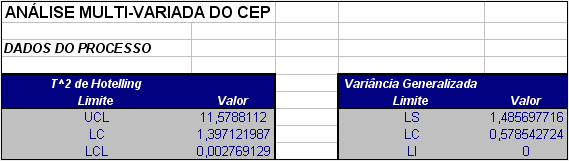
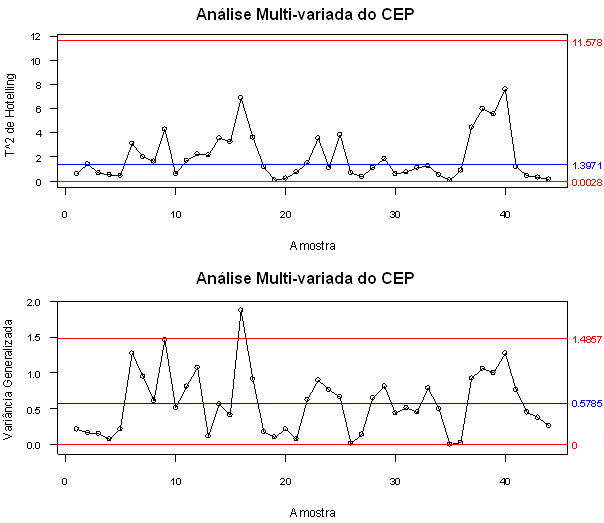
Figura 2.7.3: Gráficos T² de Hotelling e Variância Generalizada.
Podemos notar que o processo não manteve-se estável ao longo do período considerado.
Para entender como executar essa função do Software Action, você pode consultar o manual do usuário.
b) 7.2 - Gráficos de controle multivariados para observações com réplicas
A seguir apresentamos a construção dos gráficos de controle multivariados para observações com réplicas.
Para introduzir o conceito desses gráficos vamos considerar a entrada de dados, de forma geral, conforme a Tabela 2.7.9. Podemos observar agora que esses dados possuem réplicas.
| Variáveis | ||||
|---|---|---|---|---|
| Amostra | $ X_1 $ | $ X_2 $ | $ \cdots $ | $ X_p $ |
| 1 | $ X_{111} $ | $ X_{211} $ | $ \cdots $ | $ X_{p11} $ |
| 1 | $ X_{112} $ | $ X_{212} $ | $ \cdots $ | $ X_{p12} $ |
| $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ |
| 1 | $ X_{11n} $ | $ X_{21n} $ | $ \cdots $ | $ X_{p1n} $ |
| 2 | $ X_{121} $ | $ X_{221} $ | $ \cdots $ | $ X_{p21} $ |
| 2 | $ X_{122} $ | $ X_{222} $ | $ \cdots $ | $ X_{p22} $ |
| $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ |
| 2 | $ X_{12n} $ | $ X_{22n} $ | $ \cdots $ | $ X_{p2n} $ |
| 3 | $ X_{131} $ | $ X_{231} $ | $ \cdots $ | $ X_{p31} $ |
| 3 | $ X_{132} $ | $ X_{232} $ | $ \cdots $ | $ X_{p32} $ |
| $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ |
| 3 | $ X_{13n} $ | $ X_{23n} $ | $ \cdots $ | $ X_{p3n} $ |
| m | $ X_{1m1} $ | $ X_{2m1} $ | $ \cdots $ | $ X_{pm1} $ |
| m | $ X_{1m2} $ | $ X_{2m2} $ | $ \cdots $ | $ X_{pm2} $ |
| $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ |
| m | $ X_{1mn} $ | $ X_{2mn} $ | $ \cdots $ | $ X_{pmn} $ |
Tabela 2.7.9: Entrada de dados.
$ refere-se a k-ésima observação na j-ésima amostra da i-ésima variável.
Aqui $i = 1, …, p$ ; $j = 1, …, m$ e $k = 1, …, n$.
Para o cálculo da estatística T² de Hotelling devemos seguir os passos abaixo:
- Calcular a média dentro de cada amostra para cada variável
$$\overline{X}_{ij.} = \dfrac{1}{n} \sum_{k=1}^{n} X_{ijk} \qquad \hbox{para} \quad i = 1, \ldots, p$$
- Calcular o vetor de médias gerais por
$$\overline{X}_{…} = \dfrac{1}{m}\sum^{m}_{j=1}\overline{X}_{.j.}$$
- Calcular o vetor de variâncias amostrais para cada amostra
$$S^2_{ij.} = \dfrac{1}{n - 1}\sum^{n}_{k=1}(X_{ijk} - \overline{X}_{ij.})^2 \qquad {para}~i = 1, \ldots, p$$
- Calcular as p(p - 1)/2 covariâncias amostrais, denotadas por $ S^2_{ilj}, $ para cada amostra
$$S^2_{ilj} = \dfrac{1}{n - 1}\sum^{n}_{k=1}(X_{ijk} - \overline{X}_{ij.})(X_{ljk} - \overline{X}_{lj.}) \qquad \hbox{para}~i \neq l = 1, \ldots, p$$
- Construir a matriz de covariância amostral S da seguinte forma
$$S = \left(\begin{array}{cccc} S^2_{11} \qquad S^2_{12} \qquad \cdots \qquad S^2_{1p} \cr S^2_{21} \qquad S^2_{22} \qquad \cdots \qquad S^2_{2p} \cr \vdots \qquad ~~~ \vdots \qquad ~\cdots \qquad ~\vdots \cr S^2_{p1} \qquad S^2_{p2} \qquad \cdots \qquad S^2_{pp} \end{array} \right)$$
em que
$$S^2_{ii} = \dfrac{1}{m}\sum^{m}_{j=1}S^2_{iij}, \qquad \hbox{para}~i = 1, \ldots, p$$
$$S^2_{il} = \dfrac{1}{m}\sum^{m}_{j=1}S^2_{ilj}, \qquad \hbox{para}~i \neq l = 1, \ldots, p$$
- Calcular a estatística T² da seguinte forma
$$T_j^2 = n(\overline{X}_{.j.} - \overline{X}_{…})S^{-1}(\overline{X}_{.j.} - \overline{X}_{…}), \hbox{para cada}~j = 1, …, m$$
Limites de Controle para o gráfico de T²
Temos que a estatística $ T_j^2~\sim~\left(\dfrac{(mn - m)p}{mn - m - p + 1}\right)F_{(p,~mn - m - p + 1)}, $ para n > 1 (ver Johnson (2002)).
Limite inferior de controle (Montgomery (2001)):
$$LIC = \dfrac{p(m-1)(n-1)}{(mn - m - p + 1)}F_{\left(\alpha/2;~p;~mn-m-p+1\right)}$$
Linha Central (Montgomery (2001)):
$$LC = \dfrac{p(m-1)(n-1)}{(mn - m - p +1)}F_{\left(0,50;~p;~mn-m-p+1\right)}$$
Limite superior de controle (Montgomery (2001)):
$$LSC = \dfrac{p(m-1)(n-1)}{(mn - m - p + 1)}F_{\left(1-\alpha/2;~p;~mn-m-p+1\right)}$$
em que n = tamanho de cada amostra, m = número de amostras e p = quantidade de características.
Limites de Controle para a variância generalizada
$\mid S \mid$ determinante da matriz de covariância amostral, variância generalizada (Johnson (2002)).
Limite inferior de controle (Montgomery (2001)):
$$LIC = \dfrac{\mid S \mid}{b_1}(b_1 - 3\sqrt{b_2})$$
Linha Central (Montgomery (2001)):
$$LC = \mid S \mid$$
Limite superior de controle (Montgomery (2001)):
$$LSC = \dfrac{\mid S \mid}{b_1}(b_1 + 3\sqrt{b_2})$$
em que
$$b_1 = \dfrac{1}{(n-1)^p}\prod_{i=1}^p(n-i)$$
$$b_2 = \dfrac{1}{(n-1)^{2p}}\prod_{i=1}^p(n-i)\left[\prod_{j=1}^p(n-j+2) - \prod_{j=1}^p(n-j)\right]$$
sendo $p$ = número de variáveis e $n$ = número de observações em cada grupo.
Exemplo 7.2.1:
Um químico está interessado em verificar a relação entre a quantidade de horas que determinados corpos-de-prova ficam submetidos à uma estufa e a porcentagem (%) de umidade neles contida. A estufa foi mantida a temperatura constante e tomamos amostras de tamanho 5 para cada dia. Os dados estão dispostos na Tabela 2.7.10.
| Data da Medição | CP | Número de horas | Umidade(%) | Data da Medição | CP | Número de horas | Umidade(%) |
|---|---|---|---|---|---|---|---|
| 1/1/2001 | 1 | 1 | 7 | 1/6/2001 | 1 | 3 | 5,8 |
| 2 | 2 | 6,5 | 2 | 3 | 5,6 | ||
| 3 | 4 | 6 | 3 | 2 | 4 | ||
| 4 | 6 | 7 | 4 | 2 | 4 | ||
| 5 | 4 | 7 | 5 | 5 | 5,8 | ||
| 1/2/2001 | 1 | 2 | 7 | 1/7/2001 | 1 | 4 | 5,2 |
| 2 | 2 | 7 | 2 | 6 | 6,4 | ||
| 3 | 4 | 6,2 | 3 | 2 | 4,5 | ||
| 4 | 1 | 6 | 4 | 3 | 1,5 | ||
| 5 | 1 | 5,2 | 5 | 3 | 5,6 | ||
| 1/3/2001 | 1 | 5 | 7 | 1/8/2001 | 1 | 6 | 6 |
| 2 | 2 | 5,4 | 2 | 3 | 5,8 | ||
| 3 | 5 | 7 | 3 | 7 | 7 | ||
| 4 | 3 | 7 | 4 | 4 | 4,5 | ||
| 5 | 2 | 1,4 | 5 | 3 | 5,2 | ||
| 1/4/2001 | 1 | 4 | 6 | 1/9/2001 | 1 | 5 | 5,6 |
| 2 | 4 | 6,2 | 2 | 4 | 4,5 | ||
| 3 | 4 | 3,5 | 3 | 2 | 4,5 | ||
| 4 | 2 | 4,5 | 4 | 1 | 6 | ||
| 5 | 2 | 3 | 5 | 3 | 2 | ||
| 1/5/2001 | 1 | 3 | 4,2 | 1/10/2001 | 1 | 3 | 5,2 |
| 2 | 3 | 6,5 | 2 | 4 | 6 | ||
| 3 | 2 | 2,2 | 3 | 6 | 5,5 | ||
| 4 | 4 | 5,5 | 4 | 3 | 7 | ||
| 5 | 3 | 6 | 5 | 2 | 6,5 |
Tabela 2.7.10: Dados do experimento.
Primeiramente precisamos verificar se as variáveis a serem analisadas são correlacionadas. Para isso podemos utilizar a ferramenta Matriz de Correlação do Software Action.
Neste exemplo consideraremos que existe correlação entre as variáveis Número de horas e Umidade apenas para trabalhar com as mesmas conjuntamente e exemplificar os cálculos com detalhes.
Cuidado!
A correlação deve sempre ser analisada no caso multivariado para que os resultados não sejam mascarados.
Para a primeira amostra (1/1/2001), temos:
$$S_{11}^2 = \dfrac{1}{4}[(1 - 3,4)^2 + (2 - 3,4)^2 + (4 - 3,4)^2 + (6 - 3,4)^2 + (4 - 3,4)^2] = 3,8$$
$$S_{22}^2 = \dfrac{1}{4}[(7 - 6,7)^2 + (6,5 - 6,7)^2 + (6 - 6,7)^2 + (7 - 6,7)^2 + (7 - 6,7)^2] = 0,2$$
$$S_{12} = \dfrac{1}{4}[(1 - 3,4)(7 - 6,7) + (2 - 3,4)(6,5 - 6,7) + (4 - 3,4)(6 - 6,7) + (6 - 3,4)(7 - 6,7)~+$$
$$+~(4 - 3,4)(7 - 6,7)] = 0,025$$
Cálculo dos limites de controle para T² de Hotelling
O cálculo da estatística T² para a primeira amostra é dado por
$$T^2 = n(\overline{X} - \overline{\overline{X}})S^{-1}(\overline{X} - \overline{\overline{X}})$$
$$= 5 \ast [0,12 \qquad 1,3] \ast \begin{bmatrix} ~0,5427404 \qquad ~-0,2021607 \cr -0,2022607 \qquad ~0,5752761 \cr \end{bmatrix} \ast \begin{bmatrix} 0,12 \cr 1,3 \cr \end{bmatrix} = $$
$$= 4,58479$$
Na tabela a seguir temos as médias e variâncias para o gráfico T² calculadas para todas as amostras.
| Amostra | $ \overline{X}_1 $ | $ \overline{X}_2 $ | $ S_{1}^2 $ | $ S_{2}^2 $ | $ S_{12} $ | $ T^2 $ |
|---|---|---|---|---|---|---|
| 1 | 3,4 | 6,7 | 3,8 | 0,2 | 0,025 | 4,58479 |
| 2 | 2 | 6,28 | 1,5 | 0,572 | 0,3 | 8,95074 |
| 3 | 3,4 | 5,56 | 2,3 | 5,888 | 2,52 | 0,0739 |
| 4 | 3,2 | 4,64 | 1,2 | 2,073 | 0,89 | 1,55585 |
| 5 | 3 | 4,88 | 0,5 | 2,977 | 0,825 | 0,69618 |
| 6 | 3 | 5,04 | 1,5 | 0,908 | 0,9 | 0,38176 |
| 7 | 3,6 | 4,64 | 2,3 | 3,553 | 1,495 | 2,43094 |
| 8 | 4,6 | 5,7 | 3,3 | 0,87 | 1,225 | 4,18667 |
| 9 | 3 | 4,52 | 2,5 | 2,427 | -0,2 | 1,9421 |
| 10 | 3,6 | 6,04 | 2,3 | 0,533 | -0,53 | 1,04202 |
| soma | 32,8 | 54 | 21,2 | 20,001 | 7,45 | 25,84495 |
| média | 3,28 | 5,4 | 2,12 | 2,0001 | 0,745 | 2,584495 |
Tabela 2.7.11: Médias e Variâncias para o gráfico T².
Com isso, podemos construir os limites de controle do gráfico T², com um nível de confiança 3σ = 99,73%, dados a seguir.
Limite inferior de controle
$$LIC = \dfrac{p(m-1)(n-1)}{(mn - m - p + 1)}F_{\left(\alpha/2;~p;~mn-m-p+1\right)} = \dfrac{2(10 - 1)(5 - 1)}{(10 \ast 5 - 10 - 2 + 1)}F_{\left(0,00135;~2;~39\right)}$$
$$= 1,846154 \ast 0,0013509 = 0,0025$$
Limite central
$$LC = \dfrac{p(m-1)(n-1)}{(mn - m - p + 1)}F_{\left(0,50;~p;~mn-m-p+1\right)} = \dfrac{2(10 - 1)(5 - 1)}{(10 \ast 5 - 10 - 2 + 1)}F_{\left(0,50;~2;~39\right)}$$
$$= 1,846154 \ast 0,7056138 = 1,302672$$
Limite superior de controle
$$LSC = \dfrac{p(m-1)(n-1)}{(mn - m - p + 1)}F_{\left(1-\alpha/2;~p;~mn-m-p+1\right)} = \dfrac{2(10 - 1)(5 - 1)}{(10 \ast 5 - 10 - 2 + 1)}F_{\left(0,99865;~2;~39\right)}$$
$$= 1,846154 \ast 7,8650 = 14,520$$
Cálculo dos limites de controle para a variância generalizada
Vamos agora construir os limites de controle para a variância generalizada, os quais são dados por
$$LIC = \dfrac{\mid S \mid}{b_1}(b_1 - 3\sqrt{b_2}) = \dfrac{3,685}{0,75}(0,75 - 3\sqrt{0,84375}) = -9,85$$
Como o valor obtido para o LIC foi negativo, tomamos como valor mínimo o zero. Sendo assim, assumimos LIC = 0.
$$LC = ~\mid S \mid ~= det\begin{bmatrix} 2,12 \qquad 0,745 \cr 0,745 \qquad 2,001 \cr \end{bmatrix} = 3,685$$
$$LSC = \dfrac{\mid S \mid}{b_1}(b_1 + 3\sqrt{b_2}) = \dfrac{3,685}{0,75}(0,75 + 3\sqrt{0,84375}) = 17,225$$
A seguir temos os resultados obtidos pelo Software Action para esse exemplo.
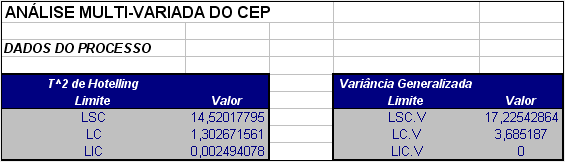
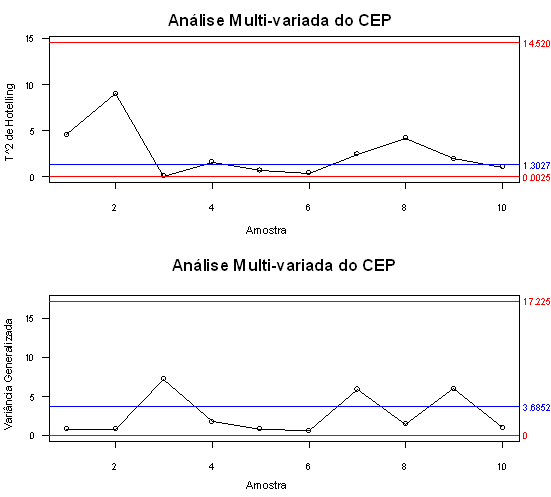
Figura 2.7.4: Gráficos T² e Variância generalizada.
Podemos notar pelos gráficos que o processo manteve-se estável ao longo do período.
Para entender como executar essa função do Software Action, você pode consultar o manual do usuário.