16. Ensaio de Proficiência
Os métodos estatísticos cada vez mais vêm sendo reconhecidos como um importante instrumento para diagnosticar e otimizar a gestão e a operação de diversos sistemas, desde os sistemas humanos aos mais complexos sistemas físicos. As aplicações destes métodos, vêm desempenhando um papel importante na solução de muitos problemas da indústria à agricultura, passando pelos setores socioeconômicos, administrativo e de saúde. Além do que, grande parte das mais avançadas pesquisas científicas em diversas áreas do conhecimento dependem cada vez mais dos métodos estatísticos.
Especificamente na indústria, observamos que o uso de técnicas estatísticas extremamente simples pode ajudar a manter a qualidade de produtos dentro de um determinado nível. Na maioria das vezes, os métodos estatísticos empregados contribuem para o aumento da produção ou até mesmo para a redução de custos, sem que nenhum investimento adicional ou que medidas de expansão industrial precisem ser tomadas. Dos diversos métodos estatísticos que podemos empregar, vamos desenvolver um procedimento para avaliar estatisticamente os programas de ensaios de proficiência.
Os programas de ensaios de proficiência são muito utilizados em comparações inter laboratoriais com o intuito de determinar o desempenho dos laboratórios participantes na realização de ensaios (ou calibrações) específicos e para monitorar a consistência e comparabilidade dos dados. Comparações inter laboratoriais são conduzidas não somente para analisar laboratórios, como também para avaliar métodos e padrões, ver ISO/IEC 17043:2010 [9].
Os ensaios de proficiência (EP) por meio de comparações inter laboratoriais são utilizados de forma corrente pelos organismos de acreditamento (INMETRO), com o objetivo de avaliar e acompanhar a capacidade de medição dos laboratórios. Eles são reconhecidos internacionalmente como um elemento importante para o estabelecimento da confiança mútua entre os laboratórios de diferentes países e entre organismos nacionais de acreditamento de laboratórios. Um programa de comparação inter laboratorial envolvendo diversos laboratórios requer uma estrutura organizacional adequada e um forte comprometimento dos participantes no cumprimento das condições preestabelecidas em documento de orientação.
1 - Introdução
As Comparações Interlaboratoriais foram definidas segundo a norma ISO/IEC 17043:2010 [9] como a organização, desempenho e avaliação de medidas ou testes com os mesmos itens ou itens similares por dois ou mais laboratórios de acordo com condições predeterminadas. Comparações interlaboratoriais são conduzidas não somente para analisar laboratórios, como também para avaliar métodos e padrões. A seguir, vamos citar algumas finalidades para as comparações interlaboratoriais:
- Avaliar o desempenho de laboratórios para testes específicos, medições, monitoramento e desempenho contínuo dos laboratórios;
- Identificar problemas em laboratórios e início de ações de melhoria, como por exemplo:
- testes ou procedimentos de medição inadequados;
- eficácia de treinamento de pessoal;
- supervisão ou calibração de equipamentos.
- Estabelecimento da eficácia e da comparabilidade dos métodos de ensaio ou medição;
- Prestação de confiança adicional aos clientes do laboratório;
- Identificação de diferenças interlaboratoriais;
- Educação de laboratórios com base nos resultados de tais comparações participantes;
- Validação dos pedidos de incerteza;
- Avaliação das características de desempenho de um método, muitas vezes descrita como estudos colaborativos;
- Atribuição de valores e materiais de referência, avaliação de sua adequação para uso em teste específico ou procedimentos de medição;
- Apoio para demonstrações de equivalência de medidas de Institutos Nacionais de Metrologia através de comparações suplementares realizadas em nome do Bureau Internacional de Pesos e Medidas (BIPM) e as organizações regionais de metrologia associados.
Os ensaios de proficiência envolvem a utilização de comparações entre laboratórios para a determinação da performance de laboratórios, como mencionados nos itens 1 a 7. Os ensaios de proficiência não abordam os itens 8 a 10, pois a competência dos laboratórios é assumido nestas aplicações, mas estas aplicações podem ser utilizadas para fornecer manifestações independentes de competência dos laboratórios.
A necessidade de confiança no desempenho dos laboratórios não é apenas essencial para os laboratórios e seus clientes, mas também para outras partes interessadas como, organismos reguladores de acreditação de laboratórios (INMETRO) e outras organizações que especificam os requisitos para laboratórios. A norma ISO/IEC 17011 [12] (2005), cita que é necessário um organismo de acreditação gerenciar a participação e o desempenho dos laboratórios em ensaios de proficiência.
Há uma necessidade crescente de ensaios de proficiência para outras atividades de avaliação da conformidade, tais como, inspeção ou certificação do produto. Se for relevante os interessados deverão documentar suas políticas para a participação em ensaios de proficiência e tais políticas documentadas devem estar disponíveis publicamente para os laboratórios e outras partes interessadas. As questões que devem ser abordadas nas políticas de participação para os regimes específicos de ensaios de proficiência incluem:
- Se a participação em programas específicos de ensaios de proficiência é obrigatório ou voluntário;
- A frequência de participação;
- Os critérios utilizados pelo interessado para julgar o desempenho satisfatório ou insatisfatório;
- A obrigatoriedade dos laboratórios em participar e acompanhar ensaios de proficiência, se o desempenho é considerado insatisfatório;
- A forma como os resultados dos ensaios de proficiência serão utilizados na avaliação de desempenho e as decisões subsequentes;
- detalhes da política do interessado em preservar a confidencialidade dos participantes.
A seguir vamos descrever os métodos de ensaio de proficiência.
2 - Métodos de Ensaio de Proficiência
Os métodos de Ensaios de Proficiência (EP) dependem da natureza do item ou material sob teste, do método de ensaio em uso e do número de laboratórios participantes. Existem seis tipos distintos de EP, discutidos na ISO/IEC 17043:2010 [9], dentre elas citamos apenas quatro, que são:
- Esquema sequencial: quando um ou mais itens de testes de proficiência são distribuídas sequencialmente para testes ou medição e devolvidos ao prestador de ensaio de proficiência a intervalos regulares;
- Regime simultâneo: quando os itens de testes de proficiência são distribuídos para teste simultâneo ou medição dentro de um período de tempo definido;
- Regime contínuo: quando os itens de testes de proficiência são fornecidos em intervalos regulares, por exemplo, programas externos de avaliação da qualidade (EQA).
Neste conteúdo, vamos descrever com detalhes apenas o esquema sequencial. Em adição ao monitoramento da consistência e comparabilidade dos dados obtidos em ensaios, o programa de EP pode contribuir para a melhora dos dados coletados pelos laboratórios, veja Richardson et al.11, por exemplo.
A análise dos dados obtidos em um EP segue 4 passos básicos, que são comuns para todos os tipos de programas, que são:
- Determinar o Valor de Referência;
- Fazer a comparação dos resultados;
- Determinar uma estatística de performance;
- Determinação preliminar de proficiência, ou seja, teste de homogeneidade e estabilidade.
Os resultados dos participantes devem ser comparados com os valores ou respostas que mais demonstrarem competência com o método. Valores de referência podem ser escolhidos para avaliar os participantes com justiça e ainda para estimular o acordo entre os laboratórios. Existem uma variedade de métodos comuns para determinar o valor de referência. Uma delas é o valor de referência pelo valor de consenso dos participantes (média das medições), ou pelo resultado da medição de um laboratório com experiência internacional (via calibração). Ainda, existem outras formas para determinar o valor de referência descritos na ISO/IEC 17043:2010 [9]. Estes são dois dos procedimentos mais comuns usados em programas de acreditação com EP de rotina.
No caso de valores de consenso, é importante realizar uma análise de valores extremos (para mais detalhes ver Teste de Grubbs), pois a presença destes pode prejudicar a análise. Uma observação considerada valor extremo não pode ser utilizada, pois essa pode sub ou super estimar a média das observações, no qual, é um dos estimadores do valor de consenso.
Após a determinação do valor de referência, o próximo passo consiste em transformar às medições de cada participante em estatísticas de desempenho. O objetivo é medir a diferença entre as medições dos laboratórios com o valor de referência, de modo, a permitir a comparação com um critério definido. Atualmente, a comparação é feita de forma direta e a ISO/IEC 17043:2010 [9] propõe o erro normalizado ($E_n$), que é expresso por
$$E_n=\frac{\mid y - \mu_{x} \mid}{\sqrt{U^{2}_{lab} +U^{2}_{ref}}}$$
no qual,
- y é a medição do laboratório participante e
- $μ_x$ é a média do valor de referência.
As notações Uref e Ulab correspondem à metade do valor da amplitude do intervalo de 95% para μx e Y, respectivamente. Esses parâmetros são determinados antes da análise e são considerados valores conhecidos. O escore En descreve a diferença entre as medições dos laboratórios e a média do valor de referência relativo a variabilidade envolvida na diferença.
Neste caso, cada medição do laboratório é comparada com o valor de referência via teste de hipótese individual. No entanto, em várias situações, estamos interessados em estabelecer comparações múltiplas para avaliar a performance do grupo de laboratórios participantes com respeito ao valor de referência. Entretanto, esta comparação múltipla não é possível considerando o escore $E_n$.
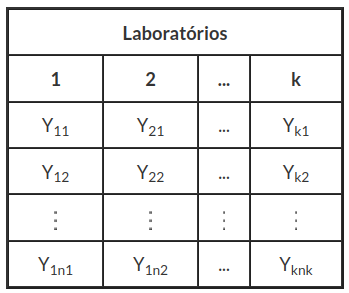
Tabela 2.1: Dados dos laboratórios.
Um importante aspecto do nosso modelo são as componentes de variância. Usamos informação externa sobre o sistema de medição para estimar essas componentes. Em geral, um sistema de medição tem imperfeições que incorporam erros no resultado de uma medição. Tradicionalmente, entendemos que um erro possui duas componentes, denominadas, aleatória e sistemática (ver mais detalhes em MSA 4ª edição). É assumido que, após a correção, o valor esperado do erro vindo desse efeito sistemático seja zero, porém, com variância positiva.
Tomamos, por exemplo, um EP em que o mesmo item é sequencialmente distribuído entre os participantes, de modo, que cada participante realiza várias medições em vários pontos (níveis ou patamares). Uma aplicação para isto é o caso de um motor sequencialmente distribuído entre 10 laboratórios, em que cada um realiza 5 medições de potência para cada um dos 18 pontos de rotação. Uma forma de apresentar os dados obtidos pode ser observado na tabela (2.2), no qual Yijk representa o valor (observado) da k-ésima medição, realizada no j-ésimo patamar pelo i-ésimo laboratório.
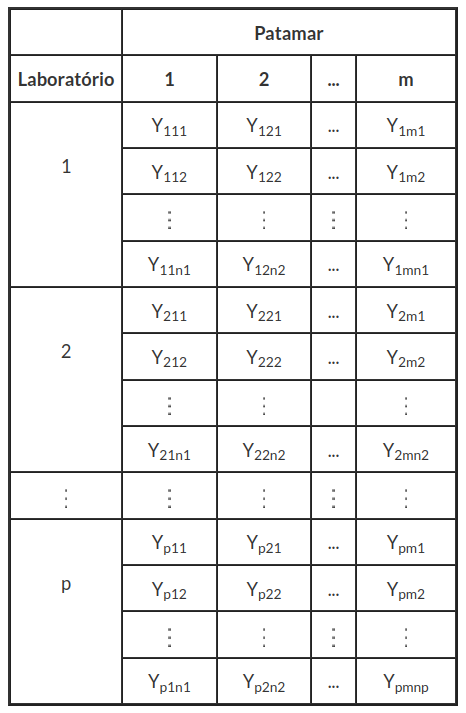
Tabela 2.2: Modelo em que o item é sequencialmente distribuído entre os participantes.
Novamente, a ISO/IEC 17043:2010 [9] propõe o erro normalizado para avaliar a competência dos laboratórios participante do EP, no entanto, sabemos que o escore En não nos possibilita realizar comparações múltiplas. Em nosso exemplo, teríamos que calcular 10*18 = 180 vezes o escore En, pois agora temos 18 patamares e 10 laboratórios.
Um importante aspecto para o desenvolvimento de um produto é a qualidade das medições e seu desempenho. Por exemplo, se uma empresa desenvolve um motor para a indústria automobilística, é importante que ela saiba maximizar a potência do motor e minimizar o custo e emissões de gases. Se essa empresa tem algum problema relacionado com as medições da potência do motor, será difícil ela saber qual é o real desempenho do produto. Consequentemente, essa empresa pode tomar decisões erradas durante o desenvolvimento do motor, o qual, em geral, tem altos custos. Portanto, é importante que a empresa saiba definir de forma apropriada o seu sistema de medição.
2.1 - Determinação preliminar de proficiência
Para garantir a confiança necessária ao Ensaio de Proficiência, por exemplo, em Motores. O artefato foi desenvolvido com base na norma ILAC-G12:2000. Esta norma descreve os requisitos do sistema da qualidade do fabricante e os procedimentos necessários para garantir a estabilidade e consistência do artefato.
Consistência do artefato ao longo do ensaio
O laboratório de referência deve ensaiar o artefato no início e no final do ensaio de proficiência, de acordo com a logística com alguma descrita em procedimento. Critérios para a homogeneidade e estabilidade adequada deve ser estabelecida e deve ser baseada no efeito que a heterogeneidade e a instabilidade terá sobre a avaliação do desempenho dos participantes. A seguir, descrevemos algumas observações descritas na norma ISO/IEC 17043:2010 [9]:
- Os requisitos são destinados a garantir que cada participante receba os itens de teste de proficiência, afim de que permaneça estável ao longo do ensaio de proficiência.
- Ter um cuidadoso planejamento, fabricação e transporte necessários para conseguir um item de proficiência estável, geralmente testes são necessários para confirmá-la.
- Em alguns casos, não é viável que os itens do teste de proficiência sejam submetidas a ensaios de estabilidade e homogeneidade. Tais casos podem incluir, por exemplo, quando o material disponível é limitado para preparar itens de ensaio de proficiência.
- Em alguns casos, os materiais que não são suficientemente homogêneos ou estáveis, em tais casos, eles ainda podem ser úteis como itens de teste de proficiência, desde que as incertezas dos valores atribuídos ou a avaliação de resultados leve em conta isso (ver B.3.1.3 e ISO 13528:2005 [19], anexo B);
- Considerações sobre a homogeneidade e estabilidade são discutidas no Guia ISO 34 [17], ISO Guia 35 [18] e ISO 13528:2005 [19].
Os procedimentos para a avaliação da homogeneidade e estabilidade devem ser documentados e realizados, quando aplicável, de acordo com os experimentos estatísticos apropriados. Sempre que possível, o coordenador de ensaios de proficiência devem utilizar estatísticamente uma selecção aleatória de um número representativo de itens de teste de proficiência de todo o lote de um material de teste, afim de avaliar a homogeneidade do material.
A avaliação da homogeneidade será normalmente realizada após os itens (artefato) do teste de proficiência foram embalados antes da distribuição para os participantes. O objetivo principal da consistência do artefato é demonstrar ser suficientemente estável para garantir que eles não sofrerão nenhuma mudança significativa durante todo o período do ensaio de proficiência, incluindo condições de armazenagem e transporte. Quando isto não for possível, a estabilidade deve ser quantificado e considerado como um componente adicional da incerteza de medida associados com o valor atribuído ao elemento de teste de proficiência, e/ou tidos em conta nos critérios de avaliação.
Quando os artefatos do ensaios de proficiência de rodadas anteriores são mantidos para uso futuro, os valores das propriedades a serem determinadas no programa de ensaios de proficiência devem ser confirmados pelo coordenador de ensaios de proficiência antes da distribuição. Nos casos em que testes de homogeneidade e estabilidade não são viáveis, o coordenador de ensaios de proficiência devem demonstrar que os procedimentos utilizados para coletar, produzir, embalar e distribuir os itens de testes de proficiência são suficientes para o propósito do ensaio de proficiência.
Exemplo
O laboratório de referência ensaiou o artefato no início e no final do ensaio de proficiência, de acordo com umaa logística descrita em procedimento. A Tabela 2.1.1 apresenta as medições da variável Potência Corrigida por faixa de rotação obtidas em ambos os ensaios.
| Rodada Inicial | Rodada Inicial | Rodada Final | Rodada Final | ||
|---|---|---|---|---|---|
| Faixa | Média | Desvio Padrão | Média | Desvio Padrão | Tendência |
| 1200 | 8,93 | 0,062 | 8,99 | 0,046 | -0,06 |
| 1600 | 12,61 | 0,035 | 12,69 | 0,08 | -0,08 |
| 2000 | 16,05 | 0,046 | 16,18 | 0,037 | -0,13 |
| 2400 | 19,55 | 0,078 | 19,73 | 0,081 | -0,18 |
| 2800 | 24,87 | 0,086 | 25,12 | 0,14 | -0,25 |
| 3000 | 27,04 | 0,072 | 27,26 | 0,12 | -0,22 |
| 3200 | 28,53 | 0,068 | 28,81 | 0,092 | -0,28 |
| 3600 | 31,74 | 0,111 | 31,91 | 0,084 | -0,17 |
| 4000 | 34,22 | 0,171 | 34,48 | 0,171 | -0,26 |
| 4400 | 37,35 | 0,14 | 37,68 | 0,186 | -0,33 |
| 4800 | 41,33 | 0,166 | 41,74 | 0,218 | -0,41 |
| 5200 | 44,54 | 0,241 | 44,67 | 0,187 | -0,13 |
| 5400 | 46,53 | 0,277 | 46,69 | 0,151 | -0,16 |
| 5600 | 47,62 | 0,208 | 47,93 | 0,169 | -0,32 |
| 5800 | 48,68 | 0,261 | 49,01 | 0,254 | -0,32 |
| 6000 | 49,59 | 0,203 | 49,61 | 0,235 | -0,02 |
| 6200 | 50,02 | 0,365 | 50,19 | 0,211 | -0,16 |
| 6400 | 50,24 | 0,318 | 50,61 | 0,178 | -0,36 |
Tabela 2.1.1: Média das medições do laboratório de referência.
Calculamos a tendência do artefato durante as rodadas (início e fim).
| Rotação | Média | Tendência | $ u_c(\text{ref}) $ | k | U |
|---|---|---|---|---|---|
| 1200 | 8,963 | -0,063 | 0,073 | 2 | 0,147 |
| 1600 | 12,648 | -0,077 | 0,102 | 2 | 0,205 |
| 2000 | 16,115 | -0,126 | 0,13 | 2 | 0,259 |
| 2400 | 19,641 | -0,182 | 0,16 | 2 | 0,32 |
| 2800 | 24,998 | -0,248 | 0,205 | 2 | 0,41 |
| 3000 | 27,152 | -0,216 | 0,22 | 2 | 0,439 |
| 3200 | 28,667 | -0,282 | 0,233 | 2 | 0,465 |
| 3600 | 31,825 | -0,169 | 0,255 | 2 | 0,51 |
| 4000 | 34,353 | -0,258 | 0,28 | 2 | 0,559 |
| 4400 | 37,516 | -0,333 | 0,306 | 2 | 0,611 |
| 4800 | 41,537 | -0,411 | 0,34 | 2 | 0,681 |
| 5200 | 44,604 | -0,132 | 0,359 | 2 | 0,718 |
| 5400 | 46,609 | -0,157 | 0,375 | 2 | 0,751 |
| 5600 | 47,775 | -0,316 | 0,386 | 2 | 0,771 |
| 5800 | 48,844 | -0,323 | 0,397 | 2 | 0,795 |
| 6000 | 49,601 | -0,02 | 0,398 | 2 | 0,795 |
| 6200 | 50,103 | -0,164 | 0,407 | 2 | 0,814 |
| 6400 | 50,424 | -0,365 | 0,41 | 2 | 0,821 |
Tabela 2.1.2: Resumo com os valores de média das medições, tendência e incerteza combinada e expandida do laboratório de referência.
A Tabela 2.1.3 apresenta o teste associado ao erro normalizado (para mais detalhes ver Estatísticas de Performance), como o erro normalizado em todas as faixas de rotação é menor que 1, concluímos que as duas rodadas de medicões do laboratório de referência são compatíveis. Portanto, o artefato apresentou um comportamento estável ao longo do ensaio de proficiência.
| Rotação | Tendência do lab | Valor de Referência | Tendência | U | Erro Normalizado (En) | W | P-valor |
|---|---|---|---|---|---|---|---|
| 1200 | -0,063 | 0 | -0,063 | 0,14 | 0,45 | 4,053 | 0,044 |
| 1600 | -0,077 | 0 | -0,077 | 0,195 | 0,394 | 3,099 | 0,078 |
| 2000 | -0,126 | 0 | -0,126 | 0,247 | 0,51 | 5,212 | 0,022 |
| 2400 | -0,182 | 0 | -0,182 | 0,304 | 0,597 | 7,131 | 0,008 |
| 2800 | -0,248 | 0 | -0,248 | 0,39 | 0,635 | 8,059 | 0,005 |
| 3000 | -0,216 | 0 | -0,216 | 0,418 | 0,517 | 5,348 | 0,021 |
| 3200 | -0,282 | 0 | -0,282 | 0,443 | 0,637 | 8,104 | 0,004 |
| 3600 | -0,169 | 0 | -0,169 | 0,484 | 0,349 | 2,438 | 0,118 |
| 4000 | -0,258 | 0 | -0,258 | 0,532 | 0,485 | 4,705 | 0,03 |
| 4400 | -0,333 | 0 | -0,333 | 0,582 | 0,572 | 6,537 | 0,011 |
| 4800 | -0,411 | 0 | -0,411 | 0,648 | 0,633 | 8,02 | 0,005 |
| 5200 | -0,132 | 0 | -0,132 | 0,683 | 0,194 | 0,751 | 0,386 |
| 5400 | -0,157 | 0 | -0,157 | 0,714 | 0,221 | 0,973 | 0,324 |
| 5600 | -0,316 | 0 | -0,316 | 0,733 | 0,431 | 3,723 | 0,054 |
| 5800 | -0,323 | 0 | -0,323 | 0,756 | 0,428 | 3,658 | 0,056 |
| 6000 | -0,02 | 0 | -0,02 | 0,755 | 0,027 | 0,015 | 0,904 |
| 6200 | -0,164 | 0 | -0,164 | 0,774 | 0,212 | 0,895 | 0,344 |
| 6400 | -0,365 | 0 | -0,365 | 0,781 | 0,467 | 4,355 | 0,037 |
Tabela 2.1.3: Homogeneidade do Artefato por faixa de rotação.
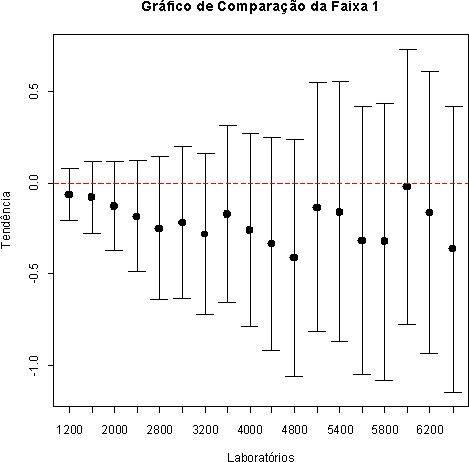
Tabela 2.1.2: Homogeneidade do Artefato por faixa de rotação.
2.2 - Comparação dos resultados
Nesta seção vamos descrever três dos seis tipos distintos de ensaio de proficiência (EP), discutidos na ISO/IEC 17043:2010 [9], dentre elas citamos apenas quatro, que são:
- Esquema sequencial: onde um ou mais itens de testes de proficiência são distribuídas sequencialmente para testes ou medição e devolvidos ao prestador de ensaio de proficiência a intervalos regulares;
- Regime simultâneo: onde os itens de testes de proficiência são distribuídos para teste simultâneo ou medição dentro de um período de tempo definido;
- Regime contínuo: onde os itens de testes de proficiência são fornecidos em intervalos regulares, por exemplo, programas externos de avaliação da qualidade (EQA).
A seguir descrevemos o esquema de comparação sequencial.
Esquemas de comparação de medição sequencial
É onde um único item de teste é distribuído sequencialmente dentre os participantes, com estes enviando o item para o próximo laboratório ou ao coordenador para manutenção. Este procedimento é comum em comparações de padrões de calibração, e os resultados das medições, juntamente com as incertezas padrão, devem ser enviadas ao coordenador. A figura 2.2.1 ilustra como é feito essa comparação.
(imagem em falta)
Figura 2.2.1: Esquema de comparação sequencial.
Os resultados das medições individuais são comparados com o valor designado pela referência estabelecida de comum acordo com os participantes. O coordenador deve levar em conta a incerteza de medição de cada participante. Pode ser difícil comparar os resultados com base nos grupos, como por exemplo, pode haver relativamente poucos participantes com capacidades de medição que se aproximam uns dos outros.
Esquemas envolvendo a participação sequencial pode levar tempo (em alguns casos anos) para ser concluído. Isto provoca uma série de dificuldades, tais como
- Assegurar a estabilidade do produto;
- Acompanhamento rigoroso da circulação entre os participantes e o tempo permitido para a medição de participantes individuais;
- Necessidade de fornecer feedback sobre o desempenho individual durante a implementação do sistema, em vez de esperar até que ele termine.
Os artefatos ou itens do teste de proficiência utilizados neste tipo de ensaio de proficiência podemos citar, por exemplo, os padrões de referência de medição (resistores, micrômetros etc), ou em ensaios biológicos, lâminas histológicas com diagnóstico confirmado.
Os ensaios que seguem este esquema de comparação, mas que se limitam a situações em que um único participante é testado independente são frequentemente chamados de “auditorias de medição”. Em algumas situações, o valor de referência para um item ou artefato de ensaio de proficiência pode ser determinada por consenso, depois todos os participantes (em algumas situações um subconjunto de participantes) completaram a medição de comparação.
Esquemas de participação simultânea
Ensaios de proficiência com participação simultânea geralmente envolvem sub-amostras selecionadas aleatoriamente a partir de uma fonte de material a ser distribuído simultaneamente aos participantes para o teste simultâneo.
Em alguns sistemas, os participantes são obrigados a recolher amostras, que são considerados os itens de teste de proficiência para análise. Após a conclusão do teste, os resultados são devolvidos ao coordenador dos ensaios de proficiência e comparado com o valor de referência, para dar uma indicação do desempenho de cada um dos participantes e o grupo como um todo.
Exemplos de itens de teste de proficiência utilizados neste tipo de comparação inclui alimentos, fluidos corporais, produtos agrícolas, a água, os solos, minerais e outros materiais ambientais. Em alguns casos, porções separadas de materiais de referência previamente estabelecidos são circuladas. Conselhos ou comentários educacionais são tipicamente parte do relatório devolvidas aos participantes pelo coordenador de ensaios de proficiência com o objetivo de promover a melhoria no desempenho.
Regimes de valor conhecido usam valores de referência que são determinadas de forma independente dos participantes e envolvem a preparação de itens de ensaio de proficiência com um número de mensurados ou características conhecidas.
Materiais de referência certificados também podem ser usados nesses regimes, assim como seu valor certificado e incerteza de medida pode ser utilizada diretamente. A comparação direta também pode ser feita entre um item de ensaio de proficiência e um material de referência certificado em condições de repetibilidade. No entanto, cuidados devem ser tomados para garantir que o material de referência certificado seja muito semelhante a um item de ensaio de proficiência. Itens do teste de proficiência de rodadas de ensaios de proficiência anteriores podem ser usados neste tipo de esquema, se o item demonstrar estabilidade.
Programas externos de avaliação da qualidade (EQA)
A maioria dos programas EQA são projetados para fornecer informações sobre o caminho completo do fluxo de trabalho do laboratório e não apenas os processos de teste. Esses programas são esquemas contínuos, que incluem o longo prazo de acompanhamento de desempenho do laboratório.
Uma característica típica de programas EQA é fornecer educação aos participantes e promover a melhoria da qualidade. Consultorias e treinamento compreendem parte do relatório devolvidas aos participantes para atingir este objetivo. Alguns programas EQA avaliam o desempenho das fases de pré e pós analíticos dos testes , bem como toda a fase analítica.
Em tais programas, a natureza do item teste de proficiência podem diferir significativamente do que é utilizado nos esquemas tradicionais de ensaios de proficiência. O item “teste de proficiência” pode ser um estudo de questionário ou caso circulou pelo provedor EQA a cada participante para o retorno de respostas específicas. Alternativamente, a informação pré analítica pode acompanhar o item de teste de proficiência, que exige que o participante selecione uma abordagem apropriada para testes e interpretação dos resultados, e não apenas para e não apenas para realizar o teste.
Na “revisão” esquemas de amostragem, os participantes podem ser obrigados a fornecer o “teste de proficiência” para o provedor EQA. Isto pode assumir a forma de uma amostra processada ou amostra, por exemplo, lâmina corada ou tecido fixo.
Para os dados de laboratório podemos exemplificar:
- Resultados de testes;
- Relatórios de laboratório;
- Relatórios de qualidade garantia/registros de controle.
Para documentação podemos exemplificar:
- Procedimentos;
- Critérios de verificação do método.
2.3 - Determinação do valor de referência e sua incerteza
De acordo com a ISO/IEC 17043:2010 [9], alguns procedimentos podem ser usados para estabelecer o valor de referência e sua incerteza. Nesta norma, os valores de referência mais comuns utilizados são:
- Valores conhecidos: resultados determinados por formulação específica do item do ensaio de proficiência (por exemplo, fabricação ou diluição);
- Valores certificados: determinado pelo teste definitivo ou métodos de medição (por ensaios quantitativos);
- Valores por laboratório referência: determinado por análise, medição ou comparação do item de teste de proficiência ao lado de um material de referência ou padrão, rastreável a um padrão internacional;
- Valores de consenso dos participantes especialistas: especialistas (que podem, em algumas situações, ser laboratórios referência) devem ter competência comprovada na determinação do(s) mensurando(s) em teste, validados utilizando métodos conhecidos por serem altamente precisos e comparáveis aos métodos gerais;
- Valores de consenso dos participantes: usando métodos estatísticos descritos na ISO 13528 [15] e da IUPAC Protocolo Internacional Harmonizado, e com a consideração dos efeitos de outliers.
Neste estudo vamos utilizar os procedimentos 3 e 4, para determinar o valor de referência.
- Consenso entre os participantes (média das medições);
- Consenso entre as rodadas de um laboratório com experiência internacional (via calibração).
Consenso entre os Participantes
Determinado através do consenso entre as medições dos laboratórios. Antes de realizar este procedimento é preciso verificar a existência de valores extremos. Para isso, podemos utilizar o Teste de Valor Extremo (Grubbs), descrito no conteúdo Teste de Valor Extremo (Grubbs). Com as medições dos laboratórios não considerados valores extremos, temos que
$$VR=\displaystyle\frac{1}{p}\sum^{p}_{i=1}y_i$$
em que:
- $y_i$: Representa a média das medições do i-ésimo laboratório;
- p: Representa o número de laboratórios, cujas as medidas não são consideradas valores extremos.
Para calcularmos o valor de referência por consenso entre os participantes, procedemos da seguinte forma:
$$U(\text{ref})=~2 \times \sqrt{u_{\text{ag}}^2(\text{labs})}$$
ou caso considerarmos a incerteza devido ao artefato (motor), temos
$$U(\text{ref})=~2 \times \sqrt{u_{\text{ag}}^2(\text{labs})+u^2(\text{motor})}$$
em que,
- U(ref): Representa a incerteza expandida da referência;
- u(motor): Representa a incerteza padrão associada a variabilidade intrínseca do artefato (VR × 0,25%).
A incerteza agrupada do laboratório é dada por:
$$u_{\text{ag}}(\text{labs}) = \sqrt{\displaystyle\frac{1}{p^2}\sum^{p}_{i=1}u^2(\text{lab}_i)}$$
- $u_{ag}$(labs): Representa a incerteza agrupada do laboratório;
- u($lab_i$): Representa a incerteza padrão da medição do i-ésimo laboratório;
Podemos ilustrar como exemplo, o ensaio em que utilizamos o artefato (motor). Assim, a incerteza do laboratório é calculado da seguinte forma:
$$u(\text{lab}_i)=\sqrt{u^2(\text{cal})+u^2(\delta)}$$
- u(cal): Representa a incerteza da calibração do banco;
- u(δ): Representa a incerteza devido a Repetibilidade;
Exemplo 2.2.1
O laboratório em um EP ensaiou o artefato, de acordo com uma logística descrita em procedimento. A Tabela 2.2.1 apresenta as medições da variável Potência Corrigida na faixa de rotação de 2000 rpm.
| Lab | Potência Corrigida | Lab | Potência Corrigida |
|---|---|---|---|
| 1 | 27 | 4 | 27,4 |
| 1 | 26,8 | 4 | 27,4 |
| 1 | 27 | 4 | 27,4 |
| 1 | 26,8 | 4 | 27,4 |
| 1 | 26,9 | 4 | 27,5 |
| 2 | 27,41 | 5 | 27,06 |
| 2 | 27,43 | 5 | 27,33 |
| 2 | 26,97 | 5 | 27,01 |
| 2 | 27,27 | 5 | 26,97 |
| 2 | 27,62 | 5 | 27,13 |
| 3 | 26,43 | 6 | 27,23 |
| 3 | 26,37 | 6 | 27,33 |
| 3 | 26,41 | 6 | 27,24 |
| 3 | 26,45 | 6 | 27,18 |
| 3 | 26,37 | 6 | 27,30 |
Tabela 2.2.1: Medidas de Potência Corrigida na faixa de 2000 rpm.
A seguir, vamos fazer um resumo descritivo, para isto vamos usar o Action.
(imagem em falta)
Figura 2.2.1: Saída do resumo descritivo usando o Action.
Neste exemplo, vamos tomar o laboratório 2, os demais casos é calculado de forma análoga. O laboratório 1 apresentou uma incerteza devido à calibração do banco de u(cal)=0,164 kW e a incerteza devido a repetibilidade foi calculada no resumo descritivo (ver figura 2.2.1), que é dado pelo desvio padrão da média (para mais detalhes acesse o conteúdo incerteza de medição), isto é, temos que incerteza devido a repetibilidade é u(δ)=0,045 kW.
Assim, a incerteza combinada do laboratório 1 é calculado da seguinte forma:
$$u(\text{lab}_1)=\sqrt{0,164^2+0,045^2}=0,17~kW$$
Logo, a incerteza expandida do laboratório 1 é calculada da seguinte forma:
$$U(\text{lab}_1)=0,17\times 2=0,34~kW$$
A seguir, na tabela 2.2.2 apresentamos um resumo de todos os laboratórios.
| Laboratório | u(cal) | u(δ) | u($lab_i$) | U($lab_i$) | k |
|---|---|---|---|---|---|
| 1 | 0,164 | 0,045 | 0,170 | 0,34 | 2 |
| 2 | 0,259 | 0,057 | 0,265 | 0,53 | 2 |
| 3 | 0,354 | 0,016 | 0,355 | 0,71 | 2 |
| 4 | 0,150 | 0,02 | 0,152 | 0,30 | 2 |
| 5 | 0,410 | 0,063 | 0,415 | 0,83 | 2 |
| 6 | 0,258 | 0,027 | 0,259 | 0,52 | 2 |
Tabela 2.2.2: Resumo do cálculo de incerteza para os laboratórios.
Como a incerteza padrão associada a variabilidade intrínseca do artefato (VR × 0,25%), então temos que:
$$VR=\displaystyle\frac{1}{p}\sum^{p}_{i=1}y_i=\frac{26,9+\dots+27,3}{6}=27,1~kW$$
$$u(\text{motor})=\frac{0,25}{100}\times 27,1=0,068~kW$$
Agora, vamos calcular a incerteza agrupada.
$$u_{\text{ag}}(\text{labs}) = \sqrt{\displaystyle\frac{1}{p^2}\sum^{p}_{i=1}u^2(\text{lab}_i)}=\sqrt{\frac{1}{6^2}\sum^6_{i=1}0,17^2+\dots+0,259^2}=0,1163~kW$$
Portanto, a incerteza expandida do valor de referência é dado por:
$$U(\text{ref})=~2 \times \sqrt{u_{\text{ag}}^2(\text{labs})+u^2(\text{motor})}=0,269~kW$$
Teste de Valor Extremo (Grubbs)
Este teste é desenvolvido para verificar a presença de valores extremos em observações amostrais. Valores extremos podem ser considerados como manifestações da variabilidade aleatória inerente aos dados, ou um erro no cálculo durante a coleta dos dados e até mesmo uma anotação precipitada pelo operador.
Existem vários critérios para testar valores extremos. Para todos eles calculamos uma estatística de performance e comparamos com um valor crítico, baseado na teoria de amostras aleatórias, para decidirmos se existe ou não uma observação considerada como um valor extremo.
No teste de Grubbs, usamos a seguinte estatística
$$Z~=~\frac{|x_i ~-~\overline{x} |}{s}$$
em que:
- $x_i$: É uma observação da amostra x1, x2, …, xn;
- $ \overline{X} $: É a média amostral;
- s: É o desvio padrão amostral.
Esta estatística testa as seguintes hipóteses
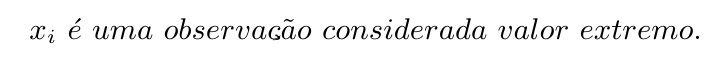
(há elementos em falta na equação acima)
Rejeitamos a hipótese $ H_0 $, com nível de significância $ \alpha $, se $ Z> Z_c $, em que $ Z_c $ é um valor crítico baseado na distribuição de Z e encontra-se tabelado (ver F. E. Grubbs (1969) [16]) para alguns valores de $ \alpha $.
Exemplo 2.2.2
O laboratório em um EP ensaiou o artefato, de acordo com uma logística descrita em procedimento. A Tabela 2.2.2 apresenta as medições da variável Potência Corrigida na faixa de rotação de 1200 rpm.
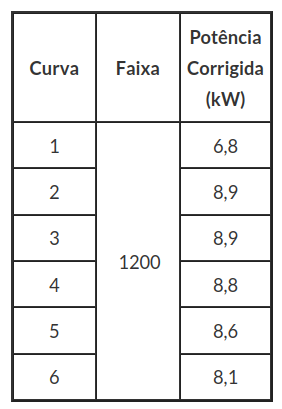
Tabela 2.2.2: Medidas de Potência Corrigida na faixa de 1200 rpm.
Vamos calcular a média e o desvio padrão:
$$\overline{X}=\frac{6,8+8,9+\dots+8,1}{6}=8,35$$
$$s=\sqrt{\frac{(6,8-8,38)^2+\dots+(8,1-8,35)^2}{6-1}}=0,8167$$
Com isso, vamos calcular para o ponto 1 o teste de Grubbs, usando a seguinte estatística
$$Z=\frac{|X_i-\overline{X}|}{s}=\frac{|X_1-\overline{X}|}{s}=\frac{|6,8-8,35|}{0,8167}=1,89788$$
Como $ Z> 1,887 $ então, essa medida é um valor extremo (outlier).
(imagem em falta)
Consenso entre as Rodadas de um laboratório com experiência internacional
Determinado através do consenso entre as medições das duas rodadas do Laboratório Referência. Com isso, temos que
$$VR~=~\displaystyle\frac{1}{p}\sum^{p}_{i=1}y_i$$
em que:
- $y_i$: Representa a média das medições da i-ésima rodada;
- p: Representa o número de rodadas realizadas pelo Laboratório Referência (p=2).
$$U(\text{ref})=~2 \times \sqrt{u^2_{\text{ag}}(\text{Lref})+u^2(\text{motor})}$$
e
$$u_{\text{ag}}(\text{ref}) = \sqrt{\frac{u^2(\text{rod}_1)+u^2({\text{rod}_2})}{2}},$$
em que:
- U(ref): representa a incerteza expandida da referência;
- $u_{ag}$(Lref): representa a incerteza agrupada das duas rodadas do laboratório referência;
- u($rod_i$): representa a incerteza padrão da medição da i-ésima rodada, para i=1,2;
- u(motor): representa a incerteza padrão associada a variabilidade intrínseca do artefato (VR × 0,25%).
Exemplo 2.2.3
O laboratório de referência ensaiou o artefato no início e no final do EP em um esquema de comparação sequencial, de acordo com uma logística descrita em procedimento. A Tabela 2.2.3 apresenta as medições da variável Potência Corrigida na faixa de rotação de 1200 rpm.
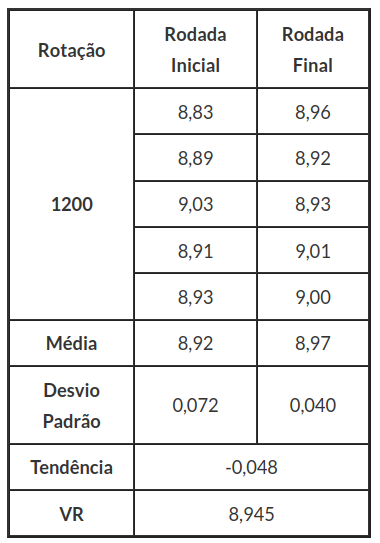
Tabela 2.2.3: Medidas de Potência Corrigida na faixa de 1200 rpm para o Laboratório de Referência.
Depois de analisarmos a consistência do artefato (para mais detalhes veja na seção Determinação preliminar de proficiência), vamos determinar o valor de referência e sua incerteza. Para isto, calculamos da seguinte forma:
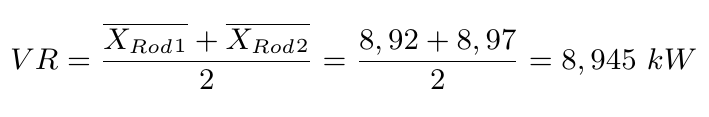
O laboratório de referência apresentou uma incerteza devido à calibração do banco de u(cal)=0,165 kW e a incerteza devido a repetibilidade foi apresentada na tabela 2.2.3. Primeiramente, vamos calcular a incerteza agrupada do laboratório de referência.
$$u_{\text{ag}}(\text{Lref})=\sqrt{u^2(cal)+u^2(\delta_1)+u^2(\delta_2)}=\sqrt{0,165^2+0,0322^2+0,0179^2}=0,169~kW$$
em que
$$u(\delta_1)=\frac{s_1}{\sqrt{5}}=\frac{0,072}{\sqrt{5}}=0,0322~kW,\quad\text{e}\quad u(\delta_2)=\frac{s_2}{\sqrt{5}}=\frac{0,04}{\sqrt{5}}=0,0179~kW$$
Agora, vamos calcular a incerteza do motor.
$$u(\text{motor})=\frac{0,25}{100}\times8,945=0,02236~kW$$
Assim, a incerteza do laboratório de referência é dada por:
$$U(\text{ref})=~2 \times \sqrt{u^2_{\text{ag}}(\text{Lref})+u^2(\text{motor})}=2\times\sqrt{0,169^2+0,02236^2}=0,56~kW$$
2.4 - Estatística de performance
Para avaliar o desempenho e performance dos resultados obtidos, vamos usar o teste do Erro Normalizado sugerido pela ISO/IEC 17043:2010 [9], o teste de tendência segundo Leão, Aoki e Silva (2009) [14] e o teste da Tendência e Linearidade de acordo com Leão, Aoki e Silva (2009) [14].
2.4.1 - Erro Normalizado
O teste do Erro Normalizado testa a compatibilidade dos resultados das medições do laboratório com respeito ao valor de referência. Neste caso, a norma ISO/IEC 17043:2010 [9] propõe a seguinte estatística:
Erro Normalizado - $ E_n $
$$E_n=\frac{|\text{Res}_{\text{lab}}-VR|}{\sqrt{U^2(\text{lab})+U^2(\text{ref})}}$$
em que:
- $Res_{lab}$: É o resultado do laboratório participante;
- VR: É o valor de referência;
- U(lab): é a incerteza expandida do laboratório participante;
- U(ref): é a incerteza expandida do valor de referência;
- Tendência =$Res_{lab}$-VR
.
- Laboratório Compatível: Laboratório cujo resultado da calibração para um determinado artefato circulante obteve um erro normalizado (En) menor ou igual a unidade.
- Laboratório não Compatível: Laboratório cujo resultado da calibração para um determinado artefato circulante obteve um erro normalizado (En) maior que a unidade.
A Figura ilustra a representação gráfica dos resultados desta comparação.
(imagem em falta)
Exemplo 2.4.1.1
O laboratório em um EP ensaiou o artefato, de acordo com uma logística descrita em procedimento. A tabela 2.4.1.1 apresenta o resumo dos dados.
| Laboratório | Média do laboratório | VR | Tendência | $U_{lab}$ | $U_{ref}$ | U | $E_n$ |
|---|---|---|---|---|---|---|---|
| 1 | 15,809 | 15,698 | 0,111 | 0,304 | 0,442 | 0,536 | 0,208 |
| 2 | 15,335 | 15,698 | -0,363 | 0,272 | 0,442 | 0,519 | 0,700 |
| 3 | 15,778 | 15,698 | 0,080 | 0,115 | 0,442 | 0,457 | 0,175 |
| 4 | 15,918 | 15,698 | 0,220 | 0,334 | 0,442 | 0,554 | 0,397 |
| 5 | 15,885 | 15,698 | 0,188 | 0,801 | 0,442 | 0,915 | 0,205 |
| 6 | 16,019 | 15,698 | 0,321 | 0,370 | 0,442 | 0,577 | 0,557 |
| 7 | 15,461 | 15,698 | -0,237 | 0,393 | 0,442 | 0,592 | 0,401 |
| 8 | 15,900 | 15,698 | 0,202 | 0,582 | 0,442 | 0,731 | 0,277 |
Tabela 2.4.1.1: Resumo do EP na faixa de 2000 rpm.
A seguir, vamos calcular o erro normalizado para o laboratório 2. Primeiramente vamos calcular o módulo da tendência.
$$|\text{Tendência}|=|\text{Res}_{\text{lab}_2}-VR|=|15,698-15,335|=0,363$$
e
$$U=\sqrt{U^2(\text{lab}_2)+U^2(\text{ref})}=\sqrt{0,272^2+0,442^2}=0,519$$
Assim, calculamos o erro normalizado En para o laboratório 2.
$$E_n=\frac{|\text{Res}_{\text{lab}_2}-VR|}{\sqrt{U^2(\text{lab}_2)+U^2(\text{ref})}}=\frac{0,363}{0,519}=0,7$$
Como $E_n$= 0,7 < 1, então concluímos que o laboratório 2 está compatível em relação ao valor de referência.
2.4.2 - Teste de Tendência
O teste de tendência testa a compatibilidade dos resultados das medições do laboratório com respeito ao valor de referência. Neste caso, vamos utilizar o teste da razão de verossimilhança generalizada proposto por Leão, Aoki e Silva (2009) [14].
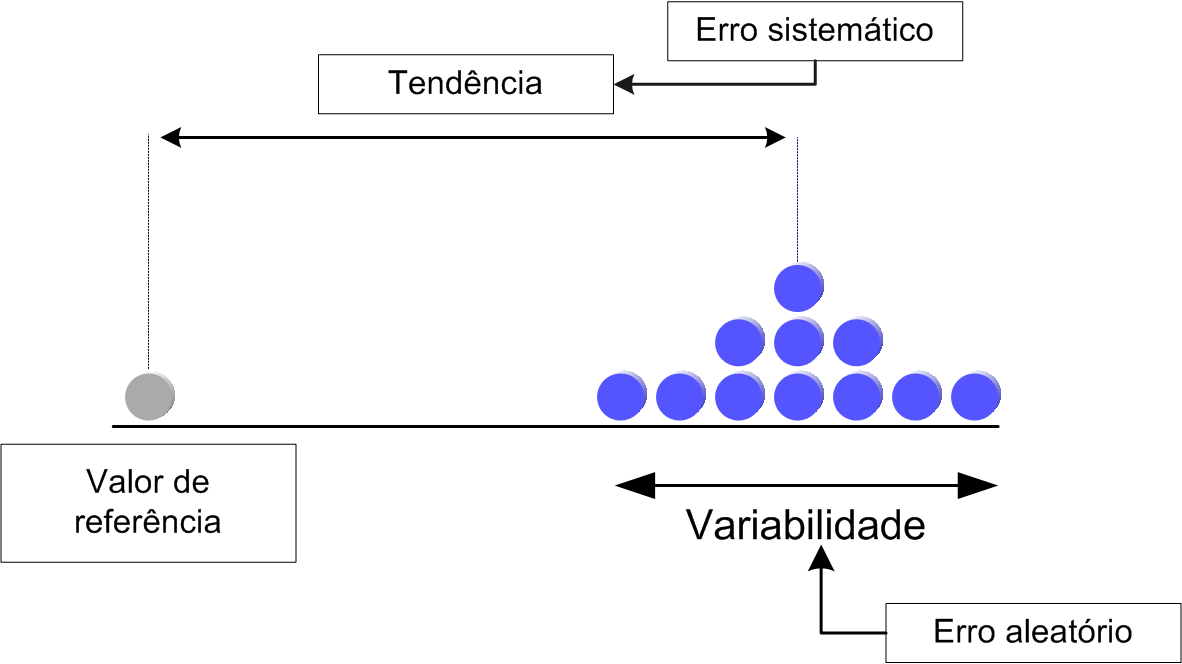
Para desenvolver o teste, foi considerado o seguinte modelo
$$Y_{ij}=\alpha_i+X+\epsilon_{ij},~j = 1,\ldots ,n_i~;~i=1,\ldots,k,~~(2.4.1)$$
em que $ Y_{ij} $ representa a j-ésima medição do i-ésimo laboratório, $ \alpha_i $ representa o parâmetro de tendência do i-ésimo laboratório em relação a $ X $ (valor de referência) e $ \epsilon_{ij} $ representa o erro de medição associado ao i-ésimo laboratório na j-ésima medição.
Com o modelo dado por (2.4.1), testamos a competência do laboratório conforme as seguintes hipóteses
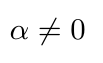
(há elementos em falta na equação acima)
Com isso, a estatística utilizada para o teste é
$$W~=~\hat{\alpha}^\top~(J^\top \Sigma^{-1} J)~\hat{\alpha}$$
em que
- α: Representa o estimador do parâmetro de tendência;
- J: Representa um vetor n x 1 de constantes;
- Σ: Representa uma matriz n x n de constantes. Esta matriz é formada por funções das incertezas combinadas, tanto do laboratório, quanto do valor de referência.
Temos que a distribuição da estatística é
$$W\sim\chi^2_{1,\tau}~~ \text{(não central)}~(2.4.2)$$
em que $ \tau = \displaystyle\frac{1}{2} \alpha^\top(J^\top\Sigma^{-1}J)\alpha. $
Sob $\alpha = 0 $, temos que $ \tau=0 $. Logo, $ W\sim\chi^2_1 $ (central) e pelo teste da razão da verossimilhança generalizada, rejeitamos $ H_0 $ se $ W \geq w_0 $, em que $ w_0 $ é um valor obtido da distribuição qui-quadrado com 1 grau de liberdade e nível de significância $ \eta $. Portanto, se não rejeitamos a hipótese $ H_0 $, podemos dizer que a medição do laboratório é TRVG-Satisfatório.
Podemos também calcular o p-valor, o qual é o menor valor para o qual rejeitamos a hipótese $ H_0 $. Este é calculado por
$$P(W> W_{obs}).$$
Exemplo 2.4.2.1
Considere os dados do exemplo 2.4.1.1. A tabela 2.4.2.1 apresenta os dados necessários para o cálculo da estatística W.
| Laboratório | Tendência | $U_{lab}$ | $U_{ref}$ | $n_i$ |
|---|---|---|---|---|
| 1 | 0,111 | 0,304 | 0,442 | 5 |
| 2 | -0,363 | 0,272 | 0,442 | 24 |
| 3 | 0,080 | 0,115 | 0,442 | 18 |
| 4 | 0,220 | 0,334 | 0,442 | 9 |
| 5 | 0,188 | 0,801 | 0,442 | 16 |
| 6 | 0,321 | 0,370 | 0,442 | 16 |
| 7 | -0,237 | 0,393 | 0,442 | 28 |
| 8 | 0,202 | 0,582 | 0,442 | 16 |
Tabela 2.4.2.1: Dados para o cálculo da estatística W.
Inicialmente, para calcularmos a estatística W, dividimos as incertezas expandidas por k. Vamos tomar o laboratório 1:
$$u^2(\text{lab}_1)=\left(\frac{U(\text{lab}_1)}{k}\right)^2=\left(\frac{0,304}{2}\right)^2=0,023,\quad \text{e}\quad u^2(\text{ref})=\left(\frac{U(\text{ref})}{k}\right)^2=\left(\frac{0,442}{2}\right)^2=0,0488$$
Agora, dividimos a incerteza do laboratório 1 pela quantidade de medidas do laboratório no ponto de rotação de 2000 rpm.
$$\hat{\sigma}^2_x=\frac{u^2(\text{lab}_1)}{n_1}=\frac{0,023}{5}=0,00461$$
Com isso, temos que
$$\hat{\sigma}^2_x+u^2(\text{ref})=0,00461+0,0488=0,053$$
Portanto, a estatística W é
$$W=\frac{\hat{\alpha}^2_1}{\hat{\sigma}^2_x+u^2(\text{ref})}=\frac{0,0123}{0,053}=0,233$$
Como dito anteriormente, $ W\sim\chi^2_1 $ (central). Assim, calculamos o p-valor, que é o menor valor para o qual rejeitamos a hipótese $\alpha=0 $.
$$P(W> W_{obs})=0,63$$
Portanto, não rejeitamos a hipótese $H_0$, isto é, temos evidências que a tendência não é significativa ao nível de significância 5%.
A seguir, apresentamos um resumo para todos os laboratórios.
| Tendência $ \alpha_i $ | $U_{lab}$ | $U_{ref}$ | $n_i$ | $u^2(lab)$ | $u^2(ref)$ | $u^2(lab)/n_i$ | $(u^2(lab)/n_i)+u^2(ref)$ | W | P-valor |
|---|---|---|---|---|---|---|---|---|---|
| 0,111 | 0,304 | 0,442 | 5 | 0,0231 | 0,0488 | 0,00461 | 0,0534 | 0,233 | 0,63 |
| -0,363 | 0,272 | 0,442 | 24 | 0,0184 | 0,0488 | 0,00077 | 0,0496 | 2,659 | 0,1 |
| 0,080 | 0,115 | 0,442 | 18 | 0,0033 | 0,0488 | 0,00018 | 0,0490 | 0,131 | 0,72 |
| 0,220 | 0,334 | 0,442 | 9 | 0,0279 | 0,0488 | 0,00310 | 0,0519 | 0,933 | 0,33 |
| 0,188 | 0,801 | 0,442 | 16 | 0,1603 | 0,0488 | 0,01002 | 0,0588 | 0,598 | 0,44 |
| 0,321 | 0,370 | 0,442 | 16 | 0,0343 | 0,0488 | 0,00214 | 0,0510 | 2,022 | 0,16 |
| -0,237 | 0,393 | 0,442 | 28 | 0,0387 | 0,0488 | 0,00138 | 0,0502 | 1,119 | 0,29 |
| 0,202 | 0,582 | 0,442 | 16 | 0,0846 | 0,0488 | 0,00529 | 0,0541 | 0,756 | 0,38 |
Tabela 2.4.2.2: Resumo do cálculo da estatística $W_i$.
2.4.3 - Teste de Tendência e Linearidade
O teste de tendência e linearidade, proposto por Leão, Aoki e Silva (2009) [14], testa a compatibilidade dos resultados das medições do laboratório com respeito ao valor de referência, para todos os pontos de medição. Neste caso, vamos utilizar a estatística de Wald, conforme Sen e Singer (2000) [13]. Para desenvolver o teste, foi considerado o seguinte modelo
$$y_{ijk}=\alpha_{i}+\beta_{i}x_{j}~\quad(2.4.3.1),$$
$$Y_{ijk}=y_{ijk}+e_{ijk}~,$$
em que, i=1,…,p, j=1,…,m, e k=1,…,ni. Dessa forma, temos que Yijk (valor observado) é sujeito ao erro de medição e assumimos que yijk satisfaz o relacionamento linear ultra-estrutural com o
valor verdadeiro xj (não observável). No modelo (2.4.3.1) temos que:
αi: representa a tendência aditiva do i-ésimo laboratório;
βi: representa a tendência multiplicativa do i-ésimo laboratório;
xj: representa o “verdadeiro” valor da característica a ser medida. Assumimos que
xj v.a.ind. ∼ $ N(\mu_{xj} , \sigma^2_{xj}) $;
$ \mu_{xj} $: representa o parâmetro de locação;
σxj: representa o parâmetro de escala e é considerado conhecido.
ϵijk: representa o erro aleatório na realização da k-ésima medição, no j-ésimo patamar pelo i-ésimo laboratório. Assumimos que
eijk v.a.ind. ∼ N(0, σ2ij);
σij: representa o parâmetro de escala e é considerado conhecido.
Consideramos ainda que xj é independente de eijk.
O objetivo desta análise é comparar a tendência aditiva (αi) e multiplicativa (βi) de cada laboratório (i) com o valor de referência, que neste caso, resulta em α = 0 e β = 1. Aqui, vamos considerar o primeiro dos p laboratórios como sendo o laboratório de referência, com isso, e considerando as premissas iniciais, temos que:
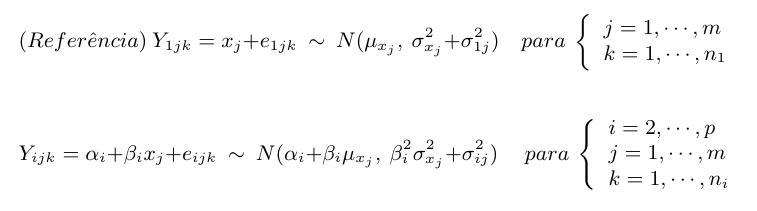
Considerando o modelo proposto, testamos a competência do laboratório desenvolvendo os seguintes testes:
- Hipótese 1: Vamos testar as seguintes hipóteses
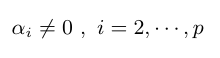
(há elementos em falta na equação acima)
Neste caso, estamos testando se a tendência aditiva do laboratório pode ser considerada nula.
- Hipótese 2: Vamos testar as seguintes hipóteses
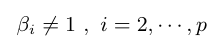
(há elementos em falta na equação acima)
Neste caso, estamos testando se a tendência multiplicativa do laboratório pode ser considerada igual a um.
- Hipótese 3: Vamos testar as seguintes hipóteses
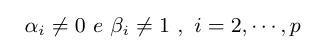
(há elementos em falta na equação acima)
Neste caso, estamos testando se a tendência aditiva é nula e se a tendência multiplicativa pode ser considerada igual a um.
As estatísticas utilizadas para a realização dos testes são:
- Teste 1:
$$Qw_{1i}=\frac{\widehat{\alpha}^2_i}{\upsilon_{\alpha_i \alpha_i}}\quad\text{para}~i=2,\cdots, p.$$
- Teste 2:
$$Qw_{2i}=\frac{(\widehat{\beta}_i - 1)^2}{\upsilon_{\beta_i\beta_i}}\quad\text{para}~i=2,\cdots, p.$$
- Teste 3:
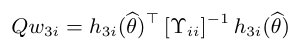
em que
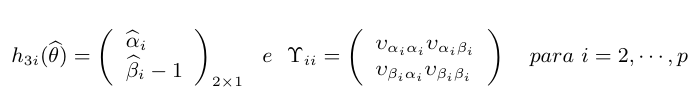

Independente do teste a ser realizado, conforme Sen e Singer (2000) [13] (teorema 5.6.3, pág. 240), temos que, sob $H_0$ a estatística $ Qw\sim\chi^2_1. $ Com isso, rejeitamos $H_0$ se Qw ≥ qw, em que qw é um valor obtido da distribuição qui-quadrado com 1 grau de liberdade e nível de significância $ \eta $. Portanto, se não rejeitamos a hipótese $H_0$, podemos dizer que a medição do laboratório é Qw-Satisfatório.
Podemos também calcular o p-valor, o qual é o menor valor para o qual rejeitamos a hipótese $H_0$. Este, é calculado por
$$P(Q_w> Q_{w_{obs}}).$$
Gráfico de tendência e linearidade
Em uma análise individual, vamos apresentar um gráfico com as tendências (tijk) de cada laboratório, para toda a faixa de medição. Aqui, definimos tendência como a diferença entre as medições do laboratório e o valor verdadeiro do motor, ou seja, tijk = Yijk − μxj. Além disso, ilustramos no gráfico, o intervalo de confiança de 99% para a tendência média, que é dado por
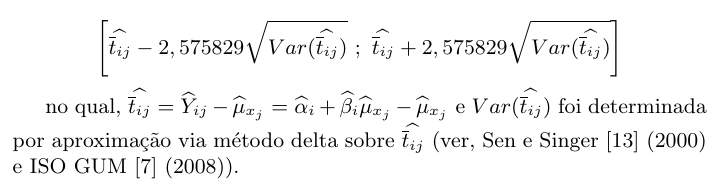
Exemplo 2.4.3.1
O laboratório em um EP ensaiou o artefato, de acordo com uma logística descrita em procedimento. Vamos considerar o estudo de tendência e linearidade para o laboratório 1.
| 1200 | 2000 | 3000 | 3600 | 4400 | 5200 | 5600 | 6000 | 6400 |
|---|---|---|---|---|---|---|---|---|
| 8,89 | 15,84 | 26,84 | 31,41 | 37,19 | 44,35 | 47,49 | 49,92 | 50,92 |
| 8,83 | 15,80 | 26,61 | 31,31 | 37,12 | 44,35 | 47,33 | 49,76 | 50,74 |
| 8,86 | 15,80 | 26,86 | 31,40 | 37,24 | 44,28 | 47,56 | 49,98 | 50,89 |
| 8,85 | 15,79 | 26,85 | 31,40 | 37,17 | 44,31 | 47,60 | 49,90 | 50,84 |
| 8,88 | 15,81 | 26,92 | 31,50 | 37,32 | 44,40 | 47,79 | 49,96 | 50,94 |
Tabela 2.4.3.1: Medidas de Potência corrigida para cada faixa de rotação do laboratório 1.
| 1200 | 2000 | 3000 | 3600 | 4400 | 5200 | 5600 | 6000 | 6400 |
|---|---|---|---|---|---|---|---|---|
| 8,74 | 15,70 | 26,47 | 31,13 | 36,91 | 43,81 | 46,87 | 48,65 | 49,52 |
Tabela 2.4.3.2: Medidas de Potência corrigida para cada faixa de rotação do laboratório de referência.
| Lab | 1200 | 2000 | 3000 | 3600 | 4400 | 5200 | 5600 | 6000 | 6400 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0,085 | 0,152 | 0,258 | 0,302 | 0,357 | 0,426 | 0,457 | 0,479 | 0,489 |
Tabela 2.4.3.3: Incerteza combinada da Potência corrigida para cada faixa de rotação do laboratório 1.
| 1200 | 2000 | 3000 | 3600 | 4400 | 5200 | 5600 | 6000 | 6400 |
|---|---|---|---|---|---|---|---|---|
| 0,123 | 0,221 | 0,373 | 0,439 | 0,518 | 0,614 | 0,656 | 0,681 | 0,692 |
Tabela 2.4.3.4: Incerteza combinada da Potência corrigida para cada faixa de rotação do laboratório de referência.
| Rotação | $n_i$ | Média | Desvio Padrão | Amplitude |
|---|---|---|---|---|
| 1200 | 5 | 8,86 | 0,025 | 0,062 |
| 2000 | 5 | 15,81 | 0,020 | 0,050 |
| 3000 | 5 | 26,81 | 0,121 | 0,311 |
| 3600 | 5 | 31,40 | 0,067 | 0,189 |
| 4400 | 5 | 37,21 | 0,075 | 0,199 |
| 5200 | 5 | 44,34 | 0,043 | 0,114 |
| 5600 | 5 | 47,55 | 0,165 | 0,452 |
| 6000 | 5 | 49,90 | 0,086 | 0,222 |
| 6400 | 5 | 50,87 | 0,082 | 0,205 |
Tabela 2.4.3.5: Estatística Descritiva para as medidas de potência corrigida para cada faixa de rotação do laboratório 1.
Veja a seguir os resultados obtidos pelo software Action para o exemplo.
(imagem em falta)
Figura 2.4.3.1: Resultados do teste de Tendência e Linearidade obtidos pelo software Action.
(imagem em falta)
Figura 2.4.3.2: Gráfico do teste de Tendência e Linearidade obtidos pelo software Action.
A partir dos resultados obtidos na Figura 2.4.3.1 e Figura 2.4.3.2, verificamos que o laboratório 1 não apresenta medições satisfatórias, pois no teste conjunto das tendências aditivas e multiplicativas (hipótese 3) rejeitamos $H_0$, pois o p-valor=0,016 está abaixo do nível de significância de 0,05. Além disso, ao testarmos somente a hipótese de tendência aditiva nula, percebemos que não rejeitamos $H_0$, pois o p-valor é igual a 0,714. Para a tendência multiplicativa, rejeitamos a hipótese $H_0$ de tendência multiplicativa igual a 1, pois o p-valor é igual a 0,047 (considerando o nível de significância de 0,05). Portanto, o laboratório precisa avaliar melhor o seu sistema de medição, uma vez que apresenta linearidade significativa e um padrão de tendências positivas.
3 - Aplicações do Ensaio de Proficiência
Nesta seção, vamos mostrar algumas aplicações do Ensaio de Proficiência. Todos os casos apresentados são reais e foram elaborados pelo cliente com a participação da equipe ESTATCAMP.
3.1 - Ensaio de Proficiência para Potência Efetiva Líquida do Motor
O objetivo de um sistema de medição é determinar o valor de uma quantidade particular a ser medida, no nosso exemplo, a potência do motor. Uma medição começa com uma especificação apropriada da quantidade a ser medida, com a definição do método e do procedimento de medição. A potência do motor (P) é o produto do Torque (T), obtido pelo motor, pela rotação (R) associada. Além disso, é bem conhecido que a potência do motor é influenciada pela altitude. Infelizmente, os laboratórios que realizam os ensaios de motores estão localizados em diferentes lugares com diferentes altitudes. Consequentemente, é necessário especificar um fator de correção (FC) de modo a ajustar as medições dos laboratórios para uma altitude padrão (nível do mar). O método de medição, especificado pela indústria automobilística, para medir a potência do motor é o dispositivo dinamométrico com “célula de carga”. Finalmente, o procedimento de medição descreve como utilizar o dispositivo dinamométrico para obter as medições de potência do motor, ou seja, ele define como conectar o motor com o dispositivo e o valor de rotação do motor durante as medições. Todas essas definições estão descritas no padrão ABNT NBR ISO 1585 [10].
No EP, o motor é distribuído sequencialmente entre os participantes, de modo, que cada laboratório, após realizar as medições de potência do motor em diferentes pontos de rotação, enviasse o motor ao próximo participante. A seguir, vamos descrever as especificações do Artefato (Motor Gasolina):
- Fornecedor: GM Powertrain;
- Modelo: 1:0 MPFI;
- Combustível: E25;
- Taxa de Compressão: 9,4 : 1;
- Quantidade de Óleo: 2,66 kg;
- Especicação do Óleo: Texaco Energy 2 - SAE 5W30 SL.
Os laboratórios participantes são
- Robert Bosch
- Mahle Metal Leve
- Ford
- Instituto Mauá de Tecnologia
- Magneti Marelli
- KSPG Automotive Brazil
- Delphi
- GM Powertrain
Renault
Cada Laboratorio deve fazer 5 curvas com este motor. As fontes de incerteza necessários para o EP são:
- Incerteza herdada do banco de ensaio;
- Repetitividade;
- Incerteza devido ao artefato.
Um ponto importante de nossa analise esta na utilização de uma variabilidade intrínseca ao artefato. Definimos que esta variabilidade intrínseca esta associada a tecnologia do motor e a sua produção. Para isto, adotamos um desvio padrão de 0,25% da leitura em potência corrigida (kW) associado ao artefato. Por exemplo, para uma medida de 50 kW, associamos um desvio padrão de 0,002550kW = 0,125kW, devido ao motor gasolina (artefato). Desta forma, esta variabilidade intrnseca do artefato e considerada como uma fonte de incerteza adicional.
A figura 3.1.1 ilustra o motor e seus componentes, dispostos dentro da embalagem utilizada para transportá-los.
(imagem em falta)
Figura 3.1.1: Detalhe do motor e seus componentes dispostos dentro da embalagem de transporte.
A figura 3.1.2 ilustra o motor acoplado ao dispositivo dinamométrico em um dos laboratórios participantes.
(imagem em falta)
Figura 3.1.2: Detalhe do motor acoplado ao dispositivo dinamométrico.
(imagem em falta)
Figura 3.1.3: Detalhe do motor acoplado ao dispositivo dinamométrico.
(imagem em falta)
Após realizadas as medições, cada laboratório deve calcular sua incerteza associada ao valor de potência corrigida. Na sequência, podemos usar qualquer uma das aplicações para a metodologia desenvolvida para avaliarmos a competência dos laboratórios participantes no EP. Podemos considerar, por exemplo, que o valor de referência é obtido pelo valor de consenso entre os laboratórios participantes.
3.1.1 - Análise da Consistência do Artefato
O ensaio de proficiência foi realizado para a variável Potência Corrigida obtida no ensaio de um motor Gasolina, conforme a NBR ISO 1585/1996 [10].
$${Potência}={Torque}\times{Rotação}$$
$${Potência Corrigida}={Potência}\times{Fator de Correção}$$
$${Fator de Correção}=\left(\frac{99}{P_{as}}\right)^{1,2}\times\left(\frac{T_{adm}}{298}\right)^{0,6}$$
em que,
- $P_{as}$: Representa a pressão do ar seco (kPa);
- $T_{adm}$: Representa a temperatura de admissão (Kelvin).
Além disso, foram consideradas as seguintes faixas de rotação:
Faixas de Rotação (rpm):
| 1200 | 2000 | 3000 | 3600 | 4400 | 5200 | 5600 | 6000 | 6400 |
|---|
Um dos laboratórios ensaiou o artefato no início e no final do ensaio de proficiência, de acordo com a logística descrita em procedimento. A seguir, apresentamos um resumo descritivo da medições das rodadas inicial e final por faixa de rotação.
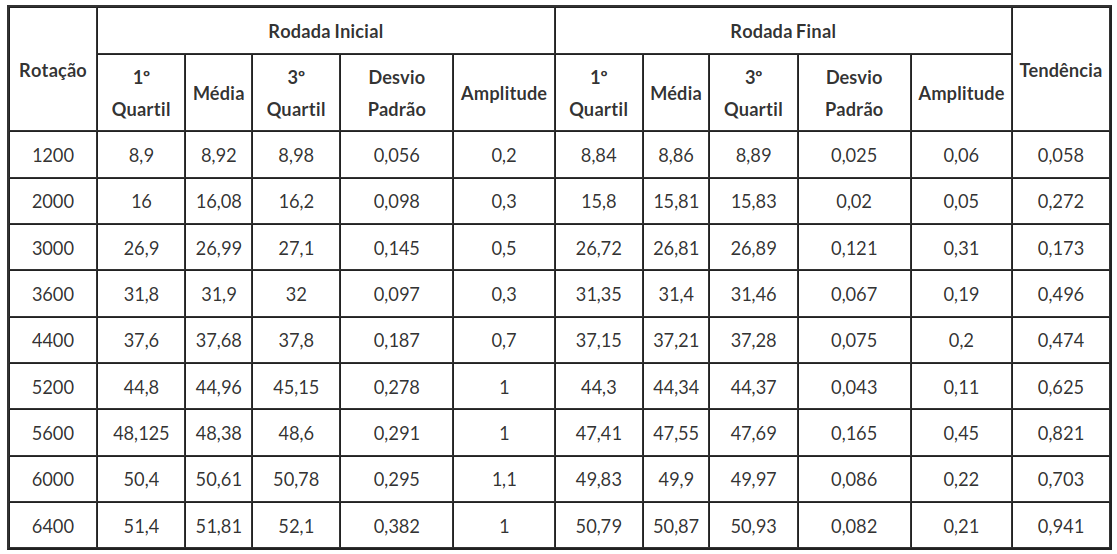
Figura 3.1.1.1: Estatística descritiva das rodadas final e inicial.
(imagem em falta)
Figura 3.1.1.1: Boxplot da potência corrigida da rodada inicial por faixa de rotação.
(imagem em falta)
Figura 3.1.1.2: Boxplot da potência corrigida da rodada final por faixa de rotação.
(imagem em falta)
Figura 3.1.1.3: Comparação entre as Rodadas Final e Inicial.
Por exemplo, tomando a faixa de Rotação 1200 temos:
Tendência
$${Tendência}=\overline{Rod}_i-\overline{Rod}_f=8,92-8,86=0,058$$
| Rotação | $ \overline{\text{Rod}}_i $ | $ \overline{\text{Rod}}_f $ | Tendência | k | U(ref) |
|---|---|---|---|---|---|
| 1200 | 8,92 | 8,86 | 0,058 | 2 | 0,17 |
| 2000 | 16,08 | 15,81 | 0,272 | 2 | 0,3 |
| 3000 | 26,99 | 26,81 | 0,173 | 2 | 0,52 |
| 3600 | 31,9 | 31,4 | 0,496 | 2 | 0,6 |
| 4400 | 37,68 | 37,21 | 0,474 | 2 | 0,71 |
| 5200 | 44,96 | 44,34 | 0,625 | 2 | 0,85 |
| 5600 | 48,38 | 47,55 | 0,821 | 2 | 0,93 |
| 6000 | 50,61 | 49,9 | 0,703 | 2 | 0,96 |
| 6400 | 51,81 | 50,87 | 0,941 | 2 | 0,98 |
Tabela 3.1.1.2: Comparação entre as Rodadas Final e Inicial.
A Tabela 3.1.1.3 apresenta o teste associado ao erro normalizado. Temos que o erro normalizado em todas as faixas de rotação é menor que 1. Concluímos que as duas rodadas de medições do laboratório são compatíveis.
Portanto, o artefato apresentou um comportamento estável ao longo do ensaio de proficiência.
| Rotação | Tendência do laboratório | VR | Tendência | U | $E_n$ | W | P-valor |
|---|---|---|---|---|---|---|---|
| 1200 | 0,058 | 0 | 0,058 | 0,170 | 0,341 | 0,465 | 0,495 |
| 2000 | 0,272 | 0 | 0,272 | 0,302 | 0,901 | 3,246 | 0,072 |
| 3000 | 0,173 | 0 | 0,173 | 0,520 | 0,332 | 0,442 | 0,506 |
| 3600 | 0,496 | 0 | 0,496 | 0,602 | 0,824 | 2,716 | 0,099 |
| 4400 | 0,474 | 0 | 0,474 | 0,711 | 0,667 | 1,780 | 0,182 |
| 5200 | 0,625 | 0 | 0,625 | 0,850 | 0,735 | 2,158 | 0,142 |
| 5600 | 0,821 | 0 | 0,821 | 0,925 | 0,888 | 3,152 | 0,076 |
| 6000 | 0,703 | 0 | 0,703 | 0,958 | 0,734 | 2,154 | 0,142 |
| 6400 | 0,941 | 0 | 0,941 | 0,983 | 0,957 | 3,661 | 0,056 |
Tabela 3.1.1.3: Homogeneidade do artefato por faixa de rotação.
(imagem em falta)
Figura 3.1.1.4: Gráfico da comparação entre as Rodadas Final e Inicial.
3.1.2 - Teste de compatibilidade
Nesta seção apresentamos os gráficos e as principais estatísticas descritivas para a variável potência corrigida ao longo da faixa de rotação, em seguida vamos realizar os testes de compatibilidade entre os resultados dos laboratórios e o valor de referência. Para este último vamos utilizar o Erro Normalizado (para mais detalhes veja Estatística de Performance). Nesta aplicação vamos tomar as faixas de rotação de 1200 e 2000 rpm e foi definido valor de referência de consenso (para mais detalhes veja determinação do valor de referência e sua incerteza). A seguir apresentamos os gráficos de dispersão da média da potência corrigida de cada laboratório por faixa de rotação.
(imagem em falta)
Figura 3.1.2.1: Curvas médias por laboratório.
(imagem em falta)
Figura 3.1.2.2: Gráfico de dispersão por laboratório e para todas as faixas de rotação.
A seguir, vamos tomar como exemplo os pontos de 1200 e 2000 rpm, os demais pontos é calculado de forma análoga. Nas figuras 3.1.2.3 e 3.1.2.4, temos os gráficos de dispersão e um boxplot da potência corrigida para as faixas de 1200 e 2000 rpm. Na tabela 3.1.2.1 temos as estatísticas descritiva dos dados e, na tabela 3.1.2.2 vemos o resultado do teste de valor extremo (ver determinação do valor de referência e sua incerteza), em seguida, o cálculo dos valores de referência: Consenso entre os Participantes.
| Rotação | Mínimo | 1º Quartil | Média | Mediana | Desvio Padrão | 3º Quartil | Máximo |
|---|---|---|---|---|---|---|---|
| 1200 | 8,46 | 8,6 | 8,74 | 8,75 | 0,15 | 8,85 | 9,13 |
| 2000 | 15,05 | 15,45 | 15,7 | 15,76 | 0,28 | 15,94 | 16,35 |
Tabela 3.1.2.1: Estatística descritiva para as faixas de 1200 e 2000 rpm.
(imagem em falta)
Figura 3.1.2.3: Gráficos de dispersão e boxplot para a faixa de rotação 1200.
(imagem em falta)
Figura 3.1.2.4: Gráficos de dispersão e boxplot para a faixa de rotação 2000.
Tomando como exemplo o laboratório 1 temos:
$$Z~=~\frac{|x_i ~-~\bar{x} |}{s}=\frac{|8,86 ~-~8,78 |}{0,13}=0,65~({Rotação 1200})$$
$$Z~=~\frac{|x_i ~-~\bar{x} |}{s}=\frac{|15,81 ~-~15,76 |}{0,24}=0,19~({Rotação 2000})$$
Como não existem valores extremos para a faixa de 1200 rpm, o valor de referência - VR é dado pela média das medições de todos os laboratórios, com a respectiva incerteza expandida, segundo a Tabela 3.1.2.2.
$$VR~=\frac{\displaystyle\sum^{8}_{i=1}y_i}{8}=\frac{8,86+\dots+8,71}{8}=8,78$$
$$U_{ref}=~2 \times \sqrt{\sum^{8}_{i=1}\frac{u^2(lab_i)}{8}}=2 \times \sqrt{\frac{0,085^2+\dots+0,159^2}{8}}=0,25$$
Logo, para a faixa de rotação de 1200 rpm temos que$ VR=8,78~kW;~U=0,25~kW. $
De forma similar, para a faixa de 2000 rpm, o valor de referência - VR é dado pela média das medições de todos os laboratórios, com a respectiva incerteza expandida, segundo a Tabela 3.1.2.2.
$$VR~=\frac{\displaystyle\sum^{8}_{i=1}y_i}{8}=\frac{15,81+\dots+15,9}{8}=15,76$$
$$U_{ref}=~2 \times \sqrt{\sum^{8}_{i=1}\frac{u^2(lab_i)}{8}}=2 \times \sqrt{\frac{0,152^2+\dots+0,291^2}{8}}=0,44$$
Logo, para a faixa de rotação de 2000 rpm temos que $ VR=15,76~kW;~U=0,44~kW. $
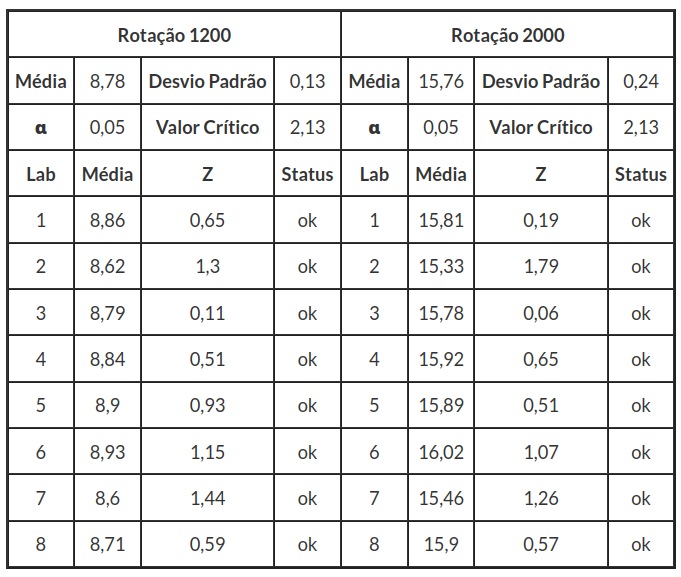
Tabela 3.1.2.2: Teste de Grubbs para detecção de outliers.
Tomando como exemplo o laboratório 1 e para a faixa de 1200 rpm temos:
Erro Normalizado - $ E_n $
$$E_n~=~\frac{\mid Res_{lab}~-~VR\mid}{\sqrt{U^2_{lab}~+~U^2_{ref}}}=\frac{\mid 8,862~-~8,744\mid}{\sqrt{0,153^2~+~0,246^2}}=0,393$$
| Laboratório | Média do lab. | VR | Tendência | $U_{lab}$ | $U_{ref}$ | U | $E_n$ | W | P-valor |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 8,86 | 8,78 | 0,081 | 0,170 | 0,246 | 0,299 | 0,272 | 0,398 | 0,528 |
| 2 | 8,62 | 8,78 | -0,164 | 0,153 | 0,246 | 0,289 | 0,566 | 1,745 | 0,187 |
| 3 | 8,79 | 8,78 | 0,014 | 0,064 | 0,246 | 0,254 | 0,054 | 0,012 | 0,912 |
| 4 | 8,84 | 8,78 | 0,064 | 0,185 | 0,246 | 0,308 | 0,207 | 0,252 | 0,615 |
| 5 | 8,90 | 8,78 | 0,116 | 0,448 | 0,246 | 0,511 | 0,227 | 0,740 | 0,390 |
| 6 | 8,93 | 8,78 | 0,144 | 0,206 | 0,246 | 0,321 | 0,449 | 1,318 | 0,251 |
| 7 | 8,60 | 8,78 | -0,181 | 0,218 | 0,246 | 0,329 | 0,550 | 2,103 | 0,147 |
| 8 | 8,71 | 8,78 | -0,075 | 0,319 | 0,246 | 0,402 | 0,185 | 0,333 | 0,564 |
Tabela 3.1.2.3: Comparação EN - faixa 1200.
(imagem em falta)
Figura 3.1.2.5: Gráfico da Comparação - faixa 1200.
Tomando como exemplo o laboratório 1 e para a faixa de 2000 rpm temos:
Erro Normalizado - $ E_n $
$$E_n~=~\frac{\mid Res_{lab}~-~VR\mid}{\sqrt{U^2_{lab}~+~U^2_{ref}}}=\frac{\mid 15,809~-~15,698\mid}{\sqrt{0,304^2~+~0,442^2}}=0,208$$
| Laboratório | Média do lab. | VR | Tendência | $U_{lab}$ | $U_{ref}$ | U | $E_n$ | W | P-valor |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 15,81 | 15,76 | 0,046 | 0,304 | 0,442 | 0,536 | 0,086 | 0,040 | 0,842 |
| 2 | 15,33 | 15,76 | -0,428 | 0,272 | 0,442 | 0,519 | 0,826 | 3,701 | 0,054 |
| 3 | 15,78 | 15,76 | 0,015 | 0,115 | 0,442 | 0,457 | 0,032 | 0,004 | 0,947 |
| 4 | 15,92 | 15,76 | 0,155 | 0,334 | 0,442 | 0,554 | 0,279 | 0,461 | 0,497 |
| 5 | 15,89 | 15,76 | 0,122 | 0,801 | 0,442 | 0,915 | 0,134 | 0,254 | 0,614 |
| 6 | 16,02 | 15,76 | 0,256 | 0,370 | 0,442 | 0,577 | 0,444 | 1,284 | 0,257 |
| 7 | 15,46 | 15,76 | -0,302 | 0,393 | 0,442 | 0,592 | 0,511 | 1,820 | 0,177 |
| 8 | 15,90 | 15,76 | 0,137 | 0,582 | 0,442 | 0,731 | 0,188 | 0,347 | 0,556 |
Tabela 3.1.2.4: Comparação EN - faixa 2000.
(imagem em falta)
Figura 3.1.2.6: Gráfico da Comparação - faixa 2000.
Extrapolando os resultados para as demais faixas de rotação e dado que as demais faixas são compatíveis com a referência. Portanto, todos os laboratórios são compatíveis com a referência para cada faixa de rotação.
3.1.3 - Análise de Tendência e Linearidade
Em situações onde os laboratórios medem várias vezes em vários pontos e a variável em análise apresenta variações naturais, utilizou-se o modelo com erro nas variáveis (para mais detalhes veja Estatística de Performance). Nesta seção vamos tomar como exemplo os laboratórios 1 e 2, os demais laboratórios é calculado de forma análoga.
Considerando o modelo proposto na seção Tendência e Linearidade, testamos a competência do laboratório desenvolvendo os seguintes testes:
- Hipótese 1: Vamos testar as seguintes hipóteses
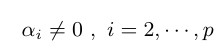
(há elementos em falta na equação acima)
Neste caso, estamos testando se a tendência aditiva do laboratório pode ser considerada nula.
- Hipótese 2: Vamos testar as seguintes hipóteses
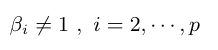
(há elementos em falta na equação acima)
Neste caso, estamos testando se a tendência multiplicativa do laboratório pode ser considerada igual a um.
- Hipótese 3: Vamos testar as seguintes hipóteses
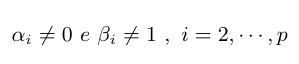
(há elementos em falta na equação acima)
Neste caso, estamos testando se a tendência aditiva é nula e se a tendência multiplicativa pode ser considerada igual a um.
A seguir apresentamos um resumo dos dados dos laboratórios 1 e 2, para aplicarmos a tendência e linearidade.
Laboratório Rotação Mínimo 1º Quartil Média 3º Quartil Máximo Desvio Padrão Amplitude Frequência
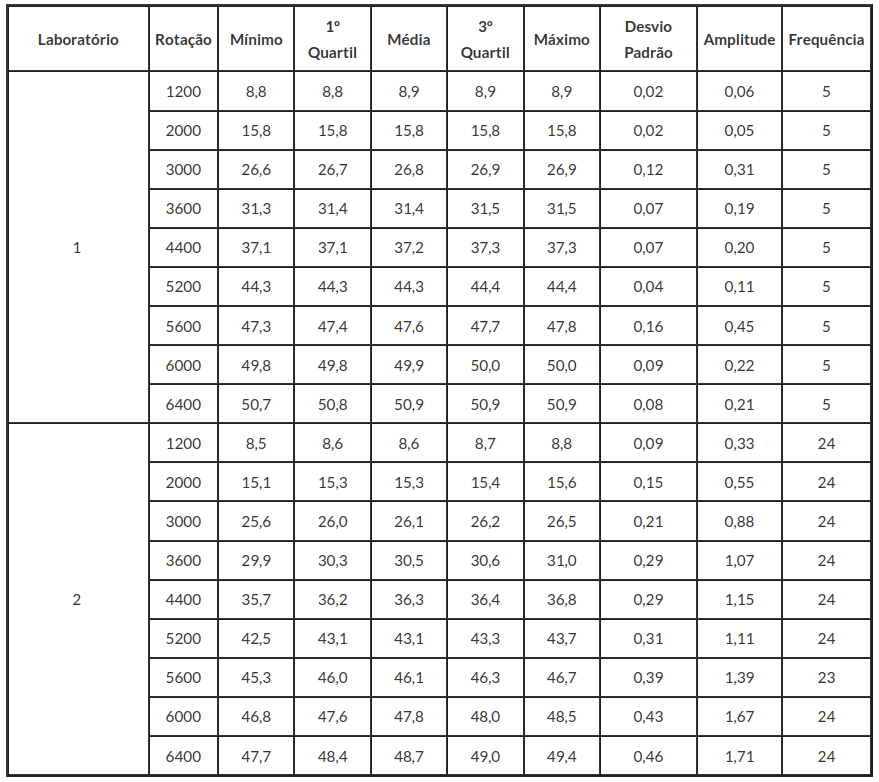
Tabela 3.1.3.1: Estatísticas Descritivas para as medidas de potência corrigida para cada faixa de rotação dos laboratórios 1 e 2.
| 1200 | 2000 | 3000 | 3600 | 4400 | 5200 | 5600 | 6000 | 6400 |
|---|---|---|---|---|---|---|---|---|
| 8,74 | 15,70 | 26,47 | 31,13 | 36,91 | 43,81 | 46,87 | 48,65 | 49,52 |
Tabela 2.3.3.2: Medidas de Potência corrigida para cada faixa de rotação do laboratório de referência.
| Lab | 1200 | 2000 | 3000 | 3600 | 4400 | 5200 | 5600 | 6000 | 6400 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0,085 | 0,152 | 0,258 | 0,302 | 0,357 | 0,426 | 0,457 | 0,479 | 0,489 |
Tabela 3.1.3.2: Incerteza combinada da Potência corrigida para cada faixa de rotação do laboratório 1.
| 1200 | 2000 | 3000 | 3600 | 4400 | 5200 | 5600 | 6000 | 6400 |
|---|---|---|---|---|---|---|---|---|
| 0,123 | 0,221 | 0,373 | 0,439 | 0,518 | 0,614 | 0,656 | 0,681 | 0,692 |
Tabela 3.1.3.3: Incerteza combinada da Potência corrigida para cada faixa de rotação do laboratório de referência.
Veja a seguir os resultados obtidos pelo software Action para o exemplo.
(imagem em falta)
Figura 3.1.3.1: Resultados do teste de Tendência e Linearidade obtidos pelo software Action.
(imagem em falta)
Figura 3.1.3.2: Gráfico do teste de Tendência e Linearidade obtidos pelo software Action.
A partir dos resultados obtidos na Figura 2.3.3.1 e Figura 2.3.3.2, verificamos que o laboratório 1 não apresenta medições satisfatórias, pois no teste conjunto das tendências aditivas e multiplicativas (hipótese 3) rejeitamos $H_0$, pois o p-valor=0,016 está abaixo do nível de significância de 0,05. Além disso, ao testarmos somente a hipótese de tendência aditiva nula, percebemos que não rejeitamos $H_0$, pois o p-valor é igual a 0,714. Para a tendência multiplicativa, rejeitamos a hipótese $H_0$ de tendência multiplicativa igual a 1, pois o p-valor é igual a 0,047 (considerando o nível de significância de 0,05). Portanto, o laboratório precisa avaliar melhor o seu sistema de medição, uma vez que apresenta linearidade significativa e um padrão de tendências positivas.
Agora para o laboratório 2 obtemos os seguintes resultados:
(imagem em falta)
Figura 3.1.3.3: Resultados do teste de Tendência e Linearidade obtidos pelo software Action.
(imagem em falta)
Figura 3.1.3.4: Gráfico do teste de Tendência e Linearidade obtidos pelo software Action.
A partir dos resultados obtidos na Figura 2.3.3.3 e Figura 2.3.3.4, verificamos que o laboratório 2, assim como o laboratório 1, não apresenta medições satisfatórias, pois no teste conjunto das tendências aditivas e multiplicativas (hipótese 3) rejeitamos $H_0$, pois o p-valor=0,016 está abaixo do nível de significância de 0,05. Além disso, ao testarmos somente a hipótese de tendência aditiva nula, percebemos que não rejeitamos $H_0$, pois o p-valor é igual a 0,95. Para a tendência multiplicativa, rejeitamos a hipótese $H_0$ de tendência multiplicativa igual a 1, pois o p-valor é igual a 0,022 (considerando o nível de significância de 0,05). Portanto, o laboratório precisa avaliar melhor o seu sistema de medição, uma vez que apresenta linearidade significativa e, diferentemente do laboratório 1, apresenta um padrão de tendências negativas.
3.2 - Ensaio de Proficiência para comitê de vidraria
Neste EP, um mesmo item é sequencialmente distribuído entre os participantes, de modo que cada participante realiza várias medições no mesmo ponto (nível ou patamar). Um balão volumétrico de 50 mL é sequencialmente distribuído entre 6 laboratórios, em que cada um realiza 10 medições do volume. Uma forma de apresentar os dados obtidos, pode ser observado na tabela 3.2.1, em que Yij representa a j-ésima medição realizada pelo i-ésimo laboratório.
Laboratórios:
| 1 | 2 | … | k |
|---|---|---|---|
| $Y_{11}$ | $Y_{21}$ | … | $Y_{k1}$ |
| $Y_{12}$ | $Y_{22}$ | … | $Y_{k2}$ |
| $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \vdots $ |
| $Y_{1n1}$ | $Y_{1n2}$ | … | $Y_{knk}$ |
Tabela 3.2.1: Dados dos laboratórios.
Devido ao fato de que todos os laboratórios medem o mesmo item, precisamos de um modelo que considera uma possível dependência entre todas as medições.
Neste EP, um balão volumétrico de 50 mL, ilustrado na figura 3.2.1, é distribuído de forma sequencial para 6 laboratórios participantes. Os participantes realizam 10 medições do volume do balão volumétrico.
O procedimento consiste em completar o balão com água e obter o valor de volume pela equação de medição definida por:
$$V=\left(\frac{m_{H_2O}}{\rho_{H_2O}-\rho_{\text{Ar}}}\right)\left(1-\frac{\rho_{\text{Ar}}}{\rho_{mass}}\right)\left[1-\omega(t_{H_2O}-t_{\text{ref}})\right]+\varepsilon~~(3.2.1)$$
em que
- $V$: representa o volume do balão volumétrico;
- $t_{ref}$: representa a temperatura de referência da água (20,0ºC);
- $t_{H2O}$: representa a temperatura da água durante o ensaio (19,9ºC);
- $m_{H2O}$: representa a massa da água (49,852 g);
- $ρ_{H2O}$: representa a massa específica da água (0,9983 g/cm3);
- $ρ_{Ar}$: representa a massa específica do ar (0,00110852 g/cm3);
- $ρ_{mass}$: representa a massa da massa padrão (7,8 g/cm3);
- $ω$: representa um fator de correção.
- $ε$: representa a repetibilidade.
(imagem em falta)
Figura 3.2.1: Ilustração do balão volumétrico de 50 mL.
Os seis laboratórios devem calcular a incerteza combinada através da equação de medição (3.2.1), conforme descrito na ISO GUM (2008). Assim, a incerteza combinada para o volume é dado por:
$$u^2_c(V)=\left(\frac{\partial V}{\partial m_{H_2O}}\right)^2 u^2(m_{H_2O})+\left( \frac{\partial V}{\partial\rho_{H_2O}}\right)^2 u^2(\rho_{H_2O})+\left( \frac{\partial V}{\partial t_{H_2O}} \right)^2 u^2(t_{H_2O})+$$
$$+\left(\frac{\partial V}{\partial \rho_{\text{Ar}}} \right)^2 u^2(\rho_{\text{Ar}})+\left(\frac{\partial V}{\partial \rho_{\text{mass}}}\right)^2 u^2(\rho_{\text{mass}})+u^2(\varepsilon).$$
A seguir, apresentamos as informações necessárias para calcularmos a incerteza combinada do volume.
| Equipamento | Incerteza |
|---|---|
| Balança | 0,0004 g |
| Barômetro | 0,76 mbar |
| Termômetro 1 | 0,05 ºC |
| Termômetro 2 | 0,3 ºC |
| Termohigrógrafo | 4,00% |
| Densímetro | 0,0003 g/mL |
| Massas | 0,03 mg |
Tabela 3.2.2: Informações para o cálculo de incerteza.
Com as informações obtidas pela tabela 3.2.2, calculamos a incerteza combinada e expandida dos 6 laboratórios (para mais detalhes consulte o conteúdo Incerteza de Medição). Os resultados do ensaio de proficiência para o comitê está resumido na tabela 3.2.3.
| Observação | L1 | L2 | L3 | L4 | L5 | L6 |
|---|---|---|---|---|---|---|
| 1 | 49,927 | 49,993 | 49,984 | 49,987 | 49,966 | 49,88 |
| 2 | 49,937 | 49,994 | 49,984 | 49,987 | 49,965 | 49,904 |
| 3 | 49,904 | 49,994 | 49,979 | 49,99 | 49,966 | 49,917 |
| 4 | 49,913 | 49,994 | 49,977 | 49,987 | 49,967 | 49,915 |
| 5 | 49,924 | 49,995 | 49,985 | 49,989 | 49,966 | 49,914 |
| 6 | 49,928 | 49,995 | 49,987 | 49,987 | 49,969 | 49,907 |
| 7 | 49,93 | 49,995 | 49,988 | 49,989 | 49,965 | 49,871 |
| 8 | 49,931 | 49,995 | 49,986 | 49,985 | 49,965 | 49,897 |
| 9 | 49,925 | 49,995 | 49,987 | 49,989 | 49,967 | 49,895 |
| 10 | 49,91 | 49,995 | 49,986 | 49,984 | 49,968 | 49,918 |
| Média | 49,923 | 49,994 | 49,984 | 49,987 | 49,966 | 49,902 |
| $u_c$(lab) | 0,004 | 0,014 | 0,008 | 0,003 | 0,009 | 0,01 |
| U(lab) | 0,008 | 0,028 | 0,016 | 0,006 | 0,018 | 0,02 |
Tabela 3.2.3: Medições de volume (mL): EP de vidraria.
Da figura 3.2.2 observamos que os laboratórios L1 e L6 apresentam medições um pouco distantes dos demais laboratórios.
(imagem em falta)
Figura 3.2.2: Boxplot do EP de vidraria.
O valor de referência para este EP são determinados por um processo de calibração. Em nossa aplicação, o laboratório L5 é reconhecido como tendo competência, que excede a competência dos outros laboratórios, para calibrar o item de interesse (balão volumétrico), pois ele é um membro da RBC (Rede Brasileira de Calibração) e também, é um membro de programas internacionais de EP. Por essa razão, vamos considerar sua média e desvio padrão como a referência, isto é, $ \overline{X_{\text{ref}}} = 49,9664 $, $ u_{\text{ref}} = 0,009 $ e $ U_{ref} = 0,018. $
Para testar a consistência do grupo de laboratórios temos as hipóteses

(há elementos em falta na equação acima)
e consideramos $ C={\bf I}_k $ e $ {\bf a}={\bf 0}_k $, com isso, podemos testar as seguintes hipóteses conjuntas:
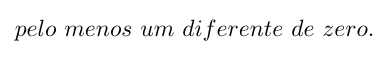
(há elementos em falta na equação acima)
Se rejeitarmos $ H_0 $, concluímos que o grupo de laboratórios não é consistente. Neste caso, passamos a desenvolver os testes individuais com respeito ao valor de referência. Então, vamos testar as seguintes hipóteses:
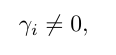
(há elementos em falta na equação acima)
para $ i=1,\ldots,k $ (neste caso, vamos considerar em (3.2.2) que $ C $ é um vetor linha ($ 1 \times k $) com $ 1 $ na i-ésima posição e zero nas demais, e $ a = 0 $). Se não rejeitarmos $ H_0 $, concluímos que as medições do i-ésimo laboratório são TRVG-satisfatórias.
Na sequência, o primeiro passo é identificar a ocorrência de outliers, para isto, vamos utilizar o teste de Grubbs (para mais detalhes veja Teste de valor extremo (Grubbs)). A tabela 3.2.4 resume os resultados obtidos pelo teste de Grubbs.
| Média | 49,958 | Desvio Padrão | 0,0395 |
|---|---|---|---|
| alpha | 0,05 | Valor Crítico | 1,72 |
| Laboratório | Média | Z | Status |
| L1 | 49,923 | 0,83 | ok |
| L2 | 49,995 | 0,85 | ok |
| L3 | 49,984 | 0,61 | ok |
| L4 | 49,987 | 0,68 | ok |
| L6 | 49,902 | 1,32 | ok |
Tabela 3.2.4: Teste de Grubbs (Teste de Valor Extremo).
Na tabela 3.2.4, apresentamos as estimativas da tendência, os resultados dos testes via estatística do teste W para os laboratórios individuais, bem como, o escore do teste En.
| Teste | Laboratório | Média do lab. | VR | Tendência | $U_{lab}$ | $U_{ref}$ | U | $E_n$ | W | P-valor |
|---|---|---|---|---|---|---|---|---|---|---|
| L1 x L5 | L1 | 49,923 | 49,966 | -0,0431 | 0,016 | 0,018 | 0,024 | 1,8 | 21,3 | 4,02E-06 |
| L2 x L5 | L2 | 49,995 | 49,966 | 0,0285 | 0,028 | 0,018 | 0,033 | 0,9 | 8,1 | 0,0045 |
| L3 x L5 | L3 | 49,984 | 49,966 | 0,0183 | 0,016 | 0,018 | 0,024 | 0,8 | 3,8 | 0,05 |
| L4 x L5 | L4 | 49,987 | 49,966 | 0,0214 | 0,006 | 0,018 | 0,019 | 1 | 5,6 | 0,018 |
| L6 x L5 | L6 | 49,902 | 49,966 | -0,0642 | 0,02 | 0,018 | 0,027 | 2,4 | 45,3 | 1,70E-11 |
Tabela 3.2.4: Tendência e testes para a competência dos cinco laboratórios.
Considerando α= 0,01 (nível de significância do teste) para decidir entre as hipóteses, rejeitamos a hipótese de que a tendência dos laboratórios são todas nulas e assim, concluímos que o grupo de laboratórios não é consistente. Além disso, segue dos testes de comparações múltiplas que somente as medições dos laboratórios L3 e L4 são TRVG-satisfatórias (p-valores 0,05 e 0,018, respectivamente). No entanto, segue do escore En que as medições dos laboratórios L2, L3 e L4 são satisfatórias (En ≤ 1). Observe que as medições do laboratório L2 são En-satisfatórias, mas elas não são TRVG-satisfatórias. Isto, é uma consequência da magnitude do seu desvio padrão combinado (s=0,014) o qual, é o maior desvio padrão entre os participantes.
(imagem em falta)
Figura 3.2.3: Gráfico da comparação da compatibilidade dos laboratórios.
Termos e definições
Nesta seção apresentamos alguns termos e definições descritos na norma ABNT NBR ISO/IEC 17043:2010 [9].
- Coordenador: uma ou mais pessoas com a responsabilidade de organizar e gerenciar todas as atividades envolvidas na operação de um programa de ensaios de proficiência;
- Comparação inter laboratorial: organização, desempenho e avaliação de medidas ou testes com os mesmos ou similares itens por dois ou mais laboratórios de acordo com condições predeterminadas;
- Outlier: observação de um conjunto de dados que parece ser incompatível com o resto do conjunto; NOTA: Um outlier pode ser proveniente de uma população diferente, ou ser o resultado de uma digitação incorreta ou outro erro grosseiro.
- Participante: laboratório, organização ou indivíduo que recebe itens de testes de proficiência e envia os resultados para a revisão pelo coordenador do ensaio de proficiência; NOTA: Em alguns casos, o participante pode ser um organismo de inspeção.
- Ensaios de proficiência: avaliação de desempenho dos participantes em relação a critérios pré-estabelecidos por meio de comparações inter laboratoriais;
- Item do ensaio de proficiência: amostra do produto, artefato, material de referência, parte do equipamento, medida padrão, conjunto de dados ou outras informações utilizadas para o ensaio de proficiência;
- Coordenador dos ensaios de proficiência: organização que assume a responsabilidade por todas as tarefas do desenvolvimento e operação de um programa de ensaios de proficiência;
- Programa de ensaios de proficiência: ensaios de proficiência concebido e operado por um ou mais ciclos de uma área especificada de teste, medição, calibração ou inspeção; NOTA: Um programa de ensaios de proficiência pode abranger um determinado tipo de ensaio, calibração, inspeção ou uma série de testes, calibrações ou verificações dos itens do teste de proficiência.
Referências Bibliográficas
[1] WEEC DOC. 19-1990: Guidelines for the Expression of the Uncertainity of Measurement in Calibration.
[2] WEEC DOC. 15-1987: International Measurements Audits.
[3] WEEC: International Inter-Laboratory Comparisons - A Tool for Gaining Mutual Confidence in Calibration and Testing Results - K. Brinkmann.
[4] Minuta básica “Comparações Interlaboratoriais” DICLA - GT-2.
[5] NIT-DICLA-026 (2008), ``Requisitos sobre a participação dos laboratórios de ensaio e calibração em atividades de ensaio de proficiência''.
[6] EAL -P7 - 1996 - EAL Interlaboratory Comparisons.
[7] ISO GUM (2008), Avaliação de dados de Medição - Guia para a expressão de incerteza de medição, 1ª edição brasileira.
[8] DOQ-CGCRE-005 - Orientações para a Organização de Comparações Interlaboratoriais pelas Comissões Técnicas da DICLA, Ver. 00, Setembro 2002.
[9] ISO/IEC 17043:2010. Conformity assessment-general requirements for Proficiency Testing, 2010.
[10] ABNT NBR ISO 1585 - Veículos Rodoviários - Código de ensaio de motores - Potência Líquida Efetiva, Rio de Janeiro, 1996.
[11] Richardson, H., Wood, D., Whitby, J., Lannigan, R., and Fleming, C. (1996). Quality Improvement of Diagnostic Microbiology Through a Peer-group Proficiency Assessment Program: a 20 year Experience in Ontario. Archives of Pathology and Laboratory Medicine, 120, 445-455.
[12] ISO/IEC 17011:2005. Avaliação da conformidade - Requisitos gerais para organismos de acreditação acreditação dos organismos de avaliação da conformidade, 2005.
[13] Sen, P. K. and Singer J. M. (2000) - Large Sample Methods in Statistics: An introduction with applications, Chapman & Hall.
[14] Leão, D. P. Jr., Aoki, R. e Silva, G. F., (2009) - Statistical Analysis of Bias and Linearity.
[15] ISO 13528:2005, Statistical methods for use in proficiency testing by interlaboratory comparisons.
[16] F. E. Grubbs (1969) - Procedures for Detecting Outlying Observations in Samples, Technometrics, TCTMTA, Vol. 11, No. 4, pp. 1-21.
[17] ISO Guide 34, General requirements for the competence of reference material producers.
[18] ISO Guide 35, Reference materials — General and statistical principles for certification.
[19] ISO 13528:2005, Statistical methods for use in proficiency testing by interlaboratory comparisons;.