Estabilidade Acelerado
Arrhenius
O objetivo principal das funções de estabilidade é determinar as taxas de reações químicas e físicas e sua relação com as condições de armazenamento, como temperatura, umidade e luz de um medicamento de tal forma que seja possível determinar o tempo de validade, ou seja, o intervalo de tempo que se espera que o medicamento permaneça dentro das especificações após a fabricação. Para isso, geralmente são realizados testes de estabilidade acelerado.
De acordo com a diretriz de estabilidade do FDA de 1987, um teste de estabilidade acelerado é um estudo de estabilidade de curto prazo conduzido sob condições exageradas ou estressadas (como temperatura alta, umidade de 75% ou mais, exposição a vários comprimentos de onda de radiação eletromagnética e armazenamento em um recipiente aberto) para aumentar a taxa de degradação química ou física de uma substância ou produto farmacêutico. Com esse tipo de estudo, é possível estimar os parâmetros cinéticos da taxa de reação e, assim, a vida útil prevista nas condições de armazenamento do mercado pode então ser obtida por extrapolação.
Existem alguns modelos para relacionar a taxa de reação de degradação e a temperatura correspondente e, assim, poder prever a vida útil do medicamento. Entre os modelos existentes, a equação de Arrhenius é a mais frequentemente empregada.
Se uma reação com duas entidades $A$ e $B$ é $A + B \rightarrow C$, a taxa de reação é dada por $$ \frac{dY(t)}{dt}= -K_{r_A+r_B}[A]^{r_A}[B]^{r_B},$$ em que a reação é dita ser da ordem $r_A+r_B$, onde $dY(t)/dt$ é um quociente diferencial entre a concentração e o tempo, $Y(t)$ é a concentração da espécie em estudo no tempo $t$, $[A]$ e $[B]$ representam as concentrações de $A$ e $B$, e $K$ é uma constante de velocidade. Na indústria farmacêutica estamos interessados apenas nas ordens inteiras de uma reação (ou seja, 0, 1 e 2). Nos concentramos nas reações de ordem zero e de primeira ordem pois na indústria farmacêutica a reação de primeira ordem é provavelmente o modelo mais comumente empregado para descrever a decomposição e a degradação dos ingredientes ativos de um medicamento, a reação de ordem zero é usada ocasionalmente e a reação de segunda ordem raramente é adotada.
A equação diferencial para uma reação de ordem zero é dada por $$ \frac{dY(t)}{dt}= -K_0$$ onde $K_0$ é a taxa constante de ordem zero, que é expressa como unidade de concentração por unidade de tempo. Integrando ambos os lados da equação em relação ao tempo, obtemos $$Y(t) = C_0 - K_0t$$ em que $C_0$ é uma constante. Seja $Y(0)$ a concentração inicial no tempo 0, podemos reescrever a equação acima, considerando $C_0 = Y(0)$, da seguinte forma $$Y(t) - Y(0) = - K_0t.$$
Ou seja, baseado na reação de ordem zero, um medicamento se degrada a uma taxa constante ao longo do tempo que é independente de ambas as concentrações no tempo inicial e no tempo $t$.
Porém, a reação mais empregada na prática é a reação de primeira ordem e, considerando que a quantidade de degradação é proporcional à concentração no tempo $t$, a equação diferencial correspondente a reação de primeira ordem é dada por $$ \frac{dY(t)}{dt}= -K_1Y(t)$$ em que $K_1$ é a taxa constante de primeira ordem. Similarmente ao caso anterior, integrando ambos os lados, resultamos em $$\ln [Y(t)] = C_1 - K_1t$$ em que $\ln$ denota o logaritmo natural e $C_1$ é uma constante. Reescrevendo a equação com a concentração inicial $Y(0)$, pode-se mostrar que $$\ln \left[\frac{Y(t)}{Y(0)} \right]= - K_1t.$$ Assim, vemos que a degradação de um medicamento descrito por uma reação de primeira ordem pode ser caracterizada por uma constante de taxa para o logaritmo das concentrações.
Em situações de testes de estabilidade térmica acelerada, as amostras de medicamentos são geralmente armazenadas ao longo do tempo em diferentes temperaturas. Estudaremos aqui um métodos para determinar a concentração de uma amostra que foi armazenada ao longo do tempo $t$ (geralmente expresso em dias ou meses) à temperatura $T$. A temperatura absoluta é usada para o estudo da relação entre a constante de velocidade e a temperatura. Para talo, cada amostra armazenada a uma temperatura elevada ao longo do tempo $t$ é analisada lado a lado com uma amostra armazenada pelo mesmo período de tempo, mas a uma temperatura mais baixa na qual nenhuma degradação apreciável pode ocorrer. Então, a concentração da amostra armazenada na temperatura elevada é expressa como uma porcentagem da amostra na temperatura mais baixa.
Uma vez que a concentração inicial no tempo 0 é 100% da reivindicação do rótulo sem erro, ou seja, $Y (0) = 100$, as equações para as reações de ordem zero e de primeira ordem tornam-se, respectivamente,
$$ \begin{equation} Y(t) = 100 -K_0t \tag{3.1} \end{equation} $$
e
$$ \begin{equation} \ln [Y(t)] = \ln [100] -K_1t. \tag{3.2} \end{equation} $$
No estágio inicial de desenvolvimento do medicamento, é necessário projetar a taxa de degradação na temperatura de armazenamento padrão com base nos dados coletados de testes acelerados de estabilidade térmica em temperaturas elevadas. Para isso, primeiro precisamos estabelecer a relação entre a constante de taxa e a temperatura. A relação entre a constante de taxa (ou taxa de reação) e a temperatura absoluta pode ser expressa pela equação de Arrhenius.
Equação de Arrhenius
A equação de Arrhenius é uma relação funcional e, de acordo com ela, a relação entre a taxa de reação e a temperatura absoluta pode ser descrita segundo a expressão $$\frac{d \ln[K]}{dT} = \frac{E}{RT^2}$$ em que
- $K$ é a taxa constante;
- $E$ é a energia de ativação, normalmente em elétrons-volts;
- $R$ é a constante de Boltzmann e
- $T$ é a temperatura absoluta Kelvin.
A temperatura é usualmente medida em graus Celsius e, assim, é necessário convertê-la para graus Kelvin através da seguinte expressão $$\text{ºKelvin} = \text{ºC}+ 273,15 $$ em que ºKelvin é a temperatura em graus Kelvin e ºC é a temperatura em graus Celsius.
Integrando ambos os lados da equação de Arrhenius e isolando $K$, obtemos que
$$ \begin{equation} K = A\exp\left(-\dfrac{E}{R \times T}\right) \tag{3.3} \end{equation} $$
em que $A$ é um fator de frequência.
Substituindo Eq. 3.3 em 3.1 e 3.2, obtemos
$$ \begin{equation} \frac{Y(t) - 100}{t} = -A\exp\left(-\dfrac{E}{R \times T}\right) \tag{3.4} \end{equation} $$
e
$$ \begin{equation} \frac{\ln [Y(t)/100]}{t} = -A\exp\left(-\dfrac{E}{R \times T}\right). \tag{3.5} \end{equation} $$
Nas duas equações acima, as quantidades no lado esquerdo são a degradação por unidade de tempo com base na escala original da concentração para a reação de ordem zero ou na escala logarítmica da concentração para a reação de primeira ordem e podem ser interpretados como as taxas de reação observadas que podem ser usadas para a estimativa dos parâmetros desconhecidos $A$ e $-E / R$ na Equação 3.3. Porém, é preferível usar o negativo das taxas de reação observada (dadas em 3.4 e 3.5) para o propósito de estimar os parâmetros $A$ e $-E / R$.
Considere $Y_{i j}$ a concentração de uma amostra armazenada após o tempo $t_j$ à temperatura $T_i$, onde $i = 1, 2,. . ., I$ e $j = 1,. . ., J$ e todos os $Y_{i j}$ são expressos em termos de porcentagem. Defina a degradação para as reações de ordem zero e de primeira ordem, respectivamente, como $$D_{ij}(0) = Y_{ij} - 100$$ e $$D_{ij}(1) = \ln[Y_{ij}/100].$$
As taxas de reação negativa ou as taxas de degradação negativas por unidade de tempo são dadas, respectivamente, por $$K_{ij}(0) = -\frac{D_{ij}(0)}{t_j} = -\frac{100 - Y_{ij}}{t_j}$$ e $$K_{ij}(1) = -\frac{D_{ij}(1)}{t_j} = -\frac{\ln[100/Y_{ij}]}{t_j}$$ em que $i = 1, 2, . . ., I$ e $j = 1, 2, . . ., J $.
A seguir, descreveremos o método de obtenção da estimativa de constantes de taxas e os parâmetros desconhecidos na equação de Arrhenius. Com base nas estimativas dos parâmetros desconhecidos e seus desvios-padrão estimados e covariância, um período de data de expiração experimental projetado pode ser obtido usando a relação dada nas Equações 3.4 e 3.5. A partir das Equações 3.1 e 3.2, a degradação no tempo $t_j$ pode ser expressa pelo seguinte modelo de regressão linear sem intercepto $$D_{ij}(h) = \beta_i(h)t_j + e_{ij}$$ em que $\beta_i(h) = -K_{hi}$, $h$ é a ordem da reação, $h=0,1$, $e_{ij}$ são os erros aleatórios e assumimos que $e_{ij}\sim N (0,\sigma_{i}^{2}(h))$. O modelo de regressão linear simples sem intercepto, dado acima, deve ser estimado por meio do método dos mínimos quadrados para a estimativa da constante de taxa para cada combinação de pontos de tempo e temperatura.
Com as constantes de taxa estimadas em cada temperatura, as estimativas dos parâmetros desconhecidos na Equação de Arrhenius 3.3 são encontradas ajustando um modelo de regressão linear (ou ponderada) ao logaritmo das constantes de taxa estimadas $\ln [b_i ( h)]$ com a temperatura como variável independente, em que $b_i$ é a estimativa de mínimos quadrados para $\beta_i$. Uma vez que o teste típico de estabilidade térmica acelerada é geralmente conduzido em três ou quatro temperaturas elevadas diferentes, a inferência estatística sobre os parâmetros desconhecidos na equação de Arrhenius é então baseada em apenas um ou dois graus de liberdade. Para superar esta desvantagem, pode-se considerar a utilização da taxa de degradação negativa observada por unidade de tempo ou taxas de reação negativas observadas $K_{ i j} (h)$, $h = 0, 1$, $i = 1,. . ., I$ e $j = 1,. . ., J$. Como resultado, todas as observações são usadas para estimar os dois parâmetros desconhecidos na equação de Arrhenius e, consequentemente, inferência estatística sobre o período de data de expiração provisório pode ser obtida com base em uma estimativa da variância do erro com $I$ $J - 2$ graus de liberdade.
Assim, para obter uma estimativa do período de validade, precisamos obter a taxa de reação média prevista na temperatura de armazenamento de comercialização para a ordem de reação $h$, em que consideramos $h=1$. Essa estimação pode ser feita considerando o seguinte modelo de regressão $$\ln(K(h))=\alpha(h)+\beta(h)X$$ em que
- $K(h)$: taxa constante de ordem $h$ estimada para temperatura;
- $h$: ordem de reação de degradação, sendo $h = 1$;
- $\alpha(h)$: fator constante;
- $\beta(h)$: parâmetro do modelo;
- $X$: inversa de temperatura absoluta Kelvin, ou seja, $X=1/T$.
Por fim, com a estimação do modelo acima realizada, pode-se verificar que a degradação prevista após o tempo $t$ na temperatura de armazenamento de comercialização $T$ é dada por $$\hat{D}(h) = -\exp[\widehat{\ln(K(h))}]t.$$
Arrhenius Modificada
Sabe-se que umidade relativa, umidade absoluta e pressão de vapor de água são linearmente correlacionadas em temperatura constante, o que significa que não importa quais dessas medidas de umidade são usadas para modelar a taxa de degradação. No entanto, ao modelar os efeitos combinados de temperatura e umidade na taxa de degradação, diferentes descritores de umidade resultam em modelos diferentes. Assim, diferentemente do Capítulo Arrhenius, em que foi considerado apenas a temperatura, neste capítulo trataremos de uma modificação da equação de Arrhenius que leva em consideração a combinação de temperatura e umidade relativa na taxa de degradação.
Apresentaremos aqui uma modificação na equação de Arrhenius para que tenhamos um modelo em que a taxa de degradação aumenta exponencialmente com a umidade relativa. Este é um modelo combinado de temperatura e umidade no qual a umidade relativa é usada para descrever a umidade, ou seja, é um modelo que incorpora uma dependência de Arrhenius da temperatura juntamente com os efeitos da umidade. Proposto por Genton e Kesselring (1977) \cite{Genton and Kesselring}; Waterman e Adami (2005) \cite{Waterman and Adami}; Waterman et al. (2007) \cite{Waterman et al} e Waterman (2009) \cite{Waterman}, a equação de Arrhenius modificada é dada por
$$ \begin{equation} K = A\times \exp\left(-\dfrac{E_0}{R \times T}\right)\times \exp(B\times RH), \tag{3.6} \end{equation} $$
e aplicando o logaritmo, temos
$$ \begin{equation} \ln K = \ln A -\dfrac{E_a}{R \times T} + B\times RH. \tag{3.7} \end{equation} $$
A explicação desse modelo vem do fato dele ser amplamente empírico por natureza e de que sabe-se que a umidade relativa afeta a mobilidade molecular e, portanto, aumenta a frequência de colisão e a constante pré-exponencial da Equação de Arrhenius.
Nenhum termo de interação (termo cruzado) é proposto neste modelo, ou seja, a temperatura da taxa de degradação é independente da umidade relativa e a umidade da taxa de degradação é independente da temperatura. O uso da umidade relativa (RH) e não da pressão de vapor (VP) ou umidade absoluta (AH) se deve ao fato de que a RH fornece o melhor ajuste dos dados experimentais. Estudos em muitos produtos diferentes forneceram suporte para este modelo.
A Equação 3.7 pode ser visualizada em termos de um gráfico tridimensional em que a variável de resposta, $\ln k$, está em um plano com uma inclinação de $-E_a/R$ ao longo do eixo de temperatura e uma inclinação de $B$ ao longo do eixo de umidade relativa, mostrando como o termo $E_a$ é um parâmetro de “sensibilidade à temperatura” e $B$ é um parâmetro de “sensibilidade à umidade”.
Os coeficientes $A$, $-E_a/R$ e $B$ podem ser calculados por meio de regressão não linear múltipla da Equação \ref{3.6} ou regressão linear múltipla da Equação \ref{3.6}. A regressão linear múltipla usa $\ln k$ como a variável medida (resposta) e $1/T(K^{-1})$ e %$RH$ como variáveis de entrada.
Estimação
Modelo de degradação linear
Ao monitorar-se a degradação química de produtos farmacêuticos, o resultado medido é dado normalmente como porcentagem em massa do produto de degradação em relação à massa total da substância medicamentosa e suas impurezas relacionadas. Esse resultado pode ser expresso como $\%\text{Deg}_t$, onde $t$ é o tempo gasto para obtê-lo. Para calcular a taxa de degradação, $k$, é preciso conhecer $\%\text{Deg}$ e o tempo de armazenamento $t$. Se $\%\text{Deg}$ aumenta linearmente com o tempo, podemos formular a seguinte expressão para calcular a taxa de degradação:
$$ \begin{equation} K = \dfrac{\%\text{Deg}_t}{\text{tempo}(t)} \quad(\text{ordem zero}) \tag{3.8} \end{equation} $$
onde a referência “ordem zero” é usada para dizer que a velocidade da reação permanece inalterada a medida que diminui a substância reagente, ou seja, é constante (elevada a zero). As unidades comumente utilizadas para calcular a taxa $k$ são a porcentagem ($\%$) ao mês ou ao dia. Dessa forma, os resultados podem ser comparados com os limites de especificação que também são usualmente dados em porcentagem. É importante ressaltar que a maioria das reações de ordem zero são na verdade reações de primeira ou segunda ordem, que, devido ao consumo do reagente, são interrompidas antes que a taxa de degradação comece a diminuir visivelmente resultando em uma degradação aparentemente linear.
Perfis de degradação não linear
Ao tratar-se de produtos farmacêuticos sólidos, perfis de degradação não linear são muito mais comuns de se encontrar que perfis lineares. Citamos abaixo alguns dos motivos que levam a essa não linearidade:
- Mecanismos de degradação química complexos: o mecanismo de degradação de alguns produtos pode envolver várias etapas reversíveis, concorrentes ou consecutivas.
- Estados físicos heterogêneos: podem haver diferentes estados físicos e ambientes de IFA, e cada estado pode exibir uma suscetibilidade diferente à degradação. Além disso, os estados físicos da amostras podem modificar-se ao longo do tempo resultando em diferentes níveis de degradação.
- Limites de degradação $%\text{Deg}_{\infty}$ desconhecidos e menores que 100%: pode ocorrer quando a taxa de reação é proporcional ao reagente limitante prestes a ser consumido ou quando apenas uma pequena proporção de IFA esteja em um estado reativo.
- Processos físicos e de estado sólido não lineares: ocorre quando há nucleação, difusão ou contração de volume no estado sólido. Dessa forma a taxa limite de velocidade do processo de degradação prossegue através de cinética não linear.
- Ambientes onde a umidade varia: a taxa de degradação para a maioria dos produtos é significativamente afetada pela umidade, por exemplo, produtos embalados podem apresentar aumento na umidade pois a umidade dentro da embalagem normalmente aumentará lentamente em direção à do ambiente externo como resultado da permeação de umidade através da embalagem. Dessa forma, a taxa de degradação vê-se afetada.
Quando se surge qualquer um dos tipos de perfil de degradação não linear citados acima, a necessidade de encontrar um valor “$k$” para modelar os efeitos de temperatura e umidade geralmente não é trivial. Mas é importante se certificar que perfis de degradação semelhantes sejam obtidos em diferentes condições de temperatura e umidade.
Apresentamos, na Tabela 3.1, modelos cinéticos para processos comuns de degradação não linear de estado sólido, que são as expressões cinéticas de degradação de zero, primeira e segunda ordem.
| Modelo Cinético | Fórmula Diferencial $\left(\dfrac{d\alpha}{dt}=\right)$ | Fórmula Integral $\left(k=\right)$ | Fórmula Integral $\left(\alpha=\right)$ |
|---|---|---|---|
| Ordem Zero | $k$ | $\dfrac{\alpha}{t}$ | $kt$ |
| Primeira Ordem | $k(1-\alpha)$ | $\dfrac{-Ln(1-\alpha)}{t}$ | $1-e^{-kt}$ |
| Segunda Ordem | $k{(1-\alpha)}^2$ | $\dfrac{{(1-\alpha)}^{-1}-1}{t}$ | $1-\dfrac{1}{1+kt}$ |
O objetivo de aplicar uma abordagem de modelo cinético é extrair uma constante de taxa significativa, $k$, da curva de degradação versus tempo, que é então usada como a variável de resposta no modelo de estabilidade acelerado com temperatura e umidade. Modelos cinéticos estão disponíveis para uma variedade de processos e mecanismos de degradação, alguns dos quais estão listados na Tabela 3.1, em que as expressões cinéticas listadas podem ser pensadas como opções para a transformação linear da curva de degradação. A terceira coluna da Tabela 3.1 mostra como pode ser calculado a partir de $\alpha$ (a extensão da degradação ou grau de conversão) e o tempo ($t$); $\alpha$ neste contexto pode ser calculado usando a seguinte equação:
$$ \begin{equation*} \alpha = \dfrac{\% \text{Deg}_t}{ \% \text{Deg} _{\infty}} \end{equation*} $$
Muitas vezes, o nível de degradação do produto no início do estudo estabilidade preditiva acelerada ($\%\text{Deg}_{0}$) é diferente de zero, caso em que pode ser preferível definir $\alpha$ usando a seguinte equação:
$$ \begin{equation*} \alpha = \frac{\%\text{Deg}_t - \%\text{Deg}_0}{\%\text{Deg}_\infty - \%\text{Deg}_0}, \end{equation*} $$
em que o limite de degradação ($%\text{Deg}{\infty}$) é um parâmetro que dificilmente será conhecido a priori; portanto, normalmente é deixado em 100% ou é estimado a partir dos perfis de degradação (ou seja, é usado um ``parâmetro de ajuste de modelo'' adicional). Consideraremos que $\%\text{Deg}{\infty} = 100\%$.
Coeficiente Q10
Conforme o Guia 16 \cite{Guia16}, a equação de Arrhenius permite calcular a variação da constante de velocidade de uma reação química conforme a temperatura. Essa equação aplicada a alimentos ajuda a entender como a deterioração ou degradação dos componentes do alimento varia com a temperatura. Em geral, à medida que a temperatura aumenta, a taxa de deterioração dos alimentos também aumenta devido ao acréscimo da energia cinética das moléculas envolvidas nas reações de degradação.
Em consequência, o modelo clássico de Arrhenius pode ser utilizado, o que permite que as previsões sejam feitas para a validade e sobredosagem de um produto.
O Guia menciona o uso de coeficiente Q10 na determinação de prazos de validade de alimentos. Q10 é uma ferramenta que auxilia a análise de dados de estudos acelerados ao estimar como a taxa de degradação de alimentos, enzimas ou outros produtos biológicos muda com o acréscimo de 10ºC de temperatura.
O coeficiente é dado pelo quociente entre as velocidades de reação a uma determinada temperatura e a uma temperatura 10°C mais baixa. A fórmula geral para o coeficiente Q10 é a seguinte:
$$Q10= \dfrac{K_{T_2}}{K_{T_1}}\hspace{5cm}$$ onde:
- $K_{T_2}$ é a taxa de degradação medida a uma temperatura $T_2$ ($T_2=T_1+10ºC$).
- $K_{T_1}$ é a taxa de degradação medida a uma temperatura $T_1$.
Em outras palavras, o coeficiente compara a taxa de degradação de um produto em duas temperaturas diferentes e fornece uma estimativa de quanto a taxa de degradação aumenta para cada aumento de 10ºC na temperatura. Assim, o objetivo principal dos testes acelerados é determinar o valor de Q10 e poder, desta forma, estimar a validade de um produto em condições de temperatura inferior.
Por exemplo, se o coeficiente Q10 for 2, significa que a taxa de degradação dobra com o aumento de 10ºC de temperatura. Neste caso, se o tempo de armazenamento de um estudo de estabilidade acelerado para um produto é de 6 meses, a confiança para a determinação do prazo de validade em uma temperatura 10ºC mais baixa pode ser de 12 meses, o dobro.
Recomenda-se que, quando possível, os estudos acelerados sejam realizados em dois ou mais pontos de temperatura elevados, particularmente, quando é necessária uma vida útil prolongada. Contudo, não deve ser utilizado quando as condições de temperaturas elevadas causam mudanças físicas no alimento, tais como derretimento, suavização, fissuração ou separação de fases ou quando o produto contiver ingredientes sensíveis à temperatura, como, por exemplo, a maioria dos probióticos.
Relação de Q10 e Arrhenius
A seguir, veremos a conexão do coeficiente $Q_{10}$ com a equação Arrhenius. Como visto nas expressões \ref{eqOrdem0A} e \ref{eqOrdem1A}, as taxas de reação observadas podem ser expressas em
- Cinética ordem zero: $$ Y(t, T)=100-K_0(T) t \quad \text { ou } \quad \frac{Y(t, T)-100}{t}=-K_0(T), $$
- Cinética ordem um $$ \ln \big(Y(t, T) \big) = \ln(100) - K_1(T) t \quad \text { ou } \quad \frac{\ln \big(Y(t, T) \big) - \ln(100)}{t}=-K_1(T), $$
onde $K_h$ é taxa da reação química no qual $h$ representa a ordem que varia entre 0 e 1, $Y(t)$ é a concentração no tempo $t$, $T$ a temperatura em grau Kelvin e $t$: tempo. Ao substituirmos as expressões na equação de Arrhenius \ref{eqArrhenius}, obtemos:
$$
\begin{cases}\frac{Y(t, T)-100}{t}=-A \exp \left(-\frac{E}{R \times T}\right), & h=0, \\
\frac{\ln \big(Y(t, T) \big) - \ln(100)}{t}=-A \exp \left(-\frac{E}{R \times T}\right), & h=1.\end{cases}
$$
Tomamos por $Q_{T2 - T1}$ a razão entre as taxas de degradação em duas faixas de temperatura, isto é,
$$ Q_{T_2-T_1}=\frac{K_h(T_2)}{K_h(T_1)} $$
no qual $K_h(T_i)$ representa a taxa de degração a temperatura $T_i$ para $i = 1, 2$, sob ordem $h$. Conforme sugerido pela ANVISA, tomamos $T_2 - T_1 = 10$.
Assim, pela equação Arrhenius, obtemos que
$$ Q_{10}=\frac{K_h(T_2)}{K_h(T_1)}=\exp \left[\frac{E}{R}\left(\frac{1}{T_1}-\frac{1}{T_2}\right)\right] $$
e
$$ E=\frac{R \ln ( Q_{10})}{\left(\frac{1}{T_1}-\frac{1}{T_2}\right)}. $$
Procedimento para determinar o prazo de validade
Para estimar o prazo de validade do produto na temperatura de referência, por exemplo $T_{\text{ref}} = 30$ºC, primeiramente determinamos o prazo de validade $t_2$ obtido na temperatura acelerada $T_2$. Esse prazo corresponde ao ponto em que a reta ajustada intercepta o limite inferior de especificação, ou seja, $Y(t_2, T_2) = LIE$. Nosso objetivo é estimar o tempo $t_{ref}$ tal que $Y(t_{ref}, T_{ref}) = LIE$, que pode ser obtido por meio da relação:
$$t_{ref} = t_2 \cdot Q_{10}$$.
A seguir, apresenta-se um breve procedimento para essa estiamtiva:
- Realizar estudo de estabilidade na temperatura $T_2$, utilizando regressão linear simples com, no mínimo, 5 pontos de tempo.
- Realizar estudo de estabilidade na temperatura $T_1$, também por meio de regressão linear simples, com no mínimo de 3 pontos de tempo.
- Calcular o coeficiente $Q_{10}$, definido como a razão entre os coeficientes angulares obtidos nas duas temperaturas $Q_{10} = \frac{K_2}{K_1}$.
- Determinar o prazo de validade $t_{\text{ref}}$ para a temperatura de referência $T_{\text{ref}}$, aplicando a relação com o tempo estimado em $T_2$.
Nas etapas de ajuste por regressão linear simples:
- As concentrações devem ser previamente realinhadas, de modo que o valor inicial corresponda a 100%.
- O coeficiente de determinação $R^2$ dos modelos ajustados não deve ser inferior a 0,7 a fim de garantir que a extrapolação de tendência seja válida.
- Conclui-se que o método não é apropriado, e que não é possível determinar o prazo de validade, quando:
- A reta ajustada em $T_2$ não intercepta o $LIE$.
- Os coeficientes angulares de ambas as retas ajustadas não são negativos.
Exemplo
Estabilidade acelerado - Arrhenius
Com o intuito de exemplificar o teste de estabilidade acelerado, considere o conjunto de dados encontrado na Tabela \ref{tab_dados_Ace}, em que contém informações de temperatura, em graus Celsius, tempo em meses de exposição do medicamento àquela temperatura, teor de certa substância do medicamento e a degradação. O intuito é estimar a taxa de degradação em uma temperatura de 50ºC.
| Temperatura | Tempo | Lote 1 (Teor/Degradação) | Lote 2 (Teor/Degradação) | Lote 3 (Teor/Degradação) |
|---|---|---|---|---|
| 25 | 3 | 100,2 / 0,001998 | 100,2 / 0,001998 | 98,8 / -0,012073 |
| 6 | 98,8 / -0,012073 | 99 / -0,01005 | 98,2 / -0,018164 | |
| 9 | 98,4 / -0,016129 | 98,2 / -0,018164 | 96,6 / -0,034591 | |
| 12 | 97,3 / -0,027371 | 96,9 / -0,031491 | 96 / -0,040822 | |
| 30 | 3 | 99,4 / -0,006018 | 99,4 / -0,006018 | 99 / -0,01005 |
| 6 | 98,2 / -0,018164 | 98,6 / -0,014099 | 98,4 / -0,016129 | |
| 9 | 96,5 / -0,035627 | 96,9 / -0,031491 | 95,5 / -0,046044 | |
| 12 | 95,9 / -0,041864 | 96,3 / -0,037702 | 95,1 / -0,050241 | |
| 40 | 1 | 98,6 / -0,014099 | 98,8 / -0,012073 | 98,8 / -0,012073 |
| 2 | 99 / -0,01005 | 98,4 / -0,016129 | 97,4 / -0,026344 | |
| 3 | 98,4 / -0,016129 | 96,3 / -0,037702 | 97,8 / -0,022246 | |
| 6 | 96,3 / -0,037702 | 95,7 / -0,043952 | 95,3 / -0,04814 |
Primeiro, devemos estimar a tendência $K_i$ de cada temperatura por meio da regressão linear com a variável dependente Tempo e a variável independente Degradação. A tendência estimada corresponde à estimativa do parâmetro de coeficiente angular no modelo.
Temperatura 25º
| Estimativa | Desvio Padrão | P-valor | |
|---|---|---|---|
| Tempo | -0,003621 | 0,000218 | 0 |
Temperatura 30º
| Estimativa | Desvio Padrão | P-valor | |
|---|---|---|---|
| Tempo | -0,003621 | 0,000218 | 0 |
Temperatura 40º
| Estimativa | Desvio Padrão | P-valor | |
|---|---|---|---|
| Tempo | -0,007669 | 0,000589 | 0 |
A partir dessas taxas estimadas, ajustamos um novo modelo de regressão linear, ou seja, ajustamos um modelo de regressão linear com os seguintes dados:
| Temperatura | $\boldsymbol{\beta}$ | Temperatura (Kelvin) | Temperatura Inversa | ln(K) |
|---|---|---|---|---|
| 25 | -0,002571 | 298,15 | 0,003354 | -5,963647 |
| 30 | -0,003621 | 303,15 | 0,003299 | -5,621091 |
| 40 | -0,007669 | 313,15 | 0,003193 | -4,870624 |
Ajustando o modelo de regressão linear com os $\beta$s e os valores de $\ln(K)$, obtemos a seguinte estimativa:
| Estimativa | Desvio Padrão | P-valor | |
|---|---|---|---|
| Intercepto | 16,982618 | 0,772592 | 0,028942 |
| Temperatura Inversa | -6845,696541 | 235,35261 | 0,021878 |
Assim, o modelo ajustado é dado por $$\ln(K(h)) = 16,982618 - 6845,696541 X$$ em que $X=1/T$ e $T$ é a temperatura Kelvin.
Queremos, nesse exemplo, estimar a taxa de degradação para a temperatura de 50ºC. Assim, calculamos o inverso da temperatura Kelvin e aplicamos esse valor no modelo ajustado, isto é, $$ \frac{1}{T} = \frac{1}{50+273,15} = \frac{1}{323,15} = 0,003095$$ e então $$\widehat{\ln(K)} = 16,982618 - 6845,696541\ast 0,003095 = -4,201651$$
Assim $$\hat{K}=\exp( -4,201651) = -0,014971.$$
Portanto, a taxa de degradação ajustada para a temperatura de 50ºC é dada por -0,014971, isto é, estima-se que o medicamento perde aproximadamente 1,5% de teor da substância analisada por mês, se exposto à temperatura de 50ºC.
Estabilidade acelerado - Arrhenius Modificada
Com a intenção de exemplificar o teste de estabilidade acelerado (Arrhenius Modificado), consideremos o conjunto de dados encontrado na Tabela \ref{tab_dados_ASAP}, que contém informações de temperatura, em graus Celsius, umidade, a duração em dias da exposição daquele medicamento àquela temperatura e umidade além do nível de degradação. O intuito é estimar a taxa de degradação para uma temperatura de 25ºC e umidade de 60%RH ao longo de 365 dias.
| Duração (Dias) | Temperatura (C) | Umidade (%RH) | Nível Degradação (%) |
|---|---|---|---|
| 14 | 50 | 75 | 0,42 |
| 14 | 60 | 40 | 0,45 |
| 14 | 70 | 10 | 0,62 |
| 2 | 70 | 75 | 0,66 |
| 2 | 80 | 40 | 0,65 |
Primeiro, estimamos a taxa de degradação ($K$) em cada condição combinada por temperatura e umidade diferente, por meio do modelo linear:
$$ \begin{equation} K = \dfrac{%\text{Deg}_t}{\text{tempo}(t)} \end{equation} $$
em que
- $\%Deg_t$: porcentagem de degradação até o tempo $t$, é obtida subtraindo degradação observada no tempo $t$ da degradação inicial ($\%Deg_0 = 0,05$);
- $t$: duração de tempo.
A seguir, apresentamos os dados com as taxas estimadas.
| Duração (Dias) | Condição | Degradação | %Deg_t | K |
|---|---|---|---|---|
| 14 | 50°C/75%RH | 0,42 | 0,37 | 0,0264 |
| 14 | 60°C/40%RH | 0,45 | 0,4 | 0,0286 |
| 14 | 70°C/10%RH | 0,62 | 0,57 | 0,0407 |
| 2 | 70°C/75%RH | 0,66 | 0,61 | 0,305 |
| 2 | 80°C/40%RH | 0,65 | 0,6 | 0,3 |
A partir das taxas estimadas, ajustamos um modelo de regressão linear múltiplo segundo a equação Arrhenius Modificado dada por:
$$ \begin{equation} \ln K = \ln A \dfrac{E_a}{R}\times \dfrac{1}{T}+B\times RH \end{equation} $$
em que
-
$\ln K$: é a variável resposta sendo $K$ a taxa de degradação estimada; - $\ln A$: fator constante;
- $E_a/R$: coeficiente angular associado à temperatura;
- $1/T$: inversa da temperatura absoluta Kelvin;
- $B$: coeficiente angular associado à umidade relativa;
- $RH$: umidade relativa
Os dados utilizados para a realização do ajuste do modelo linear múltiplo são apresentados na tabela a seguir.
| Condição | Temperatura Inversa | Umidade (%RH) | ln K |
|---|---|---|---|
| 50°C/75%RH | 0,0031 | 75 | -3,6333 |
| 60°C/40%RH | 0,003 | 40 | -3,5553 |
| 70°C/10%RH | 0,0029 | 10 | -3,2012 |
| 70°C/75%RH | 0,0029 | 75 | -1,1874 |
| 80°C/40%RH | 0,0028 | 40 | -1,2040 |
O seguinte passo será realizar uma análise da variância (ANOVA) para testar a influência da temperatura e da umidade no modelo.
| G.L. | Soma de Quadrados | Quadrado Médio | Estat. F. | P-valor | |
|---|---|---|---|---|---|
| Temperatura Inversa | 1 | 3,8542 | 3,8542 | 1069,3304 | 0,0009 |
| Umidade (%RH) | 1 | 2,4151 | 2,4151 | 670,0593 | 0,0015 |
| Resíduos | 2 | 0,0072 | 0,0036 |
Na Tabela \ref{tab_ANOVA} vemos que o p-valor é menor que 0,05 para temperatura e umidade, logo concluímos que ambas variáveis são influentes no modelo. Ajustando o modelo de regressão linear múltipla com os valores de $Ln(K)$ obtemos as seguintes estimativas:
| Estimativa | Desvio Padrão | Estat. t. | P-valor | |
|---|---|---|---|---|
| Ln A | 36,0193 | 0,9603 | 37,5094 | 0,0007 |
| Temperatura Inversa | -13581,7589 | 333,4129 | -40,7395 | 0,0006 |
| Umidade (%RH) | 0,0314 | 0,0012 | 25,8855 | 0,0015 |
Queremos, nesse exemplo, estimar a taxa de degradação para a temperatura de 25$^{\circ}$C e umidade de 60%RH por 365 dias. Assim, calculamos o inverso da temperatura Kelvin e aplicamos esses valores no modelo ajustado, isto é, $$ \frac{1}{T} = \frac{1}{25+257,5} = \frac{1}{282,5} = 0,003354$$ e então $$\widehat{\ln(K)} = 36,019 + (- 13581,759)\ast 0,003354 + 0,0314\ast 60 = -7,64978$$ assim $$\hat{K}=\exp( -7,64978) = -0,000476147.$$
Ao multiplicar esse valor por 365 dias $$-0,000476146\ast 365 = 0,173793.$$
Portanto, a taxa de degradação predita na temperatura 25$^{\circ}$C e umidade 60%RH por 365 dias é de 0,173793, isto é, estima-se que o medicamento perde aproximadamente 17,38% de teor da substância analisada por ano, se exposto a uma temperatura de 25$^{\circ}$C e umidade de 60%RH.
Estabilidade acelerado - Coeficiente Q10
Com o intuito de exemplificar o método Q10 para estimar a degradação de alimentos e assim obter o prazo de validade de alimentos, considere o conjunto de dados da tabela abaixo. Essa tabela contém dados de uma determinada substância (Vitamina C) junto com a temperatura, em graus Celsius, o tempo em meses de exposição do produto àquela temperatura, os lotes e o teor obtido da substância. Foi calculada também a taxa de degradação do teor para cada tempo e temperatura. O intuito é calcular o coeficiente Q10 e estudar a degradação para obter o prazo de validade da substância para as temperaturas de 30ºC e 40ºC com $LIE$ = 80.
| Lote | Tempo | Temperatura | Resposta | Resposta' |
|---|---|---|---|---|
| 1 | 0 | 30 | 117,92 | 100 |
| 1 | 3 | 30 | 113,26 | 96,0 |
| 1 | 6 | 30 | 110,11 | 93,4 |
| 1 | 9 | 30 | 106,08 | 90,0 |
| 2 | 0 | 30 | 117,98 | 100 |
| 2 | 3 | 30 | 114,06 | 96,7 |
| 2 | 6 | 30 | 110,46 | 93,6 |
| 2 | 9 | 30 | 105,51 | 89,4 |
| 3 | 0 | 30 | 117,58 | 100 |
| 3 | 3 | 30 | 113,82 | 96,8 |
| 3 | 6 | 30 | 110,66 | 94,1 |
| 3 | 9 | 30 | 106,60 | 90,7 |
| 1 | 0 | 40 | 115,20 | 100 |
| 1 | 3 | 40 | 103,11 | 89,5 |
| 1 | 6 | 40 | 91,39 | 79,3 |
| 2 | 0 | 40 | 115,94 | 100 |
| 2 | 3 | 40 | 107,25 | 92,5 |
| 2 | 6 | 40 | 91,54 | 79,0 |
| 3 | 0 | 40 | 117,45 | 100 |
| 3 | 3 | 40 | 102,13 | 87,0 |
| 3 | 6 | 40 | 85,85 | 73,1 |
Inicialmente, foram realizados estudos de estabilidade para determinar a taxa de degradação $K$ em diferentes temperaturas. As respostas foram escaladas para que o valor inicial corresponda a 100%, além disso, assumiu-se que a reação de degradação segue uma cinética de ordem 0 ($K$ constante ao longo do tempo).
Primeiro, devemos estimar a tendência $K_i$ de cada temperatura por meio da regressão linear com a variável independente Tempo. A tendência estimada corresponde à estimativa do parâmetro de coeficiente angular no modelo.
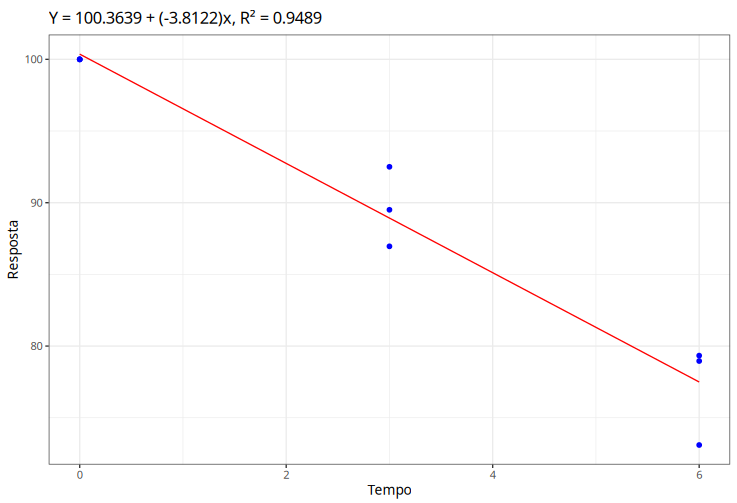
- Temperatura 40º: Ajuste do modelo de regressão linear simples para a temperatura de 40º
| Estimativa | Desvio padrão | Estat. t | P-valor | |
|---|---|---|---|---|
| Intercepto | 100,363947 | 1,295130 | 77,493320 | 0 |
| Tempo | -3,812158 | 0,334401 | -11,399952 | 0,000009 |
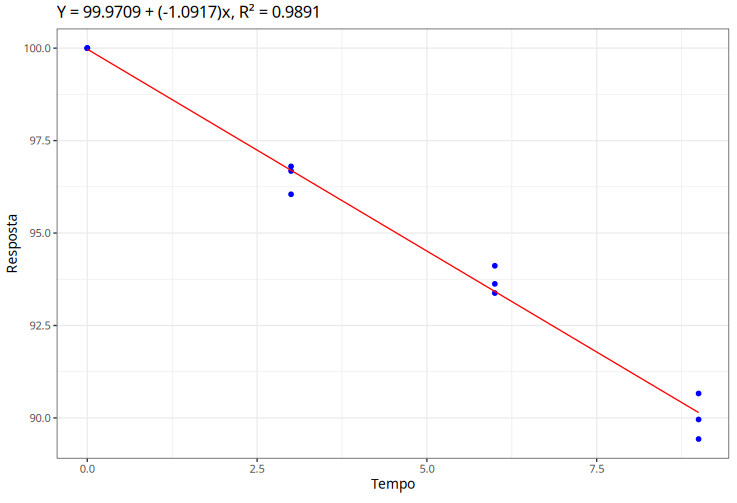
- Temperatura 30º: Ajuste do modelo de regressão linear simples para a temperatura de 30º
| Estimativa | Desvio padrão | Estat. t | P-valor | |
|---|---|---|---|---|
| Intercepto | 99,970859 | 99,970859 | 491,673658 | 0 |
| Tempo | -1,091734 | 0,036228 | -30,135304 | 0 |
Para calcular o valor do coeficiente Q10, procedemos com a divisão dos coeficientes angulares:
$$Q_{10}=\frac{k_2}{k_1}=\frac{-3,812}{-1,092}=3,492$$
A reta ajustada para a temperatura 40ºC intercepta o $LIE$ antes de 4 unidades no eixo x, temos que $t_2=5$.
A estimativa do prazo de validade na temperatura de referência (30°C) é dada por:
$$ t_{\text{ref}} = t_2 \cdot Q_{10} = 5\cdot 3,492 \approx 17 $$.
Assim, o prazo de validade estimado para a temperatura de 30°C é de aproximadamente 17 unidade de tempo.
Seguem as saídas do Action Stat:
 $$
$$