Análise de tendência no estudo de estabilidade

Modelo estatístico

O tempo de expiração ou tempo de prateleira é definido mediante um estudo de estabilidade de longa duração. Para determinar o tempo de prateleira de um produto farmacêutico, tem-se como referência a Resolução da Diretoria Colegiada RDC Nº318 e o guia Q1E do ICH. Estes guias recomendam utilizar pelo menos 3 lotes de fabricação para incluir a variação entre lotes na determinação do tempo de prateleira.

Apesar de se poder calcular um tempo de prateleira para cada lote individualmente, é desejável estabelecer um único tempo de prateleira válido para todos os lotes de fabricação. Antes de se combinar os dados de estabilidade, precisa-se avaliar a similaridade entre os lotes. A técnica estatística utilizada para essa avaliação é a ANCOVA (Análise de Covariância), onde tempo é a covariável e testa se existe uma diferença ou variação significativa nas curvas de tendência entre os lotes.

Então, para definir o modelo de estudo que avalia a similaridade entre os lotes, precisa-se inicialmente definir a matriz de planejamento dos lotes. Suponha que tenha $K$ lotes em análise, através de variável dummy, tem-se a seguinte matriz de planejamento com $K-1$ colunas: $$ \begin{array} {c}\mathrm{Lote~1}\to \cr \mathrm{Lote~2}\to \cr \mathrm{Lote~3}\to \cr \mathrm{Lote~4}\to \cr \vdots \cr \mathrm{Lote~K}\to \end{array}\quad \begin{bmatrix} 0 & 0 & 0 & 0 & \cdots & 0 \cr 1 & 0 & 0 & 0 & \cdots & 0 \cr 0 & 1 & 0 & 0 & \cdots & 0 \cr 0 & 0 & 1 & 0 & \cdots & 0 \cr & & \vdots & & \ddots & \vdots \cr 0 & 0 & 0 & 0 & \cdots & 1 \end{bmatrix} $$

Para cada lote $ i $, tem-se $ n_i $ observações relacionadas aos tempos $ t_{ij} $ e as interações entre tempo e lotes, com $ i=1,2,…,K $ e $ j=1,…,n_i $. Portanto, pode-se definir o modelo de regressão linear:

$$ \begin{equation} Y = X \beta + \varepsilon, \tag{1} \end{equation} $$

em que:

alt text

$$ \begin{align*} Y&=\begin{bmatrix} y_1 \cr y_2 \cr y_3 \cr \vdots \cr y_n \end{bmatrix}; \beta=\begin{bmatrix} \beta_0 \cr \beta_1 \cr \beta_2 \cr \beta_3 \cr \vdots \cr \beta_{2 K-1} \end{bmatrix}; \varepsilon=\begin{bmatrix} \varepsilon_1 \cr \varepsilon_2 \cr \varepsilon_3 \cr \vdots \cr \varepsilon_n \end{bmatrix} \hspace{5cm} \end{align*} $$

onde $X$ é uma matriz de $n \times 2K$ e $ n = \sum_{i=1}^K n_i $. O modelo (1) possui $p=2K-1$ parâmetros.

Admite-se que os erros experimentais $ \varepsilon_{ij} $ são independentes e identicamente distribuídos com média zero e variância $ \sigma^2 $.

Então, pode-se interpretar o modelo de forma separada por lote:

Lote 1: $Y_{1j} = \beta_0 + \beta_1\cdot t_{1j}+\varepsilon_{1j}$
Lote 2: $Y_{n2} = (\beta_0 + \beta_2)+(\beta_1 + \beta_{K+1})\cdot t_{n2}+\varepsilon_{n2}$
Lote 3: $Y_{n3} =(\beta_0 + \beta_3)+(\beta_1 + \beta_{K+2})\cdot t_{n3}+\varepsilon_{n3}$

$\vdots$
Lote K: $Y_{nK} =(\beta_0 + \beta_K)+(\beta_1 + \beta_{2K-1})\cdot t_{nK}+\varepsilon_{nK}$

em que $ Y_{n_i}, t_{n_i} $ e $ \varepsilon_{n_i}$ são as partições dos vetores por lote, com $ i=1,2,…,K $,

Estimativa dos Parâmetros

A estimação dos parâmetros $\beta$ no modelo (1) é obtida via método de mínimos quadrados na forma:

$$ \begin{align*} \varepsilon^\top\varepsilon &= \left(Y - X\beta\right)^\top\left(Y-X\beta\right) \cr % &= Y^\top Y -2Y^\top X\beta + \beta^\top X^\top X\beta . &= Y^\top Y -2 \beta^\top X^\top Y + \beta^\top X^\top X\beta. \end{align*} $$

Para encontrar o mínimo de $\varepsilon^\top\varepsilon$ deriva-se em função de $\beta$ e iguala-se a zero: $$ \dfrac{\partial\varepsilon^\top\varepsilon}{\partial\beta} = 0 - 2X^\top Y + 2X^\top X \beta = 0, $$ logo, a solução é a estimativa do $\beta$ dada por $$ \begin{equation} \widehat{\beta} = \left(X^\top X\right)^{-1}X^\top Y. \tag{2} \end{equation} $$

Portanto, o ajuste do modelo de regressão e o vetor de resíduos do modelo são definidos por:

$$\widehat{Y} = X\widehat{\beta}\quad \quad \text{e} \quad \quad e = Y - \widehat{Y} .$$

Propriedades

Para o modelo de regressão definido têm-se as seguintes propriedades:

$\mathbb{E}\left[\widehat{\beta}\right] = \beta$;
$Cov\left[\widehat{\beta}\right] = \sigma^2\left(X^\top X\right)^{-1}$;
$SQE = Y^\top\left(\mathbb{I} - X\left(X^\top X\right)^{-1}X^\top\right)Y = Y^\top\left(\mathbb{I} - \mathbb{H}\right)Y$;
$\widehat{\sigma}^2 = QME = \dfrac{SQE}{n - 2K}$.

Em notação matricial, as seguintes expressões são válidas para a soma de quadrados:

$SQT = Y^\top Y - \dfrac{Y^\top \mathbb{J} Y}{n}$;
$SQR = Y^\top\left(\mathbb{H} - \dfrac{\mathbb{J}}{n}\right)Y$;
$SQE = Y^\top Y - \widehat{\beta}^\top X^\top Y$;

sendo que $\mathbb{I}$ representa a matriz identidade, $\mathbb{H} = X\left(X^\top X\right)^{-1}X^\top$ a matriz Hat e $\mathbb{J} = \begin{bmatrix} 1 & \cdots & 1 \cr \vdots & \ddots & \vdots \cr 1 & \cdots & 1 \end{bmatrix}$.

Testes de comparação de curvas

A similaridade entre os lotes é avaliada pelos testes de hipóteses de igualdade dos interceptos e igualdade dos coeficientes angulares das curvas de tendência dos lotes. O guia do FDA recomenda um nível de significância de $0,25$ para concluir os testes.

Ajusta-se o modelo contendo o Tempo, o Lote e a interação entre esses dois fatores. Nesse modelo, se a igualdade dos coeficientes angulares (paralelismo) for rejeitada tem-se a adoção do modelo completo, ou seja, o modelo de regressão irá conter as covariáveis Tempo, Lote e a interação Tempo e Lote. Caso a igualdade dos coeficientes angulares não seja rejeitada, ajusta-se o modelo considerando o Tempo e o Lote. Após esse ajuste é verificado a significância do fator Lote, caso ele seja significativo adota-se o modelo considerando o Tempo e o Lote, caso ele seja não significativo adota-se apenas um modelo considerando o Tempo. Essa abordagem é conhecida como ANOVA sequencial.

ANOVA sequencial

Dado um modelo de regressão linear completo, considerando todos os fatores, isto é, um modelo com o Tempo, Lote e a interação entre esses dois fatores:

$$ \begin{equation} \begin{split} Y = \beta_0 + \beta_1 \cdot\text{Tempo} + \beta_2 \cdot \text{Lote2} + \cdots + \beta_{k} \cdot\text{LoteK} + \hspace{2cm} \cr \beta_{k + 1} \cdot\text{Tempo} \cdot \text{Lote1} + \cdots + \beta_{2K-1} \cdot\text{Tempo} \cdot\text{LoteK} + \epsilon \end{split} \tag{3} \end{equation} $$

Para avaliar esse modelo realiza-se uma ANOVA e efetua-se um teste $F$ parcial para as seguintes hipóteses: $$ \begin{cases} H_{0}:\beta_{K+1}=\beta_{K+2}=\cdots=\beta_{2K-1}=0;\cr H_{1}: \text{Pelo menos um é diferente}. \end{cases} $$

As hipóteses acima dizem respeito ao paralelismo das retas de regressão, em outras palavras, caso a hipótese nula ($H_0$) não seja rejeitada é possível dizer que todos os lotes possuem uma mesma tendência.

Caso $H_0$ seja rejeitada, conclui-se que não há paralelismo. Nesse caso, é realizada a abordagem com o modelo completo tal como o apresentado em Eq. (3). Caso $H_0$ não seja rejeitada, ajusta-se um modelo contendo apenas o Tempo e o Lote, sem considerar a interação entre eles. Em outros termos:

$$ \begin{equation} Y = \beta_0 + \beta_1 \cdot \text{Tempo} + \beta_2 \cdot \text{Lote2} + \cdots + \beta_{k}\cdot \text{LoteK} + \epsilon \tag{4} \end{equation} $$

Agora, no modelo acima, é avaliada a significância do fator lote, quer dizer, por intermédio do teste $F$ parcial são avaliadas as seguintes hipóteses: $$ \begin{cases} H_{0}:\beta_2=\beta_3=\cdots=\beta_K=0;\cr H_{1}: \text{Pelo menos um é diferente}. \end{cases} $$

As hipóteses acima referem-se ao intercepto das retas de regressão. Em outras palavras, caso a hipótese nula não seja rejeitada pode-se dizer que todos os lotes possuem um mesmo intercepto.

Se a hipótese nula for rejeitada será utilizado o modelo sem interação, tal como o apresentado em Eq. (4). Caso a hipótese nula não seja rejeitada, será considerado um único modelo para todos os dados sem o fator Lote, isto é, o seguinte modelo:

$$ \begin{equation} Y = \beta_0 + \beta_1 \cdot \text{Tempo} + \epsilon. \tag{5} \end{equation} $$

Teste de igualdade dos coeficientes angulares (Paralelismo)

Primeiramente, estamos interessados em testar se há ou não diferença entre os coeficientes angulares de cada modelo, ou seja, se as retas ajustadas são ou não paralelas. Se não houver diferença significativa entre os coeficientes, os valores do subconjunto do vetor de parâmetros $ \beta $ que são correspondentes a uma alteração no coeficiente angular, ou seja, $ \beta_{K+1},\beta_{K+2},\cdots,\beta_{2K-1} $, são nulos e as retas ajustadas são paralelas. Assim, queremos testar as hipóteses: $$ \begin{cases} H_{0a}:\beta_{K+1}=\beta_{K+2}=\cdots=\beta_{2K-1}=0;\cr H_{1a}: \text{Pelo menos um é diferente}. \end{cases} $$

Na Figura 1, podemos ver um exemplo ilustrativo em que, no primeiro caso, não rejeitamos $ H_{0a} $ pois há paralelismo entre as retas ajustadas e, portanto, os coeficientes angulares são iguais e os valores de $ \beta_{K+1},\beta_{K+2},\cdots,\beta_{2K-1} $ são nulos. No segundo caso, rejeitamos $ H_{0a} $ pois concluímos que as retas ajustadas não são paralelas e, portanto, os coeficientes angulares são diferentes e os parâmetros $ \beta_{K+1},\beta_{K+2},\cdots,\beta_{2K-1} $ são significativos. 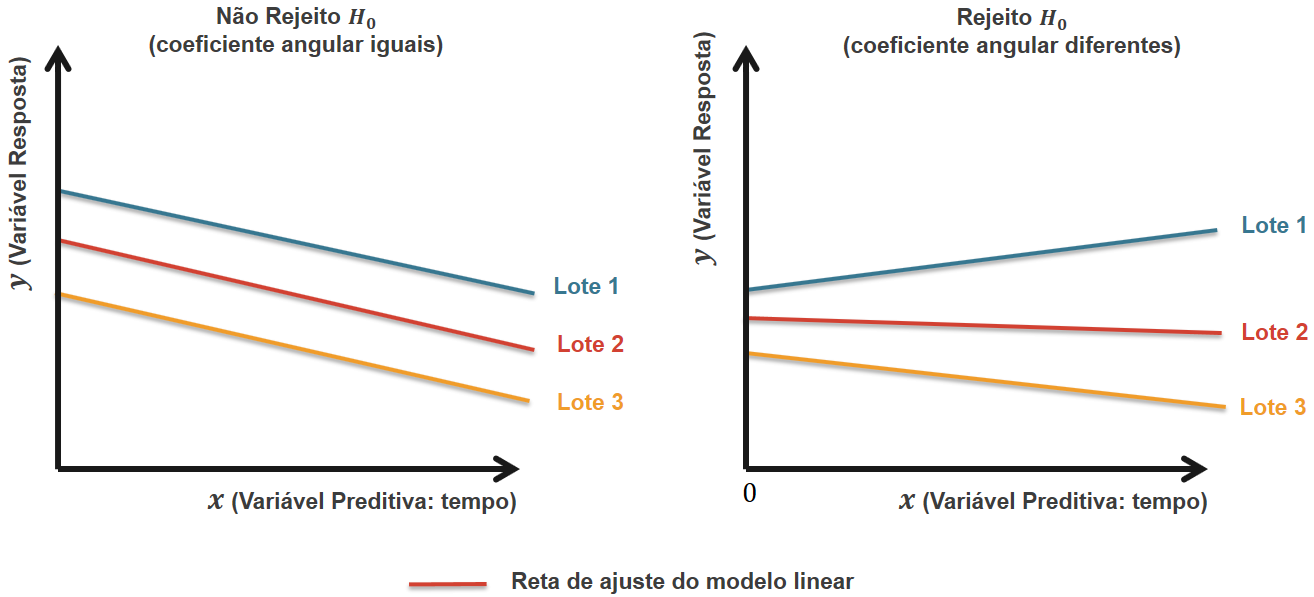parallel (Figura 1)

Imagem ilustrativa das hipoteses do teste do paralelismo

Como queremos determinar se um subconjunto de parâmetros são significan- tes ao modelo de regressão, precisamos utilizar o Teste $F$ Parcial. Para isso, consideramos a seguinte partição do vetor de parâmetros $\beta$:

$$\beta=\begin{bmatrix}\beta_{0}\cr \beta_{1}\cr \vdots\cr\beta_{2K-1}\end{bmatrix}=\begin{bmatrix}\beta_{R2}\cr\beta_{R2^c}\end{bmatrix}.$$

em que $ \beta_{R2^c} $ são os parâmetros em que temos interesse em testar e $ \beta_{R2} $ são os demais parâmetros do vetor $ \beta $:

$$\beta_{R2}=\begin{bmatrix}\beta_{0}\cr\beta_{1}\cr\vdots\cr\beta_{K}\end{bmatrix}\quad{e}\quad\beta_{R2^c}=\begin{bmatrix}\beta_{K+1}\cr\beta_{K+2}\cr\vdots\cr\beta_{2K-1}\end{bmatrix}.$$

Assim, particionamos também a matriz $ X $, de forma que a partição $ X_{R2} $ esteja associada aos vetores de $ \beta_{R2} $ e $ X_{R2^c} $ aos valores de $ \beta_{R2^c} $, como a seguir:

$$X=[X_{R2}\quad X_{R2^c}]$$

em que: $$ X_{R_2}=\left[\begin{array}{cccccccc} 1 & t_{11} & 0 & 0 & 0 & 0 & \cdots & 0 \cr 1 & t_{12} & 0 & 0 & 0 & 0 & \cdots & 0 \cr 1 & t_{13} & 0 & 0 & 0 & 0 & \cdots & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots \cr 1 & t_{1 n_1} & 0 & 0 & 0 & 0 & \cdots & 0 \cr 1 & t_{21} & 1 & 0 & 0 & 0 & \cdots & 0 \cr 1 & t_{22} & 1 & 0 & 0 & 0 & \cdots & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots \cr 1 & t_{2 n_2} & 1 & 0 & 0 & 0 & \cdots & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \cdots & \vdots \cr 1 & t_{K n_K} & 0 & 0 & 0 & 0 & \cdots & 1 \end{array}\right] \quad \text { e } \quad X_{R_2^C}=\left[\begin{array}{cclc} 0 & 0 & \cdots & 0 \cr 0 & 0 & \cdots & 0 \cr 0 & 0 & \cdots & 0 \cr \vdots & \vdots & \cdots & \vdots \cr 0 & 0 & \cdots & 0 \cr t_{21} & 0 & \cdots & 0 \cr t_{22} & 0 & \cdots & 0 \cr \vdots & \vdots & \cdots & \vdots \cr t_{2 n_2} & 0 & \cdots & 0 \cr \vdots & \vdots & \cdots & \vdots \cr 0 & 0 & \cdots & t_{K n_K} \end{array}\right]. $$

Estamos interessados apenas no quanto o subconjunto $ {\beta_{K+1},\beta_{K+2},\cdots,\beta_{2K-1}} $ influencia a regressão, ou seja, queremos testar a soma do quadrado adicional de $ \beta_{R2^c}=\begin{bmatrix}\beta_{K+1}\cr\beta_{K+2}\cr\cdots\cr\beta_{2K-1}\end{bmatrix} $ no modelo que já possui $ \beta_{R2}=\begin{bmatrix}\beta_{0}\cr\beta_{1}\cr\cdots\cr\beta_{K}\end{bmatrix}$. A soma de quadrados referente aos parâmetros da hipótese nula é dada por: $$ \begin{align*} SQR(\beta_{R2^c} \mid \beta_{R2})&= SQR(\beta_{K+1},\beta_{K+2},\cdots,\beta_{2K-1} \mid \beta_{0}, \beta_{1}, \cdots, \beta_{K})\cr &= SQR(\beta) - SQR(\beta_{0}, \beta_{1}, \cdots, \beta_{K})\cr &= SQR(\beta) - SQR(\beta_{R2}) \end{align*} $$

Para encontrar $ SQR(\beta_{R2}) $, vamos considerar o modelo sob a hipótese nula $ H_{0a} $, assumindo os valores de $ \beta_{R2^c} $ como nulos. Chamamos esse modelo de reduzido: $$Y = X_{R2}\beta_{R2} + \varepsilon$$

Calculando a soma de quadrados da regressão do modelo reduzido tem-se:

$$SQR\left(\beta_{R2}\right) = \widehat{\beta}_{R2}^\top X_{R2}^\top Y - \dfrac{Y^{\top}\mathbb{J}Y}{n}.$$

A $SQR\left(\beta_{R2^C} \mid \beta_{R2}\right) $ possui $K-1$ graus de liberdade. Desta forma, podem-se calcular a estatística do teste $F$ por:

$$F_P = \dfrac{\dfrac{SQR\left(\beta_{R2^C} \mid \beta_{R2}\right)}{K-1}}{QME} \sim F_{(K-1, n-2K)}$$ em que $F_P$ possui distribuição $F$ com $K-1$ e $n-2K$ graus de liberdade. O $p-$ valor do teste é dado por:

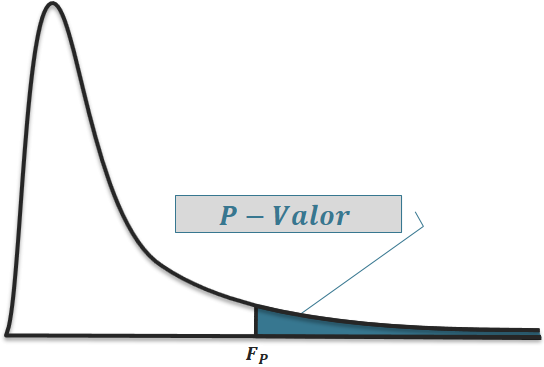
$$p-\text{valor} = \mathbb{P}\left(F_{(K-1,n-2K)} > F_P \right | H_0).$$ parallel-p

(Figura 2)

Imagem ilustrativa do p-valor para o teste de paralelismo

Adotando o nível de significância de $ \alpha = 0,25 $, se

$p-$valor $> \alpha $ não rejeitamos a hipótese nula e concluímos que os coeficientes angulares são iguais.
$p-$valor $\leq \alpha $ rejeitamos a hipótese nula e concluímos que os coeficientes angulares são diferentes.

Teste de igualdade dos interceptos

Caso ocorra a rejeição da hipótese nula no teste de paralelismo, é abordado o modelo completo na Eq. (3) e, portanto, o teste de igualdade de intercepto não é avaliado. Caso contrário, estamos interessados em testar se há ou não diferença entre os interceptos do modelo para cada lote. Se não houver diferença, os valores do subconjunto $ {\beta_2,\beta_3,\cdots,\beta_K} $ do vetor de parâmetros $ \beta $, correspondente aos interceptos, são nulos. Assim, estamos interessados em testar as hipóteses: $$ \begin{cases} H_{0b}:\beta_2=\beta_3=\cdots=\beta_K=0;\cr H_{1b}: \text{Pelo menos um é diferente}. \end{cases} $$

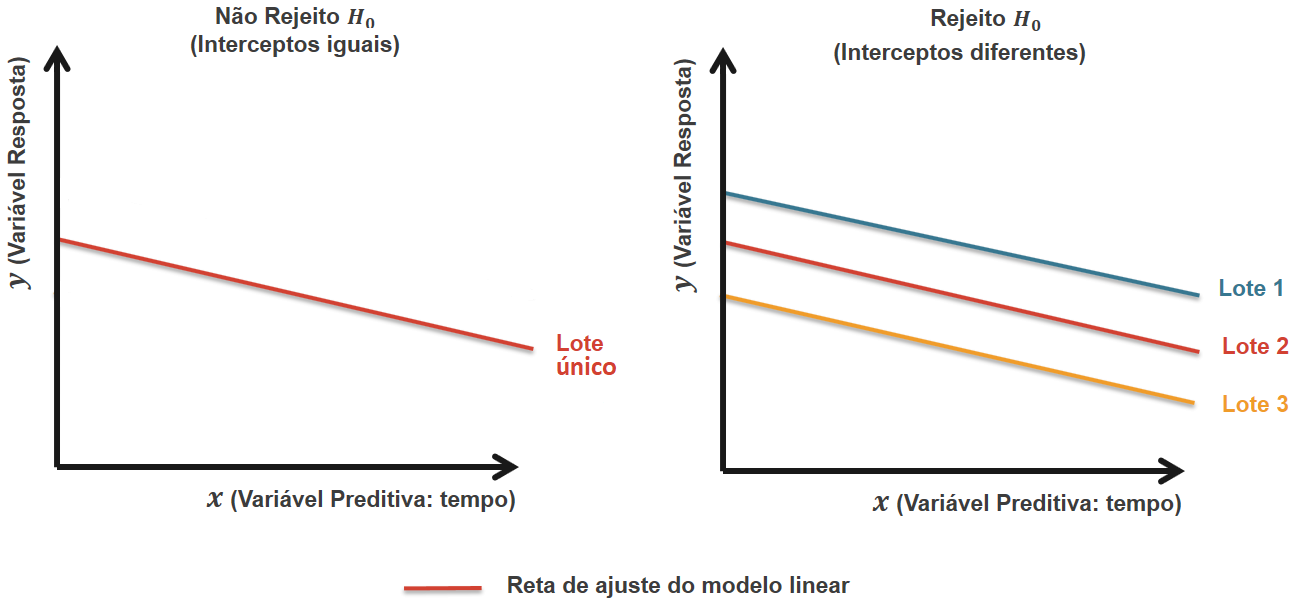
intercep

(Figura 3)

Imagem ilustrativa das hipoteses do teste de igualdade do intercepto

Na Figura 3, podemos ver um exemplo ilustrativo em que, no primeiro caso não rejeitaríamos $ H_{0b} $, pois os interceptos são iguais, e no segundo caso rejeitaríamos a hipótese nula, pois os lotes influenciam de forma significativa o intercepto de cada modelo.

Ao verificar essas hipóteses, devemos, então, utilizar o Teste $F$ Parcial como fizemos no teste do paralelismo. Consideramos a seguinte partição do vetor de parâmetros $ \beta $: $$\beta=\begin{bmatrix}\beta_{R1}\cr\beta_{R1^c}\end{bmatrix}$$ em que $ \beta_{R1^c} $ são os parâmetros em que temos interesse em testar e $ \beta_{R1} $ são os demais parâmetros do vetor $ \beta $. No caso do teste do Intercepto com $K$ lotes temos: $$\beta_{R1}=\begin{bmatrix}\beta_{0}\cr\beta_{1}\end{bmatrix} \quad \text{e} \quad \beta_{R1^c}=\begin{bmatrix}\beta_{2}\cr\beta_{3}\cr\vdots\cr\beta{K}\end{bmatrix}$$

Particionamos a matriz X de forma que a partição $ X_{R1} $ esteja relacionada ao subconjunto de $ \beta_{R1} $ e $ X_{R1^c} $ relacionada ao subconjunto de $ \beta_{R1^c}$

Assim, temos: $$X=[X_{R1}\quad X_{R1^c}]$$ em que $$ X_{R_1}=\left[\begin{array}{cc} 1 & t_{11} \cr 1 & t_{12} \cr 1 & t_{13} \cr \vdots & \vdots \cr 1 & t_{1 n_1} \cr 1 & t_{21} \cr 1 & t_{22} \cr \vdots & \vdots \cr 1 & t_{2 n_2} \cr \vdots & \vdots \cr 1 & t_{K n_K} \end{array}\right] \quad \text { e } \quad X_{R_1^C}=\left[\begin{array}{cccccc} 0 & 0 & 0 & 0 & \cdots & 0 \cr 0 & 0 & 0 & 0 & \cdots & 0 \cr 0 & 0 & 0 & 0 & \cdots & 0 \cr \vdots & \vdots & \vdots & \vdots & \cdots & \vdots \cr 0 & 0 & 0 & 0 & \cdots & 0 \cr 1 & 0 & 0 & 0 & \cdots & 0 \cr 1 & 0 & 0 & 0 & \cdots & 0 \cr \vdots & \vdots & \vdots & \vdots & \cdots & \vdots \cr 1 & 0 & 0 & 0 & \cdots & 0 \cr \vdots & \vdots & \vdots & \vdots & \cdots & \vdots \cr 0 & 0 & 0 & 0 & \cdots & 1 \end{array}\right] $$

Estamos interessados no quanto o subconjunto $\beta_2, \cdots, \beta_K$ influencia a regressão, ou seja, queremos testar a soma do quadrado adicional de $ \beta_{R1^c}=\begin{bmatrix}\beta_{2}\cr\vdots\cr\beta_{K}\end{bmatrix}$ no modelo que já possui $ \beta_{R1}=\begin{bmatrix}\beta_{0}\cr\beta_{1}\end{bmatrix} $. A soma de quadrados referente aos parâmetros da $H_{0b}$ é dada por: $$ \begin{align*} SQR(\beta_{R1^C} \mid \beta_{R1}) &= SQR(\beta_2,\cdots,\beta_K \mid \beta_0, \beta_1)\cr &= SQR(\beta_{R2}) - SQR(\beta_{R1}) \end{align*} $$

Para encontrar $ SQR(\beta_{R1}) $, vamos considerar o modelo sob a hipótese nula $ H_{0b} $, assumindo os valores de $ \beta_{R1^c} $ como nulos. Chamamos esse modelo de reduzido: $$Y = X_{R1}\beta_{R1} + \varepsilon.$$ Calculando a soma de quadrados da regressão do modelo reduzido tem-se: $$SQR\left(\beta_{R1}\right) = \widehat{\beta}_{R1}^\top X_{R1}^\top Y - \dfrac{Y^{\top}\mathbb{J}Y}{n}.$$

A $SQR(\beta_{R1^C} \mid \beta_{R1})$ possui $K-1$ graus de liberdade. Desta forma, pode-se calcular a estatística do teste $F$ por: $$F_I = \dfrac{\dfrac{SQR(\beta_{R1^C} \mid \beta_{R1})}{K-1}}{QME} \sim F_{(K-1, n-2K)}$$ em que $F_I$ possui distribuição $F$ com $K-1$ e $n-K-1$ graus de liberdade e o $p-$valor do teste dado por:

$$p-\text{valor} = \mathbb{P}\left(F_{(K-1,n-K-1)} > F_I \right | H_0)$$

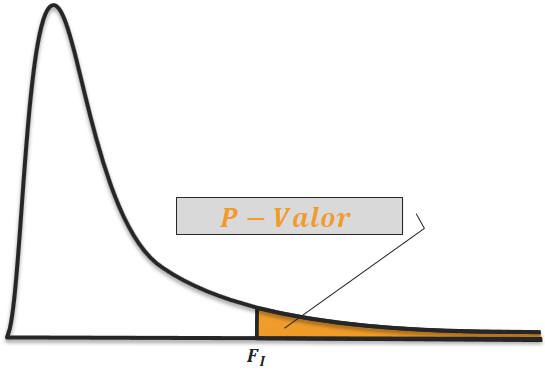
parallel-p

(Figura 4)

Imagem ilustrativa do $p-$valor para o teste de igualdade do intercepto

Adotando o nível de significância de $ \alpha = 0,25$, temos que se:

$p-$valor $> \alpha $ não rejeitamos a hipótese nula e concluímos que os interceptos são iguais para todos os lotes.
$p-$valor $\leq \alpha $ rejeitamos a hipótese nula e concluímos que os interceptos não são iguais para todos os lotes.

Tempo de prateleira

[!IMPORTANT] Tempo de prateleira é o tempo no qual o intervalo de confiança para a resposta média toca o limite de especificação. Para se determinar o tempo de prateleira, precisa-se determinar o tempo no qual o intervalo de confiança (95%) para a resposta média toca a especificação.

Tempo de prateleira é o tempo no qual o intervalo de confiança para a resposta média toca o limite de especificação. Para se determinar o tempo de prateleira, precisa-se determinar o tempo no qual o intervalo de confiança (95%) para a resposta média toca a especificação. A partir dos resultados dos testes de hipóteses do intercepto e do paralelismo, pode-se ter três possíveis cenários:

Cenário 1: Interceptos e coeficientes angulares iguais para todos os lotes (Pooling data). Nesse caso ajusta-se somente um modelo de regressão simples desconsiderando os lotes;

Cenário 2: Interceptos diferentes mas coeficientes angulares iguais para todos os lotes. Nesse cenário ajusta-se somente um modelo de regressão mas altera-se o valor do intercepto para cada lote;

Cenário 3: Coeficientes angulares diferentes para todos os lotes. Nesse cenário ajusta-se somente um modelo de regressão mas altera-se o valor do coeficiente angular para cada lote.

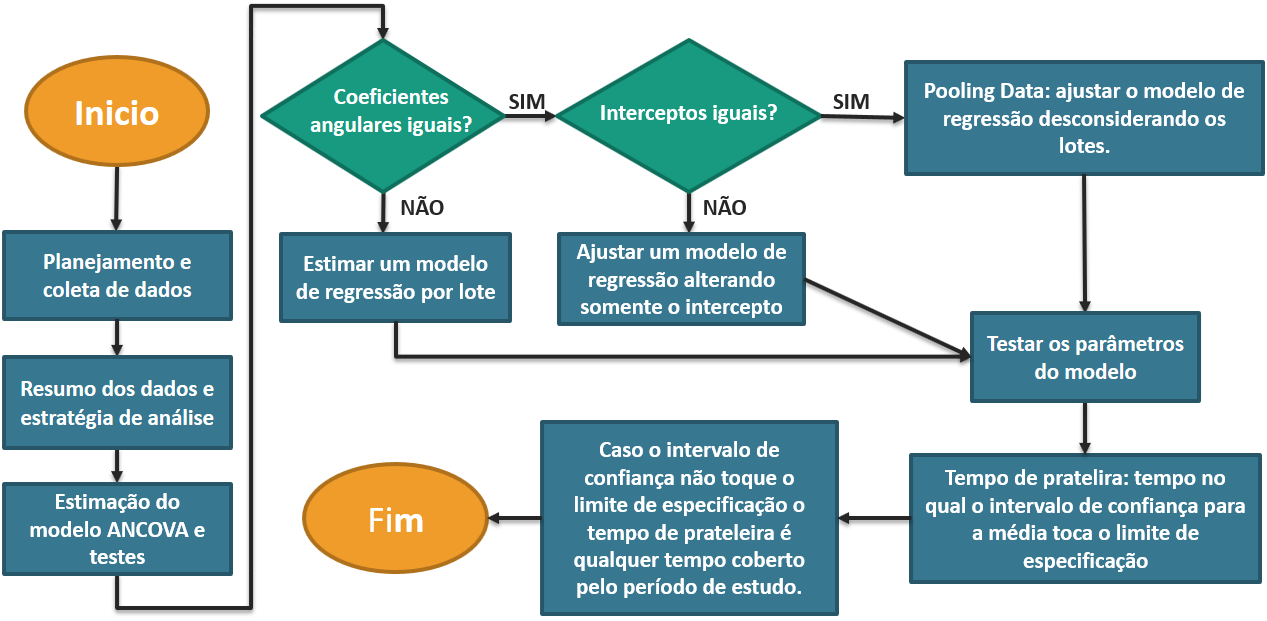fluxo-shelflife (Figura 5)

Fluxograma da análise de estabilidade e determinação do tempo de prateleira

Intervalo de confiança

Para o cálculo do intervalo de confiança, no cenário 1 tem-se apenas um modelo de regressão com os dados de todos os lotes. $$ IC\left(\mu_{Y \mid x}, 100(1-\alpha)\%\right) = \left[ \widehat{\beta}_0 + \widehat{\beta}_1 x_t \pm \widehat{\sigma}t_{(n-2)}\sqrt{\frac{1}{n}+\frac{\left(x_t - \bar{x}\right)^2}{S_{xx}}}\right] $$ em que:

$\mu_{Y|x}$: é a resposta média de $Y$ dado $x$ no tempo $t$;
$x_t$: é o tempo em que deseja-se realizar a previsão e $\bar{x}$ é a média dos tempos do modelo;
$\widehat{\beta}_0$ e $\widehat{\beta}_1$: são as estimativas dos parâmetros do modelo;
$\widehat{\sigma} = \frac{1}{n-2}\left(S_{yy} - \frac{S_{xy}^2}{S_{xx}}\right)$: é a estimativa do desvio padrão do modelo;
$S_{xx} = \sum_{i=1}^n\left(x_i - \bar{x}\right)^2; S_{yy} = \sum_{i=1}^n\left(y_i - \bar{y}\right)^2$ e $ S_{xy} = \sum_{i=1}^n\left(x_i - \bar{x}\right)\left(y_i - \bar{y}\right)$;
$t_{n-2}$: é o percentil de $\left(1-\frac{\alpha}{2}\right)%$ da distribuição t-student com $n-2$ graus de liberdade.

Nos cenários 2 e 3 é necessário utilizar a notação matricial para estimar o intervalo de confiança. Considere um vetor de valores $x_i = \left[1, x_{i1}, x_{i2}, …, x_{ip}\right]$ em que $x_i$ é o tempo para cada lote em que se deseja estimar o intervalo de confiança para o ajuste, em outras palavras, o $x_i$ é o $i$-ésimo vetor da matriz de delineamento da regressão $X$. Então,

$$IC\left(\mu_{Y|x}^i, 100(1-\alpha)\%\right) = \left[ x_i^\top \widehat{\beta} \pm t_{(n-p-1)} \widehat{\sigma} \sqrt{x_i^\top\left(X^\top X\right)^{-1}x_i}\right]$$ em que:

$\mu_{Y|x}^i$: é o tempo de resposta médio de $Y$ dado $x$ para $i$-ésima obervação;
$\widehat{\beta}$: é o vetor de estimativas dos parâmetros da regressão;
$p$: numero de covariáveis utilizadas no modelo de regressão;
$\widehat{\sigma} = \sqrt{\frac{SQE}{n-p-1}} = \sqrt{QME}$: é a estimativa do desvio padrão do modelo;
$t_{n-p-1}$: é o percentil de $\left(1-\frac{\alpha}{2}\right)%$ da distribuição t-student com $n-p-1$ graus de liberdade;
$x_i$: vetor referente a $i$-ésima linha da matriz de delineamento;
$X$: matriz de delineamento da regressão.

Determinação do tempo de prateleira

Desta forma, para o cálculo do tempo de prateleira, o FDA indica o seguinte procedimento Figura 5:

Precisa-se, inicialmente, de um conjunto de informações respeitando os requisitos básicos mencionados acima. Nesse conjunto de dados precisa-se sempre utilizar o nível de concentração (Teor) do produto farmacêutico em medida de porcentagem;
Elabora-se o modelo ANCOVA para testar a homogeneidade entre os lotes, isto é, se realiza os testes de comparação de curvas;
Ajusta-se o modelo indicado dependendo do resultado obtido no teste de comparação de curvas, tem-se as três possíveis situações:
- Um único modelo todos os lotes (caso em que não foi detectado diferença significativa ao nível de significância de 0,25 entre os lotes);
- Um modelo por lote, alterando somente o valor do intercepto (situação em que apenas o teste de igualdade de intercepto é significativo ao nível de 0,25);
- Modelos diferentes para cada lote (cenário em que o teste do paralelismo é rejeitado ao nível de significância de 0,25);
Fixam-se os limites de aceitação para o produto farmacêutico em estudo, usualmente o limite inferior é fixado em 90% e o superior em 110%. Nesse passo decide-se também qual dos limites será necessário utilizar: somente inferior, superior ou ambos. Essa decisão é tomada pelo analista e depende do produto farmacêutico em estudo;
Utilizando o modelo ajustado, realiza-se uma previsão com intervalo de confiança de 95% (esse valor pode ser alterado dependendo do estudo) para os próximos meses em que se deseja verificar a validade do produto;
Para os meses definidos no item anterior, verifica-se se o intervalo de confiança estimado ultrapassa os limites de aceitação fixados. O mês anterior ao qual o limite de aceitação for ultrapassado pelo intervalo de confiança é o Tempo de Prateleira para o modelo/lote em questão;
Repete-se os passos 5 e 6 para todos os modelos ajustados (caso haja mais de um modelo), o Tempo de Prateleira do produto farmacêutico será o menor tempo encontrado dentre todos os modelos estudados.

Em alguns estudos, têm-se casos em que o intervalo de confiança estimado não ultrapassa os limites de detecção fixados, nesses casos se diz que não foi possível encontrar o tempo de expedição para o período de avaliado no estudo.

Limites de liberação

Os limites de liberação serão verificados através do cálculo de IRL. O IRL (Internal Release Limits) é uma faixa de especificação calculada com base nas variações de processo (produção e análise) e nas alterações sofridas pelo produto ao longo do estudo de estabilidade de longa duração. Comparando o IRL com os resultados obtidos e com as especificações de liberação atuais, é possível verificar se os produtos atendem as especificações por toda sua vida útil.

Nos cálculos são levados em consideração os limites de especificação, a degradação do produto ao longo do tempo determinado pelo estudo de estabilidade de longa duração (tendência) e a variação esperada decorrente do processo e das análises (banda de confiança). No cálculo dos limites de liberação têm-se três possíveis cenários:

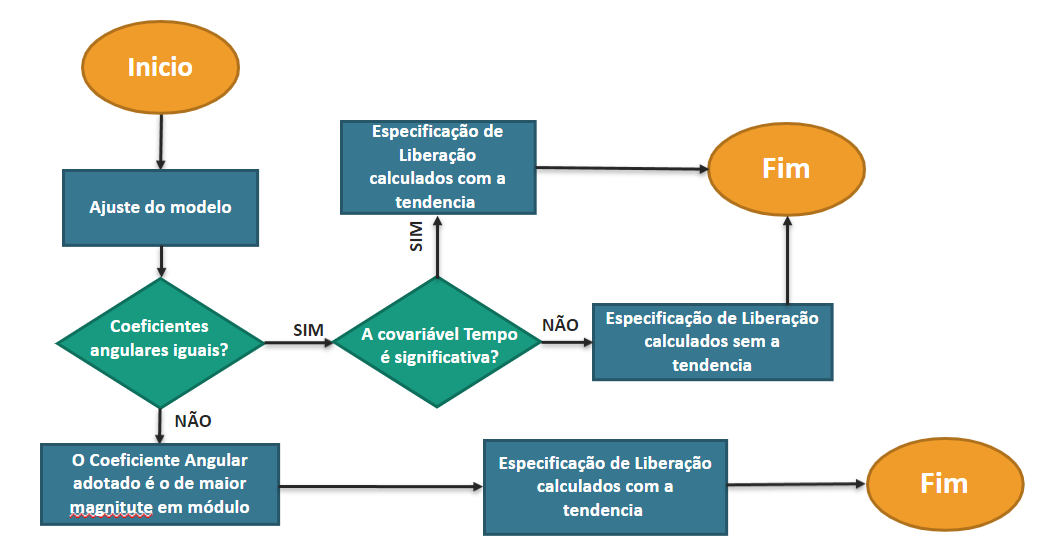
fluxo-IRL

(Figura 7)

Fluxograma do cálculo dos limites de liberação

Interação Significativa

A Tendência será calculada com base no coeficiente angular com maior magnitude em módulo. Seja $(\beta_1 + \beta_{K+1}, \beta_1 + \beta_{K+2}, …, \beta_1 + \beta_{2K-1})$ os coeficientes angulares para os diferentes lotes. Considere $$\beta_M = \max{|\beta_1 + \beta_{K+1}|, |\beta_1 + \beta_{K+2}|, …, |\beta_1 + \beta_{2k-1}|},$$ $t$ o tempo de prateleira obtido e $BC$ a banda de confiança no ponto $x_t$.

Então os limites de liberação são calculados por $$ LSL = \begin{cases} LSE - \beta_M \cdot t - BC, \qquad \text{se $\beta_M > 0$};\cr LSE - BC, \qquad \qquad \qquad \text{se $\beta_M \leq 0$}. \end{cases} $$

$$ \begin{equation*} LIL = \begin{cases} LIE + \beta_M \cdot t + BC, \qquad \text{se $\beta_M < 0$};\cr LIE + BC, \qquad \qquad \qquad \text{se $\beta_M \geq 0$}.\end{cases} \end{equation*} $$ em que:

$BC = t_{(1-\alpha/2, n-p-1)} \hat{\sigma} \sqrt{x_t^\top (X^\top X)^{-1}x_t}$: representa a metade da amplitude do intervalo de confiança, $X$ a matriz de delineamento do modelo;
$t$: tempo de prateleira obtido;
$x_t$: vetor da matrix $X$ no tempo $t$ e para o lote com maior coeficiente angular em módulo.

Interação Não Significativa e Tempo Significativo

Neste caso os lotes não apresentam interação com o tempo, ou seja, tem-se um único coeficiente angular. Se a covariável tempo for significativa o cálculo dos limites de liberação deve levar em consideração o coeficiente angular associado ao tempo $\beta_{1}$, o tempo de prateleira obtido $t$ e a banda de confiança $BC$ associado ao tempo $t$. $$ \begin{equation*} LSL = \begin{cases} LSE - \beta_1 \cdot t - BC, \qquad \text{se $\beta_1 > 0$};\cr LSE - BC, \qquad \qquad \qquad \text{se $\beta_1 \leq 0$}.\end{cases} \end{equation*} $$

$$ \begin{equation*} LIL = \begin{cases} LIE + \beta_1 \cdot t + BC, \qquad \text{se $\beta_1 < 0$};\cr LIE + BC, \qquad \qquad \qquad \text{se $\beta_1 \geq 0$}.\end{cases} \end{equation*} $$ em que:

$BC = t_{(1-\alpha/2, n-p-1)} \hat{\sigma} \sqrt{x_t^\top (X^\top X)^{-1}x_t}$: representa a metade da amplitude do intervalo de confiança, $X$ a matriz de delineamento do modelo;
$t$: tempo de prateleira obtido;
$x_t$: Para o cenário 2, representa o vetor da matrix $X$ no tempo $t$ e para o primeiro lote que mais possui dados. Caso seja o cenário 1, tem-se somente $x_t = [1, t]^\top$.

Interação Não Significativa e Tempo Não Significativo

Quando o tempo não for significativo, o limite de liberação será calculado sem a Tendência.

$$LSL = LSE - BC$$

$$LIL = LIE + BC$$

em que:

$BC = t_{(1-\alpha/2, n-p-1)} \hat{\sigma} \sqrt{x_t^\top (X^\top X)^{-1}x_t}$: representa a metade da amplitude do intervalo de confiança, $X$ a matriz de delineamento do modelo;
$x_t$: Para o cenário 2, representa o vetor da matriz $X$ no tempo $t$ e para o primeiro lote que mais possui dados. Caso seja o cenário 1, tem-se somente $x_t = [1, t]^\top$. $t$ é o tempo de prateleira obtido.

Legenda:

$LSL$: Limite superior de liberação
$LIL$: Limite inferior de liberação
$LSE$: Limite superior de especificação
$LIE$: Limite inferior de especificação

Quando se tem somente um limite de especificação, o limite de liberação a ser apresentado será o correspondente. A única diferença nos cálculos apresentados acima é que o quantil da distribuição t-student será com relação a $\alpha$ e não mais $\frac{\alpha}{2}$.

O fluxograma na Figura 7 ilustra as passagens para os cálculos das especificações de liberação descritas acima.

Fora de Tendência

Conforme preconizado na RDC 318, os resultados fora de tendência (ou seja, aqueles resultados que, durante a análise de tendência não foram coerentes com o comportamento observado) devem ter as causas para o desvio apresentadas. O motivo dessa requisição é a necessidade de avaliar o modelo como um todo e evitar distorções relacionadas a erros diversos, que podem comprometer a análise estatística. Para demonstrar que determinado resultado está fora da tendência, recomenda-se um teste estatístico adequado para apontar outliers.

Os outliers ou pontos influentes são identificados na Análise dos Resíduos do modelo. Os resíduos que são definidos como $ e_i=Y_i-\widehat{Y}_i $, que corresponde a diferença entre o valor observado e o valor ajustado pelo modelo. Entretanto, para uma melhor detecção de outliers em $Y$, diversas formas ``padronizadas'' foram propostas. No caso do estudo de estabilidade, vamos utilizar os resíduos padronizados.

Existem inúmeras maneiras de se expressar o vetor de resíduos $e$ que nos será útil. $$e=Y-\widehat{Y}=Y-X\widehat{\beta}=Y - \mathbb{H}Y=(I-\mathbb{H})Y.$$

A matriz de covariâncias dos resíduos é,

$$Cov[e]=Cov[(I-\mathbb{H})Y]=(I-\mathbb{H})Var(Y)(I-\mathbb{H})^\top$$ $$=\sigma^2(I-\mathbb{H})(I-\mathbb{H})^\top=\sigma^2(I-\mathbb{H}),$$

no qual $ \mathbb{H}=X(X^\top X)^{-1} X^\top $ é a matriz chapéu Hat e $ X $ a matriz do modelo.

Assim, definimos os resíduos padronizados por

$$r_{i}=\frac{e_i}{\sqrt{QME(1-h_{ii})}},~i=1,2,\ldots,n,$$

com $ \hat{\sigma}^2=QME $ e $ h_{ii} $ o $ i $-ésimo elemento da matriz chapéu $\mathbb{H}$.

Os resíduos padronizados tem variâncias constantes $ Var(r_i)=1 $ o que consequentemente torna muito prática a procura por outliers, que são observações distantes das demais. Em geral, as observações com resíduo padronizado fora do intervalo $ -3\leq r_i \leq 3 $ deve são considerados outliers ou pontos influentes.

Uma melhor maneira de visualizar o comportamento dos resíduos do modelo é através de uma análise gráfica. Após calculado os resíduos padronizados, construímos um gráfico em que os valores dos resíduos são apresentados de acordo com os valores ajustados.

Exemplo 1 - Iguais coeficientes angulares e iguais interceptos

Considere um experimento em estudo na Tabela 1, no qual foi medida a degradação de uma droga para 3 lotes.

Tabela 1: Dados de degradação de uma droga com o passar do tempo para diferentes lotes
Lote 1		Lote 2		Lote 3
Tempo	Medições	Tempo	Medições	Tempo	Medições
0	97,6827	0	102,0645	0	102,6337
3	104,4361	3	95,6986	3	102,2354
6	101,4657	6	95,0475	6	107,4803
9	101,2829	9	100,6914	9	99,3431
12	101,4556	12	96,7143	12	101,1194
18	96,7930	18	101,9347	18	100,1674
24	98,4863	24	101,3223	24	97,2033
36	104,8448			36	102,3533

Então, para a estimação do modelo ANCOVA, temos a seguinte matriz $X$: $$ \begin{align*} X=& \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 \cr 1 & 3 & 0 & 0 & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr 1 & 36 & 0 & 0 & 0 & 0 \cr 1 & 0 & 1 & 0 & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr 1 & 24 & 1 & 0 & 24 & 0 \cr 1 & 0 & 0 & 1 & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr 1 & 36 & 0 & 1 & 0 & 36 \cr \end{bmatrix};~ Y=\begin{bmatrix} 97,6827 \cr 104,4361 \cr \vdots \cr 104,8448 \cr 102,0645\cr \vdots\cr 101,3223\cr 102,6337\cr \vdots\cr 102,3533 \end{bmatrix}.\cr &\text{\scriptsize ~~(1) \quad (2) \quad (3) \quad (4) \quad (5) \quad (6) } \end{align*} $$

A interpretação fica da seguinte forma

(1) Intercepto,

(2) Tempo,

(3) Lote 2,

(4) Lote 3,

(5) Interação entre Tempo e o Lote 2,

(6) Interação entre Tempo e o Lote 3.

Pela Eq. (2), a estimativa dos parâmetros do modelo completo é dada por: $$ \widehat{\beta}=\begin{bmatrix} 100,2107\cr 0,0441\cr -2,5291\cr 2,5551\cr 0,0907\cr -0,1329 \end{bmatrix}, $$ e a equação do modelo completo $$ Y = 100,2107 + 0,0441 \cdot\text{Tempo} -2,5291 \cdot\text{Lote2} + 2,5551 \cdot\text{Lote3} + 0,0907 \cdot\text{Tempo} \cdot\text{Lote2} -0,1329 \cdot\text{Tempo} \cdot\text{Lote3}. $$

Assim, tem-se a equação para cada lote:

Lote 1: $Y = 100,2107 + 0,0441 \cdot \text{Tempo}$;
Lote 2: $Y = (100,2107 -2,5291) + (0,0441 + 0,0907) \cdot \text{Tempo};$
Lote 3: $Y = (100,2107 + 2,5551) + (0,0441 -0,1329) \cdot \text{Tempo}$.

E as somas dos quadrados: $$SQT = Y^\top Y - \dfrac{Y^\top \mathbb{J} Y}{n} = 207,2812,$$

$$SQE=Y^\top Y - \widehat{\beta}^\top X^\top Y=165,3966,$$

$$SQR = SQT - SQE = 41,8846,$$

$$\widehat{\sigma}^2=QME=\dfrac{SQE}{n-2K}=\dfrac{165,3966}{23-6}=9,7292.$$

Para aplicar o teste de paralelismo, temos os seguintes hipósteses: $$ \begin{cases} H_{0}:\beta_{2}=\beta_{5}=0;\cr \text{Pelo menos um é diferente}. \end{cases} $$

Particionamos o vetor: $$\beta_{R2}=\begin{bmatrix}\beta_{0}\cr\beta_{1}\cr\beta_{2}\cr\beta_{3}\end{bmatrix}\quad{e}\quad\beta_{R2^c}=\begin{bmatrix}\beta_{4}\cr\beta_{5}\end{bmatrix} $$

A estimativa do parâmetro $ \beta_{R2} $ no modelo reduzida fica: $$ \widehat{\beta}_{R2} = \left( X_{R2}^{\top} X \right)^{-1} X_{R2}^{\top} Y = \begin{bmatrix} 100,7353\cr 0,0052\cr -1,7215\cr 0,7611 \end{bmatrix}. $$

Calculando a soma de quadrados da regressão do modelo reduzido tem-se:

$$SQR\left(\beta_{R2}\right) = \widehat{\beta}_{R2}^\top X_{R2}^\top Y - \dfrac{Y^{\top}\mathbb{J}Y}{n} = 24,2455$$

Então, a soma de quadrados referente aos parâmetros da hipótese nula é dada por:

$$SQR\left(\beta_{R2^c}|\beta_{R2}\right) = SQR\left(\beta\right) - SQR\left(\beta_{R2}\right) = 41,8846 - 24,2455 = 17,6391$$

Desta forma, pode-se calcular a estatística do teste $F$ por:

$$F_P = \dfrac{\dfrac{SQR\left(\beta_{R2^c} \mid \beta_{R2}\right)}{K-1}}{QME} = \dfrac{\dfrac{17,6391}{2}}{9,7292} = 0,9065$$ e o $p$-valor do teste por: $$p-\text{valor} = \mathbb{P}\left(F_{(2, 17)} > 0,9065\right) = 0,4226.$$

Como o $p-$valor é maior que 0,25, concluímos que o coeficientes angulares são iguais para os lotes.

No teste de paralelismo não se tem evidência para rejeitar a hipótese nula ao nível de significância de 0,25 e, portanto, conclui-se que um mesmo coeficiente angular pode ser ajustado para todos os lotes. Desse modo ajusta-se o modelo com $\beta_{R2}$ descrito na Eq. (4): $$Y = 100,7353 + 0,0052 \cdot \text{Tempo} -1,7215 \cdot \text{Lote2} + 0,7611 \cdot \text{Lote3} $$

Assim, tem-se a equação para cada lote:

Lote 1: $Y = 100,7353 + 0,0052 \cdot\text{Tempo}$;
Lote 2: $Y = (100,7353 -1,7215) + 0,0052 \cdot \text{Tempo}$;
Lote 3: $Y = (100,7353 + 0,7611) + 0,0052 \cdot \text{Tempo}$.

A soma dos quadrados dos resíduos fica: $$SQE=SQT - SQR(\beta_{R2}) =207,2812 - 24,2455 = 183,0357$$ e a estimativa da variabilidade é dada por

$$\widehat{\sigma}^2=QME=\dfrac{SQE}{n-K-1}=\frac{183,0357}{23-3-1}=9,6335.$$

Para realizar o teste de igualdade do intercepto utiliza-se o Teste $F$ parcial, com as hipóteses: $$ \begin{cases} H_{0}:\beta_2=\beta_3=0;\cr \text{Pelo menos um é diferente}. \end{cases} $$ O subconjunto de parâmetros de interesse é dado por: $$\beta_{R1}=\begin{bmatrix}\beta_{0}\cr\beta_{1}\end{bmatrix}\quad\text{e }\beta_{R1^c}=\begin{bmatrix}\beta_{2}\cr\beta_{3}\end{bmatrix}.$$

A estimativa do parâmetro $ \beta_{R1} $ fica: $$\widehat{\beta}_{R1}=\left(X_{R1}^{\top}X_{R1}\right)^{-1}X_{R1}^{\top}Y =\begin{bmatrix}100,3110\cr0,0184\end{bmatrix} $$

Para o Teste $F$ parcial, calcula-se primeiro a soma dos quadrados da regressão do modelo reduzido: $$SQR\left(\beta_{R1}\right) = \widehat{\beta}_{R1}^\top X_{R1}^\top Y - \dfrac{Y^{\top}\mathbb{J}Y}{n} = 0,846$$

A soma dos quadrados referente aos parâmetros da hipótese nula: $$SQR\left(\beta_{R1^c}|\beta_{R1}\right) = SQR\left(\beta_{R2}\right) - SQR\left(\beta_{R1}\right) = 24,2455 - 0,846 = 23,4$$

Assim a estatística do teste $F$ parcial calculada:

$$F_I = \dfrac{\dfrac{SQR\left(\beta_{R2^C} \mid \beta_{R1}\right)}{K-1}}{QME} = \dfrac{\dfrac{23,4}{2}}{9,6335} = 1,2145$$

A estatística $F_I$ tem distribuição $F$ com $2$ e $19$ graus de liberdade, o p-valor é dado por:

$$p-\text{valor} = \mathbb{P}\left(F_{(2,19)} > 1,2145\right) = 0,3189$$

Como $p-\text{valor} = 0,3189 > 0,25$ não rejeita-se a hipótese nula e conclui-se a favor da hipótese de igualdade de interceptos. Prossegue-se com um modelo de regressão linear simples para todo o conjunto de dados. Portanto, o modelo é dado por:

$$Y = 100,311 + 0,0184 \cdot \text{Tempo}.$$

O exemplo tem o limite inferior de aceitação fixado em 90% e o limite superior em 110%. Desejamos realizar previsões da resposta média para, nesse caso, os próximos 36 meses com um intervalo de confiança de 95%.

No caso do cenário 1, tem-se um mesmo intercepto para todos lote e apenas um coeficiente angular para o modelo, então o intervalo de confiança é dado por: $$IC\left(\mu_{Y|x}, 100(1-\alpha)\%\right) = \left[ \widehat{\beta}_0 + \widehat{\beta}_1 x_t \pm \widehat{\sigma}t_{(n-2)}\sqrt{\frac{1}{n}+\frac{\left(x_t - \bar{x}\right)^2}{S_{xx}}}\right].$$

Para o exemplo calcula-se os limites do intervalo de confiança do tempo (mês) $ x_t = 36$: $$ \widehat{\beta}_0= 100,311 \text{ e } \widehat{\beta}_1 = 0,0184$$

$$SQE=SQT - SQR(\beta_{R1}) = 207,2812 - 0,846 = 206,435$$ $$\widehat{\sigma} = \sqrt{\widehat{\sigma}^2} =\sqrt{QME} = \sqrt{\dfrac{SQE}{23-2}} = \sqrt{\dfrac{206,435}{21}} = \sqrt{9,8302} = 3,1353$$

$$t_{(1-\alpha/2; 23-2)} = t_{(0,975; 21)} = 2,0796$$

$$\sqrt{\frac{1}{n}+\frac{\left(x_t - \bar{x}\right)^2}{S_{xx}}} = \sqrt{\frac{1}{23}+\frac{\left(36 - 12,5217\right)^2}{2495,739}} = 0,5141.$$

Finalmente, $$IC_{Inf}({y_{36}},95\%)= 100,311 + 0,0184 \cdot 36 - 3,1353\cdot2,0796\cdot0,5141 = 97,6214$$ $$IC_{Sup}({y_{36}},95\%)= 100,311 + 0,0184 \cdot 36 + 3,1353\cdot2,0796\cdot0,5141= 104,3262$$

Tem-se que $ IC_{Inf}({y_{36}},95\%) = 97,6214 > 90 $ e $ IC_{Sup}({y_{36}},95\%) = 104,3262 < 110 $, portanto ainda não encontra-se a data de expiração por um período de 36 meses. Desse modo, com Action Stat, obtem-se o gráfico de análise de tendência apresentada na Figura 6.

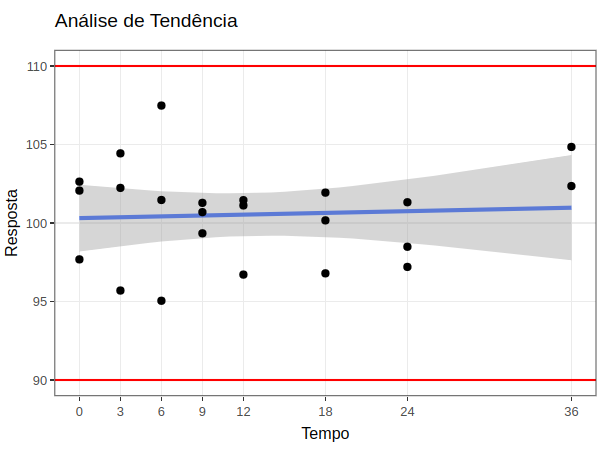
ex1-scatter

(Figura 6)

Análise de tendência para o estudo de estabilidade

Tem-se as seguintes constantes para os cálculos dos limites de liberação:

$$\text{prazo de validade } t=36 \text{ e, portanto, } x_t = [1, 36]^\top$$ $$BC = t_{(1-\alpha/2, n-2)} \hat{\sigma} \sqrt{x_t^\top (X^\top X)^{-1}x_t} = 3,3524$$

Como a covariável tempo não foi significativa para o exemplo, tem-se que os limites de liberação são dados por

$$ LSL = LSE - BC = 110 - 3,3524 = 106,648$$

$$ LIL = LIE + BC =90 + 3,3524 = 93,352.$$

Com o exemplo 1, calculamos os resíduos e contruímos os gráficos utilizando o apoio computacional do Action Stat.

A linha pontilhada verde representa o intervalo (-3,3) na Figura 8. Como temos nenhum resíduo fora dos intervalos, não identificamos pontos extremos ou outliers para esse caso.

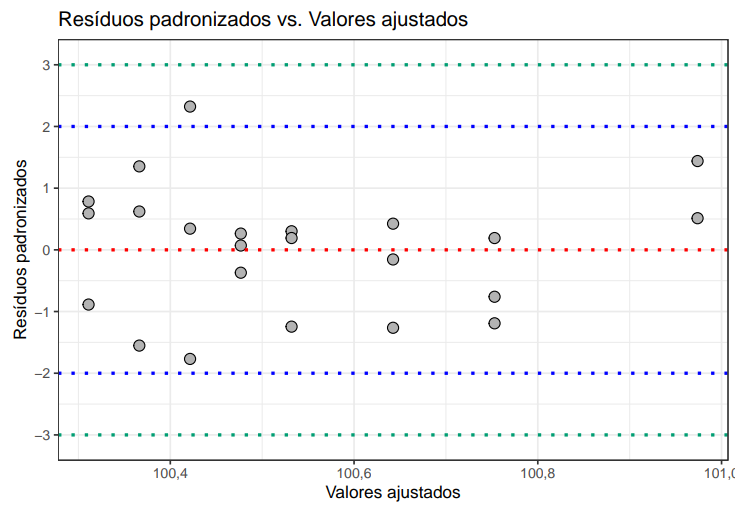
ex1-oot

(Figura 8)

Análise dos resíduos (Padronizados)

Exemplo 2 - Diferentes interceptos e mesmo coeficiente angular

Considere um experimento na Tabela 2, no qual foi medida a degradação de uma droga para 5 lotes (BV, AJ, AN66, AV634, BZ8331). Para cada lote, medi-se a concentração em diferentes níveis de tempo. O objetivo é avaliar a estabilidade da concentração de uma droga, e avaliar a similaridade entre as curvas de degradação e calcular o tempo de prateleira.

Tabela 2: Dados de degradação de uma droga com o passar do tempo para diferentes lotes
Tempo (meses)	BV	AJ	AN66	AV634	BZ8331
0	104,7	101,04	99,32	103,52	102,16
3		106,42	101,92	106,34	98,66
6		105,04	99,78	104,26	102,62
9		105,2	98,88	104,08	100,16
12	104,54	104,74	99,6	102,44	98,54
18		102,02	99,66	102,38
24	105,54	101,56	98,26	104,18
36		104,32	99,24

Inicialmente, é necessário estimar o modelo ANCOVA completo, tal que: $$Y = X\beta + \varepsilon$$

Se considerar o lote AJ como lote de referência, a matriz $X$ é da seguinte forma: $$ \begin{align*} X=& \begin{bmatrix} 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr 1 & 24 & 0 & 0 & 1 & 0 & 0 & 0 & 24 & 0 \cr 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr 1 & 36 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \cr 1 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr 1 & 36 & 1 & 0 & 0 & 0 & 36 & 0 & 0 & 0 \cr 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr 1 & 24 & 0 & 1 & 0 & 0 & 0 & 24 & 0 & 0 \cr 1 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \cr \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \cr 1 & 12 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 12 \cr \end{bmatrix};~ Y=\begin{bmatrix} 104,7 \cr \vdots \cr 105,54 \cr 101,04\cr \vdots \cr 104,32\cr 99,32\cr \vdots\cr 99,24 \cr 103,52\cr \vdots \cr 104,18\cr 102,16\cr \vdots \cr 98,54 \end{bmatrix}\cr &\text{\scriptsize ~~(1) \quad(2) \quad(3) ~~(4) ~~~(5) ~~(6) \quad(7) \quad(8) \quad(9) \quad(10) } \end{align*} $$ (1) Intercepto,

(2) Tempo,

(3) Lote AN66,

(4) Lote AV634,

(5) Lote BV,

(6) Lote BZ8331,

(7) Interação entre Tempo e o Lote AN66,

(8) Interação entre Tempo e o Lote AV634,

(9) Interação entre Tempo e o Lote BV,

(10) Interação entre Tempo e o Lote BZ8331.

Dessa forma, tem-se por objetivo estimar o vetor de parâmetros $\beta$ e encontrar o modelo ANCOVA por:

$$\widehat{\beta} = \left(X^\top X\right)^{-1}X^\top Y = \begin{bmatrix} \widehat{\beta}_0; \widehat{\beta}_1; \widehat{\beta}_2; \widehat{\beta}_3; \widehat{\beta}_4; \widehat{\beta}_5; \widehat{\beta}_6; \widehat{\beta}_7; \widehat{\beta}_8; \widehat{\beta}_9 \end{bmatrix}^\top$$

Sabe-se que a soma de quadrados do erro $(SQE)$ satisfaz:

$$\dfrac{SQE}{\sigma^2}\sim\chi^{2}_{n-2K}.$$

Portanto, um estimador não viciado para $\sigma^2$ é dado por:

$$\widehat{\sigma}^2=QME=\dfrac{SQE}{n-2K}.$$

Efetuando os cálculos, encontra-se a estimativa das somas de quadrados:

$$SQT=Y^\top Y - \dfrac{Y^\top \mathbb{J} Y}{n}=193,8994$$ $$SQE=Y^\top\left(\mathbb{I} - \mathbb{H}\right)Y=53,592$$

e a estimativa da variabilidade é dada por:

$$\widehat{\sigma}^2=QME=\dfrac{SQE}{n-2K}=\frac{53,592}{31-10}=2,552.$$

Na sequência, analisa-se o teste de paralelismo. No teste de paralelismo, também utiliza-se o Teste $F$ parcial, com as hipóteses:

$$ \begin{cases} H_0: \beta_6 = \beta_7 = \beta_8 = \beta_9 = 0 \cr H_1: \text{pelo menos um é diferente}\end{cases} $$

Calculando a soma de quadrados da regressão do modelo reduzido tem-se:

$$SQR\left(\beta_{R2}\right) = \widehat{\beta}_{R2}^\top X_{R2}^\top Y - \dfrac{Y^{\top}\mathbb{J}Y}{n} = 136,321.$$

Então, a soma de quadrados referente aos parâmetros da hipótese nula é dada por:

$$SQR\left(\beta_{R2^C} \mid \beta_{R2}\right) = SQR\left(\beta\right) - SQR\left(\beta_{R2}\right) = 140,307 - 136,321 = 3,985.$$

Desta forma, pode-se calcular a estatística do teste F por:

$$F_P = \dfrac{\dfrac{SQR\left(\beta_{R2^C} \mid \beta_{R2}\right)}{K-1}}{QME} = \dfrac{\dfrac{3,985}{4}}{2,552} = 0,3903.$$

Em que $F_P$ possui distribuição $F$ com $K-1$ e $n-2K$ graus de liberdade. Calcula-se o p-valor do teste por:

$$p-\text{valor} = \mathbb{P}\left(F_{(4, 21)} > 0,3903\right) = 0,81$$

No teste de paralelismo não tem-se evidências para rejeitar a hipótese nula ao nível de significância de 0,25 e, desse modo, conclui-se que um mesmo coeficiente angular pode ser ajustado para todos os lotes.

Desse modo, agora, ajusta-se o seguinte modelo:

$$Y = \beta_0 + \beta_1\cdot Tempo+\beta_2\cdot LoteAN66+\beta_3\cdot LoteAV634+\beta_4\cdot LoteBV+\beta_5\cdot LoteBZ8331+\epsilon$$

e dele obtém-se:

$$SQE=Y^\top\left(\mathbb{I} - \mathbb{H}\right)Y=57,578$$

e a estimativa da variabilidade é dada por:

$$\widehat{\sigma}^2=QME=\dfrac{SQE}{n-K-1}=\frac{53,592}{31-5-1}=2,303.$$

E, por meio do teste $F$ parcial, avalia-se a hipótese de igualdade de interceptos.

$$ \begin{cases} H_0: \beta_2 = \beta_3 = \beta_4 = \beta_5 = 0 \cr H_1: \text{pelo menos um é diferente} \end{cases} $$

Para o Teste $F$ parcial, calcula-se primeiro a soma dos quadrados da regressão do modelo reduzido:

$$SQR\left(\beta_{R1}\right) = \widehat{\beta}_{R1}^\top X_{R1}^\top Y - \dfrac{Y^{\top}\mathbb{J}Y}{n} = 2,0220.$$

E a soma dos quadrados referente aos parâmetros da hipótese nula:

$$SQR\left(\beta_{R1^C} \mid \beta_{R1}\right) = SQR\left(\beta\right) - SQR\left(\beta_{R1}\right) = 136,3220 - 2,022 = 134,3.$$

Assim a estatística do teste $F$ parcial calculada é:

$$F = \dfrac{\dfrac{SQR\left(\beta_{R1^C} \mid \beta_{R1}\right)}{K-1}}{QME} = \dfrac{\dfrac{134,3}{4}}{2,303} = 14,5788.$$

A estatística $F$ tem distribuição $F$ com $4$ e $25$ graus de liberdade, o p-valor é dado por:

$$p-\text{valor} = \mathbb{P}\left(F_{(4,25)} > 14,5788\right) \approx 0,00.$$

Como o $p-$valor do teste de igualdade de interceptos é inferior ao nível de significância de $25%$, tem-se a rejeição da hipótese nula.

O próximo passo é estimar o modelo de regressão para o estudo. Observe que o teste de paralelismo identificou que $\beta_6=\beta_7=\beta_8=\beta_9=0$, isto é equivalente a um modelo sem interação entre os lotes e o tempo. Portanto, ajustando o modelo sem interação entre tempo e lote, encontra-se as seguintes estimativas: $$ \widehat{\beta}=\left[104,27;-0,0357; -4,21;-0,0216;1,08;-3,632\right]^\top$$

Desta forma, pode-se separar o modelo por lote, note que a base para o cálculo do Intercepto é utilizando o Lote AJ.

\begin{align*} \text{Lote AJ:}~ Y &= 104,27 -0,0357\cdot Tempo \cr \text{Lote AN66:}~ Y &= (104,27 - 4,21) -0,0357\cdot Tempo \cr \text{Lote AV634:}~ Y &= (104,27 -0,0216) - 0,0357\cdot Tempo\cr \text{Lote BV:}~ Y &= (104,27 + 1,08) -0,0357\cdot Tempo \cr \text{Lote BV:}~ Y &=(104,27 -3,632)-0,0357\cdot Tempo \end{align*}

Observe que existe apenas um modelo geral para o estudo, nesses modelos separados por lote ocorre apenas a atribuição de valores às covariáveis (0 ou 1) dependendo do lote de interesse.

$$SQE = SQT-SQR\left(\beta_{R2}\right) =193,8994 -136,321 = 57,578.$$

Utilizando o Action Stat tem-se os seguintes resultados:

ANOVA sequencial

Modelo com interação

	G.L.	Soma de Quadrados	Quadrado Médio	Estat. F	P-valor
Tempo	1	2,02	2,00	0,79	0,38
Lote	4	134,30	33,57	13,16	0,00
Tempo:Lote	4	3,99	1,00	0,39	0,81
Resíduos	21	53,59	2,55

Modelo sem interação

	G.L.	Soma de Quadrados	Quadrado Médio	Estat. F	P-valor
Tempo	1	2,02	2,02	0,88	0,36
Lote	4	134,30	33,57	14,58	0,00
Resíduos	25	57,58	2,30

Modelo de regressão

	Estimativa	Desvio Padrão	Estat.t	P-valor
Intercepto	104,27	0,66	157,82	0,00
Tempo	-0,04	0,03	-1,25	0,22
LoteAN66	-4,21	0,76	-5,55	0,00
LoteAV634	-0,02	0,79	-0,03	0,98
LoteBV	1,08	1,03	1,05	0,30
LoteBZ8331	-3,63	0,89	-4,08	0,00

Em seguida, fixa-se o limite inferior de aceitação em 90% e o limite superior em 110%. É necessário realizar previsões da resposta média por lote para os próximos 24 meses com um intervalo de confiança de 95%. Esse caso trata-se do cenário 2, tem-se um intercepto para cada lote e apenas um coeficiente angular para o modelo, então o intervalo de confiança é dado por: $$IC\left(\mu_{Y|x}^i, 100(1-\alpha)\%\right) = \left[ x_i^\top \widehat{\beta} \pm t_{(n-p-1)} \widehat{\sigma} \sqrt{x_i^\top\left(X^\top X\right)^{-1}x_i} \text{ } \right].$$

Para o exemplo calcula-se os limites do intervalo de confiança do tempo (mês) $t = 24 $ e o lote $ BV $, para o cálculo tem-se os seguinte valores:

$$ x_{24}=\left[1,24,0,0,1,0\right]^\top $$

$$ \hat{\beta}=\left[104,27;-0,0357; -4,21;-0,0216;1,08;-3,632\right]^\top $$

Então, $$ \widehat{y_{24}} = x_{24}^{\top} \widehat{\beta} = 104,4980$$ $$\widehat{\sigma} = \sqrt{\widehat{\sigma^2}} =\sqrt{QME} = \sqrt{\dfrac{SQE}{31-4-2}} = \sqrt{\dfrac{57,578}{25}} = 1,518$$

$$t_{(1-\alpha/2; 31-4-2)} = t_{(0,975; 25)} = 2,0595$$

$$\sqrt{x_{24}^\top(X^\top X)^{-1}x_{24}} = 0,6199$$

Finalmente,

$$IC_{Inf}({y_{24}},95\%)= 104,4980 - 1,518 \cdot 2,0595 \cdot 0,6199 = 102,56$$

$$IC_{Sup}({y_{24}},95\%)= 104,4980 + 1,518 \cdot 2,0595 \cdot 0,6199 = 106,44$$

Tem-se que $ IC_{Inf}({y_{24}},95%) = 102,56 > 90 $ e $ IC_{Sup}({y_{24}},95\%) = 106,44 < 110 $, portanto ainda não encontra-se a data de expiração.

Continuando os cálculos para todos os lotes para todos os 24 meses com o Action Stat, ressalta-se que em 24 meses não foi identificado um limite inferior de degradação abaixo de 90% ou um limite superior acima de 110% . Nessa situação, se diz que o produto suporta um prazo de validade de 24 meses.

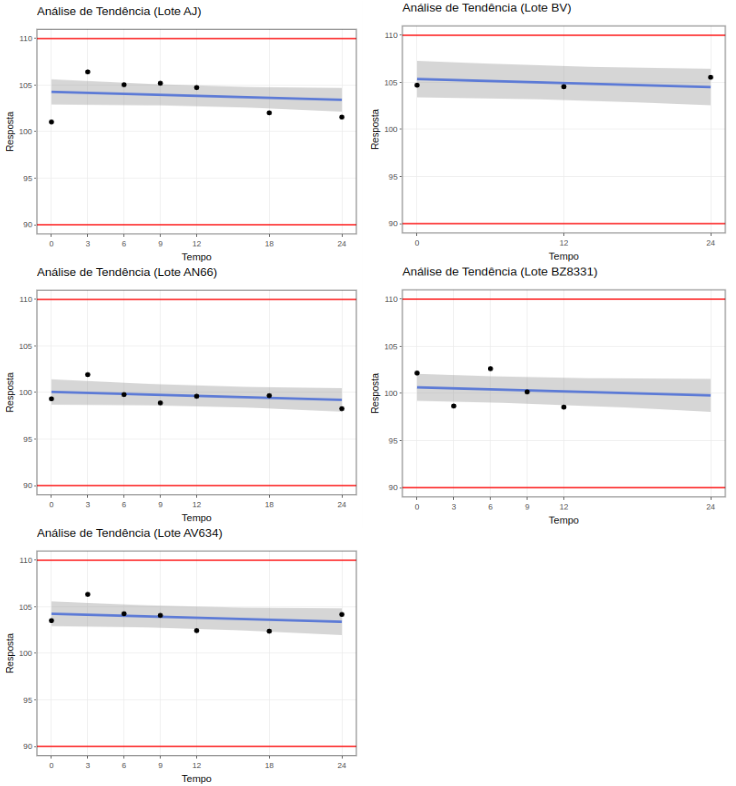
ex2-scatter

(Figura 9)

Análise de tendência

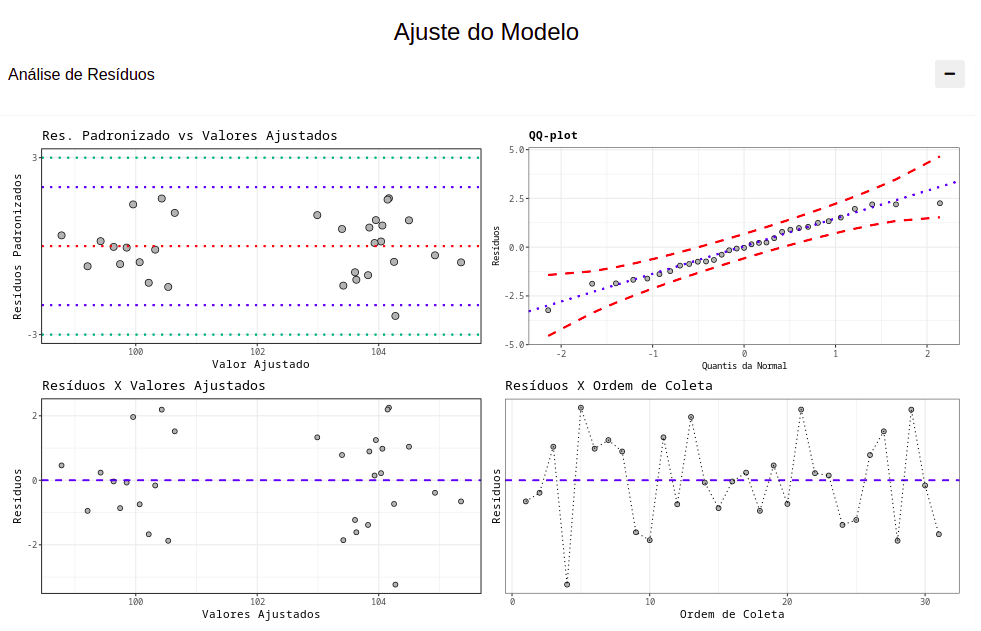
ex2-4em1

(Figura 10)

Análise de resíduos

Para esta aplicação, tem-se as seguintes constantes para os cálculos dos limites de liberação: $$t = 24 \text{ e, portanto, } x_t = [1, 24, 0, 0, 0, 0]^T$$

$$BC = t_{(1-\alpha/2, n-p-1)} \hat{\sigma} \sqrt{x_t^T (X^TX)^{-1}x_t} = 1,2659$$

Como o tempo não foi significativo para o estudo, tem-se que os limites de liberação são dados por

$$ LSL = LSE - BC = 110 - 1,27 = 108,73$$ $$ LIL = LIE + BC =90 + 1,27 = 91,27.$$

Exemplo 3 - Diferentes coeficientes angulares

Apresenta-se uma exemplificação para quando rejeita-se a hipótese de igualdade de coeficientes angulares. Considere-se para essa exemplificação dos dados na Tabela 3:

Tabela 3: Dados de degradação de uma droga com o passar do tempo para diferentes lotes
Tempo	A	B	C
0	101,615842	104,3506	104,647
3	99,29220985	103,4975	106,3846
6	99,0759734	97,5835	100,0886
9	100,0949979	101,4073	101,1726
12	100,421851	99,0102	101,7178
18	99,10443276	98,744	103,8475
24	101,0260878	96,2554	106,0826
36	100,0835435	—	101,5334

Estima-se o vetor de parâmetros $\beta$ e encontra-se o modelo ANCOVA por:

Sabe-se que a soma de quadrados do erro $(SQE)$ satisfaz:

$$\dfrac{SQE}{\sigma^2}\sim\chi^{2}_{n-2K}.$$

Portanto, um estimador não viciado para $\sigma^2$ é dado por:

$$\widehat{\sigma}^2=QME=\dfrac{SQE}{n-2K}.$$

Efetuando os cálculos, encontra-se a estimativa das somas de quadrados: $$SQT=Y^\top Y - \dfrac{Y^\top \mathbb{J} Y}{n}=150,6342$$ $$SQE=Y^\top\left(\mathbb{I} - \mathbb{H}\right)Y=64,5769$$ e a estimativa da variabilidade é dada por

$$\widehat{\sigma}^2=QME=\dfrac{SQE}{n-2K}=\frac{64,5769}{23-6}=3,7986.$$

Na sequência analisa-se as hipóteses de paralelismo. Por meio do teste $F$ parcial avalia-se as seguintes hipóteses:

$$ \begin{cases} H_0: \beta_4 = \beta_5 = 0 \cr H_1: \text{pelo menos um é diferente}\end{cases} $$

Calculando a soma de quadrados da regressão do modelo reduzido tem-se:

$$SQR\left(\beta_{R2}\right) = \widehat{\beta}_{R2}^\top X_{R2}^\top Y - \dfrac{Y^{\top}\mathbb{J}Y}{n} =58,3261$$

Então, a soma de quadrados referente aos parâmetros da hipótese nula é dada por:

$$SQR\left(\beta_{R2^C} \mid \beta_{R2}\right) = SQR\left(\beta\right) - SQR\left(\beta_{R2}\right) = 86,0573 - 58,3261 = 27,7312$$

Desta forma, pode-se calcular a estatística do teste F por:

$$F_P = \dfrac{\dfrac{SQR\left(\beta_{R2^C} \mid \beta_{R2}\right) }{K-1}}{QME} = \dfrac{\dfrac{27,7312}{2}}{3,7986} = 3,6502$$

Em que $F_P$ possui distribuição $F$ com $K-1$ e $n-2K$ graus de liberdade. Calcula-se o p-valor do teste por:

$$p-valor = \mathbb{P}\left(F_{(2, 17)} > 3,6502)\right) = 0,0480$$

No teste de Paralelismo tem-se evidência para rejeitar a hipótese nula ao nível de significância de 0,25 e concluí-se que deve-se ajustar diferentes coeficientes angulares para os lotes.

Desse modo, como houve a rejeição da hipótese nula do teste de paralelismo, ajusta-se um modelo contendo o tempo, o fator lote e a interação entre eles. Encontra-se as seguintes estimativas: $$ \widehat{\beta}=\left[ 100,0879 ; 0,0001 ; 3,0136 ; 3,3992 ; -0,2899 ; -0,0225 \right]^\top $$

Desta forma, pode-se separar o modelo por lote, note que a base para o cálculo do Intercepto é utilizando o lote A.

Lote A: $Y = 100,08787 + 0,00011 \cdot \text{Tempo} $
Lote B: $Y = (100,08787 + 3,01357) + (0,00011 + 0,28963) \cdot \text{Tempo} $
Lote C: $Y =(100,08787 + 3,39918) + (0,00011 - 0,02232) \cdot \text{Tempo}$

Observe que tem-se apenas um modelo geral para o estudo, nesses modelos separados por lote ocorre apenas a atribuição de valores (0 ou 1) às covariáveis dependendo do lote de interesse. Utilizando o Action Stat tem-se os seguintes resultados:

ANCOVA

	G.L.	Soma de Quadrados	Quadrado Médio	Estat. F	P-valor
Tempo	1	6,0817	6,0815	1,6010	0,2228
Lote	2	52,2446	26,1223	6,8768	0,0065
Lote:Tempo	2	27,7312	13,8656	3,6502	0,0480
Resíduos	17	64,5769	3,7986

Modelo de regressão

	Estimativa	Desvio Padrão	Estat.t	P-valor
Intercepto	100,0879	1,0778	92,8637	0,0000
Tempo	0,0001	0,0614	0,0018	0,9966
LoteB	3,0136	1,6249	1,8547	0,0811
LoteC	3,3992	1,5242	2,2301	0,0395
LoteB:Tempo	-0,2899	0,1123	-2,5808	0,0194
LoteC:Tempo	-0,0225	0,0868	-0,2596	0,7983

$$IC\left(\mu^i_{Y|x}, 100(1-\alpha)\%\right) = \left[ x_i^\top \widehat{\beta} \pm t_{(n-p-1)} \widehat{\sigma} \sqrt{x_i^\top\left(X^\top X\right)^{-1}x_i}\right].$$

Para o exemplo, será calculado os limites do intervalo de confiança do tempo (mês) $ t_i = 24 $ e o lote A, para o cálculo tem-se os seguinte valores:

$$ x_{24}=\left[1,24,0,0,0,0\right]^\top $$ $$\widehat{\beta}=\left[ 100,0879; 0,0001; 3,0136; 3,3992; -0,2899 ; 0,0225 \right]^\top $$

Então, $$\widehat{y_{24}} = x_{24}^{\top}\widehat{\beta} = 100,0905$$ $$\widehat{\sigma} = \sqrt{\widehat{\sigma^2}} =\sqrt{QME} = \sqrt{\dfrac{SQE}{23-5-1}} = \sqrt{\dfrac{64,5769}{17}} = 1,9490$$ $$t_{(1-\alpha/2; 23-5-1)} = t_{(0,975; 17)} = 2,1098$$ $$\sqrt{x_{24}^\top (X^\top X)^{-1}x_{24}} = 0,4841$$

Finalmente, $$IC_{Inf}({y_{24}},95\%)= 100,0905 - 2,1098 \cdot 1,9490 \cdot 0,4841 = 98,04977$$ $$IC_{Sup}({y_{24}},95\%)= 100,0905 + 2,1098 \cdot 1,9490 \cdot 0,4841 = 102,13126$$

Tem-se que $ IC_{Inf}({y_{24}},95\%) = 98,04977 > 90 $ e $ IC_{Sup}({y_{24}},95\%) = 102,13126 < 110 $, portanto ainda não encontra-se a data de expiração para o lote A.

Continuando os cálculos para todos os lotes para todos os 24 meses com o Action Stat, observa-se que em 24 meses não foi identificado um limite inferior de degradação abaixo de 90% ou um limite superior acima de 110% . Nessa situação, se diz que o produto suporta um prazo de validade de 24 meses.

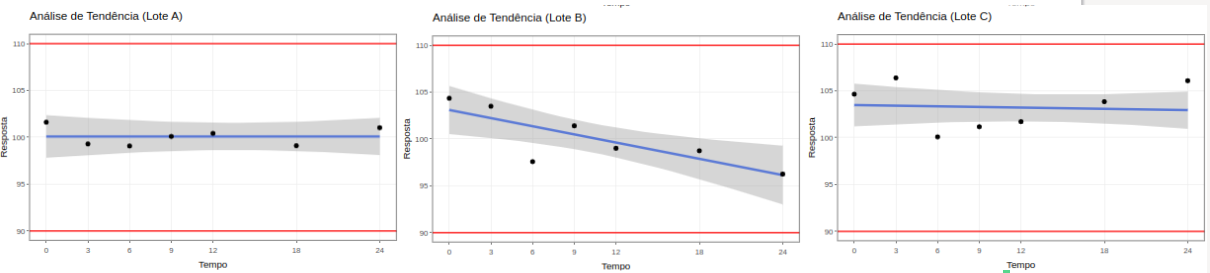
ex3-scatter

(Figura 11)

Análise de tendência

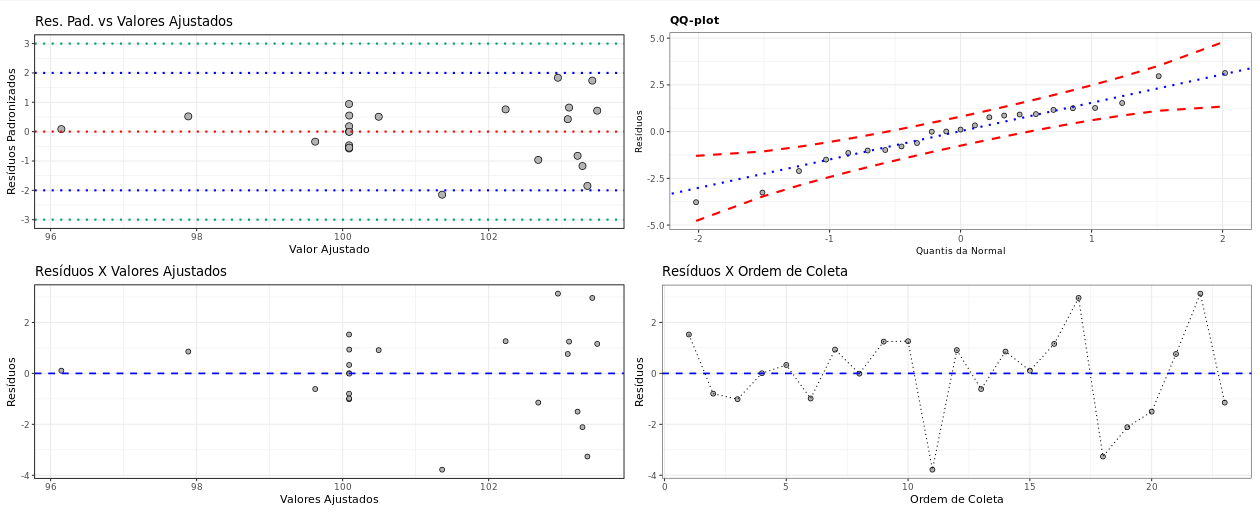
ex3-4em1

(Figura 12)

Análise de resíduos

Para esta aplicação, o prazo de prateleira foi 24 meses e o lote 2 possui o maior magnitude de inclinação $\beta_M=-0,2899$. Desse modo, tem-se o cálculo dos limites de liberação. $$t = 24 \text{ e, portanto, } x_t = [1, 24, 1, 0, 24, 0]^\top $$

$$BC = t_{(1-\alpha/2, n-p-1)} \widehat{\sigma} \sqrt{x_t^\top (X^\top X)^{-1}x_t} = 3,2126$$

Como, para esse caso, tem-se que a interação entre o tempo e o lote foi significativa os limites de liberação são: $$ \begin{align*} LSL &= \begin{cases} LSE - \beta_M \cdot t - BC, \qquad \text{se $\beta_M > 0$};\cr LSE - BC, ~~\qquad \quad \qquad \text{se $\beta_M \leq 0$}.\end{cases} \cr \Rightarrow LSL &= 110 - (-0,28974) \cdot 24 - 3,2126 = 93,2126\cr LIL &= \begin{cases} LIE + \beta_M \cdot t + BC, \qquad \text{se $\beta_M < 0$};\cr LIE + BC, ~~\qquad \quad \qquad \text{se $\beta_M \geq 0$}.\end{cases}\cr \Rightarrow LIL &= 90 + 3,2126 = 100,7896. \end{align*} $$

August 26, 2025: new changes (42d3c89a)