17. Finanças

No mercado financeiro, um mercado que ganha cada vez mais destaque é o mercado de derivativos. É no mercado de derivativos que são negociados contratos que tem por objetivo a proteção do agente econômico contra o risco de flutuação do mercado.

Relacionado a negociação dos derivativos, duas questões surgem naturalmente

• Qual o preço justo do derivativo?
• O que fazer com o dinheiro recebido da venda do derivativo?

No livro de finanças, vamos estudar diferentes modelos para responder tais questões, mas primeiro vamos apresentar os tipos de mercado e os principais contratos negociados no mercado de derivativos.

1 - Mercado Financeiro

O mercado financeiro é o mercado onde os recursos excedentes da economia (poupança) são direcionados para o financiamento de empresas e de novos projetos. No mercado financeiro tradicional, o dinheiro depositado no banco é utilizado pelas instituições financeiras para financiar alguns setores da economia. Por essa intermediação os bancos cobram do tomador do empréstimo uma taxa (spread) para cobrir os custos de transação e o risco envolvido no empréstimo.

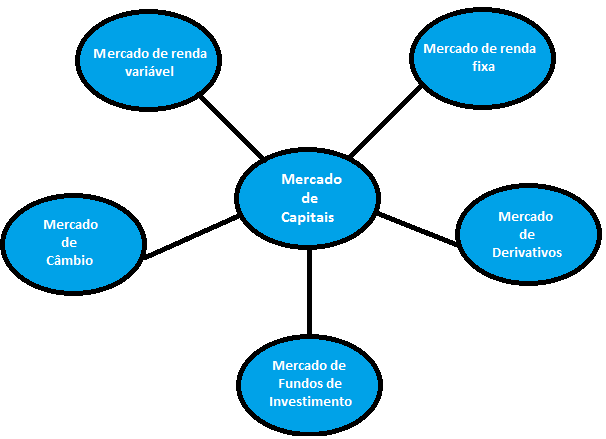
O mercado de capitais faz parte do mercado financeiro. No mercado de capitais, os recursos dos poupadores são destinados a promoção do desenvolvimento econômico de forma direta, isto é, de projetos e empresas. É no mercado de capitais que empresas que precisam de recursos conseguem financiamento por meio de emissão de títulos, vendidos diretamente aos poupadores e investidores, sem intermediação bancária.

O repasse dos recursos dos poupadores e investidores às empresas podem ser feito de duas formas:

• Dívidas: Os investidores compram títulos emitidos pelas empresas que precisam de dinheiro. Estes títulos dão aos investidores o direito de receber a quantia emprestada mais juros. Os títulos são chamados de títulos de dívida e o mercado é conhecido como mercado de renda fixa.
• Ações: Os investidores compram títulos emitidos pelas empresas que precisam de dinheiro. Os títulos não garantem remuneração fixa aos investidores. A remuneração dos títulos são os dividendos, parte do lucro que uma empresa de capital aberto possui.

O mercado de capitais é fundamental para o crescimento de um país, pois sem ele muitos projetos não conseguiriam sair do papel por falta de financiamento. Muitas empresas perderiam a competitividade e dificilmente conseguiriam desenvolver-se.

A colocação inicial dos títulos no mercado é chamado de lançamento no mercado primário. A negociação desses títulos após a oferta inicial é feita em mercados secundários específicos. No Brasil temos:

• A bolsa de valores para as ações.
• A Cetip (Central de Custódia e de Liquidação Financeira de Títulos Privados) para os títulos de dívida das empresas.
• O Selic (Sistema Especial de Liquidação e Custódia) para títulos públicos.

O Mercado de Capitais no Brasil pode ser esquematizado da seguinte forma:

Mercado de renda variável

No mercado de renda variável são negociados Ações. Uma ação é a menor parcela do capital de uma empresa. É um título que não garante remuneração predeterminada aos investidores. A remuneração da ação, é determinada pela capacidade da empresa em gerar lucros. Aquele que compra uma ação de uma determinada empresa, se torna sócio da mesma.

Há dois tipos básicos de ações:

• Ordinárias: confere ao detentor o direito de voto nas assembleias, mas os dividendos da empresa pode não ser prioritário para este tipo de ação.
• Preferenciais: o acionista não participa das decisões estratégicas da empresa, por outro lado tem prioridade no recebimento de dividendos.

O preço da ação está intimamente relacionado com a oferta e a procura da mesma. Quando a perspectiva de lucro da empresa é boa, a procura pela ação aumenta, existindo uma relação de causa no aumento do preço da ação. Quando a perspectiva de lucro da empresa é baixo, a procura pela ação cai, o que causa uma diminuição no preço da ação.

No Brasil a Bolsa de Valores que negocia ações é a Bovespa.

Mercado de renda fixa

O mercado de renda fixa tem como característica a negociação de títulos de dívidas, que permitem o recebimento da quantia emprestada mais juros previamente determinado. Os títulos de renda fixa garantem rendimentos predeterminados como, por exemplo, taxa de juros pré-fixada ou pós-fixada.

Investir em títulos de renda fixa é uma forma de investimento seguro. A explicação para este fato é que os títulos de renda fixa são atrelados a taxa de juros e taxas de juros são normalmente menos voláteis do que ações.

Os títulos são chamados de privados quando emitidos por instituições privadas e público quando emitido pelo governo municipal, estadual ou federal. Os títulos públicos federais são negociados entre bancos e instituições financeiras por meio do Selic. Já os títulos privados são negociados e liquidados por meio do Cetip.

Mercado de Câmbio

O mercado de câmbio é o ambiente onde se realiza as operações de câmbio (negociação de moeda estrangeira) entre os agentes autorizados pelo Banco Central e entre estes e seus clientes. Os compradores e vendedores são normalmente exportadores, importadores, turistas e investidores.

O órgão regulador deste mercado é o BACEN. É ele que autoriza quem pode negociar moedas estrangeiras.

Um conceito de fundamental importância neste mercado é a taxa de câmbio. A taxa de câmbio é expressa em unidades de uma moeda com relação a unidade de outra moeda.

Se a quantidade de unidades de determinada moeda necessárias para se adquirir uma outra moeda aumentar, diz-se que essa moeda se desvalorizou ou se depreciou em relação à outra; caso essa quantidade se reduza, diz-se que a moeda apreciou ou valorizou em relação à outra.

A variação da taxa de câmbio pode ser influenciada por fatores domésticos, como a posição das reservas cambiais, a situação do balanço de pagamentos, a condução da política econômica etc. Fatores externos também podem interferir na taxa de câmbio, como a evolução das taxas de juro internacionais (comparativamente às taxas de juros domésticas), pois podem determinar o fluxo de moeda dos investidores.

Mercado de Fundos de Investimento

Um fundo de investimento, é uma forma de aplicação financeira, formada pela união de vários investidores para realização de um investimento financeiro. É constituído tal qual um condomínio, onde os investidores visam um determinado objetivo ou um retorno esperado em comum.

A administração e a gestão do fundo são realizadas por especialistas contratados. Os administradores tratam dos aspectos jurídicos e legais do fundo, os gestores da estratégia de montagem da carteira de ativos do fundo, visando o maior lucro possível com o menor nível de risco.

Os fundos de investimento conferem ao investidor melhores condições de remuneração no mercado, devido à administração profissional, e por lidarem com um volume de recursos extremamente expressivo. É uma alternativa para investidores obterem rentabilidade de ativos de renda fixa e ações sem necessariamente conhecer o mercado.

Fundos também diluem o risco de grandes perdas, uma vez que a carteira pode ser composta por diversos ativos.

2 - Derivativos

Definição 2.1

Derivativos são instrumentos financeiros cujo valor depende (ou deriva) do valor de outras variáveis. Os derivativos podem depender de “quase qualquer coisa” por exemplo, do preço de suínos ou quantidade de neve que cai em uma estação de esqui.

Ativos: Bens ou direitos possuídos por uma empresa ou fundo de investimento. Para fundos de investimento, representa todos os títulos (títulos públicos, títulos privados, ações, commodities) que compõe a carteira.

Neste capítulo, vamos apresentar os principais exemplos de derivativos.

Forward contract

O forward contract é um tipo de derivativo. É um acordo de compra ou venda de um ativo em um tempo futuro (pré-especificado) por um determinado preço (pré-especificado).

O forward contract é negociado no mercado de balcão, geralmente este contrato é realizado entre duas instituições financeiras ou entre uma instituição financeira e um cliente. Ao ser realizado um forward contract, uma das partes assume a long position, ou seja, concorda em comprar os ativos em uma certa data por um certo preço. A outra parte assume a short position, ou seja, concorda em vender os ativos por um certo preço em uma certa data.

Exemplo 2.1

Definição 2.2

Denominamos de payoff ao lucro (ou compensação) de um derivativo.

Para forward contract o payoff é a diferença entre o valor combinado e o real valor do ativo na data de entrega.

O payoff de um long forward contract para uma unidade do ativo é

$$S_T - K$$

onde

$ S_T $: é o strike price (ou preço de exercício) é o preço do ativo na maturidade

$ K $ : é o preço combinado no contrato

Abaixo apresentamos o gráfico do payoff de um long forward contract

(imagem em falta)

Considerando o exemplo anterior, se a taxa de câmbio em 22/12/2010 for $ (reais) 1,750 $, o valor do payoff do forward contract será de

$$(reais) 2.800,00 (= (reais)175.000,00 - (reais)172.200,00).$$

O payoff de um short forward contract é

$$K-S_T$$

Abaixo apresentamos o gráfico do payoff de um short forward contract

(imagem em falta)

Future contract

Future contract é outro tipo de derivativo, mas este é negociado apenas na Bolsa de Valores. Se assemelha muito ao forward contract, uma das diferenças é que o future contract é padronizado, ou seja, é especificado a quantidade de ativo negociado por contrato, o período de entrega, o strike price e a quantidade máxima que um especulador pode ter do ativo. O objetivo da padronização é garantir uma maior liquidez do contrato.

No future contract uma das partes assume uma long future position (comprador) e a outra assume uma short future position (vendedor).

O payoff de um future contract é o mesmo payoff do forward contract.

Exemplo 2.2

Um produtor de café situado em Ribeirão Preto está interessado em vender $ 1000 $ sacas de café daqui a três meses. Já um fabricante situado em Recife, vai precisar comprar 1000 sacas de café daqui a três meses. Ambos procuram corretores na bolsa de valores e firmam um contrato futuro. Cada contrato futuro de café negocia 100 sacas, assim ambos terão de firmarem 10 contratos. Suponha que o preço de exercício seja $ (reais) 340,00 $.

O produtor de café assume uma short future position no contrato enquanto o fabricante assume um long future position.

Suponha que no dia de exercício do contrato o café esteja cotado em $ (reais) 335,00 $. O payoff do produtor é

$$10\times ~ ( (reais) 34 000,00 - (reais) 33 500,00 ) = (reais) 5 000,00 $$

Opções

Opções também são exemplos de derivativos. Opções são negociadas nas Bolsas de valores e em instituições financeiras. Uma opção fornece ao comprador um direito. Se é um direito e não uma obrigação, o comprador pode escolher em não exercer o direito e permitir a expiração da opção. O comprador deve pagar pela compra da opção.

Há dois tipos de opções: a call option (direito de comprar) e a put option (direito de vender).

O preço especificado no contrato é denominado preço de exercício ou Strike Price e a data especificada no contrato é denominada data de expiração ou maturidade.

A Call option dá ao comprador o direito de comprar um ativo a um preço pré-fixado (Strike price ou K) durante o período de vigência do contrato.

Suponha que a opção seja exercida no tempo $ t\in (0,T] $,

• Se $ S_t> K $, o comprador ganha a diferença $ S_t-K $;
• Se $ S_t< K $, o comprador não exerce a opção.

Assim, a função payoff de uma call option é:

$$\max (0 ,S_t-K)$$

Abaixo apresentamos o gráfico do payoff de opção de compra

A put option dá ao comprador o direito de vender o ativo especificado por um preço pré-fixado durante o período de vigência do contrato. O comprador paga um preço por esse direito. Suponha que a opção seja exercida no tempo $ t\in (0,T] $,

• Se $ S_t< K $, o comprador ganha a diferença $ K-S_t $;
• Se $ S_t> K $, o comprador não exerce a opção.

Assim, a função payoff de uma opção de venda é

$$\max(0,K-S_t).$$

Abaixo apresentamos o gráfico do payoff de uma long put option

Temos diversos tipos de opções existentes. As duas mais utilizadas são

• American Option: pode ser exercida a qualquer momento anterior a data de expiração;
• European Option: pode ser exercida somente na data de expiração;

Temos 4 tipos de participantes no mercado de opções:

• Comprador de uma call option;
• Vendedor de uma call option;
• Comprador de uma put option;
• Vendedor de uma put option;

Exemplo 2.3

Considere uma situação onde o investidor compra uma “European call option” com “Strike price” de $ (reais) 60 $ para comprar 100 ações da Microsoft. Suponha que o valor atual é de $ (reais) 58 $, que a data de expiração é de quatro meses e o preço de opção de compra é $ (reais) 5 $. O investimento inicial é de $ (reais) 500 $. Como temos uma opção Europeia, o comprador só pode exercer na data de expiração. Se o preço da ação na data de expiração, for menor que $ (reais) 60 $, o investidor não exercerá seu direito. Neste caso o investidor perde seu investimento inicial. Se o preço da ação estiver acima de $ (reais) 60 $ na data de expiração, o investidor exerce seu direito e compra a ação. Suponha que a ação vale $ (reais) 75 $ na data de expiração. Ao exercer a opção o investidor compra 100 ações por $ (reais) 60 $ e imediatamente as vende por $ (reais) 75 $.

2.1 - Especificação de um contrato

Em contratos realizados fora da Bolsa (ex. forward contract), são os participantes que decidem quais condições devem ser satisfeitas na negociação. Já nos contratos futuros e opções certas especificações são impostas no contrato pelo Bolsa de valores, por exemplo:

• Ativo
• Tamanho do contrato
• Local de entrega
• Dividendos
• Posição limite
• Variação mínima de apregoação

O objetivo destas especificações são o de facilitar a liquidez do contrato

Ativo

A bolsa de valores especifica qual o tipo de ativo está sendo negociado no contrato, ação, treasury bond, commoditie, entre outros.

Quando o ativo é um commoditie pode haver uma variação na qualidade do ativo, que é avaliada no mercado. Assim quando o ativo é especificado é importante que a Bolsa estipule os graus de aceitação da commoditie.

Exemplo 2.1.1

Em um contrato futuro de soja em grão tipo exportação a BM&F especifica que os limites máximos de aceitação do ativo-objeto é no máximo 14% de umidade, 1% de matérias estranhas e impurezas, 30% de quebrados, 8% de esverdeados, 8% de avariados e 18,5% de conteúdo de óleo.

Exemplo 2.1.2

Em um contrato futuro de Ouro a BM&F especifica que, cada lote padrão negocia 250 gramas de ouro, a variação mínima de apregoação é de $ (reais) 0,001 $, o teor de pureza é de 999,0 partes de ouro fino para cada 1.000 partes de metal e os ativos aceitos como margem são dinheiro, ouro, títulos públicos e privados e ações.

Ativos financeiros geralmente estão bem definidos. Por exemplo não existe a necessidade de especificar os graus de aceitação da moeda japonesa yen. Contudo existe características interessantes em Bonds e notas do tesouro em contratos futuros. Uma característica do Treasury bond é ter maturidade maior do que 15 anos.

Tamanho do contrato

O tamanho do contrato especifica a quantidade de ativo que será entregue por contrato. O tamanho do contrato é uma importante decisão para a bolsa de valores. Se o tamanho do contrato for muito grande, muitos investidores que desejam se proteger de pequenas exposições serão incapazes de utilizar a bolsa. Por outro lado se o tamanho do contrato for pequeno, negociá-los será caro pois a cada negociação existe um custo associado.

Exemplo 2.1.3

Em um contrato futuro de Soja em grão tipo exportação, cada contrato negocia 450 sacas de 60 quilos cada.

Exemplo 2.1.4

Em um contrato futuro de Café Arábica, cada contrato negocia 100 sacas de 60 quilos cada.

Local de entrega

O local de entrega é um fator importante para o future contract pois para commodities existe um custo de transporte envolvido na negociação. Assim a bolsa de valores especifica um local adequado para a entrega do ativo.

Exemplo 2.1.5

No contrato futuro de Café Arábica a entrega deve ser feita em armazéns cadastrados pela BM&F. No caso de entrega em localidades diferentes do município de São Paulo, haverá dedução do custo de frete para apuração do valor de liquidação.

Dividendos

Dividendos são uma parcela do lucro apurado por uma sociedade anônima, distribuída aos acionistas por ocasião do encerramento do exercício social.

Posição limite

A posição limite é o número máximo de contratos que um especulador pode possuir.

3 - Taxa de juros

Antes de determinar o preço de uma opção é importante saber como trabalhar com a taxa de juros. A afirmação de que a taxa de juros em depósito bancário é de 10 % ao ano pode não parecer ambígua, mas precisamos saber como essa taxa é composta. Considere o seguinte exemplo ilustrativo.

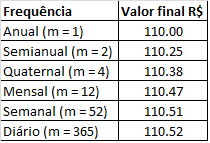
Em um investimento de $ (reais) 100,00 $ a taxa de juros é composta de forma anual, ou seja, daqui a um ano o valor do investimento será de,

$$(reais) 100,00 \times 1,1 = (reais) 110,00 $$

Agora, suponha que o mesmo valor é investido a uma taxa de juros composta de forma semianual. O valor final do investimento será de,

$$(reais) 100,00 \times 1,05 \times 1,05 = (reais) 110,25 $$

Portanto, é importante saber a maneira de como a taxa de juros é composta, pois para diferentes maneiras temos diferentes valores. Observe a tabela abaixo e veja o valor final do investimento para diferentes frequências

Para generalizar o resultado, suponha que uma quantidade A é investida para n anos com taxa R por ano. O valor final do investimento é

$$A(1+R)^n $$

Se a taxa é composta m vezes por ano, o valor final do investimento é

$$A(1+\frac{R}{m})^{nm} $$

Composição contínua

Quando m tende ao infinito, dizemos que a taxa é de composição contínua. Pode ser provado que para um investimento A, com taxa de composição contínua em n anos com taxa R, aumenta para

$$Ae^{Rn}$$

no qual e = 2.71828

4 - Modelo de um período

Nesta seção, vamos apresentar o modelo de $ 1 $ período. Este, é o modelo mais simples para precificação de opções. Contudo, é fundamental pelo fato de que muito dos conceitos apresentados aqui, serão utilizados em modelos mais complexos como, por exemplo, no modelo de Black e Scholes.

No mercado de 1 período, vamos trabalhar com dois ativos bases. Considere o conjunto de tempos $ T=(0,1) $, ou seja temos apenas um tempo inicial e um tempo final.

Ativo livre de risco (Bond)

Seja $ B_t $ o valor do ativo livre de risco no tempo $ t $. Definimos $ B_t $ como

$$B_t=(1+r)^t\ \ \ \ t\in T$$

A taxa $ r $ representa o quanto o ativo livre de risco cresce em uma unidade de tempo.

Ativo de risco (Ação)

Seja $ \bar{S}_t $ o valor do ativo de risco no tempo $ t $. Supomos que o preço do ativo de risco no tempo $ t=1 $ assume apenas dois valores

$$\bar{S}_1/S_0\in (u, d)$$

com respectivas probabilidades

$$\mathbb{P}(\bar{S}_1/S_0=u)=p\ \ \ \mathbb{P}(\bar{S}_1/S_0=d)=1-p,$$

no qual $ S_0 $ é o preço inicial da ação.

No modelo de um período, o ativo de risco é uma variável aleatória sobre um espaço de probabilidade $ (\Omega, \mathcal{F}, \mathbb{P}) $ que pode assumir apenas dois valores no tempo $ t=1 $, ou seja, em uma unidade de tempo ou o preço do ativo sobe uma taxa $ u $ ou cai uma taxa $ d $.

Para este modelo de mercado fazer sentido, vamos fazer a seguinte suposição,

$$d< (1+r)< u.$$

A justificativa para tal suposição é: se por exemplo $ (1+r)< d $, não faria sentido investir no Bond sendo que por menor que seja o rendimento da ação, ainda assim é maior do que o rendimento do Bond.

O objetivo desta seção é calcular o preço e o hedging de uma opção, em particular o preço e o hedging de uma european call option. Para podermos precificar e fazer o hedging de um derivativo, precisamos saber quanto o mesmo rende no tempo de maturidade. Chamamos de função payoff o rendimento do derivativo no tempo de maturidade. A seguir definimos formalmente a função payoff.

Definição 4.1

A função payoff $ C $ de um derivativo, é uma variável aleatória $ \mathcal{F} $-mensurável.

Como já apresentado na seção de derivativos, a função payoff para uma european call option no tempo de maturidade $ t=1 $ é dada por

$$C=(\bar{S}_1-K)^{+}$$

Questão

A função payoff da european call option é uma variável aleatória que pode assumir apenas dois valores. Por que para o cálculo do valor inicial da opção, simplesmente não calculamos a média da variável aleatória $ C_1 $ e descontamos a valor presente?

A justificativa para não utilizarmos tal método é que a média do preço da opção depende diretamente da probabilidade de alta e de baixa do preço do ativo. Assim, para diferentes probabilidades temos diferentes preços para a opção. Queremos uma abordagem que evite este tipo de problema e para alcançarmos tal objetivo, os conceitos procedentes são fundamentais.

No mercado de um período, podemos trabalhar com dois ativos. Assim, o conceito de estratégia se faz necessário.

Definição 4.2

Uma estratégia é um par $ \phi_t=(\alpha_t, \beta_t) $ tal que

• $ \alpha_t $ : representa a quantidade investida na ação no tempo $ t $;
• $ \beta_t $: representa a quantidade investida no bond no tempo $ t $.

Ao investir nestes dois ativos, estamos montando um portfolio. Uma questão de interesse é saber qual o valor do portfólio no tempo $ t\in T $, o que motiva a definição abaixo.

Definição 4.3

Seja $ \phi $ uma estratégia no mercado de um período. O valor do portfólio $ V_0(\phi) $ no tempo $ t=0 $ é definido por

$$=\alpha_t\bar{S}_t+\beta_tB_t, \ \ \ t\in T$$

(há elementos em falta na equação acima)

Dado o valor do portfólio e a estratégia $ \alpha $, podemos obter a estratégia $ \beta $ por

$$\beta_t=\frac{V_t-\alpha_tS_t}{B_t}$$

Definição 4.4

Uma estratégia $ \phi_t = (\alpha_t, \beta_t) $ é auto-financiável, se

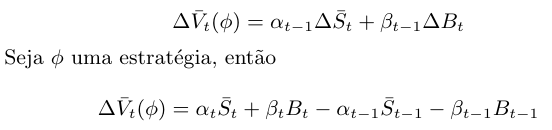
$$=\alpha_{t}\bar{S}_t+\beta_{t}B_t-\alpha_{t-1}\bar{S}_{t-1}-\beta_{t-1}B_{t-1}-\alpha_{t-1}\bar{S}_t+\alpha_{t-1}\bar{S}_t\beta_{t-1}B_t-\beta_{t-1}B_t$$

$$=\alpha_{t-1}\Delta\bar{S}_t+\beta_{t-1}\Delta B_t+\bar{S}_t\Delta\alpha_t+B_t\Delta\beta_t$$

A estratégia $ \phi $ é auto-financiável, se

$$\bar{S}_t\Delta\alpha_t+B_t\Delta\beta_t=0.$$

Ou seja, uma estratégia $ \phi $ é auto-financiável se não existe investimento e nem retirada de dinheiro do portfolio.

Definimos o valor do portfólio descontado como

$$=\frac{\bar{V}_t(\phi)}{B_t}$$

(há elementos em falta na equação acima)

Proposição 4.1

Seja $ \phi $ uma estratégia auto-financiável. Então

$$V_1(\phi)=V_0(\phi)+\alpha_{t-1}\Delta S_t$$

prova:

$$\Delta V_t(\phi)=V_t(\phi)-V_{t-1}(\phi)=\alpha_tS_t+\beta_t-\alpha_{t-1}S_{t-1}-\beta_{t-1}$$

$$=\alpha_t S_t+\beta_t-\alpha_{t-1}S_{t-1}-\beta_{t-1} -\alpha_{t-1}S_t+\alpha_{t-1}S_t$$

$$=\alpha_{t-1}\Delta S_t + S_t\Delta \alpha_t +\beta_t-\beta_{t-1}$$

Como a estratégia é auto-financiável, vale que

$$S_{t}\Delta \alpha_t + \beta_t-\beta_{t-1}=0,$$

então

$$V_1(\phi)= V_0(\phi) + \alpha_0 (S_1-S_0)$$

$ \square $

Note que o preço do portfolio descontado, depende somente da estratégia $ \alpha $ agora.

Para calcularmos o hedging, vamos supor que existe uma estratégia auto-financiável $ \phi $ tal que o valor do payoff $ C $ descontado

$$B_t^{-1}C=V_1(\phi)$$

.

Assim, temos o seguinte sistema de equações

$$B_1^{-1}C_1^u=V_0(\phi)+\alpha_0(S_1^u-S_0)$$

$$B_1^{-1}C_1^d=V_0(\phi)+\alpha_0(S_1^d-S_0)$$

Resolvendo o sistema de equações na variável $ \alpha $, temos que

$$\alpha_0=\frac{C_1^u-C_1^d}{\bar{S}_1^u-\bar{S}_1^d}.$$

e

$$V_0(\phi)=B^{-1}_1\left(C^u\frac{1+r-d}{u-d}+C^d\frac{u-1-r}{u-d}\right).$$

Se denotarmos

$$\frac{1+r-d}{u-d}=\hat{p} \ \ \ e \ \ \ \frac{u-1-r}{u-d}= 1-\hat{p},$$

temos

$$V_0(\phi)=B^{-1}_1\left( C^u\hat{p}+C^d(1-\hat{p})\right).$$

Se considerarmos uma probabilidade $ \hat{\mathbb{P}} $ de tal forma que

$$\hat{\mathbb{P}}(S_1/S_0 = u) = \hat{p} \ \ e \ \ \hat{\mathbb{P}}(S_1/S_0 = d)=1-\hat{p}.$$

Então,

$$V_0(\phi)=\mathbb{E}_{\hat{\mathbb{P}}}[B_1^{-1}C].$$

Chamamos a probabilidade $ \hat{\mathbb{P}} $ de probabilidade de risco neutro.

Preço e hedging da European Call Option

Exemplo 4.1

Assumimos que o preço atual de um ativo e de $ (reais)280 $, e depois de três meses o preco do ativo pode subir para $ (reais)320 $ ou declinar para $ (reais)260 $. Qual o preco justo e o hedging para uma European Call Option com tempo de maturidade de 3 meses, strike price $ K = (reais)280 $ e uma taxa de juros 5% para os três meses?

Suponha que o investidor trabalhe com uma probabilidade de 80% para queda do valor do ativo e 20% para subida do valor do ativo.Com esta probabilidade em mãos, o preco final do ativo $ S_T $ pode ser visto como uma variavel aleatoria que assume dois valores $ S_d = 260; S_u = 320 $ e tem funcão de probabilidade

$$\mathbb{P} (S_T = S_d = 260 ) = 0.8 ~~ \mathbb{P} ( S_T = S_u = 320 ) = 0.2 $$

Com isso, temos a seguinte função payoff

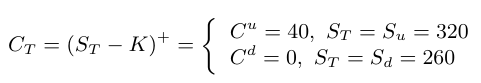
Desta forma, o valor esperado da função payoff descontado a taxa de juros é dado por

$$ \mathbb{E} [(1+ r)^{-1} C_T] = 0,2 \ast 40 \ast (1,05)^{-1} = 7,62 $$

Obviamente que o valor esperado acima depende da probabilidade associada ao payoff. Como comentado acima, esta estratégia de precificação não é conveniente para o mercado. Abaixo, calculamos a estrategia e o preço inicial com os resultados obtidos ao decorrer deste capítulo.

Primeiro vamos obter a taxa de crescimento e a taxa de queda do ativo

$$u=\frac{320}{280}=1,1428 \ \ \ e \ \ \ d=\frac{260}{280}=0,9285.$$

O valor da estratégia $ \alpha_0 $ é

$$\alpha_0=\frac{40-0}{320-260}=\frac{2}{3}$$

ou seja, precisamos comprar dois terços da ação.

Com a taxa de crescimento e a taxa de queda, podemos calcular a probabilidade de risco neutra

$$\hat{p}=\frac{1,05-0,92}{1,1428-0,9285}=0,5666 \ \ e \ \ 1-\hat{p}=\frac{1,1428-1,05}{1,1428-0,9285}=0,4334.$$

O preço inicial da european call option é

$$V_0(\phi)= (1,05)^{-1}(40\times 0,5666)=21,59$$

5 - Modelo de n períodos

Também conhecido como modelo de Cox-Ross-Rubistein, este modelo é uma extensão direta do modelo de um período. Neste modelo, discretizamos o intervalo $ [0,T] $ em $ n $ instantes $ 0=t_1< t_2<\dots< t_n=T $ e então calculamos o preço e o hedging do derivativo em cada tempo $ t_i $ para $ i\in(2,\dots,n) $. A seguir, apresentamos a composição do mercado de Cox-Ross-Rubistein.

No modelo de Cox-Ross-Rubistein, trabalhamos com dois ativos bases, são eles: um ativo de risco (Ação) e um ativo livre de risco (Bond).

• Ativo livre de risco (Bond)

O valor no tempo t de um Bond, é dado por

$$B_t = (1+r)^t\ \ \ \forall t\in\underline{T}$$

com $ r $ constante positiva. Observe que $ B_t $ é determinístico.

• Ativo de risco (Ação)

Para cada tempo $ t\in (t_2, t_3,\dots,t_n) $, o preço da ação é um variável aleatória da forma

$$\frac{S_t}{S_{t-1}}\in (u,d)$$

ou seja, em cada instante o preço sobre uma taxa $ u $ ou cai uma taxa $ d $

com probabilidades

$$\mathbb{P}(S_t=uS_{t-1}|S_{t-1},\dots,S_0)=p\ \ e \ \ \mathbb{P}(S_t=dS_{t-1}|S_{t-1},\dots,S_0)=1-p.$$

Da maneira como definimos a dinâmica do preço da ação, o processo de evolução do preço da ação é uma árvore binomial. O nome árvore binomial tem relação com os ramos que em cada tempo o preço da ação pode assumir. A imagem abaixo, esclarece o porque deste processo ser chamado de árvore binomial.

Para prosseguir será necessário definirmos o que é uma estratégia.

Definição 5.1

Uma estratégia $ \phi $ é um processo composto por dois processos previsíveis $ \alpha_t $ e $ \beta_t $ respectivamente especificados

• $ \alpha_t $ : número de ações possuídas no tempo $ [t,t+1) $
• $ \beta_t $: montante investido em um bond no período $ [t,t+1) $

Para o cálculo do preço da opção, vamos utilizar um método regressor, que ajusta a dinâmica do portfolio no início de cada período. Assim, seremos capazes de replicar o payoff no tempo $ T $.

Definição 5.2

O processo do valor do portfolio no tempo $ t $ é definido como

$$V_t(\phi)=\alpha_{t-1}S_t+\beta_{t-1}(1+r)$$

Dado uma maturidade fixa $ T $, vamos iniciar a análise considerando o último período, $ [T-1,T] $. Vamos assumir que o portfolio replicante do payoff é estabelecido em $ T-1 $ e permanece fixo até o tempo $ T $. Ou seja, vamos estabelecer uma estratégia $ \phi=(\alpha,\beta) $ no início do período $ [T-1,T] $ de forma que o valor do portfolio $ V_T(\phi) $ no tempo $ T $

$$V_T(\phi)=\alpha_TS_T+\beta_T(1+r)$$

replique o payoff $ C_T $, isto é, $ V_T(\phi)=C_T $.

Nesta linhagem de raciocínio, temos que

$$\alpha_{T-1}S_T+\beta_{T-1}(1+r)=(S_T-K)^{+}$$

Da suposição que $ S_t=uS_{t-1} $ ou $ S_t=dS_{t-1} $, temos o sistema de equações abaixo

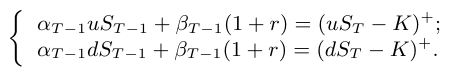
6 - Modelo de Black e Scholes

Uma maneira de se proteger de riscos futuros no mercado financeiro são os derivativos. Dentre os derivativos, o mercado de opção é um dos mais importante. Relacionado com uma opção temos as seguintes questões:

1. Qual o preço justo de uma opção?
2. Qual a estratégia de hedging?

O primeiro problema, é de interesse de ambas as partes do contrato. O comprador quer pagar o mínimo possível e o vendedor quer receber o máximo possível. Já o segundo problema é de total interesse do vendedor da opção: com o dinheiro na mão, qual estratégia permite que na expiração da opção, ele tenha dinheiro suficiente para pagar o comprador?

Nesta seção, vamos trabalhar estes problemas no mercado de Black e Scholes. Neste modelo de mercado temos dois tipos de ativos base. Os ativos livres de risco (money market account) e os ativos com risco (ações). Neste sentido, considere $ B_t $ como sendo o valor do money market account no tempo $ t $. A dinâmica do preço do money market account segue a equação diferencial ordinária da forma

$$dB_t = rB_t dt \quad \text{e} \quad B_0 = 1$$

que possui solução única dada por

$$B_t = e^{rt}.$$

Podemos notar que o modelo para o preço do money market account é determinístico, ou seja, o preço é conhecido para todo o instante de tempo. Assim, não existe risco relacionado ao money market account.

Na sequência, vamos modelar o preço da ação. Considere $ \bar{S}_t $ como sendo o valor da ação no tempo $ t $. A dinâmica do preço da ação segue a equação diferencial estocástica

$$d\bar{S}_t = \mu \bar{S}_t dt + \sigma \bar{S}_t dW_t$$

tal que o preço inicial é $ S_0 $ e $ W_t $ é o processo de Wiener (movimento browniano). Também assumimos que $ \mu $ e $ \sigma $ são constantes conhecidas. Podemos notar que o termo $ \sigma \bar{S}_t dW_t $ funciona como um ruído no modelo, ou seja, ele associa uma incerteza ao preço da ação no tempo t, o que implica que o preço final do ativo de risco (ação) é desconhecido. Já o termo $ \mu \bar{S}_t dt $ representa um crescimento linear do preço do ativo de risco. Neste caso, $ \mu $ é conhecido com taxa média de retorno e $ \sigma $ é a volatilidade do ativo.

Para garantirmos a existência e a unicidade da solução da equação diferencial estocástica para o preço, basta observarmos que as funções $ f(t,x)=\mu x $ e $ g(t,x)=\sigma x $ satisfazem as condições de Lipschitz e de crescimento polinomial. Para mais detalhes sobre existência e unicidade de soluções para equações diferenciais estocásticas, veja Equação diferencial estocástica.

O próximo resultado nos fornece uma solução analítica para a equação diferencial estocástica do ativo de risco.

Proposição 6.1

O único processo que satisfaz a equação diferencial estocástica do preço da ação é dada por

$$\bar{S}_t = S_0\exp\left(\left(\mu -\frac{\sigma^2}{2} \right)t + \sigma W_t\right).$$

A verificação deste resultado pode ser encontrada no Exemplo 10.5.1 e segue, diretamente, da aplicação da Fórmula de Itô. A fim de simular o processo de preços, podemos utilizar o algoritmo composto pelos passos abaixo.

1. Simulamos o movimento Browniano $ W_t $, conforme o algoritmo apresentado na Seção Movimento Browniano.
2. Calculamos

$$\bar{S}_t = S_0\exp\left(\left(\mu-\frac{\sigma^2}{2}\right)t+\sigma W_t\right).$$

Na figura a seguir, utilizando os valores $ S_0 = 100 $, $ \mu = 0,1 $ e $ \sigma = 0,4 $ e o intervalo de tempo $ [0,1] $ particionado em intervalos iguais de tamanho $ h = \frac{1}{500} $, simulamos algumas trajetórias para o processo de preços.

(imagem em falta)

Definição 6.1

Dizemos que $ C_T $ é a função payoff associada a um derivativo com maturidade $ T $ e ativo subjacente (ou, base) $ \bar{S}_t $, se

$$C_T=g(\bar{S}_t, \ \forall \ t\in[0,T]),$$

para alguma função $ g $.

Dizemos que uma função payoff é independente da trajetória se $ C_T=g(\bar{S}_T) $, ou seja, se o payoff depende apenas do instante final do ativo subjacente. A seguir, apresentamos exemplos de funções payoff.

Exemplo 6.1

A função payoff de uma call option europeia é dada por

$$C_T=(\bar{S}_T-K)^{+}$$

Podemos notar que o payoff de uma call option europeia é independente da trajetória, pois a função $ C_T $ só depende do preço do ativo no instante $ T $.

Exemplo 6.2

A função payoff de uma opção do tipo barreira é dada por

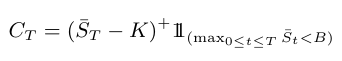
A função payoff de uma opção do tipo barreira é dependente da trajetória do processo de preço do ativo com risco, pois se para algum tempo $ t\in [0,T] $ o preço $ \bar{S}(t) $ ultrapassar o valor de barreira $ B $ então $ C_T = 0 $.

A seguir, apresentamos os conceitos de estratégia de negociação e estratégia auto-financiável, necessários para o cálculo do preço da opção.

Definição 6.2

Uma estratégia de negociação é um par $ \phi(t)=(\alpha_t,\beta_t) $ de processos estocásticos progressivamente mensuráveis sobre o espaço de probabilidade $ (\Omega ,\mathcal{F},\mathbb{P}) $, no qual

• $ \alpha_t $: representa a quantidade de ativos com risco (ações) no tempo $ t $;
• $ \beta_t $: quantidade de ativos sem risco (money market account) no tempo $ t $.

A partir da estratégia de negociação $ \phi $, vamos definir o capital do investidor associado à estratégia $ \phi $.

Definição 6.3

Seja $ \phi_t=(\alpha_t,\beta_t) $ uma estratégia de negociação. Definimos o processo $ V_t(\phi) $ como

$$V_t(\phi)=\alpha_t\bar{S}_t+\beta_tB_t, \quad 0 \leq t \leq T$$

que representa o valor do portfolio composto do ativo de risco e do money market account no tempo $ t $.

Definição 6.4

Uma estratégia de negociação $ \phi_t=(\alpha_t,\beta_t) $ sobre o intervalo $ [0, T] $ é auto-financiável, se o processo portfolio satisfaz a seguinte igualdade:

$$V_t(\phi)=V_0(\phi)+\int_0^t\alpha_ud\bar{S}_u+\int_0^t\beta_udB_u$$

Para entender a definição acima, vamos derivar o processo de portfolio de forma heurística na variável $ t $

$$\frac{dV_t(\phi)}{dt}=\alpha_t\frac{d\bar{S}_t}{dt}+\frac{d\alpha_t}{dt}\bar{S}_t+\frac{dB_t}{dt}\beta_t+\frac{d\beta_t}{dt}B_t.$$

A estratégia $ \phi $ é auto-financiável, se a condição abaixo for satisfeita

$$\frac{d\alpha_t}{dt}\bar{S}_t=-\frac{d\beta_t}{dt}B_t.$$

O que a definição está dizendo é que não existe investimento e nem retirada de dinheiro do processo de portfólio, ou seja, se aumentarmos a quantidade investida na ação, diminuímos a quantidade investida no money market account.

Na sequência, vamos verificar que existe uma probabilidade $ \mathbb{Q} $ que torna o preço do ativo descontado um martingale. Seja $ S_t=B^{-1}_t\bar{S}_t $ o processo que representa o preço da ação descontado no tempo $ t $. Assim, obtemos que

$$\frac{\bar{S}_t}{B_t} = S_0 \exp\left[\left( (\mu-r)-\frac{\sigma}{2}\right)t+\sigma W_t \right].$$

Assim, a equação diferencial estocástica para o preço da ação descontada é dada por:

$$dS_t=(\mu-r)S_tdt+\sigma S_tdW_t.$$

Agora, defina o processo estocástico $ W^{*}_t $ como

$$W^{*}_t=W_t+\frac{(\mu-r)}{\sigma}.$$

Então, temos que

$$dW^{*}_t=dW_t+\frac{\mu-r}{\sigma}dt.$$

O Teorema de Girsanov garante que existe uma única probabilidade $ \mathbb{Q} $ dada por

$$\mathbb{Q}(A)=\int_A\exp\left(-\frac{\mu-r}{\sigma}dW_t - \frac{(\mu - r)^2}{2\sigma^2}dt \right) d\mathbb{P}$$

tal que o processo estocástico $ W^{*}_t $ seja um martingale sobre $ \mathbb{Q} $.

Assim,

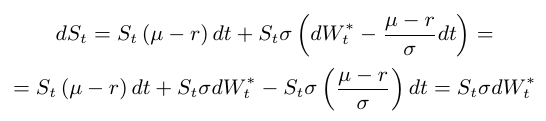
e, portanto, $ S_t $ é um martingale sob a probabilidade $ \mathbb{Q} $.

Lema 6.1

Considere $ \phi=(\alpha,\beta) $ uma estratégia auto-financiável. Defina o processo portfólio descontado como

$$V^{*}_t(\phi)=B^{-1}_tV_t(\phi).$$

Então, o processo portfólio descontado é um martingale sob a probabilidade $ \mathbb{Q} $, na forma

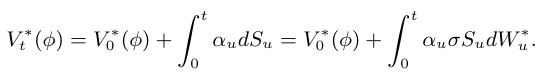
Demonstração

Utilizando a fórmula de integração por partes, temos que

$$dV_t^{*}(\phi)=V_t(\phi)dB^{-1}_t+B^{-1}_tdV_t(\phi)$$

$$=\left(\alpha_t\bar{S}_t+\beta_tB_t\right)dB^{-1}_t+B^{-1}_t\left(d\bar{S}_t\alpha_t+\beta_tdB_t\right)$$

$$=\alpha_t\left(\bar{S}_tdB^{-1}_t+B^{-1}_td\bar{S}_t\right)+\beta_t\left(B_tdB^{-1}_t+B^{-1}_tdB_t\right).$$

Como $ \beta_t\left(B_tdB^{-1}_t+B^{-1}_tdB_t\right) = \beta_td\left(B^{-1}_tB_t\right)=0 $, temos que

$$dV_t^{*}(\phi)=\alpha_t\left(\bar{S}_tdB^{-1}_t+B^{-1}_td\bar{S}_t\right)$$

$$=\alpha_tdS_t,$$

o que implica que

Definição 6.5

$$C_TB^{-1}_T = V^{\ast}_T(\phi)=V^{\ast}_0(\phi)+\int_0^T\alpha_udS_u.$$

Agora, iremos apresentar um resultado fundamental do cálculo estocástico, e que será de extrema importância para precificação de opções. Este resultado é conhecido como Teorema de Representação de Martingales.

Teorema 6.1 (Teorema de Representação de Martigales)

$$X_T=\mathbb{E}[X]+\int_0^T\theta_tdW_t.$$

Teorema 6.2

Seja $ C_T $ a função payoff de uma opção. Suponha que $ C_T $ seja atingível. Então, o preço justo da opção é dado por

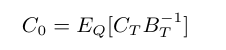
e sua estratégia de hedging é dada por

$$\alpha_t=\frac{\theta_t}{S_t\sigma}$$

em que $ \theta $ é o integrando do Teorema de representação de Martingales.

Demonstração

Do Lema 6.1, temos que

$$V^{\ast}_T(\phi) = V^{\ast}_0(\phi) + \int_0^T\alpha_udS_u = V^{\ast}_0(\phi) + \int_0^T\alpha_u\sigma S_udW^{\ast}_u.$$

Como, por hipótese, o payoff é atingível, temos que $ V^{\ast}_T(\phi) = C_TB^{-1}_T $ de onde segue que o preço justo da opção é $ V^{\ast}_0(\phi) $ e a estratégia de hedging é dada por $ \alpha $. Porém, como $ C_TB^{-1}_t $ é, por hipótese $ \mathbb{Q} $-quadrado integrável e $ \mathbb{F} $-mensurável, segue do Teorema de Representação de Martingales, que existe um único processo previsível $ \theta $ tal que

$$\alpha_t = \frac{\theta_t}{\sigma S_t}$$

concluindo a demonstração.

$ \square $

Corolário 6.1

Se a função $ C_T \in C^2 $. Então a estratégia de hedging é dada por

$$\alpha_t = \frac{\partial C_t}{\partial S_t} = \frac{\partial V^{\ast}_t(\phi)}{\partial S_t}.$$

Demonstração

O objetivo agora, é determinar o processo previsível $ \theta $. Suponha que $ V^{\ast}_t(\phi) $ seja uma função contínua de $ t $ e $ S_t $ e, além disso, que possua derivadas parciais até segunda ordem contínuas. Relembramos que o processo do preço descontado do ativo $ S $ é dado segundo a equação diferencial estocástica

$$dS_t = S_t\sigma dW^{\ast}_t,$$

sendo, portanto, um processo de Itô. Aplicando a fórmula de Itô para a função $ V^{\ast}_t(\phi) $, temos que

$$V^{\ast}_t(\phi) = V^{\ast}_0(\phi) + \int_0^t\sigma S_u\frac{\partial V^{\ast}_u(\phi)}{\partial S_u}dW^{\ast}_u + \int_0^t\left[\frac{\partial V^{\ast}_u(\phi)}{\partial u} + \frac{1}{2}\frac{\partial^2V^{\ast}_u(\phi)}{\partial S^2_u}\sigma^2S^2_u\right]du.$$

Mas, do Lema 6.1, temos que $ V^{\ast}_t(\phi) = V^{\ast}_0(\phi) + \int_0^t\alpha_u\sigma S_udW^{\ast}_u $, portanto, temos que

$$\theta_t = \sigma S_t\frac{\partial V^{\ast}_u(\phi)}{\partial S_u}$$

e a estratégia de hedging é dada por

$$\alpha_t=\frac{\partial V^{\ast}_t(\phi)}{dS_t},$$

como queríamos demonstrar.

$ \square $

O método comentado acima, consiste em encontrar uma probabilidade $ \mathbb{Q} $ de forma que o processo estocástico $ W^{*}(t)=W(t)+\frac{(\mu-r)}{\sigma}t $ seja um movimento browniano sobre $ \mathbb{Q} $, e então calcular o valor esperado do payoff descontado sobre $ \mathbb{Q} $. Este método é comumente chamado de método da $ \textit{Medida Martingale Equivalente} $.

Exemplo 6.3

Considere uma opção de compra europeia (europeian call option), cuja função payoff é dada por

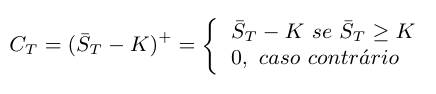
Neste caso, o preço da opção é dado por

$$\mathbb{E}_{\mathbb{Q}}\left[C_TB_T^{-1}\right] = S_0\Phi(d_1) - Ke^{-rT}\Phi(d_2)$$

em que

$$d_1 = \frac{\ln\left(\frac{S_0}{K}\right)+\left(r+\frac{\sigma^2}{2}\right)T}{\sigma\sqrt{T}}$$

e

$$d_2 = d_1 - \sigma\sqrt{T}.$$

Além disso, a estratégia de hedging, no instante inicial, é dada por

$$\alpha_0= \Phi(d_1).$$

De fato, temos que

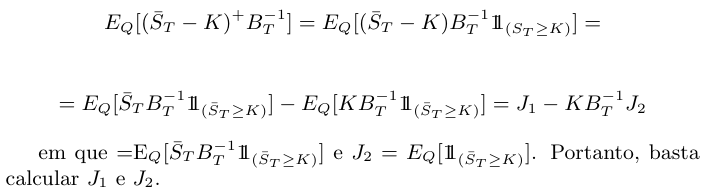
(há elementos em falta na equação acima)

Inicialmente, vamos calcular $ \mathbb{J}_2 $.

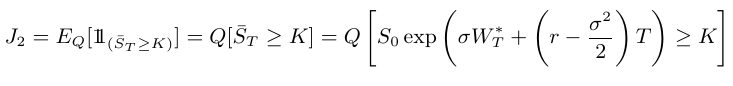
de onde concluímos que

$$\mathbb{J}_2 =\mathbb{Q}\left[ -\sigma W^{\ast}_T\leq\ln \left(\frac{S_0}{K}\right)+\left(r - \frac{\sigma^2}{2}\right)T\right]=\mathbb{Q}\left[ - \frac{W^{\ast}_T}{\sqrt{T}}\leq\frac{\ln \left(\frac{S_0}{K}\right)+\left(r - \frac{\sigma^2}{2}\right)T}{\sigma\sqrt{T}}\right].$$

Como $ -\frac{W^{*}_T}{\sqrt{T}} \sim N(0,1) $, temos que

$$\mathbb{J}_2=\Phi\left(\frac{\ln\left(\frac{S_0}{K}\right)+\left(r-\frac{\sigma^2}{2}\right)T}{\sigma\sqrt{T}}\right)$$

em que $ \Phi $ é a distribuição acumulada da normal. A fim de calcular $ \mathbb{J}_1 $, é necessário fazer uma nova mudança de probabilidade. Para isto, considere

$$\mathbb{Q}^{\ast}(A) = \int_A\exp\left(\sigma W^{*}_T - \frac{\sigma^2}{2} \right) d\mathbb{Q}$$

Como anteriormente, temos que $ \hat{W}_t=W^{*}_t-\sigma t $ é um $ \mathbb{Q}^{\ast} $-movimento browniano e, então,

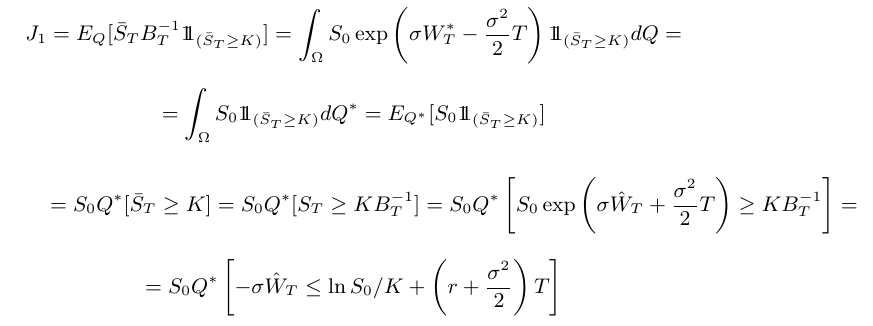
de onde concluímos que

$$\mathbb{J}_1=S_0\Phi\left(\frac{\ln{S_0/K}+(r+\frac{\sigma^2}{2})T}{\sigma\sqrt{T}}\right)$$

Portanto o preço de uma call option europeia é dado por

$$C_0 = S_0\Phi(d_1) - KB^{-1}_T\Phi(d_2),$$

com

$$d_1=\frac{\ln{S_0/K}+(r+\frac{\sigma^2}{2})T}{\sigma\sqrt{T}} \ \ \text{e} \ \ d_2=d_1-\sigma\sqrt{T}.$$

Para o cálculo da estratégia de hedging no instante inicial, temos que

$$\alpha_0 = \frac{\partial}{\partial S_t}\mathbb{E}_{\mathbb{Q}}\left[(\bar{S}_T-K)^{+}B_T^{-1}\right] = \frac{\partial}{\partial S_t}\left(S_t\Phi(d_1) - Ke^{-rT}\Phi(d_2)\right) = \Phi(d_1) + S_t\Phi^{\prime}(d_1) - Ke^{-rT}\Phi^{\prime}(d_2)$$

de onde segue que

$$\alpha_0 = \Phi(d_1) + S_t\frac{1}{\sqrt{2\pi}}e^{-\frac{d_1^2}{2}}\frac{\partial d_1}{\partial S_0} - Ke^{-rT}\frac{1}{\sqrt{2\pi}}e^{-\frac{d_2^2}{2}}\frac{\partial d_1}{\partial S_0} = \Phi(d_1) + \left(S_t\frac{1}{\sqrt{2\pi}}e^{-\frac{d_1^2}{2}}-Ke^{-rT}\frac{1}{\sqrt{2\pi}}e^{-\frac{d_2^2}{2}}\right)\frac{\partial d_1}{\partial S_0}.$$

Porém, temos que

$$Ke^{-rT}e^{-\frac{d_2^2}{2}} = Ke^{-rT}e^{-\frac{\left(d_1+\sigma\sqrt{T}\right)^2}{2}}=Ke^{-rT}e^{-\frac{d_1^2}{2}}e^{\sigma\sqrt{T}d_1-\frac{\sigma^2T}{2}} = Ke^{-rT}e^{-\frac{d_1^2}{2}}e^{\ln S_t/K + \left(r+\frac{\sigma^2}{2}\right)T-\frac{\sigma^2T}{2}}$$

e, portanto,

$$Ke^{-rT}e^{-\frac{d_2^2}{2}} = Ke^{-rT}e^{-\frac{d_1^2}{2}}\frac{S_t}{K}e^{rT} = S_te^{-\frac{d_1^2}{2}}$$

e, desta forma, concluímos que $ \alpha_0 = \Phi(d_1) $.

Ressaltamos que, de forma análoga, a partir de um simples argumento de translação, podemos calcular o preço da opção $ \mathbb{E}_{\mathbb{Q}}[C_TB_T^{-1}|\mathcal{F_t}] $ e a estratégia de hedging $ \alpha_t $ em qualquer instante $ 0\leq t \ < \ T $, respectivamente, por

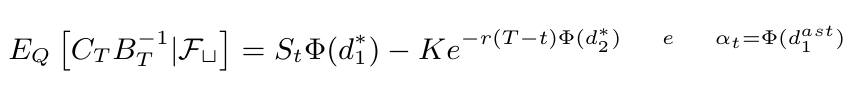
em que

$$d_1^{ast} = \frac{\ln\left(\ln\frac{S_t}{K}\right)+\left(r+\frac{\sigma^2}{2}\right)(T-t)}{\sigma\sqrt{T-t}} \quad \ \text{e} \ \quad d_2 = d_1 - \sigma\sqrt{T-t}.$$

Equação Diferencial Parcial de Black e Scholes

Vamos assumir que o preço da opção satisfaz

$$C_t=v(S_t,t)$$

para alguma função $\mathbb{R}_{+}\times[0,T]\rightarrow\mathbb{R} $.

(há elementos em falta na equação acima)

Definição 6.5

Dizemos que uma estratégia $ \Gamma_t=(\alpha_t ,\beta_t) $ sobre o intervalo $ [0,T] $ é auto financiável, se o processo de portfolio $\ V_t(\Gamma) $, definido como

$$V_t(\Gamma)=\alpha_t S_t+\beta_tB_t,\ \ \forall t\in [0,T],$$

satisfaz a seguinte condição

$$V_t(\Gamma )=V_0(\Gamma)+\int_0^t\alpha_u dS_u+\int_0^t\beta_udB_u,\ \ \forall t\in [0,T].$$

Vamos assumir também que a estratégia de replicação $ \Gamma_t $ tem a seguinte forma.

$$\Gamma_t=(\alpha_t, \beta_t)=(g(S_t,t),h(S_t,t))$$

para $ t\in[0,T] $ e $\mathbb{R}_{+}\times [0,T]\rightarrow\mathbb{R} $ funções.

(há elementos em falta na equação acima)

O processo do portfolio é dado por

$$V_t(\Gamma) = g(S_t,t)S_t+h(S_t,t)B_t$$

Então

$$dV_t(\Gamma)=g(S_t,t)dS_t+h(S_t,t)dB_t$$

Utilizando a EDE do preço da ação e a EDO do money market account, temos que

$$dV_t(\Gamma)=g(S_t,t)(\mu S_t dt+\sigma S_t dW_t)+h(S_t,t)rB_t dt$$

$$=g(S_t,t)(\mu S_tdt+\sigma S_tdW_t)+h(S_t,t)rB_tdt+rg(S_t,t)S_tdt-rg(S_t,t)S_tdt$$

$$= (\mu-r)g(S_t,t)S_tdt+\sigma S_tg(S_t,t)dW_t+rv(S_t,t)dt$$

Isolando $ h(S_t,t) $ de $ v(S_t,t)=g(S_t,t)S_t+h(S_t,t)B_t $ temos que

$$\beta_t=h(S_t,t)=B_t^{-1}(v(S_t,t)-g(S_t,t)S_t)$$

Vamos assumir que a função $ v $ é uma função diferenciável até a segunda ordem e que suas derivadas são contínuas. Assim, podemos aplicar a fórmula de Itô.

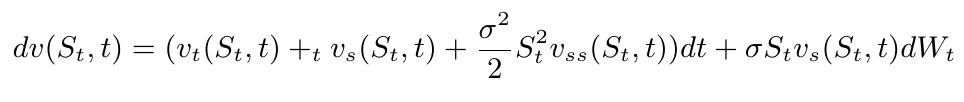
Defina o processo $ Y_t $ como

$$Y_t = v(S_t,t)-V_t(\Gamma)$$

Combinando os diferenciais, temos

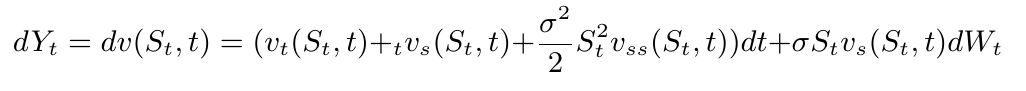
$$-((\mu-r)g(S_t,t)S_tdt+\sigma S_tg(S_t,t)dW_t+rv(S_t,t)dt)$$

como os processos são idênticos, $ Y_t = 0 $ para todo $ t\in[0,T] $. Da unicidade da decomposição de Doob-Meyer, temos que

$$\int_0^t\sigma S_u(g(S_u,u)-v_s(S_u,u))dW_u = 0$$

Da isometria de Itô, a equação anterior é equivalente a:

$$\int_0^t\sigma S_u^2(g(S_u,u)-v_s(S_u,u))^2du=0,$$

como o integrando é positivo, temos que

$$g(S_t,t) = v_s(S_t,t),\ \ \forall (S_t,t)\in\mathbb{R}_{+}\times[0,T]$$

$$v_t(S_t,t)+\frac{\sigma^2}{2}S_t^2v_{ss}(S_t,t)+rS_tv_s(S_t,t)-rv(S_t,t)$$