18. Incerteza de Medição

Ao relatarmos o resultado da medição de uma grandeza física é obrigatório que seja dado alguma indicação quantitativa da qualidade do resultado, de tal forma que aqueles que utilizam o resultado da medição possam avaliar sua confiabilidade. Sem essa indicação, os resultados da medição não podem ser comparados, sejam entre eles mesmos ou com valores de referência fornecidos em uma especificação ou norma. Portanto, é necessário que haja um procedimento implementado de fácil compreensão e de aceitação geral para caracterizar a qualidade do resultado da medição, isto é, para avaliar e expressar sua incerteza.

O conceito de incerteza de medição será utilizado como um atributo quantificável para determinar a qualidade de um sistema de medição. Neste módulo, vamos discutir em detalhes o conceito de incerteza de medição e apresentar várias aplicações na calibração de equipamentos de medição e em ensaios. Nosso texto foi baseado na norma ISO GUM (2008).

1 - Fundamentos do Cálculo de Incerteza em Medição

Medição

O objetivo de uma medição é determinar o valor do mensurando, isto é, o valor da grandeza específica a ser medida. A medição começa com uma apropriada especificação da grandeza, do método e procedimento de medição.

Em geral, o resultado de uma medição é uma aproximação ou estimativa do valor da grandeza. Assim, o resultado da medição somente está completo se estiver acompanhado da incerteza da estimativa.

Na prática, a especificação ou definição da grandeza é consequência da exatidão (accuracy) desejada. Para atender a exatidão requerida, a grandeza deve ser especificada de tal forma que esta tenha um único valor para os propósitos práticos associados.

Exemplo 1.1

Considere uma haste de 75mm onde a exatidão requerida é de micrômetros. Neste caso, sua especificação deve incluir a temperatura e pressão. Por outro lado, se o comprimento da haste deve ser determinado em milímetros, sua especificação não requer a definição da temperatura e pressão.

Na grande maioria dos casos, o resultado da medição é determinado através de uma série de leituras obtidas sob condições de repetitividade. Variações obtidas nas leituras repetidas são consequência de fatores que afetam os resultados das leituras.

Além disso, o modelo matemático da medição, que transforma as leituras repetidas no resultado da medição é crítico, pois incluí fatores que não são totalmente conhecidos. Assim, a variação obtida nas leituras repetidas e a falta de informação do modelo matemático, contribuem para a incerteza do resultado da medição.

Medição

É o conjunto de operações com objetivo de determinar o valor de uma grandeza. Estas operações podem ser realizadas automaticamente.

Medir

É um processo experimental pelo qual o valor momentâneo de uma grandeza física (grandeza a medir) é determinado como múltiplo e/ou uma fração de uma unidade, estabelecida por um padrão, e reconhecida internacionalmente.

Incerteza de Medição

Parâmetro associado ao resultado da medição, que caracteriza a dispersão de valores que podem ser atribuídos ao mensurando.

1.1 - Erros, Efeitos e Correções

Em geral, uma medição tem imperfeições que dão origem a um erro no resultado da medição. Tradicionalmente, o erro é visto como tendo dois componentes, um componente aleatório e um componente sistemático. É importante deixarmos claro que erro é um conceito idealizado e os erros não podem ser conhecidos exatamente. Uma discussão detalhada sobre erro de medição pode ser encontrada no apêndice D da norma ISO GUM (2008).

O erro aleatório se origina de variações temporais ou espaciais e ocorre de forma imprevisível. Os efeitos de tais variações (daqui para a frente denominaremos efeitos aleatórios) são a causa de variações em observações repetidas da grandeza. Embora não seja possível compensar o erro aleatório de um resultado de medição, ele pode geralmente ser reduzido aumentando-se o número de observações. Sua esperança ou valor esperado é zero.

O erro sistemático, assim como o erro aleatório, não pode ser eliminado, porém ele, frequentemente, pode ser reduzido. Se um erro sistemático se origina de um efeito reconhecido de uma grandeza de influência em um resultado de medição, daqui para diante denominado como efeito sistemático, o efeito pode ser quantificado e, se for significativo com relação à exatidão requerida da medição, uma correção ou fator de correção pode ser aplicado para compensar o efeito. Suponhamos, que, após esta correção, a esperança da distribuição de probabilidade associada ao erro sistemático seja zero.

Como dissemos, o erro é um conceito idealizado e os erros não podem ser conhecidos exatamente. Na prática, associamos uma variável aleatória (por exemplo, a distribuição normal) para representar o erro de medição, como pode ser observado na Figura 1.1.1. Outras distribuições de probabilidade também podem ser utilizadas, por exemplo, associamos o erro devido a resolução do instrumento de medição com a distribuição retangular (ou, uniforme).

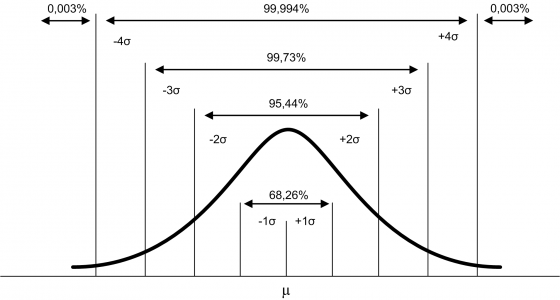
Figura 1.1.1: Representação do erro de medição.

Muitas vezes, utilizamos o desvio padrão amostral da média de uma série de observações para estudar o comportamento do erro aleatório. Entretanto, o desvio padrão amostral da média não é o erro aleatório, embora ele assim seja designado em algumas publicações. Ele é, em vez disso, uma medida de incerteza da média devido a efeitos aleatórios. O valor exato do erro da média, que se origina destes efeitos, não pode ser conhecido. Devemos tomar muito cuidado em distinguir entre os termos “erro'' e “incerteza''. Eles não são sinônimos, ao contrário, representam conceitos completamente diferentes.

A incerteza de uma correção aplicada a um resultado de medição, para compensar um efeito sistemático, não é o erro sistemático. É, ao contrário, uma medida de incerteza do resultado devido ao conhecimento incompleto do valor requerido da correção. O erro originado da compensação imperfeita de um efeito sistemático não pode ser exatamente conhecido. Os termos “erro'' e “incerteza'' devem ser usados apropriadamente e devemos tomar cuidado em distinguir um do outro. Supomos que o resultado de uma medição tenha sido corrigido para todos os efeitos sistemáticos reconhecidos como significativos e que todo esforço tenha sido feito para identificar tais efeitos.

Exemplo 1.1.1

Uma correção devido à impedância finita de um voltímetro usado para medir uma diferença de potencial (a grandeza) através de um resistor de alta impedância é aplicada para reduzir o efeito sistemático sobre no resultado da medição proveniente do efeito de carregamento do voltímetro. Entretanto, os valores da impedância do voltímetro e do resistor, que são usados para estimar o valor da correção e são obtidos a partir de outras medidas, são incertos. Essas incertezas são usadas para avaliar a componente de incerteza da determinação de diferença de potencial originada da correção e, assim, do efeito sistemático devido à impedância finita do voltímetro.

Frequentemente, os instrumentos e sistemas de medição são ajustados com base em padrões de medição e materiais de referência para eliminar os efeitos sistemáticos. Contudo, as incertezas associadas a esses padrões e materiais ainda devem ser levadas em consideração.

1.2 - Incerteza de Medição

A incerteza do resultado de uma medição reflete a falta de conhecimento associado ao valor da grandeza a ser medida. O resultado de uma medição, mesmo após correção devido aos efeitos relativos a erros sistemáticos reconhecidos, é somente uma estimativa do valor da grandeza devido a incerteza proveniente dos efeitos dos erros aleatórios e da correção imperfeita do resultado para efeitos devido aos erros sistemáticos.

O resultado de uma medição (após correção) pode, sem que se perceba, estar muito próximo do valor da grandeza (e, assim, ter um erro desprezível), muito embora possa ter uma incerteza grande. Portanto, a incerteza do resultado de uma medição não deve ser confundida com o erro desconhecido remanescente.

Na prática, existem muitas fontes possíveis de incerteza em uma medição, incluindo:

a) Definição incompleta da grandeza;

b) Falhas na definição da grandeza;

c) Amostragem não-representativa - A amostra medida pode não representar a grandeza definida;

d) Conhecimento inadequado dos efeitos das condições ambientais sobre a medição ou medição imperfeita das condições ambientais;

e) Erro de tendência pessoal na leitura de instrumentos analógicos;

f) Resolução finita do instrumento ou limiar de mobilidade;

g) Valores inexatos dos padrões de medição e materiais de referência;

h) Valores inexatos de constantes e de outros parâmetros obtidos de fontes externas e usados no algoritmo para obtenção de dados;

i) Aproximações e suposições incorporadas ao método e procedimento de medição;

j) Variações nas observações repetidas da grandeza sob condições aparentemente idênticas.

Essas fontes não são necessariamente independentes e algumas das fontes de (a) a (i) podem contribuir para a fonte (j). Naturalmente, um efeito sistemático não reconhecido não pode ser levado em consideração na avaliação da incerteza do resultado de uma medição, porém contribui para seu erro.

Em algumas publicações, os componentes da incerteza são categorizados como “aleatório'' e “sistemático'' e são associados com erros provenientes de efeitos aleatórios e de efeitos sistemáticos conhecidos, respectivamente. Tal categorização de componentes de incerteza pode se tornar ambígua quando aplicada genericamente. Por exemplo, um componente “aleatório'' de incerteza em uma medição pode se tornar um componente “sistemático'' da incerteza em outra medição na qual o resultado da primeira medição é usado como dado de entrada. Categorizando os métodos de avaliação (ou, cálculo) dos componentes de incerteza, em vez de fazermos com os próprios componentes, evitamos tal ambiguidade. Ao mesmo tempo, isto não impede designar componentes individuais que tenham sido avaliados pelos dois diferentes métodos em grupos distintos, a serem usados para uma finalidade em particular.

A recomendação da norma ISO GUM (2008) consiste em dividirmos os componentes de incerteza em dois tipos, denominados “A” e “B”. Estas categorias são aplicados ao método de avaliação da incerteza e não tem relação com as palavras aleatório ou sistemático. A incerteza associada a correção de um efeito relacionado a um erro sistemático pode ser obtido por uma avaliação do tipo A ou por uma avaliação do tipo B.

O propósito da classificação Tipo A e Tipo B é de indicar as duas maneiras diferentes de avaliar os componentes da incerteza e serve apenas para discussão. A classificação não se propõe a indicar que haja qualquer diferença na natureza dos componentes. Ambos os tipos de avaliação são baseados em distribuições de probabilidade e os componentes de incerteza resultantes de cada tipo são quantificados por variâncias ou desvios padrão.

A variância estimada $ u^2 $, caracterizando um componente de incerteza obtido de uma avaliação do Tipo A, é calculada a partir de uma série de observações repetidas, através da variância amostral da média das medidas $ s^2/n $. O desvio padrão estimado $ u=s/\sqrt{n} $ é denominado incerteza padrão do Tipo A. Para um componente de incerteza obtido por uma avaliação do Tipo B, a variância estimada $ u^2 $ é avaliada através do conhecimento disponível, e o desvio padrão estimado $ u $ é, por vezes, denominado incerteza padrão do Tipo B.

Assim, uma incerteza padrão do Tipo A é obtida a partir de uma função densidade de probabilidade derivada da observação de uma distribuição de frequência, enquanto que a incerteza padrão do Tipo B é obtida de uma suposta função densidade de probabilidade, baseada no grau de credibilidade de que um evento vá ocorrer (frequentemente chamada probabilidade subjetiva). Ambos os enfoques empregam interpretações reconhecidas de probabilidade. Uma avaliação do Tipo B de um componente de incerteza é usualmente baseada em um conjunto de informações comparativamente confiáveis.

A incerteza padrão do resultado de uma medição, quando este resultado for obtido de valores de outras grandezas, é denominada incerteza padrão combinada e designada por $ u_c $. Ela é o desvio padrão estimado, associado com o resultado, obtida a partir de todos os componentes de variância e covariância, independente de como tenham sido avaliados, usando o que é denominado, de lei da propagação de incerteza.

Para satisfazer as necessidades de algumas aplicações industriais e comerciais, assim como a requisitos nas áreas da saúde e segurança, uma incerteza expandida $ U $ é obtida multiplicando-se a incerteza padrão combinada $ u_c $ por um fator de abrangência $ k $. A finalidade pretendida para $ U $ é fornecer um intervalo em torno do resultado de uma medição com o qual se espera abranger uma grande fração da distribuição de valores que poderiam razoavelmente ser atribuída a grandeza. A escolha de $ k $, o qual está geralmente na faixa de 2 a 3, é baseada na probabilidade de abrangência ou nível da confiança requerido do intervalo.

O fator de abrangência $ k $ deve sempre ser declarado de forma que a incerteza padrão da grandeza medida possa ser recuperada para uso no cálculo de incerteza padrão combinada de outros resultados de medição que possam depender dessa grandeza.

Se houver variação de todas as grandezas das quais o resultado de uma medição depende, sua incerteza poderá ser calculada por meios estatísticos. Entretanto, uma vez que isso, na prática, raramente é possível, devido a tempo e recursos limitados, a incerteza de um resultado de medição é, geralmente, avaliada quando utilizamos um modelo matemático da medição e a lei de propagação da incerteza. Assim, está implícita a suposição de que uma medição pode ser modelada matematicamente até o grau imposto pela exatidão requerida na medição.

Uma vez que o modelo matemático pode ser incompleto, todas as grandezas relevantes devem ser variadas até a maior extensão prática possível, de modo que a avaliação da incerteza possa ser baseada, tanto quanto possível, nos dados observados.

Sempre que factível, o uso de modelos empíricos da medição, fundamentados em dados quantitativos e colecionados ao longo do tempo, e o uso de padrões de verificação e gráficos de controle que possam indicar se uma medição está sob controle estatístico, devem ser parte do esforço de obtenção de avaliações confiáveis de incerteza. O modelo matemático deverá sempre ser revisado quando os dados observados, incluindo o resultado de determinações independentes da mesma grandeza, demonstrarem que o modelo está incompleto. Um experimento bem projetado facilita as avaliações confiáveis da incerteza e é uma parte importante da arte de medição.

De forma a decidir se um sistema de medição está funcionando adequadamente, a variarbilidade observada experimentalmente de seus valores de saída, conforme medida pelo seu desvio padrão observado é, frequentemente, comparada com o desvio padrão previsto, obtido através da combinação dos vários componentes da incerteza que caracterizam a medição. Em tais casos, somente aqueles componentes (obtidos de avaliações Tipo A ou Tipo B) que poderiam contribuir para a variabilidade experimentalmente observada destes valores de saída devem ser considerados.

Tal análise pode ser facilitada, quando reunimos aqueles componentes que contribuem para a variabilidade e aqueles que não o fazem em dois grupos separados e adequadamente rotulados.

Em alguns casos, a incerteza de uma correção para um efeito sistemático não precisa ser incluída na avaliação da incerteza de um resultado de medição. Embora a incerteza tenha sido avaliada, ela pode ser ignorada se sua contribuição para a incerteza padrão combinada de um resultado de medição é insignificante. Se o valor da própria correção for insignificante relativamente à incerteza padrão combinada, ele também pode ser ignorado.

Muitas vezes ocorre na prática, especialmente no domínio da metrologia legal, que um equipamento é ensaiado através de uma comparação com um padrão de medição e as incertezas associadas com o padrão e com o procedimento de comparação são desprezíveis relativamente à exatidão requerida do ensaio. Um exemplo é o uso de um conjunto de padrões de massa bem calibrados para verificar a exatidão de uma balança comercial. Em tais casos, como os componentes da incerteza são pequenos o bastante para serem ignorados, a medição pode ser vista como determinação do erro do equipamento sob ensaio.

Exemplo 1.2.1

Um padrão de tensão Zener de alta qualidade é calibrado por comparação com uma referência de tensão de efeito Josephson baseado no valor convencional da constante Josephson recomendada para uso internacional pelo CIPM. A incerteza padrão combinada relativa $ u_c(V_S)/V_S $ da diferença de potencial calibrada $ V_S $ é relatada em termos do valor convencional, mas $ u_c(V_S)/V_S $ é $ 4\times10^{-7} $ quando $ V_S $ é relatada em termos da unidade SI da diferença de potencial, volt($ V $), por causa da incerteza adicional associada com o valor SI da constante Josephson.

Erros grosseiros no registro ou na análise dos dados podem introduzir um erro desconhecido significativo no resultado de uma medição. Grandes erros grosseiros podem ser, geralmente, identificados por uma revisão apropriada dos dados. Pequenos erros grosseiros podem ser mascarados por variações aleatórios, ou até mesmo podem aparecer como tais. Medidas de incerteza não são projetadas para levar em conta tais erros.

A avaliação da incerteza não é uma tarefa de rotina nem uma tarefa puramente matemática, ela depende de conhecimento detalhado da natureza da grandeza e da medição. A qualidade e utilidade da incerteza indicada para o resultado de uma medição, dependem, portanto, e em última análise, da compreensão, análise crítica e integridade daqueles que contribuem para o estabelecimento de seu valor.

Resultado da medição

Encontramos a expressão de um resultado de medição incompleta caso esta não se apresente com a declaração da incerteza de medição associada. A incerteza de um resultado define uma faixa de valores em torno da média das medições, dentro da qual o valor verdadeiro da grandeza se encontra com nível de confiança estabelecido.

$${Resultado} = {Média~(das~medidas)} - {Erro~Sistemático} \pm {IM~(Incerteza)}$$

Embora não seja ainda de entendimento geral e até mesmo algumas vezes de desconhecimento de alguns, cumpre-nos observar que dentre as parcelas mostradas na expressão do resultado de uma medição a IM (incerteza de medição) é a mais importante, até mesmo do que a média (das medidas) e mereceria uma maior compreensão e aplicação.

Vejamos um exemplo em que a um metrologista fosse solicitado para medir as dimensões do seu laboratório de metrologia para a preparação de um layout, e este não dispusesse de trena ou qualquer outro meio de medição. Neste poderíamos utilizar as dimensões padronizadas das placas do piso (por exemplo Paviflex, 30 $ \times $ 30 cm) e após uma contagem do número de placas em cada lado emitir um resultado de medição como o seguinte: 4,0 $ \times $ 4,0 m $ \pm $ 0,15 m.

Metrologicamente falando, o resultado da sua medição está correto mesmo se o solicitante não estivesse satisfeito com a IM apresentada e neste caso o mesmo poderia propor uma alteração no procedimento de medição utilizado, como por exemplo, o uso de uma trena.

Sob o mesmo ponto de vista, errado estaria se a medição fosse feita, por exemplo, com uma trena e o resultado apresentado fosse: 4,010 $ \times $ 4,047 m (sem a declaração da IM).

Fluxo para o Cálculo de Incerteza

(imagem em falta)

1.3 - Avaliação da Incerteza Padrão

Em muitos casos, uma grandeza $ \mathbf{y} $ não é medida diretamente, mas é determinada em função de $ n $ outras grandezas $ \mathbf{x_1, x_2,\dots, x_n} $, através de uma relação funcional $ \mathbf{f} $, que vem a ser

$$\mathbf{y = f (x_1, x_2,\dots, x_n)}.$$

As grandezas de entrada $ \mathbf{x_1, x_2,\dots, x_n} $, sobre o qual o valor de saída $ \mathbf{y} $ depende, pode ser uma medida ou depender de outras variáveis, incluindo correções e fatores de correções para efeitos sistemáticos. A função $ \mathbf{f} $ pode ser determinada experimentalmente, ou existe somente, como um algoritmo que pode ser avaliado numericamente.

As grandezas de entradas $ \mathbf{x_1, x_2,\dots, x_n} $ podem ser caracterizadas como:

• Quantidade cujos valores e incertezas são determinados diretamente da medição. Esses valores e incertezas podem ser obtidos de uma simples observação, repetidas observações ou julgamentos baseados na experiência.

Também podem envolver as determinações de correções para indicação dos instrumentos e correções por grandezas de influências, tais como: temperatura ambiente, pressão barométrica e umidade;

• Valores e incertezas, os quais são conduzidos para uma medição de fontes externas, tais como:

grandezas associadas com calibração de padrões, certificados de materiais de referência e referência de informações obtidas através de manuais.

Exemplo 1.3.1

Para medirmos o volume, podemos utilizar o seguinte método

$$Vol=\frac{Massa}{Densidade}$$

, onde a grandeza volume é obtida através das grandezas massa e densidade.

A estimativa do desvio padrão, associado com cada estimativa de entrada $ \mathbf{x_i} $ é denominada de \textbf{incerteza padrão} e indicada por $ \mathbf{u(x_i)} $.

A estimativa do desvio padrão, associado com a estimativa do resultado de medição $ \mathbf{y} $, é denominada incerteza padrão combinada e indicada por $ \mathbf{u_c(y)} $, e é determinada pela combinação das incertezas padrão associada com as estimativas de entrada ($ \mathbf{x_i} $). Cada estimativa de entrada $ \mathbf{x_i} $ e sua incerteza associada $ \mathbf{u(x_i)} $ são obtidas pela distribuição dos valores de uma grandeza de entrada ($ \mathbf{x_i} $).

A avaliação da incerteza de medição “Tipo A” é baseada na distribuição de frequência, enquanto que a avaliação “Tipo B” é baseada em informações disponíveis da variabilidade da grandeza de entrada ($ \mathbf{x}_\mathbf{i} $).

Exemplo 1.3.2

(NIS 3003, 1995) Calibração de uma massa padrão com valor nominal 10kg de classe M1, utilizando um comparador. Neste caso, obtemos a equação da massa desconhecida $ W_{X} $, por

$$W_{X} = W_{S} + D_{S} + \delta C + Ab + \Delta W.$$

Na prática não aplicamos correções para esta classe de massa e o comparador tem linearidade desconhecida. Entretanto, associamos incertezas para estas contribuições.

Símbolo	Fonte de Incerteza	Tipo	Limites	Média
$ W_{S} $	Massa padrão	B	± 30mg (k=2)	10kg
$ D_{S} $	Deriva (drift) massa padrão	B	± 15mg	0
$ \delta C $	Linearidade do comparador	B	± 10mg	0
$ Ab $	Efeito do ar	B	± 10mg	0
$ \Delta W $	Repetitividade	A

Exemplo 1.3.3

Determinar a incerteza da área de um círculo cujo diâmetro foi medido experimentalmente através de um sistema de medição denominado paquímetro.

Valor do diâmetro obtido com o paquímetro com resolução de 0,01 mm e incerteza expandida U= 0,02 mm (k = 2):

Leituras	Diâmetro
1	10,28
2	10,26
3	10,28
4	10,3
5	10,28

A expressão para o cálculo da área é dada por

$$y=\frac{1}{4}\pi d^2,$$

Exemplo 1.3.4

Determinar a incerteza de medição na composição de dois blocos padrão, que foram medidos pelo mesmo sistema de medição.

• Bloco 1

Dimensão nominal: 10 mm.

Incerteza Expandida: $ u(x_1)=0,0077~mm $ para $ k = 2 $.

• Bloco 2

Dimensão nominal: 20 mm.

Incerteza Expandida: $ u(x_2)=0,084~mm $ para $ k = 2 $.

O resultado da combinação dos blocos pode ser expresso matematicamente por

$$\mathbf{y = x_1 + x_2}$$

1.4 - Incerteza do Tipo A

Na grande maioria dos casos, a melhor estimativa para o valor esperado de uma quantidade que varia aleatoriamente e para o qual temos n leituras independentes k obtidas sob condições de repetitividade, corresponde a média aritmética.

Assim, quando a estimativa de uma grandeza de entrada $ x_i $ tem sido obtida de n medidas sob condições de repetitividade, a incerteza padrão $ \mathbf{u(x_i)} $ é obtida pela estimativa da variância da média. Esta é dada por

$$s_{\overline{X}}=\frac{s}{\sqrt{n}},$$

em que n número de medidas e s desvio padrão correspondente às n leituras.

Exemplo 1.4.1

Voltando ao Exemplo 1.3.2. Considerando o processo de calibração da massa padrão do exemplo anterior, o avaliador realizou cinco medidas da diferença entre a massa padrão e a massa desconhecida. Os resultados estão abaixo.

Leitura 1	15 mg
Leitura 2	25 mg
Leitura 3	20 mg
Leitura 4	13 mg
Leitura 5	18 mg
Média	18,20 mg
Desvio Padrão	4,66 mg
Desvio Padrão da Média	2,08 mg

Calculando a Incerteza do Tipo A, obtemos:

$$ u(\varepsilon)=\frac{s}{\sqrt{n}}=\frac{4,66}{\sqrt{5}}=2,08~ mg $$

Exemplo 1.4.1

Voltando ao Exemplo 1.3.3.

Leituras	Diâmetro	Área
1	10,28	82,99963
2	10,26	82,67699
3	10,28	82,99963
4	10,3	83,3229
5	10,28	82,99963
Média das Leituras	10,28	82,99976
Desvio Padrão das Leituras	0,014142	0,228364
Desvio Padrão da Média das Leituras	0,006325	0,102128

Para a grandeza Área, Incerteza do Tipo A é dada por:

$$ u(\varepsilon)=\frac{s}{\sqrt{n}}=\frac{0,228364}{\sqrt{5}}=0,102128~ mm^2 $$

1.5 - Incerteza do Tipo B

Para uma estimativa de uma grandeza de entrada $ \mathbf{x_i} $, que não tenha sido obtida de observações repetidas, a variância estimada $ \mathbf{u^{2}(x_i)} $ ou a incerteza padrão $ \mathbf{u(x_i)} $ é avaliada pelo julgamento específico baseado em todas as informações disponíveis na variabilidade de $ \mathbf{x_i} $. No conjunto destas informações, incluímos:

a) Informações prévias de medição;

b) Experiência ou conhecimento geral do comportamento e propriedades dos instrumentos e materiais relevantes;

c) Especificações do fabricante;

d) Informações de certificados de calibração e outras especificações;

e) Incerteza transmitida pelas informações de referências obtidas de manuais.

Por conveniência, $ \mathbf{u^{2}(x_i)} $ e $ \mathbf{u(x_i)} $ avaliados desta maneira são chamados de Variância Tipo B e Incerteza Padrão Tipo B, respectivamente.

O propósito de usar várias informações disponíveis para a avaliação da incerteza padrão do Tipo B é para buscar um discernimento baseado na experiência e nos conhecimentos gerais, e é uma habilidade que pode ser obtida com a prática. É reconhecido que uma avaliação da incerteza pelo Tipo B pode ser tanto confiável quanto a do Tipo A, especialmente na situação em que a avaliação do Tipo A é baseada na comparação de pequenos números de observações estatisticamente independentes (ISO GUM, 2008).

A seguir, são apresentados 4 suposições disponíveis para as grandezas de entradas de influência $ \mathbf{x_i} $, para a avaliação da incerteza padrão Tipo B.

Caso 1

Se a estimativa $ \mathbf{x_i} $ é retirada da especificação do fabricante, certificados de calibração, manuais ou outras fontes, sua incerteza padrão $ \mathbf{u(x_i)} $ é simplesmente o valor citado dividido pelo multiplicador.

Exemplo 1.5.1

Voltando ao exemplo 1.3.2 o certificado de calibração afirma que a massa padrão com valor nominal de 10kg de classe M1 tem como incerteza $ 30~ mg $ para o nível de confiança com k = 2.

A incerteza da massa padrão, é então

$$\mathbf{u(W_S)= \frac{30~mg}{2} =15~mg}.$$

A incerteza de $ \mathbf{x_i} $ não necessariamente é relatada como um múltiplo de um desvio padrão, como abordado acima. Em vez disso, podemos encontrar uma declaração que a incerteza declarada possui 90%, 95% ou 99% de nível de confiança.

Salvo indicação contrária, poderá assumir que uma distribuição normal (ou t-Student) será utilizada para o cálculo da incerteza declarada, e a incerteza padrão $ \mathbf{u(x_i)} $ pode ser encontrada dividindo-se a incerteza declarada por um fator k, apropriado da distribuição normal.

Exemplo 1.5.2

Um certificado de calibração afirma que a resistência de um resistor padrão $ R_S $ de valor nominal $ 10\Omega $ é $ 10,000742 \Omega $ a 23ºC e com incerteza de $ 129 \mu\Omega $, definindo um intervalo com nível de significância de 99%.

A incerteza padrão é dada por

$$u(R_S)= \frac{129}{2,58} = 50~\mu \Omega.$$

Neste caso, utilizamos a tabela da distribuição Normal para determinar o valor de k.

Exemplo 1.5.3

Voltando ao exemplo 1.3.4.

A incerteza padrão obtemos $ u(x_i) $ de cada bloco é obtido dividindo a incerteza expandida pelo fator k. Assim

$$u(x_1) = 0,077 / 2 =0,0385$$

$$u(x_2) = 0,084 / 2 =0,042$$

Exemplo 1.5.4

Voltando ao exemplo 1.3.3

A incerteza expandida do paquímetro, definida no certificado de calibração do mesmo, é de 0,02 com fator de abrangência k=2. Desta forma, a incerteza herdada do equipamento é de

$$u(d)=\frac{0,02}{2}=0,01~mm$$

Caso 2

Em alguns casos, pode ser possível estimar somente os limites (limite superior $ \mathbf{a_+} $ e inferior $ \mathbf{a_-} $) para $ \mathbf{x_i} $, por exemplo, quando a grandeza de influência é a variação da temperatura. Neste caso, consideramos que a probabilidade de que o valor de $ \mathbf{x_i} $ se encontre dentro do intervalo $ \mathbf{a_-} $ até $ \mathbf{a_+} $, para todo propósito prático, é igual a 1 e a probabilidade que $ \mathbf{x_i} $ esteja fora deste intervalo é essencialmente zero. Se não há conhecimento

específico sobre a possibilidade do valor $ \mathbf{x_i} $ estar dentro do intervalo, pode-se somente admitir que, é igualmente provável encontrá-lo por toda parte, dentro do intervalo (uma distribuição uniforme ou retangular).

Logo $ \mathbf{x_i} $ é o ponto médio do intervalo, onde:

$ \mathbf{x_i = \frac{(a_-+ a_+)}{2}} $, cuja variância associada é dada por

$$\mathbf{u^2(x_i) = \frac{(a_+-a_-)^2}{12}}.$$

Se a diferença entre os limites $ \mathbf{(a_+ - a_-)} $, é representada por $ \mathbf{2a} $, ou seja, os limites são simétricos, então a equação para variância será

$$\mathbf{u^2(x_i) = \frac{a^2}{3}}.$$

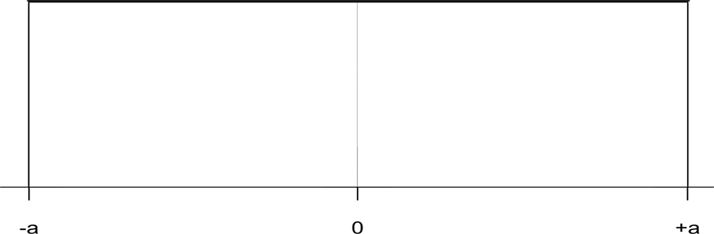
$$u=\frac{base}{2\sqrt{3}}=\frac{2a}{2\sqrt{3}}=\frac{a}{\sqrt{3}}.$$

Exemplo 1.5.5

Um manual estabelece que o valor do coeficiente linear de expansão térmica de um bloco padrão de aço é determinado por $ \alpha_S = 11,5 \times 10^{-6}~^{\circ} C^{-1} $ e que o “erro'' neste valor não deve exceder $ 2 \times 10^{-6}~^{\circ} C^{-1} $. Baseado nesta informação limitada, é razoável assumir que o

coeficiente de expansão térmica pertença ao intervalo: $ 9,5 \times10^{-6}~^{\circ} C^{-1} $ até $ 13,5 \times 10^{-6}~^{\circ} C^{-1} $, com probabilidade 1. A incerteza padrão do coeficiente de expansão térmica é dado por

$$u(\alpha_S)=\frac{(2\times 10^{-6})}{\sqrt{3}}=1,2 \times 10^{-6}~^{\circ} C^{-1}.$$

Caso 3

Os limites superiores e inferiores $ \mathbf{a_-~{e}~a_+} $ para uma grandeza de entrada $ \mathbf{x_i} $ podem não ser simétricos, ou seja, se o limite inferior é escrito como $ \mathbf{a_- = x_i - b_-} $ e o limite superior como $ \mathbf{a_+ = x_i + b_+} $, então $ \mathbf{b_- \neq~ b_+} $. Neste caso, $ \mathbf{x_i} $ não é o centro do intervalo $ \mathbf{(a_-,a_+)} $ e a distribuição de probabilidade de $ \mathbf{x_i} $ não pode ser uniforme. Entretanto, pode não existir informação suficiente para escolher uma distribuição apropriada e diferentes modelos conduzirão para diferentes expressões para a variância.

Na ausência de tais informações, uma simples aproximação é

$$u^2(x_i)=\frac{(b_+ + b_-)^2}{12}=\frac{(a_+ + a_-)^2}{12}$$

que corresponde a variância da distribuição retangular com comprimento $ \mathbf{b_- + b_+} $.

Exemplo 1.5.6

Exemplo 1.5.7

Voltando ao Exemplo 1.3.2 da calibração da massa padrão, vamos estimar as incertezas padrão do Tipo B.

Símbolo	Fonte de Incerteza	Limites	Distribuição	Incerteza
$ W_S $	Massa Padrão	$ \pm $ 30 mg	Normal	$ \frac{30}{2} = $15 mg
$ D_S $	Deriva (drift) massa padrão	$ \pm $ 15 mg	Retangular	$ \frac{15}{\sqrt{3}}= $8,66 mg
$ \delta_C $	Linearidade do comparador	$ \pm $ 10 mg	Retangular	$ \frac{10}{\sqrt{3}}= $5,77 mg
Ab	Efeito do ar	$ \pm $ 10 mg	Retangular	$ \frac{10}{\sqrt{3}}= $5,77 mg

Exemplo 1.5.8

Voltando ao exemplo 1.3.3

A resolução do paquímetro segue uma distribuição retangular com base dada pela própria resolução que é de 0,01 mm. Assim, a incerteza devido a resolução é

$$u({Res}_d)=\frac{{Res}_d}{2\sqrt{3}}=\frac{0,01}{2\sqrt{3}}=0,002887~mm$$

Caso 4

Nos casos acima não temos informação sobre os valor da grandeza $ X_i $, apenas que ela se encontra dentro dos limites especicados. Por isso, assumimos que os valores da grandeza são equiprováveis dentro destes limites, e que tem probabilidade zero de estar fora destes limites. Muitas vezes é mais realista assumirmos que valores perto dos limites especificados são menos prováveis do que valores próximos ao centro. Neste caso, é razoável trocarmos a distribuição triangular. Assumindo uma distribuição triangular para a grandeza $ X_i $, obtemos como média $ \mathbf{x_i = (a_+ + a_-) / 2} $ com incerteza associada $ \mathbf{u^2(x_i) = a^2 / 6} $.

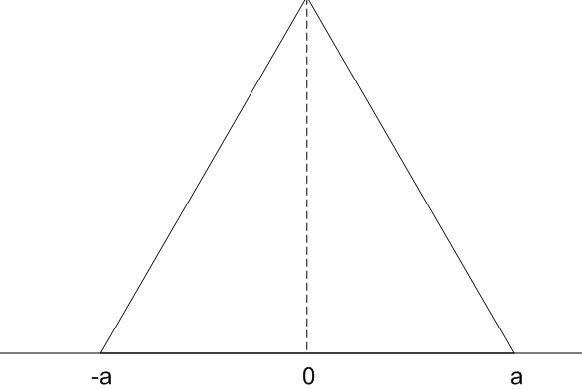
Assim,

$$u=\frac{base}{2\sqrt{6}}=\frac{2a}{2\sqrt{6}}=\frac{a}{\sqrt{6}}.$$

1.6 - Incerteza Padrão combinada

Quando a incerteza do resultado do mensurado $ \mathbf{y} $ é obtida pela combinação das incertezas padrão das estimativas de entrada $ \mathbf{x_1, x_2,\dots, x_N} $, esta incerteza combinada da estimativa $ \mathbf{y} $ é representada por $ \mathbf{u_c(y)} $ e denominada de incerteza padrão combinada.

As estimativas de entrada $ x_1, x_2,\dots, x_N $, podem ser classificadas como grandezas:

• Estatisticamente independentes ou não correlacionadas;
• Estatisticamente dependentes ou correlacionadas.

Grandezas de entrada não correlacionadas

Para as grandezas estatisticamente independentes, consideramos as séries de medições que foram realizadas com diferentes sistemas de medição. Neste caso, a incerteza padrão combinada $ \mathbf{u_c(y)} $ é a raiz quadrada positiva da variância combinada.

A expressão para se determinar esta incerteza padrão combinada no caso não correlacionado é apresentada por

$$u^2_c(y)=\sum_{i=1}^N\left(\frac{\partial y}{\partial x_i}\right)^2u^2(x_i),~~~(1.6.1)$$

em que $ u(x_i) $ é a incerteza padrão associada com a grandeza de entrada X$ _i $. As derivadas parciais ($ \partial f/\partial x_i $) calculadas no ponto $ x_i $ são denominadas coeficientes de sensibilidade, pois descrevem como a estimativa de y varia com pequenas mudanças nos valores das estimativas das grandezas de entrada $ \mathbf{x_1,x_2,\dots, x_N} $.

Exemplo 1.6.1

Voltando ao Exemplo 1.3.2. Na calibração da massa padrão, obtemos a seguinte incerteza combinada

$$u_c(W_X)=\sqrt{u^2(W_s) + u^2(D_s) + u^2(\delta C) + u^2(Ab) + u^2(\Delta W)} =$$

$$=\sqrt{(15)^2 + (8,66)^2 + (5,77)^2 + (5,77)^2 + (2,08)^2} = 19,26~mg.$$

Exemplo 1.6.1

Voltando ao Exemplo 1.3.3, obtemos:

Admitimos que $ \frac{1}{4} $ e $ \pi $ são constantes isentas de incerteza ou com incertezas desprezíveis, somente a variável $ d $ é considerada para cálculo da incerteza. Primeiramente calcularemos o coeficiente de sensibilidade da seguinte forma

$$\frac{\partial y}{\partial d}=\frac{\pi~d}{2}$$

Assim, a incerteza combinada da área é calculada da seguinte forma

$$u_c(y)~=\sqrt{\left(\frac{\pi d}{2}\right)^2~(u^2(d)+u^2({Res}_d))+u^2(\varepsilon)}=$$

$$=\sqrt{\left(\frac{3,1415\times 10,28}{2}\right)^2~(0,01^2+0,002887^2)+0,102128^2}=0,196669~mm^2$$

um segundo modo de expressarmos a incerteza é como incerteza combinada relativa e calculamos da seguinte forma

$$\frac{ u^2_{c}(y)}{y^2}~=~\frac{\left(\frac{\pi~d}{2}\right)^2(u^2(d)+u^2({Res}_d))}{\left(\frac{\pi~d^2}{4}\right)^2}+\frac{u^2(\varepsilon)}{\left(\frac{\pi~d^2}{4}\right)^2}=$$

$$=\frac{4~(u^2(d)+u^2(Res_d))}{d^2}+\frac{16~u^2(\varepsilon)}{(\pi~d^2)^2}$$

Assim a incerteza relativa é expressa como

$$u_{cr}(y)=\frac{2~\sqrt{u^2(d)+u^2(Res_d)+\frac{4~u^2(\varepsilon)}{(\pi~d^2)^2}}}{d}$$

Substituindo os valores do exemplo, obtemos a incerteza combinada relativa

$$u_{cr}(y)=\frac{2~\sqrt{0,01^2+0,002887^2+\frac{4~0,102128^2}{(\pi~10,28^2)^2}}}{10,28}=0,00237$$

À partir da incerteza combinada relativa, obtemos a incerteza combinada da Área na forma:

$$u_c(y)=u_{cr}(y)\times {Área}=0,00237\times 82,99963=0,196709~mm^2.$$

Grandezas de entrada correlacionadas

Para as grandezas estatisticamente dependentes, consideramos as séries de medições que foram realizadas com os mesmos sistemas de medição, ou seja, consideremos o seguinte modelo matemático

$$y=x_i+x_j,~~~i=j=1,\dots,N$$

Neste caso, a covariância estimada deve ser considerada como uma contribuição adicional para a incerteza. A expressão para se determinar esta incerteza padrão combinada no caso correlacionado é apresentada por

$$u^2_c(y)=\displaystyle\sum^N_{i=1}\sum^N_{j=1}\frac{\partial y}{\partial x_i}\frac{\partial y}{\partial x_j}u(x_i,x_j)=$$

$$=\underbrace{\sum^N_{i=1}\left[\frac{\partial y}{\partial x_i}\right]^2 u^2(x_i)}_{(I)}+\underbrace{2\sum^{N-1}_{i=1}\sum^N_{j=i+1}\frac{\partial y}{\partial x_i}\frac{\partial y}{\partial x_j}u(x_i,x_j)}_{(II)}~~(1.6.2)$$

em que, $ u(x_i,x_j)=u(x_j,x_i) $ é a incerteza correlacionada, associada as grandezas de entrada $ X_i $ e $ X_j $.

Assim, dividindo e multiplicando a equação (1.6.1) por $ u(x_i)u(x_j), $ em (II)obtemos

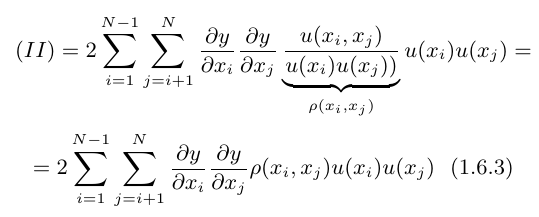
em que $ \rho(x_i,x_j) $ é o grau de correlação entre $ x_i $ e $ x_j $ com $ \rho(x_i,x_j)=\rho(x_j,x_i) $ e tomando $ -1\leq \rho(x_i,x_j)\leq 1. $ Logo, substituindo a equação (1.6.3) na equação (1.6.2), obtemos

$$u^2_c(y)=\sum^N_{i=1}\left[\frac{\partial y}{\partial x_i}\right]^2 u^2(x_i)+2\sum^{N-1}_{i=1}\sum^N_{j=i+1}\frac{\partial y}{\partial x_i}\frac{\partial y}{\partial x_j}\rho(x_i,x_j)u(x_i)u(x_j)~~(1.6.4)$$

Se as variáveis $ x_i $ e $ x_j $ são independentes, temos que $ \rho(x_i,x_j)=0, $ e a equação (1.6.4) se reduz a equação (1.6.1). Tomaremos o caso extremo em que $ \rho(x_i,x_j)=1, $ obtemos equação aproximada da incerteza de medição no caso correlacionado da seguinte forma

$$u^2_c(y)\approx\sum^N_{i=1}\left[\frac{\partial y}{\partial x_i}\right]^2 u^2(x_i)+2\sum^{N-1}_{i=1}\sum^N_{j=i+1}\frac{\partial y}{\partial x_i}\frac{\partial y}{\partial x_j}u(x_i)u(x_j)~~(1.6.5)$$

Exemplo 1.6.2

Voltando ao exemplo 1.3.4. Então, obtemos a expressão (1.6.5) da seguinte forma

$$u^2(y)=\frac{\partial y}{\partial x_1}u^2(x_1)+\frac{\partial y}{\partial x_2}u^2(x_2)+2\frac{\partial y}{\partial x_1}\frac{\partial y}{\partial x_2}u(x_1)u(x_2)~~(*)$$

Da expressão do exemplo 1.3.4, obtemos os coeficientes de sensibilidade:

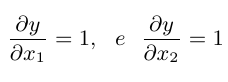
Assim, obtemos a expressão (*) da seguinte forma

$$u^2(y)=1~u^2(x_1)+1~u^2(x_2)+2~u(x_1)u(x_2)=$$

$$=(u(x_1)+u(x_2))^2$$

Daí, obtemos a seguinte equação

$$u(y)=u(x_1)+u(x_2)$$

Substituindo os valores, temos

$$u(y)=0,0385+0,042=0,0805~mm$$

1.7 - Incerteza Expandida

Embora a incerteza combinada $ u_c(y) $ possa ser universalmente usada para expressar a incerteza de um resultado de medição (devido a necessidade de algumas indústrias e aplicações comerciais, bem como requisitos em áreas de saúde e segurança) é frequentemente necessário apresentar uma medida de incerteza que defina um intervalo sobre o resultado de medição. Neste caso, a incerteza compreende uma fração da distribuição dos valores, que podem ser razoavelmente atribuídos para um mensurando, denominada de Incerteza Expandida U. Este requisito foi reconhecido pelo Working Group e Recomendações do CIPM, INC (1981).

A incerteza expandida U é obtida pela multiplicação da incerteza padrão combinada $ u_c(y) $ por um fator k.

$$U = k \times u_c(y)$$

O valor do fator k é escolhido com base no nível de confiança requerido para o intervalo. Em geral, k é usado entre 2 e 3. Portanto, para aplicações especiais, k poderá ser determinado conforme o nível de confiança requerido, de acordo com a distribuição normal ou t-Student.

A Namas (NIS 3003 , 1995) recomenda que o fator k seja igual a 2 para calcular a incerteza expandida. Este valor corresponde a aproximadamente 95% de confiança. Entretanto, se as contribuições para a incerteza relativa a repetitividade for grande comparadas com as outras distribuições e o número de repetições for pequeno, existe uma possibilidade de que a distribuição de probabilidade normal não seja adequada. Neste caso, o fator k=2 nos garante um nível de confiança menor que 95%. Aqui, devemos utilizar a distribuição t-Student para encontrar o valor do fator k que garante 95%.

Regra: Se a incerteza do Tipo A for menor que metade da incerteza combinada, vamos utilizar o fator $ k = 2. $ Caso contrário, devemos utilizar a distribuição t-Student para obtermos o valor de k que nos garante um intervalo com 95% confiança. A norma ISO GUM [ver. 2008] recomenda a utilização da equação de Welch-Satterwaite para calcular o grau de liberdade, baseado nos graus de liberdade de cada fonte de incerteza. A fórmula para tal cálculo é dada por

$$\upsilon_{eff}=\displaystyle\frac{u_c^4(y)}{\displaystyle\sum_{i=1}^N u_i^4(y)/\nu_i}= \frac{u_c^4(y)}{u_A^4(y)/\nu_A}=\left(\frac{u_c(y)}{u_A(y)}\right)^4 \nu_A,$$

em que $ u_i(y)=|\frac{\partial f}{\partial x_i}|u(x_i) $, $ \nu_i $ representa os graus de liberdade do fator de incerteza i e $ \nu_A $ representa os graus de liberdade do Tipo A. Para contribuições da incerteza Tipo A, consideramos como graus de liberdade o número de leitura menos 1 vez o número de pontos de calibração. Para os graus de liberdade referente a contribuições da incerteza Tipo B, vamos considerar $ \upsilon_i $ igual a infinito.

Exemplo 1.4.1

Suponha que um sistema de medição com incerteza do Tipo A, baseada em 4 observações, tenha valor $ u_i(y) $ de 3,5 unidades. Existem outras 5 fontes de incerteza do Tipo B que apresentam incerteza estimada muito pequena, de tal forma que a incerteza combinada $ u_c(y) $ seja igual a 5,7 unidades.

Como a incerteza do Tipo A é maior que metade da incerteza combinada, vamos utilizar a distribuição t-Student para determinar o fator $ \mathbf{k} $. Através da equação de Welch-Satterwaite, temos

$$\upsilon_{eff}=\frac{(5,7)^4}{((3,5)^4/(4-1))+ 0 + 0 + 0 + 0 + 0}=21,1.$$

Tomando valor de $ \upsilon_{eff} $ igual a 20, obtemos que k = 2,13.

Exemplo 1.4.2

Voltando ao Exemplo 1.3.2 da calibração da massa padrão, observe que a incerteza do Tipo A é menor que metade da incerteza combinada.

Vamos calcular os graus de liberdade efetivo

$$\upsilon_{eff}=\displaystyle\left(\frac{19,26}{2,08}\right)^4 (5-1)=29405,72$$

Assim, o fator de abrangência k será de 1,96.

Assim, a incerteza expandida é dada por

$$ U= 1,96 \times 19,26 mg = 37,7496~ mg .$$

Exemplo 1.4.3

Voltando ao Exemplo 1.3.3.

Vamos calcular os graus de liberdade efetivo

$$\upsilon_{eff}=\displaystyle\left(\frac{0,196669}{0,102128}\right)^4 (5-1)=55,00735$$

Assim, o fator de abrangência k será de 2,004045.

Logo, a incerteza expandida é dada por

$$ U= 2,004045 \times 0,196669 =0,394133~mm^2 .$$

Exemplo 1.4.4

Voltando ao Exemplo 1.3.4.

Não temos incerteza do tipo A, então o fator de abrangência k é 1,96;

Assim, a incerteza expandida é dada por

$$ U= 1,96 \times 0,0805 = 0,15778~mm .$$

1.8 - Expressão do Resultado da Medição

Nesta seção, discutimos as formas de apresentação do resultado da medição. Para facilitar ao usuário, começamos arrendondando o valor da incerteza expandida conforme a regra abaixo.

Regras de Arredondamento de Valores

Quando desejamos arredondar um número para que este seja expresso com uma certa quantidade de dígitos significativos, devemos aplicar regras convencionais de arredondamento.

Regra 1:

Se o algarismo à direita do último dígito que se pretende representar for inferior a 5, apenas desprezamos os demais dígitos à direita. Exemplo: 3,14159265 para 3,14.

Regra 2:

Se o algarismo à direita do último dígito que se pretende representar for maior que 5, adicionamos uma unidade ao último dígito representado e desprezamos os demais dígitos à direita. Exemplo: 3,14159265 para 3,1416.

Regra 3:

Se o algarismo à direita que se pretende representar for igual a 5, então o arredondamento deve ser tal que o último dígito representado depois do arredondamento deve ser par. Exemplo: 3,14159265 para 3,142.

Números de algarismo na incerteza de medição

Não existe uma regra bem definida para o número de algarismos que devem ser indicados para a incerteza de medição. Em geral, utilizamos 2 algarismos significativos, além dos zeros à esquerda. Em alguns casos, pode ser necessário utilizar mais dígitos significativos para evitar erros de arredondamento nos cálculos subsequentes. Em outros casos, não é possível atribuir mais de 1 algarismo para incerteza de medição.

Resumo:

• Incerteza de medição deve ser apresentada com 2 algarismos quando o primeiro algarismo na incerteza for 1 ou 2.
• Incerteza de medição pode ser apresentada com 1 algarismo quando o primeiro algarismo da incerteza for 3 ou maior.
• Incerteza de medição pode ser representada com 2 algarismos em qualquer caso.

De acordo com as regras acima, apresentamos os exemplos:

Incorreto	Correto
0,144 (mm)	0,14 (mm)
1,026 (s)	1 (s)
3,49 (mm)	3,5 (mm)	ou	3 (mm)
3,51 (mm)	3,5 (mm)	ou	4 (mm)
0,00514 (mm)	0,005 (mm)	ou	0,005 (mm)

Exemplo 1.8.1

Voltando ao exemplo 1.3.2

Neste caso, o resultado da medição é expresso na forma

$$10 000,000~g~+~0,018~g~\pm 0,04~g~(k=1,96),$$

ou seja

$$10 000,018~g~\pm~0,04~g~(k=1,96).$$

Exemplo 1.8.2

Voltando ao exemplo 1.3.3

Neste caso, o resultado da medição é expresso na forma

$$83,0~mm^2~\pm~0,4~mm^2~(k=2).$$

Quando relatamos o resultado de uma medição devemos:

a) Fornecer uma descrição completa de como o mensurando Y é definido;

b) Expressar o resultado da medição: Y=y +/- U e fornecer as unidades de y e U;

c) Incluir a incerteza relativa expandida U / |y|, com y $ \neq $ 0, quando apropriado;

d) Fornecer o valor de k utilizado para obter U;

e) Fornecer o nível de confiança aproximado associado com o intervalo y +/- U e explicar como foi obtido;

1.9 - Teste de Valor Extremo (Grubbs)

Este teste é desenvolvido para verificar a presença de valores extremos em observações amostrais. Valores extremos podem ser considerados como manifestações da variabilidade aleatória inerente aos dados, ou apenas um erro no cálculo durante o recolhimento dos dados e até mesmo uma anotação precipitada pelo operador.

Existem inúmeros critérios para testar valores extremos. Em todos eles, desenvolvemos o cálculo numérico amostral (estatística) e comparamos com um valor crítico baseado na teoria de amostras aleatórias, para decidirmos se existe ou não uma observação considerada valor extremo.

No teste de Grubbs, usamos a seguinte estatística

$$Z~=~\frac{| x_i ~-~\overline{x} |}{s}$$

em que

• $ x_i $: é uma observação da amostra $ x_1, x_2, \cdots, x_n $;
• $ \overline{x} $: é a média amostral;
• $ s $: é o desvio padrão amostral.

Esta estatística testa as seguintes hipóteses

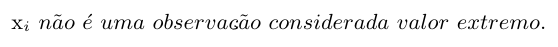
(há elementos em falta na equação acima)

Rejeitamos a hipótese $ H_0 $, com nível de significância $ \alpha $, se $ Z > Z_c $. No qual $ Z_c $ é um valor crítico baseado na distribuição de Z e encontra-se na tabela (ver F. E. Grubbs (1969)) de valores de $ \alpha $ unicaudais. Na Tabela 1.9.1 , encontramos alguns valores críticos para $ \alpha $ = 10%, 5%, 2,5%, 1% e 0,5%.

n	0,1	0,05	0,025	0,01	0,005
3	1,148	1,153	1,154	1,155	1,155
4	1,425	1,462	1,481	1,492	1,496
5	1,602	1,671	1,715	1,749	1,764
6	1,729	1,822	1,887	1,944	1,973
7	1,828	1,938	2,02	2,097	2,139
8	1,909	2,032	2,127	2,221	2,274
9	1,977	2,11	2,215	2,323	2,387
10	2,036	2,176	2,29	2,41	2,482
11	2,088	2,234	2,355	2,484	2,564
12	2,134	2,285	2,412	2,549	2,636
13	2,176	2,331	2,462	2,607	2,699
14	2,213	2,372	2,507	2,658	2,755
15	2,248	2,409	2,548	2,705	2,806
16	2,279	2,443	2,586	2,747	2,852
17	2,309	2,475	2,62	2,785	2,894
18	2,336	2,504	2,652	2,821	2,932
19	2,361	2,531	2,681	2,853	2,968
20	2,385	2,557	2,708	2,884	3,001
21	2,408	2,58	2,734	2,912	3,031
22	2,429	2,603	2,758	2,939	3,06
23	2,449	2,624	2,78	2,963	3,087
24	2,468	2,644	2,802	2,987	3,112
25	2,486	2,663	2,822	3,009	3,135
26	2,503	2,681	2,841	3,029	3,158
27	2,52	2,698	2,859	3,049	3,179
28	2,536	2,714	2,876	3,068	3,199
29	2,551	2,73	2,893	3,086	3,218
30	2,565	2,745	2,908	3,103	3,236
31	2,579	2,76	2,924	3,119	3,253
32	2,592	2,773	2,938	3,135	3,27
33	2,605	2,787	2,952	3,15	3,286
34	2,618	2,799	2,965	3,164	3,301
35	2,63	2,812	2,978	3,178	3,316
36	2,641	2,824	2,991	3,191	3,33
37	2,652	2,835	3,003	3,204	3,343
38	2,663	2,846	3,014	3,216	3,356
39	2,674	2,857	3,025	3,228	3,369
40	2,684	2,868	3,036	3,239	3,381
50	2,772	2,957	3,128	3,337	3,482
60	2,841	3,027	3,2	3,411	3,56
70	2,898	3,084	3,258	3,471	3,622
80	2,946	3,132	3,306	3,521	3,673
90	2,987	3,173	3,348	3,563	3,716
100	3,024	3,21	3,384	3,6	3,754
110	3,056	3,242	3,416	3,633	3,787
120	3,086	3,271	3,445	3,662	3,817
130	3,112	3,297	3,471	3,688	3,843
140	3,136	3,321	3,495	3,712	3,867

Tabela 1.9.1: Tabela do teste de Grubbs.

Exemplo 1.9.1

Considere as seguintes medições:

Medidas
11,89896
11,9596
11,89856
11,91408
12,04252
12,1531
11,94553
11,8682
11,85949
12,13373
12,6

Vamos calcular a média e o desvio padrão:

$$\overline{x}=\frac{11,89+11,95+\dots+12,6}{11}=12,02489$$

$$s=\sqrt{\frac{(11,89-12,024)^2+(11,95-12,024)^2+\dots+(12,6-12,024)^2}{11-1}}=0,215851$$

Com isso, vamos calcular para o ponto 11 o teste de Grubbs, usando a seguinte estatística

$$Z~=~\frac{| x_i ~-~\overline{x} |}{s}=\frac{|x_{11}-\overline{x}|}{s}=\frac{|12,6-12,02489|}{0,215851}=2,664396$$

Como $ Z> 2,3547, $ então, essa medida é um valor extremo (outlier).

Resultados desse exemplo obtidos com o software Action:

(imagem em falta)

Exercício 1.9.1

Considere as seguintes medições na tabela 1.9.2 e calcule a média, desvio padrão e o teste de Grubbs:

Medidas
9,988031
10,02081
9,997529
10,06985
9,995944
10,1367
9,936079
9,880081
9,99015
10,04604
11

Tabela 1.9.2: Medições.

1.10 - Comparação entre Sistemas de Medição

Vamos apresentar uma técnica para comparar dois sistemas de medição. Para ilustrar, vamos considerar um exemplo.

Exemplo 1.10.1

O diâmetro de um anel padrão pode ser medido por dois tipos de sistemas de medição. Para comparar estes sistemas de medição, um anel padrão foi medido 5 vezes por cada sistema de medição utilizando o mesmo operador. Os resultados estão abaixo.

	SM1	SM2
Média	15,601 mm	15,603 mm
Incerteza Expandida	0,001 mm	0,0015 mm

Etapa 1

Calcular a Estatística

$$EN~=~\frac{| MSM1~-~MSM2 |}{\sqrt{USM1^2~+~USM2^2}}$$

em que

• MSM1: representa a média do sistema de medição 1;
• MSM2: representa a média do sistema de medição 2;
• USM1: representa a incerteza expandida do sistema de medição 1;
• USM2: representa a incerteza expandida do sistema de medição 2.

Com isso, temos que

$$EN~=~\frac{| 15,601~-~15,603 |}{\sqrt{(0,001)^2~+~(0,0015)^2}}~=~\frac{0,002}{0,0018}~=~1,109.$$

Etapa 2

• Se EN ≤ 1, os dois sistemas de medição são compatíveis;
• Se EN > 1, os dois sistemas de medição não são compatíveis, isto é, os sistemas de medição apresentam diferenças significativas.

Como, no exemplo, EN=1,109 é maior que 1, concluímos que existe uma diferença significativa entre os dois sistemas de medição.

Exercício

Durante o processo de acreditação do laboratório de ensaio de potência efetiva líquida do motor, o INMETRO exigiu um estudo de comparação inter laboratorial. Com o motor em marcha lenta, foi realizado um ensaio de potência pelo laboratório participante e um laboratório de referência. Com os dados apresentados na tabela abaixo, calcule o erro normalizado e faça as devidas conclusões.

	Lab Ref	Laboratório
Média	11,601	12,613
Incerteza Expandida	0,3	0,4

2 - Análise e interpretação do Certificado de Calibração

A Comprovação Metrológica geralmente inclui calibração ou verificação, qualquer ajuste ou reparo necessário, recalibração, comparação com os requisitos metrológicos para o uso pretendido do equipamento, assim como qualquer etiqueta ou lacre necessários. Para alcançarmos ela, necessitamos que a adequação do equipamento de medição para seu uso tenha sido demonstrada e documentada. Em resumo, definimos a comprovação metrológica como sendo o conjunto de operações necessária para assegurar que um equipamento de medição atenda aos requisitos do seu uso pretendido. Esta seção foi elaborada com base na norma ABNT NBR ISO 10012:2004.

Os requisitos para o uso pretendido incluem:

• Amplitude;
• Resolução;
• Erro Máximo Permissível.

Apresentamos um diagrama dos processo envolvidos na comprovação metrológica na Figura 2.1

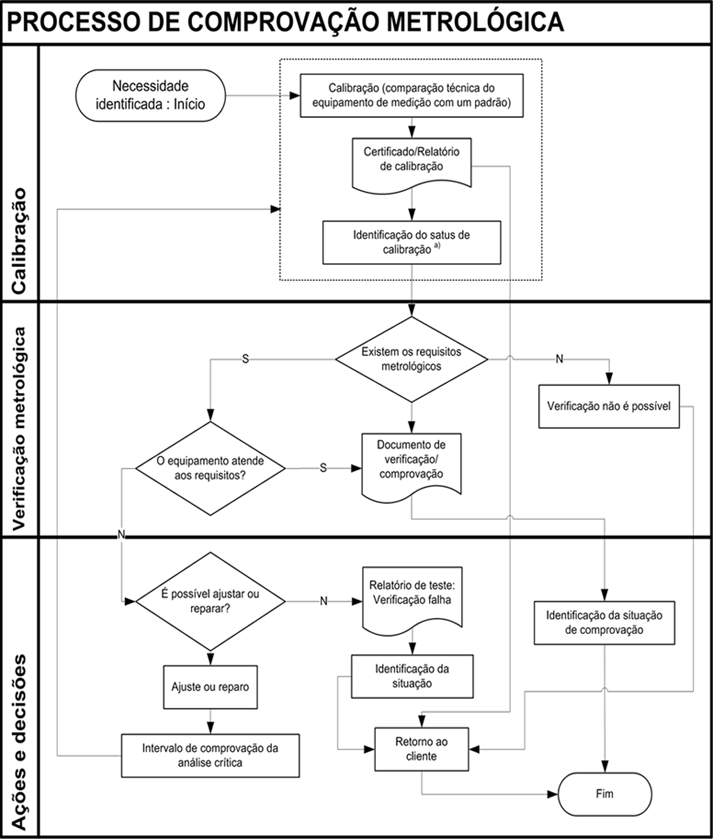
Figura 2.1: Processo de Comprovação Metrológica para equipamentos de medição.

Requisitos metrológicos são derivados de requisitos para o produto. Estes requisitos são necessários tanto para o equipamento de medição, quanto para os processos de medição. Estes também podem ser expressos como erros máximos permissíveis, incerteza permissível, faixa, estabilidade, resolução, condições ambientais ou habilidades do operador.

A orientação é que temos que especificar os processos de medição e o equipamento de medição que estão sujeitos às provisões da Norma ABNT NBR ISO 10012:2004. Com a decisão sobre o escopo e a extensão do sistema de gestão da medição, devemos levar em consideração os riscos e as consequências de falhas do cumprimento dos requisitos metrológicos.

Nota: o sistema de gestão de medição consiste em:

• no controle de processos de medições indicados;
• comprovação metrológica de equipamento de medição e dos processos de suporte necessários (conforme Figura 2.1).

A recalibração de um equipamento de medição não é necessária se o equipamento já estiver em uma situação de calibração válida. O procedimento de comprovação metrológica pode incluir métodos para verificarmos que a incerteza de medição e/ou erros de equipamento de medição estão dentro dos limites permissíveis especificados nos requisitos metrológicos. As informações pertinentes à ela deve estar prontamente disponível para o operador, incluindo quaisquer limitações ou requisitos especiais.

Função Metrológica

A função metrológica deve ser definida pela organização. A Alta Direção da organização deve assegurar a disponibilidade dos recursos necessários para estabelecer e manter a função metrológica. A função metrológica pode ser um departamento único ou estar distribuída em toda a organização.

A gestão da função metrológica deve estabelecer, documentar e manter o sistema de gestão de medição e continuamente melhorar a sua eficiência.

Intervalos de Comprovação Metrológica

A orientação para os métodos usados para a determinação ou mudança dos intervalos entre comprovações metrológicas é de que devemos descrever em procedimentos documentados. Devemos analisar criticamente e ajustarmos quando necessário para assegurar a contínua conformidade dos requisitos metrológicos especificados. Para determinação dos intervalos de comprovação metrológicas podemos usar dados obtidos de histórias de calibração, comprovação metrológica e avanços de tecnologia e conhecimento. Ao usarmos registros utilizando técnicas como Controle Estatístico de Processo (CEP), elas podem ser úteis para a determinação da necessidade ou não de alterar os intervalos de comprovação metrológica.

Segundo (OIML D10), o intervalo de calibração pode ser igual ao intervalo de comprovação metrológica.

Outro ponto importante é que cada vez que reparamos, ajustamos ou modificamos um equipamento de medição não conforme o intervalo de comprovação metrológica deve ser analisado criticamente.

Controle de ajustes de equipamento

Para o controle de ajustes de equipamento devemos ter alguns cuidados como:

• Acessos aos meios de ajustes e dispositivos sobre equipamentos de medição comprovados, cuja posição afeta o desempenho, devemos selá-los ou de alguma forma protegê-los afim de prevenir mudanças não autorizadas;
• Devemos projetar ou implementar selos ou proteções de tal forma que mudanças não autorizadas sejam detectadas;
• Devemos incluir ações a serem tomadas quando selos ou proteções são violados, danificados, contornados ou faltando.

Um ponto importante é que não aplicamos o requisito para a selagem para meios ou dispositivos de ajustes que são intencionalmente posicionadas pelo usuário sem a necessidade de referências externas, por exemplo os ajustes de zero. É importante também previnirmos de alterações não autorizadas em programas de computadores e nos procedimentos da organização.

As decisões sobre o selamento, os controles ou ajustes dos materiais de selagem e dos selos, tais como etiquetas, soldas, fios, tinta, normalmente são deixadas para a função metrológica e que a implementação de um programa de selagem sejam documentadas pela mesma. Mas vale lembrar que, nem todos os equipamentos de medição têm a possibilidade de serem selados.

Registros do processo de comprovação metrológica

Um processo importante dentro da comprovação metrológica são os registros do processo de comprovação metrológica, eles devem ser datados e aprovados por uma pessoa autorizada para atestar a correção dos resultados, como apropriado e os mesmos devem ser mantidos e estar disponíveis.

O tempo mínimo de registros depende de muitos fatores, incluindo os requisitos do cliente, requisitos estatutários ou regulamentares e responsabilidade do fabricante. Os registros relacionados com padrões de medição podem precisar ser mantidos indefinidamente. Devemos demonstrar nos registros de comprovação metrológica se cada item do equipamento satisfaz os requisitos metrológicos especificados e neles devemos incluir, quando necessário a:

• Descrição e identificação única do fabricante do equipamento, tipo, número de série etc;
• Data na qual a comprovação metrológica foi completada;
• Resultado da comprovação metrológica;
• Intervalo fixado para a comprovação metrológica;
• Identificação do procedimento de comprovação metrológica;
• Erros máximos permissíveis definidos;
• Condições ambientais pertinentes e declaração sobre quaisquer correções necessárias;
• Incertezas envolvidas na calibração do equipamento;
• Detalhes de qualquer manutenção, tais como ajustes, reparos ou modificações realizadas;
• Quaisquer limitações de uso;
• Identificação das pessoas que realizam a comprovação metrológica;
• Identificação das pessoas responsáveis pela correção da informação registrada;
• Identificação única (como número da série) de qualquer relatório ou certificado de calibração e outros documentos pertinentes;
• Evidência da rastreabilidade dos resultados de calibração;
• Requisitos metrológicos para o uso pretendido;
• Resultado da calibração após e onde requerido antes de qualquer ajuste, modificação ou reparo.

A orientação segundo ABNT NBR 10012:2004 é que os resultados de calibração sejam registrados de forma que a rastreabilidade de todas medições possa ser demonstrada e de forma que os resultados das calibrações possam ser reproduzidos sob condições próximas das condições originais. Algumas vezes, o resultado da verificação é incluído no relatório ou certificado de calibração onde é declarado se o equipamento está em conformidade (ou falha de conformidade) com os requisitos especificados. Os requisitos podem ser manuscritos, ou datilografados, ou microfilmados, ou meio eletrônico, ou meio magnético, ou em outro meio de informação.

O erro máximo permissível pode ser determinado pela função metrológica ou por referência às especificações publicadas do fabricante do equipamento de medição. É importante saber que a função metrológica deve assegurar que somente pessoas autorizadas sejam permitidos para gerar, emendar, emitir ou apagar registros.

Análise do Certificado de Calibração

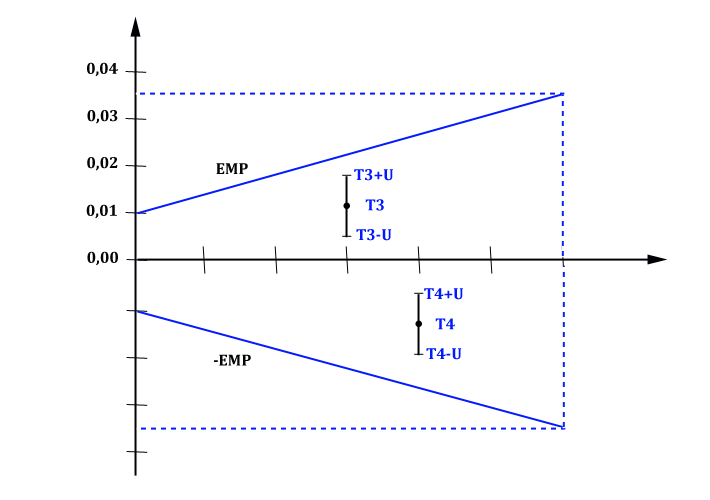
Como dissemos, a função metrológica deve definir uma estratégia para avaliar cada equipamento de medição, que é um requisito obrigatório, segundo item 5.5.2 da norma ISO/IEC 17025 [9]. Uma das formas mais utilizadas consiste em definir o erro máximo permissível (EMP), através da tolerância de produto ou especificações do fabricante, e compará-la com o resultado da calibração do equipamento. Para isto, tomamos

$$EMP=\frac{\text{Menor tolerância medida}}{J},~~~ \text{com}~~J = (5; 15].$$

O mais utilizado é $ J=10 $. Assim

$$EMP=\frac{\text{Tolerância}}{10}.$$

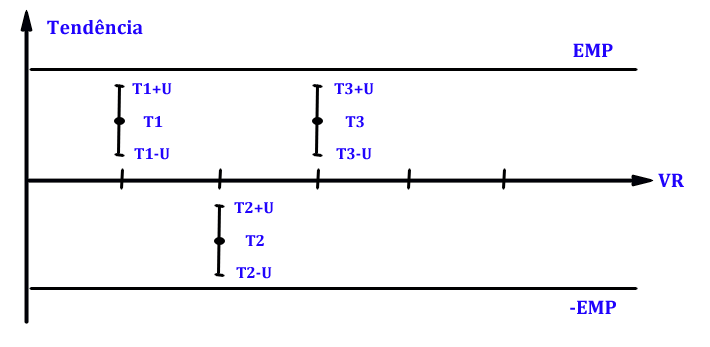
Critério

$$\max_i\left(\mid T_i \mid + U(i) \right) \leq EMP,\quad i=1,\dots,n$$

para todo ponto de calibração ($ i $ representa o ponto de calibração e $ n $ o número de pontos de calibração).

A comprovação metrológica no caso em que o EMP é função das leituras é discutido abaixo.

$$ EMP=\pm~(a + b\times leitura)$$

$$a=0,01$$

$$b=0,01$$

Critério

$ |T_i| + U(i) \leq EMP(i) $, para todo ponto de calibração ($ i $ representa o ponto de calibração).

Exemplo 2.1.1

Suponha que temos uma tolerância de 1 g para as massas padrão. Após a calibração das massas, obtivemos as seguintes informações do certificado de calibração. Essas informações estão apresentadas na Tabela 2.1.1

Ponto (g)	Tendência (g)	U (g)	k
1000	0,009	0,015	2
1000	0,01	0,015	2
1000	0,016	0,015	2
1000	0,01	0,015	2
5000	-0,014	0,075	2
5000	-0,069	0,075	2
5000	-0,043	0,075	2
5000	0,025	0,075	2

Tabela 2.1.1: Certificado de Calibração.

Considerando J=10, temos que

$$EMP=\frac{\text{Tolerância}}{10}=0,1~g.$$

A Tabela 2.1.2 apresenta o critério de aprovação $ (|T|+U \leq EMP) $ para as oito massas padrão. Como podemos ver, duas massas de 5 kg foram reprovadas. Com isso, o certificado de calibração cujo os valores foram apresentados na Tabela 2.1.1, não está aprovado.

Ponto (g)	|T|+U	Critério
1000	0,024	Aprovado
1000	0,025	Aprovado
1000	0,031	Aprovado
1000	0,025	Aprovado
5000	0,089	Aprovado
5000	0,144	Reprovado
5000	0,118	Reprovado
5000	0,1	Aprovado

Tabela 2.1.2: Critério de Aprovação.

Exemplo 2.1.2

Vamos aplicar a comprovação metrológica em uma bureta graduada. Suponha que a bureta controla um processo de tolerância de 2 mL para as medidas de volume. Na Figura 2.1.3 apresentamos o certificado de calibração da bureta graduada.

(imagem em falta)

Valor nominal	Média	Correção |C|	Incerteza Expandida	Fator de abrangência (k)	Graus de liberdade efetivo (veff)
5	4,9077	0,0923	0,002	2,37	10
15	14,8280	0,1720	0,003	2,20	15
25	24,9328	0,0678	0,003	2,06	44

Tabela 2.1.3: Tabela resumida do certificado de calibração.

Considerando J=10, temos que

$$EMP=\frac{\text{Tolerância}}{10}=\frac{2}{10}=0,2.$$

A Tabela 2.1.3 apresenta o critério de aprovação $ (|C|+U \leq EMP) $ para as três medições padrões de volume. Como podemos ver, todas as faixas de volume estão aprovadas.

Ponto (mL)	|C|+U	Critério
5	0,0943	Aprovado
15	0,175	Aprovado
25	0,0708	Aprovado

Tabela 2.1.3: Critério de Aprovação.

TUR (Test Uncertainty Ratio)

O processo de calibração envolve uma comparação entre o Equipamento de Medição e um padrão, tendo melhores requisitos metrológicos. A comparação entre a exatidão da unidade sob teste e a exatidão do padrão é conhecia como razão entre as exatidões de teste (TAR). No entanto, esta razão não considera outras fontes potenciais de erro do processo de calibração. A comparação entre a exatidão da unidade sob teste e a incerteza de calibração estimada é conhecida como uma relação entre as incertezas de teste (TUR). Esta relação é mais confiável, porque considera as fontes de erro envolvidas no processo de calibração que o TAR não considera.

A relação entre as incertezas de teste (TUR) é uma medida da capacidade de um determinado instrumento e/ou processo de medição atender uma especificação de produto (ou processo). Desta forma, TUR é a razão entre a tolerância e/ou especificação do produto e a incerteza presente no teste desta especificação ou tolerância. Historicamente, uma regra muito utilizada é a de que o TUR deve ser de pelo menos 10:1. Quanto maior a razão, melhor o desempenho do teste. Atualmente, uma proporção de 4:1 ou mesmo 3:1 são considerados aceitáveis em alguns casos. Isto é devido principalmente ao melhor desempenho dos equipamentos de fabricação. Em muitos casos, não temos um equipamento com uma incerteza pequena suficiente para um TUR 10:1, ou é muito caro para a aplicação.

Há duas principais aplicações para o TUR:

• O primeiro é na calibração de instrumentos de medição e equipamentos;
• O segundo é na inspeção de componentes fabricados.

De forma geral, temos a seguinte equação para o TUR:

$${TUR}=\frac{{Tolerância~ou~EMP}}{{Incerteza~Expandida}}$$

À partir disto, notamos que a razão TUR compara a variação admissível para o mensurando (o numerador) com a variabilidade associada com a medição do mensurando (o denominador).

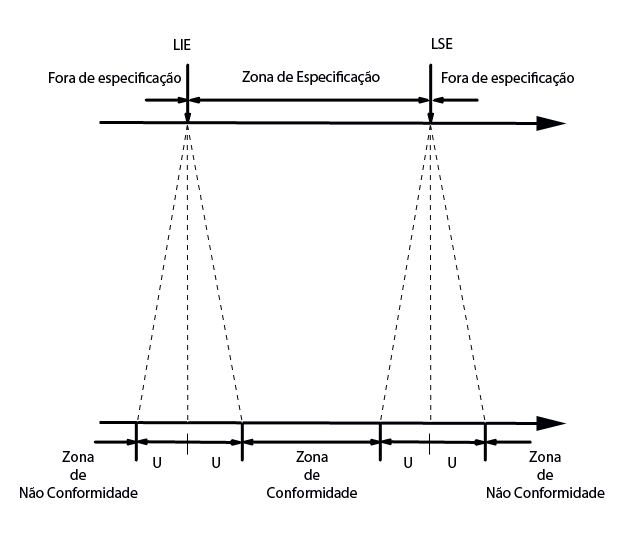
Figura 2.1.3: Relação entre a zona de especificação e a zona de conformidade.

A figura (2.1.3), nos mostra a relação entre a zona de especificação e a zona de conformidade. Se o “verdadeiro valor” do mensurando está dentro da zona de especificação, temos que a especificação é satisfeita, caso contrário, o mensurando está fora de especificação. No entanto, nunca podemos conhecer o “verdadeiro valor” do mensurando conforme citamos no módulo 2. Afim de indicar se o mensurando está ou não fora da especificação, temos que conhecer a incerteza no processo de medição. Isso é mostrado na parte inferior da linha horizontal da figura. Se o mensurando está na zona de conformidade, temos confiança de que o verdadeiro valor está dentro da especificação. Da mesma forma, se o mensurando está na zona de não conformidade, temos confiança de que o verdadeiro valor está fora de especificação. Para a região de incerteza mostrado entre conformidade e não conformidade, não temos confiança suficiente para determinar se a peça ou produto está conforme ou não.

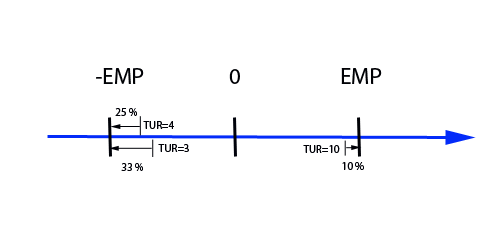
Figura 2.1.4: Influência do TUR no resultado final de uma calibração.

Como visto anteriormente, devido ao melhor desempenho dos equipamentos, consideramos TUR ≥ 5 como uma relação aceitável na escolha de um equipamento, e um TUR ≥ 3 na escolha do padrão de calibração, o que assegura e permite que a incerteza do padrão não interfira significativamente na comprovação metrológica. A Figura (2.1.4) ilustra o comprometimento da incerteza do padrão em relação ao erro máximo permissível, em função de diferentes TUR adotados.

3 - Aplicações do Cálculo de Incerteza em Calibrações

Apresentaremos nos próximos módulos, algumas aplicações da Incerteza de Medição para calibrações , para exemplificar o procedimento dos cálculos e os passos iniciais antes de iniciarmos o cálculo da incerteza de medição.

3.1 - Cálculo de Incerteza de um Relógio Comparador

Considere o processo de calibração de um relógio de resolução de 0,01 mm. Esta calibração é realizada por comparação utilizando-se um calibrador de relógio. O calibrador apresenta uma resolução 0,001mm com incerteza expandida de 0,001mm com k=2. Os resultados são apresentados na Tabela 3.1.1

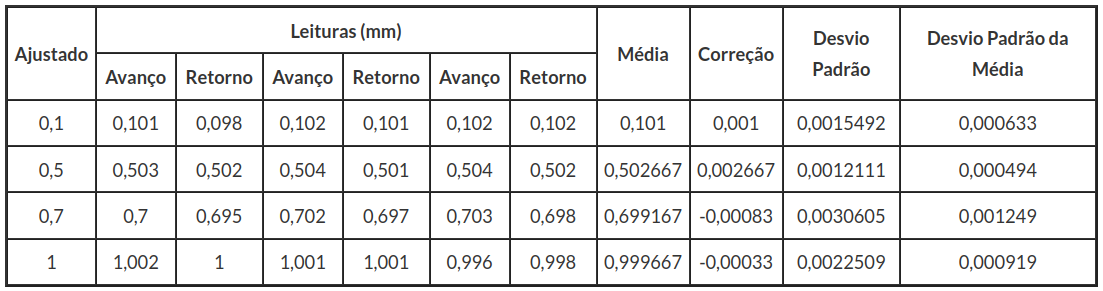
Tabela 3.1.1: Tabela de dados.

Método de Medição

A calibração corresponde a diferença entre as medições do relógio e do calibrador

$$d = l - l_S$$

onde

• $ l $: representa a leitura ajustada no relógio comparador;
• $ l_S $: representa a leitura obtida pelo calibrador.

Modelo Matemático

Os desvios obtidos apresentam as seguintes fontes de incerteza

$$d~=~\Delta_l~+~Res(Rel)~+~Res(Cal)~+~{Histerese}$$

Então

$$l= d + l_s = ~\Delta_l~+~Res(Rel)~+~Res(Cal)~+~Histerese~ +~ l_s,$$

onde,

• $Δ_l$: representa a diferença observada entre a medição do relógio e a medição do calibrador repetitividade;
• Res(Rel): resolução do relógio;
• Res(Cal): resolução do calibrador;
• $l_s$: representa a contribuição do padrão;
• Histerese: máxima diferença entre a medição no avanço e no retorno.

Incerteza Combinada

Através da equação de propagação da incerteza, temos que a expressão da incerteza combinada é dada por

$$u_c(d)=\sqrt{~u^2(\Delta_l)~+~u^2(Res(Rel))~+~u^2(Res(Cal))~+~u^2(l_s)~+~u^2({Histerese})}$$

Cálculo da Incerteza Padrão das Grandezas de Entrada

A seguir, vamos calcular a incerteza de cada fonte.

Repetitividade ($ \Delta_l $)

Incerteza do Tipo A.

Vamos tomar como exemplo o ponto 0,5 mm. Assim, temos

$$u(\Delta_l)~=~\frac{s}{\sqrt{n}}=\frac{0,00121106}{\sqrt{6}}=0,000494413$$

em que

• $ u(\Delta_l) $: representa a incerteza do Tipo A;
• $ s $: representa o desvio padrão das leituras no ponto de calibração $ i $;
• $ n $: representa o número de leituras no ponto de calibração $ i $.

Incerteza Herdada do Padrão $ (u(l_s)) $

Distribuição: Normal.

$$u(l_s)=\frac{U(L_s)}{k}=\frac{0,001}{2}=0,0005$$

Resolução do Calibrador $ (Res(Cal)) $

Distribuição: Retangular.

$$u(Res(Cal))=\frac{Res(Cal)}{2\sqrt{3}}=\frac{0,001}{2\sqrt{3}}=0,000288675$$

Resolução do Relógio $ (Res(Rel)) $

Distribuição: Retangular.

$$u(Res(Rel))=\frac{Res(Rel)}{2\sqrt{3}}=\frac{0,01}{2\sqrt{3}}=0,00288675$$

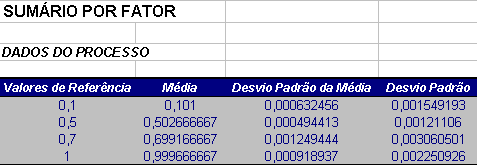
Cálculo da Histerese

Referência	Média do Avanço	Média do Retorno	|Histerese|
0,1	0,101667	0,100333	0,0013333
0,5	0,503667	0,501667	0,002
0,7	0,701667	0,696667	0,005
1	0,999667	0,999667	0

Para o ponto de calibração de 0,5 mm temos:

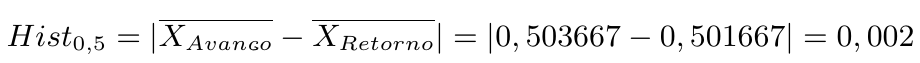
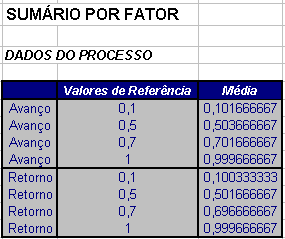
Cálculo da Incerteza Combinada

$$u_c(d)=\sqrt{~u^2(\Delta_l)~+~u^2(Res(Rel))~+~u^2(Res(Cal))~+~u^2(l_s)~+~u^2({Histerese})}=$$

$$=\sqrt{(0,00049)^2~+~(0,002887)^2~+~(0,0002887)^2~+~(0,0005)^2~+~(0,00057)^2}$$

$$=0,00304$$

Graus de Liberdade Efetivo

$$\nu_{eff}~=~\left(\frac{u_c(d)}{u(\Delta_l)}\right)^4~\nu_A~=\left(\frac{0,00304}{0,00049}\right)^4~(6-1)=7151,07$$

Através da tabela t-Student, encontramos $ k=1,96 $

Incerteza Expandida

$$U~=~k~\times~u_c(d)~=1,96\times~0,00304=0,00596$$

O resumo do cálculo de incerteza de medição para o relógio comparador, está na tabela a seguir.

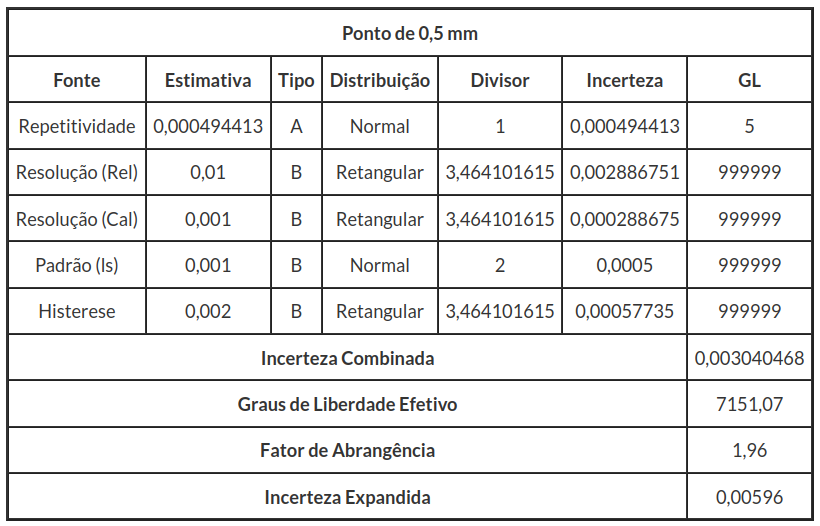
O relógio de medição é utilizado para medir, com uma tolerância de 0,2mm. Faremos agora, um estudo da comprovação metrológica.

Considerando $ J=10 $, temos que

$$EMP=\frac{{Tolerância}}{10}=\frac{0,2}{10}=0,02~mm$$

$$|T|+U=|0,0026|+0,00596=0,00863\leq 0,02=EMP$$

Portanto, para o ponto de 0,5 mm, foi aprovada.

3.2 - Cálculo de Incerteza de um Micrômetro Externo

Considere o processo de calibração de um micrômetro externo digital de resolução de 0,001mm. Esta calibração é realizada por comparação utilizando-se um jogo de blocos padrão. O resultados são apresentados na Tabela 3.2.1.

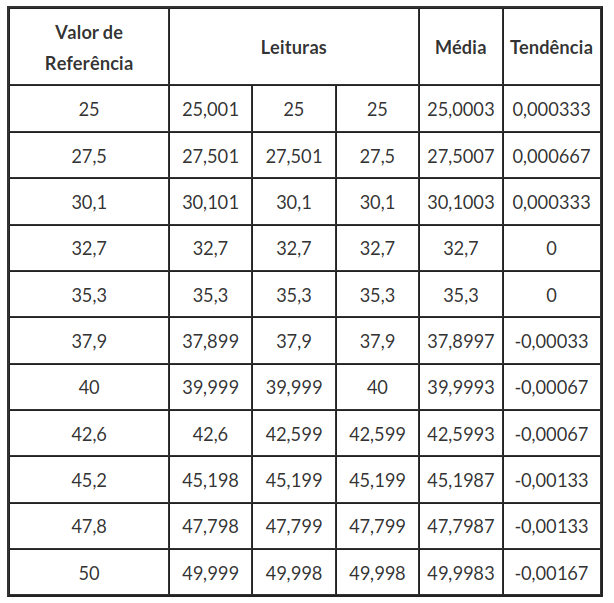
Tabela 3.2.1: Dados da medição.

Método de Medição

A leitura de um bloco padrão corresponde a diferença entre seus comprimentos

$$ d = l - l_S $$

onde,

• l: representa a leitura obtida pelo micrômetro;
• lS: representa o comprimento do bloco padrão para uma temperatura de 20ºC.

A correção devido a variação de temperatura é dada por

$$d = l (1+ \alpha~\theta )-l_S (1+\alpha_S~\theta_S)$$

onde,

• $ \alpha $ e $ \alpha_S $: correspondem aos coeficientes de expansão térmica do micrômetro (escala) e do bloco padrão utilizado na medição, respectivamente;
• $ \theta $ e $ \theta_S $: correspondem a diferença de temperatura do micrômetro e o bloco padrão, em relação a $ 20ordm;C $, respectivamente.

Modelo Matemático

A leitura, do comprimento do bloco, obtida no micrômetro é dada por

$$l=\frac{d~+~l_S(1 + \alpha_S~\theta_S)}{1+ \alpha~\theta}~~(3.2.1)$$

Mutiplicando e dividindo por ($ 1 - \alpha~\theta $), obtemos

$$l=\frac{[d~+~l_S(1+\alpha_S~\theta_S)]}{1+\alpha~\theta}~\frac{(1-\alpha~\theta)}{(1-\alpha~\theta)}$$

$$=\frac{d~(1-\alpha~\theta)~+~l_S(1 + \alpha_S~\theta_S)(1-\alpha~\theta)}{1~-~(\alpha~\theta)^2}$$

Simplificando a equação acima em relação aos termos desprezíveis, podemos aproximar o valor do bloco padrão, por

$$l~=~d~+~l_S~+ l_S(\alpha_S~\theta_S~-~\alpha~\theta)$$

Ao denotarmos a diferença entre as temperaturas do micrômetro e do bloco padrão, por

$$\delta\theta~=~\theta~-~\theta_S$$

e a diferença entre os coeficientes de expansão térmica do micrômetro e do bloco padrão, por

$$\delta\alpha~=~\alpha~-~\alpha_S$$

obtemos que

$$l~=~d~+~l_S~-~l_S(\delta\alpha~\theta~+~\delta\theta\alpha_S~)$$

Os desvios obtidos apresentam as seguintes fontes de incerteza

$$d=\Delta_l~+~Res~+~Ep$$

em que,

• $Δ_l$ : representa a diferença observada no comprimento do bloco padrão (repetitividade); medida do micrômetro - medida do bloco padrão;
• Res : representa a resolução do micrômetro;
• Ep : representa o paralelismo do micrômetro.

Assim, a equação matemática do comprimento do bloco é:

$$l~=~\Delta_l~+~Res~+~Ep~+ l_S~- l_S(\delta\alpha~\theta~+~\delta\theta~\alpha_S~)$$

Fontes de incerteza

• Resolução (Res): A resolução do micrômetro é de 0,001mm. Esta variável é considerada com média zero e limites de variação definido pela resolução do equipamento;
• Incerteza herdada do bloco padrão ($l_S$): Esta variável tem média dada pelo valor do padrão com desvio padrão definido pela incerteza combinada, ambos declarados no certificado de calibração;
• Paralelismo ($E_p$): O paralelismo entre as faces é considerada uma variável com média zero e limites de variação de $ \pm~0,0003mm $ (resultado obtido via um paralelo óptico);
• Correções de temperatura: Antes da calibração, tomamos cuidado para assegurar que o jogo de bloco padrão e o micrômetro estejam à mesma temperatura ambiente da sala de medição;

Além disso, as fontes de incerteza $ \theta,~\delta\alpha,~\delta\theta,~\alpha_S~ $ são assumidas não correlacionadas. Através da equação (3.2.1), leitura obtida no micrômetro para o comprimento do bloco, observamos que o valor estimado para comprimento é dado por

$$l = ({Média~do~desvios}) + l_S$$

OBS: Esta equação é a estimativa da medição do micrômetro que é obtida desconsiderando as variáveis que tem média zero.

Avaliação da Incerteza Combinada (uc(l))

Através da equação de propagação da incerteza, temos que

$$u^2_c(l)~=~c^2_{l_S}~u^2(l_S)~+~c^2_d~u^2(d)~+~c^2_{\alpha_S}~u^2(\alpha_S)~+~c^2_\theta~u^2(\theta)~+~c^2_{\delta\alpha}~u^2(\delta\alpha)~+~c^2_{\delta\theta}~u^2(\delta\theta)$$

Onde os coeficientes de sensibilidade avaliados no ponto da média são dados por:

• $ c_{l_S}~=~1~-~(\delta\alpha~\theta~+~\delta\theta~\alpha_S)~=~1 $;
• $ c_d~=~1 $;
• $ c_{\alpha_S}~=~-~l_S~\delta\alpha~=~0~({Média de}~ \delta\alpha~{ é igual a zero)} $;
• $ c_{\theta}~=~-~l_S~\delta\theta~=~0~({Média de}~\delta\theta~{é igual a zero}) $;
• $ c_{\delta\alpha}~=~-~l_S~\theta $;
• $ c_{\delta\theta}~=~-~l_S~\alpha $.
• Com isso, a expressão incerteza combinada é dada por

$$u_c(l)~=\sqrt{u^2(l_S)~+~u^2(\Delta_l)~+~u^2(Res)~+~u^2(Ep)~+~(~-~l_S~\theta)^2~u^2(\delta\alpha)~+~(~-~l_S~\alpha)^2~u^2(\delta\theta)}$$

Cálculo da Incerteza Padrão das grandezas de entrada

A seguir, vamos calcular a incerteza de cada fonte.

Padrão de referência (lS)

Distribuição: Normal

Bloco Padrão	Incerteza Expandida (mm)	Fator de Abrangência	Incerteza Combinada
25	0,00008	2	0,00004
27,5	0,00007	2	0,000035
30,1	0,00009	2	0,000045
32,7	0,00008	2	0,00004
35,3	0,00008	2	0,00004
37,9	0,00008	2	0,00004
40	0,00009	2	0,000045
42,6	0,00009	2	0,000045
45,2	0,00009	2	0,000045
47,8	0,00008	2	0,00004
50	0,00009	2	0,000045

Tabela 3.2.2: Cálculo da incerteza padrão.

Paralelismo (Ep)

Distribuição : Retangular

$ u(Ep)=\frac{0,0006}{2\sqrt{3}}=0,000173 $

Resolução do micrômetro (Res)

Distribuição: Retangular

$ u(Res)=\frac{0,001}{2\sqrt{3}}=0,000289 $

Diferença entre os coeficientes de expansão térmico ($ \delta\alpha $)

Distribuição: Retangular

$ u(\delta\alpha)=\frac{3,98\times 10^{-6}}{2\sqrt{3}}=1,15\times 10^{-6} $

Diferença entre a temperatura do micrômetro e a temperatura de referência $ t_0 = 20 {}^\circ C~(\theta) $

Foi registrado uma temperatura média de $ 19,9 {}^\circ C $, resultando em $ \theta=19,9 - 20 =-0,1 {}^\circ C $.

Diferença de temperatura entre o micrômetro e o bloco padrão ($ \delta\theta $)

Distribuição: Retangular

$ u(\delta\theta)=\frac{0,3999}{2\sqrt{3}}=0,11547 $

Coeficiente de expansão térmica ($ \alpha_S $)

Média de $ 11,5 \times 10^{-6}~{}^\circ C^{-1} $.

Cálculo da Incerteza do tipo A~($ u(\Delta_l) $

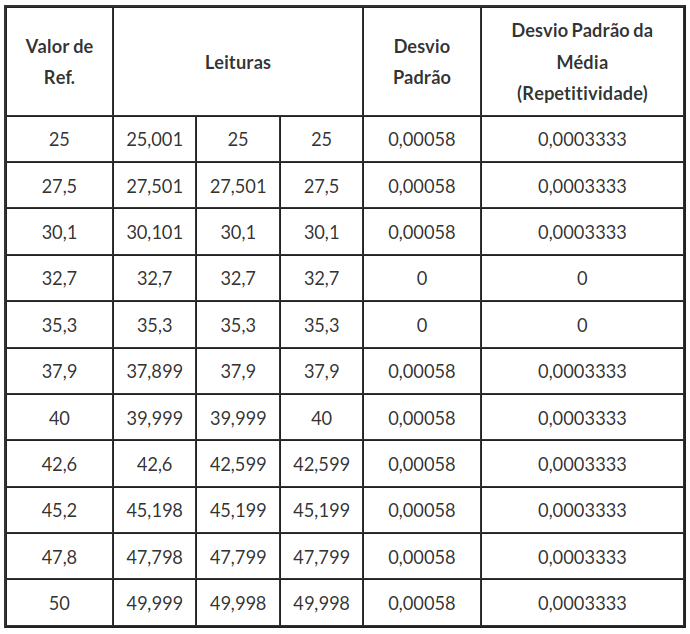
Tabela 3.2.3: Cálculo da incerteza tipo A.

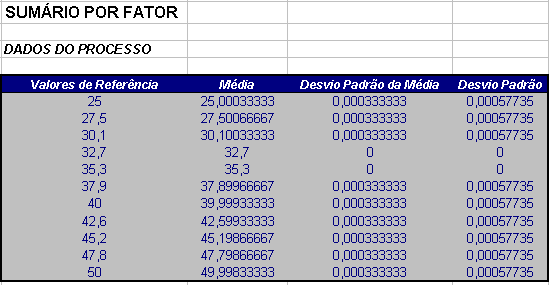
Cálculo dos Coeficientes de Sensibilidade

Valor de Referência	$ |i_S\times\theta| $	$ |l_S\times\alpha| $
25	$ 25\times 0,1=2,5 $	$ 25\times0,0000115=0,0002875 $
27,5	$ 27,5\times 0,1=2,75 $	$ 27,5\times0,0000115=0,0003163 $
30,1	$ 30,1\times 0,1=3,01 $	$ 30,1\times0,0000115=0,0003462 $
32,7	$ 32,7\times 0,1=3,27 $	$ 32,7\times0,0000115=0,0003761 $
35,3	$ 35,3\times 0,1=3,53 $	$ 35,3\times0,0000115=0,0004069 $
37,9	$ 37,9\times 0,1=3,79 $	$ 37,9\times0,0000115=0,0004369 $
40	$ 40\times 0,1=4 $	$ 40\times0,0000115=0,00046 $
42,6	$ 42,6\times 0,1=4,26 $	$ 42,6\times0,0000115=0,0004899 $
45,2	$ 45,2\times 0,1=4,52 $	$ 45,2\times0,0000115=0,0005198 $
47,8	$ 47,8\times 0,1=4,78 $	$ 47,8\times0,0000115=0,0005497 $
50	$ 50\times 0,1=5 $	$ 50\times0,0000115=0,000575 $

Tabela 3.2.4: Cálculo dos coeficientes de sensibilidade.

Contribuição para a Incerteza

Valor de Referência	$ |l_S \theta|\times u(\delta\alpha) $	$ |l_S\alpha|\times u(\delta \theta) $
25	$ 2,5\times0,00000115=0,0000029 $	$ 0,0002875\times0,11547=0,000033 $
27,5	$ 2,75\times0,00000115=0,0000032 $	$ 0,0003163\times0,11547=0,000037 $
30,1	$ 3,01\times0,00000115=0,0000035 $	$ 0,0003462\times0,11547=0,00004 $
32,7	$ 3,27\times0,00000115=0,0000038 $	$ 0,0003761\times0,11547=0,000043 $
35,3	$ 3,53\times0,00000115=0,0000041 $	$ 0,0004059\times0,11547=0,000047 $
37,9	$ 3,79\times0,00000115=0,0000044 $	$ 0,0004359\times0,11547=0,00005 $
40	$ 4\times0,00000115=0,0000046 $	$ 0,00046\times0,11547=0,000053 $
42,6	$ 4,26\times0,00000115=0,0000049 $	$ 0,0004899\times0,11547=0,000057 $
45,2	$ 4,52\times0,00000115=0,0000052 $	$ 0,0005198\times0,11547=0,00006 $
47,8	$ 4,78\times0,00000115=0,0000055 $	$ 0,0005497\times0,11547=0,000063 $
50	$ 5\times0,00000115=0,0000058 $	$ 0,000575\times0,11547=0,000066 $

Tabela 3.2.5: Contribuição para a Incerteza Combinada

Incerteza Combinada ($ u_c(l) $)

Planilha de Cálculo de Incerteza

A incerteza combinada é dada por:

$$u_c(l)=\sqrt{u^2(l_S)~+~u^2(\Delta_l)~+~u^2(Res)~+~u^2(Ep)~+~(~-~l_S~\theta)^2~u^2(\delta\alpha)~+~(~-~l_S~\alpha)^2~u^2(\delta\theta)}$$

$$u_c(l)=\sqrt{0,00004^2+0,0003^2+0,00029^2+0,00017^2+(2,5)^2~(1,15\times10^{-6})^2+(0,00028)^2~0,11^2}$$

$$=0,0004766$$

VR	$ u(l_S) $	$ u(\Delta_l) $	$ u(Res) $	$ u(Ep) $	$ |-l_S\thteta|\times u(\delta\alpha) $	$ |-l_S\thteta|\times u(\delta\theta) $	$ u_c(l) $
25	0,00004	0,00033	0,00029	0,00017	0,0000029	0,000033	0,00047
27,5	0,000035	0,00033	0,00029	0,00017	0,0000032	0,000037	0,00047
30,1	0,000045	0,00033	0,00029	0,00017	0,0000035	0,00004	0,00047
32,7	0,00004	0	0,00029	0,00017	0,0000038	0,000043	0,00034
35,3	0,00004	0	0,00029	0,00017	0,0000041	0,000047	0,00034
37,9	0,00004	0,00033	0,00029	0,00017	0,0000044	0,00005	0,00048
40	0,000045	0,00033	0,00029	0,00017	0,0000046	0,000053	0,00048
42,6	0,000045	0,00033	0,00029	0,00017	0,0000049	0,000057	0,00048
45,2	0,000045	0,00033	0,00029	0,00017	0,0000052	0,00006	0,00048
47,8	0,00004	0,00033	0,00029	0,00017	0,0000055	0,000063	0,00048
50	0,000045	0,00033	0,00029	0,00017	0,0000058	0,000066	0,00048

Tabela 3.2.6: Cálculo da Incerteza Combinada - Por Ponto

Na Tabela (3.2.6), calculamos a incerteza combinada para cada ponto de calibração.

Graus de liberdade efetivo

$$\nu_{eff}(l)~=~\left(\frac{u_c(l)}{u(\Delta_l)}\right)^4~\nu_A=\left(\frac{0,00047}{0,000333}\right)^4~(3-1)=8,36$$

Através da tabela t-Student encontramos k =2,31

Incerteza Expandida (U(l))

$$U(l)~=~k~\times~u_c(l)=2,31\times 0,0004766=0,0011$$

Assim, resumimos os resultados do cálculo de incerteza no ponto de 25mm na Tabela (3.2.7)

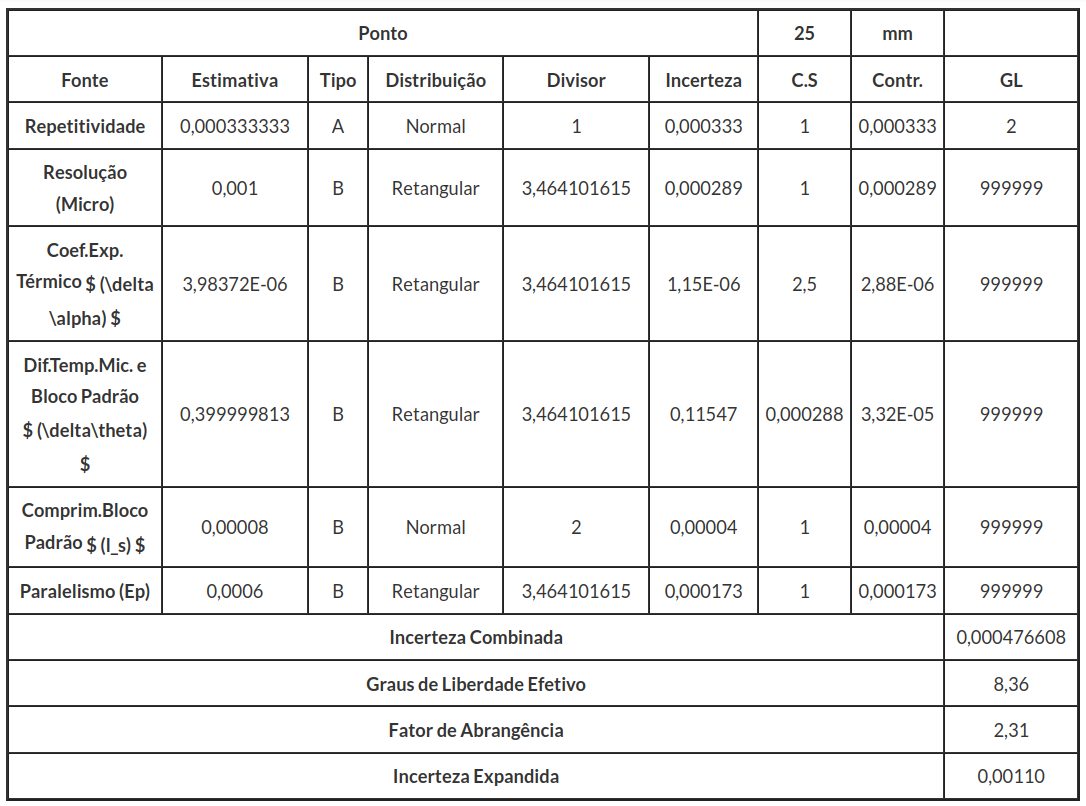
Tabela 3.6.7: Resultados do Cálculo de Incerteza para o ponto de 25 mm.

Avaliação da incerteza

Suponha que este equipamento seja utilizado para medir uma tolerância de 0,02 mm.

Considerando J=10, temos que

$$EMP=\frac{{Tolerância}}{10}=\frac{0,02}{10}=0,002~mm$$

$$|T|+U=|0,00033|+0,0011=0,00243\leq 0,002=EMP$$

Portanto, para o ponto de 25 mm, foi aprovada.

3.3 - Cálculo de Incerteza de um Manômetro

Considere o processo de calibração de um manômetro em comparação com um manômetro padrão, conforme figura 3.3.1.

Figura 3.3.1: Manômetro.

Os dados referentes aos equipamentos envolvidos na calibração são dados por:

Objeto a ser calibrado

Manômetro.

Resolução: $ 1 kgf/cm^2 $.

Faixa de Indicação (faixa nominal): $ 0 - 160 kgf/cm^2 $.

Padrão de referência

Manômetro padrão.

Resolução: $ 0,1 kgf/cm^2 $

Incerteza expandida - $ U = 0,1(porcentagem)~(k=2) $ (em relação ao fundo de escala).

Temperatura durante a calibração: $ 22~\pm~1{}^\circ C $.

Faixa de indicação (faixa nominal): $ 0 - 200 kgf/cm^2 $.

Resultados

A bancada foi ajustada com o manômetro (a ser calibrado) e as leituras foram realizadas com o padrão. A Tabela 3.3.1 apresenta os dados.

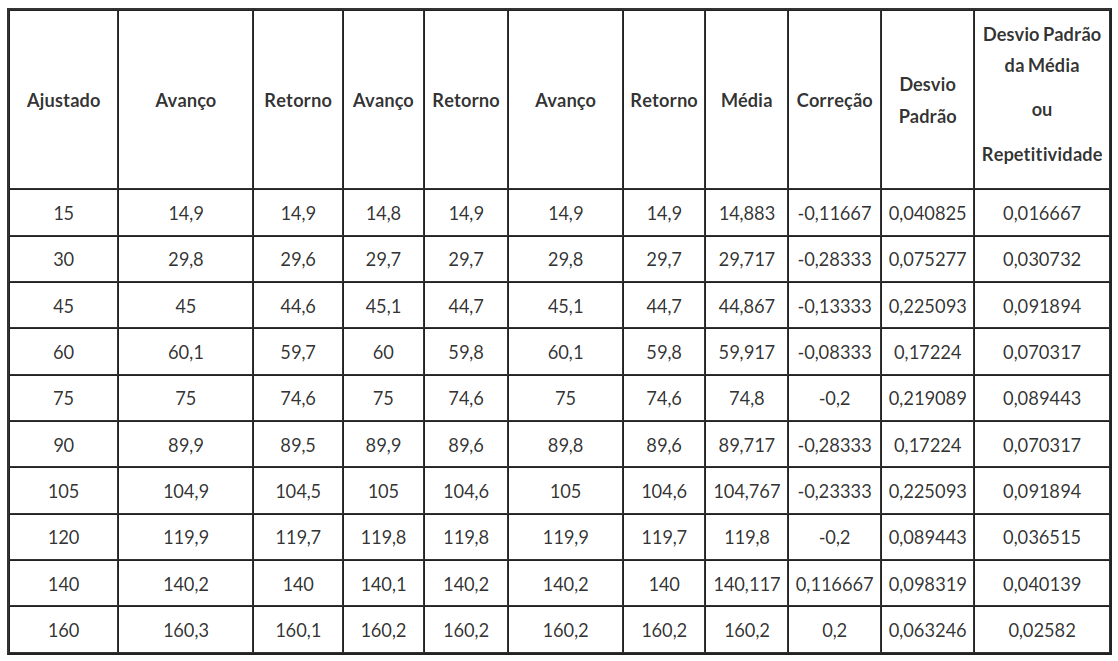
Tabela 3.3.1:Tabela de dados para o manômetro.

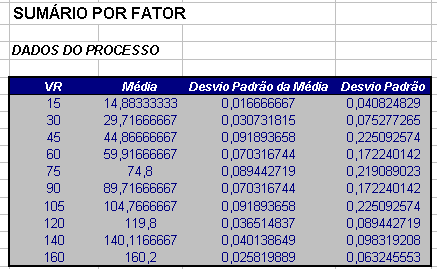
Equação Matemática

$${Desvio} = {Medida~do~Manômetro} - {Manômetro~padrão}$$

Fontes de Incerteza

• Repetitividade - Tipo A;
• Resolução do manômetro;
• Resolução do manômetro padrão;
• Incerteza herdada do padrão $ U = 0,1(porcentagem)~(k=2) $.

Porcentagem tomada em relação ao fundo de escala

$$U = \frac{U(unidade)}{200}~100(porcentagem).$$

Então

$$U(unidade)~=~\frac{U((porcentagem))}{100}~200$$

$$u_{c}~=~\frac{U(unidade)}{k}$$

Histerese

$$U(hist)=|\overline{{Avanço}}-\overline{{Retorno}}|$$

$$u(hist)=\cfrac{U(hist)}{2\sqrt{3}}$$

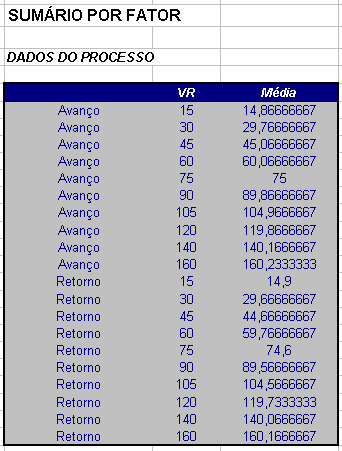
Resultados Obtidos da Histerese:

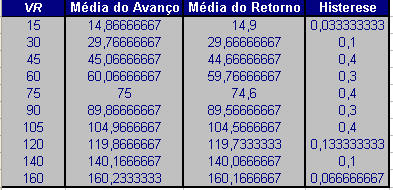
Incerteza Combinada

Através da equação de propagação da incerteza, temos que a expressão da incerteza combinada para o manômetro é dada por

$$u_c(M)=\sqrt{~u^2(\Delta_l)~+~u^2(Res(man))~+~u^2(Res(padra))~+~u^2(h_{Pad})~+~u^2(Hist)}$$

em que,

$ u(\Delta_l) $: representa a incerteza devido a repetitividade;

$ u(Res(man)) $: representa a incerteza devido a resolução do manômetro;

$ u(Res(padra)) $: representa a incerteza devido a resolução do manômetro padrão;

$ u(h_{Pad}) $: representa a incerteza herdada do manômetro padrão;

$ u(Hist) $: representa a incerteza devido a histerese.

Cálculo da Incerteza Padrão das Grandezas de Entrada

A seguir, vamos calcular a incerteza de cada fonte.

Repetitividade ($ \Delta_l $)

Incerteza do Tipo A.

$$u(\Delta_l) = \frac{s}{\sqrt{n}}$$

em que

$ u(\Delta_l) $: representa a incerteza do Tipo A ou incerteza devido a repetitividade;

$ s $: representa o desvio padrão das faixa de medição;

n: representa o número de pontos de calibração.

Incerteza Herdada do Manômetro Padrão $ (u(h_{Pad})) $

Distribuição: Normal.

$ u(h_{Pad}) =\frac{0,1(porcentagem)\text{Fundo de Escala}}{2}=\frac{0,001\times 200}{2}=0,1 $

Resolução do Manômetro Padrão $ (u(Res(padra))) $

Distribuição: Retangular.

$ u(Res(padra)) =\frac{0,1}{2\sqrt{3}}=0,0288 $

Resolução do Manômetro $ (u(Res(man))) $

Distribuição: Retangular.

$ u(Res(man)) =\frac{1}{2\sqrt{3}}=0,288 $

Cálculo da Histerese

Faixa	Média do Avanço	Média do Retorno	|Histerese|
15	14,867	14,9	0,033333
30	29,767	29,667	0,1
45	45,0667	44,667	0,4
60	60,067	59,767	0,3
75	75	74,667	0,333333
90	89,867	89,567	0,3
105	104,9	104,567	0,333333
120	119,867	119,733	0,133333
140	140,1	140,067	0,033333
160	160,233	160,233	0

Histerese da faixa de 30 $ kgf $:

$$U(hist)=|\overline{{Avanço}}-\overline{{Retorno}}|=|29,767-29,667|=0,1$$

$$u(hist)=\cfrac{U(hist)}{2\sqrt{3}}=\frac{0,1}{2\sqrt{3}}=0,0288$$

Cálculo da Incerteza do Manômetro

Incerteza Combinada

$$u_c(M)=\sqrt{~u^2(\Delta_l)~+~u^2(Res(man))~+~u^2(Res(padra))~+~u^2(h_{Pad})~+~u^2(Hist)}=$$

$$=\sqrt{(0,030731815)^2~+~(0,288675135)^2~+~(0,02887)^2~+~(0,1)^2~+~(0,028867)^2}=$$

$$=0,3097$$

Graus de Liberdade Efetivo

$$\nu_{eff}~=~\left(\frac{u_c(M)}{u(\Delta_l)}\right)^4~\nu_A=\left(\frac{0,3097}{0,0307}\right)^4~(6-1)=51600,84$$

Através da tabela t-Student, encontramos $ k =2 $

Incerteza Expandida

$$U=k\times u_c(M)=2\times 0,3097=0,6194=0,62~kgf/cm^2$$

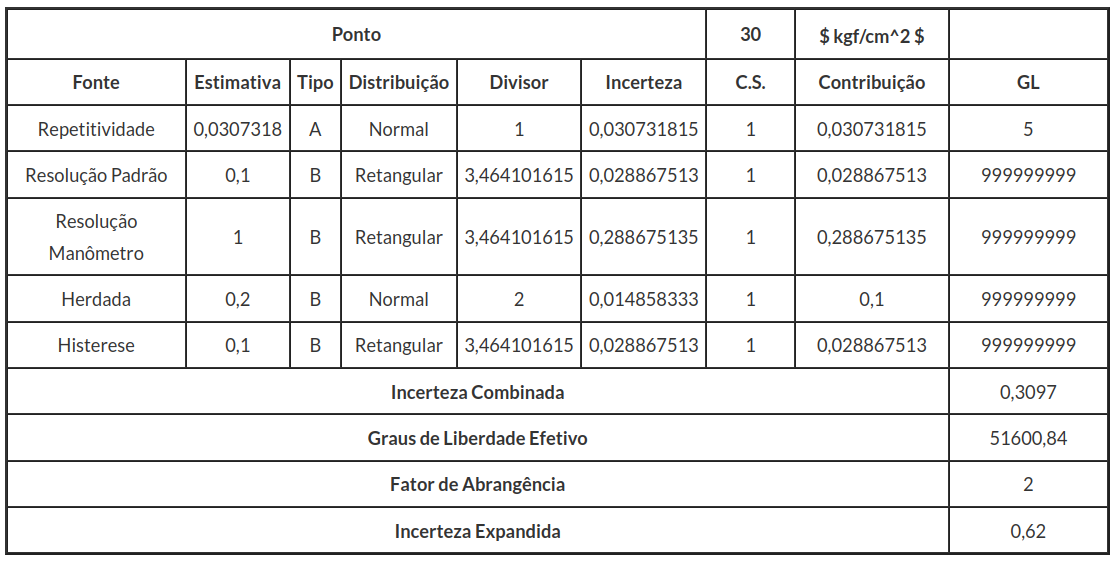
Expressão da Incerteza em Porcentagem

$$U = \frac{U(unidade)}{\overline{M}}~100(porcentagem)$$

para a faixa de 30 $ kgf/cm^2 $ temos

$$U = \frac{0,619}{29,717}~100(porcentagem)=2,08(porcentagem)$$

O manômetro é utilizado para medir uma tolerância de $ 10kgf/cm^2 $. Faremos agora, um estudo da comprovação metrológica.

Considerando $ J=10 $, temos que

$$EMP=\frac{{Tolerância}}{10}=\frac{10}{10}=1~kgf/cm^2$$

$$|T|+U=|-0,283|+0,619=0,902\leq 1=EMP$$

Portanto, para o ponto de $ 30~kgf/cm^2 $, foi aprovada.

3.4 - Cálculo de Incerteza de um Voltímetro Digital

Considere a calibração de um voltímetro digital por comparação.

Código: VO341.

Série: 006-C.

Descrição: voltímetro digital.

Menor Div: $ 0,1~mV $.

Unidade: $ mV $.

Faixa de leitura: $ 0 $ a $ 200~mV $.

Temperatura ambiente: 20 $ plusmn; 3^oC $.

Padrão de referência

Multímetro digital HP - 3458$ ^A $.

Resolução: $ 0,01mV $.

Incerteza expandida - $ U = \pm0,001(porcentagem) $ com $ k=2 $ (em relação ao fundo de escala).

Drift (instabilidade) = $ \pm 0,002mV $.

Faixa de leitura: $ 0 $ a $ 200~mV $.

Resultados:

A bancada foi ajustada com o voltímetro digital (a ser calibrado) e as leituras foram realizadas com o padrão. A Tabela 3.4.1 apresenta os dados.

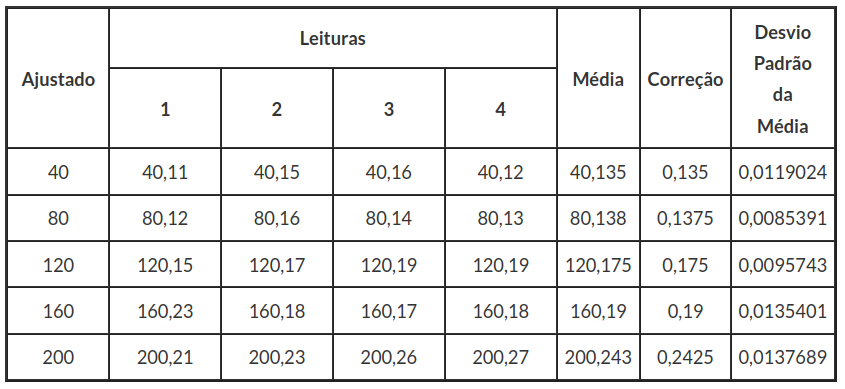
Tabela 3.4.1: Tabela dos dados.

Modelo Matemático

$${Desvio} = {Voltagem~indicada~no~equipamento~em~calibração}~-~{Voltagem~do~padrão~de~referência}.$$

Planilha de Incerteza

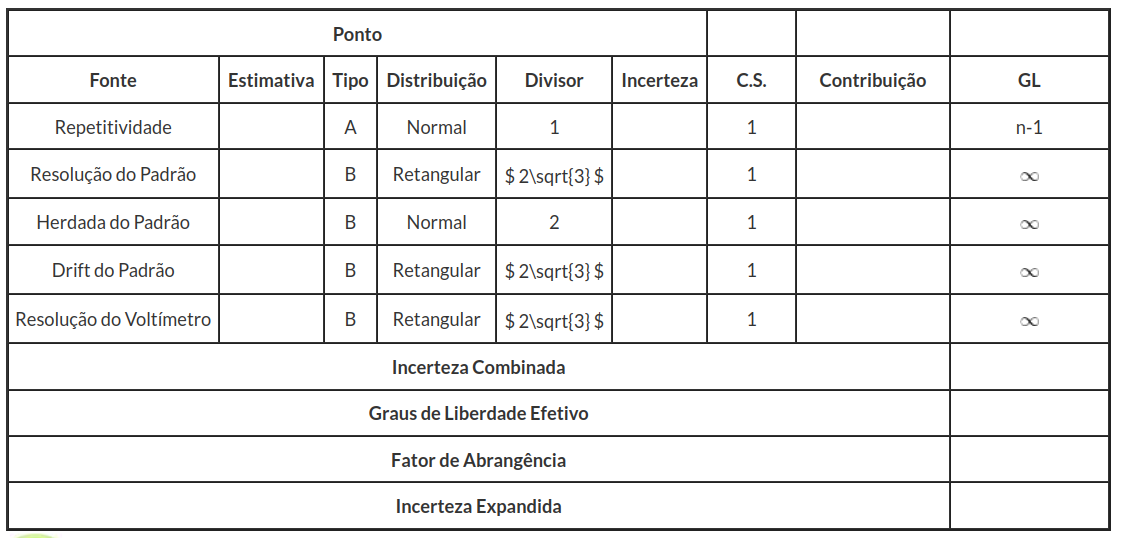
Incerteza Combinada

$$u_c(Volt)=\sqrt{~u^2(\Delta_l)~+~u^2(Res(Pad))~+~u^2(Res({Volt}))~+~u^2(Pad)~+~u^2({Drift})}=$$

$$=\sqrt{(0,0119)^2~+~(0,0028)^2~+~(0,0011)^2~+~(0,001)^2~+~(0,0288)^2}$$

$$=0,03139$$

Graus de Liberdade Efetivo

$$\upsilon_{eff}= \left(\frac{u_c(y)}{u_A(y)}\right)^4\nu_A =$$

$$= \left(\frac{0,03139}{0,0119}\right)^4(4-1) =145,22$$

Incerteza Expandida

$$U(Volt)=u_c(Volt)\times k=$$

$$=0,03139\times 1,9765=0,062052$$

Assim, obtemos os seguintes resultados:

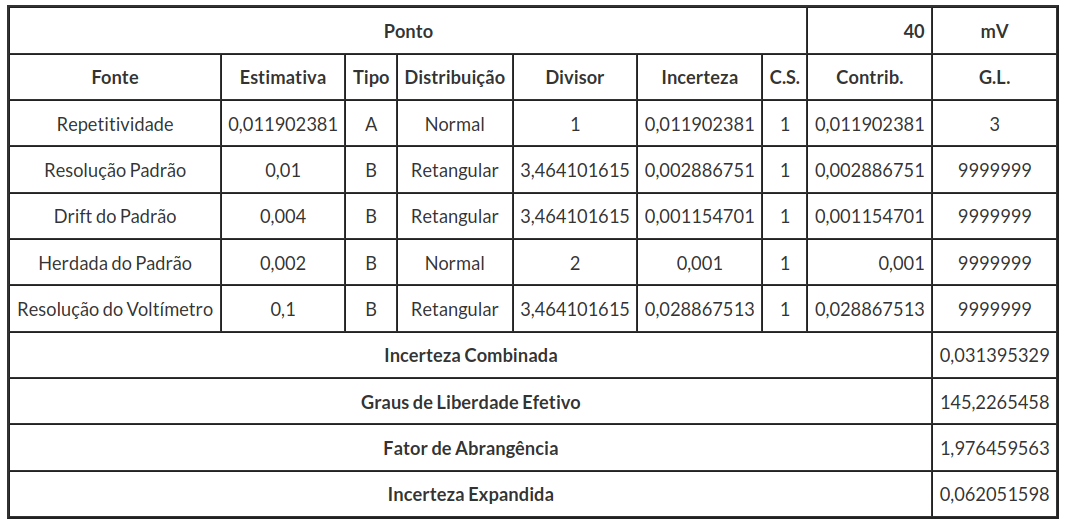
Avaliação da incerteza: Suponha que este equipamento seja utilizado para medir uma tolerância de 3$ mV $. Faremos uma análise crítica da capacidade deste equipamento para medir tal tolerância.

Critério:

$$|T|+U\leq EMP$$

Definimos o Erro Máximo Permissível (EMP) para J=10

$$EMP=\frac{{Tolerância}}{J}=\frac{3}{10}=0,3$$

$$|T|+U=|0,103|+0,062=0,19705\leq 0,3=EMP$$

Portanto, para o ponto de $ 40~mV $, foi aprovada.

3.5 - Cálculo de Incerteza de um Termômetro

Objeto a ser calibrado

Termômetro.

Resolução: $ 0,5^oC $.

Faixa de Indicação (faixa nominal): $ 0~ a~ 100^oC $.

Padrão de referência

Termômetro padrão.

Resolução: $ 0,1 $ºC

Incerteza expandida: $ U = 0,25^oC~(k=2) $.

Faixa de indicação (faixa nominal): $ -40~ a~ 500^oC $.

Banho

Falta de Homogeneidade do Banho: $ \pm 0,05^o C $

Resultados

A bancada foi ajustada com o termômetro (a ser calibrado) e as leituras foram realizadas com o padrão. A Tabela 3.5.1 apresenta os dados.

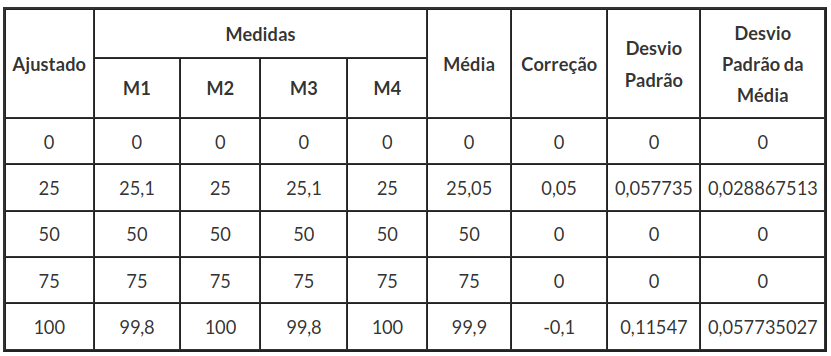
Tabela 3.5.1: Tabela de dados para o termômetro.

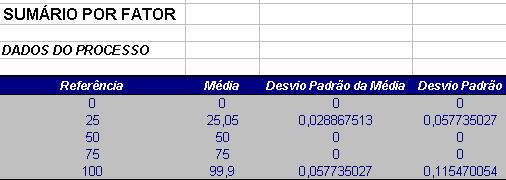
Equação Matemática

$${Desvio} = {Medida~do~termômetro} - {termômetro~padrão}$$

Fontes de Incerteza

• Repetitividade - Tipo A;
• Resolução do termômetro;
• Resolução do termômetro padrão;
• Incerteza herdada do padrão;
• Falta de Homogeneidade do Banho.

Incerteza Combinada

Através da equação de propagação da incerteza, temos que a expressão da incerteza combinada para o termômetro é dada por

$$u_c(M)=\sqrt{~u^2(\Delta_l)~+~u^2(Res(term))~+~u^2(Res(pad))~+~u^2(h_{Pad})~+~u^2(Banho)}$$

onde

• $ u(\Delta_l) $: representa a incerteza devido a repetitividade;
• $ u(Res(term)) $: representa a incerteza devido a resolução do termômetro;
• $ u(Res(pad)) $: representa a incerteza devido a resolução do termômetro padrão;
• $ u(h_{Pad}) $: representa a incerteza herdada do termômetro padrão;
• $ u(Banho) $: representa a incerteza devido a falta de homogeneidade do banho.

Cálculo da Incerteza Padrão das Grandezas de Entrada

A seguir, vamos calcular a incerteza de cada fonte.

Repetitividade ($ \Delta_l $)

Incerteza do Tipo A.

$$u(\Delta_l) = \frac{s}{\sqrt{n}}$$

para a faixa de $ 25^oC $ temos

$$u(\Delta_l) =\frac{0,0577}{\sqrt{4}}=0,028$$

onde

$ u(\Delta_l) $: representa a incerteza do Tipo A ou incerteza devido a repetitividade;

$ s $: representa o desvio padrão das faixa de medição;

n: representa o número de pontos de calibração.

Incerteza Herdada do termômetro Padrão $ (u(h_{Pad})) $

Distribuição: Normal.

$ u(h_{Pad}) =\frac{0,25}{2}=0,125 $

Resolução do termômetro Padrão $ (u(Res(pad))) $

Distribuição: Retangular.

$ u(Res(pad)) =\frac{0,1}{2\sqrt{3}}=0,028 $

Resolução do termômetro $ (u(Res(term))) $

Distribuição: Retangular.

$ u(Res(term)) =\frac{0,5}{2\sqrt{3}}=0,144 $

Cálculo da Incerteza do termômetro

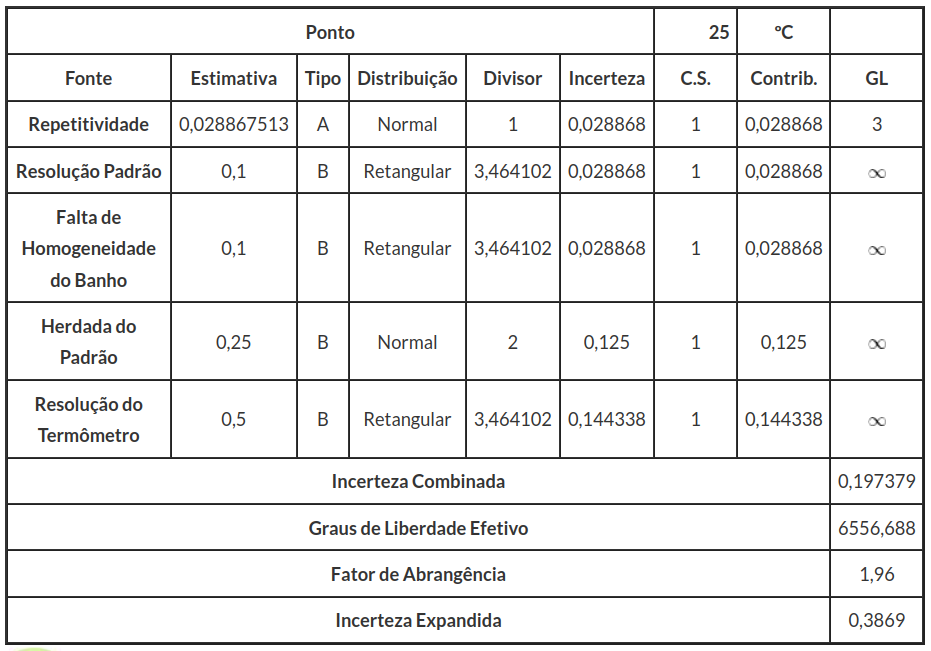
Incerteza combinada

$$u_c(Term)=\sqrt{(0,028)^2~+~(0,028)^2~+~(0,028)^2~+~(0,125)^2~+~(0,144)^2}=0,1973$$

Graus de liberdade efetivo

$$\nu_{eff}~=~\left(\frac{u_c(Term)}{u(\Delta_l)}\right)^4~\nu_A~=$$

$$=~\left(\frac{0,195789}{0,028}\right)^4~(4-1)~=6556,68$$

Através da tabela t-Student, encontramos $ k =1,96 $

Incerteza Expandida

$$U~=~k~\times~u_c(Term)~=1,96\times 0,1973=0,3869$$

O termômetro é utilizado para medir uma tolerância de $ 5ordm;C $. Faremos agora, um estudo da comprovação metrológica.

Considerando $ J=10 $, temos que

$$EMP=\frac{{Tolerância}}{10}=\frac{5}{10}=0,5^oC$$

$$|T|+U=|0,05|+0,3869=0,43693\leq 0,5=EMP$$

Portanto, para o ponto de $ 25^oC $, foi aprovada.

3.6 - Cálculo de incerteza de um Termopar tipo N a 1000ºC

Considere o processo de calibração de um termopar do tipo N. Esta calibração é realizada por comparação utilizando dois termopares do tipo R em um forno horizontal na temperatura de 1000ºC. As forças eletromotrizes (fem) geradas pelos termopares são medidas por um voltímetro digital por meio de uma chave seletora. As referências dos termopares são à 0ºC e o termopar a ser calibrado é conectado ao ponto de referência utilizando cabos de compensação.

Para calcularmos a incerteza, vamos dividir em dois passos, primeiro calculamos a incerteza da temperatura da junção quente do termopar a ser calibrado, em seguida a tensão entre os fios do termopar com a junção fria a 0ºC durante a calibração.

Incerteza devido a temperatura da junção quente

A seguir, apresentamos a equação de medição da temperatura da junção quente.

$$t_X=t_S\left(V_{iS}+\delta V_{iS1}+\delta V_{iS2}+\delta V_R-\frac{\delta t_{0S}}{C_{S0}}\right)+\delta t_D+\delta t_F+\delta t_S$$

$$\cong t_S(V_{iS})+C_S~\delta V_{iS1}+C_S~\delta V_{iS2}+C_S~\delta V_R-\frac{C_S}{C_{S0}}\delta t_{0S}+\delta t_D+\delta t_F+\delta t_S$$

em que

• temperatura do termômetro de referência em termos de tensão com a junção fria a 0ºC (certificado de calibração) em ºC. Do certificado temos que U(tS)=0,3ºC com k=2;
• indicação do voltímetro em μV;
• correções da tensão obtida à partir da calibração do voltímetro em μV. Do certificado temos que U=2 μV com k=2;
• correções da tensão devido à resolução limitada do voltímetro em μV. Aqui usamos um microvoltímetro de 4 1/2 dígitos na faixa de 10 mV, resultando nos limites de resolução de ±0,5 μV;
• correção da tensão devido aos efeitos de contato da chave inversora em μV. As tensões parasitas residuais de “offset” devido aos contatos da chave foram estimadas como zero dentro dos limites de ±2 μV;
• correções da temperatura devido ao desvio da temperatura de referência em relação ao valor em ºC. A temperatura do ponto de referência de cada termopar é conhecida como sendo 0ºC dentro dos limites ±0,1 ºC ;
• sensibilidade dos termopares em termos de tensão na temperatura de medição de 1000ºC em ºC/μV, neste caso o valor é de 0,077ºC/μV;
• sensibilidade dos termopares em termos de tensão na temperatura de referência a 0ºC em ºC/μV;
• variação dos valores dos termômetros de referência desde a sua última calibração devido à deriva em ºC. A partir de calibrações anteriores as derivas foram estimadas como sendo zero dentro dos limites de ±0,3 ºC;
• correção de temperatura devido à não uniformidade da temperatura do forno em ºC. Neste caso, os desvios da não homogeneidade de temperatura na região de medição estão dentro de ±1 ºC;
• desvio padrão agrupado entre a 1ª referência, 2ª referência e o termopar a ser calibrado.

Primeiramente, vamos calcular o desvio padrão agrupado $ t_S, $ para isto observe a seguinte tabela.

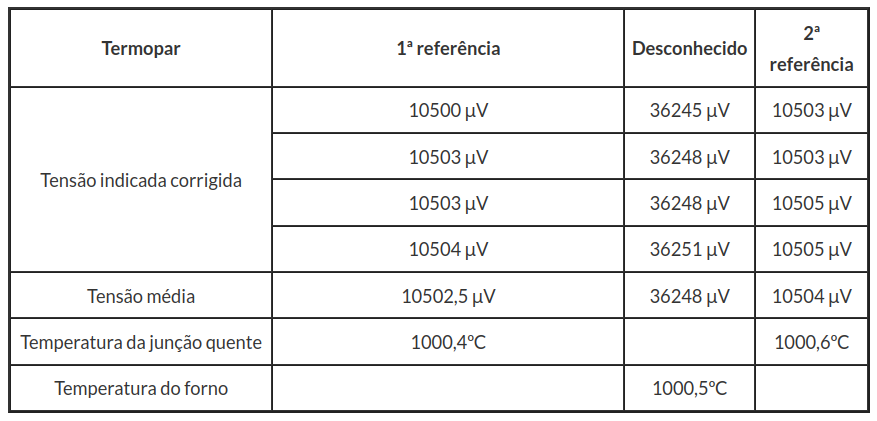
Convertendo a tensão em temperatura temos que

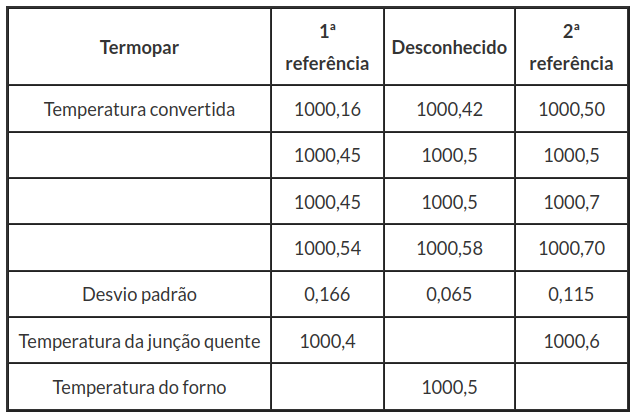
Assim, o desvio padrão agrupado é dada por

$$s_p=u(t_S)=\sqrt{\frac{(n_1-1)s^2_1+(n_2-1)s^2_2+(n_3-1)s^2_3}{n_1+n_2+n_3-3}}=0,1ordm;C$$

A seguir, apresentamos os dados para o cálculo de incerteza:

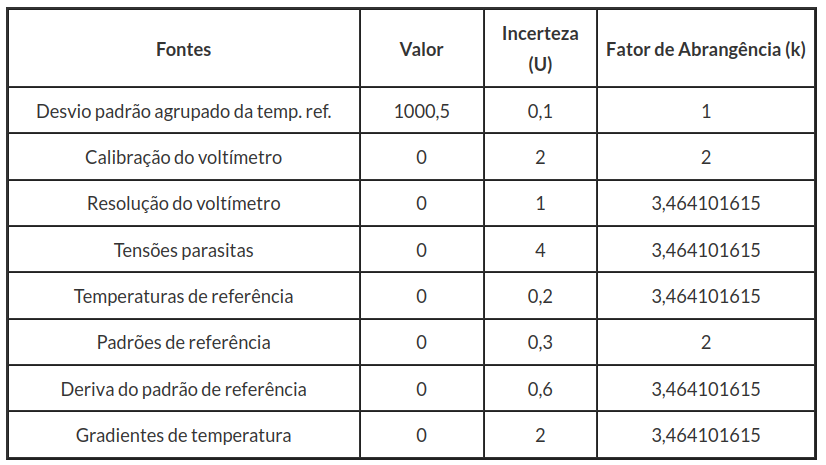
Com isso, a incerteza combinada é dada por:

$$u^2_c(t_X)=u^2(t_S)+\left(\frac{\partial t_X}{\partial \delta V_{iS1}}\right)^2 u^2(\delta V_{iS1})+\left(\frac{\partial t_X}{\partial \delta V_{iS2}}\right)^2 u^2(\delta V_{iS2})+\left(\frac{\partial t_X}{\partial \delta V_{R}}\right)^2 u^2(\delta V_{R})+$$

$$+\left(\frac{\partial t_X}{\partial \delta t_{0S}}\right)^2 u^2(\delta t_{0S})+\left(\frac{\partial t_X}{\partial \delta t_{D}}\right)^2 u^2(\delta t_{D})+\left(\frac{\partial t_X}{\partial \delta t_{F}}\right)^2 u^2(\delta t_{F})+u^2(\delta t_S)=$$

$$=0,1^2+0,077^2 1^2+0,077^2 0,29^2+0,077^2 1,15^2+(-0,407)^2 0,058^2+1^2 0,173^2+1^2 0,577^2+0,15^2$$

em que

$$\left(\frac{\partial t_X}{\partial \delta V_{iS1}}\right)=\left(\frac{\partial t_X}{\partial \delta V_{iS2}}\right)=\left(\frac{\partial t_X}{\partial \delta V_{R}}\right)=C_S=0,077$$

$$\left(\frac{\partial t_X}{\partial \delta t_{0S}}\right)=\frac{-C_S}{C_{S0}}=-\frac{0,077}{0,189}=-0,407$$

$$\left(\frac{\partial t_X}{\partial \delta t_{D}}\right)=\left(\frac{\partial t_X}{\partial \delta t_{F}}\right)=1$$

Logo, a incerteza combinada é dada por

$$u_c(t_X)=0,641$$

Assim, a incerteza expandida é dada por:

$$U(t_X)=k\times u_c(t_X)=2\times 0,641=1,282$$

Como temos apenas incerteza do tipo B, então adotamos $ k=2. $

A seguir, apresentamos um resumo do cálculo de incerteza.

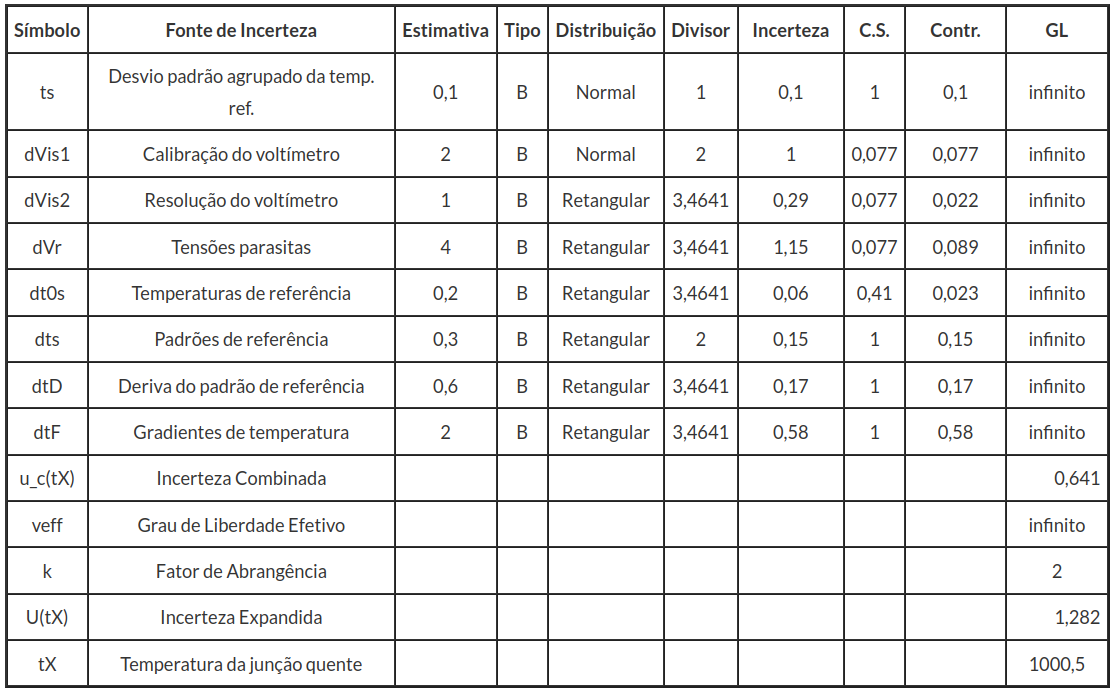
Incerteza devido a fem do termopar a ser calibrado

A seguir, apresentamos a equação de medição da tensão entre os fios do termopar com a junção fria (de referência) a 0ºC, durante a calibração.

$$V_X\cong V_X(t_X)+\frac{\Delta t}{C_X}-\frac{\delta t_{0X}}{C_{X0}}$$

$$=V_{iX}+\delta V_{iX1}+\delta V_{iX2}+\delta V_R+\delta V_{LX}+\frac{\Delta t}{C_X}-\frac{\delta t_{0X}}{C_{X0}}$$

em que

• indicação do voltímetro em μV;
• correções da tensão obtida à partir da calibração do voltímetro em μV. Do certificado temos que U=2 μV com k=2;
• correções da tensão devido à resolução limitada do voltímetro em μV. Aqui usamos um microvoltímetro de 4 1/2 dígitos na faixa de 10 mV, resultando nos limites de resolução de ±0,5 μV;
• correção da tensão devido aos efeitos de contato da chave inversora em μV. As tensões parasitas residuais de “offset” devido aos contatos da chave foram estimadas como zero dentro dos limites de ±2 μV;
• correções da temperatura devido ao desvio da temperatura de referência em relação ao valor em ºC. A temperatura do ponto de referência de cada termopar é conhecida como sendo 0ºC dentro dos limites ±0,1 ºC;
• sensibilidade dos termopares em termos de tensão na temperatura de medição de 1000ºC em ºC/μV, neste caso o valor é de 0,026ºC/μV;
• sensibilidade dos termopares em termos de tensão na temperatura de referência a 0ºC em ºC/μV, neste caso o valor é de 0,039ºC/μV;
• ponto de calibração da temperatura do termopar;
• desvio da temperatura do ponto de calibração em relação a temperatura do forno, em ºC;
• correção de tensão devido aos cabos de compensação (faixa de 0 a 40ºC). As diferenças de tensão entre os cabos e os fios do termopar estão entre os limites ±5 μV.

Primeiramente, vamos calcular a repetibilidade.

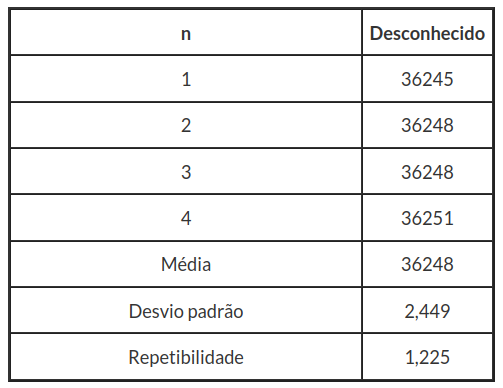
$$u(V_{iX})=\frac{s}{\sqrt{n}}=\frac{2,449}{\sqrt{4}}=1,225$$

A seguir, apresentamos os dados para o cálculo de incerteza:

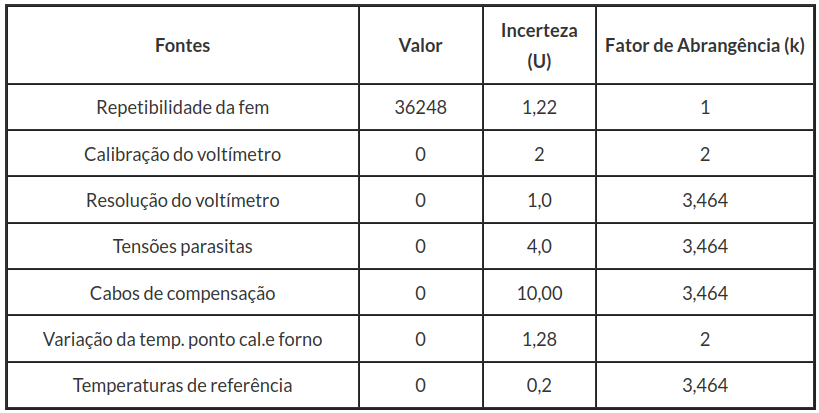
Com isso, a incerteza combinada é dada por:

$$u_c(V_X)=u^2(V_{iX})+\left(\frac{\partial V_X}{\partial \delta V_{iX1}}\right)^2 u^2(\delta V_{iX1})+\left(\frac{\partial V_X}{\partial \delta V_{iX2}}\right)^2 u^2(\delta V_{iX2})+\left(\frac{\partial V_X}{\partial \delta V_{R}}\right)^2 u^2(\delta V_{R})+$$

$$+\left(\frac{\partial V_X}{\partial \delta V_{LX}}\right)^2 u^2(\delta V_{LX})+\left(\frac{\partial V_X}{\partial \Delta t}\right)^2 u^2(\Delta t)+\left(\frac{\partial V_X}{\partial \delta t_{0X}}\right)^2 u^2(\delta t_{0X})=$$

$$=1,225^2+1^2~1^2+1^2~0,29^2+1^2~1,15^2+1^2~2,89^2+38,5^2~0,641^2+25,6^2~0,058^2$$

em que

$$\left(\frac{\partial V_X}{\partial \delta V_{iX1}}\right)=\left(\frac{\partial V_X}{\partial \delta V_{iX2}}\right)=\left(\frac{\partial V_X}{\partial \delta V_{R}}\right)=\left(\frac{\partial V_X}{\partial \delta V_{LX}}\right)=1$$

$$\left(\frac{\partial V_X}{\partial \Delta t}\right)=\frac{1}{C_{X}}=38,5$$

$$\left(\frac{\partial V_X}{\partial \delta t_{0X}}\right)=\frac{1}{C_{X0}}=25,6$$

Logo, a incerteza combinada é dada por

$$u_c(V_X)=24,94$$

Assim, a incerteza expandida é dada por:

$$U(V_X)=k\times u_c(V_X)=2\times 24,94=49,88$$

em que k é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de aproximadamente 95,45%.

$$\nu_{eff}(V_X)=\frac{u^4(V_X)}{u^4(V_{iX})}(n-1)=\frac{24,94^4}{1,22^4}=515856,11$$

A seguir, apresentamos um resumo do cálculo de incerteza.

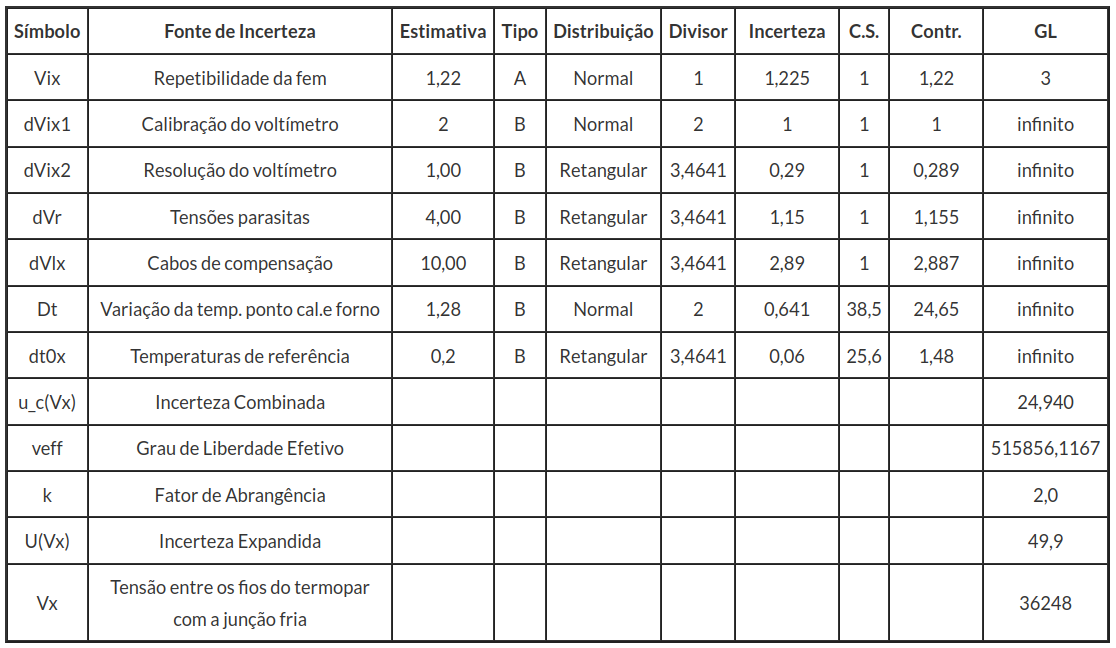
3.7 - Cálculo de incerteza de um Paquímetro

Considere o processo de calibração de um paquímetro digital de alcance 20 mm e resolução de 0,01 mm. Esta calibração é realizada por comparação utilizando-se um calibrador de paquímetros eblocos padrões de referência. Em cada patamar do ensaio obtemos um desvio de calibração ΔL que é a diferença entre indicado pelo instrumento a calibrar e o valor convencionalmente verdadeiro do padrão de referência. Dado pela seguinte equação:

$$d=L-L_s$$

em que

• L: representa a leitura obtida pelo paquímetro;
• $L_S$: representa o comprimento do bloco padrão para uma temperatura de 20ºC.

Um outro fator determinante nesta equação de medição é a temperatura, com isso a correção devido à temperatura é dada por:

$$d=L(1+\alpha\theta)-L_s(1+\alpha_s \theta_s)$$

em que,

• $ \alpha $ e $ \alpha_s $: correspondem aos coeficientes de expansão térmica do paquímetro (escala) e do bloco padrão utilizado na medição, respectivamente;
• $ \theta $ e $ \theta_s $: correspondem a diferença de temperatura do paquímetro e o bloco padrão, em relação a 20ºC, respectivamente.

Modelo Matemático

A leitura, do comprimento do bloco, obtida no paquímetro é dada por

$$L=\frac{d+L_s(1+\alpha_s \theta_s)}{(1+\alpha \theta)}\quad (*)$$

Multiplicando e dividindo por $ (1-\alpha_X\theta) $, obtemos

$$L=\frac{d+L_s(1+\alpha_s \theta_s)}{(1+\alpha \theta)}\frac{(1-\alpha\theta)}{(1-\alpha\theta)}=\frac{d(1-\alpha \theta)+L_S(1+\alpha_s\theta_s)(1-\alpha\theta)}{1-(\alpha\theta)^2}$$

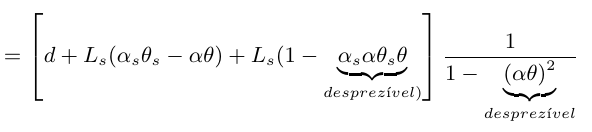
Simplificando a equação acima em relação aos termos desprezíveis, podemos aproximar o valor do bloco padrão, por

$$L=d+L_S+L_S(\alpha_s\theta_s-\alpha\theta)$$

Ao denotarmos a diferença entre as temperaturas do paquímetro e do bloco padrão, por

$$\delta\theta=\theta-\theta_s$$

e a diferença entre os coeficientes de expansão térmica do paquímetro e do bloco padrão, por

$$\delta\alpha=\alpha-\alpha_s$$

obtemos que

$$L=d+L_s-L_s(\delta\alpha\times \theta+\delta\theta\times \alpha_s)$$

Os desvios obtidos apresentam as seguintes fontes de incerteza

$$d=\Delta_L+\text{Res}+E_p$$

em que,

ΔL : representa a diferença observada no comprimento do bloco padrão (repetitividade); medida do paquímetro - medida do bloco padrão;

Res : representa a resolução do paquímetro;

Ep : representa o paralelismo do paquímetro.

Assim, a equação matemática do comprimento do bloco é:

$$L=\Delta_L+\text{Res}+E_p+L_s-L_s(\delta\alpha\times \theta+\delta\theta\times \alpha_s)$$

Fontes de incerteza

• Resolução (Res): A resolução do paquímetro é de 0,01mm. Esta variável é considerada com média zero e limites de variação definido pela resolução do equipamento;
• Incerteza herdada do bloco padrão (LS): Esta variável tem média dada pelo valor do padrão com desvio padrão definido pela incerteza combinada, ambos declarados no certificado de calibração (U=0,0008 mm, k=2);
• Paralelismo (Ep): O paralelismo entre as faces é considerada uma variável com média zero e limites de variação de ±0,0025mm (resultado obtido como a máxima diferença entre as leituras com os blocos padrão em pontos distintos nas hastes de medição);
• Correções de temperatura: Antes da calibração, tomamos cuidado para assegurar que o jogo de bloco padrão e o micrômetro estejam à mesma temperatura ambiente da sala de medição;

1. Diferença de temperatura entre o micrômetro e o bloco padrão (δθ): diferença máxima de ±0,2ºC, com média zero;
2. Coeficiente de expansão térmico do bloco padrão (αs): média de 11,5×10-6ºC-1 com limite de ±2×10-6ºC-1;
3. Diferença entre os coeficientes de expansão térmica (δα): média zero com limites ±2×10-6ºC-1;
4. Diferença entre a temperatura do paquímetro e a temperatura de referência tr=20ºC (θ): limites de ±0,2ºC.

Além disso, as fontes de incerteza θ, δα, δθ e αs são assumidas não correlacionadas. Através da equação (*), leitura obtida no paquímetro para o comprimento do bloco, observamos que o valor estimado para comprimento é dado por

$$L = (\text{Média do desvios}) + L_s$$

OBS: Esta equação é a estimativa da medição do paquímetro que é obtida desconsiderando as variáveis que tem média zero.

Avaliação da Incerteza Combinada (uc(L))

Através da equação de propagação da incerteza, temos que

$$u_c(L)=\sqrt{c^2_{L_s}~u^2(L_s)+c^2_d~u^2(d)+c^2_{\alpha_s}~u^2(\alpha_s)+c^2_\theta~u^2(\theta)+c^2_{\delta\alpha}~u^2(\delta\alpha)+c^2_{\delta\theta}~u^2(\delta\theta)}$$

em que os coeficientes de sensibilidade avaliados no ponto da média são dados por:

• $ c_{L_s}=\dfrac{\partial L}{\partial L_s}=1-\underbrace{(\delta\alpha~\theta~+~\delta\theta~\alpha_S)}_{\text{desprezível}}=1 $;
• $ c_d=\dfrac{\partial L}{\partial d}=1 $;
• $ c_{\alpha_s}=\dfrac{\partial L}{\partial \alpha_s}=-L_s~\delta\alpha=0 $ (Média de $ \delta\alpha $ é igual a zero);
• $ c_{\theta}=\dfrac{\partial L}{\partial \theta}=-L_s~\delta\theta=0 $ (Média de $ \delta\theta $ é igual a zero);
• $ c_{\delta\alpha}=\dfrac{\partial L}{\partial \delta\alpha}=-L_s~\theta $;
• $ c_{\delta\theta}=\dfrac{\partial L}{\partial \delta \theta}=-L_s~\alpha $.

Com isso, a expressão incerteza combinada é dada por

$$u_c(L)=\sqrt{u^2(L_s)+u^2(\Delta_l)~+~u^2(Res)~+~u^2(Ep)+(-L_s~\theta)^2~u^2(\delta\alpha)+(-L_s~\alpha)^2~u^2(\delta\theta)}$$

Cálculo da Incerteza Padrão das grandezas de entrada

A seguir, vamos calcular a incerteza de cada fonte.

Padrão de referência ($L_S$)

Distribuição: Normal

$$u(L_s)=\dfrac{0,008}{2}=0,004$$

Paralelismo ($E_p$)

Distribuição : Retangular

$$u(E_p)=\dfrac{0,005}{2\sqrt{3}}=0,002887$$

Resolução do paquímetro (Res)

Distribuição: Retangular

$$u(Res)=\dfrac{0,01}{2\sqrt{3}}=0,0014$$

Diferença entre os coeficientes de expansão térmico ($ \delta\alpha $)

Distribuição: Retangular

$ u(\delta\alpha)=\dfrac{4\times 10^{-6}}{2\sqrt{3}}=1,15\times 10^{-6} $

Diferença entre a temperatura do paquímetro e a temperatura de referência $t_0$=20ºC (θ)

Foi registrado uma temperatura média de 20,2ºC, resultando em θ=20,2-20 =0,2ºC.

Diferença de temperatura entre o paquímetro e o bloco padrão (δθ)

Distribuição: Retangular

$$u(\delta\theta)=\dfrac{0,4}{2\sqrt{3}}=0,115$$

Coeficiente de expansão térmica ($ \alpha_s $)

Média de 11,5 x 10-6 ºC-1.

Cálculo da Incerteza do tipo A u(ΔL)

A seguir, vamos calcular a repetibilidade (incerteza do tipo A)

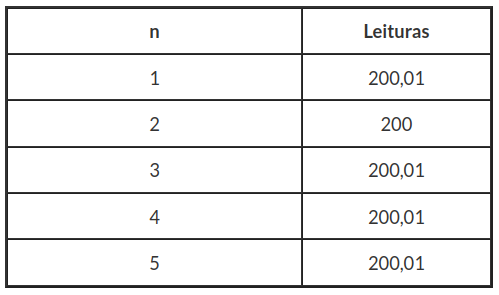
Tabela 3.2.3: Cálculo da incerteza tipo A.

A incerteza do tipo A é calculada da seguinte forma:

$$u(\Delta L)=\dfrac{s}{\sqrt{n}}=\frac{0,004472}{\sqrt{5}}=0,002~\text{mm}$$

Agora, vamos calcular aplicando o Action.

(imagem em falta)

Incerteza combinada

Com isso, a incerteza combinada é dada por

$$u^2_c(L)=u^2(L_s)+u^2(\Delta_l)+u^2(Res)+u^2(Ep)+(-L_s~\theta)^2~u^2(\delta\alpha)+(-L_s~\alpha)^2~u^2(\delta\theta)=$$

$$=0,004^2+0,002^2+0,005^2+0,0014^2+$$

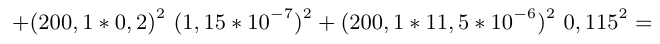
Assim, temos que

$$u_c(L)=0,0069~\text{mm}$$

Graus de liberdade efetivo

$$\nu_{eff}(L)~=~\left(\frac{u_c(L)}{u(\Delta_L)}\right)^4~(n-1)=\left(\frac{0,0069}{0,002}\right)^4~(5-1)=555,92$$

Através da tabela t-Student encontramos k =2

Incerteza Expandida (U(L))

$$U(L)=k\times u_c(L)=2\times 0,0069=0,014~\text{mm}$$

Assim, resumimos os resultados do cálculo de incerteza no ponto de 200 mm a seguir

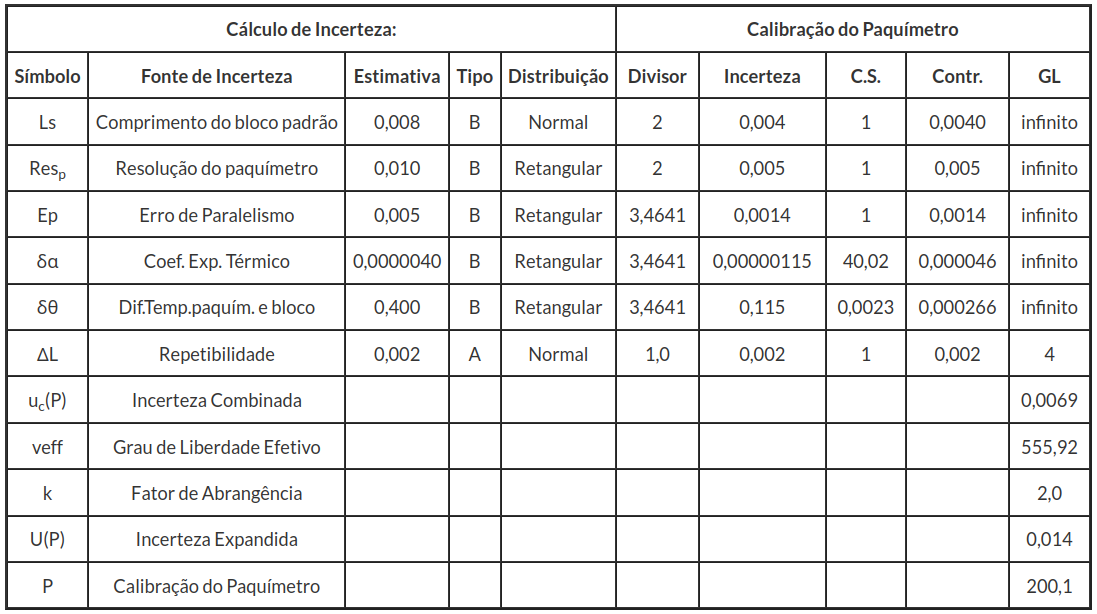
3.8 - Cálculo de incerteza de uma Trena

Considere o processo de calibração de uma trena em comparação com uma régua graduada, conforme figura.

(imagem em falta)

Figura 3.13.1: Esquema de medição.

Os dados referentes aos equipamentos envolvidos na calibração são dados por:

Objeto a ser calibrado: trena de fita de aço (5 m).

Resolução: $ 1 $ mm.

Faixa de Indicação (faixa nominal): $ 0 - 5000 $ mm .

Padrão de referência 1: régua graduada.

Resolução: $ 0,01 $ mm.

Incerteza expandida: $ U = 0,02~\text{mm}~(k=2). $

Padrão de referência 2: lupa graduada.

Resolução: $ 0,01 $ mm.

Incerteza expandida: $ U = 0,004~mm~(k=2). $

Temperatura durante a calibração: $ 20~\pm~6{}^\circ C $.

Faixa de indicação (faixa nominal): $ 1000 - 5000 mm $

(imagem em falta)

Figura 3.13.2: Medição por comparação.

Equação de medição

$${Desvio} = \text{Medida da trena} - \underbrace{(\text{Medida da Régua graduada}+\text{Medida da Lupa graduada})}_{\text{P}=\text{medidas do padrão}}$$

Fontes de Incerteza

• ε: Repetitividade - Tipo A;
• $Res_T$: Resolução da trena;
• $Res_R$: Resolução da régua graduada;
• $Res_L$: Resolução da lupa graduada;
• R: Incerteza herdada do padrão 1 (régua graduada);
• L: Incerteza herdada do padrão 2 (lupa graduada);

Neta aplicação, vamos tomar o ponto de 2000 mm. Desta forma, observe a seguinte tabela.

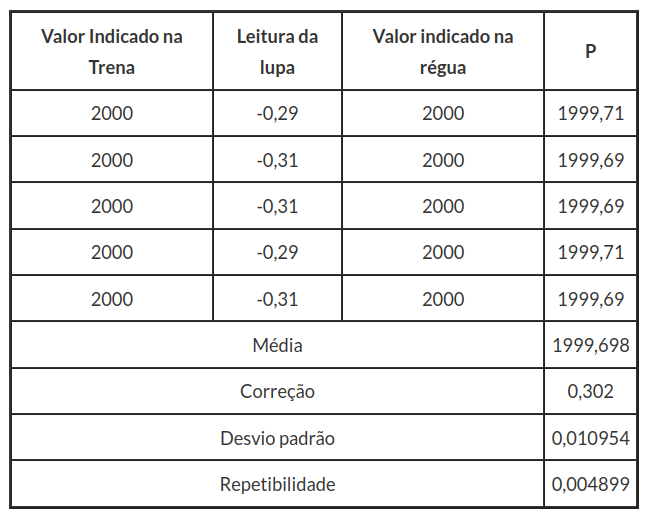
Incerteza Combinada

Através da equação de propagação da incerteza, temos que a expressão da incerteza combinada para a trena da seguinte forma.

$$u_c(T)=\sqrt{u^2(\varepsilon)+u^2(\text{Res}_T)+u^2(\text{Res}_L)+u^2(\text{Res}_R)+u^2(L)+u^2(R)}$$

Cálculo da Incerteza Padrão das Grandezas de Entrada

A seguir, vamos calcular a incerteza de cada fonte.

Repetitividade (ε)

Incerteza do Tipo A.

$$u(\varepsilon)=\frac{s}{\sqrt{n}}=\frac{0,010954}{\sqrt{5}}=0,004899$$

em que

s: representa o desvio padrão da faixa de medição;

n: representa o número de pontos de calibração.

Incerteza Herdada da Régua Graduada Padrão (u(R))

Distribuição: Normal.

$$u(R)=\frac{0,02}{2}=0,01$$

Incerteza Herdada da Lupa Graduada Padrão (u(R))

Distribuição: Normal.

$$u(R)=\frac{0,004}{2}=0,002$$

Resolução da Régua Graduada Padrão (u($Res_R$)) e da Lupa Graduada Padrão (u($Res_L$))

Distribuição: Retangular.

$$u(Res_R)=u(Res_L)=\frac{0,01}{2\sqrt{3}}=0,00289$$

Resolução da Trena (u($Res_T$))

Distribuição: Retangular.

$$u(Res_T)=\frac{1}{2\sqrt{3}}=0,289$$

Com isso, a incerteza combinada é dada por:

$$u_c(T)=\sqrt{0,289^2+0,00289^2+0,00289^2+0,01^2+0,002^2+0,004899^2}=0,289$$

Agora, vamos calcular os graus de liberdade efetivo da seguinte forma:

$$\nu_{eff}(T)=\frac{u^4_c(T)}{u^4(\varepsilon)}(n-1)=\frac{0,289^2}{0,004899^4}*4=48392892$$

Logo a incerteza expandida é dada por:

$$U(T)=k\times u_c(T)=2\times 0,289=0,58~\text{mm}$$

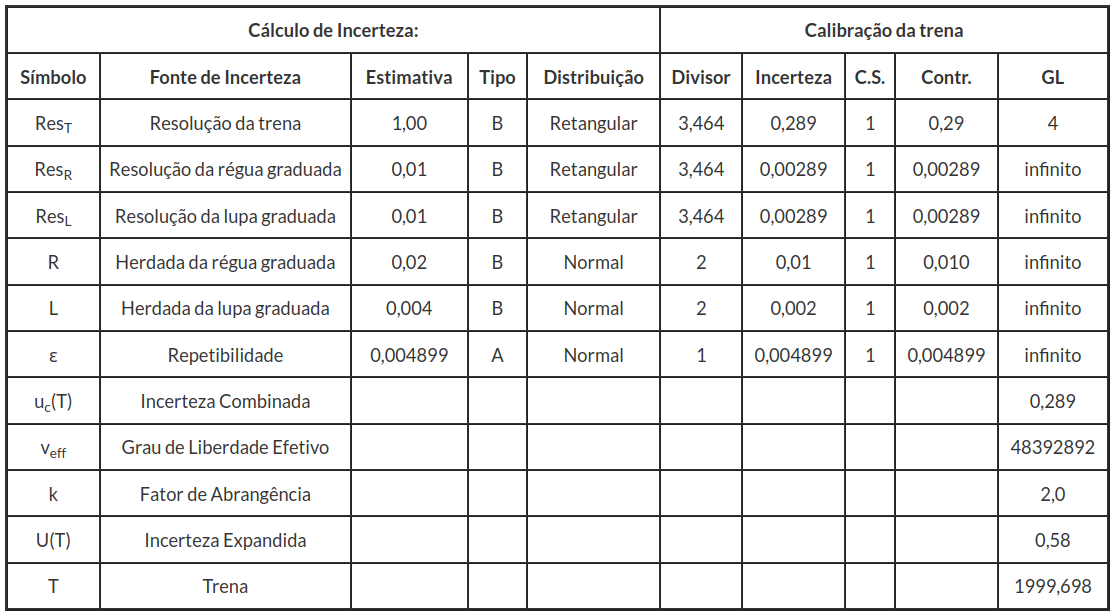
4 - Aplicações do Cálculo de Incerteza em Ensaios

Apresentaremos nos próximos módulos, algumas aplicações da Incerteza de Medição para ensaios, para exemplificar o procedimento dos cálculos e os passos iniciais antes de iniciarmos o cálculo da incerteza de medição.

4.1 - Cálculo de incerteza para Sistema de Medição de Dureza

Sistema de medição de dureza: Brinell (2,5/62,5)

Considere o sistema de medição de dureza de uma peça dentada (foto 4.1.1) na escala Brinell (2,5/62,5). Ao medirmos a dureza da peça em um determinado ponto, provocamos uma alteração na peça em torno deste ponto e consequentemente, não podemos repetir a medição da dureza nesta região. Assim, podemos interpretar o sistema de medição de dureza como um sistema não replicável. Porém, em algumas aplicações, existe uma região na peça em que a dureza é homogênea e neste caso, podemos utilizar esta região para avaliarmos a medição de dureza, considerando este sistema como replicável. Em resumo, dependendo das características da peça a ser medida, podemos interpretar o sistema de medição de dureza como replicável ou não.

Na aplicação que faremos a seguir, temos uma região bastante homogênea em relação à dureza, fato que nos permite considerar o sistema de medição como replicável. Apesar de termos uma região com dureza homogênea, esta não é constante e esta variação (mesmo que pequena) será adicionada à repetitividade do sistema de medição.

No cálculo de incerteza para o sistema de medição de dureza vamos adotar como fontes de incerteza o durômetro, a resolução do durômetro, a repetibilidade do ensaio, e a reprodutibilidade do estudo de R&R. A seguir apresentamos o fluxograma do cálculo de incerteza.

(imagem em falta)

Na sequência, apresentamos uma descrição do sistema de medição.

Fase 1

Descrição do Sistema de Medição

Utilizamos esta fase para realizarmos uma revisão do sistema de medição e o planejamento para a aplicação do MSA. Aqui, é importante definirmos a equipe responsável pela análise, os setores que aplicam o sistema de medição e a necessidade da medição. Por exemplo, a peça que medimos a dureza (Foto 5.7.1) afeta principalmente a segurança do usuário final. Por isso, é importante que tenhamos um sistema de medição confiável.

(imagem em falta)

Figura 4.1.1: foto da peça (material Alumínio Extrudado).

Para a característica dureza, o cliente especificou uma tolerância de 4,5 HB. Para esta aplicação, temos uma exatidão mínima requerida de 0,45 HB.

Para que a equipe possa conhecer melhor o sistema de medição e sua aplicação, fazemos uma análise de cenário através das seguintes questões:

• Importância/impacto no produto?
• Reclamações de Clientes?
• Histórico de Falhas?
• É característica especial?
• Condições Ambientais?
• Sistema de medição é utilizado para CEP?

Fase 2

Método de Medição:

A fase I nos prepara para fazermos uma boa descrição do sistema de medição. Assim, reunimos a equipe para realizarmos a descrição do sistema de medição e elaborarmos o diagrama de Ishikawa.

Descrição do sistema de medição de dureza: Brinell (2,5/62,5)

1. Selecionar a escala no equipamento
2. Limpar da peça
3. Posicionar o durômetro
4. Aplicar carga
5. Realizar leitura

Também definimos as variáveis de parametrização do Sistema de Medição

• Variável: Dureza;
• Descrição: medida realizada em 2,5/62,5 HB;
• Especificação: tolerância de 4,5 HB.

Outro ponto importante para a análise do sistema de medição é o diagrama de Ishikawa, ou diagrama de causa e Efeito. Com toda a equipe reunida (nesta fase é importante contarmos com a presença de operadores), realizamos um brainstorming sobre as principais causas de variação no sistema de medição. O diagrama de Ishikawa é fundamental para definirmos os pontos críticos e a técnicas estatísticas que utilizaremos para avaliar o sistema de medição.

Diagrama de Causa e Efeito (Ishikawa)

(imagem em falta)

Um dos itens crítico de um sistema de medição são os equipamentos utilizados para realizarmos as medições. Os equipamentos são calibrados por laboratórios apropriados e os certificados de calibração devem ser avaliados criticamente com relação a critérios previamente definidos. Nesta aplicação, o durômetro (Reicherter modelo 187,5/2,5) tem resolução de 0,1 HB, é calibrado anualmente e tem erro máximo permissível de 0,9 HB. Com isso, garantimos a exatidão requerida de 0,45 HRC. Na sequência, apresentamos uma foto do durômetro.

(imagem em falta)

Com a descrição do sistema de medição e o diagrama de Ishikawa planejamos a aplicação das técnicas estatísticas. Na maioria dos processos, realizamos basicamente três análises: estabilidade, RR e tendência e linearidade. A seguir, descrevemos o planejamento para aplicação das análises estatísticas.

Fase 3

Planejamento dos Estudos.

• Estabilidade: Selecionamos 1 peça para ser medida ao longo do tempo. Nesta aplicação, faremos três subgrupos racionais de medições por dia durante uma semana (18 subgrupos).
• Tendência: A mesma peça selecionada para a estabilidade será utilizada para o estudo de tendência. Neste caso, definimos o valor de referência em um sistema de medição confiável, neste exemplo, utilizamos o sistema de medição do cliente.
• Repetitividade: 10 peças de lotes de produção “distintos”, sendo 3 medições por peça realizados em ordem aleatória.
• Reprodutibilidade: selecionamos 3 operadores.
• Linearidade: Não se aplica, pois a faixa de medição é pequena.

Após a coleta de dados, vamos executar a análise estatística.

Estabilidade

AMOSTRA UTILIZADA: ALUMÍNIO EXTRUDADO

Subgurpo	Data	Horário	Pessoa	Equipamento	Escala	Medida 1	Medida 2	Medida 3
1	20/05/2013	manhã	A	REICHERTER	2,5 / 62,5	74,7	74,3	73,9
2	23/05/2013	tarde	A	REICHERTER	2,5 / 62,5	74,3	75,9	76,3
3	24/05/2013	tarde	B	REICHERTER	2,5 / 62,5	77,5	74,7	75,5
4	04/06/2013	tarde	C	REICHERTER	2,5 / 62,5	74,7	75,5	76,3
5	23/05/2013	manhã	A	REICHERTER	2,5 / 62,5	76,7	75,1	75,9
6	27/05/2013	manhã	B	REICHERTER	2,5 / 62,5	75,0	76,3	75,9
7	24/05/2013	manhã	C	REICHERTER	2,5 / 62,5	76,3	75,9	75,9
8	28/05/2013	tarde	A	REICHERTER	2,5 / 62,5	75,1	74,7	75,1
9	29/05/2013	tarde	B	REICHERTER	2,5 / 62,5	75,5	75,1	74,3
10	06/06/2013	tarde	C	REICHERTER	2,5 / 62,5	74,7	75,1	76,3
11	28/05/2013	manhã	A	REICHERTER	2,5 / 62,5	75,9	75,1	75,9
12	07/06/2013	manhã	B	REICHERTER	2,5 / 62,5	75,5	74,7	75,9
13	07/06/2013	manhã	C	REICHERTER	2,5 / 62,5	73,2	75,5	74,7
14	04/06/2013	tarde	A	REICHERTER	2,5 / 62,5	75,5	75,5	74,7
15	04/06/2013	tarde	B	REICHERTER	2,5 / 62,5	75,6	75,1	75,5
16	07/06/2013	tarde	C	REICHERTER	2,5 / 62,5	76,3	75,1	73,9
17	04/06/2013	manhã	A	REICHERTER	2,5 / 62,5	75,1	75,5	75,9
18	10/06/2013	manhã	B	REICHERTER	2,5 / 62,5	75,1	75,1	74,3
21	10/06/2013	manhã	C	REICHERTER	2,5 / 62,5	76,3	73,9	73,2

Resultados desse exemplo obtidos com o software Action:

(imagem em falta)

(imagem em falta)

Algumas sugestões de conclusão

Sistema estável ao longo do tempo. Todos os pontos estão dentro das linhas de controle.

RR - Repetitividade e Reprodutibilidade

Escala Brinell 2,5 / 62,5:

Peça	Operador	Medida
1	1	74,3
2	1	72,8
3	1	73,5
4	1	74,7
5	1	74,3
6	1	75,9
7	1	75,5
8	1	75,5
9	1	75,1
10	1	76,7
1	1	72,8
2	1	74,3
3	1	74,7
4	1	74,7
5	1	75,5
6	1	75,5
7	1	75,9
8	1	75,9
9	1	72,8
10	1	74,3
1	1	72,8
2	1	76,3
3	1	76,7
4	1	76,3
5	1	75,1
6	1	75,5
7	1	75,5
8	1	75,9
9	1	75,9
10	1	75,1
1	2	75,9
2	2	75,5
3	2	76,3
4	2	75,1
5	2	75,1
6	2	75,1
7	2	75,1
8	2	74,7
9	2	75,9
10	2	75,5
1	2	75,1
2	2	76,3
3	2	75,1
4	2	75,9
5	2	74,3
6	2	74,3
7	2	73,9
8	2	75,1
9	2	75,9
10	2	75,9
1	2	74,7
2	2	75,5
3	2	75,9
4	2	75,9
5	2	74,7
6	2	75,9
7	2	75,1
8	2	75,9
9	2	76,4
10	2	75,1
1	3	73,2
2	3	70,2
3	3	77,1
4	3	74,7
5	3	76,3
6	3	75,1
7	3	76,7
8	3	76,7
9	3	76,3
10	3	75,9
1	3	75,7
2	3	76,3
3	3	76,3
4	3	73,2
5	3	73,9
6	3	74,3
7	3	75,1
8	3	74,3
9	3	75,1
10	3	75,1
1	3	74,7
2	3	74,7
3	3	76,3
4	3	75,5
5	3	76,3
6	3	73,9
7	3	75,5
8	3	75,1
9	3	75,9
10	3	75,1

Resultados desse exemplo obtidos com o software Action:

(imagem em falta)

(imagem em falta)

(imagem em falta)

Algumas sugestões de conclusão

Análise gráfica:

No gráfico por operador observamos um comportamento similar com repeito à medição de dureza.

Análise da variabilidade:

A variabilidade do operador é nula.

Portanto, a incerteza devido a reprodutibilidade é zero.

Tendência

Peças	VR	Medidas
1	72,7	75,1
2	72,7	74,7
3	72,7	75,5
4	72,7	75,5
5	72,7	74,7
6	72,7	75,1
7	72,7	75,9
8	72,7	74,7
9	72,7	74,3
10	72,7	75,1
11	72,7	73,9
12	72,7	75,9

(imagem em falta)

(imagem em falta)

Algumas sugestões de conclusão

Como o zero não faz parte do intervalo de confiança, consideramos o que sistema de medição apresenta tendência significativa ao nível de confiança de 95%.

Cálculo de incerteza

Equação de medição

Esta seção é dedicada ao cálculo de incerteza para a dureza (equação 4.1.1). A seguir apresentamos a equação de medição.

$$D=I+\text{Res}_I+R+\varepsilon~(4.1.1)$$

em que:

• $ D $: representa a dureza, em (HB);
• $ I $: representa o instrumento medidor de dureza (durômetro), em (HB). Temos que $ I $ tem distribuição normal com incerteza $ u(I) $ e fator de abrangência k obtidos via certificado de calibração do durômetro;
• $ Res_I $: representa a resolução do instrumento. Temos que $ u(Res_I) $ tem distribuição retangular (ou uniforme) no intervalo $ \left(-\frac{{Res}_I}{2},\frac{{Res}_I}{2}\right). $ Logo a incerteza devido à resolução será dada por:

$$u(Res_I)=\frac{{Res}_I}{2\sqrt{3}}$$

• $ R $: representa a reprodutibilidade em $ (HB). $ Temos que $ R $ tem distribuição normal com incerteza $ u(R) $ obtidos no ensaio de Reprodutibilidade. A reprodutibilidade representa a variabilidade associada à aplicação do método de medição pelos operadores;
• $ \varepsilon $: representa a repetitividade. Podemos supor que a distribuição da média das medições tem distribuição normal. Logo, podemos estimar sua incerteza (desvio padrão da média) como:

$$u(\varepsilon) = \frac{s}{\sqrt{n}},$$

em que $ s^2=\frac{1}{n-1}\displaystyle\sum_{i=1}^{n}(x_i -\overline{X})^2 $ é a variância amostral e $ \overline{X} = \frac{1}{n} \displaystyle\sum^{n_{i=1}} x_i $ é a média amostral.

Incerteza Combinada

A incerteza combinada para a dureza é dada por

$$u_c(D)=\sqrt{u^2(I)+u^2(\text{Res}_I)+u^2(R)+u^2(\varepsilon)}$$

Incerteza Expandida

A incerteza expandida para a dureza é dada por

$$U(D)=u_c(D)\times k$$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de aproximadamente 95,45 %.

$$\nu_{eff}(D)=\frac{u^4_c(D)}{u^4(\varepsilon)}(n-1)$$

Ensaio de dureza

Agora vamos calcular a incerteza para o sistema de medição de dureza, para isto, realizamos três medições para o ensaio de dureza, os dados estão na tabela.

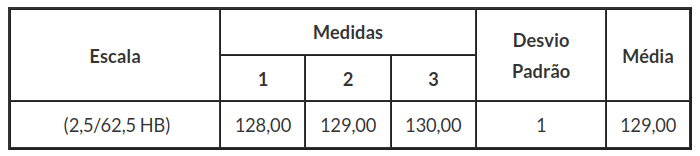
Vamos calcular a média e repetibilidade da seguinte forma

$$\overline{X}=\frac{128+129+130}{3}=129\quad\text{e}\quad u(\varepsilon)=\frac{s}{\sqrt{3}}=\frac{1}{\sqrt{3}}=0,577$$

Do certificado de calibração do durômetro, obtemos que a incerteza devido ao durômetro é de $ u(I)=0,61~HB $ e $ k=2 $ e resolução $ u(Res_I)=1~HB. $ Do estudo de RR, obtemos uma incerteza desprezível. Com isso, calculamos a incerteza combinada para a dureza da seguinte forma:

$$u_c(D)=\sqrt{u^2(I)+u^2(\text{Res}_I)+u^2(R)+u^2(\varepsilon)}=\sqrt{0,305^2+0,289^2+0,577^2+0^2}=0,71$$

A incerteza expandida para a dureza é dada por

$$U(D) =u_c(D)\times k=0,71\times 2,78=1,97$$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de aproximadamente 95,45%.

$$\nu_{eff}(D)=\frac{u^4_c(D)}{u^4(\varepsilon)}(n-1)=\frac{0,71^4}{0,577^4}(3-1)=4,58$$

A seguir, apresentamos um resumo do cálculo de incerteza para o ensaio de dureza na escala Brinell (2,5/62,5 HB).

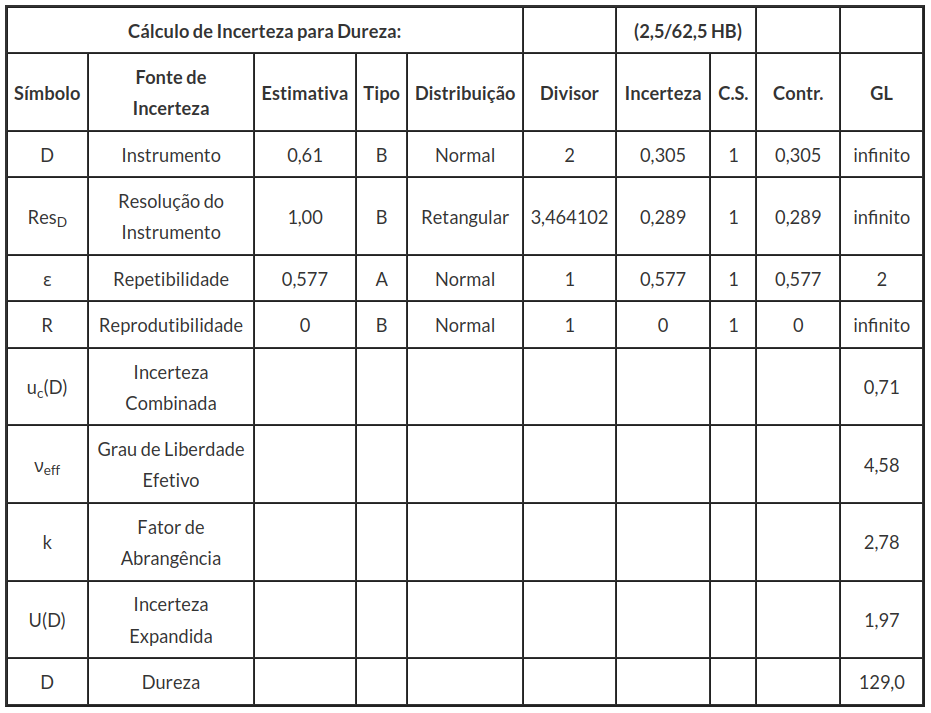
4.2 - Cálculo de Incerteza para Compressão Lateral de Copos

Para realizarmos o cálculo da incerteza associada ao ensaio de compressão lateral de copos, realizamos um levantamento inicial sobre as possíveis fontes de variabilidade que afetavam o ensaio. A Figura 4.2.1 apresenta o diagrama de Ishikawa do processo.

(imagem em falta)

Figura 4.2.1: Gráfico de Ishikawa.

A partir do diagrama, foram confeccionados alguns experimentos para a estimação da variabilidade das fontes relacionadas.

Estudos de Estabilidade

Primeiramente, precisamos atestar a estabilidade do sistema de medição. Para isto, tomamos 100 medições durante 20 dias, ou seja, a cada dia medimos 5 vezes o sistema de medição. As medições estão apresentadas na tabela a seguir:

ID DO SUBGRUPO	1	2	3	4	5	6	7	8	9	10
HORA	09:30	14:30	09:30	14:30	09:30	14:30	09:30	14:30	09:30	14:30
DATA: DIA/MÊS	25/abr	26/abr	27/abr	28/abr	29/abr	30/abr	1/mai	2/mai	3/mai	4/mai
$ x_1 $	1,123	1,124	1,098	1,074	1,117	1,07	1,089	1,118	1,113	1,325
$ x_2 $	1,18	0,947	1,185	1,14	1,057	1,066	1,173	0,968	1,095	1,19
$ x_3 $	1,006	1,115	1,137	1,05	1,022	1,102	1,087	0,993	0,979	1,139
$ x_4 $	1,07	1,047	0,989	1,101	1,046	1,31	1,135	1,041	1,092	1,213
$ x_5 $	0,92	1,281	1,134	1,17	1,068	1,181	1,024	1,147	1,061	1,074
SOMA VAL. INDIVIDUAIS	5,3	5,51	5,54	5,54	5,31	5,73	5,51	5,27	5,34	5,94
MÉDIA $ \overline{X} $	1,06	1,1	1,11	1,11	1,06	1,15	1,1	1,05	1,07	1,19
AMPLITUDE $ R $	0,26	0,33	0,2	0,12	0,1	0,24	0,15	0,18	0,13	0,25
ID DO SUBGRUPO	11	12	13	14	15	16	17	18	19	20
HORA	09:30	14:30	09:30	14:30	09:30	14:30	09:30	14:30	09:30	14:30
DATA: DIA/MÊS	5/mai	6/mai	7/mai	8/mai	9/mai	10/mai	11/mai	12/mai	13/mai	14/mai
$ x_1 $	1,197	1,085	1,089	1,137	1,169	1,081	1,045	1,099	1,19	1,045
$ x_2 $	1,101	1,108	1,149	1,188	1,085	1,051	1,093	1,004	1,246	1,082
$ x_3 $	1,052	1,031	1,129	1,147	1,195	0,963	1,218	1,104	1,073	1,112
$ x_4 $	1,194	1,143	1,19	1,183	1,103	1,212	1,171	1,162	1,074	1,219
$ x_5 $	1,052	1,124	1,157	1,071	0,958	1,07	1,086	1,06	1,087	1,228
SOMA VAL. INDIVIDUAIS	5,6	5,49	5,71	5,73	5,51	5,38	5,61	5,43	5,67	5,69
MÉDIA $ \overline{X} $	1,12	1,1	1,14	1,15	1,1	1,08	1,12	1,09	1,13	1,14
AMPLITUDE $ R $	0,15	0,11	0,1	0,12	0,24	0,25	0,17	0,16	0,17	0,18

Com isso, temos a carta de estabilidade ($ \overline{X} ~{e}~R $) a seguir:

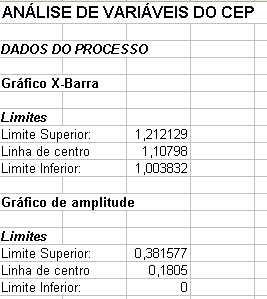
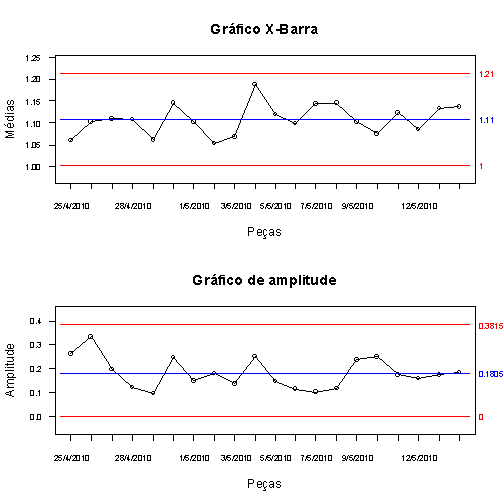
Figura 4.2.1: Gráfico de Estabilidade.

4.2.1 - Experimentos

Experimento 1: Variação no Copo

Aqui, estamos interessados em avaliar se a variação na medição do copo é significativa. Este experimento segue o seguinte procedimento:

• Amostrar um copo e medir três vezes no mesmo ponto;
• Repetir o procedimento em 10 copos.

Para obtermos a estimativa da variabilidade dentro do copo, vamos utilizar a técnica de ANOVA 1 fator (Copo) - efeito aleatório.

Experimento 2: Variação devido ao deslocamento da medição

Aqui, estamos interessados em avaliar se o deslocamento da medição no mesmo copo (radial e axial) é significativo. Este experimento segue o seguinte procedimento:

• Amostrar um copo e medir três vezes em cada ponto, deslocando no sentido altura, radial e axial;
• Repetir o procedimento em três copos.

Para obtermos a estimativa da variabilidade devido ao deslocamento, vamos utilizar as técnicas de componentes de variância e ANOVA 2 fatores (Copo e Deslocamento) - efeito aleatório.

Experimento 3: Variação devido ao ângulo de medição

Aqui, estamos interessados em avaliar se o ângulo formado entre a boca do copo e a base de medição é significativo. Este experimento segue o seguinte procedimento:

• Amostrar um copo e medir três vezes em cada ponto variando o número de lâminas posicionadas no fundo do copo na medição de um ponto para o outro;
• Repetir o procedimento em três copos.

Para obtermos a estimativa da variabilidade devido ao ângulo, vamos utilizar as técnicas de componentes de variância e ANOVA 2 fatores (Copo e Deslocamento) - efeito aleatório.

Experimento 4: Variação devido a temperatura ambiente

Aqui, estamos interessados em avaliar se a temperatura ambiente influência no resultado das medições. Este experimento segue o seguinte procedimento:

• Amostrar um copo e medir três vezes em cada ponto e anotar a temperatura ambiente;
• Repetir o procedimento em três copos.

Para obtermos a estimativa da variabilidade devido a temperatura, vamos utilizar a técnica de regressão linear simples.

Estimação das Fontes de Incerteza Obtidas nos Experimentos para copos tipo PS

Variabilidade do copo $ u_c(\epsilon_2) $

Aqui, vamos utilizar a técnica de anova com 1 fator para estimar a variabilidade no mesmo copo.

A Tabela 4.2.1.1 apresenta as medições realizadas no copo PS.

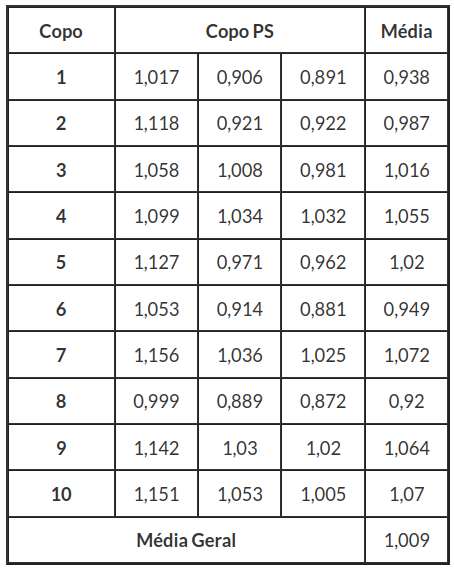
Tabela 4.2.1.1: Medições de Resistência no Copo PS.

O modelo estatístico para este experimento é:

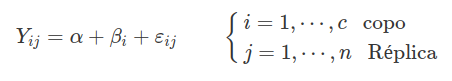
em que:

• $Y_{ij}$: representa a j-ésima medição no i-ésimo copo;
• $α$ é a média das medições;
• $β_i$ é o efeito do copo;
• $ε_{ij}$ é o erro de replicação.

Para calcularmos a $ SQ_T $, vamos calcular primeiramente a variância amostral de todos os dados, ou seja,

$$S^2_g=\frac{(1,017 - 1,009)^2+(0,906 -1,009)^2+\dots+(1,053-1,009)^2+(1,005 - 1,009)^2}{30-1}=0,007$$

Com isso, temos que

$$SQ_T=(c * n - 1)~S^2_g=(10 * 3 - 1)~0,007=0,20538$$

Para calcularmos a soma de quadrados devido ao copo ($ SQ_C $), vamos calcular primeiramente a variância amostral da coluna média, ou seja,

$$S^2_c=\frac{(0,938 - 1,009)^2+(0,987-1,009)^2+\dots+(1,064 - 1,009)^2+(1,070 - 1,009)^2}{10-1}=0,003$$

Com isso, temos que

$$SQ_C =n~(c - 1)~S^2_c=3~(10 - 1)~0,003=0,09001$$

Logo, temos que

$$SQ_E =SQ_T - SQ_C=0,20538 - 0,09001=0,11537$$

Os graus de liberdade são:

Com isso, o quadrado médio é:

$$QM_C =\frac{SQ_C}{c - 1}=\frac{0,09001}{9}=0,010$$

$$QM_E=\frac{SQ_E}{c (n - 1)}=\frac{0,115371}{20}=0,005769$$

A Figura 4.2.1.1 apresenta o resumo da análise de variância.

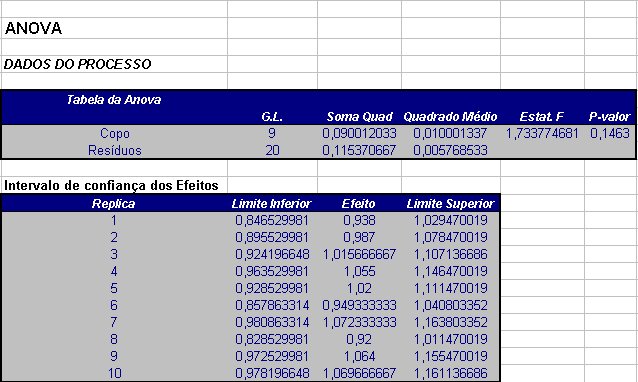
Figura 4.2.1.1: Análise de Variância (ANOVA).

Aqui, temos que p-valor é dado por:

$$P(F_{9;~20}>~1,73)=0,1463$$

Portanto, temos que a estimativa da variabilidade dentro do copo é:

$$u_c(\epsilon_2)=0$$

Fonte de variação devido ao deslocamento da medição $ u_c(\epsilon_3) $

Nesta aplicação usamos novamente uma anova, porém, uma ANOVA two-way, ou seja, dois fatores.

A Tabela 4.2.1.2 apresenta as medições realizadas no copo PS, a coluna Ponto representa o ponto de medição.

Copo	Ponto	Resistência em 10 mm (N)
1	1	1,079
1	2	1,024
1	3	1,062
1	4	1,005
1	5	1,035
2	1	1,066
2	2	0,888
2	3	0,962
2	4	1,005
2	5	1,045
3	1	1,119
3	2	0,984
3	3	1,107
3	4	1,069
3	5	1,042
4	1	1,126
4	2	1,022
4	3	1,149
4	4	1,09
4	5	1,073
5	1	1,182
5	2	1,078
5	3	1,025
5	4	1,168
5	5	1,013
	Média	1,057

Tabela 4.2.1.2: Tabela de Dados com relação ao Deslocamento do Ponto de Medição.

O modelo estatístico para este experimento é:

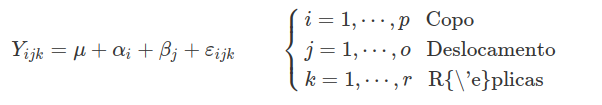
em que:

• $Y_{ijk}$ representa a k-ésima medição no j-ésimo Fator 2 no i-ésima copo;
• $μ$ é a média das medições;
• $α_i$ é o efeito do copo;
• $β_j$ é o efeito do Fator Deslocamento;
• $ε_{ijk}$ é o erro de replicação.

Para calcularmos as somas de quadrados, precisamos primeiramente calcular as seguintes variâncias amostrais :

$$S^2_=\frac{1}{p~o~r~-~1}\sum^{p~o~r}_{l=1}(y_{l}~-~\overline{y})^2=0,00435$$

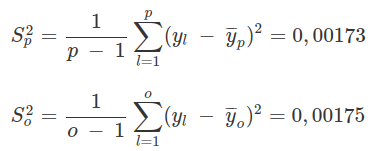
em que sabemos que

$$SQ_{\text{Total}}=(p~o~r - 1)~S^2_g = (24)~S^2_g = 0,104484$$

$$SQ_{\text{Copo}}=o~r~(p - 1)~S^2_p = 5~(4)~S^2_p=0,034567$$

$$SQ_{\text{Deslc}}=p~r~(o - 1)~S^2_o = 5~(4)~S^2_o=0,034983$$

$$SQ_{\text{Erro}}=SQ_{\text{Total}} - SQ_{\text{Deslc}} - SQ_{\text{Copo}}=0,034934$$

Os graus de liberdade são:

Efeito	Graus de Liberdade
Copo	$ p-1=4 $
Deslocamento	$ o-1=4 $
Erro	$ por-p-o-1=16 $
Total	$ por-1=24 $

Com isso, o quadrado médio é:

$$QM_{\text{Copo}}=\frac{SQ_{\text{Copo}}}{p - 1}=\frac{0,034567}{4}=0,008642$$

$$QM_{\text{Deslc}}=\frac{SQ_{\text{Deslc}}}{o - 1}=\frac{0,034983}{4}=0,008746$$

$$QM_{\text{Erro}}=\frac{SQ_{\text{Erro}}}{por-p-o+1}=\frac{0,034934}{16}=0,002183$$

A tabela abaixo apresenta o resumo da análise de variância.

(imagem em falta)

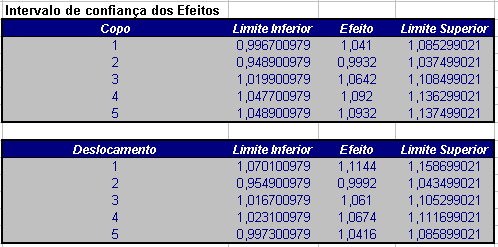
Aqui, temos que p-valor é dado por:

Copo $ P(F_{4;~16}~> 3,95)= 0,02029 $

Deslocamento $ P(F_{4;~16}> 4,00)=0,01943 $

Desta forma, como o deslocamento é significativo para o modelo, temos que a estimativa de incerteza associada ao deslocamento é dada por:

$$u_c(\epsilon_3)=\sqrt{QM_{\text{Erro}}}=0,046$$

Fonte de variação devido ao ângulo de medição $ u_c(\epsilon_4) $

Aqui, também usamos a técnica de anova dois fatores. A Tabela 4.2.1.3 apresenta as medições realizadas no copo PS.

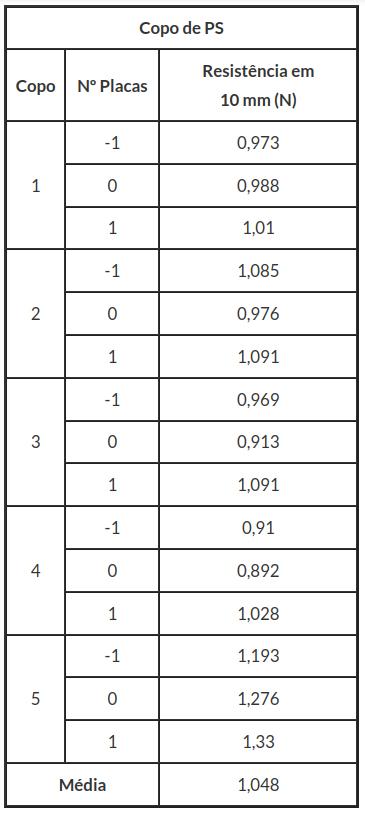
Tabela 4.2.1.3: Tabela de dados com relação ao ângulo do ponto de medição.

O modelo estatístico para este experimento é:

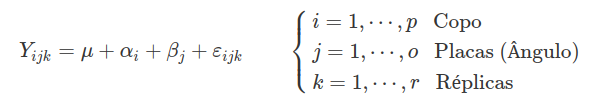
em que:

• $Y_{ijk}$ representa a k-ésima medição no j-ésimo Fator 2 no i-ésimo copo;
• $μ$ é a média das medições;
• $α_i$ é o efeito do copo;
• $β_j$ é o efeito do fator placas (ângulo);
• $ε_{ijk}$ é o erro de replicação.

Para calcularmos as somas de quadrados, precisamos primeiramente calcular as seguintes variâncias amostrais:

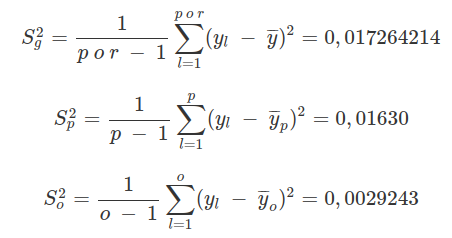
em que sabemos que

Os graus de liberdade são:

Efeito	Graus de Liberdade
Copo	$ p-1=4 $
Placas	$ o-1=2 $
Erro	$ por-p-o-1=8 $
Total	$ por-1=14 $

Com isso, o quadrado médio é:

$$QM_{\text{Copo}}=\frac{SQ_{\text{Copo}}}{p - 1}=\frac{0,1956}{4}= 0,0489$$

$$QM_{\text{Placa}}=\frac{SQ_{\text{Placa}}}{o - 1}=\frac{0,029243}{2}=0,0146$$

$$QM_{\text{Erro}}=\frac{SQ_{\text{Erro}}}{por-p-o+1}=\frac{0,016837}{8}=0,002105$$

A tabela abaixo apresenta o resumo da analise de variância.

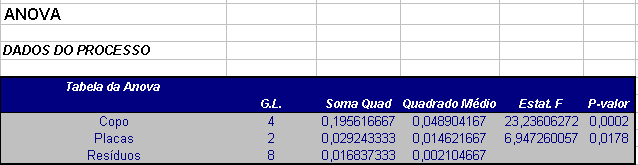
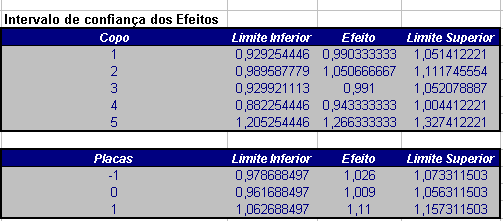
Figura 4.2.1.4: Tabela de Análise de Variância

Aqui, temos que p-valor é dado por:

Copo $ P(F_{4;~9}> 12,76600)= 0,0002 $

Placas $ P(F_{1;~9}> 3,02895)=0,0178 $

Aqui verificamos que o fator placas, ou seja, o ângulo de medição são significativos.

Portanto, a estimativa da incerteza devido ao ângulo é:

$$u_c(\epsilon_4) =\sqrt{QM_{\text{Erro}}}=0,046$$

Fonte de variação devido à temperatura ambiente $ u_c(\epsilon_5) $

Aqui, usamos a técnica de regressão linear para determinar as fontes de incerteza para o experimento. A Tabela 4.2.1.4 apresenta as medições de resistência, levando-se em consideração o valor da temperatura ambiente.

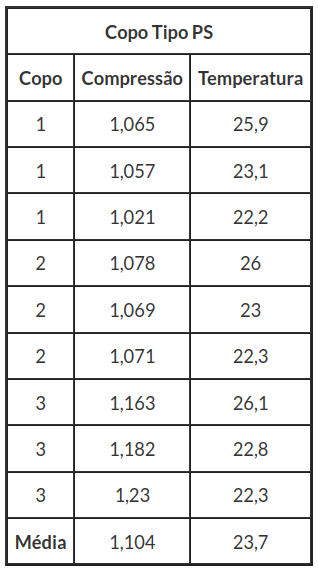
Tabela 4.2.1.4: Tabela de dados com relação a Temperatura Ambiente.

Primeiramente, determinamos as médias das variáveis resistência ($ Y $) e temperatura ($ X $). Facilmente, obtemos $ \overline{x}=23,744 $ e $ \overline{y} = 1,104 $. Assim, podemos encontrar as somas de quadrados empíricas.

$$S_{xx}=\sum^n_{i=1}(x_i-\overline{x})^2= 23,7022$$

$$S_{yy}=\sum^n_{i=1}(y_i-\overline{y})^2= 0,03905$$

$$S_{xy}=\sum^n_{i=1}(x_i-\overline{x})(y_i-\overline{y})=-0,0272$$

A seguir, utilizamos as somas de quadrados empíricas para encontrarmos as estimativas dos parâmetros da reta de regressão.

$$\hat{\beta_1}=\frac{S_{xy}}{S_{xx}} = \frac{-0,0272}{23,7022}=-0,00114757$$

$$\hat{\beta}_0=\overline{y} - \hat{\beta}_1\overline{x} = 1,104-0,0011475 \times 23,744 = 1,1312484$$

O modelo ajustado é dado por:

$$\hat{Y}~=~1,1312484~ -~ 0,00114757~X$$

A Figura 4.2.1.5 apresenta a relação entre as variáveis, bem como, a reta ajustada.

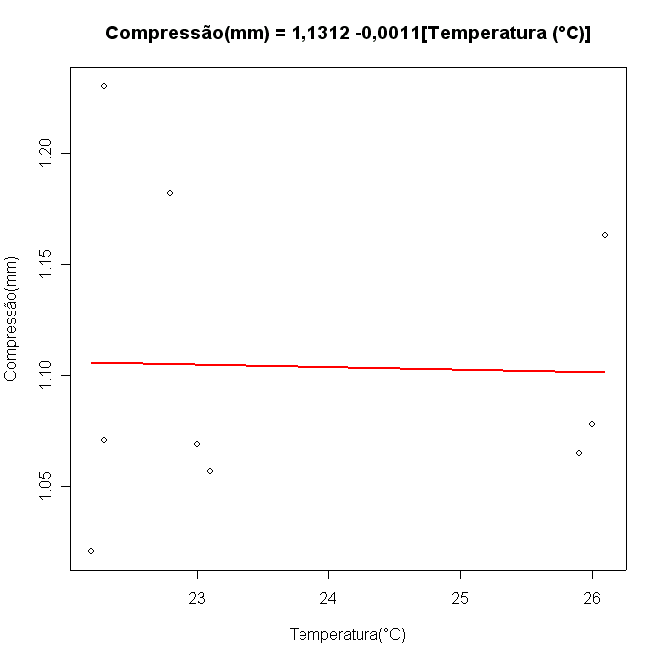
Figura 4.2.1.5: Gráfico do modelo ajustado.

A estimativa da variabilidade associada à regressão é dada por:

$$QM_E=\frac{SQ_E}{n-2}$$

Temos que $ SQ_E $ é a soma de quadrados devido ao erro aleatório, e é calculada por:

$$SQ_E=\sum^n_{i=1}(y_i-\overline{y})^2 - \hat{\beta_1}S_{xy}=\sum^n_{i=1} (y_i - 1,104)^2-(-0,0282)(-0,001147)=0,039$$

Com isso, temos que

$$QM_E=\frac{SQ_E}{n-2}=\frac{0,039}{7}=0,005574$$

A Tabela 4.2.1.7 apresenta os valores dos coeficientes para o modelo apresentado, como também a análise da significância dos coeficientes.

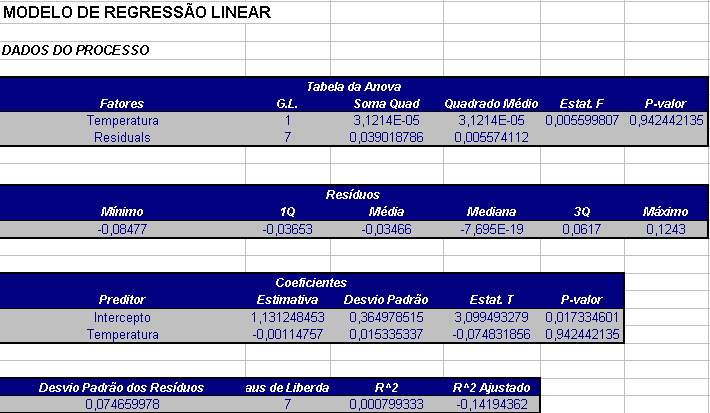
Figura 4.2.1.7: Tabela dos Coeficientes.

Aqui, temos que p-valor é dado por:

Temperatura $ P(T_{7}>-0,075)=0,9424 $

Podemos verificar na Figura 4.2.1.7 que o p-valor do coeficiente da temperatura apresenta valor acima de 5%. Logo, podemos concluir que a temperatura não é significativa.

4.2.2 - Cálculo de Incerteza para o Ensaio de Compressão Lateral de Copos

$ \mathbf{\checkmark} $Equação de Medição

A expressão 4.2.2 representa a equação de medição utilizada para a obtenção da resistência a compressão.

$$R=\text{Herd} (CG)+\text{res}(CG)+\Delta+\varepsilon_2+\varepsilon_3+\varepsilon_4+\varepsilon_5 \quad(4.2.2)$$

em que,

1. R: representa a resistência a compressão no copo descartável (N);

2. Res(CG): Representa a resolução da célula de carga (N). Podemos supor que a resolução tem distribuição Retangular (ou Uniforme) no intervalo (-Res(CG)/2,Res(CG)/2), no qual Res(CG) é a resolução do banco. Logo a incerteza devida a resolução será dada por: u(Res(CG))=Res(CG)/(2√3);

3. Herd(CG): Representa a célula de carga (N). Temos que Herd(CG) tem distribuição Normal com incerteza (u(Herd(CG))) e o fator de abrangência obtidos via certificado de calibração;

4. Δ: Representa o erro aleatório devido a célula de carga (N). Podemos supor que a distribuição da média das medições (repetitividade) tem distribuição Normal.

Logo podemos estimar a sua incerteza (desvio padrão) como u(Δ)=s/√n,

no qual, $ s^2=\displaystyle\frac{1}{n-1}\sum_{i=1}^{n}(x_i -\overline{X})^2 $ é a variância amostral e $ \overline{X}=\displaystyle\frac{1}{n}\sum^{n_{i=1}}x_i $ é a média amostral;

5. ε2: representa o erro aleatório devido a variação no mesmo copo. Vamos considerar que ε2~ N(0,σ2(copo)). Para estimarmos σ2 vamos utilizar a técnica de componentes de variância (ANOVA 1 fator - efeito aleatório), considerando os dados obtidos no seguinte experimento:

• Amostrar um copo e medir três vezes no mesmo ponto;
• o procedimento em 10 copos;

6. ε3: representa o erro aleatório devido ao deslocamento na realização das medições. Vamos considerar que ε3~ N(0,σ2(desloc)). Para estimarmos σ2 vamos utilizar a técnica de componentes de variância (ANOVA 2 fatores - efeito aleatório), considerando os dados obtidos no seguinte experimento:

• Amostrar um copo e medir três vezes em cada ponto, deslocando no sentido altura, radial e axial;
• Repetir o procedimento em três copos;

7. ε4: representa o erro aleatório devido ao ângulo na boca do copo. Vamos considerar que ε4~ N(0, σ2(angulo)). Para estimarmos σ2 vamos utilizar a técnica de componentes de variância (ANOVA 2 fatores - efeito aleatório), considerando os dados obtidos no seguinte experimento:

• Amostrar um copo e medir três vezes em cada ponto variando o número de lâminas posicionadas no fundo do copo na medição de um ponto para o outro;
• Repetir o procedimento em três copos;

8. ε5 : representa a influência da temperatura ambiente no resultado das medições. Vamos considerar que ε5~ N(0, σ2(temp)). Para estimarmos σ2 vamos utilizar a técnica de regressão linear simples:

• Este experimento segue o seguinte procedimento:
• Amostrar um copo e medir três vezes em cada ponto e anotar a temperatura ambiente;

Repetir o procedimento em três copos.

$ \mathbf{\checkmark} $Incerteza Combinada ($ u_{c}(R) $)

A incerteza combinada associada à resistência é dada por:

$$u_c(R)=\sqrt{u^2(\text{Res}(CG))+u^2(\text{Herd}(CG))+u^2(\Delta)+u^2(\epsilon_2)+u^2(\epsilon_3)+u^2(\epsilon_4)+u^2(\epsilon_5)}~~(4.2.2.1)$$

em que $ u^2(.) $ é a contribuição de cada fonte de incerteza. A expressão (4.2.2.1) representa a incerteza combinada da resistência dos copos.

$ \mathbf{\checkmark} $Incerteza Expandida ($ U(R) $)

Aqui, a expressão (4.2.2.2) representa a incerteza expandida para a resistência lateral dos copos.

$$U(R)=k\times u_c(R)~~(4.2.2.2)$$

no qual $ k $ (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(R) $ graus de liberdade e confiança de 95%. Aqui, os graus de liberdade são dados por:

$$\nu_{eff}(R)=\frac{u^4_c(R)}{u^4(\Delta)}(n-1) $$

Aplicação

Copo	Resistência
1	1,017
2	0,906
3	0,891
4	1,118
5	0,921
6	0,922
7	1,058
8	1,008
9	0,981
10	1,099
11	1,034
12	1,032
13	1,127
14	0,971
15	0,962
16	1,053
17	0,914
18	0,881
19	1,156
20	1,036
21	1,025
22	0,999
23	0,889
24	0,872
25	1,142
26	1,03
27	1,02
28	1,151
29	1,053
30	1,005
Desvio Padrão	0,084155583

A repetitividade é dada por:

$$u(\Delta)=\frac{0,084155583}{\sqrt{30}}=0,002805186$$

Valores obtidos pelos experimentos e pelos certificados de calibração

Fontes	Incerteza (U)	Fator de Abrangência (k)
Variabilidade dentro do copo	0,075950	1
Deslocamento de Medição	0,036228	1
Ângulo de Medição	0,049989	1
Temperatura Ambiente	0,074650	1
Resolução da Célula de Carga	0,000098	3,464101615
Herdada da Célula de Carga	0,008100	2
Repetitividade	0,002805186	1

Assim calculamos da seguinte forma:

$ \mathbf{\checkmark} $Incerteza Combinada ($ u_{c}(R) $)

A incerteza combinada associada à resistência é dada por:

$$u_c(R)=\sqrt{u^2(\text{Res}(CG))+u^2(\text{Herd}(CG))+u^2(\Delta)+u^2(\epsilon_2)+u^2(\epsilon_3)+u^2(\epsilon_4)+u^2(\epsilon_5)}$$

$$=\sqrt{(2,83\times10^{-5})^2+0,00405^2+0,0028^2+0,0795^2+0,036^2+0,049^2+0,074^2}=$$

$$=0,1232$$

$ \mathbf{\checkmark} $Incerteza Expandida ($ U(R) $)

$$U(R)=k\times u_c(R)=1,96\times 0,1232=0,2464$$

no qual $ k $ (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(R) $ graus de liberdade e confiança de 95%. Aqui, os graus de liberdade são dados por:

$$\nu_{eff}(R)=\frac{u^4_c(R)}{u^4(\Delta)}(n-1) ==\frac{0,1232^4}{0,0028^4}(30-1) =\infty$$

Assim,temos que $ k=1,96 $

O resumo dos cálculos é apresentado na tabela 4.2.2.1

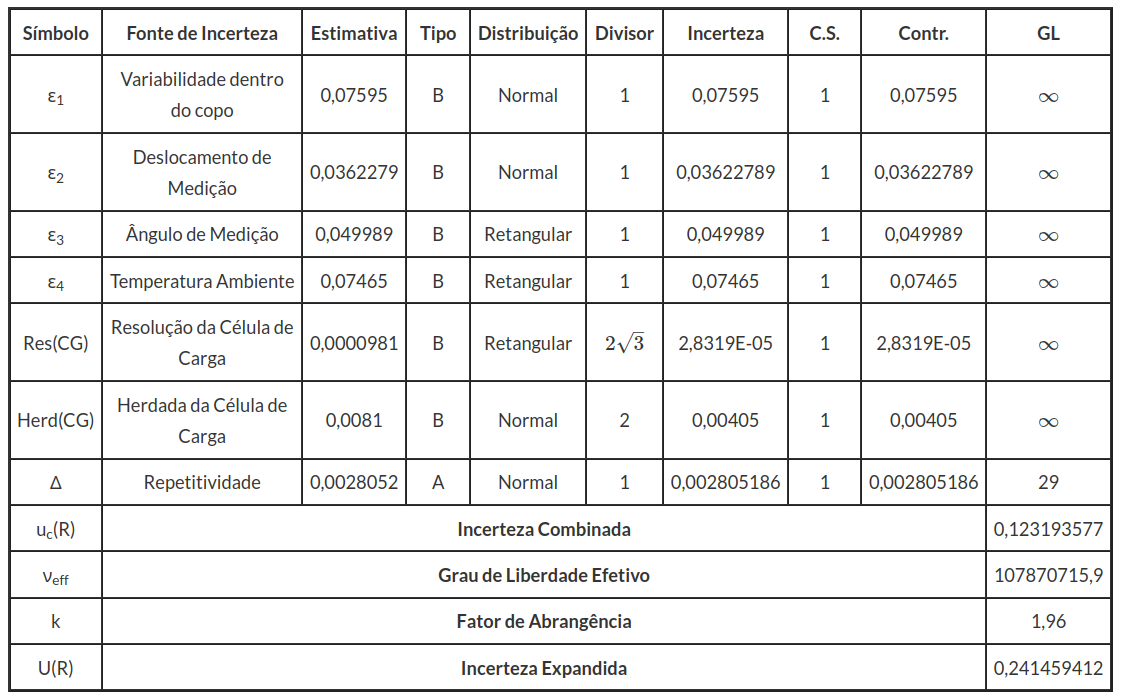
Tabela 4.2.2.1: Resultado do Cálculo de Incerteza para o Ensaio de Compressão Lateral de Copos.

4.3 - Cálculo de Incerteza para Barra Radial e Terminal de Direção

OBJETIVO

Elaborar o procedimento cálculo de Incerteza para Barra Radial e Terminal de Direção para:

• Folga Radial em milímetros (mm);

Desenvolver o estudo de Estabilidade para Barra Radial e Terminal de Direção para:

• Folga Radial em milímetros (mm);

Desenvolver o estudo de Repetitividade e Reprodutitividade para Barra Radial e Terminal de Direção para:

• Folga Radial em milímetros (mm);

Estudo de Estabilidade

a. Selecionar e identificar uma peça;

b. Realizar ensaio de CEP

i. Tamanho da amostra: 1 medição;

ii. Frequência: 2 vezes dia;

iii. Realizar 20 subgrupos;

iv. Diário de Bordo: Data, Hora, Pessoa, Temperatura ambiente;

v. OBS: realizar toda a montagem do sistema em cada medição;

Após realizado o experimento, obtemos os seguintes resultados:

Subgrupo	Data	Horário	Temp. Ambiente (ºC)	Folga Radial (mm)
1	27/7/2009	09:10	18	0,5439
2	28/7/2009	10:06	19	0,5655
3	29/7/2009	08:20	17	0,5414
4	30/7/2009	08:00	16	0,5444
5	30/7/2009	13:00	18	0,5397
6	31/7/2009	08:00	10	0,5664
7	31/7/2009	13:00	14	0,547
8	3/8/2009	08:00	15	0,5451
9	3/8/2009	13:00	17	0,5566
10	4/8/2009	08:00	13	0,5408
11	4/8/2009	13:00	18	0,544
12	5/8/2009	08:00	16	0,5435
13	5/8/2009	13:00	19	0,5365
14	6/8/2009	08:00	17	0,5335
15	6/8/2009	13:00	18	0,527
16	7/8/2009	08:00	16	0,5366
17	7/8/2009	13:00	17	0,5444
18	10/8/2009	08:00	15	0,5313
19	10/8/2009	13:00	17	0,5449
20	11/8/2009	08:00	14	0,5431

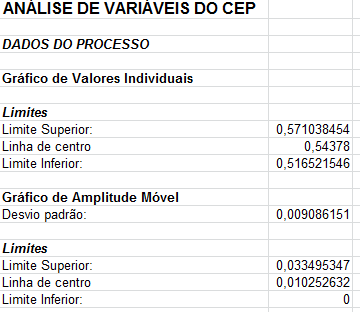
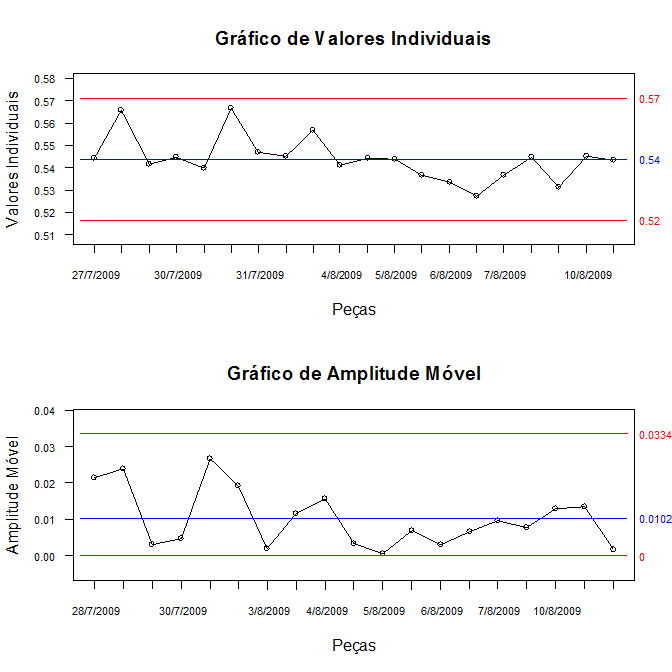
Figura 4.3.1: Gráfico de Estabilidade.

Após o estudo de estabilidade, concluímos que o sistema é estável ao longo do tempo.

4.3.1 - Ensaio de RR (Repetitividade e Reprodutividade)

Agora, descreveremos o procedimento e as variáveis envolvidas para o estudo do RR

Experimento

a. Selecionaremos 3 peças de modelos diferentes;

b. Selecionaremos 2 operadores;

c. Cada operador realizará 3 medições em cada peça;

Para mais detalhes sobre o conteúdo sobre o estudo de RR, entre no conteúdo MSA 4ºedição módulo RR.

Ordem	Pessoa	Peça	Folga Radial
1	A	1	0,5439
2	A	3	0,584
3	B	2	0,5898
4	B	1	0,5437
5	B	1	0,5413
6	A	3	0,4594
7	A	2	0,586
8	B	3	0,4564
9	B	3	0,4488
10	A	1	0,5655
11	A	2	0,59
12	A	2	0,5697
13	A	3	0,4766
14	B	2	0,5545
15	B	2	0,5646
16	B	1	0,56
17	B	3	0,4681
18	A	1	0,5414

Após o experimento, obtemos os seguintes resultados:

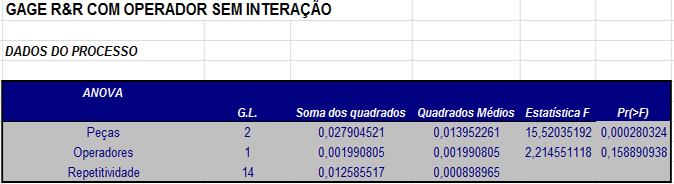
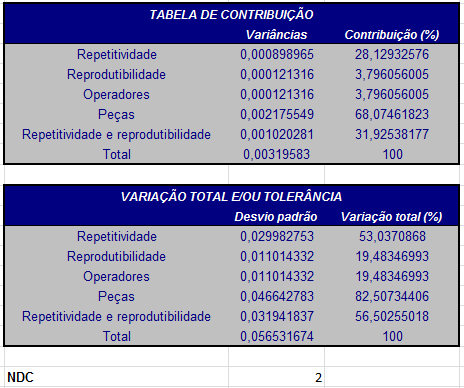
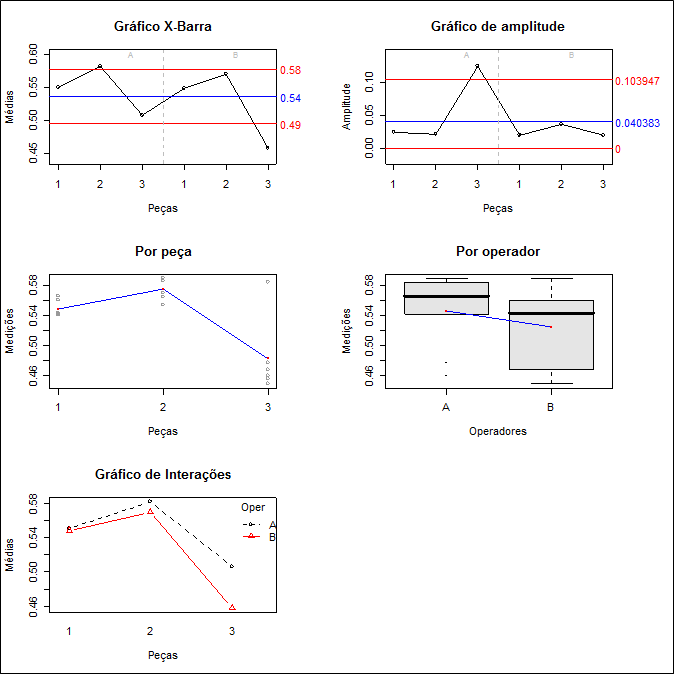
À partir do estudo do RR, estimamos a incerteza devido a Repetitividade e Reprodutitividade (RR). Assim,

$$u(\varepsilon)=0,032$$

4.3.2 - Incerteza de medição para Barra Radial e Terminal de Direção

Este módulo descreve os procedimentos e variáveis envolvidas para o cálculo de incerteza.

Equação de Medição

$$F_r=I+{Res}_I+\varepsilon+\delta$$

em que:

• $F_r$: Folga Radial em(mm);
• I: Herdada do Instrumento (Caneta de medição da folga) em (mm);
• $Res_I$: Resolução do Intrumento em (mm);
• ε: representa o erro aleatório devido a repetitividade e a reprodutividade;
• δ: representa o erro aleatório devido a repetitividade.

Incerteza Combinada u(Fr)

A incerteza combinada para a folga radial é dada por

$$u_c(F_r)=\sqrt{u^2(I)+u^2({Res}_I)+u^2(\varepsilon)+u^2(\delta)}$$

Incerteza Expandida U(Fr)

A incerteza expandida para a folga radial é dada por

$$U(F_r)=k\times u_c(F_r)$$

em que,

k é o fator de abrangência, dado pelo quantil da distribuição t-Student com νeff (Fr) graus de liberdade e confiança de 95%. e os graus de liberdade dados por:

$$\nu_{eff}(F_r)=\frac{u^4_c(F_r)}{\frac{u^4(I)}{\infty}+\frac{u^4(Res_I)}{\infty}+\frac{u^4(\varepsilon)}{\infty}+\frac{u^4(\delta)}{n-1}}$$

Aplicação

Medidas da folga radial

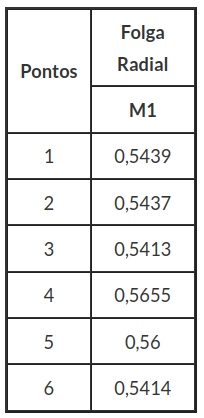
A incerteza devido a repetitividade é dada por:

$$u(\delta)=\frac{s}{\sqrt{n}}=\frac{0,0106}{\sqrt{6}}=0,0043$$

A incerteza devido ao RR $ (u(\varepsilon)=0,032) $, foi obtida no módulo 4.3.1

Do certificado de calibração obtemos a incerteza do instrumento e a resolução do instrumento.

Assim, o resumo das incertezas estão na tabela 4.3.2.1

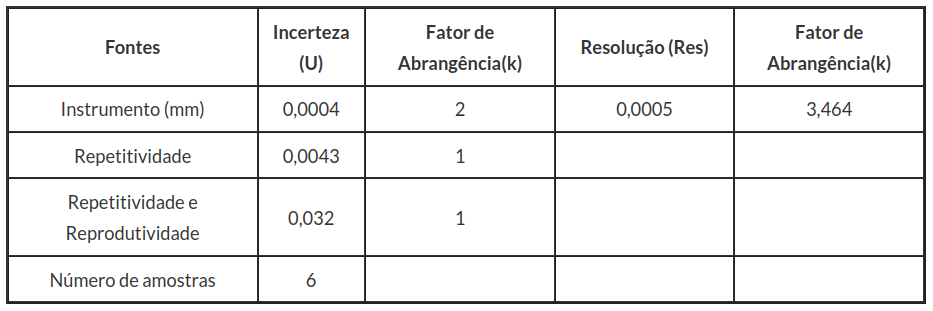
Tabela 4.3.2.1: Resumo das incertezas.

Calcularemos a incerteza combinada da seguinte forma:

$$u_c(F_r)=\sqrt{u^2(I)+u^2({Res}_I)+u^2(\varepsilon)+u^2(\delta)}=$$

$$=\sqrt{0,0002^2+0,00014^2+0,032^2+0,0043^2}=0,032$$

À partir da incerteza combinada, calcularemos a incerteza expandida com a seguir

$$U(F_r)=k\times u_c(F_r)=1,96\times 0,032=0,063$$

k é o fator de abrangência, dado pelo quantil da distribuição t-Student com νeff (FA) graus de liberdade e confiança de 95%. e os graus de liberdade dados por:

$$\nu_{eff}(F_r)=\frac{u^4_c(F_r)}{\frac{u^4(I)}{\infty}+\frac{u^4(Res_I)}{\infty}+\frac{u^4(\varepsilon)}{\infty}+\frac{u^4(\delta)}{n-1}}=$$

$$=\frac{0,0032^4}{\frac{0,0002^4}{\infty}+\frac{0,00014^4}{\infty}+\frac{0,032^4}{\infty}+\frac{0,0043^4}{6-1}}=15282,64$$

Assim, o resumo dos cálculos estão descritos na tabela abaixo:

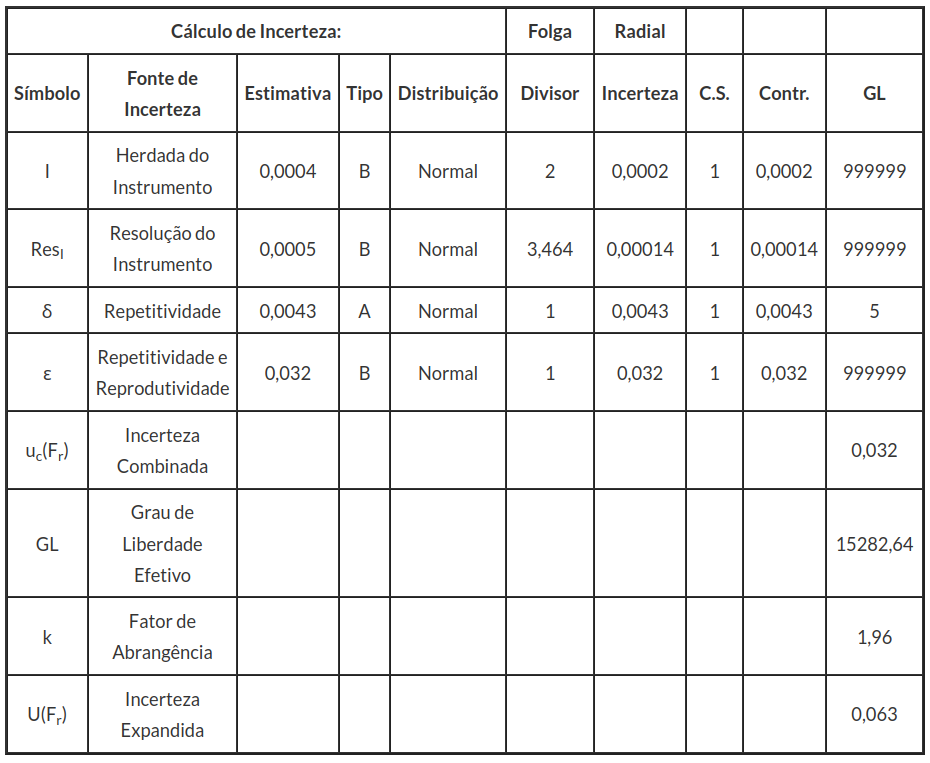
em que

C.S. : coeficiente de sensibilidade

Contr.: contribuição.

GL: graus de liberdade.

4.4 - Cálculo de Incerteza para Potência Efetiva Líquida motor ciclo Otto

Neste módulo, descrevemos o cálculo de incerteza referente ao ensaio de potência efetiva líquida para motores ciclo Otto (motores gasolina). O ensaio é realizado conforme norma ISO 1585.

4.4.1 - Torque

$ \mathbf{\checkmark} $Equação de Medição

A expressão 4.4.1.1 representa a equação de medição utilizada para a obtenção do torque. Neste caso temos:

$$T = M ~ g ~ L ~ (1 - \delta_T) + ResB + \Delta + hist~~(4.4.1.1)$$

em que

• M: Representa a Massa (kg). Temos que M tem distribuição normal com incerteza (u(M)) e o fator de abrangência obtidos via certificado de calibração;
• g: Representa a aceleração da gravidade (m/s2). Temos que g tem distribuição normal com incerteza (u(g)) e o fator de abrangência obtidos via certificado de calibração;
• L: Representa o Comprimento do Braço (m). Temos que L tem distribuição normal com incerteza (u(L)) e o fator de abrangência obtidos via certificado de calibração;
• $ \delta_T $: Representa a influência da temperatura ambiente no comprimento do Braço. Para tratar esta fonte de incerteza vamos considerar a situação de pior caso. Considere $ \delta_T $ uma variável aleatória com distribuição retangular onde os limites são dados por:

$$LI_{\delta_T} = - \alpha \times \Delta_T ~~{e}~~LS_{\delta_T} = \alpha \times \Delta_T,$$

em que

• $ \alpha $: Coeficiente de dilatação térmica do aço (11,5 x 10-6ºC-1);
• $ \Delta_T $: Máxima variação da temperatura encontrada no laboratório. Como o coeficiente de dilatação térmica tem como unidade ºC-1 e o $ \Delta_T $ tem como unidade ºC, concluímos que $ \delta_T $ não tem unidade. Podemos estimar a incerteza devido a influência da temperatura como:

$$u(\delta_T) = \frac{LS_{\delta_T} - LI_{\delta_T}}{2\sqrt{3}};$$

• $Res_B$: Representa a Resolução do Banco (Nm). Podemos supor que a resolução tem distribuição retangular (ou uniforme) no intervalo $ \left(-\frac{ResB}{2},~\frac{ResB}{2}\right) $, em que ResB é a resolução do banco. Logo, a incerteza devida a resolução será dada por:

$$u(ResB) = \frac{ResB}{2\sqrt{3}};$$

• $ \Delta $: Representa a Repetitividade (Nm). Podemos supor que a distribuição da média das medições tem distribuição normal. Logo, podemos estimar a sua incerteza (desvio padrão) como

$$u(\Delta) = \frac{s}{\sqrt{n}},$$

em que $ s^2 = \frac{1}{n-1} \displaystyle\sum_{i=1}^{n} (x_i -\overline{X})^2 $ é a variância amostral e $ \overline{X} = \frac{1}{n}\displaystyle \sum^{n_{i=1}} x_i $ a média amostral;

• hist: Representa a histerese (Nm). Temos que a histerese tem distribuição retangular no intervalo (MR, MA) se MR ≤ MA ou (MA, MR) se MA < MR, em que MA: médias das medições no avanço e MR é a médias no retorno.

Logo, a sua incerteza será dada por:

$$u(hist) = \frac{\mid M_A - M_R \mid}{2\sqrt{3}}.$$

$ \mathbf{\checkmark} $Incerteza Combinada ($ u_{c}(T) $)

A incerteza combinada para a grandeza torque é dada por:

$$u^2_c(T)=\left(\frac{\partial T}{\partial M}\right)^2 u^2(M)+\left(\frac{\partial T}{\partial g}\right)^2 u^2(g) +\left(\frac{\partial T}{\partial L}\right)^2 u^2(L)+\left(\frac{\partial T}{\partial \delta_T}\right)^2 u^2(\delta_T)$$

$$+\left(\frac{\partial T}{\partial ResB}\right)^2 u^2(ResB)+ \left(\frac{\partial T}{\partial \Delta}\right)^2 u^2(\Delta)+ \left(\frac{\partial T}{\partial hist}\right)^2 u^2(hist)~~(4.4.1.2)$$

em que

$$\left(\frac{\partial T}{\partial M}\right)=g~L~(1-\delta_T)$$

$$\left(\frac{\partial T}{\partial g}\right)=M~L~(1-\delta_T)$$

$$\left(\frac{\partial T}{\partial L}\right)=M~g~(1-\delta_T)$$

$$\left(\frac{\partial T}{\partial \delta_T}\right)=M~g~L$$

$$\left(\frac{\partial T}{\partial ResB}\right)=1$$

$$\left(\frac{\partial T}{\partial \Delta}\right)=1$$

$$\left(\frac{\partial T}{\partial hist}\right)=1$$

em que $ u^2(.) $ é a contribuição de cada fonte de incerteza. A expressão 4.4.1.2 representa a incerteza combinada do torque.

$ \mathbf{\checkmark} $Incerteza Combinada Relativa ($ u_{r}(T) $)

A incerteza combinada relativa para o torque é dada por:

$$\frac{u^2_c(T)}{T^2}=\left[\frac{g ~ L ~ (1 - \delta_T)}{T}\right]^2 ~ u^2(M) + \left[\frac{M ~ L ~(1 - \delta_T)}{T}\right]^2 ~ u^2(g) + \left[\frac{M ~ g ~(1 -\delta_T)}{T}\right]^2 ~ u^2(L)$$

$$+ \left(\frac{- M ~ g ~L}{T}\right)^2 ~u^2(\delta_T)+ \frac{u^2(ResB)}{T^2} +\frac{u^2(\Delta)}{T^2} +\frac{u^2(hist)}{T^2}$$

sendo $ T = M~g~L~(1 - \delta_T) $. Fazendo $ u_{r} =\sqrt{\frac{u^2_c(T)}{T^2}} $, temos que:

$$u_r(T)=\sqrt{\frac{u^2(M)}{M^2}+\frac{u^2(g)}{g^2}+\frac{u^2(L)}{L^2}+\frac{u^2(\delta_T)}{(\delta_T-1)^2} + \frac{u^2(Res_B)}{T^2}+\frac{u^2(\Delta)}{T^2} + \frac{u^2(hist)}{T^2}}$$

$$=\sqrt{u_{r}^2(M) + u_{r}^2(g) + u_{r}^2(L) + u_{r}^2(\delta_T) + u_{r}^2(Res_B) + u_{r}^2(Hist)}~~(4.4.1.3)$$

A expressão 4.4.1.3 representa a incerteza combinada relativa do torque, sendo que $ u_{r}^2(.) $ é a incerteza de contribuição relativa para cada fonte padrão.

$ \mathbf{\checkmark} $Incerteza Expandida ($ U(T) $)

A expressão 4.4.1.4 representa a incerteza expandida relativa para o torque

$$U(T) = k*u_r(T)~~(4.4.1.4)$$

em que k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(T) $ graus de liberdade e confiança de 95%. Os graus de liberdade são dados por:

$$\nu_{eff}(T) =\frac{(u_r(T))^4}{{\frac{u^4(\Delta)}{n - 1} +\frac{u^4(M)}{\infty} + \frac{u^4(g)}{\infty}+\frac{u^4(L)}{\infty} + \frac{u^4(\delta t)}{\infty}}+\frac{u^4(ResB)}{\infty} + \frac{u^4(hist)}{\infty}}$$

A Tabela 4.4.1.1 apresenta o resumo para o cálculo da incerteza da grandeza Torque.

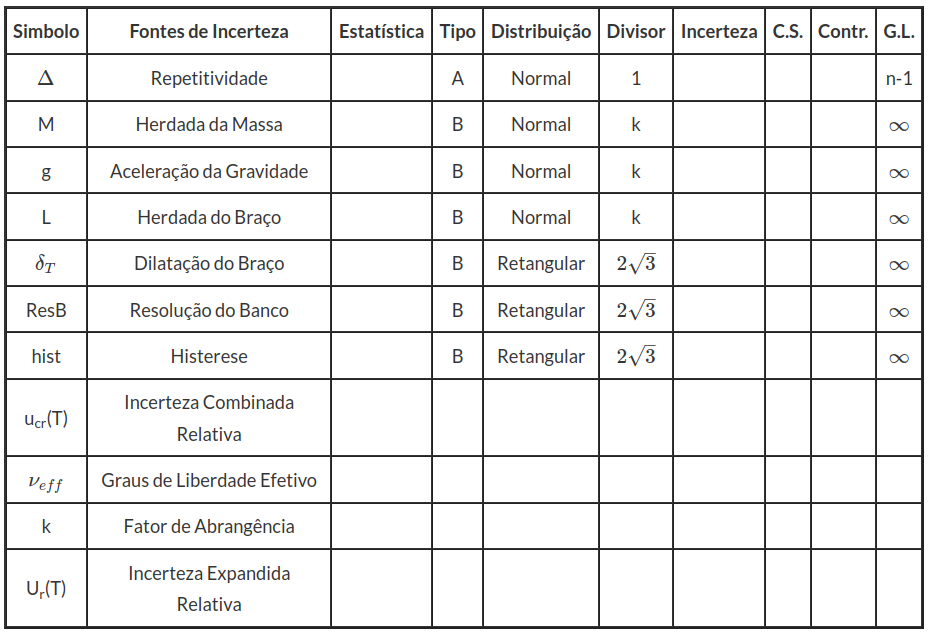
C.S. Coeficiente de Sensibilidade

Contr. Contribuição

G.L. Graus de Liberdade

Como é realizado a calibração em vários pontos, teremos um cálculo de incerteza para o respectivo ponto. No

entanto, por determinação técnica, vamos expressar uma única incerteza para toda faixa de leituras (10 a 160 Nm).

Neste sentido, podemos considerar duas técnicas: determinar a máxima incerteza entre as já calculadas, ou ainda, considerar a incerteza expandida agrupada (expressão (4.4.1.5))

$$U_a(T) = 2~\sqrt{\frac{\displaystyle\sum_{i=1}^{p}\left(\frac{U_{i}(T)}{k_i}\right)^2 }{p} }~~(4.4.1.5)$$

em que

• $ U_{i}(T) $: Representa a incerteza expandida para o i-ésimo ponto;
• $ k_i $: Representa o fator de abrangência para o i-ésimo ponto;
• $ p $: Representa o número de pontos de calibração.

Aplicação

A Tabela 4.4.1.2 apresenta todas a medições da calibração de torque.

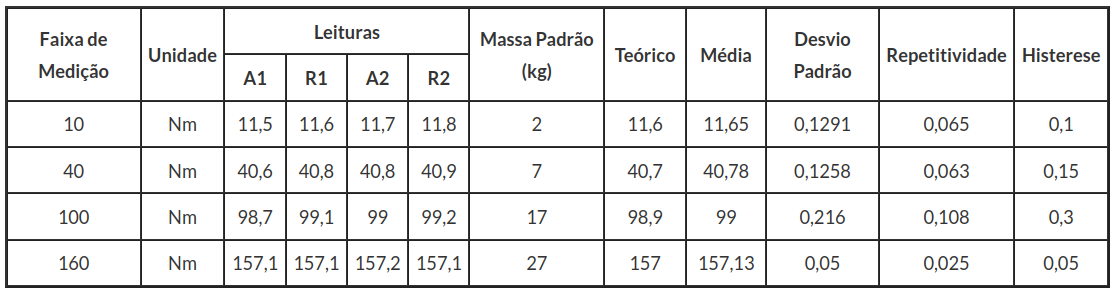
Tabela 4.4.1.2: Medições para calibração de torque.

Aqui, o comprimento do braço é 0,59421 m e a aceleração da gravidade 9,7864598 m/s2. A calibração abrange a faixa de 10 a 160 Nm porém, vamos apresentar o cálculo de incerteza para o ponto de 10 Nm. Para isso, as informações necessárias são:

• Incerteza expandida da massa de 2 kg (u(M2)) é 0,00021069, com k = 4,303 (valores declarado no certificado de calibração);
• Incerteza devido a gravidade (u(g)) é 0,0000005. Aqui, o valor de k = 2 (valores declarado no certificado de calibração);
• Incerteza expandida do comprimento do braço (u(L)) é 0,00018, com k = 2 (valores declarado no certificado de calibração);
• Incerteza devido à dilatação do braço ($ u(\delta_T) $). Temos que:

$ \alpha = 11,5 ordm; \times 10^{-6} C^{-1} $ e

$ \Delta T = \max(T) - \min(T) = 28 - 20 = 8 ordm;C, $

Logo,

$$LI_{\delta_T}=- \alpha \times \Delta_T = -(11,5 \times 10^{-6}) \times 8 = -92 \times 10^{-6} ~~{e}$$

$$LS_{\delta_T}=\alpha \times \Delta_T = (11,5 \times 10^{-6}) \times 8 = 92 \times 10^{-6},$$

Portanto,

$$u(\delta_T)=\frac{92 \times 10^{-6} - (-92 \times 10^{-6})}{\sqrt{12}} = \frac{0,000184}{2\sqrt{3}}= 0,00005311 ~~{e}$$

$$\delta_T=\frac{92 \times 10^{-6} - (-92 \times 10^{-6})}{2} = 0;$$

• Resolução do banco (u(ResB)) é 0,6 Nm;
• Repetitividade ($ u(\Delta) $) é o desvio padrão da média. Para a faixa de 10 Nm temos 0,065 Nm;
• Histerese (u(hist)) é 0,1 Nm.

Neste ponto (10 Nm), temos que:

$$T=M ~ g ~ L ~ (1 - \delta_T)$$

$$=2 \times 9,7864598 \times 0,59421 \times (1 - 0)$$

$$=11,63042.$$

A incerteza combinada relativa

$$u_r(T)=\sqrt{\frac{u^2(M)}{M^2} + \frac{u^2(g)}{g^2} + \frac{u^2(L)}{L^2} + \frac{u^2(\delta_T)}{(\delta_T-1)^2} + \frac{u^2(ResB)}{T^2} + \frac{u^2(\Delta)}{T^2} + \frac{u^2(hist)}{T^2}}$$

$$=\sqrt{\left(\frac{0,00021069 / 4,303}{2} \right)^2 + \left(\frac{0,0000005 / 2}{9,7864598}\right)^2 + \left(\frac{0,00018 / 2}{0,59421}\right)^2 }$$

$$\overline{+ \left( \frac{0,000184 / 2\sqrt{3}}{1} \right)^2 + \left(\frac{0,6 / 2\sqrt{3}}{11,63042} \right)^2 + \left(\frac{0,065 / 1}{11,63042}\right)^2 + \left(\frac{0,1 / 2\sqrt{3}}{11,63042}\right)^2}$$

$$=0,0161.$$

Os graus de liberdade são:

$$\nu_{eff}(T)=\frac{(u_r(T))^4}{\frac{u^4(\Delta) / M}{n - 1}}$$

$$=\frac{0,1880668^4}{\frac{(0,065 / 11,63042)^4}{3}}$$

$$=206,604.$$

Considerando os graus de liberdade efetivo e uma confiança de aproximadamente 95%, temos pela tabela da distribuição t-student, que o fator de abrangência é 1,968613. Com isso, a incerteza expandida relativa para a variável torque é dada por:

$$U(T)=k \times u_r(T)$$

$$=1,970855 \times 0,0161$$

$$=0,0317.$$

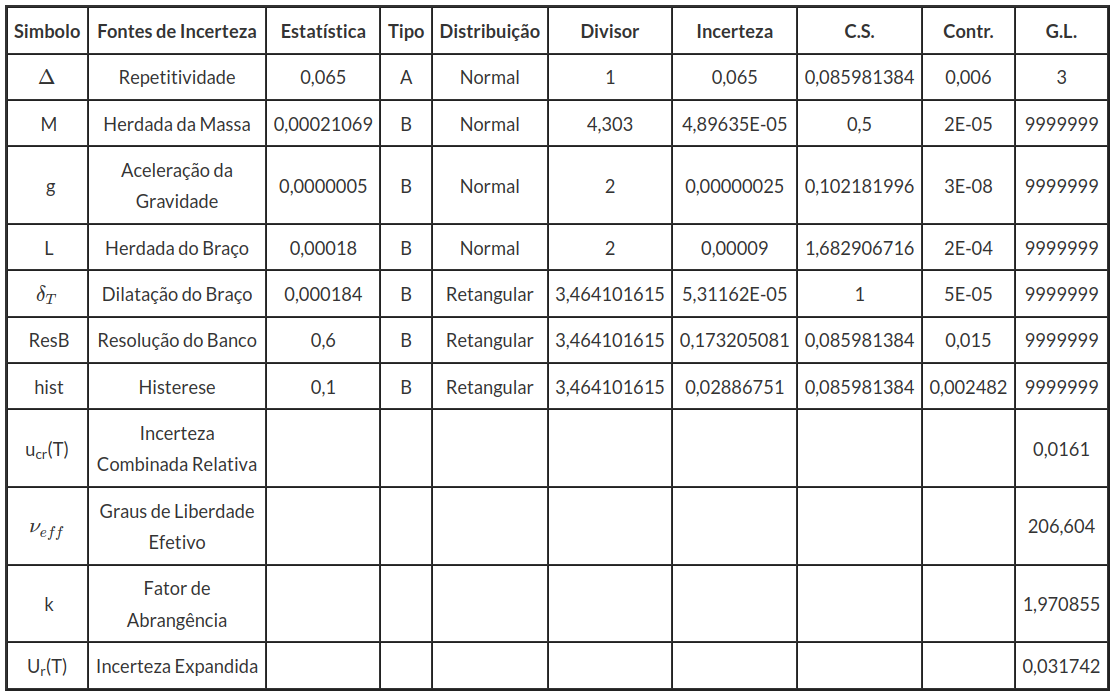
Tabela 4.4.1.3: Resumo do cálculo de incerteza para o Torque.

A Tabela 4.4.1.4 apresenta o resultado das incertezas expandidas e seus respectivos fatores de abrangência para todos os pontos de medição.

Pontos	$ u_{ci} $	k	$ U_i $
1	0,01609	1,97143	0,03171
2	0,00465	1,96982	0,00917
3	0,00225	2,00575	0,00451
4	0,00113	1,96049	0,00221
$ U_e $	Agrupada	0,016934

Tabela 4.4.1.4: Incertezas por ponto de medição.

Por determinação técnica, vamos expressar uma única incerteza para toda a faixa de leituras. Neste sentido, vamos considerar a incerteza expandida agrupada:

$$U(T)=2~\sqrt{\frac{\sum_{i=1}^{p}\left(\frac{U_{i}(T)}{k_i}\right)^2}{p}}$$

$$=2 \sqrt{\frac{\left(\frac{0,03171}{1,97143}\right)^2 + \ldots + \left(\frac{0,00221}{1,96049}\right)^2}{4}}$$

$$=0,016934.$$

Portanto, a incerteza expandida relativa para o torque, na faixa de 40 a 160 Nm, é 1,6934 % da leitura.

4.4.2 - Potência

Nesta seção vamos apresentar o procedimento de cálculo de incerteza para a calibração de Potência. Note que o procedimento de calibração aqui empregado é feito de forma indireta, ou seja, a calibração da grandeza potência é estritamente dependente das calibrações da Rotação e Torque.

O método de medição, especificado pela indústria automobilística, para medir a potência do motor é o dispositivo dinamométrico com “célula de carga” (ver figura 4.4.2.1).

Figura 4.4.2.1: Dispositivo dinamométrico para medição da potência do motor.

$ \mathbf{\checkmark} $ Equação de Medição

$$Pot = \frac{Rot \times Torque}{\theta}$$

• Pot: Representa o resultado da medição de Potência (kW);
• Rot: Representa o resultado da medição de Rotação (rpm). Temos que Rot tem distribuição normal com incerteza (u(Rot)) e o fator de abrangência k;
• Torque: Representa o resultado da medição de Torque (Nm). Temos que Torque tem distribuição normal com incerteza (u(Torque)) e o fator de abrangência determinados como no módulo (4.4.1 Torque).
• $ \theta $: Representa uma constante. Logo, $ \theta $ não tem incerteza.

$ \mathbf{\checkmark} $Incerteza Combinada ($ u_{c}(Pot) $)

A incerteza combinada para a potência é dada por:

$$u^2_c(Pot)=\left(\frac{\partial Pot}{\partial Rot}\right)^2 u^2(Rot)+\left(\frac{\partial Pot}{\partial Torque}\right)^2 u^2(Torque)$$

$$=\left(\frac{Torque}{\theta}\right)^2 u^2(Rot) + \left(\frac{Rot}{\theta}\right)^2 u^2(Torque) $$

Logo,

$$u_c(Pot) = \sqrt{\left(\frac{Torque}{\theta}\right)^2 u^2(Rot) + \left(\frac{Rot}{\theta}\right)^2 u^2(Torque)}$$

$ \mathbf{\checkmark} $Incerteza Combinada Relativa ($ u_{r}(Pot) $)

Dividindo $ u_c^2(Pot) $ por $ Pot^2 $ obtemos a incerteza combinada relativa para a potência como:

$$u_{r}(Pot)=\sqrt{\left(\frac{1}{Rot}\right)^2 u^2(Rot) + \left(\frac{1}{Torque}\right)^2 u^2(Torque)}$$

$$=\sqrt{u_{r}^2(Rot) + u_{r}^2(Pot)}$$

Note que, como a calibração da grandeza potência depende das calibrações de Rotação e torque, as estratégia aqui aplicada será tomar a incerteza relativa agrupada para toda a faixa de leitura de ambas as grandezas de entrada, tendo assim uma única incerteza relativa para a grandeza potência referente a toda faixa de leitura.

$ \mathbf{\checkmark} $] Incerteza Expandida ($ U(Pot) $)

A expressão 4.4.2.1 representa a incerteza expandida relativa para a potência

$$U(Pot) = k \times u_r(Pot)~~(4.4.2.1)$$

em que k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(Pot) $ graus de liberdade e confiança de 95%. Aqui, consideraremos os graus de liberdade igual a infinito, pois só temos fontes do tipo B. Logo, adotaremos k = 2.

A Tabela 4.4.2.1 apresenta o resumo para o cálculo da incerteza da potência, considerando as incertezas combinadas das grandezas de entrada.

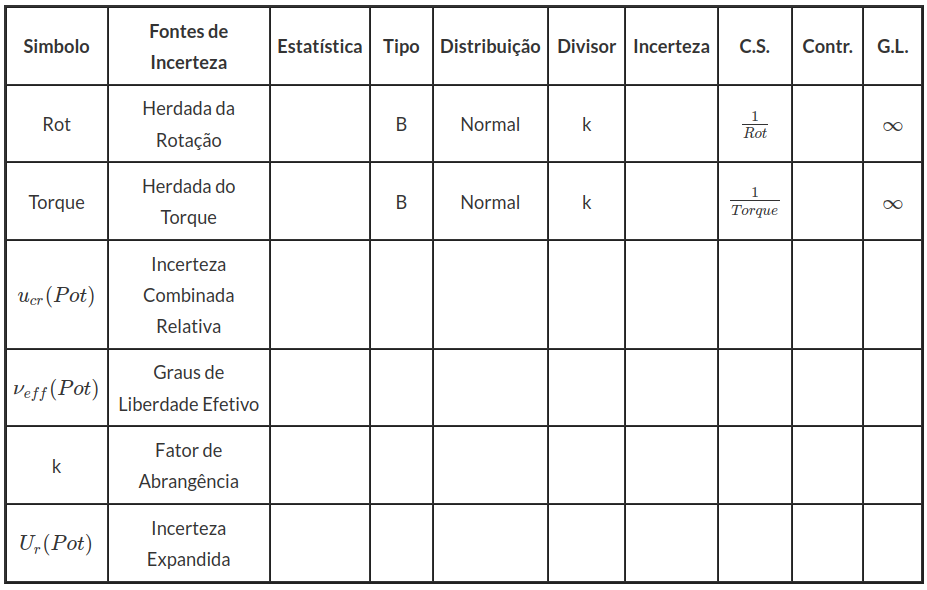
C.S. Coeficiente de Sensibilidade

Contr. Contribuição

G.L. Graus de Liberdade

Tabela 4.4.2.1: Resumo do Cálculo de Incerteza para a Potência.

A Tabela 4.4.2.2 apresenta o resumo para o cálculo da incerteza da potência, considerando as incertezas combinadas relativas das grandezas de entrada.

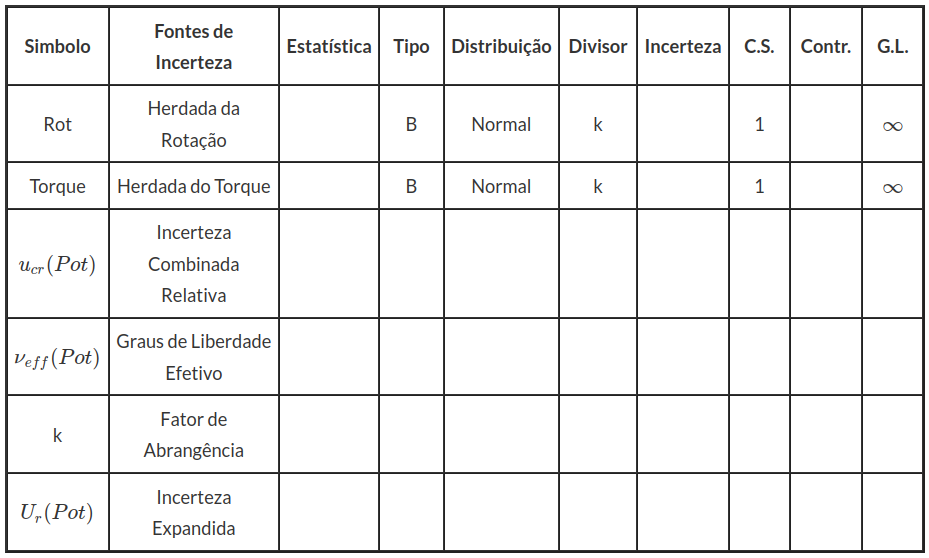
C.S. Coeficiente de Sensibilidade

Contr. Contribuição

G.L. Graus de Liberdade

Tabela 4.4.2.2: Resumo do Cálculo de Incerteza para a Potência.

Aplicação

Agora vamos apresentar uma aplicação para o cálculo da incerteza expandida da variável potência. As informações necessárias para o cálculo são:

Incerteza expandida relativa herdada da Rotação (u(Rot)) é 0,000935 (ou 0,0935% do valor de lido), com fator de abrangência k = 2;

Incerteza expandida relativa herdada do Torque (u(Torque)) é 0,016933 (ou 1,6933% do valor lido), com fator de abrangência k = 2.

A incerteza combinada relativa para a potência é dada por:

$$u_{r}(Pot)=\sqrt{\left(\frac{u^2(Rot)}{Rot}\right)^2 + \left(\frac{u^2(Torque)}{Torque}\right)^2}$$

$$=\sqrt{u_r^2(Rot) + u_r^2(Torque)}$$

$$=\sqrt{\left(\frac{0,000935}{2}\right)^2 + \left(\frac{0,016933}{2}\right)^2}$$

$$=0,00848.$$

Como não temos incerteza do tipo A, vamos considerar que os graus de liberdade são infinito. Com isso, o fator de abrangência é k = 2. Portanto, a incerteza expandida relativa para a potência é dada por:

$$U(Pot)=k \times u_{r}(Pot)=2 \times 0,00848=0,01695.$$

Portanto, a incerteza relativa da potência para toda a faixa de leituras é 1,695% do valor lido.

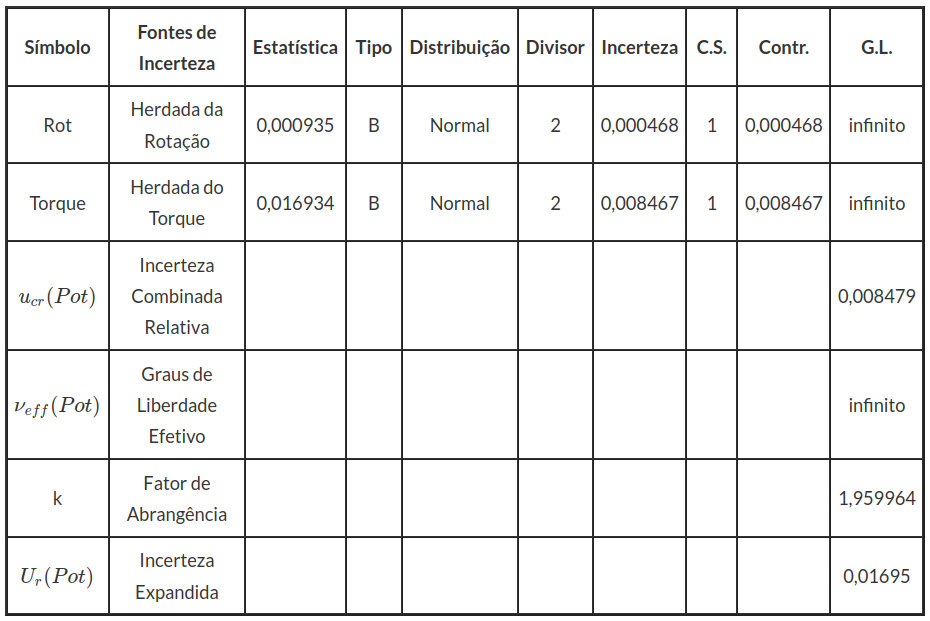
Tabela 4.4.2.3: Resumo do Cálculo de Incerteza para a grandeza Potência.

4.4.3 - Fator de Correção - Motor OTTO

$ \mathbf{\checkmark} $Equação de Medição

A expressão 4.4.3.1 representa a equação de medição utilizada para a obtenção do Fator de correção. Neste caso é dada por:

$$F_c=\left(\frac{99}{P_{as}}\right)^{1,2}~\left(\frac{T_{adm}}{298}\right)^{0,6}~~(4.4.3.1)$$

• $P_{as}$: Representa a pressão do ar seco (kPa). Temos que $ P_{as} $ tem distribuição normal com incerteza (u($P_{as}$)) e fator de abrangência k.
• $T_{adm}$: Representa a temperatura de admissão (Kelvin). Temos que $T_{adm}$ tem distribuição normal com incerteza u(Tadm) e fator de abrangência k.

$ \mathbf{\checkmark} $Incerteza Combinada ($ u_{c}(F_c) $)

A incerteza combinada para a grandeza Fator de Correção é

$$u_c(F_c)=\sqrt{ \left(\frac{\partial F_c}{\partial P_{as}}\right)^2~u^2(P_{as}) + \left(\frac{\partial F_c}{\partial T_{adm}}\right)^2~u^2(T_{adm})}$$

$$=\sqrt{\left[1,2\left(\frac{T_{adm}}{298}\right)^{0,6}\left(\frac{99}{P_{as}}\right)^{0,2}\left(\frac{99}{(P_{as})^2}\right)\right]^2u^2(P_{as})+\left[\frac{0,6}{298} \left(\frac{99}{P_{as}}\right)^{1,2}\left(\frac{298}{T_{adm}}\right)^{0,4} \right]^2~u^2(T_{adm})}$$

$ \mathbf{\checkmark} $Incerteza Expandida ($ U(F_c) $)

A expressão 4.4.3.2 representa a incerteza expandida para o Fator de Correção

$$ U(F_c) = k\times u_{c}(F_c)~~(4.4.3.2)$$

em que k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(F_c) $ graus de liberdade e confiança de 95%. Como não temos incerteza do tipo A, vamos considerar que os graus de liberdade são infinito. Com isso, o fator de abrangência é k = 2.

A Tabela 4.4.3.1 apresenta o resumo para o cálculo da incerteza da grandeza Fator de correção.

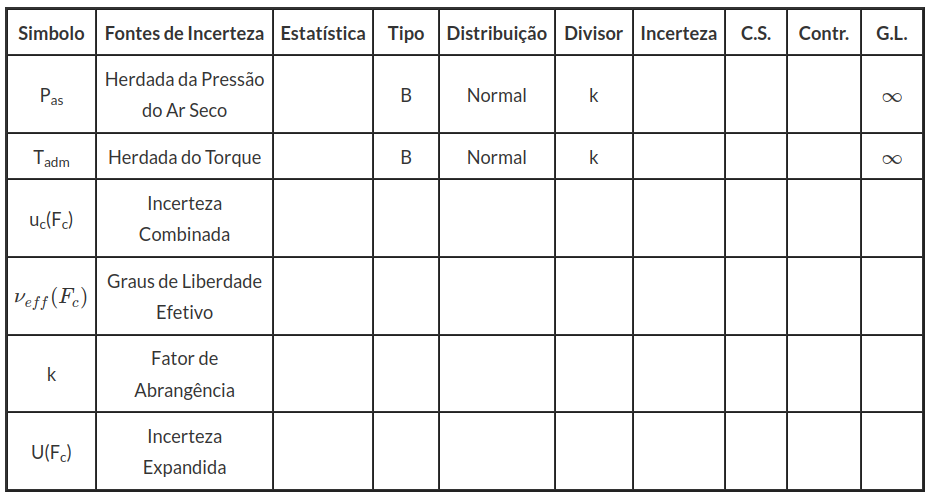
C.S. Coeficiente de Sensibilidade

Contr. Contribuição

G.L. Graus de Liberdade

Tabela 4.4.3.1: Resumo do Cálculo de Incerteza para o Fator de Correção.

Aplicação

As informações necessárias para o cálculo são:

• A incerteza expandida herdada de temperatura de admissão é 0,4908189ºC com fator de abrangência 2,03218340.

No ensaio, a temperatura de admissão não pode ultrapassar 25ºC. É este valor (25 ºC) que vamos utilizar para o cálculo do coeficiente de sensibilidade;

A incerteza expandida herdada da pressão do ar seco (Considerando um DewPoint) é 0,169187429kPa com fator de abrangência k=2. Aqui, vamos utilizar uma pressão igual a 91,25493838kPa.

Assim,

$$F_c=\left(\frac{99}{P_{as}}\right)^{1,2}~\left(\frac{T_{adm}}{298}\right)^{0,6}$$

$$=\left(\frac{99}{91,25493838}\right)^{1,2}~\left(\frac{273+25}{298}\right)^{0,6}$$

$$=1,10269291.$$

A incerteza combinada é:

$$u_{c}(F_c)=\sqrt{ \left(\frac{\partial F_c}{\partial P_{as}}\right)^2~u^2(P_{as}) + \left(\frac{\partial F_c}{\partial T_{adm}}\right)^2~u^2(T_{adm})}$$

$$=\sqrt{ \left(0,014500382\right)^2~\left(\frac{0,169187429}{2} \right)^2 + \left(0,002220187\right)^2~\left(\frac{0,4908189}{2,03218340} \right)^2}=$$

$$=0,001338723.$$

Como não temos incerteza do tipo A, vamos considerar que os graus de liberdade são infinito. Com isso, o fator de abrangência é k = 2.

Desta forma, a incerteza expandida para o fator de correção é:

$$U(F_c)=2 \times u_{c}(F_c)=2 \times 0,001338723=0,00267746.$$

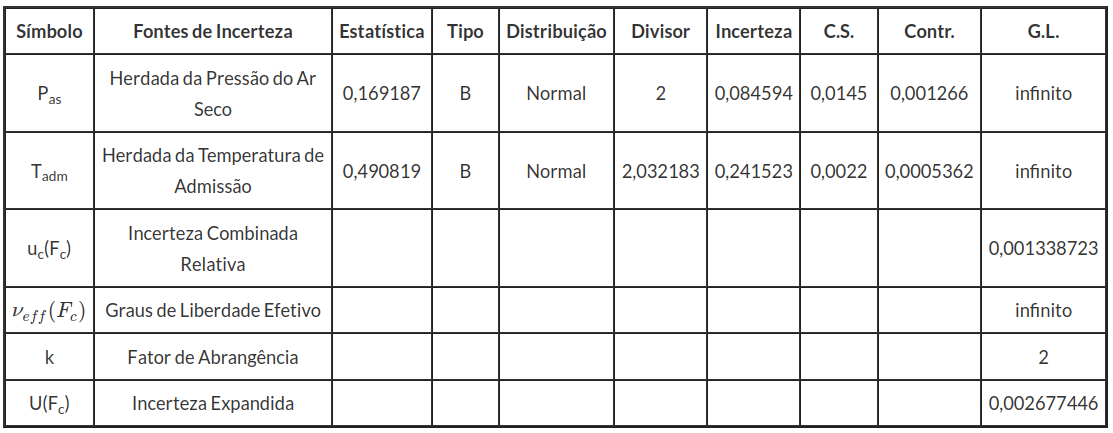
Tabela 4.4.3.2: Resumo do Cálculo de Incerteza para a grandeza Fator de Correção.

Calcularemos a incerteza relativa do fator de correção do motor OTTO da seguinte forma:

$$U_r(F_c)=\frac{U(F_c)}{F_c}=\frac{0,002677446}{1,10269291}=0,0024281.$$

Portanto, a incerteza relativa do fator de correção do motor OTTO é 0,243% do valor lido.

OBS: As aplicações via Higroclip, Bulbo seco e Bulbo úmido são similares à esta acima, com a pressão do ar seco herdada conforme o equipamento utilizado.

4.4.4 - Torque Corrigido

O procedimento aqui empregado será de forma a obtermos uma incerteza para toda a faixa de medição de torque corrigido. Desta forma:

$ \mathbf{\checkmark} $Equação de Medição

A expressão 4.4.4.1 representa a equação de medição utilizada para a obtenção do torque corrigido. Neste caso, temos:

$$T_c = T \times F_c~~(4.4.4.1)$$

em que

• $T_c$: Representa o Torque Corrigido;
• $T$: Representa o Torque. Temos que T tem distribuição normal com incerteza agrupada U(T) e fator de abrangência k;
• $F_c$: Representa o Fator de Correção. Temos que $F_c$ tem distribuição normal com incerteza U($F_c$) e fator de abrangência k.

$ \mathbf{\checkmark} $Incerteza Combinada $ (u_{c}) $

A incerteza combinada para a grandeza torque corrigido é dada por:

$$u_{c}^2(T_c)=\left(\frac{\partial T_C}{\partial T} \right)^2 u^2(T) + \left(\frac{\partial T_C}{\partial F_c} \right)^2 u^2(F_c)$$

$$=F_c^2~ u^2(T) + T^2~ u^2(F_c)$$

Logo,

$$u_{c}^2(T_C) = \sqrt{F_c^2 u^2(T) + T^2 u^2(F_c)}~~(4.4.4.2)$$

em que $ u^2(.) $ é a contribuição de cada fonte de incerteza. A expressão 4.4.4.2 representa a incerteza combinada do torque corrigido.

$ \mathbf{\checkmark} $Incerteza Combinada Relativa ($ u_{r} $)

A incerteza combinada relativa para o torque corrigido é dada por:

$$\frac{u_{r}^2(T_C)}{T_C^2}=\frac{F_c^2}{T \times F_c} u^2(T) + \frac{T^2}{T \times F_c}u^2(F_c)$$

$$=\left( \frac{F_c}{T} \right)^2 u^2(T) + \left( \frac{T}{F_c} \right)^2 u^2(F_c)$$

$$=u_r^2(T) + u_r^2(F_c)$$

Assim, temos que:

$$u_{r}(T_c) = \sqrt{u_r^2(T) + u_r^2(F_c)}~~(4.4.4.3)$$

sendo $ u_{r}^2(.) $ a incerteza de contribuição relativa para cada fonte padrão. A expressão 4.4.4.3 representa a incerteza combinada relativa do torque corrigido.

$ \mathbf{\checkmark} $Incerteza Expandida ($ U(T_c) $)

A expressão 4.4.4.4 representa a incerteza expandida relativa para o torque corrigido

$$U(T_c) = k*u_{r}(T_c)~~(4.4.4.4)$$

em que k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(T_c) $ graus de liberdade e confiança de 95%.Os graus de liberdade são dados por:

$$\nu_{eff}(T_c) =\frac{(u_r(T_c))^4}{\frac{u_r^4(T)}{\infty} + \frac{u_r^4(F_c)}{\infty}}$$

A Tabela 4.4.4.1 apresenta o resumo para o cálculo da incerteza da grandeza Torque Corrigido.

A Tabela 4.4.4.1 apresenta o resumo para o cálculo da incerteza do torque corrigido, considerando as incertezas combinadas das grandezas de entrada.

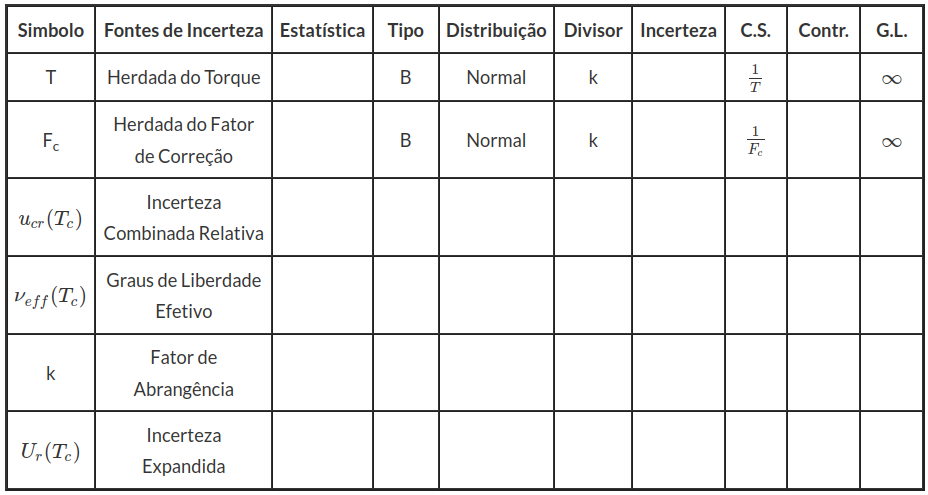
C.S. Coeficiente de Sensibilidade

Contr. Contribuição

G.L. Graus de Liberdade

Tabela 4.4.4.1: Resumo do Cálculo de Incerteza para o torque corrigido.

A Tabela 4.4.4.2 apresenta o resumo para o cálculo da incerteza do torque corrigido, considerando as incertezas combinadas relativas das grandezas de entrada.

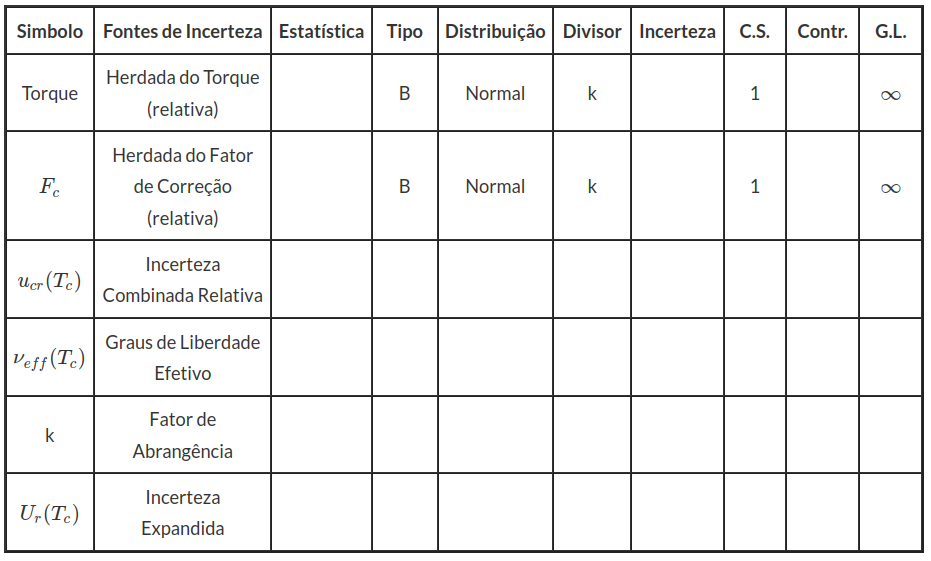
C.S. Coeficiente de Sensibilidade

Contr. Contribuição

G.L. Graus de Liberdade

Tabela 4.4.4.2: Resumo do Cálculo de Incerteza para o torque corrigido.

Aplicação

As informações necessárias para o cálculo de incerteza do torque corrigido são:

• A incerteza expandida relativa herdada do fator de correção é 0,002428, com k=2;
• A incerteza expandida relativa agrupada herdada do torque é 0,016934, com k=2.

Assim,

$$u_{r}(T_C)=\sqrt{\left( \frac{u(T)}{T} \right)^2 +\left( \frac{u(F_c)}{F_c} \right)^2}$$

$$=\sqrt{\left( u_{r}(T) \right)^2 +\left( u_{r}(F_c) \right)^2}$$

$$=\sqrt{\left( \frac{0,016934}{2} \right)^2 + \left( \frac{0,002428}{2}\right)^2}$$

$$=\sqrt{(0,008467)^2 +(0,001214)^2}$$

$$=0,008553.$$

Como não temos incerteza do tipo A, vamos considerar que os graus de liberdade são infinito. Com isso, o fator de abrangência é k = 2. Desta forma, a incerteza expandida relativa para o torque corrigido é:

$$U(T_C)=2 \times u_{cr}(T_C)=2 \times 0,008553=0,0171.$$

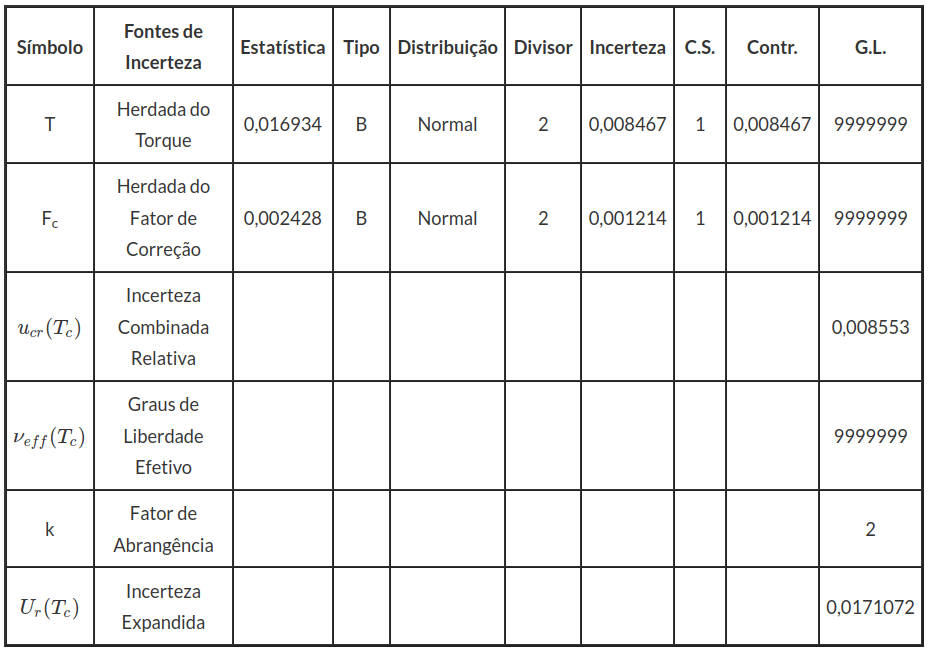
Tabela 4.4.4.3: Resumo do Cálculo de Incerteza para a grandeza Torque Corrigido.

Portanto, a incerteza relativa do Torque Corrigido é 1,71% do valor lido.

4.4.5 - Potência Corrigida

O procedimento aqui empregado será de forma a obtermos uma incerteza para toda a faixa de medição da potência corrigida. Desta forma:

$ \mathbf{\checkmark} $Equação de Medição

A expressão 4.4.5.1 representa a equação de medição utilizada para a obtenção da potência corrigida. Neste caso, temos:

$$P_c = P \times F_c~~(4.4.5.1)$$

em que

• $P_c$: Representa a Potência Corrigida;
• P: Representa a Potência. Temos que P tem distribuição normal com incerteza relativa U(P) e fator de abrangência calculado no módulo 4.4.2 Potência;
• $F_c$: Representa o Fator de Correção. Temos que $ F_c $ tem distribuição normal com incerteza U($F_c$) e fator de abrangência calculado no módulo 4.4.3 Fator de Correção do Motor OTTO;

$ \mathbf{\checkmark} $Incerteza Combinada $ (u_{c}) $

A incerteza combinada para a grandeza Potência Corrigida é dada por:

$$u_{c}^2(P_c)=\left(\frac{\partial P_c}{\partial P} \right)^2 u^2(P) + \left( \frac{\partial P_c}{\partial F_c} \right)^2 u^2(F_c)$$

$$=F_c^2~ u^2(P) + T^2~ u^2(F_c)$$

Logo,

$$u_{c}^2(P_c)=\sqrt{F_c^2 u^2(P) + P^2 u^2(F_c)}~~(4.4.6.2)$$

em que $ u^2(.) $ é a contribuição de cada fonte de incerteza. A expressão 4.4.5.2 representa a incerteza combinada da Potência Corrigida.

$ \mathbf{\checkmark} $Incerteza Combinada Relativa ($ u_{r} $)

A incerteza combinada relativa para a Potência Corrigida é dada por:

$$\frac{u_{c}^2(P_c)}{P_c^2}=\frac{F_c^2}{P \times F_c} u^2(P) + \frac{P^2}{P \times F_c}u^2(F_c)$$

$$=\left( \frac{F_c}{P} \right)^2 u^2(P) + \left( \frac{P}{F_c} \right)^2 u^2(F_c)$$

Assim, temos que:

$$u_{r}(P_c)=\sqrt{\left( \frac{1}{P} \right)^2 u^2(P) + \left( \frac{1}{F_c} \right)^2 u^2(F_c)}$$

$$=\sqrt{u_r^2(P) + u_r^2(F_c)}~~(4.4.5.3)$$

sendo $ u_{r}^2(.) $ a incerteza de contribuição relativa para cada fonte padrão. A expressão 4.4.5.3 representa a incerteza combinada relativa da potência corrigida.

$ \mathbf{\checkmark} $Incerteza Expandida ($ U(P_c) $)

A expressão 4.4.5.4 representa a incerteza expandida relativa para a Potência Corrigida

$$U(P_c) = k*u_{r}(P_C)~~(4.4.5.4)$$

em que k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(P_c) $ graus de liberdade e confiança de 95%. Os graus de liberdade são dados por:

$$\nu_{eff}(P_c) =\frac{(u_r(P_c))^4}{\frac{u_r^4(P)}{\infty} + \frac{u_r^4(F_c)}{\infty}}$$

A Tabela 4.4.5.1 apresenta o resumo para o cálculo da incerteza da grandeza Potência Corrigida.

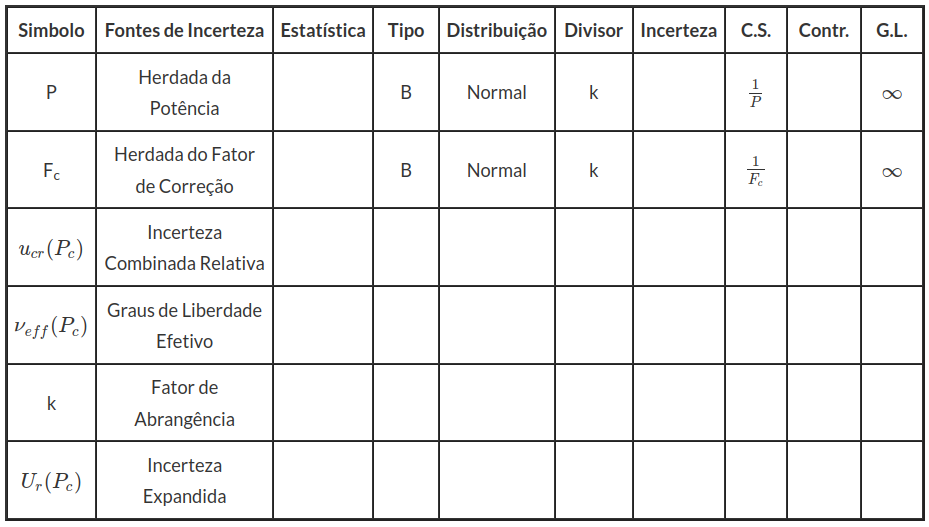
C.S. Coeficiente de Sensibilidade

Contr. Contribuição

G.L. Graus de Liberdade

Tabela 4.4.5.1: Resumo do Cálculo de Incerteza para a Potência Corrigida.

A Tabela 4.4.5.2 apresenta o resumo para o cálculo da incerteza da potência corrigida, considerando as incertezas combinadas relativas das grandezas de entrada.

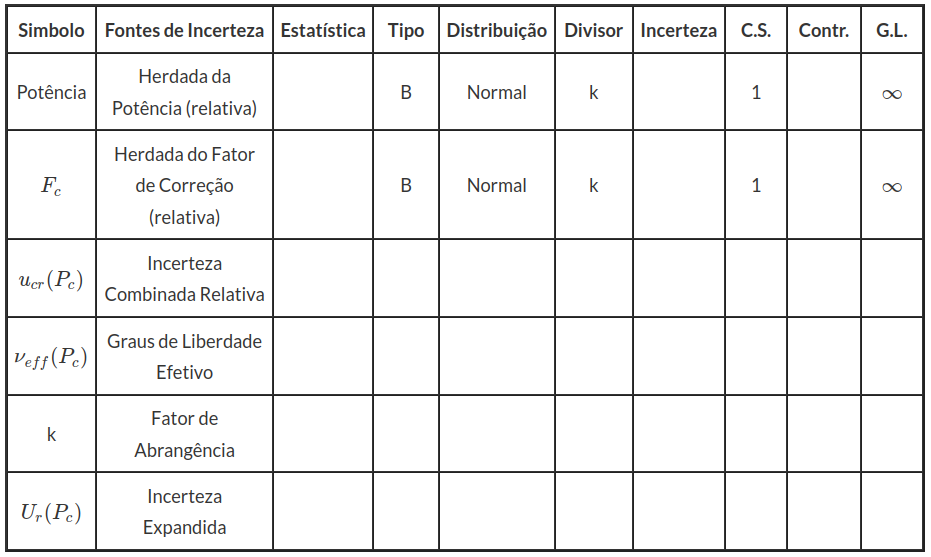
C.S. Coeficiente de Sensibilidade

Contr. Contribuição

G.L. Graus de Liberdade

Tabela 4.4.5.2: Resumo do Cálculo de Incerteza para a Potência corrigida.

Aplicação

As informações necessárias para o cálculo de incerteza da potência corrigida são:

A incerteza expandida relativa herdada do fator de correção é 0,0024281, com k=2;

A incerteza expandida relativa herdada da potência é 0,01695, com k=2.

Assim,

$$u_{r}(P_c)=\sqrt{\left(\frac{u(P)}{P} \right)^2 + \left( \frac{u(F_c)}{F_c} \right)^2}$$

$$=\sqrt{\left(u_{r}(P) \right)^2 +\left(u_{r}(F_c) \right)^2}$$

$$=\sqrt{\left(\frac{0,0024281}{2} \right)^2 + \left( \frac{0,01695}{2}\right)^2}$$

$$=\sqrt{(0,001214)^2 +(0,008475)^2}$$

$$=0,008561515.$$

Como não temos incerteza do tipo A, vamos considerar que os graus de liberdade são infinito. Com isso, o fator de abrangência é k = 2. Desta forma, a incerteza expandida relativa para a potência corrigida é:

$$U(P_C) =2 \times u_{cr}(P_C)=2 \times 0,0085561515=0,01712303.$$

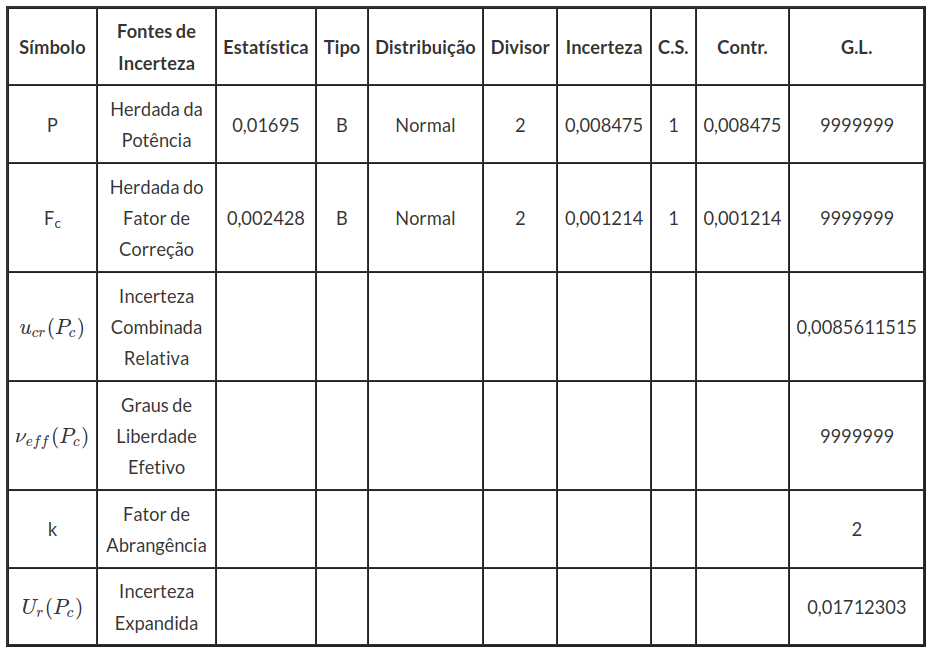
Tabela 4.4.5.3: Resumo do Cálculo de Incerteza para a grandeza Potência Corrigida.

Portanto, a incerteza relativa do Potência Corrigida é 1,712% do valor lido.

4.4.6 - Ensaio de Repetitividade e Reprodutibilidade

Nessa seção vamos realizar um ensaio de repetitividade e reprodutibilidade para potência efetiva líquida do motor ciclo OTTO. Neste ensaio, consideramos um experimento fatorial completo com os fatores Período (Manhã e Tarde) e Equipe (I e II) e 4 réplicas. este experimento foi realizado nos seguintes pontos de rotação: 1200, 2000, 3000, 3600, 4400, 5200, 5600, 6000 e 6400. Os dados para rotação de 6400 estão apresentados abaixo.

Potência Corrigida	Período	Equipe
51,4	Tarde	I
51,9	Tarde	I
51,4	Manha	I
51,4	Manha	I
51,3	Tarde	II
51,3	Tarde	II
51,7	Manha	I
51,9	Manha	I
52,1	Tarde	I
52,2	Tarde	I
52,3	Manha	II
52,3	Manha	II
52,1	Tarde	II
51,4	Tarde	II
52,1	Manha	II
52,1	Manha	II

Tabela 4.4.6.1: Dados no ponto de 6400 rpm.

A seguir apresentamos uma análise descritiva dos dados

Período	Equipe	Mínimo	1º Quartil	Média	Mediana	3º Quartil	Máximo	Desvio Padrão	Amplitude
Manha	I	51,4	51,4	51,6	51,6	51,9	51,9	0,24	0,5
Manha	II	52,1	52,1	52,2	52,2	52,3	52,3	0,12	0,2
Tarde	I	51,4	51,5	51,9	52,0	52,2	52,2	0,36	0,8
Tarde	II	51,3	51,3	51,5	51,4	51,9	52,1	0,39	0,8

Tabela 4.4.6.2: Estatísticas descritivas.

O gráfico de interações é apresentado abaixo

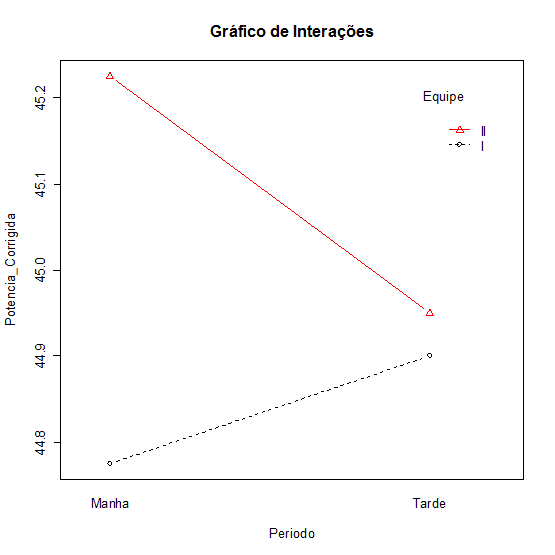
Figura 4.4.6.1: Gráfico de Interações.

Através da técnica de ANOVA com efeitos aleatórios determinamos a repetitividade do método no ponto de 6400 rpm.

Como podemos observar na tabela da ANOVA, tanto o fator período quanto o fator equipe foram considerados não significativos com $ \alpha=0,05. $ Neste caso a repetitividade foi de 0,38204 kW. De forma geral, temos a tabela 4.4.6.3.

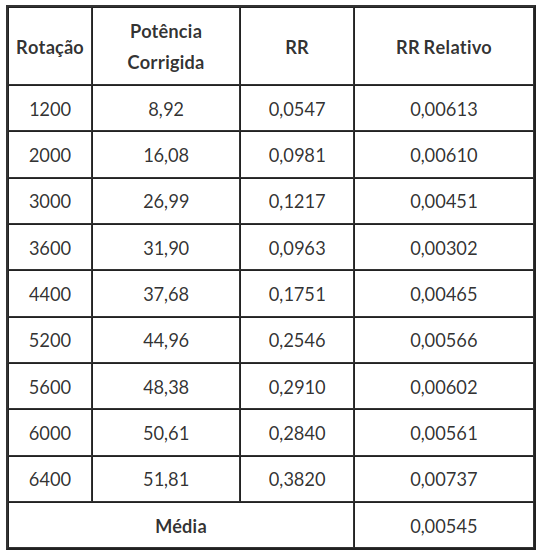
Tabela 4.4.6.3: Repetitividade e Reprodutibilidade Relativo.

4.4.7 - Incerteza do Ensaio Potência Efetiva Líquida

Nesta fase, vamos combinar a incerteza efetiva na calibração com a incerteza devido a repetitividade e reprodutibilidade do método de ensaio. Para isto, tomamos a seguinte equação de medição:

$ \mathbf{\checkmark} $Equação de Medição

A expressão 4.4.7.1 representa a equação de medição utilizada para a obtenção da potência efetiva líquida do motor ciclo OTTO. Neste caso temos:

$$PEL=P_c+\varepsilon~~(4.4.7.1)$$

em que

• PEL: Representa a Potência efetiva do motor;
• $P_c$: Representa a Potência corrigida. Temos que $P_c$ tem distribuição normal com incerteza relativa $U_r$($P_c$) e fator de abrangência calculado no módulo 4.4.6 Potência Corrigida;
• ε: Representa a Repetitividade e Reprodutibilidade. Podemos supor que a $ \varepsilon $ tem distribuição normal com média zero e desvio padrão calculada no módulo Ensaio de RR.

$ \mathbf{\checkmark} $Incerteza Combinada ($ u_{c}(PEL) $)

A incerteza combinada relativa para a Potência efetiva do motor é dada por:

$$u_{cr}(PEL)=\sqrt{u^2_r(P_c)+u^2_r(\varepsilon)}~~(4.4.7.2)$$

sendo $ u_{r}^2(.) $ a incerteza de contribuição relativa para cada fonte padrão. A expressão (4.4.7.2) representa a incerteza combinada relativa da potência efetiva do motor.

$ \mathbf{\checkmark} $Incerteza Expandida ($ U(PEL) $)

A expressão 4.4.7.3 representa a incerteza expandida relativa para a Potência Efetiva Líquida.

$$U(PEL) = k*u_{cr}(PEL)~~(4.4.7.3)$$

em que k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(PEL) $ graus de liberdade e confiança de 95%. Os graus de liberdade são dados por:

$$\nu_{eff}(PEL) =\frac{(u_{cr}(PEL))^4}{\frac{u_r^4(P_c)}{\infty} + \frac{u_r^4(\varepsilon)}{\infty}}$$

A Tabela 4.4.7.1 apresenta o resumo para o cálculo da incerteza da potência efetiva líquida do motor.

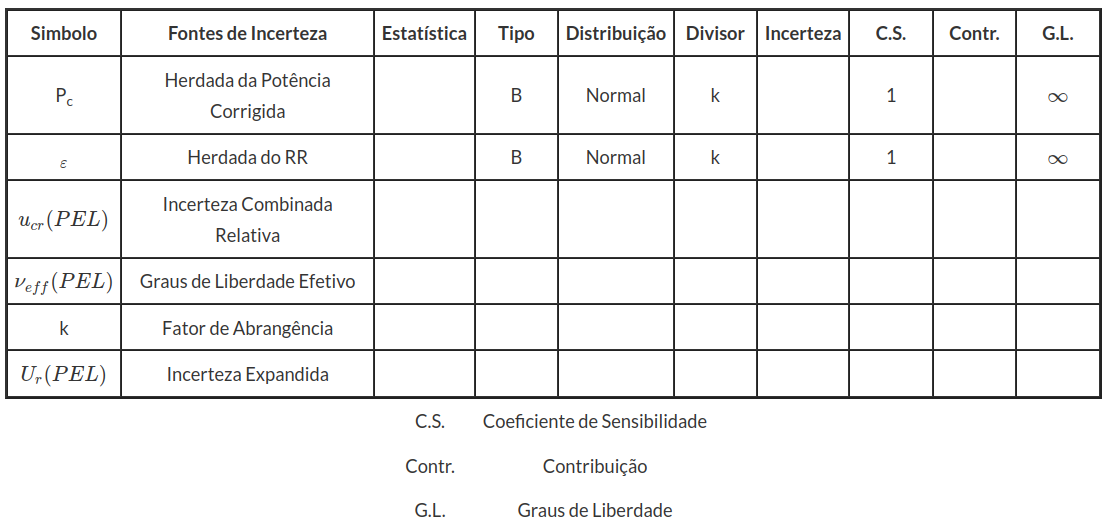
Tabela 4.4.7.1: Resumo do Cálculo de Incerteza para a Potência Efetiva Líquida.

Aplicação

As informações necessárias para o cálculo de incerteza da potência efetiva líquida do motor são:

A incerteza expandida relativa herdada da potência corrigida é 0,01712303, com k=2;

A incerteza expandida relativa herdada da potência é 0,00545.

Assim,

$$u_{r}(PEL)=\sqrt{\left(u_{r}(P_c) \right)^2 +\left(u_{r}(\varepsilon) \right)^2}$$

$$=\sqrt{\left(\frac{0,01712303}{2} \right)^2 + 0,00545^2}$$

$$=0,01015045.$$

Como não temos incerteza do tipo A, vamos considerar que os graus de liberdade são infinito. Com isso, o fator de abrangência é k = 2. Desta forma, a incerteza expandida relativa para a potência efetiva líquida do motor é:

$$U(PEL) =2 \times u_{cr}(PEL)=2 \times 0,01015045=0,0203.$$

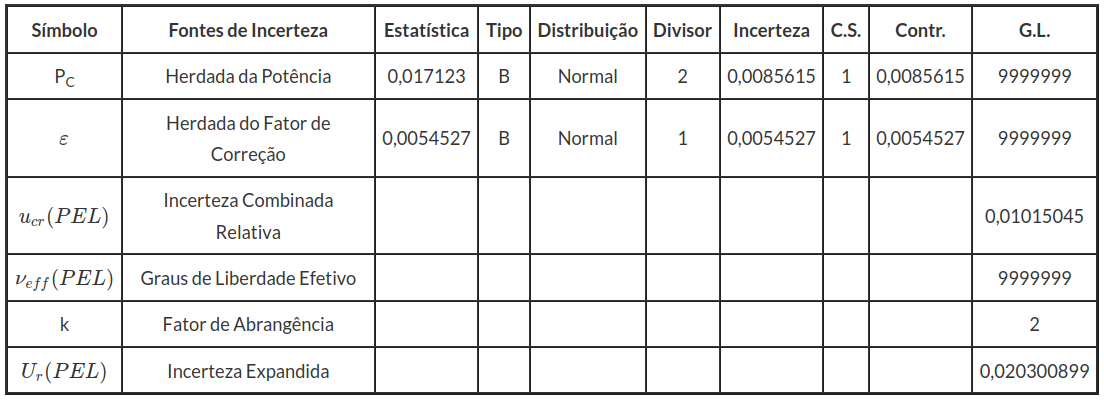
Tabela 4.4.7.3: Resumo do Cálculo de Incerteza para a grandeza Potência efetiva Líquida.

Portanto, a incerteza relativa da Potência Efetiva Líquida do motor ciclo OTTO é 2,03% do valor lido.

4.5 - Cálculo de Incerteza para Migração à partir de materiais

Esta aplicação é referente ao cálculo de incerteza para determinar a migração específica de um certo composto químico à partir de materiais, embalagens e equipamentos plásticos, por meio de sua extração em simulantes de alimentos, a uma determinada condição de temperatura e tempo de contato, e posterior análise quantitativa por cromatografia gasosa e detecção por ionização de chama com um padrão interno de referência.

A migração específica deste composto é determinada em simulante aquoso (água destilada, solução de ácido acético em água destilada ou soluções de etanol em água destilada). Após a etapa de extração e adição de padrão interno, a concentração do composto químico é determinada diretamente por cromatografia gasosa nos simulantes.

O ensaio é dividido em duas partes principais, a calibração do cromatógrafo e a medição da amostra. Para calibrar o cromatógrafo, vamos preparar soluções padrão e realizar a curva de calibração do equipamento.

4.5.1 - Cálculo de Incerteza devido às Soluções

Primeiramente, para calibração do cromatógrafo, temos a fase de preparação das soluções que descrevemos a seguir:

1. Preparação da solução Mãe do padrão primário (6 mg/mL), ou seja, pesamos 0,15 g em uma balança analítica do padrão primário em um balão volumétrico de 25 mL;

2. Preparação da solução Mãe do padrão secundário (6 mg/mL), ou seja, pesamos 0,6 g em uma balança analítica do padrão secundário em um balão volumétrico de 100 mL;

3. Preparação das soluções Filhas dos padrões primário e secundário. Em balões volumétricos de 25 mL os volumes adicionados com pipeta volumétrica de cada solução mãe de padrão primário (item 1) e padrão secundário (item 2);

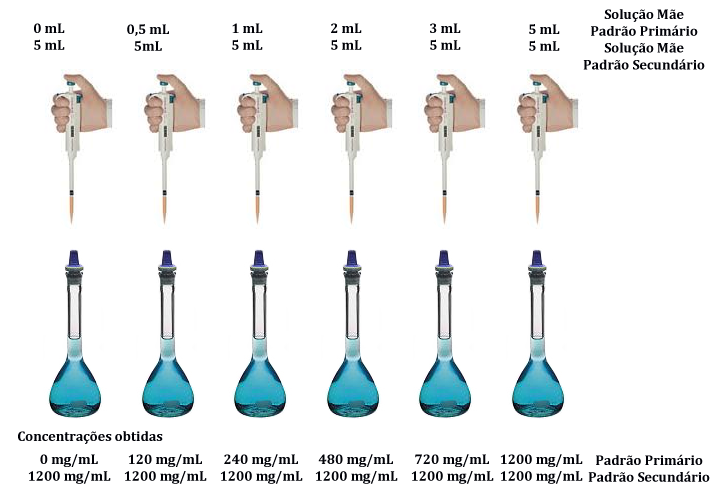
4. Preparação das soluções Netas dos padrões primário e secundário. Pipetar com auxílio de uma micropipeta volumétrica de 5 mL do simulante aquoso em uma série de frascos do amostrador de espaço-livre de 20 mL. Em seguida, adicionar com uma micropipeta volumétrica calibrada 100 μL de cada uma das soluções preparadas. Cada solução de ver preparada em duplicata. Assim, as soluções estarão prontas para análise no amostrador de espaço-livre e injeção no cromatógrafo a gás com detector de ionização de chama.

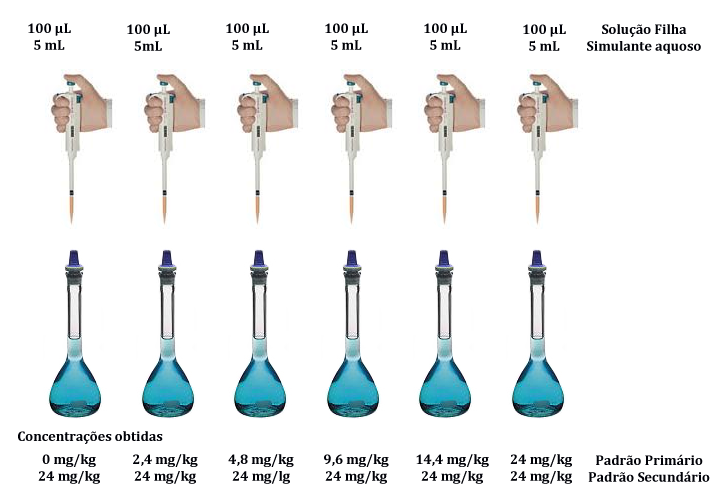
Solução Mãe do composto químico

$ \mathbf{\checkmark} $Equação de Medição

A expressão (4.5.1.1) representa a equação de medição utilizada para a grandeza concentração mãe, neste caso temos:

$$S_{M1}~=~\left(\frac{M}{V(1~-~\alpha \Delta)}\right)\times P~~(4.5.1.1)$$

• V: representa o Volume, mL. Temos que $ V $ tem distribuição normal com incerteza u(V) e o fator de abrangência dados pelo certificado de calibração;
• $ \alpha $: representa o coeficiente de expansão volumétrico, ºC-1. Podemos supor que a $ \alpha $ tem distribuição retangular (ou uniforme) no intervalo $ \left(-\frac{\alpha}{2},~\frac{\alpha}{2}\right) $, em que $ \alpha $ é o coeficiente de expansão volumétrico. Logo a incerteza devido ao coeficiente de expansão volumétrico será dada por:

$$u(\alpha) = \frac{\alpha}{2\sqrt{3}};$$

• $ \Delta $: representa a diferença entre a temperatura final e inicial ($ \Delta~=~t_f~-~t_i $), ºC;
• M: representa a massa $ (g) $. Possui duas fontes de incerteza:

a) Herdada da balança, temos que $ M $ tem distribuição normal com incerteza $ u(M) $ e o fator de abrangência k.

b) ResM: Representa a Resolução da balança (g). Podemos supor que a resolução tem distribuição retangular (ou uniforme) no intervalo $ \left(-\frac{ResM}{2},~\frac{ResM}{2}\right) $, em que ResM é a resolução do balança. Logo a incerteza devida a resolução será dada por:

$$u(ResM) = \frac{ResM}{2\sqrt{3}}$$

• P: representa a Pureza. No entanto, será considerada uma constante, ou seja, uma variável com incerteza associada desprezível;

$ \mathbf{\checkmark} $ Incerteza Combinada

$ u_c(S_{M1})=\sqrt{\left(\frac{\partial S_{M1}}{\partial M}\right)^2 (u^2(M)+u^2(Res_M))+\left(\frac{\partial S_{M1}}{\partial V}\right)^2 u^2(V)+\left(\frac{\partial S_{M1}}{\partial \alpha}\right)^2 u^2(\alpha)+ \left(\frac{\partial S_{M1}}{\partial \Delta} \right)^2 u^2(\Delta)} $

em que,

$$\left(\frac{\partial S_{M1}}{\partial M}\right)=\left(\frac{1}{V(1~-~\alpha \Delta)}\right)\times P=\frac{S_{M1}}{M}$$

$$\left(\frac{\partial S_{M1}}{\partial V}\right) =\left(\frac{M}{V^2(1~-~\alpha \Delta)}\right)\times P=\frac{S_{M1}}{V}$$

$$\left(\frac{\partial S_{M1}}{\partial \alpha}\right)=\left(\frac{M\times\Delta\times V}{V(1~-~\alpha \Delta)^2}\right)\times P=\frac{S_{M1}\times\Delta\times V}{(1-\alpha \Delta)}$$

$$\left(\frac{\partial S_{M1}}{\partial \Delta}\right)=\left(\frac{M\times\alpha\times V}{V(1~-~\alpha \Delta)^2}\right)\times P=\frac{S_{M1}\times\alpha\times V}{(1-\alpha \Delta)}$$

$ \mathbf{\checkmark} $Incerteza Expandida ($ U(S_{M1}) $)

Aqui, a expressão (4.5.1.2) representa a incerteza expandida para a concentração mãe.

$$U(S_{M1}) = k\times u_c(S_{M1})~~(4.5.1.2)$$

em que k (fator de abrangência), que é o quantil da distribuição t-Student com $ \nu_{eff}(S_{M1}) $ graus de liberdade e confiança de 95%. Os graus de liberdade são dados por:

$$\nu_{eff}(S_{M1})=\frac{(u_c(S_{M1}))^4}{\frac{u^4(M)}{\infty}+\frac{u^4(V)}{\infty}+\frac{u^4(\alpha)}{\infty} + \frac{u^4(\Delta)}{\infty} +\frac{u^4(ResM)}{\infty}}$$

Para efetuar os cálculos da calibração, as informações necessárias são:

Fontes	Valor	Incerteza (U)	Fator de Abrangência (k)	Resolução (Res)	Fator de Abrangência (k)
Massa (mg)	150	0,1	2,52	0,1	3,464101615
Volume (mL)	25	0,008	2,231
Coef.Expansão (ºC-1)	0,0001	0,000001	3,464101615
Dif.Temperatura (ºC)	0,5	0,005	3,464101615
Pureza	0,99	0	1,96

Incerteza Combinada ($ u_{c}(S_{M1}) $)

A incerteza combinada para a grandeza concentração mãe é dada por:

$ u_c(S_{M1})=\sqrt{\left(\frac{\partial S_{M1}}{\partial M}\right)^2 (u^2(M)+u^2(Res_M))+\left(\frac{\partial S_{M1}}{\partial V}\right)^2 u^2(V)+\left(\frac{\partial S_{M1}}{\partial \alpha}\right)^2 u^2(\alpha)+ \left(\frac{\partial S_{M1}}{\partial \Delta} \right)^2 u^2(\Delta)} $

$$=0,002121917$$

em que

$$\left(\frac{\partial S_{M1}}{\partial M}\right)=\left(\frac{1}{V(1~-~\alpha \Delta)}\right)\times P=\frac{S_{M1}}{M}=0,03960198$$

$$\left(\frac{\partial S_{M1}}{\partial V}\right)=\left(\frac{M}{V^2(1~-~\alpha \Delta)}\right)\times P=\frac{S_{M1}}{V}=0,237611881$$

$$\left(\frac{\partial S_{M1}}{\partial \alpha}\right)=\left(\frac{M\times\Delta\times V}{V(1~-~\alpha \Delta)^2}\right)\times P=\frac{S_{M1}\times\Delta\times V}{(1-\alpha \Delta)}=74,25742556$$

$$\left(\frac{\partial S_{M1}}{\partial \Delta}\right)=\left(\frac{M\times\alpha\times V}{V(1~-~\alpha \Delta)^2}\right)\times P=\frac{S_{M1}\times\alpha\times V}{(1-\alpha \Delta)}=0,014851485$$

Incerteza Expandida ($ U(S_{M1}) $)

$$U(S_{M1}) = k\times u_c(S_{M1})=1,95996563\times0,002121917=0,004158885$$

Os graus de liberdade são dados por:

$$\nu_{eff}(S_{M1}) =\frac{(u_c(S_{M1}))^4}{\frac{u^4(M)}{\infty}+\frac{u^4(V)}{\infty}+\frac{u^4(\alpha)}{\infty} + \frac{u^4(\Delta)}{\infty}+\frac{u^4(ResM)}{\infty}}\rightarrow\infty $$

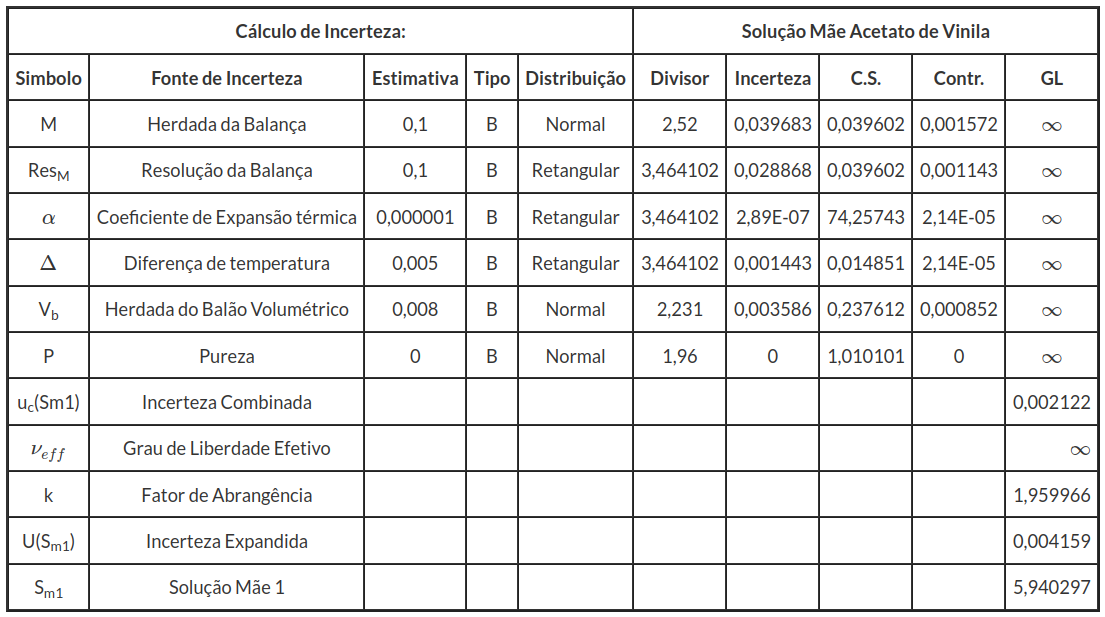
Concentração da Solução Filha

$ \mathbf{\checkmark} $ Equação de Medição

A expressão (4.5.1.3) representa a equação de medição utilizada para a grandeza concentração filha, neste caso temos:

$$S_{F}~=~\frac{V_{p1}\times(1-\alpha_{p1}\Delta)\times S_{M1}}{V_b~(1~-~\alpha_b\Delta)}~~(4.5.1.3)$$

em que

• $V_{p1}$: representa o Volume da pipeta da solução mãe do composto químico, mL. Temos que Vp1 tem distribuição normal com incerteza $ u(V_{p1}) $ e o fator de abrangência dado pelo certificado de calibração;
• $V_{b1}$: representa o Volume do balão da solução mãe do composto, mL. Temos que Vb1 tem distribuição normal com incerteza $ u(V_{b1}) $ e o fator de abrangência dado pelo certificado de calibração;
• $ \alpha_{p1} $: representa o coeficiente de expansão volumétrico da pipeta, ºC-1. Podemos supor que a $ \alpha_{p1} $ tem distribuição retangular (ou uniforme) no intervalo $ \left(-\frac{\alpha_{p1}}{2},~\frac{\alpha_{p1}}{2}\right) $,

em que $ \alpha_{p1} $ é o coeficiente de expansão volumétrico. Logo a incerteza devido ao coeficiente de expansão volumétrico será dada por:

$$u(\alpha_{p1}) = \frac{\alpha_{p1}}{2\sqrt{3}};$$

• $ \alpha_{b1} $: representa o coeficiente de expansão volumétrico do balão, ºC-1. Podemos supor que a $ \alpha_{b1} $ tem distribuição retangular (ou uniforme) no intervalo $ \left(-\frac{\alpha_{b1}}{2},~\frac{\alpha_{b1}}{2}\right) $,

em que $ \alpha_{b1} $ é o coeficiente de expansão volumétrico. Logo a incerteza devido ao coeficiente de expansão volumétrico será dada por:

$$u(\alpha_{b1}) = \frac{\alpha_{b1}}{2\sqrt{3}};$$

• $ \Delta $: representa a a diferença entre a temperatura final e inicial ($ \Delta~=~t_f~-~t_i $), ºC;
• $S_{M1}$: representa a incerteza herdada da concentração mãe, mg/mL. Temos que SM1 tem distribuição normal com incerteza $ U(S_{M1}) $ e o fator de abrangência calculado no tópico anterior;

$ \mathbf{\checkmark} $ Incerteza Combinada ($ u_{c}(S_F) $)

A incerteza combinada para a grandeza concentração mãe é dada por:

$$u^2_c(S_F)=\left(\frac{\partial S_F}{\partial V_{p1}}\right)^2 u^2(V_{p1})+\left(\frac{\partial S_F}{\partial V_{b}}\right)^2 u^2(V_{b})+\left(\frac{\partial S_F}{\partial \alpha_{p1}}\right)^2 u^2(\alpha_{p1}) +\left(\frac{\partial S_F}{\partial \alpha_{b}}\right)^2 u^2(\alpha_{b})+ $$

$$+\left(\frac{\partial S_F}{\partial \Delta} \right)^2 u^2(\Delta) + \left(\frac{\partial S_F}{\partial S_{M1}} \right)^2 u^2(S_{M1})$$

em que

$$\left(\frac{\partial S_F}{\partial V_{p1}}\right)=\left(\frac{(1-\alpha_{p1}\Delta)\times S_{M1}}{V_b(1-\alpha_b \Delta)}\right)=\frac{S_F}{V_{p1}}$$

$$\left(\frac{\partial S_F}{\partial V_b}\right)=\frac{V_{p1}\times(1-\alpha_{p1}\Delta)\times S_{M1}}{V_b^2(1-\alpha_b \Delta)}=\frac{S_F}{V_b}$$

$$\left(\frac{\partial S_F}{\partial \alpha_{p1}}\right)=\left(\frac{V_{p1}\times\Delta\times S_{M1}}{V_b(1-\alpha_b \Delta)}\right)$$

$$\left(\frac{\partial S_F}{\partial \alpha_b}\right)=\left(\frac{V_{p1}\times(1-\alpha_{p1}\Delta)\times S_{M1}}{V_b(1-\alpha_b\Delta)^2}\right)\times\Delta=\frac{S_F\times\Delta}{(1-\alpha_b\Delta)}$$

$$\left(\frac{\partial S_F}{\partial \Delta}\right)=\left(\frac{V_{p1}\times S_{M1}\times(\alpha_b-\alpha_{p1})}{(1-\alpha_b \Delta)^2}\right)$$

$$\left(\frac{\partial S_F}{\partial S_{M1}}\right)=\frac{V_{p1}\times(1-\alpha_{p1}\Delta) }{V_b(1-\alpha_b\Delta)}=\frac{S_F}{S_{M1}}$$

em que, $ u^2(.) $ é a contribuição de cada fonte de incerteza.

$ \mathbf{\checkmark} $ Incerteza Expandida ($ U(S_F) $)

A expressão (4.5.1.4) representa a incerteza expandida para a concentração filha.

$$U(S_F) = k\times u_c(S_F)$$

em que k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(S_F) $ graus de liberdade e confiança de 95%. Como neste cálculo estamos trabalhando apenas com incertezas do tipo B, então o equivale a $ \nu_{eff}(S_F)=\infty $

Para a solução filha são preparadas 6 soluções, para nossa aplicação faremos para a solução filha 2. Para efetuar os cálculos da calibração, as informações necessárias são:

Fontes	Valor	Incerteza (U)	Fator de Abrangência (k)
Volume do Balão (mL)	25	0,008	2,231
Volume da Pipeta 1 (mL)	0,5	0,0011	2,31
Coef.Expansão balão (ºC-1)	0,0001	0,000001	3,464102
Coef.Expansão pipeta 1 (ºC-1)	0,00012	0,0000012	3,464102
Dif.Temperatura (ºC)	0,5	0,005	3,464102
Solução Mãe 1	5,940297	0,004158886	1,959966357

Aplicando os valores da tabela obtemos os seguintes resultados:

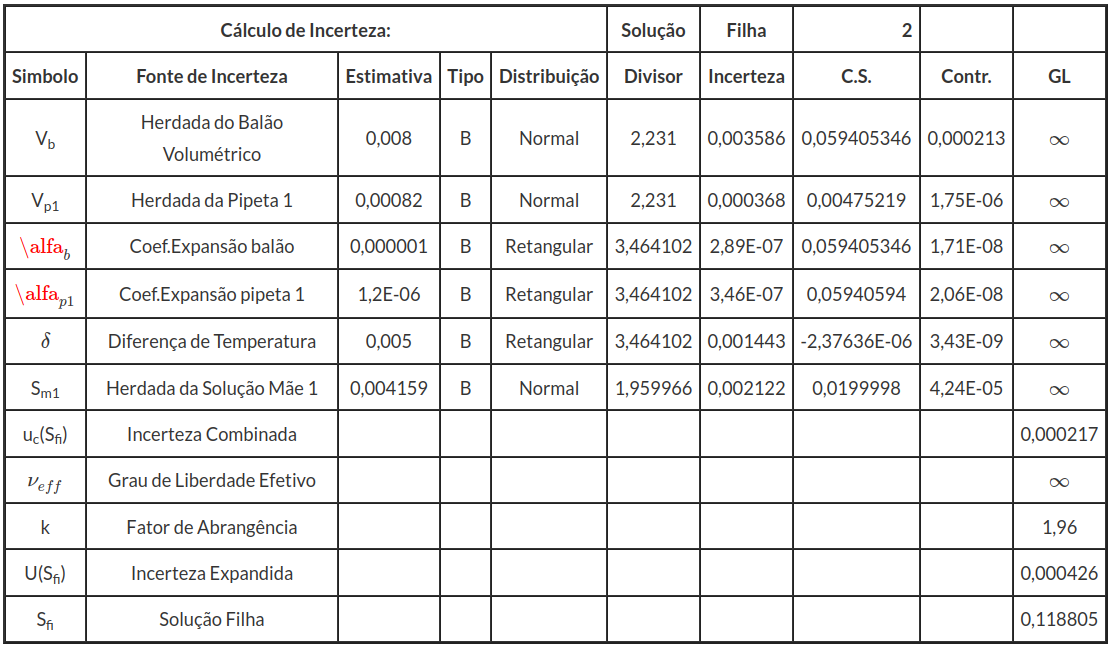
Concentração da Solução Neta

Agora, vamos considerar o cálculo de incerteza para as concentrações netas.

$ \mathbf{\checkmark} $ Equação de Medição

A expressão (4.5.1.5) representa a equação de medição utilizada para a grandeza concentração filha, neste caso temos:

$$S_{N}=\frac{V_{\mu pf}(1-\alpha_{\mu pf} \Delta)}{V_{\mu pf}(1-\alpha_{\mu pf} \Delta)+V_{\mu ps}(1-\alpha_{\mu ps} \Delta)}\times S_{F}+\varepsilon~~(4.5.1.5)$$

em que

• $ V_{\mu pf} $: representa o Volume da micro pipeta da solução filha, $ mL $. Temos que $ V_{\mu pf} $ tem distribuição normal com incerteza $ u(V_{\mu pf}) $ e o fator de abrangência dado pelo certificado;
• $ V_{\mu ps} $: representa o Volume da micro pipeta do simulante, $ mL $. Temos que $ V_{\mu ps} $ tem distribuição normal com incerteza $ u(V_{\mu ps}) $ e o fator de abrangência dado pelo certificado;
• $ \alpha_{\mu pf} $: representa o coeficiente de expansão volumétrico da micro pipeta, $ {}^\circ C^{-1} $. Podemos supor que a $ \alpha_{\mu pf} $ tem distribuição retangular (ou uniforme) no intervalo $ \left(-\frac{\alpha_{\mu pf}}{2},~\frac{\alpha_{\mu pf}}{2}\right) $, em que $ \alpha_{\mu pf} $ é o coeficiente de expansão volumétrico. Logo a incerteza devido ao coeficiente de expansão volumétrico será dada por:

$$u(\alpha_{\mu pf}) = \frac{\alpha_{\mu pf}}{2\sqrt{3}};$$

• $ \alpha_{\mu ps} $: representa o coeficiente de expansão volumétrico da micro pipeta, $ {}^\circ C^{-1} $. Podemos supor que a $ \alpha_{\mu ps} $ tem distribuição retangular (ou uniforme) no intervalo $ \left(-\frac{\alpha_{\mu ps}}{2},~\frac{\alpha_{\mu ps}}{2}\right) $, em que $ \alpha_{\mu ps} $ é o coeficiente de expansão volumétrico. Logo a incerteza devido ao coeficiente de expansão volumétrico será dada por:

$$u(\alpha_{\mu ps}) = \frac{\alpha_{\mu ps}}{2\sqrt{3}};$$

• $ \Delta $: representa a a diferença entre a temperatura final e inicial ($ \Delta~=~t_f~-~t_i $), $ {}^\circ C $;
• $ S_F $: representa a incerteza herdada da concentração filha, mg/mL. Temos que $ S_F $ tem distribuição normal com incerteza $ U(S_F) $ e o fator de abrangência calculado na seção anterior;
• $ \varepsilon $: representa a repetitividade. Podemos supor que a distribuição da média das medições tem distribuição normal. Logo, podemos estimar sua incerteza (desvio padrão da média) como:

$$u(\varepsilon) = \frac{s}{\sqrt{n}},$$

em que $ s^2 = \frac{1}{n-1} \displaystyle\sum_{i=1}^{n} (x_i -\overline{X})^2 $ é a variância amostral e $ \overline{X} = \frac{1}{n}\displaystyle \sum^{n_{i=1}} x_i $ é a média amostral;

$ \mathbf{\checkmark} $ Incerteza Combinada ($ u_{c}(S_N) $)

A incerteza combinada para a grandeza concentração neta é dada por:

$$u_c^2(S_N)=\left(\frac{\partial S_N}{\partial V_{\mu pf}}\right)^2 u^2(V_{\mu pf})+\left(\frac{\partial S_N}{\partial V_{\mu ps}}\right)^2 u^2(V_{\mu ps})+\left(\frac{\partial S_N}{\partial \alpha_{\mu pf}}\right)^2 u^2(\alpha_{\mu pf}) +\left(\frac{\partial S_N}{\partial \alpha_{\mu ps}}\right)^2 u^2(\alpha_{\mu ps}) +$$

$$+\left(\frac{\partial S_N}{\partial \Delta} \right)^2 u^2(\Delta) + \left(\frac{\partial S_N}{\partial S_F} \right)^2 u^2(S_F)+ u^2(\varepsilon)$$

em que,

$$\left(\frac{\partial S_N}{\partial V_{\mu pf}}\right)=\frac{V_{\mu ps}(1-\alpha_{\mu pf} \Delta)(1-\alpha_{\mu ps} \Delta)}{(V_{\mu pf}(1-\alpha_{\mu pf} \Delta)+V_{\mu ps}(1-\alpha_{\mu ps} \Delta))^2}\times S_{F}$$

$$\left(\frac{\partial S_N}{\partial V_{\mu ps}}\right)=\frac{V_{\mu pf}(1-\alpha_{\mu pf} \Delta)(1-\alpha_{\mu ps} \Delta)}{(V_{\mu pf}(1-\alpha_{\mu pf} \Delta)+V_{\mu ps}(1-\alpha_{\mu ps} \Delta))^2}\times S_{F}$$

$$\left(\frac{\partial S_N}{\partial \alpha_{\mu pf}}\right)=\frac{V_{\mu ps} V_{\mu pf}\Delta(1-\alpha_{\mu ps} \Delta)}{(V_{\mu pf}(1-\alpha_{\mu pf} \Delta)+V_{\mu ps}(1-\alpha_{\mu ps} \Delta))^2}\times S_{F}$$

$$\left(\frac{\partial S_N}{\partial \alpha_{\mu ps}}\right)=\frac{V_{\mu ps} V_{\mu pf}\Delta(1-\alpha_{\mu pf} \Delta)}{(V_{\mu pf}(1-\alpha_{\mu pf} \Delta)+V_{\mu ps}(1-\alpha_{\mu ps} \Delta))^2}\times S_{F}$$

$$\left(\frac{\partial S_N}{\partial \Delta}\right)=\frac{V_{\mu ps} V_{\mu pf}(\alpha_{\mu ps}-\alpha_{\mu pf})}{(V_{\mu pf}(1-\alpha_{\mu pf} \Delta)+V_{\mu ps}(1-\alpha_{\mu ps} \Delta))^2}\times S_{F}$$

$$\left(\frac{\partial S_N}{\partial S_F}\right)=\frac{V_{\mu pf}(1-\alpha_{\mu pf} \Delta)}{V_{\mu pf}(1-\alpha_{\mu pf} \Delta)+V_{\mu ps}(1-\alpha_{\mu ps} \Delta)}=\frac{S_N}{S_F}$$

em que, $ u^2(.) $ é a contribuição de cada fonte de incerteza.

$ \mathbf{\checkmark} $ Incerteza Expandida ($ U(S_N) $)

A expressão (4.5.1.6) representa a incerteza expandida relativa para a concentração neta.

$$U(S_N) = k\times u_c(S_N)~~(4.5.1.6)$$

em que k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(S_N) $ graus de liberdade e confiança de 95%. Como neste cálculo estamos trabalhando apenas com incertezas do tipo B, então o equivale a $ \nu_{eff}(S_N)=\infty $

Para as soluções netas são preparadas 6 soluções, para nossa aplicação faremos para a solução neta 2. Para efetuar os cálculos da calibração, as informações necessárias são:

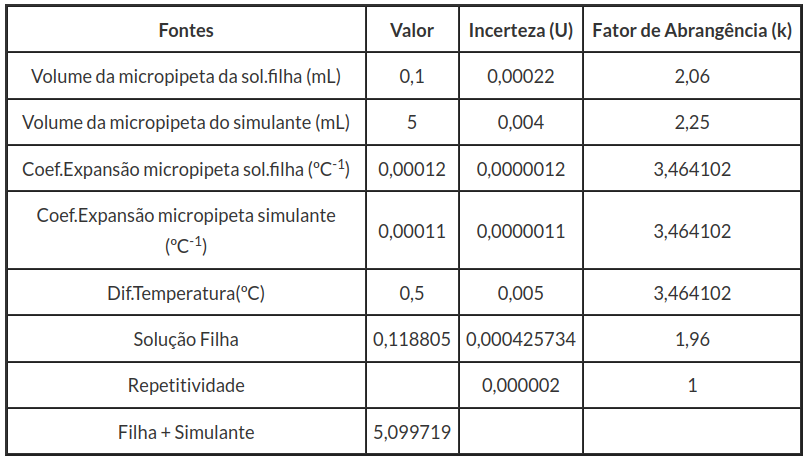
Aplicando os valores da tabela obtemos os seguintes resultados:

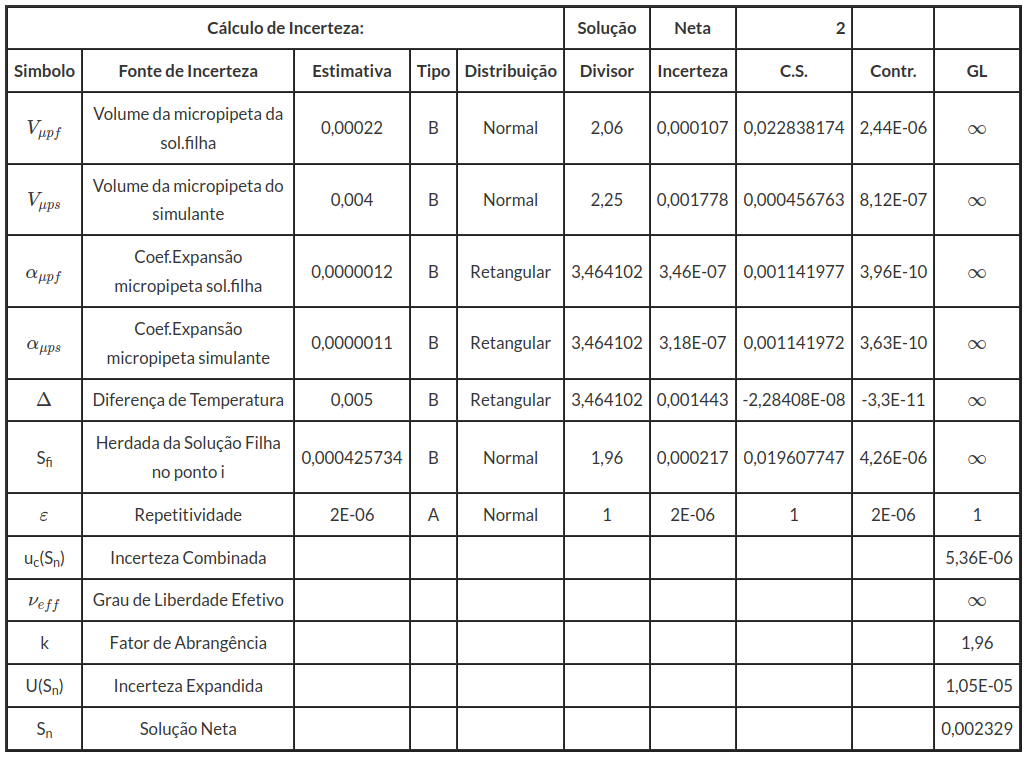
4.5.2 - Cálculo de Incerteza devido ao Cromatógrafo

Incerteza Devido a Regressão

Vamos considerar a seguinte relação linear entre intensidade e concentração:

$$Y_{ij} = \beta_0 + \beta_1~x_{i} + \varepsilon_{ij}~~~~ i =1,\cdots, n;$$

em que,

• $ Y_{ij} $: representa a i-ésima medição de intensidade referente a i-ésima Área;
• $ X_{i} $: representa a Área referente a i-ésima Concentração;
• $ \beta_0 $: representa o coeficiente linear;
• $ \beta_1 $: representa o coeficiente angular;
• $ \varepsilon_{ij} $: representa o j-ésimo erro cometido na medição da i-ésima Concentração. Consideramos que os $ \varepsilon_{ij}~\overset{i.i.d.}{\sim}~N(0,\sigma^2), $ ou seja, são independentes e identicamente distribuídos com distribuição Normal com média zero e variância $ \sigma^2. $

Pelo método dos mínimos quadrados, temos que

$$\hat{\beta_1}=\frac{S_{xy}}{S_{xx}}~~e~~\hat{\beta_0}=\overline{y}-\hat{\beta_1}\overline{x}$$

em que,

$ S_{xx} = \displaystyle\sum^n_{i=1} (x_i-\overline{x})^2 = \sum^n_{i=1} x_i^2- 2\overline{x}\sum^n_{i=1} x_i+n\overline{x}^2 = \sum^n_{i=1} x_i^2-n\overline{x}^2; $

$ S_{xy} =\displaystyle \sum^n_{i=1} (x_i-\overline{x})(y_i-\overline{y}) =\sum^n_{i=1}(x_i-\overline{x})y_i; $

$ \overline{y} = \displaystyle\frac{1}{n} \sum^n_{i=1} (y_i) $ representa a média das leituras de área;

$ \overline{x} = \displaystyle\frac{1}{n} \sum^n_{i=1} (x_i) $ representa a média das leituras de concentração.

Na prática, temos interesse em predizer o valor de Área ($ x $) dado uma observação em Concentração ($ y $). Então, dado $ y_0 $ observado, tomamos como estimativa

$$\hat{x_0} = \frac{y_0-\hat{\beta_0} }{\hat{\beta_1}}~.$$

A variância da estimativa $ \hat{x_0} $ é dada por (Veja Brown, 1993, pg. 26)

$$\widehat{Var(\hat{x_0})} = \frac{QME}{\hat{\beta_1}^2}~.$$

A tabela (4.5.2.1) apresenta os dados utilizados na regressão linear.

X	Y
Concentracao	Area
0	0
0	0
2,329493525	0,137554
2,329493525	0,129687
4,65898705	0,283453
4,65898705	0,258843
9,3179741	0,561361
9,3179741	0,514503
13,97696115	0,808883
13,97696115	0,796494
23,29493525	1,42358
23,29493525	1,41858

Tabela 4.5.2.1: Conjunto de dados para aplicação do modelo de regressão linear.

Aplicando o modelo de regressão linear (para mais detalhes acesse o conteúdo Análise de Regressão), obtemos as seguintes estimativas dos parâmetros:

$ \hat{\beta_0}=-0,013364664 $;

$ \hat{\beta_1}= 0,060596425 $;

$ \sigma $ é estimado pelo $ QME $ da seguinte forma:

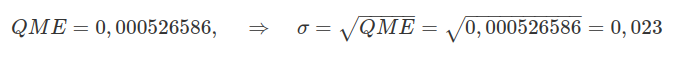
Com isso, a estimativa da incerteza, para concentração,devido a regressão é:

$$u(Reg)=\sqrt{\frac{QME}{\hat{\beta_1}^2}}=\frac{\sigma_{{resíduos}}}{\hat{\beta_1}} =\frac{0,023}{0,0606} =0,38$$

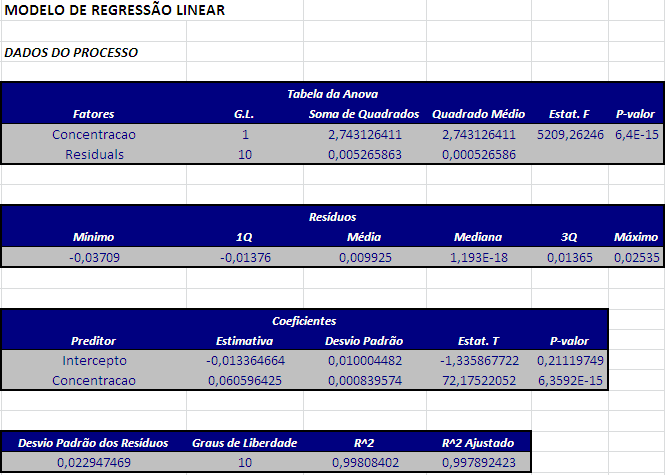
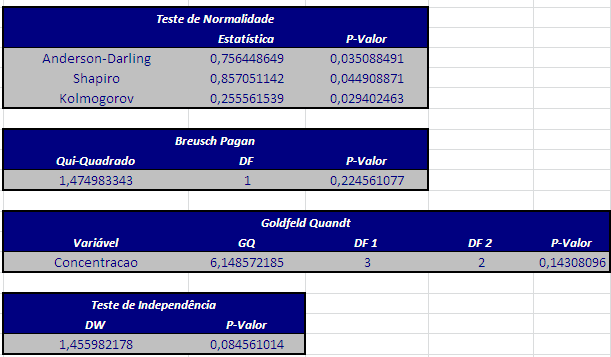
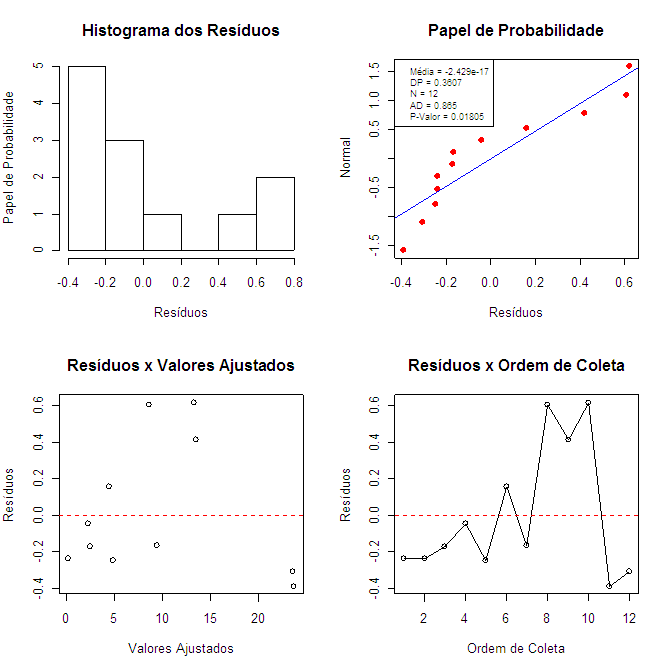
Incerteza devido ao Cromatógrafo

$ \mathbf{\checkmark} $ Equação de Medição

A expressão (4.5.2.1) representa a equação de medição utilizada para o cromatógrafo, neste caso temos:

$$Crom~=~S+Reg~~~(4.5.2.1)$$

em que,

• $ Crom $: representa o Cromatógrafo, $ mg/kg $;
• $ S $: representa a concentração da solução neta i, onde $ i~=~1,\dots,6 $, $ mg/kg $. Temos que $ S $ tem distribuição normal com incerteza $ u(S) $ e o fator de abrangência calculado no módulo Incerteza devido às soluções;
• $ Reg $: representa a incerteza devido a regressão, $ mg/kg $. Temos que $ Reg $ tem distribuição normal com incerteza $ u(Reg) $ e o fator de abrangência calculado no tópico anterior.

$ \mathbf{\checkmark} $ Incerteza Combinada ($ u_{c}(Crom) $)

A incerteza combinada para o cromatógrafo é dada por:

$$u_c^2(Crom)=\sqrt{u^2(S)+u^2(Reg)}$$

em que, $ u^2(.) $ é a contribuição de cada fonte de incerteza.

$ \mathbf{\checkmark} $Incerteza Expandida ($ U(Crom) $)

Aqui, a expressão (4.5.2.2) representa a incerteza expandida para o cromatógrafo.

$$U(Crom) = k\times u_c(Crom)~~(4.5.2.2)$$

em que $ k $ (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(Crom) $ graus de liberdade e confiança de 95%. Como neste cálculo estamos trabalhando apenas com ncertezas do tipo B, então os graus de liberdade efetivo equivale a $ \nu_{eff}(Crom)=\infty $

Para efetuar os cálculos, as informações necessárias são:

Fontes	Valor	Incerteza (U)	Fator de Abrangência (k)
Solução Neta 1	25,626	0,010508869	1,96
Desv.Pad.Resíduos	0,022947469
Coef.da Conc. (Beta1)	0,060596425
Tipo de Simulante	1

Aplicando os valores da tabela obtemos os seguintes resultados:

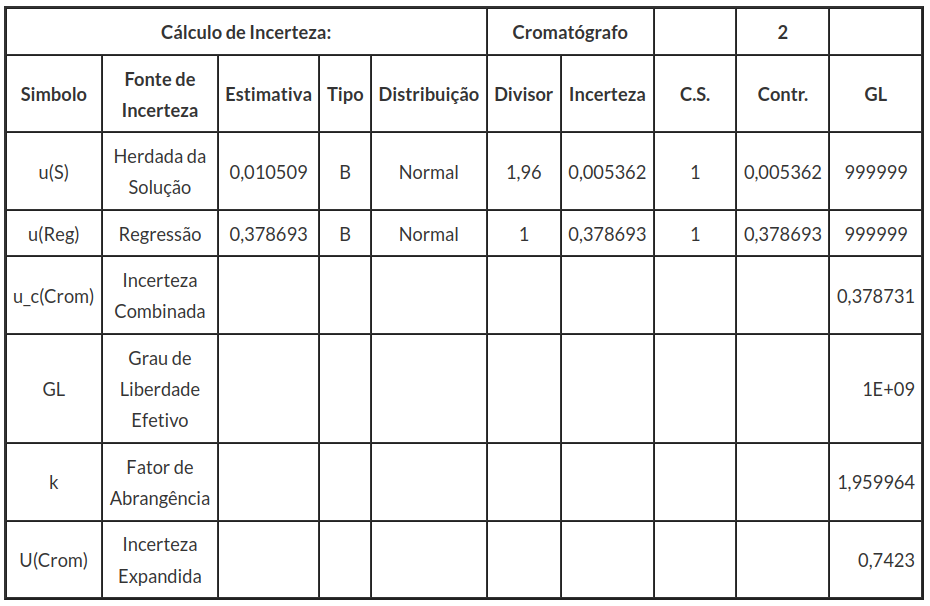
Resultado Final da incerteza devido ao cromatógrafo

Calcularemos a Incerteza Relativa ($ U_{relativa} $) para a concentração 2 os demais pontos o cálculo é análogo.

$$Conc_{2}=25,626$$

$$U_{relativa}(S_{2})=\frac{U(S_{2})}{Conc_{2}}= \frac{0,742300523}{25,626}=0,028966695$$

4.5.3 - Ensaio

$ \mathbf{\checkmark} $ Equação de Medição

A expressão (4.5.3.1) representa a equação de medição utilizada para a obtenção da solução relativa ao ensaio, neste caso temos:

$$Sol_i = \frac{A_{P}}{A_{PI}~\beta_1}-\frac{\beta_0}{\beta_1}+\varepsilon\;~~~i=1,\dots,6~~(4.5.3.1)$$

em que,

• $ Sol_i $: representa a solução i relativo ao ensaio, $ i=1,\dots,6 $, em $ mg/kg $;
• $ A_{P} $: representa a medição de área do padrão primário no Cromatógrafo(Crom). Temos que $ A_{P} $ assume distribuição normal com incerteza $ u(A_{P})=u(Crom_P) $ e fator de abrangência dado no módulo Incerteza devido ao Cromatógrafo;
• $ A_{PI} $: representa a medição de área do padrão secundário no Cromatógrafo(Crom). Temos que $ A_{PI} $ assume distribuição normal com incerteza $ u(A_{PI})=u(Crom_{PI}) $ e fator de abrangência dado no módulo Incerteza devido ao Cromatógrafo;
• $ \varepsilon $: representa a repetitividade. Podemos supor que a distribuição da média das medições tem distribuição normal. Logo, podemos estimar sua incerteza (desvio padrão da média) como:

$$u(\varepsilon) = \frac{s}{\sqrt{n}},$$

$ \mathbf{\checkmark} $ Incerteza Combinada ($ u_{c}(Sol_i) $)

A incerteza combinada para a grandeza solução relativa ao ensaio é dada por:

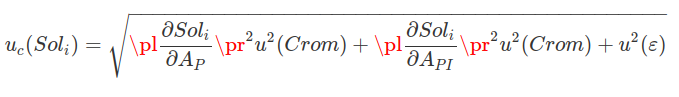
em que,

$$\left(\frac{\partial Sol_i}{\partial A_{P}}\right)=\frac{1}{A_{PI}~\beta_1}$$

$$\left(\frac{\partial Sol_i}{\partial A_{PI}}\right)=\frac{A_{P}}{A^2_{PI}~\beta_1}$$

em que, $ u_c^2(.) $ é a contribuição de cada fonte de incerteza.

$ \mathbf{\checkmark} $ Incerteza Expandida ($ U(Sol_i) $)

Aqui, a expressão (4.5.3.2) representa a incerteza expandida para o ensaio.

$$U(Sol_i)~=~k\times u_c(Sol_i)~~(4.5.3.2)$$

em que $ k $ (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(Sol_i) $ graus de liberdade e confiança de 95%.

$$\nu_{eff}(Sol_i)=\frac{u^4(Sol_i)}{\frac{u^4(A_{P})}{\infty}+\frac{u^4(A_{PI})}{\infty}+\frac{u^4(\varepsilon)}{n-1}}$$

Para efetuar os cálculos do ensaio, as informações necessárias são:

Fontes	Valor	Incerteza (U)	Fator de Abrangência (k)
Área do padrão primário	47,5558	0,90639002	1,96
Área do padrão secundário	345,724	6,589328966	1,96
Repetitividade		0,002727375	1
Coeficiente linear (Intercepto)	-0,01336
Coef. Angular	0,060596

Aplicando os valores da tabela obtemos os seguintes resultados:

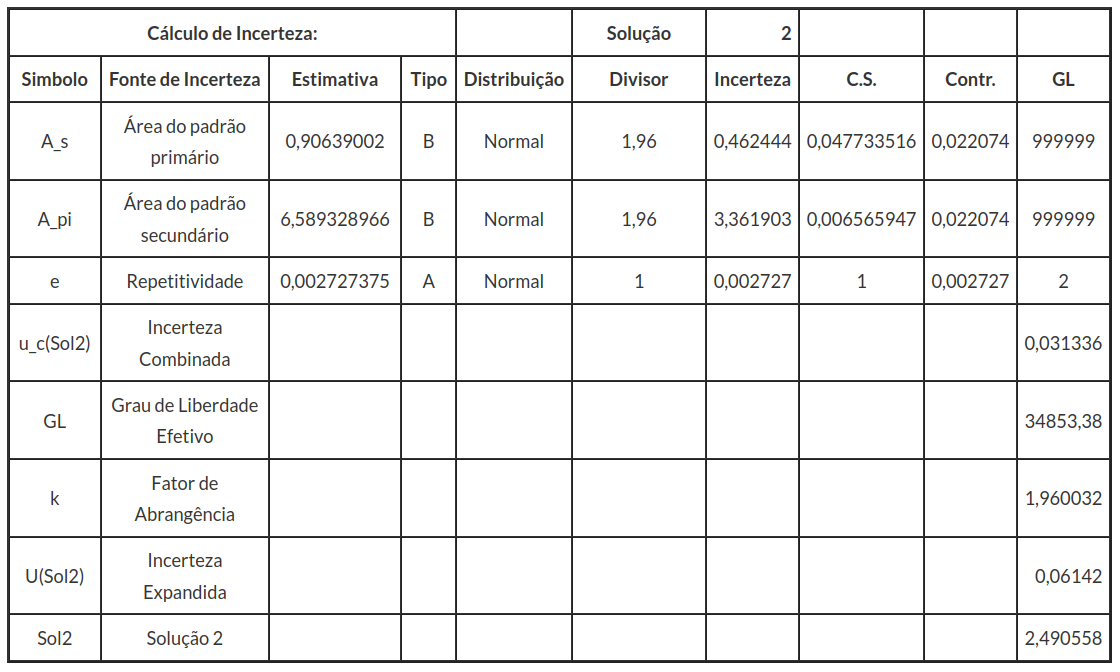
Cálculo da incerteza relativa

Seja, $ \overline{Sol_i} $ é a média das solução relativa ao ensaio, para $ i=1,\dots, 6 $. Para Concentração 2 temos:

$$U_{relativo}=\frac{U(Sol_2)}{\overline{Sol_2}}=\frac{0,061420392}{2,49518586}=0,024615558$$

Assim, o cálculo da incerteza em porcentagem:

$$U((porcentagem))=U_{relativo}\times100(porcentagem)=2,46(porcentagem)$$

4.6 - Cálculo de Incerteza para Impedância

Nesta seção, vamos aplicar o cálculo de incerteza para o ensaio de impedância, que pode ser definida como a carga resistiva total de um circuito de corrente alternada (CA). A impedância é composta à partir de dois efeitos:

1. Quando um determinado componente eletrônico cria uma resistência e gasta energia em forma de calor (Efeito Joule), chamamos este efeito de resistência;
2. Quando um determinado componente eletrônico não gasta energia em forma de calor temos a reatância.

Assim, quando estão presentes a resistência e reatância denominamos de impedância.

4.6.1 - Cálculo de incerteza para corrente elétrica

Considere um ensaio de corrente utilizando um multímetro. São realizadas 5 leituras na unidade de mili ampère (mA). Temos que, a instabilidade do multímetro é ± 0,2%.

A expressão (4.6.1.1) representa a equação de medição utilizada para a obtenção da corrente

$$I = M+ Res+Inst+\Delta\quad\text{(4.6.1.1)}$$

em que

• I: Representa a corrente elétrica;
• M: Representa a tensão no multímetro padrão do laboratório;
• Res: Resolução do multímetro;
• Inst: Instabilidade do multímetro;
• Δ: Representa a leitura do equipamento.

Incerteza Combinada ($ u_c(I) $)

A incerteza combinada para a corrente é dada por

$$u_c(I) = \sqrt{u^2(herd_{M}) + u^2(Res) + u^2(Inst) + u^2(\Delta)}.$$

Incerteza Expandida ($ U(I) $)

A expressão (4.6.1.2) representa a incerteza expandida para a corrente.

$$U(I)=k \times u_c(I)\quad \text{(4.6.1.2)}$$

em que

k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(I) $ graus de liberdade e confiança de 95%. Os graus de liberdade são dados por

$$\nu_{eff}(I) = \frac{u^4_c(I)}{u^4(\Delta)}(n-1).$$

A Tabela (4.6.2.3) apresenta as leituras para o cálculo da repetibilidade.

n	Leituras (mA)
1	500,41
2	500,32
3	501,75
4	498,06
5	496,71
Média	499,45
Desvio padrão	2,025
Repetibilidade	0,9058

Tabela 4.6.2.1: Dados para o ensaio do canal de corrente.

Os dados necessários para esta aplicação são:

A incerteza do multímetro U($herd_M$)=1% da leitura com k=2;

A resolução do multímetro res(M) = 0,1% da leitura ;

A instabilidade do multímetro inst(M) = 0,4% da leitura;

A repetitividade (%) é dada por: $ u(\Delta)=\dfrac{s}{\sqrt{n}}=\dfrac{2,025}{\sqrt{5}} = 0,9058. $

A incerteza combinada para a corrente é dada por

$$u_c(I)=\sqrt{u^2(herd_{M})+u^2(Res)+u^2(Inst)+u^2(\Delta)}=\sqrt{2,49^2+0,0144^2+0,58^2+0,9058^2}=$$

$$=2,722$$

Com isso, a incerteza expandida é dada por:

$$U(I)=k\times u_c(I)=2\times 2,722=5,5$$

em que os graus de liberdade efetivo é calculada da seguinte forma:

$$\nu_{eff}(I)=\left(\frac{u_c(I)}{u(\Delta)}\right)^4(n-1)=\left(\frac{2,722}{0,9058}\right)^4\times 4=326,27$$

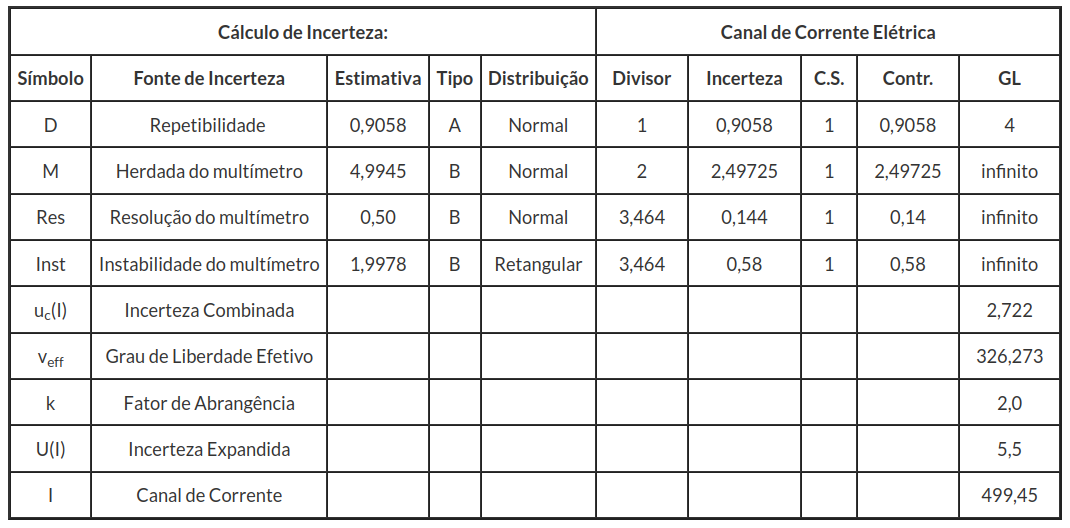
4.6.2 - Cálculo de incerteza para tensão elétrica

Considere um ensaio de corrente utilizando um multímetro. São realizadas 5 leituras na unidade de milivolt (mV). Temos que, a instabilidade do multímetro é ± 0,2%.

A expressão (4.6.2.1) representa a equação de medição utilizada para a obtenção da corrente

$$T = M+ Res+Inst+\Delta\quad\text{(4.6.2.1)}$$

em que

• T: Representa a tensão elétrica;
• M: Representa a tensão no multímetro padrão do laboratório.
• Res: Resolução do multímetro.
• Inst: Instabilidade do multímetro.
• Δ: Representa a leitura do equipamento.

Incerteza Combinada ($ u_c(T) $)

A incerteza combinada para a corrente é dada por

$$u_c(T) = \sqrt{u^2(herd_{M}) + u^2(Res) + u^2(Inst) + u^2(\Delta)}.$$

Incerteza Expandida ($ U(T) $)

A expressão (4.6.2.2) representa a incerteza expandida para a tensão elétrica.

$$U(T)=k \times u_c(T)\quad \text{(4.6.2.2)}$$

em que

k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(T) $ graus de liberdade e confiança de 95%. Os graus de liberdade são dados por

$$\nu_{eff}(T) = \frac{u^4_c(T)}{u^4(\Delta)}(n-1).$$

A Tabela (4.6.2.3) apresenta as leituras para o cálculo da repetibilidade.

n	Leituras (mV)
1	97,761
2	102,488
3	100,87
4	98,941
5	100,51
Média	100,114
Desvio padrão	1,822
Repetibilidade	0,815

Os dados necessários para esta aplicação são:

A incerteza do multímetro U($herd_M$)=1% da leitura com k=2;

A resolução do multímetro res(M) = 0,1% da leitura;

A instabilidade do multímetro inst(M) = 0,4% da leitura;

A repetitividade é dada por: $ u(\Delta)=\dfrac{s}{\sqrt{n}}=\dfrac{1,822}{\sqrt{5}}= 0,815. $

A incerteza combinada para a corrente é dada por

$$u_c(T)=\sqrt{u^2(herd_{M})+u^2(Res)+u^2(Inst)+ u^2(\Delta)}=\sqrt{0,501^2+0,0289^2+0,01155^2+0,815^2}=$$

$$=0,964$$

Com isso, a incerteza expandida é dada por:

$$U(I)=k\times u_c(I)=2,4\times 0,964=2,31$$

em que os graus de liberdade efetivo é calculada da seguinte forma:

$$\nu_{eff}(T)=\left(\frac{u_c(T)}{u(\Delta)}\right)^4(n-1)=\left(\frac{0,964}{0,815}\right)^4\times 4=7,82$$

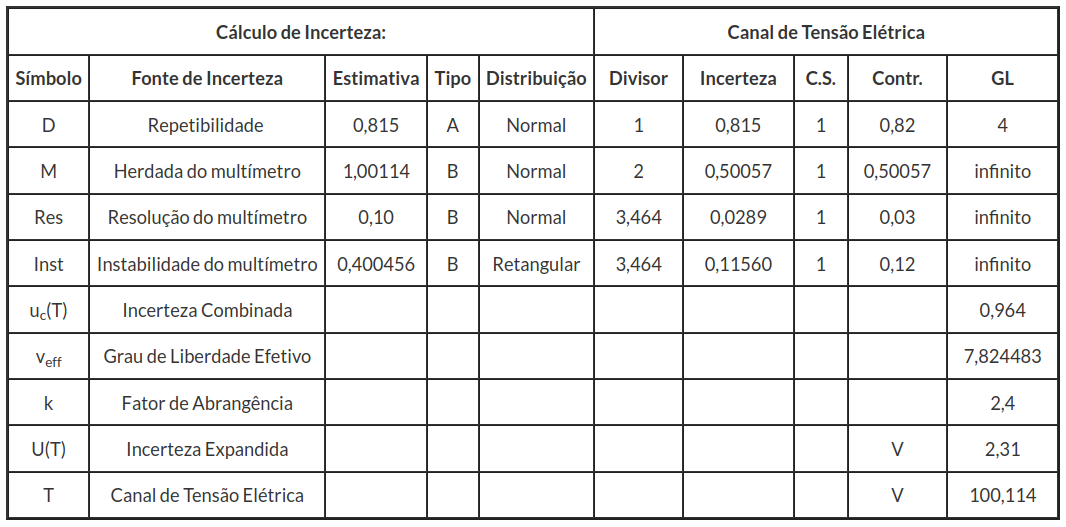
4.6.3 - Cálculo de Incerteza no Ensaio de Impedância

Considere um ensaio de impedância utilizando os dados das seções 4.6.1 (corrente elétrica) e 4.6.2 (tensão elétrica).

Equação de Medição

A expressão (4.6.3.1) representa a equação de medição utilizada para a obtenção da impedância

$$R = \frac{V}{I}\quad (4.6.3.1)$$

em que

• R: Representa a impedância;
• V: Representa a medição de tensão;
• I: Representa a medição de corrente.

Incerteza Combinada (uc(R))

A incerteza combinada para a impedância é dada por

$$u_c(R)=\sqrt{\left(\frac{\partial R}{\partial V}\right)^2 u^2(V)+\left(\frac{\partial R}{\partial I}\right)^2 u^2(I)}$$

$$=\sqrt{\left(\frac{1}{I}\right)^2 u^2(V) +\left(-\frac{V}{I^2}\right)^2 u^2(I)}.$$

Incerteza Expandida (U(R))

A expressão (4.6.3.2) representa a incerteza expandida para a impedância.

$$U(R) = k \times u_c(R)\quad (4.6.3.2)$$

em que k (fator de abrangência) é o quantil da distribuição t-Student com $ \nu_{eff}(R) $ graus de liberdade e confiança de 95%.

A Tabela (4.6.3.3) apresenta o resumo para o cálculo da incerteza da impedância.

n	Leituras (mV)	Leituras (mA)	Impedância
1	97,761	500,41	0,195
2	102,488	500,32	0,205
3	100,87	501,75	0,201
4	98,941	498,06	0,199
5	100,51	496,71	0,202
Média	100,114	499,45	0,200
Desvio padrão	1,822	2,0254	0,00362
Repetibilidade	0,815	0,9058	0,00162

Os dados necessários para esta aplicação são:

A incerteza herdada da tensão $ U(V) = 2,341 $ V com $ k=2,429 $;

A incerteza herdada da corrente $ U(I) = 0,0055 $ A com $ k=2 $;

A incerteza combinada para a impedância é dada por

$$u_c(R)=\sqrt{\left(\frac{1}{I}\right)^2 u^2(V) +\left(-\frac{V}{I^2}\right)^2 u^2(I)}=$$

$$=\sqrt{\left(\frac{1}{0,499}\right)^2 0,964^2+\left(-\frac{100,1}{0,499^2}\right)^2 0,0055^2}=$$

$$2,218~$$

Considerando os graus de liberdade efetivo e uma confiança de aproximadamente 95%, temos pela tabela da distribuição t-Student que o fator de abrangência é k=2. Com isso, a incerteza expandida para a variável impedância é dada por

$$U=k\times u_c(R)=2\times 2,218=4,44~\Omega$$

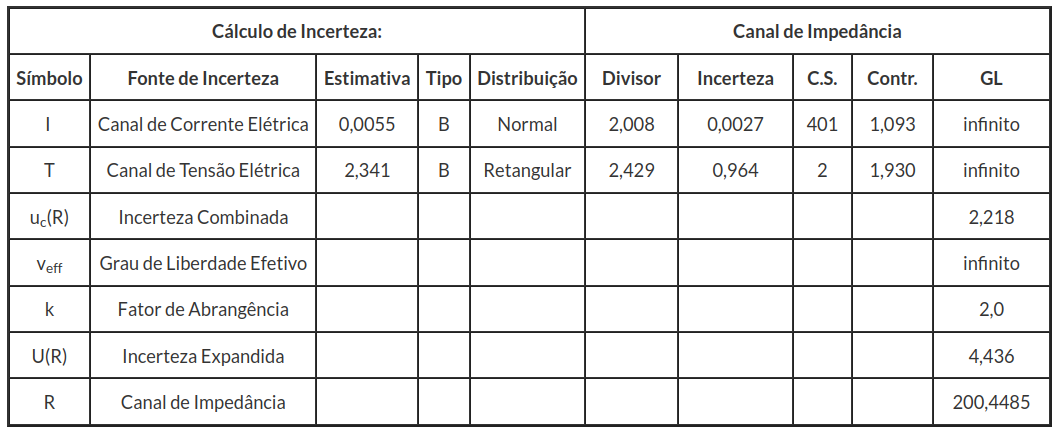
4.7- Ensaio de Medição de Área Superficial Especifica

Descrição do Ensaio

Nessa seção descrevemos os ensaios da Área Superficial Especifica. A seguir, apresentamos um fluxograma do cálculo de incerteza.

(imagem em falta)

4.7.1 - Massa (Balança)

Massa (Balança)

Esta seção é dedicada ao cálculo de incerteza da massa, que leva em conta apenas as incertezas da balança e da resolução da balança . A expressão (4.7.1.1) apresenta a equação de medição da massa (balança)

$$M_{B} = B + \text{Res}_B \quad \text{(4.7.1.1)}$$

em que

• $M_B$: representa a massa (Balança), em $ (g); $
• $B$: representa a balança em $ (g). $ Temos que $ B $ tem distribuição normal com incerteza $ u(B) $ e fator de abrangência dado pelo certificado de calibração da balança;
• $Res_B$: representa a resolução da balança em $ (g). $ Temos que $ u(Res_B) $ tem distribuição retangular (ou uniforme) no intervalo $ \left(-\frac{{Res_B}}{2},\frac{{Res_B}}{2}\right). $ Logo a incerteza devido à resolução será dada por:

$$u(Res_{B})=\frac{{Res}_{B}}{2\sqrt{3}}$$

Incerteza combinada ($ u_c(M_B) $):

A incerteza combinada da massa é dada pela expressão (4.7.1.2)

$$u_c(M_B)=\sqrt{u^2(B)+u^2(\text{Res}_B)} \quad \text{(4.7.1.2)}.$$

Incerteza Expandida ($ U(M_B) $):

A incerteza expandida da massa é dada pela expressão (4.7.1.3)

$$U(M_B) =u_c(M_B)\times k \quad \text{(4.7.1.3)}$$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de aproximadamente 95,45%. Como não temos incerteza do tipo A, adotamos $ k=2. $

Aplicação:

A seguir, vamos calcular a incerteza da massa (balança), para isto necessitamos dos dados da tabela apresentada a seguir:

Fontes	Incerteza (U)	Fator de Abrangência (k)
Balança	0,0002	2
Resolução da Balança	0,0001	2

A incerteza combinada da massa é dada por

$$u_c(M_B)=\sqrt{u^2(B)+u^2(\text{Res}_B)}=\sqrt{0,0001^2+(2,88675\times 10^{-5})^2}=0,000104083.$$

A incerteza expandida da massa é dada por

$$U(M_B) =u_c(M_B)\times k=0,000104083\times 2=0,000208167$$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de aproximadamente 95,45%. Como não temos incerteza do tipo A, adotamos $ k=2. $

A seguir, apresentamos um resumo dos resultados.

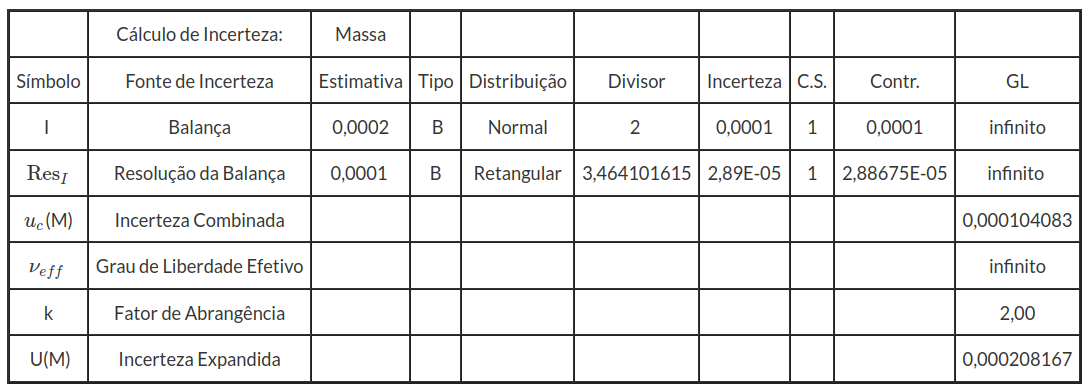
4.7.2 - Massa da amostra desgaseificada

Massa da amostra desgaseificada

Esta seção é dedicada ao cálculo de incerteza da massa da amostra desgaseificada. A amostra seca é obtida quando passamos a amostra pelo Vac Prep por 40 minutos a 200ºC, após este tempo esperamos a amostra esfriar. A seguir apresentamos a equação de medição.

Equação de Medição:

A expressão (4.7.2.1) representa a equação de medição utilizada da massa da amostra desgaseificada, neste caso temos:

$$M_{A} = M_D- M_T+ \varepsilon \quad \text{(4.7.2.1)} $$

em que

• $M_A$: representa a massa da amostra, em $ (g); $
• $M_T, M_D$ representam as massas do tubo e do tubo mais a amostra desgaseificada, em $ (g). $ Temos que $ M_T $ e $ M_D $ têm distribuição normal com incerteza $ u(M_B) $ e fator de abrangência k obtido na seção (4.7.1);
• $ \varepsilon $: representa a repetitividade. Podemos supor que a distribuição da média das medições tem distribuição normal. Logo, podemos estimar sua incerteza (desvio padrão da média) como:

$$u(\epsilon) = \frac{s}{\sqrt{n}},$$

em que

$$s^2 = \frac{1}{n-1} \sum^{n}_{i=1} (x_i -\overline{X})^2$$

é a variância amostral e

$$\overline{X} = \frac{1}{n} \sum^{n_{i=1}} x_i$$

é a média amostral.

Incerteza Combinada:

A incerteza combinada da massa da amostra é dada pela expressão (4.7.2.2)

$$u_c(M_A)=\sqrt{u^2(M_D)+u^2(M_T)+u^2(\varepsilon)} \quad \text{(4.7.2.2)}$$

Incerteza Expandida:

A incerteza expandida da massa da amostra é apresentada na expressão (4.7.2.3)

$$U(M_A) =u_c(M_A)\times k \quad \text{(4.7.2.3)}$$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de aproximadamente 95%.

$$\nu_{eff}(M_A)=\frac{u^4(M_A)}{u^4(\varepsilon)}(n-1) $$

Aplicação:

A seguir, vamos calcular a incerteza da massa da amostra desgaseificada, para isto necessitamos dos dados da tabela a seguir:

Fontes	Valor	Incerteza (U)	Fator de Abrangência (k)
Massa (Tara)	16,42	0,000208167	2,00
Massa desgaseificada	17,10	0,000208167	2,00
Repetitividade		0	1

A incerteza combinada da massa da amostra é dada por

$$u_c(M_A)=\sqrt{u^2(M_D)+u^2(M_T)+u^2(\varepsilon)}=\sqrt{0,000104083^2+0,000104083^2+0^2}= 0,000147196.$$

A incerteza expandida da massa da amostra é dada por

$$U(M_A) =u_c(M_A)\times k=0,000147196\times 2=0,000294392$$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de aproximadamente 95%. Como a repetibilidade é zero, temos que $ \nu_{eff}=\infty, $ consequentemente temos $ k=2. $ Para calcularmos a massa da amostra desgaseificada, basta aplicarmos a equação (4.7.2.1)

$$M_{A} = M_D- M_T=17,1006-16,43=0,6696$$

A seguir, apresentamos um resumo dos resultados.

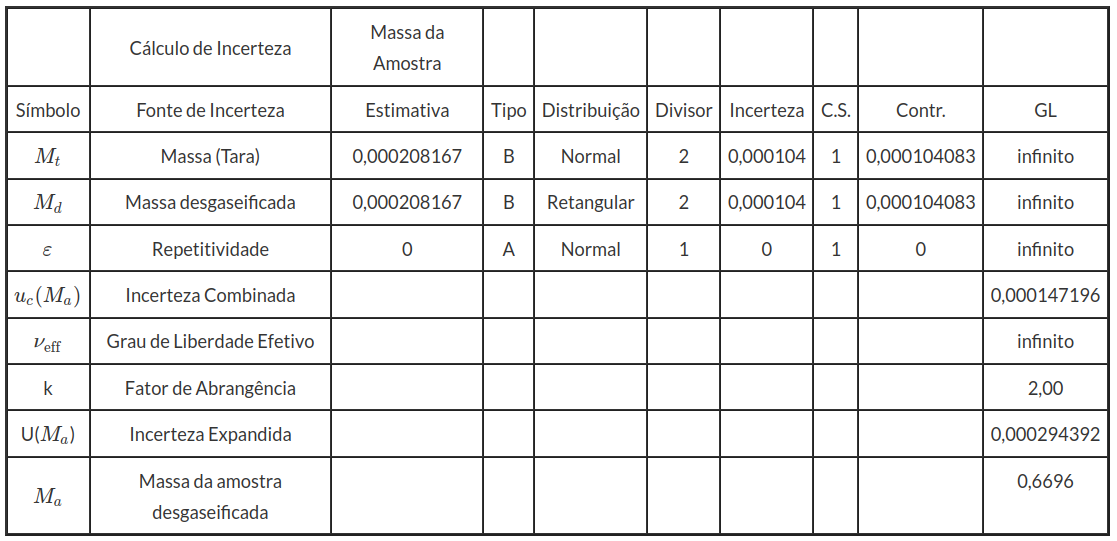
4.7.3 - Incerteza devido à regressão

Incerteza devido à regressão

Vamos considerar a seguinte relação linear entre $ 1/[Q(P_0/P-1)] $ e pressão relativa:

$$Y_{ij} = \beta_0 + \beta_1~x_{i} + \varepsilon_{ij}~~~~ i =1,\cdots, n;$$

em que,

• $ Y_{ij} $: representa a i-ésima medição de $ 1/[Q(P_0/P-1)] $ referente a i-ésima pressão relativa;
• $ X_{i} $: representa a pressão relativa referente a i-ésima $ 1/[Q(P_0/P-1)] $;
• $ \beta_0 $: representa o coeficiente linear;
• $ \beta_1 $: representa o coeficiente angular;
• $ \varepsilon_{ij} $: representa o j-ésimo erro cometido na medição da i-ésima $ 1/[Q(P_0/P-1)] $. Consideramos que os $ \varepsilon_{ij} $ são independentes e identicamente distribuídos com distribuição normal com média zero e variância $ \sigma^2, $ ou seja, $ \varepsilon_{ij}\overset{i.i.d.}{\sim}N(0,\sigma^2) $ .

Pelo método dos mínimos quadrados, obtemos que

$$\widehat{\beta_1}=\frac{S_{xy}}{S_{xx}}\quad \text{e} \quad \widehat{\beta}_0=\overline{y}-\widehat{\beta_1}\overline{x}$$

em que,

• $ S_{xx} = \displaystyle\sum_{i=1}^{n} (x_i-\overline{x})^2 = \sum_{i=1}^{n}x_i^2- 2\overline{x}\sum_{i=1}^{n} x_i+n\overline{x}^2 = \sum_{i=1}^{n} x_i^2-n\overline{x}^2; $
• $ S_{xy} = \displaystyle\sum_{i=1}^{n}(x_i-\overline{x})(y_i-\overline{y}) =\sum_{i=1}^{n}(x_i-\overline{x})y_i; $
• $ \overline{y} = \frac{1}{n}\displaystyle \sum_{i=1}^{n}(y_i) $ representa a média das leituras de área;
• $ \overline{x} = \frac{1}{n}\displaystyle \sum_{i=1}^{n}(x_i) $ representa a média das leituras de concentração.

Agora vamos deduzir a incerteza devido ao volume de gás adsorvido quando a superfície do sólido está completamente coberta por uma monocamada ($ Q_m $). Para isto, à partir da equação da reta obtemos:

$$Y= \beta_0+\beta_1 X_i$$

$$\dfrac{1}{Q(P_0/P-1)} = \beta_0+\beta_1 \dfrac{P}{P_0} \quad \text{(4.7.3.1)}$$

$$\dfrac{1}{Q(P_0/P-1)} = \dfrac{1}{Q_m\times C}+\dfrac{C-1}{Q_m\times C} \dfrac{P}{P_0} \quad \text {(4.7.3.2)}$$

Relacionando (4.7.3.1) e (4.7.3.2) obtemos que

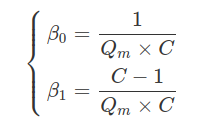
além disso,

$$\quad Q_m=\dfrac{1}{\beta_0+\beta_1}$$

Agora, vamos utilizar o método delta para calcularmos a variabilidade de $ Q_m $ (para mais detalhes consulte Incerteza devido a curva de calibração: Método Delta). Temos que:

$$\text{Var}(Q_m) \approx \left(\dfrac{\partial Q_m}{\partial \beta_0}\right)^2 \text{Var}(\widehat{\beta}_0)+\left(\dfrac{\partial Q_m}{\partial \beta_1}\right)^2 \text{Var}(\widehat{\beta}_1) + 2\left( \dfrac{\partial Q_m}{\partial \beta_0} \dfrac{\partial Q_m}{\partial \beta_1}\right)\text{Cov}(\widehat{\beta}_0, \widehat{\beta}_1)=$$

$$ \approx \left(-\dfrac{1}{(\widehat{\beta}_0+\widehat{\beta}_1)^2}\right)^2 \text{Var}(\widehat{\beta}_0)+\left(-\dfrac{1}{(\widehat{\beta}_0+\widehat{\beta}_1)^2}\right)^2 \text{Var}(\widehat{\beta}_1)+2\left(-\dfrac{1}{(\widehat{\beta}_0+\widehat{\beta}_1)^2}\right)^2\text{Cov}(\widehat{\beta}_0, \widehat{\beta}_1)=$$

$$ \approx \left(-\dfrac{1}{(\widehat{\beta}_0+\widehat{\beta}_1)^2}\right)^2 [\text{Var}(\widehat{\beta}_0)+\text{Var}(\widehat{\beta}_1)+2\text{Cov}(\widehat{\beta}_0, \widehat{\beta}_1)]$$

Portanto, a incerteza devido ao volume de gás adsorvido quando a superfície do sólido está completamente coberta por uma monocamada ($ Q_m $) é dada por:

$$u(Q_m)=\sqrt{\left(-\dfrac{1}{(\widehat{\beta}_0+\widehat{\beta}_1)^2}\right)^2 [u^2(\widehat{\beta}_0)+u^2(\widehat{\beta}_1) +2\text{Cov}(\widehat{\beta}_0, \widehat{\beta}_1)} ]\quad \text{e} \quad Q_m=\dfrac{1}{(\widehat{\beta}_0+\widehat{\beta}_1)}$$

Aplicação

A seguir, segue os dados utilizados na regressão linear. Vale lembrar que a variável resposta $ Y=1/Q(P_0/P-1) $ e variável explicativa é $ X=P/P_0. $ Com isso, obtemos os dados para a curva de calibração.

$ \bf X $	$ \bf Y $
0,050500102	0,008679
0,087812073	0,014308
0,125881379	0,019918
0,162958319	0,025366
0,201177794	0,031032

A seguir, apresentamos os resultados obtidos pelo software Action.

(imagem em falta)

(imagem em falta)

Além disso, utilizando o software Action, obtemos que $ \text{Cov}(\widehat{\beta}_0, \widehat{\beta}_1)=-1,89784e^{-08} $, neste caso, consideraremos a covariância entre os parâmetros sendo nula.

Fontes	Valor	Incerteza (U)	Fator de Abrangência (k)
Intercepto	0,001248178	5,30388E-05	1
Coeficiente Angular	0,148110327	0,000388617	1

Portanto, a incerteza devido ao volume de gás adsorvido quando a superfície do sólido está completamente coberta por uma monocamada ($ Q_m $) é dada por:

$$u(Q_m)=\sqrt{ \left(-\dfrac{1}{(\widehat{\beta}_0+\widehat{\beta}_1)^2}\right)^2 [u^2(\widehat{\beta}_0)+u^2(\widehat{\beta}_1)]}=$$

$$= \sqrt{\left(-\dfrac{1}{(0,001248178 + 0,148110327)^2}\right)^2 [(5,3\times 10^{-5})^2+(0,000388617)^2]}=$$

$$=0,017582036$$

e

$$Q_m=\dfrac{1}{(\widehat{\beta}_0+\widehat{\beta}_1)}=\dfrac{1}{(0,001248178 + 0,148110327)}=6,6953$$

A seguir, apresentamos um resumo dos resultados.

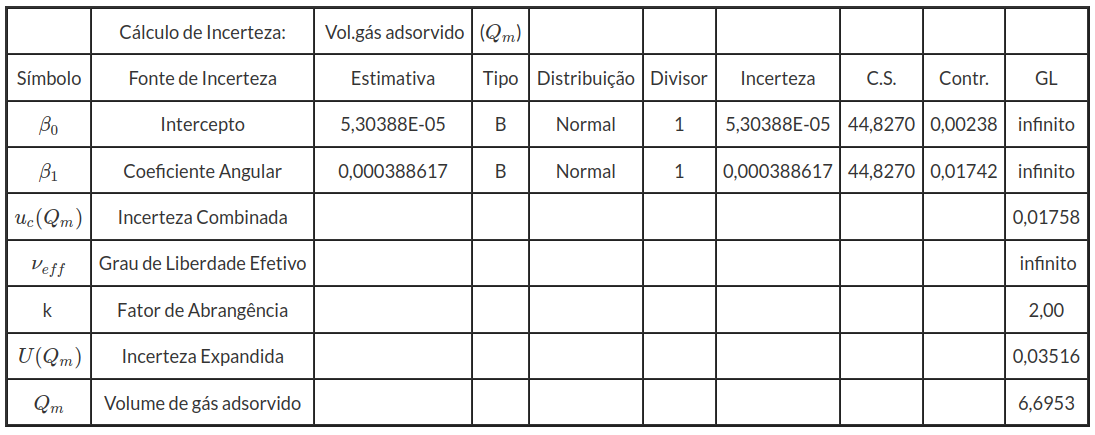
4.7.4 - Área superficial específica

Área Superficial Específica

Esta seção é dedicada ao cálculo de incerteza para Área Superficial Especifica. A seguir apresentamos a equação de medição.

Equação de Medição

A expressão (4.7.4.1) representa a equação de medição utilizada para Área Superficial Especifica, neste caso temos:

$$S_{\text{SE}}= \dfrac{Q_m\times L_{av}\times A_{ad}}{M_v} \quad \text{(4.7.4.1)}$$

em que

• $ S_{SE} $ representa a área superficial específica, em $ (m^2/g); $
• $ Q_m $ representa o volume de gás adsorvido quando a superfície do sólido está completamente coberta por uma mono camada, em $ (cm^3/g). $ Temos que $ Q_m $ tem distribuição normal com incerteza $ u(Q_m) $ obtido na seção (4.7.3);
• $ L_{av} $ representa o número de Avogadro, cujo valor desta constante é de 6,022$ \times 10^{23}. $ Temos que $ L_{av} $ é uma constante e consequentemente não possui incerteza associada;
• $ A_{ad} $ representa a área de seção transversal da uma molécula de adsorbato, cujo valor desta constante é de 0,162$ \times 10^{-18}m^2. $ Temos que $ A_{ad} $ é uma constante e consequentemente não possui incerteza associada;
• $ M_v $ representa o volume ocupado por 1 mol da molécula de adsorbato, cujo valor desta constante é de 2,2414$ \times 10^{4}cm^3. $ Temos que $ M_{v} $ é uma constante e consequentemente não possui incerteza associada;

Incerteza Combinada

A incerteza combinada do ensaio de Determinação da Área Superficial Especifica é dada pela expressão (4.7.4.2)

$$u_c(S_{SE})=\sqrt{\left(\dfrac{\partial S_{SE}}{\partial Q_m}\right)^2 u^2(Q_m)} \quad \text{(4.7.4.2)}$$

em que

$$\left(\dfrac{\partial S_{SE}}{\partial Q_m}\right)=\dfrac{L_{av}\times A_{ad}}{M_v}$$

Incerteza Expandida

A incerteza expandida é dada pela expressão (4.7.4.3)

$$U(S_{SE}) =u_c(S_{SE})\times k \quad \text{(4.7.4.3)}$$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de 95(porcentagem). Como não temos incerteza do tipo A, adotamos $ k=2. $

Aplicação

A seguir, vamos calcular a incerteza para Área Superficial Especifica. Vale lembrar que da seção (\ref{Regre}) obtemos a incerteza do volume do gás adsorvido. Afim de calcular a incerteza devido a área superficial específica, necessitamos das constantes dadas na tabela.

Fontes	Valor	Incerteza (U)	Fator de Abrangência (k)
Volume de gás adsorvido	6,695300041	0,035164071	2,00
Número de Avogadro	6,022$ \times 10^{23} $
Área da seção transversal	1,62$ \times 10^{-19} $
Vol. de 1 mol	22414

Incerteza Combinada

A incerteza combinada para Área Superficial Especifica é dada por

$$u_c(S_{SE})=\sqrt{\left(\dfrac{\partial S_{SE}}{\partial Q_m}\right)^2 u^2(Q_m)}=$$

$$=\sqrt{\left(4,352476131\right)^2 0,017582036^2}=$$

$$= 0,07652539$$

em que

$$\left(\dfrac{\partial S_{SE}}{\partial Q_m}\right)=\dfrac{L_{av}\times A_{ad}}{M_v}=\dfrac{6,022\times 10^{23}\times 1,62\times 10^{-19}}{22414} =4,352476131$$

Incerteza Expandida

A incerteza expandida é dada por

$$U(S_{SE}) =u_c(S_{SE})\times k=0,07652539 \times 2=0,15~m^2/g$$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de 95(porcentagem). Como não temos incerteza do tipo A, adotamos $ k=2. $

Já a área superficial específica é dada por:

$$S_{\text{SE}}= \dfrac{Q_m\times L_{av}\times A_{ad}}{M_v} =\dfrac{6,695300041 \times 6,022\times 10^{23}\times 1,62\times 10^{-19}}{22414} =29,14$$

A seguir, apresentamos um resumo dos resultados.

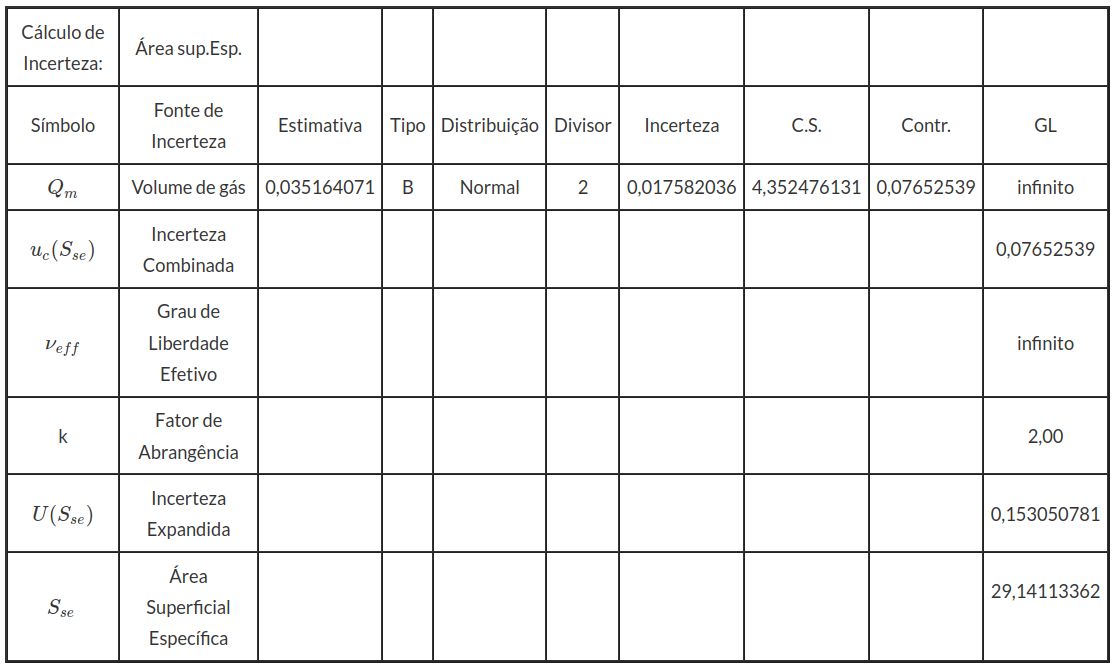
4.7.5 - Ensaio de Repetibilidade e Reprodutibilidade (R&R)

Ensaio de Repetibilidade e Reprodutibilidade (R&R):

Nesta seção, descrevemos o estudo da Repetitividade e Reprodutibilidade para o ensaio de determinação da área superficial específica. Neste estudo, selecionamos 2 operadores, 3 peças e medimos 6 vezes cada peça. A tabela a seguir corresponde ao planejamento do estudo.

Peça	Analista	Resultado
2	1	53,96
3	2	125,95
3	1	127,19
2	1	53,19
2	2	52,93
1	2	29,66
3	1	126,19
3	1	126,78
1	2	29,65
1	1	29,64
2	1	53,75
3	2	126,24
3	2	126
2	2	52,69
1	1	30,09
1	1	29,83
2	2	52,84
1	2	29,35

A seguir, apresentamos os resultados para o ensaio de determinação de área superficial específica.

	ANOVA
	G.L.	Soma dos quadrados	Quadrados Médios	Estatística F	Pr(>F)
Peças	2	30578,17781	15289,08891	224015,9547	2,9083E-32
Operadores	1	1,94045	1,94045	28,43150183	0,000105824
Repetitividade	14	0,9555	0,06825

	VARIAÇÃO TOTAL E/OU TOLERÂNCIA
	Desvio padrão ($ m^2/g $)	Tolerância (%)
Repetitividade	0,261	9,80
Reprodutibilidade	0,456	17,10
Operadores	0,456	17,10
Peças	50,479	1892,98
Repetitividade e reprodutibilidade	0,526	19,71
Total	50,482	1893,08

À partir dos resultados obtidos, temos que a estimativa da incerteza devido a repetitividade e reprodutibilidade é $ u(RR)=0,526~m^2/g. $ Para mais detalhes veja MSA 4º edição.

(imagem em falta)

4.7.6 - Ensaio de Determinação da Área Superficial Específica

Ensaio de Determinação da Área Superficial Específica

Esta seção é dedicada ao cálculo de incerteza para o ensaio de Determinação da Área Superficial Especifica. A seguir apresentamos a equação de medição.

Equação de Medição

A expressão (4.7.6.1) representa a equação de medição utilizada para o ensaio de Determinação da Área Superficial Especifica, neste caso temos:

$$S_{\text{BET}}=S_{\text{SE}}+\text{Pad}+RR \quad \text{(4.7.6.1)}$$

em que

• $ S_{BET} $ representa a determinação da área superficial específica (BET), em $ (m^2/g); $
• $ S_{SE} $ representa a área superficial específica, em $ (m^2/g). $ Temos que $ S_{\text{SE}} $ tem distribuição normal com incerteza $ u(S_{\text{SE}}) $ obtido na seção (4.7.4);
• Pad: representa o certificado do padrão, em $ (m^2/g). $ Temos que Pad tem distribuição normal com incerteza $ u(\text{Pad}) $ obtido na via certificado do padrão;
• $ RR $: representa a repetitividade e reprodutibilidade em (N): Temos que RR tem distribuição normal com incerteza $ u(RR) $ obtidos no ensaio de RR (seção 4.7.5);

Incerteza Combinada

A incerteza combinada do ensaio de Determinação da Área Superficial Especifica é dada pela expressão (4.7.6.2)

$$u_c(S_{\text{BET}})=\sqrt{u^2(S_{\text{SE}})+u^2(\text{Pad})+u^2(RR)} \quad \text{(4.7.6.2)}$$

Incerteza Expandida

A incerteza expandida é dada pela expressão (4.7.6.3)

$$U(S_{\text{BET}}) =u_c(S_{\text{BET}})\times k \quad \text{(4.7.6.3)}$$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de 95%. Como não temos incerteza do tipo A, adotamos $ k=2. $

Aplicação

A seguir, vamos calcular a incerteza para o Ensaio da Área Superficial Especifica. A seguir apresentamos os dados para calcularmos a incerteza.

Fontes	Valor	Incerteza (U)	Fator de Abrangência (k)
Área Superficial Específica	29,14	0,07652539	1
Certificado do padrão		0,75	2
Repetitividade e Reprodutibilidade		0,525616041	1

A incerteza combinada do ensaio de Determinação da Área Superficial Especifica é dada por

$$u_c(S_{\text{BET}})=\sqrt{u^2(S_{\text{SE}})+u^2(\text{Pad})+u^2(RR)}=$$

$$=\sqrt{0,07652539^2+0,375^2+0,525616041^2}=$$

$$= 0,650194862$$

A incerteza expandida é dada por

$$U(S_{\text{BET}}) =u_c(S_{\text{BET}})\times k= 0,650194862\times 2=1,3 $$

em que $ k $ é o fator de abrangência e este é obtido à partir da distribuição t-Student com $ \nu_{eff} $ graus de liberdade e nível de confiança de 95%. Como não temos incerteza do tipo A, adotamos $ k=2. $

A seguir, apresentamos um resumo dos resultados do ensaio de determinação de área superficial específica.

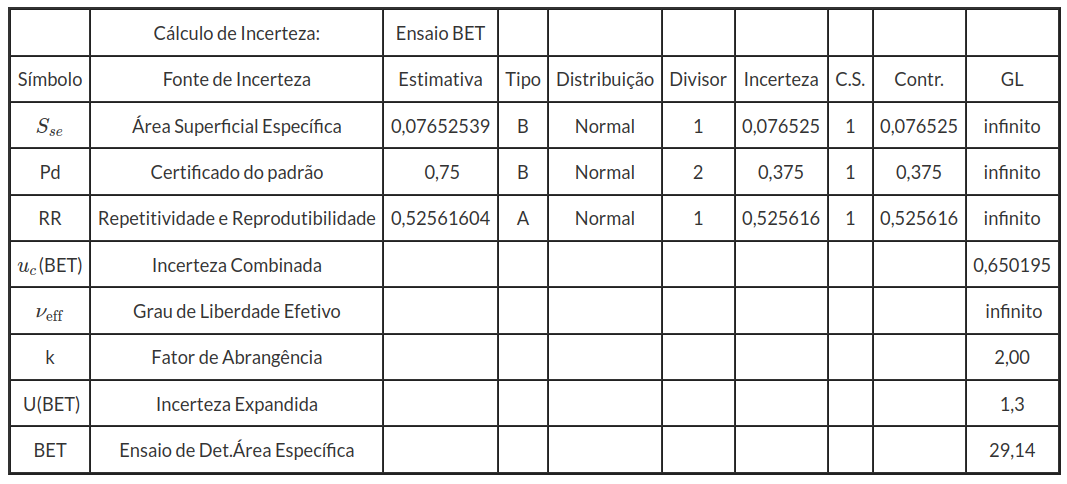
5 - Parâmetros Característicos de um Sistema de Medição

Para caracterizar o comportamento metrológico de um sistema de medição, são empregados alguns parâmetros metrológicos. Estes parâmetros podem ser expressos na forma de um simples número, uma faixa de valores ou na forma de um gráfico. Aqui, são descritos os principais parâmetros.

Faixa nominal

Faixa Nominal ou Intervalo Nominal é o conjunto de valores compreendidos entre duas indicações extremas arredondadas ou aproximadas, obtido com um posicionamento particular dos comandos de um instrumento de medição ou sistema de medição, utilizado para designar este posicionamento. Um intervalo nominal de indicações é geralmente expresso em termos de seu menor e maior valor.

Exemplos:

• Termômetro: 100ºC a 200ºC;
• Manômetro: 0 bar a 20 bar;
• Contador: 5 dígitos (isto é 99999 pulsos).

Quando o limite inferior é zero, a faixa nominal pode ser definida unicamente em termos do limite superior.

Exemplo:

A faixa nominal de 0V a 100V é expressa como “100V”.

Amplitude da faixa nominal

A amplitude da faixa nominal é a diferença, em módulo, entre os dois limites de uma faixa nominal de -10V a +10V a amplitude da faixa nominal é 20V. Em algumas áreas, a diferença entre o maior e o menor valor é denominado faixa.

Faixa de medição

A faixa de medição, também denominada faixa de trabalho, é o conjunto de valores de um mensurando para o qual admitimos que o erro de um instrumento de medição é mantido dentro dos limites especificados.

Exemplo:

Num relógio apalpador a faixa de medição é de $ -~50\mu m $ a $ +50\mu m $.

A faixa de medição é menor ou, no máximo, igual a faixa nominal. O valor da faixa de medição pode ser obtidas através:

• Do manual de operação do sistema de medição (SM);
• De sinais gravados sobre a escala;
• Das especificações de normas técnicas;
• Dos relatórios de calibração.

Divisão de escala

É a parte de uma escala compreendida entre duas marcas sucessivas quaisquer.

Comprimento de uma divisão

É a distância entre duas marcas sucessivas quaisquer, medidas ao longo da linha do comprimento de escala. O comprimento de uma divisão é expresso em unidades de comprimento, qualquer que seja a unidade mensurada ou a unidade marcada sobre a escala.

Valor de uma divisão

O valor de uma divisão é a diferença entre os valores de escala correspondentes a duas marcas sucessivas.

Condições estipulada de funcionamento

Condição de funcionamento que deve ser cumprida durante uma medição para que um instrumento de medição ou um sistema de medição funcione como projetado. Elas especificam os intervalos de valores para a grandeza medida e para as grandezas de influência.

Condições limite de funcionamento

Condição extrema de funcionamento que um instrumento de medição ou sistema de medição deve suportar sem dano e sem degradação das suas propriedades metrológicas especificadas quando, subsequentemente, é operado nas suas condições estipuladas de funcionamento. Esta condição podem diferir para armazenamento, transporte e funcionamento. Elas também podem compreender valores limites para a grandeza medida e para as grandezas de influência.

Condições de funcionamento de referência

As condições de referência são as condições usuais prescritas para ensaio de desempenho de um instrumento de medição ou de um sistema de medição ou para inter comparação de resultados de medições. Estas condições geralmente incluem os valores de referência ou as faixas de referência para as grandezas de influência que afetam o instrumento de medição. Estas também especificam os intervalos de valores do mensurando e das grandezas de influência. Na IEC 60050-300, item 311-06-02, o termo “reference condition” refere-se a uma condição de funcionamento na qual a incerteza de medição instrumental especificada é a menor possível.

Característico de resposta

É a relação entre um estímulo e a resposta correspondente, sob condições definidas.

Exemplo:

A força elemotriz (fem) de um termopar como função da temperatura. A relação poderá ser expressa na forma de uma equação matemática, uma tabela numérica ou um gráfico.

Sensibilidade

A sensibilidade é caracterizada pelo quociente entre a variação duma indicação dum sistema de medição e a variação correspondente do valor da grandeza medida. Nos instrumentos com indicador de ponteiro comumente se estabelece a sensibilidade como sendo a relação entre o deslocamento da extremidade do ponteiro em (mm) e o valor unitário da grandeza a medir.

Limiar de mobilidade

É a maior variação no estimulo (valor de uma grandeza medida) que não produz variação detectável na resposta de um instrumento de medição, sendo a variação no sinal de entrada lenta e uniforme. O limiar de mobilidade (também chamado threshold) pode depender, por exemplo, de ruído (interno e externo) ou atrito. Pode depender também do valor do estímulo.

Resolução

Resolução é o menor variação da grandeza medida que causa uma variação perceptível na indicação correspondente. A resolução pode depender, por exemplo, de ruído (interno ou externo) ou de atrito, ou ainda do valor da grandeza medida. A avaliação da resolução é executada em função do tipo de instrumento:

a) Para dispositivo mostrador digital, a resolução é a variação na indicação quando o dígito menos significativo varia de uma unidade.

b) Nos sistemas de medição com dispositivo mostrador analógico, a resolução é função das limitações do executor da leitura, da qualidade do indicador e da própria necessidade de leituras mais ou menos criteriosas.

Estabilidade

A estabilidade é a aptidão de um instrumento de medição em conservar constantes suas características metrológicas ao longo do tempo. A estabilidade pode ser quantificada de várias maneiras. Exemplo: Pelo tempo no qual a característica metrológica varia de um valor determinado, ou em termos de variação de uma característica em um determinado período de tempo.

Discrição

Caracteriza a aptidão de um instrumento de medição em não alterar o valor do mensurado.

Exemplo:

Uma balança é um instrumento discreto para medição de massas, pois o sistema de medição não altera o valor da massa. Um termômetro de resistência que aquece o meio ambiente no qual a temperatura está sob medição não é discreto.

Deriva

A deriva é a variação da indicação ao longo do tempo, contínua ou incremental, devida a variações nas propriedades metrológicas de um instrumento de medição. A deriva não está relacionada a uma variação na grandeza medida, nem a uma variação de qualquer grandeza de influência identificada.

Tempo de resposta

É o intervalo entre o instante em que o estímulo (valor de entrada de um instrumento de medição ou um sistema de medição) é submetido a uma variação brusca entre dois valores constantes especificados e o instante em que a indicação correspondente se mantém entre limites especificados em torno do seu valor final em regime estável.

Exatidão de um instrumento de medição

A exatidão, também denominada de acurácia, é a aptidão de um instrumento de medição par dar respostas próximas a um valor verdadeiro, ou ainda pode ser definido como grau de concordância entre um valor medido e um valor verdadeiro de um mensurando. A exatidão é um conceito qualitativo, não devendo ser confundido com precisão.

Classe de exatidão

Classe de instrumentos de medição ou de sistemas de medição que satisfazem requisitos metrológicos estabelecidos, destinados a manter os erros de medição ou as incertezas de medição instrumentais dentro de limites especificados, sob condições de funcionamento especificadas. Este conceito é aplicado a medidas materializadas. Uma classe de exatidão é usualmente indicada por um número ou símbolo adotado por convenção e denominado de índice de classe.

Exemplo:

Jogo de blocos padrão classe 0.

Erro de indicação em um instrumento de medição

Este erro é determinado pela diferença da indicação de um instrumento de medição e um valor verdadeiro da grandeza de entrada correspondente. Na prática, uma vez que um valor verdadeiro não pode ser determinado, é utilizado um valor verdadeiro convencional. Este conceito de erro é aplicado principalmente quando o instrumento é comparado a um padrão de referência. Para uma medida materializada, o erro é caracterizado entre a indicação e o valor atribuído a ela.

Erros máximos admissíveis

Erros máximos admissíveis ou erros máximos permissíveis é um valor extremo do erro de medição, com respeito a um valor de referência conhecido, admitido por especificações ou regulamentos para uma dada medição, instrumento de medição ou sistema de medição. Este também é denominado de limites de erros admissíveis ou erro máximo tolerado.

Tendência

A tendência ou erro de justeza é o erro sistemático da indicação de um instrumento de medição (também denominada: bias of a measuring instrument, erreur de justesse) definido como a média de repetidas indicações e um valor de referência. A tendência de um instrumento de medição é normalmente estimada pela média dos erros de indicação de um número apropriado de medições repetidas.

Isenção de tendência

Aptidão de um instrumento de medição em dar indicações isentas de erros sistemáticos.

Repetitividade

A repetitividade é a aptidão de um instrumento de medição em fornecer indicações muito próximas, em repetidas aplicações do mesmo mensurando, sob as mesmas condições de medição. Estas condições incluem:

• Redução ao mínimo das variáveis devido ao observador;
• Mesmo procedimento de medição;
• Mesmo avaliador;
• Mesmo equipamento de medição, sendo utilizado nas mesmas condições;
• Mesmo local;
• Repetições em um curto período de tempo.

A repetitividade pode ser expressa quantitativamente em termos das características de dispersão das indicações.

Histerese

A histerese de um instrumento de medição é um erro de medição, que ocorre quando há diferença entre a medida, para um dado valor do mensurado quando esta foi atingida por valores crescentes, e a medida quando atingida por valores decrescentes do mensurado. Este valor poderá ser diferente se o ciclo de carregamento e descarregamento for completo ou parcial. A histerese é um fenômeno bastante típico nos instrumentos mecânicos, tendo como fonte de erro, principalmente, folgas e deformações associadas ao atrito.

Referências Bibliográficas

[1] CIPM (1981) INC, BIPM Proc. Verb. Com. Int. Poids et Mesures, vol. 18, Metrologia (1992), 43-44 (English).

[2] ISO GUM (2008), Avaliação de dados de Medição - Guia para a expressão de incerteza de medição, 1ª edição brasileira.

[3] NIS 3003, The Expression of Uncertainty and Confidence in Measurement for Calibrations, Edition 8, may 1995.

[4] Versão Brasileira do Documento de Referência EA-4/02, Expressão da Incerteza em Medição, Volumes I e II.

[5] Montgomery, D. C. (1997), Design and Analysis of Experiments, Fourth Edition - Ed. John Wiley & Sons.

[6] Ripley, B. D. (1987),Stochastic Simulation, Wiley: New York.

[7] Wichmann, B. A. e Hill, I. D. (1982), “Algorithm AS 183: An Efficient and Portable Pseudo-random Number Generator”, Applied Statistics, vol 31, p 188-190.

[8] ABNT NBR ISO 10012. Sistemas de gestão de medição – requisitos para os processos de medição e equipamentos de medição. Rio de Janeiro: ABNT – Associação Brasileira de Normas Técnicas, 2004.

[9] ABNT NBR ISO/IEC 17025. Requisitos gerais para competência de laboratório de teste e calibração. Rio de Janeiro: ABNT – Associação Brasileira de Normas Técnicas, 1999.

[10] D. Deaver. Guardbanding and the world of iso guide 25 is there only one way? Fluke Corporation, NCSL, 1998.

[11] S.A. Khanam and E. Morse. Test uncertainty & test uncertainty ratio (tur).

[12] Grubbs, Frank E (1969), Procedures for detecting outlying observations in samples, Taylor & Francis Group, vol 11, p 1-21.