21. Simulação Monte Carlo

A aleatoriedade dos métodos de simulação se baseiam na geração de uma sequência de variáveis aleatórias independentes $ X_1,X_2,\ldots,X_n $ uniformemente distribuídas no intervalo $ [0,1] $. As primeiras técnicas utilizadas para gerar números aleatórios utilizavam processos físicos, que eram aceitos como aleatórios, por exemplo, o jogo de moedas, jogo de dados, entre outros. Os primeiros experimentos descritos datam do século XVIII, aqui citamos o experimento de Buffon. Uma das mais famosas tabelas de números supostamente aleatórios, a RAND (1955), continha 1 milhão de dígitos gerados por ruídos eletrônicos. Entretanto, para a grande maioria das tabelas de números aleatórios obtidos por processos físicos foram detectados vícios e dependências.

Ao invés de desenvolver máquinas mais eficientes para gerar números aleatórios, os pioneiros da teoria de computação propuseram a geração de números que se “assemelham” aos números aleatórios, através de sequências determinísticas. Por exemplo, Von Neumann propôs o método “middle square”: inciado com 8653, é tomado seu quadrado (74874409) e consequentemente extraídos seus elementos do meio com quatro dígitos (8744), e assim por diante.

A técnica conhecida como Monte Carlo surgiu através de trabalhos de diversos matemáticos. Stanislaw Ulam, matemático polonês, que participou do Projeto Manhattan e propôs a Teller-Ulam desenho de armas termonucleares, usou esta ideia para este projeto. Enquanto em Los Alamos, sugeriu que o método Monte Carlo para avaliar integrais matemáticas complicadas que surgem na teoria de reações nucleares em cadeia. Esta sugestão levou ao desenvolvimento do método de simulação Monte Carlo por Von Neumann, Metropolis e outros.

Von Neumann foi tomado pela idéia de fazer a amostragem estatística utilizando técnicas de simulação por computador. A abordagem pareceu ser especialmente adequada para explorar o comportamento de reações em cadeia de nêutrons em dispositivos de fissão. Em particular, a taxa de multiplicação de nêutrons podia ser estimada e usada para predizer o comportamento explosivo das diversas armas de fissão nuclear. Hoje o método de simulação Monte Carlo é utilizado não somente para cálculo de integrais, mas também como ferramenta para simularmos comportamentos estocásticos, como por exemplo, em estudos do mercado financeiro.

1 - Números Pseudo-Aleatórios

Como dito anteriormente, os métodos de simulação estocástica são baseados na habilidade de geração e números aleatórios que representam uma variável aleatória distribuída uniformemente em $ [0,1] $. Na prática, não é possível gerar de forma realmente aleatória valores de uma distribuição uniforme, entretanto, é possível gerar, de forma determinística, uma sequência de valores que parecem ser aleatórios e uniformemente distribuídos no intervalo $ [0,1] $. Neste sentido, geramos o que são conhecidos por números pseudo-aleatórios.

Definição

Uma sequência de números pseudo-aleatórios $ (U_i)_{i\geq 1} $ é uma sequência determinística de números do intervalo $ [0,1] $ que, embora tenham sido gerados de forma determinística, parecem ser aleatórios e distribuídos uniformemente. Além disso, esta sequência possui propriedades estatísticas relevantes.

Entendemos por propriedades estatísticas relevantes que, qualquer teste estatístico aplicado para detectar desvios da aleatoriedade não rejeite a hipótese de aleatoriedade. Uma das principais propriedades de uma sequência de números pseudo-aleatórios é a falta de previsibilidade. Por exemplo, no método proposto por Von Neumann, se iniciarmos por $ 2.100 $ obtemos $ 4.100, 8.100, 6.100, 2.100, 4.100, \dots $, que nos leva a recusar tal método, pois dependendo da condição inicial, podemos gerar uma sequência com período muito pequeno, neste caso 4.

A falta de previsibilidade dos números pseudo-aleatórios estabelece uma conexão entre a geração de tais números e a criptografia, a arte ou ciência de transformar sequências aparentemente aleatórias em dados originais (informações).

A seguir, vamos apresentar um dos tipos de geradores de números pseudo-aleatórios mais utilizados na prática, conhecido como método dos geradores congruenciais. Tais métodos são derivados da ciência da criptografia. No método dos geradores congruenciais, começamos com um valor inicial $ X_0 $, denominado semente e, então, de forma recursiva, calculamos sucessivos valores $ X_n $ com $ n\geq 1 $ da forma

$$X_i=(aX_i+c) \ \text{mod} \ M,$$

em que $ a, c $ e $ M $ são números inteiros positivos. Neste método, $ d \ \text{mod} \ M $ corresponde ao resto da divisão de $ d $ por $ M $. É importante observar que, desta forma, cada valor $ X_n $ pertence ao conjunto $ (0,1,\ldots,M-1) $. Por exemplo, se tomarmos $ M=16 $, $ a=1 $ e $ c=1 $, obtemos $ 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,0,1,\dots $. O segredo de tais geradores está nos valores de $ M $, $ a $ e $ c $ que nos fornecem o maior período possível. Para detalhes sobre tais geradores, ver Ripley (1987). De forma a determinar um número entre $ 0 $ e $ 1 $, basta dividi-lo por $ M $, isto é, consideramos a sequência

$$Y_i = \frac{X_i}{M}.$$

Exemplo 1.1

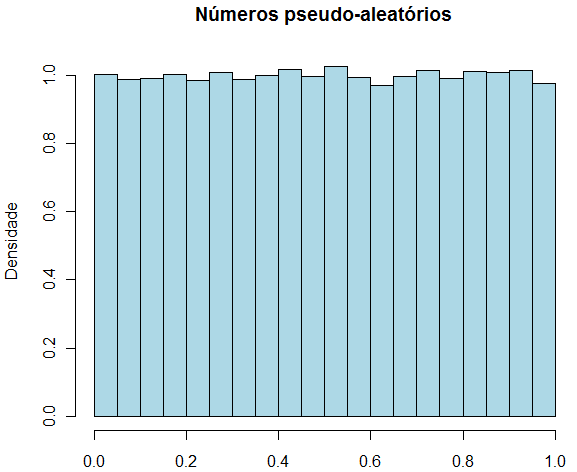
A seguir, aplicamos o método baseado nos valores $ X_0 = 100 $, $ a = 25 $, $ c = 1313 $, $ M= 1.987.345 $ para a simulação de $ 100.000 $ valores. O histograma dos valores gerados fornece evidências de que os valores estão uniformemente distribuídos no intervalo $ [0,1] $.

1.1 - Cálculo de integrais

Uma das principais aplicações para a simulação de números pseudo-aleatórios e ideia básica para o desenvolvimento do método de simulação Monte Carlo foi o cálculo de integrais. Neste sentido, seja $g: \mathbb{R}\rightarrow\mathbb{R} $ uma função real de variável real e considere o problema de se calcular

$$\theta =\int_0^1g(x)dx.$$

A fim de calcular esta integral, observamos que, se $ U $ é uma variável aleatória distribuída uniformemente no intervalo $ [0,1] $, isto é, $ U\sim U[0,1] $, então sua função densidade de probabilidade $ f_U $ é dada por

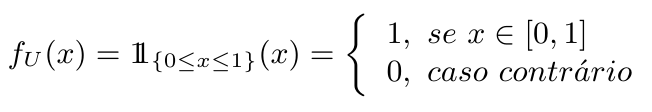
Além disso, o valor esperado de $ U $ é calculado por

$$\mathbb{E}(U) = \int_0^1f_U(x)dx = \int_0^1dx.$$

Em particular, temos que a variável aleatória $ g(U) $ tem valor esperado dado por

$$\mathbb{E}(g(U)) = \int_0^1g(x)f_U(x)dx = \int_0^1g(x)dx = \theta.$$

Portanto, se $ U_1,\ldots,U_n $ são variáveis aleatórias independentes e uniformemente distribuídas em $ [0,1] $, então $ g(U_1),\ldots,g(U_n) $ são variáveis aleatórias independentes com média $ \theta $. Desta forma, pela Lei Forte dos Grandes Números (Lei Forte de Kolmogorov), temos que

$$\sum_{i=1}^n\frac{g(U_i)}{n}\rightarrow\mathbb{E}\left[g(U)\right] = \theta$$

quando $ n\rightarrow\infty $ com probabilidade $ 1 $.

Conclusão: Podemos aproximar $ \theta $ a partir da geração de uma grande quantidade de números aleatórios $ U_1,U_2,\ldots,U_n $ com distribuição uniforme em $ [0,1] $ e então, calcular a aproximação como sendo a média

$$\hat{\theta_n} = \sum_{i=1}^n\frac{g(U_i)}{n}.$$

Desta forma, o seguinte algoritmo pode ser utilizado para o cálculo de $ \theta = \int_0^1g(x)dx $.

1. Calcular $ n $ números aleatórios $ U_1,U_2,\ldots,U_n $ uniformemente distribuídos em $ [0,1] $ utilizando o método do gerador congruencial.
2. Calcular $ g(U_1),g(U_2),\ldots,g(U_n) $.
3. Calcular a média desses valores.

Exemplo 1.1.1

Calcular uma aproximação para a integral

$$\theta = \int_0^1\text{sen}(x)dx.$$

Inicialmente, calcularemos esta integral de forma analítica. Uma função primitiva para a função $ g(x) = \ \text{sen}(x) $ é a função $ G(x) = -\cos(x) $, portanto, temos que o valor exato para $ \theta $ é dado por

$$\theta = \int_0^1\text{sen}(x)dx = -\cos(x)\Big|^{1}_0 = -\cos(1) + \cos(0) = -0,5403023 + 1 = 0,4596977.$$

A seguir, aplicamos o algoritmo acima para calcular uma aproximação para $ \theta $ baseado no algoritmo acima e em diversos valores diferentes de $ n $. Baseado na Lei Forte dos Grandes Números, esperamos que, conforme $ n $ cresça, o resultado se aproxime do verdadeiro valor.

100	0,4727
1.000	0,4646
10.000	0,4637
100.000	0,4601

Para o caso mais geral, em que precisamos calcular a integral

$$\theta = \int_a^bg(x)dx$$

em que os limites de integração não são, necessariamente, $ 0 $ e $ 1 $, é necessário realizar a seguinte substituição de variáveis

$$y = \frac{x-a}{b-a} \Rightarrow dy = \frac{dx}{b-a}$$

e, portanto,

$$\theta = \int_a^bg(x)dx = \int_0^1g(a+y(b-a))(b-a)dy = \int_0^1h(y)dy$$

em que $h: \mathbb{R}\rightarrow\mathbb{R} $ é dado por

$$h(y) = (b-a)g(a+y(b-a))$$

e, desta forma, o problema fica reduzido para o caso anterior. O seguinte algoritmo pode ser utilizado para o cálculo de $ \theta = \int_a^bg(x)dx $.

1. Calcular $ n $ números aleatórios $ U_1,U_2,\ldots,U_n $ uniformemente distribuídos em $ [0,1] $ utilizando o método do gerador congruencial.
2. Calcular os valores $ Y_i = (b-a)g(a + U_i(b-a)) $ com $ i = 1,\ldots, n $.
3. Calcular a média dos valores $ Y_i $ com $ i = 1,\ldots,n $.

Exemplo 1.1.2

Calcular a integral

$$\theta = \int_3^7x^3dx.$$

Resolvendo de forma analítica, temos que

$$\theta = \int_3^7x^3dx = \frac{x^4}{4}\Big|^7_3= 580.$$

Utilizando o algoritmo acima para a aproximação da integral temos, para diversos valores de $ n $, os resultados obtidos são dados na tabela abaixo.

100	590,2108
1.000	585,2604
10.000	582,5689
100.000	580,3870

De forma análoga a anterior, quando queremos calcular a integral imprópria

$$\theta = \int_0^{\infty}g(x)dx,$$

basta aplicar a seguinte substituição de variáveis

$$y = \frac{1}{x+1} \Rightarrow dy = -\frac{dx}{(x+1)^2} = -y^2dx$$

e assim, obtemos que

$$\theta = \int_0^{\infty}g(x)dx = \int_1^0-\frac{g\left(\frac{1}{y}-1\right)}{y^2}dy = \int_0^1\frac{g\left(\frac{1}{y}-1\right)}{y^2}dy = \int_0^1h(y)dy$$

reduzindo a integral para o caso inicial.

Observação 1.1.1

Se $ g $ é uma função quadrado integrável e considerarmos

$$ \sigma_g^2 := \int_0^1(g(x)-\theta)^2dx$$

então o erro $ \hat{\theta}_n - \theta $ na estimativa de Monte Carlo é uma variável aleatória com distribuição normal com média $ 0 $ e desvio-padrão $ \sigma_g/\sqrt{n} $ de forma que, a aproximação, de fato, torna-se melhor conforme o crescimento do valor de $ n $. O parâmetro $ \sigma_g $ é desconhecido, mas pode ser estimado usando o desvio-padrão amostral

$$s_g = \sqrt{\frac{1}{n-1}\sum_{i=1}^n\left(g(U_i)-\hat{\theta}_n\right)^2}.$$

Desta forma, as funções dos valores simulados $ g(U_1),\ldots,g(U_n) $ não fornecem, somente, o valor da integral $ \theta $ como também fornecem uma estimativa para o erro cometido na estimativa.

Observação 1.1.2

A forma do erro padrão $ \sigma_g/\sqrt{n} $ é uma propriedade central do método de Monte Carlo, de modo que, para diminuir este erro pela metade, é necessário aumentar o número de simulações por uma fator de quatro. Desta forma, a convergência é da ordem de raiz quadrada, devido ao fator $ \sqrt{n} $ no denominador do erro padrão. Como alternativa a este método, o erro na regra dos trapézios, dado por

$$\theta = \frac{g(0)+g(1)}{2n}+\frac{1}{n}\sum_{i=1}^{n-1}g\left(\frac{i}{n}\right)$$

é da ordem $ O(n^{-2}) $, pelo menos para funções de classe $ C^2 $. Desta forma, o método de Monte Carlo não é um método competitivo para calcular integrais de dimensão 1.

Entretanto, o método de simulação Monte Carlo, torna-se uma ferramenta computacional poderosa para calcular integrais pelo fato de que a ordem de convergência $ O(n^{-\frac{1}{2}}) $ não se restringe ao intervalo unitário. Na verdade, os passos acima, podem ser aplicados para estimar integrais sobre $ [0,1]^d $ para todas as dimensões $ d $. É claro que, quando mudamos as dimensões, mudando a função $ g $ e quando mudamos $ g $, também mudamos $ \sigma_g $, porém o erro padrão permanece da forma $ \sigma_g/\sqrt{n} $ para a estimativa de Monte Carlo. Isto quer dizer que a convergência de ordem $ O(n^{-\frac{1}{2}}) $ permanece a mesma para todo $ d $. Em contrapartida, o erro avaliado utilizando a regra dos trapézios em dimensão $ d $ é da ordem $ O(n^{-\frac{2}{d}}) $ para funções de classe $ C^2 $. Desta forma, conforme o número de dimensões aumenta, na regra dos trapézios, a taxa de convergência fica cada vez pior, enquanto que no método de Monte Carlo, ela permanece inalterada. Portanto, o método de Monte Carlo é muito atrativo para o cálculo de integrais múltiplas quando muitas dimensões estão em jogo. Na prática, quando o número de dimensões é $ d = 4 $, as taxas de convergência são iguais, porém, a partir de $ d \ > \ 4 $, o método de Monte Carlo torna-se superior.

Considere então $g: \mathbb{R}^d\rightarrow \mathbb{R} $ e suponha que o interesse seja calcular

$$\theta = \int_0^1\int_0^1\ldots\int_0^1g(x_1,x_2,\ldots,x_d)dx_1dx_2\ldots dx_d.$$

De forma análoga, temos que $ \theta = \mathbb{E}\left[g(U_1,U_2,\ldots,U_d)\right] $ em que $ U_1,\ldots,U_d $ são variáveis aleatórias independentes e uniformemente distribuídas em $ [0,1] $. Desta forma, para calcular uma aproximação para $ \theta $, basta simular $ n $ conjuntos independentes de $ d $ variáveis aleatórias independentes e uniformente distribuídas em $ [0,1] $ dados por $ (U^1_1,U^1_2,\ldots,U^1_d), (U^2_1,U^2_2,\ldots,U^2_d),\ldots,(U^n_1,U^n_2,\ldots,U^n_d) $ e então a estimativa para $ \theta $ é dada por

$$\hat{\theta} = \frac{1}{n}\sum_{i=1}^ng\left(U^i_1,U^i_2,\ldots,U^i_d\right).$$

Exemplo 1.1.3

Estimar o valor de $ \pi $ numericamente.

Para calcular o valor de $ \pi $, considere a circunferência de raio unitário inscrita no quadrado de vértices $ (-1,-1), (-1,1), (1,-1) $ e $ (1,1) $ como mostrado na figura abaixo.

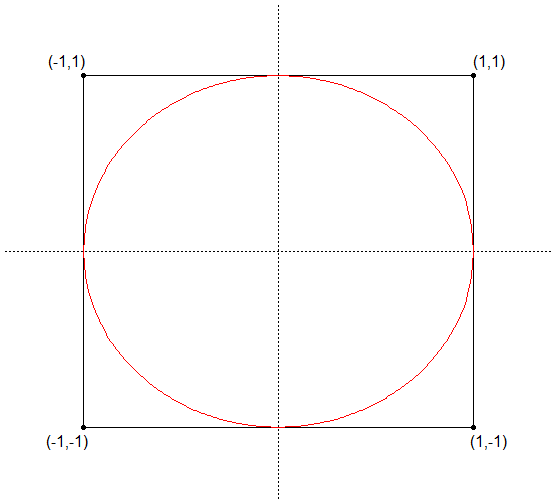
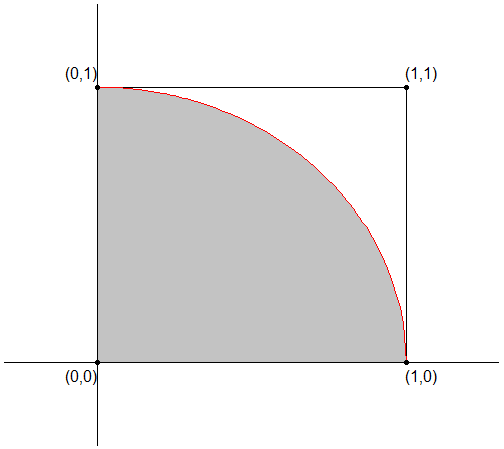
Desta forma, seja $ g: \mathbb{R}^2\rightarrow\mathbb{R} $ dada por

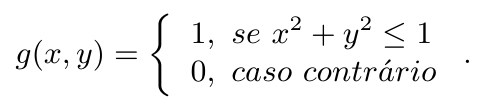
Então, se tomarmos $ U_1 $ e $ U_2 $ duas variáveis aleatórias uniformes em $ [0,1] $ independentes, temos que

$$\frac{\pi}{4} = \mathbb{E}\left[g(U_1,U_2)\right] = \mathbb{P}\left(X^2 + Y^2 \leq 1\right)$$

Desta forma, para aproximar $ \frac{\pi}{4} $, basta simular uma quantidade $ n $ conjuntos independentes de $ 2 $ variáveis aleatórias $ U_1 $ e $ U_2 $ uniformemente distribuídas no intervalo $ [0,1] $ e verificar a quantidade de pontos $ (U_1,U_2) $ do total que estão dentro da região hachurada, isto é, para cada par gerado $ (U^i_1,U^i_2) $ verificamos se $ g(U^i_1,U^i_2) = 1 $ ou se $ g(U^i_1,U^i_2) = 0 $. Desta forma, temos que

$$\frac{pi}{4} \approx \frac{1}{n}\sum_{i=1}^ng(U^i_1,U^i_2) \Rightarrow \pi \approx 4\frac{1}{n}\sum_{i=1}^ng(U^i_1,U^i_2).$$

Na figura a seguir, os pontos azuis são aqueles cujas coordenadas $ (U^i_1,U^i_2) $ são tais que $ g(U^i_1,U^i_2) = 1 $ e os verdes são aqueles em que $ g(U^i_1,U^i_2) = 0 $.

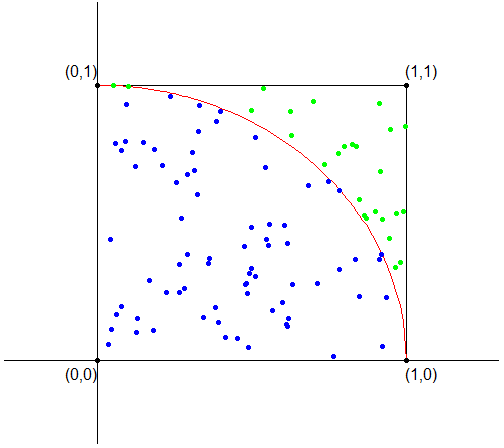
O algoritmo para a aproximação de $ \pi $ pode ser escrito considerando os passos abaixo.

1. Geramos os valores $ U^i_1 $ e $ U^i_2 $ independentes e distribuídos uniformemente em $ [0,1] $, para $ i = 1,\ldots,n $.
2. Verificamos se $ g(U^i_1,U^i_2) = 1 $ ou se $ g(U^i_1,U^i_2) = 0 $, isto é, se o par ordenado pertence a região $ R $ ou não.
3. Aproximamos o valor de $ \pi $ por

$$\pi = 4\frac{1}{n}\sum_{i=1}^ng(U^i_1,U^i_2).$$

Apresentamos a seguir, as aproximações obtidas para $ \pi $ seguindo o algoritmo descrito acima e utilizando os valores $ n = 100 $, $ n = 1.000 $, $ n = 10.000 $ e $ n = 100.000 $.

100	3.2
1.000	3.096
10.000	3.1264
100.000	3.14628

2 - Método da Transforma Inversa

Uma vez que temos uma forma eficiente de simular variáveis aleatórias uniformemente distribuídas em $ [0,1] $, o foco agora é estender este resultado para a simulação de outros modelos probabilísticos. Neste sentido, apresentamos um método bastante utilizado: o método da transformada inversa.

Suponha que queremos simular amostras aleatórias de uma variável aleatória $ X $ com função de distribuição $ F $, isto é, queremos gerar uma variável aleatória $ X $ com a propriedade $ F_X(x) = \mathbb{P}(X\leq x) $ para todo $ x $. Neste caso, geramos uma variável aleatória $ U $ uniformemente distribuída em $ [0,1] $, isto é, $ U\sim U[0,1] $ e então, o método da transforma inversa estabelece que a variável aleatória $ X = F_X^{-1}(U) $. O método pode ser ilustrado na figura abaixo para uma distribuição acumulada hipotética $ F $.

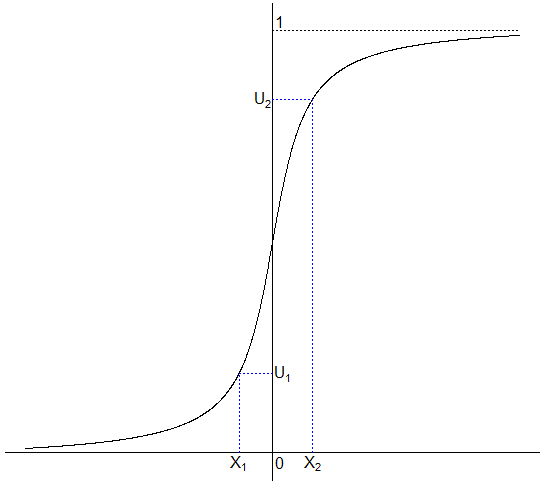
Para verificar que o método da transformada inversa, de fato, é capaz de gerar valores de uma distribuição com função de distribuição acumulada $ F_X $, basta verificar que

$$\mathbb{P}(X\leq x) = \mathbb{P}(F^{-1}(U)\leq x) = \mathbb{P}(U \leq F(x)) = F(x)$$

em que a segunda igualdade segue do fato de que, para $ F^{-1} $ como definimos, os eventos $ (F^{-1}(u)\leq x) $ e $ (u\leq F(x)) $ coincidem para todo $ u $ e $ x $. A última igualdade segue do fato de

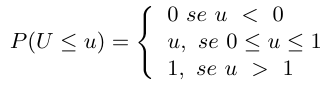
Podemos interpretar o valor $ U $ do método da transformada inversa como sendo o percentil aleatório. Se $ F_X $ é contínua e a variável aleatória $ X $ tem distribuição $ F_X $, então $ X $ tem mesma probabilidade de cair entre, digamos, o 20º e o 30º percentis, assim como o 85º e o 95º percentis. Em outras palavras, o percentil é uniformemente distribuído. Desta forma, o método da transformada inversa, seleciona um percentil uniformemente e então aplica este valor ao correspondente valor da variável aleatória.

A fim de entender de maneira prática o método, apresentamos duas aplicações: a primeira, em que queremos simular uma variável aleatória discreta e a segunda, em que queremos simular uma variável aleatória contínua.

Simulação de variáveis aleatórias discretas

Suponha que queremos gerar uma variável aleatória discreta $ X $ que possui função distribuição de probabilidade dada por

$$F_X(x) = \mathbb{P}[X = x_j] = p_j, \quad j=0,1,…, \quad \sum_j p_j = 1$$

Para isso, geramos um número aleatória $ U $ tal que $ U $ possui distribuição uniforme no intervalo $ [0,1] $. Então,

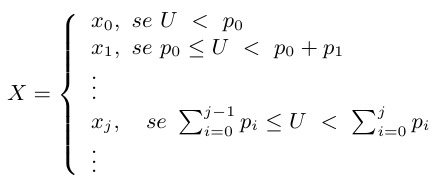
Portanto, se para $ 0 \ < \ a \ < \ b \ < 1, \mathbb{P}(a \le U \le b) = b-a $ temos que

$$\mathbb{P} (X = x_j ) = \mathbb{P} \Bigg ( \sum_{i=1}^{j-1} p_i \le U \le \sum_{i=0}^j p_i \Bigg ) = p_j$$

Desta forma, $ X $ tem a distribuição desejada acima.

Em outras palavras, após gerarmos um número aleatório $ U $ nós determinamos o valor de $ X $ identificando o intervalo $ [F_X(x_{j-1}), F_X(x_j)] $ para o qual $ U $ pertence, o qual é equivalente a encontrar a função inversa de $ F_X(U) $.

Uma forma prática de utlizar o método da transformada inversa é seguir o algoritmo:

1. Gere um número aleatório $ U $ de uma distribuição uniforme $ [0,1] $;
2. Se $ U \ < \ p_0 $ faça $ X = x_0 $ e pare por aqui;
3. Caso contrário, se $ U \ < \ p_0 + p_1 $ faça $ X = x_1 $ e pare por aqui;
4. Caso contrário, se $ U \ < \ p_0 + p_1 + p_2 $ faça $ X = x_2 $ e pare por aqui;
5. $ \vdots $

Exemplo 2.1

Vamos simular uma variável aleatória $ X $ que possui a seguinte distribuição de probabilidades.

$$p_1 = 0,20, \quad p_2 = 0,15, \quad p_3 = 0,25, \quad p_4 = 0,40, \quad \text{onde } p_j = \mathbb{P} (X = j )$$

Então, seguindo o algoritmo temos

1. Se $ U \ < \ 0,20 $ faça $ X = 1 $ e pare por aqui;
2. Se $ U \ < \ 0,35 $ faça $ X = 2 $ e pare por aqui;
3. Se $ U \ < \ 0,60 $ faça $ X = 3 $ e pare por aqui;
4. Caso contrário, $ X = 4 $.

Utilizando o algoritmo acima, obtivemos os seguintes resultados ao simular $ n = 100 $, $ n = 1.000 $, $ n = 10.000 $ e $ n = 100.000 $ valores desta variável aleatória.

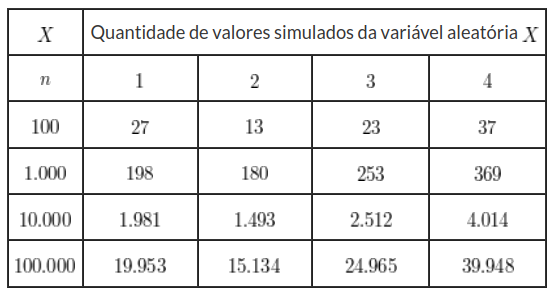
Simulação de variáveis aleatórias contínuas

Para simular variáveis aleatórias contínuas, a ideia é análoga. Para utilizar o método da transformada inversa para variáveis aleatórias contínuas, basicamente, basta utilizar a inversa da função de distribuição acumulada. Entretanto, em alguns casos, podemos tornar o método mais eficiente a partir de simples modificações.

Exemplo 2.2

Suponha que queremos simular valores de uma variável aleatória contínua $ X $ que possui função de distribuição acumulada $ F_X(x) = x^n $ para $ 0 \ > \ x \ > \ 1 $.

Neste caso, temos que a inversa da função $ F_X(x) = x^n $ é dada por $ f(x) = x^{\frac{1}{n}} $ de forma que

$$x = F^{-1}_X(u) \ \Longrightarrow \ x = u^{\frac{1}{n}}$$

e então, para gerar uma variável aleatória $ X $ a partir de um número aleatório $ U $, basta calcular

$$X = U^{\frac{1}{n}}.$$

A seguir, utilizamos o método da transformada inversa para a simulação de variáveis aleatórias dos principais modelos probabilísticos discretos e contínuos.

2.1 - Modelos Probabilísticos Discretos

Nesta seção, utilizamos o método da transformada inversa discreta para simular variáveis aleatórias dos principais modelos probabilísticos discretos. Os modelos apresentados são: modelo binomial, modelo de Poisson e modelo geométrico.

2.1.1 - Simulação do Modelo Binomial

Seja $ X $ o número de sucessos obtidos na realização de $ n $ ensaios de Bernoulli independentes. Diremos que $ X $ tem distribuição binomial com parâmetros $ n $ e $ p $, em que $ p $ é a probabilidade de sucesso em cada ensaio, se sua função de probabilidade for dada por

$$\mathbb{P}[X=k]=\frac{n!}{k!(n-k)!}p^k(1-p)^{n-k}, \quad i = 0,1,…,n$$

Então, utilizamos o método de transformação inversa através da identidade recursiva

$$\mathbb{P}[x = k+1] = \frac{n-k}{k+1} \frac{p}{1-p} \mathbb{P}[X=k]$$

onde $ k $ é o valor atual, $ \mathbb{P}[X=k] $ é a probabilidade de $ X $ se igual a $ k $. Denotando por $ F(k) $ a função distribuição acumulada de $ k $ , podemos gerar valores aleatórios de uma distribuição binomial com parâmetros $ n $ e $ p $ seguindo o seguinte algoritmo:

1. Geramos um número aleatório U de uma distribuição uniforme no intervalo $ [0,1] $.
2. Iniciamos os valores: $ c = p/(1-p) $, $ k = 0 $, $ pr = (1-p)^n, F = pr $.
3. Se $ U \ < \ F $, $ X = k $ e pare por aqui.
4. Caso contrário, $ pr = [c(n-k)/(k+1)]pr $, $ F = F + pr $, $ k = k+1 $
5. Volte ao passo 3.

Este algoritmo irá checar se $ X= 0, X=1…, X= n $, portanto, o número de tentativas para encontrar o valor de $ X $ será sempre $ 1 + X $.

Exemplo 2.2.1

Vamos gerar um número seguindo uma distribuição Binomial [5,0.3].

Gerando $ U = 0,23 $, temos que:

$$c = \frac{0,3}{1 - 0,3} = 0,43$$

$$F = pr = (1 -0,3)^5 = 0,17$$

Seguindo o algoritmo no passo 3 temos que $ U \ > \ F $, portanto

$$pr = [0,43(5-1)/(0 + 1)]0,17 = 0,29$$

$$F = 0,17 + 0,29 = 0,46$$

$$k = 1$$

Como $ U \ < \ F $, segue que o número gerado é $ X = 1. $

2.1.2 - Simulação do Modelo de Poisson

Dizemos que uma variável aleatória discreta $ X $ segue a distribuição de Poisson com parâmetro $ \lambda $, $ \lambda \ > 0 $, se sua função de probabilidade for dada por

$$p_k = \mathbb{P}(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}.$$

Desta forma, para determinarmos uma relação a ser utilizada no método da transformada inversa fazemos

$$\frac{p_{k+1}}{p_k} = \frac{\frac{e^{-\lambda}\lambda^{k+1}}{(k+1)!}}{\frac{e^{-\lambda}\lambda^k}{k!}} \ \Longrightarrow \ p_{k+1} = \frac{\lambda}{k+1}p_k, \quad k \ge 0$$

Utilizando a recursão acima para gerarmos a probabilidade do próximo evento quando necessário, o algorítimo para gerar variáveis aleatórias de Poisson com média $ \lambda $ é dado por

1 - Geramos um número aleatório U de uma distribuição uniforme no intervalo $ [0,1] $.

2 - Iniciamos os valores: $ k = 0 $, $ p = e^{-\lambda} $, $ F = p $.

3 - Se $ U \ < \ F $, $ X = k $ e pare por aqui.

4 - Caso contrário, $ p = \lambda p / (k+1) $, $ F = F + p $, $ k = k+1 $

5 - Volte ao passo 3.

Exemplo 2.1.2.1

Vamos gerar um número seguindo uma distribuição de Poisson com parâmetro $ \lambda = 2 $. Seguindo o algoritmo, suponha inicialmente que geramos U = 0,37. Então,

$$k = 0$$

$$p = e^{-2} \approx 0,13$$

$$F = 0,13$$

Como $ U \ > \ F $

$$p = (2\ast 0,13)/(0+1) = 0,26$$

$$F = 0,13 + 0,26 = 0,39$$

$$k = 1$$

Neste caso temos $ U \ < \ F $ então, o número gerado é $ X = 1 $.

2.1.3 - Simulação do Modelo Geometrico

Seja $ X $ a variável aleatória que fornece o número de falhas até o primeiro sucesso. Dizemos que $ X $ é uma variável aleatória discreta com distribuição Geométrica de parâmetro $ p $, $ 0 \ < \ p \ < \ 1 $, se sua função de probabilidade é dada por

$$\mathbb{P}\left(X=j\right)=(1-p)^{j-1}p, \quad j=1,2,\ldots$$

fazendo $ q = (1 - p) $ podemos reescrever a equação acima

$$\mathbb{P}\left(X=j\right) = q^{j-1}p, \ \text{para} \ \quad j=1,2,\ldots.$$

Como $ X $ representa o número de falhas até o primeiro sucesso, sendo que cada tentativa tem probabilidade $ p $ de sucesso, podemos escrever

$$\sum_{i=1}^{j-1}\mathbb{P} (X=i) = 1 - \mathbb{P}(X \ > \ j-1) = 1 - q^{j-1}, \quad j=1,2,\ldots.$$

Desta forma, seja $ U $ um número aleatório de uma distribuição uniforme (0,1). Podemos gerar um valor de $ X $ fazendo $ X = j $ quando

$$1 - q^{j-1} \le U \ < \ 1 - q^{j} \quad \Longrightarrow \quad q^{j} \ < \ U-1 \le q^{j-1}.$$

Note que $ (U-1) $ também possui distribuição uniforme (0,1), então, como $ U $ é um número aleatório, podemos escrever

$$q^{j} \ < \ U \le q^{j-1}.$$

Então, podemos definir

Utilizando a expressão acima encontramos um problema quando $ 0 \ < \ q \ <\ 1 $, $ \log(q) $ é negativo e mudaria o sinal da inequação. Para contrariar este problema, utilizamos a notação $ \text{Int}() $

$$X = \ \text{Int}\left(\frac{\log(U)}{\log(q)}\right) + 1$$

em que $ \text{Int}(z) $ representa a parte inteira de $ z $.

Exemplo 2.1.3.1

Vamos gerar um número seguindo uma distribuição Geométrica com $ p = 0,6 $.

Segue que $ q = 0,4 $, então, dado que foi gerado $ U = 0,82 $ aleatoriamente, temos

$$X = \ \text{Int} \left(\frac{\log(0,82)}{\log(0,4)} \right) + 1 = 1$$

2.2 - Métodos Probabilísticos Contínuos

Nesta seção, apresentamos métodos de simulação de variáveis aleatórias para os principais modelos probabilísticos contínuos.

2.2.1 - Simulação do Modelo Uniforme [a,b]

Para gerar valores de uniformemente distribuídos no intervalo $ [a,b] $, isto $ U \sim U[a,b] $, basta calcularmos a função de distribuição acumulada $ F_X $, na forma

$$F_X(x)=\int_{a}^{x}\frac{1}{b-a}dx=\frac{x-a}{b-a}, \ \text{para todo} \ a\leq x\leq b.$$

Considere $ U $ uma variável aleatória uniformemente distribuída em $ [0,1] $. Então $ F_X(X)=U $ e com isso, obtemos que,

$$\frac{X-a}{b-a}=U, \quad t\text{ou seja,} \quad X = a+(b-a)U.$$

Assim, podemos gerar amostras de variáveis aleatórias com distribuição uniforme $ [a,b] $, através o seguinte algoritmo:

1º) Gerar Uniforme $ [0,1] $;

2º) Aplicar a fórmula $ X=a+(b-a)U $.

Exemplo 2.2.1.1

Vamos gerar 2 números segundo uma distribuição uniforme com $ a=3 $ e $ b=5 $. Considerando os números gerados aleatoriamente sendo 0,27 e 0,51, em uma distribuição $ U[3,5] $ temos que

$$X_1 = 3+(5-3)\times 0,27 = 3,54.$$

e

$$X_2 = 3+(5-3)\times 0,51 = 4,02.$$

Exercício 2.2.1.1

A partir da tabela de números aleatórios, gerar uma amostra de $ 5 $ números segundo a distribuição uniforme com $ a=12 $ e $ b=19 $.

2.2.2 - Simulação do Modelo Triangular [a,b]

Considere $ U $ uma variável aleatória uniformemente distribuída em $ [0,1] $, então $ F_X(X)=U $ e com isso, para $ 0\leq U\leq \frac{1}{2} $, então, temos que

$$F_X(X)=U, \ \text{ou seja,} \ \frac{2(X-a)^2}{(b-a)^2}=U.$$

Isolando $ X $, temos que

$$X=a+\sqrt{\frac{U}{2}}(b-a),\quad {para } 0\leq U\leq\frac{1}{2}.$$

No caso em que $ \frac{1}{2}\leq U\leq 1 $, temos

$$\frac{1}{2}+\frac{(b-a)^2-4(b-X)^2}{2(b-a)^2}=U,$$

e, desta forma, isolando $ X $,

$$X=b-(b-a)\sqrt{\frac{1-U}{2}}.$$

Portanto, no geral podemos definir

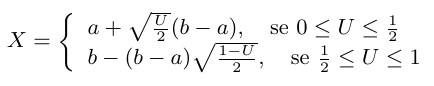
Assim, podemos gerar amostras de variáveis aleatórias com distribuição triangular no intervalo $ [a,b] $, através do seguinte algoritmo:

1º) Gerar uma amostra de uma variável aleatória $ U $ com distribuição uniforme $ [0,1] $;

2º) Se $ 0\leq U\leq\frac{1}{2} $, aplicar a fórmula $ X=a+\sqrt{\frac{U}{2}}(b-a) $;

3º) Se $ \frac{1}{2}\leq U\leq1 $, aplicar a fórmula $ X=b-(b-a)\sqrt{\frac{1-U}{2}} $.

Outro algoritmo muito utilizado para distribuições Triangulares é o seguinte:

1º) Gerar duas uniformes $ [0,1] $ independentes $ U_1 $ e $ U_2 $;

2º) Aplicar a fórmula $ X=a+(b-a)\left(\frac{U_1+U_2}{2}\right). $

Exercício 2.2.2.1

A partir da tabela de números aleatórios, gerar uma amostra de $ 5 $ números segundo a distribuição triangular com $ a=12 $ e $ b=19 $.

2.2.3 - Simulação do Modelo Normal

Definição 2.2.3.1

A variável aleatória contínua $ X $ tem distribuição normal com média $ \mu $ e variância $ \sigma^2 $ se sua função densidade de probabilidade for dada por

$$f(x)=\frac{1}{\displaystyle\sqrt{2\pi\sigma^{2}}}\exp\left[-\frac{1}{2}\left(\frac{\displaystyle x-\mu}{\displaystyle\sigma}\right)^{2}\right],~ -\infty \ < \ x \ < \ +\infty,$$

em que $ -\infty \ < \ \mu \ < \ \infty $ e $ 0 \ < \ \sigma^2 \ < \ \infty $.

Na Figura 1 ilustramos algumas curvas da distribuição normal para diversos valores de $ \mu $ e $ \sigma^2 $. Note que a distribuição normal tende a forma de “sino”.

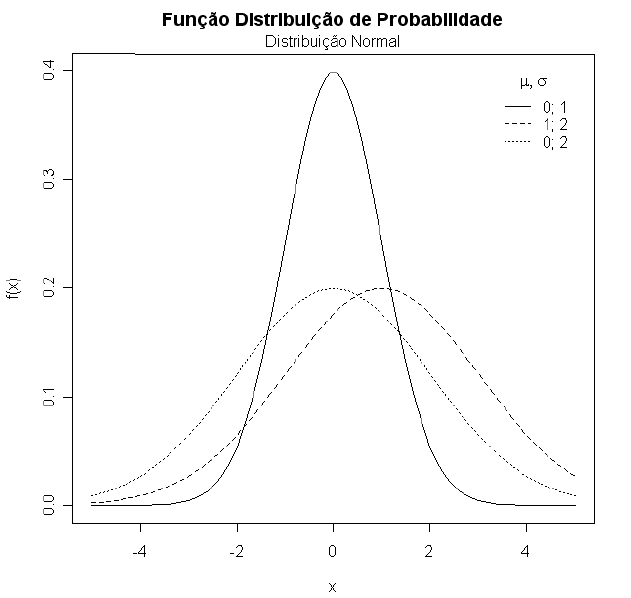
Figura 1: Função densidade de probabilidade da distribuição normal para diversos valores de $ \mu $ e $ \sigma $.

A seguir, apresentamos as principais propriedades da distribuição normal:

Propriedades

1. $ \mathbb{E}(X)=\mu $;
2. $ \text{Var}(X)=\sigma^2 $;
3. $ f(x)\rightarrow0 $ quando $ x\rightarrow\pm\infty $;
4. $ \mu-\sigma $ e $ \mu+\sigma $ são pontos de inflexão de $ f(x) $;
5. $ x=\mu $ é ponto de máximo de $ f(x) $, e o valor máximo é $ \displaystyle\frac{1}{\sqrt{2\pi\sigma}} $;
6. $ f(x) $ é simétrica ao redor de $ x=\mu $, isto é, $ f(\mu+x)=f(\mu-x) $, para todo $ -\infty< x<+\infty $.

Notação: Se $ X $ tem distribuição normal, com média $ \mu $ e variância $ \sigma^2 $, escrevemos:

$$X \sim N(\mu,\sigma^2).$$

Quando $ \mu=0 $ e $ \sigma^2=1 $, temos uma normal padrão ou reduzida, e escrevemos $ N(0,1). $

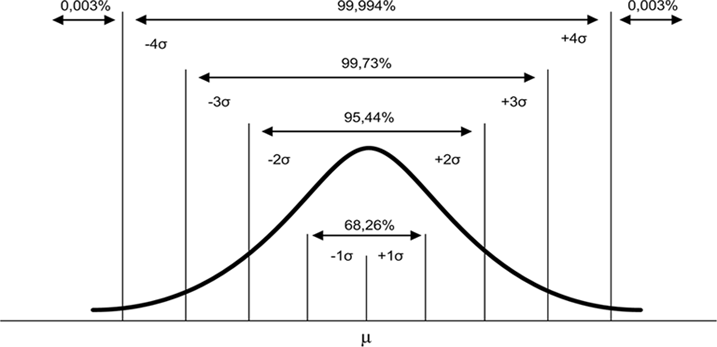
Figura 2: Função densidade de probabilidade da distribuição normal.

A Figura 2 ilustra o conceito básico das métricas de sistema da qualidade onde as peças são manufaturadas e avaliadas a porcentagem (ou PPM) de peças fora de especificação, ver Tabela 1.

Especificações	Porcentagem	PPM de defeitos
$ \pm 1\sigma $	68,27	317300
$ \pm 2\sigma $	95,45	54500
$ \pm 3\sigma $	99,73	2700
$ \pm 4\sigma $	99,9937	63
$ \pm 5\sigma $	99,999943	0,57
$ \pm 6\sigma $	99,9999998	0,002

Tabela 1: Métricas de Sistema da Qualidade.

O modelo normal é utilizado nas seguintes situações:

• Não temos apenas informação sobre os limites de variação da variável em estudo, ou não queremos fixar os limites para a variável em estudo;
• Admitimos que a variável se distribui simetricamente em torno da média e com probabilidade determinadas conforme gráfico e tabela acima.

O método mais utilizado para simular a distribuição normal foi proposto por Box e Muller (1958):

1º) Gerar uma variável aleatória $ U_1 $ com distribuição uniforme $ [0,1] $, e tomar $ Z = 2\pi U_1 $;

2º) Gerar uma variável aleatória $ U_2 $ com distribuição uniforme $ [0,1] $, e tomar $ E=-\ln(U_2) $ e $ R=\sqrt{2E} $;

3º) Tomar $ X=R\cos(Z) $ e $ Y=R\sin(Z) $ como amostras independentes da distribuição normal com média zero e desvio padrão 1;

Para obtermos amostras de uma distribuição normal com média $ \mu $ e desvio padrão $ \sigma $, basta aplicarmos a seguinte transformação:

$$\theta=\mu+\sigma X.$$

Exemplo 2.2.3.1

Solução: Temos que $ \mu=10.000 $, $ \sigma=1.500 $ e seja $ X= $depósito

a)

$$\mathbb{P}(X\leq10.000)=\mathbb{P}\left(\frac{X-10.000}{1.500}<\frac{10.000-10.000}{1.500}\right)=\mathbb{P}(Z\leq 0)=0,5=50(porcentagem);$$

b)

$$\mathbb{P}(X\geq10.000)=\mathbb{P}(Z\geq0)= 1 - \mathbb{P}(Z \leq 0) = 0,5=50(porcentagem);$$

c)

$$\mathbb{P}(12.000< X< 15.000)=\mathbb{P}\left[\frac{12.000-10.000}{1.500}\leq Z\leq\frac{15.000-10.000}{1.500}\right]$$

$$=\mathbb{P}\left[\frac{4}{3}\leq Z\leq\frac{10}{3}\right]=\mathbb{P}(1,33\leq Z\leq3,33)$$

$$=0,4997-0,40824=0,09133=9(porcentagem)$$

d)

$$\mathbb{P}(X\geq 20.000)=\mathbb{P}\left(\ Z \geq\frac{20.000-10.000}{1.500}\right)=\mathbb{P}(Z\geq6,67)\cong0.$$

2.2.4 - Simulação do Modelo Gama

Definição 2.2.4.1

Uma variável aleatória contínua $ X $ tem distribuição de Gama com parâmetros $ r,\lambda> 0 $, se sua função densidade de probabilidade for dada por

$$f(x)=\frac{x^{r-1}}{\Gamma(r)\lambda^r}e^{-\frac{x}{\lambda}},\quad {para~todo~} x \ > \ 0,$$

sendo:

• $ \lambda: $ primeiro parâmetro de forma;
• $ r: $ segundo parâmetro de forma.

Na Figura 1 ilustramos a distribuição Gama para diversos valores de $ \lambda $ e $ r $.

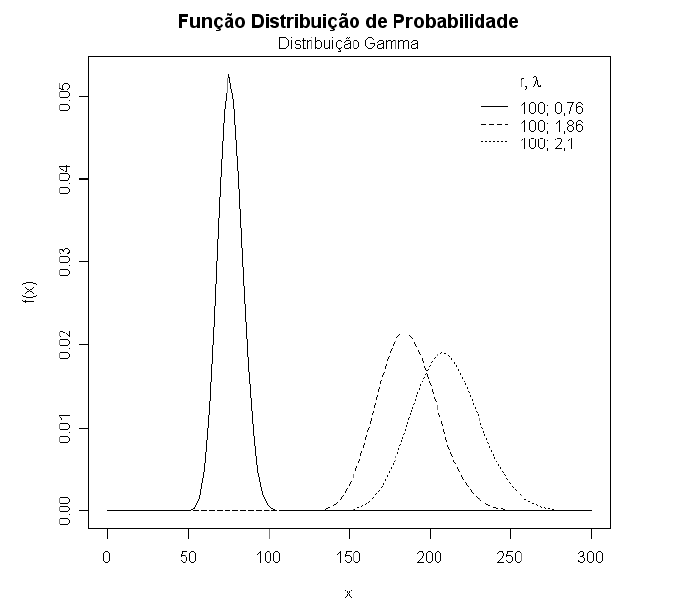
Figura 1: Função densidade de probabilidade da distribuição Gama para diversos valores de $ \lambda $ e $ r $.

Propriedades

i) $ \mathbb{E}(X)=r\lambda $;

ii) $ \text{Var}(X)=r\lambda^2. $

O modelo Gama é utilizado na seguinte situação:

• A distribuição da variável se comporta como no gráfico acima.
• Não temos como estabelecer limites para a variável aleatória, exceto que nunca é menor que zero.

Considere $ U $ uma variável aleatória com distribuição uniforme $ [0,1] $, então $ X=\displaystyle\frac{U^{-(r+1)}}{\Gamma(r)\lambda^r}e^{-\frac{U}{\lambda}} $ tem distribuição Gamma com parâmetros e $ r $ e $ \lambda $. Assim, temos o seguinte algoritmo para simular a distribuição de Gamma:

1º) Gerar uma variável aleatória $ U $ com distribuição uniforme $ [0,1] $;

2º) Aplicar a fórmula: $ X=\frac{U^{-(r+1)}}{\Gamma(r)\lambda^r}e^{-\frac{U}{\lambda}}. $

Exemplo 2.2.4.1

O fluxo de caixa (FC) para o próximo mês segue distribuição Gama com parâmetros $ \lambda=30 $ e $ r=5200 $. Esta variável aleatória tem média igual a $ 156.000 $. Encontrar o desvio padrão e a probabilidade dos seguintes eventos:

a) O Fluxo de Caixa é inferior a 150.000,00 (reais);

b) O Fluxo de Caixa está entre 158.000,00 (reais) e 161.000,00 (reais);

c) O Fluxo de Caixa é inferior a 157.000,00 (reais).

Antes de calcularmos tais probabilidades, vamos apresentar o gráfico da função densidade de probabilidade:

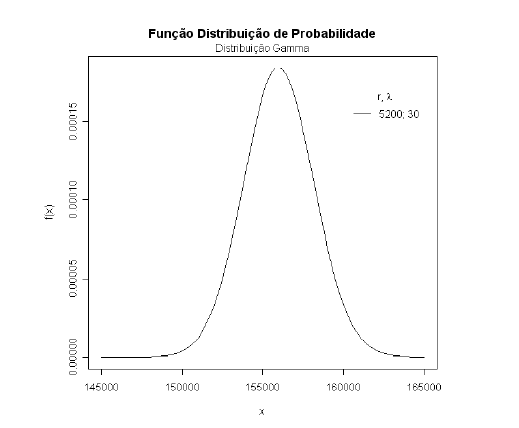
Figura 2: Função densidade de probabilidade da distribuição Gama para $ \lambda=30 $ e $ r=5.200 $, exemplo 1.

a) $ \mathbb{P}[\text{FC} \ < \ 150.000]=0,0025 $;

b)

$$\mathbb{P}[158.000\leq \ \text{FC} \ \leq 161.000]=\mathbb{P}[\text{FC} \ \leq161.000]-\mathbb{P}[\text{FC} \ \leq \ 158.000] = 0,98-0,8226=0,1574;$$

c) $ \mathbb{P}[\text{FC} \ < \ 157.000]=0,6794. $

2.2.5 - Simulação do Modelo Exponencial

A distribuição exponencial se caracteriza por ter uma função de taxa de falha constante. A distribuição exponencial é a única com esta propriedade. Ela é considerada uma das mais simples em termos matemáticos. Esta distribuição tem sido usada extensivamente como um modelo para o tempo de vida de certos produtos e materiais. Ela descreve adequadamente o tempo de vida de óleos isolantes e dielétricos entre outros.

Definição 2.2.5.1

Uma variável aleatória contínua $ X $, que tome todos os valores não-negativos, terá uma distribuição exponencial com parâmetro $ \lambda> 0 $, se sua função densidade de probabilidade for dada por

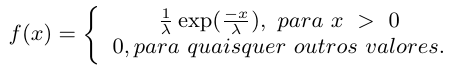
Na Figura 1 apresentamos alguns gráficos da distribuição exponencial para diversos valores de $ \lambda $.

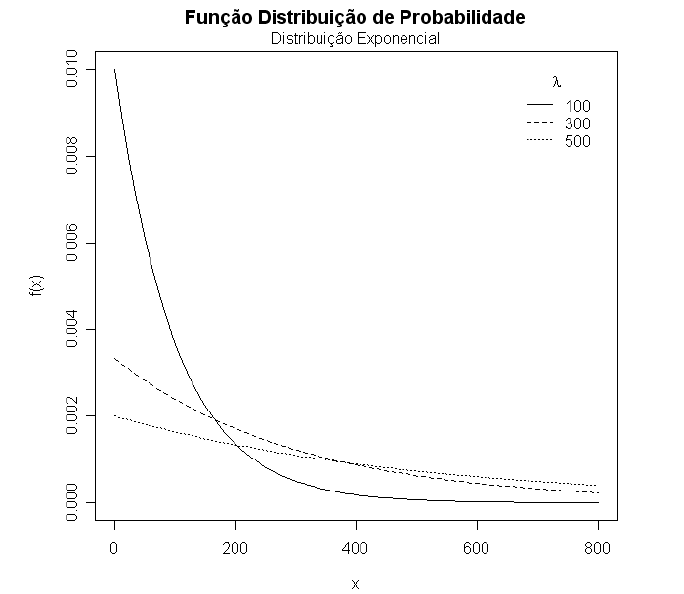
Figura 1: Função densidade de probabilidade da distribuição exponencial para diversos valores de $ \lambda $.

Propriedades

i) $ \mathbb{E}(X)=\lambda $;

ii) $ \text{Var}(X)=\lambda^2 $;

iii) $ f(x)\rightarrow 0 $ quando $ x\rightarrow +\infty $.

O modelo exponencial é utilizado na seguinte situação:

• Temos informação de que a distribuição da variável aleatória é assimétrica e se comporta como o gráfico acima;
• Não temos como estabelecer limites para a variável aleatória, exceto que nunca é menor que zero.

Para simularmos a distribuição exponencial, considere $ U $ uma variável aleatória com distribuição uniforme $ [0,1] $, então $ X=-\lambda\ln(U) $ tem distribuição exponencial com parâmetro $ \lambda $. Assim, temos o seguinte algoritmo para simular a distribuição exponencial:

1º) Gerar uma variável aleatória $ U $ com distribuição uniforme $ [0,1] $;

2º) Aplicar a fórmula: $ X=-\lambda\ln(U) $.

Exemplo 2.2.5.1

Suponha que o fluxo de caixa em um determinado instante de tempo segue uma distribuição exponencial com parâmetro $ \lambda=500 $ (média). Assim, a função densidade de probabilidade é dada por:

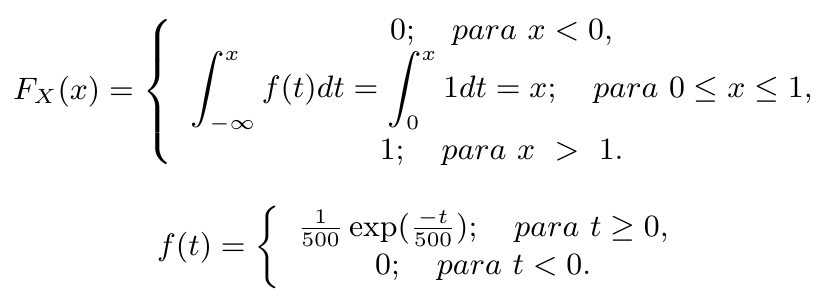
Segue-se que o fluxo médio é $ E(T)= 500 $ horas, e a probabilidade de que seja maior do que a média é:

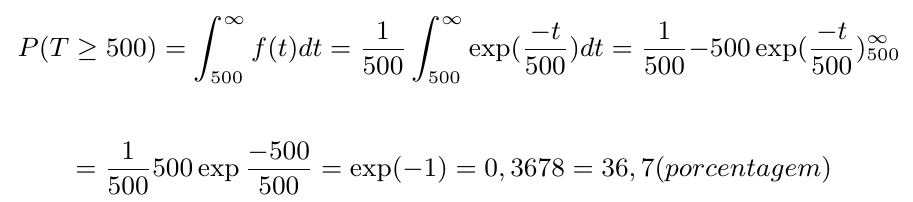
2.2.6 - Simulação do Modelo Weibull

A Distribuição de Weibull foi proposta originalmente por W. Weibull (1954) em estudos relacionados ao tempo de falha devido a fadiga de metais. Ela é frequentemente usada para descrever o tempo de vida de produtos industriais. A sua popularidade em aplicações práticas deve-se ao fato dela apresentar uma grande variedade de formas, todas com uma propriedade básica: a sua função de taxa de falha é monótona. Isto é, ou ela é crescente ou decrescente ou constante. Ela descreve adequadamente vida de mancais, componentes eletrônicos, cerâmicas, capacitores e dielétricos.

Definição 2.2.6.1

Uma variável aleatória contínua $ X $ uma distribuição de Weibull com parâmetros $ \alpha,\delta,\gamma> 0 $, se sua função densidade de probabilidade for dada por

$$f(t,\alpha,\delta,\gamma)=\frac{\delta}{\alpha}\left(\frac{t-\gamma}{\alpha}\right)^\delta\exp\left[-\left(\frac{t-\gamma}{\alpha}\right)^\delta\right],~t\leq\gamma { e } \alpha,\delta>0,$$

em que:

• $ \alpha $ parâmetro de escala, proporcional à média da variável aleatória;
• $ \delta $ parâmetro de forma, determina a forma mais ou menos achatada da fdp;
• $ \gamma $ parâmetro de locação, limite inferior para a variável aleatória.

A função densidade de probabilidade da distribuição de Weibull com parâmetro de locação ($ \gamma $) igual a zero é dada por:

$$f(t,\alpha,\delta)=\frac{\delta}{\alpha}\left(\frac{t}{\alpha}\right)^{\delta-}\exp\left[-\left(\frac{t}{\alpha}\right)^\delta\right],~t\leq0 {~e~} \alpha,\delta \ > \ 0.$$

Na Figura 1 apresentamos a curva da distribuição Weibull para diversos valores de $ \alpha $, $ \delta $ e $ \gamma $.

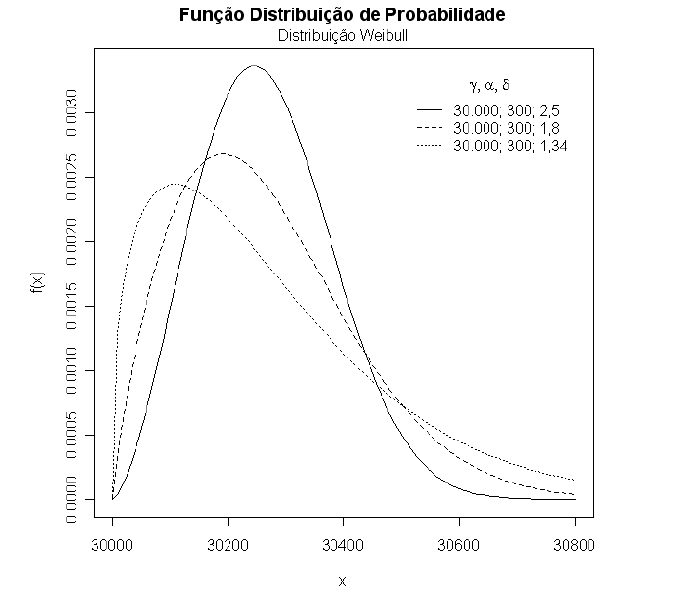
Figura 1: Função densidade de probabilidade da distribuição Weibull para diversos valores de $ \gamma $, $ \alpha $ e $ \delta $.

Propriedades

i) $ \mathbb{E}(X)=\alpha\Gamma\left(1+\frac{1}{\delta}\right) $;

ii) $ \text{Var}(X)=\alpha^2 ( \Gamma\left(1+\frac{2}{\delta}\right)-\left[\Gamma\left(1+\frac{1}{\delta}\right)\right]^2) $.

Dado que temos a informação de que a distribuição da variável aleatória é assimétrica e se comporta como o gráfico acima, estabelecemos apenas limite inferior para a variável aleatória.

Considere $ U $ uma variável aleatória com distribuição uniforme $ [0,1] $, então $ X=-\alpha[\ln(U)]^{\frac{1}{\delta}} $ tem distribuição Weibull com parâmetros e $ \alpha $ e $ \delta $. Assim, temos o seguinte algoritmo para simular a distribuição de Weibull:

1º) Gerar uma variável aleatória $ U $ com distribuição uniforme $ [0,1] $;

2º) Aplicar a fórmula: $ X=-\alpha[\ln(U)]^{\frac{1}{\delta}}. $

Exemplo 2.2.6.1

Para um certo tipo de tubo, os valores de escala $ \alpha $ e de forma $ \delta $ são iguais a $ 19,7 $ e $ 41,7 $ kwh. Qual a probabilidade deste tipo de tubo cumprir no mínimo $ 985 $ h?

$$P[X> 985]=1-\int_{0}^{0,985}\frac{\delta}{\alpha}\left(\frac{t}{\alpha}\right)^{\delta-1}\exp\left[-\frac{t}{\alpha}^\delta\right]dt=\exp\left[-\left(\frac{0,985}{\alpha}\right)^\delta\right]$$

$$=\exp\left[-\left(\frac{0,985}{19,7}\right)^{1,7}\right]=0,994.$$

Sendo assim, temos que a probabilidade deste tipo suportar no mínimo $ 985 $ h é de $ 99,4 (porcentagem) $.

3 - Método de Aceitação-Rejeição

O método de aceitação-rejeição está entre os mecanismos mais utilizados para geração de números aleatórios. Basicamente, este método gera amostras de uma distribuição de interesse a partir da geração de candidatos de uma distribuição conveniente (conhecida) e então, rejeitando um subconjunto dos candidatos gerados. O mecanismo de rejeição é construído de forma que, a amostra que será aceita segue, de fato, a distribuição de interesse.

Desta forma, suponha que queremos gerar valores aleatórios de uma densidade de probabilidade $ f $ definida em um algum conjunto $ \mathcal{X} $. Neste caso, este subconjunto pode ser um subconjunto da reta real $ \mathbb{R} $, de $ \mathbb{R}^d $ ou de um conjunto mais geral. Seja $ g $ uma densidade em $ \mathcal{X} $ a partir da qual sabemos gerar valores aleatórios e com a propriedade de que

$$f(x)\leq cg(x) \ \text{para todo} \ x\in\mathcal{X}$$

para alguma constante $ c $. No método de aceitação-rejeição, geramos um elemento $ X $ a partir da densidade $ g $ e aceitamos o elemento com probabilidade $ f(X)/cg(X) $. Este método pode ser implementado ao gerar um elemento $ U $ distribuido uniformemente em $ (0,1) $ e então, aceitamos $ X $ se $ U\leq f(X)/cg(X) $. Se $ X $ é rejeitado, um novo candidato é amostrado de $ g $ e repetimos o teste de aceitação. O processo se repete até que o teste de aceitação seja positivo; o valor aceito é um elemento selecionado de $ f $.

Algoritmo

O algoritmo do método de aceitação-rejeição pode ser apresentado nos passos abaixo.

1. Simula-se o valor $ X $ com densidade $ g $
2. Gera-se um número aleatório $ U\sim U(0,1) $
3. Se $ U\leq f(X)/cg(X) $, aceita-se o valor $ X $ e pare. Caso contrário, retorna-se ao passo 1.

Exemplo 3.1

Suponha que queremos simular uma variável aleatória $ X $ que assume os valores $ 1,2,\ldots,10 $ com probabilidade $ 0,11; 0,12; 0,09; 0,08; 0,12; 0,10; 0,09; 0,09; 0,10; 0,10 $, respectivamente. Desta forma, temos que a densidade que queremos simular é dada por $ f(x) = \mathbb{P}(X = x) $. Utilizaremos o método de aceitação-rejeição para resolver o problema a partir da densidade uniforme discreta em $ 1,2,\ldots,10 $, isto é, $ g(x) = \mathbb{P}(Y = x) = 1/10 $ para $ x = 1,\ldots,10 $. Para isto, escolhemos $ c $ da forma

$$c = \max_{x}\frac{g(x)}{f(x)} = \frac{0,12}{0,1} = 1,2$$

O algoritmo será da seguinte forma:

1. Na primeira etapa, geramos um valor aleatório $ U_1\sim U(0,1) $ e tomamos $ Y = \text{int}(10U_1) + 1 $. Desta forma, estaremos gerando um número aleatório da variável aleatória uniforme discreta em $ 1,2,\ldots,10 $.

2. No segundo passo, geramos um número aleatório $ U\sim U(0,1) $.

3. Se

$$U \leq \frac{f(Y)}{cg(Y)}=\frac{f(Y)}{1,2\times 0,1} = \frac{f(Y)}{0,12}$$

então $ X = Y $ e o algoritmo para. Senão, volte ao Passo 1.

Para verificar a validade do método de aceitação-rejeição, seja $ Y $ uma amostra obtida pelo algoritmo. Neste caso, $ Y $ tem a distribuição de $ X $ condicional ao fato de que $ U\leq f(X)/cg(X) $. Assim, para qualquer $ A\subseteq\mathcal{X} $, temos que

$$\mathbb{P}(Y\in A) = \mathbb{P}\left(X\in A|U\leq \frac{f(X)}{cg(X)}\right) = \frac{\mathbb{P}\left(X\in A, U\leq \frac{f(X)}{cg(X)}\right)}{\mathbb{P}\left(U\leq \frac{f(X)}{cg(X)}\right)}.$$

Portanto, dado $ X $, a probabilidade de $ U\leq f(X)/cg(X) $ é, simplesmente, $ f(X)/cg(X) $, já que $ U $ é uniforme, de forma que o denominador na equação acima é dado por

$$\mathbb{P}\left(U\leq \frac{f(X)}{cg(X)}\right) - \int_{\mathcal{X}}\frac{f(x)}{cg(x)}g(x)dx = \frac{1}{c}$$

e então, concluímos que

$$\mathbb{P}\left(Y\in A\right) = c\mathbb{P}\left(X\in A, U\leq\frac{f(X)}{cg(X)}\right) = c\int_A\frac{f(x)}{cg(x)}g(x)dx = \int_Af(x)dx.$$

Como $ A $ é arbitrário, segue que $ Y $ tem a densidade $ f $. Além disso, temos que a probabilidade de aceitação em cada tentativa é igual a $ 1/c $. Como o número de tentativas são independentes, o número de candidatos gerados até que um seja aceito possui distribuição geométrica com média $ c $.

4 - Risco de Investimentos em Finanças

4.1 - Introdução

A ideia de incerteza está sempre relacionada à ocorrência de acontecimentos futuros. Enquanto que a ideia de risco está relacionada ao grau de incerteza que atribuímos às possíveis situações futuras. Alguns autores fazem distinção entre incerteza e risco, considerando incerteza uma situação em que não se atribuiu qualquer probabilidade de forma objetiva, mas sim subjetiva.

A ideia de probabilidade objetiva refere-se aquela que é calculada através de informações e conhecimentos passados ou com base em uma sequência de dados reais. Já a probabilidade subjetiva refere-se à probabilidade estabelecida de forma qualitativa, ou seja, sem uma base de dados como suporte, podendo ser com base em uma avaliação de especialistas, com na intuição ou na experiência de profissionais da área, refletindo a crença pessoal sobre a ocorrência de determinado evento.

Já o risco para esses autores é tratado como uma situação em que podemos associar uma determinada distribuição de probabilidade. Neste sentido, podemos dizer que toda situação de risco admite um certo grau de incerteza, mas não o contrário, ou seja, a incerteza apresenta-se como uma condição necessária para o risco, mas não suficiente, isto devido à necessidade de atribuirmos uma probabilidade para o conceito de risco.

As medidas mais comuns para avaliar o risco são as medidas dispersão variância, desvio padrão e coeficiente de variação ou a probabilidade associada a um evento de sucesso, as quais estão relacionadas ao retorno do investimento.

• $ \mu = E(X)= \sum x_i \quad p(x_i) $ (Esperança);
• $ \sigma^2 = Var(X) = E(X^2)-E^2(X) $ (Variância);
• $ \sigma = \sqrt{[Var(X)]} $ (Desvio Padrão); e
• $ CV = \frac{\sigma}{\mu} \times 100 $ (Coeficiente de Variação).

A seguir, apresentamos os principais métodos utilizados para avaliação de investimentos.

4.2 - Avaliação de Investimentos

Na avaliação tradicional de investimentos os instrumentos mais utilizados são: Taxa Interna de Retorno (TIR), Índice de Lucratividade (IL), Valor Anual Equivalente Uniforme (VAEU), Payback e o Valor Atual Líquido (VAL) ou Recuperação de Capital. Estes métodos de avaliação de investimentos nos proporcionarão condições para aceitarmos ou rejeitarmos um investimento.

Na análise tradicional desses métodos, os fluxos de caixa futuros e taxa de desconto são determinados sem incerteza, o que simplifica a análise, porém a torna menos real. Para uma análise mais real deve-se considerar que existe incerteza quanto aos eventos futuros. Inicialmente apresentaremos os métodos acima de forma convencional e posteriormente focaremos nossa atenção sobre o método do valor atual líquido, mais amplamente aceito, e incorporaremos o conceito de grau de incerteza, ao qual associaremos uma distribuição de probabilidade.

4.2.1 - Método da Taxa Interna de Retorno (TIR)

Este método baseia-se no fluxo de caixa descontado para o cálculo da taxa interna de retorno, podendo ser definido como a taxa de desconto que torna o valor atual líquido do investimento igual a zero, expresso da seguinte forma:

$${TIR} = \sum \limits_{t=1}^{n} \frac{FC_t}{(1+i)^t}$$

sendo que

$ FC_t $ = Fluxo de Caixa do Projeto;

$ i $ = Taxa de Juros do Projeto; e

$ n $ = Tempo de Vida do Projeto.

Na decisão quanto ao projeto de investimento, quando se considera o método da taxa interna de retorno, deve-se considerar essa taxa como a taxa de desconto. Quando a taxa interna de retorno for maior que a taxa de desconto o investimento é considerado atrativo, caso contrário deverá ser rejeitado do ponto de vista econômico. Como a taxa interna de retorno é calculada sobre os fluxos de caixa da empresa e sobre o investimento total de empresa, deve-se considerar o custo de capital da empresa, ou seja, o investimento deverá ser recomendado se a TIR for maior que o custo de capital, caso contrário deverá ser rejeitado.

4.2.2 - Método do Índice de Lucratividade (IL)

O método do índice de lucratividade é um método que considera a razão entre o valor atual líquido do investimento e o Valor Inicial do Investimento (I$ _0 $), para uma dada taxa de desconto. O método de IL pode ser expresso da seguinte forma:

$${IL_t} = \frac{\sum \limits_{t=1}^{n} \frac{FC_t}{(1+i)^t}}{I_0}.$$

Como mostra a expressão acima, o projeto será recomendável sempre que o IL for superior a 1, dado que a expressão do numerador, fluxo de caixa somado ao valor residual do investimento, teria que ser maior que o valor do investimento inicial. Portanto, quanto maior o índice mais atrativo será o investimento. Por outro lado, caso o IL seja menor que 1 o investimento deverá ser rejeitado.

4.2.3 - Método do Tempo de Recuperação do Capital (Payback)

É um método que considera a extensão do tempo que seria suficiente para que os fluxos de caixa gerados pelo projeto cubra o investimento inicial. Este método está relacionado a uma ideia aparentemente simples, qual seja, ao tempo de recuperação do capital, portanto, quanto mais rápido o fluxo de caixa futuro proporcionar a recuperação do capital, maior a atratividade de se realizar o investimento.

Embora dificilmente as empresas não utilizem apenas o método do Payback como um único critério para tomar uma decisão sobre a realização de um investimento, é um instrumento que deve ser utilizado de forma auxiliar e complementar na tomada de decisão, principalmente na comparação de dois projetos. A utilização unicamente desse critério de avaliação de investimento pode ser comprometedora, já que sua análise restringe-se apenas ao período de recuperação de capital não considerando os períodos subsequentes, fundamentais para a análise do investimento.

4.2.4 - Método do Valor Anual Uniforme Equivalente (VAUE)

Este método procura encontrar uma série anual uniforme equivalente de um fluxo de caixa do investimento, considerando uma dada taxa mínima de atratividade. Esse método pode ser utilizado também para converter o desembolso de um fluxo de caixa e os seus benefícios no custo anual uniforme equivalente e no benefício anual uniforme equivalente, respectivamente. Assim, uma vez transformados os custos e os benefícios de um fluxo de caixa em seus respectivos valores anuais uniforme equivalente podemos compará-los.

$${VAUE} = \sum \limits_{t=1}^n \frac{FC_t}{(1+i)^t} \times \left[\frac{i \times (1+i)^t}{(1+i)^t -1}\right]$$

em que

$ FC_t $ = Fluxo de Caixa do Projeto;

$ i $ = Taxa de Juros do Projeto;

$ n $ = Tempo de Vida do Projeto.

sendo que o primeiro termo do lado direito da expressão é o valor atual de um fluxo de caixa e o segundo termo é o fator de recuperação do capital de uma série uniforme.

4.2.5 - Método do Valor Atual Líquido (VAL)

Na utilização do VAL como instrumento de avaliação de um dado investimento estamos interessados em saber se o projeto possui um valor maior que o seu custo, ou seja, é a soma dos valores dos fluxos de caixas futuros descontados a uma determinada taxa de juros obtidos durante o tempo de vida do projeto menos o investimento inicial, podendo ser um valor negativo ou positivo.

Para que o VAL atual seja positivo, o retorno esperado do investimento deve ser maior que o seu custo de oportunidade. Portanto, uma elevação no custo de oportunidade do investimento, isto é, da taxa de juros, implicará em uma redução no VAL do projeto, podendo até torná-lo negativo em dado horizonte de planejamento.

$${VAL} = - I_0 + \sum \limits_{t=1}^{n} \frac{FC_t}{(1+i)^t}$$

em que

$ FC_t $ = Fluxo de Caixa do Projeto;

$ i $ = Taxa de Juros do Projeto;

$ n $ = Tempo de Vida do Projeto; e

$ I_0 $ = Investimento Inicial.

Exemplo 4.2.5.1

Obter o Valor Atual Líquido (VAL) de um investimentos que tem as seguintes características:

Um previsão de fluxo de caixa futuro de $ (reais) $ 45.000,00 no ano $ t_1 $; $ (reais) $ 50.000,00 em $ t_2 $; $ (reais) $ 40.000,00 em $ t_3 $; $ (reais) $ 45.000,00 em $ t_4 $; e (reais) 55.000,00 em $ t_5 $.

Consideremos:

T = 5 anos;

$ I_0 = (reais) 150.000,00 $; e

$ i = 10(porcentagem). $

O Valor Atual Líquido desse Investimento será:

$${VAL} = - I_0 + \sum \limits_{t=1}^5 \frac{FC_t}{(1+i)^t}$$

$${VAL} = - 150.000 + \left[\frac{45.000}{(1+0,10)} + \frac{50.000}{(1+0,10)^2} + \frac{40.000}{(1+0,10)^3} + \frac{45.000}{(1+0,10)^4} + \frac{55.000}{(1+0,10)^5}\right]$$

$${VAL} = - 150.000 + 177.170,30$$

$${VAL} = 27.170,30.$$

4.2.6 - Aleatoriedade dos Parâmetros

Nos modelos de capitalização apresentados as variáveis utilizadas, a taxa de juros, o fluxo de caixa, o período são considerados variáveis aleatórias. Na prática, consideramos apenas uma destas variáveis como aleatória em cada análise, em geral, tomamos o fluxo de caixa como variável aleatória.

Ao admitirmos que o FC é uma variável aleatória, pois não temos como saber seu valor em um momento específico do tempo, calculamos o valor esperado do valor atual líquido $ \mathbb{E} \text{[VAL]} $ por:

$$\mathbb{E}\text{[VAL]} = \sum \limits_{t=1}^n \mathbb{E}\left[ \frac{FC_t}{(1+i)^t} \right]$$

A variância do valor atual líquido $ \text{Var[VAL]} $ será:

$$\text{Var[VAL]}= \sum \limits_{i=1}^n \text{Var} \left[ \frac{FC_t}{(1+i)^t} \right]$$

O desvio padrão do valor atual líquido é denominado por $ \sigma[VAL] $ que é dado pela raiz quadrada da variância, isto é:

$$\sigma \text{[VAL]} = \sqrt{ \text{Var[VAL]}}$$

O Exemplo 4.2.5.1 apresenta um Valor Atual Líquido positivo, o que significa que as soma dos fluxos de caixa descontados é superior ao valor do investimento, ou seja, o investimento vale a pena ser feito. No entanto, deve-se ressaltar que consideramos uma situação em condições que não há incerteza, ou seja, os fluxos de caixa futuros são certos.

Na análise de projetos de investimentos devemos ter um certo cuidado com o tipo de risco de consideramos, já que quando fazemos qualquer aplicação em qualquer ativo real ou financeiro estamos assumindo algum tipo de risco. O risco total a que qualquer investimento está submetido apresenta-se da seguinte forma: risco sistemático e risco não sistemático.

O risco sistemático ou conjuntural é definido como aquele risco devido ao sistema econômico, político e social idiossincrático de qualquer mercado, ou seja, o risco determinado pela situação conjuntural de uma nação. Em tais condições indica-se a diversificação na administração de portfólio de ativos como medida de redução de risco, apesar de não ser possível elimina-lo por completo.

Já o risco não sistemático é aquele risco que é inerente ao próprio ativo, ou seja, é um risco específico de um dado ativo real ou financeiro, não impactando nos demais ativos de um portfólio.

Quando tomamos uma decisão em fazer qualquer aplicação, devemos analisar as possíveis condições de retorno considerando diferentes situações ou estado de natureza, para isso podemos aplicar algumas metodologias tais como: análise de uma situação otimista e pessimista, análise de cenários e análise de sensibilidade.

Na avaliação de duas situações, uma otimista e a outra pessimista busca-se avaliar o retorno do projeto fazendo estimativas pessimistas e otimistas sobre os parâmetros de interesse.

Na análise de cenários busca-se elencar as principais variáveis que tem influência sobre a decisão a ser tomada. Uma vez identificadas as variáveis de impacto fixam-se os parâmetros e formam-se os vários cenários. Esta análise, geralmente é feita por um grupo de pessoas da área ou especialistas.

4.3 - Análise de Cenários

A análise de cenários pode ser melhor entendida através do seguinte exemplo:

Exemplo 4.3.1

Considere a possibilidade de um investidor comprar títulos da dívida (C-bond) do governo brasileiro para um prazo de 6 meses. Conforme dados da Gazeta Mercantil, sabemos que tais títulos estão sendo negociados a uma cotação de cerca de $ 50(porcentagem) $ do valor de face no mercado e com um risco Brasil na mesma data atingindo 2.449 pontos.

Estamos interessados aqui em fazer uma avaliação do valor do C-bond daqui a seis meses. Um grupo de analistas de mercado admitiu os seguintes cenários:

Cenário 1: O governo propõe uma renegociação da dívida das atuais condições, o que provoca uma redução em seu valor de mercado para 20 centavos de dólar do valor de face;

Cenário 3: O governo paga a dívida em reais, mas com a condição de que caso seja convertida exige um ágio de $ 25(porcentagem) $;

Cenário 3: O governo cumpre seus compromissos em dólar.

O mesmo grupo de analista admite as seguintes probabilidades aos eventos acima:

$ \mathbb{P}(C_1)=0,20 $, $ \mathbb{P}(C_2)=0,70 $, $ \mathbb{P}(C_3)=0,10 $ e, portanto, $ \sum \limits_{k=1}^3 \mathbb{P}(C)=1. $

Como a forma de pagamento dos títulos no mercado internacional é feita de forma linear podemos aplicar a seguinte expressão de capitalização simples:

$${Para~o~Valor~Futuro:~} F=A(1 + i \times n)$$

$${Para~o~Valor~Atual:~} A = \frac{F}{(1 + i \times n)}$$

$${Para~o~Valor~dos~Juros:~} i = \frac{F}{A \times n}$$

Como os detentores dos títulos da dívida externa brasileira estão interessados em saber o valor do título daqui a seis meses, temos:

$${Valor~Esperado~dos~títulos:~} \mathbb{E} [C-bond] = 0,20 \times 0,20 + 0,75 \times 0,70 + 1,00 \times 0,10 = 0,665$$

$$\Longrightarrow \mathbb{E} [C-bond^2] = 0,20^2 \times 0,20 + 0,75^2 \times 0,70 + 1,00^2 \times 0,10 = 0,50175$$

$${Desvio~Padrão:~} \sigma [C-bond] = \sqrt{0,5018-0,665^2} = 0,244$$

Os valores acima nos mostram que o valor médio do título da dívida do governo daqui a seis meses é: 0,665 e com um Desvio Padrão de 0,244.

Como o objetivo é obter o valor do título e o seu desvio no momento atual, aplicamos a forma de valor atual para juros linear, admitindo também uma taxa de $ 20(porcentagem) $ ao ano, isto é, próxima do risco Brasil, temos os seguintes valores:

$$E[VAC-bond] = \frac{E[C-bond]}{1 + i \times n}= \frac{0,665}{1 + 0,20 \times \frac{180}{365}}=0,6053$$

$$\sigma[VAC-bond] = \frac{\sigma[C-bond]}{1 + i \times n}= \frac{0,244}{1 + 0,20 \times \frac{180}{365}}= 0,2221.$$

Na análise acima, admitimos que a taxa de juros (i) e o período são fixos, apenas o C-bond é uma variável aleatória.

Os resultados anteriores nos dizem que o título da dívida do governo vale em média $ 57,80(porcentagem) $ do seu valor de face com um desvio de 28,58 centavos de dólar, o que significa que o valor do título está entre 28,22 e 86,38 centavos de dólar.

Podemos também utilizar o coeficiente de variação como uma medida de dispersão relativa:

$$CV = \frac{0,2221}{0,6053} \times 100 = 36,69$$

onde nos indica que um desvio com relação à média de $ 36,69(porcentagem) $, isto é, existe um risco muito elevado para os títulos do governo.

A título de exercício e de curiosidade,o leitor poderia calcular o valor médio e o desvio dos valores futuro e atual do C-bond considerando a avaliação feita pelo Megainvestidor George Soros, em que atribui uma probabilidade de $ 50(porcentagem) $ de reestruturação da dívida do governo brasileiro

4.4 - Análise de Sensibilidade

Na análise de sensibilidade são feitas estimativas otimistas e pessimistas sobre um grupo de variáveis que tem impacto no retorno do investimento. As variáveis que influenciam o Valor Atual Líquido ou Retorno sobre o investimento, tais como participação de mercado, vendas, custos variáveis e fixos entre outras são estimadas atribuindo diferentes valores e estados da natureza. A análise pode ser feita de forma mais simplificada assumindo independência entre as variáveis, isto é, atribui-se valores diferentes a apenas uma variável e mantém as outras constantes ou de forma mais complexa e real assumindo que são interdependentes.

Exemplo 4.4.1

Vamos considerar que uma determinada empresa faça um investimento inicial de 150.000.000 dólares e apresente as seguintes informações referentes à expectativa de ganho futuro nos próximos dez anos:

1. Considere que o preço do produto seja vendido por $ U$ 30,00 a unidade;
2. Imagine que a dimensão do mercado seja 75 milhões de produtos e que a empresa tenha uma participação de $ 20(porcentagem) $ do mercado;
3. Que o custo por unidade seja de $ 80(porcentagem) $ do preço vendido, isto é, de $ U$ 24,00;
4. O custo de oportunidade do capital é de $ 18(porcentagem) $ ao ano (taxa Selic).

Vamos assumir também que o investimento tenha sido feito através da compra de um equipamento com vida útil de 10 anos, sendo depreciado linearmente e que taxa de imposto de renda seja de $ 30(porcentagem) $ sobre lucro antes do imposto de renda.

	Valor (Dólares)
Receita Total (1)	450.000,00
Custos Variáveis (2)	360.000,00
Custos Fixos (3)	40.000,00
Depreciação (4)	15.000,00
LAIR (5)	35.000,00
IR (6)	10.500,00
Lucro Líquid (7)	24.500,00
Fluxo de Caixa (4+7)	39.500,00

A depreciação é adicionada ao fluxo de caixa devido ao fato de não representar uma saída efetiva de dinheiro.

Utilizando o método do valor atual líquido temos:

$$\text{VAL} = -150.000 + \sum \limits_{i=1}^{10} \frac{39500}{1,18^10}=27.517,41.$$

O Valor Atual Líquido positivo acima nos indica que o investimento a priori deveria ser feito. No entanto, antes de se tomar tal decisão baseada apenas na previsão dos valores da tabela acima, deve-se identificar as variáveis que podem ter maior influência sobre o valor atual líquido e atribuir alguma variação em suas estimativas e assim analisar o impacto no VAL.

Como tomar decisão apenas nas previsões da tabela acima pode ser muito otimismo, devemos considerar a possibilidade dessas previsões não serem as reais. Para isso, fazemos uma análise de sensibilidade sobre algumas variáveis que impactam no fluxo de caixa da empresa e, consequentemente, sobre o VAL.

Vamos agora considerar as seguintes alterações nas variáveis que influenciam no fluxo de caixa da empresa:

1. A empresa resolve elevar o preço por unidade em $ 20(porcentagem) $, isto é, passando para $ U$36,00;
2. Com a elevação no preço a participação de mercado da firma que era de $ 20(porcentagem) $ do total passa para $ 14(porcentagem) $, o que significa uma redução de $ 30(porcentagem) $ em sua participação de mercado;
3. A redução na participação de mercado provocou também uma redução nos custos variáveis da empresa de $ 15(porcentagem) $, dado que houve uma redução nos fatores de produção considerados variáveis.

Considerando que as variáveis alteradas acima estejam relacionadas podemos obter as seguintes conclusões:

• O efeito da elevação no preço do produto em $ 20(porcentagem) $ provocando uma redução na quantidade vendida de $ 30(porcentagem) $ implica que o produto possui elasticidade-preço da demanda positiva, isto é, uma elevação no preço provocou uma redução na quantidade proporcionalmente maior que a redução no preço.

Elasticidade-preço da demanda:

(há elementos em falta na equação acima)

$ \Delta $Q: representa a variação quantidade vendida;

$ \Delta $P: representa a variação nos preços;

P: preço; e

Q: quantidade vendida.

• Com a redução na participação de mercado houve consequentemente uma redução nos custos variáveis da empresa. No entanto, como a redução nos custos variáveis foi de $ 15(porcentagem) $, enquanto a redução na participação de mercado foi de $ 30(porcentagem) $, isto é, uma redução proporcionalmente menor que a redução na utilização de fatores de produção variáveis, dizemos que existe uma elasticidade-despesa positiva.

Elasticidade-despesa:

(há elementos em falta na equação acima)

$ \Delta $Q: representa a variação quantidade vendida;

$ \Delta $CT: representa a variação nos custos;

CT: custo de produção; e

Q: quantidade vendida.

Com as informações acima vamos elaborar uma nova previsão para o fluxo de caixa da empresa e para o valor atual líquido. Na análise de sensibilidade feita aqui consideramos que existe uma interdependência entre a variáveis que influenciam o VAL, tornando a análise mais real do que se fosse feita considerando independência entre as variáveis. Dessa forma, a previsão dos fluxos de caixa futuros se apresentariam da seguinte forma:

	Valor (Dólares)
Receita Total (1)	478.000,00
Custos Variáveis (2)	306.000,00
Custos Fixos (3)	40.000,00
Depreciação (4)	15.000,00
LAIR (5)	17.000,00
IR (6)	5.100,00
Lucro Líquid (7)	11.900,00
Fluxo de Caixa (4+7)	26.900,00

Utilizando o método do valor atual líquido temos:

$$\text{VAL} = -150.000 + \sum \limits_{i=1}^{10} \frac{26900}{1,18^{10}}=-29.109,08.$$

O resultado acima nos mostra um valor atual líquido negativo, indicando que o investimento deixou de ser atrativo. Isto ocorreu devido à alteração no preço do produto e uma possível redução na participação do mercado, impactando também em outras variáveis, já que existe uma interdependência entre as variáveis que influenciam o fluxo de caixa da empresa e que devem ser consideradas na análise de investimentos.

A consideração das elasticidades na elaboração da análise de investimento é de grande importância, já que nos dá uma ideia de como a variação em uma variável pode afetar as outras variáveis. O exemplo acima nos proporciona uma ideia de como devemos fazer uma análise de sensibilidade considerando a interdependência entre as variáveis, ou seja, na análise de sensibilidade devemos considerar valores otimistas, pessimistas e aqueles mais prováveis para cada variável. Em uma análise mais complexa seria de grande utilidade investigar o comportamento do projeto considerando diferentes cenários e várias combinações.

Na análise acima consideramos que o produto foi negociado em um mercado próximo de competitivo, em que a elasticidade-preço da demanda é positiva, no entanto, o leitor poderia, como exercício, considerar um mercado próximo de oligopólio em que a elasticidade preço da demanda é negativa.

Em muitas situações seria conveniente apresentar a questão de como as variáveis impactam no VAL da seguinte forma: Qual a quantidade de vendas ou aumentos no preço, por exemplo, que poderá tornar o projeto inconveniente, ou seja, com um valor atual líquido negativo. Ou ainda, a partir de qual volume de vendas a empresa passaria a ter um VAL positivo? Esta abordagem é conhecida como análise de ponto de equilíbrio.

Para respondermos a questão acima teríamos que encontrar o ponto em que o valor atual líquido fosse igual a zero e aí obter o volume de vendas compatível com o VAL = 0. Assim, no exemplo teríamos que encontrar o volume de vendas em que resultasse no seguinte:

$$\text{VAL}= -150.000 + \sum \limits_{i=1}^{10} \frac{FC_t}{(1+i)^t}= 0.$$

Neste caso, encontraríamos o seguinte fluxo de caixa para o que o valor atual líquido fosse igual a zero:

$$FC = \frac{150.000}{\frac{(1+i)^n - 1}{(1+i)^n \times i}} = \frac{150.000}{\frac{(1+0,18)^{10} - 1}{(1+0.18)^{10} \times 0,18}} = \frac{150.000}{4,494} = 33.377,20.$$

onde o denominador é o fator de valor atual para uma série uniforme com uma taxa de $ 18(porcentagem) $ ao ano e um período de 10 anos. O valor de $ U$ 33.377,20 representa o fluxo de caixa que a empresa teria caso o seu valor atual líquido fosse igual a zero.

	Valor (Dólares)
Receita Total (1)	406.265,20
Custos Variáveis (2)	325.012,56
Custos Fixos (3)	40.000,00
Depreciação (4)	15.000,00
LAIR (5)	26.253,14
IR (6)	7.875,94
Lucro Líquid (7)	18.377,20
Fluxo de Caixa (4+7)	33.377,20

Assim, uma vez encontrado o fluxo de caixa acima teríamos o seguinte valor atual líquido do investimento:

$$\text{VAL} = -150.000 + \sum \limits_{i=1}^{10} \frac{33.377,20}{(1+i)^{10}}= 0.$$

Com a receita total de $ U$ 406.265,70, para o mesmo preço de venda teríamos que ter o volume de vendas reduzido de $ U$15.000.000,00 para $ U$13.542.000,00 aproximadamente, ou seja, um volume de vendas que nos proporcionasse um valor atual líquido igual a zero. Portanto isto responderia nossa questão inicial, qual seja, a partir de qual volume de vendas passaríamos a obter um valor atual líquido positivo. Neste exemplo, por simplicidade, estamos supondo que as outras variáveis estão se mantendo constantes.

(imagem em falta)

Nesta análise de ponto de equilíbrio outras questões de caráter similar poderiam ser feitas com relação, por exemplo, ao custo de oportunidade do capital investido, isto é, qual seria a taxa de atratividade mínima que pudesse proporcionar um valor atual líquido positivo. O mesmo poderia ser feito para outras variáveis de interesse.

Em uma análise mais complexa e real poderíamos considerar o efeito da mudança de várias variáveis econômicas, simultaneamente que afetariam o valor atual líquido do projeto de investimento. Essa análise combinando todas possíveis alterações nas variáveis pode ser feita via simulação Monte Carlo, a qual trataremos mais adiante.

A avaliação do VAL é feita sobre o fluxo de caixa futuro descontados a uma determinada taxa de juros, no entanto, o problema aqui é conhecer com certeza qual será o fluxo de caixa futuro do investimento. Para introduzirmos a ideia de risco considerando a distribuição de probabilidade que o valor atual líquido poderá assumir vamos apresentar o seguinte exemplo:

Exemplo 4.4.2

Considere a compra de uma máquina com um dado fluxo de caixa a uma taxa de atratividade de 10(porcentagem) ao ano e com as seguintes probabilidades de alteração nos valores dos fluxos de caixa. Vamos assumir a seguinte sequência de fluxos de caixa $ (F_k )_{k=3} = (F_1, F_2, F_3 ) $ com as seguintes probabilidades $ \mathbb{P}(F_1), $ $ \mathbb{P}(F_2), $ $ \mathbb{P}(F_3), $ dadas abaixo. Além disso, admitimos que as variáveis fluxo de caixa (FC) são independentes entre os tempos específicos.

$ \bold{F_1} $	$ \bold{\mathbb{P}(F_1)} $	$ \bold{F_2} $	$ \bold{\mathbb{P}(F_2)} $	$ \bold{F_3} $	$ \bold{\mathbb{P}(F_3)} $
500	0,7	600	0,6	550	0,7
650	0,2	550	0,4	600	0,3
600	0,1

Para cada fluxo acima temos mais de uma alternativa, isto é, para o fluxo temos três possibilidades de ocorrências 500 com probabilidade 0,70, 650 com probabilidade 0.20 e 600 com probabilidade 0,10. O nosso problema aqui é determinar o valor esperado $ \mathbb{E} \text{[VAL]} $ e o desvio padrão $ \sigma \text{[VAL]} $ do valor atual líquido.

A distribuição de $ F_1 $ terá $ k_1=3 $ elementos, $ F_2 $ terá $ k_1=2 $ e $ F_3 $ com $ k_1=2, $ isto é, teremos o total de $ k_1 \times k_2 \times k_3 = 12 $ elementos. Para cada combinação de fluxos de caixa entre os períodos, teremos um correspondente valor atual líquido. No total temos 12 $ (3 \ast 2 \ast 2) $ combinações possíveis. A seguir, calculamos a VAL de cada combinação:

(imagem em falta)

$$\text{VAL}_1 = \frac{500}{1,10} + \frac{600}{1,10^2} + \frac{550}{1,10^3} = 1.363,64$$

$$\text{VAL}_2 = \frac{500}{1,10} + \frac{600}{1,10^2} + \frac{500}{1,10^3} = 1.326,07$$

(imagem em falta)

$$\text{VAL}_3 = \frac{600}{1,10} + \frac{600}{1,10^2} + \frac{550}{1,10^3} = 1.454,55$$

$$\text{VAL}_4 = \frac{500}{1,10} + \frac{550}{1,10^2} + \frac{550}{1,10^3} = 1.322,31$$

(imagem em falta)

$$\text{VAL}_5 = \frac{550}{1,10} + \frac{550}{1,10^2} + \frac{550}{1,10^3} = 1.367,69$$

$$\text{VAL}_6 = \frac{600}{1,10} + \frac{550}{1,10^2} + \frac{550}{1,10^3} = 1.413,22$$

(imagem em falta)

$$\text{VAL}_7 = \frac{500}{1,10} + \frac{600}{1,10^2} + \frac{600}{1,10^3} = 1.401,20$$

$$\text{VAL}_8 = \frac{550}{1,10} + \frac{600}{1,10^2} + \frac{600}{1,10^3} = 1.446,66$$

(imagem em falta)

$$\text{VAL}_9= \frac{600}{1,10} + \frac{600}{1,10^2} + \frac{600}{1,10^3} = 1.492,11$$

$$\text{VAL}_{10} = \frac{500}{1,10} + \frac{550}{1,10^2} + \frac{600}{1,10^3} = 1.359,88$$

(imagem em falta)

$$\text{VAL}_{11}= \frac{550}{1,10} + \frac{550}{1,10^2} + \frac{600}{1,10^3} = 1.405,33$$

$$\text{VAL}_{12} = \frac{600}{1,10} + \frac{550}{1,10^2} + \frac{600}{1,10^3} = 1.450,79$$

Fluxo	$ \text{Val} $	$ \mathbb{P}\text{[Val]} $	$ \mathbb{E}\text{[Val]} $	$ \mathbb{E}\text{[Val]} \times \mathbb{P}\text{[Val]} $
1	1.363,08	0,294	400,75	546.248,20
2	1.409,08	0,084	118,36	166.782,54
3	1.454,53	0,042	61,09	88.857,62
4	1.322,31	0,196	259,17	364.454,06
5	1.367.69	0,056	76,59	111.841,10
6	1.413,22	0,028	39,29	55.638,38
7	1.401,20	0,126	176,55	247.383,54
8	1.446,66	0,036	52,08	75.341,70
9	1.492,11	0,018	26,86	40.075,06
10	1.359,88	0,084	114,23	155.338,98
11	1.405,33	0,024	33,73	47.398,86
12	1.450,79	0,012	17,41	25.257,40
Total	-	1	1376,11	1.924.617,44

A probabilidade de cada combinação foi calculada assumindo a independência entre os períodos. O valor esperado e desvio padrão para os fluxos de caixa descontado são obtidos da seguinte forma:

$$\mathbb{E}\text{[VAL]} = \sum \text{VAL} \times \mathbb{P}\text{[VAL]} = 1.376,11$$

$$\mathbb{E}\text{[VAL}^2\text{]} = \sum \text{VAL}^2 \times \mathbb{P}\text{[VAL]} = 1.924.617,44$$

$$\sigma\text{[VAL]} = \sqrt{1.924.617,44 - 1.376,11^2} = 175,89.$$

Os resultados acima nos indicam um valor médio do fluxo de caixa descontado de 1.376,11, com um desvio padrão de 175,89. Logicamente na avaliação de se o investimento deveria ser feito ou não depende do valor do investimento inicial, e consequentemente, do valor atual líquido ser positivo ou negativo.

Poderíamos também calcular o coeficiente de variação, o qual representa uma medida relativa da dispersão associada ao investimento, ou seja, uma medida do risco, definida como a razão do desvio pela média:

$$CV = \frac{175,89}{1.376,11} = 0,1278.$$

O coeficiente de variação acima nos indica que existe um risco associado ao projeto de cerca de $ 12,78(porcentagem) $, significando um pequeno grau de dispersão relativa. Caso tenha-se um outro projeto seria interessante comparar os dois coeficientes, sendo que escolha com relação ao índice se daria para aquele que fosse menor.

O exemplo acima apresenta uma ideia de como a distribuição de um fluxo de caixa descontado, a uma determinada taxa de juros, é construída quando o investimento é analisado considerando o risco. No entanto, existem situações em que estamos interessados na transformação de determinada quantia em dinheiro em uma série de pagamentos uniformes equivalente. Por exemplo, dado o valor atual líquido de um determinado valor, qual a série anual equivalente deste valor atual líquido, já que dificilmente teríamos uma previsão de fluxos de caixa futuros iguais.

Nesse sentido, quando a finalidade for transformar os fluxos de caixa descontados, para um dado custo de oportunidade, em uma série anual uniforme equivalente utilizamos o método do Valor Anual Uniforme Equivalente - VAUE. Vamos apresentar abaixo um exemplo com o VAUE considerando uma situação em que existe incerteza.

Exemplo 4.4.3

Considere que a compra de uma máquina proporcione um valor anual uniforme dado inicialmente pelo seguinte fluxo de caixa e com as seguintes probabilidades:

$ \bold{F_1} $	$ \bold{\mathbb{P}(F_1)} $	$ \bold{F_2} $	$ \bold{\mathbb{P}(F_2)} $
150	0,8	170	0,7
120	0,1	120	0,3
80	0,1

O valor esperado dos fluxos $ F_1 $ e do $ F_2 $ são:

$$F_{\mu_1} = 150 \times 0,80 + 120 \times 0,10 + 80 \times 0,10 = 140$$

$$F_{\mu_2} = 170 \times 0,70 + 120 \times 0,30 = 155$$

E desvio padrão dos fluxos de caixa por:

$$\mathbb{E}[F_1^2] = \sum \limits_{t=1}^3 F_1 \times \mathbb{P}(F_1) = 150^2 \times 0,80 + 120^2 \times 0,10 + 80 \times 0,10 = 20.080$$

$$\mathbb{E}[F_2^2] = \sum \limits_{t=1}^2 F_1 \times \mathbb{P}(F_2) = 170^2 \times 0,70 + 120^2 \times 0,30 = 24.550$$

$$S(F_1)= \sqrt{\mathbb{E}[F_1^2] - \mathbb{E}[F_1]^2} = 20.080 - 140^2 = 21,91 $$

$$S(F_2)= \sqrt{\mathbb{E}[F_2^2] - \mathbb{E}[F_2]^2} = 24.550 - 155^2 = 22,91, $$

portanto o desvio será dado por:

$$\sqrt{\sum \limits_{t=1}^2[S(F_t)]^2 + 2 \times \sum S_1(F_1) \times S_2(F_2)} = 44,81.$$

Estamos interessados aqui no cálculo do valor atual líquido da série anual uniforme. Para isso vamos considerar um período de cinco anos a um custo de oportunidade de $ 10(porcentagem) $ ao ano. Neste caso, portanto, temos o seguinte VAL esperado:

$$\mathbb{E}\text{[VAL]} = \mathbb{E}[F_t] \times \frac{(1+i)^n - 1}{(1+i)^n \times i} = 559,14,$$

sendo que $ \mathbb{E}[F_t] $ é a série uniforme dos fluxos de caixa, que por simplificação é considerada como a média geral:

$ \sum\limits_{t=1}^T \frac{F_t}{n}=147,50, $ e o segundo termo do lado direito da equação é o fator de valor atual de uma série anual uniforme equivalente, dado pela soma dos termos de uma progressão geométrica. Já o desvio padrão do valor anual uniforme e seus coeficientes são representados respectivamente por:

$$S\text{[VAL]} = S(F_t) \times \sqrt{\frac{(1+i)^{2n}-1}{[(1+i)^2-1]\times (1+i)^{2n}}+ \frac{2}{i} \sum \limits_{t=1}^{n-1} \frac{(1+i)^{n-1}-1}{(1+i)^{n+t}}}$$

$$S\text{[VAL]} = 44,81 \times \sqrt{2,9260 + \frac{2}{0,10} \times 0,3102} = 135,40$$

$$CV = \frac{S\text{[VAL]}}{\mathbb{E}\text{[VAL]}} \times 100 = \frac{135,40}{559,14} \times 100 = 0,2422$$

O valor de 559,14 representa o valor atual de uma série uniforme, dada pelos fluxos de caixa de 147,50 em cinco anos a uma taxa de juros de 10(porcentagem) ao ano. Já o valor de 135,40 representa o desvio padrão do valor atual líquido da série anual uniforme. Enquanto, o CV de 24,22(porcentagem) significa uma dispersão relativa de grau médio do valor anual uniforme.

4.5 - Distribuição de Probabilidades

Quando analisamos um projeto de investimento envolvendo risco devemos considerar a distribuição de probabilidade que melhor pode representar o conjunto de valores que estamos interessados. Dentre os métodos de avaliação de investimentos, o mais extensivamente utilizado é o método do fluxo de caixa descontado ou valor atual líquido do projeto. Neste método, como já descrito, estamos interessados nos fluxos de caixa futuros que o investimento irá proporcionar, que será atualizado a dado custo de oportunidade. Neste sentido, teríamos que identificar uma distribuição de probabilidade para cada variável que tenha influência sobre o fluxo de caixa.

Mostraremos alguns exemplos de como algumas distribuições de probabilidade podem ser utilizadas em diferentes situações na análise de investimentos.

A seguir apresentaremos um exemplo de uma distribuição binomial. Uma distribuição binomial tem uma sequência de $ n $ experimentos idênticos e independentes e possui a seguinte representação: As observações $ X_1, X_2,\ldots,X_k $ têm distribuição binomial com parâmetros $ (n , p) $ e tamanho amostral $ n, $ onde cada experimento admite dois resultados: sucesso com probabilidade $ p $ ou insucesso com probabilidade $ (1 - p). $

A distribuição binomial pode ser escrita como:

$$\mathbb{P}(X = k) = \binom{n}{k} p^k (1-p)^{n-k}, \quad k=0,1,2,\ldots,n.$$

Exemplo 4.5.1

Suponha que uma máquina tenha sido adquirida de um certo fornecedor sem conhecer o valor atual líquido de cada máquina. No entanto, sabe-se que existem as seguintes possibilidades quanto ao valor atual líquido de cada máquina:

$$E_1 = {\text{VAL} \ > \ 0} \quad \text{e} \quad E_2 = {\text{VAL} \ > \ 0}.$$

Um grupo de especialistas analisando as máquinas disponíveis para compra atribuiu as seguintes probabilidades para os eventos possíveis:

$$\mathbb{P}(E_1) = p = 0,70 \quad {e} \quad \mathbb{P}(E_2) = 1 - p = 0,30.$$

De um total de 10 máquinas, queremos saber a probabilidade de 7 máquinas terem um $ \text{VAL} \ > \ 0 $ e de 3 máquinas terem um $ \text{VAL}\ > \ 0. $

Para sabermos tal probabilidade aplicamos a fórmula da binomial.

$$\binom{10}{3} 0,7^7 (1-0,7)^3= 0,2668.$$

O resultado acima nos indica existe $ 26,68(porcentagem) $ de probabilidade de 7 máquinas terem um $ \text{VAL} \ > \ 0 $ e de 3 máquinas terem um $ \text{VAL} \ > \ 0 $.

Uma extensão da distribuição binomial é a distribuição multinomial. Uma distribuição multinomial tem uma seqüência de $ n $ experimentos idênticos e independentes. As observações $ X_1, X_2,\ldots,X_k $ têm distribuição multinomial com parâmetros $ \theta_1, \theta_2,\ldots, \theta_k $ e tamanho amostral $ n, $ representada por:

$$\mathbb{P}(X_1, X_2,\ldots,X_k|\theta_1, \theta_2,\ldots, \theta_k) = \frac{n!}{X_1! X_2!\ldots X_k!} \theta_1^{x_1} \theta_2^{x_2} \ldots \theta_k^{x_k}.$$

Exemplo 4.5.2

Suponha que uma máquina tenha sido adquirida de um certo fornecedor sem conhecer o valor atual líquido de cada máquina. No entanto, sabe-se que existem as seguintes possibilidades quanto ao valor atual líquido de cada máquina:

$$E_1 = {150 \leq \text{VAL} \leq 190}; \quad E_2 = {130 \leq \text{VAL} \leq 150} \quad \text{e} \quad E_3 = {80 \leq \text{VAL} \leq 100}.$$

Um grupo de especialistas juntamente com as informações dos fornecedores analisando as máquinas disponíveis para compra atribuiu as seguintes probabilidades para os eventos:

$$\mathbb{P}(E_1) = \theta_1 = 0,50; \quad \mathbb{P}(E_2) = \theta_2 = 0,30 \quad \text{e} \quad \mathbb{P}(E_3) = \theta_3 = 0,20.$$

De um total de 10 máquinas, queremos saber a probabilidade de 5 máquinas terem um VAL entre 150 e 190, de 3 máquinas terem um VAL entre 130 e 150 e de 2 máquinas terem um VAL entre 80 e 100.

Para sabermos tal probabilidade utilizamos a distribuição multinomial.

$$\frac{10!}{5!3!2!} \times 0,50^5 \times 0,30^3 \times 0,20^2 = 0,085 = 8,5(porcentagem).$$

O resultado anterior nos indica existe $ 8,5(porcentagem) $ de probabilidade de 5 máquinas terem um VAL entre 150 e 190, de 3 máquinas terem um VAL entre 150 e 130 e 2 máquinas terem um VAL entre 80 e 100.

4.6 - Simulação Estocástica

Exemplo 4.6.1

Vamos considerar que uma determinada empresa faça um investimento e apresente as seguintes informações referentes à expectativa de ganho futuro nos próximos dez anos:

1. Considere que o preço do produto seja vendido por 30,00 (reais) a unidade;
2. Imagine que a dimensão do mercado seja 75 milhões de produtos e que a empresa tenha uma participação de $ 20(porcentagem) $ do mercado;
3. Que o custo por unidade seja de $ 80(porcentagem) $ do preço vendido, isto é, de 24,00 (reais)
4. O custo de oportunidade do capital de $ 18(porcentagem) $ ao ano (taxa selic).

Vamos assumir também que o investimento tenha sido feito atraves da compra de um equipamento com vida útil de 10 anos, sendo depreciado linearmente e que a taxa de imposto de renda seja de $ 30(porcentagem) $ sobre lucro antes do imposto de renda.

Investimento: 150.000,00	Valor
Receita Total (1)	450.000,00
Custos Variáveis (2)	360.000,00
Custos Fixos (3)	40.000,00
Depreciação (4)	15.000,00
LAIR (5)	35.000,00
IR (6)	10.500,00
Lucro Líquido (7)	24.500,00
Fluxo de Caixa (4+7)	39.500,00

A conta depreciação e adicionada ao fluxo de caixa devido ao fato de não representar uma saída efetiva de dinheiro.

Utilizando o método do valor atual líquido temos:

$$\text{VAL} = -150.000 + \sum \limits_{t=1}^{10} \frac{39500}{1,18^{t}}=27.517,41.$$

Para realizarmos a simulação estocástica, vamos estabelecer as relações entre as variaveis estabelecidas na tabela acima. Em geral, não podemos assumir que as variaveis são independentes.

Abaixo, apresentamos uma sugestão para simular o fluxo de caixa. Repetimos os 9 passos descritos abaixo 3 mil vezes e analisamos o risco contido no investimento.

1. Receita Total (RT) = Valor unitário do Produto (VUP) $\times$ Quantidade Vendida (QV)

Para simularmos a receita total (RT), vamos simular a quantidade vendida (QV) e tomar o valor unitário do produto (VUP) como fixo. Para isto, seguimos os passos:

1. Estudar a variável aleatória de interesse (QV). Analisar dados históricos e/ou a experiência do pessoal envolvido;
2. Determinar a distribuição que melhor descreve o comportamento da variavel. Neste caso, a partir de um modelo de series temporais para previsão de vendas, concluímos que a distribuição que melhor descreve o comportamento de vendas é uma distribuição normal com media de 14.000 e desvio padrão 1.000.
3. Gerar uma amostra da quantidade vendida (QV) utilizando simulação monte Carlo, denominada QV-S.

Assim, simulamos a receita total (RT) por ano fazendo:

$$\text{RT-S} = \text{VUP} \ast \text{QV-S}$$

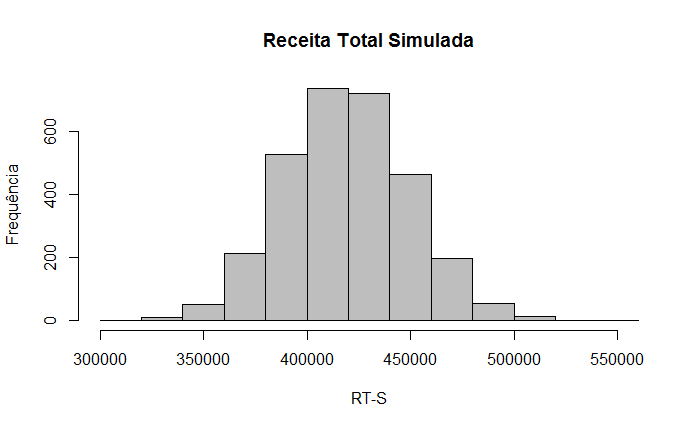
$ \text{2) Custo Variável (CV) = p} \ast \text{RT} $

O custo variável corresponde a uma porcentagem do valor da receita total (RT). No exemplo, consideramos que $ p=0,8 $. Aqui, vamos simular a porcentagem do RT que corresponde ao custo variável (CV). Através de dados históricos, determinamos que $ p $ varia entre $ 0,75 $ e $ 0,85 $. Esta é a única informação que temos sobre p. Assim, vamos modelar a variabilidade (o comportamento) da variável aleatória p via a distribuição uniforme entre $ [0,75; 0,85] $, para obtermos p-S. Com isso, simulamos o custo variável (CV-S) a cada ano por:

$$\text{CV-S = p-S} \ast \text{RT-S}$$

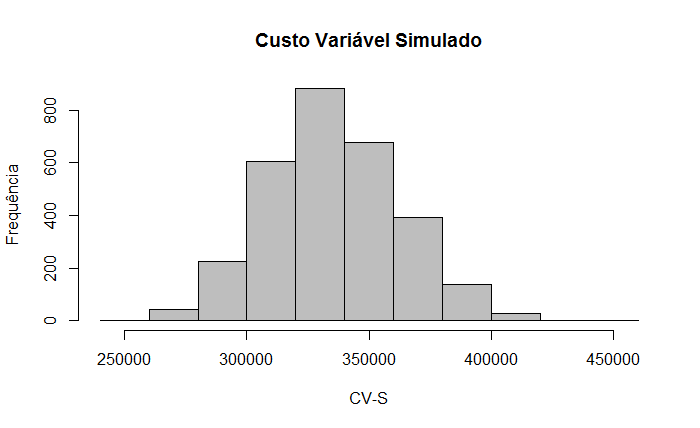
$ \text{3) Custo fixo (CF)} $

Este custo, como o proprio nome diz, é fixo. Assim, não estipulamos nenhuma distribuição de probabilidade.

$ \text{4) Depreciação (D)} $

A depreciação apresenta um comportamento fixo durante o projeto de investimento.

$ \text{5) LAIR} $

Esta variável aleatória e função das outras variáveis. Assim, obtemos uma amostra da variável aleatória LAIR em cada ano por:

$$\text{LAIR-S} = \text{RT-S} - \text{CV-S} - \text{CF} - \text{D}$$

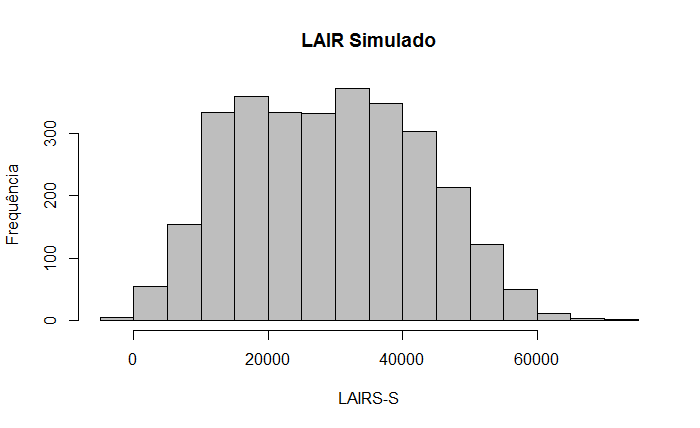
$ \text{6) IR} $

O imposto de renda (IR) corresponde a uma taxa i do valor do LAIR. No exemplo, consideramos que $ i = 30(porcentagem) $. Assim, podemos obter uma amostra do IR via

$$\text{IR-S} = 0,30 \ast \text{LAIRS-S}$$

$ \text{7) Lucro Líquido (LL)} $

Esta variavel aleatória é função das outras variáveis. Assim, obtemos uma amostra da variável aleatória LL em cada ano por:

$$\text{LL-S} = \text{LAIR-S} - \text{IR-S}$$

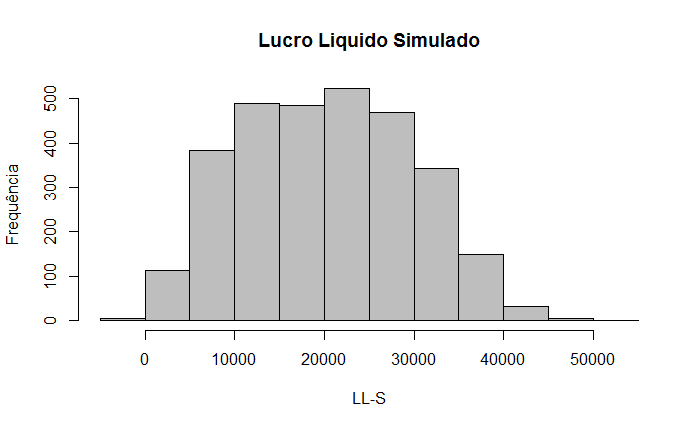
$ \text{8) Fluxo de Caixa }(FC_t) $

Esta variável aleatória é função das outras variáveis. Assim, para cada ano $ t $ obtemos uma amostra da variável aleatória FC por:

$$FC_t-S = \text{D} + \text{LL-S}$$

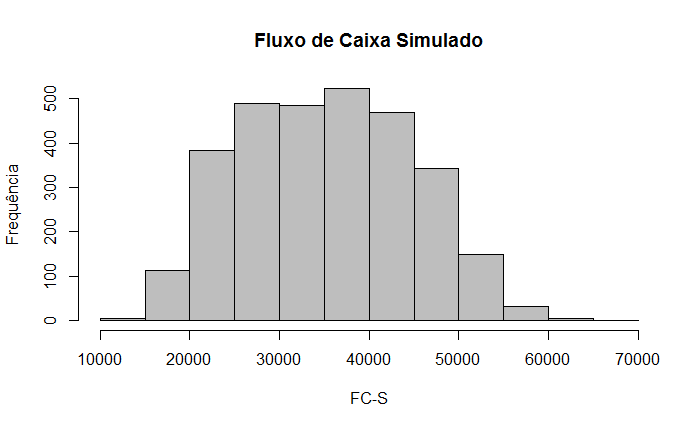
Repetimos os 8 passos acima para todos os anos da simulação, no caso deste exemplo 10 anos, para então podermos calcular o valor atual liquido do investimento.

$ \text{9) Valor Atual Liquido (VAL) em 10 anos} $

Para obtermos uma amostra do Valor Atual Líquido (VAL) considerando 10 anos, vamos simular o Fluxo de Caixa (FC) para cada ano, via o modelo discutido de (1) a (8), inclusive podemos modificar alguns parâmetros conforme alteramos o ano. Na sequência, obtemos uma amostra do VAL por

$$\text{VAL-S} = -150.000+\sum\limits_{t=1}^{t=10} {\frac{FC_t }{(1,18)^t}}$$

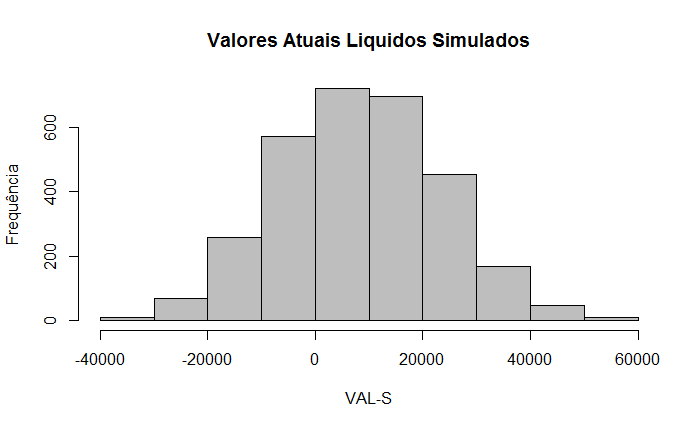
Segue que, nesta simulação repetida 3 mil vezes encontramos um risco de 30,3% de obter prejuízo no investimento.

Exercício 4.6.1

Assumir que o investimento inicial é uma variável aleatória e, assumir parâmetros distintos para as variáveis ao longo do tempo. Por exemplo, podemos admitir que o Valor Unitário do Produto (VUP) é função do tempo.

Um dos elementos mais importantes para uma boa análise de um projeto de experimento é a veracidade do modelo proposto. Abaixo, apresentamos uma forma de modelar a correlação entre as variaveis.

O efeito da elevação no preço do produto em $ 20(porcentagem) $ provocando uma redução na quantidade vendida de $ 30(porcentagem) $ implica que o produto possui elasticidade-preco da demanda positiva, isto é, uma elevação no preço provocou uma redução na quantidade vendida proporcionalmente maior que a redução no preço.

Elasticidade-preço da demanda: $ \varepsilon_p = \frac{\Delta QV}{\Delta P} \times \frac{P}{QV} = \frac{(15.000 - 10.500)}{(30-36)} \times \frac{30}{15.000} = -1,5 $

$ \Delta QV $: representa a variação quantidade vendida;

$ \Delta P $: representa a variação nos preços;

$ P $: preço de venda;

$ QV $: quantidade vendida.

Através de uma relação linear, tomamos

$$\text{QV} =a + b \ast \text{VUP}$$

Com isso, para quaisquer dois valores VUP$ _{1} $ e VUP$ _{2} $, obtemos que

$$\frac{\Delta QV}{\Delta VUP}=\frac{QV_2 -QV_1 }{VUP_2 -VUP_1 }=b$$

Observe que b apresenta como unidade quantidade por, para tornarmos b um valor relativo (sem unidade), vamos dividir pela razão QV / VUP.

(há elementos em falta na equação acima)

Assim, obtemos que a elasticidade é dada por:

$$\varepsilon _P =\frac{\Delta QV}{\Delta VUP}\frac{VUP_1 }{QV_1 }$$

Então, podemos interpretar a elasticidade como a proporção de variação de uma variável em relação à outra. No nosso exemplo, a redução percentual da QV é 1,5 da proporção de aumento do VUP.

Para simularmos a Receita Total (RT), vamos simular o VUP e obter a simulação da quantidade vendida através da elasticidade. Aqui, também vamos considerar a elasticidade como variável aleatória. Observe que,

$$\frac{\Delta QV}{\Delta VUP}=\varepsilon _P \ast \frac{QV_1 }{VUP_1 }$$

Assim, obtemos que

$$\Delta QV = \Delta VUP \ast \varepsilon_P \ast \frac{QV}{VUP_1}$$

Portanto, concluímos que

$$QV_2 = QV_1 + \Delta VUP \ast \varepsilon_p \ast \frac{QV_1}{VUP_1}$$

Aqui vamos simular três fluxos distintos: $ FC_1; FC_2 = \cdots = FC_6; FC_7 = \cdots = FC_{10} $. Na sequência, estabelecemos os passos para gerarmos o Fluxo de Caixa no instante de tempo $ t_1 $:

a) Gerar o Valor Unitario do Produto no instante $ t_1 $ $ (\text{VUP}_1) $. Vamos assumir que o $ \text{VUP} $ tem distribuição triangular com limite inferior 29 e limite superior igual a 31.

b) Gerar quantidade vendida no instante $ t_1 $ $ (\text{QV}_1) $ via uma distribuição triangular com limite inferior a $ 14.500 $ e limite superior de $ 15.500 $;

Obter a receita total simulada via equação: $ \text{RT-S} = \text{VUP-S} \ast \text{QV-S} $. A seguir, repetimos os mesmos passos dos itens $ (2) $ a $ (8) $ para obtermos o fluxo de caixa no instante $ t_1 $. Para obtermos o FC no instante $ t_2 $, vamos utilizar a seguinte politica de elevação de preços. Vamos subir em uma unidade monetária o valor esperado do Valor Unitário do Produto $ ( \mathbb{E} (\text{VUP})) $.

c) Vamos simular $ \text{VUP}_2 $ (no instante $ t_2 $) via uma distribuição triangular com limite inferior a 30 e limite superior 32;

d) A elasticidade preço da demanda é simulada através de uma distribuição triangular com limite inferior de –1,6 e limite superior de –1,4;

e) Através da $ \text{VUP}_1 $ e da elasticidade, obtemos

$$QV_2 = QV_1 + \Delta VUP \ast \varepsilon_p \ast \frac{QV_1}{VUP_1}$$

f) Gerar da Receita Total $ (RT) $ e repetir os passos dos itens $ (2) $ a $ (8) $ para obtermos uma amostra de fluxo de caixa $ (FC_2) $ no instante $ t2 $.

Por simplicidade, vamos considerar que o fluxo de caixa é constante até o instante $ t_2 $. Na realidade, estamos considerando que $ FC_2 = FC_3 = FC_4 = FC_5 = FC_6 $. Nos instantes $ t_7 $ até $ t_{10} $, vamos considerar que o valor esperado do Valor Unitário do produto sobe para 32 unidades monetárias. Assim, devemos repetir os passos (c), (d), (e) e (f) acima, para estabelecer o fluxo de caixa nos instantes $ t_7 $ até $ t_{10} $.

Após obtermos os fluxos de caixa em cada instante de tempo, podemos calcular o VAL via a fórmula:

$$\text{VAL-S} = -150.000 + \sum_{t=1}^{t=10} \frac{FC_t}{(1,18)^t}$$

Na sequência, vamos introduzir a elasticidade-despesa na simulação estocástica.

Com a redução na participação de mercado houve consequentemente uma redução nos custos variáveis da empresa. No entanto, como a redução nos custos variáveis foi de $ 15(porcentagem) $, enquanto a redução na participação de mercado foi de 30%, isto é, uma redução proporcionalmente menor que a redução na utilização de fatores de produção variáveis, dizemos que existe uma elasticidade-despesa positiva. A Elasticidade-despesa é dada por:

$$ \varepsilon_d = \frac{(\Delta CV)}{(\Delta QV)} \times \frac{QV}{CV} = \frac{(360.000 - 306.000)}{(15.000 - 10.500)} \times \frac{15.000}{360.000} = 0,5$$

$ \Delta QV $: representa a variação da quantidade vendida;

$ \Delta CV $: representa a variação nos custos total da variável;

$ CV $: custo total variável;

$ QV $: quantidade vendida.

Com as informações acima vamos elaborar uma nova previsão para o fluxo de caixa da empresa e para o valor atual líquido. Na análise de sensibilidade feita aqui consideramos que existe uma interdependência entre a variáveis que influenciam no $ \text{VAL} $, tornando a análise mais real do que se fosse feita considerando independência entre as variáveis.

Através de uma relação linear tomamos

$$CV = a + b\ast QV$$

Com isso, para quaisquer valores $ QV_1 $ e $ QV_2 $, obtemos que

$$\frac{\Delta CV}{\Delta QV} = \frac{CV_2 - CV_1}{QV_2 - QV_1} = b$$

Observe que b apresenta como unidade quantidade por, para tornarmos b um valor relativo (sem unidade), vamos dividir pela razão QV / CV. Assim, obtemos que a elasticidade é dada por:

(há elementos em falta na equação acima)

$$\varepsilon_P = \frac{\Delta CV}{\Delta QV} \ast \frac{QV_1}{CV_1}$$

Assim, podemos interpretar a elasticidade como a proporção de variação de uma variável em relação à outra. No nosso exemplo, a redução percentual da CV é 0,5 da proporção de redução da QV.

Para simularmos o Custo Variável (CV), simulamos a Quantidade Vendida (QV) e a elasticidade. Assim, obtemos que

$$CV_2 = CV_1 + \Delta QV \ast \varepsilon_P \ast \frac{CV_1}{QV_1}$$