19. Planejamento de Experimento

O conhecimento é a chave para a inovação e lucro, porém a aquisição de conhecimento pode ser complexa, demorada e custosa. Para termos sucesso, precisamos aprender a aprender. Esta é a chave para a geração de ideias, melhoria de processos, desenvolvimento de novos produtos. Uma ideia inicial (ou modelo) conduz a um processo de dedução de certas consequências necessárias que podem ser comparadas com dados. Quando há uma discrepância entre as consequências e os dados, somos conduzidos a um processo chamado indução, para modificar o nosso modelo inicial. Sendo assim, iniciamos um novo ciclo, em que modificamos o nosso modelo e comparamos com dados (antigos ou novos). Consequentemente, somos conduzidos a novas modificações e ganho de conhecimento.

Suponha que queremos resolver um problema em particular e a partir de uma certa especulação inicial, temos algumas ideias relevantes para solucioná-lo. Desta forma, vamos buscar dados que garantam ou refutem a nossa teoria. Algumas vezes, os fatos e os dados obtidos confirmam a nossa conjectura e, neste caso, o nosso problema estará resolvido. No entanto, frequentemente, nossa ideia inicial está parcialmente correta ou as vezes, totalmente errada. Neste caso, teremos que continuar pesquisando.

Em qualquer área de pesquisa, estamos interessados em saber quais variáveis são determinantes para obtermos sucesso, assim como limites inferior e superior de valores destas variáveis. Por exemplo, em um processo de retífica estamos interessados em saber quais variáveis são determinantes para um bom acabamento da peça. Em um processo de cura de resinas termorrígidas, a temperatura de cura e a quantidade de catalisador são variáveis importantes na determinação do tempo total de cura da resina polimérica. Com isso, estamos interessados em determinar valores adequados para estas variáveis de forma a manter nosso processo de acordo com as necessidades dos clientes.

Para estudarmos o comportamento das variáveis que influenciam em nossa pesquisa, realizamos EXPERIMENTOS. Para isto, escolhemos, de acordo com a conveniência do pesquisador, níveis para as variáveis de interesse e executamos experimentos em combinações dos níveis destas variáveis. O planejamento experimental é uma destas técnicas, que atualmente vem sendo usadas em grande escala. Por meio dele, pesquisadores determinam as variáveis que exercem maior influência no desempenho de um determinado processo. Esse é um dos objetivos do planejamento de experimento que em inglês é denominado Design Of Experiments (DOE).

1 - Introdução

Experimento

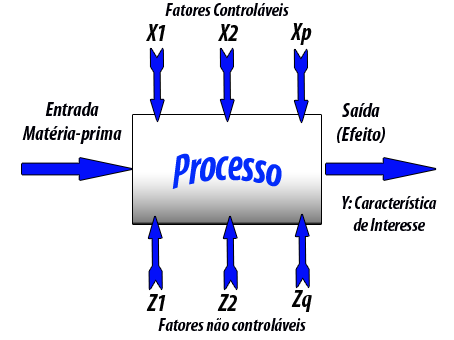
É um procedimento no qual alterações propositais são feitas nas variáveis de entrada de um processo ou sistema, de modo que se possa avaliar as possíveis alterações sofrida pela variável resposta, como também as razões de sua alteração.

Objetivos de um experimento planejado

• redução da variação do processo e melhor concordância entre os valores obtidos e os valores pretendidos;
• redução do tempo do processo;
• redução do custo operacional;
• melhoria no rendimento do processo.

Para obtermos sucesso na utilização destas técnicas, é necessário definir características da qualidade e todos os possíveis fatores que podem afetar estas características. Na sequência, realizamos um experimento para determinar relações entre as entradas ($ X_1 $ e $ X_2 $) e saídas ($ Y $).

Algumas aplicações típicas do planejamento de experimentos

• avaliação e comparação de configurações básicas de projeto;
• avaliação de diferentes materiais;
• seleção de parâmetros de projeto;
• determinação de parâmetros de projeto que melhorem o desempenho de produtos.
• obtenção de produtos que sejam mais fáceis de fabricar, que sejam projetados, desenvolvidos e produzidos em menos tempo, que tenham melhor desempenho e confiabilidade que os produzidos pelos competidores.

Três princípios básicos de um planejamento de experimentos

• replicação;
• aleatoriedade;
• blocagem.

Fazer um experimento com réplicas é muito importante por dois motivos. O primeiro é que isto permite a obtenção do erro experimental. A estimativa desse erro é básica para verificar se as diferenças observadas nos dados são estatisticamente diferentes. O segundo motivo se refere ao fato de que, se a média de uma amostra for usada para estimar o efeito de um fator no experimento, a replicação permite a obtenção de uma estimativa mais precisa desse efeito.

Os métodos estatísticos requerem que as observações, ou os erros, sejam variáveis aleatórias distribuídas independentemente. Os experimentos, com suas réplicas, devem ser realizados de forma aleatória, de modo a garantir a distribuição equânime de todos os fatores não considerados. Por exemplo, ao realizarmos um experimento para determinar as variáveis determinantes do acabamento da peça em uma retífica, devemos cuidar da aleatoriedade na execução do experimento, pois fatores críticos que não estão no estudo, como temperatura ambiente e lote de matéria prima, podem influenciar as variáveis de interesse de forma diferenciada, o que compromete a independência e a variabilidade entre os erros experimentais.

A blocagem é uma técnica extremamente importante, utilizada com o objetivo de aumentar a precisão de um experimento. Em certos processos, podemos controlar e avaliar, sistematicamente, a variabilidade resultante da presença de fatores conhecidos que perturbam o sistema, mas que não temos interesse em estudá-los. A blocagem é usada, por exemplo, quando uma determinada medida experimental é feita por duas diferentes pessoas, levando a uma possível não homogeneidade nos dados. Um outro exemplo seria quando um determinado produto é produzido sob as mesmas condições operacionais, mas em diferentes bateladas. De modo a evitar a não homogeneidade, é melhor tratar cada pessoa e batelada como um bloco.

Os experimentos devem ser realizados sequencialmente. O primeiro deles, denominado experimento de peneiramento (screening experiment), é usado para determinar que variáveis são importantes (variáveis críticas). Os experimentos subsequentes são usados para definir os níveis das variáveis críticas identificadas anteriormente, que resultam em um melhor desempenho do processo.

Em resumo, o que se quer aqui é obter um modelo matemático apropriado para descrever um certo fenômeno, utilizando o mínimo possível de experimentos. O planejamento experimental permite eficiência e economia no processo experimental e o uso de métodos estatísticos na análise dos dados obtidos resulta em objetividade científica nas conclusões.

Os métodos básicos usados para realizar um eficiente planejamento experimental têm como objetivos:

i. A seleção do melhor modelo entre uma série de modelos plausíveis;

ii. A estimação eficiente de parâmetros do modelo selecionado.

Todo planejamento experimental começa com uma série inicial de experimentos, com o objetivo de definir as variáveis e os níveis importantes. Podemos ter variáveis qualitativas (tipo de catalisador, tipo de equipamento, operador, etc.) e quantitativas (temperatura, pressão, concentração índice de inflação, ph do meio, etc.). Os resultados devem ser analisados e modificações pertinentes devem ser feitas no planejamento experimental. A Figura 1 apresenta um resumo desta estratégia inicial.

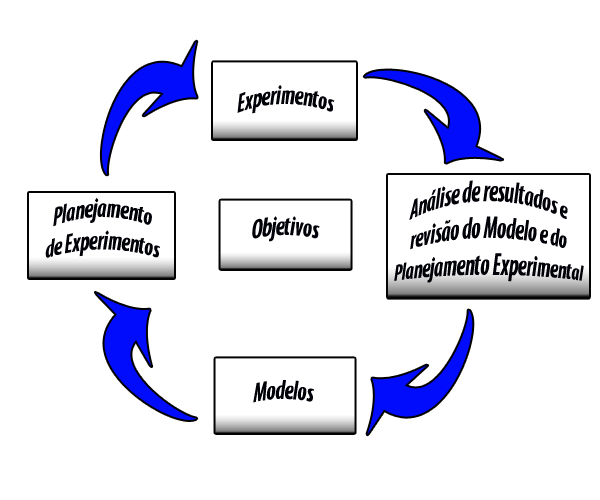
Figura 1: Fluxograma DOE.

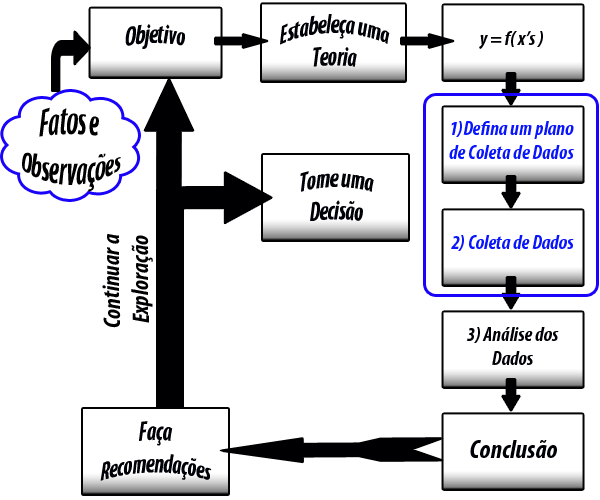
É importante frisar que os métodos que serão descritos aqui não substituem a imaginação e o bom senso, mas eles ajudam a economizar tempo e dinheiro, uma vez que eles conduzem à objetividade da análise de resultados. Antes de começar a realizar os experimentos, os objetivos e os critérios devem estar bem claros, de modo a dar subsídios para a escolha:

1. das variáveis envolvidas nos experimentos;
2. da faixa de variação das variáveis selecionadas;
3. dos níveis escolhidos para essas variáveis. No caso de muitos fatores, é melhor escolher inicialmente dois níveis;
4. da variável de resposta;
5. do planejamento experimental. Nessa etapa, há que se considerar o tamanho da amostra (número de réplicas), a seleção de uma ordem de realização dos tratamentos e se há vantagem em fazer a blocagem dos experimentos; dos métodos de análise dos resultados dos experimentos. Os métodos estatísticos são usados para guiar uma tomada objetiva de decisão.

2 - Definições

Experimentos Fatoriais

Este tipo de planejamento experimental é adequado para estudar, de forma eficiente e econômica, o efeito conjunto de vários fatores sobre uma variável resposta de interesse. De um modo geral, cada fator poderia ser observado em vários níveis, porém os experimentos mais utilizados na indústria são os experimentos fatoriais em que cada fator assume apenas dois níveis, por exemplo dois valores de temperatura, dois níveis de um reagente, e principalmente duas características qualitativas de um determinado fator, por exemplo uma peça “com” ou “sem” determinada característica. Geralmente, deseja-se comparar o nível atual de trabalho de determinado fator com um novo nível deste fator, para verificar se o nível atual proporciona um bom aproveitamento do processo ou se este poderia ter resultados melhores utilizando um novo nível.

Efeitos

O efeito de um fator pode ser definido como a mudança sofrida pela variável resposta quando passamos do nível baixo do fator para o nível mais alto.

Considere um experimento fatorial em que cada fator tenha dois níveis e r repetições para cada tratamento (combinações de níveis). Uma maneira especial de representar os tratamentos é usando a representação dos efeitos, como descrita abaixo:

Notação:

• Atribua os sinais de - se nível baixo e + se nível alto para cada um dos fatores, ou;
• Atribua valor 0 ou 1 aos níveis de cada um dos fatores;
• Denotar a presença ou ausência do nível alto do fator, isto é:

[0] = Ambos os fatores estão ausentes (ambos em nível baixo);

[a] = Somente o fator A está presente (nível alto em A e baixo em B);

[b] = Somente o fator B está presente (nível alto em B e baixo em A); e

[ab] = Ambos os fatores AB estão presentes (ambos em nível alto).

Interações

Se o comportamento de um fator não é o mesmo nos dois níveis de outro fator, dizemos que existe interação entre os fatores. Matematicamente, o efeito da interação entre dois fatores é a metade da diferença entre os efeitos de um fator nos níveis do outro fator.

Interação: A interação ocorre entre dois ou mais fatores se o efeito de um fator na resposta depende do nível dos outros fatores.

Para maiores informações, você pode consultar o conteúdo Análise Estatística do livro ANOVA.

3 - Experimentos Fatoriais Completos

Um Experimento Fatorial Completo inclui todas as possíveis combinações entre os níveis dos fatores do experimento. Assim, em um experimento aleatório completo todos os tratamentos possíveis devem ser utilizados no experimento, mas a ordem das corridas é aleatorizada. A aleatorização é essencial para uma boa conclusão, pois o experimentador não pode estar certo de todas as variáveis que influenciam o experimento, portanto desta maneira nos certificamos de que um maior número de variáveis externas ao experimento influenciam de maneira igual. Mesmo que alguém possa identificar e controlar algumas dessas variáveis, complicações não planejadas são comuns. A aleatorização não evita complicações dentro do experimento, mas oferece alguma proteção contra o vício do experimento.

Passos para a construção de um experimento aleatório completo

1. Enumere todas as combinações entre níveis dos fatores. De 1 a N. Inclua as réplicas.
2. Gere uma sequência de números aleatórios para a sequência de 1 até N, utilizando tabelas de números aleatórios ou o computador.
3. Conduza o experimento seguindo a sequência obtida na aleatorização.

Os planejamentos de experimentos devem, quando possível, incluir réplicas. Devemos trabalhar com o maior número de réplicas possíveis, pois assim, utilizamos mais informação sobre o nível de trabalho. Desta forma vários testes permitirão estimar a variância do erro do experimento e ainda investigar a adequabilidade do modelo ajustado. Quando possível, devemos balancear as combinações para um número igual de vezes. O único requisito é que seja feito um número suficiente de réplicas para obter uma estimativa satisfatória do erro experimental.

3.1 - Experimentos Fatoriais 2^k

Os experimentos fatoriais $ 2^k $ têm k fatores, com dois níveis cada.

Um esquema de um experimento fatorial pode ser visto da seguinte maneira:

(imagem em falta)

Exemplo 3.1.1

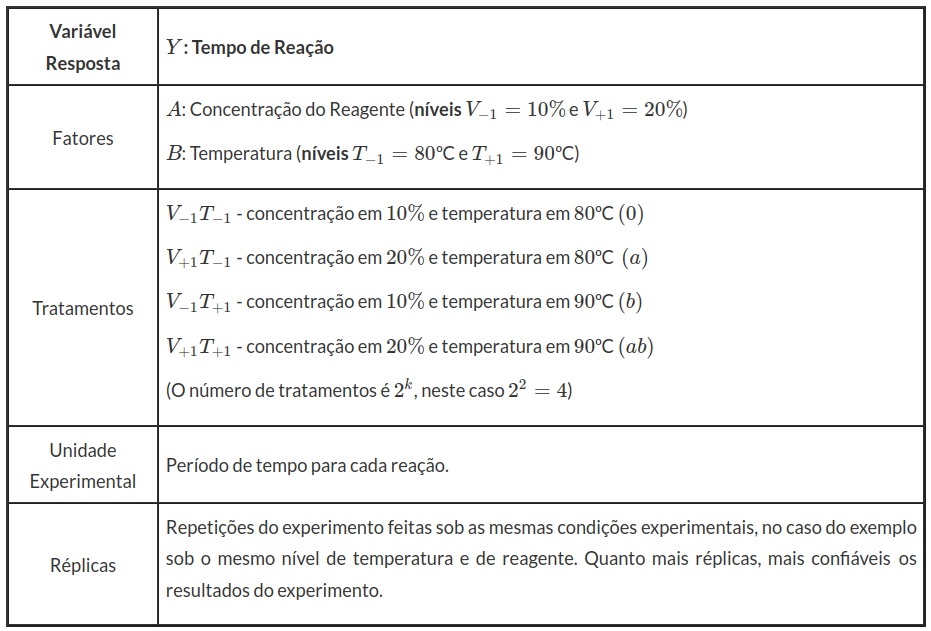
Estudar o efeito no tempo de uma determinada reação química com a variação de temperatura e concentração de um reagente, como mostra o esquema a seguir.

(imagem em falta)

Para o exemplo acima, podemos definir:

Os experimentos $ 2^k $ constituem uma importante classe de planejamento pois:

• O número de ensaios envolvidos na realização desses experimentos é relativamente pequeno.
• A região experimental nestes experimentos pode ser restrita, porém pode indicar tendências e determinar uma melhor (ou mais adequada) direção para novos experimentos.
• Estes experimentos podem ser “aumentados” com a inclusão de novos níveis e/ou novos fatores.

Aleatorização

A aleatorização é um procedimento que conduz as combinações dos níveis dos fatores em uma sequência de tratamentos de maneira que os tratamento sejam embaralhados.

Suponha que tem-se um experimento com 3 fatores, sendo eles: Tipo de Metal (ferro, alumínio), Porosidade (poroso, não poroso) e Tipo de Lubrificante (A, B, C e D). Tem-se

$${Número Total de Tratamentos}=2\times2\times4=16$$

Assim, enumera-se cada tratamento como na Tabela a seguir e gera-se um sequência de números aleatórios de 1 a 16, por exemplo a sequência {8, 15, 2, 12, 16, 6, 7, 11, 10, 14, 9, 1, 3, 4, 13, 5}.

Na Tabela mostramos a ordem das corridas.

Combinação	Tipo de metal	Porosidade	Lubrificante	Ordem	Corrida
1	ferro	poroso	A	1	8
2	ferro	poroso	B	2	15
3	ferro	poroso	C	3	2
4	ferro	poroso	D	4	12
5	ferro	não poroso	A	5	16
6	ferro	não poroso	B	6	6
7	ferro	não poroso	C	7	7
8	ferro	não poroso	D	8	11
9	alumínio	poroso	A	9	10
10	alumínio	poroso	B	10	14
11	alumínio	poroso	C	11	9
12	alumínio	poroso	D	12	1
13	alumínio	não poroso	A	13	3
14	alumínio	não poroso	B	14	4
15	alumínio	não poroso	C	15	13
16	alumínio	não poroso	D	16	5

3.1.1 - Experimentos fatoriais 2^2

Considere um experimento fatorial completo com somente 2 fatores.

Temos $ 2^2 $ = 4 combinações entre os níveis dos fatores.

Considere o Exemplo 3.1.1, onde deseja-se estudar o efeito no tempo de uma determinada reação química com a variação de temperatura e concentração de um reagente. Tínhamos que

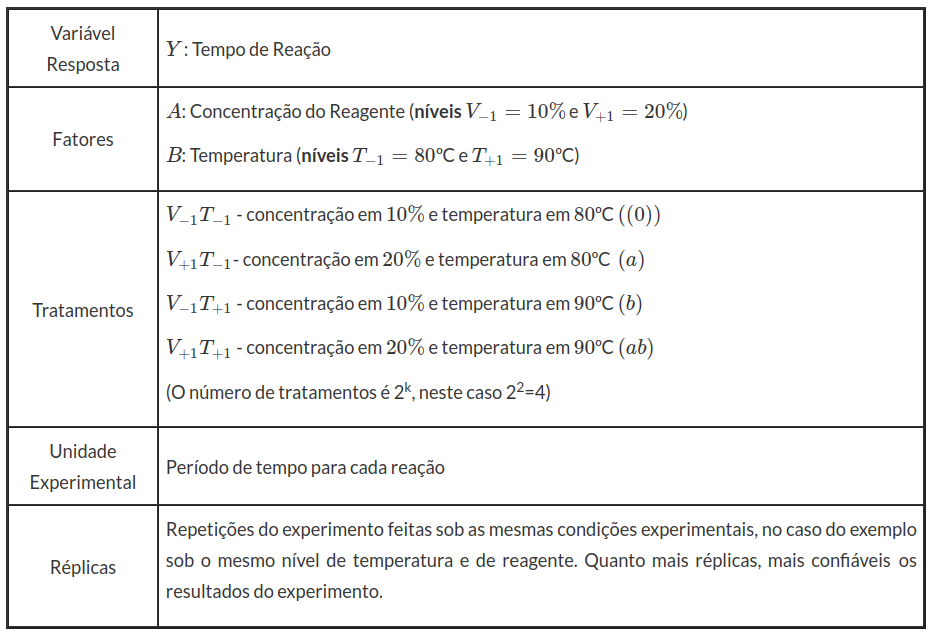
Considere 3 réplicas deste experimento (completo), com os dados abaixo, e a ordem de execução entre parênteses:

Tratamento	A	B	Y1	Y2	Y3	Y
0	-1	-1	26,6(1)	22,0(7)	22,8(10)	23,8
(a)	1	-1	40,9(4)	36,4(9)	36,7(12)	38
(b)	-1	1	11,8(3)	15,9(8)	14,3(11)	14
(ab)	1	1	34,0(2)	29,0(5)	33,6(6)	32,2

Primeiramente fazemos um gráfico com as médias dos valores de $ Y $ para os diferentes tratamentos:

(imagem em falta)

Observamos que a melhor configuração seria A- e B+. No entanto, a interação entre A e B pode ser significativa, assim nada podemos concluir neste momento.

Sejam:

• $ \overline{Y_{A+}} $ a média de Y com o fator A no nível + (alto);
• $ \overline{Y_{A-}} $ a média de Y com o fator A no nível - (baixo); e assim para os demais fatores.

Calcula-se o efeito médio do fator A como sendo

$$A=\overline{Y_{A+}}-\overline{Y_{A-}}=\frac{ab+a}{2}-\frac{b+(0)}{2}=\frac{32,2+38}{2}-\frac{23,8+14}{2}=16,2$$

e analogamente o efeito médio do fator B é dado por

$$B=\overline{Y_{B+}}-\overline{Y_{B-}}=\frac{ab+b}{2}-\frac{a+(0)}{2}=\frac{14+32,2}{2}-\frac{23,8+38}{2}=-7,8.$$

Para encontrar o efeito da interação entre os fatores A e B fazemos

$$AB=\frac{ab-a}{2}-\frac{b-(0)}{2}=\frac{32,2-38}{2}-\frac{14-23,8}{2}=-2,9-(-4,9)=2$$

Gráfico de Interações

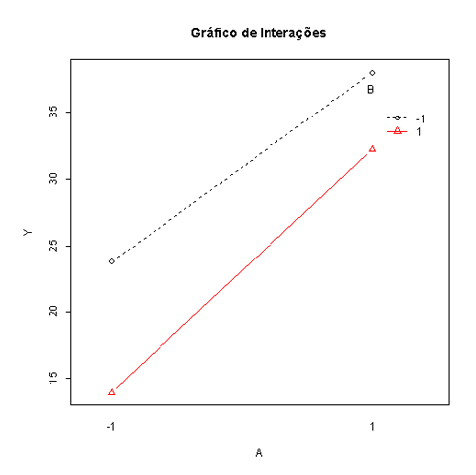
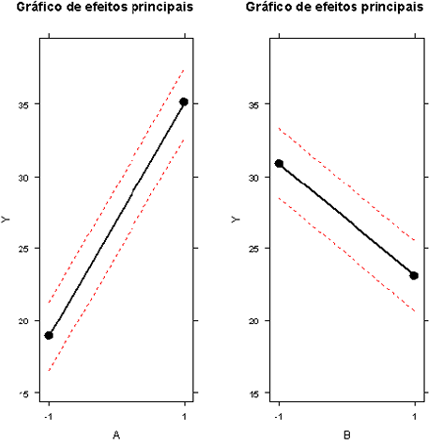
Gráfico de Efeitos principais

3.1.2 - Análise dos efeitos via ANOVA

Na análise de um experimento usando a Tabela da ANOVA é possível quantificar a parcela da variabilidade total que é devida a cada fator e à interação entre eles.

Para isto, seja $ y_{ijk} $ a k-ésima observação no nível i de A e j de B. Em geral, i = 1, …, a; j = 1, …,b; k = 1, …, r; onde a e b são os números de níveis de A e B, respectivamente e r é o número de réplicas do experimento. No caso de experimentos com 2 níveis para cada fator, a = b = 2.

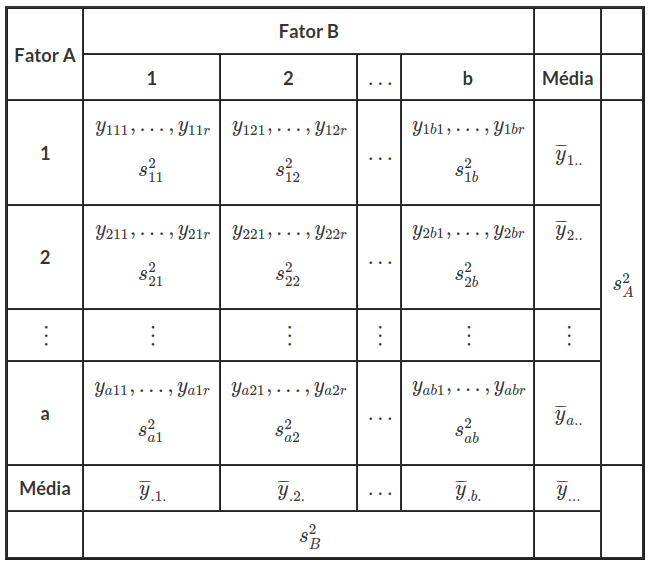
Os resultados da tabela são obtidos da seguinte forma:

• $ y_{i\cdot\cdot}=\displaystyle\sum_{j=1}^{b}\sum_{k=1}^{r}y_{ijk}~ $, a soma de todas as observações no nível i de A e $ \overline{y_{i\cdot\cdot}}=\cfrac{y_{i\cdot\cdot}}{br},~ $ a média destas observações, para i = 1, …, a.
• $ y_{\cdot j\cdot}=\displaystyle\sum_{i=1}^{a}\sum_{k=1}^{r}y_{ijk}~ $, a soma de todas as observações no nível j de B e $ \overline{y_{\cdot j\cdot}}=\cfrac{y_{\cdot j\cdot} }{ar} $, a média destas observações, para j = 1, …, b.
• $ y_{i j \cdot}=\displaystyle\sum_{k=1}^{r}y_{ijk}~ $, a soma de todas as observações que têm nível i de A e j de B (ao mesmo tempo) e $ ~\overline{y_{i j \cdot}}=\cfrac{y_{i j \cdot}}{r},~ $ a média destas observações, para i = 1, …, a; j = 1, …, b.
• $ y_{\cdot\cdot\cdot}=\displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{r} y_{ijk},~ $ a soma de todas as observações e $ ~\overline{y_{\cdot\cdot\cdot}}=\cfrac{y_{\cdot\cdot\cdot}}{abr}~ $ a média geral das observações.

Para quantificar a variação referente a cada fator e a interação entre eles é preciso separar a Soma de Quadrados Total (SQT), que representa a variação total. Para isso, vamos mostrar que

$$SQ_T = SQ_A + SQ_B + SQ_{AB} + SQ_E$$

onde

$$SQ_A=br\sum_{i=1}^{a}(\overline{y_{i..}}-\overline{y_{…}})^{2}=\displaystyle\cfrac{1}{br}\sum_{i=1}^{a}y_{i\cdot\cdot}^2-\cfrac{y_{\cdot\cdot\cdot}^2}{abr}$$

$$SQ_B=ar\sum_{j=1}^{b}(\overline{y_{. j.}}-\overline{y_{…}})^{2}=\displaystyle\cfrac{1}{ar}\sum_{j=1}^{b}y_{\cdot j\cdot}^2-\cfrac{y_{\cdot\cdot\cdot}^2}{abr}$$

e a soma de quadrados do efeito da interação

$$SQ_{AB}=r\sum_{i=1}^{a}\sum_{j=1}^{b}(\overline{y_{ij.}}-\overline{y_{i..}}-\overline{y_{.j.}}-\overline{y_{…}})^{2}=\cfrac{1}{r}\sum_{i=1}^{a}\sum_{j=1}^{b}y_{ij\cdot}^2-\cfrac{y_{\cdot\cdot\cdot}^2}{abr}-SQ_A-SQ_B.$$

Temos também que a Soma de Quadrados Total é dada por

$$SQ_{T}=\displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{r}(y_{i j k }-\overline{y_{\cdot\cdot\cdot}})^2=\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{r}y_{ij k }^2-\cfrac{y_{\cdot\cdot\cdot}^2}{abr}$$

e finalmente a Soma de Quadrados dos Erros

$$SQ_{E}=\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{r}(y_{i j k}- \overline{y_{i j\cdot}})^2=\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{r}y_{i jk}^2-\cfrac{1}{r} \sum_{i=1}^{a}\sum_{j=1}^{b}y_{i j \cdot}^2.$$

Como estamos trabalhando com experimentos fatoriais $ 2^2 $ então tomando $ a=b=2 $ temos

$$SQ_A=br\displaystyle\sum_{i=1}^{a}(\overline{y_{i..}}-\overline{y_{…}})^2=2 r [(\overline{y_{2..}}-\overline{y_{…}})+(\overline{y_{1..}}-\overline{y_{…}})]^2$$

ou seja,

$$SQ_A= 2 r \left[\left(\overline{y_{2..}}-\frac{\overline{y_{2..}}+\overline{y_{1..}}}{2}\right)+\left(\overline{y_{1..}}-\frac{\overline{y_{2..}}+\overline{y_{1..}}}{2}\right)\right]^2= 2 r\left[\left(\frac{\overline{y_{2..}}-\overline{y_{1..}}}{2}\right)+\left(\cfrac{\overline{y_{1..}}-\overline{y_{2..}}}{2}\right)\right]^2$$

e então, concluímos que

$$SQ_A=4 r\left(\displaystyle\cfrac{\overline{y_{2..}}-\overline{y_{1..}}}{2}\right)^2=r(\overline{y_{2..}}-\overline{y_{1..}})^2=r ({efeito de A})^2$$

Para os experimentos fatoriais $ 2^2, $ tem-se:

$$SQ_A = r ({efeito de A})^2$$

$$SQ_B=r ({efeito de B})^2~{ e }$$

$$SQ_{AB}=r({efeito de AB})^2.$$

Assim, constrói-se a Tabela da ANOVA:

Fonte de Variação	Graus de Liberdade	Soma de Quadrados	Quadrados Médios	Estatística F
$ A $	$ a-1 $	$ SQ_A $	$ QM_A=\displaystyle\frac{SQ_A}{a-1} $	$ \displaystyle\frac{QM_A}{QM_E} $
$ B $	$ b-1 $	$ SQ_B $	$ QM_B=\displaystyle\frac{SQ_B}{b-1} $	$ \displaystyle\frac{QM_B}{QM_E} $
$ AB $	$ (a-1)(b-1) $	$ SQ_{AB} $	$ QM_{AB}=\displaystyle\frac{SQ_{AB}}{(a-1)(b-1)} $	$ \displaystyle\frac{QM_{AB}}{QM_E} $
$ Erro $	$ ab(r-1) $	$ SQ_E $	$ QM_{E}=\displaystyle\frac{SQ_{E}}{ab(r-1)} $
$ Total $	$ abr-1 $	$ SQ_T $

Exemplo 3.2.1.1

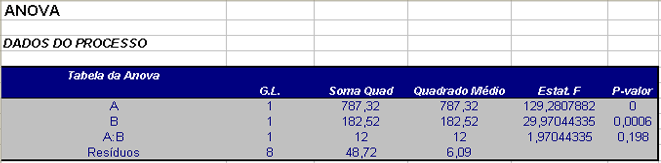
Considerando novamente os dados do Exemplo 3.1.1, onde desejava-se estudar os efeitos da temperatura e concentração do reagente no tempo de reação, construiu-se a Tabela da ANOVA para verificar se os efeitos dos fatores e da interação entre eles são significativos.

Fonte	G.L.	Soma de Quadrados	Quadrado Médio	Estatística F	P-valor
A	1	787,32	787,32	129,28	0
B	1	182,52	182,52	29,97	0,0006
A:B	1	12	12	1,97	0,198
Resíduos	8	48,72	6,09
Total	11	1030,56

Para o fator A, temos que $ F_{obs} = 129,28> F_{0,95;1;8}=5,32 $, portanto o fator A é significativo. Já para o fator B, temos que $ F_{obs} = 29,97> F_{0,95;1;8}=5,32, $, portanto o fator B também é significativo. Mas a interação não é significativa, pois $ F_{AB}=1,97< F_{0,95;1;8}=5,32 $.

Vamos observar as mudanças quando passamos de um nível para o outro:

$$\overline{y_{1..}}=(26,6+11,8+22+15,9+22,8+14,3)/6=18,9$$

$$\overline{y_{2..}}=(40,9+34+36,4+29+36,7+33,6)/6=35,1$$

$$\overline{y_{.1.}}=(26,6+40,9+22+36,4+22,8+36,7)/6=30,9$$

$$\overline{y_{.2.}}=(11,8+34+15,9+29+14,3+33,6)/6=23,1$$

Portanto, a melhor configuração para se obter o menor tempo de reação é $ A_- $ e $ B_+ $, ou seja, a concentração em $ 10(porcentagem) $ e a temperatura em $ 90 $ºC.

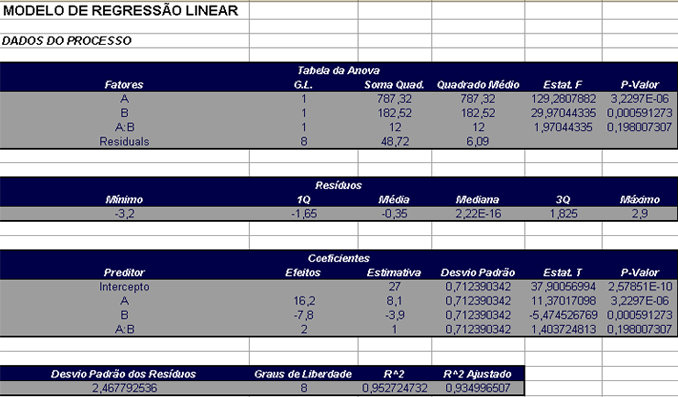
Resultados obtidos pelo software Action.

3.1.3 - Análise dos efeitos via regressão linear

Uma outra forma de analisar os efeitos dos fatores e das interações é definir um modelo de regressão linear, por exemplo, para um experimento com 2 fatores A e B, o modelo é definido da seguinte forma

$$Y=\beta_{0}+\beta_{1}X_{i}+\beta_{2}X_{j}+\beta_{12}X_{i}X_{j}+\varepsilon$$

em que

• $ \beta_{0} $ é a média geral da resposta
• $ X_{i} $ assume valor -1 ou 1, dependendo do nível do fator A
• $ X_{j} $assume valor -1 ou 1, dependendo do nível do fator B
• $ X_{ij} = X_{i}X_{j} $.

As constantes desconhecidas βj são denominadas parâmetros e ε representa o erro experimental, isto é, a variabilidade devido a fatores aleatórios não controlados no experimento.

De forma geral, o modelo de regressão linear é dado por

$$Y = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + … +\beta_{k}x_{k}+ \varepsilon$$

Estimação dos Parâmetros

O método de mínimos quadrados é o mais utilizado para estimar os parâmetros do modelo de regressão linear. Para isso, consideramos p variáveis explicativas x, p+1 parâmetros do modelo e n observações, com n > p.

Os dados de uma regressão linear podem ser representados da seguinte forma:

$ \mathbf{Y} $	$ \mathbf{x}_{1} $	$ \mathbf{x}_{2} $	$ \dots $	$ \mathbf{x}_{p} $
$ y_{1} $	$ x_{11} $	$ x_{12} $	$ \dots $	$ x_{1p} $
$ y_{2} $	$ x_{21} $	$ x_{22} $	$ \dots $	$ x_{2p} $
$ \vdots $	$ \vdots $	$ \vdots $	$ \ddots $	$ \vdots $
$ y_{n} $	$ x_{n1} $	$ x_{n2} $	$ \dots $	$ x_{np} $

Hipóteses: ε é uma variável aleatória tal que:

$$E[\varepsilon]=0~{e}~Var[\varepsilon]=\sigma^{2}$$

Consideremos o modelo,

$$y_{i}=\beta_{0}+\beta_{1}x_{i1}+\beta_{2}x_{i2}+…+\beta_{p}x_{ip}+\varepsilon_{i}=\sum^{p}_{j=1}\beta_{j}x_{ij} + \varepsilon_{i}~~(3.1.3.1)$$

Também, supomos que os erros experimentais εi são não correlacionados, possuem média zero e variância constante.

O método dos mínimos quadrados determina valores dos β’s da equação (3.1.3.1), para os quais a soma dos quadrados dos erros εi, seja minimizada. Como podemos ver no livro de Análise de Regressão no capítulo 2.3 Estimação dos Parâmetros do Modelo, os estimadores dos β’s são dados por:

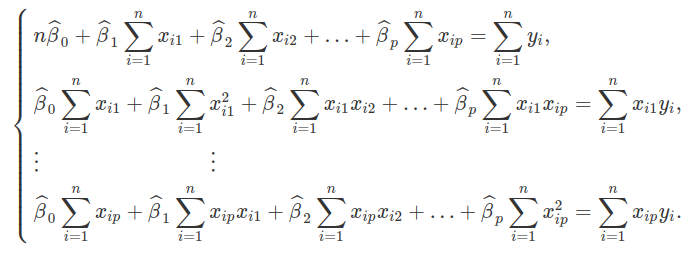
Este sistema de equações é resolvido por um método apropriado que utiliza a notação matricial. O modelo de regressão pode ser escrito na seguinte forma matricial

$$Y = X \beta + \varepsilon$$

onde

Seguindo esta notação, os estimadores de β devem satisfazer

$$\widehat{\beta}=(X^\prime X)^{-1} X^\prime Y$$

e o modelo de regressão linear ajustado e o vetor de resíduos são, respectivamente:

$$\widehat{Y}=X\widehat{\beta} \quad \hbox{e} \quad \varepsilon=Y-\widehat{Y}.$$

Exemplo 3.1.3.1

Um experimento fatorial 22 pode ser representado conforme a tabela abaixo

Y	I	X1	X2	X1 x X2
0	1	-1	-1	+1
a	1	+1	-1	-1
b	1	-1	+1	-1
ab	1	+1	+1	+1

Matricialmente, podemos expressar o modelo da seguinte forma:

$$\mathbf{Y}=X\beta+\varepsilon$$

onde

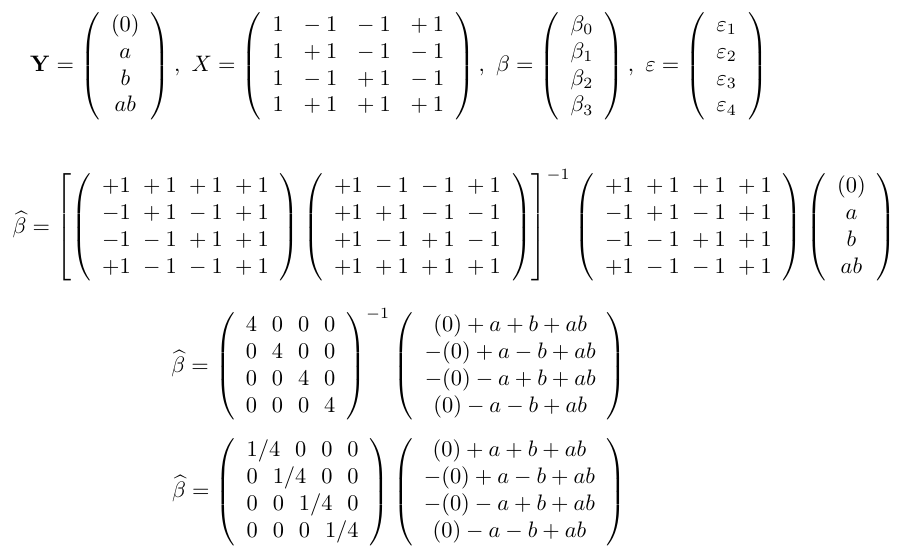
para todo i = 1, …, n.

Assim tem-se:

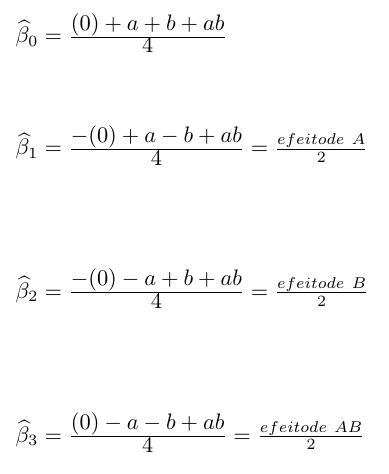
Observe que os estimadores $ \widehat{\beta}_1,~\widehat{\beta}_2,~\widehat{\beta}_3 $ correspondem ao efeito do fator A dividido por 2, efeito do fator B dividido por 2 e efeito da interação AB dividido por 2, respectivamente.

Exemplo 3.1.3.2

Calcular os coeficientes do modelo.

A	B	AB	Y1	Y2	Y3	$ \overline{ Y} $	Tratamento
-1	-1	+1	28	25	27	26,67	(0)
+1	-1	-1	36	32	32	33,33	a
-1	+1	-1	18	19	23	20,00	b
+1	+1	+1	31	30	29	30,00	ab

$$Média~Geral: \quad \widehat{\beta_0}=(26,67+33,33+20+30)/4=27,50$$

$$Efeito~de~A: \quad \widehat{\beta_1}=(-26,67+33,33-20+30)/4=4,17$$

$$Efeito~de~B: \quad \widehat{\beta_2}=(-26,67-33,33+20+30)/4=-2,50$$

$$Efeito~de~AB: \quad \widehat{\beta_3}=(26,67-33,33-20+30)/4=0,84$$

Desta forma, modelo ajustado é

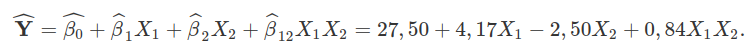
Propriedades dos estimadores de mínimos quadrados

Temos que

Testes sobre os parâmetros individuais

Estes testes são muito importantes para verificar a influência de cada variável no modelo. Por exemplo, o modelo pode ser mais eficiente com a inclusão de outras variáveis ou com a exclusão de variáveis que estão no modelo. As hipóteses são definidas por:

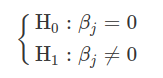
Se a hipótese $ H_0 $ é verdadeira, a variável independente $ X_j $ pode ser retirada do modelo. A estatística do teste é dada por

$$t_{0}=\cfrac{\displaystyle \widehat{\beta}_{j}}{\displaystyle \sqrt{\widehat{\sigma}^{2}C_{jj}}}$$

onde $ C_{jj} $ é um elemento da diagonal da matriz $ (X^\prime X)^{-1} $ correspondente a $ \widehat{\beta}_j $.

O critério do teste é dado a seguir:

• Rejeitamos $ H_0 $ se $ \mid t_0 \mid> t_{(\alpha/2, n-k-1)} $;
• Caso contrário não rejeitamos a hipótese nula.
• O P-valor é dado por

$$2*P\left[~t_{n-k-1}> \mid t_0 \mid ~\displaystyle/~H_0~\right]$$

Exemplo 3.1.3.3

Considere novamente os dados do Exemplo 3.1.1,

a) Obter as estimativas dos parâmetros do modelo;

b) Fazer testes de hipóteses para analisar a significância dos parâmetros.

Tratamento	$ A $	$ B $	$ Y_1 $	$ Y_2 $	$ Y_3 $	$ \overline{Y} $
(0)	-1	-1	26,6(1)	22,0(7)	22,8(10)	23,8
(a)	+1	-1	40,9(4)	36,4(9)	36,7(12)	38
(b)	-1	+1	11,8(3)	15,9(8)	14,3(11)	14
(ab)	+1	+1	34,0(2)	29,0(5)	33,6(6)	32,2

O modelo, na forma matricial é $ Y=\mathbf{X}\beta+\varepsilon, $ com

Portanto

$$\widehat{\beta_0}=27$$

$$\widehat{\beta_1}=\displaystyle\frac{{efeito~de~A}}{2}=8,1$$

$$\widehat{\beta_2}=\displaystyle\frac{{efeito~de~B}}{2}=-3,9$$

$$\widehat{\beta_3}=\displaystyle\frac{{efeito~de~AB}}{2}=1$$

Os efeitos dos fatores e da interação já foram vistos no Exemplo 1.1.1, e são:

$$A=16,2~~{ e }~~B=-7,8~~{ e }~~AB=2.$$

como já havíamos obtido anteriormente no Exemplo 3.1.1.

O modelo ajustado é

$$\widehat{Y} = 27 + 8,1 X_{i} -3,9 X_{j} + 1 X_{i}X_{j}.$$

onde

• $ x_i $ assume valor -1 ou 1, dependendo do nível do fator A
• $ x_j $ assume valor -1 ou 1, dependendo do nível do fator B
• $ x_{ij}=x_{i}x_j $.

Testes de significâncias para os parâmetros $ \beta_1, \beta_2, \beta_3. $

Estatística de teste

$$t_{0}=\cfrac{\displaystyle \widehat{\beta}_{j}}{\displaystyle \sqrt{\widehat{\sigma}^{2}C_{jj}}}$$

onde $ C_{jj} $ é o elemento da matriz $ (X^\prime X)^{-1} $ correspondente a $ \widehat{\beta}_j $.

A matriz $ X^\prime X $ neste caso é dada por

ou seja,

$$C_{11}=C_{22}=C_{33}=\cfrac{1}{12}=0,0833$$

e

$$\widehat{\sigma}^2=\displaystyle\cfrac{SQ_E}{n-k-1}$$

,

onde $ SQ_E=\mathbf{Y}^\prime\mathbf{Y}-\beta^\prime X^\prime \mathbf{Y}=9778,56-9729,84=48,72. $

Assim,

$$\widehat{\sigma}^2=\cfrac{SQ_E}{n-k-1}=\frac{48,72}{12-3-1}=6,09,$$

Calcula-se os valores das estatísticas para os parâmetro do modelo

Para $ \beta_1 $:

$ t_0=\cfrac{8,1}{\sqrt{6,09*0,0833}}=\cfrac{8,1}{\sqrt{0,507297}}=\cfrac{8,1}{0,7122479}=11,37 $

Para $ \beta_2 $:

$ t_0=\cfrac{-3,9}{\sqrt{6,09*0,0833}}=\cfrac{-3,9}{\sqrt{0,507297}}=\cfrac{-3,9}{0,7122479}=-5,47 $

Para $ \beta_3 $:

$ t_0=\cfrac{1}{\sqrt{6,09*0,0833}}=\cfrac{1}{\sqrt{0,507297}}=\cfrac{1}{0,7122479}=1,4 $

Construindo uma Tabela com os valores acima e os p-valores temos

Termo	Efeito	Coeficiente da Regressão	Desvio Padrão	T	P-valor
Média Geral		27	0,7124	37,9	0
A	16,2	8,1	0,7124	11,37	0
B	-7,8	-3,9	0,7124	-5,47	0,0005
A*B	2	1	0,7124	1,4	0,198

O critério do teste é dado por:

• Rejeitamos $ H_0 $ se $ |t_0| > t_{\alpha/2,n-k-1} $;
• Caso contrário não rejeitamos a hipótese nula.

O valor de $ t_{0,025;12-3-1}= 2,306 $ e assim concluímos que, com nível α = 5%, que os fatores A e B são significativos e a interação AB não é significativa. Basta então ver que os coeficientes da regressão de A e B são respectivamente 8,1 e -3,9 e como estamos interessados em obter a menor resposta (menor tempo de reação), escolhemos os níveis A-B+.

3.2 - Experimentos Fatoriais 2^3

Exemplo 3.2.1

Considere o processo de colagem de um circuito integrado em uma base.

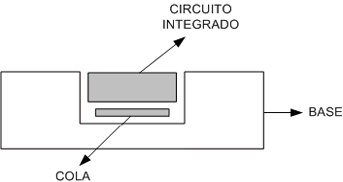
Neste caso teremos:

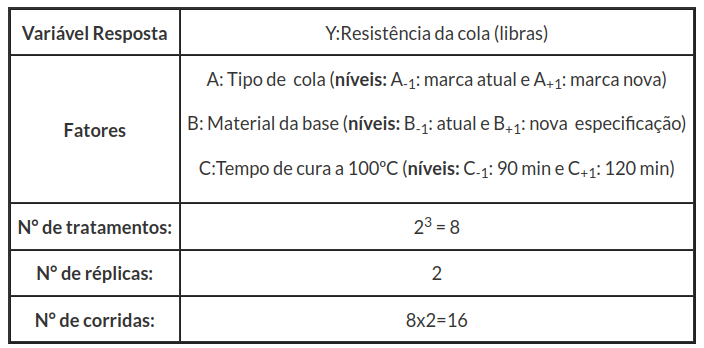
Os dados do experimento são apresentados na tabela a seguir. Os números entre parênteses representam a ordem das corridas:

Tratamento	A	B	C	$ Y_1 $	$ Y_2 $	$ \overline{Y} $
(0)	-1	-1	-1	82,9 (1)	88,6 (7)	85,75
a	+1	-1	-1	95,0 (6)	96,4(13)	95,7
b	-1	+1	-1	80,0 (2)	78,6 (14)	79,3
c	-1	-1	+1	93,1 (3)	94,7 (7)	93,9
ab	+1	+1	-1	105,0 (8)	103,6 (10)	104,3
ac	+1	-1	+1	104,0 (9)	101,2 (16)	102,6
bc	-1	+1	+1	89,7 (5)	86,9 (15)	88,3
abc	+1	+1	+1	114,0 (11)	111,8 (12)	112,9

3.2.1 - Análise gráfica

Gráfico de Médias para resistência da cola.

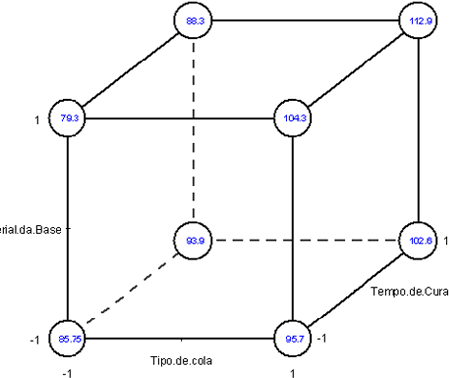
Figura 3.2.1.1: Valores médios para a colagem para 2 níveis de A (tipo de cola), B (material da base) e C (tempo de cura).

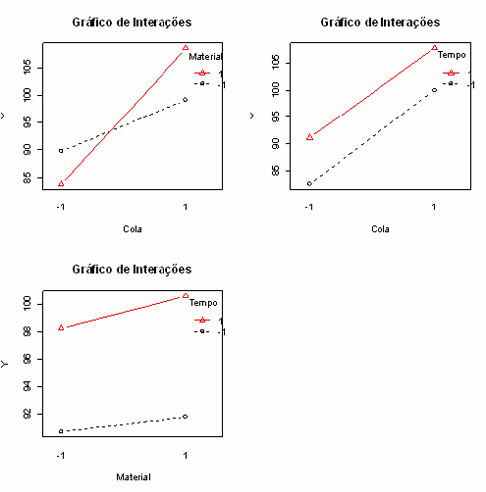
Figura 3.2.1.2: Efeitos das interações entre os fatores $ A $ (tipo de cola), $ B $ (material da base) e $ C $ (tempo de cura).

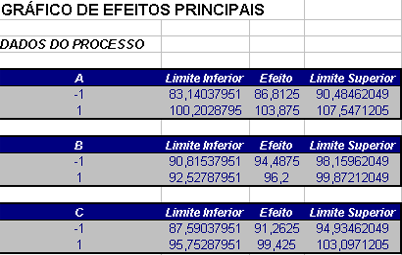
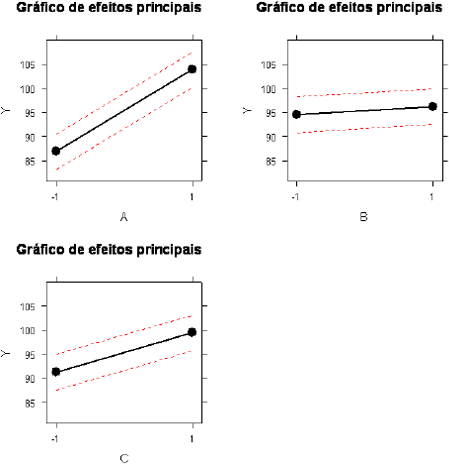
Figura 3.2.1.3: Efeitos principais entre os fatores $ A $ (tipo de cola), $ B $ (material da base) e $ C $ (tempo de cura).

3.2.2 - Cálculo dos efeitos

Pode-se calcular os efeitos principais dos fatores e das interações por cálculos diretos, como segue, ou usando o modelo linear.

$$A=\overline{Y_{A+}}-\overline{Y_{A-}}=\frac{a+ab+ac+abc}{4n}-\frac{(0)+b+c+bc}{4n}$$

$$B=\overline{Y_{B+}}-\overline{Y_{B-}}=\frac{b+ab+bc+abc}{4n}-\frac{(0)+a+c+ac}{4n}$$

$$C=\overline{Y_{C+}}-\overline{Y_{C-}}=\frac{c+ac+bc+abc}{4n}-\frac{(0)+a+b+ab}{4n}$$

$$AB=\frac{(0)+c+ab+abc}{4n}-\frac{a+b+ac+bc}{4n}$$

$$AC=\frac{(0)+b+ac+abc}{4n}-\frac{a+c+ab+bc}{4n}$$

$$BC=\frac{(0)+a+bc+abc}{4n}-\frac{b+c+ab+ac}{4n}$$

$$ABC=\frac{a+b+c+abc}{4n}-\frac{(0)+ab+ac+bc}{4n}$$

Exemplo 3.2.2.1

Considerando a tabela a seguir (Exemplo 3.2.1), calcular os efeitos principais.

Tratamento	$ A $	$ B $	$ C $	$ AB $	$ AC $	$ BC $	$ ABC $	$ Y_1 $	$ Y_2 $	$ \overline{Y} $
0	-1	-1	-1	1	1	1	-1	82,90	88,60	85,75
a	1	-1	-1	-1	-1	1	1	95	96,40	95,70
b	-1	1	-1	-1	1	-1	1	80	78,60	79,30
c	-1	-1	1	1	-1	-1	1	93,10	94,70	93,90
ab	1	1	-1	1	-1	-1	-1	105	103,60	104,30
ac	1	-1	1	-1	1	-1	-1	104	101,20	102,60
bc	-1	1	1	-1	-1	1	-1	89,70	86,90	88,30
abc	1	1	1	1	1	1	1	114	111,80	112,90

$$A=\frac{95+105+\ldots+111,8}{8}-\frac{82,9+80+\ldots+86,9}{8}=103,875-86,8125=17,0625$$

$$B=\frac{80+78,6+\ldots+111,8}{8}-\frac{82,9+88,6+\ldots+101,2}{8}= 96,20-94,4875=1,7125$$

$$C=\frac{93,1+94,7+\ldots+111,8}{8}-\frac{82,9+88,6+\ldots+103,6}{8}=99,425-91,2625=8,1625$$

$$AB=\frac{82,9+88,6+\ldots+111,8}{8}-\frac{95+96,4+\ldots+86,9}{8}= 99,2125+91,475=7,7375$$

$$AC=\frac{82,9+88,6+\ldots+ 111,8}{8}-\frac{95+96,4+\ldots+86,9}{8}=95,1375-95,55=-0,4125$$

$$BC=\frac{82,9+88,6+\ldots+111,8}{8}-\frac{80+78,6+\ldots+101,2}{8}=95,6625-95,025=0,6375$$

$$ABC=\frac{95+96,4+\ldots+111,8}{8}-\frac{82,9+88,6+\ldots+86,9}{8}=95,45-95,2375=0,2125$$

Resultados obtido pelo software Action

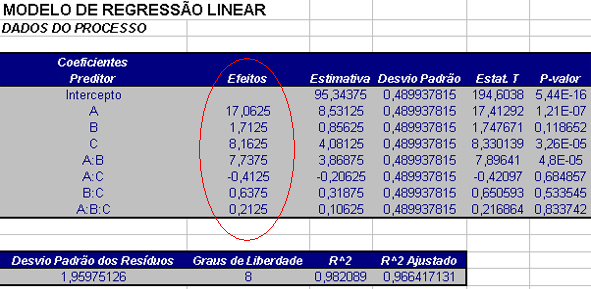
3.2.3 - Modelo Linear

Outra forma de calcular os efeitos principais é utilizando o modelo de regressão:

Cálculo dos efeitos principais usando modelo linear:

$$Y=\beta_0+\beta_1 x_1+\beta_2x_2+\beta_3 x_3+\beta_{12}x_1x_2+\beta_{13}x_1x_3+ \beta_{23}x_2x_3+\beta_{123}x_1x_2x_3+\varepsilon,~~(3.2.1)$$

a) $ x_{1} $, $ x_{2} $ e $ x_{3} $ são variáveis correspondentes aos fatores A, B e C;

b) Os coeficientes da regressão são $ \beta_{0} $, $ \beta_{1} $, $ \beta_{2} $, $ \beta_{3} $, $ \beta_{12} $, $ \beta_{13} $, $ \beta_{23} $ e $ \beta_{123} $;

c) ε é um componente de erro aleatório envolvido no modelo (erro experimental).

Para os dados do Exemplo 3.2.1, obter as estimativas dos parâmetros do modelo linear.

Na forma matricial, temos que:

$$Y=X\beta+\varepsilon$$

com

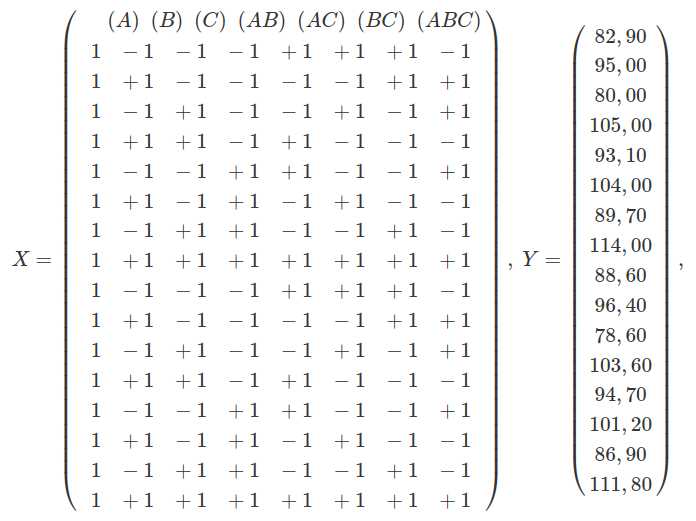
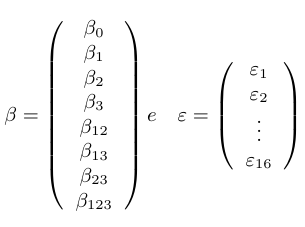
Podemos estimar $ \beta $ utilizando

Assim podemos obter os efeitos dos fatores e interações, que é duas vezes o coeficiente da regressão correspondente, ou seja, $ A=17,0625 $, $ B=1,7125 $, $ C=8,1625 $, $ AB=7,7375 $, $ AC=-0,4125 $, $ BC=0,6375 $ e $ ABC=0,2125 $.

Resultados obtidos pelo software Action

3.2.4 - Tabela da ANOVA

Outra forma de analisar os efeitos dos fatores e das interações é por meio da tabela da ANOVA.

Em um experimento fatorial $ 2^3 $, a forma geral desta tabela é obtida considerando $ y_{ijkl} $ a l-ésima observação no nível i de A, j de B e k de C. Em geral, i = 1, …, a; j = 1, …, b; k = 1, …, c; l = 1, …, r; onde a, b e c são o número de níveis de A, B e C, respectivamente e r é o número de réplicas do experimento.

Para o caso do experimento $ 2^3 $ temos 2 níveis para cada fator, desta forma, a = b = c = 2.

Além disso, devemos considerar que:

• $ y_{i\cdot\cdot\cdot}=\displaystyle\sum_{j=1}^{b}\sum_{k=1}^{c}\sum_{l=1}^{r}y_{ijkl} $ é a soma de todas as observações no nível i de A e $ \overline{y_{i\cdot\cdot\cdot}}=\displaystyle\cfrac{y_{i\cdot\cdot\cdot}}{bcr} $ é a média destas observações, para $ i=1,\ldots,a $

Analogamente,

• $ y_{\cdot j\cdot\cdot}=\displaystyle\sum_{i=1}^{a}\sum_{k=1}^{c}\sum_{l=1}^{r}y_{ijkl} $e $ \overline{y_{\cdot j\cdot\cdot}}=\displaystyle\cfrac{\displaystyle y_{\cdot j\cdot\cdot}}{acr} $, para $ j=1,\ldots,b $
• $ y_{\cdot \cdot k\cdot}=\displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{l=1}^{r}y_{ijkl} $ e $ \overline{y_{\cdot \cdot k\cdot}}=\displaystyle\cfrac{\displaystyle y_{\cdot \cdot k\cdot}}{abr} $, para $ k=1,\ldots,c $
• $ y_{ij\cdot\cdot}=\displaystyle\sum_{k=1}^{c}\sum_{l=1}^{r}y_{ijkl} $ é a soma de todas as observações que têm nível i de A e j de B (ao mesmo tempo) e $ \overline{y_{i\cdot\cdot}}=\displaystyle\cfrac{y_{i j \cdot\cdot}}{cr} $ é a média destas observações, para $ i=1,\ldots,a;j=1,\ldots,b $

Analogamente,

• $ y_{i \cdot k\cdot}=\displaystyle\sum_{j=1}^{b}\sum_{l=1}^{r}y_{ijkl} $ e $ \overline{y_{i \cdot k\cdot}}\displaystyle\cfrac{y_{i \cdot k \cdot}}{br} $, para $ i=1,\ldots,a;k=1,\ldots,c $
• $ y_{\cdot j k\cdot}=\displaystyle\sum_{i=1}^{a} \sum_{l=1}^{r} y_{ijkl} $ e $ \overline{y_{\cdot j k\cdot}}=\displaystyle\cfrac{y_{\cdot j k\cdot}}{ar} $, para $ j=1,\ldots,b;k=1,\ldots,c $
• $ y_{i j k\cdot}=\displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{c} y_{ijkl} $ é a soma de todas as observações que têm nível $ i $ de $ A $, $ j $ de $ B $ e $ k $ de $ C $ (ao mesmo tempo) e $ \overline{y_{i j k\cdot}}=\displaystyle\frac{y_{i j k\cdot}}{abc} $ é a média destas observações, para $ i=1,\ldots,a;j=1,\ldots,b;k=1,\ldots,c $
• $ y_{\cdot\cdot\cdot\cdot}=\displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{c} \sum_{l=1}^{r} y_{ijkl} $ é a soma de todas as observações e $ \overline{Y_{\cdot\cdot\cdot\cdot}}=\displaystyle\cfrac{Y_{\cdot\cdot\cdot\cdot}}{abcr} $ é a média geral das observações.

Desta forma, tem-se as somas de quadrados dos efeitos principais

$$SQ_A=\displaystyle\cfrac{1}{bcr}\displaystyle\sum_{i=1}^{a}y_{i\cdot\cdot\cdot}^2-\cfrac{y_{\cdot\cdot\cdot\cdot}^2}{abcr}$$

$$SQ_B=\displaystyle\cfrac{1}{acr}\displaystyle\sum_{j=1}^{b}y_{\cdot j\cdot\cdot}^2- \cfrac{y_{\cdot\cdot\cdot\cdot}^2}{abcr}$$

$$SQ_C=\displaystyle\cfrac{1}{abr}\displaystyle\sum_{k=1}^{c}y_{\cdot\cdot\cdot}^2- \cfrac{y_{\cdot\cdot\cdot\cdot}^2}{abcr}$$

As somas de quadrados dos efeitos das interações

$$SQ_{AB}=\displaystyle\cfrac{1}{cr}\displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}y_{ij\cdot\cdot}^2-\displaystyle\cfrac{y_{\cdot\cdot\cdot\cdot}^2}{abcr}-SQ_A-SQ_B$$

$$SQ_{AC}=\displaystyle\cfrac{1}{br}\displaystyle\sum_{i=1}^{a}\sum_{k=1}^{c}y_{i\cdot k\cdot}^2-\displaystyle\cfrac{y_{\cdot\cdot\cdot\cdot}^2}{abcr}-SQ_A-SQ_C$$

$$SQ_{BC}=\displaystyle\cfrac{1}{ar}\displaystyle\sum_{j=1}^{b}\sum_{k=1}^{c}y_{\cdot j k\cdot}^2-\displaystyle\cfrac{y_{\cdot\cdot\cdot\cdot}^2}{abcr}-SQ_B-SQ_C$$

$$SQ_{ABC}=\displaystyle\cfrac{1}{r}\displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{c}y_{ijk\cdot}^2-\cfrac{y_{\cdot\cdot\cdot\cdot}^2}{abcr}-SQ_A-SQ_B-SQ_C-SQ_{AB}-SQ_{AC}-SQ_{BC}$$

A Soma de Quadrados Total é dada por

$$SQ_{T}=\displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{c}\sum_{l=1}^{r}y_{i j k l}^2-\displaystyle\cfrac{y_{\cdot\cdot\cdot\cdot}^2}{abcr}$$

e, finalmente, a Soma de Quadrados dos Erros

$$SQ_{E}=\displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{c}\sum_{l=1}^{r}y_{i j k l}^2-\cfrac{1}{r} \displaystyle\sum_{i=1}^{a}\sum_{j=1}^{b}\sum_{k=1}^{c}y_{i j k \cdot}^2.$$

Fonte de Variação	Soma de Quadrados	Graus de Liberdade	Quadrados Médios	Estatística F
$ A $	$ SQ_A $	$ a-1 $	$ QM_A=\displaystyle\frac{SQ_A}{a-1} $	$ \displaystyle\frac{QM_A}{QM_E} $
$ B $	$ SQ_B $	$ b-1 $	$ QM_B=\displaystyle\frac{SQ_B}{b-1} $	$ \displaystyle\frac{QM_B}{QM_E} $
$ C $	$ SQ_C $	$ c-1 $	$ QM_C=\displaystyle\frac{SQ_C}{c-1} $	$ \displaystyle\frac{QM_C}{QM_E} $
$ AB $	$ SQ_{AB} $	$ (a-1)(b-1) $	$ QM_{AB}=\displaystyle\frac{SQ_{AB}}{(a-1)(b-1)} $	$ \displaystyle\frac{QM_{AB}}{QM_E} $
$ AC $	$ SQ_{AC} $	$ (a-1)(c-1) $	$ QM_{AC}=\displaystyle\frac{SQ_{AC}}{(a-1)(c-1)} $	$ \displaystyle\frac{QM_{AC}}{QM_E} $
$ BC $	$ SQ_{BC} $	$ (b-1)(c-1) $	$ QM_{BC}=\displaystyle\frac{SQ_{BC}}{(b-1)(c-1)} $	$ \displaystyle\frac{QM_{BC}}{QM_E} $
$ ABC $	$ SQ_{ABC} $	$ (a-1)(b-1)(c-1) $	$ QM_{ABC}=\displaystyle\frac{SQ_{ABC}}{(a-1)(b-1)(c-1)} $	$ \displaystyle\frac{QM_{ABC}}{QM_E} $
$ Erro $	$ SQ_{E} $	$ abc(r-1) $	$ QM_{E}=\displaystyle\frac{SQ_{E}}{abc(r-1)} $
$ Total $	$ SQ_{T} $	$ abcr-1 $

Tabela 3.2.4.1: Tabela de Análise de Variância para Experimentos Fatoriais do tipo $ 2^3 $.

Para maiores informações, consulte o módulo ANOVA.

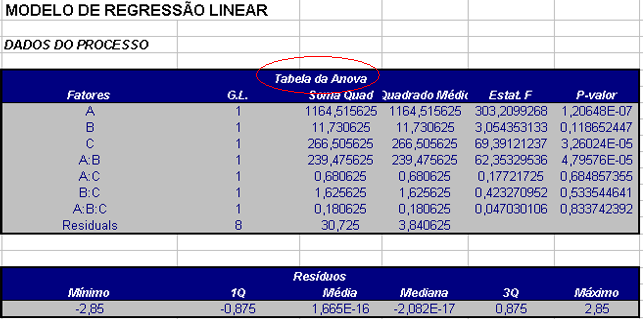
Exemplo 3.2.4.1

Fazer a análise de variância e cálculos dos testes estatísticos para

Fonte de Variação	Soma de Quadrados	Graus de Liberdade	Quadrado Médio	Estatística F	P-valor
A	1164,52	1	1164,52	303,21	0,000
B	11,73	1	11,73	3,05	0,119
C	266,51	1	266,51	69,39	0,000
AB	239,48	1	239,48	62,35	0,000
AC	0,68	1	0,68	0,18	0,685
BC	1,63	1	1,63	0,42	0,534
ABC	0,18	1	0,18	0,05	0,834
Erro	30,72	8	3,84
Total	1715,44	15

Relembrando: A é o tipo de cola, B é o material da base, C é o tempo de cura.

Como os valores de p para A, C e AB são menores que α = 5% esses fatores são significativos, porém o fator B não é significativo, como notou-se nos gráficos de efeitos principais.

Calcula-se os valores dos testes para os parâmetros $β_1, β_2, β_3, β_{12}, β_{13}, β_{23}, β_{123}$, obtidos no Exemplo 3.2.1.

Conclusões:

• Os fatores A, C e AB são significativos, mas B não;
• O coeficiente de regressão de A é maior, em módulo, que o de AB, então podemos olhar apenas para os níveis de A e C;
• Como os coeficientes da regressão de ambos são positivos, concluímos que A e C são melhores no nível +1; e
• Como B não é significativo, é melhor conservar o nível atual -1. Portanto a melhor configuração seria A+, B-, C+.

Resultados obtidos pelo software Action

3.3 - Experimentos Fatoriais sem Réplicas

Em algumas situações, o número de combinações dos fatores do experimento (tratamentos) é grande. Nestes casos, recursos podem estar disponíveis apenas para uma única execução do projeto, ou seja, o experimento não possuirá réplicas.

Um risco evidente quando se conduz um experimento sem réplicas é que o modelo ajustado pode levar a conclusões erradas. Além disto, neste caso não há estimativa interna de erro (erro puro).

Existem alguns método para tratar estes experimento, dentre elas citamos os métodos de Lenth e Daniel que são métodos objetivos para decidir quais efeitos são significativos na análise de experimentos sem réplicas, nas situações em que o modelo está saturado e assim, não há graus de liberdade para estimar a variância do erro. Consequentemente, é proposto um método para estimar uma quantidade semelhante ao erro padrão, chamado de pseudo erro padrão ou PSE.

3.3.1 Gráfico da Probabilidade Normal e Half-Normal

A utilização dos gráficos de probabilidade normal e half-normal para identificar efeitos possivelmente ativos (efeitos não nulos do ponto de vista estatístico). No estudo de experimento fatoriais sem réplicas Cuthbert Daniel (1959) propôs um método que avalia estes efeitos ativos. A ideia de Daniel é bastante utilizada até os dias atuais por ser simples e conseguir apontar a direção correta dos efeitos em grande parte dos experimentos.

A aplicação eficaz desses gráficos depende do fato das estimativas dos efeitos terem a mesma variância, e os pontos em que temos “efeitos esparsos” são detectados pelo método. Segundo Daniel, esperamos que apenas uma pequena fração dos contrastes sejam ativos dentre todos aqueles envolvidos no estudo. Nestes gráficos, os efeitos cujos pontos estiverem claramente afastados de uma reta imaginária, formada pela nuvem de pontos, serão julgados ativos.

Sejam $ \hat{c_1},\hat{c_2},\dots,\hat{c_n} $, os $ n $ efeitos estimados. Denote por $ \hat{c_{(i)}}, $ o i-ésimo dos $ n $ efeitos ordenados, $ \hat{c_{(1)}},\hat{c_{(2)}},\dots,\hat{c}_{(n)} $. Dessa forma, o gráfico de probabilidade normal pode ser obtido dispondo-se os pontos em um gráfico cujas coordenadas $ (x,y) $ são dadas por

$$\left(\hat{c}_{(i)},\Phi^{-1}\left[\frac{(i-0,5)}{n}\right]\right)$$

em que $ \Phi^{-1}(.) $ é a função de distribuição acumulada da normal padrão. Alguns autores comentam sobre a preferência de utilizar o gráfico half-normal ao invés do gráfico de probabilidade normal. Segundo eles, uma das vantagens de utilizar o half-normal é o fato de que os efeitos possivelmente ativos vão se apresentar no canto superior direito do gráfico. O gráfico de probabilidade half-normal é obtido a partir da marcação dos pontos cujas coordenadas $ (x,y) $ são dadas por

$$\left(|\hat{c}_{(i)}|,\Phi^{-1}\left[0,5+\frac{(i-0,5)}{n}\right]\right)$$

Exemplo 3.3.1

Um determinado produto químico é produzido em um vaso de pressão. Com o objetivo de estudar quais fatores influenciam na taxa de filtração do produto (Y), foi realizado um experimento fatorial em que se considerou 4 fatores: A (temperatura), B (pressão), C (concentração de formaldeido) e D (velocidade de agitação). Cada fator é observado em dois níveis. Segue na Tabela 3.3.1.1 a matriz de planejamento e a resposta dos dados, considerando um experimento sem réplicas.

Tratamento	$ A $	$ B $	$ C $	$ D $	$ Y $
0	-1	-1	-1	-1	45
a	1	-1	-1	-1	71
b	-1	1	-1	-1	48
ab	1	1	-1	-1	65
c	-1	-1	1	-1	68
ac	1	-1	1	-1	60
bc	-1	1	1	-1	80
abc	1	1	1	-1	65
d	-1	-1	-1	1	43
ad	1	-1	-1	1	100
bd	-1	1	-1	1	45
abd	1	1	-1	1	104
cd	-1	-1	1	1	75
acd	1	-1	1	1	86
bcd	-1	1	1	1	70
abcd	1	1	1	1	96

Tabela 3.3.1.1: Experimento - Taxa de filtração do produto.

Primeiramente, vamos calcular os pontos do gráfico. Após calculados os efeitos estimados $ \hat{c_i} $ em seguida calculamos $ (i-0,5)/n. $ Após este passo, calculamos os quantis da normal padrão $ \Phi^{-1}\left[\frac{(i-0,5)}{n}\right]. $ Por fim, ordenamos os efeitos estimados em módulo $ |\hat{c}_{(i)}|. $

Observe os resultado na tabela a seguir.

i	$ \hat{c}_i $	$ \dfrac{i-0,5}{n} $	$ \Phi^{-1}\left[\frac{(i-0,5)}{n}\right] $	$ \hat{c}_{(i)} $
1	21,625	0,033333	-1,83391	0,125
2	3,125	0,1	-1,28155	0,375
3	9,875	0,166667	-0,96742	1,125
4	14,625	0,233333	-0,72791	1,375
5	0,125	0,3	-0,5244	1,625
6	-18,125	0,366667	-0,34069	1,875
7	2,375	0,433333	-0,16789	2,375
8	16,625	0,5	0	2,625
9	-0,375	0,566667	0,167894	3,125
10	-1,125	0,633333	0,340695	4,125
11	1,875	0,7	0,524401	9,875
12	4,125	0,766667	0,727913	14,625
13	-1,625	0,833333	0,967422	16,625
14	-2,625	0,9	1,281552	18,125
15	1,375	0,966667	1,833915	21,625

Conforme dito anteriormente plotamos um gráfico de coordenadas:

$$\left(|\hat{c}_{(i)}|,\Phi^{-1}\left[\frac{(i-0,5)}{n}\right]\right)$$

Agora, para os dois percentis calculamos os índices dos quantis

$ j_k=1+(n-1)*\text{percentis},\quad k=1,2 $

Com isso, temos

$$j_1=1+(15-1)*0,25=4,5\quad \text{e}\quad j_2=1+(15-1)*0,75=11,5$$

Como os índices são números inteiros, vamos truncar os índices anteriores:

$$l_1=4\quad \text{e}\quad l_2=11$$

Também, tomamos os maiores inteiros dos índices $ j_k $ para $ k=1,2 $

$$h_1=[j_1]=5\quad\text{e}\quad h_2=[j_2]=12$$

e calculamos $ w_k=j_k–l_k,\quad k=1,2, $ e obtemos

$$w_1=4,5-4=0,5\quad\text{e}\quad w_2=11,5-11=0,5$$

Outra informação importante são os quantis iniciais

$ q_0=\hat{c}_{(i)}[l_k]=(-1,125\quad 4,125)^T $

Logo, obtemos os quantis empíricos

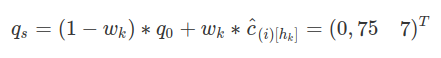
Calculados $ q_s $ e os quantis da normal padrão, calculamos o coeficiente angular da reta, para isto usamos a fórmula $ y-y_0=m*(x-x_0) $

$$m=\dfrac{\Phi^{-1}(0,75)-\Phi^{-1}(0,25)}{7-(-0,75)}=0,2632155$$

e o intercepto é zero.

Portanto, obtemos o gráfico da direita a seguir. Vale lembrar que o da esquerda é o clássico QQ-Plot.

(imagem em falta)

Figura 3.3.1.1: Gráfico de papel de probabilidade normal e half-normal (Daniel Plot).

3.3.2 Método de Lenth

O método de Lenth tem sido considerado por muitos autores na literatura como um método muito eficiente, quando trabalhamos com análise de experimentos fatoriais sem réplicas. Um ponto para análise destes experimentos, é o estudo de um número grande de contrastes e que as estimativas destes contrastes tenham a mesma variabilidade. O método de Lenth, assim como Daniel, parte do princípio de que tenhamos apenas poucos “efeitos esparsos'' (efeitos dispersos), que o autor trata como efeitos ativos (diferente de zero), ou seja, efeitos significativamente não nulos do ponto de vista estatístico.

Considere um experimento fatorial com dois níveis e suponha que existam $ m $$ k_1,k_2,\dots,k_m $ contrastes $ c_1,c_2,\dots,c_m $ ou efeitos estimados independentes e que eles têm a mesma variância, denotada por $ \tau^2 $ com distribuição Normal $ N(k_i,\sigma^2). $ Sendo $ N $ o número de observações, por exemplo, temos que $ m=N-1 $ no caso de modelo saturado. Desta forma, temos que cada contraste ou efeito estimado é dado por

$$c=\overline{y_{+}}-\overline{y_{-}},$$

sendo que $ \overline{y_{+}} $ é a média das $ N/2 $ observações no nível “alto'' do fator em questão e $ \overline{y_{-}} $ é a média das $ N/2 $ observações no nível “baixo''. Como já mencionado, cada contraste tem a mesma variância $ \tau^2=4 \sigma^2/N $, em que $ \sigma^2 $ é a variância do erro.

Sejam $ c_{1}, c_{2}, …, c_{m} $ os contrastes ou efeitos estimados, com $ m=N-1 $. Inicialmente, calculamos a quantidade

$$s_{0}=1,5 \times \text{mediana} (|c_{j}|)\quad j=1,\dots,m.$$

Então, calculamos o pseudo erro padrão (PSE) como sendo

$$ PSE = 1,5 \times \text{mediana}(|c_{j}|:|c_{j}|\leq2,5 s_{0})\quad j=1,\dots,m, $$

sendo que o termo PSE é um estimador para $ \tau^2. $ Notamos que $ s_0 $ e $ PSE $ são bastante similares, com uma pequena diferença na mediana do $ PSE, $ que é mais restrita. Esta restrição é devido aos pontos ativos e é descrita no artigo Russel Lenth (1989), que é feita para obtermos estimativas consistentes para $ \tau. $

Em relação ao critério de decisão de quais efeitos são significativos, definimos uma margem de erro dos contrastes $ c_{i} $, denotada por ME. O valor da margem de erro é dada por

$$ME = t_{(1-\frac{\alpha}{2};d)} \times PSE,$$

sendo que $ t_{(1-\frac{\alpha}{2};d)} $ é o quantil $ (1-\frac{\alpha}{2}) $ da distribuição t-student com $ d $ graus de liberdade e $ \alpha $ é o nível de significância adotado. (Geralmente, utilizamos $ d=m/3 $ e $ \alpha=0,05 $). Assim, temos que ME é uma margem de erro para $ c_i $ com confiança aproximada de $ 95(porcentagem) $. Contrastes que excedem o valor de ME em valor absoluto são considerados significativos com nível de significância de $ 95(porcentagem) $, por exemplo.

Entretanto, quando há um grande número de contrastes $ m $, esperamos que uma ou duas estimativas de contrastes não significativos excedam o valor de ME, conduzindo a uma falsa conclusão. Desta forma, a fim de tratar estes casos, é definida uma margem de erro simultânea, que será denotada por SME. Esta medida é calculada multiplicando o pseudo erro padrão PSE por um fator $ t_{\gamma;d} $. De fato,

$$SME = t_{\gamma;d} \times PSE,$$

em que

$$\gamma=(1+0,95^{1/m})/2.$$

A constante $ \gamma $ vem do fato de que as estimativas dos contrastes são independentes. É usual construir um gráfico para exibir as informações aqui calculadas. Para isto, construímos um gráfico de barra mostrando os valores absolutos das estimativas dos contrastes ou efeitos estimados e adicionamos linhas de referências com os valores de ME e SME. Os contrastes cujas barras estendem a linha SME são considerados ativos. Já aqueles cujas barras não estendem a linha de referência ME são considerados inativos. Os contrastes cujas barras estão entre as linhas de referências ME e SME requerem um cuidado maior na decisão. A região entre as linhas ME e SME é dita região de incerteza e é necessário um bom argumento para decidir se o(s) contraste(s) é(são) significativo(s) ou não.

Critérios para avaliar os efeitos

• Intervalo de Confiança

O efeito é aceitável ao nível de significância $ \alpha $ se o efeito pertencer ao intervalo de confiança $ (1-\alpha )\times $ 100% com limites:

• $ LI=\hat{c}_j-ME,\quad \text{Limite Inferior} $
• $ LS=\hat{c}_j+ME,\quad \text{Limite Superior}\quad j=1,\dots,m $
• Teste de Hipóteses:

Outro modo de avaliarmos os efeitos, é através do teste de hipóteses:

Para isto, calculamos a estatística de Lenth, dada por:

$$T_{L_j}=\frac{|\hat{c}_j|}{PSE}\sim t_{(d)},\quad j=1,\dots,k$$

sendo $ PSE $ o pseudo erro padrão, $ d $ o número de contrastes dividido por 3 e $ t_{(d)} $ a distribuição t-Student com $ d $ graus de liberdade. Portanto, obtemos a seguinte regra de decisão para um nível de significância $ \alpha. $

• Se $ |T_{L_j}| > t_{(d;1-\alpha/2)} $ rejeitamos $ H_0, $ ou seja, o efeito é significativo do ponto de vista estatístico;
• Se $ |T_{L_j}| \leq t_{(d;1-\alpha/2)} $ não rejeitamos $ H_0, $ ou seja, efeito não é significativo do ponto de vista estatístico.
• P-valor:

representa o menor nível de significância para o qual rejeitamos $ H_0 $. Logo, para um nível de significância = 0,05 adotado, rejeitamos $ H_0 $ se o P-valor obtido for menor que 0,05, enquanto que não rejeitamos $ H_0 $ se o P-valor for maior que 0,05. Para o teste t, o P-valor é calculado na forma

$$\text{p-valor}=2\times P[t_d>|T_{L_j}|~|~H_0]$$

Com isso, rejeitamos $ H_0 $ quando o p-valor for menor que o nível de significância $ \alpha $ proposto (usualmente 0,05), caso contrário (p-valor > $ \alpha $) não rejeitamos $ H_0. $

Exemplo 3.3.2

Considerando os dados do Exemplo 3.3.1 em que o objetivo é estudar quais fatores influenciam na taxa de filtração do produto (Y) e utilizando a Tabela 3.3.1.1, calcula-se as estimativas dos efeitos (efeitos principais) por cálculos diretos ou usando o modelo linear, como visto na Seção 3.2.2. As estimativas dos efeitos são dadas pela Tabela 3.3.2.1.

Termo	Estimativa dos Efeitos
A	21,625
B	3,125
C	9,875
D	14,625
AB	0,125
AC	-18,125
AD	16,625
BC	2,375
BD	-0,375
CD	-1,125
ABC	1,875
ABD	4,125
ACD	-1,625
BCD	-2,625
ABCD	1,375

Tabela 3.3.2.1: Estimativas dos efeitos dos fatores.

Com os valores da Tabela 3.3.1.2, calculamos os valores de PSE, ME e SME. De fato,

$$s_{0}=1,5 \times \text{mediana} (21,625; 3,125; …; 2,625; 1,375) =3,938.$$

Desta forma, tem-se que

$$ PSE = 1,5 \times \text{mediana}(|c_{j}|:|c_{j}|\leq2,5 s_{0}) = 1,5 \times \text{mediana} (|c_{j}|: |c_{j}|\leq9,844) = 2,625. $$

Adotando $ \alpha=0,05 $ e $ m=15 $, tem-se que $ d=5 $. Logo, $ t_{(0,975;5)}=2,571 $, $ \gamma=(1+0,95^{1/15})/2=0,998 $ e consequentemente, $ t_{0,998;5}=5,219 $. Portanto, segue que a margem de erro ME e a margem de erro simultânea SME são dados por

$$SME = 13,699 \ \hbox{e} \ ME = 6,748.$$

Vamos adotar o efeito A para calcularmos o intervalo de confiança e a estatística t. Assim, o intervalo de confiança é dado por:

$$LI=\hat{c}_j-ME=21,625-6,748$$

$$LS=\hat{c}_j+ME=21,625+6,748$$

E a estatística do teste:

$$T_{L_j}=\frac{|\hat{c}_j|}{PSE}=\frac{21,625}{2,625}=8,238$$

Logo o p-valor é dado por:

$$\text{p-valor}=2\times P[t_d>|T_{L_j}|~|~H_0]=2\times P[t_d>|8,238|~|~H_0]=0,0002$$

Resultados desse exemplo obtidos com o software Action:

(imagem em falta)

(imagem em falta)

Tabela 3.3.2.2: Análise do experimento sem réplicas

(imagem em falta)

Figura 3.3.2.1: Gráfico dos efeitos pelo método de Lenth.

Portanto, pelos resultados obtidos, temos que os fatores A, C, D, A:C e A:D são significativos.

3.3.3 - Experimento de Youden

O estudo da robustez é geralmente parte de desenvolvimento do método. Caso não seja estudado durante o desenvolvimento do método, existe a necessidade de se realizar tal estudo. De acordo com INMETRO, a robustez mede a sensibilidade que este apresenta face à pequenas variações nas condições experimentais que podem ser expressas como uma lista de materiais da amostra, analitos, condições de armazenamento, ambiental e/ou amostra, condições de preparação em que o método pode ser aplicado ou apresentado, sujeitas à pequenas modificações. Para todas as condições experimentais que possam, na prática, estar sujeitas a variações (por exemplo, estabilidade dos reagentes, a composição da amostra) quaisquer alterações podem afetar o resultado analítico e este deve ser indicado.

Por exemplo, a robustez de um método cromatográfico é avaliada pela variação de parâmetros como a concentração do solvente orgânico, pH e força iônica da fase móvel em HPLC, bem como o tempo de extração, agitação etc. As mudanças introduzidas refletem as alterações que podem ocorrer quando um método é transferido para outros laboratórios, analistas ou equipamentos. Visando essas mudanças o INMETRO recomenda o teste de Youden, que permite avaliar se modificações no método tem diferenças significativas. Outro ponto que pode avaliado neste método, é que podemos ordenar se uma combinação de influências podem causar diferenças significativas nos resultados finais. Neste método são realizados oito ensaios separadamente, visando determinar quais efeitos das diferentes etapas no procedimento analítico afetam o resultado. A tabela de planejamento pelo método de Youden é dado por:

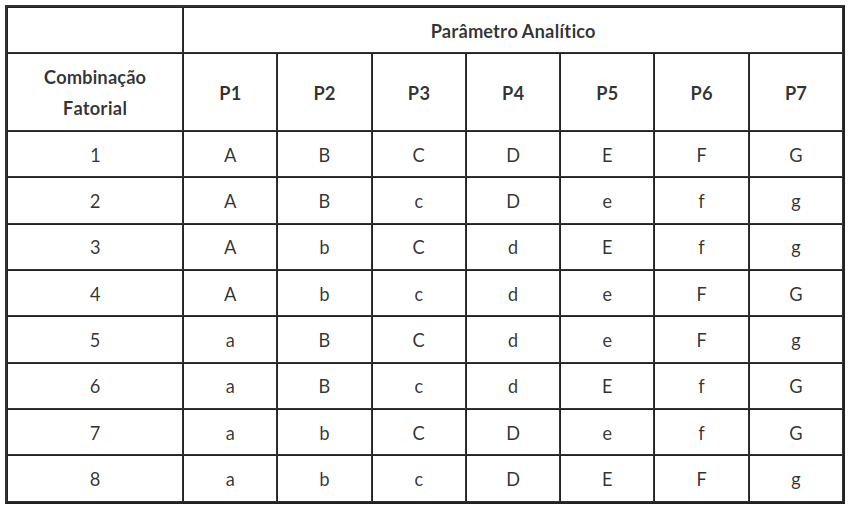
Tabela 3.3.1: Planejamento experimental para avaliar a robustez pelo método de Youden.

Em cada parâmetro analítico da tabela (3.3.1), definimos o nível alto (letra maiúscula) como $ (+) $ e o nível baixo (letra minúscula) como $ (-). $ Assim, obtemos a tabela (3.3.2).

Tabela 3.3.2: Planejamento experimental para avaliar a robustez pelo método de Youden recodificado.

Para a analisar o experimento de Youden, primeiramente são calculados os efeitos apara cada parâmetro analítico, em seguida utilizamos o método de Lenth para avaliar se os efeitos ativos são significativos. Vamos aplicar estes conceitos no seguinte exemplo extraído do artigo de Isabela C. e Pianete.

Exemplo 3.3.2

Com objetivo de avaliar a robustez do método cromatográfico para a quantificação de lumefantrina, no experimento de Youden, e determinar parâmetros analíticos que apresentam maior influência nos resultados finais da análise. Sete parâmetros analíticos foram selecionados e pequenas variações foram induzidas nos valores nominais do método.

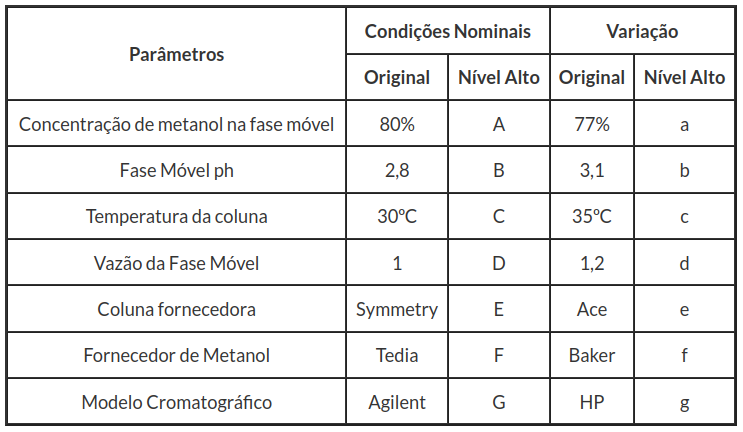
Tabela 3.3.3: Parâmetros analíticos.

Utilizando o experimento de Youden obtemos a seguinte tabela:

P1	P2	P3	P4	P5	P6	P7	Resposta
1	1	1	1	1	1	1	99,63
1	1	-1	1	-1	-1	-1	99,8
1	-1	1	-1	1	-1	-1	99,85
1	-1	-1	-1	-1	1	1	99,63
-1	1	1	-1	-1	1	-1	99,48
-1	1	-1	-1	1	-1	1	99,64
-1	-1	1	1	-1	-1	1	99,6
-1	-1	-1	1	1	1	-1	99,51

Tabela 3.3.4: Conjunto de dados.

Termo	Estimativa dos efeitos
P1	0,17
P2	-0,01
P3	-0,005
P4	-0,015
P5	0,03
P6	-0,16
P7	-0,035

Tabela 3.3.5: Estimativa dos efeitos.

Com os valores da Tabela (3.3.5), calculamos os valores de PSE, ME e SME. Primeiramente, calculamos $ s_0 $ da seguinte forma

$$s_{0}=1,5 \times mediana (|c_{j}|)=1,5 \times mediana (0,005; 0,01; …; 0,015; 0,035) =0,03.$$

Desta forma, tem-se que

$$ PSE = 1,5 \times mediana(|c_{j}|:|c_{j}|\leq2,5 s_{0}) = 1,5 \times mediana (|c_{j}|: |c_{j}|\leq 0,075) = 0,0225. $$

Adotando $ \alpha=0,05 $ e $ m=7 $, tem-se que $ d=2,333 $. Logo, $ t_{(0,975;2,333)}=3,76412307 $, $ \gamma=(1+0,95^{1/7})/2=0,996 $ e consequentemente, $ t_{0,996;2,333}=9,01 $. Portanto, segue que a margem de erro ME e a margem de erro simultânea SME são dados por

$$SME= t_{(0,975;2,333)} \times PSE=0,20269 \ \hbox{e} \ ME =t_{0,996;2,333} \times PSE=0,08493.$$

Vamos adotar o efeito 1 para calcularmos o intervalo de confiança e a estatística t. Assim, o intervalo de confiança é dado por:

$$LI=\hat{c}_1-ME=0,17-0,08493=0,0853$$

$$LS=\hat{c}_1-ME=0,17+0,08493=0,2547$$

A estatística t no ponto 1 é dado por:

$$T_{L_1}=\frac{|\hat{c}_i|}{PSE}=\frac{|0,17|}{0,0225}=7,5556$$

com o quantil da distribuição t-Student $ t_{0,975,2,333}, $ ou calculamos o p-valor à partir da distribuição t-Student com $ 2,333 $ graus de liberdade e com nível de significância $ \alpha=0,05. $ Logo, p-valor é dado por:

$$p-valor=2\times P[t_d> |T_{L_j}|~|~H_0]=2\times P[t_d> |7,5556|~|~H_0]=0,005$$

Como o p-valor é menor que o $ \alpha $ adotado (0,05), rejeitamos $ H_0 $ ao nível de significância de 5%. Portanto, a temperatura da coluna a vazão da faze móvel tem efeitos ativos. Para saber detalhes da influência destes dois parâmetros consulte o artigo de Isabela C. e Pianete.

Veja a seguir os resultados obtidos pelo software Action Stat para o mesmo exemplo.

(imagem em falta)

Tabela 3.3.6: Análise do experimento sem réplicas pelo método de Lenth.

(imagem em falta)

Tabela 3.3.7: Gráfico dos efeitos pelo método de Lenth.

(imagem em falta)

Tabela 3.3.8: Gráfico de papel de probabilidade half-normal (Daniel Plot).

4 - Experimentos fatoriais em blocos

A medida que o número de fatores de um experimento aumenta torna-se inviável realizar todas as corridas sob condições homogêneas, como por exemplo, coletar os dados todos no mesmo dia, utilizar o mesmo lote de matéria prima ou manter o mesmo operador. Ou então pode ser de interesse realizar um experimento que garanta tratamento igual para diferentes condições encontradas na prática. Nestes casos, utilizamos os experimentos fatoriais em blocos.

4.1 - Blocos para experimentos fatoriais $2^k$

Para realizar um experimento fatorial $ 2^k $ com n réplicas sob condições não homogêneas podemos considerar cada conjunto dessas condições como um bloco e realizar as réplicas em blocos diferentes. Além disso, as corridas devem ser feitas de forma aleatória.

Para situações em que não é possível fazer uma réplica completa de um experimento fatorial em um único bloco utiliza-se uma técnica denominada de confundimento. Esta técnica faz com que certos efeitos de interação fiquem indistinguíveis dos blocos, ou confundidos com os blocos.

Considerando um planejamento fatorial $ 2^k $ em $ 2^p $ blocos, sendo p < k, pode-se delinear este experimento em dois blocos, quatro blocos, oito blocos e assim por diante.

4.1.1 - Dois blocos

Supondo um experimento fatorial $ 2^2 $ com uma única réplica tem-se quatro possíveis combinações. Muitas vezes, os recursos disponíveis, como por exemplo, a matéria prima não é suficiente para realizar as quatro combinações, mas apenas duas delas. Neste caso, pode-se considerar cada tipo de matéria prima como um bloco, o que permite alocar duas combinações para cada bloco.

Verifica-se na Figura 4.1.1.1 uma maneira de alocar as combinações possíveis em blocos diferentes. No bloco 1 observa-se as combinações [(0), ab] e no bloco 2 as combinações [a,b], sendo que a ordem das corridas é aleatória.

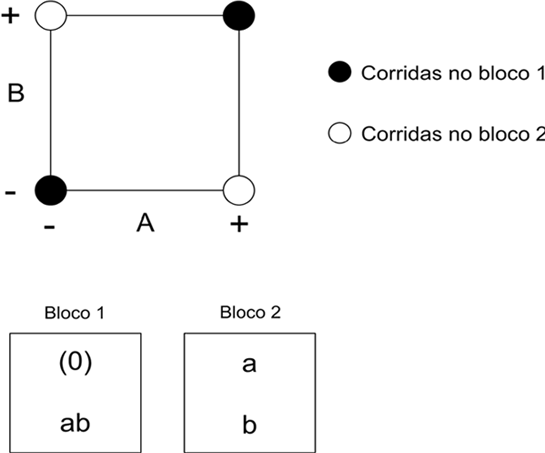
Figura 4.1.1.1: Um delineamento $ 2^2 $ em dois blocos. forma geométrica (superior) e quatro corridas em dois blocos (inferior).

Cálculo dos efeitos

Os procedimentos para estimar os efeitos principais de A e B são os mesmos usados para estimativas em experimentos que não são delineados em blocos.

$$A=\frac{1}{2}\left[ab+a-b-(0)\right]$$

$$B=\frac{1}{2}\left[ab+b-a-(0)\right]$$

Nota-se que os dois efeitos principais não são afetados pelos blocos, pois para cada estimativa existe uma combinação de tratamento mais e outra menos em cada bloco. Ou seja, qualquer combinação entre os blocos 1 e 2 será cancelada.

A estimativa do efeito da interação é dada por:

$$AB=\frac{1}{2}\left[ab+(0)-a-b\right]$$

Como os dois tratamentos com sinal positivo [ab e (0)] estão no bloco 1 e os dois com o sinal negativo [a e b] estão no bloco 2, o efeito da interação é idêntico nos blocos. Portanto AB está confundida com os blocos.

De maneira geral, se a interação for assinalada com sinal positivo considera-se o bloco 1 e quando for assinalada com sinal negativo, o bloco 2 desta forma, a interação fica confundida com os blocos. Na prática determina-se que as interações de maior ordem sejam confundidas com os blocos, de acordo com a Tabela 4.1.1.1.

Tabela 4.1.1.1: Planejamento Fatorial 22 em dois blocos

O caso mostrado na Tabela 4.1.1.1 é o mais simples para experimentos fatoriais $ 2^k $ com dois blocos. A seguir verificamos um exemplo de um experimento $ 2^4 $ em dois blocos.

Exemplo 4.1.1.1

Uma empresa fabricante de bolos quer reduzir as reclamações relacionadas a dureza de sua massa. Para isso delineou um experimento $ 2^3 $, com duas réplicas, com os fatores definidos da seguinte forma:

• A - Açúcar;
• B - Leite;
• C - Fermento.

Para realizar este experimento foram produzidos bolos com variações de 2 níveis de fatores. Entretanto, os bolos foram assados em um forno com 2 divisões que permitem somente 4 bolos cada, desta forma, o forno caracteriza um novo fator de influência. Por isso, o forno foi considerado um bloco, de acordo com a sua posição. o experimento e os dados coletados são mostrados na tabela a seguir.

Réplica	Bloco	A	B	C	Leveza
1	1	-1	-1	-1	0,539
1	1	1	1	-1	0,446
1	1	1	-1	1	0,306
1	1	-1	1	1	0,371
1	2	1	-1	-1	0,411
1	2	-1	1	-1	0,602
1	2	-1	-1	1	0,369
1	2	1	1	1	0,295
2	1	-1	-1	-1	0,459
2	2	-1	-1	1	0,430
2	1	1	1	-1	0,372
2	2	1	1	1	0,246
2	2	1	-1	-1	0,354
2	2	-1	1	-1	0,622
2	1	1	-1	1	0,357
2	1	-1	1	1	0,310

Exemplo 4.1.1.2

As lâmpadas fluorescentes são equipamentos que utilizam descargas elétricas para produzir energia luminosa. Para o seu funcionamento necessitam de equipamentos auxiliares, os reatores, que visam controlar e estabilizar a corrente elétrica. O tempo de vida das lâmpadas e a quantidade de luz que elas produzem dependem do rendimento dos reatores. O reator é um produto composto, basicamente, de chapas de aço, fio esmaltado, resina (para encapsulamento) e capacitores (quando necessário).

Uma indústria fabricante de reatores quer melhorar o rendimento de seu produto em 10 %.

Para chegar as alternativas para a melhoria do produto, decidiram fazer um experimento fatorial levando em conta os fatores:

• A - Peso do Núcleo de Aço,
• B - Peso do Fio de Cobre,
• C - Temperatura de Cura da Resina e
• D - Tipo de Capacitor.

Cada fator foi estudado em dois níveis e os dados obtidos em dois dias diferentes com 8 tratamentos em cada dia. Portanto temos um experimento $ 2^4 $ em dois blocos com o confundimento da interação ABCD.

A	B	C	D	ABCD	Bloco	Rendimento
-1	-1	-1	-1	1	2	3,6
1	-1	-1	-1	-1	1	4,9
-1	1	-1	-1	-1	1	3,4
1	1	-1	-1	1	2	5,4
-1	-1	1	-1	-1	1	6
1	-1	1	-1	1	2	4,9
-1	1	1	-1	1	2	5,1
1	1	1	1-	-1	1	4,5
-1	-1	-1	1	-1	1	3,4
1	-1	-1	1	1	2	7,9
-1	1	-1	1	1	2	3,2
1	1	-1	1	-1	1	7,6
-1	-1	1	1	1	2	5,3
1	-1	1	1	-1	1	7,3
-1	1	1	1	-1	1	5,7
1	1	1	1	1	2	6,5

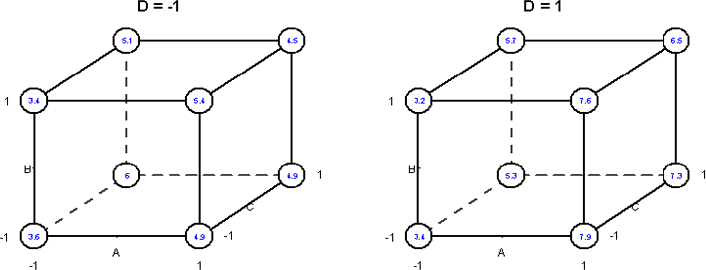
Figura 4.1.1.2: Gráfico de média para o Exemplo 4.1.1.2.

Verificamos a seguir os gráficos da representação geométrica, dos efeitos principais e da interação, para os dados de rendimento dos reatores, respectivamente.

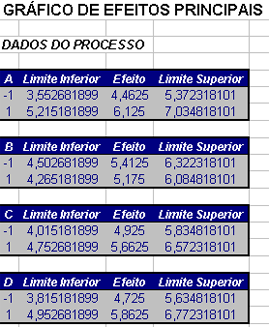
Tabela 4.1.1.2: Tabela dos Efeitos Principais.

Verificamos na Figura 4.1.1.2 a representação geométrica do experimento e os valores de cada combinação, pois o experimento foi realizado sem réplicas.

As estimativas dos efeitos principais e das interações obtidas pelo modelo de regressão são mostrados na Tabela 4.1.1.2.

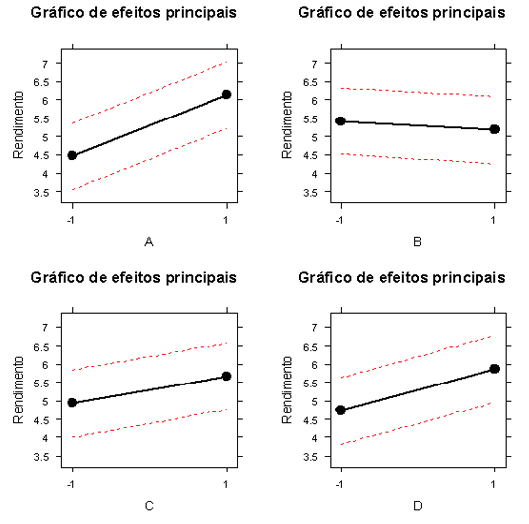
Figura 4.1.1.3: Gráfico dos Efeitos principais para o Exemplo 4.1.2.1.

De acordo com a análise gráfica da Figura 4.1.1.3 verificamos indícios de que a mudança do nível -1 para o nível 1 dos fatores A (Peso de núcleo de aço), C (Temperatura de cura da resina) e D (Tipo de Capacitor) aumentam o rendimento dos reatores.

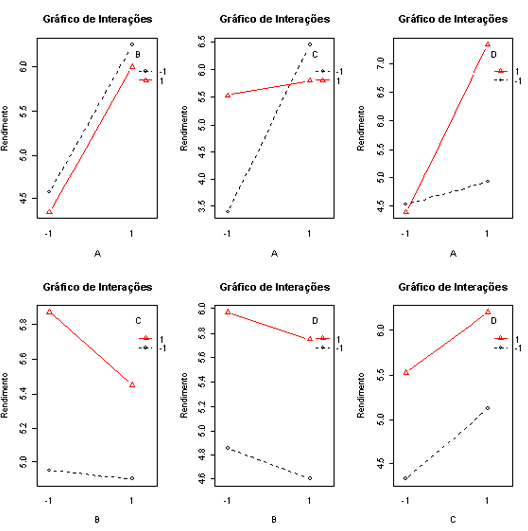
Figura 4.1.1.4: Gráfico de Interações para o Exemplo 4.1.2.1.

Verificamos na Figura 4.1.1.4 indícios da existência das interações AC e AD.

Obtemos então os efeitos dos fatores e das interações através de modelo de regressão:

Termo	Efeito	Coef. Regressão
Média Geral		5,2938
Bloco		-0,0562
Peso núcleo	1,6625	0,8313
Peso fio	-0,2375	-0,1188
Temperatura	0,7375	0,3687
Capacitor	1,1375	0,5688
Peso nucleo * Peso fio	-0,0125	-0,0062
Peso nucleo * Temperatura	-1,3875	-0,6938
Peso nucleo * Capacitor	1,2625	0,6312
Peso fio * Temperatura	-0,1875	-0,0937
Peso fio * Capacitor	0,0125	0,0063
Temperatura * Capacitor	-0,0625	-0,0312
Peso nucleo * Peso fio* Temperatura	-0,1625	-0,0812
Peso nucleo * Peso fio * Capacitor	-0,3125	-0,1563
Peso nucleo * Temperatura * Capacitor	-0,1375	-0,0688
Peso fio * Temperatura * Capacitor	0,2125	0,1063

Neste caso, como não temos réplicas, não existe soma de quadrados do erro (estamos estimando 16 coeficientes com 16 equações).

Uma saída neste caso é aplicar o método de Lenth para decidir que efeitos são significativos, como mostra a Figura 4.1.1.5.

(imagem em falta)

(imagem em falta)

(imagem em falta)

(imagem em falta)

Figura 4.1.1.5: Método de Lenth para os Efeitos do Exemplo 4.1.1.2.

(imagem em falta)

Figura 4.1.1.6: Daniel Plot para o Exemplo 4.1.1.2.

De acordo com as análises gráficas notamos que os fatores A, C e D e as interações AC e AD influenciam no rendimento dos reatores. Desta forma, podemos ajustar um novo modelo linear para estimar os seus efeitos.

Os termos significativos de acordo com a Figura 4.1.1.5 são A, C, D, AC e AD. Ajustamos então um novo modelo linear e estimamos os efeitos de cada fator e das interações significativas:

Termo	Efeito	Coeficiente da Regressão	Desvio Padrão	T	P
Média Geral		5,2938	0,0888	59,61	0
Bloco		0,0562	0,0888	0,63	0,542
A	1,6625	0,8313	0,0888	9,36	0
C	0,7375	0,3688	0,0888	4,15	0,002
D	1,1375	0,5687	0,0888	6,4	0
AC	-1,3875	-0,6938	0,0888	-7,81	0
AD	1,2625	0,6312	0,0888	7,11	0

Tabela 4.1.1.3: Tabela de coeficientes de regressão e efeitos para o Exemplo 4.1.1.2.

Na sequência construímos a Tabela ANOVA, utilizando também como fonte de variação o bloco considerado.

Fonte de Variação	Soma de Quadrados	Graus de Liberdade	Quadrados Médios	Estatística F	P-valor
Bloco	0,05	1	0,05	0,4	0,54
A	11,06	1	11,06	87,62	0
C	2,18	1	2,18	17,24	0
D	5,18	1	5,18	41,02	0
AC	7,7	1	7,7	61,03	0
AD	6,38	1	6,38	50,53	0
Erro	1,14	9	0,13
Total	33,67	15

Tabela 4.1.1.4: Tabela da ANOVA para o Exemplo 4.1.1.2.

Olhando para os coeficientes obtidos pela regressão na Tabela 4.1.1.4 vemos que os fatores e as interações consideradas realmente são significativos.

Resultados obtidos pelo software Action

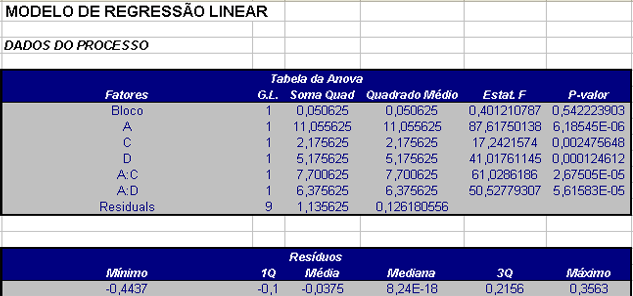
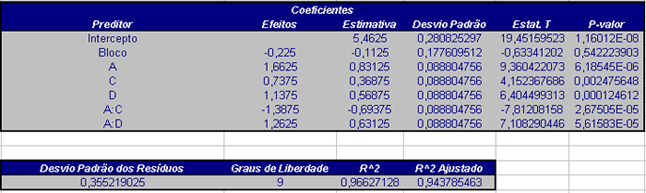
Tabela 4.1.1.7 resultados da Tabela da ANOVA obtidos no Action.

Os resultados mostrados na Tabela 4.1.1.7 confirmam os indícios verificados na análise gráfica, que os fatores A, C e D e as interações AC e AD são significativas ao nível α = 0,05, ou seja, eles influenciam no rendimento do reator. Portanto, a melhor configuração para aumentar o rendimento dos reatores é manter o nível do fator “B” e fixar os níveis dos fatores A, C e D no nível 1.

4.1.2 - Quatro ou mais blocos

Além dos delineamentos já discutidos é possível construir um experimento fatorial do tipo $ 2^k $ dividido em quatro blocos com $ \frac{2^k}{4}=2^{k-2} $ observações em cada bloco. Este delineamento é útil quando o número de fatores é grande (k ≥ 4) e o tamanho dos blocos é pequeno.

Como um exemplo, considere um experimento fatorial $ 2^5 $. Cada bloco é composto por 8 corridas, resultando assim em 4 blocos. Considerando, por exemplo, os efeitos de ABC e CDE para serem confundidos com os blocos, o delineamento do experimento é dado de acordo com a Tabela 4.1.2.1.

	A	B	C	D	E	ABC	CDE	Blocos
0	-1	-1	-1	-1	-1	-1	-1	1
(a)	1	-1	-1	-1	-1	1	-1	3
(b)	-1	1	-1	-1	-1	1	-1	3
(ab)	1	1	-1	-1	-1	-1	-1	1
(c)	-1	-1	1	-1	-1	1	1	4
(ac)	1	-1	1	-1	-1	-1	1	2
(bc)	-1	1	1	-1	-1	-1	1	2
(abc)	1	1	1	-1	-1	1	1	4
(d)	-1	-1	-1	1	-1	-1	1	2
(ad)	1	-1	-1	1	-1	1	1	4
(bd)	-1	1	-1	1	-1	1	1	4
(abd)	1	1	-1	1	-1	-1	1	2
(cd)	-1	-1	1	1	-1	1	-1	3
(acd)	1	-1	1	1	-1	-1	-1	1
(bcd)	-1	1	1	1	-1	-1	-1	1
(abcd)	1	1	1	1	-1	1	-1	3
(e)	-1	-1	-1	-1	1	-1	1	2
(ae)	1	-1	-1	-1	1	1	1	4
(be)	-1	1	-1	-1	1	1	1	4
(abe)	1	1	-1	-1	1	-1	1	2
(ce)	-1	-1	1	-1	1	1	-1	3
(ace)	1	-1	1	-1	1	-1	-1	1
(bce)	-1	1	1	-1	1	-1	-1	1
(abce)	1	1	1	-1	1	1	-1	3
(de)	-1	-1	-1	1	1	-1	-1	1
(ade)	1	-1	-1	1	1	1	-1	3
(bde)	-1	1	-1	1	1	1	-1	3
(abde)	1	1	-1	1	1	-1	-1	1
(cde)	-1	-1	1	1	1	1	1	4
(acde)	1	-1	1	1	1	-1	1	2
(bcde)	-1	1	1	1	1	-1	1	2
(abcde)	1	1	1	1	1	1	1	4

Tabela 4.1.2.1: Delineamento do experimento fatorial $ 2^5 $ em 4 blocos.

Observamos que a forma como o experimento foi delineado resultou em exatamente quatro combinações de sinais diferentes, para as 32 observações, que correspondem aos 4 blocos do experimento. Para compor os blocos consideramos todas as corridas que estão em (-,-) no bloco 1, (-,+) no bloco 2, (+,-) no bloco 3 e por fim, (+,+) no bloco 4, conforme a Tabela 4.1.2.2. Neste caso, qualquer interação adicionada a ABC e CDE serão confundidas com os blocos, já que existem quatro blocos com 3 graus de liberdade e também ABC e CDE tem 1 grau de liberdade. O efeito geral de ABC e CDE é definido como o produto entre eles, da seguinte forma:

$$(ABC)(CDE)=ABC^2DE=ABDE, {(pois }~ C^2=1, { sempre)}$$

assim, o efeito de ABDE também é confundido com os blocos.

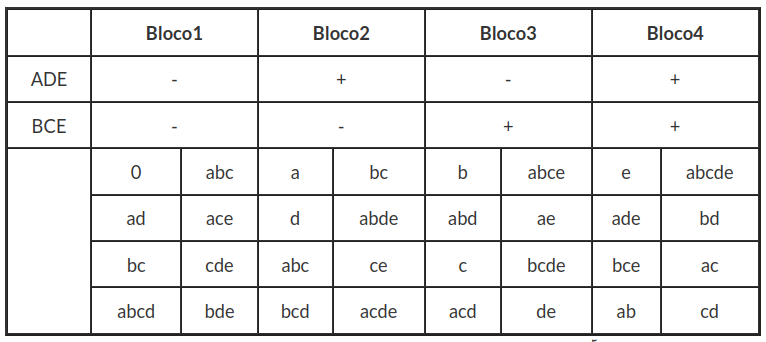
Tabela 4.1.2.2: Resumo do delineamento do experimento fatorial $ 2^5 $ em 4 blocos.

O procedimento geral para construir um delineamento $ 2^k $ em quatro blocos consiste em escolher dois efeitos para gerar os blocos, assim, temos automaticamente um terceiro efeito confundido com os dois primeiros. Os efeitos escolhidos para serem confundidos devem ser cuidadosamente selecionados, para não escolher efeitos que realmente são importantes para o experimento.

Este procedimento pode ser estendido para um número maior de blocos. É possível construir um delineamento fatorial de $ 2^k $ em p blocos, onde p < k, de $ 2^k-p $ combinações cada bloco. Para isso, basta escolher p efeitos independentes para confundir com blocos (independentes significa que nenhum efeito principal está generalizado com as interações). A seguir verifica-se alguns exemplos de efeitos que podem ser confundidos.

$$(ABEF)(ABCD)=A^2B^2CDEF = CDEF$$

$$(ABEF)(ACE)= A^2BCE^2F=BCF$$

$$(ABCD)(ACE) = A^2BC^2ED=BDE$$

$$(ABEF)(ABCD)(ACE) = A^3B^2C^2DE^2F=ADF$$

Existem muitos procedimentos para construção e análise de delineamentos fatoriais com k fatores e dois níveis. A Tabela 4.1.2.3 mostra a estrutura de blocos para Experimentos Fatoriais $ 2^k $.

Nº de fatores k	Nº de blocos 2p	Tam. do bloco 2k-p	Efeito escolhido	Interações Confundidas
3	2	4	ABC	ABC
	4	2	AB,AC	AB,AC,BC
4	2	8	ABCD	ABCD
	4	4	ABC,ACD	ABC,ACD,BD
	8	2	AB,BC,CD	AB,BC,CD,AC,BD,AD,ABCD
5	2	16	ABCDE	ABCDE
	4	8	ABC,CDE	ABC,CDE,ABDE
	8	4	ABE,BCE,CDE	ABE,BCE,CDE,AC,ABCD,BD,ADE
	16	2	AB,AC,CD,DE	Todos os fatores de 2º grau, 4º grau (15 interações)
6	2	32	ABCDEF	ABCDEF
	4	16	ABCF,CDEF	ABCF,CDEF,ABDE
	8	8	ABEF,ABCD,ACE	ABEF,ABCD,ACE,BCF,BDE,CDEF,ADF
	16	4	ABF,ACF,BDF,DEF	ABE,ACF,BDF,DEF,BC,ABCD,ABDE,AD,ACDE, CE,BDF,BCDEF,ABCEF,AEF,BE
	32	2	AB,BC,CD,DE,EF	Todos os fatores de 2º grau, 4º grau, 6º grau (31 interações)
7	2	64	ABCDEFG	ABCDEFG
	4	32	ABCFG,CDEFG	ABCFG,CDEFG,ABDE
	8	16	ABC,DEF,AFG	ABC,DEF,AFG,ABCDEF,DCFG,ADEG,BCDEFG
	16	8	ABD,EFG,CDE,ADG	ABCD,EFG,CDE,ADG,ABCDEFG,ABE,ACG, CDFG,ADEF,ACEG,ABFG,BCEF,BDEG,ACF,BDF
	32	4	ABG,BCG,CDG,DEG,EFG	ABG,BCG,CDG,DEG,EFG,AC,BC,DE,DF,AE,BE,ABCD, ABDE,ABEF,BCDE,BCEF,CDEF,ABCEDFG,ADG,ACDEG,ACEFG, ABDFG,ABCEG,BEG,BDEFG,CFG,ADEF,ACDF,ABCF,AFG
	64	2	AB,BC,CD,DE,EF,FG	Todos os fatores de 2º grau, 4º grau, 6º grau (63 interações)

Tabela 4.1.2.3: Estrutura de Blocos para Experimentos Fatoriais 2k.

5 - Experimentos Fatoriais Fracionados

A medida que o número de fatores em um experimento fatorial $ 2^k $ aumenta, o número de corridas também aumenta e consequentemente o número de interações de ordem alta. Se o condutor do experimento assumir que estas interações não são úteis para o experimento, pois são difíceis de interpretar, então, os efeitos principais e das interações de baixa ordem serão fundamentais, desta forma, eles deverão ser obtidos mesmo que seja realizada apenas uma fração deste experimento.

Estes tipos de experimentos denominam-se experimentos fatoriais fracionados. Na prática das indústrias, este tipo de experimento é muito utilizado, pois permite reduzir o número de corridas e consequentemente o custo de realização do experimento.

A maior aplicação prática deste tipo de experimento fatorial é na seleção de variáveis. Nesta aplicação, consideramos um grande número de variáveis ou fatores que podem influenciar no sistema ou processo. Neste caso, o experimento fatorial é fracionado a fim de identificar quais variáveis ou fatores influenciam no processo e, posteriormente, realizar um experimento mais detalhado, somente com os fatores que influenciam.

Estes experimentos fatoriais estão fundamentalmente baseados em três ideias:

• Efeitos principais: Na presença de muitas variáveis, o sistema ou processo será dirigido por alguns efeitos principais e interações de baixa ordem.
• Propriedades projetivas: Fatoriais fracionados podem ser projetados para que os fatores mais significantes tenham os maiores efeitos.
• Experimentos sequenciais: É possível combinar as corridas de dois (ou mais) fatoriais fracionados para montar sequencialidade em delineamentos grandes para estimar os fatores e interações de interesse.

5.1 - Meia fração de um experimento fatorial fracionado

• Temos um experimento com três fatores com dois níveis cada;
• Serão executados metade dos 8 tratamentos;

Considere a situação onde temos um experimento com três fatores com dois níveis cada, mas por questões de custo somente metade dos 8 tratamentos serão executados.

A Tabela 4.1.1 representa um delineamento do tipo $ 2^3 $.

Suponha que neste caso selecionemos quatro tratamentos a, b, c e abc como nossa meia fração. Note que neste caso temos ainda as interações de segunda ordem, mas escolhemos definir como a meia fração os termos que tem sinal positivo na coluna ABC.

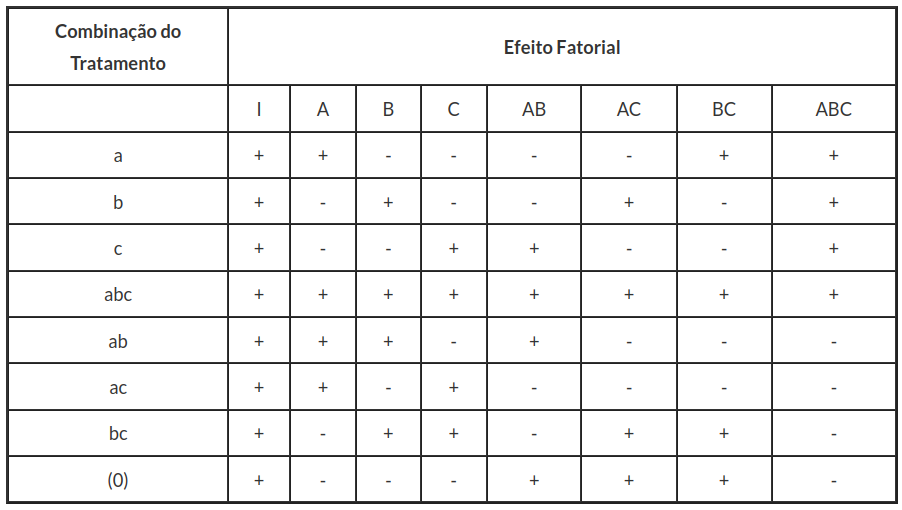
Tabela 5.1.1: Fatorial Fracionado 23.

As combinações do tratamento no delineamento fatorial 23-1 rendem três graus de liberdade para estimar os efeitos principais. Que podem ser definidos como:

$$A=\frac{1}{2}(a-b-c+abc)$$

$$B=\frac{1}{2}(-a+b-c+abc)$$

$$C=\frac{1}{2}(-a-b+c+abc)$$

Para saber se o fator A está confundido com algum outro fator, podemos fazer o cálculo

$$A=A \times I=A \times ABC=A^2 \times BC$$

$$(A^2 \text{ é sempre 1 })$$

$$A=BC$$

de onde concluímos que A está confundido com AB. De forma análoga, mostramos que B está confundido com AC e que C está confundindo com AB. Os efeitos das interações de 2ª ordem são dados por

$${BC}=\frac{1}{2}(a-b-c+abc).$$

$${AC}=\frac{1}{2}(-a+b-c+abc).$$

$${AB}=\frac{1}{2}(-a-b+c+abc).$$

ou seja, é impossível diferenciar entre A e Bc, B e AC, e C e AB. Quando estimamos A, B e C, estamos na verdade estimando A + BC, B + AC e C + AB. Quando dois ou mais efeitos tem essa propriedade são chamados de aliases. Neste caso A e BC são aliases, B e AC são aliases e C e AB são aliases. Indicamos as aliases pelas notações IA → A + BC, IB → B + AC e IC → C + AB

A meia fração I=+ABC é chamada de fração principal.

Se selecionarmos a outra meia fração, isto é, I' = -ABC, os tratamentos associados com o sinal menos na coluna ABC as aliases (ou fatores confundidos) seriam neste caso

$${A}=A*-ABC=-BC$$

$${B}=B*-ABC=-AC$$

$${C}=C*-ABC=-AB$$

Ou seja, estaremos estimando na verdade A - BC, B - AC e C - AB. E as aliases são indicadas por I’A = A - BC, I’B = B - AC, I’C = C - AB

Se efetuarmos as corridas de ambas as meias frações, todas as 8 corridas associadas com o experimento experimento completo 23 estarão disponíveis. Desta forma, podemos obter as estimativas de todos os efeitos analisando as 8 corridas como um experimento completo 23 em dois blocos de quatro corridas cada. Isto implica que, considerando IA → A + BC e I’A → A - BC

$$\frac{1}{2}(I_A + I_A) = \frac{1}{2}(A+BC+A-BC) \rightarrow A$$

e também

$$\frac{1}{2}(I_A - I_A)=\frac{1}{2}(A+BC-A+BC) \rightarrow BC$$

Portanto, todas as três partes das combinações lineares são demonstradas da seguinte maneira:

X	$ \frac{1}{2}(I_A + I_A) $	$ \frac{1}{2}(I_A - I_A) $
A	A	BC
B	B	AC
C	C	AB

5.1.1 - Resoluções dos experimentos fatoriais fracionados

Para resolver os experimentos fatoriais fracionados, são utilizados três tipos de resoluções:

1. Resolução do tipo III: Estas são as resoluções nos quais nenhum efeito principal está relacionado com qualquer outro efeito principal, mas podem estar relacionado com interações de segunda ordem que por sua vez podem estar relacionadas também com interações de segunda ordem ou de ordem superior. O planejamento $ 2^{3-1} $ na Tabela 5.1.1.1 segue resolução do tipo III $ (2^{3-1}_{III}). $
2. Resolução do tipo IV: Esta resolução determina que nenhum efeito principal está relacionado com outro efeito principal ou então interação de segunda ordem, mas as interações de segunda ordem estão relacionadas entre si. Um planejamento $ 2^{4-1} $ com $ I=ABCD $ segue resolução do tipo IV $ (2^{4-1}_{IV}) $
3. Resolução do tipo V: Estes são os experimentos em que nem os efeitos principais ou as interações de segundo grau estão relacionados com os efeitos principais ou as interações de segundo grau, mas as interações de segundo grau podem estar relacionadas com interações de terceiro ou maior grau. Um planejamento $ 2^{5-1} $ com $ I=ABCDE $ segue resolução do tipo V $ (2^{5-1}_V) $

Construindo meias frações

Uma meia fração de um experimento $2^k$ da resolução mais alta, pode ser construído escrevendo um delineamento básico consistindo de corridas para um fatorial completo do tipo $2^{k-1}$ e então adicionando-se o k-ésimo fator, identificando-o com os mais e menos, que representam os níveis da interação de maior ordem ABC…(K - 1). Portanto, o fatorial fracionado ($2^{3-1}III$) pode ser obtido por um fatorial completo $2^2$ e então, equacionando-se as interações de segunda ordem AB com C. A fração alternativa, desta forma, -AB com C. Podemos entender melhor este procedimento da seguinte forma.

Tabela 5.1.1.1: Duas meias frações de um planejamento $ 2^3 $.

Resultados obtido pelo software Action

Exemplo 5.1.1.1

Um experimentador quer avaliar o comportamento do desgaste do pinhão do motor de uma máquina colheitadeira de cana, em relação a quatro fatores: abertura da lateral do chassi, janela da caneca, formato do disco e formato do rolo. O objetivo é determinar qual configuração estabelece um menor desgaste do pinhão. Utilizando 8 máquinas do mesmo modelo, mesmo ano de fabricação e utilizando a mesma frente de trabalho, realizamos um experimento fatorial fracionado $2^{4-1}$ com três réplicas. As unidades experimentais foram de 250 horas de trabalho por réplica. Os dados são dados na tabela a seguir.

Lateral chassi (LC)	Janela caneca (JC)	Formato disco (FD)	Rolo (R)	Desgaste
menor	com janela	sem recorte	com furo	0,2233
menor	sem janela	com recorte	com furo	0,1233
menor	sem janela	com recorte	com furo	0,1300
maior	sem janela	com recorte	sem furo	0,1867
menor	com janela	sem recorte	com furo	0,2533
menor	sem janela	com recorte	com furo	0,1700
menor	com janela	com recorte	sem furo	0,2400
menor	sem janela	sem recorte	sem furo	0,3033
maior	com janela	com recorte	com furo	0,1933
maior	com janela	sem recorte	sem furo	0,2500
maior	com janela	com recorte	com furo	0,1900
maior	com janela	sem recorte	sem furo	0,2533
maior	sem janela	sem recorte	com furo	0,2067
menor	com janela	com recorte	sem furo	0,2033
maior	com janela	com recorte	com furo	0,1767
menor	sem janela	sem recorte	sem furo	0,2200
menor	sem janela	sem recorte	sem furo	0,2133
maior	sem janela	com recorte	sem furo	0,1800
maior	com janela	sem recorte	sem furo	0,2333
maior	sem janela	com recorte	sem furo	0,1967
maior	sem janela	sem recorte	com furo	0,2100
maior	sem janela	sem recorte	com furo	0,2033
menor	com janela	sem recorte	com furo	0,2067
menor	com janela	com recorte	sem furo	0,1967

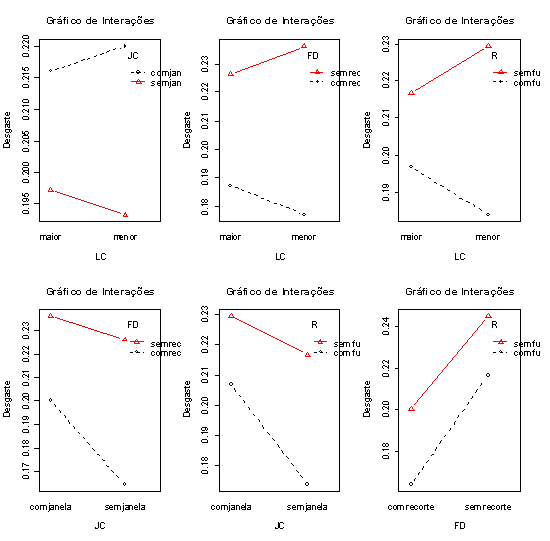
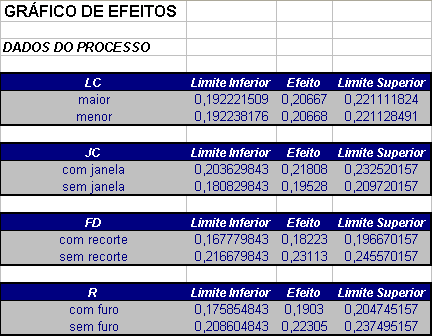
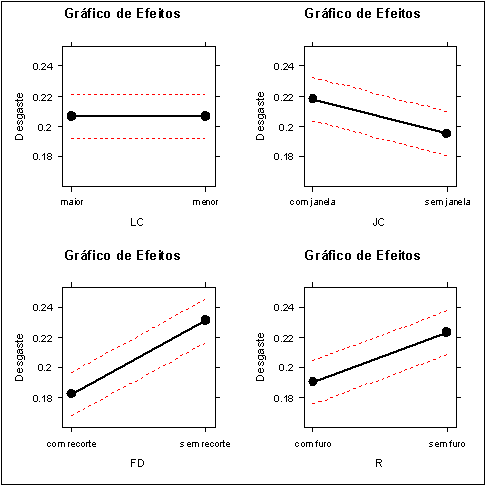
5.2 - Fatoriais fracionados sequenciais

Usando planejamentos fatoriais fracionados podemos ter uma grande economia e eficiência no experimento, particularmente se o experimento for conduzido sequencialmente. Por exemplo, suponha que tenhamos que investigar um fatorial k = 4 fatores ($ 2^4 $ = 16). Porém é preferível termos um experimento pela metade, ou seja, $ (2^{4-1}_{IV}) $ fatorial com 8 corridas, analisar os resultados e então decidir qual o melhor conjunto para correr em seguida. Se for necessário desenvolver ambiguidades é preferível que o experimento seja conduzido de maneira alternada até completar o fatorial. Quando este método for escolhido, ambas as frações do fatorial representam blocos do planejamento completo, com a maior ordem das interações confundida com os blocos (ABCD). Podemos afirmar que os experimentos sequenciais podem perder informação, mas apenas nas interações mais altas. De outra maneira podemos também aprender o suficiente com a primeira fração e poderemos fazer novas análises dos dados, excluir fatores, interações e até aumentar o intervalo de varredura de certas variáveis.

Exemplo 5.2.1

Considere a taxa de filtragem definida na tabela a seguir. A taxa de filtragem depende dos fatores envolvidos no processo:

• Temperatura (A);
• Pressão (B);
• Concentração de gás (utilizado para esterilização) (C);
• Taxa de filtragem (D).

Iremos utilizar a resolução $ 2_{IV}^{4-1} $ com I = ABCD. O experimento básico tem o número necessário de corridas, mas somente três fatores (colunas). Para encontrar o nível do quarto fator fazemos D = ABC. Então o nível D em cada corrida é definido como o produto dos sinais de + e - nas colunas A, B e C. Como o gerador ABCD é positivo, este experimento $ 2^{4-1}_{IV} $ é chamado fração principal.

Tabela 5.2.1: Planejamento $ 2^{4-1}_{IV} $ com a relação definida I=ABCD.

O experimento está ilustrado segundo a figura abaixo

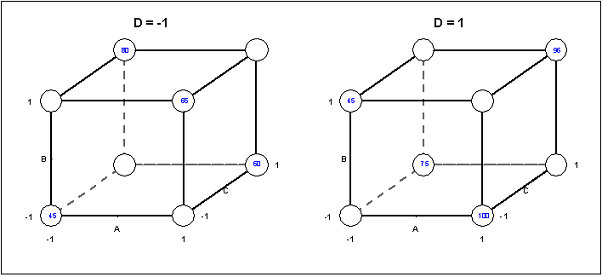
Figura 5.2.1: Planejamento do tipo $ 2^{4-1}_{IV} $ para a taxa de Filtragem.

Como seriam analisados se apenas metade do fatorial fosse considerado? Mais ainda, que análises poderíamos fazer sabendo que os fatores A, C e D e as interações AC e AD são todas diferentes de zero?

Neste caso estaremos usando um fatorial com resolução IV, $ (2^{4-1}) $. Usando ainda as definições do experimento podemos escrever que os efeitos principais e suas estruturas de aliases estão relacionados com a interações de terceira ordem; ou seja,

$$A=A*ABCD=A^2BCD=BCD$$

$$B=B*ABCD=AB^2CD=ACD$$

$$C=C*ABCD=ABC^2D=ABD$$

$$D=D*ABCD=ABCD^2=ABC$$

Cada interação de segunda ordem está relacionada com outra relação de segunda:

$$AB=CD,~AC=BD,~BC=AD.$$

As estimativas dos efeitos obtidos do experimento são:

$$A = \overline{Y_{A+}} - \overline{Y_{A-}} = \frac{100+65+60+96}{4}-\frac{45+45+75+80}{4}= 80,25-61,25=19$$

$$B = \overline{Y_{B+}} - \overline{Y_{B-}} = \frac{45+65+75+60}{4}-\frac{45+100+75+60}{4}=71,50-70=1,50$$

$$C = \overline{Y_{C+}} - \overline{Y_{C-}} = \frac{75+60+80+96}{4}-\frac{45+100+45+65}{4}=77,75-63,75=14$$

$$D = \overline{Y_{D+}} - \overline{Y_{D-}} = \frac{100+45+75+96}{4}-\frac{45+65+60+80}{4}=79-62,50=16,50$$

$$AB = \overline{Y_{AB+}} - \overline{Y_{AB-}} = \frac{45+65+75+96}{4}-\frac{100+45+60+80}{4}=70,25-72,25=-1$$

$$AC = \overline{Y_{AC+}} - \overline{Y_{AC-}} = \frac{45+45+60+96}{4}-\frac{100+65+75+80}{4}=61,50-80=-18,50$$

$$AD = \overline{Y_{AD+}} - \overline{Y_{AD-}} = \frac{45+100+80+96}{4}-\frac{45+65+75+60}{4}=80,25-61,25=19$$

Os resultados obtidos no Action são dados a seguir

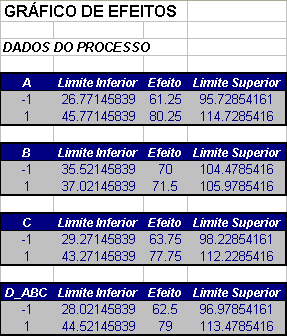
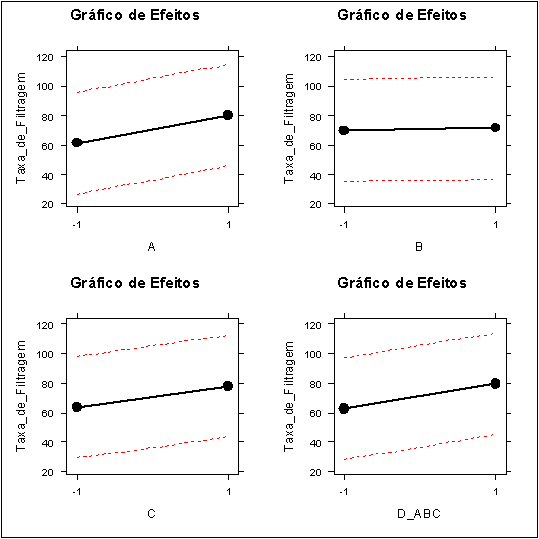
Exercício 5.2.2

Deseja-se verificar a quantidade de alimento que migra através de uma embalagem num processo de estocagem de acordo com quatro fatores. Para cada um dos fatores temos os seguintes níveis:

• A: tempo de estufa (em minutos) nos níveis 27 e 33;
• B: temperatura de estufa (em ºC) nos níveis 17 e 23;
• C: temperatura de tara (em ºC) nos níveis 90 e 120;
• D: tempo de resfriamento (em minutos) nos níveis 2 e 4.

Neste caso, temos 4 fatores, o que nos daria 16 corridas se fôssemos executar o experimento completo. Decidimos então fracionar o experimento em duas partes e executar 4 réplicas. Os dados são apresentados na tabela a seguir.

Repetição	A	B	C	D	Migração
1	27	17	90	2	11,0933
2	27	17	90	2	15,4800
3	27	17	90	2	12,7600
4	27	17	90	2	9,6267
1	27	17	120	4	1,7733
2	27	17	120	4	5,7733
3	27	17	120	4	4,2533
4	27	17	120	4	3,6667
1	33	17	90	4	1,5333
2	33	17	90	4	0,8533
3	33	17	90	4	5,1467
4	33	17	90	4	5,6267
1	33	17	120	2	3,0533
2	33	17	120	2	8,7067
3	33	17	120	2	6,2533
4	33	17	120	2	6,8933
1	27	23	90	4	10,7067
2	27	23	90	4	13,0400
3	27	23	90	4	11,6667
4	27	23	90	4	12,7333
1	27	23	120	2	13,5467
2	27	23	120	2	11,4267
3	27	23	120	2	8,2533
4	27	23	120	2	7,4533
1	33	23	90	2	18,0800
2	33	23	90	2	17,2000
3	33	23	90	2	19,2400
4	33	23	90	2	16,5067
1	33	23	120	4	5,4533
2	33	23	120	4	11,9467
3	33	23	120	4	12,9200
4	33	23	120	4	13,1867

Tabela 5.2.3: Conjunto de dados.

5.2.1 - Um quarto de fração de um planejamento 2^k

Para um número grande de fatores, pequenas frações de um planejamento fatorial fracionado podem ser úteis. Considere neste caso uma fração de um quarto de um planejamento $ 2^k $. Este planejamento contém $ 2^{k-2} $ corridas e é frequentemente considerado um planejamento fatorial fracionado do tipo $ 2^{k-2} $. Um planejamento deste tipo pode ser construído simplesmente escrevendo um experimento fatorial completo com $ (k-2) $ fatores e então associando as duas colunas com os geradores, isto é, escolher as interações que envolvem os primeiros $ (k-2) $ fatores. Portanto um quarto do experimento terá dois geradores. Se escolhermos como os geradores $ P $ e $ Q $, então $ I=P $ e $ I=Q $ são chamadas relações geradoras para o experimento. Seus sinais (+ ou -) definem que parte dos quartos de fração será produzida. Lembramos também que todos os quartos definidos por $ \pm P $ e $ \pm Q $ fazem parte da mesma família, e ainda, podemos assumir que quando temos os dois geradores positivos temos o quarto principal.

Considere um planejamento $ 2^{6-2} $, suponha que escolhamos

$$I=ABCE~~{ e }~~I=BCDF$$

como os geradores. Matricialmente podemos descrever o experimento como mostra a Tabela 5.2.1.1.

Corridas	A	B	C	D	E=ABC	F=BCD
1	-	-	-	-	-	-
2	+	-	-	-	+	-
3	-	+	-	-	+	+
4	+	+	-	-	-	+
5	-	-	+	-	+	+
6	+	-	+	-	-	+
7	-	+	+	-	-	-
8	+	+	+	-	+	-
9	-	-	-	+	-	+
10	+	-	-	+	+	+
11	-	+	-	+	+	-
12	+	+	-	+	-	-
13	-	-	+	+	+	-
14	+	-	+	+	-	-
15	-	+	+	+	-	+
16	+	+	+	+	+	+

Tabela 5.2.1.1: Experimento fatorial fracionado $ 2^{6-2} $.

Uma outra forma de obter um quarto da fração é gerar o experimento $ 2^6 $ e dividi-lo em 4 blocos, conforme já tratado no capítulo anterior. Isso resultará em um experimento fatorial fracionado $ 2^{6-2}, $ com geradores ABCF e CDEF (conforme Tabela 4.1.3.3) Quando considerarmos o bloco onde ambos os geradores são positivos a fração será chamada fração principal.

A interação entre os geradores $ ABCE $ e $ BCDF $ é $ ADEF $, portanto a relação completa para o experimento é

$$I=ABCE=BCDF=ADEF.$$

Por exemplo, para encontrar os aliases de $ A $ podemos fazer:

• $ A*ABCE=AABCE=BCE $, pois $ AA=1 $ sempre ($ A $ só assume os valores +1 ou -1),
• $ A* BCDF=ABCDF, $ e
• $ A*ADEF=AADEF=DEF $, novamente pois $ AA=1 $.

Assim, vemos que quando estimarmos $ A $, estaremos estimando $ A+BCE+DEF+ABCDF $. Na Tabela 5.2.1.2 mostramos a estrutura completa de aliases para este caso.

$ A = BCE = DEF = ABCDF $	$ AD = EF = ABCF = BCDE $
$ B = ACE = CDF = ABDEF $	$ AE = BC = DF = ABCDEF $
$ C = ABE = BDF = ACDEF $	$ AF = DE = ABCD = BCEF $
$ D = AEF = BCF = ABCDE $	$ BD = CF = ABEF = ACDE $
$ E = ABC = ADF = BCDEF $	$ BF = CD = ABDE = ACEF $
$ F = ADE = BCD = ABCEF $	$ ABD = ACF = BEF = CDE $
$ AB = CE = ACDF = BDEF $	$ ABF = ACD = BDE = CEF $
$ AC = BE = ABDF = CDEF $

Tabela 5.2.1.2: Estrutura de aliases para o experimento com $ I=ABCE=BCDF=ADEF $.

Exemplo 5.2.1.1

(Montgomery, 1997) Algumas peças manufaturadas em um processo de moldagem por injeção têm mostrado encolhimento excessivo. Uma equipe de qualidade decidiu então utilizar um experimento para reduzir este encolhimento. Foram investigados seis fatores, cada um com dois níveis:

[A - ] temperatura do molde,

[B - ] velocidade do parafuso,

[C - ] duração do processo,

[D - ] templo de ciclo,

[E - ] tamanho da porta, e

[F - ] pressão.

O objetivo é estudar como cada fator afeta o encolhimento das peças, e ainda verificar quais fatores interagem entre si.

A equipe decidiu usar um experimento fatorial fracionado (um quarto da fração), isto é equivalente a fazer um experimento com 16 corridas. O experimento está representado na tabela a seguir.

Calculando os efeitos principais, temos que:

A = 13,875, B = 35,625, C = -0,875, D = 1,375, E = 0,375, F = 0,375, AB = 11,875, AC = -1,625, AD = -5,375, AE = -1,875, AF = 0,625, BC = -1,875, BD = -0,125, BE = -1,625, BF = -0,125, CD = -0,125, CE = 11,875, CF = -0,125, DE = 0,625,

DF = -1,875 e EF = -5,375.

Os maiores efeitos principais foram obtidos em A, B e na interação AB, portanto esses fatores são os mais importantes para o modelo. O modelo ajustado para esses parâmetros é:

$$Encolhimento=27,31+6,94A+17,81B + 5,94AB.$$

Os desvios padrão e algumas estatísticas referentes ao modelo estão na tabela a seguir.

Preditor	Estimativa	Desvio Padrão	Estat. T	P-Valor
Intercepto	27,3125	1,138232365	23,99554	1,65E+11
A	6,9375	1,138232365	6,094977	5,38E+05
B	17,8125	1,138232365	15,64927	2,39E+09
A:B	5,9375	1,138232365	5,216422	0,000216

Resultados obtidos pelo software Action

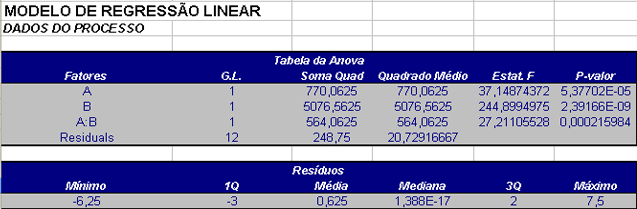
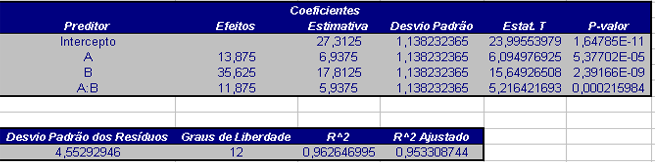
6 - Superfície de Resposta

Introdução a modelos de superfície de resposta

As técnicas de superfície de resposta são ferramentas matemáticas muito úteis quando estamos interessados na otimização de um processo em que temos a influência de vários fatores em uma variável resposta, ou seja, os modelos de superfície de resposta podem ser explorados para determinar condições ótimas para se trabalhar ou a sensibilidade da variável resposta a mudanças dos níveis dos fatores de interesse.

Basicamente, as diretrizes para se trabalhar com um modelo de superfície de resposta são:

• Amostragem;
• Modelagem;
• Otimização.

1. Amostragem: definimos o número de ensaios que vamos executar, já pensando nos modelos que iremos implementar.
2. Modelagem e Testes de Hipóteses: ajustamos os modelos e analisamos os ajustes obtidos.
3. Otimização: obtemos a configuração ótima dos níveis dos fatores de interesse, entre os intervalos considerados, e verificamos a necessidade de realizar novamente o experimento considerando novos níveis para os fatores.

Podemos dividir os modelos de Planejamento de Experimentos, em geral, em dois tipos:

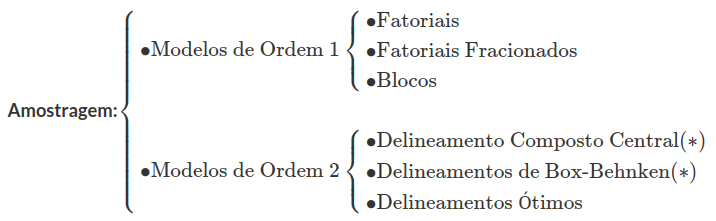
Neste capítulo iremos considerar os modelos marcados com $ (\ast) $, que são os modelos de superfície de resposta. Para a modelagem/análise dos modelos de superfície de resposta podem ser utilizadas as seguintes técnicas:

E para a otimização do modelo ajustado podem ser utilizadas as técnicas:

Para a fase de otimização, é importante ressaltar que a visualização gráfica da superfície de resposta é possível quando temos até 2 fatores. Para um problema com mais fatores essa visualização não é mais possível e é necessário utilizar técnicas numéricas. As técnicas de Steepest Ascent e Descent são utilizadas quando ainda não foi atingida a configuração ótima dentro dos intervalos considerados e é necessário extrapolar para outros níveis na direção mais interessante. As técnicas de simulações são utilizadas para verificar um possível comportamento quando considerarmos situações que não foram observadas.

É importante ressaltar que ao considerar modelos quadráticos é essencial a inclusão de réplicas no experimento, devido à necessidade de detectar o grau de curvatura do modelo. Portanto, sempre que possível inclua réplicas no experimento.

A ideia básica das técnicas de superfície de resposta é considerar que existe uma relação entre as variáveis $ x_1, \ldots,x_k $ e $ y $

$$y=f(x_1, \ldots,x_k,\beta)$$

que é desconhecida, mas que podemos aproximar esta função por uma relação polinomial, por exemplo, do tipo

$$y= \beta_0+\beta_1 x_1+\beta_2 x_2+\ldots+\beta_kx_k+\beta_{11}x_1^2+\ldots+\beta_{kk}x_k^2+\beta_{12}x_1 x_2+\beta_{13}x_1 x_3+\ldots+\beta_{(k-1)k}x_{k-1}x_k+\varepsilon.~~(1.5.1)$$

Assim chamaremos de superfície de resposta a curva dada pela relação

$$E(y)=f(x_1, \ldots,x_k, \beta).$$

A expressão (5.1) é denominada modelo de segunda ordem de superfície de resposta (os termos têm, no máximo, ordem 2). O termo $ \varepsilon $ é o erro aleatório envolvido no modelo, e tem suposições de distribuição de acordo com cada problema. Os $ \beta $’s são os coeficientes do modelo de regressão.Esse modelo é interessante e muito útil para descrever dados experimentais nos quais a curvatura é abundante. Mas isto não implica que em todos os sistemas contendo curvatura este modelo tem bom ajuste. Existem vários casos em que é necessário um modelo mais complexo, e em alguns casos raros pode até ser necessário utilizar termos cúbicos, para alcançar um ajuste adequado. Em outros casos a curvatura pode ser facilmente manuseada utilizando uma transformação logaritmo na resposta, por exemplo, com $ k=2 $

$$\ln y=\beta_0+\beta_1 x_1+\beta_2 x_2+\beta_{12} x_1 x_2.$$

6.1 - Experimentos para Superfície de Resposta de segunda ordem

A importância de utilizarmos delineamentos do tipo superfície de resposta está no fato de possibilitar conclusões mais gerais do que os experimentos fatoriais. Quando executamos um experimento fatorial, definimos alguns níveis dos fatores para trabalhar e verificamos qual é a melhor configuração dentre os níveis dos fatores considerados. Já as técnicas de superfície de resposta nos possibilitam verificar qual é a melhor configuração para os níveis em todo o intervalo considerado. Isso se deve à possível curvatura que o modelo incorpora. Além disso, podemos também verificar se a configuração ótima faz parte do intervalo considerado ou se há necessidade de executar um novo experimento considerando novos níveis dos fatores. Muitas vezes após ajustarmos um modelo fatorial do tipo $ 2^k $, percebemos que nenhuma das configurações está razoável ou percebemos uma falta de ajuste no modelo. Neste caso, poderíamos acrescentar novos níveis nos fatores propondo um experimento fatorial do tipo $ 3^k $ ou $ 4^k $, por exemplo. Porém o custo seria muito mais elevado e poderíamos novamente não chegar a boas conclusões.

Uma boa alternativa, neste caso, seria propor um modelo com curvatura que teria um custo muito mais baixo do que um experimento fatorial, com vários níveis de fatores e que ainda facilitaria a conclusão com respeito à níveis que otimizam a resposta.

É desejável que um experimento de superfície de resposta tenha algumas boas características, entre elas:

• Bom ajuste aos dados;
• Forneça informação suficiente para realizar um teste de falta de ajuste (lack of fit) e para estimar o erro puro;
• Permita fácil ampliação dos dados;
• Seja robusto à presença de outliers nos dados e no controle de níveis dos fatores;
• Tenha um custo razoável;
• Permita que os experimentos sejam realizados em blocos; e
• Tenha variância de predição constante.

Considerando que existe uma relação entre as variáveis $ x_1, … , x_k $ e $ Y=f(x_1, … , x_k, β) $ que é desconhecida, mas que podemos aproximá-la utilizando uma relação linear quadrática ou de ordem superior de acordo com as necessidades de cada problema.

Nos experimentos para superfície de resposta quando um estudo fatorial envolve fatores quantitativos, geralmente, aproximamos por um modelo de regressão polinomial de segunda ordem. A justificativa é que os efeitos principais e efeitos de segunda ordem, geralmente captam a “essência” da função de resposta, pois os efeitos de terceira ordem e superiores são geralmente sem importância. Assim, temos que para o nível $ X_j $ do j-ésimo fator quantitativo é:

$$E[Y]=\beta_0+\beta_1X_1+\dots+\beta_kX_k+\beta_{11}X^2_1+\dots+\beta_{kk}X^2_{k}+\beta_{12}X_1~X_2+\dots+\beta_{k-1,k}X_{k-1}X_k~~(6.2.1)$$

em que o nível $ X_j $ do j-ésimo fator é:

$$X_j=\frac{\text{nível atual}-\frac{\text{maior nível} + \text{menor nível}}{2}}{\frac{\text{maior nível} -\text{menor nível}}{2}}$$

Ao planejarmos um experimento de superfície de resposta, uma exigência mínima é que o experimento seja capaz de proporcionar estimativas de $ p=\frac{(k+1)(k+2)}{2} $ parâmetros no modelo (6.2.1). Por exemplo, com $ k $=2 temos $ p=\frac{(2+1)(2+2)}{2}=6. $ Assim, temos que:

$$Y=\beta_0+\beta_1 X_1+\beta_2 X_2+\beta_{11}X^2_{1}+\beta_{22}X^2_{2}+\beta_{12}X_{1}X_{2}$$

Um experimento fatorial fracionado de resolução V ou superior, em um estudo de dois níveis fatoriais, irá fornecer estimativas lineares para os efeitos principais. Todos os efeitos de dois fatores e de interação são confundidos apenas com efeitos de ordem superior. No entanto, pelo menos três níveis de cada fator devem estar presentes para obtermos estimativas quadráticas de $ k $ efeitos principais.

Um tipo de experimento que fornece estimativas de todos os parâmetros no modelo regressão (6.2.1) é o planejamento fatorial completo com cada fator em três níveis, ou seja, $ 3^k $ em que $ k $ denota o número de fatores no estudo. Um certo número de limitações práticas estão associados aos experimentos fatoriais completos $ 3^k $. Uma das principais, é que o número de tratamentos necessários para um experimento $ 3^k $ cresce rapidamente com o número de fatores. Outra desvantagem é que cada um dos fatores aparece em exatamente três níveis, não sendo possível testar a presença de efeitos principais cúbicos ou de ordem superior.

Nos modelos de superfície de resposta foram desenvolvidos estimativas com base no modelo de segunda ordem (6.2.1) que superam as limitações de modelos $ 3^k $, como por exemplo, Experimentos de Composição Central que são experimentos de usos gerais amplamente utilizados na prática.

Para executar a análise dos modelos de superfície de resposta, podemos recorrer a diferentes técnicas, dependendo do que está sendo analisado. A visualização da superfície de resposta para uma primeira análise só é possível quando temos no máximo 2 fatores. Quando temos até 3 fatores podemos utilizar curvas de nível. Entretanto, para modelos de ordem maior são necessárias técnicas numéricas e a visualização gráfica não é possível. Para quatro ou mais fatores, podemos utilizar técnicas que não são descritas neste conteúdo.

6.1.1 Experimento Composto Central

Os experimentos composto central são os mais populares dentre os planejamentos de experimentos de segunda ordem. Basicamente, estes experimentos são compostos de um ponto central, que será executado com réplicas e dará uma estimativa interna do erro puro e de pontos axiais, que irão determinar os termos quadráticos. Esses experimentos são de dois níveis totais ou fatoriais fracionados que foram aumentados com um pequeno número de tratamentos, cuidadosamente escolhidos, para permitir a estimativa do modelo de superfície de resposta de segunda ordem.

Na figura 6.1.1.1(a) temos um exemplo de experimento fatorial $ 2^2 $, já na figura 6.1.1.1(b) temos um experimento composto central que obtemos somando um ponto único ao centro e quatro pontos da estrela (também chamados de pontos axiais). Um ponto de estrela é aquela em que todos os fatores são fixados em suas médias dos níveis. As coordenadas dos quatro pontos da estrela na Figura 6.1.1.1(b) são (-1,0), (1,0), (0,-1), e (0,1). Resumindo, os quatro pontos da estrela estão localizados nos centros de cada uma das quatro arestas da região experimental.

(imagem em falta)

Figura 6.1.1.1: (a) Experimento fatorial $ 2^2 $, (b) Experimento composto central com $ \alpha=1 $, (c) Experimento de composição central com $ \alpha=\sqrt{2}. $

A distância entre um ponto de estrela e o ponto central em unidades é $ \alpha. $ Note que, na figura 6.1.1.1(b) os pontos da estrela estão a uma distância de uma unidade à partir do centro, ou seja, $ \alpha=1. $ As vezes, é possível colocar os pontos da estrela para além da região experimental definida pelos limites superiores e inferiores originais dos fatores, como é mostrado na Figura 6.1.1.1(c) em que apresentamos um experimento composto central em que os pontos da estrela estão localizados a uma distância $ \alpha=\sqrt{2} $ à partir do centro. Como pode ser visto , cada fator é executado em mais de cinco níveis distintos quando $ \alpha $ é maior do que 1, enquanto o uso de $ \alpha $ é composto de apenas três níveis distintos para cada fator, como mostrado na Figura 6.1.1.1(b). Uma vantagem de fixar $ \alpha $ maior do que 1, portanto, é que os testes para efeitos de curvatura cúbicos e quadráticos poderão ser conduzidos.

Agora, definimos alguns componetes importantes para os experimentos de composição central:

1. $ 2^{k-f} $ pontos de vértice: a base de qualquer experimento composto central é um experimento fatorial completo de 2 níveis ou experimento fatorial fracionado de resolução V ou maior, em que k é o número de fatores e f é o número de níveis de fração de um experimento fatorial $ 2^2. $ Este componente é fornecido por estimação dos efeitos principais lineares e todos os efeitos de interação dois a dois. Geralmente, usamos para os pontos de vértices os níveis $ (\pm 1, \dots, \pm 1). $

2. $ 2 k $ pontos de estrela: a combinação destes níveis do fator permite a estimativa de todos efeitos quadráticos principais. Quando temos $ \alpha> 1, $ podemos conduzir testes de significância para ordens grandes de efeitos de curvatura. Geralmente, usamos para os pontos de estrela os níveis $ (\pm \alpha, \dots, 0),~(0,\pm\alpha,\dots,0) $ etc.

3. $ n_0 $ pontos de centro: se $ n_0> 1, $ uma estimação do erro puro para $ \sigma^2 $ pode ser avaliada e um teste de falta de ajuste é possível. As coordenadas dos pontos de centro são $ (0,\dots,0). $

Com as definições feitas até o momento, o termo experimento composto central refere-se à família de planejamentos de experimentos de segunda ordem. Porém, podemos ter diversos delineamentos dependendo dos pontos de vértice $ \alpha $ e nas extensões das repetições. Nesses experimentos, podemos ter repetições no ponto central, nos pontos de vértices e pontos de estrela. Assim, temos que $ n_c $ é o número de réplicas em cada ponto de vértice e $ n_s $ o número de réplicas em cada ponto da estrela. Agora, definimos o número de corridas experimentais como:

1. $ 2^{k-f}n_c: $ número de corridas experimentais dos pontos de vértice;
2. $ 2~k~n_s: $ número de corridas experimentais dos pontos da estrela;
3. $ n_T=2^{k-f}n_c+2~k~n_s+n_0: $ número de corridas do experimento.

Na tabela 6.1.1.1, temos alguns experimentos de composição central usuais.

Número de fatores	2	3	4	5	6	7	8
Experimento fatorial (base)	$ 2^2 $	$ 2^3 $	$ 2^4 $	$ 2^{5-1}_V $	$ 2^{6-1}_V $	$ 2^{7-1}_V $	$ 2^{8-2}_V $
Pontos de estrela	4	6	8	10	12	14	16
Pontos de centro	1	1	1	1	1	1	1
$ \alpha~(n_c=n_s=1) $	1,414214	1,6818	2	2	2,3784	2,8284	3,3636
Total de corridas $ (n_c=n_s=1,n_0=4) $	12	18	28	30	48	82	84

Tabela 6.1.1.1: Experimentos de composição central usuais.

Agora, mostramos algumas diretrizes para a construção de um experimento de composição central:

• Determinar o número de réplicas do ponto central;
• Determinar os pontos axiais do modelo; e
• Construção da matriz de planejamento.

Exemplo 6.1.1.1

(Montgomery, 1985) Na análise de um processo químico vamos desenvolver um modelo de superfície de resposta de ordem 2 para relacionar o tempo de reação e a temperatura em relação ao rendimento do produto. Na tabela 6.1.1.1.1, temos os dados originais antes do planejamento de composição central.

Tempo	Temperatura	Produto (rendimento %)
80	170	76,5
80	180	77
90	170	78
90	180	79,5
85	175	79,9
85	175	80,3
85	175	80
85	175	79,7
85	175	79,8
92,07	175	78,4
77,93	175	75,6
85	182,07	78,5
85	167,93	77

Tabela 6.1.1.1.1: Dados do processo químico.

A seguir, montaremos um experimento de composição central como na tabela 6.1.1.1.2. Na figura 6.1.1.1.1 temos a ilustração do planejamento.

(imagem em falta)

Figura 6.1.1.1.1: Planejamento de composição central com $ \alpha=\sqrt{2}. $

x1	x2	Produto (rendimento %)
-1	-1	76,5
-1	1	77
1	-1	78
1	1	79,5
0	0	79,9
0	0	80,3
0	0	80
0	0	79,7
0	0	79,8
$ \sqrt{2} $	0	78,4
$ -\sqrt{2} $	0	75,6
0	$ \sqrt{2} $	78,5
0	$ -\sqrt{2} $	77

Tabela 6.1.1.1.2: Tabela do Planejamento de composição central com $ \alpha=\sqrt{2}. $

Assim, modelamos os dados da seguinte forma:

$$Y=\beta_0+\beta_1 x_1+\beta_2 x_2+\beta_{11} x^2_1+\beta_{22} x^2_2+\beta_{12}x_1 x_2+\varepsilon_{12}$$

em que

• Y representa o produto que é o rendimento do produto em %;
• $ x_1 $ representa a variável explicativa tempo em segundos;
• $ x_2 $ representa a variável explicativa temperatura em ºC;
• $ \varepsilon_{12} $ é a variável aleatória que representa o erro experimental;
• $ \beta_0 $, $ \beta_1 $, $ \beta_2 $, $ \beta_{11} $, $ \beta_{22} $ e $ \beta_{12} $ são os parâmetros do modelo, que são estimados, e que definem a regressão polinomial de segunda ordem.

Usando o Software Action obtemos os seguintes resultados:

(imagem em falta)

(imagem em falta)

(imagem em falta)

(imagem em falta)

(imagem em falta)

(imagem em falta)

(imagem em falta)

Exemplo 6.1.1.2

(Montgomery, 1985) Suponha que estamos interessados em desenvolver um modelo de superfície de resposta para relacionar o rendimento de uma reação (%) contra temperatura e tempo de reação.

Os dados estão na tabela abaixo:

Temperatura (ºC)	111	115	125	135	139
Tempo (s)	258	270	300	330	342

Podemos padronizar as medidas, para facilitar a interpretação, transformando-as em valores no intervalo [-1, 1]. A equação para a transformação é:

$$x_{i} = \frac{\xi_{i} - \frac{[\max(\xi_{i}) + \min(\xi_{i})]}{2}}{\frac{[\max(\xi_{i}) - \min(\xi_{i})]}{2}}.$$

Denominando a variável Temperatura $ (x_1) $ e o Tempo $ (x_2), $ temos:

$$x_1=\displaystyle\frac{{Temperatura}-125}{14}$$

$$x_2=\displaystyle\frac{{Tempo}-300}{42}$$

Os valores, transformados, de x1 e x2 são:

x1	x2	y
-0,714	-0,714	88,55
-0,714	0,714	86,29
0,714	-0,714	85,8
0,714	0,714	80,44
-1	0	85,5
1	0	85,39
0	-1	86,22
0	1	85,7
0	0	90,21
0	0	90,85
0	0	91,31

Neste caso, podemos ilustrar o experimento com ponto central como mostra a Figura 6.1.1.2.1, em que cada ponto representa uma corrida. Note que temos 3 pontos centrais.

(imagem em falta)

Figura 6.1.1.2.1: Descrição do experimento com ponto central, para este exemplo.

Poderíamos tentar ajustar um modelo de primeira ordem, mas como mostra a Figura 6.1.1.2.2, isto não seria uma boa alternativa.

(imagem em falta)

Figura 6.1.1.2.2: Ajuste linear para os dados.

Uma alternativa mais adequada seria o ajuste quadrático, como mostra a Figura 6.1.1.2.3.

(imagem em falta)

Figura 6.1.1.2.3: Ajuste quadrático para os dados.

Neste caso, o modelo será do tipo

$$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\beta_3 x_1^2+\beta_4 x_2^2 +\beta_5x_1 x_2, \text{ em que }$$

$ x_1 $	$ x_2 $	$ x^2_1 $	$ x^2_2 $	$x1:x2 $
-0,714	-0,714	0,51	0,51	0,51
-0,714	0,714	0,51	0,51	-0,51
0,714	-0,714	0,51	0,51	-0,51
0,714	0,714	0,51	0,51	0,51
-1	0	1	0	0
1	0	1	0	0
0	-1	0	1	0
0	1	0	1	0
0	0	0	0	0
0	0	0	0	0
0	0	0	0	0

Note que as três últimas linhas correspondem ao ponto central $ (x_1=x_2=0) $, então podemos considerar a regressão linear

$ Y= X\beta+\varepsilon, $ com

e assim, o modelo ajustado será dado por

$$\widehat{y}=90,794 - 1,547 x_1 - 1,476 x_2 - 5,514 x_2^2- 1,519 x_1 x_2.$$

(imagem em falta)

Figura 6.1.1.2.4: Superfície ajustada.

(imagem em falta)

Figura 6.1.1.2.5: Curvas de contorno para a superfície ajustada.

Nas Figuras 6.1.1.2.4 e 6.1.1.2.5 podemos observar a superfície ajustada, e as curvas de contorno, respectivamente.

Para encontrar a resposta máxima, podemos igualar as derivadas da função $ \widehat{y}, $ em relação às variáveis $ x_1 $ e $ x_2, $ a 0. Ou seja, calculamos

$$\frac{\partial \widehat{y}}{\partial x_1}=\beta_1+2,\beta_3 x_1+\beta_5 x_2=0$$

$$\frac{\partial \widehat{y}}{\partial x_2}=\beta_2+2 ,\beta_4 x_1+\beta_5 x_1=0$$

$$\frac{\partial \widehat{y}}{\partial x_1}=-1,547-2 \times 5,514 x_1 - 1,519 x_2 = 0$$

$$\frac{\partial \widehat{y}}{\partial x_2}=-1,476- 2 \times 4,999 x_2 - 1,519 x_1=0$$

e para resolver o sistema

ou seja, os valores de $ x_1 $ e $ x_2 $ que maximizam a resposta são respectivamente $ -0,123 $ e $ -0,129 $, e o rendimento máximo da reação é $ \widehat{y}=90,98(porcentagem). $

Nas variáveis originais, obteríamos

$ Temperatura_{ótima}=123,28~ºC~e~tempo_{ótimo}=294,58 $

ou de forma aproximada,

Temperatura = 123 ºC e Tempo = 294 segundos.

6.1.2 Experimento de Box-Behnken

Planejamentos de composição central são os mais utilizados no que diz respeito a planejamentos de superfície de resposta de ordem 2, entretanto existem outros tipos de modelos. Box-Behnken (1960) desenvolveu uma família de planejamentos de 3 níveis eficientes para modelar superfície de resposta de ordem 2.

Os planejamentos de Box-Behnken diferem dos planejamentos de composição central de duas maneiras. Em primeiro lugar, apenas 3 níveis para cada fator são empregados. Em segundo lugar, os planejamentos Box-Behnken não têm pontos de vértices, sendo assim, algumas vezes, preferidos ao invés de planejamentos de composição central, pois quando há restrições físicas ou econômicas, eles impedem a utilização de pontos de vértices, ou seja, quando todos os níveis dos fatores estão em um extremo.

Os experimentos de Box-Behnken são caracterizados por planejamento de experimentos com 3 níveis dos fatores e por modelos de segunda ordem. Este planejamento está baseado em experimentos com blocos incompletos balanceados. Basicamente, fixamos uma das variáveis em zero e um fatorial $ 2^2 $ é executado com as outras duas variáveis.

Quando utilizar um experimento de Box-Behnken: Em alguns experimentos de superfície de resposta, necessitamos utilizar fatores com 3 níveis (baixo, médio e alto), neste caso os experimentos de Box-Behnken são uma boa alternativa para o experimentos de composição central. Além disto, existe informação suficiente para realizarmos um teste de falta de ajuste (lack of fit). Uma outra característica interessante neste tipo de experimento é a simetria da disposição dos pontos no cubo. Um experimento de Box-Behnken com k = 3 pode ser dado por:

x1	x2	x3
-1	-1	0
-1	1	0
1	-1	0
1	1	0
-1	0	-1
-1	0	1
1	0	-1
1	0	1
0	-1	-1
0	-1	1
0	1	-1
0	1	1
0	0	0

e representado como na Figura 6.1.2.1

(imagem em falta)

Figura 6.1.2.1: Experimento de Box-Behnken com k=3.

Exemplo 6.1.2.1

Um passo importante na produção de uma resina de poliamida é adição de aminas. Foi imaginado que a maneira de adição tem um profundo efeito na distribuição do peso molecular da resina. Três variáveis foram então consideradas: temperatura da amina (x1, ºC), agitação (x2, RPM) e a taxa de adição (x3, 1/min). Como é difícil determinar os níveis de adição e agitação, 3 níveis foram considerados e um experimento de Box-Behnken foi proposto como abaixo.

Nível	Temperatura	Agitação	Taxa	$x_1$	$x_2$	$x_3$
Alto	200	10	25	1	1	1
Médio	175	7,5	20	0	0	0
Baixo	150	5	15	-1	-1	-1

O experimento foi realizado e foram obtidas as seguintes respostas:

$x_1$	$x_2$	$x_3$	y
-1	-1	0	53
1	-1	0	58
-1	1	0	59
1	1	0	56
-1	0	-1	64
1	0	-1	45
-1	0	1	35
1	0	1	60
0	-1	-1	59
0	1	-1	64
0	-1	1	53
0	1	1	65
0	0	0	65
0	0	0	59
0	0	0	62

Os coeficientes da regressão, os respectivos desvios padrão e os valores observados da estatística T e o P-valor do modelo quadrático são dados na tabela 6.1.2.1:

Tabela 6.1.2.1: Tabela da ANOVA e das estimativas dos parâmetros do modelo polinomial de 2º ordem.

(imagem em falta)

Tabela 6.1.2.2: Tabela do Teste de Falta de Ajuste e dos resíduos.

(imagem em falta)

Figura 6.1.2.2: Gráficos da análise de resíduos, papel de probabilidade etc.

(imagem em falta)

Figura 6.1.2.3: Gráfico de Contorno (curvas de nível).

(imagem em falta)

Figura 6.1.2.4: Gráfico de contorno (Áreas).

(imagem em falta)

Figura 6.1.2.5: Gráfico de superfície.

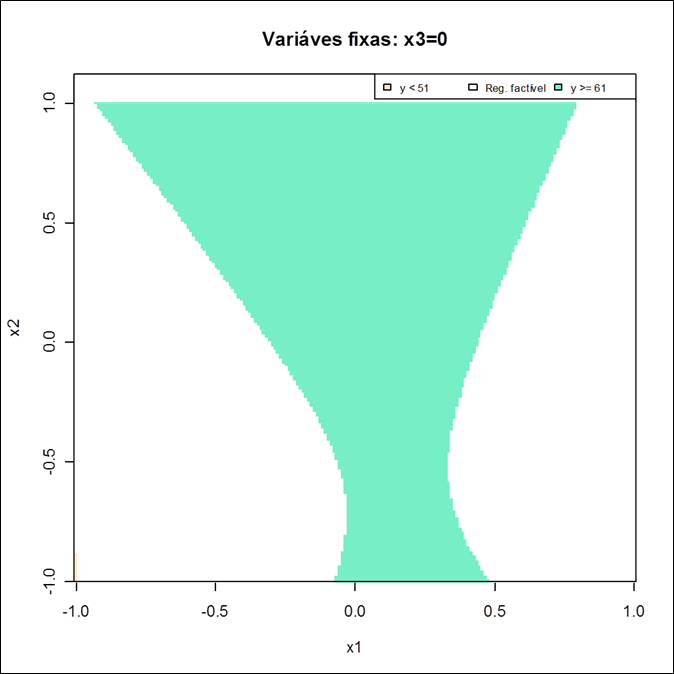
Figura 6.1.2.6: Gráfico da região factível.

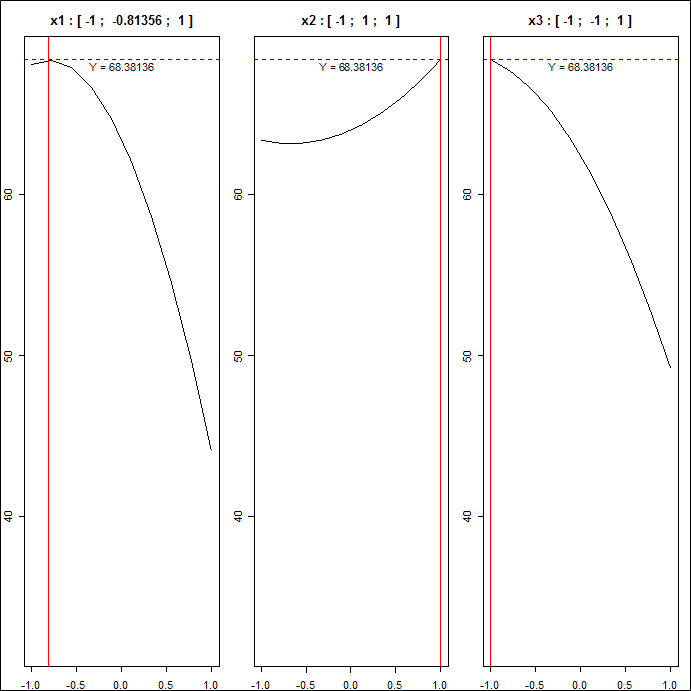
Figura 6.1.2.7: Gráfico de Otimização.

6.2 - Método de Superfície de Resposta

Em muitas situações temos interesse em avaliar as relações existentes entre os principais fatores que compõem um processo e uma variável resposta de interesse. Nestas situações, temos como objetivo, determinar qual é a condição de operação do processo que levará à obtenção de um valor ótimo para a variável resposta. De modo geral, podemos representar o relacionamento existente entre uma variável resposta de interesse ($ Y $) e $ k $ fatores do processo ($w_1$, $w_2$, …, $w_k$) por uma expressão do tipo

$$Y= f(w_1, w_2,\ldots, w_k) + \varepsilon$$

em que $ \varepsilon $ representa um componente de erro aleatório, que leva em consideração a variação observada na variável resposta que não é explicada pelos fatores $w_1$, $w_2$, …, $w_k$. Dizemos que a função $ f $ define uma superfície de resposta.

• Uma superfície de resposta é a figura obtida quando uma variável resposta é representada graficamente em função de um ou mais fatores do processo.

Observe que à partir da forma matemática da função $ f $ é possível encontrar qual condição de operação que leva ao ponto ótimo (máximo, mínimo ou alvo) da variável resposta. No entanto, na maioria das situações práticas, a forma matemática da função $ f $ não é conhecida, sendo então, necessário estimá-la por meio do emprego de dados amostrais. Como usualmente é difícil encontrar uma função que seja adequada para descrever a relação existente entre $w_1$, $w_2$, …, $w_k$ e $ Y $, em todas as possíveis condições de operação do processo. Concentramos, nesse capítulo, a atenção em faixas estreitas de valores das variáveis $w_1$, $w_2$, …, $w_k$, de forma que seja possível ajustar equações simples, tais como polinômios de primeira e segunda ordem, que forneçam informações sobre como devemos conduzir o processo para encontrar a região ótima de operação. É importante destacar que na maioria das situações, a determinação de $ f $ não constitui o interesse principal do estudo, sendo apenas uma etapa necessária para a obtenção da condição ótima na qual o processo deve ser operado.

Exemplo 6.2.1

Realizamos um experimento para verificar o tempo de reação (min), devido a concentração de reagente (A), nos níveis 10% e 20% e da temperatura (B), nos níveis 80°C e 90°C. O experimento foi realizado com 3 réplicas e os dados coletados estão na tabela a seguir.

Tratamento	A	B	Y1	Y2	Y3	Média (Y)
(o)	-1	-1	26,6(1)	22,0(7)	22,8(10)	23,8
a	1	-1	40,9(4)	36,4(9)	36,7(12)	38
b	-1	1	11,8(3)	15,9(8)	14,3(11)	14
ab	1	1	34,0(2)	29,0(5)	33,6(6)	32,2

Na tabela, os valores entre parênteses indicam a ordem (sequência) de realização dos tratamentos.

No ajuste do modelo encontramos os seguintes resultados:

(imagem em falta)

Tabela 6.2.1: Resultados obtidos para o ajuste do modelo linear.

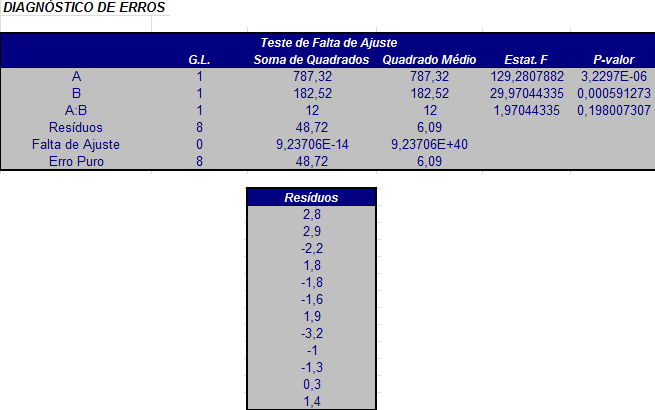
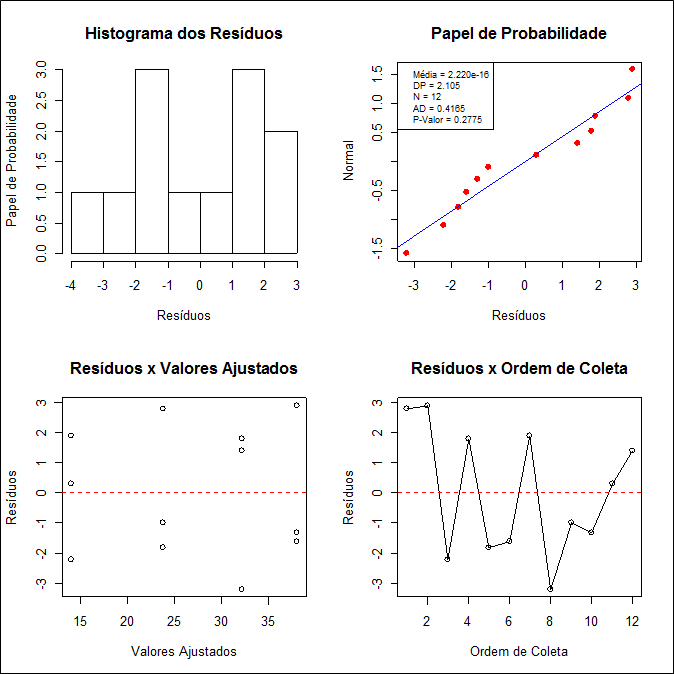
No ajuste do modelo tem-se que a interação AB não é significativa, portanto o melhor modelo para representar os dados não inclui a interação

$$y = 27 + 8,1 A - 3,9 B$$

Uma superfície de resposta para o modelo 5.2 é apresentada a seguir.

(imagem em falta)

(imagem em falta)

Figura 6.2.2: Superfície de resposta para o modelo

Nesta figura, f(A,B) é representada graficamente em função dos níveis de A e B. A variável resposta $ Y $ é então obtida como uma superfície no espaço tridimensional.

Para a superfície de resposta mostrada acima, se forem fixados alguns valores de interesse para a variável resposta $ Y $ obtemos, no plano, curvas denominadas curvas de nível ou curvas de contorno.

(imagem em falta)

(imagem em falta)

(imagem em falta)

Figura 6.2.3: Superfície de resposta para o modelo

Na Figura 6.2.3 os valores da legenda, a direita, são os valores fixados para a variável resposta $ Y $. Nesta figura cada curva de nível corresponde a uma altura particular da superfície de resposta.

De modo geral, quando estão envolvidos $ k $ fatores $x_1$, $x_2$, …, $x_k$ é usual construir as curvas de nível considerando pares de fatores de interesse (x1, x2). Assim, uma curva de nível identifica os valores dos fatores para os quais a variável resposta é constante.

Conforme já mencionado, usualmente a forma da relação existente entre a variável resposta e os fatores do processo é desconhecida. Portanto, a primeira etapa do método de superfície de resposta consiste na determinação de uma equação que represente, de forma aproximada, o relacionamento existente entre as variáveis do experimento. Frequentemente, quando se tem interesse em considerar uma pequena região da superfície de resposta, afastada do ponto ótimo, que é o ponto que maximiza ou minimiza a variável resposta, quase não existe curvatura na superfície. Neste caso, podemos empregar o modelo de primeira ordem apresentado abaixo para representar o relacionamento entre as variáveis:

$$y=\beta_0+\beta_1 x_1+\beta_2 x_2+\ldots+\beta_k x_k+\varepsilon$$

Nas proximidades do ponto ótimo, mesmo para pequenas regiões da superfície, na maioria das vezes a curvatura é mais acentuada, sendo então necessário utilizar um polinômio de ordem mais elevada para representar o relacionamento entre $ Y $ e $x_1$, $x_2$, …, $x_k$. Usualmente, um modelo de segunda ordem é empregado.

É importante destacar que o método de superfície de resposta é um procedimento sequencial. Apresentaremos a seguir, de forma resumida, uma visão geral das etapas para a determinação da condição ótima de operação de um processo, por meio do emprego do método de superfície de resposta.

Realizou-se um experimento fatorial $2^2$; com os resultados descritos na tabela a seguir.

Tempo	Temperatura	$x_1$	$x_2$	Pureza
30	150	-1	-1	39,3
30	160	-1	1	40
40	150	1	-1	40,9
40	160	1	1	41,5
35	155	0	0	40,3
35	155	0	0	40,5
35	155	0	0	40,7
35	155	0	0	40,2
35	155	0	0	40,6

Tabela 6.2.2: Resultados obtidos para o ajuste do modelo linear.

(imagem em falta)

Plotar gráficos de contorno e superfície

(imagem em falta)

Figura 6.2.4: Gráfico de Contorno (Linhas).

(imagem em falta)

Figura 6.2.5: Gráfico de Contorno (Áreas).

O Gráfico de Superfície 3D abre em uma nova janela e o usuário consegue rotacionar a superfície para analisar melhor o gráfico.

(imagem em falta)

Figura 6.2.6: Gráfico de Superfície (Estática).

A Região Factível é a parte branca do gráfico.

(imagem em falta)

Figura 6.2.7: Gráfico da Região Factível.

6.2.1 - Métodos de Otimização

Geralmente, a forma da relação existente entre a variável resposta e os fatores do processo é desconhecida. Portanto, a primeira etapa do método de superfície de resposta consiste na determinação de uma equação que represente, de forma aproximada, o relacionamento existente entre a resposta $ Y $ e os fatores do processo $x_1$, $x_2$, …, $x_k$.

Frequentemente, quando consideramos uma pequena região da superfície de resposta, afastada do ponto ótimo, quase não existe curvatura na superfície. Neste caso, podemos empregar o modelo de primeira ordem. Nas proximidades do ótimo, mesmo para pequenas regiões da superfície, na maioria das vezes a curvatura é mais acentuada, sendo necessário utilizar um polinômio de ordem mais elevada para representar o relacionamento entre a resposta $ Y $ e os fatores do processo $x_1$, $x_2$, …, $x_k$. Usualmente, um modelo de segunda ordem é empregado.

É importante destacarmos, que o método de superfície de resposta é um procedimento sequencial. Apresentamos a seguir, de forma resumida, uma visão geral das etapas para a determinação da condição ótima de operação de um processo, por meio do método de superfície de resposta.

Visão Geral das Etapas para a Determinação da Condição Ótima de Operação de um Processo, por meio do Método de Superfície de Resposta:

• Relacionamos os fatores que possam exercer efeitos significativos sobre a variável resposta de interesse.
• Planejamos um experimento que permita a identificação dos fatores influentes dentre aqueles relacionados no item 1. Nesta etapa, geralmente são utilizados os experimentos fatoriais 2k descritos anteriormente.
• Eliminamos os fatores detectados como não influentes na etapa anterior e avaliamos a necessidade de inclusão de novos fatores no estudo. Observe que esta necessidade pode ser o resultado da aprendizagem resultante da realização do experimento na etapa 2. Caso não seja necessário incluir novos fatores, devemos realizar a etapa 4. Caso contrário, devemos retornar à etapa 2.
• Realizamos um experimento mais detalhado, envolvendo apenas os fatores que exercem efeitos significativos sobre a variável resposta. O objetivo desta etapa consiste em ajustar um modelo que possa representar o relacionamento existente entre os fatores influentes e a resposta. Geralmente, este experimento é realizado em uma pequena região centrada na condição atual de operação do processo.
• À partir do modelo ajustado no item 4, realizamos uma análise que permitirá a determinação da condição ótima de operação do processo.

A forma de realização desta análise será detalhada ao longo desta seção mas, de modo geral, as seguintes diretrizes devem ser observadas:

• No item 4 usualmente é ajustado um modelo de primeira ordem. Inicialmente esperamos estar afastados do ponto ótimo de operação do processo e como nesta situação é comum haver apenas uma leve curvatura na verdadeira relação funcional entre as variáveis, um modelo de primeira ordem fornecerá uma boa aproximação para esta relação.
• O modelo de primeira ordem será o ponto de partida para que possamos caminhar sequencialmente, de forma rápida e eficiente, para as proximidades do ponto ótimo.
• Em etapas subsequentes da análise, quando as vizinhanças do ponto ótimo já estiverem sido alcançadas, será necessário ajustar um modelo de ordem mais elevada. Já que nestas regiões a curvatura presente na superfície de resposta será mais acentuada.
• A interpretação deste modelo permitirá que a condição ótima de operação do processo possa ser alcançada.

Exemplo 6.2.1.1

Realizamos um experimento fatorial $2^2$; com os resultados descritos na tabela a seguir.

Tempo	Temperatura	$ x_1 $	$ x_2 $	Pureza
30	150	-1	-1	39,3
30	160	-1	1	40
40	150	1	-1	40,9
40	160	1	1	41,5
35	155	0	0	40,3
35	155	0	0	40,5
35	155	0	0	40,7
35	155	0	0	40,2
35	155	0	0	40,6

(imagem em falta)

Figura 6.2.1: Gráfico de Otimização.

6.2.2 - Método da máxima inclinação ascendente (descendente)

Nesta seção será detalhado as etapas 4 e 5 do procedimento para a determinação da condição ótima de operação de um processo por meio do método de superfície de resposta.

Usualmente, o ponto de início da experimentação está distante da condição ótima de operação do processo a qual desejamos conhecer. Nesta situação, o objetivo será aproximar do ótimo de forma mais rápida e econômica possível.

Um procedimento que permite o alcance deste objetivo é o método da máxima inclinação ascendente (descendente), quando o objetivo é o de maximização (minimização) da resposta. Este método parte do pressuposto que, caminharemos sequencialmente ao longo da direção de máxima inclinação ascendente, isto é, na direção e no sentido em que ocorre o aumento máximo da variável resposta. Por outro lado, se o objetivo é o de minimização da resposta, caminharemos sequencialmente ao longo da direção de máxima inclinação descendente, ou seja, na direção e no sentido em que acontece a máxima diminuição da variável resposta. O método da máxima inclinação ascendente (descendente) é constituído pelas etapas apresentadas a seguir.

Etapas do Método de Máxima Inclinação Ascendente (Descendente):

1. Realizamos um experimento com o objetivo de ajustar um modelo de primeira ordem em uma pequena região de interesse definida pelas variáveis $ x_1,x_2,\ldots, x_k $. Geralmente esta região engloba a condição usual de operação do processo, que na maioria das situações está longe do ótimo. Nesta região é comum que a superfície de resposta apresente apenas uma leve curvatura, sendo então ajustado por um modelo de primeira ordem. O modelo de primeira ordem ajustado nessa região de interesse é dado pela equação

$$\begin{equation*}\displaystyle\widehat{y} = \widehat{\beta_0} + \sum_{i=1}^{k} \widehat{\beta_i} x_i\end{equation*}$$

Para esta superfície, as curvas de nível são uma série de retas paralelas (primeira ordem), conforme está apresentado na Figura (6.2.2.1).

2. Utilizamos a informação obtida na etapa 1 para determinar a direção de máxima inclinação ascendente (descendente). A direção de máxima inclinação ascendente (descendente) é a direção na qual $ y $ aumenta (diminui) mais rapidamente. Esta direção é perpendicular às curvas de nível e é tomada a partir do centro da região de interesse.

3. Conduzimos uma série de experimentos ao longo da direção de máxima inclinação ascendente (descendente) até que seja encontrada uma região onde não é observado nenhum aumento (decréscimo) na variável resposta.

4. Repetimos as etapas 1, 2 e 3 a partir da nova região determinada na etapa 3. Esta repetição deve ser realizada enquanto não for detectada a falta de ajuste do modelo de primeira ordem.

5. Quando for detectada a falta de ajuste do modelo de primeira ordem, realizamos experimentos adicionais para obter uma estimação mais precisa da condição ótima de operação do processo. Esta estimação, na maioria das vezes, envolverá o ajuste de um modelo de segunda ordem.

$$\begin{equation*}\displaystyle\widehat{y}=\beta_0 + \sum_{i=1}^k \widehat{\beta}_i x_i +\sum_{i=1}^k \widehat{\beta}_{i} x_i^2 + \sum_{i=1}^k \sum_{j=i+1}^k \widehat{\beta}_{ij} x_i x_j + \varepsilon\end{equation*}$$

(imagem em falta)

Figura 6.2.2.1: Superfície de resposta de primeira ordem e direção da inclinação ascendente.

A necessidade de ajuste de um modelo de segunda ordem, geralmente, é uma indicação em que as vizinhanças do ponto ótimo foram alcançadas.

As etapas 1 a 4 do método da máxima inclinação ascendente (descendente) são ilustradas no exemplo a seguir e a etapa 5 é descrita na próxima seção.

Exemplo 6.2.2.1

Um engenheiro químico está interessado em determinar as condições de operação que maximize o rendimento de um processo. Duas variáveis de controle afetam a resposta:

• tempo da reação química (w1)
• temperatura (w2).

O processo está operando com um tempo de reação de 35 minutos e uma temperatura de 155°F, com um rendimento em torno de 40%. O experimentador decidiu avaliar o processo na região de (30, 40) minutos e (150, 160)°F. Para simplificar a interpretação as variáveis foram transformadas, utilizando:

$$x_i = \frac{w_i + \displaystyle\frac{\text{máx}(w_i) - \text{mín}(w_i)}{2}}{\displaystyle\frac{\text{máx}(w_i) - \text{mín}(w_i)}{2}}$$

Realizamos um experimento fatorial 22, com os resultados descritos na tabela a seguir.

Tempo	Temperatura	x1	x2	Pureza
30	150	-1	-1	39,3
30	160	-1	1	40
40	150	1	-1	40,9
40	160	1	1	41,5
35	155	0	0	40,3
35	155	0	0	40,5
35	155	0	0	40,7
35	155	0	0	40,2
35	155	0	0	40,6

Fatores	G.L.	Soma de Quadrados	Quadrado Médio	Estat. F	P-valor
x1	1	2,4025	2,4025	68,75199	0,000417
x2	1	0,4225	0,4225	12,09062	0,017713
x1:x2	1	0,0025	0,0025	0,071542	0,799787
Residuals	5	0,174722	0,034944

Tabela 6.2.2.1:Análise de variância.

Na tabela da ANOVA, notamos que a interação entre as duas variáveis não é significativa, pois o p-valor está muito acima do nível de significância $ \alpha=0,05, $ portanto o melhor modelo não inclui a interação.

(imagem em falta)

Para entender como executar essa função do Software Action, você pode consultar o manual do usuário.

Portanto o modelo que mais se adéqua aos dados é

$$y = 40,45 + 0,775 x_1 + 0,325 x_2.$$

Para o teste de significância foi obtido p-valor muito pequeno o que indicou que o rendimento está relacionado com o tempo da reação química e a temperatura. Abaixo, apresentamos uma análise dos parâmetros do modelo

A direção de máxima inclinação ascendente é a direção na qual o rendimento da reação química aumenta mais rapidamente. Esta direção é perpendicular às curvas de nível e é tomada a partir do centro da região na qual foi ajustado o modelo na etapa anterior. É possível mostrar que os passos que devem ser dados ao longo da direção de máxima inclinação ascendente são obtidos por meio da promoção dos fatores do processo, de acréscimos proporcionais dos coeficientes de regressão $ j. $

O detalhamento do procedimento pode ser encontrado abaixo:

a) Escolher o valor da alteração que será sofrida por um dos fatores w1, …, wk à partir do centro do intervalo de variação deste fator.

Esta alteração irá gerar uma nova condição de operação do processo, em relação a este fator, na qual será coletada uma nova observação da variável resposta. O fator considerado (wi) deverá ser aquele cujo efeito sobre a variável resposta é mais conhecido pelo responsável, pelo experimento e/ou àquele que possuí coeficiente de regressão de maior valor absoluto. A magnitude de variação que será sofrida por este fator (wi) deve ser tal que não implique em um afastamento muito grande de onde foi ajustado o modelo e ao mesmo tempo, devemos provocar uma variação significativa na variável resposta. O sinal de wi deve ser escolhido de acordo com os critérios:

i) Se o ponto ótimo é máximo, $ \Delta w_i $ tem o mesmo sinal de bi.

ii)Se o ponto ótimo é mínimo, $ \Delta w_i $ tem o sinal oposto ao de bi.

b) Expressar o acréscimo $ \Delta w_i $ sob a forma codificada

$$x_i = \frac{2 (w_i - C_i)}{A_i},$$

sendo que:

• Ci: centro do intervalo de variação do fator considerado; e
• Ai: amplitude do intervalo de variação do fator considerado.

Assim, o acréscimo $ \Delta x_i $ é calculado por

$$\Delta x_i = \frac{2 \Delta w_i}{A_i}$$

c) Calcular o valor da variação que será sofrida pelos outros fatores, sob a forma codificada.

$$\Delta x_j = \frac{b_{j+1}}{\frac{b_j}{\Delta x_j }}, \quad \forall j \neq i.$$

Estas alterações devem definir a nova condição de operação do processo na qual será coletada as observações da resposta.

d) Converter os $ \Delta x_j $ dos fatores sob a forma codificada para as alterações $ \Delta w_j $ dos fatores sob a forma original.

$$\Delta w_i = \Delta x_i \frac{A_j}{2}.$$

e) Obter a nova condição de operação do processo: (C1 + w1, …, Ck + wk);

f) Obter valores de resposta do processo para a nova condição de operação do processo e comparar com os valores obtido na condição anterior em (C1, …, Ck):

i) Ponto de Máximo:

Se o valor da resposta do processo para a nova condição de operação do processo (C1 + w1, …, Ck + wk) for maior ou igual à resposta média obtida em (C1, …, Ck), retornar à etapa a) anterior com a nova especificação do processo.

Vale a pena destacar que é usual considerar os mesmos valores xj determinados na primeira interação do método, o que torna desnecessário a realização dos passos b), c) e d).

Se o valor da variável resposta obtido para a nova condição de operação for menor que a resposta média obtida em (C1, …, Ck), encerre a experimentação ao longo desta direção de máxima inclinação ascendente.

ii) Ponto de mínimo (vale as mesmas considerações) que para o ponto de máximo.

Voltando ao exemplo, temos:

a) Escolher o valor da alteração que será sofrida pelo fator tempo da reação (w1), a partir do centro do intervalo de variação deste fator.

$$\Delta w_1 = 5 , {minutos};$$

b)Expressar o acréscimo $ \Delta w_1 $ de forma codificada

$$\Delta x_1 = \frac{2 \Delta w_1}{A_1} = \frac{2 \times 5}{10}=1.$$

c) Calcular o valor da alteração, sob a forma codificada, que será sofrida pelo fator temperatura (x2), a partir do centro do intervalo de variação deste fator (155° F).

$$\Delta x_1 = \frac{b_2}{\frac{b_1}{\Delta x_1}} = \frac{0,325}{0,775}=0,42.$$

d) Converter a nova condição de operação do processo na qual será coletada a observação do rendimento

$$\Delta w_2 = \Delta x_2 \frac{A_2}{2} = 0,42 \frac{10}{2}=2,1.$$

e) Nova condição de operação

$$(C_1 + w_1, \ldots, C_k + w_k) = ( 35 + 5 ; 155 + 2) = (40 , 157)$$

f) Comparar o valor da variável resposta obtido para a nova condição de operação definida no item anterior com a resposta média obtida em (C1 , C2).

Resultado obtido para otimização do processo

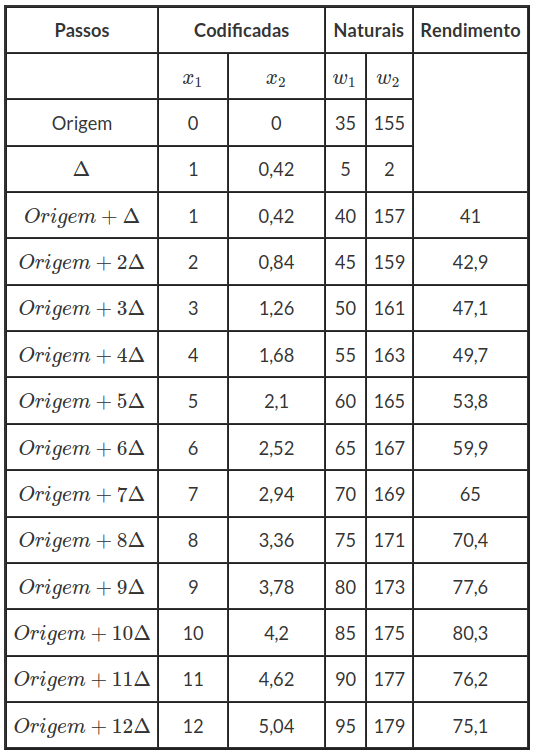
(imagem em falta)

7 - Aplicações do DOE

7.1 - Modelo para granulometria de material residual

Esta aplicação tem como objetivo minimizar a granulometria de material residual indesejado em certo produto na produção do mesmo. Para isto, foi feito um planejamento de experimento no qual foram selecionados as variáveis:

1. Damper
2. Drenagem
3. Corrente
4. APS D90
5. APS D50
6. Peneira 45 μm

A variável reposta deste modelo é a peneira 45 μm​, que é a quantidade de resíduos de materiais indesejados que ficaram retidos na peneira. As variáveis APS D90 e D50 representam a distribuição do tamanho de partículas do resíduo dadas em (%). A corrente é o fluxo de ar do duto, já a drenagem representa a quantidade de dias para a secagem do material e por fim o damper mede o controle do fluxo de material. A seguir apresentamos os resultados do experimento.

Damper	Drenagem	Corrente	APS D50	APS D90	Peneira 45 μm
25	7	40	12,4	25,5	0,02
25	7	40	12,2	24,2	0,02
25	7	40	12,6	24,5	0,02
25	7	60	11,4	23,6	0,02
25	7	60	11,4	23,4	0,01
25	7	60	11,4	23,1	0,01
25	7	75	10,3	21,2	0,01
25	7	75	10,4	20,9	0,01
25	7	75	10,5	20,9	0,00
50	7	75	13,3	27,4	0,00
50	7	75	13,4	27,4	0,00
50	7	75	13,5	27,5	0,00
50	7	60	13,1	27,6	0,00
50	7	60	13,2	27,7	0,00
50	7	60	13,7	28,2	0,00
50	7	40	13,6	29,1	0,00
50	7	40	13,8	29,6	0,01
50	7	40	13,9	29,8	0,01
75	7	40	16,8	39,5	0,31
75	7	40	16,7	39,1	0,36
75	7	40	16,4	38,8	0,38
75	7	60	15,8	37,8	0,39
75	7	60	15,7	37,6	0,37
75	7	60	15,6	37,6	0,37
75	7	75	15,2	35,8	0,24
75	7	75	15,1	35,6	0,22
75	7	75	15,0	35,7	0,24
50	7	60	12,9	28,8	0,06
50	7	60	13,0	28,3	0,07
50	7	60	13,0	27,5	0,06
50	7	60	12,7	27,1	0,04
50	7	60	12,6	26,3	0,03
50	7	60	12,5	26,4	0,03
50	7	60	11,9	25,5	0,02
50	7	60	12,3	26,1	0,02
50	7	60	12,6	26,6	0,02
50	7	60	11,5	25,0	0,02
50	7	60	11,6	25,1	0,03
50	7	60	11,8	25,3	0,03
50	7	60	14,5	33,0	0,04
50	7	60	14,7	33,5	0,03
50	7	60	14,9	33,7	0,03
50	7	60	13,7	28,4	0,02
50	7	60	13,4	28,3	0,03
50	7	60	13,7	28,4	0,02
25	30	40	11,9	25,6	0,02
25	30	40	11,7	25,0	0,02
25	30	40	11,6	23,8	0,02
25	30	60	11,0	22,5	0,00
25	30	60	11,0	22,3	0,00
25	30	60	10,9	21,6	0,00
25	30	75	10,2	21,0	0,01
25	30	75	10,0	20,5	0,02
25	30	75	10,0	20,1	0,01
50	30	75	12,9	26,4	0,01
50	30	75	13,4	26,4	0,02
50	30	75	13,2	26,7	0,01
50	30	60	12,8	26,4	0,02
50	30	60	12,5	25,9	0,01
50	30	60	13,1	26,7	0,01
50	30	40	12,8	27,2	0,04
50	30	40	13,0	27,6	0,02
50	30	40	13,2	27,9	0,02
75	30	40	13,7	30,9	0,06
75	30	40	13,6	30,9	0,07
75	30	40	14,0	30,7	0,18
75	30	60	14,1	31,70	0,04
75	30	60	14,0	31,7	0,02
75	30	60	13,9	31,6	0,07
75	30	75	14,5	32,3	0,05
75	30	75	14,4	32,1	0,05
75	30	75	14,4	32,1	0,05
50	30	70	11,0	21,5	0,04
50	30	70	11,1	21,6	0,03
50	30	70	11,2	21,6	0,05
50	30	60	12,0	24,9	0,04
50	30	60	12,1	24,6	0,03
50	30	60	12,1	24,5	0,03

7.1.1 - Ajuste do modelo completo

Considerando o modelo de regressão linear múltipla com todas as variáveis explicativas enunciadas na seção modelo de granulometria de material residual, verificamos inicialmente se há problemas de colinearidade e de multicolinearidade entre as variáveis envolvidas.

Usando o Software Action obtemos os seguintes resultados:

(imagem em falta)

Tabela 7.1.1: Matriz de correlação para as covariáveis do modelo.

Analisando a Tabela 7.1.1 observamos que as variáveis APS D50 e APS D90 tem correlação superior a 0,9. Desta forma, vamos eliminar a covariável do APS D50 do modelo. Após avaliarmos a colinearidade entre as covariáveis envolvidas, realizamos um diagnóstico de outlier afim de detectar se alguma observação é outlier e ponto influente.

(imagem em falta)

Figura 7.1.1: Boxplot do hii, leverage, Resíduos padronizados e studentizados versus valores ajustados.

Agora, vamos fazer o diagnóstico de outliers. Pela Figura 5.3.1 observamos que a observação 48, 66 e 69 são outliers em Y pois os valores dos resíduos studentizados e padronizados são maiores que 3.

(imagem em falta)

Tabela 7.1.2: Teste de Bonferroni para outliers.

Afim de confirmar a análise gráfica, pelo teste de Bonferroni da Tabela 7.1.2 apenas a observação 66 rejeita a hipótese de que não é um outlier.

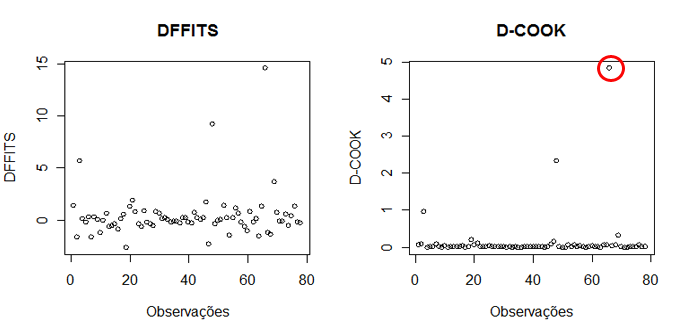
Figura 7.1.2: Gráficos das medidas de influência das observações.

Pela Figura 7.1.2 percebemos que além de outliers, a observação 66 é um ponto influente pois os seus valores de $ D_i $ (Distância de Cook) é maior que 1.

7.1.2 - Análise gráfica

O objetivo deste modelo é otimizar a quantidade mínima de flocos de resíduos indesejados na peneira de 45 μm (próximo de zero). Assim, devido à prática e em relação a custos, definimos algumas condições de contorno para as variáveis. A seguir, segue as condições de contorno:

• APS (D50): entre 11,0 a 20
• APS (D90): máximo de 28,0.
• Peneira 45µm: máximo de 0,03 g.
• Tempo de drenagem: 0 a 30 dias

As variáveis APS (D50) e (D90), representam distribuição granulomética acumulada de resíduo de um certo tipo de material (50% e 90% respectivamente). Já a variável Drenagem, representa o tempo de drenagem, mais especificamente, o tempo em que o material é mantido para secagem. O Damper representa a abertura do sistema para a passagem de material e a corrente a velocidade com o material passa pelo damper. E por fim, a Peneira 45μm representa o quanto sobrou de resíduo indesejado de um certo tipo de material na peneira.

Inicialmente, vamos realizar análises gráficas, afim de ter uma visão geral.

(imagem em falta)

Figura 7.1.2.1: Gráfico da região factível APS D50 x APS D90 fixando as variáveis Damper, Drenagem e Corrente.

(imagem em falta)

Figura 7.1.2.2: Gráfico da região factível APS D50 x APS D90 fixando as variáveis Damper, Drenagem e Corrente.

(imagem em falta)

Figura 5.3.2.3: Gráfico da região factível APS D50 x APS D90 fixando as variáveis Damper, Drenagem e Corrente.

Após a análise dos gráficos das regiões factíveis, observamos que para uma drenagem de 7 dias temos que trabalhar com APS D90 de 23 μm de resíduo, pois com isto chegamos ao limite inferior de 11 μm de resíduo para APS D50. Notamos também que, fixando a drenagem em 7 dias e a corrente em 60, quando aumentamos o damper, aumentamos o APS D50, podendo ser atingir no máximo 15 μm para um damper de 75. Uma observação importante é que devemos avaliar as faixas brancas, pois elas são as regiões equivalentes a peneira de 45μm que retém de 0 a 0,03 g de resíduo indesejado. Porém, fixando a drenagem em 30 dias e a corrente em 60, quando aumentamos o damper de 25 para 50, aumentamos o APS D50 com no máximo de 15 μm de resíduo de material a 50%. Agora, quando aumentamos o damper de 50 para 75, diminuímos o APS D50 atingindo máximo aproximadamente 12 μm.

Outros tipos de gráficos podem ser aplicados para o modelo como os gráficos de contorno e superfície. A seguir, apresentamos alguns gráficos.

(imagem em falta)

Figura 7.1.2.4: Gráfico de contorno (linhas).

(imagem em falta)

Figura 7.1.2.5: Gráfico de contorno (Áreas).

(imagem em falta)

Figura 7.1.2.6: Gráfico da superfície de resposta.

Observe que, pelos gráficos das figuras 5.3.2.4 e 5.3.2.5, fixando a corrente em 50, o APS D50 em 12 μm e APS D90 em 23,1 μm, obtemos para um damper de 30 que a drenagem é livre de 7 a 30 dias para obtermos 0 g na peneira de 45 μm.

7.1.3 - Modelo Final

Conforme analisado na seção ajuste do modelo completo observamos que as variáveis APS D50 e APS D90 tem correlação superior a 0,9. Desta forma, vamos eliminar a covariável do APS D50 do modelo. Após avaliarmos a colinearidade entre as covariáveis envolvidas, a observação 66 é um ponto influente pois os seus valores de $ D_i $ (Distância de Cook) é maior que 1. Assim, vamos retirar esta observação do modelo.

Portanto, o modelo final é dado por:

$$Y=\beta_0+\beta_1 x_{1}+\beta_2 x_{2}+\beta_3 x_{3}+\beta_3 x_{3}+\beta_4 x_{4}+\beta_6 x_{1}:x_{2}+\dots+\beta_{32} x_{1}:x_{2}:x_{3}:x_{4}~~~(7.1.3.1)$$

em que

• Y: é a peneira de 45 μm;
• $β_0$: é o intercepto;
• $x_1 $: é a variável damper;
• $x_2 $: é a variável drenagem;
• $x_3 $: é a variável corrente;
• $x_4 $: é a variável APS D90;
• $β_i $: são os coeficientes do modelo para as variáveis x1, x2, x3 , x4e as interações dois a dois, três a três etc entre estas variáveis, para i=1,…,32.

A seguir, vamos apresentar os resultados obtidos pelo software Action.

(imagem em falta)

Tabela 7.1.3.1: Tabela da ANOVA.

No ajuste do modelo com as variáveis Damper, Drenagem, Corrente, APS D90 e todas as interações como variáveis explicativas da variável Peneira 45 μm, observamos que o modelo é significativo ao nível de significância de 5%. Fato visto também na tabela 7.1.3.2 na tabela com teste individual dos parâmetros.

(imagem em falta)

Tabela 7.1.3.2: Tabela com a estimativa dos parâmetros do modelo.

O $ R^2 $ é uma medida descritiva da qualidade do ajuste obtido. Em geral referimo-nos ao $ R^2 $ como a quantidade de variabilidade nos dados que é explicada pelo modelo de regressão ajustado. Neste caso obtemos $ R^2 $=0,97.

Tabela 7.1.3.3: Tabela com o desvio padrão dos resíduos, graus de liberdade e medidas de associação $ R^2 $ e $ R^2 $ ajustado.

Um valor grande de $ R^2 $ não significa uma reta mais inclinada, além do mais, ele não leva em consideração a falta de ajuste do modelo. O $ R^2 $ poderá ser grande, mesmo que y e x estejam não linearmente relacionados. Dessa forma, temos que $ R^2 $ não deve ser observado sozinho, mas sempre aliado a outros diagnósticos do modelo. Logo, para reforçar o ajuste do modelo, vamos analisar a falta de ajuste do modelo 7.1.3.1.

Agora, vamos testar a seguinte hipótese:

Temos inicialmente

$$ (y_{ij}-\hat{y}_i)=(y_{ij}-\bar{y}_{i.})-(\bar{y}_{i.}-\hat{y}_{i}).$$

Disto, calculamos a soma de quadrados separadamente para o Falta de Ajuste.

$$SQE=\sum_{i=1}^m\sum_{j=1}^{n_i}(y_{ij}-\overline{y_{i.}})^2 +\sum_{i=1}^m \sum_{j=1}^{n_i}(\hat{y}_{ij}-\overline{y_{i}})^2$$

$$=0,00135+0,01448771=0,01583771.$$

$$QM_{LOF}=\frac{SQ_{LOF}}{m-p-1}=\frac{0,01448771}{48}= 0,000301827.$$

$$QM_{PE}=\frac{SQ_{PE}}{n-m}=\frac{0,00135}{10} =0,000135.$$

Podemos então, calcular a estatística F, com base nos quadrados médios, sabendo que neste exemplo os valores de m=122 e n=132.

$$F_0=\frac{QM_{LOF}}{QM_{PE}} = \frac{0,000301827}{0,000135}= 2,2357.$$

Se $ H_0 $ é verdadeiro, obtemos que $ F_0 \sim F_{(48;10)}. $

Com isso, rejeitamos $ H_0 $ se $ F_0> F_{(48; 10)} $. Como $ F_{(48;10)}=2,64, $ então temos $ F_0< F_{(48;10)}. $ Assim, não temos evidências de rejeitar $ H_0. $ A seguir, vamos calcular o p-valor.

$$\text{P-valor}=P[F_{(48; 10)}> F_0]= 0,08512.$$

Temos a seguir a Tabela ANOVA com o Falta de Ajuste dos dados com réplicas.

(imagem em falta)

Tabela 7.1.3.4: Tabela do teste de falta de ajuste (Lack of Fit).

Portanto, não rejeitamos a hipótese de que o modelo linear é adequado, isto é, o modelo linear é adequado.

A seguir apresentamos alguns diagnósticos do modelo final como o diagnóstico de outliers e pontos influentes.

(imagem em falta)

Figura 5.3.3.1: Gráfico do diagnóstico de outliers.

(imagem em falta)

Figura 7.1.3.2: Gráfico do diagnóstico de pontos influentes.

Agora, vamos avaliar a homocedasticidade (variância constante dos erros εi) do modelo. A partir da tabela 5.3.3.5, obtemos que a variável APS D90 é a responsável pela heteroscedasticidade do modelo (p-valor desprezível). Assim, não podemos mais dizer que os Estimadores de Mínimos Quadrados são os melhores estimadores de variância mínima variância para $ \beta, $ embora ainda possam ser não viciados.

(imagem em falta)

Tabela 7.1.3.5: Tabela do diagnóstico de homocedasticidade.

A seguir, como não obtemos estimadores de mínimos quadrados com variância mínima, vamos na próxima seção fazer a previsão do modelo ajustado e alguns gráficos de otimização do modelo final.

7.1.4 - Previsão e métodos de otimização do modelo

Nesta seção, vamos estudar os métodos de otimização e previsão do modelo ajustado final obtido na seção 7.1.3. Primeiramente, vamos fazer uma análise gráfica. Nesta análise, vamos fixar a corrente em 60 e o APS D90 em 21. Usando o software Action temos os seguintes resultados:

(imagem em falta)

Figura 7.1.4.1: Gráfico de Contorno ou curvas de nível (linhas).

(imagem em falta)

Figura 7.1.4.2: Gráfico de Contorno ou curvas de nível (Áreas).

(imagem em falta)

Figura 7.1.4.3: Gráfico de Superfície de Resposta.

Avaliando os gráficos 7.1.4.1 e 7.1.3.2 observamos que para drenagem até 20 dias, temos que trabalhar com damper acima de 50 (área azul claro e verde médio), afim de obtermos mínimo de resíduo de material na peneira de 45 μm (de 0 a 0,03 g). Agora, para drenagem acima de 25 dias, temos que trabalhar com damper mais baixo (abaixo de 40) afim de obtermos os mesmos resultados para a peneira de 45 μm.

A seguir, apresentamos a previsão para algumas configurações nas variáveis damper, drenagem, corrente e APS D90.

(imagem em falta)

As linhas amarelas, são algumas configurações que atendem a necessidade da medição, que visa atender ao mínimo de massa de resíduos de material indesejado, dentro do intervalo de 0 a 0,03 gramas. Por fim, vamos analisar o gráfico de otimização do modelo de regressão. Para isto, vamos analisar em duas situações, a primeira com o tempo de drenagem mais baixo, em seguida com tempo mais alto. A seguir, apresentamos os gráficos.

(imagem em falta)

(imagem em falta)

Note que, para obtermos praticamente zero de resíduos de material na peneira de 45 μm, necessitamos de pelo meno 11 dias de drenagem, com 25 de damper, 74,9 de corrente e 20,5 de APS D90. Agora, com tempo de drenagem de 30 dias, damper 25, corrente 75 e APS D90 de 21,65, obtemos zero de resíduos na peneira e 45 μm. Portanto, podemos obter zero de resíduos de material dependendo do tempo de drenagem.

Referências Bibliográficas

[1] Bussab, W. O. & Morettin, P. A. (1987), Estatística Básica, 4a Edição, Atual Editora: São Paulo.

[2] Magalhães, M. N. & Lima, A. C. P. (2001), Noções de Probabilidade e Estatística, Editora USP: São Paulo.

[3] Mason, R. L., Gunst, R. F. & Hess, J. L. (1989), Statistical Design and Analysis of Experiments: with applications do Engineering and Science, John Wiley & Sons: New York.

[4] Meyer, P. L. (1983), Probabilidade: Aplicações à Estatística, segunda edição, Livros técnicos e Científicos Editora: Rio Janeiro.

[5] Montgomery, D. C. (1985), Introduction to Statistical Quality Control, John Wiley: New York.

[6] Montgomery, D. C. (1997), Design and Analysis of Experiments, John Wiley and Sons: New York.

[7] Neter, J. & Kutner, M. H. & Wasserman, W. & Nachststein, C. J. (1996) Applied Linear Statistical Models. Forth Edition, Ed. Irwin.

[8] R Development Core Team (2007). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. ISBN 3-900051-07-0, URL http://www.R-project.org.

[9] Schmidt, S. R. & Launsby, R. G. (1997), Understanding Industrial Designed Experiments, Air Academic Press: Colorado.

[10] Vieira, S. e Hoffmann, R. (1989) Estatística Experimental. Editora Atlas, São Paulo.

[11] Isabela da Costa César and Gerson Antônio Pianetti. Robustness evaluation of the chromatographic method for the quantitation of lumefantrine using youden’s test. Brazilian Journal of Pharmaceutical Sciences, 45(2):235{240, 2009.

[12] Cuthbert Daniel. Use of half-normal plots in interpreting factorial two-level experiments. Technometrics, 1(4):311{341, 1959.

[13] Coordenacão Geral de Acreditacão. Orientacão sobre validacão de metodos analticos. Technical report, DOQ-CGCRE-008, revis~ao 3, 2010.

[14] Russell V Lenth. Quick and easy analysis of unreplicated factorials. Technometrics, 31(4):469{473, 1989.