8.2 Variáveis Aleatórias

Dado um fenômeno aleatório qualquer, com um certo espaço amostral, desejamos estudar a estrutura probabilística de quantidades associadas a esse fenômeno. Por exemplo, ao descrever uma peça manufaturada podemos empregar duas classificações: “defeituosa” ou “não defeituosa”. Para facilitar a análise, vamos atribuir um número real a cada resultado do experimento. Assim podemos atribuir o valor 0 às peças não defeituosas e 1 às defeituosas. Nós podemos entender por variável aleatória uma função que associa a cada elemento do espaço amostral (neste exemplo os elementos são “defeituosa”, “não defeituosa”) um número real. Denotaremos as variáveis aleatórias por letras maiúsculas.

Definição 2.1

Consideremos um experimento e $ \Omega $ o espaço amostral associado a esse experimento. Uma função X, que associa a cada elemento $ \omega \in \Omega $ um número real, $ X(\omega) $, é denominada variável aleatória (v.a.). Ou seja, variável aleatória é um característico numérico do resultado de um experimento.

As variáveis aleatórias são fundamentais para as aplicações, pois elas representam as características de interesse em uma população. Por exemplo, em uma linha de usinagem de peças estamos interessados em controlar o diâmetro das peças produzidas. Neste caso, o resultado da medição do diâmetro é a variável aleatória de interesse. Em um ensaio clínico, estamos interessados em avaliar o tempo de vida dos pacientes e neste caso, a tempo de vida corresponde à variável aleatória.

Exemplo 2.1

Considere três lançamentos independentes de uma moeda equilibrada. Seja C cara e K coroa. O espaço amostral deste experimento é S={(C,C,C); (C,C,K); (C,K,C); (K,C,C); (C,K,K); (K,C,K); (K,K,C); (K,K,K)}. Podemos definir a variável aleatória X: “número de caras obtidas nos três lançamentos”. Por exemplo, temos que X((C,C,C)) = 3 e X((K,C,C))=2.

Exemplo 2.2

Escolher um ponto ao acaso no quadrado unitário, ou seja, escolher um par ordenado $ (x,y) \in [0,1] \times [0,1] $. Então $ \Omega=[0,1]\times [0,1] $ e como exemplo de variável aleatória o produto das duas coordenadas $ X(\omega)= x y $., para todo $ w =(x,y) \in \Omega $.

Em geral, não é qualquer função com domínio no espaço amostral e imagem na reta que é uma variável aleatória. Para espaços amostrais infinitos não enumeráveis, dizemos que a função $ X: \Omega \rightarrow \Bbb{R} $ é uma variável aleatória se o conjunto $ { w \in \Omega : X(w) \leq x } $ é um evento (pertence a $ \sigma $-álgebra de eventos em $ \Omega $), para todo $ x \in \Bbb{R} $

2.1 - Função de distribuição acumulada

A função de distribuição acumulada descreve como probabilidades são associadas aos valores ou aos intervalos de valores de uma variável aleatória. Ela representa a probabilidade de uma variável aleatória ser menor ou igual a um valor real $ x $. Na seção distribuição de probabilidade na reta, mostramos que variável aleatória e função de distribuição acumulada são sinônimos. Desta forma, podemos definir variáveis aleatórias através da sua função de distribuição acumulada. Na sequência, vamos definir e estudar propriedades da função de distribuição acumulada. Para isto, tomamos o espaço de probabilidade $ (\Omega , {\cal F} , \mathbb{P}) $.

Definição 2.1.1

A função de distribuição acumulada de uma variável aleatória $ X $ definida sobre $ (\Omega , \mathcal{F} , \mathbb{P}) $ é uma função que a cada número real $ x \in \mathbb{R} $ associa o valor

$$F(x)=\mathbb{P}\left(X\leq x\right) \in [0,1].$$

A notação $ (X \leq x) $ é usada para designar o conjunto $ {\omega\in \Omega : X(\omega) \leq x} $, isto é, denota a imagem inversa do intervalo $ (-\infty,x] $ pela variável aleatória X. Com isso, podemos observar que a função de distribuição acumulada $ F $ tem como domínio os números reais $ (\Bbb{R}) $ e imagem o intervalo $ [0,1] $.

O conhecimento da função de distribuição acumulada é suficiente para entendermos o comportamento de uma variável aleatória. Mesmo que a variável assuma valores apenas num subconjunto dos reais, a função de distribuição é definida em toda a reta. Ela é chamada de função de distribuição acumulada, pois acumula as probabilidades dos valores inferiores ou iguais a x.

Exemplo 2.1.1

Consideremos o Exemplo 2.1. Vamos encontrar a função distribuição acumulada de $ X $: “número de caras obtidas nos três lançamentos”.

Os valores que $ X $ pode assumir são $ 0,1,2 $ e $ 3 $. Portanto,

$$\mathbb{P}(X=0)=\mathbb{P}((KKK))=\frac{1}{2}\times\frac{1}{2}\times\frac{1}{2}=\frac{1}{8}.$$

$$\mathbb{P}(X=1)=\mathbb{P}((CKK))+\mathbb{P}((KCK))+\mathbb{P}((KKC))=\frac{3}{8}.$$

$$\mathbb{P}(X=2)=\mathbb{P}((CCK))+\mathbb{P}((CKC))+\mathbb{P}((KCC))=\frac{3}{8}.$$

$$\mathbb{P}(X=3)=\mathbb{P}((CCC))=\frac{1}{8}.$$

Portanto,

$$\text{se} \ x \ < \ 0 \Rightarrow \mathbb{P}(X\leq x) = 0,$$

$$\text{se} \ 0\leq x \ < \ 1 \Rightarrow \mathbb{P}(X\leq x) = \mathbb{P}(X = 0) = \frac{1}{8},$$

$$\text{se} \ 1\leq x \ < \ 2 \Rightarrow \mathbb{P}(X\leq x) = \mathbb{P}(X = 0) + \mathbb{P}(X = 1) = \frac{1}{8} + \frac{3}{8} = \frac{1}{2},$$

$$\text{se} \ 2\leq x \ < \ 3 \Rightarrow \mathbb{P}(X\leq x) = \mathbb{P}(X = 0) + \mathbb{P}(X = 1) + \mathbb{P}(X = 2) = \frac{1}{8} + \frac{3}{8} + \frac{3}{8} = \frac{7}{8} \ \text{e}$$

$$\text{se} \ x\geq 3, \Rightarrow \mathbb{P}(X\leq x) = \mathbb{P}(X = 0) + \mathbb{P}(X = 1) + \mathbb{P}(X = 2) + \mathbb{P}(X = 3) = 1.$$

Desta forma, temos que a função de distribuição acumulada de $ X $ é dada por

Exemplo 2.1.2

O tempo de validade, em meses, de um óleo lubrificante num certo equipamento está sendo estudado. Seja $ \Omega = {\omega\in \Bbb{R} : 6 \ < \ \omega \leq 8} $. Uma variável de interesse é o próprio tempo de validade e, nesse caso, definimos $ X(\omega) = \omega; \ \forall \ \omega\in \Omega $. Por exemplo, podemos tomar a seguinte função de distribuição acumulada de $ X $:

Observe que neste exemplo, definimos diretamente a Função de Distribuição Acumulada (FDA) ao invés da probabilidade. Na maioria das aplicações, partimos da FDA para definirmos o modelo probabilístico.

A função de distribuição acumulada de uma variável aleatória $ X $ têm três propriedades básicas:

1. $ 0\leq F(x)\leq 1 $, $ \lim_{x \rightarrow -\infty} F(x) =0 $ e $ \lim_{x \rightarrow \infty} F(x)=1 $;

2. $ F $ é não decrescente.

3. $ F $ é uma função contínua à direita e tem limite à esquerda.

Demonstração

(1) Se $ x \rightarrow - \infty $, então $ (X\leq x)\downarrow \emptyset $ e assim $ F(x)=\mathbb{P}(X\leq x)\downarrow 0 $. Se $ x \rightarrow + \infty $, então $ (X\leq x)\uparrow \Omega $ e assim $ F(x)=\mathbb{P}(X\leq x)\uparrow 1 $.

(2) $ F $ não decrescente é equivalente a $ x\leq y\Rightarrow (X\leq x)\subset (X\leq y) \Rightarrow F(x)=\mathbb{P}(X\leq x)\leq \mathbb{P}(X\leq y)=F(y) $

(3) $ F $ é contínua a direita é equivalente a se $ x_n\downarrow x $, então $ (X\leq x_n) $ é um sequência decrescente de eventos aleatórios e $ \displaystyle \bigcap_{n\geq 1}[X\leq x_n]= ([X\leq x) $, pois $ X\leq x $ se, e somente se, $ X\leq x_n{ }\forall n $. Assim, concluímos que

$$F(x_n)=\mathbb{P}(X\leq x_n)\downarrow \mathbb{P}(X\leq x)=F(x)$$

Exemplo 2.1.3

Para o lançamento de uma moeda, temos que $ \Omega = (\text{cara}, \text{coroa}) $ e que $ \mathbb{P}(\text{cara}) = \mathbb{P}(\text{coroa}) = \frac{1}{2} $. Definimos uma variável aleatória $ X:\Omega\rightarrow\mathbb{R} $ da seguinte forma:

Para obter a função de distribuição acumulada da variável aleatória $ X $, é conveniente separar os vários casos, de acordo com os valores da variável.

Para $ x \ < \ 0 $, $ \mathbb{P}(X \leq x) = 0 $, uma vez que o menor valor assumido pela variável $ X $ é $ 0 $. No intervalo $ 0 \leq x \ < \ 1 $, temos que $ \mathbb{P}(X \leq x) = \mathbb{P}(X = 0) = 1/2 $. E, para $ x \geq 1 $, temos que $ \mathbb{P}(X \leq x) = \mathbb{P}(X = 0) + \mathbb{P}(X = 1) = 1 $. Dessa forma, $ F(x) = \mathbb{P}(X \leq x) $ foi definida para todo $ x $ real. Assim, temos

O seguinte resultado, nos diz que qualquer função $ F $ que satisfaz as propriedades básicas (1, 2 e3) é a função de distribuição acumulada de alguma variável aleatória na reta. A demonstração deste resultado está na seção distribuição de probabilidade na reta.

Teorema 2.1.1

Toda função $ F $ satisfazendo as propriedades básicas é uma função de distribuição acumulada de alguma variável aleatória.

A partir deste resultado, podemos definir variáveis aleatórias através da sua respectiva função de distribuição acumulada.

Exemplo 2.1.4

Seja $ X $ é uma variável aleatória com distribuição exponencial de parâmetro $ \lambda > 0 $, qual a distribuição da variável aleatória $ Y=\min(\lambda,X) $? Faça a decomposição de $ F_Y $.

(a) Distribuição de Y é dada por

(a1) $ Y< \lambda $ e $ \mathbb{P}(Y\leq y)=0 $

(a2) $ Y=\lambda $ temos que

$$\mathbb{P}(Y\leq y)=\mathbb{P}(Y=\lambda)=\mathbb{P}(X\leq \lambda)=1-e^{-\lambda^2}$$

(a3) $ Y> \lambda $

$$\mathbb{P}(Y\leq y)=\mathbb{P}(X\leq x)=1-e^{-\lambda x}$$

b) Decomposição de $ F_Y $

(b1) $ F_{Y_d}: $

e então, $ F_Y(y)=F_{Y_d}(y)+F_{Y_{ab}}(y), \forall y \in \mathbb{R} $ o que implica que $ F_{Y_s}=0 $ para qualquer $ y\in \mathbb{R} $.

Exemplo 2.1.5

Cinco pontos são escolhidos, independentemente e ao acaso, do intervalo $ [0,1] $. Seja $ X $ o número de pontos que pertencem ao intervalo $ [0,c] $ no qual $ 0< c< 1 $. Qual a distribuição X?

É a repetição de ensaios com mesma probabilidade de sucesso de $ p $ e independentes, no qual

$$p=\frac{comp[0,c]}{comp[0,1]}=c.$$

Então, $ X $ tem distribuição binomial com parâmetro $ 5 $ e $ p $.

Exemplo 2.1.6

Determine a distribuição do tempo de espera até o segundo sucesso em uma sequência de ensaios de Bernoulli com probabilidade $ p $ de sucesso.

Seja $ X $ a variável aleatória que designa o tempo de espera até o segundo sucesso. Note que a probabilidade de ocorrer 2 sucessos em $ k(k\geq 2) $ é $ p^2(1-p)^{k-2} $. Agora o último ensaio ocorre na última posição então o primeiro ensaio pode ocorrer em qualquer das posições anteriores. Assim,

$$\mathbb{P}(X=k)=(k-1)p^2(1-p)^{k-2}, k=2,3,\dots$$

Exemplo 2.1.7

Uma massa radioativa emite partículas segundo um processo de Poisson a uma taxa média de 10 partículas por segundo. Um contador é colocado ao lado da massa. Suponha que cada partícula emitida atinge o contador com probabilidade de $ 1/10 $, que o contador registra todas as partículas que o atingem, e que não há iteração entre as partículas(elas se movimentam independentemente).

(a) Qual a distribuição de $ X_i= $ número de partículas emitidas até o tempo $ t,t> 0 $?

Temos $ (X_t)_{t> 0} $ é a probabilidade de Poisson então

(b) Prove que $ Y_t $ tem distribuições de Poisson, onde $ Y_t $ é o número de partículas registradas (contadas) até o tempo t, $ t> 0 $. Qual o parâmetro?

$$Y_t=\text{número de partículas registradas.}$$

Agora

$$[Y_t=n]=\bigcup_{k=n}^\infty \left([Y_t=n]\cap [X_t=k]\right)$$

o que implica que

$$\mathbb{P}(Y_t=n)=\sum_{k=n}^\infty \mathbb{P}(Y_t=n,X_t=k)=\sum_{k=n}{\infty}\mathbb{P}(Y_t=n|X_t=n)\mathbb{P}(X_t=k)$$

Agora,

Então

$$\mathbb{P}(Y_t=n)=\sum_{k=n}^\infty \frac{k!}{(n-k)!n!}\left(\frac{1}{10}\right)^n \left(\frac{9}{10}\right)^{k-n}\frac{(\lambda t)^k}{n!} c^{\lambda t}= \frac{(\lambda t)^n \left(\frac{1}{10}\right)^n}{n!}e^{-\lambda t}\sum_{k=n}^\infty \frac{\left(\frac{9}{10}\lambda t\right)^{k-n}}{(k-n)!}$$

$$=\frac{\left(\frac{\lambda t}{10}\right)^n e^{-\lambda t}}{10} $$

Então, $ Y_t\sim Poisson\left(\frac{\lambda}{10}t\right) $

2.1.1 - Distribuição de probabilidade na reta

A fim de construir a probabilidade na reta real $ \mathbb{R} $, vamos construir, inicialmente, os conjuntos de Borel da reta. Neste sentido, considere a classe dos intervalos abertos à esquerda e fechados à direita da forma

$$(a,b] = {x\in\mathbb{R}: a \ < \ x\leq b}$$

para quaisquer $ a $ e $ b $ tais que $ -\infty\leq a \ < \ b \ < \ \infty $.

Observação 2.1.1.1

Consideramos o intervalo $ (a,\infty] $ como sendo o intervalo aberto $ (a,\infty) $. Esta consideração é importante para que o complementar de um intervalo $ (-\infty,b] $ dado por $ (\infty,b]^c = (b,\infty) = (b,\infty] $ seja um elemento da classe.

Seja $ \mathcal{A} $ a classe de subconjuntos de $ \mathbb{R} $ composta pelo conjunto vazio $ \varnothing $ e dos conjuntos que podem ser escritos como uma união finita de intervalos disjuntos da forma $ (a,b] $, isto é,

$$A\in\mathcal{A} \ \text{se} \ A = \varnothing \ \text{ou} \ A = \bigcup_{i=1}^n(a_i,b_i], \ \text{com} \ (a_i,b_i]\cap (a_j,b_j] = \varnothing \ \text{se} \ i\neq j \ \text{e} \ n \ < \ \infty.$$

Proposição 2.1.1.1

A classe $ \mathcal{A} $ é uma álgebra.

Demonstração

De fato, para que $ \mathcal{A} $ seja uma álgebra, basta verificar as seguintes condições:

1. $ \varnothing\in\mathcal{A} $;

2. Se $ A,B\in\mathcal{A} $ então $ A\cap B\in\mathcal{A} $.

3. Se $ A\in\mathcal{A} $, então $ A^c\in\mathcal{A} $.

O item 1) é imediato da definição da classe $ \mathcal{A} $. Para verificar o item 2), seja $ A,B\in\mathcal{A} $ e observamos que, se ou $ A = \varnothing $ ou $ B = \varnothing $, então $ A\cap B = \varnothing \in\mathcal{A} $. Suponha que

$$A = \bigcup_{i=1}^n(a_i,b_i] \ \text{com} \ (a_i,b_i]\cap(a_j,b_j] = \varnothing \ \text{se} \ i\neq j \ \text{e} \ B = \bigcup_{k=1}^m(c_k,d_k] \ \text{com} \ (c_k,d_k]\cap(c_l,d_l] = \varnothing \ \text{se} \ k\neq l.$$

Segue então que

$$A\cap B = \left(\bigcup_{i=1}^n(a_i,b_i]\right)\bigcap\left(\bigcup_{k=1}^m(c_k,d_k]\right) = \bigcup_{i=1}^n\bigcup_{k=1}^m\left((a_i,b_i]\cap(c_k,d_k]\right).$$

Mas, para $ i = 1,\ldots,n $ e $ k = 1,\ldots, m $ temos que

de modo que $ A\cap B $ pode ser escrito como uma união finita de elementos da forma $ (a,b] $. Portanto, $ A\cap B \in\mathcal{A} $. Basta agora verificar o item 3). Se $ A = \varnothing $, então $ A^c = \mathbb{R} = (-\infty,\infty) $ que pode ser escrito na forma

$$\mathbb{R} = (-\infty,\infty) = (-\infty,0]\cup(0,\infty]\in\mathcal{A}.$$

Para o caso em que $ A = \cup_{i=1}^n(a_i,b_i] $, com $ (a_i,b_i]\cap(a_j,b_j] = \varnothing $ se $ i\neq j $, podemos reescrever $ A $ da forma

$$A = \bigcup_{j=1}^n(a_{i_j},b_{i_j}]$$

de forma que

$$-\infty \leq a_{i_1} \ < b_{i_1} \leq a_{i_2} \ < \ b_{i_2} \leq \ldots \leq a_{i_n} \ < \ b_{i_n} \leq \infty$$

e então, temos que

$$A^c = \left(\bigcup_{j=1}^n(a_{i_j},b_{i_j}]\right)^c = (-\infty,a_{i_1}]\cup (b_{i_1},a_{i_2}] \cup \ldots \cup (b_{i_{n-1}},a_{i_n}] \cup (b_{i_n},\infty] \in \mathcal{A}.$$

completando a demonstração.

É importante observar que, apesar da classe $ \mathcal{A} $ ser uma álgebra, como demonstrado Pela Proposição 2.1.1.1, ela não é uma $ \sigma $-álgebra. De fato, a propriedade $ \sigma $-aditiva não é satisfeita. Basta tomar os conjuntos $ A_n\in\mathcal{A} $ dados por $ A_n = (0,1-\frac{1}{n}] $. Desta forma temos que

$$\bigcup_{n=1}^{\infty}A_n = (0,1)\notin \mathcal{A}.$$

Definição 2.1.1.1

Seja $ \sigma(\mathcal{A}) $ a $ \sigma $-álgebra gerada pela classe de eventos $ \mathcal{A} $. Esta $ \sigma $-álgebra desempenha um papel fundamental em análise e é chamada de $ \sigma $-álgebra de Borel de subconjunto da reta $ \mathbb{R} $, denotada por $ \mathfrak{B}(\mathbb{R}) $. Seus conjuntos são denominados conjuntos de Borel da reta ou de borelianos da reta.

Observação 2.1.1.2

Se $ \mathcal{I} $ é a classe de intervalos da forma $ (a,b] $ e $ \sigma(\mathcal{I}) $ é a menor $ \sigma $-álgebra de conjuntos que contém $ \mathcal{I} $, podemos verificar que $ \sigma(\mathcal{I}) $ é a $ \sigma $-álgebra de Borel. Em outras palavras, podemos obter a $ \sigma $-álgebra de Borel a partir de $ \mathcal{I} $ sem a álgebra $ \mathcal{A} $, já que $ \sigma(\mathcal{I}) = \sigma(\alpha(\mathcal{I})) $.

A $ \sigma $-álgebra de Borel não contém somente os intervalos da forma $ (a,b] $, mas também os conjuntos unitários da forma $ (a) $ e os intervalos da forma $ (a,b) $, $ [a,b] $, $ [a,b) $, $ (-\infty,b) $ e $ (a,\infty) $. De fato, temos que

$$(a,b) = \bigcup_{n=1}^{\infty}\left(a,b-\frac{1}{n}\right], \ a \ < \ b,$$

$$[a,b] = \bigcap_{n=1}^{\infty}\left(a-\frac{1}{n},b\right], \ a \ < \ b,$$

$$(a)=\bigcap_{n=1}^{\infty}\left(a-\frac{1}{n},a\right]$$

e todos os demais elementos são construídos a partir destes três.

Também ressaltamos que $ \mathfrak{B}(\mathbb{R}) $ pode ser construída a partir de quaisquer classes de intervalos das formas mencionadas acima ao invés dos intervalos do tipo $ (a,b] $, já que todas as $ \sigma $-álgebras mínimas geradas por essas classes de intervalos são as mesmas, isto é, $ \mathfrak{B}(\mathbb{R}) $.

Observação 2.1.1.3

O espaço mensurável $ (\mathbb{R},\mathfrak{B}(\mathbb{R})) $ também pode ser denotado por $ (\mathbb{R},\mathfrak{B}) $.

A seguir, demonstramos o Teorema 2.1.1 enunciado na Seção 2.1.

Teorema 2.1.1.1

Toda função $ F $ satisfazendo as propriedades básicas é uma função de distribuição acumulada de alguma variável aleatória.

Demonstração

Suponhamos que a função $ F $ satisfaça as propriedades básicas. Vamos construir uma variável aleatória $ X $ de forma que a função de distribuição acumulada $ F_X $ seja igual a $ F $, isto é, $ F_X=F $. Seja $ \mathbb{P} $ uma probabilidade definida nos borelianos da reta $ \mathfrak{B}(\mathbb{R}) $ de tal forma que $ \mathbb{P}[(-\infty,x)]=F(x) $ para qualquer $ x $ no conjunto dos números reais. Desta forma basta definirmos $ X(\omega)=\omega $ para qualquer $ \omega $ percente ao conjunto dos números reais. Assim o resultado segue, basta construirmos a probabilidade da seguinte forma

$$F_X(x) = \mathbb{P}\left(X(\omega)\leq x\right) = \mathbb{P}\left((-\infty,x]\right)=F\left(x\right),$$

$$1 - F_X(x) = 1-\mathbb{P}\left(X(\omega)\leq x\right) = \mathbb{P}\left((x,\infty)\right)=1-F\left(x\right),$$

$$F_X(b) - F_X(a) = \mathbb{P}\left(a \ < \ X\leq b\right) = \mathbb{P}\left((a,b]\right)=F\left(b\right)-F\left(a\right)$$

e definir $ \mathbb{P} $ na álgebra $ \mathcal{A} $ da forma

$$\mathbb{P}\left((a,b]\cup (c,d]\right)=F(b)-F(a)+F(d)-F(c),$$

para os intervalos $ (a,b], (c, d] $ tal que $ (a,b]\cap (c,d] = \varnothing $. Agora basta usarmos o Teorema de Extensão de Carathéodory ( que será enunciado e demonstrado abaixo para este caso). Assim, após construirmos a probabilidade, temos que $ F $ será uma função de distribuição acumulada da variável aleatória $ X $ definida acima.

Uma demonstração alternativa para o Teorema 2.1.1.1 pode ser dada da seguinte forma.

Seja $ \Omega=(0,1) $, $ \mathcal{F} $ a sigma-álgebra de borel e $ \mathbb{P} $ a medida de Lebesgue ou distribuição uniforme. Para $ \omega \in (0,1) $, considere

$$X(\omega)=\sup{(y:F(y) \ < \ \omega)}.$$

Se mostrarmos que

$${(\omega : X(\omega)\leq x)}={(\omega:\omega \leq F(x))},$$

então o resultado segue imediatamente uma vez que $ \mathbb{P}(\omega:\omega\leq F(x))=F(x) $. De fato, temos que, se $ \omega\leq F(x) $ então $ X(\omega)\leq x $, uma vez que $ x \notin {y:F(y) \ < \ \omega} $. Por outro lado temos que, se $ \omega \ < \ F(x) $, então como $ F $ é continua a direita temos que existe um $ \epsilon \ > \ 0 $ tal que

$$F(x+\epsilon) \ < \ \omega \ \text{e} \ X(\omega)\geq x+\epsilon \ > \ x.$$

Assim temos que $\mathbb{P}({\omega : X(\omega)\leq x})=\mathbb{P}({\omega:\omega \leq F(x)})=F(x)$. Para demostrarmos o teorema de extensão de carathéodory vamos necessitar de alguns resultados, enunciados nos lemas a seguir.

Lema 2.1.1.1

Seja $ \mathbb{P} $ uma probabilidade definida em uma álgebra $ \mathcal{F}_0 $ de subconjuntos de $ \Omega $. Suponha que $ A_1,A_2,\cdots\in \mathcal{F}_0 $ com $ A_1\subset A_2 \subset \ldots $ com limite $ A $ e os conjuntos $ A^{\prime}_1,A^{\prime}_2,\cdots\in \mathcal{F}_0 $ com $ A^{\prime}_1\subset A^{\prime}_2 \subset \cdots $ com limite $ A^{\prime} $ (com $ A $ e $ A^{\prime} $ não necessariamente em $ \mathcal{F}_0 $). Se $ A\subset A^{\prime} $ então

$$\lim_{m\rightarrow \infty}\mathbb{P}(A_m)\leq \lim_{n\rightarrow \infty}\mathbb{P}(A^{\prime}_n).$$

Se $ A=A^{\prime} $ temos imediatamente que

$$\lim_{m\rightarrow \infty}\mathbb{P}(A_m)= \lim_{n\rightarrow \infty}\mathbb{P}(A^{\prime}_n).$$

Demonstração

Seja $ m $ fixo, então $ A_m\cap A^{\prime}_n \uparrow A_m\cap A^{\prime}=A_m $ e, portanto,

$$\mathbb{P}\left(A_m\cap A^{\prime}_n\right)\rightarrow \mathbb{P}\left(A_m\right).$$

Como $ \mathbb{P}\left(A_m\cap A^{\prime}_n\right)\leq \mathbb{P}\left(A^{\prime}_n\right) $ então

$$\mathbb{P}\left(A_m\right)=\lim_{n\rightarrow \infty}\mathbb{P}\left(A_m\cap A^{\prime}_n\right)\leq\lim_{n\rightarrow \infty}\mathbb{P}(A^{\prime}_n).$$

Assim, basta tomarmos os limite em $ m $ e teremos que

$$\lim_{m\rightarrow \infty}\mathbb{P}\left(A_m\right)\leq\lim_{n\rightarrow \infty}\mathbb{P}\left(A^{\prime}_n\right)$$

e o resultado segue.

Lema 2.1.1.2

Seja $ \mathbb{P} $ uma medida probabilidade definida em uma álgebra $ \mathcal{F}_0 $ de subconjuntos de $ \Omega $. Seja $ \mathcal{G} $ a coleção de todos os conjuntos que são limites de sequências crescentes de conjuntos de $ \mathcal{F}_0 $. Então $ \mathbb{P}^{\ast} $ definida em $ \mathcal{G} $ de tal forma que

$$\mathbb{P}^{\ast}(A)=\lim_{n\rightarrow \infty}\mathbb{P}(A_n)$$

é uma extensão de $ \mathbb{P} $ em $ \mathcal{G} $ e $ \mathbb{P}^{\ast}(B)=\mathbb{P}(B) \ \forall \ B\in \mathcal{F}_0 $. Além disso $ \mathbb{P}^{\ast} $ é uma probabilidade.

Demonstração

É imediato ver que $ \mathbb{P}^{\ast}=\mathbb{P} $ em $ \mathcal{F}_0 $. Assim basta mostramos que $ \mathbb{P}^{\ast} $ é uma probabilidade, ou seja, que

1. $ \mathbb{P}^{\ast}(\emptyset)=0 $, $ \mathbb{P}^{\ast}(\Omega)=1 $ e que $ 0\leq \mathbb{P}^{\ast}(A)\leq 1\forall A\in \mathcal{G} $.

2. Se $ G_1, G_2\in \mathcal{G} $ então $ G_1\cup G_2 $ e $ G_1\cap G_2 \in \mathcal{G} $ e ainda $ \mathbb{P}^{\ast}(G_1\cup G_2)+\mathbb{P}^{\ast}(G_1\cap G_2)=\mathbb{P}^{\ast}(G_1)+\mathbb{P}^{\ast}(G_2) $.

3. Se $ G_1,G_2\in \mathcal{G} $ então $ G_1\subset G_2 $ então $ \mathbb{P}^{\ast}(G_1)\leq \mathbb{P}^{\ast}(G_2) $.

4. Se $ G_n \in \mathcal{G} $, com $ n\in\mathbb{N} $ e $ G_n\uparrow G $ então $ G\in \mathcal{G} $ e $ \mathbb{P}^{\ast}(G_n)\rightarrow \mathbb{P}^{\ast}(G) $.

(1.) É imediato pelo fato de $ \mathbb{P}^{\ast}=\mathbb{P} $ em $ \mathcal{F}_0. $

(2.) Seja $ A_{n_1}\in \mathcal{F}_0 $ e $ A_{n_2}\in \mathcal{F}_0 $, tal que $ A_{n_1}\uparrow G_1 $ e $ A_{n_2}\uparrow G_2 $ então, como $ \mathbb{P}(A_{n_1}\cup A_{n_2})+\mathbb{P}(A_{n_1}\cap A_{n_2})=\mathbb{P}(A_{n_1})+\mathbb{P}(A_{n_2}) $, basta tomarmos o limite em $ n $ e o resultado segue.

(3.) O resultado segue imediatamente pelo Lema 2.1.1.1.

(4.) Como $ G $ é uma união enumerável de conjuntos de $ \mathcal{F_0} $ então $ G\in \mathcal{G} $. Pois para cada $ n $ podemos encontrar conjuntos $ A_{n_m}\in \mathcal{F}_0 $ com $ A_{n_m}\uparrow G_n $. Desta forma seja

$$D_m=A_1\cup A_2\cup\cdots\cup A_{n_m}.$$

Então $ D_m $ é uma sequência crescente de conjuntos de $ \mathcal{F}_0 $ e, além disso

$$A_{n_m}\subset D_m \subset G_m, \ \forall \ n\leq m. \ \text{(1)}$$

e, portanto,

$$\mathbb{P}(A_{n_m})\leq \mathbb{P}(D_m)\leq \mathbb{P}^{\ast}(G_m), \ \forall \ n \leq m. \ \text{(2)}$$

Se $ m\rightarrow \infty $, obtemos por (1) que

$$G_n\subset\displaystyle \bigcup_{m=1}^{\infty}D_m\subset G,$$

assim tomando $ n\rightarrow \infty $ concluímos que $ D_m\uparrow G $ e, portanto,

$$\mathbb{P}(D_m)\rightarrow \mathbb{P}^{\ast}(G)$$

tomando o limite em $ m $ obtemos por (2) que

$$\mathbb{P}^{\ast}(G_n)\leq\lim_{m\rightarrow \infty}\mathbb{P}(D_m)\leq \lim_{m\rightarrow\infty}\mathbb{P}^{\ast}(G_m).$$

Assim, tomando o limite em $ n $ concluímos que

$$\lim_{n\rightarrow}\mathbb{P}^{\ast}(G_n)=\lim_{m\rightarrow \infty}\mathbb{P}(D_m)=\mathbb{P}^{\ast}(G)$$

e, portanto, o resultado segue.

Lema 2.1.1.3

Seja $ \mathcal{G} $ uma classe de subconjuntos do conjunto $ \Omega $, $ \mathbb{P} $ uma probabilidade definida em $ \mathcal{G} $ tal que, $ \mathbb{P} $ e $ \mathcal{G} $ satisfaça as condições do Lema 2.1.1.2. Desta forma definimos para cada $ A\in \Omega $,

$$\mathbb{P}^{\ast}(A)=\inf{(\mathbb{P}(G):G\in\mathcal{G}, G\supset A)}.$$

Então $ \mathbb{P}^{\ast}=\mathbb{P} $ em $ \mathcal{G} $ e $ \mathbb{P}^{\ast} $ é uma probabilidade.

Demonstração

É imediato ver que $ \mathbb{P}^{\ast}=\mathbb{P} $ em $ \mathcal{G} $. Assim basta mostramos que $ \mathbb{P}^{\ast} $ é uma probabilidade, ou seja, que

1. $ \mathbb{P}^{\ast}(\emptyset)=0 $, $ \mathbb{P}^{\ast}(\Omega)=1 $ e que $ 0\leq \mathbb{P}^{\ast}(A)\leq 1 \ \forall \ A\in \Omega $.

2. $ \mathbb{P}^{\ast}(G_1\cup G_2)+\mathbb{P}^{\ast}(G_1\cap G_2)=\mathbb{P}^{\ast}(G_1)+\mathbb{P}^{\ast}(G_2) $

3. Se $ A\subset B $ então $ \mathbb{P}^{\ast}(A)\leq \mathbb{P}^{\ast}(B) $

4. Se $ A_n\uparrow A $, então $ \mathbb{P}^{\ast}(A_n)\rightarrow \mathbb{P}^{\ast}(A) $.

(1.) É imediato pelo fato de $ \mathbb{P}^{\ast}=\mathbb{P} $ em $ \mathcal{G} $.

(2.) Se $ \epsilon \ > \ 0 $, escolha $ G_1,G_2\in \mathcal{G} $, tal que $ G_1\supset A $, $ G_2\supset B $ tal que $ \mathbb{P}(G_1)\leq \mathbb{P}^{\ast}(A)+\epsilon/2 $, $ \mathbb{P}(G_2)\leq \mathbb{P}^{\ast}(B)+\epsilon/2 $ e, pelo Lema 2.1.2 temos que

$$\mathbb{P}^{\ast}(A)+\mathbb{P}^{\ast}(B)+\epsilon\geq \mathbb{P}(G_1)+\mathbb{P}(G_2)=\mathbb{P}(G_1\cup G_2)+\mathbb{P}(G_1\cap G_2)\geq \mathbb{P}^{\ast}(A\cup B)+\mathbb{P}^{\ast}(A\cap B).$$

Como $ \epsilon $ é arbitrário, temos que o resultado segue.

(3.) Segue da definição de $ \mathbb{P}^{\ast} $.

(4.) Pelo item anterior temos que $ \mathbb{P}^{\ast}(A)\geq \displaystyle \lim_{n\rightarrow \infty}\mathbb{P}^{\ast}(A_n) $. Se $ \epsilon \ > \ 0 $ para cada $ n $ podemos escolher $ G_n\in\mathcal{G} $, $ G_n\supset A $, tal que

$$\mathbb{P}(G_n)\leq \mathbb{P}^{\ast}(A_n)+\epsilon2^{-n}.$$

Agora tomemos

$$A=\displaystyle \bigcup_{n=1}^{\infty}A_n\subset \bigcup_{n=1}^{\infty}G_n\in \mathcal{G}.$$

Portanto

$$\mathbb{P}^{\ast}(A)\stackrel{item 3.}{\leq} \mathbb{P}^{\ast}\left(\bigcup_{n=1}^{\infty}G_n\right)\stackrel{item 1.}{=}\mathbb{P}\left(\bigcup_{n=1}^{\infty}G_n\right)=\lim_{n\rightarrow \infty}\mathbb{P}\left(\bigcup_{k=1}^{n}G_n\right)$$

pelo Lema 2.1.1.2(4.). Assim basta provarmos que

$$\mathbb{P}\left(\bigcup_{i=1}^{n}G_i\right)\leq \mathbb{P}^{\ast}(A_n)+\epsilon\sum_{i=1}^{n}2^{-i}.$$

Mostremos este fato por indução. Para $ n=1 $ é verdadeiro pela forma como escolhemos $ G_1 $. Suponha válido para $ n $, aplicando o Lema 2.1.1.2(2.) para o conjunto $ \bigcup_{i=1}^{n}G_i $ e $ G_{n+1} $ obtemos

$$\mathbb{P}\left(\bigcup_{i=1}^{n+1}G_i\right)=\mathbb{P}\left(\bigcup_{i=1}^{n}G_i\right)+\mathbb{P}(G_{n+1})-\mathbb{P}\left(\left(\bigcup_{i=1}^{n}G_i\right)\cap G_{n+1}\right).$$

Agora como $ \bigcup_{i=1}^{n}G_i\cap G_{n+1}\supset G_n\cap G_{n+1}\supset A_n\cap A_{n+1}=A_n $, então, utilizando a hipótese de indução, temos que

$$\mathbb{P}\left(\bigcup_{i=1}^{n+1}G_i\right)\leq \mathbb{P}^{\ast}(A_n)+\epsilon\sum_{i=1}^{n}2^{-i}+\mathbb{P}^{\ast}(A_{n+1})+\epsilon 2^{-(n+1)}-\mathbb{P}^{\ast}(A_n)\leq \mathbb{P}^{\ast}(A_{n+1})+\epsilon\sum_{i=1}^{n+1}2^{-i}$$

portanto, o resultado segue.

Lema 2.1.1.4

Sobre as hipóteses do Lema 2.1.1.2 com $ \mathbb{P} $ definida no Lema 2.1.1.3. Seja $ \mathcal{H}={H\subset \Omega : \mathbb{P}(H)+\mathbb{P}(H^c)\leq 1} $ então $ \mathcal{H} $ é uma $ \sigma $-álgebra e $ \mathbb{P} $ é uma probabilidade em $ \mathcal{H} $.

Teorema 2.1.2 (Teorema de Extensão de Carathéodory)

Seja $ \mathbb{P} $ uma medida probabilidade definida em uma álgebra $ \mathcal{F}_0 $ de subconjuntos de $ \Omega $. Então $ \mathbb{P} $ tem uma única extensão para a menor $ \sigma $-álgebra ($ \mathcal{F} $) gerada por $ \mathcal{F}_0 $.

Demonstração

Como $ \mathbb{P} $ é uma medida finita, segue imediatamente dos lemas anteriores que $ \mathbb{P} $ pode ser estendido para $ \sigma(\mathcal{F}_0) $.

2.2 - Variável aleatória discreta

Definição 2.2.1

Seja $ X $ uma variável aleatória (v.a.). Se o número de valores possíveis de $ X $ for enumerável (finito ou infinito), dizemos que $ X $ é uma variável aleatória discreta. Isto é, os possíveis valores de $ X $ podem ser postos em lista como $ x_1,x_2,\ldots $. No caso finito, a lista possui um valor final $ x_n $, e no caso infinito, a lista continua indefinidamente.

Exemplo 2.2.1

Suponha que, após um exame médico, pessoas sejam diagnosticadas como tendo diabetes (D) e não tendo diabetes (N). Admita que três pessoas sejam escolhidas ao acaso e classificadas de acordo com esse esquema.

O espaço amostral é dado por

$ \Omega=(DDD, DDN, DND, NDD, NND, NDN, DNN, NNN) $

Nosso interesse é saber quantas pessoas com diabetes foram encontradas, não interessando a ordem em que tenham sido selecionadas. Isto é, desejamos estudar a variável aleatória $ X $, a qual atribui a cada resultado $ \omega \in \Omega $ o número de pessoas com diabetes. Consequentemente, o conjunto dos possíveis valores de $ X $ é $ (0, 1, 2, 3) $, ou seja, $ X $ é uma variável aleatória discreta.

Definição 2.2.2

Seja $ X $ uma variável aleatória discreta. A cada possível resultado $ x_i $ associaremos um número $ p(x_i) = \mathbb{P}\left(X = x_i\right) $, denominado probabilidade de $ x_i $. Os números $ p(x_i) $, $ i = 1, 2, \ldots $ devem satisfazer as seguintes condições:

1. $ p(x_i) \geq 0 $ para todo $ i $;

2. $ \displaystyle \sum_{i=1}^\infty p(x_i)=1 $.

A função $ p $ é denominada função de probabilidade da variável aleatória $ X $.

Definição 2.2.3

A coleção de pares $ (x_i, p(x_i)) $; $ i = 1, 2, \ldots $ é algumas vezes denominada distribuição de probabilidade de $ X $. Assim, podemos falar que a distribuição de probabilidades de uma variável aleatória discreta $ X $, definida em um espaço amostral $ \Omega $, é uma tabela que associa a cada valor de $ X $ sua probabilidade.

Exemplo 2.2.2

Considere que uma moeda é lançada duas vezes. Seja $ X $ a função definida no espaço amostral que é igual ao número de caras nos dois lançamentos ($ C $ - Cara e $ K $ - Coroa).

Temos na Tabela a seguir a distribuição de probabilidade referente a variável aleatória X.

Valores de X	Pontos amostrais	Probabilidade
0	KK	1/4
1	KC, CK	1/2
2	CC	1/4

Os valores das probabilidades, na tabela acima, são obtidos da seguinte maneira:

$$\mathbb{P}\left(X=0\right) = \mathbb{P}((KK)) = \frac{1}{4}.$$

$$\mathbb{P}\left(X=1\right) = \mathbb{P}((CK)) + \mathbb{P}((KC)) = \frac{1}{2}.$$

$$\mathbb{P}\left(X=2\right) = \mathbb{P}((CC)) = \frac{1}{4}.$$

Definição 2.2.4

O quantil $ q100(porcentagem)% $ ($ 0 \leq q \leq 1 $) de uma variável aleatória discreta $ X $ é o menor valor de $ x $ para o qual

$$F(x)=\mathbb{P}(X\leq x)\geq q.$$

Já o percentil $ p100(porcentagem)% $ de um valor $ x $ é o valor da distribuição acumulada em $ x $, ou seja,

$$p=F(x)=\mathbb{P}(X\leq x).$$

Relação entre a função de distribuição acumulada e a distribuição de probabilidade discreta

Seja $ X $ uma variável aleatória discreta cuja distribuição de probabilidade associa aos valores $ x_1,x_2,\ldots $ as respectivas probabilidades $ \mathbb{P}(X=x_1),\mathbb{P}(X=x_2),\ldots $.

Como os valores de $ X $ são mutuamente exclusivos, temos que a função de distribuição acumulada é dada por

$$F(x)=\sum_{i\in A_x}\mathbb{P}(X=x_i), \ \text{com} \ A_x=(i: x_i\leq x).$$

Assim, dada a distribuição de probabilidade de uma variável aleatória discreta, conseguimos determinar sua função de distribuição acumulada, ou ainda, dada a função de distribuição acumulada, podemos determinar a sua distribuição de probabilidade.

Exemplo 2.2.3

Considere dois lançamentos independentes de uma moeda equilibrada. Com o espaço de probabilidade usual, defina $ X $ como sendo o número de caras nos dois lançamentos. Determine a função de distribuição acumulada de $ X $.

A variável $ X $ é discreta e sua distribuição de probabilidade será dada por

$ x_i $	$ 0 $	$ 1 $	$ 2 $
$ P(X = x_i) $	$ \frac{1}{4} $	$ \frac{1}{2} $	$ \frac{1}{4} $

A função de distribuição acumulada correspondente será:

2.3 - Variável aleatória contínua

Definição 2.3.1

Seja $ X $ uma variável aleatória. Suponha que o contradomínio ($ \mathbb{R}_x $) de $ X $ seja um intervalo ou uma coleção de intervalos. Então diremos que $ X $ é uma variável aleatória contínua.

Os exemplos abaixo ajudam a ilustrar esse conceito.

Exemplo 2.3.1

Uma válvula eletrônica é instalada em um circuito, seja $ X $ o período de tempo em a válvula funciona.

Neste caso, $ X $ é uma variável aleatória contínua podendo tomar valores nos reais positivos, ou seja, o subconjunto dos números reais $ [0,\infty) $.

Exemplo 2.3.2

Um navio petroleiro sofre um acidente no qual seu casco é rompido e o óleo é derramado. Seja $ Y $ a variável aleatória que determina a área atingida pelo óleo do navio.

Neste caso, temos que a variável $ Y $ é uma variável continua a qual também assume valores em no subconjunto dos números reais $ [0,\infty) $.

Definição 2.3.2

Dizemos que $ X $ é uma variável aleatória absolutamente contínua se existe uma função $ f_X:\mathbb{R}\rightarrow[0,+\infty) $ denominada função densidade de probabilidade e abreviada por f.d.p, que satisfaz às seguintes propriedades:

1. $ f(x)\geq 0 $, para todo $ x \in\mathbb{R}_x $

2. $ \displaystyle\int_{-\infty}^\infty f(x)dx=1 $

Além disso, definimos para qualquer $ c, d \in \mathbb{R}_x $, com $ c \ < \ d $ que

$$\mathbb{P}(c \ < \ X \ < \ d)=\int_c^d f(x)dx.$$

Vale a pena notar que, da forma como a probabilidade foi definida, a probabilidade de um ponto isolado é sempre zero, ou seja, $ \mathbb{P}(X=c)=\displaystyle \int_{c}^{c} f(x)dx=0 $. Desta forma, podemos concluir que, quando $ X $ é uma variável aleatória contínua, a probabilidade de ocorrer um valor especifico é zero.

Observação

Se $ X $ é uma variável aleatória absolutamente contínua, então

$$\frac{\partial }{\partial x}F_X(x)=f_X(x)$$

Exemplo 2.3.3

Suponha que escolhamos um número ao acaso no intervalo $ [0,1] $. Qual a probabilidade de escolhermos o número $ 0,54 $?

É zero justamente pelo que foi dito acima, todo ponto isolado em uma variável continua tem probabilidade zero.

Exemplo 2.3.4

Seja $ A={(x: -1 \ < \ x \ < \ 5)} $ e seja $ X $ uma variável aleatória tal que sua função densidade de probabilidade seja $ f(x) $ definida abaixo, com $ c $ sendo uma constante. Qual deve ser o valor da constante $ c $?

Como $ f $ é uma função densidade de probabilidade ela deve satisfazer a condição que

$$\int_{- \infty}^{\infty}f(x)dx=1 \Rightarrow \int_{-1}^{5}c dx = c \cdot (5-(-1))=6c=1 \Rightarrow c=\frac{1}{6}.$$

Exemplo 2.3.5

Consideremos uma variável aleatória $ X $ com densidade abaixo:

Determine o valor de c.

Para isto basta integrarmos a função f(x) em todo o seu domínio, lembrando que esta integral deve ter valor 1. Assim

$$\int_{-\infty}^{\infty} f(x)=1 \Rightarrow \int_{0}^{1}c[x^2 + x]=c \int_{0}^{1}x^2+x=c\left[\frac{x^3}{3}+\frac{x^2}{2} \right]^{1}_{0}=c\left(\frac{1}{3}+\frac{1}{2} \right)=\frac{5c}{6}=1 \Rightarrow c=\frac{6}{5}.$$

Exemplo 2.3.6

Seja $ X $ uma variável contínua com f.d.p.

Portanto, a função de distribuição acumulada é dada por

Exemplo 2.3.7

Suponha que o Lucro Líquido ($ LL $) de uma empresa para o ano futuro esteja entre $ a = 12.000 $ e $ b = 20.000 $. Além disso, temos informações suficientes para supor que o $ LL $ esteja concentrado em torno do valor médio do intervalo, isto é, em torno de $ (a+b)/2 = 16.000. $ Com isso, podemos modelar a distribuição de $ LL $ via uma forma triangular, como na Figura a seguir.

Observe que a função de distribuição de probabilidade é construída de forma que a área total abaixo da curva é igual a 1, note também que ela está concentrada em torno do ponto médio do intervalo (16.000) e se distribui linearmente do ponto médio aos extremos do intervalo. De forma geral, a função distribuição de probabilidade de uma distribuição triangular é dada por:

Exemplo 2.3.8

Seja $ X:\Omega\rightarrow \mathbb{R} $ uma variável aleatória absolutamente contínua com função distribuição de probabilidade (f.d.p.) dada por

$$f_X(x)=\frac{1}{\sqrt{2~\pi}}~e^{\frac{-x^2}{2}}, \ \infty \ < \ x \ < \ \infty.$$

Neste caso, dizemos que $ X $ tem distribuição Normal.

Resolução

Para que $ f_X $ seja uma f.d.p, basta mostrarmos que

$$\int^{\infty}_{-\infty}f_X(s)ds=1.$$

Então, tomamos

e, a partir da mudança de variáveis $ x = r\cos\theta $ e $ y = r\text{sen}\theta $, temos que

Exemplo 2.3.9

Seja X uma variável aleatória com densidade

(a) Determine o valor da constante c.

$$1=\int_{-\infty}^\infty f(x)dx=\int_{-1}^1 cx^2dx=c\frac{x^3}{3}\bigg|_{-1}^1= c\frac{2}{3}\Rightarrow c=\frac{3}{2}$$

(b) Ache o valor $ \alpha $ tal que $ F_X(\alpha)=\frac{1}{4} $.($ \alpha $ é o primeiro quartil da distribuição de X.)

$$\frac{1}{4}=F_X(\alpha)=\int_{-\infty}^\alpha f(x)dx=\int_{-1}^\alpha \frac{3}{2}x^2 dx=\frac{x^3}{2}\bigg|_{-1}^\alpha=\frac{\alpha^3}{2}+\frac{1}{2}\Rightarrow \frac{\alpha^3}{2}=-\frac{1}{4}\Rightarrow \alpha=-\frac{1}{\sqrt[3]{2}}.$$

Exemplo 2.3.10

Uma variável aleatória X tem função de distribuição

Qual é a densidade de X?

$$f(x)=\frac{dF(x)}{dx}$$

quando F for diferenciável em $ x $ então

Exemplo 2.3.11

Seja X uma variável aleatória com densidade

Seja $ Y=\max (X,c) $, no qual $ c $ é uma constante $ c > 0 $.

(a) Ache a função de distribuição de Y.

Vamos dividir em três etapas primeiramente

(a1) $ y< c $ isso implica que $ \mathbb{P}(Y\leq y)=0 $

(a2) $ y=c $ o que implica que

$$\mathbb{P}(Y\leq y)=\mathbb{P}(X\leq c)=\int_0^c \frac{1}{(1+x)^2}dx=-\frac{1}{1+x}\bigg|_0^c=1-\frac{1}{1+c}=\frac{c}{1+c}$$

(a3) $ y> 0 $ o que implica que

$$\mathbb{P}(Y\leq y)=\mathbb{P}(Y< y)=\int_0^y \frac{1}{(1+x)^2}dx=-\frac{1}{1+x}\bigg|_0^y=\frac{y}{1+y}$$

Assim,

(b) Decomponha $ F_Y $ em suas partes discreta, absolutamente contínua e singular.

(b1) Parte discreta $ F_{Y_d} $, temos que

(b2) $ F_{Y_{ab}} $ tal que

$$F_{Y_{ab}}=\int_{-\infty}^y f_Y(x) dx,$$

então $ F_{Y_s}(y)=0, \forall y\in \mathbb{R} $.

Exemplo 2.3.12

Determine a densidade de $ Y=(b-a)X+a $, no qual $ X\sim U[0,1] $. É a densidade da distribuição uniforme em $ [a,b] $, e escrevemos $ Y\sim U[a,b] $. Faça o gráfico da função de distribuição de Y.

Agora

Exemplo 2.3.13

Se X tem densidade $ f(x)= \frac{e^{-|x|}}{2} $, $ -\infty< x< \infty $, qual a distribuição de $ Y=|X| $?

$$\mathbb{P}(Y\leq y)=\mathbb{P}(|X|< y)=\mathbb{P}(-y\leq X \leq y)=\int_{-y}^y \frac{e^{-|x|}}{2}dx=\int_0^y e^{-x}dx=-e^{-x}\bigg|_0^y=1-e^{-y}$$

Então temos que $ Y\sim Exp(1) $.

2.4 - Vetores Aleatórios

Nesta seção, vamos introduzir o conceito de vetor aleatório e estudar suas principais características. Por facilidade de notação, vamos considerar apenas vetores bidimensionais. Assim, dizemos que o par ordenado $ (X,Y) $ é um vetor aleatório se seus componentes $ X $ e $ Y $ são variáveis aleatórias.

Exemplo 2.4.1

Considere o experimento de selecionar um ponto ao acaso no quadrado unitário

$$\mathcal{R}=(0 \ < \ x \ < \ 1 \ \text{e} \ 0 \ < \ y \ < \ 1).$$

Denotamos por $ X $ e $ Y $ a primeira e a segunda coordenada do ponto selecionado, respectivamente. Com isso, temos um vetor $ (X,Y) $ que corresponde ao ponto selecionado.

Neste contexto, definimos para duas variáveis aleatórias $ X $ e $ Y $ a função de distribuição acumulada conjunta da seguinte forma:

Definição 2.4.1

a) Um vetor $ Z=(X,Y) $ cujos componentes $ X $ e $ Y $ são variáveis aleatórias é denominado vetor aleatório.

b) A função de distribuição acumulada de $ Z $ é definida como sendo uma função $ F_Z=F_{X,Y}: \mathbb{R}^2 \rightarrow [0,1] $ tal que

$$F_{X,Y}(x,y) = \mathbb{P}\left((X \leq x) \cap (Y \leq y)\right) = \mathbb{P}\left(X \leq x , Y \leq y\right); \ \forall(x,y) \ \in \mathbb{R}^2.$$

A distribuição acumulada de $ X $ pode ser obtida a partir da distribuição acumulada de $ Z $ da seguinte forma:

$$F_{X}(a) = \mathbb{P}(X \leq a)=\mathbb{P}(X \leq a, Y < \infty) = \mathbb{P}(\lim_{b\to \infty}(X\leq a,Y \leq b))=\lim_{b\to \infty}\mathbb{P}(X \leq a, Y \leq b)$$

de onde concluímos que

$$F_X(a) = \lim_{b \to \infty}F(a,b).$$

Analogamente, podemos obter a distribuição marginal de $ Y $.

Propriedades da função de distribuição acumulada

P1. A função de distribuição acumulada $ F_Z $ é não decrescente em cada variável, isto é, se $ x_1 \leq x_2 $, então

$$F_Z(x_1,y) \leq F_Z(x_2,y) \ \forall \ y \in \mathbb{R}$$

P2. $ F_Z $ é contínua à direita e tem limite à esquerda em cada variável, isto é, se $ x_n \downarrow x $ então

$$F_X(x_n,y) \downarrow F_X(x,y) \ \forall \ y \in \mathbb{R}.$$

P3. Temos que

$$\lim_{x \rightarrow -\infty}F_Z(x,y)=0.$$

Dado uma função $ g:\mathbb{R}^2\rightarrow \mathbb{R} $ uma função qualquer, o operador diferença é definido por

$$\Delta_{a_1,b_1} g(x,y)=g(b_1,y)-g(a_1,y) \quad \text{e} \quad \Delta_{a_2,b_2} g(x,y)=g(x,b_2)-g(x,a_2),$$

no qual $ -\infty < a_i< b_i< \infty $ para $ i=1,2 $. Assim, temos que

$$\Delta_{a_1,b_1}\Delta_{a_2,b_2}g(x,y)=\Delta_{a_1,b_1}\left[g(x,b_2)-g(x,a_1)\right]=g(b_1,b_2)-g(a_1,b_2)-g(b_2,a_1)+g(a_1,a_2).$$

Com isso, temos a seguinte propriedade.

P4. Temos que $ \Delta_{a_1,b_1}\Delta_{a_2,b_2}F(x,y) \geq 1. $

Essa quarta propriedade é de fundamental importância, pois sem ela podemos encontrar uma função que satisfaz P1,P2 e P3 porém apresenta probabilidade negativa como podemos ver no exemplo abaixo. Esta propriedade vale para cada componente do vetor.

Exemplo 2.4.2

A região em vermelho representa $ F(x,y)=0 $. Note que F satisfaz as três propriedades, porém não é uma função de distribuição, pois

$$0\leq \mathbb{P}[0< X\leq 1,0< Y \leq 1]=\mathbb{P}[X\leq 1, 0< Y\leq 1]-\mathbb{P}[X\leq 0,0< Y\leq 1]=$$

$$\mathbb{P}[X\leq 1, Y\leq 1]-\mathbb{P}[X\leq 1, Y\leq 0]-\mathbb{P}(X\leq 0,Y\leq 1)+\mathbb{P}[X\leq 0,Y\leq 0]=$$

$$F(1,1)-F(1,0)-F(0,1)+F(0,0)=1-1-1+0=-1$$

o que é um absurdo.

Teorema 2.4.1

Dado uma função $ F $ satisfazendo as propriedades P1, P2, P3 e P4, então existe um vetor aleatório $ (X_1,X_2) $ em $ (\mathbb{R}^2,\mathfrak{B}(\mathbb{R}^2),\mathbb{P}) $ tal que

$$\mathbb{P}(X_1\leq x_1, X_2\leq x_2)=F(x_1,x_2)$$

ou seja, P1, P2, P3 e P4 são suficientes para caracterizar uma função de distribuição

Demonstração: Esse teorema pode ser visto em sua forma geral em distribuição de probabilidade no $ \mathbb{R}^n $.

Dizemos que um vetor aleatório $ Z=(X,Y) $ é discreto se as variáveis aleatórias $ X $ e $ Y $ são discretas.

Definição 2.4.2

Se $ Z=(X,Y) $ é um vetor aleatório discreto, definimos a função de probabilidade conjunta de X e Y por

$$p(x,y)=\mathbb{P}(X=x,Y=y).$$

A função de probabilidade marginal de $ X $ pode ser obtida de $ p(x,y) $ por

$$p_X(x)=\mathbb{P}(X=x)=\sum_{y} p(x,y).$$

E, similarmente, a função de probabilidade marginal de $ Y $ pode ser obtida de $ p(x,y) $ por

$$p_Y(y)=\mathbb{P}(Y=y)=\sum_{x} p(x,y).$$

Exemplo 2.4.3

Considere uma urna contendo $ 3 $ bolas vermelhas, $ 4 $ brancas e $ 5 $ azuis de onde são selecionadas $ 3 $ bolas ao acaso e sem reposição. Se $ X $ e $ Y $ denotam, respectivamente, o número de bolas vermelhas e brancas escolhidas, então a função de probabilidade conjunta de $ X $ e $ Y $, $ p(i,j) = \mathbb{P}(X=i,Y=j) $, é dada por

Estas probabilidades podem ser expressas em forma de tabela, como mostrado abaixo. Observe que a função de probabilidade de $ X $ é obtida ao calcularmos as somas das linhas, enquanto que a função de probabilidade de $ Y $ é obtida ao calcularmos as somas das colunas. Como as funções de probabilidades individuais de $ X $ e $ Y $ aparecem na margem da tabela, são chamadas de funções de probabilidades marginais de $ X $ e $ Y $ respectivamente.

i\j	0	1	2	3	$ \mathbb{P}(X=i) $
0	$ \frac{10}{220} $	$ \frac{40}{220} $	$ \frac{30}{220} $	$ \frac{4}{220} $	$ \frac{84}{220} $
1	$ \frac{30}{220} $	$ \frac{60}{220} $	$ \frac{18}{220} $	0	$ \frac{108}{220} $
2	$ \frac{15}{220} $	$ \frac{12}{220} $	0	0	$ \frac{27}{220} $
3	$ \frac{1}{220} $	0	0	0	$ \frac{1}{220} $
$ \mathbb{P}(Y=j) $	$ \frac{56}{220} $	$ \frac{112}{220} $	$ \frac{48}{220} $	$ \frac{4}{220} $

Definição 2.4.3

Dizemos que $ X $ e $ Y $ são conjuntamente contínuas se existe uma função $ f(x,y) $ definida para todos reais $ x $ e $ y $, tal que

$$\mathbb{P}\left((X,Y)\in (a_1 , b_1) \times (a_2 , b_2)\right)=\int_{a_2}^{b_2}\int_{a_1}^{b_1} f(x,y)dxdy.$$

para todo $ -\infty \ < \ a_i \ < \ b_i \ < \ \infty $ com $ i=1,2 $. A função $ f(x,y) $ é denominada função densidade de probabilidade conjunta de $ X $ e $ Y $.

Se $ X $ e $ Y $ são conjuntamente contínuas, então elas são individualmente contínuas e suas funções densidades de probabilidade podem ser obtidas da seguinte forma

$$\mathbb{P}\left(X\in A\right)=\mathbb{P}\left(X\in A,Y\in(-\infty,\infty)\right)=\int_A\int_{-\infty}^{\infty} f(x,y) dydx=\int_A f_X(x)dx$$

em que $ f_X(x)=\displaystyle \int_{-\infty}^{\infty} f(x,y)dy $ é a função densidade de probabilidade de $ X $. Similarmente, a função densidade de probabilidade de $ Y $ é dada por

$$f_Y(y)=\int_{-\infty}^{\infty} f(x,y)dx$$

Exemplo 2.4.3

A função densidade conjunta de $ X $ e $ Y $ é dada por

Calcule (a) $ \mathbb{P}\left(X \ > \ 1, Y \ < \ 1\right) $, (b) $ \mathbb{P}\left(X \ < \ Y\right) $ e (c) $ \mathbb{P}\left(X \ < \ a\right) $.

(a) Temos que

$$\mathbb{P}\left(X \ > \ 1, Y \ < \ 1\right)=\int_0^1\int_1^{\infty} 2e^{-x}e^{-2y}dxdy = e^{-1}(1-e^{-2}).$$

(b) Temos que

$$\mathbb{P}\left(X \ < \ Y\right)=\int\int_{{(x,y):x \ < \ y}}2e^{-x}e^{-2y}dxdy=\int_{0}^{\infty}\int_0^y 2e^{-x}e^{-2y}dxdy=\int_0^\infty 2e^{-3y}(e^y-1)dy=\frac{1}{3}.$$

(c) Temos que

$$\mathbb{P}\left(X \ < \ a\right)=\int_0^a\int_0^{\infty}2e^{-2y}e^{-x}dydx=1-e^{-a}.$$

Exemplo 2.4.4

Seja $ A((x,y)\in \mathbb{R}^2 | 1\leq x \leq 3; 1\leq y \leq 5) $. Consideremos o vetor aleatório $ (X,Y) $ tal que sua função densidade de probabilidade é definida abaixo.

Determine o valor de $ c $ e encontre as distribuições marginais de $ X $ e $ Y $.

Como a função densidade de probabilidade integrada em todo seu domínio deve ter valor igual a 1, temos que

Agora para encontrar a fdp marginal de $ X $, basta integramos a densidade conjunta em todo seu domínio de $ Y $, ou seja,

$$f_X(x)= \displaystyle \int_{-\infty}^{\infty}f(x,y)dy = \int_{1}^{5}\frac{1}{8} = \frac{4}{8}=\frac{1}{2}.$$

Assim a distribuição marginal de $ X $ é

Calculemos agora a marginal de Y

$$f_Y(y)= \int_{-\infty}^{\infty}f(x,y)dx = \int_{1}^{3}\frac{1}{8} = \frac{2}{8}=\frac{1}{4}.$$

Portanto a marginal de Y é dada por

Exemplo 2.4.5

Suponha que uma urna contenha $ 6 $ bolas enumeradas $ 1,2,3,4,5 $ e $ 6 $. Duas bolas são retiradas ao acaso e sem reposição. Seja $ X $ o número da primeira bola e $ Y $ o da segunda bola. Qual a distribuição conjunta de $ X $ e $ Y $?

Note que, como as bolas são retiradas sem reposição, então não existe a possibilidade de retirarmos bolas iguais, ou seja, com a mesma numeração em ambas as retiradas, portanto $ \mathbb{P}(X=i,Y=i)=0 $. Além disso, como as bolas são retiradas ao acaso temos que não existe preferência por nenhuma das bolas. Assim $ \mathbb{P}(X=i,Y=j) $ para $ i\neq j $ é dada por

$$\mathbb{P}(X=i,Y=j)=\mathbb{P}(Y = j|X=i)\mathbb{P}(X=i) = \frac{1}{5}\cdot \frac{1}{6}=\frac{1}{30}.$$

Exemplo 2.4.6

(a) Demonstre que a função

não é função de distribuição de um vetor aleatório.

Seja $ I_X=(0,1] $ e $ I_Y=(0,1] $ então

$$F(x,y)=F(1,1)-F(1,0)-F(0,1)+F(0,0)=1-e^{-2}-1+e^{-1}+0=2e^{-1}-e^{-2}-1=-0,3995 $$

Portanto $ F $ não é função de distribuição pois não vale.

$ F(x,y)\geq 0 $, todo $ I_X $ e $ I_Y $ intervalo de números reais.

(b) Mostre que a seguinte função é função de distribuição de algum $ (X,Y) $

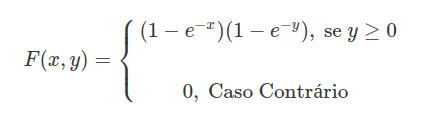
Seja $ \bar{X}\sim Exp(1) $ e $ \bar{Y}\sim Exp(1) $ e $ \bar{X} $ independentes $ \bar{Y} $ então

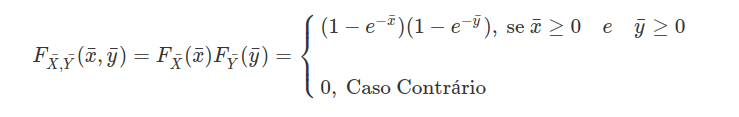
Assim $ F_{\bar{X},\bar{Y}}(x,y)=F(x,y) $, $ \forall x,\forall y \in \mathbb{R} $. Então $ (X,Y) $ é função de algum particular $ (X,Y) $ pois é função de cada $ (\bar{x},\bar{y}) $

Exemplo 2.4.7

Uma urna contém três bolas numeradas 1,2 e 3. Duas bolas são tiradas sucessivamente da urna, ao acaso e sem reposição. Seja $ X $ o número da primeira bola tirada e Y o número da segunda.

(a) Descreva a distribuição conjunta de X e Y.

Todas os resultados possíveis do experimento são equiprováveis, então a função de probabilidade é dada por

$$\mathbb{P}(X=1,Y=1)=\mathbb{P}(1,1)=0$$

$$\mathbb{P}(1,2)=\frac{1}{6}$$

$$\mathbb{P}(1,3)=\frac{1}{6}$$

$$\mathbb{P}(2,1)=\frac{1}{6}$$

$$\mathbb{P}(2,2)=0$$

$$\mathbb{P}(2,3)=\frac{1}{6}$$

$$\mathbb{P}(3,1)=\frac{1}{6}$$

$$\mathbb{P}(3,2)=\frac{1}{6}$$

$$\mathbb{P}(3,3)=0$$

(b) Calcule $ \mathbb{P}(X< Y). $

Pelas probabilidades acima temos que

$$\mathbb{P}(X< Y)=\mathbb{P}(1,2)+\mathbb{P}(1,3)+\mathbb{P}(2,3)=3\frac{1}{6}=\frac{1}{2}=\mathbb{P}(X> Y).$$

Exemplo 2.4.8

Dizemos que a distribuição conjunta de $ X_1,\dots, X_n $ é invariante para permutação se toda permutação das $ X_i $ tem a mesma distribuição, i.e., se

$$X_{\pi_1},X_{\pi_2},\dots, X_{\pi_n}\sim (X_1,\dots, X_n)$$

para toda permutação $ (\pi_1,\dots, \pi_n) $ do vetor $ (1,\dots,n) $.

(a) Mostre que se $ (X,Y)\sim (Y,X) $ e X e Y possuem densidade conjunta $ f(x,y) $, então

$$\mathbb{P}(X< Y)=\mathbb{P}(X> Y)=1/2$$

com $ \mathbb{P}(X=Y)=0 $.

Temos que

$$\mathbb{P}(X< Y)=\int_{-\infty}^\infty \int_x^\infty f_{XY}(x,y)dxdy$$

trocando as varáveis $ x^\prime=y $ e $ y^\prime=x $ e

$$\int_{-\infty}^\infty \int_{y^\prime}^\infty f_{X,Y}(y^\prime, x^\prime)dx^\prime dy^\prime=\int_{-\infty}^\infty \int_{y^\prime}^\infty f(y^\prime, x^\prime)dxdy=\int_{-\infty}^\infty \int_{y^\prime}^\infty f(x^\prime,y^\prime)dxdy=\mathbb{P}(Y< X)$$

Agora $ \mathbb{P}(X=Y)=0 $, pois F é absolutamente contínua e $ \lambda^2(B)=0 $ no qual

$$B=({(x,y): x=y})$$

então

$$\mathbb{P}(\Omega)=\mathbb{P}\left([X> Y]\bigcup [Y> X]\bigcup [X=Y]\right)$$

o implica que

$$1=\mathbb{P}(X> Y)+\mathbb{P}(Y> X)+\mathbb{P}(X=Y)=2\mathbb{P}(X> Y)$$

então, obtemos que

$$\mathbb{P}(X> Y)=\mathbb{P}(X< Y)=\frac{1}{2}$$

(b) Generalize o item (a), provando que se a distribuição conjunta de $ X_1,\dots, X_n $ é invariante para permutações e $ X_1, \dots, X_n $ possuem densidade conjunta $ f(x_1,\dots,x_n) $, então

$$\mathbb{P}(X_1< X_2< \dots < X_n)=\mathbb{P}(X_{\pi_1}< X_{\pi_2}< \dots < X_{\pi_n})=\frac{1}{n!}$$

e $ \mathbb{P}(X_i=X_j\text{ para algum par } (i,j)\text{ tal que }i\neq j)=0 $.

$$\mathbb{P}(X_1< X_2< \dots < X_n)=\int_{-\infty}^{\infty}\int_{-\infty}^{x_n}\int_{-\infty}^{x_{n-1}}\dots\int_{-\infty}^{x_2}f(x_1,x_2,\dots, x_n)dx_1dx_2\dots dx_n$$

Fazendo uma troca de variáveis $ X_1=X_{\pi_1} $$ \dots $$ X_n=X_{\pi_n} $ temos que

$$\int_{-\infty}^{\infty}\int_{-\infty}^{x_n}\int_{-\infty}^{x_{n-1}}\dots\int_{-\infty}^{x_2}f(x_1,x_2,\dots, x_n)dx_1dx_2\dots dx_n$$

$$=\int_{-\infty}^{\infty}\int_{-\infty}^{x_{\pi_n}}\int_{-\infty}^{x_{\pi_{n-1}}}\dots\int_{-\infty}^{\pi_2}f(x_{\pi_1},x_{\pi_2},\dots, x_{\pi_n})dx_{\pi_1}dx_{\pi_2}\dots dx_{\pi_n}$$

$$=\int_{-\infty}^{\infty}\int_{-\infty}^{x_{\pi_n}}\int_{-\infty}^{x_{\pi_{n-1}}}\dots\int_{-\infty}^{\pi_2}f(x_1,x_2,\dots, x_n)dx_1dx_2\dots dx_n$$

Agora sendo $ B={(X_i=X_j : \text{ para algum } (i,j) \text{ tal que } i\neq j)}\subset\mathbb{R}^n $ e $ \lambda^n(B)=0 $. Assim como

$ F_{X_1,X_2, \dots X_n} $ é absolutamente contínua o que implica que $ \mathbb{P}(B)=0 $. Agora

$$\Omega=\left(\bigcup_{\pi_1,\pi_2,\dots, \pi_n} [X_{\pi_1}< X_{\pi_2}< \dots < X_{\pi_n}]\right)\bigcup B$$

com $ {\pi_1,\pi_2,\dots, \pi_n} $ sendo permutações de $ (X_1,X_2,\dots, X_n) $ então

$$1=n!\mathbb{P}(X_1< X_2< \dots < X_n)$$

o que implica que

$$\mathbb{P}(X_1< X_2< \dots < X_n)=\frac{1}{n!}.$$

Exemplo 2.4.9

Dizemos que a distribuição conjunta de $ X_1,\dots, X_n $ é invariante para permutação se toda permutação das $ X_i $ tem a mesma distribuição, i.e., se

$$X_{\pi_1},X_{\pi_2},\dots, X_{\pi_n}\sim (X_1,\dots, X_n)$$

para toda permutação $ (\pi_1,\dots, \pi_n) $ do vetor $ (1,\dots,n) $.

(a) Mostre que se $ (X,Y)\sim (Y,X) $ e X e Y possuem densidade conjunta $ f(x,y) $, então

$$\mathbb{P}(X< Y)=\mathbb{P}(X> Y)=1/2$$

com $ \mathbb{P}(X=Y)=0 $.

Temos que

$$\mathbb{P}(X< Y)=\int_{-\infty}^\infty \int_x^\infty f_{XY}(x,y)dxdy$$

trocando as varáveis $ x^\prime=y $ e $ y^\prime=x $ e

$$\int_{-\infty}^\infty \int_{y^\prime}^\infty f_{X,Y}(y^\prime, x^\prime)dx^\prime dy^\prime=\int_{-\infty}^\infty \int_{y^\prime}^\infty f(y^\prime, x^\prime)dxdy=\int_{-\infty}^\infty \int_{y^\prime}^\infty f(x^\prime,y^\prime)dxdy=\mathbb{P}(Y< X)$$

Agora $ \mathbb{P}(X=Y)=0 $, pois F é absolutamente contínua e $ \lambda^2(B)=0 $ no qual

$$B=({(x,y): x=y}) $$

então

$$\mathbb{P}(\Omega)=\mathbb{P}\left([X> Y]\bigcup [Y> X]\bigcup [X=Y]\right)$$

o implica que

$$1=\mathbb{P}(X> Y)+\mathbb{P}(Y> X)+\mathbb{P}(X=Y)=2\mathbb{P}(X> Y)$$

então, obtemos que

$$\mathbb{P}(X> Y)=\mathbb{P}(X< Y)=\frac{1}{2}$$

(b) Generalize o item (a), provando que se a distribuição conjunta de $ X_1,\dots, X_n $ é invariante para permutações e $ X_1, \dots, X_n $ possuem densidade conjunta $ f(x_1,\dots,x_n) $, então

$$\mathbb{P}(X_1< X_2< \dots < X_n)=\mathbb{P}(X_{\pi_1}< X_{\pi_2}< \dots < X_{\pi_n})=\frac{1}{n!}$$

e $ \mathbb{P}(X_i=X_j\text{ para algum par } (i,j)\text{ tal que }i\neq j)=0 $.

$$\mathbb{P}(X_1< X_2< \dots < X_n)=\int_{-\infty}^{\infty}\int_{-\infty}^{x_n}\int_{-\infty}^{x_{n-1}}\dots\int_{-\infty}^{x_2}f(x_1,x_2,\dots, x_n)dx_1dx_2\dots dx_n$$

Fazendo uma troca de variáveis $ X_1=X_{\pi_1} $$ \dots $$ X_n=X_{\pi_n} $ temos que

$$\int_{-\infty}^{\infty}\int_{-\infty}^{x_n}\int_{-\infty}^{x_{n-1}}\dots\int_{-\infty}^{x_2}f(x_1,x_2,\dots, x_n)dx_1dx_2\dots dx_n$$

$$=\int_{-\infty}^{\infty}\int_{-\infty}^{x_{\pi_n}}\int_{-\infty}^{x_{\pi_{n-1}}}\dots\int_{-\infty}^{\pi_2}f(x_{\pi_1},x_{\pi_2},\dots, x_{\pi_n})dx_{\pi_1}dx_{\pi_2}\dots dx_{\pi_n}$$

$$=\int_{-\infty}^{\infty}\int_{-\infty}^{x_{\pi_n}}\int_{-\infty}^{x_{\pi_{n-1}}}\dots\int_{-\infty}^{\pi_2}f(x_1,x_2,\dots, x_n)dx_1dx_2\dots dx_n$$

Agora sendo $ B={(X_i=X_j : \text{ para algum } (i,j) \text{ tal que } i\neq j)}\subset\mathbb{R}^n $ e $ \lambda^n(B)=0 $. Assim como $ F_{X_1,X_2, \dots X_n} $ é absolutamente contínua o que implica que $ \mathbb{P}(B)=0 $. Agora

$$\Omega=\left(\bigcup_{\pi_1,\pi_2,\dots, \pi_n} [X_{\pi_1}< X_{\pi_2}< \dots < X_{\pi_n}]\right)\bigcup B$$

com $ {\pi_1,\pi_2,\dots, \pi_n} $ sendo permutações de $ (X_1,X_2,\dots, X_n) $ então

$$1=n!\mathbb{P}(X_1< X_2< \dots < X_n)$$

o que implica que

$$\mathbb{P}(X_1< X_2< \dots < X_n)=\frac{1}{n!}.$$

Exemplo 2.4.10

Seleciona-se, ao acaso, um ponto do circulo unitário $({(x,y):x^2+y^2\leq 1}).$ Sejam X e Y as coordenadas do ponto selecionado.

(a) Qual a densidade conjunta de X e Y?

$ (X,Y) $ é uniforme no circulo unitário, então $ A={(x,y):x^2+y^2=1} $. A área $ A=\pi $, então

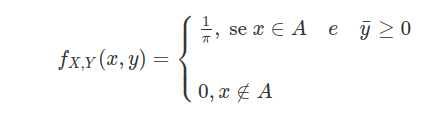
(b) Determine $ \mathbb{P}(X< Y), \mathbb{P}(X> Y) $

Agora pelo item (a) $ (X,Y)\sim (Y,X) $ então explicando o exercício 19(a)

$$\mathbb{P}(X< Y)=\mathbb{P}(Y< X)=\frac{1}{2}$$

e $ \mathbb{P}(X=Y)=0 $

Exemplo 2.4.11

Seleciona-se, ao acaso, um ponto do quadrado unitário $ {((x,y):0\leq x\leq 1, 0\leq y\leq 1)} $. Sejam $ X $ e $ Y $ as coordenadas do ponto selecionado.

(a) Qual a densidade conjunta de X e Y ?

$ (X,Y) $ é uniforme em $ A={(x,y): 0\leq x\leq 1, 0\leq y\leq 1} $. A area $ A=1 $ então

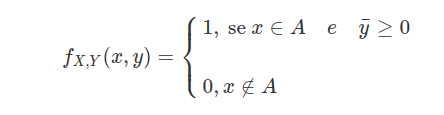
(b) Calcule $ \mathbb{P}\left(\bigg|\frac{Y}{X-1}\bigg|\leq \frac{1}{2}\right) $.

$$\mathbb{P}\left(\bigg|\frac{Y}{X-1}\bigg|\leq \frac{1}{2}\right)=\mathbb{P}\left(-\frac{1}{2}\leq \frac{Y}{X}-1\leq \frac{1}{2}\right)=\mathbb{P}\left(\frac{1}{2}\leq \frac{Y}{X}\leq \frac{3}{2}\right)$$

$$=\int_{0}^{2/3}\int_{1/2}^{3/2}1dxdy+\int_{2/3}^1 \int_{2/2}^1 1dxdy=\left[\frac{x^2}{2}\right]^{2/3}_{0}+\left[x-\frac{x^2}{4}\right]_{2/3}^1=\frac{2}{9}+\frac{3}{4}-\frac{2}{3}+\frac{1}{9}=\frac{5}{12}$$

(c) Calcule $ \mathbb{P}\left(Y\geq X|Y\geq \frac{1}{2}\right) $.

$$\mathbb{P}\left(Y\geq X|Y\geq \frac{1}{2}\right)=\int_{1/4}^{1/2}\int_{\sqrt{x}}^{2x}dydx+\int_{1/2}^1\int_{\sqrt{x}}^1 1dydx$$

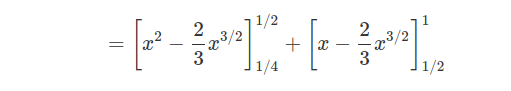
$$=\frac{1}{4}-\frac{1}{16}+\frac{2}{3}\left(\frac{1}{4}\right)^{3/2}+ \frac{1}{3}-\frac{1}{2}=10,416(porcentagem)%$$

2.4.1 - Distribuição de probabilidade no $R^n$

Os Borelianos de $R^n$

Nesta seção, vamos trabalhar com $ \mathbb{R}^n=\mathbb{R}\times\mathbb{R}\times\cdots\times\mathbb{R} $, o conjunto das n-uplas ordenadas. Nosso primeiro objetivo consiste em construir a $ \sigma $-álgebra de Borel correspondente ao $ \mathbb{R}^n $. Neste caso, o conjunto gerador da $ \sigma $-álgebra de Borel é dado pelos retângulos de $ \mathbb{R}^n $. Os intervalos aberto à esquerda e fechados à direita serão definidos na forma

$$(a,b]=\left(x \in \mathbb{R}: a < x \leq b \right),$$

para todo $ a $ e $ b $ tais que $ -\infty \leq a < b < \infty $. O intervalo $ (a ,\infty] $ é tomado como $ (a,\infty) $, esta convenção é necessária para que o complementar do intervalo $ (\infty,b] $ seja um intervalo da mesma forma (aberto à esquerda e fechado à direita).

Definição 2.4.1.1

Para $ I_k=(a_k,b_k] $ um intervalo, o conjunto $ I=I_1\times I_2\times \cdots\times I_n $ definido por,

$$(x\in \mathbb{R}^n| x_k\in I_k, k=1,\dots,n)$$

é denominado de retângulo de lados $ I_k $, com $ k=1,\cdots,n $. O conjunto de todos os retângulos I, será denotado por $ \mathcal{I} $. De forma geral, um conjunto $ A=A_1\times A_2\times \cdots\times A_n $ é denominado de retângulo (ou cilindro) de lados $ A_i $. Se $ A_i \in \mathfrak{B}(\mathbb{R}) $ dizemos que $ A $ é um retângulo (ou cilindro) de lados borelianos.

Definição 2.4.1.2

A $ \sigma $-álgebra de Borel de subconjuntos de $ \mathbb{R}^n $, denotada por $ \mathfrak{B}(\mathbb{R}^n) $, é a menor $ \sigma $-álgebra gerada por todos os retângulos de $ \mathbb{R}^n $, isto é,$ \mathfrak{B}(\mathbb{R}^n)=\sigma(\mathcal{I}) $.

Da mesma forma que os intervalos geram a $ \sigma $-álgebra de Borel na reta, os retângulos de lados representados por intervalos geram a $ \sigma $-álgebra de Borel do $ \mathbb{R}^n $. Na sequência, mostraremos que a $ \mathfrak{B}(\mathbb{R}^n) $ também pode ser definida como a menor $ \sigma $-álgebra que contém os retângulos com lados Borelianos. Considere

$$\mathcal{R}=(A=A_1\times \cdots\times A_n: A_i \in \beta(\mathbb{R})),$$

a classe dos retângulos com lados Borelianos. Denotamos por

$$ \sigma(\mathfrak{B}(\mathbb{R})\times\mathfrak{B}(\mathbb{R})\times\cdots\times \mathfrak{B}(\mathbb{R}))=\sigma(\mathcal{R}).$$

Exercício

Mostre que a classe dos retângulos $ \mathcal{I} $ e a classe dos retângulos de lados Borelianos $ \mathcal{R} $ formam uma semi-álgebra.

Teorema 2.4.1.1

Temos que, $ \mathfrak{B}(\mathbb{R}^n)=\sigma(\mathcal{I})=\sigma(\mathfrak{B}(\mathbb{R})\times\mathfrak{B}(\mathbb{R})\times\cdots\times \mathfrak{B}(\mathbb{R})) $

Demonstração

Note que o resultado é trivial se $ n=1 $. Vamos mostrar o caso $ n=2 $. Definimos por

$$\mathcal{C}=(B_1\times B_2: B_i\in \mathfrak{B}(\mathbb{R}), i=1,2),$$

a classe dos retângulos com lados Borelianos.

Sabemos que que $ \mathcal{I}\subset \mathcal{C} $, logo é imediato que

$$\mathfrak{B}(\mathbb{R}^2)=\sigma(\mathcal{I})\subset \sigma(\mathcal{C})=\mathfrak{B}(\mathbb{R})\otimes\mathfrak{B}(\mathbb{R})$$

Assim resta-nos apenas mostrar que

$$\mathfrak{B}(\mathbb{R})\otimes\mathfrak{B}(\mathbb{R})\subset\mathfrak{B}(\mathbb{R}^2)$$

Na sequência, considere $ \mathfrak{C} $ uma classe de subconjuntos de $ \mathbb{R}^2 $ e $ B\subset\mathbb{R}^2 $. Então, ao definirmos

$$\mathfrak{C}\cap B=(A\cap B:A\in\mathfrak{{C}}),$$

vamos provar que

$$\sigma(\mathfrak{C}\cap B)=\sigma(\mathfrak{C})\cap B.$$

Como $ \mathfrak{C}\subset \sigma(\mathfrak{C}) $, concluímos que

$$\mathfrak{C}\cap B\subset \sigma(\mathfrak{C})\cap B$$

Além disso, temos que $ \sigma(\mathfrak{C})\cap B $ é uma $ \sigma $-álgebra (exercício). Assim, obtemos que

$$\sigma(\mathfrak{C}\cap B)\subset \sigma(\mathfrak{C})\cap B$$

Na sequência, vamos mostrar

$$\sigma(\mathfrak{C})\cap B\subset \sigma(\mathfrak{C}\cap B) $$

Para isso, tomamos $ \mathcal{C}_B={A\in\sigma(\mathfrak{C}):A\cap B\in \sigma(\mathfrak{C}\cap B)} $. Desde que $ \sigma(\mathfrak{C}) $ e $ \sigma(\mathfrak{C}\cap B) $ são $ \sigma $-álgebras, obtemos que $ \mathcal{C}_B $ também é uma $ \sigma $-álgebra, Portanto, temos que

$$\mathfrak{C}\subset\mathcal{C}_B\subset \sigma(\mathfrak{C})$$

O que implica que $ \mathcal{C}_B= \sigma(\mathfrak{C}) $. Assim, concluímos que

$$A\cap B\in \sigma(\mathfrak{C}\cap B)$$

para todo $ A\in\mathfrak{C} $. Consequentemente $ \sigma(\mathfrak{C})\cap B\subset \sigma(\mathfrak{C}\cap B) $.

Para terminarmos a demonstração do teorema, considere os seguintes conjuntos $ \mathcal{B}\times \mathbb{R}=(B\times \mathbb{R}| B\in\mathfrak{B}(\mathbb{R})) $ e $ \mathbb{R}\times \mathcal{B}=(\mathbb{R}\times B| B\in\mathfrak{B}(\mathbb{R})) $.

Então dado $ B_1\times B_2 $, com $ B_1,B_2\in \mathfrak{B}(\mathbb{R}) $, temos que

$$B_1\times B_2=(B_1\times \mathbb{R})\cap (\mathbb{R}\times B_2) \in\sigma(I_1 \times \mathbb{R})\cap (B_2\times \mathbb{R})= \sigma((I_1 \times \mathbb{R})\cap (B_2\times \mathbb{R}))\subset\sigma ((I_1\times \mathbb{R})\cap (I_2\times\mathbb{R}))=\sigma(\mathcal{I})$$

no qual, $ I_i $ é o conjunto de todos os intervalos de $ \mathbb{R} $ correspondente a $ i $-ésima coordenada, com $ i=1,2 $.. Portanto o resultado segue.

Como a $ \sigma $-álgebra de Borel do $ \mathcal{R}^n $ é gerada pelo produto “direto” da $ \sigma $-álgebra de Borel de cada coordenada, esta também pode ser denotada por $ \mathfrak{B}(\mathbb{R})\otimes\mathfrak{B}(\mathbb{R})\otimes\cdots\otimes \mathfrak{B}(\mathbb{R})=\sigma(\mathcal{R}). $

Distribuição de probabilidade no $R^n$

Suponha $ \mathbb{P} $ uma probabilidade no espaço mensurável $ (\mathbb{R}^n,\mathfrak{B}(\mathbb{R}^n)) $. A função

$$F_n(x_1,\dots,x_n)=\mathbb{P}((-\infty,x_1]\times (-\infty,x_2]\times\dots\times(-\infty,x_n])$$

é denominada função de distribuição da probabilidade $ \mathbb{P} $. Usaremos uma notação mais compacta, a qual será denotada da seguinte forma

$$F_n(x)=\mathbb{P}((-\infty,x])$$

no qual $ x=(x_1,\dots,x_n) $ e $ (-\infty,x]=(-\infty,x_1]\times (-\infty,x_2]\times\dots\times(-\infty,x_n] $. Na sequência, introduzimos o operador diferença $ \Delta_{a_i,b_i}:\mathbb{R}^n\rightarrow \mathbb{R} $ definido por

$$\Delta_{a_i,b_i}F_n(x)=F_n(x_1,\dots,x_{i-1},b_i,x_{i+1},\dots,x_n)-F_n(x_1,\dots,x_{i-1},a_i,x_{i+1},\dots,x_n),$$

no qual $ a_i\leq b_i $ para $ i=1, \cdots , n $. Com esta notação, temos que

$$\Delta_{a_1,b_1}\dots\Delta_{a_n,b_n} F_n(x)=\mathbb{P}((a,b])$$

no qual $ (a,b]=(a_1,b_1]\times\dots\times(a_n,b_n] $. Como no exemplo 2.4.2 mostrado na seção anterior no caso multidimensional em geral $ \mathbb{P}((a,b])\neq F_n(b)-F_n(a) $, com $ a=(a_1,\dots,a_n) $ e $ b=(b_1,\dots,b_n) $. Além disso como $ \mathbb{P} $ é positiva temos que

P1

$$\Delta_{a_1,b_1}\dots\Delta_{a_n,b_n} F_n(x)\geq 0$$

Da continuidade a direita de $ \mathbb{P} $, temos que $ F_n $ também é contínua a direita, ou seja, se uma sequência $ (x^{k})_{k\in\mathbb{N}} $ e $ x^k\downarrow x $, com $ x^k=(x_1^k,\dots,x_n^k) $ então

P2

$$F_n(x^k)\downarrow F_n(x),\quad k\rightarrow \infty.$$

Além disso,

P3

$$\displaystyle\lim_{x\rightarrow \infty}F_n(x)=1$$

e

P4

$$\displaystyle \lim_{x\downarrow y}F_n(x)=0$$

se pelo menos uma coordenada de $ y $ é $ -\infty $.

Definição 2.4.1.3

Uma função de distribuição $ n $-dimensional em $ \mathbb{R}^n $ é uma função $ F=F_n(x_1,\dots,x_n) $ com as propriedades P1,P2,P3,P4.

Nosso objetivo é mostrar que se $ F $ é uma função de distribuição, então existe uma única probabilidade $ \mathbb{P} $ definida em $ (\mathbb{R}^n,\mathfrak{B}(\mathbb{R}^n)) $, tal que

$$\mathbb{P}((a,b])=\Delta_{a_1,b_1}\dots\Delta_{a_n,b_n} F_n(x).$$

Para isso, vamos construir uma probabilidade definida na álgebra gerada pelos retângulos e então, usaremos o teorema de extensão. Relembramos que $ \mathcal{I} $ denota semi-álgebra composta pelos retângulos de lados compostos por intervalos na forma $ I_k = (a_k , b_k] $, com $ k=1,\cdots,n $.

Lema 2.4.1.1

Seja $ F $ uma função de distribuição em $ \mathbb{R}^n $. Tomamos a função de conjunto $ \mathbb{P_F} $ sobre a semi-álgebra $ \mathcal{I} $ na forma

Demonstração

Note que, pela definição de $ F $, $ \mathbb{P_F} $ é não negativa em $ \mathcal{I} $ e $ \mathbb{P_F}(\emptyset)=0 $ . Agora para mostrar a aditividade finita, considere o caso n=2, consideraremos somente esse caso, por simplicidade da notação, a demonstração para o caso geral pode ser estendida naturalmente, a partir deste caso.

Assim considere

$$\displaystyle \bigcup_{m=1}^{k}I_m\in \mathcal{I}$$

onde $ I_m $ são elementos disjuntos $ \mathcal{I} $. Primeiramente vamos considerar o caso em que $ I_m $ tem lados disjuntos. Desta forma, podemos rescrever

$$\displaystyle \bigcup_{m=1}^k I_m=\bigcup_{i=1}^{K_1}\bigcup_{j=1}^{K_2} I_{i,j}$$

Onde

$$\displaystyle \bigcup_{m=1}^k I_m= (a^0,a^{K_1}]\times(b^0,b^{K_2}]$$

e

$$I_{i,j}=(a^{i-1},a^{i}]\times (b^{j-1},b^{j}].$$

no qual $ I_m $ é um dos $ I_{i,i} $.

Agora fixando $ i $, temos que

$$\displaystyle \sum_{j=1}^{K_2}\mathbb{P}(I_{i,j})=\sum_{j=1}^{K_2}(F(a^i,b^j)-F(a^i, b^{j-1})-F(a^{i-1},b^j)+F(a^{i-1},b^{j-1}))=$$

$$\displaystyle \sum_{j=1}^{K_2}(F(a^i, b^j)-F(a^i,b^{j-1}))-\sum_{j=1}^{K_2}(F(a^{i-1},b^j)-F(a^{i-1},b^{j-1}))=$$

$$\displaystyle (F(a^i,b^{K_2})-F(a^i,b^0))-(F(a^{i-1},b^{K_2})-F(a^{i-1},b^0))=$$

$$\displaystyle \Delta_{a^{i-1},a^{i}}\Delta_{b^0,b^{K_2}} F(x_1,x_2)$$

Logo, obtemos que

$$\displaystyle \sum_{i=1}^{K_1}\sum_{j=1}^{K_2}\mathbb{P_F}(I_{i,j})=\sum_{j=1}^{K_2}\Delta^1_{a^{i-1},a^{i}}\Delta^2_{b^0,b^{K_2}}F(x_1,x_2)=$$

como

$$\displaystyle \sum_{i}^{K_1}\sum_{j=1}^{K_2}\mathbb{P_F}(I_{i,j})=\displaystyle \bigcup_{m=1}^k\mathbb{P_F}(I_m)$$

$$\displaystyle \sum_{i=1}^{K_1}((F(a^i,b^{K_2})-F(a^i,b^0))-(F(a^{i-1},b^{K_2})-F(a^{i-1},b^0)))=$$

$$\sum_{i=1}^{K_1}(F(a^i,b^{K_2})-F(a^i,b^0))-\sum_{i=1}^{K_1}(F(a^{i-1},b^{K_2})-F(a^{i-1},b^0))=$$

$$F(a^{K_1},b^{K_2})-F(a^0,b^{K_2})-F(a^{K_1},b^0)-F(a^{K_1},b^0)+F(a^0,b^0)=$$

$$\Delta^1_{a^{0},a^{K_1}}\Delta^2_{b^{0},b^{K_2}}F(x_1,x_2)=$$

$$\mathbb{P_F}((a^0,b^{K_2}]\times(a^{K_1},b^{K_2}])=\mathbb{P_F}\left(\bigcup_{m=1}^{k}I_m\right)$$

Como

$$\displaystyle \sum_{i=1}^{K_1}\sum_{j=1}^{K_2}\mathbb{P_F}(I_{i,j})=\sum_{m=1}^k \mathbb{P_F}(I_m)$$

Segue que

$$\mathbb{P_F}\left(\bigcup_{m=1}^{k}I_m\right)=\displaystyle \sum_{i=1}^{K_1}\sum_{j=1}^{K_2}\mathbb{P_F}(I_{i,j})=\sum_{m=1}^k \mathbb{P_F}(I_m)$$

Agora para o caso geral, pode sempre ser reduzido ao caso onde os lados dos retângulos são disjuntos. Por exemplo se

$$I_m=(u_1^{m},u_2^{m}]\times(v_1^m,v_2^m],\quad m=1,\dots,k$$

Assim basta colocar os valores em ordem crescente os valores distintos

$$u_1^{1},u_2^{1}, u_1^2,u_2^{2},\dots,u_1^{k}, u_2^{k}\quad e \quad v_1^{1},v_2^{1}, v_1^2,v_2^{2},\dots,v_1^{k}, v_2^{k}$$

respectivamente por

$$a^0< a^{1}<\dots< a^{K_1}\quad e \quad b^{0}< b^{1}<\dots< b^{K_2}$$

Então

$$\displaystyle \bigcup_{m=1}^k I_m=\bigcup_{i=1}^{K_1}\bigcup_{j=1}^{K_2} (a^{i-1},a^{i}]\times (b^{j-1},b^{j}]$$

Pelo caso anterior temos que

$$\displaystyle \mathbb{P_F}\left(\bigcup_{m=1}^k I_m\right)=\sum_{i=1}^{K_1}\sum_{j=1}^{K_2}\mathbb{P_F}\left((a^{i-1},a^{i}]\times(b^{j-1},b^{j}]\right)$$

Note que cada $ I_m $ é união de elementos disjuntos com lados disjuntos da forma $ (a^{i-1},a^{i}]\times(b^{j-1},b^{j}] $, logo cada $ I_m $ é soma dos seus termos correspondentes $ \mathbb{P}\left((a^{i-1},a^{i}]\times(b^{j-1},b^{i}]\right) $. Assim novamente usando o caso disjunto obtemos que

$$\displaystyle \mathbb{P_F}\left(\bigcup_{m=1}^k I_m\right)=\sum_{i=1}^{K_1}\sum_{j=1}^{K_2}\mathbb{P_F}\left((a^{i-1},a^{i}]\times(b^{j-1},b^{j}]\right)=\sum_{m=1}^{k}\mathbb{P}_{F}\left(I_m\right)$$

Portanto temos que $ \mathbb{P_F} $ é finitamente aditiva em $ \mathcal{I} $

Lema 2.4.1.2

Seja $ F $ uma função de distribuição em $ \mathbb{R}^n $ e

$$\mathbb{P_F}((a,b])=\Delta_{a_1,b_1}\dots\Delta_{a_n,b_n} F_n(x)$$

.

Considere em $ \mathcal{I} $ os retângulos na forma

$$R_k=(a_1^k,b_1^k]\times \cdots\times (a_n^k,b_n^k], \quad -\infty\leq a^k_{i}\leq b_i^k\leq \infty$$

com

$$\displaystyle R\subset \bigcup_{k=1}^{\infty} R_k$$

com $ R\mathcal{I} $. Então

$$\displaystyle \mathbb{P_F}(R)\leq \sum_{k=1}^{\infty}\mathbb{P_F}(R_k)$$

Demonstração:

Primeiramente notemos que para $ h> 0 $

$$\displaystyle \mathbb{P_F}((a_1^k,b_1^k+h]\times \cdots\times (a_n^k,b_n^k+h])=\Delta^1_{a_1^k,b_1^k+h}\cdots \Delta^n_{a_n^k,b_n^k+h}F(x_1,\dots,x_n)$$

Assim, devido a continuidade a direita de F em cada coordenada, segue que

$$\displaystyle \lim_{h\rightarrow 0} \mathbb{P_F}((a_1^k,b_1^k+h]\times \cdots\times (a_n^k,b_n^k+h])=\lim_{h\rightarrow 0}\Delta^1_{a_1^k,b_1^k+h}\cdots \Delta^n_{a_n^k,b_n^k+h}F(x_1,\dots,x_n)=$$

$$\Delta^1_{a_1^k,b_1^k}\cdots \Delta^n_{a_n^k,b_n^k}F(x_1,\dots,x_n)=\mathbb{P_F}((a_1^k,b_1^k]\times \cdots\times (a_n^k,b_n^k])$$

Desta forma, dado $ \epsilon> 0 $, existe um $ h_k $, tal que

$$\displaystyle \mathbb{P_F}((a_1^k,b_1^k+h_k]\times \cdots\times (a_n^k,b_n^k+h_k])=\mathbb{P_F}((a_1^k,b_1^k]\times \cdots\times (a_n^k,b_n^k])+\frac{\epsilon}{2^k}$$

Primeiramente vamos considerar o caso em que $ R=(a_1^0,b_1^0]\times \cdots\times (a_n^0,b_n^0] $, para $ -\infty< a^k_{i}< b_i^k< \infty $. Assim para $ h> 0 $ temos

$$\displaystyle [a_1^0+h,b_1^0]\times \cdots\times [a_n^0+h,b_n^0]\subset R\subset\bigcup_{k=1}^{\infty}(a_1^k,b_1^k+h_k]\times \cdots\times (a_n^k,b_n^k+h_k]$$

Mas $ [a_1^0+h,b_1^0]\times \cdots\times [a_n^0+h,b_n^0] $ é um conjunto compacto de $ \mathbb{R}^n $ e portanto pelo teorema de Heine-Borel toda cobertura aberta admite uma subcobertura finita. Em nosso caso a nossa cobertura aberta é

$$\displaystyle \bigcup_{k=1}^{\infty}(a_1^k,b_1^k+h_k]\times \cdots\times (a_n^k,b_n^k+h_k]$$

Logo para algum $ K $ temos que

$$\displaystyle [a_1^0+h,b_1^0]\times \cdots\times [a_n^0+h,b_n^0]\subset\displaystyle \bigcup_{k=1}^{K}(a_1^k,b_1^k+h_k]\times \cdots\times (a_n^k,b_n^k+h_k]$$

Além disso, como $ \mathbb{P_F} $ é finitamente aditiva pelo Lema 2.4.1.1, temos que ela trivialmente monótona e sub-aditiva, e portanto

$$\displaystyle \mathbb{P_F}((a_1^0+h,b_1^0]\times \cdots\times (a_n^0+h,b_n^0])\leq \sum_{k=1}^{K}\mathbb{P_F}((a_1^k,b_1^k+h_k]\times \cdots\times (a_n^k,b_n^k+h_k]) $$

Pela equação acima temos que

$$\sum_{k=1}^{K}\mathbb{P_F}((a_1^k,b_1^k+h_k]\times \cdots\times (a_n^k,b_n^k+h_k])\leq \sum_{k=1}^{\infty}\left(\mathbb{P_F}((a_1^k,b_1^k]\times \cdots\times (a_n^k,b_n^k])+\frac{\epsilon}{2^k}\right)=$$

$$\sum_{k=1}^{\infty}\left(\mathbb{P_F}((a_1^k,b_1^k]\times \cdots\times (a_n^k,b_n^k])\right)+\epsilon=\sum_{k=1}^{\infty}\mathbb{P_F}(R_k)+\epsilon$$

Por outro lado temos que F é continua a direita em cada coordenada então

$$\displaystyle \lim_{h\rightarrow 0}\displaystyle \mathbb{P_F}((a_1^0+h,b_1^0]\times \cdots\times (a_n^0+h,b_n^0])=\lim_{h\rightarrow 0}\Delta^1_{a_1^0+h,b_1^0}\cdots \Delta^n_{a_n^0+h,b_n^0}F(x_1,\dots,x_n)=$$

$$\Delta^1_{a_1^k,b_1^k}\cdots \Delta^n_{a_n^0,b_n^0}F(x_1,\dots,x_n)=\mathbb{P_F}((a_1^0,b_1^0]\times \cdots\times (a_n^0,b_n^0])=\mathbb{P_F}(R)$$

Portanto

$$\displaystyle \mathbb{P_F}(R)\leq \sum_{k=1}^\infty \mathbb{P_F}(R_k)+\epsilon$$

Como $ \epsilon $ é arbitrário temos

$$\displaystyle \mathbb{P_F}(R)\leq \sum_{k=1}^\infty \mathbb{P_F}(R_k)$$

Para o caso em que $ R $ não é finito considere

$$R^N=R\cap ((-N,N]\times\cdots\times (-N,N])$$

Logico que $ R^N $ é limitado e ainda

$$\displaystyle R^N\subset R^{N+1}\subset R\subset \bigcup_{k=1}^{\infty}R_k$$

Então pelo resultado anterior temos que

$$\displaystyle \mathbb{P_F}(R^N)\leq \sum_{k=1}^{\infty}\mathbb{P}(R_k), \quad \forall N$$

Como $ F $ é monótona em cada coordenada, tomando o limite em N tendendo a infinito, o resultado segue.

Lema 2.4.1.3

$ \mathbb{P_F} $ é $ \sigma $-aditiva em $ \mathcal{I} $

Demonstração:

Seja $ \displaystyle \bigcup_{k=1}^{\infty}R_k \in \mathcal{I} $, no qual $ R_k\in\mathcal{I}^n $ e $ R_j\cap R_i=\emptyset $ se $ i\neq j $.

Pelo Lema 2.4.1.1 temos que $ \mathbb{P_F} $ é finitamente aditiva, logo monótona. Assim

$$\displaystyle \sum_{k=1}^{N}\mathbb{P}(R_k)=\mathbb{P_F}\left(\bigcup_{k=1}^{N} R_k\right)\leq \mathbb{P_F}\left(\bigcup_{k=1}^{\infty}R_k\right), \quad \forall N\in\mathbb{N}$$

Agora tomando $ N\rightarrow \infty $ temos que

$$\displaystyle \sum_{k=1}^{\infty}\mathbb{P}(R_k)\leq \mathbb{P_F}\left(\bigcup_{k=1}^{\infty}R_k\right).$$

Por outro pela lema 2.4.1.2 temos que

$$\mathbb{P_F}\left(\bigcup_{k=1}^{\infty} R_k\right)\leq \sum_{k=1}^{\infty}\mathbb{P_F}(R_k)$$

Portanto

$$\mathbb{P_F}\left(\bigcup_{k=1}^{\infty} R_k\right)= \sum_{k=1}^{\infty}\mathbb{P_F}(R_k)$$

E o resultado segue

Até esse ponto mostrarmos que $ \mathbb{P_F} $ é $ \sigma $-aditiva na semi-álgebra porém precisamos de $ \mathbb{P_F} $ seja definida na $ \sigma $-algebra e ainda seja $ \sigma $-aditiva. Na proposição a seguir mostraremos que podemos extender $ \mathbb{P_F} $ para uma álgebra de maneira única. Para enfim podermos invocar o Teorema de Caratheodory e finalmente extender nossa medida para a $ \sigma $-álgebra.

A proposição a seguir nos diz que se temos uma medida de probabilidade qualquer (a qual chamaremos de $ \lambda $), definida apenas na semi-álgebra e ainda se ela for $ \sigma $-aditiva, então existe uma única extensão desta medida de probabilidade para a álgebra, tal que essa extensão seja $ \sigma $-aditiva na algebra.

Uma extensão natural de $ \lambda: \mathcal{I}\rightarrow \mathbb{R}^n $ a qual chamaremos de $ \mu:\mathcal{A}(\mathcal{I})\rightarrow \mathbb{R}^n $, seja $ A\in\mathcal{A}(\mathcal{I}) $ então $ A $ pode ser escrito como

$$A=\displaystyle \bigcup_{i=1}^{n} I_i$$

e a extesão natural de $ \lambda $ é dada por

$$\mu(A)=\displaystyle \sum_{i=1}^{n}\lambda(I_i).$$

A proposição a seguir mostra que essa extensão é unica.

Proposição 2.4.1.1

Seja $ \lambda: \mathcal{I}\rightarrow \mathbb{R}^n $, uma função positiva e $ \sigma $-aditiva definida em uma semi-álgebra $ \mathcal{I} $. Então existe uma única extensão, $ \sigma $-aditiva, de $ \lambda $ para a álgebra $ \mathcal{A}(\mathcal{I}) $.

Demonstração:

Primeiramente considere $ \lambda $ finitamente aditiva em $ \mathcal{I} $ e seja $ A\in\mathcal{A}(\mathcal{I}) $ então $ A $ pode ser escrito como

$$A=\displaystyle \bigcup_{i=1}^{n} I_i$$

no qual os conjuntos $ I_i $ são elementos disjuntos de $ \mathcal{I} $. Então defina $ \mu: \mathcal{A}(\mathcal{I})\rightarrow [0,1] $ com $ \mu\mid_{\mathcal{I}}=\lambda $.

$$\mu(A)=\displaystyle \sum_{i=1}^{n}\lambda(I_i)$$

A função $ \mu $ está bem definida, e por definição estende $ \lambda $. Para ver que $ \mu $ está bem definida considere

$$\displaystyle \sum_{i=1}^{n}I_i=A=\bigcup_{j=1}^{m} R_j$$

para conjuntos disjuntos $ R_j\in\mathcal{I} $, então

$$\mu(A)=\displaystyle \sum_{i=1}^{n}\lambda(I_i)=\sum_{i=1}^{n}\mu(I_i)=\sum_{j=1}^{m}\mu(R_j)=\sum_{j=1}^{m}\lambda(R_j)=\mu(A)$$

De fato, considere

$$I_i\cap R_j, \quad i=1,\cdots,n, \quad j=1,\cdots,m$$

são elementos disjuntos de $ \mathcal{I} $ e

$$\displaystyle \bigcup_{j=1}^{m}(I_i\cap R_j)= I_i \quad e \quad \displaystyle \bigcup_{i=1}^{n}(I_i\cap R_j)=R_j$$

Então

$$\displaystyle \mu(A)=\sum_{i=1}^n \lambda(I_i)=\sum_{i=1}^n\lambda\left(\displaystyle \bigcup_{j=1}^{m}(I_i\cap R_j)\right)=$$

$$\displaystyle \sum_{i=1}^n \sum_{j=1}^m \lambda(I_i\cap R_j)=\sum_{j=1}^m \sum_{i=1}^n \lambda(I_i\cap R_j)=\sum_{j=1}^m\lambda\left(\displaystyle \bigcup_{i=1}^{n}(I_i\cap R_j)\right)=\sum_{j=1}^m\lambda(R_j)=\sum_{j=1}^m\mu(R_j)$$

Portanto $ \mu $ está bem definida em $ \mathcal{A}(\mathcal{I}) $. Agora vamos mostrar que $ \mu $ é finitamente aditiva. Assim, considere os conjuntos $ A,B\in \mathcal{A}(\mathcal{I}) $, com $ A\cap B=\emptyset $, como então podemos reescrever $ A $ e $ B $ da seguinte forma

$$\displaystyle A=\bigcup_{i=1}^{n}(I_i)\quad \quad e \quad \quad B=\bigcup_{i=1}^{n}R_j$$

onde $ I_i\cap I_{i^\prime}=\emptyset $ para $ i\neq i^\prime $ e $ R_j\cap R_{j^\prime}=\emptyset $ para $ j\neq j^\prime $ e $ I_i,R_j\in \mathcal{I} $. Note que como $ A\cap B=\emptyset $ então

$$I_i\cap R_j=\emptyset \quad \quad e \quad \quad A\cup B= \displaystyle\bigcup_{i=1}^{n}I_i\cup \bigcup_{j=1}^{m}R_j$$

Então pela definição de $ \mu $ temos

$$\displaystyle \mu(A\cup B)=\sum_{i=1}^{n}\mu(I_i)+\sum_{j=1}^{m}\mu(R_j)=\mu(A)+\mu(B)$$

Logo por indução temos que $ \mu $ é finitamente aditiva em $ \mathcal{A}(\mathcal{I}) $. Para mostrar a unicidade de $ \mu $ seja $ \theta:\mathcal{A}(\mathcal{I})\rightarrow [0,1] $ com $ \theta\mid_{\mathcal{I}}=\lambda $ e $ \theta $ finitamente aditiva. Então para

$$\displaystyle A\in\mathcal{A}(\mathcal{I}),\quad A=\bigcup_{i=1}^n I_i,\quad \quad I_i\cap I_j=\emptyset$$

como $ \theta $ é finitamente aditiva e $ \theta\mid_{\mathcal{I}}=\lambda=\mu\mid_{\mathcal{I}} $ temos

$$\mu(A)=\displaystyle \sum_{i=1}^n\mu(I_i)=\sum_{i=1}^n\lambda(I_i)=\sum_{i=1}^n\theta(I_i)=\theta(A)$$

o que implica que

$$\mu=\theta$$

e portanto única.

Agora suponha $ \lambda $$ \sigma $-aditiva, então mostremos que $ \mu $ também é $ \sigma $-aditiva em $ \mathcal{A}(\mathcal{I}) $. De fato, considere

$ (A_j)_{j\in\mathbb{N}} $ uma sequência disjunta em $ \mathcal{A}(\mathcal{I}) $. Como cada $ A_j\in\mathcal{A}(\mathcal{I}) $, temos que existem conjuntos disjuntos $ I^j_i\in\mathcal{I} $, tais que

$$A_j=\displaystyle \bigcup_{i=1}^{m_j}I^j_i$$

Assim

$$\displaystyle A=\bigcup_{j=1}^{\infty} A_j =\bigcup_{j=1}^{\infty}\bigcup_{i=1}^{m_j}I^j_i$$

Desta forma, temos duas possibilidades para $ A $, ou $ A\in\mathcal{A}(\mathcal{I}) $ ou $ A\notin \mathcal{A}(\mathcal{I}) $. Vamos supor inicialmente que $ A\in\mathcal{A}(\mathcal{I}) $. Então como cada $ A_i\cap A_j=\emptyset $ para $ i\neq j $ temos que todos os $ I^j_i $ são disjuntos. e como $ \lambda $ é $ sigma $-aditiva logo

$$\displaystyle \mu(A)=\lambda(A)=\lambda\left(\bigcup_{j=1}^{\infty}\bigcup_{i=1}^{m_j}I^j_i\right)=\sum_{j=1}^{\infty}\sum_{i=1}^{m_j}\lambda(I^j_i)=$$

$$\displaystyle \sum_{j=1}^{\infty}\sum_{i=1}^{m_j}\mu(I^j_i)=\sum_{j=1}^{\infty}\mu\left(\bigcup_{i=1}^{m_j}I^j_i\right)=\sum_{j=1}^{\infty}\mu(A_j)$$

portanto $ \mu $ é $ \sigma $-aditiva em $ \mathcal{A}(\mathcal{I}) $, se $ A\in\mathcal{I} $.

Agora considere o caso em que $ A\notin\mathcal{I} $. Então temos que $ A\in\mathcal{A}(\mathcal{I}) $, portanto

$$A=\displaystyle \bigcup_{i=1}^{n} I_i, \quad \quad \bigcup_{j=1}^{\infty} A_j=A=\bigcup_{i=1}^{n} I_i$$

Desta forma

$$\displaystyle I_i=A\cap I_i=\left(\bigcup_{j=1}^{\infty} A_j\right)\cap I_i=\bigcup_{j=1}^{\infty}(A_j\cap I_i)$$

como $ I_i\in\mathcal{I} $ temos que pelo caso anterior que

$$\mu(I_i)=\displaystyle \sum_{j=1}^{\infty}\mu(A_j\cap I_i)$$

Além disso, temos que

$$A_j=\displaystyle \bigcup_{i=1}^n (A_j\cap I_i)$$

como $ S_i $ são disjuntos temos que

$$(A_j\cap I_i)\cap (A_j\cap I_n), \quad n\neq i$$

segue então, pela aditividade finita de $ \mu $ temos

$$\mu(A_j)=\displaystyle \sum_{i=1}^n (A_j\cap I_i)$$

Então

$$\displaystyle \mu(A)=\mu\left(\bigcup_{i=1}^{n} I_i\right)=\sum_{i=1}^n \mu(I_i)$$

E pela equação anterior temos que

$$\displaystyle \sum_{i=1}^n \mu(I_i)=\sum_{i=1}^n\sum_{j=1}^\infty\mu(A_j\cap I_i)$$

como todos os termos da serie são positivos então podemos permutar a soma e obtemos que

$$\displaystyle \sum_{i=1}^n\sum_{j=1}^\infty\mu(A_j\cap I_i)=\sum_{j=1}^\infty\sum_{i=1}^n\mu(A_j\cap I_i)=\sum_{j=1}^\infty\mu\left(\bigcup_{i=1}^{n}(A_j\cap I_i)\right)=\sum_{j=1}^\infty\mu(A_j)$$

Logo $ \mu $ é $ \sigma $-aditivo em $ \mathcal{A}(\mathcal{I}) $ e o resultado segue.

Note que $ \mathbb{P_F} $ satisfaz as condições da proposição, por isso existe uma única extensão de $ \mathbb{P_F} $, tal que $ \mathbb{P_F} $ é $ \sigma $-aditiva na álgebra, desta forma basta-nos apenas estender $ \mathbb{P_F} $ para a $ \sigma $-álgebra, como vemos no teorema a seguir.

Teorema 2.4.1.2

Dado uma função de distribuição $ F $ com as propriedades P1,P2,P3,P4 então existe uma única medida de probabilidade $ \mathbb{P} $ tal que

$$\mathbb{P}((a,b])=\Delta_{a_1,b_1}\dots\Delta_{a_n,b_n} F_n(x)$$

Demonstração

Pelos Lemas anteriores, e usando o teorema de extensão o resultado segue

2.5 - Variáveis aleatórias independentes

Neste tópico, vamos introduzir o conceito de variáveis aleatórias independentes e derivar critérios para avaliar a independência entre variáveis aleatórias. Seja $ X=(X_1,X_2, \ldots , X_n) $ um vetor aleatório.

Definição informal

As variáveis aleatórias $ X_1, X_2, \ldots ,X_n $ são independentes se, e somente se, qualquer grupo de eventos definidos pelas variáveis “individuais” são independentes.

Definição 2.5.1

As variáveis aleatórias $ (X_1,\ldots ,X_n) $ são independentes se, e somente se, para quaisquer conjuntos de números reais $ B_1,B_2,\ldots ,B_n $ com $ B_i \in X_i, \ \forall \ i=1, \ldots ,n $ temos que

$$\mathbb{P}(X_1 \in B_1,\ldots , X_n \in B_n)=\mathbb{P}(X_1 \in B_1)\ldots \mathbb{P}(X_n \in B_n).$$

Critério para independência

a) Se $ X_1,X_2, \ldots , X_n $ são variáveis aleatórias independentes,então

$$F_{X_1,X_2, \ldots , X_n}(x_1,x_2, \ldots ,x_n)=\prod^n_{i=1}F_{X_i}(x_i), \ \forall (x_1, \ldots x_n) \in \mathbb{R}^n$$

b) Reciprocamente, se existem funções $ F_1,F_2, \dots ,F_n $ tais que

$$\lim_{x_i\rightarrow \infty}F_i(x_i)=1, \ \forall \ i=1, \ldots ,n \ \text{e} \ F_{X_1, \dots ,X_n}(x_1,…,x_n)=\prod^n_{i=1}F_{i}(x_i), \ \forall \ (x_1, \ldots ,x_n) \in \mathbb{R}^n$$

então as variáveis aleatórias $ (X_1,\dots ,X_n) $ são independentes e $ F_{X_i} = F_i $ para todo $ i=1, \ldots , n $.

Demonstração

O item (a) é consequência direta da definição, basta tomarmos $ B_i=(-\infty , x_i] $. Na sequência, vamos mostrar a parte (b). Inicialmente vamos mostrar que $ F_i=F_{X_i} $. Para isto,

$$F_{X_i}(x_i)=\lim_{x_1\rightarrow\infty} \dots \lim_{x_{i-1} \rightarrow \infty}\lim_{x_{i+1}\rightarrow \infty} \dots \lim_{x_n\rightarrow \infty}F_{X_1, \dots , X_n}(x_1, \cdots , x_n)$$

de onde segue que

$$F_{X_i}(x_i)=\lim_{x_1\rightarrow \infty}F_1(x_1) \dots \lim_{x_{i-1} \rightarrow \infty}F_{i-1}(x_{i-1}) F_i(x_i) \lim_{x_{i+1} \rightarrow \infty}F_{i+1}(x_{i+1}) \ldots \lim_{x_n \rightarrow \infty}F_n(x_n)=F_i(x_i).$$

Portanto, concluímos que $ F_{X_i}(x_i)=F_i(x_i) $.

Agora, para mostrar que as variáveis aleatórias são independentes, precisamos mostrar que a Definição 2.5.1 é válida para quaisquer borelianos $ B_i $ com $ i=1,\ldots,n $. Sabemos que para $ B_i=(-\infty ,x_i] $,

$$\mathbb{P}\left(X_1 \in B_1, \ldots , X_n \in B_n\right) = F_{X_1, \ldots ,X_n}(x_1, \ldots , x_n)=F_{X_1}(x_1)\ldots F_{X_n}(x_n)=\prod^n_{i=1}\mathbb{P}\left(X_i \in B_i\right).$$

Por facilidade de notação, vamos considerar o caso em que $ n=2 $. Se tomarmos $ B_i=(a_i,b_i] $ para todo $ i=1,2 $, obtemos que

$ \mathbb{P}\left(X_1 \in B_1, X_2 \in B_2\right)=\mathbb{P}\left(a_1 \ < \ X_1 \leq b_1,a_2 \ < \ X_2 \leq b_2\right) $

$$=F_{X_1,X_2}(b_1,b_2) - F_{X_1,X_2}(b_1,a_2) - F_{X_1,X_2}(a_1,b_2)+F_{X_1,X_2}(a_1,a_2)$$

$$=F_{X_1}(b_1)F_{X_2}(b_2)-F_{X_1}(b_1)F_{X_2}(a_2)-F_{X_1}(a_1)F_{X_2}(b_2)+F_{X_1}(a_1)F_{X_2}(a_2)$$

$$=\left(F_{X_1}(b_1)-F_{X_1}(a_1)\right)\left(F_{X_2}(b_2)-F_{X_2}(a_2)\right)$$

$$=\mathbb{P}\left(a_1 < X_1 \leq b_1\right) \mathbb{P}\left(a_2 < X_2 \leq b_2\right).$$

Utilizando resultados da teoria da medida (Teorema da Classe monótona) podemos mostrar que a relação de independência é válida para qualquer boreliano. Com isto, segue o resultado.

Este critério nos diz que as variáveis aleatórias $ X_1, \cdots , X_n $ são independentes se, e só se, sua função de distribuição conjunta fatora e cada fator converge para $ 1 $ quando $ x_i \rightarrow \infty $. Observe que não é preciso verificar se $ F_i $ é uma função de distribuição acumulada. Na sequência, vamos adaptar o critério acima para variáveis aleatórias continuas.

Corolário 2.5.1

Critério de independência no caso absolutamente contínuo.

a) Se $ X_1,X_2, \dots ,X_n $ são variáveis aleatórias independentes com f.d.p. conjunta $ f_{X_1,\dots ,X_n} $ então

$ f_{X_1,\dots ,X_n}(x_1, \cdots,x_n)=\prod^n_{i=1}f_{X_i}(x_i)~~~~~~~\forall (x_1,\dots, x_n) \in \mathbb{R}^n $

b) Reciprocamente se $ X_1,X_2,\dots ,X_n $ tem f.d.p. conjunta $ f_{X_1,\cdots,X_n}(x_1,\dots,x_n)=\prod^n_{i=1}f_{i}(x_i) $ no qual $ 0 \leq f_i $ e

$ \int^{\infty}_{-\infty}f_i(s_i)ds_i =1 ~~~~~~\forall (x_1,\dots ,x_n) \in \mathbb{R}^n $.

Então as variáveis aleatórias $ X_1,\dots ,X_n $ são independentes e $ f_{X_i}(x_i)=f_i(x_i)~~~~~~ \forall x_i \in \mathbb{R}^n $.

Demonstração

a) Se $ X_1,\dots ,X_n $ são independentes

$ F_{X_1,\dots ,X_n}=\prod^n_{i=1}F_{X_i}(x_i)=\prod^n_{i=1}\int^{x_i}_{-\infty}f_{X_i}(s_1)ds_1=\int^{x_1}_{-\infty}\dots \int^{x_n}_{-\infty} f_{X_1}(s_1)\dots f_{X_n}(s_n)ds_1 \dots ds_n $

Portanto, temos que

$$f_{X_1,\dots ,X_n}(x_1,\dots ,x_n)=\prod^n_{i=1}f_{X_i}(x_i)$$

b) Por outro lado, temos que

$$F_{X_1,\dots ,X_n}(x_1 , \cdots , x_n)=\int^{x_1}_{-\infty}\dots \int^{x_n}_{-\infty}f_{X_1,\dots ,X_n}(x_1,\dots ,x_n) ds_1\dots ds_n =\prod_{i=1}^n\int^{x_i}_{-\infty}f_i(s_i)ds_i.$$

Com isso, concluímos que

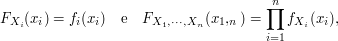
para todo $ (x_1,\cdots,x_n) \in \Bbb{R}^n $. Segue o resultado.

Da mesma forma, podemos derivar um critéria para independência no caso de variáveis aleatórias discretas.

Corolário 2.5.2

As variáveis aleatórias discretas $ X_1 , \cdots , X_n $ são independentes se, e só se,

$$\mathbb{P}\left(X_1 = x_1, \cdots , X_n = x_n\right) = \prod_{i=1}^n \mathbb{P}\left(X_i = x_i\right).$$

Na sequência, vamos apresentar alguns exemplos.

Exemplo 2.5.1

Considere n + m lançamentos de um dado. Fixemos um valor $ i\in(1,2,3,4,5,6) $ e sejam X a variável aleatória que conta o número de vezes que o valor i apareceu nos n primeiros lançamentos e Y a variável aleatória que conta o número de vezes que o valor i apareceu nos m últimos lançamentos.

Como os lançamentos são todos independentes, então para $ x \ < \ n $ e $ y \ < \ m $ temos

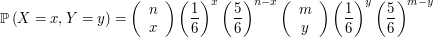
de onde segue que

$$\mathbb{P}\left(X=x,Y=y\right)=\mathbb{P}\left(X=x\right)\mathbb{P}\left(Y=y\right).$$

Exemplo 2.5.2

Suponha que $ X $ e $ Y $ tenham distribuição conjunta dada pela seguinte tabela:

$ X $	$ 1 $	$ 2 $	$ 3 $
$ 1 $	$ 0 $	$ 1/5 $	$ 0 $
$ 2 $	$ 1/5 $	$ 1/5 $	$ 1/5 $
$ 3 $	$ 0 $	$ 1/5 $	$ 0 $

Determine as distribuições marginais e diga se $ X $ e $ Y $ são independentes. Para encontrarmos a distribuição marginal de $ X $ basta somarmos as linhas relativas a cada valor de $ X $ e para encontrar a distribuição marginal de $ Y $, basta somarmos as colunas relativas a cada valor de $ Y $. Desta forma, obtemos que

$ X $	$ 1 $	$ 2 $	$ 3 $	Marginal de $ X $
$ 1 $	$ 0 $	$ 1/5 $	$ 0 $	$ 1/5 $
$ 2 $	$ 1/5 $	$ 1/5 $	$ 1/5 $	$ 3/5 $
$ 3 $	$ 0 $	$ 1/5 $	$ 0 $	$ 1/5 $
Marginal de $ Y $	$ 1/5 $	$ 3/5 $	$ 1/5 $

Observamos que $ X $ e $ Y $ não são independentes, pois $ \frac{1}{5}=\mathbb{P}(X=2,Y=2)\neq \mathbb{P}(X=2)\mathbb{P}(Y=2)=\frac{9}{25} $.

Exemplo 2.5.3

Sejam $ X $ e $ Y $ variáveis aleatórias independentes com distribuição comum dada por

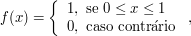
Encontre a função de distribuição acumulada de $ Z=X+Y $.

$$F(z)=\mathbb{P}(X+Y\leq z)=\displaystyle \int \int_{B_z}f(x,y)dx dy,$$

no qual $ B_z = ((x,y): x+y \leq z) $. Para $ 0 ≤ z ≤ 1 $

$$F(z)=\int_{0}^{z}\int_{0}^{z-x}1 dy dx=\frac{z^2}{2}.$$

Para $ 1 \ < \ z \leq 2 $, temos que

$$F(z)=\displaystyle \int_{0}^{z-1}\int_{0}^{1}1 dydx+\int_{z-1}^{1}\int_{0}^{z-x}1dydx=z-1 + \frac{2z-z^2}{2}=\frac{4z-z^2-2}{2}$$

Portanto a função de distribuição acumulada de Z é dada por

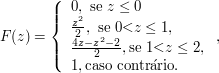
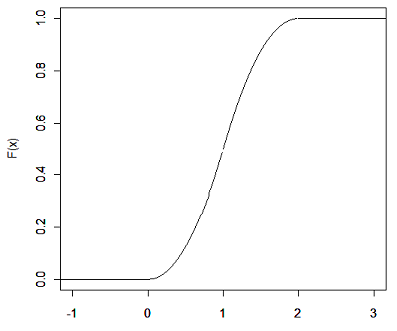
Exemplo 2.5.4

Sejam $ X $ e $ Y $ variáveis aleatórias com distribuição dada no exemplo 2.5.3. Qual a densidade conjunta de $ Z = X-Y $?

$$F(z)=\mathbb{P}(X-Y\leq z)=\int \int_{B_z}f(x,y)dx dy,$$

em que $ B_z = ((x,y): x-y \leq z) $. Para $ -1\leq z \leq 0 $. Então

$$F(z)=\int_{0}^{1+z}\int_{x-z}^{1}1 dy dx=\frac{(z+1)^2}{2}.$$

Para $ 0 \ < \ z \leq 1 $, temos que

$$F(z)=1-\int_{z}^{1}\int_{0}^{x-z}1 dydx=1-\frac{(z-1)^2}{2}$$

Portanto a função de distribuição acumulada de Z é dada por

Exemplo 2.5.5 (Critério para independência no caso discreto)

(a) Sejam $ X $ e $ Y $ variáveis aleatórias discretas, tomando respectivamente os valores $ x_1,x_2, \dots $ e $ y_1,y_2,\dots $. Prove que $ X $ e $ Y $ são independentes se, e somente se,

$$\mathbb{P}(X=x_i,Y=y_j)=\mathbb{P}(X=x_i)\mathbb{P}(Y=y_j)$$

para todo $ i,j $.

Temos pela definição de independência que:

$ X $ independente de $ Y $ se, e somente se, para todo par de Borelianos $ B_1 $ e $ B_2 $:

$$\mathbb{P}(X\in B_1, Y\in B_2)=\mathbb{P}(X\in B_1)\mathbb{P}(X\in B_2)$$

Então, ($ \Rightarrow $) para cada $ (i,j) $ basta tomar $ B_1=(x_i) $ e $ B_2=(y_j) $ então a independência implica que

$$\mathbb{P}(X=x_i, Y=y_j)=\mathbb{P}(X=x_i)\mathbb{P}(Y=y_j)$$

Para a volta, sejam $ B_1 $ e $ B_2 $ borelianos quaisquer

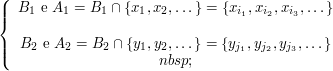
$$\mathbb{P}(X\in B_1, Y\in B_2)=\mathbb{P}(X\in A_1, Y\in A_2)=\sum_k \sum_m \mathbb{P}(X=x_{i_k}, Y=y_{j_m})$$

$$=\sum_k\sum_m \mathbb{P}(X=x_{i_k})\mathbb{P}(Y=y_{j_m})=\left(\sum_{k}\mathbb{P}(X=x_{i_k}\right)\left(\sum_m \mathbb{P}(Y=y_{j_m})\right)$$

$$\mathbb{P}(X\in A_1)\mathbb{P}(X\in A_2)=\mathbb{P}(X\in B_1)\mathbb{P}(Y\in B_2)$$

(b) Mostre que se $ X $ e $ Y $ tomam somente um número finito de valores, digamos $ x_1, \dots, x_m $ e $ y_1, \dots,y_n $, então X e Y são independentes se

$$\mathbb{P}(X=x_i,Y=y_j)=\mathbb{P}(X=x_i)\mathbb{P}(Y=y_j)$$

para $ 1\leq i\leq m-1 $, (Em outras palavras, para provar a independência, basta verificar (m-1)(n-1) equações)

Se

$$\mathbb{P}(X=x_i, Y=y_j)=\mathbb{P}(X=x_i)\mathbb{P}(Y=y_j)$$

para $ i=1,2, \dots, m-1 $ e $ j=1,2,\dots,n $. Então,

$$\mathbb{P}(X=x_{m}, Y=y_j)=\mathbb{P}(Y=y_j)\left(\mathbb{P}(X=x_1,Y=y_j)+\dots+\mathbb{P}(X=x_{m-1},Y=y_j)\right)$$

$$=\mathbb{P}(Y=y_j)-\mathbb{P}(Y=y_j)\left(\mathbb{P}(X=x_1)+\dots+\mathbb{P}(X=x_{m-1})\right)$$

$$=\mathbb{P}(Y=y_j)-\mathbb{P}(X=x_1)\left[1-\mathbb{P}(X=x_m)\right]=\mathbb{P}(Y=y_j)\mathbb{P}(X=x_m), \quad \quad j=1,2,\dots,n$$

Analogamente temos que

$$\mathbb{P}(X=x_i, Y=y_n)=\mathbb{P}(X=x_i)\mathbb{P}(Y=y_n)$$

Das equações acima e usando o item (a) isso implica que $ X $ e $ Y $ são independentes.

(c) Generalize o item (a) para o caso de n variáveis aleatórias. Compare com os critérios de independência e explique por que é suficiente verificar se a função de probabilidade conjunta é igual ao produto de n funções de probabilidade unidimensionais.

$ X_1,X_2,\dots , X_n $ são v.a discretas, onde $ X_i $ assume os valores $ x_i^1,x_i^2, \dots $.

Então $ X_1, X_2, \dots, X_n $ são independentes se, e somente se,

$$\mathbb{P}(X_1=x_i^{i_1},X_2=x_i^{i_2},\dots, X_n=x_i^{i_n})=\mathbb{P}(X_1=x_i^{i_1})\mathbb{P}(X_2=x_i^{i_2})\dots\mathbb{P}( X_n=x_i^{i_n})\quad \quad \forall i_1, i_2, \dots, i_n$$

Agora, isto é o suficiente, pois para todo Boreliano $ B $, temos que

$$\mathbb{P}(X_i\in B)=\mathbb{P}(A)$$

no qual $ A\subset (x_1^1,x_2^2,\dots ) $, é generalizado o raciocínio do item (a).

$$\mathbb{P}(X_1\in B_1, \dots, X_n\in B_n)=\mathbb{P}(X_1\in B_1)\dots \mathbb{P}(X_n\in B_n).$$

Exemplo 2.5.6

Demonstre ou exiba um contra-exemplo: se X,Y e Z são independentes 2 a 2, então elas são independentes.

Contra-Exemplo: W v.a no qual

$$\mathbb{P}(W=1)=\mathbb{P}(W=2)=\mathbb{P}(W=3)=\mathbb{P}(W=4)=\frac{1}{4}$$

X v.a. discreta

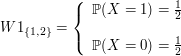
Y v.a. discreta

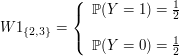
Z v.a. discreta

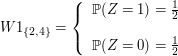
Então,

$$\mathbb{P}(X=1,Y=1)=\mathbb{P}(W=2)=\frac{1}{4}=\frac{1}{2}\frac{1}{2}=\mathbb{P}(X=1)\mathbb{P}(Y=1)$$

o que implica que $ X $ e $ Y $ são independentes

$$\mathbb{P}(Y=1,Z=1)=\mathbb{P}(W=2)=\frac{1}{4}=\frac{1}{2}\frac{1}{2}=\mathbb{P}(Y=1)\mathbb{P}(Z=1)$$

o que implica que $ Y $ e $ Z $ são independentes

$$\mathbb{P}(X=1,Z=1)=\mathbb{P}(W=2)=\frac{1}{4}=\frac{1}{2}\frac{1}{2}=\mathbb{P}(X=1)\mathbb{P}(Z=1)$$

o que implica que $ X $ e $ Z $ são independentes. Agora $ X,Y, Z $ não são independentes pois,

$$\mathbb{P}(X=1, Y=1, Z=1)=\mathbb{P}(W=2)=\frac{1}{4}\neq \mathbb{P}(X=1)\mathbb{P}(Y=1)\mathbb{P}(Z=1)$$

pois

$$\mathbb{P}(X=1)\mathbb{P}(Y=1)\mathbb{P}(Z=1)=\frac{1}{2}\frac{1}{2}\frac{1}{2}=\frac{1}{8}$$

Exemplo 2.5.7

Ache a densidade conjunta e as distribuições marginais das variáveis aleatórias X e Y cuja funções de distribuição conjunta está no exemplo 2.4.6, X e Y são independentes ?

Temos

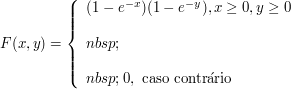
então,

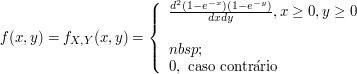
Portanto,

$$f_X(x)=\int_{-\infty}^\infty f(x,y)dy=e^{-x}\int_0^\infty e^{-y}dy=e^{-x}$$

$$f_Y(y)=\int_{-\infty}^\infty f(x,y)dy=e^{-y}\int_0^\infty e^{-x}dx=e^{-y}$$

então $ X\sim Exp(1) $ e $ Y\sim Exp(1) $. Agora, como

$$f_{X,Y}(x,y)=f_X(x)f_Y(y)$$

e

$$\int_{-\infty}^\infty f_X(x)dx=1$$

e

$$\int_{-\infty}^\infty f_Y(y)dy=1$$

então, X e Y são independentes.

Exemplo 2.5.8

Determine as distribuições marginais das variáveis aleatórias discretas X e Y definidas no exemplo 2.4.7. X e Y são independentes?

Temos da resolução do exemplo 2.4.7

$$\mathbb{P}(X=1)=\mathbb{P}(X=2)=\mathbb{P}(X=3)=\frac{1}{3}$$

$$\mathbb{P}(Y=1)=\mathbb{P}(Y=2)=\mathbb{P}(Y=3)=\frac{1}{3}$$

Agora, então

$$\mathbb{P}(X=1,Y=1)=0\neq \mathbb{P}(X=1)\mathbb{P}(Y=1)$$

pois,

$$\mathbb{P}(X=1)\mathbb{P}(Y=1)=\frac{1}{3}\frac{1}{3}=\frac{1}{9}$$

o que implica que pelo exemplo 2.5.5 $ X $ e $ Y $ não são independentes.

Exemplo 2.5.9

Demonstre a que:

Se $ f(x,y) $ é densidade conjunta de $ X $ e $ Y $ então $ X $ tem densidade dada por:

$$f_X(x)=\int_{-\infty}^\infty f(x,y)dy$$

Vejamos se $ f_X $ assim obtida verifica a definição de densidade de X

$$\int_{-\infty}^x\int_{-\infty}^\infty f(x,y)dydx=\int_{-\infty}^\infty \int_{-\infty}^x f(x,y) dx dy$$

$$= \mathbb{P}(X\leq x, -\infty < Y < \infty)=\mathbb{P}(X\leq x)=F_X(x)$$

então o resultado vale.

Exemplo 2.5.10

Sejam X, Y e Z independente, cada uma tendo distribuição uniforme em $ [0,1] $. Qual a probabilidade da equação quadrática

$$Xt^2+Yt+Z=0$$

ter raízes reais ?

Temos

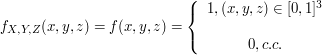
Definimos $ A=(Xt^2+Yt+Z=0, \text{ tem raizes reais })=(Y^2-4XZ\geq 0) $. Então,

$$\mathbb{P}(A)=\mathbb{P}([Y^2-4XZ\geq 0])=\int_{y^2-4xz> 0} f_{X,Y,Z}(x,y,z)dxdy dz=\displaystyle \int_0^1\left[\frac{y^2}{4}+\int_{y^2/4}^1\int_{0}^{y^2/4x}1dzdx\right]dy=\int_0^1\left[\frac{y^2}{4}+\frac{y^2}{4}\int_{y^2/4}^1 \frac{1}{x}\right]dy$$

$$=\int_0^1\left[\frac{y^2}{4}-\frac{y^2}{4}\ln\left(\frac{y^2}{4}\right)\right]dy=\int_0^1 \frac{y^2}{4}\left(1+ln(4)\right)dy-\frac{1}{2}\int_0^1 y^2 \ln(y)dy$$

$$\left[\frac{y^3}{12}(1+\ln(4))\right]_0^1-\frac{1}{2}\int_0^1 y^2 \ln(y)dy=\frac{1}{12}(1+\ln(4))-\frac{1}{2}\int_0^1 y^2 \ln(y)dy$$

Agora, para resolver

$$\frac{1}{2}\int_0^1 y^2 \ln(y)dy$$

vamos fazer uma mudança de variável, $ y=e^{-v} $ e $ dy=e^{-v}dv $, então temos

$$-\frac{1}{2}\int_0^1 e^{-2v} ve^{-v}dv=\frac{1}{2}\int_0^\infty v e^{-3v}$$

temos que $ u=v $ e $ e^{-3v}dv=dw $ o que implica que $ w=\frac{-e^{-3v}}{3} $, desta forma

$$\frac{1}{2}\int_0^\infty v e^{-3v}=\frac{1}{2}\left[-v\frac{e^{-3v}}{3}\bigg|_0^\infty+\int_0^\infty \frac{e^{-3v}}{3}dv\right]=\frac{1}{18}$$

Desta forma, $ \mathbb{P}(A)=\frac{\ln(4)}{12}+\frac{1}{12}+\frac{1}{18}= 0,2544 $

Exemplo 2.5.11

Sejam X e Y variáveis aleatórias independentes, com $ X\sim U[0,a] $ e $ Y\sim U[a,a+b] $, no qual $ a> 0 $, $ b> 0 $. Qual a probabilidade de que os três segmentos $ [0,X] $, $ [X,Y] $, $ [Y,a+b] $ possam formar um triângulo?

Defina as seguintes variáveis aleatórias

$$S_1=X=(\text{Comprimento do Seguimento } [0,X])$$

$$S_2=Y-X=(\text{Comprimento do Seguimento } [X,Y])$$

$$S_3=(a+b)-Y=(\text{Comprimento do Seguimento } [Y,a+b])$$

As condições geométrica para que $ S_1,S_2 $ e $ S_3 $ possam formar um triangulo são:

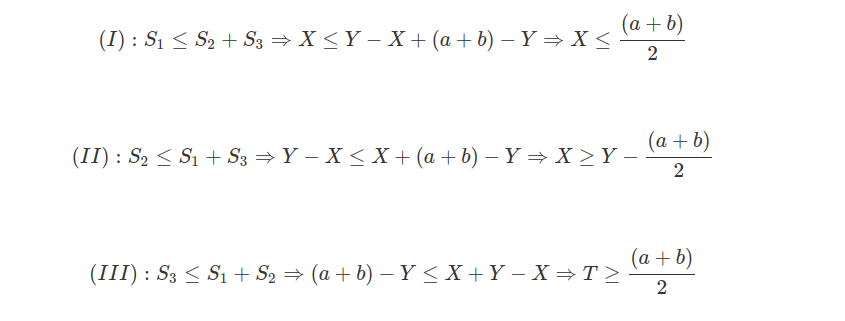
Seja $ E $=evento é possível somar em triângulos com $ [0,X] $, $ [X,Y] $ e $ [Y,a+b] $. Então

$$E=\left[X\leq \frac{a+b}{2}\right]\cap \left[X\geq Y-\frac{a+b}{2}\right]\cap\left[Y\geq \frac{a+b}{2}\right]$$

$ A=((x,y); \text{Valem (I), (II), (III)}) $ e Assim

$$\mathbb{P}(E)=\int_A\int f_{X,Y}(x,y)dxdy=\int_{A\cap([0,a]\times[a,a+b])}\int \frac{1}{ba}dxdy=\frac{1}{ba}\times Area(A\cap([0,a]\times [a,a+b])).$$

Agora, tomando $ a\geq b $, então

$$Area(A\cap([0,a]\times [a,a+b]))=\frac{b}{2}\left(\frac{a+b}{2}-\frac{a-b}{2}\right)=\frac{b^2}{2}$$

Desta forma,

$$\mathbb{P}(E)=\frac{b^2}{2ba}=\frac{b}{2a}$$

Agora, supomos $ a< b $, então

Então,

$$\mathbb{P}\left(A\cap([0,a]\times[a,a+b])\right)=\frac{a}{2}\left(\frac{(a+b)}{2}+a-\frac{(a+b)}{2}\right)=\frac{a^2}{2}$$

Assim,

$$\mathbb{P}(E)=\frac{a^2}{2ba}\Rightarrow \mathbb{P}(E)=\frac{a}{2b}.$$

Resumindo, temos que

$$\mathbb{P}(E)=\frac{\min(a,b)}{2\max(a,b)}.$$

Exemplo 2.5.12

Demonstre: se a variável aleatória X é independente de si mesma, então X é constante com probabilidade 1(i.e., existe uma constante c tal que $ \mathbb{P}(X=c)=1 $).

Se X é independente de X então pela definição de independência para todo par de Borelianos $ B_1 $ e $ B_2 $:

$$\mathbb{P}(X\in B_1, X\in B_2)=\mathbb{P}(X\in B_1)\mathbb{P}(X\in B_2)$$

Agora vamos escolher uma classe de Borelianos que caracteriza a distribuição de X:

$$B_1=B_2=[X\leq x]$$

então para todo $ x\in \mathbb{R} $.

$$F_X(x)=\mathbb{P}([X\leq x])=\mathbb{P}([X\leq x]\cap [X\leq x])=\mathbb{P}^2([X\leq x])=(F_X(x))^2$$

o que implica que $ F_X(x)=0 $ ou $ F_X(x)=1 $ para todo $ x\in \mathbb{R} $. Assim como $ F $ é não decrescente então existe um $ c\in \mathbb{R} $ tal que

$$\mathbb{P}(X=c)=1.$$

Exemplo 2.5.13

Suponha que as vidas úteis $ T_1 $ e $ T_2 $ de máquinas I e II sejam variáveis aleatórias independentes tendo distribuições exponenciais com, respectivamente, parâmetro $ \lambda_1 $ e $ \lambda_2 $. Um inspetor escolhe uma das máquinas ao acaso, cada uma tendo a mesma probabilidade de ser a escolhida, e depois observa a máquina escolhida durante a vida útil dela. (Suponha que a escolha seja independente das vidas.)

(a) Determine a densidade de T, onde T é a vida observada

Defina $ E $ v.a. que designa a maquina escolhida $ E=0 $ maquina I e $ E=1 $ a maquina II. Então,

$$\mathbb{P}(E=0)=\mathbb{P}(E=1)=\frac{1}{2}\Rightarrow \mathbb{P}\left([E=0]\cup [E=1]\right)=1$$

Agora

$$\mathbb{P}(T\leq t)=\mathbb{P}\left([T\leq t]\cap ([E=1]\cup [E=0])\right)$$

$$=\mathbb{P}\left(([T\leq t]\cap [E=1])\bigcup ([T\leq t]\cap [E=0])\right)=\mathbb{P}\left(([T\leq t]\cap [E=1])\right)+ \mathbb{P}\left(([T\leq t]\cap [E=0])\right)$$

$$=\mathbb{P}\left(T\leq t| E=1\right)\mathbb{P}\left(E=1\right)+\mathbb{P}(T\leq t| E=0)\mathbb{P}(E=0)$$

Agora, temos

$$\mathbb{P}(T\leq t| E=1)=\mathbb{T_2\leq t}=1-e^{-\lambda_2 t}$$

$$\mathbb{P}(T\leq t| E=0)=\mathbb{T_1\leq t}=1-e^{-\lambda_1 t}$$

E portanto:

$$\mathbb{P}(T\leq t)=\frac{1}{2}\left(1-e^{-\lambda_2 t}\right)+\frac{1}{2}\left(1-e^{-\lambda_1 t}\right)=1-\frac{1}{2}\left(e^{-\lambda_1 t}+e^{-\lambda_2 t}\right), \quad \quad t> 0$$

e então

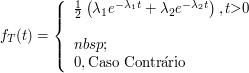
(b) Suponha que o inspetor parou de observar a máquina escolhida depois de cem horas, com a máquina ainda funcionando. Qual a probabilidade condicional da máquina escolhida ter sido a máquina I?

$$\mathbb{P}\left(E=0|T> 100\right)=\frac{\mathbb{P}\left(E=0 \cap [T> 100]\right)}{\mathbb{P}\left(T> 100\right)} =\frac{\mathbb{P}\left(T> 100| E=0\right)\mathbb{P}\left(E=0\right)}{\mathbb{P}\left(T> 100\right)}$$

$$=\frac{\mathbb{P}\left(T_1> 100\right)\mathbb{P}\left(E=0\right)}{\mathbb{P}\left(T> 100\right)}=\frac{e^{-\lambda_1 100}\frac{1}{2}}{\frac{1}{2}(e^{-\lambda_1 100}+e^{-\lambda_2 100})}=\frac{e^{\lambda_1 100}}{e^{-\lambda_1 100}+e^{\lambda_2 100}}$$

(c) Qual a distribuição de $ T $ se $ \lambda_1=\lambda_2=\lambda $?

De (a), temos que

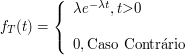
Exemplo 2.5.14

Suponhamos que os tempos que dois estudantes demoram para resolverem um problema sejam independentes e exponenciais com parâmetro $ \lambda > 0 $. Calcule a probabilidade do primeiro estudante demorar pelo menos duas vezes o tempo do segundo para resolver o problema?

$$T_1=(\text{ Tempo que o primeiro estudante demora})$$

$$T_2=(\text{ Tempo que o segundo estudante demora})$$

com $ T_1 \sim exp(\lambda) $ e $ T_2 \sim exp(\lambda) $, com $ T_1 $ e $ T_2 $ são independentes. Então,

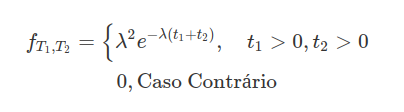
Assim,

$$\mathbb{P}(T_1\geq 2 T_2)=\int_A\int f_{T_1,T_2}(t_1,t_2)dt_1dt_2$$

com $ A={((t_1,t_2): 0 < t_1 \quad e \quad t_2\leq 2t_1)} $. Então,

$$\mathbb{P}(T_1\geq 2T_2)=\int_0^\infty \int_0^{t_1/2} \lambda^2 e^{-\lambda t_1}e^{-\lambda t_2}dt_2dt_1=\int_0^\infty \lambda e^{-\lambda t_1}\left[-e^{-\lambda t_2}\right]_0^{t_1/2}dt_1$$

$$=\int_0^\infty \lambda e^{-\lambda t_1}\left(1-e^{-\lambda t_1/2}\right)dt_1=\int_0^\infty \lambda e^{-\lambda t_1}dt_1-\int_0^\infty \lambda e^{-\lambda \frac{3t_1}{2}}dt_1$$

$$=1+\left[\frac{3}{2}e^{-\lambda \frac{3}{2}t_1}\right]_0^\infty=1-\frac{2}{3}=\frac{1}{3}$$

Exemplo 2.5.15

Um ponto é selecionado, ao acaso (i.e., conforme a distribuição uniforme) do seguinte quadrado:

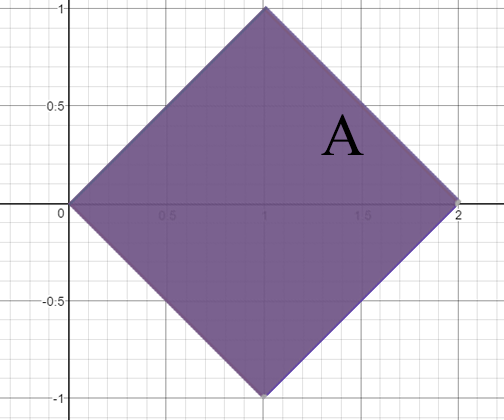
Sejam X e Y as coordenadas do ponto selecionado

(a) Qual a densidade conjunta de X e Y ?

Tendo $ A={((x,y): |x|+|y|\leq 1)} $, então como $ (X,Y)\sim U(A) $, ou seja

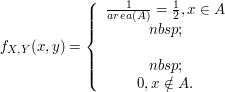
(b) Obtenha a densidade marginal de X.

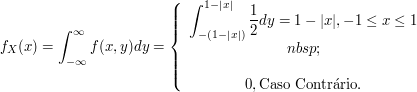
(c) X e Y são independentes?

Não, pois $ \exists B\subset A $, $ (x,y)\in B $ o que implica $ f(x,y)\neq f_X(x)f_Y(y) $ e com a medida de Lebesgue de $ B $ maior que zero.

Pois, analogamente

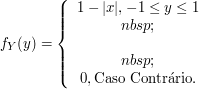
Então, seja $ B\subset A $ tal que $ (x,y)\in B $, o que implica que $ (1-|x|)(1-|y|)\notin \frac{1}{2} $ então a medida de lebesgue de B é maior que zero o que implica que $ X $ e $ Y $ não são independentes.

2.6 - Distribuição condicional: caso discreto

Como para dois eventos quaisquer $ E $ e $ F $, a probabilidade condicional de $ E $ dado $ F $ é definida, desde que $ \mathbb{P}(F) \ > \ 0 $, por

$$\mathbb{P}(E|F)=\frac{\mathbb{P}(E\cap F)}{\mathbb{P}(F)}$$

então, se $ X $ e $ Y $ são variáveis aleatórias discretas, é natural definir a função de probabilidade condicional de $ X $ dado que $ Y=y $, por

$$p_{X|Y}(x|y)=\mathbb{P}(X=x|Y=y)=\frac{\mathbb{P}(X=x,Y=y)}{\mathbb{P}(Y=y)}=\frac{p(x,y)}{p_Y(y)}$$

para todos os valores de y tais que $ p_Y(y) \ > \ 0 $. Similarmente, a função de distribuição acumulada da probabilidade condicional de $ X $ dado que $ Y=y $ é definida, para todo $ y $ tal que $ p_Y(y) > 0 $, por

$$F_{X|Y}(x|y)=\mathbb{P}(X\leq x| Y\leq y)=\sum_{a\leq x}p_{X|Y}(a|y)$$

Se $ X $ é independente de $ Y $, então a função de probabilidade condicional e a função de distribuição acumulada são as mesmas do caso não condicional. Isto acontece pois, se $ X $ é independente de $ Y $, então

$$p_{X|Y}(x|y)=\mathbb{P}(X=x|Y=y)=\frac{\mathbb{P}(X=x,Y=y)}{\mathbb{P}(Y=y)}=\frac{\mathbb{P}(X=x)\mathbb{P}(Y=y)}{\mathbb{P}(Y=y)}=\mathbb{P}(X=x).$$

Exemplo 2.6.1

Suponha que $ p(x,y) $, a função de probabilidade conjunta de $ X $ e $ Y $ seja dada por

$$p(0,0)=0,4 \qquad p(0,1)=0,2 \qquad p(1,0)=0,1 \qquad p(1,1)=0,3.$$

Calcule a função de probabilidade condicional de $ X $, dado que $ Y=1 $.

Primeiramente, observamos que

$$p_Y(1)=\sum_{x}p(x,1)=p(0,1)+p(1,1)=0,5.$$

Então

$$p_{X|Y}(0|1)=\frac{p(0,1)}{p_Y(1)}=\frac{2}{5}$$

e

$$p_{X|Y}(1|1)=\frac{p(1,1)}{p_Y(1)}=\frac{3}{5}.$$

Exemplo 2.6.2

Em uma prova com $ 10 $ perguntas de verdadeiro ou falso, qual a probabilidade de acertarmos todas as perguntas, se respondermos todas de forma aleatória? E se respondêssemos de forma aleatória, mas soubermos que existem mais respostas verdadeiras do que falsa?

Considere o evento $ A=(\text{acertar todas as questões}) $. Como existem $ 2^{10}=1024 $ possíveis combinações, então a probabilidade de respondermos todas as respostas corretas respondendo apenas de forma aleatória é dada por

$$\mathbb{P}(A)=1/1024.$$

Seja $ B $ o conjunto dos pontos com mais resposta verdadeira do que falsa.

Então o número de elementos de $ B $ é

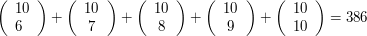
e portanto $ \mathbb{P}(A|B)=\frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)}=\frac{1}{386} $.

Exemplo 2.6.3

Suponha que uma urna contenha $ 6 $ dados, em que $ 3 $ deles são honestos e os outros $ 3 $ são viciados. Os dados viciados apresentam a seguinte probabilidade $ \mathbb{P}(1)=1/2 $ e $ \mathbb{P}(2) = \mathbb{P}(3) = \mathbb{P}(4) = \mathbb{P}(5) = \mathbb{P}(6)=1/10 $. Retira-se um dado ao acaso da urna. Qual a probabilidade dele ser viciado, sabendo que em dois lançamentos o resultado foi 1?

Considere os eventos $ A=(\text{O dado ser viciado}) $, $ B=(\text{Sair o número 1 na primeira e na segunda jogada}) $.

Queremos encontrar $ \mathbb{P}(A|B) $, mas pelo Teorema 1.4.3 temos que

$$\mathbb{P}(A|B)= \frac{\mathbb{P}(B|A)\mathbb{P}(A)}{\mathbb{P}(B)}.$$

Calculemos então cada uma das probabilidades.

$$\mathbb{P}(B|A)=\mathbb{P}({(Sair 1 na primeira Jogada)}|A) \mathbb{P}({(Sair 1 na segunda Jogada)}|A)=\frac{1}{2}\frac{1}{2}=\frac{1}{4},$$

$$\mathbb{P}(A)=\frac{3}{6}=\frac{1}{2}$$

Para encontramos $ \mathbb{P}(B) $, basta utilizarmos o Teorema 1.4.2.

$$\mathbb{P}(B)=\mathbb{P}(B\cap A)+\mathbb{P}(B\cap A^{C})=\mathbb{P}(B|A)\mathbb{P}(A)+\mathbb{P}(B|A^{C})=\frac{1}{4}\frac{1}{2}+\frac{1}{36}\frac{1}{2}=\frac{10}{72}.$$

Portanto

$$\mathbb{P}(A|B)=\frac{1/8}{10/72}=\frac{9}{10}.$$

Assim a probabilidade de que o dado seja viciado dado que saiu duas vezes o número 1 é de 90%.

Exemplo 2.6.4

Suponha as mesmas condições do exemplo acima (Exemplo 2.6.3). Sabendo que em $ 3 $ lançamentos em nenhum deles o resultado foi $ 1 $, qual a probabilidade de que o dado seja viciado?

Considere os eventos $ A=(\text{O dado é viciado}) $ e $ B_i=(\text{Sair um número diferente de 1 na i-ésima jogada}) $ e seja $ C= B_1 \cap B_2 \cap B_3 $. Queremos encontrar a probabilidade de $ \mathbb{P}(A|C) $.

Usando o Teorema 1.4.3, temos que

$$\mathbb{P}(A| C)=\frac{\mathbb{P}(C|A)\mathbb{P}(A)}{\mathbb{P}(C)}.$$

Calculemos então cada uma das probabilidades.

$$\mathbb{P}(C|A)=\mathbb{P}(B_1|A)\mathbb{P}(B_2|A)\mathbb{P}(B_3|A)=\frac{1}{2}\frac{1}{2}\frac{1}{2}=\frac{1}{8},$$

$$\mathbb{P}(A)=\frac{3}{6}=\frac{1}{2}.$$

Para encontramos $ \mathbb{P}(C) $, basta utilizarmos o Teorema 1.4.2.

$$\mathbb{P}(C)=\mathbb{P}(C\cap A)+\mathbb{P}(C\cap A^{C})=\mathbb{P}(C|A)\mathbb{P}(A)+\mathbb{P}(C|A^{C})=\frac{1}{8}\frac{1}{2}+\frac{5^3}{6^3}\frac{1}{2}=\frac{152}{432}.$$

Portanto

$$\mathbb{P}(A|B)=\frac{1/16}{152/432}=\frac{27}{152} \thickapprox 0,1776.$$

Portanto dado que não saiu o número 1 nos três primeiros lançamentos, temos uma chance de aproximadamente 18% que o dado seja viciado.

Exemplo 2.6.5

Sejam $ X_1 $ e $ X_2 $ variáveis aleatórias independentes, cada uma com distribuição geométrica definida por

$$ \mathbb{P}(X_i=n)=p(1-p)^n, n=0,1,2,\dots; \quad i=1,2;$$

no qual $ 0< p < 1. $.(Observação: esta versão da distribuição geométrica corresponde à distribuição do número de fracassos antes do primeiro sucesso em uma sequência de ensaios de Bernoulli.)

(a) Calcule $ \mathbb{P}(X_1=X_2) $ e $ \mathbb{P}(X_1< X_2) $.

$$\mathbb{P}(X_1=X_2)=\sum_{n=0}^\infty \mathbb{P}(X_1=X_2=n)=\sum_{n=0}^\infty \mathbb{P}(X_1=n)\mathbb{P}(X_2=n)$$

$$\sum_{n=0}^\infty p^2[(1-p)^2]^n=\frac{p^2}{1-(1-p)^2}=\frac{p^2}{-p^2+2p}=\frac{p}{2-p}$$

Agora $ \mathbb{P}(X_1> X_2)=\mathbb{P}(X_2> X_1) $ (simetria) então

$$\mathbb{P}(X_1> X_2)+\mathbb{P}(X_2> X_1)+\mathbb{P}(X_1= X_2)=1$$

o que implica

$$\mathbb{P}(X_1> X_2)=\frac{1-\mathbb{P}(X_1=X_2)}{2}$$

o que implica que

$$\mathbb{P}(X_1> X_2)=\frac{\frac{2-p-p}{2-p}}{2}=\frac{2-2p}{4-2p}=\frac{1-p}{2-p}$$

(b) Determine a distribuição condicional de $ X_1 $ dada $ X_1+X_2 $.

$$\mathbb{P}(X_1=k|X_1+X_2=n)=\frac{\mathbb{P}(X_1=k,X_1+X_2=n)}{\mathbb{P}(X_1+X_2=n)}=\frac{\mathbb{P}(X_1=k,X_2=n+k)}{\mathbb{P}(X_1+X_2=n)}$$

$$\frac{\mathbb{P}(X_1=k)\mathbb{P}(X_2=n-k)}{\mathbb{P}(X_1+X_2=n)}$$

Agora:

$$\mathbb{P}(X_1+X_2=n)=\sum_{k=0}^n\mathbb{P}(X_1=k,X_2=n-k)=\sum_{k=0}^n \mathbb{P}(X_1=k)\mathbb{P}(X_2=n-k)$$

$$\sum_{k=0}^n p^2(1-p)^n=(n+1)p^2(1-p)^n$$

Então:

$$\mathbb{P}(X_1=k|X_1+X_2=n)=\frac{p(1-p)^kp(1-p)^{n-k}}{(n+1)p^2(1-p)^n}=\frac{1}{n+1}$$

com $ k=0,1,\dots,n $. Assim, esta distribuição é uniforme nos pontos $ k=0,1,\dots,n $

Exemplo 2.6.6

Uma certa lâmpada tem uma vida, em horas, tendo distribuição exponencial de parâmetro 1. Um jogador acende a lâmpada e, enquanto a lâmpada ainda estiver acesa, lança um dado equilibrado de quinze em quinze segundos. Qual o número espero de 3’s lançados pelo jogador até a lâmpada se apagar ?

$$T\sim Exp\left(\frac{1}{3600}s\right)$$

$ [T/15] $= número de vezes que o jogador lança o dado enquanto a lâmpada estava acesa. O experimento lançamento de dado e obtenção ou não de 3 é um ensaio de bernoulli condicionado a T.

$$\mathbb{P}(X=k|T=t)=\binom{[T/15]}{k}p^k(1-p)^{[T/15]^{-k}},k=0,1,\dots,[T/15]$$

e $ p=\frac{1}{6} $. Então, $ \mathbb{E}(X|T)=p[T/15] $ e $ \mathbb{E}(X)=\mathbb{E}\left(\mathbb{E}(X|T)\right)=\frac{1}{6}\mathbb{E}([T/15]) $. Agora,

$$\mathbb{P}([T/15]\geq k)=\mathbb{P}(T> 15k)=e^{-\frac{15}{3600}k}=e^{-\frac{1}{240}k}.$$

Assim

$$\mathbb{E}([T/15])=\sum_{k=0}^\infty \left(e^{-\frac{1}{240}}\right)^k=\frac{1}{1-e^{-\frac{1}{240}}}$$

Assim, $ \mathbb{E}(X)=\frac{1}{6}\frac{1}{1-e^{-1/240}}=40,08 $

Exemplo 2.6.7

Partículas chegam em um contador segundo um processo de Poisson com parâmetro $ \lambda $. Em um determinado tempo $ t $, produz-se uma voltagem, multiplicando o número de partículas que já entraram no contador por um fator que é independente desse número e que tem densidade:

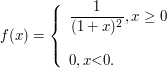
Ache a probabilidade da voltagem produzida ser menor que 1.

$$X=Nk$$

no qual, k tem densidade

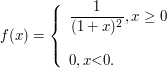
e $ N\sim Poisson(\lambda t) $. Agora

$$\mathbb{P}(X< 1)=\mathbb{P}(0\leq X< 1)=\mathbb{P}(X=0)+\mathbb{P}(0< X< 1)$$

Agora

$$\mathbb{P}(X=0)=\mathbb{P}(N=0,k \quad\text{qualquer}\quad)+\mathbb{P}(N\quad \text{qualquer} \quad,k=0)=e^{-\lambda t}$$

Porém, se $ 0< X < 1 $ se, e somente se,

$$(0< k< \frac{1}{n})\Rightarrow \mathbb{P}\left(0< k < \frac{1}{n}\right)=\int_{0}^{1/n}\frac{1}{(1+x)^2}dx$$

fazendo uma substituição $ 1+x=y $ e $ dx=dy $.

$$\int_{0}^{1/n}\frac{1}{(1+x)^2}dx=-\frac{1}{y}\bigg|_1^{1+\frac{1}{n}}=1-\frac{1}{1+\frac{1}{n}}=\frac{n+1-n}{n+1}=\frac{1}{n+1}, \quad n=1,2,\dots.$$

Assim,

$$\mathbb{P}(X< 1)=\mathbb{P}(X=0)+\sum_{n=1}^\infty \mathbb{P}\left(0< k< \frac{1}{n}\right)\mathbb{P}(N=n) $$

$$=e^{-\lambda t}+\sum_{n=1}^\infty \frac{(\lambda t)^n}{(n+1)!}e^{-\lambda t}=e^{-\lambda t}\left(1+\frac{1}{\lambda t }\sum_{k=2}^\infty \frac{(\lambda t)^k}{k!}\right)$$

$$=e^{-\lambda t}\left[1+\frac{1}{\lambda t}\left(e^{\lambda t}-1-\lambda t\right)\right]=\frac{1}{\lambda t}[1-e^{-\lambda t}]$$

Exemplo 2.6.8

Mostre que se X é uma variável aleatória tendo distribuição simétrica em torno de zero, e se $ \mathbb{P}(X=0)=0 $, então a distribuição condicional de $ X^2 $ dado que $ X> 0 $ é igual à própria distribuição de $ X^2 $.

X tem distribuição simétrica em torno de zero se, e somente se, $ \mathbb{P}(X\leq -x)=\mathbb{P}(X\geq x), \forall x \in \mathbb{R} $. Além disso $ \mathbb{P}(X=0)=0 $ o que implica que $ \mathbb{P}(0< X \leq x)=\mathbb{P}(-x\leq X < 0) $ para todo $ x> 0 $. Queremos provar que

$$\mathbb{P}(X^2\leq x| X> 0)=\mathbb{P}(X^2\leq x)$$

Agora

$$\mathbb{P}(X^2\leq x | X> 0)=\frac{\mathbb{P}(X^2\leq x, X> 0)}{\mathbb{P}(X> 0)}=\frac{\mathbb{P}(0> X\leq \sqrt{x})}{\mathbb{P}(X> 0)}$$

e

$$\mathbb{P}(X^2\leq x | X< 0)=\frac{\mathbb{P}(X^2\leq x, X< 0)}{\mathbb{P}(X> 0)}=\frac{\mathbb{P}(-\sqrt{x}\leq X< 0)}{\mathbb{P}(X> 0)}$$

Temos então que

$$\mathbb{P}(X^2\leq x | X< 0)=\mathbb{P}(X^2\leq x | X> 0)$$

são iguais pela simetria em torno de zero, para todo $ x> 0 $. Então,

$$\mathbb{P}(X^2\leq x)=\mathbb{P}(X^2\leq x| X> 0)\mathbb{P}(X> 0)+\mathbb{P}(X^2\leq x|X=0)\mathbb{P}(X=0)\mathbb{P}(X^2\leq x | X< 0)$$

$$=\mathbb{P}(X^2\leq x |X> 0)\frac{1}{2}+\mathbb{P}(X^2\leq x| X> 0)\frac{1}{2}=\mathbb{P}(X^2\leq x|X> 0), \quad \forall x > 0$$

e para $ X=0 $ temos

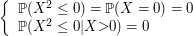
Da equação acima e do fato que

$$\mathbb{P}(X^2\leq x|X> 0), \quad \forall x > 0$$

temos então que $ X^2 $ e $ X^2|X> 0 $ são identicamente distribuídas (A distribuição é determinada pela f distribuição de probabilidade)

Exemplo 2.6.9

Partículas radioativas chegam a um contador segundo um processo de Poisson com uma taxa média de três por segundo, mas o contador registra somente cada segunda partícula (i.e., são registradas somente as partículas número $ 2,4,6,\dots $).

(a) Seja $ X_t $ o número de partículas registradas até o tempo t. É $ ({X_t: t\geq 0}) $ um processo de Poisson? Se for, qual o parâmetro ? Se não for, explique o porquê.

$ (Y_t)_{t\geq 0} $ é processo de Poisson, se e somente se, $ \mathbb{P}(Y_t=k)=\frac{\lambda t }{k!}e^{-\lambda t} $. Agora,

$$\mathbb{P}(X_t=k)=\mathbb{P}(Y_t=2k\quad\text{ou}\quad Y_t=2k+1)=\left[\frac{(\lambda t)^{2k}}{(2k)!}+\frac{(\lambda t)^{2k+1}}{(2k+1)!}\right] e^{-\lambda t}$$

então $ X_t $ não é processo de Poisson.

(b) Supondo que o contador registrou exatamente uma partícula durante o primeiro segundo, qual a probabilidade de que ele não registre mais partícula alguma antes do tempo 2?

$$\mathbb{P}(X_2=X_1| X_1=1)=\frac{\mathbb{P}(X_2=X_1=1)}{\mathbb{P}(X_1=1)}$$

$$=\frac{\mathbb{P}(Y_1=2, Y_2-Y_1=0)+\mathbb{P}(Y_1=2,Y_2-Y_1=1)+\mathbb{P}(Y_1=3,Y_2Y_1=0)}{\mathbb{P}(Y_1=2)+\mathbb{P}(Y_1=3)}$$

Agora $ Y_1\sim Poisson(\lambda) $ e $ Y_2-Y_1\sim Poisson(\lambda) $ são independentes. Então,

$$\mathbb{P}(X_2=X_1|X_1=1)=\frac{\mathbb{P}(Y_1=2)\left(\mathbb{P}(Y_2-Y_1=1)+\mathbb{P}(Y_2-Y_1=0)\right)\mathbb{P}(Y_1=1)\mathbb{P}(Y_2-Y_1=0)}{ \mathbb{P}(Y_1=2)+\mathbb{P}(Y_1=3)}$$

$$=\frac{\frac{\lambda^2}{2}e^{-\lambda t }(\lambda+1)e^{-\lambda t}+\frac{\lambda^3}{6}e^{-\lambda t}e^{-\lambda t}}{\frac{\lambda^2}{2}e^{-\lambda t}+\frac{\lambda^3}{6}e^{-\lambda t}}$$

$$=\frac{e^{-\lambda t}\lambda^2\left(\frac{\lambda+1}{2}+\frac{1}{6}\right)}{\lambda^2\left(\frac{1}{2}+\frac{\lambda}{6}\right)}=\frac{3\lambda +4}{\lambda+3}e^{-\lambda t}$$

Exemplo 2.6.10

Um contador recebe impulsos de duas fontes independentes, A e B. Fonte A gera impulsos conforme um processo de Poisson com parâmetro $ \lambda > 0 $, enquanto a fonte B gera impulsos segundo um processo de Poisson com parâmetro $ \xi > 0 $. Suponha que o contador registre todo impulso gerado pelas duas fontes.

(a) Seja $ X_t $ o número de impulsos registrados pelo contador até o tempo $ t, t > 0 $ ($ X_0=0 $). Explique porque $ ({X_t: t\geq 0}) $ é um processo de Poisson (basta uma explicação intuitiva). Qual o parâmetro?

É um processo de Poisson por que:

a) Incrementos independentes

b) Incrementos estacionários

c) Não chegam 2 simultaneamente e com parâmetro $ \lambda+\xi $.

(b) Qual a probabilidade de que o primeiro impulso registrado seja da fonte A?

Sabemos que $ X_{\lambda} $ e $ X_{\lambda+\xi}-X_{\xi} $ são independentes com $ X_{\lambda}\sim Poisson(\lambda) $ e $ X_{\lambda+\xi}-X_{\lambda}\sim Poisson(\xi) $. Então

$$\mathbb{P}(X_{\lambda}=1|X_{\lambda+\xi}=1)=\frac{\lambda}{\lambda+\xi}$$

(c) Dado que exatamente 100 impulsos foram contados durante a primeira unidade de tempo, qual a distribuição que você atribuiria ao número emitido pela fonte A?

$$\mathbb{P}(X_\lambda=k| X_{\lambda+\xi}=100)=\binom{100}{k}\left( \frac{\lambda}{\lambda+\xi}\right)^k\left( \frac{\xi}{\lambda+\xi}\right)^{100-k},$$

$ k=0,1,\dots,100 $ sendo uma $ Binomal\left(100,\frac{\lambda}{\lambda+\xi}\right) $

Exemplo 2.6.11

Diz-se que $ X=(X_1,\dots, X_k) $ tem distribuição multinomial com parâmetros $ p_1,\dots ,p_k $ e n, no qual $ p_i\geq 0 $ e $ \displaystyle \sum_{i=1}^k p_i=1 $, se

$$\mathbb{P}(X=(j_1, \dots, j_k))=\frac{n!}{j_1!j_2!\dots j_k!}p_1^{j_1}p_2^{j_2}\dots p_k^{j_k}$$

para toda escolha de $ j_1,\dots, j_k $ inteiros não-negativos tais que $ \sum_{\ell=1}^k j_\ell =n $.

(a) Prove que $ X_i\sim b(n,p_i), i=1,\dots,k. $

Temos que:

$$\mathbb{P}(X_i=m)=\sum_{(j_1,\dots, j_k)}\frac{n!}{j_1!\dots j_{i-1}!m!j_{i+1}!\dots j_k!}p_1^{j_1}p_2^{j_2}\dots p_1^m\dots p_k^{j_k}$$

no qual $ j_{\ell}\geq 0 $ e $ \sum_{\ell\neq i}^k j_\ell=n-m $.

Então,

$$\frac{n!}{m!}p_i^m \sum \frac{1}{j_1!\dots j_k!}p_1^m\dots p_k^{j_k}$$

Agora dividindo e multiplicando por $ (1-p_i)^{n-m} $, temos

$$\mathbb{P}(X_1=m)=\frac{n!}{m!(n-m)!}p_i^m(1-p_i)^{n-m}\sum \frac{(m-n)!}{j_1!\dots j_k!}\left(\frac{p_i}{1-p_i}\right)^{j_1} \dots \left(\frac{p_i}{1-p_i}\right)^{j_k}$$

mas o lado direito da equação representa uma multinomial, e portanto é igual a 1. Logo temos que $ X_i\sim b(n,p_i),\quad i=1,2,\dots,k $

(b) Sejam $ 0< s_1< s_2< \dots< s_k=t. $ Mostre que no processo de Poisson, dado que $ X_t=n, $ a distribuição condicional de $ X_{s_1},X_{s_2}-X_{s_1}, \dots , X_t-X_{s_{k-1}} $ é multinomial com parâmetros $ \frac{s_1}{t},\frac{s_2-s_1}{t}, \dots, 1- \frac{s_{k-1}}{t} $ e n. (Note que essa distribuição não depende do parâmetro $ \lambda $ do processo.)

Dado que até o instante t chegaram n partículas, a distribuição dos tempos de chegada é igual a de uma amostra aleatória de n elementos de uma v.a. uniforme em $ [0,t] $. Assim a distribuição em questão será:

$$\mathbb{P}(X_{s_1}=j_1,X_{{s_2}}-X_{s_1}=j_2, \dots, X_{t}-X_{s_{k-1}}=j_k|X_t=n)=\frac{n!}{j_1!\dots j_k!}p_1^{j_1}\dots p_k^{j_k}$$

para $ (j_1,j_2,\dots,j_k) $ tal que $ \sum_{j=1}^k j_i=n $ e $ j_i $ inteiro não negativo caso contrário é zero o que implica que é uma multinomial.

Exemplo 2.6.12

Uma exposição funciona pelo período de T horas. Visitantes chegam à exposição segundo um processo de Poisson com taxa $ \lambda $ visitantes/hora. Os visitantes permanecem na exposição até o fim do período. Calcule o tempo médio total gasto pelos visitantes na exposição. %Dado que chegou um só visitante durante as T horas, qual a média do tempo que ele permanece na exposição ?

Seja $ Y(T) $ número de visitantes que chegam até T, o que implica que $ Y(T)\sim Poisson(\lambda T) $ e então sendo $ T_1,T_2,\dots, T_n $ os tempos de chegada do n-visitantes, temos que $ T_i $ independentes $ T_j $ e $ T_i\sim U[0,T] $$ i=1,2,\dots,n $ e

$$\mathbb{E}(T_i)=\frac{T}{2}$$

para qualquer i. Então, seja $ X= $ tempo médio total gasto pelos visitantes na exposição:

$$\mathbb{E}(X|Y=n)=\sum_{i=1}^n (T-T_i)=nT - \sum_{i=1}^n T_i.$$

Agora, então

$$\mathbb{E}(X|Y=n)=nT-\sum_{i=1}^n \mathbb{E}(T_i)=nT-\frac{nT}{2}=n\frac{T}{2}.$$

Então $ \mathbb{E}(X)=\mathbb{E}\left(\mathbb{E}(X|Y=n)\right)=\frac{T}{2}\mathbb{E}(Y)=\frac{T^2}{2}\lambda $

Exemplo 2.6.13

Suponha que o número de passas num bolo inglês tenha distribuição de Poisson de parâmetro 60. Um jogador compra um bolo, tira todas as passas uma por uma e reparte as passas entre ele e você da seguinte maneira: depois da extração de cada passa ele joga uma moeda equilibrada, dando a passa para você se der cara, comedo ele mesmo a passa se der coroa. Qual a distribuição do número de passas que você recebe ? A esperança?

Temos que $ X= $ número de passas que você recebe e $ Y= $ número de passas extraídas. Assim, $ X|Y=n\sim b\left(n,\frac{1}{2}\right) $ então

$$\mathbb{P}(X=k)=\sum_{n=k}^\infty \mathbb{P}(X=k|Y=n)\mathbb{P}(Y=n)=\sum_{n=1}^\infty \frac{n!}{(n-k)!k!}\left(\frac{1}{2}\right)^{n} \frac{\lambda^n}{n!}e^{-\lambda}$$

$$=\frac{e^{-\lambda}\left(\frac{\lambda}{2}\right)^k}{k!}\sum_{n=k}^\infty \frac{\left(\frac{\lambda}{2}\right)^{n-k}}{(n-k)!}$$

$$=\frac{e^{-\lambda}\left(\frac{\lambda}{2}\right)^ke^{\lambda/2}}{k!}=\frac{\left(\frac{\lambda}{2}\right)^ke^{-\lambda}}{k!}$$

ou seja $ X\sim Poisson\left(\frac{\lambda}{2}\right) $, como $ \lambda/2=30 $. Agora

$$\mathbb{E}(X|Y=n)=n\frac{1}{2}$$

o que implica que

$$\mathbb{E}(X)=\mathbb{E}\left(\mathbb{E}(X|Y=n)\right)=\frac{1}{2}\mathbb{E}(n)=\frac{1}{2}60=30.$$

Exemplo 2.6.14

Sejam X e Y independentes tais que $ X\sim b(m,p) $ e $ Y \sim b(n,p) $. Obtenha a distribuição condicional de X dada $ X+Y $. Como se chama essa distribuição?

Sabemos que se $ X\sim b(m,p) $ e $ Y\sim b(n,p) $ são independentes o que implica que $ X+Y\sim b(m+n,p) $. Assim,

$$\mathbb{P}(X=k|X+Y=z)=\frac{\mathbb{P}(X=k,X+Y=z)}{\mathbb{P}(X+Y=z)}=\frac{\mathbb{P}(X=k)\mathbb{P}(Y=z-k)}{\mathbb{P}(X+Y=z)}$$

$$=\frac{\binom{m}{k}p^k(1-p)^{m-k}\binom{n}{z-k}p^{k-z}(1-p)^{n-(k-z)}}{\binom{m+n}{z}p^z(1-p)^{m+n-z}}=\frac{\binom{m}{k}\binom{n}{k-z}}{\binom{m+n}{z}}$$

que é uma distribuição hipergeométrica com $ N=m+n $ e $ D=m $.

Exemplo 2.6.15

Duas fontes radioativas, I e II, emitem partículas (independentemente) segundo processos de Poisson com, respectivamente, parâmetro $ \lambda $ e $ \xi $. Seja $ Z_t $ o número total de partículas emitidas até o instante t, para $ t\geq 0 $. Dado que $ Z_t=k $, onde $ k> 0 $, qual a probabilidade condicional da última partícula emitida antes do instante t ter sido da fonte I? (A resposta é igual à do exemplo 2.6.10 (b). Um possível método de verificação: use o exemplo 1.4.13(e), com $ A_n $ o evento “n partículas emitidas até o instante t pela fonta I”.)

Temos que $ X_t\sim Poisson(\lambda) $ e $ X_{2t}\sim Poisson(\xi) $ independentes o que implica que $ Z_t=X_t+X_{2t}\sim Poisson(\lambda+\xi) $. Assim dado que chegam k partículas $ X_{\lambda+\xi}=k $, os tempos de chegadas $ T_1,T_2,\dots,T_k $ são variáveis aleatórias uniforme em $ [0,\lambda+\xi] $ então, a probabilidade da última ter sido da fonte I é

$$\mathbb{P}(\text{última é da fonte I})=\frac{\lambda}{\lambda+\xi}$$

Exemplo 2.6.16

Considere um processo de Poisson com parâmetro $ \lambda> 0 $.

(a) Para $ t> 0 $ fixo, seja $ Z_t $ o tempo transcorrido até o instante t desde a ocorrência (“chegada”) imediatamente anterior. ($ Z_t=t $ se não houve nenhuma chegada em $ (0,t] $.) Calcule a distribuição de $ Z_t $.(Note que distribuição é aproximadamente exponencial quando t é grande.)

Então, $ (X_t)_{t\geq 0} $ é um processo de Poisson $ Z_t= $ tempo transcorrendo até o instante t desde a ocorrência imediata anterior. Para $ z< 0 $ e $ \mathbb{P}(Z_t\leq z)=0 $ (pois Z é v.a. não-negativa), $ \mathbb{P}(Z_t=0)=\mathbb{P}(\text{chega 1 partícula em t=0})=0 $. Agora, para $ 0< z< t $:

$$\mathbb{P}(Z_t> z)=\mathbb{P}(\text{não ocorrer nenhuma chegada em} [t-z,t])=e^{-\lambda z}$$

então $ \mathbb{P}(Z_t\leq z)=1-e^{-\lambda z} $. Agora para $ z\geq t $

$$\mathbb{P}(Z_t=t)=\mathbb{P}(\text{não ocorrer nenhuma chegada em }[0,t])=e^{-\lambda t}$$

e também $ \mathbb{P}(Z_t\leq t)=1 $ o que implica que $ \mathbb{P}(Z_t\leq z)=1 $ para $ z\geq t $. Então a distribuição de $ Z_t $ será

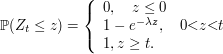
Obs: Quando $ t\rightarrow \infty $, esta distribuição converge fracamente para o distribuição $ Exp(\lambda) $.

(b) Se $ T_{n+1} $ é o tempo transcorrido entre a $ n- $ésima chegada e a chegada número $ n+1 $, qual a distribuição de $ T_{n+1} $? Determine a distribuição de $ W_t= $ tempo que transcorre entre o instante t e a próxima chegada.

Sabemos que os tempos de espera são variáveis aleatórias independentes e identicamente distribuídas com distribuição $ Exp(\lambda) $, então

$ T_{n+1}\sim Exp(\lambda) $, assim:

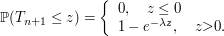
Agora, seja $ W_t= $ tempos transcorridos entre o instante t e as próximas chegadas. $ W_t $ é uma variável aleatória não-decrescentes e

$$\mathbb{P}(W_t=0)=\mathbb{P}(\text{ocorreu uma chegada em }t)=0$$

Agora $ w> 0 $, temos

$$\mathbb{P}(W_t> w)=\mathbb{P}(\text{não ocorreu nenhuma chegada em }[t,t+w])=e^{-\lambda w}$$

o que implica que

$$\mathbb{P}(W_t\leq w)=1-e^{-\lambda w}$$

então $ W_t $ tem distribuição

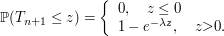
(c) Mostre que $ Z_t+W_t $, o tempo entre as chegadas que “cercam” o instante t, é estocasticamente estritamente maior que $ T_{n+1} $, i.e,

$$\mathbb{P}(Z_t+W_t\leq x)< \mathbb{P}(T_{n+1}\leq x)$$

$ \forall x> 0. $(Esse é o “paradoxo do tempo de espera”.)

Temos $ Z_t $ e $ W_t $ são independentes então para $ \rho\leq t $, temos

$$\mathbb{P}(Z_t+W_t\leq \rho)=\int_0^\rho \int_0^{\rho-z}\lambda^2e^{-\lambda z}e^{-\lambda w}dwdz$$

$$=\int_0^\rho \lambda e^{-\lambda z}\left[-e^{-\lambda z}\right]_0^{\rho-z}dz=\int_0^\rho \lambda e^{-\lambda z}(1-e^{-\lambda(\rho -z)})dz$$

$$=\int_0^\rho \lambda e^{-\lambda z}dz-\int_0^\rho \lambda e^{-\lambda \rho}dz=1-e^{-\lambda\rho}-\lambda \rho e^{-\lambda \rho}< 1-e^{-\lambda \rho}.$$

Agora para $ \rho\geq t $, temos

$$\mathbb{P}(Z_t+W_t\leq \rho)=\int_0^t\int_0^{\rho-z}\lambda^2 e^{-\lambda z}e^{-\lambda w}dwdz=\int_0^t \lambda e^{-\lambda z}dz-\int_0^t \lambda e^{-\lambda \rho}dz=1-e^{-\lambda t}-\lambda te^{-\lambda \rho}$$

Assim $ \rho\geq t $:

$$\mathbb{P}(Z_t+W_t\leq \rho)=1-e^{-\lambda t}-\lambda te^{-\lambda \rho}$$

Agora $ \rho\geq t $ o que implica que

$$e^{-\lambda t}\geq e^{-\lambda \rho}$$

então como $ \lambda t e^{-\lambda t}> 0 $, temos que

$$\mathbb{P}(Z_t+W_t\leq \rho)< 1-e^{-\lambda \rho}$$

Resumindo tudo, temos que

$$Z_t+W_t$$

é estocasticamente maior que $ T_{n+1} $.

Exemplo 2.6.17

Seja $ X_1,X_2,\dots $ uma sequência de variáveis aleatórias independentes e identicamente distribuídas tendo distribuição exponencial com média $ \frac{1}{\lambda} $, no qual $ \lambda > 0 $. Para $ t> 0 $ fixo, seja $ N=\max{n\geq 0: S_n\leq t} $, no qual $ S_0=0 $ ou igual a t. Mostre que N tem distribuição Poisson com média $ \lambda t. $

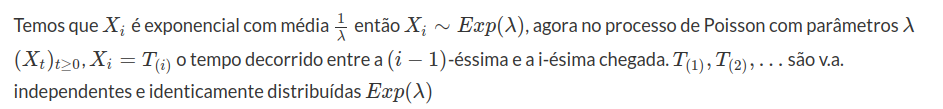
Então

$$[N=m]=[\max{n\geq 0:S_n\leq t}]=[T_{(m)}\leq t< T_{(m+1)}]=[X_t=m]$$

então

$$\mathbb{P}(N=m)=\mathbb{P}(X_t=m)=\frac{(\lambda t)^m}{m!}e^{\lambda t}\sim Poisson(\lambda t)$$

o que implica que $ \mathbb{E}(N)=\lambda t $.

2.7 - Distribuição condicional: caso contínuo

Se $ X $ e $ Y $ são variáveis aleatórias com função densidade de probabilidade conjunta $ f(x,y) $, então a função densidade de probabilidade de $ X $, dado que $ Y=y $ é definida para todos os valores $ y $ tais que $ f_Y(y) \ > \ 0 $, por

$$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}$$

Para motivar esta definição, multiplicamos o lado esquerdo da equação por $ dx $ e o lado direito por $ (dx dy)/dy $. Desta forma, obtemos

$$f_{X|Y}(x|y)dx=\frac{f(x,y)dxdy}{f_Y(y)dy}\approx \frac{\mathbb{P}(x\leq X\leq x+dx,y\leq Y\leq y+dy)}{\mathbb{P}(y\leq Y\leq y+dy)}$$

ou seja,

$$f_{X|Y}(x|y)dx=\mathbb{P}(x\leq X\leq x+dx|y\leq Y\leq y+dy).$$

Em outras palavras, para pequenos valores de $ dx $ e $ dy $, $ f_{X|Y}(x|y)dx $ representa a probabilidade condicional de $ X $ estar entre $ x $ e $ x+dx $, dado que $ Y $ está entre $ y+dy $.

O uso de densidades condicionais nos permite definir probabilidades condicionais de eventos associados com uma variável aleatória quando é dado o valor de uma segunda variável aleatória. Isto é, se $ X $ e $ Y $ são conjuntamente distribuídas, então para qualquer conjunto $ A $,

$$\mathbb{P}(X\in A|Y=y)=\int_A f_{X|Y}(x|y) dx$$

Em particular, tomando A=(-∞,a], podemos definir a função de distribuição acumulada de $ X $, dado que $ Y=y $, por

$$F_{X|Y}(a|y)=\mathbb{P}(X\leq a|Y=y)=\int_{-\infty}^a f_{X|Y}(x|y) dx.$$

Além disso, temos que

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_X(x|Y=t)dF_Y(t), \forall (x,y)\in \mathbb{R}^2$$

No qual a integral acima é a integral de Lebesgue.

Exemplo 2.7.1

A densidade conjunta de $ X $ e $ Y $ é dada por

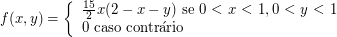
Calcule a densidade condicional de $ X $, dado que $ Y=y $, quando $ 0 \ < \ y \ < \ 1 $.

Para $ 0 \ < \ x \ < \ 1 $, $ 0 \ < \ y \ < \ 1 $, temos que

$$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}=\frac{f(x,y)}{\int_{-\infty}^{\infty} f(x,y)dx}=\frac{x(2-x-y)}{\int_0^1 x(2-x-y)dx}$$

ou seja,

$$f_{X|Y}(x|y)=\frac{x(2-x-y)}{\frac{2}{3}-\frac{y}{2}}=\frac{6x(2-x-y)}{4-3y}.$$

Se $ X $ e $ Y $ são variáveis aleatórias contínuas independentes, a densidade condicional de $ X $, dado $ Y=y $, é justamente a densidade não condicional de $ X $. Isto ocorre pois, no caso independente, temos que

$$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}=\frac{f_X(x)f_Y(y)}{f_Y(y)}=f_X(x)$$

Também podemos falar de distribuições condicionais quando as variáveis aleatórias não são nem conjuntamente contínuas, nem conjuntamente discretas. Por exemplo, suponha que $ X $ é uma variável aleatória contínua com função densidade de probabilidade $ f $ e $ N $ é uma variável aleatória discreta e considere a distribuição condicional de $ X $ dado que $ N=n $. Então

$$\frac{\mathbb{P}(x \ < \ X \ < \ x+dx|N=n)}{dx}=\frac{\mathbb{P}(N=n|x \ < \ X \ < x+dx)}{\mathbb{P}(N=n)}\frac{\mathbb{P}(x \ < \ X \ < \ x+dx)}{dx}$$

e, fazendo $ dx $ tender a $ 0 $, temos que

$$\lim_{dx\to 0}\frac{\mathbb{P}(x \ < \ X \ < \ x+dx|N=n)}{dx}=\frac{\mathbb{P}(N=n|X=x)}{\mathbb{P}(N=n)}f(x)$$

o que nos mostra que a densidade condicional de $ X $ dado que $ N=n $ é dada por

$$f_{X|N}(x|n)=\frac{\mathbb{P}(N=n|X=x)}{\mathbb{P}(N=n)}f(x).$$

Exemplo 2.7.2

Suponha que $ Y $ possua densidade $ f_Y(y) $ e que a distribuição condicional de X, dado que $ Y=y $, possua densidade $ f(x|y) $, para todo $ y $ (ou pelo menos para “quase todo” valor possível de Y). Demonstre que

$$f(x,y)= f_Y(y)f(x|y)$$

é a densidade conjunta de $ X $ e $ Y $.

Temos por

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_X(x|Y=t)dF_Y(t), (x,y)\in \mathbb{R}^2$$

que

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_X(x|Y=y)dF_Y(t)$$

Agora se $ Y $ e $ X|Y $ são distribuições absolutamente contínuas então

$$dF_Y(y)=f_Y(y)dy$$

e

$$F_X(X|Y=y)=\int_{-\infty}^x f_{X|Y=y}(x)dx$$

Assim,

$$F_{X,Y}(x,y)=\int_{-\infty}^y \left[\int_{-\infty}^x f_{X|Y=y}(x)dx\right]f_Y(y)dy= \int_{-\infty}^y \int_{-\infty}^x f_{X|Y=y}(x) f_Y(y)dxdy$$

Então, pela definição de densidade de probabilidade

$$f_{X,Y}(x,y)=f_{X|Y=y}(x)f_Y(y)$$

Exemplo 2.7.3

Considere o seguinte experimento de duas etapas: primeiro, escolhe-se um ponto $ x $ de acordo com a distribuição uniforme em (0,1); depois escolhe-se um ponto $ y $ de acordo com a distribuição uniforme em $ (-x,x) $. Se o vetor aleatório $ (X,Y) $ representar o resultado do experimento, qual será a densidade conjunta de X e Y ? A densidade marginal de Y? A densidade condicional de X dada Y?

Temos que $ X\sim U[0,1] $ o que implica

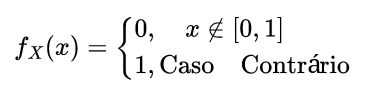
então utilizando o exemplo 2.7.2 :

$$f_{X,Y}(x,y)=f_{Y|X=x}(y)f_X(x)$$

então

e o resultado segue

Exemplo 2.7.4

Observam-se duas lâmpadas durante suas vidas úteis. Suponha as vidas independentes e exponenciais de parâmetro $ \lambda $. Sejam X o tempo de queima da primeira lâmpada a queimar e Y o tempo de queima da segunda a queimar ($ X\leq Y $).

(a) Qual a distribuição condicional de X dada Y?

Sejam $ Z_1\sim Exp(\lambda) $ e $ Z_2\sim Exp(\lambda) $ independentes e $ X=\min(Z_1,Z_2) $ e $ Y=\max(Z_1,Z_2) $. Então

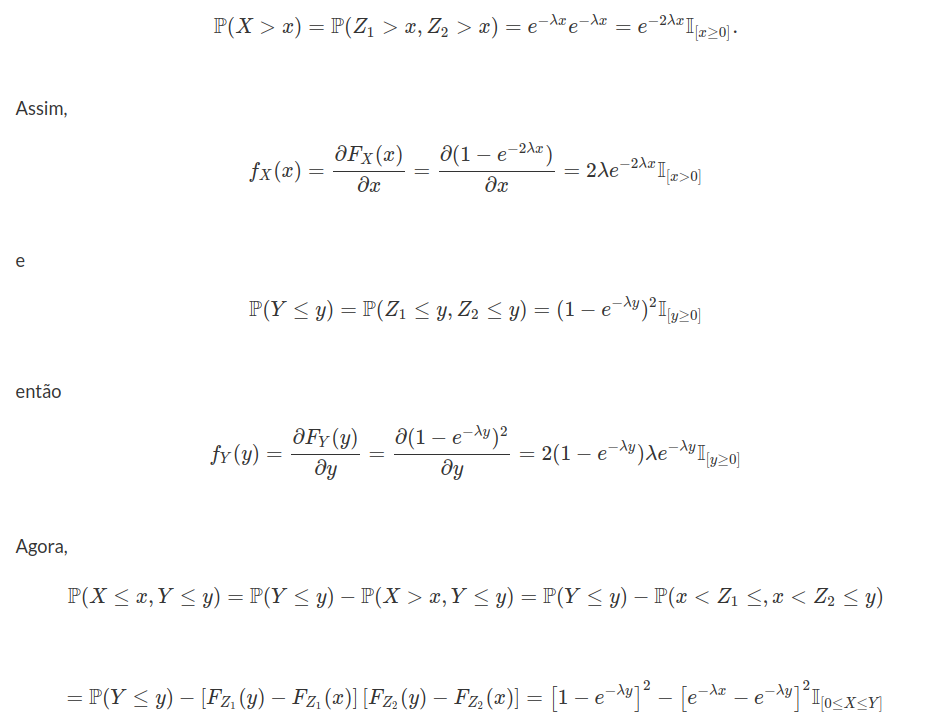
Assim,

$$f_{X,Y}(x,y)=\frac{\partial^2 F_{X,Y}(x,y)}{\partial x\partial y}=\frac{\partial}{\partial x}\left[2(1-e^{-\lambda y})\lambda e^{-\lambda y} -2(e^{-\lambda x}-e^{-\lambda y})\lambda e^{-\lambda y}=2\lambda^2 e^{-\lambda x}e^{-\lambda y}\right]$$

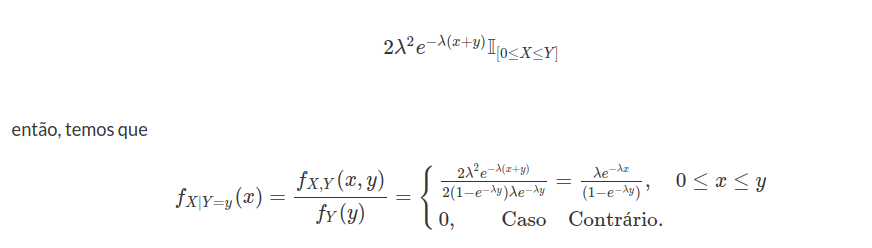
(b) Qual a distribuição de Y dada X?

Exemplo 2.7.5

Suponha que (X,Y) possua distribuição uniforme em A, onde A é uma região de área positiva. Mostre que a distribuição condicional de X dado que $ Y=y $ é uniforme em $ A_y $, a secção de A por y, onde definimos $ A_y={(x:(x,y)\in A)}$.

Seja $ (X,Y)\sim U(A) $ se, e comente se, $ \mathbb{P}(B\in \mathcal{B}^2)=\frac{\text{área}(B\cap A)}{\text{área}(A)} $

Agora como $ \text{Área}(A)> 0 $ o que implica $ (X,Y) $ é variáveis aleatórias absolutamente contínuas e

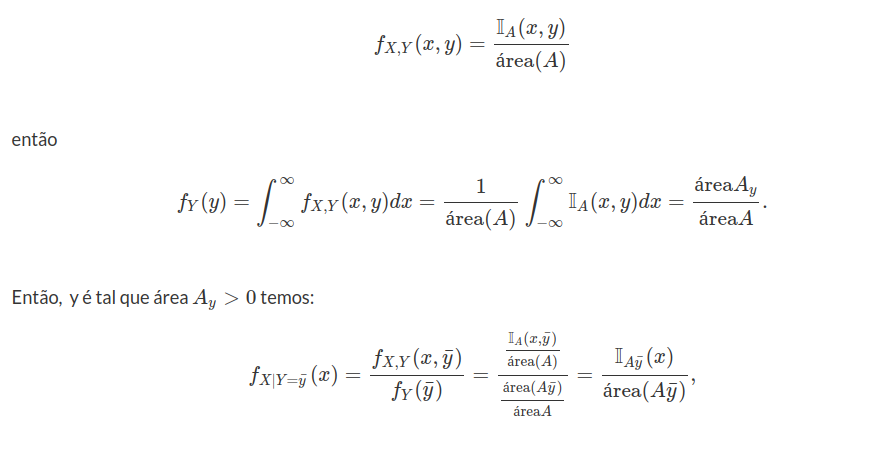
então $ X|Y=\bar{y} $ é uniforme em $ A\bar{y} $

Exemplo 2.7.6

Demonstre que se $ \mathbb{P}(X\in B| Y=y)=\mathbb{P}(X\in B) $ para todo $ B\in \mathcal{B} $ e $ y\in \mathbb{R}, $ então $ X $ e $ Y $ são independentes, de modo que $ X $ e $ Y $ são independentes se, e somente se, a distribuição condicional não depende do valor de Y.

Temos que

$$\mathbb{P}(X\leq x| Y=y)=\mathbb{P}(X\leq x)$$

o que implica que $ F_{X|Y=y}(x)=F_X(x) $ então, por

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_X(x|Y=t)dF_Y(t), (x,y)\in \mathbb{R}^2$$

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_{X|Y=y}(x)dF_Y(y)=\int_{-\infty}^y F_X(x)dF_Y(y)-F_X(x)\int_{-\infty}^y dF_Y(y)=F_X(x)F_Y(y)$$

o que implica que X e Y são independentes. Agora, pelo caso II vemos que $ X,Y $ independentes implica que

$$\mathbb{P}(X\in B|Y=y)=\mathbb{P}(X\in B)$$

com $ B\in \mathcal{B} $ e $ y\in \mathbb{R} $.

Exemplo 2.7.7

19- Seja X uma variável aleatória com densidade $ f(x) $, no qual f é contínua. Qual a distribuição condicional de X dada $ |X| $? Verifique sua resposta.

Dado que $ |X|=y $ os valores possíveis de X são $ -y $ e $ y $ então a distribuição de X dado $ |X|=y $ deverá ser concentradas nos pontos $ -y $ e $ y $ e, pelo princípio da preservação das chances relativas, temos que

$$\mathbb{P}(X=y| |X|=y)=\frac{f_X(y)}{f_X(y)+f_X(-y)}$$

e

$$\mathbb{P}(X=-y| |X|=y)=\frac{f_X(-y)}{f_X(y)+f_X(-y)}$$

Agora, verifiquemos a $ \mathbb{P}(X\in B| Y=y)=\lim_{\Delta y\rightarrow 0}\mathbb{P}(X\in B| Y\in I) $, no qual I é um intervalo que contém y, de comprimento $ \Delta y $. Seja $ B\subset \mathcal{B} $ no qual $ B $ é intervalo aberto de extremos racionais que contém y e $ I=(r_1,r_2)\cup(-r_2,-r_1) $ no qual $ r_1< y < r_2 $. Então

$$\lim_{\Delta y\rightarrow 0}\mathbb{P}(B\in \mathcal{B}|y\in I)=\lim_{\Delta \rightarrow 0}\frac{\mathbb{P}(B\in \mathcal{B},y\in I)}{\mathbb{P}(y\in I)}.$$

Agora,

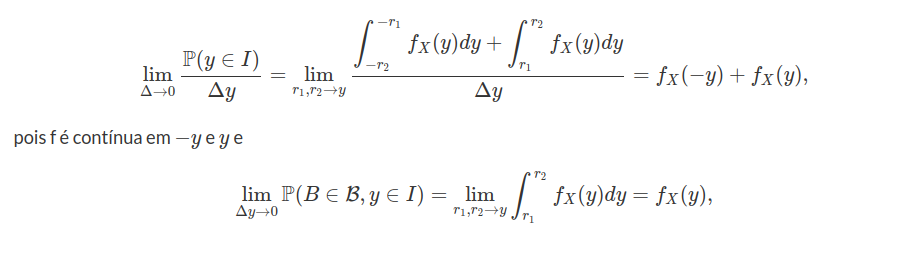
pois f é contínua em $ y $ então

$$\mathbb{P}(X=y||X|=y)=\frac{f_X(y)}{f_X(y)+f_X(-y)}.$$

Analogamente para $ -y $ teremos:

$$\mathbb{P}(X=-y||X|=y)=\frac{f_X(-y)}{f_X(y)+f_X(-y)}.$$

Isto define a distribuição condicional.

Exemplo 2.7.8

Sejam $ X $ e $ Y $ independentes, cada uma com distribuição $ N(0,\sigma^2) $. Qual a distribuição condicional de X dado $ \sqrt{X^2+Y^2} $?

Sabemos pelo exemplo 2.6.14 que:

$$\frac{(X,Y)}{\sqrt{X^2+Y^2}=z}$$

é uniforme em $ A_z $, no qual

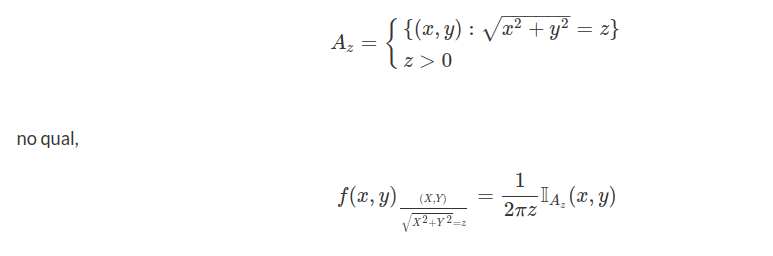
Agora aplicando o princípio da substituição temos que

$$\frac{(X,Y)}{\sqrt{X^2+Y^2}=z}\sim \left(\frac{(X)}{\sqrt{X^2+Y^2}=z},\frac{(Y)}{\sqrt{X^2+Y^2}=z}\right)$$

então:

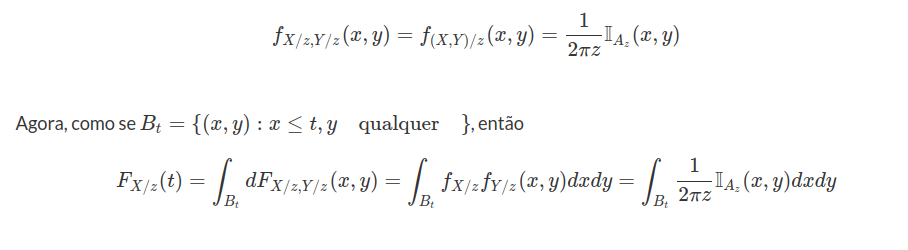
$$=\frac{1}{2\pi z}\int_{B_t\cap A_z}dxdy=\frac{1}{2\pi z}\text{Comp}(B_t\cap A_z)$$

Agora para $ 0< t< z $, temos que

$$\text{Comp}(B_t^c\cap A_z)=2z\arccos\left(\frac{t}{z}\right)$$

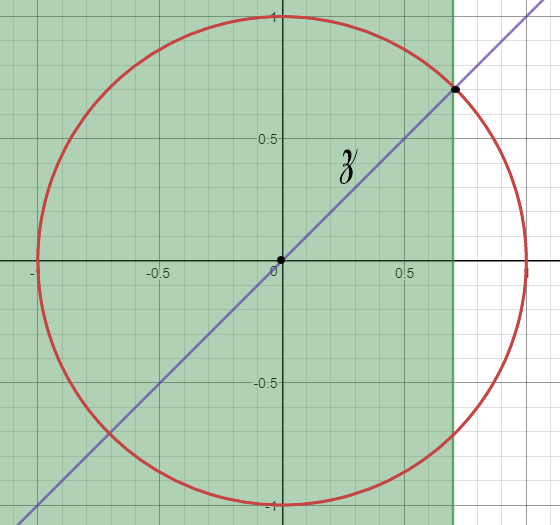
Assim

$$F_{X/z}(t)=\frac{2\pi z-\text{Comp}(B_t^c\cap A_z)}{2\pi z}=1-\frac{1}{\pi}\arccos\left(\frac{t}{z}\right)$$

Então, por analogia, observamos que $ X/z $ é simétrica em torno de zero e assim

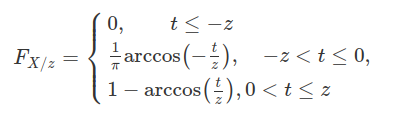
Agora como $ X/Z $ é simétrico em torno de zero e limitada (e portanto integrável) temos que

$$\mathbb{E}\left(X|\sqrt{X^2+Y^2}\right)=0$$

Exemplo 2.7.9

Explique como os casos abaixos podem ser consideradas consequências do princípio da preservação de chances relativas.

\textbf{Caso I:} Y é variável aleatória discreta e assume os valores $ y_1,y_2, \dots $. Temos que se $ B_1=[X\leq x_1] $, $ B_2=[X\leq x_2] $, assim para $ y_n $ tal que

$$\mathbb{P}(Y=y_n)> 0$$

temos

$$\frac{\mathbb{P}(X\leq x_1|Y=y_n)}{\mathbb{P}(X\leq x_2|Y=y_n)}=\frac{\frac{\mathbb{P}(X\leq x_1,Y=y_n)}{\mathbb{P}(Y=y_n)}}{\frac{\mathbb{P}(X\leq x_2,Y=y_n)}{\mathbb{P}(X\leq x_2,Y=y_n)}}=\frac{\mathbb{P}(X\leq x_1,Y=y_n)}{\mathbb{P}(X\leq x_2,Y=y_n)}$$

Então, as chamas relativas são preservadas e podemos considerar a divisão por

$$\mathbb{P}(Y=y_n)$$

como uma normalização pois

$$\mathbb{P}(Y=y_n)=\lim_{x\rightarrow \infty}\mathbb{P}(X\leq x, Y=y_n)$$

\textbf{Caso II:} $ X $ e $ Y $ são variáveis aleatórias independentes, então se

$$\mathbb{P}(Y=y)> 0$$

Então, temos que

$$\frac{\mathbb{P}(X\leq x_1|Y=y)}{\mathbb{P}(X\leq x_2|Y=y)}=\frac{\mathbb{P}(X\leq x_1)}{\mathbb{P}(X\leq x_2)}$$

$$=\frac{\mathbb{P}(X\leq x_1)\mathbb{P}(Y=y)}{\mathbb{P}(X\leq x_2)\mathbb{P}(Y=y)}=\frac{\mathbb{P}(X\leq x_1,Y=y)}{\mathbb{P}(X\leq x_2,Y=y)}$$

Então, as chances relativas também neste caso são preservadas e podemos considerar

$$\lim_{x\rightarrow \infty}\mathbb{P}(X\leq x, Y=y)=\mathbb{P}(Y=y).$$

Exemplo 2.7.10

Sejam X e Y o mínimo e o máximo de duas variáveis aleatórias independentes com distribuição comum $ Exp(\lambda) $, no qual $ \lambda > 0 $. Mostre de duas maneiras que $ Y-X| X\sim Exp(\lambda) $

(a) A partir da densidade conjunta de X e Y-X.

Temos $ T_1\sim Exp(\lambda) $$ T_2\sim Exp(\lambda) $ com $ T_1 $ e $ T_2 $ são independentes. Seja $ X=\min(T_1,T_2) $ então

$$\mathbb{P}(X\leq x)=1-\mathbb{P}(X> x)=1-\mathbb{P}(T_1> x)\mathbb{P}(T_2> x)=1-e^{-2\lambda x}$$

e $ Y=\max(T_1,T_2) $ então $ \mathbb{P}(Y\leq y)=\mathbb{P}(T_1\leq y)\mathbb{P}(T_2\leq y)=\left(1-e^{-\lambda y}\right)^2 $, $ y\geq 0 $ e também

$$\mathbb{P}(X\leq x, Y\leq y)=\mathbb{P}(Y\leq y)-\mathbb{P}(X> x, Y\leq y)=\mathbb{P}(Y\leq y)-\mathbb{P}(x< T_1\leq y,x< T_2\leq y)$$

$$=\mathbb{P}(Y\leq y)-\left[F_{T_1}(y)-F_{T_1}(x)\right]^2=\left(1- e^{-\lambda y}\right)^2-\left(e^{-\lambda x}-e^{-\lambda y}\right)^2, \quad \quad 0\leq x\leq y$$

então

$$f_X(x)=\frac{\partial F_X(x)}{\partial x}=\frac{\partial}{\partial x}[1-e^{-2\lambda x}]=2\lambda e^{-2\lambda x}, \quad x> 0$$

$$f_Y(y)=\frac{\partial F_Y(y)}{\partial y}=\frac{\partial}{\partial y}[1-e^{-2\lambda y}]^2=2\lambda e^{-\lambda y}(1-e^{\lambda y}), \quad y> 0$$

$$f_{X,Y}(x,y)=\frac{\partial^2 F_{X,Y}(x,y)}{\partial y\partial x}=\frac{\partial}{\partial y\partial x}[(1-e^{-2\lambda x})^2-(e^{-\lambda x}-e^{-\lambda y})^2]=\frac{\partial}{\partial y}\left(2\lambda e^{-\lambda x}(e^{-\lambda x}-e^{-\lambda y})\right)=2\lambda^2 e^{-\lambda (x+y)}, \quad 0\leq x\leq y$$

Agora, aplicando o método do Jacobiano, obteremos a distribuição conjunta de W e Z, no qual:

$ W=X $ e $ Z=Y-X $ o que implica que $ X=W $, $ Y=Z+W $ então

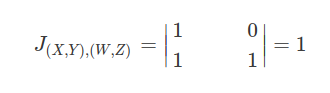
Desta forma,

$$f_{W,Z}(w,z)=|J_{(X,Y),(W,Z)}|f_{X,Y}(w,z-w)=2\lambda^2e^{-\lambda (z+2w)}, w\geq 0 \quad \quad z\geq 0,$$

então, usando o caso $ III $, temos que se $ f_W(w)> 0 $ ou seja $ w=x> 0 $.

$$f_{Z|W=w}(z)=\frac{f_{W,Z}(w,z)}{f_W(w)}=\frac{2\lambda^2e^{-\lambda(z+2w)}}{2\lambda e^{-2\lambda w}}=\lambda e^{-\lambda z}, z\geq 0 \quad \quad w\geq 0$$

ou seja, $ Z|W=w\sim Exp(\lambda) $ para qualquer $ w=x\geq 0 $.

(b) Utilizando o princípio da substituição e o resultado do exemplo 16b.

Pelo princípio da substituição temos que $ (Y-X)|X=x\sim Y-x| X=x $. Então

$$\mathbb{P}(Y-X\leq w|X=x)=\mathbb{P}(Y-x\leq w| X=x)=\mathbb{P}(Y\leq w+x| X=x)$$

Agora, pelo exercício 16b, temos que

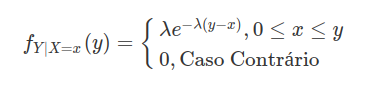
Então,

$$\mathbb{P}(Y\leq w+x|X=x)=\int_{x}^{w+x}\lambda e^{-\lambda (y-x)}dy=e^{-\lambda(y-x)}\bigg|_{x}^{w+x}=1-e^{-\lambda w}, \quad w> 0$$

Então $ (Y-X)|X=x\sim Exp(\lambda) $ para todo $ x\geq 0 $.

Exemplo 2.7.11

(a) Seja $ X=(X_1,\dots, X_n) $ um vetor aleatório com densidade $ f(x_1,\dots,x_n) $. Use o princípio da preservação de chances relativas para obter dado $ (X_{k+1},\dots, X_n)=(x_{k+1},\dots,x_n) $, onde $ 1\leq k\leq n-1 $.

Usando o princípio da preservação de chances relativas, temos que

$$f_{(X_1,X_2,\dots,X_k)|(X_{k+1},\dots,X_n)=(x_{k+1},\dots,x_n)}(x_1,\dots,x_k)=\frac{f_{X_1,X_2,\dots,X_n}(x_1,x_2,\dots,x_n)}{ \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\dots\int_{-\infty}^{\infty}f_{X_1,X_2,\dots,X_n}(x_1,\dots,x_n)dx_1dx_2\dots dx_k }$$

$$=\frac{f_{X_1,X_2,\dots,X_n}(x_1,x_2,\dots,x_n)}{f_{X_{k+1},\dots,X_n}(x_{k+1},\dots,x_n)}$$

(b) Sejam $ X_1, X_2 e X_2 $ independentes com distribuição comum $ U[0,1] $, com $ X_{(1)}, X_{(2)} $ e $ X_{(3)} $ as estatísticas de ordem. Determine a distribuição condicional de $ X_{(2)} $ dadas $ X_{(1)} $ e $ X_{(3)} $

Temos pelo exemplo 2.5.5:

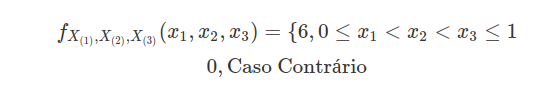
então

$$f_{X_{(1)},X_{(3)}}(x_1,x_3)=\int_{-\infty}^\infty f_{X_{(1)},X_{(2)},X_{(3)}}(x_1,x_2,x_3)dx_2=6\int_{x_1}^{x_3}dx_2=6(x_3-x_1), \quad0\leq x_1< x_3\leq 1.$$

Agora, aplicando o item (a):

$$f_{X_{(2)}|(X_{(1)},X_{(3)})}(x_2)=\frac{6}{6(x_3-x_1)}=\frac{1}{x_3-x_1},\quad 0\leq x_1< x_2< x_3\leq 1.$$

Então, $ X_{(2)}|X_{(1)},X_{(3)} $ será uma variável aleatória uniforme em $ [x_1,x_3] $ no caso de $ 0\leq x_1< x_3\leq 1 $.

Exemplo 2.7.12

Sejam $ X_1,\dots, X_n $ variáveis aleatórias independentes e identicamente distribuídas, com distribuição contínua F. Seja $ X=\max_{1\leq i\leq n}X_i $.

(a) Mostre que para todo $ k=1,2, \dots, n, $

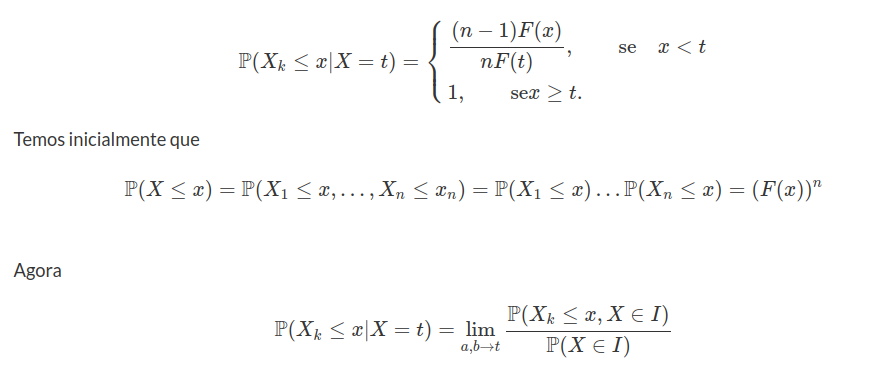
no qual $ I=(a,b) $ com $ a< t< b $. Tomemos incialmente $ x\in [0,t) $ então:

$$[X_k\leq x,X\in I]=[X_k\leq x,a< X< b]=[X_k\leq x]\cap [a< X< b]$$

no qual,

$$[a< X< b]=\bigcup_{i=1}^n \left([X_i> a]\bigcap_{i=1}^n [X_i< b]\right)$$

então

$$[X_k\leq x, X\in I]=\bigcup_{i=1}^n \left([X_i> a]\cap [X_k\leq x]\bigcap [X_i< b]\right)$$

para a e b suficientemente entre próximas de t, no qual $ 0< x< a< t< b $.

$$\mathbb{P}([X_k\leq x,X\in I])=\sum_{i=1}^n \mathbb{P}\left([X_i> a]\cap [X_k\leq x]\bigcap_{i=1}^n [X_i< b]\right)$$

$$=(n-1)\left[F(b^-)\right]^{n-2}\left[F(b^-)-F(a)\right]F(x)=(n-1)\left[F(b)\right]^{n-2}\left[F(b)-F(a)\right]F(x)$$

Agora, temos também que

$$\mathbb{P}(X\in I)=\mathbb{P}(a< X< b)=\left[F(b^-)\right]^n-\left[F(a)\right]^n=\left[F(b)\right]^n-\left[F(a)\right]^n$$

Então,

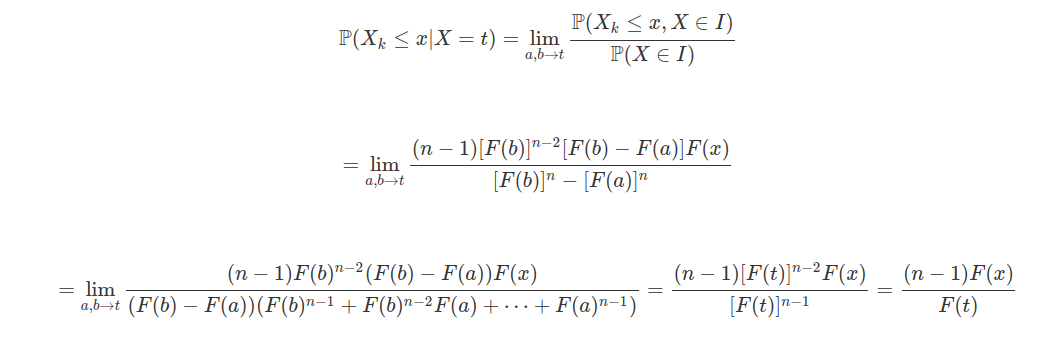
Agora para

$$\mathbb{P}(X_k\leq t,X\in I)=\sum_{i=1}^n \mathbb{P}\left([X_i> a]\bigcap_{i=1}^n[X_i< b]\right)=n[F(b)-F(a)][F(b)]^{n-1}$$

então

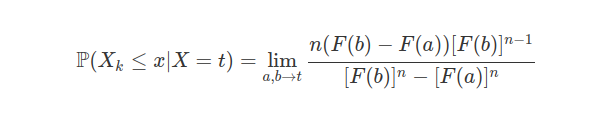
$$=\frac{n[F(t)]^{n-1}}{n[F(t)]^{n-1}}=1$$

Agora, como $ \mathbb{P}(X_k\leq | X=t) $ é contínua a direita, temos que

$$\mathbb{P}(X_k\leq t| X=t)=\lim_{h\downarrow t}\mathbb{P}(X_k\leq h| X=t)=1$$

Assim,

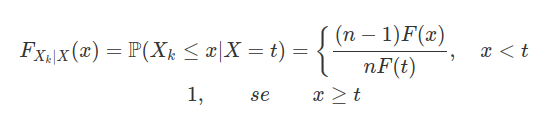
Então

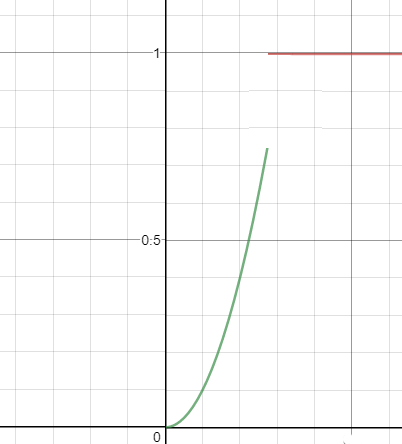
Com o tamanho do salto da figura sendo

$$\mathbb{P}(X_k=t|X=t)=1-\frac{(n-1)}{n}=\frac{1}{n}$$

(b) Suponha F diferenciável. Existe densidade condicional no item (a)?

Como visto no gráfico do item a a distribuição de $ X_k|X=t $ é mista de discreta e contínua. Assim, a densidade condicional é a densidade da parte contínua e é igual a

$$f_{X_k|X=t}(x)=\frac{(n-1)}{n}\frac{f(x)}{F(t)}$$

no qual

$$f(x)=\frac{\partial F(x)}{x}, x< t.$$

Exemplo 2.7.13

Suponha que $ Y $ possua densidade $ f_Y(y) $ e que a distribuição condicional de X, dado que $ Y=y $, possua densidade $ f(x|y) $, para todo $ y $ (ou pelo menos para “quase todo” valor possível de Y). Demonstre que

$$f(x,y)= f_Y(y)f(x|y)$$

é a densidade conjunta de $ X $ e $ Y $.

Temos que

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_X(x|Y=y)dF_Y(t)$$

Agora se $ Y $ e $ X|Y $ são distribuições absolutamente contínuas então

$$dF_Y(y)=f_Y(y)dy$$

e

$$F_X(X|Y=y)=\int_{-\infty}^x f_{X|Y=y}(x)dx$$

Assim,

$$F_{X,Y}(x,y)=\int_{-\infty}^y \left[\int_{-\infty}^x f_{X|Y=y}(x)dx\right]f_Y(y)dy= \int_{-\infty}^y \int_{-\infty}^x f_{X|Y=y}(x) f_Y(y)dxdy$$

Então, pela definição de densidade de probabilidade

$$f_{X,Y}(x,y)=f_{X|Y=y}(x)f_Y(y)$$

Exemplo 2.7.14

Considere o seguinte experimento de duas etapas: primeiro, escolhe-se um ponto $ x $ de acordo com a distribuição uniforme em (0,1); depois escolhe-se um ponto $ y $ de acordo com a distribuição uniforme em $ (-x,x) $. Se o vetor aleatório $ (X,Y) $ representar o resultado do experimento, qual será a densidade conjunta de X e Y ? A densidade marginal de Y? A densidade condicional de X dada Y?

Temos que $ X\sim U[0,1] $ o que implica

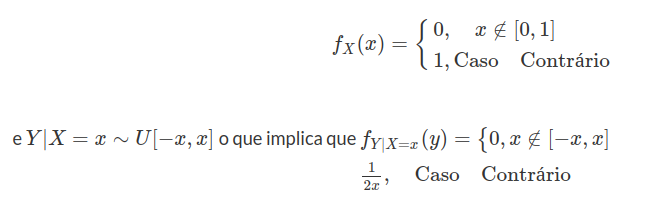
então utilizando o exemplo 2.7.2:

$$f_{X,Y}(x,y)=f_{Y|X=x}(y)f_X(x)$$

então

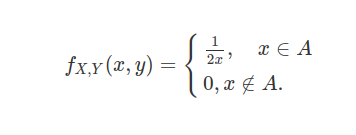
com $ A={(x,y):0\leq x\leq 1 \quad e \quad -x\leq y\leq x} $ e portanto

$$f_Y(y)=\int_{-\infty}^\infty f_{X,Y}(x,y)dx=\int_{|y|}^1\frac{1}{2x}dx=\frac{1}{2}\left[\ln(x)\right]_{|y|}^1=-\frac{1}{2}\ln(|y|),\quad -1\leq y\leq 1.$$

Agora, aplicando que X e Y tendo densidade conjunta

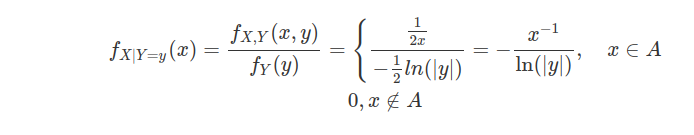
e o resultado segue

Exemplo 2.7.15

Observam-se duas lâmpadas durante suas vidas úteis. Suponha as vidas independentes e exponenciais de parâmetro $ \lambda $. Sejam X o tempo de queima da primeira lâmpada a queimar e Y o tempo de queima da segunda a queimar ($ X\leq Y $).

(a) Qual a distribuição condicional de X dada Y?

Sejam $ Z_1\sim Exp(\lambda) $ e $ Z_2\sim Exp(\lambda) $ independentes e $ X=\min(Z_1,Z_2) $ e $ Y=\max(Z_1,Z_2) $. Então

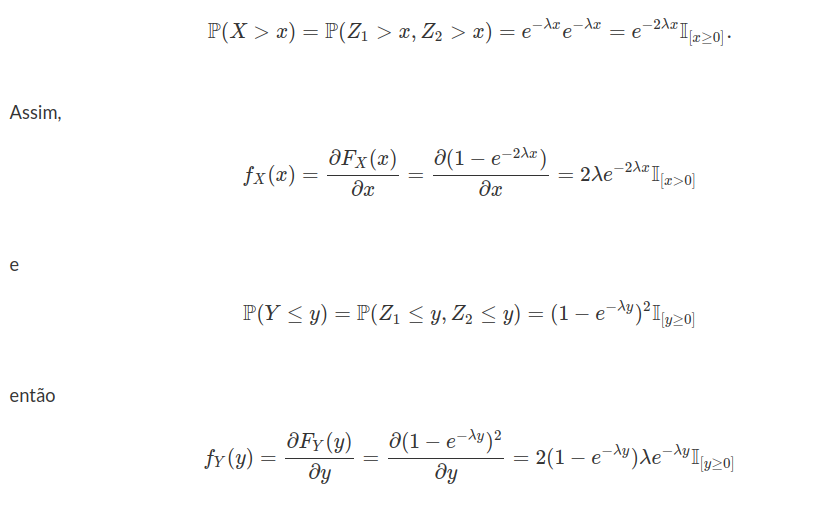
Agora,

$$\mathbb{P}(X\leq x,Y\leq y)=\mathbb{P}(Y\leq y)-\mathbb{P}(X> x,Y\leq y)=\mathbb{P}(Y\leq y)-\mathbb{P}(x< Z_1\leq, x< Z_2\leq y)$$

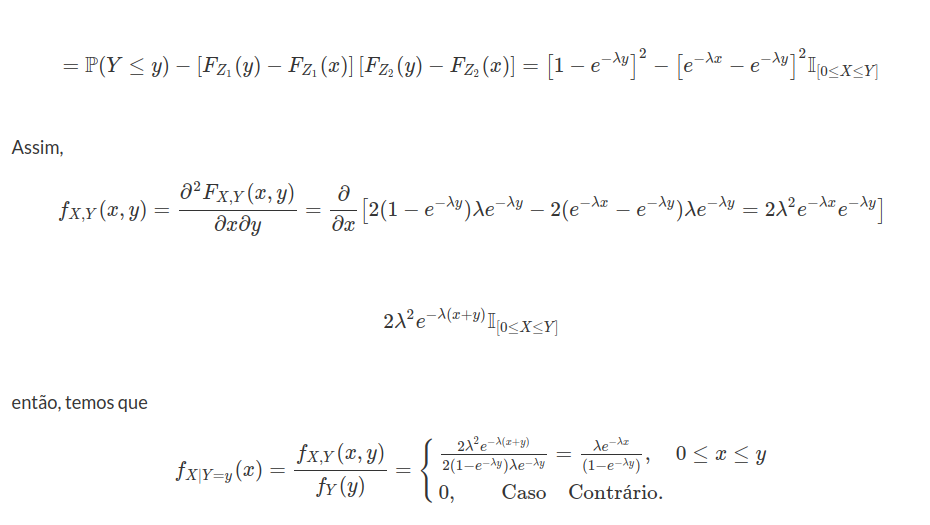
(b) Qual a distribuição de Y dada X?

Exemplo 2.7.16

Suponha que (X,Y) possua distribuição uniforme em A, onde A é uma região de área positiva. Mostre que a distribuição condicional de X dado que $ Y=y $ é uniforme em $ A_y $, a secção de A por y, onde definimos $ A_y={x:(x,y)\in A} $.

Seja $ (X,Y)\sim U(A) $ se, e comente se, $ \mathbb{P}(B\in \mathcal{B}^2)=\frac{\text{área}(B\cap A)}{\text{área}(A)} $

Agora como $ \text{Área}(A)> 0 $ o que implica $ (X,Y) $ é variáveis aleatórias absolutamente contínuas e

então $ X|Y=\bar{y} $ é uniforme em $ A\bar{y} $

Exemplo 2.7.17

Demonstre que se $ \mathbb{P}(X\in B| Y=y)=\mathbb{P}(X\in B) $ para todo $ B\in \mathcal{B} $ e $ y\in \mathbb{R}, $ então $ X $ e $ Y $ são independentes, de modo que $ X $ e $ Y $ são independentes se, e somente se, a distribuição condicional não depende do valor de Y.

Temos que

$$\mathbb{P}(X\leq x| Y=y)=\mathbb{P}(X\leq x)$$

o que implica que $ F_{X|Y=y}(x)=F_X(x) $ então, pela relação

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_X(x|Y=t)dF_Y(t),(x,y)\in \mathbb{R}^2$$

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_{X|Y=y}(x)dF_Y(y)=\int_{-\infty}^y F_X(x)dF_Y(y)-F_X(x)\int_{-\infty}^y dF_Y(y)=F_X(x)F_Y(y)$$

o que implica que X e Y são independentes. Agora, pelo caso II vemos que $ X,Y $ independentes implica que

$$\mathbb{P}(X\in B|Y=y)=\mathbb{P}(X\in B)$$

com $ B\in \mathcal{B} $ e $ y\in \mathbb{R} $.

\end{example}

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_X(x|Y=t)dF_Y(t), (x,y)\in \mathbb{R}^2$$

2.8 - Distribuição de probabilidade conjunta de funções de variáveis aleatórias

Sejam $ X_1 $ e $ X_2 $ variáveis aleatórias conjuntamente contínuas com densidade de probabilidade conjunta $ f_{X_1,X_2} $. Algumas vezes estamos interessados em obter a distribuição conjunta das variáveis aleatórias $ Y_1 $ e $ Y_2 $ que são funções de $ X_1 $ e $ X_2 $. Especificamente, suponha que $ Y_1=g_1(X_1,X_2) $ e $ Y_2=g_2(X_1,X_2) $ para funções $ g_1 $ e $ g_2 $.

Assuma que as funções $ g_1 $ e $ g_2 $ satisfaçam as seguintes condições:

1. As equações $ y_1=g_1(x_1,x_2) $ e $ y_2=g_2(x_1,x_2) $ podem ser unicamente resolvidas para $ x_1 $ e $ x_2 $ nos termos de $ y_1 $ e $ y_2 $ com soluções dadas por, digamos, $ x_1=h_1(y_1,y_2) $ e $ x_2=h_2(y_1,y_2) $

2. As funções $ g_1 $ e $ g_2 $ tem derivadas parciais contínuas em todos os pontos $ (x_1,x_2) $ e são tais que o seguinte determinante $ 2times;2 $

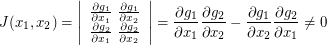
para todos os pontos $ (x_1,x_2) $. Sob essas duas condições podemos mostrar que as variáveis aleatórias $ Y_1 $ e $ Y_2 $ são continuamente conjuntas com função densidade conjunta dada por

$$f_{Y_1Y_2}(y_1,y_2)=f_{X_1,X_2}(x_1,x_2)|J(x_1,x_2)|^{-1}$$

em que $ x_1=h_1(y_1,y_2) $ e $ x_2=h_2(y_1,y_2) $.

Exemplo 2.8.1

Sejam $ X_1 $ e $ X_2 $ variáveis aleatórias conjuntamente contínuas com função densidade de probabilidade conjunta $ f_{X_1,X_2} $. Sejam $ Y_1=X_1+X_2 $ e $ Y_2=X_1-X_2 $. Encontre a função densidade acumulada de $ Y_1 $ e $ Y_2 $ em termos de $ f_{X_1,X_2} $.

Seja $ g_1(x_1,x_2)=x_1+x_2 $ e $ g_2(x_1,x_2)=x_1-x_2 $. Então

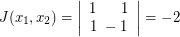
Além disso, as equações $ y_1=x_1+x_2 $ e $ y_2=x_1-x_2 $ têm como soluções $ x_1=(y_1+y_2)/2 $ e $ x_2=(y_1-y_2)/2 $ e então, segue que a densidade desejada é dada por

$$f_{Y_1,Y_2}(y_1,y_2)=\frac{1}{2}f_{X_1,X_2}\left(\frac{y_1+y_2}{2},\frac{y_1-y_2}{2}\right)$$

Soma de variáveis aleatórias e multiplicação por constante

É importante ser capaz de calcular a distribuição de $ aX + bY $ a partir das distribuições de $ X $ e $ Y $ quando $ X $ e $ Y $ são independentes, e $ a $ e $ b $ são constantes.

Teorema 2.8.1

Suponha que $ X $ e $ Y $ são variáveis aleatórias contínuas com função densidade de probabilidade conjunta $ f $ e seja $ Z=aX+bY $. Então

$$F_Z(z)= \int_{-\infty}^{z} \int_{- \infty}^{\infty}\frac{1}{|a|}f\left(\frac{s-bt}{a},t\right)dtds.$$

Demonstração

De fato, temos que

$$F_Z(z)=\mathbb{P}(Z\leq z)=\mathbb{P}(aX+bY \leq z)=\int_{ax+by\leq z}f(t)dt= \int_{-\infty}^{\infty}\int_{- \infty}^{\frac{z-by}{a}}f(x,y)dx dy.$$

Considerando a mudança de variável $ s=ax+by $ e $ t=y $, temos que $ s=ax+bt \Rightarrow x=\frac{s-bt}{a} $ e que além disso o determinante da matriz jacobiana é dado por

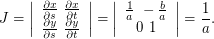
portanto

$$\int_{-\infty}^{\infty}\int_{- \infty}^{z}\left|\frac{1}{a}\right| f\left(\frac{s-bt}{a},t\right)ds dt= \int_{-\infty}^{z}\int_{- \infty}^{\infty}\frac{1}{|a|}f\left(\frac{s-bt}{a},t\right)dt ds$$

e, assim concluímos que a fdp da variável aleatória $ Z = aX+bY $ é dada por

$$f_Z(s)=\int_{- \infty}^{\infty}\frac{1}{|a|}f\left(\frac{s-bt}{a},t\right)dt,$$

e que a sua função de distribuição acumulada é dada por

$$F_Z(z)= \displaystyle \int_{-\infty}^{z} \int_{- \infty}^{\infty}\frac{1}{|a|}f\left(\frac{s-bt}{a},t\right)dtds.$$

Teorema 2.8.2

Suponha que $ X $ e $ Y $ são variáveis aleatórias contínuas independentes com funções densidades de probabilidades $ f_X $ e $ f_Y $ e seja $ Z=aX+bY $. Então

$$F_Z(z)= \int_{-\infty}^{z} \int_{- \infty}^{\infty}\frac{1}{|a|}f_X\left(\frac{s-bt}{a}\right)f_Y(t)dtds.$$

Para verificar que este teorema é verdadeiro, basta aplicars o Teorema 2.8.1 e utilizarmos a hipótese de independência das variáveis $ X $ e $ Y $. Portanto $ f(\frac{s-bt}{a},t)=f_X(\frac{s-bt}{a})f_Y(t) $ e o resultado segue.

Quando $ a $ e $ b $ são iguais a $ 1 $ então $ f_{Z}(s) $ é chamada de convolução das distribuições $ f_X $ e $ f_Y $.

Exemplo 2.8.2

Seja $ A=({(x,y):0\leq x \leq 1, 0\leq y \leq 1 \ \text{e} \ x+y\leq 1}) $, ou seja, A é um triângulo. Suponha que $ X $ e $ Y $ tenham densidade conjunta dada por

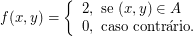
Qual a distribuição de $ Z = X+Y $?

Para calcular essa distribuição basta usarmos o teorema 2.8.2 no qual $ a=1 $ e $ b=2 $, então neste caso

$$F_Z(z)=\int_{-\infty}^{z} \int_{- \infty}^{\infty}\frac{1}{|a|}f\left(\frac{s-bt}{a},t\right) dt ds=\int_{0}^{z}\int_{0}^{z-x}2 dy dx=z^{2}$$

Teorema 2.8.3

Seja $ X $ uma variável aleatória com densidade de probabilidade $ f_X $. Então a densidade de probabilidade de $ X^{2n} $ é dada por

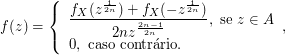
no qual o conjunto $ A $ depende da variável aleatória $ X $.

Seja $ Z=X^{2n} $. Temos então que:

$$F_Z(z)=\mathbb{P}(Z\leq z)=\mathbb{P}(X^{2n}\leq z)=\mathbb{P}(|X|\leq z^{\frac{1}{2n}})=\mathbb{P}(-z^{\frac{1}{2n}}\leq X \leq z^{\frac{1}{2n}})$$

de onde segue que

$$F_Z(z)=\int_{-z^{\frac{2}{2n}}}^{-z^{\frac{2}{2n}}}f_X(t)dt=\int_{-z^{\frac{2}{2n}}}^{0}f_X(t)+\int_{0}^{-z^{\frac{2}{2n}}}f_X(t)$$

e, utilizando o teorema de cálculo de mudança de variável, segue que

$$\int_{-z^{\frac{2}{2n}}}^{0}f_X(t)dt+\int_{0}^{-z^{\frac{2}{2n}}}f_X(t)dt=\int_{0}^{z}\frac{f_X(-z^{\frac{1}{2n}})}{2nz^{\frac{2n-1}{2n}}}+\int_{0}^{z}\frac{f_X(z^{\frac{1}{2n}})}{2nz^{\frac{2n-1}{2n}}}=\int_{0}^{z}\frac{f_X(z^{\frac{1}{2n}})+f_X(-z^{\frac{1}{2n}})}{2nz^{\frac{2n-1}{2n}}}.$$

Assim a fdp de $ Z $ é dada por

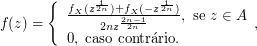
em que $ A $ depende da variável aleatória $ X $.

Teorema 2.8.4

Seja $ X $ uma variável aleatória com densidade de probabilidade $ f_X $. Então a densidade de probabilidade de $ X^2 $ é dada por

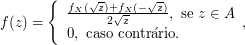
em que $ A $ depende da variável aleatória $ X $.

Demonstração

Basta aplicar o Teorema 2.8.3 com $ n=1 $ e o resultado segue.

Exemplo 2.8.3

Suponha que $ X $ é uma variável aleatória com densidade de probabilidade dada por

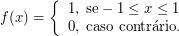
Qual a densidade de probabilidade de $ X^4 $?

Para resolvermos este exemplo basta utilizar o Teorema 2.8.3 com $ n=2 $, assim temos que a função densidade de probabilidade de $ Z = X^4 $ é dada por

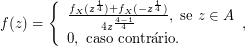
ou seja,

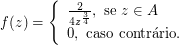
em que $ A $ depende da variável aleatória $ X $, e neste caso $ A=(z \in \mathbb{R}| 0\leq z \leq 1) $.

Teorema 2.8.5

Suponha que $ X $ é uma variável aleatória com densidade de probabilidade $ f_X $. Então a densidade de probabilidade de $ Y = |X| $ é dada por

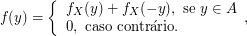
em que $ A $ depende da variável aleatória $ X $.

Seja $ Y=|X| $, então

$$F_Y(y)=\mathbb{P}(Y\leq y)=\mathbb{P}(|X|\leq y)=\mathbb{P}(-y\leq X \leq y)=\int_{-y}^{y}f_X(t)dt=\int_{0}^{y}f_X(t)dt+\int_{-y}^{0}f_X(t)dt$$

de onde segue que

$$F_Y(y)=\int_{0}^{y}f(t)+f(-t)dt.$$

Portanto a fdp de $ Y $ é dada por

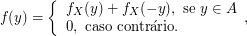
em que o conjunto $ A $ depende da variável aleatória $ X $.

Exemplo 2.8.4

Sejam $ X $ e $ Y $ variáveis aleatórias independentes com distribuição uniforme em $ [\Theta -1/2, \Theta+1/2] $, no qual $ \Theta \in \mathbb{R} $. Prove que a distribuição de $ X-Y $ não depende de $ \Theta $, achando sua densidade.

$ X $ e $ Y $ independentes implica que

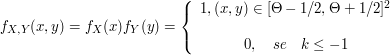
Assim, considere $ k\leq 0 $:

(imagem em falta)

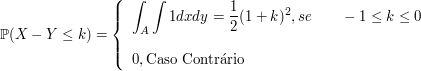
Analogamente, por simetria para $ k> 0 $

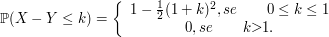
Então,

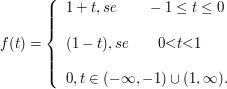
Exemplo 2.8.5

Sejam as variáveis aleatórias $ X_1, \dots, X_n $ independentes e exponenciais com parâmetros $ \alpha_1, \dots, \alpha_n $.

(a) Mostre que a distribuição de $ Y=\min_{1\leq i\leq n} X_i $ é exponencial. Qual o parâmetro ?

Considere $ y> 0 $

$$\mathbb{P}(Y> y)=\mathbb{P}(X_1> y,\dots, X_n>)=\prod_{i=1}^n \mathbb{P}(X_i> y)=e^{-(\sum_{i=1}^n\alpha_i)y}$$

o que implica que

$$\mathbb{P}(Y\leq y)=1-e^{-(\sum_{n}^\infty \alpha_i)y}$$

Agora considere $ y\leq 0 $

$$\mathbb{P}(Y> y)=1$$

o que implica que

$$\mathbb{P}(Y\leq y)=0$$

Então $ Y\sim Exp\left(\sum_{i=1}^n \alpha_i \right) $

(b) Prove que para $ k=1,\dots,n $

$$\mathbb{P}(X_k=\min_{1\leq i\leq n} X_i)=\frac{\alpha_k}{\alpha_1+\dots+\alpha_n}.$$

Temos que o evento

$$[X_k=\min_{1\leq i\leq n} Y_i]=[X_k\leq \min_{i\neq k}]$$

Agora, fazendo $ U_k=\min_{i\neq k} X_i $, temos que $ X_k $ e $ U_k $ são independentes então

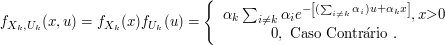
Então

$$\mathbb{P}\left(X_k=\min_{1\leq i \leq n} X_i\right)=\mathbb{P}\left([X_k\leq U_k]\right)=\int_0^\infty \int_0^u \alpha_u\left(\sum_{i\neq k}\alpha_i\right)e^{-\left(\sum_{i\neq k}\alpha_i\right)u}e^{-\alpha_k x}dx du$$

$$=\int_0^\infty \left(\sum_{i\neq k}\alpha_i\right)e^{-\left(\sum_{i\neq k}\alpha_i\right)u}\left[-e^{-\alpha_u x}\right]_0^u du= \int_0^\infty \left(\sum_{i\neq k}\alpha_i\right)e^{-\left(\sum_{i\neq k}\alpha_i\right)u} \left(1-e^{-\alpha_k u}\right)du $$

$$=1-\frac{\sum_{i\neq k}\alpha_i }{\sum_{i=1}^n \alpha_i}=\frac{\alpha_k}{\alpha_1+\dots +\alpha_n}$$

Exemplo 2.8.6

Seja $ X $ uma variável aleatória cuja função de distribuição F é uma função contínua na reta. Prove que a distribuição de $ Y=F(X) $ é $ U[0,1] $.

Suponha que $ F $ é estritamente crescente e contínua, então existe inversa

$$F^{-1}:[0,1]\rightarrow \mathbb{R}$$

e portanto sejam $ a,b\in [0,1] $, $ a< b $:

$$\mathbb{P}(a< Y \leq b)=\mathbb{P}(a< F(X)\leq b)=\mathbb{P}(F^{-1}(a)< X\leq F^{-1}(b))=F(F^{-1}(b))-F(F^{-1}(a))=b-a$$

então como $ \mathbb{P}(0\leq Y\leq 1)=1 $, temos que $ Y\sim U[0,1] $.

Caso geral, se $ F $ é contínua, não-decrescente em $ \mathbb{F} $ e contínua, com $ \lim_{x\rightarrow \infty}F(x)=1 $ e $ \lim_{x\rightarrow -\infty}F(x)=0 $. Então $ F $ será constante em uma união disjuntas enumerável de intervalos fechados, ou seja no conjunto

$$A=\bigcup_{i} I_i$$

no qual $ I_i=[a_i,b_i] $, com $ a_i< b_i< a_{i+1}< b_{i+1} $, para todo $ i \in \mathbb{N} $. E também $ F $ será estritamente em

$$B=\mathbb{R}-A=\bigcup_j J_j$$

no qual $ J_j=(b_j,a_{j+1}) $. Então, $ F $ é estritamente crescente quando restrita a B. Se $ x\in \mathbb{R} $ e $ x\notin B $, o que implica que existe um $ i_2 $ tal que $ a_{i_2}\leq x\leq b_{i_2} $ com $ F(x)=F(a_{i_2})=F(b_{i_2}) $. Desta forma,

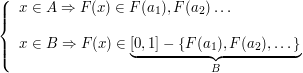
Desta forma temos que a função

$ F|_B: B\rightarrow F(B) $, então $ F|_B $ é contínua e estritamente crescente, o que implica que existe uma função

$$(F|_B)^{-1}:[0,1]\rightarrow B.$$

Agora, sejam $ w,z\in [0,1] $ e $ w< z $. Então,

$$\mathbb{P}(w< Y\leq z)=\mathbb{P}(w< F(X)\leq z)$$

temos então 4 possibilidades

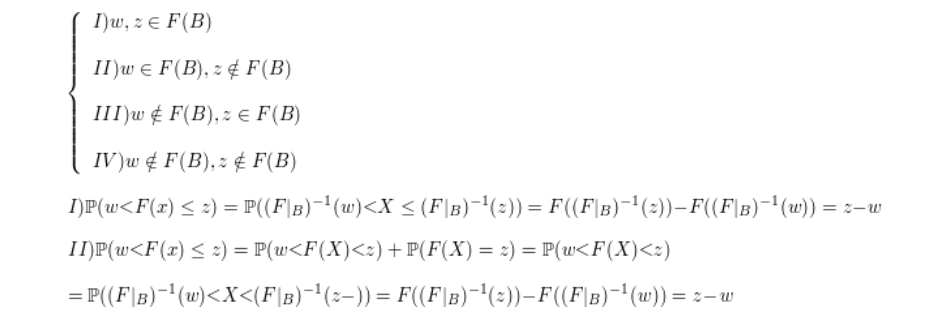
observe que $ \mathbb{P}(F(X)=z)=0 $, pois

$ \mathbb{P}(F(X)=z)=\mathbb{P}(a_{i_j}\leq X\leq b_{i_j})=F(b_{i_j})-F(a_{i_j})=0 $

Para o caso $ III $ e $ IV $, é analogo, com isso temos que $ Y\sim U[0,1] $.

Exemplo 2.8.7

(a) As variáveis $ X,Y $ e $ Z $ são independentes, cada uma uniformemente distribuída no intervalo $ [0,1] $. Determine

$$\mathbb{P}(X< Y < Z)$$

e

$$\mathbb{P}(X\leq Y\leq Z)?$$

Como $ X,Y $ e $ Z $ são independentes então

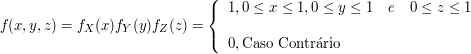
então:

$$\mathbb{P}(X\leq Y\leq Z)=\mathbb{P}(X\leq Y\leq Z)=\mathbb{P}(X< Y< Z)=\int_0^1\int_0^z\int_0^y 1dxdydz=\int_0^1\int_0^z ydydz=\int_0^1\frac{z^2}{2}dz=\frac{1}{6}$$

(b) Se $ X,Y $ e $ Z $ são independentes e independentes e identicamente distribuídas, e a função de distribuição comum F é contínua, qual é

$$\mathbb{P}(X< Y< Z)?$$

Temos

$$\mathbb{P}(X< Y< Z)=\mathbb{P}(X\leq Y \leq Z)$$

pois é absolutamente contínua. Como $ F $ contínua não decrescente e $ F(x)\geq 0 $, para $ \forall x $.

$$\mathbb{P}(F(x)\leq F(y)\leq F(z))=\frac{1}{6}$$

pelo exemplo 2.8.6 pelo item (a).

Exemplo 2.8.8

(a) Sejam X e Y independentes com distribuições de Poisson tendo, respectivamente, parâmetro $ \lambda_1 $ e $ \lambda_2 $. Mostre que $ X+Y \sim Poisson(\lambda_1+\lambda_2) $.

$$[X+Y=k]=\bigcup_{n=0}^k ([X=n]\cap[Y=k-n]), k=0,1,2,\dots$$

então

$$\mathbb{P}(X+Y=k)=\sum_{n=0}^k \mathbb{P}(X=n,Y=k-n)=\sum_{n=0}^k \mathbb{P}(X=n)\mathbb{P}(Y=k-n)=\sum_{n=0}^k \frac{\lambda_1^n}{n!}e^{-\lambda_1}\frac{\lambda_2^{k-n}}{(k-n)!}e^{-\lambda_2}$$

$$=\frac{e^{-(\lambda_1+\lambda_2)}}{k!}\sum_{n=0}^k \left(\frac{k!}{n!(k-n)!}\lambda_1^n\lambda_2^{k-n}\right)=\frac{e^{-(\lambda_1+\lambda_2)}}{k!} \sum_{n=0}^k\binom{k}{n}\lambda_1^n \lambda_2^{k-n}=\frac{(\lambda_1+\lambda_2)^k}{k!}e^{-(\lambda_1+\lambda_2)}, k=0,1,2, \dots$$

Assim, $ X+Y\sim Poisson(\lambda_1+\lambda_2) $.

(b)Mostre que se $ X_1, \dots, X_n $ são independentes tais que $ X_i\sim Poisson(\lambda_i) $, $ i=1, \dots, n $, então $ X_1+\dots +X_n \sim Poisson(\lambda_1+\dots+ \lambda_n) $.

Temos pelo item(a) que $ X_1+X_2\sim Poisson(\lambda_1+\lambda_2) $. Agora, suponhamos que $ (2< m< n) $ e

$$X_1+X_2+\dots +X_m\sim Poisson(\lambda_1+\dots +\lambda_m).$$

Então, como $ (X_1+X_2+\dots +X_m) $ e $ X_{m+1} $ são independentes (pela propriedade hereditária) então pelo item (a)

$$X_1+X_2+\dots+X_{m+1}\sim Poisson(\lambda_1+\lambda_2+\dots+\lambda_{m+1})$$

Então por indução:

$$X_1+X_2+\dots+X_n\sim Poisson(\lambda_1+\dots+\lambda_n)$$

E portanto o resultado segue.

Exemplo 2.8.9

Certo supermercado tem duas entradas, A e B. Fregueses entram pela entrada A conforme um processo de Poisson com taxa média de 15 fregueses por minuto. Pela entrada B, entram fregueses conforme outro processo de Poisson, independente do primeiro, a uma taxa média de 10 por minuto.

(a) Seja $ X_t $ o número total de fregueses que entram no supermercado até o instante $ t $ (inclusive), para $ t\geq 0 $. Então $ ({X_t:t\geq 0}) $ também é processo de Poisson. Qual o parâmetro deste processo?

É um processo de Poisson com parâmetro $ \lambda=\lambda_1+\lambda_2=10+15=25 $. O parâmetro de $ ({X_t:t\geq 0}) $ é $ \lambda=\lambda_1+\lambda_2 $, pois fixando um determinado t, temos

$$X_t=A_t+B_t$$

no qual

$$A_t=(\text{ Variável do número de fregueses que entram até } t \text{ por } A)$$

$$B_t=(\text{ Variável do número de fregueses que entram até } t \text{ por } B)$$

$ A_t\sim Poisson(\lambda_1 t) $ e $ B_t\sim Poisson(\lambda_1 t) $ e $ A_t $ independente de $ B_t $

pelo item (a) do exemplo 2.8.8. O que implica que $ X_t\sim Poisson[(\lambda_1+\lambda_2)t]=25t $.

(b) Seja $ T_1 $ o tempo em que o primeiro freguês entra pela entrada A, com $ V_1 $ o tempo em que o primeiro freguês entra pela entrada $ B $. Ache a distribuição de $ \min(T_1,V_1) $, o mínimo dos dois tempos.

Temos $ T_1\sim Exp(\lambda_1) $ e $ V_1\sim Exp(\lambda_2) $ com $ T_1 $ independente de $ V_1 $. Assim, para $ m> 0 $, temos

$$\mathbb{P}(M=\min(T_1,V_1)> m)=\mathbb{P}(T_1> m, V_1> m)=\mathbb{P}(T_1> m)\mathbb{P}(V_1> m)=e^{-\lambda_1 m}e^{-\lambda_2 m}=e^{-(\lambda_1+\lambda_2)m}$$

o que implica que $ M\sim Exp(\lambda_1+\lambda_2=25) $

(c)Determine a probabilidade de que o primeiro freguês a entrar no mercado entre pela entrada A.

$$\mathbb{P}(T_1=\min(T_1,V_1))=\frac{\lambda_1}{\lambda_1+\lambda_2}=\frac{15}{10+15}=\frac{3}{5}$$

no qual a primeira igualdade segue do exemplo 2.8.5.

Exemplo 2.8.10

Seja A o seguinte triângulo:

(imagem em falta)

(a) Determine o valor da constante c.

Temos que

$$1=\int_{-\infty}^\infty \int_{-\infty}^\infty f(x,y)dxdy=c\int_{A}\int dxdy=c Area(A)=c\frac{1}{2}\Rightarrow c=2.$$

(b) Calcule a distribuição de X, a de Y e a de $ Z=X+Y $.

A distribuição de X:

$$F_X(x)=\int_{-\infty}^{\infty}\int_{-\infty}^{t-x}f(x,y)dydx=2\int_0^t\int_{0}^{t-x}dydx=2\int_0^t(t-x)dx=2\left[tx-\frac{x^2}{2}\right]_0^t=t^2, \quad \quad 0\leq t\leq 1.$$

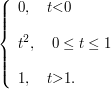
(c) X e Y são independentes ? Por que ?

Não, pois

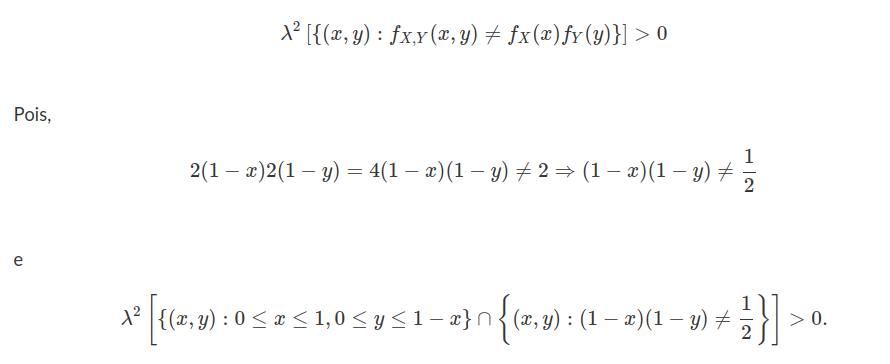
Exemplo 2.8.11

então $ 0\leq z\leq 1 $.

$$\mathbb{P}(Z\leq z)=\mathbb{P}(X^2+Y^2\leq z)=\int_{x^2+y^2\leq z}\int f_{X,Y}(x,y)dxdy=$$

$$\int_{x^2+y^2\leq z}\int \frac{1}{\pi}\mathbb{I}_A dxdy=\frac{1}{\pi}Area\left[{(x,y):x^2+y^2\leq z}\cap A\right]=\frac{\pi z^2}{\pi}=z^2$$

Portanto, temos que $ Z\sim U[0,1] $.

Exemplo 2.8.12

Sejam $ X $ e $ Y $ variáveis aleatórias independentes, tendo distribuição comum $ U[0,1] $.

(a) Qual a densidade da variável aleatória $ Z=X+Y $?

Para $ 0\leq z\leq 1 $, temos

$$P(X+Y\leq z)=\int_{z-1}^1\int_0^{z-x}1dydx=\left[zx-\frac{x^2}{2}\right]^{1}_{z-1}=-\frac{1}{2}\left(1-z(z-1)\right)$$

e $ z< 0 $, para

$$\mathbb{P}(X+Y\leq z)=0$$

e para $ z> 0 $, temos

$$\mathbb{P}(X+Y\leq z)=1$$

então

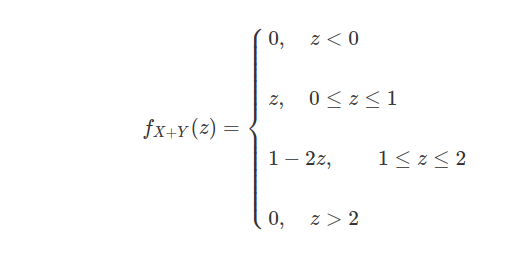
(b) Ache a probabilidade da equação quadrático $ Xt^2+Yt+Z=0 $ ter raízes reais.

Temos que $ Xt^2+Yt+Z $ tem raizes reais se

$$Y^2-4XZ=Y^2-4X(X+Y)> 0$$

o que implica que

$$Y^2-4XY-4X> 0$$

raizes

$$y_k=\frac{4X\pm \sqrt{16X^2+16X^2}}{2}=2X(1\pm \sqrt{2})$$

(imagem em falta)

Então, seja $ E $ o evento $ Xt^2+Yt+Z $ tem reais

$$\mathbb{P}(E)=\int_B\int f_{X,Y}(x,y)dxdy=\int_B\int dxdy=Area(B)=\frac{1}{4(1+\sqrt{2})}=0,10355$$

Exemplo 2.8.13

Dizemos que X tem distribuição de Weibull com parâmetro $ \alpha $ e $ \lambda $ se $ X $ tem densidade

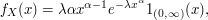
onde $ \alpha> 0 $ e $ \lambda > 0 $. Suponha que a vida útil de certo tipo de máquina i.e, o tempo que ele funciona até pifar, possua distribuição $ Weibull(\alpha,\lambda) $. Colocam-se em funcionamento, simultaneamente, n dessas máquinas. Qual a distribuição do tempo de espera até alguma máquina pifar?

Temos $ X_1, X_2, \dots, X_n $ variáveis aleatórias independentes que designam a vida útil das $ n $ máquinas

$$\mathbb{P}(X_1> x_1)=\int_{x_1}^\infty f_{X_1}(x)dx$$

se $ x_1> 0 $ então

$$\mathbb{P}(X_1> x_1)=\int_{x_1}^\infty \lambda \alpha x^{\alpha-1} e^{-\lambda x^\alpha}dx$$

fazendo uma mudança de variável $ y=\lambda x^{\alpha} $ e $ dy=\lambda x^{\alpha-1}dx $ então temos

$$\int_{x_1}^\infty \lambda \alpha x^{\alpha-1} e^{-\lambda x^\alpha}dx=\int_{\lambda x_1^\alpha}^\infty \lambda e^{-\lambda y}dy=\left[\right]_{\lambda x_1^\alpha}^\infty =e^{-\lambda x_1^\alpha}, x_1> 0$$

Desta forma temos que

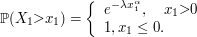
Agora $ Z=\min(X_1,\dots,X_n) $ tempo até alguma máquina pifar.

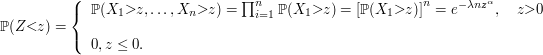
então,

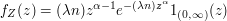
o que implica que

$ Z\sim Weibull(\alpha,n\lambda) $.

Exemplo 2.8.14

Sejam $ X $ e $ Y $ variáveis aleatórias independentes, X tendo distribuição de Poisson com parâmetro $ \lambda=5 $, e $ Y $ tendo distribuição uniforme em $ [0,1] $. Ache a densidade de $ Z=X+Y $.

Primeiramente definimos $ \lceil x\rceil $ como sendo a parte inteira de $ x $. Assim, temos que

$$[X+Y\leq z]=[X\leq \lceil z\rceil-1] \bigcup [X=\lceil z\rceil,y\leq z-\lceil z\rceil ]$$

então se $ z> 0 $ temos

$$F_Z(z)= \mathbb{P}(X\leq \lceil z\rceil -1 )+\mathbb{P}(X= \lceil z\rceil, 0\leq y\leq z- \lceil z\rceil)$$

Pela independência, temos que

$$\sum_{k=0}^{ \lceil z\rceil-1} \frac{\lambda^k}{k!}e^{-5}+\frac{\lambda^{ \lceil z\rceil}}{ \lceil z\rceil!}e^{-5}(z- \lceil z\rceil)$$

Agora, se $ z\leq 0 $ então $ F_{Z}(z)=0 $

Desta forma temos que

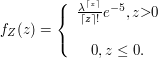
Exemplo 2.8.15

Lança-se um dado equilibrado duas vezes, independentemente. Sejam $ X $ e $ Y $ as variáveis aleatórias que representam os números obtidos em respectivamente, o primeiro e o segundo lançamento.

(a) Determine $ \mathbb{P}(X=Y) $

$ X $ independente $ Y $ pelo exemplo 2.5.5 e

$$\mathbb{P}(X=x, Y=y)=\frac{1}{36}$$

para qualquer $ x,y\in (1,2,\dots, 6) $. Então,

$$\mathbb{P}(X=Y)=\sum_{k=1}^{6}\mathbb{P}(X=k,Y=k)=6\frac{1}{36}=\frac{1}{6}$$

(b) Descreva a distribuição de $ W=|X-Y| $

$$\mathbb{P}(W=0)=6\frac{1}{36}=\frac{1}{6}$$

$$\mathbb{P}(W=1)=2\frac{5}{36}=\frac{5}{18}$$

$$\mathbb{P}(W=2)=2\frac{4}{36}=\frac{2}{9}$$

$$\mathbb{P}(W=3)=2\frac{3}{36}=\frac{1}{6}$$

$$\mathbb{P}(W=4)=2\frac{2}{36}=\frac{1}{9}$$

$$\mathbb{P}(W=6)=2\frac{1}{36}=\frac{1}{18}$$

$$\mathbb{P}(W\in (0,1,2,3,4,5,6))=0$$

(c) Seja

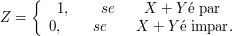
Explique por que X e Z são, ou não são, independentes.

Temos $ \mathbb{P}(Z=0)=\mathbb{P}(Z=1)=\frac{(5\cdot 3)+(3\cdot 3)}{36}=\frac{1}{2} $

e ainda

$$\mathbb{P}(X=x,Z=1)=\frac{3}{36}=\frac{1}{12}=\mathbb{P}(X=x)\mathbb{P}(Z=1)=\frac{1}{6}\frac{1}{2}$$

e

$$\mathbb{P}(X=x,Z=0)=\frac{3}{36}=\frac{1}{12}=\mathbb{P}(X=x)\mathbb{P}(Z=1)=\frac{1}{6}\frac{1}{2}$$

Então, pelo exercício 22 implica que X e Z são independentes.

Exemplo 2.8.16

Escolhe-se um ponto ao acaso(i.e. conforme a distribuição uniforme) dos lados do quadrado de vértices $ (1,1);(1,-1);(-1,-1) $ e $ (-1,1) $. Sejam $ X $ e $ Y $ as coordenadas do ponto escolhido.

(a) Determine a distribuição de $ X+Y $.

Temos que

$$\mathbb{P}(A)=\frac{Comp(A\cap L)}{L}$$

no qual $ L=({(x,y):(|x|=1 \text{ ou } |y|=1) \text{ e } x^2+y^2\leq 1}) $ e $ Comp(L)=8 $. Então,

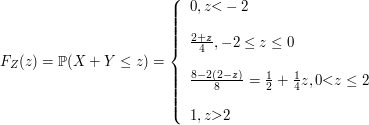
(b) Ache $ \mathbb{P}(W> 0) $, no qual $ W $ é o máximo de $ X $ e $ Y $.

$$\mathbb{P}(W> 0)=\frac{Comp(C\cap L)}{L}$$

com $ C=({(-1,1)\times (-1,1)}-{(x,y):x\leq 0 \text{ e } y\leq 0 }) $ então $ Comp(C\cap L)=6 $ o que implica que

$$\mathbb{P}(W> 0)=\frac{Comp(C\cap L)}{L}=\frac{6}{8}=\frac{3}{4}$$

Exemplo 2.8.17

Sejam X e Y variáveis aleatórias independentes com distribuição comum $ N(0,1) $. Mostre que $ U=\frac{X+Y}{\sqrt{2}} $ e $ V=\frac{X-Y}{\sqrt{2}} $ também são independentes e $ N(0,1) $.

$$f_{X,Y}(x,y)=\frac{1}{2\pi}e^{-\frac{1}{2}(x^2+y^2)}, \quad -\infty< x,y< \infty$$

Agora, seja $ U=\frac{X+Y}{\sqrt{2}} $$ V=\frac{X-Y}{\sqrt{2}} $ e então temos $ X=\frac{U+V}{\sqrt{2}} $ e $ Y=\frac{U-V}{\sqrt{2}} $. Assim,

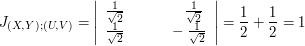
Então:

$$f_{U,V}(u,v)=\bigg| J_{(X,Y),(U,V)}\bigg|f_{X,Y}\left(\frac{u+v}{\sqrt{2}},\frac{u-v}{\sqrt{2}}\right)=\frac{1}{2\pi} e^{-\frac{1}{2}\left(\frac{(u+v)^2}{2}+\frac{(u-v)^2}{2}\right)}=\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}u^2} \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}v^2}$$

com $ -\infty< u< \infty $ e $ -\infty< v< \infty $

Então $ U\sim N(0,1) $ e $ V\sim N(0,1) $ e U independente V.

Exemplo 2.8.18

Sejam X e Y variáveis aleatórias independentes com distribuição comum $ U[0,1] $. Ache a densidade conjunta de $ W $ e $ Z $, onde $ W=X+Y $ e $ Z=X-Y $. $ W $ e $ Z $ são independentes ?

Temos $ X\sim U[0,1] $ e $ Y\sim U[0,1] $ com X e Y independente o que implica que

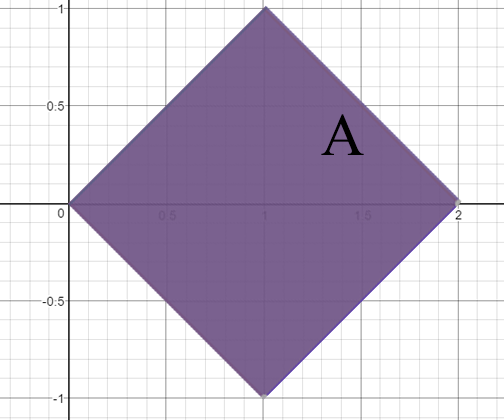
Assim,

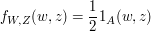
Temos que W e Z não são independentes, é análogo ao exemplo 2.5.15.

Exemplo 2.8.19

Suponha que $ X $ seja uma variável aleatória com distribuição $ N(0,1) $. Calcule a densidade de $ Y=X^4 $ e a $ Z=1/X $. Y e Z possuem densidade conjunta? Por que?

Como $ X\sim N(0,1) $ o que implica que $ f_X(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} $ com $ -\infty < x< \infty $.

(a) $ Y=X^4 $

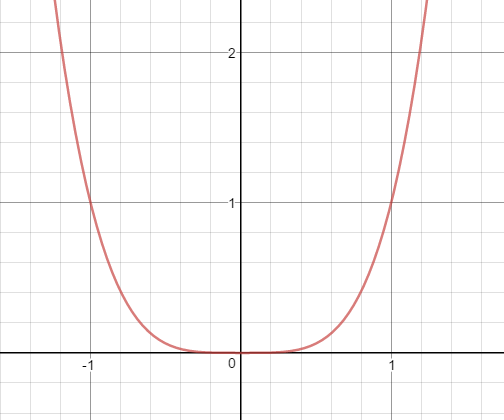
Seja $ G_0=(0,\infty) $, $ G_1=(0,\infty) $ e $ G_2=(-\infty,0) $ então,

$ Y_1: G_1\rightarrow G_0 $ temos que $ y_1=x^4 $ o que implica que $ h^{-1}_1(y)=y_1^{1/4} $ e $ Y_2: G_2\rightarrow G_0 $ e $ y_2=x^4 $ o que implica que $ h^{-1}_2(y)=-(y)^{1/4} $.

Assim

$$J_1(x,y)=\frac{dh^{-1}_1}{dy}=\frac{1}{4}y^{-3/4}$$

e

$$J_2(x,y)=\frac{dh^{-1}_2}{dy}=-\frac{1}{4}y^{-3/4}$$

então

$$f_Y=\bigg|J_1(x,y)\bigg|f_X(h^{-1}_1 (y))\bigg|J_2(x,y)\bigg|f_X(h^{-1}_2 (y))$$

então temos que

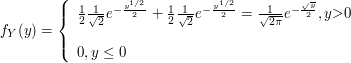
(b) $ Z=\frac{1}{X} $ o que implica que $ h^{-1}(z)=\frac{1}{z} $ o que implica que $ J_{X,Z}=-\frac{1}{z^2} $, então

$$f_Z(z)=\bigg|J(x,z)\bigg|f_Z(h^{-1}(z))=\frac{1}{z^2}\frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2z^2}}, -\infty < z < \infty$$

Temos que $ Y $ e $ Z $ não possuem densidade conjunta pois $ (Y,Z) $ possui distribuição singular. Isto acontece pois existe um conjunto

$$A\subset \mathbb{R}$$

tal que $ \mathbb{P}((Y,Z)\in A)=1 $ e $ \lambda^2(A)=0 $ onde $ A=({(y,z): z^4 y=1}) $

Exemplo 2.8.20

Seja X uma variável aleatória possuindo densidade $ f(x) $.

(a) Ache a densidade de $ Y=|X| $ pelo método básico, obtendo a função de distribuição de X e derivando-a.

Temo que

$$\mathbb{P}(Y\leq y)=\mathbb{P}(|X|\leq y)=\mathbb{P}(-y\leq X\leq y)$$

como $ X $ é uma variável contínua então

$$\mathbb{P}(-y\leq X\leq y)=\mathbb{P}(-y< X\leq y)=F_X(y)-F_X(-y), y> 0$$

e $ \mathbb{P}(Y\leq y)=0 $, $ y< 0 $ então

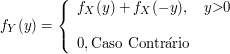
(b) Ache a densidade de Y pelo método do jacobiano.

Considere $ G_0=(0,\infty) $, $ G_1=(0,\infty) $, $ G_2=(-\infty,0) $. Assim defina

$$Y_1: G_1\rightarrow G_0$$

com $ y_1=x $, o que implica que $ h_1^{-1}(y)=y $ então $ J(x,y_1)=1 $. Da mesma forma, defina

$$Y_2: G_2\rightarrow G_0$$

com $ y_2=-x $, o que implica que $ h_1^{-1}(y)=-y $ então $ J(x,y_2)=-1 $. Então,

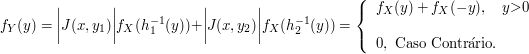
Exemplo 2.8.21

Suponha que $ X,Y $ e $ Z $ possuam densidade conjunta

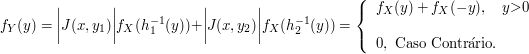
Obtenha a densidade da variável aleatória $ W=X+Y+Z $ de duas maneiras diferentes.

Primeiramente vamos fazer usando o método básico:

$$\mathbb{P}(W\leq w)=\mathbb{P}(X+Y+Z\leq w)=\int_0^w\int_0^{w-x}\int_{0}^{w-(x+y)}\frac{6}{1+x+y+z} dz dy dx$$

Então, a primeira integral é dada por

$$I=\int_0^{w-(x+y)}\frac{6}{1+x+y+z}dz$$

fazendo uma mudança de variável $ v=1+x+y+z $ e $ dv=dz $ então

$$I=\int_0^{w-(x+y)}\frac{6}{1+x+y+z}dz=6\int_{1+x+y}^{w+1}\frac{1}{v}dv=6\left(\ln(v)\right)_{1+x+y}^{w+1}=6\left[\ln(w+1)-\ln( 1+x+y)\right]$$

a segunda integral

$$II=\int_0^{w-x}6\left[\ln(w+1)-\ln( 1+x+y)\right]dy=6\left((\ln(w+1))(w-x)+\int_0^{w-x}\ln(1+x+y)dy\right)$$

Novamente fazendo uma mudança de variável $ v=1+x+y $ e $ dv=dx $ temos que

$$\int_{1+x}^{w+1}\ln(v)dv=\left[v \ln(v)-v\right]_{1+x}^{w+1}=(w+1)\ln(w+1)-(w+1)-(1+x)\ln(1+x)+(1+x)$$

então temos que

$$II=6\left((\ln(w+1))(w-x)+(w+1)\ln(w+1)-(w+1)-(1+x)\ln(1+x)+(1+x)\right)$$

e por fim, a terceira integral

$$III=\int_0^w 6\left((\ln(w+1))(w-x)+(w+1)\ln(w+1)-(w+1)-(1+x)\ln(1+x)+(1+x)\right)dx= 6\left(xw(\ln(w+1))-\frac{x^2}{2}\ln(w+1)+x(w+1)\ln(w+1)-x(w+1)+x+\frac{x^2}{2}\right)_0^{w}=3(2w+1)^2\ln(w+1)-\frac{9}{2}w^2+3w-3$$

Então,

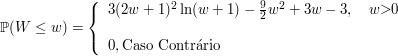
Método Jacobiano:

Definimos $ W=X+Y+Z $, $ U=X $ e $ T=Y $ então $ X=U $, $ Y=T $ e $ Z=W-U-T $ e

Exemplo 2.8.22

Sejam X e Y variáveis aleatórias independentes com distribuição comum $ exp(\lambda) $. Prove que $ Z=\frac{X}{X+Y}\sim U[0,1] $.

Usando, o método do Jacobiano e fazendo:

$ W=X $ e $ Z=\frac{X}{X+Y} $ o que implica que $ X=W $ e $ Y=W\left(\frac{1}{z}-1\right) $ então

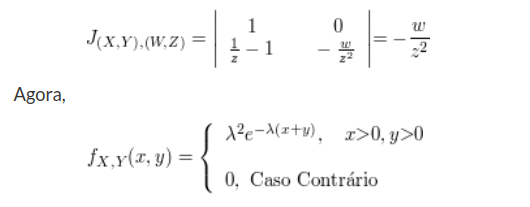
Assim,

$$f_{Z}(z)=\int_{-\infty}^{\infty}f_{W,Z}(w,z)dz.$$

Então, para $ 0< z < 1 $ temos que

$$f_{Z}(z)=\int_{0}^{\infty}\frac{w}{z^2}\lambda^2 e^{-\lambda \left(\frac{w}{z}\right)}dz$$

fazendo uma mudança $ v=\frac{\lambda w}{z} $ e $ dv=\frac{\lambda}{z}dw $ então

$$f_{Z}(z)=\int_0^{\infty}v e^{-v}dv=1$$

Então, $ Z\sim U[0,1] $, pois f caracteriza a lei de Z.

Exemplo 2.8.23 (Extensão do método do jacobiano para o caso de k infinito.)

Seja $ Y=g(X) $, no qual $ X=(X_1,X_2, \dots , X_n) $ e $ Y=(Y_1,Y_2, \dots, Y_n) $. Suponhamos que $ G,G_1, G_2, \dots $ sejam sub-regiões abertas de $ \mathbb{R}^n $ tais que $ G_1,G_2,\dots $ sejam disjuntas e

$$\mathbb{P}\left(X\in \bigcup_n G_n\right)=1$$

no qual $ J_n(x,y) $ é o jacobiano de $ h^{(n)} $.

Seja $ B\subset G $, sob as condições acima, temos:

$$\mathbb{P}(Y\in B)=\mathbb{P}(g(X)\in B)=\sum_{\ell =1}^{\infty}\mathbb{P}(g(X)\in B, X \in G_\ell)=\sum_{\ell=1}^\infty \mathbb{P}(X \in h^{\ell}(B))=$$

$$\sum_{\ell=1}^\infty \int\dots_{h^{\ell}(B)}\int f(x_1,x_2,\dots, x_n)dx_1dx_2\dots dx_n$$

$$=\sum_{\ell=1}^\infty \int\dots_B \int f(h^{(\ell)}(y))|J_\ell(x,y)|dy_1dy_2\dots dy_n$$

como o integrando é contínuo e limitador temos que

$$\sum_{\ell=1}^\infty \int\dots_B \int f(h^{(\ell)}(y))|J_\ell(x,y)|dy_1dy_2\dots dy_n=\int\dots_B \int \sum_{\ell=1}^\infty f(h^{(\ell)}(y))|J_\ell(x,y)|dy_1dy_2\dots dy_n$$

portanto o resultado segue.

Exemplo 2.8.24

Se $ X $ possui densidade $ f(x) $, qual a densidade de $ Y=\cos(X) $?

Defina, $ G=(0,\infty) $ e $ G_k=(k\pi, (k+1)\pi) $. Assim, $ \mathbb{P}\left(X\in \bigcup_{k\in \mathbb{Z}}\right)=1 $ pois temos que X é absolutamente contínua então a $ \mathbb{P}\left(X=k\pi,k\in \mathbb{Z}\right)=0 $. Temos também que $ Y=cosX $ é biunívoca em $ G_k $, então a função inversa existe e é dada por $ X=h^{(k)}(y)=\arccos(y-k\pi) $

$$\frac{dh^{(k)}}{dy}=-\frac{1}{\sqrt{1-y^2}}$$

que é contínua em $ G $, para todo $ k \in \mathbb{Z} $. Então, valem as condições do exemplo 2.8.23 e portanto temos que

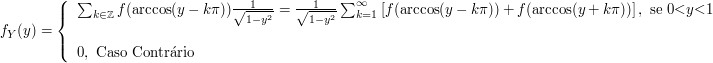
Exemplo 2.8.25

Sejam X e Y variável aleatória independentes, tendo distribuição comum $ U[0,1] $, e sejam $ R=\sqrt{2\log(1/(1-X))} $ e $ \Theta = \pi(2Y-1) $.

(a) Mostre que $ \Theta \sim U[-\pi,\pi] $ e que $ R $ tem distribuição de Rayleigh com densidade

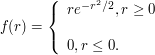
Inicialmente considere $ X,Y \sim U[0,1] $ e independentes o que implica que

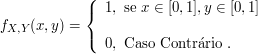
Usando o Método do Jacabiano, definimos

$$R=\sqrt{2\log\left(\frac{1}{1-X}\right)}$$

o que implica $ \frac{\mathbb{R}^2}{2}=\log\left(\frac{1}{(1-X)}\right) $ o que implica que

$$X-1=e^{-r^2/2}$$

o que implica que $ x=e^{-r^2/2}-1 $. Definimos também que

$$\Theta=\pi(2Y-1)$$

o que implica que $ 2Y-1 $ o que implica que $ Y=\frac{1}{2}\left(\frac{\Theta}{\pi}+1\right) $. Então:

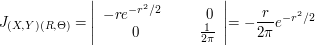
Desta forma,

$$f_{R,\Theta}(r,\theta)=\bigg|J_{(X,Z),(R,\Theta)}\bigg|f_{X,Y}\left(e^{-r^2/2}+1,\frac{1}{2}\left(\frac{\theta}{\pi}+1\right)\right) = \frac{r}{2\pi}e^{-r^2/2}f_{X,Y}\left(e^{-r^2/2}+1,\frac{1}{2}\left(\frac{\theta}{\pi}+1\right)\right)$$

o que implica que

Então,

$$J_{(R,\Theta);(Z,W)}=\frac{1}{J_{(Z,W);(R,\Theta)}}=\frac{1}{R}$$

Desta forma,

$$f_{Z,W}(z,w)=\bigg|J_{(R,\Theta);(Z,W)}\bigg|f_{R,\Theta}(h^{-1}(r),h^{-1}(\theta))=\frac{1}{r}\frac{1}{2\pi}re^{-\frac{z^2+w^2}{2}} = \frac{1}{\sqrt{2\pi}}e^{-z^2/2}\frac{1}{\sqrt{2\pi}}e^{-w^2/2}, \quad -\infty< z< \infty, \quad -\infty < w< \infty$$

Então, Z é independente de W e $ Z,W\sim N(0,1) $

Exemplo 2.8.26

(a) Se $ X $ e $ Y $ tem densidade conjunta $ f(x,y) $, ache a densidade conjunta de $ W $ e $ Z $, no qual $ W=aX+b $ e $ Z=cY+d $, $ a> 0 $, $ c> 0 $, $ b,d \in \mathbb{R} $.

Usando o método Jacobiano, temos que

$ W=aX+b $ o que implica que $ X=\frac{1}{a}\left(W-b\right) $ e $ Z=cY+d $ o que implica que $ Y=\frac{1}{c}(Z-d) $. Então,

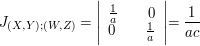
e portanto,

$$f_{W,Z}(w,z)=\bigg|J_{(X,Y);(W,Z)}\bigg|f_{X,Y}\left(\frac{1}{a}\left(w-b\right),\frac{1}{c}(z-d)\right)= \frac{1}{ab}f_{X,Y}\left(\frac{1}{a}\left(w-b\right),\frac{1}{c}(z-d)\right)$$

para $ -\infty< w< \infty $ e $ -\infty< z< \infty $

(b) Seja $ (X,Y) $ um vetor aleatório tendo distribuição normal bivariada com densidade dada no Exemplo 2.1.13. Qual a densidade de

$$(W,Z)=\left(\frac{X-\mu_1}{\sigma_1}, \frac{Y-\mu_2}{\sigma_2}\right)?$$

Que distribuição é essa ?

Temos que

$$f_{X,Y}(x,y)=\frac{1}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1-\rho^2)}\left[\left(\frac{X-\mu_1}{\sigma_1}\right)^2- 2\rho\left(\frac{X-\mu_1}{\sigma_1}\right)\left(\frac{y-\mu_2}{\sigma_2}\right)+\left(\frac{y-\mu_2}{\sigma_2}\right)^2\right]\right),$$

no qual $ \sigma_1> 0 $, $ \sigma_2> 0 $, $ -1< \rho < 1 $, $ \mu_1\in \mathbb{R} $ e $ \mu_2\in \mathbb{R} $.

Agora, temos que $ W=\frac{X-\mu_1}{\sigma_1} $ o que implica que se $ a=\frac{1}{\sigma_1} $ e $ b=-\frac{\mu_1}{\sigma_1} $ o que implica que $ W=aX+b $.

Então, temos que $ Z=\frac{Y-\mu_2}{\sigma_2} $ o que implica que se $ c=\frac{1}{\sigma_2} $ e $ b=-\frac{\mu_2}{\sigma_2} $ o que implica que $ Z=cY+d $.

Usando o item (a) temos que

$$f_{W,Z}(w,z)=\frac{\sigma_1 \sigma_2}{2\pi\sigma_1\sigma_2\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1+\rho^2)}\left[w^2-2\rho wz+z^2\right]\right) = \frac{1}{2\pi\sqrt{1-\rho^2}}\exp\left(-\frac{1}{2(1+\rho^2)}\left[w^2-2\rho wz+z^2\right]\right)$$

com $ -\infty< w< \infty $ e $ -\infty< z< \infty $. A qual é um distribuição normal bivariada com coeficiente de correlação $ \rho $. No qual, $ W\sim N(0,1) $ e $ Z\sim N(0,1) $.

Exemplo 2.8.27

Exemplo 2.8.28

Suponha que $ X_1,X_2,\dots, X_n $ formem uma amostra aleatória de uma distribuição com densidade $ f(x) $. Mostre que

$$\mathbb{P}(X_1< \dots < X_n)=\frac{1}{n!}$$

e que

$$\mathbb{P}(X_i=X_j \text{ para algum par } (i,j) \text{ tal que } i \neq j)=0$$

Temos que se $ X_1,X_2, \dots X_n $ são uma amostra aleatória, então são variáveis aleatórias independentes e identicamente distribuídas então $ X_1,X_2, \dots X_n $ é invariantes para permutações e possuem densidade conjunta $ [f(X_1),f(X_2),\dots, f(X_n)] $ assim pelo exemplo 2.4.9(b) temos que

$$\mathbb{P}(X_1< \dots < X_n)=\frac{1}{n!}$$

e

$$\mathbb{P}(X_i=X_j \text{ para algum par } (i,j) \text{ tal que } i \neq j)=0$$

Exemplo 2.8.29

Suponha que $ X_1,X_2, \dots X_n $ sejam independentes e identicamente distribuídas, com densidade comum $ f $. Mostre que a densidade conjunta de

$$U=\min_{1\leq i\leq n} X_i \quad \quad\quad \quad e \quad \quad \quad \quad V=\max_{1\leq i \leq n}X_i$$

é

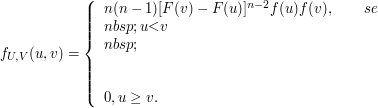
Temos que

$$\mathbb{P}(V\leq v)=\mathbb{P}(X_1< v, \dots, X_n< v)=\left[\mathbb{P}(X_1\leq v)\right]^n=\left[F(v)\right]^n$$

isso devido ser independente e identicamente distribuídos. Então, temos que

$$F_{U,V}(u,v)=\mathbb{P}(U\leq u, V\leq v)=\mathbb{P}(V\leq v)-\mathbb{P}(U> u, V\leq v)=\left[F(v)\right]^n -\mathbb{P}(U> u, V\leq v)$$

Agora, temos que

$$\mathbb{P}(U> u, V\leq v)=\mathbb{P}(u< X_1\leq v, u< X_2\leq v, \dots , u< X_n\leq v)$$

como é independente e identicamente distribuídos temos que

$$\mathbb{P}(U> u, V\leq v)=\left[\mathbb{P}(u< X_1\leq v)\right]^n =\left[F(v)-F(u)\right]^n$$

Portanto temos que

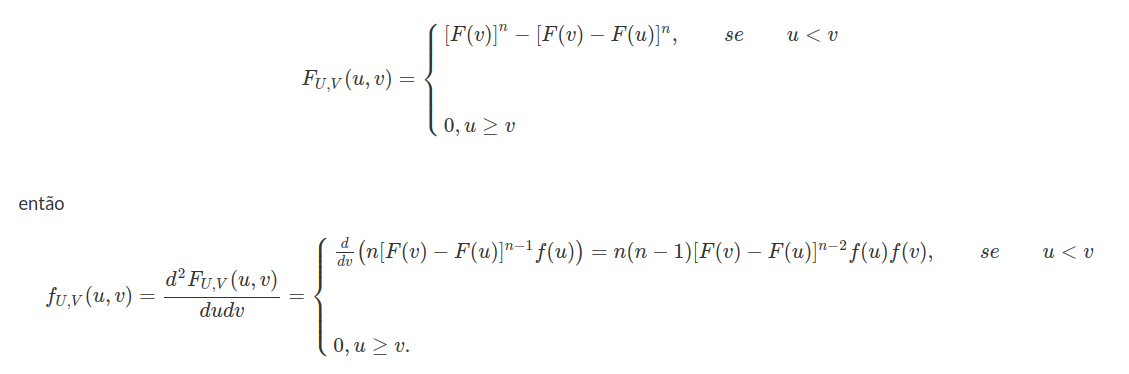
Exemplo 2.8.30

Sejam $ X_1,X_2, \dots X_n $ variáveis independentes e identicamente distribuídas, com densidade $ U[0,\theta] $, no qual $ \theta > 0 $. Sejam

$$U=\min_{1\leq i\leq n} X_i \quad \quad\quad \quad e \quad \quad \quad \quad V=\max_{1\leq i \leq n}X_i$$

(a)Prove que a densidade conjunta de $ (U,V) $ é

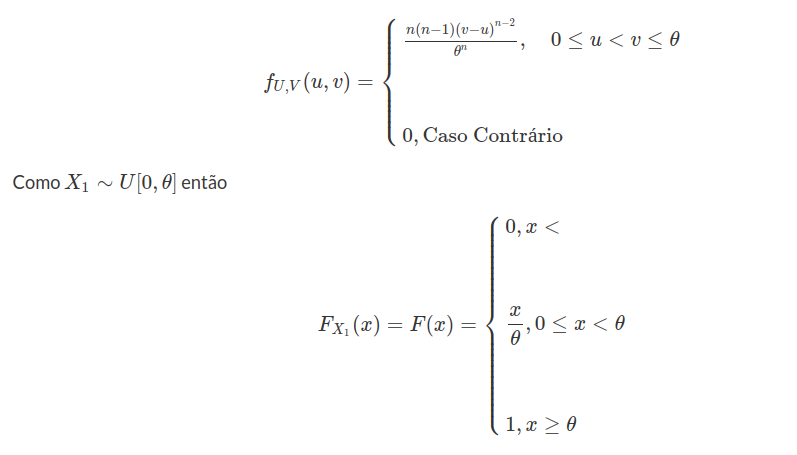
e

Temos que

$$F_W(w)=\mathbb{P}(W\leq w)=\mathbb{P}(V-U\leq w)=\int_0^w \int_0^v f(u,v)du dv+\int_w^\theta \int_{v-w}^v f(u,v)dudv$$

no qual

$$\int_0^w \int_0^v f(u,v)du dv= \int_0^w \int_0^v\frac{n(n-1)(v-u)^{n-2}}{\theta^n}dudv$$

fazendo uma mudança de variável $ x=v-u $ e $ dx=-du $ então

$$\int_0^w \int_0^v\frac{n(n-1)(v-u)^{n-2}}{\theta^n}dudv=\int_0^w \frac{n(n-1)}{\theta^n}\int_{0}^v x^{n-2}dx=\int_0^w \frac{n(n-1)}{\theta^n(n-1)}v^{n-1}dv=\left[\frac{w}{\theta^n}\frac{v^n}{n}\right]_0^w=\left(\frac{w}{\theta}\right)^n $$

Também temos que

$$\int_w^\theta \int_{v-w}^v f(u,v)dudv=\int_w^\theta \int_{v-w}^v \frac{n(n-1)(v-u)^{n-2}}{\theta^n}dudv$$

fazendo novamente uma mudança de variável $ x=v-u $ e $ dx=-du $ então

$$\int_w^\theta \int_{v-w}^v \frac{n(n-1)(v-u)^{n-2}}{\theta^n}dudv=\int_w^\theta \frac{n(n-1)}{\theta^n}\int_0^w x^{n-2}dx=\frac{n(n-1)}{\theta^n(n-1)}\int_w^\theta w^{n-1}dv=\frac{nw^{n-1}}{\theta^n}(\theta-w)=n\left(\frac{w^{n-1}}{\theta^{n-1}}-\frac{w^n}{\theta^n}\right)$$

Então,

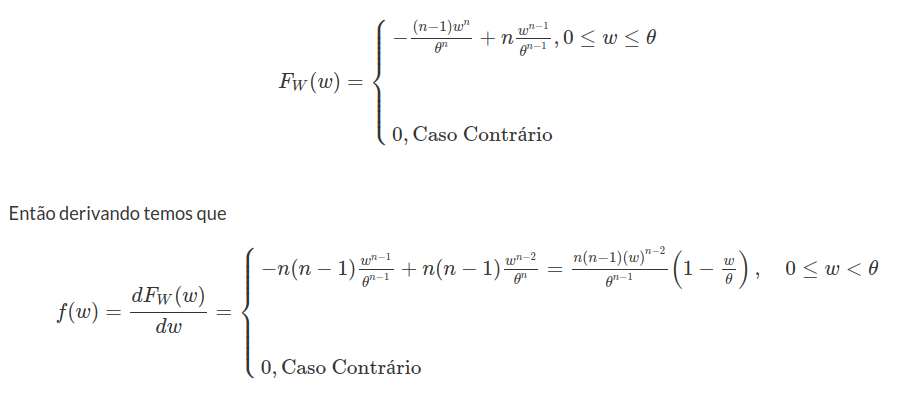
Exemplo 2.8.31

Se $ X_1,X_2, \dots, X_n $ são independentes com distribuição comum $ U[0,1] $, mostre que

$$-2n\ln Y\sim \chi^2(2n),$$

no qual Y é a média geométrica das $ X_i $ definida por

$$Y=\left(\prod_{i=1}^n X_i\right)^{1/n}$$

Temos que se $ X_1\sim U[0,1] $ então pelo exemplo 2.4.6, $ \ln(X_1) \sim Exp(1)=\Gamma(1,1) $ (ver Observação 6.12.2 ).

Então:

$$n\ln(Y)=-\ln(Y^n)=-\ln\left(\prod_{i=1}^n X_i\right)=-\sum_{i=1}^n \ln(X_i).$$

Agora pela propriedade hereditária da independência e com distribuição $ \Gamma(1,1) $. Assim,

$$-n\ln(Y)\sim \Gamma(n,1)$$

Agora, fazendo $ Z=-n\ln(Y) $. Então, seja $ W=2Z $.

$$f_W(w)=\frac{1}{2}f_Z(w/2)=\frac{1}{2}\frac{1}{\Gamma(n)}\left(\frac{w}{2}\right)^{n-1}e^{-w/2}, \quad \quad w> 0.$$

Então, $ W=2n\ln Y\sim \Gamma\left(n,\frac{1}{2}\right) $. Agora como $ \chi^2(n) $ tem a mesma distribuição de $ \Gamma\left(\frac{n}{2},\frac{1}{2}\right) $(Observação 6.3.1 ) .

Além disso, temos que $ \chi^2(2n) $ tem a mesma distribuição de $ \Gamma\left(n,\frac{1}{2}\right) $, o que implica que $ -2n\ln(Y)\sim \chi^2(2n) $

Exemplo 2.8.32

Mostre que se $ X\sim t(1) $, então X tem distribuição de Cauchy

Pela definição da variável t de student temos que se $ Z $ e $ Y $ independentes com $ Z\sim N(0,1) $ e $ Y\sim \chi^2(n) $ então

$$\frac{Z}{\sqrt{Y/n}}\sim t(n)$$

Agora se $ n=1 $, defina $ W=\sqrt{Y} $ o que implica que $ Y=W^2 $, usando o método Jacobiano temos que $ J_{(Y,W)}=2W $ e então:

2.9 - Construção de variáveis aleatórias

Nesta seção construímos uma variável aleatória associada à distribuição de probabilidade discreta $ f $. Primeiramente, definimos que uma partição $ \mathcal{K} $ do $ S^{\infty} $, no qual $ S^\infty $ é o espaço de Cantor, é uma classe finita de conjuntos $ K_{1}, \ldots, K_{n} $ que satisfaz

(i) $ K_{i} \in S^\infty, \ i=1, \ldots,n $;

(ii) $ \displaystyle\bigcup_{i=1}^{n}K_{i} = S^{\infty} $;

(iii) $ K_{j}\displaystyle\bigcap K_{l}=\emptyset, ~~j,l=1, \ldots,n ~\hbox{e}~j\neq l $.

Denotamos por $ S(\mathcal{A}) $ conjunto de todas as funções $ X:S^{\infty}\rightarrow \mathbb{R} $ tais que

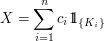
com $ K_1, \ldots, K_{n} $ uma partição do $ S^{\infty} $ e $ c_{i} \in \mathbb{R} $, $ i=1,\ldots,n $. Os elementos de $ S(\mathcal{A}) $ são denominados variáveis aleatórias (ou funções mensuráveis).

Teorema 2.9.1

Consideremos o espaço de probabilidade ($ S^{\infty}, \mathcal{A}, \mathbb{P} $).

$$\mathbb{P}\left(\omega: X(\omega)=c_{i}\right) = \eta(i)$$

Demonstração

Consideremos $ (B_{1},B_{2},\ldots,B_{2^{j}}) $ um conjunto enumerável qualquer tal que

$$\Delta_{j} =(\pi_{1}^{-1}((\omega_{1}))\cap \ldots \cap\pi_{1}^{-1}((\omega_{j})): (\omega_{1},\omega_{2},\ldots,\omega_{J})\in S^{j}) = (B_{1},B_{2},\ldots,B_{2^{j}}).$$

Consideramos

$$A_{1} = B_{1}\cup \cdots \cup B_{j_{1}}$$

$$\vdots$$

$$A_{i}=B_{j_1+\cdots+j_{i-1}}\cup \cdots \cup B_{j_{1}+ \cdots + j_{i}},$$

para $ i=1,2,\ldots,n $. Assim, obtemos uma variável aleatória $ X $

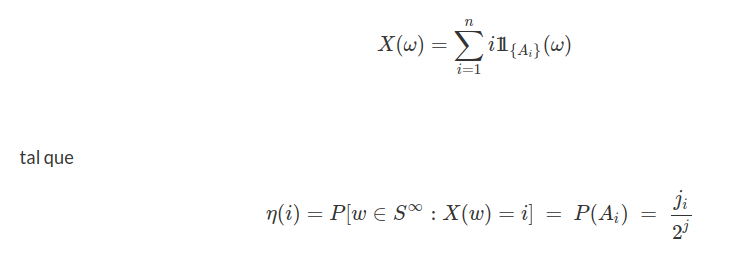
A probabilidade imagem $ P $ é a distribuição de probabilidade discreta $ \eta(i) $ associada à variável aleatória $ X $ definida anteriormente.

Por outro lado, dado $ X = \sum_{i=1}^{n}c_i1!!1_{(K_{i})} $ uma variável aleatória obtemos que $ \eta(i) = P[K_{i}] $.

Observe que a representação da variável aleatória $ X $ não é única: qualquer permutação dos elementos de $ \Delta_j $ nos conduz a uma variável aleatória distinta. Por isso, fixamos a enumeração definida por $ \Delta_j $.