8.3 Valor Esperado

Na tentativa de resumir o comportamento de uma variável aleatória vamos estudar uma medida que estuda a tendência central da variável aleatória, chamada de esperança ou valor esperado de uma variável aleatória. Para ilustrar os vários momentos em que lidamos com o valor esperado vamos apresentar alguns exemplos.

Exemplo 3.1

Em um restaurante quando pedimos nossa comida e perguntamos para o garçom quanto tempo leva para ficar pronto, ele vai nos fornecer um valor esperado, ou seja, o tempo médio em que a comida deve demorar a ficar pronta.

Exemplo 3.2

Quando estamos em um ponto de ônibus e perguntamos para a pessoa ao lado, quanto tempo leva até que o próximo ônibus venha, ela prontamente vai nos dar o valor esperado, o qual ela conseguiu constatar depois de algum tempo de experiência.

Nos exemplos acima o garçom e a pessoa que esperava no ponto de ônibus resumiram toda a informação de um modelo em um único número, o valor esperado. Nesta seção iremos estudar como se obter a esperança ou valor esperado de uma variável aleatória, estudaremos algumas de suas propriedades, e também a função geradora de momentos, responsável por gerar todos os limites centrais.

3.1 - Valor esperado de variáveis aleatórias discretas e de vetores discretos

Definição 3.1.1

Seja $ X $ uma variável aleatória discreta que assume os valores $ (x_1,x_2,\ldots) $e seja $ p(x) $ a função de probabilidade de $ X $, isto é, $ p(x_i) = \mathbb{P}(X = x_i) $. Então, o valor esperado de $ X $, também chamado de esperança de $ X $ e denotado por $ \mathbb{E}(X) $ ou $ \mu_X $, é definido por

$$\mathbb{E}(X)= \mu_X=\sum_{i=1}^\infty x_i p(x_i) = \sum_{i=1}^\infty x_i\mathbb{P}(X = x_i).$$

Este número também é denominado valor médio ou expectância de X. Observamos que o valor esperado $ \mathbb{E}(X) $ só está definido se a série acima for absolutamente convergente, ou seja, se

$$\mathbb{E}(X)=\sum_{i=1}^{\infty} |x_i| \mathbb{P}(X=x_i) \ < \ \infty.$$

Observação 3.1.1

Se $ X $ tomar apenas um número finito de valores, a expressão acima se torna $ \mathbb{E}(X)=\sum_{i=1}^n x_i\mathbb{P}(X=x_i) $. Neste caso, o valor esperado pode ser considerado como uma média ponderada dos possíveis valores $ x_1,x_2,\ldots,x_n $. Se todos esses valores possíveis forem equiprováveis, $ \mathbb{E}(X)=\frac{1}{n}\displaystyle\sum_{i=1}^n x_i $, que representa a média aritmética simples dos n possíveis valores.

Exemplo 3.1.1

Consideremos o lançamento de um dado equilibrado. Consideremos a variável aleatória $ X = \ \text{``número da face voltada para cima} $. Calcular o valor esperado de $ X $.

Sabemos que os valores possíveis de $ X $ são $ (1, 2, 3, 4, 5, 6) $ e que esses valores são equiprováveis. Assim,

$$\mathbb{E}(X)=\frac{1}{6}(1+2+3+4+5+6)=\frac{7}{2}.$$

Observação 3.1.2

Este exemplo ilustra claramente que $ \mathbb{E}(X) $ não é o resultado que podemos esperar quando $ X $ for observado uma única vez. De fato, temos que $ \mathbb{E}(X) = 7/2 $ nem é um possível valor de $ X $. Esse valor na verdade significa que se jogássemos o dado um grande número de vezes e depois calculássemos a média aritmética dos vários resultados, esperaríamos que essa média ficasse próxima de 7/2 e quanto maior fosse o número de vezes que o dado fosse lançado, mais a média aritmética se aproximaria de 7/2.

Dado $ X $ uma variável aleatória discreta assumindo valores em $ \mathcal{R}_X=(x_1, x_2, \cdots ) $ e com função de distribuição $ p_X $. Seja $ g: \Bbb{R} \rightarrow \Bbb{R} $ uma função real. A variável aleatória $ Y=g(X) $ tem função de distribuição dada por

$$ p_Y (y) = \mathbb{P} [ Y = y] = \sum_{(x \in \mathcal{R}_X:g(x) = y)}\mathbb{P}[X=x]. $$

Assim, obtemos o seguinte resultado.

Teorema 3.1.1

Seja $ X $ uma variável aleatória discreta que assume valores em $ \mathcal{R}_X $ com função de probabilidade $ p(x) $ e $ g: \mathbb{R} \rightarrow \mathbb{R} $ uma função. Temos então que

$$\mathbb{E}[g(X)]= \sum_{x_i\in\mathcal{R}_X}g(x_i)p(x_i) = \sum_{x_i\in\mathcal{R}_X}g(x_i)\mathbb{P}(X=x_i).$$

De fato, considerando a variável aleatória $ Y $ dada por $ Y=g(X) $, temos que

$$\mathbb{E}(Y)=\sum_{y\in\mathcal{R}_Y} y \mathbb{P}(Y = y) =\sum_{y\in\mathcal{R}_Y} \sum_{(x:g(x)=y)}g(x) \mathbb{P}(X = x)$$

de onde concluímos que

$$\mathbb{E}[g(X)] = \sum_{i=1}^{n}g(x_i)\mathbb{P}(X = x_i)$$

Exemplo 3.1.2

Seja $ X $ uma variável aleatória com distribuição de probabilidade dada na tabela abaixo:

$ X $	-2	-1	0	1	2
$ \mathbb{P}(X = x) $	1/5	1/5	1/5	1/5	1/5

e seja $ g(X)=X^{2} $. Vamos calcular o valor esperado de $ X $ e de $ g(X) $.

O valor esperado de $ X $ é dado por

$$\mathbb{E}(X)= \sum_{i=1}^{5}x_i \mathbb{P}(X = x_i)=-2\frac{1}{5}-1\frac{1}{5}+0\frac{1}{5}+1\frac{1}{5}+2\frac{1}{5}=0.$$

Para calcularmos a esperança de $ g(X) $, existem duas possibilidades: utilizando o Teorema 3.1.1 ou através da forma tradicional, isto é, encontrando a distribuição de probabilidade da variável $ Y = g(X) $. Através do Teorema 3.1.1 temos que:

$$\mathbb{E}[g(X)]=\sum_{i=1}^{5}g(x_i)\mathbb{P}(X = x_i)=(-2)^2\frac{1}{5}-1^2\frac{1}{5}+0^2\frac{1}{5}+1^2\frac{1}{5}+2^2\frac{1}{5}=2.$$

Para o cálculo através da forma tradicional, inicialmente devemos encontrar a distribuição de probabilidade de $ g(X) $, que é dada por

$ g(X) $	0	1	4
$ \mathbb{P}(g(X) = g(x)) $	1/5	2/5	2/5

e então, temos que

$$\mathbb{E}[g(X)]=\sum_{i=1}^{3} g(x_i)\mathbb{P}(g(X) = g(x_i))= 0\frac{1}{5}+1\frac{2}{5}+4\frac{2}{5}=2.$$

Exemplo 3.1.3

Uma indústria alimentícia está participando de três licitações públicas, com lucros possíveis de 30, 50 e 60 mil reais, respectivamente. Se a probabilidade dessa indústria vencer as licitações são de 0,3; 0,7 e 0,2 respectivamente, qual o valor esperado do lucro desta indústria?

Neste caso basta aplicarmos diretamente a definição de valor esperado, ou seja:

$$\mathbb{E}(X)=0,3~\cdot ~ 30 + 0,7~ \cdot ~50 + 0,2~ \cdot~ 60=56.$$

Assim, o valor esperado do lucro desta indústria nas licitações é de 56 mil reais.

Valor esperado e funções de vetores aleatórios discretos

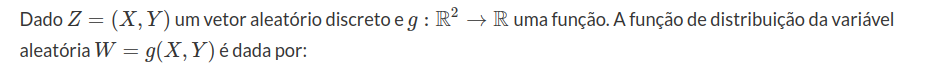
$$\mathbb{P}\left[W=w\right]=\mathbb{P}\left[(X,Y) \in B_w\right],$$

Definição 3.1.2

$$\mathbb{E}[g(\widetilde{Z})]=\sum_{x\in\mathcal{R}_X}\sum_{y\in\mathcal{R}_Y}g(x,y)p(x,y) = \sum_{x\in\mathcal{R}_X}\sum_{y\in\mathcal{R}_Y}g(x,y)\mathbb{P}(X = x; Y = y).$$

Observação 3.1.3

A Definição 3.1.2 acima pode ser generalizada para o caso em que temos uma vetor aleatório n-dimensional.

Definição 3.1.3

Seja $ \widetilde{Z} = (X,Y) $ um vetor aleatório bidimensional discreto, $ p(x,y) $ a função de probabilidade conjunta de $ \widetilde{Z} $ e $ p_{X}(x) $ e $ p_{Y}(y) $ as funções de probabilidade marginais das variáveis $ X $ e $ Y $ respectivamente. Então, temos que o valor esperado das variáveis $ X $ e $ Y $ são dados por

$$\mathbb{E}(X) = \sum_{x\in\mathcal{R}_X}xp_X(x) \quad \text{e} \quad \mathbb{E}(Y) = \sum_{y\in\mathcal{R}_Y}yp_Y(y).$$

Além disso, temos que o valor esperado do vetor aleatório $ \widetilde{Z} $ é dado por

$$\mathbb{E}(\widetilde{Z}) = (\mathbb{E}(X),\mathbb{E}(Y))$$

Exemplo 3.1.4

Suponha que uma máquina seja utilizada para determinada tarefa de manhã e para outra tarefa à tarde. Suponha que o número de vezes que a máquina apresenta problema de manhã e à tarde sejam representados, respectivamente, por variáveis aleatórias $ X $ e $ Y $ com função de probabilidade conjunta.

X\Y	0	1	2	$ p_X(x) $
0	0,1	0,2	0,2	0,5
1	0,04	0,08	0,08	0,2
2	0,06	0,12	0,12	0,3
$ p_Y(y) $	0,2	0,4	0,4	1

Neste caso, temos que

$$\mathbb{E}(X) = \sum_{x\in\mathcal{R}_X}xp_X(x) = 0\cdot 0,5 + 1 \cdot 0,2 + 2\cdot 0,3 = 0,8.$$

$$\mathbb{E}(Y) = \sum_{y\in\mathcal{R}_Y}yp_Y(y) = 0\cdot 0,2 + 1 \cdot 0,4 + 2\cdot 0,4 = 1,2.$$

De onde segue que $ \mathbb{E}(\widetilde{Z}) = (\mathbb{E}(X),\mathbb{E}(Y)) = (0,8;1,2) $.

Seja $ g(X,Y) = XY $. Então o valor esperado de $ g(X,Y) $ é dado por

$$\mathbb{E}(g(X,Y)) = 0\cdot 0\cdot p(0,0) + 0\cdot 1\cdot p(0,1) + \ldots + 2\cdot 2\cdot p(2,2) = 0,96.$$

Observe que, neste exemplo, para todo $ (x,y)\in\mathcal{R}_X\times\mathcal{R}_Y $, temos que $ p(x,y) = p_X(x)\cdot p_Y(y) $ e, portanto, do Corolário 2.5.2 concluímos que $ X $ e $ Y $ são independentes.

3.2 - Valor esperado de variáveis aleatórias contínuas e de vetores contínuos

Definição 3.2.1

Seja $ X $ uma variável aleatória contínua com função densidade de probabilidade $ f(x) $. Definimos o valor esperado ou esperança matemática ou média de $ X $ por

$$\mathbb{E}(X)=\int_{-\infty}^{\infty}xf(x) dx,$$

desde que a integral esteja bem definida.

Observação 3.2.1

1. Se a variável é limitada, o cálculo é feito sem ambiguidade e a existência do valor esperado está assegurada. No caso não limitado, podem aparecer situações indefinidas do tipo $ \infty-\infty $, em que diremos que a esperança não existe. Assim, temos que $ \mathbb{E}(X) $ vai estar bem definida se a integral, em pelo menos um desses intervalos, for finita; isto é

$$\int_{-\infty}^0 xf(x)dx \ < \ \infty \qquad \text{e} \qquad \int_0^\infty xf(x)dx \ < \ \infty.$$

2. A interpretação de $ \mathbb{E}(X) $ para o caso contínuo é similar ao mencionado para variáveis aleatórias discretas.

3. Se $ g:\mathbb{R}\rightarrow\mathbb{R} $ é uma função mensurável, então $ \mathbb{E}(g(X))=\int_{-\infty}^{\infty}g(x)f(x)dx. $

Exemplo 3.2.1

Seja $ X $ o tempo (em minutos) durante o qual um equipamento elétrico é utilizado em carga máxima, em um certo período de tempo especificado. Então, $ X $ é uma variável aleatória contínua e sua fdp é dada por

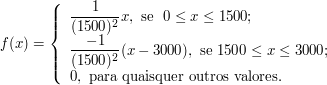
Calcular o valor esperado de $ X $.

$$\mathbb{E}(X)=\int_{-\infty}^\infty xf(x)dx=\frac{1}{(1500)(1500)}\left[ \int_0^{1500} x^2dx-\int_ {1500}^{3000} x(x-3000)dx\right]=1500 \ \hbox{minutos}.$$

Exemplo 3.2.2

Seja a função de densidade de uma variável aleatória de $ X $ dada por

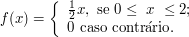
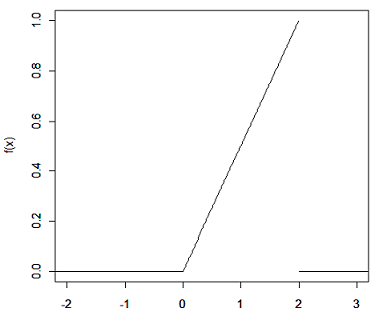
Encontre o valor esperado de $ X $.

Pela definição 3.2.1, temos que:

$$\mathbb{E}(X)=\int_{-\infty}^{\infty}xf(x) dx=\int_{0}^{2}xf(x)=\int_{0}^{2}\frac{1}{2}x^2=\frac{4}{3}.$$

Assim $ \mathbb{E}(X)=4/3 $.

Exemplo 3.2.3

Seja $ X $ uma variável aleatória com função densidade de probabilidade dada por:

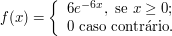
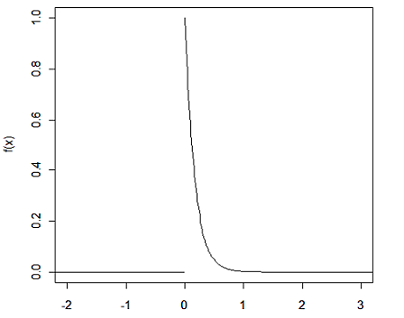
Encontre o valor esperado da variável aleatória $ X $.

$$\mathbb{E}(X)= \int_{-\infty}^{\infty}xf(x) dx=\int_{0}^{\infty}6xe^{-6 x}dx=6\int_{0}^{\infty}xe^{-6x}dx.$$

Resolvendo a integral por partes concluímos que

$$6\left[\frac{xe^{-6 x}}{-6}-\int_{0}^{\infty} \frac{e^{-6 x}}{-6}dx \right]=6 \left[ \frac{xe^{-6 x}}{-6}- \frac{e^{-6 x}}{36} \right]^{\infty}_{0}= \frac{1}{6}$$

Exemplo 3.2.4

Seja $ X $ uma variável aleatória com função densidade dada por

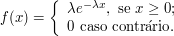
Encontre o valor esperado da variável aleatória $ X $ e de $ X^2 $

$$\mathbb{E}(X)=\int_{-\infty}^{\infty}xf(x) dx=\int_{0}^{\infty}x\lambda e^{-\lambda x}dx=\lambda\int_{0}^{\infty}xe^{-\lambda x}dx$$

Resolvendo a integral por partes concluímos que

$$\lambda\left[\frac{xe^{-\lambda x}}{-\lambda}-\int_{0}^{\infty}\frac{e^{-\lambda x}}{-\lambda}dx \right]=\lambda \left[ \frac{xe^{-\lambda x}}{-\lambda}- \frac{e^{-\lambda x}}{\lambda^2} \right]^{\infty}_{0}=\frac{1}{\lambda}.$$

Agora calculamos o valor esperado de $ X^2 $ usando o item 3 da Observação 3.2.1.

$$\mathbb{E}(X^2)=\int_{-\infty}^{\infty}g(x)f(x)dx=\int_{0}^{\infty}x^2\lambda e^{-\lambda x}dx.$$

Resolvendo a integral por partes, obtemos que

$$\lambda \int_{0}^{\infty}x^2 \lambda e^{-\lambda x} dx = \lambda \left[x^2\frac{e^{-\lambda x}}{-\lambda}-2x \frac{e^{-\lambda x}}{\lambda^2}+ 2\frac{e^{-\lambda x}}{-\lambda^3} \right]_{0}^{\infty}=\frac{2}{\lambda^2}.$$

Exemplo 3.2.5

Seja $ X $ uma variável aleatória com função densidade de probabilidade dada abaixo

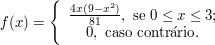
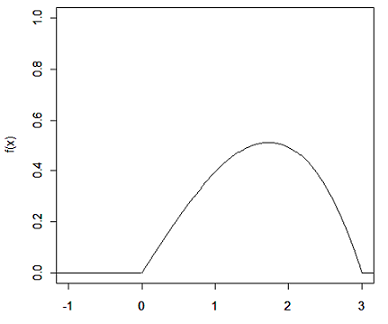
Determine o valor esperado de $ X $.

$$\mathbb{E}(X)= \frac{4}{81}\int_{0}^{3}x^2 (9-x^2)dx=\frac{8}{5}.$$

Valor esperado e funções de vetores aleatórios contínuos

Definição 3.2.2

Seja $ \widetilde{Z} = (X,Y) $ um vetor aleatório bidimensional contínuo, $ f(x,y) $ a função densidade de probabilidade conjunta de $ \widetilde{Z} $ e $ f_X(x) $ e $ f_Y(y) $ as funções densidade de probabilidade marginais de $ X $ e $ Y $ respectivamente. Então, temos que o valor esperado das variáveis aleatórias $ X $ e $ Y $ são dados por

$$\mathbb{E}(X) = \int_{-\infty}^{\infty}xf_X(x)dx \quad \text{e} \quad \mathbb{E}(Y) = \int_{-\infty}^{\infty}yf_Y(y)dy.$$

Além disso, temos que o valor esperado do vetor aleatório bidimensional $ \widetilde{Z} $ é dado por

$$\mathbb{E}(\widetilde{Z})=(\mathbb{E}(X),\mathbb{E}(Y)).$$

Definição 3.2.3

Seja $ \widetilde{Z} = (X,Y) $ um vetor aleatório bidimensional contínuo, $ f(x,y) $ a função densidade de probabilidade conjunta de $ \widetilde{Z} $ e $ g:\mathbb{R}^2\rightarrow\mathbb{R} $ uma função real Borel mensurável. Então, definimos o valor esperado da variável aleatória $ g(\widetilde{Z}) $ por

$$\mathbb{E}[g(\widetilde{Z})] = \mathbb{E}[g(X,Y)] = \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}g(x,y)f(x,y)dxdy.$$

Observação 3.2.2

As Definições 3.2.2 e 3.2.3 acima podem ser generalizadas para o caso n-dimensional de forma natural.

Exemplo 3.2.6

Duas características do desempenho do motor de um foguete são o empuxo ($ X $) e a taxa de mistura ($ Y $). Suponha que $ (X,Y) $ seja uma variável aleatória bidimensional contínua com função densidade de probabilidade conjunta dada por

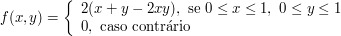
Neste caso, temos que as funções densidade de probabilidade marginais de $ X $ e $ Y $ são dadas respectivamente, por

$$f_X(x)=\int_{-\infty}^{\infty}f(x,y)dy=\int_0^12(x+y-2xy)dy = 2\left(xy+\frac{y^2}{2}-xy^2\right)\big|_0^1 = 1, \ \text{se} \ 0\leq x\leq 1.$$

Ou seja,

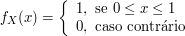
e

$$f_Y(y)=\int_{-\infty}^{\infty}f(x,y)dx=\int_0^12(x+y-2xy)dx = 2\left(\frac{x^2}{2}+xy-x^2y\right) \big|_0^1 = 1, \ \text{se} \ 0\leq y\leq 1.$$

Ou seja,

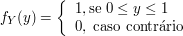
Portanto, concluímos que

$$\mathbb{E}(X) = \int_{-\infty}^{\infty}xf_X(x)dx = \int_0^1xdx = \frac{1}{2} \quad \text{e} \quad \mathbb{E}(Y) = \int_{-\infty}^{\infty}yf_Y(y)dy = \int_0^1ydy = \frac{1}{2}.$$

Se $ \widetilde{Z} = (X,Y) $ segue então que

$$\mathbb{E}(\widetilde{Z}) = (\mathbb{E}(X),\mathbb{E}(Y)) = \left(\frac{1}{2},\frac{1}{2}\right).$$

3.3 - Propriedades do valor esperado

Nesta seção, veremos algumas importantes propriedades do valor esperado de uma variável aleatória. Em cada caso, admitimos que todos os valores esperados mencionados, existem.

P1. Se $ X=c $ com $ c $ uma constante real, então $ \mathbb{E}(X)=c $.

De fato, se $ X $ é uma variável aleatória discreta, temos que

$$\mathbb{E}(X) =\sum_{\mathcal{R}_X}x\mathbb{P}(X=x) = c\mathbb{P}(X=c) = c\cdot 1=c$$

P2. Seja $ c $ uma constante real e $ X $ uma variável aleatória. Então,

$$\mathbb{E}(cX) = c\mathbb{E}(X)$$

De fato, no caso discreto temos que

$$\mathbb{E}(cX)=\sum_{x\in\mathcal{R}_X}cx\mathbb{P}(X = x)=c\sum_{x\in\mathcal{R}_X}x\mathbb{P}(X = x)= c\mathbb{E}(X).$$

De modo análogo, temos no caso contínuo, que

$$\mathbb{E}(cX)=\int_{-\infty}^{\infty}cxf(x)dx=c\int_{-\infty}^{\infty}xf(x)dx=c\mathbb{E}(X)$$

P3. Sejam $ X $ e $ Y $ duas variáveis aleatórias quaisquer. Então,

$$\mathbb{E}(X + Y) = \mathbb{E}(X) + \mathbb{E}(Y).$$

De fato, no caso discreto, considere $ p(x,y) $ a função de probabilidade conjunta e $ p_X(x) $ e $ p_Y(y) $ as funções de probabilidade marginais de $ X $ e $ Y $ respectivamente. Então, temos que

$$\mathbb{E}(X+Y)=\sum_{y\in\mathcal{R}_Y}\sum_{x\in\mathcal{R}_X}(x+y)p(x,y)=\sum_{x\in\mathcal{R}_X}\sum_{y\in\mathcal{R}_Y}xp(x,y)+\sum_{y\in\mathcal{R}_Y}\sum_{x\in\mathcal{R}_X}yf(x,y)$$

de onde segue que

$$\mathbb{E}(X+Y)\sum_{x\in\mathcal{R}_X}xp_X(x) +\sum_{y\in\mathcal{R}_Y}yp_Y(y).$$

Portanto, concluímos que

$$\mathbb{E}(X+Y)=\mathbb{E}(X)+\mathbb{E}(Y).$$

Se $ X $ e $ Y $ são variáveis aleatórias contínuas, considere $ f(x,y) $ a função densidade de probabilidade conjunta e $ f_X(x) $ e $ f_Y(y) $ as funções densidade de probabilidade marginais de $ X $ e $ Y $ respectivamente. Então

$$\mathbb{E}(X+Y)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(x+y)f(x,y)dxdy=\int_{-\infty}^{\infty}x\left(\int_{-\infty}^{\infty}f(x,y)dy\right)dx+\int_{-\infty}^{\infty}y\left(\int_{-\infty}^{\infty}f(x,y)dx\right)dy.$$

ou seja,

$$\mathbb{E}(X+Y)=\int_{-\infty}^{\infty}xf_X(x,y)dx+\int_{-\infty}^{\infty}yf_Y(x,y)dy=\mathbb{E}(X)+\mathbb{E}(Y)$$

demonstrando o resultado.

P4. Sejam $ n $ variáveis aleatórias $ X_1,\ldots,X_n $. Então,

$$\mathbb{E}(X_1+X_2+\ldots+X_n)=\mathbb{E}(X_1)+\mathbb{E}(X_2)+\ldots+\mathbb{E}(X_n).$$

A demonstração deste caso é análoga a anterior. Basta fazer uma indução sobre $ n $.

P5. Sejam $ X $ e $ Y $ variáveis aleatórias independentes. Então,

$$\mathbb{E}(XY) = \mathbb{E}(X)\mathbb{E}(Y).$$

De fato, suponha que $ X $ e $ Y $ são variáveis aleatórias independentes com função de probabilidade conjunta $ p(x,y) $ para o caso discreto ou função densidade de probabilidade conjunta $ f(x,y) $ para o caso contínuo. Como, por hipótese, $ X $ e $ Y $ são independentes, temos do Teorema 3.1.2 que

$$p(x,y) = p_X(x) \cdot p_Y(y)$$

no caso discreto e do Teorema 3.2.1 que

$$f(x,y) = f_X(x)\cdot f_Y(y)$$

no caso contínuo. Desta forma, se $ X $ e $ Y $ são variáveis aleatórias discretas independentes, temos que

$$\mathbb{E}(XY)=\sum_{x\in\mathcal{R}_X}\sum_{y\in\mathcal{R}_Y}xyp(x,y)= \sum_{x\in\mathcal{R}_X}\sum_{y\in\mathcal{R}_Y}xyp_X(x)p_Y(y)= \sum_{x\in\mathcal{R}_X}xp_X(x)\sum_{y\in\mathcal{R}_Y}yp_Y(y)$$

de onde segue que

$$\mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y).$$

Analogamente, para o caso contínuo, temos que

$$\mathbb{E}(XY)=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf(x,y)dxdy=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xyf_X(x)f_Y(y)dxdy$$

ou seja,

$$\mathbb{E}(XY)=\int_{-\infty}^{\infty}xf_X(x)\left(\int_{-\infty}^{\infty}yf_Y(y)dy\right)dx=\mathbb{E}(X)\mathbb{E}(Y).$$

demonstrando assim o resultado.

P6 (Desigualdade de Jensen). Seja $ f:\mathbb{R}\rightarrow\mathbb{R} $ uma função convexa e $ X $ uma variável aleatória integrável, ou seja, $ E(X)\leq \infty $. Então temos que

$$\mathbb{E}(f(X))\geq f(\mathbb{E}(X)).$$

Ressaltamos que uma função é dita convexa se seu gráfico for convexo, ou seja, dado quaisquer pontos $ a,b\in \mathbb{R} $ a reta que passa pelos pares ordenados $ (a,f(a)) $ e $ (b,f(b)) $ não intercepta o gráfico de $ f $ em nenhum ponto no intervalo $ (a,b) $.

Uma definição equivalente seria que para quaisquer $ x, y \in [a,b] $ e para todo $ t\in [0,1] $ temos que:

$$f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)$$

De fato se $ f $ é uma função convexa então dado um par ordenado $ (y,f(y)) $ no gráfico de $ f $, temos que existe uma reta $ r $ tal que a reta passa pelo ponto $ (y,f(y)) $ e deixa a curva $ f $ toda acima dela, ou seja, existe um $ \lambda\in\mathbb{R} $ tal que $ r(x)=\lambda(x-y)+f(y) $.

Então temos que

$$f(x)\geq r(x)=\lambda(x-y)+f(y),~~~\forall x \in\mathbb{R}.$$

Portanto, se aplicarmos o valor esperado em ambos os lados obtemos:

$$\mathbb{E}(f(X))\geq \mathbb{E}(r(X))=f(y)+\lambda(\mathbb{E}(X)-y).$$

E, tomando $ y=\mathbb{E}(X) $, o resultado segue.

Teorema 3.3.1

Seja X uma variável aleatória, $ \varphi(x) $ uma função real mensurável. Então

$$\mathbb{E}(\varphi(X))=\int y dF_{\varphi(X)}(y)=\int \varphi(x)dF_X(x),$$

no qual a existência de uma das integrais implica a existência da outra e a igualdade das duas.

Exemplo 3.3.1

Dizemos que a distribuição de X é simétrica (em torno de zero) se $ \mathbb{P}(X\geq x)=\mathbb{P}(X\leq -x) $ para todo $ x\in \mathbb{R} $, e que sua distribuição é simétrica em torno de $ \mu $ se

$$\mathbb{P}(X\geq \mu +x)=\mathbb{P}(X\leq \mu -x) \forall x \in \mathbb{R}$$

(a) Prove: Se a distribuição de X é simétrica em torno de $ \mu $ e se X é simétrica em torno de $ \mu $ e se X é integrável, então $ \mathbb{E}(X)=\mu $

Primeiramente vamos provar para $ \mu=0 $. Se $ \mu=0 $ isso implica que X é integrável e tem distribuição simétrica em zero o que implica que

$$\mathbb{P}(X\geq 0)=\mathbb{P}(X\leq -x)$$

o que implica que

$$(1-F_X(x))=F_X(-x)$$

Logo temos que

$$\mathbb{E}(X)=\int_0^\infty (1-F_X(x))dx-\int_{-\infty}^0 F_X(x)dx$$

Fazendo uma mudança de variável temos que

$$\mathbb{E}(X)=\int_0^\infty (1-F_X(x))dx-\int_{0}^\infty F_X(-x)dx=0$$

Agora, para $ \mu\neq 0 $, temos que $ X $ é integrável e tem distribuição simétrica em $ \mu $, ou seja,

$$\mathbb{P}(X\geq \mu+x)=\mathbb{P}(X\leq \mu - x), \quad \quad \forall x\in \mathbb{R}$$

Assim, definimos $ Y=X-\mu $ então $ Y\leq X $, e como X é integrável implica que Y é integrável, pois

$ Y=X-\mu $ o que implica

$$|X|-\mu \leq |X-\mu|=|Y|=|X-\mu|\leq |X|+\mu$$

Agora $ Y $ é simétrica em zero, pois

$$\mathbb{P}(Y\geq y)=\mathbb{P}(X-\mu \geq y)=\mathbb{P}(X\geq \mu +y)=\mathbb{P}(X\leq \mu-y)=\mathbb{P}(X-\mu\leq -y)=\mathbb{P}(Y\leq -y)$$

Então, pelo caso em que $ \mu=0 $ temos que $ \mathbb{E}(Y)=0 $.

(b) Suponha que X possua densidade $ f(x) $. Mostre que se $ f(\mu+x)=f(\mu-x) $$ \forall x $, então a distribuição de X é simétrica em torno de $ \mu $. Enuncie e prove a propriedade análoga para o caso discreto.

$$\mathbb{P}(X\geq \mu +x)=\int_{\mu+x}^\infty f_X(x)dx$$

Fazendo uma mudança de variável $ y=2\mu-x $ e $ dy=-dx $, temos que

$$\int_{\mu+x}^\infty f_X(x)dx=-\int_{\mu-x}^{-\infty} f_X(2\mu+y)dy=\int_{-\infty}^{\mu-x}f_X(2\mu+y)dy=\int_{-\infty}^{\mu-x}f_X(y)dy=\mathbb{P}(X\leq \mu +x)$$

Caso Discreto: Suponha que X possui função de probabilidade $ p $. Mostre que se

$$\mathbb{P}(\mu+x)=\mathbb{P}(\mu-x), \quad \quad \forall x$$

então a distribuição de X é simétrica em torno de $ \mu $.

$$\mathbb{P}(X\geq \mu +x)=\sum_{\mu+x}^\infty \mathbb{P}(x)$$

tomando $ y=\mu-x $ temos que

$$\sum_{\mu+x}^\infty \mathbb{P}(x)=\sum_{-x}^{-\infty} \mathbb{P}(\mu-y)=\sum_{-\infty}^{-x}\mathbb{P}(\mu+y)=\sum_{-\infty}^{\mu-x}\mathbb{P}(X)=\mathbb{P}(X\leq \mu-x)$$

e o resultado segue.

(c)Qual o ponto de simetria das distribuições das seguintes variáveis aleatórias? Dê a esperança de cada variável aleatória, se existir.

(i) $ X\sim N(\mu,\sigma^2) $.

Temos que

$$f(x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2}, \quad \quad x\in \mathbb{R}$$

temos que :

$$f(\mu-x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(\mu-x-\mu)^2}=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}x^2}, \quad \quad x\in \mathbb{R}$$

e

$$f(\mu+x)=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(\mu+x-\mu)^2}=\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}x^2}, \quad \quad x\in \mathbb{R}$$

pelo item (b) X é simétrica em torno de $ \mu $.

$$\mathbb{E}(X)=\int_{-\infty}^\infty x \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2\sigma^2}(x-\mu)^2}$$

tomando $ y=\frac{x-\mu}{\sigma} $ e $ x=\sigma y +\mu $ e $ dx=\sigma dy $ então

$$\mathbb{E}(X)=\int_{-\infty}^\infty (\sigma y+\mu)\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}y^2}\sigma dy= \frac{\sigma}{\sqrt{2 \pi}}\int_{-\infty}^\infty y e^{-\frac{1}{2}y^2}dy+\mu \int_{-\infty}^\infty \frac{1}{\sqrt{2\pi}}e^{-\frac{1}{2}y^2}dy= \frac{\sigma}{\sqrt{2\pi}}\left[-e^{-\frac{1}{2}y^2}\right]_{-\infty}^{\infty}+\mu=\mu$$

(ii)$ X\sim Cauchy(M,b) $ i.e., $ f(x)=\frac{b}{\pi[b^2+(x-M)^2]}, \quad \quad x \in \mathbb{R} $

$$f(M-x)=\frac{b}{\pi[b^2+(M-x-M)^2]}=\frac{b}{\pi(b^2+x^2)}$$

e

$$f(M+x)=\frac{b}{\pi[b^2+(M+x-M)^2]}=\frac{b}{\pi(b^2+x^2)}$$

então pelo item (b) X é simétrica em M.

$$\mathbb{E}(X)=\int_{-\infty}^\infty x\frac{b}{\pi[b^2+(x-M)^2]}dx$$

tomando $ y=x-M $, $ x=y+M $ e $ dx=dy $ temos então que

$$\mathbb{E}(X)=\frac{2}{\pi}\int_{-\infty}^\infty (y+M)\frac{b}{b^2+y^2}dy=\frac{b}{\pi}\int_0^{\infty}\frac{2y}{b^2+y^2}dy+\frac{2bM}{\pi}\int_{0}^\infty \frac{1}{b^2+y^2}dy$$

então, temos que

$$\frac{b}{\pi}\int_0^{\infty}\frac{2y}{b^2+y^2}dy+\frac{2bM}{\pi}\int_{0}^\infty \frac{1}{b^2+y^2}dy=\frac{b}{\pi}\lim_{a\rightarrow \infty}\left(\ln(b^2+y^2)\right)_0^\infty+\frac{2bM}{\pi}\left[\frac{1}{\pi}arctg\left(\frac{M}{b}\right)\right]_0^\infty= 0$$

(iii)$ X\sim U[a,b] $

Assim,

$$\mathbb{E}(X)=\int_{-\infty}^\infty x f_X(x)dx=\int_a^b\frac{x}{b-a}dx=\frac{1}{b-a}\left[\frac{x^2}{2}\right]^b_a=\frac{1}{2}\frac{b^2-a^2}{(b-a)}=\frac{a+b}{2}$$

(iv)$ X \sim b\left(n, \frac{1}{2}\right) $

$$\mathbb{P}(x)=\binom{n}{x}\left(\frac{1}{2}\right)^2, x=0,1,2, \dots, n-1,n.$$

Agora, temos que

$$\mathbb{P}\left(x+\frac{n}{2}\right)=\binom{n}{x+\frac{n}{2}}\left(\frac{1}{2}\right)^n$$

$$\mathbb{P}\left(-x+\frac{n}{2}\right)=\binom{n}{-x+\frac{n}{2}}\left(\frac{1}{2}\right)^n$$

que são iguais pois $ x+\frac{n}{2}=n-\left(x-\frac{n}{2}\right) $. X é integrável, pois $ 0\leq X \leq n $, então pelo item (a):

$$\mathbb{E}(X)=\frac{n}{2}$$

(v) X tal que $ F_X $ é função de Cantor

Por construção X é simétrica em torno de $ \frac{1}{2} $ e como é limitada $ 0\leq \mathbb{E}(X)\leq 1 $ o que implica que $ \mathbb{E}(X)=\frac{1}{2} $

(vi) X tendo distribuição de Laplace (ou exponencial dupla):

$$f(x)=\frac{\lambda}{2}e^{-\lambda |x-\mu|}, \quad x \in \mathbb{R}$$

Temos que

$$f(\mu -x)=\frac{\lambda}{2}e^{-\lambda |\mu-x-\mu|}=\frac{\lambda}{2}e^{-\lambda |x|}, \quad x \in \mathbb{R}$$

e

$$f(\mu+ x)=\frac{\lambda}{2}e^{-\lambda |\mu+x-\mu|}=\frac{\lambda}{2}e^{-\lambda |x|}, \quad x \in \mathbb{R}$$

ou seja, é simétrica em torno de $ \mu $.

Agora

$$\mathbb{E}(X)=\int_{-\infty}^\infty x \frac{\lambda}{2}e^{-\lambda |x-\mu|}dx$$

definindo $ x-\mu=y $, $ x=y+\mu $ e $ dx=dy $ temos

$$\mathbb{E}(X)=\int_{-\infty}^\infty (y+\mu) \frac{\lambda}{2}e^{-\lambda |y|}dy= \int_{-\infty}^0 (y+\mu) \frac{\lambda}{2}e^{-\lambda |y|}dy +\int_{0}^\infty (y+\mu) \frac{\lambda}{2}e^{-\lambda |y|}dy = \mu$$

Exemplo 3.3.2

Seja X uma variável aleatória tendo distribuição logística com densidade

$$f(x)=\frac{e^{-x}}{(1+e^{-x})^2}, \quad x \in \mathbb{R}.$$

(a) Prove que a distribuição de X é simétrica em torno de zero

$$\frac{f(x)}{f(-x)}=\frac{\frac{e^{-x}}{(1+e^{-x})^2}}{\frac{e^{x}}{(1+e^{x})^2}}=\frac{e^{-x}(1+e^{x})^2}{e^{x}(1+e^{-x})^2}= \frac{e^{-x}+e^{x}+2}{e^{x}+e^{-x}+2}=1\Rightarrow f(x)=f(-x).$$

Assim pelo exemplo 3.3.1 é simétrica em torno de zero.

(b) Determine se X tem esperança finita, Se tiver ache o valor.

Sabemos X é integrável se, e somente se, $ \mathbb{E}(|X|)< \infty $

Assim

$$\mathbb{E}(|X|)=\int_0^\infty x dF_{|X|}(x)=\int_0^\infty x \left[f(x)+f(x)\right]dx=2\int_0^\infty x\frac{e^{-x}}{(1+e^{-x})^2}dx$$

Definimos, $ t=e^{-x} $, $ x=-\ln(t) $ e $ dx=-\frac{1}{t}dt $ e então

$$2\int_0^\infty x\frac{e^{-x}}{(1+e^{-x})^2}dx=2\int_0^1 \ln(t)\frac{t}{(1+t)^2}\left(\frac{1}{t}\right)dt=-2\int_0^1 \frac{\ln(t)}{(1+t)^2}dt$$

Novamente fazendo uma mudança de variável, $ u=\ln(t) $ o que implica que $ du=\frac{1}{t}dt $ e $ dv=\frac{1}{(1+t)^2}dt $ o que implica que $ v=-(1+t)^{-1} $. Então, temos que

$$-2\int_0^1 \frac{\ln(t)}{(1+t)^2}dt=-2\left(\left[-\frac{\ln(t)}{1+t}\right]_0^1+ \int_0^1 \frac{1}{t(t+1)}dt\right)=$$

$$-2\left(-\frac{\ln(t)}{1+t}+\ln\left(\frac{1+t}{t}\right)\right)_0^1 = -2\left[\ln(t)^{1/(t+1)}\left(\frac{1+t}{t}\right)\right]=$$

$$ -2 \left[\frac{t}{1+t}\ln(t)+\ln(1+t)\right]_0^1=2\ln(2)$$

então $ X $ é integrável pelo exemplo 3.3.1 temos que $ \mathbb{E}(X)=0 $.

(c)Obtenha a densidade de $ Y=e^{Y} $ e ache $ \mathbb{E}(Y). $

Temos que

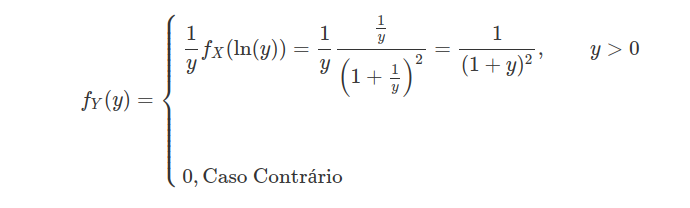
Assim,

$$\mathbb{E}(Y)=\int_0^\infty \frac{y}{(1+y)^2}dy$$

fazendo uma mudança de variável $ u=y $ o que implica que $ du=dy $ e $ dv=\frac{dy}{(1+y)^2} $ que implica que $ v=-\frac{1}{1+y} $, temos então que

$$\int_0^\infty \frac{y}{(1+y)^2}dy=\left[-\frac{y}{1+y}\right]_0^\infty + \int_0^\infty \frac{1}{1+y}dy= \infty$$

Exemplo 3.3.3

Calcule $ \mathbb{E}(X) $ se $ X $ possui densidade $ f(x) $, onde:

(a) f é a densidade dada

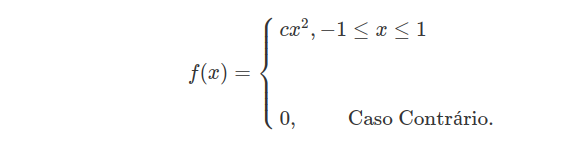
Então, a esperança é dada por

$$\mathbb{E}(X)=\int_{-1}^1 x f(x)dx=\int_{-1}^1 cx^3 dx =\left[\frac{cx^4}{4}\right]_{-1}^1=0$$

(b) $ f(x)=\displaystyle \frac{1}{(1+x)^2} $ se $ x > 0; $$ f(x)=0 $ se $ x\leq 0 $.

Pelo item (c) do exemplo 3.3.2 $ \mathbb{E}(X)=\infty $.

Exemplo 3.3.4

Calcule $ \mathbb{E}(X) $ neste caso.

Temos então

$$\mathbb{E}(X)=\int_0^\infty x f(x)dx=\int_0^\infty \lambda \alpha x^{\alpha}e^{-\lambda x^{\alpha}}dx$$

fazendo mudança de variável $ y=\lambda x^\alpha $, $ x=\left(\frac{y}{\lambda}\right)^{1/\alpha} $ com $ dx=\frac{1}{\lambda^{1/\alpha}}\frac{1}{\alpha} y^{\frac{1}{\alpha}-1} $, então temos que

$$\int_0^\infty \lambda \alpha x^{\alpha}e^{-\lambda x^{\alpha}}dx=\int_0^\infty \alpha y e^{-y}\frac{1}{\alpha}\frac{y^{1/\alpha - 1}}{\lambda^{1/\alpha}} dy = \lambda^{-\frac{1}{\alpha}}\int_{0}^\infty y^{1/\alpha}e^{-y}dy= \lambda^{-1/\alpha} \Gamma(1+1/\alpha)$$

Exemplo 3.3.5

Sejam $ X $ e $ Y $ variáveis aleatórias independentes com distribuição comum $ U[0,1] $. Calcule $ \mathbb{E}(Z) $ e $ \mathbb{E}(W) $, com $ Z=\min(X,Y) $ e $ W=\max(X,Y) $

Temos que

então,

$$\mathbb{E}(Z)=\int_0^1 \mathbb{P}(Z> z)dz= \int_0^1 (1-z)^2dz=-\frac{(1-z)^3}{3}\Biggl|_0^1 =\frac{1}{3}$$

Agora

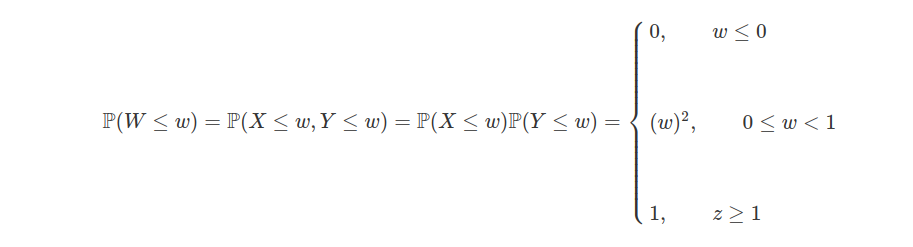
Então,

$$\mathbb{E}(W)=\int_0^\infty \mathbb{P}(W> z)dz= \int_0^1 (1-w)^2dz=w\Biggl|_0^1- \frac{w^3}{3}\Biggl|_0^1 =\frac{2}{3}$$

Exemplo 3.3.6

Um jogador vai lançando uma moeda honesta. Ele para depois de lançar ou duas caras sucessivas ou duas coras sucessivas. Qual a esperança do número de lançamentos ?

Seja $ X $ o número de lançamentos, primeiramente vamos considerar $ X=n $, com $ n $ par, ou seja, $ n=2k $ para $ k\in \mathbb{N} $. Então,

$$\mathbb{P}(X> 2k)=2p^k(1-p)^k=2\left(\frac{1}{2}\right)^k\left(\frac{1}{2}\right)^k=2\left(\frac{1}{2}\right)^{2k}=2\left(\frac{1}{2}\right)^n$$

Agora considere $ n=2k+1 $, então

$$\mathbb{P}(X> 2k+1)=p^k(1-p)^{k+1}+p^{k+1}(1-p)^{k}=2\left(\frac{1}{2}\right)^{2k+1} =2\left(\frac{1}{2}\right)^n$$

e

$$\mathbb{P}(X> 0)=\mathbb{P}(X\geq 1)=1$$

Então,

$$\mathbb{E}(X)=\displaystyle \sum_{n=0}^\infty \mathbb{P}(X> 0)=2+\sum_{n=2}^\infty 2\left(\frac{1}{2}\right)^n=2+\frac{1}{1-\frac{1}{2}}=3$$

Exemplo 3.3.7

Uma urna contém n bolas numeradas $ 1,2, \dots,n $. Uma pessoa tira uma bola e a devolve, tira outra e a devolve, continuando até tirar uma bola pela segunda vez. Seja X o número total de retiradas necessárias para obter essa repetição

(a) Ache a distribuição de X

Temos que $ [X> k]= $ as k primeiras bolas retiradas são diferentes, $ k=2,\dots, (n-1) $. Então,

$$\mathbb{P}(X> k)=\frac{C_n^k}{n^k}=\frac{n}{n}\frac{n-1}{n}\frac{n-2}{n}\dots \frac{n-k}{n} = \left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\dots \left(1-\frac{k}{n}\right)$$

e

$$\mathbb{P}(X> 0)=\mathbb{P}(X\geq 1)=1$$

e

$$\mathbb{P}(X\geq k)=0, k\geq n$$

(b) Mostre que

$$\mathbb{E}(X)=2+\left(1-\frac{1}{n}\right)+\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)+\dots +\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\dots \left(1-\frac{n-1}{n}\right)$$

Temos que $ X $ é uma variável não negativa, e pelo item (a) temos que

$$\mathbb{E}(X)=\sum_{n=0}^\infty \mathbb{P}(X> n)=2+\left(1-\frac{1}{n}\right)+\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)+\dots +\left(1-\frac{1}{n}\right)\left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right)\dots \left(1-\frac{n-1}{n}\right)$$

Exemplo 3.3.8

Sejam X e Y variáveis aleatórias. Se $ F_X(x)\leq F_Y(x) $ para todo $ x\in \mathbb{R} $, dizemos que X é estocasticamente maior que Y. Prove que se X é estocasticamente maior que Y, então $ \mathbb{E}(X)\geq \mathbb{E}(Y) $ (se $ \mathbb{E}(X) $ e $ \mathbb{E}(Y) $ existem )

Temos que

$$\mathbb{E}(X)=\int_0^\infty (1-F_X(x))dx-\int_{-\infty}^0 F_X(x)dx$$

e

$$\mathbb{E}(Y)=\int_0^\infty (1-F_Y(y))dy-\int_{-\infty}^0 F_Y(y)dy$$

Agora, como

$$F_X(x)\leq F_Y(x), \forall x\in \mathbb{R}$$

o que implica que

$$\int_{-\infty}^0 F_{X}(x)dx\leq \int_{-\infty}^0 F_Y(y)dy $$

e

$$(1-F_X(x))\geq (1-F_Y(x)), \forall x\in \mathbb{R}$$

o que implica que

$$\int_{0}^\infty(1- F_{X}(x))dx\leq \int_{0}^\infty (1-F_Y(y))dy $$

Então temos que

$$\mathbb{E}(X)\geq \mathbb{E}(Y).$$

Exemplo 3.3.9

Dois componentes eletrônicos vão ser testados simultaneamente. Suponha que a “vida” em horas de cada componente é exponencialmente distribuída com parâmetro $ \lambda $, e que as vidas dos componentes são independentes. Calcule:

(a) A esperança do tempo até a primeira falha de um dos componentes.

Temos que $ T_1\sim \exp(\lambda) $ independente $ T_2\sim \exp(\lambda) $ então

$$[T> t ]=[T_1> t]\cap [T_2> t] $$

Então,

$$\mathbb{P}(T> t)=\mathbb{P}(T_1> t) \mathbb{P}(T_2> t)= e^{-\lambda t}e^{-\lambda t}=e^{-2\lambda t}$$

Assim, como

$$\mathbb{E}(T)=\int_0^\infty \mathbb{P}(T> t)dt=\int_0^\infty e^{-2\lambda t}=-\frac{e^{-2\lambda}}{2\lambda}\Bigg|_0^\infty = \frac{1}{2\lambda}$$

(b) A esperança do tempo até ambos os componentes falharem.

Para isso, temos que

$$[T\leq t ]=[T_1\leq t]\cap [T_2\leq t] $$

o que implica que

$$\mathbb{P}(T\leq t)=\mathbb{P}(T_1\leq t) \mathbb{P}(T_2\leq t)= \left(1-e^{-\lambda t}\right)^2$$

Como T é uma variável não-negativa então

$$\mathbb{E}(T)=\int_0^\infty \mathbb{P}(T> t)dt=\int_0^\infty \left(e^{-2\lambda t}+2e^{-\lambda t}\right)dt=\frac{3}{2\lambda}$$

Exemplo 3.3.10

Dois jogadores lançam moedas simultaneamente até obterem o primeiro casamento (ie. ou duas caras ou duas coroas ). Se os dois lançam “cara” simultaneamente, ganha o jogador I, se ambos lançam “coroa”, ganha o jogador II. Por exemplo, se os dois obtêm “cara” no primeiro lançamento, então o jogo termina e o jogador I ganha o jogo. Suponha que a moeda do jogador I seja honesta, mas que a moeda do outro não necessariamente ou seja, tendo probabilidade $ p $ de “cara”, $ 0< p< 1 $.

(a) Calcule a esperança do número de lançamentos (i.e., o número de vezes que o jogador I lança a moeda até terminar o jogo).

Defina

então

$$\mathbb{P}(X_i=0)=\frac{1}{2}=\mathbb{P}(X_i=1)$$

e

$$\mathbb{P}(Y_i=0)=p,\quad \quad \quad \mathbb{P}(Y_i=1)=1-p$$

Vamos definir os seguintes conjuntos

$$G_i^{I}=(\text{Ganha o jogador I no Lançamento i})$$

$$G_i^{II}=(\text{Ganha o jogador II no Lançamento i})$$

e ainda

$$C_i=(\text{nem o jogador I e o jogador II no lançamento i e então o jogo continua.})$$

Assim temos que

$$\mathbb{P}\left(G_i^{I}\bigg| C_{i-1}\right)=\mathbb{P}(X_i+Y_i=0)=\mathbb{P}(X_i=0)\mathbb{P}(Y_i=0)=\frac{1}{2}p$$

$$\mathbb{P}\left(G_i^{II}\bigg| C_{i-1}\right)=\mathbb{P}(X_i+Y_i=2)=\mathbb{P}(X_i=1)\mathbb{P}(Y_i=1)=\frac{1}{2}(1-p)$$

$$\mathbb{P}\left(C_i\bigg| C_{i-1}\right)=\mathbb{P}(X_i+Y_i=1)=$$

$$\mathbb{P}(X_i=0)\mathbb{P}(Y_i=1)+ \mathbb{P}(X_i=1)\mathbb{P}(Y_i=0)=$$

$$ \frac{1}{2}p+\frac{1}{2}(1-p)=\frac{1}{2}$$

Seja $ Z $ a variável aleatória que conta o número de lançamentos até o jogo acabar. Então, temos que

$$\mathbb{P}(Z> n)=\mathbb{P}(C_1)\mathbb{P}\left(C_2\bigg|C_1\right)\mathbb{P}\left(C_3\bigg|C_1\cap C_2\right) \dots \mathbb{P}\left(C_n\bigg|C_1\cap C_2\cap \dots \cap C_{n-1}\right)$$

$$= \mathbb{P}\left(C_1\right)\mathbb{P}\left(C_2\bigg|C_1\right)\dots \mathbb{P}\left(C_n\bigg|C_{n-1}\right)=$$

$$\left(\frac{1}{2}\right)^n, \quad n=0,1,2, \dots$$

Como Z é uma variável não negativa, temos que

$$\mathbb{E}(Z)=\sum_{n=0}^\infty \mathbb{P}(Z> n)=\sum_{n=0}^\infty\left(\frac{1}{2}\right)^n =\frac{1}{1-\frac{1}{2}}=2$$

(b) Ache a probabilidade do jogador I ganhar o jogo (mais cedo ou mais tarde)

Defina

$$W=(\text{Jogador ganha o Jogo})$$

e

$$W_i=(\text{Jogador ganha o Jogo no lançamento i}).$$

Então $ W=\displaystyle \bigcup_{i=1}^\infty W_i $ pela $ \sigma $-aditividade temos que

$$\mathbb{P}(W)=\sum_{n=1}^\infty \mathbb{P}(W_n)$$

Agora

$$\mathbb{P}(W_n)=\mathbb{P}(C_1)\mathbb{P}\left(C_2\bigg|C_1\right)\dots \mathbb{P}\left(C_{n-1}\bigg|C_{n-2}\right) \mathbb{P}\left(G^{I}_{n}\bigg|C_{n-1}\right)=\left(\frac{1}{2}\right)^{n-1}\frac{1}{2}p$$

Então,

$$\mathbb{P}(W)=\sum_{n=1}^\infty \left(\frac{1}{2}\right)^n p=\frac{\frac{1}{2}}{1-\frac{1}{2}}p=p$$

Exemplo 3.3.11

Jogadores I e II tem 200,00 reais. Lança-se uma moeda com probabilidade $ p $ de dar cara (0< p < 1). Se der cara, o jogador I recebe 100,00 reais do II, se der coroa, I paga 100,00 reais ao II. Continua-se lançando a moeda, independentemente, até um dos jogadores perder tudo, i.e., até um deles ficar com os 400,00 reais. Determine $ \mathbb{E}(N) $, no qual N é o número de lançamentos até terminar o jogo.

Defina $ X_i=\text{número de caras até a jogada i} $, $ Y_i=\text{ número de coroas até a jogada i} $ o jogo só acaba na i-ésima jogada se $ |X_i-Y_i|=2 $. Assim, considere primeiramente $ n $ um número par e $ n=2k $ então

$$[N> n]=[X_i=k]\cap [Y_i=k]$$

Então,

$$\mathbb{P}(N> n)=p^k(1-p)^k=[p(1-p)]^k$$

Agora, se n é impar então

$$[N> n]=\left([X_i=k]\cap[Y_i=k+1]\right)\bigcup \left([X_i=k+1]\cap[Y_i=k]\right)$$

o que implica que

$$\mathbb{P}(N> n)=p^k(1-p)^{k+1}+p^{k+1}(1-p)^{k}=p^k(1-p)^k[p(1-p)]=p^k(1-p)^k$$

com

$$\mathbb{P}(N> 0)=\mathbb{P}(N> 1)=0$$

Assim,

$$\mathbb{E}(N)=\sum_{n=0}^\infty \mathbb{P}(N> n)=2+\sum_{k=1}^\infty \mathbb{P}(N> 2k)+\sum_{k=1}^\infty \mathbb{P}(N> 2k+1)=2\frac{2p(1-p)}{1-p(1-p)}=\frac{4p(1-p)}{1-p(1-p)}$$

Exemplo 3.3.12

Prove que o critério de integrabilidade ainda vale se “$ \geq $” é substituído por “$ > $”, isto é, X é integrável se, e somente se,

$$\sum_{n=1}^\infty \mathbb{P}(|X|> n)< \infty.$$

Temos que $ X $ é integrável se, e somente, se $ |X| $ é integrável

Agora $ \mathbb{E}(|X|)\leq \mathbb{E}(|X|)+1 $. Porém,

$$\mathbb{E}(|X|)=\sum_{n=0}^\infty \mathbb{P}(|X|> n)=\mathbb{P}(|X|> 0)+ \sum_{n=1}^\infty \mathbb{P}(|X|> n)$$

então,

$$\sum_{n=0}^\infty \mathbb{P}(|X|> n)\leq \mathbb{E}(|X|)\leq 1+\sum_{n=1}^\infty \mathbb{P}(|X|> n)$$

Assim,

$$\sum_{n=1}^\infty \mathbb{P}(|X|> n)\leq \mathbb{E}(|X|)\leq 2+\sum_{n=1}^\infty \mathbb{P}(|X|> n).$$

Então,

$$\mathbb{E}(|X|)> \infty$$

se, e somente se,

$$\sum_{n=1}^\infty \mathbb{P}(|X|> n)< \infty$$

Exemplo 3.3.13

Verifique que a desigualdade de Jensen ainda vale se a função $ \varphi $ é convexa em um intervalo (a,b) tal que

$$\mathbb{P}(a< X < b)=1,$$

no qual admitimos a possibilidade de $ a=-\infty $ ou $ b=\infty $.

Exemplo 3.3.14

Sejam X e Y variáveis aleatórias com densidade conjunta $ f(x,y) $. Verifique se $ \mathbb{E}(aX+bY)=a\mathbb{E}(X)+b\mathbb{E}(Y) $ para esse caso.(Suponha $ \mathbb{E}(X) $ e $ \mathbb{E}(Y) $ finito)

Sabemos que se a X e Y tem densidade conjunta $ f(x,y) $ então:

$$\mathbb{E}(aX+bY)=\int_{-\infty}^\infty \int_{-\infty}^\infty(ax+by)f_{X,Y}(x,y)dxdy=\int_{-\infty}^\infty \int_{-\infty}^\infty a x f_{X,Y}(x,y)dxdy +\int_{-\infty}^\infty \int_{-\infty}^\infty by f_{X,Y}(x,y)dxdy$$

e

$$a\mathbb{E}(X)+b\mathbb{E}(Y)=a\int_{-\infty}^\infty x f_X(x)dx+b\int_{-\infty}^\infty yf_Y(y)dy$$

Mas,

$$\int_{-\infty}^\infty \int_{-\infty}^\infty a x f_{X,Y}(x,y)dxdy +\int_{-\infty}^\infty \int_{-\infty}^\infty by f_{X,Y}(x,y)dxdy=a\int_{-\infty}^\infty x f_X(x)dx+b\int_{-\infty}^\infty yf_Y(y)dy=a\mathbb{E}(X)+b\mathbb{E}(Y)$$

Portanto,

$ \mathbb{E}(aX+bY)=a\mathbb{E}(X)+b\mathbb{E}(Y) $.

Exemplo 3.3.15

Suponha que $ X\sim U[0,1] $. Determine os valores de $ t(t\in \mathbb{R}) $ tais que $ \mathbb{E}(X^t) $ é finita. Qual o valor da esperança nesse caso?

$$\mathbb{E}(X^t)=\int_{-\infty}^\infty x^t f_X(x)dx$$

Agora se $ X\sim U[0,1] $, então $ f_X(x)={1}_{[0,1]} $. Logo,

$$\mathbb{E}(X^t)=\int_0^1 x^tdx=\frac{x^{t+1}}{t+1}\Biggl|_0^1=\frac{1}{t+1}$$

Portanto, $ \mathbb{E}(X^t)\leq \infty $ o que implica que $ t\neq -1 $, assim $ t\in \mathbb{R}-(-1) $ o que implica que $ \mathbb{E}(X^t)=\frac{1}{1+t}< \infty. $

Exemplo 3.3.16

Calcule $ \mathbb{E}(e^X) $, no qual X tem densidade Logística

$$\frac{e^{-x}}{(1+e^{-x})^2}$$

$ x\in \mathbb{R} $, utilizando o Teorema 3.3.1. Compare com o resultado obtido no exemplo 3.3.2(c).

Pelo Teorema 3.3.1 temos:

$$\mathbb{E}(e^x)= \int_{-\infty}^\infty e^x \frac{e^{-x}}{(1+e^{-x})^2}dx=\int_{-\infty}^\infty \frac{1}{(1+e^{-x})^2}dx=\int_{-\infty}^0 \frac{1}{(1+e^{-x})^2}dx+\int_{0}^\infty \frac{1}{(1+e^{-x})^2}dx $$

Agora, fazendo uma mudança de variável $ y=e^{-x} $ e $ dy=\frac{e^{-x}}{y}dx $

$$\int_{-\infty}^0 \frac{1}{(1+e^{-x})^2}dx=\int_0^1\frac{1}{y\left(1+\frac{1}{y}\right)^2}dy=\int_0^1 \frac{y}{(1+y)^2}dy$$

novamente fazendo uma mudança de variável $ z=1+y $ e $ dz=dy $

$$\int_0^1 \frac{y}{(1+y)^2}dy=\int_1^2 \frac{z-1}{z^2}dz= \ln z\Biggl|_1^2 +\frac{1}{z}\Biggl|_1^2=\ln 2-\frac{1}{2}.$$

Temos que

$$\int_{0}^\infty \frac{1}{(1+e^{-x})^2}dx=\infty$$

pois

$$\frac{1}{(1+e^{-x})^2}\geq 0, \quad \quad x\in \mathbb{R}_{+}$$

e

$$\lim_{x\rightarrow \infty}\frac{1}{(1+e^{-x})^2}=1$$

Então,

$$\mathbb{E}(e^{x})=\ln2- \frac{1}{2}+\infty=\infty$$

Exemplo 3.3.17

Calcule a esperança de

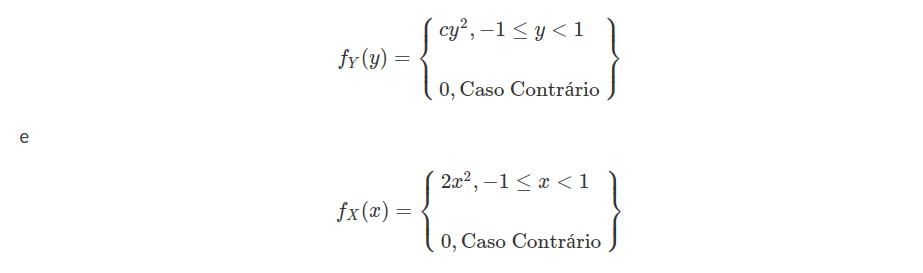
Para o primeiro caso, temos que

$$\mathbb{E}(Y)=\int_{-\infty}^\infty f_Y(y)dy=\int_{-1}^1 cy^3dy=\frac{cy^4}{4}\Biggl|_{-1}^{1}=0$$

Para o segundo caso temos que

$$\mathbb{E}(X)=\int_{-\infty}^\infty f_X(x)dx=\int_{0}^1 3y^3dx=\frac{3y^4}{4}\Biggl|_{0}^{1}=\frac{3}{4}$$

Exemplo 3.3.18

Seja X o tempo de espera até o primeiro sucesso em uma sequência de ensaios de Bernoulli tendo probabilidade $ p $ de sucesso em cada ensaio. Calcule $ \mathbb{E}(X^2) $

$$\mathbb{P}(X=k)=p(1-p)^{k-1},\quad \quad k=1,2, \dots $$

para $ 0< p< 1 $, então

$$\mathbb{E}(X^2)=\sum_{k=1}^\infty \left(k^2 p (1-p)^{k-1}\right)=p\sum_{k=1}^\infty \left(k^2 (1-p)^{k-1}\right)$$

para simplificar a notação vamos definir $ q:=(1-p) $, então vamos mostrar que

$$\sum_{k=1}^\infty \left(k^2 q^{k-1}\right)=\frac{1+q}{(1-q)^3}$$

Para isso, observe que

$$\sum_{k=1}^\infty \left(k^2 q^{k-1}\right)=1+4q+9q^2+16q^3+\dots =\sum_{k=1}^\infty q^{k-1}+3q+8q^2+15q^3+\dots$$

$$=\left(\sum_{k=1}^\infty q^{k-1}\right)+3q(1+q+q^2+q^3+\dots)+5q^2+12q^3+21q^4+\dots =\left(\sum_{k=1}^\infty q^{k-1}\right)(1+3q)+5q^2(\sum_{k=1}^\infty q^{k-1})+7q^3+16q^4+\dots$$

$$=\left(\sum_{k=1}^\infty q^{k-1}\right)(1+3q+5q^2+7q^3+9q^4+\dots)=\left(\sum_{k=1}^\infty q^{k-1}\right)\left(\sum_{k=1}^\infty (2k-1)q^{k-1}\right)$$

Então temos que

$$\left(\sum_{k=1}^\infty k^2 q^{k-1}\right)=\left(\sum_{k=1}^\infty q^{k-1}\right)\left[2\left(\sum_{k=1}^\infty q^{k-1}\right)-\left(\sum_{k=1}^\infty k q^{k-1}\right)\right]$$

Mas, é conhecido que

$$\left(\sum_{k=1}^\infty q^{k-1}\right)=\frac{1}{1-q}$$

e

$$\left(\sum_{k=1}^\infty kq^{k-1}\right)=\frac{1}{(1-q)^2}$$

Então, temos que

$$\left(\sum_{k=1}^\infty k^2 q^{k-1}\right)=\left(\frac{1}{1-q}\right)\left[\frac{2}{(1-q)^2}-\frac{1}{1-q}\right]=\frac{1}{1-q}\left( \frac{2-1+q}{(1-q)^2}\right)=\frac{1+q}{(1-q)^3}$$

Desta forma temos que

$$\mathbb{E}(X^2)=p\frac{1+q}{(1-q)^3}=\frac{2-p}{p^2}$$

3.4 - Momentos

Seja $ X $ uma variável aleatória. Se $ \mathbb{E}(X^r) \ < \ \infty $, dizemos que $ \mathbb{E}(X^r) $ é o r-ésimo momento de $ X $.

O r-ésimo momento em torno de $ \alpha\in\mathbb{R} $ é definido como sendo $ \mathbb{E}((X-\alpha)^r) $, caso este valor esperado exista. Se $ \alpha=\mathbb{E}(X) $ então ele é chamado de r-ésimo momento central. Observamos que $ \text{Var}(X)=\mathbb{E}[(X-\mathbb{E}(X))^2] $, ou seja, a variância $ \text{Var}(X) $ é definida como sendo o segundo momento central. Uma definição mais detalhada da variância e de suas propriedades pode ser encontrada na Seção 4.

Função geradora de momentos

Definição 3.4.1

Seja $ X $ uma variável aleatória. A função geradora de momentos da variável $ X $ é definida como sendo a função

$$M_{X}(t)=\mathbb{E}(e^{tX})$$

desde que $ \mathbb{E}(e^{tX}) $ exista em algum intervalo do tipo $ (-h,h) $ para algum número real $ h \ > \ 0 $.

A função geradora de momentos possui esse nome pois, a partir dela, podemos encontrar todos os momentos da variável aleatória $ X $ (quando estes existem). A função só precisa estar definida em uma vizinhança do ponto zero, pois os momentos serão obtidos através de sucessivas diferenciações aplicadas em zero, utilizando o resultado abaixo.

Teorema 3.4.1

Seja $ X $ uma variável aleatória. Como $ \mathbb{E}(e^{tX}) $ está definido para $ t\in (-h,h) $ para algum $ h\in\mathbb{R} $, temos que

$$M_{X}^{(n)}(t)=\frac{d^n}{dt^n}\mathbb{E}\left(e^{tX}\right)=\mathbb{E}\left(\frac{d^n}{dt^n}e^{tX}\right) = \mathbb{E}\left(X^ne^{tX}\right).$$

Observamos que

$$M_{X}^\prime(t)=\frac{d}{dt}\mathbb{E}\left(e^{tX}\right)=\mathbb{E}\left(\frac{d}{dt}e^{tX}\right)=\mathbb{E}\left(Xe^{tX}\right)$$

e, no ponto $ t = 0 $ temos que $ M_{X}^\prime(0)=\mathbb{E}(X) $. Similarmente temos que:

$$M_{X}^{\prime\prime}(t)=\frac{d^2}{dt^2}\mathbb{E}\left(e^{tX}\right)=\mathbb{E}\left(\frac{d^2}{dt^2}e^{tX}\right)=\mathbb{E}\left(X^2e^{tX}\right)$$

e, se calcularmos $ M_X^{\prime\prime}(t) $ no ponto $ t=0 $, temos que $ M_{X}^{\prime\prime}(0)=\mathbb{E}(X^2) $. Por indução, é fácil perceber que:

$$M_{X}^{(n)}(t)=\frac{d^n}{dt^n}\mathbb{E}\left(e^{tX}\right)=\mathbb{E}\left(X^ne^{tX}\right).$$

de onde segue que $ M_X^{(n)}(0) = \mathbb{E}(X^n) $.

Portanto, se queremos encontrar o n-ésimo momento da variável aleatória $ X $, basta derivarmos sua função geradores de momentos (quando esta existir) $ n $ vezes e então calcular o seu valor no ponto $ t = 0 $.

Função geradora de momentos de variáveis aleatórias discretas

Definição 3.4.2

Seja $ X $ uma variável aleatória discreta que assume valores em $ \mathcal{R}_X $. A função geradora de momentos de $ X $, quando existe, é então calculada da seguinte forma:

$$M_{X}(t)=\mathbb{E}\left(e^{tX}\right)=\sum_{x\in\mathcal{R}_X}e^{tx}p(x),$$

em que $ p(x) $ é a função de probabilidade da variável aleatória $ X $, isto é, $ p(x) = \mathbb{P}(X=x) $.

A seguir, apresentamos alguns exemplos de funções geradoras de momentos para algumas variáveis aleatórias discretas (veremos com mais detalhes essas variáveis aleatórias na seção 5).

Exemplo 3.4.1

Seja $ X $ uma variável aleatória discreta com distribuição binomial com parâmetros $ n $ e $ p $, ou seja, $ X\sim b(n,p) $. Então

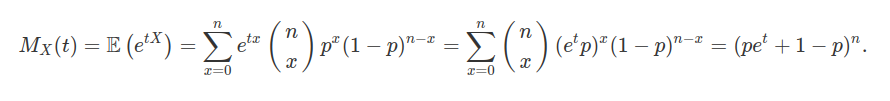
Podemos encontrar a média e a variância através da função geradora de momentos. Assim

$$M^\prime_X(t)=\frac{d}{dt}(p e^t+ 1-p)^n=n(pe^t+1-p)^{n-1}pe^t.$$

Então como $ \mathbb{E}(X)=M^\prime_X(0)=n(p+1-p)^{n-1}p=np $.

Para encontrarmos a variância basta derivarmos mais uma vez a função $ M_X(t) $. Assim temos que:

$$M^{\prime\prime}_X(t)=\frac{d^2}{dt^2}(p e^t+ 1-p)^n=n(n-1)(pe^t+1-p)^{n-2}pe^t pe^t+pe^t n(pe^t+1-p)^{n-1}$$

e, portanto,

$$M^{\prime\prime}_X(t)=n(n-1)(pe^t+1-p)^{n-2}(pe^t)^2+npe^t (pe^t+1-p)^{n-1}.$$

Logo, segue que $ \mathbb{E}\left(X^2\right)=M^{\prime\prime}_X(0)=n(n-1)p^2+ pn $, então obtemos que:

$$\text{Var}(X)=\mathbb{E}(X^2)-\mathbb{E}^2(X)=[n(n-1)p^2+pn] -(np)^2=np^2(n-1)+np-n^2p^2=np(1-p).$$

Exemplo 3.4.2

Seja $ X $ uma variável aleatória discreta com distribuição de Poisson, com parâmetro $ \lambda $, ou seja, $ X\sim Po({\lambda}) $. Então

$$M_{X}(t)=\mathbb{E}[e^{tX}]=\sum_{k=0}^{\infty}\frac{e^{tk}e^{\lambda}\lambda^k}{k!}=e^{-\lambda}\sum_{k=0}^{\infty}\frac{(\lambda e^t)^k}{k!}=e^{-\lambda}e^{\lambda e^t}=e^{\lambda[e^t-1]}.$$

Exemplo 3.4.3

Seja $ X $ uma variável aleatória discreta com distribuição geométrica com parâmetro p, ou seja, $ X\sim \ \text{Geo}(p) $. Então

$$M_{X}(t)=\mathbb{E}[e^{tX}]=\sum_{k=0}^{\infty}e^{tk}(1-p)^{k-1}p=\frac{pe^{t}}{1-(1-p)e^t}.$$

A tabela abaixo resume a função geradora de momentos de algumas das principais distribuições discretas já vistas acima.

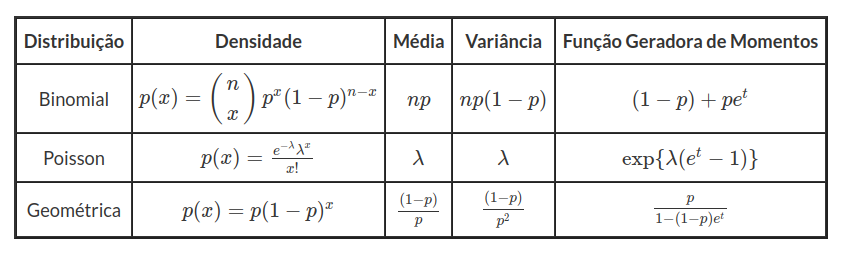
Exemplo 3.4.4

Vamos encontrar a função geradora de momentos para calcular a variável aleatória da soma de Poisson independentes, assim sendo, seja $ X~\sim ~Po(\lambda_1) $ e $ Y~\sim ~Po(\lambda_2) $.

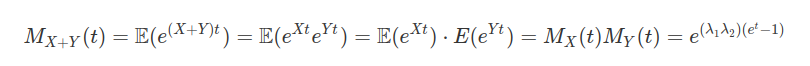
Pela unicidade da função geradora de momentos, temos que a soma de variáveis aleatórias independentes que seguem uma distribuição de Poisson, também possui uma distribuição de Poisson. Ou seja, $ X+Y~\sim ~Po(\lambda_1+\lambda_2) $. Por indução finita podemos concluir que se $ X_i~\sim ~Po(\lambda_i) $, então $ \displaystyle\sum_{i=1}^{n}X_i~\sim ~Po\left(\displaystyle\sum_{i=1}^{n}\lambda_i \right) $.

Exemplo 3.4.5

Vamos utilizar a função geradora de momentos para encontrar a distribuição de $ X+Y $, sabendo que $ X $ e $ Y $ são independentes com $ X~\sim ~b(n,p) $ e $ Y~\sim ~b(m,p) $.

$$M_{X+Y}(t)=\mathbb{E}(e^{(X+Y)t})=\mathbb{E}(e^{Xt}e^{Yt})=\mathbb{E}(e^{Xt})\mathbb{E}(e^{Yt})=M_X(t)M_Y(t)=(pe^t+ 1-p)^{m+n}.$$

Da mesma forma que o exemplo anterior concluímos pela unicidade da função geradora de momentos que $ X+Y~\sim ~b(m+n,p) $. Assim por indução finita concluímos que $ X_i~\sim ~ b(n_i,p) $, então $ \displaystyle\sum_{i=1}^{k}X_i~\sim ~b\left(\displaystyle\sum_{i=1}^{k}n_i,p \right) $

Função geradora de momentos de variáveis aleatórias contínuas

Assim como foi definido para variáveis aleatórias discretas, temos a seguinte definição para a função geradora de momentos de uma variável aleatória contínua

Definição 3.4.3

Seja $ X $ uma variável aleatória contínua. A função geradora de momentos, também denotada por $ M_X(t) $ é dada por:

$$M_{X}(t)=\mathbb{E}[e^{tX}]=\int_{-\infty}^{\infty}e^{tx}f(x)dx$$

em que $ f(x) $ é a função densidade de probabilidade de $ X $. A seguir, vamos calcular a função geradora de momentos para algumas variáveis aleatórias contínuas, sendo que veremos cada uma delas com mais detalhes no seção 6.

Exemplo 3.4.6

Seja $ X $ uma variável aleatória contínua com distribuição exponencial de parâmetro $ \lambda $, ou seja, $ X\sim \ \text{Exp}(\lambda) $. Então, temos que

$$M_{X}(t)=\mathbb{E}[e^{tX}]=\int_{-\infty}^{\infty}e^{tx}\lambda e^{-\lambda x}dx=\lambda \int_{0}^{\infty}e^{-(\lambda-t)x}dx=\frac{\lambda}{\lambda -t},~~~t<\lambda.$$

Exemplo 3.4.7

Seja $ X $ uma variável aleatória contínua com distribuição normal com média $ \mu=0 $ e variância $ \sigma^2=1 $, ou seja, $ X\sim N(0,1) $. Então

$$M_{X}(t)=\mathbb{E}[e^{tX}]=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{tx}e^{-x^2/2}dx=\frac{e^{t^2/2}}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-(x-t)^2/2}dx=e^{t^2/2}.$$

Exemplo 3.4.8

Seja $ X $ uma variável aleatória contínua com distribuição normal com média $ \mu $ e variância $ \sigma^2 $, ou seja, $ X \sim N(\mu,\sigma^2) $ e seja $ Z\sim N(0,1) $. Então $ X=\sigma Z+\mu $. Assim sendo, podemos usar a função geradora de momentos de $ Z $ para calcular a função geradora de momentos de X, da seguinte forma:

$$M_X(t)=\mathbb{E}[e^{tX}]=\mathbb{E}[e^{t(\sigma Z+ \mu)}]=e^{t\mu}\mathbb{E}[e^{t\sigma Z}]=e^{t\mu}e^{\frac{(t\sigma)^2}{2}}=\exp\left(\frac{\sigma^2 t^2}{2}+ \mu t\right).$$

Vamos calcular a variância e a média de X a partir da função geradora de momentos.

$$M^\prime_X(t)=\frac{d}{dt}\exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)=(\mu+t\sigma^2)\exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)$$

e

$$M^{\prime\prime}_X(t)=\frac{d^2}{dt^2}\exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)=(\mu+ t\sigma^2)^2 \exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)+ \sigma^2 \exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)$$

E, portanto, $ \mathbb{E}[X]=M^\prime_X(0)=\mu $ e $ \mathbb{E}[X^2]=\mu^2+\sigma^2 $ de onde segue que a variância é dada por

$$\text{Var}(X)=\mathbb{E}(X^2)-\mathbb{E}^2(X)=\mu^2-\sigma^2-\mu^2=\sigma^2.$$

Uma demonstração alternativa deste fato pode ser vista no seção 6.2.

Exemplo 3.4.9

Se $ X\sim N(\mu_1,\sigma_1^2) $ e $ Y\sim N(\mu_2,\sigma_2^2) $ são variáveis aleatórias independentes, então $ X+Y\sim N(\mu_1+ \mu_2,\sigma_1^2+\sigma_2^2) $.

De fato,

$$M_{X+Y}(t)=\mathbb{E}(e^{(X+Y)t})=\mathbb{E}(e^{Xt}e^{Yt})=\mathbb{E}(e^{Xt})\mathbb{E}(e^{Yt})=M_X(t)M_Y(t)$$

de onde segue que

$$M_{X+Y}(t)=\exp\left(\frac{\sigma_1^2 t^2}{2}+ \mu_1 t\right)\exp\left(\frac{\sigma_2^2 t^2}{2}+ \mu_2 t\right)=\exp\left( \frac{(\sigma_1^2+\sigma_2^2)t^2}{2}+(\mu_1+\mu_2)t\right).$$

Assim pela unicidade da função geradora de momentos concluímos que $ X+Y\sim N(\mu_1+ \mu_2,\sigma_1^2+\sigma_2^2) $. Por indução finita podemos concluir que se $ X_i~\sim ~ N(\mu_i,\sigma_i^2) $, então $ \displaystyle\sum_{i=1}^{k}X_i~\sim ~N\left(\displaystyle\sum_{i=1}^{k}\mu_i,\sum_{i=1}^{k}\sigma_i\right) $.

Exemplo 3.4.10

Suponha que a variável aleatória X tenha a seguinte densidade “triangular”:

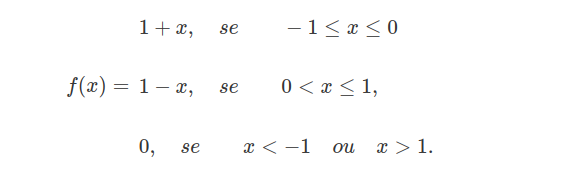
Calcule $ \mathbb{E}(X) $ e $ Var(X) $.

$$\mathbb{E}\left(X\right)=\int_{-\infty}^\infty x f(x)dx=\int_{-1}^0 x(1+x)dx+\int_{0}^1x(1-x)dx=\left[\frac{x^2}{2}+\frac{x^3}{3}\right]_{-1}^0+ \left[\frac{x^2}{2}+\frac{x^3}{3}\right]_{0}^1=-\frac{1}{2}+\frac{1}{3}+\frac{1}{2}-\frac{1}{3}=0$$

$$\mathbb{E}(X^2)=\int_{-\infty}^\infty x^2 f(x)dx =\int_{-1}^0x^2(1+x)dx+\int_{0}^1 x^2(1+x)dx=\left[\frac{x^3}{3}+\frac{x^4}{4}\right]_{-1}^0 + \left[\frac{x^3}{3}+\frac{x^4}{4}\right]_{0}^1=\frac{1}{3}-\frac{1}{4}+\frac{1}{3}-\frac{1}{4}=\frac{1}{6}$$

Então,

$$Var(X)=\mathbb{E}(X^2)-\mathbb{E}^2(X)=\frac{1}{6}$$

Exemplo 3.4.11

(a) Prove: se a variável aleatória X é limitada, então tem momentos finitos de toda ordem.

X é limitada o que implica que existe $ k> 0 $ tal que $ |X|< k $ o que implica que $ \mathbb{E}(|X|)< k $ o que implica que X é integrável. Agora, se X é limitada $ |X|^t< k^t $, $ t> 0 $ o que implica que $ \mathbb{E}(|X|^t)< k^t $ o que implica que $ X^t $ é integrável. Assim, X terá momentos finitos de toda ordem.

(b) Seja A um evento aleatória. Calcule todos os momentos absolutos da variáveis aleatória $ X={1}_A $.

Temos que $ X^t=\left({1}_A\right)^t={1}_A $ o que implica que

$$\mathbb{E}(X^t)=\mathbb{E}(X)=\mathbb{E}({1}_A)=\int_A f_x(x)dx=\mathbb{P}(X\in A), \forall t \in A$$

(c) Demonstre: se $ X\sim N(\mu,\sigma^2) $, então todos os momentos absolutos de X são finitos.

(d) Seja $ X\sim Cauchy(0,1) $.

Quais são os momentos absolutos finitos de X?

Exemplo 3.4.12

Obtenha as variância de $ Z $ e $ W $ dadas por

Agora, já sabemos que $ \mathbb{E}(Z)=\frac{1}{3} $ e $ \mathbb{E}(W)=\frac{2}{3} $. Agora,

$$\mathbb{E}(Z^2)=\int_{-\infty}^\infty z^2f_Z(z)dz =\int_0^1 2z^2(1-z)dz=\left(\frac{2}{3}z^3-\frac{z^4}{2}\right)_0^1=\frac{2}{3}-\frac{1}{2}=\frac{1}{6}$$

e

$$\mathbb{E}(W^2)=\int_{-\infty}^\infty w^2f_W(w)dw =\int_0^1 2w^3dw=\left(\frac{w^4}{2}\right)_0^1=\frac{1}{2}$$

Então,

$$Var(Z)=\mathbb{E}(Z^2)-\mathbb{E}^2(Z)=\frac{1}{6}-\frac{1}{9}=\frac{1}{18}$$

$$Var(W)=\mathbb{E}(W^2)-\mathbb{E}^2(W)=\frac{1}{2}-\frac{4}{9}=\frac{1}{18}$$

Exemplo 3.4.13

Através de experimentos estatísticos, determina-se que a duração de um certo tipo de chamada telefônica satisfaz a relação

$$\mathbb{P}(T> t)=ae^{-\lambda t}+(1-a)e^{-\xi t}$$

$ t\geq 0 $, no qual $ 0\leq a\leq 1 $, $ \lambda > 0 $, $ \xi > 0 $. Ache a média e a variância de T.

Temos que T é uma variável não-negativa, então:

$$\mathbb{E}(T)=\int_0^\infty \mathbb{P}(T> t)dt=\int_0^\infty a e^{-\lambda t}dt+\int_0^\infty (1-a)e^{-\xi t}dt= a \int_0^\infty e^{-\lambda t}dt+(1-a)\int_0^\infty e^{-\xi t}dt$$

o que implica que $ \mathbb{E}(T)=\frac{a}{\lambda}+\frac{(1-a)}{\xi} $. Agora $ T^2 $ é também variável aleatória não-negativa, então:

$$\mathbb{E}(T^2)=2\int_0^\infty t \mathbb{P}(T> t)dt=2\left( a \int_0^\infty te^{-\lambda t}dt+(1-a)\int_0^\infty t e^{-\xi t}dt\right)=2\left[\frac{a}{\lambda^2}+\frac{(1-a)}{\xi^2}\right]$$

Assim,

$$Var(T)=\mathbb{E}(T^2)-\left(\mathbb{E}(T)\right)^2=2\left[\frac{a}{\lambda^2}+\frac{1-a}{\xi^2}\right]- \left[\frac{a}{\lambda}-\frac{1-a}{\xi}\right]^2$$

Exemplo 3.4.14

Prove que se X assume valores somente no intervalo $ [a,b] $, então $ a\leq \mathbb{E}(X)\leq b $ e $ Var(X)\leq \frac{(b-a)^2}{4} $. Exiba uma variável aleatória que atinge a variância máxima.

Defina uma variável $ Y $ tal que $ 0\leq Y \leq 1 $ o que implica que $ 0\leq \mathbb{E}(Y)\leq 1 $. Agora, seja m uma mediana de Y então

$$Var(Y)=Var(Y-m)\leq \mathbb{E}(Y-m)^2=\int_0^m (Y-m)^2 dF_Y+ \int_m^1 (Y-m)^2 dF_Y\leq m^2 \mathbb{P}(Y\leq m)+ (1-m^2)\mathbb{P}(Y\geq m) \leq \frac{1}{2}m^2+\frac{1}{2}(1- m^2)=m^2- m +\frac{1}{2}=\left(m-\frac{1}{2}\right)^2+\frac{1}{4}\leq \frac{1}{4}$$

Resumindo $ Var(Y)\leq \frac{1}{4} $. Agora tome $ Y-(b-a)X+a $ o que implica que $ Var(Y)=(b-a)^2Var(X)\leq \frac{(b-a)^2}{4} $ e $ \mathbb{E}(Y)=(b-a)\mathbb{E}(X)+a $ o que implica que $ a\leq \mathbb{E}(Y)\leq b $. A variável aleatória que atinge a variância maxima é

$$\mathbb{P}(X=a)=\mathbb{P}(X=b)=\frac{1}{2}$$

Exemplo 3.4.15

Demonstre que a desigualdade de Jensen é estrita, isto é, $ \mathbb{E}(\varphi(X))> \varphi\left(\mathbb{E}(X)\right) $, se a função $ \varphi $ é estritamente convexa e X não é constante.

Temos que $ \varphi(x) $ é estritamente convexa. Então, para $ X\neq X_0 $ temos

$$\varphi(x)> \varphi(x_0)+\lambda (x-x_0)$$

Agora, fazendo $ X_0=\mathbb{E}(X) $ e como

$$\mathbb{P}(X\neq X_0)=\mathbb{P}(X\neq \mathbb{E}(X))=\mathbb{P}(|X-\mathbb{E}(X)|> 0)$$

pois $ \mathbb{P}(X=X_0)< 1, $ para todo $ X_0\in \mathbb{R} $ (X não é constante), então:

$$\mathbb{E}(\varphi(X))> \varphi(X_0)+\lambda \mathbb{E}(X-X_0)=\varphi(\mathbb{E}(X)).$$

Exemplo 3.4.16

Sejam $ X_1,\dots, X_n $ variáveis aleatórias independentes com $ \mathbb{E}(X_j)=\mu_j $ e $ Var(X_j)=\sigma_j^2 $. Considere combinações lineares

$$Y=\sum_{j=1}^n p_j X_j$$

no qual $ p_j\geq 0 $ e

$$\sum_{j=1}^n p_j =1$$

Prove que $ Var(Y) $. Prove que $ Var(Y) $ é minimizada pela escolha de

$$p_j=\frac{\sigma_j^{-2}}{\sum_{i=1}^n \sigma_i^{-2}}, \quad \quad j=1, \dots, n.$$

Temos, com $ X_1, \dots, X_n $ são variável aleatória independentes

$$Var(Y)=Var\left(\sum_{j=1}^n p_jX_j\right)=\sum_{j=1}^n p_j^2\left(Var(X_j)\right)=\sum_{j=1}^n p_j^2\sigma^2_j.$$

Para resolver esse problema usaremos o método do lagrange, então queremos:

$$\min_{p_1,p_2,\dots,p_j}\sum_{j=1}^n p_j^2 \sigma_j^2$$

com $ \sum_{j=1}^n p_j=1 $ e $ p_j> 0, \forall j=1, \dots, n. $

Então,

$$L=\sum_{j=1}^n p_j^2\sigma_j^2+\lambda\left(1-\sum_{j=1}^n p_j\right)$$

então, $ \frac{dL}{dp_j=0} $ o que implica que

$$2p_j\sigma_k^2-\lambda =0$$

o que implica que $ p_j=\frac{\lambda}{2}\sigma^{-2}_j $. Assim,

$$\sum_{j=1}^n p_j=\frac{\lambda}{2}\sum_{j=1}^n \sigma^{-2}_j=1 $$

o que implica que

$$\lambda=\frac{2}{\displaystyle \sum_{j=1}^n \sigma_j^{-2}}$$

substituindo temos que

$$p_j=\frac{\sigma_j^{-2}}{\displaystyle \sum_{j=1}^n \sigma_j^{-2}}$$

para $ j=1,2,\dots,n $, o qual é um ponto de mínimo pois

$$\frac{d^2L}{d^2 p_j}=2\sigma_j^2> 0$$

para $ j=1,2,\dots,n $.

Exemplo 3.4.17

Sejam X e Y variáveis aleatórias com variâncias finitas. Mostre que se $ Var(X)\neq Var(Y) $, então $ X+Y $ e $ X-Y $ não são independentes

Primeiramente observe que

$$\mathbb{E}[(X+Y)(X-Y)]=\mathbb{E}[X^2-Y^2]=\mathbb{E}(X^2)-\mathbb{E}(Y^2)$$

Como tem variância finita então temos que

$$\mathbb{E}(X^2)-\mathbb{E}(Y^2)=Var(X)+\left(\mathbb{E}(X)\right)^2-Var(Y)-\left(\mathbb{E}(Y)\right)^2$$

$$=\left(\mathbb{E}(X)-\mathbb{E}(Y)\right)+\left(Var(X)-Var(Y)\right)=\mathbb{E}(X+Y)\mathbb{E}(X-Y)+Var(X)-Var(Y)$$

Então temos que

$$\mathbb{E}[(X+Y)(X-Y)]=\mathbb{E}(X+Y)\mathbb{E}(X-Y)+Var(X)-Var(Y)$$

Agora desde que $ Var(X)\neq Var(Y) $, temos que (X+Y) e (X-Y) não são independentes pois isso implica que

$$\mathbb{E}[(X+Y)(X-Y)]\neq \mathbb{E}(X+Y)\mathbb{E}(X-Y)$$

(pois se fossem independentes teríamos que $ \mathbb{E}[(X+Y)(X-Y)]= \mathbb{E}(X+Y)\mathbb{E}(X-Y) $)

Exemplo 3.4.18

Seja X uma variável aleatória tendo distribuição $ b(n,p) $. Mostre que X tem a mesma distribuição de $ X_1+\dots +X_n $, com $ X_i $ sendo variáveis aleatórias independentes e identicamente distribuídas que assumem apenas os valores 0,1. Calcule a esperança e a variância de X.

Provaremos que isto vale quando $ \mathbb{P}(X_i=1)=p $ para $ i=1,2,\dots,n. $

Agora, note que

$$\left[X_1+\dots +X_n=k\right]=\bigcup_{(i_1,i_2,\dots, i_n)\in \Pi}\left([X_{i_1}=1]\cap[X_{i_k}=1]\cap[X_{i_{k}+1}=0]\cap \dots \cap [X_{i_n}=0]\right)$$

no qual $ \Pi $ é o conjunto de todas as permutações $ (1,2,3,\dots,n) $. Então

$$\mathbb{P}(X_1+\dots+X_n=k)=\sum_{(i_1,i_2,\dots, i_n)\in \Pi} \left(\mathbb{P}(X_1=1)\right)^k\left(1-\mathbb{P}(X_1=1)\right)^{n-k}=\binom{n}{k}p^k(1-p)^{n-k}, k=0,1,\dots,n.$$

Assim, $ X_1+\dots X_n \sim b(n,p) $. Desta maneira;

$$\mathbb{E}(X)=\mathbb{E}(X_1+\dots +X_n)=n\mathbb{E}(X_1)=n(0(1-p)+1p)=np$$

$$Var(X)=Var(X_1+\dots+X_n)=nVar(X_1)$$

Mas

$$\mathbb{E}(X_1^2)=0^2(1-p)+1^2p=p$$

Então,

$$Var(X_1)=\mathbb{E}(X_1^2)-\left(X_1\right)^2=p-p^2=p(1-p)$$

Desta forma temos que

$$Var(X)=np(1-p)$$

Exemplo 3.4.19

Seja (X,Y) uniformemente distribuído na seguinte região:

(imagem em falta)

Calcule $ Cov(X,Y) $.

Temos que $ Cov(X,Y)=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y) $. Agora, X é simétrico em torno de zero e limitado então integrável, então pelo exemplo 3.3.1, temos que $ \mathbb{E}(X)=0 $.

Então, $ Cov(X,Y)=\mathbb{E}(XY) $. Agora, $ A=A_1\cup A_2 $, com $ A_1=((x,y): 0\leq x \leq 1, x-1\leq y\leq 1) $ e $ A_2=((x,y): -1\leq x< 0, -x-1\leq y\leq 1) $, então a Area de $ A=3 $ logo

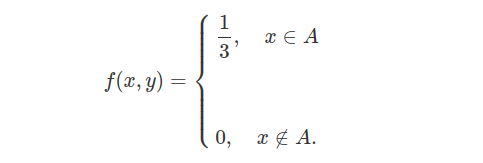
Então,

$$\mathbb{E}(XY)=\int xy f(x,y)dxdy=\int_0^1\int_{x-1}^1 \frac{xy}{3}dxdy+\int_{-1}^0\int_{-x-1}^1 \frac{xy}{3}dxdy = \frac{1}{3}\int_{0}^1 x\left[\frac{y^2}{2}\right]_{x-1}^1dx + \frac{1}{3}\int_{-1}^0 x\left[\frac{y^2}{2}\right]_{-x-1}^1dx$$

$$=-\frac{1}{6}\left(\int_{0}^1 x^2(x-2)dx +\int_{-1}^0 x^2(x+2)dx\right)=-\frac{1}{6}\left(\left[\frac{x^4}{4}-\frac{2x^3}{3}\right]_0^1 +\left[\frac{x^4}{4}+\frac{2x^3}{3}\right]_{-1}^0\right) $$

$$=0$$

3.5 - Esperança Condicional

Neste módulo, vamos definir e apresentar as principais propriedades de esperança condicional, como uma extensão do conceito de probabilidade condicional. Aqui, apresentamos o conceito de esperança condicional através de uma abordagem simples e repleta de exemplos. A definição de esperança condicional com respeito a uma $ \sigma $-álgebra pode ser encontrado na seção esperança condicional com respeito a uma sigma-álgebra.

Considere $ (\Omega, \mathcal{F}, \mathbb{P}) $ um espaço de probabilidade. A probabilidade condicional do evento $ A $ dado o evento $ B $ é definida por

$$\displaystyle \mathbb{P}(A|B)=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)}$$

assumindo que $ \mathbb{P}(B)> 0 $. Dados $ X $ e $ Y $ variáveis aleatórias discretas assumindo valores $ \mathcal{R}_X=(x_1, x_2, \cdots , x_n) $ e $ \mathcal{R}_Y=(y_1, y_2, \cdots , y_m) $, respectivamente. Uma definição natural para esperança condicional de $ X $ dado $ Y=y $ é dada por

$$\displaystyle \mathbb{E}[X|Y=y]=\sum_{x\in \mathcal{R}_X}x\mathbb{P}[X=x|Y=y], \quad y \in \mathcal{R}_Y.$$

Assim, obtemos que a esperança condicional da variável aleatória $ X $ dado a variável aleatória $ Y $, denotada por $ \mathbb{E}[X\mid Y] $, é uma função da variável aleatória $ Y $ e com isso, a esperança condicional também é uma variável aleatória. Portanto, temos que

$$ \mathbb{E} \left[\mathbb{E}[X\mid Y]\right]=\sum_{y \in \mathcal{R}_Y} \mathbb{E}[X\mid Y=y] \mathbb{P}[Y=y]=\sum_{y \in \mathcal{R}_Y}\sum_{x\in \mathcal{R}_X}x\mathbb{P}[X=x|Y=y]\mathbb{P}[Y=y]=$$

$$\sum_{y \in \mathcal{R}_Y}\sum_{x\in \mathcal{R}_X}x \frac{\mathbb{P}[X=x;Y=y]}{\mathbb{P}[Y=y]}\mathbb{P}[Y=y]=\sum_{x\in \mathcal{R}_X}x \sum_{y \in \mathcal{R}_Y}\mathbb{P}[X=x;Y=y]=\sum_{x\in \mathcal{R}_X}x\mathbb{P}[X=x]=\mathbb{E}[X].$$

Na sequência, tomamos $ X $ e $ Y $ variáveis aleatórias discretas assumindo valores nos conjuntos enumeráveis $ \mathcal{R}_X=(x_1, x_2, \cdots) $ e $ \mathcal{R}_Y=(y_1, y_2, \cdots) $, respectivamente. A esperança condicional de $ X $ dado $ Y $ é definida na forma

$$\mathbb{E}[X|Y=y]=\sum_{x\in \mathcal{R}_X}x\mathbb{P}[X=x|Y=y],$$

caso esta série esteja bem definida para todo $ y \in \mathbb{R}_Y $. Da mesma forma, se $ \mathbb{E}\mid X \mid <\infty $, obtemos que $ \mathbb{E}[\mathbb{E}(X\mid Y)]=\mathbb{E}(X) $.

Considere $ I_x=1!!1_{(X=x)} $ a função indicadora do evento $ (X=x) $, que assume valor $ 1 $ se $ X=x $ ou zero caso contrário. Neste caso, a esperança conditional de $ I_x $ dado a variável aleatória $ Y $ é dada por

$$\mathbb{E}[I_x\mid Y] = \sum_{i=0}^{1}i\mathbb{P}[I_x=i\mid Y=y]= \mathbb{P}[X=x\mid Y=y],$$

para todo $ x \in \mathcal{R}_X $ e $ y \in \mathcal{R}_Y $. Assim, obtemos que a probabilidade condicional é uma caso particular da esperança condicional e consequentemente, uma variável aleatória. Neste caso, obtemos que $ \mathbb{E}[\mathbb{P}[X=x\mid Y]]=\mathbb{E}[\mathbb{E}[I_x\mid Y]]=\mathbb{E}[I_x]=\mathbb{P}[X=x] $.

Agora, considere $ (X,Y) $ um vetor aleatório absolutamente contínuo com função densidade de probabilidade conjunta $ f_{X,Y} $. A função densidade condicional de $ X $ dado $ Y $ é definida por

$$\displaystyle f_{X|Y}(x,y)=\frac{f_{X,Y}(x,y)}{f_{Y}(y)},$$

no qual $ f_Y $ é a função densidade de probabilidade da variável aleatória $ Y $. Por definição, temos que

$$\mathbb{P}[a\leq X \leq b\mid y-\epsilon \leq Y \leq y+\epsilon]=\frac{\mathbb{P}[a\leq X \leq b;y-\epsilon \leq Y \leq y+\epsilon]}{\mathbb{P}[y-\epsilon \leq Y \leq y+\epsilon]}=\frac{\int_{a}^{b}\int_{y-\epsilon}^{y+\epsilon} f_{X,Y}(x,t)dxdt}{\int_{y-\epsilon}^{y+\epsilon}f_Y(t) dt}=$$

$$\frac{\int_{y-\epsilon}^{y+\epsilon} \int_{a}^{b}f_{X,Y}(x,t)dxdt}{\int_{y-\epsilon}^{y+\epsilon}f_Y(t) dt} \sim \int_{a}^b \frac{f_{X,Y}(x,y)}{f_Y(y)}dx,$$

para $ \epsilon > 0 $ suficientemente pequeno.

Então, a probabilidade condicional neste caso é definida por

$$\displaystyle \mathbb{P}(a\leq X\leq b|Y=y)=\int_{a}^b f_{X|Y}(x,y)dx$$

e a esperança condicional da variável aleatória $ X $ dado a variável aleatória $ Y $ é definida por

$$\displaystyle \mathbb{E}[X|Y=y]=\int_{-\infty}^{\infty}xf_{X|Y}(x,y)dx.$$

Proposição 3.5.1

Sejam $ X $ e $ Y $ variáveis aleatórias absolutamente contínuas então

$$\displaystyle \mathbb{E}[X]=\mathbb{E}[\mathbb{E}(X\mid Y)]=\int_{-\infty}^{\infty}\mathbb{E}[X|Y=y]f_{Y}(y)dy$$

Demonstração:

$$\displaystyle \mathbb{E}[X]=\int_{-\infty}^{\infty}\mathbb{E}[X|Y=y]f_{Y}(y)dy$$

$$=\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf_{X|Y}(x,y)f_Y(y)dxdy$$

$$=\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}x\frac{f_{X,Y}(x,y)}{f_{Y}(y)}f_Y(y)dydx$$

$$=\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf_{X,Y}(x,y)dydx$$

$$=\displaystyle\int_{-\infty}^{\infty}x\int_{-\infty}^{\infty} f_{X,Y}(x,y)dydx$$

$$=\displaystyle \int_{-\infty}^{\infty}xf_X(x)dx=\mathbb{E}[X]$$

Exemplo 3.5.1

Um dado honesto é lançado até a ocorrência do númeor $ 6 $. Seja Y a variável aleatória que conta o número de vezes que lançamos o dado até a ocorrência do número $ 6 $ e $ X $ a variável aleatória que conta o número de uns que tivemos nestes lançamentos. Vamos calcular $ \mathbb{E}[X|Y=y] $. O evento $ Y=y $, significa que lançamos os dado $ y $ vezes nos quais, $ y-1 $ vezes não obtivemos o número $ 6 $ e então no $ y $-ésimo lançamento obtivemos o número $ 6 $. Assim, dado $ Y=y $, temos que X tem distribuição binomial $ B(n,p) $, com $ n=y-1 $ e $ p=\frac{1}{5} $, pois temos $ y-1 $ possibilidades de ter ocorrido o número $ 1 $. De fato, como sabemos que dentro destes $ n $ lançamentos o número $ 6 $ não pode ter ocorrido, temos apenas a possibilidade dos seguintes resultados $ (1,2,3,4,5) $, com probabilidade iguais para cada um deles. Logo, a probabilidade de corrência do evento de interesse (sair o número $ 1 $) é $ p=1/5 $. Então, temos que

$$\displaystyle \mathbb{E}[X|Y=y]=np=\frac{y-1}{5}$$

Como a esperança condicional é uma função da variável aleatória $ Y $, sabemos que $ \mathbb{E}[X|Y] $ é uma variável aleatória. No exemplo, temos que

$$\mathbb{E}[X|Y=y]=\displaystyle \frac{y-1}{5},$$

e assim, a variável aleatória esperança condicional é dada por

$$\mathbb{E}[X|Y]=\displaystyle \frac{Y-1}{5}.$$

Exemplo 3.5.2

Utilizando o mesmo exemplo anterior vamos calcular $ \mathbb{E}[X^2|Y] $.

Note que novamente $ \mathbb{E}[X|Y=y] $ é uma binomial, e ainda sua a variança é dada por

$$\mathbb{E}[X^2|Y=y]-(\mathbb{E}[X|Y=y])^2=np(1-p)=\displaystyle \frac{4(y-1)}{25}$$

Sabemos do exemplo 3.5.1 que

$$\displaystyle \mathbb{E}[X^2|Y=y]-\left(\frac{y-1}{5}\right)^2=\frac{4(y-1)}{25}$$

Portanto

$$\displaystyle \mathbb{E}[X^2|Y=y]=\frac{(y-1)^2}{25}+\frac{4(y-1)}{25}$$

Assim, temos que

$$\displaystyle \mathbb{E}[X^2|Y]=\frac{(Y-1)^2}{25}+\frac{4(Y-1)}{25}=\frac{Y^2+2Y-3}{25}$$

Exemplo 3.5.3

Sejam $ X,Y\stackrel{iid}{\sim}B(n,p) $. Calcule $ \mathbb{E}[X|X+Y=y] $.

Para isso, primeiramente vamos calcular a probabilidade condicional de $ X $ dado $ X+Y=m $. Para $ k\leq \min(n,m) $,

$$\mathbb{P}(X=k|X+Y=m)=\displaystyle \frac{\mathbb{P}(X=k,X+Y=m)}{\mathbb{P}(X+Y=m)}$$

$$=\displaystyle \frac{\mathbb{P}(X=k, Y=m-k)}{\mathbb{P}(X+Y=m)}$$

$$=\displaystyle \frac{\mathbb{P}(X=k)\mathbb{P}(Y=m-k)}{\mathbb{P}(X+Y=m)}$$

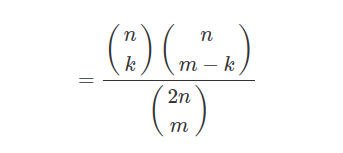
Usamos o fato de que $ X+Y $ é uma binomial $ 2n $ e $ p $. Portanto, a distribuição de X, dado $ X+Y=m $, tem distribuição hipergeométrica e obtemos

$$\displaystyle \mathbb{E}[X|X+Y=m]=\frac{m}{2}$$

Exemplo 3.5.4

Suponha X e Y com densidade conjunta dada por

$$f(x,y)=\displaystyle\frac{e^{-x/y}e^{-y}}{y},~~0< x<\infty,~~0< y< \infty$$

Calcule $ \mathbb{E}[X|Y=y] $.

Para isso vamos primeiramente calcular a densidade condicional

$$f_{X|Y}(x|y)=\displaystyle \frac{f(x,y)}{f_Y(y)}=\frac{f(x,y)}{\int_{0}^{\infty}f_{X,Y}(x,y)}dx$$

$$=\displaystyle \frac{e^{-x/y}e^{-y}}{y\int_{0}^{\infty}e^{-x/y}e^{-y}/y}$$

$$=\displaystyle \frac{e^{-x/y}}{y}$$

Portanto a distribuição condicional de $ X $ dado $ Y=y $, tem distribuição exponencial com média y.

Então

$$\displaystyle \mathbb{E}[X|Y=y]=\int_{0}^{\infty}\frac{x}{y}e^{-x/y}dx=y\Rightarrow \mathbb{E}[X|Y]=Y$$

Exemplo 3.5.5

Sejam X e Z variáveis aleatórias em $ (\Omega, \mathbb{A}, \mathbb{P}) $

(a)Mostre que para A e B borelianos,

Então, se $ x\in A $ o que implica que

$$\mathbb{P}(X\in A| X=x)=1$$

o que implica que

$$\mathbb{P}(Z\in B,X\in A|X=x)=\mathbb{P}(Z\in B|X=x)=\mathbb{P}(Z\in B|X=x)$$

Agora se $ x\notin A $, então $ \mathbb{P}(X\in | X=x)=0 $ então

$$\mathbb{P}(Z\in B,X\in A| X=x)\leq \mathbb{P}(X\in A| X=x)=0$$

o que implica que

$$\mathbb{P}(Z\in B, X\in A|X=x)=0\Rightarrow \mathbb{P}(Z\in B, X\in A| X=x)=0$$

(b) Mostre que se $ \mathbb{P}(Z\in B|X=x)\geq \frac{1}{2} $, para todo $ x\in A $, então $ \mathbb{P}(Z\in B|X\in A)\geq \frac{1}{2} $

temos que:

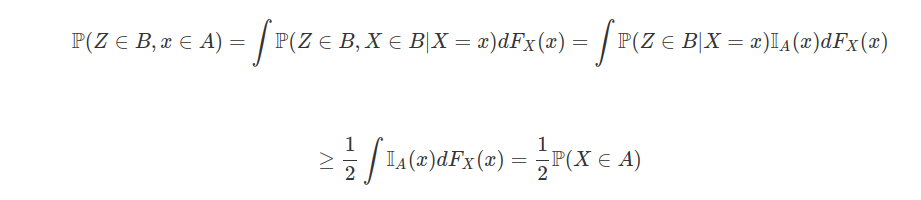
Agora se assumirmos

$$\mathbb{P}(X\in A)> 0,$$

então

$$\mathbb{P}(Z\in B|X\in A)=\frac{\mathbb{P}(Z\in B,X\in A)}{\mathbb{P}(X\in A)}\geq \frac{\frac{1}{2}\mathbb{P}(X\in A)}{\mathbb{P}(X\in A)}\geq \frac{1}{2}$$

(c) Sejam X e Y independentes tais que $ \mathbb{P}(Y\geq 0)\geq \frac{1}{2} $. Demonstre que $ \mathbb{P}(X+Y\geq a| X\geq a)\geq \frac{1}{2} $.

Assumimos que $ \mathbb{P}(X\geq a)> 0 $, então:

$$\mathbb{P}(X+Y\geq a | X\geq a)=\frac{\mathbb{P}(X+Y\geq a, X\geq a)}{\mathbb{P}(X\geq a)}\geq \frac{\mathbb{P}(Y\geq 0, X\geq 0)}{\mathbb{P}(X\geq a)}$$

$$=\frac{\mathbb{P}(Y\geq 0)\mathbb{P}(X\geq a)}{\mathbb{P}(X\geq a)}=\mathbb{P}(Y\geq 0)\geq \frac{1}{2}$$

Agora, se $ \mathbb{P}(X\geq a)=0 $, podemos definir arbitrariamente e assumimos que

$$\mathbb{P}(X+Y\geq a| X\geq a)=\frac{1}{2}$$

da igualdade acima de do fato de $ \mathbb{P}(Y\geq 0)\geq \frac{1}{2} $, e portanto o resultado segue.

Exemplo 3.5.6

Prove: se X é constante quase certamente, i.e., $ \mathbb{P}(X=c)=1 $, então $ \mathbb{P}(X=c| Y=y)=1 $. Deduza a propriedade se $ X=c $, para alguma constante c, então

$$\mathbb{E}(X|Y)=c$$

Tomemos, $ I=(a,b) $ no qual $ a,b\in \mathbb{Q} $ e $ a< y< b $, então

$$\mathbb{P}(X=c, Y\in I)=\mathbb{P}(Y\in I)$$

pois $ \mathbb{P}(X=C)=1 $. Assim, temos que

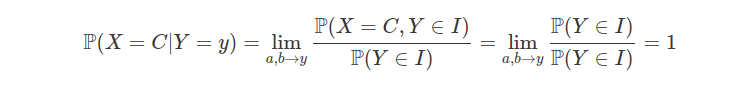
Então,

$$\mathbb{E}(X|Y=y)=C\mathbb{P}(X=C|Y=y)=C$$

se $ \mathbb{P}(X=C)=1 $.

Exemplo 3.5.7

Sejam X e Y variáveis aleatórias tais que $ \mathbb{E}(X^2)< \infty $ e $ \mathbb{E}(Y^2)< \infty $. Demostre que $ Cov(X,Y)=Cov(X, \mathbb{E}(Y|X)) $.

Inicialmente, temos por Cauchy-Schwarz que XY é integrável, pois

$$\mathbb{E}(|XY|)\leq \sqrt{\mathbb{E}(X^2)\mathbb{E}(Y^2)}< \infty$$

Naturalmente como X e Y são integráveis então usamos a propriedade básica

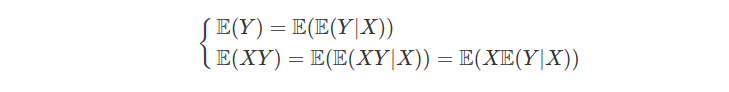
$$Cov(X,Y)=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y)=\mathbb{E}(X\mathbb{E}(Y|X))-\mathbb{E}(X)(\mathbb{E}(Y|X))=Cov(X,\mathbb{E}(Y|X))$$

Exemplo 3.5.8

Suponho que X e Y possuam densidade conjunta

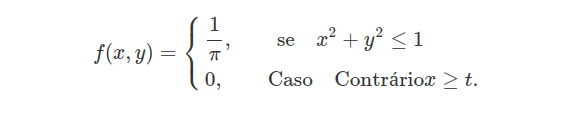
(a) Ache a distribuição condicional de Y dada X. Calcule $ \mathbb{E}(Y|X) $.

Usando o exemplo 2.7.5, no qual $ A=((x,y)\in \mathbb{R}^2,x^2+y^2\leq 1) $

temos que $ Y|X=x $ tem distribuição uniforme em $ A_X $, no qual $ A_X=(y:(x,y)\in A)=[-\sqrt{1-x^2},\sqrt{1-x^2}] $

Assim,

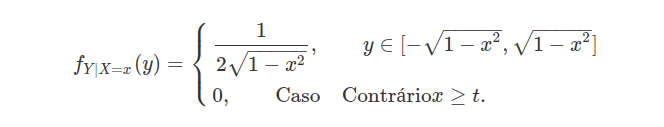
(b) X e Y são independentes? Por que ?

Não, pois

e então para $ (x,y)\in A $ temos que

$$f_X(x)f_Y(y)=\frac{4}{\pi^2}[(1-x^2)(1-y^2)]^{1/2}\neq \frac{1}{\pi}=f_{X,Y}(x,y)$$

Assim, $ ((x,y):f_{X,Y}(x,y)\neq f_X(x)f_Y(y))\subset A $, e A tem medida de Lebesgue positiva $ (Area(A)=\pi) $, então $ X $ e $ Y $ não são independentes.

(c) Prove que X e Y são não-correlacionadas

Pelos Exemplo 3.5.8:

$$COV(X,Y)=COV(X,\mathbb{E}(Y|X))=\mathbb{E}(X\mathbb{E}(Y|X))-\mathbb{E}(X)\mathbb{E}(\mathbb{E}(Y|X))=\mathbb{E}(X.0)-\mathbb{E}(X)0=0$$

então X e Y não são correlacionado.

Exemplo 3.5.9

Seja X uma variável aleatória Cauchy-padrão.

(a) Conforme a Definição 4.3, qual é $ \mathbb{E}(X||X|=y) $?

Como X é simetria em torno de zero, utilizando o exemplo 2.6.12, temos que

$$\mathbb{P}(X=y||X|=y)=\mathbb{P}(X=-y||X|=y)=\frac{1}{2}$$

Então,

$$\mathbb{E}(X||X|=y)=y\frac{1}{2}+(-y)\frac{1}{2}=0$$

(b) Deduza que $ \mathbb{E}(\mathbb{E}(X||X|))=0 $.

Do item (a)

$$\mathbb{E}(X||X|=y)=0$$

então $ \mathbb{E}(\mathbb{E}(X||X|))=\mathbb{E}(X||X|)=0 $

(c) A propriedade básica $ \mathbb{E}(\mathbb{E}(X|Y))=\mathbb{E}(X) $ não vale nesse caso. Existe uma contradição nisso?

Não, ocorre que a propriedade básica foi provada usando a hipótese que X seja integrável, o que não acontece neste caso;

Exemplo 3.5.10

Se $ X\geq 0 $, ocorre que $ \mathbb{E}(X)=\mathbb{E}(\mathbb{E}(X|Y)) $ sem a hipótese de integrabilidade de X. Prove esse resultado quando X e Y são discretas.

Se X é uma variável aleatória e $ X\geq 0 $ então $ X|Y=y $ é uma variável aleatória discreta e não-negativa assim

$$\mathbb{E}(X|Y=y)=\sum_{n=0}^\infty \mathbb{P}(X> n|Y=y)$$

Agora Y é variável aleatória discreta toma os valores em $ y_m $, $ m=\pm 1, \pm 2, \dots $, então

$$\mathbb{P}(X\in B| Y=y_n)=\frac{\mathbb{P}(X\in B, Y=y_m)}{\mathbb{P}(Y=y_m)}$$

para $ \mathbb{P}(Y=y_m)> 0 $, então

$$\mathbb{E}(X|Y=y_m)=\sum_{n=0}^\infty \mathbb{P}(X> n| Y=y_n)=\sum_{n=0}^\infty \frac{\mathbb{P}(X> n, Y=y_m)}{\mathbb{P}(Y=y_m)}$$

E então

$$\mathbb{E}(\mathbb{E}(X|Y))=\sum_{m\in \mathbb{Z}}\mathbb{P}(Y=y_m)\sum_{n=0}^\infty \frac{\mathbb{P}(X> n, Y=y_m)}{\mathbb{P}(Y=y_m)} = \sum_{m\in \mathbb{Z}}\sum_{n=0}\mathbb{P}(X> n, Y=y_m)$$

Agora, como $ \mathbb{P}(X> n, Y=y_m)\geq 0 $, para todo $ n\geq 0 $ e $ m\in \mathbb{Z}^\star $, podemos inverter as somatórias e

$$\mathbb{E}(\mathbb{E}(X|Y))=\sum_{n=0}\sum_{m\in \mathbb{Z}^\star}\mathbb{P}(X> n,Y=y_m)=\sum_{n=0}\mathbb{P}([X> n]\bigcup_{m\in \mathbb{Z}^\star}[y=y_m])$$

$$\sum_{n=0}^\infty \mathbb{P}([X> n]\cap \Omega)=\sum_{n=0}^\infty \mathbb{P}(X> n)=\mathbb{E}(X)$$

Exemplo 3.5.11

O número de acidentes que ocorrem em certa fábrica em uma semana é uma variável aleatória com média $ \mu $ e variância $ \sigma^2 $. Os números de indivíduos feridos nos diferentes acidentes são independentes e identicamente distribuídos com média $ \xi $ e variância $ \tau^2 $, e são independentes do número de acidentes. Determine a média e a variância do número de indivíduos feridos em uma semana.

Seja $ N $=número de acidentes em uma semana: Variável aleatória discreta e não-negativa com

e $ X=F_1+F_2+\dots+F_N $ número de feridos em uma semana. Temos que $ X $ também é variável aleatória discreta e não-negativa e então pelo exemplo 3.5.10 vale a propriedade básica, então:

$$\mathbb{E}(X)=\mathbb{E}(\mathbb{E}(X|N=n)).$$

Agora

$$\mathbb{E}(X|N=n)=\mathbb{E}(F_1+\dots+F_N)=N\mathbb{E}(F_1)=N$$

então $ \mathbb{E}(X)=\mathbb{E}(N\xi)=\xi\mathbb{E}(N)=\xi\mu $

Temos também que $ X^2 $ é v.a. discreta e não-negativa e então:

$$\mathbb{E}(X^2)=\mathbb{E}(\mathbb{E}(X^2|N=n))$$

Agora

$$\mathbb{E}(X^2|N=n)=\mathbb{E}((F_1+\dots+F_N)^2)=Var(F_1+\dots+F_N)+\left(\mathbb{E}(F_1+\dots+F_n)\right)^2$$

$$=NVar(F_1)+(N\mathbb{E}(F_1))^2=N\tau^2+N^2\xi^2$$

Assim,

$$\mathbb{E}(X^2)=\mathbb{E}(N\tau^2+N^2\xi^2)=\tau^2\mathbb{E}(N)+\xi^2\mathbb{E}(N^2)=\tau^2\mu+\xi^2(\sigma^2+\mu^2)$$

E então

$$Var(X)=\mathbb{E}(X^2)-(\mathbb{E}(X))^2=\tau^2\mu+\xi^2(\sigma^2+\mu^2)-(\xi\mu)^2=\tau^2\mu+\xi^2\sigma^2$$

Exemplo 3.5.12

Calcule $ \mathbb{E}(X_{(2)}|X_{(1)},X_{(3)}) $, no qual $ X_{(1)},X_{(2)} $ e $ X_{(3)} $ são as estatísticas de ordem de uma amostra aleatória da $ U[0,1] $.

Pelo exemplo 3.5.5(b), temos que $ X_{(2)}|(X_{(1)},X_{(3)})=(x_{(1)},x_{(3)})\sim U[x_{(1)}],x_{(3)} $, então

$$\mathbb{E}(X_{(2)}|X_{(1)},X_{(3)})=\frac{X_{(1)}+X_{(3)}}{2}$$

Exemplo 3.5.13

Seja X uma variável aleatória com distribuição exponencial de parâmetro 1. Seja $ t> 0 $ fixo. Ache $ \mathbb{E}(X|\max(X,t)) $ e $ \mathbb{E}(X|\min(X,t)) $.

Sejam $ Z=\max(X,t) $ e $ W=\min(X,t) $. Vamos obter inicialmente a distribuição de $ X|Z=z $

\textbf{a1)} $ 0\leq t\leq z $ então $ \max(X,t)=z> t\Rightarrow X=z $. Assim o nosso candidato a distribuição condicional será

$$\mathbb{P}(X=z)=1$$

o que implica que

$$\mathbb{E}(X|z)=z$$

a2) $ z=t $ então usando o princípio da preservadas das chances relativas, o candidato a distribuição condicional será

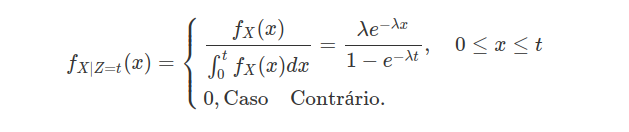
Formalmente deveríamos verificar

$$\mathbb{P}(X\in B| Y=y)=\lim_{\Delta y\rightarrow 0}\mathbb{P}(X\in B| Y\in I)$$

ou

$$F_{X,Y}(x,y)=\int_{-\infty}^y F_X(x|Y=t)dF_Y(t),(x,y)\in \mathbb{R}^2$$

para validar as escolhas das distribuições condicionais, mas supondo que estas sejam o mesmos corretas temos que

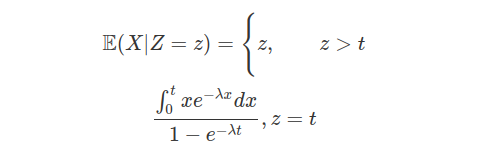
Agora fazendo uma substituição $ x=u $ e $ \lambda e^{-\lambda x}dx=dv $ e

$$\frac{\int_0^tx e^{-\lambda x}dx}{1-e^{-\lambda t}}=\frac{-xe^{-\lambda x}\big|_0^t+\int_0^t e^{-\lambda x}dx}{1-e^{-\lambda t}}$$

$$=\frac{\frac{1}{\lambda}(1-e^{-\lambda t})-te^{-\lambda t}}{(1-e^{-\lambda t})}=\frac{1}{\lambda} -\frac{te^{-\lambda t}}{(1-e^{-\lambda t})},z=t$$

Então,

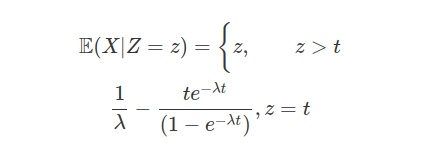
Analogamente, concluímos que a distribuição $ X|W=w $ será

b1) $ 0\leq w< t $ o que implica que $ \min(X,t)=w< t $ o que implica que $ X-w $. Então,

$$\mathbb{P}(X=w)=1$$

\textbf{b2)} $ W=t $, pelo princípio da preservação da chances relativas temos

Exemplo 3.5.14

Mostre que se X e Y são variáveis aleatórias, então

$$F_{X,Y}(x,y)\leq \sqrt{F_X(x)F_Y(y)}$$

então, aplicando a desigualdade de Cauchy-Schwarz, então

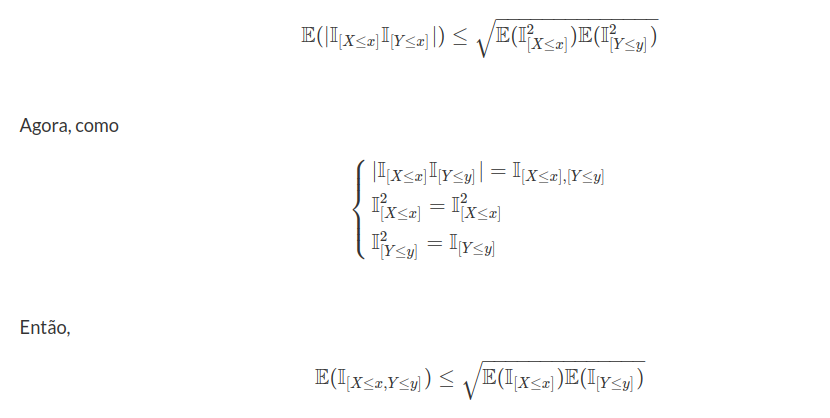
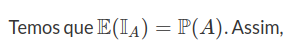
$$\mathbb{P}(X\leq x, Y\leq y)\leq \sqrt{\mathbb{P}(X\leq x)\mathbb{P}(Y\leq y)}\Rightarrow F_{X,Y}(x,y)\leq \sqrt{F_X(x)F_Y(y)}.$$

Exemplo 3.5.15

Seja $ (X,Y) $ um vetor aleatória bidimensional. Suponha que $ (i) $ X tem distribuição exponencial com parâmetro $ \frac{1}{2} $ e $ (ii) $ para cada $ x> 0, $ a distribuição condicional de Y dado que $ X=x $ é $ U[0,x^2] $. Em outras palavras, $ X\sim Exp\left(\frac{1}{2}\right) $ e $ Y|X=x\sim U[0,x^2] $.

(a) Qual a distribuição de $ Z=Y|X^2=t $?

O nossa candidato será $ Z\sim U[0,t] $, verificaremos isto usando

$$\mathbb{P}(X\in B| Y=y)=\lim_{\Delta y\rightarrow 0}\mathbb{P}(X\in B| Y\in I)$$

Seja $ I=(a,b) $ no qual $ 0< a< t< b $, assim

$$\mathbb{P}(X^2\in I)=\mathbb{P}(a< X^2< b)=\mathbb{P}(\sqrt{a}< X<\sqrt{b})=\mathbb{P}(X\in I^{1/2})$$

no qual, $ I^{1/2}=(a^{1/2},b^{1/2}) $ e $ t^{1/2}\in I^{1/2} $. Além disso,

$$\displaystyle \lim_{a\rightarrow t, b\rightarrow t}\frac{\mathbb{P}(Y\in B, X^2\in I)}{\mathbb{P}(X^2\in I)}=\lim_{a\rightarrow t, b\rightarrow t}\frac{\mathbb{P}(Y\in B, X\in I^{1/2})}{\mathbb{P}(X\in I^{1/2})}$$

$$=\lim_{\sqrt{a}\rightarrow t, \sqrt{b}\rightarrow t}\frac{\mathbb{P}(Y\in B, X^2\in I)}{\mathbb{P}(X^2\in I)}=\mathbb{P}(Y\in B| X=\sqrt{t})$$

por hipótese temos que $ Y|X=x\sim U[0,x^2]. $

$$\mathbb{P}(Y\in B| X=\sqrt{t})=\frac{Comp(B\cap [0,t])}{t}$$

Então $ Y|X^2=t\sim U[0,t] $.

(b) Calcule $ \mathbb{E}(X) $, $ \mathbb{E}(Y) $ e $ Cov(X,Y) $.

Inicialmente $ \mathbb{E}(X)=\mathbb{E}(\exp(\frac{1}{2}))=2 $ e como $ Y $ é v.a. não-negativa, através da propriedade fundamental $ Y $Exemplo 3.5.11, temos

$$\mathbb{E}(Y)=\mathbb{E}(\mathbb{E}(Y|X=x))$$

Agora $ \mathbb{E}(Y|X=x)=\frac{x^2}{2} $, então

$$\mathbb{E}(Y)=\mathbb{E}\left(\frac{X^2}{2}\right)=\frac{1}{2} \mathbb{E}(X^2)=4$$

A última igualdade decorre do fato que $ X\sim \exp(1/2) $ e então $ \mathbb{E}(X^2)=\frac{2}{(1/2)^2}=8 $. Analogamente $ XY $ é v.a. não negativa, então

$$\mathbb{E}(XY)=\mathbb{E}(\mathbb{E}(XY|X))$$

Pelo princípio de substituição temos

$$\mathbb{E}(X\mathbb{E}(Y|X))=\mathbb{E}(XX^2/2)=\frac{1}{2}\mathbb{E}(X^3)=24$$

no qual a última igualdade decorre de $ X\sim \exp(1/2) $ e $ \mathbb{E}(X^3)=\frac{6}{(1/2)^3}=48 $. Então,

$$Cov(X,Y)=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y)=24-2(4)=16$$

Exemplo 3.5.16

Sejam X e Y variáveis aleatórias tais que $ Y $ tem esperança finita.

(a) Mostre que a variância condicional de Y dada X, como definida no exemplo 2.7.2, é a variância da distribuição condicional.

$$Var(Y|X=x)=\mathbb{E}[(Y|X=x)^2]-[\mathbb{E}(Y|X=x)]^2=\mathbb{E}(Y^2|X=x)-\mathbb{E}^2(Y|X=x)$$

(b) Demonstre que $ Var(Y)=\mathbb{E}(Var(Y|X))+Var(\mathbb{E}(Y|X)) $, i.e., a variância de Y é a soma da esperança da variância condicional e a variância da esperança condicional.

Supomos que $ Var(Y)< \infty $ se, e somente se, $ \mathbb{E}(Y^2)< \infty $.

$$\mathbb{E}(Var(X|Y))=\mathbb{E}(\mathbb{E}(Y^2|X))-\mathbb{E}(\mathbb{E}^2(Y|X))=\mathbb{E}(Y^2)-\mathbb{E}(\mathbb{E}^2(Y|X))$$

no qual a ultima igualdade temos que $ \mathbb{E}(Y^2)< \infty $ e $ Y^2 $ é integrável. Além disso, temos que

$$Var(\mathbb{E}(Y|X))=\mathbb{E}(\mathbb{E}^2(Y|X))-\left(\mathbb{E}(\mathbb{E}(Y|X))\right)^2=\mathbb{E}(\mathbb{E}^2(Y|X))-(\mathbb{E}(Y))^2$$

Então

$$\mathbb{E}(Var(X|Y))+Var(\mathbb{E}(Y|X))=\mathbb{E}(Y^2)-\mathbb{E}^2(Y)=Var(Y)$$

Exemplo 3.5.17

Sejam X e Y variáveis aleatórias com segundos momentos finitos, e seja Z uma outra variável aleatória. Demonstre a seguinte fórmula:

$$Cov(X,Y)=\mathbb{E}(Cov(X,Y)|Z)+Cov(\mathbb{E}(X|Z), \mathbb{E}(Y|Z)),$$

no qual $ Cov((X,Y)|Z)=\mathbb{E}(XY|Z)-\mathbb{E}(X|Z)\mathbb{E}(Y|Z) $.

Como $ \mathbb{E}(Y^2)< \infty $ e $ \mathbb{E}(X^2)< \infty $, então $ Y^2,X^2,Y,X $ são integráveis e portanto por Cauchy-Schwarz $ XY $ é integrável

$$\mathbb{E}(Cov(X,Y)|Z)=\mathbb{E}(\mathbb{E}(XY|Z))-\mathbb{E}(\mathbb{E}(X|Z)\mathbb{E}(Y|X))=\mathbb{E}(XY)- \mathbb{E}(\mathbb{E}(X|Z))\mathbb{E}(Y|Z)$$

e

$$Cov(\mathbb{E}(X|Z),\mathbb{E}(Y|Z))=\mathbb{E}(\mathbb{E}(X|Z)\mathbb{E}(Y|Z))-(\mathbb{E}(\mathbb{E}(X|Z))\mathbb{E}(\mathbb{E}(Y|Z)))$$

$$\mathbb{E}(\mathbb{E}(X|Z)\mathbb{E}(Y|Z))-\mathbb{E}(X)\mathbb{E}(Y)$$

Então

$$\mathbb{E}(Cov(X,Y)|Z)+Cov(\mathbb{E}(X|Z),\mathbb{E}(Y|Z))=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y)=Cov(X,Y)$$

Exemplo 3.5.18

Suponha que em um temporal, o número X de gotas de chuva que caem no IMPA durante um segundo tenha distribuição de Poisson com parâmetro $ \lambda> 0 $, no qual $ \lambda $ representa a intensidade de chuva. Suponha que o parâmetro $ \lambda $ seja uma variável aleatória que tenha distribuição gama com parâmetros $ \alpha> 0 $ e $ \beta=1 $, i.e. que sua densidade seja dada por

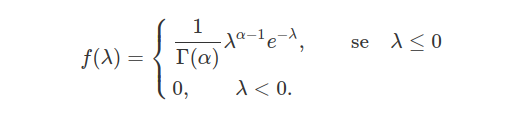
(a) Mostre que

$$\mathbb{P}(X=k)=\frac{\Gamma(k+\alpha)}{\Gamma(\alpha)\Gamma(k+1)}\left(\frac{1}{2}\right)^{k+\alpha}, k=0,1,2,\dots$$

Temos que: $ X|\lambda=s\sim Poisson(s) $, então

$$\mathbb{P}(X=k)=\int_{-\infty}^\infty \mathbb{P}(X=k|\lambda=s)dF_{\lambda}(s)=\int_0^\infty \left(\frac{s^k}{k!}e^{-s}\right)\frac{1}{\Gamma(\alpha)}s^{\alpha-1}e^{-s}ds$$

$$=\frac{\Gamma(k+\alpha)}{\Gamma(\alpha)\Gamma(k+1)}\int_0^\infty \frac{s^{k+\alpha-1}e^{-2s}}{\Gamma(k+\alpha)} e^{-2s}ds = \frac{\Gamma(k+\alpha)}{\Gamma(\alpha)\Gamma(k+1)}\frac{1}{2^{k+\alpha-1}}\int_0^\infty \frac{2s^{(k+\alpha)-1}e^{-2\lambda}}{\Gamma(k+\alpha)}ds$$

fazendo uma mudança de variável $ t=2s $ e $ dt=2ds $ então

$$\frac{\Gamma(k+\alpha)}{\Gamma(\alpha)\Gamma(k+1)}\left(\frac{1}{2}\right)^{k+\alpha-1}\frac{1}{2}\int_0^\infty \frac{t^{k+\alpha-1}}{\Gamma(k+\alpha)}e^{-t}dt=\frac{\Gamma(k+\alpha)}{\Gamma(\alpha)\Gamma(k+1)}\left(\frac{1}{2}\right)^{k+\alpha-1}\frac{1}{2}$$

para $ k=1,2,\dots. $

(b) Usando métodos probabilísticos, demonstre que

$$\sum_{k=1}^\infty \binom{k+n-1}{n}\frac{1}{2^k}=2^n,\quad\quad para\quad n=1,2,\dots.$$

Temos que,

$$\mathbb{E}(X)=\mathbb{E}(\mathbb{E}(X|s=\lambda)),$$

Agora $ X|s=\lambda\sim Poisson(\lambda) $ então $ \mathbb{E}(X|s=\lambda)=\lambda $. Então,

$$\mathbb{E}(X)=\mathbb{E}(\mathbb{E}(X|s=\lambda))=\int_0^\infty \frac{\lambda \lambda^{\alpha-1}e^{-\lambda}}{\Gamma(\lambda)}d\lambda$$

$$=\frac{\Gamma(\alpha+1)}{\Gamma(\alpha)}\int_0^\infty \frac{\lambda^\alpha}{\Gamma(\alpha+1)}e^{-\lambda}d\lambda=\frac{\Gamma(\alpha+1)}{\Gamma(\alpha)}=\alpha$$

Agora, calculando a esperança de X e pela definição e pelo item (a) temos que

$$\mathbb{E}(X)=\displaystyle \sum_{k=0}^\infty k\mathbb{P}(X=k)=\sum_{k=0}^\infty k\frac{\Gamma(k+\alpha)}{\Gamma(\alpha)\Gamma(k+1)}\left(\frac{1}{2}\right)^{k+\alpha}$$

$$=\sum_{k=1}^\infty \frac{\Gamma(k+\alpha)}{\Gamma(\alpha)\Gamma(k)}\left(\frac{1}{2}\right)^{k+\alpha}=\sum_{k=1}^\infty \frac{(k+\alpha-1)!}{(\alpha-1)!(k-1)!}\frac{1}{2^{k+\alpha}}$$

$$=\alpha\frac{1}{2^{\alpha}}\sum_{k=1}^\infty \binom{k+\alpha-1}{\alpha}\frac{1}{2^k}$$

Agora, utilizando as igualdades acima, temos que

$$\alpha\frac{1}{2^{\alpha}}\sum_{k=1}^\infty \binom{k+\alpha-1}{\alpha}\frac{1}{2^k}=\alpha$$

o que implica que

$$\sum_{k=1}^\infty \binom{k+\alpha-1}{\alpha}\frac{1}{2^k}=2^{\alpha}$$

Agora, fazendo $ n=\alpha=1,2,3,\dots $ temos que

$$\sum_{k=1}^\infty \binom{k+n-1}{n}\frac{1}{2^k}=2^{n},\quad\quad n=1,2,3,\dots$$

Exemplo 3.5.19

Calcule $ \mathbb{E}(X_k|X=t) $ no exercício 23;

Temos que $ X_k $ é uma variável aleatória com distribuição

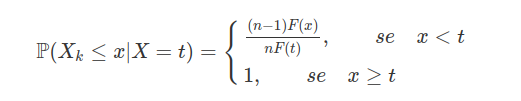
temos que

$$\mathbb{E}(X)=-\int_{-\infty}^0 F_X(x)dx+\int_0^\infty(1-F_X(x))dx$$

Então,

$$\mathbb{E}(X_k|X=t)=-\int_{-\infty}^0 F_{X_k|X=t}(x)dx+\int_0^\infty(1-F_{X_k|X=t}(x))dx$$

Agora, se $ t\leq 0 $, então

$$\mathbb{E}(X_k|X=t)=-\left[\int_{-\infty}^t \frac{(n-1)F(x)}{nF(t)}dx+\int_t^0 dx\right]=t-\frac{(n-1)}{nF(t)}\int_{-\infty}^t F(x)dx$$

e se $ t> 0 $, temos

$$\mathbb{E}(X_k|X=t)=-\int_{-\infty}^0 \frac{(n-1)}{n}\frac{F(x)}{F(t)}dx+\int_0^t\left(1-\frac{n-1}{n}\frac{F(x)}{F(t)}\right)dx$$

$$=-\frac{(n-1)}{nF(t)}\int_{-\infty}^0 F(x)dx+t-\frac{(n-1)}{nF(t)}dx=t-\frac{(n-1)}{nF(t)}\int_{-\infty}^tF(x)dx$$

Então pelas equações acima temos que

$$\mathbb{E}(X_k|X=t)=t-\frac{(n-1)}{nF(t)}\int_{-\infty}^0F(x)dx, \quad\quad \forall t \in \mathbb{R}$$

Exemplo 3.5.20

Determine $ \mathbb{E}(X|Y) $ e $ \mathbb{E}(Y|X) $ no exemplo 2.7.3. Calcule $ Cov(X,Y) $. $ X $ e $ Y $ são independentes?

$ f_{X,Y}(x,y)=\frac{1}{2x},\quad\quad (x,y)\in A, $ no qual $ A=((x,y):0\leq x\leq 1,-x\leq y\leq x) $. Pelo princípio da preservação das chamas relativa, temos que

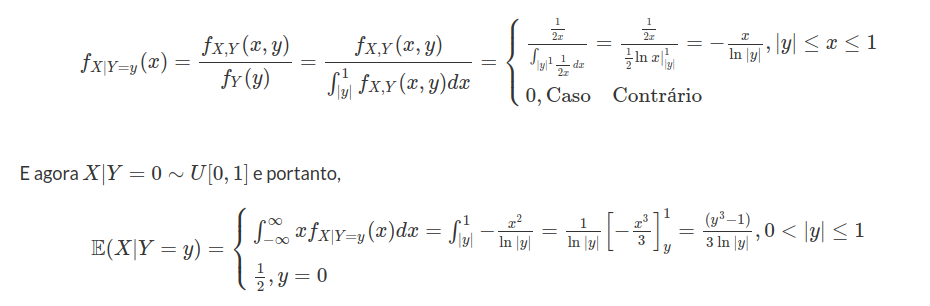
Temos também que: $ Y|X=x\sim U[-x,x]\Rightarrow \mathbb{E}(Y|X=x)=0, x\in [0,1] $. Agora temos também que $ Y $ é integrável pois $ |y|\leq 1 $ e $ XY $ é integrável pois $ |XY|=|X||Y|\leq 1 $. Então,

$$Cov(X,Y)=\mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y)=\mathbb{E}(\mathbb{E}(XY|X))-\mathbb{E}(X)\mathbb{E}(Y|X)=\mathbb{E}(X\mathbb{E}(Y|X=x)) -\mathbb{E}(X)\mathbb{E}(\mathbb{E}(Y|X))=\mathbb{E}(X 0)-\mathbb{E}(X)\mathbb{E}(0)=0$$

No entanto X e Y não são independentes pois para $ (x,y)\in B=(A^c\cap [0,1]\times(-1,1)) $.

$$f_X(x)f_Y(y)=1(-\ln{(|y|)})=-\ln{|y|}\neq 0=f_{X,Y}(x,y)$$

Como a medida de Lebesgue de $ B $ é não nula então $ X $ e $ Y $ não são independentes.

Exemplo 3.5.21

Seleciona-se ao acaso um número entre 0 e 1. Se x é o número selecionado, lança-se n vezes uma moeda com probabilidade x de dar “cara”. Seja Y a variável aleatória que representa o número de caras lançadas.

(a)Y é variável aleatória discreta ou contínua?

$ Y $ é variável discreta pois os resultados possíveis de Y são $ 0,1,2,3,\dots $

(b) Calcule a esperança e a variância de Y.

$ Y $ e $ Y^2 $ são v.a. não-negativas então para elas vale a propriedades básicas temos que $ X\sim U[0,1] $ o que implica que $ \mathbb{E}(X)=1/2 $ e $ \mathbb{E}(X^2)=1/3 $ e $ Y|X=x\sim b(n,x) $ o que implica $ \mathbb{E}(Y|X=x)=nx $ e $ \mathbb{E}(Y^2|X=x)=nx(1-x)+(nx)^2 $. E então

$$\mathbb{E}(Y)=\mathbb{E}(\mathbb{E}(Y|X=x))=\mathbb{E}(nX)=n\mathbb{E}(X)=\frac{n}{2}$$

e

$$\mathbb{E}(Y^2)=\mathbb{E}(\mathbb{E}(Y^2|X=x))=\mathbb{E}(nX-nX^2+n^2X^2)=n\mathbb{E}(X)+n(n-1)\mathbb{E}(X^2)=\frac{n}{2}+\frac{n(n-1)}{3}$$

e portanto,

$$Var(Y)=\mathbb{E}(Y^2)-\mathbb{E}^2(Y)=\frac{n}{2}+\frac{n(n-1)}{3}-\frac{n^2}{4}=\frac{6n+4n^2-4n-3n^2}{12}\Rightarrow Var(Y)=\frac{n(n+2)}{12}$$

Exemplo 3.5.22

(a) Demonstre que se $ X $ e $ Y $ são independentes, então

$$\mathbb{P}(X< Y)=\int_{-\infty}^\infty (1-F_{Y}(x))dF_X(x).$$

$$=\mathbb{E}(1-F_Y(x))=\int_{-\infty}^\infty (1-F_Y(x))dF_X(x)$$

(b)Sejam X e Y independentes, X exponencial de parâmetro $ \lambda $ e Y uniforme em $ [0,\lambda] $, no qual $ \lambda> 0 $. Calcule

$$\mathbb{P}(X< Y),\mathbb{P}(X> Y)$$

e

$$\mathbb{P}(X= Y)$$

Neste caso, temos que

$$\mathbb{P}(X< y)=\int_{-\infty}^\infty (1-F_Y(x))dF_X(x)=\int_0^\lambda (1-x/\lambda)\lambda e^{-\lambda x}dx+ \int_{\lambda}^\infty (1-1)\lambda e^{-\lambda x}dx$$

$$=\int_0^\lambda \lambda e^{-\lambda x}dx-\frac{1}{\lambda}\int_0^\lambda x\lambda e^{-\lambda x}dx=1-e^{-\lambda^2}-\frac{1}{\lambda}\int_0^\lambda x\lambda e^{-\lambda x}dx$$

Agora,

$$\int_0^\lambda x\lambda e^{-\lambda x}dx=-xe^{-\lambda x}\bigg|_0^{\lambda}+\int_0^\lambda e^{-\lambda x}dx=-\lambda e^{-\lambda^2}-\frac{e^{-\lambda x}}{\lambda}\bigg|_0^\lambda$$

$$=-\lambda e^{-\lambda^2}+\frac{1}{\lambda}-\frac{1}{\lambda}e^{-\lambda^2}$$

Então,

$$\mathbb{P}(X< y)=1-e^{-\lambda^2}+e^{-\lambda^2}-\frac{1}{\lambda^2}+\frac{1}{\lambda^2}e^{-\lambda^2} =1-\frac{1}{\lambda^2}(1-e^{-\lambda^2})$$

Agora

$$\mathbb{P}(Y< X)=\int_{-\infty}^\infty (1-F_X(y))dF_Y(y)=\int_0^\lambda e^{-\lambda y}\frac{1}{\lambda}dy=-\frac{e^{-\lambda y}}{\lambda^2}\bigg|_0^\lambda=\frac{1}{\lambda^2}(1-e^{-\lambda^2})$$

E como

$$\mathbb{P}(X> Y)+\mathbb{P}(X< Y)+\mathbb{P}(X=Y)=1,$$

pois $ \Omega=[X> Y]\cup[X< Y]\cup [X=Y] $ temos

$$\mathbb{P}(X=Y)=1-\mathbb{P}(X> Y)-\mathbb{P}(X< Y)=1-\frac{1}{\lambda^2}(1-e^{-\lambda^2})=1$$

Exemplo 3.5.23

Fregueses entram em um supermercado conforme um processo de Poisson com parâmetro $ \lambda $. Há luz no supermercado enquanto não queima um fusível instalado no tempo $ t=0 $, e cuja vida útil T tem distribuição exponencial com parâmetro $ \xi $. Qual o número esperado de fregueses que entram no supermercado enquanto há luz?

Temos que $ (X_t)_{t\geq 0} $ é um processo de $ Poisson(\lambda) $ e T é variável aleatória $ Exp(\xi) $ então $ \mathbb{E}(T)=\frac{1}{\xi} $

Y é número de fregueses que entram no supermercado enquanto a luz. Assim $ Y=X_T $, no qual T é uma variável aleatória com distribuição $ Exp(\lambda) $. Agora $ (Y|T=t)= X_t\sim Poisson(\lambda t) $ o que implica que $ \mathbb{E}(Y|T=t)=\lambda t $. Mas Y é v.a. não negativa, então para ela vale a propriedade básica e então

$$\mathbb{E}(Y)=\mathbb{E}(\mathbb{E}(Y|T=t))=\mathbb{E}(\lambda T)=\lambda\mathbb{E}(T)=\frac{\lambda}{\xi}$$

3.5.1 - Propriedades da Esperança Condicional

Teorema 3.5.1.1

Seja X,Y e Z v.a’s e $ a,b\in\mathbb{R} $ e $ g:\mathbb{R}\rightarrow \mathbb{R} $. Assumindo que todas as esperanças condicionais a seguir existem, temos que

P1) $ \mathbb{E}[a|Y]=a $

P2) $ \mathbb{E}[aX+bY|Z]=a\mathbb{E}[X|Z]+b\mathbb{E}[Y|Z] $

P3) $ \mathbb{E}[X|Y]\geq 0 $ se $ X\geq 0 $

P4) $ \mathbb{E}[X|Y]=\mathbb{E}[X] $ se X é independente de Y.

P5) $ \mathbb{E}[\mathbb{E}[X|Y]]=\mathbb{E}[X] $

P6) $ \mathbb{E}[Xg(Y)|Y]=g(Y)\mathbb{E}[X|Y] $. Em particular $ \mathbb{E}[g(Y)|X]=g(Y) $

P7) $ \mathbb{E}[X|Y,g(Y)]=\mathbb{E}[X|Y] $

P8) $ \mathbb{E}[\mathbb{E}[X|Y,Z]|Y]=\mathbb{E}[X|Y] $

Demonstração

As demonstrações serão feitas para o caso contínuo, para fazer o caso discreto é feito de forma similar

P1)

$$\mathbb{E}[a|Y]=a\mathbb{P}(a|Y)=a$$

P2)Primeiramente note que

$$\mathbb{E}[aX+bY|Z]=\displaystyle \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(ax+by) f_{X,Y|Z}(X,Y|Z)dxdy$$

$$=\displaystyle a\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf_{X,Y|Z}(X,Y|Z)dydx+b\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}y f_{X,Y|Z}(X,Y|Z)dxdy$$

$$=\displaystyle a\int_{-\infty}^{\infty}x\left[\int_{-\infty}^{\infty}f_{X,Y|Z}(X,Y|Z)dy\right]dx+b\int_{-\infty}^{\infty}y\left[\int_{-\infty}^{\infty} f_{X,Y|Z}(X,Y|Z)dx\right]dy$$

$$=\displaystyle a\int_{-\infty}^{\infty}xf_{X|Z}(X|Z)dx+\displaystyle b\int_{-\infty}^{\infty}yf_{Y|Z}(Y|Z)dy$$

$$=a\mathbb{E}[X|Z]+b\mathbb{E}[Y|Z]$$

P3)Suponha $ X\geq 0 $ então

$$\mathbb{E}[X|Y]=\displaystyle \int_{-\infty}^{\infty}xf_{X|Y}(x|Y)dx=\int_{0}^{\infty}xf_{X|Y}(x|Y)dx\geq 0,$$

pois $ f_{X|Y}(x|Y)\geq 0 $

P4)Se X e Y são independente temos que

$$\displaystyle f_{X|Y}(x|y)=\frac{f_{X,Y}(x,y)}{f_Y(y)}=\frac{f_{X}(x)f_Y(y)}{f_Y(y)}=f_X(x)$$

então

$$\displaystyle\mathbb{E}[X|Y]=\int_{-\infty}^{\infty}xf_{X|Y}(x|y)dx=\int_{-\infty}^{\infty}xf_{X}(x)dx=\mathbb{E}[X]$$

P5)Basta notar que

$$\displaystyle \mathbb{E}[\mathbb{E}[X|Y]]=\int_{-\infty}^{\infty}\mathbb{E}[X|Y=y]f_Y(y)dy$$

$$=\displaystyle\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf_{X|Y}(x|y)f_Y(y)dydx$$

$$=\displaystyle\int_{-\infty}^{\infty}x\int_{-\infty}^{\infty}\frac{f_{X,Y}(x,y)}{f_Y(y)}f_Y(y)dydx$$

$$=\displaystyle\int_{-\infty}^{\infty}x\int_{-\infty}^{\infty}f_{X,Y}(x,y)dydx$$

$$=\displaystyle\int_{-\infty}^{\infty}xf_{X}(x)dx$$

$$=\mathbb{E}[X]$$

P6)Note que

$$\mathbb{E}[Xg(Y)|Y=y]=\displaystyle \int_{-\infty}^{\infty}xg(y)f_{X|Y}(x|Y=y)dx$$

$$\displaystyle g(y)\int_{-\infty}^{\infty}xf_{X|Y}(x|Y=y)dx=g(y)\mathbb{E}[X|Y=y]\Rightarrow g(Y))\mathbb{E}[X|Y]$$

P7)Observe que

$$\mathbb{E}[X|Y=y,g(y)]=\displaystyle \int_{-\infty}^{\infty}xf_{X|Y,g(Y)}(x|y,g(y))dx$$

$$=\displaystyle \int_{-\infty}^{\infty}x\frac{f_{X,Y,g(Y)}(x,y,g(y))}{f_{Y,g(Y)}(y,g(y))}dx$$

$$=\displaystyle \int_{-\infty}^{\infty}x\frac{f_{X,Y,g(Y)}(x,y,g(y))}{f_{g(Y)|Y}(g(y)|y)}dx$$

$$=\displaystyle \int_{-\infty}^{\infty}x\frac{f_{X,g(Y)|Y}(x,g(y)|y)f_Y(y)}{g(y)f_{Y}(y)}dx$$

$$=\displaystyle \int_{-\infty}^{\infty}x\frac{g(y)f_{X|Y}(x|y)f_Y(y)}{g(y)f_{Y}(y)}dx$$

$$=\displaystyle \int_{-\infty}^{\infty}xf_{X|Y}(x|y)dx=\mathbb{E}[X|Y]$$

P8)É importante ter em mente que $ \mathbb{E}[X|Y,Z] $ é uma variável aleatória, por isso

$$\mathbb{E}[\mathbb{E}[X|Y,Z]|Y=y]=\displaystyle \int_{-\infty}^{\infty}\mathbb{E}[X|Y=y,Z=z]f_{Z|Y}(z|y)dz$$

$$=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}xf_{X|Y,Z}(x|y,z)f_{Z|Y}(z|y)dzdx$$

$$=\int_{-\infty}^{\infty}x\int_{-\infty}^{\infty}\frac{f_{X,Y,Z}(x,y,z)}{f_{Z,Y}(z,y)}\frac{f_{Z,Y}(z,y)}{f_Y(y)}dzdx$$

$$=\int_{-\infty}^{\infty}x\int_{-\infty}^{\infty}\frac{f_{X,Y,Z}(x,y,z)}{f_Y(y)}dzdx$$

$$=\int_{-\infty}^{\infty}x\int_{-\infty}^{\infty}f_{X,Z|Y}(x,z|y)dzdx$$

$$=\int_{-\infty}^{\infty}xf_{X|Y}(x|y)dx=\mathbb{E}(X|Y=y)\Rightarrow \mathbb{E}[\mathbb{E}[X|Y,Z]|Y]=\mathbb{E}[X|Y]$$

Exemplo 3.5.1.1

Seja $ X,Y\stackrel{iid}{\sim}U(0,1) $, e $ Z=X+Y $. Encontre $ \mathbb{E}[Z|X],\mathbb{E}[XZ|X],\mathbb{E}[X|Z],\mathbb{E}[XZ|Z] $.

Vamos começar pelos mais simples

$$\displaystyle\mathbb{E}[Z|X]=\mathbb{E}[X+Y|X]=\mathbb{E}[X|X]+\mathbb{E}[Y|X]\stackrel{P4,P6}{=}X+\mathbb{E}[Y]=X+\frac{1}{2}$$

Agora

$$\mathbb{E}[XZ|X]\stackrel{P6}{=}X\mathbb{E}[Z|X]=X(X+\frac{1}{2})$$

Para calcular $ \mathbb{E}[X|Z] $, precisamos encontrar a densidade conjunta de X e Z. Precisamos encontrar imagem do quadrado $ 0\leq x,y\leq 1 $ através da nossa transformação $ X, Z=X+Y $, para mais detalhes consulte a seção 2.8 de probabilidade conjunta. Para verificar a nossa transformação, basta verificar o que ocorre nas bordas, já que nossa transformação é linear.

$$(x,y)=(0,0)\rightarrow (0,0)$$

$$(x,y)=(0,1)\rightarrow (0,1)$$

$$(x,y)=(1,0)\rightarrow (1,1)$$

$$(x,y)=(1,1)\rightarrow (1,2)$$

formando uma paralelogramo como na figura

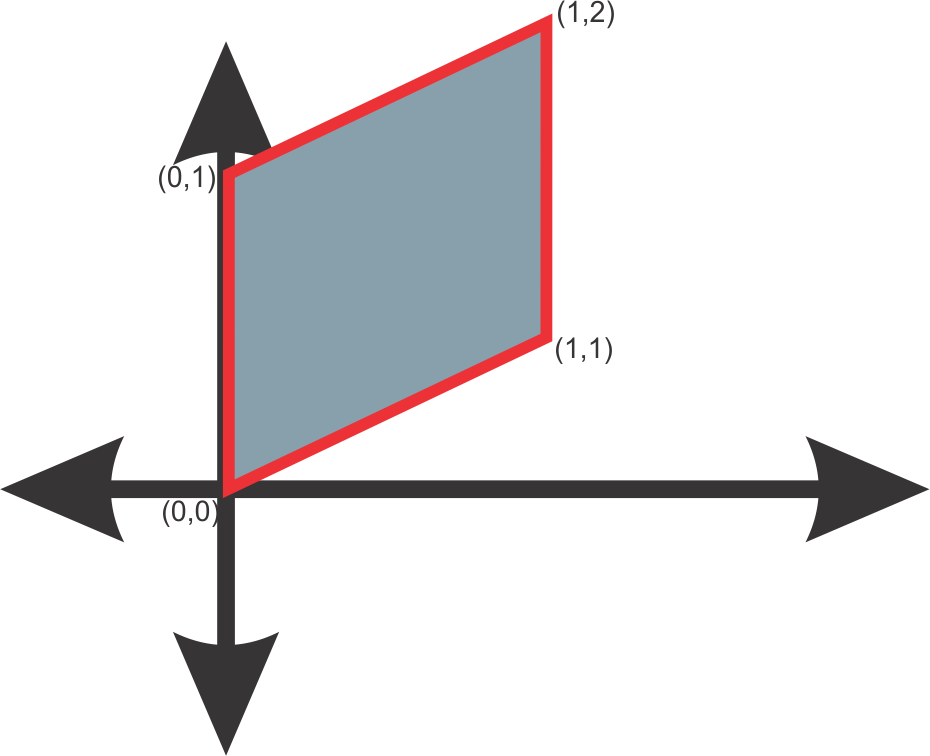
Note que a área do paralelogramo é 1, portanto a densidade conjunta é dada por

Resolvendo as integrais temos que

$$\mathbb{E}[X|Z=z]=z/2$$

Portanto

$$\mathbb{E}[X|Z]=Z/2 $$

E por fim temos que

$$\mathbb{E}[XZ|Z]\stackrel{P6}{=}Z\mathbb{E}[X|Z]=Z(Z/2)=Z^2/2$$

Exemplo 3.5.1.2

Seja $ (X_n)_{n\in\mathbb{N}} $ uma sequência de variáveis aleatórias iid com média $ \mu $ e variância $ \sigma^2 $. Seja $ N $ uma variável aleatória que assume valores nos naturais. Defina

$$\displaystyle S_N=\sum_{i=1}^N X_i$$

observe que $ S_N $ é uma variável aleatória cuja a quantidade de termos varia de acordo com o valor que a variável $ N $ assume. Queremos encontrar $ \mathbb{E}[S_N|N] $ e $ \mathbb{S}^2_{N|N} $ e calcule $ Var[S_N] $.

Para isso considere

$$\mathbb{E}[S_N^2|N=n]=\displaystyle \sum_{i=1}^n \mathbb{E}[X_i]=n\mu\Rightarrow \mathbb{E}[S_N|N]=N\mu$$

Agora como $ X_i $ são independente temos

$$\mathbb{E}[S_N^2|N=n]-\left(\mathbb{E}[S_N|N=n]\right)=Var[S_N|N=n]=\sum_{i=1}^n Var[X_i]=n\sigma^2\Rightarrow Var[S_N|N]=N\sigma^2$$

o que implica que

$$\mathbb{E}[S_N^2|N]=N\sigma^2+N^2\mu^2$$

Agora usando P5, temos

$$\mathbb{E}[S_N]=\mathbb{E}[\mathbb{E}[S_N|N]]=\mathbb{E}[N\mu]=\mu\mathbb{E}[N]$$

E ainda

$$\mathbb{E}[S_N^2]=\mathbb{E}[\mathbb{E}[S_N^2|N]]=\mathbb{E}[N\sigma^2+N\mu^2]=\sigma^2\mathbb{E}[N]+\mu^2\mathbb{E}[N^2]$$

Finalmente temos que a variância de $ S_N $ é

$$Var[S_N]=\mathbb{E}[S^2_N]-\left(\mathbb{E}[S_N]\right)^2=\sigma^2\mathbb{E}[N]+\mu^2Var[N]$$

Exemplo 3.5.1.3

Suponha que o numero de clientes que entram em supermercado em um dia é uma variável aleatória com média 100. Suponha também que o montante gasto neste supermercado por cada cliente é uma variável aleatória independente com média de 40 reais, suponha também que o montante gasto pelos clientes é independente do total de clientes no dia, ou seja, se o supermercado está cheio ou vazio a quantidade que cada cliente gasta independe disto. Qual é o valor esperado do montante total de dinheiro que entra neste supermercado ?

Se tomarmos N como o total de clientes que entram no supermercado e $ X_i $ como sendo o valor que cada cliente gasta, então queremos calcular

$$\displaystyle \mathbb{E}\left[\sum_{i=1}^N X_i\right]$$

utilizando o exemplo 3.5.1.2 temos

$$\mathbb{E}[S_N]=\mathbb{E}[N]\mathbb{E}[X_i]=100\star40=(reais)4000,00$$