8.4 Variância de Variáveis Aleatórias

Suponhamos que, para uma variável aleatória $ X $, verificamos que $ \mathbb{E}(X) = 2 $. Qual o significado disso? Como vimos acima, significa que se considerarmos um grande número de observações de $ X $, digamos $ x_1, x_2,\ldots,x_n $, ao calcularmos a média desses valores, ela estará próxima de 2, se $ n $ for grande.

Suponhamos, por exemplo, que $ X $ representa a duração de vida de lâmpadas que estão sendo recebidas de um fabricante, e que $ \mathbb{E}(X) = 1000 $ horas. Isto pode significar que a maioria das lâmpadas deve durar um período de tempo compreendido entre 900 horas e 1100 horas. Poderia significar também que as lâmpadas são formadas por dois tipos muito diferentes: cerca da metade são de muita boa qualidade e durarão aproximadamente 1400 horas, enquanto que a outra metade é de muito má qualidade e durarão aproximadamente 600 horas.

Assim, existe uma necessidade óbvia de se introduzir uma medida que possa distinguir entre essas duas situações.

Definição 4.1

Seja $ X $ uma variável aleatória. Definimos a variância de $ X $, denotada por $ \text{Var}(X) $ ou $ \sigma^2_X $ por

$$\text{Var}(X)=\mathbb{E}\left[\left(X-\mathbb{E}(X)\right)^2\right].$$

A raiz quadrada positiva da variância $ \text{Var}(X) $ é denominada de desvio-padrão de $ X $ e denotado por $ \sigma_X $.

Observação

O número $ \text{Var}(X) $ é expresso por unidades quadradas de $ X $. Isto é, se $ X $ for medido em horas, então $ \text{Var}(X) $ é expressa em (horas)².

O cálculo de $ \text{Var}(X) $ pode ser simplificado com o auxílio do seguinte resultado.

Propriedade

A variância de uma variável aleatória $ X $ pode ser calculada da seguinte forma

$$\text{Var}(X)=\mathbb{E}(X^2)-[\mathbb{E}(X)]^2.$$

De fato, desenvolvendo $ \mathbb{E}\left[\left(X-\mathbb{E}(X)\right)^2\right] $ e empregando as propriedades já estabelecidas de valor esperado, obtemos

$$\text{Var}(X)=\mathbb{E}\left[\left(X-\mathbb{E}(X)\right)^2\right]=\mathbb{E}\left(X^2-2X\mathbb{E}(X)+[\mathbb{E}(X)]^2\right)$$

ou seja

$$\text{Var}(X)=\mathbb{E}(X^2)-2\mathbb{E}(X)\mathbb{E}(X)+[\mathbb{E}(X)]^2=\mathbb{E}(X^2)-[\mathbb{E}(X)]^2.$$

Exemplo 4.1

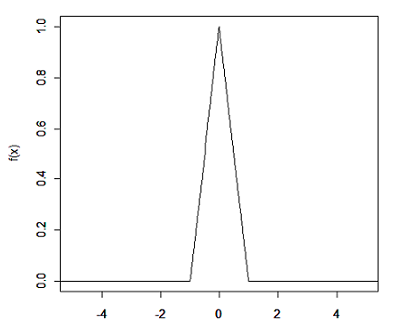
Suponhamos que $ X $ seja uma variável aleatória contínua com fdp

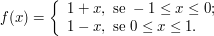
Calcule $ \text{Var}(X) $.

Temos que

$$\mathbb{E}(X)=\int_{-1}^0x(1+x)dx+\int_0^1x(1-x)dx=\left(\frac{x^3}{3}+\frac{x^2}{2}\right)_{-1}^0+\left(\frac{x^2}{2}-\frac{x^3}{3}\right)_0^1=0$$

e

$$\mathbb{E}(X^2)=\int_{-1}^0x^2(1+x)dx+\int_0^1x^2(1-x)dx=\left(\frac{x^4}{4}+\frac{x^3}{3}\right)_{-1}^0+\left(\frac{x^3}{3}-\frac{x^4}{4}\right)_0^1=\frac{1}{6}$$

portanto, temos que

$$\text{Var}(X)=\mathbb{E}(X^2)-[\mathbb{E}(X)]^2=\frac{1}{6}.$$

Exemplo 4.2

Utilizando o exemplo 3.2.5 cujo a função densidade de probabilidade da variável aleatória $ X $ é dada por

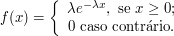
Neste exemplo calculamos os valores esperados de $ X $ e de $ X^2 $, os quais são dados por

$$\mathbb{E}(X)=\frac{1}{\lambda}$$

e

$$\mathbb{E}(X^2)= \frac{2}{\lambda^2}.$$

Desta forma, a variância de $ X $ é dada por

$$\text{Var}(X)=\mathbb{E}(X^2)-\mathbb{E}^2(X)=\frac{1}{\lambda^2}-\left(\frac{1}{\lambda}\right)^2=\frac{1}{\lambda^2}.$$

E portanto, $ \text{Var}(X)=\frac{1}{\lambda^2} $.

4.1 - Propriedades da variância

Existem várias propriedades importantes para a variância de uma variável aleatória. A seguir, enunciamos algumas delas.

P1) Se $ c $ for uma constante, então

$$\text{Var}(X+c)=\text{Var}(X).$$

De fato, temos que

$$\text{Var}(X+c)=\mathbb{E}[(X+c)^2]-[\mathbb{E}(X+c)]^2=\mathbb{E}[X^2+2cX+c^2]-[\mathbb{E}(X)+c]^2$$

portanto

$$\text{Var}(X+c)=\mathbb{E}(X^2)-[\mathbb{E}(X)]^2=\text{Var}(X).$$

Observação

Esta propriedade é intuitivamente evidente, porque somar uma constante a um resultado $ X $ não altera sua variabilidade.

P2) Se $ c $ for uma constante, então

$$\text{Var}(cX)=c^2\text{Var}(X)$$

De fato, temos que

$$\text{Var}(cX)=c^2\mathbb{E}(X^2)-c^2[\mathbb{E}(X)]^2=c^2\text{Var}(X).$$

P3) Se $ X $ e $ Y $ forem variáveis aleatórias independentes, então

$$\text{Var}(X+Y)=\text{Var}(X)+\text{Var}(Y).$$

De fato, temos que

$$\text{Var}(X+Y)=\mathbb{E}[(X+Y)^2]-[\mathbb{E}(X+Y)]^2$$

ou seja

$$\text{Var}(X+Y)=\mathbb{E}(X^2)+2\mathbb{E}(X)\mathbb{E}(Y)+\mathbb{E}(Y^2)-[\mathbb{E}(X)]^2-2\mathbb{E}(X)\mathbb{E}(Y)-[\mathbb{E}(Y)]^2=\text{Var}(X) +\text{Var}(Y).$$

Observação

É importante compreender que a variância não é, em geral, aditiva, como o valor esperado. Com a hipótese complementar de independência, a P3 fica válida.

P4) Sejam $ X_1,\ldots,X_n $ variáveis aleatórias independentes. Então,

$$\text{Var}(X_1+\ldots+X_n)=\text{Var}(X_1)+\ldots+\text{Var}(X_n).$$

Esta propriedade segue direto da anterior. Basta fazer uma indução sobre $ n $.

4.2 - Covariância e Coeficiente de Correlação

Em probabilidade, a covariância de duas variáveis X e Y é uma medida da variabilidade conjunta destas variáveis aleatórias. Se as variáveis tem covariância positiva tendem a mostrar um comportamento semelhante, ou seja, os menores(maiores) valores da variável X corresponde aos menores(maiores) da variável Y . Se a covariância é negativa então as variáveis tendem a mostrar um comportamento oposto, ou seja, os menores(maiores) valores da variável X corresponde aos maiores(menores) da variável Y.

Assim, podemos ver que o sinal da covariância mostra a tendência na relação linear entre as variáveis.

Definição 4.2.1

Sejam $ X $ e $ Y $ variáveis aleatórias integráveis. Então a covariância entre X e Y é definida por

$$Cov(X,Y)=\mathbb{E}[(X-\mathbb{E}(X))(Y-\mathbb{E}(Y))],$$

se essa esperança existe, então pela linearidade da esperança temos que

$$Cov(X,Y)=\mathbb{E}(XY-Y\mathbb{E}(X)-X\mathbb{E}(Y)+\mathbb{E}(X)\mathbb{E}(Y))=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y)$$

Assim, temos que existe a covariância entre duas variáveis integráveis se, e somente se, existe a esperança $ \mathbb{E}(XY) $.

De fato, se existe a covariância entre duas variáveis integráveis então temos que

$$Cov(X,Y)=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y)< \infty\Rightarrow\mathbb{E}(XY)\leq \mathbb{E}(X)\mathbb{E}(Y)< \infty$$

desde que X e Y são integráveis.

Agora existe $ \mathbb{E}(XY) $ e as variáveis X e Y são integráveis então temos que $ \mathbb{E}(XY)< \infty $ e $ \mathbb{E}(X)< \infty $ e $ \mathbb{E}(Y)< \infty $ então temos que a $ Cov(XY)< \infty $.

Se $ Cov(X,Y)=0 $, dizemos que $ X $ e $ Y $ são não-correlacionado. Se X e Y são independentes e integráveis, então são não-correlacionado, poies neste caso

$$\mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y)$$

mas é claro que $ \mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y) $ não implica que em independência, ou seja, a covariância zero não necessariamente implica independência.

Teorema 4.2.1

Sejam $ X_1,\dots, X_n $ variáveis aleatórias integráveis. Então,

$$Var\left(\sum_{i=1}^n X_i\right)=\sum_{i=1}^n Var(X_i)]+2\sum_{i< j}Cov(X_i,X_j).$$

Em particular se $ Cov(X_i,X_j)=0 $ para $ i\neq j $ então

$$Var\left(\sum_{i=1}^n X_i\right)=\sum_{i=1}^nVar(X_i)$$

Demonstração

$$Var(X_1+\dots+X_n)=\mathbb{E}(X_1+\dots+X_n-\mathbb{E}(X_1+\dots+X_n))^2$$

$$=\mathbb{E}(X_1-\mathbb{E}(X_1)+\dots+X_n-\mathbb{E}(X_n))^2$$

$$=\mathbb{E}\left[\sum_{i=1}^n\sum_{j=1}^n (X_i-\mathbb{E}(X_i))(X_j-\mathbb{E}(X_j))\right]$$

$$=\mathbb{E}\left[\sum_{i=1}^n(X_i-\mathbb{E}(X_i))^2+\sum_{i\neq j}(X_i-\mathbb{E}(X_i))(X_j-\mathbb{E}(X_j))\right]$$

$$=\mathbb{E}\left(\sum_{i=1}^n (X_i-\mathbb{E}(X_i))^2+2\sum_{i< j}(X_i-\mathbb{E}(X_i))(X_j-\mathbb{E}(X_j))\right)$$

$$=\sum_{i=1}^n Var(X_i)+2\sum_{i< j}Cov(X_i,X_j)$$

Portanto o resultado segue.

Corolário 4.2.1

Se $ X_1,\dots, X_n $ são independentes e integráveis, então

$$Var(X_1+\dots+X_n)=\sum_{i=1}^n Var(X_i).$$

A magnitude da covariância não é fácil de interpretar. A versão normalizada da covariância (coeficiente de correlação) entretanto, mostra por sua magnitude a força da relação linear. Assim, agora X e Y sejam variáveis aleatórias integráveis, com variâncias positivas e finitas. Dizemos que a variável aleatória $ \displaystyle \frac{X-\mathbb{E}(X)}{\sigma_X} $ é uma padronização de X, pois expressa o valor de X em unidades padronizadas (desvio padrão). Um variável aleatória padronizada possuí esperança zero e variância 1.

A covariância padronizada, chama-se coeficiente de correlação entre X e Y, o qual denotaremos por $ \rho(X,Y) $

Definição 4.2.2

Seja X e Y variáveis aleatórias integráveis então o coeficiente de correlação entre X e Y é dado por

$$\rho(X,Y):=\frac{Cov(X,Y)}{\sigma_X \sigma_Y}=\mathbb{E}\left[\left(\frac{X-\mathbb{E}(X)}{\sigma_X}\right) \left(\frac{Y-\mathbb{E}(Y)}{\sigma_Y}\right)\right]$$

Proposição 4.2.1

O coeficiente de correlação é independente da escola e transação da variáveis, ou seja,

$$\rho(X,Y)=\rho(aX+b,cY+d)$$

para $ a< 0 $, $ c< 0 $.

Demonstração

De fato, primeiramente observe que

$$\sigma_{aX+b}=\sqrt{Var(aX+b)}=\sqrt{a^2Var(X)}=a\sqrt{Var(X)}=a\sigma_X$$

$$\sigma_{cY+d}=\sqrt{Var(cY+d)}=\sqrt{c^2Var(Y)}=c\sqrt{Var(Y)}=c\sigma_Y$$

e portanto

$$\rho(aX+b,cY+d)=\mathbb{E}\left[\left(\frac{aX+b-\mathbb{E}(aX+b)}{\sigma_{aX+b}}\right) \left(\frac{cY+d-\mathbb{E}(cY+d)}{\sigma_{cY+d}}\right)\right]$$

$$=\mathbb{E}\left[\left(\frac{aX-\mathbb{E}(aX)}{\sigma_{aX+b}}\right) \left(\frac{cY-\mathbb{E}(cY)}{\sigma_{cY+d}}\right)\right]$$

$$=\mathbb{E}\left[\left(\frac{a(X-\mathbb{E}(X))}{\sigma_{aX+b}}\right) \left(\frac{c(Y-\mathbb{E}(Y))}{\sigma_{cY+d}}\right)\right]$$

$$=\mathbb{E}\left[\left(\frac{a(X-\mathbb{E}(X))}{a\sigma_{X}}\right) \left(\frac{c(Y-\mathbb{E}(Y))}{c\sigma_{Y}}\right)\right]$$

$$=\mathbb{E}\left[\left(\frac{X-\mathbb{E}(X)}{\sigma_{X}}\right) \left(\frac{Y-\mathbb{E}(Y)}{\sigma_{Y}}\right)\right]$$

$$=\rho(X,Y)$$

A seguir temos uma proposição com algumas propriedades do coeficiente linear.

Proposição 4.2.2

Sejam X e Y variáveis aleatórias com variâncias finitas e positivas. Então:

a) $ -1\leq \rho(X,Y)\leq 1 $

b) $ \rho(X,Y)=1 $ se, e somente se, $ \mathbb{P}(Y=aX+b)=1 $ para algum $ a> 0 $, $ b\in \mathbb{R} $.

c) $ \rho(X,Y)=-1\Leftrightarrow \mathbb{P}(Y=aX+b)=1 $ para algum $ a< 0, \quad b\in \mathbb{R}. $

Demonstração

(a) Como

$$0\leq \left(\frac{X-\mathbb{E}(X)}{\sigma_X}-\frac{Y-\mathbb{E}(Y)}{\sigma_Y}\right)^2,$$

temos

$$0\leq \mathbb{E}\left(\frac{X-\mathbb{E}(X)}{\sigma_X}-\frac{Y-\mathbb{E}(Y)}{\sigma_Y}\right)^2$$

$$=\mathbb{E}\left(\frac{X-\mathbb{E}(X)}{\sigma_X}\right)^2+\mathbb{E}\left(\frac{Y-\mathbb{E}(Y)}{\sigma_Y}\right)^2- \frac{2}{\sigma_X\sigma_Y}\mathbb{E}[(X-\mathbb{E}(X))(Y-\mathbb{E}(Y))]$$

$$=\frac{Var(X)}{\sigma^2_X}+\frac{Var(Y)}{\sigma^2_Y}-\frac{2Cov(X,Y)}{\sigma_X\sigma_Y}=2-2\rho(X,Y).$$

Logo $ \rho(X,Y)\leq 1. $

Substituindo o sinal “$ - $” por “$ + $” na expressão acima temos que

$$0\leq 2+2\rho(X,Y)$$

isto é $ \rho(X,Y)\geq -1 $. Portanto, (a) segue.

Agora se $ \rho=1 $ então temos que

$$0=2-2\rho(X,Y)=\frac{Var(X)}{\sigma^2_X}+\frac{Var(Y)}{\sigma^2_Y}- \frac{2Cov(X,Y)}{\sigma_X\sigma_Y}=\mathbb{E}\left(\frac{X-\mathbb{E}(X)}{\sigma_X}-\frac{Y-\mathbb{E}(Y)}{\sigma_Y}\right)^2$$

Então,

$$\mathbb{E}\left(\frac{X-\mathbb{E}(X)}{\sigma_X}-\frac{Y-\mathbb{E}(Y)}{\sigma_Y}\right)^2=0$$

ou seja,

$$\mathbb{E}\left(\frac{X-\mathbb{E}(X)}{\sigma_X}\right)=\mathbb{E}\left(\frac{Y-\mathbb{E}(Y)}{\sigma_Y}\right)$$

Desde que, X e Y são positivas temos que

$$\mathbb{P}\left(\frac{X-\mathbb{E}(X)}{\sigma_X}-\frac{Y-\mathbb{E}(Y)}{\sigma_Y}\right)=1$$

ou seja,

$$Y=\mathbb{E}(Y)+\frac{\sigma_Y}{\sigma_X}(X-\mathbb{E})$$

quase certamente. Para a volta basta tomar $ a=\frac{\sigma_Y}{\sigma_X} $ e $ b=\mathbb{E}(Y)-\frac{\sigma_Y}{\sigma_X}\mathbb{E}(X) $.

Agora se $ \rho(X,Y)=-1 $, então

$$\mathbb{E}\left(\frac{X-\mathbb{E}(X)}{\sigma_X}+\frac{Y-\mathbb{E}(Y)}{\sigma_Y}\right)=0$$

e

$$Y=\mathbb{E}(Y)-\frac{\sigma_Y}{\sigma_X}(X-\mathbb{E}(X))$$

com probabilidade 1. Neste caso, $ a=-\frac{\sigma_Y}{\sigma_X} $ e $ b=\mathbb{E}(Y)+\frac{\sigma_Y}{\sigma_X}\mathbb{E}(X) $.

Por outro lado, se $ \mathbb{P}(Y=aX+b)=1 $ para algum $ a\neq 0 $, temos

$$\rho(X,Y)=\mathbb{E}\left[\left(\frac{X-\mathbb{E}(X)}{\sigma_X}\right)\left(\frac{aX+b-a\mathbb{E}(X)-b}{\sqrt{a^2\sigma^2_X}}\right)\right]$$

$$=\frac{a}{|a|}\mathbb{E}\left(\frac{X-\mathbb{E}(X)}{\sigma_X}\right)^2=\frac{a}{|a|}=\text{sinal}(a)$$

Uma alta correlação entre X e Y, i.e. se $ \rho(X,Y) $ próximo de 1, significa que o valor de $ Y $ tende a acompanhar o de X.

Exemplo 4.2.1

Mostre que se $ \mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y) $ e X e Y assumem apenas valores $ 0 $ e $ 1 $ então X e Y são independentes.

De fato, observe que:

$$\mathbb{E}(X)=0\mathbb{P}(X=0)+1\mathbb{P}(X=1)=\mathbb{P}(X=1)$$

$$\mathbb{E}(Y)=0\mathbb{P}(Y=0)+1\mathbb{P}(Y=1)=\mathbb{P}(Y=1)$$

e

$$\mathbb{E}(XY)=0\mathbb{P}(X=0,Y=0)+0\mathbb{P}(X=0,Y=1)+0\mathbb{P}(X=1,Y=0)+1\mathbb{P}(X=1,Y=1)=\mathbb{P}(X=1,Y=1)$$

Mas como por hipótese $ \mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y) $ então temos que

$$\mathbb{E}(XY)=\mathbb{P}(X=1,Y=1)=\mathbb{E}(X)\mathbb{E}(Y)=\mathbb{P}(X=1)\mathbb{P}(Y=1)$$

Agora observe que

$$\mathbb{P}(X=0,Y=1)=\mathbb{P}(Y=1)-\mathbb{P}(X=1,Y=1)=\mathbb{P}(Y=1)-\mathbb{P}(X=1)\mathbb{P}(Y=1)=\mathbb{P}(Y=1) \left(1-\mathbb{P}(X=1)\right)=\mathbb{P}(Y=1)\mathbb{P}(X=0)$$

e

$$\mathbb{P}(X=0,Y=0)=\mathbb{P}(X=0)-\mathbb{P}(X=0,Y=1)=\mathbb{P}(X=0)(1-\mathbb{P}(Y=1))=\mathbb{P}(X=0)=\mathbb{P}(X=0)\mathbb{P}(Y=0)$$

Pelas equações acima obtemos a independência.

Exemplo 4.2.2

Se X assume apenas valores $ a $ e $ b $, Y assume apenas os valores c e d e $ Cov(X,Y)=0 $, então X e Y são independentes

De fato, considere que $ W $ e $ Z $ assumem apenas valores 0 e 1. Então

$$X=(b-a)W+a$$

e

$$Y=(d-c)Z+c$$

Então,

$$XY=[(b-a)W+a][(d-c)Z+c]=(b-a)(d-c)WZ+a(d-c)Z+c(b-a)W+ac$$

e portanto

$$\mathbb{E}(XY)=(b-a)(d-c)\mathbb{E}(WZ)+a(d-c)\mathbb{E}(Z)+c(b-a)\mathbb{E}(W)+ac$$

e temos que

$$\mathbb{E}(X)=(b-a)\mathbb{E}(W)+a$$

e

$$\mathbb{E}(Y)=(d-c)\mathbb{E}(Z)+c$$

o que implica que

$$\mathbb{E}(X)\mathbb{E}(Y)=(b-a)(d-c)\mathbb{E}(W)\mathbb{E}(Z)+a(d-c)\mathbb{E}(Z)+c(b-a)\mathbb{E}(W)+ac$$

Como a $ Cov(X,Y)=0 $ e

$$0=Cov(X,Y)=(b-a)(d-c)Cov(W,Z)$$

e ainda

$$Cov(XY)=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}(Y)=(b-a)(d-c)\mathbb{E}(WZ)+a(d-c)\mathbb{E}(Z)+c(b-a)\mathbb{E}(W)+ac - (b-a)(d-c)\mathbb{E}(W)\mathbb{E}(Z)+a(d-c)\mathbb{E}(Z)+c(b-a)\mathbb{E}(W)+ac $$

$$(b-a)(d-c)[\mathbb{E}(WZ)-\mathbb{E}(W)\mathbb{E}(Z)]=(b-a)(d-c)Cov(W,Z)$$

Agora se $ Cov(X,Y)=0 $ então como $ (a-b)(d-c)\neq 0 $, pois $ b> a $ e $ d> c $ o que implica que pelo exemplo anterior temos que

$$Cov(W,Z)=0$$

o que implica que $ W $ e $ Z $ são independentes o que implica que $ (b-a)W+a $ e $ (d-c)Z+c $ são independentes e portanto X e Y são independente.

Exemplo 4.2.3

Se X e Y são independentes com variância finita, então

$$Var(XY)=Var(X)Var(Y)+\mathbb{E}(X)^2Var(Y)+\mathbb{E}(Y)^2Var(X)$$

Para isso observe que

$$Var(X)Var(Y)+\mathbb{E}(X)^2Var(Y)+\mathbb{E}(Y)^2Var(X)=\left(\mathbb{E}(X^2)-\mathbb{E}^2(X)\right)\left(\mathbb{E}(Y^2)-\mathbb{E}^2(Y)\right) $$

$$+\left(\mathbb{E}^2(X)\right) \left(\mathbb{E}(Y^2)-\mathbb{E}^2(Y)\right)+ \left(\mathbb{E}^2(Y)\right)\left(\mathbb{E}(X^2)-\mathbb{E}^2(X)\right)$$

$$=\mathbb{E}^2(X)\mathbb{E}(Y^2)-\mathbb{E}^2(X)\mathbb{E}^2(Y)+\mathbb{E}(X^2)\mathbb{E}^2(Y)-\mathbb{E}^2(X)\mathbb{E}^2(Y) + \mathbb{E}(X^2)\mathbb{E}(X^2)-\mathbb{E}(X^2)\mathbb{E}^2(Y)-\mathbb{E}^2(X)\mathbb{E}(Y^2)+\mathbb{E}^2(X)\mathbb{E}^2(Y)$$

$$=\mathbb{E}(X^2)\mathbb{E}(Y^2)-\mathbb{E}^2(X)\mathbb{E}^2(Y)=\mathbb{E}((XY)^2)-\mathbb{E}^2(XY)=Var(XY)$$

portanto o resultado segue.

Proposição 4.2.3

A covariância é bilinear, ou seja,

$$Cov\left(\sum_{i=1}^n a_iX_i, \sum_{j=1}^m b_jY_j\right)=\sum_{j=1}^m\sum_{i=1}^n a_i b_j Cov(X_i,Y_j)$$

no qual $ a_i $ e $ b_j $ são números reais e $ Var(X_i) $, $ Var(Y_j) $ são finitas.

Demonstração

Como as variâncias são finitas então $ \mathbb{E}(X_iY_j)< \infty $, e pela desigualdade de Cauchy-Schwartz a $ Cov(X_i,Y_j) $. Assim

$$Cov\left(\sum_{i=1}^n a_iX_i, \sum_{j=1}^n b_jY_j\right)=\mathbb{E}\left(\sum_{i=1}^n a_iX_i\sum_{j=1}^n b_jY_j\right)-\mathbb{E}\left(\sum_{i=1}^n a_i X_i\right)\mathbb{E}\left(\sum_{j=1}^m b_j Y_j\right)$$

$$=\mathbb{E}\left(\sum_{j=1}^m\sum_{i=1}^n a_i b_jX_iY_j\right)-\mathbb{E}\left(\sum_{i=1}^n a_iX_i\right)\mathbb{E}\left(\sum_{j=1}^m b_jY_j\right)$$

Pela linearidade da esperança temos que

$$Cov\left(\sum_{i=1}^n a_iX_i, \sum_{j=1}^n b_jY_j\right)=\sum_{j=1}^n\sum_{i=1}^m a_ib_j\mathbb{E}(X_i Y_j)-\left(\sum_{i=1}^n a_i\mathbb{E}(X_i)\right)\left(\sum_{j=1}^m b_j\mathbb{E}(Y_j)\right)$$

$$=\sum_{i=1}^n \sum_{j=1}^m a_ib_j \left(\mathbb{E}(X_iY_j)-\mathbb{E}(X_i)\mathbb{E}(Y_i)\right)=\sum_{j=1}^m\sum_{i=1}^n a_ib_jCov(X_i,Y_j)$$

portanto o resultado segue.

Exemplo 4.2.4

Sejam $ (X_1,\dots X_n, Y_1, \dots, Y_m) $ um vetor aleatória $ (m+n) $-dimensional tal que $ Var(X_i)=Var(Y_j)=1 $ e $ \rho(X_i,X_j)=\rho_1 $ e $ \rho(Y_i,Y_j)=\rho_2 $ para todo $ i\neq j $ e $ \rho(X_i,Y_j)=\rho_3 $. Se $ U=X_1+\dots+X_m $ e $ V=Y_1+\dots+Y_n $, então prove que o coeficiente de correlação

$$\rho(U,V)=\frac{\sqrt{mn}\rho_3}{\sqrt{1+(m-1)\rho_1}\sqrt{1+(n-1)\rho_2}}$$

Para isso, observe que

$$Cov(U,V)=Cov\left(\sum_{i=1}^n X_i,\sum_{j=1}^m Y_j\right)=\sum_{i=1}^n\sum_{j=1}^mCov(X_i, Y_j)=mn(\rho_3\sqrt{Var(X_1)}\sqrt{Var(Y_1)})=mn\rho_3$$

Agora

$$\sigma_U^2=Var\left(\sum_{i=1}^nX_i\right)=\sum_{i=1}^nVar(X_i)+2\sum_{i< j}Cov(X_i,X_j)=n+2n(n-1)\rho_1=n(1+(n-1)\rho_1)$$

Igualmente obtemos que

$$\sigma_V^2=Var\left(\sum_{i=1}^mY_i\right)=\sum_{i=1}^mVar(Y_i)+2\sum_{i< j}Cov(Y_i,Y_j)=m(1+(m-1)\rho_2)$$

Então,

$$\rho(U,V)=\frac{Cov(U,V)}{\sigma_U\sigma_V}=\frac{\sqrt{mn}\rho_3}{\sqrt{1+(m-1)\rho_1}\sqrt{1+(n-1)\rho_2}}$$

e portanto o resultado segue.

Exemplo 4.2.5

Sejam X, Y e Z variáveis independentes com distribuição comum $ U[0,1] $. Calcule a esperança e a variância de $ W=(X+Y)Z $.

Primeiramente note que

$$\mathbb{E}(X)=\frac{1}{2}$$

e

$$\mathbb{E}(X^2)=\frac{1}{3}$$

Agora usando a independência, temos que

$$\mathbb{E}(W)=\mathbb{E}(X+Y)\mathbb{E}(Z)=\mathbb{E}(X)\mathbb{E}(Z)+\mathbb{E}(Y)\mathbb{E}(Z)=\left(\frac{1}{2}+\frac{1}{2}\right)\frac{1}{2}=\frac{1}{2}$$

e usando o Exemplo 4.2.3, temos que

$$Var[(X+Y)Z]=Var(X+Y)Var(Z)+\mathbb{E}(X+Y)^2Var(Z)+\mathbb{E}(Z)^2Var(X+Y)=\frac{5}{36}$$