8.5 Modelos Probabilísticos Discretos

A seguir veremos os principais modelos probabilísticos discretos, alguns dos quais já utilizados em seções anteriores. Os principais modelos são: uniforme discreto, Bernoulli, binomial, geométrico, Poisson e o Hipergeométrico. Cada um deles será analisado individualmente.

Os assuntos tratados a seguir podem ser encontrados com mais detalhes no livro do Barry R. James e Murray R. Spiegel.

5.1 - Distribuição binomial

Para construir o modelo binomial vamos introduzir uma sequência de ensaios de Bernoulli. Tal sequência é definida por meio das seguintes condições:

• Em cada ensaio considera-se somente a ocorrência ou não-ocorrência de um certo evento que será denominado sucesso (S) e cuja não-ocorrência será denominada falha (F).
• Os ensaios são independentes.
• A probabilidade de sucesso, que denotaremos por p é a mesma para cada ensaio. A probabilidade de falha será denotada por 1-p.

Para um experimento que consiste na realização de $ n $ ensaios independentes de Bernoulli, o espaço amostral pode ser considerado como o conjunto de n-uplas, em que cada posição há um sucesso (S) ou uma falha (F).

A probabilidade de um ponto amostral com sucessos nos $ k $ primeiros ensaios e falhas nos $ n-k $ ensaios seguintes é $ p^k(1-p)^{n-k}. $

Note que esta é a probabilidade de qualquer ponto com $ k $ sucessos e $ n-k $ falhas. O número de pontos do espaço amostral que satisfaz essa condição é igual ao número de maneiras com que podemos escolher $ k $ ensaios para a ocorrência de sucesso dentre o total de $ n $ ensaios, pois nos $ n-k $ restantes deverão ocorrer falhas. Este número é igual ao número de combinações de $ n $ elementos tomados $ k $ a $ k $, ou seja,

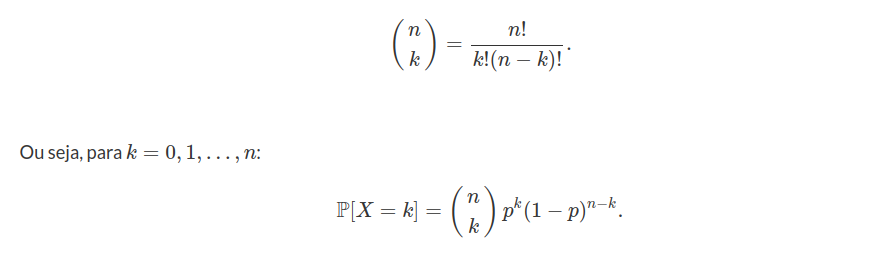
Definição 5.1.1

Seja $ X $ o número de sucessos obtidos na realização de $ n $ ensaios de Bernoulli independentes. Diremos que $ X $ tem distribuição binomial com parâmetros $ n $ e $ p $, em que $ p $ é a probabilidade de sucesso em cada ensaio, se sua função de probabilidade for dada por

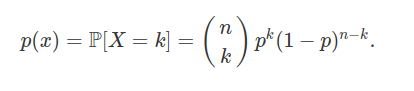
Usaremos a notação $ X \sim b(n,p) $.

Exemplo 5.1.1

Suponha que numa linha de produção a probabilidade de se obter uma peça defeituosa (sucesso) é $ p = 0,1 $. Toma-se uma amostra de 10 peças para serem inspecionadas. Qual a probabilidade de se obter:

1. Uma peça defeituosa?

2. Nenhuma peça defeituosa?

3. Duas peças defeituosas?

4. No mínimo duas peças defeituosas?

5. No máximo duas peças defeituosas?

Solução

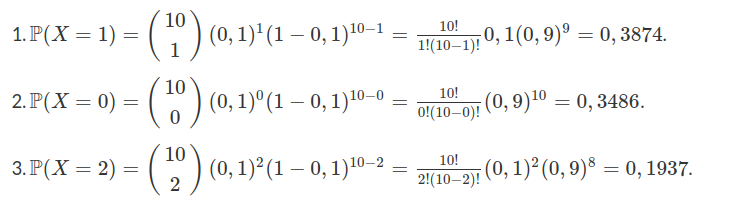
4. $ \mathbb{P}(X\geq 2)=\mathbb{P}(X=2)+\mathbb{P}(X=3)+\ldots+\mathbb{P}(X=9)+\mathbb{P}(X=10) $.

ou seja, $ \mathbb{P}(X\geq 2)=1-[\mathbb{P}(X=0)+\mathbb{P}(X=1)]=0,2639 $.

5. $ \mathbb{P}(X\leq 2)=\mathbb{P}(X=0)+\mathbb{P}(X=1)+\mathbb{P}(X=2)=0,9298 $.

Exemplo 5.1.2

Suponha que um aluno pretende fazer um teste de múltipla escolha com 10 questões e cinco alternativas por questão respondendo cada uma das questões de forma aleatória. Qual é probabilidade dele acertar no máximo 3 questões?

Como cada questão apresenta cinco alternativas e o aluno pretende respondê-las ao acaso temos que a probabilidade de sucesso em cada questão, ou seja, probabilidade dele escolher a alternativa correta é de 1/5. Desta forma, podemos definir as seguintes variáveis aleatórias com distribuição de Bernoulli

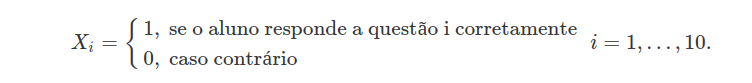
Temos que, para todo $ i $, a probabilidade de sucesso é $ p=0,2 $ (já que temos 5 alternativas disponíveis). Desta forma, $ \mathbb{P}(X_i = 1) = 0,2 $. Se definirmos $ X $ como sendo a variável aleatória que assume o número total de acertos na prova, temos que

$$X = \sum_{i=1}^{10}X_i\sim b(10;0,2),$$

isto é, $ X $ tem distribuição binomial com parâmetros $ n = 10 $ e $ p = 0,2 $. Como queremos saber a probabilidade do aluno acertar no máximo 3 questões, queremos encontrar o valor de $ \mathbb{P}(X\leq 3) $. Assim

$$\mathbb{P}(X\leq 3)=\mathbb{P}(X=0)+\mathbb{P}(X=1)+\mathbb{P}(X=2)+\mathbb{P}(X=3).$$

Portanto

$$P(X\leq 3)=\sum_{i=0}^{3} \left( \begin{array}{c} 10\ i \end{array} \right) (0,2)^i (1-0,2)^{10-i}\thickapprox 0,879.$$

Logo, a probabilidade de que o aluno acerte no máximo 3 questões é de aproximadamente 0,879.

Exemplo 5.1.3

Uma moeda não viciada é lançada várias vezes. Qual a probabilidade de que obtermos 5 caras antes de obtermos 3 coroas?

Vamos considerar como sucesso a obtenção de cara em cada lançamento da moeda. Desta forma queremos obter 5 sucessos antes de obtermos 3 fracassos. Mas isto só é possível se jogarmos a moeda pelo menos 5 vezes e no máximo 7 vezes, pois em menos de 5 jogadas não é possível obtermos 5 caras e em 8 jogadas ou mais, já temos que ter obtido as 5 caras, pois caso contrário vamos ter obtido 3 coroas, ou mais o que não é o intuito.

Considere as variáveis aleatórias $ X_i\sim b(i,0,5) $, definidas como sendo o número de sucessos obtidos em $ i $ lançamentos da moeda com $ i = 5,6,7 $. Sendo assim precisamos calcular $ \mathbb{P}(X_i=5) $ para cada $ i $.

Portanto a probabilidade de obtermos 5 caras antes de 3 coroas é:

$$\mathbb{P}(X_5 =5)+\mathbb{P}(X_6=5)+\mathbb{P}(X_7=5)= \sum_{i=5}^7\left(\begin{array}{c} i\ 5 \end{array} \right) (1/2)^5 (1-1/2)^{i-5}\thickapprox 0,23.$$

Exemplo 5.1.4

(Problema da caixa de fosforo de Banach) Suponha que um homem ande sempre com duas caixas de fósforos com $ n $ palitos cada uma. Suponha também que cada vez que ele necessite usar um fósforo ele pegue de forma aleatória em qualquer uma das caixas. Como ele é uma pessoa distraída quando ele pega o último palito da caixa de fósforos ele não se lembra de joga-la fora. Qual a probabilidade de que quando ele perceba que uma das caixas está vazia a outra contenha exatamente $ k $ fósforos?

Para facilitar a resolução do problema vamos numerar as caixas de fósforo. Vamos calcular inicialmente a probabilidade de que, quando o homem percebe que a caixa de fósforo número 1 está vazia, a caixa de fósforo número 2 contém exatamente $ k $ palitos. Consideremos como sucesso a retirada de um palito da caixa número 1.

Seja $ A $ o evento “Retirar um fósforo da caixa número 1, mas a caixa 1 está vazia e a caixa de número 2 contém exatamente $ k $ fósforos. O evento $ A $ ocorre se, e somente se, o $ n+1 $-ésimo sucesso, ocorre na retirada de número $ n+1+n-k $.

Em outras palavras para que o evento $ A $ ocorra é necessário que nas $ n+1 $ vezes que obtemos sucesso, ou seja, que retiramos fósforo da caixa 1, já tenhamos realizado $ n+1+n-k $ experimentos. Com isso em mente, concluímos que deve haver n sucessos nos 2n-k primeiros experimentos, e deve haver sucesso na vez seguinte.

Assim

Função Geradora de Momentos, Valor Esperado e Variância

Seja $ X $ uma variável aleatória com distribuição Binomial$ (n,p) $. Então a função geradora de momentos de $ X $, $ M_X(t) $ é dada por

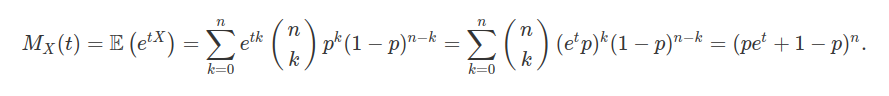
em que, na última igualdade, utilizamos a fórmula do binômio de Newton. Podemos encontrar a média e a variância de $ X $ através da função geradora de momentos. Assim

$$M^\prime_X(t)= \frac{d}{dt}(p e^t+ 1-p)^n=n(pe^t+1-p)^{n-1}pe^t$$

e, como $ \mathbb{E}(X)=M^\prime_X(0) $, segue que $ \mathbb{E}(X)=n(p+1-p)^{n-1}p=np $.

Para encontrarmos a variância basta derivarmos mais uma vez a função $ M_X(t) $.

Assim temos que:

$$M^{\prime\prime}_X(t)=\frac{d^2}{dt^2}(p e^t+ 1-p)^n=n(n-1)(pe^t+1-p)^{n-2}(pe^t)^2+npe^t (pe^t+1-p)^{n-1}.$$

E, portanto, obtemos que $ \mathbb{E}(X^2)=M^{\prime\prime}_X(0)=n(n-1)p^2+ pn $. Desta forma, $ \text{Var}(X) $ pode ser calculada por

$$\text{Var}(X)=\mathbb{E}(X^2)-\mathbb{E}^2(X)=[n(n-1)p^2+pn] -(np)^2=n^2p^2-np^2+np-n^2p^2=np(1-p).$$

Portanto o valor esperado representa o número médio de sucessos. Por definição, temos que

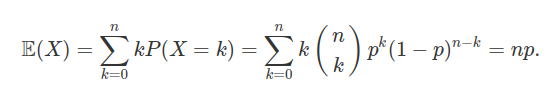
A variância $ \text{Var}(X) $ é dada por

$$\text{Var}(X)=\mathbb{E}\left(\left(X-\mathbb{E}(X)\right)^2\right)=\mathbb{E}(X^2)-\left(\mathbb{E}(X)\right)^2=np(1-p).$$

5.2 - Distribuição de Poisson

Em muitas situações nos deparamos com a situação em que o número de ensaios $ n $ é grande ($ n\rightarrow \infty $) e $ p $ é pequeno ($ p\rightarrow 0 $), no cálculo da função binomial, o que nos leva a algumas dificuldades, pois, como podemos analisar, para $ n $ muito grande e $ p $ pequeno, fica relativamente difícil calcularmos a probabilidade de $ k $ sucessos a partir do modelo binomial, isto é, utilizando a função de probabilidade

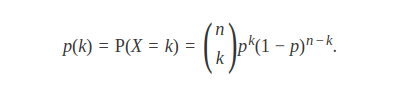
Observamos que podemos reescrever a expressão acima da seguinte forma

$$\mathbb{P}(X=k)=\frac{n!}{k!(n-k)!}p^k\frac{n^k}{n^k}\left(1-\frac{np}{n}\right)^{n-k}=\frac{n!}{k!(n-k)!}\frac{(np)^k}{n^k}\left(1-\frac{np}{n}\right)^{n-k}$$

e, tomando $ \lambda = np $, segue que

$$\mathbb{P}(X = k)=\frac{n(n-1)\cdots(n-k+1)}{k!}\frac{\lambda^k}{n^k}\left(1-\frac{\lambda}{n}\right)^{n-k}=\frac{\lambda^k}{k!}1\left(1-\frac{1}{n}\right)\dots\left(1-\frac{k-1}{n}\right)\left(1-\frac{\lambda}{n}\right)^{n-k}.$$

Se tomarmos o limite quando $ n\rightarrow \infty $, obtemos que

$$\lim_{n\rightarrow \infty}1\left(1-\frac{1}{n}\right)\dots\left(1-\frac{k-1}{n}\right)=1$$

e

$$\lim_{n\rightarrow \infty}\left(1-\frac{\lambda}{n}\right)^{n-k}=\lim_{n\rightarrow \infty}\left(1-\frac{\lambda}{n}\right)^{n}=e^{-\lambda}$$

para $ k = 0,1,\ldots $ e $ e\approx 2,718 $.

Assim temos que

$$\lim_{n\rightarrow \infty}\mathbb{P}(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}.$$

Tal expressão é devida a Poisson e é muito utilizada para calcular probabilidades de ocorrências de defeitos “raros” em sistemas e componentes.

Definição 5.2.1

Uma variável aleatória discreta $ X $ segue a distribuição de Poisson com parâmetro $ \lambda $, $ \lambda \ > 0 $, se sua função de probabilidade for dada por

$$\mathbb{P}(X=k)=\frac{e^{-\lambda}\lambda^k}{k!}.$$

Utilizamos a notação $ X \sim \ \text{Poisson}(\lambda) $ ou $ X\sim \ \text{Po}(\lambda) $. O parâmetro $ \lambda $ indica a taxa de ocorrência por unidade medida.

Exemplo 5.2.1

Considere um processo que têm uma taxa de $ 0,2 $ defeitos por unidade. Qual a probabilidade de uma unidade qualquer apresentar:

a) dois defeitos?

b) um defeito?

c) zero defeito?

Solução

Neste caso, temos que $ X \sim \ \text{Poisson}(\lambda) $ com $ \lambda=0,2 $. Então

a) $ \displaystyle\mathbb{P}(X=2)=\frac{e^{-0,2}(0,2)^2}{2!}=0,0164 $;

b. $ \displaystyle\mathbb{P}(X=1)=\frac{e^{-0,2}(0,2)^1}{1!}=0,1637 $;

c. $ \displaystyle\mathbb{P}(X=0)=\frac{e^{-0,2}(0,2)^0}{0!}=0,8187 $.

Exemplo 5.2.2

Suponha que uma aplicação de tinta em um automóvel é feita de forma mecânica, e pode produzir defeitos de fabricação, como bolhas ou áreas mal pintadas, de acordo com uma variável aleatória $ X $ que segue uma distribuição de Poisson de parâmetro $ \lambda=1 $. Suponha que sorteamos um carro ao acaso para que sua pintura seja inspecionada, qual a probabilidade de encontrarmos, pelo menos, $ 1 $ defeito? E qual a probabilidade de encontrarmos de $ 2 $ a $ 4 $ defeitos?

A probabilidade de encontrarmos pelo menos um defeito é dada por:

$$\mathbb{P}(X\geq 1)=1-\mathbb{P}(X< 1)=1-\frac{e^{-1}1^0}{0!}=1-e^{-1}\approx 0,63212.$$

Já a probabilidade de encontrarmos entre 2 e 4 defeitos é de

$$\mathbb{P}(2\leq X\leq 4)=\mathbb{P}(X=2)+\mathbb{P}(X=3)+\mathbb{P}(X=4)=\frac{e^{-1}1^2}{2!}+\frac{e^{-1}1^3}{3!}+\frac{e^{-1}1^4}{4!}\approx 0,26058.$$

Exemplo 5.2.3

Suponha que 10% das crianças de um determinado bairro do Rio de Janeiro prefiram sorvete de baunilha ao de chocolate. Qual a probabilidade de que, se entrevistarmos $ 10 $ crianças deste bairro, exatamente $ 2 $ duas prefiram soverte de baunilha?

Podemos resolver este problema de duas maneiras. A primeira é a partir da utilização da distribuição binomial com parâmetros $ n=10 $ e $ p=0,1 $. A segunda, através da distribuição de Poisson de parâmetro $ \lambda = np = 1 $ que, embora não seja tão exata quanto a binomial, é bem mais simples de ser calculada. Calculemos primeiramente pela distribuição binomial.

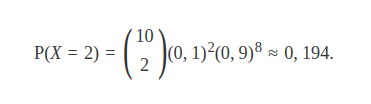
Já pelo método de Poisson temos

$$\mathbb{P}(X=2)=\frac{e^{-1}}{2!}\approx 0,184.$$

Embora pelo método de Poisson tenhamos um erro associado a aproximação da distribuição binomial (que é a distribuição exata), este erro, em muitos casos, não chega a ser significativo.

Exemplo 5.2.4

Suponhamos que em uma indústria farmacêutica 0,001% de um determinado medicamento sai da linha de produção somente com o excipiente, ou seja, sem nenhum princípio ativo. Qual a probabilidade de que em uma amostra de 4 mil medicamentos mais de 2 deles esteja somente com o excipiente.

Vamos calcular esta probabilidade usando a aproximação de poisson, pois além de ser uma aproximação muito boa neste caso é bem mais fácil de ser calculada.

Para usarmos a distribuição de Poisson primeiramente devemos encontrar o $ \lambda $, o qual é dado por $ \lambda=n\times p=4000\times 0,00001=0,04 $. Assim

$$\mathbb{P}(X\geq 2)=1-\mathbb{P}(X=0)-\mathbb{P}(X=1)=1-\displaystyle \frac{0,04^0e^{-0,04}}{0!}-\frac{0,04^1 e^{-0,04}}{1!}\approx 1-0,999221\approx 0,00078.$$

Assim a probabilidade de que existam mais de 2 medicamentos com apenas o excipiente é de 0,078%.

Função Geradora de Momentos, Valor Esperado e Variância

Seja $ X $ uma variável aleatória discreta com distribuição de Poisson, com parâmetro $ \lambda $, ou seja, $ X\sim \ \text{Poisson}(\lambda) $. Então sua função geradora de momentos é dada por:

$$M_{X}(t)=\mathbb{E}[e^{tX}]=\sum_{k=0}^{\infty}\frac{e^{tk}e^{\lambda}\lambda^k}{k!}=e^{-\lambda}\sum_{k=0}^{\infty}\frac{(\lambda e^t)^k}{k!}=e^{-\lambda}e^{\lambda e^t}=e^{\lambda[e^t-1]}.$$

O valor esperado de $ X $, que frequentemente é chamado de taxa de defeitos, é dado por:

$$\mathbb{E}(X)=\sum_{k=0}^\infty k\frac{e^{-\lambda}\lambda^k}{k!}=\sum_{k=1}^{\infty}\lambda \left[\frac{e^{-\lambda}\lambda^{k-1}}{(k-1)!}\right]=\lambda e^{-\lambda}\sum_{k=1}^{\infty}\left[\frac{\lambda^{k-1}}{(k-1)!}\right]=\lambda e^{-\lambda}\sum_{k=0}^{\infty}\left[\frac{\lambda^k}{k!}\right] = \lambda e^{-\lambda}e^{\lambda}=\lambda.$$

Outra forma de calcularmos o valor esperando é utilizando a função geradora de momentos, pois $ M^\prime(0)=\mathbb{E}(X) $. Desta forma temos que:

$$M^\prime(t)=\frac{d}{dt}\exp(\lambda(\exp(t)-1))=\lambda \exp(\lambda(e^t - 1)+t)$$

e então,

$$\mathbb{E}(X) = M^\prime(0)=\lambda \exp(1-1+0)=\lambda.$$

Da mesma forma como feito para a esperança vamos usar a função gerradora de momentos para calcular a a variância, pois temos que $ \mathbb{E}[X^2]=M^{\prime\prime}(0) $. Assim

$$M^{\prime\prime}(t)=\lambda(e^{\lambda(e^t - 1)+t}(\lambda e^t +1))$$

e então,

$$\mathbb{E}(X^2) = M^{\prime\prime}(0)=\lambda(\lambda+1)$$

de onde segue que

$$\text{Var}(X)=\mathbb{E}(X^2)-(\mathbb{E}(X))^2=\lambda(\lambda+1)-\lambda^2=\lambda.$$

5.3 - Distribuição geométrica

Consideremos uma sequência ilimitada de ensaios de Bernoulli, com probabilidade de sucesso p em cada ensaio. Designemos sucesso por $ S $ e falha por $ F $. Realizamos os ensaios até que ocorra o primeiro sucesso.

O espaço amostral para este experimento é o conjunto $ (S, FS, FFS, FFFS,\ldots) $.

Ou seja, um elemento típico desse espaço amostral é uma sequência de $ n $ em que nos $ n-1 $ primeiros ensaios temos $ F $ e na $ n $-ésima temos S.

A distribuição geométrica apresenta duas parametrizações importantes, que têm interpretações distintas. Uma das parametrizações da função geométrica conta o número de falhas até que ocorra o primeiro sucesso. Notemos que nessa parametrização podemos incluir o zero como sendo um possível resultado, pois podemos ter sucesso já no primeiro ensaio de Bernoulli.

A segunda parametrização da geométrica conta o número de ensaios de bernoulli necessário para se obter um sucesso. Assim nessa parametrização não é possível se ter o zero, portanto nessa parametrização da geométrica o domínio será os números naturais sem o zero.

Geométrica (conta o número de falhas até o sucesso.)

Definição 5.3.1

Seja $ X $ a variável aleatória que fornece o número de falhas até o primeiro sucesso. A variável $ X $ tem distribuição Geométrica com parâmetro $ p $, $ 0 \ < \ p \ < \ 1 $, se sua função de probabilidade é dada por

$$\mathbb{P}\left(X=j\right)=(1-p)^jp, \quad j=0,1,\ldots$$

Usaremos a notação $ X \sim \ \text{Geo}(p) $.

O evento $ [X=j] $ ocorre se, e somente se, ocorrem somente falhas nos $ j $ primeiros ensaios e sucesso no $ (j+1) $-ésimo ensaio.

A distribuição geométrica tem uma propriedade que serve para caracterizá-la no conjunto das distribuições discretas:

Propriedade 5.3.1

Se $ X $ é variável aleatória discreta com distribuição geométrica, então, para todo $ j,k = 1,2,\ldots $ temos que:

$$\mathbb{P}\left(X> t+s|X\geq s\right)=\mathbb{P}\left(X> t\right).$$

Este resultado reflete a falta de memória ou de desgaste da distribuição geométrica.

Demonstração

De fato, temos que

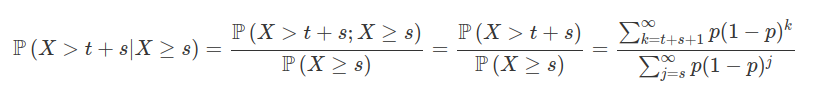
de onde segue que

$$\mathbb{P}\left(X> t+s|X\geq s\right)=\frac{1-p\sum_{k=0}^{t+s}(1-p)^k}{1-p\sum_{j=0}^{s-1}(1-p)^j}=\frac{(1-p)^{t+s+1}}{(1-p)^{s}}=(1-p)^{t+1}=1-p\sum_{k=0}^{t}(1-p)^k$$

e, portanto,

$$\mathbb{P}\left(X> t+s|X\geq s\right)=\sum_{k=t+1}^{\infty}p(1-p)^k=\mathbb{P}\left(X> t\right).$$

Portanto a distribuição geométrica apresenta a propriedade de perda de momória. Vale notar que ela é a única distribuição discreta com essa característica.

Propriedade 5.3.2

Seja $ h(k)=\displaystyle \frac{\mathbb{P}\left(X=k\right)}{\mathbb{P}\left(X\geq k\right)} $ mostre que se $ X\sim Geo(p) $ então h(k)=p

De fato,

$$h(k)=\frac{\mathbb{P}\left(X=k\right)}{\mathbb{P}\left(X\geq k\right)}=\frac{p(1-p)^k}{\sum_{j=k}^{\infty}p(1-p)^j}=\frac{p(1-p)^k}{1-\sum_{j=0}^{k-1}p(1-p)^j}=\frac{(1-p)^{k}p}{(1-p)^{k}}=p.$$

Notemos que h(k) é muito usado em análise de sobrevivência e representa a função risco.

Exemplo 5.3.1

Considere o experimento em que uma moeda viciada é lançada sucessivas vezes, até que ocorra a primeira cara. Seja $ X $ a variável aleatória que conta o número de coroas obtidos no experimento (ou seja, a quantidade de lançamentos anteriores a obtenção da primeira cara). Sabendo que a probabilidade de cara é de $ 0,4 $, qual é a probabilidade de $ \mathbb{P}(2\leq X< 4) $ e a probabilidade de $ \mathbb{P}(X> 1| X\leq 2) $.

Observamos que

$$\mathbb{P}(2\leq X< 4)=\mathbb{P}(X=2)+\mathbb{P}(X=3)=0,6^2\cdot 0,4+0,6^3\cdot 0,4=0,2304.$$

Vamos calcular agora $ \mathbb{P}(X> 1| X\leq 2) $.

$$\mathbb{P}(X> 1| X\leq 2)=\frac{\mathbb{P}(X> 1\cap X\leq 2)}{\mathbb{P}(X\leq2)}=\frac{\mathbb{P}(X=2)}{\mathbb{P}(X=0)+\mathbb{P}(X=1)+\mathbb{P}(X=2)}=\frac{0,144}{0,784}=0,18367.$$

Exemplo 5.3.2

Um pesquisador está realizando um experimentos químico independentes e sabe que a probabilidade de que cada experimento apresente uma reação positiva é $ 0,3 $. Qual é a probabilidade de que menos de 5 reações negativas ocorram antes da primeira positiva?

Para resolver este problema, considere $ X $ como sendo a variável aleatória que representa o número de reações negativas até a ocorrência da primeira positiva. Neste caso, temos que $ X\sim \ \text{Geo}(0,3) $ e então

$$\mathbb{P}(X \ < \ 5) = \sum_{i=0}^4\mathbb{P}(X=i)=0,3+0,7\cdot 0,3 + 0,7^2\cdot 0,3 + 0,7^3\cdot 0,3 + 0,7^4\cdot 0,3 = 0,83193.$$

Exemplo 5.3.3

Considerando o exemplo 5.3.1, qual a probabilidade de que $ X\geq 1 $.

$$\mathbb{P}(X\geq 1)=1-\mathbb{P}(X< 1)=1-\mathbb{P}(X=0)=1-0,4=0,6.$$

Função Geradora de Momentos, Valor Esperado e Variância

Seja $ X $ uma variável aleatória discreta com distribuição geométrica. Então a função geradora de momentos é dada por:

$$M_{X}(t)=\mathbb{E}\left(e^{tX}\right)=\sum_{k=0}^{\infty}e^{tk}(1-p)^{k}p=p\sum_{k=0}^{\infty}(e^{t})^{k}(1-p)^{k}=p\sum_{k=0}^{\infty}[e^{t}(1-p)]^{k} =\frac{p}{1-(1-p)e^t}.$$

Desta forma, o valor esperado de $ X $ é dado por

$$\mathbb{E}(X)=\sum_{j=0}^\infty j(1-p)^jp=p\sum_{j=0}^\infty j(1-p)^j=p(1-p)\sum_{j=0}^\infty j(1-p)^{j-1}=\frac{p(1-p)}{p^2}.$$

ou seja,

$$\mathbb{E}(X)=\frac{1-p}{p}.$$

Podemos calcular o valor esperado de $ X $ através da função geradora de momentos, sabendo que $ \mathbb{E}(X) = M^\prime(0) $. Para isto, temos que

$$M^\prime_X(t)=-\frac{(1-p)pe^t}{((p-1)e^t+1)^2}.$$

Assim o valor esperado é dado por:

$$\mathbb{E}(X)=M^\prime_X(0)=-\frac{(p-1)pe^0}{((p-1)e^0+1)^2}=-\frac{(p-1)p}{((p-1)+1)^2}=-\frac{(p-1)p}{p^2}=\frac{(1-p)}{p}.$$

Também podemos utilizar a função geradora de momentos para calcular a variância da variável $ X $, sabendo que $ \mathbb{E}(X^2) = M^{\prime\prime}(0) $. Para isto, temos que

$$M^{\prime\prime}_X(t)=\frac{(p-1)pe^t((p-1)e^t -1)}{((p-1)e^t+1)^3}$$

e, portanto

$$\mathbb{E}(X^2)=M^{\prime\prime}_X(0)=\frac{(p-1)p((p-1)-1)}{((p-1)+1)^3}=\frac{p(p-1)(p-2)}{p^3}=\frac{p^3-3p^2+2p}{p^3}$$

e a variância é dada por

$$\text{Var}(X)=\mathbb{E}(X^2)-\mathbb{E}^2(X)=\frac{p^3-3p^2+2p}{p^3}-\frac{(1-p)^2}{p^2}=\frac{1-p}{p^2}.$$

Geométrica (conta o número ensaios para se obter um sucesso.)

Definição 5.3.2

Seja $ X $ a variável aleatória que fornece o número de ensaios de Bernoulli realizados até a obtenção do primeiro sucesso. A variável $ X $ tem distribuição Geométrica com parâmetro $ p $, $ 0 \ < \ p \ < \ 1 $, se sua função de probabilidade é dada por

$$\mathbb{P}(X=j)=(1-p)^{j-1} p, \quad j=1,2,\ldots$$

Usaremos a notação X $ \sim $ Geo(p).

Observação 5.3.1

Observe que, nesta parametrização os valores possíveis assumidos pela variável aleatória $ X $ são $ \mathcal{R}_X = (1,2,\ldots) $ e que a probabilidade de $ X $ ser igual ao valor $ k $ é igual a probabilidade de $ X $ ser igual a $ k-1 $ na parametrização anterior.

Exemplo 5.3.4

Um dado honesto é lançado sucessivas vezes até que apareça pela primeira vez a face 1. Seja $ X $ a variável aleatória que conta o número de ensaios até que corra o primeiro $ 1 $. Qual a probabilidade de obtermos $ 1 $ no terceiro lançamento.

Como o dado é honesto, a probabilidade de, em um lançamento, obtermos qualquer face é igual a 1/6. Neste caso, a probabilidade de se obter a face $ 1 $ (sucesso) é $ 1/6 $ e a probabilidade de se obter qualquer outra face (fracasso) é $ 5/6 $. Podemos definir a variável aleatória

Neste caso, $ Y\sim \ \text{Bernoulli}(1/6) $ e, se definirmos $ X $ como sendo a variável que representa o número de lançamentos até a obtenção do primeiro sucesso (aparecimento da face 1), temos que $ X \sim \ \text{Geo}(1/6) $. Portanto, se estamos interessados no cálculo da probabilidade de obter $ 1 $ no terceiro lançamento, precisamos calcular $ \mathbb{P}(X = 3) $, ou seja,

$$\mathbb{P}(X=3)=(1-p)^2p=\left(1-\frac{1}{6}\right)^2\frac{1}{6}=\left(\frac{5}{6}\right)^2\frac{1}{6}=\frac{5^2}{6^3}\approx 0,115741.$$

Exemplo 5.3.5

Um pesquisador está produzindo um novo tipo de vacina para ser usada em seres humanos. Através de testes em animais ele chegou à conclusão de que esta vacina tem probabilidade de matar o usuário em 0,1% dos casos. Por causa das leis do país onde será aplicada, a vacina deve ter sua produção suspensa após ocorrer sua primeira morte.

Se admitirmos como sendo a ocorrência da morte do paciente como um sucesso então $ p=0,001 $. Assim, se $ X $ é o número de pessoas que tomarão a vacina até a ocorrência da primeira morte, temos que $ X $ tem uma distribuição geométrica com parâmetro $ p $, isto é, $ X\sim \ \text{Geo}(0,001) $, e a probabilidade de que a primeira morte ocorra na $ k $-ésima aplicação da vacina é

$$\mathbb{P}(X=k)=0,001(1-0,001)^k-1.$$

Analisando a função podemos verificar que conforme aumenta o número de pessoas que tomam a vacina maior é a chance de que uma pessoa morra e a produção seja interrompida.

Exemplo 5.3.6

Voltando ao Exemplo 5.3.4 vamos calcular $ \mathbb{P}\left(3 \leq X\leq 5\right) $.

$$\mathbb{P}\left(n\leq X \leq m\right)=\mathbb{P}\left(X\leq m\right)-\mathbb{P}\left(X \ < \ n\right)=\sum_{j=1}^{m}p(1-p)^{j-1}-\sum_{j=1}^{n-1}p(1-p)^{j-1}=\sum_{j=n}^{m}p(1-p)^{j-1}.$$

Assim

$$\mathbb{P}\left(3\leq X\leq 5\right)=\sum_{j=3}^{5}\frac{1}{6}(\frac{5}{6})^{j-1}=\frac{25}{216}+\frac{125}{1296}+\frac{625}{7776}\approx 0,29257.$$

Observe que as duas parametrizações estão intimamente ligadas. De fato, suponha que $ Y $ seja uma variável aleatória geométrica com a parametrização anterior e com parâmetro $ p $, isto é:

$$\mathbb{P}\left(Y=k\right)=p(1-p)^{k}$$

e suponha que $ X $ seja uma distribuição geométrica com a parametrização atual e com o mesmo parâmetro $ p $, ou seja:

$$\mathbb{P}\left(X=k\right)=p(1-p)^{k-1}.$$

Assim

$$\mathbb{P}\left(Y=k\right)=p(1-p)^{k}=p(1-p)^{(k+1)-1}=\mathbb{P}\left(X=k+1\right)$$

e, portanto,

$$\mathbb{P}\left(Y> m+n|Y\geq n\right)=\mathbb{P}\left(Y> m\right)=\mathbb{P}\left(X> m+1\right).$$

Por outro lado

$$\mathbb{P}\left(Y> m+n|Y\geq n\right)=\frac{\mathbb{P}\left(Y > m+n\right)}{\mathbb{P}\left(Y\geq n\right)}=\frac{\mathbb{P}\left(X> m+n+1\right)}{\mathbb{P}\left(X\geq n+1\right)}=\mathbb{P}\left(X> m+1\right).$$

tomando $ s = n+1 $, temos que:

$$\mathbb{P}\left(X> m+s|X\geq s\right)=\mathbb{P}\left(X> m+1\right).$$

Exemplo 5.3.7

Seja $ h(k)=\displaystyle \frac{\mathbb{P}\left(X=k\right)}{\mathbb{P}\left(X\geq k\right)} $. Mostre que se $ X\sim \ \text{Geo}(p) $ então $ h(k)=p $.

De fato,

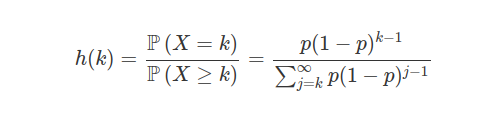
de onde segue que

$$h(k)=\frac{p(1-p)^{k-1}}{1-\sum_{j=1}^{k-1}p(1-p)^j}=\frac{(1-p)^{k-1}p}{(1-p)^{k-1}}=p.$$

Função Geradora de Momentos, Valor Esperado e Variância

Seja $ X $ uma variável aleatória discreta com distribuição geométrica de parâmetro $ p $. Assim a função geradora de momentos é dada por

$$M_{X}(t)=\mathbb{E}[e^{tX}]=pe^{t}\sum_{k=0}^{\infty}(e^{t})^{k-1}(1-p)^{k-1}=pe^{t}\sum_{k=0}^{\infty}[e^{t}(1-p)]^{k-1}=\frac{p}{(1-p)}\sum^\infty_{k=0}[e^t(1-p)]^k=\frac{p}{(1-p)(1-(1-p)e^t)}.$$

Agora vamos calcular o valor esperado.

$$\mathbb{E}(X)=\sum_{j=0}^\infty j(1-p)^{j-1}p=p\sum_{j=0}^\infty j(1-p)^{j-1}=\frac{p}{p^2}.$$

Assim, temos que

$$\mathbb{E}\left(X\right)=\frac{1}{p}.$$

Outra forma de calcularmos o valor esperado é usando a função geradora de momentos. Desta forma

$$M^\prime_X(t)=\frac{pe^t}{((1-p)e^t+1)^2}.$$

Como $ \mathbb{E}(X) = M^\prime_X(0 $, temos que

$$\mathbb{E}(X) = M^\prime_X(0)=\frac{p}{((p-1)+1)^2}=\frac{1}{p}.$$

Também podemos utilizar a função geradora de momentos para calcular a variância desta variável aleatória, já que $ \mathbb{E}(X^2) = M^{\prime\prime}_X(0) $. Então

$$M_X^{\prime\prime}(t)=-\frac{pe^t((p-1)e^t-1)}{((p-1)e^t+1)^3}$$

e, portanto,

$$\mathbb{E}(X^2) = M_X^{\prime\prime}(0)=-\frac{p(p-2)}{p^3}=-\frac{(p-2)}{p^2}=\frac{2-p}{p^2}.$$

Logo, a variância de $ X $ é dada por

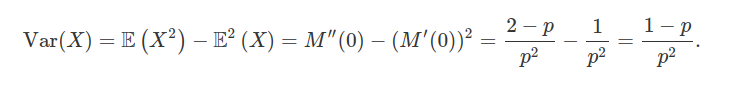
5.4 - Distribuição hipergeométrica

Considere uma população com $ N $ objetos nos quais $ M $ são classificados como do tipo $ A $ e $ N-M $ são classificados como do tipo $ B $. Por exemplo, em um lote de $ 100 $ ($ N $) peças temos $ 10 $ ($ M $) peças defeituosas e $ 90 $ ($ N-M $) peças conformes. Tomamos uma amostra ao acaso, sem reposição e não ordenada de $ n $ objetos. Seja $ X $ a variável aleatória que conta o número de objetos classificados como do tipo $ A $ na amostra. Então a distribuição de probabilidade de $ X $ é dada por:

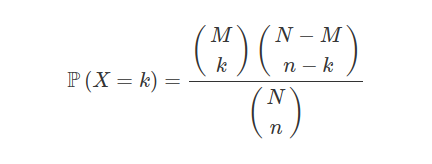
sendo $ k $ inteiro e $ \max(0,n-(N-M))\leq k \leq \min(M,n) $.

Definição 5.4.1

Diremos que uma variável aleatória $ X $ tem distribuição hipergeométrica de parâmetros $ M $, $ N $ e $ n $ se sua função de probabilidade for dada da maneira acima. Denotamos $ X \sim \ \text{Hgeo}(M,N,n) $

Exemplo 5.4.1

Seja $ X $ a variável aleatória que segue o modelo hipergeométrico com parâmetros $ N=10 $, $ M=5 $ e $ n=4 $. Determine a probabilidade $ \mathbb{P}(X\leq 1) $.

Para calcular a probabilidade procurada precisamos.

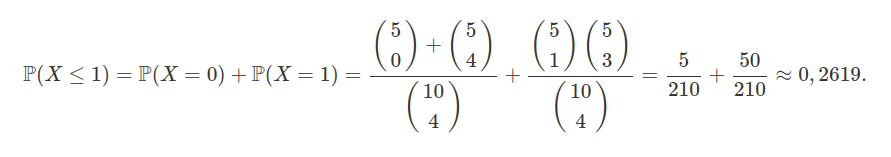
Exemplo 5.4.2

Uma empresa fabrica um tipo de tomada que são embalados em lote de $ 25 $ unidades. Para aceitar o lote enviado por essa fábrica, o controle de qualidade da empresa tomou o seguinte procedimento: sorteia-se um lote e desse lote selecionam-se $ 8 $ tomadas para teste, sem reposição. Se for constatado, no máximo, duas tomadas defeituosas, aceita-se o lote fornecido pela fábrica. Se o lote sorteada tiver $ 7 $ peças defeituosas, qual a probabilidade de se aceitar o lote?

Observamos aqui que o tamanho da população é o tamanho do lote, ou seja, $ N=25 $, das quais temos $ M = 7 $ defeituosas e sorteamos uma amostra de tamanho $ n=8 $. Então, seja $ X $ a variável aleatória que representa o número de peças defeituosas encontradas na amostra. Desta forma $ X\sim \ \text{Hgeo}(7, 25, 8) $ e então, a probabilidade de se aceitar o lote é igual a probabilidade de que $ X $ seja menor ou igual a $ 2 $, ou seja,

$$\mathbb{P}\left(\hbox{aceitar o lote}\right)=\mathbb{P}[X\leq 2]=\mathbb{P}(X=0)+\mathbb{P}(X=1)+\mathbb{P}(X=2)$$

ou seja,

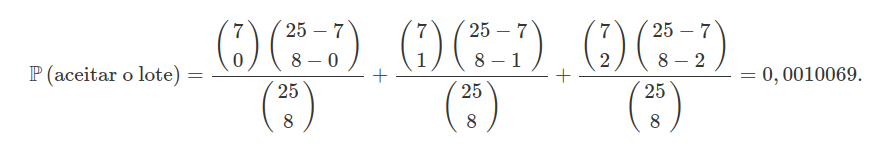
Exemplo 5.4.3

Suponha que $ 3 $ moedas comemorativas foram colocadas por engano em um cofrinho no qual já haviam algumas moedas comuns, o qual ficou contendo um total de $ 12 $ moedas. Suponha que, devido a dificuldade de tirar as moedas do cofrinho sem quebrá-lo, vamos retirar ao acaso um total de $ 4 $ moedas, qual a probabilidade de retirarmos no mínimo $ 1 $ moeda comemorativa?

Observemos que o modelo hipergeométrico se encaixa bem ao nosso problema com $ N=12 $, $ M=3 $ e $ n=4 $. Seja $ X $ a variável aleatória que conta o número de moedas comemorativas retiradas do cofrinho.

Então, estamos interessado no cálculo de $ \mathbb{P}(X\geq 1) $ que é dado por

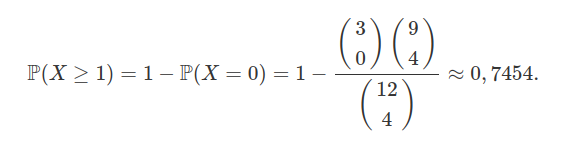
Exemplo 5.4.4

Uma urna contém $ 10 $ bolas, das quais $ 6 $ são brancas e $ 4 $ pretas. Suponha que décimos retirar $ 5 $ bolas da urna qual a probabilidade de que das $ 5 $ bolas retiradas $ 3 $ sejam brancas?

Para este problema basta usarmos a distribuição hipergeométrica, com $ M=6 $, $ k=3 $, $ N=10 $ e $ n=5 $.

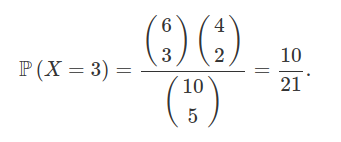
Exemplo 5.4.5

Vamos mostrar que quando a população é muito grande a distribuição hipergeométrica converge para uma binomial, ou seja, se $ X\sim \ \text{Hgeo}(M,N,n) $, então

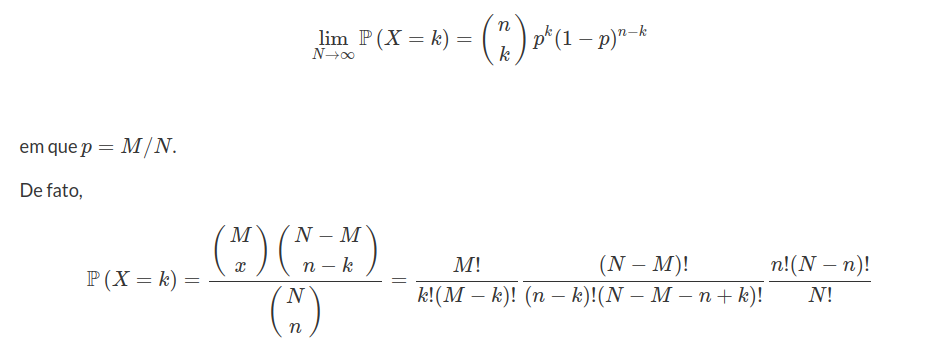
de onde segue que

$$\mathbb{P}\left(X=k\right)=\frac{n!}{k!(n-k)!}\frac{M!}{(M-k)!}\frac{(N-M)!}{(N-M-n+k)!}\frac{(N-n)!}{N!}$$

e daí

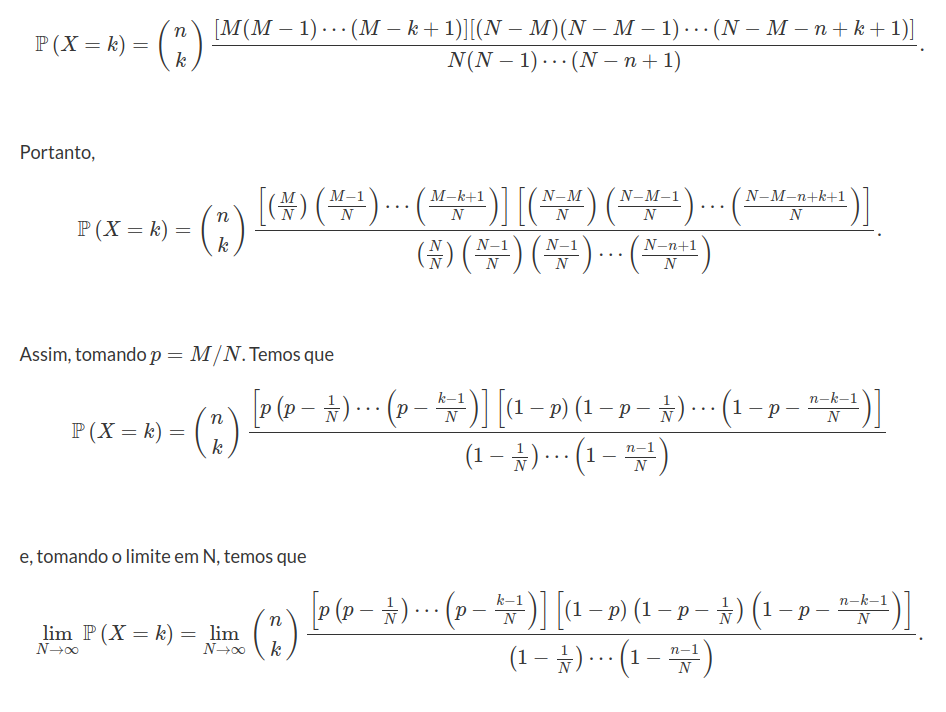
de onde podemos concluir que

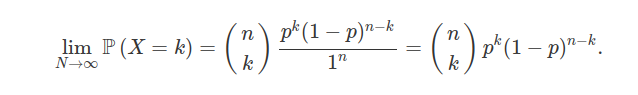
Função Geradora de Momentos, Valor Esperado e Variância

A função geradora de momentos da hipergeométrica existe, mas ela é escrita dependendo de uma função introduzida por Gauss conhecida como função hipergeométrica. Essa função é a solução da seguinte equação diferencial:

$$x(x-1)\frac{d^2}{dx^2}y + [(a+b+1)x-c]\frac{d}{dx}y+aby=0.$$

A função hipergeométrica é dada por:

$$F(a,b,c,x)=1+\frac{ab}{c}x+\frac{a(a+1)b(b+1)}{2c(c+1)}x^2+\frac{a(a+1)(a+2)b(b+1)(b+2)}{6c(c+1)(c+2)}x^3\cdots$$

que pode ser escrita como

$$F(a,b,c,x)=1+ \sum_{i=0}^{\infty}\frac{(a+i)!(b+i)!c!}{i!(a-1)!(b-1)!(c+i)!}x^{i+1}.$$

Assim a função geradora de momentos da distribuição hipergeométrica é dada por:

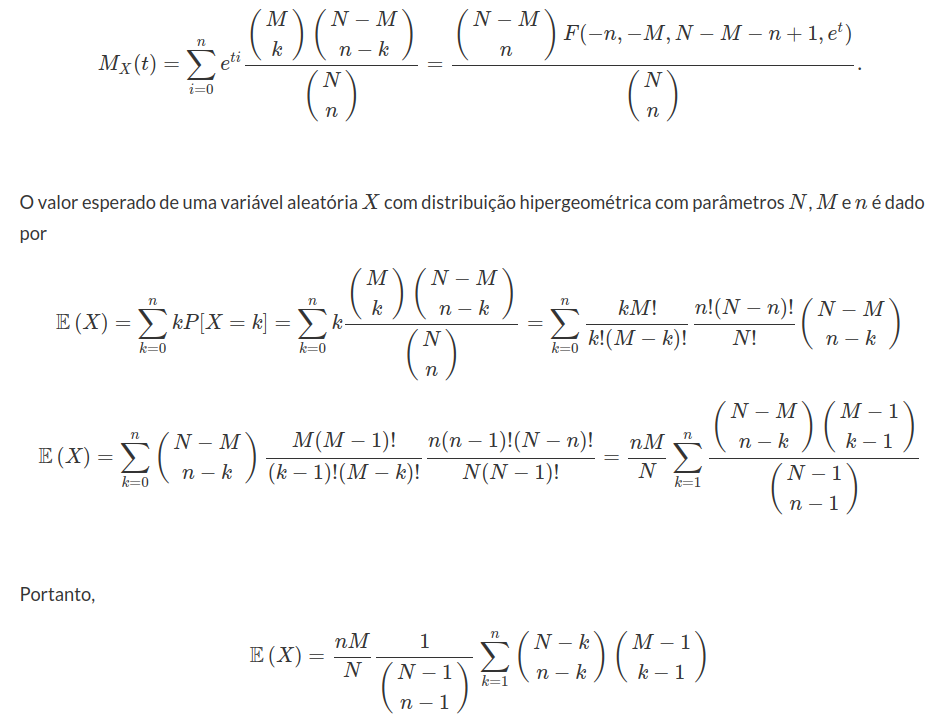
e, assim,

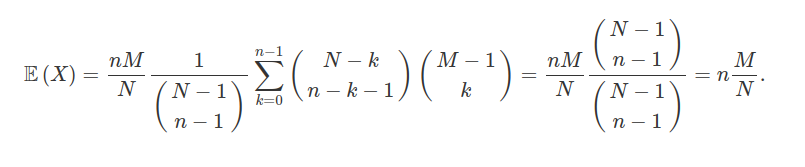
Vamos agora calcular a variância.

$$\mathbb{E}\left(X^2\right)=\sum_{k=0}^{n}k^2\mathbb{P}\left(X=k\right)=\sum_{k=0}^{n}[k(k-1)+k]\mathbb{P}\left(X=k\right)=\sum_{k=0}^{n}x(x-1)\mathbb{P}\left(X=k\right)+\sum_{k=0}^{n}x\mathbb{P}\left(X=k\right)=$$

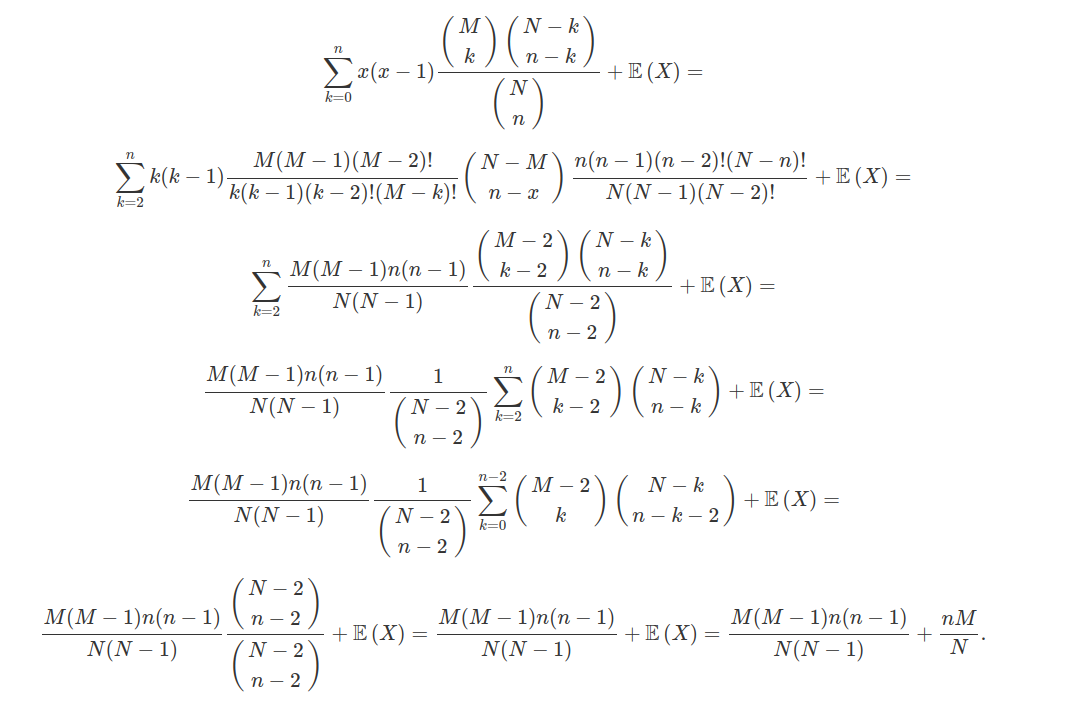
Então, a variância é dada por

$$\text{Var}\left(X\right)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=\frac{M(M-1)n(n-1)}{N(N-1)}+\frac{nM}{N}-\left(\frac{nM}{N}\right)^2=n\frac{M}{N}\frac{(N-M)}{N}\left(1-\frac{n-1}{N-1}\right)$$

5.5 - Distribuição multinomial

Considere um experimento dividido em $ n $ ensaios independentes, no qual cada ensaio resulta em um número finito $ k $ de valores possíveis com probabilidades $ p_1,p_2,\ldots,p_k $ (de modo que $ p_i \geq 0 $ para $ i = 1,\ldots,k $ e $ \displaystyleΣ\sum_{i=1}^kp_i=1 $).Tomando a variável aleatória $ X_i $ que representa o número de vezes que o índice $ i $ foi observado nos $ n $ ensaios, o vetor $ X = (X_1,\ldots,X_k) $ segue uma distribuição multinomial com parâmetros $ n $ e $ p $ onde $ p = (p_1,\ldots,p_k) $.

Com isso, sua distribuição de probabilidade é dada por

$$\mathbb{P}(X_1=n_1,\ldots,X_k=n_k)=\frac{n!}{n_1!\times\ldots\times n_k!}\times p_1^{n_1}\times p_2^{n_2}\times\ldots\times p_k^{n_k}.$$

Definição 5.5.1

Diremos que um vetor aleatório $ X = (X_1,\ldots,X_k) $ segue uma distribuição multinomial com parâmetros $ n $ e $ p = (p_1,\ldots,p_k) $ se sua função de probabilidade for dada por

$$\mathbb{P}(X_1=n_1,\ldots,X_k=n_k)=\frac{n!}{n_1!\times\ldots\times n_k!}\times p_1^{n_1}\times p_2^{n_2}\times\ldots\times p_k^{n_k}.$$

Denotamos $ X \sim \ \text{Multi}(n,p_1,\ldots,p_k) $.

Exemplo 5.5.1

Os seguintes eventos podem ocorrer com um pacote enviado pelo correio: chegar em perfeito estado, chegar danificado ou perder-se pelo caminho. As probabilidades desses eventos são, respectivamente $ 0,7 $, $ 0,2 $ e $ 0,1 $. Foram enviados recentemente $ 10 $ pacotes pelo correio. Qual a probabilidade de $ 6 $ chegarem corretamente ao destino, $ 2 $ serem perdidos e os outros $ 2 $ avariados?

Defina as seguintes variáveis aleatórias:

$ X_1 $: número de pacotes que chegaram corretamente e sem danos;

$ X_2 $: número de pacotes que chegaram avariados;

$ X_3 $: número de pacotes que se perderam pelo caminho.

Então $ X_1+X_2+X_3=n=10 $ e $ p_1+p_2+p_3=0,7+0,2+0,1=1 $. Logo,

$$\mathbb{P}(X_1=6,X_2=2,X_3=2)=\frac{10!}{6!2!2!}\times(0,7)^6\times(0,2)^2\times(0,1)^2=0,059.$$

Exemplo 5.5.2

Uma caixa contendo $ 12 $ bolas, das quais $ 5 $ são vermelhas, $ 4 $ brancas e $ 3 $ azuis. Suponha que seja retirada $ 5 $ bolas ao acaso e com reposição. Qual a probabilidade de que sejam retiradas $ 2 $ bolas vermelhas, $ 2 $ brancas e $ 1 $ azul.

Primeiramente temos que calcular a probabilidade de retirarmos uma bola branca:

$$\mathbb{P}(B)=\displaystyle \frac{4}{12}$$

a probabilidade de retirarmos uma bola vermelha:

$$\mathbb{P}(V)=\displaystyle \frac{5}{12}$$

e a probabilidade de retirarmos uma bola azul:

$$\mathbb{P}(A)=\displaystyle \frac{3}{12}$$

Assim usando a formula da multinomial temos que

$$\mathbb{P}(V=2,B=2,A=1)=\frac{5!}{2!2!1!}\left(\frac{5}{12}\right)^2\left(\frac{4}{12}\right)^2\left(\frac{3}{12}\right)=\frac{3000}{20736}\approx 0,144675.$$

Função Geradora de Momentos, Valor Esperado e Variância

Se $ X\sim \ \text{Multi}(n,p_1,\cdots, p_k) $ então sua função geradora de momentos é dada por:

$$M_X(t)=\mathbb{E}\left(e^{tX}\right)=\sum_{x}e^{tx}P[X=k]=\sum_{j_1}^{n}\cdots\sum_{j_k}^{n}e^{tj_1}\cdots e^{tj_k}\frac{n!}{j_1!\cdots j_k}p_1^{j_1}\cdots p_k^{j_k}=\left(\sum_{i=1}^{n}p_ie^{t_i}\right)^n.$$

O valor esperado do número de vezes em que o índice $ i $ é observado é dado por

$$\mathbb{E}(X_i)=np_i$$

e a variância

$$\text{Var}(X_i)=np_i(1-p_i).$$

5.6 - Binomial negativa

Seja $ X $ uma variável aleatória que conta o número de tentativas necessárias para se obter $ k $ sucessos, em $ n $ ensaios de Bernoulli com probabilidade $ p $ em cada ensaio. Notemos que neste caso o último ensaio será o $ k $-ésimo sucesso. Essa variável é conhecida como binomial negativa. Na verdade a binomial negativa é a soma de $ k $ variáveis geométricas com parâmetros iguais a $ p $. Neste caso, temos que a probabilidade de realizarmos $ x $ ensaios é dada por

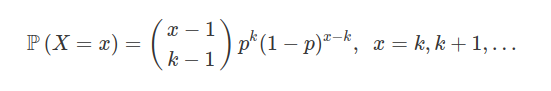
Definição 5.6.1

Seja $ X $ uma variável aleatória que fornece o número de ensaios até o $ k $-ésimo sucesso. Assim $ X $ tem uma distribuição binomial negativa com parâmetro $ p\in (0,1) $, se sua função de probabilidade é dada por:

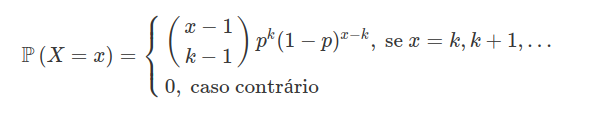
Usualmente utilizamos a notação $ X\sim BN(p,k) $.

Exemplo 5.6.1

Suponha que, para se ganhar um jogo de dados seja necessário obter $ 3 $ vezes a face voltada para cima do dado com o número de $ 1 $. Sendo que o número de lançamentos devem ser $ 6 $ e devemos obter a face $ 1 $ voltada para cima pela terceira vez no sexto lançamento. Supondo que o dado seja honesto, qual será a probabilidade de vencermos o jogo.

De fato, como o dado é honesto temos que a probabilidade de sair o face $ 1 $ é $ 1/6 $, portanto usando a formula da binomial negativa temos que:

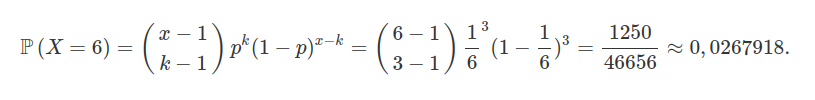
Exemplo 5.6.2

Suponha que um vendedor de automóveis tem, além de seu salário, uma bonificação de $ 200 $ reais por cada automóvel que ele venda. Suponha também que ele necessite vender, no mínimo, $ 5 $ automóveis por mês para que ele não seja despedido. Qual a probabilidade do vendedor ser despedido no mês de fevereiro, dado que ele trabalha todos os dias, inclusive finais de semana e feriados. Suponha que ele consiga vender no máximo 1 automóvel por dia com probabilidade de 0,2.

Para que ele seja despedido no mês de fevereiro ele precisa vender, no máximo, 4 automóveis durante todo o mês. Desta forma, considere $ X_i $ a variável aleatória que representa a quantidade de dias necessários para vender $ i $ carros. Neste caso, temos que $ X_i\sim \ \text{BN}(0,2;i) $ e então

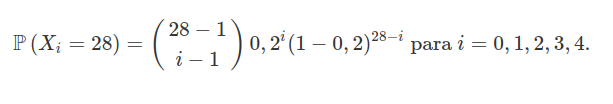
Portanto,

$$\mathbb{P}\left(X_0=28\right)=(0,8)^{28}=0,001934.$$

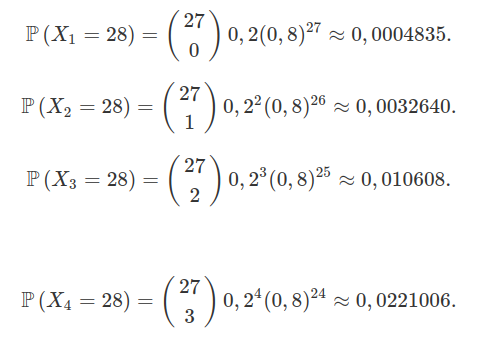
Portanto, a probabilidade dele ser mandado embora no mês de fevereiro é dada por

$$\mathbb{P}\left(\text{Ser demitido}\right)=\sum_{i=0}^{4}\mathbb{P}\left(X_i=28\right)\approx 0,0364561.$$

Exemplo 5.6.3

Suponha que em uma fábrica produz resistência para chuveiros, com uma taxa de defeitos de $ 2(porcentagem)% $. Qual a probabilidade de que em uma inspeção de $ 10 $ resistências se tenha $ 3 $ resistências defeituosas sendo que a terceira defeituosa seja exatamente a décima inspecionada.

Seja $ X $ o número de resistências inspecionadas até que encontremos a terceira defeituosa. Então temos que $ X \sim \ \text{BN}(0,02;3) $ e

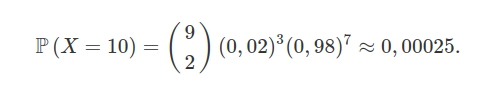
Função Geradora de Momentos, Valor Esperado e Variância

Seja $ X $ um variável aleatória discreta Binomial negativa com parâmetros $ p $ e $ k $. Então a função geradora de momentos de $ X $ é dada por

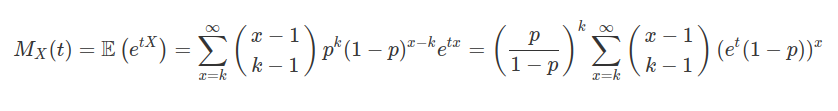
de onde segue que

$$M_X(t) = \left(\frac{p}{1-p}\right)^{k}(e^t(1-p))^k\sum_{x=0}^{\infty}\frac{(k+x)!}{x!k!}((1-p)e^t)^{x}=\frac{(pe^t)^k}{[1-(1-p)e^t]^k}=\frac{p^k}{[e^{-t}+p-1]^k}.$$

Portanto a função geradora de momentos da Binomial negativa é dada por:

$$M_X(t) = \frac{p^k}{[e^{-t}+p-1]^k}$$

Utilizando a função geradora de momentos vamos calcular o valor esperado, temos que

$$M^\prime_X(t)=\frac{kp^k}{e^{t}(p+e^{-t}-1)^{k+1}}$$

de onde concluímos que

$$\mathbb{E}(X) = M^\prime_X(0)=\frac{kp^{k}}{(p+e^{0}-1)^{k+1}e^{0}}=\frac{kp^k}{(p)^{k+1}}=\frac{k}{p}.$$

Vamos calcular agora $ \mathbb{E}\left(X^2\right) $ utilizando a função geradora de momentos.

$$M'';_X(t)=\frac{kp^k (k-(p-1)e^t)(p+e^{-t}-1)^{-k}}{((p-1)e^{t}+1)^2}.$$

E então,

$$\mathbb{E}\left(X^2\right)=M'';_X(0)=\frac{k(k-p+1)}{p^2}.$$

Agora estamos em posição de calcular o valor da variância de $ X $ que é dada por

$$\text{Var}(X)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=\frac{k(k-p+1)}{p^2}-\frac{k^2}{p^2}=\frac{k(1-p)}{p^2}.$$