8.6 Modelos Probabilísticos Contínuos

A seguir apresentamos os principais modelos probabilísticos contínuos, suas propriedades e aplicações.

Essas distribuições contínuas podem ser encontradas com mais detalhes nos livro do Barry R. James e Murray R. Spiegel, A. N. Shiryaev, Philip E. Protter, Howard M. Taylor & Samuel Karlin e Sheldon Ross.

6.1 - Distribuição uniforme

A distribuição uniforme é a mais simples distribuição contínua, entretanto uma das mais importantes e utilizadas dentro da teoria de probabilidade. A distribuição uniforme tem uma importante característica a qual a probabilidade de acontecer um fenômeno de mesmo comprimento é a mesma.

Definição 6.1.1

Uma variável aleatória $ X $ tem distribuição Uniforme no intervalo $ [a,b] $ se sua função densidade de probabilidade for dada por:

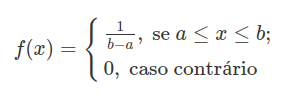
O gráfico abaixo ilustra a função densidade da distribuição uniforme com parâmetros a=0 e b=1.

Exemplo 6.1.1

A ocorrência de panes em qualquer ponto de uma rede telefônica de $ 7 $ km foi modelada por uma distribuição Uniforme no intervalo $ [0, 7] $. Qual é a probabilidade de que uma pane venha a ocorrer nos primeiros $ 800 $ metros? E qual a probabilidade de que ocorra nos $ 3 $ km centrais da rede?

A função densidade da distribuição Uniforme é dada por $ f(x)=\frac{1}{7} $ se $ 0\leq x\leq 7 $ e zero, caso contrário. Assim, a probabilidade de ocorrer pane nos primeiros 800 metros é

$$\mathbb{P}\left(X\leq 0,8\right)=\int_0^{0,8} f(x)dx=\frac{0,8-0}{7}=0,1142.$$

e a probabilidade de ocorrer pane nos 3 km centrais da rede é

$$\mathbb{P}\left(2\leq X\leq 5\right)=\int_2^5f(x)dx=\mathbb{P}\left(X\leq 5\right)-\mathbb{P}\left(X\leq 2\right)=5/7-2/7\approx 0,4285.$$

Exemplo 6.1.2

Suponha que $ Y ~\sim ~U[0,5] $. Qual a probabilidade que a equação $ 4x^2+4Yx+4=0 $, tenha ambas as raízes reais?

Primeiramente observemos que para que uma equação de segundo grau tenha raízes reais é necessário que o discriminante da equação de segundo grau seja maior ou igual a zero, ou seja, que a fórmula abaixo seja maior ou igual a zero.

$$\Delta = 16Y^2-64\geq 0 \Rightarrow Y^2 \geq 4.$$

Assim queremos encontrar $ \mathbb{P}(Y^2\geq 4) $. Então vamos encontrar a função densidade de probabilidade para $ Y^2 $, usando o teorema 2.8.3, temos que

$$F(t)=\mathbb{P}(Y^2\leq t)=\mathbb{P}(-\sqrt{t}\leq Y \leq \sqrt{t})=\mathbb{P}(0\leq Y \sqrt{t})=\int_{0}^{\sqrt{t}}f_Y(x)dx=\int_{0}^{\sqrt{t}}\frac{1}{5}dx=\frac{\sqrt{t}}{5}.$$

Portanto a função densidade de probabilidade de $ Y^2 $ é dada por

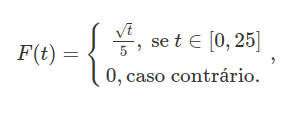
Com isso em mãos agora basta encontramos $ \mathbb{P}(Y^2 \geq 4) $, que é dada por

$$\mathbb{P}(Y^2\geq 4)=1-\mathbb{P}(Y^2< 4)=1-F(2)=1-\frac{\sqrt{4}}{5}=\frac{3}{5}.$$

Assim a probabilidade de que ambas as raízes sejam reais é de $ 3/5 $.

Exemplo 6.1.3

Suponha que um casal marque de se encontrar em uma pizzaria as 20:30h, e que o tempo de chegada seja uniformemente distribuído para ambos, mas que a distribuição do homem seja uniforme entre 20:15 e 20:45 e da mulher entre 20h e 21h. Assim sendo seja $ X $ a distribuição de probabilidade do tempo de chegada do homem. Então $ X \sim \ U(-15,15) $ e $ Y $ a distribuição de probabilidade do tempo de chegada da mulher, ou seja, $ Y \sim \ U(-30,30) $. Qual a probabilidade de que nenhum dos dois espere o outro por mais de $ 5 $ minutos?

Para que nenhum dos dois espere por mais de $ 5 $ minutos é necessário que $ |X-Y|\leq 5 $, sendo assim temos que

$$\mathbb{P}(|X-Y|\leq 5)=\mathbb{P}(-5\leq X-Y \leq 5)=\mathbb{P}(Y-5\leq X \leq Y+5).$$

Então

$$\mathbb{P}(|X-Y|\leq 5)=\int_{-15}^{15}\int_{y-5}^{y+5}f_Y(t)f_X(s)dsdt =\int_{-15}^{15}\int_{y-5}^{y+5} \frac{1}{1800}dsdt=\int_{-15}^{15}\frac{1}{180}dt=\frac{1}{6}.$$

Portanto a probabilidade de que nenhum dos dois espere por mais que $ 5 $ minutos é de $ 1/6 $.

Exemplo 6.1.4

Sejam $ X $ e $ Y $ variáveis aleatórias independentes com distribuição comum dada por

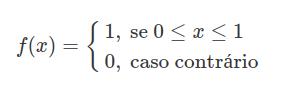
Encontre a função de distribuição acumulada de $ Z=X+Y $ ?

$$F(z)=\mathbb{P}(X+Y\leq z)=\int \int_{B_z}f(x,y)dx dy.$$

Para $ 0\leq z \leq 1 $

$$F(z)= \int_{0}^{z}\int_{0}^{z-x}1 dy dx=\frac{z^2}{2}.$$

Para $ 0 < z \leq 2 $,

$$F(z)=\displaystyle \int_{0}^{z-1}\int_{0}^{1}1 dydx+\int_{z-1}{1}\int_{0}^{z-x}1dydx=z-1 + \frac{2z-z^2}{2}=\frac{4z-z^2-2}{2}.$$

Portanto a função de distribuição acumulada de $ Z $ é dada por

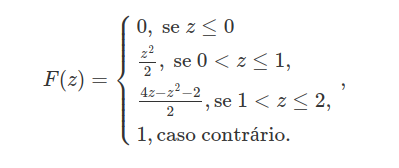
Exemplo 6.1.5

Sejam $ X $ e $ Y $ variáveis aleatórias com distribuição uniforme em $ [0,1] $ e independentes. Qual a densidade conjunta de $ Z=X-Y $?

$$F(z)=\mathbb{P}(X-Y\leq z)=\int \int_{B_z}f(x,y)dx dy.$$

Para $ -1\leq z \leq 0 $

$$F(z)\displaystyle \int_{-z}^{1}\int_{0}^{x-z}1 dx dy=\frac{1-3z^2-2z}{2}$$

Para $ 0 < z \leq 1 $

$$F(z)=1-\displaystyle \int_{0}^{1-z}\int_{x-z}^{1}1 dydx=1-\frac{(1-z^2)^2}{2}$$

Portanto a função de distribuição acumulada de $ Z $ é dada por

Função Geradora de Momentos, Valor Esperado e Variância

Seja $ X $ uma variável contínua com distribuição uniforme então sua função geradora de momentos é dada por:

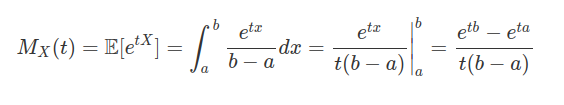
O valor esperado de uma variável aleatória $ X $ com distribuição uniforme é dado por

$$\mathbb{E}(X)=\int_a^b x\frac{1}{b-a}dx=\frac{a+b}{2}$$

Outra forma de calcularmos é utilizando a função geradora de momentos.

$$M^\prime_X(t)=\frac{e^{at}(at-1)+e^{bt}(1-bt)}{t^2(a-b)}$$

de onde segue que

$$\mathbb{E}(X) = M^\prime_X(0)=\lim_{t\rightarrow 0}\frac{e^{at}(at-1)+e^{bt}(1-bt)}{t^2(a-b)}.$$

Aplicando a regra de L’Hospital (uma vez que, no limite, tanto o numerador quanto o numerador vão para zero, temos que

$$M^\prime_X(0)=\lim_{t\rightarrow 0}\frac{t(e^{at}a^2-e^{bt}b^2)}{2t(a-b)}=\frac{(a-b)(a+b)}{2(a-b)}=\frac{a+b}{2}$$

e, portanto,

$$\mathbb{E}(X) = \frac{a+b}{2}.$$

Calculemos agora $ E[X^2] $ a partir da função geradora de momentos.

$$M^{\prime\prime}_X(t)=\frac{e^{at}(a^2t^2-2at+2)-e^{bt}(b^2 t^2-2bt+2)}{t^3(a-b)}.$$

E então,

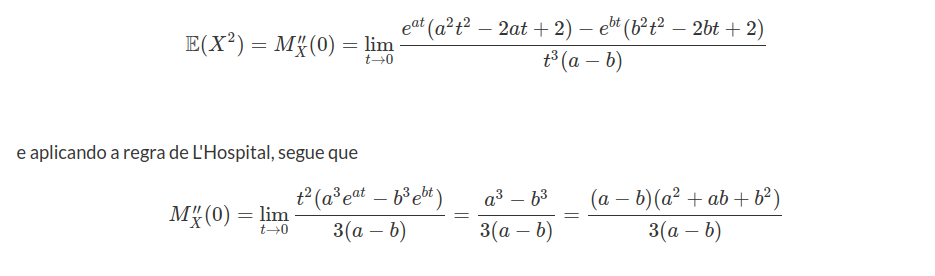
Desta forma, temos que a variância $ \text{Var}(X) $ é dada por

$$\text{Var}\left(X\right)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=M^{\prime\prime}_X(0)-(M^\prime_X(0))^2=\frac{(a^2+ab+b^2)}{3}-\left(\frac{(a+b)}{2}\right)^2=\frac{b^2-2ab+a^2}{12}.$$

Assim

$$\text{Var}(X)=\mathbb{E}(X^2)-\mathbb{E}^2(X)=\frac{(b-a)^2}{12}.$$

6.2 - Distribuição Normal

A distribuição normal conhecida também como distribuição gaussiana é sem dúvida a mais importante distribuição contínua. Sua importância se deve a vários fatores, entre eles podemos citar o teorema central do limite, o qual é um resultado fundamental em aplicações práticas e teóricas, pois ele garante que mesmo que os dados não sejam distribuídos segundo uma normal a média dos dados converge para uma distribuição normal conforme o número de dados aumenta. Além disso diversos estudos práticos tem como resultado uma distribuição normal. Podemos citar como exemplo a altura de uma determinada população em geral segue uma distribuição normal. Entre outras características físicas e sociais tem um comportamento gaussiano, ou seja, segue uma distribuição normal.

Definição 6.2.1

Uma variável aleatória contínua $X$ tem distribuição Normal se sua função densidade de probabilidade for dada por:

$$f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2\right], \quad x\in(-\infty,\infty).$$

Usamos a notação $X\sim N(\mu,\sigma^2).$

A variação natural de muitos processos industriais é realmente aleatória. Embora as distribuições de muitos processos possam assumir uma variedade de formas, muitas variáveis observadas possuem uma distribuição de frequências que é, aproximadamente, uma distribuição de probabilidade Normal.

Probabilidade é a chance real de ocorrer um determinado evento, isto é, a chance de ocorrer uma medida em um determinado intervalo. Por exemplo, a frequência relativa deste intervalo, observada à partir de uma amostra de medidas, é a aproximação da probabilidade. E a distribuição de frequências é a aproximação da distribuição de probabilidades.

A distribuição é normal quando tem a forma de “sino”:

Para achar a área sob a curva normal devemos conhecer dois valores numéricos, a média $\mu$ e o desvio padrão $\sigma$. A Figura a seguir mostra algumas áreas importantes:

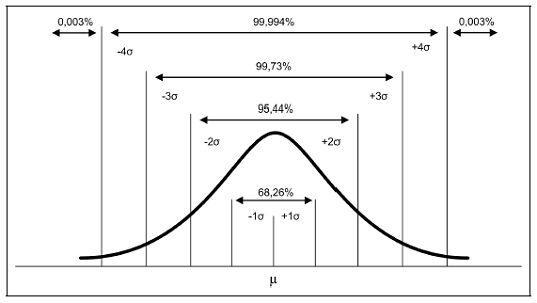
Quando $\mu$ e $\sigma$ são desconhecidos (caso mais comum), estes valores serão estimados por $\overline{X}$ e $s$, respectivamente, a partir da amostra, em que $\overline{X}=\displaystyle\frac{1}{n}\sum_{i=1}^{n}x_i$ e $s=\sqrt{\displaystyle\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\overline{X})^2}$

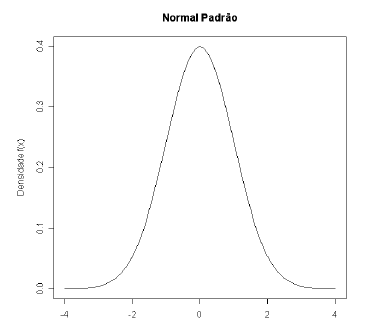
Para cada valor de $\mu$ e/ou $\sigma$ temos uma curva de distribuição de probabilidade. Porém, para se calcular áreas específicas, faz-se uso de uma distribuição particular: a “distribuição normal padronizada”, também chamada de Standartizada ou reduzida, o qual é a distribuição normal com $\mu=0$ e $\sigma=1$. Para obter tal distribuição, isto é, quando se tem uma variável $X$ com distribuição normal com média $\mu$ diferente de $0$ (zero) e/ou desvio padrão $\sigma$ diferente de $1$ (um), devemos reduzi-la a uma variável $Z$, efetuando o seguinte cálculo

$$Z=\frac{x-\mu}{\sigma}.$$

Assim, a distribuição passa a ter média $\mu=0$ e desvio padrão $\sigma= 1$. Pelo fato da distribuição ser simétrica em relação à média $\mu= 0$, a área à direita é igual a área à esquerda de $\mu$. Por ser uma distribuição muito usada, existem tabelas a qual encontramos a resolução de suas integrais. Assim, a tabela fornece áreas acima de valores não negativos que vão desde $0,00$ até $4,09$. Veja o gráfico da curva Normal padronizada na Figura abaixo.

Exemplo 6.2.1

Calcular a área sob a curva para $Z$ maior que $2,75$.

A área sob a curva normal para $Z$ maior do que $2,75$ é dada por

$$\mathbb{P}(Z\geq 2,75)= \int_{2,75}^{\infty}\frac{1}{\sqrt{2\pi}}\exp\left[-\frac{x^2}{2}\right]=1-0,9970=0,003;$$

ou seja, a probabilidade de $Z$ ser maior do que $2,75$ é $0,3(porcentagem)%$.

Exemplo 6.2.2

Determine a área sob a curva de uma normal padronizada para $z$ entre $-0,204$ e $1,93$.

Para este cálculo, precisamos determinar:

$$\mathbb{P}(-0,20 \leq Z\leq 1,93)=\mathbb{P}(Z\leq 1,93)-\mathbb{P}(Z\leq -0,2)=0,9732-0,4207=0,5525.$$

Assim, a área que procuramos é $0,5525$.

Exemplo 6.2.3

Suponha que a espessura média de arruelas produzidas em uma fábrica tenha distribuição normal com média $11,15$mm e desvio padrão $2,238$mm. Qual a porcentagem de arruelas que tem espessura entre $8,70$mm e $14,70$mm?

Para encontrar a porcentagem de arruelas com a espessura desejada devemos encontrar a área abaixo da curva normal, compreendida entre os pontos $8,70$ e $14,70$mm.

Para isso, temos que encontrar dois pontos da distribuição normal padronizada.

O primeiro ponto é

$$Z_1 = \frac{8,70 - 11,15 }{2,238} = -1,09.$$

A área para valores maiores do que $-1,09$ é $0,8621$, ou seja, $86,21(porcentagem)%$. Portanto, a área para valores menores do que $-1,09$ é de $0,1379$.

O segundo ponto é:

$$Z_2 = \frac{14,70 - 11,15 }{2,238} = 1,58.$$

A área para valores maiores do que $1,58$ é $0,0571$, ou seja, $5,71(porcentagem)%$. Logo, o que procuramos é a área entre $Z_1$ e $Z_2$, que é dada por

$$1 - (0,1379 + 0,0571) = 1 - 0,195 = 0,8050.$$

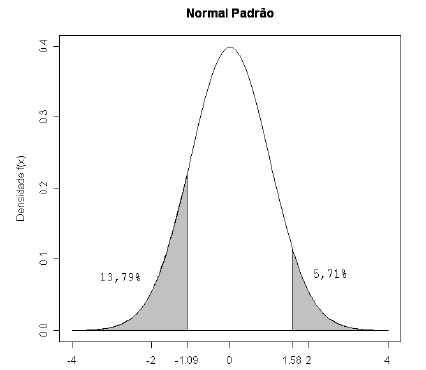
Logo, a porcentagem de arruelas com espessura entre $8,70$ e $14,70$ (limites de tolerância da especificação) é de $80,50(porcentagem)%$.

Exemplo 6.2.4

Suponha que o peso médio de $800$ porcos de uma certa fazenda é de $64$kg, e o desvio padrão é de $15$kg. Supondo que este peso seja distribuído de forma normal, quantos porcos pesarão entre $42$kg e $73$kg.

Para resolvermos este problema primeiramente devemos padroniza-lo, ou seja,

$$Z=\frac{x-64}{15} \sim N(0,1).$$

Então o valor padronizado de $42$kg é de $\frac{42-64}{15}\approx -1,47$ e de $73$kg é de $0,6$.

Assim a probabilidade é de

$$\mathbb{P}(-1,47 \leq Z\leq 0,6)=\mathbb{P}(Z\leq 0,6)-\mathbb{P}(Z\leq -1,47)=0,7257-0,0708=0,6549.$$

Portanto, o número aproximado que se espera de porcos entre $42$kg e $73$kg é $800\cdot 0,6549\approx 524$.

Exemplo 6.2.5

Suponha que $X$ siga uma distribuição normal com média $0$ e variância $1$, ou seja, $X~ \sim ~N(0,1)$. Então $Y=\sigma X+\mu~\sim ~N(\mu,\sigma^2)$.

De fato,

$$F_Y(y)=\mathbb{P}(Y\leq y)=\mathbb{P}(\sigma X + \mu \leq y)=\mathbb{P}\left(X\leq \frac{y-\mu}{\sigma}\right)=\int_{-\infty}^{y}\frac{1}{\sqrt{2\pi\sigma^2}}exp(\frac{-(t-\mu)^2}{2\sigma^2})dt.$$

E portanto, concluímos que $Y~\sim ~N(\mu,\sigma)$.

Exemplo 6.2.6

Suponha que $X$ seja uma variável aleatória tal que $X~\sim ~N(\mu;\sigma^2)$. Seja $Y=aX+b$, mostremos que $Y$ também tem distribuição normal, sabendo que a e b são constantes reais.

De fato,

$$F_Y(y)=\mathbb{P}(Y\leq y)=\mathbb{P}(aX+b\leq y)=\mathbb{P}\left(X\leq\displaystyle \frac{y-b}{a}\right)=\int_{-\infty}^{\frac{y-b}{a}}f_{X}(t)dt$$

Fazendo uma mudança de variável; s=at+b temos que $\frac{dt}{ds}=\frac{1}{a}$ e então

$$F_Y(y)=\int_{-\infty}^{y}\frac{1}{|a|}f_{X}\left(\frac{s-b}{a}\right)ds=\int_{-\infty}^{y}\frac{1}{|a|}\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{1}{2}\left(\frac{\frac{s-b}{a}-\mu}{\sigma}\right)^2\right]ds$$

de onde concluímos que

$$F_Y(y)=\int_{-\infty}^{y}\frac{1}{\sqrt{a^2}}\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[-\frac{1}{2}\left(\frac{s-(a\mu+b)}{a\sigma}\right)^2\right]=\int_{-\infty}^{y}\frac{1}{\sqrt{2\pi a^2\sigma^2}}\exp\left[-\frac{1}{2}\left(\frac{s-(a\mu+b)}{a\sigma}\right)^2\right]$$

e, portanto $Y~\sim ~N[a\mu+b;(a\sigma)^2].$

6.2.1 - Propriedades da distribuição normal

Vamos calcular a função geradora de momentos para uma variável aleatória com distribuição normal. Inicialmente, trataremos do caso em que a variável $X$ possui uma distribuição padronizada para tratar do caso geral posteriormente. Portanto, considere inicialmente que $X\sim N(0,1)$. Então sua função geradora de momentos é dada por

$$M_{X}(t)=\mathbb{E}\left(e^{tX}\right)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{tx}e^{-x^2/2}dx=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{(x^2-2tx)/2}=\frac{e^{t^2/2}}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{-(x-t)^2/2}dx$$

de onde concluímos que

$$M_X(t) = e^{t^2/2}.$$

Agora vamos calcular a função geradora de momentos para uma variável aleatória Z, tal que $Z\sim N(\mu,\sigma)$. Lembremo-nos de que $Z=\sigma X +\mu$ com $X\sim N(0,1)$. Assim

$$M_Z(t)=\mathbb{E}\left(e^{tZ}\right)=\mathbb{E}\left(e^{t(\sigma X+ \mu)}\right)=e^{t\mu}\mathbb{E}\left(e^{t\sigma X}\right)=e^{t\mu}e^{\frac{(t\sigma)^2}{2}}=\exp\left(\frac{\sigma^2 t^2}{2}+ \mu t\right).$$

Se $X$ tem distribuição Normal, podemos calcular o valor esperado de $X$ a partir da função geradora de momentos.

$$M^\prime_X(t)=\frac{d}{dt}\exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)=(\mu+t\sigma^2)\exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)$$

e assim

$$\mathbb{E}\left(X\right)=M^\prime_X(0)=(\mu+0\sigma^2)e^{\frac{\sigma^20}{2}+\mu 0}=\mu$$

Agora iremos calcular a variância de $X$ utilizando a função geradora de momentos.

$$M^{\prime\prime}_X(t)=\frac{d^2}{dt^2}\exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)=(\mu+ t\sigma^2)^2 \exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)+ \sigma^2 \exp\left(\frac{\sigma^2t^2}{2}+ \mu t\right)$$

Desta forma temos que

$$\mathbb{E}\left(X^2\right)=M^{\prime\prime}_X(0)=(\mu+ 0\sigma^2)^2 \exp\left(\frac{\sigma^20^2}{2}+ \mu 0\right)+ \sigma^2 \exp\left(\frac{\sigma^20^2}{2}+\mu 0\right)=\mu^2+\sigma^2$$

e, portanto

$$\text{Var}\left(X\right)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=\mu^2+\sigma^2-\mu_2=\sigma^2.$$

6.3 - Distribuição qui-quadrado

A distribuição qui-quadrada pode ser interpretada de duas formas, como um caso particular da distribuição gamma, que será analisada mais adiante, ou como sendo a soma de normais padronizadas ao quadrado. Tome $X_i\sim N(0,1)$ então

$$\sum_{j=1}^{r}X^2_j=\chi^{2}_{r}.$$

Esse fato será demonstrado no teorema 6.3.1.

Definição 6.3.1

Uma variável aleatória contínua $X$ tem distribuição qui-quadrado com $\nu$ graus de liberdade se sua função densidade for dada por:

$$f(x)=\frac{1}{2^{\nu/2}\Gamma(\nu/2)}x^{(v/2)-1}\exp\left(-\frac{x}{2}\right); \ \nu \ > \ 0, \ x \ > \ 0$$

sendo $\Gamma(\omega)=\displaystyle\int_0^{\infty}x^{\omega-1}e^{-x}dx, \ \omega \ > \ 0$. Denotamos $X\sim \chi_{\nu}^2$.

O gráfico abaixo mostra a função qui-quadrado com 2 graus de liberdade.

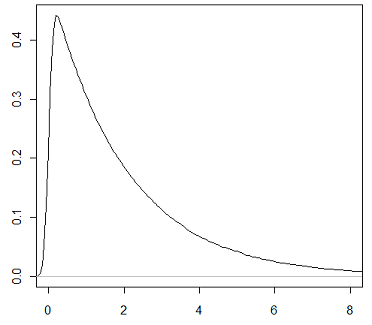
Notemos pelo gráfico da distribuição qui-quadrado que ela é assimétrica e positiva, isto vale para qualquer grau de liberdade. Sua positividade é fácil de ser verificada, pois ela é soma de normais ao quadrado, portanto só pode ser positiva. A distribuição qui-quadrado possui diversas aplicações na inferência estatística.

Para entender a ideia de graus de liberdade, consideremos um conjunto de dados qualquer. Graus de liberdade é o número de valores deste conjunto de dados que podem variar após terem sido impostas certas restrições a todos os valores. Por exemplo, consideremos que $10$ estudantes obtiveram em um teste média $8,0$. Assim, a soma das $10$ notas deve ser $80$ (restrição). Portanto, neste caso, temos um grau de liberdade de $10-1=9$, pois as nove primeiras notas podem ser escolhidas aleatoriamente, contudo a $10$ª nota deve ser igual a [$80$ - (soma das $9$ primeiras)].

Observação 6.3.1

Se $X~\sim ~\chi^{2}_{\nu}$, então temos que $X~\sim ~Gamma(\frac{\nu}{2},\frac{1}{2})$, ou seja a distribuição qui-quadrado é um caso particular da distribuição Gama. A distribuição Gama será apresentada no tópico 6.9.

Exemplo 6.3.1

Suponha que $y_1, \ldots,y_n$ sejam variáveis aleatórias normais independentes e identicamente distribuídas com média $\mu$ e desvio padrão $\sigma$. Então, temos que a estatística

$$Q_n=\frac{\displaystyle \sum_{i=1}^n(y_i-\overline{y})^2}{\sigma^2}=\frac{(n-1)s^2}{\sigma^2}$$

tem distribuição qui-quadrado com $(n-1)$ graus de liberdade, onde $s$ é o desvio padrão amostral.

O número de graus de liberdade de uma soma de quadrados corresponde ao número de elementos independentes na soma de quadrados. Considerando novamente $y_1,\ldots,y_n$ variáveis aleatórias normais independentes e identicamente distribuídas com média $\mu$ e desvio padrão $\sigma$, temos que os elementos da soma de quadrados $y_1-\overline{y},y_2-\overline{y},\ldots,y_n-\overline{y}$ não são todos independentes. Na realidade, somente $(n - 1)$ destes elementos são independentes, implicando que $s$ tem $(n - 1)$ graus de liberdade. Podemos encontrar mais detalhes sobre isso na apostila de inferência.

Exemplo 6.3.2

Suponha agora que $X$ segue uma distribuição qui-quadrado com $17$ graus de liberdade e queremos encontrar $x_1$ e $x_2$ tais que $P(x_1 \leq X \leq x_2)=0,95$. Para isto notemos que

$$\mathbb{P}(x_1 \leq X \leq x_2)=\mathbb{P}(X \leq x_2)-P(X \leq x_1)=0,95$$

o que implica que

$$\mathbb{P}(x_1\leq X\leq x_2) = 0,975-0,025=\mathbb{P}(X\leq 30,191)-\mathbb{P}(X\leq 7,564).$$

Assim $x_1=7,564$ e $x_2=30,191$.

Observação 6.3.1

Observamos que poderíamos ter encontrado outros valores de $x_1$ e $x_2$ para os quais $\mathbb{P}(x_1\leq X\leq x_2) = 0,95$, porém, na prática, sempre buscamos por valores de forma que as probabilidade $\mathbb{P}(X \ < \ x_1) =\mathbb{P}(X \ > \ x_2)$.

Exemplo 6.3.3

Seja $X$ uma variável aleatória com distribuição normal padronizada. Vamos mostrar que $X^2$, segue uma distribuição $\chi^2$ com um grau de liberdade.

Seja $Y=X^2$, então

$$\mathbb{P}(Y\leq y)=\mathbb{P}(-\sqrt{y}\leq X \leq \sqrt{y})=\displaystyle\frac{1}{\sqrt{2\pi}}\int_{-\sqrt{y}}^{\sqrt{y}}e^{-\frac{x^2}{2}}dx=\frac{2}{\sqrt{2\pi}}\int_{0}^{\sqrt{y}}e^{-\frac{x^2}{2}}dx.$$

Observe que na última igualdade foi usado o fato da função normal padronizada ser simétrica em torno de zero. Agora basta apenas fazermos uma mudança de variável tomando $t=\sqrt{y}$, então $\displaystyle \frac{dt}{dx}=\displaystyle \frac{t^{-\frac{1}{2}}}{2}$, assim obtemos que:

$$\mathbb{P}(Y\leq y)=\frac{1}{\sqrt{2}\sqrt{\pi}}\int_{0}^{y}t^{-\frac{1}{2}}e^{-\frac{t}{2}}dt.$$

Aqui vale uma observação, para mostramos que $Y$ segue uma distribuição qui-quadrado, precisamos usar o fato de que $\Gamma\left(\frac{1}{2}\right)=\sqrt{\pi}$, e portanto a distribuição acima é uma $\chi^2_1$.

Teorema 6.3.1

Sejam $X_i~\sim ~N(0,1)$ variáveis aleatórias independentes, com $i=1, \cdots , \nu$ e $\nu \in \Bbb{N}$. Então $Z=\displaystyle \sum_{i=1}^{\nu}(X_i)^2$ segue uma distribuição qui-quadrado com $\nu$ graus de liberdade.

Vamos demonstrar este teorema via a função geradora de momentos. Como as variáveis aleatórias $X_1 , \cdots , X_n$ são independentes, temos que

$$M_Z(t)=\mathbb{E}[e^{tZ}]=\mathbb{E}\left(e^{t\left(\sum_{i=1}^{\nu}(X_i)\right)}\right)=\mathbb{E}\left(\prod_{i=1}^{\nu}e^{t(X_i)^2}\right)= \prod_{i=1}^{\nu}\mathbb{E}\left(e^{t(X_i)^2}\right).$$

Mas

$$\mathbb{E}\left(e^{t(X_i)^2}\right)=\int e^{tx_i^2}\left(\frac{1}{\sqrt{2\pi}}\right)e^{-(1/2)x_i^2}dx_i=\int \frac{1}{\sqrt{2\pi}}e^{-(1/2)(1-2t)x_i^2}dx_i$$

e, portanto,

$$\mathbb{E}\left(e^{t(X_i)^2}\right)=\frac{1}{\sqrt{1-2t}}\int\frac{\sqrt{1-2t}}{\sqrt{2\pi}}e^{-(1/2)(1-2t)x_i^2}dx_i=\left(\frac{1}{1-2t}\right)^{\frac{1}{2}}$$

em que a última integral é igual a 1, pois se trata justamente de uma normal com média zero e variância $1/(1-2t)$. Portanto,

$$\mathbb{E}\left(e^{tZ}\right)\prod_{i=1}^{\nu}\mathbb{E}\left(e^{tX_i}\right)= \prod_{i=1}^{\nu}\frac{1}{\sqrt{1-2t}}=\left(\frac{1}{1-2t}\right)^{\nu/2}.$$

corresponde a função geradora de momentos da distribuição qui-quadrado com $\nu$ graus de liberdade. E o resultado segue.

Função Geradora de Momentos, Valor Esperado e Variância

Como visto no Teorema 6.3.1, se $X$ é uma variável aleatória com distribuição qui-quadrado com $\nu$ graus de liberdades, sua função geradora de momentos é dada por:

$$M_X(t)=\mathbb{E}\left(e^{tX}\right)=\left(\frac{1}{1-2t}\right)^{\frac{\nu}{2}}.$$

Desta forma, temos que

$$M^\prime_X(t)=\nu\left(\frac{1}{1-2t}\right)^{\frac{\nu+2}{2}}$$

e

$$M^{\prime\prime}_X(t)=(\nu^2+2\nu)\left(\frac{1}{1-2t}\right)^{\frac{\nu+4}{2}}.$$

Portanto, podemos calcular o valor de esperado e a variância da variável $X$. De fato, temos que

$$\mathbb{E}\left(X\right)=M^\prime_X(0)=\nu\left(\frac{1}{1}\right)^{\frac{\nu+2}{2}}=\nu$$

e

$$\text{Var}\left(X\right)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=M^{\prime\prime}_X(0)-(M^\prime_X(0))^2$$

de onde concluímos que

$$\text{Var}\left(X\right)=(\nu^2+2\nu)\left(\frac{1}{1}\right)^{\frac{\nu+4}{2}}-\nu^2=\nu^2+2\nu-\nu^2=2\nu.$$

6.4 - Distribuição t de Student

A distribuição t de Student é uma das distribuições mais utilizadas na estatística, com aplicações que vão desde a modelagem estatística até testes de hipóteses.

Definição 6.4.1

Uma variável aleatória contínua $X$ tem distribuição $t$ de Student com $\nu$ graus de liberdade se sua função densidade de probabilidade é dada por

$$f(x)=\frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\sqrt{\nu\pi}\Gamma\left(\frac{\nu}{2}\right)}\left(1+\frac{x^2}{\nu}\right)^{-\left(\frac{\nu+1}{2}\right)}\qquad x \in(-\infty,\infty).$$

Utilizamos a notação $X\sim t_\nu$.

Propriedades da distribuição t de Student

• A função densidade da distribuição t de Student tem a mesma forma em sino da distribuição Normal, mas reflete a maior variabilidade (com curvas mais alargadas) que é de se esperar em amostras pequenas.
• Quanto maior o grau de liberdade, mais a distribuição t de Student se aproxima da distribuição Normal.

Abaixo temos um gráfico da função densidade de um t de Student com 10 graus de liberdade.

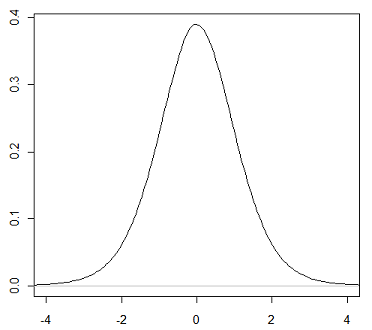
Exemplo 6.4.1

Considere $X_1 , \ldots , X_n$ variáveis aleatórias independentes e com distribuição normal com média $\mu$ e desvio padrão $\sigma$. Então, a variável

$$t=\frac{\overline{X}-\mu}{s/\sqrt{n}}$$

onde $s$ é o desvio padrão amostral, tem distribuição $t$ de Student com $n-1$ graus de liberdade. Este fato é decorrente do teorema a seguir.

Teorema 6.4.1

Considere $Z$ e $V$ duas variáveis aleatórias independentes tal que $Z\sim N(0,1)$ e $V\sim\chi_k^2$. Defina $X$ como sendo uma variável aleatória de tal forma que

$$X=\frac{Z}{\sqrt{V/k}}.$$

Temos que a variável aleatória $X$ tem distribuição $t$ de Student com $k$ graus de liberdade.

Demonstração

A função densidade de probabilidade conjunta de $Z$ e $V$ é dada por

$$f_{Z,V}(z,v) = \frac{1}{\sqrt{2\pi}}\frac{1}{\Gamma(k/2)}\left(\frac{1}{2}\right)^{k/2} u^{(k/2)-1}e^{-v/2}e^{-z^2/2}1!!1_{(0,\infty)}(v).$$

Considerando a transformação

$$X = \frac{Z}{\sqrt{V/k}} \quad \hbox{e} \quad Y = V$$

o jacobiano é $\sqrt{y/k}$ e então

$$f_{X,Y}(x,y) = \sqrt{\frac{y}{k}}\frac{1}{\sqrt{2\pi}}\frac{1}{\Gamma(k/2)}\left(\frac{1}{2}\right)^{k/2}y^{(k/2)-1}e^{-y/2}e^{-x^2y/2k}1!!1_{(0,\infty)}(y)$$

e

$$f_X(x) = \int_{-\infty}^{\infty}f_{X,Y}(x,y)dy=\frac{1}{\sqrt{2k\pi}}\frac{1}{\Gamma(k/2)}\left( \frac{1}{2}\right)^{k/2}\int_0^\infty y^{k/2-1+1/2}e^{-1/2(1+x^2/k)y}dy.$$

Na sequência, ao fazermos a mudança de variável

$$w = y \frac{1}{2} \left( 1 + \frac{x^2}{k} \right),$$

obtemos que

$$f_X(x) = \frac{\Gamma[(k+1)/2]}{\Gamma(k/2)}\frac{1}{\sqrt{k\pi}}\frac{1}{(1+x^2/k)^{(k+1)/2}}$$

que é a função densidade de probabilidade de uma distribuição $t$ com $k$ graus de liberdade.

Função geradora de momentos, Valor esperado e Variância

A função geradora de momentos da $t$ de Student não está definida para todos os graus de liberdade, entretanto podemos encontrar os momentos da função t de Student para alguns graus de liberdade.

Desta forma seja $X \sim t_{\nu}$, então

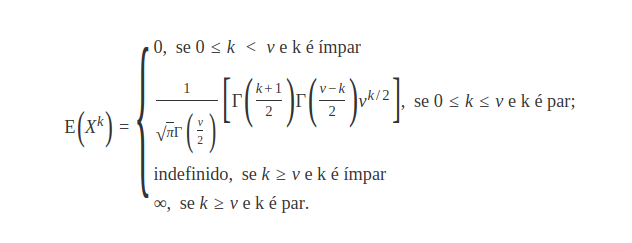
O valor esperado da $t$ de student, é zero se $\nu \ > \ 1$ caso contrário não está definido. Basta observarmos que $\mathbb{E}\left(X\right)=\mathbb{E}\left(X^1\right)$, ou seja, utilizando a formula dos momentos temos que $k$ é ímpar e assim, está definido apenas se $\nu \ > k=1$.

Utilizando a fórmula dos momentos da distribuição $t$ de Student podemos calcular a variância de $X$.

6.5 - Distribuição t de Student não-central

Em probabilidade e estatística, a distribuição $t$ não central generaliza a distribuição $t$ de Student. Assim como a distribuição $t$ central, a distribuição $t$ não central é inicialmente utilizada em inferência estatística, especialmente em análise do poder.

Definição 6.5.1

Sejam $Z\sim N(\lambda,1)$ e $U\sim\chi_n^2$, com Z e U independentes. Então

$$t_{n,\lambda}\sim\frac{Z}{\sqrt{\frac{U}{n}}}$$

tem distribuição $t$ não central com parâmetro de não centralidade $\lambda$.

O gráfico abaixo mostra a função densidade de uma $t$ de Student com $6$ graus de liberdade não centralizada onde o parâmetro de não centralidade é $10$. Notemos que o gráfico de sua função densidade é apenas uma $t$ de student com $6$ graus de liberdade transladada.

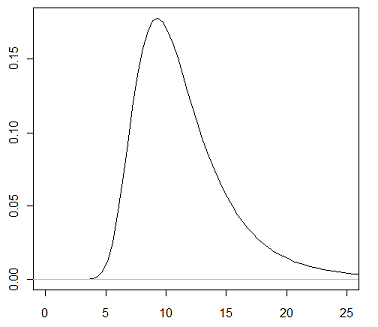
6.6 - Distribuição F de Snedecor

A distribuição F de Snedecor também conhecida como distribuição de Fisher é frequentemente utilizada na inferência estatística para análise da variância, mais detalhes pode ser encontrado na apostila de inferência.

Definição 6.6.1

Uma variável aleatória contínua $X$ tem distribuição $F$ de Snedecor com $n$ graus de liberdade no numerador e $m$ graus de liberdade no denominador se sua função densidade de probabilidade é definida por

$$f(x)=\frac{\Gamma\left[\frac{m+n}{2}\right]\left(\frac{m}{n}\right)^{\frac{m}{2}}x^{\frac{m}{2}-1}}{\Gamma\left[\frac{m}{2}\right]\Gamma\left[\frac{n}{2}\right]\left[\left(\frac{m}{n}\right)x+1\right]^{\frac{m+n}{2}}}\qquad x\in [0,\infty)$$

Neste caso, utilizamos a notação $X\sim F(m,n)$.

O gráfico abaixo ilustra a função densidade da distribuição $F$ de Snedecor com parâmetros $m=3$ e $n=2$.

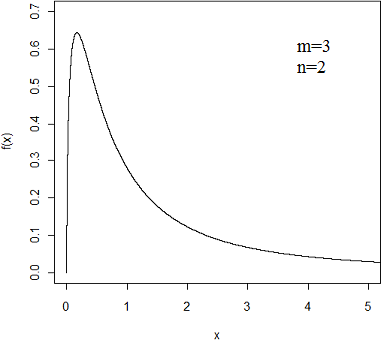
Exemplo 6.6.1

Um importante exemplo da distribuição $F$ de Snedecor corresponde a estatística $F$. Suponha que temos duas populações independentes tendo distribuições normais com variâncias iguais a $\sigma^2$. Considere $Y_{11},\ldots,Y_{1n}$ uma amostra aleatória da primeira população com $n$ observações e $Y_{21},\ldots,Y_{2m}$ uma amostra aleatória da segunda população com $m$ observações. Então, a estatística

$$F=\frac{\frac{(n-1)s_1}{(n-1)\sigma^2}}{\frac{(m-1)s_2}{(m-1)\sigma^2}}$$

tem distribuição $F$ de Snedecor com $(n-1)$ graus de liberdade no numerador e $(m-1)$ graus de liberdade no denominador, onde $s_1$ e $s_2$ sãos os desvios padrão amostrais da primeira e da segunda amostra, respectivamente.

Teorema 6.6.1

Considere $Q_n$ e $Q_m$ variáveis aleatórias com distribuição qui-quadrado com $n$ e $m$ graus de liberdade, respectivamente. Além disso, suponha que estas variáveis aleatórias são independentes. Então a variável aleatória

$$F=\frac{Q_m/m}{Q_n/n}$$

tem distribuição $F$ de Snedecor com $m$ graus de liberdade no numerador e $n$ graus de liberdade no denominador.

Demonstração

Seja $X$ uma variável aleatória positiva com função densidade de probabilidade $f_X$ e $Y$ uma variável aleatória com função densidade $f_Y$. Suponha que as variáveis aleatórias $X$ e $Y$ sejam independentes. Neste caso, a função densidade de probabilidade conjunta é dada por $f_{XY} = f_X f_Y$. Considere a fração $Z=\frac{Y}{X}$. Neste caso, a função densidade conjunta do quociente $Z$ é dada por

$$\mathbb{P}\left(Z\leq z\right)=\mathbb{P}\left(\frac{Y}{X}\leq z\right)=\mathbb{P}\left((X,Y) \in B_z \right),$$

em que $B_z = ((x,y) \in [0, \infty) \times \Bbb{R} : y \leq zx )$. Assim temos que

$$F_{Z}(z)= \mathbb{P}\left((X,Y) \in B_z\right) = \int_{0}^{\infty}\int_{-\infty}^{zx}f_{XY}(x,y)dydx$$

Considerando a mudança de variável $y=xw$; temos que:

$$F_{Z}(z)=\int_{0}^{\infty}\int_{-\infty}^{z}xf_{XY}(x,xw)dwdx=\int_{-\infty}^{z}\int_{0}^{\infty}xf_{XY}(x,xw)dxdw.$$

Assim, a função densidade de probabilidade de $Z$ é dada por

$$f_{Z}(z)=\int_{0}^{\infty}xf_{XY}(x,xz)dx.$$

Como $X$ e $Y$ são independentes, a distribuição conjunta do quociente é dada por

$$f_{Z}(z)=\int_{0}^{\infty}xf_{X}(x)f_{Y}(xz)$$

Portanto a distribuição do quociente $Z=\frac{Y}{X}$, com $Y\sim \chi^2_m$ e $X\sim \chi^2_n$ é dada por:

$$f_Z(z)=\int_{0}^{\infty}x\frac{x^{(n/2)-1}e^{-x/2}}{\Gamma\left(\frac{n}{2}\right)2^{n/2}}\frac{(xz)^{(m/2)-1}e^{-xz/2}}{\Gamma\left(\frac{m}{2}\right)2^{m/2}}dx$$

de onde concluímos que

$$f_Z(z)=\frac{z^{(m/2)-1}}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)2^{(m+n)/2}}\int_{0}^{\infty}x^{(m+n)/2-1}e^{-x(z+1)/2}dx$$

lembrando que $\displaystyle\Gamma(x)=\int_{0}^{\infty}t^{x-1}e^{-t}dt$. Fazendo a substituição $\displaystyle t=x\left(\frac{z+1}{2}\right)$ e reorganizando a integral acima temos que:

$$f_Z(z)=\frac{z^{(m/2)-1}}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)2^{(m+n)/2}} \frac{1}{\left(\frac{z+1}{2}^{(m+n)/2}\right)}\int_{0}^{\infty}t^{(m+n)/2 - 1}e^{-t}dt=\frac{\Gamma{\left(\frac{m+n}{2}\right)}z^{(m/2)-1}}{\Gamma{\left(\frac{m}{2}\right)}\Gamma{\left(\frac{n}{2}\right)}(z+1)^{(m+n)/2}}.$$

Para finalizar, tomamos $W=\frac{Y/m}{X/n}$ e, neste caso, temos que

$$\mathbb{P}\left(W \leq w\right)=\mathbb{P}\left(\frac{Y/m}{X/m} \leq w \right)=\mathbb{P}\left(\frac{Y}{X} \leq \frac{m}{n} w \right)= \int_{0}^{\frac{m}{n}w} f_{Z}(z)dz.$$

Ao realizarmos a transformação de variáveis $t=(n/m)z$, concluímos que

$$\mathbb{P}\left(W \leq w\right)= \int_{0}^w f_Z (tm/n) (m/n) dt$$

Ao substituirmos, concluímos que $W$ segue uma distribuição $F$ com $m$ graus de liberdade no numerador e $n$ graus de liberdade no denominador.

Por construção, o quadrado da distribuição t-Student com $\nu$ graus de liberdade tem distribuição F com $1$ grau de liberdade no numerador e $\nu$ graus de liberdade no denominador.

Função Geradora de Momentos, Valor Esperado e Variância

Não existe função geradora de momentos para a distribuição $F$ de Snedecor.

Assim vamos calcular o valor esperado de X com $X\sim F(m,n)$.

$$\mathbb{E}\left(X\right)=\int_{0}^{\infty}x\frac{\Gamma{\left(\frac{m+n}{2}\right)}\left(\frac{m}{n}\right)^{(m/2)-1}x^{(m/2)-1}}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)\left(1+\frac{m}{n}x\right)^{(m+n)/2}}=\frac{\Gamma{\left(\frac{m+n}{2}\right)}\left(\frac{m}{n}\right)^{(m/2)-1}}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)} \int_{0}^{\infty}\displaystyle \frac{x^{(m/2)}}{\left(1+\frac{m}{n}x\right)^{(m+n)/2}}$$

e, portanto,

$$\mathbb{E}\left(X\right)=\frac{n}{(n-2)}, \ \text{se} \ n \ > \ 2.$$

A variância da distribuição $X\sim F(m,n)$ é dada por

$$\text{Var}\left(X\right)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=\frac{2n^2(m+n-2)}{m(n-2)^2(m-4)}, \ \text{se} \ n \ > \ 4.$$

6.7 - Distribuição F não-central

Na teoria de probabilidades e estatística, a distribuição $F$ não central é uma distribuição de probabilidade contínua que é uma generalização da distribuição $F$ comum. Ela descreve a distribuição do quociente $\frac{X/n_1}{Y/n_2}$, onde o numerador $X$ tem uma distribuição qui-quadrado não central com $n_1$ graus de liberdade e o denominador $Y$ tem distribuição qui-quadrado com $n_2$ graus de liberdade. Além disso, $X$ e $Y$ são independentes.

Definição 6.7.1

Se $X\sim\chi_{n_1}^2(\lambda)$ e $Y\sim\chi_{n_2}^2$, e ainda, $X$ e $Y$ são independentes, então:

$$\frac{\frac{X}{n_1}}{\frac{Y}{n_2}}\sim F_{n_1,n_2}(\lambda)$$

com $\lambda=\frac{1}{2}\mu$ (parâmetro de não centralidade). Neste caso, dizemos que $F$ tem uma distribuição $F$ não central.

O gráfico abaixo ilustra a função densidade da distribuição $F$ de Snedecor com parâmetros $n_1=3$, $n_2=2$ e parâmetro de não-centralidade $\lambda=4$.

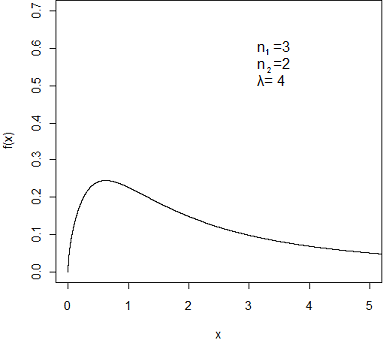
6.8 - Distribuição de Cauchy

A distribuição de Cauchy pode ser considerada uma distribuição patológica, pois ela não apresenta média e variância. Entretanto a distribuição de Cauchy tem sua importância em diversas áreas do conhecimento científico na física por exemplo essa distribuição é solução de um equação diferencial que descreve um determinado tipo de oscilador, em matemática é uma das soluções para a equação de Laplace, entre diversas outras finalidades. A distribuição de Cauchy, cujo o nome foi dado em homenagem ao famoso matemático Augustin-louis Cauchy apesar de suas particularidades tem diversas propriedades importantes que iremos analisar a seguir.

Definição 6.8.1

Uma variável aleatória contínua $X$ tem distribuição de Cauchy com parâmetros $\alpha$ e $\beta$ se sua função densidade de probabilidades e sua função de distribuição forem definidas, respectivamente, por

$$f(x)=\frac{1}{\pi\beta\left[1+\left[\frac{x-\alpha}{\beta}\right]^2\right]}\qquad x\in(-\infty,\infty)$$

$$F(x)=\frac{1}{2}+\pi^{-1}\arctan\left(\frac{x-\alpha}{\beta}\right), \ -\infty \ < \ x \ < \ \infty$$

onde $\alpha$ e $\beta$ são parâmetros de locação e de escala, respectivamente.

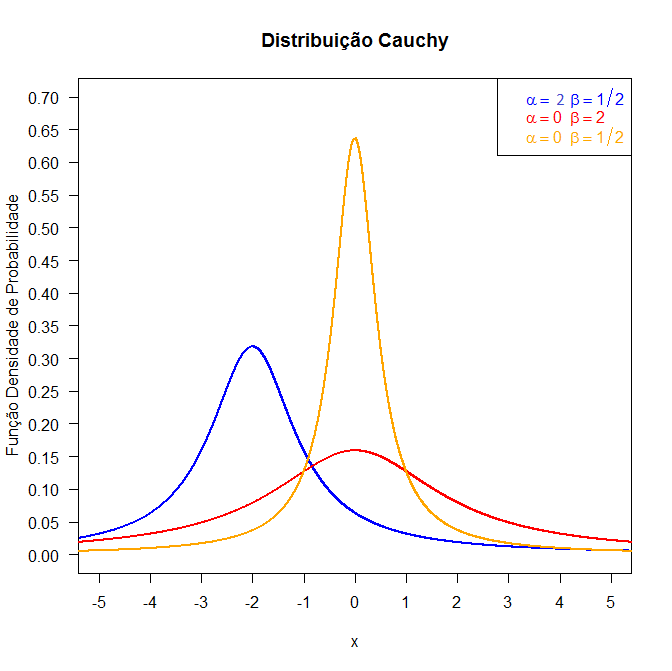
Figura 6.8.1: Gráfico da função densidade da distribuição Cauchy.

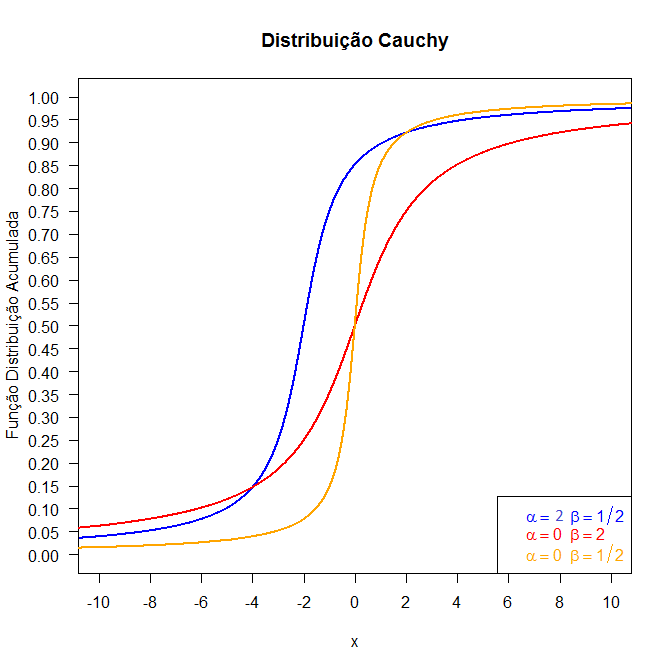
Figura 6.8.2: Gráfico da função distribuição acumulada da distribuição Cauchy para diversos valores de α e β.

A distribuição de Cauchy satisfaz as seguintes propriedades:

• A mediana da distribuição é $ \alpha^4 $ e o primeiro e o terceiro quartis são iguais $ \alpha-\beta $ e $ \alpha+\beta $, respectivamente;
• A sua média não é definida, logo ela também não tem desvio padrão;
• A distribuição de Cauchy pode ser simulada como a razão entre duas normais independentes;
• A forma padrão da distribuição de Cauchy é obtida fazendo $ \alpha=0 $ e $ \beta = 1 $

$$f(x)=\frac{1}{\pi}~\cdot ~\left(\frac{1}{1+x^2}\right), \ -\infty \ < \ x \ < \ \infty;$$

• Estabelecendo algumas comparações, podemos referir que ambas as distribuições Normal e Cauchy são simétricas. A principal diferença entre elas é que na distribuição de Cauchy as abas são mais alongadas e mais achatadas.

Exemplo 6.8.1

Seja $X$ uma variável aleatória contínua com distribuição uniforme no intervalo $\left[\displaystyle \frac{-\pi}{2};\frac{\pi}{2}\right]$. Prove que $Y=a \tan{(X)}$, $a \ > \ 0$ segue uma distribuição de Cauchy com parâmetros $\alpha=0$ e $\beta=a$.

Primeiramente devemos encontrar a função densidade de probabilidade de $X$. Como $X$ segue uma distribuição uniforme temos que:

$$f(x)=\frac{1}{b-a}=\frac{1}{\frac{\pi}{2}-\frac{-\pi}{2}}=\frac{1}{\pi}$$

e então

$$\mathbb{P}(Y\leq y)=\mathbb{P}(a\tan{(X)}\leq y)=\mathbb{P}\left(\tan{(X)}\leq \frac{y}{a}\right)=\mathbb{P}\left(X\leq \tan^{-1}{\left(\frac{y}{a}\right)}\right)=\int_{-\infty}^{\tan^{-1}{\left(\frac{y}{a}\right)}}\frac{1}{\pi}dx.$$

Assim fazendo uma mudança de variável $t=\tan^{-1}{\left(\frac{y}{a}\right)}$, teremos $\displaystyle \frac{dt}{dy}=\frac{a}{y^2+a^2}$. E portanto pelo teorema da mudança de variável temos que:

$$\int_{0}^{\tan^{-1}{\left(\frac{y}{a}\right)}}\frac{1}{\pi}dx=\int_{-\infty}^{t}\frac{1}{\pi}\left(\frac{a}{y^2+a^2}\right)dy.$$

Portanto $Y$ segue uma distribuição de Cauchy com $\alpha=0$ e $\beta=a$.

Função Geradora de Momentos, Valor Esperado e Variância

A distribuição de Cauchy não apresenta função geradora de momentos, sua esperança também não está definida e como consequência sua variância também não.

6.9 - Distribuição Gama

A distribuição gama é uma das mais gerais distribuições, pois diversas distribuições são caso particular dela como por exemplo a exponencial, a qui-quadrado, entre outras. Essa distribuição tem como suas principais aplicações à análise de tempo de vida de produtos.

Definição 6.9.1

Uma variável aleatória $X$ tem distribuição Gama com parâmetros $\alpha \ > \ 0$ (também denominado parâmetro de forma) e $\beta \ > \ 0$ (parâmetro de taxa), denotando-se $X \sim \ \text{Gama}(\alpha,\beta)$, se sua função densidade é dada por

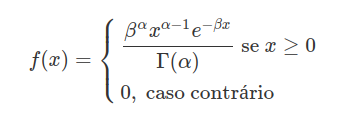
Os gráficos aproximados das funções de distribuição e de densidade para $\alpha = 2$ e $\beta = 0,5$ são apresentados, respectivamente, nas seguintes figuras

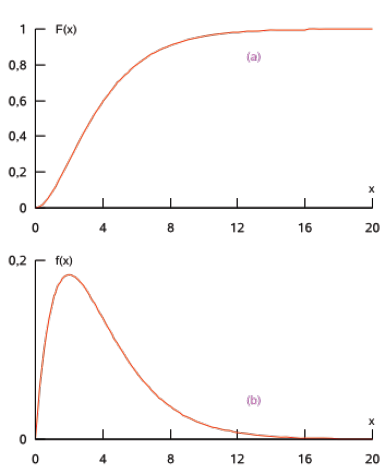
Observação 6.9.1

Em algumas referências, é usado um parâmetro de escala $\theta \ > \ 0$ equivalente ao inverso do parâmetro de taxa, isto é, $\beta=\frac{1}{\theta}$. E a função densidade anterior é escrita como

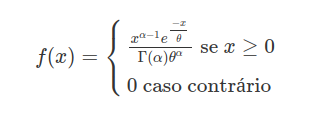
Teorema 6.9.1

Suponha que $(X_i)_i$ seja uma sequência de variáveis aleatórias independentes, tais que $X_i\sim \ \text{Gama}(\alpha_i,\beta)$. Então

$$\sum_{i=1}^{k}X_i\sim \ \text{Gama}\left(\sum_{i=1}^{k}\alpha_i,\beta\right).$$

Para demonstrar esse fato vamos utilizar da função geradora de momentos, mas antes vamos encontrar a função geradora da distribuição gamma.

$$M_X(t)=E[e^{tX}]=\int_{0}^{\infty}e^{tx}x^{\alpha-1}e^{-\beta x}\frac{\beta^\alpha}{\Gamma(\alpha)}=\frac{\beta^{\alpha}}{\Gamma(\alpha)}\int_{0}^{\infty}x^{\alpha-1}e^{-(\beta-t)x}dx=\frac{\beta^\alpha}{\Gamma(\alpha)}\frac{\Gamma(\alpha)}{(\beta-t)^{\alpha}}.$$

Portanto,

$$M_X(t) =\left(\frac{\beta}{\beta-t}\right)^{\alpha}.$$

Assim mostramos que $\displaystyle \sum_{i=1}^{k}X_i\sim \ \text{Gama}(\sum_{i=1}^{k}\alpha_i,\beta)$. De fato,

$$M_{\sum_{i=1}^{k}X_i}(t)=\mathbb{E}\left(e^{t(\sum_{i=1}^{k}x_i)}\right)= \mathbb{E}\left(\prod_{i=1}^{k}e^{tx_i}\right)=\prod_{i=1}^{k}\mathbb{E}\left(e^{tx_i}\right) =\prod_{i=1}^{k}\left(\frac{\beta}{\beta-t}\right)^{\alpha_i}=\left(\frac{\beta}{\beta-t}\right)^{\sum_{i=1}^{k}\alpha_i}.$$

Portanto $\displaystyle \sum_{i=1}^{k}X_i\sim \ \text{Gama}(\sum_{i=1}^{k}\alpha_i,\beta)$.

Com a demonstração deste teorema, mostramos também que soma de distribuições qui-quadradado independentes tem distribuição qui-quadrado, com a soma dos graus de liberdade.

Função Geradora de Momentos, Valor Esperado e Variância

Vamos utilizar a função geradora de momentos para calcular a média e a variância da distribuição gamma. Assim seja $X$ uma variável aleatória, tal que $X\sim \ \text{Gama}(\alpha,\beta)$, então sua função geradora de momentos é dada por:

$$M_X(t)=\mathbb{E}\left(e^{tX}\right)=\int_{0}^{\infty}e^{tx}x^{\alpha-1}e^{-\beta x}\frac{\beta^\alpha}{\Gamma(\alpha)}=\frac{\beta^{\alpha}}{\Gamma(\alpha)}\int_{0}^{\infty}x^{\alpha-1}e^{-(\beta-t)x}dx=\frac{\beta^\alpha}{\Gamma(\alpha)}\frac{\Gamma(\alpha)}{(\beta-t)^{\alpha}}$$

Portanto, concluímos qeu

$$M_X(t) =\left(\frac{\beta}{\beta-t}\right)^{\alpha}.$$

Para calcularmos o valor esperado e a variância vamos necessitar do primeiro e do segundo momento, assim basta derivarmos a função geradora de momentos.

$$M^\prime_X(t)=\frac{\alpha}{\beta-t}\left(\frac{\beta}{\beta-t}\right)^\alpha$$

e

$$M^{\prime\prime}_X(t)=\frac{\alpha(\alpha+1)}{(\beta-t)^2}\left(\frac{\beta}{\beta-t}\right)^\alpha.$$

Desta forma, o valor esperado de $X$ é dado por:

$$\mathbb{E}(X)= M^{\prime}_X(0)=\frac{\alpha}{\beta}\left(\frac{\beta}{\beta}\right)^\alpha=\frac{\alpha}{\beta}$$

e sua variância é dada por

$$\text{Var}(X)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=M^{\prime\prime}_X(0)-(M^\prime_X(0))^2=\frac{\alpha(\alpha+1)}{\beta^2}-\left(\frac{\alpha}{\beta}\right)^2\displaystyle =\frac{\alpha}{\beta^2}.$$

Observação 6.9.2

É importante observar que, no caso em que utilizamos a distribuição Gama com o parâmetro de escala $\theta = \frac{1}{\beta} \ > \ 0$ para a variável aleatória $X$, temos que

$$\mathbb{E}\left(X\right) = \alpha\theta \quad \text{e} \quad \text{Var}\left(X\right) = \alpha\theta^2$$

Exemplo 6.9.1

Seja $ X\sim Gamma(\alpha,\beta) $, então $ cX\sim Gamma(\alpha,\beta/c) $.

De fato, pela função geradora de momentos temos que

$$M_{cX}(t)=\mathbb{E}(e^{tcx})=\int_0^\infty e^{tcx}x^{\alpha-1}e^{-\beta x} \frac{\beta^\alpha}{\Gamma(\alpha)} dx$$

$$=\frac{\beta^\alpha}{\Gamma(\alpha)} \int_0^\infty x^{\alpha-1}e^{-(\beta-ct) x} \frac{\beta^\alpha}{\Gamma(\alpha)} dx=\left(\frac{\beta}{(\beta-ct)}\right)^\alpha$$

$$=\left(\frac{\beta/c}{\frac{1}{c}(\beta-ct)}\right)^\alpha=\left(\frac{\beta/c}{(\beta/c-t)}\right)^\alpha$$

Portanto o resultado segue.

6.10 - Distribuição Beta

A distribuição Beta é frequentemente usada para modelarmos a proporção, ou modelagem de objetos que pertenceção ao intervalo $(0,1)$, pois essa distribuição está definida neste intervalo. Devido a grande versatilidade de uma variável aleatória $X$ com distribuição beta para modelar funções densidade de probabilidade no intervalo $(0,1)$ e pela possibilidade de generalizar essa versatilidade para qualquer variável aleatória $Y$ restrita a um intervalo finito $(m,n)$, bastando para isso utilizar a relação $Y = (n - m)X + m$, o modelo beta tem inúmeras aplicações para representar quantidades físicas cujos valores estejam restritos a um intervalo identificável.

Definição 6.10.1

A distribuição Beta é uma distribuição de probabilidade contínua, com dois parâmetros $\alpha$ e $\beta$ cuja função de densidade para valores $0 \ < \ x \ < \ 1$ é

$$f(x)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1}\quad x\in(0,1) \ \text{e} \ \alpha,\beta \ > \ 0$$

No modelo, os parâmetros $\alpha$ e $\beta$ definem a forma da distribuição. Se $\alpha = \beta$, a distribuição é simétrica, se $\alpha \ > \ \beta$, a assimetria é negativa e, no caso de $\alpha \ < \ \beta$, sua assimetria é positiva.

Observação 6.10.1

A distribuição beta não apresenta forma fechada para sua função de distribuição acumulada.

• Note que se α = β = 1, a densidade de Beta se reduz à Uniforme no intervalo (0,1).
• A densidade beta é apropriada para modelar proporções, por causa do seu domínio (o intervalo (0,1)) e também pela variedade de formas que a densidade pode assumir, de acordo com os valores especificados de α e β.

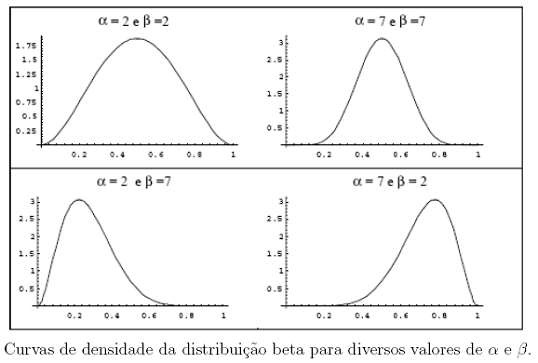
Função Geradora de Momentos, Valor Esperado e Variância

A função geradora de momentos da distribuição beta é complicada e envolve a chamada função hipergeométrica confluente a qual é solução de uma equação diferencial chamada equação diferencial hipergeométrica confluente, também conhecida como função de Whittaker. Entretanto podemos encontrar a sua função de momentos, dada da seguinte forma:

$$\mathbb{E}\left(X^k\right)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\int_{0}^{1}x^{\alpha +k-1}(1-x)^{\beta-1}dx=\displaystyle \frac{\Gamma(\alpha+\beta)\Gamma(\alpha+k)}{\Gamma(\alpha+\beta+k)\Gamma(\alpha)}.$$

Com a função de momentos em mãos podemos encontrar o valor esperado e a variância.

$$\mathbb{E}(X)=\frac{\Gamma(\alpha+\beta)\Gamma(\alpha+1)}{\Gamma(\alpha+\beta+1)\Gamma(\alpha)}=\displaystyle \frac{\Gamma(\alpha+\beta)\alpha\Gamma(\alpha)}{(\alpha+\beta)\Gamma(\alpha+\beta)\Gamma(\alpha)}=\displaystyle \frac{\alpha}{\alpha+\beta}$$

Para o cálculo da variância necessitamos de $\mathbb{E}\left(X^2\right)$, que é dado por

$$\mathbb{E}\left(X^2\right)=\frac{\Gamma(\alpha+\beta)\Gamma(\alpha+2)}{\Gamma(\alpha+\beta+2)\Gamma(\alpha)}=\frac{\Gamma(\alpha+\beta)(\alpha+1)\alpha\Gamma(\alpha)}{(\alpha+\beta+1)(\alpha+\beta)\Gamma(\alpha+\beta)\Gamma(\alpha)}=\frac{(\alpha+1)\alpha}{(\alpha+\beta+1)(\alpha+\beta)}.$$

Portanto, temos que

$$\text{Var}(X)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=\frac{(\alpha+1)\alpha}{(\alpha+\beta+1)(\alpha+\beta)}-\frac{\alpha^2}{(\alpha+\beta)^2}\displaystyle =\frac{\alpha\beta}{(\alpha+\beta+1)(\alpha+\beta)^2}.$$

6.11 - Distribuição Beta não-central

Distribuição 6.11.1

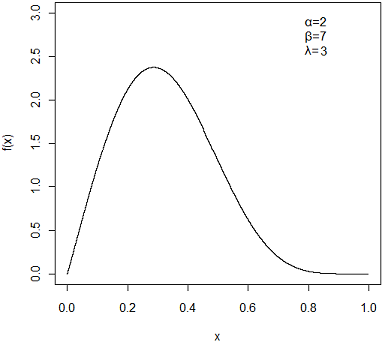
A distribuição Beta não central é uma generalização da distribuição Beta. Sejam $Z_1\sim\chi_m^2(\lambda)$ e $Z_2\sim\chi_n^2$. Então, define-se a distribuição beta não central pela razão

$$\frac{Z_1}{Z_1+Z_2}\sim \ \text{Beta}(\alpha,\beta,\lambda).$$

O gráfico abaixo mostra a distribuição beta não central com $\alpha=2$, $\beta=7$ e $\lambda=3$.

6.12 - Distribuição Exponencial

Esta é uma distribuição que se caracteriza por ter uma função de taxa de falha constante. A distribuição exponencial é a única com esta propriedade. Ela é considerada uma das mais simples em termos matemáticos. Esta distribuição tem sido usada extensivamente como um modelo para o tempo de vida de certos produtos e materiais. Ela descreve adequadamente o tempo de vida de óleos isolantes e dielétricos, entre outros.

Definição 6.12.1

A variável aleatória $X$ tem distribuição Exponencial com parâmetro $\lambda$, $\lambda \ > \ 0$, se tiver função densidade de probabilidade dada por:

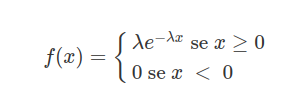
em que $\lambda$ é o parâmetro de taxa da distribuição e deve satisfazer $\lambda \ > \ 0$. Neste caso, $\lambda$ é o tempo médio de vida e $x$ é um tempo de falha. O parâmetro deve ter a mesma unidade do tempo da falha $x$. Isto é, se $x$ é medido em horas, $\lambda$ também será medido em horas.

A função de distribuição acumulada $F(x)$ é dada por

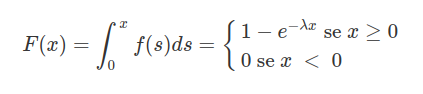
Utilizamos a notação $X\sim \ \text{Exp}(\lambda)$.

Observação 6.12.1

A distribuição Exponencial pode ser parametrizada de uma forma alternativa segundo a função densidade de probabilidade dada por

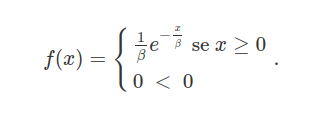
Neste caso, dizemos que $\beta \ > 0$ é o parâmetro de escala da distribuição e é o inverso do parâmetro taxa na definição acima. Neste definição alternativa, a variável aleatória $X$ pode ser interpretada como a duração de tempo em que um sistema mecânico ou biológico sobrevive. Para este caso, denotamos $X\sim \ \text{Exp}(\beta)$ e, infelizmente, esta definição alternativa torna-se ambígua. Neste caso, devemos verificar qual das duas especificações está sendo utilizada quando escrevemos $X\sim \ \text{Exp}(\lambda)$. Ou seja, devemos sempre verificar se $\lambda$ está se referindo ao parâmetro taxa ou ao parâmetro escala da distribuição.

Deixamos claro aqui que, a menos que especifiquemos o contrário, sempre que escrevemos $X\sim \ \text{Exp}(\lambda)$ estamos nos referindo à parametrização em que $\lambda$ é o parâmetro taxa.

Observação 6.12.2

Notem que a função exponencial, na verdade, é um caso particular da função Gama, pois se $X\sim \ \text{Exp}(\lambda)$, então $X\sim \ \text{Gama}(1,\lambda)$

O gráfico abaixo mostra a distribuição exponencial com parâmetros $\lambda=1/2, 1$ e $3/2$.

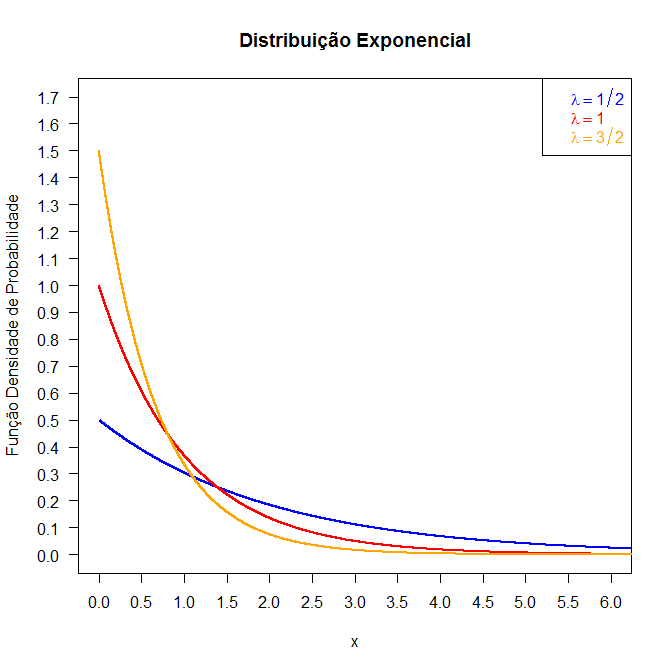
Figura 6.12.1: Gráfico da função densidade para distribuição Exponencial.

Exemplo 6.12.1

O tempo até a falha do ventilador de motores a diesel tem uma distribuição Exponencial com parâmetro $\lambda = \frac{1}{28700}$ horas. Qual a probabilidade de um destes ventiladores falhar nas primeiras 24000 horas de funcionamento?

$$\mathbb{P}[0\leq X\leq 24000]=\int_0^{24000}f(x)dx=\int_0^{24000}\frac{1}{28700}\exp\left(-\frac{x}{28.700}\right)=0,567.$$

Ou seja, a probabilidade de um destes ventiladores falhar nas primeiras $24000$ horas de funcionamento é de, aproximadamente, 56,7%.

Exemplo 6.12.2

Suponha que o tempo de vida de uma determinada espécie de inseto tenha uma distribuição exponencial de parâmetro $\lambda=1/12$ dia. Suponha também que estes insetos atinjam a maturidade sexual após $3$ dias de seu nascimento. Qual a função densidade de probabilidade, em dias, dos insetos que conseguem se reproduzir? E qual a probabilidade de que um inseto reprodutor viva mais de $24$ dias?

Seja $X$ a distribuição do tempo de vida dos insetos, e $Y$ a distribuição do tempo de vida dos insetos que chegam a reprodução. Observem que $Y=X+3$, assim

$$F_Y(y)=\mathbb{P}(Y\leq y)=\mathbb{P}(X+3\leq y)=\mathbb{P}(X\leq y-3)=F_X(y-3).$$

Portanto, a função densidade de probabilidade de $Y$ é dada por

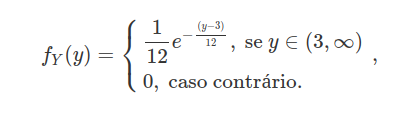
Agora falta encontramos qual a probabilidade de que o inseto reprodutor dure mais de 24 dias. Usando a densidade acima temos que

$$\mathbb{P}(Y \ > \ 24)=1-\mathbb{P}(Y\leq 24)=1-F_Y(24)=1-\int_{-\infty}^{24}f_Y(y)dy=1-\int_{3}^{24}\frac{1}{12}e^{-\frac{(y-3)}{12}}\approx 0,1738.$$

Exemplo 6.12.3

Uma fábrica utiliza dois métodos para a produção de lâmpadas. 70% das lâmpadas são produzidas pelo método $A$ e as demais pelo método $B$. A duração da lâmpada depende do método pelo qual ela foi produzida, sendo que as produzidas pelo método $A$ seguem uma distribuição exponencial com parâmetro $1/80$ e as do método $B$ seguem uma exponencial de parâmetro $1/100$. Qual a probabilidade de que, se escolhermos uma lâmpada ao acaso, ela dure mais de $100$ horas?

Sejam $X_A\sim \ \text{Exp}(1/80)$ e $X_B\sim \text{Exp}(1/100)$ e considere os evento C={Uma lâmpada durar mais de 100 horas}, A={A lâmpada ter sido fabricada pelo método A} e B={A lâmpada ter sido fabricada pelo método B}. Assim usando o teorema 1.4.2 obtemos que

$$\mathbb{P}(C)=\mathbb{P}(C|A)\mathbb{P}(A)+\mathbb{P}(C|B)\mathbb{P}(B)=\mathbb{P}(X_A\geq 100)0,7+\mathbb{P}(X_B\geq 100)0,3$$

e, portanto,

$$\mathbb{P}(C)=0,7\int_{100}^{\infty}\frac{1}{80}e^{-\frac{x}{80}}dx+0,3\int_{100}^{\infty}\frac{1}{100}e^{-\frac{x}{100}}dx\approx 0,2+0,11=0,31.$$

Portanto a probabilidade de que uma lâmpada escolhida ao acaso dure mais de 100 horas é de 31%.

Exemplo 6.12.4

Sabendo que $X \ \sim \ \text{Exp}(1)$, qual a função densidade de probabilidade de $Y=e^{-X}$.

Sabemos que a densidade de $X$ é dada por

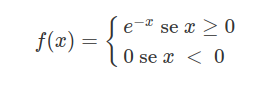
Assim

$$F_Y(y)=P(Y\leq y)=P(e^{-X}\leq y)=P(X\geq -\ln{y})=1-P(X\leq -\ln{y})=1-F_X(-\ln{y})$$

e portanto concluímos que

$$f_Y(y)=\displaystyle \frac{d F_Y(y)}{dy}=\frac{d[1-F_X(-\ln{y})]}{dy}=-f_X(-\ln{y})\left(-\frac{1}{y}\right)=\frac{f_X(-\ln{y})}{y}=\frac{e^{-(-\ln{y})}}{y}=1.$$

Portanto $Y$ segue uma distribuição uniforme em (0,1).

Função Geradora de Momentos, Valor Esperado e Variância

Seja $X$ um variável aleatória com distribuição exponencial com parâmetro $\lambda$. Então sua função geradora de momentos é dada por:

$$M_X(t)=\mathbb{E}\left(e^{tX}\right)=\int_{0}^{\infty}\lambda e^{-\lambda x}dx=\int_{0}^{\infty}\lambda e^{(t-\lambda)x}=\left|^{\infty}_0\frac{\lambda}{t-\lambda}\right.=\frac{\lambda}{\lambda-t}.$$

Temos que o valor esperado e a variância de uma variável aleatória X com distribuição exponencial com parâmetro λ são dados, respectivamente, por

$$\mathbb{E}(X)=\int_{-\infty}^{\infty}xf(x) dx=\int_{0}^{\infty}x\lambda e^{-\lambda x}dx=\lambda\int_{0}^{\infty}xe^{-\frac{1}{\lambda} x}dx$$

e, resolvendo esta integral por partes concluímos que

$$\mathbb{E}(X)= \frac{1}{\lambda}$$

Portanto, o valor esperado de $X$ é $\frac{1}{\lambda}$. Para encontrar a variância de $X$, vamos primeiramente calcular o valor esperado de $X^2$.

$$\mathbb{E}(X^2)=\int_{-\infty}^{\infty}g(x)f(x)dx=\int_{0}^{\infty}x^2\lambda e^{-\lambda x}dx$$

e, resolvendo a integral por partes, obtemos que

$$\mathbb{E}(X^2) = \frac{2}{\lambda^2}.$$

Portanto a variância de $X$ é dada por

$$\text{Var}(X)=\mathbb{E}(X^2 )-\mathbb{E}^2(X)=\frac{2}{\lambda^2}-\frac{1}{\lambda^2}=\frac{1}{\lambda^2}.$$

Assim, o valor esperado e a variância de $X$ são dados, respectivamente por:

$$\mathbb{E}(X)=\frac{1}{\lambda} ~~~ Var(X)=\frac{1}{\lambda^2}.$$

Podemos calcular também o valor esperado e a variância utilizando a função geradora de momentos

$$M^\prime_X(t)=\frac{\lambda}{(\lambda -t )^2}$$

e

$$M^{\prime\prime}_X(t)=\frac{2\lambda}{(\lambda-t)^3}.$$

Portanto, o valor esperado e a variância podem ser calculados por

$$\mathbb{E}\left(X\right)=M^\prime_X(0)=\frac{1}{\lambda}$$

e

$$\text{Var}\left(X\right)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=M^{\prime\prime}_X(0)-(M^\prime_X(0))=\frac{2}{\lambda^2}-\frac{1}{\lambda^2}=\frac{1}{\lambda^2}.$$

Observação 6.12.3

Quando estamos trabalhando com a distribuição exponencial parametrizada com o parâmetro escala $\beta \ > \ 0$ temos que

$$\mathbb{E}\left(X\right) = \beta \quad \text{e} \quad \text{Var}\left(X\right) = \beta^2.$$

Não demonstraremos estas propriedades, mas ressaltamos que elas são imediatas a partir do fato de que $\beta = \frac{1}{\lambda}$ em que $\lambda$ é parâmetro taxa.

6.13 - Distribuição Weibull

A distribuição Weibull foi proposta originalmente por W. Weibull (1954) em estudos relacionados ao tempo de falha devido a fadiga de metais. Ela é frequentemente usada para descrever o tempo de vida de produtos industriais. A sua popularidade em aplicações práticas deve-se ao fato dela apresentar uma grande variedade de formas, todas com uma propriedade básica: a sua função de taxa de falha é monótona. Isto é, ou ela é crescente ou decrescente ou constante. Ela descreve adequadamente a vida de mananciais, componentes eletrônicos, cerâmicas, capacitores e dielétricos. Podemos encontrar mais detalhes sobre a distribuição weibull na apostila de confiabilidade.

Definição 6.13.1

Uma variável aleatória $X$ tem distribuição Weibull se tiver função densidade de probabilidade dada por:

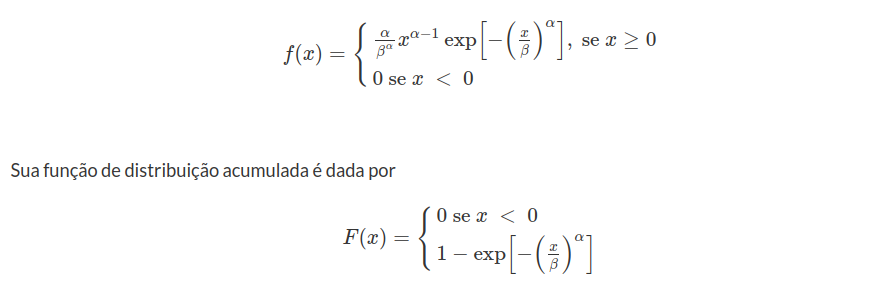
O gráfico abaixo mostra a distribuição Weibull fixando o parâmetro $\alpha=2$ e variando o parâmetro β=0,5, 1,5 e 3.

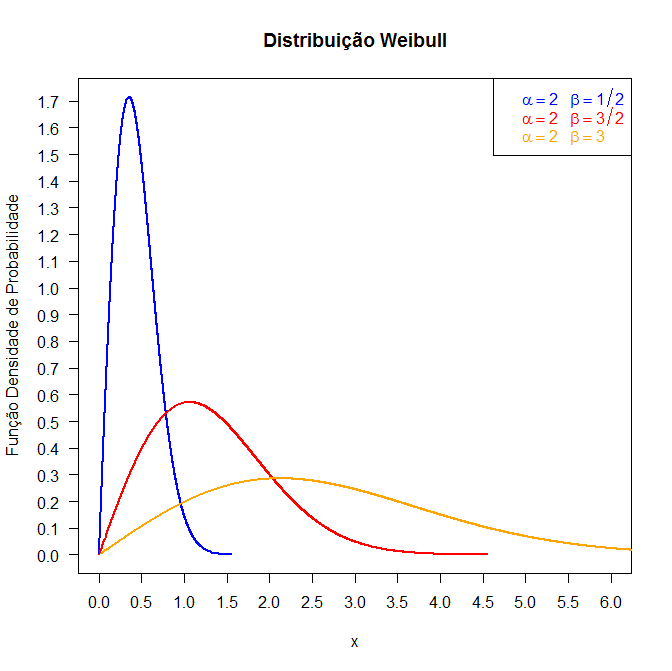
Figura 6.13.1: Gráfico da função densidade da distribuição Weibull.

Função Geradora de Momentos, Valor Esperado e Variância

A função geradora de momentos da função Weibull não tem uma forma fechada, entretanto podemos encontrá-la.

$$\mathbb{E}\left(X^{k}\right)=\int_{0}^{\infty}x^k\frac{\alpha}{\beta^{\alpha}}x^{\alpha-1}e^{-(x/\beta)^{\alpha}}$$

Assim fazendo uma substituição $t=\displaystyle \left(\frac{x}{\beta}\right)^\alpha$, temos que

$$t=\left(\frac{x}{\beta}\right)^\alpha, \quad dt=\frac{\alpha}{\beta^\alpha}x^{\alpha-1}dx \quad \text{e} \quad x^{k}=(t\beta^\alpha)^{k/\alpha}=t^{k/\alpha}\beta^{k}$$

e, desta forma

$$\mathbb{E}\left(X^k\right)=\int_{0}^{\infty}t^{k/\alpha}\beta^{k}e^{-t}dt=\beta^{k}\Gamma\left(\frac{k}{\alpha}+1\right).$$

Assim, sendo $X$ uma variável aleatória com distribuição Weibull, o valor esperado de $X$ é dado por

$$\mathbb{E}(X)=\beta\Gamma\left[1+\left(\frac{1}{\alpha}\right)\right]$$

e a variância é dada por

$$\text{Var}(X)=\mathbb{E}\left(X^2\right)-\mathbb{E}^2\left(X\right)=\beta^{2}\Gamma\left(\frac{2}{\alpha}+1\right)-\left(\beta\Gamma\left(\frac{1}{\alpha}+1\right)\right)^2$$

de onde concluímos que

$$\text{Var}(X)=\beta^2\left(\Gamma\left[1+\left(\frac{2}{\alpha}\right)\right]-\Gamma[1+(1+\alpha)]^2\right)$$

6.14 - Distribuição Gumbel (ou valor extremo)

A distribuição Gumbel ou valor extremo surge quando se toma o logaritmo de uma variável com a distribuição Weibull. Isto é, se a variável $X$ tem uma distribuição Weibull, então a variável $Y = \log(X)$ tem uma distribuição Gumbel. Podemos encontrar mais detalhes sobre essa distribuição na apostila de confiabilidade.

Definição 6.14.1

Uma variável $Y$ tem distribuição Gumbel se tiver função densidade de probabilidade dada por

$$f(x)=\frac{1}{\sigma}\exp\left[\frac{x-\mu}{\sigma}-\exp\left(\frac{x-\mu}{\sigma}\right)\right]\qquad x\in (-\infty,\infty)$$

em que $\sigma=1/\delta$ e $\mu=\log(\alpha)$.

O gráfico abaixo mostra a distribuição gumbel com parâmetros $\mu=0.5$ e $\sigma=2$.

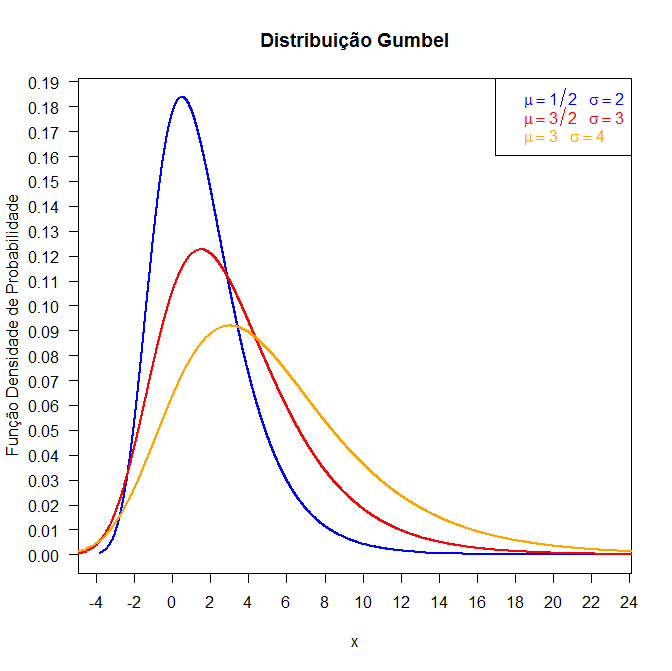
Figura 6.14.1: Gráfico da função densidade da distribuição Gumbel.

Distribuições de valores extremos foram obtidos como limitantes das distribuições de maiores (ou menores) valores em amostras aleatórias de tamanho de amostra crescente. Para obter uma distribuição limitante não degenerada é necessário “reduzir” o maior valor real através da aplicação de uma transformação linear com coeficientes que dependem do tamanho da amostra. Este processo é análogo à normalização embora não limitado a esta sequência particular de transformações lineares.

Se $X_1,\dots,X_n$ são variáveis aleatórias independentes com função densidade de probabilidade comum

$$p_{X_j}(x)=f(x),\quad j=1,\dots, n$$

então a função de distribuição acumulada de $\widetilde{X}_n=\max(X_1,\dots,X_n)$ é dada por

$$F_{\widetilde{X}_n}(x)=[F(x)]^n=\left[\int^x_{-\infty}f(s)ds\right]^n$$

Quando n tende ao infinito, temos que para qualquer valor fixo de x

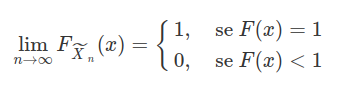
que é uma distribuição degenerada.

Há uma distribuição limitante de interesse, que encontramos como a distribuição limitante de uma sequência de valores transformados “reduzidos”, como por exemplo $(a_n \widetilde{X}_n+b_n)$ em que $a_n$ e $b_n$ podem depender n, mas não de x.

Para distinguirmos a função distribuição acumulada limitante do “reduzido” maior valor de $F(x),$ denotamos por $G(x).$ Então, uma vez que o maior dos valores $Nn$ de $X_1,\dots, X_{Nm}$ é também a maior dos $N$ valores

$$\max(X_{(j-1)n+1},X_{(j-1)n+2},\dots, X_{(j)n}),\quad j=1,\dots,N$$

Com isso, segue que $G(x)$ satisfaz a seguinte equação

$$[G(x)]^N=G(a_N x+b_N)\quad(6.14.1)$$

A distribuição de Gumbel é obtida tomando $a_N=1.$ Logo, temos que

$$[G(x)]^N=G(x+b_N)$$

desde que $G(x+b_N)$ é satisfeita, temos que

$$[G(x)]^{NM}=[G(x+b_N)]^M=G(x+b_N+b_M)$$

Com isso, temos que $b_N+b_M=b_{NM}.$ Assim,

$$b_n=\sigma\log N,\quad \text{com}~\sigma~\text{constante} $$

Tomando o logaritmo duas vezes em (6.14.1) e substituindo o valor de $b_n$ obtemos

$$\log N+\log(-\log G(x))=\log(-\log G(x+\sigma \log N))\quad (6.14.2)$$

Agora, denotamos

$$h(x)=\log(-\log G(x))$$

Logo, de (6.14.2) obtemos que

$$h(x)=h(0)-\frac{x}{\sigma}$$

Desde que $h(x)$ decresce quando x cresce, para $\sigma> 0.$ Da equação anterior obtemos que

$$-\log G(x)=\exp\left(-\frac{x-\sigma h(0)}{\sigma}\right)=\exp\left(-\frac{x-\mu}{\sigma}\right)$$

em que $\mu=\sigma \log(-\log G(0)).$ Portanto

$$G(x)=\exp\left(-\exp\left(-\frac{x-\mu}{\sigma}\right)\right).$$

Para o mínimo temos que

$$H(x)=\mathbb{P}[\min(X_1,\dots,X_n)> x]=1-G(x)=1-\exp\left(-\exp\left(-\frac{x-\mu}{\sigma}\right)\right).$$

Vale lembrar que existem 3 tipos de distribuições do tipo Valor Extremo. O tipo abordado nesta seção é a distribuição Valor Extremo do tipo 1 ou distribuição Gumbel. A seguir, vamos apresentar as formas padronizadas para a distribuição do máximo e do mínimo.

Para o máximo temos:

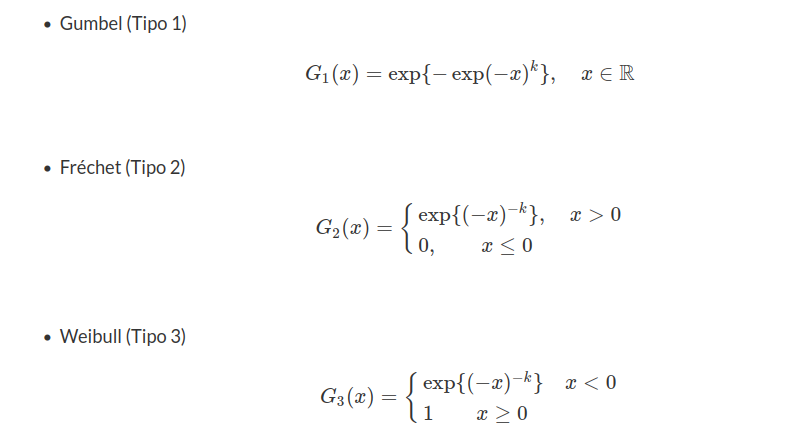
Para o mínimo temos:

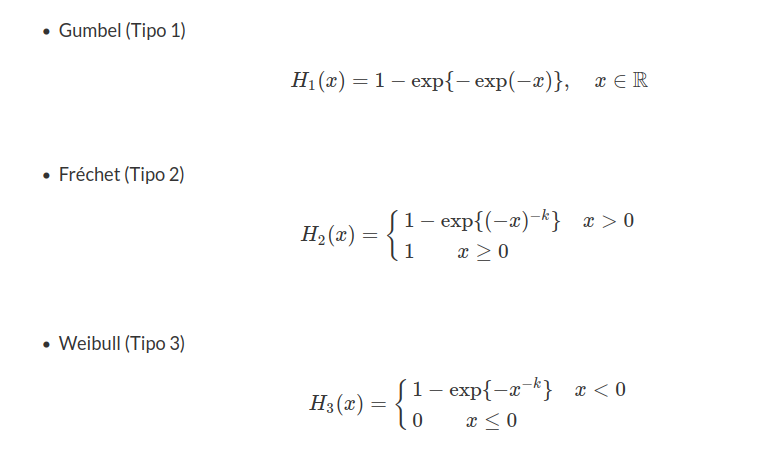
A seguir, resumimos as formas de distribuições limitantes para máximos e mínimos de sete distribuições contínuas mais utilizadas.

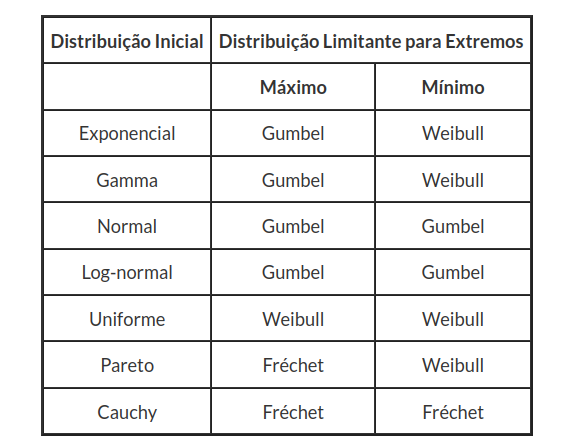
Função Geradora de Momentos, Valor Esperado e Variância

Seja $X$ uma variável aleatória com distribuição Gumbel, observamos que se $\mu=0$ e $\sigma=1,$ a distribuição de $Y=\dfrac{X-\mu}{\sigma},$ obtemos a forma padrão

$$f(y)=\exp(-y-e^{-y})$$

Assim, a variável $Z=\exp(-(X-\mu)/\sigma)=e^{-Y}$ tem distribuição exponencial

$$f(z)=e^{-z},\quad z\geq 0$$

Disto, segue que

$$\mathbb{E}[\exp\left(\frac{t(X-\mu)}{\sigma}\right)]=\mathbb{E}[Z^{-t}]=\Gamma(1-t),\quad \text{para}~t< 1.$$

Portanto, a função geradora de momentos de X é dada por

$$M_X(t)=\mathbb{E}[e^{tX}]=e^{t\mu}\Gamma(1-\sigma t), \quad \sigma|t|< 1$$

e a função geradora acumulada é dada por

$$\kappa(t)=\mu t-\log \Gamma(1-\sigma t)$$

Com isso, o valor esperado de X é dado por

$$\kappa_1(t)=\mathbb{E}[X]=\mu -\sigma\psi(1)=\mu-\gamma \sigma$$

em que $\gamma\approx 0,5772$ é conhecida constante de Euler.

As funções geradoras de ordem superior são dadas por:

$$\kappa_i(t)=(-\sigma)^i\psi^{(i-1)}(1),\quad i\geq 2$$

em que $\psi(.)$ é a função digama.

Portanto, a variância é dada por

$$\text{Var}(X)=\dfrac{1}{6}\pi^2\sigma^2$$

6.15 - Distribuição log-normal

Assim como a distribuição Weibull, a distribuição Log-Normal é muito usada para caracterizar tempo de vida de produtos e materiais. Isto inclui fadiga de metal, semicondutores, diodos e isolação elétrica. Podemos encontrar mais detalhes sobre essa distribuição na apostila de confiabilidade.

Definição 6.15.1

Uma variável aleatória $X$ tem distribuição Log-Normal se sua função densidade de probabilidade for dada por:

em que $\mu\in\mathbb{R}$ é a média do logaritmo do tempo de falha e $\sigma \ > \ 0$ é o desvio padrão.

Existe uma relação entre as distribuições Log-Normal e Normal similar à relação existente entre as distribuições Weibull e do Valor Extremo. Como o nome sugere o logaritmo de uma variável com distribuição Log-Normal com parâmetros $\mu$ e $\sigma$ tem uma distribuição Normal com média $\mu$ e desvio padrão $\sigma$. Esta relação significância que dados provenientes de uma distribuição Log-Normal podem ser analisados segundo uma distribuição Normal se trabalharmos com o logaritmo dos dados ao invés dos valores originais.

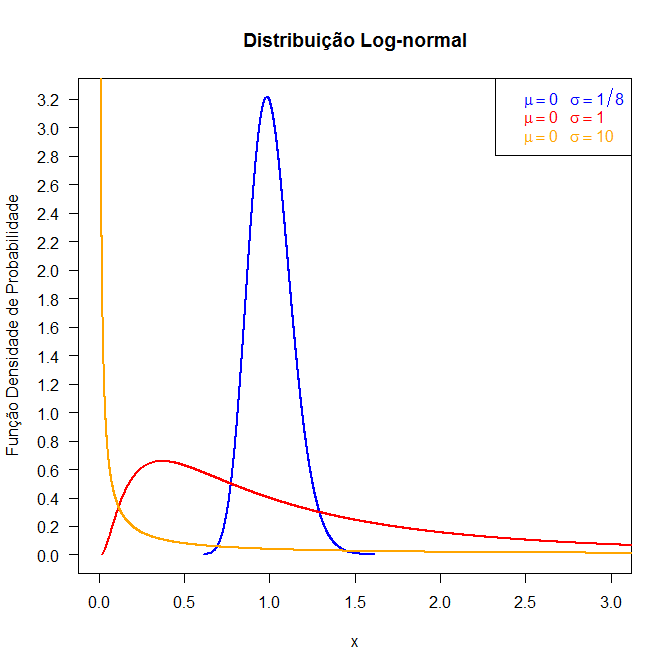
Figura 6.15.1: Gráfico da função densidade da distribuição Log-normal.

Exemplo 6.15.1

Se $X$ segue uma distribuição normal padronizada então, $Y=e^X$ tem distribuição log-normal com parâmetros $\mu=0$ e $\sigma=1$.

De fato se $X$ segue uma distribuição normal padrão, então temos que

$$F_Y(y)=\mathbb{P}(Y\leq y)=\mathbb{P}(e^X\leq y)=\mathbb{P}(X\leq \ln{y})=\int_{-\infty}^{\ln{y}}f_X(x)dx=\int_{\infty}^{\ln{y}}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx.$$

Fazendo uma mudança de variável temos que

$$\int_{\infty}^{\ln{y}}\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx=\int_{0}^{y}\frac{1}{x}\frac{1}{\sqrt{2\pi}}e^{-\frac{\ln{x}^2}{2}}dx$$

e, portanto, a função densidade de probabilidade de $Y$ é uma log-normal com os parâmetros ditos anteriormente.

Função Geradora de Momentos, Valor Esperado e Variância

A função geradora de momentos da log-normal não está definida nos números reais. O valor esperado e a variância da distribuição Log-Normal são dados respectivamente por:

$$\mathbb{E}(X)=\exp\left(\mu+\frac{\sigma^2}{2}\right) \qquad \text{e} \qquad \text{Var}(X)=\exp(2\mu+\sigma^2)(\exp(\sigma^2)-1).$$

6.16 - Distribuição Logística

A função de crescimento logístico foi proposta inicialmente para estudos demográficos, isto é, para estudos de crescimento populacional humano. No livro de Balakrishnan, também cita aplicações como dados de produção agrícola e crescimento de mortalidades. A seguir apresentamos a definição.

Definição 6.16.1

Seja X variável aleatória contínua, dizemos que X tem distribuição Logística com parâmetros de locação μ e de escala s, se a função densidade de probabilidade (f.d.p.) é dada por:

$$f(x)=\frac{\exp\left(\frac{x-\mu}{s}\right)}{s\left(1+\exp\left(\frac{x-\mu}{s}\right)\right)^2},\quad x,\mu\in \mathbb{R},~~\sigma> 0.$$

e sua correspondente função distribuição acumulada (F.D.A.) é dada por:

$$F(x)=\frac{1}{1+\exp\left(-\frac{x-\mu}{s}\right)},\quad x,\mu\in \mathbb{R},~~\sigma> 0.$$

Notação

$X\sim L\left(\mu,s\right)$.

Algumas vezes, para facilitar os cálculos, trabalhamos com a variável aleatória

$$Z=\frac{X-\mu}{s}$$

com f.d.p. dada por:

$$f(x)=\frac{e^{-z}}{(1+e^{-z})^2},\quad z\in \mathbb{R}.$$

e com F.D.A. dada por:

$$F(z)=\frac{1}{1+e^{-z}},\quad z\in\mathbb{R}.$$

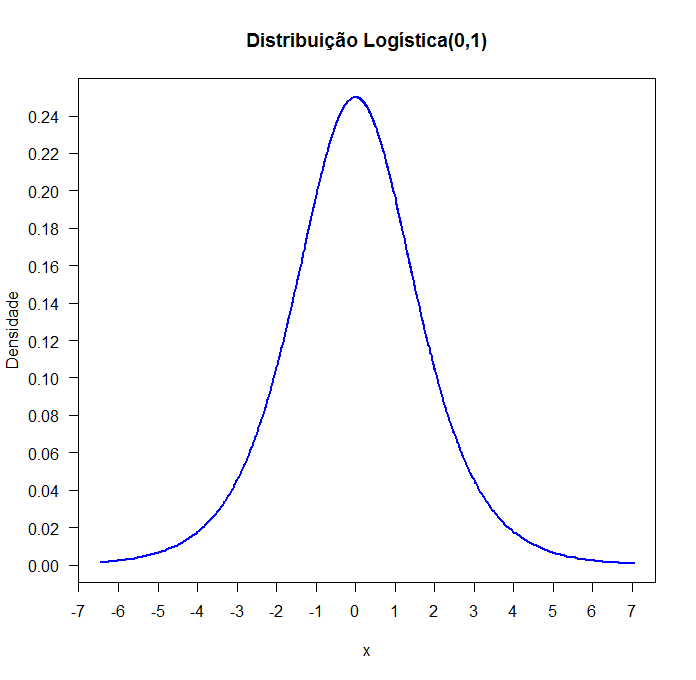
Figura 6.16.1: Função densidade de probabilidade da distribuição L(0,1).

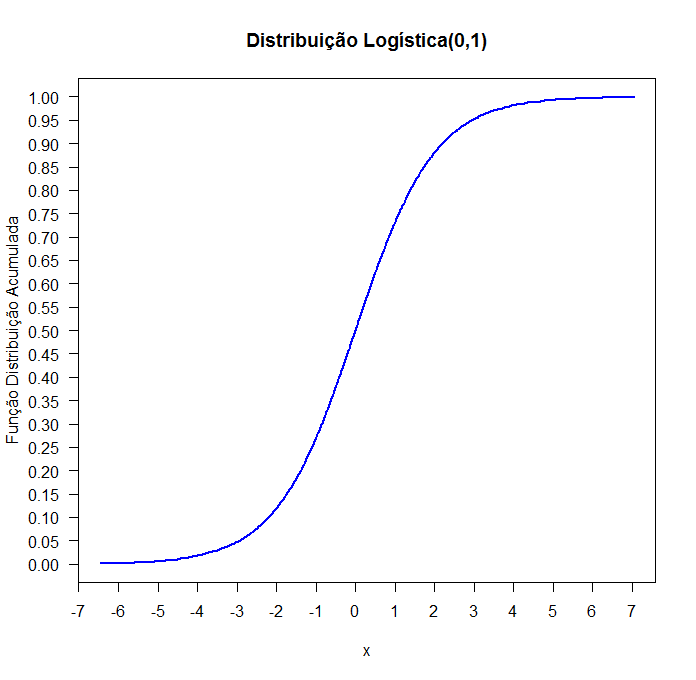
Figura 6.16.2: Função Distribuição Acumulada da distribuição L(0,1).

Função Geradora de Momentos, valor esperado, variância

Agora, vamos estudar a função geradora de momentos da distribuição Logística, para isto, afim de facilitar os cálculos vamos estudar as bases características e suas propriedades da população logística através da variável aleatória Z. Com isso, a função geradora de momentos de Z é:

$$M_Z(t)=\mathbb{E}(e^{tZ})=\int^\infty_{-\infty}\frac{e^{-(1-t)z}}{(1+e^{-z})^2}dz\quad (6.16.1)$$

Fazemos agora uma mudança de variável da seguinte maneira:

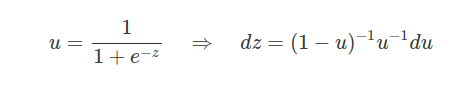
Voltando em (6.16.1) temos que

$$=\int^1_0 u^t(1-u)^t du= B(1+t,1-t)=\Gamma(1+t)\Gamma(1-t)$$

Agora, definimos função geradora acumulada de Z é obtida quando

$$K_Z(t)=\ln M_Z(t)=\ln \Gamma(1+t)+\ln \Gamma(1-t)$$

Derivando em relação a t e aplicando em t=0 temos que

$$\mathbb{E}[Z]=\frac{\Gamma^\prime(1)}{\Gamma(1)}-\frac{\Gamma^\prime(1)}{\Gamma(1)}=\psi^\prime(1)-\psi^\prime(1)=0$$

e

$$\text{Var}(Z)=2[\psi^{\prime\prime}(1)-(\psi^\prime(1))^2]=\frac{\pi^2}{3}$$

Aplicando o valor esperado e variância em ambos os lados em $Z=\frac{\pi(X-\mu)}{\sigma \sqrt{3}}$ obtemos que

$$\mathbb{E}(X)=\mu+\frac{\sigma\sqrt{3}}{\pi}\mathbb{E}(Z)=\mu$$

e

$$\text{Var}(X)=\frac{3\sigma^2}{\pi^2}\text{Var}(Z)=\sigma^2.$$

Exemplo 6.16.1

Seja X variável aleatória contínua com f.d.p. $f_{X}$(x). Então a v.a. $Y=-\ln\left(\frac{e^{-x}}{1-e^{-x}}\right)$ é v.a. com distribuição logística se, e somente se, X tem distribuição exponencial com parâmetro λ=1.

De fato, suponhamos que X tem distribuição exponencial, i.e., para λ=1 temos que

$$f_X(x)=e^{-x}, \quad x\in (0,\infty)$$

Desde que $Y=-\ln\left(\frac{e^{-x}}{1-e^{-x}}\right)$ para $y\in (0,\infty).$

Assim,

$$x=\ln\left(\frac{1+e^{-y}}{e^{-y}}\right)\quad \text{e}\quad |J|=\frac{1}{1+e^{-y}}$$

Com isso, temos que

$$f_Y(y)=|J|f_X(y)=\frac{e^{-y}}{(1+e^{-y})^2},\quad y\in\mathbb{R}$$

Por outro lado, suponhamos que Y é uma v.a. com distribuição logística, então a função distribuição de X é dada por:

$$F_X(x)=\mathbb{P}[X\leq x]=\mathbb{P}\left[\ln\left(\frac{1+e^{-y}}{e^{-y}}\right)\leq x\right]= \mathbb{P}[y\leq \ln(e^{x}-1)]=1-e^{-x}$$

que é a função distribuição da distribuição exponencial com parâmetro λ=1.

Exemplo 6.16.2

Em um experimento realizado por um laboratório, determinou que a concentração de strotitium-90 presentas em uma amostra de leite não devem ultrapassar 9,22 micromicrocuries por litro. Supondo que a concentração de strotitium-90 tenha distribuição logística com parâmetro de locação μ=8,2 e de escala de σ=1, qual a probabilidade da amostra de leite atender a especificação?

A probabilidade é dada por:

$$\mathbb{P}[X\leq 9,22]=\frac{1}{1+\exp\left(-\frac{\pi(x-8,2)}{1\sqrt{3}}\right)}=0,8641$$

Portanto, a probabilidade da amostra de leite atender a especificação é de 86,4%.

Observação 6.16.1

Vale lembrar que a parametrização do software Action é dada por:

$$f(x)=\frac{\exp\left(-\frac{(x-\mu)}{\sigma}\right)}{\left(1+\exp\left(-\frac{(x-\mu)}{\sigma}\right)\right)^2},\quad x,\mu\in \mathbb{R},~~\sigma> 0.$$

Com isso, a resolução do exercício anterior é dada por

$$\mathbb{P}[X\leq 9,22]=\dfrac{1}{1+\exp\left(-\frac{(x-8,2)}{1}\right)}=0,731.$$

6.17 - Distribuições truncadas

Uma distribuição de probabilidade truncada é uma distribuição condicional resultante da restrição do domínio de alguma outra distribuição de probabilidade. Por exemplo, ao examinar as datas de nascimentos de crianças de uma escola, é intuitivo esperar que as idades dessas crianças estejam dentro de um intervalo pois a escola matricula somente crianças dentro de alguma faixa etária especificada.

Definição

Seja $Y$ uma variável aleatória com função densidade de probabilidade $g(y)$ e função de distribuição $G(y), y \in \Re$. A distribuição de probabilidade da variável aleatória $X$, que representa a distribuição de $Y$ no intervalo $[a, b]$, com $-\infty \ < \ a \ < \ b \ < \ \infty$, é uma distribuição de probabilidade truncada

A função densidade de probabilidade é dada por:

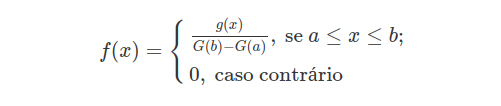
(1)

Demonstração

Temos que,

$$P(X=x)=P(Y=y|\ a\leq x\leq b)=\dfrac{P(Y=y;\ a\leq x\leq b)}{P(\ a\leq x\leq b)}=\dfrac{P(Y=y)}{P(\ a\leq x\leq b)}=\dfrac{g(y)}{G(b)-G(a)}$$

A função de distribuição é dada por

$$F(x)=\dfrac{G(max[min(x,b),a])-G(a)}{G(b)-G(a)};\ a\leq x\leq b.$$

Nesse caso, o trucamento é chamado intervalar ou truncamento duplo, pois restringimos a distribuição em um intervalo fechado $[a, b]$. Quando a restrição ocorre em apenas um lado, temos o truncamento simples, simples à direita para $(-\infty, b]$ ou simples à esquerda para $[a, \infty)$

6.17.1 - Distribuição normal truncada

A distribuição normal truncada é uma distribuição de probabilidade de uma variável aleatória normal delimitada inferiormente, superiormente ou ambos. Essa distribuição tem ampla aplicação em estatística e econometria, por exemplo, ela é usada para modelar saídas binárias no modelo probito e modelar dados com censura no modelo tobito. Para detalhes de exemplos em econometria veja Greene, William H. (2003).

Definição

Seja $Y$ uma variável aleatória $N(\mu,\sigma^2)$ com função densidade de probabilidade

$$g(y)=\frac{1}{\sigma\sqrt{2\pi}}\exp\left\lbrace-\frac{(y-\mu)^2}{2\sigma^2}\right\rbrace, y \in \Re$$

e função de distribuição

$$G(y) = \int_{-\infty}^y g(z) dz.$$

A variável aleatória contínua $X$ tem distribuição normal truncada em $[a,b]$ com os parâmetros $\mu, \sigma^2$ se sua função densidade de probabilidade for dada por

Notação

$$X \sim NT(\mu,\sigma^2;a,b)$$

Demonstração

A demonstração ocorre direto da equação (1).

Note que

$$g(x) = \dfrac{1}{\sigma \sqrt{2\pi} } \exp \left\lbrace -\dfrac{1}{2} \left( \dfrac{x-\mu}{\sigma} \right)^2 \right\rbrace = \dfrac{1}{\sigma}\dfrac{1}{\sqrt{2\pi} } \exp \left\lbrace -\dfrac{1}{2} \left( \dfrac{x-\mu}{\sigma} \right)^2 \right\rbrace = \dfrac{1}{\sigma} \phi \left( \dfrac{x-\mu}{\sigma} \right)$$

No caso em que o truncamento é simples à direita, temos

$$f(x) = P( X = x) = P( Y=y | y \leq b) = \dfrac { P( Y=y ; y \leq b ) }{ P( y \leq b) } = \dfrac{P(Y=y)}{ P( y \leq b) } = \dfrac{ g(y) }{G(b)}$$

No caso em que o truncamento é simples à esquerda, temos

$$f(x) = P( X = x) = P( Y=y | y \geq a) = \dfrac { P( Y=y ; y \geq a ) }{ P( y \geq a) } = \dfrac{P(Y=y)}{ P( y \geq a) } = \dfrac{ g(y) }{1-G(a)}$$

A função de distribuição é dada por:

$$F(x) = \dfrac{ G(x) - G(a) }{ G(b) - G(a) } = \dfrac{ \Phi( \frac{x-\mu}{\sigma} ) - \Phi( \frac{a-\mu}{\sigma} ) }{ \Phi( \frac{b-\mu}{\sigma} ) - \Phi( \frac{a-\mu}{\sigma} ) },$$

onde $\Phi(\cdot)$ é a função de distribuição da normal padrão.

Demonstração

$$F(x) = \int_a^x f(x)dx = \int_a^x \dfrac{ g(x) }{ G(b) - G(a) } dx = \dfrac{1}{G(b) - G(a)} \int_a^x g(x) dx = \dfrac{ G(x) - G(a) }{ G(b) - G(a) }$$

A esperança é dada por:

$$E(X) = \mu + \dfrac{ \phi \left( \frac{a-\mu}{\sigma} \right) - \phi \left( \frac{b-\mu}{\sigma} \right) }{ \Phi \left( \frac{b-\mu}{\sigma} \right) - \Phi \left( \frac{a-\mu}{\sigma} \right) } \sigma,$$

em que $\phi(\cdot)$ é a f.d.p. e $\Phi(\cdot)$ é a função de distribuição da distribuição normal padrão.

• Quando o truncamento é simples à direita, temos,

$$E(X) = E(Y | Y \leq b) = \mu -\sigma \dfrac{\phi \left( \frac{b-\mu}{\sigma} \right) }{ G(b) }$$

• Quando o truncamento é simples à esquerda, temos,

$$E(X) = E(Y | Y \geq a) = \mu +\sigma \lambda( \alpha ),$$

em que $\alpha = \dfrac{ a-\mu }{ \sigma }$ e $\lambda( \alpha ) = \dfrac{ \phi( \alpha )}{ 1 - G(a) }$

A variância é dada por:

$$Var(X) = \left[ 1 + \dfrac{ \left( \dfrac{a - \mu}{\sigma } \right) \phi \left( \dfrac{a - \mu}{\sigma } \right) - \left( \dfrac{b - \mu}{\sigma } \right) \phi \left( \dfrac{b - \mu}{\sigma } \right) }{ G(b) - G(a) } \right] \sigma^2 - \left[ \dfrac{ \phi \left( \dfrac{a - \mu}{\sigma } \right) - \phi \left( \dfrac{b - \mu}{\sigma } \right) } { G(b) - G(a) } \right]^2 \sigma^2,$$

em que $\phi(\cdot)$ é a função densidade de probabilidade da distribuição normal padrão.

• Quando o truncamento é simples à direita, temos,

$$Var(X) = Var( Y | Y \leq b) = \sigma^2 \left[ 1 - \beta \dfrac{ \phi(\beta) }{ G(b) } - \left( \dfrac{ \phi( \beta) }{ G(b) } \right)^2 \right],$$

em que $\beta = \dfrac{b - \mu}{ \sigma }$

• Quando o truncamento é simples à esquerda, temos,

$$Var(X) = Var( Y | Y \geq a) = \sigma^2 [ 1 - \delta( \alpha ) ],$$

em que $\alpha = \dfrac{ a-\mu }{ \sigma }, \delta( \alpha ) = \lambda(\alpha) [ \lambda(\alpha) - \alpha ]$ e $\lambda( \alpha ) = \dfrac{ \phi( \alpha )}{ 1 - G(a) }$

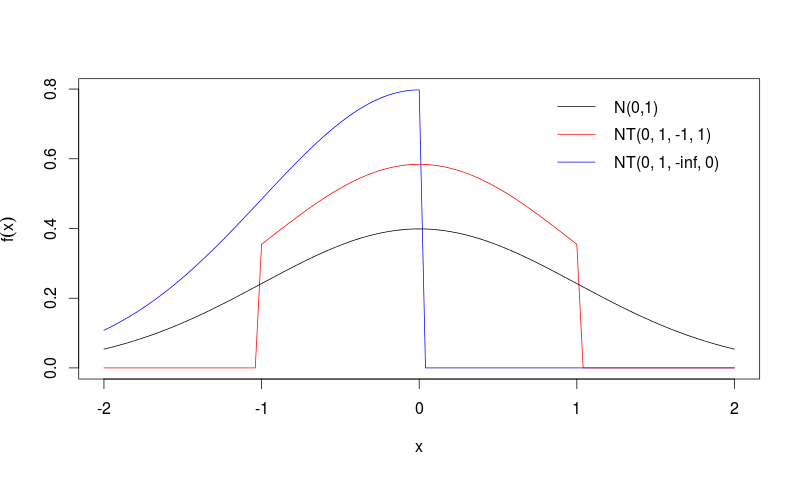
Figura 1: Exemplos de curvas da distribuição normal truncada

Exemplo 6.17.1.1

Considere o Exemplo 6.2.4 em que o peso médio de 800 porcos de uma fazenda é de 64kg e o desvio padrão é de 15kg. Suponha que este peso seja distribuído de forma normal. Entretanto, devido à sua raça, cada porco peso no mínimo 30kg e no máximo 120kg. Quantos porcos pesarão entre 42kg e 73kg?

Seja $ X_i $ a variável aleatória que representa o peso de um porco.

Como admitido no enunciado, $ X_i \sim NT(64, 15^2; 30, 120), i=1, \ldots, 800. $ Assim, a probabilidade de um porco $ i $ estar entre 42kg e 73kg é

$$P( 42 \leq X_i \leq 73) = P( X_i \leq 73) - P(X_i \leq 42) = F(73) - F(42),$$

em que $ F(\cdot) $ é a função de distribuição de $ X $.

Utilizando a fórmula da função de distribuição, temos,

$$P( 42 \leq X_i \leq 73) = F(73) - F(42) =$$

$$= \dfrac{ \Phi\left( \dfrac{73-64}{15} \right) - \Phi\left( \dfrac{30-64}{15} \right) }{ \Phi\left( \dfrac{120-64}{15} \right) - \Phi\left( \dfrac{30-64}{15} \right) } - \dfrac{ \Phi\left( \dfrac{42-64}{15} \right) - \Phi\left( \dfrac{30-64}{15} \right) }{ \Phi\left( \dfrac{120-64}{15} \right) - \Phi\left( \dfrac{30-64}{15} \right) } =$$

$$=\dfrac{ 0,7257 - 0,0117 }{0,999 - 0,0117} - \dfrac{ 0,0712 - 0,0117 }{ 0,999 - 0,0117 } =$$

$$= \dfrac{0,714}{0,9882} - \dfrac{0,0595}{0,9882} =$$

$$= 0,7225 - 0,0602 = 0,6623 (66,23(porcentagem))$$

Portanto, a quantidade esperada de porcos entre 42kg e 73kg é de $ 800 \times 0,6623 = 529,8523 \approx 530 $

A área hachurada do gráfico da Figura 2, representa a probabilidade do porco pesar entre 42kg e 73kg, como calculado acima.

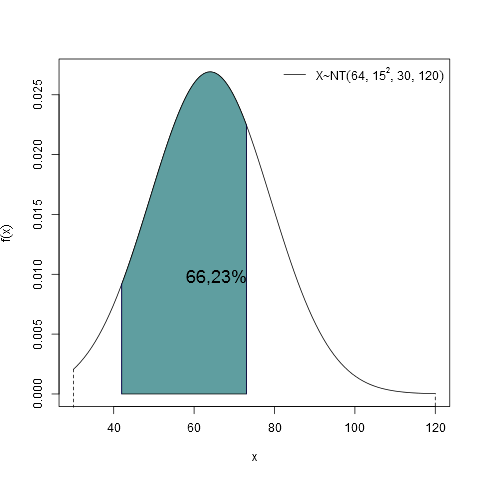
Figura 2: Gráfico da distribuição normal com média 64, desvio padrão 15, truncada de 30 a 120, destacando a área entre 42 e 73.

Exemplo 6.17.1.2

Suponha que o peso de uma melancia seja normalmente distribuído com média 7kg e desvio padrão de 2,5kg. As melancias abaixo de 3kg são descartadas pelo produtor e não são repassadas para o mercado.

a) Calcule o peso médio esperado e o desvio padrão de uma melancia no mercado.

Usando a fórmula da esperança para o truncamento simples à esquerda temos,

$$\alpha = \dfrac{ a-\mu }{ \sigma } = \frac{3-7}{2,5} = -1,6$$

e

$$\lambda( \alpha ) = \lambda( -1,6 ) = \dfrac{ \phi( -1,6 )}{ 1 - \Phi \left( \dfrac{3-7}{2,5} \right) } =\dfrac{ \phi( -1,6 )}{ 1 - \Phi \left( -1,6 \right) } = \dfrac{0,1109}{0,9452} = 0,1173$$

Assim,

$$E(X) = \mu + \sigma \lambda(\alpha) = 7 + 2,5 \times 0,1173 = 7,2933Kg \approx 7,3Kg$$

Variância e desvio padrão:

Agora,

$$\delta(\alpha) = \lambda(\alpha)[ \lambda(\alpha)-1 ] = 0,1173(0,1173-1) = -0,1035$$

Assim,

$$\text{Var}(X) = \sigma^2 (1 - \delta(\alpha) ) = 2,5^2 (1 -(-0,1035)) = 6,8971$$

Extraindo a raiz quadrada da variância chegamos ao desvio padrão

$$s = \sqrt{\text{Var}(X)} = \sqrt{6,8971} = 2,6262kg \approx 2,6kg$$

6.18 - Distribuições mistas

Uma distribuição de probabilidade mista é uma mistura de duas ou mais distribuições de probabilidades, por exemplo, uma distribuição $N(\mu, \sigma^2)$ e uma $\exp(\lambda)$. Essas distribuições são chamadas de componentes mistas.

A distribuição mista é contínua quando todas as componentes mistas também são e sua função densidade de probabilidade pode ser chamada de Densidade Mista. A função de distribuição acumulada da distribuição mista (ou função densidade de probabilidade se existir) pode ser expressa como uma combinação linear de outras funções de distribuição (ou funções densidades), isto é, uma soma ponderada, com pesos não negativos que somam 1. Os pesos associados para cada componente são chamados de pesos mistos ou somente pesos. O número de componentes pode ser finito, infinito e enumerável ou infinito e não enumerável. As componentes mistas são chamadas de distribuições compostas quando são enumeráveis ou infinitas e não enumeráveis.

Conjunto Finito e Infinito Enumerável

Dado um conjunto finito de funções densidades de probabilidade $p_1(x), p_2(x), \ldots, p_n(x)$, ou funções de distribuições $P_1(x), P_2(x), \ldots, P_n(x)$ e seus respectivos pesos $w_1, w_2, \ldots, w_n$ com $w_i \geq 0$ e $\displaystyle\sum_{i=1}^n w_i = 1, i=1, \ldots\ n$, a função densidade da distribuição mista, $f$, ou sua função de distribuição, $F$, são dadas, respectivamente, por,

$$ f(x) = \sum_{i=1}^n w_i p_i(x) $$ $$ F(x) = \sum_{i=1}^n w_i P_i(x).$$

O caso em que o conjunto das componentes é finito tem-se que $n$ é finito e nos casos em que esse conjunto é infinito enumerável tem-se que $n = \infty$.

Conjunto Infinito Não Enumerável

Chama-se de distribuição de probabilidade composta os casos em que o conjunto das componentes é infinito não enumerável. Considere a função densidade de probabilidade da componente $a$ dada por $p(x;a), a \in A$ e seu respectivo peso $w(a)$ tal que $\int_A w(a) da = 1, w(a) \geq 0$. Assim,

A função densidade de probabilidade mista é dada por

$$ f(x) = \int_A w(a) p(x;a) da $$

e a função de distribuição é dada por,

$$ F(x) = \int_A w(a) P(x;a) da, $$

em que $P(x;a)$ é a função de distribuição da componente $a$.

Distribuição Mista de famílias de distribuições paramétrica

As componentes mistas fazem partes de uma mesma família de distribuição paramétrica, por exemplo a distribuição normal, com diferentes valores para os parâmetros. Nesse caso, a função densidade de probabilidade pode ser escrita por,

$$f(x; a_1, \ldots, a_n) = \sum_{i=1}^n w_i p(x;a_i) \text{ no caso uniparamétrico,}$$

$$ f(x; a_1, \ldots, a_n, b_1, \ldots, b_n) = \sum_{i=1}^n w_i p(x;a_i,b_i) \text{ para dois parâmetros, e assim por diante.}$$

Momentos

Sejam $X_1, \ldots, X_n$ variáveis aleatórias de $n$ distribuições compostas e seja $X$ a variável aleatória da distribuição mista. Assim, para qualquer função $H(.)$, desde que $E[H(X_i)]$ exista, e assumindo que as densidades da distribuições componentes $p_i(x)$ existam,

$$E[H(X)] = \int_{-\infty}^\infty H(x) \sum_{i=1}^n w_i p_i(x) dx = \sum_{i=1}^n \int_{-\infty}^\infty p_i(x)H(x)dx = \sum_{i=1}^n w_i E[H(X_i)] $$

Para $H(X) = X^j$, tem-se que o j-ésimo momento de $X$ é simplesmente a média ponderada dos j-ésimos momentos das componentes, isto é,

$$ E[X^j] = \sum_{i=1}^n w_i E[X_i^j] $$.

O momento central $H(X) = (X - \mu)^j$ envolve uma expansão binomial,

$$ E[(X-\mu)^j] = \sum_{i=1}^n w_i E[(X_i - \mu)^j] = \sum_{i=1}^n w_i E[(X_i - \mu_i + \mu_i - \mu)^j] = \sum_{i=1}^n \sum_{k=0}^j \binom{j}{k} (\mu_i - \mu)^{j-k} w_i E[ (X_i-\mu_i)^k ], $$

em que $\mu_i$ denota a média da i-ésima componente.

6.18.1 - Distribuição Normal Mista

A distribuição normal mista é a mistura de duas ou mais distribuições normais, ou seja, as distribuições compostas são normais. Essa distribuição é geralmente usada para modelar dados cujo pico e caldas são maiores do que a normal. A Figura 6.18.1 representa o histograma de um conjunto de dados simulados e a curva normal com a mesma média e variância usadas na simulação. Note que a distribuição empírica é mais alta e possui caldas mais longas comparadas à distribuição normal. Para maiores detalhes sobre a distribuição normal mista veja Sylvia Frühwirth-Schnatter (2006)

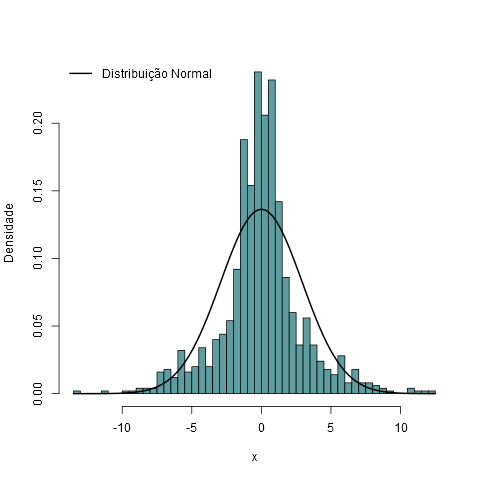
Figura 6.18.1: Histograma de uma distribuição normal mista com a curva da distribuição normal.

Definição

Sejam $X_1, X_2, \ldots, X_n$ variáveis aleatórias com distribuição normal em que suas funções densidades de probabilidade são dadas, respectivamente, por $p_1, p_2, \ldots, p_n$, em que $p_i \sim N(\mu_i,\sigma^2_i), i=1,\ldots,n.$

A função densidade de probabilidade da distribuição normal mista é dada por,

$$ f(x) = \sum_{i=1}^n w_i p_i(x) = \sum_{i=1}^n w_i \dfrac{1}{\sigma_i \sqrt{2\pi}} \exp \left\lbrace \dfrac{ -(x-\mu_i)^2}{ 2 \sigma^2_i } \right\rbrace, $$

em que, $\sum_{i=1}^n w_i = 1$

A função de distribuição é dada por,

$$F(x) = \sum_{i=1}^n w_i \Phi \left( \dfrac{x-\mu_i}{\sigma_i} \right),$$

em que $\Phi(\cdot)$ é a função de distribuição da $N(0,1)$

Notação: $X\sim\text{Normal Mista}(\boldsymbol\mu, \boldsymbol\sigma^2, \mathbf{w})$

em que $\boldsymbol\mu= (\mu_1, \mu_2, \cdots, \mu_n)$, $\boldsymbol\sigma^2=(\sigma^2_1, \sigma^2_2, \cdots, \sigma^2_n)$ e $\mathbf{w} = (w_1, w_2, \cdots, w_n)$

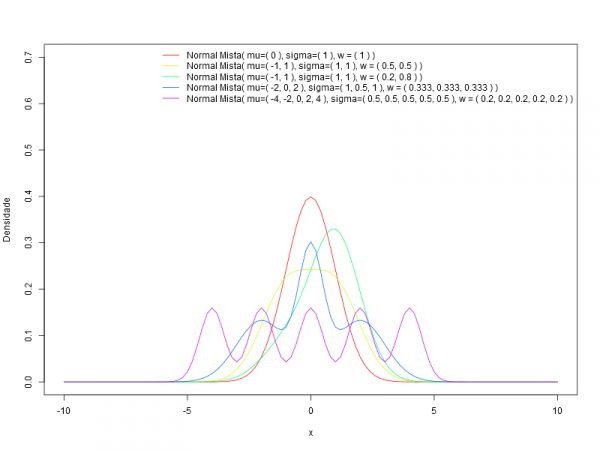
Figura 6.18.2: Curva da função densidade de probabilidade da distribuição normal mista

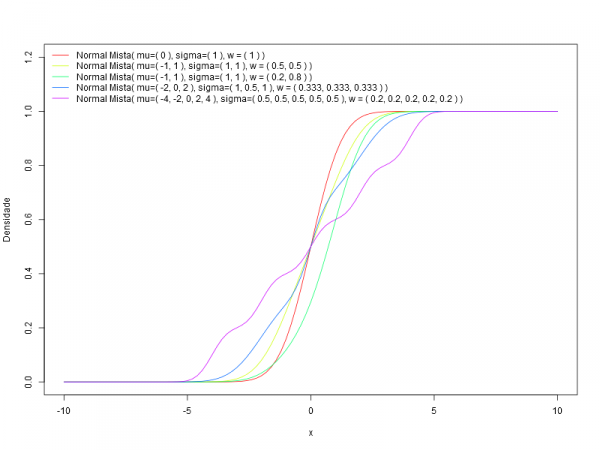
Figura 6.18.3: Curva da função de distribuição da normal mista

Esperança e Variância

Como vimos na seção 6.18 Distribuições Mistas, a esperança e a variância da distribuição normal mista são dadas por,

$$E(X) = \sum_{i=1}^n w_i E[X_i] = \sum_{i=1}^n w_i \mu_i$$

$$Var(X) = E[(X-\mu)^2] = \sum_{i=1}^n w_i( (\mu_i-\mu)^2 + \sigma^2_i )$$

Exemplo 6.18.1.1

Médias iguais e variâncias diferentes}

Considere duas populações tais que $X_1 \sim N(0,1)$ e $X_2 \sim N(0,25)$. Calculando a esperança e a variância, considerando $w_1=w_2=1/2$ temos,

$$E(X) = \left(\frac{1}{2} \times 0 \right) + \left( \frac{1}{2} \times 0 \right) = 0$$

$$Var(X) = \frac{1}{2} \left[ (0-0)^2 + 1 \right] + \frac{1}{2} \left[ (0-0)^2 + 25 \right] = \frac{1}{2} ( 1 + 25 ) = 26 \times \frac{1}{2} = 13$$

Geralmente quando as médias são iguais a densidade se assemelha a de uma distribuição normal, entretanto com as caldas mais longas e com o pico mais alto. No gráfico da Figura 6.18.4, é apresentado o histograma desses dados simulados e as curvas da distribuição normal e da normal mista.

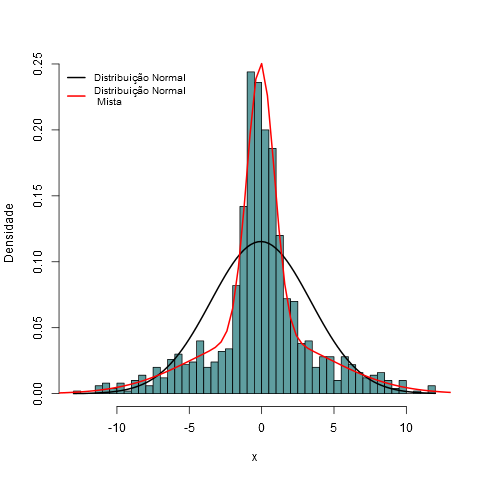
Figura 6.18.4: Distribuição normal mista. Componentes mistas com médias iguais e variâncias diferentes

Exemplo 6.18.1.2

Médias diferentes

Considere duas populações tais que $X_1 \sim N(0,1)$ e $X_2 \sim N(5,1)$. Calculando a esperança e a variância, considerando $w_1=w_2=1/2$ temos,

$$ E(X) = (\frac{1}{2} \times 0) + (\frac{1}{2} \times 5) = 0 + \frac{5}{2} = \frac{5}{2}$$

$$ Var(X) = \frac{1}{2} \left[ (0-5/2)^2 + 1 \right] + \frac{1}{2} \left[ (5-5/2)^2 + 1 \right] = \frac{1}{2} \left[ 25/4 + 1 + 25/4 + 1 \right] = \frac{1}{2} \times \frac{29}{2} = \frac{29}{4}$$

Geralmente quando as médias são diferentes a densidade da distribuição mista apresenta picos referentes as médias $\mu_i$ das componentes. No gráfico da Figura 6.18.5, é apresentado o histograma desses dados simulados e as curvas da distribuição normal e da normal mista.

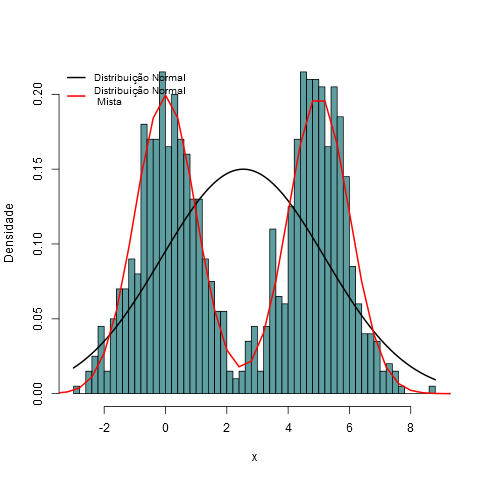
Figura 6.18.5: Distribuição normal mista. Componentes mistas com médias diferentes

6.19 - Distribuição de Rayleigh

A distribuição de Rayleigh, homenagem ao Físico e matemático inglês John William Strutt conhecido como o terceiro barão de Rayleigh, é uma distribuição de probabilidade contínua para valores positivos. Geralmente, essa distribuição é observada quando a magnitude global de um vetor está relacionada com os seus componentes de direção. Por exemplo, quando a velocidade do vento é analisada em duas direções, ou seja, um vetor de componentes bidimensional. Assumindo que as componentes são independentes e normalmente distribuídas com média zero e variâncias iguais, então a velocidade geral do vento tem um a distribuição de Rayleigh. Veja Siddiqui, M. M. (1964) para mais detalhes.

Teorema

Sejam $ U \sim N(0, \sigma^2) $ e $ V \sim N(0, \sigma^2) $ variáveis aleatórias independentes. Então, $ X = \sqrt{ U^2 + V^2 } $ segue uma distribuição de Rayleigh.

Notação: $ R \sim \text{Rayleigh}(\sigma) $

Dessa maneira, a função densidade de probabilidade $ f $ e a função de distribuição $ F $ são dadas, respectivamente, por,

$$f(x;\sigma) = \dfrac{x}{\sigma^2} \exp \left\lbrace \dfrac{-x^2}{2 \sigma^2} \right\rbrace$$

$$F(x) = 1 - \exp \left\lbrace \dfrac{-x^2}{2 \sigma^2} \right\rbrace; x \geq 0; \sigma > 0$$

Os gráficos da função densidade de probabilidade e da função de distribuição para $ \sigma = 1, 2, 3, 4, 5 $ estão apresentados na Figura 1.

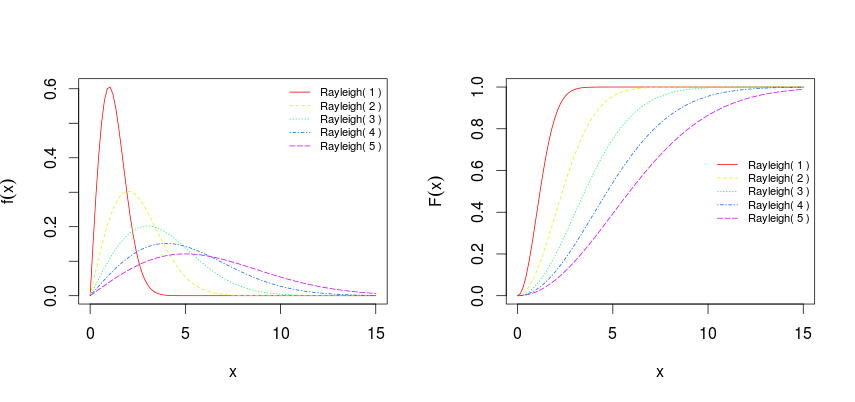
Figura 1: Curvas das funções densidades de probabilidade (gráfico da esquerda) e as curvas das funções de distribuições (gráfico a direita) para $ \sigma = 1, 2, 3, 4, 5 $

Demonstração

Sejam $ U \sim N(0, \sigma^2) $ e $ V \sim N(0, \sigma^2) $. A função densidade de probabilidade conjunta de $ U $ e $ V $ é

$$f(u,v)=f(u)f(v)=\left[ \dfrac{1}{\sigma \sqrt{2\pi}} \exp\left\lbrace \dfrac{-u^2}{2\sigma^2} \right\rbrace \right] \times \left[ \dfrac{1}{\sigma \sqrt{2\pi}} \exp\left\lbrace \dfrac{-v^2}{2\sigma^2} \right\rbrace \right] =$$

$$=\dfrac{1}{2 \pi \sigma^2 } \exp\left\lbrace \dfrac{-(u^2 + v^2)}{ 2\sigma^2 } \right\rbrace =$$

$$=\dfrac{1}{2\pi\sigma^2} \exp \left\lbrace \frac{-1}{2} \left( \frac{u^2}{\sigma^2} + \frac{v^2}{\sigma^2} \right) \right\rbrace$$

$$= \dfrac{1}{2\pi\sigma^2} \exp \left\lbrace \frac{-1}{2} \left( \dfrac{u^2 + v^2}{ \sigma^2 } \right) \right\rbrace, (u,v) \in \Re^2$$

Agora, a função de distribuição é

$$F(x)=P(X \leq x)=\int_{A_x} f(u,v) d(u,v) = \int_{A_x} \dfrac{1}{2\pi\sigma^2} \exp \left\lbrace \frac{-1}{2} \left( \dfrac{u^2 + v^2}{ \sigma^2 } \right) \right\rbrace d(u,v)$$

em que $ A_x = ((u,v) \in \Re^2 : u^2 + v^2 \leq x^2) $

Mudando para coordenadas polares, temos

$$u = r \cos(\theta)$$

$$v = r \text{sen}(\theta)$$

Assim,

$$u^2 + v^2 = r^2 \cos^2(\theta) + r^2 \text{sen}^2(\theta) = r^2 ( \cos^2(\theta) + \text{sen}^2(\theta)) = r^2.$$

Portanto,

$$F(x)=\int_0^{2\pi} \int_0^x \dfrac{1}{2 \pi \sigma^2} \exp \left\lbrace -\dfrac{r^2}{2 \sigma^2} \right\rbrace r dr d\theta$$

$$=\dfrac{1}{2 \pi \sigma^2} \int_0^{2\pi} d\theta \int_0^x \exp \left\lbrace -\dfrac{r^2}{2 \sigma^2} \right\rbrace r dr$$

$$=\dfrac{1}{\sigma^2} \int_0^x \exp \left\lbrace -\dfrac{r^2}{2 \sigma^2} \right\rbrace r dr$$

$$=\int_0^x \dfrac{r}{\sigma^2} \exp \left\lbrace -\dfrac{r^2}{2 \sigma^2} \right\rbrace dr$$

$$=\int_0^x f(r) dr$$

Portanto, a função densidade de probabilidade de $ X $ é,

$$f(x)=\dfrac{x}{\sigma^2} \exp \left\lbrace -\dfrac{x^2}{2 \sigma^2} \right\rbrace, x \geq 0$$

Para mostrar a função de distribuição, basta resolver,

$$F(x)=\int_0^x f(r)dr = \int_0^x \dfrac{r}{\sigma^2} \exp \left( -\dfrac{r^2}{2\sigma^2} \right) dr$$

Substituindo $ z=r^2 $ e $ dz = 2r dr $ em (2), temos,

$$F(x) = \int_0^{x^2} \dfrac{1}{2\sigma^2} e^{-z / 2\sigma^2} dz = -\exp \left( -\dfrac{z}{2\sigma^2} \right)_0^{x^2} = 1 - \exp \left( -\dfrac{x^2}{2\sigma^2} \right) \square$$

A esperança e a variância são dados, respectivamente, por,

$$E(X)=\sigma \sqrt{\dfrac{\pi}{2}} \approx 1,253 \sigma \qquad \qquad (3)$$

$$Var(X)=\dfrac{4-\pi}{2} \sigma^2 \approx 0,429 \sigma^2 \qquad \qquad (4)$$

Exemplo

Sejam $ U $ e $ V $ variáveis aleatórias contínuas e independentes com $ U \sim N(0, 1) $ e $ V \sim N(0, 1) $. Seja $ X = \sqrt{U^2 + V^2} $

a) Calcule a esperança e a variância da distribuição de $ X $

Sabemos que $ X \sim \text{Rayleigh}(1) $. Portanto, pela equação 3, a esperança é dada por,

$$E(X) = \sqrt{\dfrac{\pi}{2}}\sigma \approx 1,253 \sigma \approx 1,253$$

E pela equação 4 a variância de $ X $ é dada por,

$$ Var(X) = \dfrac{4-\pi}{2} \sigma^2 = 0,429$$

Neste caso em que $ \sigma = 1 $ a distribuição de $ X $ é denominada \emph{Rayleigh Padrão}

b) Calcule a área sob a curva de $ X $ maior que $ 1 $.

A área sob a curva da distribuição de $ X $ maior que $ 1 $ é dada por

$$P( X > 1 ) = 1 - P( X \leq 1 ) = 1 - F(1) = 1 - \left[ 1 - \exp\left( -\dfrac{1}{2} \right) \right] = e^{-1/2} \approx 0,6065 \text{ ou } 60,65(porcentagem)%$$

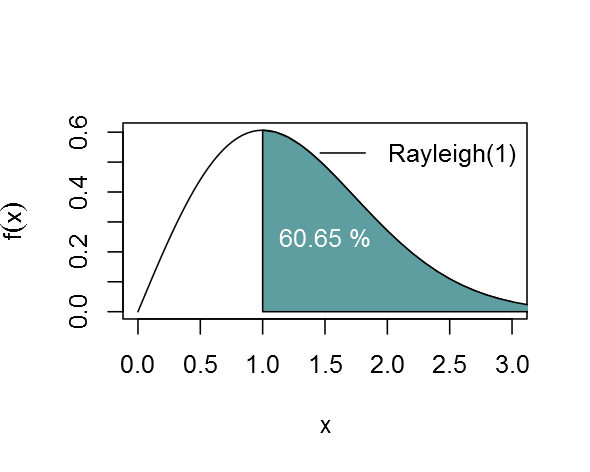
Figura 2: Curva da distribuição de Rayleigh para $ \sigma =1 $. A área hachurada representa $ P(X > 1) $

6.20 - Distribuição normal dobrada

A distribuição normal dobrada é a distribuição dos valores absolutos de uma variável aleatória com distribuição normal. O nome vem do fato dos valores da distribuição normal no intervalo $ \mathbf{(-\infty, 0]} $ “sobreporem” os valores no intervalo $ \mathbf{ [0, \infty) } $, ou seja, os valores negativos da distribuição normal dobram na parte positiva (ver Figura 1). Um dos primeiros exemplos, segundo \emph{Tsagris, 2014}, nos anos 60, foi o uso da distribuição normal dobrada para estudar a magnitude do desvio do alinhamento de um automóvel (magnitude of deviation of an automobile strut alignment). Veja TSAGRIS, Michail; at al. (2014) para maiores detalhes.

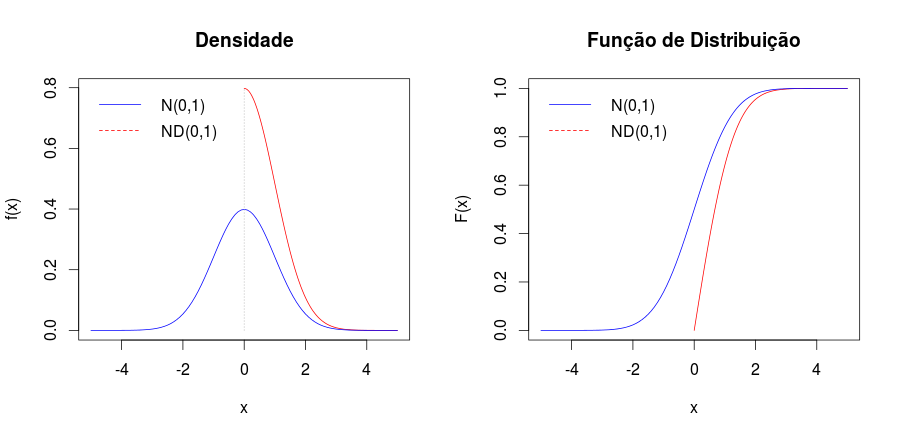
Figura 6.20.1: Distribuição normal vs Distribuição Normal Dobrada

Definição

Sejam $ Y \sim N( \mu, \sigma^2 ) $ com função densidade de probabilidade dada por

$$f(y) = \dfrac{1}{\sqrt{2 \pi \sigma^2}} e^{ -\frac{(y-\mu)^2}{ 2 \sigma^2 } }, -\infty < y < \infty$$

Assim, $ X = |Y| $ tem distribuição normal dobrada com os parâmetros $ (\mu, \sigma^2) $ e sua função densidade de probabilidade é dada por

$$f(x) = \dfrac{1}{\sqrt{2 \pi \sigma^2}} \left[ e^{ -\frac{(x-\mu)^2}{ 2 \sigma^2 } } + e^{ -\frac{(x+\mu)^2}{ 2 \sigma^2 } } \right], x \geq 0$$

Notação:$ X \sim ND( \mu, \sigma^2 ) $

Propriedade

Seja $ Z \sim N(0,1) $. Assim, $ X = |\mu + \sigma Z| \sim ND( \mu, \sigma^2 ) $.

A função de distribuição de $ X $ é dada por

$$F_X(x)=\Phi \left( \dfrac{x-\mu}{\sigma} \right) - \Phi \left( \frac{-x - \mu}{\sigma} \right)=\Phi \left( \dfrac{x-\mu}{\sigma} \right) + \left[ \Phi \left( \frac{x + \mu}{\sigma} \right) -1 \right]$$

$$=\dfrac{1}{\sqrt{2\pi\sigma^2}} \left\lbrace \exp \left[ -\dfrac{(y+\mu)^2}{2\sigma^2} \right] + \exp \left[ -\dfrac{(y-\mu)^2}{2\sigma^2} \right] \right\rbrace dy \qquad \qquad (1)$$

Demonstração:

$$F_X(x) = P(X \leq x) = P (|Y| \leq x ) = P(|\mu + Z\sigma| \leq x) = P(-x \leq \mu + Z\sigma \leq x) $$ $$ = P \left( \dfrac{-x-\mu}{\sigma} \leq Z \leq \dfrac{x-\mu}{\sigma} \right) = \Phi \left( \dfrac{x-\mu}{\sigma} \right) - \Phi \left( \frac{-x - \mu}{\sigma} \right) \square$$

Também podemos escrever a função de distribuição de $ X $ em termos da função erro (erf),

$$F_X(x; \mu, \sigma) = \dfrac{1}{2} \left[ erf \left( \dfrac{x + \mu}{\sigma\sqrt{2}} \right) + erf \left( \dfrac{x - \mu}{\sigma\sqrt{2}} \right) \right],$$

em que a função erro (erf) é definida por,

$$erf(x) = \dfrac{2}{ \sqrt{\pi} } \int_0^x e^{-t^2} dt$$

A esperança é dada por,

$$E(X) = \mu \left[ 1 - 2\Phi \left( \dfrac{-\mu}{\sigma} \right) \right] + \sigma \sqrt{ \dfrac{2}{\pi} } \exp \left( -\dfrac{ \mu^2 }{ 2\sigma^2} \right)$$

Demonstração:

$$E(X) = E( |\mu + \sigma Z| )$$

Note que $ |\mu + \sigma Z| \geq 0 \Leftrightarrow Z lt; -\dfrac{\mu}{\sigma} $ ou $ Z \geq -\dfrac{\mu}{\sigma} $.

Assim,

$$E( |\mu + \sigma Z| )=E( \mu + \sigma Z | Z \geq -\frac{\mu}{\sigma} ) + E( -\mu - \sigma Z | Z lt;-\frac{\mu}{\sigma} )$$

$$=E( \mu + \sigma Z | Z \geq -\frac{\mu}{\sigma} ) - E( \mu + \sigma Z | Z lt;-\frac{\mu}{\sigma} )$$

$$=E( \mu + \sigma Z ) - E( \mu + \sigma Z | Z lt;-\frac{\mu}{\sigma} )- E( \mu + \sigma Z | Z lt;-\frac{\mu}{\sigma} )$$

$$=E( \mu + \sigma Z ) - 2E( \mu + \sigma Z | Z lt;-\frac{\mu}{\sigma} )$$

$$=\mu -2\mu \Phi(-\mu/\sigma) - 2\sigma E(Z | Z \leq - \dfrac{\mu}{\sigma})$$

$$=\mu \left[ 1 -2\Phi(-\mu/\sigma) \right] - 2\sigma E(Z | Z \leq - \dfrac{\mu}{\sigma}) \qquad (1)$$

Mas,

$$E(Z | Z \leq - \dfrac{\mu}{\sigma}) = \int_{-\infty}^{\mu/\sigma} z \dfrac{1}{ \sqrt{2 \pi} } e^{-z^2/2} dz$$

Fazendo a mudança de variável $ u = z^2/2 $, temos

$$E(Z | Z \leq - \dfrac{\mu}{\sigma}) = \int_{\infty}^{\mu^2/2\sigma^2} \dfrac{1}{ \sqrt{2 \pi} } e^{-u} du = - \int_{\mu^2/2\sigma^2}^{\infty} \dfrac{1}{ \sqrt{2 \pi} } e^{-u} du = - \dfrac{1}{ \sqrt{2\pi} } e^{-\mu^2/2\sigma^2} \qquad (2)$$

Substituindo (2) em (1), temos

$$\mu \left[ 1 -2\Phi(-\mu/\sigma) \right] + 2\sigma \dfrac{1}{ \sqrt{2\pi} } e^{-\mu^2/2\sigma^2} = \mu \left[ 1 - 2\Phi(-\mu/\sigma) \right] + \sigma \sqrt{ \dfrac{2}{\pi} } e^{-\mu^2/2\sigma^2} \square$$

A variância é dada por,

$$Var(X) = \mu^2 + \sigma^2 - \left\lbrace \mu \left[ 1 - 2\Phi \left( \dfrac{-\mu}{\sigma} \right) \right] + \sigma \sqrt{ \dfrac{2}{\pi} } \exp \left( -\dfrac{ \mu^2 }{ 2\sigma^2} \right) \right\rbrace^2$$

Demonstração:

Note que,

$$E(X^2) = E(Y^2) = Var(Y) + [E(Y)]^2 = \sigma^2 + \mu^2$$

Assim,

$$ Var(X) = E(X^2) - [E(X)]^2 $$ $$ Var(X) = \mu^2 + \sigma^2 - \left\lbrace \mu \left[ 1 - 2\Phi \left( \dfrac{-\mu}{\sigma} \right) \right] + \sigma \sqrt{ \dfrac{2}{\pi} } \exp \left( -\dfrac{ \mu^2 }{ 2\sigma^2} \right) \right\rbrace^2 $$

Propriedade:

Seja $ W = |\sigma Z| = \sigma |Z| $, em que $ Z \sim N(0,1) $, a distribuição de $ W $ é uma \textbf{distribuição seminormal} com o parâmetro de escala $ \sigma $. A função de distribuição, $ F(w) $, e a função densidade de probabilidade $ f(w) $, são dadas, respectivamente, por,

$$F(w) = 2 \Phi \left( \dfrac{y}{\sigma} \right) - 1, y \in [0, \infty),$$

em que $\Phi(\cdot)$ é a função de distribuição da distribuição normal padrão.

$$ f(w) = \dfrac{2}{\sigma} \phi \left( \dfrac{y}{\sigma} \right), y \in [0, \infty),$$

em que $\phi(\cdot)$ é a função densidade da distribuição normal padrão.

Exemplo 1

Para exemplificar o cálculo da esperança e variância da distribuição normal dobrada considere $ Y \sim N(0,1) $. Sabemos que $ X = |Y| \sim ND(0,1) $. Assim, a esperança e a variância de $ X $ são dadas por,TeX Embedding failed!

$$ E(X) = \mu \left[ 1 - 2\Phi \left( \dfrac{-\mu}{\sigma} \right) \right] + \sigma \sqrt{ \dfrac{2}{\pi} } \exp \left( -\dfrac{ \mu^2 }{ 2\sigma^2} \right) = 0 \left[ 1 - 2\Phi \left( \dfrac{-0}{1} \right) \right] + 1 \sqrt{ \dfrac{2}{\pi} } \exp \left( -\dfrac{ 0^2 }{ 2*1^2} \right) $$ $$=0 + \sqrt{\dfrac{2}{\pi}} e^0 = \sqrt{\dfrac{2}{\pi}} * 1 = \sqrt{\dfrac{2}{\pi}} = 0, 798 $$

$$ Var(X) = E(X^2) - [E(X)]^2 = \mu^2 + \sigma^2 - [E(X)]^2 = 0 + 1 - 0,798^2 = 1 - 0,637 = 0,363 $$

Portanto, $ E(X) = 0,798 $ e $ Var(X)= 0,363 $.

Podemos notar que os parâmetros $ \mu $ e $ \sigma^2 $ representam, respectivamente, a esperança e a variância somente da v.a. $ Y $ e não da v.a. $ X $.

Exemplo 2

Seja $ X $ uma variável aleatória contínua com distribuição normal dobrada com $ \mu=0 $ e $ \sigma^2 = 4 $, ou seja, $ X \sim ND(0,4) $. Calcule a probabilidade de $ X \leq 2 $.

Sabemos que $ X = |Y| $, em que $ Y \sim N(0,4) $. Assim, a probabilidade de $ X \leq 2 $ é dada por,

$$ P( X \leq 2 ) = P( -2 \leq Y \leq 2 ) = P( \frac{-2 - 0}{ 2 } \leq \frac{Y- 0}{2} \leq \frac{2 - 0}{2} ) = P( -1 \leq Z \leq 1 ), $$

em que $ Z \sim N(0,1) $.

Assim,

$$ P( X \leq 2 ) = \Phi(1) - \Phi(-1) = 0,8413 - 0,1587 = 0,6826, $$

Ou seja, $ 68,26(porcentagem)% $

Exemplo 3

Suponha que uma fábrica produz uma peça cilíndrica cuja medida do diâmetro tem distribuição normal dobrada com os parâmetros $ \mu=0,04 $cm e $ \sigma^2 = 0,02^2 = 0,0004 $cm. Seja $ X $ a variável aleatória que representa essa medida. Assim, $ X \sim ND(0,04 ; 0,0004) $. Suponha também que os limites de engenharia são $ LIE = 0,01 $cm e $ LSE = 0,07 $cm. Qual é a probabilidade da fábrica produzir uma peça fora dos limites especificados?

Queremos saber,

$$ P[ (X < 0,01) \cup (X > 0,07)] $$

Temos,

$$ P[ (X < 0,01) \cup (X > 0,07)] = P(X < 0,01) + P(X > 0,07) - P[ (X < 0,01) \cap (X > 0,07)] = $$

$$ = P(X < 0,01) + P(X > 0,07), $$

pois $ P[ (X < 0,01) \cap (X > 0,07)] = 0 $

Dessa maneira,

$$ P(X < 0,01) + P(X > 0,07) = P(X < 0,01) + 1 - P(X \leq 0,07) $$

$$ = 1 + F_X(0,01) - F_X(0,07), $$

em que $ F_X(\cdot) $ é a f.d.a. de $ X. $

Pela equação 1, temos

$$F_X(0,01)=\Phi \left( \dfrac{ x - \mu }{ \sigma } \right) - \Phi \left( \dfrac{ -x - \mu }{ \sigma } \right) = \Phi \left( \dfrac{ 0,01 - 0,04 }{ 0,02 } \right) - \Phi \left( \dfrac{ -0,01 - 0,04 }{ 0,02 } \right)=$$

$$=\Phi \left( -1,5 \right) - \Phi \left( -2,5 \right) = 0,0668 - 0 = 0,0606$$

$$F_X(0,07)=\Phi \left( \dfrac{ x - \mu }{ \sigma } \right) - \Phi \left( \dfrac{ -x - \mu }{ \sigma } \right) = \Phi \left( \dfrac{0,07 - 0,04 }{ 0,02 } \right) - \Phi \left( \dfrac{ -0,07 - 0,04 }{ 0,02 } \right)=$$

$$= \Phi \left( 1 \right) - \Phi \left( -5 \right) = 0,8413 - 0 = 0,8413$$

Finalmente,

$$ P[ (X < 0,01) \cup (X > 0,07)] = 1 + F_X(0,01) - F_X(0,07) = 1 + 0,0606 - 0,8413 = 0,2193 $$

Portanto, a probabilidade da fábrica produzir uma peça fora dos limites especificados é de $ 21,93(porcentagem)% $.

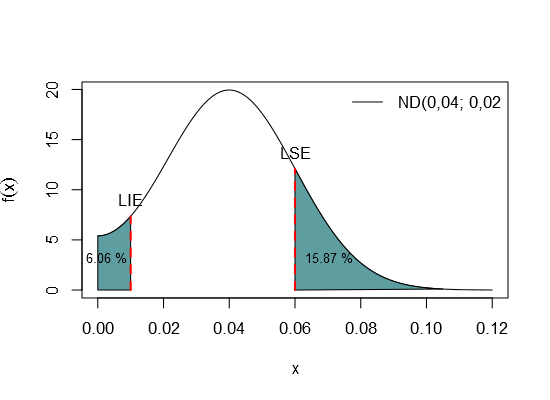
Figura 6.20.2: Curva da distribuição normal dobrada com $ \mu=0,04 $ e $ \sigma^2=0,02^2 $. A área hachurada do lado esquerdo é a probabilidade de produzir uma peça abaixo do limite inferior de engenharia e a área hachurada do lado direito é a probabilidade de produzir uma peça acima do limite superior de engenharia

6.21 Distribuição de Rice

A distribuição de Rice é uma distribuição de probabilidade contínua para valores positivos. Geralmente, essa distribuição é observada quando a magnitude global de um vetor está relacionada com os seus componentes de direção. Por exemplo, quando a velocidade do vento é analisada em duas direções, ou seja, um vetor de componentes bidimensional. Assumindo que as componentes são independentes e normalmente distribuídas com variâncias iguais, então a velocidade geral do vento tem uma distribuição de Rice. Veja Sijbers, Jan, et al. (1998) para mais detalhes.

Observação

Definição

Seja $X$ uma variável aleatória contínua com distribuição de Rice com média $v$ e variância $\sigma^2$. A função densidade de probabilidade $f(\cdot)$ é dada por,

$$f( x | v, \sigma^2) = \dfrac{x}{\sigma^2} \exp \left( \dfrac{ -(x^2 + v^2) }{2\sigma^2} \right) I_0 \left( \dfrac{xv}{\sigma^2} \right); x,v \in \Re; \sigma^2 > 0$$

em que,

$$I_{\alpha}(z) = \sum_{m=0}^\infty \dfrac{1}{ m! \Gamma(m + \alpha + 1) } \left( \dfrac{z}{2} \right)^{2m+\alpha}, \alpha \in \Re,$$

é a função modificada de Bessel do primeiro tipo de ordem $\alpha$.

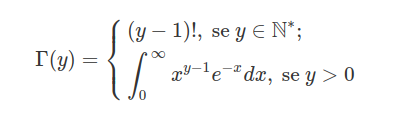
é a função Gama.

A função de distribuição $F(\cdot)$ é dada por

$$F(x | v, \sigma) = 1- Q_1 \left( \dfrac{v}{\sigma}, \dfrac{x}{\sigma} \right),$$

em que,

$$Q_M(a,b) = \int_a^\infty x \left( \dfrac{x}{a} \right)^{M-1} \exp \left( - \dfrac{x^2 + a^2}{2} \right) I_{M-1}(ax) dx$$

chamada Função-Q Marcum (Marcum Q-Function)

O gráfico da Figura 6.21.1 ilustra a forma da função densidade de probabilidade e da função de distribuição de Rice para alguns valores de $v$ e $\sigma$

Figura 6.21.1: Função densidade de probabilidade (à esquerda) e a função de distribuição (à direita) da distribuição de Rice

Momentos

Os momentos de ordem 1, $m_1$, e de ordem 2, $m_2$, são dados por,

$$m_1 = \sigma \sqrt{ \dfrac{\pi}{2}} L_{1/2} \left( \dfrac{-v^2}{2 \sigma^2} \right)$$

$$m_2 = 2\sigma^2 + v^2$$

Assim, a esperança de $X$ é dada por,

$$E(X) = m_1 = \sigma \sqrt{ \dfrac{\pi}{2}} L_{1/2} \left( \dfrac{-v^2}{2 \sigma^2} \right),$$

ou pode ser escrito da forma reduzida como,

$$L_n(x) = \sum_{k=0}^n \binom{n}{k} \dfrac{ (-1)^k }{k!} x^k$$

Vale lembrar que $L_n$ é o polinômio de Laguerre de ordem n.

A variância de $X$ é dada por,

$$Var(X) = m_2 - m_1^2 = 2\sigma^2 + v^2 - \dfrac{\pi \sigma^2}{2} L^2_{1/2} \left( \dfrac{-v^2}{2\sigma^2} \right)$$

Exemplo 6.21.1

$$f(x| 0, \sigma^2) = \dfrac{x}{\sigma^2} \exp{ \left[ \dfrac{-(x^2+0^2)}{2\sigma^2} \right] } I_0( \frac{x*0}{\sigma^2} ) = \dfrac{x}{\sigma^2} \exp{ \left[ \dfrac{-(x^2)}{2\sigma^2} \right] } I_0( 0 ),$$

Mas,

Assim,

$$f(x| 0, \sigma^2) = \dfrac{x}{\sigma^2} \exp{ \left[ \dfrac{-(x^2)}{2\sigma^2} \right] }, x \in \Re.$$

6.22 - Distribuição normal estendida

A distribuição normal estendida resulta da superposição de distribuições normais com o mesmo desvio padrão e que apresentam mudanças de locação sistemáticas (tendências e ciclos). A Figura abaixo exemplifica a distribuição normal estendida. A distribuição normal estendida definida aqui foi embasada no manual Volkswagen AG VW 101 31.

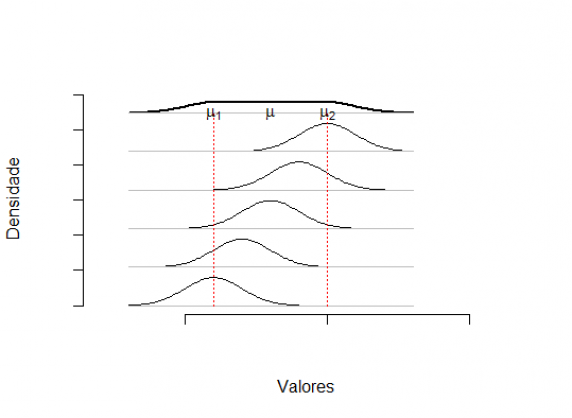
Figura 6.22.1

Definição

Seja $X$ uma variável aleatória contínua com distribuição normal estendida. Então, sua função densidade de probabilidade é:

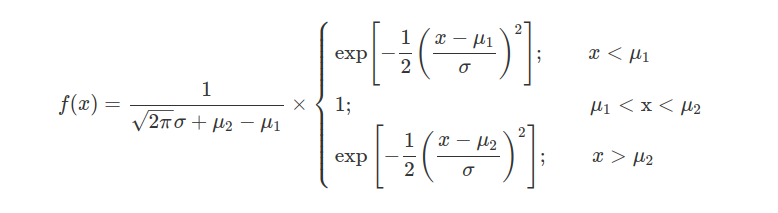
Em que,

• μ1 e μ2 são as médias das distribuições normais que limitam a distribuição normal estendida (como pode ser visto no gráfico da Figura 6.22.1)
• σ é o desvio padrão das distribuições normais que limitam a distribuição normal estendida.

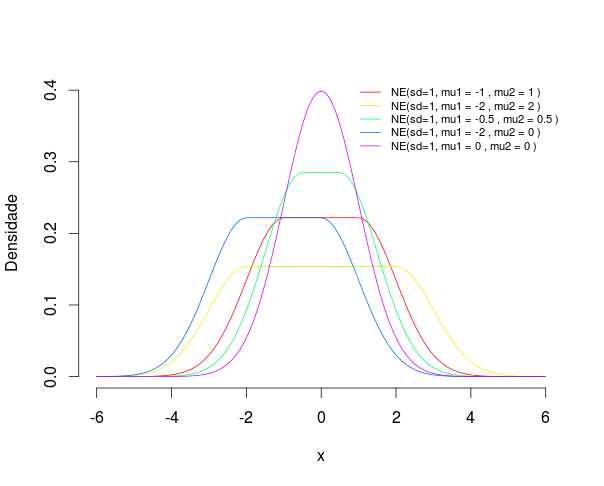
Figura 6.22.2: Gráfico da função densidade da distribuição normal estendida

6.22.3: Gráfico da função de distribuição acumulada da normal estendida.

Notação: $X \sim NE(\mu_1, \mu_2, \sigma)$

A esperança de X é dada por:

$$ E[X] = \int_{-\infty}^{\infty} x f(x) dx$$

$$E[X] = \dfrac{1}{\sqrt{2\pi}\sigma+\mu_2 - \mu_1} \times \left\lbrace \int_{-\infty}^{\mu_1} x \exp{ \left[ -\dfrac{1}{2} \left(\dfrac{x-\mu_1}{\sigma}\right)^2 \right]}+\int_{\mu_1}^{\mu_2} x dx + \int_{\mu_2}^{\infty} x \exp{\left[-\dfrac{1}{2}\left(\dfrac{x-\mu_2}{\sigma}\right)^2\right]}\right\rbrace$$

A variância de X é dada por:

$$Var(X) = E[X^2] - (E[X])^2$$

em que,

$$E[X^2] = \int_{-\infty}^\infty x^2 f(x) dx$$

Exemplo 6.22.1

Seja X uma variável aleatória contínua com distribuição normal estendida com $\mu_1=1, \mu_2=3$ e $\sigma=1$. Calcule:

• A densidade de X no ponto X = 2

Seja $f(x)$ a função densidade de probabilidade de X no ponto X = 2. Utilizando a função densidade de probabilidade da distribuição normal estendida acima, note que $\mu_1 < 2 < \mu_2$. Assim, temos que

$$f(2)=\dfrac{1}{\sqrt{2\pi}\times 1 + 3 - 1}=\dfrac{1}{\sqrt{2\pi} + 2} \approx 0,2219$$

Observação

Note que a densidade de $X$ sempre valerá $0,2219$ para qualquer valor de $x$ no intervalo $(1,3)$

• A área sob a curva de X tal que $ P(X < 1) $

Sabemos que

$$P(X<1)=\int_{-\infty}^{1} f(x) dx = \dfrac{1}{\sigma*\sqrt{2\pi}+\mu_2 -\mu_1}\int_{-\infty}^{1}\exp{\left[-\dfrac{1}{2}\left(\dfrac{x-\mu_1}{\sigma}\right)^2\right]}dx$$

Substituindo $z = \dfrac{x-\mu_1}{\sigma}$, temos que $dz=\dfrac{1}{\sigma}dx$.

Para $x=-\infty$ temos $z=-\infty$ e para $x=1$ temos $z=\dfrac{1-\mu_1}{\sigma}=\dfrac{1-1}{1}=0$. Assim,

$$P(X<1)=\dfrac{\sigma}{\sigma*\sqrt{2\pi}+\mu_2-\mu_1}\int_{-\infty}^0\exp\left( -\dfrac{z^2}{2}\right)dz$$

Agora, multiplicando a equação acima por $\dfrac{\sqrt{2\pi}}{\sqrt{2\pi}}$, temos,

$$P(X<1)=\dfrac{\sigma\sqrt{2\pi}}{\sigma*\sqrt{2\pi}+\mu_2-\mu_1}\int_{-\infty}^0\dfrac{1}{\sqrt{2\pi}}\exp\left(-\dfrac{z^2}{2}\right)dz$$

$$P(X<1)=\dfrac{\sigma\sqrt{2\pi}}{\sigma*\sqrt{2\pi}+\mu_2-\mu_1}\Phi(0),$$

em que $\Phi(\cdot)$ é a função de distribuição da normal padrão.

Olhando para a tabela da distribuição normal padrão ou calculando no Action, temos $\Phi(0) = 1/2$. Portanto,

$$P(X<1)=\dfrac{1*\sqrt{2\pi}}{1*\sqrt{2\pi}+3-1}*\dfrac{1}{2}=\dfrac{\sqrt{2\pi}}{2(\sqrt{2\pi}+2)}\approx 0,2781$$