8.7 Convergência de variáveis aleatórias

O teorema central do limite é um resultado fundamental com diversas aplicações. Mesmo quando a distribuição da população de eventos não segue uma distribuição Normal, a distribuição da média dos dados converge para a distribuição Normal conforme o tamanho da amostra aumenta. Assim, qualquer que seja a distribuição da amostra, para um número suficientemente grande de observações, a distribuição de probabilidade da média se aproxima da distribuição Normal com média $ \mu $ e variância $ \frac{\sigma^2}{n} $, nos quais $ \mu $ é a média e $ \sigma^2 $ é a variância da população. Para ilustrar, considere uma população $ X $ que possui distribuição exponencial com parâmetro $ \lambda = 1 $, isto é, $ X\sim \ \text{Exp}(1) $. Vamos realizar um estudo da distribuição amostral de $ \overline{X} $.

Inicialmente, vamos plotar o histograma da população que possui distribuição exponencial com parâmetro $ \lambda =1 $ e tamanho de amostra 500.

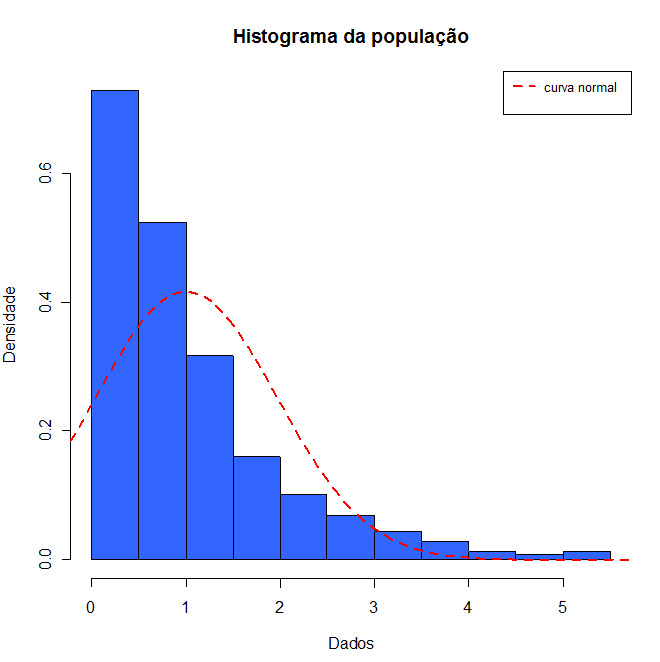
Figura 7.1: histograma dos dados da população com distribuição exponencial com parâmetro λ=1.

Note que o gráfico do conjunto de dados segue uma distribuição não simétrica, diferente da curva da distribuição Normal (linha vermelha). Vamos fazer um resumo descritivo dos dados da população.

Figura 7.2: Resumo descritivo da população.

Observamos que no caso de toda população, a média a média populacional é aproximadamente 1 e o desvio padrão da média é dada por $ \dfrac{s}{\sqrt{n}}=\dfrac{0,95961}{\sqrt{500}}=0,042915. $ Afim de aplicar o teorema do limite central (TCL), vamos tomar 1000 amostras aleatórias dessa população, cujo tamanho da amostra é dois. De cada uma destas 1000 amostras calculamos a média, em seguida verificamos o comportamento dos dados. A seguir, vamos plotar o histograma dos dados e fazer um resumo descritivo.

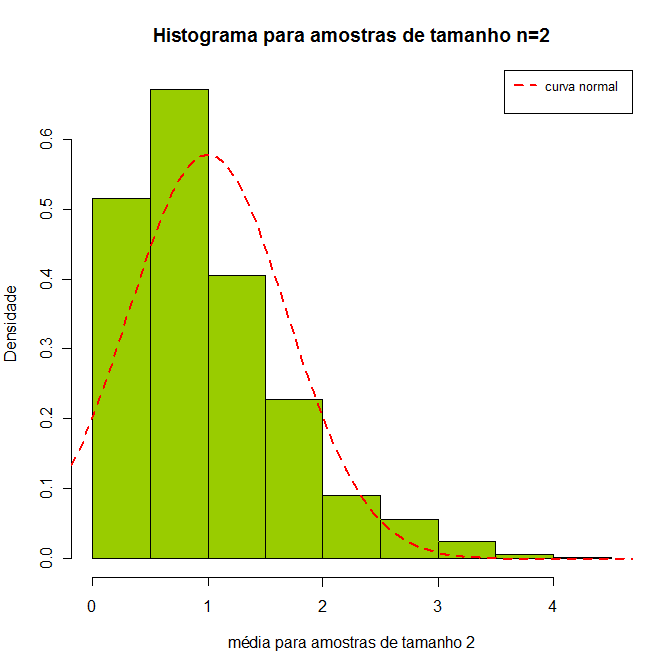
Figura 7.3: histograma usando grupos de 2.

Figura 7.4: Resumo descritivo para amostras de tamanho 2.

Com amostras de tamanho 2, ainda não obtemos resultados satisfatórios. Com isso, vamos tomar 1000 amostras aleatórias de tamanho 10. De cada uma destas 1000 amostras calculamos a média, em seguida verificamos o comportamento dos dados. A seguir, vamos plotar o histograma dos dados e fazer um resumo descritivo.

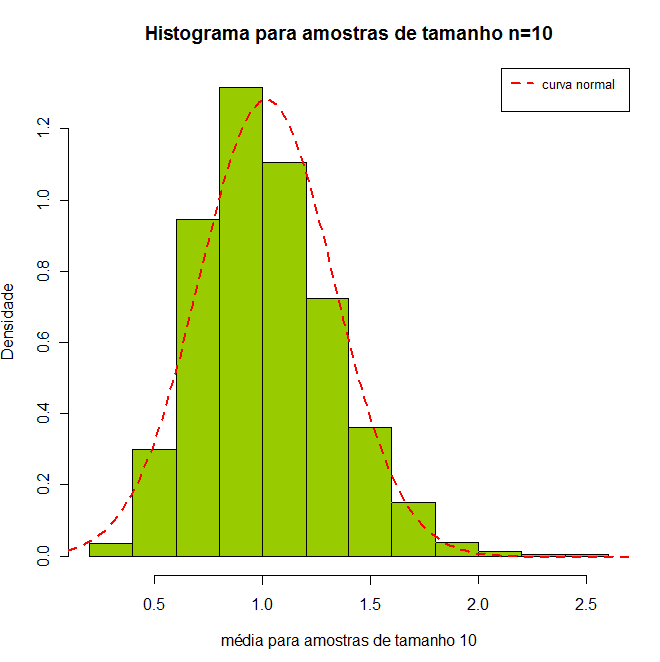
Figura 7.5: histograma para amostras de tamanho $ n=10. $

Figura 7.6: Resumo descritivo para amostras de tamanho 10.

Agora, para amostras de tamanho 2, ainda não obtemos resultados satisfatórios. Por fim, vamos tomar 1000 amostras aleatórias de tamanho 250. De cada uma destas 1000 amostras calculamos a média, em seguida verificamos o comportamento dos dados. A seguir, vamos plotar o histograma dos dados e fazer um resumo descritivo.

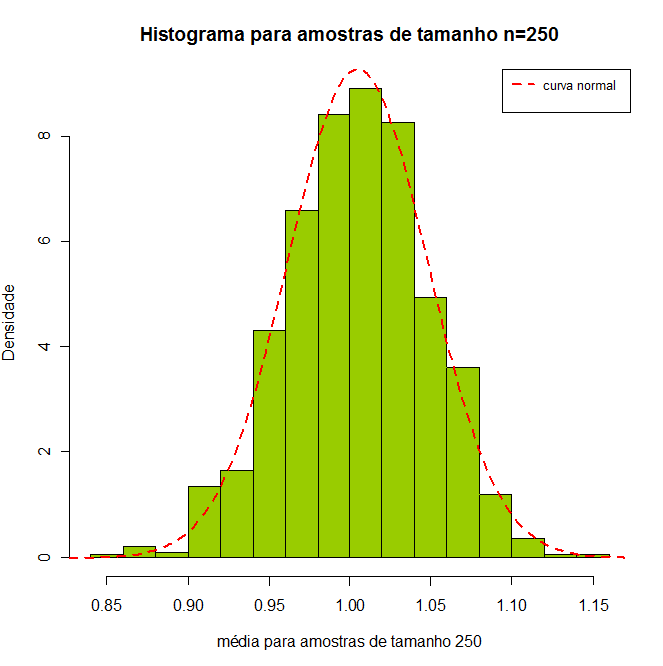
Figura 7.7: histograma para amostras de tamanho $ n=250. $

Figura 7.8: Resumo descritivo para amostras de tamanho 250.

Como percebemos este gráfico já possui uma distribuição similar a da distribuição Normal. Da distribuição da média populacional obtemos $ \mu=\overline{X}=1 $ e $ \sigma_{\overline{X}}=\dfrac{s}{\sqrt{n}}=\dfrac{0,95961}{\sqrt{500}}=0,042915. $ Observamos pela figura 7.8 que a diferença entre os dados com amostras de tamanho 250 e a distribuição da média empírica (erro) é de 0,004 para a média e de 0,00012 para o desvio padrão. Para reforçar isto, vamos realizar um teste de normalidade (para mais detalhes consulte o conteúdo de inferência estatística), em que realizamos o seguinte teste de hipótese (para mais detalhes consulte o conteúdo teste de hipóteses):

(imagem em falta)

Figura 7.9: Teste de normalidade segundo critério de Anderson e Darling.

Notamos que à partir do teste de Anderson e Darling, obtemos um p-valor de 0,53 (para mais detalhes consulte o conteúdo cálculo e interpretação do p-valor). Então, existe forte evidência de que os dados provém de uma distribuição Normal. A seguir, apresentamos um gráfico resumindo todos os passos deste estudo.

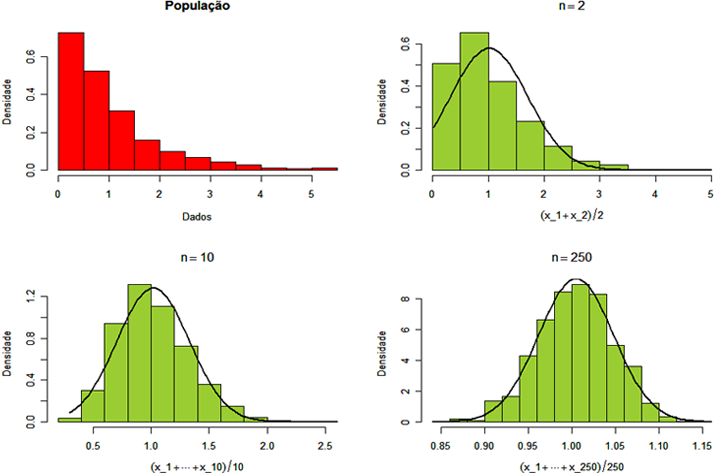
Figura 7.10: Todos os passos do estudo.

Logo, quando a distribuição da população não seguem uma distribuição Normal, a distribuição da média dos dados converge para a distribuição Normal conforme o tamanho da amostra aumenta.

Portanto, o teorema central do limite (TCL) pode ser resumido como. Para amostras grandes, a distribuição amostral da média pode ser aproximada pela distribuição Normal. Mais especificamente, consideramos uma amostra aleatória simples de tamanho n, retirada de uma população com média μ e variância σ2. Representando tal amostra por n variáveis aleatórias independentes X1,…,Xn, e denotando sua média por $ \overline{X} $, temos pelo teorema central do limite, que quando n for suficientemente grande, a variável Z dada por

$$\frac{\overline{X}-\mu}{\sigma / \sqrt{n}}$$

tem distribuição aproximadamente Normal com média 0 e variância 1 (N(0,1)).

A lei dos grandes números é um dos principais teoremas assintóticos da estatística. Intuitivamente, visualizamos através de um gráfico (figura 7.10) a lei dos grandes números, que diz que a média aritmética dos valores observados tendem a esperança da variável aleatória.

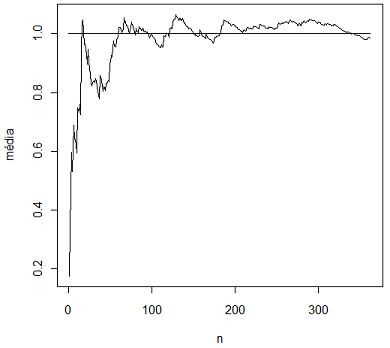
Figura 7.11: Ideia intuitiva da lei dos grandes números.

No gráfico a linha reta representa a média da variável aleatória, enquanto que a outra linha representa a média dos valores observados. Notemos que conforme aumenta o número de observações a média aritmética dos valores observados tende para a média da variável aleatórios.

A seguir, vamos mostrar os resultados com detalhes sobre a lei dos grandes números e do teorema central do limite (TCL).

7.1 - Tipos de Convergência

Neste módulo, apresentamos os principais tipos de convergência estocástica e suas relações.

7.1.1 - Convergências em probabilidade e quase certa

Nesta seção, vamos estudar as convergências em probabilidades e quase certa, porém, inicialmente vamos apresentar um resultado importante, que é o lema de Borel-Cantelli.

Definição 7.1.1.1

Seja $(A_n)_{n\geq 1}$ uma sequência de eventos aleatórios então o limite superior da sequência é definido como

Lema 7.1.1.1 (Lema de Borel-Cantelli)

Seja $(A_n)_{n\geq 1}$ uma sequência de eventos aleatórios. Temos que:

Assim, seja $B_n=\displaystyle \bigcup_{k=n}^{\infty}A_k$, note que $B_n \supset \displaystyle \bigcup_{k=n}^{n+m}A_k $, para qualquer $m \in \mathbb{N}$, e portanto $B_n^c \subset \left(\displaystyle \bigcup_{k=n}^{n+m}A_k\right)^c=\displaystyle \bigcap_{k=n}^{n+m}A_k^{c}$ (essa igualdade é válida pelas leis de De Morgan).

Logo, para todo m temos

$$1-\mathbb{P}(B_n)=\mathbb{P}(B_n^c)\leq \mathbb{P}\left(\displaystyle \bigcap_{k=n}^{n+m}A_k^{c}\right).$$

Como cada $A_i$ são independentes então obtemos que

$$\mathbb{P}\left(\displaystyle \bigcap_{k=n}^{n+m}A_k^{c}\right)=\prod_{k=n}^{n+m}\mathbb{P}(A_k^c)=\prod_{k=n}^{n+m}(1-\mathbb{P}(A_k)).$$

Notemos que $1-p\leq e^{-p}$ para $0\leq p \leq 1$, temos então que:

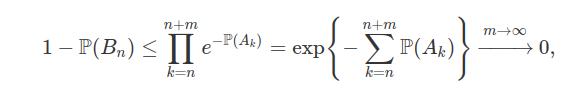
pois por hipótese temos que $\displaystyle \sum_{n=1}^{\infty}\mathbb{P}(A_n)=\infty$. Portanto $\mathbb{P}(B_n)=1$, para todo $n\geq 1$.

$\Box$

Exemplo 7.1.1.1

Seja $(X_n)_{n\geq 1}$ uma sequência de variáveis aleatórias independentes tal que, $X_n\sim \text{Bernoulli}(p_n)$, $0 \ < \ p_n \ < \ 1$, $n\geq 1.$

Pelo lema de Borel-Cantelli, temos que

Se $\displaystyle\sum^\infty_{n=1}p_n \ < \ \infty$ então $\mathbb{P}([X_n=1],i.v.)=0$

Se $\displaystyle\sum^\infty_{n=1}p_n=\infty$ então $\mathbb{P}([X_n=1],i.v.)=1$

Exemplo 7.1.1.2

Seja $(X_n)_{n\geq 1}$ uma sequência de variáveis aleatórias independentes com $X_n\sim \text{Exp}(1).$ Defina $Y_n=\frac{X_n}{\log(n)}$ para $n\geq1.$ Discuta a convergência em probabilidade e quase certa.

Note que

$$\mathbb{P}\left(X_n \ > \ x\right)=e^{-x},\quad x \ > \ 0,~n\geq 1$$

e portanto,

$$\mathbb{P}\left(X_n \ > \ \alpha \log n\right)=e^{-\alpha\log n}=\dfrac{1}{n^\alpha},\quad ~n\geq 1$$

Então, pelo lema de Borel-Cantelli,

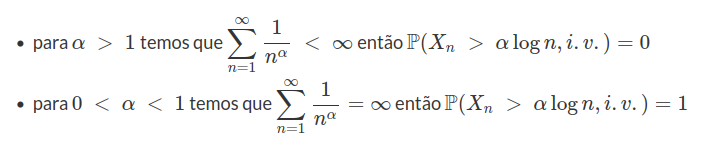
Agora, vamos apresentar as definições de convergências em probabilidades e quase certa.

Definição 7.1.1.2: (Convergência em probabilidade)

A principal ideia da convergência em probabilidade é que, quando n é arbitrariamente grande, a probabilidade da diferença $|X_n-X|$ ser maior do que qualquer número positivo $\varepsilon$ tende a zero.

Definição 7.1.1.3: (Convergência quase certa)

Teorema 7.1.1.1: (Critério de convergência quase certa)

Sejam $(X_n)_{n\geq 1}$ uma sequência de variáveis aleatórias e $X$ uma variável aleatória. Então $X_n$ converge quase certamente para $X$ se, e somente se, para todo $j\geq1$

$$\mathbb{P}\left(|X_n-X|\geq \frac{1}{j} \ \text{i.v.} \right)=0$$

Demonstração:

Um sequência de funções converge se para todo $j\geq 1,$ existe $n\geq 1$ tal que $k\geq n$ implica

$$|X_k(\omega)-X(\omega)| \ < \ \frac{1}{j}$$

equivalentemente

A seguir, apresentamos dois exemplos relacionados com as convergências quase certa e em probabilidade. Na sequência, apresentamos um resultado que comprova que convergência quase certa implica em convergência em probabilidade.

Exemplo 7.1.1.3

Exemplo 7.1.1.4

Teorema 7.1.1.2

Teorema 7.1.1.3

Teorema 7.1.1.4

Teorema 7.1.1.5

Teorema 7.1.1.6

Sejam $(X_n)_{n\geq 1}$ uma sequência de variáveis aleatórias, $X$ uma variável aleatória e $g$ uma função contínua a valores reais. Se $X_n$ converge em probabilidade para $X$ então $g(X_n)$ converge em probabilidade para $g(X)$.

Demonstração:

Inicialmente, suponha que $g$ é uniformemente contínua. Então, dado $\varepsilon \ > \ 0$, existe um $\delta \ > \ 0$ tal que $|g(X_n) - g(x)| \ < \ \varepsilon$ sempre que $|X_n-X| \ < \ \delta$. Neste caso, temos que

logo converge em probabilidade.

$\Box$

Teorema 7.1.1.7: (O limite em probabilidade é “único”)

Definição 7.1.1.4

Teorema 7.1.1.8

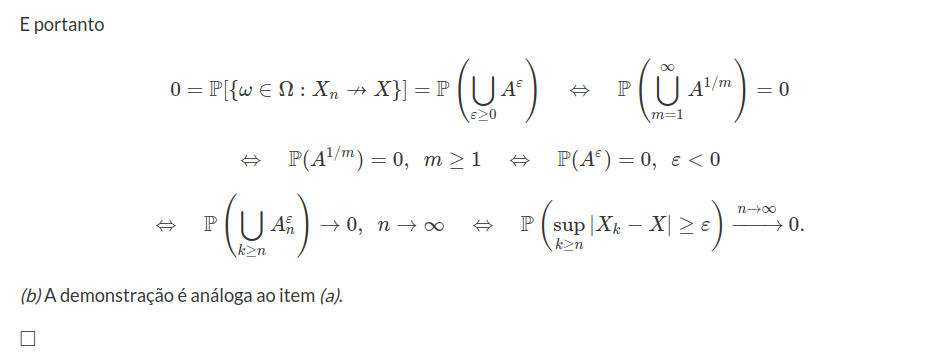
Exemplo 7.1.1.5

Exemplo 7.1.1.6

Exemplo 7.1.1.7

Seja $(X_n)_{n\geq 1}$ uma sequência de v.a’s independentes definidas em $(\Omega, \mathcal{A}, \mathbb{P})$, tal que $X_n\sim U(0,a_n)$, com $a_n \ > \ 0$, $n\geq 1$. Então

(a) Supondo $a_n=n$, prove que, com probabilidade 1, existe um número infinito de v.a’s $X_n$ que assumem valores menores que 1 e um número infinito $X_n$ que assumem valores maiores do que 2.

(b) Com considerações análogas as do item (a) decida sobre a convergência quase certa, no caso em que $a_n=n^2$, $n\geq 1$.

(a) Temos que:

$$\mathbb{P}(X_n \ < \ 1)= \int_{0}^{1}\frac{1}{n}dx_n=\frac{1}{n}$$

Como $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n}=\infty$, então pelo Lema de Borel-Cantelli, concluímos que $\mathbb{P}(X_n \ < \ 1;~ i.v.)=1$.

Agora para

$$\mathbb{P}(X_n \ > \ 2)= \int_{2}^{n}\frac{1}{n}=\frac{n-2}{n}.$$

Como $\displaystyle \sum_{n=1}^{\infty}\frac{n-2}{n}=\infty,$ então pelo Lema de Borel-Cantelli, concluímos que $\mathbb{P}(X_n \ > \ 2;~ i.v.)=1$.

Agora do fato de existirem infitos valores menores do que 1 e infinitos valores maiores que 2, concluímos que a sequência de v.a’s $(X_n)_{n\geq 1}$ não converge quase-certamente.

(b) Temos que,

$$\mathbb{P}(X_n \ < \ 1)= \int_{0}^{1}\frac{1}{n^2}dx_n=\frac{1}{n^2}$$

Como $\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2} \ < \ \infty$, então pelo Lema de Borel-Cantelli, concluímos que $\mathbb{P}(X_n \ < \ 1;~ i.v.)=0$.

$$\mathbb{P}(X_n \ > \ 2)=\displaystyle \int_{2}^{n^2}\frac{1}{n^2}dx_n=1-\frac{2}{n^2}$$

Como $\displaystyle \sum_{n=1}^{\infty}1-\frac{2}{n^2}=\infty,$ então pelo Lema de Borel-Cantelli, concluímos que $\mathbb{P}(X_n \ > \ 2;~ i.v.)=1$.

Exemplo 7.1.1.8

Considere X uma v.a. e $(X_n)_{n\geq 1}$ uma sequência de v.a’s definidas sobre $(\Omega,\mathcal{A},\mathbb{P})$, tal que a distribuição conjunta de $(X_n,X)$ seja dada por:

$$\mathbb{P}(X_n=0,X=0)=\displaystyle \frac{n}{3(n+1)}$$

$$\mathbb{P}(X_n=1,X=0)=\displaystyle \frac{1}{3(n+1)}$$

$$\mathbb{P}(X_n=0,X=1)=\displaystyle \frac{n}{3}$$

$$\mathbb{P}(X_n=1,X=1)=\displaystyle \frac{1}{3}$$

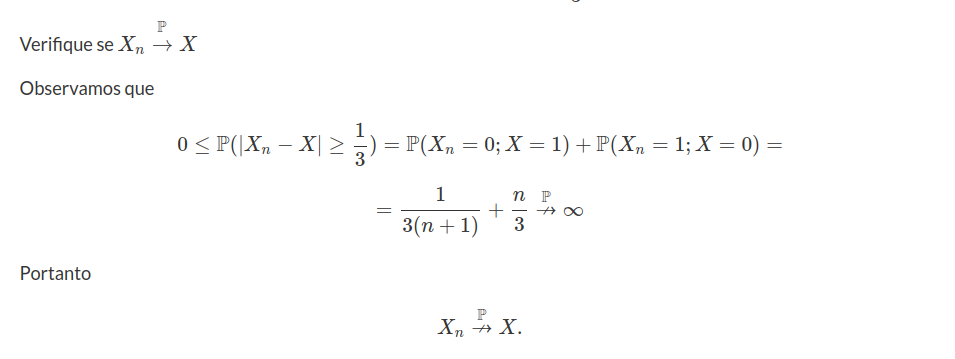
Para finalizar esta seção, vamos apresentar um diagrama dos principais resultados.

Figura 7.1.1.1: Diagrama de implicações entre os tipos de convergência.

7.1.2 - Convergência em distribuição ou Convergência fraca

Nesta seção, vamos discutir algumas características da convergência em distribuição ou convergência fraca das medidas de probabilidades. A seguir, apresentamos a seguinte definição.

Definição 7.1.2.1

Exemplo 7.1.2.1

Teorema 7.1.2.1

Sejam $F$ uma função de distribuição acumulada e $(F_{n})_{n\geq 1}$ uma sequência de funções de distribuição acumulada. Se $F_{n}\rightarrow F$ então, para toda função $g:\mathbb{R}\rightarrow\mathbb{R}$ contínua e limitada temos que:

$$\displaystyle\int{g(x)dF_n(x)}\rightarrow \int{g(x)dF(x)}.$$

Este teorema é conhecido como teorema de Helly Bray.

Demonstração:

Queremos mostrar que $\displaystyle\int{g(x)dF_n(x)}\rightarrow \int{g(x)dF(x)}$. Para isso, precisamos mostrar que

$$\displaystyle\left|\displaystyle\int{g(x)dF_n(x)}-\int{g(x)dF(x)}\right| \ < \ \varepsilon,~~\forall \ \varepsilon \ > \ 0.$$

Sejam $-\infty \ < \ a \ < \ b \ < \ \infty$. Podemos dividir a diferença entre as integrais acima da seguinte forma:

$$\int{g(x)dF_n(x)}-\int{g(x)dF(x)}= A - B$$

em que

$$A = \int_{-\infty}^{a}{g(x)dF_n(x)} +\int_{a}^{b}{g(x)dF_n(x)}+\int_{b}^{\infty}{g(x)dF_n(x)}$$

e

$$B = \int_{-\infty}^{a}{g(x)dF(x)}+\int_{a}^{b}{g(x)dF(x)}+\int_{b}^{\infty}g(x)dF(x).$$

Por hipótese temos que $g$ é uma função limitada e, portanto, $c=\sup_{x\in \mathbb{R}}|g(x)| \ < \ \infty$. Seja $\varepsilon \ > \ 0$ arbitrário. Usando a desigualdade triangular temos que

$$\displaystyle\left|\displaystyle\int{g(x)dF_n(x)} - \int{g(x)dF(x)}\right|\leq \left|\int g(x)dF_n-\int_{a}^{b}g(x)dF_n(x)\right|+$$

$$+\left|\int_{a}^{b}g(x)dF_n(x)-\int_{a}^{b}g(x)dF(x)\right|+\left|\int_{a}^{b}g(x)dF(x)-\int g(x)dF(x)\right|.$$

Notemos o seguinte fato:

$$\displaystyle\left|\int_{-\infty}^{a}g(x)dF_n(x)-\int_{-\infty}^{a}g(x)dF(x)\right|\leq\int_{-\infty}^{a}cdF_n(x)+\int_{-\infty}^{a}cdF(x)=c[F_n(a)+F(a)].$$

Se $a$ é suficientemente pequeno, como $F$ é não decrescente temos que para $F(a)$ também será pequeno, e o mesmo vale para $F_n(a)$. Desta forma concluímos que para cada $\varepsilon_0 \ > \ 0$ existe um a tal que:

$$c[F_n(a)-F(a)] \ < \ \varepsilon_0$$

Analogamente temos:

$$\displaystyle \left|\int_{b}^{\infty}g(x)dF_n(x)-\int_{b}^{\infty}g(x)dF(x)\right|\leq \int_{b}^{\infty}cdF_n(x)-\int_{b}^{\infty}cdF(x)=c[F_n(b)-F(b)].$$

Para $b$ suficientemente grande temos que:

$$c[F_n(b)-F(b)] \ < \ \varepsilon_2.$$

Agora basta mostrarmos que:

$$\displaystyle\left|\int_{a}^{b}g(x)dF_n(x)-\int_{a}^{b}g(x)dF(x)\right| \ < \ \varepsilon_3.$$

Como por hipótese g é contínua e limitada, temos que no intervalo fechado $[a,b]$ a função g é uniformemente contínua, pois toda função contínua defina em um compacto é uniformemente contínua.

Lembrando que um compacto nos reais é um conjunto fechado e limitado.

Assim, vamos considerar a seguinte partição do intervalo [a,b]:

$$x_0=a \ < \ x_1 \ < \ \cdots \ < \ x_m=b.$$

Para $x\in\mathbb{R}$, com $x_i \ < \ x \ < \ x_{i+1}$ temos que:

$$g(x)-g(x_i) \ < \ \varepsilon_4,~~\forall i,$$

Para $\varepsilon_4 \ > \ 0$. Vamos definir uma função $g_j(x)=g(x_i)$ para todo $x\in(x_i,x_i+1)$, observemos que $g_j$ é uma função constante, desta forma mostremos o seguinte fato:

$$\displaystyle\int_{a}^{b}g(x_i)dF_n(x)=\sum_{i=0}^{m-1}g(x_i)[F_n(x_{i+1})-F_n(x_i)]\rightarrow\sum_{i=0}^{m-1}g(x_i)[F(x_{i+1})-F(x_i)]=\int_{a}^{b}g_j(x)dF(x).$$

Esta convergência decorre do fato de que por hipótese $F_n$ converge para F.

Desta forma temos que para qualquer $\varepsilon \ > \ 0$ existe um n suficientemente grande tal que:

$$\displaystyle \left|\int_{a}^{b}g_m(x)dF_n(x)-\int_{a}^{b}g_m(x)dF(x)\right|\leq\varepsilon_5.$$

Mas

$$\left|\int_{a}^{b}g(x)dF_n(x)-\int_{a}^{b}g(x)dF(x)\right|\leq$$

$$\left|\int_{a}^{b}g(x)dF_n-\int_{a}^{b}g_m(x)dF_n\right|+\left|\int_{a}^{b}g_m(x)dF_n(x)-\int_{a}^{b}g_m(x)dF(x)\right|+$$

$$+\left|\int_{a}^{b}g_m(x)dF(x)-\int_{a}^{b}g(x)dF(x)\right|\leq\left|\int_{a}^{b}\varepsilon_4dF_n+\varepsilon_5+\int_{a}^{b}\varepsilon_4dF_n\right|\leq\varepsilon_5+ 2\varepsilon_4.$$

Portanto podemos concluir que:

$$\left|\int g(x)dF_n(x)-\int g(x)dF(x)\right|\rightarrow 0,$$

$\Box$

Com isso, podemos ter uma definição alternativa, dada por

Definição 7.1.2.2

Dizemos que uma sequência de variáveis aleatórias $(X_n)_{n\geq 1}$ converge em distribuição para a variável aleatória $X$, se

$$\mathbb{E}[f(X_n)]\rightarrow \mathbb{E}[f(X)$$

para toda função contínua e limitada $f$.

Teorema 7.1.2.2

Sejam $(F_n)_{n\geq 1}$ uma sequência de funções de distribuição acumulada e $(\varphi_n)$ uma sequência de funções características, com $\varphi_n$ sendo a função característica de $F_n$. Se $\varphi_n$ converge pontualmente para $\varphi$ e $\varphi$ é contínua em zero, então existe uma função $F$ tal que $F_n \rightarrow F$ tal que $\varphi$ é a função característica de $F$.

Demonstração:

Vamos omitir a prova deste teorema por ser uma prova muito técnica, entretanto ela pode ser encontrada no livro do Barry James e em alguns outros livros que aparecem nas referências.

$\Box$

Proposição 7.1.2.1

Demonstração:

Pelo Teorema 7.1.2.2 concluímos que uma função característica define a função de distribuição acumulada de forma única. Como a função característica da distribuição normal é $e^{-t^{2}/2}$ temos que decorre imediatamente do Teorema 7.1.2.2 que $X_n$ converge para a distribuição normal.

$\Box$

Teorema 7.1.2.3

Sejam $(X_n)_{n\geq 1}$ uma sequência de variáveis aleatórias, $X$ uma variável aleatória e $g$ uma função contínua a valores reais. Se $X_n$ converge em distribuição para $X$ então $g(X_n)$ também converge em distribuição para $g(X)$.

Demonstração:

Por hipótese temos que $X_n$ converge em distribuição para $X$. Assim para mostrarmos que $g(X_n)$ converge em distribuição para $g(X)$. Basta mostrarmos a convergência das funções características. Temos, por definição que

$$\varphi_{g(X_n)}(t)=\mathbb{E}[e^{itg(X_n)}]=\mathbb{E}[\cos{(tg(X_n))}]+i~\mathbb{E}[\text{sen}{(tg(X_n))}].$$

Mas $\cos$ e $\text{sen}$ são funções contínuas e limitadas e assim do Teorema 7.1.2.1 decorre que:

$$\varphi_{g(X_n)}\rightarrow \varphi_{g(X)}.$$

Portanto $g(X_n)$ converge em distribuição para $g(X)$.

$\Box$

Teorema 7.1.2.4 (Slutsky)

i) $X_n+Y_n$ converge em distribuição para $X+Y.$

ii) $X_n-Y_n$ converge em distribuição para $X-Y.$

iii) $X_nY_n$ converge em distribuição para $YX.$

iv) se $Y\neq 0$ e $\mathbb{P}(Y_n\neq 0)=1$, então $\displaystyle \frac{X_n}{Y_n}$ converge em distribuição para $\displaystyle \frac{X}{Y}$.

Demonstração:

i) Basta mostrarmos que $\varphi_{X_n+Y_n}(t)\rightarrow \varphi_{X+Y}(t)$, mas temos

$$\varphi_{X_n+Y_n}=\mathbb{E}[e^{it(X_n+Y_n)}]=\mathbb{E}[e^{it(X_n+Y)}]+\mathbb{E}[e^{itX_n}(e^{itY_n}-e^{itY})].$$

Como $\mathbb{E}[e^{itX_n}]=\varphi_{X_n}(t)\rightarrow \varphi_X(t)$, e portanto

$$\mathbb{E}[e^{it(X_n+Y)}]=e^{itY}\mathbb{E}[e^{itX_n}]\rightarrow e^{itY}\varphi_X=\varphi_{X+Y}(t).$$

Desta forma, precisamos mostrar apenas que $\mathbb{E}[e^{itX_n}(e^{itY_n}-e^{itY})]\rightarrow 0$.

$$|\mathbb{E}[e^{itX_n}(e^{itY_n}-e^{itY})]|\leq \mathbb{E}[|e^{itX_n}(e^{it Y_n}e^{itY})|]=\mathbb{E}[e^{itY_n}-e^{itY}],$$

pois $|e^{itX_n}|=1$, assim precisamos apenas mostrar que $\mathbb{E}[|e^{it(Y_n-Y)}|]\rightarrow 0$. Mas esse fato é consequência do teorema da convergência dominada.

ii) Esta convergência é imediata de i), pois $-Y_n\rightarrow -Y$.

iii) Vamos supor primeiramente que $Y=0.$ Assim queremos mostrar que $Y_nX_n$ converge em probabilidade para 0, pois convergência em probabilidade implica em convergência distribuição.

Portanto sejam $\varepsilon,~\delta \ > \ 0$ e $x \ < \ 0 \ < \ y$ pontos de continuidade de $F_X$, tais que $F_X(y)-F_X(x)=\mathbb{P}[x \ < \ X \leq y] \ > \ 1-\delta$. Como por hipótese $X_n$ converge em distribuição para $X$, temos que

$$\mathbb{P}[x \ < \ X_n \leq y]=F_{X_n}(y)-F_{X_n}(x) \ > \ 1-\delta$$

para um $n$ suficientemente grande. Além disso, definimos $M=\max(y,-x).$ Então a convergência em probabilidade de $Y_n$ para zero implica que $\mathbb{P}[|Y_n| \ < \ \varepsilon/M] \ > \ 1-\delta$ para $n$ suficientemente grande.

$$\mathbb{P}[x \ < \ X_n \ < \ y, |Y| \ < \ \varepsilon/M] \ >1-2\delta.$$

isto decorre da P10.

Além disso, temos que $x \ < \ X_n \ < \ y$ e $|Y_n| \ < \ \frac{\varepsilon}{M}$ o que implica que $|X_nY_n| \ < \ \varepsilon$.

Logo $\mathbb{P}[|X_nY_n| \ < \ \varepsilon] \ > \ 1-2\delta$ para $n$ suficientemente grande.

Portanto temos que para todo $\varepsilon \ > \ 0$ temos que $\mathbb{P}[|X_nY_n| \ < \ \varepsilon]\rightarrow 1$, ou seja $X_nY_n$ converge em probabilidade para zero.

Para demonstrarmos o caso geral em que $Y=c$, basta analisarmos o seguinte fato

$$Y_nX_n=YX_n+(Yn-Y)X_n$$

e $Y_n-Y$ converge em probabilidade para zero, assim segue do caso em que $Y=0$ que $(Y_n-Y)X_n$ converge em probabilidade para zero.

Além disso, temos que

$$\varphi_{cX_n}(t)=\varphi_{X_n}(ct)\rightarrow \varphi_{X}(ct)=\varphi_{cX}(t)=\varphi_{YX}(t),$$

Assim do Teorema 7.1.2.5 decorre que $YX_n$ converge $YX$. Agora o resultado segue imediatamente do item i), pois temos a soma de dois termos em que um que converge em probabilidade para zero e outro converge em distribuição para $YX$.

iv) Notemos que do Teorema 7.1.2.4 que $\frac{1}{Y_n}$ converge em probabilidade para $\frac{1}{Y}$ e em seguida basta aplicarmos o item iii) que o resultado segue.

$\Box$

Teorema 7.1.2.4 (Cramér-Wold)

Demonstração:

Para iniciarmos essa demonstração vamos definir a função característica de um vetor aleatório.

Assim, consideramos um vetor j-dimensional $\widetilde{X}=(X_1,\cdots,X_j)$ a função característica de $\widetilde{X}$ é a função $\varphi_{\widetilde{X}}:\mathbb{R}^j\rightarrow C$ a qual é definida por:

$$\displaystyle\varphi_{\widetilde{X}}(t_1,\cdots,t_j)=\mathbb{E}\left[\exp\left(i\sum_{k=1}^{j}t_jX_j\right)\right]=E\left[e^{i\widetilde{t} \widetilde{X}}\right].$$

Agora com a definição da função característica para um vetor aleatório em mãos podemos finalmente partir para a demonstração do teorema de Cramér-Wold.

Suponhamos que $\sum_{j=1}^{k}t_jX_{nj}$ converge em distribuição para

$$\sum_{j=1}^{k}t_jX_{j}$$

Neste caso temos que:

$$\varphi_{X_n}(t_1,\cdots,t_k)=\mathbb{E}[e^{i\sum_{j=1}^{k}t_jX_{nj}}]$$

$$\varphi_{\sum_{j=1}^{k}t_jX_{nj}}(1)\rightarrow\varphi_{\sum_{j=1}^{k}tjXj}(1)=\varphi_{\widetilde{X}}(t_1,\cdots,t_k)$$

Assim decorre imediatamente que como $\varphi_{\widetilde{X_n}}\rightarrow\varphi_{\widetilde{X}}$ que $\widetilde{X_n}$ converge em distribuição para $X$.

Agora vamos supor o caso contrário, suponha que $X_n$ converge em distribuição para $X$.

Assim notemos que:

$$\varphi_{\sum_{j=1}^{k}tjX_{nj}}=E\left[e^{it\sum_{j=1}^{k}t_jX_{nj}}\right]=E\left[e^{i \sum_{j=1}^{k}tt_jX_{nj}}\right]=$$

$$=\varphi_{\widetilde{X_n}}(tt_1,\cdots,tt_k)\rightarrow\varphi_{\widetilde{X}}(tt_1,\cdots,tt_k)=\varphi_{\sum_{j=1}^{k}t_jX_j}(t).$$

Portanto $$\sum_{j=1}^{k}t_jX_{nj}$$

converge em distribuição para $$\sum_{j=1}^{k}t_jX_{j}$$

$\Box$

Proposição 7.1.2.2

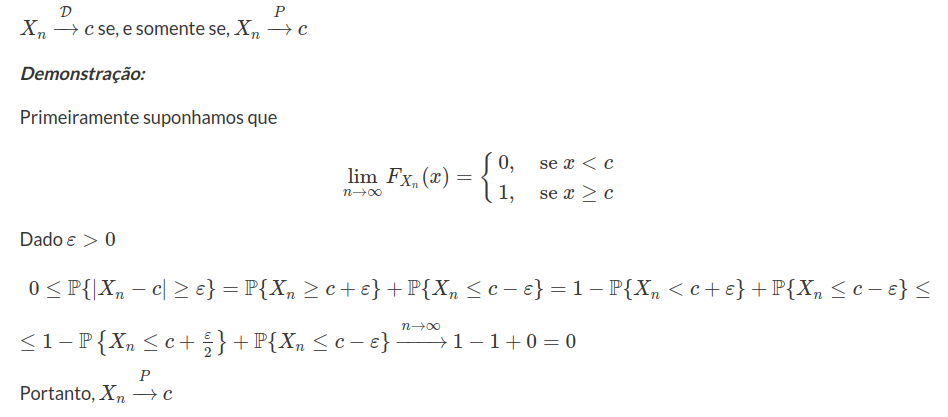
Reciprocamente, seja $F_n$ a função distribuição acumulada de $X_n,~n\geq 1.$ Fixamos $x\in\mathbb{R}$ para todo $x$ ponto de continuidade de $F$. Então para todo $\varepsilon>0$

$$\mathbb{P}(X_n\leq x)\leq\mathbb{P}(X\leq x+\varepsilon)+\mathbb{P}(X_n\leq x~;~X> x+\varepsilon)\leq \mathbb{P}(X\leq x+\varepsilon)+\mathbb{P}(|X_n-c|>\varepsilon)~~(7.1.2.1)$$

e similarmente

$$\mathbb{P}(X_n\leq x)\geq\mathbb{P}(X\leq x-\varepsilon)-\mathbb{P}(|X_n-c|>\varepsilon)~~(7.1.2.2)$$

Logo, de (7.1.2.1) e (7.1.2.2) obtemos que

$$F(x-\varepsilon)-\mathbb{P}(|X_n-c|> \varepsilon)\leq F_n(x)\leq F(x+\varepsilon)+\mathbb{P}(|X_n-c|>\varepsilon)$$

$\Box$

Teorema 7.1.2.5

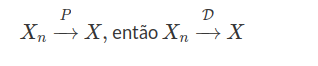
Demonstração:

Basta, usar a volta da proposição 7.1.2.2 trocando c por $X.$

$\Box$

Proposição 7.1.2.3: (Caso discreto)

$\Box$

Exemplo 7.1.2.2

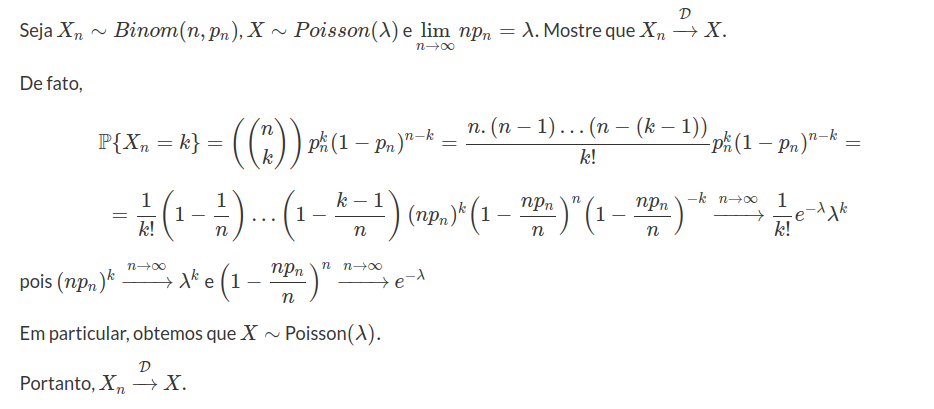
Exemplo 7.1.2.3

Portanto segue o resultado.

Agora, apresentamos um exemplo de uma sequência de variáveis aleatórias a qual converge em probabilidade e em média p para X $\forall p\geq 1$, mas não converge quase certamente.

Exemplo 7.1.2.4

Para finalizar esta seção, vamos apresentar um diagrama dos principais resultados.

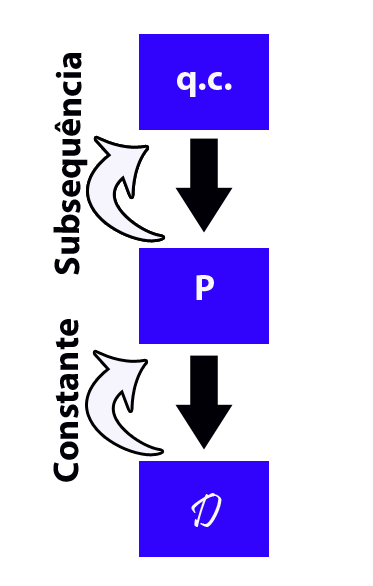
Figura 7.1.2.1: Diagrama de implicações entre os tipos de convergência.

7.1.3 - Convergência em média p

Nesta seção, vamos estudar as convergências em média p, porém, inicialmente necessitamos de desigualdades importantes como por exemplo as desigualdades de Markov e Chebyshev. Chebyshev estabeleceu uma simples desigualdade que permitiu uma prova trivial da Lei dos Fraca dos Grandes Números. A seguir, apresentamos as principais desigualdades.

Proposição 7.1.3.1 (Desigualdade de Markov)

Seja X uma variável aleatória não negativa, ou seja, que assume apenas valores reais positivos. Então temos que para qualquer $\varepsilon > 0$:

$$\mathbb{P}[X > \varepsilon]\leq \displaystyle \frac{\mathbb{E}[X]}{\varepsilon}$$

Demonstração:

Para todo $\varepsilon > 0$, observe que

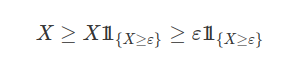
Logo, $\mathbb{E}[X]\geq \varepsilon \mathbb{P}(X\geq \varepsilon)$

Portanto, $\mathbb{P}(X\geq \varepsilon ) \leq \dfrac{\mathbb{E}[X]}{\varepsilon}$ segue a desigualdade de Markov.

$\Box$

Proposição 7.1.3.2 (Desigualdade de Chebyshev)

Seja X uma variável aleatória tal que $\mathbb{E}(X)< \infty$, $\text{Var}(X)<\infty$ e $\varepsilon > 0$ então:

$$\mathbb{P}[|X-\mathbb{E}[X]|> \varepsilon]\leq \displaystyle \frac{\text{Var}(X)}{\varepsilon^2}.$$

Demonstração:

Primeiramente vamos definir uma variável aleatória $Y=(X-\mathbb{E}[X])^2.$ Note que a variável Y satisfaz as hipóteses da desigualdade de Markov, pois Y é uma variável não negativa. Assim, temos que:

$$\mathbb{P}[Y> \varepsilon^2]\leq \displaystyle \dfrac{\mathbb{E}[Y]}{\varepsilon^2}=\dfrac{\mathbb{E}[(X-\mathbb{E}[X])^2]}{\varepsilon^2}$$

Por definição temos que $\mathbb{E}[(X-\mathbb{E}[X])^2]=\text{Var}[X],$ então

$$\mathbb{P}[Y> \varepsilon^2]\leq \displaystyle \frac{\text{Var}[X]}{\varepsilon^2}.$$

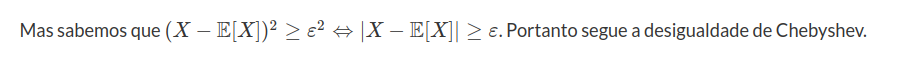
$\Box$

A seguir, vamos enunciar uma desigualdade importante, que é a desigualdade de Jensen, muito utilizada na teoria das probabilidades. Johan Valdemar Jensen, engenheiro de telecomunicações dinamarquês, publicou esta desigualdade em 1906 na Acta Matemática.

Proposição 7.1.3.3 (Desigualdade de Jensen)

Seja X uma variável aleatória, então para toda a variável aleatória $X\in \mathcal{L}^1(\mathbb{P})$ tal que $-\infty\leq a< X< b\leq +\infty$ e $\varphi: (a,b)\rightarrow \mathbb{R}$ convexa

$$\varphi(\mathbb{E}[X])\leq \mathbb{E}[\varphi(X)]$$

Demonstração:

Ideia intuitiva: (Caso particular) Seja $\varphi(x)=x^2$ uma função $\varphi: (a,b)\rightarrow \mathbb{R}$ convexa. Vimos na seção variância de variáveis aleatórias que

$$\text{Var}(X)=\mathbb{E}(X^2)-[\mathbb{E}(X)]^2.$$

Podemos rescrever como

$$\mathbb{E}(X^2)=\underbrace{\text{Var}(X)}_{\geq 0}+[\mathbb{E}(X)]^2\geq [\mathbb{E}(X)]^2$$

O caso geral, pode ser visto no artigo de Johan L. W. V. Jensen. Podemos ver uma outra demonstração no conteúdo Propriedades do valor esperado.

$\Box$

Proposição 7.1.3.4 (Desigualdade de Cauchy-Schwartz)

Sejam X e Y uma variáveis aleatórias, tais que $\mathbb{E}[X^2]<\infty$ e $\mathbb{E}[Y^2]<\infty,$ então

$$\mathbb{E}[|X|.|Y|]\leq \sqrt{\mathbb{E}[X^2]\mathbb{E}[Y^2]}$$

Demonstração:

Para $\lambda\in \mathbb{R},$

$$0\leq\mathbb{E}\left[(\lambda|X|+|Y|)^2\right]=\mathbb{E}[\lambda^2|X|^2+2\lambda|X|.|Y|+|Y|^2]=\lambda^2\mathbb{E}[X^2]+2\lambda\mathbb{E}[|X|.|Y|]+\mathbb{E}[|Y|^2]$$

Usamos a ideia do discriminante na solução da equação do 2º grau da seguinte forma

$$\Delta=4(\mathbb{E}[|X|.|Y|])^2-4\mathbb{E}[|X|^2]\mathbb{E}[|Y|^2]\leq0$$

Portanto,

$$\mathbb{E}[|X|.|Y|]\leq \sqrt{\mathbb{E}[X^2]\mathbb{E}[Y^2]}$$

$\Box$

Com isso, vamos definir a convergência em média p da seguinte forma.

Definição 7.1.3.1

Considere $X$ uma variável aleatória com $\mathbb{E}[|X|^p]< \infty$ e $(X_n)_{n\geq 1}$ sequência de variáveis aleatórias. Dizemos que $X_n$ converge em média p para X ou converge em $\mathcal{L}^p$ para X (caso queira saber mais sobre os espaço $\mathcal{L}^p$ consulte o conteúdo Propriedades do espaço L^p) se

$$\lim_{n\rightarrow\infty}\mathbb{E}\left[|X_n-X|^p\right]=0,\quad \text{para}~p\geq 1$$

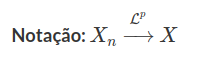
Observação

quando $p=2,$ dizemos que converge em média quadrática.

Teorema 7.1.3.1

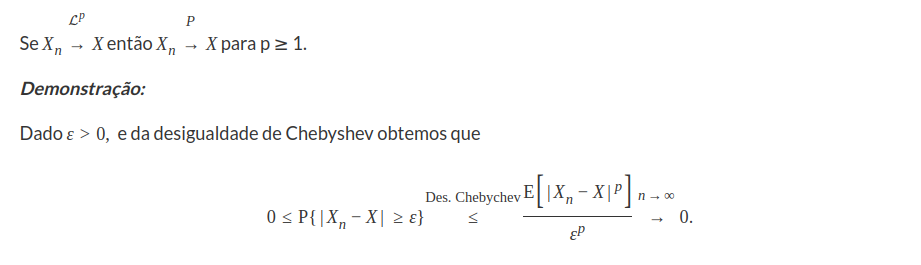
$\Box$

Lema 7.1.3.1

$\Box$

Teorema 7.1.3.2

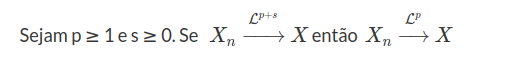
Demonstração:

Consideramos $q=p+s$ e pela desigualdade de Jensen obtemos que

$$\left(\mathbb{E}|X_n-X|^p\right)^{\frac{1}{p}}\leq \left(\mathbb{E}|X_n-X|^q\right)^{\frac{1}{q}}\rightarrow 0$$

$\Box$

No caso particular, temos que se $X_{n}$ converge em média quadrática para X, então também $X_{n}$ converge em média para X (lema 7.1.3.1). No teorema 7.1.3.1 vimos que se $X_{n}$ converge em média p para X então converge em probabilidade, porém a recíproca nem sempre é verdadeira. A seguir, apresentamos um caso particular em que vale a volta.

Teorema 7.1.3.3 (Caso dominado)

$\Box$

Teorema 7.1.3.4

Seja $(X_n)$ uma sequência de variáveis aleatórias não negativas tal que

$X_n\stackrel{q.c}{\rightarrow}X$ e $\mathbb{E}[X_n]\rightarrow \mathbb{E}[X]$, então $X_n\stackrel{\mathcal{L}^1}{\rightarrow}X$

Demonstração:

Para n suficientemente grande temos que $\mathbb{E}[X_n]< \infty$ e temos que

o que prova o resultado.

$\Box$

Exemplo 7.1.3.1

Exemplo 7.1.3.2

$$\varepsilon\leq |X-Y|\leq |X_n-X|+|X_n-Y|$$

Agora, observamos os seguintes eventos

$$[|X-Y|\geq \varepsilon]\subseteq [|X_n-X|\geq \frac{\varepsilon}{2}]\cup[|X_n-Y|\geq \frac{\varepsilon}{2}].$$

Logo,

$$0\leq \mathbb{P}[|X-Y|\geq \varepsilon]\leq \mathbb{P}[|X_n-X|\geq \frac{\varepsilon}{2}]+[|X_n-Y|\geq \frac{\varepsilon}{2}]\rightarrow 0$$

o que implica que $\mathbb{P}[|X-Y|\geq \varepsilon]\rightarrow 0,~\forall \varepsilon> 0$

Portanto, $$\mathbb{P}[|X-Y|> 0]=\lim_{n\rightarrow \infty}\mathbb{P}\left(|X-Y|> \frac{1}{n}\right)=0.$$

Exemplo 7.1.3.3

Exemplo 7.1.3.4

Logo converge quase certamente e portanto converge em probabilidade. Mas observe que não converge em média p para $X=0$, pois

$$\lim_{n\rightarrow\infty} \mathbb{E}[|X_n|^p]=\lim_{n\rightarrow\infty} \frac{e^{np}}{n^2}=\infty, ~~\forall p\geq 1.$$

Exemplo 7.1.3.5

Suponha $(X_n)_{n\geq 1}$ uma sequência de v.a’s tal que

$$\mathbb{P}(X=0)=1-\displaystyle \frac{1}{n}$$

$$\mathbb{P}(X_n=1)=\displaystyle \frac{1}{2n}=\mathbb{P}(X_n=-1).$$

Mostre que $X_n\stackrel{P}{\rightarrow} 0$ e $X_n\stackrel{\mathcal{L}^p}{\rightarrow} 0,$ para todo p≥1.

Primeiramente vamos mostrar que $X_n\stackrel{P}{\rightarrow} 0.$ Para isto, dado ε>0,

$$\mathbb{P}(|X_n-0|\geq \varepsilon)=\mathbb{P}(X_n=0;X=0)+\mathbb{P}(X_n=0;X=1)+\mathbb{P}(X_n=0;X=-1)=$$

Portanto $X_n\stackrel{\mathcal{L}^p}{\rightarrow} 0.$

Exemplo 7.1.3.6

Para $c\in\mathbb{R}$, constante, mostre que $X_n\stackrel{\mathcal{L}^2}{\rightarrow} c$ se, e somente se, $\mathbb{E}[X_n]\rightarrow c$ e $Var[X_n]\rightarrow 0$.

Primeiramente supomos que $X_n\stackrel{\mathcal{L}^2}{\rightarrow} c$.

$$\mathbb{E}\left[(X_n-c)^2\right]=\mathbb{E}\left[(X_n-\mathbb{E}[X_n]+\mathbb{E}[X_n]-c)^2\right]=$$

$$=\mathbb{E}\left[(X_n-\mathbb{E}[X_n])^2\right]+\mathbb{E}\left[(\mathbb{E}[X_n]-c)^2\right]-2\mathbb{E}\left[(X_n-\mathbb{E}[X_n])\right]\mathbb{E}\left[(\mathbb{E}[X_n]-c)\right]=$$

Portanto $X_n\stackrel{\mathcal{L}^2}{\rightarrow} c.$

Uniformemente integrável e limitado em $\mathcal{L}^1$

A principal preocupação entre as relações dos tipos de convergência estocástica é saber se é uma condição necessária e suficiente. Para isto vamos introduzir o conceito de Uniformemente Integrável (UI) e limitado em $\mathcal{L}^1.$ A seguir, vamos apresentar resultados e definições para mostrar que uma condição necessária e suficiente para que a convergência em média p para X, implique em convergência em probabilidade.

Definição 7.1.3.2

Obs: (caso queira saber mais sobre os espaço $\mathcal{L}^p$ consulte o conteúdo Propriedades do espaço L^p)

Observamos que $\mathbb{X}$ é limitada em $\mathcal{L}^1$ se, e somente se $I_{\mathbb{X}}(1)< \infty.$

Definição 7.1.3.3

Logo, se $\mathbb{X}$ é limitada em $\mathcal{L}^p$ para algum p$\in(1,\infty)$ então $\mathbb{X}$ é U.I.

Lema 7.1.3.1

Seja $(\Omega,\mathcal{A},\mathbb{P})$ espaço de probabilidade fixado e X uma variável aleatória integrável e o conjunto

que é uma contradição.

$\Box$

A seguir, apresentamos uma outra caracterização de U.I.

Lema 7.1.3.2

Seja $\mathbb{X}$ uma família de variáveis aleatórias. Então $\mathbb{X}$ é U.I. se, e somente se,

Portanto, $\mathbb{X}$ é U.I.

$\Box$

Agora, necessitamos de uma definição e um resultado que são de grande importância para demonstração do último resultado deste assunto.

Definição 7.1.3.4

Teorema 7.1.3.5

Demonstração:

Vamos omitir esta demonstração, pois necessitamos de resultados de análise funcional.

$\Box$

Finalmente, vamos provar o resultado que mostra a condição necessária e suficiente para que a convergência em média p para X, implique em convergência em probabilidade.

Teorema 7.1.3.6

Seja $(X_n)_{n\geq 1}$ uma sequência de variáveis aleatórias e X variável aleatória. Obtemos as seguintes equivalências:

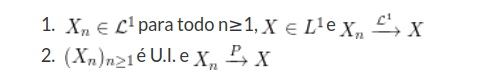
Demonstração:

Inicialmente, vamos enunciar o lema de Fatou.

Lema de Fatou

Considere $(X_n)_{n\geq 1}$ sequência de variáveis aleatórias não negativas. Então pelo Teorema da Convergência Monótona temos que $\mathbb{E}[\liminf Xn]\leq\liminf_n \mathbb{E}[X_n].$

Logo, pelo lema de Fatou $\mathbb{E}[|X|]\leq\displaystyle\liminf_k \mathbb{E}[|X_{n_k}|]<\infty.$

Com isso, dado ε > 0, existe um K < ∞ tal que para todo n ≥ 1, temos que

Como tomamos um ε > 0 arbritrário, podemos concluir que (2)$\rightarrow$(1).

$\Box$

Para finalizar esta seção, vamos apresentar um diagrama dos principais resultados.

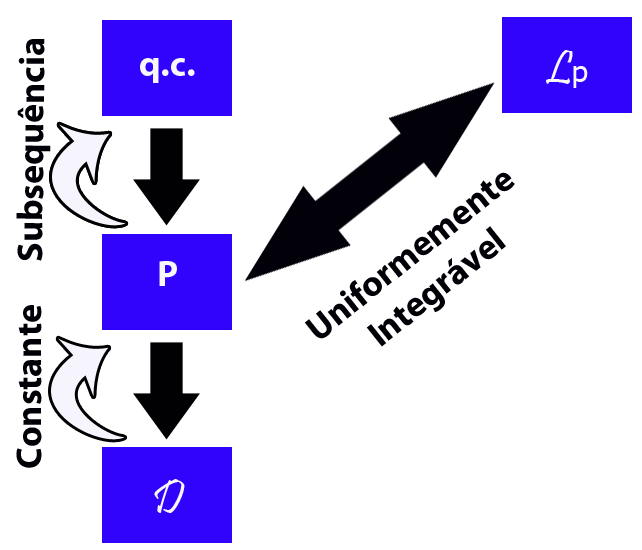
Figura 7.1.3.1: Diagrama de implicações entre os tipos de convergência.

7.2 - Lei dos Grandes Números

A lei dos grandes números foi primeiramente provada pelo matemático James Bernoulli na quarta parte de seu livro Ars Conjectandi publicado em 1713. Como acontece na maioria dos casos, a prova dada por Bernoulli é muito mais difícil do que a realizada com a desigualdade de Chebyshev. Chebyshev desenvolveu sua desigualdade (uma generalização da desigualdade de Markov) para demonstrar uma forma mais geral da Lei dos Grandes Números.

A lei dos grandes números é uma das principais leis assintóticas da estatística, sua ideia é bastante intuitiva, mas de grande importância. Antes de enunciarmos esta lei, vamos tentar analisar a ideia intuitiva dela.

Por exemplo, seja X uma variável aleatória que representa o lançamento de uma moeda honesta, no qual $X(cara)=1$ e $X(coroa)=0.$ Se lançarmos essa moeda n vezes então temos que a média aritmética dos valores observados tendem a 1/2, ou seja, tendem a $\mathbb{E}[X].$ A lei dos grandes números nos diz que a média aritmética dos valores observados tendem a esperança da variável aleatória.

Um outro exemplo, é quando lançamos um dado equilibrado, com as faces numeradas de 1 a 6. A probabilidade de obtermos o número 4 é de $\dfrac{1}{6}=0,16666\dots,$ pois os eventos são equiprováveis. Vamos simular os resultados no computador da seguinte forma. Primeiramente lançamos os dados 100 vezes e anotamos quantas vezes a face 4 aparece nos resultados e por fim calculamos a proporção de vezes que a face 4 aparece. Repetimos isto para 1000 e 10000 lançamentos. Assim, obtemos os seguintes resultados:

Lançamentos	Face do dado igual a 4	Proporção de face igual a 4
100	11	0,11
1000	159	0,159
10000	1660	0,166

Observe que quanto maior o número de lançamentos do dado, mais o resultado experimental se aproxima da probabilidade esperada.

7.2.1 - Lei Fraca dos Grandes Números

Fundada no final do século XIX, a escola de São Petersburgo produziu grandes matemáticos russos com grandes contribuições à Lei dos Grandes Números. Chebyshev influenciado por grandes matemáticos russos, publicou o importante livro Fundamentos da teoria matemática de probabilidades, que fazem parte das linhas estudadas por Daniel Bernoulli e Euler em São Petersburgo. Chebyshev foi o primeiro a raciocinar sistematicamente em termos de variáveis aleatórias e seus momentos. Chebyshev estabeleceu uma simples desigualdade que permitiu uma prova trivial da Lei Fraca dos Grandes Números.

Antes de definirmos e demonstrarmos formalmente a Lei Fraca dos Grandes Números, vamos necessitar de conhecimento de convergência em probabilidade e quase certa e de algumas desigualdades importantes , como as desigualdades de Markov e Chebyshev (para mais detalhes consulte o conteúdo de convergência de variáveis aleatórias).

A principal diferença entre a lei fraca e a lei forte dos grandes números é que a primeira converge em probabilidade e a segunda converge quase certamente. A convergência em probabilidade é uma convergência mais fraca que a convergência quase certa, pois se houver convergência quase certa há convergência em probabilidade. Vejamos isto através da seguinte proposição.

Proposição 7.1.1.1

Se uma sequência de variáveis aleatórias $Y_n$ sobre um espaço de probabilidade $(\Omega , \mathcal{F} , \mathbb{P} )$ converge quase certamente para uma variável aleatória $Y $ então $Y_n \to Y$ em probabilidade.

Demonstração:

Dado $\varepsilon > \ 0 $ tome $ S_m = ( Y_m : Y_m - Y > \varepsilon ) $ para todo $m \in \mathbb{N} $.

Como $Y_m \to Y $ quase certamente, temos

$\mathbb{P}(\limsup S_m ) \leq \limsup \mathbb{P}(S_m ) = 0 $ e $\mathbb{P}(S_m ) \ge 0$ para todo $m \in \mathbb{N} $. Assim temos $\mathbb{P}(S_m ) \to 0$

$\Box$

Teorema 7.1.1.1 (Lei Fraca de Chebyshev)

Sejam $X_i$ uma sequência enumerável de variáveis aleatórias independentes dois a dois. Se a sequência $X_i$ tem variância finita e uniformemente limitada, ou seja, existe uma constante $c\in \mathbb{R}$ tal que $\text{Var}[X_i]\leq c$. Então a sequência $X_i$ satisfaz a Lei Fraca dos Grandes Números:

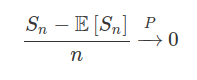
em que $\displaystyle S_n=\sum_{i=1}^{n}X_i$

Demonstração:

Como $X_i$ são independentes temos que $\text{Var}\left[S_n\right]=\displaystyle\sum_{i=1}^{n}\text{Var}[X_i]\leq nc,$ logo as hipóteses da desigualdade de Chebyshev são satisfeitas.

Portanto, temos que

$$\mathbb{P}\left[\left|\displaystyle S_n - \mathbb{E}\left[S_n\right]\right|\right]\geq \varepsilon n]\leq\displaystyle \dfrac{\text{Var}\left[S_n\right]}{\varepsilon^2 n^2}\leq\dfrac{c}{\varepsilon^2 n^2}\rightarrow 0,~~\text{quando} ~~ n\rightarrow \infty.$$

$\Box$

Teorema 7.1.1.1 (Lei Fraca de Khintchine)

Sejam $X_i$ uma sequência enumerável de variáveis aleatórias independentes e identicamente distribuídas e integráveis com média $\mu.$ Então $X_i,~i\in\mathbb{N}$ satisfazem a Lei Fraca do Grandes Números:

$$\frac{S_n}{n}\stackrel{P}{\rightarrow}\mu$$

Demonstração:

De fato, como as $X_n$ são independentes e identicamente distribuídos e usando a função característica (para mais detalhes consulte o conteúdo Função Característica ou Transformada de Fourier), temos que

$$\varphi_{S_n/n}(t)=\left(\varphi_{X_1}\left(\frac{t}{n}\right)\right)^n=\left(1+it\frac{\mu}{n}+r_1\left(\frac{t}{n}\right)\right)^n$$

em que $\frac{r_1(t)}{t}\stackrel{t\rightarrow 0}\longrightarrow0.$ Disto, obtemos que

$$\varphi_{S_n/n}(t)\stackrel{n\rightarrow \infty}\longrightarrow e^{it\mu},\quad \forall ~t\in \mathbb{R}$$

Pelo teorema da continuidade de Lévy, temos que

$$\frac{S_n}{n}\stackrel{\mathcal{D}}\rightarrow\mu$$

Mas como $\mu$ é constante, temos que

$$\frac{S_n}{n}\stackrel{P}\rightarrow\mu$$

$\Box$

Proposição 7.1.1.4

Sejam $X_1,\dots,X_n$ variáveis aleatórias independentes com $E[X_i]=\mu$ e $\text{Var}(X_i)=\sigma^2$ para $i=1,2,\dots,n.$ Então, para todos $\varepsilon> 0$ temos:

$$\mathbb{P}\left[\left|\frac{S_n}{n}-\mu\right|\geq \varepsilon \right]\leq \dfrac{\sigma^2}{n\varepsilon^2}$$

Demonstração:

Seja $S_n=X_1+\dots+X_n,$ aplicamos a desigualdade de Chebyshev e obtemos que

$$\mathbb{P}\left[\left|\frac{S_n}{n}-\mu\right|\geq \varepsilon \right]\leq \dfrac{\text{Var}\left(\frac{S_n}{n}\right)}{\varepsilon^2}=\dfrac{\sigma^2}{n\varepsilon^2}$$

$\Box$

A primeira lei dos grandes números foi proposta por Bernoulli em 1713 e é um caso particular da lei fraca de Chebychev, a qual é proposta como a proposição abaixo.

Proposição 7.1.1.5 (Lei Fraca dos Grandes Números de Bernoulli)

Seja $X_i$ uma sequência de ensaios de bernoulli independentes, com mesma probabilidade de sucesso. Então

$\displaystyle \frac{S_n}{n}\stackrel{P}\rightarrow p$

em que $S_n=\displaystyle\sum^n_{i=1}X_i$

Demonstração:

Podemos demonstrar esse resultado de duas formas. A primeira delas basta observarmos que $p=\mathbb{E}[X_i]$ e $\text{Var}[X_i]=p(1-p)$, e portanto a sequência $X_i$ tem variância uniformemente limitada. Assim, as hipóteses do teorema anterior são satisfeitas o que implica que:

$\displaystyle \frac{S_n-np}{n}=\frac{S_n}{n}-p\stackrel{P}\rightarrow 0$

ou seja,

$\displaystyle \frac{S_n}{n}\stackrel{P}\rightarrow p.$

A outra maneira de demonstrarmos este resultado seria usando a desigualdade de Chebychev. Como as hipóteses da desigualdade são satisfeitas, temos que

$$\mathbb{P}[|\displaystyle S_n-\mathbb{E}[S_n]|\geq \varepsilon n]=\mathbb{P}[|S_n -np]|\geq \varepsilon n]\leq\displaystyle \frac{\text{Var}[S_n]}{\varepsilon^2 n^2}\leq\frac{p(1-p)}{\varepsilon^2 n^2}\rightarrow 0,$$

quando $n\rightarrow \infty$, ou equivalentemente $\displaystyle \frac{S_n}{n}\stackrel{P}\rightarrow p.$

$\Box$

Para finalizarmos esta seção, vamos apresentar alguns exemplo para fixarmos os conceitos apresentados.

Exemplo 7.1.1.1

Seja $X_i$ uma sequência de variáveis aleatórias, mostre que se $\mathbb{E}[X_i]\rightarrow \alpha$ e $\text{Var}[X_i]\rightarrow 0$, então $X_n\stackrel{P}\rightarrow\alpha$.

Como $\mathbb{E}[X_i]\rightarrow \alpha$ temos que para cada $\varepsilon > 0$, existe $n_0$ tal que $|\mathbb{E}[X_n]-\alpha|<\dfrac{\varepsilon}{2}$ para $n\geq n_0$.

Assim, para todo $n\geq n_0$ temos que:

$$[|X_n-\alpha|> \varepsilon]\subseteq[|X_n-\mathbb{E}[X_n]|> \dfrac{\varepsilon}{2}],$$

pois

$$\varepsilon < |X_n-\alpha|=|X_n-\mathbb{E}[X_n]+\mathbb{E}[X_n]-\alpha|\leq|X_n-\mathbb{E}[X_n]|+|\mathbb{E}[X_n]-\alpha|\leq|X_n-\mathbb{E}[X_n]|+\dfrac{\varepsilon}{2}$$

Logo,

$$|X_n-\mathbb{E}[X_n]|+\dfrac{\varepsilon}{2}>\varepsilon\quad \rightarrow\quad |X_n-\mathbb{E}[X_n]|> \dfrac{\varepsilon}{2}$$

Mas pela desigualdade de Chebyshev para todo $n\geq 1$.

$\mathbb{P}(|X_n-\mathbb{E}[X_n]|>\dfrac{\varepsilon}{2})\leq\displaystyle\dfrac{4}{\varepsilon^2}\text{Var}(X_n).$

Portanto para todo $n\geq n_0,$

$\mathbb{P}(|X_n-\alpha|> \varepsilon)\leq \dfrac{4}{\varepsilon^2}\text{Var}[X_n],$

mas como $\text{\text{Var}}[X_n]\rightarrow 0$, quando $n\rightarrow \infty$, concluímos que $X_n \stackrel{P}\rightarrow \alpha$.

Exemplo 7.1.1.2

Suponha que em uma fábrica borracha o número de borrachas produzidas por dia seja uma variável aleatória X com média $\mu=70$. Estime a probabilidade de que a produção diária seja maior que 210.

Neste caso basta usarmos a desigualdade de Markov, e obtemos o seguinte resultado:

$\mathbb{P}(X\geq 210)\leq\displaystyle\dfrac{\mathbb{E}[X]}{210}=\frac{70}{210}=\dfrac{1}{3}.$

Exemplo 7.1.1.3

Se no exemplo acima a variância de X é igual a 20, qual a probabilidade de que a produção do dia esteja entre 40 e 100 borrachas produzidas ?

Utilizando a desigualdade de Chebyshev, obtemos que:

$\mathbb{P}(|X-\mathbb{E}[X]|\geq 30)=\displaystyle\dfrac{\text{Var}[X]}{30^2}=\dfrac{20}{30^2}=\dfrac{1}{45}$

ou seja,

$\mathbb{P}(X-\mathbb{E}[X]\leq 30)=1-\mathbb{P}(X-\mathbb{E}[X]\geq 30)=1-\displaystyle \dfrac{1}{45}=\dfrac{44}{45}\approx 0,977.$

Desta forma a probabilidade de que a produção do dia esteja entre 40 e 100 borrachas produzidas é de aproximadamente 97,7%.

Exemplo 7.1.1.4

Portanto $\mathbb{P}[B_n]=\mathbb{P}[A_n]\rightarrow 0$

Exemplo 7.1.1.5

Uma variável com variância zero é um valor determinístico.

De fato, seja X uma variável aleatória com variância zero $\text{Var}(X)=0,$ pela desigualdade de Chebyshev temos que

$$\mathbb{P}[|X-\mu|\geq k]\leq \dfrac{\text{Var}(X)}{k^2}\quad \rightarrow \quad \mathbb{P}[|X-\mu|>0]=0$$

Portanto, $X=\mu$ com probabilidade 1, isto é, é determinístico.

Exemplo 7.1.1.6

Um candidato a prefeito da cidade de São Carlos gostaria de ter uma ideia de quantos votos receberá nas próximas eleições. Para isto, foi feito uma pesquisa com os cidadães, em que $p$ representa a proporção de votos do candidato com $0\leq p< 1.$ Quantas pessoas devem ser entrevistadas com 95% de confiança para que o valor de $p$ tenha sido determinado com erro inferior a 5%, supondo que as escolhas de cada pessoa sejam independentes.

Seja $n$ o número de candidatos, denotamos $X_i, ~i=1,\dots,n$ a variável aleatória de Bernoulli que assume valor 1, com probabilidade p, se a i-ésima pessoa entrevistada declara a intenção de votar no candidato. Assume o valor 0, com probabilidade $1-p$ caso contrário.

Note que $S_n=X_1+\dots+X_n\sim b(n,p)$ (para mais detalhes consulte distribuição binomial). Assim, $\frac{S_n}{n}$ é uma aproximação do valor de $p$ que é desconhecido.

Logo, do enunciado, queremos

$$\mathbb{P}\left[\left|\frac{S_n}{n}-p\right|\leq 0,05\right]\geq 0,95$$

Da proposição 7.1.1.4 temos que

$$\mathbb{P}\left[\left|\frac{S_n}{n}-p\right|\geq 0,05\right]\leq \frac{p(1-p)}{n(0,05)^2}\leq \frac{1}{4n~(0,05)^2}, \quad\text{pois}~p(1-p)\leq \frac{1}{4}\quad (7.1.1.1)$$

A probabilidade do lado esquerdo de (7.1.1.1) é o complementar à probabilidade desejada, isto é, $1-0,95=0,05.$

Logo,

$$\frac{1}{4n(0,05)^2}\leq 0,05\quad \rightarrow \quad n\geq 2000.$$

Portanto, devemos entrevistar pelo menos 2000 pessoas.

Exemplo 7.1.1.7

$$\mathbb{P}(A_n)\rightarrow 0$$

o que implica que

E o resultado segue

Exemplo 7.1.1.8

Sejam $ X_1,X_2,\dots $ variáveis aleatórias independentes com distribuição comum $ Poisson(\lambda) $. Qual o limite em probabilidade da sequência $ (Y_n)_{n\geq 1} $, no qual

$$Y_n=\frac{X_1^2+\dots+X^2_n}{n}$$

Temos que $ \mathbb{E}(X_1^2)=Var(X_1)+[\mathbb{E}(X_1)]^2=\lambda+\lambda^2=\lambda(\lambda+1) $. Agora sejam $ Z_i=X^2_i, i=1,2,\dots $ variável aleatória que serão independentes pela “propriedade hereditária”, identicamente distribuídas e integráveis. Então, pela Lei Fraca de Khintchine

$$Y_n=\frac{X_1^2+\dots+X_n^2}{n}\stackrel{\mathbb{P}}{\rightarrow} \mathbb{E}(X_1^2)=\lambda(\lambda+1)$$

Exemplo 7.1.1.9

Seja $ (X_n)_{n\geq 1} $ uma sequência de variáveis aleatórias. Prove que se $ \mathbb{E}(X_n)\rightarrow \alpha $.

Sejam $ \epsilon > 0 $ qualquer e

$$A_n=[|X_n-\alpha|\geq \epsilon]=[|X_n-\mathbb{E}(X_n)+\mathbb{E}(X_n)-\alpha|\geq \epsilon]$$

$$B_n=[(|X_n-\mathbb{E}(X_n)|+|\mathbb{E}(X_n)-\alpha|)\geq \epsilon]$$

Agora $ \omega \in A_n $ o que implica que $ \omega \in B_n $ pois

$$(|X_n-\mathbb{E}(X_n)|+|\mathbb{E}(X_n)-\alpha|)\geq |X_n-\alpha|\geq \epsilon$$

Então $ A_n\subset B_n $ o que implica que

$$\mathbb{P}(A_n)\leq \mathbb{P}(B_n)$$

No entanto, através da desigualdade clássica de Chebyshev-Bienayme. Temos

$$\mathbb{P}(A_n)\leq \mathbb{P}(B_n)=\mathbb{P}((|X_n-\mathbb{E}(X_n)|+|\mathbb{E}(X_n)-\alpha|)\geq \epsilon)$$

$$=\mathbb{P}((|X_n-\mathbb{E}(X_n)|)\geq \epsilon-|\mathbb{E}(X_n)-\alpha|)\leq \frac{Var(X_n)}{[\epsilon-|\mathbb{E}(X_n-\alpha)|]^2}\rightarrow 0$$

Exemplo 7.1.1.10

Sejam $ X_1,X_2,\dots $ variáveis aleatórias independentes tais que $ X_1=0 $ e para $ j\geq 2 $, $ X_j $ é variável aleatória discreta satisfazendo

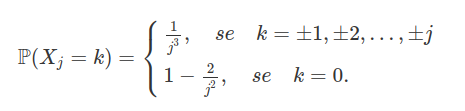
Prove que

$$\frac{\displaystyle \sum_{j=1}^n X_j}{n^\alpha}\stackrel{\mathbb{P}}{\longrightarrow} 0$$

quando $ n\rightarrow \infty $, se $ \alpha > \frac{1}{2} $.

Temos que por conta da simetria $ \mathbb{E}(X_j)=0 $ para $ j=1,2,\dots $ e

$$Var(X_j)=2\sum_{k=1}^n k^3\frac{1}{j^3}=\frac{2}{j^3}\sum_{k=1}^n k^2=\frac{j(j+1)(2j+1)}{6j^3}=\frac{2j^2+3j+1}{3j^2}$$

$$=\frac{2}{3}+\frac{1}{j}+\frac{1}{3j^2}\leq 2$$

Agora

$$Var\left(\sum_{j=1}^n X_j\right)=\sum_{j=1}^n Var X_j\leq 2n$$

Aplicando a desigualdade de Chebyshev-Bienayme temos

$$\mathbb{P}\left(\bigg|\frac{\sum_{j=1}^n X_j}{n^\alpha}\bigg|\geq \epsilon \right)=\mathbb{P}\left(|\sum_{j=1}^n X_j|\geq n^{\alpha}\epsilon\right)$$

$$\leq \frac{Var\left(\sum_{j=1}^n X_j\right)}{n^{2\alpha}\epsilon^2}\leq \frac{2}{n^{2\alpha-1}\epsilon^2}\rightarrow 0$$

Exemplo 7.1.1.11

Seja S uma sequência finita de caras e coroas. Demonstre que se uma moeda não necessariamente honesta( com probabilidade de cara igual a p, $ 0< p< 1 $) for jogada independentemente um número infinito de vezes então S sairá infinitas vezes na sequência obtida, com probabilidade 1.

Teremos

$$\Omega=(W=(\omega_1,\omega_2,\dots),\quad no\quad qual\quad \omega_i=1 \quad ou\quad \omega_i=0,\quad todo\quad i)$$

Seja $ S_k $ a sequência finita(de k elementos) de caras e coroas

$$S_k=(s_1,s_2,\dots,s_k)$$

no qual $ s_i\in (0,1) $ e $ i=1,\dots,k $. Agora, seja a sequência de eventos aleatórios

$$A_1=(\text{a ocorrência da sequência} S_k\text{nos k primeiros ensaios})$$

\colorbox[rgb]{1,1,0}{Revisar}

$$A_2=(\text{a ocorrência da sequência} S_k\text{nos (k+1)2k primeiros ensaios})$$

$ \vdots $

$$A_n=(\text{a ocorrência da sequência} S_k\text{nos k primeiros ensaios})$$

ou seja, $A_n=(\omega\in \Omega: \omega_{(n-1)k+i}=s_i, i=1,\dots,k)$ no qual $ A_1,A_2,\dots $ são eventos aleatórios independentes pois os ensaios são independentes, então temos

$$\mathbb{P}(A_n)=p^j(1-p)^{k-j}=q$$

no qual $ S_k $ tem $ j $ caras e $ k-j $ coroas. Agora $ \sum_{n=1}^\infty \mathbb{P}(A_n)=\sum_{n=1}^\infty q=\infty $. Como $ A_1,A_2,\dots $ são eventos aleatórios independentes aplicando o teorema de Borel-Cantelli, temos

$$\mathbb{P}(A_n,\quad i.o)=1$$

No entanto, sendo $ \mathcal{S} $ o evento “ocorrência de S infinitas vezes”, temos

$$\mathcal{S}\supset [A_n,\quad i.o.]$$

o que implica que $ \mathbb{P}(\mathcal{S})\geq \mathbb{P}(A_n,\quad i.o)=1 $ o que implica que $ \mathbb{P}(\mathcal{S})=1 $

Exemplo 7.1.1.12

Sejam $ X_1,X_2,\dots $ variáveis aleatórias independentes tais que $ X_n $ tem distribuição $ U[0,a_n] $, no qual $ a_n> 0 $. Mostre

(a) Se $ a_n=n^2 $, então com probabilidade 1, somente um número finito das $ X_n $ toma valores menores que 1.

Seja $ A_n=[X_n< 1] $. Então $ A_1,A_2,\dots $ são eventos aleatórios independentes pois $ A_i $ depende apenas de $ X_i $. E

$$\mathbb{P}(A_n)=\mathbb{P}([X_n< 1])=\frac{1}{n^2}, \quad n=1,2,\dots$$

Então,

$$\sum_{n=1}^\infty \mathbb{P}(A_n)=\sum_{n=1}^\infty \frac{1}{n^2}< \infty$$

o que implica por Borel-Cantelli que

$$\mathbb{P}(A_n,\quad i.o)=0$$

o que implica que $ \mathbb{P}(A_n,\quad f.o.)=1 $.

(b) Se $ a_n=n, $ então com probabilidade 1, um número infinito das $ X_n $ toma valores menores que 1.

Então,

$$\sum_{n=1}^\infty \mathbb{P}(A_n)=\mathbb{P}([X_n< 1])=\frac{1}{n}=\infty$$

por Borel-Cantelli e por $ A_n $ ser independentes, isso implica que

$$\mathbb{P}(A_n,\quad i.o)=1$$

Exemplo 7.1.1.13

Sejam $ X_1, X_2,\dots $ variáveis aleatórias independentes tais que $ \mathbb{P}(X_n=1)=1/n, \mathbb{P}(X_n=0)=1-1/n $. Mostre que $ X_n\stackrel{\mathbb{P}}{\rightarrow}0 $ mas $ \mathbb{P}(X_n\rightarrow 0)=0. $

Para todo $ \epsilon> 0, $

$$\mathbb{P}(|X_n|\geq \epsilon)\leq \mathbb{P}(X_n=1)=\frac{1}{n}\stackrel{n\rightarrow\infty}{\longrightarrow} 0$$

Seja $ A_n=[X_n\neq 0] $, então $ A_1,A_2,\dots $ são independentes pois $ A_i $ depende de $ X_i $. Então,

$$\mathbb{P}(A_n)=\mathbb{P}([X_n\neq 0])=\mathbb{P}(X_n=1)=\frac{1}{n}.$$

Agora,

$$\sum_{n=1}^\infty \mathbb{P}(A_n)=\sum_{n=1}^\infty \frac{1}{n}=\infty$$

por Borel-Cantelli temos que $ \mathbb{P}(A_n,\quad i.o.)=1 $. Então, um número infinito de $ X_i $ são diferentes de zero. Então,

$$\mathbb{P}(\omega\in \Omega: X_n(\omega)\nrightarrow 0)=1$$

o que implica que

$$\mathbb{P}(\omega\in\Omega:X_n(\omega)\rightarrow 0)=0$$

Exemplo 7.1.1.14

Sejam $ X_1,X_2, \dots $ variáveis aleatórias independentes e identicamente distribuídas com distribuição exponencial de parâmetro 1. Mostre que

$$\displaystyle \mathbb{P}\left(\frac{X_n}{\ln(n)}> 1 \text{infinitas}\quad \text{vezes}\right)=1$$

mas

$$\displaystyle \mathbb{P}\left(\frac{X_n}{\ln(n)}> 2 \text{infinitas}\quad \text{vezes}\right)=0$$

Primeiramente vamos mostrar que

$$\displaystyle \mathbb{P}\left(\frac{X_n}{\ln(n)}> 1 \text{infinitas}\quad \text{vezes}\right)=1$$

Seja $ A_n=\left[\frac{X_n}{\ln{(n)}}> 1\right] $ o que implica que $ A_1, A_2, \dots $ são independentes pois $ A_i $ depende apenas de $ X_i $ que são variáveis aleatórias independentes. Agora,

$$\mathbb{P}(A_n)=\mathbb{P}\left(\left[\frac{X_n}{\ln(n)> 1}\right]\right)=\mathbb{P}(X_n> \ln(n))=e^{-\ln(n)}=\frac{1}{n}$$

então pelo lema de Borel-Cantelli temos que

$$\displaystyle \sum_{n=1}^\infty \mathbb{P}(A_n)=\sum_{n=1}^\infty \frac{1}{n}=\infty$$

o que implica que $ \mathbb{P}(A_n,\quad i.o.)=1 $.

Agora vamos mostrar que

$$\displaystyle \mathbb{P}\left(\frac{X_n}{\ln(n)}> 2 \text{infinitas}\quad \text{vezes}\right)=0$$

Analogamente seja $ B_n=\left[\frac{X_n}{\ln{n}}> 2\right] $, novamente temos que $ B_i $ são independentes. Agora

$$\mathbb{P}(B_n)=\mathbb{P}\left(\frac{X_n}{\ln(n)}> 2\right)=\mathbb{P}(X_n> 2\ln(n))=e^{-2\ln(n)}=\frac{1}{n^2}$$

Então

$$\sum_{n=1}^\infty\mathbb{P}(B_n)=\sum_{n=1}^\infty \frac{1}{n^2}< \infty$$

pelo teorema de Borel-Cantelli temos que $ \mathbb{P}(B_n,\quad i.o)=0 $. E o resultado segue.

Exemplo 7.1.1.15

Sejam $ X_1,X_2, \dots $ variáveis aleatórias tais que

$$\mathbb{P}(X_n=0)=1-\frac{1}{n^2},\mathbb{P}(X_n=n^2)=\frac{1}{n^2}$$

para $ n=1,2,\dots $. Demonstre que $ X_n $ converge quase certamente (ache o limite X), mas $ \mathbb{E}(X^m_n)\nrightarrow \mathbb{E}(X^m) $ quando $ n\rightarrow \infty $, para todo $ m=1,2,\dots $.

Vamos mostrar que $ X_n\rightarrow 0 $ q.c.

Seja $ A_n=[X_n\neq 0] $ o que implica que $ \mathbb{P}(A_n)=\mathbb{P}(X_n\neq 0)=1-\mathbb{P}(X_n=0)=\frac{1}{n^2} $ então

$$\sum_{n=1}^\infty \mathbb{P}(A_n)=\sum_{n=1}^\infty \frac{1}{n^2}< \infty$$

o que implica que $ \mathbb{P}(A_n,\quad i.o.)=0 $ o que implica que

$$\mathbb{P}(X_n\neq 0\quad\text{um número finito de vezes})=1$$

o que implica que $ \mathbb{P}(X_n\rightarrow 0)=1 $ o que implica que $ X_n\stackrel{q.c.}{\rightarrow}0 $

Agora vamos mostrar que

$$\mathbb{E}(X_n^m)\nrightarrow \mathbb{E}(X^m)$$

Temos que

$$\mathbb{P}(X_n^m=0)=\mathbb{P}(X_n=0)=1-\frac{1}{n^2}$$

Além disso,

$$\mathbb{P}(X_n^m=n^{2m})=\mathbb{P}(X_n=n^2)=\frac{1}{n^2}$$

Então,

$$\mathbb{E}(X_n^m)=n^{2m}\frac{1}{n^2}=n^{2(m-1)}$$

e ainda

$$\mathbb{E}(X^m)=\mathbb{E}(0)=0$$

Exemplo 7.1.1.16

Sejam $ X_1,X_2, \dots $ variáveis aleatórias

(a) Demonstre: se $ \sum_{n=1}^\infty \mathbb{P}(|X_n|> n)< \infty $, então

$$\limsup_{n\rightarrow \infty} \frac{|X_n|}{n}\leq 1$$

quase certamente.

Note que

$$\sum_{n=1}^\infty \mathbb{P}(|X_n|> n)=\sum_{n=1}^\infty \mathbb{P}\left(\frac{|X_n|}{n}> 1\right)< \infty$$

Seja $ A_n=\left[\frac{|X_n|}{n}> 1\right] $ então pelo lema de Borel-Cantelli temos

$$\mathbb{P}(A_n,\quad i.o)=0$$

o que implica que

$$\mathbb{P}\left(\frac{|X_n|}{n}> 1,\quad \text{finita vezes}\right)=1$$

o que implica que

$$\mathbb{P}\left(\omega:\frac{|X_n(\omega)|}{n}> 1,\quad \text{finita vezes}\right)=1$$

o que implica que

$$\frac{|X_n(\omega)|}{n}> 1$$

finitas vezes, implica que

$$\frac{|X_n(\omega)|}{n}\leq 1$$

para n suficientemente grande, o que implica que

$$\liminf_{n\rightarrow \infty}\frac{|X_n(\omega)|}{n}\leq 1$$

Então, defina \frac{|X_n(\omega)|}{n}> 1,\quad \text{finita vezes}) $ e \limsup_{n\rightarrow \infty}\frac{|X_n(\omega)|}{n}\leq 1) $. Então, $ A\subset B $ e portanto

$$\mathbb{P}(B)\geq \mathbb{P}(A)=1.$$

(b) Se as $ X_n $ são identicamente distribuídas e integráveis, demonstre que

$$\limsup_{n\rightarrow \infty }\frac{|X_n|}{n}\leq 1$$

quase certamente.

Note que,

$$\sum_{n=1}^\infty \mathbb{P}(|X_n|> n)=\sum_{n=1}^\infty \mathbb{P}(|X_1|> n)$$

$$=\sum_{n=0}^\infty \mathbb{P}(|X_1|> n)-\mathbb{P}(|X_1|> 0)=\sum_{n=0}^\infty \mathbb{P}(|X_1|> n)-1$$

Agora, como $ X_1 $ é integrável, temos pelo critério da integrabilidade que

$$\sum_{n=0}^\infty \mathbb{P}(|X_1|\geq n)=\sum_{n=0}^\infty \mathbb{P}(|X_1|> n)< \infty$$

então

$$\sum_{n=1}^\infty \mathbb{P}(|X_n|> n)< \infty$$

o que implica que $ \mathbb{P}(B)=1 $.

Exemplo 7.1.1.17

Sejam $ X_1,X_2,\dots $ variáveis aleatórias independentes e identicamente distribuídas tais que $ X_1\sim U[0,1] $. Prove que $ n^{-X_n}\rightarrow 0 $ em probabilidade, mas $ n^{-X_n} $ não converge quase certamente para 0.

(a)

$$\mathbb{P}(n^{-X_n}\geq \epsilon)=\mathbb{P}(-X_n\ln(x)\geq \ln(\epsilon))=\mathbb{P}(X_1\ln(n)\geq \ln(\epsilon))$$

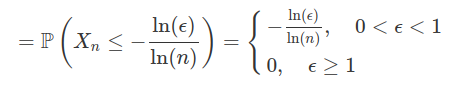
então, qualquer $ \epsilon > 0 $,

$$\mathbb{P}(n^{-X_n}\geq \epsilon)\leq \frac{\ln(\epsilon)}{\ln(n)}\stackrel{\longrightarrow}{n\rightarrow \infty} 0.$$

(b)Sejam os eventos: $ A_n=[n^{-X_n}\neq 0] $ então $ A_1,A_2,\dots $ eventos independentes e

$$\mathbb{P}(A_n)=\mathbb{P}(n^{-X_n}\neq 0)=\mathbb{P}(n^{-X_1}\neq 0)$$

$$=\left(1,\quad n=1\ \mathbb{P}(-X_1\neq 0)=\mathbb{P}(X_1\neq 0)=1,\quad n> 1\right.$$

Então $ \mathbb{P}(A_n)=1 $, para qualquer n. Então,

$$\sum_{n=1}^\infty \mathbb{P}(A_n)=\sum_{n=1}^\infty 1=\infty$$

Agora, como $ A_1,A_2, \dots $ são independentes o que implica pelo Lema de Borel-Cantelli

$$\mathbb{P}(A_n,\quad i.o)=1$$

o que implica que

$$\mathbb{P}(\omega: n^{-X_n(\omega)}\neq 0,\quad i.o.)=1\Rightarrow \mathbb{P}(\omega:n^{-X_n(\omega)}\nrightarrow 0)=1$$

$$\Rightarrow \mathbb{P}\left(\omega:n^{-X_n(\omega)}\rightarrow 0\right)=0\Rightarrow n^{-X_n}\nrightarrow 0$$

Exemplo 7.1.1.18

a) Provaremos incialmente que para cada n existe $ b_n $ tal que

$$\mathbb{P}(|X_n|> \frac{b_n}{n})< \frac{1}{n^2}$$

Para isso, vamos fixar um determinado n, e seja $ (Y_m^n)_{m\geq 1} $ uma sequência de número reais onde

$$Y_m^n=\mathbb{P}\left(|X_n|> \frac{m}{n}\right)$$

Temos que

$$\lim_{m\rightarrow \infty} Y_m^n=\lim_{m\rightarrow \infty}\left[\mathbb{P}\left(\frac{m^-}{n}\right)-1+\mathbb{P}\left(\frac{m}{n}\right)\right] = 0-1+1=0$$

Então dado $ \epsilon> 0 $ existe $ m_0(\epsilon)\in \mathbb{N} $ tal que $ m\geq m_0 $ o que implica que

$$\bigg|\mathbb{P}\left(|X_n|> \frac{m}{m_0}\right)\bigg|< \frac{1}{\epsilon}.$$

Tome em $ \epsilon=\frac{1}{n^2} $ e tomemos $ b_n=m_0\left(\frac{1}{n^2}\right) $ então

$$\mathbb{P}\left(|X_n|> \frac{b_n}{n}\right)< \frac{1}{n^2}$$

Repetindo o procedimento acima descrito obtemos todos os $ b_n\in \mathbb{N}^\star \subset \mathbb{R}^+_\star $.

b) Agora temos fazendo $ \epsilon > 0 $ e

$$A_n=\left[\bigg|\frac{X_n}{b_n}\bigg|> \epsilon\right]$$

o que implica que existe $ n_0(\epsilon) $, tal que $ n> n_0 $ o que implica que

$ \frac{1}{n}< \epsilon $ e $ n> n_0 $.

$$\omega\in \left[\bigg|\frac{X_n}{b_n}\bigg|> \frac{1}{n}\right]$$

o que implica que

$$\mathbb{P}(A_n)\leq \mathbb{P}\left(\bigg|\frac{X_n}{b_n}\bigg|> \frac{1}{n}\right)$$

Então,

$$\sum_{n=1}^\infty \mathbb{P}(A_n)=\sum_{n=1}^\infty \mathbb{P}(A_n)+ \sum_{n> n_0} \mathbb{P}(A_n)$$

$$\leq n_0+\sum_{n> n_0}\mathbb{P}\left(\bigg|\frac{X_n}{b_n}\bigg|> \frac{1}{n}\right)\leq n_0+ \sum_{n> n_0}\frac{1}{n^2}< \infty$$

Então, pelo Lema de Borel-Cantelli.

$$\mathbb{P}(A_n,\quad i.o.)=0$$

o que implica que para qualquer $ \epsilon> 0 $ temos

$$\mathbb{P}\left(\omega:\bigg|\frac{X_n(\omega)}{b_n}\bigg|> \epsilon,i.o.\right)=0$$

o que implica que

$$\mathbb{P}\left(\omega:\bigg|\frac{X_n(\omega)}{b_n}\bigg|\leq \epsilon, \quad n \text{suficientemente grande}\right)=1$$

o que implica que

$$\mathbb{P}\left(\omega:\bigg|\frac{X_n(\omega)}{b_n}\bigg|\rightarrow 0\right)=1$$

então

$$\frac{X_n}{b_n}\rightarrow 0.$$

Na próxima seção, vamos estudar a Lei Forte dos Grandes Números.

7.2.2 - Lei Forte dos Grandes Números

Após estudarmos a Lei Fraca do Grandes Números, vamos estudar agora a Lei Forte dos Grandes Números. A principal diferença da Lei Fraca é que ao invés da convergência em probabilidade, temos a convergência quase certa como dita na seção anterior. Os detalhes destes dois tipos de convergência, foi amplamente discutido na seção convergências em probabilidade e quase certa. A seguir, apresentamos os principais resultados para Lei Forte dos Grandes Números.

Teorema 7.1.2.1

Sejam $ (X_i)_{i\geq 1} $ uma sequência de variáveis aleatórias independentes e identicamente distribuídas. Se $ \mathbb{E}[|X_1|]=\infty $, então com probabilidade 1, a sequência

$ \displaystyle \frac{|S_n|}{n} = \frac{|X_1 + \cdots + X_n|}{n}, $

não é limitada.

Demonstração:

Sabemos que $ \mathbb{E}[|X_1|]=\infty $, então como consequência temos que $ \displaystyle \mathbb{E}\left[\frac{|X_1|}{k}\right]=\frac{\mathbb{E}[|X_1|]}{k}=\infty $.

Então mostremos primeiramente que $ \displaystyle\sum_{n=1}^{\infty}\mathbb{P}(|X|\geq n)\leq \mathbb{E}[|X|]\leq 1+\displaystyle\sum_{n=1}^{\infty}\mathbb{P}(|X|\geq n) $, para qualquer variável aleatória X.

De fato, se $ x\geq 0 $, seja $ [x] $ o maior número inteiro menor ou igual a $ x $. Então a variável aleatória $ [|X|] $ assume valor k quando $ k\leq |X|< k+1 $ e portanto

$$0\leq [|X|]\leq |X|\leq [|X|]+1,$$

Assim pela linearidade e pela monotonicidade da esperança, temos que:

$$0\leq \mathbb{E}([|X|])\leq \mathbb{E}[|X|]\leq \mathbb{E}([|X|])+1,$$

Como [|X|] é uma variável aleatória que assume apenas valores inteiros temos que

$$\mathbb{E}([|X|])=1-F_X[0]+1-F_X[1]+1-F_X[2]\cdots=\displaystyle \sum_{n=0}^{\infty}1-F[n]=\sum_{n=0}^{\infty}\mathbb{P}[X> n].$$

Desta forma temos que $ \mathbb{E}([|X|])=\displaystyle\sum_{n=0}^{\infty}\mathbb{P}[[|X|]\geq n]=\sum_{n=0}^{\infty}\mathbb{P}[|X|\geq n] $. Logo

$$\sum_{n=0}^{\infty}\mathbb{P}[|X|> n]\leq \mathbb{E}|X|\leq 1+\sum_{n=0}^{\infty}\mathbb{P}[|X|> n].$$

Assim $ \displaystyle\sum_{n=0}^{\infty}\mathbb{P}\left[\frac{|X_1|}{k}> n\right]=\infty $ para qualquer $ k\in \mathbb{N} $. Como as variáveis $ X_n $ são identicamente distribuídas temos que:

$$\displaystyle\sum_{n=0}^{\infty}\mathbb{P}\left[\frac{|X_1|}{k}> n\right]=\displaystyle\sum_{n=0}^{\infty}\mathbb{P}\left[\frac{|X_n|}{k}> n\right]=\displaystyle\sum_{n=0}^{\infty}\mathbb{P}\left[\frac{|X_n|}{n}> k\right].$$

Como os $ X_n $ são independentes, os eventos $ A_n=\left[\frac{|X_n|}{n}\geq k\right] $ são independentes, desta forma usando o lema de Borel Cantelli

$$\mathbb{P}\left(\limsup \displaystyle\frac{|X_n|}{n}\geq k\right)=1.$$

Seja $ B_k=\left[\limsup \displaystyle \frac{|X_n|}{n}\geq k\right] $, temos então

$$\mathbb{P}\left(\displaystyle \bigcap_{k=1}^{\infty}B_k\right)=1,$$

pois a intersecção de um número enumerável de eventos de probabilidade 1 também tem probabilidade 1, como demonstrado na Propriedade 12. Mas o evento $ \displaystyle \bigcap_{k=1}^{\infty}B_k $ é o evento “a $ \displaystyle\frac{|X_n|}{n}\geq k $ é ilimitada”. Assim basta provarmos que se $ \displaystyle\frac{|X_n|}{n} $ é ilimitada, então $ \displaystyle \frac{|S_n|}{n} $ também é ilimitada. Agora, com $ S_0=0 $, temos

$$\displaystyle\frac{|X_n|}{n}=\frac{|S_n-S_{n-1}|}{n}\leq \frac{|S_n|}{n}+\frac{|S_{n-1}|}{n},$$

para $ n \in \mathbb{N} $. Portanto, se $ \frac{X_n}{n} $ é ilimitada, então $ \frac{|S_n|}{n} $ é ilimitada ou $ \frac{|S_{n-1}|}{n} $. Mas se $ n\geq 2 $, temos que

$$\frac{|S_{n-1}|}{n}=\frac{|S_{n-1}|}{n-1} \frac{n-1}{n}$$

e $ \frac{1}{2}\leq \frac{n-1}{n}< 1 $, de modo que $ \frac{|S_{n-1}|}{n} $ é ilimitada se, e somente se,$ \frac{|S_n|}{n} $ também é, pois $ \frac{|S_{n-1}|}{n-1} $ e $ \frac{S_n}{n} $ formam a mesma sequência.

$ \Box $

Teorema 7.1.2.2

Seja $ X_i $ uma sequência de variáveis aleatórias independentes tais que $ \mathbb{E}[X_n]=0 $ e a $ \text{Var}[X_n]\leq \infty $. Então para todo $ \lambda> 0 $,

$ \mathbb{P}\left[\displaystyle\max_{1\leq k \leq n}|\sum_{i=1}^{k}X_i|\geq \lambda\right]\leq \displaystyle \sum_{k=1}^{n}\frac{\text{Var}[X_k]}{\lambda^2}. $

Demonstração:

Para facilitar a notação seja $ S_n=\displaystyle\sum_{i=1}^{n}X_i $. Observemos que:

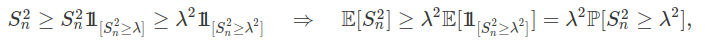
Mas isto implica que :

$$\mathbb{P}(|S_n|\geq \lambda)\leq \displaystyle \frac{1}{\lambda^2}\mathbb{E}[S_n^2]=\frac{\text{Var}[S_n]}{\lambda^2}.$$

Nossa meta é encontrar uma cota superior para $ \mathbb{P}\left[\displaystyle \max_{1\leq k\leq n}S_k^2\geq \lambda^2\right] $, para isto consideramos $ A=\left(\displaystyle\max_{1\leq k\leq n}S_k^2\geq \lambda^2\right) $.

Vamos decompor A da seguinte forma:

$$A_1=[S_1^2\geq \lambda^2]$$

$$A_2=[S_1^2< \lambda^2,S_2^2\geq \lambda^2]$$

$$A_k=[S_1^2< \lambda^2,S_2^2< \lambda^2,\cdots,S_{k-1}< \lambda^2,S_k^2\geq \lambda^2]$$

Note que os $ A_k $ são disjuntos 2 a 2 e $ A=\displaystyle\bigcup_{k=1}^{n}A_k $:

Concluímos que

$$\mathbb{E}[S_n^2]\geq \displaystyle \sum_{k=1}^{n}\lambda^2\mathbb{P}[A_k]=\lambda^2\mathbb{P}[A]$$

Assim

$$\mathbb{P}(A)\leq \displaystyle \frac{\mathbb{E}[S_n^2]}{\lambda^2}=\frac{\text{Var}[S_n]}{\lambda^2}.$$

$ \Box $

Teorema 7.1.2.3 (Primeira Lei Forte de Kolmogorov)

Seja $ (X_i)_{i\geq 1} $ uma sequência de variáveis aleatórias independentes e integráveis, e suponha que:

$ \displaystyle \sum_{i=1}^{\infty}\frac{\text{Var}[X_i]}{i^2}< \infty,\quad (7.1.2.1) $ (condição de Kolmogorov)

então

$ \displaystyle\sum^n_{i=1}\frac{X_i -\mathbb{E}[X_i]}{n}\rightarrow 0, ~~ \text{quase certamente}. $

Demonstração:

Vamos redefinir a nossa sequência de variáveis aleatórias de forma que esperança seja zero. Para isto, seja $ Y_i=X_i-\mathbb{E}[X_i] $, assim $ \mathbb{E}[Y_i]=0 $ e $ \text{Var}[Y_i]=\text{Var}[X_i] $, por P1 da variância.

Desta forma queremos mostrar que

$ \displaystyle\sum_{i=1}^{\infty}\frac{Y_i}{n}\rightarrow 0, ~~ \text{quase certamente}. $

Vale salientar que é equivalente mostrarmos que

$ \displaystyle \max_{2^n< k< 2^{n+1}}\frac{|S_k|}{k}\rightarrow 0,~~ \text{quase certamente}, $

quando $ n\rightarrow \infty, $ em que $ S_k=\displaystyle\sum^k_{i=1}Y_i. $

Agora, para cada m fixo, temos que

$ \mathbb{P}\left(\displaystyle \max_{2^n< k< 2^{n+1}}\frac{|S_k|}{k}\geq \frac{1}{m}\right)\leq \mathbb{P}\left(\displaystyle \max_{2^n< k< 2^{n+1}}\frac{|S_k|}{k}\geq \frac{2^n}{m}\right)\leq \mathbb{P}\left(\displaystyle \max_{1< k < 2^{n+1}}\frac{|S_k|}{k}\geq \frac{2^n}{m}\right) $

$ \leq \displaystyle\frac{m^2}{4^n}\displaystyle\sum^{2^{n+1}}_{k=1}\text{Var}(Y_k), $

Notemos que a última desigualdade é válida pelo Teorema 7.1.2.2. Desta forma temos

$$\displaystyle \sum_{n=1}^{\infty}\mathbb{P}\left(\max_{2^n< k\leq 2^{n+1}}\frac{S_k}{k}\geq \frac{1}{m}\right)\leq m^2 \displaystyle\sum_{n=1}^{\infty}\left(\frac{1}{4^n}\sum_{k=1}^{2^{n+1}}\text{Var} (Y_k)\right)=m^2\displaystyle\sum_{k=1}^{\infty}\displaystyle~\sum_{n:2^{n+1}\geq k}\left(\frac{\text{Var}(Y_k)}{4^n}\right)$$

$$=m^2\displaystyle\sum_{k=1}^{\infty}\left(\text{Var}(Y_k)\displaystyle\sum_{n:2^{n+1}\geq k}^{\infty}\frac{1}{4^n}\right)$$

Observe que

$\displaystyle\sum_{n:2^{n+1}\geq k}\frac{1}{4^n}< \frac{16}{3k^2},$

Portanto

$ \displaystyle \sum_{n=1}^{\infty} \mathbb{P}\left(\max_{2^{n}< k < 2^{n+1}}\displaystyle\frac{S_k}{k}\right)\leq \frac{(4m)^2}{3}\sum_{k=1}^{\infty}\frac{\text{Var}(Y_k)}{k^2}< \infty. $

Assim usando o lema de Borel Cantelli temos que

$ \displaystyle\mathbb{P}\left(\limsup_{n\rightarrow \infty}A_n\right)=0, $

no qual $ A_n=\left[\displaystyle \max_{2^n< k \leq 2^{n+1}}\frac{S_k}{k}\geq\frac{1}{m}\right]. $

Logo, $ \mathbb{P}(\displaystyle\liminf_{n\rightarrow \infty}A_n)=1 $, pois se $ \mathbb{P}\left(\limsup A_n\right)=0 $ temos que para cada m fixo a probabilidade de que $ \displaystyle \max_{2^n< k< 2^{n+1}}\frac{S_k}{k} $ assuma um valor maior que $ \frac{1}{m} $ é 0.

Assim a probabilidade de que $ \displaystyle \max_{2^n< k< 2^{n+1}}\frac{|S_k|}{k} $ assuma um valor maior que zero um número finito de vezes é 1. Logo,

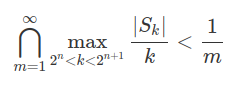
deve ocorrer para todo n a partir de um índice, ou seja, temos que

$ \forall m, 0\leq\displaystyle \max_{2^n< k< 2^{n+1}}\frac{|S_k|}{k} < \frac{1}{m} $ para todo n a partir de um índice.

Portanto concluímos que $ \displaystyle \max_{2^n< k< 2^{n+1}}\frac{|S_k|}{k}\rightarrow 0 $ quase certamente.

$ \Box $

Uma observação importante é que a condição de Kolmogorov (7.1.2.1) é suficiente, mas não é necessária para lei forte dos grandes números. Podemos construir exemplos tais que $ \displaystyle \sum_{i=1}^{\infty}\frac{\text{Var}[X_i]}{i^2}= \infty $ e que satisfaçam a lei dos grandes números.

Exemplo 7.1.2.1

Valor esperado infinito implica em variância infinita.

De fato, seja $ X $ uma variável aleatória tal que $ \mathbb{E}[X]=\infty. $

Por definição, temos que $ \text{Var}(X)=\mathbb{E}[X^2]-\mathbb{E}^2[X]. $

Mas, $ \mathbb{E}[X]=\infty $ e $ \mathbb{E}[X^2]\geq\mathbb{E}^2[X]. $

Portanto, $ \text{Var}(X)=\infty $

Em particular, variáveis aleatórias com valor esperado infinito não satisfazem a condição de Kolmogorov e consequentemente não há garantias que cumpra a lei dos grandes números.

Proposição 7.1.2.2

Seja X uma variável aleatória e seja F sua função de distribuição acumulada. Então,

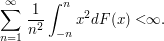
Demonstração:

Vamos relembrar o seguinte fato, o qual vamos utilizar para a demonstração desta proposição.

$ \displaystyle \sum_{n=j}^{n^2}< \frac{2}{j} $

Como

$ \displaystyle\int_{-n}^{n}x^2dF(x)=\sum_{j=-n+1}^{n}\int_{j-1}^{j}x^2dF(x) $

Assim temos que:

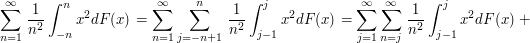
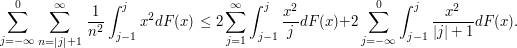
Como $ \frac{x^2}{j}\leq x $ em $ (j-1,j] $, $ j< 1 $, e $ \frac{x^2}{|j|+1}\leq |x| $ em $ (j-1,j] $, para j\leq 0, temos

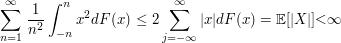
$ \Box $

Teorema 7.1.2.4 (A Lei Forte de Kolmogorov)

Seja $ X_i $ uma sequência de variáveis aleatórias independentes e identicamente distribuídas e com $ \mathbb{E}[X_i]=\mu < \infty $. Então

$ \displaystyle \sum_{i=1}^{n}\frac{X_i}{n}\rightarrow \mu, {quase certamente}. $

Demonstração:

Vale observar neste momento que basta mostrarmos para $ \mu=0 $, pois no caso geral em que $ \mu\neq 0 $ fazermos uma mudança de variável, usando $ G_n=X_n-\mu. $ Neste caso as variáveis aleatórias $ G_n $ serão independentes e indenticamentes distribuidas com $ \mathbb{E}[G_n]=0 $.

Seja $ Y_n $ definida da seguinte forma.

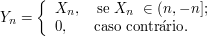
E seja $ Z_n=X_n-Y_n\quad\Rightarrow\quad X_n=Y_n+Z_n $

$$\frac{X_1+\cdots+X_n}{n}=\frac{Y_1+\cdots+Y_n}{n}+\frac{Z_1+\cdots+Z_n}{n}$$

Vamos dividir a demonstração deste teorema em três partes.

Primeiro mostramos que $ \displaystyle\frac{Z_1+\cdots+Z_n}{n}\rightarrow 0 $ quase certamente.

Observamos que $ Z_n\neq 0\Leftrightarrow Y_n\neq X_n\rightarrow X_n \notin (-n,n] $.

Assim,

$$\mathbb{P}(Z_n\neq 0)=\mathbb{P}(X_n\notin (-n,n])< \mathbb{P}(|X_n|> n).$$

Mas os eventos $ A_n=[Z_n\neq 0] $ satisfazem

$$\displaystyle\sum_{n=1}^{\infty}\mathbb{P}(A_n)\leq \sum_{n=1}^{\infty}\mathbb{P}(|X_n|\geq n)$$

Notemos que se os $ X_i $ são identicamentes distribuídos, então temos que:

$$\sum_{n=1}^{\infty}\mathbb{P}(|X_n|\geq n)=\sum_{n=1}^{\infty}\mathbb{P}(|X_1|\geq n)< \infty,$$

no qual a última passagem é consequência da intregabilidade de $ X_1 $.

Assim pelo lema de Borel-Cantelli decorre que $ \mathbb{P}(\displaystyle\limsup_{n\rightarrow \infty}A_n)=0 $, o que implica que:

$$\mathbb{P}(\displaystyle\limsup_{n\rightarrow \infty}Z_n\neq 0)=0$$

Ou seja,

$$\mathbb{P}(\displaystyle\liminf_{n\rightarrow \infty}A_n)=1\quad\Rightarrow\quad \mathbb{P}(Z_m=0)=1$$

com $ m> n $ para algum n suficientemente grande, isto é, $ Z_n\rightarrow 0 $ e ainda

$$\displaystyle\frac{Z_1+\cdots+Z_n}{n}\rightarrow 0\quad\Rightarrow\quad \mathbb{P}\left(\frac{Z_1+\cdots+Z_n}{n}\rightarrow 0\right)=1$$

Logo $ \displaystyle\frac{Z_1+\cdots+Z_n}{n}\rightarrow 0 $ quase certamente.

Mostramos agora que $ \displaystyle \frac{Y_1+\cdots+Y_n}{n}-\frac{\mathbb{E}[Y_1]+\cdots+\mathbb{E}[Y_n]}{n}\rightarrow 0 $ quase certamente.

Como por hipótese $ X_i $ são identicamente distribuídos, então temos que $ F_{X_1}=\cdots=F_{X_n} $.

Notemos que

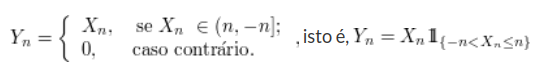
Logo o teorema segue, pois

$ A=\displaystyle\left[\frac{Z_1+\cdots+Z_n}{n}\rightarrow 0\right] $ e $ B=\displaystyle\left[\frac{Y_1+\cdots+Y_n}{n}-\frac{\mathbb{E}[Y_1]+\cdots+\mathbb{E}[Y_n]}{n}\rightarrow 0\right] $.

Portanto $ \displaystyle \frac{X_1+\cdots+X_n}{n}\rightarrow 0 $ quase certamente e no caso mais geral:

$ \displaystyle\frac{X_1+\cdots+X_n}{n}\rightarrow \mu,\quad\text{quase certamente} $

$ \Box $

Teorema 7.1.2.5 (Cantelli)

Seja $ (X_i)_{i\in\mathbb{N}} $ uma sequência de variáveis aleatórias com quarto momento finito, e seja

$$E[|X_n-E[X_n]|^4]\leq C$$

com $ C\in \mathbb{R} $. Então quando $ n\rightarrow \infty $

$$\frac{S_n-E[S_n]}{n}\stackrel{q.c}{\rightarrow} 0 $$

Demonstração:

Sem perda de generalidade podemos assumir que $ \mathbb{E}[X_n]=0 $, pois caso não seja, redefinirmos $ X_n=X_n-\mathbb{E}[X_n] $. Assim para mostramos que $ \dfrac{S_n}{n}\rightarrow 0 $ quase certamente basta mostramos que

$$\displaystyle \sum^\infty_{n=1} \mathbb{P}\left(\left|\dfrac{S_n}{n}\right|\geq \epsilon\right)< \infty,~~~\forall \epsilon > 0$$

Utilizando a desigualdade de Chebyshev, basta mostrarmos que

$$\displaystyle \sum^\infty_{n=1} \mathbb{E}\left(\left|\dfrac{S_n}{n}\right|^4\right)< \infty.$$

Note que $ S_n=(X_1+\cdots X_n)^4 $, logo

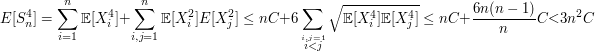
Logo

$$\mathbb{E}\left[\left(\frac{S_n}{n}\right)^4\right]< 3\frac{C}{n^2}$$

Assim

$$\sum^\infty_{n=1} \mathbb{E}\left[\left(\frac{S_n}{n}\right)^4\right]< 3C \sum^\infty_{n=1} \frac{1}{n^2}< \infty$$

E portanto, segue o resultado.

$ \Box $

Teorema 7.1.2.6 (Kolmogorov)

$$\displaystyle \sum^\infty_{n=1} \frac{Var[S_n]}{b^2_n}< \infty$$

Então

$$\displaystyle \frac{S_n-E[S_n]}{n}\stackrel{q.c}{\rightarrow} 0$$

Demonstração:

Vamos omitir a demonstração deste resultado, porém ela pode ser encontrada no livro do Shiryaev.

$ \Box $

Para finalizarmos esta seção, vamos apresentar alguns exemplo para fixarmos os conceitos apresentados.

Exemplo 7.1.2.2

Exemplo 7.1.2.3

Seja $ (X_i)_{i\geq 1} $ uma sequência de variáveis aleatórias independentes e identicamente distribuídas, com distribuição exponencial de parâmetro $ 1 $. Mostremos que:

$ \mathbb{P}\left(\displaystyle\limsup_{n \rightarrow \infty}\frac{X_n}{\log n}> 1\right)=1. $

Para mostrarmos isso basta mostrarmos que $ \displaystyle \sum_{i=1}^{\infty}A_i=\infty $. Assim primeiramente vamos definir o evento $ A_i=(X_i> \log i) $ para $ i\geq 1 $. Como cada $ A_i $ são eventos independentes. Portanto

$ \mathbb{P}(A_i)=\mathbb{P}(X_i> \log i)=e^{-\log{i}}=\displaystyle \frac{1}{i}. $

Desta forma concluímos que:

$ \displaystyle \sum_{i=1}^{\infty}\mathbb{P}(A_i)=\sum_{i=1}^{\infty}\frac{1}{i}=\infty $

consequentemente pelo lema de Borel-Cantelli concluímos que $ \mathbb{P}\left(\displaystyle\limsup_{n \rightarrow \infty}\frac{X_n}{\log n}> 1\right)=1 $ como queríamos demonstrar.

Exemplo 7.1.2.4

Podemos generalizar o exemplo 7.1.2.3 proposto acima, da seguinte forma seja $ X_i $ uma sequência de variáveis aleatórias independentes e identicamente distribuídas, com distribuição exponencial de parâmetro $ \lambda $. Mostremos que:

$ \mathbb{P}\left(\displaystyle\limsup_{n \rightarrow \infty}\frac{X_n}{\log n}> \frac{1}{\lambda}\right)=1. $

A demonstração segue da mesma forma, basta definirmos o conjunto $ A_i=(X_i> \log i) $ para $ i\geq 1 $. Assim

$ \mathbb{P}(A_i)=\mathbb{P}(X_i> \frac{\log i}{\lambda})=e^{-\lambda\frac{\log{i}}{\lambda}}=\displaystyle \frac{1}{i}. $

E portanto concluímos que

$ \displaystyle \sum_{i=1}^{\infty}\mathbb{P}(A_i)=\sum_{i=1}^{\infty}\frac{1}{i}=\infty $

usando novamente o lema de Borel-Cantelli concluímos que $ \mathbb{P}\left(\displaystyle\limsup_{n \rightarrow \infty}\frac{X_n}{\log n}> \frac{1}{\lambda}\right)=1. $

Exemplo 7.1.2.5

Seja $ (X_i)_{i\geq 1} $ uma sequência de variáveis aleatória independentes com distribuição Poisson com parâmetro $ \lambda $. Qual é o limite em probabilidade da sequência $ Y_n $, em que $ Y_n=\dfrac{X_1^2+\cdots+X_n^2}{n} $?

Para resolvermos esse exemplo basta utilizarmos o a lei forte de Kolmogorov, que vamos obter um resultado ainda mais forte. Pela lei forte de Kolmogorov temos que $ Y_n\rightarrow \mathbb{E}[X_1^2] $. Como $ X_1 $ segue uma Poisson temos o seguinte:

$ \lambda=\text{Var}[X_1]=\mathbb{E}[X_1^2]-\mathbb{E}^2[X_1]=\mathbb{E}[X_1^2]-\lambda^2 \quad\Rightarrow\quad \mathbb{E}[X_1^2]=\lambda(1+\lambda) $

Assim pela lei forte de Kolmogorov, temos que $ Y_n\rightarrow \lambda(1+\lambda) $ quase certamente, ou seja, $ Y_n $ converge em probabilidade para $ \lambda(1-\lambda) $.

Exemplo 7.1.2.6 (Método Monte Carlo)

Talvez uma das mais importantes aplicações da lei dos grandes números seja no Método Monte Carlo, que é um método computacional para calcular integrais. Assim, seja $ f $ uma função contínua com imagem no intervalo [0,1] e $ X_1,c_1,X_2,c_2 \cdots $ uma sequência de variáveis aleatórias independentes uniformes no [0,1]. Tomamos

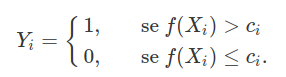
Então

$$\mathbb{E}[Y_1]=\mathbb{P}(f(X_1)> c_1)=\displaystyle \int_{0}^{1}f(x)dx$$

Portanto, pela lei forte dos grandes números temos que:

$$\displaystyle \frac{1}{n}\sum_{i=1}^{n}Y_i\rightarrow \int_{0}^{1}f(x)dx , \quad \text{P-quase certamente}$$

Exemplo 7.1.2.7

Seja $ (X_n)_{n\geq 1} $ uma sequência de variáveis aleatórias independentes e identicamente distribuídas com $ \mathbb{E}[X_1]=\mu $ e $ \text{Var}[X_1]=\sigma^2, $ com $ 0,< \sigma^2< \infty. $ Mostre que

$$\dfrac{\displaystyle\sum^n_{j=1}X_j}{\displaystyle\sqrt{n\sum^n_{j=1}X^2_j}}\xrightarrow{q.c.}\dfrac{\mu}{\sqrt{\mu^2+\sigma^2}}$$

De fato, da 1ª lei de Kolmogorov temos que

$$\sum^n_{j=1}X_j\xrightarrow{q.c.}\mu\quad\text{e}\quad \sum^n_{j=1}\frac{X_j}{n}\xrightarrow{q.c.}\mu$$

Também temos que

$$\sum^n_{j=1}\frac{X^2_j}{n}\xrightarrow{q.c.}\sigma^2+\mu^2$$

Uma observação importante é que se $ X_n\xrightarrow{q.c.}X $ então $ g(X_n)\xrightarrow{q.c.}g(X) $ para g contínua.

Logo, $ X_n\xrightarrow{q.c.}X,~Y_n\xrightarrow{q.c.}Y $ isto implica que $ \dfrac{X_n}{Y_n}\xrightarrow{q.c.}\dfrac{X}{Y} $

Portanto, vale a tese.

Exemplo 7.1.2.8

Sejam $ X_1, X_2, \dots $ independentes e identicamente distribuídas, com $ X_1\sim U[0,1] $. Ache o limite quase certo da média geométrica

$$\left(\prod_{k=1}^n X_k\right)^{1/n}$$

Seja $ Y_n=\left(\prod_{k=1}^n X_k\right)^{\frac{1}{n}} $ o que implica que

$$\ln(Y_n)=\frac{\sum_{k=1}^n\ln(X_k)}{n}$$

Chamaremos de $ Z_i=\ln(X_i) $, $ i=1,2,\dots $. Então, $ Z_1,Z_2,\dots $ é uma equivalência de variáveis aleatórias independentes e identicamente distribuídas, pois $ Z_i $ depende apenas de $ X_i $ que são independentes e identicamente distribuídas. Além disso, temos que

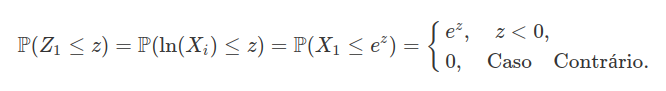
Então,

$$\mathbb{E}(Z_1)=\int_{-\infty}^0 z^2e^{z}dz$$

fazendo uma mudança de variável temos que $ t=-z $. Então, temos

$$\int_{-\infty}^0 z^2e^{z}dz=-\int_0^\infty t^2e^{-t}dt=-1$$

Então, aplicando a lei forte de Kolmogorov para $ Z_1,Z_2,\dots $ temos que

$$\frac{Z_1+Z_2+\dots+Z_n}{n}\stackrel{q.c.}{\longrightarrow}\mathbb{E}(Z_1)=-1$$

Então,

$$\ln(Y_n)\stackrel{q.c.}{\longrightarrow}-1$$

o que implica que

$$\mathbb{P}(\omega:\ln(Y_n(\omega))\rightarrow -1)=1.$$

Agora, como $ f(u)=e^{u} $ é uma função contínua, então se

$$\ln(Y_n(\omega))\rightarrow -1$$

o que implica que

$$e^{\ln(Y_n(\omega))}\rightarrow e^{-1}$$

o que implica que

$$Y_n(\omega)\rightarrow e^{-1}$$

Assim, se

$$\omega\in [\omega:\ln(Y_n(\omega))\rightarrow -1]\Rightarrow \omega \in [\omega: Y_n(\omega)\rightarrow e^{-1}]$$

então

$$\mathbb{P}(\omega: Y_n(\omega)\rightarrow e^{-1})\geq \mathbb{P}(\omega:\ln(Y_n(\omega))\rightarrow -1)=1$$

o que implica que $ Y_n\stackrel{q.c.}{\longrightarrow}e^{-1} $.

Exemplo 7.1.2.9

Demonstre: se $ X_1,X_2,\dots $ são independentes e identicamente distribuídas, com $ \mathbb{E}(X_1)=1=Var(X_1) $, então

$$\displaystyle \frac{\displaystyle \sum_{i=1}^n X_i}{\displaystyle \sqrt{n\sum_{i=1}^n X_i^2}}\rightarrow \frac{1}{\sqrt{2}},\text{quase}\quad\text{certamente}.$$

Como $ X_1,X_2,\dots $ é uma sequência de variáveis aleatórias integráveis, aplicando a lei forte de Kolmogorov, temos que

$$\frac{\sum_{i=1}^n X_i}{n}\stackrel{q.c.}{\rightarrow} \mathbb{E}(X_1)=1$$

isto, se e somente se,

$$\mathbb{P}\left(\omega: \frac{\sum_{i=1}^n X_i(\omega)}{n}\rightarrow 1\right)=1$$

Agora, seja $ Y_i=X_i^2 $, $ i=1,2,\dots $, então $ Y_1,Y_2,\dots $ e sequência de variáveis aleatórias independentes pois $ Y_i $ depende apenas de $ X_i $. Além disso, são integráveis pois $ \mathbb{E}(Y_1)=\mathbb{E}(X_1^2)=Var(X_1)+\left(\mathbb{E}(X_1)\right)^2=1+1=2 $. Então, aplicando a lei forte de Kolmogorov e esta sequência,

$$\frac{\sum_{i=1}^n Y_i}{n}=\frac{\sum_{i=1}^n X_i^2}{n}\rightarrow 2$$

mas isso, se, e somente se,

$$\mathbb{P}\left(\omega: \frac{\sum_{i=1}^nX_1^2}{n}\rightarrow 2\right)=1$$

Agora, definindo $ A:=\left(\omega: \frac{\sum_{i=1}^nX_1}{n}\rightarrow 1\right) $ e $ B:=\left(\omega: \frac{\sum_{i=1}^nX_1^2}{n}\rightarrow 2\right)$.

Então, como

$$\mathbb{P}(A)=\mathbb{P}(B)=1$$

então

$$\mathbb{P}(A\cap B)=1$$

o que implica que

$$\mathbb{P}\left(\omega: \frac{\sum_{i=1}^nX_1(\omega)}{n}\rightarrow 1, \frac{\sum_{i=1}^nX_1^2(\omega)}{n}\rightarrow 2\right)=1$$

Agora se $ \omega $ é tal que

$$\frac{\sum_{i=1}^nX_1}{n}\rightarrow 1\quad\quad e \quad\quad \frac{\sum_{i=1}^nX_1^2}{n}\rightarrow 2$$

Assim, como $ f(t)=\sqrt{t} $ é uma função contínua então, temos que

$$\frac{\sum_{i=1}^nX_1}{n}\rightarrow 1\quad\quad e \quad\quad \sqrt{\frac{\sum_{i=1}^nX_1^2}{n}}\rightarrow \sqrt{2}$$

Agora, observe que se $ \lim_{n\rightarrow \infty}a_n\neq 0 $ e $ \lim_{n\rightarrow \infty}b_n\neq 0 $ então $ \lim_{n\rightarrow \infty}\frac{a_n}{b_n}\neq \frac{a}{b} $ e portanto,

$$\frac{\frac{\sum_{i=1}^nX_1}{n}}{\sqrt{\frac{\sum_{i=1}^nX_1^2}{n}}}\rightarrow \frac{1}{\sqrt{2}}$$

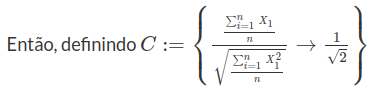
desta forma, temos que $ \omega\in (A\cap B)\Rightarrow \omega \in C $. Assim,

$$\mathbb{P}(C)\geq \mathbb{P}(A\cap B)=1$$

o que implica que

$$\frac{\frac{\sum_{i=1}^nX_1}{n}}{\sqrt{\frac{\sum_{i=1}^nX_1^2}{n}}}\stackrel{q.c}{\longrightarrow}\frac{\sqrt{2}}{2}$$

Exemplo 7.1.2.10

Seja $ 0< \theta < 1/2 $. Prove que se $ X_1,X_2, \dots $ são independentes tais que $ \mathbb{P}(X_n=n^\theta)=\frac{1}{2}=\mathbb{P}(X_n=-n^\theta) $, então

$$\frac{X_1+\dots+X_n}{n}\rightarrow 0$$

quase certamente.

Temos que $ \mathbb{E}(X_n)=0 $ pois é uma variável aleatória limitada e simétrica e

$$Var(X_n)=\mathbb{E}(X_n^2)=2\frac{1}{2}n^{2\theta}=n^{2\theta}$$

e portanto,

$$\displaystyle \sum_{n=0}^\infty \frac{Var(X_n)}{n^2}=\sum_{n=0}^\infty n^{2(\theta-1)}< \infty,$$

pois $ 0< \theta< \frac{1}{2} $. Agora, utilizando a primeira Lei Forte de Kolmogorov, que diz que se $ X_1,X_2,\dots $ é uma sequência de variáveis aleatórias independentes e

$$\sum_{n=1}^\infty \frac{Var(X_n)}{n^2}< \infty$$

então

$$\frac{X_1+\dots+X_n}{n}\stackrel{q.c.}{\longrightarrow} \frac{\mathbb{E}(X_1+\dots+X_n)}{n}=0$$

Exemplo 7.1.2.11

Sejam $ X_1,X_2,\dots $ variáveis aleatórias independentes com densidade comum

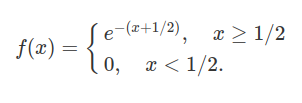
Demonstre que $ S_n\rightarrow \infty $ quase certamente, no qual $ S_n=X_1+\dots+X_n. $

Temos que

$$\mathbb{E}(X_1)=\int_{-1/2}^\infty xe^{-x+1/2}dx$$

fazendo uma mudança de variáveis, temos que $ y=x+\frac{1}{2} $, $ dy=dx $ e $ x=y-\frac{1}{2} $ e temos que

$$\int_0^\infty y(e^{-y})dy-\frac{1}{2}\int_0^\infty e^{-y}dy=1-\frac{1}{2}=\frac{1}{2}$$

Então, como $ X_1,X_2,\dots $ variáveis aleatórias e integráveis pela lei forte de Kolmogorov

$$\frac{X_1+X_2+\dots+X_n}{n}\stackrel{q.c.}{\rightarrow} \frac{1}{2}$$

se, e somente se,

$$\mathbb{P}\left(\omega: \frac{X_1(\omega)+X_2(\omega)+\dots+X_n(\omega)}{n}\rightarrow \frac{1}{2}\right)=1$$

Agora, seja o evento

$$A=\left(\omega:\frac{X_1(\omega)+X_2(\omega)+\dots+X_n(\omega)}{n}\rightarrow \frac{1}{2}\right)$$

Então, se $ \omega \in A $ então

$$\frac{X_1(\omega)+X_2(\omega)+\dots+X_n(\omega)}{n}\rightarrow \frac{1}{2}$$

o que implica que

$$X_1(\omega)+X_2(\omega)+\dots+X_n(\omega)\rightarrow \infty.$$

Assim, definindo

$$B:=\left(\omega: X_1(\omega)+X_2(\omega)+\dots+X_n(\omega)\rightarrow \infty\right)$$

Temos $ \omega \in B $, ou seja, $ A\subset B $ o que implica

$$\mathbb{P}(B)\geq \mathbb{P}(A)=1$$

o que implica que $ S_n\rightarrow \infty. $ E o resultado segue.

Exemplo 7.1.2.12

Sejam $ X_1,X_2,\dots $ independentes e identicamente distribuídas com média $ \mu_1 $ e variância $ \sigma^2_1 $ e sejam $ Y_1,Y_2,\dots $ independentes e identicamente distribuídas com média $ \mu_2 $ e variáveis aleatórias $ Z_1,Z_2,\dots $ da seguinte maneira: joga-se uma moeda honesta e define-se $ Z_1=X_1 $ se dá cara e $ Z_1=Y_1 $ se dá coroa. Depois joga-se de novo, definindo-se $ Z_2=X_2 $ se dá cara e $ Z_2=Y_2 $ se dá coroa. Depois joga-se de novo, definindo-se $ Z_2=X_2 $ se dá cara e $ Z_2=Y_2 $ se dá coroa, etc. (ad infinitum). Suponha que todas as $ Xs $ e $ Ys $ são independentes e que os lançamentos da moeda não dependem das $ Xs $ e $ Ys $. Explique se a sequência $ Z_1,Z_2,\dots $ obedece a Lei Forte dos Grandes Números. Se obedece, qual o limite de

$$\bar{Z}_n=\frac{Z_1+\dots+Z_n}{n}$$

Seja $ M_i $ variáveis aleatórias que representa o resultado da moeda no i-ésimo ensaio. Então definimos $ M_i(\omega)=1 $ se $ \omega= $cara e $ M_i(\omega)=0 $ o que implica $ \omega= $coroa. Como a moeda é honesta temos que

$$\mathbb{P}(M_i=1)=\mathbb{P}(M_i=0)=\frac{1}{2}.$$

Além disto, $ X_1,X_2,\dots, Y_1,Y_2,\dots, M_1,M_2,\dots $ são variáveis aleatórias independentes pois $ Z_i $ só depende de $ X_i,Y_i $ e $ M_i $ o que implica que $ Z_1,Z_2,\dots $ são variáveis independentes. Agora

$$\mathbb{P}(Z_i\leq z)=\mathbb{P}(Z_i\leq z,[M_i=1]\cup[M_i=0])$$

$$=\mathbb{P}(Z_i\leq z,[M_i=1])+\mathbb{P}(Z_i\leq z,[M_i=0])=\mathbb{P}(M_i=1)\mathbb{P}(Z_i\leq z|M_i=1)+\mathbb{P}(M_i=0)\mathbb{P}(Z_i\leq z|M_i=0)$$

$$=\frac{1}{2}\mathbb{P}(X_i\leq z)+\frac{1}{2}\mathbb{P}(Y_i\leq z)=\frac{1}{2}\left[F_{X_1}(z)+F_{Y_1}(z)\right]$$

Então $ Z_1,Z_2,\dots $ são variáveis aleatória identicamente distribuídas e

$$\mathbb{E}(Z_1)=\int_{-\infty}^\infty z dF_Z(z)=\frac{1}{2}\int_{-\infty}^\infty z dF_{X_1}(z)+\frac{1}{2}\int_{-\infty}^\infty zdF_{Y_1}(z)=\frac{1}{2}\left(\mu_1+\mu_2\right)$$

e $ Z_1,Z_2,\dots $ são variáveis integráveis. Assim, pela lei forte de Kolmogorov é aplicável e resulta em

$$\frac{Z_1+Z_2+\dots+Z_n}{n}\stackrel{q.c.}{\rightarrow} \frac{1}{2}\left(\mu_1+\mu_2\right)$$

e o resultado segue.

Exemplo 7.1.2.13

Sejam $ X_1,X_2,\dots $ variáveis aleatórias independentes tais que $ X_k\sim b(n_k,p) $, no qual $ 0< p< 1 $.

(a) Qual a distribuição de $ S_n=\sum_{k=1}^n X_k? $

Vejamos, primeiro $ S_2=X_1+X_2 $ então para $ 0\leq n\leq n_1+n_2 $.

$$\mathbb{P}(S_2=n)=\sum_{k=1}^n\mathbb{P}(X_1=k,X_2=n-k)=\sum_{k=1}^n\mathbb{P}(X_1=k)\mathbb{P}(X_2=n-k)$$

$$=\sum_{k=1}^n\binom{n_1}{k}p^k(1-p)^{n_1-k}\binom{n_2}{n-k}p^{n-k}(1-p)^{n_2-n-k}$$

$$=p^n(1-p)^{(n_1+n_2)-k}\sum_{k=1}^n\binom{n_1}{k}\binom{n_2}{n-k}=\binom{n_1+n_2}{n}p^n(1-p)^{(n_1+n_2)-k}$$

Vamos precisar de alguns fatos importantes. Se $ X_1\sim b(n_1,p) $ e independente de $ X_2\sim b(n_2,p) $, então $ X_1+X_2\sim b(n_1+n_2,p) $. Então, se $ S_3=(X_1+X_2)+X_3 $ no qual $ (X_1+X_2) $ é independente de $ X_3 $, então temos que $ (X_1+X_2)+X_3\sim b(n_1+n_2+n_3,p) $. Por indução, temos que

$$S_n\sim b\left(\sum_{k=^1}^n n_k,p\right).$$

(b) Se $ n_k\leq \sqrt{k} $, mostre que a sequência satisfaz a Lei Forte.

Agora $ Var(X_k)=n_kp(1-p) $ então supondo $ n_k\leq \sqrt{k} $

$$\sum_{k=1}^\infty \frac{Var(X_k)}{k^2}=\sum_{k=1}^\infty \frac{n_k(1-p)p}{k^2}\leq \sum_{k=1}^\infty \frac{\sqrt{k}p(1-p)}{k^2}$$

$$=p(1-p)\sum_{k=1}^\infty \frac{1}{k^{3/2}}< \infty$$

Então, aplicando a primeira lei forte de Kolmogorov, temos que

$$\frac{S_n-\mathbb{E}(S_n)}{n}\stackrel{q.c}{\rightarrow}0$$

e o resultado segue

Exemplo 7.1.2.14

Uma massa radioativa emite partículas segundo um processo de Poisson com parâmetro $ \lambda > 0 $. Sejam $ T_1,T_2,\dots $ os tempos transcorridos entre emissões sucessivas. Ache o

$$\lim_{n\rightarrow \infty}\frac{T_1^2+\dots+T_n^2}{n}$$

É limite quase certo ou em probabilidade ?

Sabemos que em um processo de Poisson $ T_1,T_2,\dots $ é sequência variáveis aleatórias independentes e identicamente distribuídas, com $ T_1\sim Exp(\lambda) $. Então, pela propriedade da hereditariedade da independência, $ T_1^2,T_2^2,\dots $ é uma sequência de variáveis aleatórias independentes e também identicamente distribuídas e

$$\mathbb{E}(T_1^2)=\int_0^\infty t^2\lambda e^{-\lambda t}dt= Var(T_1)+\left[\mathbb{E}(T_1)\right]^2=\frac{1}{\lambda^2}+\frac{1}{\lambda^2}=\frac{1}{\lambda^2}$$

Então, $ T_1^2,T_2^2,\dots $ é uma sequência variáveis aleatória independentes identicamente distribuídas e integráveis. Aplicando a Lei forte de Kolmogorov

$$\frac{T_1^2+T_2^2+\dots+T_n^2}{n}\rightarrow \mathbb{E}(T_1^2)=\frac{2}{\lambda^2}$$

E o resultado segue.

Exemplo 7.1.2.15

Sejam $ X_1,X_2,\dots $ independentes com distribuição comum $ N(0,1) $. Qual o limite quase certo de

$$\frac{X_1^2+\dots+X^2_n}{(X_1-1)^2+\dots+(X_n-1)^2}?$$

Primeiramente temos pela Lei Forte de Kolmogorov que $ X_1^2,X_2^2,\dots $ é uma sequência de variáveis aleatórias independentes (propriedade hereditária) e identicamente distribuídas e integráveis ($ \mathbb{E}(X_i^2)=Var(X_i)=1,\quad i=1,2,\dots $)

$$\frac{X_1^2+\dots X_n^2}{n}\stackrel{q.c.}{\rightarrow} 1$$

o que implica que

$$\mathbb{P}\left(\omega:\frac{X_1^2(\omega)+\dots+X_n^2(\omega)}{n}\rightarrow 1\right)=1$$

Seja,

$$A=\left(\omega: \frac{X_1^2+\dots+X_n^2}{n}\rightarrow 1\right)$$

então $ \mathbb{P}(A)=1 $. Então, defina a sequência

$$(X_1-1)^2,\dots (X_n-1)^2$$

de variáveis aleatórias independentes e identicamente distribuídas e integráveis, pois

$$\mathbb{E}(X_1-1)^2=\mathbb{E}(X_1^2-2X_1+1)=\mathbb{E}(X_1^2)+1=1+1=2$$

Assim sendo, defina

$$B=\left(\omega: \frac{(X_1-1)^2(\omega)+\dots+(X_n-1)^2(\omega)}{n}\rightarrow 2\right)$$

temos pela lei forte de Kolmogorov, temos

$$\frac{(X_1-1)^2+\dots+(X_n-1)^2}{n}\rightarrow 2$$

o que implica que $ \mathbb{P}(B)=1 $. Agora se $ \omega \in (A\cap B) $. Então, $ \omega \in A $ o que implica que

$$\frac{X_1^2(\omega)+\dots+X_n^2(\omega)}{n}\rightarrow 1$$

e $ \omega \in B $ temos

$$\frac{(X_1-1)^2(\omega)+\dots+(X_n-1)^2(\omega)}{n}\rightarrow 2$$

Desta forma, $ \omega \in A\cap B $

$$\frac{X_1^2(\omega)+\dots+X_n^2(\omega)}{(X_1-1)^2(\omega)+\dots+(X_n-1)^2(\omega)}\rightarrow \frac{1}{2}$$

Sendo,

$$C=\left(\omega:\frac{X_1^2(\omega)+\dots+X_n^2(\omega)}{(X_1-1)^2(\omega)+\dots+(X_n-1)^2(\omega)}> \frac{1}{2}\right).$$

Temos $ (A\cap B)\subset C $ e então

$$\mathbb{P}(C)\geq \mathbb{P}(A\cap B)=1$$

pois $ \mathbb{P}(A)=1 $ e $ \mathbb{P}(B)=1 $ então $ \mathbb{P}(C)=1 $ o que implica que

$$\frac{X_1^2+\dots+X_n^2}{(X_1-1)^2+\dots+(X_n-1)^2}\rightarrow\frac{1}{2}$$

portanto o resultado segue.

Exemplo 7.1.2.16

Sejam $ X_1,X_2,\dots $ variáveis aleatórias independentes tais que $ X_n\sim U[0,n], \quad n=1,2,\dots $. Chame o n-ésimo ensaio de sucesso se $ X_{2n}> X_{2n-1} $, fracasso se $ X_{2n}\leq X_{2n-1} $, para $ n=1,2,\dots $. Determine a probabilidade de haver sucesso no n-ésimo ensaio e ache o limite(se existir) de $ S_n/n $, no qual $ S_n= $número de sucessos nos primeiros n ensaios. Esse limite e o limite em probabilidade e/ou quase certo?

Defina

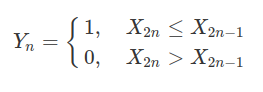
e $ B_n=[X_{2n},X_{2n-1}] $

Teremos que

$$p_n=\mathbb{P}(Y_n=1)=\mathbb{P}(X_{2n}\leq X_{2n-1})=\int_{B_n}f_{X_{2n},X_{2n-1}}(x_{2n},x_{2n-1})dx_{2n}dx_{2n-1}.$$

Agora, como $ X_{2n} $ é independente de $ X_{2n-1} $, o que implica que

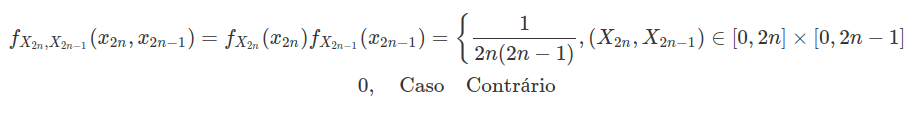
então

$$p_n=\frac{1}{2n(2n-1)}Vol(B\cap A)=\frac{(2n-1)^2}{4n(2n-1)}=\frac{2n-1}{4n}=\frac{1}{2}-\frac{1}{4n}$$

Assim, a sequência $ Y_1,Y_2,\dots $ é variável aleatória independente, com

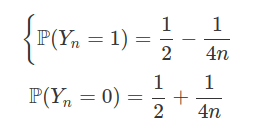
Então

$$\mathbb{E}(Y_n)=p_n=\frac{1}{2}-\frac{1}{4n}$$

e

$$Var(Y_n)=p_n(1-p_n)=\frac{1}{4}-\frac{1}{16n^2}.$$

Assim,

$$\sum_{n=1}^\infty \frac{Var(Y_n)}{n^2}=\sum_{n=1}^\infty \frac{1}{4n^2}-\sum_{n=1}^\infty \frac{16}{n^4}< \infty$$

Usando a primeira lei forte de Kolmogorov, temos

$$\frac{S_n}{n}=\frac{Y_1+\dots+Y_n}{n}\rightarrow \frac{\mathbb{E}(S_n)}{n}$$

com

$$\frac{\mathbb{E}(S_n)}{n}=\frac{\frac{1}{2}-n-\sum_{k=1}^n \frac{1}{4k}}{n}=\frac{1}{2}-\frac{1}{4n}\sum_{k=1}^n\frac{1}{4k}$$

Desta forma, definindo

$$A=(\omega: \frac{S_n}{n}\rightarrow \frac{1}{2}-\frac{1}{4n}\sum_{k=1}^n\frac{1}{k})$$

temos que $ \mathbb{P}(A)=1 $. Agora

$$\lim_{n\rightarrow \infty}\left(\frac{1}{2}-\frac{1}{4n}\sum_{k=1}^n\frac{1}{k}\right)=a$$

então seja $B=\left(\omega: \frac{S_n}{n}\rightarrow a\right)$, então $ \omega\in A $ o que implica que $ \omega \in B $ o que implica $ A\subset B $ o que implica que $ \mathbb{P}(B)\geq \mathbb{P}(A)=1 $ o que implica que

$$\frac{S_n}{n}\stackrel{q.c.}{\longrightarrow} a.$$

Exemplo 7.1.2.17

A lei forte para variáveis aleatórias independentes, identicamente distribuídas e integráveis pode ser estendida ao acaso de esperanças infinitas, se admitirmos limites infinitos. Em particular, se $ X_1,X_2,\dots $ são independentes e identicamente distribuídas tais que $ \mathbb{E}(X_n)=\infty $, então

$$S_n/n\rightarrow \infty$$

quase certamente. Prove esse resultado em 3 etapas:

(a) Para $ m $ inteiro positivo fixo, seja $ Y_n $ o truncamento de $ X_n $ em $ m $

Mas

$$\mathbb{E}(X_1)=\int_{0}^\infty (1-F_{X_1}(x))dx-\int_{-\infty}^0 F_{X_1}(x)dx$$

Agora como $ \mathbb{E}(X_1)=\infty $ isto implica que

$$\int_{-\infty}^0 F_{X_1}(x)dx< \infty.$$

Assim

$$\mathbb{E}(Y_1)=\int_{0}^\infty (1-F_{Y_1}(y))dy-\int_{-\infty}^0 F_{Y_1}(y)dy=\int_0^m(1-F_{X_1}(y))dy-\int_{-\infty}^0 F_{X_1}(y)dy$$

como

$$\int_{-\infty}^0 F_{X_1}(y)dy< \infty$$

então

$$0\leq \int_0^m(1-F_{X_1}(y))dy\leq \int_0^m dy=m< \infty $$

Portanto, $ \mathbb{E}(Y_1)< \infty $. Então, utilizando a Lei forte de Kolmogorov

$$\frac{Y_1+\dots+Y_n}{n}\rightarrow \mathbb{E}(Y_1)$$

mas isso se, e somente se,

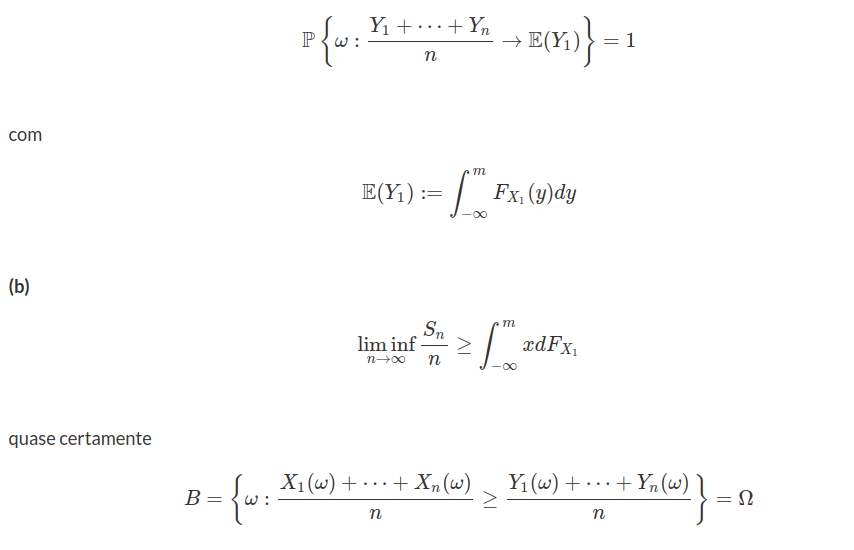
e

$$A=\left(\omega \frac{Y_1(\omega)+\dots+Y_n(\omega)}{n}\rightarrow \mathbb{E}(Y_1)\right)$$

Se $ \omega \in A\cap B $, $ \omega \in B_m $ o que implica que

$$\frac{X_1(\omega)+\dots+X_n(\omega)}{n}\geq \frac{Y_1(\omega)+\dots+Y_n(\omega)}{n}$$

se $ \omega \in A $ isto implica que

$$\lim_{n\rightarrow \infty}\frac{Y_1(\omega)+\dots+Y_n(\omega)}{n}=\mathbb{E}(Y_1)$$

Logo se $ \omega\in A\cap B $, isto implica que

$$\liminf_{n\rightarrow \infty}\frac{X_1(\omega)+\dots+X_n(\omega)}{n}\geq \mathbb{E}(Y_1)$$

Definindo $C_m=\left(\omega : \liminf_{n\rightarrow \infty}\frac{S_n(\omega)}{n}\geq \mathbb{E}(Y_1)\right)$, temos então que $ C_m\supset A\cap B $. O que implica que

$$\mathbb{P}(C_m)> \mathbb{P}(A\cap B)=1$$

pois $ \mathbb{P}(A)=\mathbb{P}(B)=1 $. Assim,

$$\liminf_{n\rightarrow \infty}\frac{S_n}{n}\geq \mathbb{E}(Y_1)=\int_{-\infty}^m xdF_{X_1}(x).$$

(c) $ \frac{S_n}{n}\rightarrow \infty $ quase certamente.

Agora, se dado qualquer $ M> 0 $, temos que existe $ n_0 $ tal que $ n> n_0 $ o que implica que

$$\frac{S_n}{n}> M$$

Então, $ \frac{S_n}{n}\rightarrow \infty $. Como $ \mathbb{E}(Y_1(m))\rightarrow \mathbb{E}(X_1)=\infty $, então dado $ M> 0 $ existe $ m_0 $ tal que $ m> m_0 $ o que implica que

$$\mathbb{E}(Y_1(m))> M$$

Então se $ \omega \in C_m $, para $ m> m_0 $, isto implica que

$$\liminf_{n\rightarrow \infty}\frac{S_n(\omega)}{n}\geq \mathbb{E}(Y_1(m))> M\Rightarrow \frac{S_n(\omega)}{n}\rightarrow \infty.$$

Sendo $D=\left(\omega: \frac{S_n(\omega)}{n}\rightarrow \infty\right)$

se $ \omega \in C_m\Rightarrow \omega \in D $

o que implica que

$$\mathbb{P}(D)\geq \mathbb{P}(C_m)=1$$

o que implica

$$\frac{S_n}{n}\stackrel{q.c.}{\longrightarrow} \infty$$

Exemplo 7.1.2.18

Sejam $ X_1,X_2,\dots $ variáveis aleatórias independentes, identicamente distribuídas e integráveis. Determine

$$\lim_{n\rightarrow \infty}\mathbb{E}(X_1|X_1+X_2+\dots+X_n)$$

Qual o tipo de convergência?

Como $ X_1,X_2,\dots $ variáveis aleatórias independentes, identicamente distribuídas e integráveis

$$\mathbb{E}\left(X_1|X_1+\dots+X_n\right)=\mathbb{E}\left(X_2|X_1+\dots+X_n\right)=\dots=\mathbb{E}\left(X_n|X_1+\dots+X_n\right)$$

o que implica que

$$\mathbb{E}\left(X_1+\dots+X_n|X_1+\dots+X_n\right)=n\mathbb{E}\left(X_1|X_1+\dots+X_n\right)$$

o que implica que

$$\mathbb{E}\left(X_1+\dots+X_n|X_1+\dots+X_n\right)=n\mathbb{E}\left(X_1|X_1+\dots+X_n\right)$$

o que nos leva a

$$X_1+\dots+X_n=n\mathbb{E}\left(X_1|X_1+\dots+X_n\right)\Rightarrow \mathbb{E}\left(X_1|X_1+\dots+X_n\right)=\frac{X_1+\dots+X_n}{n}$$

Agora, pela lei forte de Kolmogorov, temos

$$\mathbb{E}\left(X_1|X_1+\dots+X_n\right)=\frac{X_1+\dots+X_n}{n}\stackrel{q.c}{\longrightarrow} \mathbb{E}(X_1)$$

Exemplo 7.1.2.19

(a)$ \alpha_n=1/2, \forall n $

Agora

$$\mathbb{P}(X_1=x_1,X_2=x_2,\dots,X_n=x_n)=\mathbb{P}(X_1=x_1,X_2=x_2,\dots,X_{n-1}=x_{n-1})\mathbb{P}(X_n=x_n|X_1=x_1,X_2=x_2,\dots,X_{n-1}=x_{n-1})$$

Como

$$\mathbb{P}(X_n=X_{n-1}|X_1=x_1,X_2=x_2,\dots,X_{n-1}=x_{n-1})=\frac{1}{2}=\mathbb{P}(X_n\neq X_{n-1}|X_1=x_1,X_2=x_2,\dots,X_{n-1}=x_{n-1})$$

Temos por indução

$$\mathbb{P}(|X_1=x_1,X_2=x_2,\dots,X_{n}=x_{n})=\left(\frac{1}{2}\right)^{n}=\mathbb{P}(X_1=X_{1})\dots\mathbb{P}(X_{n}=x_{n})$$

para todo $ x_1,x_2,\dots, x_n $, então para todo n $ (X_1,X_2,\dots,X_n) $ são variáveis aleatórias independentes o que implica que a sequência de variáveis aleatórias independentes e identicamente distribuída e integráveis $ \left(\mathbb{E}(X_1)=\frac{1}{2}\right) $. Assim, pela lei forte de Kolmogorov temos que

$$Y_n=\frac{1}{n}(X_1+\dots+X_n)\stackrel{q.c}{\longrightarrow}\frac{1}{2}.$$

(b)$ \sum \alpha_n $ converge

Se $ \sum \alpha_n $ converge, isto implica que para todo $ \epsilon > 0 $ existe $ n_0 $ tal que $ n> n_0 $ o que implica que

$$\sum_{k=n}^\infty \alpha_n< \epsilon$$

Seja $A_n:=[X_{n+1}\neq X_n]$ e

$$\mathbb{P}(A_n)=\mathbb{P}(X_{n+1}\neq X_n)=1-\mathbb{P}(X_{n+1}=X_n)$$

Agora

$$\mathbb{P}(X_{n+1}=X_n)=\sum_{(x_1,\dots,x_n)}\mathbb{P}(X_{n+1}=x_n|X_1=x_1,\dots,X_n=x_n)\mathbb{P}(X_1=x_1,\dots,X_n=x_n)$$

$$=(1-\alpha_n)\sum_{(x_1,\dots,x_n)}\mathbb{P}(X_1=x_1,\dots,X_n=x_n)=1-\alpha_n$$

Assim, $ \mathbb{P}(\alpha_n) $, o que implica que

$$\sum_{n=1}^\infty \mathbb{P}(A_n)=\sum_{n=1}^\infty \alpha < \infty $$

o que implica pelo lema de Borel-Cantelli

$$\mathbb{P}(A_n,\quad i.o)=0$$

então

$$\mathbb{P}(X_{n+1}=x_n,\quad i.o)=0$$

o que implica que

$$\mathbb{P}(X_{n+1}=x_n,\quad n \text{suficientemente}\quad \text{grande}\quad (n> n_0))=1$$

o que implica que

e

$$C=\left(\omega \frac{S_n(\omega)}{n}\rightarrow \frac{1}{2}\right)$$

Temos que $ \omega\in A $ implica que $ \omega \in B $ o que implica que

$$\mathbb{P}(B)\geq \mathbb{P}(A)=1\Rightarrow \mathbb{P}(B)=1$$

e $ \omega \in C $ o que implica que $ \omega \notin B \Rightarrow (B\cap C)=\emptyset $ o que implica que

$$\mathbb{P}(C)\leq 1-\mathbb{P}(B)=1-1=0$$

o que implica que

$$\mathbb{P}(C)=\mathbb{P}\left(\frac{S_n}{n}\rightarrow \frac{1}{2}\right)=0$$

o que implica que

$$\frac{S_n}{n}\stackrel{q.c.}{\longrightarrow}\frac{1}{2}.$$

Agora, provaremos também que

$$\frac{S_n}{n}\stackrel{\mathbb{P}}{\nrightarrow}\frac{1}{2}$$

como um contra-exemplo seja $ 0=\alpha_1=\dots=\alpha_n=\dots $ então $ \sum_{i=1}^\infty \alpha_i=0< \infty $ e então

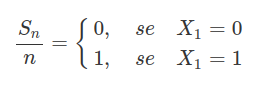
o que implica que

$$\mathbb{P}\left(\frac{S_n}{n}=0\right)=\mathbb{P}(X_1=0)=\frac{1}{2}$$

e

$$\mathbb{P}\left(\frac{S_n}{n}=1\right)=\mathbb{P}(X_1=1)=\frac{1}{2}$$

Agora, seja $ 0< \epsilon < \frac{1}{2} $, então

$$\mathbb{P}\left(\bigg|\frac{S_n}{n}-\frac{1}{2}\bigg|\geq \epsilon\right)=1$$

pois se $ \frac{S_n}{n}=0 $ o que implica que

$$\bigg|\frac{S_n}{n}-\frac{1}{2}\bigg|=\frac{1}{2}$$

ou $ \frac{S_n}{n}=1 $ o que implica que

$$\bigg|\frac{S_n}{n}-\frac{1}{2}\bigg|=\frac{1}{2}$$

Assim,

$$\lim_{n\rightarrow \infty }\mathbb{P}\left(\bigg|\frac{S_n}{n}-\frac{1}{2}\bigg|\geq \epsilon\right)=1\neq 0$$

o que implica que

$$\frac{1}{2}\nrightarrow \frac{1}{2}$$

Exemplo 7.1.2.20

Sejam $ X_1,X_2,\dots $ independentes tais que $ \mathbb{E}(X_n)=0, \forall n $. Demonstre que se

$$\sum_{n=1}^\infty Var(X_n)< \infty$$

então $ \mathbb{E}(\sup_{n> 1}|S_n|)< \infty $, no qual $ S_n=X_1+\dots+X_n. $

Pelo critério da integrabilidade temos que

$$\mathbb{E}\left(\sup_{n\geq 1}|S_n|\right)< \infty$$

se, e somente se

$$\sum_{k=0}^\infty \mathbb{P}\left(\sup_{n\geq 1}|S_n|> k\right)< \infty$$

Agora pela desigualdade de Kolmogorov, temos que

$$\mathbb{P}\left(\max_{1\leq k\leq n_0}|S_k|> k\right)\leq \frac{1}{k^2}\sum_{i=1}^{n_0}Var(X_i),k> 0$$

Agora, se $ \sup_{n\geq 1}|S_n|> k $ pela definição de supremo, temos que existe $ n_0 $ tal que $ |S_{n_0}|> k $ o que implica que

$$\max_{1\leq k\leq n_0}|S_n|\geq k.$$

Assim, $ \omega \in A=[\sup_{n\geq 1}|S_n|> k] $ o que implica que $ \omega \in [\max_{1\leq n\leq n_0}|S_n|\geq k] $ então

$$\mathbb{P}(\sup_{n\geq 1}|S_n|> k)\leq \mathbb{P}(\max_{1< n< n_1}|S_n|\leq k)$$

Pela desigualdade de Kolmogorov

$$\mathbb{P}(\max_{1< n< n_1}|S_n|\leq k)\leq \frac{1}{k^2}\sum_{i=1}^{n_0} Var(X_i)\leq \frac{1}{k^2}\sum_{i=1}^\infty Var(X_i)$$

Assim, $ k> 0 $ o que implica que

$$\mathbb{P}(\sup_{n\geq 1}|S_n|> k)=\mathbb{P}(\sup_{n\geq 1}|S_n|> 0)+\sum_{k=1}^\infty \mathbb{P}(\sup_{n\geq 1}|S_n|> k)$$

$$\leq 1+\sum_{k=1}^\infty \frac{1}{k^2}\sum_{i=1}^\infty Var(X_i)$$

Como

$$\sum_{i=1}^\infty Var(X_i)< \infty$$

então

$$\sum_{k=0}^\infty \mathbb{P}\left(\sup_{n\geq 1}|S_n|< k\right)\leq 1+\sum_{i=1}^\infty Var(X_i)\sum_{i=1}^\infty \frac{1}{k^2}$$

o que implica que

$$\sum_{k=0}^\infty \mathbb{P}(\sup_{n\geq 1}|S_n|)< \infty$$

7.3 - Teorema Central do Limite

Na história da teoria de probabilidades, Chebyshev foi o primeiro a utilizar o métodos dos momentos. Em seguida seu aluno Andrei Markov, usou o método dos momentos para dar uma prova rigorosa do Teorema Central do Limite. Outro de seus famosos estudantes, Alexander Lyapunov, posteriormente usou o conceito de funções características para dar uma prova mais simples desse importante teorema.

O teorema central do limite consiste em um importante teorema da teoria assintótica, no qual a ideia central baseia-se em encontrar a distribuição da somas parciais normalizadas, o qual demonstramos que converge para a distribuição normal padronizada. Entretanto para que possamos demonstrar esse importante resultado, vamos necessitar de alguns pré-requisitos, como por exemplo:

• A transformada de Fourier

• Convergência fraca (em distribuição).

Nas próximas seções, dedicamos uma parte dela as funções características, comunmente chamado de transformada de Fourier. Finalizamos com a seção em que apresentamos as principais definições e demonstrações do Teorema Central do Limite.

7.3.1 - Função Característica ou Transformada de Fourier

A transformada de Fourier, também conhecida dentro da área da estatística como função característica, tem aplicações nas mais diversas áreas do conhecimento científico, como por exemplo, no processamento de sinais e imagens, na física quântica, entre outros. Além deste operador vamos necessitar de vários resultados relevantes dentro da área de probabilidade, o qual usamos na demonstração do teorema central do limite (TCL).

Na seção Momentos, estudamos a função geradora de momentos. Do ponto de vista teórico a função característica ou transformada de Fourier é bem mais robusta que a função geradora de momentos, pois:

• é definida para qualquer distribuição;
• determina a convergência em distribuição;
• gera momentos.

De certa forma, a função característica é mais funcional, porém do ponto de vista prático, muitos pesquisadores preferem trabalhar com a função geradora de momentos, pois a função característica envolve números complexos. A seguir, apresentamos algumas definição e resultados para a função característica.

Definição 7.2.1.1

Seja X uma variável aleatória. Então a função característica (transformada de Fourier) de X é uma função $\varphi:\mathbb{R} \rightarrow \mathbb{C}$ definida por: $$\varphi(t)=\varphi_X(t)=\mathbb{E}(e^{itX})=\displaystyle\int_{\mathbb{R}} e^{(itx)}dF_X(x),$$

no qual definimos $$\mathbb{E}(e^{itX})=\mathbb{E}(\cos(t X))+i~\mathbb{E}(\sin(t X)),~~~~t\in\mathbb{R}.$$

Observação (fórmula de Euler)

$e^{itX}=\cos(tX)+i~\sin(tX)$

Como a função característica é determinada pela sua função de distribuição, temos que se X e Y são identicamente distribuídos então: $$\varphi_X=\varphi_Y.$$

Após demonstrarmos algumas propriedades da função característica, vamos mostrar uma proposição importante, que mostra que a função característica de X determina a função de distribuição acumulada de X.

Proposição 7.2.1.1

A função característica é uma função limitada por 1.

Demonstração:

De fato, pela definição temos que $$|\varphi_{X}(t)|=|\mathbb{E}[e^{itX}]|=\sqrt{\mathbb{E}^2[\cos{(tX)}]+\mathbb{E}^2[\sin{(tX)}]}$$

Assim, temos que $$\sqrt{\mathbb{E}^2[\cos{(tX)}]+\mathbb{E}^2[\sin{(tX)}]}\leq \sqrt{\mathbb{E}[\cos^2{(tX)}]+\mathbb{E}[\sin^2{(tX)}]}=\sqrt{\mathbb{E}[\underbrace{\cos^2{(tX)}+\sin^2{(tX)}}_{1}]}=1$$

A desigualdade apresentada é devido a P6 da esperança. Portanto, a função característica é limitada por 1. $\Box$

Proposição 7.2.1.2

Se X e Y são duas variáveis aleatórias independentes então $\varphi_{X+Y}=\varphi_X(t)\varphi_Y(t).$

Demonstração:

De fato, temos que: $$\varphi_{X+Y}(t)=\mathbb{E}[e^{it(X+Y)}]=\mathbb{E}[e^{itX}~e^{itY}]=\mathbb{E}[(\cos{(tX)}+i~\sin{(tX)})(\cos{(tY)}+i~\sin{(tY)})]$$

Como X e Y são independentes temos que: $$\mathbb{E}[\cos{(tX)}+i~\sin{(tX)}]~\mathbb{E}[\cos{(tY)}+i~\sin{(tY)}]=\mathbb{E}[e^{iX}]~\mathbb{E}[e^{iY}]=\varphi_X(t)\varphi_Y(t)$$

$\Box$

Um resultado geral da proposição 7.2.1.2, é que se uma família finita de variáveis aleatórias $X_1\cdots X_n$ são independentes e $S_n=X_1,\dots,X_n$, então $$\varphi_{S_n}=\prod_{i=1}^{n}\varphi_{X_i}$$

De fato, $$\varphi_{S_n}=\mathbb{E}[e^{it(X_1+\dots+X_n)}]=\mathbb{E}[e^{itX_1}e^{it X_2}\dots e^{it X_n}]\overset{\text{indep.}}{=}\mathbb{E}[e^{it X_1}]\dots\mathbb{E}[e^{it X_n}]=\prod^n_{i=1}\varphi_{X_i}$$

Proposição 7.2.1.3

Se $X=aY+b,$ então $\varphi_X(t)=\varphi_{aY+b}(t)=e^{itb}\varphi_Y(at)$

Demonstração:

De fato, $$\varphi_{X}(t)=\varphi_{aY+b}(t)=\mathbb{E}[e^{it(aY+b)}]=\mathbb{E}[e^{itaY}~e^{itb}]=e^{itb}\mathbb{E}[e^{itaY}]=e^{itb}\varphi_Y(at)$$

$\Box$

Proposição 7.2.1.4

A função característica $\varphi_X$ também gera momentos.

Demonstração:

$$\frac{d^n}{dt^n}\varphi_X(t)\mid_{t=0}=i^n\mathbb{E}[X^n],\quad \text{se}~\mathbb{E}|X|^n< \infty.$$

Note que, se $\mathbb{E}|X|^n< \infty,$ então $$\varphi_X(t)=\varphi(0)+\varphi^\prime(0)t+\varphi^{\prime\prime}(0)\frac{t^2}{2!}+\dots+\varphi^{(n)}(0)\frac{t^n}{n!}+r_n(t)=$$ $$\overset{(\text{Obs})}{=}1+i(\mathbb{E}[X])t-\frac{\mathbb{E}[X^2]}{2!}t^2+\dots+i^n\frac{\mathbb{E}[X^n]}{n!}t^n+r_n(t)$$

Obs: $\dfrac{r_n(t)}{t^n}\stackrel{t\rightarrow 0}\rightarrow 0$

$\Box$

Corolário 7.2.1.1:

Se $\mathbb{E}[|X|^n]< \infty$ para algum $n\geq 1,$ então $\varphi_X$ possui k derivadas contínuas para todo $k\leq n$ e ainda temos que: $$\displaystyle \varphi_X^{(k)}(t)=\int_{\mathbb{R}}(ix)^k e^{itx}dF_X(x).$$

E portanto; $\varphi_X^{k}(0)=i^k~\mathbb{E}[X^k]$.

Demonstração:

Para demonstrarmos esse fato vamos nos utilizar da definição de derivada. Notemos primeiramente que: $$\displaystyle\frac{\varphi(t+h)-\varphi(t)}{h}=\int_{\mathbb{R}} \frac{e^{i(t+h)x}-e^{itx}}{h}dF(x)=\int_{\mathbb{R}} e^{itx}\left(\frac{e^{ihx}-1}{h}\right)dF(x)=\mathbb{E}\left[e^{itX}\left(\frac{e^{ihX}-1}{h}\right)\right].$$

Como $\frac{(e^{ithx}-1)}{h}\rightarrow ix$ quando $h\rightarrow 0,$ obtemos que: $$\displaystyle \mathbb{E}\left[e^{itx}\left(\frac{e^{ihX}-1}{h}\right)\right]\rightarrow i~\mathbb{E}[Xe^{itX}].$$

Vamos demonstrar o caso geral por indução. Suponhamos que $$\displaystyle \varphi^{(n)}(t)=\int(ix)^n e^{itx}dF_X(x),$$

Mostremos que é válido para (n+1).

De fato, $$\frac{\varphi^{(n+1)}(t+h)-\varphi^{(n+1)}(t)}{h}=\int_{\mathbb{R}} \frac{(ix)^{n+1} e^{i(t+h)x}-(ix)^n e^{itx}}{h}dF_X(x)=\int_{\mathbb{R}} (ix)^{n+1} e^{itx}\left(\frac{e^{ihx}-1}{h}\right)=$$ $$=\mathbb{E}\left[(iX)^{n+1} e^{itX}\left(\frac{e^{ithX}-1}{h}\right)\right].$$

Mas como $$\mathbb{E}\left[e^{itX}\frac{(e^{ithX}-1)}{h}\right]\rightarrow i~\mathbb{E}[Xe^{itX}].$$

Para encontrarmos $\varphi_{X}^{(k)}(0)=i^k\mathbb{E}[X^k]$, basta tomarmos $t=0$.

Portanto, temos que

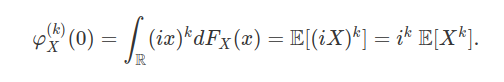
$\Box$

A função característica de uma variável aleatória X determina a função de distribuição acumulada de X, ou seja, dado a sua função característica podemos determinar qual é a sua função de distribuição acumulada. Este fato decorre de uma formula conhecida como formula da inversão.

Teorema 7.2.1.1 (Fórmula da inversão)

Se x e y são pontos de continuidade de F tais que x $<$ y, então $$F(y)-F(x)=\displaystyle\frac{1}{2\pi}\lim_{u\rightarrow\infty}\int_{-u}^{u}\frac{e^{-itx}-e^{-ity}}{it}\varphi(t)dt.$$

Demonstração:

Para demonstrarmos esse teorema vamos necessitar do teorema da convergência dominada, o qual é enunciado abaixo.

Teorema da convergência dominada

Seja $(X_n)_{n\geq 1}$ uma sequência de variáveis aleatórias tal que $X_n\rightarrow X$ quase certamente e existe uma variável aleatória Y não negativa tal que $|X_n|\leq Y$ com $\mathbb{E}[Y]<\infty,$ então para $\mathbb{E}[X]<\infty,$ temos que $$\mathbb{E}[X_n]\rightarrow \mathbb{E}[X],\quad \text{quando}~~ n\rightarrow \infty.$$

Voltando a demonstração do teorema 7.2.1.1 vamos definir uma integral iterada $$I(u):=\displaystyle\int_{-u}^{u}\frac{e^{-itx}-e^{-ity}}{it}\varphi(t)dt=\int_{-u}^{u}\left(\int_{-\infty}^{\infty}\frac{e^{-itx}-e^{-ity}}{it}e^{itz}dF(z)\right)dt.$$

Neste momento é importante relembrarmos que $$\lim_{t\rightarrow 0}\frac{e^{-itx}-e^{ity}}{it}=y-x$$

e ainda que a integral de Dirichlet é dada por: $$\displaystyle\lim_{u\rightarrow\infty}\int_{0}^{u}\frac{\sin{(t)}}{t}dt=\frac{\pi}{2}.$$

Assim temos que: $$I(u)=\displaystyle\int_{-\infty}^{\infty}\left(\int_{-u}^{u}\frac{e^{it(z-x)}-e^{it(z-y)}}{it}dt\right)dF(z).$$

Portanto $$I(u)=\displaystyle\int_{-\infty}^{\infty}\left(2\int_{0}^{u}\displaystyle \frac{\sin{t(z-x)}}{t}-2\int_{0}^{u}\frac{\sin{t(z-y)}}{t}\right)dF(z)$$

Neste momento basta usarmos o teorema da convergência dominada, ou seja, precisamos encontrar uma variável aleatória tal que $H_u(X)\rightarrow Y$ e mostrar que para todo $H_u(X)$ existe uma variável Z tal que $H_u(X)< Z$, no qual $H_u(X)=\displaystyle 2\int_{0}^{u}\frac{\sin{t(z-x)}}{t}dt-2\int_{0}^{u}\frac{\sin{t(z-y)}}{t}dt.$

De fato, aplicando o limite em $H_u(X)$ e utilizando o resultado da integral de Dirichlet podemos encontrar o seguinte cenário. Como $x< y$ temos que:

se $z< x$ então $(z-x)$ e $(z-y)$ são menores que zero temos que: $$H_u(X)=\lim_{u\rightarrow \infty}2\int_{0}^{u}\frac{\sin{t(z-x)}}{t}dt -2\int_{0}^{u}\frac{\sin{t(z-y)}}{t}dt=$$ $$\quad\lim_{u\rightarrow \infty}-2\int_{0}^{-(z-x)u}\frac{\sin{t}}{t}+2\int_{0}^{-(z-y)u}\frac{\sin{t}}{t}=-\pi+\pi=0.$$

Analogamente temos que se $z> y$ temos que também é $H_u(X)=0$

Por outro lado se $z=x$ temos que $(z-x)=0$ e $(z-y)< 0$ então teremos que: $$H_u(X)=\displaystyle \lim_{u\rightarrow \infty}2\int_{0}^{u}\frac{\sin{t(z-x)}}{t}dt-2\int_{0}^{u}\frac{\sin{t(z-y)}}{t}dt =\lim_{u\rightarrow \infty}2\int_{0}^{t(z-y)}\frac{\sin{t}}{t}dt=\pi.$$

Podemos notar que se $z=y$ temos também que $H_u(t)=\pi$. Por último se $x< z < y$, assim temos que $z-x> 0$ e ainda $z-y< 0$. $$H_u(X)=\displaystyle \lim_{u\rightarrow \infty}2\int_{0}^{u}\frac{\sin{t(z-x)}}{t}-2\int_{0}^{u}\frac{\sin{t(z-x)}}{t} = 2\int_{0}^{u(z-x)}\frac{\sin{t}}{t}+2\int_{0}^{-u(z-y)}\frac{\sin{t}}{t}=2\pi$$

Assim temos que: $H_u(X)\rightarrow \pi~ I_{[X=x]}+2\pi ~I_{[x< X < y]}+\pi ~I_{X=y}=Y$ quando $u\rightarrow \infty.$

Neste momento basta encontrarmos uma variável que limita Y, como por exemplo: $$Z=4\pi~ I_{x\leq X\leq y}$$

Assim usando o teorema da convergência dominada podemos concluir que: $$\displaystyle\lim_{u\rightarrow \infty}\mathbb{E}[H_u(X)]=\mathbb{E}[Y]=\pi~ \mathbb{P}(X=x)+2\pi ~\mathbb{P}(x< X < y)+\pi ~\mathbb{P}(X=y).$$

Notemos que da forma como $H_u(X)$ foi definido temos que: $$\displaystyle\lim_{u\rightarrow \infty} I(u)=\displaystyle \mathbb{E}[H_u(t)]=\pi ~\mathbb{P}(X=x)+2\pi ~\mathbb{P}(x< X < y)+\pi~ \mathbb{P}(X=y).$$

Assim concluímos a demonstração do teorema.

$\Box$

Proposição 7.2.1.5

A variável aleatória X tem função característica real para todo t se, e somente se, X tem distribuição simétrica em torno de zero.

Demonstração:

De fato, notemos que X tem distribuição simétrica em torno de zero se, e somente se, $\mathbb{P}(X\leq x)=\mathbb{P}(X\geq -x)$ para qualquer $x \in \mathbb{R}$, ou seja, $F_{-X}=F_{X}$ no qual X e -X são identicamente distribuídas.

Mas pelo teorema temos que $F_X=F_{-X}$ se, e somente se, suas funções característica são iguais, ou seja, $\varphi_X=\varphi_{-X}$. Desta forma X é simétrica em zero se, e somente se, $\varphi_X(t)=\varphi_{-X}(t)=\overline{\varphi_{-X}(-t)}$.

A última igualdade decorre do fato de que,

$\displaystyle \overline{\varphi_X(t)}=\varphi_{X}(t)$, pois $\cos{(-tX)}=\cos{(tX)}$ e $\sin{(-tX)}=-\sin{(tX)}$ e portanto temos que: $$\varphi_X(-t)=\mathbb{E}[\cos{(-tX)}+i~\sin{(-tX)}]=\mathbb{E}[\cos{(-tX)}]+i~\mathbb{E}[\sin{(-tX)}]=$$ $$=\mathbb{E}[\cos{(tX)}]-i~\mathbb{E}[\sin{(tX)}]=\mathbb{E}[\cos{(tX)}-i~\sin{(tX)}]=$$ $$=\overline{\mathbb{E}[e^{itX}]}=\overline{\varphi_{X}(t)}$$

Assim podemos concluir que: $$\varphi_{X}(t)=\varphi_{-X}(t)=\overline{\varphi_{-X}(-t)}=\overline{\mathbb{E}[e^{i(-t)(-X)}]}=\overline{\mathbb{E}[e^{itX}]}=\overline{\varphi_X(t)},$$

ou seja, $\varphi_X(t)=\overline{\varphi_X(t)}$ mas um número complexo só é igual ao seu conjugado se, e somente se, ele for real, e portanto concluímos nossa demonstração.

$\Box$

A seguir, vamos demonstrar o teorema de unicidade, isto é, que a função de distribuição $F=F(x)$ é determinado unicamente pela função característica $\varphi=\varphi(t).$

Teorema 7.2.1.2 (Unicidade)

Seja $F$ e $G$ as funções de distribuição com as mesmas funções características, isto é, $$\int_{\mathbb{R}}e^{itx}dF(x)=\int_{\mathbb{R}}e^{itx}dG(x), \quad \text{para todo}~ t\in \mathbb{R}.$$

Então $F(x)\equiv G(x)$

Demosntração:

Escolhemos $a,b\in\mathbb{R},$ dado $\varepsilon>0$ e consideramos a função $f^{\varepsilon}(x).$ Vamos mostrar que $$\int_{\mathbb{R}}f^{\varepsilon}(x)dF(x)=\int_{\mathbb{R}}f^{\varepsilon}(x)dG(x)$$

Para isto, seja $n> 0$ suficientemente grande, para que $[a-\varepsilon,b+\varepsilon]\subseteq [-n,n]$ e sequência $(\delta_n)$ tal que $\delta_n$ é limitada por 1 e $\delta_n\downarrow 0,$ quando $n\rightarrow \infty.$ Como qualquer função contínua em $[-n,n]$ tem valores iguais nos extremos.

Logo, $f^{\varepsilon}(x)$ pode ser aproximada uniformemente por polinômios trigonométricos (teorema de Weierstrass). $$F^\varepsilon_n(x)=\sum_k a_k \exp\left(i\pi x \frac{k}{n}\right)$$

tal que $$\sup_{-n\leq x\leq n}|f^\varepsilon(x)-f^\varepsilon_n(x)|\leq \delta_n$$

Estendendo a função periódica $f_n(x)$ para todo $\mathbb{R}.$ Note que, $$\sup_{x}|f^\varepsilon_n(x)|\leq 2$$

Então pela hipótese temos que $$\int_{\mathbb{R}}f^\varepsilon_n(x)dF(x)=\int_{\mathbb{R}}f^\varepsilon_n(x)dG(x)$$

Daí, obtemos que

$$\left|\int_{\mathbb{R}}f^\varepsilon_n(x)dF(x)-\int_{\mathbb{R}}f^\varepsilon_n(x)dG(x)\right|=\left|\int^n_{-n}f^\varepsilon(x)dF(x)-\int^n_{-n}f^\varepsilon(x)dG(x)\right|$$

$$\leq\left|\int^n_{-n}f^\varepsilon_n(x)dF(x)-\int^n_{-n}f^\varepsilon_n(x)dG(x)\right|+2\delta_n$$

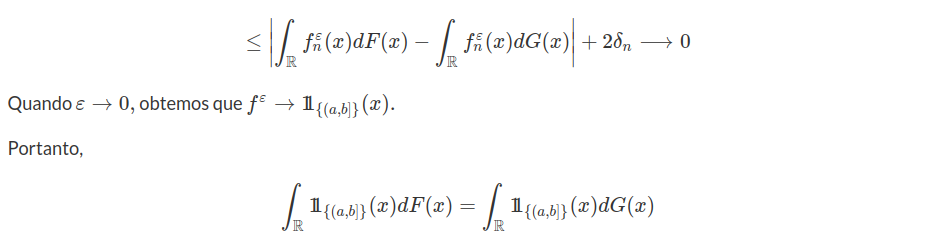
e do teorema fundamental do cálculo $F(b)-F(a)=G(b)-G(a)$ e desde que $a$ e $b$ sejam arbitrários temos que $F(x)=G(x)$ para todo $x\in \mathbb{R}$

$\Box$

Apresentamos a seguir a função característica de algumas das principais distribuições de probabilidade.

Exemplo 7.2.1.1

Suponha que $X~\sim ~B(n,p)$

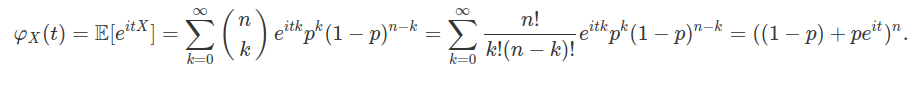
Exemplo 7.2.1.2

Suponha que $X~\sim ~\text{Poisson}(\lambda)$. $$\varphi_{X}(t)=\mathbb{E}[e^{itX}]=\sum_{k=0}^{\infty}e^{itk}e^{-\lambda}\frac{\lambda^k}{k!}=e^{-\lambda}\sum_{k=0}^{\infty}\frac{(\lambda e^{it})^{n}}{n!}=e^{-\lambda}e^{\lambda e^{it}}=\exp(\lambda(e^{it}-1)).$$

Exemplo 7.2.1.3

Suponha que $X~\sim ~N(0,1)$ $$\varphi_X(t)=\mathbb{E}[e^{itX}]=\displaystyle \int_{-\infty}^{\infty}e^{itx}dF_X(x)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{\infty}e^{itx}e^{-(x^2)/2}dx=e^{-t^2/2}\displaystyle \int_{-\infty}^{\infty}e^{-(x-it)^2/2}dx=e^{-t^2/2}$$

Para concluímos a última igualdade necessitamos de um resultado de análise complexa, que é o teorema de Cauchy. Este teorema diz que uma função analítica integrada sobre um caminho fechado no plano complexo tem integral nula. Usando esse resultado e com alguma manipulação algébrica concluímos a última igualdade.

Exemplo 7.2.1.4

Suponha que $X~\sim ~U[a,b],$ então $$\varphi_X (t)=\mathbb{E}[e^{itX}]=\int^b_a e^{itx}\dfrac{1}{b-a}dx=\dfrac{e^{itb}-e^{ita}}{it(b-a)}$$

Abaixo segue uma tabela com algumas funções características das principais distribuições.

Distribuição	Função Característica
Binomial	$ [(1-p)+pe^{it}]^n $
Binomial Negativa	$ \left[\dfrac{p}{(1-(1-p)e^{it})}\right]^r $
Poisson	$ \exp(\lambda(e^{it}-1)) $
Normal	$ \exp\left(i\mu t-\dfrac{(\sigma t)^2}{2}\right) $
Gamma	$ \left[1-\dfrac{it}{\theta}\right]^{-\lambda} $

Um assunto muito importante e que foi dedicado uma seção é a Lei Fraca do Grandes Números (para mais detalhes acesse LFGN), que pode ser demonstrada através do método da função característica. A seguir, vamos demonstrar o seguinte teorema.

Teorema 7.2.1.3 (Lei Fraca dos Grandes Números)

Seja $(X_i)_{i\geq 1}$ sequência de variáveis aleatórias independentes e identicamente distribuídos com $\mathbb{E}[X_1] < \infty,$ $S_n=X_1+\dots+X_n$ e $\mathbb{E}[X_1]=\mu.$ Então $\dfrac{S_n}{n}\stackrel{P}\rightarrow \mu$ tal que para todo $\varepsilon> 0$

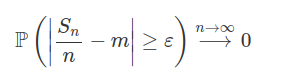
Demonstração:

Seja $\varphi(t)=\mathbb{E}[e^{it X_1}]$ e $\varphi_{S_n/n}(t)=\mathbb{E}[e^{it\frac{S_n}{n}}].$ Da hipótese temos que as variáveis aleatórias são i.i.d’s, então

$\varphi_{S_n/n}(t)=\left[\varphi\left(\frac{t}{n}\right)\right]^n$

Pela proposição 7.2.1.4, temos que $$\varphi(t)=1+it\mu+r(t), \quad \text{quando} t\rightarrow 0$$

Assim, para cada $t\in\mathbb{R}$ $$\varphi\left(\frac{t}{n}\right)=1+i\frac{t}{n}\mu+r(\frac{1}{n}),\quad\text{qaundo}~t\rightarrow \infty $$

Logo, $$\varphi_{S_n/n}(t)=\left[1+i\frac{t}{n}\mu+r(\frac{1}{n})\right]^n\rightarrow e^{it\mu}$$

A função $\varphi(t)=e^{it\mu}$ é contínua no zero e é a função característica da distribuição de probabilidade que é concentrada em $\mu.$ Portanto, $\dfrac{S_n}{n}\stackrel{\mathcal{D}}\rightarrow\mu$. Como $\mu$ é uma constante obtemos que (ver Proposição 7.1.2.2 em Convergência em distribuição) a convergência também ocorre em probabilidade, $$\dfrac{S_n}{n}\stackrel{P}\rightarrow \mu.$$

$\Box$

7.3.2 - Teorema Central do Limite

O teorema central do limite nos remete à convergência de somas de variáveis aleatórias para uma distribuição normal e é considerado, pela sua importância na teoria e em aplicações, como o teorema básico mais central da probabilidade. A palavra central para esse teorema limite foi dado pelo matemático George Polya. O nome mais usual é “Teorema Central do Limite” que deixa explícito que o adjetivo central se refere ao teorema e não ao limite.

Para demonstrarmos o Teorema Central do Limite necessitamos de dois assuntos importantes, que são as funções características vista na seção anterior (para mais detalhes consulte Função Característica ou Transformada de Fourier) e a convergência em distribuição vista na seção de convergência de variáveis aleatórias (para mais detalhes consulte Convergência de variáveis aleatórias). Com todas as ferramentas necessárias em mãos, podemos finalmente demonstrar algumas versões do teorema central do limite. No entanto, Helland demonstrou que existe apenas um teorema central do limite, que os demais são todos casos particulares. Entretanto a demonstração deste resultado é complexa e exige uma teoria mais avançada que a desenvolvida aqui. Este conteúdo é abordado no tópico Teorema Central do Limite para soma de variáveis aleatórias dependentes.

Teorema 7.3.2.1

Demonstração:

Primeiramente vamos supor que $X_n$ tem média zero $(\mu=0).$ Podemos supor este fato sem perda de generalidade, pois se $\mu\neq 0,$ definimos $Y_n=X_n-\mu$. Pelo teorema 7.2.2.2, basta mostrarmos que: $$\varphi_{S_n/\sigma\sqrt{n}}(t)\rightarrow e^{-t^2/2},\forall t \in \mathbb{R}.$$

Utilizando a Proposição 7.2.1.2 e a Proposição 7.2.1.3, concluímos que $$\varphi_{S_n/\sigma\sqrt{n}}(t)=\varphi_{S_n}\left(\frac{t}{\sigma\sqrt{n}}\right)=\prod_{k=1}^{n}\varphi_{X_k}\left(\frac{t}{\sigma\sqrt{n}}\right)=\left(\varphi_{X_1}\left(\frac{t}{\varphi\sqrt{n}}\right)\right)^{n},$$

Como por hipótese $X_n$ apresenta variância limitada, temos que $\varphi$ apresenta pelo menos duas derivadas contínuas.

Desta forma, utilizando da formula de Taylor, temos que $$\varphi(t)=\varphi(0)+\varphi^{\prime}(0)t+\varphi^{\prime\prime}(\theta(t))\frac{t^2}{2},$$

no qual $|\theta(t)|\leq|t|$.

Logo, $$\varphi(t)=\varphi(0)+\varphi^{\prime}(0)t+\varphi^{\prime\prime}(\theta(t))\frac{t^2}{2}+\frac{t^2}{2}[\varphi^{\prime\prime}(\theta(t))-\varphi^{\prime\prime}(0)],$$

com $\varphi^{\prime\prime}(\theta(t))-\varphi(0)\rightarrow 0$ quando $t\rightarrow 0$.

Como $\varphi(0)=1$, e pelo corolário 7.2.1.1 concluímos que $\varphi^{\prime}(0)=i\mu=0$ e $\varphi^{\prime\prime}(0)=i^2\mathbb{E}[X_1^{2}]=-\mathbb{E}[X_1^2]=-\sigma^2.$

Assim, temos que $$\varphi(t)=1-\frac{\sigma^2 t^2}{2}+\frac{t^2}{2}~o(t),$$

no qual $\displaystyle \lim_{t\rightarrow 0}o(t)=0.$ Por isso, para cada t fixo, $$\varphi^{n}\left(\frac{t}{\sigma\sqrt{n}}\right)=\left[1-\frac{t^2}{2n}+\frac{t^2}{2\sigma^2 n}~o\left(\frac{t}{\sigma\sqrt{n}}\right)\right]^n= \left[ 1-\frac{t^2}{2n}\left(1-\frac{1}{\sigma^2}~o\left(\frac{t}{\sigma\sqrt{n}}\right)\right) \right]^n\rightarrow e^{-t^2/2},$$

pois $1-\dfrac{1}{\sigma^2}~o\left(\frac{t}{\sigma\sqrt{n}}\right)\rightarrow 1$ quando $n \rightarrow \infty$ e para números complexos, $c_n\rightarrow c \rightarrow \left(1+\frac{c_n}{n}\right)^n\rightarrow e^c$.

E portanto o resultado segue.

$\Box$

A condição de Lindeberg é um resultado muito importante para o teorema central do limite, pois é uma condição suficiente e para certas condições também é necessária. A condição de Lindeberg é enunciada da seguinte forma.

Definição 7.3.2.1 (Condição de Lindeberg)

$$\text{Para todo}~\epsilon> 0,\quad\quad\displaystyle\lim_{n\rightarrow\infty}\frac{1}{s_n^2}\sum_{k=1}^{n}\int_{(x;~|x-\mu_k|> \epsilon s_n)}(x-\mu_k)^2dF_k(x)=0\quad (\text{Lind})$$

Corolário 7.3.2.1

Sejam $X_1 , X_2 , \cdots$ variáveis aleatórias independentes e identicamente distribuídas com distribuição binomial com parâmetro $p~(0 < p < 1)$. Então $$\displaystyle\frac{S_n -np}{\sqrt{np(1-p)}}$$

converge em distribuição para uma normal padronizada $(N(0,1)).$

Demonstração:

Este teorema também ficou conhecido como Teorema Central do Limite de De Moivre e Laplace. Sua demonstração segue quase que imediatamente do teorema 7.3.2.1.

Basta observar que os $X_i^\prime s$ são independentes e identicamente distribuídas com média $\mu=p$ e variância $\sigma^2=p(1-p)$ e o resultado segue.

$\Box$

Agora, vamos fazer algumas observações sobre o ponto de vista intuitivo da condição de Lindeberg.

Notemos que a condição de Lindeberg significa, que de certa forma, as parcelas $\displaystyle\frac{X_k-\mu_k}{s_n}$ da soma $\displaystyle \frac{S_n-\mathbb{E}[S_n]}{s_n}$ são uniformemente pequenas se n for muito grande.

Um exemplo para esse fato é notarmos que a condição de Lindeberg implica $\displaystyle\max_{1\leq k\leq n}\frac{\sigma_k^2}{s_n^2}\rightarrow 0$

Assim para n grande, as variâncias das parcelas são uniformemente pequenas em relação à variância da soma. Esse fato pode ser observado da seguinte forma.

Notemos que para todo k $$\displaystyle\frac{\sigma^2_k}{s_n^2}=\frac{1}{s_n^2}\int_{|x-\mu_k|\leq \epsilon s_n}(x-\mu_k)^2dF_k(x)+\frac{1}{s_n^2}\int_{|x-\mu_k|> \epsilon s_n}(x-\mu_k)^2dF_k(x)\leq $$ $$\leq \displaystyle \frac{1}{s_n^2}\int_{|x-\mu_k|\leq \epsilon s_n}\epsilon^2 s_n^2dF_k(x)+\frac{1}{s_n^2}\sum_{j=1}^{n}\int_{|x-\mu_k|> \epsilon s_n}(x-\mu_j)^2dF_j(x)\leq$$ $$\leq \displaystyle\frac{1}{s_n^2}\int_{-\infty}^{\infty}\epsilon^2 s_n^2dF_k(x)+\frac{1}{s^2_n}\sum_{j=1}^{n}\int_{|x-\mu_j|> \epsilon s_n}(x-\mu_j)^2dF_j(x).$$

Como a primeira parcela é igual a $\epsilon^2$ que não depende de k, então temos que $$\displaystyle\max_{1\leq k \leq n}\frac{\sigma^2_k}{s_n^2}\leq \epsilon^2 + \frac{1}{s_n^2}\sum_{k=1}^n\int_{|x-\mu_k|> \epsilon s_n}(x-\mu_k)^2dF_k(x),$$

no qual converge para $\epsilon^2$, pela condição de Linderberg.

Logo, como vale para todo $\epsilon> 0$, temos $\displaystyle\max {\frac{\sigma_k^2}{s_n^2}}\rightarrow 0$.

Notem que intuitivamente isso nos diz que a soma de pequenas quantidades independentes com média zero tem aproximadamente uma distribuição normal.

Um exemplo deste fato intuitivo é quando consideramos a altura média da população brasileira. A diferença entre da altura de uma pessoa qualquer e a média tem distribuição normal com média zero e variância $\sigma^2.$ Notemos que cada pessoa contribui com uma parcela pequena.

Teorema 7.3.2.2

Seja $(X_i)_{i\geq 1}$ uma sequência de variáveis aleatórias independentes e quadrado integráveis, para algum $\text{Var}(X_n)=\sigma_n^2>0$ e $\mathbb{E}[X_n]=\mu_n.$ Definimos

$S_n=X_1+\cdots+X_n$

$s_n=\sqrt{\text{Var}(S_n)}=\sqrt{\sigma^2_1+\cdots+\sigma_{n}^2}.$

Então

$\displaystyle\frac{S_n-\mathbb{E}[S_n]}{s_n}$ converge em distribuição para $N(0,1)$ quando $n\rightarrow \infty$.

Demonstração:

É suficiente que a condição de Lindeberg seja satisfeita: $$\forall\epsilon> 0,\quad\quad\displaystyle\lim_{n\rightarrow\infty}\frac{1}{s_n^2}\sum_{k=1}^{n}\int_{(x;~|x-\mu_k|> \epsilon s_n)}(x-\mu_k)^2dF_k(x)=0\quad (\text{Lind})$$

Agora, vamos mostrar que as funções características das somas parciais padronizadas convergem para a função característica da $N(0,1)$ para qualquer t, da mesma forma como mostramos que a função característica converge então converge em distribuição.

Desta forma mostramos que: $$\displaystyle\varphi_{((S_n-\mathbb{E}[S_n])/s_n)}(t)=\prod_{k=1}^{n}\mathbb{E}[e^{it((X_k-\mu_k)/s_n)}]\rightarrow e^{-\frac{t^2}{2}}$$

Primeiramente fixamos t, além disso vamos utilizar as duas versões da fórmula de Taylor aplicada à função $g(x)=e^{itx}$. $$\displaystyle e^{itx}=1+itx+\gamma_1(x)\frac{t^2 x^2}{2},$$

em que $|\gamma_1(x)|\leq 1$ $$\displaystyle e^{itx}=1+itx-\frac{t^2 x^2}{2}+\gamma_{2}(x)\frac{t^3 x^3}{6},$$

em que $|\gamma_2(x)|\leq 1$

Seja $\epsilon > 0$ e ainda $|x|> \epsilon$ para a primeira formula de Taylor e na segunda para $|x|\leq \epsilon$. Assim podemos escrever $e^{itx}$ da seguinte forma geral: $$\displaystyle e^{itx}=1+itx-\frac{t^2 x^2}{2}+\theta_{\epsilon}(x),\quad (7.3.2.1)$$

no qual,

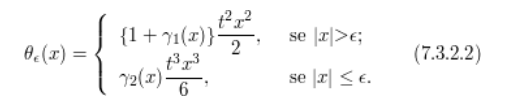
Consequentemente, $$\displaystyle \mathbb{E}\left[\exp\left(it\left(\frac{X_k-\mu_k}{s_n}\right)\right)\right]=\int \exp\left(it\left(\frac{x-\mu_k}{s_n}\right)\right)dF_k(x)\overset{\text{eq.}~(7.3.2.1)}{=}$$ $$=\int \left(1+it\left(\frac{x-\mu_k}{s_n}\right)-\frac{t^2}{2}\left(\frac{x-\mu_k}{s_n}\right)^2+\underbrace{\theta_{\epsilon}}_{\text{eq.}~(7.3.2.2)}\left(\frac{x-\mu_k}{s_n}\right)\right)dF_k(x)=$$ $$\displaystyle=1+it~\mathbb{E}\left[\frac{X_k-\mu_k}{s_n}\right]-\frac{t^2}{2}\mathbb{E}\left[\left(\frac{X_k-\mu_k}{s_n}\right)^2\right]+$$ $$+\frac{t^2}{2}\int_{|x-\mu_k|> \epsilon s_n}\left(1+\gamma_1\left(\frac{x-\mu_k}{s_n}\right)\left(\frac{x-\mu_k}{s_n}\right)^2\right)dF_k(x)+$$ $$+\frac{t^3}{6}\int_{|x-\mu_k|\leq \epsilon s_n}\gamma_2\left(\frac{x-\mu_k}{s_n}\right)\left(\frac{x-\mu_k}{s_n}\right)^3 dF_k(x)$$

Como $\mathbb{E}[X_k]=\mu_k$ e $\text{Var}[X_k]=\sigma_k^2$, temos

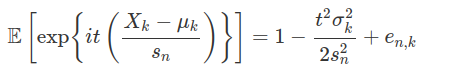
no qual o resto $e_{n,k}$ satisfaz a seguinte desigualdade

$$\displaystyle |e_{n,k}|\leq t^2 \int_{|x-\mu_k|> \epsilon s_n}\left(\frac{x-\mu_k}{s_n}\right)^2 dF_k (x)+\frac{|t|^3}{6}\int_{|x-\mu_k|\leq \epsilon s_n}\epsilon \left(\frac{x-\mu_k}{s_n}\right)^2dF_k(x)\leq$$ $$\displaystyle \leq \frac{t^2}{s_n^2}\int_{|x-\mu_k|> \epsilon s_n}(x-\mu_k)^2dF_k(x)+\frac{\epsilon |t|^3}{6s_n^2}\int_{-\infty}^{\infty}(x-\mu_k)^2dF_k(x).$$

Temos então

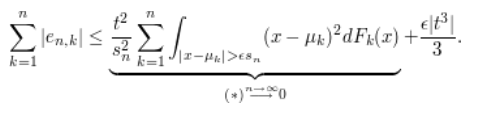
Pela condição de Linderberg, $(*)$ tende a zero quando $n\rightarrow \infty$. Logo, para n suficientemente grande,

$\displaystyle \sum_{k=1}^{n}|e_{n,k}|\leq \frac{\epsilon |t|^3}{3}$

Então vamos tomar uma sequência de $\epsilon$’s que converge para zero. Tome $\epsilon=\displaystyle \frac{1}{j}$, existe $n_j$ tal que para $n\geq n_j$,

$\displaystyle \sum_{k=1}^{n}|e_{n,k}|\leq \frac{|t|^3}{3j}\rightarrow 0,$

no qual o resto $e_{n,k}$ são determinados pela fórmula baseada em $\epsilon=\frac{1}{j}$. Assim

$\displaystyle\varphi_{((S_n-\mathbb{E}[S_n])/s_n)}(t)=\prod_{k=1}^{n}\left(1-\frac{t^2\sigma^2_k}{2 s_n^2}+e_{n,k}\right)$

Se tomarmos $e_{n,k}\rightarrow 0$. Desta forma basta provarmos que $\displaystyle \prod_{k=1}^{n}\left(1-\frac{t^2\sigma^2_k}{2 s_n^2}\right)\rightarrow e^{-t^2/2}$.

De fato, isto acontece, pois no caso de variáveis independentes e identicamente distribuídas, com $c_n\rightarrow c$ implica que $\displaystyle\left(1+\frac{c_n}{n}\right)^n\rightarrow e^c.$

$\Box$

Proposição 7.3.2.1:

Seja $(X_i)_{i\geq 1}$ uma sequência de variáveis aleatórias independentes e identicamente distribuídas com $\mathbb{E}[X_n]=\mu$ e $\text{Var}[X_n]=\sigma^2$, em que $0< \sigma^2 < \infty$

$\dfrac{S_n-n\mu}{\sigma\sqrt{n}}\overset{\mathcal{D}}{\rightarrow} N(0,1)$

Demonstração:

Vamos verificar a condição de Linderberg: $s^2_n=n\sigma^2$ e para $\epsilon> 0$, $$\displaystyle \frac{1}{n\sigma^2}\sum_{k=1}^{n}\int_{|x-\mu|\leq \epsilon \sigma \sqrt{n}}(x-\mu)^2dF_k(x)=$$ $$=\frac{1}{\sigma^2}\int_{|x-\mu|\leq \epsilon \sigma \sqrt{n}}(x-\mu)^2dF_1(x)\rightarrow \frac{1}{\sigma^2}\int_{-\infty}^{\infty}(x-\mu)^2dF_1(x)=\frac{\sigma^2}{\sigma^2}=1$$

em que a última convergência decorre da definição da integral e a igualdade para $\sigma^2$ decorre da definição da variância.

$\Box$

Definição 7.3.2.2 (Condição de Lyapunov)

Proposição 7.3.2.2

A condição de Lyapunov implica na condição de Lindeberg.

Demonstração:

Suponhamos a condição de Lyapunov satisfeita, isto é, para algum $\delta> 0$

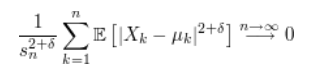
Para $\varepsilon> 0,$ então $$\mathbb{E}\left[|X_k-\mu_k|^{2+\delta}\right]=\int_{\mathbb{R}}|x-\mu_k|^{2+\delta}dF_k(x)\geq \int_{(x;~x|x-\mu_k|\geq \varepsilon s_n)}|x-\mu_k|^{2+\delta}dF_k(x)$$

$\displaystyle\geq (\varepsilon s_n)^\delta \int_{(x;~|x-\mu_k|\geq \varepsilon s_n)}(x-\mu_k)^2dF_k(x)$

Portanto, $$\frac{1}{s^2_n}\sum^n_{k=1}\int_{(x;~x|x-\mu_k|\geq \varepsilon s_n)}(x-\mu_k)^2dF_k(x)\leq \frac{1}{\varepsilon^\delta}\frac{1}{s^{2+\delta}_{n}}\sum^n_{k=1}\mathbb{E}\left[|X_k-\mu_k|^{2+\delta}\right]$$

$\Box$

Proposição 7.3.2.3

Seja $(X_i)_{i\geq 1}$ uma sequência de variáveis aleatórias independentes e satisfaz as condições de Lyapunov. Então $\dfrac{S_n-\mathbb{E}[S_n]}{s_n}$ converge em distribuição $N(0,1).$

Demonstração:

Para demonstrarmos essa proposição basta verificarmos a condição de Lyapunov, pois esta implica na condição de Lindeberg.

Para $\varepsilon > 0$, da proposição 7.3.2.2, temos que

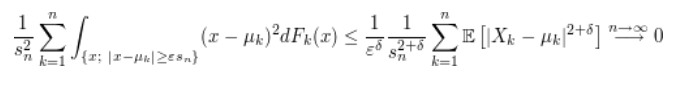
$\Box$

Proposição 7.3.2.4

Seja $(X_i)_{i\geq 1}$ uma sequência de variáveis aleatórias independentes tal que para todo $n\geq 1$ $$|X_k|\leq K\leq \infty$$

em que $K$ é uma constante e $s_n\rightarrow\infty,$ quando $n\rightarrow\infty.$ Então $$\frac{1}{s^2_n}\sum^n_{k=1}\int_{(x;~|x-\mu_k|\geq \varepsilon s_n)}|x-\mu_k|^2dF_k(x)\leq (2K)^2\frac{\sigma^2_k}{\varepsilon^2~s^2_n}$$

e satifaz as condições do Teorema Central do Limite.

Demonstração:

Seja as hipóteses satisfeitas então pela desigualdade de Chebyshev temos que

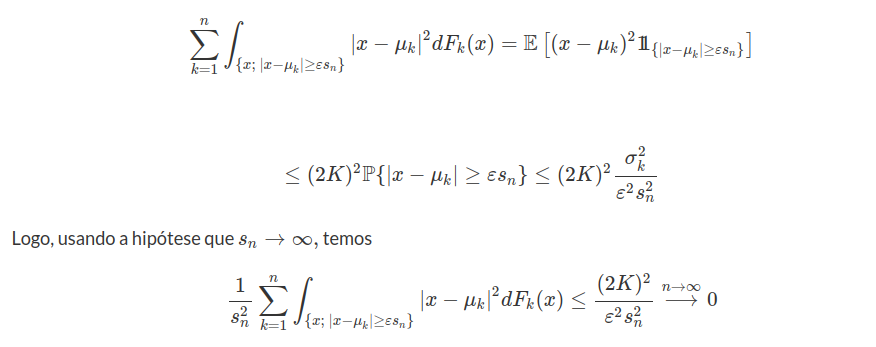
Portanto, a condição de Lindeberg é satisfeita e com isso o Teorema Central do Limite é verificado.

$\Box$

Exemplo 7.3.2.2

Exemplo 7.3.2.3

Um candidato a prefeito da cidade de São Carlos gostaria de ter uma ideia de quantos votos receberá nas próximas eleições. Para isto, foi feito uma pesquisa com os cidadães, em que $p$ representa a proporção de votos do candidato com $0\leq p< 1.$ Quantas pessoas devem ser entrevistadas com 95% de confiança para que o valor de $p$ tenha sido determinado com erro inferior a 5%, supondo que as escolhas de cada pessoa sejam independentes.

Seja $n$ o número de candidatos, denotamos $X_i, ~i=1,\dots,n$ a variável aleatória de Bernoulli que assume valor 1, com probabilidade p, se a i-ésima pessoa entrevistada declara a intenção de votar no candidato. Assume o valor 0, com probabilidade $1-p$ caso contrário.

Assim, temos que $\mathbb{P}[X_i=1]=p$ e $\mathbb{P}[X_i=0]=1-p.$ Consequentemente, $\mathbb{E}[X_i]=p$ e $\text{Var}(X_i)=p(1-p)$ para todo $i=1,\dots,n.$

Logo, do enunciado queremos $n$ mínimo de modo que $$\mathbb{P}\left[\left|\frac{S_n}{n}-p\right|\leq 0,05\right]\geq 0,95$$

em que $S_n=X_1+\dots+X_n.$

Mas, temos que $$\mathbb{P}\left[\left|\frac{S_n}{n}-p\right|\leq0,05\right]=\mathbb{P}\left[-0,05\leq \frac{S_n-np}{n}\leq 0,05\right]=$$ $$=\mathbb{P}\left[-0,05\sqrt{\frac{n}{p(1-p)}}\leq \frac{S_n-np}{\sqrt{np(1-p)}}\leq 0,05\sqrt{\frac{n}{p(1-p)}}\right]\geq 0,95$$

Pelo TCL, temos que para $n$ suficientemente grande $$\Phi\left(0,05\sqrt{\frac{n}{p(1-p)}}\right)-\Phi\left(-0,05\sqrt{\frac{n}{p(1-p)}}\right)\geq 0,95$$

Logo, basta escolhermos $n$ tal que

$$0,05\sqrt{\frac{n}{p(1-p)}}\overset{(\text{Obs.})}{\geq} 1,96\quad\rightarrow\quad n\geq \left(\frac{1,96}{0,05}\right)^2p(1-p)$$

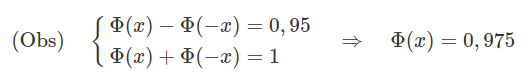
Como $p(1-p)\leq \frac{1}{4},$ temos que $$n\geq \left(\frac{1,96}{0,05}\right)^2\frac{1}{4}\approx384,16$$

Portanto, devemos entrevistar pelo menos 385 eleitores.