8.8 Esperança de variáveis aleatórias

Considere $(\Omega,\mathcal{F})$ um espaço mensurável, no qual $\mathcal{F}$ é uma $\sigma$-álgebra em $\Omega$. Denotamos por $\mathbb{P}: \mathcal{F}\rightarrow [0,1]$ uma probabilidade sobre $(\Omega, \mathcal{F})$. A probabilidade $\mathbb{P}$ é uma função de conjunto $\sigma$-aditiva com $\mathbb{P}(\Omega)=1$, ver Noções de Probabilidade. Para uma discussão detalhada sobre a construção da probabilidade ver teorema de extensão de caratheodory.Neste módulo, vamos nos dedicar a estudar o funcional linear e positivo, denominado esperança ou integral de lebesgue.

Seja $X:\Omega \rightarrow \mathbb{R}$ uma função. Para todo $A \subset \mathbb{R}$, definimos $$X^{-1}(A)=(\omega\in \Omega |X(\omega)\in A)$$ a imagem inversa da função $X$. As propriedades de imagem inversa listadas abaixo serão utilizadas na sequência: $$X^{-1}(\emptyset)=\emptyset$$ $$X^{-1}(A^c)=(X^{-1}(A))^{c}$$ $$\displaystyle X^{-1}\left(\bigcup_{i}A_i\right)=\bigcup_{i}X^{-1}(A_i)$$ $$\displaystyle X^{-1}\left(\bigcap_{i}A_i\right)=\bigcap_{i}X^{-1}(A_i).$$ Denotamos por $X^{-1}(\mathcal{E})$ a classe de subconjuntos $X^{-1}(C)$ no qual $C \in \mathcal{E}$. Com essas propriedades não é difícil notar que a imagem inversa de uma $\sigma$-álgebra define uma $\sigma$-álgebra.

Dizemos que $X$ é uma função mensurável se $X^{-1}(A)\in \mathcal{F}$ para todo $A\in \mathcal{B},$ no qual $\mathcal{B}$ é a $\sigma$-álgebra de borel definida nos reais. Para facilidade de notação, neste módulo, vamos identificar variáveis aleatórias com funções mesuráveis, sem necessariamente mencionar uma probabilidade sobre o espaço mensurável.

Definição 8.1

Lema 8.1

Demonstração

Propriedades da função Indicadora

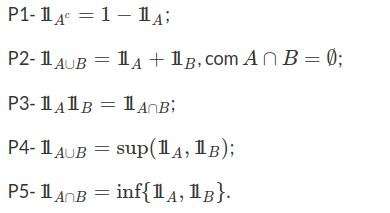
Definição 8.2

Definimos uma variável aleatória simples, na forma

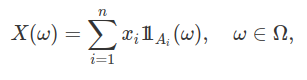
no qual $x_i\in \mathbb{R}$ são números reais distintos e $(A_i:i=1,2, \cdots , n) \subset \mathcal{F}$ é uma partição de $\Omega$, isto é, $A_i\cap A_j=\emptyset$, se $i\neq j$ e $ \cup_i A_i = \Omega$.

Lema 8.2

O conjunto $\mathfrak{E}$ composto pelas variáveis aleatórias simples é um espaço vetorial.

Demonstração

também são variáveis aleatórias simples. Portanto, a classe $\mathfrak{E}$ tem uma estrtura de lattice. Para qualquer função $X: \Omega \rightarrow \mathbb{R}$, as seguintes fórmula são válidas:

(1) $\sup(-X,-Y)=- \inf(X,Y)$;

(2) $\sup(X,Y)+\in(X,Y)=X+Y$.

Denotamos por $X^{+}=\sup(X,0)$ e por $X^{-}=\sup(-X,0)=-\inf(X,0)$ duas funções não negativas. Assim, obtemos que $X=X^{+} - X^{-}$ e $\mid X\mid = X^{+}+X^{-}$.

Definição 8.3

Dados $(\Omega, \mathcal{F} , \mathbb{P})$ um espaço de probabilidade e $X:\Omega \rightarrow \mathbb{R}$ uma função, dizemos que $X$ é uma variável aleatória se $(\omega \in \Omega: X(w) \leq x) \in \mathcal{F}$ para todo $x \in \mathbb{R}$.

Lema 8.3

Toda variável aleatória $X$ é uma função mensurável.

Demonstração: Vamos mostrar que para todo boreliano $B \in \mathcal{B}$, temos que $X^{-1}(B) \in \mathcal{F}$. Desde que $X$ é uma variável aleatória, sabemos que esta propriedade é válida para $B=(- \infty, b]$ com $b \in\mathbb{R}$. Utilizando o fato de que $\mathcal{F}$ é ma $\sigma$-álgebra, concluímos que

(1) $X^{-1} ((a, \infty))=X^{-1} \left( (- \infty , a]^c \right)= \left[ X^{-1} ((-\infty, a])\right]^c \in \mathcal{F}$;

(2) $X^{-1} ((a,b]) = X^{-1} ((-\infty,b] \cap (a, \infty))= X^{1}((-\infty , b]) \cap X^{-1} ((a, \infty)) \in \mathcal{F}$.

para todo $-\infty \leq a < b < \infty$. Denotamos por $\mathcal{D} = ( B \subset \mathbb{R}: X^{-1} (B) \in \mathcal{F})$. Como consequência da propriedade (2), concluímos que $\mathcal{D}$ contém a semiálgebra formada pelos intervalos $\mathcal{R} = ((a,b]: -\infty \leq a < b < \infty)$. Desde que a $\sigma$-álgebra de Borel é gerada pelos intervalos $\mathcal{R}$, basta mostrarmos que $\mathcal{D}$ é uma $\sigma$-álgebra. Assim, temos que

(a) $X^{-1} (\emptyset)=\emptyset \in \mathcal{F}$;

(b) Suponha que $B \in \mathcal{D}$, então $X^{-1}(B^c) = \left(X^{-1}(B)\right)^c \in \mathcal{F}$;

(c) Sejam $A_1 , A_2, \cdots$ elementos de $\mathcal{D}$, então temos que $X^{-1} \left(\cup_{i=1}^\infty A_i \right) = \cup_{i=1}^\infty X^{-1}(A_i) \in \mathcal{F}.$

Portanto, obtemos que $\mathcal{D}$ é uma $\sigma$-álgebra e segue o lema.

Lema 8.4

Seja $X:\Omega \rightarrow \mathbb{R}$ uma função tal que $(\omega \in \Omega: X(\omega) < x) \in \mathcal{F}$ para todo $x \in \mathbb{R}$. Então, temos que $X$ é uma variável aleatória.

Demonstração: Basta observarmos que $$X^{-1} ((-\infty,b])=X^{-1} \left(\cap_{n=1}^{\infty} (-\infty, b+ \frac{1}{n})\right) = \cap_{n=1}^{\infty} X^{-1} ((-\infty, b+ \frac{1}{n})) \in \mathcal{F},$$ para todo $b \in \mathbb{R}$. Segue o lema.

Com os lemas 8.3 e 8.4, concluímos que se $X:\Omega \rightarrow \mathbb{R}$ satisfaz $(\omega \in \Omega: X(\omega)\geq a) \in \mathcal{F}$ para todo $a \in \mathbb{R}$, então $X$ também é uma variável aleatória. Dados $X$ e $Y$ variáveis aleatórias, temos que $g=\sup (X,Y)$ também é uma variável aleatória, pois $$(\omega \in \Omega:g(\omega) \leq b)=(\omega \in \Omega:X(\omega) \leq b)\cap (\omega \in \Omega: Y(\omega) \leq b) \in \mathcal{F},$$ para todo $b \in \mathbb{R}$. Da mesma forma, podemos mostrar que $Z=\inf (X,Y)$ é uma variável aleatória. A seguir, vamos caracterizar variáveis aleatórias através de sequências de variáveis aleatórias simples. Este fato será importante na definição da esperança ou da integral de lebesgue.

Teorema 8.1

Uma função $X: \Omega \rightarrow \mathbb{R}$ é uma variável aleatória se, e só se, existe uma sequência de variáveis aleatórias simples $(X_n) \subset \mathfrak{E}$ tal que $X_n(\omega) \rightarrow X(\omega)$ para todo $\omega \in \Omega$. Para todo variável aleatória positiva $Y$, existe uma sequência não decrescente de variáveis aleatórias simples $(Y_n)$ que converge pontualmente para $Y$. Além disso, esta sequência pode ser tomada de tal forma que o limite seja uniforme em todo subconjunto de $\Omega$ para o qual $Y$ é limitada acima.

Demonstração: Suponha que existe uma sequência de variáveis aleatórias simples $(X_n)$ que converge pontualmente para $X$. Ao definirmos $g_n=\sup_{k \geq n} X_k$, obtemos que $(\omega \in \Omega: g_n(\omega) \leq b) = \cap_{k \geq n} ( \omega \in \Omega : X_k(\omega) \leq b) \in \mathcal{F}$, para todo $b \in \mathbb{R}$ e $n \in \mathbb{N}$. Desta forma, obtemos que $g_n$ é uma variável aleatória para todo $n$. Desde que $X_n$ converge pontualmente para $X$, sabemos que $$X = \lim \sup_n X_n = \inf_{n \geq 1} \sup_{n \geq k} X_k = \inf_{n \geq 1} g_n.$$ Assim, concluímos que $(\omega \in \Omega: X(\omega) > a)=\cap_{n=1}^{\infty} (\omega \in \Omega: g_n(\omega) > a ) \in \mathcal{F}$ para todo $a \in \mathbb{R}$. Portanto, obtemos que $X$ é uma variável aleatória.

Por outro lado, suponha que $X$ seja uma variável aleatória. Desde que $X=X^+ - X^-$ é a diferença de duas variáveis aleatórias positivas, basta mostrarmos que toda variável aleatória positiva é limite pontual de variáveis aleatórias simples. Seja $X$ uma variável aleatória positiva, para $n=0,1,2,3,\cdots$ e $0\leq k\leq 2^{2n}-1$ tomamos $$E_n^k= X^{-1}((k2^{-n},(k+1)2^{-n}]) \quad \text{e} \quad F_n=X^{-1}((2^n,\infty]).$$

Assim, definimos a variável aleatória simples

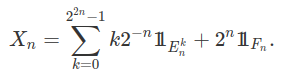
Note que $X_n\leq X_{n+1}$, para todo n, e ainda que $0\leq X-X_n\leq 2^n$, no conjunto onde $X\leq 2^n$, logo quando $ n\rightarrow \infty$ temos que $X_n\rightarrow X$ pontualmente e uniformemente nos conjuntos no qual X é limitado. Com isso, obtemos o teorema.

Para ilustrar a aproximação de variáveis aleatórias por variáveis aleatórias simples, consideramos as figuras abaixo.

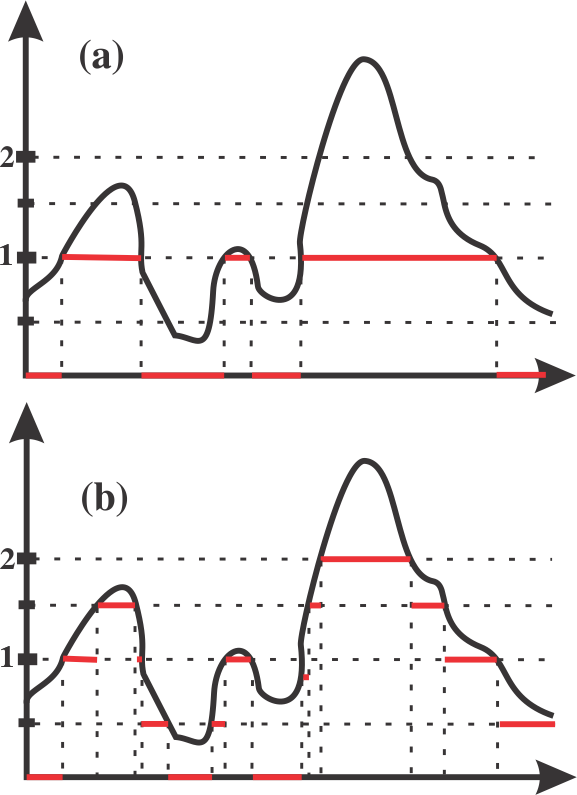
Na figura (a) temos em vermelho a função $X_0$ e na figura (b) também em vermelho temos $X_1$, podemos notar que conforme n cresce $X_n$ aproxima-se cada vez mais e ainda $X_n\leq X_{n+1}$. Como consequência do teorema 8.1, obtemos a seguinte proposição

Proposição 8.1

Sejam $X, Y$ funções mensuráveis, então

(a) $cX$;

(b) $X+Y$;

(c) $XY$;

(d) $X/Y$, se $Y(\omega)\neq 0$.

são funções mensuráveis.

Demonstração: Exercício.

Através da proposição 8.1, concluímos que a classe de variáveis aleatórias apresenta uma estrutura de álgebra. Além disso, se $(X_n)$ é uma sequência de variáveis aleatórias, as funções $Y=\sup_n X_n$ e $Z=\inf_n X_n$ também são variáveis aleatórias. Desta forma, para toda sequência $(X_n)$ de variáveis aleatórias, temos que $\lim \sup_n X_n$ e $\lim \inf_n X_n$ também são variáveis aleatórias. O conjunto de convergência da sequência $(X_n)$ é definido por $$(\omega \in \Omega: \lim \inf_n X_n = \lim \sup_n X_n) \in \mathcal{F}.$$ Assim, o limite de toda sequência convergente de variáveis aleatórias também é uma variável aleatória.

Dado $Y$ uma variável aleatória definida sobre $(\Omega, \mathcal{F} , \mathbb{P})$ e $\beta \subset \mathcal{F}$ uma sub-$\sigma$-álgebra. Dizemos que $Y$ é mensurável com respeito a $\beta$ se $\sigma$-álgebra gerada pela variável aleatória $Y$, definida por $\beta(Y)=(Y^{-1}(B):B \in \mathcal{B})$, está contida em $\beta$.

Proposição 8.2

Considere $\beta(X)$ a $\sigma$-álgebra gerada pela variável aleatória $X$. Uma variável aleatória $Y$ é mensurável com respeito a $\beta(X)$ se, e só se, $Y=f(X)$ no qual $f:\mathbb{R} \rightarrow \mathbb{R}$ é uma função mensurável.

Demonstração: Se $Y=f(X)$ no qual $f$ é uma função mensurável, temos que $Y$ é mensurável com respeito a $\sigma$-álgebra $\beta(X)$ (exercíco). Na sequência, vamos mostrar que se $Y$ é uma variável aleatória mensurável com respeito a $\beta(X)$, então $Y$ tem a forma $Y=f(X)$. Inicialmente, consideramos o caso em que $Y$ é uma variável aleatória simples. Por definição, existe uma partição finita $(B_i:i=1,2, \cdots ,n)$ de $\Omega$ tal que

Seja $Y$ uma variável aleatória mensurável com respeito a $\beta(X)$ que não é uma variável aleatória simples. Tomamos $(Y_n)$ uma sequência de variáveis aleatórias simples mesnuráveis com respeito a $\beta(X)$ tal que $Y=\lim_n Y_n$. Sabemos que $Y_n = f_n(X)$ no qual $f_n:\mathbb{R} \rightarrow \mathbb{R}$ é uma função mensurável. Desta forma, ao definirmos $f=\lim_n f_n$, concluímos que $f$ é mensurável e $Y=f(X)$. Segue a proposição.

8.1 - Integral de Lebesgue

Seja $(\Omega, \mathcal{F},\mathbb{P})$ um espaço de probabilidade e $X$ uma variável aleatória definida sobre $(\Omega, \mathcal{F}, \mathbb{P})$. Neste módulo, vamos definir a esperança da variável aleatória $X$, ou integral de Lebesgue de $X$. Na seção esperança de variáveis aelatórias, introduzimos as variáveis aleatórias simples na forma

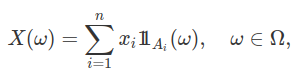
nos quais $(x_i)$ são números reais distintos e $(A_i) \subset \mathcal{F}$ uma partição finita de $\Omega$. Desta forma, definimos a esperança ou integral da variável aleatória simples $X$, por $$\mathbb{E} [X]=\sum_{i=1}^n x_i \mathbb{P}(A_i).$$ Aqui, utilizaremos a notação $$\mathbb{E}[X],~~ \int X(\omega)d\mathbb{P}(\omega),~~\int Xd\mathbb{P},~~\text{ou simplesmente quando não houver confusão } \int Xd\mathbb{P}.$$

O funcional $\mathbb{E}$ toma elementos no espaço das variáveis aleatórias simples $X \in \mathfrak{E}$ e os transforma em números reais $\mathbb{E}(X)$. Desta forma, dizemos que $\mathbb{E}: \mathfrak{E} \rightarrow \mathbb{R}$ é um funcional. Dizemos que um funcional $\mathbb{G}:\mathfrak{E}\rightarrow \mathbb{R}$ é positivo se $\mathbb{G}(X)\geq 0$ sempre que $X\geq 0$. Na sequência, derivamos algumas propriedades do funcional esperança.

Proposição 8.2.1

Demonstração

Pela definição da esperança, temos que

$$\lim\mathbb{P}({X_n> \epsilon})+\epsilon=\epsilon$$

o que implica que $$0\leq \lim E[X_n]\leq \epsilon$$

como $\epsilon$ é arbitrário temos que $$\lim E[X_n]=0$$

Mostramos anteriormente que qualquer variável aleatória positiva pode ser aproximada por uma sequência de variáveis aleatórias simples. Assim, podemos estender a nossa definição de esperança para toda variável aleatória positiva.

Teorema 8.2.1

Seja $X$ uma variável aleatória positiva e $(X_n)$ uma sequência de variáveis aleatórias simples que converge pontualmente para $X$. Desta forma, definimos $$\mathbb{E}[X]=\lim_{n \rightarrow \infty} \mathbb{E}[X_n].$$ Além disso, a esperança satisfaz as seguintes propriedades:

(a) $0 \leq \mathbb{E}[X] \leq \infty$, para toda variável aleatória positiva $X$;

(b) $\mathbb{E} [cX]=c\mathbb{E}[X]$ para todo variável aleatória positiva $X$ e constante real $c \geq 0$. Além disso, se $X,Y$ são variáveis aleatórias positivas, temos que $\mathbb{E}[X+Y]=\mathbb{E}[X]+\mathbb{E}[Y]$;

(c) Se $X\leq Y$ são variáveis aleatórias positivas, temos que $\mathbb{E}[X] \leq \mathbb{E}[Y]$;

(d) Dado $(X_n)$ uma sequência crescente de variáveis aleatórias positivas, então temos que $\mathbb{E}[\lim_{n\rightarrow \infty} X_n]=\lim_{n \rightarrow \infty} \mathbb{E}[X_n]$.

Demonstração: Inicialmente, vamos mostrar que a definição de esperança está bem definida. Neste caso, precisamos mostrar que a definição da esperança é independente da sequência de variáveis aleatórias simples. Sejam $(X_n)$ e $(Y_n)$ duas sequências crescentes de variáveis aleatórias simples, vamos mostrar que se $\lim_mX_m\leq \lim_n Y_n$, então temos que $\lim_m \mathbb{E}[X_m] \leq \lim_n \mathbb{E}[Y_n].$ Como as sequência são monótonas, temos que $$\lim_n \inf(X_m , Y_n)=X_m\quad m \geq 1,$$ em $\mathfrak{E}$. Assim, como $\mathbb{E}$ é um funcional linear positivo com a propriedade de continuidade monótona em $\mathfrak{E}$, temos que $$\lim_n \mathbb{E}[Y_n]\geq\lim_n \mathbb{E}[\inf(X_m,Y_n)]=\mathbb{E}[X_m], \quad m\geq 1.$$ Assim, ao tomarmos o limite quando $m \rightarrow \infty$, concluímos que $\lim_m \mathbb{E}[X_m] \leq \lim_n \mathbb{E}[Y_n].$

Como consequência, temos que se $X=\lim_n X_n$ a expressão $\lim_n \mathbb{E}[X_n]$ depende somente de $X$ e não da sequência de variáveis aleatórias simples $(X_n)$. Como consequência obtemos os itens (a) e (c). Para provarmos o item (b), basta observarmos que se $X=\lim_n X_n$ e $Y=\lim_n Y_n$ temos que $cX=c\lim_nX_n$ e $X+Y=\lim_n(X_n+Y_n)$. Na sequência, aplicamos a definição de esperança de ma variável aleatória positiva.

Para provar (d), tomamos $X_n=\lim_mY_{m,n}$ no qual $(Y_{m,n}:m\geq 1)$ é uma sequência de variáveis aleatórias simples para todo $n\geq 1$. Ao denotarmos por $Z_m=\sup_{n\leq m}Y_{m,n} \in \mathfrak{E}$ para todo $m\geq 1$, obtemos que $Y_{m,n}\leq Z_m\leq X_m$ e, obviamente, $\mathbb{E}[Y_{m,n}]\leq \mathbb{E}[Z_m]\leq \mathbb{E}[X_m]$ para todo $m\geq n$. Além disso, sabemos que $Z_m\leq Z_{m+1}$ o que implica que $\mathbb{E}[Z_m]\leq \mathbb{E}[Z_{m+1}]$. Desta forma, ao tomarmos o limite, concluímos que $$\lim_m X_m=\lim_m Z_m\quad \text{então}\quad \lim_m\mathbb{E}[X_m]=\lim_m \mathbb{E}[Z_m]=\mathbb{E}\left[\lim_m Z_m\right].$$ Com isso, obtemos o teorema.

Com a proposição acima, definimos esperança para qualquer variável aleatória positiva, mesmo que a esperança seja $\infty$. Agora, se $X$ é uma variável aleatória qualquer, sabemos que $X=X^+-X^-$ e $\mid X\mid=X^++X^-$, nos quais $X^+=\sup(X,0)$ e $X^-=-\inf (X,0)$. Assim, dizemos que a variável aleatória $X$ é integrável se $\mathbb{E}[X^+]< \infty$ e $\mathbb{E}[X^-]< \infty$, em particular, isto é válido para toda variável aleatória limitada. Para toda variável aleatória $X$ integrável, definimos $\mathbb{E}[X]=\mathbb{E}[X^+]-\mathbb{E}[X^-]$. Assim, obtemos uma extensão da esperança para todas variáveis aleatórias que são integráveis, que é linear, positiva e satisfaz a propriedade de continuidade monótona (ver teorema 8.2.2). A definição de esperança pode ser ampliada para a classe de variáveis aleatórias quase integráveis. Uma variável aleatória $X$ é denominada quase integrável se pelo menos um dos membros $\mathbb{E}[X^+]$ ou $\mathbb{E}[X^-]$ for finito. Neste caso, definimos $\mathbb{E}[X]=\mathbb{E}[X^+]-\mathbb{E}[X^-]$.

Teorema 8.2.2 (Esperança de uma variável Aleatória)

Dado $(\Omega, \mathcal{F}, \mathbb{P})$ um espaço de probabilidade, a esperança $\mathbb{E}$ definida sobre o espaço de todas as variáveis aleatórias quase integráveis satisfaz as seguinte propriedades:

(a) Temos que $-\infty \leq \mathbb{E}[X] \leq \infty$ para toda variável aleatória quase integrável $X$. A esperança é finita se, e só se, a variável aleatória for integrável. Além disso, se $X\geq 0$, então obtemos que $\mathbb{E}[X]\geq 0$;

(b) Temos que $\mathbb{E}[cX]=c\mathbb{E}[X]$ para toda constante finita $c$. Além disso, temos que $\mathbb{E}[X+Y]=\mathbb{E}[X]+\mathbb{E}[Y]$, se $X^+$ e $Y^+$ (ou, $X^-$ e $Y^-$) são integráveis;

(c) Se $X \leq Y$, então $\mathbb{E}[X]\leq \mathbb{E}[Y]$;

Teorema 8.2.3

Seja $(X_n)$ uma sequência de variáveis aleatórias positivas e $X=\displaystyle \sum_{n=1}^{\infty}X_n$ então $\mathbb{E}[X]=\displaystyle \sum_{n=1}^{\infty}\mathbb{E}[X_n]$.

Demonstração

$$\mathbb{E}[X_1+X_2]=\lim \mathbb{E}[Y_n+Z_n]=\lim \left(\mathbb{E}[Y_n]+\mathbb{E}[Z_n]\right)=\lim \mathbb{E}[Y_n]+\lim \mathbb{E}[Z_n]= \mathbb{E}[X_1]+\mathbb{E}[X_2]$$

Por indução temos que $$\displaystyle \mathbb{E}[\sum_{i=1}^{n}X_i]=\sum_{i}^{n} \mathbb{E}[X_i]$$

Agora pelo teorema da convergência monótona, temos que $$\mathbb{E}[\sum_{i=1}^{\infty}X_i] =\mathbb{E}[\lim_n \sum_{i=1}^{n}X_i]=\lim \sum_{i=1}^{n}\mathbb{E}[X_i]=\sum_{i=1}^{\infty}\mathbb{E}[X_i].$$ Portanto o resultado segue.

Corolário 8.2.1 (Lema de Fatou-Lebesgue)

Seja $(X_n)$ uma sequência de variáveis aleatórias e Y e Z variáveis aleatórias integráveis, então $$X_n\leq Y\rightarrow E[\limsup X_n]\geq \limsup \mathbb{E}[X_n]$$ $$X_n\geq Z\rightarrow \mathbb{E}[\liminf X_n]\leq \liminf \mathbb{E}[X_n]$$

Em particular, se a sequência $(X_n)$ é convergente e se existe uma variável aleatória integrável U tal que $|X_n|\leq U$, então $\mathbb{E}[\lim X_n]=\lim \mathbb{E}[X_n]$.

Demonstração

Para o caso em que $-U\leq X_n\leq U$ com U integrável, temos que $$E[\liminf X_n]\leq \liminf E[X_n]\leq \limsup E[X_n]\leq E[\limsup X_n].$$ Como a sequência $(X_n)$ é por hipótese convergente, isto implica que o limite existe logo $$\lim_n E[X_n]=E[\lim X_n].$$ Segue o corolário.

Proposição 8.2.2

Seja X e Y variáveis aleatórias independentes com $\mathbb{E}[|X|]< \infty$ e $\mathbb{E}[|Y|]< \infty$. Então $\mathbb{E}[|XY|]< \infty$ e

$$\mathbb{E}[XY]=\mathbb{E}[X]\mathbb{E}[Y]$$

Demonstração

Primeiramente considere $X\geq 0$ e $Y\geq 0$. Tomando

Mudança de Variável

Corolário 8.2.2

$$\int_{\Omega} (g\circ X)(\omega)\mathbb{P}(d\omega)=\lim_n\int_{\Omega} (g_n\circ X)(\omega)\mathbb{P}(d\omega)=\lim_n\int_{-\infty}^{\infty} g_n(x)\mathbb{P}_X(dx)=\int_{-\infty}^{\infty} g(x)\mathbb{P}_X(dx).$$ Segue o corolário.

Um ponto imporante deste corolário é que apesar de lidarmos com variáveis aleatórias positivas, não precisamos da hipótese de integrabilidade. A seguir, vamos estender este corolário para variáveis aleatórias gerais com a hipótese de integrabilidade.

Corolário 8.2.3

8.2 - Propriedades do espaço L^p

Vamos denotar por $ L^p=L^p(\Omega,\mathcal{F},\mathbb{P}) $, com $ 0\leq p\leq \infty $ o espaço das variáveis aleatórias tal que $ \mathbb{E}[|X|^p]=\displaystyle \int Xd\mathbb{P}< \infty $, ou seja, para $ 0\leq p< \infty $ temos

$$L^p=(X:\Omega\rightarrow \mathbb{R}; X \text{ é mensurável e }\mathbb{E}[|X|^p]< \infty),$$

para $ p=\infty $ temos que

$$L^\infty=(X:\Omega \rightarrow \mathbb{R}; X \text{ é mensurável e existe uma constante C tal que } |X(\omega)|\leq C, \quad q.c. \quad em \quad\Omega).$$

Existe uma norma tradicional desse espaço, a qual é definida da seguinte forma:

$$||X||_p=\mathbb{E}^{1/p}[|X|^p]$$

Apenas relembrando para que $ ||\cdot|| $ seja uma norma é necessário que:

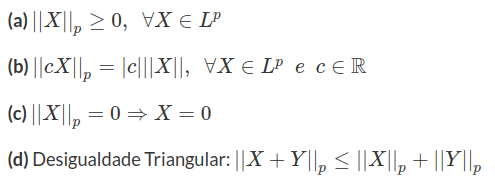
Note que para que $ ||\cdot|| $ seja uma norma, precisamos criar uma classe de equivalência. Assim dizemos que $ X\equiv Y $ se, e somente se, $ \mathbb{P}(X=Y)=1 $.

Primeiramente mostre que de fato é uma classe de equivalência. Para que seja uma classe de equivalência é preciso satisfazer 3 propriedades:

(a) Reflexiva: $ X\equiv X $

(b) Simétrica: $ X\equiv Y \Rightarrow Y\equiv X $

(c) Transitiva: $ X\equiv Y ~e~Y\equiv Z\Rightarrow X\equiv Z $

Demonstração

(a) De fato, $ X\equiv X $, pois $ \mathbb{P}(X=X)=1 $.

(b) De fato, $ X\equiv Y \Rightarrow Y\equiv X $, pois $ \mathbb{P}(X=Y)=1=\mathbb{P}(Y=X) $.

(c) De fato, $ X\equiv Y ~e~Y\equiv Z\Rightarrow X\equiv Z $, pois $ \mathbb{P}(X=Y)=1=\mathbb{P}(Y=Z)\Rightarrow \mathbb{P}(X=Z)=1 $.

Assim dentro da classe de equivale temos que $ ||\cdot||_p $ de fato é uma norma.

Vamos apresentar nesse momento algumas propriedades fundamentais do espaço $ L^p $.

Notação

Vamos usar $ L^{q} $ para representar o expoente conjugado do $ L^p $, ou seja, $ \displaystyle \frac{1}{p}+\frac{1}{q}=1 $.

Proposição 8.2.1 (Desigualdade de Young)

Seja p e q conjugados então para todo número real não-negativo $ a $ e $ b $, para $ 1\leq p\leq \infty $ temos

$$ab\leq \displaystyle \frac{a^p}{p}+\frac{b^q}{q}$$

Demonstração

Vamos dividir em casos. Caso $ ab=0 $ é trivial.

Caso $ a^p=b^q $, como $ p $ e $ q $ são conjugados temos $ 1/p+1/q=1 $

$$ab=a(b^q)^{1/q}=aa^{p/q}=a^{p/p}a^{p/q}=a^{p(1/p+1/q)}=a^p1=a^{p}\displaystyle\left(\frac{1}{p}+\frac{1}{q}\right)=\frac{a^P}{p}+\frac{b^q}{q}$$

Agora se $ a^p\neq b^q $, então usando a função exponencial, a qual é estritamente convexa temos (a derivada segunda é maior que zero em todo ponto). Então para todo $ t\in (0,1) $ e $ x,y \in \mathbb{R} $ com $ x\neq y $, temos

$$e^{tx+(1-t)y}\leq t e^x+(1-t)e^y$$

Assim tomando $ t=1/p $ o que implica $ 1-t=1/q $ e $ x=\ln a^p $ e $ y=\ln b^q $ temos que

$$\displaystyle ab=e^{\ln ab}=exp\left(\frac{\ln a^p}{p}+\frac{\ln b^q}{q}\right)\leq \frac{e^{\ln a^p}}{p}\frac{e^{\ln b^q}}{q}=\frac{a^p}{p}+\frac{b^q}{q}$$

Teorema 8.2.1 (Desigualdade de Hölder)

Seja f e g uma variável aleatória, tal que $ f\in L^p $, com $ 1\leq p\leq \infty $ e $ g\in L^{q} $. Então $ fg\in L^1 $ e

$$||fg||_1\leq ||f||_p||g||_q$$

Demonstração

Pela desigualdade de Young, temos que

integrando de ambos os lados, obtemos que

$$|fg|_1\leq \frac{|f|_p}{p}+\frac{|g|_q}{q}=1$$

Portanto o resultado segue. Para o caso geral, basta tomar $ f=f/|f|_p $ e $ g=g/|g|_q $ e o resultado segue.

A desigualdade de Hölder pode ser estendida para k funções.

Proposição 8.2.2 (Desigualdade de Minkowski)

Se $ 1\leq p\leq \infty $ e $ f,g\in L^p $, então $ f+g\in L^p $ e

$$|f+g|_p\leq |f|_p+|g|_p$$

Demonstração

Para o caso $ p=1 $ basta integrarmos a desigualdade

$$|f(x)+g(x)|\leq |f(x)|+|g(x)|$$

Agora se $ 1< p< \infty $, então sabemos que

$$|f(x)+g(x)|^p\leq (|f(x)|+|g(x)|)^p\leq 2^p (|f(x)|^p+|g(x)|^p)$$

o que implica que $ f+g\in L^p $. A seguir considere

$$|f(x)+g(x)|^p=|f(x)+g(x)|^{p-1}|f(x)+g(x)|\leq |f(x)+g(x)|^{p-1}|f(x)|+|f(x)+g(x)|^{p-1}|g(x)|$$

Como $ (p-1)q=p $ isso implica que $ |f+g|^{(p-1)}\in L^q $, então podemos aplicar a desigualdade de Hölder. Logo

$$||f||f+g|^{p-1}|_1\leq |f|_p|(f+g)^{p-1}|_q$$

$$||g||f+g|^{p-1}|_1\leq |g|_p|(f+g)^{p-1}|_q$$

Agora integrando de ambos os lados

$$|f(x)+g(x)|^p\leq |f(x)+g(x)|^{p-1}|f(x)|+|f(x)+g(x)|^{p-1}|g(x)|$$

e usando as desigualdades acima obtemos

$$|f+g|_p^p\leq |f|_p|(f+g)^{p-1}|_q+|g|_p|(f+g)^{p-1}|_q$$

Além disso, note que

$$|(f+g)^{p-1}|_q=\mathbb{E}[|f+g|^{(p-1)q}]^{1/q}=\mathbb{E}[|f+g|^{p}]^{p/pq}=|(f+g)|_p^{p/q}$$

Portanto

$$|f+g|_p^p\leq |f|_p|(f+g)|_p^{p/q}+|g|_p|(f+g)|_p^{p/q}$$

o que implica que dividindo ambos os lados por $ |(f+g)|_p^{p/q} $ temos

$$|f+g|_p^{p(1-1/q)}=|f+g|_p\leq |f|_p+|g|_p$$

Portanto o resultado segue

Teorema 8.2.2

$ L^p $ é um espaço vetorial e $ ||\cdot||_p $ é uma norma para qualquer $ p\geq 0 $

Demonstração

Usando a desigualdade de Minkowski e as classes de equivalência o resultado segue.

Definição 8.2.1

Um espaço é dito ser um espaço de Banach se é um espaço vetorial normado e completo.

Teorema 8.2.3 (Fischer-Riesz)

$ L^p $ é um espaço de Banach.

Demonstração

Como consequência temos que $ g(\omega) $ tem limite finito quase certamente em $ \Omega $, com $ g\in L^p $. Além disso, temos que para $ m\geq j\geq 2 $, temos que:

$$|f_{n_m}(\omega)-f_{n_j}(\omega)|\leq |f_{n_m}(\omega)-f_{n_{m-1}}(\omega)|+\dots+|f_{n_{n+1}}(\omega)-f_{n_{j}}(\omega)|\leq g(\omega)-g_{n_{j-1}}(\omega)$$

isto ocorre quase certamente em $ \Omega $. Agora temos que $ f_n(x) $ é de Cauchy e portanto converge para um limite finito, digamos $ f(x) $. Assim temos que q.c

$$|f(\omega)-f_n(\omega)|\leq g(\omega), \quad n\geq 2$$

Além disso, $ f\in L^p $, pois

$$|f|_p=|f-f_n+f_n|_p\leq |f-f_n|_p+|f_n|_p\leq |g|_p+|f_n|_p\leq \infty$$

Finalmente desde que

$$|f_n(x)-f(x)|^p\rightarrow 0\quad e \quad |f_n-f|^p\leq g^p\in L^1$$

pelo teorema da Convergência dominada temos que

$$|f_n-f|_p\rightarrow 0$$

Portanto o resultado segue.

Proposição 8.2.3 (Desigualdade de Jensen)

Seja $ f:\mathbb{R}\rightarrow\mathbb{R} $ uma função convexa e $ X\in L^1 $. Então temos que

$$\mathbb{E}(f(X))\geq f(\mathbb{E}(X)).$$

Demonstração

Ressaltamos que uma função é dita convexa se seu gráfico for convexo, ou seja, dado quaisquer pontos $ a,b\in \mathbb{R} $ a reta que passa pelos pares ordenados $ (a,f(a)) $ e $ (b,f(b)) $ não intercepta o gráfico de $ f $ em nenhum ponto no intervalo $ (a,b) $.

Uma definição equivalente seria que para quaisquer $ x, y \in [a,b] $ e para todo $ t\in [0,1] $ temos que:

$$f(tx+(1-t)y)\leq tf(x)+(1-t)f(y)$$

De fato se $ f $ é uma função convexa então dado um par ordenado $ (y,f(y)) $ no gráfico de $ f $, temos que existe uma reta $ r $ tal que a reta passa pelo ponto $ (y,f(y)) $ e deixa a curva $ f $ toda acima dela, ou seja, existe um $ \lambda\in\mathbb{R} $ tal que $ r(x)=\lambda(x-y)+f(y) $.

Então temos que

$$f(x)\geq r(x)=\lambda(x-y)+f(y),~~~\forall x \in\mathbb{R}.$$

Portanto, se aplicarmos o valor esperado em ambos os lados obtemos:

$$\mathbb{E}(f(X))\geq \mathbb{E}(r(X))=f(y)+\lambda(\mathbb{E}(X)-y).$$

E, tomando $ y=\mathbb{E}(X) $, o resultado segue.

Teorema 8.2.4

Seja $ (f_n)_{n\in\mathbb{N}} $ um sequência tal que $ f_n\in L^p $ e seja $ f\in L^p $, tal que $ ||f_n-f||_p\rightarrow 0 $.

Então existe uma subsequência $ (f_{n_k}) $ e existe $ h\in L^p $, talque:

(a)$ f_{n_k}\stackrel{q.c}{\rightarrow}f $

(b)$ |f_{n_k}|\leq h $ quase certamente para qualquer $ k\geq 0 $

Lema 8.2.1 (Desigualdade Chebyshev)

Seja $ f\in L^p $ para $ 1\leq p\leq \infty $. Então

$$\mathbb{P}({x:|f(x)|> \alpha})\leq \displaystyle \left(\frac{|f|_p}{\alpha}\right)^p$$

Demonstração

Seja $ E_{\alpha}=(x:|f(x)|> \alpha) $. Então

$$|f|^p_p=\displaystyle \int_{\Omega}|f|^pd\mathbb{P}\geq \int_{E_{\alpha}}|f|^p d\mathbb{P}\geq \alpha^p \int_{E_\alpha}d\mathbb{P}=\alpha^p\mathbb{P}(E_\alpha).$$

Portanto o resultado segue.

Definição 8.2.2

Definição 8.2.3

Definição 8.2.4

Um espaço E é dito ser separavél se possui um subconjunto D enumerável e denso em E.

Neste instante vamos mostrar que o espaço $ L^p $ é reflexivo e separável e o espaço dual de $ L^p $ é o seu expoente conjugado $ L^q $, não demonstraremos esses resultados, porém eles podem ser encontrados em qualquer livro de análise funcional a exemplo do Brezis.

Definição 8.2.5

Seja X um espaço de Banach. Dizemos que X é um espaço uniformemente convexo se, para todo $ \epsilon > 0 $, existe $ \delta> 0 $ tal que, se $ |x|\leq 1 $, $ |y|\leq 1 $ e $ |x-y|> \epsilon $, então

$$\displaystyle \left|\frac{x+y}{2}\right|< 1-\delta$$

Teorema 8.2.5 (Milman-Pettis)

Se X é um espaço de Banach uniformemente convexo, então X é reflexivo

Lema.8.2.2 (Desigualdade de Clarkson)

Se $ f,g \in L^p $, $ 1< p< \infty $

$ 1^\circ $ Desigualdade de Clarkson. Se $ p\geq 2 $, então

$$\displaystyle \left|\frac{f+g}{2}\right|^p_p+\left|\frac{f-g}{2}\right|^p_p\leq \frac{1}{2}(|f|_p^p+|g|^p_p)$$

$ 2^\circ $ Desigualdade de Clarkson. Se $ 1< p< 2 $, então

$$\displaystyle \left|\frac{f+g}{2}\right|^q_p+\left|\frac{f-g}{2}\right|^q_p\leq \frac{1}{2^{q-1}}(|f|_p^p+|g|^p_p)^{q-1}$$

Demonstração

Para primeira desigualdade de Clarkson, note que

$$a^p+b^p\leq (a^2+b^2)^{p/2}$$

tomando $ a=\displaystyle \frac{\alpha +\beta}{2} $ e $ b=\displaystyle \frac{\alpha-\beta}{2} $. Então

$$\left(\displaystyle \frac{\alpha +\beta}{2}\right)^p+\left(\displaystyle \frac{\alpha-\beta}{2}\right)^p\leq \left(\left(\displaystyle \frac{\alpha +\beta}{2}\right)^2+\left(\displaystyle \frac{\alpha-\beta}{2}\right)^2\right)^{p/2}$$

$$=\left(\displaystyle \frac{\alpha^2}{2}\frac{\beta^2}{2}\right)^{p/2}$$

$$\displaystyle \leq \frac{|\alpha|^p}{2}+\frac{|\beta|^p}{2}$$

Agora basta integramos e a desigualdade segue. Na segunda desigualdade de Clarkson, no que basta mostrarmos que

$$\left|\displaystyle \frac{\alpha +\beta}{2}\right|^q+\left|\displaystyle \frac{\alpha-\beta}{2}\right|^q\leq \frac{1}{2^{q-1}} (|\alpha|^p+|b|^p)^{q-1}$$

É equivalente mostrar que

$$\left|\frac{1+t}{2}\right|^{q}+\left|\frac{1-t}{2}\right|^q\leq \frac{1}{2^{q-1}}(1+t^p)^{q-1}$$

para $ 0\leq t\leq 1 $. Note que para $ t=1 $ e $ t=0 $ a desigualdade segue trivialmente. Para, então seja $ 0< t< 1 $, fazendo uma mudança de variável temos

$$t=\displaystyle \frac{1-s}{1+s}$$

com $ 0< s < 1 $ então a equação acima é dada por

$$\displaystyle \frac{1}{2}[(1+s)^q+(1-s)^p]-(1+s^q)^p-1\geq 0$$

Assim, fazendo uma expansão por serie de potencia temos

$$\displaystyle \frac{1}{2}\sum_{k=0}^\infty \binom{p}{k}s^k+\frac{1}{2}\sum_{k=0}^\infty \binom{p}{k}(-s)^k-\sum_{k=0}^\infty \binom{p-1}{k}s^{qk}=$$

$$\displaystyle \sum_{k=1}^\infty \left[\binom{p}{2k}s^{2k}-\binom{p-1}{2k-1}s^{q(2k-1)}-\binom{p-1}{2k}s^{2qk}\right]$$

no qual é convergente para $ 0\leq s\leq 1 $. Assim, basta provar que cada termo dela é positivo para $ 0< s < 1 $ e desta forma o resultado segue. Após algumas manipulações algébricas temos que o $ k $-ésimo termo da série é dado por

$$\displaystyle \frac{(2-p)(3-p)\cdots (2k-p)}{(2k-1)!}s^{2k}\left[\frac{1-s^{(2^k-p)/(p-1)}}{(2k-p)/(p-1)}-\frac{1-s^{2k/(p-1)}}{2k/(p-1)}\right]$$

Como $ p< 2 $, temos que

$$\displaystyle \frac{(2-p)(3-p)\cdots (2k-p)}{(2k-1)!}s^{2k}> 0$$

Além disso, desde que a função $ f(x)=(1-s^x)/x $ é decrescente para $ x> 0 $ e pelo fato de que

$$\displaystyle 0< \frac{(2k-p)}{(p-1)}< \frac{2k}{(p-1)} $$

o que implica que

$$\displaystyle \left[\frac{1-s^{(2^k-p)/(p-1)}}{(2k-p)/(p-1)}-\frac{1-s^{2k/(p-1)}}{2k/(p-1)}\right]> 0$$

portanto o k-ésimo termo é sempre positivo e como a serie é convergente temos que

$$\displaystyle \frac{1}{2}[(1+s)^q+(1-s)^p]-(1+s^q)^p-1\geq 0$$

o que implica que

$$\left|\frac{1+t}{2}\right|^{q}+\left|\frac{1-t}{2}\right|^q\leq \frac{1}{2^{q-1}}(1+t^p)^{q-1}$$

é verdadeira e portanto

$$\left|\displaystyle \frac{\alpha +\beta}{2}\right|^q+\left|\displaystyle \frac{\alpha-\beta}{2}\right|^q\leq \frac{1}{2^{q-1}} (|\alpha|^p+|b|^p)^{q-1}$$

Assim, basta integrarmos os dois lados da desigualdade e portanto temos que a segunda desigualdade de Clarkson é válida.

Teorema 8.2.6

$ L^p $ é um espaço uniformemente convexo para qualquer $ 1< p< \infty $.

Demonstração

Dado $ \epsilon> 0 $, sejam $ f,g \in L^p $ tais que

$$|f|_p=|g|_p=1\quad e \quad |f-g |> \epsilon$$

Se $ p\geq 2 $, então usando a primeira desigualdade de Clarkson temos

$$\displaystyle \left|\frac{f+g}{2}\right|_p^p\leq\frac{1}{2}(|f|^p_p+|g|_p^p)-\left|\frac{f-g}{2}\right|^p_p\leq 1-\frac{\epsilon^p}{2^p} $$

tomando $ \delta =\displaystyle 1-\left(\frac{1-\epsilon^p}{2^p}\right)^{1/p} $ temos que

$$\displaystyle \left|\frac{f+g}{2}\right|_p< 1-\delta$$

o que mostra que $ L^p $ é uniformemente convexo para $ p\geq 2 $. Para $ 1< p\leq 2 $, usando a segunda desigualdade de Clarkson temos

$$\displaystyle \left|\frac{f+g}{2}\right|^q_p\leq \frac{1}{2^{q-1}}(|f|^p_p+|g|_p^p)^{q-1}-\left|\frac{f-g}{2}\right|^q_p$$

$$1-\frac{\epsilon^q}{2^q}$$

tomando $ \delta =\displaystyle 1-\left(1-\frac{\epsilon^q}{2^q}\right)^{1/q} $

Portanto temos que $ L^p $ é um espaço uniformemente convexo para qualquer $ 1< p< \infty $.

Teorema 8.2.7

$ L^p $ é um espaço reflexivo para qualquer $ 1< p< \infty $

Demonstração

Note que $ L^p $ é um espaço de Banach. Portanto, pelo teorema 8.2.6 ele é uniformemente convexo e assim reflexivo pelo teorema de Milman-Pettis

Teorema 8.2.8

O espaço das funções contínuas $ C(\mathbb{R}^n) $ é denso em $ L^p $

Teorema 8.2.9

$ L^p $ é separável para qualquer $ p\geq 1 $.

Demonstração

Assim escolhendo de maneira que $ \delta |R|^{1/p}< \epsilon $ obtemos

$$|f-f_2|_p\leq 2\epsilon$$

Isso concluí a demonstração no caso em que $ \Omega=\mathbb{R}^n $.

No caso geral em que $ \Omega\subset \mathbb{R}^n $, vemos que podemos estender cada função de $ L^p(\Omega) $ como sendo zero fora de $ \Omega $. Dessa forma,

vemos que $ L^p(\Omega) $ pode ser visto com um subespaço fechado de $ L^p(\mathbb{R}^n) $. Existe uma isometria canônica e portanto temos que é separável.

Teorema 8.2.10

O $ L^\infty $ não é separável.

Demonstração

Seja $ \Omega \subset \mathbb{R}^n $ um aberto, então escolhemos $ \Lambda \subset \Omega $ um aberto, com $ \Lambda \neq \Omega $ de tal forma que a projeção de $ \Lambda $ sobre a primeira coordenada continha um intervalo $ [a,b] $. Então definimos um subconjunto $ B_t $ de $ \Lambda $ como

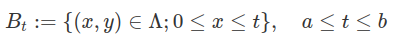
Neste caso, para $ t, s\in[0,1] $ com $ t\neq s $, temos

$$|u_t-u_s|_\infty=1$$

$$B_{u_t}=(f\in L^\infty;|f-u_t|< 1/2)$$

Proposição 8.2.4

O espaço $ L^1 $ não é reflexivo.

Demonstração

Suponha que $ L^1 $ seja reflexivo. Neste caso, ele seria reflexivo e separável. Consequentemente o seu dual $ (L^1)^\star=L^\infty $ seria separável o que é um absurdo.

É importante notarmos que como o espaço $ L^p $ é um espaço de Banach, ou seja, um espaço completo toda sequência é convergente se, e somente se, é uma sequência de Cauchy.

Lema 8.2.3

Suponhamos que $ p_0\leq p_1 $. Então

$$L^{p_1}\subset L^{p_0}$$

Além disso, para toda $ f\in L^{p_1} $

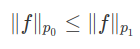
ou seja, a inclusão de $ L^{p_1} $ em $ L^{p_0} $ é um operador limitado

Demonstração

Defina $ F:=|f|^{p_0}\in L^{p_1/p_0} $, com $ f\in L^{p_1} $, podemos assumir sem perda de generalidade que $ p_1> p_0 $, então defina $ p=\displaystyle \frac{p_1}{p_0}> 1 $ e seu expoente conjugado, dado por

$$q=\displaystyle \frac{p_1}{p_1-p_0}.$$

Aplicamos a Desigualdade de Hölder:

$$\displaystyle \int_{\Omega}Fd\mathbb{P}\leq \left(\int_\Omega 1d\mathbb{P}\right)^{1/q}\left(\int_{\Omega}F^pd\mathbb{P}\right)^{1/p}$$

$$\leq \mathbb{P}(\Omega)^{1-\frac{p_0}{p_1}}\left(\int_{\Omega}|f|^{p_1}d\mathbb{P}\right)^{p_0/p_1}$$

$$=|f|^{p_0}_{p_1},$$

o que implica que

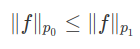
Covariância e o Produto interno

Definição 8.2.6

Seja $ Cov(\cdot,\cdot):L^2\times L^2\rightarrow \mathbb{R} $ na qual é definida por

$$Cov(X,Y)=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{E}[Y]$$

Note que a $ Cov(\cdot,\cdot) $ está bem definida para $ X,Y \in L^2 $, pois nesse caso basta usar a desigualdade de Hölder e obtemos que

$$\mathbb{E}[XY]\leq \mathbb{E}[X^2]\mathbb{E}[Y^2]< \infty$$

o que implica que $ Cov(\cdot,\cdot) $, se $ X,Y \notin L^2 $, não podemos garantir que a $ Cov(\cdot,\cdot) $ exista.

Proposição 8.2.5

A Covariância é simétrica e bilinear

Demonstração

Simetria: $ Cov(X,Y)=Cov(Y,X) $, para $ X,Y\in L^2 $

De fato,

$$Cov(X,Y)=\mathbb{E}(XY)-\mathbb{E}(X)\mathbb{Y}=\mathbb{E}(YX)-\mathbb{E}(Y)\mathbb{X}=Cov(Y,X)$$

Bilinear: $ Cov(aX+bY,W)=aCov(X,W)+bCov(Y,W) $, para $ X,Y,W\in L^2 $ e $ a,b\in \mathbb{R} $

De fato,

$$Cov(aX+bY,W)=\mathbb{E}([aX+bY]W)-\mathbb{E}(aX+bY)\mathbb{E}(W)=$$

$$\mathbb{E}(aXW+bYW)-[a\mathbb{E}(X)\mathbb{E}(W)+b\mathbb{E}(Y)\mathbb{E}(W)]=$$

$$a\mathbb{E}(XW)+b\mathbb{E}(YW)-a\mathbb{E}(X)\mathbb{E}(W)-b\mathbb{E}(Y)\mathbb{E}(W)=$$

$$a(\mathbb{E}(XW)-\mathbb{E}(X)\mathbb{E}(W))+b(\mathbb{E}(YW)-\mathbb{E}(Y)\mathbb{E}(W))=$$

$$aCov(X,W)+bCov(Y,W)$$

Portanto o resultado segue

Definição 8.2.7 (Produto interno)

Seja $ \langle\cdot,\cdot\rangle:V\times V\rightarrow K $, no qual, V é um espaço vetorial. No qual essa função tem as seguintes propriedades

(i) Simetria: $ \langle u,v\rangle=\langle v,u\rangle $

(ii) Bilinearidade: $ \langle au+bv,w\rangle=a\langle u,w\rangle+b\langle v,w\rangle $, com $ a,b \in\mathbb{R} $

(iii) Positividade: $ \langle u,u\rangle\geq 0 $ e é igual a zero se, e somente se, $ u=0 $

Muita propriedades de covariância podem ser facilmente obtida se pudermos identificar a covariância como um produto interno. Note que, ela satisfaz todas as propriedades de produto interno exceto o fato de ser igual a zero se, e somente se, $ X=0 $ isto ocorre para $ X=c $ com $ c $ constante é chamada de semi-positividade.

Então, assim criamos a seguinte classe de equivalência $ \mathbb{P}[X-Y=c]=1 $ para alguma constante $ c\in \mathbb{R} $, o que implica que a covariância define um produto interno sobre a classe de equivalência, este é o subespaço de variáveis aleatórias com segundo momento finito e esperança zero. Neste subespaço, a covariância é exatamente o produto interno de $ L^2 $.

Neste caso vamos mostrar a desigualdade de Cauchy-Schwarz, que nada mais é que um caso particular da desigualdade de Hölder, para normas que provem de um produto interno.

Proposição 8.2.6 (Desigualdade de Cauchy-Schwarz)

Seja $ X,Y \in L^2 $, com $ \mathbb{E}(X)=0=\mathbb{E}(Y) $, então

$$|Cov(X,Y)|\leq|X|_2|Y|_2$$

Demonstração

Segue diretamente da Desigualdade de Hölder.

8.3 - Convergência de Soma de variáveis aleatórias

Sabemos que a serie $\displaystyle \sum_{n=1}^{\infty} 1/n$ diverge, e ainda que $\displaystyle \sum_{n=1}^{\infty} (-1)^n/n$ converge. Entretanto a pergunta que fica será que se $P(X_n=1)=P(X_n=-1)=1/2$ a $\displaystyle \sum_{n=1}^{\infty} X_n/n$ converge ? Como podemos analisar a convergência de uma serie aleatória ? $$A_1=(\omega|\displaystyle \sum_{n=1}^{\infty} X_n/n~~ converge )$$

esse é o conjunto dos pontos para o qual a serie converge. Mas adiante vamos demonstrar pelo Teorema de Kolmogorov conhecido como “lei zero-um” $P(A_1)$

pode ser apenas 0 ou 1.

Definição 8.3.1

$\xi$ é uma $\sigma$-álgebra chamada de $\sigma$-álgebra calda, é também conhecida como $\sigma$-álgebra terminal ou álgebra assintótica.

Observação

Note que para todo evento $A\in \xi$ temos que A é independente de $X_1,\cdots, X_n$ para todo n finito.

Assim para todo $k\geq 1$ temos que $$A_1=(\omega|\displaystyle \sum_{n=1}^{\infty} X_n/n ~~converge )=(\omega|\displaystyle \sum_{n=k}^{\infty} X_n/n ~~converge)\in \mathcal{F}_k$$

Temos que $A_1\in \displaystyle \bigcap_{ k=1}^{\infty} \mathcal{F}_k^{\infty}=\xi$. Da mesma forma temos que, se $X_1,X_2,\cdots$ é uma sequência qualquer, $$A_2=(\displaystyle \sum_{n=1}^{\infty}X_n~~ converge)\in \xi$$

Além disso, temos que $$A_3=(X_n \in I_n\text{para um numero infinito de n})$$

onde $I_n$ pertence a $\sigma$-álgebra de borel. Logo se consideramos as variáveis independentes temos que pelo lema de Borel-Cantelli, segue que:

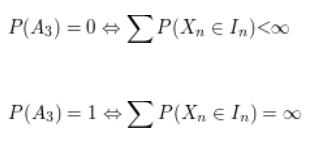
Assim a probabilidade de $A_3$ pode assumir apenas valor 0 ou 1, dependendo apenas da convergência ou não da serie. Isto é conhecida como Lei 0-1 de Borel.

Lema 8.3.1

Seja $\mathcal{B}$ uma algebra então, para qualquer $\epsilon> 0$ e $B\in\mathcal{F}$, com $\sigma{(\mathcal{B})}=\mathcal{F}$, existe $A\in\mathcal{B}$ tal que $$P(A\Delta B)\leq \epsilon$$

Teorema 8.3.1

Lei zero-um de Kolmogorov. Seja $(X_n)_{n\in \mathbb{N}}$ uma sequência de variáveis aleatórias independentes e seja $A\in \xi$. A $P(A)$ assume apenas valor zero ou um.

Demonstração

portanto $$P(A_n)\rightarrow P(A), P(A_n\cap A)\rightarrow P(A)$$

Entretanto $A\in \xi$ e portanto A é independente de $A_n$ para todo $n\geq 1$. E portanto o resultado segue.

Corolário 8.3.1

Seja $Y$ uma variável aleatória mensurável em relação a $\sigma$-álgebra cauda $\xi$. Então existe $c \in\mathbb{R}$ talque P(Y=c)=1.

Demonstração

Primeiramente observe que como $Y$ é $\xi$-mensurável então para qualquer $A\in\sigma(Y)\subset \xi$, então $$P(Y\in B_1\cap Y=B_2)=P(Y\in B_1)P(Y\in B_2), \forall B_i\in\mathfrak{B}$$

com $\mathfrak{B}$ sendo a $\sigma$-álgebra de Borel. Assim, considere a probabilidade do evento $[Y \leq x]$ é 0 ou 1, pois $$P([Y \leq x])=P([Y \leq x]\cap[Y \leq x])=P([Y \leq x])P([Y \leq x])=P^2([Y \leq x])$$

Portanto, a função de distribuição de Y tem um único ponto de salto, que é o supremo do conjunto $(x\in \mathbb{R} : P(Y \leq x) = 0)$. Assim seja $c=sup(x\in \mathbb{R} : P(Y \leq x) = 0)$, então $$P(Y=c)=1$$

o que implica que Y=c quase certamente.

Teorema 8.3.2

a) Se $p=1/2$, então $P(S_n=0, i.v.)=1$, onde i.v.=infinita vezes.

b) Se $p\neq 1/2$, então $P(S_n=0,i.v.)=0$

Demonstração

a) Note primeiramente que $B={[S_n=0,i.v.]}$ não pertence a $\sigma$-álgebra $\xi$ logo não é imediato que $P(B)=0$ ou $P(B)=1$. É suficiente provar que o evento $$A=(\displaystyle \limsup \frac{S_n}{\sqrt{n}}=\infty,\liminf \frac{S_n}{\sqrt{n}}=-\infty)$$

que $P(A)=1$, como $A\subset B$. Pois, é equivalente considerarmos o seguinte caso.

Como queremos usar o lema de Borel-Cantelli precisamos olhar para uma sequência independente. Assim considere uma subsequência $n_1< n_2< \cdots$ de números inteiros. Então para qualquer evento $(C_k)$ talque cada $C_k$ depende apenas de $(X_{n_k +1},X_{n_k +2},\cdots, X_{n_{k +1}})$ são independentes e o lema de Borel-Cantelli pode ser aplicado. Assim seja $n_k< m_k < n_{k+1}$ e definimos $$C_k=(X_{n_k+1}+\cdots+X_{m_k}\leq -n_k)\cap(X_{m_k+1}+\cdots +X_{n_{k+1}}\geq m_k)$$

é importante notar que escolhemos definir $C_k$ desta forma devido a sabermos do seguinte fato $$S_{n_k}=X_1+\cdots +X_{n_k}\leq n_k$$

pois $X_i=\pm 1$. Portanto $(\omega \in C_k)\rightarrow S_{n_k}\leq 0$. Por outro lado como $S_{m_k}\geq -m_k$, então adicionando temos que $$(\omega\in C_k)\rightarrow S_{n_{k+1}}\geq 0$$

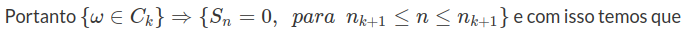
$(C_k, i.v.)\subset (S_n=0,i.v.)$

Assim basta provarmos que existe $n_k$ e $m_k$ talque $\sum P(C_k)=\infty$, e usando Borel-Cantelli temos $P[C_k,i.v]=1$, o que implica que $P[S_n=0,i.v.]=1$. Notemos primeiramente que dado qualquer $0<\alpha<1$, e um inteiro $k\geq 1$, existe um inteiro $p_k$, talque $$P(|S_{p_k}|=k)\leq \alpha$$

Defina $n_k, m_k$ da seguinte forma $n_1=1$, $m_k=n_k+p_k$ e $n_{k+1}=m_k+p_k$. Assim $P(C_k)$ é dado da seguinte forma $$P(C_k)=P(X_{n_k+1}+\cdots+X_{m_k}\leq - n_k)P(X_{m_k+1}+\cdots+X_{n_{k+1}}\geq m_k)$$

Pela simetria temos que $$P(C_k)=\frac{1}{4}P(|X_{n_k+1}+\cdots+X_{m_k}|\geq n_k)P(|X_{m_k+1}+\cdots+X_{n_{k+1}}|\geq m_k)$$

Além disso note que a distribuição de $P(S_{n+j}-S_n)=P(S_j)$, então temos que $$P(C_k)=\frac{1}{4}P(|X_{1}+\cdots+X_{m_k-n_k}|\geq n_k)P(|X_{1}+\cdots+X_{n_{k+1}-m_k}|\geq m_k)\geq \frac{1}{4}(1-\alpha)^2$$

o que implica que $$\displaystyle \sum_{k=1}^{\infty} P(C_k)\geq \sum_{k=1}^{\infty}\frac{1}{4}(1-\alpha)^2=\infty$$

Portanto por Borel-Cantelli temos que $P(S_n=0,i.v.)=1$.

(b) Análogo a letra (a) porém usando o complementar.

Teorema 8.3.3: (Lei 0-1 de Hewitt-Savage)

Seja $X_1,X_2,\cdots$ uma sequência de variáveis aleatórias iid, e $$A=(\omega | (X_1,X_2,\cdots)\in B)$$

um evento simétrico. Então P(A)=0 ou P(A)=1

Demonstração

Seja $A=[X\in B]$ um evento simétrico. Seja $B_n\in \mathfrak{B}(R^n)$, com $\mathfrak{B}(R^n)$ a $\sigma$-álgebra de borel do $R^n$, tal que para $A_n=(\omega | (X_1,\cdots, X_n)\in B_n)$ com

$P(A\Delta A_n)\rightarrow 0, ~~ n\rightarrow \infty$

Então $P(A_n)\rightarrow P(A)$. Assim como A é simétrico então $$P(A_n\cap A_n)=P((X_1,\cdots X_n)\in B_n;(X_{n+1}, \cdots X_{2n})\in B_n)$$

E pela independência dos $X_i$ temos que $$P((X_1,\cdots X_n)\in B_n;(X_{n+1}, \cdots X_{2n})\in B_n)=P((X_1,\cdots X_n)\in B_n)P((X_{n+1}, \cdots X_{2n})\in B_n)$$

Assim quando $n\rightarrow \infty$ temos que $$P(A)=P^2(A)$$

o que implica que P(A)=0 ou P(A)=1.

Exemplo 8.3.1

Suponha $(X_n)_{n\geq 1}$ uma sequência de v.a’s tal que $P(X=0)=1-\displaystyle \frac{1}{n}$, $P(X_n=1)=\displaystyle \frac{1}{2n}=P(X_n=-1)$. Mostre que $X_n\stackrel{P}{\rightarrow} 0$ e $X_n\stackrel{L^p}{\rightarrow} 0$.

Primeiramente mostremos que $X_n\stackrel{P}{\rightarrow} 0$, $$P(|X_n|\geq \epsilon)=P(X_n=1)+P(X_n=-1)$$ $$=\displaystyle \frac{1}{2n}+\frac{1}{2n}=\frac{1}{n}.$$

Como $$\displaystyle \lim_{n\rightarrow}P(|X_n|\geq \epsilon)=0$$

Portanto concluímos que, $$X_n\stackrel{P}{\rightarrow} 0.$$

Agora mostremos que $X_n\stackrel{L^p}{\rightarrow} 0$.

Temos que $$E[|X_n|^p]=\displaystyle \frac{1}{n}$$

Como $$\displaystyle \lim_{n\rightarrow}E[|X_n|^p]=0$$

E portanto o resultado segue.

Exemplo 8.3.2

Para $c\in\mathbb{R}$, constante, mostre que $X_n\stackrel{L^2}{\rightarrow} c$ se, e somente se, $E[X_n]\rightarrow c$ e $Var[X_n]\rightarrow 0$.

Primeiramente vamos supor que $X_n\stackrel{L^2}{\rightarrow} c$. Como $X_n\stackrel{L^2}{\rightarrow} 0$ temos que $$E[|X_n-c|^2]\rightarrow 0\rightarrow Var[X_n]+(E[X_n]-c)^2\rightarrow 0$$ $$\rightarrow Var[X_n]\rightarrow 0$$

e $$(E[X_n]-c)^2\rightarrow 0\rightarrow E[X_n]\rightarrow 0$$

como queríamos demonstrar

Agora suponha que $E[X_n]\rightarrow c$ e $Var[X_n]\rightarrow 0$. Note que $$E[|X_n-c|^2]=Var[X_n]+(E[X_n]+c)^2\rightarrow 0$$

8.4 - Variáveis Aleatórias com segundo momento finito.

Discutimos algumas propriedades dos espaços $L^p$ na seção. Nesta seção vamos trabalhar com o espaço $L^2$, o qual é um espaço de Banach. Dentro deste contexto, ou seja, dentro do contexto de variáveis aleatórias de $L^2$, vamos introduzir uma visão geométrica dentro deste espaço.

Para essa seção todas as variáveis aleatórias consideradas serão variáveis pertencentes a $L^2$.

Assim como $L^2$ tem estrutura de espaço vetorial, assim vamos definir um produto interno e a norma induzida por esse produto interno.

Seja $X,Y\in L^2$ $$(X,Y)=E[XY]$$

é fácil ver que $(X,Y)$ é um produto interno e além disso, que a norma induzida por esse produto interno é dada por $$||X||=E^{1/2}[|X^2|]$$

o qual já mostramos que é uma norma na seção de propriedades do espaço $L^p$. Assim para introduzirmos nossa visão geométrica nesse espaço, agora que temos nossa definição de produto interno nesse espaço, podemos definir ortogonalidade.

Definição 8.4.1

Dizemos que X e Y são variáveis ortogonais se, $(XY)=E[XY]=0$

Note que, duas variáveis são não correlacionadas se elas tem covariância nula, isto implica que $Cov(X,Y)=0\rightarrow E[XY]=E[X]E[Y]$, o que implica que variáveis aleatórias ortogonais são não correlacionadas.

Definição 8.4.2

Dizemos que M é um sistema de variáveis ortogonais se, X é ortogonal a Y para todo $X,Y\in M$.

Definição 8.4.3

Dizemos que M é um sistema ortonormal se é um sistema ortogonal e além disso para todo $X\in M$ temos que $||X||=1$.

Observação

Podemos fazer uma analogia com álgebra linear, quando temos uma base ortonormal por exemplo para o $R^2$, sendo essa por exemplo $M=((0,1);(1,0))$. Porém existe uma pequena peculiaridade no $L^2$, ele é um espaço com dimensão infinita e portanto a base ortonormal do espaço todo é uma conjunto M com infinitos termos. Lembrando que como $L^2$ é um espaço de Hilbert (para $L^p$, com $p\neq 2$, temos que $L^p$ não é Hilbert) e como mostramos na seção de propriedades do espaço $L^p$ temos que $L^2$ é separável. Além disso, temos que todo espaço de Hilbert separável admite uma base ortonormal.

Teorema 8.4.1

Todo espaço H separável e de Hilbert tem uma base ortonormal.

Demonstração

Seja $(v_n)$ um subconjunto enumerável denso em H (esse conjunto existe a prova pode ser encontrada no Brezis). Seja um espaço linear $F_k$ cujo a base é formada por $(v_1, \dots, v_k)$. A sequência de espaços $(F_k)$ é não decrescentes e finita dimensional e ainda $\displaystyle \bigcup_{k=1}^{\infty}F_k$ é denso em H. Tome o vetor $e_1$ base ortonormal de $F_1$. Se $F_1\neq F_2$, então existe $e_2$ tal que $(e_1,e_2)$ são base ortonormais para $F_2$. Repetindo essa construção encontramos uma base ortonormal enumerável para H.

8.4.1 - Melhor estimador da média quadrática

Seja $M=(X_1,X_2,\cdots, X_n)$ uma sistema ortonormal e X uma variável aleatória qualquer com $X\in L^2$. Podemos encontrar uma classe estimadores lineares. Basta notarmos que $$E[|X-\displaystyle \sum_{i=1}^{n}a_iX_i|^2]=||X-\displaystyle \sum_{i=1}^{n}a_iX_i||^2 =\left(X-\displaystyle \sum_{i=1}^{n}a_iX_i,X-\displaystyle \sum_{i=1}^{n}a_iX_i\right)$$ $$||X||^2 -2\displaystyle \sum_{i=1}^{n}a_i(X,X_i)+\left(\displaystyle \sum_{i=1}^{n}a_iX_i,\displaystyle \sum_{i=1}^{n}a_iX_i \right)$$ $$=||X||^2 -2\displaystyle \sum_{i=1}^{n}a_i(X,X_i)+ \sum_{i=1}^{n}a_i^2$$ $$=||X||^2 -\displaystyle \sum_{i=1}^{n}|(X,X_i)|^2+ \sum_{i=1}^{n}|a_i-(X,X_i)|^2$$ $$\geq ||X||^2- \displaystyle \sum_{i=1}^{n}|(X,X_i)|$$

Assim o $\inf E[|X-\displaystyle \sum_{i=1}^{n}a_iX_i|^2]$ é $a_i=(X,X_i)$. Desta forma, podemos escrever X em termos de $X_i$ da melhor forma possivel. Com $a_i=(X,X_i)$, escrevemos $$\widehat{X}=\displaystyle \sum_{i=1}^{n}(X,X_i)X_i$$

Como dizemos na observação a base para o espaço $L^p$ tem dimensão infinita. E como mostrado no teorema sempre podemos encontrar uma base ortonormal $M=(X_1,X_2,\dots)$, utilizando essa base existe uma importante desigualdade conhecida como desigualdade de Bessel’s. A qual diz que $\forall X \in L^2$, temos que $$\displaystyle \sum_{i=1}^{\infty}|(X,X_i)|^2\leq ||X||^2$$

com a igualdade sendo verificada se, e somente se, $$X=\displaystyle \sum_{i=1}^{\infty}(X,X_i)X_i$$

Além disso, é importante dizermos que se consideramos todos os estimadores $e\in L^2$ de X, que são função de $X_i$, temos que o melhor estimador é dado por $$\widehat{X}=E(X|X_1,\dots, X_n)$$

(imagem em falta)

Uma visão geométrica a esse respeito por ser analisada na figura. Onde A é um subconjunto de $L^2$ e além disso, A é gerado pelo sistema ortonormal M. Note que $\widehat{X}$ (em vermelho) é a projeção de X(em preto) no conjunto A.