8.9 Fundamentos da Teoria da Probabilidade

A teoria da probabilidade apresentada neste portal está fundamentada na base axiomática de Kolmogorov, nos quais os elementos estocásticos são definidos sobre o espaço de probabilidade $(\Omega, \mathcal{F} , \mathbb{P})$:

a) $\Omega$ um espaço abstrato;

b) $\mathcal{F}$ uma $\sigma$-álgebra formada por subconjuntos de $\Omega$;

c) $\mathbb{P}$ uma probabilidade sobre $\mathcal{F}$;

Apesar do modelo axiomático de Kolmogorov ser universalmente aceito, em 1948, exemplos publicados por Dieudonné (1948), Andersen e Jessen (1948), Doob (1948) e Jessen (1948), abalaram o modelo de Kolmogorov.

1. [Dieudonné] Existe um espaço mensurável $(\Omega , \mathcal{F})$, uma probabilidade $\mathbb{P}$ sobre $\mathcal{F}$ e uma sub-$\sigma$-álgebra $\mathcal{A} \subset \mathcal{F}$ para o qual não existe uma função $\nu(\omega , E)$ definida para todo $\omega \in \Omega$ e $E \in \mathcal{F}$ com as seguintes propriedades:

a) Para todo $\omega \in \Omega$, temos que $\nu(\omega , \cdot)$ é uma probabilidade sobre $\mathcal{F}$;

b) Para todo $E \in \mathcal{F}$, a função $\nu(\cdot , E)$ é $\mathcal{A}$-mensurável;

c) Para todo $A \in \mathcal{A}$ e $E \in \mathcal{F}$, temos que $$\mathbb{P} (A \cap E) = \int_A \nu(\omega , E) \mathbb{P}(d \omega).$$ O teorema de Radon-Nikodym nos mostra a existência de uma função satisfazendo (a) e (b), porém, a propriedade (c) nem sempre é válida como mostra Dieudonné. Neste caso, não garantimos a existência de probabilidade condicional regular. Desta forma se tomarmos $f: \Omega \rightarrow \mathbb{R}$ uma função $\mathcal{F}$-mensurável e integrável, apesar da esperança condicional de $f$ dado a sub-$\sigma$-álgebra $\mathcal{A}$ existir, esta não pode ser escrita como a integral (de Lebesgue) em relação a probabilidade condicional.

2. [Doob, Jessen] Considere $(\Omega, \mathcal{F}, \mathbb{P})$ um espaço de probabilidade e $f$ e $g$ duas variáveis aleatórias definidas sobre $(\Omega, \mathcal{F}, \mathbb{P})$. Dizemos que estas variáveis aleatórias são independentes, se $$\mathbb{P}[f^{-1} (A) \cap g^{-1}(B)] = \mathbb{P}[f^{-1} (A) ] \mathbb{P}[g^{-1}(B)] ~ ~ (1)$$ para $A$ e $B$ nos quais as probabilidade acima estejam bem definidas. Entretanto, existe um espaço de probabilidade $(\Omega, \mathcal{F}, \mathbb{P})$ e variáveis aleatórias $f$ e $g$ para os quais $(1)$ é válido para todo boreliano do reta, mas não para todo subconjunto da reta no qual $(1)$ esteja bem definido.

Esta questão é necessária para expressarmos a definição de independência em termos da função característica das variáveis aleatórias, pois a função característica determina a probabilidade da variável aleatória pertencer a borelianos da reta. Desta forma, a propriedade da função característica conjunta de $(f,g)$ ser o produto das funções características de $f$ e $g$ é equivalente a validade de $(1)$ apenas para borelianos.

3. [Andersen e Jessen] Considere $((\Omega_n , \mathcal{F}_n) : n \geq 1)$ uma sequência de espaços mensuráveis. Tomamos $\Omega = \prod \Omega_n$ o espaço produto com $\mathcal{F}$ a $\sigma$-álgebra produto. Existe uma sequência de espaços mensuráveis $((\Omega_n , \mathcal{F}_n) : n \geq 1)$ e uma função de conjunto $\mathbb{P} : \mathcal{F} \rightarrow [0,1]$ tal que a marginal de $\mathbb{P}$ sobre $\mathcal{F}_n$ é $\sigma$-aditiva para todo $n \in \geq 1$, embora a função de conjunto $\mathbb{P}$ sobre $\mathcal{F}$ não é $\sigma$-aditiva.

Este exemplo nos mostra que o teorema de Extensão de Kolmogorov não pode ser estendido para uma sequência qualquer de espaços mensuráveis.

Nos exemplos acima, observamos que conceitos fundamentais (intuítivos) da teoria da probabilidade são violados. Assim, podemos concluir que o modelo de Kolmogorov é muito geral e que modelos mais restritivos, nos quais os problemas acima não acontecem devem ser considerados. No livro de Gnedenko e Kolmogorov (1949) foi proposto o conceito de espaço de probabilidade perfeito para tratar a questão (2). No apêndice da versão inglesa deste livro, Doob, inspirado em parte pelo conceito de separabilidade de Marczewski (1938) e Halmos e von Neumann (1942), mostrou que para espaços de probabilidade perfeito os problemas (1) e (2) não ocorrem. Como consequência do teorem VIII em Ryll-Nardzewski (1954), concluímos que a questão (3) também não ocorre para espaços de probabilidade perfeito. A utilização da separabilidade de Halmos e von Neumann (1942) tinha por objetivo caracterizar via isomorfismos espaços de probabilidade abstratos através do espaço $([0,1] , \Sigma , m)$, no qual $\Sigma$ corresponde a $\sigma$-álgebra de Lebesgue e $m$ a medida de lebesgue (ver módulo “Medida de Lebesgue”).

Ao analisar o teorema de Extensão de kolmogorov, Marczewski (1954) observou que a aproximação da probabilidade de borelianos pela probabilidade de compactos é importante. Assim, Marczewski introduziu o conceito de espaço de probabilidade compacto e estabeleceu uma versão abstrata do teorema de extensão de Kolmogorov (ver módulo “Probabilidade Produto”). Em Jirina (1954) foi mostrado que a questão $(1)$ não ocorre se o espaço de probabilidade for separável e compacto.

O que distingue este módulo de fundamentos da teoria de probabilidade dos trabalhos citados acima é que ao invés de caracterizarmos os espaços de probabilidade nos quais os problemas acima não ocorrem, caracterizamos os espaços mensuráveis nos quais tais questões não ocorrem, independente da probabilidade sobre estes espaços mensuráveis. Estes espaços mensuráveis, denominados espaços de Radon, foram introduzidos por Leão, Fragoso e Rufino (1999).

Seleção Universalmente Mensurável

Considere dois espaços mensuráveis $(\Omega_1 , \mathcal{F}_1)$ e $(\Omega_2 , \mathcal{F}_2)$, um retângulo mensurável em $\Omega_1 \times \Omega_2$ é um subconjunto na forma

A demonstração da existência de seleção universalmente mensurável será realizada dentro deste módulo na máxima generalidade possível. A seguir, vamos exemplificar a necessidade dos teoremas de seleção mensurável em problemas de otimização estocástica. Tomamos $f:\Omega \times E \rightarrow \mathbb{R}^\star$ uma função mensurável, no qual $\mathbb{R}^\star= \mathbb{R} \cup (-\infty,\infty)$ corresponde ao conjunto de número reais aumentado. Definimos,

$$f^{\star}(\omega) = \inf_{ u \in E} f(u, \omega) ~ ~ ; ~ ~ \omega \in \Bbb{R}.$$ O problema da seleção mensurável pode ser formulado da seguinte forma. Dado $\epsilon > 0$, existe um seletor mensurável $\phi : \Omega \rightarrow E$, tal que

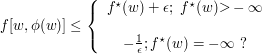
Também, podemos definir o problema de seleção na forma. Seja,

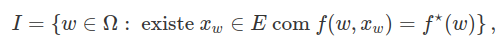
o conjunto no qual o ínfimo ocorre. Assim, requeremos que além da equação acima ϕ satisfaça

$$f[w, \phi(w)] = f^{\star}(w) ~ ~ ; ~ ~ w \in I .$$

De forma geral, não necessariamente existe uma função mensurável $\phi$ (seletor) que satisfaça as condições acima. Outra questão que surge com o poblema de otimização descrito acima é a questão da mensurabilidade da função $f^\star$. Para mostrarmos estes resultados, vamos utilizar o Corolário do Teorema 5.5 em Leese(1978) em conjunto com o Teorema II.8 em Dellacherie (1980), a fim de apresentarmos um teorema de seleção para conjuntos universalmente mensuráveis. A seguir, apresentamos alguns conceitos que serão utilizados neste módulo.

Definições

Considere um espaço mensurável $(\Omega, \mathcal{F})$ e $A \subset \Omega$ um subconjunto qualquer, definimos por

Definição 9.2 (Espaço Mensurável Separado e Espaço Mensurável Separável)

O espaço mensurável $(\Omega, \mathcal{F})$ é denominado separado se os átomos de $\Omega$ são seus pontos (singletons). Também dizemos que o espaço mensrável $(\Omega, \mathcal{F})$ é separável, se existe uma sequência de elementos de $\mathcal{F}$ que gera $\mathcal{F}$. Neste caso, existe uma sequência $\mathcal{A} = (A_1 , A_2 , \cdots ) \subset \mathcal{F}$ tal que $\sigma(\mathcal{A})=\mathcal{F}$.

Considere $(\Omega , \mathcal{F})$ um espaço mensurável não separado, podemos definir a transformação canônica que associa elementos $w \in \Omega$ às classes de equivalência definidas pela relação $R$. Com isso, podemos construir o espaço quociente (quotient space) $\dot{\Omega} $, imagem de $\Omega$ pela transformação canônica, e uma $\sigma$-álgebra $\dot{\mathcal{F}}$ também consistindo das imagens em $\dot{\Omega}$ de elementos de $\mathcal{F}$ pela transformação canônica gerada pela relação $R$. Assim, obtemos um espaço separado $(\dot{\Omega} , \dot{\mathcal{F}})$ associado ao espaço mensurável $(\Omega , \mathcal{F})$. Com esta construção, dado um espaço mensurável qualquer podemos construir um espaço mensurável separado via a transformação canônica induzida por $R$.

Uma das principais estratégias para estudar espaços mensuráveis consiste em compará-los com outros espaços mensuráveis através de funções apropriadas. A seguir, apresentamos duas destas funções.

Definição 9.3

(Isomorfismo)

Dois espaços mensuráveis são ditos isomorfos se existe uma bijeção entre estes que seja mensurável e tenha inversa mensurável, tal bijeção é denominada isomorfismo mensurável.

(Homeomorfismo)

Da mesma forma, dois espaços topológicos são homeomorfos se existe uma bijeção entre estes que seja contínua e tenha inversa contínua, tal bijeção é denominada homeomorfismo.

Com o isomorfismo mensurável conseguimos transportar propriedades associadas com a mensurabilidade, como a separabilidade. Por outro lado, homeomorfismos são utilizados para transportar propriedades topológicas de conjuntos. Na próximo módulo, vamos explorar estas propriedades.

Definição 9.4

1- (Espaço Métrico)

Seja $ X $ um conjunto qualquer. Uma métrica definida sobre $ X $ é uma função $ {\displaystyle d:X\times X\to \mathbb{R}} $ que satisfaz as seguintes propriedades:

$${\displaystyle d(x,y)\geq 0\ \ \forall x,y\in X}$$

e

$${\displaystyle d(x,y)=0\iff x=y}$$

$${\displaystyle d(x,y)=d(y,x)\ \ \forall x,y\in X}$$

$${\displaystyle d(x,z)\leq d(x,y)+d(y,z)\ \ \forall x,y,z\in X}$$

essa propriedade é conhecida como (desigualdade triangular).

Então o par $ (X,d) $ é chamado espaço métrico.

2- (Espaço Topologico)

Uma topologia associada a um conjunto $ X $ é uma coleção $ \tau $ de partes de $ X $, denominados os abertos da topologia, com as seguintes propriedades:

$$\varnothing , X \in \tau;$$

Se

$$A_1,A_2 \in \tau,\text{ então } A_1\cap A_2\in\tau;$$

Dada uma família arbitrária

$$(A_\lambda)_{\lambda\in L},\text{ com } A_\lambda\in\tau, \forall\lambda\in L,\text{ tem-se }(\bigcup_{\lambda\in L}A_{\lambda})\in\tau.$$

Um espaço topológico é um par $ ( X, \tau) $ onde $ X $ é um conjunto e $ \tau $ é uma topologia em $ X $.

3- (Espaço de Hausdorff)

Um espaço de Hausdorff (ou espaço topológico separado) é um espaço topológico no qual quaisquer dois pontos distintos têm vizinhanças disjuntas.

4- (Espaço de Borel)

Um espaço topológico $ X $ é denominado Borel se este for homeomórfico a um subconjunto de Borel de um espaço métrico completo e separável.

5- (Espaço Polonês)

Um espaço topológico $ X $ é denominado Polonês se é um espaço métrico completo e separável.

6-(Conjunto Compacto)

Seja $ F $ um espaço topológico com topologia $ \tau $. Um subconjunto $ X \subset F $ é dito compacto, se dado uma coleção de abertos $ (A_\lambda)_\lambda \subset \tau $, tal que $ X\subset\bigcup_{\lambda}A_\lambda $ então existe uma sub-coleção $ (A_{\lambda_1}, A_{\lambda_2}, \dots , A_{\lambda_n}) $ finita tal que $ X\subset \bigcup_{i=1}^n A_{\lambda_i} $.

Notação: Considere $ \mathcal{H} $ uma família de subconjuntos de um espaço $ X $, usaremos a notação

$$\mathcal{H}_{\sigma},~~ \mathcal{H}_{\delta}\text{ e } \mathcal{H}_c$$

para denotar, respectivamente, a família de uniões enumeráveis, intersecções enumeráveis e complementos de elementos de $ \mathcal{H} $. Se $ X $ é um espaço topológico, usaremos os símbolos

$$F(X), ~~ G(X) \text{ e } K(X)$$

para denotar, respectivamente, a classe dos subconjuntos fechados, abertos e compactos de $ X $.

Conjunto de Souslin

A seguir, vamos introduzir a principal classe de conjuntos associados aos teoremas de seleção mensurável, denominados conjuntos de Souslin. Considere $ \mathbb{N} $ o conjunto dos números naturais, equipado com a topologia discreta. Indicaremos por $ \Sigma $ o espaço das sequências finitas de elementos de $ \mathbb{N} $ equipado com a topologia produto e $ \mathbb{N}^{\mathbb{N}} $ o espaço das sequências de elementos de $ \mathbb{N} $ equipado com a topologia produto. Podemos identificar o espaço $ \mathbb{N}^{\mathbb{N}} $ com o espaço $ I $ dos números irracionais do $ [0,1] $ via a transformação $ \Psi : \mathbb{N}^{\mathbb{N}} \rightarrow I $, definida por

$$ \Psi (\sigma) = \frac{1}{\sigma_1} ~ + ~ \frac{1}{\sigma_2} ~ + ~ \cdots $$

no qual $ \sigma=(\sigma_1, \sigma_2, \cdots) \in \mathbb{N}^{\mathbb{N}} $. Além disso, a topologia do $ \mathbb{N}^{\mathbb{N}} $ coincide com a topologia em $ I $ herdada do $ [0,1] $, isto é, com a topologia da reta restrita ao conjunto I.

Se $ \sigma \in \mathbb{N}^{\mathbb{N}} $ e $ n \geq 0 $, usamos o símbolo $ \sigma|n $ para denotar a sequência finita

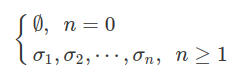
Definição 9.5

Considere $ X $ um espaço qualquer e $ \mathcal{H} $ uma classe de subconjuntos de $ X $. Um esquema de Souslin é uma função $ S : \Sigma \rightarrow \mathcal{H} $, isto é, para todo elemento $ \sigma \in \mathbb{N}^{\mathbb{N}} $, temos que

$$ S[\sigma|n] ~ \in ~ \mathcal{H} $$

O núcleo de um esquema de Souslin $ S $ é definido por

$$ \displaystyle N(S) = \bigcup_{\sigma \in \mathbb{N}^{\mathbb{N}}} \bigcap_{n=1}^{\infty} S[ \sigma|n] .$$

Para cada $ \sigma \in \mathbb{N}^{\mathbb{N}} $ tomamos uma família enumerável $ (S(\sigma|n))_{n \geq 1} $ de elementos de $ \mathcal{H} $ no qual aplicamos a operação

$$ \displaystyle \bigcap_{n=1}^{\infty} S[\sigma|n] .$$

O conjunto

$$ \displaystyle A = \bigcup_{\sigma \in \mathbb{N}^{\mathbb{N}}}\bigcap_{n=1}^{\infty} S[\sigma|n] $$

A notação $ s \leq t $, onde $ s \in \Sigma $ e $ t \in \Sigma ~ {ou} ~ \mathbb{N}^{\mathbb{N}} $, significa que $ t $ começa com a sequência $ s $. Por exemplo, $ s=(2,4,5,9) $ e $ t=(2,4,5,9,10,15,19) $. Um esquema de Souslin $ S $ é denominado regular se $ S(t) \subset S(s) $ para todo $ s \leq t $. Se $ \mathcal{H} $ for fechado por intersecção finita, podemos definir um esquema de Souslin regular

$$ S^{\prime}(s) = \bigcap_{r \leq s} S(r) ,$$

que tem o mesmo núcleo que $ \mathcal{H} $. Portanto, sempre que $ \mathcal{H} $ for fechada por intersecção finita, usaremos esquemas de Souslin regulares.

Uma discussão detalhada sobre operações de Souslin pode ser encontrado em Kuratowski (1966) e Rogers (1980). Observe que todo $ A\in \mathcal{H} $-Souslin tem representação da forma:

$$A=\bigcup_{\sigma \in \mathbb{N}^{\mathbb{N}}} \bigcap_{n=1}^{\infty} S[ \sigma|n]$$

com $ S[ \sigma|n] \in \mathcal{H} $. A seguir, vamos definir espaço analíticos em espaços de Hausdorff da mesma forma que Choquet (1954).

Definição 9.6 (Conjuntos Analítico)

Em espaços topológicos, existem diferentes formas de se definir conjuntos analíticos, porém Rogers (1980) mostra que todas são equivalentes. Para uma discussão detalhada sobre conjuntos analíticos ver Rogers (1980). Uma forma útil de definir conjuntos é analíticos em um espaço Polonês são conjuntos obtidos pela aplicação das operações de Souslin aos conjuntos fechados do espaço.

Definição 9.7 (Conjuntos E-Analíticos)

Considere $ E \subset F $ onde $ F $ é um conjunto analítico, dizemos que um subconjunto $ H \subset E $ é $ E $-analítico se existe $ A^{\prime} \in A(F) $ tal que

$$ H = A^{\prime} \cap E $$

Na realidade, definimos o traço dos conjuntos analíticos em $ F $ sobre o subconjunto $ E $.

9.1. - Espaços de Radon

Nesta seção, vamos explorar a estratégia de isomorfismo entre espaços mensuráveis para transportarmos propriedades entre estes espaços. Inicialmente, mostraremos que todo espaço mensurável separável e separado (Hausdorff) é homoeomorfo a um subconjunto do espaço de Cantor. Com isso, podemos transportar propriedades do espaço de Cantor para estes espaços mensuráveis (separável e separado). Dizemos que um espaço mensurável $ (\Omega , \mathcal{F}) $ é Radon, se, e só se, é isomorfo a um subconjunto $ U \subset S^\infty $ universalmente mensurável. Esta estratégia de “isomorfismo mensurável” também será utilizada para demonstrar nosso teorema de selação mensurável. Considere um espaço mensurável $ (\Omega, \mathcal{F}) $ e $ A \subset \Omega $ um subconjunto qualquer, definimos por

$$\mathcal{F}_A = { B \cap A : B \in \mathcal{F} }$$

a $ \sigma $-álgebra traço de $ \mathcal{F} $ sobre $ A \subset \Omega $. Os átomos de $ \mathcal{F} $ são classes de equivalência em $ \Omega $ dada pela relação $ w \sim w^{\prime} $ se, e somente se,

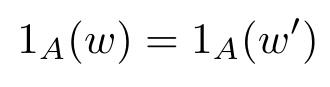
para todo $ A \in \mathcal{F} $ no qual $ 1_{A} $ é a função indicadora.

Definição 9.1.1

O espaço mensurável $ (\Omega , \mathcal{F}) $ é chamado de Hausdorff ou separado, se os átomos são pontos de $ \Omega $. Se existe uma sequência de elementos de $ \mathcal{F} $ que gera $ \mathcal{F} $, então dizemos que $ \mathcal{F} $ é separável.

Considere $ (\Omega , \mathcal{F}) $ é um espaço mensurável separável, tal que a sequência $ (E_n) $ gera a $ \sigma $-álgebra $ \mathcal{F} $. Então, para cada $ w \in \Omega $, definimos

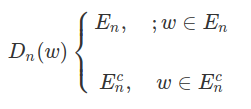
e

$$ Z_{w} ~ = ~ D_1 (w) \cap D_2 (w) \cap \cdots . $$

Com estes elementos, obtemos de Marczewski (1938) os seguintes Lemas.

Lema 9.1.1

Seja $ (\Omega , \mathcal{F}) $ um espaço mensurável separável tal que $ \mathcal{F} = \sigma((E_n )) $. Então, para todo $ w_1 $, $ w_2 \in \Omega $ temos que $ w_1 \sim w_2 $ se, e somente se, $ Z_{w_1} = Z_{w_2} $.

Demonstração: $ \forall \omega_1, \omega_2\in \Omega $ temos que se $ \omega_1\sim \omega_2 $ temo que

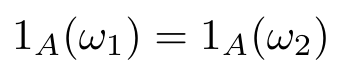
para todo $ A\in \mathcal{F} $ em particular para todo $ (E_n) $, logo

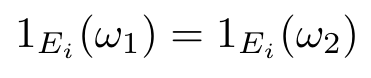
para todo $ i $ mas isso implica que $ D_i(\omega_1)=D_i(\omega_2) $ para todo i, o que implica que

$$Z_{\omega_1}=Z_{\omega_2}.$$

Por outro lado temos que se $ Z_{\omega_1}=Z_{\omega_2} $, então temos que

$$D_i(\omega_1)=D_i(\omega_2)$$

para todo i, logo temos que

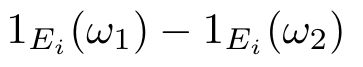
portanto o resultado segue.

Lema 9.1.2

Um espaço mensurável $ (\Omega , \mathcal{F}) $ é separável e separado se, se e somente se, existe uma sequência $ ( E_n ) $ que separa os pontos em $ (\Omega , \mathcal{F}) $.

Demonstração: Se $ (\Omega , \mathcal{F}) $ é um espaço mensurável de Hausdorff, obtemos que do Lema 9.1.1 que $ w_1 \sim w_2 $ se, e somente se, $ w_1=Z_{w_1} = Z_{w_2} = w_2 $. Portanto, a sequência $ ( E_n ) $ separa pontos em $ (\Omega , \mathcal{F}) $,i.e.,

i) $ \mathcal{F} = \sigma( (E_n )) $;

ii) Para todo $ w_1 $, $ w_2 \in \Omega $ $ (w_1 \neq w_2) $ existe um $ m \in \Bbb{N} $ tal que $ 1_{E_m}(w_1) \neq 1_{E_m}(w_2) $.

A partir destas propriedades básicas dos espaços mensuráveis separável e separado, podemos definir uma topologia $ \tau_{\Omega} $ em $ \Omega $ tal que $ \mathcal{F} = \sigma(\tau_{\Omega}) $, Considere $ (\Omega , \mathcal{F}) $ um espaço mensurável separável e separado. Então, existe uma sequência $ (E_n ) $ que separa os pontos em $ \Omega $. Seja $ {\mathcal V}_0 $ a classe de subconjunto de $ \Omega $ que contém os $ E_n $ e $ E_{n}^c $. Denotamos que $ {\mathcal V}_1 $ a classe obtida por operações finitas de interseções de elementos de $ {\mathcal V}_0 $. Portanto, a classe $ {\mathcal V}_1 $ define uma base para a topologia

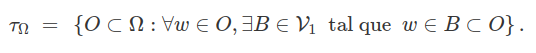
Através do Teorema 2 em Blackwell (1956) sabemos que a função $ \rho_{\Omega}: \Omega \times \Omega \rightarrow [0, \infty) $, definida por

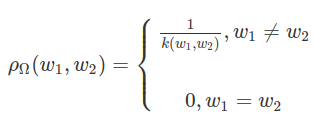
no qual $ k(w_1 , w_2) $ é o menor $ n \in \Bbb{N} $ para o qual $ 1_{E_n}(w_1) \neq 1_{E_n}(w_2) $, define uma métrica em $ \Omega $. Além disso, a topologia gerada pela métrica $ \rho_{\Omega} $ coincide com $ \tau_{\Omega} $. Desde que $ {\mathcal V}_1 $ é uma base para $ \tau_{\Omega} $ e gera $ \mathcal{F} $, concluimos que $ \mathcal{F}=\sigma(\tau_{\Omega}) $.

Utilizamos propriedades de mensurabilidade para construir uma topologia adequada $ (\mathcal{F}=\sigma(\tau_{\Omega})) $ relacionada um espaço mensurável $ (\Omega , \mathcal{F}) $ separável e separado. Por outro lado, sabemos que para todo espaço topológico $ X $ com topologia $ \tau_X $ separável e Hausdorff, a $ \sigma $-álgebra gerada pelos abertos desta topologia $ \beta = \sigma(\tau_X) $, nos fornece um espaço mensurável $ (X, \beta) $ separável e separado (Hausdorff). A partir deste fato, podemos estudar homeomorfismo (ou isomofirmos) entre espaços mensuráveis na presença da topologia $ \tau_{\Omega} $.

Na sequência, vamos introduzir a principal classe de espaços de probabilidade relaionados com os espaços mensuráveis separável e separado, denominados espaço de probabilidade compacto.

Definição 9.1.2 (Espaço de probabilidade Compacto)

Dado um conjunto abstrato $ \Omega $ com uma classe de subconjuntos $ {\mathcal C} $, dizemos que $ {\mathcal C} $ é uma Classe Compacta, se para toda sequência $ (C_n : n \geq 1) $ em $ {\mathcal C} $ com intersecção $ \cap_{n \geq 1} C_n = \emptyset $ existe um inteiro $ n_0 $ tal que $ \displaystyle \bigcap_{n \leq n_0} C_n = \emptyset $. Para um espaço de probabilidade, dizemos que a tripla $ (\Omega , \mathcal{F}, \mathbb{P}) $ é compacto se existe uma classe de compactoa $ {\mathcal C} \subset \mathcal{F} $ tal que

$$\mathbb{P}(A) ~ = ~ \sup { \mathbb{P}(C) : C \subset A , C \in {\mathcal C} }, A \in \mathcal{F}.$$

O espaço de Cantor $ (S^\infty $ com a $ \sigma $-álgebra produto e a probabilidade usual $ \mathbb{P} $ contruída através de experimentos de Bernoulli consiste no principal exemplo de espaço de probabilidade compacto. Da forma geral, se $ (\Omega , \mathcal{F} , \mathbb{P}) $ é um espaço de probabilidade no qual $ \Omega $ é um espaço topológico separável e Hausdorff, $ \mathcal{F} $ a $ \sigma $-álgebra de Borel e $ \mathbb{P} $ uma probabilidade regular, isto é,

$$\mathbb{P}(A) = \sup (\mathbb{P}(D) : D\subset A, ~\text{compacto na topologia de} ~\Omega),\quad A \in \mathcal{F}$$

obtemos que $ (\Omega , \mathcal{F} , \mathbb{P}) $ é um espaço de probabilidade compacto.

A classe dos espaços de probabilidade compacto apresenta diversas propiredades, para maiores detalhes ver Leão, fragoso e Rufino (1999). A seguir, apresentamos um conceito sobre espaços de probabilidade amplamento estudados na literatura.

Definição 9.1.3 (Espaço Perfeito)

Um espaço de probabilidade $ (\Omega , \mathcal{F}, \mathbb{P}) $ é dito ser perfeito se para qualquer função mensurável $ f: \Omega \rightarrow\Bbb{R} $ existe um conjunto de Borel $ B $ tal que $ B \subset f(\Omega) $ e $ \mathbb{P}[f^{-1}(B)] = 1 $. Se a $ \sigma $-álgebra $ \mathcal{F} $ é separável, é bem conhecido que a perfeição e a compacidade são equivalentes, como apresentado em Tortrat (1977, Proposition 3).

A seguir, vamos estabelecer um homeomorfismo entre um espaço mensurável separável e separado com um subconjunto do Espaço de Cantor. Iniciamos com uma breve introdução das principais propriedades do espaço de Cantor, apresentadas e demonstradas na seção “Espaco de Cantor”. Seja $ S $ o espaço composto pelos elementos $ 0 $ e $ 1 $, e

$$ S^{\infty} ~ = ~ S \times S \times S \times \cdots . $$

O espaço $ S^{\infty} $ é denominado espaço de Cantor. Considere $ \pi_{k}: S^{\infty} \rightarrow S $ a projeção coordenada $ (k \in \Bbb{N}) $, definida por

$$ \pi_k (w) ~ = ~ w_k ~ ~ ; ~ ~ w = (w_1 , w_2 , \cdots ) \in S^{\infty} ~ { e }~ k \in \Bbb{N}. $$

Com essas projeções coordenadas, definimos a classe dos cilindros de $ S^{\infty} $ com base em $ S $, na forma

$$ \mathbb{P}(B) ~ = ~ \delta(B) ~ ~ ; ~ ~ \forall ~ B \in {\mathcal C}. $$

Ao denotamos por $ \mathcal{E} $ a classe de subconjuntos de $ S^{\infty} $ composta por interseções enumeráveis de elementos de $ \mathcal{C} $, temos que

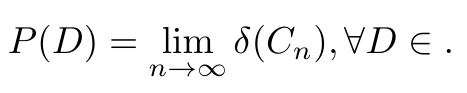
no qual $ ( C_n ) $ é uma sequência monótona decrescente de elementos que $ {\mathcal C} $ tal que $ D = \cap C_n $, e

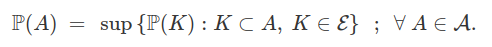
Além disso, temos que $ \mathcal{E} $ é uma classe compacta, pois é obtida a partir de interseções enumeráveis de elementos de $ {\mathcal C} $), ver a seção probabilidades compactas.

Considere o espaço de Cantor equipado com a topologia metrizável induzida pela métrica de Blackwell’s, denotada por $ \tau $. Então, obtemos que o espaço de Cantor é compacto e metrizável tal que

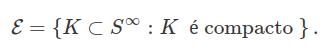
Como definido anteiormente, dois espaço são ditos isomorfos se existe uma bijeção entre eles, que é mensurável e tem inversa mensurável. Tal bijeção é denominada isomorfismo mensurável.

Seja $ (\Omega , \mathcal{F}) $ um espaço mensurável separável e separado tal que a sequência $ ( E_ n ) $ separa os pontos em $ \Omega $. A função Característica de Marczewski (1938) (MCF) na forma

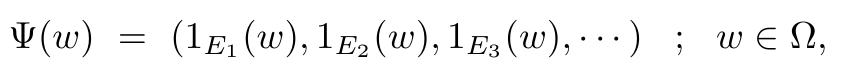
associa elementos de $ \Omega $ com elementos do espaço de Cantor.

Ao equiparmos $ \Omega $ com a topologia $ \tau_{\Omega} $, obtemos que MCF estabelece um homeomorfismo entre $ \Omega $ e $ U $, com $ U (\subset S^{\infty}) $ dotadado com a topologia induzida por $ \tau $ em $ U $. Além disso, os elementos da sequência $ (E_n) $, o qual separa pontos em $ \Omega $, estão abertos e fechados em $ \tau_{\Omega} $ [Marczewski (1938)]. Em particular, está função estabelece um isomorfismo entre $ (\Omega , \mathcal{F}) $ e $ (U , \beta(U)) $ no qual $ U \subset S^{\infty} $ e $ \beta(U) $ é um traço da $ \sigma $-álgebra.

Considere $ K $ o conjunto composto de números reais $ x $ da forma $ x=2 \sum_{i=1}^n x_i / 3^i $, onde cada $ x_i $ é igual a zero ou 1. Uma vez que cada série converge, $ K $ é uma coleção de números reais a qual podemos metrizar pela métrica usual. Além disso, podemos ver que $ K $ é um homeomorfismo para $ S^{\infty} $ [Pervin (1964), Theorem 8.3.2]. Portanto, concluimos que para todo espaço mensurável de Hausdorff $ (\Omega , \mathcal{F}) $, se dotamos $ \Omega $ com a topologia $ \tau_{\Omega} $ e $ K $ com a topologia usual obtemos que $ \Omega $ é homeomorfo a um subconjunto de $ K $ (ou $ [0,1] $).

Seja $ (\Omega , \mathcal{F}) $ um espaço mensurável seperável de Hausdorff, então podemos definir uma topologia separável e metrizável $ (\tau_{\Omega}) $ em $ \Omega $ tal que $ \Psi: \Omega \rightarrow U $ estabelece um homeomorfismo entre $ \Omega $ e $ U $, no qual $ U $ é dotado is com a topologia induzida por $ \tau $ em $ U $. A seguir caracterizaremos a classe compacta de subconjuntos de $ \Omega $.

Lema 9.1.3

Seja $ {\mathcal K}_{\Omega} $ a classe de subconjunto compactos de $ \Omega $. Então, temos que

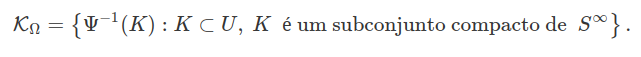
Demonstração

Considere $ C $ um subconjunto compacto de $ \Omega $. Desde que $ \Psi $ é um homeomorfismo, a restrição $ \Psi : C \rightarrow S^{\infty} $ é uma função contínua.

Resulta da compacidade de $ C $ que $ \Psi(C) $ é também compacto [Royden (1988), prop. 4, pg. 191]. Portanto,

Por outro lado, seja $ K \subset U $ ser um conjunto compacto de $ S^{\infty} $. Usando os mesmos argumentos concluímos que $ \Psi^{-1}(K) $ é um subconjunto compacto de $ \Omega $.

Seja $ Y $ um espaço métrico compacto dotado com $ \sigma $-algebra de Borel $ \beta(Y) $. Considere $ U \subset Y $ dotado com a $ \sigma $-álgebra traço de $ \beta(Y) $ em $ U $ denotado por $ \beta(U) $ e a topologia herdada de $ Y $.

Portanto, a proposição seguinte é uma consequência dos argumentos estabelecido acima e Marczewski (1938).

Proposição 9.1.1

Para espaço mensurável $ (\Omega , \mathcal{F}) $, os seguintes item são equivalentes

a) $ (\Omega , \mathcal{F}) $ é um espaço mensurável separável de Haussdorff;

b) Existe um isomorfismo mensurável entre $ (\Omega , \mathcal{F}) $ and $ (U, \beta(U)) $, no qual $ U $ é um subconjunto de um espaço métrico compacto;

c) Existe uma topologia $ \delta_{\Omega} $ em $ \Omega $ que gera $ \mathcal{F} $ e um homeomorfismo $ \phi: \Omega \rightarrow U $, no qual $ U $ é um subconjunto de um espaço métrico compacto dotado com a topologia herdada de $ Y $;

d) Existe uma topologia metrizável separável $ \delta_{\Omega} $ em $ \Omega $ tal que $ \mathcal{F} = \sigma(\tau_{\Omega}) $.

Dado um espaço mensurável $ (E , \mathcal{E}) $, denotamos por $ \mathcal{E}^{\lambda} $ o completamento de $ \mathcal{E} $ com respeito a probabilidade $ \lambda $ neste espaço. A $ \sigma $-álgebra universal $ \mathcal{E}^\star $ definida por

$$ \mathcal{E}^\star ~ = ~ \bigcap_{\lambda} \mathcal{E}^{\lambda}, $$

no qual a interseção tomando sobre todas as probabilidade $ \lambda $ em $ (E , \mathcal{E}) $. O conjunto contendo em $ \mathcal{E}^\star $ é chamado universalmente mensurável.

Seja $ Y $ um espaço métrico dotado com a $ \sigma $-algebra Borel $ \beta(Y) $. Dizemos que $ (\Omega , \mathcal{F}) $ é um espaço de Radon se existe um isomorfismo $ \phi : (\Omega, \mathcal{F}) \rightarrow (U, \beta(U)) $, no qual $ U \in \beta(Y)^\star $ e $ \beta(U) = { A \cap U : A \in \beta(Y) } $, o traço de $ \beta(Y) $ em $ U $. Note que

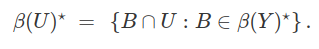
O próximo teorema fornece uma caracterização de espaços de Radon que ajuda a compreender esse conceito e perceber melhor o quão rico é a estrutura desse espaço.

Teorema 9.1.1

Considere $ (\Omega , \mathcal{F}) $ um espaço mensurável, então os seguintes itens são equivalentes:

1) $ (\Omega , \mathcal{F}) $ é um espaço de Radon,

2) $ (\Omega , \mathcal{F}) $ é um espaço mensurável separável e Hausdorff e para cada probabilidade $ \mathbb{P} $, o espaço de probabilidade $ (\Omega , \mathcal{F}, \mathbb{P}) $ é compacto (ou perfeito).

3) Existe uma sequência $ (E_n) $ que separa os pontos em $ (\Omega, \mathcal{F}) $ e MCF estabelece um homeomorfismo entre $ \Omega $ (dotado com a topologia $ \tau_{\Omega} $) e um subconjunto universalmente mensurável $ U $ de $ S^{\infty} $ dotado com com a topologia induzida,

4) Existe uma topologia $ \delta_{\Omega} $ em $ \Omega $ que gera $ \mathcal{F} $ e um homeomorfismo $ \phi: \Omega \rightarrow U $, no qual $ U $ é um subconjunto universalmente mensurável de um espaço métrico dotado $ Y $ denotado com a topologia herdada de $ Y $;

5) Existe uma sequência $ ( E_n ) \subset \mathcal{F} $ tal que o MCF estabelece um isomorfismo entre $ \Omega $ e $ U $, no qual $ U $ é um subconjunto universalmente mensurável de $ S^{\infty} $;

6) Existe uma topologia separável metrizável $ \tau_{\Omega} $ em $ \Omega $ que gera $ \mathcal{F} $ e para cada probabilidade $ \mathbb{P} $ em $ (\Omega , \mathcal{F}) $, temos que

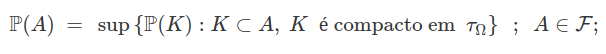
7) Existe uma topologia metrizável e separável $ \tau_{\Omega} $ em $ \Omega $ que gera $ \mathcal{F} $ e para cada probabilidade $ \mathbb{P} $ em $ (\Omega , \mathcal{F}) $, temos que

8) $ (\Omega , \mathcal{F}) $ é um espaço mensurável separável e Haussdorff e para cada probabilidade $ \mathbb{P} $ e o MCF $ \Psi: \Omega \rightarrow U $, existe um subconjunto $ B \subset U $ com $ B \in \mathcal{A} $ e $ \mathbb{P}[\Psi^{-1} (B) ]=1 $

Demonstração

Do Teorema 2.1 em Leão, Fragoso e Ruffino (1999) temos que (1) e (2) são equivalente. Se $ (\Omega , \mathcal{F}) $ é um espaço de Radon, então $ (\Omega , \mathcal{F}) $ é separável e Hausdorff. Portanto, existe uma sequência $ (E_n) $ que separa os pontos em $ (\Omega, \mathcal{F}) $

Lema 9.1.2. Agora, se dotarmos $ \Omega $ com a topologia $ \tau_{\Omega} $ obtemos que MCF estabelece um homeomorfismo entre $ \Omega $ e $ U $, no qual $ U $ é dotado com a topologia induzida por $ S^{\infty} $. Além disso, do Corolário 2.1 em Leão, Fragoso e Ruffino (1999) temos que $ U $ é universalmente mensurável. Assim, concluímos que (1) implica (3). Além disso, podemos ver que (3) implica (1).

Agora para provar que (3) implica (4), é suficiente definir que $ \delta_{\Omega} = \tau_{\Omega} $. E por outro lado, se (4) é válido, temos que $ (\Omega , \mathcal{F}) $ é um espaço de Radon. Portanto (4) implica (3). Para mostrar que (1) e (5) são equivalente, é suficiente ver que (3) e (5) são equivalentes. A seguir, seja $ (\Omega , \mathcal{F}) $ um espaço de Radon e $ \mathbb{P} $ uma probabilidade. O MCF $ \Psi $ estabelece um isomorfismo entre $ (\Omega , \mathcal{F}) $ e $ (U , \beta(U)) $, no qual $ U $ é um subconjunto universalmente mensurável de $ S^{\infty} $. Considere $ (\Psi_{\star} \mathbb{P}) $ a imagem da probabilidade em $ (U , \beta(U)) $. Desde que $ U $ é universalmente mensurável, podemos extender $ (\Psi_{\star}\mathbb{P}) $ em $ (\Omega , \mathcal{A}^{\star}) $, no qual $ \mathcal{A}^{\star} $ corresponde a $ \sigma $-álgebra universal. Então, obtemos que

A equivalência das afirmações (6) e (7) resulta das observações da Definição 1.1 em De La Rue (1993). Finalmente, conluímos que do Lema 3 em Sazonov (1965, Theorem 3, pg. 245) que (1) e (8) são equivalentes.

Seja $ (\Omega , \mathcal{F}) $ um espaço de Radon, então a seguinte versão do MCF.

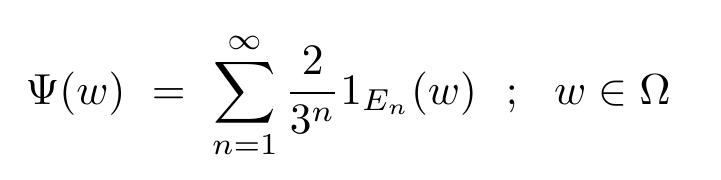
estabelece um homeomorfismo entre $ \Omega $ (dotado da topologia $ \tau_{\Omega} $) e $ V $, no qual $ V $ é um subconjunto universalmente mensurável $ [0,1] $ com a topologia herdada. Assim, um resultado similar do Teorema 9.1.1 poderia ser obtido substituindo $ S^{\infty} $ e $ U $ pelo $ [0,1] $ e $ V $, respectivamente.

Definição 9.1.4 (Quase Isormoficos)

Dizemos que dois espaços de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ e $ (E , \mathcal{E}, \mu) $ são quase isomorfos, se existe um subconjunto $ \Omega_0 \in \mathcal{F} $ e $ E_0 \in \mathcal{E} $ com $ \mathbb{P}(\Omega_0) = \mu(E_0)=1 $ satisfazendo

a) Existe um isomorfismo mensurável $ \Phi $ entre $ (\Omega_0 , \mathcal{F}_0) $ e $ (E_0 , \mathcal{E}_0) $, no qual $ \mathcal{F}_0 $ $ (\mathcal{E}_0) $ corresponde ao traço da $ \sigma $-álgebra de $ \mathcal{F} $ $ (\mathcal{E}) $ em $ \Omega_0 $ $ (E_0) $;

b) Para qualquer $ A \in \mathcal{F} $, temos que

$$ \mathbb{P}(A) ~ = ~ \mathbb{P}\left[ A \cap \Omega_0 \right] ~ = ~ \mu \left[ \Phi (A \cap \Omega_0) \right]. $$

Considere $ \mathbb{P} $ uma medida de probabilidade não atômica em um espaço de Radon $ (\Omega , \mathcal{F}) $ (i.e., $ \mathbb{P}((w)) = 0 $, para qualquer $ w \in \Omega $). Então, seguindo a mesma linha para provar que os Teoremas 1 e 2 em Halmos and von-Neumann (1942, pg. 335 e 339) [veja, Leão (1999)], obtemos que o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ e $ ([0,1] ,\beta([0,1]) , m) $ são quase isomorfo, no qual $ m $ denota a medida de Lebesgue. Além disso, temos que $ \Phi=(g^{-1} \circ \Psi) $, no qual

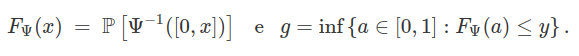
Teorema 9.1.2

O espaço mensurável separável e Hausdorff $ (\Omega , \mathcal{F}) $ é Radon, se, e somente se, para cada probabilidade não atômica $ \nu $, o espaço de probabilidade $ (\Omega , \mathcal{F} , \nu) $ é quase isomorfo ao $ ([0,1], \beta([0,1]), m) $.

Demonstração

Se $ (\Omega , \mathcal{F}) $ é um espaço de Radon, é suficiente definir $ \Phi=(g^{-1} \circ \Psi) $. Por outro lado, se existe $ \Omega_0 \in \mathcal{F} $ e $ E_0 \in \beta([0,1]) $ com $ \nu(\Omega_0)=m(E_0)=1 $ satisfazendo (a) e (b), obtemos de Ryll-Nardzewski (1953, Teorema VII, pg. 129) que o espaço de probabilidades é completo $ (\Omega , \mathcal{F}^{\nu} , \nu) $ é perfeito. Além disso, é conhecido que um espaço de probabilidades $ (\Omega , \mathcal{F} , \nu) $ é perfeito se, e somente se, o espaço é completo $ (\Omega , \mathcal{F}^{\nu} , \nu) $ é também perfeito [Sazonov (1965), Prop. (d), pg. 239]. Então, para todo probabilidade não atômica $ \mathbb{P} $ em $ (\Omega , \mathcal{F}) $, o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ é perfeito (ou compacto). Em seguida, estenderemos esta propriedade para uma probabilidade arbitrária. Considere $ \mathbb{P} $ uma probabilidade em $ (\Omega , \mathcal{F}) $, então para cada $ a> 0 $, o conjunto

$$( w \in \Omega : \mathbb{P}( { w }) > a )$$

é finita. Além disso, a coleção de todos os pontos $ w \in \Omega $ tal que $ \mathbb{P}((w))> 0 $ é finita ou enumerável. Então, podemos enumerar $ w_1, w_2, \cdots $ tal que $ \mathbb{P}((w_1)) \leq \mathbb{P}((w_2)) \leq \cdots $. Para cada $ n \geq 1 $, definimos

$$ M_n ~ = ~ \mathbb{P}((w_n)) $$

e

$$ M_0 ~ = ~ 1 - \sum_{n=1}^{\infty} M_n . $$

Considere $ M_{n+1} = 0 $ se não houver mais de $ n $ pontos com probabilidade positiva. Denotamos $ \Omega_0 = \Omega - \cup_{n \geq 1} (w_n) $, vamos admitir que $ M_0 > 0 $, caso contrario, é trivial. Desde que $ \Omega_0 \in \mathcal{F} $, obtemos que

$$ \mathbb{P}_{0} (A) ~ = ~ \frac{\mathbb{P}(A \cap \Omega_0)}{M_0}, \quad \quad A \in \mathcal{F} $$

define uma probabilidade não atômica sobre $ (\Omega , \mathcal{F}) $. Então, o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}_0) $ é perfeito (ou compacto). Além disso, podemos dividir a probabilidade $ \mathbb{P} $ em duas partes

$$ \mathbb{P}(A) ~ = ~ \mathbb{P}(A \cap \Omega_0) ~ + ~ \mathbb{P}(A \cap \Omega_{0}^{c}) ~=~ \mathbb{P}(A \cap \Omega_0) ~ + ~ \sum_{ (w_k) \in A \cap \Omega_{0}^{c} } \mathbb{P}((w_k)). $$

Assim, o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ é compacto. Desde que $ \mathbb{P} $ é arbitrário, concluímos que $ (\Omega , \mathcal{F}) $ é um espaço de Radon Teorema 9.1.1. Portanto o resultado segue.

A partir dos argumentos acima obtemos os seguintes resultados.

Corolário 9.1.1

O espaço separável mensurável e Hausdorff $ (\Omega , \mathcal{F}) $ é um espaço de Radon se, e somente se, para toda probabilidade não atômica $ \mathbb{P} $, o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ é perfeito (ou compacto).

Seja $ l $ uma probabilidade definida em $ (S^{\infty} , \mathcal{A}) $ tal que

$$ l \left[ \pi_{1}^{-1} ( ( w_1 )) \cap \cdots \cap \pi_{n}^{-1} ((w_n)) \right] ~ = ~ \frac{1}{2^n} $$

no qual $ (w_1 , \cdots , w_n) \in S^n $ e $ n \geq 1 $.

Corolário 9.1.2

O espaço mensurável $ (\Omega , \mathcal{F}) $ é um espaço de Radon se, e somente se, para toda probabilidade não atômica $ \mathbb{P} $, o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ é quase isomórfico para o espaço de probabilidade $ (S^{\infty} , \mathcal{A} , l) $.

Demonstração

Podemos ver que a expansão diádica estabelece um quase isomorfismo entre os espaços de probabilidade $ (S^{\infty} , \mathcal{A} , l) $ e $ ([0,1], \beta([0,1]), m) $ [veja, Leão (1999), Capitulo 02]. Então, concluímos que do Teorema 9.1.2 que $ (\Omega , \mathcal{F}) $ é Radon se, e somente se, para cada probabilidade não atômica $ \mathbb{P} $, o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ é quase isomorfo o espaço de probabilidade $ (S^{\infty} , \mathcal{A} , l) $.

Corolário 9.1.3

O espaço mensurável separável e Hausdorff $ (\Omega , \mathcal{F}) $ é um espaço de Radon se, e somente se, para toda probabilidade $ \mathbb{P} $, o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ é quase isomorfo para o espaço de probabilidade $ (\Omega_1 , \mathcal{F}_1 , \mathbb{P}_1) $, no qual

i) $ \Omega_1 = [0 , M_0] \cup (x_n) $ tal que $ x_n = 1 + \frac{1}{n} $

ii) $ \mathcal{F}_1 = \sigma \left( \beta([0,M_0]); (x_n ) \right) $

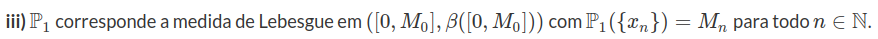
Demonstração

Seja $ \mathbb{P} $ um probabilidade sobre em $ (\Omega , \mathcal{F}) $, suponha o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ é quase isomorfo $ (\Omega_1 , \mathcal{F}_1 , \mathbb{P}_1) $. Desde que $ (\Omega_1, \mathcal{F}_1 , \mathbb{P}_1) $ é compacto, obtemos que $ (\Omega, \mathcal{F} , \mathbb{P}) $ é também compacto [Ryll-Nardzewski (1953), Lema, pg. 126]. Então, concluímos que $ (\Omega , \mathcal{F}) $ é um espaço de Radon (Teorema 9.1.1).

Por outro lado, considere $ (\Omega , \mathcal{F}) $ é um espaço de Radon. Se $ \mathbb{P} $ é uma probabilidade é suficiente aplicar o Teorema 9.1.2. Considere $ \Omega_0 = \Omega - \cup_{n \geq 1} (w_n) $, vamos admitir que $ M_0 > 0 $, caso contrário é trivial.

Usando o fato que $ \Omega_0 \in \mathcal{F} $, obtemos que $ \mathcal{F}_0 =( A \in \mathcal{F} : A \subset \Omega_0 ) $ corresponde ao traço $ \sigma $-álgebra de $ \mathcal{F} $ em $ \Omega_0 $ e

$$ \mathbb{P}_{0} (A) ~ = ~ \frac{\mathbb{P}(A \cap \Omega_0)}{M_0}, \quad \quad A \in \mathcal{F}, $$

define um probabilidade não atômica em $ (\Omega_0 , \mathcal{F}_0) $.

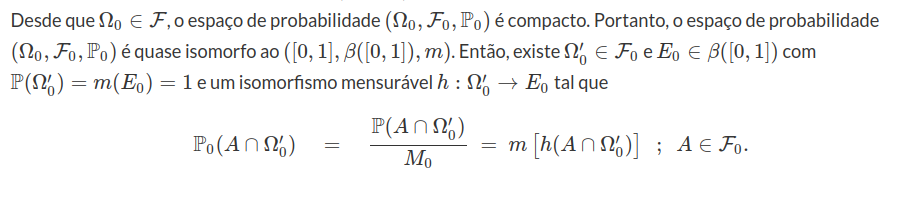
Portanto,

$$ \mathbb{P}(A \cap \Omega_{0}^{\prime}) ~ = ~ M_0 ~ m[h(A \cap \Omega_{0}^{\prime})] ~ = ~ m \left[ (M_0 h)(A \cap \Omega_{0}^{\prime}) \right] ~ ~ ; ~ ~ A \in \mathcal{F}_0 , $$

$$ \mathbb{P}\left(\Omega_{0}^{\prime}\right) ~ = ~ m \left(E_{0}^{\prime}\right) ~ = ~ M_0 . $$

Então, concluímos que o espaço de probabilidade $ (\Omega_0 , \mathcal{F}_0 , \mathbb{P}_0) $ and $ ([0,M_0] , \beta([0,M_0]), m) $ são quase isomorfas. Finalmente, concluímos que o espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ e $ (\Omega_1 , \mathcal{F}_1 , \mathbb{P}_1) $ são quase isomorfos. Portanto o resultado segue.

Considere $ (\Omega , \mathcal{F}) $ um espaço mensurável separável e Hausdorff e seja $ (E_n) $ uma sequência tal que $ \mathcal{F}= \sigma((E_n)) $. Em seguida, caracterizamos os espaços Radon através das propriedades de funções definidas na algebra gerada por $ (E_n) $.

Primeiramente, vamos estabelecer uma conexão entre subespaços universalmente mensurável $ U $ de um espaço de Cantor o conjunto de funções definidas no traço da álgebra cilindros em $ U $. Então, usaremos este resultado para caracterizar os espaços de Radon.

Lema 9.1.4

Considere $ U $ um subconjunto de $ S^{\infty} $, então as seguintes afirmações são equivalentes:

a) $ U $ é universalmente mensurável;

b) Para cada probabilidade $ \mathbb{P} $ em $ (S^{\infty}, \mathcal{A}) $, temos que

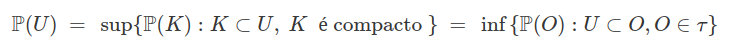
c) Considere $ \mathcal{C}_U $ o traço da algebra $ \mathcal{C} $ em $ U $ $ (\mathcal{C}_U = {C \cap U : C \in \mathcal{C} }) $. Todo conjunto de funções $ \mu: \mathcal{C}_U \rightarrow [0,1] $ que é aditivo finito $ \mu(U)=1 $ é também $ \sigma $-aditiva.

Demonstração

Desde que $ S^{\infty} $ é um espaço métrico compacto e $ \mathcal{A} $ é Borel $ \sigma $-álgebra, concluímos do Teorema 9.1.1 que (a) e

(b) são equivalentes. A seguir, vamos mostrar que (b) e (c) são equivalentes. Suponha que (b) é válido e considere um conjunto de funções

$$ \mu^{\star} (C) ~ = ~ \mu(C \cap U) ~ ~ ; ~ ~ C \in \mathcal{C} , $$

definida $ \mathcal{C} $. Então, $ \mu^{\star} $ é finitamente aditiva e $ \mu^{\star}(S^{\infty})=1 $. Resulta da compacidade de $ \mathcal{C} $ que $ \mu^{\star} $ é também $ \sigma $-aditiva. Portanto, usando ao Teorema de extensão Carathéodory, obtemos que uma única probabilidade $ \mathbb{P} $ em $ (S^{\infty},\mathcal{A}) $ que se estende $ \mu^{\star} $. A seguir, vamos mostrar que $ \mathbb{P}(U)=1 $.

Seja $ F $ ser um conjunto fechado (ou compacto) tal que $ U \subset F $. Então, existe uma sequência monótona decrescente $ (C_n ) \subset \mathcal{C} $ tal que $ \cap C_n = F $. Portanto,

$$ \mathbb{P}(F) ~ = ~ \lim_{n \rightarrow \infty} \mathbb{P}(C_n) ~ = ~ \lim_{n \rightarrow \infty} \mu^{\star} (C_n) ~ = ~ \lim_{n \rightarrow \infty} \mu(C_n \cap U) ~ = ~ 1 . $$

Então, se $ U $ é fechado obtemos que $ \mathbb{P}(U)=1 $. Para todo conjunto aberto $ O $, existe uma sequência $ (C_n) \subset \mathcal{C} $ tal que

$$ \bigcup_{k=1}^{\infty} C_k ~ = ~ O . $$

Suponha que $ U \subset O $ e $ O \neq U $, então existe $ n_0 \in \Bbb{N} $ satisfazendo

$$ U \subset \bigcup_{k=1}^{n_0} C_k ~ = ~ S_{n_0}~ \in ~ \mathcal{C} . $$

Portanto, temos que

$$ \mathbb{P}(O) ~ \geq ~ \mathbb{P}\left( S_{n_0} \right)~ = ~ \mu^{\star} \left( S_{n_0} \right) ~ = ~ \mu \left( S_{n_0} \cap U \right) ~ = ~\mu(U) ~ = ~ 1 . $$

Então, concluímos que $ \mathbb{P}(O)=1 $ para todo conjunto aberto $ O $ tal que $ U \subset O $ e $ U \neq O $. Usando o fato, que para todo conjunto universalmente mensurável $ A $ tal que $ U \subset A $ and $ A \neq U $, denotamos que

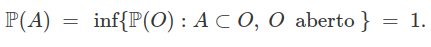
Desde que $ U $ é universalmente mensurável, obtemos que $ U_x = U \cup (x) $ é também universalmente mensurável, para todo $ x \in U^c $. Então, temos que

$$\mathbb{P}\left( U_x \right) ~ = ~ 1 ~ ~ ; ~ ~ x \in U^c . $$

Portanto, concluímos que $ \mathbb{P}(U) = 1 $. Então, a restrição $ \mathbb{P}_U $ de $ \mathbb{P} $ em $ (U , \mathcal{A}_U) $ satisfaz

$$ \mathbb{P}_U(C \cap U) ~ = ~ \mathbb{P}(C \cap U) ~ = ~ \mathbb{P}(C) ~ = ~ \mu^{\star} (C) ~= ~ \mu(C \cap U)~ ~ ; ~ ~ C \in \mathcal{C} . $$

Então, obtemos que $ \mathbb{P}_U $ é uma probabilidade em $ (U , \mathcal{A}_U) $ o qual estende $ \mu $.

A seguir, vamos estabelecer que (c) implica (b). Para provar que, usaremos a noção de probabilidade condicional regular.

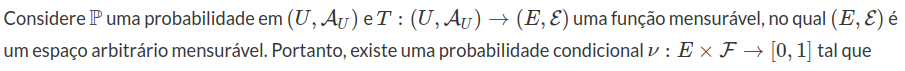
$$ \mathbb{P}(A \cap T^{-1}(B)) ~ = ~ \int_{B} \nu(x,A) (T_{\star}P)(dx), $$

i) Para todo $ x \in E $, temos que $ \mu(x, \cdot) $ é uma probabilidade em $ (U , \mathcal{A}_U) $;

ii) Para todo $ A \in \mathcal{A}_U $, temos que $ \mu( \cdot , A) $ é uma função mensurável.

A partir das propriedades das probabilidades condicional $ \nu( \cdot ; U) = 1 ~ (T_{\star}P)-a.e. $ e para cada sequência $ ( A_n ) \subset \mathcal{A}_U $ dois a dois disjuntos, obtemos que

$$ \nu \left( \cdot , \bigcup_n A_n \right) ~ = ~ \sum_{n=1}^{\infty} \nu \left( \cdot , A_n \right)~ ~ ; ~ ~ (T_{\star}P)-a.e. . $$

Portanto, o conjunto $ M_1 = ( x \in E : \nu(x , U) =1 ) $ pertence a $ \mathcal{E} $ and $ (T_{\star}P)(M_1)=1 $. Além disso, para cada sequência finita $ C_1 , \cdots , C_n $ de elementos de $ \mathcal{C}_U $, o conjunto

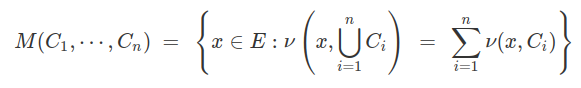
pertence a $ \mathcal{E} $ e $ (T_{\star}P)[M(C_1 , \cdots , C_n)]=1 $. Assim, se denotamos

$$ M_2 ~ = ~ \bigcup M(C_1 , \cdots , C_n), $$

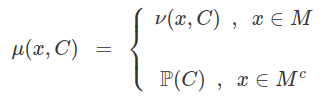
para todo $ C \in \mathcal{C}_U $. Então, para cada $ x \in E $, o conjunto de função $ \mu(x , \cdot) : \mathcal{C}_U \rightarrow [0,1] $ é finita aditiva e $ \mu(x , U)=1 $.

Resulta da hipótese (c) que $ \mu(x , \cdot) $ é $ \sigma $-aditiva em $ \mathcal{C}_U $. Assim, função de ajuste pode ser estendida a uma probabilidade em $ \mathcal{A}_U $, também denotamos por $ \mu(x, \cdot) $. Para qualquer $ C \in \mathcal{C}_U $ e $ B \in \mathcal{E} $, temos que

$$ \mathbb{P}(C \cap T^{-1}(B)) ~ = ~ \int_{B} \nu(x , C) (T_{\star}P)(dx) ~ = ~ \int_{B} \mu(x,C) (T_{\star}P)(dx).$$

Desde que $ \mathcal{C}_U $ é a álgebra gerada $ \mathcal{A}_U $, concluímos que a equação acima é válida para todo $ A \in \mathcal{A}_U $. Portanto, $ \mu $ é uma probabilidade regular. Finalmente, decorre pelo Teorema 3.2 em Leão, Fragoso e Ruffino (1999) que $ U $ é universalmente mensurável.

Teorema 9.1.3

Seja $ (\Omega , \mathcal{F}) $ um espaço mensurável separável e Hausdorff e $ (E_n) $ uma sequência tal que $ \mathcal{F}= \sigma((E_n)) $. A álgebra gerada por $ (E_n) $ é denotada por $ \mathcal G $. Então, $ (\Omega , \mathcal{F}) $ é um espaço de Radon se, e somente se, qualquer função de conjunto finitamente aditiva $ \mu:{\mathcal G} \rightarrow [0,1] $ satisfazendo $ \mu(\Omega) =1 $ também é $ \sigma $-aditiva na álgebra $ \mathcal{G} $.

Demonstração: Considere $ (\Omega , \mathcal{F}) $ um espaço separável e Hausdorff, então, o MCF estabelece uma isomorfismo mensurável entre $ (\Omega , \mathcal{F}) $ e $ (U, \beta(U)) $, no qual $ U $ é um subconjunto de $ S^{\infty} $ (Proposição 9.1.1). Além disso, para cada $ n \in \Bbb{N} $, obtemos que

$$ \Psi(E_n) ~ = ~ \pi_{n}^{-1} ((1)) \cap U . $$

Portanto, concluimos que $ \Psi({\mathcal G}) = \mathcal{C}_U $ e $ \Psi^{-1} (\mathcal{C}_U)= {\mathcal G} $. Usando esse fato, para cada função $ \mu $ definida em $ {\mathcal G} $, podemos definir que

$ \Psi_{\star}\mu $ em $ \mathcal{C}_U $ induzida por $ \mu $, satisfazendo

$$ \Psi_{\star}\mu(D) ~ = ~ \mu \left[ \Psi^{-1} (D) \right] ~ ~ ; ~ D \in \mathcal{C}_U . $$

Além disso, $ \mu $ é finito aditivo se, e somente se, $ \Psi_{\star}\mu $ é também finito aditivo.

Agora, se $ (\Omega , \mathcal{F}) $ é um espaço de Radon, concluímos que $ U $ é universalmente mensurável (Teorema 9.1.1). Então, segue do Lema 9.1.4 que $ \Psi_{\star}\mu $ é $ \sigma $-aditiva. Então, obtemos que $ \mu $ também é $ \sigma $-aditiva.

Portanto, segue do Lema 9.1.4 que $ U $ é universalmente mensurável. Finalmente, usando o Teorema 9.1.1 concluímos que $ (\Omega , \mathcal{F}) $ é um espaço de Radon.

9.2 - Seleção Universalmente Mensurável

Dado um espaço mensurável $ (\Omega , \mathcal{F}) $, vamos estudar a classe dos subconjuntos universalmente mensuráveis de $ \Omega $ e propriedades das funções universalmente mensuráveis. Entre os principais resultados desta seção, vamos mostrar que a $ \sigma $-álgebra universal é fechada por operações de Souslin e por composição de funções universalmente mensurável. Na sequência, vamos estabelecer o teorema de seleção mensurável e aplicações. Fechamos esta seção com uma apresentação dos espaços de Souslin.

Definição 9.2.1 (Conjuntos Nulos e Espaço completo)

Considere $ (\Omega, \mathcal{F} ,\mathbb{P}) $ um espaço de probabilidade, um conjunto $ N \subset \Omega $ é denominado $ \mathbb{P} $-nulo se existe $ A \in \mathcal{F} $ com $ \mathbb{P}(A)=0 $ tal que $ N \subset A $. Com isso dizemos que um espaço de probabilidade $ (\Omega , \mathcal{F} ,\mathbb{P}) $ é completo se a $ \sigma $-álgebra $ \mathcal{F} $ contém todos os conjuntos $ \mathbb{P} $-nulos de $ \Omega $. Denotaremos por $ \mathcal{N} $ a classe de todos os conjuntos $ \mathbb{P} $-nulos. Dado um espaço $ (\Omega , \mathcal{F} ,\mathbb{P}) $ qualquer é possível ``completarmos'' este espaço de probabilidade com os conjuntos $ \mathbb{P} $-nulos, na forma [Neveu (1965); pp. 16, prop. I.4.5]: definimos a $ \sigma $-álgebra

$$\mathcal{F}_p = \mathcal{F} \cup \mathcal{N} $$

no qual cada elemento $ B \in \mathcal{F}_p $ é união de um elemento de $ \mathcal{F} $ com um elemento de $ \mathcal{N} $. Para estendermos a probabilidade $ \mathbb{P} $ para $ \mathcal{F}_p $, basta definirmos

$$ \bar{\mathbb{P}}(A \cup N) = \mathbb{P}(A) ~ ~ ~ ; ~ ~ ~ A \in \mathcal{F} { e } ~ ~ N \in \mathcal{N} $$

sobre $ \mathcal{F}_p $. Com isso, obtemos um outro espaço de probabilidade $ (\Omega , \mathcal{F}_p , \bar{\mathbb{P}}) $ que é completo.

Definição 9.2.2 ($ \sigma $-álgebra universal e conjuntos universalmente mensuráveis)

Denotamos por $ \mathcal{P}(\Omega) $ o conjunto de todas as probabilidades definidas sobre $ (\Omega , \mathcal{F}) $, Então, podemos definir

$$ \bar{\mathcal{F}} = \bigcap_{p \in \mathcal{P}(\Omega)} ~ \mathcal{F}_p $$

a qual chamaremos de $ \sigma $-álgebra universal. Se um conjunto $ E $ pertence a $ \bar{\mathcal{F}} $, dizemos que $ E $ é universalmente mensurável. Por construção, se $ E $ é universalmente mensurável, então

$$ E = A \cup N $$

nos quais $ A \in \mathcal{F} $ e $ N $ é um conjunto $ p $-nulo para toda probabilidade $ p \in \mathcal{P}(\Omega) $. Desta forma, toda probabilidade sobre $ (\Omega , \mathcal{F}) $ pode ser estendida para $ (\Omega , \bar{\mathcal{F}}) $. A seguir, vamos utilizar um teorema de Lusin [Doob (1984), pg. 751] para mostrar que a $ \sigma $-álgebra universal $ \bar{\mathcal{F}} $ é fechada por operações de Souslin.

Proposição 9.2.1

Considere $ (\Omega, \mathcal{F}) $ um espaço mensurável e $ S $ um esquema de Souslin para $ \bar{\mathcal{F}} $. Então $ N(S) $ é universalmente mensurável. Em outras palavras, a $ \sigma $-álgebra universal é fechada por operações de Souslin.

Demonstração: Aplicando o teorema de Lusin [Doob (1984), pg. 751], obtemos que para toda probabilidade $ p \in \mathcal{P}(\Omega) $

$$ \bar{\mathcal{F}} \subset \mathcal{S} \left[ \bar{\mathcal{F}} \right] \subset \mathcal{S} \left[ \mathcal{F}_p \right] \subset \mathcal{F}_p $$

Desde que o resultado acima é válido para todo $ p \in \mathcal{P}(\Omega) $, obtemos

$$ \bar{\mathcal{F}} \subset \mathcal{S} \left[ \bar{\mathcal{F}} \right] \subset \bigcap_{p \in \mathcal{P}(\Omega)} \mathcal{F}_p = \bar{\mathcal{F}}$$

portanto, $ \bar{\mathcal{F}} = \mathcal{S}[ \bar{\mathcal{F}} ] $, segue a proposição

Na sequência, vamos definir e estudar algumas propriedades de funções universalmente mensuráveis.

Definição 9.2.3

Considere $ (\Omega , \mathcal{F}) $ e $ (Y, \beta) $ espaços mensuráveis e $ f:D \rightarrow Y $, onde $ D \subset \Omega $. Se $ D \in \bar{\mathcal{F}} $ e $ f^{-1}(B) \in \bar{\mathcal{F}} $ para todo $ B \in \beta $, $ f $ é denominada universalmente mensurável.

Lema 9.2.1

Considere $ (\Omega , \mathcal{F}) $ um espaço mensurável e $ E \subset \Omega $. Então $ E \in \bar{\mathcal{F}} $ se, e só se, dado $ p \in \mathcal{P}(\Omega) $, existe $ B \in \mathcal{F} $ tal que $ p(E \Delta B) = 0 $.

Demonstração: Se $ E \in \bar{\mathcal{F}} $, então $ E \in \mathcal{F}_p $ para todo $ p \in \mathcal{P}(\Omega) $.

Com isso,

$$ E = B \cup N $$

onde $ N $ é um conjunto $ p $-nulo (para toda probabilidade $ p \in \mathcal{P}(\Omega) $) e $ B \in \mathcal{F} $. Agora,

$$ E \Delta B = (E - B) \cup (B - E) = N \cup \emptyset = N $$

Portanto, concluímos que

$$ p[E \Delta B] = p(N) = 0 $$

Agora suponha que para qualquer $ p \in \mathcal{P}(\Omega) $, existe $ B \in \mathcal{F} $ tal que $ p(E \Delta B) = 0 $. Temos que

$$ E \Delta B = (B \cap E^c) \cup (E \cap B^c) $$

Assim,

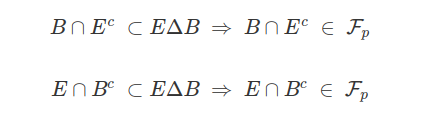
Por outro lado, temos que

$$ E \cap B = B - [B \cap E^c] = B \cap [B \cap E^c]^c $$

Desde que,

$$ B \cap E^c ~ \in ~ \mathcal{F}_p ~ \Rightarrow ~ [B \cap E^c]^c ~ \in ~ \mathcal{F}_p $$

Obtemos que $ E \cap B \in \mathcal{F}_p $. Agora,

$$ E = (E \cap B) \cup (E \cap B^c) $$

Mas, $ E \cap B \in \mathcal{F}_p $ e $ E \cap B^c \in \mathcal{F}_p $, portanto

$$ E \in \mathcal{F}_p ~ ~ ; ~ ~ \forall ~ p \in \mathcal{P}(\Omega) $$

Outra importante propriedade da $ \sigma $-álgebra universal é que esta é fechada por composição de funções, como mostraremos no lema a seguir.

Lema 9.2.2

Considere $ (\Omega, \mathcal{F}) $, $ (Y, \beta) $ e $ (W, \mathcal{A}) $ espaços mensuráveis e $ D \in \bar{\mathcal{F}} $, $ E \in \bar{\beta} $. Suponha que $ f : D \rightarrow Y $ e $ g : E \rightarrow W $ sejam universalmente mensuráveis e $ f(D) \subset E $. Então, a composição $ g \circ f $ é universalmente mensurável.

Demonstração: Devemos mostrar que para todo $ B \in \mathcal{A} $, o conjunto $ f^{-1} [ g^{-1} (B)] \in \bar{\mathcal{F}} $. Desde que $ g^{-1}(B) \in \bar{\beta} $, basta mostrarmos que $ f^{-1}(A) \in \bar{\mathcal{F}} $ para todo $ A \in \bar{\beta} $. Para qualquer $ p \in \mathcal{P}(\Omega) $, definimos

$$ p^{\prime} [C] = p [ f^{-1}(C) ] ~ ~ ; ~ ~ \forall C \in \beta $$

Para $ A \in \bar{\beta} $ (fixo), considere $ V \in \beta $ tal que

$$ 0 = ~ p^{\prime}[V \Delta A] = \mathbb{P}[ f^{-1}(V) \Delta f^{-1}(A)] $$

Agora, temos que $ f^{-1}(V) \in \bar{\mathcal{F}} $, então $ f^{-1}(V)= B \cup N $ onde $ B \in \mathcal{F} $ e $ N $ é um conjunto $ p $-nulo. Portanto, existe $ B \in \mathcal{F} $ tal que

$$ p [ B \Delta f^{-1}(A) ] = 0 $$

com isso, o resultado segue do lema 9.2.1.

Como consequência da demonstração deste Lema, obtemos o seguinte resultado.

Corolario 9.2.1

Considere $ (\Omega, \mathcal{F}) $ e $ (Y, \beta) $ espaços mensuráveis e $ D \in \bar{\mathcal{F}} $ e $ f: D \rightarrow Y $ uma função unversalmente mensurável. Então, para todo $ B \in \bar{\beta} $ temos que $ f^{-1}(B) \in \bar{\mathcal{F}} $.

Acima, estudamos algumas propriedades elementares sobre mensurabilidade universal, que utilizaremos para generalizar o teorema de seleção universalmente mensurável proposto por Bertsekas e Shreve (1978, prop. 7.50, pp. 184).

Seleção Universalmente Mensurável

Na sequência, vamos utilizar Teorema 5.5 em Leese (1978) para estabelecer um teorema de uniformização de conjuntos universalmente mensuráveis. Dado dois espaços $ \Omega_1 $ e $ \Omega_2 $, denotamos por $ \Omega_1 \times \Omega_2 $ o produto Cartesiano de $ \Omega_1 $ e $ \Omega_2 $. Se $ A $ é um subconjunto arbitrário de $ \Omega_1 \times \Omega_2 $, denotamos por $ A_{w_1} $ a seção de $ A $ em $ w_1 $, isto é, um subconjunto de $ \Omega_2 $ definido por

onde $ A_1 \in \mathcal{F}_1 $ e $ A_2 \in \mathcal{F}_2 $. A classe de todos os retângulos mensuráveis forma uma semi-álgebra de subconjuntos de $ \Omega_1\times \Omega_2 $ e denotaremos por $ \mathcal{F}_1 \times \mathcal{F}_2 $a $ \sigma $-álgebra gerada pela semi-álgebra de retângulos mensuráveis [ver módulo “Espaço Produto”] .

Considere $ \mathbb{N} $ o conjunto dos números naturais. Denotamos por $ \Sigma $ o espaço das sequências finitas $ i|n=(i_1 , i_2, \cdots , i_n) $ de elementos de $ \mathbb{N} $. O espaço produto $ \mathbb{N}^{\mathbb{N}} $ corresponde ao espaço das sequências de elementos de $ \mathbb{N} $. A seguir, vamos introduzir a principal classe de conjuntos associados aos teoremas de seleção mensurável, denominados conjuntos de Souslin. Considere $ \Omega $ um espaço qualquer e $ (A_{i|n} : n \geq 1) $ uma sequência de subconjuntos de $ \Omega $ indexada por $ i|n $, com $ i \in \mathbb{N}^{\mathbb{N}} $. Assim, dizemos que o conjunto

$$A ~ = ~ \bigcup_{i \in \Bbb{N}^{\Bbb{N}}} ~ \bigcap_{n=1}^{\infty} A_{(i_1, \cdots , i_n)}$$

é obtido da coleção de subconjuntos $ (A_{i|n}: n \in \mathbb{N} , ~ i \in \mathbb{N}^{\mathbb{N}}) $ por operações de Souslin. Se $ \mathcal{H} $ é uma classe de subconjuntos de $ \Omega $, a classe dos conjuntos obtidos por operações de Soulin para sequências de conjuntos em $ \mathcal{H} $ é denominada $ \mathcal{H} $-Souslin. Dados $ \Omega $ um espaço qualquer e $ \mathcal{H}_1 $ e $ \mathcal{H}_2 $ duas classes de subonjuntos de $ \Omega $ contendo o vazio (Paving), são válidas as seguinte afirmações (Bertsekas and Shreve (1978, Teorema 7.35):

a) Se $ \mathcal{H}_1 \subset \mathcal{H}_2 $, temos a classe de conjuntos $ \mathcal{H}_1 $-Souslin está contida na classe de conjuntos $ \mathcal{H}_2 $-Souslin;

b) A classe de conjuntos $ \mathcal{H}_1 $ está contida na classe de conjuntos $ \mathcal{H}_1 $-Souslin;

c) A classe $ \mathcal{H}_1 $-Souslin coincide com a classe ($ \mathcal{H}_1 $-Souslin)-Souslin.

Considere $ (\Omega , \mathcal{F}) $ um espaço mensurável separável e Hausdorff. Um subconjunto $ A \subset \Omega $ é denominado analítico se $ A \in \mathcal{F} $-Souslin. Diversas definições de subconjuntos analíticos podem ser encontrados na literatura [ver, Kuratowski (1966)]. A seguir, estabelecemos a definição de espaço de Souslin.

Definição de Espaço de Souslin

Seja $ (\Omega , \mathcal{F}) $ um espaço mensurável separável e Hausdorff. Dizemos que o espaço mensurável $ (\Omega , \mathcal{F}) $ é Souslin ( Radon , Borel) se existe um isomorfismo mensurável $ \phi : \Omega \rightarrow U $ no qual $ U \subset Y $ é um subconjunto analítico (universalmente mensurável, Borel) de $ Y $ um espaço metrizável compacto com a $ \sigma $-álgebra de Borel $ \beta(Y) $.

Na definição acima, tomamos $ U $ com a $ \sigma $-álgebra traço de $ \beta(Y) $. Com esta notação, vamos apresentar alguns resultados sobre os espaços de Souslin, que utilizaremos durante este trabalho. Começamos com caracterizações dos subconjuntos analíticos dos espaços de Souslin.

Lema

Considere $ (\Omega , \mathcal{F}) $ um espaço de Souslin e $ A \subset \Omega $. Então, as seguintes afirmações são equivalentes:

a) $ A $ é um subconjunto analítico;

b) $ A \in F(\Omega) $-Souslin, no qual $ F(\Omega) $ corresponde a classe dos subconjuntos fechados de $ \Omega $ com a topologia $ \tau_{\Omega} $.

c) O espaço mensurável $ (A , \mathcal{F}_A) $ é Souslin, no qual $ \mathcal{F}_A $ corresponde ao traço da $ \sigma $-álgebra $ \mathcal{F} $ sobre $ A $.

d) Existe uma função contínua $ f : \mathbb{N}^{\mathbb{N}} \rightarrow A $ no qual $ f(\mathbb{N}^{\mathbb{N}}) = A $.

Prova: Vamos mostrar que (a) e b são equivalentes. Desde que $ \Omega $ com a topologia $ \tau_{\Omega} $ é um espaço metrizável e separável, obtemos que todo subconjunto aberto é união de subconjuntos fechados [Bertsekas and Shreve (1978), lema 7.2, pg. 105]. Assim, temos que todo aberto de $ \Omega $ pode ser obtido por operações de Souslin de conjuntos fechados. Desde que $ \mathcal{F} $ corresponde a $ \sigma $-álgebra de Borel, obtemos $ \mathcal{F} \subset F(\Omega) $-Souslin. Com isso, obtemos que a classe dos conjuntos $ \mathcal{F} $-Souslin está contida na classe $ F(\Omega) $-Souslin [Bertsekas and Shreve (1978) , prop. 7.35, pg. 158]. Por outro lado, como $ F(\Omega) \subset \mathcal{F} $, concluímos que a classe $ F(\Omega) $-Souslin está contida na classe $ \mathcal{F} $-Souslin. Portanto, estas classes coincidem. Para mostrarmos que (a) e (c) são equivalentes, basta aplicamos o teorema 19 em Dellacherie e Meyer (1978, pg. 48). Na sequência, vamos mostrar que (c) e (d) são equivalentes. Considere $ (A , \mathcal{F}_ A) $ um subconjunto de Souslin, existe um homeomorfismo $ \Psi : A \rightarrow U $ no qual $ U \subset [0,1] $ é analítico. Utilizando a proposição 7.37 em Bertsekas e Shreve (1978, pg. 164), obtemos que existe uma função $ f: \mathbb{N}^{\mathbb{N}} \rightarrow U $ contínua com imagem $ f[\mathbb{N}^{\mathbb{N}}] = U $. Assim, a função

$$g(x) ~ = ~ \Psi^{-1} \left[ f(x) \right] ~ ~ ; ~ ~ x ~ \in ~ \mathbb{N}^{\mathbb{N}}$$

é contínua e $ g[\mathbb{N}^{\mathbb{N}}]=A $.

Por outro lado, se existe uma função $ f: \Bbb{N}^{\Bbb{N}} \rightarrow A $ contínua e com imagem $ f[\mathbb{N}^{\mathbb{N}}]=A $, vamos mostrar que $ A $ é analítico. Desde que $ (\Omega , \mathcal{F}) $ é um espaço de Souslin, o espaço mensurável $ (A , F_A) $ é separável e Hausdorff. Assim, existe um homeomorfismo $ \Psi:A \rightarrow U $ onde $ U \subset [0,1] $. Com isso, a função

$$h(x) ~ = ~ \Psi \left[ f(x) \right] ~ ~ ; ~ ~ x ~ \in ~ \mathbb{N}^{\mathbb{N}} $$

é contínua e $ g[\mathbb{N}^{\mathbb{N}}]=U $. Desta forma, obtemos da proposição 7.37 em Bertsekas e Shreve (1978, pg. 164) que $ U $ é analítico. Segue o resultado.

A seguir, apresentamos uma propriedade dos subconjuntos analíticos de um espaço de Souslin.

Lema:

Considere $ (\Omega , \mathcal{F}) $ e $ (E , \mathcal{E}) $ dois espaços de Souslin e $ f: \Omega \rightarrow E $ uma função mensurável. Então, se $ A $ é um subconjunto analítico de $ \Omega $, a imagem $ f(A) $ é um subconjunto analítico de $ E $. Por outro lado, se $ B \subset E $ é analítico, obtemos que $ f^{-1}(B)\subset \Omega $ também é um conjunto analítico.

Prova: Suponha que $ A \subset \Omega $ seja um conjunto analítico. Então, existe um homeomorfismo $ \Psi_1 : A \rightarrow U_1 $, no qual $ U_1 $ é um subconjunto analítico do $ [0,1] $. Assim, temos que a função

$$(f \circ \Psi_{1}^{-1}) (x) ~ ~ f \left[ \Psi_{1}^{-1} (x) \right] ~ ~ ; ~ ~ x \in U_1$$

é mensurável e $ (f \circ \Psi_{1}^{-1})(U_1)=f(A)=C $. Desde que $ C $ é um subconjunto do espaço de Souslin $ (E , \mathcal{E}) $, o espaço mensurável $ (C , \mathcal{E}_C) $ é separável e Hausdorff. Então, existe um homeomorfismo $ \Psi_2: C \rightarrow U_2 $, no qual $ U_2 $ é um subconjunto do $ [0,1] $. Desta forma, a função

$$(\Psi_2 \circ f \circ \psi_{1}^{-1}) (x) ~ = ~ \psi_2 \left( f \left[ \Psi_{1}^{-1} (x) \right] \right) ~ ~ ; ~ ~x \in U_1 $$

é mensurável e tem como imagem $ (\Psi_2 \circ f \circ \psi_{1}^{-1}) (U_1) = U_2 $. Desta forma, utilizando o lema 7.40 em Bertsekas e Shreve (1978, pg. 165), obtemos que $ U_2 \subset [0,1] $ é analítico. Desde que $ \Psi_2: C \rightarrow U_2 $ estabelece um homeomorfismo, obtemos que $ C \subset E $ é analítico. Segue o resultado.

Como consequência dos lemas, obtemos o seguinte resultado.

Teorema 9.2.1

Considere $ (\Omega , \mathcal{F}) $ um espaço mensurável, $ (E , \mathcal{E}) $ um espaço de Souslin e $ H $ um conjunto $ (\bar{\mathcal{F}} \times \mathcal{E}) $-Souslin. Então, temos que

a) $ Proj_{\Omega} (H) \in \bar{\mathcal{F}} $;

b) Existe uma função $ f: Proj_{\Omega} \rightarrow E $ que é universalmente mensurável e $ (\omega, f(\omega)) \in H $ para todo $ \omega \in Proj_{\Omega}[H] $.

Prova: Seja $ R $ a classe de todos os retângulos mensuráveis $ B \times C $, no qual $ B \in \bar{\mathcal{F}} $ e $ C \in F(E) $. Vamos mostrar que $ H $ é $ R $-Souslin. Para isto, considere $ \mathcal{C} $ a classe de todos os conjuntos $ R $-Souslin cujo complementar também é $ R $-Souslin. Portanto, temos que $ \mathcal{C} $ é uma $ \sigma $-álgebra [Dellacherie e Meyer (1978), pp. 43, teo. 12]. Para todo $ B \in \bar{\mathcal{F}} $ e $ F \in F(E) $, temos que

Como $ B^c \times F $ e $ \Omega \times F^c $ são conjuntos $ R $-Souslin, obtemos que $ (B \times F)^c $ também é $ R $-Souslin. Por outro lado, temos que $ \sigma $-álgebra $ \bar{\mathcal{F}} \times \mathcal{E} $ é gerada pelos retângulos em $ R $. Assim, concluímos que $ \bar{\mathcal{F}} \times \mathcal{E} \subset \mathcal{C} $. Desta forma, os elementos de $ \bar{\mathcal{F}} \times \mathcal{E} $ são $ R $-Souslin. Com isso, obtemos do teorema 7.35 em Bertsekas e Shrere que $ H $ também é um conjunto $ R $-Souslin. Utilizando o teorema 5.5 em Leese (1978), obtemos que:

a) $ Proj_{\Omega} (H) \in \bar{\mathcal{F}} $

b) Existe uma função $ f: Proj_{\Omega} \rightarrow E $ que é universalmente mensurável e $ (\omega, f(\omega)) \in H $ para todo $ \omega \in Proj_{\Omega}[H] $. Segue o resultado.

Como aplicação deste resultado, vamos generalizar o teorema de seleção universalmente mensurável apresentado por Bertsekas e Shreve (1978).

Proposição 9.2.2

Considere os espaços $ (\Omega , \mathcal{F}) $ e $ (E, \beta_{E}) $ satisfazendo as hipóteses do teorema 9.2.1 e $ D \in \bar{\mathcal{F}} \times \beta_{E} $. Seja $ f : D \rightarrow \mathbb{R}^\star $ uma função $ \bar{\mathcal{F}} \times \beta_{E} $-mensurável, definimos $ f^{\star} : Proj_{\Omega}[D] \rightarrow \mathbb{R}^\star $ por

$$f^{\star}(w) = \inf_{x \in E} ~ f(w , x)$$

a) A função $ f^{\star} $ é universalmente mensurável e para todo $ \epsilon > 0 $, existe uma função $ \phi : Proj_{\Omega}[D] \rightarrow E $ tal que $ Gr[\phi] \subset D $ e para todo $ w \in Proj_{\Omega} [D] $

Demonstração: Observe que,

Agora seja $ w \in (w \in Proj_{\Omega}(D) : f^{\star}(w) < b) $ isto implica que

$$\inf_{x\in E} f(w,x)< b$$

o que implica que dado $ \epsilon\geq 0 $ existe $ x^\prime \in E $ tal que

$$f(w,x^\prime)-\epsilon < b \Rightarrow f(w,x^\prime)< b+\epsilon$$

Desde que $ \epsilon $ é arbitrário obtemos que existe um $ x^{\epsilon/2}\in E $ tal que

$$f(w,x^{\epsilon/2})< b$$

O que implica que $ w\in Proj_{\Omega} \left[ \left( (w,x) \in D : f(w,x)< b \right) \right] $ e portanto

$$( w \in Proj_{\Omega}(D) : f^{\star}(w) < b ) = Proj_{\Omega} [ ( (w,x) \in D : f(w,x) < b ) ]$$

Desde que $ f $ é uma função $ \bar{\mathcal{F}} \times \beta_{E} $-mensurável, segue do Teorema 9.2.1 a que $ f^{\star} : Proj_{\Omega}[D]\rightarrow \mathbb{R}^{\star} $ é universalmente mensurável. Para todo $ k= \cdots, -2, -1, 0 , 1, 2, \cdots $, definimos

$$ A(k) = ( (w,x) \in D : f(w,x) \leq k \epsilon ) $$

que pertence a $ \sigma $-álgebra $ \bar{\mathcal{F}} \times \beta_{E} $, pois $ f $ é $ (\bar{\mathcal{F}} \times \beta_{E}) $-mensurável. Os conjuntos,

$$ B(k) = ( w \in Proj_{\Omega}(D) : (k-1) \epsilon \leq f^{\star}(w) < k \epsilon ) $$

são universalmente mensuráveis ($ \bar{\mathcal{F}} $-mensuráveis), pois $ f^{\star} $ é universalmente mensurável. O conjunto,

$$ B(\infty) = ( w \in Proj_{\Omega}(D) : f^{\star}(w) = \infty )$$

é universalmente mensurável, pois

$$ B(\infty) = \bigcap_{r \in \mathbb{Q}^\star} ~ ( w \in Proj_{\Omega} (D) : f^{\star}(w) > r ) $$

Da mesma forma, o conjunto

$$ B(- \infty) = ( w \in Proj_{\Omega}(D) : f^{\star} = - \infty ) $$

é universalmente mensurável, pois

$$ B(\infty) = \bigcap_{r \in \mathbb{Q}^\star} ~ ( w \in Proj_{\Omega} (D) : f^{\star} (w) < r ) $$

Aplicando o Teorema 9.2.1 ao conjunto $ A(k) \in \bar{\mathcal{F}} \times \beta_E $, sabemos que existe uma função universalmente mensurável $ \phi_k : Proj_{\Omega}(A(k)) \rightarrow E $ tal que $ Gr[\phi_k] \in A(k) $. Da mesma forma, aplicando o Teorema 9.2.1 ao conjunto D, existe uma função universalmente mensurável $ \phi^{\star} : Proj_{\Omega}(D) \rightarrow E $ tal que $ Gr[\phi^{\star}] \in D $. Considere $ {k}^{\star} $ um inteiro tal que $ k^{\star} \leq -\frac{1}{\epsilon^2} $, com isso, definimos uma função $ \phi : Proj_{\Omega}(D) \rightarrow E $, por

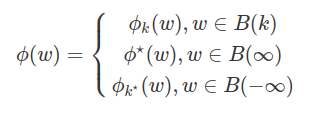
Desde que,

$$ B(k) ~ \subset ~ Proj_{\Omega} [ A(k)] $$

e

$$ B( - \infty) ~ \subset ~ Proj_{\Omega}[A(k)] $$

para todo $ k= \cdots, -1,0,1, \cdots $, obtemos que $ \phi $ está bem definido. Além disso, $ \phi $ é universalmente mensurável e $ Gr[\phi] \subset D $.

Se tomarmos $ w \in B(k) $, temos que

$$ f[w, \phi(w)] = f [ w , \phi_k(w) ] ~ \leq ~ k \epsilon ~ \leq ~ f^{\star}(w) ~ + ~ \epsilon $$

Agora, se $ w \in B(\infty) $, então $ f(w,x) = + \infty $ para todo $ x \in D_w $, que implica em $ f[w, \phi(w)] = f[w, \phi^{\star}] = f^{\star}(w)= \infty $. Para finalizar, se tomarmos $ w \in B(- \infty) $, temos

$$ f[w, \phi(w)] = f[w, \phi_{k^{\star}} (w)] ~ \leq ~ k^{\star} \epsilon ~ \leq ~ - \frac{1}{\epsilon} $$

Portanto, $ \phi $ tem as propriedades requeridas e segue a parte (a). Para mostrarmos a parte (b), considere o conjunto $ F \subset \Omega \times E \times\mathbb{R}^\star $ definido por

$$ F = ( (w,x,b) \in \Omega \times E \times \mathbb{R}^\star : f (w,x) \leq b ) $$

Vamos mostrar que $ F \in \bar{\mathcal{F}} \times \beta_{E} \times \beta_{\mathbb{R}^\star} $. Seja $ k \in \mathbb{N} $, $ r \in \mathbb{Q}^\star $ e o conjunto

$$ C[r;k] = ( (w,x) \in D : f(w,x) \leq r ) ~ \times ~ ( b \in \mathbb{R}^\star : r \leq b + \frac{1}{k} ) $$

Desde que,

$$ ( (w,x) \in D : f(w,x) \leq r ) ~ \in ~ \bar{\mathcal{F}} \times \beta_{E} $$

e

$$ ( b \in \mathbb{R}^\star : r \leq b + \frac{1}{k} ) ~ \in ~ \beta_{\mathbb{R}^\star} $$

temos que $ C[r,k] \subset \bar{\mathcal{F}} \times \beta_{E} \times \beta_{\mathbb{R}^\star} $. Como

$$ F = \bigcap_{k=1}^{\infty} ~ \bigcup_{r \in \mathbb{Q}^\star} C[r;k] $$

obtemos que $ F \in \bar{\mathcal{F}} \times \beta_{E} \times \beta_{\mathbb{R}^\star} $. Aplicando o Teorema 9.2.1, concluímos que

$$ A = Proj_{(\Omega \times \mathbb{R}^\star} (F) ~ \in ~ \stackrel{-}{\mathcal{F}} \times \stackrel{-}{\beta_{\mathbb{R}^\star}} $$

A transformação $ T : Proj_{\Omega}(D) \rightarrow \Omega \times \mathbb{R}^\star $, definida por

$$ T(w) = (w, f^{\star}(w)) $$

é $ (\bar{\mathcal{F}}; \bar{\mathcal{F}} \times \beta_{\mathbb{R}^\star}) $-mensurável, pois para todo $ C \in \bar{\mathcal{F}} \times \beta_{\mathbb{R}^\star} $, temos que

$$T^{-1}(C) = ( w \in Proj_{\Omega}(C) : f^{\star}(w) \in C_w )$$

Como consequência do Teorema 9.2.1 e o fato de que $ C_w \in \beta_{\mathbb{R}^\star} $ [Neveu (1965), prop. III.1.2, pg. 71], a transformação $ T $ é $ (\bar{\mathcal{F}}; \bar{\mathcal{F}} \times \beta_{\mathbb{R}^\star}) $-mensurável. Além disso, temos que

$$I = ( w \in Proj_{\Omega}(D) : (w, f^{\star}(w)) \in A ) = T^{-1}(A)$$

Portanto, segue do corolário 9.2.1, que $ T^{-1}(A) \in \bar{\mathcal{F}} $ e assim, o conjunto $ I $ é universalmente mensurável. Como $ F \in \bar{\mathcal{F}} \times \beta_{E} \times \beta_{\mathbb{R}^\star} $, segue do teorema 9.2.1 que, existe uma função $ \rho : A \rightarrow E $ universalmente mensurável [$ ( \bar{\mathcal{F}} \times \stackrel{-}{\beta_{\mathbb{R}^\star}}; \beta_{E} ) $-mensurável] tal que $ (w, \rho(w,b),b) \in F $ para todo $ (w,b) \in A $. Com isso, definimos $ \psi: I \rightarrow E $, por

$$ \psi (w) = \rho[w, f^{\star}(w)] = (\rho \circ T)(w) ; w \in I $$

Então, como consequência do lema 9.2.2 a função $ \psi $ é universalmente mensurável e por construção

$$ f[w, \psi(w)] ~ \leq ~ f^{\star}(w) ~ ~ ; ~ ~ w \in I $$

Portanto,

$$ f[w, \psi(w)] = f^{\star}(w) ~ ~ ; ~ ~ w \in I $$