12. Processo Estocástico

Processo estocástico é uma coleção de variáveis aleatórias que, em geral, são utilizadas para estudar a evolução de fenômenos (ou sistemas) que são observados ao longo do tempo. Assim, ao invés de descrevermos o sistema através de equações determinísticas (como, equações diferenciais ordinárias), que dado uma condição inicial, conhecemos toda a evolução do sistema, vamos utilizar processos estocásticos, para o qual, dado uma condição inicial, ainda temos diversas trajetórias possíveis para a evolução do sistema.

1 - Base Estocástica

O processo estocástico é uma coleção de variáveis aleatórias que descreve a evolução de um sistema ao longo do tempo. Assim, a evolução da informação acumulada ao longo do tempo é fundamental para estudarmos o comportamento do sistema. Esta evolução da informação é definida através de uma coleção encaixante de $ \sigma $-álgebras, denominada filtragem. O conceito de filtragem foi introduzido por Doob e corresponde a uma das principais ferramentas para estudarmos processos estocásticos

Dado um espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $, uma filtragem é uma coleção de sub-$ \sigma $-álgebras$ ( \mathcal{F_t} : t \geq 0 ) $ de $ \mathcal{F} $ tal que $ \mathcal{F_s} \subset \mathcal{F_t} $ para $ s \leq t $. Podemos interpretar $ \mathcal{F_t} $ como a $ \sigma $-álgebra dos eventos que ocorrerarm até o tempo $ t $ e a filtragem $(\mathcal{F_t} : t \geq 0)$ como a coleção de $ \sigma $-álgebras que representam a evolução da informação do sistema.

Definição 1.1

Dado uma filtragem $ \mathbb{F} $ associamos as seguintes filtragens:

$$\mathcal{F_{t^+}}=\displaystyle \bigcap_{s> t}\mathcal{F_s},$$

para todo $ t \geq 0 $ e

$$\mathcal{F_{t^-}}=\sigma( \displaystyle \bigcup_{s< t}\mathcal{F_s})=\bigvee_{s\leq t} \mathcal{F_s},$$

para todo $ t> 0 $. Para $ t=0 $ utilizamos $ \mathcal{F_{0^-}}=\mathcal{F_0} $.

Definição 1.2

Dizemos que uma filtragem $ \mathbb{F} $ é contínua a direita se $ \mathcal{F_t}=\mathcal{F_{t^+}}, $ para todo $ t \geq 0 $. Para facilitar a notação tomamos $ \mathcal{F_{\infty}}=\mathcal{F} $ e ainda

$$\displaystyle \mathcal{F_{\infty^-}}=\bigvee_{s\in\mathbb{R_{+}}}\mathcal{F_s}.$$

Lembrando que o símbolo $ \bigvee $ significa que é a $ \sigma $-álgebra gerada pela união das $ \mathcal{F_s} $, pois união de $ \sigma $-álgebra nem sempre é $ \sigma $-álgebra. A base estocástica $ \mathfrak{B}=(\Omega,\mathcal{F},\mathbb{F},\mathbb{P}) $ é chamada também de espaço de probabilidade filtrado.

Definição 1.3

Dizemos que uma base estocástica $ \mathfrak{B}=(\Omega,\mathcal{F},\mathbb{F},\mathbb{P}) $ satisfaz as hipóteses usuais da teoria geral de processos estocásticos se:

(i) O espaço $ (\Omega,\mathcal{F},\mathbb{P}) $ é completo.

(ii) $ \mathbb{F} $ é $ \mathbb{P} $-completada, isto é, $ \mathcal{F_0} $ contém todos os conjuntos $ \mathbb{P} $-nulos da $ \sigma $-álgebra $ \mathcal{F} $. Neste caso, temos que todo conjunto $ F $ que pertence ao $ \mathbb{P} $ completamento de $ \mathcal{F} $ com $ \mathbb{P}(F)=0 $ também pertence a $ \mathcal{F_t} $ para todo $ t \geq 0 $.;

(iii) A filtragem $ \mathcal{F} $ é contínua à direita.

1.1 - Tempos de Parada

Considere $ T $ uma variável aleatória que pode ser interpretada como o tempo de ocorrência de um fenômeno que depende “casualmente” da evolução do sistema. Aqui, casualidade significa que, para cada tempo $ t \geq 0 $, a resposta à questão: o fenômeno já ocorreu? depende somente da informação acumulada sobre o sistema até o tempo $ t \geq 0 $. Assim, o conjunto $ ( T \leq t ) $ deve ser um elemento da $ \sigma $-álgebra $ \mathcal{F_t} $. Seja $ \mathfrak{B}=(\Omega,\mathcal{F},\mathbb{F},\mathbb{P}) $ a base estocástica que carrega toda a informação acumulada sobre o sistema ao longo do tempo.

Definição 1.1.1

Seja $ T $ uma variável aleatória, tal que $T:\Omega \rightarrow \overline{\mathbb{R_+}}$, com $ \overline{\mathbb{R}}_+=[0,\infty] $, a parte dos positivos da reta estendida (incluindo o $ \infty $). Então dizemos que $ T $ é um $ \mathbb{F} $-tempo de parada se, e somente se,

$$(T\leq t)\in \mathcal{F_t}, \quad t \geq 0.$$

Observação

Note que $ T $ é um tempo de parada segundo alguma filtragem, ou seja, se mudarmos a filtragem pode ser que ele deixe de ser um tempo de parada. Além disso, usamos frequentemente o termo tempo de parada ao invés de $ \mathbb{F} $-tempo de parada, quando não houver dúvidas em relação a qual filtragem estamos nos referindo, ressaltamos também que $(T\leq t)=(\omega\in \Omega:T(\omega)\leq t)$

Proposição 1.1.1

Algumas propriedades de tempos de parada.

i) Se $ T $ é um tempo de parada com respeito à filtragem $ \mathbb{F} $, então $ (T< t)\in \mathcal{F_t} $ para todo $ t\geq 0 $

ii) Se $ T(\omega)=a, ~\forall \omega \in \Omega $, para qualquer constante $ a\in \overline{\mathbb{R}}_+ $. Então, $ T $ é um tempo de parada.

iii) Se $ T $ é um tempo de parada e $ a\in \overline{\mathbb{R}}_+ $ uma constante, então T+a também é um tempo de parada.

iv) Se $ T $ e $ S $ são tempos de parada sobre a mesma filtragem, então $ S+T $ também é um tempo de parada.

v) Se $ T $ e $ S $ são tempos de parada com respeito a mesma filtragem, então $ \min(S,T) $ e $ \max(S,T) $ também são tempos de parada.

vi) Se $ T $ é um tempo de parada e $ a\in \overline{\mathbb{R}}_+ $ uma constante, então $ \min(T,a) $ é um $ \mathcal{F}_a $- tempo de parada.

Demonstração

i) Note que $ (T< t)\in \mathcal{F_t} $, é equivalente a $ (T\leq t-1/n)\in \mathcal{F_t} $.

De fato, note que $ (T\leq t-1/n)\in \mathcal{F_{t-1/n}}\subset\mathcal{F_{t}} $ e portanto

$$(T< t )=\displaystyle \bigcup_{n\geq 1}(T\leq t-1/n)\in \mathcal{F_t},$$

para todo $ t \geq 0 $. Observe que entretanto $ (T< t)\in \mathcal{F_t} $ não implica $ (T\leq t)\in \mathcal{F_t} $, a menos que a filtragem seja contínua a direita. Neste caso, as definições são equivalentes.

ii) De fato, note que se $ T(\omega)=a, \forall \omega \in \Omega $ então para $ t< a $ temos que

$$(T\leq t)=\emptyset \in \mathcal{F_t}, \forall t< a,$$

pois $ \mathcal{F_t} $ é $ \sigma $-álgebra. Agora se $ t\geq a $ então

$$(T\leq t)=\Omega \in \mathcal{F_t},$$

para todo $ t \geq 0 $. Portanto $ T $ é um tempo parada.

iii) Temos que $ T $ é um tempo de parada logo, $ (T\leq k)\in \mathcal{F}_k $. Vamos mostrar que $ S=T+t $ também é um tempo de parada, ou seja, $ (S\leq k)\in\mathcal{F}_k $. Basta notar que se $ k< t $ então

$$(S\leq k)=\emptyset\Rightarrow (S\leq k)\in \mathcal{F}_k,~~\forall k< t.$$

Agora suponha que $ k\geq t $, então temos que

$$(S\leq k)=(T+t\leq k)=(T\leq k-t)\in\mathcal{F}_{k-t}\Rightarrow(S\leq k)\in \mathcal{F}_k,$$

pois $ \mathcal{F}_{k-t}\subset \mathcal{F}_k,~~\forall k\geq t. $ E o resultado segue.

iv) Seja $ t> 0 $, então

$$(T+S> t)=(T=0, S> t)\cup (0< T< t, T+S> t)\cup (T> t, S=0 )\cup(T\geq t, S > 0).$$

Como da um desses eventos pertence a $ \sigma $-álgebra $ \mathcal{F_t} $, então temos que a união também pertence e portanto $ S $ é tempo de parada e o resultado segue.

v) Note que, $ (\max(T,S)\leq t)=(S\leq t)\cap(T\leq t) $ e como $ (S\leq t)\in\mathcal{F_t} $ e $ (S\leq t)\in\mathcal{F_t} $, pois são tempos de parada e como $ \mathcal{F_t} $ é $ \sigma $-álgebra temos que

$$(\max(T,S)\leq t)=(S\leq t)\cap(T\leq t)\in \mathcal{F_t},$$

para todo $ t \geq 0 $. Para o mínimo basta observar que $ (\min(T,S)\leq t)=(S\leq t)\cup(T\leq t) $ e o resultado segue de forma análoga.

vi) De fato, basta notar que se $ t\leq a $ temos que

$$(\min(T,a)\leq t)=(T\leq t)\in\mathcal{F_t}\subset\mathcal{F}_a.$$

Por outro lado, se $ t\geq a $ então:

$$(\min(T,a)\leq t)=\Omega \in \mathcal{F}_a.$$

Portanto o resultado segue.

Teorema 1.1.1

Seja $ (T_n,n\geq 1) $ uma familia de $ \mathbb{F} $ tempos de parada. Então $ \sup_{n}T_n $ é um $ \mathbb{F} $ tempo de parada, e ainda $ \inf_n T_n $ é um $ (\mathcal{F}_{t+}) $ tempo de parada.

Demonstração

De fato, basta notar que

$$\displaystyle (\sup_{n}T_n \leq t)=\bigcap_n (T_n\leq t)\in\mathcal{F_t}$$

$$\displaystyle (\inf_{n}T_n \leq t)=\bigcup_{m\leq 1}\bigcap_{n\geq 1}(T_n< t+\frac{1}{m})\in\bigcap_{m\leq 1}\mathcal{F}_{t+\frac{1}{m}}=\mathcal{F}_{t+}$$

Observação

Em particular podemos notar que se $ \mathcal{F_t} $ é contínua a direita, então o $ \limsup T_n $ e $ \liminf T_n $ e o $ \lim T_n $ (caso existe) são $ \mathbb{F} $ tempos de parada.

Exemplo 1.1.1

Se $X: \Omega \times [0,\infty) \rightarrow \mathbb{R}$ é um processo estocástico com trajetórias contínuas à direita (ou contínuas à esquerda) e $ \mathbb{F} $ uma filtragem contínua à direita. Também admitimos que $ X(t) $ é $ \mathcal{F_t} $-mensurável para todo $ t \geq 0 $. Neste caso, dizemos que $ X $ é adaptado à filtragem $ \mathbb{F} $. Definimos $ T $ por:

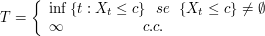
Então $ T $ é um tempo de parada.

Demonstração

Temos que $ (T> t)=(X(s)< c ~\forall s\in [0,t]) $. Como $ X $ é contínuo à direita (ou contínuo à esquerda) obtemos que:

$$\bigcap_{s \in [0,t]}~\displaystyle (X(s)< c)=\bigcup_{n=1}^{\infty}\bigcap_{k=0}^{2^n}(X(kt/2^n)< c)\in \mathcal{F_t},$$

para todo $ t \geq 0 $. Portanto o resultado segue.

$ \Box $

Considere $ (\Omega, \mathcal{F}, \mathbb{P}) $ um espaço de probabilidade, $ \mathbb{F} $ uma filtragem e $ T $ um tempo de parada. Na sequência, vamos definir a $ \sigma $-álgebra $ \mathcal{F_t} $ que representa as informações até o tempo $ T $.

Definição 1.1.2

i) Se $ T $ é um tempo de parada denotamos por $\mathcal{F_t}=(A\in \mathcal{F}:A\cap {T\leq t}\in\mathcal{F_t}, \forall t\in\mathbb{R_+})$.

ii) Se $ T $ é um tempo de parada denotamos por $ \mathcal{F_{T^-}} $ a $ \sigma $-álgebra gerada por $ \mathcal{F_0} $ e todos os conjuntos da forma $ A\cap (t< T) $, com $ A \in \mathcal{F_t} $ e $ t \geq 0 $.

A $ \sigma $-álgebra $ \mathcal{F_{T^-}} $ representas os eventos anteriores ao tempo de parada $ T $. Observe que $ \mathcal{F_{T^-}} $ também é a $ \sigma $-álgebra gerada pela seguinte família de subconjuntos de $ \mathcal{F} $,

$$(F \cap {t \leq T}: F \in \mathcal{F_{t^-}}, t \geq 0).$$

Note que a definição (i) acima apresenta algumas sutilezas, como por exemplo, será que de fato, $ \mathcal{F_t} $ é uma $ \sigma $-álgebra. Além disso, se tomarmos $ T=t $ para alguma constante $ t \geq 0 $, devemos obter que $ \mathcal{F_t}=\mathcal{F_t} $.

Proposição 1.1.2

A definição 1.1.2 (i) está bem definida.

Demonstração

Primeiramente mostremos que $ \mathcal{F_t} $ é de fato uma $ \sigma $-álgebra. De fato, $ \emptyset\in \mathcal{F_t} $, pois $ \emptyset \cap(T\leq t)=\emptyset \in \mathcal{F_t}, \forall t \in \mathbb{R_+} $. Mostremos que se $ A\in \mathcal{F_t} $ então $ A^c \in \mathcal{F_t} $. De fato, se

$$A\in \mathcal{F_t}\Rightarrow A\cap (T\leq t)\in \mathcal{F_t},\forall t \in \mathcal{R}_+.$$

Mas isso implica que $ (A\cap(T\leq t))^c\in \mathcal{F_t}, \forall t \in \mathbb{R_+} $, pois $ \mathcal{F_t} $ é $ \sigma $-álgebra. Além disso, como

$$(T\leq t)\in \mathcal{F_t}, \forall t\in \mathbb{R_+},$$

obtemos que

$$(A\cap(T\leq t))^c\cap (T\leq t)=A^c\cap(T\leq t)\in \mathcal{F_t}, \forall t\in \mathbb{R_+}.$$

Portanto temos que $ A^c\in \mathcal{F_t}. $

A seguir, tomamos $ A_1,A_2,\cdots \in \mathcal{F_t} $ uma sequência de conjuntos disjuntos, mostremos que $ \displaystyle \bigcup_{i=1}^{\infty}A_i\in \mathcal{F_t} $. De fato, basta notar que $ A_i\cap (T\leq t)\in \mathcal{F_t},\forall t\in \mathbb{R_+} ~e~ \forall i\in \mathbb{N}. $ Assim, obtemos que

$$\displaystyle \left(\bigcup_{i=1}^{\infty}A_i\right)\cap(T\leq t)=\bigcup_{i=1}^{\infty}\left(A_i\cap(T\leq t)\right)\Rightarrow \bigcup_{i=1}^{\infty}A_i\in \mathcal{F_t}.$$

Como consequência, obtemos que $ \mathcal{F_t} $ é uma $ \sigma $-álgebra.

Agora mostremos que se $ T=t $ para alguma constante $ t \geq 0 $, então $ \mathcal{F_t}=\mathcal{F_t} $. Na realidade, basta notarmos que se $ k< t $, então o conjunto $ (T\leq k)=\emptyset $ e se $ k\geq t $, então o conjunto $ (T\leq k)=\Omega $. Assim, obtemos que

$$A\cap\emptyset=\emptyset\in \mathcal{F}_k,\forall k< t$$

e

$$A\cap \Omega=A\in \mathcal{F}_k, \forall k\geq t \Leftrightarrow A\in\mathcal{F_t}.$$

Como consequência, concluímos que $ \mathcal{F_t}=\mathcal{F_t} $, e portanto não existe ambiguidade na notação.

$ \Box $

Teorema 1.1.2

Se $ T $ é um $ \mathbb{F}=(\mathcal{F_t}: t \geq 0) $ tempo de parada, então $ \mathcal{F_{T-}}\subset \mathcal{F_t} $ e T é $ \mathcal{F_{T-}} $-mensurável e portanto $ \mathcal{F_t} $-mensurável

Demonstração

Para mostramos que $ \mathcal{F_{T-}}\subset \mathcal{F_t} $, basta mostramos que o geradores de $ \mathcal{F_{T-}} $ pertencem a $ \mathcal{F_t} $. De fato, note que

$$\mathcal{F_0}\subset \mathcal{F_t}$$

para todo $ t \geq 0 $ e, ainda que

$$A_s \cap(s< T)\cap(T\leq t)=A_s\cap(s< T\leq t )\in \mathcal{F_t},~ \forall s,t\in [0,\infty)$$

com $ A_s\in\mathcal{F_s} $. Com isso concluimos que $ \mathcal{F_{T-}}\subset \mathcal{F_t} $. Agora para mostrar que T é $ \mathcal{F_{T-}} $-mensurável basta mostar que $ (T> a)\in\mathcal{F_{T-}}, ~\forall a \geq 0 $ e que $ (T=0)\in\mathcal{F_{T-}} $, o que de fato ocorre por que esses conjuntos são alguns dos geradores de $ \mathcal{F_{T-}} $.

$ \Box $

Teorema 1.1.3

Seja $ T $ um $\mathbb{F}=(\mathcal{F_t}:t\geq 0)$ tempo de parada e $S:\Omega\rightarrow [0,\infty]$ uma variável aleatória $ \mathcal{F_t} $-mensurável tal que $ S\geq T $, então S é um tempo de parada.

Demonstração

De fato, basta notar que

$$(S\leq t)=(S\leq t)\cap(T\leq t)\cup (S\leq t )\cap(T> t)$$

Entretanto como $ S\geq T $ temos que $ (S\leq t )\cap(T> t)=\emptyset $. Além disso, como $ S $ é $ \mathcal{F_t} $-mensurável, temos que $ (S\leq t)\in \mathcal{F_t} $ e portanto por definição temos que $ (S\leq t )\cap(T\leq t)\in \mathcal{F_t} $

$ \Box $

Uma consequência do teorema 1.1.3: acima é o corolário abaixo

Corolário 1.1.1

Qualquer tempo de parada pode ser aproximado por uma sequência decrescente $ (S_n,n\geq 1) $ de $\mathbb{F}=(\mathcal{F_t}:t \geq 0)$ tempos de parada assumindo um número enumerável de valores.

Demonstração

Basta tomarmos

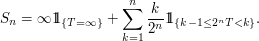
$ \Box $

Teorema 1.1.4

Sejam $ S $ e $ T $ dois $\mathbb{F}=(\mathcal{F_t}: t \geq 0)$ tempos de parada. Para todo $ A\in \mathcal{F_s} $ temos que $ A\cap(S\leq T)\in \mathcal{F_t} $ e $ A\cap (S< T)\in \mathcal{F_{T-}} $.

Demonstração

Para todo $ t\geq 0 $,

$$A\cap (S\leq T)\cap (T\leq t)=A\cap (S\leq t)\cap (T\leq t )\cap(\min{(S, t)}\leq \min{(T,t)})$$

Agora $ (\min{(S, t)}\leq \min{(T,t)})\in\mathcal{F_t} $, desde que $ \min{(S, t)} $ e $ \min{(T,t)} $ são $ \mathcal{F_t} $-mensurável, além disso $ A\cap (S\leq t)\in \mathcal{F_t} $, pois $ A\in\mathcal{F_s}\subset\mathcal{F_t} $ e claro como $ (T\leq t) $ é tempo de parada temos que $ (T\leq t)\in\mathcal{F_t} $, desta forma temos que $ A\cap (S\leq T)\cap (T\leq t)\in \mathcal{F_t}, ~\forall t\geq 0 $. Portanto concluímos que $ A\cap(S\leq T)\in \mathcal{F_t} $.

A segunda implicação deve-se ao fato de

$$A\cap (S< T)=\displaystyle \bigcup_{r\in \mathbb{Q}}A\cap (S\leq r)\cap(r\leq T)\in\mathcal{F_{T-}}$$

pois $ A\cap (S\leq r)\in \mathcal{F_{r}} $ e portanto $ A\cap (S\leq r)\cap(r\leq T) $ é um gerador de $ \mathcal{F_{T-}} $.

$ \Box $

Teorema 1.1.5

Sejam $ S $ e $ T $ dois $\mathbb{F}=(\mathcal{F_t}:t\geq 0)$ tempos de parada tal que $ S\leq T $. Então $ \mathcal{F_s}\subset\mathcal{F_t} $ e $ \mathcal{F_{S-}}\subset\mathcal{F_{T-}} $

Demonstração

Para concluirmos esse teorema, basta observarmos que $ A\cap(S\leq T)\in\mathcal{F_s} $, para todo $ A\in \mathcal{F_s} $, por que $ (S\leq T)=\Omega $, logo $ \mathcal{F_s}\subset \mathcal{F_t} $. Agora $ \mathcal{F_{S-}}\subset\mathcal{F_{T-}} $, pois todos os geradores de $ \mathcal{F_{S-}} $ também são geradores de $ \mathcal{F_{T-}} $, pois se $ A\in\mathcal{F_t} $

$$A\cap(t< S)=A\cap(t< S)\cap(t< T)=B\cap(t< T)$$

com $ B\in\mathcal{F_t} $. Portanto o resultado segue.

$ \Box $

Teorema 1.1.6

Seja $ (T_n,n\geq 1) $ uma sequência monótona de $\mathbb{F}=(\mathcal{F_t}:t\geq 0)$ tempos de parada, no qual $ \mathbb{F} $ contínua a direita. Então

i) Se $ (T_n, n\geq 1) $ é descrescente $ \mathcal{F_t}=\displaystyle \bigcap_{n\geq 1}\mathcal{F_{T_n}} $

ii) Se $ (T_n, n\geq 1) $ é crescente $ \mathcal{F_{T-}}=\displaystyle \bigvee_{n\geq 1}\mathcal{F_{T_n-}} $

Demonstração

Primeiramente note que $ T=\displaystyle \lim_n T_n $ é um tempo de parada, como demonstrado no teorema 1.1.1.

i) Pelo teorema 1.1.5 temos que $ \mathcal{F_t}\subset\mathcal{F_{T_n}},~\forall n\geq 1 $, portanto $ \mathcal{F_t}\subset\displaystyle \bigcap_{n\geq 1}\mathcal{F_{T_n}} $.

Inversamente seja $ A\in\mathcal{F_{T_n}}~\forall n\geq 1 $, logo para todo n temos que

$$A\cap (T_n< t)\in \mathcal{F_t}, ~\forall t\geq 0$$

Portanto temos que $ A\cap (T< t)\in \mathcal{F_t}, ~\forall t\geq 0 $, como $ \mathcal{F_t} $ é uma filtragem contínua a direita, temos que $ A\cap (T\leq t)\in \mathcal{F_t}, ~\forall t\geq 0 $, o que implica que $ A\in \mathcal{F_t} $.

ii) Pelo teorema 1.1.5 temos que $ \mathcal{F_{T_n-}}\subset \mathcal{F_{T-}},~\forall n\geq 1 $ e portanto

$$\displaystyle \bigvee_{n\geq 1}\mathcal{F_{T_n-}}\subset\mathcal{F_{T-}}$$

Inversamente seja $ A_s \cap (s< T) $ um gerador de $ \mathcal{F_{T-}} $, com $ A_s \in \mathcal{F_s} $. Note que $ A_s \cap(s< T) $, também está contido em $ \displaystyle \bigvee_{n\geq 1}\mathcal{F_{T_n-}} $, pois $ A_s \cap (s< T)=\displaystyle \lim_n A_s \cap(s< T_n) $. E portanto o resultado segue.

$ \Box $

Proposição 1.1.3

Se $ A\in\mathcal{F_t} $, então

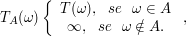
é um $ \mathbb{F} $-tempo de parada.

Demonstração

Vamos mostrar que $ (T_A\leq t)\in \mathcal{F_t} $. Basta notar que se $ A\in\mathcal{F_t} $, então $ A\cap(T\leq t)\in \mathcal{F_t}, ~ \forall t $. Assim temos que

$$(T_A\leq t)=A\cap(T\leq t)\in \mathcal{F_t},\forall t.$$

Portanto o resultado segue.

$ \Box $

Teorema 1.1.7

Se $ T $ é um $ \mathcal{F_t} $ tempo de parada e $ A\in\mathcal{F_\infty}=\mathcal{F}=\displaystyle \bigvee_{t\geq 0}\mathcal{F_t} $ o evento $ A\cap(T=\infty)\in \mathcal{F_{T-}} $

Demonstração

Primeiramente defina $G=(B\in\mathcal{F}:B\cap{T=\infty}\in \mathcal{F_{T-}})$, note que $ G $ é $ \sigma $-álgebra. De fato,

$ \emptyset \in G $, pois $ \emptyset\cap(T=\infty)=\emptyset\in\mathcal{F_{T-}} $. Da mesma forma temos que

$ \Omega \cap (T=\infty)=(T=\infty)\in \mathcal{F_{T-}} $. Além disso, se $ A_0,A_1,A_2,\cdots \in G $ então

$ A_i\cap(T=\infty)\in \mathcal{F_{T-}},~\forall i\geq 0 $. Assim, como $ \mathcal{F_{T-}} $ é $ \sigma $-álgebra, obtemos que $ \bigcap_{n\geq 0}A_n(T=\infty)\in\mathcal{F_{T-}} $ e portanto $ \bigcap_{n\geq 0}A_n $, logo $ G $ é $ \sigma $-álgebra.

Assim precisamos mostrar que $ \mathcal{F_n}\subset G, \forall \mathcal{F_n} $,e, como consequência $ \mathcal{F_\infty}\subset G $ e o resultado segue.

Então seja $ A\in\mathcal{F_n} $. Temos que $ A\cap(T=\infty)=\displaystyle \bigcap_{m\geq n}(A\cap(m< T))\in \mathcal{F_{T-}} $, pois $ A\cap(m< T) $ é um gerador de $ \mathcal{F_{T-}} $, sempre que $ m\geq n $. Finalizando a prova.

$ \Box $

Teorema 1.1.8

Sejam $ S $ e $ T $ dois $\mathbb{F}=(\mathcal{F_t}:t\geq 0)$ tempos de parada satisfazendo $ S\leq T $. Se além disso, $ S< T $ quando $ (0< T< \infty) $, então $ \mathcal{F_s}\subset \mathcal{F_{T-}} $

Demonstração

Para todo $ A\in \mathcal{F_s} $, podemos escrever o conjunto $ A $ da seguinte forma, $ (A\cap(S=0))\cup(S< T)\cup(A\cap(T=\infty)) $.

Mas note que $ A\cap (S=0)\in \mathcal{F_0} $, pela definição de $ \mathcal{F_s} $ e ainda temos que $ (S< T)\in \mathcal{T-} $ pelo Teorema 1.1.4. e por fim temos que $ A\cap(T=\infty)\in \mathcal{F_{T-}} $ pelo teorema anterior. Portanto o resultado segue.

$ \Box $

Corolário 1.1.2

Seja $ (T_n,n\geq 1) $ uma sequência monótona de $ \mathbb{F} $ tempos de parada, com $ \mathbb{F} $ contínua a direita. Então

i) Se $ (T_n,n\geq 1) $ e decrescente e se para todo $ n\geq 1 $ temos que $ T< T_n $ quando $ (0< T_n< \infty) $, então $ \mathcal{F_t}=\displaystyle \bigcap_{n\geq 1}\mathcal{F_{T_n-}} $

ii) Se $ (T_n,n\geq 1) $ e crescente e se para todo $ n\geq 1 $ temos que $ T_n< T $ quando $ (0< T< \infty) $, então

$ \mathcal{F_{T-}}=\displaystyle \bigvee_{n\geq 1}\mathcal{F_{T_n}} $

Demonstração

É consequência imediata do teorema 1.1.6 e dos teoremas 1.1.7 e teorema 1.1.8.

2 - Processo Estocástico

Considere $ (\Omega, \mathcal{F} , \mathbb{F}, \mathbb{P}) $ uma base estocástica, no qual $ (\Omega , \mathcal{F} , P) $ é um espaço de probabilidade e $\mathbb{F}=(\mathcal{F_t}: t \geq 0)$ uma filtragem. Neste módulo, vamos introduzir o conceito de processo estocástico e suas principais propriedades.

Definição 2.1

Seja $ (\Omega, \mathcal{F}, \mathbb{F},\mathbb{P}) $ uma base estocástica e $ X $ um processo estocástico com conjunto de índices $ T $ e espaço de estados $ (E,\mathcal{E}) $.

Definição 2.2

Um processo $ X $ é adaptado a filtragem $ \mathbb{F} $, se $ X(t) $ é $ \mathcal{F_t} $-mensurável para todo $ t \in T $. Muitas vezes, dizemos que o processo $ X $ é não antecipativo. O processo $ X $ é denominado mensurável se a transformação $X:(T\times \Omega, \beta_T \times \mathcal{F}) \rightarrow (E,\mathcal{E})$ é mensurável no qual $ \beta_T $ denota a $ \sigma $-álgebra de Borel do conjunto de índices $ T $.

Na sequência, tomamos como conjunto de índices $ T \subset [0, \infty] $. Um processo estocástico $ X $ é dito progressivamente mensurável, se para todo $ t\in T $ a transformação $ X $ restrita a $ ([0,t] \cap T)\times \Omega $ é $ \beta_{[0,t]} \times \mathcal{F_t} $-mensurável, no qual $ \beta_{[0,t]} $ denota a $ \sigma $-álgebra de Borel dos subconjuntos de $ [0,t]\cap T $.

Definição 2.3

A filtragem interna de um processo é definida como sendo

$$\mathcal{F_t}=\sigma(X_s:s\leq t),\quad t\geq 0.$$

Obviamente, que todo processo $ X $ é adaptado e progressivamente mensurável com respeito a sua filtragem interna.

Suponha que o espaço de estados $ E $ seja um espaço topológico com $ \mathcal{E} $ a $ \sigma $-álgebra de Borel (gerada pelos abertos da topologia). Um processo estocástico $ X $ é denominado contínuo à direita (cad) se este possui trajetória contínuas à direita. Da forma análoga, o processo $ X $ é contínuo à esquerda (cag) se este possui trajetórias contínuas à esquerda. Também, dizemos que o processo estocástico $ X $ é contínuo se este tem trajetórias contínuas e dizemos $ X $ é cadlag se possui trajetórias contínuas à direita e com limites à esquerda.

Teorema 2.4

Todo Processo $ X $ adaptado e cad (respectivamente, cag) é progressivamente mensurável.

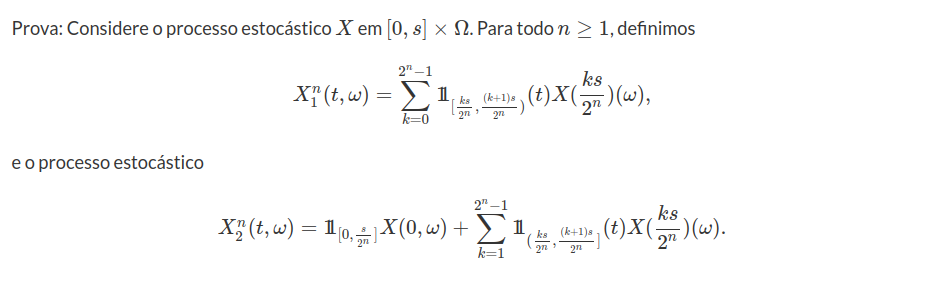
Desde que $ X $ é adaptado, os processo estocásticos $ X^n_1 $ e $ X^n_2 $ são $ \beta_{[0,s]}\times \mathcal{F_s} $-mensurável em $ [0,s] \times \Omega $. Se $ X $ é cad (respectivamente, cag) a sequência n \geq 1) $ (respectivamente, n \geq 1) $) converge em $ [0,s] \times \Omega $ para $ X $. Portanto, obtemos que $ X $ é progressivamente mensurável. Segue o teorema.

Considere $ (\Omega, \mathcal{F}, \mathbb{F}, \mathbb{P}) $ uma base estocástica. Dizemos que um subconjunto $ O \subset [0, \infty) \times \Omega $ é opcional se este pertence a $ \sigma $-álgebra $ \mathcal{O} $ gerada pelos processos estocásticos cadlag à valores nos reais. Um processo estocástico $ X $ a valores no espaço topológico $ E $ é denominado opcional se este for $ \mathcal{O} $-mensurável. Como consequência do teorema 2.4 temos que $ \mathcal{O} \subset \mathcal{M}_1 $.

A $ \sigma $-álgebra $ \mathcal{P} $ de subconjuntos de $ [0, \infty) \times \Omega $ gerada pelos processos adaptados e contínuos à valores reais é denominada previsível. Um processo estocástico $ X $ a valores no espaço topológico $ E $ é denominado previsível se este for $ \mathcal{P} $-mensurável.

Teorema 2.5

(1) A seguinte inclusão é válida: $ \mathcal{P} \subset \mathcal{O} $.

(2) A $ \sigma $-álgebra $ \mathcal{P} $ é gerada pelos processos adaptados e cag e pelas seguintes classes de conjuntos:

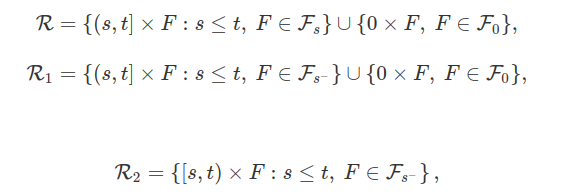
no qual tomamos $ \mathcal{F_{0^-}}=\mathcal{F_{0}} $.

Prova: Como $ \mathcal{P} $ é a $ \sigma $-álgebra gerada pelos processos contínuos concluímos que facilmente que $ \mathcal{P} \subset \mathcal{O} $. Da mesma forma, temos que $ \mathcal{P} \subset \mathcal{P}^\prime $, no qual $ \mathcal{P}^\prime $ corresponde a $ \sigma $-álgebra gerada pelos processos adaptados e cag.

converge de forma pontual para $ X $ sobre $ [0, \infty )\times \Omega $. Com isso, obtemos que $ \mathcal{P}^\prime \subset \sigma(\mathcal{R}) $ e $ \mathcal{P} \subset \sigma(\mathcal{R}) $.

Para provarmos a igualdade entre $ \mathcal{P} $, $ \sigma(\mathcal{R}) $ e $ \mathcal{P}^\prime $ é suficiente mostrarmos $ \sigma(\mathcal{R}) \subset \mathcal{P} $. Para isto, tomamos $ (s,t] \times F \in \mathcal{R} $. Então, existe uma sequência $ (\varphi_n) $ de funções contínuas a valores positivos tal que

Como consequência, obtemos que

$$\sigma(\mathcal{R}_1) \subset \sigma(\mathcal{R}_2)=\sigma(\mathcal{R}_2^\prime)\subset \sigma(\mathcal{R}_1^\prime)=\sigma(\mathcal{R}_1).$$

Obtemos diretamente da definição $ \sigma(\mathcal{R}_1) \subset \sigma(\mathcal{R}) $. Por outro lado, sabemos que

o gráfico do tempo de parada $ T $.

Lema 2.6

Lema 2.7

Lema 2.8

Teorema 2.9

Teorema 2.10

Ao denotarmos por $ \mathcal{T} $ a classe de todos os tempos de parada, obtemos que

A seguir, estabelecemos uma construção da $ \sigma $-álgebraprevisível por intervalos estocástico.

Teorema 2.11

Considere $ (\Omega, \mathcal{F}, \mathbb{F}, \mathbb{P}) $ uma base estocástica. Ao denotarmos por $ \mathcal{T} $ a classe de todos os tempos de parada, obtemos que

$$\mathcal{P}=\sigma ([0, S]: S \in \mathcal{T}) = \sigma(]S,T] ~ ~ \text{e} ~ ~ (0) \times F, ~ F \in \mathcal{F}_0).$$

Segue o teorema.

Dado $ X $ um processo estocástico cadlag, denotamos por $ X^- $ a versão contínua à esquerda de $ X $ definida por $ X^-(t) = \lim_{n \rightarrow \infty} X \left(t-\frac{1}{n} \right)= X(t^-) $. O salto de $ X $ é dado por $ \Delta X(t) = X(t) - X^-(t) $. Então, o processo $ X^{-} $ é previsível. Além disso, se $ X $ for previsível, então $ \Delta X $ também é previsível.

Definição 2.12

Um conjunto estocástico $ B $ é denominado magro se,

$$B = \bigcup_{n=1}^\infty [T_n],$$

no qual $ (T_n : n \geq 1) $ é uma sequência de tempos de parada.

Lema 2.13

Teorema 2.12

Construção de Processo Estocástico

Dados $ (\Omega ,\mathcal{F},\mathbb{P}) $ um espaço de probabilidade, $ T $ um conjunto de índices qualquer e $ X_t : \Omega \rightarrow \Bbb{R} $ uma variável aleatória para todo $ t \in T $. Sejam $ t_1 , \cdots, t_n $ elementos de $ T $ e $ x_1, \cdots , x_n $ elementos em $ \Bbb{R} $ ou $ + \infty, - \infty $. Definimos a função de distribuição $ n $-dimensional de $ (X_{t_1}, \cdots,X_{t_n}) $, por

$$ F_{t_1, \cdots, t_n} (x_1, \cdots, x_n)=\mathbb{P}\left[ \cap_{i=1}^{n} \left(\omega\in \Omega:X_{t_1}(\omega) \leq x_i \right) \right]. $$

Quando $ n \in \mathbb{N} $ e os pontos $ t_i $’s em $ T $ variam, obtemos uma família de distribuições $ n $-dimensionais $ ( F_{t_1, \cdots t_n}:t_i \in T , n \in \mathbb{N} ) $.

Definição 2.6

Desde que $ (\omega: X_t (\omega)<\infty )=\Omega $ para todo $ t \in T $, temos

$$F_{t_1, \cdots, t_n} (x_1, \cdots, x_{n-1}, \infty) ~ = ~ F_{t_1, \cdots,t_{n-1}} (x_1, \cdots,x_{n-1})$$

e

$$F_{t_{i_1},\cdots,t_{i_n}} (x_{i_1},\cdots,x_{i_n})=F_{t_1,\cdots,t_n} (x_1,\cdots,x_n),$$

no qual $ (i_1,\cdots,i_n) $ é qualquer permutação de $ (1,\cdots,n) $. Estas relações são denominadas condições de compatibilidade de Kolmogorov da família $ (F_{t_1,\cdots t_n}:t_i \in T,n \in \mathbb{N} ) $.

Portanto, qualquer família de variáveis aleatórias $ (X_t:t \in T) $ sobre um espaço de probabilidade determina uma classe compatível de funções de distribuição finito dimensionais. Entretanto, existe um problema básico que é a existência do espaço de probabilidade $ (\Omega, \mathcal{F},\mathbb{P}) $ suportando a família de variáveis aleatórias. Um resultado fundamental de Kolmogorov nos diz que uma família compatível de distribuições finito dimensionais nos produz um espaço de probabilidade e uma coleção de variáveis aleatórias sobre este tal que suas distribuições finito dimensionais são iguais a classe compatível de distribuições. Entretanto, extensões do teorema de Kolmogorov para espaços mais gerais do que a reta $ (X_{t}(\omega)\in \mathbb{R}) $ não necessariamente são válido [Halmos (1950), pg. 150, ex. 3]. Na seção produto de espaços mensuráveis, vamos construir uma $ \sigma $-álgebra no espaço produto. Com isso, na seção probabilidade sobre o espaço produto, construímos uma probabilidade sobre o espaço produto que suporta a coleção de variáveis aleatórias $ (X_t:t\geq 0) $.

2.1 - Produto de espaços mensuráveis

Nesta seção, vamos definir o produto qualquer de espaços mensuráveis e construir uma $ \sigma $- álgebra sobre este espaço produto de tal forma que esta $ \sigma $- álgebra tenha algumas propriedades importantes. O produto de espaços mensuráveis é utilizado em diversas aplicações na teoria de probabilidade, como a construção de processos estocásticos, tais como a cadeia de markov e o movimento browniano.

Considere uma classe arbitrária de conjuntos $ ( \Omega_t : t \in T ) $ com $ \Omega_t \neq \emptyset $ para todo $ t \in T $, no qual $ T $ é um conjunto de índices. O espaço produto pode ser definido como

$$ \prod_{t \in T} \Omega_t \ = \ \left( { conjunto~das~famílias} \ w = (w_t : t \in T ) \ { com } \ w_t \in \Omega_t \right). $$

Para qualquer $ S \subset T $, também denotamos o espaço produto por $ \prod_S \Omega_s $ o espaço produto dos conjuntos $ \left( \Omega_s : s \in T \right) $. Em particular se $ \Omega_t = \Omega \ \forall t \in T $ denotaremos o espaço produto por $ \prod_{t \in T} \Omega_t \ = \Omega^T $ que é denominado o espaço das aplicações $ w : T \to \Omega $.

Exemplo 2.2.1

Considere $ T = (1,2,3) $, com $ \Omega_t = \mathbb{R}, \ \ \forall t \in T $. Então

$$\prod_{t=1}^3 \Omega_t = \prod_{t= 1}^3 \mathbb{R} = \mathbb{R}^3$$

Exemplo 2.2.2

Considere $ T = \mathbb{N} $, com $ \Omega_t = \mathbb{R}, \ \ \forall t \in T $. Então

$$ \prod_{t\in T} \Omega_t = \prod_{t\in\mathbb{N}} \mathbb{R} = \mathbb{R}^{\infty}=(\omega=(\omega_1,\omega_2,\cdots):-\infty< \omega_i<\infty,i=1,2,\cdots), $$

corresponde ao espaço das sequências ordenadas de números reais.

A seguir faremos algumas definições que serão utilizadas na construção da $ \sigma $-álgebra produto.

Definição 2.2.1

Dada um classe arbitrária de conjuntos $ ( \Omega_t : t \in T) $, no qual T é um conjunto de índices qualquer, definimos

a- aplicação coordenada em $ s \in T $ : a transformação $ X_s : \prod_T \Omega_t \to \ \Omega_s $, tal que $ X_s (w) = w_s $ para todo $ w\in \prod_T \Omega_t $. Esta aplicação pode ser interpretada como o estado da trajetória $ w $ no instante s.

b- seção : Para qualquer subconjunto $ S \subset T $, a seção para $ w_S = ( \omega_s : s \in S ) $ de uma parte $ A \in \prod_T \Omega_t \ \hbox{em} \ \prod_{u \in S^c } \Omega_u $ é definido por:

$$ A_{\omega_S } = ( ( \omega_u : u \in S^c ) :( \omega_t : t \in T ) \in A ) $$

c- cilindro : Uma parte $ A \in \prod_T \Omega_t $ é denominado cilindro de base B em $ \prod_{s \in S } \Omega_s $, com $ S \subset T $, se este for da forma:

$$ A \ = \ B \times \prod_{u \in S^c } \Omega_u $$

Portanto A é um cilindro de base B em $ \prod_{s \in S} \Omega_s $, se e só se, suas seções $ A_{\omega_{S^c}} $ são independentes de $ \omega_{S^c } $, no qual $ A_{\omega_{S^c}} = B $.

d- retângulo : Um retângulo em $ \prod_T \Omega_t $ é um subconjunto da forma:

$$ \prod_T A_t \ = \ ( \omega \in \prod_T \Omega_t : \omega_t \in A_t \ (t \in T ) ) $$

no qual $ A_t = \Omega_t $ exceto um número finito de $ t \in T $.

e- projeção : Para todo $ S \subset T $ e $ A \in \prod_T \Omega_t $, a transformação

$$ \pi_S (A) = ( ( \omega_s :s \in S ) :A_{\omega_S} \neq \emptyset ) $$

é denominado projeção da parte A nas coordenadas de S.

Para fins ilustrativos, vamos exemplificar as definições anteriores.

Exemplo 2.2.3

No caso do espaço das sequências ordenadas de números reais, denotada por $ \mathbb{R}^{\infty} $, a transformação coordenada $ X_n:\mathbb{R}^{\infty}\rightarrow \mathbb{R} $ é tomada na forma $ X_n(\omega)=\omega_n $, no qual $ \omega=(\omega_1,\omega_2,\cdots)\in \mathbb{R}^{\infty} $. Para qualquer subconjunto $ S\subset \mathbb{N} $, a seção para $ \omega_{S}=(\omega_s:s\in S) $ de uma parte $ A\subset \mathbb{R}^{\infty} $ em $ \mathbb{R}^{S^c} $ é dada por

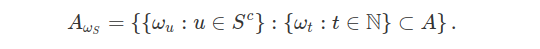
Da mesma forma, dado $ B\subset \mathbb{R}^S $, um cilindro de base $ B $ é dado por $ A=B\times \mathbb{R}^{S^c} $. Por exemplo, se $ S=(1,2,\cdots,n) $, temos que $ B\subset \mathbb{R}^n $ e assim, $ A $ é um cilindro com base no $ \mathbb{R}^n $ na forma

$$A=B\times\mathbb{R}\times \mathbb{R}\times \cdots .$$

Além disso, um retângulo em $ \mathbb{R}^{\infty} $ é um subconjunto na forma

$$ \prod_{t\in \mathbb{N}}A_t=\left(\omega=(\omega_1,\omega_2,\cdots)\in \mathbb{R}^{\infty}:\omega_t\in A_t,t\in T\right), $$

no qual $ A_t=\mathbb{R} $ exceto um número finito de índices $ t \in \mathbb{N} $. Assim, ao tomarmos $ (A_1,A_2,\cdots ,A_n) $ subconjuntos dos números reais, obtemos que $ R=A_1\times A_2\times \cdots \times A_n \times \mathbb{R}\times \mathbb{R}\times \cdots $ é um retângulo de lados $ (A_1,\cdots ,A_n) $.

Para construir a $ \sigma $-álgebra produto, vamos usar as mesmas ideias que são utilizadas para construção da topologia produto. A principal exigência para a construção da topologia produto é que esta deve ser a menor topologia que faz cada aplicação coordenada contínua. Aqui, vamos trocar continuidade por mensurabilidade. Desta forma, queremos definir uma $ \sigma $-álgebra produto nos quais as transformações coordenadas sejam mensuráveis. Para isto, vamos definir a $ \sigma $-álgebra produto através da classe dos retângulos com lados mensuráveis.

Proposição 2.1.1

Considere $ ((\Omega_t , \mathfrak{F}_t ) : t \in T) $ uma família de espaços mensuráveis. Então o conjunto de todos os retângulos mensuráveis de $ \prod_T \Omega_t $, isto é, todos os retângulos $ \prod_T A_t $ tais que $ A_t \in \mathfrak{F}_t $, com $ A_t = \Omega_t $ exceto um número finito de t’s, formam uma semi-álgebra.

Demonstração

Vamos denotar por $ C $ a classe de todos os retângulos mensuráveis. Na sequência, vamos mostrar que a classe $ C $ é uma semi-álgebra. Sabemos que $ \prod_T \Omega_t $ é um retângulo mensurável, para isto basta tomarmos $ \Omega_t = A_t $ para todo $ t\in T $. Da mesma forma, o conjunto $ \emptyset $ é um conjunto um retângulo mensurável, pois basta tomarmos $ A_t \ = \ \emptyset $ para algum $ t \in T $.

Agora, vamos mostrar que a classe $ C $ é fechada por intersecção finita. Com esta finalidade, tomamos os retângulos mensuráveis $ B_1 \ e \ B_2 $, no qual $ B_i $ tem $ n_i $ componentes diferente de $ \Omega_t $, para $ i=1,2 $. Sem perda de generalidade podemos assumir que $ n_1 \leq n_2 $, assim temos que

$$B_1 \cap B_2 = (\prod_T A_t )\cap (\prod_T F_t) = $$

$$ = \left[ (A_{t_1} \times \dots \times A_{t_{n_1}}) \times \prod_{t \neq t_1 , \dots t_{n_1}} \Omega_t \right] \cap \left[ (F_{t_1 } \times \dots \times F_{t_{n_2}} ) \times \prod_{t \neq t_1 , \dots t_{n_2}} \Omega_t \right] = $$

$$ = \left[ (A_{t_1 }\cap F_{t_1 }) \times \dots \times (A_{t_{n_1}}\cap F_{t_{n_1}})\times (\Omega_{t_{n_1+1}}\cap F_{t_{n_1+1}})\times (\Omega_{t_{n_2}}\cap F_{t_{n_2}}))\times \prod_{t \neq t_1 , \dots t_{n_2}} \Omega_t \right] \in C.$$

Com isso concluímos que $ C $ é fechada por intersecção finita. Para finalizar, vamos mostrar que o complementar é união finita disjunta de elementos de $ C $. Para isto, tomamos,

$$A = A_1 \times A_2 \times \prod_{t\neq t_1 , t_2 } \Omega_t.$$

Então, temos que

$$A^c = A^c_{t_1 } \times A_{t_2 } \times \prod_{t\neq t_1 , t_2 } \Omega_t\cup A^{c}_{t_2}\times \prod_{t\neq t_2 } \Omega_t.$$

Assim, segue a proposição.

O ponto principal para a demonstração desta proposição concentra-se na restrição ‘'$ A_t = \Omega_t $ exceto para um número finito de índices t’', na definição de retângulo mensurável.

Assim, construímos uma semi-álgebra via os retângulos mensuráveis. Na sequência, acrescentando a classe dos retângulos mensuráveis uniões finitas (disjuntas 2 a 2) de retângulos mensuráveis obtemos uma álgebra. A álgebra dos retângulos mensuráveis será denotada por $ \mathcal{E} $. A $ \sigma $-álgebra gerada por esta álgebra, denotada por:

$$\beta^T=\bigotimes_T \mathcal{F_t}=\sigma(\mathcal{E})$$

é denominada $ \sigma $-álgebra produto. Para todo $ S \subset T $, vamos denotar por $ \beta^S $ a $ \sigma $-álgebra produto sobre o espaço $ \prod_S \Omega_s $. Por construção $ \beta^S $ é a menor $ \sigma $-álgebra que contém os retângulos mensuráveis. Com isso construímos o espaço mensurável produto

$$\prod_T (\Omega_t , \mathcal{F_t} ) = (\prod_T \Omega_t , \beta^T ).$$

Exemplo 2.2.4

No caso do $ \mathbb{R}^{\infty} $, temos que a $ \sigma $-álgebra gerada pelos retângulos mensuráveis será denotada por $ \beta^{\infty} $. Assim, concluímos que

$$\prod_{\mathbb{N}}(\mathbb{R},\mathcal{F})=(\mathbb{R}^{\infty},\beta^{\infty}),$$

no qual $ \mathcal{F} $ é a $ \sigma $-álgebra de Borel de $ \mathbb{R} $. Dado $ n \in \mathbb{N} $ um número natural, a construção da $ \sigma $-álgebra produto no $ \mathbb{R}^n $ através de retângulos mensuráveis está descrita em Distribuição de Probabilidade no $ \mathbb{R}^n $ e pode ser visto como um caso particular da contrução acima.

A principal característica da $ \sigma $-álgebra produto é que esta foi construída a partir dos retângulos mensuráveis e então, a partir de conjuntos que dependem apenas de um número finito de coordenadas. Na sequência, vamos explorar esta característica para apresentar algumas propriedades interessantes para a $ \sigma $-álgebra produto. Inicialmente, precisamos verificar se nossa forma de construção atende ao propósito básico de que esta é a menor $ \sigma $-álgebra cujas aplicações coordenadas sejam mensuráveis. Considere a aplicação coordenada $ X_s : \prod_T \Omega_t \to \Omega_s $, então

$$ \forall A \in {\cal F_s} \rightarrow X_{s}^{-1}(A) = A \times \prod_{t \neq s} \Omega_t $$

é um retângulo mensurável. Portanto, concluímos que $ \beta^T $ é a menor $ \sigma $-álgebra cujas aplicações coordenadas são mensuráveis. Além disso, a equação acima nos apresenta um fato importante, pois

$$ A \times \prod_{t \neq s} \Omega_t $$

é um cilindro de base $ A \in \mathcal{F_s} $. Com esta observação, podemos elaborar uma outra forma de construção da $ \sigma $-álgebra produto via os cilindros mensuráveis de base com dimensão finita. Esta estratégia foi aplicada na construção do espaço de Cantor $ S^\infty $ com sua respectiva $ \sigma $-álgebra produto $ \mathcal{F} $.

Para isto, introduzimos a seguinte notação,

$$ D ~ = ~ ( S \subset T ~ : ~ S ~ {finito} ) ~ ~ \text{e} ~ ~ C_S ~ = ~ ({família~dos~cilindros~com~base~em} ~ ~ \beta^S)~ ~ ; ~ ~ S\in D. $$

Para todo $ S \subset T $, a projeção coordenada $ X_{S} $ leva elementos de $ \prod_T \Omega_t $ em elementos de $ \prod_{S} \Omega_s $. Agora, se tomarmos $ S \in D $ e $ B \in \beta^S $, obtemos que

$$X_{S}^{-1} (B) ~ = ~ B \times \prod_{t \not \in S} \Omega_t $$

é um cilindro de base $ B \in \beta^S $. Desta forma, temos que $ C_S=(X^{-1}(B):B\in \beta^S) $. Vamos utilizar esta notação para denotarmos os cilindros mensuráveis no espaço produto. Na sequência, vamos mostrar como podemos obter a $ \sigma $-álgebra produto via os cilindros mensuráveis de dimensião finita.

Lema 2.1.1

A classe de subconjuntos $ \prod_T \Omega_t $, definida por

$$\mathcal{A}=\cup_{S\in D}C_S$$

é uma álgebra. Além disso, temos $ \beta^T=\sigma(\mathcal{A}) $.

Demonstração

Vamos mostrar que $ {\cal A} $ é uma álgebra. Sabemos que $ \emptyset, ~ \Omega^T ~ \in ~ {\cal A} $, pois

$$ \emptyset= \emptyset \times \prod_{t \neq t_1} \Omega_t ~ = ~ X_{(t_1)}^{-1}( \emptyset) ~ ~ \text{e} ~ ~ \Omega^T=\Omega_{t_1} \times \prod_{t \neq t_1} \Omega_t ~ = ~ X_{(t_1)}^{-1}(\Omega_{t_1}) ;; ;;; \forall ~ t_1 \in T.$$

Na sequência, tomamos $ A_1, A_2 \in \mathcal{A} $, na forma

$$A_1=X_{S_1}^{-1}(B_1) ~ ~ \text{e} ~ ~ A_2=X_{S_2}^{-1}(B_2)$$

com $ B_i\in \beta^{S_i} $, no qual $ S_i \in D $ para $ i=1,2 $. Assim, obtemos que

$$ A_1 \cap A_2=X_{(S_1 \cup S_2)}^{-1} (B_1 \cap B_2).$$

Agora, para todo $ A=X_{S}^{-1}(B) $, temos que

$$A^c =\left(X_{S}^{-1}(B)\right)^c=X_{S}^{-1}(B^c).$$

Com isso, concluímos que $ \mathcal{A} $ é uma álgebra.

Na sequência, vamos mostrar que $ \sigma(\mathcal{A}) = \beta^T $. Para isto, basta mostrarmos que $ C_{S} \subset \beta^T $ para todo $ S\in D $. Desde que a classe de conjuntos $ \mathcal{G}=(B\in\beta^S:X^{-1}_{S}(B)\in \beta^T) $ é uma $ \sigma $-álgebra e contém os retângulos mensuráveis, concluímos que $ X^{-1}_{S}(B)\in \beta^S $ para todo $ B\in \beta^S $. Portanto, concluímos o lema.

Na sequência, apresentamos mais caracterizações da $ \sigma $-álgebra produto. Denotamos por $ \mathcal{L} $ a classe de todos os subconjuntos finitos ou enumeráveis de índices. Para todo $ S\in \mathcal{L} $, definimos a projeção coordenada $ X_{S}:\prod_T \Omega_t \rightarrow \prod_S \Omega_s $ por $ X_{S}((\omega_t:t\in T))=(\omega_s:s\in S) $. Denotamos por $ \mathcal{H}_{S}=(X^{-1}_{S}(B):B\in \beta^S) $ a classe dos cilindros com base em $ \beta^S $, no qual $ S $ é um subconjunto finito ou enumerável de índices $ (S\in \mathcal{L}) $. Com esta notação, obtemos a seguinte proposição.

Proposição 2.1.2

A classe de de conjuntos $ \mathcal{F}=\cup_{S\in \mathcal{L}}\mathcal{H}_{S} $ é uma $ \sigma $-álgebra que coincide com a $ \sigma $-álgebra produto $ \beta^T $.

Demonstração

Obviamente que o vazio e $ \prod_T \Omega_t $ estão em $ \mathcal{F} $. Seja $ A\in \mathcal{F} $. Então, existe $ S\in \mathcal{L} $ e $ B\in \beta^S $ tal que $ A=X_{S}^{-1}(B) $. Desta forma, temos que $ A^c=[X^{-1}_{S}(B)]^c=X^{-1}_{S}(B^c)\in \mathcal{F} $, pois $ B^c\in \beta^S $. Na sequência, tomamos $ A_1, A_2, \cdots \in \mathcal{F} $. Então, existe $ S_i\in \mathcal{L} $ e $ B_i\in \beta^{S_i} $ tal que $ A_i=X^{-1}_{S}(B_i) $ para todo $ i=1,2,\cdots $. Com isso, obtemos que

$$\cup_{i=1}^{\infty}A_i=\cup_{i=1}^{\infty}X^{-1}_{S_i}(B_i)=X^{-1}_{\cup_i S_i}\left(\cup_{i=1}^{\infty}B_i\right)\in \mathcal{F},$$

pois temos que união enumerável de conjuntos enumeráveis é enumerável e $ \cup_i B_i \in \beta^{\cup_i S_i} $. Portanto, obtemos que $ \mathcal{F} $ é uma $ \sigma $-álgebra.

Na sequência, vamos mostrar que $ \mathcal{F} $ coincide com a $ \sigma $-álgebra produto $ \beta^T $. Desde que $ \beta^T=\sigma(\mathcal{A})\subset \mathcal{F} $, basta mostrarmos que $ X_{S}^{-1}(B)\in \beta^T $, para todo $ B\in \beta^S $ e $ S\in \mathcal{L} $. Para isto, dados $ S_1,S_2\in \mathcal{L} $ subconjuntos de índices tais que $ S_1\subset S_2 $, definimos a projeção coordenada $ X_{S2,S_1}:\prod_{t\in S_2} \Omega_t \rightarrow \prod_{u\in S_1} \Omega_u $ por $ X_{S_2,S_1}((\omega_t:t\in S_2))=(\omega_u :u\in S_1) $. Considere $ S\in \mathcal{L} $ um subconjunto enumerável de índices e $ S^{\prime} \subset S $ um subconjunto finito. Então, para todo $ B\in \beta^{S^{\prime}} $, sabemos que $ X^{-1}_{S,S^{\prime}}(B)\in \beta^{S} $. Além disso, temos que $ X_{S}^{-1}\left(X^{-1}_{S,S^\prime}(B)\right)=X^{-1}_{S^\prime}(B). $ Desde que a classe $ \mathcal{G}=(H\in \beta^S:X^{-1}_{S}(H)\in \beta^{\infty}) $ é uma $ \sigma $-álgebra e contém os cilindros de base finita, concluímos que $ \mathcal{G}=\beta^S $. Portanto, segue o lema.

A seguir, fechamos esta seção apresentando consequências da proposição acima.

Corolário 2.1.1

Se tomarmos o espaço produto $ (\prod_T \Omega_t , \beta^T) $ e $ S \subset T $, obtemos que os espaços mensuráveis $ (\Omega^S, \beta^S) $ e $ (\Omega^{S^c}, \beta^{S^c}) $ tem como produto $ (\prod_T \Omega_t, \beta^T) $ e toda seção

$$ A_{w_S} ~=~ \left( (w_u : u \in S^c ) : ( w_t : t \in T ) \in A \right) $$

com $ A \in \beta^T $ é mensurável em $ (\prod_{S^c} \Omega_u, \beta^{S^c}) $,

Em particular, se $ A $ é um cilindro em $ \prod_T \Omega_t $ com base $ B $ em $ \prod_S \Omega_s $, segue que $ A $ é mensurável em $ \beta^T $ se, e só se, $ B $ é mensurável em $ \beta^S $. Além disso, para toda função $X: \prod_{T} t \rightarrow \Bbb{R}$ mensurável, a seção

$$ X_{ ( w_S )} (w_{S^c}) ~ = ~ X \left[ w_{S} , w_{S^c} \right] $$

é mensurável sobre $ (\prod_{S^c} \Omega_u , \prod_{S^c} \beta_u) $.

Demonstração

Vamos mostrar que $ \beta^S\otimes \beta^{S^c}=\beta^T $. Se tomarmos $ A_1 \in \beta^{S} $ e $ A_2 \in \beta^{S^c} $, segue da proposição acima que, existe $ S_1,S_2 \subset T $ enumeráveis, tal que

$$ A_1 \times A_2 ~ \in ~ \beta^{S_1 \cup S_2} ~ \subset ~ \beta^{T} $$

Então,

$$ \beta^{S} \otimes \beta^{S^c} ~ \subset ~ \beta^T $$

Por outro lado, se tomarmos $ A \in \beta^T $, existe $ S^{\prime} \subset T $ enumerável, tal que $ A \in \beta^{S^{\prime}} $. Assim, definindo

$$ S_1 ~ = ~ S^{\prime} \cap S ~ ~ ~ {e} ~ ~ ~ S_{2}~ = ~ S^{\prime} \cap S^c $$

obtemos da proposição acima, que

$$ A ~ \in ~ \beta^{S_1 \cup S_2} ~ \subset ~ \beta^{S} \otimes \beta^{S^c} $$

Portanto,

$$ \beta^{S} \otimes \beta^{S^c} ~ = ~ \beta^T $$

Na sequência, se denotarmos por

$$ C_{w_S} ~ = ~ \left( A\subset\prod_T\Omega_t:A_{w_S} \in \beta^{S^c} \right) $$

com $ S \subset T $, obtemos que todo retângulo mensurável pertence a $ C_{w_S} $ e que esta classe é fechada por complementação e intersecção enumerável. Portanto,

$$ \beta^T ~ \subset ~ C_{w_S}.$$

Com isso, provamos o corolário.

Através do corolário acima, concluímos que se tomarmos $ ( S_i : i \in I ) $ uma partição de $ T $, então

$$ \prod_{T} ( \Omega_t , F_t ) ~ = ~ \prod_{i \in I} \left( \prod_{S_i} \Omega_s ,\beta^{S_i} \right) $$

Corolário 2.1.2

Todo subconjunto mensurável de $ \Omega^T $ e toda variável aleatória definida sobre $ (\Omega^T, \beta^T) $ depende somente de um número enumerável de coordenadas.

Portanto, através de uma família de espaços mensuráveis, construímos o espaço mensurável produto e estudamos algumas propriedades deste. Na próxima seção, vamos construir uma probabilidade sobre o espaço mensurável produto.

Espaços mensurável $ (\mathbb{R}^n,\beta(\mathbb{R}^n)) $

Na sequência, tomamos o espaço dos $ n $-pares ordenados $ \mathbb{R}^n=\mathbb{R}\times\mathbb{R}\times\cdots\times\mathbb{R} $. A partir dos resultados acima, vamos construir a $ \sigma $-álgebra produto no $ \mathbb{R}^n $ através de retângulos com base nos intervalos finitos.

Definição 2.1.1

O conjunto $ I=I_1\times I_2\times \cdots\times I_n $, com $ I_k=(a_k,b_k] $, definido por

$$ (x\in \mathbb{R}^n : x_k\in I_k, k=1,\dots,n) $$

é denominado de retângulo de lados $ I_i $. O conjunto de todos os retângulos I, será denotado por $ \mathcal{I} $. De forma geral, um conjunto $ A=A_1\times A_2\times \cdots\times A_n $ é chamado de retângulo de lados $ A_i $. Se $ A_i \in \beta(\mathbb{R}) $ dizemos que $ A $ é um retângulo de lados borelianos.

Definição 2.1.2

A $ \sigma $-álgebra de Borel de subconjuntos de $ \mathbb{R}^n $ é denotada por $ \beta(\mathbb{R}^n) $ e é a menor $ \sigma $-álgebra gerada por todos os retângulos de $ \mathbb{R}^n $ ($ \sigma(\mathcal{I}) $). Outra forma de gerarmos a $ \sigma $-álgebra de Borel é

$$\sigma(\beta(\mathbb{R})\times\beta(\mathbb{R})\times\cdots\times \beta(\mathbb{R}))$$

ou seja, é a menor $ \sigma $-álgebra que contém os retângulos com lados Borelianos, é comum essa $ \sigma $-álgebra ser denotada por

$$\beta(\mathbb{R})\otimes\beta(\mathbb{R})\otimes\cdots\otimes \beta(\mathbb{R})$$

Observação

É importante dizer que

$$\beta(\mathbb{R})\times\beta(\mathbb{R})\times\cdots\times \beta(\mathbb{R})\neq \beta(\mathbb{R})\otimes\beta(\mathbb{R})\otimes\cdots\otimes \beta(\mathbb{R})$$

mais do que isso $ \beta(\mathbb{R})\times\beta(\mathbb{R})\times\cdots\times \beta(\mathbb{R}) $ não é uma $ \sigma $-álgebra.

Teorema 2.1.1

$ \sigma(\mathcal{I})=\beta(\mathbb{R}^n)=\beta(\mathbb{R})\otimes\beta(\mathbb{R})\otimes\cdots\otimes \beta(\mathbb{R})=\sigma(\beta(\mathbb{R})\times\beta(\mathbb{R})\times\cdots\times \beta(\mathbb{R})) $

Demonstração

Note que o resultado é trivial se $ n=1 $. Assim sendo considere primeiramente $ n=2 $, e defina

$$ \mathcal{C}=(B_1\times B_2: B_i\in \beta(\mathbb{R}), i=1,2) $$

Note que, é óbvio que $ \mathcal{I}\subset \mathcal{C} $, logo é imediato que

$$\beta(\mathbb{R}^2)=\sigma(\mathcal{I})\subset \sigma(\mathcal{C})=\beta(\mathbb{R})\otimes\beta(\mathbb{R}).$$

Assim, basta mostrarmos que

$$\beta(\mathbb{R})\otimes\beta(\mathbb{R})\subset\beta(\mathbb{R}^2)$$

Para isso, vamos mostrar que dado uma classe $ \mathfrak{C} $ de subconjuntos de $ \mathbb{R} $, e seja $ B\subset\mathbb{R} $, temos que

$$ \mathfrak{C}\cap B=(A\cap B:A\in\mathfrak{{C}}). $$

Claro que, como $ \mathfrak{C}\subset \sigma(\mathfrak{C}) $ então

$$\mathfrak{C}\cap B\subset \sigma(\mathfrak{C})\cap B$$

Como $ \sigma(\mathfrak{C})\cap B $ é uma $ \sigma $-álgebra temos então que

$$\sigma(\mathfrak{C}\cap B)\subset \sigma(\mathfrak{C})\cap B$$

Agora vamos mostrar

$$\sigma(\mathfrak{C})\cap B\subset \sigma(\mathfrak{C}\cap B) $$

Para isso considere $ \mathcal{C}_B=(A\in\sigma(\mathfrak{C}):A\cap B\in \sigma(\mathfrak{C}\cap B)) $, a qual é uma $ \sigma $-álgebra, portanto

$$\mathfrak{C}\subset\mathcal{C}_B\subset \sigma(\mathfrak{C})$$

O que implica que $ \mathcal{C}_B= \sigma(\mathfrak{C}) $ o que implica que

$$A\cap B\in \sigma(\mathfrak{C}\cap B)$$

para todo $ A\in\mathfrak{C} $ e consequentemente $ \sigma(\mathfrak{C})\cap B\subset \sigma(\mathfrak{C}\cap B) $. O que finalmente implica que $ \mathfrak{C}\cap B=(A\cap B:A\in\mathfrak{{C}}) $. Com isso em mente, considere os seguinte conjuntos $ \mathcal{B}\times \mathbb{R}=(B\times \mathbb{R}| B\in\beta(\mathbb{R})) $ e $ \mathbb{R}\times \mathcal{B}=(\mathbb{R}\times B| B\in\beta(\mathbb{R})) $.

Então dado $ B_1\times B_2 $, com $ B_1,B_2\in \beta(\mathbb{R}) $, temos que

$$B_1\times B_2=(B_1\times \mathbb{R})\cap (\mathbb{R}\times B_2) \in \sigma(I_1\times \mathbb{R})\cap (B_2\times \mathbb{R})= \sigma((I_1\times \mathbb{R})\cap (B_2\times \mathbb{R}))\subset\sigma ((I_1\times \mathbb{R})\cap (I_2\cap \mathbb{R}))=\sigma(\mathcal{I})$$

no qual, $ I_i $ é o conjunto de todos os intervalos de $ \mathbb{R} $. Portanto o resultado segue.

Espaço mensurável $ (\mathbb{R}^\infty,\beta(\mathbb{R}^\infty) $

Este espaço mensurável é um dos espaços mais importante na teoria de probabilidade, pois é base para a construção de diversos modelos. Dizemos que $ x\in \mathbb{R}^\infty $ se $ x=(x_1,x_2,\dots) $ com $ -\infty< x_i< \infty, k\in\mathbb{N} $. Denotamos por $ I_k=(a_k,b_k] $ um intervalo e $ B_k $ um boreliano em $ \beta(\mathbb{R}) $. Nesse caso tomamos as seguintes classes de cilindros de base finita

$$ C(I_1\times\dots\times I_n)=(x\in\mathbb{R}^\infty: x=(x_1,x_2,\dots), x_1\in I_1,\dots,x_n\in I_n), $$

$$ C(B_1\times\dots B_n)=(x\in\mathbb{R}^\infty: x=(x_1,x_2,\dots), x_1\in B_1,\dots,x_n\in B_n) $$

$$ C(B^n)=(x\in\mathbb{R}^\infty: x=(x_1,x_2,\dots,x_n)\in B^n) $$

no qual $ B^n $ é um boreliano de $ \beta(\mathbb{R}^n) $. É importante notarmos que cada cilindro na forma $ C(B_1\times\dots B_n) $, ou mesmo $ C(B^n) $, pode ser definido como um cilindro com base em $ \mathbb{R}^{n+k} $, para qualquer $ k\in \mathbb{N} $, pois

$$C(B_1\times\dots B_n)=C(B_1\times\dots B_n\times \underbrace{\mathbb{R}\times\dots\times\mathbb{R}}_{k~ vezes}) ~ ~ \text{e} ~ ~ C(B^n)=C(B^{n+k})$$

no qual $ B^{n+k}=B^n\times \underbrace{\mathbb{R}\times \dots \times \mathbb{R}}_{k~vezes} $.

É fácil vermos que as classes de cilindros na formas $ C(B_1\times\dots B_n) $ e $ C(B^n) $ são álgebras, pois $ \emptyset \in C(B_1\times\dots B_n) $ e $ \emptyset \in C(B^n) $. Além disso, também é fácil observarmos que a união disjuntas destes cilindros também é um cilindro. Denotamos por $ \mathcal{A} $, $ \mathcal{A}_1 $ e $ \mathcal{A}_2 $ a álgebra gerada respectivamente pelas classes de cilindros $ C(I_1\times\dots\times I_n) $, $ C(B_1\times\dots B_n) $ e $ C(B^n $. Sejam $ \beta(\mathbb{R}^\infty) $, $ \beta_1(\mathbb{R}^\infty) $ e $ \beta_2(\mathbb{R}^\infty) $ a menor $ \sigma $-álgebra que contem estas classes de cilindros $ C(I_1\times\dots\times I_n) $, $ C(B_1\times\dots B_n) $ e $ C(B^n) $ respectivamente. Por construção, temos que

$$\beta(\mathbb{R}^\infty)\subset \beta_1(\mathbb{R}^\infty)\subset \beta_2(\mathbb{R}^\infty),$$

pois temos que $ C(I_1\times\dots\times I_n)\subset C(B_1\times\dots B_n)\subset C(B^n) $. Mostraremos que na verdade essas $ \sigma $-álgebras são identicas.

Teorema 2.1.2

$ \beta(\mathbb{R}^\infty)= \beta_1(\mathbb{R}^\infty)= \beta_2(\mathbb{R}^\infty) $

Demonstração

Para mostrar isso, como $ \beta(\mathbb{R}^\infty)\subset \beta_1(\mathbb{R}^\infty)\subset \beta_2(\mathbb{R}^\infty) $, basta mostrarmos que

$$\beta_2(\mathbb{R}^\infty)\subset \beta(\mathbb{R}^\infty)$$

De fato, considere o conjunto

$$ \mathcal{C}_n=(A\subset \mathbb{R}^n: (x\in \mathbb{R}^\infty:(x_1,x_2,\dots,x_n)\in A)\in \beta(\mathbb{R}^\infty)) $$

para $ n\in \mathbb{N} $. Seja $ B^n\in \beta(\mathbb{R}^n) $. Então,

$$B^n\in \mathcal{C}_n\subset \beta(\mathbb{R}^\infty)$$

pois $ (x\in\mathbb{R}^\infty: (x_1,x_2,\dots,x_n)\in B^n)\in \beta(\mathbb{R}^\infty) $. Mas $ \mathcal{C}_n $ também é uma $ \sigma $-álgebra de $ \mathbb{R}^\infty $, e portanto

$$\beta(\mathbb{R}^n)\subset\sigma(\mathcal{C}_n)=\mathcal{C}_n\subset\beta(\mathbb{R}^\infty)$$

Consequentemente pela definição de $ \beta_2(\mathbb{R}^\infty) $, temos que

$$\beta_2(\mathbb{R}^\infty)\subset\mathcal{C}_n\subset\beta(\mathbb{R}^\infty)$$

E portanto o resultado segue.

Daqui por diante descreveremos $ \beta(\mathbb{R}^\infty) $ como os conjuntos de Borel em $ \mathbb{R}^\infty $.

Espaço mensurável $ (\mathbb{R}^T,\beta(\mathbb{R}^T)) $

O espaço $ \mathbb{R}^T $ no qual T é um conjunto arbitrário é uma coleção de funções reais $ (x:T \rightarrow \mathbb{R}) $ com domínio em $ T $ e imagem na reta. Em geral, estamos interessados no caso em que $ T $ é um conjunto não enumerável do conjunto de números reais. Por simplicidade, podemos tomamos $ T=[0,\infty) $. Da mesma forma, consideramos três tipos de cilindros definidos como

$$ C_{t_1,t_2,\dots,t_n}(I_1\times\dots\times I_n)=(x\in\mathbb{R}^T: x_{t_1}\in I_1,\dots,x_{t_n}\in I_n), $$

$$ C_{t_1,t_2,\dots,t_n}(B_1\times\dots B_n)=(x\in\mathbb{R}^T: x_{t_1}\in B_1,\dots,x_{t_n}\in B_n), $$

$$ C_{t_1,t_2,\dots,t_n}(B^n)=(x\in\mathbb{R}^T: x=(x_{t_1},x_{t_2},\dots,x_{t_n})\in B^n) $$

definimos então $ I_k=(a_k,b_k] $ e $ B_k $ um boreliano de $ \beta(\mathbb{R}) $ e $ B^n $ é um boreliano de $ \beta(\mathbb{R}^n) $. Vamos então definir a $ \sigma $-álgebras geradas pelos cilindros $ \beta(\mathbb{R}^T) $, $ \beta_1(\mathbb{R}^T) $ e $ \beta_2(\mathbb{R}^T) $ geradas respectivamente $ C_{t_1,t_2,\dots,t_n}(I_1\times\dots\times I_n) $, $ C_{t_1,t_2,\dots,t_n}(B_1\times\dots B_n) $ e $ C_{t_1,t_2,\dots,t_n}(B^n) $.

É fácil ver que

$$\beta(\mathbb{R}^T)\subset \beta_1(\mathbb{R}^T)\subset \beta_2(\mathbb{R}^T)$$

É importante notar que assim como no caso anterior

$$\beta(\mathbb{R}^T)=\beta_1(\mathbb{R}^T)=\beta_2(\mathbb{R}^T)$$

Teorema 2.1.3

Seja $ T $ qualquer conjunto não enumerável. Então $ \beta(\mathbb{R}^T)=\beta_1(\mathbb{R}^T)=\beta_2(\mathbb{R}^T) $. Além disso, para todo conjunto $ A\in\beta(\mathbb{R}^T) $ existe um conjunto enumerável de índices $ t_1,t_2,\dots $ de $ T $ e um conjunto de Borel $ B\in \beta(\mathbb{R}^\infty) $ tal que

$$ A=(x\in\mathbb{R}^T: (x_{t_1},x_{t_2},\dots)\in B). $$

Demonstração

Desde que a $ \sigma $-álgebra gerada pelos retângulos coincide com a $ \sigma $-álgebra gerad pelos cilindros de base finita, concluímos que

$$\beta_1(\mathbb{R}^T)=\beta_2(\mathbb{R}^T).$$

Além disso, mostramos que a $ \sigma (I^n) $ gerada pelos intervalos do $ \mathbb{R^n} $ coincide com a $ \sigma $-álgebra de Borel do $ \mathbb{R}^n $. Assim, mostramos a igualdade entre as três $ \sigma $-álgebras. A partir da Proposição 2.1.2 obtemos o teorema.

O interessante do teorema anterior é que ele nos mostra que a $ \sigma $-algebra $ \beta(\mathbb{R}^T) $ é determinada por restrições no máximo em um conjunto enumeráveis de pontos imposta sobre as funções $ x=(x_t), ~t\in T $. Daí segue, em particular, que o conjunto

$$ A_1=(x\in\mathbb{R}^{[0,1]}: \sup x_t< C, \forall t\in [0,1]), $$

o qual depende do comportamento da função em um conjunto não-enumerável de pontos não pertence a $ \sigma $-álgebra produto $ \mathbb{R}^{[0,1]}) $. Para verificarmos isso, suponha que $ A_1\in \beta(\mathbb{R}^{[0,1]}) $. Então pelo teorema anterior existe $ (t_1^0,t_2^0,\dots) $ and um conjunto $ B^0\in \beta(\mathbb{R}^\infty) $ tal que

$$ \left(x\in\mathbb{R}^T:\sup_t x_t< C,~t\in[0,1]\right)=(x\in\mathbb{R}^{[0,1]}:(x_{t^0_1},x_{t^0_2},\dots)\in B^0). $$

Podemos então notar, que a função $ y_t=C-1 $ pertence a $ A_1 $, e consequentemente $ (y_{t_1^0},y_{t_2}^0,\dots)\in B^0 $. Agora considere a função

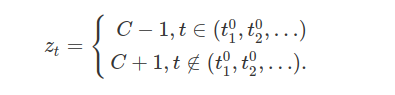
Então claro que

$$(y_{t_1^0},y_{t_2}^0,\dots)=(z_{t_1^0},z_{t_2}^0,\dots)$$

Desde que o conjunto $ A_1 $ são não-mensurável com respeito a $ \sigma $-álgebra $ \beta(\mathbb{R}^{[0,1]}) $ é o espaço de todas as funções $ x=(x_t) $ $ t\in [0,1] $ é natural que se considere como sendo a menor classe de funções para as quais esses conjuntos são mensuráveis.

Espaço mensurável $ (C(T),\beta(C(T))) $

Seja $ T=[0,1] $ e seja $ C(T) $ o espaço das funções continua $ x=(x_t) $ $ 0\leq t\leq 1 $. Esse espaço é um espaço métrico com a métrica

$$\rho(x,y)=\sup_{t\in T}|x_t-y_t|.$$

Iremos considerar duas $ \sigma $-álgebras em $ C(T) $, $ \beta(C(T)) $, gerada pelos cilindros

$$ C_{t_1,t_2,\dots,t_n}(b_1\times\dots\times b_n)=(x\in C(T):x_{t_1}< b_1,\dots,x_{t_n}< b_n), $$

a qual chamaremos $ \beta(C(T)) $ e a $ \sigma $-algebra gerada pelos abertos com respeito as métricas $ \rho(x,y) $ a qual chamaremos $ \beta_0(C(T)) $.

Vamos mostrar que ambas são idênticas, assim seja $ B=(x:x_{t_0}< b) $ claro que $ B $ é um cilindro, e ainda é aberto, disto segue

$$ (x:x_{t_1}< b_1,\dots , x_{t_n}< b_n )\in \beta_0(C(T)) $$

o que implica $ \beta(C(T))\subset \beta_0(C(T)) $.

Inversamente considere o conjunto $ B_\rho=(y\in C(T):y\in S_{\rho}(x^0)) $, no qual $ x^0 $ é um elemento de $ C(T) $ e

$$ S_{\rho}(x^0)=(x\in C:\sup_{t\in T}|x_t-x^0_t|< \rho) $$

é uma bola aberta com centro em $ x^0 $. Desde que as funções em $ C $ e são continuas,

$$ B_{\rho}=(y\in C(T): y\in S_{\rho}(x^0))=\left(y\in C(T):\max_t |y_t-x_t^0|< \rho\right)=\bigcap_{t_k}\left(y\in C(T): |y_{t_k}-x_{t_k}^0|< \rho\right)\in \beta(C(T)). $$

no qual $ t_k $ são pontos racionais de $ [0,1] $. Portanto $ \beta_0(C(T))\subset \beta(C(T)) $, o que implica $ \beta_0(C(T))=\beta(C(T)) $.

Espaço mensurável $ (D(T),\beta(D(T))) $

$ D(T) $ é o espaço das funções $ x=(x_t)_{t\in T} $ continuas as direita, com $ T=[0,1] $

Da mesma forma, como acontece com o espaço das funções contínuas, podemos introduzir uma métrica

$$ d(x,y)=\inf \left(\epsilon > 0: \exists \lambda \in \Lambda : \sup_t |x_t-y_{\lambda(t)}|\leq \epsilon \right) $$

onde $ \Lambda $ é um conjunto de funções $ \lambda =\lambda(t) $ estritamente crescente, o qual é continua de $ [0,1] $ e temos $ \lambda(0)=0 $, $ \lambda(1)=1 $.

Essa métrica foi introduzida por Skorohod e é uma métrica muito importante para esse espaço. E da mesma forma que o espaço das funções contínuas a $ \sigma $-algebra gerada pelos abertos da topologia de Skorohod é igual a $ \sigma $-algebra gerada pelos cilindros de $ D(T) $.

2.2 - Probabilidade sobre o espaço produto

Nesta seção vamos construir uma probabilidade sobre o espaço produto de espaços mensuráveis. Considere que o espaço de probabilidade $ (\Omega_t , \mathcal{F_t}, \mathbb{P}_t) $ seja compacto para todo $ t \in T $, no qual $ T $ é uma família de índices. Denotamos por $ D=( u: u \subset T, ~ u ~\text{subconjunto finito}) $ a classe de todos os subconjuntos finitos de $ T $. Suponha que a família de probabilidades $ (\mathbb{P_u}: u \in D) $ satisfaça as condições de compatibilidade de Kolmogorov, então, vamos mostrar que existe uma única probabilidade sobre o espaço produto que estende a família de probabilidades $ (\mathbb{P_u}: u \in D) $. Como toda probabilidade no $ (\mathbb{R}^n , \beta(\mathbb{R}^n)) $ é compacta, Kolmogorov mostrou que existe uma probabilidade $ \mathbb{P} $ sobre $ (\mathbb{R}^T ,\beta^T) $ se ,e só se, a família de probabilidades $ (\mathbb{P_u}: u \in D) $ satisfaz a condição de compatibilidade.

As condições de compatibilidade de Kolmogorov podem ser expressas numa forma mais sistemática usando a seguinte abstração devido a Bochner (1955). Para ilustração, seja $ \Omega_t=\mathbb{R} $, $ T\subset [0,\infty) $ e $ \beta^u $ a $ \sigma $-álgebra de Borel do $ \mathbb{R}^u $, com $ u=(t_1, \cdots, t_n) \subset T $. Denotamos por $ \mathbb{P_{u}} $ a probabilidade de Lebesgue-Stieltjes determinada pela função de distribuição $ F_{t_1, \cdots, t_n} $, na forma

$$\mathbb{P_{u}} (A) ~ = ~ \int_{A} \cdots \int d F_{t_1, \cdots, t_n} (dx_1, \cdots, x_n) ~ ~ ; ~ ~ A \in \beta^u.$$

Então a família de distribuições $ ( F_{t_1, \cdots, t_n} : t_i \in T, i \in \mathbb{N} ) $ é equivalente ao conjunto $ (P_{u}: u \in D ) $ de probabilidades, no qual $ D $ é o conjunto de todos os subconjuntos finitos de $ T $. Portanto, vamos traduzir as condições de compatibilidade de Kolmogorov para a família de probabilidades $ (\mathbb{P_{u}}:u\in D) $.

Se $ u $ e $ v $ é um par de elementos de $ D $, denotamos por $ u < v $ a relação $ u \subset v $. Neste caso, dizemos que$ D $ é um conjunto dirigido, isto é, $ (D, < ) $ é um conjunto parcialmente ordenado e para quaisquer dois elementos de $ D $ existe um terceiro (a união) que contém ambos. Se $ u < v $ denotamos por $ \pi_{uv} $ a projeção coordenada do $ \mathbb{R}^v $ em $ \mathbb{R}^u $. Portanto, as condições de compatibilidade tomam a forma

$$ \mathbb{P_{u}} ~ = ~ \mathbb{P}_{v} \circ \pi^{-1}_{uv} \qquad \qquad (1). $$

Considere uma família de espaços mensuráveis $ ((\Omega_t, \mathcal{F_t} ) : t \in T ) $ e $ D $ o conjunto dirigido formado por todos os subconjuntos finito de $ T $. Para facilitar a notação, tomamos

$$ \Omega^u ~ = ~ \prod_{t \in u} \Omega_t ~ ~ ; ~ ~ \beta^u ~ = ~ \otimes_{t \in u} \mathcal{F_t} $$

e $ \mathbb{P_u} : \beta^u \rightarrow [0,1] $ uma probabilidade para cada $ u \in D $. A família $ ( \mathbb{P_u} : u \in D ) $ é denominada compatível se (1) é válido para todo par $ u \ < \ v $ (em $ D $). Então, dado a família $ ( (\Omega^u , \beta^u , \mathbb{P_u} , \pi_{uv}) : u < v \in D ) $, procuramos por uma probabilidade $ \mathbb{P} $ sobre o espaço produto $ (\Omega^T , \beta^T) $ tal que sua $ u $-marginal seja $ \mathbb{P_u} $ para todo $ u \in D $.

A família $ ( (\Omega^u , \beta^u , \mathbb{P_u} , \pi_{uv}) : u < v \in D ) $ é denominada sistema projetivo de espaços de probabilidade se a classe $ ( \mathbb{P}_u : u \in D ) $ é compatível. Dizemos que o sistema projetivo admite um limite projetivo se existe uma probabilidade $ \mathbb{P} $ sobre $ (\Omega^T , \beta^T) $, tal que

$$ \mathbb{P_{u}} ~ = ~ \mathbb{P} \circ \pi^{-1}_{u} ,$$

para todo $ u \in D $

Na sequência, vamos demonstrar o teorema de Kolmogorov-Bochner em etapas. Para isto, vamos utilizar a notação e resultados da seção anterior, sobre a construção de espaços produto. Mais uma vez, dado uma família de espaços mensuráveis $ ((\Omega_t , \mathcal{F_t} : t \in T ) $, construímos o espaço mensurável produto

$$ \prod_{T} ( \Omega_t , \mathcal{F_t}) ~ = ~ ( \Omega^T , \beta^T) $$

no qual

$$\Omega^T ~ = ~ \prod_{T} \Omega_t ~ ~ ; ~ ~ \beta^T ~ = ~ \sigma \left[ \cup_{u \in D} C_u \right] $$

e

$$C_u ~ = ~ \left( A \subset \Omega^T : A = \pi^{-1}_u (B), ~ B \in \beta^u \right)$$

corresponde a classe dos cilindros com base em $ \beta^u $. Vamos denotar por

$$ \mathcal{A} ~ = ~ \cup_{u \in D} C_u,$$

a álgebra formada pelos cilindros de base finita.

Proposição 2.2.1

Dado uma família de espaços mensuráveis $ ((\Omega_t , \mathcal{F_t} : t \in T ) $ e uma família de probabilidades $ (\mathbb{P_u} : u \in D ) $, existe uma função de conjunto $ \mathbb{P} $ sobre a álgebra $ \mathcal{A} $ satisfazendo

$$\mathbb{P_u} ~ = ~ \mathbb{P} \circ \pi^{-1}_u ~ ~ ; ~ ~ u \in D \qquad \qquad (2)$$

se, e só se, a família $ (\mathbb{P_u} : u \in D ) $ é compatível.

Demonstração

As projeções coordenadas satisfazem a regra de composição

$$\pi_{uv} \circ \pi_{v \gamma} ~ = ~ \pi_{u \gamma} $$

para todo $ u \ < v \ < \ \gamma $ com $ \pi_{uu} $ a função identidade. Suponha que existe uma função de conjunto $ \mathbb{P} $ sobre $ \mathcal{A} $ tal que

$$\mathbb{P_u} ~ = ~ \mathbb{P} \circ \pi^{-1}_u ~ ~ ; ~ ~ u \in D .$$

Então, para todo $ A \in \beta^u $ e $ u \ < \ v $ em $ D $, temos que $ \pi_{u} = \pi_{uv} \circ \pi_v $ e

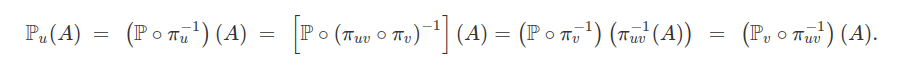
Assim, temos que

$$\mathbb{P_u} ~ = ~ \mathbb{P_v} \circ \pi^{-1}_{uv} $$

e a família $ (\mathbb{P_u} : u \in D ) $ é compatível.

Por outro lado, se a família $ (\mathbb{P_u} : u \in D ) $ é compatível, podemos construir uma função de conjunto $ \mathbb{P} $ sobre a ágebra $ \mathcal{A} $ satisfazendo (2). Para todo elemento $ A \in \mathcal{A} $, existe $ u \in D $ e $ B \in \beta^u $ tal que $ A ~ = ~ \pi^{-1}_u (B) $. Assim, definimos

$$\mathbb{P}(A) ~ = ~ \mathbb{P_u} (B) ~ ~ ; ~ ~ u \in D.$$

Na sequência, vamos mostrar que a função de conjunto $ \mathbb{P} $ está bem definida. Suponha que $ A \in \mathcal{A} $ tenha duas representações, isto é, existe $ u,v \in D $, $ B_1 \in \beta^u $ e $ B_2 \in \beta^v $, tal que

$$A ~ = ~ \pi_{u}^{-1} (B_1) ~ = ~ \pi_{v}^{-1} (B_2).$$

Como $ D $ é um conjunto dirigido, existe $ \gamma \in D $ tal que $ u \ < \ \gamma $ e $ v \ < \ \gamma $. Desde que, $ \pi_u = \pi_{u \gamma} \circ \pi_{\gamma} $ e $ \pi_v = \pi_{v \gamma} \circ \pi_{\gamma} $, temos

$$\pi_{\gamma}^{-1} \circ \pi_{u \gamma}^{-1}(B_1) ~ = ~ \pi^{-1}_u (B_1) ~ = ~ A ~ = ~ \pi^{-1}_v (B_2)~ = ~ \pi_{\gamma}^{-1} \circ \pi^{-1}_{v \gamma}(B_2) \qquad \qquad (3).$$

Além disso, como $ \pi_{\gamma} ( \Omega^T) = \Omega^{\gamma} $, a relação (3) no diz que

$$\pi_{u \gamma}^{-1}(B_1) ~ = ~ \pi^{-1}_{v \gamma}(B_2).$$

Então, utilizando a compatibilidade da família $ (\mathbb{P_u} : u \in D ) $, obtemos

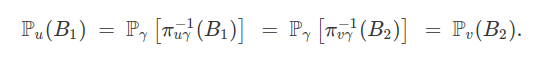
Portanto, a função de conjunto $ \mathbb{P} $ definida sobre $ \mathcal{A} $ está bem definida. Com isso, concluímos a proposição.

Através desta proposição, definimos uma função de conjunto $ \mathbb{P} $ sobre a álgebra $ A $, na forma

$$\mathbb{P}(A) ~ = ~ \mathbb{P_u} (B) \quad (4)$$

no qual $ A= \pi^{-1}_u (B) $ para algum $ u \in D $ e $ B \in \beta^u $. Na sequência, vamos mostrar que esta função de conjunto satisfaz algumas propriedades interessantes.

Lema 2.2.1

A função de conjunto $ \mathbb{P} $ é não negativa, finitamente aditiva sobre a álgebra $ \mathcal{A} $ e $ \mathbb{P}(\Omega^T) = 1 $.

Demonstração

Desde que $ \mathbb{P_u} $ é não negativa $ (u \in D) $, obtemos que $ \mathbb{P} $ é não negativa. Se tomarmos $ A $ e $ B $ em $ \mathcal{A} $ disjuntos, existem $ u,v \in D $, $ A_1 \in \beta^u $ e $ B_1 \in \beta^v $, tais que

$$A ~ = ~ \pi_u^{-1} (A_1) ~ ~ ; ~ ~ B ~ = ~ \pi_{v}^{-1} (B_1).$$

Como $ D $ é um conjunto dirigido, existe $ \gamma \in D $ tal que $ u \ < \ \gamma $ e $ v \ < \ \gamma $,com

$$A ~ = ~ \pi_{\gamma}^{-1} \left[ \pi^{-1}_{u \gamma} (A_1) \right] ~ ~ ; ~ ~ B ~ = ~ \pi_{\gamma}^{-1} \left[ \pi^{-1}_{v \gamma} (A_2) \right].$$

Ao denotarmos por

$$A_{\gamma} ~ = ~ \pi_{u \gamma}^{-1}(A_1) ~ ~ ; ~ ~ B_{\gamma} ~ = ~ \pi^{-1}_{v \gamma} (A_2),$$

obtemos que $ A_{\gamma} $ e $ B_{\gamma} $ são elementos de $ \beta^{\gamma} $ e disjuntos, pois $ A $ e $ B $ são disjuntos. Com isso, temos que

Ao utilizarmos a equação (3), temos

$$\mathbb{P} \left( \Omega^T \right) ~ = ~ \mathbb{P_{u}} \left( \Omega^{u} \right) ~ = ~ 1 ~ ~ ; ~ ~ u \in D.$$

Com estes resultados preliminares, podemos apresentar e demonstrar uma versão do teorema de Kolmogorov-Bochner, que não utiliza hipóteses topológicas. Nossa construção está baseada no conceito de probabilidade compacta, que nos garante que a probabilidade de um conjunto da $ \sigma $-álgebra pode ser aproximado pela probabilidade de um subconjunto que pertence a uma classe compacta.

Teorema 2.2.1

Considere $ ((\Omega_t , \mathcal{F_t} : t \in T ) $ uma família de espaços mensuráveis e uma família compatível $ (\mathbb{P_u} : u \in D ) $ de probabilidades . Se, para todo $ t \in T $, a probabilidade $ \mathbb{P_t} $ é compacta. Então, o sistema projetivo $ ( (\Omega^u , \beta^u , \mathbb{P_u} , \pi_{uv} ) : u < v \in D ) $ tem um único limite projetivo.

Demonstração

Esta demonstração será baseada nos resultados de probabilidades compactas. Vamos mostrar que a função de conjunto $ \mathbb{P} $ (definida na equação (4)) é compacta com respeito a uma semi-álgebra formada por retângulos mensuráveis. Desta forma, podemos aplicar o teorema de exntensão de probabilidades compactas para mostrarmos a existência de um único limite projetivo.

Por hipótese, o espaço de probabilidade $ (\Omega_t , \mathcal{F_t} , \mathbb{P}_t) $ é compacto para todo $ t \in T $. Assim, sabemos que existe uma classe compacta $ \mathcal{C}_t $ composta de subconjuntos de $ \Omega_t $ tal que

$$ \mathbb{P}_t(A) = \sup ( P(C) : ~ C \subset A, ~ C \in \mathcal{C}_t). $$

Considere $ Y $ a classe de retângulos mensuráveis, na forma

$$C_t \times \prod_{s \neq t} \Omega_s $$

no qual $ C_t $ percorre a classe compacta $ \mathcal{C_t} $ e $ t $ percorre o conjunto de índices $ T $. Vamos mostrar que $ Y $ é uma classe compacta. Dado uma sequência $ (E_n)_{n \geq 1} \subset Y $, a intersecção

$$\bigcap_{n=1}^{\infty} E_{n} ~ = ~ \bigcap _{n=1}^{\infty} \left[ C_{t_n} \times \prod_{s \neq t_n} \Omega_s \right]$$

para $ C_{t_n} \in \mathcal{C}_{t_n} $ e $ t_n \in T $ com $ n \in \Bbb{N} $. Com isso, se tomarmos

$$ A_{t_k} ~ = ~ \bigcap_{ (n : t_n = t_k )} C_{t_n} $$

para $ k=1,2, \cdots $ , temos

$$\bigcap_{n=1}^{\infty} E_n ~ = ~ \bigcap _{k=1}^{\infty} \left[ A_{t_k} \times \prod_{s \neq t_k} \Omega_s \right] $$

Se $ \cap E_n = \emptyset $, existe pelo menos um $ A_{t_k} $ vazio, por exemplo $ A_{t_i} $. Como $ \mathcal{C}_{t_i} $ é uma classe compacta, existe um subconjunto finito $ J \subset (n : t_n = t_i ) $, tal que

$$ \bigcap_{J} C_{t_n} ~ = ~ \emptyset $$

o que implica em

$$\bigcap_{J} E_n ~ = ~ \emptyset $$

Com isso, a classe $ Y $ formada pelos retângulos mensuráveis é compacta. Além disso, a classe $ \mathcal{C} $ obtida via intersecções enumeráveis de elementos de $ Y $ também é compacta. Agora, considere $ A $ um retângulo mensurável, com base

$$\prod_{i=1}^{n} A_{t_i} $$

tal que $ A_{t_i} \in \mathcal{F}_{t_i} $. Para todo $ \varepsilon > 0 $, tomamos $ C_i \in C_{t_i} $ tal que

$$C_i \subset A_{t_i} ~ ~ {e} ~ ~ \mathbb{P}_{t_i}(A_{t_i}) ~ \leq ~ \mathbb{P}_{t_i}(C_i) ~ + ~ \frac{\varepsilon}{n} .$$

Agora, o conjunto

$$C ~ = ~ \bigcap_{i=1}^{n} \left[ C_i \times \prod_{t \neq t_i} \Omega_t \right] ~ \in ~ \mathcal{C} $$

e está contido em $ A $, a álgebra gerada pelos retângulos mensuráveis. Além disso,

$$A - C ~ \subset ~ \bigcup_{i=1}^{n} \left( (A_{t_i} - C_i) \times \prod_{s \neq t_i} \Omega_s \right) .$$

Assim, utilizando a aditividade finita de $ \mathbb{P} $, temos

$$\mathbb{P}(A) ~ - ~ \mathbb{P}(C) ~ \leq ~ \sum_{i=1}^n ~ \left( \mathbb{P}_{t_i}(A_{t_i}) - \mathbb{P}_{t_i} (C_i) \right) ~ \leq ~ \epsilon $$

Portanto, fazendo $ \epsilon \rightarrow 0 $, obtemos que

$$ \mathbb{P}(A) ~ = ~ \sup \left( \mathbb{P}(C) : C \subset A , A \in C \right) $$

para todo retângulo mensurável. Assim através do teorema da classe compacta, existe uma única probabilidade $ \mathbb{P} $ definida sobre o espaço das funções $ (\Omega^T, \beta^T) $ que estende a família compatível de probabilidades $ (\mathbb{P_u}: u \in D) $.

A partir do teorema de extensão de Komogorov-Bochner, mostrarmos a existência de uma única probabilidade $ \mathbb{P} $ sobre o espaço produto $ (\Omega^T, \beta^T) $ satisfazendo:

a) $ \mathbb{P} (A) = \mathbb{P_u} (B) $, no qual $ A=\pi^{-1}_u (B) $, com $ B \in \beta^u $ para algum $ u \in D $.

b) $ \mathbb{P}(A) = \sup ( \mathbb{P} (C) : C \subset \mathcal{C}) $, para todo $ A \in \beta^T $.

A seguir, apresentamos algumas aplicações do teorema de Kolmogorov-Bochner.

Distribuicao $ (\mathbb{R}^\infty,\beta(\mathbb{R}^\infty)) $

A construção da medida de probabilidade desse espaço é similar a do espaço $ \mathbb{R}^n $ na qual pode ser encontrada na seção de probabilidade, considere os retângulos de $ \mathbb{R}^\infty $ definidos como

$$ I_n(B)=(x\in\mathbb{R}^\infty:(x_1,x_2,\dots,x_n)\in B), ~B\in\beta(\mathbb{R}^n) $$

Seja $ \mathbb{P} $ uma medida de probabilidade em $ (\mathbb{R}^\infty,\beta(\mathbb{R}^\infty)) $. Para $ n=1,2,\dots $, temos

$$\mathbb{P}_n(B)=\mathbb{P}(I_n(B)),~ B\in\beta(\mathbb{R}^n)$$

A sequência de medida de probabilidade $ \mathbb{P}_1,\mathbb{P}_2,\dots,\mathbb{P}_n $, definida respectivamente em $ ((\mathbb{R},\beta(\mathbb{R})), (\mathbb{R}^2,\beta(\mathbb{R}^2)),\dots,(\mathbb{R}^n,\beta(\mathbb{R}^n))) $, temos então a seguinte propriedade

$$\mathbb{P}_{n+1}(B\times \mathbb{R})=\mathbb{P}_n(B)$$

para $ n=1,2,\dots $

Teorema 2.2.2

Seja $ \mathbb{P}_1,\mathbb{P}_2,\dots $ uma sequência de medidas de probabilidade em $ ((\mathbb{R},\beta(\mathbb{R})), (\mathbb{R}^2,\beta(\mathbb{R}^2)),\dots) $ tal que

$$\mathbb{P}_{n+1}(B\times \mathbb{R})=\mathbb{P}_n(B)$$

Então existe uma única medida de probabilidade $ \mathbb{P} $ em $ (\mathbb{R}^\infty, \beta(\mathbb{R}^\infty)) $, tal que

$$\mathbb{P}(I_n(B))=\mathbb{P}(B), ~B\in\beta(\mathbb{R}^n)$$

para $ n=1,2,\dots $

Demonstração

Seja $ B^n\in \beta(\mathbb{R}^n) $ e seja $ I_n(B^n) $ um cilindro com base $ B^n $. Atribuímos a medida $ \mathbb{P}(I_n(B^n)) $ para o cilindro tomando

$$\mathbb{P}(I_n(B^n))=\mathbb{P}_n(B^n)$$

Vamos mostrar que em virtude da condição de consistência, essa definição é consistente, isto é, o valor de $ \mathbb{P}(I_n(B^n)) $ é independente da representação do conjunto $ I_n(B^n) $. De fato, considere o mesmo cilindro representado de duas formas

$$I_n(B^n)=I_{n+k}(B^{n+k})$$

Disto segue que se $ (x_1,\dots,x_{n+k})\in\mathbb{R}^{n+k} $, temos que

$$(x_1,\dots,x_n)\in B^n\Leftrightarrow (x_1,\dots,x_{n+k})\in B^{n+k},$$

Com isso, temos que

$$ \mathbb{P_n}(B^n)=\mathbb{P_{n+1}}\left((x_1,\dots,x_{n+1}):(x_1,\dots,x_n)\in B^{n}\right) $$

$$ =\mathbb{P_{n+1}}\left((x_1,\dots,x_{n+2}):(x_1,\dots,x_{n+1})\in B^{n}\right) $$

$$=\dots=\mathbb{P}_{n+k}(B^{n+k})$$

Seja $ \mathcal{A}(\mathbb{R}^\infty) $ denota a coleção de todos os cilindros $ \bar{B}^n=I_n(B^n) $, $ B^n\in \mathbb{R}^n $, $ n=1,2,\dots $ .

Agora seja $ \bar{B}_1,\dots,\bar{B}_k $ conjuntos disjuntos em $ \mathcal{A}(\mathbb{R}^\infty) $. Podemos assumir sem perda de generalidade que $ \bar{B}_i=I_n(B_i^n), ~i=1,\dots,k $ para algum $ n $, no qual $ B^n_1,\dots,B^n_k $ são conjuntos disjuntos em $ \beta(\mathbb{R}^n) $. Então,

$$\mathbb{P}\left(\sum_{i=1}^k \bar{B}_i\right)=\mathbb{P}\left(\sum_{i=1}^k I_n{B}^n_i\right)=\mathbb{P}_n\left(\sum_{i=1}^k B^n_i\right)= \sum_{i=1}^k\mathbb{P}_n\left( B^n_i\right)=\sum_{i=1}^k\mathbb{P}\left( \bar{B}_i\right)$$

Isto implica que a função $ \mathbb{P} $ é finitamente aditiva na algebra $ \mathcal{A}(\mathbb{R}^\infty) $. Agora precisamos mostrar $ \mathbb{P} $ é continua em zero, isto é, se a sequência de conjuntos $ \bar{B}_n\downarrow \emptyset $, $ n\rightarrow \infty $, então $ \mathbb{P}(\bar{B}_n)\rightarrow 0 $ quando $ n\rightarrow \infty $. Para isso, suponha o contrario, isto é,

$$\lim_{n\rightarrow \infty}\mathbb{P}(\bar{B}_n)=\delta> 0.$$

Suponha sem perda de generalidade que $ (\bar{B}_n) $ tem a forma

$$ \bar{B}_n=(x\in\mathbb{R}^\infty:(x_1,\dots,x_n)\in B_n)~ B_n\in \beta(\mathbb{R}^n) $$

Para demonstrar isso vamos precisar de uma propriedade da medida de probabilidade $ \mathbb{P}_n $ no espaço $ (\mathbb{R}^n,\beta(\mathbb{R}^n)) $. Se $ B_n\in \beta(\mathbb{R}^n) $, para $ \delta> 0 $ dado podemos encontrar um compacto $ A_n\beta(\mathbb{R}^n) $ dado $ A_n\subset B_n $ e

$$\mathbb{P}_n(Bn-A_n)\leq \frac{\delta}{2^{n+1}}$$

Portanto se

$$ \bar{A}_n=(x\in \mathbb{R}^\infty:(x_1,x_2,\dots,x_n)\in A_n), $$

temos que

$$\mathbb{P}(\bar{B}_n-\bar{A}_n)=\mathbb{P}_n(B_n-A_n)\leq \frac{\delta}{2^{n+1}}$$

Seja $ \displaystyle \bar{C_n}=\bigcap_{k=1}^n \bar{A_k} $ e seja $ C_n $ tal que

$$ \bar{C}_n=(x\in \mathbb{R}^\infty:(x_1,x_2,\dots,x_n)\in C_n) $$

Então, desde que o conjuntos $ \bar{B}_n $ é decrescente, obtemos

$$ \mathbb{P}(\bar{B_n}-\bar{C_n})\leq \displaystyle \sum_{k=1}^{n}\mathbb{P}(\bar{B_n}-\bar{A_k})\leq\sum_{k=1}^{n}\mathbb{P}(\bar{B_k}-\bar{A_k})\leq \frac{\delta}{2} $$

Mas por hipótese

$$\displaystyle \lim_n \mathbb{P}(\bar{B}_n)> 0$$

e portanto $ \displaystyle \lim_n\mathbb{P}(\bar{C}_n)\geq \frac{\delta}{2} $, o que contradiz o fato de que $ \bar{C}_n\downarrow 0 $.

Vamos escolher um ponto $ \bar{x}^{(n)}=(x^{(n)}_1,x^{(n)}_2,\dots)\in \bar{C}_n $. Então $ (x^{(n)}_1,x^{(n)}_2,\dots,x^{(n)}_n)\in C_n $ para $ n\geq 1 $.

Seja $ (n_1) $ uma subsequência de $ (n) $ tal que $ x^{(n_1)}_1\rightarrow x_1^0 $, onde $ x^0_1 $ é um ponto de $ C_1 $. (Sabemos que tal sequência existe desde que $ x_1^{(n)}\in C_1 $ e $ C_1 $ é compacto). Então selecione uma subsequência de $ (n_2) $ de $ (n_1) $ tal que $ (x^{(n_2)}_1,x^{(n_2)}_2)\rightarrow (x^{(0)}_1,x^{0}_2)\in C_2 $. Similarmente seja

$$(x^{(n_k)}_1,\dots,x^{(n_k)}_k)\rightarrow (x^{(0)}_1,\dots,x^{(0)}_k)\in C_k$$

Finalmente forma a sequência de diagonais $ (m_k) $, no qual $ m_k $ é o k-ésimo termo de $ (n_k) $. Então $ x_i^{(m_k)}\rightarrow x_i $ como $ m_k\rightarrow \infty $ por $ i=1,2,\dots $, e $ (x^0_1,x^0_2,\dots)\in \bar{C}_n $ para $ n=1,2,\dots $, o qual evidentemente contradiz a afirmação que $ \bar{C}_n\downarrow \emptyset $, $ n\rightarrow \infty $. Isto completa a demonstração do Teorema.

Distribuição $ (\mathbb{R}^{T},\beta(\mathbb{R}^T)) $

Seja $ T $ o conjunto de índice $ t\in T $ e $ \mathbb{R_t} $ a reta real correspondente ao índice $ t $. Considere um conjunto desordenado $ \tau=[t_1,\dots,t_n] $ de indices distintos $ t_i $, $ t_i\in T, ~ n\geq 1 $, e $ \mathbb{P_\tau} $ seja a medida de probabilidade no espaço $ (\mathbb{R}^{\tau},\beta(\mathbb{R}^{\tau})) $, no qual $ \mathbb{R}^{\tau}=\mathbb{R}_{t_1}\times \mathbb{R}_{t_2}\times\dots\times \mathbb{R}_{t_n} $.

Dizemos que uma familia de medidas de probabilidades $ (\mathbb{P}_\tau) $, com $ \tau $ varia entre todos os conjuntos finitos e desordenados, é consistente se, para todos os conjuntos $ \tau=[t_1,t_2,\dots,t_n] $ e $ \sigma=[s_1,\dots,s_k] $ tal que $ \sigma\subset \tau $, temos que

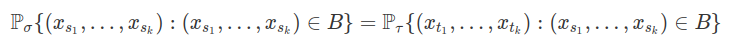
para todo $ B\in \beta(\mathbb{R}^\sigma) $.

Teorema 2.2.3

Seja $ (\mathbb{P}_\tau) $ uma familia de probabilidade consistente em $ (\mathbb{R}^\tau,\beta(\mathbb{R}^\tau)) $. Então existe uma única probilidade $ \mathbb{P} $ em $ (\mathbb{R}^T,\beta(\mathbb{R}^T)) $ tal que

$$\mathbb{P}(I_\tau(B))=\mathbb{P}_\tau(B)$$

para todo conjunto $ \tau=[t_1,\dots,t_n] $ com diferentes indices $ t_i\in T, ~ B\in \beta(\mathbb{R}^\tau) $ e $ I_\tau (B)=(x\in \mathbb{R}^T:(x_{t_1},\dots,x_{t_n})\in B) $.

Demonstração

Seja um conjunto $ \bar{B}\in \beta(\mathbb{R}^T) $. Então, pelo Teorema 2.1.3 da seção anterior temos que existe um conjunto enumerável $ S=(s_1,s_2,\dots)\subset T $ tal que $ \bar{B}=(x\in \mathbb{R}^T:(x_{s_1},x_{s_2},\dots)\in B) $ no qual $ B\in \beta(\mathbb{R}^S) $, $ \mathbb{R}^S=\mathbb{R}_{s_1}\times\mathbb{R}_{s_2}\times \dots $. Ou seja,

$$\bar{B}=I_{S}(B)$$

é um cilindro com base $ B \in \beta(\mathbb{R}^S) $. Desta forma, podemos definir uma função $ \mathbb{P} $ definida da seguinte forma

$$\mathbb{P}(I_S(B))=\mathbb{P}_S(B),$$

no qual a existência da medida $ \mathbb{P}_S $ é garantida pelo Teorema 2.1.3 da seção anterior.

Agora a medida $ \mathbb{P} $, iremos demonstrar a sua existência nesse teorema, para isso primeiramente vamos mostrar a consistência da definição a cima, ou seja, queremos mostrar que $ \mathbb{P}(\bar{B}) $, para todas as possíveis representação de $ \bar{B} $.

Seja $ \bar{B}=I_{S_1}(B_1) $ e $ \bar{B}=I_{S_2}(B_2) $ então $ \bar{B}=I_{S_1\cup S_2}(B_3) $, para algum $ B_3\in \beta(\mathbb{R}^{S_1\cup S_2}) $, portanto é suficiente mostrar que se $ S\subset A $ e $ B\in \beta(\mathbb{R}^S) $, então $ \mathbb{P}_{A}(B^\prime)=\mathbb{P}_S(B) $, no qual

$$ B^\prime=((x_{a_1},x_{a_2},\dots)\in \mathbb{R}^{A}: (x_{s_1},x_{s_2},\dots)\in B) $$

com $ A=(a_1,a_2,\dots) $ e $ S={s_1,s_2,\dots} $, porém a consistência devido a consistência admitida para conjuntos finitos e ao Teorema 2.1.3 da seção anterior temos que $ \mathbb{P}(\bar{B}) $ independe da representação de $ \bar{B} $.

$$\mathbb{P}\left(\displaystyle \sum_{n=1}^\infty \bar{B}_n\right)=\mathbb{P}\left(\displaystyle \sum_{n=1}^\infty I_S(B_n)\right)=\mathbb{P}_S\left(\displaystyle \sum_{n=1}^\infty B_n\right)=\displaystyle \sum_{n=1}^\infty \mathbb{P}_S\left( B_n\right)$$

$$=\displaystyle \sum_{n=1}^\infty \mathbb{P}\left( I_S(B_n)\right)=\displaystyle \sum_{n=1}^\infty\mathbb{P}\left( \bar{B}_n\right)$$

Então, pela propriedade $ \mathbb{P}(I_\tau(B))=\mathbb{P}_\tau(B) $, o resultado segue.

Exemplo 2.2.1

Considere o caso em que $ T=[0,\infty) $. Então $ \mathbb{R}^T $ é o espaço de todas as funções reais $ x=(x_t)_{t\geq 0} $. O exemplo mais famoso de medida de probabilidade desse espaço é a medida de Wiener, a qual é construída da seguinte forma.

Considere a familia $ (\phi_t(y|x))_{t\geq 0} $ de densidades Gaussian como função de $ y $ para $ x $ fixado.

$$\phi_t(y|x)=\displaystyle \frac{1}{\sqrt{2\pi t}}e^{-(y-x)^2/2t}, ~y\in \mathbb{R}.$$

e para cada $ \tau=[t_1,\dots,t_n] $, $ t_1< t_2< \dots < t_n $, e para cada conjunto

$$B=I_1\times \dots\times I_n, ~~ I_k=(a_k,b_k),$$

construímos a medida $ \mathbb{P}_{\tau}(B) $ de acordo com a fórmula

O significado intuitivo deste método de atribuição de uma medida ao cilindro.

2.3 - Processo de Bernoulli

O processo de Bernoulli é definido como uma família finita ou enumerável de variáveis aleatórias assumindo valores binários dados por $ 0 $ e $ 1 $. Desta forma, temos um processo estocástico a tempo discreto e a valores no conjunto $ S=(0,1) $. Como as variáveis aleatórias são binárias, a existência do processo de Bernoulli está garantida pela construção do espaço de Cantor. A seguir, mostramos como o teorema de extensão de Kolmogorov também pode ser utilizado na construção do processo de Bernoulli.

Considere $ \Omega $ um espaço amostral (diferente do vazio) e $ A_1 , A_2 ,\dots $ uma sequência de eventos, isto é, subconjuntos de $ \Omega $. Dado a sequência de eventos, definimos uma sequência de funções

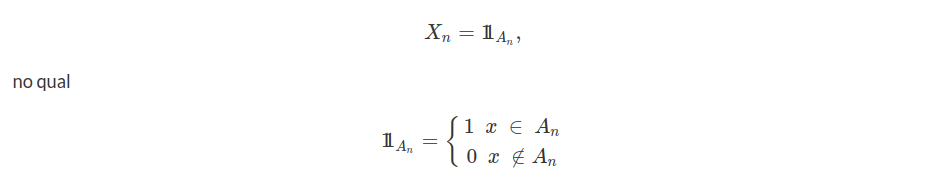
Para cada função $ X_n $ associamos uma probabilidade em $ \Omega $, na forma

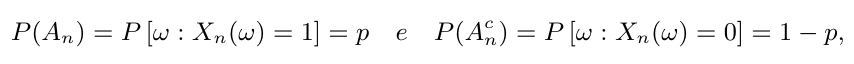
nos quais $ 0 < p < 1 $, $ \mathbb{P}(\emptyset )=0 $ e $ \mathbb{P}(\Omega )=1 $.

Para aplicarmos o teorema de extensão de Kolmogorov, precisamos de um conjunto de distribuições finito dimensionais satisfazendo a condição de compatibilidade de Kolmogorov. Para isto, admitimos que as probabilidade conjuntas seja definidas por

$$ \mathbb{P} \left[ \cap_{j=1}^n \left(\omega : X_j (\omega)=i_j \right) \right] = p^{\sum_{j=1}^n i_j } (1-p)^{n-\sum_{j=1}^n i_j}, $$

para todo família finita $ (i_1, \cdots , i_n) \in S^n $. Desta forma, temos uma distribuição de probabilidade definida sobre $ \Omega $ com a $ \sigma $-álgebra finita dada por $ \mathcal{A}_n = \sigma (A_1, A_2 , \cdots , A_n) $. Para detalhes sobre a construção da família de probabilidades ver a seção sobre o espaço de Cantor. Por construçao, a família de probabilidades finito dimensionais satisfaz a condição de compatibilidade de Kolmogorov e assim, existe uma única probabilidade $ \mathbb{P} $ sobre $ \Omega $ com a $ \sigma $-álgebra $ \mathcal{F} $ gerada pela sequência de eventos $ (A1, A_2 , \cdots ) $ tal que

$$ \mathbb{P} \left[ \cap_{j=1}^n \left(\omega : X_j (\omega)=i_j \right) \right] = p^{\sum_{j=1}^n i_j } (1-p)^{n-\sum_{j=1}^n i_j}, $$

para todo família finita $ (i_1, \cdots , i_n) \in S^n $, para todo $ n \geq 1 $. A partir do teorema de extensão de Kolmogorov, existe um espaço de probabilidade $ \Omega, \mathcal{F} , \mathbb{P}) $ no qual $ (X_1 , X_2 , \cdots ) $ é uma sequência de variáveis aleatórias independentes e identicamente distribuídas (iid) com $ \mathbb{P}[X_j=1]=p $ para todo $ j \geq 1 $.

Definição 2.3.1

O processo estocástico $ X=(X_n: n \geq 1) $, nos quais $ X_1, X_2, \cdots $ são variáveis iid com com $ \mathbb{P}[X_j=1]=p $ para todo $ 0 < p < 1 $ e $ j \geq 1 $ é denominado processo de Bernoulli.

Exemplo 2.3.1

Suponha que uma fábrica de lentes de contato produza lentes de contatos que apresente defeitos que distorcem a imagem com probabilidade $ p = 0,96 $ de que haja erro na lente. Definimos $ X_n $ como 1 ou 0 se apresenta algum erro de distorção na n-ésima lente produzida ou se não apresenta, respectivamente. Assumindo que a produção da lente ocorra de forma independente, as variáveis aleatórias $ X_1,X_2,\cdots $ são independentes. Então $ X=(X_n;n = 1,2,\cdots) $ é um processo de Bernoulli com probabilidade de sucesso $ \mathbb{P}(X_n= 1) = p = 0,96 $.

a) Qual a probabilidade das duas primeiras lentes terem defeitos e as duas subsequentes não tenha ?

$$\mathbb{P}(X_1= X_2= 0,X_3= X_4= 1) \stackrel{indep}{=} \mathbb{P}(X_1= 0)\mathbb{P}(X_2= 0)\mathbb{P}(X_3= 1)\mathbb{P}(X_4= 1)$$

$$= (1- p)(1- p)pp = (1- p)^2p^2 = 0,9232.$$

Dado $ X=(X_i : i \geq 1) $ um processo de bernoulli, associamos um processo de contagem $ N=(N_n, n\in \mathbb{N}) $ que conta o número de sucessos, na forma

$$N_n=\displaystyle \sum^n_{i=1}X_i, \quad n \geq 1.$$

Note que podemos recuperar o processo de Bernoulli a partir do processo de contagem pois,

$$\Delta N_n=N_n-N_{n-}=X_n.$$

Como $ X_n $ segue uma distribuição de Bernoulli de parâmetro $ p $ então a esperança e a variância de $ X_n $ são dadas por:

$$E[X_n]=E[X_n^2]=E[X_n^3]=E[X_n^4]=\cdots =p \quad \text{e} \quad Var[X_n]=p-p^2=p(1-p).$$

Além disso, temos que:

$$E[b^{X_n}]=b^0\mathbb{P}[X_n=0]+b\mathbb{P}[X_n=1]=b(1-p)+bp.$$

Podemos generalizar da seguinte forma

$$E[f(X_n)]=f(0)\mathbb{P}[X_n=0]+f(1)\mathbb{P}[X_n=1]=f(0)(1-q)+f(1)p.$$

Quanto ao processo de contagem, dado n fixado, temos que

$$E[N_n]=E[\displaystyle \sum_{i=1}^{n}X_i]=\sum_{i=1}^{n}E[X_i]=\sum_{i=1}^{n}p=np.$$

Como $ X_j $’s são independentes temos que

$$Var[N_n]=Var[\sum_{i=1}^{n}X_i]=\sum_{i=1}^{n}Var[X_n]=\sum_{i=1}^{n}(1-p)p=np(1-p).$$

Dado que $ X_n $ tem distribuição de Bernoulli, o processo de contagem $ N_n $ tem distribuição binomial. Portanto temos que

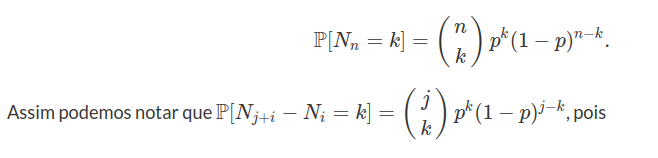
$$\displaystyle N_{j+i}-N_i=\sum_{w=i+1}^{j+i}X_w=\sum_{w=1}^{j}X_{i+w}.$$

Lema 2.3.1

Para qualquer $ m,n \in \mathbb{N} $ temos que

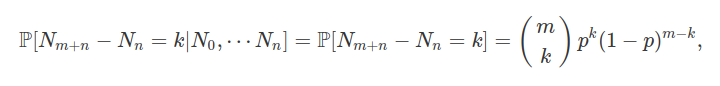
para todo $ k=0, \cdots , m $.

Demonstração

Notemos primeiramente que a variável $ N_j $ depende exclusivamente das variáveis $ X_0,\cdots,X_j $ assim conhecer $ N_0,\cdots,N_n $ é equivalente a conhecer $ X_0,\cdots,X_n $. Além disso, temos que $ X_0,\cdots,X_n $ é independente de $ X_{n+1},\cdots,X_m $ e portanto, temos que

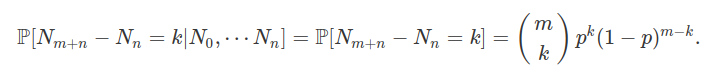
3 - Esperança Condicional: caso geral

Na módulo de probabilidade, apresentamos a esperança condicional para variáveis aleatória discretas e absolutamente contínuas de forma simples e intuítiva. Aqui, faremos uma discussão detalhada sobre esperança condicional com respeito a uma $ \sigma $-álgebra. Para isto, começamos com o conceito de probabilidade condicional dado uma partição finita do espaço amostral.

3.1 - Probabilidade Condicional para uma partição

Seja $ (\Omega,\mathcal{A},\mathbb{P}) $ um espaço de probabilidade e $ \mathcal{D}=(D_1,\cdots, D_k) $ uma partição finita de $ \Omega $ tal que $ D_i\in \mathcal{A}, \mathbb{P}(D_i)> 0, $ para todo $ i\in (1,\cdots,k)) $ e $ \displaystyle \cup_{i=1}^{k} D_i=\Omega $. Dado $ A \in \mathcal{A} $ um evento, tomamos $ \mathbb{P}(A|D_i) $ a probabilidade condicional do evento $ A $ dado $ D_i $.

Para a família finita de probabilidades condicionais $ (\mathbb{P}(A|D_i), i=1,\cdots,k) $, associamos a variável aleatória

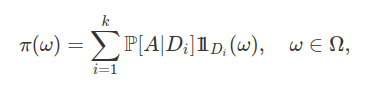
assumindo valor $ \mathbb{P}(A|D_i) $ no elemento $ D_i $ da partição $ \mathcal{D} $. Note que a variável aleatória $ \pi $ está associada especificamente a partição $ \mathcal{D} $ e será denominada probabilidade condicional do evento $ A $ dado a partição $ \mathcal{D} $. Utilizaremos a seguinte notação

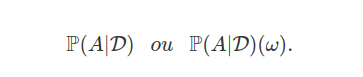
Como consequência da definição da probabilidade condicional dada uma partição, temos que

$$\mathbb{P}(\cup_{i=1}^n A_i \mid \mathcal{D})(\omega)=\sum_{i=1}^{\infty} \mathbb{P}(A_i \mid \mathcal{D})(\omega), \quad \omega \in \Omega,$$

no qual $ (A_i) \subset \mathcal{A} $ é uma sequência de eventos disjuntos $ (A_i \cap A_j = \emptyset, ~ i \neq j) $. Se tomarmos $ \mathcal{D} $ a partição trivial, ou seja, $ \mathcal{D}=(\Omega) $, então

$$\mathbb{P}(A|\mathcal{D})=\mathbb{P}(A|\Omega)=\mathbb{P}(A), \quad A \in \mathcal{A}.$$

Assim, a probabilidade condicional com respeito a partição $ \mathcal{D} $ é uma função $ \mathbb{P}(\cdot \mid \mathcal{D}): \mathcal{A} \times \Omega \rightarrow [0,1] $ satisfazendo

(i) Para todo $ A \in \mathcal{A} $, temos que $ \mathbb{P}(A \mid \mathcal{D}): \Omega \rightarrow [0,1] $ é uma variável aleatória;

(ii) Para todo $ \omega \in \Omega $, temos que $ \mathbb{P}(\cdot \mid \mathcal{D}) (\omega): \mathcal{A} \rightarrow [0,1] $ é uma probabilidade.

Desde que a probabilidade condicional é uma variável aleatória simples, para todo $ A \in \mathcal{A} $, temos que

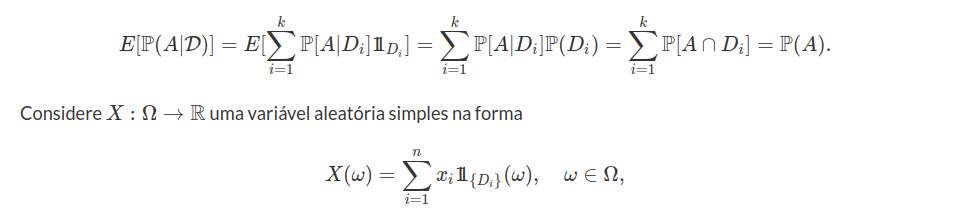
nos quais $ D_i = ( \omega \in \Omega: X(\omega)=x_i) $, $ \mathcal{R}_X=(x_1, \cdots , x_n) $ números distintos e $ \mathcal{D}_X=(D_1, \cdots ,D_n) $ a partição induzida pela variável aleatória $ X $. A probabilidade condicional $ \mathbb{P}(\cdot \mid \mathcal{D}_X) $ será denotada por $ \mathbb{P}(\cdot \mid X) $ e denominada probabilidade condicional dado a variável aleatória $ X $. Da mesma forma, temos que $ \mathbb{P}(A \mid X=x_i) = \mathbb{P}(A \mid D_i) $, para todo $ i=1,2, \cdots, n $ e $ A \in \mathcal{A} $.

Dados $ X_1, \cdots , X_k $ variáveis aleatórias simples, denotamos por $ \mathcal{D}_{X_1,\cdots , X_k} $ a partição induzida pelo vetor de variáveis aleatórias $ (X_1, \cdots , X_k) $, na forma

$$ D_{x_1, \cdots , x_k}=(\omega \in \Omega: X_1(\omega)=x_1, \cdots , X_k=x_k), \quad (x_1,\cdots , x_k) \in \mathcal{R}_{X_1} \times \cdots \times \mathcal{R}_{X_k}, $$

3.2 - Esperança Condicional para uma partição

Sejam $ (\Omega,\mathcal{A},\mathbb{P}) $ um espaço de probabilidade e $ \mathcal{D}=(D_1,\cdots, D_k) $ uma partição finita de $ \Omega $. Uma variável aleatória simples é dada por

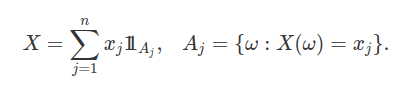
Sabemos que a esperança de uma variável aleatória simples é uma combinação linear dos elementos do conjunto de probabilidades $ (\mathbb{P}(D_1), \cdots , \mathbb{P}(D_k)) $, na forma

$$\mathbb{E}[X]=\displaystyle \sum_{j=1}^{n}x_j \mathbb{P}(A_j)$$

De forma similar, podemos definir a esperança condicional de $ X $ dado uma partição finita $ \mathcal{D} $ como uma combinação linear dos elementos da família de probabilidades condicionais $ (\mathbb{P}(A_1 \mid \mathcal{D}), \cdots , \mathbb{P}(A_n \mid \mathcal{D}) $. Na seção probabilidade condicional dado uma partição, definimos a probabilidade condicional do evento $ A \in \mathcal{A} $ dado a partição $ \mathcal{D} $, por

Assim, chegamos a seguinte definição de esperança condicional.

Definição 3.2.1

A esperança condicional da variável aleatória simples $ X $ dado a partição finita $ \mathcal{D}=(D_1, \cdots , D_k) $ é definida pela forma

$$\displaystyle \mathbb{E}[X|\mathcal{D}]=\sum_{j=1}^{n}x_j \mathbb{P}(A_j|\mathcal{D}).$$

Observe que a esperança condicional $ \mathbb{E}[X|\mathcal{D}] $ é uma variável aleatória. Além disso, para todo $ \omega \in D_i $, temos que $ \mathbb{E}(X \mid \mathcal{D})(\omega)=\sum_j x_j \mathbb{P}(A_j \mid D_i) $. Como consequência, denotamos por

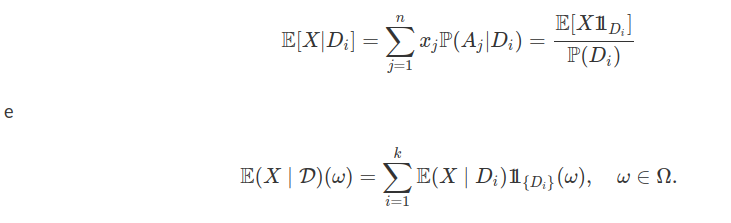
A seguir, vamos apresentar propriedades da esperança condicional.

Proposição 3.2.1

Sejam $ X $ e $ Y $ variáveis aleatórias simples e $ a,b\in \mathbb{R} $, e ainda $ C $ uma função constante. Então as seguintes propriedades são satisfeitas.

(i) $ \mathbb{E}[aX+bY|\mathcal{D}]=a\mathbb{E}[X|\mathcal{D}]+b\mathbb{E}[Y|\mathcal{D}] $;

(ii) $ \mathbb{E}[X|\Omega]=\mathbb{E}[X] $;

(iii) $ \mathbb{E}[C|\mathcal{D}]=C $;

(v) Temos que $ \mathbb{E}[\mathbb{E}[X|\mathcal{D}]]=\mathbb{E}[X] $;

no qual $ \mathcal{D} $ é uma partição finita de $ \Omega $.

Demonstração

Os itens (i)-(iv) são consequências direta da definição. Para provarmos o item (v), basta aplicarmos o fato de que a esperança da probabilidade condicional do evento $ A_j $ dado a partição $ \mathcal{D} $ é $ \mathbb{P}(A_j) $, de fato

$$\mathbb{E}[\mathbb{E}[X|\mathcal{D}]]=\mathbb{E}[\displaystyle \sum_{j=1}^{n}x_j\mathbb{P}(A_j|\mathcal{D})]= \sum_{j=1}^{n}x_j\mathbb{E}[\mathbb{P}(A_j|\mathcal{D})]=\sum_{j=1}^{n}x_j\mathbb{P}(A_j)=\mathbb{E}[X].$$

Segue a proposição.

Considere $ \mathcal{D}=(D_1, \cdots , D_k) $ uma partição finita de $ \Omega $. Neste caso, a $ \sigma $-álgebra gerada por $ \mathcal{D} $, que será denotada por $ \sigma(\mathcal{D}) $, é a classe formada por união de elementos de $ \mathcal{D} $ e o conjunto vazio. Dado $ Y $ uma variável aleatória simples, dizemos que $ Y $ é mensurável com respeito a $ \sigma(\mathcal{D}) $ (ou, com respeito a partição $ \mathcal{D} $), se a $ \sigma(Y)\subset \sigma(\mathcal{D}) $

Lema 3.2.1

Dado $ \mathcal{D} $ uma partição de $ \Omega $. Uma variável aleatória simples $ Y $ é mensurável com respeito a $ \sigma(\mathcal{D}) $ se, e só se, $ Y $ pode ser representada na forma

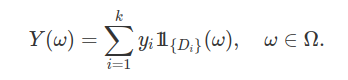
Demonstração

Basta aplicarmos o teorema da representação de Doob.

Dados duas partições finitas $ \mathcal{D_1} $ e $ \mathcal{D_2} $, dizemos que $ \mathcal{D_2} $ é mais fina que $ \mathcal{D_1} $, se para todo elemento $ D\in \mathcal{D_1} $, existe uma família $ (F_1, \cdots , F_m) \subset \mathcal{D}_2 $ tal que $ D=F_1\cup \cdots \cup F_m $. Assim, obtemos que $ \mathcal{D_2} $ é mais fina que $ \mathcal{D_1} $ se, e só se, $ \sigma(\mathcal{D_1})\subset \sigma(\mathcal{D_2}) $ (exercício).

Considere $ \mathcal{D}=(D_1, \cdots , D_k) $ uma partição de $ \Omega $ e $ Y $ uma variável aleatória simples na forma

Teorema 3.2.1

Considere $ Y $ uma variável aleatória simples, $ \mathcal{D} $ uma partição finita de $ \Omega $. A esperança condicional de $ Y $ dado $ \mathcal{D} $ é a única variável aleatória $g:\Omega \rightarrow \mathbb{R}$ satisfazendo

(i) $ g $ é mensurável com respeito a $ \sigma(\mathcal{D}) $;

(ii) Para todo $ F\in\sigma(\mathcal{D}) $, temos que

Observe que esta equação é válida para todo elemento da $ \sigma $-álgebra gerada pela partição $ \mathcal{D} $. Além disso, ela caracteriza a esperança condicional no seguinte sentido: a esperança condicional é a única variável aleatória simples, mensurável com respeito a $ \sigma(\mathcal{D}) $ e satisfazendo (1). Na sequência, apresentamos algumas propriedades da esperança condicional

Proposição 3.2.2

Sejam $ X $ uma variável aleatória simples e $ Y $ uma variável aleatória mensurável com respeito $ \sigma(\mathcal{D}) $. Então, temos que

$$\mathbb{E}[X Y \mid \mathcal{D}]=Y\mathbb{E}[X \mid \mathcal{D}].$$

Demonstração

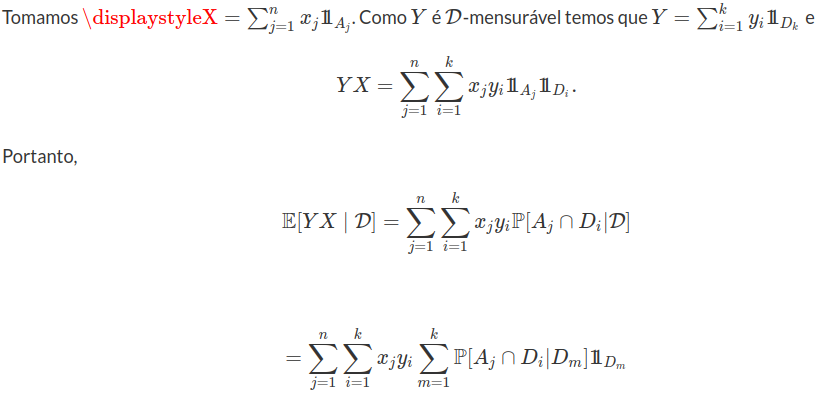
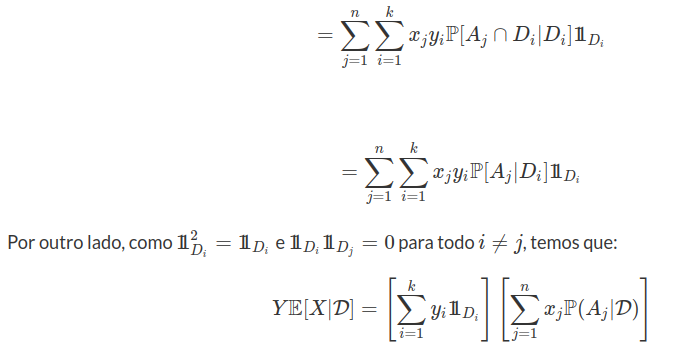
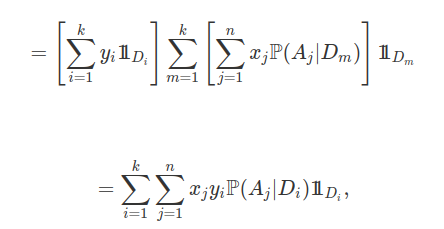
Segue a proposição.

Na sequência, vamos mostrar a propriedade de “torre” da esperança condicional.

Proposição 3.2.3

Considere $ \mathcal{D_1} $ e $ \mathcal{D_2} $ partições de $ \Omega $ tal que $ \sigma(\mathcal{D_1})\subset\sigma(\mathcal{D_2}) $. Para todo variável aleatória simples $ X $, temos que

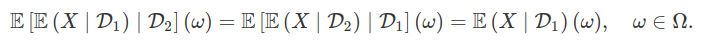
Demonstração

Desde que $ \mathbb{E}(X \mid \mathcal{D_1}) $ é uma variável aleatória simples mensurável com respeito a $ \sigma(\mathcal{D_2}) $, segue da proposição 3.2.2 que

$$\mathbb{E}\left[\mathbb{E}\left(X \mid \mathcal{D_1}\right) \mid \mathcal{D_2}\right]=\mathbb{E}\left(X \mid \mathcal{D_1}\right).$$

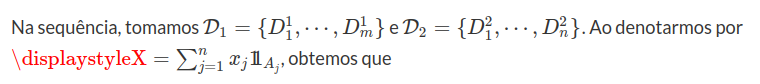
$$\mathbb{E}\left[\mathbb{E}\left(X \mid \mathcal{D_2}\right) \mid \mathcal{D_1}\right]=\displaystyle \mathbb{E}\left[\sum_{j=1}^{n}x_j\mathbb{P}(A_j|\mathcal{D_2})\mid \mathcal{D_1}\right].$$

Assim, basta mostrarmos que $ \mathbb{E}[\mathbb{P}(A_j|\mathcal{D_2})|\mathcal{D_1}]=\mathbb{P}(A_j|\mathcal{D_1}) $. Notemos primeiramente que

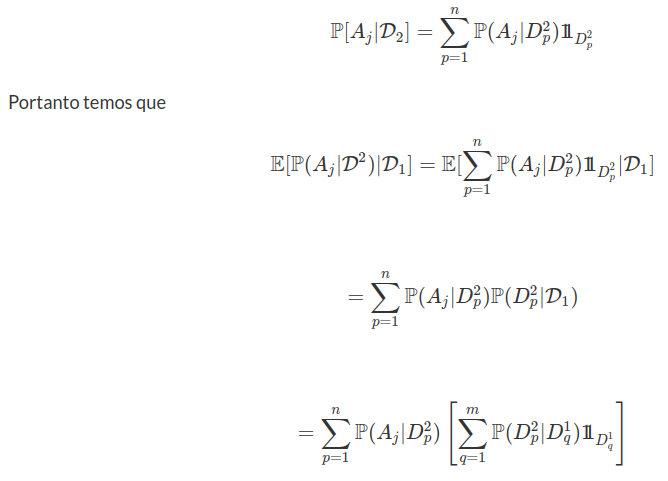
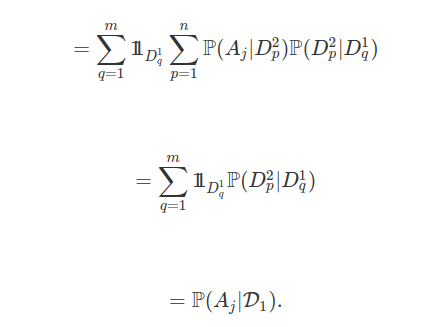
Segue a proposição.

Proposição 3.2.4

Sejam $ X $ e $ Y $ variáveis aleatórias independentes, com $ \mathbb{E}(|X|)< \infty $ e $ \mathbb{E}(|Y|)< \infty $. Então, temos que $ \mathbb{E}(XY)=\mathbb{E}(X)\mathbb{E}(Y) $.

Demonstração

Primeiramente considere o caso em que $ X\geq 0 $ e $ Y\geq 0 $. Seja

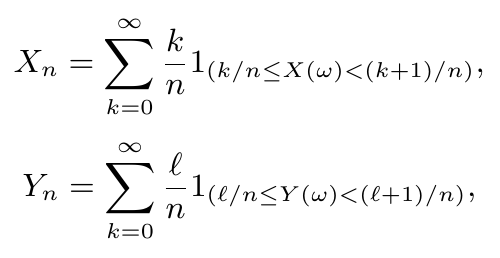
Então $ X_n\leq X $, $ |X_n-X|\leq 1/n $ e $ Y_n\leq Y $, $ |Y_n-Y|\leq 1/n $. Desde que $ \mathbb{E}(X)< \infty $ e $ \mathbb{E}(Y)< \infty $. Assim, segue do teorema da convergência dominada que

$$\lim_{n\rightarrow \infty} \mathbb{E}(X_n)=\mathbb{E}(X)$$

$$\lim_{n\rightarrow \infty} \mathbb{E}(Y_n)=\mathbb{E}(Y).$$

Além do mais, desde que $ X $ e $ Y $ são independente,

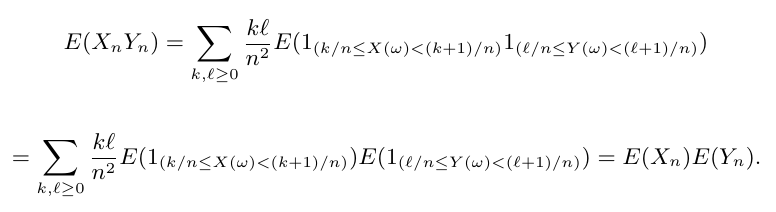
Agora note que

$$|\mathbb{E}(XY)-\mathbb{E}(X_n Y_n)|\leq \mathbb{E}(|XY-X_nY_n|) $$

$$\leq \mathbb{E}(|X||Y-Y_n|)+\leq \mathbb{E}(|Y_n||X-X_n|)\leq\displaystyle \frac{1}{n} \mathbb{E}(X)+\frac{1}{n}\mathbb{E}\left(Y+\frac{1}{n}\right)\rightarrow 0, ~n\rightarrow \infty.$$

Portanto,

$$\displaystyle \mathbb{E}(XY)=\lim_{n\rightarrow \infty}\mathbb{E}(X_nY_n)=\lim_{n\rightarrow \infty}\mathbb{E}(X_n)\lim_{n\rightarrow \infty}\mathbb{E}(Y_n).$$

De modo geral se reduz a seguinte representação

$$X=X^+ +X^-$$

$$Y=Y^+ +Y^-$$

$$XY=X^+Y^+ -X^-Y^+ -X^+Y^- X^-Y^-.$$

E isto completa a prova.

3.3 - Esperança Condicional com respeito a uma sigma-álgebra

Considere $ (\Omega,\mathcal{F},\mathbb{P}) $ um espaço de probabilidade e $ \mathcal{G} $ uma $ \sigma $-álgebra tal que $ \mathcal{G}\subset\mathcal{F} $. Seja $ X $ uma variável aleatória positiva e $ Q $ uma medida definida sobre $ (\Omega , \mathcal{G}) $, na forma

Como consequência, apresentamos a seguinte definição da esperança condicional.

Definição 3.3.1

A esperança condicional de uma variável aleatória positiva $ X $ dado a $ \sigma $-álgebra $ \mathcal{G}~(\subset \mathcal{F}) $, denotada por $ \mathbb{E}[X|\mathcal{G}] $, é a única $ (\mathbb{P}-q.c.) $ variável aleatória satisfazendo

i) $ \mathbb{E}[X|\mathcal{G}] $ é $ \mathcal{G} $-mensurável

ii) Para todo $ A\in \mathcal{G} $

$$\displaystyle \int_{A}X d \mathbb{P}=\int_{A}\mathbb{E}[X|\mathcal{G}]d\mathbb{P}.$$

​A esperança condicional de uma variável aleatória qualquer $ X $ com respeito a uma $ \sigma $-álgebra é dada por

$$\mathbb{E}[X|\mathcal{G}]=\mathbb{E}[X^+|\mathcal{G}]-\mathbb{E}[X^-|\mathcal{G}],$$

caso $ \mathbb{E}[X^+|\mathcal{G}] < \infty $ ou $ \mathbb{E}[X^-|\mathcal{G}])< \infty, $ nos quais $ X^+=\max(X,0) $ e $ X^-=\min(-X,0) $. Podemos definir também a variância condicional da seguinte forma.

Definição 3.3.2

Seja $ X $ uma variável aleatória quase integrável e $ \mathbb{E}[X|\mathcal{G}] $ a esperança condicional com respeito a $ \sigma $-álgebra $ \mathcal{G} $. Então a variância condicional é dada por

$$Var[X|\mathcal{G}]=\mathbb{E}[(X-\mathbb{E}[X|\mathcal{G}])^2|\mathcal{G}]$$

Definição 3.3.3

Dado $ B\in \mathcal{F} $, a probabilidade condicional de $ B $ dado a $ \sigma $-álgebra $ \mathcal{G} $ é definido por

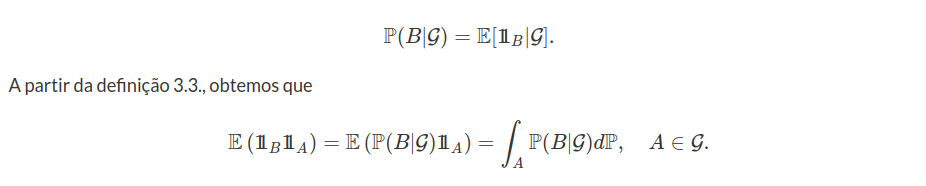
Dado $ \mathcal{D}=(D_1, \cdots , D_k) $ uma partição finita de $ \Omega $, definimos e estudamos propriedades da esperança condicional com respeito a partição $ \mathcal{D} $. A seguir, vamos verificar que esta definição de esperança condicional está coerente com a definição via $ \sigma $-álgebra. O lema abaixo foi demonstrado no módulo anterior.

Lema 3.3.1

Seja $ X $ uma variável aleatória $ \sigma(\mathcal{D}) $-mensurável. Então $ X $ pode ser representado da forma

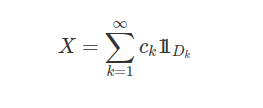
com $ c_k\in \mathbb{R} $, ou seja, $ X $ é constante em $ D_k $.

Proposição 3.3.1

Se $ \mathcal{G}=\sigma(\mathcal{D}) $, com $ \mathcal{D} $ sendo uma partição e seja $ X $ uma variável aleatória tal que, $ \mathbb{E}[X] <\infty $.

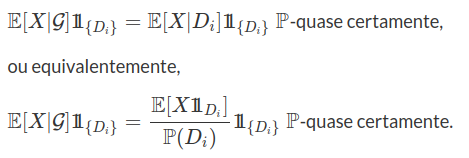
Demonstração

De acordo com o lema anterior temos que $ \mathbb{E}[X|\mathcal{G}]=c_i $ em $ D_i $, onde $ c_i\in \mathbb{R} $, Mas

$$\displaystyle\int_{D_i}X d\mathbb{P}=\int_{D_i}\mathbb{E}[X|\mathcal{G}] d\mathbb{P}=c_i\mathbb{P}(D_i).$$

Assim, temos que

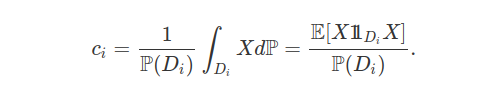
Portanto o resultado segue.

Agora vamos demonstrar algumas propriedades da esperança condicional dado uma $ \sigma $-àlgebra

Propriedades da Esperança condicional

P1: Se $ C $ é uma constante e $ X=C $, quase certamente, então $ \mathbb{E}[X|\mathcal{G}]=C $, quase certamente.

P2: A esperança condicional é linear, sejam c e b constantes e X e Y variáveis aleatórias. Então,

$$\mathbb{E}[cX+bY|\mathcal{G}]=c\mathbb{E}[X|\mathcal{G}]+b\mathbb{E}[Y|\mathcal{G}]~\mathbb{P}-q.c.$$

P3: Se $ X\leq Y $ quase certamente, então $ \mathbb{E}[X|\mathcal{G}]\leq \mathbb{E}[Y|\mathcal{G}]~\mathbb{P}-q.c. $

P4: Seja $ \mathcal{G} \subset \mathcal{F} $ uma $ \sigma $-álgebra e $ \sigma(X) $ a $ \sigma $-álgebra gerada pela variável aleatória X, com $ \sigma(X)\subset\mathcal{G} $. Então

$$\mathbb{E}[X|\mathcal{G}]=X~\mathbb{P}-q.c..$$

P5: Seja X uma variável aleatória e as $ \sigma $-álgebras $ \mathcal{G}_1\subset\mathcal{G}_2 $. Então,

a) $ \mathbb{E}[X|\mathcal{G}_1]=\mathbb{E}[\mathbb{E}[X|\mathcal{G}_1]|\mathcal{G}_2]~\mathbb{P}-q.c. $ e

b) $ \mathbb{E}[X|\mathcal{G}_1]=\mathbb{E}[\mathbb{E}[X|\mathcal{G}_2]|\mathcal{G}_1]~\mathbb{P}-q.c. $

P6: Se a variável aleatória $ X $ e a $ \sigma $-álgebra $ \mathcal{G} $ são independentes, obtemos que

$$\mathbb{E}[X|\mathcal{G}]=\mathbb{E}[X]~\mathbb{P}-q.c..$$

Em particular se X e Y são variáveis aleatórias independentes então $ \mathbb{E}[X|Y]=\mathbb{E}[X]~\mathbb{P}-q.c. $.

P7: A esperança de $ X $ e a esperança de $ \mathbb{E}[X|\mathcal{G}] $ são as mesmas, ou seja

$$\mathbb{E}[X]=\mathbb{E}\left[\mathbb{E}[X|\mathcal{G}]\right]~\mathbb{P}-q.c..$$

Demonstração

P1 - Claro que a função constante é mensurável com respeito a $ \mathcal{G} $. Assim basta verificar se

$$\displaystyle \int_{A}X d\mathbb{P}=\int_{A}C dP, ~ A\in \mathcal{G}.$$

Entretanto por hipótese temos que $ X=C $ quase certamente, então essa equação é satisfeita e o resultado segue.

P2 - A propriedade 2 é consequência direta de propriedades da integral,

$$\displaystyle \int_{A}(cX+bY)d\mathbb{P}=c\int_{A}X d\mathbb{P}+b\int_{A}Y d\mathbb{P}=c\int_{A}\mathbb{E}[X|\mathcal{G}] d\mathbb{P}+b\int_{A}\mathbb{E}[Y|\mathcal{G}] d\mathbb{P}=$$

$$\int_{A}\left(c\mathbb{E}[X|\mathcal{G}]+b\mathbb{E}[X|\mathcal{G}] \right)d\mathbb{P}.$$

e portanto o resultado segue.

P3 - Se $ X\leq Y $ quase certamente, então

$$\displaystyle \int_{A}X d\mathbb{P} \leq \int_{A}Y d\mathbb{P}, ~ A \in \mathcal{G}$$

mais isso implica que

$$\displaystyle \int_{A}\mathbb{E}[X|\mathcal{G}] d\mathbb{P} \leq \int_{A}\mathbb{E}[Y|\mathcal{G}] d\mathbb{P}, ~ A \in \mathcal{G}$$

e portanto o resultado segue.

P4 - Desde que $ \sigma(X)\subset \mathcal{G} $, temos então que $ X $ é $ \mathcal{G} $-mensurável, logo

$$\displaystyle \int_AXd\mathbb{P}=\int_A\mathbb{E}(X|\mathcal{G})d\mathbb{P}, ~A\in\mathcal{G}$$

o que implica que $ X=\mathbb{E}(X|\mathcal{G}) $ $ \mathbb{P} $-q.c.

E portanto o resultado segue.

P5 - a) De fato, seja $ A\in \mathcal{G}_1 $ então

$$\displaystyle \int_A \mathbb{E}(X|\mathcal{G}_1)d\mathbb{P}=\int_AXd\mathbb{P}$$

desde que $ \mathcal{G}_1\subset\mathcal{G}_2 $, temos que $ A\in \mathcal{G}_1 $ implica em $ A\in \mathcal{G}_2 $ então

$$\displaystyle \int_{A}\mathbb{E}(X|\mathcal{G}_2)d\mathbb{P}=\int_A\mathbb{E}[\mathbb{E}(X|\mathcal{G}_1)|\mathcal{G}_2]d\mathbb{P}=\int_AXd\mathbb{P}$$

E portanto o resultado segue

b) Seja $ A\in \mathcal{G}_1 $ e $ Y=\mathbb{E}[X|\mathcal{G}_1] $

$$\displaystyle \int_A Yd\mathbb{P}=\int_A Xd\mathbb{P}$$

Por outro lado por P4 temos que desde que $ A\in \mathcal{G}_1\subset\mathcal{G}_2 $

$$\displaystyle \int_A\mathbb{E}[\mathbb{E}[X|\mathcal{G}_2]|\mathcal{G}_1]d\mathbb{P}=\int_A\mathbb{E}[X|\mathcal{G}_2]d\mathbb{P}=\int_A\mathbb{E}(X|\mathcal{G}_1)d\mathbb{P}=\int_A Xd\mathbb{P}$$

então o resultado segue.

P6 - Temos que desde que $ \mathbb{E}[X] $ é $ \mathcal{G} $-mensurável, temos apenas que verificar que

$$\displaystyle \int_A X d\mathbb{P} =\int_A \mathbb{E}[X]d\mathbb{P},\quad A\in \mathcal{G}$$

P7 - Tome primeiramente a $ \sigma $-álgebra trivial $ \mathcal{G}_1=(\emptyset,\Omega) $. Então seja $ A\in \mathcal{G}_1 $, temos

$$\displaystyle \int_{A}\mathbb{E}[X|\mathcal{G}_1]d\mathbb{P}=\int_{A}X d\mathbb{P}.$$

claro que, $ A\in \mathcal{G}_1\subset\mathcal{G} $ então

$$\displaystyle \int_{A}\mathbb{E}[\mathbb{E}[X|\mathcal{G}_1]|\mathcal{G}]d\mathbb{P}=\int_{A}\mathbb{E}[X|\mathcal{G}]=\int_{A}X d\mathbb{P}$$

e portanto o resultado segue

Abaixo definiremos algumas desigualdades importantes para esperança.

Teorema 3.3.4

Seja $ (X_n)_n\in\mathbb{N} $ uma sequência de variáveis aleatórias. Então

i) Se $ |X_n|\leq Y $, $ \mathbb{E}[Y]< \infty $ e $ X_n\rightarrow X $ quase certamente, então

$$\mathbb{E}[X_n|\mathcal{G}]\rightarrow \mathbb{E}[X|\mathcal{G}]~quase~certamente$$

e

$$\mathbb{E}[|X_n-X||\mathcal{G}]\rightarrow 0~quase~certamente$$

ii) Se $ X_n\geq Y $, $ \mathbb{E}[Y]> -\infty $ e $ X_n\uparrow X $ quase certamente, então

$$\mathbb{E}[X_n|\mathcal{G}]\uparrow \mathbb{E}[X|\mathcal{G}]~quase~certamente$$

iii) Se $ X_n\leq Y $, $ \mathbb{E}[Y]< \infty $ e $ X_n\downarrow X $ quase certamente, então

$$\mathbb{E}[X_n|\mathcal{G}]\downarrow \mathbb{E}[X|\mathcal{G}]~quase~certamente$$

iv) Se $ X_n\geq Y $, $ \mathbb{E}[Y]> -\infty $, então

$$\mathbb{E}[\liminf X_n|\mathcal{G}]\leq\liminf \mathbb{E}[X_n|\mathcal{G}]~quase~certamente$$

v) Se $ X_n\leq Y $, $ \mathbb{E}[Y]<\infty $, então

$$\mathbb{E}[\limsup X_n|\mathcal{G}]\geq\limsup \mathbb{E}[X_n|\mathcal{G}]~quase~certamente$$

vi) Se $ X_n\geq 0 $, então

$$\displaystyle \mathbb{E}[\sum X_n|\mathcal{G}]=\sum \mathbb{E}[X_n|\mathcal{G}]~quase~certamente$$

Demonstração

i)Seja $ W_n= \sup_{m\geq n |X_n-X|} $. Como $ X_n \rightarrow X $ quase certamente, temos que $ W_n\downarrow 0 $ quase certamente. A esperança $ \mathbb{E}[X_n] $ e $ \mathbb{E}[X] $ são finitas, assim usando as propriedades de esperança condicional temos que:

$$|\mathbb{E}[X_n|\mathcal{G}]-\mathbb{E}[X|\mathcal{G}]|=|\mathbb{E}[X_n-X|\mathcal{G}]|\leq \mathbb{E}[|X_n-X||\mathcal{G}]\leq \mathbb{E}[W_n|\mathcal{G}].$$

Desde que$ \mathbb{E}[W_{n+1}|\mathcal{G}]\leq \mathbb{E}[W_n|\mathcal{G}] $ quase certamente, e assim o $ \lim_n \mathbb{E}[W_n|\mathcal{G}]=h $ existe quase certamente. Então

$$0\leq \int_{\Omega}h d\mathbb{P}\leq \int_{\Omega}\mathbb{E}[W_n|\mathcal{G}]d\mathbb{P}=\int_{\Omega}W_nd\mathbb{P}\rightarrow 0, ~ n\rightarrow \infty,$$

onde a ultima igualdade decorre do teorema da convergência dominada, o qual é um teorema muito importante dentro da teoria da medida. Assim $ \int_{\Omega}hd\mathbb{P}=0 $ implica pelas propriedades de esperança condicional, isto implica que h=0 quase certamente. E portanto o resultado segue.

ii) Primeiro seja, $ Y=0 $. Desde que $ \mathbb{E}[X_n|\mathcal{G}]\leq \mathbb{E}[X_{n+1}|\mathcal{G}] $ quase certamente. Seja $ \lim_{n}\mathbb{E}[X_n|\mathcal{G}]=W(\omega) $ existe quase certamente. Então a equação

$$\int_{A}X_n d\mathbb{P}=\int_A \mathbb{E}[X_n|\mathcal{G}]d\mathbb{P}, ~ A\in \mathcal{G},$$

e pelo teorema da convergência monótona, temos que

$$\int_A X_nd\mathbb{P}=\int_A W d\mathbb{P}, ~ A \in \mathcal{G}$$

Consequentemente $ X=W $ quase certamente. E portanto o resultado segue.

iii) O resultado segue do resultado anterior.

iv) Seja $ W_n= \inf_{m\geq n}X_m $, então $ X_n\uparrow X $, onde $ W=\liminf X_n $. Usando ii) $ \mathbb{E}[W_n|\mathcal{G}]\uparrow \mathbb{E}[W|\mathcal{G}] $ quase certamente. Portanto,

$$\mathbb{E}[W|\mathcal{G}]=\lim_{n}\mathbb{E}[W_n|\mathcal{G}]=\liminf \mathbb{E}[W_n|\mathcal{G}]\leq \liminf \mathbb{E}[X_n|\mathcal{G}]$$

e o resultado segue.

v) Segue do iv)

vi) Se $ X_n \geq 0 $, pelas propriedades de esperança condicional temos que

$$\mathbb{E}\left[\displaystyle \sum_{k=1}^{n}X_k|\mathcal{G}\right]=\sum_{k=1}^{n}\mathbb{E}[X_k|\mathcal{G}]$$

Assim uma utilizando ii), e o resultado segue.

Proposição 3.3.2

Seja $ \mathcal{G} $ uma $ \sigma $-álgebra e $ \sigma(X) $ a $ \sigma $-álgebra gerada pela variável aleatória X, com $ \sigma(X)\subset\mathcal{G} $. Ao tomarmos $ Y $ uma variável aleatória qualquer, obtemos que

$$\mathbb{E}[XY|\mathcal{G}]=X\mathbb{E}[Y|\mathcal{G}]~\mathbb{P}-q.c..$$

Em particular se $ X $ é uma função da variável $ Z $, então $ \sigma(X)\subset\sigma(Z) $ e,

$$\mathbb{E}[XY|Z]=X\mathbb{E}[Y|Z]~\mathbb{P}-q.c..$$

Demonstração

Considere primeiramente $ Y=1_{B} $ e $ B\in \mathcal{G} $. Então, para todo $ A\in \mathcal{G} $,

$$\displaystyle \int_A XYd\mathbb{P}=\int_{A\cap B} Xd\mathbb{P}=\int_{A\cap B}\mathbb{E}(X|\mathcal{G})d\mathbb{P}=\int_{A}{1}_B\mathbb{E}(X|\mathcal{G})d\mathbb{P}=\int_A Y\mathbb{E}(X|\mathcal{G})d\mathbb{P}$$

Então, pela propriedade de aditividade da integral temos que

$$\displaystyle \int_A XYd\mathbb{P}=\int_A Y\mathbb{E}(X|\mathcal{G})d\mathbb{P},~A\in\mathcal{G}$$

é valido para $ Y=\displaystyle \sum_{k=1}^n y_k {1}_{B_k} $, $ B_k\in \mathcal{G} $, o que implica que

$$\mathbb{E}(XY|\mathcal{G})=Y\mathbb{E}(X|\mathcal{G})$$

Agora seja $ Y $ qualquer variável $ \mathcal{G} $-mensurável com $ \mathbb{E}(|Y|)< \infty $ e seja $ (Y_n)_{n\geq 1} $ uma sequência de variáveis tal que $ |Y_n|\leq Y $ e $ Y_n\rightarrow Y $. Então como é valido para variáveis simples temos que

$$\mathbb{E}(XY_n|\mathcal{G})=Y_n\mathbb{E}(X|\mathcal{G})$$

Claro que $ |XY_n|\leq |XY| $, com $ |XY|< \infty $. Portanto pelo teorema 3.3.4 temos que

$$\mathbb{E}(XY_n|\mathcal{G})\rightarrow \mathbb{E}(XY|\mathcal{G})$$

E portanto o resultado segue.

3.4 - Teorema de Radon-Nikodym

Um dos problemas mais comuns estudados em análise matemática é encontrar uma representação conveniente para algumas funções especiais. Por exemplo, sobre certas condições, pode-se representar um funcional linear sobre um espaço de Hilbert em termos de um produto escalar dado. Uma situação similar ocorre na teoria da medida. Dado duas medidas $ \nu $ e $ \mu $ sobre um espaço mensurável $ (X,\mathcal{F}) $, uma questão importante que surge é se conseguimos representar $ \nu $ em termos de $ \mu $ através de algum operador linear. O teorema de Radon-Nikodym garante tal representação sobre certas hipóteses.

Definição 3.4.1

Uma medida sinal sobre um espaço mensurável $ (X,\mathcal{F}) $ é uma função a valores reais estendidos $ \nu $ definida para conjuntos de $ \mathcal{F} $ satisfazendo

• $ \nu $ assume no máximo um dos valores $ +\infty $, $ -\infty $;
• $ \nu(\emptyset)=0 $;

Outro conceito importantíssimo é a noção de conjunto positivo e conjunto negativo.

Definição 3.4.2

Um conjunto $ A $ é dito ser positivo, se para qualquer subconjunto $ E\subset A $, temos que $ \nu(E)\geq 0 $. Similarmente, dizemos que $ B $ é um conjunto negativo se, para qualquer subconjunto $ E\subset B $, temos que $ \nu(E)\leq 0 $.

Lema 3.4.1

Todo subconjunto mensurável de um conjunto positivo é ele mesmo positivo. A união de uma coleção enumerável de conjuntos positivos é um conjunto positivo.

Prova:

A primeira afirmação sai direto da definição de conjunto positivo.

Seja $ A $ a união de uma sequência de conjuntos positivos. Se $ E $ é qualquer subconjunto mensurável de A. Defina

$$E_n=E\cap(A_n-\cup_{i=1}^{n-1}A_i)$$

Cada $ E_n $ é um subconjunto mensurável de $ A_n $ e portanto $ \nu(E_n)\geq 0 $. Desde que $ E_n $ são disjuntos e $ E=\cup_{n=1}^{\infty}E_n $, da definição de medida, temos que

$$\nu(E)=\nu(\cup_{n=1}^{\infty})=\sum_{n=1}^{\infty}\nu(E_n)\geq 0.$$

Então $ A $ é um conjunto positivo.

$ \square $

Lema 3.4.2

Seja $ E $ um conjunto mensurável tal que $ 0 < \nu(E)<\infty $. Então existe um conjunto positivo $ A\subset E $ com $ \nu(A)> 0 $.

Prova:

Se $ E $ é um conjunto positivo, não há nada a provar. Suponha que $ E $ não seja um conjunto positivo. Então ele contém conjuntos de medida não positiva. Seja $ n_1 $ o menor inteiro positivo tal que existe um conjunto mensurável $ E_1\subset E $ com $ \nu(E)< -\frac{1}{n_1} $.

Procedendo indutivamente, se $ E-\cup_{i=1}^{k-1}E_i $, ainda não for um conjunto positivo, seja $ n_k $ o menor inteiro positivo para o qual existe um conjunto mensurável $ E_k $ tal que $ E_k -\cup_{i=1}^{k-1}E_i $ e $ \nu(E_k)< -\frac{1}{n_k} $.

Defina $A:=E-\cup_{i=1}^{\infty}E_i$. Vamos mostrar que $ A $ é um conjunto positivo.

Note que $ E=A\cup(\cup_{i=1}^{\infty}E_i) $ e que esta é uma união disjunta. Entã, temos que

$$\nu(E)=\nu(A)+\nu(\cup_{i=1}^{\infty}E_i).$$

Por outro lado, temos que

$$\sum_{i=1}^{\infty}|\nu(E_i)|=|\nu(\cup_{i=1}^{\infty}E_i)|\leq |\nu(E)|< \infty.$$

Então $ \sum_{i=1}^{\infty}\nu(E_i) $ converge absolutamente. Assim, vale que

$$\nu(E)=\nu(A)+\sum_{i=1}^{\infty}\nu(E_i).$$

Desde que $ |\nu(E_k)|=-\nu(E_k)\geq \frac{1}{n_k} $. Do critério da comparação, como $ \sum_{i=1}^{\infty}|\nu(E_i)|<\infty $ converge, segue quea série $ \sum_{i=1}^{\infty}\frac{1}{n_i} $ converge. Então $ \frac{1}{n_k}\rightarrow 0 $ quando $ k\rightarrow \infty $, isto é, $ \lim_{k\rightarrow \infty}n_k=\infty $.

Como $ n_k\rightarrow\infty $, existe $ k $ tal que $ (n_k-1)^{-1}\leq\varepsilon $.

Suponha que $ A $ contém um conjunto $ C $ com medida menor do que $ -(n_k-1)^{-1} $. Observe que $ C\subseteq A\subseteq E-\cup_{i=1}^{k-1}E_i $ e

$$\nu(C)<-\frac{1}{n_k-1}<-\frac{1}{n_k}$$

Temos uma contradição, desde que $ n_k $ é o menor inteiro positivo para o qual existe um conjunto mensurável $ E_k\subset E-\cup_{i=1}^{k-1}E_i $ tal que $ \nu(E_k)< -\frac{1}{n_k} $. Então o conjunto $ A $ não pode conter conjuntos mensuráveis com medida menor do que $ -(n_k-1)^{-1} $, qual é maior do que $ -\varepsilon $. Então $ A $ nã contém conjuntos com medida menor do que $ -\varepsilon $. Como $ \varepsilon $ é arbitrário, segue que $ A $ não contém conjuntos com medida negativa, e portanto é um conjunto positivo.

$ \square $

Teorema 3.4.1 (Teorema da Decomposição de Hahn)

Seja $ \nu $ medida sinal sobre $ (X,\mathcal{F}) $. Então, existe um conjunto positivo $ A $ e um conjunto negativo $ B $ tal que

$$X=A\cup B\ \ \ e \ \ \ A\cap B=\emptyset.$$

Prova:

Como $ \nu $ assume no máximo um valor de $ -\infty $ ou $ +\infty $, vamos assumir que $ -\infty\leq\nu(E)<\infty $ para qualquer conjunto mensurável $ E $.

Seja

$$ \lambda:=\sup(\nu(A):A \text{é conjuto positivo com respeito a $\nu$}) $$

Como $ \emptyset $ é positivo e $ \nu(\emptyset)=0 $, temos que $ \lambda\geq 0 $.

Então

$$\nu(A)=\nu(A_i)+\nu(A-A_i)\geq\nu(A_i)$$

para todo $ i $. Assim,

$$\lambda=\lim_{n\to\infty}n(A_i)\leq \nu(A)\leq\lambda$$

Temos então

$$\nu(A)=\lambda$$

Seja $ B=X-A $. Vamos mostrar que $ B $ é um conjunto negativo. Suponha que $ E $ é um subconjunto positivo de $ B $. Então $ E $ e $ A $ são disjuntos e $ E\cup A $ é um conjunto positivo.

$$\lambda\geq\nu(E\cup A)=\nu(E)+\nu(A)=\nu(E)+\lambda.$$

Como $ \lambda<\infty $, temos que $ \nu(E)=0 $. Se $ B $ contém um conjunto com medida positiva, pelo Lema 3.4.2 existe um subconjunto positivo $ A\subset E $ tal que $ \nu(A)>0 $. Então $ B $ é um conjunto negativo.

$ \square $

Definição 3.4.3

Se $ (X,\mathcal{F}) $ é um espaço mensurável e $ \mu $ e $ \nu $ duas medidas sinais sobre $ \mathcal{F} $, dizemos que $ \mu $ e $ \nu $ são mutuamente singulares, $ \mu\perp\nu $, se existe dois conjuntos $ A $ e $ B $ no qual $ A\cup B=X $ e para todo subconjunto mensurável $ E $,

$$|\mu|(A\cap E)=|\nu|(E\cap B)=0.$$

Teorema 3.4.2 (Teorema da Decomposição de Jordan)

Seja $ \nu $ uma medida sinal sobre o espaço mensurável $ (X,\mathcal{F}) $. Então existem duas medidas mutuamente singulares $ \nu^{+} $ e $ \nu^{-} $ sobre $ (X,\mathcal{F}) $ tal que

$$\nu=\nu^{+}-\nu^{-}$$

e o par $ (\nu^{+},\nu^{-}) $ é único.

Prova:

Seja $ A $ e $ B $ a decomposição de Hahn para $ \nu $. Defina \mathcal{F}\rightarrow[0,+\infty] $ e \mathcal{F}\rightarrow[0,+\infty] $ por

$$\nu^{+}(E)=\nu(E\cap A).$$

$$\nu^{-}(E)=-\nu(E\cap B).$$

Como $ A $ e $ B $ são respectivamente conjunto positivo e negativo, temos que $ \nu^{+} $ e $ \nu^{-} $ são medidas não negativas.

Agora, vamos verificar que $ \nu^{+} $ e $ \nu^{-} $ são mutuamente singulares.

Desde que $ A $ e $ B $ são conjuntos mensuráveis disjuntos, então

$$\nu^{+}(B\cap E)=\nu(E\cap (A\cap B))=\nu(\emptyset)=0$$

$$\nu^{-}(A\cap E)=\nu(E\cap (A\cap B))=\nu(\emptyset)=0$$

Para todo conjunto mensurável $ E $, temos que $ \nu^{+} $ e $ \nu^{-} $ são mutuamente singulares. Vamos checar que $ \nu=\nu^{+}-\nu^{-} $.

$$\nu(E)=\nu(E\cap X)=\nu(E\cap (A\cup B))=\nu(E\cap A)+\nu(E\cap B)=\nu^{+}(E)-\nu^{-}(E).$$

Só nos resta mostrar que a decomposição é única. Seja $ X=A^{\prime}\cup B^{\prime} $ outra decomposição de Hahn para $ \nu $. Vamos mostrar que $ \nu(E\cap A)=\nu(E\cap A^{\prime}) $ e $ \nu(E\cap B)=\nu(E\cap B^{\prime}) $. Observe que $ E\cap (A-A^{\prime})\subset A $ então $ \nu(E\cap (A-A^{\prime}))\geq 0 $ e $ E\cap (A-A^{\prime})\subset B^{\prime} $ então $ \nu(E\cap (A-A^{\prime}))\leq0 $. Assim, $ \nu(E\cap (A-A^{\prime}))=0 $, e por simetria $ \nu(E\cap (A^{\prime}-A))=0 $.

Note que $ A\cup A^{\prime}=A\cup (A^{\prime}-A) $, então

$$\nu(E\cap (A\cup A^{\prime}))=\nu(E\cap(A\cup (A-A^{\prime})))\nu(E\cap A)+\nu(E\cap(A^{\prime}-A))=\nu(E\cap A).$$

e

$$\nu(E\cap (A\cup A^{\prime}))=\nu(E\cap(A^{\prime}\cup (A-A^{\prime}))=\nu(E\cap A^{\prime})+\nu(E\cap(A-A^{\prime}))=\nu(E\cap A^{\prime}).$$

Similarmente, podemos mostrar que $ \nu(E\cap B)=\nu(E\cap B^{\prime}) $.

$ \square $

Definição 3.4.4

Se $ (X,\mathcal{F}) $ é um espaço mensurável e $ \mu $ e $ \nu $ medidas sinais sobre $ \mathcal{F} $, dizemos que $ \nu $ é absolutamente contínua com respeito a $ \mu $, $ \nu\ll\mu $, se $ \nu(E)=0 $ para todo conjunto mensurável $ E $ para qual $ |\nu|(E)=0 $.

Proposição 3.4.1

Se $ \nu $ e $ \mu $ são medidas sinais, então as condições

1. $ \nu\ll\mu $
2. $ \nu^{+}\ll\mu $ e $ \nu^{-}\ll\mu $
3. $ |\nu|\ll|\mu| $

são equivalentes.

Prova:

$ 1\rightarrow 2 $.

Seja E conjunto mensurável tal que $ |\mu|(E)=0 $. Então

$$0\leq|\mu|(A\cap E)\leq|\mu|(E)=0$$

Similarmente, $ |\mu|(B\cap E)=0 $. E $ \nu\ll\mu $, temos que $ \nu(A\cap E)=0 $ e $ \nu(B\cap E)=0 $, isto é, $ \nu^{+}(E)=\nu^{-}(E)=0 $. Assim, $ \nu^{+}\ll\mu $ e $\nu^{-}\ll\mu $.

$ 2\rightarrow 3 $.

Seja $ E $ um conjunto mensurável tal que $ |\mu|(E)=0. $ Então

$$\nu^{+}\ll\mu\Rightarrow\nu^{+}(E)=0.$$

$$\nu^{-}\ll\mu\Rightarrow\nu^{-}(E)=0.$$

Então, $ |\nu|(E)=\nu^{+}(E)+\nu^{-}(E)=0+0=0 $. E portanto

$$|\nu|\ll|\mu|.$$

$ 3\rightarrow 1 $.

Seja $ E $ conjunto mensurável tal que $ |\nu|(E)=0. $ Desde que $ |\nu|\ll|\mu| $, temos que $ |\nu|(E)=0 $. Como $ 0\leq\nu^{+}(E)\leq|\nu|(E)=0 $, então $ \nu^{+}(E)=0 $. Similarmente $ \nu^{-}(E)=0 $. Como $ \nu(E)=\nu^{+}(E)-\nu^{-}(E)=0-0=0 $. Portanto $ \nu\ll\mu $.

Lema 3.4.3

Se $ \nu $ e $ \mu $ são medidas finitas tal que $ \nu\ll\mu $ e $ \nu $ não é identicamente nula, então existe um número positivo $ \epsilon $ e um conjunto mensurável $ A $ tal que $ \nu(A)>0 $ e $ A $ um conjunto mensurável positivo para a medida sinal $ \nu-\epsilon\mu $.

Prova:

Para cada $ n=1,2,3,\dots $, considere a medida sinal $ \nu-\frac{1}{n}\mu $ e seja $ X=A_n\cup B_n $ a decomposição de Hahn com respeito a medida $ \nu-\frac{1}{n}\mu $. Seja $ A_0=\cup_{n=1}^{\infty}A_n $ e $ B_0=\cap_{n=1}^{\infty}B_n $.

Como $ B_0\subset B_n $ para cada $ n\in\mathbb{Z}_{+} $, como cada $ B_n $ é um conjunto negativo, temos que

$$0\leq\nu(B_0)\leq\frac{1}{n}\mu(B_0)$$

para todo $ n\in\mathbb{Z}_{+} $. Assim, $ \nu(B_0)=0 $.

Note que $ X=A_0\cup B_0 $ é uma união disjunta. Se $ \nu(A_0)=0 $ então $ \nu(X)=\nu(A_0)+\nu(B_0)=0+0=0 $, ou seja, $ \nu(X)=0 $, mas como $ \nu $ não é identicamente nula, então $ \mu(A_0)> 0 $.

Como $ \nu\ll\mu $, temos que $ \nu(A_0)> 0 $. Por outro lado

$$0<\mu(A_0)=\mu(\cup_{n=1}^{\infty}A_n)\leq\sum_{n=1}^{\infty}\mu(A_n).$$

Então, para no mínimo um $ N $, devemos ter $ \mu(A_N)> 0 $. Defina

$$A=A_N\ \ e\ \ \epsilon=\frac{1}{N}$$

Portanto temos que

$$\mu(A)> 0\ \ \ e\ \ \ \nu(A)-\epsilon\mu(A)> 0.$$

$ \square $

Teorema 3.4.3 (Teorema de Radon-Nikodym para medidas finitas)

Seja $ (X,\mathcal{F}, \mu) $ é um espaço de medida, com $ \mu $ medida finita. Se $ \nu $ é uma medida finita sobre $ \mathcal{F} $ absolutamente contínua com respeito a medida $ \mu $, então existe uma função mensurável finita $ f $ sobre $ X $ tal que

$$\nu(E)=\int_{E}fd\mu\ \ \ \ \ (1)$$

para todo conjunto mensurável $ E $. A função $ f $ é única no sentido que se $ g $ é uma função que satisfaz $ (1) $, então $ f=g $ quase certamente.

Prova:

Seja $ \mathcal{C} $ a classe das funções não negativas, integráveis com respeito a $ \mu $ tal que $ \int_Ef d\mu\leq \nu(E) $ para todo conjunto mensurável $ E $ e defina

$$ \alpha=\sup\left(\int f d\mu:f\in\mathcal{C}\right) $$

Note que $ \mathcal{C}\neq\emptyset $ uma vez que $ 0\in\mathcal{C} $. Mais ainda,

$$0\leq\int f d\mu\leq\nu(X)<\infty\ \ \ \text{para toda}\ f\in\mathcal{C}.$$

o que implica que $ 0\leq\alpha<\infty $.

Desde que $ \alpha $ é um ponto limite do conjunto $ \left(\int f d\mu:f\in\mathcal{C}\right) $, então existe uma sequência de funções em $ \mathcal{C} $ tal que $ \alpha=\lim_{n\to\infty}\int f_n d\mu $. Seja $ E $ um conjunto mensurável e $ n $ um inteiro positivo. Defina a função $ g_n:X\rightarrow [0,\infty] $, por

$$g_n=\max(f_1,f_2,\dots,f_n).$$

Seja

$$A_i=E\cap(\cap_{k=1,k}^n(f_i-f_k)^{-1}([0,\infty)))$$

para $ i=1,2,\dots,n $. Defina

$$E_1=A_1, E_2=A_2-A_1,\dots, E_n=A_n-\cup_{i=1}^{n-1}A_i.$$

Temos que $ f_0(x)=\lim_{n\to\infty}g_n(x) $

Como $ (g_n) $ é uma sequência de funções não decrescente que converge pontualmente para $ f_0 $, pelo teorema da convergência monótona, temos que

$$\int_Xf_0d\mu=\lim_{n\to\infty}\int_Xg_nd\mu$$

Como cada $ g_n\in\mathcal{C} $, então

$$\int_xg_nd\mu\leq\alpha$$

para todo $ n $, então

$$\int_Xf_0d\mu=\lim_{n\to\infty}\int_Xg_nd\mu\leq\alpha .$$

Também $ f_n\leq g_n $ para todo $ n $, temos

$$\int_Xf_nd\mu\leq\int_Xg_nd\mu$$

Então

$$\alpha=\lim_{n\to\infty}\int_Xf_nd\mu\leq\lim_{n\to\infty}\int_Xg_nd\mu=\int_Xf_0d\mu.$$

Portanto

$$\int_Xf_0d\mu=\alpha.$$

Mais ainda,

$$\int_Ef_0d\mu=\lim_{n\to\infty}\int_Eg_nd\mu\leq\lim_{n\to\infty}\nu(E)=\nu(E).$$

Então $ f_0\in\mathcal{C} $.

Seja $ \nu_0:\mathcal{M}\rightarrow [0,\infty] $ função dada por

$$\nu_0(E)=\nu(E)-\int_Efd\mu.$$

Observação: $ \nu_0 $ é uma medida finita e que $ \nu_0\ll \mu $.

Vamos mostrar que $ \nu_0 $ é identicamente zero. Suponha que não. Então $ \nu_0 $ satisfaz a hipótese do lema 3.4.3 e portanto, existe $ \epsilon> 0 $ e um conjunto mensurável $ A $ tal que $ \mu(A)> 0 $ e $ A $ é um conjunto positivo para $ \nu_0-\epsilon\mu $.

Seja $ E $ mensurável, então $ E\cap A\subset A $ é mensurável e como $ A $ é positivo para $ \nu_0-\epsilon\mu $, temos que $ \nu_0(E\cap A)-\epsilon\mu(E\cap A)\geq 0 $, isto é, $ \epsilon\mu(E\cap A)\leq \nu_o(A\cap E)=\nu(E\cap A)-\int_{E\cap A}fd\mu $

$$\int_Egd\mu=\int_ef d\mu+\epsilon\mu(E\cap A)=\int_{E\cap A}f d\mu+\int_{E-A}f d\mu+\epsilon\mu(E\cap A)$$

$$\leq \int_{E-A}f d\mu+\nu(E\cap A)\leq \nu(E-A)+\nu(E\cap A)=\nu(E).$$

Então $ g\in\mathcal{C} $. Contudo, $ \int_Xg d\mu=\int_X f d\mu+\epsilon\mu(A)> \alpha $, temos uma contradição desde que $ \alpha $ é o supremo do conjunto $ \left(\int_X f d\mu:f\in\mathcal{C}\right) $ e $ \int_X g d\mu\in\left(\int_Xf d\mu\right) $. Então $ \nu_0(E)=0 $ para qualquer conjunto mensurável $ E $, isto é

$$\nu(E)=\int_E fd\mu$$

Agora, vamos mostrar a unicidade de $ f $. Seja $ g $ outra função não negativa mensurável satisfazendo $ (1) $. Desde que $ \nu(E)<\infty $ para todo $ E\in\mathcal{F} $, então

$$0=\nu(E)-\nu(E)=\int_Eg d\mu-\int_Ef d\mu=\int_E(g-f) d\mu$$

para todo $ E\in \mathcal{F} $. Então, temos que $ f=g $ quase certamente.

$ \square $

5 - Cadeia de Markov

A cadeia de markov é um processo estocástico caracterizado por seu estado futuro depender apenas do seu estado atual, sendo que os estados passados não influenciam no estado futuro. O nome cadeia de markov foi dado em homenagem ao matemático russo Andrey Markov.

Definição 5.1

Um processo de Markov $ {X_t} $ é um processo estocástico com a propriedade de que, dado o valor de $ X_t $ os valores de $ X_s $, para $ t \ < \ s $ não são influenciados pelos valores de $ X_u $ para $ u \ < \ t $. Ou seja, a probabilidade de qualquer comportamento futuro do processo, quando o seu estado atual é conhecida exatamente, não é alterada pela conhecimento adicional sobre seu comportamento passado.

Se o conjunto de índice for discreto então a propriedade da cadeia de markov é dada da seguinte forma

$ \mathbb{P}[X_{n}=x_n|X_0=x_0, \cdots, X_{n-1}=x_{n-1}]=\mathbb{P}[X_{n}=x_{n}|X_{n-1}=x_{n-1}]= $

$ \mathbb{P}(x_{n-1},x_{n}) $.

Vamos trabalhar apenas com o conjunto de índice discreto, assim notamos que a cadeia e markov é um processo de estados

Definimos a probabilidade de transição de n-passos como:

$$p_n (i, j ) = \mathbb{P} (X_{n+m} = j | X_m = i ) $$

Exemplo 5.1

Seja $ (X_t) $ um processo estocástico com $X_i: \Omega \rightarrow\mathbb{N}$, no qual $ \mathbb{N} $ é o conjuntos dos naturais com o zero. Definamos o seguinte que:

$$\mathbb{P_k(i,i+1)}=\mathbb{P}[X_k=i+1|X_{k-1}=i]=p$$

$$\mathbb{P_k(i,i-1)}=\mathbb{P}[X_k=i-1|X_{k-1}=i]=q$$

$$\mathbb{P_k(i,i)}=\mathbb{P}[X_k=i|X_{k-1}=i]=1-(p+q)$$

Esse processo é chamado de processo de nascimento e morte, pois no fundo estamos dizendo que existem apenas 3 possibilidades em cada instantes

• Nascer - acrescentar um novo elemento com probabilidade de que isso ocorra sendo p.
• Morrer - diminuir um novo elemento com probabilidade de que isso ocorra sendo q.
• Nada - não acrescentar, nem diminuir com probabilidade $ 1-(p+q) $.

Notemos que no processo de nascimento e morte, a probabilidade de acrescentar, diminuir ou nada acontecer não depende do tamanho atual da população, ou seja, não depende de i.

Teorema 5.1 (Chapman - Kolmogorov)

Dado uma cadeia de Markov $ (X_t) $ com o espaço de estados E, ou seja, E é o conjunto dos possíveis valores de $ X_i $ e a probabilidade de transição $ \mathbb{P}_k(\cdot,\cdot) $. Para $ n < m $ temos que

$$\displaystyle \mathbb{P}[X_{m}= j|X_{n} = i]=\sum_{m=1}^{\infty}\mathbb{P}_{m-k} [x_m , j] \mathbb{P}_{k-n}[i ,x_m]$$

Demonstração

Primeiramente lembremos que $ \displaystyle \mathbb{P}[A|B]=\mathbb{P}[A\cap \Omega|B]=\frac{\mathbb{P}[A\cap \Omega ;B]}{\mathbb{P}[B]} $, podemos encontrar mais detalhes sobre a probabilidade condicional na apostila de probabilidade.

Assim, temos que

$$\displaystyle \mathbb{P}[X_{m}=j|X_{n}=y]=\mathbb{P}\left[(X_{m}=j)\bigcap \left(\bigcup_{p=1}^{\infty}(X_k=x_p)\right)|X_{n}=i\right]$$

Observe que $ ((X_{m}=j)\cap(X_k=x_p))\cap((X_{m}=j)\cap(X_k=x_p))=\emptyset $, se $ j\neq i $, ou seja eles são dois a dois disjuntos assim:

$$\displaystyle \mathbb{P}[X_{m}=j|X_{n}=i]=\sum_{p=1}^{\infty}\mathbb{P}\left[(X_{m}=j)\cap(X_k=x_p)|X_{n}=i\right]$$

$$\displaystyle \sum_{p=1}^{\infty}\mathbb{P}[X_{m}=j|(X_k=x_p)\cap X_{n}=i]\mathbb{P}[X_k=x_p|X_{n}=i]$$

$$\displaystyle \sum_{p=1}^{\infty}\mathbb{P}[X_{m}=j|X_k=x_p]\mathbb{P}_{k}(i,x_p)=\sum_{p=1}^{\infty}\mathbb{P}_{k-n}(i, x_p)\mathbb{P}_{m-k} (x_p , j)$$

E portanto o resultado segue.

Uma notação muito usada e útil é a notação matricial que nos fornece toda informação sobre os estados de transição.

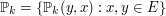
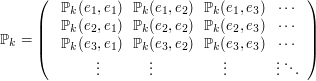
Essa matriz é conhecida como matriz de transição.

Exemplo 5.2

Usando a notação matricial qual seria a matriz de transição do exemplo 5.1. A matrix de transição do processo de nascimento e morte é dada por:

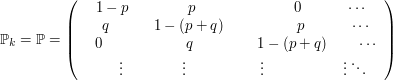
Exemplo 5.3

Suponha que uma concessionária tem a seguinte estratégia para um determinado veículo modelo de veículo de seu estoque. Todo sexta-feira a noite quando a concessionária fecha ela contabiliza o número de veículos deste modelo e faz um pedido para o fornecedor que lhe entrega na segunda-feira pela manhã antes da concessionária abrir novamente.

• Se há veículos no estoque, a concessionária não faz nenhum pedido
• Se não há veículos no estoque, a concessionária pede 3 veículos ao fornecedor
• Caso durante a semana este modelo de veículo termine no estoque, ele não será vendido até a semana seguinte.

Assim definamos nosso processo $ X_n $ como sendo o número de veículos na sexta feira da semana n, e $ X_0 $ como sendo o número inicial de veículos.

Definimos $ D_i $ a demanda da semana i. Suponha que $ D_1,D_2, D_3, \cdots \sim Po(\lambda) $ e sejam independentes, ou seja, $ D_i $ tem distribuição poisson com parâmetro $ \lambda $. Para mais detalhes sobre a distribuição poisson consulte apostila de probabilidade.

Desta forma nossa variável

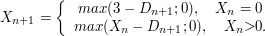
A primeira coisa que devemos fazer é verificar se esse processo é uma cadeia de markov se a resposta for afirmativa então devemos encontrar sua matriz de transição.

Notemos que nosso processo tem apenas 4 fases possíveis, ou seja, nosso espaço de fase é dado por:

$$E=(0,1,2,3)$$

$$\mathbb{P}[X_{n+1}=x_{n+1}|X_0=x_0,X_1=x_1,\cdots, X_{n}=x_n]$$

Se $ x_n=0 $, então

$$\mathbb{P}[X_{n+1}=x_{n+1}|X_0=x_0,X_1=x_1,\cdots, X_{n}=0]=$$

$$\mathbb{P}[max(3-D_{n+1},0)x_{n+1}|X_0=x_0,X_1=x_1,\cdots, X_{n}=0]=$$

$$\mathbb{P}[max(3-D_{n+1},0)x_{n+1}| X_{n}=0]$$

Se $ x_n> 0 $

$$\mathbb{P}[X_{n+1}=x_{n+1}|X_0=x_0,X_1=x_1,\cdots, X_{n}=x_{n}]=$$

$$\mathbb{P}[max(x_n-D_{n+1},0)=x_{n+1}|X_0=x_0,X_1=x_1,\cdots, X_{n}=x_n]=$$

$$\mathbb{P}[max(x_n-D_{n+1},0)x_{n+1}| X_{n}=x_{n}]$$

.

Agora estamos em posição de calcular a matriz de transição.

O interessante da cadeia de markov é que dado um estado inicial, podemos calcular a distribuição assintótica do sistema.

Definição 5.2

Uma cadeia de markov é dita ser homogênea se a probabilidade de transição for estacionária, ou seja, se a probabilidade de transição não depender da etapa n.

Teorema 5.2

Seja $ {X_n} $ um processo markoviano, então dado um estado inicial $ \mu_0 $ temos que

$$\displaystyle \mu_n=\mu_0\prod_{i=1}^{n}\mathbb{P}_i$$

Se o a cadeia de markov for homogênea então $ \mu_n=\mu_0 \mathbb{P}^{n} $.

Demonstração

Como $ \mu_0 $ é o estado inicial então temos que $ \mu_0=(\mathbb{P}[X_0=0], \mathbb{P}[X_0=1], \mathbb{P}[X_0=2], \cdots) $. Assim

$$\mu_1=(\mathbb{P}[X_1=0|X_0], \mathbb{P}[X_1=1|X_0], \mathbb{P}[X_1=2|X_0], \cdots)$$

Agora usando a equação de Chapman-Kolmogorov, temos que

$$\mu_1=\mu_0 \mathbb{P}_1$$

.

Assim por indução temos que

$$\mu_n=\mu_0 \prod_{j=1}^{n}\mathbb{P}_j$$

E portanto o resultado segue.

Exemplo 5.4

Seja uma cadeia de markov $ (X_t) $ homogênea com o espaço de transição $ E=(0,1,2) $ e a seguinte matriz de transição:

Calcule $ \mathbb{P}[X_2=1; X_3=1|X_1=0] $ e $ \mathbb{P}[X_1=0; X_2=0|X_0=2] $.

Basta observarmos que:

$$\displaystyle \mathbb{P}[X_2=1; X_3=1|X_1=0]=\frac{\mathbb{P}[X_2=1; X_3=1|X_1=0]}{\mathbb{P}[X_2=1;X_1=0]}=$$

$$\frac{\mathbb{P}[X_3=1|X_2=1;X_1=0]}{\mathbb{P}[X_2=1;X_1=0]}\mathbb{P}[X_2=1|X_1=0]$$

$$\displaystyle \mathbb{P}[ X_3=1|X_2=1;X_1=0]\mathbb{P}[X_2=1|X_1=0]=$$

$$\mathbb{P}[ X_3=1|X_2=1]\mathbb{P}[X_2=1|X_1=0]=(0,1)(0,17)=0,017$$

Da mesma forma temos que

$$\mathbb{P}[X_1=0; X_2=0|X_0=2]=\mathbb{P}[X_2=0|X_1=0]\mathbb{P}[X_1=0|X_0=2]=(0,73)(0,68)=0,4964 $$

Exemplo 5.5

Seja uma cadeia de markov $ (X_t) $ homogênea com o espaço de transição $ E=(0,1,2) $ e a seguinte matriz de transição:

E com a seguinte condição inicial $ \mu_{0}=[0,2; 0,8; 0] $

Calcule $ \mathbb{P}[X_0=1; X_1=0; X_2=2] $

Observemos que

$ \mathbb{P}[X_0=1; X_1=0; X_2=2]=\mathbb{P}[X_2=2| X_1=0; X_0=1]\mathbb{P}[X_0=1; X_1=0]=\mathbb{P}[X_2=2| X_1=0]\mathbb{P}[X_1=0| X_0=1]\mathbb{P}[X_0=1]=(0,1)(0,55)(0,8)=0,044 $

Exemplo 5.6

Suponha que 3 bolas brancas e 3 bolas pretas são distribuídas em uma urna de tal forma que cada urna tenha exatamente 3 bolas. Suponha que em cada etapa uma bola de cada urna é selecionada e trocada de urna. Seja $ X_n $ o numero de bolas brancas na urna 1. Seja $ (X_t) $ o processo estocástico associado.

i) Esse processo é um processo markoviano?

ii) Se o estado inicial do sistema é $ X_0=1 $, ou seja, $ \mu_0=(0, 1, 0, 0) $. Qual a probabilidade de $ X_2 $ ser igual a 0?

iii) Se $ \mu_0=(1/4, 1/4, 1/4, 1/4) $ calcule $ \mu_{10} $

iv) Se $ \mu_{1/4,2/4, 0, 1/4} $ calcule $ \mu_{10} $.

i) Primeiramente definíamos as seguintes variáveis aleatórias

$ B_{n}^1 $={Pegar uma bola branca na urna um na etapa n.}

$ B_{n}^2 $={Pegar uma bola branca na urna dois na etapa n.}

Notemos que $ B_n^1, B_{n}^2 $, pode assumir apenas o valor 0 ou 1, pois vamos pegar uma única bola em cada etapa. Assim $ B_n^1 $ será 1 se pegarmos uma bola branca na urna 1 e zero caso contrário e o mesmo vale para $ B_n^{2} $ só que para a urna 2.

Portanto temos que o nosso processo $ X_n $ será dado da seguinte forma:

$$X_n=X_{n-1}-B_n^1+B_n^2$$

Ou seja o número de bolas brancas na etapa n depende do numero de bolas que tínhamos na etapa anterior, menos o $ B_n^1 $ que é o número de bolas brancas que tiramos da urna 1, mais $ B_n^2 $ que é o número de bolas brancas que tiramos da urna 2. Assim temos que:

$$\mathbb{P}[X_n=x_n| X_{n-1}=x_{n-1}]=\mathbb{P}[X_{n-1}-B_n^1+B_n^2=x_n| X_{n-1}=x_{n-1}]=$$

$$\mathbb{P}[B_n^2-B_n^1=x_n-X_{n-1}| X_{n-1}=x_{n-1}]=$$

$$\mathbb{P}[B_n^2-B_n^1=x_n-x_{n-1}| X_{n-1}=x_{n-1}]$$

Como $ B_n^1 $ e $ B_n^2 $ assumem apenas valores 0 ou 1, então temos que $ B_n^2-B_n^1 $ pode assumir apenas o valores -1, 0 e 1.

Calculemos primeiramente então

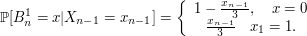
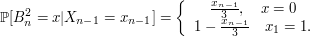
Notemos que:

$$\mathbb{P}[B_n^{2}=0;B_n^{1}=1|X_{n-1}=x_{n-1}]=\mathbb{P}[B_n^{2}=0|X_{n-1}=x_{n-1}]\mathbb{P}[B_n^{1}=1|X_{n-1}=x_{n-1}]=\left(\frac{x_{n-1}}{3}\right)^2$$

$$\mathbb{P}[B_n^{2}=0;B_n^{1}=0|X_{n-1}=x_{n-1}]+\mathbb{P}[B_n^{2}=1;B_n^{1}=1|X_{n-1}=x_{n-1}]=$$

$$\mathbb{P}[B_n^{2}=0|X_{n-1}=x_{n-1}]\mathbb{P}[B_n^{1}=0|X_{n-1}=x_{n-1}]+\mathbb{P}[B_n^{2}=1|X_{n-1}=x_{n-1}]\mathbb{P}[B_n^{1}=1|X_{n-1}=x_{n-1}]$$

$$=\left[2\frac{x_{n-1}}{3}\left(1-\frac{x_{n-1}}{3}\right)\right]$$

$$\mathbb{P}[B_n^{2}=1;B_n^{1}=0|X_{n-1}=x_{n-1}]=\mathbb{P}[B_n^{2}=1|X_{n-1}=x_{n-1}]\mathbb{P}[B_n^{1}=0|X_{n-1}=x_{n-1}]=\left(1-\frac{x_{n-1}}{3}\right)^2$$

Desta forma temos que:

$$\mathbb{P}[B_n^2-B_n^1=x_{n}-x_{n-1}|X_{n-1}=x_{n-1}] =$$

Portanto concluímos que $ X_n $ é de fato uma cadeia de markov homogênea.

ii) Por definição temos que

$$\mu_n=(\mathbb{P}[X_n=0], \mathbb{P}[X_n=1], \mathbb{P}[X_n=2], \mathbb{P}[X_n=3])$$

Assim para encontrarmos $ \mathbb{P}[X_2=0] $, basta encontrarmos $ \mu_2 $. Entretanto pela equação de Chapman-Kolmogorov temos que

$$\mu_2=\mu_0 \mathbb{P}^2$$

Lembrando que nosso $ \mu_0=[0, 1, 0, 0] $ assim temos que:

$$\mu_2(4/81, 41/81, 32/81, 4/81)$$

Portanto temos que, $ \mathbb{P}[X_2=0]=41/81 $

iii) Para encontrarmos $ \mu_{10} $ basta utilizarmos a equação de Chapman-Kolmogorov, desta forma temos que

$$\mu_{10}=\mu_0 \mathbb{P}^{10}$$

Para encontrarmos $ \mathbb{P}^10 $ usamos métodos computacionais, com $ \mu_0=(1/4, 1/4, 1/4, 1/4) $

$$\mu_{10}=(0,05; 0,45; 0,45; 0,05)$$

iv) Idêntico ao item anterior, basta mudarmos $ \mu_0=(1/4, 2/4, 0, 1/4) $

$$\mu_{10}=(0,05; 0,45; 0,45; 0,05)$$

Notemos que o resultado foi o mesmo do item anterior apesar de ter uma condição inicial distinta. Isso nos indica que após um determinado número de etapas nossa $ \mu_n $ passa a não depender mais da sua condição inicial.

Exemplo 5.7

Generalize o exemplo 5.6 para o caso de N bolas brancas e N bolas pretas.

Primeiramente definíamos as seguintes variáveis aleatórias

$ B_{n}^1 $={Pegar uma bola branca na urna um na etapa n.}

$ B_{n}^2 $={Pegar uma bola branca na urna dois na etapa n.}

Notemos que $ B_n^1, B_{n}^2 $, pode assumir apenas o valor 0 ou 1, pois vamos pegar uma única bola em cada etapa. Assim $ B_n^1 $ será 1 se pegarmos uma bola branca na urna 1 e zero caso contrário e o mesmo vale para $ B_n^{2} $ só que para a urna 2.

Portanto temos que o nosso processo $ X_n $ será dado da seguinte forma:

$$X_n=X_{n-1}-B_n^1+B_n^2$$

Ou seja o número de bolas brancas na etapa n depende do numero de bolas que tínhamos na etapa anterior, menos o $ B_n^1 $ que é o número de bolas brancas que tiramos da urna 1, mais $ B_n^2 $ que é o número de bolas brancas que tiramos da urna 2. Assim temos que:

$$\mathbb{P}[X_n=x_n| X_{n-1}=x_{n-1}]=\mathbb{P}[X_{n-1}-B_n^1+B_n^2=x_n| X_{n-1}=x_{n-1}]=$$

$$\mathbb{P}[B_n^2-B_n^1=x_n-X_{n-1}| X_{n-1}=x_{n-1}]=\mathbb{P}[B_n^2-B_n^1=x_n-x_{n-1}| X_{n-1}=x_{n-1}]$$

Como $ B_n^1 $ e $ B_n^2 $ assumem apenas valores 0 ou 1, então temos que $ B_n^2-B_n^1 $ pode assumir apenas o valores -1, 0 e 1.

Calculemos primeiramente então

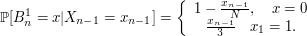
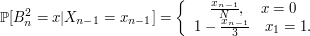
Notemos que:

$$\mathbb{P}[B_n^{2}=0;B_n^{1}=1|X_{n-1}=x_{n-1}]=\mathbb{P}[B_n^{2}=0|X_{n-1}=x_{n-1}]\mathbb{P}[B_n^{1}=1|X_{n-1}=x_{n-1}]=\left(\frac{x_{n-1}}{N}\right)^2$$

$$\mathbb{P}[B_n^{2}=0;B_n^{1}=0|X_{n-1}=x_{n-1}]+\mathbb{P}[B_n^{2}=1;B_n^{1}=1|X_{n-1}=x_{n-1}]=$$

$$\mathbb{P}[B_n^{2}=0|X_{n-1}=x_{n-1}]\mathbb{P}[B_n^{1}=0|X_{n-1}=x_{n-1}]+ \mathbb{P}[B_n^{2}=1|X_{n-1}=x_{n-1}]\mathbb{P}[B_n^{1}=1|X_{n-1}=x_{n-1}]$$

$$=\left[2\frac{x_{n-1}}{N}\left(1-\frac{x_{n-1}}{3}\right)\right]$$

$$\mathbb{P}[B_n^{2}=1;B_n^{1}=0|X_{n-1}=x_{n-1}]=\mathbb{P}[B_n^{2}=1|X_{n-1}=x_{n-1}]\mathbb{P}[B_n^{1}=0|X_{n-1}=x_{n-1}]=\left(1-\frac{x_{n-1}}{N}\right)^2$$

Desta forma temos que:

$$\displaystyle \mathbb{P}[B_n^2-B_n^1=x_{n}-x_{n-1}|X_{n-1}=x_{n-1}] = $$

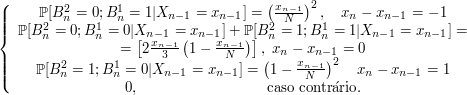
Assim a matriz de transição do processo $ X_n $ é dada

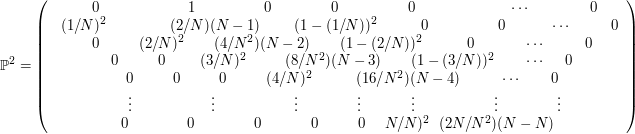
Concluímos também que para o caso geral de N bolas a matriz permanece homogênea.

Exemplo 5.8

Talvez o exemplo mais simples de cadeia de markov seja o exemplo de um movimento completamente determinado, o qual pode ser definido da seguinte forma seja $ \mathbb{P} $ uma matriz de transição com apenas zeros e uns. Assim para cada estado i existe um estado g(i) tal que

$\mathbb{P}({i,g(i)})=1 $ , $ \mathbb{P}({i,j})=0,~\forall j \neq g(i)$

Notemos que isso significa que se estamos no estado i necessariamente no próximo estado estaremos no estado g(i). Notemos que nesse caso basta sabermos o instante inicial e então saberemos todo o futuro, pois se $ X_0=i $ então

$X_1=g(1) $, $ X_2=g(g(1))=g^{(2)}(1),~~\cdots X_{n}=g^{(n)}(1)$

Observação

Muitas vezes apenas olhando para a matriz de transição podemos verificar se as variáveis são $ X_0, X_1, X_2,\cdots $ formão variáveis independentes e identicamente distribuídas, ou seja, com distribuição comum. Basta apenas que a matriz de transição seja homogênea e suas linhas sejam idênticas.

5.1 - Tempos de Paradas na cadeia de Markov

Uma importante propriedade da cadeia de Markov é quando usamos uma forma de dizer o passado em relação ao tempo, ou seja, quando a informação passada é aleatória e temporal. Essa variável é conhecida como tempo de parada, e cadeia de markov com essa propriedade é conhecida como tempo de Markov.

Definição 5.1.1

Seja $ (X_n:~n=0,1,2\cdots) $ um processo estocástico com um espaço de estado enumerável definida no espaço de probabilidade $ (\Omega,\mathcal{F},\mathbb{P}) $. Uma variável aleatórial $ \tau $ definida neste espaço de probabilidade é dita ser um tempo de parada se:

(i) Se assumir valores não negativos inteiros, sendo que existe a possibilidade dela assumir o valor $ +\infty $

(ii) Para todo inteiro não negativo m o evento $ (\omega:\tau (\omega)\leq m) $ é determinado por $ X_0,X_1,X_2,\cdots,X_m $.

Observe que essa definição é um caso particular da definição de tempo de parada anterior, pois essa definição refere-se apenas a um espaço enumerável e não a um espaço contínuo como dito anteriormente.

Intuitivamente, se $ \tau $ é um tempo de parada, então ele será parado ou não pelo tempo m o qual é decidido pela observação do processo estocástico até o momento m. Por exemplo consideremos o primeiro tempo de parada $ \tau_y $ o processo $ X_n $ atinge o estado x, definido por:

$$ \tau_y (\omega)=\inf(n\geq 0: X_n(\omega)=x). $$

Se $ \omega $ é tal que $ X_n\neq x $ para qualquer n, ou seja, o processo nunca assume o valor x, então é claro que $ \tau_x(\omega)=\infty $. Observe que a seguinte igualdade é válida

$$ (\omega:\tau_x(\omega)\leq m)=\displaystyle \bigcup_{n=0}^{m}(\omega: X_n(\omega)=x). $$

Teorema 5.1.1

Toda cadeia de Markov tem a propriedade forte de markov se para todo tempo de parada $ \tau $, a distribuição condicional do processo após $ \tau $, o qual é dado por $ X_\tau^{+}=(Y_{\tau+n}:n=0,1,2,\cdots) $, dado que o passado até o tempo $ \tau $ é dado como sendo $ \mathbb{P}_{X_{\tau}} $ no conjunto

Demonstração

Escolhemos um m e k inteiros não negativos com m fixo, e k um tempo tal que $ 0\leq m_1< m_2< \cdots < m_{k} $ e estados $ i_0,i_1,\cdots , i_m $, $ j_1,j_2,\cdots, j_k $. Então

$$\mathbb{P}(X_{\tau+m_1}=j_1,X_{\tau+m_2}=j_2,\cdots, X_{\tau+m_k}=j_k|\tau=m, X_0=i_0,\cdots, X_m=i_m)=$$

$$\mathbb{P}(X_{m+m_1}=j_1,X_{m+m_2}=j_2,\cdots, X_{m+m_k}=j_k|\tau=m, X_0=i_0,\cdots, X_m=i_m)$$

Agora se $ (\tau=m) $ não é consistente com o evento $ (X_0=i_0,\cdots, X_m=i_m) $ então $ (\tau=m, X_0=i_0,\cdots, X_m=i_m)=\emptyset $, por outro lado se $ (\tau=m) $ é consistente com o evento $ (X_0=i_0,\cdots, X_m=i_m) $ então $ (\tau=m, X_0=i_0,\cdots, X_m=i_m)=(X_0=i_0,\cdots, X_m=i_m) $. Portanto temos que

$$\mathbb{P}(X_{m+m_1}=j_1,X_{m+m_2}=j_2,\cdots, X_{m+m_k}=j_k|\tau=m, X_0=i_0,\cdots, X_m=i_m)=$$

$$\mathbb{P}(X_{m+m_1}=j_1,X_{m+m_2}=j_2,\cdots, X_{m+m_k}=j_k|X_0=i_0,\cdots, X_m=i_m)$$

Usando a propriedade da cadeia de Markov temos que

$$\mathbb{P}(X_{m+m_1}=j_1,X_{m+m_2}=j_2,\cdots, X_{m+m_k}=j_k|X_0=i_0,\cdots, X_m=i_m)=$$

$$\mathbb{P}(X_{m+m_1}=j_1,X_{m+m_2}=j_2,\cdots, X_{m+m_k}=j_k|X_m=i_m)=$$

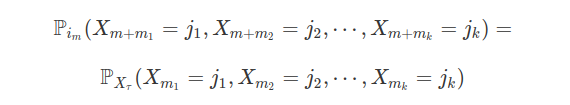
no conjunto $ (\tau =m) $. Como m é fixo porém arbitrário e portanto $ m< \infty $, temos então que o resultado segue.

5.2 - Classificação de Estados em uma Cadeia de Markov

Uma importante caracterização da cadeia de markov seria a classificação dos estados.

Definição 5.2.1

O estado j é dito acessível pelo estado i se j pode ser alcançado a partir do estado i por um número finito de passos. Se dois estados i e j são acessíveis ou seja j é acessível a i e i é acessível a j então dizemos são comunicado.

Probabilisticamente temos que essa definição implica que

$ i \rightarrow j $ (j é acessível de i) se para algum $ 0\leq n< \infty $, $ \mathbb{P}_{i,j}^n > 0 $

$ j \rightarrow i $ (i é acessível de j) se para algum $ 0\leq n< \infty $, $ \mathbb{P}_{j,i}^n > 0 $

$ i \leftrightarrow j $ (i e j são comunicados) se para algum $ 0\leq n< \infty $, e se para algum $ 0\leq m< \infty $ $ \mathbb{P}^n_{i,j} > 0 $ $ \mathbb{P}_{j,i}^m > 0 $

Reciprocamente temos que

$ i \rightarrow j $ (j não é acessível de i) se para todo $ 0\leq n< \infty $, $ \mathbb{P}_{i,j}^n = 0 $

$ j \rightarrow i $ (i não é acessível de j) se para todo $ 0\leq n< \infty $, $ \mathbb{P}_{j,i}^n = 0 $

$ i \leftrightarrow j $ (i e j não são comunicados) se para todo $ 0\leq n< \infty $, e se para todo $ 0\leq m< \infty $ $ \mathbb{P}^n_{i,j}=0 $ $ \mathbb{P}_{j,i}^m= 0 $.

Notemos que como consequência desta definição temos que a relação de comunicação é uma relação de equivalência:

i) Reflexiva

De fato é reflexiva pois $ i\leftrightarrow i $ basta tomarmos n=0.

ii) Simétrica

Se $ i\leftrightarrow j $, então $ j\leftrightarrow i $

iii) Transitividade

Se $ i\leftrightarrow j $, e $ j\leftrightarrow k $, então $ i\leftrightarrow k $

Sabemos que existe dois inteiros r e s tal que:

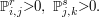
Mas temos que

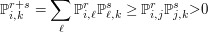
Logo temos que $ i\rightarrow k $. Similarmente mostramos que existe um inteiro n tal que

$$\mathbb{P}^{n}_{k,i}> 0$$

Portanto $ k\rightarrow i $. Combinando esses dois resultados temos que $ i\leftrightarrow k $.

Definição 5.2.2

Se a cadeia de markov tem todos os estados pertence a uma única classe de equivalência, então ele é dito irredutível.

Definição 5.2.3

Um estado é dito recorrente se e somente se, partindo deste estado eventualmente retornamos ao mesmo estado, ou seja, um estado é recorrente é

se existe um $ n> 0 $ tal que $ f_{i,i}^{\star}=1 $, no qual $ f_{i,i}^{\star}=1 $ é definido da seguinte forma

$$f^{n}_{i,i}=\mathbb{P}[X_n=i,X_r\neq i|X_0=i]$$ $$r\in(1,2,\cdots,n-1)$$

então

$$f_{i,i}^{\star}=\displaystyle \sum_{n=1}^{\infty}f^{n}_{i,i}$$

note que $ f^{n}_{i,i} $ é a probabilidade de começarmos em i e retornarmos para i, em um tempo n.

Em termos de probabilidade temos temos que um estado é dito recorrente se e somente se $ f_{i,i}^{\star}=1 $.

Quando o estado i é recorrente podemos definir,

$$\mu_i=\sum_{n=1}^{\infty}n f_{i,i}^{n}$$

note que $ \mu $ define o valor esperado do numero de passos necessários para que retorne ao estado i. O qual é chamado de tempo de recorrência. Portanto $ \mu_i $ pode ser chamado de média de recorrência do estado i.

Usando a média de recorrência podemos classificar o seu estado recorrência nula ou recorrência

Dizemos que um estado recorrente é dito se um estado recorrente nulo se e somente se o tempo média recorrente é $ \infty $, ou seja, se $ \mu_i $.

Dizemos que um estado tem recorrência positiva se, e somente se, o tempo médio recorrente é finito, ou seja, $ \mu_{i} $.

Definição 5.2.4

Um estado é dito ser transiente se, e somente se, partindo do estado i, existe uma probabilidade positiva do processo não eventualmente retornar a este estado.

Isto implica que $ f^{\star}_{i,i}< 1 $.

Outra forma de classificarmos os estados em recorrente e transiente pode ser dado em termos das probabilidade $ \mathbb{P}_{i,i}^{n} $ que é a probabilidade do processo ocupar o estado i depois de n passos, dado que o estado inicial também foi i.

Teorema 5.2.1

i) Um estado i é recorrente se

$$\displaystyle \sum_{n=1}^{\infty}\mathbb{P}_{i,i}^{n}=\infty$$

ii) Um estado i é transiente se

$$\displaystyle \sum_{n=1}^{\infty}\mathbb{P}_{i,i}^{n}< \infty$$

Demonstração

Os estados de equivalência $ \displaystyle \sum_{n}f_{i,i}^{n}=1 $ e $ \displaystyle \sum_{n}\mathbb{P}_{i,i}^{n}=\infty $ o que nos mostra claramente a distinção entre $ f_{i,i}^{n} $ e $ \mathbb{P}^{n}_{i,i} $. $ f_{i,i}^{n} $ nos refere a probabilidade do primeiro retorno de i em n passos e $ \displaystyle \sum_{n}f_{i,i}^{n} $ é a probabilidade do processo retornar a i eventualmente.

Seja $ Q_{ii}^{(N)} $ a probabilidade de partindo do estado i que a cadeia de markov retorne a este estado pelo menos N vezes. Então se tomarmos $ N\rightarrow \infty $ é a probabilidade de retornar infinita vezes no estado i. É claro que se o estado é recorrente então temos que

$$\displaystyle \lim_{N\rightarrow \infty}Q_{ii}^{(N)}=1$$

e por outro lado se o estado é dito ser transiente então temos que

$$\displaystyle \lim_{N\rightarrow \infty}Q_{ii}^{(N)}=0$$

Definição 5.2.5

O período de um estado i é definido como sendo o maior divisor comum de todos os inteiros $ n\geq 1 $, para o qual $ \mathbb{P}^{n}_{ii}> 0 $. Quando o período é 1, o estado é dito ser aperiódico.

Exemplo 5.2.1

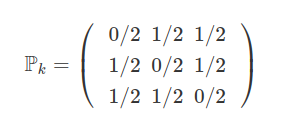
Analisando a matriz podemos ver que os todos os estados se interligam além disso $ \mathbb{P}_{ii}^{n}> 0 $, para $ n\geq 1 $, portanto o período que é o máximo divisor comum é 1.

Como todos os estados comunicam-se temos que existe uma única classe de equivalência.

Exemplo 5.2.2

Observando a matriz que todos os estados se comunicam, pois $ 1\rightarrow 4\rightarrow 3\rightarrow 1 $ ou $ 1\rightarrow 4\rightarrow 2\rightarrow 4\rightarrow 3 \rightarrow 1 $.

Portanto todos os estados pertencem a mesma classe de equivalência. Além disso temos que $ \mathbb{P}_{ii}^{n}> 0 $ é válido apenas para n=3, n=6 ou múltiplos de deles e portanto temos que o período que é o máximo divisor comum é 3.

Exemplo 5.2.3

Um exemplo clássico de um processo Markoviano, seria o chamado passeio aleatório nos inteiros. Nesse exemplo podemos imaginar uma partícula qualquer, que se movimenta de acordo com a seguinte lei:

$$p(i,i+1)=p e p(i,i-1)=1-p$$

Note que essa partícula apenas se movimenta para frente dando um passo ou para trás dando apenas um passo. A respeito desse exemplo podemos nos fazer diversas perguntas, como por exemplo o sobre quais condições o passeio aleatório é recorrente?

Note que o passeio aleatório é uma cadeia irredutível. Assim basta mostrarmos que um estado é recorrente que os demais também serão recorrentes. Vamos considerar a origem observe que para a partícula saindo da origem voltar a ela, necessitará de um número par de passos, pois nossa cadeia dá apenas um passo para frente ou para trás. Assim se n é ímpar $ \mathbb{P}^n_{0,0}=0 $, então

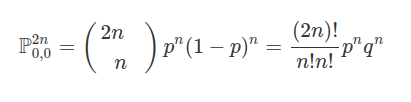
Podemos usar a formula de Stirling

$$\displaystyle \lim_{n\rightarrow \infty}\frac{n!}{n^ne^n\sqrt{2\pi n}}=1$$

Com alguma manipulação algebrica, temos que

$$\displaystyle \lim_{n\rightarrow \infty}\frac{\mathbb{P}^{2n}(0,0)}{(4pq)^n/\sqrt{\pi n}}=1$$

Observe que quando $ p\neq 1/2 $ temos que $ 4pq< 1 $ e que quando $ p=1/2 $ temos que $ 4pq=1 $. Assim quando $ p=1/2 $ a série $ \displaystyle\sum_{n=1}^{\infty}\mathbb{P}^{2n}_{0,0} $ diverge e quando $ p\neq 1/2 $ a serie converge pois é basicamente a serie geométrica. Logo pelo Teorema 5.2.1, temos que o passeio aleatório é recorrente se, e somente se p=1/2.

Exemplo 5.2.4

Suponha que tenhamos 10 bolas, 5 pretas e 5 brancas e duas urnas A e B nas quais, são colocadas aleatoriamente 5 bolas em cada uma. Em cada passo 1 bola de cada urna é retirada e colocada na outra. Seja $ X_n= $número de bolas brancas na urna A, na etapa n. Qual a matriz de transição da cadeia.

Primeiramente note que temos um processo markoviano, pois claramente

$$\mathbb{P}(X_{n+1}=j|X_n=i_n,\cdots,X_0=i_0)=\mathbb{P}(X_{n+1}=j|X_n=i_n)$$

Calculemos nossa matriz de transição. Observe que para que o número de bolas se mantenha é necessário retirar duas bolas de mesma cor em cada urna. Assim

$$\mathbb{P}_{i,i}=\displaystyle \frac{i}{5}\frac{5-i}{5}+\frac{5-i}{5}\frac{i}{5}=\frac{2}{25}i(5-i)$$

Para que o número de bolas brancas aumente na urna A devemos pegar uma bola preta nela e uma bola branca na urna B. Então

$$\mathbb{P}{i,i+1}=\frac{5-i}{5}\frac{5-i}{5}=\frac{(5-i)^2}{25}$$

Para que o número de bolas brancas diminua na urna A devemos pegar uma bola branca nela e uma bola preta na urna B. Então

$$\mathbb{P}_{i,i-1}=\frac{i}{5}\frac{i}{5}=\frac{i^2}{25}$$

Logo a matriz de transição é dada por:

Exemplo 5.2.5 (Cadeia de Ehrenfest.)

Considere r bolas rotuladas de 1 a r. Algumas estão na caixa 1 e outras na caixa 2. A cada passo um número é escolhido aleatoriamente e a bola correspondente é movida de sua caixa para a outra. Seja $ X_n= $número de bolas na caixa 1 após n passos. Qual a matriz de transição deste processo ?

Primeiramente temos que

$$\mathbb{P}_{0,1}=1$$

$$\mathbb{P}_{r,r-1}=1$$

Para $ 0< i < r $ temos que

$$\mathbb{P}{i,i}=0$$

$$\displaystyle \mathbb{P}{i,i-1}=\frac{i}{r}$$

$$\displaystyle \mathbb{P}_{i,i+1}=\frac{(r-i)}{r}$$

Como exemplo tomemos r=4, então

Definição 5.2.5

$$\mathbb{P}(T_j< \infty|X_0=i)=0$$

com $ T_j=\inf(n\geq 1 |X_n=j) $.

Teorema 5.2.2

Um classe finita é recorrente se, e somente se é fechado.

Demonstração

Iremos provar por contradição, assim seja $ \mathcal{C} $ uma classe finita fechada e transiente. Seja i e j em $ \mathcal{C} $. Pelo Teorema 5.2.1 temos que

$$\displaystyle \lim_{n\rightarrow \infty}\mathbb{P}^{n}_{i,j}=0$$

e então

$$\displaystyle \sum_{j\in\mathcal{C}}\lim_{n\rightarrow \infty}\mathbb{P}^{n}_{i,j}=0$$

Como $ \mathcal{C} $ é uma classe finita, podemos permutar o limite com a somatória.

$$\displaystyle \lim_{n\rightarrow \infty}\sum_{j\in \mathcal{C}}\mathbb{P}_{i,j}^{n}=0$$

mas $ \displaystyle \sum_{j\in\mathcal{C}}\mathbb{P}^n_{i,j}=\mathbb{P}(X_n\in \mathcal{C}|X_0=i) $. Desde que a classe é fechada temos que a soma das probabilidades dever ser igual a 1. O que contradiz a equação acima. Assim temos que $ \mathcal{C} $ é recorrente. O que mostra o resultado.

Exemplo 5.2.6

Seja $ S=(1,2,3,4,5,6) $ e a matriz de transição

Encontre todas as classes e determine qual é transiente e qual é recorrente.

Primeiramente observe o diagrama que nos ajuda a identificar as classes.

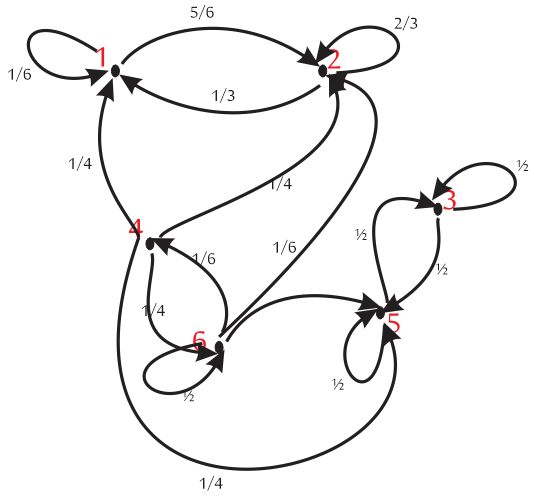
Pelo diagrama podemos identificar as seguinte classes:

$$C_1=(1,2)\text{ recorrente}$$

$$C_2=(3,5)\text{ recorrente}$$

$$C_3=(4,6)\text{ transiente}$$

$ C_1 $ e $ C_2 $ são classes recorrentes, pois são fechadas pelo Teorema 5.2.2.

$ C_3 $ é transiente, pois não é fechada e portanto não recorrente.

Exemplo 5.2.7

Dê um exemplo de uma classe fechada infinita a qual é transiente.

Um exemplo é o passeio aleatório, é fácil ver que este é fechado, pois todos os estados pertence a mesma classe.

Além disso, como $ S=\mathbb{Z} $ que é infinito enumerável, então temos uma classe fechada e infinita.

Como todos os estados pertence a mesma classe para mostrar que é transiente basta mostrar que

$$\sum_{n=0}^{\infty}p_n(0,0)> \infty$$

pela contra-positiva do Teorema 5.2.1.

Assim defina o passeio aleatório da seguinte forma:

$$p(i,i+1)=p$$

$$p(i,i-1)=1-p=q$$

Pelo exemplo 5.2.3, temos que

$$\sum_{n=0}^{\infty}p_n(0,0)> \infty$$

se, e somente se $ p\neq 1/2 $. Logo para $ p\neq 1/2 $ o passeio aleatório é transiente.

5.3 - Autovalores e Cadeias Irredutíveis

Seja P uma matriz de transição e seja $ \lambda $ os autovalores da matriz P, o qual é definido da seguinte forma

$$PX=\lambda X$$

A solução desta equação quando X é um vetor não nulo temos que X é chamado de autovetor e $ \lambda $ é o autovalor. Podemos reescrever a equação da seguinte forma:

$$|\lambda I- P|=0$$

Seja $ \Lambda = \lambda I $, seja $ M $ uma matriz onde os autovetores de P, onde os autovalores compõem a matriz M em forma de coluna.

Assim P é dito diagonalizável se P pode ser escrito como sendo

$$P=M\Lambda M^{-1}$$

$$P^2=(M\Lambda M^{-1})(M\Lambda M^{-1})=M\Lambda^2 M^{-1}$$

Por indução temos que $ P^n=M\Lambda^n M^{-1} $

Exemplo 5.3.1

Seja

o que implica que

$$x_{12}=x_{11}$$

Além disso temos que

$$1/2(x_{11}+x_{12})=x_{12}$$

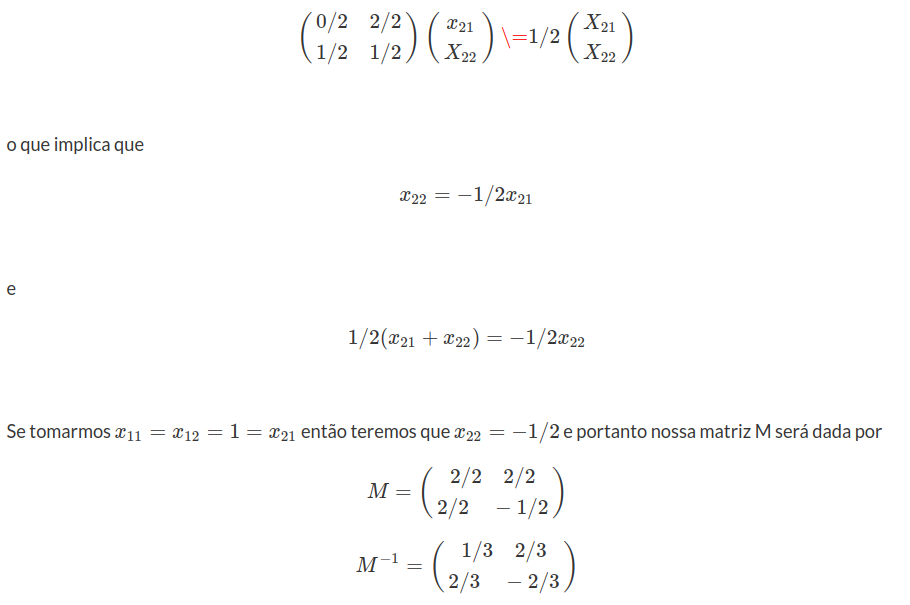
Assim temos que $ P=M\lambda M^{-1} $ e portanto $ P^n =M\lambda^{n} M^{-1} $

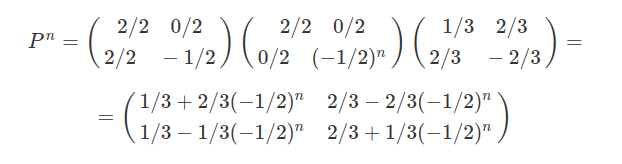
Uma enorme de informação a respeito de uma cadeia de markov finita pode ser retirada a partir da natureza dos autovalores associados a matriz de probabilidade de transição, como por exemplo pelo teorema de Perron-Frobenius da teoria de matrizes temos que existe um autovalor $ r $ chamado de autovalor de perron-frobenius, tal que para qualquer outro autovalor $ \lambda $ temos que $ |\lambda|\leq r $, se $ r $ for menor ou igual a $ 1 $, então temos que a cadeia de markov é irredutível, mas isso vale apenas para cadeias finitas. Além disso o número de autovalores unitários em modulo nos fornece a periodicidade das cadeias de markov periódicas.

Teorema 5.3.1 (lema de Kemeny-Snell)

Seja P uma matriz estocástica (m$ \times $ m) sm nenhum elemento zero. Seja $ \epsilon $ a menor entrada de P. Seja X qualquer vetor coluna com $ m $ componentes, e com o menor componente dado por $ a_0 $ e o maior dado por $ b_0 $. Seja $ a_1 $ e $ b_1 $ o mínimo e o máximo componente respectivamente de PX. Então

$$a_1\geq a_0$$

$$b1\leq b_0$$

e

$$b_1-a_1\leq (1-2\epsilon)(b_0-a_0)$$

A demonstração pode ser encontrada no livro Bhat e Miller e também no artigo Kemeny-Snell (1959).

Note que esse lema implica que o poder da matriz probabilidade de transição P é crescente e o mínimo e o máximo de cada coluna correspondente fica mais próximo e portanto no limite $ \displaystyle \lim_{n\rightarrow \infty}P^n $ todos os elementos de uma mesma coluna serão idênticos, ou seja, teremos linhas idênticas.

Esse teorema nos ajuda a determinar o comportamento limite de uma cadeia de markov.

5.4 - Comportamento Limite

O comportamento limite descreve bem o comportamento do processo estocástico em si, por que de modo geral a convergência é rápida, isto não ocorre apenas se entra em uma região critica, a qual nem sempre existe. Além disso, de modo geral é mais fácil trabalhar com o limite o processo.

Observe que o teorema 5.3.1 da seção anterior nos dá uma taxa de convergência $ (1-2\epsilon) $. Pelo teorema 5.3.1 anterior como ele garante que as linhas são idênticas temos que $ \displaystyle \lim_{n\rightarrow \infty}P_{ij}^n=\pi_{j}, \forall i ~e~ \forall j \in(1,2,\cdots,m) $.

Teorema 5.4.1

Seja $ \displaystyle \lim_{n\rightarrow \infty}P_{ij}^n=\pi_{j}; \forall i ~e~ \forall j \in(1,2,\cdots,m) $, então existe uma constante c e uma constante r com $ c > 0 $ e $ 0> r> 1 $, tal que

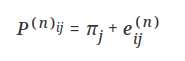
onde

$$|e^{(n)}_{ij}|\leq c r^n$$

Quando a matriz de transição não tem nenhum zero então c=1.

Demonstração

Do teorema 4.3.1 anterior podemos escrever

$$|e^{(n)}_{ij}|\leq b_n-a_n=d_n$$

onde $ d_n $ é o maior dos $ d^{(j)}_n\leq (1-2\epsilon)^n, \forall n\geq 1 $. A constante c e r podem ser obtidas comom $ c=(1-2\epsilon_N)^{-1} $ e $ r=(1-2\epsilon_N)^{1/N} $, no qual N é o menor valor de $ P^n $, para o qual $ P^n $ não tem nenhum elemento zero.

Em termos pratico podemos encontrar

$$N_{\alpha}^{\star}=min\left(n|P_{ij}^{(n)}-\pi_j|< \alpha\right)$$

$$=min\left(n|e^{(n)}_{ij}|< \alpha\right)$$

$$=cr^n< \alpha$$

Quando P não tem nenhum elemento igual a zero, temos que a desigualdade $ r^n<\alpha $.

Teorema 5.4.2

$$\displaystyle \lim_{n\rightarrow \infty}P^{(n)}_{ii}=\frac{1}{\mu_i}$$

ii)Seja j um outro estado que pertence a mesma classe de equivalência de i e seja $ P^{(n)}_{ji} $ a probabilidade do n-ésimo passo com transição de $ i\rightarrow i $. Então

$$\displaystyle \lim_{n\rightarrow \infty}P^{(n)}_{ji}=\displaystyle \lim_{n\rightarrow \infty}P^{(n)}_{ii}.$$

Definição 5.4.1

Suponha que $ p=(p_1,p_2,\cdots) $ é um vetor de probabilidade tal que $ \sum p_i=1 $. Então a distribuição de probabilidade $ (p_i) $ é dita estacionária, com P sendo a matriz de transição de probabiliaade então

$$p=pP$$

Teorema 5.4.3

Em uma cadeia de Markov irredutível com estados ergótico, a probabilidade limite $ p $ satisfaz a equação

$$p_j=\displaystyle \sum_{i=0}^{\infty}p_iP_ij,~~ j=0,1,2,\cdots$$

e

$$\sum p_j=1$$

A distribuição limite é estacionária.

Demonstração

Note que a distribuição limite é estacionária, pois

$$p_j=\displaystyle \sum_{i=0}^{\infty}p_iP_{ij}$$

$ p_k=\displaystyle \sum_{j=0}^{\infty}p_jP_jk=\displaystyle \sum_{i=0}^{\infty}p_i\sum_{j=0}^{\infty} P_{ij}P_jk=\sum_{i=0}^{\infty}p_iP^{(2)}_{ik}=\cdots \sum_{i=0}^{\infty}p_i P^{(n)}_{ij},~~ n\geq 1. $

o que demonstra que ela é estacionária.

Exemplo 5.4.1

Vendedor de uma determinada empresa, pode visitar três cidades A,B e C para vender o seu produto. Mas para ir para essas cidades ele segue algumas regras caso ele esteja na cidade A ele escolhe ir para a cidade B com probabilidade $ 2/3 $ e com probabilidade $ 1/3 $. Se ele estiver na cidade B ele vai para cidade A com probabilidade $ 3/8 $ e para cidade C com probabilidade 1/2 e permanece na mesma cidade com probabilidade $ 1/8 $. Caso ele esteja na cidade C ele vai para cidade A ou para cidade B com probabilidade $ 1/2 $. A pergunta que fica, qual seria a probabilidade de ele visitar a cidade A, B e C a longo prazo.

A matriz de transição da cadeia de Markov é dada por

Assim

$$\displaystyle p_A=\frac{3}{8}p_B+\frac{1}{2}p_B$$

$$\displaystyle p_B=\frac{2}{3}p_A+\frac{1}{8}p_B+\frac{1}{2}p_C$$

$$\displaystyle p_C=\frac{1}{3}p_A+\frac{1}{2}p_B$$

Lembrando que as equações não são independentes, pois existe uma condição

$$p_A+p_B+p_C=1.$$

Combinando todas as equações temos que

$$p_A+p_B+p_C=1$$

$$4p_A-9p_B+8p_C=0$$

$$2p_A+3p_B-6p_C=0$$

Com resolvendo as equações temos que

$$p_A=0,3 ~p_B=0,4 ~p_C=0,3$$

ou seja, podemos dizer que o vendedor vai para cidade A, C e B respectivamente $ 30(porcentagem) , 30(porcentagem) e 40(porcentagem) $.

Exemplo 5.4.2

Suponha que queremos avaliar o número de acidentes em uma determinada rodovia. Assim seja X a variável aleatória que conta o número de acidentes. Definida da seguinte forma

Nº $ 0~ 1~\geq 2 $

Pr $ p~q~r $

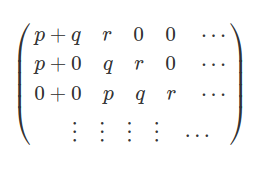
pelo teorema 5.4.3 $ p=(p_0,p_1,\cdots) $ é o vetor da probabilidade limite

Usando a matriz de transição temos que $ pP=p $ logo

$$(p+q)p_0+pp_1=p_0$$

$$rp_0+qp_1+pp_2=p_1$$

$$rp_1+qp_2+pp_3=p_2$$

$$\vdots$$

da primeira equação temos que:

$$p p_1=(1-p-q)p_0=rp_0$$

$$p_1=\displaystyle \frac{r}{q}p_0.$$

da segunda equação

$$p p_2=(1-p-q)p_1=rp_1$$

$$p_2=\displaystyle \frac{r}{q}p_1=\displaystyle \left(\frac{r}{q}\right)^2 p_0$$

Procedendo da mesma forma temos que

$$p_n=\displaystyle \left(\frac{r}{q}\right)^n p_0$$

Por outro lado temos que

$$\displaystyle p_0\sum_{n=1}^{\infty}\left(\frac{r}{p}\right)^n=1$$

$$\displaystyle \left(1-\frac{r}{p}\right)^{-1}p_0=1$$

$$p_0=\displaystyle 1-\frac{r}{p}$$

Assim de modo geral,

$$p_n=\displaystyle \left(1-\frac{r}{p}\right)\left(\frac{r}{p}\right)^n$$

Exemplo 5.4.3

Consideremos uma modificação do exemplo anterior. Seja o número de chegadas dada pela tabela abaixo:

Nº $ 0~ 1 ~ 2 ~ \geq 3 $

Pr $ p ~q ~ r~ s $

com p+q+r+s=1

A matriz de transição é dada por

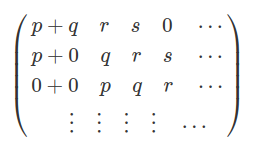
Note que as equações correspondente ao modelo são:

$$(p+q)p_0+p p_1=p_0$$

$$rp_0+qp_1+pp_2=p_1$$

$$sp_0+rp_1+qp_2+pp_3=p_2$$

$$sp_1+rp_2+qp_3+pp_4=p_3$$

$$\vdots$$

Multiplicando apropriadamente potências de z, onde $ |z|< 1 $, assim temos

$$(p+q)p_0+p p_1=p_0$$

$$rp_0z+qp_1z+pp_2z=p_1z$$

$$sp_0z^2+rp_1z^2+qp_2z^2+pp_3z^2=p_2z^2$$

$$sp_1z^3+rp_2z^3+qp_3z^3+pp_4z^3=p_3z^3$$

$$\vdots$$

Somando essas equações e escrevendo $ \sum_{i=0}^{\infty}p_iz^i=K $, após algumas simplificações temos que:

$$p p_0+sz^2 K+rzK+qzK+qK+\displaystyle\frac{p}{z}[K-p_0]=K$$

$$\displaystyle \left(sz^2+rz+q+\frac{p}{z}-1\right)K=\left(\frac{p}{z}-p\right)p_0$$

$$[sz^3+rz^2+(q-1)z+p]K=p(1-z)p_0$$

dando assim

$$K=\displaystyle \frac{p(1-z)p_0}{sz^3+rz^2+(q-1)z+p}$$

5.5 - Existência da Cadeia de Markov

Para garantir a existência da cadeia de markov, vamos construir um espaço de probabilidade para tal processo estocástico.

Considerando um experimento, vamos descrever o espaço de probabilidade $ (\Omega , \mathcal{F} , \mu ) $. Para uma variável aleatória $ X $ que toma valores em

$$X : \Omega \to \Re$$

O espaço amostral é no máximo um conjunto enumerável de valores, ou seja:

$$\Omega = (\omega_n ;n \in \mathbb{N} ) $$

A $ \sigma - $álgebra é a classe de subconjuntos do espaço amostral,

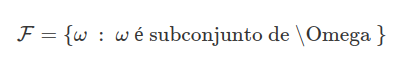
e a probabilidade é

$$\mu : \mathcal{F} \to [0 ,1]$$

o qual $ \mu $ é a probabilidade do instante inicial da cadeia.

Agora em um segundo instante, vamos definir um espaço de probabilidade para um vetor de variáveis aleatórias $ X = (X_1 , X_2 , \dots , X_n ) $

O espaço amostral para o vetor aleatória é o espaço amostral produto:

$$ \Omega^n = \Omega \times \Omega \times \dots \times \Omega $$

A $ \sigma - $álgebra é a $ \sigma - $álgebra produto, ou seja:

$$ \mathcal{F}^n = \mathcal{F} \times \mathcal{F} \times \dots \times \mathcal{F} $$

Como as variáveis aleatórias $ X_1 , X_2 , \dots X_n $ não são independentes, existe probabilidade de transição entre as variáveis, não podemos proceder da mesma forma como no processo de Bernoulli. Mas da teorema de Bayes, temos:

$$ \mu(A|B) = \frac{\mu(A , B) }{\mu (B) }$$

ou seja,

$$ \mu(A , B) = \mu (A|B) \mu (B) $$

E como a probabilidade de transição de um estado para outro é conhecido, definimos a probabilidade sobre o vetor aleatório como

$$\eta (X_1 = i_1 , X_2 = i_2 ,\dots , X_n = i_n ) = \eta (X_1 = i_1 ) \eta (X_2 = i_2 | X_1 = i_1) \dots \eta (X_n = i_n | X_{n-1} = i_{n-1} ) $$

Assim temos um espaço de probabilidade $ (\Omega^n , \mathcal{F}^n , \eta ) $ para o vetor aleatório.

Agora queremos estender esta estrutura para uma sequência de variáveis aleatórias $ X = (X_1 , X_2 , \dots ) $

O espaço amostral para um sequência de variáveis aleatórias é

$$ \Omega^{\infty } = \Omega \times \Omega \times \dots $$

A $ \sigma - $álgebra é a $ \sigma - $álgebra produto

$$\mathcal{G} = \mathcal{F} \times \mathcal{F} \times \dots = \otimes \mathcal{F} $$

e a função de probabilidade $ \mathbb{P} $ é definida da seguinte forma

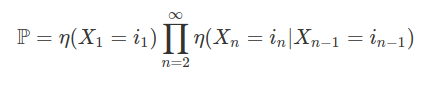
Assim, temos um espaço de probabilidade $ (\Omega^{\infty} , \mathcal{G} , \mathbb{P} ) $ para a cadeia de Markov. Portanto a existência é garantida.

6 - Martingale

O nome Martingale foi intoduzido na literatura de probabilidade por Ville em 1939 e o termo martingale foi detalhado por Doob nas décadas de 40 e 50. A teoria de martingale, assim como a teoria de probabilidade, tem origem na teoria de jogos de azar. A ideia de martingale expressa o conceito de jogo justo.

Considere um jogo de azar com duas possibilidades, o apostador ganha ou perde sua aposta. O termo martingale vem da estratégia de jogo denominada “la grand martingale”, uma estratégia no qual o apostador dobra sua aposta a cada perda. Se o apostador dobra sua aposta a cada perda, na primeira vez que ganhar, vai recuperar todo o dinheiro investido e ainda terá um pequeno lucro. Desde que em qualquer jogo sempre temos uma chance positiva de ganhar, esta estratégia nos garante lucro sempre.

Um martingale é um modelo probabilístico para o jogo justo. O que é um jogo justo? Considere o seguinte exemplo. Um dado é jogado e você ganha uma unidade monetária se o resultado for $ 1, 2 $ ou $ 3 $ e você perde a mesma quantidade se o valor for $ 4, 5 $ pu $ 6 $. Neste caso, o ganho esperado é zero, o que significa que não podemos ganhar sistematicamente. Denotamos por $ Y_n $ a fortuna do apostador na etapa $ n $, ou seja, $ Y_n= X_0 + X_1 + \cdots + X_n $, nos quais $ X_0 $ é a fortuna inicial do apostador e $ X_i $ é o resultado do jogo na etapa $ i $. Por construção, temos que $ X_i=1 $ ou $ X_i=-1 $ com probabilidade $ 0,5 $ para todo $ i=1, \cdots , n $. Além disso, assumimos que as variáveis aleatórias $ X_1, \cdots , X_n $ são independentes. Desta forma, o processo estocástico $ (Y_n: n \geq 1) $ é um martingale.

A questão é: qual a característica essencial de um martigale. Confome ilustrado no exemplo, o martingale mantém saltos de tamanho esperado zero ao longo das etapas. A consequência é que o valor esperado de $ Y_{n+1} $ dado $ Y_n $ é o mesmo valor da etapa $ n $ (ou seja, $ Y_n $). Outra questão importante é como podemos nos beneficiar do conceito de martingale. Suponha que o processo de interesse seja um martingale. Então, se nós conhecemos o estado atual do processo, também temos uma infomação valiosa sobre seu futuro. Sabemos que o valor esperado de amanhã é igual ao valor de hoje, que é conhecido. Em qualquer área de aplicação, ter conhecimentos sosbre o futuro é essencial. Para maiores detalhes ver Modelo de Black e Scholes.

Definição 6.1

Lema 6.1

Seja X um processo estocástico discreto, então X é um martingale se, e somente se, $ \mathbb{E}[X_n|\mathcal{F_s}]=X_s $, para qualquer $ n \geq s $.

Demonstração

De fato, suponha que $ \mathbb{E}[X_n|\mathcal{F_s}]=X_s $, para qualquer $ s< n $, então ao tomarmos $ s=n-1 $ chegamos a definição de martingale. Agora suponha que X é um martingale, logo

Definição 6.2

Seja $ (Y_n,n\geq 1) $ um processo estocástico e seja $ (\mathcal{F_n},n\geq 1) $ uma filtragem. Se

$$\mathbb{E}[Y_n|\mathcal{F}_{n-1}]=0,$$

dizemos que $ (Y_n, \mathcal{F_n}, n\geq 1) $ é um martingale array difference.

A seguir apresentamos alguns exemplos de martingales.

Exemplo 6.1

$$X_n=X_{n-1} + V_n \eta_n, \quad X_0=0.$$

É natural admitirmos que a aposta $ V_n $ investida na $ n $-ésima rodada pode depender dos resultados das rodadas anteriores, isto é, depende de $ V_1, \cdots , V_{n-1} $ e $ \eta_1, \cdots , \eta_{n-1} $. Em outras palavras, tomamos $ \mathcal{F_0} = (\Omega, \emptyset) $ e $ \mathcal{F_n} = \sigma (\eta_1, \cdots , \eta_n) $. Neste caso, obtemos que a estratégia do jogador na rodada $ n $, dada por $ V_n $, é $ \mathcal{F}_{n-1} $-mensurável. Então, dizemos que a estratégia $ V_n $ é previsível. Ao denotarmos $ Y_n = \eta_1 + \cdots + \eta_n $, concluímos que

$$X_n = \sum_{i=1}^n V_i \Delta Y_i, \quad n \geq 1,$$

no qual $ \Delta Y_i = Y_i - Y_{i-1} $.

Do ponto de vista do jogador, dizemos que o jogo é justo (favorável ou desfavorável) se, para qualquer rodada do jogo, temos que

$$\mathbb{E} [X_{n+1} - X_n \mid \mathcal{F_n}] = 0 \quad (\geq 0, \leq 0).$$

$$\sum_{i=1}^n 2^{i-1} = 2^n - 1.$$

Portanto, se obtivermos $ \eta_{n+1}=1 $, concluímos que

$$X_{n+1} = X_n + V_{n+1}= -(2^n - 1) + 2^n =1.$$

Na prática de jogos de azar, este sistema de jogo (dobra a aposta a cada rodada perdida e para o jogo assim que ganhar) é denominado martingale. Como dissemos, esta é a origem do termo matemático “Martingale”.

Exemplo 6.2

Consideramos o exemplo 1, se quisermos ao invés de ir para casa apenas 1 real mais rico quisermos ir $ x $ reais mais rico, basta apostarmos no primeiro lançamento x reais e ir dobrando nos lançamentos seguintes.

Exemplo 6.3

Seja T uma variável aleatória integrável e seja $ (\mathbb{F}=\mathcal{F_n}, n\geq 1) $ uma filtragem. Tomamos

$$T_n=\mathbb{E}[T|\mathcal{F_n}],$$

para cada $ n\geq 1 $. Desde que

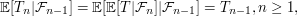
concluímos que $ (T_n : n \geq 1) $ é um martingale.

Exemplo 6.4

Sejam $ (Y_n : n \geq 1) $ variáveis aleatórias independentes com $ \mathbb{E}[Y_j]=1 $ para todo $ j\geq 1 $. Então, o processo estocástico $ X=(X_n : n \geq 1) $ com $ \displaystyle X_n=\prod_{k=1}^{n}Y_k $ e $ \mathcal{F_n}=\sigma(Y_j:j=1,\cdots n) $ é um martingale. Basta notarmos que

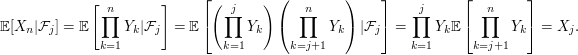
6.1 - Estruturas que mantém a propriedade martingale.

Nessa seção vamos estudar algumas estruturas que preservam a propriedade martingale ou a propriedade supermartingale.

Teorema 6.1.1

Sejam $ X= (X_n : n \geq 1) $ um martingale com respeito a filtragem $ \mathbb{F} $ e $ f: \mathbb{R} \rightarrow \mathbb{R} $ uma função convexa tal que $ \mathbb{E} \mid f(X_n)\mid < \infty $. Então, o processo estocástico $ Y=(f(X_n): n \geq 1) $ é um submartingale.

Demonstração

Como aplicação da desingualdade de Jensen (ver, propriedade da esperança condicional), obtemos que

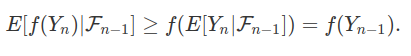
$ \Box $ Como a função $ \mid \mid^p $ para $ p \leq 1 $ é convexa, obtemos o seguinte Corolário.

Corolário 6.1.2

Para $ p\geq 1 $ se $ (Y_n, n\geq 1) $ é um martingale com $ E[|Y_n|^{p}]< \infty $ para $ n\geq 1 $, então $ (|Y_n|^{p}, n\geq 1) $ é um submartingale.

Demonstração

A demonstração deste corolário é imediata, pois basta usarmos os teorema1 e lembrarmos que é $ |\cdot|^{p} $ é uma função convexa.

$ \Box $

Considere $ (\Omega, \mathcal{F}, \mathbb{P}) $ um espaço de probabilidade e $ X=(X_n: n \geq 0) $ um martingale que representa um jogo. Denotamos por $ \mathbb{F}^X $ a filtragem interna associada ao jogo $ X=(X_i : i \geq 1) $. Tomamos por $ C=(C_i : i \geq 1) $ um processo estocástico que representa a aposta do jogador em cada etapa. É intuítivo supormos que o valor de $ C_i $ depende somente da história do jogo até a etapa $ i-1 $. Este princípio, denominado “previsível” , nos garante qe $ C_i $ é $ \mathcal{F}^X_{i-1} $-mensurável. O ganho do jogador na etapa $ n $ é dado por $ C_n (X_n - X_{n-1}) $ e o total acumulado até a etapa $ n $ é dado por

$$Y_n = X_0 + \sum_{i=1}^n C_i (X_i - X_{i-1}), \quad n \geq 1 \quad {e} \quad Y_0=X_0.$$

O processo estocástico $ Y=(Y_n: \geq 1 ) $ é denominado “transformação martingale”. Este é o análogo discreto da integral estocástica. Com isso, motivamos as seguintes definições.

Definição 6.1.1

Um processo estocástico $ X=(X_n : n \geq 1) $ é denominado previsível para a filtragem $ \mathbb{F}=(\mathcal{F_n} ; n \geq 1) $ se, $ X_n $ é $ \mathcal{F}_{n-1} $-mensurável, para todo $ n\geq 1 $.

Definição 6.1.2

Sejam $ M=(M_n: n \geq 0) $ e $ X=(X_i:i \geq 1) $ dois processos estocásticos. Definimos o processo $ X.M $ com $ (X.M)_0=0 $ na forma

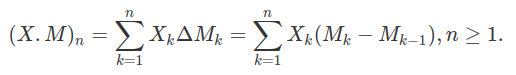
Dizemos que $ X.M $ é a integral estocástica discreta de $ X $ com respeito a $ M $. Se $ M $ é um super ou um sub-martingale, dizemos que é uma transformação martingale de $ M $ por $ X. $

A seguir, vamos utilizar a definição de integral estocástica para introduzirmos transformações que preservam a propriedade martingale.

Teorema 6.1.3

Seja $ X $ um processo previsível tal que para todo $ n $ existe uma constante $ K_n $ tal que $ |X_1|,\dots,|X_n|\leq K_n. $ Se $ M $ é um martingale, então o processo estocástico $ X.M $ também é um martingale. Se $ X $ também é não negativo e $ M $ é um (super)submartingale, obtemos que $ X.M $ também é um (super)submartingale.

Demonstração

Consideramos $ Y=X.M, $ a integral estocástica. Então, $ Y $ é um processo adaptado. Se $ |X_n|\leq K_n $ q.c. para todo $ n $, obtemos que

$$\mathbb{E}|Y_n|\leq 2K_n\sum_{k\leq n}\mathbb{E}|M_k|< \infty.$$

Agora suponhamos que $ M $ é um submartingale e $ X $ não negativo. Então

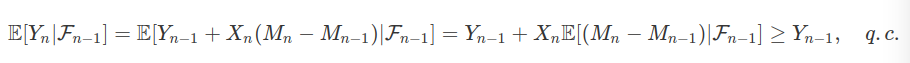
Portanto, $ Y $ também é um submartingale. Se M é um martingale, a última desigualdade é uma igualdade, independentemente do sinal de $ X_n. $ Isso implica que $ Y $ é um martingale.

$ \Box $

Seja $ Y=(Y_n, n\geq 0) $ um martingale que representa o ganho acumulado de um jogador até a $ n $-ésima rodada. Neste jogo, gostaríamos de construir uma estrutura probabilística que possibilitasse ao jogador parar o jogo em alguma etapa finita $ n $ com ganho positivo. Além disso, esta parada opcional deve preservar a propriedade martingale. Esta estrutura é denominada tempo de parada, uma das mais importantes armas dentro da abrangente teoria de processos estocásticos. Para relembrar o conceito de tempo de parada, dado $ (\Omega , \mathcal{F}, \mathbb{P}) $ um espaço de probabilidade e $ \mathbb{F}= (\mathcal{F_n} : n \geq 1 ) $ uma filtragem, dizemos que uma variável aleatória positiva e discreta $\tau : \Omega \rightarrow \mathbb{N}$ é um tempo de parada se $ (\tau = n ) \in \mathcal{F_n} $ para todo $ n \geq 1 $.

Seja $ Y=(Y_{n},\mathcal{F_n},n\geq 1) $ um martingale e $ \tau $ um tempo de parada, tomamos

$$Y_{n}^{(\tau)}(\omega)=Y_{min(\tau(\omega),n)}(\omega) = Y_{\tau(\omega)\wedge n}(\omega), \quad \omega \in \Omega.$$

Assim, sobre o o conjunto $ (\omega \in \Omega : \tau (\omega)=n) $ teremos a sequência

$$Y_1, Y_2, \cdots, Y_{n- 1}, Y_{n}, Y_n, \cdots .$$

Por definição, temos que $ Y_n=Y_n^{(\tau)} $ para $ \tau\geq n $ e $ Y_{n}^{(\tau)}=Y_{n-1}^{(\tau)}=Y_{\tau} $ para $ \tau< n $. Desta forma, sobre o evento $ [\tau\geq n] $, obtemos que

$$(Y_1^{(\tau)}, Y_2^{(\tau)}, \cdots, Y_{n-1}^{(\tau)})=(Y_1,Y_2,\cdots, Y_{n-1}).$$

Suponha $ Y=(Y_{n},\mathcal{F_n},n\geq 0) $ um martingale e $ \tau $ um tempo de parada. Assim, temos que

Corolário 6.1.4

Seja $ M $ um (super,sub)martingale e $ \tau $ um $ \mathbb{F} $-tempo de parada. Então o processo parado $ M^\tau $ também é um (super,sub)martingale.

É importante sabermos se a propriedade martingale $ (\mathbb{E} X_n = \mathbb{E} X_{n-1}) $ se mantém quando a etapa $ n $ é subtituída por um tempo de parada. A principal diferença entre os dois casos é que $ n $ é constante e $ \tau $ é uma variável aleatória que depende da trajetória. A seguir, apresentamos o teorema da parada opcional de Doob. Dado $ \tau $ um tempo de parada, definimos

$$ \mathcal{F_{\tau}} = (A \in \mathcal{F}: A \cap (\tau = n) \in \mathcal{F_n}, \quad \forall n \geq 1). $$

Esta classe de eventos é uma $ \sigma $-álgebra, que é denominada $ \sigma $-álgebra dos eventos anteriores ao tempo de parada $ \tau $.

Teorema 6.1.4

Seja M um (sub)martingale e seja $ \tau,\kappa $ dois tempos de parada tal que $ \kappa\leq \tau\leq K $ para alguma constante $ K $ positiva. Então

$$\mathbb{E}(M_\tau|\mathcal{F}_\kappa)\overset{(\geq)}{=}M_\kappa, \quad q.c.\quad (6.1.1)$$

Um processo $ M $ adaptado e integrável é um martingale se, e somente se,

$$\mathbb{E}(M_\tau)=\mathbb{E}(M_\kappa),$$

para quaisquer pares de tempos de parada limitados $ \kappa\leq \tau. $

Demonstração

Suponha que $ M $ seja um martingale. Definimos o processo

Pela definição de $ \mathcal{F}_\tau $ temos que

$$(\kappa^A\leq n)=(A\cap (\kappa \leq n))\cup (A^c\cap (K\leq n))\in \mathcal{F_n},$$

para todo $ n \geq 1 $. Com isso, obtemos que $ \kappa^A $ e $ \tau^A $ são tempos de parada tal que $ \kappa^A\leq \tau^A\leq K $. De forma análoga temos que $ \mathbb{E}(M_{\tau^A})=\mathbb{E}(M_{\kappa^A}), $ isto é,

$$\int_A M_\kappa~d\mathbb{P}+\int_{A^c} M_K~d\mathbb{P}=\int_A M_\tau~d\mathbb{P}+\int_{A^c} M_K~d\mathbb{P} \quad (6.1.2)$$

com $ \displaystyle\int_A M_\kappa~d\mathbb{P}=\int_A M_\tau~d\mathbb{P}. $

Assim, com $ M $ um processo adaptado com $ \mathbb{E}(M_{\tau})=\mathbb{E}(M_{\kappa}), $ para cada par limitado $ \kappa\leq \tau $ de tempos de parada. Tomamos $ \kappa=n-1 $ e $ \tau=n $ e o procedimento usado para tempos de parada truncados $ \kappa^A $ e $ \tau^A $ para $ A\in \mathcal{F}_{n-1}. $ Então de (6.1.2) para $ A\in \mathcal{F}_{n-1} $ e para os tempos de parada $ \kappa^A $ e $ \tau^A $ implica que $ \mathbb{E}[M_n|\mathcal{F}_{n-1}]=M_{n-1}, $ em outras palavras, $ M $ é um martingale.

Para $ M $ sub-martingale o procedimento é análogo.

$ \Box $

6.2 - Decomposição de Doob

Considere $ (\Omega, \mathcal{F}, \mathbb{P}) $ um espaço de probabilidade, $ \mathbb{F}=( \mathcal{F_n}: n \geq 0 ) $ uma filtragem e $ Z=(Z_n:n \geq 1 ) $ um processo estocástico adaptado à filtragem $ \mathbb{F} $, satisfazendo $ \mathbb{E}\mid Z_n \mid < \infty $. Então, o processo estocástico $ Z $ pode ser decomposto na soma de um martingale e um processo previsível. Este ressultado, motivado pela teoria de integral estocástica, tem diversas aplicações que vamos estudar ao longo deste texto.

Definição 6.2.1

Um processo estocástico $ X=(X_n:n\geq 1) $ é previsível se $ X_n $ for $ \mathcal{F}_{n-1} $-mensurável para todo $ n \geq 1 $.

A seguir apresentamos o teorema da decomposição de Doob.

Teorema 6.2.1

Seja $ Z=(Z_n : n \geq 1) $ um processo estocástico adaptado à filtragem $ \mathbb{F}=(\mathcal{F_n} :n \geq 0) $ tal que $ \mathbb{E}\mid Z_n \mid < \infty $. Então o processo pode ser decomposto de forma única em

$$Z=M+A$$

no qual M é um martingale e A é um processo previsível, satisfazendo:

$$M_n=Z_0+\displaystyle\sum_{\ell=1}^{n}\left[Z_\ell-\mathbb{E}[Z_\ell|\mathcal{F}_{\ell-1}]\right] \quad {e} \quad A_n=\displaystyle\sum_{\ell=1}^{n}\left[\mathbb{E}[Z_\ell|\mathcal{F}_{\ell-1}]-Z_{\ell-1}\right].$$

Demonstração

Vamos mostrar por indução

$$Z_0=0=M_0+A_0.$$

Para $ n=1 $, temos que

$$Z_1=Z_0+Z_1-\mathbb{E}[Z_1|\mathcal{F_0}]+ \mathbb{E}[Z_1|\mathcal{F_0}]-Z_0 =M_1+A_1.$$

Para $ n=2 $, temos que

$$Z_2=Z_0+Z_1-\mathbb{E}[Z_1|\mathcal{F_0}]+ \mathbb{E}[Z_1|\mathcal{F_0}]-Z_0 + Z_2- \mathbb{E}[Z_2|\mathcal{F}_1]+ \mathbb{E}[Z_2|\mathcal{F}_1]-Z_1 =M_2+A_2.$$

Suponha que essa propriedade seja válida para n-1, vamos mostrar que também vale para n. Considere

$$Z_n=Z_{n-1}+Z_n-\mathbb{E}[Z_n|\mathcal{F}_{n-1}]+\mathbb{E}[Z_n|\mathcal{F}_{n-1}]- Z_{n-1} =$$

$$ =M_{n-1}+A_{n-1}+Z_n-\mathbb{E}[Z_n|\mathcal{F}_{n-1}]+\mathbb{E}[Z_n|\mathcal{F}_{n-1}]- Z_{n-1}= $$

$$ =M_n+A_n. $$

Agora vamos mostrar que $ M_n $ é um martingale

Logo é previsível.

A unicidade da decomposição é uma aplicação do conceito de previsível. Suponha que tenhamos duas decomposições $ M^1 + A^1 = M^2 + A^2 $. Então, temos que $ X=M^1 - M^2 = A^1 - A^2 $. Desde que $ A^1 - A^2 $ é previsível e $ M^1 - M^2 $ um martingale, concluímos que $ X $ é um martingale previsível, então

$$X_{n-1}=\mathbb{E}[X_n \mid \mathcal{F}_{n-1}]=X_n,$$

o que ocorre somente se $ X=0 $. Portanto, temos a unicidade da decomposição de Doob.

$ \Box $

Considere $ X=( X_n ; n \geq 1) $ um submartingale. Por construção, o processo previsível $ A=( A_n: n \geq 1) $ é não descrescente. Além disso, o processo previsível $ A $ é denominado compensador relacionado ao processo estocástico $ X $.

6.2.1 - Variação quadrática Previsível

O conceito de variação quadrática de um martingale deriva da decomposição de Doob. Seja $ M $ um martingale com $ \mathbb{E} \mid X_n \mid^2 < \infty $ para todo $ n \geq 1 $. Como consequência da desigualdade de Jensen, sabemos que $ M^2 $ é um submartingale, pois

$$\mathbb{E}[M^2_\ell|\mathcal{F}_{\ell-1}]\geq \left(\mathbb{E}[M_\ell|\mathcal{F}_{\ell-1}]\right)^2=M^2_{\ell-1}, \ell \geq 1.$$

Como consequência da decomposição de Doob, existe um único processo previsível não decrescente, denotado por $ < M,M> $, tal que

$$M^2_\ell-< M,M> _\ell=\overline{M}_\ell, \quad \ell \geq1$$

é um martingale. O processo estocástico $ < M,M> $ é denominado variação quadrática previsível. A partir da decompsição de Doob e da definição de martingale, obtemos que

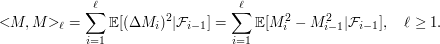
Para todo $ \ell \leq k $, concluímos que

$$\mathbb{E} [(M_k - M_\ell)^2 | \mathcal{F}_{\ell}] = \mathbb{E} [M^2_k - M^2_\ell | \mathcal{F}_{\ell} ]= \mathbb{E} [< M,M> _k - < M,M> _\ell | \mathcal{F}_\ell].$$

Em particular, obtemos que $ \mathbb{E} \mid X_i \mid^2 = \mathbb{E} < M,M> _i $ para todo $ i \geq 1 $.

Suponha $ M $ um martingale com $ M_0=0 $ e $ M_i = \xi_1 + \cdots + \xi_i $, no qual $ (\xi_i : i \geq 1) $ é uma sequência de variáveis aleatórias independentes com $ \mathbb{E} \xi_i=0 $ e $ \mathbb{E} \xi_i^2 < \infty $. Então, a variação quadrática previsível é dada por

$$ < M,M> _i=\mathbb{E} M^2_i = Var(\xi_1) + \cdots + Var(\xi_i),$$

que é determinística e coincide com a variância.

Considere $ X=(X_n : n \geq 1) $ e $ Y=(Y_n : n \geq 1) $ martingales com $ \mathbb{E} \mid X_n \mid^2 < \infty $ e $ \mathbb{E} \mid Y_n \mid^2 < \infty $ para todo $ n \geq 1 $. Definimos a variação cruzada previsível por

$$< X,Y> _i=\frac{1}{4} \left[ < X+Y,X+Y> _i\right]-< X-Y,X-Y> _i.$$

Facilmente, podemos mostrar que $ X_n Y_n - < X,Y> _n $ é um martingale e portanto, para todo $ \ell \leq k $, temos que

$$\mathbb{E} \left[ (X_k - X_\ell) (Y_k - Y_\ell) \mid \mathcal{F}_\ell\right]=\mathbb{E} \left[ (< X,Y> _k - < X,Y> _\ell) \mid \mathcal{F}_\ell\right].$$

Ao tomarmos $ X_n = \xi_1 + \cdots + \xi_n $ e $ Y_n = \eta_1 + \cdots + \eta_n $, nos quais $ (\xi_i) $ e $ (\eta_i) $ são sequências de variáveis aleatórias independentes com $ \mathbb{E} \xi_i=\mathbb{E} \eta_i=0 $, $ \mathbb{E} \xi_i^2 < \infty $ e $ \mathbb{E} \eta_i^2 < \infty $, obtemos que o processo variação cruzada previsível é dado por

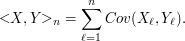
Tomamos $ C=(C_i : i \geq 1 ) $ um processo previsível limitado e $ X=(X_i : i \geq 1 ) $ uma martingale. Sabemos que a transformação martingale $ Y=C \cdot X $ também é um martingale. Neste caso, temos que

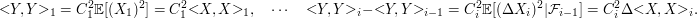
Como consequência, obtemos que

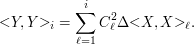
Da mesma forma, temos que

$$A_2= A_1 + \mathbb{E}\left[ \left(X_2 -X_1\right) \mid \mathcal{F}_1 \right]=A_2 = A_1 + \mathbb{E}\left[ \left(X_2 -X_1\right) \mid X_1 \right].$$

Se $ X_1=1 $, temos que $ X_2-X_1=0 $. Assim concluímos que $ \mathbb{E} \left[ \left( X_2 - X_1 \right) \mid X_1=1 \right] =0 $. Por outro lado, temos que

$$\mathbb{E} \left[ X_2 - X_1 \mid X_1=0 \right] = \mathbb{E} \left[ X_2 \mid X_1=0 \right]=\frac{\mathbb{P}[W=2]}{\mathbb{P}[W \geq 2]}.$$

Desta forma, obtemos que

Assim, obtemos uma relação um a um entre a taxa de risco e a distribuição de uma variável aleatória discreta. A partir desta caracterização podemos estudar variáveis aleatórias discretas através do modelo de intensidade multiplicativo de Aalen e consequentemente da teoria de martingales. A seguir, vamos calcular o processo variação quadrática associado ao martingale $ M=X-A $, na forma

$$M_\ell^2=2\sum_{i=1}^{\ell}M_{i-1}\Delta M_i+\sum_{i=1}^{\ell}[\Delta M_i]^2.$$

De fato,

$$2\sum_{i=1}^{\ell}M_{i-1}\Delta M_i + \sum_{i=1}^{\ell}[\Delta M_i]^2 =2\sum_{i=1}^{\ell}M_i[ M_i-M_{i-1}]+\sum_{i=1}^{\ell}[M_i-M_{i-1}]^2=$$

$$=\sum_{i=1}^{\ell}2M^2_i- 2M_iM_{i-1}+\sum_{i=1}^{\ell}[M^2_i-2M_iM_{i-1}+M^2_{i-1}]=\sum_{i=1}^{\ell}M^{2}_i-M^{2}_{i-1}=M^{2}_\ell-M^{2}_0=M^{2}_\ell,$$

pois $ M_0=0 $. Mas por outro lado temos que

$$[\Delta M_\ell]^2= [\Delta X_\ell-\Delta A_\ell]^2=[\Delta X_\ell]^2-2\Delta X_\ell\Delta A_\ell+[\Delta A_\ell]^2.$$

Desta forma temos que

$$M_\ell^2= 2 \sum_{i=1}^{\ell}M_{i-1}\Delta M_i+\sum_{i=1}^{\ell}[\Delta M_i]^2=$$

$$=2\sum_{i=1}^{\ell}M_{i-1}\Delta M_i+\sum_{i=1}^{\ell}[\Delta X_i]^2-2\sum_{i=1}^{\ell}\Delta X_i\Delta A_i+\sum_{i=1}^{\ell}[\Delta A_i]^2=$$

$$=2\sum_{i=1}^{\ell}M_{i-1}\Delta M_i+\sum_{i=1}^{\ell}[\Delta X_i]-2\sum_{i=1}^{\ell}\Delta X_i\Delta A_i+\sum_{i=1}^{\ell}[\Delta A_i]^2=$$

$$\stackrel{\Delta X=\Delta M+\Delta A}{=} 2 \sum_{i=1}^{\ell}M_{i-1}\Delta M_i+ \sum_{i=1}^{\ell}\Delta M_i+\sum_{i=1}^{\ell}\Delta A_i-2\sum_{i=1}^{\ell}\Delta X_i\Delta M_i-\sum_{i=1}^{\ell}[\Delta A_i]^2$$

$$= \sum_{i=1}^{\ell}[2M_{i-1}+1-2\Delta A_i]\Delta M_{i}+ \sum_{i=1}^{\ell}\Delta A_i[1-\Delta A_i].$$

Notamos que $ \displaystyle \sum_{i=1}^{\ell}\Delta A_i[1-\Delta A_i] $ é a parte previsível. Para verificar esse fato, basta observarmos que

$$\displaystyle\sum_{i=1}^{\ell}[2M(_{i-1}+1-2\Delta A_i]\Delta M(i)$$

é um martingale, pois $ C_i=[2M(_{i-1}+1-2\Delta A_i] $ é previsível. Portanto, como a decomposição é única temos que

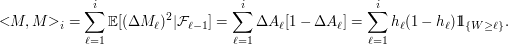
6.3 - Convergência para martingales

Neste módulo, vamos apresentar os principais resultados sobre convergência de martingales. Aqui, vamos estender os resultados de convergência para sequências de variáveis aleatórias independentes para sequências que formam a estrutura martingale. Vamos mostrar que é válido a lei dos grandes números e o teorema central do limite sem a hipótese de independência das variáveis aleatórias.

6.3.1 - Martingales Uniformemente Integráveis

Integrabilidade uniforme desempenha papel importante quando se estuda convergência de martingales. Na seção convergência em média p, mostramos que a integrabilidade uniforme é condição necessária e suficiente para que a convergência em média seja consequência da convergência em probabilidade. Aqui, vamos mostrar que o mesmo resultado é válido para uma sequência de variáveis aleatórias que tem a propriedade martingale.

Definição de Integrabilidade Uniforme para sequências de variáveis aleatórias

A coleção $ (X_i)_{i\in I} $ de variáveis aleatórias é chamada uniformemente integrável (UI) se

Observação

Vale lembrar que uma família UI é limitada em $ \mathcal{L}^1, $ mas a recíproca é falsa. Por outro lado, se uma família é limitada em $ \mathcal{L}^p, $ para algum $ p> 1, $ então é UI.

A seguir apresentamos o primeiro resultado para famílias UI.

Teorema 6.3.1.1

Seja $ X\in \mathcal{L}^1. $ Então a classe

$$ (\mathbb{E}[X|\mathcal{G}]: ~\mathcal{G}~\text{uma sub-}\sigma\text{-álgebra de }~\mathcal{F}) $$

é UI.

Demonstração

Como $ X\in \mathcal{L}^1, $ obtemos que para todo $ \varepsilon> 0 $ existe um $ \delta> 0 $ tal que sempre que $ \mathbb{P}(A)\leq \delta, $ então

$ \Box $

Agora, apresentamos a definição de martingales UI’s.

Definição 6.3.1.2

Um martingale $ X=(X_n : n \geq 0) $ é um martingale uniformemente integrável, se $ X $ é um martingale e a coleção de variáveis aleatórias $ (X_n) $ é uma família UI.

A partir desta definição, apresentamos o seguinte resultado.

Teorema 6.3.1.2 Teorema de Convergência para martingales UI:

Seja $ X=(X_n : n \geq 0) $ um martingale. As seguintes afirmações são equivalentes.

(i) $ X $ é um martingale uniformemente integrável;

(ii) $ X_n $ converge q.c. e em $ \mathcal{L}^1(\Omega,\mathcal{F},\mathbb{P}) $ para uma variável aleatória limite $ X_\infty $ com $ \mathbb{E} \mid X_{\infty} \mid < \infty $;

(iii) Existe $ Z\in\mathcal{L}^1(\Omega,\mathcal{F},\mathbb{P}) $ tal que $ X_n=\mathbb{E}[Z|\mathbb{F}_n] $ P-q.c. para todo $ n\geq 0. $

Demonstração

(i)$ \Rightarrow $(ii) Como $ X $ é um martingale UI, obtemos que $ \sup_n \mathbb{E} \mid X_n \mid < \infty $. Assim, como consequência do lema de upcrossing de Doob concluímos que $ X_\infty = \lim_n X_N $ existe e é finito quase certamente. Como $ X $ é UI concluímos que $ X_n \rightarrow X_\infty $em média, isto é,

$$\mathbb{E} \mid X_n - X_\infty \mid \rightarrow 0, ~ ~ n \uparrow \infty.$$

(ii)$ \Rightarrow $(iii) Seja $ Z=X_\infty\in \mathcal{L}^1. $ Vamos mostrar que $ X_n=\mathbb{E}[Z|\mathcal{F_n}] $ q.c.

De fato, para $ m\geq n $ e pela propriedade de martingale obtemos que

$$\parallel X_n-\mathbb{E}[X_\infty|\mathcal{F_n}] \parallel_1=\parallel \mathbb{E}[X_n-X_\infty|\mathcal{F_n}] \parallel_1\leq \parallel X_n-X_\infty\parallel_1\xrightarrow{m\rightarrow\infty}0.$$

(iii)$ \Rightarrow $(i) Notamos que da propriedade de esperança condicional $ \mathbb{E}[Z|\mathcal{F_n}] $ é um martingale. Por fim, a integrabilidade uniforme é obtida do teorema 6.3.1.1.

$ \Box $

Observação 6.3.1.3

Se $ X $ é um martingale UI e $ T $ é um tempo de parada, no qual também pode ter o valor $ \infty, $ então podemos obter de forma única que

Teorema 6.3.1.3 [Parada opcional para martingales UI]

Seja $ X $ um martingale UI e $ S $ e $ T $ tempos de parada com $ S\leq T. $ Então

$$\mathbb{E}[X_T|\mathcal{F}_S]=X_S,\quad \text{P-q.c.}$$

Demonstração

Observamos que $ \mathbb{E}[X_\infty|\mathcal{F}_T]=X_T $ P-q.c. para qualquer tempo de parada $ T. $

De fato, desde que $ X_T\in \mathcal{L}^1 $ e $ |X_n|\leq \mathbb{E}(|X_\infty|~|\mathcal{F}_T) $ obtemos que

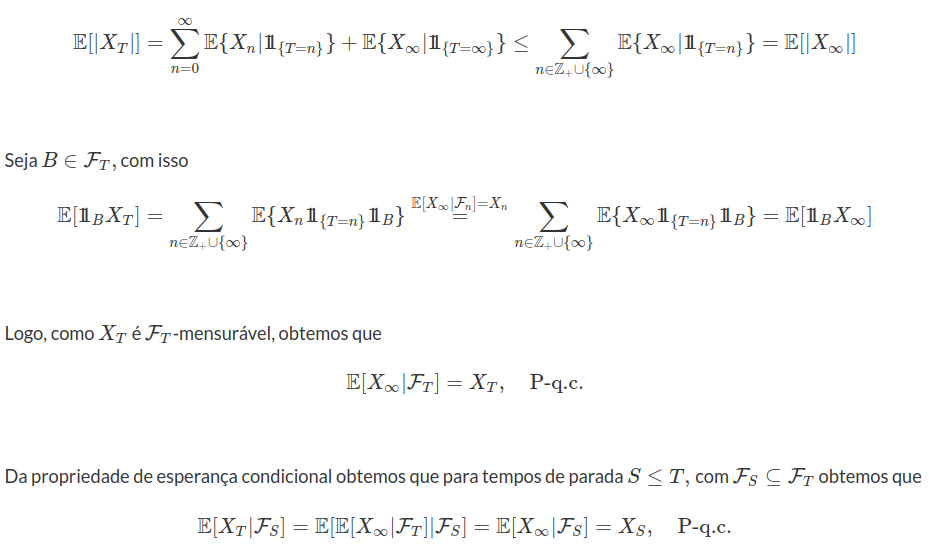
$ \Box $

6.3.2 - Upcrossings

No módulo martingales uniformemente integráveis, mostramos que uma sequência de variáveis aleatórias que forma a estrutura martingale tem limite se e só se, a sequência de variáveis aleatórias for uniformemente integrável. Neste módulo, vamos estender este resultado supermartingales (ou submartingales).

O número de vezes que um processo estocástico “passa” de forma crescente ou descrescente através de um intervalo é denominado número de upcrossings e respectivamente, número de downcrossings do processo. O número de upcrossings será denotado por $ U_\infty (a,b) $. Por definição, sabemos que $ U_\infty ([a,b]) $ assume valores inteiros não negativos ou é infinito. De forma similar, o número de downcrossings será denotado por $ D_\infty (a,b) $ e também assume valores inteiros não negativos ou é infinito.

O significado de upcrossings para a convergência de processo estocástico é devido ao seguinte critério para convergência de uma sequência de números reais. Uma sequenência de números reais $ (x_n : n \geq 1) $ converge para um real extendido $ (\mathbb{R} \cup (-\infty , \infty)) $ se e só se o número de upcrossings for finito para todo $ a < b $. Na realidade, denotamos por

$$L = \liminf_{n \rightarrow \infty} x_n \quad \text{e} \quad U= \limsup_{n \rightarrow \infty} x_n .$$

Então, temos que $ L \leq U $ e a sequência converge se e só se $ L=U $. Suponha que a sequência seja convergente. Se $ a < L $ então, existe $ N $ tal que $ x_n > a $ para todo $ n \geq N $. Como consequência, todo upcrossing do intervalo $ [a,b] $ deve começar antes de $ N $ e então, o número de upcrossings $ U_\infty (a,b) \leq N $ é finito. Por outro lado, se $ L \leq a $ então $ U=L < b $ e assim, podemos concluir que $ x_n < b $ para todo $ n \geq N $ e algum $ N $. Mais uma vez, obtemos que $ U_\infty (a,b) \leq N $.

Contrariamente, suponha que a sequência $ (x_n) $ não converge e assim $ U > L $. Escolha $ a < b $ no intervalo $ (L.U) $. Para qualquer inteiro positivo $ n $, existe $ r > n $ tal que $ x_r > b $ e um $ s > n $ com $ x_s < a $. Este fato nos permite definir duas sequência $ (s_k) $ e $ (t_k) $ por $ t_0=0 $ e

$$ s_k = \inf ( m \geq t_{k-1}: x_m \leq a) \quad \text{e} \quad t_k = \inf ( m \geq s_{k}: x_m \geq b), $$

para todo $ k \geq 1 $. Por construção, temos que $ s_1 < t_1 < s_2 < \cdots $ e $ x_{s_k} \leq a < b \leq x_{t_k} $ para todo $ k \geq 1 $. Portanto, concluímos que $ U_\infty (a,b) = \infty $.

A seguir, vamos utilizar a estratégia de Doob para adaptarmos o teorema de upcrossing que caracteriza sequências de números convergentes para processos estocásticos. A desigualdade de upcrossings de Doob nos fornece uma limitação uniforme para o número de upcrossings (e downcrossings) de uma sequência de variáveis aleatórias que forma uma estrutura martingale.

Seja X um supermartingale e $ a< b $ dois números reais. Um upcrossing é um par $ (X_k,X_\ell) $ tal que

$$X_k\leq a< b\leq X_\ell.$$

Em outras palavras o processo completa um upcrossing se para um determinado tempo ele está abaixo de $ a $ e então após alguns passos ele ultrapassa $ b. $ Denotamos $ U_N(a,b) $ como sendo o número de upcrossing até o tempo N. Podemos definir o upcrossing através dos tempos de paradas,

$$\tau_0=0,$$

$$ \tau_1=\inf(n> 0: X_n\leq a), $$

$$ \tau_2=\inf(n> \tau_1: X_n\geq b), $$

$$\vdots$$

$$ \tau_{2k-1}=\inf(n> \tau_{2k-2}: X_n\leq a), $$

$$ \tau_{2k}=\inf(n> \tau_{2k-1}: X_n\geq b), $$

$$\vdots$$

No gráfico os pontos em vermelho representam os upcrossing.

Para qualquer inteiro N definimos

$$ U_N(a,b)=\sup(n\geq 0:\tau_{2n}\leq N). $$

Dado $ x \in \mathbb{R} $ uma constante, denotamos por $ x^+=\max (x,0) $ e $ x^-=-\min (x,0) $. Na Figura ilustrativa, temos $ U_N(a,b) = 3 $.

Lema 6.3.1 (Upcrossing de Doob)

Seja $ X=(X_n : n \geq 0) $ um supermartingale. Para qualquer inteiro N, temos

$$\displaystyle E[U_N(a,b)]\leq \frac{1}{b-a}E[(a-X_N)^+ ]\leq \frac{1}{b-a}(|a|+E[X_N]).$$

Demonstração:

Seja

$$D=\displaystyle \sum_{k=1}^{N}\left[X_{\tau_{2k\wedge N}}-X_{\tau_{2k-1\wedge N}}\right].$$

Se para algum $ \ell $ temos que

$$\tau_{2\ell-1}< N< \tau_{2\ell},$$

dizemos que temos um upcrossing incompleto. Portanto, temos que

$$D\geq (b-a)U_N(a,b)+R_N,$$

no qual o resíduo $ R_N $ satisfaz $ R_N=0 $ se não existe upcrossing incompleto, ou $ R_N\geq X_{N}-a $, se existe algum upcrossing incompleto. Desde que $ X $ é um supermartingale e $ \tau_i\wedge N $ é um tempo de parada limitado, temos que

$$E[D]\leq 0.$$

Assim, obtemos que

$$\displaystyle E[U_N(a,b)]\leq \frac{1}{b-a}E[-R_N]\leq \frac{1}{b-a}E[(a-X_N)^+]\leq \frac{1}{b-a}(|a|+E[|X_N|]).$$

$ \Box $

Corolário 6.3.1

Sejam $ a,b \in \mathbb{R} $, com $ a< b $ e $ X=(X_n : n \geq 0) $ um supermartingale limitado em $ L^1 $ em que

$$\sup_{n}E[|X_n|]< \infty.$$

Se denotarmos por $ U_{\infty}[a,b]:=\uparrow \lim_N U_N[a,b] $, obtemos que $ (b-a)E[U_\infty[a,b]]\leq |a|+\sup_{n}E[|X_n|]< \infty $. Como consequência, concluímos que $ P(U_\infty [a,b]=\infty)=0. $

Demonstração

Pelo Lema anterior temos que para $ n\in\mathbb{N} $,

$$(b-a)E[U_N[a,b]]\leq |a|+E[|X_N|]\leq |a|+\sup_n E[|X_n|].$$

Ao tomarmos o limite quando $ N\uparrow \infty $, concluímos que o resultado é consequência do teorema da convergência monótona.

$ \Box $

Definimos a $ \sigma $-álgebra “limite” como sendo

$$\mathcal{F}_{\infty}=\sigma\left(\bigcup_n\mathcal{F_n}\right).$$

Teorema 6.3.2

Seja X um supermatingale limitado em $ L^1 $, ou seja,

$$\sup_n E[|X_n|]< \infty.$$

Então $ \lim X_n $ existe e é finito quase certamente. Definimos por $ X_\infty (\omega):=\limsup X_n(\omega), \forall \omega $, então temos que $ X_\infty $ é variável aleatória $ \mathcal{F_\infty} $-mensurável e $ X_\infty= \lim X_n $ quase certamente.

Demonstração

Seja $ \overline{\mathbb{R}}=[-\infty,\infty] $. Assim definimos o conjunto

$$A=(\omega\in\Omega|\liminf X_n< \limsup X_n)$$

$$ =\bigcup_{(a,b\in \mathbb{Q}:a< b)}\left(\omega\in \Omega| \liminf X_n(\omega)< a < b< \limsup X_n(\omega)\right):=\bigcup_{(a,b\in \mathbb{Q})} A_{a,b} $$

Note que

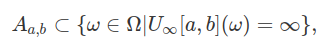
Mas utilizando o corolário anterior temos que $ P(A_{a,b})=0 $. Como $ A $ é uma união enumerável temos que $ P(A)=0 $, e portanto

$$ X_\infty := \lim X_n $$

existe quase certamente em $ \overline{\mathbb{R}} $. Assim nos resta mostrar penas que $ E[|X_\infty|]< \infty $. Pelo lema de fatou

$$E[|X_\infty|]=E[\liminf |X_n|]\leq \liminf E[|X_n|]\leq sup E[|X_n|]< \infty$$

o que implica que $ P(X_\infty< \infty)=1 $.

$ \Box $

A seguir, apresentamos uma demonstração alternativa para o lema dos upcrossings de Doob.

Lema 6.3.2 [Lema dos upcrossing de Doob]

Seja $ M $ uma supermartingale. Em seguida, para todo $ a< b, $ o número de upcrossings $ U_n[a, b] $ do intervalo $ [a, b] $ é uma variável aleatória $ \mathcal{F_n} $-mensurável e satisfaz

$$(b-a)\mathbb{E}\left(U_n[a,b]\right)\leq \mathbb{E}\left[(M_n-a)^-\right]$$

O número total de upcrossings $ U_\infty[a,b] $ é $ \mathcal{F_\infty} $-mensurável.

Demonstração

Definimos $ Y=X.M, $ com isso, o processo $ X $ é igual a 0, até $ M $ cair abaixo do nível a, então permanece até $ M $ ficar acima de b e assim por diante. Assim, cada upcrossing concluído de $ [a, b] $ aumenta o valor de Y, pelo menos, $ b - a. $ Se o último upcrossing ainda não foi completado no tempo n, então esta pode reduzir Y por, no máximo, $ (M_n - a)^-. $

Veja a ilustração a seguir:

Logo, a desigualdade fundamental com $ Y_0\doteq 0. $

$$Y_n\geq (b-a)U_n[a,b]-(M_n - a)^-\quad (6.3.1)$$

Vale lembrar que $ Y=X.M $ é um super-martingale, fato visto no lema 6.1.1 (para mais detalhes consulte estruturas que mantém a propriedade de martingale).

Em particular, $ \mathbb{E}[Y_n]\leq \mathbb{E}[Y_0]=0. $ Portanto, para concluir este resultado, basta aplicarmos a esperança em ambos os lado em (6.3.1).

$ \Box $

6.3.3 - Teoremas de convergência para martingales

Inicialmente vamos apresentar algumas desigualdades importantes, para em seguida mostrar os principais resultados de convergência para martingales.

Teorema 6.3.3.1 [Desigualdade do submartingale de Doob]

Seja M um submartingale, para todo $ \lambda > 0,~ n\geq 1 $

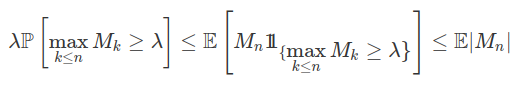
Demonstração

Definimos o tempo de parada $ \tau=n\wedge \inf(k;~M_k\geq \lambda) $ com $ \tau\leq n. $ Assim, temos que $ \mathbb{E}[M_n]\geq \mathbb{E}[M_\tau]. $

Como consequência, concluímos que

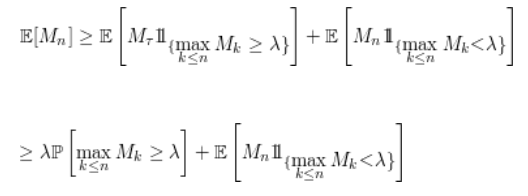
Portanto, temos um lado da desigualdade, a outra parte é imediata.

$ \Box $

Teorema 6.3.3.2 [Desigualdade $ \mathcal{L}^p $ de Doob]

Se $ M $ é um martingale ou um submartingale não negativo e $ p> 1. $ Então para todo $ n\geq 1 $ temos que

$$\mathbb{E}\left[\max_{k\geq n}|M_n|^p\right]\leq \left(\frac{p}{1-p}\right)^p\mathbb{E}|M_n|^p$$

Demonstração

Consideramos $ M^*=\max_{k\geq n}|M_n| $ e $ M $ definido sobre o espaço de probabilidade $ (\Omega,\mathcal{F},\mathbb{P}). $ Assim, para qualquer $ m\geq 1 $ obtemos que

$$\mathbb{E}[(M^*\wedge m)^p]=\int_{\omega}(M^*(\omega)\wedge m)^p d\mathbb{P}(\omega)=\int_{\omega}\int^{(M^*(\omega)\wedge m)}_0 px^{p-1}dx~ d\mathbb{P}(\omega)=$$

$$=p\int_\omega|M_n(\omega)|\int^{M^*(\omega)\wedge m}_0 x^{p-2}~dx~d\mathbb{P}(\omega)=$$

$$=\frac{p}{p-1}\mathbb{E}[|M_n|(M^*(\omega)\wedge m)^{p-1}]$$

Usando a desigualdade de Hölder com $ \frac{1}{p}+\frac{1}{q}=1 $ obtemos que

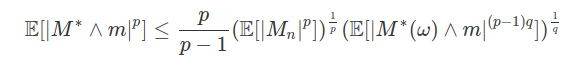
Para $ p> 1 $ obtemos que $ q=\frac{p}{p-1}, $ iso implica que

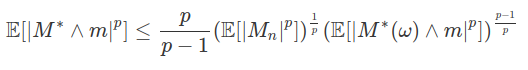
Elevando a p dos dois lados obtemos que

$$\mathbb{E}[|M^*\wedge m|^p]\leq \left(\frac{p}{p-1}\right)^p\mathbb{E}[|M_n|^p]$$

Para completar a demonstração, basta $ m $ tender ao infinito.

$ \Box $

Corolário 6.3.2.1

Seja $ M $ um martingale quadrado integrável. Então existe um único processo previsível crescente $ A $ com $ A_0=0 $ tal que $ M^2-A $ é um martingale. Além disso, a variável aleatória $ A_{n+1}-A_n $ é uma versão da variância condicional de $ M_n $ dado $ \mathcal{F}_{n-1}, $ isto é,

$$A_{n+1}-A_n=\mathbb{E}\left[(M_n-\mathbb{E}[M_n|\mathcal{F}_{n-1}])^2|\mathcal{F}_{n-1}\right]=\mathbb{E}\left[(M_n-M_{n-1})^2|\mathcal{F}_{n-1}\right]\quad P\text{-}q.c.$$

Concluímos que o teorema de Pitágoras é válido para martingales quadrados integráveis.

$$\mathbb{E}[M^2_n]=\mathbb{E}[M^2_0]+\sum^n_{k=1}\mathbb{E}[(M_n-M_{n-1})^2]$$

O processo $ A $ é chamado de processo de variação quadrática previsível de $ M $ e denotado por $ \langle M\rangle. $

Demonstração

Pela desigualdade de Jensen, temos que $ M^2 $ é um submartingale. Como $ M $ é um martingale, temos que

$$\mathbb{E}\left[(M_n-M_{n-1})^2|\mathcal{F}_{n-1}\right]=\mathbb{E}\left[M^2_n+M^2_{n-1}-2M_n M_{n-1}|\mathcal{F}_{n-1}\right]=$$

$$=\mathbb{E}\left[M_n^2|\mathcal{F_{n-1}}\right]-2M_{n-1}\mathbb{E}[M_n|\mathcal{F}_{n-1}]+M_{n-1}^2=$$

$$=\mathbb{E}\left[M^2_n|\mathcal{F_{n-1}}\right]-M^2_{n-1}=$$

$$=\mathbb{E}\left[M^2_n-M^2_{n-1}|\mathcal{F}_{n-1}\right]=A_{n}-A_{n-1}$$

$ \Box $

Definição 6.3.3.1

Definimos a $ \sigma $-álgebra “limite” como sendo

$$\mathcal{F}_{\infty}=\sigma\left(\bigcup_n\mathcal{F_n}\right)$$

Para demonstramos os teoremas de convergência consideramos $ M $ supermartingale e um intervalo compacto $ [a, b]\subset \mathbb{R}. $

Como apresentado no módulo upcrossing, o número de upcrossings no intervalo $ [a, b] $ até o tempo $ n, $, representa o número de vezes que o processo passa a partir de um nível inferior $ a $ ao um nível superior de $ b ~ (X_k \leq a < b \leq X_\ell) $.

Teorema 6.3.3.3 [Teorema da convergência de martingales de Doob]

Seja $ M $ uma supermartingale tal que é limitado em $ \mathcal{L}^1, $ então $ M_n $ converge quase certamente para um limite finito $ M_\infty $ que é $ \mathcal{F_\infty} $-mensurável quando $ n\rightarrow \infty, $ com $ \mathbb{E}|M_\infty|< \infty. $

Demonstração

Suponhamos que $ M $ é definido no espaço de probabilidade $ (\Omega, \mathcal{F}, \mathbb{P}). $ Suponha que $ M (\omega) $ não converge para um limite de $ \overline{\mathbb{R}}. $ Então existem dois racionais $ a < b $ tal que $ \liminf M_n (\omega) < a < b < \limsup M_n (\omega). $ Em particular, $ U_\infty [a, b] (\omega) =\infty. $ Pelo lema (lema upcrossings de Doob) $ \mathbb{P} (U_\infty [a, b] =\infty) = 0. $

Agora observamos que

$$A\doteq (\omega ; M(\omega)~\text{não converge para um limite em }~\overline{\mathbb{R}})\subset \bigcup_{a< b}(\omega; U_\infty [a, b] (\omega) =\infty), \quad a,b\in \mathbb{Q}.$$

Logo,

$$\mathbb{P}[A]\leq \sum_{a< b}\mathbb{P}(U_\infty[a,b]=\infty)=0,$$

Isto implica que $ M_n $ converge quase certamente para o limite $ M_\infty\in \overline{\mathbb{R}}. $ Assim, pelo lema de Fatou

$$\mathbb{E}[M_\infty]=\mathbb{E}(\liminf |M_n|)\leq \liminf \mathbb{E}|M_n|\leq \sup\mathbb{E}|M_n|< \infty.$$

Com isso, obtemos que $ M_\infty $ é finito quase certamente e é integrável. Vale lembrar que $ M_n $ é $ \mathcal{F_n} $-mensurável e portanto é $ \mathcal{F_\infty} $-mensurável, desde que $ \displaystyle M_\infty=\lim_{n\rightarrow \infty}M_n $ é o limite de aplicações $ \mathcal{F_\infty} $-mensuráveis, logo é $ \mathcal{F_\infty} $-mensurável.

$ \Box $

Teorema 6.3.3.4

Seja $ M $ um supermartingale que é limitada em $ \mathcal{L}^1. $ Então $ M_n\xrightarrow{\mathcal{L}^1}M_{\infty}, $ quando $ n\rightarrow\infty $ se, e somente se, $ (M_n)_{n\in\mathbb{Z}_+} $ é uniformemente integrável, em que $ M_\infty $ é integrável e $ \mathcal{F}_{\infty} $-mensurável. Neste caso,

$$\mathbb{E}[M_\infty| \mathcal{F_n}]\leq M_n,\quad \text{q.c.}\quad (6.3.3.1)$$

Adicionalmente, se $ M $ é um martingale, então temos uma igualdade em (6.3.3.1). Neste caso, dizemos que $ M $ é um Doob Martingale.

Demonstração

Primeiramente, observamos que do teorema da convergência de martingales de Doob que $ M_n\xrightarrow{q.c.}M_\infty, $ para $ M_\infty $ uma variável aleatória finita. Com isso, segue que $ M_n\xrightarrow{P}M_\infty, $ logo se $ (M_n)_{n\in\mathbb{Z}_+} $ é uniformemente integrável temos que $ M_n\xrightarrow{\mathcal{L}^1}M_{\infty}. $

Por outro lado suponhamos que $ M_n\xrightarrow{\mathcal{L}^1}M_{\infty}, $ desde que $ M $ seja um super-martingale, obtemos que

isto implica que $ \mathbb{E}[M_\infty| \mathcal{F_n}]\leq M_n,\quad \text{q.c.}. $

$ \Box $

Com este resultado obtemos que um martingale uniformemente integrável é limitado em $ \mathcal{L}^1 $ e são Doob martingales. Por outro lado, seja $ X $ uma variável aleatória integrável $ \mathcal{F} $-mensurável e seja $ \mathbb{F}^n=(\mathcal{F_n}, ~n=0,1,2\dots) $ a filtragem. Então $ \mathbb{E}[X|\mathcal{F_n}] $ é um Doob martingale uniformemente integrável. Para Doob martingales podemos identificar o limite explícito em termos da $ \sigma $-álgebra limite $ \mathcal{F_\infty}. $

Teorema 6.3.3.5 [Teorema upward de Lévy]

Seja $ X $ uma variável aleatória integrável, definido no espaço de probabilidade $ (\Omega, \mathcal{F},\mathbb{P}) $ e seja $ \mathbb{F}^n=(\mathcal{F_n}, ~n=0,1,2\dots) $ a filtragem com $ \mathcal{F_n}\subset \mathcal{F} $ para todo $ n. $ Então

$$\mathbb{E}[X|\mathcal{F_n}]\xrightarrow{q.c.} \mathbb{E}[X|\mathcal{F_\infty}], \quad\text{quando}~n\rightarrow\infty$$

e também em $ \mathcal{L}^1. $

Demonstração

O processo $ M_n=\mathbb{E}[X|\mathcal{F_n}] $ é uniformemente integrável, com isso é limitada em $ \mathcal{L}^1. $ Pelo teorema (6.3.3.4) $ M_n\xrightarrow{q.c.}M_\infty $ e em $ \mathcal{L}^1, $ quando $ n\rightarrow\infty $ com $ M_\infty $ integrável e $ \mathcal{F_\infty} $-mensurável. Este último basta mostrar que $ M_\infty=\mathbb{E}[X|\mathcal{F_\infty}] $ quase certamente.

De fato, observamos que

Logo, $ Q_1 $ e $ Q_2 $ concordam em $ \sigma\left(\bigcup_n\mathcal{F_n}\right). $ Este implica da definição de esperança condicional que $ M_\infty=\mathbb{E}[X|\mathcal{F_\infty}] $ quase certamente.

Finalmente, consideramos o caso especial $ X $$ \mathcal{F} $-mensurável, então $ X=X^+-X^-, $ é a diferença de duas funções não negativas $ \mathcal{F} $-mensurável. Usamos a linearidade da esperança condicional para completar a demonstração.

$ \Box $

Corolário 6.3.3.2 [Lema de Hunt]

Suponha que $ X_n\xrightarrow{q.c.}X $ e que $ |X_n|\leq Y $ quase certamente para todo n, em que $ Y $ é uma variável aleatória integrável. Além disso, suponha $ \mathcal{F_n}\subseteq \mathcal{F}_{n+1},~n\geq 1 $ sequência crescente de $ \sigma $-álgebras.

Então $ \mathbb{E}[X_n|\mathcal{F_n}]\xrightarrow{q.c.}\mathbb{E}[X|\mathcal{F_\infty}] $ em que $ \displaystyle\mathcal{F_\infty}=\sigma\left(\bigcup_n\mathcal{F_n}\right). $

Demonstração

Para $ m\in \mathbb{Z_+}, $ tomamos $ U_m=\inf_{n\geq m} X_n $ e $ V_m=\sup_{n\geq m} X_n. $ Caso $ X_m\xrightarrow{q.c.}X, $ necessariamente temos que $ V_m-U_m\xrightarrow{q.c.}0 $ quando $ m\rightarrow \infty. $

Logo, $ |V_m-U_m|\leq 2Y. $

Da convergência dominada temos que $ \mathbb{E}(V_m-U_m)\rightarrow 0, $ quando $ m\rightarrow \infty. $

De fato,

Dado $ \varepsilon> 0 $ e escolhemos $ m $ suficientemente grande tal que

$$\mathbb{E}(V_m-U_m)< \varepsilon.$$

Para $ n\geq m $ obtemos que

$$U_m\leq X_n\leq V_m, \quad q.c.\quad (6.3.3.4)$$

Disto, obtemos que

$$\mathbb{E}[U_m|\mathcal{F_n}]\leq \mathbb{E}[X_n|\mathcal{F_n}]\leq \mathbb{E}[V_m|\mathcal{F_n}], \quad q.c.$$

Os processos do lado esquerdo e direito são martingales que satisfazem as condições do teorema upward Lévy. Considerando n tendendo ao infinito obtemos

$$\mathbb{E}[U_m|\mathcal{F_\infty}]\leq \liminf\mathbb{E}[X_n|\mathcal{F_n}]\leq \limsup\mathbb{E}[X_n|\mathcal{F_n}]\leq \mathbb{E}[V_m|\mathcal{F_\infty}], \quad q.c.\quad (6.3.3.5)$$

Com isso, obtemos que

$$0\leq\mathbb{E}\left(\liminf\mathbb{E}[X_n|\mathcal{F_n}]- \limsup\mathbb{E}[X_n|\mathcal{F_n}]\right)\leq \mathbb{E}\left(\mathbb{E}[V_m|\mathcal{F_\infty}]-\mathbb{E}[U_m|\mathcal{F_\infty}]\right)$$

$$\leq\mathbb{E}(V_m-U_m)< \varepsilon$$

Considerando $ \varepsilon\downarrow 0 $ obtemos que $ \liminf\mathbb{E}[X_n|\mathcal{F_n}]= \limsup\mathbb{E}[X_n|\mathcal{F_n}] $ q.c.

Assim, $ \mathbb{E}[X_n|\mathcal{F_n}] $ converge quase certamente. Agora, para $ n\rightarrow \infty $ em (6.3.3.4) obtemos $ U_m\leq X\leq V_m $ q.c. Logo,

$$\mathbb{E}[U_m|\mathcal{F_\infty}]\leq \mathbb{E}[X|\mathcal{F_\infty}]\leq \mathbb{E}[V_m|\mathcal{F_\infty}], \quad q.c.\quad (6.3.3.6)$$

De (6.3.3.5) e (6.3.3.6) implicam que tanto $ \lim \mathbb{E}(X_n|\mathcal{F_n}) $ quanto $ \mathbb{E}(X|\mathcal{F_\infty}) $ estão q.c. entre $ V_m $ e $ U_m. $ Consequentemente temos que

$$\mathbb{E}\left|\lim \mathbb{E}(X_n|\mathcal{F_n})- \mathbb{E}(X|\mathcal{F_\infty})\right|\leq \mathbb{E}(V_m-U_m)< \varepsilon$$

Portanto, tomando $ \varepsilon\downarrow 0 $ obtemos que

$$\lim_n \mathbb{E}(X_n|\mathcal{F_n})= \mathbb{E}(X|\mathcal{F_\infty}),\quad q.c.$$

$ \Box $

A seguir, apresentamos um resultado que nos diz que um martingale $ M $ e dois tempos de parada limitados $ \kappa\leq \tau $ tal que $ E (M_{\tau} | \mathcal{F}_{\kappa}) = M_{\kappa}. $ Assim, vamos apresentar o seguinte teorema.

Teorema 6.3.3.6 [Teorema da amostragem opcional (Optional sampling)]

Seja $ M $ um (super)martingale uniformemente integrável (U.I.). Então a família de variáveis aleatórias $ (M_\tau|\tau~\text{é um tempo de parada finito}) $ é uniformemente integrável e para todo tempo de parada $ \kappa\leq \tau $ obtemos

$$\mathbb{E}(M_\tau|\mathcal{F}_{\kappa})\overset{(\leq)}{=}M_\kappa\quad P-q.c.$$

Demonstração

Consideramos apenas o caso de martingale. Do teorema (6.3.3.4) temos que $ \displaystyle M_{\infty}=\lim_{n\rightarrow \infty}M_n $ existe P-q.c. em em $ \mathcal{L}^1 $ e $ \mathbb{E}(M_{\infty}|\mathcal{F_n})=M_n. $ Agora, seja $ \tau $ um tempo de parada arbitrário e $ n\in \mathcal{N}\cup(0). $

Vale lembrar que quando $ \tau\wedge n\leq n $ isto implica que $ \mathcal{F}_{\tau\wedge n}\subseteq \mathcal{F_n}. $

Das propriedades de esperança condicional temos que para todo n

$$\mathbb{E}(M_{\infty}|\mathcal{F}_{\tau\wedge n})=\mathbb{E}[\mathbb{E}(M_{\infty}|\mathcal{F}_{n})|\mathcal{F}_{\tau\wedge n}]=\mathbb{E}(M_{n}|\mathcal{F}_{\tau\wedge n})\quad q.c.$$

Do teorema (6.1.4) (para mais detalhes consulte estruturas que mantém a propriedade de martingale) obtemos que

$$\mathbb{E}(M_{\infty}|\mathcal{F}_{\tau\wedge n})=M_{\tau\wedge n}$$

Fazendo $ n\rightarrow \infty $ implica que $ M_{\tau\wedge n}\rightarrow M_\tau $ q.c. Do teorema upward de Lévy o lado esquerdo converge q.c. em $ \mathcal{L}^1 $ para $ \mathbb{E}(M_\infty|\mathcal{G}) $ em que

$$\mathcal{G}=\sigma\left(\bigcup_{n}\mathcal{F}_{\tau\wedge n}\right)$$

Portanto,

$$\mathbb{E}(M_\infty|\mathcal{G})=M_\tau\quad P-q.c.$$

Portanto, $ \mathbb{E}(M_\infty|\mathcal{F}_{\tau})=M_\tau $ P-q.c. pois $ \mathcal{F}_\kappa\subseteq \mathcal{F}_\tau $

$ \Box $

Para a igualdade $ \mathbb{E}(M_\tau|\mathcal{F}_{\kappa})=M_\kappa $ P-q.c. no teorema anterior é necessário que $ M $ seja uniformemente integrável. Existem martingales (positivos) que são limitadas em $ \mathcal{L}^1 $ mas não são uniformemente integráveis, para os quais a igualdade falha em geral. Para super-martingales não negativos sem propriedades integrabilidade adicionais temos somente uma desigualdade. A seguir vamos apresentar o resultado que mostrar este fato.

Teorema 6.3.3.7

Seja $ M $ um super-martingale não negativo e seja $ \kappa \leq\tau $ um tempo de parada. Então

$$\mathbb{E}(M_\tau|\mathcal{F}_{\kappa})\leq M_\kappa\quad \text{P-q.c}.$$

Demonstração

Primeiramente, observamos que $ M $ é limitada em $ \mathcal{L}^1 $ com isso converge. Fixamos $ n\in \mathbb{N}\cup (0), $ pelo teorema () o super-martingale parado $ M^{\tau\wedge n} $ é um super-martingale também e ainda uniformemente integrável.

$$\mathbb{E}(M_{\tau\wedge n}|\mathcal{F}_{\kappa})=\mathbb{E}(M^{\tau\wedge n}_\infty|\mathcal{F}_{\kappa})\leq M^{\tau\wedge n}_\kappa=M_{\tau\wedge n}\quad \text{P-q.c}.$$

Agora pelo lema de Faltou condicional obtemos que

$$\mathbb{E}(M_\tau|\mathcal{F}_\kappa)\leq\mathbb{E}(\liminf M_{\tau\wedge n}|\mathcal{F}_{\kappa})$$

$$\leq\liminf \mathbb{E}(M_{\tau\wedge n}|\mathcal{F}_{\kappa})$$

$$\leq\liminf M_{\kappa\wedge n}=M_\kappa\quad \text{P-q.c}.$$

Portanto, segue o resultado.

$ \Box $

6.3.4 - Lei dos Grandes Números para martingales

Segundo Helland, martingales são generalizações de somas de i.i.d.’s de variáveis aleatórias com média zero. Para tais somas, podemos derivar a Lei dos Grandes Números, Teorema Central do Limite e a lei do Logaritmo Iterado.

A questão então é:

• que essas leis também se aplicam a martingales?
• se sim, que tipo de condições que precisamos exigir.

A seguir, apresentamos um resultado importante.

Teorema 6.3.4.1 [Lei 0-1 de Kolmogorov]

Demonstração

quando $ \mathcal{F_\infty}\subseteq \mathcal{G}_\infty. $

Portanto,

$$\mathbb{P}(A)\in (0,1).$$

$ \Box $

Teorema 6.3.4.2

Demonstração

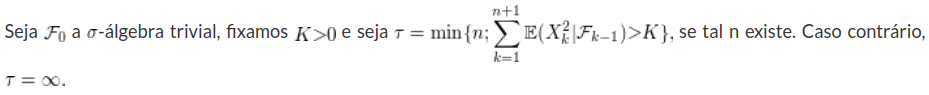
Pela desigualdade de Jensen $ (\mathbb{E}|S^\tau_n|)^2\leq \mathbb{E}[(S^\tau_n)^2]\leq K^2. $

Como consequência $ S^\tau $ é um martingale que é limitada em $ \mathcal{L}^1. $ Pelo teorema de convergência martingale, converge q.c. um limite integrável $ S_{\infty} $.

Portanto $ S_n $ converge q.c. no evento $ \tau=\infty, $ em outras palavras, no evento $ (\displaystyle\sum^\infty_{k=1}\mathbb{E}[X^2_k|\mathcal{F}_{k-1}]\leq K) $ com $ K\uparrow \infty. $

$ \Box $

Definição 6.3.4.1 [Backward martingales]

$$\mathbb{E}[X_{n+1}|\mathcal{G}_n]=X_n\quad \text{P-q.c.}$$

Teorema 6.3.4.3 [Lei Forte do Grandes Números]

Seja $ (X_n)_{n\geq 1} $ sequência de variáveis aleatórias i.i.d. em $ \mathcal{L}^1 $ com $ \mathbb{E}[X_1]=\mu. $ Seja $ S_n=X_1+\dots+X_n, $ para $ n\geq 1 $ e $ S_0=0. $ Então

$$\frac{S_n}{n}\xrightarrow{q.c.}\mu\quad \text{e}\quad \frac{S_n}{n}\xrightarrow{\mathcal{L}^1}\mu,~\text{quando}~n\rightarrow\infty.$$

Demonstração

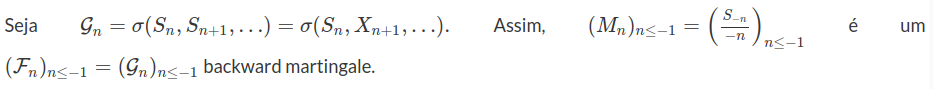
De fato, obtemos para $ m\leq -1 $ que

$$\mathbb{E}\left[M_{m+1}|\mathcal{F}_m\right]=\mathbb{E}\left[\frac{S_{-(m+1)}}{-(m+1)}|\mathcal{F}_{-m}\right]\quad (6.3.4.1)$$

Fazendo $ n=-m, $ e desde que $ X_n $ seja independente de $ X_{n+1},X_{n+2},\dots, $ obtemos que

$$\mathbb{E}\left[\frac{S_{n-1}}{n-1}|\mathcal{F}_{n}\right]=\mathbb{E}\left[\frac{S_{n}-X_n}{n-1}|\mathcal{F}_{n}\right]=\frac{S_n}{n-1}-\mathbb{E}\left[\frac{X_{n}}{n-1}|\mathcal{F}_{n}\right]\quad (6.3.4.2)$$

$$\mathbb{E}[X_1|S_n]+\dots+\mathbb{E}[X_n|S_n]=\mathbb{E}[S_n|S_n]=S_n$$

com isso, $ \mathbb{E}[X_n|S_n]=\frac{S_n}{n}. $

Logo, de (6.3.4.2) obtemos que

$$\mathbb{E}\left[\frac{S_{n-1}}{n-1}|\mathcal{F}_{n}\right]=\frac{S_n}{n-1}-\frac{1}{n-1}\underbrace{\mathbb{E}\left[X_{n}|\mathcal{F}_{n}\right]}_{S_n/n}=\frac{S_n}{n-1}-\frac{S_n}{n(n-1)}=\frac{S_n}{n}$$

Logo, pelo teorema da convergência do backward martingale obtemos que $ \frac{S_n}{n} $ converge quase certamente e em $ \mathcal{L}^1 $ quando $ n\rightarrow \infty $ para a variável aleatória $ Y=\lim \frac{S_n}{n}, $ tal que para todo $ k $

$$Y=\lim\frac{X_{k+1}+\dots+X_{k+n}}{n}$$

Assim, $ Y $ é $ \sigma(X_{k+1},\dots) $-mensurável para todo $ k $ e portanto $ \displaystyle\bigcap_k \sigma(X_{k+1},\dots) $-mensurável. Pela lei 0-1 de Kolmogorov concluímos que existe uma constante $ c\in \mathbb{R} $ tal que $ \mathbb{P}(Y=c)=1, $ mas

$$c=\mathbb{E}[Y]=\lim\mathbb{E}\left[\frac{S_n}{n}\right]=\mu.$$

$ \Box $

6.4 - Teorema Central do Limite para Martingales

Pierre Simon de Laplace (o marquês de Laplace), escreveu sobre fundamentos da teoria de probabilidade e estabeleceu os métodos de equações diferenciais e de funções geradoras de momentos, que deu uma nova formulação e uma prova heurística do teorema central do limite. O conceito de momentos foi utilizado anos depois por Chebyshev, em seguida por seu aluno Andrei Markov para dar uma prova rigorosa do teorema central do limite. Outro de seus famosos estudantes, Alexander Lyapunov, posteriormente usou o conceito de funções características para dar uma prova mais simples desse importante teorema. Markov fez estudos sobre dependência de variáveis aleatórias analisando as hoje denominadas cadeias de Markov em tempo discreto. Com a construção axiomática escrita por Henri Lebesgue e Èmile Borel, obtemos a a base necessária para o desenvolvimento dos processos estocásticos, esperança condicional. Disto possibilitou Joseph Doob e Paul Lévy o desenvolvimento da teoria de martingale, que será utilizado para demonstrar os principais resultados do teorema central do limite para variáveis aleatórias dependentes.

Os teoremas centrais do limite clássicos são generalizados imediatamente à partir das matrizes de variáveis aleatórias dependentes, que sob condições de convergência todas probabilidades, esperança e variância são condicionados com respeito ao passado conforme dito no artigo de Helland. Helland deduziu um único teorema do limite central básico, em que as condições de de convergência são em termos doa momentos de variáveis truncadas. Outra importante contribuição foi mostrar a estreita conexão entre todos os diferentes teoremas centrais do limite dependentes que apareceram nos últimos anos.

6.4.1 - Teorema Central do Limite para soma de variáveis aleatórias dependentes

Como mencionado, a propriedade de martingale substitui a suposição de independência. Teoremas centrais do limite para martingales foi iniciada em 1970 (Brown, 1971; Dvoretsky, 1972). A particular importância para o desenvolvimento da presente teoria se deve a McLeish (1974 [17]). A aplicação de processos de contagem de análise de sobrevivência, incluindo a aplicação do artigo de McLeish foi feito por Aalen durante 1974-1975.

O teorema do limite central para martingales está relacionada ao fato de que um martingale com trajetórias contínuas e um processo de variação previsível determinístico é um martingale Gaussiano, ou seja, com distribuições normais de dimensão finita. Assim, o teorema central do limite para processos de contagem associado a martingales dependem de duas condições:

(i) o tamanho dos saltos ir a zero (isto é, aproximando-se a continuidade das trajetórias);

(ii) o processo de variações previsíveis converge para uma função determinística.

Em teoria da probabilidade, a década de 1960 e 1970 foram o auge do estudo de teoremas centrais do limite para martingales. O teorema central do limite para martingales não era apenas uma generalização do clássico teorema central do limite de Lindeberg, mas que a prova foi a mesma. Era simplesmente uma questão de inserção criteriosa de esperanças condicionais, de modo que a mesma linha de prova trabalhada exatamente. Em outras palavras, a prova clássica do teorema central do limite de Lindeberg já é a prova do teorema central do limite para martingales.

Na seção Teorema Central do Limite, vimos que $ (X_n)_{n\geq 1} $ sequência de variáveis aleatórias tem como suposição a independência. Nesta seção vamos trabalhar os resultados utilizando a teoria de martingale (para mais detalhes consulte Martingale) e a ideia de matrizes triangulares que pode ser escrito como:

Definição 6.4.1.1

Suponha que para cada n ≥ 1, é dada Xn1,…,Xnn uma sequência de variáveis aleatórias independentes. Dizemos que uma matriz triangular dada por

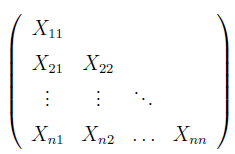
de variáveis aleatórias, no qual cada linha é independente. Porém, vamos trocar a notação de $ X_{nk} $ para $ X^n_k, $ e denotamos $ S_n=X^n_{1}+\dots+X^n_{n}. $

O teorema central do limite para somas $ S_n=X^n_{1}+\dots+X^n_{n}, $ n≥1 de variáveis aleatórias $ (X^n_1,\dots,X^n_n), $ foi estabelecido sob o pressuposto de independência, segundos momentos finitos e o limite de seus termos são desprezíveis. Nesta seção, não vamos partir do pressuposto da independência e até mesmo dos valores absolutos finitos dos momentos de primeira ordem. Com isso, supomos $ (\Omega, \mathcal{F}, \mathbb{P}) $o espaço de probabilidade completo e as sequências

$$X^n=(X^n_k,\mathcal{F}^n_k), \quad 0\leq k \leq n, ~n\geq 1$$

com $ X^n_{0}=0, $ e denotamos $ (\Omega,\mathcal{F},\mathbb{F},\mathbb{P}) $ a base estocástica com $ \mathbb{F}^{n}=(\mathcal{F}^{n}_{i},~i=0,1\dots,k) $ a filtragem (para mais detalhes consulte o conteúdo de base estocástica) definida por $ \mathcal{F}^n_0=(\emptyset,\Omega), $$ \mathcal{F}^n_k \subseteq \mathcal{F}^n_{k+1}\subseteq \mathcal{F}. $ Agora, seja para cada n, kn um tempo de parada (para mais detalhes consulte tempos de parada) com respeito a $ (\mathcal{F}^n_k)_{k\geq 0}. $ Assim, obtemos

$$X^n(t)=\sum^{k_n}_{k=0}X^n_k$$

Teorema 6.4.1.1

ara um dado $ t,~t\in [0,1], $ as seguintes condições são satisfeitas:

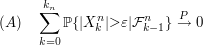
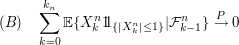
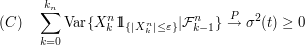
Então $ X^n(t)\overset{\mathcal{D}}{\rightarrow}N(0,\sigma^2(t)) $

Demonstração

Primeiramente, temos a seguinte observação.

Observação

Para cada $ \delta\in(0,1), $

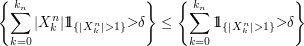
Assim,

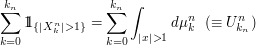
Da condição (A) obtemos que

$$V^n_{k_n}\equiv\sum^{k_n}_{k=0} \int_{|x|>1}d\nu^n_k\overset{P}{\rightarrow}0\quad (6.4.1.4)$$

e $ V^n_{k_n} $ é $ \mathcal{F}^n_{k-1} $-mensurável. Então pelo corolário 2 parágrafo 3 do capítulo 7 do livro do Shiraev [3] obtemos que

$$V^n_{k_n}\overset{P}{\rightarrow}0\quad \Rightarrow \quad U^n_{k_n}\overset{P}{\rightarrow}0\quad (6.4.1.5)$$

Também pelo corolário e da desigualdade $ \Delta U^n_{k_n}\leq 1 $ obtemos

$$U^n_{k_n}\overset{P}{\rightarrow}0\quad \Rightarrow \quad V^n_{k_n}\overset{P}{\rightarrow}0$$

De (6.4.1.3) a (6.4.1.5) temos que

$$X^n(t)=Y^n(t)+Z^n(t)$$

em que

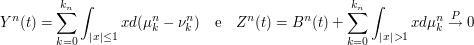
Para mostrar que $ X^n(t)\overset{\mathcal{D}}{\rightarrow}N(0,\sigma^2(t)). $ Basta mostrar que

$$Y^n(t)\overset{\mathcal{D}}{\rightarrow}N(0,\sigma^2(t))$$

Assim, seja $ Y^n(t) $ escrito da forma

$$Y^n(t)=\gamma^n_{k_n}(\varepsilon)+\Delta^n_{k_n}(\varepsilon),\quad \varepsilon\in(0,1],$$

em que

$$\gamma^n_{k_n}(\varepsilon)=\sum^{k_n}_{k=0} \int_{\varepsilon<|x|\leq1}x d(\mu^n_k-\nu^n_k)$$

$$\Delta^n_{k_n}(\varepsilon)=\sum^{k_n}_{k=0} \int_{|x|\leq \varepsilon}x d(\mu^n_k-\nu^n_k)$$

Da condição (A), obtemos $ \gamma^n_{k_n}(\varepsilon)\overset{P}{\rightarrow}0 $ quando $ n\rightarrow \infty. $ Agora, a sequência $ \Delta^n(\varepsilon)=(\Delta^n_{k}(\varepsilon),\mathcal{F}^n_{k}),1\leq k\leq n, $ é um martingale quadrado integrável com variação quadrática

Da condição (C) obtemos que

$$\langle\Delta^n(\varepsilon)\rangle_{k_n}\overset{P}{\rightarrow}\sigma^2(t)$$

Portanto, para cada $ \varepsilon\in (0,1], $

$$\max(\gamma^n_{k_n}(\varepsilon)~ ;~|\langle\Delta^n(\varepsilon)\rangle_{k_n}-\sigma^2(t)|)\overset{P}{\rightarrow}0\quad (6.4.1.6)$$

Logo, $ M^n_{k_n}\overset{\mathcal{D}}{\rightarrow}N(0,\sigma^2(t)), $ em que

$$M^n_k\equiv \Delta^n_k(\varepsilon_n)=\sum^k_{i=0}\int_{|x|\leq \varepsilon_n}x(\mu^n_i-\nu^n_i)\quad (6.4.1.7)$$

Para $ \Gamma\in \sigma(R(0)), $ seja

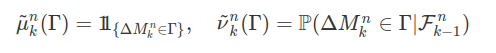
e $ \Delta M^n_k=M^n_k-M^n_{k-1},k\geq 1, M^n_0=0. $ Então o martingale quadrado integrável $ M^n=(M^n_k,\mathcal{F}^n_{k}),1\leq k\leq n, $ pode ser escrito da forma

$$M^n_k=\sum^k_{i=1}\Delta M^n_i=\sum^k_{i=1}\int_{|x|\leq 2\varepsilon_n}x d\tilde{\mu}^n_k$$

lembrando que $ |\Delta M^n_i|\leq 2\varepsilon_n $ por (6.4.1.7). Para mostrar (6.4.1.6), temos que para cada $ \lambda\in \mathbb{R}, $

$$\mathbb{E}[\exp(i\lambda M^n_{k_n})]\rightarrow \exp(-\frac{1}{2}\lambda^2\sigma^2(t))$$

Definimos

$$G^n_k=\sum^k_{j=1}\int_{|x|\leq 2\varepsilon_n}(e^{i\lambda x}-1)d\tilde{\nu}^n_j,\quad \text{e}\quad \mathcal{E}^n_k(G^n)=\prod^k_{j=1}(1+\Delta G^n_k).$$

Observe que

$$1+\Delta G^n_k=1+\int_{|x|\leq 2\varepsilon_n}(e^{i\lambda x}-1)d\tilde{\nu}^n_k = \int_{|x|\leq 2\varepsilon_a}e^{i\lambda x}d\tilde{\nu}^n_k=E[\exp(i\lambda \Delta M^n_k)|\mathcal{F}^n_{k-1}]$$

e consequentemente

$$\mathcal{E}^n_k(G^n)=\prod^k_{j=1}(1+\Delta G^n_k)$$

Agora, para cada $ \lambda\in \mathbb{R}, $ temos que

$$|\mathcal{E}^n_{k_n}(G^n)|=\left|\prod^k_{j=1}\mathbb{E}[\exp(i\lambda \Delta M^n_k)|\mathcal{F}^n_{k-1}]\right|\geq C(\lambda)>0\quad (6.4.1.8)$$

e

$$\mathcal{E}^n_{k_n}(G^n)\overset{P}{\rightarrow}\exp(-\frac{1}{2}\lambda^2\sigma^2(t))\quad (6.4.1.9)$$

Representamos $ \mathcal{E}^n_{k}(G^n) $ da forma

$$\mathcal{E}^n_{k}(G^n)=\exp(G^n_k)\prod^k_{j=1}(1+\Delta G^n_j)\exp(-\Delta G^n_j)$$

Desde que

$$\int_{|x|\leq 2\varepsilon_n}x d\tilde{\nu}^n_j=\mathbb{E}[\Delta M^n_j| \mathcal{F}^n_{j-1}]=0$$

obtemos que

$$G^n_k=\sum^k_{j=1}\int_{|x|\leq 2\varepsilon_n}(e^{i\lambda x}-1-i\lambda x)d\tilde{\nu}^n_j\quad (6.4.1.10)$$

Portanto,

$$|\Delta G^n_k| \leq\int_{|x|\leq 2\varepsilon_n}|e^{i\lambda x}-1-i\lambda x|d\tilde{\nu}^n_k~\leq~ \frac{1}{2}\lambda^2\int_{|x|\leq 2\varepsilon_n} x^2d\tilde{\nu}^n_k$$

$$\leq \frac{1}{2}\lambda^2 (2\varepsilon_n)^2 \rightarrow 0\quad (6.4.1.11)$$

e

$$\sum^k_{j=1}|\Delta G^n_k| \leq\frac{1}{2}\lambda^2\sum^k_{j=1}\int_{|x|\leq 2\varepsilon_n} x^2d\tilde{\nu}^n_j=\frac{1}{2}\lambda^2 \langle M^n\rangle_k\quad (6.1.1.12)$$

Da condição (C), obtemos que

$$\langle M^n\rangle_{k_n}\overset{P}{\rightarrow}\sigma^2(t)\quad (6.4.1.13)$$

Primeiramente, supomos que $ \langle M^n\rangle_{k}\leq a $ (P-q.c.), $ k\leq k_n, $ em que $ a\geq \sigma^2(t)+1. $ Então, de (6.4.1.11) e (6.4.1.12) obtemos

$$\prod^{k_n}_{k=1}(1+\Delta G^n_k)\exp(-\Delta G^n_k)\overset{P}{\rightarrow}1,\quad n\rightarrow \infty$$

Assim, para provar (6.4.1.9), basta que

$$G^n_{k_n}\rightarrow -\frac{1}{2}\lambda^2\sigma^2(t),\quad (6.4.1.14)$$

De (6.4.1.10), (6.4.1.11) e (6.4.1.13) temos que

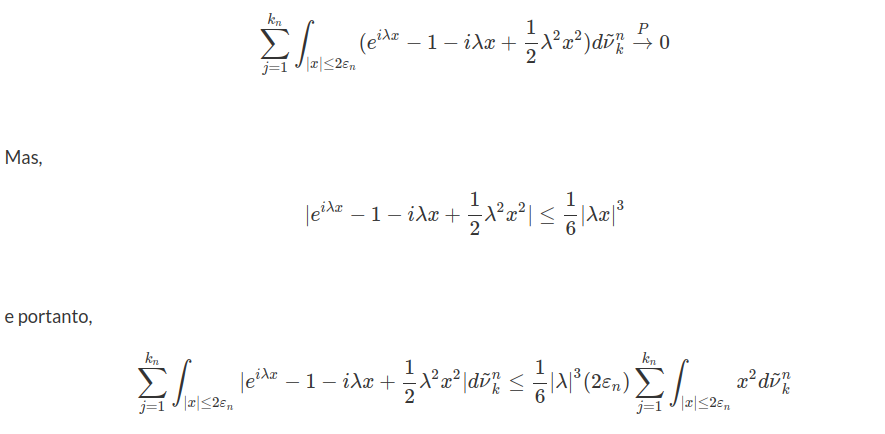
$$=\frac{1}{3}\varepsilon_n|\lambda|^3\langle M^n\rangle_{k_n}\leq \frac{1}{3}\varepsilon_n|\lambda|^3 a\overset{n\rightarrow \infty}{\longrightarrow}0$$

Portanto, se $ \langle M^n\rangle_{k_n}\leq a $ (P-q.c.), (6.4.1.14) é satisfeito e consequentemente (6.4.1.9) é satisfeito.

Agora, para verificar (6.4.1.8), desde que $ |e^{i\lambda x}-1-i\lambda x|\leq \frac{1}{2}(\lambda x)^2. $ De (6.4.1.11), temos que para n suficientemente grande

$$|\mathcal{E}^n_k(G^n)|=\left|\prod^k_{j=1}(1+\Delta G^n_i)\right|\geq \prod^k_{j=1}\left(1-\frac{1}{2}\lambda^2\Delta \langle M^n\rangle_j\right)=\exp\left(\sum^k_{j=1}\ln(1-\frac{1}{2}\lambda^2\Delta \langle M^n\rangle_j)\right)$$

Mas

$$\ln(1-\frac{1}{2}\lambda^2\Delta \langle M^n\rangle_j)\geq -\frac{\frac{1}{2}\lambda^2\Delta \langle M^n\rangle_j}{1-\frac{1}{2}\lambda^2\Delta \langle M^n\rangle_j}$$

e $ \Delta\langle M^n\rangle_j\leq (2\varepsilon_n)^2\downarrow 0, $ quando $ n\rightarrow \infty. $ Assim, existe um $ n_0=n_0(\lambda) $ tal que para todo $ n\geq n_0(\lambda), $

$$|\mathcal{E}^n_k(G^n)|\geq \exp(-\lambda^2\langle M^n\rangle_k)$$

e portanto

$$|\mathcal{E}^n_{k_n}(G^n)|\geq \exp(-\lambda^2\langle M^n\rangle_{k_n})\geq e^{-\lambda^2 a}$$

que é provado pela suposição $ \langle M^n\rangle_{k_n}\leq a $ (P-q.c.). Para removermos esta suposição, definimos

$$\tau^n=\min(k\leq k_n; \langle M^n\rangle_{k}\geq \sigma^2(t)+1)$$

tomando $ \tau^n=\infty $ se $ \langle M^n\rangle_{k}\leq \sigma^2(t)+1. $ Então para $ \overline{M}^n_k=M^n_{k \wedge \tau^n} $ obtemos que

$$\langle \overline{M}^n\rangle_{k_n}=\langle M^n\rangle_{k_n\wedge \tau^n}\leq 1+\sigma^2(t)+2\varepsilon^2_n\leq 1+\sigma^2(t)+2\varepsilon^2_1$$

como mostrado anteriormente,

$$\mathbb{E}[\exp(i\lambda\overline{M}^n_{k_n})]\rightarrow \exp\left(-\frac{1}{2}\lambda^2\sigma^2(t)\right)$$

Mas

$$\lim_n \left|\mathbb{E}\left[\exp(i\lambda{M}^n_{k_n})- \exp(i\lambda\overline{M}^n_{k_n})\right]\right|\leq 2\lim_n \mathbb{P}(\tau<\infty)=0$$

Consequentemente,

$$\lim_n \mathbb{E}[\exp(i\lambda\overline{M}^n_{k_n})]=\lim_n \mathbb{E}\left[\exp(i\lambda{M}^n_{k_n})- \exp(i\lambda\overline{M}^n_{k_n})\right]+\lim_n\mathbb{E}\left[\exp(i\lambda\overline{M}^n_{k_n})\right]=$$

$$=\exp\left(-\frac{1}{2}\lambda^2\sigma^2(t)\right)$$

Isto completa a demonstração do teorema

$ \Box $

Vale observar que muitos teoremas centrais do limite relacionados para variáveis aleatórias dependentes agora podem ser facilmente deduzidos à partir do teorema (6.4.1.1).

Nos casos em que $ X^n_1,\dots,X^n_n $ são independentes, as condições do teorema (6.4.1.1) com $ t=1, $ e $ \sigma^2=\sigma^2_1, $ obtemos

$$(a)\sum^{k_n}_{k=0}\mathbb{P}(|X^n_k|>\varepsilon)\rightarrow0$$

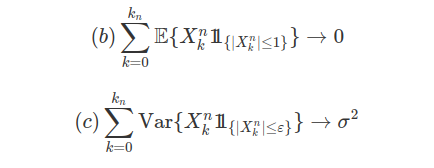
Notamos que este resultado não assume a independência e até mesmo não exige que $ X^n_k $ sejam integráveis. No caso de variáveis aleatórias independentes, esse resultado se transforma no teorema central do limite de Lindeberg. No caso em que $ \sigma^2(t)=0, $ a distribuição limitante é degenerada.

Lema 6.4.1.1

Se para um determinado $ \lambda $$ |\mathcal{E}^n(\lambda)|\geq c(\lambda)>0, n \geq 1, $ um condição suficiente para

$$\mathbb{E}[e^{i\lambda Y^n}]\rightarrow\mathbb{E}[e^{i\lambda Y}],\quad \text{i.e.}\quad \mathcal{E}^n(\lambda)\overset{P}{\rightarrow} \mathcal{E}(\lambda)\quad (6.4.1.15)$$

Demonstração

Primeiramente, seja $ \eta^n=(\eta^n_k,\mathcal{F}^n_{k}),1\leq k\leq n,\geq 1 $ a sequência estocática, denotamos

$$Y^n=\sum^n_{k=1}\eta^n_k,$$

e

$$\mathcal{E}^n(\lambda)=\prod^n_{k=1}\mathbb{E}[\exp(i\lambda \eta^n_k)|\mathcal{F}^n_{k-1}], \quad \lambda \in \mathbb{R}$$

em que $ Y $ é a v.a. com

$$\mathcal{E}(\lambda)=\mathbb{E}[e^{i\lambda Y}]$$

Agora, seja $ m^n(\lambda)=\frac{e^{i\lambda Y^n}}{\mathcal{E}^n(\lambda)}. $ Então $ |m^n(\lambda)|\leq c^{-1}(\lambda)<\infty. $ Note que $ \mathbb{E}[m^n(\lambda)]=1 $ e que da equação (6.4.1.15) e da hipótese $ \mathcal{E}^n(\lambda)\geq c(\lambda)>0, $ que $ \mathcal{E}^n(\lambda)\neq 0. $

Portanto, de (6.4.1.15) e do teorema da convergência dominada obtemos que

$$|\mathbb{E}[e^{i\lambda Y^n}]-\mathbb{E}[e^{i\lambda Y}]|=|\mathbb{E}(e^{i\lambda Y^n}-\mathcal{E}(\lambda))|=|\mathbb{E}\left(m^n(\lambda)[\mathcal{E}^n(\lambda)-\mathcal{E}(\lambda)]\right)|\leq$$

$$\leq c^{-1}(\lambda)\mathbb{E}\left|\mathcal{E}^n(\lambda)-\mathcal{E}(\lambda)\right|\overset{n\rightarrow \infty}{\longrightarrow} 0$$

$ \Box $

Corolário 6.4.1.1

Se $ X^n_1,\dots,X^n_n $ são variáveis aleatórias independentes, n≥1, então as condições (A), (B) e (C) implicam que $ X^n_1 \overset{\mathcal{D}}{\rightarrow}N(0,\sigma^2) $

Proposição 6.4.1.1

Seja $ 0< t_1< t_2<\dots< t_j<1 $ e $ \sigma^2(t_1)<\sigma^2(t_2)<\dots<\sigma^2(t_j), $ com $ \sigma^2(0)=0 $ e seja $ \varepsilon_1,\dots,\varepsilon_j $ são variáveis aleatórias normais com média zero e $ \mathbb{E}(\varepsilon^2_k)=\sigma^2(t_k)-\sigma^2(t_{k-1}). $ Resultam nos vetores (Normais) $ (W(t_1),\dots, W(t_j)) $ com $ W(t_k)=\varepsilon_1+\dots+\varepsilon_k. $

Demonstração

Suponhamos que condições (A), (B) e (C) são satisfeitas para $ t=t_1,\dots, t_j. $ Então a distribuição conjunta ($ P^n(t_1,\dots,t_j) $) para as variáveis aleatórias ($ (X^n(t_1),\dots, X^n(t_j)) $) converge fracamente para distribuição Normal $ P (t_1,\dots, t_j) $ das variáveis $ (W_{t_1},\dots, W_{t_j})$:

$$P^n(t_1,\dots,t_j) \overset{\mathcal{D}}{\rightarrow} P(t_1,\dots,t_j)$$

$ \Box $

Teorema 6.4.1.2

A condição (A) é equivalente a

$$(a) \max_{1\leq k\leq k_n}|X^n_k|\overset{P}{\rightarrow}0$$

Suponha (A) ou (a) válidos, a condição (C) é equivalente a

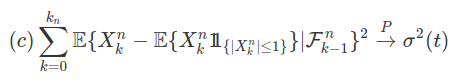
Demonstração

Para provar a primeira parte do teorema temos que dado $ \varepsilon>0, $ existe $ \delta \in (0,\varepsilon) $ e por simplicidade tomamos $ t=1. $ Desde que

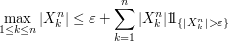
e

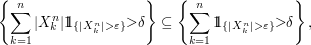
obtemos que

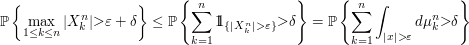
Se (A) é satisfeita, isto é,

$$\mathbb{P}\left(\sum^n_{k=1} \int_{|x|>\varepsilon}d\nu^n_k>\delta \right)\rightarrow 0.$$

então, obtemos que

$$\mathbb{P}\left(\sum^n_{k=1} \int_{|x|>\varepsilon}d\mu^n_k>\delta \right)\rightarrow 0.$$

Logo, (A) $ \Rightarrow $ (a).

Por outro lado, seja

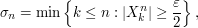
Suponhamos que $ \sigma_n=\infty $ se $ \displaystyle\max_{1\leq k \leq n}|X^n_k|\geq \frac{\varepsilon}{2}. $ Pela condição (c), $ \displaystyle \lim_n \mathbb{P}(\sigma<\infty)=0. $

Agora, observe que, para cada $ \delta\in (0,1), $ o conjunto

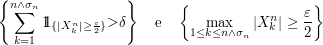
coincidem. Da condição (a)

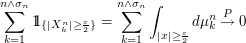
que em conjunto com a propriedade $ \lim_n \mathbb{P}(\sigma_n<\infty)=0, $ provamos que (a) $ \Rightarrow $ (A).

Agora, vamos mostrar a parte (2). Novamente supomos $ t=1, $ escolhemos $ \varepsilon\in (0,1] $ e consideramos o martingale quadrado integrável $ \Delta^n(\delta)=(\Delta^n_k(\delta),\mathcal{F}^n_k) $ para $ 1\leq k \leq n, $ com $ \delta \in (0,\varepsilon]. $ Para dado $ \varepsilon\in (0,1], $ da condição (C) temos que

$$\langle \Delta^n(\varepsilon)\rangle_n \overset{P}{\rightarrow} \sigma^2_1$$

A partir da condição (A) que para cada $ \delta \in (0,\varepsilon] $

$$\langle \Delta^n(\delta)\rangle_n \overset{P}{\rightarrow} \sigma^2_1$$

Decorre das condições (c), (A) e (a) que para cada $ \delta \in (0,\varepsilon], $

$$[ \Delta^n(\delta)]_n \overset{P}{\rightarrow} \sigma^2_1\quad (6.4.1.16)$$

em que

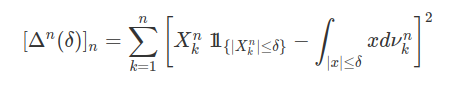
De fato, da condição (A)

$$[ \Delta^n(\delta)]_n - [ \Delta^n(1)]_n\overset{P}{\rightarrow}0\quad (6.4.1.17)$$

Mas

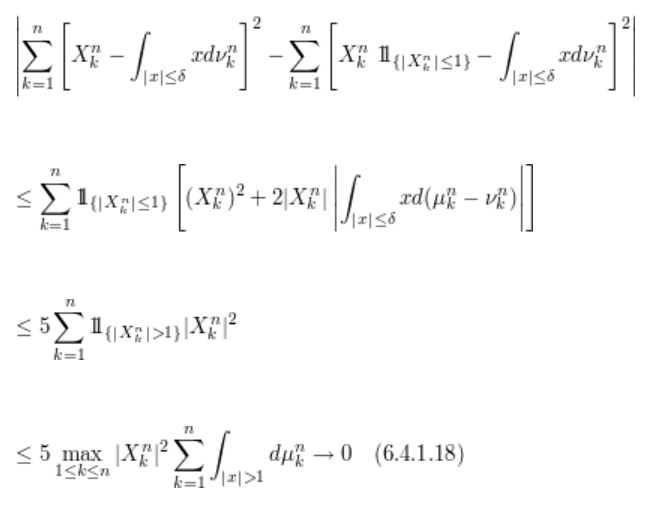
Logo, a equação (6.4.1.16) é obtido à partir de (6.4.1.17) e (6.4.1.18).

Para mostrar a equivalência das condições (C) e (c), é suficiente mostrar que a condição (C) é satisfeita. Para dado $ \varepsilon \in(0,1], $ então a condição (c) é também satisfeita para cada $a\geq 0$:

$$\lim_{\delta\rightarrow 0}\lim\sup_n \mathbb{P}(\left|[\Delta^n(\sigma)]_n-\langle \Delta^n(\delta)\rangle_n\right| > a)=0\quad (6.4.1.19)$$

Seja $ m^n_k(\delta)=[\Delta^n(\sigma)]_n-\langle \Delta^n(\delta)\rangle_n,\quad 1\leq k \leq n. $ A sequência $ m^n(\delta)=(m^n_k(\delta),\mathcal{F}^n_k) $ é um martingale quadrado integrável e $ (m^n(\delta))^2 $ é dominado pelas sequências $ [m^n(\delta)] $ e $ \langle m^n(\delta)\rangle. $

Note que

$$\leq3\delta^2 ([\Delta^n(\delta)]_n + \langle \Delta^n(\delta)\rangle_n)\quad (6.4.1.20)$$

Desde que $ [\Delta^n(\delta)] $ e $ \langle \Delta^n(\delta)\rangle $ domina uns aos outros. Disto, segue de (6.4.1.20) que $ (m^n(\delta))^2 $ é dominada pela sequências $ 6\delta^2[\Delta^n(\delta)] $ e $ 6\delta^2\langle \Delta^n(\delta)\rangle. $ Assim, se a condição (C) é satisfeita, então para $ \delta $ suficientemente pequeno $ (\delta=\frac{1}{6}b(\sigma^2_1+1)) $

$$\lim \sup_n \mathbb{P}(6\delta^2\langle \Delta^n(\delta)\rangle_n > b)=0$$

logo, pelo corolário (Shiraev [3]), obtemos de (6.4.1.19). Se a condição (c) é satisfeita então para os mesmos valores de $ \delta, $

$$\lim\sup_n \mathbb{P}(6\delta^2[ \Delta^n(\delta)]_k > b)=0\quad (6.4.1.21)$$

Desde que $ |\Delta[ \Delta^n(\delta)]_k|\leq (2\delta)^2, $ a validade de (6.4.1.19) segue de (6.4.1.21) e recorrendo ao corolário (Shiraev [3]). Isto completa a demonstração.

$ \Box $

Teorema 6.4.1.3

Para cada $ n\geq 1 $ a sequência $ X^n=(X^n_k,\mathcal{F}^n_{k}), 1\leq k\leq n, $ é um martingale difference quadrado integrável tal que

$$\mathbb{E}((X^n_k)^2)<\infty,\quad \mathbb{E}(X^n_k|\mathcal{F}^n_{k-1})=0$$

Suponha que a condição de Lindeberg é satisfeita. Assim, para $ \varepsilon>0, $

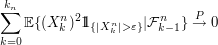
Então (C) é equivalente a

$$\langle X^n\rangle(t) \overset{P}{\rightarrow} \sigma^2(t),\quad (6.4.1.22)$$

em que a variação quadrática

Demonstração

Pela condição de Lindeberg, a equivalência da condição (C) e (6.4.1.22), da condição (c) e de (6.4.1.23) pode ser obtido calculado diretamente.

$ \Box $

Teorema 6.4.1.4

Seja o martingale difference quadrado integrável tal que $ X^n=(X^n_k,\mathcal{F}^n_{k}), $$ n\geq 1, $ para um dado $ t\in (0,1] $ satisfaz a condição de Lindeberg (L). Então

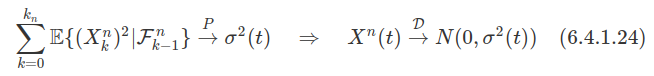
$$\sum^{k_n}_{k=0}(X^n_k)^2\overset{P}{\rightarrow} \sigma^2(t)\quad \Rightarrow \quad X^n(t)\overset{\mathcal{D}}{\rightarrow}N(0,\sigma^2(t))\quad (6.4.1.25)$$

Demonstração

A condição (A) resulta da condição Lindeberg. Quanto à condição (B), é suficiente observar que quando $ X^n $ é um martingale difference, as variáveis $ B^n(t) $ que aparece na decomposição canônica (6.4.1.2), podendo ser representada da forma

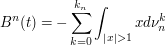
Portanto, $ B^n(t)\overset{P}{\rightarrow}0 $ pela condição de Lindeberg.

$ \Box $

O teorema fundamental desta seção (Teorema 6.4.1.1), provou que sob a hipótese dos termos que somados são uniformemente infinitesimais assintoticamente. É natural definir condições para o teorema central do limite sem tal hipótese. Para variáveis aleatórias independentes, exemplos de tais teoremas são dadas pelo Teorema 7.3.2.2 (assumindo segundos momentos finitos).

Citamos (sem prova) um análogo do primeiro destes teoremas, aplicável apenas a sequências $ X^n=(X^n_k,\mathcal{F}^n_k) $ que são martingale difference quadrados integráveis.

Seja $ F^n_k(x)=\mathbb{P}(X^n_k\leq x| \mathcal{F}^n_{k-1}) $ a função distribuição regular de $ X^n_k $ com respeito a $ \mathcal{F}^n_{k-1} $ e seja $ \Delta^n_k=\mathbb{E}[(X^n_k)^2|\mathcal{F}^n_{k-1}]. $ Assim, temos o seguinte resultado.

Teorema 6.4.1.5

Se um martingale difference quadrado integrável $ X^n=(X^n_k,\mathcal{F}^n_{k}),0\leq k \leq n, $$ n\geq 1, $ e $ X^n_{0}=0 $ satisfaz a condição

$$\sum^{k_n}_{k=0}\Delta^n_k\overset{P}{\rightarrow}\sigma^2(t), \quad 0\leq \sigma^2(t)<\infty$$

para todo $ \varepsilon>0 $

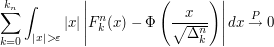
Então

$$X^n(t)\overset{\mathcal{D}}{\rightarrow}N(0,\sigma^2(t))$$

6.4.2 - Generalizações e principio da invariância

O teorema central do limite para martingales foi estendido por McLeish (1974) [17]. Assim, seja as mesmas definições da seção anterior (para mais detalhes consulte TCL para soma de v.a.’s dependentes) com a modificação de que para cada n, definimos a função aleatória $ r_n(.) $ em $ [0,\infty), $ com as seguintes propriedades:

• Cada $ r_n(t) $ é um tempo de parada com respeito a $F^n_k$, para k=0,1,…;
• A trajetória da amostra $ r_n(.) $ são valores inteiros, não decrescentes e contínuas à direita com $r_n(0)$=0.

Definimos

$$X^n(t)=\sum^{r_n(t)}_{k=1}X^n_k$$

Seja $ W $ o movimento Browniano padrão de modo que $ W(0)=0, $$ ~\mathbb{E}(W(t))=0 $ e $ ~\mathbb{E}(W(t)^2)=t. $ A integral estocástica simples $ \displaystyle X=\int g~dW $ está bem definida sempre que $ \displaystyle \int^a_0 g^2(s)~ds< \infty $ para todo $ a> 0. $

Com isso, definimos o processo gaussiano contínuo com

$$X(0)=0,~\mathbb{E}(X(t))=0~ \text{e}~ \mathbb{E}(X(t)X(u))=\displaystyle \int^{t\wedge u}_0 g^2(s)~ds.$$

A seguir apresentamos a seguinte definição.

Definição 6.4.2.1

Dizemos que $ Z_n(t) $ converge em probabilidade uniformemente no compacto para $ Z(t) $, isto é, $ Z_n(t)\xrightarrow{Pu}Z(t) $, se para todo $ a> 0 $

$$\sup_{0\leq t\leq a}|Z_n(t)-Z(t)|\xrightarrow{P}0$$

Segundo Helland (1982) [16], quando $ Z_n(.) $ e $ Z(.) $ são não decrescentes e $ Z_n(.) $ é contínua quase certamente, a definição (6.4.2.1) é equivalente a condição fraca $ Z_n(t)\xrightarrow{P}Z(t), $ para todo $ t> 0. $

Teorema 6.4.2.1

Suponha que para todo $ \varepsilon,~t> 0 $ e uma função $ f $ mensurável e não negativa tal que $ \displaystyle\int^t_0 f^2(s)ds< \infty $

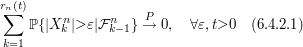
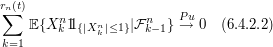
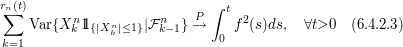
Então

$$X^n\xrightarrow{\mathcal{D}}\int f~dW.$$

Demonstração

Logo, $ \eta^n_k $ satisfaz a condição de McLeish (1974) [17] trocando t por $ \displaystyle \int^t_0 f^2(s)~ds. $

$$\sum^{r_n(t)}_{k=1}\eta^n_k\xrightarrow{\mathcal{D}}\int f~dW $$

Com isso, da equação (6.4.2.2) obtemos que

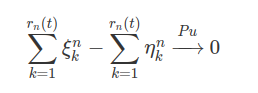
Portanto da equação (6.4.2.1) e do teorema (6.4.1.2) obtemos que para todo t

$$\mathbb{P}\left[\max_{1\leq k\leq r_n(t)}|X^n_k-\xi^n_k|\neq 0\right]\rightarrow 0,$$

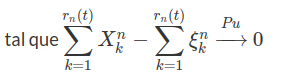
Portanto,

$$X^n\xrightarrow{\mathcal{D}}\int f~dW.$$

$ \Box $

Teorema 6.4.2.2

Considere $ (X^n_k) $ satisfazendo a condição de martingale difference e seja $ f $ função mensurável e não negativa tal que $ \displaystyle\int^t_0 f^2(s)ds< \infty $ para todo $ t> 0. $ Suponha que uma dos três conjunto de condições são satisfeitas para todo $ t> 0. $

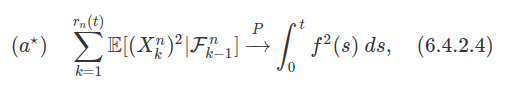
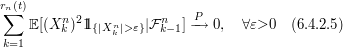
$$(b^\star)\quad\sum^{r_n(t)}_{k=1}(X^n_k)^2\xrightarrow{P}\int^t_0 f^2(s)~ds,\quad (6.4.2.6)$$

$$\mathbb{E}\left[\max_{1\leq k \leq r_n(t)}|X^n_k|\right]\rightarrow 0\quad (6.4.2.7)$$

$$(c^\star)\text{A equação (6.4.2.6) é satisfeita }\sum^{r_n(t)}_{k=1}(X^n_k)^2\xrightarrow{P}\int^t_0 f^2(s)~ds,\quad (6.4.2.8)$$

$$\mathbb{E}\left[\max_{1\leq k \leq r_n(t)}|X^n_k|\right]\rightarrow 0\quad (6.4.2.9)$$

Então

$$X^n\xrightarrow{\mathcal{D}}\int f~dW$$

Demonstração

Primeiramente, da equação (6.4.2.5) obtemos que

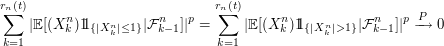
para $ p=1 $ e $ p=2. $

Logo, a condição (a$ ^\star $) implica nas hipóteses do teorema (6.4.2.1). Para a condição (b$ ^\star $) obtemos que as hipóteses do teorema (6.4.2.1) também são satisfeitas. Similarmente, obtemos que as equações (6.4.2.6), (6.4.2.9) e

$$\max_{1\leq k \leq r_n(t)}|X^n_k|\xrightarrow{P}0,\quad \forall~t>0\quad (6.4.2.10)$$

implicam nas hipóteses do teorema (6.4.2.1). Porém, a equação (6.4.2.10) é uma consequência da hipótese (6.4.2.6) válido para todo t > 0. Esta última mostra que da condição (b$ ^\star $) a equação (6.4.2.7) pode ser obtido fracamente como

$$\max_{1\leq k \leq r_n(t)}|X^n_k|\quad \text{uniformemente integrável}\quad (6.4.2.11)$$

Portanto, sob condições (a$ ^\star $) até (c$ ^\star $) obtemos $ \displaystyle X^n\xrightarrow{\mathcal{D}}\int f~dW. $

$ \Box $