Parte 2

7 - Processo de Poisson

O processo de Poisson é o processo estocástico a tempo contínuo com a estrutura mais simples. Este processo conta o número de eventos de interesse em um intervalo da reta. Por exemplo, o número de falhas de um sistema durante um intervalo de tempo. Nesta seção, vamos construir o processo de Poisson e estudar suas principais propriedades.

Seja $ (T_n)_{n> 0} $ uma sequência de variáveis aleatórias positivas estritamente crescente $ (T_0=0 \ < \ T_1 \ < \ T_2 \cdots) $ definidas na base estocástica $ \mathfrak{B}=(\Omega,\mathcal{F},\mathbb{F},\mathbb{P}) $. As variáveis aleatórias $ (T_n) $ representam os instantes de tempo nos quais o evento de interesse ocorre. Para contar o número de eventos ocorridos até o tempo $ t \geq 0 $, introduzimos a função indicadora

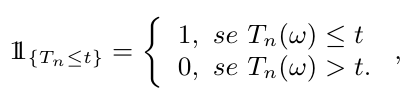
para $ n \geq 1 $. A partir destes elementos, vamos introduzir o processo de contagem dos eventos de interesse.

Definição 7.1

O processo estocástico $ N=(N_t)_{0\leq t \leq \infty} $ definido por:

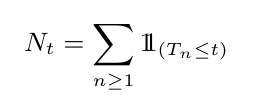
é denominado processo de contagem associado a sequência $ (T_n)_{n\geq 1}. $

Definimos também $ T= \sup_n T_n $, então

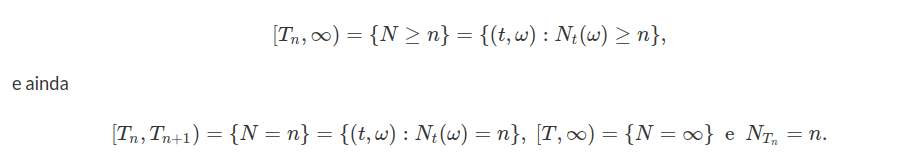
A variável aleatória T é denominada tempo de explosão do processo de contagem $ N $. Se temos $ T=\infty $ quase certamente então $ N $ é um processo de contagem não explosivo. Para um processo de contagem $ N $ não explosivo e para $ 0\leq s< t< \infty $, temos que

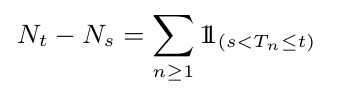
conta o numero de eventos que ocorrem entre o tempos $ s $ e $ t $ fixos.

Observação

É importante notarmos que da maneira como definimos o processo de contagem $ N $, este não necessariamente é um processo adaptado a filtagem $ \mathbb{F} $. Pois, ser um processo adaptado depende estritamente da filtragem, ou seja, o processo pode ser adaptado para uma determinada filtragem e não ser para outra. O teorema a seguir o nos diz sob qual circunstância $ N $ é um processo adaptado com respeito a filtragem $ \mathbb{F} $.

Teorema 7.1

O processo de contagem $ N $ é um processo adaptado, se e somente se, a variável aleatória $ T_n $ é um tempo de parada para to $ n \geq 1 $.

Demonstração

Suponha primeiramente que $ (T_n)_{n\geq 1} $ são tempos de parada, assim temos que o evento

$$ (N_t=n)=(\omega\in \Omega: T_n(\omega )\leq t< T_{n+1}(\omega))\in \mathcal{F_t}, $$

para todo $ n\geq 0 $. Então temos que $ N_t $ é $ \mathcal{F_t} $-mensurável e portanto N é um processo adaptado.

Agora suponha que $ N $ seja um processo adaptado, então o evento

$$(T_n\leq t)=(N_t\geq n)\in \mathcal{F_t},$$

para todo $ t \geq 0 $. Portanto temos que $ T_n $ é um tempo de parada. E o resultado segue.

Definição 7.2

Um processo estocástico $ (N_t, t\geq 0) $ é dito possuir incrementos independentes se para quaisquer $ t_1, t_2, t_3,\cdots, t_n $, com $ 0< t_1< t_2< \cdots < t_n $ temos que

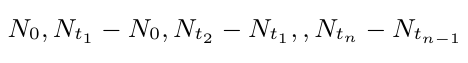
são variáveis aleatórias independentes em $ (\Omega, \mathcal{F} , \mathbb{P}) $.

Por exemplo, isto significa que o número de eventos que tenham ocorrido até tempo t (que é dado por $ N_t $) deve ser independente do número de eventos que ocorrem entre os tempos de t e t + s (isto é, $ N_{t + s}-N_t $).

Definição 7.3

Um processo estocástico $ N=(N_t, t\geq 0) $ é dito ter incrementos estacionários se $ P[N_{t+s}-N_{t}=k]=P[N_{s}=k] $, para qualquer $ t\geq 0 $ e qualquer $ k \geq 0 $.

Definição 7.4

O processo de contagem $ (N_t, t\geq 0) $adaptado na filtragem $ \mathbb{F}=(\mathcal{F_t} : t \geq 0) $ e não explosivo é dito ser um processo de Poisson se:

1. N(0)=0.
2. Incrementos independentes.
3. Incrementos estacionários.

Com o resultado a seguir, vamos mostrar que o número de saltos relacionado com o processo de Poisson segue a distribuição de Poisson, ou seja, $ N_t $ tem distribuição de Poisson com parâmetro $ \lambda t $ para algum $ \lambda > 0 $, o que justifica o nome do processo estocástico de contagem. Note que na definição do processo $ N $ em momento algum foi citado que o processo tem alguma relação com a distribuição de Poisson, obtemos isso como consequência desta definição.

Teorema 7.2

Seja N um processo de Poisson. Então, temos que

$$\mathbb{P}(N_t=n)=\frac{e^{-\lambda t}(\lambda t)^n}{n!},~\forall n\in \mathbb{N},$$

para algum $ \lambda> 0 $. Ou seja, $ N_t\sim ~Poisson(\lambda t) $. Além disso, o processo $ N $ é contínuo em probabilidade (ou seja, $ \displaystyle \lim_{t\rightarrow u}N_t=N_u $ tomando o limite em probabilidade, ou equivalentemente temos que $ \lim_{t\rightarrow u}\mathbb{P}(|N_t-N_u|\geq \epsilon)=0, ~\forall \epsilon > 0 $) .

Demonstração

Para demonstrarmos esse resultado, vamos dividi-lo em algumas etapas.

(a) Para todo $ t\geq 0 $, temos que

$$\mathbb{P}(N_t=0)=e^{-\lambda t},$$

para algum $ \lambda> 0. $

(b) $ \displaystyle \lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}(N_t\geq 2)=0. $

(c) $ \displaystyle \lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}(N_t= 1)=\lambda $, no qual $ \lambda $ é a constante que aparece em (a).

(d) E por fim o resultado desejado. Temos que

$$\mathbb{P}(N_t=n)=\frac{e^{-\lambda t}(\lambda t)^n}{n!},~\forall n\in \mathbb{N}.$$

(a) Primeiramente observe que o número de chegadas no intervalo $ [0,t+s] $ é zero se, e somente se, não existe chegada no intervalo $ [0,t] $ e no intervalo $ (t,t+s] $, ou seja, o evento $ (N_{t+s}=0) $ é igual ao evento $ (N_t=0, N_{t+s}-N_t=0) $. Por definição esses eventos são independentes, então,

$$\mathbb{P}[N_{s+t}=0]=\mathbb{P}[N_t=0, N_{t+s}-N_t=0]=\mathbb{P}[N_t=0]\mathbb{P}[N_{t+s}-N_t=0].$$

Por outro lado temos que a distribuição é estacionária. Assim, temos que

$$\mathbb{P}[N_{t+s}-N_t=0]=\mathbb{P}[N_s=0].$$

Logo, concluímos que

$$\mathbb{P}[N_{s+t}=0]=\mathbb{P}[N_t=0, N_{t+s}-N_t=0]=\mathbb{P}[N_t=0]\mathbb{P}[N_s=0].$$

Portanto, temos que a função $ g(t)=\mathbb{P}[N_t=0] $, satisfaz a seguinte condição

$$g(t+s)=g(t)g(s).$$

Por um resultado clássico de análise matemática, sabemos que apenas duas funções satisfazem essa condição, ou $ g(t)=0,~ \forall t\geq 0 $, ou

$$g(t)=e^{-\lambda t},$$

para algum $ \lambda \geq 0 $. Formalmente temos que $ \lambda\in \mathbb{R} $, porém como estamos tomando a função $ g $ igual a uma probabilidade, temos que $ \lambda $ é não negativo. Assim, basta mostrarmos que $ g(t) $ não pode ser zero para todo $ t $.

De fato, note que se $ g(t) $ for igual a $ 0 $ para todo $ t $, temos que

$$N_{s}\stackrel{d}{=}N_{t+s}-N_t\geq 1, ~ ~ \mathbb{P}-q.c.,$$

não importando quão pequeno seja $ s $. Assim sejam $ t_1< t_2< t_3< \cdots < t_n=t $, então

$$N_t=N_{t_1}+(N_{t_2}-N_{t_1})+\cdots +(N_{t_n}-N_{t_{n-1}}).$$

Desde que

$$N_{t_i}-N_{t_{i-1}}\geq 1, ~ \forall i=1,\cdots, n,$$

obtemos que $ N_t(\omega)\geq n,~ \forall n\in\mathbb{N} ~ \mathbb{P}-q.c. $. Mas isto implica que

$$N_t=\infty,$$

o que é absurdo pois por hipótese N é um processo não explosivo. Isto implica que $ g(t) $ não pode ser identicamente igual a $ 0 $. Assim, concluímos que $ g(t)=e^{-\lambda t} $ para algum $ \lambda $ não negativo. Agora, se $ \lambda =0 $, temos que $ \mathbb{P}[N_t=0]=1 $ para todo $ t \geq 0 $. Como consequência, temos que $ T_1 = \infty ~ ~ \mathbb{P}-q.c. $, o que é um absurdo, pois $ T_1 $ é uma variável aleatória. Assim, tomamos $ \lambda >0 $.

(b) Queremos mostrar que $ \displaystyle \lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}(N_t\geq 2)=0 $. Defina $ f(t)=\mathbb{P}[N_t\geq 2] $.

Note que se $ N_{t}\geq 2 $ então $ N_{t+s}\geq 2 $, ou seja, $ (N_{t}\geq 2)\subset(N_{t+s}\geq 2) $, isto implica que

$$\mathbb{P}[N_t\geq 2]\leq \mathbb{P}[N_{t+s}\geq 2],$$

ou seja, $ f(t)\leq f(t+s) $, isto é f é uma função não decrescente. Seja $ n_t=\sup(n\in\mathbb{N}: ~n\leq 1/t) $, então $ t\leq \displaystyle \frac{1}{n_t} $ e ainda $ \displaystyle \frac{1}{t}< n_t+1 $. Portanto temos que $ f(t)\leq f\left(\frac{1}{n_t}\right) $ e

$$\displaystyle 0\leq \frac{1}{t}f(t)\leq (n_t+1)f\left(\frac{1}{n_t}\right)=\frac{n_t+1}{n_t}n_t f\left(\frac{1}{n_t}\right)$$

Como temos que $ t\downarrow 0 $, isto implica que $ n_t\uparrow \infty $ e ainda $ \displaystyle \frac{(n_t+1)}{n_t}\downarrow 1 $. Desta forma é suficiente mostrar que $ \displaystyle n f\left(\frac{1}{n}\right) $ quando $ n\rightarrow \infty $.

Na sequência, dividimos o intervalo $ [0,1] $ em n subintervalos de comprimento $ 1/n $ cada, seja $ S_n(\omega) $ o número de subintervalos durante os quais houveram duas ou mais chegadas para a realização $ \omega $.

Como $ N $ tem incrementos independentes, interpretamos $ S_n $ como sendo o número de sucessos em n ensaios de Bernoulli, no qual o sucesso na k-ésima tentativa significa que houveram duas ou mais chegadas durante o k-ésimo subintervalo. Então a probabilidade de sucesso de qualquer ensaio é dada por $ p=f\left(\frac{1}{n}\right) $. Portanto temos que

$$E[S_n]=np=\displaystyle nf\left(\frac{1}{n}\right).$$

Como $ N $ é processo não explosivo, temos que para quase todo $ \omega \in \Omega $, existe um tempo minimo $ \delta(\omega)> 0 $ entre duas chegadas no [0,1]. Assim para $ n $ for suficientemente grande temos que

$$\displaystyle\frac{1}{n}< \delta(\omega).$$

Então nenhum subintervalo irá conter duas chegadas, logo $ S_n(\omega)=0 $, para quase todo $ \omega\in \Omega $. Portanto, obtemos que

$$\displaystyle \lim_{n\rightarrow \infty}S_n(\omega)=0,~\mathbb{P}-qc.$$

Além disso, temos que $ S_n $ é limitado, pois não pode ser maior que o número de chegadas que ocorrem no $ [0,1] $, ou seja, $ S_n $ é limitada por $ N_1 $, o qual o valor esperado é finito. Então, temos que

$$E[S_n]\leq E[N_1]< \infty.$$

Logo, temos que a sequência $ S_n $ é dominada. Portanto, pelo teorema da convergência dominada, temos que

$$\displaystyle \lim_{n\rightarrow \infty}nf\left(\frac{1}{n_t}\right)=\lim_{n\rightarrow \infty}E[S_n]=E[\lim_{n\rightarrow \infty} S_n]=E[0]=0,$$

o que implica que $ \displaystyle \lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}(N_t\geq 2)=0 $. Como queríamos demonstrar.

(c) Queremos mostrar que $ \displaystyle \lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}(N_t= 1)=\lambda $, no qual $ \lambda $ é a constante que aparece em (a).

Note que,

$$\mathbb{P}[N_t=1]=1-\mathbb{P}[N_t=0]-\mathbb{P}[N_t\geq 2].$$

Então, pelos itens (a) e (b) temos que

$$\displaystyle \lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}(N_t= 1)=\lim_{t\downarrow 0}\frac{1-e^{-\lambda t}}{t}-\lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}[N_t\geq 2]=\lambda.$$

E portanto o resultado segue.

(d) Por fim, iremos demonstrar o resultado principal, o qual nos diz que:

$$\mathbb{P}(N_t=n)=\frac{e^{-\lambda t}(\lambda t)^n}{n!},~\forall n\in \mathbb{N}.$$

Para isso, definimos a função

$$F(t)=E[\alpha^{N_t}], ~ com ~\alpha \in (0,1).$$

Sabemos que $ N_{t+s}=N_{t}+(N_{t+s}-N_t). $ Pela independência da variáveis aleatórias $ N_{t+s}-N_t $ e $ N_t $, temos que

$$F(t+s)=E[\alpha^{N_{t+s}}]=E[\alpha^{N_{t}+(N_{t+s}-N_t)}]=E[\alpha^{N_{t}}]E[\alpha^{N_{t+s}-N_t}]=F(t)F(s.)$$

Desta forma, obtemos que $ F(t)=0 $ ou $ F(t)=e^{tf(\alpha)} $, com $ f $ sendo a derivada $ F $ no ponto $ t=0 $. Desde que,

$$F(t)=E[\alpha^{N_t}]=\displaystyle \sum_{n=0}^{\infty}\alpha^n \mathbb{P}[N_t=n]\geq P[N_t=0]=e^{-\lambda t},$$

obtemos que $ F(t) $ não pode ser identicamente nula. Note também que $ F(0)=1 $, e $ F(t)=\displaystyle \sum_{n=0}^{\infty}\alpha^{n}\mathbb{P}[N_t=n] $, portanto sua derivada é dada por

$$f(\alpha)=\displaystyle \lim_{t\downarrow 0}\frac{1}{t}(F(t)-1)=$$

$$\displaystyle \lim_{t\downarrow 0}\frac{1}{t}\left[\mathbb{P}(N_t=0)-1\right]+\displaystyle \lim_{t\downarrow 0}\frac{1}{t}\alpha \mathbb{P}[N_t=1]+$$

$$+\displaystyle \lim_{t\downarrow 0}\frac{1}{t}\sum_{n=2}^{\infty}\alpha^n \mathbb{P}[N_t=n].$$

Mas pelo item (a) temos que

$$\displaystyle \lim_{t\downarrow 0}\frac{1}{t}\left[\mathbb{P}(N_t=0)-1\right]=\displaystyle \lim_{t\downarrow 0}\frac{1}{t}\left[e^{-\lambda t}-1\right]=-\lambda,$$

e pelo item (b), o segundo limite

$$\displaystyle \lim_{t\downarrow 0}\frac{1}{t}\alpha \mathbb{P}[N_t=1]=\alpha \lambda.$$

Além disso, pelo item (c) e para todo $ \alpha \in[0,1] $, temos que

$$0\leq \displaystyle \lim_{t\downarrow 0}\frac{1}{t}\sum_{n=2}^{\infty}\alpha^n \mathbb{P}[N_t=n]\leq $$

$$\leq \displaystyle \lim_{t\downarrow 0}\frac{1}{t}\sum_{n=2}^{\infty}\alpha^n \mathbb{P}[N_t\geq 2]=\sum_{n=2}^{\infty}\alpha^n\displaystyle \lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}[N_t\geq 2]\leq$$

$$\displaystyle \leq \sum_{n=0}^{\infty}\alpha^n\lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}[N_t\geq 2]=\frac{1}{1-\alpha}\lim_{t\downarrow 0}\frac{1}{t}\mathbb{P}[N_t\geq 2]=0.$$

Como consequência,

$$f(\alpha)=-\lambda +\lambda\alpha,~\forall \alpha \in [0,1].$$

Desta forma,

$$F(t)=e^{-\lambda t+\lambda t\alpha}.$$

Abrindo em serie de taylor em torno do zero. Temos

$$\displaystyle \sum_{n=0}^{\infty}\alpha^n \mathbb{P}[N_t=n]=\sum_{n=0}^{\infty}\frac{e^{-\lambda t}(\lambda t)^n}{n!}\alpha^n.$$

Pela igualdade da series temos que

$$\mathbb{P}[N_t=n]=\displaystyle \frac{e^{-\lambda t}(\lambda t)^n}{n!}.$$

Portanto o resultado segue.

Na sequência, vamos mostrar que o processo de Poisson é contínuo em probabilidade, ou seja,

$$\displaystyle \lim_{t\rightarrow u}\mathbb{P}(|N_t-N_u|\geq \epsilon)=0,~ \forall \epsilon \geq 0.$$

Para isso, primeiro observemos que para $ t> u $ e $ \epsilon > 1 $ temos

$$\mathbb{P}(|N_t-N_u|\geq \epsilon)=\mathbb{P}(N_t-N_u\geq \epsilon)=\mathbb{P}(N_t-N_u\neq 0)=$$

$$1-\mathbb{P}(N_t-N_u=0)=1-\mathbb{P}(N_{t-u}=0)=1-e^{-\lambda (t-u)}.$$

Da mesma forma para $ t< u $ e $ \epsilon > 1 $ temos que

$$\mathbb{P}(|N_t-N_u|\geq \epsilon)=\mathbb{P}(N_u-N_t\geq \epsilon)=\mathbb{P}(N_u-N_t\neq 0)=$$

$$1-\mathbb{P}(N_u-N_t=0)=1-\mathbb{P}(N_{u-t}=0)=1-e^{-\lambda (u-t)}.$$

Logo,

$$\mathbb{P}(|N_t-N_s|\geq \epsilon)=1-e^{-\lambda |u-t|}.$$

Além disso, temos que

$$[|N_t-N_u|\geq \epsilon]\subset [|N_t-N_u|> 0], ~ \forall \epsilon \geq 0.$$

Portanto, temos que

$$\mathbb{P}(|N_t-N_u|> 0)\geq \mathbb{P}(|N_t-N_u|\geq \epsilon) .$$

Desta forma, ao tomarmos o limite temos que

$$\displaystyle \lim_{t\rightarrow u}\mathbb{P}(|N_t-N_s|> 0)=\lim_{t\rightarrow u}1-e^{-\lambda |u-t|}=0.$$

Portanto o resultado segue.

Definição 7.5

O parâmetro $ \lambda $ associado ao processo de Poisson dado pelo teorema 7.2 é denominado de intensidade ou taxa de chegada do processo.

Corolário 7.1

O processo de Poisson com intensidade $ \lambda $ satisfaz:

(a) $ E[N_t]=\lambda t $

(b) $ Var[N_t]=\lambda t $

Demonstração

A demonstração deste fato, decorre imediatamente do teorema 7.2. Para isto, basta calcularmos a esperança e a variância de uma v.a. com distribuição de Poisson de parâmetro $ \lambda t $.

Como consequência do teorema 7.2, obtemos a seguinte caracterização infinitessimal do processo de Poisson:

i) $ \mathbb{P}[N_{t+h} - N_t = 0]=1 - \lambda h + o(h) $,

ii) $ \mathbb{P}[N_{t+h} - N_t = 1]=\lambda h + o(h) $,

iii) $ \mathbb{P}[N_{t+h} - N_t \geq 2]=o(h) $,

no qual $ o $ é uma função tal que $ o(h)/h \rightarrow 0 $ quando $ h \rightarrow 0 $. Com isso, concluímos que exceto para um conjunto de probabilidade pequena comparada com $ h > 0 $, o processo de Poisson tem distribuição de Bernoulli tomando o valor $ 0 $ com probabilidade $ 1-\lambda t $ e o valor $ 1 $ com probabilidade $ \lambda t $. Desde que o processo de Poisson tem incrementos independentes, temos que

$$N_{t+s}-N_t = \sum_{j=1}^n N_{t+jh}-N_{t+(j-1)h},$$

com $ h=s/n $, tem aproximadamente distribuição binomial com parâmetros $ (n, \lambda s/n) $. Quando $ n \rightarrow \infty $, obtemos a convergência da distribuição binomial para a distribuição de Poisson.

Como consequência direta do teorema 7.2, temos que

$$\mathbb{P}[T_1 > t] = \mathbb{P} [N_t = 0]=e^{-\lambda t}.$$

Portanto, obtemos que $ T_1 $ tem distribuição exponencial com parâmetro $ \lambda $. Da mesma forma, temos que

$$\mathbb{P}[T_{N_s + 1} -s > t] = \mathbb{P} [N_{t+s}-N_s = 0]=e^{-\lambda t},$$

no qual $ T_{N_s + 1} -s $ é o tempo de espera após $ s $ de ocorrência do evento de interesse.

Na sequência, vamos mostrar que o processo de Poisson é um processo de Markov. Seja $ N=(N_t : t \geq 0) $ um processo de Poisson com intensidade $ \lambda $. Para todo $ s,t > 0 $, tomamos

(há elementos em falta na equação acima)

$$N^s_t = N_{s+t} - N_t.$$

Proposição 7.1

Seja $ N $ um processo de Poisson com intensidade $ \lambda $. Então $ N_t-\lambda t $ e $ (N_t-\lambda t)^2 -\lambda t $ são martingales.

Demonstração

Queremos mostrar que $ M_t=N_t-\lambda t $ é um martingale. Desde que $ \mathbb{E} M_t=0 $, basta mostrarmos que $ E[M_t|\mathcal{F_s}]=M_s, $ para todo $ t \geq s. $ De fato, note primeiramente que $ \lambda t $ é uma função não aleatória e ainda que

$$E[M_t- M_s|\mathcal{F_s}]=E[N_t-\lambda t-(N_s-\lambda s)|\mathcal{F_s}]=E[N_t-N_s|\mathcal{F_s}]-\lambda(t-s).$$

Mas $ N_t-N_s $ é independente de $ \mathcal{F_s} $ pela definição do processo de Poisson. Portanto, temos que

$$E[N_t-N_s|\mathcal{F_s}]-\lambda(t-s)=E[N_t-N_s]-\lambda(t-s)=E[N_{t-s}]-\lambda(t-s)=\lambda(t-s)-\lambda(t-s)=0.$$

O que implica que,

$$E[M_t-M_s|\mathcal{F_s}]=E[M_t|\mathcal{F_s}]-M_s=0\Rightarrow E[M_t|\mathcal{F_s}]=M_s.$$

O que mostra que $ N_t-\lambda t $ é um martingale.

Agora seja $ W_t=(N_t-\lambda)^2-\lambda t=M^2_t-\lambda t $. Queremos mostrar que $ W_t $ também é um martingale, mas antes disso mostremos algumas propriedades importantes. Sabemos que $ Var(N_t)=\lambda t $. Com isso calculamos $ E[N^2_t] $, na forma

$$Var[N_t]=E[N^2_t]-E^2[N_t]=E[N^2_t]-\lambda^2 t^2=\lambda t$$

$$\Rightarrow E[N^2_t]=\lambda t +\lambda^2 t^2.$$

Além disso,

temos que

$$E[M^2_t]=E[(N_t-\lambda t)^2]=E[N^2_t-2\lambda t N_t+\lambda^2 t^2]=\lambda t$$

e

$$E[M_t M_s|\mathcal{F_s}]=M_sE[M_t|\mathcal{F_s}]=M^2_s.$$

Assim

$$E[W_t-W_s|\mathcal{F_s}]=E[M^2_t-M^2_s-\lambda(t-s)|\mathcal{F_s}]=$$

$$E[M^2_t - M^2_s-2M_sM_t+2M_sM_t-\lambda(t-s)|\mathcal{F_s}]=E[M^2_t-M^2_s+2M^2_s-2M_sM_t-\lambda(t-s)|\mathcal{F_s}]=$$

$$E[(M_t-M_s)^2-\lambda(t-s)|\mathcal{F_s}]=E[(M_t-M_s)^2]-\lambda(t-s)$$

$$E[(M_{t-s})^2]-\lambda(t-s)=\lambda(t-s)-\lambda(t-s)=0.$$

Portanto, concluímos que

$$E[W_t-W_s|\mathcal{F_s}]=0\Rightarrow E[W_t|\mathcal{F_s}]=W_s.$$

Logo temos que $ W_t $ é um martingale e o resultado segue.

Com a proposição 7.1, obtemos que o processo estocástico $ Y_t = N_t - \lambda t $ é um martingale com respeito a filtragem $ \mathbb{F} $. Além disso, temos que $ Var(Y_t)=\lambda t $. Como $ \lambda > 0 $, obtemos que

$$\mathbb{E} [N_{t+s} \mid \mathcal{F_t}]= N_s + \lambda (t-s) \geq N_s, \quad s,t \geq 0.$$

Como consequência, dizemos que o processo de Poisson $ N $ é um submartingale. A decomposição do submartingale $ N $ em um martingale $ Y $ mais um processo “determinístico” $ \lambda t $ é denominada decomposição de Doob-Meyer.

Definição 7.6

Observação

Quando não houver confusão denotaremos $ \mathbb{F}^0 $ apenas por $ \mathbb{F} $. Além disso, temos que a filtragem natural é a menor filtragem que torna $ Z $ um processo estocástico adaptado. De modo geral também temos que essa filtragem não necessariamente é completa.

Dado $ N $ um processo de Poisson com intensidade $ \lambda $, denotamos por $ \mathbb{F}^0 $ a filtragem interna relacionada com $ N $. Por definição, temos que

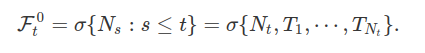
Um tempo de parada $ S $ com respeito a filtragem interna $ \mathbb{F}^0 $ é uma variável aleatória não negativa satisfazendo $ (S \leq t ) \in \mathcal{F}^0_t $ para todo $ t \geq 0. $ Para todo $ s > 0 $, temos $ S=s $ é um tempo de parada. Para todo $ n \geq 1 $, as variáveis aleatórias $ T_n $ e $ T_{N_s + 1} $ também são tempos de parada. Porém, a variável aleatória $ T_{N_s} $ não é um tempo de parada, pois para todo $ t < s $, temos que

$$(T_{N_s} \leq t )=(N_s - N_t = 0 ) \not \in \mathcal{F}^0_t.$$

Propriedades da $ \sigma $-álgebra relacionada com um tempo de parada pode ser encontrado no módulo sobre “tempos de Parada”.

Como $ T_n $ é $ \mathcal{F}^0_{T_n} $-mensurável , temos que $ T_i $ também é $ \mathcal{F}^0_{T_n} $-mensurável para todo $ i \leq n $. Com isso consluímos que $ \sigma (T_1, \cdots , T_n) \subset \mathcal{F}^0_{T_n} $. Por outro lado, como $ N(u \wedge T_n) $ é mesurável com respeito a $ \sigma (T_1, \cdots , T_n) $ para todo $ u \geq 0 $, concluímos que

$$ \sigma (T_1, \cdots , T_n) = \mathcal{F}^0_{T_n}=\sigma ( N(u \wedge T_n) : u \geq 0 ). $$

$$\mathcal{F}^0_{T_n} = \sigma (T_1, \cdots , T_n) = \mathcal{F}_{T_{n}^{-}}^0.$$

Para todo $ A \in \mathcal{F}^0_t $, obtemos do teorema de representação de Doob-Dynkin que existe uma variável $ g $ mensurável com respeito a $ \sigma $-álgebra $ \sigma(N_{t}, T_1 , \cdots , T_{N_t}) $ satisfazendo

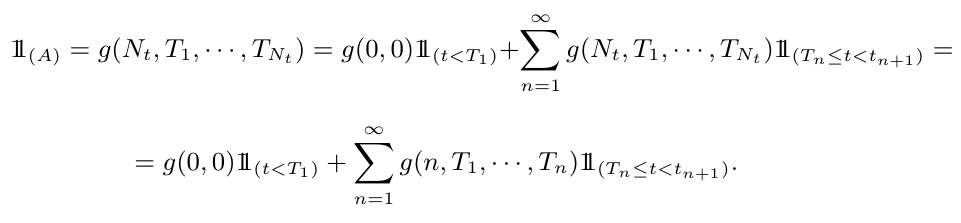
Como consequência, concluímos que

$$A = (H_0 \cap ( t < T_{1} ) ) \cup_{n=1}^\infty ( H_{n} \cap ( T_n \leq t < t_{n+1} )),$$

nos quais $ H_0 \in \mathcal{F}^0_0 $ e $ H_n \in \mathcal{F}^0_{T_n} $. Neste caso, dizemos que a filtragem interna $ \mathbb{F}^0 $ do processo de Poisson $ N $ é do tipo discreta, isto é,

$$ \mathcal{F}^0_{t} = (\cup_{n=0}^\infty ( H_{n} \cap ( T_n \leq t < t_{n+1} )) : H_0 \in \mathcal{F}^0_0, ~ ~ H_n \in \mathcal{F}^0_{T_n}) $$

para todo $ t > 0 $.

Teorema 7.3

Seja $ N=(N_t : t \geq 0) $ um processo de Poisson com intensidade $ \lambda $ e $ S $ um tempo de parada com respeito a filtragem interna de $ N $. Sobre o evento $ (S < \infty ) $ definimos

$$N^S_t = N_{S+t} - N_S, t \geq 0.$$

Condicional ao evento $ (S < \infty ) $, temos que $ N^S : N^S_t : t \geq 0 ) $ também é um processo de Poisson com intensidade $ \lambda $ independente de $ \mathcal{F}_S^o $.

Demonstração: Sabemos que se $ S $ é uma constante o resultado é válido. Na sequência, suponha que $ S $ toma valores em um sequência crescente $ (s_j: j \geq 1 ) $ de número reais positivos. Desde que $ S $ é um tempo de parada, temos que

$$(S=s_j)=(S \leq s_j) - (S \leq s_{j-1}) \in \mathcal{F}^o_{s_j},$$

para todo $ j \geq 1 $.

Para todo $ A \in \mathcal{F}^o_S $, $ 0 < t_1 < t_2 < \cdots < t_\ell $ e $ n_1, \cdots , n_\ell $ pertencente aos naturais, temos que

$$\mathbb{P} \left[ A \cap \left( \bigcap_{k=1}^\ell (N^S_{t_k} = n_k ) \right) \right] = \sum_{j=1}^\infty \mathbb{P} \left[ (S_j = s_j) \cap A \cap \left( \bigcap_{k=1}^\ell (N_{s_j+t_k} - N_{s_j} = n_k ) \right)\right]$$

$$= \sum_{j=1}^\infty \mathbb{P} \left[ (S=s_j) \cap A \right] \mathbb{P} \left[ \bigcap_{k=1}^\ell (N_{s_j+t_k} - N_{s_j} = n_k ) \right] = \mathbb{P} (A) \mathbb{P} \left[ \bigcap_{k=1}^\ell (N_{s_j+t_k} - N_{s_j} = n_k ) \right],$$

no qual utilizamos o fato de que $ (S=s_j) \cap A \in \mathcal{F}^o_{s_j} $ e o fato de que o processo de Poisson $ N $ tem incrementos estacionários. Portanto, o resultado é válido se $ S $ assume valores em uma sequência crescente de valores.

De forma geral, sabemos que qualquer tempo de parada $ S $ pode ser aproximado por uma sequência decrescente de tempos de parada $ (S_ n : n \geq 1) $, na forma

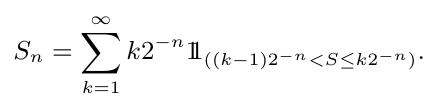
Desde que $ S_n $ assume valores em uma sequência crescente de valores, sabemos que o resultado é válido para $ S_n $. Como $ S \leq S_n $, obtemos que $ \mathcal{F}^o_{S} \subset \mathcal{F}^o_{S_n} $, para todo $ n \geq 1 $.

O fato de que $ N $ tem trajetórias contínuas à direita e de que $ A \in \mathcal{F}^o_{S} \subset \mathcal{F}^o_{S_n} $, nos leva a concluir que

$$\mathbb{P} \left[ A \cap \left( \bigcap_{k=1}^\ell (N^{S_n}_{t_k} = n_k ) \right) \right] \rightarrow \mathbb{P} \left[ A \cap \left( \bigcap_{k=1}^\ell (N^{S}_{t_k} = n_k ) \right) \right],$$

quando $ n \rightarrow \infty $. Com isso, obtemos o resultado.

Como consequência do Teorema 7.3, obtemos o seguinte corolário.

Corolário

Seja $ (S_ n : n \geq 1) $ um processo de Poisson com parâmetro $ \lambda $ e $ (T_n) $ a sequência de tempos de salto relacionado com $ N $. Tomamos os tempos de parada $ S_1=T_1 $, $ S_2=T_2 - T_1 $ e $ S_n=T_n - T_{n-1} $. As variáveis aleatórias $ S_1, S_2 , \cdots $ são independentes e identicamente distribuídas com distribuição exponencial de parâmetro $ \lambda $.

Demonstração: Sabemos que $ T_1 $ tem distribuição exponencial com parâmetro $ \lambda $. Como consequência do teorema 7.3, ao tomarmos $ S=T_n $, obtemos que $ S_n=T_n - T_{n-1} $ é o primeiro salto do processo de Poisson $ N^{T_n} $ e portanto, $ S_n $ também tem distribuição exponencial com parâmetro $ \lambda $ e é independente de $ T_1, \cdots , T_n $. Assim, concluímos que $ S_n $ é independente de $ S_1, \cdots , S_n $. Com isso, obtemos o resultado.

A seguir, apresentamos uma outra forma de definirmos o processo de Poisson que é utilizado em simulação.

Teorema 7.4

Seja $ N $ um processo de contagem. A filtragem natural de $ N $ é contínua a direita.

Demonstração

Desejamos mostrar que

$$ \bigcap_{n\geq 1} \mathcal{F}^{0}_{t+\frac{1}{n}} = \mathcal{F}^{0}_t .$$

Tome $ E = [0,\infty] $ e $ \mathcal{B} $ os borelianos de $ E $. Seja $ \Gamma $ o espaço produto dado por

$$ \Gamma = \left(\prod_{s \in [0, \infty)} E_s; \bigotimes_{s \in[0, \infty)} \mathcal{B}_s\right).$$

Definimos a relação $\pi_t: \Omega \rightarrow \Gamma$ dada por

$$ \pi_t(\omega) = s\mapsto N_{s\wedge t}(\omega).$$

Assim, temos que $ \pi_t $ é a relação que leva os elementos $ \omega $ no conjunto de funções constantes após $ t $

$$ \omega \rightarrow (N_{t\wedge s}(\omega) : \ s \in [0, \infty)). $$

Note que, por construção, $ \pi_t $ é um gerador da filtragem interna $ \mathcal{F}^0_t $, pois $ \pi_t $ tem como imagem todos os possíveis caminhos até $ N_t $, logo $ \mathcal{F}^0_t=\sigma(\pi_t) $.

Para ilustramos melhor como funciona a função $ \pi_t $ elaboramos um gráfico. Este gráfico ilustra um ponto da função $ \pi_t $. Note que, cada ponto da função $ \pi_t $ é dado como uma trajetória (uma função). O gráfico ilustra o ponto $ \pi_t(\omega) $ para $ \omega $ fixado.

(imagem em falta)

Tome agora um evento $ \Lambda $ em $ \bigcap_{n\geq 1} \mathcal{F}^{0}_{t+\frac{1}{n}} $, temos que existe um conjunto $ A \in \bigotimes_{s \in[0, \infty)} \mathcal{B}_s $ de modo que $ \Lambda = \left(\pi_{t+\frac{1}{n}} \in A\right) $.

Defina agora um conjunto $ W_n = \left(\pi_t = \pi_{t +\frac{1}{n}}\right) $, temos que como o processo $ N_t $ é não explosivo, para cada $ \omega $, existe um $ n $, de modo que a função permanece constante em $ \left[t, t+\frac{1}{n}\right] $. Logo $ \bigcup_{n\geq 1} W_n = \Omega $.

Assim

$$\Lambda= \Omega \cap \Lambda= \lim_{n\rightarrow \infty} \left( W_n \cap \Lambda\right)$$

$$= \lim_{n\rightarrow \infty} \left( W_n \cap \left(\pi_{t+\frac{1}{t}} \in A\right)\right)= \lim_{n\rightarrow \infty} \left( W_n \cap \left(\pi_{t} \in A\right)\right)$$

$$= \lim_{n\rightarrow \infty} \left( \left(\pi_{t} \in A\right)\right)$$

Concluímos que $ \Lambda \in \mathcal{F}^0_t $.

Portanto

$$\bigcap_{n\geq 1} \mathcal{F}^{0}_{t+\frac{1}{n}} \subset \mathcal{F}^{0}_t.$$

Com isso, obtemos o resultado.

Exemplo 7.1

Suponha que os defeitos que ocorrem um cano subaquático de petróleo da Petrobras acontecem de acordo com um processo de Poisson com média $ \lambda=0,1 $ por Quilômetro.

i) Qual a probabilidade de acontecer zero defeito nos primeiros 2 Quilômetros ?

ii) Dado que não houve defeito nos primeiros 2 Quilômetros. Qual a probabilidade condicional de ter um defeito entre o segundo e o terceiro Quilômetro?

i) Basta usarmos a definição do processo de Poisson $ P[(N(t+s)-N(s))=n]=e^{-\lambda t}\frac{(\lambda t)^{n}}{n!} $ assim temos que

$$P[(N(2)-N(0))=0]=e^{- 0,2}\frac{(0,2)^{0}}{0!}=e^{- 0,2}=0,8187.$$

ii) Como $ N(3)-N(2) $ é independente de $ N(2)-N(1) $, a probabilidade condicional é dada por,

$$P[N(3)-N(2)=1|N(2)-N(0)=0]=P[N(3)-N(2)=1]=e^{- 0,1}\frac{(0,1)^{1}}{1!} = e^{-0,1} = 0,09048.$$

Exemplo 7.2

Suponha que os clientes de uma determinada loja chegam de acordo com um processo de Poisson com média $ \lambda $. Seja $ N(t) $ o número de clientes que entram até o tempo t.

i) Qual é a P[N(t)=k] para $ k=0,1,\cdots $?

ii) Fixemos t, assim para $ s\in(0,t) $. Determine $ P[N(t)=n+k|N(s)=n] $ e a $ E[N(t)N(s)] $.

i)Nesta primeira questão basta usarmos a definição do processo de Poisson como temos que N(0)=0 então

$$P[(N(t+s)-N(s))=n]=e^{-\lambda t}\frac{(\lambda t)^{n}}{n!}$$

o que implica que

$$P[(N(t+0)-N(0))=k]=P[(N(t+0)-N(0))=k]=e^{-\lambda t}\frac{(\lambda t)^{k}}{k!}$$

para $ k=0,1,\cdots $

ii) Notemos que dado que

$$\displaystyle P[N(t)=n+k|N(s)=n]=\frac{P[N(t)=n+k,N(s)=n]}{P[N(s)=n]}=\frac{P[N(t)-N(s)=k,N(s)=n]}{P[N(s)=n]}=$$

$$\frac{P[N(t)-N(s)=k]P[N(s)=n]}{P[N(s)=n]}=P[N(t)-N(s)=k]=e^{-\lambda (t-s)}\frac{(\lambda (t-s))^{k}}{k!}$$

A

$$E[N(s).N(t)]=E[N(s)[N(s)+N(t)-N(s)]]=E[N^2(s)+N(s)[N(t)-N(s)]]=$$

$$E[N^2(s)]+E[N(s)[N(t)-N(s)]]=E[N^2(s)]+E[N(s)]E[N(t)-N(s)]=$$

$$\lambda s+\lambda^2 s^2+\lambda s(\lambda(t-s))=\lambda s + \lambda^2 st$$

Exemplo 7.3

Suponha que em um call center cheguem ligações de acordo com um processo de Poisson com média $ \lambda=3 $ ligações por minuto.

Qual a probabilidade de que nenhuma ligação chegue durante toda amanha das 8:00 ao 12:00.

Notemos que durante toda as 4 horas pela manha que o call center funciona para não chegar nenhuma ligação é necessário que durante todo os 240min ou seja temos queremos calcular $ P[N(240)=0]=e^{-(3)(240)}\frac{-3(240)^0}{0!}=e^{-720} $.

Exemplo 7.4

Suponha que os clientes de um supermercado cheguem a um dos caixas do mesmo de acordo com um processo de Poisson com média $ \lambda=4 $ por hora dado que o supermercado abre as 7:00 qual a probabilidade de que tenha 1 cliente por volta das 7:30 um total de 5 clientes até as 9:30 ?

Se medirmos o tempo em horas então das 7:00 as 7:30 temos meia hora e das 7:00 as 9:30 temos 2,5 horas.

$$P[N(1/2)=1;N(5/2)=5]=P[N(1/2)=1;N(5/2)-N(1/2)=4]=$$

$$P[N(1/2)=1]P[N(5/2)-N(1/2)=4]=\left[e^{-4/2}\frac{2}{1!}\right]\left[e^{-8}\frac{8^4}{4!}\right]=0,0154965.$$

Exemplo 7.5

Em certa rodovia, a intensidade média do fluxo de tráfego é de 30 carros por minuto. Um medidor é colocado na rua para registrar o número de carros

passando. Suponha válido as hipótese do processo de poison calcule:

(a) A probabilidade de que dois ou mais carros sejam registrados durante um determinado intervalo de dois segundos.

Processo de Poisson:

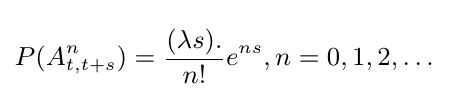
$ \lambda=30/min $. Agora,

$$\mathbb{P}\left[(A^0_{t,t+\frac{1}{30}})\cup(A^1_{t,t+\frac{1}{30}})^c\right]=1-\frac{(30\frac{1}{30})}{0!}e^{-30\frac{1}{30}}- \frac{(30\frac{1}{30})^1}{1!}e^{-30\frac{1}{30}}=1-2e^{-1}$$

(b) A probabilidade de passar mais de um minuto até registar o primeiro carro.

$$\mathbb{P}(A_{0,1}^0)=\frac{((30)1)^0}{0!}e^{-30\frac{1}{30}}=e^{-30}.$$

Exemplo 7.6

Consideremos um experimento em que será contado o número de estrelas em uma região longíqua do espaço, a região sendo de volume V. Façamos as seguintes

hipóteses, que são análogas espaciais das hipóteses do processo de Poisson:

(H1) A probabilidade de achar k estrelas na região depende somente de V.

(H2) Os números de estrelas contadas em regiões disjuntas do espaço são independentes.

(H3) Duas estrelas não ocupam o mesmo lugar.

Interpretando estas hipóteses de maneira semelhante à do processo de Poisson, obtenha o valor de $ \mathbb{P}_k(V)= $ probabilidade de achar exatamente $ k $

estrelas na região sendo considerada.

Contaremos o número de estrelas em uma determinada região V. Então, escolheremos um eixo arbitrário de coordenadas e um ponto de referência.

$$V=\frac{4}{3}\pi r^3$$

uma esfera de raio $ r $ e fazemos

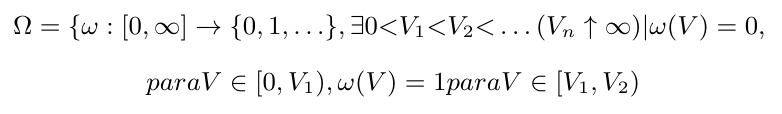
Com W=[Volume da esfera de centro $ (0,0,0) $ e raio $ r=\frac{4}{3}\pi r^3 $].

Seja o evento $ A^k_{W,V}= $[Contas exatamente k estrelas no intervalo do volume $ (W,W+V] $ ]

para $ W,V > 0 $ e $ k=0,1,2,\dots $ e assumiremos que a $ \sigma $-álgebra $ \mathcal{A} $ de conjunto de $ \Omega $ contenha todos os eventos do tipo $ A^k_{W,V} $. Com

$$ A^k_{W,V}=(\omega\in \Omega: \omega(W+V)-\omega(W)=k), \quad s,t\geq 0, k=0,1,2,\dots $$

As três hipóteses adotadas são:

(H1): Incrementos estacionário: $ \mathbb{P}(A_{W,V}^k)=\mathbb{P}(A^k_{0,V})=\mathbb{P}_k(V) $, $ \forall k=0,1,2,\dots $, $ V > 0 $.

(H3) “Chegadas” não simultâneas: $ \frac{1-\mathbb{P}_0(V)-\mathbb{P}_1(V)}{1-\mathbb{P}_0(V)}\stackrel{\rightarrow}{V\rightarrow 0} 0. $

(H2) Incrementos independentes: ($ A^k_{W,V} $ e $ A^j_{U,Z} $ são independentes para toda escolha de $ k $ e $ j $ se $ (W,W+V]\cap (U,U+Z)=\emptyset $, e temos independência também no caso de $ 3,4,5, \dots $ intervalos disjuntos)

Então, temos que

$$\mathbb{P}_k(V)=\frac{(\lambda V)^k}{k!}e^{-(\lambda V)}, k=0,1,2,\dots$$

no qual $ \lambda= $(número médio de estrelas Contadas/Volume). V=(Volume de contagem)$ \geq 0 $

Exemplo 7.7

N pontos são escolhidos, independentemente e ao acaso, de uma esfera(bola) de raio R.

(a) Calcule a probabilidade da distância entre o centro da esfera e o ponto mais proximo ser maior que r.

Seja $ A_r= $(evento distância entre centro e ponto mais próximo é maior).

$ \mathbb{P}(A_r)= $($ \mathbb{P} $( todos os pontos distanciar do centro mais que r)=$ \mathbb{P} $( do ponto distanciar mais que r).

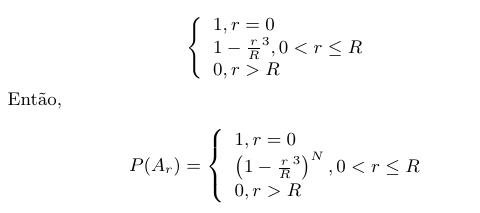
(b) Qual o limite da probabilidade obtida no item (a) quando $ r\rightarrow \infty $ e $ \frac{N}{r^3} $ e

$ \frac{N}{r^3}\rightarrow \frac{4}{3}\pi \lambda $ ? (Observação: este $ \lambda $ é o mesmo exercício anterior)

$$\lim \mathbb{P}(A_r)=\lim \left(1-\frac{r}{R}^3\right)^N=\lim \left(\left[1-\frac{r^3}{R^3}\right]^{R^3}\right)^{\frac{N}{R^3}}=\lim (e^{-r_3})^{\frac{N}{R^3}}=e^{-\frac{4}{3}\pi r^3 \lambda}$$

no qual $ V_r= $ volume da espera de centro na origem e raio $ r $.

Obs: Isto é o mesmo que $ \mathbb{P}_0(V_r) $ no exercício anterior.

Exemplo 7.8

Acende-se uma lâmpada no instante $ t=0 $. Para $ t= 0 $. Para $ t > 0 $, seja $ Q(t+\Delta t|t) $ a probabilidade condicional da lâmpada queimar

até o instante $ t+\Delta t $, dado que ficou acesa até o instante t. Suponha que

$$\forall t> 0, \quad \quad \frac{Q(t+\Delta t|t)}{\Delta t}\rightarrow \lambda t$$

quando $ \Delta t\rightarrow 0 $, onde $ \lambda > 0 $ não depende de t.(Este limite é chamada taxa de falha da lâmpada. Neste exemplo, a taxa de

falha, $ \lambda t $, é proporcional à idade)

(a) Ache a equação diferencial satisfeita pela função $ \mathbb{P}(t) $= probabilidade da lâmpada ficar acesa até o instante t. Você pode supor que a função

$ \mathbb{P} $ seja contínua, com $ \mathbb{P}(0)=1 $, e que as derivadas à direita e à esquerda sejam iguais.

$$Q(t+\Delta |t)=\mathbb{P}(T> t+\Delta t| T> t)=\frac{\mathbb{P}(T< t+\Delta t, T> t)}{\mathbb{P}(T> t)}$$

Já que as derivadas são iguais a direita e a esquerda e a função é contínua então $ \mathbb{P}(t) $ é diferenciável em todo $ t> 0 $. Assim

$$\mathbb{P}(t)=\lim_{\Delta t\rightarrow 0}\frac{\mathbb{P}(t+\Delta t)-\mathbb{P}(t)}{\Delta t}=\lim_{\Delta t\rightarrow 0}-\mathbb{P}(t)\left[1-\frac{1-\frac{\mathbb{P}(t+\Delta t)}{\mathbb{P}(t)}}{\Delta t}\right]=-\mathbb{P}(t)Q(t+\Delta t/t)=-\lambda t\mathbb{P}(t).$$

então, a equação diferencial será:

$$\mathbb{P}(t)+\lambda t \mathbb{P}(t)=0, \quad \quad \mathbb{P}(0)=1$$

(b) Resolva a equação diferencial do item (a)

$$\mathbb{P}(t)+\lambda t\mathbb{P}(t)=0 \rightarrow \frac{d\mathbb{P}}{dt}=-\lambda t \mathbb{P}(t)$$

o que implica

$$\int \frac{d\mathbb{P}}{\mathbb{P}}=\int -\lambda t dt\rightarrow \ln \mathbb{P}+C=-\frac{\lambda t^2}{2}$$

o que implica que

$$\mathbb{P}(t)=k e^{-\frac{\lambda t^2}{2}}$$

no qual $ k=e^{-c} $. Agora:

$$\mathbb{P}(0)=ke^{-\frac{\lambda 0^2}{2}}=k=1 \rightarrow \mathbb{P}(t)=e^{-\frac{\lambda t^2}{2}}, t\geq 0.$$

(c) Obtenha e resolva a equação diferencial satisfeita por $ \mathbb{P}(t) $ quando a taxa de falha é constante ($ =\lambda $).

Teremos:

$$\mathbb{P}(t)=-\mathbb{P}(t)Q(t+\Delta t|t)=-\mathbb{P}(t)\lambda$$

o implica que

$$\int \frac{d\mathbb{P}}{\mathbb{P}}=\int -\lambda dt\Rightarrow \ln \mathbb{P}(t) +C=e^{-\lambda t}\Rightarrow \mathbb{P}(t)= k e^{-\lambda t}$$

Agora $ \mathbb{P}(0)=1=k e^{-0 \lambda}=k $

o que implica que

$$\mathbb{P}(t)=e^{-\lambda t}, t\geq 0$$

Exemplo 7.9

Uma lâmpada está acesa no tempo $ t=0 $. Sempre que a lâmpada queimar, é substituída por uma lâmpada nova, embora isso não seja feito imediatamente.

Suponha que para todo $ t> 0 $;

(H1) dado que a lâmpada esteja acesa no instante t, a probabilidade dela estar queimada no instante $ t+\Delta t $, dividida por $ \Delta t $, converge para

$ \lambda $ quando $ \Delta t\rightarrow 0; $ e

(H2) dado que a lâmpada esteja queimada no instante t, a probabilidade dela estar novamente acesa em $ t+\Delta t $, divida por $ \Delta t $, converge para

$ \xi $ quando $ \Delta \rightarrow 0 $. ($ \lambda, \xi > 0. $)

(a) Seja $ \mathbb{P}(t) $ a probabilidade da lâmpada estar acesa no instante t, $ t\geq 0 $. Ache a equação diferencial satisfeita por $ \mathbb{P}(t) $.

$$\mathbb{P}_{q/a}(t+\Delta t|t)=(\text{ probabilidade de estar queimada em } t+\Delta t \text{ dado que estava acesa em } t)$$

$$\mathbb{P}_{a/q}(t+\Delta t|t)=(\text{ probabilidade de estar acesa em } t+\Delta t \text{ dado que estava queimada em } t)$$

Pela hipótese $ (H1) $,

$$\frac{\mathbb{P}_{q/a}(t+\Delta t|t)}{\Delta t}\rightarrow \lambda$$

Por (H2)

$$\frac{\mathbb{P}_{a/q}(t+\Delta t|t)}{\Delta t}\rightarrow \xi$$

e seja $ \mathbb{P}_a(t)=(\text{ probabilidade de estar acesa em t}) $. Então

$$\mathbb{P}_a(t+\Delta t)=\mathbb{P}(\text{ acesa em } t+\Delta t, \text{ acesa em } t \cup \text{queimada em } t)= $$

$$\mathbb{P}(\text{ acesa em } t+\Delta t, \text{ acesa em } t) \mathbb{P}(\text{ acesa em } t+\Delta t, \text{queimada em } t)=$$

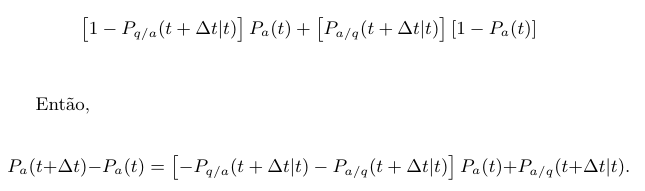
Agora sendo $ \mathbb{P}_a $ contínua e com derivados iguais a direita e esquerda e portanto diferenciável em todo t.

$$\mathbb{P}^\prime_a(t)=\lim_{\Delta t\rightarrow 0} \frac{\mathbb{P}_a(t+\Delta t)-\mathbb{P}_a(t)}{\Delta t}= \lim_{\Delta t\rightarrow 0}\mathbb{P}_a(t)\left[-\mathbb{P}_{q/a}(t+\Delta t| t){\Delta t}-\frac{\mathbb{P}_{a/q}(t+\Delta t| t)}{\Delta t}\right]+\frac{\mathbb{P}_{a/q}(t+\Delta t|t)}{\Delta t}= -\mathbb{P}_a(t)[\lambda +\xi]+\xi.$$

Então, a equação diferencial será

$$\mathbb{P}^\prime_a(t)+\mathbb{P}_a(t)[\lambda+\xi]-\xi=0, \mathbb{P}_a(0)=1.$$

(b) Resolva a equação diferencial do item (a). Determine $ \lim_{t\rightarrow \infty} \mathbb{P}(t) $.

Temos que

$$\mathbb{P}^\prime_a(t)+\mathbb{P}_a(t)[\lambda+\xi]=0$$

o que implica que

$$\mathbb{P}_a^h(t)=k e^{-(\lambda+\xi)t}$$

solução particular

$$\mathbb{P}_a(t)=C\Rightarrow C[\lambda +\xi]=\xi \Rightarrow C=\frac{\xi}{\lambda +\xi}$$

o que implica que

$$\mathbb{P}^p_a(t)=\frac{\xi}{\lambda+\xi}$$

e então

$$\mathbb{P}_a(t)=\mathbb{P}_a^h(t)+\mathbb{P}_a^p(t)=ke^{(\lambda+\xi)t}+\frac{\xi}{\lambda +\xi}, t\geq 0$$

Agora,

$$\lim_{t\rightarrow \infty}\mathbb{P}_a(t)=\frac{\xi}{\lambda+\xi}.$$

Este resultado tem um apelo intuitivo, pois se $ \xi\gg \lambda $ então

$$\lim_{t\rightarrow \infty}\mathbb{P}_a(t)\approx 1$$

ou seja, a lâmpada permanece acesa e se, $ \lambda \gg \xi $ então

$$\lim_{t\rightarrow \infty}\mathbb{P}_a(t)\approx 0$$

ou seja, a lâmpada permanece queimada. De fato, esta relação nos dá uma idéia da proporção do tempo que a lâmpada fica acesa.

Exemplo 7.10

Suponhamos que cada elemento de certa população ou morre ou se divide. (Exemplo: uma colônia de bactérias.) Façamos três hipóteses:

(H1) A probabilidade de que um elemento, vivo no instante t, venha a morrer até o instante $ t+\Delta t $, é assintoticamente equivalente a $ \mu\Delta<br /> t $(i.e., a razão dos dois converge para 1 quando $ \Delta t \rightarrow 0 $).

(H2) Um elemento vivo no instante t se divide até o instante $ t+\Delta t $ com probabilidade assintoticamente equivalente a $ \lambda \Delta t $, e produz

“netos” (i.e., se divide ao menos duas vezes) com probabilidade que, dividida por $ \Delta t $, converge para 0 quando $ \Delta t\rightarrow 0 $.

(H3) Não há interação entre os elementos, e eles morrem ou se dividem independentemente.

(a) Ache as equações diferenciais satisfeitas pelas probabilidades $ \mathbb{P}_n(t)= $ probabilidade da população conter exatamente $ n $ elementos no instante t $ (n=0,1,2, \dots; t\geq 0). $

(b) Mostre que se $ \lambda= \mu=1 $ e $ \mathbb{P}_1(0)=1 $, uma solução será

$$\mathbb{P}_0(t)=\frac{t}{1+t}; \mathbb{P}_n(t)=\frac{t^{n-1}}{(1+t)^{n+1}}, n=1,2, \dots.$$

(c) Supondo que a solução do item (b) seja a única, qual a probabilidade da população mais cedo ou mais tarde ficar extinta ?

7.1 - Construção do Processo de Poisson por Pontos Marcados

Para começar nossa construção, vamos primeiramente tomar uma partição enumerável qualquer de $ \mathbb{R} $. A partir dessa partição vamos construir nosso processo, em seguida mostraremos que a construção do processo não depende de uma particular escolha da partição.

Assim sendo seja, $ A=(A_i,i\in \mathbb{Z}) $, com $ A_i=[a_i,a_{i+1}) $ e $ a_i< a_{i+1} $. Denominaremos $ |A_i| $ o comprimento $ a_{i+1}-a_i $ do intervalo $ A_i $. Assim, como o conjunto $ A $ é uma partição temos que $ \displaystyle \bigcup_{i\in\mathbb{Z}}A_i=\mathbb{R} $ e $ A_i\cap A_j=\emptyset $ para $ i\neq j $.

Além disso, seja $ Y_i $ uma variável aleatória com distribuição Poisson de média $ \lambda|A_i| $, ou seja

$$\mathbb{P}(Y_i=k)=\displaystyle \frac{e^{-\lambda|A_i| }(\lambda|A_i|)^{k}}{k!}$$

Tome $ Y=(Y_i,\in\mathbb{Z}) $ variáveis independentes.

Para cada $ i\in\mathbb{Z} $ considere uma sequência de variáveis independentes $ (U_{j}^{i}| j=1,2,\cdots) $, uniformes no intervalo $ A_i $.

$$\mathbb{P}(U_j^i\in B\cap A_i)=\displaystyle \frac{|B\cap A_i|}{|A_i|}$$

Seja $ \mathcal{S} $ o conjunto aleatório

$$\mathcal{S}=\displaystyle \bigcup_{i\in\mathbb{Z}}S_i$$

Com $ S_i $ sendo variáveis aleatória crescentes definidas por

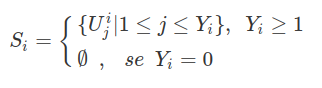
Note que $ S_i $ coloca em cada intervalo $ A_i $ exatamente $ Y_i $ pontos, sendo eles uniformentes distribuídos. Como na figura abaixo, nela temos que no intervalo $ A_i $ tem 3 pontos marcados pois $ Y_i=3 $ e $ A_{i+1} $ tem 7 pontos, pois $ Y_{i+1}=7 $, já $ A_{i+2} $ não tem nenhum ponto marcado

Agora ordenamos todos os pontos de $ \mathcal{S} $, assim seja $ (T_n)_{n\in\mathbb{Z}} $ a sequência ordenada dos pontos de $ \mathcal{S} $, definida da seguinte forma

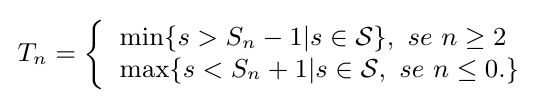
Para $ A\subset\mathbb{R} $, definimos $ N_{\mathcal{S}}(A)=(\text{ número de pontos do conjunto }\mathcal{S}\cap A) $. É claro que

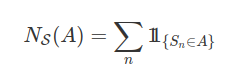
Para que nosso processo não seja explosivo necessitamos colocar uma pequena restrição, necessitamos que o processo de pontos marcados não tenha pontos de acumulação, ou seja, um intervalo no qual tenha infinitos pontos marcados.

Com isso construímos nosso processo de poisson, entretanto, necessitamos mostrar que ele de fato tem distribuição de poisson com parâmetro $ \lambda t $. O incrementos independentes e estacionários decorre da própria construção do processo.

Lema 7.3.1.1

Para cada intervalo A, a variável aleatória $ N(A) $ tem distribuição de poisson com média $ \lambda |A| $.

Demonstração

Observe que $ A\cap A_i $ são conjuntos disjuntos, e por isso as variáveis $ N(A\cap A_i) $ são independentes. Assim por construção

Por fim, basta notar que $ N(A)=\displaystyle \sum_i N(A\cap A_i) $ é uma soma de variáveis aleatórias independentes com distribuição de Poisson de médias $ \lambda |A\cap A_i| $, como os $ A_i $ são disjuntos temos que $ \displaystyle \sum_i |A\cap A_i|=|A| $. Assim, $ N(A)~\sim ~Poisson(|A|) $.

Para mais detalhes sobre esse tipo de construção o leitor pode estar consultando o livro de Ferrari e Galves.

8 - Movimento Browniano

Existem diversos fenômenos biológicos, físicos, entre outros, baseados na aleatoriedade. Um exemplo clássico, de fundamental importância, em que podemos perceber a aleatoriedade está relacionado com o movimento dos preços de ativos e índices financeiros. Apesar disso, este não é o único exemplo em que temos significantes flutuações aleatórias. Por exemplo, em biologia, temos equações diferenciais que representam interações entre predadores e presas. Tais modelos, geralmente, são escritos utilizando modelos de equações diferenciais ordinárias. Entretanto, tais populações vivem em ambientes sujeitos a eventos aleatórios que não estão previstos nestas equações. A partir do teorema central do limite, assumimos que estas influências aleatórias dos processos são acumuladas de forma a tornarem-se uma distribuição normal. Neste sentido, um dos principais processos estocásticos é o movimento Browniano.

O movimento Browniano é um processo estocástico nomeado após o botânico Robert Brown observar em 1826 o movimento aleatório do pólen em seu microscópio. Inicialmente, ele imaginou que o pólen estivesse vivo e, por isso, estaria se movimentando. Mais tarde, foi verificado que, na verdade, o movimento se dava devido a pequenos, porém incessantes impactos aleatórios do pólen com moléculas de ar. Dente algumas aplicações para o movimento Browniano, destacamos o estudo de partículas microscópicas, a variação dos preços de ativos no mercado, o ruído térmico em circuitos elétricos e, até mesmo, variações e mutações genéticas. A definição formal é dada abaixo.

Definição 8.1 (Movimento Browniano Unidimensional padrão)

Um movimento Browniano contínuo é um processo adaptado $ B=(B_t,\mathcal{F_t}:0\leq t< \infty) $, definido sobre $ (\Omega,\mathcal{A},P) $, com as seguintes propriedades:

1. $ B_0=0 $ quase certamente, isto é, $ \mathbb{P}(B_0 = 0) = 1 $;
2. Para qualquer $ 0\leq s \ < \ t $, o incremento $ B_t-B_s $ tem distribuição normal com média zero e variância t-s, isto é, $ B_t - B_s\sim N(0,t-s) $ ou

$$\mathbb{P}(a\leq B_t-B_s\leq b) = \frac{1}{\sqrt{2\pi(t-s)}}\int_a^b\exp\left(-\frac{x^2}{2(t-s)}\right).$$

3. $ B_t $ tem incrementos independentes, isto é, para quaisquer $ 0 \ < \ t_1 \ < \ t_2 \ < \ \ldots \ < \ t_n $, as variáveis aleatórias

$$B_{t_1}, B_{t_2}-B_{t_1},\ldots,B_{t_n}-B_{t_{n-1}}$$

são independentes.

4. As trajetórias de $ B_t $ são função contínuas quase certamente, isto é,

$$\mathbb{P}(B_{\cdot}(\omega) \ \text{ser contínua}) = 1.$$

O movimento Browniano também é denominado de Processo de Wiener, já que foi Wiener quem formalizou suas propriedades no século XX. Diretamente da definição do movimento browniano, concluímos que $ \mathbb{E}(B_t)=0 $, $ ~Var(B_t)=t $ e $ Cov[B_t,B_s]=min(t,s) $.

Propriedades elementares do movimento Browniano

A partir das propriedades acima, podemos simular, de maneira bastante eficiente, trajetórias do movimento Browniano. A fim de simular estas trajetórias no intervalo $ [0,T] $, consideramos os instantes $ 0 = t_0 \ < \ t_1 \ < \ t_2 \ < \ \ldots \ < t_n = T $ de forma que $ \Delta t_j = t_j -t_{j-1} = h $. Então, podemos determinar o valor de $ B_{t_j} $ a partir do valor de $ B_{t_{j-1}} $ utilizando a propriedade de incrementos independentes da forma

$$B_{t_j} = B_{t_{j-1}} + (B_{t_j} - B_{t_{j-1}}) = B_{t_{j-1}} + \sqrt{h}Z_j \ \text{com} \ Z_j\sim N(0,1) \ \text{e com} \ B_0 = 0.$$

Portanto, conhecido o valor do movimento Browniano no instante $ t_{j-1} $, para encontrar o valor $ B_{t_j} $, basta simular um valor de uma distribuição normal padrão e utilizar a fórmula acima. Desta forma, o algoritmo para simulação de uma trajetória do movimento Browniano no instante $ [0,T] $ pode ser construído a partir dos passos abaixo.

1. Definir o instante final $ T $ de simulação.
2. Definir o número $ n $ de subintervalos do intervalo $ [0,T] $.
3. O tamanho dos subintervalos é calculado da forma $ h = T/n $.
4. No instante inicial, o movimento Browniano assume o valor zero, isto é, $ B_0 = 0 $
5. Para cada $ j= 1,\ldots,n $, simulamos uma variável $ Z_j $ com distribuição normal padrão, isto é, $ Z_j\sim N(0,1) $. Então, o valor do movimento Browniano no instante $ t_j $ é dado por $ B_{t_j} = B_{t_{j-1}} + \sqrt{h}Z_j $.

Na figura a seguir, temos a simulação de 5 trajetórias do movimento Browniano no intervalo $ [0,1] $. Utilizamos $ 500 $ instantes para a partição do intervalo e, além disso, os subintervalos são igualmente espaçados com tamanho $ h = \frac{1}{500} $.

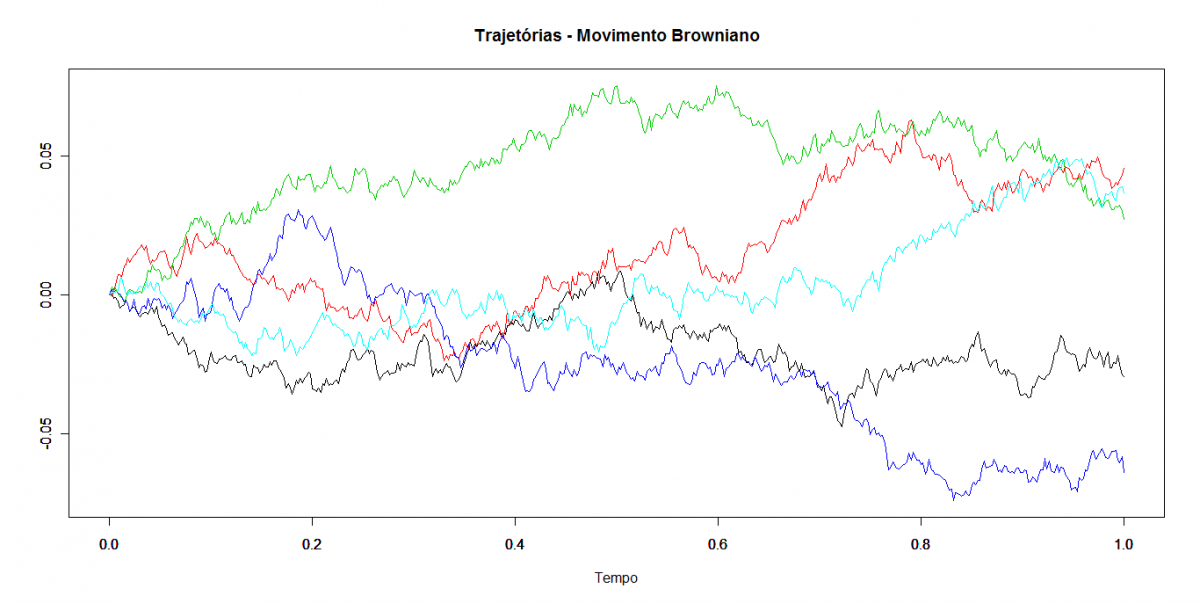
Na sequência, vamos utilizar o teorema central do limite (TCL) para apresentar uma ideia intuitiva do comportamento do movimento browniano. O TCL nos diz, que sob condições gerais, a soma de variáveis aleatórias independentes de impacto individual “pequeno” tem distribuição “aproximadamente” normal. Ao considerarmos tais somas como processos, podemos obter aproximações para o movimento browniano.

Como consequência do TCL, ao tomarmos ma sequência de variáveis aleatórias independentes e identicamente distribuídas (iid) $ \xi_1, \xi_2, \cdots $ com $ \mathbb{E}(\xi_n)=0 $ and $ Var(\xi_n)=1 $, obtemos que

$$\frac{X_n}{\sqrt{n}} \rightarrow \xi=N(0,1), \quad \text{quando} ~ n \rightarrow \infty,$$

no qual $ X_n=\xi_1, \cdots , \xi_n $ para todo $ n \geq 1 $.

Para estendermos a sequência de variáveis aleatórias $ (X_n) $ para um processos estocástico $ (X_t : t \geq 0) $ tomamos

$$X_t=X_{[t]}=X_k, \quad t \in [k,k+1), ~k\in \mathbb{N} \cup (0),$$

no qual $ [t] $ denota a parte inteira do número $ t $. Como consequência do TCL,

$$X^n_t=\frac{X_{nt}}{\sqrt{n}} \rightarrow B_t \sim N(0,t).$$

Na realidade, temos que

$$\frac{X_{nt}}{\sqrt{n}}=\frac{X_{[nt]}}{\sqrt{[nt]}}\sqrt{\frac{[nt]}{n}}\rightarrow \xi \sqrt{n} \sim N(0,t), \quad \text{quando} ~n \rightarrow \infty,$$

no qual utilizamos o fato de que $ [nt]/n \rightarrow t $ quando $ n \rightarrow \infty $ para todo $ t \geq 0 $. Portanto, para todo $ t\geq 0 $ fixo, a sequência de variáveis aleatórias $ (X^n_t) $converge em distribuição para a variável aleatória $ B_t \sim N(0,t) $. Entretanto, isto não significa que a sequência de processos estocásticos $ (X_n) $ converge, em algum sentido, para o movimento browniano. A construção do movimento browniano está na próxima seção. A seguir, apresentamos algumas propriedades elementares do movimento browniano.

Proposição 8.1

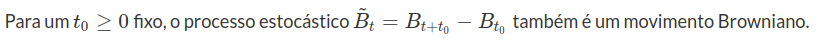
Demonstração: É imediato que $ \tilde{B}_0 = 0 $ quase certamente e que $ \tilde{B}_t $ tem trajetórias contínuas quase certamente, de forma que as condições (1) e (4) são satisfeitas. Agora, para qualquer $ s \ < \ t $, temos que

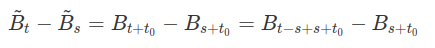
Outra importante propriedade é que o movimento Browniano não é diferenciável em qualquer ponto quase certamente. De fato, se $ t \ > \ t_0 $, o incremento $ B_{t} - B_{t_0} $ é uma variável aleatória normal com média $ 0 $ e variância $ t-t_0 $. Portanto, temos que $ (B_{t}-B_{t_0})/(t-t_0) $ é uma variável aleatória normal com média $ 0 $ e variância $ t-t_0 $. Desta forma, quando $ t\rightarrow t_0 $, a variância desta variável aleatória vai para infinito.

Proposição 8.2

Para todo $ t_0 $, temos que

$$\limsup_{t\rightarrow t_0}\left|\frac{B_t-B_{t_0}}{t-t_0}\right|=\infty \ \text{q.c}$$

o que implica que, para qualquer $ t_0 $, quase toda trajetória $ B_t $ não é diferenciável neste ponto.

Demonstração: Sem perda de generalidade, suponha que $ t_0 = 0 $ e considere o evento

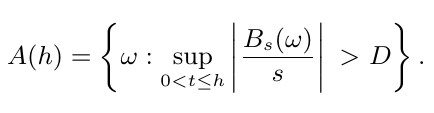
Então, para qualquer sequência $ (h_n) $ decrescente e convergindo para $ 0 $, temos que

$$A(h_n)\supset A(h_{n+1}),$$

e

$$A(h_n) \supset \left(\left|\frac{B_{h_n}}{h_n}\right| \ > \ D \right).$$

Portanto,

$$\mathbb{P}(A(h_n)) \geq \mathbb{P}\left(|B_{h_n}/\sqrt{h_n}| \ > \ D\sqrt{h_n}\right) = \mathbb{P}(|B_1| \ > \ D\sqrt{h_n}) \rightarrow 1, \ n\rightarrow \infty.$$

Então,

$$\mathbb{P}\left(\bigcap_{n=1}^{\infty}A(h_n)\right) = \lim_{n\rightarrow\infty} \mathbb{P}(A(h_n)) = 1.$$

De onde segue que

$$\sup_{0 < s \leq h_n}\left|\frac{B_s}{s}\right| \geq D \ \text{q.c para todo} \ n \ \text{e} \ D \ > 0.$$

Portanto,

$$\lim_{h\rightarrow 0}\sup_{0 < s \leq h}\left|\frac{B_s}{s}\right| = \infty \ \text{q.c}.$$

Segue a proposição.

A proposição acima nos diz que, apesar do movimento browniano ter trajetórias contínuas, estas não apresentam derivada em qualquer ponto $ 0 \leq t < \infty $.

Proposição 8.3

Demonstração

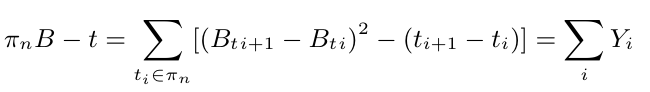
Onde $ Y_i $ são variáveis aleatórias independentes com média zero. Portanto

$$ \mathbb{E} [(\pi_n B - t)^2 ] = \mathbb{E} [(\sum_i Y_i )^2 ] = \sum_i \mathbb{E} (Y_i )^2 $$

tem distribuição qui-quadrado.

$$\mathbb{E} [(\pi_n B - t)^2]=\mathbb{E} [\sum (t_{i+1} - t_i )^2 (Z^2 -1)^2 ] = $$

$$ = \sum (t_{i+1} - t_i )^2 \mathbb{E}[(Z^2 - 1)^2 ] \leq \mathbb{E}[(Z^2 - 1)^2 ] \hbox{mesh} (\pi_n )t \to 0 $$

Na próxima seção, discutimos a questão de existência do movimento browniano.

8.1 - Construção do Movimento Browniano: Probabilidade Produto.

$$C=(\omega \in \mathbb{R}^{[0,\infty)}|(\omega(t_1),\cdots,\omega(t_n))\in A),$$

no qual $ t_i\in[0,\infty), i=1,\cdots,n $ e $ A $ pertence aos borelianos de $ \mathbb{R}^n $. Denotamos por $ \mathcal{C} $ a classe de todos os cilindros. E por fim definimos $ \mathfrak{B}(\mathbb{R}^{[0,\infty)}) $ a menor $ \sigma $-álgebra que contém $ \mathcal{C} $. Para maiores detalhes sobre a classe dos cilindros e da $ \sigma $-algebra gerada pelos cilindros, ver seção produto de espaços mensuráveis.

Definição 8.1.1

Seja $ D $ o conjunto de todas as sequências finitas $ t=(t_1,\cdots,t_n) $ de números não negativos. Suponha que para cada $ t\in D $ temos uma probabilidade $ Q_t $ em $ (R^n,\mathfrak{B}(\mathbb{R}^n)) $. A coleção $ (Q_t)_{(t\in D)} $ é denominada familia de distribuições finito dimensionais.

Definição 8.1.2

A família $ (Q_t)_{t\in D} $ é consistente se esta satifaz as condições de compatibilidade de Kolmogorov:

(a)Se $ s=(t_{i_1},\cdots, t_{i_n}) $ é uma permutação de $ t=(t_1,\cdots,t_n) $, então para qualquer $ A_i\in \mathfrak{B}(\mathbb{R}) $, temos que:

$$Q_t(A_1\times \cdots \times A_n)=Q_s(A_{i_1}\times \cdots \times A_{i_n}),$$

(b)Se $ t=(t_1,\cdots,t_n) $ com $ n\geq 1 $, $ s=(t_1,\cdots, t_{n-1}) $, e $ A\in \mathfrak{B}(\mathbb{R}^{n-1}) $, então

$$Q_t(A\times \mathbb{R})=Q_s(A).$$

Observação

Se temos uma probabilidade $ \mathbb{P} $ sobre $ (\mathbb{R}^{[0,\infty)},\mathfrak{B}(\mathbb{R}^{[0,\infty)})) $, podemos definir a família de distribuições finito dimensionais, na forma

$$Q_t(A)=\mathbb{P}[\omega \in \mathbb{R}^{[0,\infty)}|(\omega(t_1),\cdots,\omega(t_n))\in A],$$

com $ A\in \mathfrak{B}(\mathbb{R}^{n}) $.

A seguir, temos por interesse construir uma probabilidade sobre $ \mathfrak{B}(\mathbb{R}^{[0,\infty)}) $ a partir de uma família de distribuições finito dimensionais. Para isto, enunciamos o seguinte teorema.

Teorema 8.1.1

Demonstração: Desde que toda probabilidade definida sobre $ (\mathbb{R}, \mathfrak{B}(\mathbb{R})) $ é compacta, basta aplicarmos os resultados da seção probailidade sobre o espaço produto.

Assim para construirmos uma probabilidade $ \mathbb{P} $ sobre $ (\mathbb{R}^{[0,\infty)},\mathfrak{B}(\mathbb{R}^{[0,\infty)})) $ tal que o movimento browniano corresponda às projeções coordenadas, precisamos construir uma família de distribuições finito dimensionais satisfazendo as condições de compatibilidade de Kolmogorov. Por definição, a função de distribuição acumulada de $ (B_{s_1},\cdots, B_{s_n}) $, com $ 0=s_0< s_1< \cdots < s_n $ é dada por:

$$F_{s_1,\cdots , s_n}(x_1,\cdots, x_n)=\displaystyle \int_{-\infty}^{x_1}\int_{-\infty}^{x_2}\cdots\int_{-\infty}^{x_n}f(s_1,0,y_1)f(s_2-s_1,y_1,y_2) \cdots f(s_n-s_{n-1},y_{n-1},y_{n})dy_n \cdots dy_1,$$

no qual $ f(t,x,y) $ é definido como sendo

$$f(t,x,y)=\frac{1}{\sqrt{2\pi t}}e^{-(x-y)^2/2t}, t> 0, x,y\in \mathbb{R}.$$

Corolário 8.1.1

Existe uma única probabilidade $ \mathbb{P} $ em $ (\mathbb{R}^{[0,\infty)},\mathfrak{B}(\mathbb{R}^{[0,\infty)})) $, sobre a qual o processo projeção coordenada

$$W_t(\omega)=\omega(t),\omega\in\mathbb{R}^{[0,\infty)}, t> 0 $$

tem incrementos independentes e estacionários. Por construção, qualquer incremento $ W_t - W_s $ no qual $ 0 \leq s \leq t $, tem distribuição normal com média zero e variância $ t-s $.

Note que nossa construção já estaria completa se não fosse pelo fato de que construímos um processo sobre $ \mathbb{R}^{[0,\infty)} $. Porém, gostaríamos que nosso espaço amostral fosse apenas as funções contínuas, o qual é denotado por $ C[0,\infty) $, com

$$C[0,\infty)=(f\in \mathbb{R}^{[0,\infty)}| f\quad \text{contínua}).$$

Talvez o leitor pense que esse problema seja fácil de se tratar, bastaria mostrar que a probabilidade $ \mathbb{P} $ do corolário anterior é uma probabilidade em $ C[0,\infty) $. Para isto, teríamos apenas que restringir $ \mathbb{P} $ sobre $ C[0,\infty) $. Porém, o problema é que o conjunto $ C[0,\infty)\notin \mathfrak{B}(\mathbb{R}^{[0,\infty)}) $, ou seja, $ \mathbb{P}(C[0,\infty)) $ não está bem definido e portanto não podemos fazer isso. Note que isso ocorre pis $ \mathfrak{B}(\mathbb{R}^{[0,\infty)}) $ é uma $ \sigma $-álgebra pequena demais, contendo apenas funções que podem ser escritas com no máximo um número enumerável de coordenadas. Obviamente que não podemos descrever uma função continua com um número enumerável de coordenadas. Assim, vamos construir uma modificação do movimento browniano para que este tenha trajetórias contínuas quase certamente. Dados dois processos estocásticos $ X $ e $ Y $ definidos no mesmo espaço de probabilidade $ (\Omega , \mathcal{F} , \mathbb{P}) $ dizemos que $ Y $ é uma modificação de $ X $ se $ \mathbb{P} [ X_t = Y_t ]=1 $ para todo $ t \in [0, \infty) $. Entretanto, antes de falarmos dessas modificações daremos uma breve introdução sobre espaços de Hölder e algumas de suas propriedades.

Espaço de Hölder

Seja $ \Omega $ um aberto de $ \mathbb{R}^d $, denotamos $ BC(\Omega) $ e $ BC(\overline{\Omega}) $ o conjunto das funções contínuas e limitadas em $ \Omega $ e $ \overline{\Omega} $ respectivamente, com $ \overline{\Omega} $ sendo o fecho de $ \Omega $. Identificaremos $ f\in BC(\overline{\Omega}) $ com $ f|_{\Omega}\in BC(\Omega) $, para $ u\in BC(\Omega) $ e $ 0< \beta \leq 1 $ seja

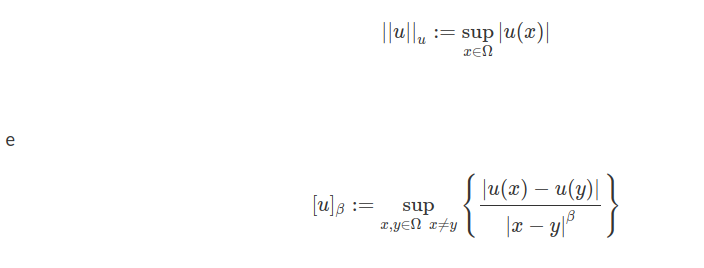
se $ [u]_{\beta}< \infty $ então u é dita Hölder-contínua com expoente de Hölder $ \beta $. A coleção de todas as funções contínuas $ \beta $-Hölder em $ \Omega $ é denotada por

$$ C^{0,\beta}(\Omega):=(u\in BC(\Omega): [u]_{\beta}< \infty ) $$

para $ u\in C^{0,\beta}(\Omega) $ seja

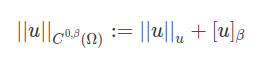
Definição 8.1.3

O espaço de Hölder $ C^{k,\beta}(\overline{\Omega}) $ consiste de todas as funções $ u\in C^k(\Omega) $ para os quais a norma

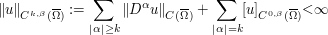
O espaço $ C^{k,\beta}(\overline{\Omega}) $ consiste das funções u, as quais tem a k-ésima derivada contínua, limitadas e com expoente de Hölder $ \beta $

Teorema 8.1.2

O espaço $ C^{k,\beta}(\overline{\Omega}) $ é Banach

Demonstração

Basta mostrarmos a completude do espaço, assim seja $ u_n\in C^{k,\beta}(\overline{\Omega}) $ uma sequência de Cauchy. Note que como o domínio é compacto e ainda $ u_n $ é limita e contínua. Então existe uma subsequência $ u_{n_k} $ a qual converge uniformemente para u, com u uma função limita de contínua em $ \overline{\Omega} $, pois limite uniforme de funções contínuas é contínua(lembre-se que se o limite não for uniforme isso não necessariamente é contínua). Assim utilizando o mesmo argumentos para as derivadas $ D^k u_n $ o resultado segue.

Lema 8.1.2

Seja $ u\in C^k(B_r) $, $ |\alpha|=k $. Então existe $ y\in B_r $, tal que

$$|D^{\alpha}u(y)|\leq \displaystyle \frac{(2k)^k}{r^k }|u|_{u}$$

Para obtermos uma versão do movimento browniano com trajetórias contínuas utilizaremos o teorema de Kolmogorov-Centsov, que nos fornece uma condição para que um processo estocástico tenha uma extensão contínua a partir de intervalos diádicos. Com esse teorema em mãos basta mostrarmos que o movimento Browniano satisfaça a condição imposta pelo teorema para obtermos a modificação contínua.

Teorema 8.1.3 (Kolmogorov-Centsov (1956))

Suponha que o processo $ X=(X_t; 0\leq t \leq T) $ definido no espaço de probabilidade $ (\Omega , \mathcal{F}, \mathbb{P}) $ satisfaça a seguinte condição

$$E[|X_t-X_s|^\alpha]\leq C |t-s|^{1+\beta},~ 0 \leq s,t\leq T,$$

para constantes positivas $ \alpha, \beta $ e $ C $. Então existe uma modificação com trajetórias contínuas, denotada por $ Y=(Y_t;~0 \leq s,t\leq T ) $ de X, o qual é localmente Hölder contínua com expoente $ \gamma $, para todo $ \gamma \in (0,\beta/\alpha) $, isto é

$$\displaystyle \mathbb{P}\left[\omega| \sup_{{0< t-s < h(\omega)~ s,t \in [0,T]}}\frac{|Y_t(\omega)-Y_s(\omega)|}{|t- s|^{\gamma}}\leq \delta \right]=1$$

no qual $ h(\omega) $ é uma variável aleatória positiva e $ \delta > 0 $ é uma constante apropriada.

Demonstração: Sem perda de generalidade vamos tomar $ T=1 $, apenas para facilitar os primeiros cálculos. Como consequência da desigualdade de Chebysev, temos que para qualquer $ \epsilon > 0 $, temos que:

$$\displaystyle P[|X_t-X_s|\geq \epsilon]\leq \frac{E[|X_t-X_s|^\alpha]}{\epsilon^{\alpha}}\leq \frac{C |t-s|^{1+\beta}}{\epsilon^{\alpha}}.$$

Como consequência, temos que $ X_s\rightarrow X_t $ em probabilidade quando $ s\rightarrow t $. Ao tomarmos $ t=k/2^n $, $ s=(k-1)/2^n $, e $ \epsilon = 2^{-\gamma n} $, no qual $ \gamma \in (0, \beta/\alpha) $, obtemos que

$$\displaystyle \mathbb{P}[|X_{k/2^n}-X_{(k-1)/2^n}|\geq 2^{-\gamma n}]\leq C2^{-n(1+\beta -\alpha\gamma)}.$$

Consequentemente temos que:

$$\displaystyle \mathbb{P}\left[\max_{1\leq k\leq 2^n}|X_{k/2^n}-X_{(k-1)/2^n}|\geq 2^{-\gamma n}\right]=\displaystyle \mathbb{P}\left[\bigcup_{k=1}^{2^n}|X_{k/2^n}-X_{(k-1)/2^n}|\geq 2^{-\gamma n}\right] \leq C2^{-n(1+\beta -\alpha\gamma)}.$$

Com isso, obtemos que

$$\displaystyle \sum_{n=1}^{\infty}\mathbb{P}\left[\max_{1\leq k\leq 2^n}|X_{k/2^n}-X_{(k-1)/2^n}|\geq 2^{-\gamma n}\right]\leq \sum_{n=1}^{\infty}C2^{-n(1+\beta -\alpha\gamma)}< \infty.$$

Logo, pelo lema de Borel-Cantelli, existe um conjunto $ \Omega^{\star}\in \mathcal{F} $ com $ \mathbb{P}(\Omega^{\star})=1 $, tal que para cada $ \omega\in \Omega^{\star} $,

$$\displaystyle \max_{1\leq k\leq 2^n}|X_{k/2^n}(\omega)-X_{(k-1)/2^n}(\omega)|< 2^{-\gamma n},~ n\geq n^{\star}(\omega), \quad (\star)$$

no qual $ n^{\star}(\omega) $ é uma variável aleatória assumindo valores inteiros positivos.

Agora, para cada $ n\geq 1 $, considere a partição $ D_n=((k/2^n))| k\in\mathbb{N}\cup (0)) $ formada pelos diádicos do intervalo $ [0,1] $. Seja $ D=\displaystyle \bigcup_{n=1}^{\infty}D_n $, o conjunto de todos os diádicos em $ [0,1] $. Ao fixarmos $ \omega \in \Omega^{\star}, ~n\geq n^{\star}(\omega) $, mostremos que para todo $ m> n $ temos que

$$|X_t(\omega)-X_s(\omega)|\leq 2 \displaystyle \sum_{j=n+1}^{m}2^{-\gamma j},~\forall t,s \in D_m, 0 < t-s < 2^{-n} \quad (\star \star).$$

Para $ m=n+1 $, temos como única possibilidade que $ t=(k/2^m) $ e $ s=((k-1)/2^m) $ e, assim, a desigualdade é consequência da equação $ (\star) $. Vamos mostrar que a desigualdade $ (\star \star) $ é válida através do princípio de indução.

Suponha que a equação $ (\star \star) $ seja válida para to $ n=n+1, \cdots , M-1 $. Tomamos $ s < t $ e $ s,t \in D_M $. Considere os número $ t^1 = \max ( u \in D_{M-1}: t \leq t) $ e $ s^1 = \max ( u \in D_{M-1} : u > s) $. Assim, obtemos as seguintes relações $ s \leq s^1 \leq t^1 \leq t $, $ s^1 - s \leq 2^{-M} $ e $ t-t^1 \leq 2^{-M} $. A partir da equação $ (\star) $, obemos que

$$\mid X_{s^1}(\omega) - X_s(\omega) \mid \leq 2^{-\gamma M} \quad \text{e} \quad \mid X_{t}(\omega) - X_{t^1}(\omega) \mid \leq 2^{-\gamma M}.$$

A partir da equação $ (\star \star) $ com $ m=M-1 $, concluímos que

$$ \mid X_t (\omega) - X_s (\omega) \mid \leq 2 ~\sum_{j=n+1}^{M-1} 2^{- \gamma j}.$$

Como consequência, obtemos $ (\star \star) $ é válido.

Mostremos agora que $ X=(X_t; t\in D) $ é uniformemente contínua em t para $ \omega \in \Omega^{\star} $. Para cada numero $ s,t\in D $ com $ 0< t-s < h(\omega)=2^{-n^{\star}(\omega)} $, selecionamos $ n\geq n^{\star}(\omega) $, tal que $ 2^{-(n+1)}\leq t-s < 2^{-n} $. Assim da desigualdade $ \star \star) $ temos que

$$|X_t(\omega)-X_s(\omega)|\leq 2 \displaystyle \sum_{j=n+1}^{\infty}2^{\gamma j}\leq \delta|t-s|^{\gamma}, ~ 0 < t-s < h(\omega)$$

no qual $ \delta=2/(1-2^{-\gamma}) $. Assim, temos que o processo é uniformemente contínuo em $ t \in D $ para $ \omega\in \Omega^{\star} $.

$$Y_t(\omega)=\lim_{s_n\rightarrow t}X_{s_n}.$$

Para finalizar, vamos mostrar que $ Y $ é uma modificação de $ X $. Sabemos que $ \mathbb{P}[X_t = Y_t]=1 $ para todo $ t \in D $. Seja $ t \in [0,1] \cap D^c $ e $ (s_n) \subset D $ tal que $ s_n \rightarrow t $, então, temos que $ X_{s_n} \rightarrow X_t $ em probabilidade e, por definição, temos que $ X_{s_n} \rightarrow Y_t $ quase certamente. Como o limite é única, concluímos que $ \mathbb{P}[X_t = Y_t] $ para todo $ t \in [0,1] $. Portanto, obtemos o resultado.

Proposição 8.1.1

$$ \mathbb{E} |B_t - B_s |^{2n} = C_n |t - s |^{n} $$

Demonstração

vamos tomar n = 1. Como o valor esperado de $ B_t - B_s $ é zero, a variância é igual ao segundo momento, assim,

$$\mathbb{E} |B_t -B_s |^2 = |t - s|.$$

A extensão para $ n > 1 $ é consequência de propriedades da distrbuição normal. Segue a proposição.

Como a Proposição 8.1.1 é válida, o teorema de Kolmogorov-Centsov nos garante que existe uma modificação do movimento browniano que é Hölder contínua. Então, existe uma modificação $ B^T $ de $ W $ tal que $ B^T $ tem trajetórias contínuas em $ [0,T] $. Tomamos

$$ \Omega_T = ( \omega : W_t(\omega) = B_t^T(\omega), ~ ~ \text{para todo número racional} ~ t \in [0,T] ) $$

tal que $ \mathbb{P}(\Omega_T)=1 $. Denotamos por

$$\tilde{\Omega} = \bigcap_{T=1}^\infty \Omega_T.$$

Para dois inteiros positivos $ T_1 $ e $ T_2 $, temos que

$$B^{T_1}_t (\omega) = B^{T_2}_t (\omega) , \quad \text{para todo número racional} ~ t \in [0, \min{T_1,T_2} ].$$

A seguir, apresentamos algumas propriedades do Movimento Browniano como a não diferenciabilidade em probabilidade.

Teorema 8.1.5

Com probabilidade 1, as trajetórias do Movimento Browniano não são diferenciáveis.

Demonstração: Vamos considerar, o caso unidimensional e, sem perda de generalidade no intervalo $ [0, 1) $. Suponha que $ (B_t )_{t \in [0, 1) } $ seja diferenciável em algum ponto $ t_0 $ no intervalo contendo $ [0, 1) $. Então em algum intervalo contendo $ t_0 $, devemos ter

$$ |B_t - B_{t_0 }| \leq K |t - t_0 | $$

para alguma constante k. Logo para pontos $ t_1 $ e $ t_2 $ suficiente próximos de $ t_0 $, temos pela desigualdade triangular, que

$$ | B_{t_1} - B_{t_2 } | \leq |B_{t_2 } - B_{t_0 }| + |B_{t_0 } - B_{t_1 }| \leq $$

$$ K(|t_2 - t_0 | + |t_0 - t_1 | ) ~~( \star )$$

Para $ i = 0, 1 e 2 $ e $ n \in \aleph $, definamos

$$t_2 (n, i) = \frac{\lfloor nt_0 \rfloor + i + 1}{n} ~e~ t_1 (n, i) = \frac{\lfloor nt_0 \rfloor + i }{n}$$

Assim, para i = 0, 1 e 2, temos que

$$\lim_{n \to \infty} t_2 (n, i) = \lim_{n \to \infty} t_1 (n, i) = t_0 $$

Portanto para n suficientemente grande, de acordo com $ \star $, temos que para i = 0, 1 e 2

$$\left |B_{\frac{\lfloor nt_0 \rfloor + i + 1}{n}} - B_{\frac{\lfloor nt_0 \rfloor + i}{n}} \right | \leq K \left ( \left |\frac{\lfloor nt_0 \rfloor + i + 1}{n} - t_0 \right | + \left | \frac{\lfloor nt_0 \rfloor + i}{n} - t_0 \right |\right ) $$

$$ \leq K \left ( \frac{i+1}{n} + \frac{i}{n} \right ) \leq \frac{5K}{n} $$

Portanto o evento $ (B_t )_{t\in [0,1)} $ é diferenciável em algum ponto $ t_0 \in [0,1) $ está contido no evento

$$A \equiv \bigcup_{k=1}^{\infty} \bigcup_{m=1}^{\infty} \bigcap_{n=m}^{\infty} \bigcup_{j=0}^{n-1} \bigcap_{i=0}^{2} \left ( \left | B_{\frac{j+i+1}{n} } - B_{\frac{j+1}{n}} \right | < \frac{5K}{n} \right ) $$

Mostraremos que A é união enumerável de eventos de probabilidade zero, de modo que concluímos que $ \mathbb{P}(A) = 0 $.

Para cada K seja

$$A_n^K \equiv \bigcup_{j=0}^{n-1} \bigcap_{i=0}^{2} \left ( \left | B_{\frac{j+i+1}{n} } - B_{\frac{j+1}{n}} \right | < \frac{5K}{n} \right ) $$

Então, A pode ser expresso como $ A = \bigcup_{k=1}^{\infty} (\liminf A_n^K ) $. Portanto basta mostrar que para cada K, $ \mathbb{P} (\liminf A_n^k ) = 0 $

$$\mathbb{P} [\liminf A_n^k] \leq \liminf \mathbb{P} [\bigcup_{j=0}^{n-1} \bigcap_{i=0}^{2} \left (\left | B_{\frac{j+i+1}{n} } - B_{\frac{j+1}{n}} \right | < \frac{5K}{n} \right ) ] \leq $$

$$ \leq \liminf \sum_{j=0}^{n-1} \mathbb{P} [\bigcap_{i=0}^{2} \left ( \left | B_{\frac{j+i+1}{n} } - B_{\frac{j+1}{n}} \right | < \frac{5K}{n} \right ) ] $$

Teorema 8.1.6

Demonstração

tem distribuição qui-quadrado.

$$\mathbb{E} [(\pi_n B - t)^2]=\mathbb{E} [\sum (t_{i+1} - t_i )^2 (Z^2 -1)^2 ] = $$

$$ = \sum (t_{i+1} - t_i )^2 \mathbb{E}[(Z^2 - 1)^2 ] \leq \mathbb{E}[(Z^2 - 1)^2 ] \hbox{mesh} (\pi_n )t \to 0 $$

Corolário 8.1.2

O movimento browniano é um martingale

$$ \mathbb{E} [B_t | \mathcal{F_s} ] = \mathbb{E} [B_t - B_s + B_s | \mathcal{F_s} ] = \mathbb{E} [B_t - B_s ] + B_s = B_s $$

o resultado acima segue da mensurabilidade de $ B_s $ em relação a $ \mathcal{F_s} $ e da independência de $ (B_t - B_s ) $ de $ \mathcal{F_s} $.

Corolário 8.1.3

O valor esperado $ \mathbb{E} [B_t B_s ] $ é igual ao $ \min (t, s ) $

8.2 - Propriedades do Espaço $C[0,\infty)$

Construímos o movimento Browniano sobre o espaço $ \mathbb{R}^{[0,\infty)} $. O espaço canônico do movimento Browniano é o $ C[0,\infty) $ e devido as suas propriedades será mais conveniente utilizarmos esse espaço amostral. Além disso podemos introduzir a seguinte métrica no espaço $ C[0,\infty) $

$$\rho(\omega_1,\omega_2)=\displaystyle \sum_{n=1}^{\infty}\frac{1}{2^n}\max_{0\leq t\leq n}(|\omega_1(t)-\omega_2(t)|\wedge 1)$$

Proposição 8.2.1

$ \rho $ é uma métrica sobre $ C[0,\infty) $ e ainda temos que $ C[0,\infty) $ um espaço métrico separável e completo.

Demonstração

i) $ \rho(\omega_1,\omega_2)\geq 0 $.

De fato, basta notar que é definido como soma de números positivos.

ii) $ \rho(\omega_1,\omega_2)= 0 \Leftrightarrow \omega_1=\omega_2 $.

De fato, note que:

$$\rho(\omega_1,\omega_2)= 0 \Leftrightarrow \displaystyle \sum_{n=1}^{\infty}\frac{1}{2^n}\max_{0\leq t\leq n}(|\omega_1(t)-\omega_2(t)|\wedge 1)=0$$

$$\Leftrightarrow \displaystyle \frac{1}{2^n}\max_{0\leq t\leq n}(|\omega_1(t)-\omega_2(t)|\wedge 1)=0, ~\forall n\in\mathbb{N}$$

$$\Leftrightarrow \displaystyle (|\omega_1(t)-\omega_2(t)|\wedge 1)=0, ~\forall t\in[0,\infty)$$

$$\Leftrightarrow \omega_1=\omega_2$$

iii) $ \rho(\omega_1,\omega_2)=\rho(\omega_2,\omega_1) $

Basta notar que $ |\omega_1(t)-\omega_2(t)|=|\omega_2(t)-\omega_1(t)| $, o que implica no resultado

iv) $ \rho(\omega_1,\omega_3)\leq \rho(\omega_1,\omega_2)+\rho(\omega_2,\omega_1) $.

De fato, observe que

$$\rho(\omega_1,\omega_3)= \displaystyle \sum_{n=1}^{\infty}\frac{1}{2^n}\max_{0\leq t\leq n}(|\omega_1(t)-\omega_3(t)|\wedge 1)$$

$$ =\displaystyle \sum_{n=1}^{\infty}\frac{1}{2^n}\max_{0\leq t\leq n}(|\omega_1(t)-\omega_2(t)+\omega_2(t)-\omega_3(t)|\wedge 1)$$

$$ \leq \displaystyle \sum_{n=1}^{\infty}\frac{1}{2^n}\max_{0\leq t\leq n}(|\omega_1(t)-\omega_2(t)|\wedge 1)+\max_{0\leq t\leq n}(|\omega_2(t)-\omega_3(t)|\wedge 1)$$

$$=\displaystyle \sum_{n=1}^{\infty}\frac{1}{2^n}\max_{0\leq t\leq n}(|\omega_1(t)-\omega_2(t)|\wedge 1)+\displaystyle \sum_{n=1}^{\infty}\frac{1}{2^n}\max_{0\leq t\leq n}(|\omega_2(t)-\omega_3(t)|\wedge 1)$$

$$=\rho(\omega_1,\omega_2)+\rho(\omega_2,\omega_1)$$

Portanto o resultado segue.

Teorema 8.2.1

Seja $ \mathfrak{C} $ a coleção de todos os cilindros finito dimensional definido como

$$C=(\omega\in C[0,\infty)|(\omega(t_1),\cdots, \omega(t_n))\in A),~n\geq 1, A\in \mathfrak{B}(\mathbb{R}^n)$$

com $ t_i\in[0,\infty), ~\forall i=1,\cdots n $. E denotamos por $ \mathfrak{G} $ a menor $ \sigma $-álgebra que contém $ \mathfrak{C} $ e ainda é a menor $ \sigma $-álgebra que contém todos os abertos de $ C[0,\infty) $

Demonstração

Primeiramente é importante definirmos os abertos de $ C[0,\infty) $, claro que como temos a nossa métrica, para definirmos os abertos basta definirmos as bolas. Assim dizemos que a bola de centro x e raio r é definida da seguinte forma

$$B(x,r)={y\in C[0,\infty)|p(x,y)< r}$$

Definimos um conjunto aberto da seguinte forma, dizemos que $ A\subset C[0,\infty) $ é um conjunto aberto se para todo $ \omega \in A $ existe um r tal que a bola $ B(\omega,r)\subset A $. Agora mostremos que $ \mathfrak{G}=\mathfrak{B}{(\mathbb{R}^n)} $, para isso temos que mostrar que $ \mathfrak{G}\subset\mathfrak{B}{(\mathbb{R}^n)} $ e que $ \mathfrak{G}\supset\mathfrak{B}{(\mathbb{R}^n)} $.

i) Mostremos primeiramente que qualquer $ \forall \omega_0\in C[0,\infty)\Rightarrow \omega_0\in C $, para algum $ C\in\mathfrak{C} $. De fato, basta escolhermos $ A\subset Im(\omega) $, com $ A\in\mathfrak{B}(\mathbb{R}) $ e escolhermos $ t=(t_1,\cdots,t_n) $, tal que $ t_i\in \omega_0^{-1}(A) $. Note que podemos fazer isso pois $ \omega_0 $ é contínua. E por fim tomamos

$$C=(\omega\in C[0,\infty)|(\omega(t_1),\cdots, \omega(t_n))\in A^n),~n\geq 1,~ A^n=(A\times\cdots\times A)\in \mathfrak{B}(\mathbb{R}^n)$$

então $ \omega_0 \in C $.

ii) Mostremos agora que $ \forall \omega \in C[0,\infty) $ e $ r\in \mathbb{R} $ temos que $ B(\omega,r)\in \mathfrak{G} $

9 - Processo de Lévy

Os processos de Lévy são utilizados para modelar o ruído em diversos tipos de aplicações. Em finanças, diversos estudos empíricos nos mostram que os processos de Lévy descrevem de forma mais realística o mercado financeiro do que modelos baseados somente no movimento browniano. No nundo “real”, observamos que o preço de diversos ativos apresentam saltos. Além disso, a distribuição empírica de ativos financeiros apresentam assimetria e curtose alta e com isso, desviam da tradicional distribuição normal. Em função disso, os processos de Lévy são uma alternativa importante na modelagem de diversos problemas reais. Neste módulo, vamos estudar a classe dos processos de Lévy e apresentar diversas aplicações em finanças.

1. $ X $ tem incrementos independentes, isto é, $ X(t) - X(s) $ é independente de $ \mathcal{F_s} $ para qualquer $ 0 \leq s< t \leq T $.

2. $ X $ é contínuo em probabilidade, isto é, para todo $ 0 \leq t\leq T $ e $ \epsilon> 0 $, temos que

$$\lim_{s \rightarrow t} \mathbb{P} (\mid X(t) - X(s) \mid > \epsilon)=0$$

.

Como consequência da condição (1), para qualquer $ 0 \leq t_0 < t_1 < \cdots < t_n $ temos que

$$X(t_0), X(t_1) - X(t_2), \cdots , X(t_n)-X(t_{n-1})$$

são variáveis aleatórias independentes. Esta propriedade de que incrementos de intervalos disjuntos são independentes é equivalente ao fato que o processo $ X $ tem incrementos independentes com respeito a filtragem interna de $ X $. A condição (2) não implica que o processo de Lévy tenha trajetórias contínuas. Por exemplo, o processo de Poisson satisfaz a condição (2). Esta condição serve para excluir os processos estocásticos com saltos em tempos determinísticos.

3. Dizemos que o processo $ X $ tem incrementos estacionários se, para tod $ 0 \leq s < t \leq T $, a distribuição da variável aleatória $ X(t)-X(s) $ depende somente de $ t-s $.

Um processo $ X $ com incrementos independentes é denominado homogêneo se este tem incrementos estacionários. De forma geral, vamos estudar processos de Lévy não homogênos. Os exemplos elementares de processos de Lévy são o processo de Poisson e o movimento browniano.

9.1 - Processo de Lévy

Nesta seção, vamos apresentar as propriedades básicas dos processos de Lévy (incrementos independentes e contínuo em probabilidade). Inicialmente, mostraremos que todo processo de Lévy tem uma modificação com trajetórias contínuas à direta e com limite à esquerda (cadlag). Como consequência, sempre que nos referirmos a um processo de Lévy assumiremos que estamos lidando com a modificação de trajetórias cadlag. Na sequência, vamos estudar a filtragem relacionada com o processo de Lévy. Neste módulo, mostraremos que a filtragem interna do processo de Lévy, devidamente completada, é contínua à direita.

Para qualquer processo de Lévy $ X $ denotamos por $ \varphi_{s,t} $ a função característica do incremento $ X(t)-X(s) $ com $ s\leq t $:

$$\varphi_{s,t}(u)=E[\exp(iu(X(t)-X(s)))],\quad u \in \mathbb{R}.$$

Como os incrementos são independentes temos que

$$\varphi_{r,s}(u)\varphi_{s,t}(u)=\varphi_{r,t}(u),~r\leq s\leq t.$$

Além disso, como o processo $ X $ é estocasticamente contínuo (ou seja contínuo em probabilidade) temos que $ \varphi_{s,t}(u) $ é uma função contínua em $ s,t $ e u.

Lema 9.1.1

Seja $ X $ um processo de Lévy. Então para todo $ u\in\mathbb{R} $, $ s,t\in [0,T] $ e $ s< t $ temos que

$$\varphi_{s,t}(u)\neq 0.$$

Demonstração

Seja $ t_0=\inf(t\geq s:\varphi_{s,t}(u)=0) $. Desde $ \varphi_{s,s}=1 $, logo $ t_0> s $. Assim, é suficiente mostrarmos que $ t_0=\infty $. Suponha que $ t_0< \infty $, então

$$\varphi_{s,t}\varphi_{t,t_0}=0~s< t< t_0.$$

Como $ \varphi_{s,t}(u)\neq 0 $, temos que $ \varphi_{t,t_0}=0 $. Da propriedade de continuidade temos que $ \varphi_{t_0,t_0}=0 $, o que contradiz o fato de que $ \varphi_{t_0,t_0}=1 $, logo o resultado segue.

Teorema 9.1.1

Seja $ X $ um processo de Levy. Definimos

$$Z_{s,t}(u)=[\varphi_{s,t}(u)]^{-1}\exp(iu (X(t)-X(s))),~s\leq t.$$

Então $ (Z_{s,t}(u) : t\geq s) $ é um $ (\mathcal{F_t}:t\geq s) $-martingale.

Demonstração

Seja $ s\leq t_0< t $. Então

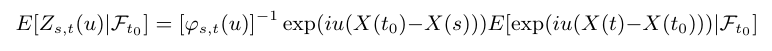
$$=\exp(iu (X(t_0)-X(s))\displaystyle \frac{\varphi_{t_0,t}(u)}{\varphi_{s,t}(u)}=Z_{s,t_0}(u).$$

Portanto o resultado segue.

A propriedade de martingale de $ Z_{s,t}(u) $ é fundamental para mostrarmos que todo processo de Lévy $ X $ tem uma modificação com trajetórias contínuas à direita e com limites à esquerda (cadlag). Na sequência, apresentamos um lema técnico.

Lema 9.1.2(Desigualdade de Ottaviani)

Suponha que $ X_1,\cdots X_n $ satisfaz a seguinte condição:

$$P(|X_k+\cdots+X_n|\geq a)\leq \alpha,~k=1\cdots n,$$

no quais $ a> 0 $ e $ \alpha\in(0,1) $ são contantes. Então para qualquer $ b> 0 $ temos que

$$\displaystyle P\left(\sup_{1\leq k\leq n}|X_1+\cdots+X_k|\geq a+b\right)\leq \frac{1}{1-\alpha}P(|X_1+\cdots+X_n|\geq b)$$

Demonstração

Tomamos

$$A_k=[|X_1+\cdots+X_k|\geq a+b]$$

$$B_k=[X_k+\cdots+X_n|\geq a],~ k=1,\cdots n ~ B_{n+1}=\emptyset$$

$$C=[|X_1+\cdots+X_n|\geq b].$$

Então,

$$\displaystyle \bigcup_{k=1}^{n} A_k\cap B^c_{k+1}\subset C$$

$$\displaystyle \sum_{k=1}^{n}P(A_1^c\cap\cdots\cap A_{k-1}^c A_k\cap B_{k+1}^c)\leq P\left(\bigcup_{k=1}^{n}A_k\cap B_{k+1}^c\right)\leq P(C).$$

Por outro lado, $ B_{k+1}^c $ é independente de $ (A_1^c\cap\cdots\cap A_{k+1}^c \cap A_k) $. Então

$$P(C)\geq \displaystyle \sum_{k=1}^{n}P(A_1^c\cap\cdots\cap A_{k-1}^c A_k\cap B_{k+1}^c)=\sum_{k=1}^nP(A_1^c\cap\cdots\cap A_{k-1}^c A_k)P(B_{k+1}^c)$$

$$\geq (1-\alpha)\displaystyle \sum_{k=1}^{n}P(A_1^c\cap\cdots\cap A_{k-1}^c A_k)=(1-\alpha)P\left(\bigcup_{k=1}^{n}A_k\right).$$

E portanto o resultado segue.

A seguir, apresentamos um lema de análise que será utilizado na demonstração do teorema 9.1.2.

Lema 9.1.3

Seja $ (x_n) $ um sequência de números reais tal que $ e^{iux_n} $ converge quando $ n \rightarrow \infty $ para quase todo $ u\in \mathbb{R} $. Então, a sequência $ (x_n) $ converge para um limite finito.

Demonstração

Vamos utilizar o critério de Cauchy para verificar a convergência da sequência $ (x_n) $. Tomamos duas sequências crescentes $ n_k $ e $ m_k $ tais que $ \lim_k n_k = \lim_k m_k= \infty $. Seja $ U $ uma variável aleatória com distribuição uniforme no intervalo $ [0,1] $. Para qualquer número real $ 0 \leq t \leq T $, por hipótese $ e^{itUx_{n_k}} $ e $ e^{itUx_{m_k}} $ convergem para a mesma variável aleatória. Portanto, temos que

$$\lim_k e^{itU(x_{n_k}-x_{m_k})}=1,\quad \mathbb{P}-\text{quase certamente}.$$

Com isso, as funções características convergem,

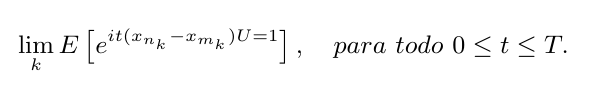
Consequentemente, temos que $ (x_{n_k}-x_{m_k})U $ converge para zero em probabilidade. Como consequência, concluímos que $ (x_{n_k}-x_{m_k}) \rightarrow 0 $.

Para simplificar a notação, denotamos $ Z_{0,t}(u) $ e $ \phi_{0,t} $ por $ Z_t(u) $ e $ \varphi_t $.

Teorema 9.1.2

Seja $ X $ um processo de Lévy definido na base estocástica $ (\Omega, \mathcal{F}, \mathbb{F}, \mathbb{P}) $ satisfazendo as hipóteses usuais. Então, existe um processo de Lévy $ Y $ também definido na base estocástica $ (\Omega, \mathcal{F}, \mathbb{F}, \mathbb{P}) $ com trajetórias contínuas à direita e com limite à esquerda (cadlag) tal que

$$\mathbb{P}\left[X(t)=Y(t)\right], \quad 0 \leq t \leq T.$$

Demonstração

Seja $ X=(X(t): 0 \leq t \leq T) $ um processo de Lévy. Inicialmente, vamos mostrar que,

$$ \mathbb{P}\left[\sup(\mid X(t) \mid: t\in [0,T]\cap \mathbb{Q} \mid)< \infty\right]=1, $$

no qual $ \mathbb{Q} $ representa o número racionais. Para cada $ 0\leq t \leq T $, definimos a função

$$g^n(t)= \mathbb{P}\left[ \mid X(T)-X(t)\mid \geq n\right] ~~\text{com}~ n\geq 1.$$

Por definição temos que $ g^n(t)\downarrow 0, $ quando $ n\rightarrow \infty. $ A seguir, vamos utilizar o teorema de Dini para mostrar que esta convergência é uniforme tem $ t $. Através da continuidade em probabilidade de $ X $, para cada $ n $ e $ t_0\in [0,T] $, temos que

$$\lim_{t\rightarrow t_0} g^n(t)=\lim_{t\rightarrow t_0} \mathbb{P}\left[\mid X(T)-X(t)\mid \geq n\right]\leq \mathbb{P}\left[\mid X(T)-X(t_0)\mid \geq n\right]=g^n(t_0).$$

Com isso, obtemos que a função $ g^n $ é semicontínua inferiormente para todo $ n \geq 1 $. Além disso, temos que $ g^n(t) \geq g^{n+1}(t) $ para todo $ 0 \leq t \leq T $ e $ n \geq 1 $. Então, pelo teorema de Dini, obtemos que

$$\lim_n \sup_{0\leq t \leq T} \mathbb{P} \left[\mid X(T)-X(t)\mid \geq n\right]=\lim_n \sup_{0\leq t \leq T} g^n(t)=0.$$

A partir da convergência uniforme, podemos escolher $ n_1 $ tal que

$$\sup_{0 \leq t \leq T} \mathbb{P}\mid \left[X(T)-X(t)\mid \geq n_1\right]< \frac{1}{2}.$$

Ao aplicarmos a desigualdade de Ottaviani com partição $ X(T)=(X(T)-X(t))+X(t) $, obtemos que

$$\mathbb{P}\left[\sup_{t\in [0,T]\cap \mathbb{Q}} \mid X(t) \mid \geq n + n_1\right] \leq 2 \mathbb{P}\left[ \mid X(T) \mid \geq n \right].$$

Com isso, concluímos que

$$ \mathbb{P}\left[\sup(\mid X(t)\mid: t\in [0,T]\cap \mathbb{Q} \mid)< \infty\right]=1. $$

Na sequência, vamos aplicar o teorema de regularidade das trajetórias ao martingale $ (Z_t(u):t \geq 0) $. Existe um subconjunto $ \Omega_0 \in \mathcal{F} $ com $ \mathbb{P}(\Omega_0)=1 $ tal que para todo $ \omega \in \Omega_0 $, temos que

(1) $ \sup_{t\in [0,T] \cap \mathbb{Q}} \mid X(T,\omega) \mid < \infty $,

(2) Para todo $ u\in \mathbb{Q} $ temos que

$$\lim_{r \in \mathbb{Q}_{+}, r \downarrow t} e^{iuX(r,\omega)}, \quad t\geq 0 \quad \text{e} \quad \lim_{r \in \mathbb{Q}_{+}, r \uparrow t} e^{iuX(r,\omega)}, \quad t> 0$$

existem e são finitos.

Como consequência de (2) e do lema 9.1.3, concluímos que

$$\lim_{r \in \mathbb{Q}_{+}, r \downarrow t} X(r,\omega), \quad t\geq 0 \quad \text{e} \quad \lim_{r \in \mathbb{Q}_{+}, r \uparrow t} X(r,\omega), \quad t> 0$$

também existem e são finitos. Assim, definimos

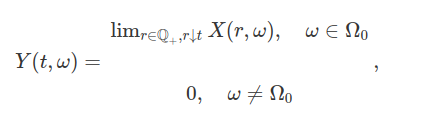
para todo $ 0 \leq t \leq T $.

Por construção $ Y $ é um processo estocástico com trajetórias contínuas à direita e com limite à esquerda (cadlag). Ao aplicarmos a propriedade de continuidade em probabilidade do processo de Lévy $ X $, obtemos que

$$\mathbb{P} \left[ X(t)=Y(t)\right]=1,\quad \text{para todo} ~ 0 \leq t \leq T.$$

Com isso, concluímos que $ Y $ é uma modificação de $ X $. Desde que a filtragem $ \mathbb{F} $ satisfaz as condições usuais, obtemos que $ Y $ é um processo $ \mathbb{F} $-adaptado. Portanto, $ Y $ também é um processo de Lévy. Assim, concluímos o teorema.

Como todo processo de Lévy admite uma modificação com trajetórias cadlag, vamos considerar somente a classe dos processos de Lévy com trajetórias cadlag.

Teorema 9.1.3

Seja $ X=(X(t):0 \leq t \leq T) $ um processo com incrementos independentes tal que $ \mathbb{E} \mid X(t) \mid < \infty $. Então $ (X(t)-m_t) $ com $ m_t=E[X(t)] $ é um martingale. Além disso, se $ d_t=Var(X(t))< \infty $ então, o processo estocástico $ (X(t)-m_t)^2-d_t $ também é um martingale.

Demonstração

Como $ X $ tem incrementos independentes, obtemos que

$$E[X(t)-X(s)|\mathcal{F_s}]=E[X(t)-X(s)]=m_t-m_s,$$

para todo $ 0 \leq s < t \leq T $. Como consequência, concluímos que

$$E[X(t)-m_t|\mathcal{F_s}]=E[X(t)-X(s)+X(s)-m_t|\mathcal{F_s}]=E[X(t)-X(s)|\mathcal{F_s}]+E[X(s)-m_t|\mathcal{F_s}]=X(s)-m_s.$$

Logo, o processo estocástico $ X-m $ é um martingale.

Na sequência, suponha que $ d_t=Var(X(t))< \infty $. Sem perda de generalidade podemos admitir que $ m_t=0 $ para todo $ 0\leq t \leq T $. Como o processo $ X $ tem incrementos independentes, obtemos que

$$ \mathbb{E} \left[\mid X(t) - X(s) \mid^2 \mid \mathcal{F_s} \right]=\mathbb{E}\mid X(t) - X(s) \mid^2, ~ ~ \mathbb{P}-q.c.$$

Desde que $ X(s) $ e $ X(t)-X(s) $ são variáveis aleatórias independentes, temos que

$$d_t=Var(X(t))=Var(X(s))+Var(X(t)-X(s))=d_s+\mathbb{E}\mid X(t)-X(s) \mid^2.$$

Por outro lado, como $ X $ é um martingale, pois admitimos que $ m_t=0 $, concluímos que

$$\mathbb{E}\left[\mid X(t)-X(s)\mid^2 \mid \mathcal{F_s}\right]= \mathbb{E}\left[\mid X(t)\mid^2 \mathcal{F_s}\right]-2X(s)\mathbb{E}\left[ X(t)\mid \mathcal{F_s}\right]+[X(s)]^2=\mathbb{E}\left[\mid X(t)\mid^2 \mid \mathcal{F_s}\right]-[X(s)]^2, ~ \mathbb{P}-q.c.$$

Utilizando as equações acima, concluímos que

$$\mathbb{E}\left[X^2(t)-d_t\right]=X^2(s)-d_s, ~ \mathbb{P}-q.c..$$

Com isso, concluímos o lema.

Considere $ X $ um processo de Lévy com $ \mathbb{E} \mid X(t) \mid < \infty $ para todo $ 0\leq t \leq T $. Como consequência do teorema 9.1.3, o processo $ X $ pode ser representado como a soma de uma média, que é determinística, mais um ruído dado por um martingale, tal que

$$X(t)=X(0)+N(t)+M(t), \quad 0\leq t \leq T,$$

no qual $ N(t)=\mathbb{E}[X(t)-X(0)] $ é uma função contínua e $ M $ é um martingale.

Se o processo de Lévy $ X $ é homogêneo, sabemos que a distribuição de probabilidade de $ X(t)-X(s) $ depende somente de $ t-s $. Assim, a função característica $ \varphi_{s,t}(u) $ do incremento $ X(t)-X(s) $ depende somente de $ t-s $:

$$\varphi_{s,t}(u)=\varphi_{t-s}(u),$$

para todo $ 0 \leq s \leq t \leq T $ e $ u \in \mathbb{R} $. Como consequência, temos que $ N(t) = \gamma t $, no qual $ \gamma $ é uma constante. Portanto, o processo de Lévy homogêneo pode ser escrito na forma

$$X(t)=X(0)+\gamma t + M(t),\quad 0 \leq t \leq T,$$

no qual $ \gamma \in \mathbb{R} $ e $ M $ é um martingale. Desde que $ \varphi_{s,t}(u)=\varphi_{t-s}(u) $, obtemos que

$$\varphi_{t+s}(u)=\varphi_{t}(u)\varphi_{s}(u),\quad s,t, \in [0,T].$$

Como $ X $ é um processo de Lévy homogêneo, a variável aleatória $ X(t) $ é infinitamente divisível, isto é,

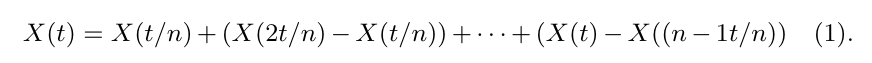
Para cada $ u \in \mathbb{R} $ e $ 0 \leq t \leq T $, denotamos

$$\Psi_t(u)=-\ln \mathbb{E}e^{iuX(t)}.$$

Como $ X(t) $ pode ser decomposto numa soma de variáveis aleatórias independentes e identicamente distribuídas (ver, (1)), temos que para quaisquer inteiros $ m $ e $ n $ que

$$m\Psi_1(u)=\Psi_m(u)=n\Psi_{m/n}(u).$$

Então,

para qualquer racional $ t $, temos que

$$t\Psi_{1}(u)=\Psi_t(u),\quad u \in \mathbb{R}.$$

$$t\Psi_{1}(u)=\Psi_t(u),\quad u \in \mathbb{R},$$

para todo $ 0 \leq t \leq T $. Como consequência, temos que

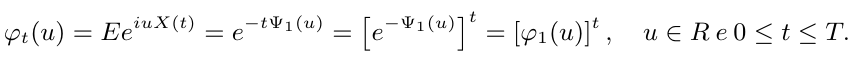
A seguir, vamos estudar proriedades da filtragem interna associada ao processo de Lévy.

Dado um processo de Lévy $ X $, a filtragem interna do processo estocástico $ X $ é definida por:

Lema 9.1.4

Para qualquer processo estocástico $ X=(X(t):0 \leq t \leq T) $ um processo estocástico, a classe

$$ \mathcal{H}=\left( \exp\left[i\left(u_0X(t_0)+\sum_{i=1}^nu_i(X(t_i)-X(t_{i-1})\right)\right]:n\geq 1, ~ (u_0,\cdots , u_n)\in \mathbb{R}^n, ~0=t_0< t_1< \cdots < t_n \right) $$

Demonstração

$$dG(x_1,\cdots ,x_n)=f(x_1,\cdots ,x_n)dF_X(x_1,\cdots ,x_n).$$

Se $ Z $ é ortogonal a classe $ \mathcal{H} $, então para todo $ (u_1,\cdots ,u_n)\in \mathbb{R}^n $, obtemos que

$$0=\mathbb{E}\left[Z\exp (-i\sum_{j=1}^n u_jX(t_{j})\right]=\int_{\mathbb{R}^n}\exp(-i\sum_{j=1}^n u_jx_j)dG(x_1,\cdots ,x_n).$$

Como consequência da formula inversa da transformada de Fourier (função característica), obtemos que $ dG=0 $. Assim, concluímos que $ Z=0 $. Portanto, temos que $ \mathcal{H} $ é total no $ L^2(\mathcal{F}^\mathbb{P}_{T}(X)) $.

$$\mathbb{E}\mid Z -Z_{\epsilon}\mid^2< \epsilon .$$

Através da primiera parte da demonstração, sabemos que $ Z $ é ortognonal a $ Z_{\epsilon} $. Assim, temos que

$$\mathbb{E}Z^2=\mathbb{E}\left[Z\bar{(Z-Z_{\epsilon})}\right]\leq \left(\mathbb{E}Z^2\mathbb{E}\mid Z-Z_{\epsilon}\mid^2\right)^{1/2}\leq(\epsilon \mathbb{E}Z^2)^2.$$

Desta forma, obtemos que $ \mathbb{E}Z^2\leq \epsilon. $ Como $ \epsilon > 0 $ é arbitrário, concluímos o lema.

Desde que o processo de Lévy é contínuo em probabilidade, isto é, ele não salta em tempos fixos, obtemos que $ \mathcal{F_t}=\mathcal{F_{t^-}} $ para todo $ 0< t \leq T $. Com a convenção de que $ \mathcal{F_0}=\mathcal{F_{0^-}} $, concluímos que $ \mathcal{F_t}=\mathcal{F}_{t^-} $ para todo $ 0 \leq t \leq T $. Na sequência, vamos mostrar que a filtragem é contínua à direita.

Teorema 9.1.4

Seja $ X $ um processo de Lévy. Então para todo $ 0\leq t \leq T $, obtemos que

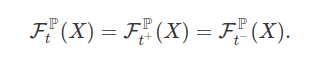
Demonstração

Para todo $ u \in \mathbb{R} $ e $ 0 \leq r \leq s $, temos que

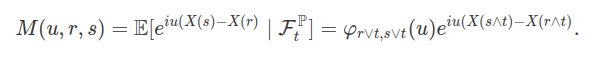
Na realidade, para $ t \geq r $, temos que

$$M(u,r,s)=\mathbb{E}[e^{iu(X(r)-X(t)}],$$

pois $ X $ tem incrementos independentes. Agora, para $ r \leq t < s $, temos que

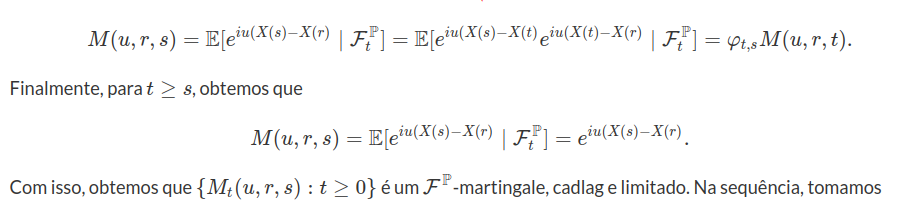
$$\eta=e^{iu_0X(0)+iu(X(t_1)-X(t_0))+ \cdots + iu_n(X(t_n)-X(t_{n-1}))},$$

para todo $ n \geq 1 $, $ (u_0,\cdots , u_n) \in \mathbb{R}^{n+1} $ e $ 0=t_0 < t_1 < \cdots < t_n $. Com isso, concluímos que

Dados $ X $ um processo de Lévy e $ T $ um tempo de parada com respeito a filtragem $ \mathbb{F}^P $, denotamo por $ X^T $ o processo de Lévy parado em $ T $, isto é, o processo $ X^T(s) = X(s \wedge T) $, para todo $ s \geq 0 $.

Lema 9.1.5

Seja $ (X_t) $ um martingale continuo a direita e $ S\leq T $ dois tempos de parada. Então $ X_S $ e $ X_T $ são integráveis e

$$E[X_T|\mathcal{F_S}]=X_S ~ q.c$$

Omitiremos a demonstração desse lema entretanto ela pode ser encontrada no livro Sheng-wu et. al. teorema 2.58.

Teorema 9.1.4

Seja $ X $ um processo de Levy homogêneo e $ S $ um tempo de parada finito. Tomamos

$$Y(t)=X(S+t)-X(S),~ 0\leq t \leq T.$$

Então

(1) $ Y $ é independente de $ \mathcal{F}_S $;

(2) $ Y $ é um processo com incrementos independentes com respeito a filtragem $ (\mathcal{F}_{S+t}:t\geq 0) $;

(3) $ Y $ tem a mesma distribuição que $ X-X(0) $.

Demonstração

Desde que $ Z_t $ é um martingale cadlag, para todo tempo de parada S temos pelo lema 9.1.2 que:

$$E[Z_{S+t}|\mathcal{F}_S]=Z_S~ q.c.$$

Então

$$E[e^{X_{S+t}-X_S}|\mathcal{F}_S]=\displaystyle \frac{\varphi_{S+t}(u)}{\varphi_S(u)=\varphi_t(u)}~q.c$$

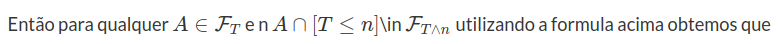1

O que implica que $ Y_t $ é independente de $ \mathcal{F}_T $. E portanto o resultado segue.

9.2 - Processo de Poisson Composto

Neste módulo, vamos estudar uma extensão do Processo de Poisson nos quais o tamanho do salto não é fixo (igual a 1), mas é representado por uma variável aleatória. O processo de Poisson composto é base para o entendermos a estrutura de salto do processo de Lévy. Considere $ (\Omega, \mathcal{F}, \mathbb{P}) $ um espaço de probabilidade completo. O processo de Poisson composto com intensidade $ \lambda > 0 $ e tamanho de saltos com distribuição $ F $ é o processo estocástico definido por $ Y(0)=0 $ e

$$Y(t) = \displaystyle\sum_{i=1}^{N(t)} J_i,$$

em que

(1) Os tamanhos dos saltos $ J_i $, $ i \in \mathbb{N} $, são v.a.s independentes e identicamente distribuidas com distribuição $ F $;

(2) $ N=(N(t):0\leq t \leq T) $ é um processo de Poisson de intensidade $ \lambda $, independente dos saltos $ (J_1, J_2, \ldots ) $.

Ao denotarmos por $ 0 = T_0 < T_1 < T_2 \ldots $ os instantes de saltos do processo de Poisson $ N $, obtemos que

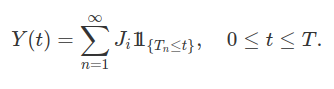
Desde que os instantes de salto são determinados por um processo de Poisson e o tamanho dos saltos são determinados por variáveis aleatórias independentes e identicamente distribuídas, obtemos que $ Y $ é um processo de Lévy homogêneo. Denotamos por $ \mathbb{F}^0 $ a filtragem interna do processo de Poisson composto e por $ \mathbb{F} $ a filtragem interna completada, ver a seção sobre base estocástica. Como $ Y $ é um processo de Lévy, sabemos que $ \mathbb{F} $ é contínua à direita. Ao longo deste módulo, sempre que nos referirmos ao processo de Poisson composto com intensidade $ \lambda $ e tamanho dos saltos com distribuição $ F $, iremos denotar por $ PPC(\lambda, F) $.

Teorema 9.2.1

Seja $ Y $ um $ PPC(\lambda, F) $. Então, temos que $ \mathbb{E}\left[Y(t)\right] = \lambda tk, $ em que $ k = \mathbb{E}\left[J_1\right] $, com $ J_1 $ é o tamanho do primeiro salto.

Demonstração

Por propriedade de esperança condicional

$$\mathbb{E}\left[Y(t)\right] = \mathbb{E}\left[ \mathbb{E}\left[Y(t)| N(t) \right]\right].$$

Sabemos que,

$$\mathbb{E}\left[\mathbb{E}\left[Y(t)\mid N(t) \right]\right]=\mathbb{E}\left[ \mathbb{E}\left[\sum_{l=1}^{N(t)} J_l\Big| N(t)\right]\right]=\sum_{n=0}^{\infty} \mathbb{E}\left[\sum_{l=1}^{N(t)} J_l \Big| N(t) =n\right] P(N(t) =n)= \sum_{n=0}^{\infty} \mathbb{E}\left[\sum_{l=1}^{n} J_l\right] P(N_t =n).$$

Além disso,

$$\mathbb{E}\left[\sum_{l=1}^{n} J_l\right]=\sum_{l=1}^{n}\mathbb{E}\left[ J_l\right]=nk.$$

Com os resultados acima, concluímos que

$$\mathbb{E}Y(t)=\sum_{n=0}^{\infty} nk P(N(t) =n)= k\sum_{n=0}^{\infty} n P(N_t =n)= k \mathbb{E}\left[N(t)\right].$$

Como $ N $ é um processo de Poisson, concluímos o teorema.

A seguir, vamos calcular a função característica associada ao processo de Poisson composto.

Teorema 9.2.2

A função característica do processo $ Y $ é dada por

$$\varphi_t(u)=\exp\left(t \int_{-\infty}^{\infty} (e^{iux} -1)\lambda F(dx)\right),$$

para todo $ u\in \mathbb{R} $ e $ 0 \leq t \leq T $.

Demonstração

Por definição, temos que

$$\varphi_t(u)=\mathbb{E}\left[e^{iuY(t)}\right]=\mathbb{E}\left[\exp{\left(iu \sum_{l=1}^{N(t)} J_l\right)}\right].$$

Via a propriedade de torre da esperança condicional, temos que

$$\mathbb{E}\exp{\left(iu \sum_{l=1}^{N(t)} J_l\right)}=\sum_{n=0}^{\infty}\mathbb{E}\left[\exp{\left(iu \sum_{l=1}^{N(t)} J_l\right)} \Big|N(t)=n\right]P(N(t)=n)=\sum_{n=0}^{\infty}\mathbb{E}\left[\exp{\left(iu \sum_{l=1}^{n} J_l\right)} \right]P(N(t)=n).$$

Como $ N $ é o processo de Poisson e $ (J_i:i \geq 1) $ são variáveis aleatórias independentes e identicamente distribuídas, concluímos que

$$\varphi_t(u) = \sum_{n=0}^{\infty} \left(\mathbb{E}\left[\exp{(iu J_1)} \right]\right)^n \frac{e^{-\lambda t}(\lambda t)^n}{n!}.$$

Desde que,

$$\mathbb{E}\left[\exp{(iu J_1)} \right] = \int_{-\infty}^{\infty} e^{iuy} F(dy),$$

obtemos que

$$\varphi_t(u)=\sum_{n=0}^{\infty} \left(\int_{-\infty}^{\infty} e^{iuy} F(dy) \right)^n \frac{e^{-\lambda t}(\lambda t)^n}{n!}=e^{-\lambda t}\sum_{n=0}^{\infty}\dfrac{\left(\lambda t \int_{-\infty}^{\infty} e^{iuy} F(dy) \right)^n}{n!}=\exp\left(-\lambda t + \lambda t \int_{-\infty}^{\infty} e^{iuy} F(dy)\right)= \exp\left(-\lambda t\left(\int_{-\infty}^{\infty} e^{iuy} F(dy) - 1\right)\right).$$

Portanto, temos que

$$\varphi_t(u)= \exp\left(-\lambda t\left(\int_{-\infty}^{\infty} e^{iuy} F(dy) - \int_{-\infty}^{\infty} 1F(dy)\right)\right)= \exp\left(t \int_{-\infty}^{\infty} (e^{iuy} -1)\lambda F(dy)\right).$$

Na sequência, vamos estudar propriedades da filtragem interna do processo de Poisson composto. Conforme definido no módulo sobre tempos de parada, dado $ R $ um tempo de parada, o conjunto de informação até $ R $ corresponde a $ \sigma $-álgebra avaliada até o tempo de parada $ R $,

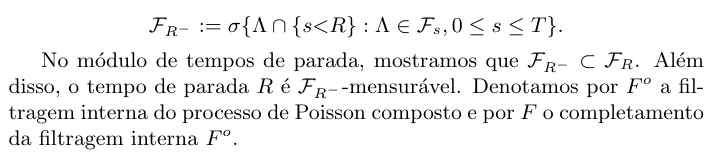
Teorema 9.2.3

Sejam $ Y $ um $ PPC(\lambda, F) $, $ T_1,T_2,\ldots $ os tempos de ocorrências dos saltos e $ J_1 $, $ J_2 $, $ \ldots $ os tamanhos dos saltos. Valem as igualdades:

(1) $ \mathcal{F}^o_{T_n}=\sigma\big((T_1, J_1); \ldots ;(T_n, J_n)\big) $;

(2) $ \mathcal{F}^o_{{T_n}^-} = \sigma\big((T_1, J_1); \ldots ;(T_{n-1}, J_{n-1}); T_n\big) $.

Demonstração

Inicialmente, mostraremos que

$$\sigma\big((T_1, J_1); \ldots ;(T_n, J_n)\big) \subset \mathcal{F}^o_{T_n}.$$

De fato, como $ T_n ~\text{é} ~\mathcal{F}^o_{T_n}{-mensurável} $, obtemos que $ T_i ~\text{é} ~ \mathcal{F}^o_{T_n}\text{-mensurável} $ para todo $ i\leq n. $

Na sequência, mostraremos que $ Y(T_n) $ é $ \mathcal{F}^o_{T_n} $-mensurável. Desde que $ \mathbb{F}^o $ é a filtragem interna do processo de Poisson composto, sabemos que $ Y $ é adaptado e progressivamente mensurável. Assim, ao tomarmos $ B $ um boreliano da reta, obtemos que

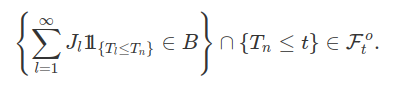
Com isso, concluímos que $ (Y(T_n) \in B) \in \mathcal{F}^o_{T_n} $. Sabemos que os saltos são dados por,

$$J_n=Y_{T_n} - Y_{T_{n-1}}.$$

Logo, obtemos que $ J_n $ é $ \mathcal{F}^o_{T_n} $-mensurável. Como consequência, temos que

$$J_i { é } \mathcal{F}^o_{T_n}{-mensurável } \forall i \leq n.$$

Para mostrarmos a recíproca, basta notarmos que $ Y(u \wedge T_n) $ é $ \sigma\left(\left(T_1, J_1\right),\ldots \left(T_n, J_n\right)\right) $-mensurável, para todo $ u \geq 0 $. De fato, como $ Y(u \wedge T_n) $ é um processo cadlag $ \mathbb{F} $-adaptado, segue a parte (1).

Na parte (2), mostraremos que $ \mathcal{F}^o_{{T_n}^-} = \sigma\big((T_1, J_1); \ldots ;(T_{n-1}, J_{n-1}); T_n\big) $. Como

$$\mathcal{F}^o_{{T_n}^{-}} = \sigma(\Lambda \cap (T_n > t)\ e \ \Lambda \in \mathcal{F}^o_t ;\ t\geq 0),$$

basta mostrarmos que a classe

$$(\Lambda \cap (T_n > t)) \subset \sigma\big((T_1, J_1); \ldots ;(T_{n-1}, J_{n-1}); T_n\big).$$

Sabemos que

Portanto, concluímos que

$$\mathcal{F}^o_{{T_n}^{-}} \subset \sigma\big((T_1, J_1); \ldots ;(T_{n-1}, J_{n-1}); T_n\big).$$

A seguir, vamos mostrar a recíproca. Como

$$\sigma\big((T_1, J_1); \ldots ;(T_{n-1}, J_{n-1})\big)= \mathcal{F}^o_{T_{n-1}} \subset \mathcal{F}^o_{T_{n^{-}}},$$

basta observarmos que que $ T_n $ é $ \mathcal{F}^o_{T_{n^{-}}} $-mensurável, ver o módulo de tempos de parada. Logo, concluímos que

$$\sigma\big((T_1, J_1); \ldots ;(T_{n-1}, J_{n-1}); T_n\big) \subset \mathcal{F}^o_{{T_n}^{-}} .$$

Segue o teorema.

Sabemos que a filtragem interna $ \mathbb{F}^o $ é dada por

$$ \mathcal{F}^o_t=\sigma(Y(s \wedge t): s \geq 0). $$

Desta forma, para todo $ n \geq 0 $, temos que

$$ \mathcal{F}^o_t \cap (T_n \leq t < T_{n+1} ) =\sigma(X(s \wedge T_n): s \geq 0) \cap (T_n \leq t < T_{n+1} ), $$

pois $ Y(s \wedge T_n(\omega), \omega)=Y(s \wedge t,\omega) $ para todo $ \omega \in (T_n \leq t < T_{n+1} ) $ para todo $ s \geq 0 $. Por construção, temos que

$$ \sigma(X(s \wedge T_n): s \geq 0) = \sigma\big((T_1, J_1); \ldots ;(T_n, J_n)\big), ~ ~ n \geq 1. $$

Como consequência do teorema 9.2.3, concluímos que

$$\mathcal{F}^o_t = \cup_{n=1}^\infty \left( \mathcal{F}^o_{T_n} \cap (T_n \leq t < T_{n+1} ) \right), ~ ~ t \geq 0,$$

no qual $ \mathcal{F_0}^o $ é a $ \sigma $-álgebra trivial. Neste caso, dizemos que a filtragem inerna do processo de Poisson composto $ Y $ é do tipo discreta.

Na sequência, vamos estudar propriedades dos saltos do processo de Poissom composto. Considere $ X $ um processo estocástico adaptado à filtragem interna $ \mathbb{F} $ do processo de Poisson composto $ Y $. Dizemos que $ X \in \textbf{B}^p $ se

$$\mathbb{E} [\sup_{0 \leq s \leq T} \mid X(t) \mid ]^p < \infty,$$

para $ p > 0 $. A seguir, vamos rever alguns conceitos introduzidos na seção sobre processo estocástico. A $ \sigma $-álgebra dos subconjuntos em $ [0, \infty) \times \Omega $ gerada pelos processos $ \mathbb{F} $-adaptados e contínuos é denominada previsível e será denotada por $ \mathcal{P} $. Da mesma forma, denotamos por $ \mathcal{O} $ a $ \sigma $-álgebra gerada pelos processo contínuos à direita e com limites à esquerda (cadlag), denominada $ \sigma $-álgebra opcional.

Definição 9.2.4

Dado um processo estocástico $ X \in \textbf{B} $. Se existe um processo $ \mathbb{F} $-previsível $ N $, tal que $ X-N $ é um $ \mathbb{F} $-martingale, dizemos que $ N $ é o compensador de $ X $.

Se$ X \in \textbf{B} $ é um processo de Lévy, sabemos que o processo $ M(t)=X(t)-\mathbb{E}(X(t)) $ é um $ \mathbb{F} $-martingale. Portanto, o compensador $ N(t) =\mathbb{E}(X(t)) $ é determinístico. Como o processo de Poisson composto pode ser escrito na forma

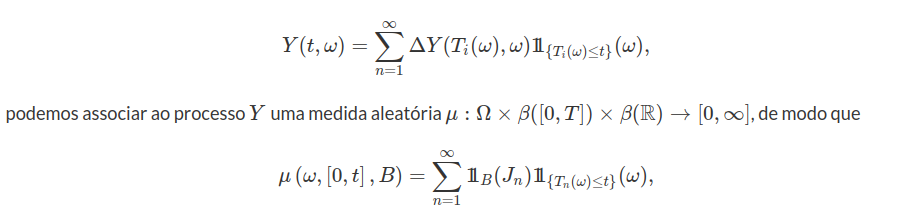
para todo $ \omega \in \Omega $, $ t \in [0,T] $ e $ B \in \beta(\mathbb{R}) $. A medida $ \mu $ caracteriza o processo $ Y $, pois

$$Y(t, \omega) = \int_0^t\int_{-\infty}^{\infty}x\mu(\omega, ds, dx), \quad t \geq 0.$$

Como os incrementos do processo de Poisson composto são independentes, obtemos que o processo estocástico $ \mu(\cdot , [0,t], B) $ também tem incrementos independentes, para todo $ B \in \beta(\mathbb{R}) $ fixo. Assim, existe uma medida $ \nu $ definida sobre $ ([0,T]\times \mathbb{R}; \beta([0,T]\times \beta(\mathbb{R}))) $, que é o compensador de $ \mu $, definida por

$$ \nu([0,t], B) = \mathbb{E}\left[\mu([0,t]\times B)\right], \quad t \geq 0 \quad {e} \quad B \in \beta(\mathbb{R}).$$

Por definição, temos que

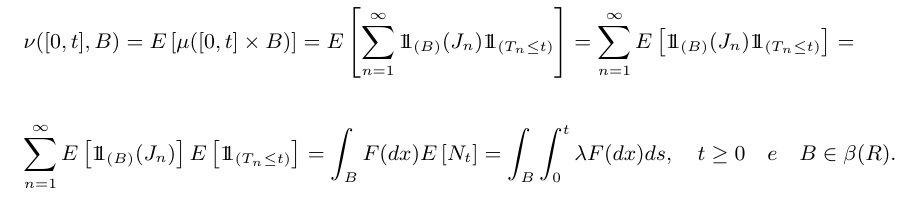
Portanto, obtemos que

$$\nu(ds, dx) = \lambda F(dx)ds \quad {e} \quad \int^{\infty}_{-\infty} x\nu([0,t], dx) = \lambda t\mathbb{E} \left[J_1\right] < \infty.$$

Nesta seção, vamos admitir que $ \mathbb{E} [J_1]^2 < \infty $. Assim, concluímos que

$$\int^{\infty}_{-\infty} |x|^2\nu([0,T], dx) = \lambda T\mathbb{E} \left[J_1\right]^2 < \infty.$$

A seguir, introduzimos o conceito de variação quadrática do processo de Poisson composto $ Y $.

Definição 9.2.5

O processo variação quadrática $ [Y,Y] $ é definido por

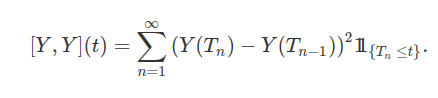
Podemos decompor o processo variação quadrática, na forma

9.3 - Processo Gamma

O processo gamma é um processo cujo os incrementos independentes tem distribuição gamma.

Definição 9.3.1

A densidade da função Gamma(a,b) com $ a > 0 $, e $ b> 0 $ é dada por

$$f_{Gamma}(x,a,b)=\frac{b^a}{\Gamma(a)}x^{a-1}exp(-xb),~x> 0$$

Assim sua função característica é dada por

$$\phi_{Gamma}(u,a,b)=(1-iu/b)^{-a}$$

Portanto o processo Gamma

$$X^{(Gamma)}=(X_t^{Gamma},t\geq 0)$$

com parâmetros a,b. Ele é definido como sendo um processo estocástico que começa em zero e é estacionário com incrementos independentes com distribuição Gamma(a,b), ou seja $ X_t^{Gamma}-X_0^{Gamma}=X_t^{Gamma} $, tem distribuição $ Gamma(at,b) $

A tripla de Lévy do processo Gamma é dado por

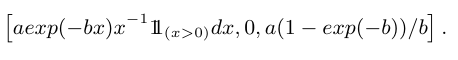
Para mais propriedades da função Gamma, entre no conteúdo de probabilidades.

9.4 - Processo Gaussiano Inverso

Definição 9.4.1

A Gaussiana Inversa é uma variável aleatória que pode ser definida como sendo o tempo que um movimento Browniano leva para atingir um determinado patamar pela primeira vez. Em outras palavras, seja $ T^{(a,b)} $ o tempo do movimento Browniano com drift $ b> 0 $, atingir o valor $ a< 0 $, ou seja, o primeiro $ s $ tal que $ (W_s+bs,~s\geq 0) $ atinja $ a $, com $ W $ sendo o movimento Browniano padrão. Esse tempo aleatório é chamado de Gamma Inversa $ IG(a,b) $, sua lei e sua função características são dadas por

$$\phi_{IG}(u,a,b)=exp(-a\sqrt{-2iu+b^2}-b)$$

Quando $ b $ tende a infinito a distribuição gaussiana inversa tende a uma normal. É importante notar que o nome inversa pode enganar já que não é uma inversa direta de uma normal(Gaussiana), o nome inversa vem do fato de que a função geradora dessa distribuição é um logaritmo, que é a função inversa da exponencial.

Assim definimos nosso processo como sendo $ X^{IG}=(X_t^{IG}, t\geq 0) $, com parâmetros $ a,b> 0 $, como sendo um processo que começa em zero e tem incrementos independentes e estacionários, tal que

$$\mathbb{E}[exp(iuX_t^{IG})]=\phi_{IG}(u,at,b)=exp(-at\sqrt{-2iu+b^2}-b)$$

A função densidade de $ IG(a,b) $ é dada por

$$f_{IG}(x,a,b)=\displaystyle \frac{a}{\sqrt{2\pi}}exp(ab)x^{-3/2}exp\left(-\frac{1}{2}(a^2x^{-1}+b^2x)\right)$$

Assim a medida de Lévy de $ IG(a,b) $ é dada por

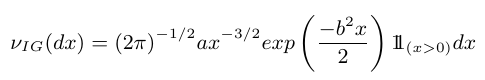
E por fim, o último componente da tripla de Lévy é dado por

$$\alpha=\displaystyle \frac{a}{b}\left(2N(b)-1\right)$$

com

$$N(x)=\displaystyle \int_{-\infty}^{x}\frac{1}{\sqrt{2\pi}}exp(-x^2/2)$$

ou seja, a acumulada da $ N(0,1) $

Assim temos a tripla de Lévy dada por

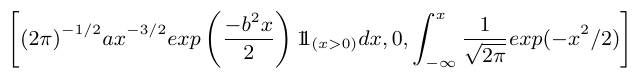
Algumas Propriedades da IG(a,b)}

Seja $ X\sim IG(a,b) $, então

$$\mathbb{E}[X^{-\alpha}]=\displaystyle \left(\frac{b}{a}\right)^{2\alpha+1}\mathbb{E}[X^{\alpha+1}],~ \alpha\in\mathbb{R}$$

Com a equação acima podemos obter a média e a variância como sendo

$$\mathbb{E}[X]=\displaystyle \frac{a}{b}$$

basta substituir $ \alpha=-1 $ e para variância

$$Var[X]=\displaystyle \frac{a}{b^3}$$

Além disso, temos a seguinte propriedade, se $ X\sim IG(a,b) $, então $ cX\sim(\sqrt{c}a,b/\sqrt{c}) $, para $ c> 0 $.

9.5 - Processo Gaussiano Inverso Generalizado

Existe uma generalização do processo Gaussiano Inverso, conhecida como Processo Gaussiano Inverso Generalizado o qual denotaremos por $ GIG(\lambda,a,b) $, sua função de densidade é dada por

$$f_{GIG}(x,\lambda,a,b)=\displaystyle \frac{(b/a)^\lambda}{2K_{\lambda}(ab)}x^{\lambda-1 }exp\left(-\frac{1}{2}(a^2x^{-1}+b^2x)\right)$$

com $ \lambda \in \mathbb{R} $ e $ a,b\geq 0 $, porém não podendo ser zero simultaneamente. A função $ K_{\lambda} $ representa a função de Bessel modificada, a qual apresentaremos mais detalhes abaixo.

A função característica é dada por

$$\phi_{GIG}(u,\lambda,a,b)=\displaystyle \frac{1}{K_{\lambda}(ab)}\left(1-\frac{2iu}{b^2}\right)^{\lambda/2}K_{\lambda}(ab\sqrt{1-2iub^{-2}})$$

Assim definimos O processo GIG como sendo um processo no qual os incrementos dos intervalos $ [s,t+s],~s,t\geq 0 $ tem função característica dada por

$$(\phi_{GIG}(u,\lambda,a,b))^t$$

onde t é o tamanho do intervalo. A medida de Lévy para esse caso é bem complicada e envolve uma densidade na reta real positiva dada abaixo

$$\displaystyle u(x)=x^{-1}exp\left(-\frac{1}{2}b^2x\right)\left(a^2\int_{0}^{\infty}exp(-xz)g(z)dz+max{0,\lambda}\right)$$

no qual

$$g(z)=\displaystyle \left(\pi^2a^2z(J_{|\lambda|}(a2\sqrt{2z})+N^2_{|\lambda|}(a\sqrt{2z}))\right)^{-1}$$

no qual, $ J_{|\lambda|} $ e $ N_{|\lambda|} $ são funções de Bessel que será definida adiante.

Propriedade

O momento da variável $ X\sim GIG(\lambda,a,b) $ é dado por

$$\mathbb{E}[X^k]=\displaystyle \left(\frac{a}{b}\right)^k \frac{K_{\lambda+k}(ab)}{K_\lambda(ab)},\quad \alpha\in\mathbb{R}$$

9.6 - Função de Bessel

10 - Cálculo Estocástico para o Movimento Browniano

O principal objetivo desta seção é estudar o cálculo estocástico com respeito ao movimento Browniano. Inicialmente, apresentamos os conceitos básicos de integral de Wiener para, depois, apresentar a integral de Itô e suas principais propriedades. Uma vez que a integral de Itô esteja apresentada, estudaremos a Fórmula de Itô e as principais propriedades relacionadas a ela. Finalmente, apresentaremos as equações diferenciais estocásticas, o teorema de Girsanov e o teorema de representação de martingales.

A ideia principal é definir de forma consistente a seguinte integral

$$\int_a^bf(t)dB_t$$

em que $ B_t $ é o movimento Browniano e $ f $ é uma função que satisfaz algumas propriedades específicas. Antes de definirmos este tipo de integral, vamos relembrar, de forma rápida os conceitos das integrais de Riemann e de Riemann-Stieltjes que serão utilizadas como inspiração no desenvolvimento da integral anterior.

Integrais de Riemann e de Riemann-Stieltjes

A fim de definir as integrais de Riemann e de Riemann-Stieltjes definida no intervalo $ [a,b] $, começamos com a seguinte definição.

Definição 10.1

Seja $ [a,b] $ um intervalo dado da reta real $ \mathbb{R} $. Uma partição $ \mathcal{P} $ de $ [a,b] $ é um conjunto finito de pontos $ x_0, x_1,\ldots,x_n $, em que

$$a = x_0\leq x_1\leq \ldots \leq x_{n-1}\leq x_n = b.$$

Escrevemos $ \Delta x_i = x_i - x_{i-1} $ para $ i = 1,\ldots, n $. Suponha agora que $ f $ seja uma função real limitada definida em $ [a,b] $. Para cada partição $ \mathcal{P} $, definimos

$$M_i = \sup_{x_{i-1}\leq x\leq x_i}f(x) \quad \text{e} \quad m_i = \inf_{x_{i-1}\leq x\leq x_i}f(x)$$

e

$$U(\mathcal{P},f) = \sum_{i=1}^nM_i\Delta x_i \quad \text{e} \quad L(\mathcal{P},f) = \sum_{i=1}^nm_i\Delta x_i$$

Finalmente, definimos as integrais de Riemann superior e inferior de $ f $ sobre o intervalo $ [a,b] $ da seguinte forma

$$\overline{\int}_a^bf(x)dx = \inf U(\mathcal{P},f) \quad \text{e} \quad \underline{\int}_a^bf(x)dx = \sup L(\mathcal{P},f)$$

em que o $ \inf $ e o $ \sup $ são tomados sobre todas as partições $ \mathcal{P} $ de $ [a,b] $.

Definição 10.2

Quando as integrais superior e inferior de $ f $ são iguais, dizemos que a função $ f $ é Riemann integrável em $ [a,b] $ e escrevemos $ f\in\mathfrak{R} $, em que $ \mathfrak{R} $ denota o conjunto das funções Riemann integráveis e o valor comum de $ \overline{\int}_a^bf(x)dx $ e $ \underline{\int}_a^bf(x)dx $ é denotado por

$$\int_a^bf(x)dx$$

Esta é a integral de Riemann de $ f $ no intervalo $ [a,b] $. Como $ f $ é limitada, existem dois números, $ m $ e $ M $ tais que

$$m\leq f(x)\leq M \qquad a\leq x\leq b$$

e, então, para todo $ \mathcal{P} $, temos que

$$m(b-a)\leq L(\mathcal{P},f)\leq U(\mathcal{P},f)\leq M(b-a)$$

de forma que os valores $ L(\mathcal{P},f) $ e $ U(\mathcal{P},f) $ foram um conjunto limitado, o que mostra que as integrais superior e inferior estão definidas para toda função limitada $ f $. De forma parecida, vamos definir a integral de Riemann-Stieltjes.

Definição 10.3

Seja $ \alpha $ uma função monótona crescente defnida em $ [a,b] $ (como $ \alpha(a) $ e $ \alpha(b) $ são finitos, segue que $ \alpha $ é limitada em $ [a,b] $). Para cada partição $ \mathcal{P} $ de $ [a,b] $, escrevemos

$$\Delta \alpha_i = \alpha(x_i) - \alpha(x_{i-1}).$$

É claro que $ \Delta \alpha_i\geq 0 $. Para qualquer função real $ f $ limitada em $ [a,b] $, definimos

$$U(\mathcal{P},f,\alpha) = \sum_{i=1}^nM_i\Delta\alpha_i \quad \text{e} \quad L(\mathcal{P},f,\alpha) = \sum_{i=1}^nm_i\Delta\alpha_i$$

em que $ M_i $ e $ m_i $ têm os mesmos significados que foram definidos na integral de Riemann. A partir disso, definimos

$$\overline{\int}_a^bf(x)d\alpha(x) = \inf U(\mathcal{P},f,\alpha) \quad \text{e} \quad \underline{\int}_a^bf(x)d\alpha(x) = \sup L(\mathcal{P},f,\alpha)$$

em que o $ \inf $ e o $ \sup $ são tomados sobre todas as partições. De forma análoga à defnição de integral de Riemann, quando $ \overline{\int}_a^bf(x)d\alpha(x) = \underline{\int}_a^bf(x)d\alpha(x) $, denotamos seu valor comum por

$$\int_a^bf(x)d\alpha(x)$$

Esta é a integral de Riemann-Stieltjes (ou simplesmente, a integral de Stieltjes) de $ f $ com respeito a $ \alpha $, sobre $ [a,b] $. Quando a integral de Riemann-Stieltjes existe, dizemos que $ f $ é integrável com respeito a $ \alpha $ no sentido de Riemann e escrevemos $ f\in\mathfrak{R}(\alpha) $.

Observação 10.1

Quando tomamos $ \alpha(x) = x $, a integral de Riemann é vista como um caso particular da integral de Riemann-Stieltjes.

10.1 - Integral de Wiener

Antes de definir a integral de Itô em sua forma mais geral, vamos tratar da integral de Wiener dada por

$$\int_a^bf(t)dB_t(\omega)$$

em que $ f $ é uma função determinística (não depende de $ \omega\in\Omega $) e $ B(t,\omega) $ é um movimento Browniano. A fim de reduzir a notação, reescreveremos a integral de Wiener da forma

$$I(f)(\omega) := \int_a^bf(t)dB_t.$$

Suponha que, para cada $ \omega\in\Omega $, queremos utilizar a fórmula de integração por partes definida na integral de Riemann-Stieltjes. Neste caso, teríamos que

$$\int_a^bf(t)dB_t = f(t)B_t\Big|_a^b- \int_a^bB_tdf(t)$$

de forma que a integral somente estará definida para uma classe bastante limitada de funções, isto é, para cada $ \omega $, $ f_t $ precisa ser uma função contínua de variação limitada. A seguir, vamos construir a integral de Wiener para funções $ f $ quadrado integráveis, não necessariamente de variação limitada.

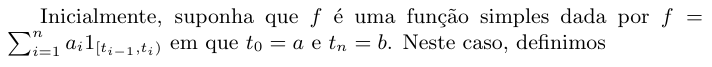
$$I(f) = \sum_{i=1}^na_i(B_{t_i} - B_{t_{i-1}}).$$

É claro que, a partir desta definição, temos que $ I(cf+dg) = cI(f) + dI(g) $ para quaisquer $ c,d\in\mathbb{R} $ e funções simples $ f $ e $ g $. O que mostra que, para funções simples, a integral satisfaz a propriedade de linearidade. Também ressaltamos que a integral independe da representação da função simples $ f $, isto é, se

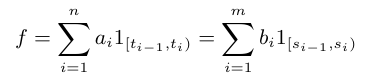
então

$$\sum_{i=1}^na_i(B_{t_i}-B_{t_{i-1}}) = \sum_{i=1}^mb_i(B_{s_i}-B_{s_{i-1}}).$$

Observação 10.1.1

Lema 10.1.1

Para uma função simples $ f $, a variável aleatória $ I(f) $ é gaussiana com média $ 0 $ e variância

$$\mathbb{E}\left[(I(f))^2\right] = \int_a^bf^2(t)dt.$$

Demonstração: Para verificar esta propriedade, é importante relembrar que uma combinação linear de variáveis aleatórias gaussianas é gaussiana. Além disso, temos que, se $ f $ é uma função simples, então

$$\mathbb{E}\left[I(f)\right] = \mathbb{E}\left[\sum_{i=1}^na_i\left(B_{t_i}-B_{t_{i-1}}\right)\right] = \sum_{i=1}^na_i\mathbb{E}\left[B_{t_i}-B_{t_{i-1}}\right] = 0$$

a partir das propriedades do movimento Browniano. Além disso,

$$\mathbb{E}\left[\left(I(f)^2\right)\right]=\mathbb{E} \left[\sum_{j,i=1}^{n}a_ia_j(B(t_i)-B(t_{i-1}))(B(t_j)-B(t_{j-1}))\right], \ \text{com}\ i,j = 1,\ldots,n.$$

Para $ i\neq j $ temos que $ \mathbb{E}[(B(t_i)-B(t_{i-1}))(B(t_j)-B(t_{j-1}))]=0 $, pois os incrementos do movimento Browniano são independentes. Além disso, para $ i=j $ temos

$$\mathbb{E}[(B(t_i)-B(t_{i-1}))^2]=t_i-t_{i-1}$$

pela definição do movimento Browniano. Portanto

$$\mathbb{E}(I^2(f))=\sum_{j,i=1}^{n}a^2_i(t_i-t_{i-1})=\int_{a}^{b}f^2(t)dt$$

a última igualdade decorre da definição da integral Riemann. E portanto o resultado segue.

Tendo definido a integral para funções simples, o próximo passo é estender nossa definição para o espaço $ L^2[a,b] $.

Definição 10.1.1

O espaço $ L^2(\Omega) $ é utilizado para denotar o espaço das variáveis aleatórias definidas em $ \Omega $ a valores reais que são quadrado integráveis e com produto interno definido por

$$\langle X, Y\rangle = \mathbb{E}(XY).$$

Da mesma forma, temos que $ L^2([a,b]) $ é o espaço das funções quadrado integráveis com o produto interno dado por

$$\langle f,g\rangle=\int_{a}^b f(s)g(s)ds,$$

para todas funções $ f,g \in L^2([a,b]) $.

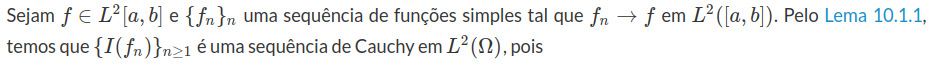
$$\mathbb{E}[(I(f_n)-I(f_m))^2]=\int_{a}^b (f_n-f_m)^2(t)dt\rightarrow 0 \ \text{quando} \ n, m \rightarrow\infty.$$

Como $ L^2(\Omega) $ é um espaço de Hilbert, temos que $ (I(f_n))_n $ converge em $ L^2(\Omega) $. Portanto definimos

$$I(f)=\lim_{n\rightarrow} I(f_n), \ \text{em} \ L^2(\Omega).$$

Uma questão natural que podemos levantar é: será que, desta forma, a integral $ I(f) $ está bem definida? Ou seja, será que esse limite independe da escolha da sequência $ (f_n)_n $?

De fato, o resultado não depende da escolha da sequência. Para mostrar isso, seja $ (g_m)_{m\geq 1} $ outra sequência tal que $ g_m\rightarrow f $ em $ L^2[a,b] $. Então

$$\mathbb{E}[|I(f_n)-I(g_m)|^2]=\mathbb{E}[|I(f_n-g_m)|^2]=\int_a^b (f_n(t)-g_m(t))^2dt\leq 2\int_{a}^b (f_n(t)-f(t))^2dt+ 2\int_a^b(g_m(t)-f(t))^2dt\rightarrow 0$$

quando $ n,m\rightarrow \infty $. Isto implica que

$$\lim_{n\rightarrow \infty}I(f_n)=\lim_{m\rightarrow \infty}I(g_m), \ \text{em} \ L^2(\Omega).$$

O que mostra que $ I(f) $ está bem definida.

Definição 10.1.2

Seja $ f\in L^2[a,b] $. A integral $ I(f) $ definida acima para funções $ f\in L^2([a,b]) $ é conhecida como integral de Wiener e denotada por

$$I(f)(\omega)=\left(\int_{a}^b f(t)dB_t\right)(\omega).$$

Por simplicidade, denotaremos esta integral por $ \int_{a}^b f(t)dB_t $ ou $ \int_{a}^b f(t)dB(t) $.

O teorema a seguir é o teorema fundamental da integral de Wiener.

Teorema 10.1.1

Para cada $ f\in L^2([a,b]) $, a integral de Wiener

$$\int_a^bf(t)dB_t$$

é uma variável aleatória gaussiana com média zero e variância $ |f|^2_{L^2([a,b])} = \int_a^bf^2(t)dt $.

Demonstração: De fato, seja $ (f_n)_n $ uma sequência de funções simples tal que $ f_n\rightarrow f $ em $ L^2([a,b]) $. Sabemos do Lema 10.1.1 que, para cada $ n $, $ I(f_n) $ é uma variável aleatória Gaussiana com média $ 0 $ e variância

$$\int_a^bf_n^2(t)dt$$

já que $ f_n $ é uma função simples para todo $ n $. Para verificar o resultado para a função $ f $, utilizamos o seguinte fato conhecido: se $ X_n $ é uma variável aleatória normal com média $ \mu_n $ e variância $ \sigma^2_n $, então $ X = \lim_{n\rightarrow\infty}X_n $ tem distribuição normal com média $ \mu = \lim_{n\rightarrow\infty}\mu_n $ e variância $ \sigma^2 = \lim_{n\rightarrow\infty} \sigma^2_n $. Portanto, temos que $ I(f) = \int_a^bf(t)dB_t $ é uma variável aleatória gaussiana com média zero, já que cada $ I(f_n) $ é uma variável aleatória normal com média zero e, além disso,

$$\mathbb{E}\left[(I(f))^2\right] = \lim_{n\rightarrow\infty}\mathbb{E}\left[(I(f_n))^2\right]= \lim_{n\rightarrow\infty}\int_a^bf_n^2(t)dt = \int_a^b\lim_{n\rightarrow\infty}f_n^2(t)dt = \int_a^bf^2(t)dt = |f|^2_{L^2([a,b])}$$

como queríamos demonstrar.

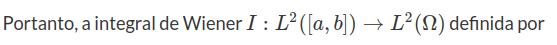
$$I(f) = \left(\int_a^bf(t)dB_t\right)(\omega)$$

é uma isometria, pois

$$|I(f)|^2_{L^2(\Omega)} = \langle I(f),I(f)\rangle = \mathbb{E}\left[I^2(f)\right] = \int_a^bf^2(t)dt = |f|^2_{L^2([a,b])}.$$

Corolário 10.1.1

Se $ f,g\in L^2([a,b]) $, então

$$\mathbb{E}\left[I(f)I(g)\right] = \int_a^bf(t)g(t)dt.$$

Em particular, se $ f $ e $ g $ são ortogonais, então as variáveis aleatórias $ I(f) $ e $ I(g) $ são independentes.

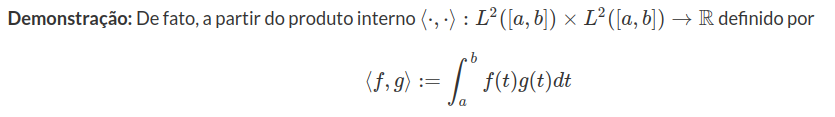
e, pela linearidade da integral de Wiener, temos que

$$\mathbb{E}\left[\left(I(f) +I(g)\right)^2\right] = \mathbb{E}\left[I^2(f+g)\right] = \int_a^b\left(f(t)+g(t)\right)^2dt = \int_a^bf^2(t)dt + 2\int_a^bf(t)g(t)dt + \int_a^bg^2(t)dt.$$

Além disso, temos que

$$\mathbb{E}\left[\left(I(f)+I(g)\right)^2\right] = \mathbb{E}\left[I^2(f) + 2I(f)I(g) + I^2(g)\right] = \int_a^bf^2(t)dt + 2\mathbb{E}\left[I(f)I(g)\right] + \int_a^bg^2(t)dt$$

e, portanto, concluímos que

$$\mathbb{E}\left[I(f)I(g)\right] = \int_a^bf(t)g(t)dt.$$

No caso particular em que $ f $ e $ g $ são ortogonais, temos que

$$\int_a^bf(t)g(t)dt = \mathbb{E}\left[I(f)I(g)\right] = \langle I(f),I(g)\rangle = 0$$

e, como as variáveis são gaussianas, temos que $ I(f) $ e $ I(g) $ são independentes.

Exemplo 10.1.1

A integral de Wiener

$$\int_0^1tdB_t$$

é uma variável aleatória gaussiana com média zero e variância $ \int_0^1t^2dt = \frac{1}{3} $.

Teorema 10.1.2

Seja $ f $ uma função contínua de variação limitada. Então, para quase todo $ \omega\in\Omega $, temos que

$$\left(\int_a^bf(t)dB_t\right)(\omega) = (\text{RS})\int_a^bf(t)dB_t(\omega)$$

em que $ (\text{RS})\int $ é a integral de Riemann-Stieltjes.

Demonstração: De fato, para cada partição $ \Delta_n = (t_0,t_1,\ldots,t_n) $ de $ [a,b] $, definimos uma função simples dada por

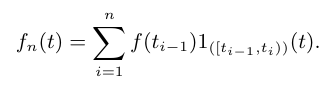
Desta forma, temos que $ f_n\rightarrow f $ em $ L^2([a,b]) $ quando $ n\rightarrow\infty $. Da definição da integral de Wiener, temos que

$$\int_a^bf(t)dB_t = \lim_{n\rightarrow\infty}I(f_n) = \lim_{n\rightarrow\infty}\int_a^bf_n(t)dB_t = \lim_{n\rightarrow\infty}\sum_{i=1}^nf(t_{i-1})\left(B_{t_i}-B_{t_{i-1}}\right) \ \text{em} \ L^2(\Omega).$$

Reciprocamente, para cada $ \omega\in\Omega $,

$$\text{(RS)}\int_a^bf(t)dB_t(\omega) = f(b)B_b(\omega) - f(a)B_a(\omega) - \lim_{n\rightarrow\infty}\sum_{i=1}^nB_{t_i}(\omega)(f(t_i) - f(t_{i-1})) = \lim_{n\rightarrow\infty}\sum_{i=1}^nf(t_{i-1})\left(B_{t_i}(\omega) - B_{t_{i-1}}(\omega)\right).$$

Como a convergência em $ L^2(\Omega) $ implica a existência de uma subsequência que converge quase certamente, escolhemos esta subsequência e temos o resultado.

Exemplo 10.1.2

Considere a integral de Riemann $ \int_0^1B_t(\omega)dt $ definida para cada $ \omega\in\Omega $. Vamos encontrar a distribuição de probabilidades desta variável aleatória.

Utilizando a fórmula de integração por partes, temos que

$$\int_0^1B_t(\omega)dt = B_t(\omega)(t-1)\Big|^1_0 - \int_0^1(t-1)dB_t(\omega) = \text{(RS)}\int_0^1(1-t)dB_t(\omega).$$

Então, pelo Teorema 10.1.2, temos que, para quase todo $ \omega\in\Omega $

$$\int_0^1B_t(\omega)dt = \left(\int_0^1(1-t)dB_t\right)(\omega)$$

em que a integral do lado direito é uma integral de Wiener, de forma que $ \int_0^1B_tdt $ e a integral de Wiener $ \int_0^1(1-t)dB_t $ têm a mesma distribuição de probabilidades, ou seja, uma distribuição Gaussiana com média zero e variância

$$\int_0^1(1-t)^2dt = \frac{1}{3}.$$

A seguir, apresentamos um importante resultado relacionando a variável aleatória definida pela integral de Wiener com martingales.

Teorema 10.1.3

Seja $ f\in L^2([a,b]) $. Então, o processo estocástico $ M_t $ definido por

$$M_t = \int_a^tf(s)dB_s, \quad a\leq t\leq b$$

é um martingale com respeito à filtragem $ \mathcal{F_t} = \sigma\left(B_s; \ s\leq t\right) $.

Demonstração: Inicialmente, mostramos que $ \mathbb{E}\left(|M_t|\right) \ < \ \infty $ para todo $ t\in[a,b] $ para que possamos considerar a esperança condicional de $ M_t $. De fato,

$$\mathbb{E}\left[|M_t|^2\right] = \int_a^tf^2(s)ds\leq \int_a^bf^2(s)ds \ < \ \infty.$$

Como $ \mathbb{E}\left[|M_t|\right] \leq\left[\mathbb{E}\left(|M_t|^2\right) \right]^{\frac{1}{2}} \ < \ \infty $, segue o resultado.

Mostremos agora que $ \mathbb{E}\left[M_t|\mathcal{F_s}\right] = M_s $ quase certamente para todo $ s\leq t $. Para isto, observamos que

$$M_t = \int_a^tf(u)dB_u = \int_a^sf(u)dB_u + \int_s^tf(u)dB_u = M_s + \int_s^tf(u)dB_u$$

e que $ M_s $ é $ \mathcal{F_s} $-mensurável. Então

$$\mathbb{E}\left[M_t|\mathcal{F_s}\right] = M_s + \mathbb{E}\left[\int_s^tf(u)dB_u\Big|\mathcal{F_s}\right].$$

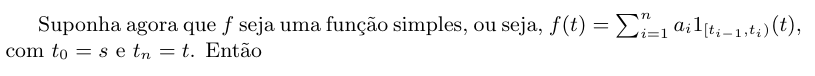
$$\int_s^tf(u)dB_u = \sum_{i=1}^na_i\left(B_{t_i} - B_{t_{i-1}}\right).$$

Porém, da propriedade de incrementos independentes do movimento Browniano, temos que $ B_{t_i}-B_{t_{i-1}} $ são independentes de $ \mathcal{F_s} $ para todo $ i = 1,\ldots,n $. Portanto, $ \mathbb{E}\left[B_{t_i}-B_{t_{i-1}}\Big|\mathcal{F_s}\right] = \mathbb{E}\left[B_{t_i}-B_{t_{i-1}}\right] = 0 $ para todo $ i $. Logo

$$\mathbb{E}\left[\int_s^tf(u)dB_u\Big|\mathcal{F_s}\right] = 0$$

e o resultado segue. Basta mostrar agora que o resultado permanece verdadeiro se tomarmos $ f\in L^2([a,b]) $. Neste caso, escolhemos uma sequência $ (f_n)_n $ de funções simples que converge para $ f $ em $ L^2([a,b]) $. Pela desigualdade condicional de Jensen, com $ \phi(x) = x^2 $, temos que

$$\left|\mathbb{E}\left[X\Big|\mathcal{F}\right]\right|^2\leq \mathbb{E}\left[X^2\Big|\mathcal{F}\right]$$

de onde concluímos que

$$\Big|\mathbb{E}\left[\int_s^t\left(f_n(u)-f(u)\right)dB_u\Big|\mathcal{F_s}\right]\Big|^2\leq \mathbb{E}\left[\left(\int_s^t\left(f_n(u)-f(u)\right)dB_u\right)^2\Big|\mathcal{F_s}\right].$$

Usamos agora a propriedade $ \mathbb{E}\left[\mathbb{E}\left[X|\mathcal{F}\right]\right] = \mathbb{E}[X] $ da esperança condicional e concluímos que

$$\mathbb{E}\left[\Big|\mathbb{E}\left[\int_s^t\left(f_n(u)-f(u)\right)dB_u\Big|\mathcal{F_s}\right]\Big|^2\right]\leq \mathbb{E}\left[\left(\int_s^t\left(f_n(u)-f(u)\right)dB_u\right)^2\right] = \int_s^t\left(f_n(u)-f(u)\right)^2du\leq\int_a^b\left(f_n(u)-f(u)\right)^2du\rightarrow 0$$

Observamos que a convegência em $ L^2(\Omega) $ implica convergência em probabilidade que implica a existência de uma subsequência que converge quase certamente. Escolhendo esta subsequência, temos que

$$\lim_{n\rightarrow\infty}\mathbb{E}\left[\int_s^tf_n(u)dB_u\Big|\mathcal{F_s}\right] = \mathbb{E}\left[\int_s^tf(u)dB_u\Big|\mathcal{F_s}\right] \ \text{quase certamente}$$

e, como $ \mathbb{E}\left[\int_s^tf_n(u)dB_u|\mathcal{F_s}\right) = 0 $, segue que $ \mathbb{E}\left[\int_s^tf(u)dB_u|\mathcal{F_s}\right]=0 $, concluindo a demonstração.

10.1.1 - Expansão em série da integral de Wiener

Seja $ (\phi_n)_n $ uma base ortonormal pra o espaço de Hilbert $ L^2([a,b]) $. Desta forma, cada função $ f\in L^2([a,b]) $ tem a seguinte expansão

$$f = \sum_{n=1}^\infty\langle f,\phi_n\rangle\phi_n \qquad (\star)$$

em que $ \langle \cdot,\cdot\rangle $ é o produto interno em $ L^2([a,b]) $ definido por $ \langle f,g\rangle = \int_a^bf(t)g(t)dt $. A partir desta expansão, temos a seguinte identidade, conhecida como identidade de Parseval e dada por

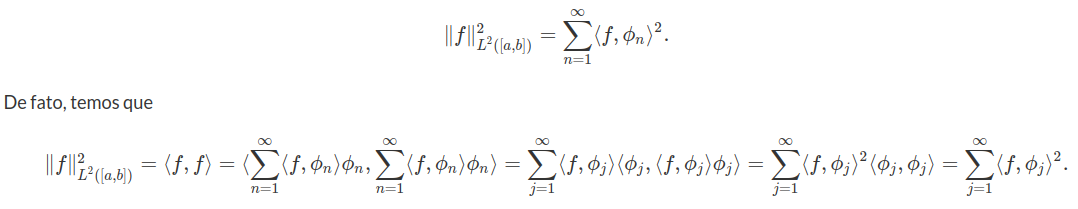
Então, tomando a integral de Wiener em ambos os lados da equação ($ \star $), temos

$$\int_a^bf(t)dB_t = \sum_{n=1}^{\infty}\langle f,\phi_n\rangle\int_a^b\phi_ndB_t.$$

Questão: A série do lado direito converge para a integral de Wiener do lado esquerdo? Em que sentido?

Inicialmente, observamos que as variáveis aleatórias $ \int_a^b\phi_ndB_t $ com $ n \geq 1 $ são independentes, uma vez que $ \phi_i $ e $ \phi_j $ são ortogonais se $ i\neq j $. Além disso, são variáveis gaussianas com média zero e variância $ \int_a^b\phi_n^2dt = \langle \phi_n,\phi_n\rangle = |\phi_n|^2_{L^2([a,b])} = 1 $. Assim, o lado direito é uma série aleatória de variáveis aleatórias independentes e igualmente distribuídas.phi

Pelo teorema da equivalência de Lévy, esta série converge quease certamente se, e somente se, converge em probabilidade e, em contrapartida, se, e somente se, converge em distribuição. Porém, a convergência em $ L^2(\Omega) $ desta série pode ser verificada facilmente. De fato, temos que

$$\mathbb{E}\left[\left(\int_a^bf(t)dB_t-\sum_{n=1}^N\langle f,\phi_n\rangle\int_a^b\phi_n(t)dB_t\right)^2\right] = \mathbb{E}\left[\left(\int_a^bf(t)dB_t\right)^2\right] - 2\sum_{n=1}^N\mathbb{E}\left[\int_a^bf(t)dB_t\langle f,\phi_n\rangle\int_a^b\phi_n(t)dB_t\right] + \mathbb{E}\left[\left(\sum_{n=1}^N\langle f,\phi_n\rangle\int_a^b\phi_n(t)dB_t\right)^2\right].$$

E então, segue que

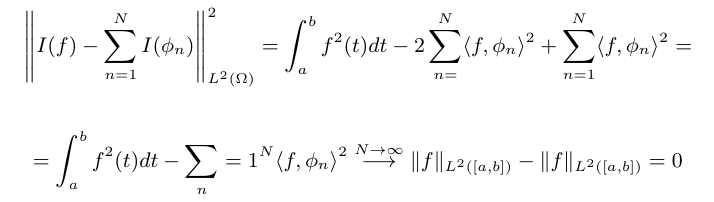
de onde concluímos que a série do lado direito converge em $ L^2(\Omega) $ para a variável aleatória do lado esquerdo e, como a convergência em $ L^2(|Omega) $ implica convergência em probabilidade, temos o resultado. A partir disso, temos o seguinte resultado

Teorema 10.1.1.1

Seja $ (\phi_n)_n $ uma base ortonormal para $ L^2([a,b]) $. Então, para cada $ f\in L^2([a,b]) $, a integral de Wiener de $ f $ possui a seguinte expansão

$$\int_a^bf(t)dB_t = \sum_{n=1}^\infty\langle f,\phi_n\rangle\int_a^b\phi_n(t)dB_t$$

com probabilidade um, em que a série converge quase certamente.

Exemplo 10.1.1.1

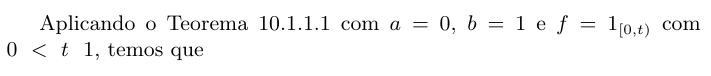
$$\int_0^1f(t)dB_t = 1(B_t - B_0) + 0(B_1- B_t) = B_t$$

e então

$$B_t(\omega) = \sum_{n=1}^{\infty}\left(\int_0^t\phi_n(s)ds\right)\left(\int_0^1\phi_n(s)dB_s(\omega)\right).$$

Desta forma, esperamos que $ B_t $ possa ser representado por

$$B_t(\omega) = \sum_{n=1}^{\infty}\xi_n(\omega)\int_0^t\phi_n(s)ds$$

em que $ \xi_n(\omega) $ são variáveis aleatórias gaussianas independentes com média zero e variância 1.

10.2 - Integral de Itô

Seja $ B_t(\omega) $ um movimento Browniano. A Integral de Itô será definida de forma a generalizar a ideia da Integral de Wiener. Neste sentido, estudaremos integrais do tipo

$$\int_a^bf(t,\omega)dB_t(\omega)$$

em que $ f(t,\omega) $ é um processo estocástico adaptado à filtragem $ \mathcal{F_t} = \sigma\left(B_s; \ s\leq t\right) $ e

$$\int_a^b\mathbb{E}\left(|f(t)|^2\right)dt \ < \ \infty.$$

É claro que, como a integral será uma generalização da Integral de Wiener, quando o integrando é uma função determinística $ f(t) $, a integral de Itô $ \int_a^bf(t)dB_t(\omega) $ é reduzida para a integral de Wiener.

Inicialmente, a teoria de integração estocástica foi motivada como um método direto para a construção de processos de difusão como soluções de equações diferenciais estocásticas. Ela também pode ser vista como motivação para martingales. Seja $ B_t $ um movimento Browniano. Suponha que $ f(t) $ seja uma função determinística definida em $ L^2([a,b]) $. Então, como vimos no Teorema 10.1.3 o processo

$$M_t = \int_a^tf(s)dB_s, \quad a\leq t\leq b$$

é um martingale. De forma análoga, queremos definir a integral estocástica

$$\int_a^bf(t,\omega)dB_t(\omega)$$

de forma que

$$M_t = \int_a^tf(s,\omega)dB_s(\omega) \quad a\leq t\leq b$$

seja um martingale.

Exemplo 10.2.1

Antes que possamos definir a integral de Itô, consideramos um exemplo simples com $ f(t,\omega) = B_t(\omega) $, de forma que a integral estocástica é dada por

$$\int_a^bB_tdB_t.$$

Considerando subintervalos $ [t_{i-1},t_i] $ e avaliarmos $ B_t $ nos extremos da partição, temos que

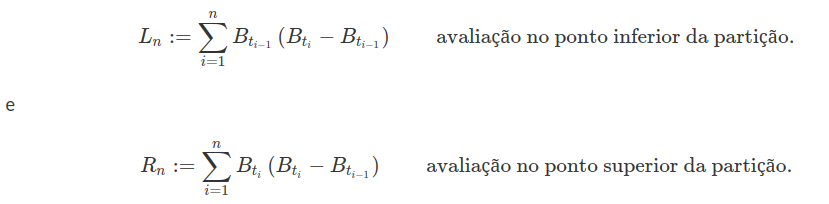
Então, segue que

$$R_n-L_n = \sum_{i=1}\left(B_{t_i}-B_{t_{i-1}}\right)^2$$

e, se $ \lim_{n\rightarrow\infty}(R_n-L^n) $ existe, ele é a variação quadrática do movimento Browniano $ B_t $.

Teorema 10.2.1

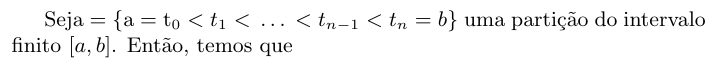
$$\sum_{i=1}^n\left(B_{t_i}-B_{t_{i-1}}\right)^2 \rightarrow b-a$$

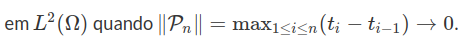
Demonstração: De fato, observamos que

$$b-a = \sum_{i=1}^n(t_i-t_{i-1})$$

e, então, tomando

$$\phi_n = \sum_{i=1}^n\left[\left(B_{t_i}-B_{t_{i-1}}\right)^2 - \left(t_i-t_{i-1}\right)\right] = \sum_{i=1}^nX_i$$

em que $ X_i = \left(B_{t_i}-B_{t_{i-1}}\right)^2-\left(t_i-t_{i-1}\right) $. Desta forma, segue que

$$\phi_n^2 = \sum_{i,j=1}^nX_iX_j. \qquad (\star)$$

Para $ i\neq j $, temos que $ \mathbb{E}\left[X_iX_j\right] = 0 $, já que $ B_t $ tem incrementos independentes e $ \mathbb{E}\left[\left(B_t-B_s\right)^2\right] = |t-s| $. Reciprocamente, temos que $ \mathbb{E}\left[\left(B_t-B_s\right)^4\right] = 3(t-s)^2 $ e, então, para $ i = j $, temos que

$$\mathbb{E}\left[X_i^2\right] = \mathbb{E}\left[\left(B_{t_i}-B_{t_{i-1}}\right)^4 - 2(t_i-t_{i-1})\left(B_{t_i}-B_{t_{i-1}}\right)^2 + (t_i-t_{i-1})^2\right] = 2(t_i-t_{i-1})^2.$$

Portanto, da equação $ (\star) $, temos que

$$\mathbb{E}\left[\phi_n^2\right] = \sum_{i=1}^n2(t_i-t_{i-1})^2\leq 2|\mathcal{P}_n|\sum_{i=1}^n(t_i-t_{i-1}) = 2(b-a)|\mathcal{P}_n|\rightarrow 0 \ \text{quando} \ |\mathcal{P}_n|\rightarrow0$$

o que mostra que $ \phi_n $ converge para zero em $ L^2(\Omega) $. Então, $ \sum_{i=1}^n\left(B_{t_i}-B_{t_{i-1}}\right)^2 $ converge para $ b-a $ em $ L^2(\Omega) $ quando $ |\mathcal{P}_n|\rightarrow 0 $.

$ \square $

Portanto, aplicando o Teorema 10.2.1, concluímos que

$$\lim_{|\mathcal{P}_n|\rightarrow 0}R_n-L_n = b-a \ \text{em} \ L^2(\Omega)$$

e $ \lim_{|\mathcal{P}_n|\rightarrow 0}R_n\neq \lim_{|\mathcal{P}_n|\rightarrow 0}L_n $. Mas o que são esses limites? Observamos que

$$R_n + L_n = \sum_{i=1}^n\left(B_{t_i}+B_{t_{i-1}}\right)\left(B_{t_i}-B_{t_{i-1}}\right) = \sum_{i=1}^n\left(B^2_{t_i}-B^2_{t_{i-1}}\right) = B^2_b-B^2_a$$

de forma que

$$R_n = \frac{1}{2}\left(B^2_b-B^2_a+\sum_{i=1}^n\left(B_{t_i}-B_{t_{i-1}}\right)2\right)$$

e

$$L_n = \frac{1}{2}\left(B^2_b-B^2_a-\sum_{i=1}^n\left(B_{t_i}-B_{t_{i-1}}\right)2\right)$$

e, utilizando o Teorema 10.2.1, temos que

$$\lim_{|\mathcal{P}_n|\rightarrow 0}R_n = \frac{1}{2}\left(B^2_b-B^2_a + (b-a)\right) \qquad (1)$$

e

$$\lim_{|\mathcal{P}_n|\rightarrow 0}L_n = \frac{1}{2}\left(B^2_b-B^2_a - (b-a)\right) \qquad (2)$$

A partir dos limites acima, qual dentre as equações (1) e (2) deve ser escolhida para ser a integral $ \int_a^bB_tdB_t $? Ou seja, qual ponto extremo do subintervalo $ [t_{i-1},t_i] $ deve ser escolhido para calcular o integrando? A fim de responder esta questão, tomamos $ a = 0 $ e $ b = t $ nas equações (1) e (2) para definir os processos estocásticos

$$R_t= \frac{1}{2}\left(B^2_t + t\right) \qquad \text{e} \qquad L_t = \frac{1}{2}\left(B^2_t - t\right).$$

Desta forma, temos que

$$\mathbb{E}\left[R_t\right] = \mathbb{E}\left[\frac{1}{2}\left(B^2_t + t\right)\right] = \frac{1}{2}\left(\mathbb{E}\left[B^2_t\right] + t\right) = t$$

$$\mathbb{E}\left[L_t\Big|\mathcal{F_s}\right] = \frac{1}{2}\mathbb{E}\left[B^2_t\Big|\mathcal{F_s}\right] - \frac{1}{2}t = \frac{1}{2}\left(\mathbb{E}\left[B^2_t - B^2_s\Big|\mathcal{F_s}\right] +\mathbb{E}\left[B^2_s\right]\right) - \frac{1}{2}t$$

de onde concluímos que

$$\mathbb{E}\left[L_t\Big|\mathcal{F_s}\right] = \frac{1}{2}\left(t-s+B^2_s\right) - \frac{1}{2}t = \frac{1}{2}\left(B^2_s-s\right) = L_s \ \text{para todo} \ s\leq t$$

Portanto, se desejamos a propriedade martingale para a integral estocástica $ \int_a^tf(s)dB_s $, devemos tomar o ponto extremo à esquerda de cada subintervalo como ponto de avaliação de $ f $.

Exemplo 10.2.2

Considere a integral

$$X_t = \int_0^tB_1dB_s; \ 0\leq t\leq 1.$$

Intuitivamente, é de se pesperar que $ X_t = B_1B_t $. Entretanto, o processo estocástico $ X_t $ não é um martingale, uma vez que $ \mathbb{E}\left[X_t\right] = \mathbb{E}\left[B_1B_t\right] = \min(1,t) = t $ que não é constante. Desta forma, a integral $ \int_0^1B_1dB_s $ não pode ser calculada desta forma se queremos obter um processo martingale. A razão para esta integral simples não estar definida (quando queremos obter martingales) é devido ao fato de que o integrando $ B_1 $ não é adaptado à filtragem $ \sigma(B_s; \ s\leq t) $ com $ 0\leq t\leq 1 $. Portanto, uma importante exigêngia para o integrando, se queremos a propriedade martingale para integral estocástica $ \int_a^tf(s)dB_s $ é que o integrando seja adapatado à filtragem $ (\mathcal{F_t}) $. Em geral, permitiremos que $ (\mathcal{F_t}) $ seja uma filtragem um pouco maior do que a gerada pelo movimento Browniano, isto é, $ \sigma(B_s; \ s\leq t) \subset \mathcal{F_t} $ para todo $ t $.

Observação 10.2.1

Do discutido acima, é importante observar que, para que a integral estocástica tenha a propriedade martingale, então devemos tomar a integral ‘‘inferior’’ em cada subintervalo. É importante destacar que, nas integrais dexo Riemann (ou Riemann-Stieltjes) o ponto do subintervalo a ser tomado é irrelevante, pois o limite é o mesmo independente do ponto escolhido. Entretanto, na integral estocástica, como pudemos ver, isto não é possível, já que cada ponto nos fornece um limite diferente e a escolha do ponto depende das propriedades que desejamos que a integral possua. Como o foco é a propriedade martingale da integral estocástica, sua definição dependerá da escolha do ponto inferior.

Definição da Integral de Itô

A fim de definir a integral de Itô, consideramos $ B_t $ um movimento Browniano fixo e uma filtragem $ (\mathcal{F_t}; \ a\leq t\leq b) $ que satisfaz as seguintes condições:

1. Para cada $ t $, $ B_t $ é $ \mathcal{F_t} $-mensurável;

2. Para qualquer $ s\leq t $, a variável aleatória $ B_t-B_s $ é independente da $ \sigma $-álgebra $ \mathcal{F_s} $.

Notação 10.2.1

Utilizaremos a notação $ L^2_{\text{ad}}([a,b]\times\Omega) $ para o espaço de todos os processos estocásticos $ f(t,\omega) $, com $ a\leq t\leq b $ e $ \omega\in\Omega $ que satisfazem as seguintes condições:

1. $ f(t,\omega) $ é adapatado à filtragem $ (\mathcal{F_t}) $.

2. $ \int_a^b\mathbb{E}\left[\left|f(t)\right|^2\right]dt \ < \ \infty $.

É imediato que, neste caso, a integral é linear, ou seja, $ I(\alpha f+\beta g) = \alpha I(f) + \beta I(g) $ para quaisquer $ \alpha,\beta\in\mathbb{R} $ e funções simples $ f $ e $ g $.

Lema 10.2.1

Seja $ f $ um processo estocástico simples em $ L^2_{\text{ad}}([a,b]\times\Omega) $ e a integral de Itô definida da forma acima. Então $ \mathbb{E}\left[I(f)\right] = 0 $ e

$$\mathbb{E}\left[\left|I(f)\right|^2\right] = \int_a^b\mathbb{E}\left[\left|f(t)\right|^2\right]dt$$

Demonstração: De fato, para cada $ 1\leq i\leq n $, temos que

$$\mathbb{E}\left[\xi_{i-1}\left(B_{t_i}-B_{t_{i-1}}\right)\right]=\mathbb{E}\left[\mathbb{E}\left[\xi_{i-1}\left(B_{t_i}-B_{t_{i-1}}\right)\Big|\mathcal{F}_{t_{i-1}}\right]\right] = \mathbb{E}\left[\xi_{i-1}\mathbb{E}\left[B_{t_i}-B_{t_{i-1}}\Big|\mathcal{F}_{t_{i-1}}\right]\right] = \mathbb{E}\left[\xi_{i-1}\mathbb{E}\left[B_{t_i}-B_{t_{i-1}}\right]\right] = 0$$

de onde segue que $ \mathbb{E}\left[I(f)\right] = 0 $. Além disso, temos que

$$I^2(f) = \sum_{i,j=1}^n\xi_{i-1}\xi_{j-1}\left(B_{t_i}-B_{t_{i-1}}\right)\left(B_{t_j}-B_{t_{j-1}}\right).$$

Observamos que, para $ i\neq j $, digamos $ i \ < \ j $,

$$\mathbb{E}\left[\xi_{i-1}\xi_{j-1}\left(B_{t_i}-B_{t_{i-1}}\right)\left(B_{t_j}-B_{t_{j-1}}\right)\right] = \mathbb{E}\left[\mathbb{E}\left[\xi_{i-1}\xi_{j-1}\left(B_{t_i}-B_{t_{i-1}}\right)\left(B_{t_j}-B_{t_{j-1}}\right)\Big|\mathcal{F}_{t_{j-1}}\right]\right]$$

e, portanto,

$$\mathbb{E}\left[\xi_{i-1}\xi_{j-1}\left(B_{t_i}-B_{t_{i-1}}\right)\left(B_{t_j}-B_{t_{j-1}}\right)\right]=\mathbb{E}\left[\xi_{i-1}\xi_{j-1}\left(B_{t_i}-B_{t_{i-1}}\right)\mathbb{E}\left[B_{t_j}-B_{t_{j-1}}\right]\right] = 0.$$

Em contrapartida, se $ i = j $, então

$$\mathbb{E}\left[\xi^2_{i-1}\left(B_{t_i}-B_{t_{i-1}}\right)^2\right] = \mathbb{E}\left[\mathbb{E}\left[\xi^2_{i-1}\left(B_{t_i}-B_{t_{i-1}}\right)^2\Big|\mathcal{F}_{t_{i-1}}\right]\right] = \mathbb{E}\left[\xi^2_{i-1}\mathbb{E}\left[\left(B_{t_i}-B_{t_{i-1}}\right)^2\Big|\mathcal{F}_{t_{i-1}}\right]\right] = \mathbb{E}\left[\xi^2_{i-1}(t_i-t_{i-1})\right] = (t_i-t_{i-1})\mathbb{E}\left[\xi^2_{i-1}\right].$$

Das equações acima, temos que

$$\mathbb{E}\left[\left|I(f)\right|^2\right] = \sum_{i=1}^n(t_i-t_{i-1})\mathbb{E}\left[\xi^2_{i-1}\right] = \int_a^b\mathbb{E}\left[\left|f(t)\right|^2\right]dt.$$

como queríamos demonstrar.

$ \square $

Por fim, usando o teorema a seguir podemos estender a definição da integral de Itô para qualquer processo $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $. Para isso, basta mostramos que existe uma sequência de processos simples que converge para $ f $.

Teorema 10.2.2

Suponha que $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $. Então existe uma sequência $ (f_n(t); \ n\geq 1) $ de processos estocásticos simples em $ L^2_{\text{ad}}([a,b]\times\Omega) $ tal que

$$\lim_{n\rightarrow\infty}\int_a^b\mathbb{E}\left[\left|f(t)-f_n(t)\right|^2\right]dt = 0.$$

Demonstração: A demonstração será dividida em casos especiais e o caso geral.

Caso1: Suponha que $ \mathbb{E}\left[f(t)f(s)\right] $ é uma função contínua de $ (t,s) $ em $ [a,b]\times[a,b] $.

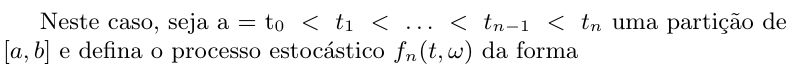
$$f_n(t) = f(t_{i-1}) \ \text{para} \ t_{i-1} \ < \ t \leq t_i.$$

Desta forma, $ (f_n(t,\omega))_n $ é uma sequência de processos estocásticos simples adaptados. Pela continuidade de $ \mathbb{E}\left[f(t)f(s)\right] $ em $ [a,b]\times[a,b] $, temos que

$$\lim_{s\rightarrow t}\mathbb{E}\left[\left|f(t)-f(s)\right|^2\right] = 0$$

o que implica que, para cada $ t\in[a,b] $,

$$\lim_{n\rightarrow\infty}\mathbb{E}\left[\left|f(t)-f_n(t)\right|^2\right] = 0.$$

Além disso, utilizando a desigualdade

$$|\alpha-\beta|^2\leq 2\left(|\alpha|^2+|\beta|^2\right)$$

segue que

$$\left|f(t)-f_n(t)\right|^2\leq 2\left(\left|f(t)\right|^2+\left|f_n(t)\right|^2\right).$$

Então, para todo $ a\leq t\leq b $, temos que

$$\mathbb{E}\left[\left|f(t)-f_n(t)\right|^2\right] \leq 2\left(\mathbb{E}\left[\left|f(t)\right|^2\right] + \mathbb{E}\left[\left|f_n(t)\right|^2\right]\right) \leq 4\sup_{a\leq s\leq b}\mathbb{E}\left[\left|f(s)\right|^2\right].$$

Portanto, aplicando o teorema da convergência dominada, concluímos que

$$\lim_{n\rightarrow\infty}\int_a^b\mathbb{E}\left[\left|f(t)-f_n(t)\right|^2\right]dt = 0.$$

Caso 2: $ f $ é limitada.

Neste caso, definimos um processo estocástico $ g_n $ dado por

$$g_n(t,\omega) = \int_0^{n(t-a)}e^{-\tau}f(t-n^{-1}\tau,\omega)d\tau.$$

Observamos que $ g_n $ é adaptado a $ \mathcal{F}_{\tau} $ e $ \int_a^b\mathbb{E}\left[\left|g_n(t)\right|^2\right]dt \ < \ \infty $.

Afirmação (a): para cada $ n $, $ \mathbb{E}\left[g_n(t)g_n(s)\right] $ é uma função contínua de $ (t,s) $.

A fim de demonstrar esta afirmação, seja $ u = t - n^{-1}\tau $ de forma que podemos reescrever $ g_n(t,\omega) $ como

$$g_n(t) = \int_a^bne^{-n(t-u)}f(u)du,$$

que podemos utilizar para verificar que

$$\lim_{t\rightarrow s}\mathbb{E}\left[\left|g_n(t)-g_n(s)\right|^2\right] = 0,$$

demonstrando a afirmação.

Afirmação (b): $ \int_a^b\mathbb{E}\left[\left|f(t)-g_n(t)\right|^2\right]dt \rightarrow 0 $ quando $ n\rightarrow \infty $.

Para verificar esta afirmação, basta notar que

$$f(t) - g_n(t) = \int_0^{\infty}e^{-\tau}\left(f(t) - f(t-n^{-1}\tau)\right)d\tau,$$

em que $ f(t) $ é uma função não zero para $ t \ < \ a $. Como $ e^{-\tau}d\tau $ é uma medida de probabilidade em $ [0,\infty) $, podemos aplicar a desigualdade de Schwarz e então, segue que

$$\left|f(t)-g_n(t)\right|^2\leq \int_0^{\infty}\left|f(t)-f(t-n^{-1}\tau)\right|^2e^{\tau}d\tau.$$

Portanto,

$$\int_a^b\mathbb{E}\left[\left|f(t)-g_n(t)\right|^2\right]dt \leq \int_a^b\int_0^{\infty}e^{\tau}\mathbb{E}\left[\left|f(t)-f(t-n^{-1}\tau)\right|^2\right]d\tau dt = \int_0^{\infty}e^{-\tau}\left(\int_a^b\mathbb{E}\left[\left|f(t)-f(t-n^{-1}\tau)\right|^2\right]dt\right)d\tau$$

de forma que

$$\int_a^b\mathbb{E}\left[\left|f(t)-g_n(t)\right|^2\right]dt\leq \int_0^{\infty}e^{\tau}\mathbb{E}\left(\int_a^b\left|f(t)-f(t-n^{-1}\tau)\right|^2dt\right)d\tau.$$

Como, por hipótese, $ f $ é limitada, temos que

$$\int_a^b\left|f(t,\cdot)-f(t-n^{-1}\tau,\cdot)\right|^2dt\rightarrow 0 \ \text{q.c}$$

quando $ n\rightarrow\infty $. Portanto, concluímos a afirmação.

A partir da afirmação (a), podemos aplicar o caso 1 em $ g_n $ para cada $ n $ para obter um processo estocástico simples $ f_n(t) $ tal que

$$\int_a^b\mathbb{E}\left[\left|g_n(t)-f_n(t)\right|^2\right]dt\leq \frac{1}{n}.$$

Então, pela afirmação (b) e a desigualdade acima, temos que

$$\lim_{n\rightarrow\infty}\int_a^b\mathbb{E}\left[\left|f(t)-f_n(t)\right|^2\right]dt = 0,$$

o que completa a demonstração para o caso 2.

Caso 3: Caso geral para $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $.

Para cada $ n $ definimos

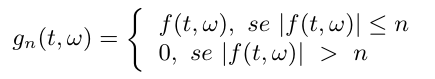
Então, pelo teorema da convergência dominada,

$$\int_a^b\mathbb{E}\left[\left|f(t)-g_n(t)\right|^2\right]dt\rightarrow 0 \ \text{quando} \ n\rightarrow \infty. \qquad (3)$$

Agora, para cada $ n $, aplicamos o caso 2 em $ g_n $ para selecionar um processo estocástico simples $ f_n(t) $ tal que

$$\int_a^b\mathbb{E}\left[\left|g_n(t)-f_n(t)\right|^2\right]dt\leq \frac{1}{n}. \qquad (4)$$

Então, das equações (3) e (4), concluímos a demonstração do resultado.

$ \square $

Ressaltamos que o Teorema 10.2.2 é de fundamental importância para a definição de integral de Itô. De fato, aplicamos o Teorema 10.2.2 para obter uma sequência $ (f_n(t,\omega))_n $ de processos estocásticos simples adaptados tal que

$$\lim_{n\rightarrow\infty}\int_a^b\mathbb{E}\left[\left|f(t)-f_n(t)\right|^2\right]dt = 0.$$

Para cada $ n $, $ I(f_n) $ está definida, já que $ f_n $ é um processo estocástico simples. Além disso, do Lema 10.2.1, temos que

$$\mathbb{E}\left[\left|I(f_n)-I(f_m)\right|^2\right] = \int_a^b\mathbb{E}\left[\left|f_n(t)-f_m(t)\right|^2\right]dt \rightarrow 0 \ \text{quando} \ n,m\rightarrow\infty$$

Definição 10.2.1

O limite $ I(f) $ definido acima é chamada de integral de Itô de $ f $ e denotada por

$$\int_a^bf(t)dB_t.$$

Assim, a integral de Itô está bem definida para $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $ e é uma aplicação linear.

O teorema a seguir é uma extensão imediada to Lema 10.2.1 e sua demonstração sera omitida.

Teorema 10.2.3

Seja $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $. Então a integral de Itô

$$I(f) = \int_a^bf(t)dB_t$$

é uma variável aleatória com $ \mathbb{E}\left[I(f)\right] = 0 $ e

$$\mathbb{E}\left[\left|I(f)\right|^2\right] = \int_a^b\mathbb{E}\left[\left|f(t)\right|^2\right]dt.$$

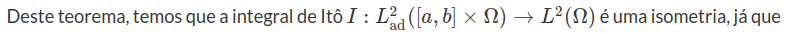
$$\left|\int_a^bf(t)dB_t\right|^2_{L^2(\Omega)} = |I(t)|^2_{L^2(\Omega)} = \langle I(f),I(f)\rangle = \mathbb{E}\left[\left|I(f)\right|^2\right] = \int_a^b\mathbb{E}\left[\left|f(t)\right|^2\right]dt = |f(t)|^2_{L^2_{\text{ad}}([a,b]\times\Omega)}.$$

Um corolário imediato é o seguinte.

Corolário 10.2.1

Para quaisquer $ f,g\in L^2_{\text{ad}}([a,b]\times\Omega) $, a seguinte igualdade ocorre

$$\mathbb{E}\left[\int_a^bf(t)dB_t\int_a^bg(t)dB_t\right] = \int_a^b\mathbb{E}\left[f(t)g(t)\right]dt.$$

Exemplo 10.2.3

Vamos verificar que

$$\int_a^bB_tdB_t = \frac{1}{2}\left(B^2_b - B^2_a - (b-a)\right)$$

Já tentamos definir esta integral. Quando utilizamos o ponto extremo à esquerda dos subintervalos de uma partição de $ [a,b] $ para o integrando, chegamos na soma $ L_n $ dada por

$$L_n = \sum_{i=1}^nB_{t_{i-1}}\left(B_{t_i}-B_{t_{i-1}}\right).$$

Se tomamos a integral como o limite de $ L_n $ quando $ n\rightarrow \infty $, temos que

$$\int_a^bB_tdB_t = \frac{1}{2}\left(B^2_b-B^2_a-(b-a)\right)$$

De fato, observamos que $ \mathbb{E}\left[B_tB_s\right] = \min(s,t) $ que é uma função contínua de $ t $ e $ s $. Então, podemos aplicar o caso 1 do Teorema 10.2.2 ao integrando $ f(t) = B_t $, ou seja, para uma partição $ \Delta_n = (a = t_0 \ < \ t_1 \ < \ \ldots \ < \ t_{n-1} \ < \ t_n = b) $ de $ [a,b] $ definimos o processo estocástico $ f_n(t) $ por

$$f_n(t) = B_{t_{i-1}} \ \text{para} \ t_{i-1} \ < \ t \leq t_i.$$

Então, da definição da integral para processos simples, temos que a integral de Itô $ \int_a^bB_tdB_t $ é dada por

$$\int_a^bB_tdB_t = \lim_{n\rightarrow\infty}I(f_n) \ \text{em} \ L^2(\Omega)$$

em que

$$I(f_n) = \sum_{i=1}^nB_{t_{i-1}}\left(B_{t_i}-B_{t_{i-1}}\right)$$

que é igual a $ L_n $. Portanto

$$\int_a^bB_tdB_t = \frac{1}{2}\left(B^2_b-B^2_a-(b-a)\right).$$

Exemplo 10.2.4

Calcular a integral

$$\int_a^bB^2_tdB_t = \frac{1}{3}\left(B^3_b-B^3_a\right)-\int_a^bB_tdt.$$

De fato, suponha que $ s \ < \ t $. Temos que

$$\mathbb{E}\left[B^2_tB^2_s\right] = \mathbb{E}\left[\left(B_t-B_s+B_s\right)^2B^2_s\right]=\mathbb{E}\left[\left(\left(B_t-B_s\right)^2 + 2B_s\left(B_t-B_s\right) + B^2_s\right)B^2_s\right] = (t-s)s + 3s^2$$

o que mostra que $ \mathbb{E}\left[B^2_tB^2_s\right] $ é uma função contínua de $ t $ e $ s $. Então, aplicamos o caso 1 para a função $ f(t) = B^2_t $.

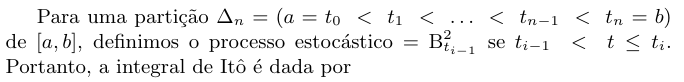
$$\int_a^bB^2_tdB_t = \lim_{n\rightarrow\infty}\sum_{i=1}^nB^2_{t_{i-1}}\left(B_{t_i}-B_{t_{i-1}}\right) \ \text{em} \ L^2(\Omega)$$

Em contrapartida, para o segundo somatório, temos que (verificar)

$$\mathbb{E}\left[\left|\sum_{i=1}^nB_{t_{i-1}}\left(B_{t_i}-B_{t_{i-1}}\right)^2 - \sum_{i=1}^nB_{t_{i-1}}(t_i-t_{i-1})\right|^2\right] = 2\sum_{i=1}^n2t_{i-1}(t_i-t_{i-1})^2\leq 2b(b-a)|\Delta_n|\stackrel{n\rightarrow\infty}{\longrightarrow}0$$

de forma que $ \sum_{i=1}^nB_{t_i}\left(B_{t_i}-B_{t_{i-1}}\right)^2 $ converge para $ \sum_{i=1}^nB_{t_{i-1}}(t_i-t_{i-1}) = \int_a^bB_tdt $ em $ L^2(\Omega) $. Portanto, concluímos que

$$\int_a^bB^2_tdB_t = \lim_{n\rightarrow\infty}\sum_{i=1}^nB^2_{t_{i-1}}\left(B_{t_i}-B_{t_{i-1}}\right) = \frac{1}{3}\left(B^3_b-B^3_a\right)-\int_a^bB_tdt$$

Exemplo 10.2.5

O processo

$$X_t = \int_0^tB^2_udB_u = \frac{1}{3}B^3_t - \int_0^tB_udu$$

é um martingale.

De fato, seja $ 0\leq s\leq t $. Inicialmente, seja $ B^3_t $ escrito como

$$B^3_t = \left(B_t-B_s\right)^3 + 3\left(B_t-B_s\right)^2B_s + 3\left(B_t-B_s\right)B^2_s + B^3_s$$

e então, tomando a esperança condicional, temos que

$$\mathbb{E}\left[B^3_t\Big|\mathcal{F_s}\right] = \mathbb{E}\left[\left(B_t-B_s\right)^3\Big|\mathcal{F_s}\right] + 3\mathbb{E}\left[\left(B_t-B_s\right)^2B_s\Big|\mathcal{F_s}\right] + 3\mathbb{E}\left[\left(B_t-B_s\right)B^2_s\Big|\mathcal{F_s}\right]+\mathbb{E}\left[B^3_s\Big|\mathcal{F_s}\right] = 3(t-s)B_s + B^3_s.$$

Além disso, temos que

$$\mathbb{E}\left[\int_0^tB_udu\Big|\mathcal{F_s}\right]= \mathbb{E}\left[\int_0^sB_udu\Big|\mathcal{F_s}\right] + \mathbb{E}\left[\int_s^tB_ud_u\Big|\mathcal{F_s}\right] = \int_0^sB_udu + \int_s^t\mathbb{E}\left[B_u|\mathcal{F_s}\right]du = \int_0^sB_udu + B_s(t-s).$$

Portanto,

$$\mathbb{E}\left[X_t\Big|\mathcal{F_s}\right] = (t-s)B_s + \frac{1}{3}B^3_s - \int_0^sB_ud_u - B_s(t-s) = \frac{1}{3}B^3_s - \int_0^sB_udu = X_s$$

o que mostra que $ X_t $ é um martingale.

Considere agora $ X_t $ com $ a\leq t\leq b $ um martingale e $ \phi $ uma função convexa tal que $ \phi(X_t) $ é integrável para cada $ t\in[a,b] $. Então $ \phi(X_t) $ é um submartingale a partir da desigualdade de Jensen. Por exemplo, com a função $ \phi(x) = |x| $, temos o submartingale $ |X_t| $.

Definição 10.2.2

Um processo estocástico $ X_t $ com $ a\leq t\leq b $ é chamado contínuo à direita se quase todas as suas trajetórias são funções contínuas à direita em $ [a,b] $, isto é,

$$\mathbb{P}\left[\left(\omega; X_t(\omega) \ \text{é contínuo à direita em} \ [a,b]\right)\right] = 1.$$

Teorema 10.2.4 (Desigualdade submartingale de Doob)

Seja $ X_t $ com $ a\leq t\leq b $ um submartingale contínuo à direita. Então, para todo $ \varepsilon \ > \ 0 $, temos que

$$\mathbb{P}\left[\left(\sup_{0\leq t\leq b}X_t\geq\varepsilon\right)\right] \leq \frac{1}{\varepsilon}\mathbb{E}\left[X_b^{+}\right]$$

em que $ X_b^{+} $ é a parte positiva de $ X_b $, isto é, $ X_b^{+} = \max_{\omega}(X_b,0) $. Em particular, se $ X_t $ é um martingale contínuo à direita, então, para todo $ \varepsilon \ > \ 0 $,

$$\mathbb{P}\left[\left(\sup_{0\leq t\leq b}|X_t|\geq\varepsilon\right)\right] \leq \frac{1}{\varepsilon}\mathbb{E}\left[\left|X_b\right|\right].$$

Demonstração: Seja $ \mathbb{Q}= (r_1,r_2,\ldots) $ uma enumeração dos números racionais em $ [a,b] $. Então, da continuidade à direita de $ X_t $, temos que

$$\sup_{a\leq t\leq b}X_t = \sup_{r\in\mathbb{Q}}X_r \ \mathbb{P}-q.c. \qquad (5)$$

Para cada $ k $, organizamos os números no conjunto $ (r_1,r_2,\ldots,r_k) $ em ordem crescente $ (r^{(k)}_1 \ < \ r^{(k)}_2 \ < \ r^{(k)}_k) $. Então, para todo $ \varepsilon \ > \ 0 $, temos que

$$\left(\sup_{r\in\mathbb{Q}}X_r \geq \varepsilon\right)=\bigcap_{n=1}^{\infty}\bigcup_{k=1}^{\infty}\left(\max_{1\leq v\leq k}X_{r^{(k)}_v} \geq \varepsilon - \frac{1}{n}\right). \qquad (6)$$

De $ (5) $ e $ (6) $, segue que

$$\mathbb{P}\left[\left(\sup_{a\leq t\leq b}X_t \geq \varepsilon\right)\right] = \mathbb{P}\left[\left(\sup_{r\in\mathbb{Q}}X_t\geq\varepsilon\right)\right] = \lim_{n\rightarrow\infty}\lim_{k\rightarrow\infty}\mathbb{P}\left[\left(\max_{1\leq v\leq k}X_{r^{(k)}_v}\geq \varepsilon - \frac{1}{n}\right)\right] \qquad (7)$$

Observamos agora que $ \left(X_{r^{(k)}_j}\right)_{j\geq 1} $ é um submartingale discreto. Então, pela desigualdade submartingalde de Doob discreta, temos que

$$\mathbb{P}\left[\left(\max_{1\leq v\leq k}X_{r^{(k)}_v} \geq \varepsilon - \frac{1}{n}\right)\right] \leq \frac{1}{\varepsilon - \frac{1}{n}}\mathbb{E}\left[X_{r^{(k)}_v}\right]. \qquad (8)$$

Também observamos que $ \left(X^{+}_{r^{(k)}_j}\right)_j $ é um submartingale. Portanto,

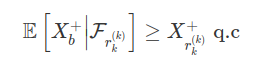
e, aplicando o valor esperado, segue que

$$\mathbb{E}\left[X_{r^{(k)}_k}^{+}\right]\leq \mathbb{E}\left[X_b^{+}\right]. \qquad (9)$$

Juntando $ (7) $, $ (8) $ e $ (9) $, temos

$$\mathbb{P}\left[\left(\sup_{a\leq t\leq b}X_t\geq \varepsilon\right)\right] \leq \frac{1}{\varepsilon}\mathbb{E}\left[X_{r^{(k)}_v}^{+}\right]\leq\frac{1}{\varepsilon}\mathbb{E}\left[X_b^{+}\right]$$

como queríamos demonstrar.

$ \square $

Processos estocásticos definidos por integrais de Itô

Seja $ B_t $ um movimento Browniano fixo e $ (\mathcal{F_t}; \ a\leq t\leq b) $ uma filtragem tal que $ B_t $ é $ \mathcal{F_t} $-mensurável e, para todo $ a\leq s \ < \ t\leq b $, $ B_t-B_s $ é independente de $ \mathcal{F_s} $. Então, temos que, para todo $ t\in[a,b] $ e $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $,

$$\int_a^t\mathbb{E}\left[\left|f^2(s)\right|\right]ds \leq \int_a^b\mathbb{E}\left[\left|f^2(s)\right|\right]ds \ < \ \infty.$$

Então, $ f\in L^2_{\text{ad}}([a,t]\times\Omega) $, o que implica que, para cada $ t\in[a,b] $, a integral estocástica $ \int_a^tf_sdB_s $ está definida. Considere um processo estocástico dado por

$$X_t = \int_a^tf_sdB_s; \ a\leq t\leq b.$$

A partir da isometria entre os espaços $ L^2_{\text{ad}}([a,b]\times\Omega) $ e $ L^2(\Omega) $, temos que

$$\mathbb{E}\left[\left|X_t\right|^2\right] = \mathbb{E}\left[\left|\int_a^tf(s)dB_s\right|^2\right] = \int_a^t\mathbb{E}\left[\left|f(s)\right|^2\right]ds \ < \ \infty$$

e, como $ \mathbb{E}\left[|X_t|\right] \leq \left[\mathbb{E}\left[\left|X_t^2\right|\right]\right]^{\frac{1}{2}} \ < \ infty $, a variável aleatória $ X_t $ é integrável para cada $ t $. Logo, podemos tomar a esperança condicional de $ X_t $ com respeito a uma $ \sigma $-álgebra $ \mathcal{F_s} $.

Teorema 10.2.5 (Propriedade martingale)

Suponha que $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $. Então, o processo estocástico

$$X_t=\int_a^tf(s)dB_s, \ a\leq t\leq b$$

é um martingale com respeito à filtragem $ (\mathcal{F_t}; \ a\leq t\leq b) $.

Demonstração: Inicialmente, considere o caso em que $ f $ é um processo estocástico simples. Precisamos mostrar que, para todo $ a\leq s \ < \ t\leq b $,

$$\mathbb{E}\left[X_t\Big|\mathcal{F_s}\right] = X_s.$$

Porém, temos que

$$X_t = \int_a^tf(s)dB_s = \int_a^sf(u)dB_u + \int_s^tf(u)dB_u = X_s + \int_s^tf(u)dB_u$$

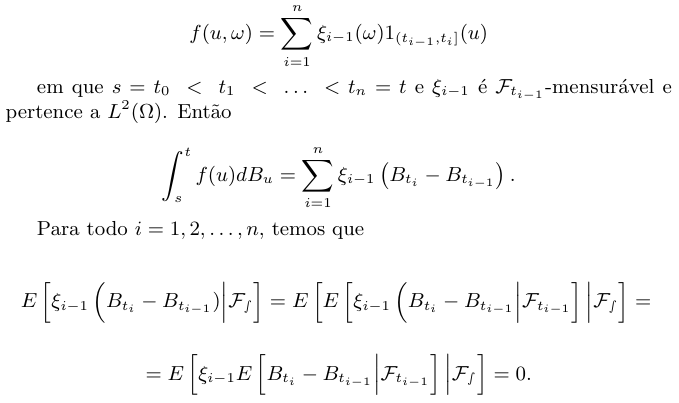
Considere agora o caso geral. Seja $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $. Tome uma sequência $ (f_n) $ de processos simples em $ L^2_{\text{ad}}([a,b]\times\Omega) $ tal que

$$\lim_{n\rightarrow\infty}\int_a^b\mathbb{E}\left[\left|f_n(u)-f(u)\right|^2\right]du = 0.$$

Para cada $ n $, definimos o processo estocástico

$$X^n_t = \int_a^tf_n(u)dB_u.$$

Neste caso, $ X^n_t $ é um martingale. De fato, para $ s \ < \ t $, escrevemos

$$X_t - X_s = (X_t - X^n_t) + (X^n_t - X^n_s) + (X^n_s - X_s)$$

e, então

$$\mathbb{E}\left[X_t-X_s\Big|\mathcal{F_s}\right] = \mathbb{E}\left[X_t-X^n_t\Big|\mathcal{F_s}\right] + \mathbb{E}\left[X^n_s - X_s\Big|\mathcal{F_s}\right]. \qquad (10)$$

Observamos que

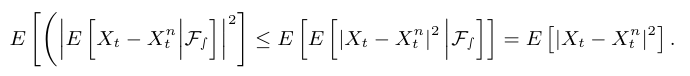
Então,

$$\mathbb{E}\left[\left|\mathbb{E}\left[X_t-X^n_t\Big|\mathcal{F_s}\right]\right|^2\right]\leq \int_a^t\mathbb{E}\left[\left|f_n(u)-f(u)\right|^2\right]du \leq\int_a^b\mathbb{E}\left[\left|f_n(u)-f(u)\right|^2\right]du \rightarrow 0 \ \text{quando} \ n\rightarrow\infty.$$

Portanto, tomando uma subsequência, se necessário, vemos que $ \mathbb{E}\left[X_t-X^n_t\Big|\mathcal{F_s}\right] $ converge quase certamente para 0. Analogamente, $ \mathbb{E}\left[X^n_s-X^s\Big|\mathcal{F_s}\right] $ converge quase certamente para 0. Então $ \mathbb{E}\left[X_t-X_s\Big|\mathcal{F_s}\right] = 0 $ q.c e $ \mathbb{E}\left[X_t\Big|\mathcal{F_s}\right] = X_s $, de forma que $ X_t $ é um martingale, concluindo a demonstração.

$ \square $

Teorema 10.2.6 (Propriedade da continuidade)

Suponha que $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $. Então o processo estocástico

$$X_t = \int_a^tf(s)dB_s, \quad a\leq t\leq b$$

é contínuo, isto é, quase todas as trajetórias são funções contínuas no intervalo $ [a,b] $.

Demonstração: Inicialmente, considere o caso em que $ f $ é um processo estocástico simples, digamos

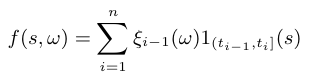
em que $ \xi_{i-1} $ é $ \mathcal{F}_{t_{i-1}} $-mensurável. Neste caso, para cada $ \omega\in\Omega $ fixo, a trajetória de $ X_t $ é dada por

$$X_t(\omega) = \sum_{i=1}^{k-1}\xi_{i-1}(\omega)\left(B_{t_i}-B_{t_{i-1}}\right) + \xi_{k-1}(\omega)\left(B_{t_i}-B_{t_{i-1}}\right)$$

para $ t_{k-1} \leq t \ < \ t_k $. Observe que, para quase todo $ \omega $, a trajetória do movimento Browniano $ B_t $ é contínua. Então, para quase todo $ \omega $, a trajetória $ X_t(\omega) $ é contínua em $ [a,b] $.

Considere agora o caso geral. Seja $ (f_n) $ uma sequência de processos estocásticos simples em $ L^2_{\text{ad}}([a,b]\times\Omega) $ tal que

$$\lim_{n\rightarrow\infty}\int_a^b\mathbb{E}\left[|f_n(s)-f(s)|^2\right]ds = 0.$$

Podemos escolher uma subsequência, se necessário, tal que

$$\int_a^b\mathbb{E}\left[\left|f_n(s)-f(s)\right|^2\right]ds\leq \frac{1}{n^6}, \ \text{para todo} \ n\geq 1.$$

Para cada $ n $, definimos um processo estocástico

$$X^n_t = \int_a^tf_n(s)dB_s, \quad a\leq t\leq b$$

e então, quase todas as trajetórias de $ X^n_t $ são contínuas. Além disso, do Teorema 10.2.5, $ X_t $ e $ X^n_t $ são martingales. Então, pela Desigualdade submartingalde de Doob, temos que

$$ \mathbb{P}\left[\left(\omega:\sup_{a\leq t\leq b}|X_t-X^n_t|\geq\frac{1}{n}\right)\right]\leq n\mathbb{E}\left[\left|X_b-X_b^n\right|\right]. $$

Da desigualdade de Schwartz,

$$\mathbb{E}\left[\left|X_b-X^n_b\right|\right]\leq\left(\mathbb{E}\left[\left|X_b-X^n_b\right|^2\right]\right)^{\frac{1}{2}} = \left(\int_a^b\left|f(s)-f_n(s)\right|^2ds\right)^{\frac{1}{2}}\leq \frac{1}{n^3}.$$

Portanto, para todo $ n\geq 1 $,

$$ \mathbb{P}\left[\left(\omega:\sup_{a\leq t\leq b}\left|X_t-X^n_t\right|\geq\frac{1}{n}\right)\right]\leq \frac{1}{n^2}. $$

Como $ \sum_{n=1}^{\infty}\frac{1}{n^2} \ < \ \infty $, pelo teorema de Borel-Cantelli, temos que

$$ \mathbb{P}\left[\limsup_{n\rightarrow\infty}\left(\omega:\sup_{a\leq t\leq b}\left|X_t-X^n_t\right|\geq\frac{1}{n}\right)\right] = 0 $$

e, tomando o complementar do evento $ (A_n \ \text{ocorre infinitas vezes}) $ temos que

$$ \mathbb{P}\left[\left(\omega:\sup_{a\leq t\leq b}\left|X_t-X^n_t\right|\geq\frac{1}{n} \ \text{ocorre um número finito de vezes}\right)\right] = 1. $$

Portanto, existe um evento $ \Omega_0 $ tal que $ \mathbb{P}\left[\Omega_0\right] = 1 $ e, para cada $ \omega\in\Omega_0 $, existe um inteiro positivo $ N(\omega) $ tal que

$$\sup_{a\leq t\leq b}\left|X_t(\omega)-X^n_t(\omega)\right| \ < \ \frac{1}{n}, \ \text{para todo} \ n\geq N(\omega).$$

Assim, para cada $ \omega\in\Omega_0 $, a sequência de funções $ X^n_t(\omega) $, com $ n\geq 1 $, converge uniformemente para $ X_t(\omega) $ em $ [a,b] $. mas, para cada $ n $, o processo estocástico $ X^n_t $ é contínuo e, então existe um evento $ \Omega_n $ com $ \mathbb{P}(\Omega_n) = 1 $ e, para qualquer $ \omega\in\Omega_n $, a função $ X^n(\omega) $ é contínua.

Finalmente, seja $ \tilde{\Omega} = \cap_{n=0}^{\infty}\Omega_n $. Então, temos que $ \mathbb{P}\left[\tilde{\Omega_n}\right] = 1 $ e, para cada $ \omega\in\tilde{\Omega} $, a sequência

$$X^n_{\cdot}(\omega), \quad n = 1,2,3,\ldots$$

é uma sequência de funções contínuas que converge uniformemente para $ X_{\cdot}(\omega) $ em $ [a,b] $. Segue que $ X_{\cdot}(\omega) $ é uma função contínua para cada $ \omega\in\tilde{\Omega} $. Então, quase todas as trajetórias dos processos estocásticos $ X_t $ são funções contínuas em $ [a,b] $. Desta forma, mostramos que $ X_t $ é um processo estocástico contínuo.

$ \square $

Extensão de integrais estocásticas

A integral de Itô foi definida para processos estocásticos $ f(t) $ que são $ \mathcal{F_t} $-adaptados e que satisfazem a condição $ \int_a^b\mathbb{E}\left[\left|f(t)\right|^2\right]dt \ < \ \infty $. Desta forma, vimos que a integral estocástica $ I(f) $ pertence a $ L^2(\Omega) $ e, portanto, é integrável. Além disso, $ X_t = \int_a^tf(s)dB_s $ com $ a\leq t\leq b $ é um martingale. A ideia agora é estender o conceito da integral de Itô $ I(f) $ para processos estocásticos $ f(t) $ que sejam $ \mathcal{F_t} $-adaptados e que satisfazem a condição $ \int_a^b\left|f(t)\right|^2dt \ < \ \infty $ quase certamente. Neste caso, a integral $ I(f) $ é uma variável aleatória, em geral, não integrável. A falta de integrabilidade de um processo estocástico leva ao conceito de martingale local.

A fim de estender o conceito de integral para esta classe maior de integrandos, fixamos um movimento Browniano $ B_t $ e uma filtragem $ \left(\mathcal{F_t}\right)_t $ com $ a\leq t\leq b $ tal que

1. para cada $ t $, $ B_t $ é $ \mathcal{F_t} $-mensurável.

2. para qualquer $ s\leq t $, a variável aleatória $ B_t - B_s $ é independente da $ \sigma $-álgebra $ \mathcal{F_s} $.

Vamos definir a integral estocástica $ \int_a^bf(t)dB_t $ para um processo estocástico $ f(t,\omega) $ que satisfaz as seguintes condições

1. $ f(t) $ é adaptado à filtragem $ \mathcal{F_t} $.

2. $ \int_a^b\left|f(t)\right|^2dt \ < \ \infty $ q.c.

Notação 10.2.2

Usaremos a notação $ \mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $ para denotar o espaço dos processos estocásticos $ f(t,\omega) $ que satisfazem as condições definidas acima.

Se $ f(t)\in L^2_{\text{ad}}([a,b]\times\Omega) $, então $ \mathbb{E}\left[\left|f(t)\right|^2\right] \ < \ \infty $ e, pelo teorema de Fubini, temos que

$$\mathbb{E}\left[\int_a^b\left|f(t)\right|^2dt\right] = \int_a^b\mathbb{E}\left[\left|f(t)\right|^2\right]dt \ < \ \infty$$

de onde concluímos que $ L^2_{\text{ad}}([a,b]\times\Omega)\subset\mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $. Desta forma temos uma classe efetivamente maior de integrandos $ f(t,\omega) $ para a integral estocástica $ \int_a^bf(t)dB_t $. A diferença crucial é a possível falta de integrabilidade do integrando $ f(t,\omega) $ com respeito à variável $ \omega $.

Exemplo 10.2.6

Considere o processo estocástico $ f(t) = e^{B^2_t} $. Temos que

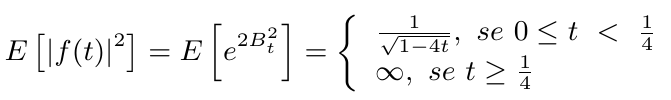
É claro que $ \int_0^1\mathbb{E}\left[\left|f(t)\right|^2\right]dt = \infty $ e então $ f\notin L^2_{\text{ad}}([0,1]\times\Omega) $. Então, $ \int_0^1e^{B^2_t}dB_t $ não é uma integral estocástica como definido anteriormente. Porém, como $ f(t) $ é uma função contínua de $ t $, $ \int_0^1\left|f(t)\right|^2dt \ < \ \infty $ q.c. Ou seja, $ f\in\mathcal{L}_{\text{ad}}(\Omega,L^2([0,1])) $.

Exemplo 10.2.7

Considere o processo estocástico $ f(t) = e^{B^k_t} $. Para qualquer inteiro $ k\geq 3 $, temos que

$$\mathbb{E}\left[\left|f(t)\right|^2\right] = \mathbb{E}\left[e^{2B^k_t}\right] = \int_{-\infty}^{\infty}e^{2x^k}\frac{1}{\sqrt{2\pi t}}e^{-\frac{x^2}{2t}}dx = \infty.$$

Então, $ f\notin L^2_{\text{ad}}([a,b]\times\Omega) $. Reciprocamente, observamos que quase todas as trajetórias de $ f(t) $ são funções contínuas e, portanto, pertencem a $ L^2([a,b]) $. Assim, temos que $ f\in\mathcal{L}_{ad}(\Omega,L^2([a,b])) $.

Observação 10.2.2

É importante observar que, em geral, são necessárias muitas contas para verificar se um processo estocástico $ \mathcal{F_t} $-adaptado pertence a $ L^2_{\text{ad}}([a,b]\times\Omega) $, porém é fácil verificar se o processo pertence a $ \mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $.

Lema 10.2.2

Seja $ f\in\mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $. Então existe uma sequência $ (f_n)_n $ em $ L^2([a,b]\times\Omega) $ tal que

$$\lim_{n\rightarrow\infty}\int_a^b\left|f_n(t)-f(t)\right|^2dt = 0 \ \text{q.c}$$

e, portanto, também em probabilidade.

Demonstração: Para cada $ n $ definimos

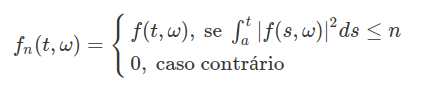
Então, $ f_n $ é adaptado à filtragem $ (\mathcal{F_t})_t $. Além disso,

$$\int_a^b\left|f_n(t)\right|^2dt = \int_a^{\tau_n(\omega)}\left|f(t)\right|^2dt \ \text{q.c}$$

em que $ \tau_n(\omega) = \sup(t; \int_a^t\left|f(s)\right|^2ds\leq n) $. Portanto, temos que

$$\int_a^b\left|f_n(t)\right|^2dt \leq n \ \text{q.c}$$

o que implica que $ \int_a^b\mathbb{E}\left[\left|f(t)\right|^2\right]dt\leq n $ e, portanto, $ f_n\in L^2_{\text{ad}}([a,b]\times\Omega) $. Seja $ \omega $ fixo. Assim que $ n $ torna-se suficientemente grande de forma que $ \int_a^b\left|f(t)\right|^2dt \ < \ n $, temos que

$$f_n(t) = f(t) \ \text{para todo} \ t\in[a,b]$$

o que implica que

$$\lim_{n\rightarrow\infty}\int_a^b\left|f_n(t)-f(t)\right|^2dt = 0.$$

Como $ \int_a^b\left|f(t)\right|^2dt \ < \ \infty $ q.c, a convergência ocorre quase certamente. Além disso, a convergência quase certa implica a convergência em probabilidade.

$ \square $

A seguir, apresentamos um lema fundamental para a definição de integral estocástica para funções $ f\in\mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $.

Lema 10.2.3

Seja $ f(t) $ um processo estocástico simples em $ L^2_{\text{ad}}([a,b]\times\Omega) $. Então a desigualdade

$$\mathbb{P}\left[\left(\left|\int_a^bf(t)dB_t\right| \ < \ \varepsilon\right)\right]\leq\frac{c}{\varepsilon^2}+\mathbb{P}\left[\left(\int_a^b\left|f(t)\right|^2dt \ > \ c\right)\right]$$

ocorre para quaisquer constantes positivas $ \varepsilon $ e $ c $.

Demonstração: Para cada constante positiva $ c $, definimos um processo estocástico $ f_c(t) $ dado por

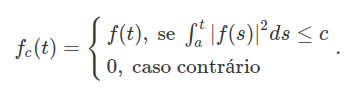
Observamos que

$$\left(\left|\int_a^bf(t)dB_t\right| \ > \ \varepsilon\right)\subset\left(\left|\int_a^bf_c(t)dB_t\right| \ > \ \varepsilon\right)\bigcup\left(\int_a^bf(t)dB_t\neq\int_a^bf_c(t)dB_t\right).$$

Então, temos que

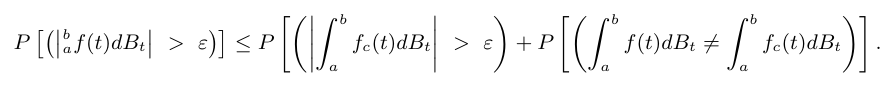
Como $ f $ é um processo estocástico simples, temos que

$$\left(\int_a^bf(t)dB_t\neq\int_a^bf_c(t)dB_t\right)\subset\left(\int_a^b\left|f(t)\right|^2dt \ > \ c\right).$$

Portanto,

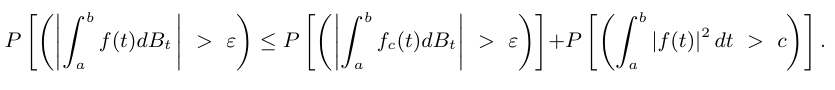
Da definição de $ f_c $, temos que $ \int_a^b\left|f_c(t)\right|^2dt\leq c $ q.c. Então $ \mathbb{E}\left[\int_a^b\left|f_c(t)\right|^2dt\right]\leq c $ e, então, podemos aplicar a desigualdade de Chebyschev ao primeiro termo da última desigualdade e

$$\mathbb{P}\left[\left(\left|\int_a^bf(t)dB_t\right| \ > \ \varepsilon\right)\right] \leq \frac{1}{\varepsilon^2}\mathbb{E}\left[\left|\int_a^bf_c(t)dB_t\right|^2\right]+\mathbb{P}\left[\left(\int_a^b\left|f(t)\right|^2dt \ > \ c\right)\right]$$

e, portanto

$$\mathbb{P}\left[\left(\left|\int_a^bf(t)dB_t\right| \ > \ \varepsilon\right)\right]\leq \frac{1}{\varepsilon^2}\int_a^b\mathbb{E}\left[\left|f_c(t)\right|^2\right]dt+\mathbb{P}\left[\left(\int_a^b\left|f(t)\right|^2dt \ > \ c\right)\right] \leq\frac{c}{\varepsilon^2}+\mathbb{P}\left[\left(\int_a^b\left|f(t)\right|^2dt \ > \ c\right)\right].$$

provando o resultado.

$ \square $

Lema 10.2.4

$$\lim_{n\rightarrow\infty}\int_a^b\left|f_n(t)-f(t)\right|^2dt = 0$$

em probabilidade.

Demonstração: Inicialmente, utilizando o Lema 10.2.2, existe uma sequência $ (g_n) $ em $ L^2_{\text{ad}}([a,b]\times\Omega) $ tal que

$$\lim_{n\rightarrow\infty}\int_a^b\left|g_n(t)-f(t)\right|^2dt = 0 \qquad (11)$$

em probabilidade. Agora, para cada $ g_n(t) $, existe um processo simples $ f_n(t) $ em $ L^2_{\text{ad}}([a,b]\times\Omega) $ tal que

$$\mathbb{E}\left[\int_a^b\left|f_n(t)-g_n(t)\right|^2dt\right] \ < \ \frac{1}{n}. \qquad (12)$$

Pela desigualdade de Young, temos que, para todo $ \varepsilon \ > \ 0 $,

$$\left(\int_a^b\left|f_n(t)-f(t)\right|^2dt \ > \ \varepsilon\right) \subset \left(\int_a^b\left|f_n(t)-g_n(t)\right|^2dt \ > \ \frac{\varepsilon}{4}\right)\bigcup\left(\int_a^b\left|g_n(t)-f(t)\right|^2dt \ > \ \frac{\varepsilon}{4}\right)$$

e, então

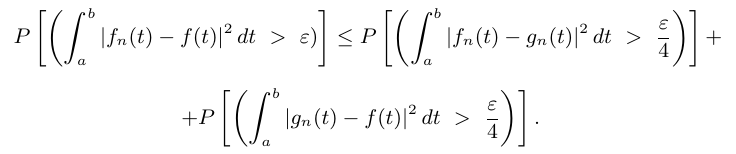
E, da desigualdade de Chebyshev, juntamente com $ (12) $, temos que

$$\mathbb{P}\left[\left(\int_a^b\left|f_n(t)-f(t)\right|^2dt \ > \ \varepsilon\right)\right] \leq\frac{4}{\varepsilon n} + \mathbb{P}\left[\left(\int_a^b\left|g_n(t)-f(t)\right|^2dt \ > \ \frac{\varepsilon}{4}\right)\right].$$

Da equação $ (11) $, segue que, para todo $ \varepsilon \ > \ 0 $,

$$\lim_{n\rightarrow\infty}\mathbb{P}\left[\left(\int_a^b\left|f_n(t)-f(t)\right|^2dt \ > \ \varepsilon\right)\right] = 0$$

como queríamos.

$ \square $

Desta forma, estamos em condições de definir a integral

$$\int_a^bf(t)dB_t$$

para $ f\in\mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $. A partir do Lema 10.2.4, podemos escolher uma sequência $ (f_n) $ de processos estocásticos simples em $ L^2([a,b]\times\Omega) $ tal que

$$\lim_{n\rightarrow\infty}\int_a^b\left|f_n(t)-f(t)\right|^2dt = 0 \qquad (13)$$

em probabilidade. Para cada $ n $, a integral estocástica

$$I(f_n) = \int_a^bf_n(t)dB_t$$

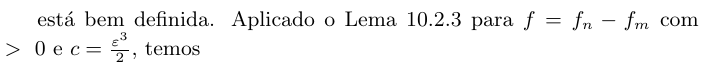
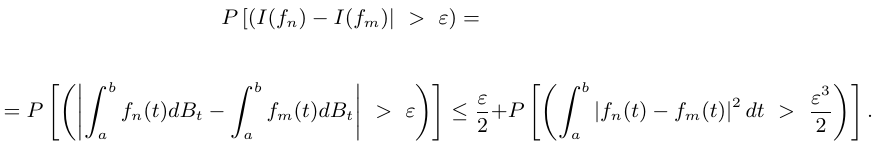
Também é importante observar que

$$\left(\int_a^b\left|f_n(t)-f_m(t)\right|dt \ > \ \frac{\varepsilon^3}{2}\right)\subset\left(\int_a^b\left|f_n(t)-f(t)\right|^2dt \ > \ \frac{\varepsilon^3}{8}\right)\bigcup\left(\int_a^b\left|f_m(t)-f(t)\right|^2dt \ > \ \frac{\varepsilon^3}{8}\right)$$

de onde temos a desigualdade

$$\mathbb{P}\left[\left(\int_a^b\left|f_n(t)-f_m(t)\right|^2dt \ > \ \frac{\varepsilon^3}{2}\right)\right]\leq \mathbb{P}\left[\left(\int_a^b\left|f_n(t)-f(t)\right|^2dt \ > \ \frac{\varepsilon^3}{8}\right)\right] + \mathbb{P}\left[\left(\int_a^b\left|f_m(t)-f(t)\right|^2dt \ > \ \frac{\varepsilon^3}{8}\right)\right].$$

De $ (13) $, temos que

$$\lim_{n\rightarrow\infty}\mathbb{P}\left[\left(\int_a^b\left|f_n(t)-f_m(t)\right|^2dt \ > \ \frac{\varepsilon^3}{2}\right)\right] = 0$$

e então, existe $ N \ > \ 1 $, tal que

$$\mathbb{P}\left[\left(\int_a^b\left|f_n(t)-f_m(t)\right|^2dt \ > \ \frac{\varepsilon^3}{2}\right)\right] \ < \ \frac{\varepsilon}{2} \ \text{para todo} \ n,m\geq N. \qquad (15)$$

De $ (14) $ e $ (15) $, segue que

$$\mathbb{P}\left[\left(\left|I(f_n)-I(f_m)\right| \ > \ \varepsilon\right)\right] \ < \ \varepsilon \ \text{para todo} \ n, m\geq N$$

o que mostra que a sequência $ (I(f_n)) $ de variáveis aleatórias converge em probabilidade. Desta forma, definimos

$$I(f) = \int_a^bf(t)dB_t = \lim_{n\rightarrow\infty}\int_a^bf_n(t)dB_t = \lim_{n\rightarrow\infty}I(f_n) \ \text{em probabilidade}$$

Observação 10.2.3

É importante observar que o limite é independente da escolha da sequência $ (f_n) $ de forma que a integral $ \int_a^bf(t)dB_t $ está bem definida. Além disso, a integral estocástica $ \int_a^bf(t)dB_t $ estende o conceito de integral estocástica de funções $ f\in L^2_{\text{ad}}([a,b]\times\Omega) $ para $ \mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $. Outra importante observação é que, se $ f\in L^2_{\text{ad}}([a,b],\Omega) $ então $ \int_a^bf(t)dB_t $ pertence a $ L^2(\Omega) $. No entanto, se $ f\in\mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $, então $ \int_a^bf(t)dB_t $ é uma variável aleat[oria e, em geral, não possui valor esperado finito.

Teorema 10.2.7

Suponha que $ f $ é um processo estocástico $ (\mathcal{F_t}) $-adaptado contínuo. Então $ f\in\mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $ e

$$\int_a^bf(t)dB_t = \lim_{|\mathcal{P}_n|\rightarrow 0}\sum_{i=1}^nf(t_{i-1})\left(B_{t_i}-B_{t_{i-1}}\right) \ \text{em probabilidade}.$$

Demonstração: De fato, observamos que, se $ \theta\in\mathcal{L}_{\text{ad}}(\Omega,L^2([a,b])) $ é dado por

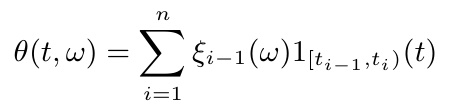
em que $ \xi_{i-1} $ é $ \mathcal{F}_{t_{i-1}} $-mensurável. Então, temos que

$$\int_a^b\theta(t)dB_t = \sum_{i=1}^n\xi_{i-1}\left(B_{t_i}-B_{t_{i-1}}\right). \qquad (16)$$

$$\int_a^b\left|f_n(t)-f(t)\right|^2dt \rightarrow 0$$

quase certamente e, então, em probabilidade, quando $ n\rightarrow\infty $. Utilizando a definição, temos que

$$\int_a^bf(t)dB_t = \lim_{\mathcal{P}_n}\int_a^bf_n(t)dB_t$$

em probabilidade. Podemos utilizar $ (16) $ com $ \theta = f_n $ e então

$$\int_a^bf_ndB_t = \sum_{i=1}^nf(t_{i-1})\left(B_{t_i}-B_{t_{i-1}}\right)$$

de onde concluímos o teorema.

Processo estocástico Associado e Martingale Local

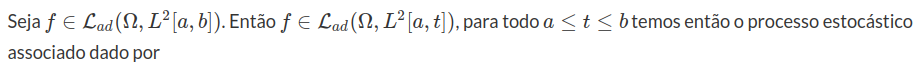
$$X_t=\int_a^tf(s)dB(s), a\leq t\leq b.$$

$ X_t $ não tem necessariamente esperança finita e por isso não faz sentido dizer que $ X_t $ é um martingale. Para isso, necessitamos generalizar o conceito de martingale. Pois, desta forma seremos capaz de cobrir a situação em que $ X_t $ não tem esperança finita. Vamos usar o conceito de tempo de parada.

Note que

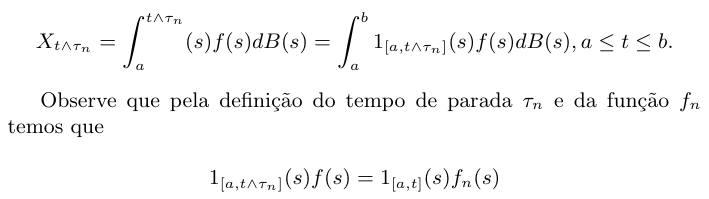
para quase todo $ \omega $. Portanto,

$$X_{t\wedge \tau_n}=\int_a^{t\wedge \tau_n}(s)f(s)dB(s)=\int_a^tf_n(s)dB(s), a\leq t\leq b.$$

Então, temos que

$$\int_a^b\mathbb{E}(|f_n(t)|^2)dt\leq n$$

O que implica que $ f_n\in L^2_{ad}([a,b],\Omega) $. Mais isso implica que $ X_{t\wedge \tau_n} $ é um martingale para cada $ n $.

Temos que $ \tau_n $ é uma sequência monótona e crescente para $ b $ quando $ n\rightarrow \infty $. Com isso, vamos fazer a seguinte definição

Definição 10.2.3 (Martingale Local)

Seja $ X_t $ um processo $ \mathcal{F_t} $ adaptado, $ a\leq t\leq b $ é chamado de um martingale Local com respeito a $ \mathcal{F_t} $ se existe uma sequência de tempos de parada $ \tau_n $, $ n\in \mathbb{N} $, tal que $ \tau_n $ é monotonamente crescente para b quase certamente quando $ n\rightarrow \infty $. E para cada $ n $ temos que $ X_{t\wedge\tau_n} $ é um martingale com respeito a $ (\mathcal{F_t};a\leq t\leq b) $.

Claro que todo martingale é um martingale local, para isso basta tomar $ \tau_n=b $ para todo $ n $. Entretanto, temos que nem todo martingale local é um martingale como o exemplo pudemos ver para o caso de

$$X_t=\int_a^tf(s)dB(s), a\leq t\leq b.$$

Desta forma, obtemos o seguinte teorema

Teorema 10.2.8

Seja $ f\in \mathcal{L}_{ad}(\Omega,L^2[a,b]) $. Então, o processo estocástico

$$X_t=\int_a^tf(s)dB(s), a\leq t\leq b.$$

é um martingale local com respeito a filtragem $ \mathcal{F_t} $ gerada pelo movimento Browniano.

Exemplo 10.2.8

Seja $ f(t)=e^{B(t)^2} $, sabemos que $ f\in \mathcal{L}_{ad}(\Omega,L^2[a,b]) $. Portanto, pelo teorema acima temos que

$$X_t=\int_a^tf(s)dB(s), a\leq t\leq b.$$

é um martingale local. Por outro lado considere o processo estocástico

$$Y_t=\int_0^t e^{B(s)^2}dB(s), 0\leq t< \frac{1}{4}.$$

é um martingale, pois

$$\mathbb{E}(|e^{B(s)^2}|^2)=\mathbb{E}(e^{2B(s)^2})=\frac{1}{\sqrt{1-4t}}, 0\leq t< 1/4$$

Lema 10.2.5

Suponha que $ f\in L^2_{ad}([a,b]\times \Omega) $. Seja

$$C=(\omega;f(t,\omega)=0, \forall t\in [a,b])$$

Então temos que

$$\int_a^bf(t)dB(t)=0$$

quase certamente em C.

Demonstração:

Defina

O que implica que

$$\mathbb{E}(|Y(\tau)|^2)=0$$

e $ Y(\tau)=0 $ quase certamente. Mas se $ \omega\in C $ então temos que $ \tau(\omega)=b $ e portanto temos que

$$Y(\tau(\omega))=\int_a^b f(s)dB(s)$$

O que mostra que $ \int_a^b f(s)dB(s)=0 $ para quase todo $ \omega\in A $.

Teorema 10.2.9

Seja $ f\in \mathcal{L}_{ad}(\Omega,L^2[a,b]) $. Então o processo estocástico

$$X_t=\int_a^t f(s)dB(s),\quad a\leq t\leq b$$

tem realização contínua.

Demonstração:

Para cada $ n $, seja $ f_n $ um processo estocástico definida por

e seja

$$X_t^{(n)}=\int_a^t f_n(s)dB(s), \quad a\leq t \leq b. $$

Então pelo Teorema 10.2.6 é um processo estocástico contínuo. Seja

$$A_n=(\omega, \int_a^b |f(t,\omega)|^2 dt \leq n)$$

$$f_n(t,\omega)=f_m(t,\omega),\quad \forall m\geq n \quad e \quad \forall t\in [a,b]$$

Portanto, pelo Lemma acima temos que $ \forall n\in A_n $,

$$X_t^{(m)}(\omega)=X_t^{(n)}(\omega), \forall m\geq n$$

e qualquer $ t\in [a,b] $. Desde que $ A=\bigcup_{n=1}^{\infty} A_n $, a igualdade acima implica que para todo $ \omega\in A $ o seguinte limite existe para todo $ t\in [a,b] $:

$$\lim_{m\rightarrow \infty}X_t^{(m)}(\omega)$$

Agora definimos o processo estocástico $ Y_t(\omega) $ por

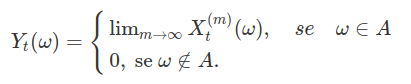
Então $ Y_t(\omega) $ é um processo estocástico contínuo. Por outro lado, da definição de integral estocástica dada pela equação acima da Observação 10.2.3 . Temos que

$$X_t=\lim_{m\rightarrow \infty}X_t^{(m)}$$

em probabilidade. Portanto, para cada $ t\in [a,b] $, $ X_t=Y_t $ quase certamente. Portanto $ Y_t $ é uma realização contínua de $ X_t $.

10.3 - Integral Estocástica para Martingales

O objetivo principal desta seção é ampliar a definição de integral estocástica. Anteriormente, definimos a integral com respeito ao movimento Browniano e o integrando $ f $ como sendo um processo adaptado e satisfazendo a condição

$$\mathbb{E}\left[\int_a^b\left|f(t)\right|^2dt\right] \ < \ \infty \ \text{q.c}.$$

Agora, o objetivo será definir a integral estocástica com respeito a um martingale $ M $ adaptado a filtragem do Movimento Browniano, isto é, uma integral do tipo

$$\int_a^bf(t)dM_t$$

em que $ M_t $ é uma martingale quadrado integrável e adaptado a filtragem do movimento Browniano. Para mostrar isso, vamos necessitar de alguns resultados técnico. Como $ M_t $ é um martingale adaptado a filtragem do Movimento Browniano, do teorema da representação martigale, existe um processo previsível $ H $ tal que

$$M_t = \int_a^bH(s)dB_s$$

Do teorema 10.2.6 da seção Integral de Itô, caso $ H(s)\in L_{ad}([a,b]\times\Omega) $, $ M_t $ é um martingale contínuo.

Intuitivamente, o “diferencial” $ dM_t $ de $ M_t $ pode ser definido por

$$dM_t = H(t)dB_t$$

e, desta forma, é razoável definir a integral estocástica com respeito a $ M_t $ por

$$\int_a^bf(t)dM_t = \int_a^bf(t)H(t)dB_t. \qquad (2)$$

Vamos mostrar que de fato, isto acontece. Mais do que isso, vamos definir a integral para todo martingale $ M_t $ adaptado a filtragem do Movimento Browniano e quadrado integrável.

Obs: nem todo martingale pode ser escrito como uma integral como mostrado acima. Um exemplo simples é o processo de poisson compensado.

Notação 10.3.1

Seja $ \left(\mathcal{F_t}; \ a\leq t\leq b\right) $ a filtragem do Movimento Browniano, em que assumimos que todas as $ \sigma $-álgebra $ \mathcal{F_t} $ são completas. Denotamos por $ \mathbb{L} $ a coleção dos processos estocásticos conjuntamente mensuráveis $ X_t $ que satisfaz a seguinte condição:

1. $ X_t $ é adaptado a $ \left(\mathcal{F_t}\right) $.

Exemplo 10.3.1

Seja $ B_t $ o Movimento Browniano. e tome $ M_t=B^{2}_t-t $. Então $ M_t\in\mathbb{L} $.

Teorema 10.3.1 (Decomposição de Doob-Meyer)

Seja $ X_t $ um submartingale com respeito a uma filtragem contínua a direita $ \left(\mathcal{F_t}; \ a\leq t\leq b\right) $. Então podemos decompor $ X_t $, de forma única, da forma

$$X_t=M_t+C_t, \quad a\leq t\leq b$$

em que $ M_t $ é um martingale com respeito a $ \left(\mathcal{F_t}; \ a\leq t\leq b\right) $ e $ C_t $ é um processo previsível, contínuo à direita e crescente quase certamente com $ \mathbb{E}\left[C_t\right] \ < \ \infty $ para todo $ t\in [a,b] $ com $ C_a = 0 $.

A demonstração deste fato para o caso discreto pode ser encontrada aqui. Para o caso contínuo, a demonstração é um pouco mais complicada e será omitida.

Definição 10.3.1

O processo estocástico previsível $ C_t $ obtido da decomposição de Doob-Meyer é chamado de compensador do submartingale $ X_t $.

É importante observar que, se $ M_t $ é um martingale quadrado integrável, então $ \mathbb{E}\left[M_t^2\right] \ < \ \infty $ e, então, podemos aplicar a desigualdade condicional de Jensen para verificar que $ M^2_t $ é um submartingale. Apresentamos, a seguir, um caso especial da Decomposição de Doob-Meyer para o submartingale $ M^2_t $.

Teorema 10.3.2

Seja $ M_t, \ a\leq t\leq b $ um martingale adaptado a filtragem do movimento browniano e quadrado integrável. Então, existe uma única decomposição da forma

$$M^2_t = L_t + A_t, \ a\leq t\leq b,$$

em que $ L_t $ é um martingale contínuo e $ A_t $ é um processo previsível, contínuo à direita e crescente tal que $ A_a = 0 $ e $ \mathbb{E}\left[A_t\right] \ < \ \infty $ para todo $ t\in [a,b] $.

Notação 10.3.2

A fim de facilitar a notação, utilizaremos $ \langle M\rangle_t $ para denotar o compensador $ A_t $ de $ M^2_t $ na decomposição de Dobb-Meyer do submartingale $ M^2_t $.

Para um martingale $ M_t $, como mostrado no teorema, podemos mostrar que o seguinte limite existe

Observação 10.3.1

Em geral, o processo de variação quadrática $ \left[M\right]_t $ de $ M_t $ não é igual ao compensador $ \langle M\rangle_t $ de $ M^2_t $. Entretanto, pela decomposição de Doob-Meyer, $ M^2_t-\langle M\rangle_t $ é um martingale. Portanto, $ \left[M\right]_t-\langle M\rangle_t $ é, também, um martingale. Além disso, $ \langle M\rangle_t $ é o único compensador previsível do processo estocástico $ \left[M\right]_t $.

Exemplo 10.3.3

Considere um movimento Browniano $ B_t $ e seja $ a = 0 $ e $ b = t $. Considerando o Teorema 10.2.1, temos que a variação quadrática de $ B_t $ é dada por $ \left[B\right]_t = t $. Além disso, temos que $ B^2_t - t $ é um martingale. Portanto, da decomposição de Doob-Meyer, temos que

$$B^2_t = \left(B^2_t-t\right) + t.$$

Portanto, o compensador de $ B^2_t $ é dado por $ \langle B\rangle_t = t $. Note, neste caso, que $ \left[B\right]_t = \langle B\rangle_t $.

Exemplo 10.3.4

Considere o martingale $ M_t = B^2_t - t $ e seja $ \left(\mathcal{F_t}\right) $ a filtragem definida de forma que $ B_t $ seja $ \mathcal{F_t} $-mensurável e $ B_t-B_s $ seja independente de $ \mathcal{F_s} $ para todo $ 0\leq s \ < \ t $. Então, para qualquer $ s \ < \ t $,

$$\mathbb{E}\left[B^4_t\Big|\mathcal{F_s}\right] = B^4_s+6(t-s)B^2_s+3(t-s)^2 \quad (3)$$

e

$$\mathbb{E}\left[B^2_t\Big|\mathcal{F_s}\right] = B^2_s + (t-s). \quad (4)$$

Como $ M_t = B^4_t - 2tB^2_t + t^2 $, obtemos que

$$\mathbb{E}\left[M^2_t\Big|\mathcal{F_s}\right] = B^4_s + (4t-6s)B^2_s + 2(t-s)^2 + s^2. \quad (5)$$

Reciprocamente, seja $ M^2_t = L_t + A_t $ a decompsição de Doob-Meyer de $ M^2_t $. Então, temos que

$$\mathbb{E}\left[M^2_t\Big|\mathcal{F_s}\right] = L_s + \mathbb{E}\left[A_t\Big|\mathcal{F_s}\right] = B^4_s - 2sB^2_s + s^2 + \mathbb{E}\left[A_t-A_s\Big|\mathcal{F_s}\right]. \quad (6)$$

Das equações $ (5) $ e $ (6) $, concluímos que

$$\mathbb{E}\left[A_t-A_s\Big|\mathcal{F_s}\right] = 4(t-s)B^2_s + 2(t-s)^2. \quad (7)$$

Agora, vemos da equação $ (4) $ que

$$\mathbb{E}\left[\int_s^tB^2_udu\Big|\mathcal{F_s}\right] = \int_s^t\mathbb{E}\left[B^2_u\Big|\mathcal{F_s}\right]du = \int_s^t\left(B^2_s+u-s\right)du = (t-s)B^2_s+\frac{1}{2}(t-s)^2. \quad (8)$$

Comparando as equações $ (7) $ e $ (8) $, é fácil verificar que

$$A_t = 4\int_0^tB^2_udu \quad (9)$$

e, portanto, o compensador de $ M^2_t = \left(B^2_t-t\right)^2 $ é dado por

$$\langle M\rangle_t = 4\int_0^tB^2_udu. \quad (10)$$

Isto implica que o processo estocástico

$$\left(B^2_t - t\right)^2 - 4\int_0^tB^2_udu$$

é um martingale. Também podemos verificar que o processo de variação quadrática de $ M_t $ é dado por $ 4\int_0^tB^2_udu $. Portanto, $ \left[M\right]_t = \langle M\rangle_t $.

Um martingale como integrando

Lema 10.3.2

Para qualquer $ s< t $ temos que

$$E[(M(t)-M(s))^2|\mathcal{F_s}]=E[\langle M\rangle_t- \langle M\rangle_s |\mathcal{F_s}]$$

Dem:

Seja $ M^2(t)=L(t)+A(t) $ a decomposição de Doob-Meyer de $ M^2(t) $. Então

$$E[(M(t)-M(s))^2|\mathcal{F_s}]=E[M^2(t)-2M(t)-M^2(s)|\mathcal{F_s}]=$$

$$E[M^2(t)|\mathcal{F_s}]-M^2(s)=E[L(t)+A(t)|\mathcal{F_s}]-L(s)-A(s)$$

$$E[A(t)-A(s)|\mathcal{F_s}]$$

Como $ A(t)=\langle M\rangle_{t} $.

Agora vamos especificar o integrando pois o caso geral que usamos no inicio desta seção não poderá ser usado, vamos ter que restringir para $ f\in L^2_{pred}([a,b]_{lt;Mgt;}\times \Omega) $, o qual é o espaço de todas os processos todos os processos $ f(t,\omega), ~ a\leq t \leq b,~ \omega \in \Omega $ satisfazendo a condição

$$\displaystyle E\left[\int_{a}^{b}|f(t)|^2 d\langle M\rangle_t\right]< \infty$$

É importante notar que como $ \langle M\rangle_t $ é um processo previsível então a integral está bem definida no intervalo fechado, ou seja, é uma integral de Riemann-Stieltjes.

Para isso, vamos definir finalmente a integral desejada, é importante notar que os métodos usados são exatamente os mesmos.

Definição 10.3.5

Defina

$$\int_{a}^{b}f(t)dM(t)$$

para $ f\in L^2_{pred}([a,b]_{\langle M\rangle}\times \Omega) $. Primeiramente definimos f um processo estocástico do tipo escada.

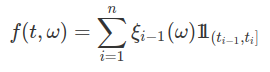
Neste caso nossa integral será definida como

$$I(f)=\displaystyle \sum_{i=1}^{n}\xi_{i-1}(M(t_i)-M(t_{i-1}))$$

Note que a nossa definição de integral claramente é linear para funções do tipo escada, ou seja, $ I(\alpha f+\beta g)=\alpha I(f)+\beta I(g) $ para qualquer $ \alpha, \beta \in\mathbb{R} $ e $ f,g \in L^2_{pred}([a,b]_{\langle M\rangle}\times \Omega) $ para f e g funções do tipo escada.

Lema 10.3.3

Seja I(f) definida acima então

$$\displaystyle E[|I(f)|^2]=E\left[\int_{a}^{b}|f(t)|^2d\langle M\rangle_t\right]$$

Dem:

Note que para $ i\neq j $, dizemos que $ i< j $ temos que

$$E[\xi_{i-1}\xi_{j-1}(M(t_i)-M(t_{i-1}))(M(t_j)-M(t_{j-1}))]=$$

$$E[E[\xi_{i-1}\xi_{j-1}(M(t_i)-M(t_{i-1}))(M(t_j)-M(t_{j-1}))|\mathcal{F}_{t_{j-1}}]]=$$

$$E[\xi_{i-1}\xi_{j-1}(M(t_i)-M(t_{i-1}))]E[(M(t_j)-M(t_{j-1}))|\mathcal{F}_{t_{j-1}}]=0$$

Portanto,

$$E[|I(f)|^2]=\displaystyle \sum_{i,j=1}^{n}E[\xi_{i-1}\xi_{j-1}(M(t_i)-M(t_{i-1}))(M(t_j)-M(t_{j-1}))]=$$

$$\displaystyle \sum_{i=1}^{n}E[\xi^2_{i-1}(M(t_i)-M(t_{i-1}))^2]=$$

$$\displaystyle \sum_{i=1}^{n}E[\xi^2_{i-1}E[(M(t_i)-M(t_{i-1}))^2|\mathcal{F}_{t_{i-1}}]]$$

Então pelo lema 10.3.2 temos que

$$E[|I(f)|^2 ]=\displaystyle \sum_{i=1}^{n}E[\xi^2_{i-1}E[\langle M\rangle_{t_i}-\langle M\rangle_{t_{i-1}}|\mathcal{F}_{t_{i-1}}]]=$$

$$\displaystyle \sum_{i=1}^{n}E[\xi^2_{i-1}(\langle M\rangle_{t_i}-\langle M\rangle_{t_{i-1}})]=$$

$$\displaystyle E\left[\sum_{i=1}^n \xi^2_{i-1}(\langle M\rangle_{t_i}-\langle M\rangle_{t_{i-1}})\right]=$$

$$\displaystyle E\left[\int_{a}^{b}|f(t)|^2d\langle M\rangle_t\right].$$

Com esses lemas em mãos vamos generalizar o nosso conceito de integral para $ f\in L^2_{pred}([a,b]_{\langle M\rangle}\times \Omega) $ agora não só para funções escadas mas para qualquer função presente nesse espaço.

Nesse ponto iremos fazer a seguinte afirmação:

Se $ f\in L^2_{pred}([a,b]_{\rangle M\rangle}\times \Omega) $ então existe uma sequência de funções $ (f_n) $ escadas com $ f_n\in L^2_{pred}([a,b]_{\langle M\rangle}\times \Omega) $ para todo n, tal que

$$\displaystyle \lim_{n\rightarrow \infty}E\left[\int_{a}^{b}|f(t)-f_n(t)|^2d\langle M\rangle_t\right]=0.$$

Então pelo Lema 10.3.2 temos que $ (I(f_n)) $ é de Cauchy em $ L^2(\Omega) $. Defina então

$$\displaystyle I(f)=\lim_{n\rightarrow \infty}I(f_n)$$

O qual é independente da sequência $ (f_n) $. Note que de fato, está bem definido pelo fato da sequência $ (I(f_n)) $ é de Cauchy em $ L^2(\Omega) $. Portanto denotamos por

$$I(f)=\displaystyle \int_{a}^{b}f(t)dM(t)$$

Teorema 10.3.2

Seja $ f\in L^2_{pred}([a,b]_{\langle M\rangle}\times \Omega) $. Então o processo estocástico

$$X_t=\displaystyle \int_{a}^{t}f(s)dM(s), a\leq t\leq b$$

é um martingale e a seguinte igualdade é verdadeira

$$\displaystyle E[|X(t)|^2]=E\left[\int_{a}^{t}|f(s)|^2d\langle M\rangle_s\right]$$

Dem:

A prova deste teorema é similar a do lema anterior.

Teorema 10.3.3

Seja $ f\in L^2_{pred}([a,b]_{\langle M\rangle}\times \Omega) $. Então o processo estocástico

$$X_t=\displaystyle \int_{a}^{t}f(s)dM(s), a\leq t \leq b,$$

é contínuo a direita com limite a esquerda quase certamente, além disso, o compensador de $ X_t^2 $ é dado por

$$\langle X\rangle_t=\displaystyle \int_{a}^{t}|f(s)|^2d\langle M\rangle_s .$$

10.4 - Fórmula de Itô

A regra básica para a diferenciação é a regra da cadeia. Se $ f $ e $ g $ são funções diferenciáveis, então $ f(g(t)) $ também é diferenciável e sua derivada é dada por

$$\frac{d}{dt}f(g(t))=\frac{d}{dt}f(g(t))\frac{d}{dt}g(t)$$

Em termos do teorema fundamental do cálculo, temos que

$$f(g(t))-f(g(a))=\int_a^t\frac{d}{ds}f(g(s))\frac{d}{ds}g(s)ds$$

No cálculo de Itô, estamos interessados em encontrar alguma relação parecida para processos estocásticos. Seja $ B(t) $ o movimento browniano e $ f $ uma função diferenciável. Considere a função composta $ f(B(t)) $. Como $ B(t) $ não é diferenciável, a igualdade

$$\frac{d}{dt}f(B(t))=\frac{d}{dt}f(B(t))\frac{d}{dt}B(t)$$

não faz sentido. Contudo quando trocamos $ \frac{d}{dt}B(t) $ por $ dB(t) $ na integral de Itô, surge a seguinte questão:

A igualdade

$$f(B(t))-f(B(a))=\int_a^t\frac{d}{dt}f(B(s))dB(s)$$

é válida para qualquer função diferenciável?

Se considerarmos a função $ f(x)=x^2 $, a igualdade anterior nos fornece que a integral estocástica é igual a:

$$B(t)^2-B(a)^2=2\int_a^tB(s)dB(s)$$

Mas como já visto na seção de integral estocástica, o verdadeiro valor para tal integral é:

$$B(t)^2-B(a)^2-(t-a)=2\int_a^tB(s)sB(s)$$

Portanto, a resposta para tal questão é negativa. Mas, existe uma fórmula para a função composta $ f(B(t)) $ que serve como regra da cadeia na forma integral para o cálculo de Itô? Sim, existe! E este resultado é conhecido como fórmula de Itô.

Considere uma partição $ \Delta_n=(t_0,t_1,\dots,t_n) $ do intervalo $ [a,t] $. Então,

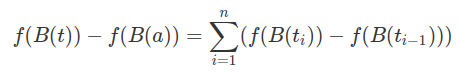
Vamos supor que $ f $ é uma função de classe $ C^2 $. A expansão de Taylor para a função $ f $ é dada por:

$$f(x)-f(x_0)=f^{\prime}(x_0)(x-x_0)+\frac{1}{2}f^{\prime\prime}(x_0+\lambda(x-x_0))(x-x_0)^2$$

para $ 0<\lambda\leq 1 $. Portanto,

$$f(B(t))-f(B(a))=\sum_{i=1}^nf^{\prime}(B(t_{i-1}))(B(t_{i})-B(t_{i-1}))$$

$$\quad{}+\frac{1}{2}\sum_{i=1}^nf^{\prime\prime}(B(t_{i-1})+\lambda_i[B(t_{i})-B(t_{i-1})])(B(t_{i})-B(t_{i-1}))^2$$

com, $ 0< \lambda_i < 1 $.

Para a primeira somatória, temos que

$$\lim_{||\Delta_n || \to 0}\sum_{i=1}^n f^{\prime}(B(t_{i-1}))(B(t_{i})-B(t_{i-1})) = \int_a^tf^{\prime}(B(s))dB(s)$$

Já para a segunda somatória, vamos mostrar que

$$\sum_{i=1}^nf^{\prime\prime}(B(t_{i-1})+\lambda_i[B(t_{i})-B(t_{i-1})])(B(t_{i})-B(t_{i-1}))^2 \rightarrow \int_a^t f^{\prime\prime}(B(s))ds$$

quando $ ||\Delta_n|| \rightarrow 0 $.

Teorema 10.4.1 (Fórmula de Itô)

Seja $ f $ uma função de classe $ C^2 $. Então

$$f(B(t))-f(B(a))=\int_a^tf^{\prime}(B(s))dB(s)+\frac{1}{2}\int_a^t f^{\prime\prime}(B(s))ds$$

Para demonstrarmos o teorema, primeiro vamos enunciar e provar dois lemas.

Lema 10.4.1

Seja $ g(x) $ uma função contínua sobre $ \mathbb{R} $. Para cada $ n\geq 1 $, seja $ \Delta_n=(t_0,t_1,\dots,t_n) $partição de $ [a,t] $ e $ 0<\lambda_i< 1 $ para $ 1\leq i\leq n $. Então existe uma subsequência de

$$\sum_{i=1}^n(g(B(t_{i-1})+\lambda_i[B(t_{i})-B(t_{i-1})])-g(B(t_i)))(B(t_{i})-B(t_{i-1}))^2\rightarrow 0$$

quase certamente, quando $ ||\Delta_n|| \rightarrow 0 $.

Prova

Seja

$$X_n =\sum_{i=1}^n(g(B(t_{i-1})+\lambda_i[B(t_{i})-B(t_{i-1})])-g(B(t_i)))(B(t_{i})-B(t_{i-1}))^2$$

.

Defina a variável aleatória

$$\xi_n=\max_{1\leq i\leq n, 0< \lambda<1}|g(B(t_{i-1})+\lambda_i[B(t_{i})-B(t_{i-1})])-g(B(t_i)))|$$

Vale que

$$|X_n|=|\sum_{i=1}^n(g(B(t_{i-1})+\lambda_i[B(t_{i})-B(t_{i-1})])-g(B(t_i)))(B(t_{i})-B(t_{i-1}))^2|$$

$$\leq \sum_{i=1}^n|(g(B(t_{i-1})+\lambda_i[B(t_{i})-B(t_{i-1})])-g(B(t_i)))|(B(t_{i})-B(t_{i-1}))^2$$

$$\leq \sum_{i=1}^n \xi_n(B(t_{i})-B(t_{i-1}))^2$$

Pela continuidade de $ g(x) $ e do movimento browniano, $ \xi_n $ converge para $ 0 $ quase certamente. Como $ \sum_{i=1}^n(B(t_{i})-B(t_{i-1}))^2 \rightarrow t-a $ em $ L^2(\Omega) $, então existe uma subsequência que converge para 0 quase certamente. Segue então que $ (X_n) $ tem uma subsequência que converge para 0 quase certamente.

Lema 10.4.2

Seja $ g(x) $ função contínua sobre $ \mathbb{R} $. Para cada $ n\geq 1 $, seja $ \Delta_n=(t_0,t_1,\dots,t_n) $ uma partição de $ [a,t] $. Então a sequência

$$S_n=\sum_{i=1}^ng(B(t_{i-1}))((B(t_i)-B(t_{i-1}))^2-(t_i-t_{i-1}))$$

converge para 0, quando $ ||\Delta_n|| \rightarrow 0 $.

Para cada $ L> 0 $, defina os eventos

$$A_{i-1}^{(L)}\equiv (|B(t_j)|\leq L \ \text{para todo} \ j\leq i-1).$$

Defina também

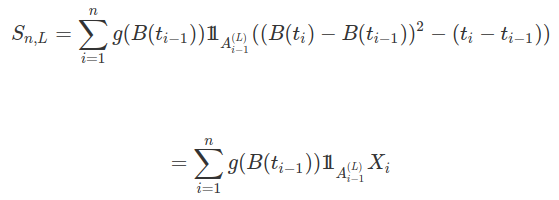
$$=\sum_{i=1}^nY_i$$

Considere $ \mathcal{F_t} = \sigma(B(s): s\leq t ) $. Então, para $ i\neq j $, digamos $ i< j $, podemos calcular a esperança condicional

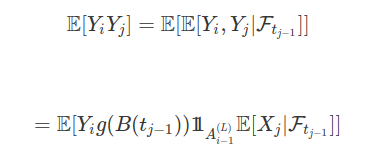
$$=0$$

Por outro lado, da definição de $ A_{i-1}^{(L)} $, segue que

$$Y_i^2\leq \max_{|x|\leq L}(|g(x)|^2)X_i^2$$

Então

$$\mathbb{E}(Y_i^2)\leq 2(t_i-t_{i-1})^2\max_{|x|\leq L}(|g(x)|^2)$$

de onde segue que

$$\mathbb{E}[S^2_{n,L}]= \sum_{i=1}^n\mathbb{E}[Y_i^2]$$

$$\leq 2\max_{|x|\leq L}(|g(x)|^2)\sum_{i=1}^n(t_i-t_{i-1})^2$$

$$\leq 2\max_{|x|\leq L}(|g(x)|^2)(t-a)\sum_{i=1}^n(t_i-t_{i-1})\rightarrow 0$$

quando $ ||\Delta_n||\rightarrow 0 $.

Assim, para qualquer $ L $ fixado maior que zero, a sequência $ S_{n,L} $ converge para $ 0 $ em $ L^2(\Omega) $ e portanto em probabilidade quando $ ||\Delta_n||\rightarrow 0 $.

Da maneira como definimos o conjunto $ A^L_{n-1} $, temos que

$$A^L_{n-1}\subset (S_n = S_{n,L})$$

que implica que

$$(S_n\neq S_{n,L})\subset (A_{n-1}^{(L)})^c\subset (\max_{a\leq s\leq t}|B(s)|> L)$$

e portanto, segue a desigualdade

$$\mathbb{P}(S_n\neq S_{n,L})\leq \mathbb{P}(\max_{a\leq s\leq t}|B(s)|> L).$$

Da desigualdade de submartingale

$$\leq 2\max_{|x|\leq L}(|g(x)|^2)\sum_{i=1}^n(t_i-t_{i-1}) \leq \frac{1}{L}\mathbb{E}[|B(t)|]=\frac{1}{L}\sqrt{\frac{2t}{\pi}}$$

então

$$\mathbb{P}(S_n\neq S_{n,L})\leq\frac{1}{L}\sqrt{\frac{2t}{\pi}}.$$

Como

$$(|S_n|> \varepsilon)\subset(|S_{n,L}|>\varepsilon)\cup(S_n\neq S_{n,L})$$

vale que

$$\mathbb{P}(|S_n|> \varepsilon)\leq\mathbb{P}(|S_{n,L}|>\varepsilon)+\mathbb{P}(S_n\neq S_{n,L})$$

$$\leq\mathbb{P}(|S_{n,L}|>\varepsilon)+\frac{1}{L}\sqrt{\frac{2t}{\pi}}$$

Escolha L suficientemente grande, de forma que $ \frac{1}{L}\sqrt{\frac{2t}{\pi}}\leq \frac{\varepsilon}{2} $. Já provamos que para qualque $ L> 0 $, $ S_{n,L} $ converge para $ 0 $, quando $ ||\Delta_n||\rightarrow 0 $. Então, existe $ n_0\geq 1 $, tal que para $ \mathbb{P}(|S_{n,L}|>\varepsilon)< \frac{\varepsilon}{2} $ para todo $ n\geq n_0 $. Provando que $ S_n $ converge para $ 0 $ em probabilidade quando $ ||\Delta_n||\rightarrow 0 $.

Na sequência, apresentamos alguns exemplos simples de aplicação da fórmula de Itô.

Exemplos

1. Considere $ f(x) = x^2 $, então temos que

$$B^2(t) = f(B(t))=\int_{0}^t 2B(s)dB(s) + \frac{1}{2}t.$$

Assim, concluímos que

$$\int_{0}^t B(s) dB(s) = \frac{B^2(t) - t}{2}.$$

2. Vamos calcular $ \mathbb{E}[B^4(t)]. $. Através da fórmula de Itô obtemos que

$$\int_{0}^t 4B^3(s)dB(s) + \frac{1}{2} \int_{0}^t12B^2(s)ds.$$

Com isso, concluímos que

$$\mathbb{E}[B^4(t)]=6\int_{0}^t \mathbb{E}[B^2(s)]ds=6\int_{0}^tsds=3t^2.$$

3. Ao tomarmos $ f(x)=\exp^{\sigma x} $, obtemos que $ f $ é diferenciável com $ f^\prime(x)=\sigma \exp^{\sigma x} $ e $ f^{\prime \prime}(x)=\sigma^2 \exp^{\sigma x} $. Como aplicação da fórmula de Itô, temos que

$$X(t)=\exp^{\sigma B(t)}=1+\int_{0}^t \sigma X(s) dB(s) + \frac{1}{2} \int_{0}^t \sigma^2 X(s) ds. $$

Na sequência, vamos calcular o valor esperado de $ X(t) $. Facilmente, obtemos que

$$\mathbb{E}[X(t)]=1+\frac{\sigma^2}{2}\int_{0}^t\mathbb{E}(X(s))ds.$$

Ao denotarmos $ y(t)=\mathbb{E}(X(t)) $, obtemos que

$$y(t)=1+\frac{\sigma^2}{2}\int_{0}^ty(s)ds \quad \text{ou} \quad dy(t)=\frac{\sigma^2}{2}y(t)dt$$

com condição inicial $ y(0)=1 $. Trivialmente, obtemos como solução $ \mathbb{E}[X(t)]=y(t)=\exp^{\frac{\sigma^2}{2}t} $.

Vamos estender a fórmula de Itô para funções que dependem da variável espacial e da variável temporal. Ou seja, como seria a formula de Itô para o caso em que temos $ f(t,x) $ uma função de $ t $ (variável temporal) e $ x $ (variável espacial). Se substituímos $ x=B(t) $ temos $ f(t,B(t)) $, note que ambas as variáveis dependem de $ t $. Em relação a primeira variável podemos usar o calculo tradicional, porém em relação a segunda temos que usar o calculo de Itô.

Assim sendo, suponha $ f(t,x) $ com derivadas parciais contínuas $ \frac{\partial f}{dt}, \quad\frac{\partial f}{dx} $ e $ \frac{\partial^2 f}{dx^2} $. Então usando a expansão por serie de Taylor obtemos

$$f(t,x)-f(s,x_0)=[f(t,x)-f(s,x)]+[f(s,x)-f(s,x_0)]$$

$$=\frac{\partial f}{dt}(s+\rho(t-s),x)(t-s)+\frac{\partial f}{dx}(s,x_0)(x-x_0)+\frac{1}{2}\frac{\partial^2 f}{dx^2}(s,x_0+\lambda(x-x_0))(x-x_0)^2$$

com $ 0< \rho < 1 $ e $ 0< \lambda < 1 $. Considere a partição $ \Delta_n=(t_0,t_1,\dots,t_{n-1}, t_n) $ para $ [a,t] $. Então

$$f(t,B(t))-f(a,B(a))=\sum_{i=1}^n\left(f(t_i,B(t_i))-f(t_{i-1},B(t_{i-1}))\right)$$

$$=\sum_{i=1}^n \frac{\partial f}{dt}(t_{i-1}+\rho(t_i-t_{i-1}),B(t_{i-1}))(t_i-t_{i-1})+\sum_{i=1}^n \frac{\partial f}{dx}(t_{i-1},B(t_{i-1}))(B(t_i)-B(t_{i-1}))+\sum_{i=1}^n \frac{\partial^2 f}{dx^2}(t_{i-1},B(t_{i-1})+\lambda(B(t_{i})-B(t_{i-1})))(B(t_i)-B(t_{i-1}))^2$$

Pela continuidade das derivadas e do movimento Browniano temos

$$\sum_{i=1}^n \frac{\partial f}{dt}(t_{i-1}+\rho(t_i-t_{i-1}),B(t_{i-1}))(t_i-t_{i-1})\rightarrow \displaystyle \int_a^t \frac{\partial f}{dt}(s,B(s))ds $$

quase certamente, quanto $ |\Delta_n|\rightarrow 0 $. Por outro lado, podemos modificar os argumentos usados nessa equação e obter

$$\sum_{i=1}^n \frac{\partial f}{dx}(t_{i-1},B(t_{i-1}))(B(t_i)-B(t_{i-1}))\rightarrow \int_a^t \frac{\partial f}{dx}(s,B(s))dB(s), $$

e

$$\sum_{i=1}^n \frac{\partial^2 f}{dx^2}(t_{i-1},B(t_{i-1})+\lambda(B(t_{i})-B(t_{i-1})))(B(t_i)-B(t_{i-1}))^2\rightarrow \int_a^t \frac{\partial^2 f}{dx^2}(s,B(s))ds.$$

Assim obtemos a seguinte formula de Itô para $ f(t,B(t)) $.

Teorema 10.4.2 (Formula de Itô Suavemente Generalizada)

Vamos estender a fórmula de Itô para funções que dependem da variável espacial e da variável temporal. Para isto, tomamos $ F:[0,T]\times \mathbb{R} \rightarrow \mathbb{R} $ uma função satisfazendo:

(i) $ \frac{\partial}{\partial t}F(t,x) $ existe para todo $ x \in \mathbb{R} $;

(ii) $ \frac{\partial}{\partial x}F(t,x) $ e $ \frac{\partial^2}{\partial^2 x}F(t,x) $ existem para todo $ 0 \leq t \leq T $.

Para facilidade de notação, se $ F $ satisfaz (i) e (ii) denotaremos $ F \in C^{1,2} $. Para toda função $ F \in C^{1,2} $, a fórmula de Itô é dada por:

$$F(t,B(t))=F(0,0)+\int_{0}^t \frac{\partial}{\partial t}F(s,B(s))ds+\int_{0}^t \frac{\partial}{\partial x}F(s,B(s))dB(s)+\frac{1}{2}\int_{0}^t\frac{\partial^2}{\partial^2 x}F(s,B(s))ds=$$

$$F(0,0)+\int_{0}^t \frac{\partial}{\partial x}F(s,B(s))dB(s)+\int_{0}^t \left[\frac{\partial}{\partial t}F(s,B(s))+\frac{1}{2} \frac{\partial^2}{\partial^2 x}F(s,B(s))\right]ds.$$

Exemplos

1. Ao tomarmos $ F(t,x)=tx $, obtemos que

$$tB(t)=\int_{0}^tB(s)ds+\int_{0}^tsdB(s).$$

2. Martingale exponencial. Considere a função $ f(t,x)=\exp[ux-\frac{u^2}{2}t] $ no qual $ u $ é uma constante positiva. Então, concluímos da fórmula de Itô que

$$X(t)=\exp[uB(t)-\frac{u^2}{2}t]=1+\int_{0}^tuX(s)dB(s).$$

3)Considere a função a função $ f(t,x)=tx^2 $. Então

$$\frac{\partial f}{dt}=x^2, \quad \frac{\partial f}{dx}=2tx, \quad \frac{\partial^2 f}{dx^2}=2t$$

Portanto, pela equação

$$tB^2(t)=2\int_0^t sB(s)dB(s)+\left(\int_0^t B^2(s)ds+\frac{1}{2}t^2\right)$$

Podemos usar a esperança condicional para mostrar que $ tB(t)^2 $ é um submartingale. Portanto, essa igualdade nos fornece a decomposição de Doob-Meyer de $ tB(t)^2 $. Desta forma temos que

$$\int_0^t sB(s)dB(s)=\frac{1}{2}tB^2(t)-\frac{1}{4}t^2-\frac{1}{2}\int_{0}^t B^2(s)ds.$$

A equação estocástica $ M(t)=B^2(t)-t $ é um martingale. Usaremos a formula de Itô para encontrar o compensador de $ M^2(t) $. Assim considere a função

$ f(t,x)=(x^2-t)^2 $. Então

$$\frac{\partial f}{\partial t}=-2(x^2-t), \quad\frac{\partial f}{\partial x}=4x(x^2-t), \quad \frac{\partial^2 f}{\partial x^2}=4(x^2-t)+8x^2.$$

Usando a formula generalizada acima temos que

$$M^2(t)=(B^2(t)-t)^2=4\int_{0}^{t}B(s)(B^2(s)-s)dB(s)+4\int_0^tB^2(s)ds.$$

Observe que a primeira integral é um martingale e a segunda é um processo integral é um processo crescente. Portanto, pelo Teorema decomposição de Doob-Meyer o compensador de $ M^2(t) $ é dado por

$$\langle M\rangle_t = 4\int_0^t B^2(s) ds.$$

Formula de Itô na formula Geral

$$X_t=X_a+\int_{a}^t f(s)dB(s)+\int_{a}^t g(s)ds, \quad a\leq t\leq b,$$

no qual $ X_a $ é $ \mathcal{F}_a- $mensurável, $ f\in \mathcal{L}_ad(\Omega,L^2[a,b]) $, e $ g\in \mathcal{L}_ad(\Omega,L^1[a,b] $. Usando a formula diferencial temos que

$$dX_t=f(t)dB(t)+g(t)dt.$$

Então iremos fazer uma formula de Itô mais geral,

Teorema 10.2.3

Seja $ X_t $ um processo de Itô dado por

$$X_t=X_a+\int_{a}^t f(s)dB(s)+\int_{a}^t g(s)ds, \quad a\leq t\leq b,$$

Suponha $ \theta(t,x) $ é uma função contínua com derivadas parcial contínuas $ \frac{\partial \theta}{\partial t}, \frac{\partial \theta}{\partial x} $ and $ \frac{\partial^2 \theta}{\partial x^2} $. Então, $ \theta(t,X_t) $ é também um processo de Itô e

$$\theta(t,X_t)=\theta(a,X_a)+\int_a^t \frac{\partial \theta}{\partial x}(s,X_s)f(s)dB(s)$$

$$+\int_a^t \left[\frac{\partial \theta}{\partial t}(s,X_s)+\frac{\partial \theta}{\partial x}(s,X_s)g(s)+\frac{1}{2}\frac{\partial^2 \theta}{\partial x^2}(s,X_s)f^2(s)ds\right]$$

Esse teorema pode ser demonstrado fazendo modificações dos argumentos do Teorema da formula de Itô 10.4.2 . Uma boa forma de se obter o resultado é usando a tabela abaixo na qual temos o resultado das multiplicações das derivadas simbolicas, ou seja, $ (dB(t))^2=dt $, $ (dt)^2=0 $.

x	dB(t)	dt
dB(t)	dt	0
dt	0	0

Então, usando a tabela e a expansão em serie de Taylor temos que o resultado segue.

Exemplos

1. Seja $ f\in \mathcal{L}_{ad}(\Omega, L^2[0,1]) $. Considere o seguinte processo de Itô.

$$X_t=\int_0^t f(s)dB(s)-\frac{1}{2}\int_0^t f^2(s)ds, 0\leq t\leq 1,$$

e a função $ \theta(x)=e^x $. Então $ dX_t=f(t)dB(t)-\frac{1}{2}f^2(t)dt $. Aplicando a expansão de serie Taylor junto com tabela acima

$$d\theta(X_t)=e^{X_t}dX_t+\frac{1}{2}e^{X_t}(dX_t)^2=e^{X_t(f(t)dB(t)-\frac{1}{2}f^2(t)dt)+\frac{1}{2}e^{X_t}f^2(t)}dt$$

$$f(t)e^{X_t}dB(t).$$

Portanto temos que

$$e^{\int_0^t f(s)dB(s)-\frac{1}{2}\int_0^tf^2(s)ds}=1+\int_{0}^t f(s)e^{\int_0^tf(u)dB(u)-\frac{1}{2}\int_0^s f^2(u)du}dB(s)$$

Portanto, temos que

$$Y(t)=e^{\int_0^t f(s)dB(s)-\frac{1}{2}\int_0^tf^2(s)ds}$$

é um martingale se $ f(t)\in L^2[0,1] $ ou seja, é uma função determinística pelo Teorema 10.2.5

e pelo teorema dessa mesma secção temos que é um martingale local, para $ f\in \mathcal{L}^2(\Omega,L^2[0,1]) $.

2. Considere a equação de Langevin

$$dX_t=\alpha dB(t)-\beta X_t dt, \quad X_0=x_0,$$

no qual $ \alpha\in \mathbb{R} $ e $ \beta> 0 $. Então, $ X_t $ é interpretado como

$$X_t=x_0+\alpha B(t)-\beta\int_0^tX_s ds$$

Podemos então usar um método de iteração e de integração por parte para derivar a solução $ X_t $ por cada caminho de $ B(t) $. Mas na verdade esse método é bem complicado. Entretanto se usarmos a formula de Itô, então podemos obter a solução de forma bem mais fácil.

Considere $ \theta(t,x)=e^{\beta t}x $. Então

$$\frac{\partial \theta}{dt}=\beta e^{\beta t}, \quad \frac{\partial \theta}{dx}= e^{\beta t},\quad \frac{\partial^2 \theta}{dx^2}=0$$

Portanto

$$d(e^{\beta t} X_t)=\beta e^{\beta t}X_tdt+ e^{\beta t}dX(t)=\beta e^{\beta t}X_t dt + e^{\beta t}(\alpha dB(t)-\beta X_t dt)$$

$$=\alpha e^{\beta t} dB(t).$$

Então, a integral estocástica é dada por

$$e^{\beta t}X_t=e^{\beta_s}X_s+\int_s^t \alpha e^{\beta_u}dB(u), s\leq t.$$

Portanto, $ X_t $ é dado por

$$X_t=e^{-\beta(t-s)}X_s+\alpha \int_s^t e^{-\beta(t-u)}dB(u), \quad s\leq t.$$

Em particular, quando $ s=0 $, temos que a solução para a equação de Langevin é dada por

$$X_t=e^{-\beta t}x_0+\alpha \int_0^t e^{-\beta(t-u)}dB(u).$$

Definição 10.4.1

A solução de $ X_t $ é chamada um processo de Ornstein-Uhlenbeck.

Teorema 10.4.3

Seja $ X_t $ um processo de Ornstein-Uhlenbeck dado por

$$X_t=e^{-\beta t}x_0+\alpha \int_0^t e^{-\beta(t-u)}dB(u).$$

Então, temos que a probabilidade condicional é dada por

$$\mathbb{P}(X_t\leq y|X_s=x)=\int_{-\infty}^y G_{\frac{\alpha^2}{2\beta}(1-e^{-2\beta(t-s)})}(e^{-\beta(t-s)}x,v)dv,\quad s< t$$

no qual $ G_t(m,v)=\frac{1}{\sqrt{2\pi t}}e^{-\frac{1}{2t}(v-m)^2} $, é uma função de densidade de uma Normal em v com média $ m $ e variância $ t $. Em particular quando $ s=0 $ e $ x=x_0 $, a variável aleatória $ X_t $ é uma Normal com média $ x_0e^{\beta t} $ e variância $ \frac{\alpha^2}{\beta}(1-e^{-2\beta t}) $.

Demonstração:

Seja $ s\leq t $. Então, dado $ X_s=x $, temos que pela equação acima

$$X_t=e^{-\beta (t-s)}x+\alpha \int_{s}^t e^{-\beta(t-u)}dB(u).$$

Note que a integral da equação acima é uma integral de Wiener, a qual é uma variável aleatória com média 0 e variância

$$\alpha^2\int_s^t e^{-2\beta(t-u)}du=\frac{\alpha^2}{2\beta}(1-e^{-2\beta(t-s)}).$$

Portanto a variável $ X_t $ é dado por $ X_s=x $ é uma normal com media $ e^{-\beta(t-s)}x $ e a variância $ \alpha^2(1-e^{2\beta (t-s)})/(2\beta) $. Portanto o resultado segue.

Formula de Itô Multidimensional

Seja $ B_1(t),B_2(t),\dots B_m(t) $ m movimento Browniano independentes. Considere o processo de Itô $ X_t^{(1)}, X_t^{(2)},\dots ,X_t^(n) $ dado por

$$X_t^{i}=X_a^{(i)}+\sum_{j=1}^m \int_a^t f_{ij}(s)dB_j(s)+\int_a^t g_i(s)ds, \quad 1\leq i\leq n,$$

no qual $ f_{ij}\in \mathcal{L}_{ad}(\Omega,L^2[a,b]) $ e $ g_i\in \mathcal{L}_{ad}(\Omega,L^1[a,b]) $ para todo $ 1\leq i\leq n $ e $ 1\leq j\leq m $. Se introduzimos a forma matricial temos

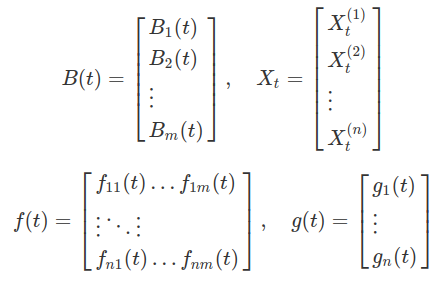
$$f(t)=\left[\begin{array}{l} f_{11}(t)\dots f_{1m}(t)\ \vdots \ddots \vdots\ f_{n1}(t)\dots f_{nm}(t)\ \end{array}\right],\quad g(t)=\left[\begin{array}{l} g_1(t)\ \vdots\ g_n(t) \end{array}\right]$$

então a equação acima pode ser escrito na forma matricial

$$X_t=X_a+\int_a^t f(s)dB(s)+\int_a^t g(s)ds,\quad \quad a \leq t\leq b.$$

Portanto podemos extender a formula de Itô para o caso multi-dimensional. Suponha $ \theta(t,x_1,\dots, x_n) $ é uma função contínua em $ [a,b]\times \mathbb{R}^n $ e com derivadas parciais contínuas $ \frac{\partial \theta}{\partial t}, \frac{\partial \theta}{\partial x_i} $ e $ \frac{\partial^2 \theta}{\partial x_i \partial x_j} $ para $ 1\leq i,j \leq n $. Então a equação diferencial estocástica de $ \theta(t,X_t^{(1)},\dots,X_t^{(n)}) $ é dado por

$$d\theta(t,X^{(1)}_t,\dots,X^{(n)}_t)$$

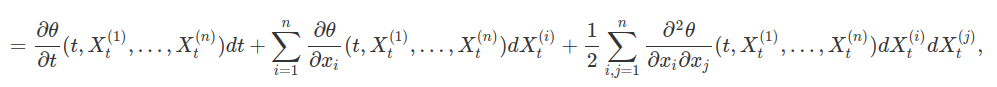
no qual o produto $ dX_t^{(i)}dX_t^{(j)} $ pode ser calculada usando a tabela abaixo

x	$ dB_j $(t)	dt
$ dB_i(t) $	$ \delta_{ij}dt $	0
dt	0	0

O produto $ dB_i(t)dB_j(t)=0 $ para $ i\neq j $. Isto decorre $ B_1(t) $ e $ B_2(t) $ dois processos independentes movimentos Browniano e seja $ \Delta_n=(t_0,t_1,\dots,t_{n-1},t_n) $ uma partição de $ [a,b] $. Então

$$\sum_{i=1}^n (B_1(t_i)-B_1(t_{i-1}))(B_2(t_i)-B_2(t_{i-1}))\rightarrow 0$$

em $ L^2(\Omega) $ como $ |\Delta_n|=\max_{1\leq i\leq n}(t_i-t_{i-1}) $ tende a zero.

Exemplos

Considere a função $ \theta\ (x,y)=xy $. Temos que $ \frac{\partial \theta}{\partial x}=y, \frac{\partial \theta}{\partial y}=x $, $ \frac{\partial^2 \theta}{\partial y\partial x}=1 $, e $ \frac{\partial^2 \theta}{\partial x^2}=\frac{\partial^2 \theta}{\partial y^2}=0 $ e $ \frac{\partial^2 \theta}{\partial x\partial y}=\frac{\partial \theta}{\partial y\partial x}=1 $. Aplicando a equação acima para $ \theta(x,y) $ para doi processos de Itô $ X_t $ e $ Y_t $ temos que

$$d(X_tY_t)=Y_tdX_t+X_tdY_t+\frac{1}{2}dX_tdY_t+\frac{1}{2}dY_tdX_t=Y_tdX_t+X_tdY_t+dX_tdY_t.$$

Portanto,

$$X_tY_t=X_aY_a+\int_a^t Y_sdX_s+\int_a^t X_sdY_s+\int_a^tdX_sdY_s.$$

A igualdade acima é chamada de formula produto de Itô. Se $ X_t $ e $ Y_t $ é dado por

$$dX_t=f(t)dB(t)+\xi(t)dt$$

e

$$dY_t=g(t)dB(t)+\eta(t)dt$$

Então a formula produtos nos fornece que

$$X_tY_t=X_aY_a+\int_a^t \left(f(s)Y_s+g(s)X_s\right)dB(s)+\int_a^t\left(\xi(s)Y_s+\eta(s)X_s+f(s)g(s)\right)ds$$

Em particular temos que, que quando $ \xi=\eta=0 $, temos que

$$X_tY_t=X_aY_a+\int_a^t\left(f(s)Y_s+g(s)X_s\right)dB(s)+\int_a^t f(s)g(s)ds.$$

This implica que o processo estocástico

$$\left(\int_a^t f(s)dB(s)\right)\left(\int_a^t g(s)dB(s)\right)-\int_a^t f(s)g(s)ds$$

é um martingale local para qualquer $ f,g \in \mathcal{L}_{ad}(\Omega,L^2[a,b]) $.

Formula de Itô para Martingales

Seja $ M(t) $ um martingale contínua a direita com limite a esquerda, tal que $ \mathbb{E}(M^2(t))< \infty $ para cada $ t\in [a,b] $. Omitiremos a demonstração do Teorema a seguir, mas salientamos que para demonstrar esse teorema devemos ter bastante cuidado, pois um martingale qualquer pode ter saltos, ou seja, pode ter partes descontínuas (um exemplo é o compensador do processo de Poisson compensado). Por conta disso, devemos tomar bastante cuidado nesses pontos de salto.

Teorema 10.4.4

Seja $ M_t $ um martingale contínuo a direita e quadrado integrável com limite a esquerda. Suponha que $ F $ seja uma função $ C^2 $. Então

$$F(M_t)=F(M_a)+\int_a^t F^\prime(M_{s-})dM_s+\frac{1}{2}\int_a^t F^{\prime\prime}(M_s)d[M]_s^c+\sum_{a\leq s\leq t}\left(F(M_s)-F(M_{s-})-F^\prime(M_{s-})\Delta M_s\right),$$

Teorema 10.4.5

Seja $ M_t $ um martingale contínuo e quadrado integrável. Suponha que $ F(t,x) $ seja uma função contínua com derivadas parciais

$$\frac{\partial F}{\partial t}, \frac{\partial F}{\partial x},\quad \frac{\partial^2 F}{\partial x^2}.$$

Então,

$$F(t,M_t)=F(a,M_a)+\int_a^t \frac{\partial F}{\partial t}(s,M_s)ds+\int_a^t \frac{\partial F}{\partial x}(s,M_s)dM_s+\frac{1}{2}\int_a^t \frac{\partial^2 F}{\partial x^2}(s,M_s)d\langle M\rangle_s$$

Teorema 10.4.6

Suponha $ M_1(t)\dots,M_n(t) $ são martingales contínuos e quadrado integráveis. Seja $ F(t,x_1,\dots, x_n) $ uma função com derivadas parciais contínuas

$$\frac{\partial F}{\partial t}, \frac{\partial F}{\partial x_i}, \quad \frac{\partial^2 F}{\partial x_i\partial x_j}$$

para $ 1\leq i,j\leq n $. Então

$$dF=\frac{\partial F}{\partial t}dt+\sum_{i=1}^n \frac{\partial F}{\partial x_i}dM_i(t)+\frac{1}{2}\sum_{i,j=1}^n \frac{\partial^2 F}{\partial x_i\partial x_j} d\langle M_i,M_j\rangle_t,$$

no qual $ \langle \cdot,\cdot\rangle $ é a variação cruzada do processo dada por

$$\langle X,Y\rangle_t=\frac{1}{4}\left(\langle X+Y\rangle_t-\langle X-Y\rangle_t\right).$$

10.5 - Equações Diferenciais Estocásticas

Nesta seção, vamos estudar a existência e unicidade da solução de uma equação diferencial estocástica. A seguir, mostramos que diferente da equação diferencial ordinária, a equação diferencial estocástica é apenas uma representação simbólica.

No cálculo de Newton, fornecer a equação diferencial ordinária

$$df(t)=\alpha(t)dt\ \ \ \text{com}\ \ \ f(0) = \beta$$

é equivalente a fornecer a equação integral

$$f(t)=\beta + \int_0^t\alpha(u)du.$$

A representação diferencial é válida se a função $ f(t) $ for diferenciável.

Já no cálculo de Itô, uma equação diferencial estocástica da forma

$$dX(t)=\sigma(t,X)dB(t)+f(t,X)dt$$

é uma representação simbólica da equação

$$X(t)=X(a)+\int_a^t\sigma(s,X(s))dB(s)+\int_a^tf(s,X(s))ds. \ \ \ \text{e}\ \ \ X(0)=x_0.$$

A representação diferencial é simbólica pelo fato de que o movimento browniano não é diferenciável, e portanto a equação

$$\frac{dX(t)}{dt}=\sigma(t,X)\frac{dB(t)}{dt}+f(t,X)$$

não faz sentido. A razão de utilizarmos a representação diferencial está na facilidade da escrita.

As equações diferencias estocástica (SDE, sigla em inglês), antes da Teoria de Itô de integração estocástica para o movimento Browniano, o método de estudo SDE era baseado em estudar seus semigrupos de transição. Isto equivalia a estudar os geradores infinitesimais de seus semigrupos, que são operadores diferenciais parciais. Assim, os estudos do Feller por exemplo foram na verdade estudos de equações diferenciais parciais, inspiradas em difusões, a qual pode ser pensada como um processo forte de Markov em $ \mathbb{R}^n $ com caminhos contínuos. Assim, na época as principais ferramentas para estudar as difusões foi as equações diferenciais de Kolmogorov e as extensões de Feller. Mas essa abordagem não permitia um estudo mas detalhado de suas propriedades.

Foi então, que Itô estudou casos em que a difusão poderia ser vista como solução de equações diferencias da forma representada acima.

Nessa seção vamos buscar resolver equações estocástica e buscar descrever a estabilidade das soluções e relacionar a solução com processos de difusão.

Exemplo 10.5.1 (Movimento Browniano Geométrico)

$$dS(t)= \mu S(t)dt+\sigma S(t)dB(t).$$

A única solução para a equação diferencial estocástica é

$$S(t)=S(0)\exp\left(\left(\mu-\frac{\sigma^2}{2}\right)t+\sigma B(t)\right).$$

Prova

Para provarmos este resultado, vamos utilizar um resultado fundamental do cálculo estocástico, conhecido como Fórmula de Itô.

Tome a função $ f $ como

$$f(t,x) = S_0\exp\left(\left(\mu-\frac{\sigma^2}{2}\right)t+\sigma x\right)$$

então,

$$\frac{df(t,x)}{dt} = \left(\mu - \frac{\sigma^2 }{2}\right) f(t, x),\ \ \frac{df(t,x)}{dx} = \sigma f(t, x)\ e \ \frac{d^2f}{dx^2 } = \sigma^2 f(t, x)$$

Aplicando a fórmula de Itô, temos que

$$f(t, W_t) = f(0,W_0 ) + \int_0^t \left[\left(\mu - \frac{\sigma^2 }{2}\right) f(s,W_s ) + \frac{\sigma^2}{2}f(s, W_s)\right] ds+ \int_0^t \sigma f(s, W_s) dW_s$$

simplificando a equação temos que

$$f(T, W_T ) = f(0,W_0 ) + \int_0^T \mu f(t,W_t ) dt + \int_0^T \sigma f(t, W_t) dW_t$$

e substituindo $ S_t $ por $ f(t,W_t) $ temos

$$\bar{S}_T = S_0 + \int_0^T \mu \bar{S}_t dt + \int_0^T \sigma \bar{S}_t dW_t$$

ou na forma de diferencial

$$d\bar{S}_t = \mu \bar{S}_t dt + \sigma \bar{S}_t dW_t$$

$ \square $

No Modelo de Black e Scholes, o movimento browniano geométrico é utilizada para modelar o comportamento de um ativo de risco.

Exemplo 10.5.2 (Equação de Langevin)

$$dX(t)=-\alpha X(t)dt+\beta dB(t),$$

com $ \alpha $ e $ \beta $ constantes positivas.

A única solução da equação acima é

$$X(t)=e^{-\beta t}x_0+\alpha\int_0^te^{-\beta(t-u)}dB(u).$$

Prova

Considere a função $ g(t,x)=e^{\alpha t}x $.

$$\frac{dg(t,x)}{dx}=e^{\alpha t}\ \ \ \frac{d^2g(t,x)}{dx^2}=0\ \ \ \ \frac{dg(t,x)}{dt}=\alpha;e^{\alpha t}x$$

Aplicando a Fórmula de Itô, temos

$$X(t)e^{\alpha t}=X(0)+\int_0^t\beta e^{\alpha u}dB(u)+\int_0^t\alpha e^{\alpha u}X(u)du-\alpha e^{\alpha u}X(u)du$$

então,

$$X(t)=e^{-\alpha t}X(0)+\int_0^t\beta e^{-\alpha(t-u)}dB(u)$$

$ \square $

Este processo é conhecido como processo de Ornstein-Uhlenbeck.

Para provarmos a existência e unicidade da solução de equações diferenciais estocásticas, primeiro vamos enunciar e provar dois lemas fundamentais. Os dois lemas consistem em desigualdades. A primeira desigualdade cobre a seguinte situação. Suponha que uma função $ \phi\in L^1[a,b] $ satisfaça a desigualdade

$$\phi(t)\leq f(t)+\beta\int_a^t\phi(s)ds, \ \ \ \forall t\in[a,b]$$

com $ f\in L^1[a,b] $ e $ \beta $ constante positiva.

Levantamos a seguinte questão. Dado a desigualdade anterior, como podemos limitar a função $ \phi(t) $ em termos de $ f(t) $ e $ \beta $?

Defina

$$g(t)=\int_a^t\phi(s)ds$$

Do teorema fundamental do cálculo

$$\frac{d}{dt}g(t)=\phi(t)\leq f(t)+\beta g(t)$$

Assim,

$$\frac{d}{dt}g(t)-\beta g(t)\leq f(t)$$

então,

$$\frac{d}{dt}\left(e^{-\beta t}g(t)\right)=e^{-\beta t}\left(\frac{d}{dt}g(t)-\beta g(t)\right)\leq e^{-\beta t}f(t)$$

Integrando no intervalo $ [a,t] $, temos que

$$e^{-\beta t}g(t)\leq\int_a^te^{-\beta s}f(s)ds$$

e portanto

$$g(t)\leq \int_a^t f(s)e^{\beta (t-s)}ds.$$

Assim, vale a desigualdade a seguir:

$$\phi(t)\leq f(t)+\beta g(t)\leq f(t)+\beta\int_a^tf(s)e^{\beta(t-s)}ds.$$

Lema 10.5.1 (Desigualdade de Bellman-Gronwall)

Suponha que $ \phi\in L^1[a,t] $ e que satisfaça

$$\phi(t)\leq f(t)+\beta\int_a^t\phi(s)ds, \ \ \ \forall t\in[a,b].$$

Então,

$$\phi(t)\leq f(t)+\beta\int_a^tf(s)e^{\beta(t-s)}ds.$$

Em particular, quando $ f(t) $ é uma constante $ \alpha $, temos que

$$\phi(t)\leq \alpha e^{\beta(t-a)}.$$

Para a segunda desigualdade, considere uma sequência de funções $ (\theta_n)_{n=1}^{\infty} $ em $ L^1[a,b] $, satisfazendo

$$\theta_{n+1}(t)\leq f(t)+\beta\int_a^t\theta_n(s)ds, \ \ \ \forall t\in [a,b]$$

com $ f\in L^1[a,b] $ e $ \beta $ constante positiva.

Será possível, limitar $ \theta_{n+1} $ em termos de $ f(t), \beta, n $ e $ \theta_1 $?

Para $ n=1 $, temos que

$$\theta_2(t)\leq f(t)+\beta\int_a^t\theta_1(s)ds.$$

Para $ n=2 $, temos que

$$\theta_3(t)\leq f(t)+\beta\int_a^t\theta_2(s)ds $$

$$\leq f(t)+\beta\int_a^tf(s)ds+\beta^2\int_a^t\int_a^s\theta_1(u)du ds$$

$$\leq f(t)+\beta\int_a^tf(s)ds+\beta^2\int_a^t(t-u)\theta_1(u)du$$

Por indução, temos que

$$\theta_{n+1}(t)\leq +\beta\int_a^tf(s)ds+\beta^2\int_a^t(t-s)f(s)ds+\dots+\beta^{n-1}\int_a^t\frac{(t-s)}{(n-2)!}^{n-2}f(s)ds+\beta^n\int_a^t\frac{(t-s)}{(n-1)!}^{n-1}\theta_1(s)ds.$$

Como

$$\sum_{k=0}^{n-2}\beta^k\frac{(t-u)}{k!}^k\leq e^{\beta(t-u)},$$

podemos simplificar $ \theta_{n+1}(t) $ por

$$\theta_{n+1}(t)\leq f(t)+\beta\int_a^tf(s)e^{\beta(t-s)}ds+\beta^n\int_a^t\frac{(t-s)}{(n-1)!}^{n-1}\theta_1(s)ds$$

Lema 10.5.2

Seja $ (\theta_n)_{n=1}^{\infty} $ sequência de funções em $ L^1[a,b] $ satisfazendo

$$\theta_{n+1}(t)\leq f(t)+\beta\int_a^t\theta_n(s)ds, \ \ \ \forall t\in [a,b]$$

Então,

$$\theta_{n+1}(t)\leq f(t)+\beta\int_a^tf(s)e^{\beta(t-s)}ds+\beta^n\int_a^t\frac{(t-s)}{(n-1)!}^{n-1}\theta_1(s)ds$$

Em particular, quando $ f(t)=\alpha $ e $ \theta_1(t)=c $, vale a seguinte desigualdade para todo $ n\geq 1 $

$$\theta_{n+1}(t)\leq \alpha e^{\beta(t-a)}+\frac{c\beta^n(t-a^n)}{n!}.$$

Vamos considerar equações diferenciais estocásticas do tipo

$$dX(t)=\sigma(t,X(t))dB(t)+f(t,X(t))dt,\ \ \ X(a)=\xi.\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)$$

Antes de provarmos o teorema de existência e unicidade da solução de uma equação diferencial estocástica (EDE), primeiro precisamos entender o que significa um processo estocástico $ X(t) $ ser solução de uma EDE.

10.5.1 - Teorema da existência e unicidade

Seja $ \sigma(t,x) $ e $ f(t,x) $ funções mensurável de $ t\in [a,b] $ e $ x\in \mathbb{R} $. Considere uma equação diferencial estocástica

$$dX_t=\sigma(t,X_t)dB(t)+f(t,X_t)dt, \quad \quad X_a=\xi,$$

o qual deve ser interpretada na verdade como

$$X_t=\xi+\int_a^t\sigma(s,X_s)dB(s)+\int_a^tf(s,X_s)ds, \quad \quad a\leq t\leq b$$

Primeiramente, precisamos definir o que significa o processo estocástico $ X_t $ acima ser solução da equação

$$X_t=\xi+\int_a^t\sigma(s,X_s)dB(s)+\int_a^tf(s,X_s)ds, \quad \quad a\leq t\leq b$$

Definição 10.5.1.1: Um processo estocástico conjuntamente mensurável $ X_t, \quad a\leq t\leq b $, é chamado da solução de equação acima, se satisfaz as seguintes condições:

1. O processo estocástico $ \sigma(t,X_t) $ pertence $ \mathcal{L}_{ad}(\Omega, L^2[a,b]) $, então

$$\int_a^t\sigma(s,X_s)dB(s)$$

é uma integral de Itô para cada $ t\in [a,b] $;

2. Quase todos os caminhos do processo estocástico $ f(t,X_t) $ pertence a $ L^1[a,b] $;

3. Para cada $ t\in [a,b] $, a equação acima, segue quase certamente.

Como vimos em exemplos na seção 10.5.1 precisamos impor condições sobre as funções $ \sigma(t,x) $ e $ f(t,x) $ para garantir as existência de uma única solução não explosiva da integral estocástica.

Então definimos as seguintes condições

Definição 10.5.1.2: Um função mensurável $ g(t,x) $ em $ [a,b]\times \mathbb{R} $ é dito satisfazer a condições de Lipschitz em $ x $ se existe uma constante $ K> 0 $ tal que

$$|g(t,x)-g(t,y)|\leq K|x-y|, \quad \quad \forall a\leq t\leq b, \quad x, y \in \mathbb{R}$$

Definição 10.5.1.3: Uma função mensurável $ g(t,x) $ em $ [a,b]\times \mathbb{R} $ é dita satisfazer um condição de crescimento linear $ x $ se existe uma constante $ K> 0 $ tal que

$$|g(t,x)|\leq K(1+|x|), \quad \quad \forall a\leq t\leq b, \quad x\in \mathbb{R}.$$

Observe as seguintes desigualdades para todo $ x\geq 0 $:

$$1+x^2\leq (1+x)^2\leq 2(1+x^2).$$

Portando a condição de crescimento linear é equivalente a existência de uma constante $ Cgt;0 $, tal que

$$|g(t,x)|^2\leq C(1+x^2), \quad \quad \forall a\leq t\leq b, \quad \quad x \in \mathbb{R}.$$

Lema 10.5.1.1: Seja $ \sigma(t,x) $ e $ f(t,x) $ uma função mensurável em $ [a,b]\times \mathbb{R} $ satisfazendo a condição de Lipschitz em $ x $. Suponha que $ \xi $ é uma variável aleatória $ \mathcal{F}_a $-mensurável com $ \mathbb{E}(\xi^2)< \infty $. Então a integral estocástica, tem no máximo um solução contínua em $ X_t $.

Demonstração: Seja $ X_t $ e $ Y_t $ duas soluções contínuas da integral estocástica. Seja $ Z_t=X_t-Y_t $. Então $ Z_t $ é um processo estocástico contínuo e

$$Z_t=\int_a^t (\sigma(s,X_s)-\sigma(s,Y_s))dB(s)+\int_a^t(f(s,X_s)-f(s,Y_s))ds$$

Usando a desigualdade $ (a+b)^2\leq 2(a^2+b^2) $ junto com

$$Z_t^2\leq 2\left[\left(\int_a^t (\sigma(s,X_s)-\sigma(s,Y_s))dB(s)\right)^2 + \left(\int_a^t (f(s,X_s)-f(s,Y_s))ds\right)^2\right]$$

Pelo condição de Lipschitz na em $ \sigma(t,x) $ temos

$$\mathbb{E}\left(\int_a^t (\sigma(s,X_s)-\sigma(s,Y_s))dB(s)\right)^2=\int_a^t \mathbb{E}\left[(\sigma(s,X_s)-\sigma(s,Y_s))^2\right]ds\leq K^2 \int_a^t \mathbb{E}(Z_s^2)ds.$$

Por outro lado, pela condição de Lipschitz a função $ f(t,x) $,

$$\left(\int_a^t (f(s,X_s)-f(s,Y_s))ds\right)^2\leq (t-a)\int_a^t(f(s,X_s)-f(s,X_s))^2ds\leq (b-a)K^2\int_a^tZ^2_sds$$

Por essas duas desigualdades temos que

$$\mathbb{E}(Z_t^2)\leq K^2 \int_a^t \mathbb{E}(Z_s^2)ds+ (b-a)K^2\int_a^t \mathbb{E}(Z^2_s)ds=2K^2(1+b-a)\int_a^t \mathbb{E}(Z^2_s)ds$$

Pela desigualdade de Bellman-Gronwall, temos que $ \mathbb{E}(Z_t^2)=0 $, para todo $ t\in[a,b] $. Portanto, $ Z_t=0 $ quase certamente para cada $ t\in[a,b] $. Seja $ (r_1,r_2,\dots) $ um conjunto enumerável de racionais no intervalo $ [a,b] $. Então para cada $ r_n $, existe um conjunto $ \Omega_n $ tal que $ \mathbb{P}(\Omega_n)=1 $ e $ Z_{r_n}(\omega)=0 $ para cada $ \omega \in \Omega_n $. Seja

$$\Omega^\prime =\bigcap_{n=1}^\infty \Omega_n$$

Então $ \mathbb{P}(\Omega^\prime)=1 $ e para cada $ \omega \in \Omega^\prime $ temos que $ Z_{r_n}(\omega)=0 $ para todo $ n $. Desde que $ Z_t $ é um processo estocástico contínuo temos que existe um $ \Omega^\star $ tal que $ \mathbb{P}(\Omega^\star)=1 $ e para cada $ \omega \in \Omega^\star $, a função $ Z_t(\omega) $ é uma função contínua em t.

Finalmente, seja $ \Omega_0=\Omega^\prime \cap \Omega^\star $. Então $ \mathbb{P}(\Omega_0)=1 $ e para cada $ \omega \in \Omega_0 $, a função $ Z_t(\omega) $ é uma função contínua que é nula em todos os números racionais que pertence a $ [a,b] $. Se segue para $ \omega \in \Omega_0 $ $ Z_t(\omega) $ é nula para todo $ t $ já que $ Z $ é contínua. Isto implica que $ X_t $ e $ Y_t $ são os mesmos processos contínuos quase certamente.

Teorema 10.5.1.1:Seja $ \sigma(t,x) $ e $ f(t,x) $ um função mensurável em $ [a,b]\times \mathbb{R} $ satisfazendo a condição de Lipschitz e de crescimento linear em $ x $. Suponha que $ \xi $ é uma variável aleatória $ \mathcal{F}_a $-mensurável com $ \mathbb{E}(\xi^2)< \infty $. Então, a integral estocástica descrita na equação acima tem uma única solução em $ X_t $.

Demonstração: A unicidade da solução contínua vem do Lema 10.5.1.1. Resta-nos mostrar a existência de uma solução.

Pela afirmação, existe uma constante $ C> 0 $ tal que a seguinte desigualdade segue, para todo $ t\in [a,b] $ e $ x,y\in \mathbb{R} $:

$$|\sigma(t,x)-\sigma(t,y)|\leq C|x-y|,$$

$$|f(t,x)-f(t,y)|\leq C|x-y|,$$

$$|\sigma(t,x)|^2\leq C(1+x^2),$$

$$|f(t,x)|^2\leq C(1+x^2).$$

Defina uma sequência $ (X_t^{(n)})_{n=1}^\infty $ de um processos estocástico contínuos indutivamente, definindo $ X_t^{(1)}=\xi $ e para $ n\geq 1 $,

$$X_t^{(n+1)}=\xi+\in_a^t \sigma(s,X_s^{(n)})dB(s)+\int_a^t f(s,X_s^{(n)})ds.$$

Obviamente, $ X_1^{(1)} $ pertence a $ L_{ad}^2([a,b]\times \Omega) $. Assumimos que por indução que o processo estocástico $ X^(n)_t $ pertence a $ L^2_{ad}([a,b]\times \Omega) $. Então pelo condição crescimento linear, temos que

$$\mathbb{E}\left(\int_a^b\sigma(t,X_t^{(n)})^2dt\right)\leq C(b-a)+C\mathbb{E}\left(\int_a^b|X_t^{(n)}|dt\right)< \infty$$

$$\int_a^t|f(s,X_s^{(n)})|ds\leq \sqrt{C(b-a)}\left(\int_a^b(1+|X_t^{(n)}|^2)dt\right)^{1/2}< \infty, \quad \quad a.s.$$

Consequentemente

$$\in_a^t \sigma(s,X_s^{(n)})dB(s)$$

é um integral de Itô, enquanto

$$\int_a^t f(s,X_s^{(n)})ds$$

é um integral de Lebesgue em $ t $ para quase todo $ \omega \in\Omega $. Então $ X_t^{(n+1)} $ é um processo estocástico contínuo e é adaptado a filtragem $ (\mathcal{F_t}) $. Além disso, desde que $ |a+b+c|^2\leq 3(a^2+b^2+c^2) $, temos que

$$|X^{(n+1)}_t|^2\leq 3\left[\xi^2+\left(\int_a^t \sigma(s,X_s^{(n)})dB(s)\right)^2+\left(\int_a^tf(s,X_s^{(n)})ds\right)^2\right],$$

juntando com a condição do crescimento linear implica que

$$\mathbb{E}\left(\int_a^b |X_t^{(n+1)}|^2\right)dt< \infty$$

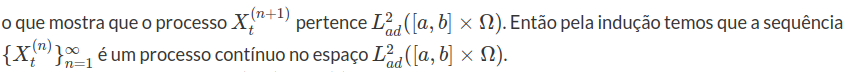
A seguir, vamos estimar $ \mathbb{E}(|X_t^{(n+1)}-X_t^{(n)}|^2) $. Para isso, defina

$$Y^{n+1}_t=\int_a^t\sigma(s,X^{(n)}_s)dB(s)$$

e

$$Z^{(n+1)}_t=\int_a^t f(s,X_s^{(n)})ds$$

Então, $ X_t^{(n+1)}=\xi+Y_t^{(n+1)}+Z_t^{(n+1)} $; Desde que $ (a+b)^2\leq 2(a^2+b^2) $, definimos

$$\mathbb{E}(|X_t^{(n+1)}-X_t^{(n)}|^2)\leq 2\left(\mathbb{E}\left(|Y_t^{(n+1)}-Y_t^{(n)}|^2\right) +\mathbb{E}\left(|Z_t^{(n+1)}-Z_t^{(n)}|^2\right)\right)$$

Pela condição de Lipschitz temos que

$$\mathbb{E}\left(|Y_t^{(n+1)}-Y_t^{(n)}|^2\right)=\int_a^t\mathbb{E}(|\sigma(s,X_s^{(n)})-\sigma(s,X_s^{(n-1)})|^2)ds$$

$$\leq C^2 \int_a^t\mathbb{E}(|X_s^{(n)}-X_s^{(n-1)}|^2)ds.$$

Similarmente, usando a condição de Lipschitz segue que

$$|Z_t^{n+1}-Z_t^{(n)}|^2\leq (b-c)C^2\int_a^t |X_s^{(n)}-X_s^{(n-1)}|^2ds.$$

Com isso, obtemos que

$$\mathbb{E}\left(|X_t^{(n+1)}-X_t^{(n)}|^2\right)\leq 2 C^2(1+b-a)\int_a^t\mathbb{E}(|X_s^{(n)}-X_s^{(n-1)}|^2)ds.$$

Por outro lado, a condição de crescimento

$$|\sigma(t,x)|^2\leq C(1+x^2),$$

$$|f(t,x)|^2\leq C(1+x^2).$$

temos que,

$$\mathbb{E}(|X_t^{(2)}-X_t^{(1)}|^2)\leq 2C^2(1+b-a)\int_a^t (1+\mathbb{E}(\xi^2))ds.$$

Então pelo Lema 10.2.4, temos que

$$\mathbb{E}(|X_t^{(n+1)}-X_t^{(n)}|^2)\leq \rho \frac{\beta^n(t-a)^n}{n!}$$

no qual $ \rho=1+\mathbb{E}(\xi^2) $ e $ \beta=2C^2(1+b-a) $. Agora observe que para qualquer $ t\in [a,b] $,

$$|X_t^{(n+1)}-X_t^{(n)}|\leq |Y_t^{(n+1)}-Y_t^{(n)}|+|Z_t^{(n+1)}-Z_t^{(n)}|.$$

Portanto temos que

$$\sup_{a\leq t\leq b}|X_t^{(n+1)}-X^{(n)}|\leq \sup_{a\leq t\leq b}|Y_t^{(n+1)}-Y_t^{(n)}|+\sup_{a\leq t\leq b}|Z_t^{n+1}-Z_t^{n}|,$$

o que implica que

$$\left(\sup_{a\leq t\leq b}|X_t^{(n+1)}-X_t^{(n)}|> \frac{1}{n^2}\right)\subset \left(\sup_{a\leq t\leq b}|Y_t^{(n+1)}-Y_t^{(n)}|> \frac{1}{2n^2}\right)\bigcup \left(\sup_{a\leq t\leq b}|Z_t^{(n+1)}-Z_t^{(n)}|> \frac{1}{2n^2}\right)$$

Portanto,

$$\mathbb{P}\left(\sup_{a\leq t\leq b}|X_t^{(n+1)}-X_t^{(n)}|> \frac{1}{n^2}\right)\leq \mathbb{P} \left(\sup_{a\leq t\leq b}|Y_t^{(n+1)}-Y_t^{(n)}|> \frac{1}{2n^2}\right)+ \mathbb{P}\left(\sup_{a\leq t\leq b}|Z_t^{(n+1)}-Z_t^{(n)}|> \frac{1}{2n^2}\right)$$

Aplicando a desigualdade de submartingale de Doob do Teorema 10.2.4 e então usando a equação EQ005 obtemos que

$$\mathbb{P}\left(\sup_{a\leq t\leq b}|Y_t^{(n+1)}-Y_t^{(n)}|> \frac{1}{2n^2}\right)\leq 4n^4\mathbb{E}(|Y_b^{(n+1)}-Y_b^{(n)}|^2)$$

$$\leq 4n^4C^2\int_a^b \mathbb{E}(|X_t^{(n)}-X_t^{(n-1)}|^2)dt\leq 4n^4C^2\rho \frac{\beta^{n-1}(b-a)^n}{n!}$$

Por outro lado usando a condição de Lipschitz da função $ f $, obtemos que

$$|Z_t^{(n+1)}-Z_t^{(n)}|^2\leq C^2(b-a)\int_a^t|X_s^{(n)}-X_s^{(n-1)}|^2ds,$$

o que implica

$$sup_{a\leq t\leq b}|Z_t^{(n+1)}-Z_t^{(n)}|^2\leq C^2(b-a)\int_a^b |X_t^{(n)}-X_t^{(n-1)}|^2ds$$

por essa desigualdade de pela desigualdade

$$\mathbb{E}(|X_t^{(n+1)}-X_t^{(n)}|^2)\leq \rho \frac{\beta^n(t-a)^n}{n!}$$

obtemos que

$$\mathbb{P}\left(\sup_{a\leq t\leq b}|Z_t^{(n+1)}-Z^{(n)}_t|> \frac{1}{2n^2}\right)\leq 4n^4\mathbb{E}\left[\left(\sup_{a\leq t\leq b}|Z^{n+1}_t-Z^{n}_t|\right)^2\right]\leq 4n^4C^2(b-a)\rho \frac{\beta^{n-1}(b-a)^n}{n!}$$

Juntando as equações acima obtemos

$$\mathbb{P}\left(\sup_{a\leq t\leq b}|X_t^{(n+1)}-X_t^{(n)}|> \frac{1}{n^2}\right)\leq \mathbb{P} \left(\sup_{a\leq t\leq b}|Y_t^{(n+1)}-Y_t^{(n)}|> \frac{1}{2n^2}\right)+ \mathbb{P}\left(\sup_{a\leq t\leq b}|Z_t^{(n+1)}-Z_t^{(n)}|> \frac{1}{2n^2}\right)$$

$$\leq 4n^4C^2\rho \frac{\beta^{n-1}(b-a)^n}{n!}+ 4n^4C^2(b-a)\rho \frac{\beta^{n-1}(b-a)^n}{n!}\leq 2\rho \frac{n^4\beta^n(b-a)^n}{n!}$$

Pelo teste da razão podemos ver que

$$2\rho\sum_{n=1}^\infty \frac{n^4\beta^n(b-a)^n}{n!}$$

é convergente, pois

$$\lim_{n\rightarrow \infty}\frac{a_{n+1}}{a_n}=\lim_{rightarrow \infty}\frac{\beta(n+1)^3(b-a)}{n^4}=0,$$

com $ a_n=\frac{n^4\beta^n(b-a)^n}{n!} $

Portanto, pelo Lema de Borel-Cantelli Lema 7.1.1.1

$$\mathbb{P}\left(\sup_{a\leq t\leq b}|X_t^{(n+1)}-X_t^{(n)}|> \frac{1}{n^2}\quad \quad i.o.\right)=0$$

Mas isso implica que

$$\xi+\sum_{n=1}^\infty (X_t^{(n+1)}-X_t^{(n)})$$

converge uniformemente em $ [a,b] $ com probabilidade 1, ou seja, converge para um elemento que vamos chamar de $ X_t $. Observe que a soma parcial

$$\xi+\sum_{n=1}^m (X_t^{(n+1)}-X_t^{(n)})=X_t^{(m+1)}$$

Portanto, com probabilidade 1, temos que

$$\lim_{n\rightarrow \infty} X_t^{(n)}=X_t$$

uniformemente para $ t\in [a,b] $. Claro que, o processo estocástico $ X_t $ é contínuo e adaptado a filtragem a $ (\mathcal{F_t}; a\leq t\leq b) $. Além do mais, temos que a equação

$$\mathbb{E}(|X_t^{(n+1)}-X_t^{(n)}|^2)\leq \rho \frac{\beta^n(t-a)^n}{n!}$$

implica que

$$|X_t^{(n+1)}-X_t^{(n)}|\leq \sqrt{\rho} \frac{\beta^{n/2}(t-a)^{n/2}}{\sqrt{n!}}$$

como $ |\cdot| $ sendo a norma de $ L^2(\Omega) $. Essa desigualdade implica que para cada t, a serie

$$\xi+\sum_{n=1}^\infty (X_t^{(n+1)}-X_t^{(n)})$$

converge em $ L^2(\Omega) $ e ainda, temos que

$$|X_t|\leq |\xi|+\sum_{n=1}^\infty\sqrt{\rho} \frac{\beta^{n/2}(t-a)^{n/2}}{\sqrt{n!}}$$

Isto segue que

$$\mathbb{E}\int_a^b|X_t|^2dt< \infty$$

Portanto, o processo estocástico $ X_t $ pertence ao espaço $ L^2_{ad}([a,b]\times\Omega)\subset \mathcal{L}_{ad}(\Omega,L^2[a,b]) $. Com isso, podemos observar que satisfaz a Definição 10.5.1.1 e ainda podemos passar o $ \lim_{n\rightarrow \infty} $ para dentro da integral e então obtemos que $ X_t $ é solução da integral estocástica e portanto, o resultado segue.

10.5.2 - Solução de Equações Diferenciais Estocásticas

Nessa seção vamos estudar algumas propriedades da solução das equações diferenciais. Seja

$$X_t=\xi+\int_a^t \sigma(s,X_s)dB(s)+\int_a^t f(s,X_s)ds, \quad \quad a\leq t\leq b,$$

com $ \sigma $ e $ f $ satisfazendo as condições de crescimento linear e de Lipschitz. Primeiramente vamos provar que a solução de $ X_t $ é um processo de Markov.

Seja $ (\mathcal{F_t},\quad a\leq t\leq b) $ a filtragem dada pelo movimento Browniano $ B(t) $, definida por $ \mathcal{F_t}=\sigma(B(s); s\leq t) $. Claro que, a solução de $ X_t $ é adaptado a filtragem .

Seja $ s\in [a,b] $ e $ x\in \mathbb{R} $ fixado e considere o seguinte

$$X_t=x+\int_s^t \sigma(u,X_u)dB(s)+\int_s^t f(u,X_u)du, s\leq t\leq b.$$

Para evitar confusão com a solução $ X_t $, usaremos $ X_t^{s,x} $ para denotar a solução da equação acima. Desde que a condição inicial $ x $ é uma constante, o qual vemos na prova do Teorema 10.5.1.1 a solução é independente de $ \mathcal{F_s} $ para $ t\in [s,b] $. Isso implica que para qualquer variável $ Z $ é $ \mathcal{F_s} $-mensurável temos a seguinte igualdade

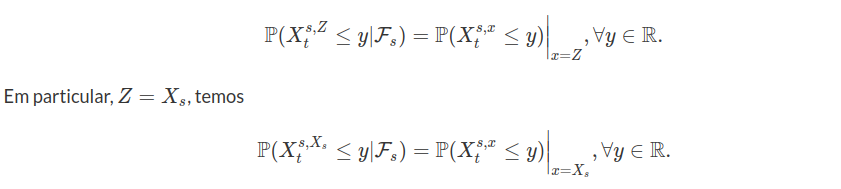
Agora, desde que $ X_t $ é uma solução da equação, temos

$$X_t=X_s+\int_s^t \sigma(u,X_u)dB(u)+\int_s^t f(u,X_u)du, \quad \quad s\leq t\leq b.$$

Mas $ X_t^{s,X_s} $ é também solução. Portanto, pela unicidade da solução temos que $ X_t=X_t^{s,X_s} $. Então, temos que

$$\mathbb{P}(X_t\leq y|\mathcal{F_s})=\mathbb{P}(X_t^{s,x}\leq y)\bigg|_{x=X_s}, \forall y\in \mathbb{R}.$$

o qual é mensurável com respeito a $ \sigma $-álgebra gerada por $ X_s $. Portanto concluímos que

$$\mathbb{P}(X_t\leq y|X_s)=\mathbb{E}[\mathbb{P}(X_t\leq y| \mathcal{F_s})|X_s]=\mathbb{P}(X_t\leq y|\mathbb{F}_s)\quad \quad \forall s< t,y\in \mathbb{R}.$$

Então pela

$$\mathbb{P}(X_t\leq x|\mathcal{F_s})=\mathbb{P}(X_t\leq x|X_s), \quad \forall s< t, x\in \mathbb{R}$$

o processo estocástico $ X_t $ é um processo de Markov. Portanto, temos que a prova do teorema a seguir

Teorema 10.5.2.1: Seja $ \sigma(t,x) $ e $ f(t,x) $ uma função mensurável em $ [a,b]\times \mathbb{R} $, satisfazendo as condições de crescimento linear e Lipschitz em x. Suponha que $ \xi $ seja uma variável $ \mathcal{F}_a $-mensurável com $ \mathbb{E}(\xi^2)< \infty $. Então, a única solução contínua da equação estocástica

$$X_t=\xi+\int_s^t \sigma(u,X_u)dB(u)+\int_s^t f(u,X_u)du, \quad \quad s\leq t\leq b.$$

é um processo de Markov.

Observe que a solução de $ X_t $ satisfaz

$$\mathbb{P}(X_t\leq y|X_s)=\mathbb{E}[\mathbb{P}(X_t\leq y| \mathcal{F_s})|X_s]=\mathbb{P}(X_t\leq y|\mathbb{F}_s)\quad \quad \forall s< t,y\in \mathbb{R}.$$

a qual é mais forte sobre do que a propriedade de Markov de $ X_t $. Na verdade a solução de $ X_t $ satisfaz propriedades ainda mais forte, a qual utiliza o conceito de tempos de parada introduzido anteriormente. Seja $ \tau $ um tempo de parada com respeito a filtragem $ (\mathcal{F_t}, a\leq t\leq b) $ dado um movimento Browniano $ B(t) $. A $ \sigma $-algebra $ \mathcal{F}_\tau $ associada com $ \tau $ é definida por

$$\mathcal{F}_\tau=(A,A\cap (\tau< t)\in \mathcal{F_t}, \forall t\in [a,b]).$$

Então, podemos provar que para qualquer tempo de parada $ \tau $ com respeito a filtragem $ (\mathcal{F_t}) $, o processo estocástico $ X_t $ satisfaz a seguinte igualdade

$$\mathbb{P}(X_{\tau+v}\leq y|\mathcal{F}_\tau)=\mathbb{P}(X_{\tau+v}\leq y| X_\tau), \quad \forall v\geq 0, y\in \mathbb{R},$$

o que pode ser entendido como $ X_{\tau(\omega)+v}(\omega)=X_b(\omega) $ se $ \tau(\omega)+v\geq b $. A equação acima é chamada de propriedade forte de Markov de $ X_t $. Note que quando $ \tau=s $ e $ v-t-s $ a equação acima se reduz novamente a

$$\mathbb{P}(X_t\leq y|X_s)=\mathbb{E}[\mathbb{P}(X_t\leq y| \mathcal{F_s})|X_s]=\mathbb{P}(X_t\leq y|\mathbb{F}_s)\quad \quad \forall s< t,y\in \mathbb{R}.$$

Então, a propriedade forte de Markov implica na equação acima a qual implica na propriedade de Markov.

Em seguida considere a integral estocástica com funções $ \sigma $ e $ f $ dependendo apenas de $ x $. Neste caso, observe que a condição de Lipschitz

$$|g(x)|\leq |g(x)-g(0)|+|g(0)|\leq K|x|+|g(0)|\leq C(1+|x|),$$

no qual $ C=\max(K,|g(0)|) $. Portanto a condição de crescimento linear decorre da condição de Lipschitz.

Teorema 10.5.2: Assumindo que $ \sigma(x) $ e $ f(x) $ são funções que satisfaz a condição de Lipschitz e seja $ x_0\in \mathbb{R} $. Então a única solução contínua da integral estocástica

$$X_t=x_0+\int_0^t\sigma(X_s)dB(s)+\int_0^t f(X_s)ds, \quad t\geq 0,$$

é um processo de Markov estacionário.

Demonstração: Seja $ s\geq 0 $ e $ x\in \mathbb{R} $ fixado e considere o seguinte equação

$$X_t=x+\int_s^t \sigma(X_u)dB(u)+\int_s^t f(X_u)du, t\geq s.$$

Seja $ X_t^{s,x} $ denotando a única solução contínua da equação acima. Então

$$X_t^{s,x}=x+\int_s^t\sigma(X^{s,x}_u)dB(u)+\int_s^t f(X_u^{s,x})du$$

Fazendo uma mudança de variável $ u=s+v $ temos

Fazendo mudança de variáveis $ t=s+w $ temos

$$X_{s+w}^{s,x}=x+\int_0^w \sigma(X^{s,x}_{s+v})d\tilde{B}_s(v)+\int_0^w f(X^{s,x}_{s+v})dv$$

Então, substituindo a variável w por t:

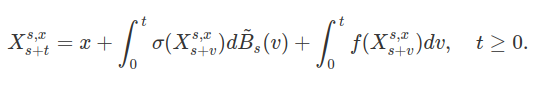
o que significa que para qualquer $ s> 0 $ fixado, o processo estocástico $ X^{s,x}_{s+t} $, $ t\geq 0 $, é uma solução de

$$Y_{t}=x+\int_0^t \sigma(Y_u)d\tilde{B}_s(v)+\int_0^w f(Y_u)du, \quad t\geq 0.$$

Do procedimento procedimento de aproximação da prova do Teorema 10.5.1 vemos então que a distribuição da solução de $ X^{s,x}_{s+t} $ é independente de s. Portanto,

$$\mathbb{P}(X^{s,x}_{s+t}\in A)=\mathbb{P}(X_t^{0,x}\in A), \quad \forall A\in \mathcal{B}(\mathbb{R}).$$

Seja $ \mathbb{P}_{s,x}(t,\cdot) $ denota a probabilidade de transição da solução $ X_t $ dada por

$$X_t=x_0+\int_0^t\sigma(X_s)dB(s)+\int_0^t f(X_s)ds, \quad t\geq 0,$$

Então, podemos reescrever

$$\mathbb{P}(X^{s,x}_{s+t}\in A)=\mathbb{P}(X_t^{0,x}\in A), \quad \forall A\in \mathcal{B}(\mathbb{R}).$$

como sendo

$$\mathbb{P_{s,x}(}s+t,A)=\mathbb{P_{0,x}}(t,A),\quad \forall A\in \mathcal{B}(\mathbb{R}).$$

Isto significa que para qualquer $ t\geq 0 $ e $ x\in \mathbb{R} $, a medida de probabilidade $ \mathbb{P}_{s,x}(s+t,\cdot) $ é independente de $ s\geq 0 $. Então o processo estocástico $ X_t $ é estacionário.

Exemplo 10.5.2.1: Considere uma equação diferencial simples

$$dX_t=X_tdB(t)+dt,\quad \quad X_0=x.$$

Pelo teorema anterior, a solução desta SDE (sigla em inglês para Equação Diferencial Estocástica) é um processo de Markov estacionário. Por outro lado, podemos resolver explicitamente a equação acima. Aplicando a formula de Itô, temos

$$d(e^{-B(t)+\frac{1}{2}t}X_t)=e^{-B(t)+\frac{1}{2}t}(dX_t-X_tdB(t))=e^{-B(t)+\frac{1}{2}t}dt$$

Integrando ambos os lados de s a t, temos

$$X_t=e^{(-B(t)-B(s))-\frac{1}{2}(t-s)}X_s+\int_s^t e^{(B(t)-B(u))-\frac{1}{2}(t-u)}du$$

Em particular

$$X_t=xe^{B(t)-\frac{1}{2}t}+\int_0^t e^{(B(t)-B(u))-\frac{1}{2}(t-u)}du$$

Além do mais,

$$X^{s,x}_{s+t}=xe^{B(s+t)-B(s)-\frac{1}{2}t}+\int_s^{s+t} e^{(B(s+t)-B(u))-\frac{1}{2}(s+t-u)}du$$

o qual, após fazer uma mudança de variável $ u=s+v $, temos

$$X^{s,x}_{s+t}=xe^{B(s+t)-B(s)-\frac{1}{2}t}+\int_0^{t} e^{(B(s+t)-B(u))-\frac{1}{2}(s+t-u)}du$$

Note que $ B(s+t)-B(s) $ é um movimento Browniano para qualquer $ s\geq 0 $ fixado. Portanto, a distribuição de $ X^{s,x}_{s+t} $ é independente de s. O que mostra que o processo $ X_t $ é um processo de Markov estacionário.

A seguir considere a dependência de uma solução de um equação diferencial estocástica em sua condição inicial. É dado pelo próximo teorema.

Teorema 10.5.2.3: Seja $ \sigma $ e $ f $ e satisfazendo a condição de Lipschitz em x, existe uma constante $ K> 0 $, tal que

$$|\sigma(t,x)-\sigma(t,y)|\leq K|x-y|, \quad \quad |f(t,x)-f(t,y)|\leq K|x-y|,$$

para todo $ t\in [a,b] $ e $ x,y \in \mathbb{R} $. Seja $ \xi,\eta \in L^2(\Omega) $ funções em $ \mathcal{F}_a $-mensurável. Assumindo que $ X^{\xi}_t $ e $ X^\eta_t $ são duas soluções para a equação diferencial estocástica

$$dX_t=\sigma(t,X_t)dB(t)+f(t,X_t)dt$$

com condição inicial $ \xi $ e $ \eta $, respectivamente. Então

$$\mathbb{E}(|X^{\xi}_t-X^{\eta}_t|^2)\leq 3 \mathbb{E}(|\xi-\eta|^2)e^{2K^2(1+b-1)(t-a)}, \quad \forall a\leq t\leq b.$$

Demonstração:

Temos que

$$X_t^\xi=\xi+\int_a^t\sigma(s,X_s^\xi)dB(s)+\int_a^t f(s,X^\xi_s)ds$$

$$X_t^\eta=\eta+\int_a^t\sigma(s,X_s^\eta)dB(s)+\int_a^t f(s,X^\eta_s)ds$$

Observação: Existe outra parte da desigualdade de Doob’s para submartingale, afirma que se $ Y_t $, $ a\leq t\leq b $ é um submartingale contínua a direita, então

$$\mathbb{E}\left(\left[\sup_{a\leq t\leq b}|Y_t|\right]^p\right)\leq q^p\mathbb{E}(|Y_b|^p),$$

no qual $ p> 1 $ e $ p^{-1}+q^{-1}=1 $. Usando essa desigualdade com $ p=2 $ e argumentos similares a prova acima, podemos obter uma estimativa mais forte para qualquer $ a\leq t\leq b $:

$$\mathbb{E}\left(\left[\sup_{a\leq t\leq b}|X^\xi_t-X^\eta_s|\right]^2\right)\leq 3\mathbb{E}(|\xi-\eta|^2)e^{3K^2(4+b-a)(t-a)},$$

Portanto,

$$|X^\xi_t-X^\eta_t|\leq |\xi-\eta|+\Big|\int_a^t(\sigma(s,X_s^\xi)-\sigma(s,X^\eta_s))dB(s)\Big|$$

$$+\Big|\int_a^t (f(s,X^\xi_s)-f(s,X^\eta_s))ds\Big|.$$

Usando a desigualdade $ (|a|+|b|+|c|)^2\leq 3(a^2+b^2+c^2) $, temos que

$$|X^\xi_t-X^\eta_t|^2\leq 3\left(|\xi-\eta|^2+\Big|\int_a^t (\sigma(s,X^\xi_s)-\sigma(s,X^\eta_s))dB(s)\Big|^2+\Big|\int_a^t (f(s,X^\xi_s)-f(s,X^\eta_s))ds\Big|^2\right)$$

$$3\left(|\xi-\eta|^2+\Big|\int_a^t (\sigma(s,X^\xi_s)-\sigma(s,X^\eta_s))dB(s)\Big|^2+(b-a)\int_a^t |f(s,X^\xi_s)-f(s,X^\eta_s)|^2ds\right)$$

Então, tomando a esperança em ambos os lados

$$\mathbb{E}(|X^\xi_t-X^\eta_t|^2)\leq 3\left(\mathbb{E}(|\xi-\eta|^2)+\mathbb{E}\left(\int_a^t |\sigma(s,X^\xi_s)-\sigma(s,X^\eta_s)|^2dB(s)\right)+\mathbb{E}\left(\int_a^t |f(s,X^\xi_s)-f(s,X^\eta_s)|^2ds\right)\right)$$

$$3\mathbb{E}(|\xi-\eta|^2)+3K^2(1+b-a)\int_a^t \mathbb{E}(|X^\xi_s-X^\eta_s|^2)ds$$

No qual a última desigualdade decorre da desigualdade de Bellman-Gronwall.

E portanto o resultado segue.

Algumas estimativas de soluções

Nesta seção, iremos provar algumas estimativas para a integral Itô e para as soluções de equações diferenciais estocásticas.

Lema 10.5.2.1: Suponha que $ h(t) $ e um processo estocástico adaptado satisfazendo

$$\displaystyle \int_a^b\mathbb{E}\left(|h(s)|^4\right)ds < \infty$$

e seja

$$\displaystyle Y_t=\int_a^t h(s) dB(s),\quad \quad a\leq t\leq b < \infty$$

Então,

$$\displaystyle \mathbb{E}(|Y_t|^4)\leq 2(17+4\sqrt{17})(t-a)\int_a^t\mathbb{E}(|h(s)|^4)ds, a\leq t\leq b.$$

Demonstração:

Aplicando a formula de Itô, temos

$$Y_t^2=2\displaystyle \int_a^t Y_sh(s)dB(s)+\int_a^th(s)^2ds.$$

A hipótese em $ h(t) $ implica que $ Y_th(t) $ pertence que $ L^2_{ad}([a,b]\times \Omega) $. Pela desigualdade $ (a+b)^2\leq 2a^2+2b^2 $,

$$Y_t^4\leq 8\left(\displaystyle \int_a^t Y_sh(s)dB(s)\right)^2+2\left(\displaystyle \int_a^t h^2(s)dB(s)\right)^2$$

Então usando o Teorema 10.2.3

$$\mathbb{E}(Y_t^4)\leq 8 \displaystyle \int_a^t \mathbb{E}(Y^2_sh(s)^2)ds+2\mathbb{E}\left(\int_a^th(s)^2ds\right)^2$$

$$\leq 8 \displaystyle \left[\int_a^t \mathbb{E}(Y^4_s)ds\right]^{1/2}\left[\int_a^t\mathbb{E}\left(h(s)^4\right)ds\right]^{1/2}+2(t-a)\int_a^t\mathbb{E}(h(s)^4)ds.$$

Integrando ambos os lados e usando desigualdade de Schwarz temos

$$\displaystyle \int_a^t\mathbb{E}\left(Y^4_s\right)ds \leq 8 \displaystyle \left[\int_a^t \int_a^s \mathbb{E}(Y^4_u)duds\right]^{1/2}\left[\int_a^t\int_a^s\mathbb{E}\left(h(u)^4\right)duds\right]^{1/2}+2\int_a^t(s-a)\int_a^s\mathbb{E}(h(u)^4)duds.$$

Mudando a ordem da integração temos que

$$\displaystyle \int_a^t\int_a^s\mathbb{E}\left(Y^4_s\right)duds = \displaystyle \int_a^t (t-u)\mathbb{E}(Y^4_u)du\leq (t-a)\int_a^t\mathbb{E}\left(Y_u^4\right)du$$

Similarmente, temos que

$$\displaystyle \int_a^t\int_a^s \mathbb{E}(h(u)^4)duds\leq (t-a)\int_a^t\mathbb{E}(h(u)^4)du$$

$$\displaystyle \int_a^t(s-a)\int_a^s \mathbb{E}(h(u)^4)duds\leq \frac{1}{2}(t-a)^2\int_a^t\mathbb{E}(h(u)^4)du$$

Agora usando as desigualdades acima e fazendo uma mudança de variável, temos que

$$\int_a^t \mathbb{E}(Y_s^4)ds \leq 8(t-a)\left[\int_a^t\mathbb{E}(Y^4_s)ds\right]^{1/2}\left[\int_a^t\mathbb{E}(h(s)^4)ds\right]^{1/2}+(t-a)^2\int_a^t\mathbb{E}(h(s)^4)ds.$$

Seja $ x=\displaystyle \int_a^t \mathbb{E}(Y^4_s)ds $ e $ y=\displaystyle \int_a^t \mathbb{E}(h(s)^4)ds $. Podemos assumir $ y\neq 0 $, por caso ele seja igual a zero, o Lema já válido. Então seja $ w=\sqrt{x}/\sqrt{y} $. Então, temos que $ w^2\leq 8(t-a)w+(t-a)^2 $, o qual temos que $ w\leq (4+|sqrt{17})(t-a) $. Segue que

$$\int_a^t\mathbb{E}(Y_s^4)ds\leq (4+\sqrt{17})^2(t-a)^2\int_a^t\mathbb{E}(h(s)^4)ds.$$

Então, o resultado segue.

Teorema 10.5.2.4: Seja $ \sigma(t,x) $ e $ f(t,x) $ satisfazendo a condição de Lipschitz em x e seguindo a condição de crescimento

$$|\sigma(t,x)|^2\leq C(1+x^2), \quad \quad \quad \quad |f(t,x)|^2\leq C(1+x^2)$$

Suponha $ \xi $ é uma variável aleatória $ \mathcal{F}_a $-mensurável com $ \mathbb{E}(\xi^4)< \infty $. Então a solução de $ X_t $ da equação estocástica

$$X_t=\xi+ \int_a^t \sigma(s,X_s)dB(s)+\int_a^t f(s,X_s)ds, \quad \quad a\leq t\leq b,$$

satisfaz a desigualdades

$$\mathbb{E}(|X_t|^4)\leq (27\mathbb{E}(\xi^4)+C_1(b-a))e^{C_1(t-a)},$$

$$\mathbb{E}(|X_t-\xi|^4)\leq C_2(1+27\mathbb{E}(\xi^4)+C_1(b-a))(t-a)^2e^{C_1(t-a)}$$

com $ C_1 $ e $ C_2 $ são dados por

$$C_1=54(2(17+4\sqrt{17})+(b-a)^2)(b-a)C^2$$

$$C_2=16(2(17+4\sqrt{17})+(b-a)^2)C^2.$$

Demonstração: Usando a desigualdades $ (a+b+c)^4\leq 27(a^4+b^4+c^4) $, Lema 10.5.2.1 e desigualdades de Holder obtemos

$$\mathbb{E}(|X_t|^4)\leq 27\mathbb{E}(\xi^4)+27\tilde{C}(t-a)\int_a^t\mathbb{E}(\sigma(s,X_s)^4)ds+ 27(t-a)^3 \int_a^t \mathbb{E}(f(s,X_s)^4)ds$$

$$\leq 27\mathbb{E}(xi^4)+27\tilde{C}(b-a)\int_a^t\mathbb{E}(\sigma(s,X_s)^4)ds+27(b-a)^3\int_a^t\mathbb{E}(f(s,X_s)^4)ds,$$

no qual $ \tilde{C}=2(17+4\sqrt{17}) $ é uma constante do Lema 10.5.2.1. Então usando a condição de crescimento e a desigualdade

$$(1+x^2)^2\leq 2(1+x^4)$$

para obter que

$$\mathbb{E}(|X_t|^4)\leq 27 \mathbb{E}(\xi^4)+C_1\int_a^t[1+\mathbb{E}(|X_s|^4)]ds,$$

no qual $ C_1=54(\tilde{C}+(b-a)^2)(b-a)C^2 $. Assim sendo, temo que

$$\mathbb{E}(|X_t|^4)\leq 27 \mathbb{E}(\xi^4)+C_1(b-a)+C_1\int_a^t \mathbb{E}(|X_s|^4)ds,$$

o que implica que a equação acima pela desigualdade de Bellman-Gronwall.

Agora usando a desigualdade $ (a+b)^4\leq 8(a^4+b^4) $, Lema 10.5.2.1 e a desigualdade de Holder obtemos que

$$\mathbb{E}(|X_t-\xi|^4)\leq 8\tilde{C}(t-a)\int_a^t \mathbb{E}(\sigma(s,X_s)^4)ds+8(t-a)^3\int_a^t \mathbb{E}(f(s,X_s)^4)ds$$

$$ 8(t-a)\left(\tilde{C}\int_a^t \mathbb{E}(\sigma(s,X_s)^4)ds+(b-a)^2\int_a^t \mathbb{E}(f(s,X_s)^4)ds\right)$$

Portanto, pela equação acima e a desigualdade $ (1+x^2)^2\leq 2(1+x^4) $,

$$\mathbb{E}(|X_t-\xi|^4)\leq 16(\tilde{C}+(b-a)^2)C^2(t-a)\int_a^t (1+\mathbb{E}(|X_s|^4))ds.$$

Além disso, pela equação acima e pela desigualdade $ e^x-1\leq xe^x $ para $ x\geq 0 $,

$$\int_a^t \mathbb{E}(|X_s|^4)ds\leq (27 \mathbb{E}(\xi^4)+C_1(b-a))(t-a)e^{C_1(t-a)}.$$

Finalmente, colocando a equação

$$\int_a^t \mathbb{E}(|X_s|^4)ds\leq (27 \mathbb{E}(\xi^4)+C_1(b-a))(t-a)e^{C_1(t-a)}.$$

na equação

$$\int_a^t \mathbb{E}(|X_s|^4)ds\leq (27 \mathbb{E}(\xi^4)+C_1(b-a))(t-a)e^{C_1(t-a)}.$$

junto com a desigualdade

$$\mathbb{E}(|X_t-\xi|^4)\leq C_2(1+27\mathbb{E}(\xi^4)+C_1(b-a))(t-a)^2e^{C_1(t-a)}$$

o resultado segue.

10.5.3 - Equações Diferenciais Estocástica Lineares

Nessa seção nossa meta é mostrar explicitamente a solução da equação diferencial estocástica linear.

Considere uma equação diferencial linear de primeira ordem

$$\frac{dx_t}{dt}=f(t)x_t+g(t), \quad \quad a\leq t\leq b, \quad \quad x_a=x,$$

no qual $ f(t) $ é uma função contínua. Para resolver essa equação diferencial,

$$\left(\frac{dx_t}{dt}-f(t)x_t\right)=g(t), \quad \quad a\leq t\leq b, \quad \quad x_a=x,$$

definimos

$$h(t)=e^{-\int_a^tf(s)ds}$$

multiplicando $ h(t) $ em ambos os lados obtemos

$$h(t)\left(\frac{dx_t}{dt}-f(t)x_t\right)=h(t)g(t)$$

Agora, note que

$$\frac{d}{dt}(h(t)x_t)=h(t)\left(\frac{dx_t}{dt}-f(t)x_t\right)$$

então obtemos que

$$\frac{d}{dt}(h(t)x_t)=h(t)g(t),$$

o qual a solução é dada por

$$h(t)x_t=x+\int_a^th(s)g(s)ds$$

Portanto, a solução de $ x_t $ é dada por

$$x_t=xh(t)^{-1}+\int_a^th(t)^{-1}h(s)g(s)ds=xe^{\int_a^t f(s)ds}+\int_a^t g(s)e^{\int_s^t f(u)du}ds.$$

Vamos utilizar as ideias acima para explorar como resolver uma equação estocástica diferencial linear, a qual é definida da forma

$$dX_t=\left(\phi(t)X_t+\theta(t)\right)dB(t)+\left(f(t)X_t+g(t)\right)dt, \quad \quad X_a=x,$$

o qual é uma expressão simbólica para

$$X_t=x+\int_a^t\left(\phi(s)X_s+\theta(s)\right)dB(s)+\int_a^t\left(f(s)X_s+g(s)\right)ds, $$

para $ a\leq t\leq b $. No mesmo mesmo espírito da equação diferencial linear, podemos ter como palpite o processo exponencial,

$$H_t=e^{-Y_t}, \quad \quad Y_t=\int_a^t f(s)ds+\int_a^t \phi(s)dB(s)-\frac{1}{2}\int_a^t \phi(s)^2ds.$$

Precisamos encontrar $ d(H_t X_t) $, pela formula de Itô para o produto, temos

$$d(H_t X_t)=H_tdX_t+X_tdH_t+(dH_t)(dX_t)$$

Aplicando a formula de Itô para encontrar $ dH_t $ como segue

$$dH_t=-H_tdY_t+\frac{1}{2}H_t(dY_t)^2$$

$$=H_t\left(-f(t)dt-\phi(t)dB(t)+\frac{1}{2}\phi^2(t)dt\right)+\frac{1}{2}H_t\phi^2(t)$$

$$=H_t\left(-f(t)dt-\phi(t)dB(t)+\phi^2(t)dt\right).$$

Assim, da equação acima e de

$$dX_t=\left(\phi(t)X_t+\theta(t)\right)dB(t)+\left(f(t)X_t+g(t)\right)dt, \quad \quad X_a=x,$$

temos que

$$(dH_t)(dX_t)=-H_t\phi(t)\left(\phi(t)X_t+\theta(t)\right)dt$$

Juntando tudo, temos que

$$d(H_tX_t)=H_t\left(dX_t-f(t)X_tdt-\phi(t)X_tdB(t)-\theta(t)\phi(t)dt\right).$$

observe que $ \left(dX_t-f(t)X_tdt-\phi(t)X_tdB(t)-\theta(t)\phi(t)dt\right) $ não é exatamente o que obteríamos movendo os termos envolvendo $ X_t $, tem um termo extra $ -\theta\phi(t) $. Mas podemos cuidar deste termo extra de forma simples, o que implica que

$$d(H_tX_t)=H_t\left(dX_t-f(t)X_tdt-\phi(t)X_tdB(t)-\theta(t)\phi(t)dt\right).$$

o que produz que

$$H_tX_t=x+\int_a^tH_s\theta(s)dB(s)+\int_a^t H_s\left(g(s)-\theta(s)\phi(s)\right)ds$$

Assim, dividindo ambos os lados por $ H_t $, obtemos as solução de $ X_t $. Desta forma, obtemos o seguinte teorema.

Teorema 10.5.3.1 - A solução da equação diferencial estocástica linear

$$dX_t=(\phi(t)X_t+\theta(t))dB(t)+(f(t)X_t+g(t))dt, \quad \quad X_a=x,$$

dada por

$$X_t=xe^{Y_t}+\int_a^t e^{Y_t-Y_s}\theta(s)dB(s)+\int_a^t e^{Y_t-Y_s}(g(s)-\theta(s)\phi(s))ds,$$

no qual,

$$Y_t=\displaystyle \int_a^t\phi(s)dB(s)+\int_a^t(f(s)-\frac{1}{2}\phi(s)^2)ds.$$

Podemos generalizar um pouco mais o Teorema acima. Para isso, suponha que $ Z_t $ é um processo de Itô e considere a equação diferencial estocástica linear

$$dX_t=(\phi(t)X_t+\theta(t))dZ(t)+(f(t)X_t+g(t))dt, \quad \quad X_a=x,$$

para resolver essa equação, temos duas opções a primeira delas é usando a formula de Itô para reescrever a equação acima e então usar o teorema e obter a solução em função de $ B(t) $.

A segunda opção é encontrar a formula em termo do processo $ Z_t $, para isso podemos simplesmente passar por cada etapa da derivação acima modificando os cálculos. A solução é dada por

$$X_t=xe^{Y_t}+\int_a^t e^{Y_t-Y_s}\theta(s)dZ_s+\int_a^t e^{Y_t-Y_s}g(s)ds-\int_a^t e^{Y_t-Y_s}\theta(s)\phi(s)d\langle Z\rangle_s$$

no qual $ d\langle Z\rangle_s $ é dado pelo Teorema 10.3.3 e

$$Y_t=\displaystyle \int_a^t \phi(s)dZ_s+\int_a^t f(s)ds-\frac{1}{2}\int_a^t \phi(s)^2d\langle Z\rangle_s$$

Desta forma, obtemos o seguinte corolário

Corolário 10.5.3.1: A solução da equação diferencial estocástica linear

$$dX_t=(\phi(t)X_t+\theta(t))dZ(t)+(f(t)X_t+g(t))dt, \quad \quad X_a=x,$$

dada por

$$X_t=xe^{Y_t}+\int_a^t e^{Y_t-Y_s}\theta(s)dZ_s+\int_a^t e^{Y_t-Y_s}g(s)ds-\int_a^t e^{Y_t-Y_s}\theta(s)\phi(s)d\langle Z\rangle_s$$

no qual,

$$Y_t=\displaystyle \int_a^t \phi(s)dZ_s+\int_a^t f(s)ds-\frac{1}{2}\int_a^t \phi(s)^2d\langle Z\rangle_s$$

com $ Z_t $ sendo um processos de Itô.

Exemplo 10.5.3.1: Seja $ dZ_t=\alpha dB(t)-\beta Z_t dt $ um processo Ornstein-Uhlenbeck e considere a equação diferencial estocástica

$$dX_t=(X_t+1)dZ_t+X_tdt, \quad \quad X_0=x$$

Podemos aplicar a formula do corolário, neste caso como $ d\langle Z\rangle_s = \alpha^2 ds $ obtemos

$$X_t=xe^{Z_t+\left(1-\frac{\alpha^2}{2}\right)}+\int_a^t e^{Z_t-Z_s+(1-\frac{1}{2}\alpha^2)(t-s)}dZ_s-\alpha^2\int_a^t e^{Z_t-Z_s+(1-\frac{1}{2}\alpha^2)(t-s)}ds$$

10.6 - Aplicações da Fórmula de Itô

Neste capítulo vamos ver que a Fórmula de Itô desempenha um papel fundamental no cálculo estocástico. Vamos verificar que no cálculo estocástico, a fórmula de Itô representa um resultado semelhante ao teorema fundamental do cálculo no cálculo clássico.

O teorema fundamental do cálculo garante que se $ F(x) $ é uma primitiva de uma função contínua $ f(x) $, então

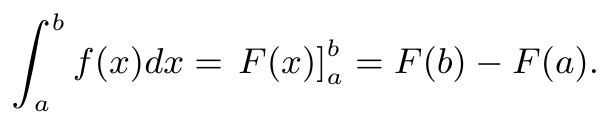
No cálculo estocástico, um resultado semelhante é obtido com a fórmula de Itô. Um processo de Itô é um processo estocástico que pode ser representado na forma,

$$X(t) = X(0) + \it_{0}^t a(s)ds + \int_{0}^tb(s) dB(s)$$

nos quais $ B $ é o movimento Browniano, $ a $ e $ b $ são processos adaptados. De forma simbólica, denotamos

$$dX(t) = a(t)dt + b(t)dB(t), \quad \text{com condição inicial}~X(0).$$

Uma equação diferencial estocástica tem a representação

$$dX(t) = a(t,X(t))dt+b(t,X(t))dB(T), \quad \text{com condição inicial}~X(0),$$

nos quais $ a $ e $ b $ são funções satisfazendo as condições usuais para existência de solução forte (ver, 10.5 - Equações Diferenciais Estocásticas). A seguir, a presentamos a formula de Itô para processos de Itô.

Teorema 10.6.1

Seja $ F \in C^{1,2} $ uma função diferenciável e $ X $ uma processo de Itô. Então, temos que

$$F(t,X(t))= F(0,X(0))+\int_{0}^t \frac{\partial}{\partial t}F(s,X(s))ds+\int_{0}^t \frac{\partial}{\partial x}F(s,X(s))a(s)ds+\int_{0}^t \frac{\partial}{\partial x}F(s,X(s))b(s)dB(s)+\frac{1}{2}\int_{0}^t \frac{\partial^2}{\partial^2 x}F(s,X(s))b^2(s)ds.$$

Demonstração: ver 10.5 - Equações Diferenciais Estocásticas.

Assim, ao tomarmos $ Y(t)=F(t,X(t)) $, obtemos que

$$dY(s)= \frac{\partial}{\partial t}F(s,X(s))ds+\frac{\partial}{\partial x}F(s,X(s))a(s)ds+\frac{\partial}{\partial x}F(s,X(s))b(s)dB(s)+\frac{1}{2} \frac{\partial^2}{\partial^2 x}F(s,X(s))b^2(s)ds.$$

Na sequência, apresentamos diversas aplicações da fórmla de Itô para processos de Itô.

Exemplo 10.6.1

Avalie a integral $ \int_0^tB(s)e^{B(s)}dB(s) $.

Note que a função do integrando na variável $ x $ é dada por $ f(x)=xe^x $. Assim,

$$F(x)=\int xe^x dx=xe^x-e^x+C$$

$$\frac{d}{dx}f(x)=xe^x+e^x\ \ \ \text{e}\ \ \frac{d}{dt}f(x)=0$$

Portanto,

$$\int_0^tB(s)e^{B(s)}dB(s)=(B(t)-1)e^{B(t)}+1-\frac{1}{2}\int_0^t(B(s)+1)e^{B(s)}ds.$$

Exemplo 10.6.2

Avalie a integral $ \int_0^t\frac{1}{1+B(s)^2}dB(s) $

Note que a função no integrando na variável $ x $ é dada por $ f(x)=\frac{1}{1+x^2} $. Assim,

$$F(x)=\int\frac{1}{1+x^2}dx=\arctan{x} +C$$

$$\frac{d}{dx}f(x)=-\frac{2x}{(1+x^2)^2}\ \ \ \text{e}\ \ \ \frac{d}{dt}f(x)=0$$

Portanto,

$$\int_0^t\frac{1}{1+B(s)^2}dB(s)= \arctan{B(t)}+\int_0^t\frac{B(s)}{(1+B(s)^2)^2}ds.$$

Decomposição e Compensadores

A fórmula de Itô possibilita encontrar a decomposição de submartingales que são funções do movimento browniano. Em particular, podemos encontrar o compensador $ \langle M\rangle_t $ de $ M^2_t $ para $ M_t=\int_0^tf(f)dB(s) $.

Seja $ f\in L^2_{ad}([a,b]\times\Omega) $ e considere o processo estocástico:

$$M_t=\int_a^tf(s)dB(s)\ \ \ \forall \ a\leq t\leq b.$$

Observe que $ M_t $ é um martingale.

Seja $ \varphi $ uma função de classe $ C^2 $. Aplicando a fórmula de Itô em $ \varphi(M_t) $, temos que

$$\varphi(M_t)=\varphi(0)+\int_a^t\frac{d}{dM_s}\varphi(M_s)f(s)dB(s)+\frac{1}{2}\int_a^t\frac{d^2}{dM^2_s}\varphi(M_s)f^2(s)ds.$$

Suponha que $ \varphi $ seja uma função convexa e que

$$\mathbb{E}\int_a^b\left|\frac{d}{dM_t}\varphi(M_t)f(t)\right|^2dt< \ \infty.$$

Da desigualdade de Jensen $ \varphi(M_t) $ é um submartingale. Note que o termo

$$\varphi(0)+\int_a^t\frac{d}{dM_s}\varphi(M_s)f(s)dB(s)$$

é um martingale. Como $ \varphi $ é uma função convexa, o processo

$$\frac{1}{2}\int_a^t\frac{d^2}{dM^2_s}\varphi(M_s)f(s)^2ds,$$

é um processo crescente. Assim, temos a decomposição de Doob-Meyer para o submartingale $ \varphi(M_t) $.

Em particular se considerarmos $ \varphi(x)=x^2 $, temos que

$$M^2_t=2\displaystyle \int_{a}^t M_s f(s)dB(s)+\int_a^t f^s(s)ds$$

Portanto, o compensador de $ M_t^2 $ para $ M(t) $ é dado por

$$\langle M\rangle_t=\int_a^t f^2(s)ds,$$

ou equivalentemente

$$d\langle M\rangle_t=f^2(t)dt=(dM_t)^2,~ \langle M\rangle_a=0$$

Em algumas situações pode ser complicado encontrar o compensador, utilizando simplesmente a aplicação direta da formula de Itô, uma alternativa interessante pode ser escrever a representação $ M_t $ como integral de Itô como podemos ver no exemplo a seguir

Exemplos 10.6.3

Considere o martingale $ M_t=B^2(t)-t $. Qual o compensador de $ M^2_t $?

Como dissemos acima, nesse exemplo seria complicado calcular o compensador usando diretamente a formula de Itô. Assim vamos primeiramente encontrar a representação de $ M_t $ como uma integral de Itô:

$$M_t=B^2(t)-t=2\displaystyle \int_0^t B(s)dB(s),$$

então $ dM_t=2B(t)dB(t) $. Então, $ d\langle M\rangle_t=(dM_t)^2=4B^2(t)dt $

Portanto, o compensador de $ M^2_t $ é dado por

$$\langle M\rangle_t=4\displaystyle \int_0^t B^2(s)dt$$

Exemplo 10.6.4

Considere

$$M_t=(B^2(t)-t)^2-4\displaystyle \int_0^tB^2(s)ds$$

é um martingale, como podemos ver pelo exemplo anterior. A fim de encontrar o compensador de $ M^2_t $, iremos primeiramente encontrar a representação de $ M_t $ como formula de Itô. Primeiramente temos que aplicando a formula de Itô, temos

$$dM_t=-2(B^2(t)-t)dt+2(B^2(t)-t)2B(t)dB(t)$$

Teorema da Caracterização de Lévy

Como podemos ver na definição de movimento Browniano, um processo estocástico é um movimento Browniano com respeito a alguma medida. A pergunta é dado um processo estocástico, podemos dizer se existe uma medida para o qual esse processo é um movimento Browniano?

Primeiramente vamos considerar um exemplo simples. Seja $ B(t) $ um movimento Browniano com respeito a medida $ \mathbb{P} $. O processo estocástico $ M_t=B(t)-t $, para $ 0\leq t\leq 1 $, é um movimento Browniano para alguma medida $ \mathbb{Q} $?

Seja $ \mathbb{Q}:\mathcal{F}\rightarrow [0,\infty) $ definida por (na seção Teorema de Girsanov mostraremos como encontrar essa medida)

$$\mathbb{Q}(A)=\int_A e^{B(1)-1/2}d\mathbb{P}, \quad A\in \mathcal{F}$$

Denotaremos $ \mathbb{E}_{\mathbb{P}} $ como sendo a esperança com respeito a $ \mathbb{P} $ and usaremos indistintamente tanto $ exp(x) $ quanto $ e^{x} $ . Temos então que

$$\mathbb{E}_\mathbb{P}(e^{B(1)})=e^{1/2}$$

o que implica que

$$\mathbb{Q}(\Omega)=\int_\Omega e^{B(1)-1/2}d\mathbb{P}=e^{1/2-1/2}=1$$

Portanto temos que $ \mathbb{Q} $ é uma medida de probabilidade, mostraremos então que $ M_t $ é de fato um movimento Browniano segundo a medida $ \mathbb{Q} $. É fácil ver que $ \mathbb{Q}(A)=0\Leftrightarrow \mathbb{P}(A) $, desta forma temos que $ \mathbb{P} $ e $ \mathbb{Q} $ são medidas equivalentes. Com isso temos que

$$1-\mathbb{Q}(\omega; M_0(\omega)=0)=\mathbb{P}(\omega; B(0,\omega)=0)=1$$

$$2-\mathbb{Q}(\omega; M_t(\omega)\hbox{ é continuo em } t)=\mathbb{P}(\omega; B(t,\omega)\hbox{ é continuo em } t)=1$$

Assim sendo, para que $ M_t $ seja um movimento Browniano, resta-nos apenas mostrar que $ M_t-M_s $ é normalmente distribuído com respeito a $ \mathbb{Q} $ com média $ 0 $ e variância $ t-s $. E também que possui incrementos independentes.

Para mostrar que $ M_t-M_s $ é normalmente distribuído com respeito a $ \mathbb{Q} $ com média $ 0 $ e variância $ t-s $, Denote que $ \mathbb{E}_\mathbb{Q} $ a esperança com respeito a medida $ \mathbb{Q} $ e seja $ 0\leq s< t \leq 1 $. Então para qualquer $ \lambda $ temos que

onde $ \mathcal{F_t}=\sigma(B(s);s\leq t) $ and $ \mathbb{E}_\mathbb{P}(\cdot|\mathcal{F_t}) $ denota a esperança condicional (para mais detalhes sobre esperança condicional click aqui) com respeito a medida $ \mathbb{P} $.

Lema 10.6.1

Seja $ f(t,x)=exp(cx-\frac{1}{2}c^2 t) $ para alguma constante fixa c. Então f é um martingale para qualquer constante c.

Demonstração:

De fato, considere

$$\frac{\partial f}{\partial t}=-\frac{1}{2}c^2 f(t,x), ~ \frac{\partial f}{\partial x}=cf(t,x), ~ \frac{\partial^2 f}{\partial x^2 }=c^2f(t,x),$$

Pela formula de Itô temos que

$$f(t,x)=1+c\int_0^t f(t,x)dB(s)$$

Portanto $ M(t) $ é um martingale para qualquer constante c.

Aplicando o Lema anterior pra o caso em que $ c=1 $ temos que $ e^{B(t)-\frac{1}{2}t} $ é um martingale e por tanto

$$\mathbb{E}_\mathbb{P}(exp(B(1)-\frac{1}{2})|\mathcal{F_t})=e^{B(t)-\frac{1}{2}t}, \forall 0\leq t\leq 1.$$

Portanto temos que

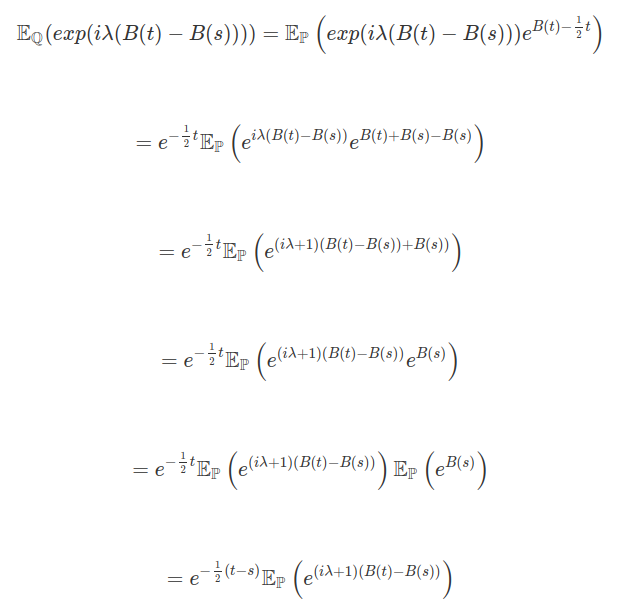
no qual a penúltima igualdade decorre da independência dos termos. Agora como

$$\mathbb{E}_{\mathbb{P}}\left(e^{(c)(B(t)-B(s))}\right)=e^{\frac{c^2}{2}(t-s)}$$

temos que

$$\mathbb{E}_{\mathbb{P}}\left(e^{(i\lambda +1)(B(t)-B(s))}\right)=e^{\frac{(i\lambda+1)^2}{2}(t-s)}=e^{\frac{1}{2}(-\lambda^2+1+2i\lambda)(t-s)}= e^{\frac{1}{2}(t-s)}e^{(-\frac{1}{2} \lambda +i\lambda)(t-s)}$$

E portanto temos que

$$\mathbb{E}_{\mathbb{Q}}(e^{i\lambda(B(t)-B(s))}) =e^{-\frac{1}{2}(t-s)}e^{\frac{1}{2}(t-s)}e^{(-\frac{1}{2} \lambda +i\lambda)(t-s)}=e^{(-\frac{1}{2} \lambda +i\lambda)(t-s)}$$

Desta forma temos que

$$\mathbb{E}_\mathbb{Q}(e^{i\lambda(M_t-M_s)})=e^{-\frac{1}{2}\lambda^2(t-s)}$$

E isto implica que $ M(t)-M(s) $ é normalmente distribuída com média 0 e variância $ t-s $ com respeito a $ \mathbb{Q} $. Agora seja $ 0\leq t_1< t_2\leq 1 $. Então para qualquer $ \lambda_1,\lambda_2\in \mathbb{R} $,

De forma indutiva podemos repetir os mesmos argumentos para o caso em que $ t_1,\dots,t_n\leq 1 $.

O que implica que $ M $ tem incrementos independentes. O que mostra que $ M(t)=B(t)-t $ é um movimento Browniano em relação a medida $ \mathbb{Q} $, Claro que $ M(t) $ não é um movimento Browniano em relação a medida $ \mathbb{P} $, pois $ \mathbb{E}_{\mathbb{P}}(M(t))=-t\neq 0 $. Entretanto fomos capaz de mostrar que existe uma medida (no caso, $ \mathbb{Q} $) na qual torna $ M(t) $ um movimento Browniano. Mas isso não responde a nossa pergunta. A pergunta é dado um processo estocástico, podemos dizer se existe uma medida para o qual esse processo é um movimento Browniano? De uma forma geral, podemos responder essa questão pelo teorema a seguir.

Teorema 10.6.2 (Teorema da Caracterização de Lévy’s)

Um processo estocástico $ M_t $ é um movimento Browniano se, e somente se, existe uma medida de probabilidade $ \mathbb{Q} $ e uma filtragem $ \mathbb{F}=(\mathcal{F_t})_t $, tal que $ M_t $ é um martingale contínuo com respeito a $ \mathbb{F} $, sobre a medida $ \mathbb{Q} $, $ \mathbb{Q}(M_0=0)=1 $ e $ \langle M\rangle_t $ a.s. com respeito a $ \mathbb{Q} $ para cada $ t $.

Demonstração:

Claro que, se $ M(t) $ é um movimento Browniano, então existe uma medida $ \mathbb{Q} $, tal que $ M_t $ é um martingale contínuo com respeito a $ \mathbb{F} $, sobre a medida $ \mathbb{Q} $, $ \mathbb{Q}(M_0=0)=1 $ e $ \langle M\rangle_t $ a.s. com respeito a $ \mathbb{Q} $ para cada $ t $.

Neste caso, basta mostrarmos que dado que existe uma medida de probabilidade $ \mathbb{Q} $ e uma filtragem $ \mathbb{F} $, tal que $ M_t $ é um martingale contínuo com respeito a $ \mathbb{F} $, sobre a medida $ \mathbb{Q} $, $ \mathbb{Q}(M_0=0)=1 $ e $ \langle M\rangle_t $ a.s. com respeito a $ \mathbb{Q} $ para cada $ t $.

Note que as condição de que $ M(t) $ é contínuo e $ \mathbb{Q}(M_0=0)=1 $ já são validas, então resta-nos mostrar apenas que tem distribuição normal e incrementos independentes com respeito a $ \mathbb{Q} $.

Para mostrar que tem distribuição normal, vamos aplicar a formula de Itô $ F(t,x)=e^{i\lambda x+\frac{1}{2}\lambda^2t} $ e obtemos

$$dF(t,M_t)=\frac{1}{2}\lambda^2 F(t,M_t)dt+i\lambda F(t,M_t)dM_t -\frac{1}{2}\lambda^2F(t,M_t)d\langle M\rangle_t$$

Por hipótese temos que $ d\langle M\rangle_t= dt $. Portanto, temos que $ dF(t,M_t)=i\lambda F(t,M_t)dM_t $, então na forma de integral temos que

$$e^{i\lambda M_t+\frac{1}{2}\lambda^2t}=1+i\lambda \int_{0}^t e^{i\lambda M_s+\frac{1}{2}\lambda^2s} dM_s$$

O implica pelo Teorema 10.3.2 que o processo estocástico $ e^{i\lambda M_t+\frac{1}{2}\lambda^2t} $ é um martingale com respeito a medida $ \mathbb{Q} $ e a filtragem $ \mathbb{F} $. Então para qualquer $ 0\leq s \leq t $,

$$\mathbb{E}_{\mathbb{Q}}\left(e^{i\lambda M_t+\frac{1}{2}\lambda^2t}|\mathcal{F_s}\right)=e^{i\lambda M_s+\frac{1}{2}\lambda^2s}$$

o que implica que

$$\mathbb{E}_{\mathbb{Q}}\left(e^{i\lambda (M_t-M_s)+\frac{1}{2}\lambda^2(t-s)}|\mathcal{F_s}\right)=0$$

e portanto

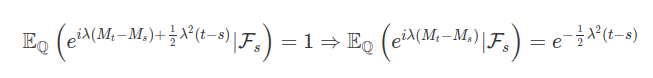
O que mostra pela função característica que $ M_t-M_s, s\leq t $, é normalmente distribuída com média zero e variância $ t-s $ sobre $ \mathbb{Q} $.

Resta-nos então, mostrar que tem incrementos independentes sobre a medida $ \mathbb{Q} $. Assim sendo, suponha que $ 0\leq t_1< t_2 $ e seja $ \lambda_1,\lambda_2\in \mathbb{R} $, qualquer então

O que implica que são independentes. De forma geral podemos repetir os mesmos argumentos de forma indutiva para mostrar para qualquer $ 0\leq t_1 < t_2< \cdots< t_n\leq 1 $. O que mostra que temos incrementos independentes para a medida $ \mathbb{Q} $. E com isso completamos a prova.

Exemplo 10.6.5

Seja $ B(t) $ um movimento Browniano com respeito a medida $ \mathbb{P} $. Considere o Processo estocástico

$$X_t=\int_{0}^tsign(B(s))dB(s).$$

Claro que $ \mathbb{P}(X_0=0)=1 $ e que $ X_t $ é um martingale contínuo com respeito a medida $ \mathbb{P} $ e a filtragem $ \mathbb{F}=(\mathcal{F_t}=\sigma(B(s); s\leq t)) $. Além disso, o compensador de $ X^2_t $ é dado por

$$\langle X\rangle_t=\int_0^t|sign B(s)|^2ds=\int_0^t1ds=t$$

Portanto, pelo Teorema de Caracterização de Lévy temos que $ X_t $ é um movimento Browniano com respeito a $ \mathbb{P} $.

Exemplo 10.6.6

Seja $ (\Omega,\mathcal{F},\mathbb{P}) $ um espaço de probabilidade e seja $ B(t), 0\leq t\leq 1 $ um movimento Browniano com respeito a esse espaço. Considere o processo estocástico $ M_t=B(t)-ct, $ no qual c é uma constante fixada. Defina $\mathbb{Q}:\mathcal{F}\rightarrow [0,\infty)$ por

$$\mathbb{Q}(A)=\int_{A}e^{cB(1)-\frac{1}{2}c^2}d\mathbb{P}, A \in \mathcal{F}$$

Temos que $ \mathbb{E}_{\mathbb{P}}(e^{cB(1)})=e^{\frac{1}{2}c^2} $. Portanto, temos que $ \mathbb{Q} $ é uma medida de probabilidade em $ (\Omega,\mathcal{F}) $. Seja $ \mathbb{F}=(\mathcal{F_t}=\sigma(B(s); s\leq t)) $ a filtragem. Note que $ \mathbb{P} $ e $ \mathbb{Q} $ são equivalentes, o que implica que $ \mathbb{Q}(M_0=0)=\mathbb{P}(B(0)=0)=1 $.

ou seja, temos que $ M_t $ é um martingale com respeito a $ \mathbb{Q} $ se, e somente se, $ X_t=M_t e^{cB(t)-\frac{1}{2}c^2 t} $ é um martingale com respeito a $ \mathbb{P} $. Aplicando a formula de Itô por $ X_t $ para encontrar

$$X_t=\int_0^t (1+cB(s)-c^2 s)e^{cB(s)-\frac{1}{2}c^2s} dB(s)$$

o que implica que $ X_t $ é um martingale com respeito a $ \mathbb{P} $. E portanto, $ M_t $ é um martingale com respeito a medida $ \mathbb{Q} $. Além disso, temos que $ dM_t=dB(t)-cdt $. Portanto,

$$d\langle M\rangle_t=(dM_t)^2=(dB(t)-cdt)^2=(dB(t))^2-2dB(t)dt -(cdt)^2=dt$$

Então pelo teorema temos que $ M_t=B(t)-ct $ é um movimento Browniano com respeito a medida $ \mathbb{Q} $ definida por

$$\mathbb{Q}(A)=\int_{A}e^{cB(1)-\frac{1}{2}c^2}d\mathbb{P}, A \in \mathcal{F}.$$

Formula de Tanaka e Tempo Local

Note que não é possível aplicar a formula de Itô para $ f(B(t)) $ com $ f(x)=|x| $ e $ x\in \mathbb{R} $. Entretanto podemos fazer uma modificação nesta função na qual, a formula de Itô poderá ser aplicada derivando uma importante propriedade do movimento Browniano.

Considere $ a\in \mathbb{R} $ um numero real fixo. Para cada $ \epsilon > 0 $, definimos um função $ f_{\epsilon} $ nos números reais por

Note que a função $ f_\epsilon $ não é de $ C^2 $, pois a sua derivada segunda é descontinua quando $ x=a\pm \epsilon $. Entretanto, podemos aplicar a formula de Itô, pelo seguinte observação

Observação 10.6.1

Seja $ B(t) $ um movimento Browniano, Então para qualquer numero real c o conjunto $ (t\in \mathbb{R}, B(t)=c) $ tem medida de Lebesgue nula q.c.. Portanto, temos a seguinte igualdade

$$f_\epsilon(B(t))=f_\epsilon(B(0))+ \displaystyle \int_0^t f^{\prime}_\epsilon(B(s))dB(s)+\frac{1}{2}\int_0^t f^{\prime\prime}_\epsilon(B(s))ds$$

$$=f_\epsilon(0)+ \displaystyle \int_0^t f^{\prime}_\epsilon(B(s))dB(s)+\frac{1}{2}\int_0^t f^{\prime\prime}_\epsilon(B(s))ds$$

Quando $ \lim_{\epsilon\rightarrow 0}f_\epsilon(B(t))=|B(t)-a| $ q.c. $ \lim_{\epsilon\rightarrow 0}f_\epsilon(0)=|a| $ e então

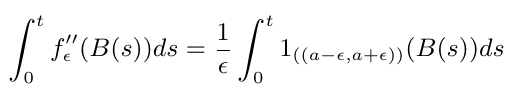
Além disso para cada $ \omega $, podemos aplicar o teorema da convergência dominada em $ B(\cdot,\omega) $ e ver que

$$\lim_{\epsilon\rightarrow 0}\displaystyle \int_0^t |f^{\prime}_\epsilon(B(s,\omega))-sgn(B(s,\omega)-a)|^2ds=0$$

Portanto, temos que

$$\lim_{\epsilon\rightarrow 0}\displaystyle \int_0^t |f^{\prime}_\epsilon(B(s))-sgn(B(s)-a)|^2ds=0 ~~ q.c.$$

Mas a convergência quase certa implica na convergência em probabilidade (ver Teorema 7.1.1.3 em Probabilidades)

e que o processo $ f^{\prime}_\epsilon(B(\cdot))\in L^2_ad([a,t]\times \Omega) $. Portanto pela Definição 10.2.1 da Integral de Itô temos que

$$\lim_{\epsilon \rightarrow 0}\displaystyle \int_0^t f^{\prime}_\epsilon(B(s))dB(s)=\int_0^t sgn(B(s)-a)dB(s)~ em ~ probabilidade$$

Então, pela equação de referencia 001, obtemos a seguinte igualdade

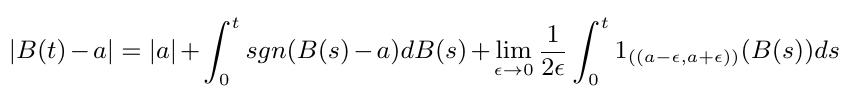
É importante observar que essa igualdade sendo válida, na verdade implica que que o limite em probabilidade existe.

Definição 10.6.1

O local time de um movimento Browniano $ B(t) $ em a, até e incluindo $ t $, é definido como sendo a variável aleatória

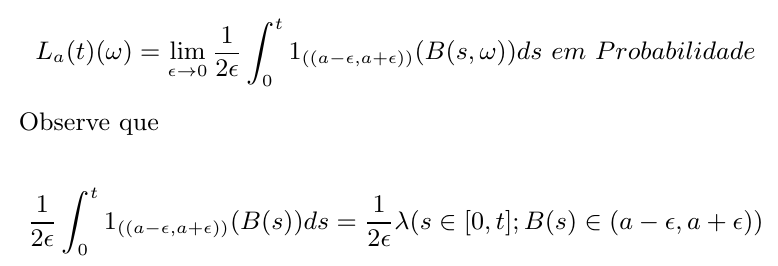
no qual, $ \lambda $ é a medida de Lebesgue. Desta forma, podemos interpretar o tempo local $ L_a(t,\omega) $ como sendo a quatia de tempo que as trajetórias do movimento Browniano gasta em a, incluindo o tempo t. Então $ L_a(t,\omega) $ é dado como sendo também

$$L_a(t)(\omega)=\lim_{\epsilon \rightarrow 0}\frac{1}{2\epsilon}\lambda(s\in[0,t]; B(s,\omega)\in (a-\epsilon,a+\epsilon))$$

Teorema 10.6.3 (Formula de Tanaka)

Seja $ B(t) $ um movimento Browniano se iniciando em 0. Então para qualquer $ a\in \mathbb{R} $,

$$|B(t)-a|=|a|+\displaystyle \int_0^t sgn(B(s)-a)dB(s)+L_a(t).$$

Note que $ B(t)-a $ é um martingale. Portanto pela desigualdade de Jensen temos que $ |B(t)-a| $ é um submartingale. Então, a formula de Tanaka nos fornece a decomposição de Doob-Meyer de $ |B(t)-a| $, pois pelo Exemplo 10.6.3, temos que

$$M_t=\displaystyle \int_0^t sgn(B(s)-a)dB(s)$$

é um movimento Browniano.

Processo Exponencial

Seja $ h $ uma função determinística com $ h\in L^2[0,T] $. Então para qualquer $ t\in [0,T] $ a integral de Wiener $ \int_0^th(s)dB(s) $ tem distribuição com média 0 e variância $ \sigma^2=\int_0^th^2(s)ds $. Portanto, temos que

$$\mathbb{E}(e^{\int_0^t h(s)}dB(s))=\frac{1}{\sqrt{2\pi \sigma}}\int_{-\infty}^{\infty}e^{x}e^{-\frac{x^2}{2\sigma^2}}dx=e^{\frac{1}{2}\int_0^t h^2(s)ds}.$$

Assim fazendo uma normalização de $ e^{\int_0^t h(s)dB(s)} $ definida por

$$Y_t=\frac{e^{\int_0^t h(s)dB(s)}}{\mathbb{E}(e^{\int_0^t}h(s)dB(s))}=e^{\int_0^th(s)dB(s)-\frac{1}{2}\int_0^t h^2(s)ds}.$$

Pelo exemplo da seção formula de Itô temos que $ Y_t $ tem a seguinte representação

$$Y_t=1+\int_0^t h(s)e^{\int_0^s h(u)dB(u)-\frac{1}{2}\int_0^s h^2(u)du}dB(s)$$

Note que $ h(s)e^{\int_0^s h(u)dB(u)-\frac{1}{2}\int_0^s h^2(u)du} \in L^2_ad([0,T]\times \Omega) $ e portanto, pelo Teorema 10.2.5 temos que $ Y_t $ é um martingale. Desta forma, vamos dar a seguinte definição

Definição 10.6.2: Definimos $ \xi_h(t) $, para cada $ h\in \mathcal{L}_{ad}(\Omega,L^2[0,T]) $ por

$$\xi_h(t)=e^{\int_0^t h(s)dB(s)-\frac{1}{2}\int_0^t h^2(s)ds}, \quad 0\leq t\leq T$$

$ \xi_h(t) $ definido acima é chamado de processo exponencial.

Aplicando a formula de Itô temos que

$$d\xi_h(t)=h(t)\xi_h(t)dB(t)$$

o que implica que

$$\xi_h(t)=1+\int_0^t h(s)\xi_h(s)dB(s),\quad 0\leq t\leq T$$

o que mostra que $ \xi_h(t) $ é um martingale local pelo Teorema 10.2.8

A questão é sobre quais condições temos que $ \xi_h(t) $ é um martingale.

Teorema 10.6.4:

Se $ h\in \mathcal{L}_{ad}(\Omega,L^2[0,T]) $ satisfaz

$$\mathbb{E}(\xi_h(t))=1$$

então $ \xi_h(t) $ é um martingale.

Demonstração: Se $ h(t) $ é uma função determinística é $ L^2[0,T] $, então temos é satisfeita, como vimos anteriormente pela equação acima é um martingale satisfaz a equação.

$$\int_A \mathbb{E}_{\mathbb{P}}(\xi_h(t)|\mathcal{F_s})d\mathbb{P}=\int_A \xi_h(t)d\mathbb{P}=\int_A d\mathbb{Q}_t=\mathbb{Q}(A).$$

Por outro lado temos que

$$\int_A \xi_h(t)d\mathbb{P}=\int_A d\mathbb{Q}_s=\mathbb{Q}(A)$$

Isto implica que $ \mathbb{E}_{\mathbb{P}}(\xi_h(t)|\mathcal{F_s})=\xi_h(s) $. Então temos que $ \xi_h(t) $ de fato é um martingale se

$$\mathbb{E}(\xi_h(t))=1$$

é satisfeita.

É importante observar que em geral verificar a equação

$$\mathbb{E}(\xi_h(t))=1$$

é difícil, existe uma condição mais forte chamada de condição de Novikov, a qual é mais de verificar, dada por

$$\mathbb{E}\left(\frac{1}{2}\int_0^T h^2(t)dt\right)$$

Novikov mostrou no artigo “On an identity for stochastic integrals” que a equação acima implica em

$$\mathbb{E}(\xi_h(t))=1$$

porém o contrário não necessariamente é verdade. Ou seja, de fato a condição de Novikov é mais forte que a condição do teorema.

Exemplo 10.6.7: Seja $ h(t)=sign(B(t)) $. Então seu processo exponencial dado por

$$\xi_h(t)=e^{\int_{0}^t sign(B(s))dB(s)-\frac{1}{2}t}$$

No exemplo 10.6.5 provamos que

$$X_t=\int_0^t sign(B(s))dB(s)$$

é um movimento browniano e portanto, temos que

$$\mathbb{E}(\xi_h(t))=e^{-\frac{1}{2}t}\mathbb{E}(e^{X_t})=e^{-\frac{1}{2}t}e^{\frac{1}{2}t}=1$$

Então a condição do teorema é satisfeita e portanto temos que $ \xi_h(t) $ é um martingale

Transformação de Medidas de Probabilidades

A fim de dar uma motivação para o importante Teorema de Girsanov, iremos apresentar um teorema e alguns exemplos que ilustram um pano de fundo interessante para conseguirmos entender a fundamental importância desse teorema.

Primeiramente considere o exemplo abaixo

Exemplo 10.6.8: Considere uma variável X tendo distribuição normal com média $ \mu $ e variância $ 1 $. Suponha que queremos saber que $ \mathbb{E}(X^4) $. Então temos 2 métodos é calcular a integral

$$\mathbb{E}(X^4)=\int_{-\infty}^{\infty}x^4 \frac{1}{\sqrt{2\pi}}e^{-(x-\mu)^2/2}dx.$$

O segundo método é fazer uma mudança de variável. Seja $ Y=X-\mu $. Então $ Y $ é uma normal padrão, neste caso podemos expressar $ X^4 $ em função de $ Y $ dada por

$$X^4=(Y+\mu)^4=Y^4+4\mu Y^3+6\mu^2 Y^2+4\mu^3 Y+\mu^4$$

Portanto, temos que

$$\mathbb{E}(X^4)=\mathbb{E}(Y^4)+4\mu\mathbb{E}(Y^3)+6\mu^2\mathbb{E}(Y^2)+4\mu^3 \mathbb{E}(Y)+\mu^4=3+6\mu^3+\mu^4$$

Observe que com a mudança de variável ficou bem mais simples encontrar $ \mathbb{E}(X^4) $

Neste caso, vamos que existe uma relação direta entre os dois métodos. Então queremos explorar essa ideia para o caso de processo estocástico. Para entender essa ideia considere o seguinte exemplo.

Exemplo 10.6.9:

Seja $ B(t) $ um movimento Browniano e considere que desejamos calcular $ \mathbb{E}(B^3(t)e^{B(1)-\frac{1}{2}}) $ para $ 0\leq t\leq 1 $. Novamente podemos usar dois métodos para resolver esse problema. O primeiro método para resolver esse problema é expressar essa variável aleatória como o produto de duas variáveis independentes

$$\mathbb{E}(B^3(t)e^{B(1)-\frac{1}{2}})=e^{-\frac{1}{2}}\mathbb{E}[(B^3(t)e^{B(t)})(e^{B(1)-B(t)})]= e^{-\frac{1}{2}\mathbb{E}(B^3(t)e^{B(t)})\mathbb{E}(e^{B(1)-B(t)})},$$

Nesse caso, podemos calcular separadamente cada uma das esperanças. Um segundo método para resolver esse problema é fazer uma mudança de medida de $ \mathbb{P} $ para $ \mathbb{Q} $ definida por

$$\mathbb{Q}(A)=\int_A e^{B(1)-1/2}d\mathbb{P}, \quad A\in \mathcal{F}$$

Então teremos a seguinte igualdade

$$=\mathbb{E}_{\mathbb{Q}}(M^3_t+3tM^2_t+3t^2M_t+t^3)=3t^2+t^3$$

Observe que fazendo a mudança de medida fica bem mais simples calcular. Com isso temos o seguinte Teorema.

Teorema 10.6.5:

Seja $ B(t) $, $ 0\leq t\leq 1 $, um movimento Browniano com respeito a medida $ \mathbb{P} $. Seja $ \mathbb{Q} $ definida por $ d\mathbb{Q}=e^{B(1)-\frac{1}{2}}d\mathbb{P} $. Então para qualquer função f tal que $ \mathbb{E}_{\mathbb{P}}(f(B(t)))< \infty $, temos que

$$\int_\Omega f(B(t)-t)d\mathbb{Q}=\int_{\Omega}f(B(t))d\mathbb{P},$$

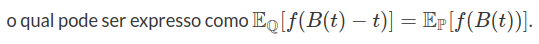
\end{theorem}

\begin{proof} Suponha que $ \alpha(t) $ seja uma função determinística. Então

$$\int_{\Omega} f(B(t)-\alpha(t))e^{B(1)-\frac{1}{2}}d\mathbb{P}=\mathbb{E}[f(B(t)-\alpha(t))e^{B(1)-\frac{1}{2}}]= \mathbb{E}(\mathbb{E}[f(B(t)-\alpha(t))e^{B(1)-\frac{1}{2}}|\mathcal{F_t}])$$

$$=\mathbb{E}[f(B(t)-\alpha(t))]\mathbb{E}[e^{B(1)-\frac{1}{2}}|\mathcal{F_t}]=\mathbb{E}[f(B(t)-\alpha(t))e^{B(t)-\frac{1}{2}t}]$$

$$=\int_{\Omega} f(B(t)-\alpha(t))e^{B(t)-\frac{1}{2}t}d\mathbb{P}$$

A ultima integral é dado por

$$\int_{\Omega}f(B(t)-\alpha(t))e^{B(t)-\frac{1}{2}t}d\mathbb{P}=\int_{-\infty}^{\infty}f(x-\alpha(t))e^{x-\frac{1}{2}t}\frac{1}{\sqrt{2\pi t}}e^{-\frac{1}{2t}x^2}dx.$$

Fazendo uma mudança de variável $ y=x-\alpha(t) $ para obter que

$$\int_{-\infty}^{\infty}f(x-\alpha(t))e^{x-\frac{1}{2}t}\frac{1}{\sqrt{2\pi t}}e^{-\frac{1}{2t}x^2}dx $$

$$=\int_{-\infty}^{\infty}f(y)e^{\frac{1}{2}(t-\alpha(t))y-\frac{1}{2t}(t-\alpha(t))^2}\frac{1}{\sqrt{2\pi t}}e^{-\frac{1}{2t}y^2}dy$$

$$=\int_{\Omega} f(B(t))e^{\frac{1}{t}(t-\alpha(t))B(t)-\frac{1}{2t}(t-\alpha(t))^2}d\mathbb{P}$$

Portanto, temos que

$$\int_{\Omega}f(B(t)-\alpha(t))e^{B(t)-\frac{1}{2}t}d\mathbb{P}=\int_{\Omega} f(B(t))e^{\frac{1}{t}(t-\alpha(t))B(t)-\frac{1}{2t}(t-\alpha(t))^2}d\mathbb{P}$$

Com isso temos que

$$\int_{\Omega} f(B(t)-\alpha(t))e^{B(1)-\frac{1}{2}}d\mathbb{P}=\int_{\Omega} f(B(t))e^{\frac{1}{t}(t-\alpha(t))B(t)-\frac{1}{2t}(t-\alpha(t))^2}d\mathbb{P}$$

Em particular se $ \alpha(t)=t $. Temos que

$$\int_{\Omega} f(B(t)-t)e^{B(1)-\frac{1}{2}}d\mathbb{P}=\int_{\Omega} f(B(t))d\mathbb{P}$$

10.7 - Teorema de Girsanov

Um resultado fundamental do cálculo estocástico é o teorema de Cameron-Martin-Girsanov. Este resltado nos diz que se mudarmos a média de um processo de Itô, provocamos uma mudança não muio radical na distribuição de probabilidade do processo.

Considere $ (\Omega, \mathcal{F},\mathbb{P}) $ um espaço de probabilidade. Podemos introduzir outra probabilidade sobre $ (\Omega, \mathcal{F}) $ de forma que obtemos outro espaço de probabilidade com o mesmo espaço amostral e a mesma $ \sigma- $álgebra de eventos.

Uma maneira fácil de se fazer isso, é considerar uma variável aleatória $ \Theta $ sobre $ (\Omega,\mathcal{F}) $ tal que

$$\Theta\geq 0\ \ e\ \ \mathbb{E}_{\mathbb{P}}[\Theta]=1,$$

no qual $ \mathbb{E}_{\mathbb{P}}[\cdot] $ denota a esperança associada a probabilidade $ \mathbb{P} $. Podemos obter uma probabilidade $ \mathbb{Q} $ sobre $ (\Omega, \mathcal{F}) $ na forma

A variável aleatória $ \Theta $ é denominada derivada de Radon-Nikodym de $ \mathbb{Q} $ com respeito a $ \mathbb{P} $. Simbolicamente, denotamos

$$\Theta=\frac{d\mathbb{P}}{d\mathbb{Q}}.$$

Se $ \mathbb{E}_{\mathbb{Q}}[\cdot] $ é a esperança definida com relação a probabilidade $ \mathbb{Q} $, sabemos que

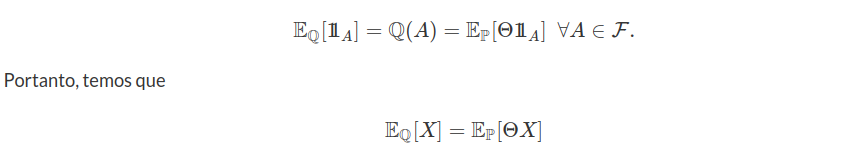
para qualquer variável aleatória $ X $ sobre $ (\Omega, \mathcal{F}). $

A seguir relacionamos a esperança condicional com respeito a probabilidade $ \mathbb{Q} $ em termos da esperança condicional da probabilidade $ \mathbb{P} $.

Proposição 10.6.1

Seja $ \mathcal{B} $ uma sigma-álgebra tal que $ \mathcal{B}\subset\mathcal{F} $. Então

Desta forma, concluímos que

$$\mathbb{Q}(A)=\tilde{\mathbb{Q}}(A)\ \ \ \forall A\in\mathcal{B},$$

o que implica que

e

$$F_{\mathbb{P}}(x)=\mathbb{P}(X\leq x)\ \ \ e\ \ \ F_{\mathbb{Q}}(x)=\mathbb{Q}(X\leq x).$$

Em geral, temos que $ F_{\mathbb{P}}(x)\neq F_{\mathbb{Q}}(x) $. Então a frase X é uma variavel aleatória normal, pode ser equivocada se trabalharmos com mais de uma probabilidade.

Exemplo 10.6.2

Considere $ (\Omega, \mathcal{F}, \mathbb{P}) $ um espaço de probabilidade e uma variável aleatória $ Z $ sobre este espaço de probabilidade, no qual

$$\mathbb{P}(Z\leq x)=\Phi(x)=\int_{-\infty}^x\frac{1}{\sqrt{2\pi}}e^{-y^2/2}dy\ \ \ x\in\mathbb{R}.$$

Claro que existe muitas variáveis aleatórias sobre $ (\Omega, \mathcal{F}, \mathbb{P}) $ tendo distribuição normal padrão.

Relacionado a variável aleatória $ Z $, sabemos que

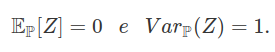
e também que

$$\mathbb{E}_{\mathbb{P}}[e^{\mu Z}]=e^{\mu^2/2}.$$

Então

$$\mathbb{E}_{\mathbb{P}}[e^{\mu Z-\mu^2/2}]=1$$

Portanto podemos introduzir a probabilidade $ \mathbb{Q} $ definida por

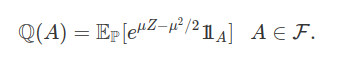
Uma questão de interesse é: qual a distribuição da variável aleatória $ Z $ com respeito a probabilidade $ \mathbb{Q} $?

Temos que

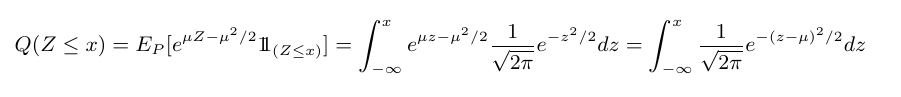
Isto é, com respeito a probabilidade $ \mathbb{Q} $, a variável aleatória $ Z $ tem distribuição normal com média $ \mu $ e variância $ 1 $.

$$\int_0^T X^2_t dt< \infty\ \ \ \mathbb{P}-a.s.$$

Defina

$$M_t:=\exp{Y_t}\ \text{no qual}\ \ Y_t:=-\frac{1}{2}\int_0^tX^2_sds+\int_0^tX_sdB_s.$$

Aplicando a fórmula de Itô em $ M_t $, temos que

$$M_t=1+\int_0^tM_sX_sdB_s.$$

Segue então que $ M_t $ é um $ \mathcal{F_t}- $martingale.

Em particular

Observe que

$$\mathbb{Q}_t(A)=\mathbb{Q}(A)\ \ \forall A\in\mathcal{F_t}.$$

Teorema 10.6.2 (Teorema de Cameron-Martin-Girsanov)

Seja $ (\Omega, \mathcal{F},\mathbb{P}) $ um espaço de probabilidade, $ B_t $ movimento browniano e $ X_t $ como definido acima. Defina

$$W_t:=B_t-\int_0^tX_sds\ \ \ t\in[0,T].$$

Então, para qualquer $ T\geq 0 $ fixado, o processo $ W_t,\ 0\leq t\leq T $ é um $ \mathcal{F_t}- $movimento browniano em $ \mathbb{R} $ com respeito a probabilidade $ \mathbb{Q} $.

Prova:

Vamos provar o teorema com o auxílio da caracterização de Levy do movimento browniano.

Um processo estocástico contínuo $ W=(W_t) $ em uum espaço de probabilidade $ (\Omega, \mathcal{F},\mathbb{P}) $ é um movimento browniano se, e somente se:

• $ W_t $ é um martingale com respeito a $ \mathcal{F_t}^{W} $

• $ W^2_t-t $ é um martingale com respeito a $ \mathcal{F_t}^{W} $

Defina

$$K_t:=M_tW_t$$

Aplicando a regra do produto para o calculo de Itô,

$$dK_t=W_tdM_t+M_tdW_t+dW_tdM_t$$

$$=W_tM_tX_tdB_t+M_t(dB_t-X_tdt)+M_tX_tdt$$

$$=\left[W_tM_tX_t+M_t\right]dB_t$$

O que implica que $ K_t=M_tW_t $ é um $ \mathcal{F_t}- $martingale co respeito a $ \mathbb{P} $.

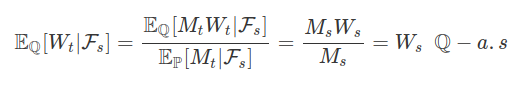
Vamos utilizar a mesma estratégia para provar que $ W_t^2-t $ é um martingale.

Seja

$$Z_t=g(W_t,t)=W_t^2-t.$$

$ W_t $ é um processo de Itô. Aplicando a fórmula de Itô na função $ g(W_t,t) $, temos que

$$dZ_t=2W_tdB_t-2W_tX_tdt$$

A regra do produto para o cálculo de Itô garante que

$$d(Z_tM_t)=dZ_tM_t+Z_tdM_t+dZ_tdM_t$$

$$=2W_tM_tdB_t-2W_tX_tM_tdt+Z_tX_tM_tdB_t+W_tX_tM_tdt$$

$$=(2W_tM_t+Z_tX_tM_t)dB_t$$

Ou seja, o processo $ Z_tM_t $ é um $ \mathcal{F_t}- $martingale com respeito a probabilidade $ \mathbb{P} $.

Aplicando a proposição 10.6.2, temos que

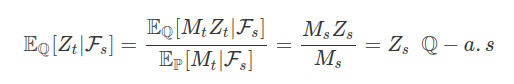
E portanto $ W_t $ é um $ \mathcal{F_t}- $movimento browniano com respeito a probabilidade $ \mathbb{Q} $.

10.8 - Representação Martingale

Seja $ W(t) $ o movimento browniano e $ \mathcal{F} $ a $ \sigma- $álgebra gerada pelo mesmo. Se $ \nu\in L^2(\Omega, [0,T]) $ então como já visto na seção Integral de Itô,

$$X_t=X_0+\int_0^t\nu dW(s)$$

é um martingale com respeito a filtragem gerada pelo movimento browniano.

Nosso interesse, é saber se podemos representar qualquer martingale com respeito a filtragem $ \mathcal{F} $ como uma média mais uma integral de Itô. O resultado que garante tal representação é conhecido como Teorema de Representação de Martingales. O objetivo desta seção e provar o teorema de representação de martingales.

Primeiro, vamos apresentar alguns resultados auxiliares.

Lema 10.8.1

$ \square $

Lema 10.8.2

O conjunto $ \mathcal{A} $, dado por

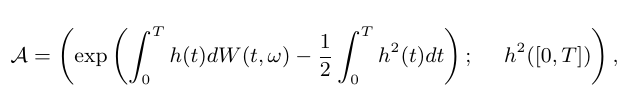
é denso em $ L^2(\mathcal{F}_T,\mathbb{P}). $

Prova:

Suponha $ g\in L^2(\mathcal{F}_T,\mathbb{P}) $ ortogonal em $ L^2(\mathcal{F}_T,\mathbb{P}) $ a todas as funções do conjunto $ \mathcal{A} $. Então, em particular

$$ G(\lambda):=\int_{\Omega}\exp(\lambda_1B_{t_1}(\omega)+\dots+\lambda_nB_{t_n}(\omega))g(\omega)d\mathbb{P}(\omega)=0 $$

para todo $ \lambda=(\lambda_1,\dots,\lambda_n)\in\mathbb{R}^n $ e todo $ t_1,\dots,t_n\in[0,T] $. A função $ G(\lambda) $ é analítica real em $ \lambda\in\mathbb{R}^n $. Então, $ G $ tem uma extensão analítica para o espaço complexo $ \mathbb{C}^n $, dada por

$$G(z)=\int_{\omega}\exp(z_1B_{t_1}(\omega)+\dots+z_nB_{t_n}(\omega))g(\omega)d\mathbb{P}(\omega)$$

para todo $ z\in\mathbb{C}^n $. Desde que $ G=0 $ sobre $ \mathbb{R}^n $ e $ G $ é analítica, $ G=0 $ sobre $ \mathbb{C}^n $. Em particular $ G(iy_1,\dots,iy_n)=0 $ para todo $ y\in\mathbb{R}^n $.

Tome $ \phi\in C^{\infty}(\mathbb{R}^n) $

$$\int_{\Omega}\phi(B_{t_1},\dots,B_{t_n})g(\omega)d\mathbb{P}(\omega)=\int_{\Omega}(2\pi)^{-n/2}\left(\int_{\mathbb{R}^n}\hat{\phi}(y)e^{i(y_1B_{t_1}+\dots+y_nB_{t_n})}dy\right)g(\omega)d\mathbb{P}(\omega)$$

$$=(2\pi)^{-n/2}\int_{\mathbb{R}^n}\hat{\phi}(y)\left(\int_{\Omega}e^{i(y_1B_{t_1}+\dots+y_nB_{t_n})}g(\omega)d\mathbb{P}(\omega)\right)dy=(2\pi)^{-n/2}\int_{\mathbb{R}^n}\hat{\phi}(y)G(iy)dy=0.$$

No qual

$$\hat{\phi}(y)=(2\pi)^{-n/2}\int_{\mathbb{R}^n}\phi(x)e^{-ixy}dx$$

é a transformada de Fourier de $ \phi $ e usando o teorema da transformada inversa de Fourier, temos que

$$\phi(x)=(2\pi)^{-n/2}\int_{\mathbb{R}^n}\hat{\phi}(y)e^{ixy}dy.$$

Assim, se $ g $ é ortogonal ao conjunto $ \mathcal{A} $, temos que $ g $ é ortogonal a um subconjunto denso de $ L^2(\mathcal{F}_T,\mathbb{P}) $, e portanto concluímos que $ g=0 $. Então o conjunto $ \mathcal{A} $ é denso em $ L^2(\mathcal{F}_T,\mathbb{P}) $.

$ \square $

Teorema 10.8.1 (Teorema da Representação de Itô)

Seja $ F\in L^2(\mathcal{F}_T, \mathbb{P}) $ uma variável aleatória. Então existe um único processo estocástico $ f(t,\omega)\in\Nu(0,T) $ tal que

$$F(\omega)=\mathbb{E}[F]+\int_0^Tf(t,\omega)dW(t,\omega).$$

Prova:

Primeiro assuma que $ F $ tenha a seguinte forma

$$F(\omega)=\exp\left(\int_0^Th(t)dW(t,\omega)-\frac{1}{2}\int_0^Th^2(t)dt\right)$$

para alguma função $ h\in L^2[0,T] $.

Defina

$$Y(t,\omega)= \exp\left(\int_0^th(t)dW(s,\omega)-\frac{1}{2}\int_0^th^2(s)ds\right)\ \ \ \ 0\leq t\leq T.$$

Aplicando a fórmula de no processo $ Y $, temos que

$$dY(t,\omega)=Y(t,\omega)h(t)dW(t,\omega)$$

então

$$Y(t)=1+\int_0^tY(s)h(s)dW(s)\ \ \ \forall t\in[0,T]$$

e assim, $ \mathbb{E}[F]=1 $. Se $ F\in L^2(\mathcal{F}_T,\mathbb{P}) $ é arbitrária, pelo lema 10.8.2 podemos aproximar $ F $ por combinações lineares de funções $ F_n $ tal que

$$F_n(\omega)=\exp\left(\int_0^Tf_n(t)dW(t)-\frac{1}{2}\int_0^Tf_n^2(t)dt\right)$$

10.9 - Integrais Multiplas

Nossa meta é definir a integral múltiplas de Wiener-Itô como

$$\int_a^b\dots\int_a^b f(t,s)dB(t)s\dots dB(s), \quad f\in L^2([a,b]^2)$$

Para isso vamos começar com a Integral dupla e em seguida vamos extender para o caso de integrais múltiplas.

Integrais Duplas

Nossa meta é definir a integral dupla de Wiener-Itô como

$$\int_a^b\int_a^b f(t,s)dB(t)sdB(s), \quad f\in L^2([a,b]^2)$$

Seja $ D=((t,s)\in [a,b]^2; t=s) $ denotamos a diagonal do quadrado $ [a,b]^2 $. Chamaremos de retângulo nessa seção um subconjunto de $ [a,b]^2 $ da forma $ [t_1,t_2)\times[s_1,s_2) $.

Definição 10.9.1: Um função escada é uma função fora da diagonal no quadrado $ [a,b]^2 $ é definida pela função da forma

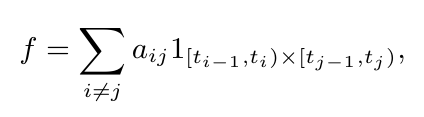
com $ a=t_0< t_1< t_2< \cdots < t_{n-1}< t_n=b $.

é uma função diagonal desde que $ A_i\bigcap D=\emptyset $. Para uma função escada fora da diagonal, temos que a integral de Wiener-Itô múltipla dada por

$$I(f)=\sum_{i\neq j}a_{ij}(B(t_i)-B(t_{i+1}))(B(t_j)-B(t_{j-1}))$$

Mas uma função escada não diagonal não tem representação única, porém $ I(f) $ é unicamente definido. Além disso, é fácil ver que

$$I(\alpha f+\beta g)=\alpha I(f)+\beta I(g)$$

para quaisquer funções escadas fora da diagonal e $ \alpha, \beta \in \mathbb{R} $.

A simetrização $ \bar{f}(t,s) $ da função $ f(t,s) $ é dada por

$$\bar{f}(t,s)=\frac{1}{2}(f(t,s)+f(s,t))$$

Claro que $ \bar{f} $ é uma função simétrica. Se $ f $ é uma função simétrica então $ \bar{f}=f $. Para a função $ f(t,s)=t $ em $ [0,1]^2 $, temos que $ \bar{f}(t,s)=\frac{1}{2}(t+s) $

Lema 10.9.1: Seja f uma função escada fora da diagonal, então $ I(f)=I(\bar{f}) $.

Demonstração

Portanto, pela definição de $ I $ temos que

$$I(f)=\left(B(t_2)-B(t_1)\right)\left(B(s_2)-B(s_1)\right)$$

$$I(\bar{f})=\frac{1}{2}\left(\left(B(t_2)-B(t_1)\right)\left(B(s_2)-B(s_1)\right)+\left(B(s_2)-B(s_1)\right)\left(B(t_2)-B(t_1)\right)\right)$$

$$=\left(B(t_2)-B(t_1)\right)\left(B(s_2)-B(s_1)\right)$$

Portanto, $ I(f)=I(\bar{f}) $ e o resultado segue.

Lema 10.9.2: Se $ f $ é uma função escada fora da diagonal, então $ \mathbb{E}(I(f))=0 $ e

$$\mathbb{E}\left(I(f)^2\right)=2\int_a^b\int_a^b \bar{f}^2(t,s)dtds$$

Demonstração:

Suponha que $ f $ tenha a seguinte representação

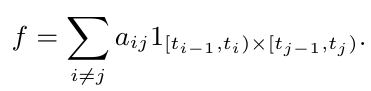
Então, temos que

$$I(f)=\sum_{i\neq j}a_{ij}(B(t_i)-B(t_{i-1}))(B(t_j)-B(t_{j-1}))$$

a esperança $ \mathbb{E}(I(f)) $ é a soma de cada termo, e portanto $ \mathbb{E}(I(f))=0 $

Para provar a equação

$$\mathbb{E}\left(I(f)^2\right)=2\int_a^b\int_a^b \bar{f}^2(t,s)dtds$$

primeiramente vamos assumir que $ f $ é simétrica. E neste caso temos que $ a_{ij}=a_{ji} $ para $ i\neq j $. Para facilitar a notação vamos definir

$ B_i=B(t_i)-B(t_{i-1}) $. Então

$$I(f)=\sum_{i\neq j}a_{ij}B_iB_j=2\sum_{i< j}a_{ij}B_iB_j$$

Portanto, temos que

$$\mathbb{E}(I^2(f))=4\sum_{i< j}\sum_{p< q}a_{ij}a_{pq}\mathbb{E}(B_iB_jB_pB_q)$$

Seja $ i< j $ fixado. Observando a posição dos intervalos, podemos ver a seguinte implicação

$$p\neq i\Rightarrow \mathbb{E}(B_iB_jB_pB_q)=0 \quad \quad \forall q > p,$$

$$q\neq j\Rightarrow \mathbb{E}(B_iB_jB_pB_q)=0 \quad \quad \forall p < q.$$

Portanto para $ i< j, $ a soma sobre $ p< q $

$$\mathbb{E}(I^2(f))=4\sum_{i< j}a^2_{ij}\mathbb{E}(B^2_iB^2_j)$$

$$=4\sum_{i< j}a^2_{ij}\mathbb{E}(B^2_iB^2_j)$$

$$=4\sum_{i< j}a^2_{ij}(t_i-t_{i-1})(t_j-t_{j-1})$$

$$=2\sum_{i\neq j}a^2_{ij}(t_i-t_{i-1})(t_j-t_{j-1})$$

$$=2\int_{a}^b\int_a^b f^2(t,s)dtds.$$

Finalmente, para qualquer escada função fora da diagonal f, temos que $ I(f)=I(\bar{f}) $ pelo Lema anterior, portanto

$$\mathbb{E}(I^2(f))=\mathbb{E}(I^2(\bar{f}))=2\int_a^b\int_a^b \bar{f}^2(t,s)dtds$$

Portanto o resultado segue.

O proximo passo iremos fazer aproximação por função escada fora da diagonal para funções gerais.

Pelo Lema 10.9.2, temos que $ \mathbb{E}(I(f)^2)=2|\bar{f}|^2 $, como $ |\bar{f}|\leq |f| $ e portanto, $ \mathbb{E}(I(f)^2)\leq 2|f|^2 $ para qualquer função escada fora da diagonal. Com essa desigualdade podemos extender essa integral para funções $ f\in L^2([a,b]^2) $, basta uma aproximação pela por funções escadas fora da diagonal.

Suponha que $ f\in L^2([a,b]^2) $. Seja $ D_{\delta} $ o conjunto dos pontos em $ [a,b]^2 $ tendo a distancia $ < \delta $ da diagonal $ D $. Para cada $ \epsilon> 0 $, podemos escolher $ \delta > 0 $ pequeno o bastante para o qual

$$\int\int_{D_\delta}f^2(t,s)dtds < \frac{\epsilon}{2}.$$

Por outro lado temos que se $ D_{\delta}^c=[a,b]^2\ D_\delta $ e considere a restrição de $ f $ para $ D_\delta^c $. Então existe uma função $ g $ da forma

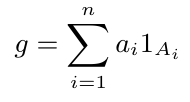
com os retângulos $ A_i\subset D_\delta^c $ para todo $ 1\leq i\leq n $ tal que

$$\int\int_{D_\delta^c}|f(t,s)-g(t,s)|^2dtds< \frac{\epsilon}{2}$$

Com isso, podemos resumir a integrais e temos que

$$\int_a^b\int_a^b |f(t,s)-g(t,s)|^2dtds < \epsilon$$

Observando que a função g desaparece no conjunto $ D_{\delta} $. Portanto a função $ g $ é uma função escada fora da diagonal, com isso obtemos o Lema abaixo:

Lema 10.9.3 Seja $ f $ uma função $ L^2([a,b]^2) $. Então existe uma sequência $ (f_n) $ de funções escadas fora da diagonal tal que

$$\lim_{n\rightarrow \infty}\int_a^b\int_a^b |f(t,s)-f_n(t,s)|^2dtds=0$$

Com isso podemos extender a integral dupla para funções $ f\in L^2([a,b]^2) $. Para cada $ f \in L^2([a,b]^2) $, podemos escolher uma sequência $ (f_n) $ de funções escadas foras da diagonal, convergindo para $ f \in L^2([a,b]^2) $. A existência desta sequência é garantida pelo Lema acima. Então pela linearidade da integral $ I $ e do Lema 10.9.2.

$$\mathbb{E}\left[(I(f_n)-I(f_m))^2\right]=2|\bar{f}_n-\bar{f}_m|^2\leq 2|f_n-f_m|^2\rightarrow 0,$$

como $ n,m\rightarrow \infty $. Portanto a sequência $ (I(f_n)) $ é uma sequência de Cauchy em $ L^2(\Omega) $. Definir

$$I(f)=\lim_{n\rightarrow \infty} I(f_n), \quad em \quad L^2(\Omega).$$

Com isso, temos que $ I $ é bem definida, ou seja, não depende da escolha de $ (f_n) $.

Definição 10.9.2: Seja $ f\in L^2([a,b]^2) $. O limite

$$I(f)=\lim_{n\rightarrow \infty} I(f_n), \quad em \quad L^2(\Omega).$$

É chamada de integral dupla de Wiener-Itô de f. Iremos usar

$$\int_a^b\int_a^b f(t,s)dB(t)dB(s)$$

para denotar a integral dupla de Wiener-Itô.

Exemplo 10.9.1: Note que a função $ f\equiv 1 $ em $ [0,1]^2 $ é uma função escada fora da diagonal. Portanto, a integral dupla de Wiener-Itô não está bem definida. Porém, definimos

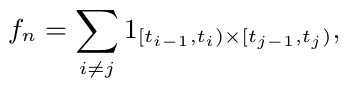
e ainda

$$I(f_n)=\sum_{i\neq j}(B(t_i)-B(t_{i+1}))(B(t_j)-B(t_{j-1}))$$

Temos que

$$I(f_n)=\sum_{i,j=1}^n(B(t_i)-B(t_{i+1}))(B(t_j)-B(t_{j-1}))-\sum_{i=1}^n \left(B(t_i)-B(t_{i-1})^2\right)$$

$$=B^2(1)-\sum_{i=1}^n \left(B(t_i)-B(t_{i-1})\right)^2.$$

Com isso, temos que

$$I(f)=\lim_{n \rightarrow \infty} I(f_n)=B^2(1)-1,$$

Portanto, temos que

$$\int_0^1\int_0^1 1dB(t)dB(s)=B^2(1)-1,$$

Com isso, temos o seguinte teorema

Teorema 10.9.1: Seja $ f(t,s)\in L^2([a,b]^2) $. Então, temos que

(a)$ I(f)=I(\bar{f}) $. Na qual, $ \bar{f} $ é a simetrização de f.

(b)$ \mathbb{E}(I(f))=0 $

(c)$ \mathbb{E}(I(f)^2)=2|\bar{f}|^2 $. No qual, $ |\cdot| $ é uma norma em $ L^2([a,b]^2) $.

Existe uma importante relação entre a integral dupla de Wiener-Itô e a integral de Itô.

Teorema 10.9.2: Seja $ f(t,s)\in L^2([a,b]^2) $. Então,

$$\int_a^b\int_a^b f(t,s)dB(t)dB(s)=2\int_a^b\left(\int_a^t \bar{f}(t,s)dB(s)\right)dB(t),$$

na qual $ \bar{t} $ é a simetrização de f.

Demonstração:

Podemos assumir sem perda de generalidade que $ s_1< s_2< t_1 < t_2 $. Pela definição de $ I(f) $ temos que

$$\int_a^b\int_a^b f(t,s)dB(t)dB(s)=(B(t_2)-B(t_1))(B(s_2)-B(s_1)).$$

Por outro lado temos que

$$\int_a^b \left[\int_a^t \bar{f}(t,s)dB(s)\right]dB(t)=\frac{1}{2}\int_{t_1}^{t_2}\left[\int_{s_1}^{s_2} 1 dB(s)\right]dB(t)$$

$$=\frac{1}{2}\int_{t_1}^{t_2}\left(B(s_2)-B(s_1)\right)dB(t)$$

$$=\frac{1}{2}\left(B(s_2)-B(s_1)\left(B(t_2)-B(t_1)\right)\right)$$

Portanto o resultado é válido. Agora usando a linearidade da integral e usando a aproximação, obtemos que o resultado é válido para $ f(t,s)\in L^2([a,b]^2) $.

Para fazermos uma generalização para funções mais gerais, vamos necessitar de algumas ferramentas que serão descritas abaixo, como o polinômio de Hermite bases ortogonais entre outros.

10.9.1 - Polinômio de Hermite

A ideia dessa seção é explicar melhor o Polinômio de Hermite, pois iremos necessitar de algumas de suas propriedades nas seções seguintes.

Assim, seja $ \mu $ uma medida Gaussiana com média 0 e variância $ \sigma> 0 $,

$$d\mu(x)=\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{1}{2\sigma}x^2}$$

Considere a sequência $ 1,x,x^2,\cdots, x^n,\cdots $ pertencentes ao espaço de Hilbert real $ L^2(\mu) $. Assim, aplicando o processo de ortogonalização de Gram-Schmidt(processo muito comum na Algebra Linear) para essa sequência, em ordem crescente de potência, para obter polinômios ortogonais $ P_0(x),P_1(x),\dots,P_n(x),\dots $ no espaço de Hilbert $ L^2(\mu) $ onde $ P_0(x)=1 $ e $ P_n(x) $ é um polinômio de grau n, com $ n\geq 1 $.

Seria possível definirmos os polinômios $ P_n $ de forma explicita?

Seja $ \theta(t,x)=e^{tx} $. A esperança de $ \theta(t,\cdot) $ com respeito a medida $ \mu $ é dada por

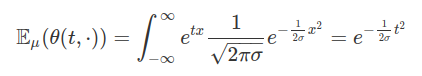
A renormalização multiplicativa $ \psi(t,x) $ de $ \theta(t,x) $ é definida por

$$\psi(t,x)=\frac{\theta(t,x)}{\mathbb{E}_{\mu}(\theta(t,\cdot))}=e^{tx-\frac{1}{2\sigma}t^2}$$

Podemos expandir a função $ \psi $ por series de potência em t. Note que coeficiente de $ t^n $ na serie depende de $ n $ $ x $ e $ \sigma $.

$$e^{tx-\frac{1}{2\sigma}t^2}=\sum_n^\infty \frac{H_n(x,\sigma)}{n!}t^n$$

no qual, $ H_n(x,\sigma)/n! $ é o coeficiente da serie. Por outro lado temos que a serie de potência

$$e^s=\sum_{n=0}^\infty s^n/n!$$

assim podemos usar essa igualdade para encontrar os coeficientes os coeficientes de $ t^n $. Assim escrevendo $ e^{tx-\frac{1}{2\sigma}x^2}=e^{tx}e^{\frac{1}{2\sigma}t^2} $ temos

$$e^{tx-\frac{1}{2\sigma}t^2}=\sum_{n=0}^\infty \frac{(xt)^n}{n!}\sum_{n=1}^\infty\frac{(-\sigma t)^n}{n!2^n}$$

Desta forma, encontramos os coeficientes de $ t^n $, $ H_n(x,\sigma) $ é dado por

$$H_n(x,\sigma)=n!\left(\frac{x^n}{n!}+\frac{x^{n-2}(-\sigma)}{(n-2)!2}+\dots+\frac{x^{n-2k}(-\sigma)^k}{(n-2k)!2^k}+\dots\right)$$

$$=x^n+\frac{n!}{(n-2)!2}(-\sigma)x^{n-2}+\dots+\frac{n!}{(n-2k)!k!2^k}(-\sigma)^k x^{n-2k}+\dots$$

Observe que

$$\frac{n!}{(n-2k)!k!2^k}=\binom{n}{2k}(2k-1)!!$$

no qual $ (2k-1)!!=(2k-1)(2k-3)\dots 3\cdot 1 $. O que implica que

$$H_n(x,\sigma)=\sum_{k=0}^{[n/2]}\binom{n}{2k}(2k-1)!!(-\sigma)^kx^{n-2k},$$

com $ [x] $ sendo a parte inteira de $ x $. Observe que $ H_n(x,\sigma) $ é um polinômio em x de grau n.

Definição 10.9.1.1:

O polinômio $ H_n(x,\sigma) $ dado acima é chamado de polinômio de Hermite de grau $ n $ com parâmetro $ \sigma $.

Teorema 10.9.1.1:

Seja $ H_n(x,\sigma) $ um polinômio de Hermite de grau n, definido acima. Então

$$H_{n}(x,\sigma)=(-\sigma)^n e^{x^2/2\sigma}D_x^ne^{-x^2/2\sigma},$$

no qual $ D_x $ é o operador diferencial na variável x.

Demonstração:

O expoente do lado esquerdo da equação pode ser reescrito como

$$-\frac{1}{2}\sigma(t-\frac{x}{\sigma})^2+\frac{x^2}{2\sigma}$$

Portanto temos que

$$e^{\frac{x^2}{2\sigma}}e^{-\frac{1}{2}\sigma(t-\frac{x}{\sigma})^2}=\sum_{n=0}^\infty \frac{H_n(x,\sigma)}{n!}t^n$$

Derivando de ambos os lados n vezes na variável t e então tomando t=0 temos

$$H_n(x,\sigma)=e^{\frac{x^2}{2\sigma}}\left(D_t^ne^{-\frac{1}{2}\sigma\left(t-\frac{x}{\sigma}\right)^2}\right)\left|_{t=0}\right.$$

Note que $ D_x^ne^{-\frac{1}{2}\sigma\left(t-\frac{x}{\sigma}\right)^2} $. Portanto,

$$H_n(x,\sigma)=e^{\frac{x^2}{2\sigma}}\left((-\sigma)^n D_x^ne^{-\frac{1}{2}\sigma\left(t-\frac{x}{\sigma}\right)^2}\right)\left|_{t=0}\right.$$

$$(-\sigma)^ne^{\frac{x^2}{2\sigma}}D^n_x e^{-\frac{x^2}{2\sigma}},$$

o que prova o resultado.

Teorema 10.9.1.2:

\begin{theorem}Seja $ \mu $ uma medida Gaussiana com média 0 e variância $ \sigma $. Então, o polinômio de Hermite $ H_n(x,\sigma) $, $ n\geq 0, $ são ortogonais em $ L^2(\mu) $. Além disso, temos que

$$\int_{-\infty}^{\infty} H_n(x,\sigma)^2d\mu(x)=n!\sigma^n, \quad\quad n\geq 0.$$

Demonstração:

Para qualquer $ t,s\in \mathbb{R} $, temos

$$e^{(t+s)x-\frac{1}{2}\sigma(t^2+s^2)}=\sum_{n,m=0}^{\infty}\frac{t^n s^m}{n!m!}H_n(x,\sigma)H_m(x,\sigma).$$

Pela equação

$$\int_{-\infty}^\infty e^{tx}\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{1}{2\sigma}x^2}dx=e^{-\frac{1}{2\sigma}t^2}$$

Temos que

$$\int_{-\infty}^\infty e^{(t+s)x-\frac{1}{2}\sigma (t^2+s^2)}dx=e^{-\frac{1}{2}\sigma (t^2+s^2)}e^{\frac{1}{2}\sigma(t+s)^2}=e^{\sigma ts}.$$

Portanto, ao integrar ambos os lados da equação

$$e^{(t+s)x-\frac{1}{2}\sigma(t^2+s^2)}=\sum_{n,m=0}^{\infty}\frac{t^n s^m}{n!m!}H_n(x,\sigma)H_m(x,\sigma).$$

Temos que,

$$e^{\sigma ts}= \sum_{n,m=0}^\infty \frac{t^n s^m}{n!m!}\int_{-\infty}^\infty H_n(x,\sigma)H_m(x,\sigma)d\mu(x).$$

Desde que o lado esquerdo é uma função produto de $ ts $, os coeficientes de $ t^n $ e $ s^m $ do lado direito são zeros quando $ n\neq m $ o que implica que

$$\int_{-\infty}^\infty H_n(x,\sigma)H_m(x,\sigma)d\mu(x)=0$$

para qualquer $ n\neq m $. E portanto, temos que os polinômios de Hermite são ortogonais em $ L^2(\mu) $. E então temos que

$$e^{\sigma ts}=\sum_{n=0}^\infty \frac{(ts)^n}{(n!)^2}\int_{-\infty}^\infty H_n(x,\sigma)^2d\mu(x)$$

Mas pela expansão em serie da função $ e^{\sigma ts} $ temos

$$e^{\sigma ts}=\sum_{n=0}^\infty \frac{\sigma^n}{n!}(ts)^n$$

Portanto, o resultado segue.

Teorema 10.9.1.3:

Seja $ \mu $ uma medida Gaussiana com média 0 e variância $ \sigma $. Então para toda função $ f\in L^2(\mu) $ existe uma única expansão em serie dada por

$$f(x)=\sum_{n=0}^\infty \alpha_n \frac{H_n(x,\sigma)}{\sqrt{n!\sigma^n}}$$

no qual os coeficientes $ \alpha_n $ são dados por

$$\alpha_n=\frac{1}{\sqrt{n!\sigma^n}}\int_{-\infty}^{\infty}f(x)H_n(x,\sigma)d\mu(x),\quad\quad\quad n\geq 0.$$

Além disso, temos que

$$|f|^2=\sum_{n=0}^\infty \alpha_n^2.$$

Abaixo temos algumas propriedades muito importante dos polinômios de Hermite:

1- Função Geradora: $ \displaystyle e^{tx-\frac{1}{2}\sigma t^2}=\sum_{n=0}^{\infty}\frac{t^n}{n!}H_n(x,\sigma) $.

2- Monômios: $ x^n=\displaystyle \sum_{k=0}^{[n/2]}\binom{n}{2k}(2k-1)!! \sigma^k H_{n-2k}(x,\sigma) $

3- Formula recursiva: $ \displaystyle H_{n+1}(x,\sigma)=xH_{n}(x,\sigma)-\sigma n H_{n-1}(x,\sigma) $

4- Derivadas: $ D_x H_{n}(x,\sigma)=nH_{n-1}(x,\sigma) $

5- Autofunção: $ (-\sigma D_x^2+xD_x)H_{n}(x,\sigma)=nH_{n}(x,\sigma) $

6- Produto: $ \displaystyle H_{n}(x,\sigma)H_{m}(x,\sigma)=\sum_{k=0}^{n\wedge m} k!\binom{n}{k}\binom{m}{k}\sigma^k H_{n+m-2k}(x,\sigma) $

7- Derivadas Parciais: $ \displaystyle \frac{\partial}{\partial \sigma}H_{n}(x,\sigma)=\frac{1}{2}\frac{\partial^2 }{\partial x^2}H_{n}(x,\sigma). $

10.9.2 - Homogeneidade no Caos

Seja $ \mu $ uma medida gaussiana com média zero e variância $ \sigma $, pelo Teorema 10.9.1.3, toda função no espaço de Hilbert $ L^2(\mu) $ tem representação única em séries de polinômio de Hermite.

O espaço de Wiener $ C(\mathbb{R},[0,1]) $ é um espaço de Banach de funções contínua a valores reais no [0,1] que se anula em zero, seja $ \mathbb{P} $ a medida de Wiener no espaço das $ C(\mathbb{R},[0,1]) $, o qual para facilitar a notação denotaremos apenas por $ C $. Agora será que existe uma versão análoga ao Teorema 10.9.1.3 funções em $ L^2(\mathbb{P}) $ no espaço de probabilidade $ (\Omega,\mathcal{F},\mathbb{P}) $, no qual, $ \mathbb{F} $ é a $ \sigma $-algebra gerada pelo movimento Browniano.

Seja $ I(f)=\displaystyle \int_a^b f(t)dB(t) $ a integral de Wiener para $ f\in L^2[a,b] $. O produto $ I(f_1)I(f_2)\dots I(f_k) $ com $ f_1,f_2,\dots, f_k \in L^2[a,b] $ é chamada de polinômio caos de ordem k.

Seja $ J_0=\mathbb{R} $ e para $ n\geq 1 $, definimos $ J_n $ como sendo o fecho linear de $ L^2(\Omega) $ e adicionando as funções constante e polinômios caóticos de grau menor ou igual a $ n $. Então temos que

$$J_0\subset J_1\subset \dots \subset J_n \subset \dots \subset L^2(\Omega)$$

Teorema 10.9.2.1:

A união $\displaystyle J:=\bigcup_{n=0}^\infty$ é denso em $ L^2(\Omega) $.

Demonstração:

Seja $ (e_n)_{n=1}^\infty $ uma base ortogonal de $ L^2([a,b]) $ e seja $ \mathcal{G}_n $ a $ \sigma $-álgebra gerada por $ I(e_1),I(e_2),\dots,I(e_n) $. Então, $ (\mathcal{G}_n) $ é uma filtragem e ainda temos que $ \sigma(\cup_n \mathcal{G}_n)=\mathcal{F} $.

Seja $ \phi\in L^2(\Omega) $ ortogonal em $ \displaystyle \bigcup_{n=0}^\infty J_n $. Então, para cada n fixado temos

$$\mathbb{E}\left[\phi I^{k_1}(e_1)I^{k_2}(e_2)\dots I^{k_n}(e_n)\right]=0, \quad \quad \forall k_1, k_2, \dots, k_n \geq 0.$$

Observe que $ I^{k_1}(e_1)I^{k_2}(e_2)\dots I^{k_n}(e_n) $ é $ \mathcal{G}_n $-mensurável. Portanto,

$$\mathbb{E}\left[\phi I^{k_1}(e_1)I^{k_2}(e_2)\dots I^{k_n}(e_n)\right]=\mathbb{E}(I^{k_1}(e_1)I^{k_2}(e_2)\dots I^{k_n}(e_n))\mathbb{E}(\phi| \mathcal{G}_n).$$

Portanto, para todo inteiro $ k_1, k_2, \dots, k_n \geq 0 $,

$$\mathbb{E}(I^{k_1}(e_1)I^{k_2}(e_2)\dots I^{k_n}(e_n))\mathbb{E}(\phi| \mathcal{G}_n)=0.$$

Mas as variáveis $ I(e_1),I(e_2),\dots,I(e_n) $ são independentes com mesma distribuição normal. Além do mais,

$$\mathbb{E}(\phi|\mathcal{G}_n)=\theta_n (I(e_1),I(e_2),\dots,I(e_n))$$

para alguma função $ \theta_n $ em $ \mathbb{R}^n $. Então, para todo $ k_1,k_2,\dots,k_n\geq 0 $,

$$\displaystyle \int_{\mathbb{R}^n}x_1^k x_2^{k_2}\dots x_n^{k_n}\theta_n(x_1,x_2,\dots, x_n)d\mu(x)=0$$

na qual, $ \mu $ é uma medida Gaussiana em $ \mathbb{R}^n $. Da equação do $ H_n(x,\sigma) $, temos que implica que

$$\displaystyle \int_{\mathbb{R}^n}H_{k_1}(x_1,1)H_{k_2}(x_2,1)\dots H_{k_n}(x_n,1)\theta_n(x_1,x_2,\dots, x_n)d\mu(x)=0$$

Mas, do Teorema 10.9.1.3 a coleção

$$(H_{k_1}(x_1,1)H_{k_2}(x_2,1)\dots H_{k_n}(x_n,1);k_1,k_2,\dots,k_n\geq 0)$$

é uma base ortogonal de $ L^2(\mathbb{R}^n,\mu) $. Portanto, $ \theta_n=0 $ quase certamente com respeito a $ \mu $. Então, pela equação acima, temos que

$$\mathbb{E}(\phi|\mathcal{G}_n)=0$$

para qualquer $ n\geq 1 $. Por outro lado, como $ \mathbb{E}(\phi|\mathcal{G}_n) $ converge para $ \phi $ em $ L^2(\Omega) $ quando $ n\rightarrow \infty $. Portanto, $ \phi=0 $ quase certamente. Portanto, o resultado segue.

Agora lembramos a sequência $ (J_n) $ é um subespaço de $ L^2(\Omega) $. Seja $ K_0=\mathbb{R} $ e para cada $ n\geq 1 $ definimos $ K_n $ o complemento ortogonal de $ J_{n-1} $ em $ J_n $, temos

$$J_n=J_{n-1}\oplus K_n $$

Então, obtemos a seguinte sequência de subespaços ortogonais

$$K_0, K_1,K_2,\dots , K_n, \dots$$

Definição 10.9.2.1:

Seja $ n $ um número inteiro não negativo. Os elementos do espaço de Hilbert no espaço $ K_n $ são chamados de caos homogêneos de ordem n.

O espaço $ K_n, n\geq 1 $, são todos infinito dimensional. O caos homogêneos de ordem 1 são variáveis homogêneas Gaussianas.

Teorema 10.9.2.2:

O espaço $ L^2(\Omega) $ é soma ortogonal direta dos espaços $ K_n $, ou seja,

$$L^2(\Omega)=\displaystyle \bigoplus_{j=0}^{\infty} K_j.$$

Para cada função $ \phi \in L^2(\Omega) $ existe uma única expansão em serie de caos homogênos

$$\phi =\displaystyle \sum_{n=0}^\infty \phi_n$$

Além disso,

$$|\phi|^2=\sum_{n=0}^\infty |\phi_n|^2$$

no qual, $ |\cdot| $ é a norma de $ L^2(\Omega) $.

Exemplo 10.9.2.1:

Seja $ f\in L^2([a,b]) $ e $ I(f)=\displaystyle \int_a^b f(t)dB(t) $. Temos

$$I^2(f)=|f|^2+(I^2(f)-|f|^2).$$

Podemos mostrar que $ I^2(f)-|f|^2 $ é ortogonal a $ K_0 $ e $ K_1 $. Portanto, $ I^2(f)-|f|^2 $ pertence a $ K_2 $. Por outro lado, considere a integral dupla de Wiener-Itô

$$\displaystyle \int_a^b\int_a^b f(t)f(s)dB(t)dB(s)$$

Pelo Teorema 10.9.2

$$\displaystyle \int_a^b\int_a^b f(t)f(s)dB(t)dB(s)=2\int_a^b f(t)\left[\int_a^t f(s)\right]dB(t)$$

$$2\int_a^b f(t)X_tdB(t)$$

no qual $ X_t=\displaystyle \int_a^b f(s)dB(s) $. Então $ dX_t=f(t)dB(t) $. Usando a formula de Itô é dada por

$$d(X^2_t)=2X_tdX_s+(dX_t)^2=2f(t)X_tdB(t)+f^2(t)dt,$$

o qual nos fornece a integral estocástica

$$\displaystyle 2 \int_a^bf(t)X_tdB(t)=X^2_b-X_a^2-\int_a^b f^2(t)dt=I^2(f)-|f|^2.$$

Das equações acima e da integral dupla de Itô-Wiener temos,

$$\displaystyle \int_a^b\int_a^b f(t)f(s)dB(t)dB(s)=I^2(f)-|f|^2$$

Essa igualdade nos mostra que o caos homogêneo $ I^2(f)-|f|^2 $ é uma integral dupla de Itô-Wiener.

Teorema 10.9.2.3:

Seja $ \mathbb{P}_n $ denota a projeção ortogonal de $ L^2(\Omega) $ em $ K_n $. Se $ f_1,\dots, f_k $ funções ortogonais não negativa em $ L^2([a,b]) $ e $ n_1,\dots,n_k $ são inteiros não negativos. Então,

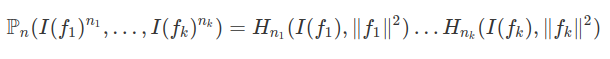
no qual $ n=n_1+\dots+n_k $. Em particular temos que

$$\mathbb{P}_n(I(f)^n)=H_n(I(f),|f|^2)$$

para qualquer função não nula $ f\in L^2[a,b] $.

Demonstração:

Afim de evitar uma notação complicada vamos provar apenas a segunda equação. Primeiro use a segunda identidade dos polinômios de Hermite, temos que

$$\displaystyle I^n(f)=H_n(I(f);|f|^2)+\frac{n(n-1)}{2}|f|^2 H_{n-2}(I(f);|f|^2)+\cdots.$$

Observe que todos os termos do lado direito, exceto o primeiro deles é ortogonal em $ K_n $, por que tem grau menor que n. Portanto para provar

$$\mathbb{P}_n(I(f)^n)=H_n(I(f),|f|^2)$$

é suficiente provar que

$$H_n(I(f),|f|^2)\perp J_{n-1}.$$

ou equivalentemente, para qualquer não negativa $ g_1,\dots,g_m\in L^2([a,b]) $ e $ 0\leq m\leq n-1 $,

$$\mathbb{E}\left(H_n(I(f),|f|^2)I(g_1)I(g_2)\dots I(g_m)\right)=0$$

Claro que podemos assumir que $ g_1,\dots,g_m $ são ortogonais. Além disso, para cada $ g_i $, podemos escrever $ g_i=c_if+h_i $ com $ c_i\in \mathbb{R} $ e $ h_i\perp f $. Portanto, afim de provar que

$$\mathbb{E}\left(H_n(I(f),|f|^2)I(g_1)I(g_2)\dots I(g_m)\right)=0$$

é suficiente para provar que para qualquer $ h_i,\cdots,h_m $ ortogonais a $ f $ e $ p+q_1+\dots+q_m\leq n-1, $

$$\mathbb{E}\left(H_n(I(f),|f|^2)I^p(f)I^{q_1}(h_1)\dots I^{q_m}(h_m)\right)=0$$

Finalmente usando que

$$\displaystyle I^n(f)=H_n(I(f);|f|^2)+\frac{n(n-1)}{2}|f|^2 H_{n-2}(I(f);|f|^2)+\cdots.$$

vemos que é suficiente provar que para qualquer $ 0\leq r+r_1+\dots +r_m\leq n-1, $

$$\mathbb{E}\left(H_n(I(f),|f|^2)H_r(I(f),|f|^2)\right)=0$$

Mas isso é verdade pelo Teorema 10.9.1.3

Exemplo 10.9.2.2:

Seja $ f\in L^2([a,b]) $ uma função não negativa. Na função geradora (equação da seção anterior), colocando $ x=I(f) $ e $ \rho=|f|^2 $ e obtemos

$$e^{tI(f)-\frac{1}{2}|f|^2 t^2}=\displaystyle \sum_{n=0}^\infty \frac{t^n}{n!}H_n(I(f),|f|^2).$$

pelo Teorema 10.9.2.3, $ H_n(I(f),|f|^2)\in K_n $ para cada $ n\geq 0 $. Portanto, pela equação acima temos uma expansão para a função $ \phi=e^{tI(f)-\frac{1}{2}|f|^2 t^2} $.

10.9.3 - Base ortogonais para o caos homogêneo

Observe que o espaço $ K_n, n\geq 1 $ é um espaço de Hilbert infinito dimensional. Iremos fixar uma base ortogonal $ (e_k)^\infty_{k=1} $ para o espaço $ L^2[a,b] $. Assim, para uma sequência $ (n_k)_{k=1}^\infty $ de inteiros não negativos com soma finita, definimos

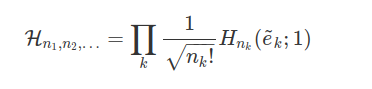
$$=\frac{1}{\sqrt{n_1!n_2!\dots}}H_{n_1}(\tilde{e}_1;1)H_{n_2}(\tilde{e}_2;1)\cdots.$$

Com $ H_0(x;1)=1 $ e existe somente um numero finito não nulos de $ n_k $’s. Portanto, o produto dessa equação é apenas um produto finito de fatores.

Lema 10.9.3.1:

Para qualquer inteiro fixo $ n\geq 1 $, a coleção de funções

$$(\mathcal{H}_{n_1,n_2,\dots; n_1+n_2+\dots =n})$$

é um subconjunto de $ K_n $. Além disso, o espaço linear expandido por essa coleção de funções é denso em $ K_n $.

Teorema 10.9.3.1:

Para qualquer inteiro fixo $ n\geq 1 $, a coleção de funções

$$(\mathcal{H}_{n_1,n_2,\dots};n_1+n_2+\dots=n)$$

é uma base ortogonal para o espaço $ K_n $ de classes homogéneos caos de ordem n.

\end{theorem}

Exemplo 10.9.3.1:

Suponha que $ f\in L^2([a,b]) $ que tenha expansão $ f=\displaystyle \sum_{n=1}^\infty a_ne_n $, onde $ a_n=\langle f,e_n\rangle $. Então a expansão de $ I(f)\in K_1\in L^2(\Omega) $ é dado por

$$I(f)=\displaystyle \sum_{n=1}^\infty a_n I(e_n).$$

Essa expansão é um caso especial do Teorema 10.9.3.1 quando $ n=1 $. Mas isso também segue do fato que a aplicação

$$I:L^2([a,b])\rightarrow L^2(\Omega)$$

é uma isometria (VER O TEOREMA 10.1.1)

Teorema 10.9.3.2

A coleção de funções

$$(\mathcal{H}_{n_1,n_2,\dots};n_1+n_2+\dots=n,n=0,1,2,\dots)$$

é uma base ortogonal para o espaço de Hilbert $ L^2(\Omega) $. Todo $ \phi\in L^2(\Omega) $ tem uma única expansão em serie

$$\phi=\displaystyle \sum_{n=0}^\infty \sum_{n_1+n_2+\dots=n} a_{n_1,n_2,\dots}\mathcal{H}_{n_1,n_2,\dots}$$

no qual, $ a_{n_1,n_2,\dots}=\displaystyle\int_{\Omega}\phi \mathcal{H}_{n_1,n_2,\dots} d\mathbb{P}. $

10.9.4 - Integrais múltiplas de Itô-Wiener

Quando olhamos Exemplo 10.9.2.1 o caos homogêneo é $ I^2(f)-|f|^2 $ para $ f\in L^2([a,b]) $ é dado por uma integral dupla de Wiener-Itô. Assim, é razoável esperar que exista uma relação biunívoca, do caos homogêneo de ordem 2 e a integral dupla. O que nos leva a questão. Todas as funções de caos homogêneo é dado por algum tipo integral de ordem $ n\geq 2 $ ?

Essa questões foram consideradas pelo Itô em 1951. Usando essas ideias vamos mostrar essa relação biunívoca.

Por simplicidade, Seja $ T\equiv [a,b] $. O objetivo desta seção é definir uma integral múltipla de Wiener-Itô

$$\displaystyle \int_{T^n}f(t_1,t_2,\dots,t_n)dB(t_1)dB(t_2)\dots dB(t_n)$$

para $ f\in L^2(T^n) $. Já temos a ideia inicial para o caso $ n=2 $ para a integral Wiener-Itô. Iremos modificar os argumentos para o o caso $ n\geq 3 $.

Seja $ D=((t_1,t_2,\dots, t_n)\in T^n, \exists i\neq j \text{ tal que } t_i=t_j) $ sendo a diagonal do conjunto de $ T^n $. Um subconjunto de $ T^n $ da forma

$$[t_1^{(1)},t_1^{(2)})\times [t_2^{(1)},t_2^{(2)})\times \dots \times [t_n^{(1)},t_n^{(2)})$$

é chamado de retângulo

O primeiro passo: Função escada fora da diagonal

A primeira função escada $ T^n $ é uma função da forma

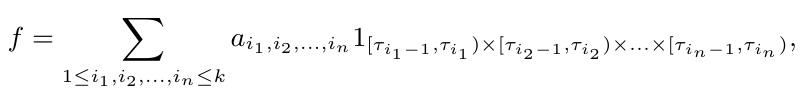
no qual, $ a=\tau_0< \tau_1 <\dots < t_k=b $. Uma função escada fora da diagonal é uma função com coeficiente satisfazendo a condição

$$a_{i_1,i_2,\dots, i_n}=0,\quad if \quad i_{p}=i_q$$

para qualquer $ p\neq q $. A condição na equação acima significa a função f desaparece no conjunto $ D $. A coleção de funções escadas fora da diagonal fora da diagonal é um espaço de vetor.

Para um função escada fora da diagonal f dada pela equação acima é dada por

$$I_n(f)=\displaystyle \sum_{1\leq i_1,i_2,\dots, i_n\leq k}a_{i_1,i_2,\dots, i_n}\xi_{i_1}\xi_{i_2}\dots \xi_{i_n}$$

no qual $ xi_{i_p}=B(\tau_{i_p})-B(\tau_{i_p-1}) $, $ 1\leq p \leq n $. O valor $ I_n(f) $ é bem definido, isto é, isto não depende da representação de f. Além disso, a aplicação $ I_n $ é linear no espaço de vetores de funções escadas fora da diagonal.

A simetrização de $ \hat{f}(t_1,t_2,\dots, t_n) $ da função $ f(t_1,t_2,\dots, t_n) $ é definida por

$$\hat{f}(t_1,t_2,\dots, t_n)=\frac{1}{n!}\sum_{\sigma}f(t_{\sigma(1)},t_{\sigma(2)},\dots, t_{\sigma(n)}),$$

no qual a somatório é sobre o conjunto de todas as permutações $ \sigma $ sobre o conjunto $ (1,2,\dots,n) $. Desde que a medida de Lebesgue é simétrica, temos

$$\displaystyle \int_{T^n}|f(t_{\sigma(1)},\dots,t_{\sigma(n)})|^2dt_1\dots dt_n=\int_{T^n}|f(t_1,\dots,t_n)|^2dt_1\dots dt_n$$

para qualquer permutação $ \sigma $. Portanto, pela desigualdade triangular temos que

$$|\hat{f}|\leq \frac{1}{n!}\displaystyle \sum_{\sigma}|f|=\frac{1}{n!}|f|=|f|.$$

Então, temos pela desigualdade triangular temos $ |\hat{f}|\leq |f| $. Em geral, a desigualdade restrita ocorre como mostramos anteriormente. Se $ f $ é uma função escada fora da diagonal, então $ \hat{f} $ é também uma função escada fora da diagonal.

Lema 10.9.4.1:

Se $ f $ é uma função escada fora da diagonal, então $ I_n(f)=I_n(\hat{f}) $.

Demonstração:

Note que $ I_n $ e o operador de simetrização são linear. Portanto, é suficiente provar o lema para o caso

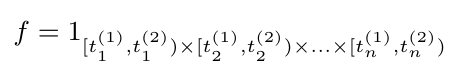
no qual o intervalos $ [t_i^{(1)},t_i^{(2)}) $, $ 1\leq i\leq n $, são disjuntos. Então, temos que

$$I_n(f)=\prod_{i=1}^n (B(t_i^{(2)})-B(t_i^{(2)}))$$

Por outro lado, a simetrização $ \hat{f} $ de $ f $ é dado por

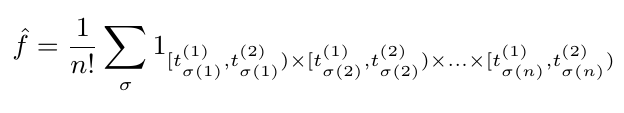
Portanto,

$$I_n(\hat{f})=\frac{1}{n!}\displaystyle \sum_{\sigma}\prod_{i=1}^n(B(t_{\sigma(i)}^{(2)})-B(t_{\sigma(i)}^{(2)}))$$

Observe que $ \displaystyle \prod_{i=1}^n (B(t_i^{(2)})-B(t_i^{(2)}))= \prod_{i=1}^n (B(t_{\sigma(i)}^{(2)})-B(t_{\sigma(i)}^{(2)})) $ para qualquer permutação $ \sigma $. Além disso, existem $ n! $ permutações do conjunto $ (1,2,\dots,n) $. Segue que

$$I_n(\hat{f})=\frac{1}{n!}\sum_{\sigma}\prod_{i=1}^n (B(t_i^{(2)})-B(t_i^{(2)}))=\prod_{i=1}^n (B(t_i^{(2)})-B(t_i^{(2)}))$$

Portanto o resultado segue.

Lema 10.9.4.2:

Se $ f $ é uma função escada fora da diagonal então $ \mathbb{E}(I_n(f))=0 $ e

$$\mathbb{E}(I_n(f))=n!\displaystyle \int_{T^n}|\hat{f}(t_1,t_2,\dots,t_n)|^2dt_1dt_2\dots dt_n.$$

O segundo passo: Aproximação por funções escadas fora da diagonal.

Seja $ D=((t_1,t_2,\dots, t_n)\in [a,b]^n; t_i=t_j, i\neq j) $ o conjunto diagonal, o qual pode ser reescrito como $ D=\displaystyle \bigcup_{i\neq j}[(t_i=t_j)\cap D] $, o que significa que $ D $ é uma união finita de intersecções de hiperplano $ (n-1) $-dimensional com o conjunto D. Portanto, a medida de Lebesgue de D é zero. Esse fato, nos permite adotar os mesmos argumentos da integral dupla.

Lemma 10.9.4.3:

Seja $ f $ uma função de $ L^2(T^n) $. Então existe uma sequência de funções escadas fora da diagonal $ (f_k) $ tal que

$$\displaystyle \lim_{k\rightarrow \infty}\int_{T^n}|f(t_1,t_2,\dots,t_n)-f_k(t_1,t_2,\dots,t_n)|^2 dt_1dt_2\dots dt_n=0$$

Agora suponha que $ f\in L^2(T^n) $. Escolha uma sequência $ (f_k) $ de funções escadas fora da diagonal convergindo para $ f\in L^(T^n) $. Pelo Lema acima essa sequência existe. Então pela linearidade e pelo Lema 10.9.4.2

$$\mathbb{E}[(I_n(f_k)-I_n(f_\ell))^2]=n!|\hat{f}_k-\hat{f}_\ell|^2\leq n!|f_k-f_\ell|^2\rightarrow 0,$$

quando $ k,\ell \rightarrow \infty $. Portanto, a sequência $ (I_n(f_k))_{k=1}^\infty $ é de Cauchy em $ L^2(\Omega) $. Defina

$$I(f)=\lim_{k\rightarrow} I(f_k),$$

em $ L^2(\Omega) $. O valor $ I_n(f) $ está bem definido, isto é, não depende da escolha da sequência $ (f_k) $ usada na equação.

Definição 10.9.4.1:

Seja $ f\in L^2(T^n) $. O limite $ I(f) $ é chamado de integral múltipla de Wiener-Itô da função $ f $ e é denotado por

$$\int_{T^n}f(t_1,t_2,\cdots, t_n)dB(t_1)dB(t_2)\dots dB(t_n)$$

No caso em que $ n=1 $, temos a integral de Wiener da função $ f $ e para o caso de $ n=2 $ a integral dupla.

Teorema 10.9.4.1: Seja $ f\in L^2(T^n) $, $ n\geq 1 $. Então, temos que

(1) $ I_n(f)=I_n(\bar{f}) $. No qual, $ \bar{f} $ é a simetrização de $ f $.

(2)$ \mathbb{E}(I_n(f))=0 $.

(3) $ \mathbb{E}(I(f)^2)=n!|\bar{f}|^2 $. Aqui, $ |\cdots| $ é a norma de $ L^2(T^n) $.

O teorema a seguir nos fornece uma igualdade para escrever a integral múltipla de Wiener-Itô como sendo uma integral interativa da integral de Itô. A qual é muito útil para calcular.

Teorema 10.9.4.2:

Seja $ f\in L^2(T^n) $, $ n\geq 2 $. Então,

$$\displaystyle \int_{T^n}f(t_1,t_2,\dots,t_n)dB(t_1)dB(t_2)\dots dB(t_n)=n!\displaystyle \int_{a}^b\dots\int_a^{t_{n-2}}\left[\int_a^{t_{n-1}}\bar{f}(t_1,t_2,\dots,t_n)dB(t_n)\right]dB(t_{n-1})\dots dB(t_{1}),$$

no qual $ \bar{f} $ é a simetrização de $ f $.

Demonstração:

É suficiente provar o teorema para o caso em que $ f $ é uma função caracterizada por retângulos disjuntos no conjunto $ D $. Pelo Lema 10.9.4.1 podemos assumir que $ f $ é da seguinte forma

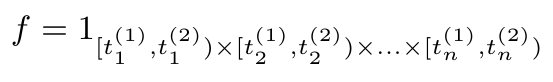
no qual, $ t_n^{(1)}< t_n^{(2)}\leq t_{n-1}^{(2)}\leq \dots \leq t_2^{(1)}< t_2^{(2)}< t_1^{(1)}< t_1^{(2)} $. Então a integral múltipla de Wiener-Itô de $ f $ é dada por

$$\displaystyle \int_{T^n}f(t_1,\dots, t_n)dB(t_1)\dots dB(t_n)=\prod_{i=1}^n(B(t_{i}^{(2)})-B(t_i^{(1)})).$$

Por outro lado temos que $ \hat{f}=\frac{1}{n!}f $ na região $ t_n< t_{n-1}< \dots < t_1 $. Portanto, temos que

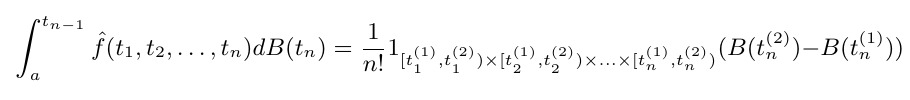
$$\displaystyle \displaystyle \int_{a}^b\dots\int_a^{t_{n-2}}\left[\int_a^{t_{n-1}}\bar{f}(t_1,t_2,\dots,t_n)dB(t_n)\right]dB(t_{n-1})\dots dB(t_{1})=\frac{1}{n!}\prod_{i=1}^n (B(t_i^{(2)})-B(t_i^{(1)})).$$

Portanto, o resultado segue.

Definição 10.9.4.2:

Seja $ g_1, \dots, g_n \in L^2[a,b] $. O produto tensorial $ g_1\otimes\dots \otimes g_n $ é definido como sendo uma função

$$g_1\otimes \dots \otimes g_n(t_1,t_2,\dots,t_n)=g_1(t_1)\dots g_n(t_n).$$

O produto tensorial $ f_1^{\otimes_{n_1}}\otimes \dots \otimes f_k^{\otimes n_k} $ o que significa que $ f_j $ é repetir $ n_j $ vezes, $ 1\leq j\leq k $.

Teorema 10.9.4.3:

Seja $ f_1,f_2,\dots,f_k $ funções não negativas ortogonais em $ L^2[a,b] $ e seja $ n_1,\dots, n_k $ inteiros positivos. Então,

$$I\left(f_1^{\otimes_{n_1}}\otimes \dots \otimes f_k^{\otimes n_k}\right)=\prod_{j=1}^{k}H_{n_j}(I(f_j);|f_j|^2),$$

no qual $ n=n_1+\dots+ n_k. $ Em particular, para qualquer função não nula $ f\in L^2[a,b] $,

$$I_n(f^{\otimes n})=H_n(I(f);|f|^2).$$

Demonstração:

Primeiramente vamos provar que

$$I_n(f^{\otimes n})=H_n(I(f);|f|^2).$$

O caso em que $ n=1 $ é óbvio. O caso para $ n=2 $ já foi provado. Assim vamos provar por indução, assumir que é válido para $ n $ e mostrar para $ n+1 $. Então, pelo Teorema 10.9.4.2 temos que

$$\displaystyle \int_{T^{n+1}}f(t_1)\dots f(t_{n+1})dB(t_1)\dots dB(t_{n+1})=(n+1)!\int_{a}^b f(t_1)X_{t_1}dB(t_1)$$

no qual, $ X_t $ é dado por

$$X_t=\int_a^t\dots \left[\int_a^{t_n}f(t_2)\dots f(t_{n+1})dB(t_{n+1})\right]\dots dB(t_2).$$

Pela Teorema 10.9.4.2 e pela indução em $ n $,

$$X_t=\displaystyle \frac{1}{n!}\int_{[a,t]^n}f(t_2)\dots f(t_{n+1})dB(t_2)\dots dB(t_{n+1})$$

$$=\frac{1}{n!}H_n\left(\displaystyle \int_a^t f(s)dB(s); \int_a^t f^2(s)ds\right).$$

Portanto, temos a seguinte igualdade

$$\displaystyle \int_{T^{n+1}}f(t_1)\dots f(t_{n+1})dB(t_1)\dots dB(t_{n+1})$$

$$=(n+1)\int_{a}^b f(t_1)H_n\left(\displaystyle \int_a^t f(s)dB(s); \int_a^t f^2(s)ds\right)dB(t_1)$$

Por outro lado, podemos aplicar a formula de Itô para $ H_{n+1}(x;\sigma) $ e obtemos que

$$dH_{n+1}\left(\displaystyle \int_a^t f(s)dB(s); \int_a^t f^2(s)ds\right)$$

$$\left(\frac{\partial}{\partial x}H_{n+1}\right)f(t)dB(t)+\frac{1}{2}\left(\frac{\partial^2}{\partial x^2}H_{n+1}\right)f^2(t)dt+\left(\frac{\partial}{\partial \sigma}H_{n+1}\right)f^2(t)dt$$

Usando as identidades do polinômino de hermite temos

$$\frac{\partial}{\partial x}H_{n+1}(x,\sigma)=(n+1)H_{n}(x,\sigma)$$

$$\frac{\partial}{\partial \sigma}H_{n+1}(x,\sigma)=-\frac{1}{2}\frac{\partial^2}{\partial x^2}H_{n+1}(x,\sigma)$$

Desta forma, obtemos

$$dH_{n+1}\left(\int_a^t f(s)dB(s),\int_a^t f^2(s)ds\right)$$

$$=(n+1)f(t)H_n\left(\int_a^t f(s)dB(s),\int_a^t f^2(s)ds\right)dB(t)$$

a qual, sobre a integração sobre $ [a,b] $, o que nos fornece a seguinte igualdade

$$H_{n+1}(I(f);|f|^2)=(n+1)\int_a^b f(t)H_n\left(\int_a^t f(s)dB(s),\int_a^t f^2(s)ds\right)dB(t)$$

O que mostra que é valido para $ n+1 $. Portanto, por indução o resultado segue para qualquer inteiro positivo $ n $ e então a equação

$$I_n(f^{\otimes n})=H_n(I(f);|f|^2)$$

é valida. Seja $ \tilde{f}=I(f) $. Para qualquer numero real $ r_1,r_2,\dots, r_k $, temos

$$e^{\sum_{i=1}^kr_i \tilde{f}_i-\frac{1}{2}\sum_{i=1}^k r_i^2|f_i|^2}=\prod_{i=1}^k e^{r_i\tilde{f}_i-\frac{1}{2}r^2_i|f_i|^2}$$

$$\displaystyle =\prod_{i=1}^k\sum_{n_i=0}^\infty \frac{r_i^{n_i}}{n_i!}H_{n_i}(\tilde{f}_i;|f_i|^2)$$

Por outro lado, temos que pela equação acima com $ t=1 $ e $ \displaystyle \sum_{i=1}^k r_i^2|f_i|^2 $,

$$e^{\sum_{i=1}^kr_i \tilde{f}_i-\frac{1}{2}\sum_{i=1}^k r_i^2|f_i|^2}=\sum_{m=0}^{\infty}\frac{1}{m!}H_m\left(\sum_{i=1}^k r_i\tilde{f}_i;\frac{1}{2}\sum_{i=1}^k r_i^2 |f_i|^2\right).$$

Então aplicando a equação

$$I_n(f^{\otimes n})=H_n(I(f);|f|^2).$$

para $ H_m $ do lado direito, temos que

$$e^{\sum_{i=1}^kr_i \tilde{f}_i-\frac{1}{2}\sum_{i=1}^k r_i^2|f_i|^2}=\sum_{m=0}^{\infty}\frac{1}{m!}\int_{T^m}\prod_{j=1}^m\left[\sum_{i=1}^k r_if_i(t_j)\right]dB(t_1)\dots dB(t_m)$$

Portanto o resultado segue comprando os coeficientes $ r_1^{n_1}r_2^{n_2}\cdots r_k^{n_k} $ no lado direito da equação.

Teorema 10.9.4.4

Seja $ n\neq m $. Então $ \mathbb{E}(I_n(f)I_m(g))=0 $ para qualquer $ f\in L^2(T^n) $ e $ g\in L^2(T^m) $.

Demonstração

É suficiente provar o teorema para $ f $ e $ g $ da seguinte forma

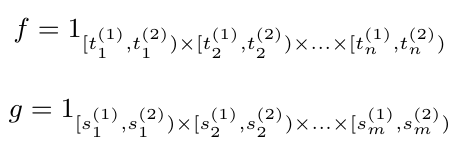
No qual, o intervalo satisfaz a seguinte condição

$$t_n^{(1)}< t_n^{(2)}\leq t_{n-1}^{(2)}\leq \cdots \leq t_2^{(1)}< t_2^{(2)}\leq t_1^{(1)}< t_1^{(2)}$$

$$s_m^{(1)}< s_m^{(2)}\leq s_{m-1}^{(2)}\leq \cdots \leq s_2^{(1)}< s_2^{(2)}\leq s_1^{(1)}< s_1^{(2)}$$

Então, $ I_n(f)I_m(g) $ é dado por

$$I_n(f)I_m(g)=\left[\prod_{i=1}^n \left(B(t_i^{(2)})-B(t_i^{(1)})\right)\right]\left[\prod_{j=1}^m \left(B(s_j^{(2)})-B(s_j^{(1)})\right)\right]$$

Agora colocando os pontos $ t $ e $ s $ juntos formando uma sequência crescente de pontos $ \tau_1< \tau_2 < \cdots< \tau_r $ com $ r\leq n+m $. Então cada fator do primeiro produto da equação acima pode ser escrito como soma de incrementos de $ B(t) $ nos $ \tau $-intervalos. Portanto, após multiplicarmos os n fatores, cada termo do primeiro produto é descrito como

$$\left(B(\tau_{i_1})-B(\tau_{i_1-1})\right)\cdots \left(B(\tau_{i_n})-B(\tau_{i_n-1})\right)$$

no qual $ \tau_{i_1}< \cdots < \tau_{i_n} $. Similarmente, cada termo do segundo produto é dado por

$$\left(B(\tau_{j_1})-B(\tau_{j_1-1})\right)\cdots \left(B(\tau_{j_m})-B(\tau_{j_m-1})\right)$$

no qual $ \tau_{j_1}< \cdots < \tau_{j_m} $.

Podemos ver que a esperança do produto é zero. Pois, $ n\neq m $ e portanto o resultado segue.

10.9.5 - Teorema de Wiener-Itô e Representação Martingale Browniana

Denotamos por $ L^2_{sym}(T^n) $ o espaço de Hilbert das funções simétricas reais quadrado integráveis de $ T^n $. Para facilitar vamos resumir os resultados mais importantes obtidos anteriormente:

1- Pelo Teorema 10.9.2.2 temos que o espaço $ L^2(\Omega) $ pode ser decomposto como soma direta ortogonais,

$$L^2(\Omega)=K_0\oplus K_1\oplus \dots \oplus K_n\oplus \cdots.$$

2- Pelo Teorema 10.9.3.2 a coleção $ (\mathcal{H}_{n_1,n_2,\dots};n_1+n_2+\dots=n) $ é uma base ortogonal para $ K_n $.

3- Pelo Teorema 10.9.4.1 $ \mathbb{E}(I_n(f)^2)=n!|f|^2 $ para qualquer $ f\in L^2_{sym}(T^n) $. Portanto a aplicação

$$\frac{1}{\sqrt{n!}}I_n:L^2_{sym}(T^n)\rightarrow L^2(\Omega)$$

é uma isometria.

4- Pelo Teorema 10.9.4.3 a integral múltipla de Wiener-Itô estão relacionadas com a integral de Wiener do polinômio de Hermite.

Teorema 10.9.5.1:

Seja $ n\geq 1 $. Se $ f\in L^2(T^n) $, então $ I_n(f)\in K_n $. Inversamente, se $ \phi \in K_n $, então existe uma única função $ f\in L^2_{sym}(T^n) $, tal que $ \phi=I_n(f) $.

Demonstração:

Seja $ f_1^{\otimes_{n_1}}\hat{\otimes}f_2^{\otimes_{n_2}}\hat{\otimes}\dots \hat{\otimes} f_k^{\otimes_{n_k}} $ a qual é a função simetrização da função $ f_1^{\otimes_{n_1}} {\otimes}f_2^{\otimes_{n_2}}{\otimes}\dots {\otimes} f_k^{\otimes_{n_k}} $ definido anteriormente. Seja $ (e_k)_{k=1}^\infty $ uma base ortogonal para $ L^2(T) $, $ T=[a,b] $. É de fato uma coleção de funções

$$\displaystyle \left(\frac{\sqrt{n!}}{\sqrt{n_1!n_2!\dots}}e^{\otimes_{n_1}}_1\hat{\otimes}e^{\otimes_{n_2}}_2\hat{\otimes} \dots ; n_1+n_2+\dots=n\right)$$

forma uma base ortogonal para $ L^2_{sym}(T^n) $.

Para provar a primeira afirmação, podemos assumir que $ f\in L^2(T^n) $ é uma função simétrica desde que $ I_n(f)=I_n(\hat{f}) $ pelo Teorema 10.9.4.1. Então, $ f $ pode ser escrita como

$$f=\displaystyle \sum_{n_1+n_2+\dots=n}a_{n_1,n_2, \dots}\frac{\sqrt{n!}}{\sqrt{n_1!n_2!\dots}}e^{\otimes_{n_1}}_1\hat{\otimes} e^{\otimes_{n_2}}_2\hat{\otimes} \dots$$

aonde o coeficiente satisfaz a condição de que

$$|f|^2=\displaystyle \sum_{n_1+n_2+\dots=n}a_{n_1,n_2, \dots}< \infty.$$

Então, usando as equação $ \mathcal{H}_{n_1,n_2,\dots} $ e o Teorema 10.9.4.3, temos que

$$I_n(f)=\displaystyle \sum_{n_1+n_2+\dots=n}a_{n_1,n_2, \dots}\frac{\sqrt{n!}}{\sqrt{n_1!n_2!\dots}}\prod_j H_{n_j}(\tilde{e}_j,1)$$

$$=\sqrt{n!}\displaystyle \sum_{n_1+n_2+\dots=n}a_{n_1,n_2, \dots} \mathcal{H}_{n_1,n_2,\dots}.$$

Portanto, pelo Teorema 10.9.3.2, temos que

$$|I_n(f)|=n!\displaystyle \sum_{n_1+n_2+\dots=n}a^2_{n_1,n_2, \dots}=n!|f|^2< \infty.$$

Segue que $ I_n(f)\in K_n $.

Inversamente, suponha que $ \phi\in K_n $. Pelo Teorema 10.9.3.2 $ \phi $ pode ser expandido como

$$\phi=\displaystyle \sum_{n_1+n_2+\dots=n}b_{n_1,n_2, \dots}\mathcal{H}_{n_1,n_2, \dots}.$$

Defina a função $ f $ em $ T^n $ por

$$f=\displaystyle \sum_{n_1+n_2+\dots=n}b_{n_1,n_2, \dots}\frac{\sqrt{n!}}{\sqrt{n_1!n_2!\dots}}e^{\otimes_{n_1}}_1\hat{\otimes} e^{\otimes_{n_2}}_2\hat{\otimes} \dots.$$

Então pelos argumentos acima temos que

$$|f|^2=\frac{1}{n!}\displaystyle \sum_{n_1+n_2+\dots=n}b_{n_1,n_2, \dots}=\frac{1}{n!}|\phi|^2< \infty.$$

Isto mostra que $ f \in L^2_{sym}(T^n) $. Além disso, podemos ver a partir dos argumentos acima temos que $ I_n(f)=\phi $. Para mostrar a unicidade, suponha que $ f,g\in L^2_{sym}(T^n) $ e $ \phi=I_n(f)=I_n(g) $. Então,

$$|f-g|=\frac{1}{\sqrt{n!}}|I_n(f-g)|=\frac{1}{\sqrt{n!}}|I_n(f)-I_n(g)|=0,$$

o que implica que $ f=g $.

Teorema 10.9.5.2 (Teorema de Wiener-Itô)

O espaço $ L^2(\Omega) $ pode ser decomposto em soma direta ortogonal

$$L^2(\Omega)=K_0\oplus K_1\oplus \dots \oplus K_n\oplus \dots ,$$

no qual, $ K_n $ consiste na integral múltipla de Wiener-Itô de ordem n. Cada função $ \phi\in L^2(\Omega) $ tem única representação como

$$\phi=\sum_{n=0}^\infty I_n(f_n), \quad \quad f_n\in L^2_{sym}(T^n),$$

e então, temos que

$$|\phi|^2=\sum_{n=0}^\infty n!|f_n|^2$$

O que nos leva a seguinte questão, $ \phi\in L^2(\Omega) $, como podemos derivar a função $ f_n,~n\geq 0 $?

Para responder essa questão, precisamos da ideia da teoria de derivada do ruido branco. Vamos explorar esse conceito de uma forma mais informal por enquanto.

Definição 10.9.5.1:

Seja $ \phi=I_n(f) $, $ f\in L^2_{sym}(T^n) $. A derivada variacional de $ \phi $ é definida como sendo

$$\frac{\delta}{\delta t}\phi=nI_{n-1}(f_n(t,\cdot)),$$

no qual, o lado direito pode ser visto como sendo 0 quando $ n=0 $. Em particular,

$$\frac{\delta}{\delta t} I(f)=f(t).$$

Suponha que $ \phi \in L^2(\Omega) $ é representado pela equação acima dada por

$$\phi=\sum_{n=0}^\infty I_n(f_n), \quad \quad f_n\in L^2_{sym}(T^n),$$

Aplicando o operador $ \frac{\delta}{\delta t} $ informalmente n vezes, temos

$$\frac{\delta^n}{\delta t_1 \delta t_2 \dots \delta t_n}\phi=n! f_n(t_1,t_2,\dots, t_n)+(n+1)!I_1(f_{n+1}(t_1,t_2,\dots, t_n,\cdot))+\cdots$$

Lembrando que $ \mathbb{E}(I_n(f))=0 $ para todo $ n\geq 1 $. Portanto, temos que tomando a esperança de ambos os lados da equação acima, obtemos o seguinte teorema.

Teorema 10.9.5.3:

Seja $ \phi \in L^2(\Omega) $. Assumindo que todas as derivadas variacionais existem e que a esperança também existe. Temos

$$f_n(t_1,t_2,\dots, t_n)=\frac{1}{n!}\mathbb{E}\left(\frac{\delta^n}{\delta t_1 \delta t_2 \dots \delta t_n}\phi\right).$$

Então, a expansão de Wiener-Itô de $ \phi $ é dada por $ \phi =\displaystyle \sum_{n=0}^\infty I_n(f_n) $.

Exemplo 10.9.5.1:

Seja $ \phi=e^{B(1)^2} $. Claro que, $ \phi \in L^2(\Omega) $. Iremos encontrar os três primeiro termos não nulos da expansão de Wiener-Itô de $ \phi $. Primeiro temos que

$$\mathbb{E}\left(e^{-B(1)^2}\right)=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^\infty e^{-x^2/2}dx=\frac{1}{\sqrt{3}}.$$

Escrevendo $ \phi $ como $ \phi=\displaystyle e^{-\left(\int_0^1 1 dB(s)\right)^2} $ e usando a equação acima obtemos

$$\frac{\delta}{\delta t_1}\phi=\phi \cdot \left(-2 \int_0^1 1 dB(s)\cdot 1\right)= -2 B(1)e^{-B(1)^2}$$

Portanto,

$$f_1(t_1)=\mathbb{E}\left[\frac{\delta}{\delta t_1}\phi\right]=0, \quad \quad \forall 0 \leq t_1 \leq 1.$$

Diferenciando mais uma vez obtemos

$$\frac{\delta^2}{\delta t_1\delta t_2}\phi=-2(1-2B(1)^2)e^{-B(1)^2},$$

A qual, tem a seguinte esperança

$$f_2(t_1,t_2)=\mathbb{E}\left[\frac{\delta^2}{\delta t_1 \delta t_2}\phi\right]=-\frac{2}{3\sqrt{3}}$$

As próximas duas derivadas variacionais de $ \phi $ são dadas por

$$\frac{\delta^3}{\delta t_1\delta t_2\delta t_3}\phi=4(3B(1)-2B(1)^3)e^{-B(1)^2}$$

$$\frac{\delta^4}{\delta t_1\delta t_2\delta t_3\delta t_4}\phi=4(3-12B(1)^2+4B(1)^4)e^{-B(1)^2}$$

Claro que, $ f_3=0 $. Pelo calculo direto, temos que

$$f(t_1,t_2,t_3,t_4)=\mathbb{E}\left(\frac{\delta^4}{\delta t_1\delta t_2\delta t_3\delta t_4}\phi\right)=\frac{4}{3\sqrt{3}}.$$

Então, temos que os três primeiro termos não negativos da expansão de Wiener-Itô temos que

$$e^{-B(1)^2}=\frac{1}{\sqrt{3}}-\frac{2}{3\sqrt{3}}I_2(1)+ \frac{4}{3\sqrt{3}}I_4(1)+\cdots.$$

Representação Martingale Browniana

Seja $ B(t) $ o movimento Browniano e seja $ T=[a,b] $ um intervalo fixado. Suponha que $ f(t) $ seja um processo estocástico em $ L^2_{ad}([a,b]\times \Omega) $. Então, pelo Teorema 10.2.5 e Teorema 10.2.6, o processo estocástico $ X_t=\displaystyle \int_a^t f(s)dB(s) $ para todo $ t\in [a,b] $. Além do mais, pelo Teorema 10.2.3 temos que $ \mathbb{E}(X^2_t)=\int_a^t \mathbb{E}(f^2(s))dt< \infty $ para $ t\in [a,b] $.

Seja $ n\geq 1 $ e considere a integral múltipla de Wiener-Itô

$$X=\int_{T^n} f(t_1,t_2,\dots, t_n)dB(t_1)dB(t_2)\dots dB(t_n)$$

no qual $ f\in L^2_{sym}(T^n) $. Pelo Teorema 10.9.4.2, X pode ser reescrito como

$$X=n!\int_a^b \int_a^{t_1}\dots \left[\int_a^{t_{n-1}}f(t_1,t_2,\dots, t_n)dB(t_n)\right]\dots dB(t_2)dB(t_1).$$

Definimos o processo estocástico $ \theta(t) $ por

$$\theta(t)=n!\int_a^t\dots \left[\int_a^{t_{n-1}}f(t_1,t_2,\dots, t_n)dB(t_n)\right]\dots dB(t_2), \quad \quad a\leq t\leq b.$$

Então, podemos escrever X como uma integral estocástica

$$X=\int_a^b \theta(t)dB(t).$$

Note que o processo estocástico $ \theta(t) $ é adaptado com respeito a filtragem $ (\mathcal{F_t}) $. Além disso, podemos usar novamente Teorema 10.9.4.2 para reescrever $ \theta(t) $ como uma integral múltipla de Wiener-Itô

$$\theta(t)=n(n-1)!\int_a^t\dots \left[\int_a^{t_{n-1}}f(t_1,t_2,\dots, t_n)dB(t_n)\right]\dots dB(t_2)$$

$$=n\int_{[a,t]^{n-1}} f(t_1,t_2,\dots, t_n)dB(t_2)\dots dB(t_n).$$

Então, aplicando o teorema 9.6.6 para obter

$$\mathbb{E}(\theta(t)^2)=n^2(n-1)!\int_{[a,t]^{n-1}}f(t,t_2,\dots,t_n)^2dt_2\dots dt_n$$

$$\leq n n! \int_{[a,b]^{n-1}}f(t,t_2,\dots,t_n)^2dt_2\dots dt_n,$$

o que implica que

$$\int_a^b \mathbb{E}(\theta(t)^2)dt\leq n n! \int_{[a,b]^n}f(t_1,t_2,\dots,t_n)^2dt_1dt_2\dots dt_n=n\mathbb{E}(X^2)< \infty.$$

Então, para $ \theta \in L^2_{ad}([a,b]\times \Omega) $ e a integral estocástica

$$X=\int_a^b \theta(t)dB(t).$$

é uma integral de Itô.

Com isso obtemos o seguinte Teorema

Teorema 10.9.5.4:

Seja $ X\in L^2(\Omega) $ e $ \mathbb{E}(X)=0 $. Então, existe uma processo estocástico $ \theta \in L^2([a,b]\times \Omega) $ tal que

$$X=\int_a^b \theta(t)dB(t).$$

Demonstração:

Pelo Teorema de Wiener-Itô, X tem uma expansão $ X=\displaystyle \sum_{n=0}^{\infty} I_n(f_n) $ com $ f_n\in L^2_{sym}(T^n) $. Mas $ f_0=\mathbb{E}(X)=0 $. Portanto, temos que

$$X=\displaystyle \sum_{n=1}^\infty I_n(f_n), \quad \quad |X|^2=\displaystyle \sum_{n=1}^\infty n!|f_n|^2.$$

Para cada $ n\geq 1 $, definimos um processo estocástico

$$\theta_n(t)=n! \int_a^t \cdots \left[\int_a^{t_{n-1}}f_n(t,t_2,\dots,t_n)dB(t_n)\right]\dots dB(t_2).$$

Pela equação acima , podemos reescrever $ \theta_n(t) $ como integrais múltiplas de Wiener-Itô

$$\theta_n(t)=n\displaystyle \int_{[a,t]^{n-1}}f_n(t,t_2,\dots,t_n)dB(t_2)\dots dB(t_n).$$

Portanto pelo Teorema 10.9.4.4, os $ \theta_n $’s são ortogonais. Definimos

$$S_n(t)=\displaystyle \sum_{k=1}^n \theta_k(t), \quad a \leq t \leq b. $$

Note que para $ I_n(f_n)=\displaystyle \int_a^b\theta_n(t) dB(t) $. Portanto, $ \mathbb{E}(I_n(f_n)^2)=\displaystyle \int_a^b\mathbb{E}(\theta_n(t)^2)dt $. Então, para qualquer $ n> m, $

$$\displaystyle \int_a^b\mathbb{E}(|S_n(t)-S_m(t)|^2)dt=\displaystyle \sum_{k=m+1}^n \int_a^b \mathbb{E}(\theta_k(t)^2)dt=\sum_{k=m+1}^n \mathbb{E}(I_k(f_k)^2)$$

o qual converge para $ 0 $ quando $ n> m \rightarrow \infty $. E isto mostra que $ \theta=\displaystyle \lim_{n\rightarrow \infty} S_n $ existe um espaço $ L^2_{ad}([a,b]\times \Omega) $. Então por

$$X=\sum_{n=1}^\infty \int_a^b \theta_n(t)dB(t)$$

temos que

$$X=\displaystyle \lim_{n\rightarrow \infty} \sum_{k=1}^n \int_a^b \theta_k(t)d B(t)=\lim_{n\rightarrow \infty}\int_a^b S_n(t)dB(t)=\int_a^b \theta(t)dB(t).$$

O que completa o teorema.

Teorema 10.9.5.5 (Teorema de Representação Martingale) :

Seja $ M_t $, $ a\leq t \leq b $, um martingale quadrado integrável com respeito $ ( \mathcal{F_t}, a\leq t\leq b ) $ e $ M_a=0 $. Então, $ M_t $ tem uma versão continua $ \tilde{M}(t) $ dado por

$$\tilde{M}(t)=\displaystyle \int_a^t \theta(s)dB(s), \quad \quad a\leq t\leq b,$$

no qual $ \theta \in L^2_{ad}([a,b]\times \Omega) $.

Demonstração:

Pela hipótese $ M_b\in L^2_B(\Omega) $ e $ \mathbb{E}(M_b)=\mathbb{E}(M_b)=0 $. Portanto, podemos aplicar o Teorema 10.9.5.4 para uma variável aleatória $ M_b $ para obtermos o processo estocástico $ \theta(t)\in L^2_{ad}([a,b]\times \Omega) $ tal que

$$M_b=\int_a^b \theta(s)dB(s)$$

Definimos um processo estocástico $ \tilde{M}(t) $ por

$$\tilde{M}(t)=\displaystyle \int_a^t \theta(s)dB(s), \quad \quad a\leq t\leq b.$$

Pelo Teorema 10.2.5 e Teorema 10.2.6, $ \tilde{M}(t) $ é um martingale contínuo com respeito a filtragem $ (\mathcal{F_t}) $. Além disso, para cada $ t\in [a,b] $,

$$M_t=\mathbb{E}\left(M_b\bigg| \mathcal{F_t}\right)=\mathbb{E}\left(\tilde{M}_b\bigg| \mathcal{F_t}\right)=\tilde{M}(t)\quad \quad a.s.$$

Portanto $ \tilde{M}(t) $ é uma versão de $ M_t $ e o resultado segue.

Referências

[1] Ross, Sheldon M. Applied probability models with optimization applications. Courier Dover Publications, 1970.

[2] Bhat, U. Narayan, and Gregory K. Miller. Elements of applied stochastic processes. J. Wiley, 1972.

[3] Shiryaev, Albert N. “Probability, volume 95 of Graduate texts in mathematics.” (1996).

[4] Protter, Philip. Stochastic Integration and Differential Equations: Version 2.1. Vol. 21. Springer Verlag, 2004.

[5] Brémaud, Pierre. Point processes and queues: Martingale dynamics. Springer, 1981.

[6] Stout, William F. Almost sure convergence. Vol. 154. New York: Academic press, 1974.

[7] Fleming, Thomas R., and David P. Harrington. Counting processes and survival analysis. Vol. 169. Wiley, 2011.

[8] Chung, Kai Lai, et al. Markov chains with stationary transition. New York: Springer, 1960.

[9] Doob, Joseph L., and Joseph L. Doob. Stochastic processes. Vol. 7. No. 2. New York: Wiley, 1953.

[11] Engle, Robert F., and Jeffrey R. Russell. “Autoregressive conditional duration: a new model for irregularly spaced transaction data.” Econometrica (1998): 1127-1162.

[12] Brezis, Haim. Functional analysis, Sobolev spaces and partial differential equations. Springer, 2010.

[13] Nelson, Edward, et al. Dynamical theories of Brownian motion. Vol. 10. Princeton: Princeton university press, 1967.

[14] Karatzas, Ioannis. Brownian motion and stochastic calculus. Ed. Steven Eugene Shreve. Vol. 113. Springer, 1991.

[15] He, Sheng-wu, Chia-kang Wang, and Jia-an Yan. Semimartingale theory and stochastic calculus. Science Press and CRC Press Inc, 1992.

[16] Inge S Helland. Central limit theorems for martingales with discrete or continuous time. Scandinavian Journal of Statistics, pages 79–94, 1982.

[17] DL McLeish. Dependent central limit theorems and invariance principles. the Annals of Probability, pages 620–628, 1974.

[18] Ferrari, P. A., and A. Galves. “Acoplamento e Processos Estocasticos. 21 Coloquio Brasileiro de Matematica IMPA.” 1997.

[19] Applebaum, David. Lévy processes and stochastic calculus. Cambridge university press, 2009.

[20] Rudin, Walter. Principles of mathematical analysis. Vol. 3. New York: McGraw-Hill, 1964.

[21] Itô, Kiyosi. “Stochastic integral.” Proceedings of the Imperial Academy 20.8 (1944): 519-524.

[22] Halmos, P. R. Measure Theory, (1950), Springer Verlag.