20. Séries Temporais
1 - Introdução
Uma série temporal é um conjunto de observações ordenadas no tempo. Alguns exemplos de séries temporais são:
- valores diários de poluição em uma cidade;
- valores mensais de temperatura registrados em uma cidade;
- índices diários da Bolsa de Valores de São Paulo;
- acidentes ocorridos nas rodovias da cidade de São Paulo durante um mês.
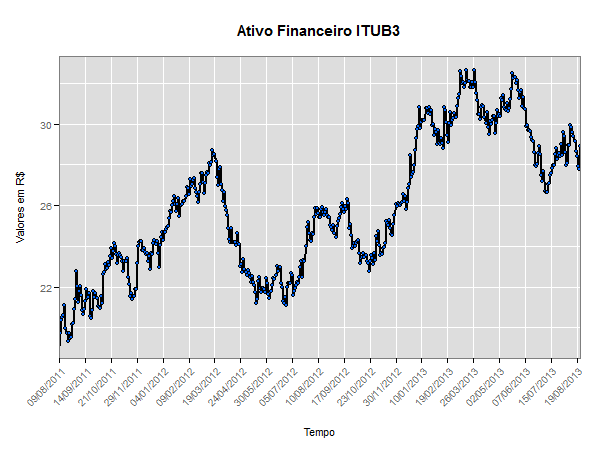
Os modelos utilizados para descrever séries temporais são processos estocásticos, isto é, processos controlados por leis probabilísticas.
Temos na literatura um número muito grande de modelos diferentes para descrever o comportamento de uma série particular. A construção destes modelos depende de vários fatores, tais como o comportamento do fenômeno ou o conhecimento a priori que temos de sua natureza e do objetivo da análise.
1.1 - Estacionariedade
Uma série temporal é dita estacionária quando ela se desenvolve no tempo aleatoriamente ao redor de uma média constante, refletindo alguma forma de equilíbrio estável. Na prática, a maioria das séries que encontramos apresentam algum tipo de não estacionariedade, por exemplo, tendência.
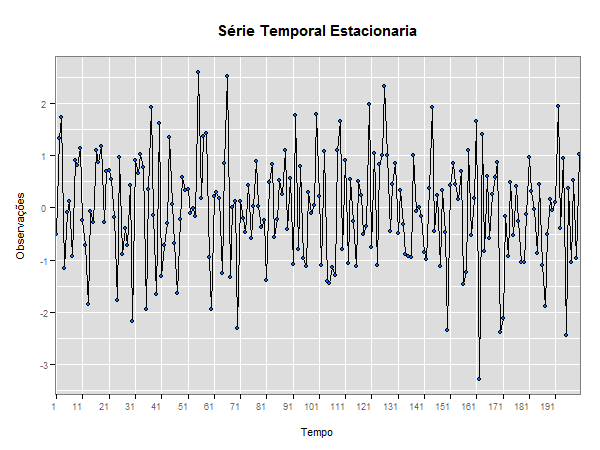
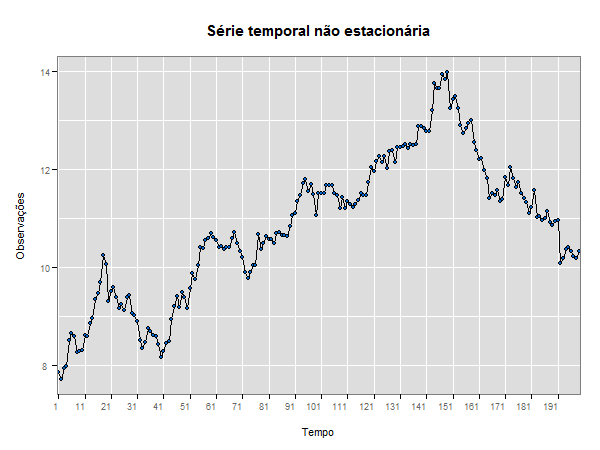
Uma série pode ser estacionária por períodos curtos ou longos, o que implica uma mudança de nível e/ou inclinação. A classe dos modelos ARIMA será capaz de descrever de maneira satisfatória séries estacionárias e séries não estacionárias que não apresentem um comportamento explosivo. Este tipo de não estacionariedade é chamado homogêneo, quando a série pode ser estacionária, flutuando ao redor de um nível, por um certo tempo, depois mudar de nível e flutuar ao redor de um novo nível e assim por diante, ou então mudar de inclinação.
A maioria dos procedimentos de análise estatística de séries temporais supõe que estas sejam estacionárias, portanto, será necessário transformar os dados originais se estes não formam uma série estacionária. A transformação mais comum consiste em tomar diferenças sucessivas da série original, até se obter uma série estacionária. A primeira diferença Z(t) é definida por
$$\Delta Z(t) = Z(t) - Z(t - 1)$$
então, a segunda diferença é
$$\Delta^2 Z(t) = \Delta[\Delta Z(t)] = \Delta[Z(t) - Z(t - 1)]$$
$$\Delta^2 Z(t) = Z(t) - 2Z(t - 1) + Z(t - 2)$$
De modo geral, a n-ésima diferença de Z(t) é
$$\Delta^n Z(t) = \Delta[\Delta^{n-1} Z(t)]$$
Normalmente, será suficiente tomar uma ou duas diferenças para que a série se torne estacionária.
1.2 - Processos Estocásticos
Definição 1.2.1
Seja $ T $ um conjunto arbitrário. Um processo estocástico é uma família $ Z = (Z(t), t \in T) $, tal que, para cada $ t \in T $, Z(t) é uma variável aleatória.
Nestas condições, um processo estocástico é uma família de variáveis aleatórias, que supomos definidas num mesmo espaço de probabilidades (Ω, A, P). O conjunto $ T $ é normalmente tomado como o conjunto dos inteiros $ Z $ = {±1, ±2, ±3,…}.
Para dizermos que um processo estocástico está especificado necessitamos de certas condições. Sejam $ t_1 $, $ t_2 $,…, $ t_n $ elementos quaisquer de $ T $ e consideremos
$$F(z_1, \dots,z_n;t_1, \dots ,t_n) = P[Z(t_1) \le z_1, \dots ,Z(t_n) \le z_n]$$
Então, o processo estocástico $ Z = (Z(t), t \in T) $ estará especificado se conhecermos as distribuições finito-dimensionais, para todo n ≥ 1. As funções de distribuição devem satisfazer as duas condições seguintes:
- (Condição de Simetria) para qualquer $ j_1 $,…,$ j_n $, dos índices 1,2,…,n temos:
$$F(z_{j_n}, \dots ,z_{j_1};t_1, \dots ,t_n) = F(z_1, \dots ,z_n;t_1, \dots ,t_n)$$
- (Condição de Compatibilidade) para m < n,
$$F(z_1, \dots ,z_m,+ \infty , \dots ,- \infty ;t_1, \dots ,t_m,t_{m+1}, \dots ,t_n) = F(z_1, \dots ,z_m;t_1, \dots ,t_m)$$
Exemplo 1.2.1
Consideramos {$ X_n $, n = 1,2,…} uma sequência de v.a. definidas no mesmo espaço amostral Ω. Aqui, $ T $ = {1,2,…} e temos um processo com parâmetro discreto, ou uma sequência aleatória. Para todo n ≥ 1, podemos escrever
$$P[X_1 = a_1, \dots , X_n = a_n] = P[X_1 = a_1]P[X_2 = a_2|X_1 = a_1] \times \dots \times$$
$$P[X_n = a_n|X_1 = a_1, \dots, X_{n-1} = a_{n-1}].$$
Aqui, os $ a_j $’s representam os estados do processo e o espaço dos estados pode ser tomado como o conjunto dos reais. O caso mais simples é aquele em que temos uma sequência {$ X_n $, n ≥ 1} de v.a. mutuamente independentes e neste caso temos
$$P[X_1 = a_1, \dots , X_n = a_n] = P[X_1 = a_1] \dots P[X_n = a_n].$$
Este exemplo é conhecido como Sequência Aleatória.
Exemplo 1.2.2
Considere uma sequência aleatória $ {\varepsilon_t \ge 1} $ com v.a. i.i.d. $ (\mu_{\varepsilon} , \sigma^2_{\varepsilon}) $. Defina a sequência
$$X_t = \varepsilon_1 + \dots + \varepsilon_t.$$
Segue-se que $ E(X_t) = t\mu_{\varepsilon} $ e $ Var(X_t) = t\sigma_{\varepsilon} $, ou seja, ambas dependem de t.
Esse exemplo é conhecido como Passeio Aleatório, e têm grande importância em econometria e finanças.
1.3 - Processos Estácionarios
Dizemos que um processo é estacionário se todas as características do comportamento do processo não são alterados no tempo, ou seja, o processo se desenvolve no tempo em torno da média, de modo que a escolha de uma origem dos tempos não é importante.
Definição 1.3.1
Um processo estocástico $ Z = (Z(t), t \in T) $ diz-se estritamente estacionário se todas as distribuições finito-dimensionais permanecem as mesmas sob translações no tempo, ou seja,
$ F(z_1, \dots , z_n;t_1 + \tau , \dots , t_n + \tau) = F(z_1, \dots , z_n;t_1, \dots , t_n), $ para quaisquer $ t_1, \dots , t_{n +\tau} $ de $ T $.
Em particular, se um processo é estritamente estacionário significa que todas as distribuições unidimensionais são invariantes sob translações do tempo, logo a média $ \mu (t) $ e variância $ V(t) $ são constantes, isto é,
$ \mu (t) = \mu, \hspace{0.3cm} V(t) = \sigma^2, $ para todo $ t \in T $.
Definição 1.3.2
Dizemos que um processo estocástico $ Z(t) = (Z(t), t \in T) $ é fracamente estacionário ou estacionário de segunda ordem se e somente se
(i) $ E[Z(t)] = \mu (t) = \mu $, constante, para todo $ t \in T $;
(ii) $ E[Z^2(t)] < \infty $, para todo $ t \in T $;
(iii) $ \gamma (t_1,t_2) = Cov[Z(t_1), Z(t_2)] $ é uma função de $ |t_1 - t_2| $.
Denominaremos simplesmente por processo estacionário quando o processo for fracamente estacionário. Iremos tratar de modelos que são apropriados para os processos estacionários homogêneos, isto é, processos cujo nível e/ou inclinação mudam com o decorrer do tempo. Tais processos podem tornar-se estacionários por meio de diferenças sucessivas.
Definição 1.3.3
Um processo estocástico $ Z = (Z(t), t \in T) $ diz-se Gaussiano (ou normal) se para qualquer conjunto $ t_1 $,$ t_2 $,…,$ t_n $ de $ T $, as v.a. Z($ t_1 $),…,Z($ t_n $) tem distribuição normal n-variada.
Se um processo for Gaussiano (ou normal) ele será determinado pelas médias e covariâncias; em particular, se ele for estacionário de segunda ordem, ele será estritamente estacionário.
Função de Autocovariância
Seja $ (X_t, t \in Z) $ um processo estacionário real discreto de média zero, sua função de autocovariância (f.a.c.v.) é definida por $ \gamma_{\tau} = E[X_tX_{t + \tau}] $.
Proposição 1.3.1
A facv $ \gamma_{\tau} $ deve satisfazer as seguintes propriedades:
(i) $ \gamma_0 > 0 $;
(ii) $ \gamma_{-\tau} = \gamma_{\tau} $;
(iii) $ |\gamma_{\tau}| \le \gamma_o $;
(iv) $ \gamma_{\tau} $ é não negativa definida, tal que $ \sum^{n}_{j = 1} \sum^{n}_{k = 1}a_ja_k\gamma_{\tau_j - \tau_k} \ge 0, $
para quaisquer números reais $ a_1, \dots , a_n, $ e $ \tau_1, \dots , \tau_n $ de $ Z $.
Prova
(i) e (ii) decorrem imediatamente da definição de $ \gamma_{\tau} $.
(iii) Basta notarmos que
$$E[X_{t + \tau} \pm X_t]^2 = E[X^2_{t + \tau} \pm 2X_{t + \tau}X_t + X^2_t] \ge 0$$
mas, sabemos que
$$X^2_{t + \tau} \pm 2X_{t + \tau}X_t + X^2_t = \gamma^2 \pm 2\gamma_{\tau} + \sigma^2 \ge 0$$
ou seja,
$$2\gamma_0 \pm 2\gamma_{\tau} \ge 0 \Longrightarrow |\gamma_{\tau}| \le \gamma_0$$
.
(iv) Temos que
$$\sum_{j = 1}^{n} \sum_{k = 1}^{n} a_ja_k\gamma_{\tau_j - \tau_k} = \sum_{j = 1}^{n} \sum_{k = 1}^{n} a_ja_kE[X_{\tau_j}X_{\tau_k}] = E[\sum_{j = 1}^{n} a_jX_{\tau_j}]^2 \ge 0$$
Note que a facv de um processo estacionário tende a zero quando $ |\tau| \rightarrow 0. $
Função de Autocorrelação
A função de autocorrelação do processo é definida por
$$\rho_{\tau} = \dfrac{\gamma_{\tau}}{\gamma_0}, \tau \in Z$$
e possui as mesmas propriedades da função de autocovariância $ \gamma_{\tau} $, exceto que agora temos $ \rho_0 = 1 $.
A função de autocorrelação é utilizada para identificarmos um modelo adequado para a série temporal.
Exemplo 1.3.1
Voltando ao Exemplo 1.2.1, temos uma sequência aleatória. Se as v.a.$ X_1 $,$ X_2 $, … tiverem todas a mesma distribuição, teremos então uma sequência de v.a. independentes e identicamente distribuídas. Neste caso, o processo $ X_n $ é estacionário. Se $ E[X_n] = \mu $ e $ Var[X_n] = \sigma^2 $, para todo $ n \ge 1 $, então temos
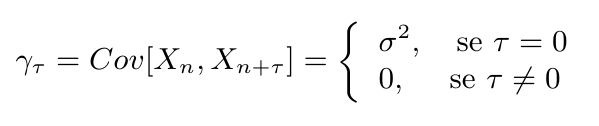
Portanto, segue que $ \rho_{\tau} = 1 $, para $ \tau = 0 $ e $ \rho_{\tau} = 0 $, caso contrário.
Exemplo 1.3.2
Dando continuidade ao Exemplo 1.2.2 temos um Passeio Aleatório. Então, temos que $ E[X_t] = t\mu_{\varepsilon} $ e $ Var[X_t] = t\sigma^2_{\varepsilon} $. Podemos notar que se trata de um processo não estacionário, pois a média e a variância dependem de t. Calculando a função de autocovariância temos
$$Cov[X_t, X_{t - k}] = Cov[\varepsilon_1 + \dots + \varepsilon_{t-k} + \dots + \varepsilon_t , \varepsilon_1 + \dots + \varepsilon_{k-t}] = (t - k)\sigma_{\varepsilon}^2$$
assim, a função de autocorrelação fica
$$\rho_t = \dfrac{t - k}{t}.$$
Operador de Retardo
Considere um processo MA(q), podemos expressa-lo utilizando um operador de retardo, denotado por B, definido por
$$B^jX_t = X_{t-j}$$
Então, podemos reescrever
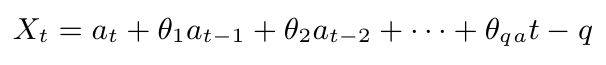
$$X_t = (1 + \theta_1B + \theta_2B^2 + \cdots + \theta_qB^q)a_t = \theta(B)a_t$$
onde $ \theta(B) $ é um polinômio de ordem q em B. Dizemos que um processo MA(q) é inversível se as raízes da equação
$$\theta (B) = 1 + \theta_1B + \theta_2B^2 + \cdots + \theta_qB^q = 0$$
estiverem fora do círculo unitário, ou seja, dado $ b_1, \dots, b_q $ soluções de $ \theta(B) = 0 $ então o processo será inversível se $ |b_j| > 1, j = 1,\dots,q $, dizemos então que o processo é estacionário.
No caso de um processo AR(p)
$$X_t = \phi_0 + \phi_1X_{t-1} + \phi_pX_{t-p} + a_t$$
Utilizando o resultado de que um processo AR(p) pode ser escrito como um processo MA infinito com coeficientes $ \omega_0 , \omega_1, \dots $, ou seja
$$X_t = \omega_0a_t + \omega_1a_{t-1} + \cdots = (\omega_0 + \omega_1B + \omega_2B^2 + \cdots)a_t = \omega(B)a_t$$
segue que um processo AR(p) será estacionário se $ \sum_j \omega_j^2 < \infty $. Os $ \omega_j $ podem ser determinados por
$$\omega_0 = 1$$
$$\omega_1 = \omega_0\phi_1$$
$$\omega_2 = \omega_1\phi_1 + \omega_0\phi_2$$
$$ \quad \vdots $$
$$\omega_i = \sum_{j=1}^i \omega_{i-j}\phi_j$$
Em um modelo misto ARMA(p,q), utilizando o operador de retardo, podemos escrever
$$X_t = \phi_1X_{t-1} + \cdots \phi_pX_{t-p} + a_t + \theta_1a_{t-1} + \cdots + \theta_qa_{t-q}$$
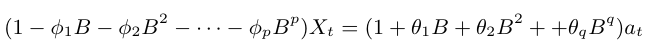
ou seja,
$$\phi(B)X_t = \theta(B)a_t$$
Os valores de $ \phi_1, \dots, \phi_p $ que tornam o processo estacionário são tais que as raízes de $ \phi(B) = 0 $ estão fora do círculo unitário. Analogamente, os valores de $ \theta_1, \dots, \theta_q $ que tornam o processo inversível são tais que as raízes de $ \theta(B) = 0 $ estão fora do círculo unitário.
Exemplo 1.3.3
Considere um processo ARMA(1,1) dado por $ X_t = 0,7X_{t-1} + a_t + 0,6a_{t-1} $. Vamos analisar se este processo é estacionário e inversível.
Escrevendo em forma dos operadores de retardo temos
$$(1 - 0,7B)X_t = (1 + 0,6B^*)a_t$$
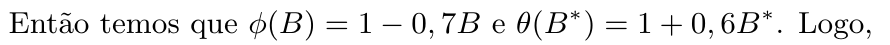
$$(1 - 0,7B) = 0 \quad \Longleftrightarrow \quad B = \dfrac{1}{0,7} = 1,43$$

Concluímos que o processo é estacionário e inversível.
1.4 - Testes de Estacionariedade
Grande parte dos recursos para séries temporais foram elaborados utilizando o conceito de estacionariedade nas séries. Uma forma geral para analisar este fato é fazendo um estudo da existência de alguma raiz dos operadores de retardos dentro do círculo unitário, denominada simplesmente por raiz unitária.
Portanto, utilizamos testes de hipóteses que em geral, possui as seguintes hipóteses:
$$H_0=\text{Existe pelo menos uma raiz dentro do círculo unitário}$$
$$H_1=\text{Não existem raízes dentro do círculo unitário}$$
Apresentamos a seguir três testes de raiz unitária, cada um com suas particularidades. Em um contexto geral, o ideal é aplicar os testes em conjunto para ter a certeza da estacionariedade da série.
1.4.1 - Teste de Dickey-Fuller Aumentado
O teste de Dickey-Fuller Aumentado é conhecido na literatura como teste ADF(Augmented Dickey-Fuller) e requer o estudo sobre a seguinte regressão:
$$\Delta y_t = \beta_1 + \beta_2t + \delta y_{t-1} + \sum^m_{i=1}\alpha_i \Delta y_{t-i} + \varepsilon_t$$
onde $ \beta_1 $ é o intercepto, também denominado como drift da série; $ \beta_2 $ é o coeficiente de tendência; $ \delta $ é o coeficiente de presença de raiz unitária e m é o número de defasagens tomadas na série.
Neste caso a hipótese nula é dada por $H_0: \delta = 0$
Fazemos uma regressão de $ \Delta y_t $ em $ y_{t-1}, \Delta y_{t-1}, \dots, \Delta y_{t+p-1} $ e calculamos a estatística T dada por
$$T = \dfrac{\hat{\delta}}{se(\hat{\delta})}$$
onde $ \hat{\delta} $ é um estimador para $ \delta $ e, $ se(\hat{\delta}) $ é um estimador para desvio padrão do erro de $ \delta $.
Os valores críticos da estatística $ T $ foram tabelados por Dickey e Fuller através de simulação Monte Carlo e variam nos casos de presença somente de intercepto, presença somente de tendência e presença de ambos.
1.4.2 - Teste de Phillips - Perron
O teste de Phillips - Perron, conhecido na literatura como teste PP é uma generalização do teste de Dickley - Fuller para os casos em que os erros $ (\varepsilon_t)_{t \in \mathbb{Z}} $ são correlacionados e, possivelmente, heterocedásticos. Então, vamos estudar a seguinte regressão
$$\Delta y_t = \beta_1 + \beta_2t + \delta y_{t-1} + \sum^m_{i=1}\alpha_i \Delta y_{t-i} + \varepsilon_t$$
Neste caso, a estatística $ Z $ é calculada por
$$Z = n \hat{\delta_n} - \dfrac{n^2\hat{\sigma}^2}{2s^2_n}\Bigg( \hat{\lambda_n}^2 - \hat{\gamma_{0,n}} \Bigg)$$
onde
$$\hat{\gamma_{j,n}} = \dfrac{1}{n} \sum^n_{i=1+j} r_ir_{i-j}$$
$$\hat{\lambda_n}^2 = \hat{\gamma_{0,n}} + 2\sum^q_{j = 1}\Bigg(1 - \dfrac{j}{q+1}\Bigg) \hat{\gamma}_{j,n}$$
$$s^2_n = \dfrac{1}{n-k} \sum^n_{i = 1} r_i^2$$
em que $ r_i $ representa o resíduo em $ y_i $ utilizando estimadores de mínimos quadrados, k é o número de covariáveis na regressão e, q é o número de defasagens utilizadas para calcular $ \hat{\lambda}^2_n $.
Note que $ Z $ trata-se de um ajuste na estatística de Dickley - Fuller. Caso o processo seja não correlacionado temos covariâncias nulas e neste caso, $ \hat{\lambda}^2_n = \hat{\gamma}_{0,n} $. Se o processo não for heterocedástico temos que $ se(\delta) = 1/n $ e então $ Z $ é dada por
$$Z = n\hat{\delta}= \dfrac{\hat{\delta}}{se(\hat{\delta})}$$
isto é, $ Z $ é a estatística de Dickley - Fuller e portanto, tem a mesma distribuição da estatística do teste ADF, calculada por Dickley - Fuller através de simulação de Monte Carlo.
1.4.3 - Teste KPSS
Teste criado por Denis Kwiatkowski , Peter C. B. Phillips, Peter Schmidt e Yongcheol Shin, denominado teste KPSS devido a seus nomes, tem por finalidade determinar estacionariedade em uma série temporal.
As hipóteses do teste são
$ H_0 = $ “A série é estacionária”
$ H_1 = $ “A série apresenta raiz unitária”
Note que as hipóteses deste teste não são iguais aos testes de Dickley - Fuller e Phillips - Perron para estacionariedade. A hipótese nula deste teste é igual às hipóteses alternativas nos testes anteriores.
Seja $ X_t, t = 1,2,\dots,N $ as observações de uma série temporal a qual queremos testar sua estacionariedade. Suponha que podemos decompor a série em componentes de tendência, passeio aleatório e erro
$$X_t = \xi t + r_t + \varepsilon_t$$
onde $ r_t $ é o passeio aleatório
$$r_t = r_{t-1} + \mu_t$$
com $ \mu_t $ i.i.d com média zero e variância $ \sigma_{\mu}^2 $.
Considere agora, $ e_t $, t = 1,2, … , N os resíduos de uma regressão em y explicado pelas componentes de tendência, passeio aleatório e intercepto. Denominamos $ \hat{\sigma_{\varepsilon}}^2 $ um estimador para a variância dos erros nesta regressão, isto é, $ \hat{\sigma_{\varepsilon}}^2 = \dfrac{SQE}{N} $. Definimos a soma parcial dos resíduos por
$$S_t = \sum^t_{i = 1} e_t, \quad t = 1, 2, \dots, T$$
então, a estatística do teste é dada por
$$LM = \sum^N_{t = 1} \dfrac{S_t^2}{N^2 \hat{\sigma}_{\varepsilon}^2}$$
É possível mostrar que a estatística $ LM $ tem distribuição que converge assintoticamente para um Movimento Browniano em que seus valores críticos são tabelados.
Para mais detalhes acesse o artigo de Kwiatkowski, Phillips, Schmidt e Shin no Journal of Econometrics em 1992.
1.5 - Modelos Para Séries Temporais
Estudaremos modelos paramétricos para séries temporais, ou seja, modelos que o número de parâmetros é finito.
Nestes modelos a análise é feita no domínio do tempo. Os mais frequentemente usados são os modelos de erro ( ou de regressão), os modelos autorregressivos e de médias móveis(ARMA) e os modelos autorregressivos integrados e de médias móveis(ARIMA).
Modelos de erro ou de regressão
Podemos escrever uma série temporal observada na seguinte forma
$ Z_t = f(t) + a_t, \quad t = 1, 2, \dots , N, $ onde $ f(t) $ é chamada sinal e $ a_t $ ruído.
Neste modelo o sinal $ f(t) $ é uma função do tempo completamente determinada e $ a_t $ é uma sequência aleatória, independente de $ f(t) $. Supõe-se que as v.a. $ a_t $ sejam não correlacionadas, tenham média zero e variância constante, isto é,
$$E[a_t] = 0, \forall t, \quad E[a^2_t] = \sigma^2_a, \forall t, \quad E[a_ta_s] = 0, s\neq t.$$
A série $ a_t $ com as características acima é conhecida como ruído branco.
Modelos ARMA
Para descrever o comportamento de séries econômicas e sociais, onde os erros observados são autocorrelacionados utilizamos modelos ARMA. Estes modelos são úteis nestes casos, uma vez que o fato de serem autocorrelacionados influencia na evolução do processo.
Há três casos particulares de modelos ARIMA que estudaremos:
- processo autorregressivo de ordem p: AR(p);
- processo de médias móveis de ordem q: MA(q)
- processo autorregressivo e de médias móveis de ordens p e q: ARMA(p,q).
Podemos generalizar estes processos de maneira adequada pelos chamados modelos autorregressivo integrados e de médias móveis de ordem p, d e q: ARIMA(p,d,q), em que d representa a inclusão de um operador sazonal.
Note que podemos descrever os três processos através do ARIMA. Por exemplo, um processo autorregressivo de ordem p, AR(p), pode ser escrito como ARIMA(p,0,0).
2 - Tendência e Sazonalidade
Na tentativa de descrever o comportamento de uma série temporal, utilizamos a decomposição da série original em três séries temporais, tendência, sazonalidade e uma componente aleatória, conhecida também como nível.
Seja {$ Z_t $, t = 1, … ,N} as observações de uma série temporal. Podemos decompor $ Z_t $ em duas formas.
Modelo aditivo
$$Z_t = T_t + S_t + a_t.$$
Modelo multiplicativo
$$Z_t = T_t \ast S_t \ast a_t,$$
onde $ T_t $ e $ S_t $representam a tendência e sazonalidade, respectivamente, enquanto $ a_t $ é uma componente aleatória, de média zero e variância $ \sigma_a^2 $.
O principal objetivo será estimar $ S_t $ e $ T_t $ e construir uma série livre de sazonalidade ou sazonalmente ajustada e sem tendência. Estimando-se $ S_t $ e $ T_t $ e subtraindo de $ Z_t $ obteremos uma estimativa da componente aleatória $ a_t $.
Em geral, as componentes $ T_t $ e $ S_t $ são bastante relacionadas e a influência da tendência sobre a componente sazonal pode ser muito forte.
2.1 - Tendências
Suponha inicialmente que a componente sazonal não esteja presente, então consideraremos o seguinte modelo
$$Z_t = T_t + a_t$$
onde $ a_t $ é uma variável aleatória com média zero e variância $ \sigma^2_a $. Alguns dos métodos mais utilizados para estimar $ T_t $ consistem em:
(i) ajustar uma função do tempo, como um polinômio ou uma exponencial;
(ii) suavizar os valores da série ao redor de um ponto, para estimar a tendência naquele ponto;
(iii) suavizar os valores da série através de sucessivos ajustes de retas de mínimos quadrados ponderados;
Após estimado a tendência em $ \hat T_t $ podemos ter a série ajustada para tendência ou livre de tendência,
$$Y_t = Z_t - \hat T_t.$$
Um procedimento que é normalmente utilizado para remover tendências é tomar sucessivas diferenças da série original até encontrar uma série estacionária.
$$\Delta Z_t = Z_t - Z_{t-1}$$
Para mais detalhes sobre como calcular uma estimativa da tendência $ \hat T_t $ consulte o livro: Análise de séries temporais(2006) / Pedro A. Morettin, Célia M. C. Toloi.
2.2 - Testes para tendência
Existe alguns testes não paramétricos úteis para detectar se há tendência em um conjunto de observações. Porém, estes testes em geral se baseiam em hipóteses que podem não estar verificadas no caso de uma série temporal, por exemplo, supor que as observações são independentes.
É necessário estar atento se existe outra componente (como $ S_t $) na série, além de $ T_t $. Precisamos eliminar esta componente antes de testar $ T_t $, pois há uma grande influência de outras componentes sobre a tendência.
Portanto, é necessário cautela ao utilizar estes testes.
2.2.1 - Teste de Wald - Wolfowitz
Para podermos aplicar este teste, precisamos inicialmente que a série temporal seja independente e identicamente distribuída.
Seja {Zt, t = 1, … , N} uma série temporal com N observações. Considere M sendo a mediana das N observações de Zt. Atribuímos a cada valor de Zt o simbolo “a” se ele for maior ou igual a M, e “b” caso ele for menor que M. Então, temos que N = (“Na” pontos “a”) + (“Nb” pontos “b”). Desta forma, teremos grupos de observações marcadas com “a” e grupos de observações marcadas com “b” ao longo da série temporal. O número total de grupos será a estatística do teste, iso é,
T = “número total de grupos com símbolos iguais”.
Consideramos as seguintes hipóteses:
$ H_0 = $ “Não Existe tendência”
$ H_1 = $ “Existe tendência”
Rejeitamos a hipótese nula H0 se tivermos um número pequeno de grupos com símbolos iguais, ou seja, se T for relativamente pequeno.
Para valores de Na e Nb superiores a 20, podemos utilizar o Teorema Central do Limite e aproximar a distribuição de T por uma normal, isto é, $ T \sim N(\mu , \sigma^2) $, onde
$$\mu = \dfrac{2N_aN_b}{N} + 1, $$
$$\sigma = \sqrt\dfrac{2N_aN_b(2N_aN_b - N)}{N^2(N-1)}.$$
Exemplo 2.2.1.1
Considere as observações abaixo referente aos índices do IBOVESPA no período de 01 de setembro de 2009 a 01 de novembro de 2009.
| t | Índice | t | Índice |
|---|---|---|---|
| 1 | 56176 | 12 | 60570 |
| 2 | 55706 | 13 | 60432 |
| 3 | 55582 | 14 | 60575 |
| 4 | 56258 | 15 | 61467 |
| 5 | 57504 | 16 | 61157 |
| 6 | 57898 | 17 | 60020 |
| 7 | 58153 | 18 | 60207 |
| 8 | 58460 | 19 | 61089 |
| 9 | 58448 | 20 | 61152 |
| 10 | 59082 | 21 | 61523 |
| 11 | 60088 | 22 | 60772 |
Gráfico da série:
(imagem em falta)
Resultados utilizando o Action:
(imagem em falta)
Note que para este exemplo a mediana é de 60054 e portanto, temos T = 4 grupos distintos com símbolos iguais. Aplicando o teste de Wald-Wolfowitz rejeitamos a hipótese nula com nível de confiança acima de 99%.
.
Exemplo 2.2.1.2
Observe abaixo o gráfico da série temporal dos valores diários de fechamento das ações da Petrobras no período de 10 de julho de 2007 a 09 de janeiro de 2008, com um total de 123 observações.
(imagem em falta)
Resultados do Action:
(imagem em falta)
Podemos fazer uma análise gráfica e notar que esta série possui tendência. Para confirmarmos esta analise, foi aplicado o teste de Wald-Wolfowitz e, portanto, rejeitamos a hipótese nula de não existência de tendência.
2.2.2 - Teste de Cox-Stuart
Considere um conjunto de observações X1,x2,…,xN. Agrupamos as observações em pares (X1,X1+c), (X2,X2+c),…, (XN-c,XN), onde c = N/2 se N for par e c = (N+1)/2 se N for ímpar. A cada par de observações associamos o sinal “-” se Xi$ < $ Xi+c e o sinal “+” se Xi$ > $ Xi+c, caso Xi = Xi+c eliminamos esta observação. Considere Nt o numero de pares onde Xi$ \neq $ Xi+c. Assim, queremos testar:
$$ H_0 = P(X_i < X_{i+c}) = P(X_i > X_{i+c}), \quad \forall i: \text{Não existe tendência}; $$
$$ H_1 = P(X_i < X_{i+c}) \neq P(X_i > X_{i+c}), \quad \forall i: \text{Existe tendência}. $$
Note que trata-se de um teste bilateral, onde a estatística do teste é dada por
T = Número de pares com sinal “+”.
Utilizamos a distribuição binomial para avaliar o teste, com os parâmetros p = 0,5 e n = Nt com hipóteses do teste bilateral.
Exemplo 2.2.2.1
Considere o Exemplo 2.2.1.1, onde as observações abaixo são referente aos índices do IBOVESPA no período de 01 de setembro de 2009 a 01 de novembro de 2009.
| t | Índice | t | Índice |
|---|---|---|---|
| 1 | 56176 | 12 | 60570 |
| 2 | 55706 | 13 | 60432 |
| 3 | 55582 | 14 | 60575 |
| 4 | 56258 | 15 | 61467 |
| 5 | 57504 | 16 | 61157 |
| 6 | 57898 | 17 | 60020 |
| 7 | 58153 | 18 | 60207 |
| 8 | 58460 | 19 | 61089 |
| 9 | 58448 | 20 | 61152 |
| 10 | 59082 | 21 | 61523 |
| 11 | 60088 | 22 | 60772 |
Gráfico da série:
(imagem em falta)
Resultados utilizando o Action:
(imagem em falta)
Portanto, rejeitamos a hipótese nula e concluímos que há tendência na série.
.
Exemplo 2.2.2.2
Utilizando o Exemplo 2.2.1.2, observe abaixo o gráfico da série temporal dos valores diários de fechamento das ações da Petrobras no período de 10 de julho de 2007 a 09 de janeiro de 2008, com um total de 123 observações.
(imagem em falta)
Resultados utilizando o Action:
(imagem em falta)
Neste exemplo temos um total de pares Nt = 62, isto é, em todos os pares (Xi, Xi+c), temos Xi$ < $ Xi+c para todos i. Portanto, rejeitamos a hipótese nula de que a série não tem tendência.
2.2.3 - Teste de Mann-Kendall
Seja as observações X1, X2,…,Xn de uma série temporal. Podemos aplicar o teste de Mann-Kendall para tendência somente se a série for serialmente independente. Então, queremos testar se as observações da série são independentes e identicamente distribuída, isto é, queremos testar as hipóteses

Sendo assim, sob $H_0$ a estatística do teste é dada por:
$$ S = \sum_{k=1}^{n-1} \sum_{j = k+1}^{n} sign(x_j - x_k)$$
onde
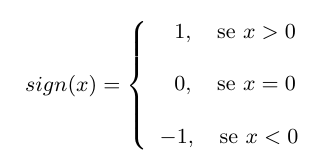
É possível mostrar que S é normalmente distribuída, ou seja, $ S \sim N(\mu, \sigma^2) $ com
$$\mu = 0$$
$$\sigma^2 = \dfrac{n(n-1)(2n+5) - \sum^{P}_{j = 1} t_j(t_j -1)(2t_j + 5)}{18}$$
em que n é o número de observações e, considerando o caso em que a série pode ter grupos com observações iguais, P é o número de grupos com observações iguais e tj é o numero de observações iguais no grupo j.
No caso em que o número de observações é superior a 30, a estatística do teste é calculada por
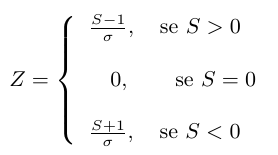
Mesmo para um número de observações inferiores a 30, podemos utilizar a estatística Z para realizarmos o teste.
Em um teste bilateral, não rejeitamos a hipótese nula H0 para um dado nível de significância $ \alpha $, se para o quantil $ Z_{\alpha /2} $ de uma distribuição normal padrão temos $ |Z| \leq Z_{\alpha /2} $.
Exemplo 2.2.3.1
Considere Exemplo 2.2.1.1, as observações abaixo são referente aos índices do IBOVESPA no período de 01 de setembro de 2009 a 01 de novembro de 2009.
| t | Índice | t | Índice |
|---|---|---|---|
| 1 | 56176 | 12 | 60570 |
| 2 | 55706 | 13 | 60432 |
| 3 | 55582 | 14 | 60575 |
| 4 | 56258 | 15 | 61467 |
| 5 | 57504 | 16 | 61157 |
| 6 | 57898 | 17 | 60020 |
| 7 | 58153 | 18 | 60207 |
| 8 | 58460 | 19 | 61089 |
| 9 | 58448 | 20 | 61152 |
| 10 | 59082 | 21 | 61523 |
| 11 | 60088 | 22 | 60772 |
Gráfico da série:
(imagem em falta)
Resultados utilizando o Action:
(imagem em falta)
Portanto, rejeitamos a hipótese nula de não existência de tendência na série.
.
Exemplo 2.2.3.2
Observe abaixo o gráfico da série temporal, do Exemplo 2.2.1.2, os valores diários de fechamento das ações da Petrobras no período de 10 de julho de 2007 a 09 de janeiro de 2008, com um total de 123 observações.
(imagem em falta)
Resultados utilizando o Action:
(imagem em falta)
Analisando os resultados, rejeitamos a hipótese nula de que as informações são independentes e identicamente distribuídas, ou seja, rejeitamos que a série não possui tendência.
2.3 - Sazonalidade
Dizemos que uma série temporal é sazonal quando os fenômenos que ocorrem durante o tempo se repete a cada período idêntico de tempo, ou seja, fenômenos que ocorrem diariamente em uma certa hora, todos os dias, ou em um certo mês em todos os anos. Um exemplo fácil de visualizar seria o aumento das vendas de passagens aéreas todos os finais de ano, ou ainda, o aumento das vendas do comércio no período do natal.
Considerando a série temporal composta pelas três componentes $S_t$, $T_t$ e $a_t$, onde $S_t$ é a componente sazonal, queremos então encontrar um estimador para $S_t$.
(imagem em falta)
2.3.1 - Sazonalidade determinística
Sazonalidade determinística é quando pressupomos um padrão sazonal regular e estável no tempo, desta forma podemos prever o comportamento sazonal perfeitamente a partir de dados anteriores.
Modelos de regressão são ótimos para séries que apresentam este tipo de sazonalidade. Então, utilizando a decomposição aditiva da série temporal temos temos
$$ T_t = \sum^m_{j=0} \beta_j t^j$$
$$S_t = \sum_{j=0}^{12}\alpha_j d_{jt}$$
onde $ d_{jt} $ são variáveis periódicas. Estamos supondo sazonalidade constante, ou seja, $ \alpha_j $ não depende de t, portanto, para uma sazonalidade determinística com período 12 temos

Assim, temos
$$ \sum_{j = 1}^{12} d_{jt} = 1, \quad t = 1, \dots , N$$
tal que a matriz de regressão é de posto m+12. Desta forma, precisamos impor a restrição abaixo para obtermos o modelo completo
$$\sum^{11}_{j = 1} \alpha_j = 0$$
assim, o modelo de posto completo é dado por
$$Z_t = \sum^m_{j = 0} \beta_j t^j + \sum^{11}_{j = 1} \alpha_j D_{jt} + a_t$$
tal que

Agora, a partir do modelo com posto completo, podemos utilizar o método dos mínimos quadrados para obter os estimadores de $ \alpha_j $ e $ \beta_j $.
2.3.2 - Sazonalidade Estocástica
Dizemos que uma série temporal possui sazonalidade estocástica quando a componente sazonal da série varia com o tempo. Este procedimento pode ser utilizado e normalmente é utilizado quando temos um padrão sazonal constante.
Dada a série temporal $ Z_t $, seja $ \hat{T_t} $ um estimador para a tendência calculado previamente, consideramos a seguinte série temporal
$$ Y_t = Z_t - \hat{T_t}.$$
Assim, considerando o caso em que temos um padrão sazonal constante, utilizaremos $ Y_t $ para estimar $ S_t $. Inicialmente, considerando os dados fornecidos anualmente, tomamos a média dos meses
$$\bar{Y_{.j}} = \frac{1}{n_j} \sum^{n_j}_{i = 1} Y_{ij}, \quad j= 1, \dots , 12;$$
em geral, a soma dos $ \bar{Y_{.j}} $ não é zero e, portanto, tomamos como estimativas das constantes sazonais
$$\hat{S_j} = \bar{Y_{.j}} - \bar{Y}, \quad \hbox{onde} \quad \bar{Y} = \frac{1}{12} \sum^{12}_{j = 1} \bar{Y_{.j}}$$
Assim, o modelo da série original $ Z_t $ pode ser escrito na forma aditiva por
$$ Z_t = T_t + S_j + a_t$$
com t = 12i + j, i = 0, 1, … ,p-1, j = 1, … ,12, onde p é o número de anos.
Então, a série livre de sazonalidade pode ser escrita como
$$Z^{\ast_t} = Z_t - \hat{S_t}.$$
Exemplo 2.3.2
Considere a série temporal AirPassengers que representa o número de passageiros mensalmente em uma empresa de transporte aéreo no período de 1949 a 1960.
Nota-se pelo gráfico da série que esta possui sazonalidade anualmente e portanto, podemos obter a série livre de sazonalidade:
(imagem em falta)
2.4 - Testes para sazonalidade deterministíca
Utilizando o modelo para sazonalidade determinística visto na seção 2.3.1, temos
$$Z_t = \sum^m_{i=0}\beta_it^i + \sum^{n_j}_{j=1}\alpha_jD_{jt} + a_t$$
então, dizemos que não existe sazonalidade determinística na série temporal se a hipótese nula de que todos os $ \alpha_j $ são nulos não for rejeitada, ou seja, se
$$H_0 : \alpha_1 = \dots = \alpha_{n_j} = 0$$
não for rejeitada.
Podemos utilizar métodos paramétricos e não paramétricos para determinar sazonalidade determinísticas e, para qualquer teste, é necessário eliminar a tendência da série se ela existir, ou seja, vamos trabalhar com a série $ Y_t = Z_t - \hat{T_t} $.
2.4.1 - Teste de Kruskal-Wallis
Supondo uma amostra de uma população, subdividida em k conjuntos de amostras de tamanho $ n_j $ cada, que varia dependendo da série que estamos trabalhando. Por exemplo, se a série for anual e temos observações mensais, isto é, nj = 12 e k representaria o número de anos.
Então, temos as seguintes amostras
$$Y_{ij}, \quad j=1,\dots,k, \ \ i=1, \dots, n_j, \quad N = \sum^k_{j=1} n_j$$
Substituímos as observações Yij por seus respectivos postos dentre todas as N observações, somamos todos os postos em cada subgrupo j, ou seja
$$R_{.j} = \sum^{n_j}_{i=1} R_{ij}, \quad j=1,\dots,k.$$
Assim, a estatística para o teste é dada por
$$H=\frac{\frac{12}{N(N+1)}\sum_{i=1}^kn_i\left(R_{i\cdot}-\frac{N+1}{2}\right)^2}{1-\frac{ \sum_{j=1}^g t_j^3-t_j}{N^3-N}}=\frac{\left(\frac{12}{N(N+1)}\sum_{i=1}^k \frac{R_i^2}{n_i} \right)-3(N+1)}{1-\frac{\sum_{j=1}^g t_j^3-t_j}{N^3-N}}$$
onde t é o número de observações repetidas no grupo j e g é o número de grupos com observações repetidas.
Sob H0, para nj suficientemente grande, ou k $ \ge $ 4, a distribuição de H pode ser aproximada por uma variável $ \chi^2 $ com k-1 graus de liberdade. Portanto, rejeitamos a hipótese nula de não existência de sazonalidade determinística se $ P_{h_0}(H \ge \chi^2_{(k-1), \alpha}) = \alpha $, tal que $ \alpha $ é o nível de significância do teste.
Exemplo 2.4.1
Consideramos novamente a série temporal AirPassengers do Exemplo 2.3.2 e aplicamos o teste de Kruskal-Wallis.
| Ano/Mês | Jan | Fev | Mar | Abr | Mai | Jun | Jul | Ago | Set | out | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1949 | 112 | 118 | 132 | 129 | 121 | 135 | 148 | 148 | 136 | 119 | 104 | 118 |
| 1950 | 115 | 126 | 141 | 135 | 125 | 149 | 170 | 170 | 158 | 133 | 114 | 140 |
| 1951 | 145 | 150 | 178 | 163 | 172 | 178 | 199 | 199 | 184 | 162 | 146 | 166 |
| 1952 | 171 | 180 | 193 | 181 | 183 | 218 | 230 | 242 | 209 | 191 | 172 | 194 |
| 1953 | 196 | 196 | 236 | 235 | 229 | 243 | 264 | 272 | 237 | 211 | 180 | 201 |
| 1954 | 204 | 188 | 235 | 227 | 234 | 264 | 302 | 293 | 259 | 229 | 203 | 229 |
| 1955 | 242 | 233 | 267 | 269 | 270 | 315 | 364 | 347 | 312 | 274 | 237 | 278 |
| 1956 | 284 | 277 | 317 | 313 | 318 | 374 | 413 | 405 | 355 | 306 | 271 | 306 |
| 1957 | 315 | 301 | 356 | 348 | 355 | 422 | 465 | 467 | 404 | 347 | 305 | 336 |
| 1958 | 340 | 318 | 362 | 348 | 363 | 435 | 491 | 505 | 404 | 359 | 310 | 337 |
| 1959 | 360 | 342 | 406 | 396 | 420 | 472 | 548 | 559 | 463 | 407 | 362 | 405 |
| 1960 | 417 | 391 | 419 | 461 | 472 | 535 | 622 | 606 | 508 | 461 | 390 | 432 |
Então, temos
$$n_j = \hbox{número de meses} = 12, \quad j = 1,2,\dots,12$$
$$N = \sum^{12}_{j=1}n_j = 144$$
Os postos de cada observação, são dados pela tabela abaixo
| Ano/mês | Jan | Fev | Mar | Abr | Mai | Jun | Jul | Ago | Set | Out | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1949 | 2,0 | 5,5 | 12,0 | 11,0 | 8,0 | 14,5 | 21,5 | 21,5 | 16,0 | 7,0 | 1,0 | 5,5 |
| 1950 | 4,0 | 10,0 | 18,0 | 14,5 | 9,0 | 23,0 | 29,5 | 29,5 | 25,0 | 13,0 | 3,0 | 17,0 |
| 1951 | 19,0 | 24,0 | 34,5 | 27,0 | 32,5 | 34,5 | 47,5 | 47,5 | 40,0 | 26,0 | 20,0 | 28,0 |
| 1952 | 31,0 | 36,5 | 43,0 | 38,0 | 39,0 | 54,0 | 59,0 | 67,5 | 52,0 | 42,0 | 32,5 | 44,0 |
| 1953 | 45,5 | 45,5 | 64,0 | 62,5 | 57,0 | 69,0 | 71,5 | 77,0 | 65,5 | 53,0 | 36,5 | 49,0 |
| 1954 | 51,0 | 41,0 | 62,5 | 55,0 | 61,0 | 71,5 | 84,0 | 82,0 | 70,0 | 57,0 | 50,0 | 57,0 |
| 1955 | 67,5 | 60,0 | 73,0 | 74,0 | 75,0 | 91,5 | 112,0 | 100,5 | 89,0 | 78,0 | 65,5 | 80,0 |
| 1956 | 81,0 | 79,0 | 93,0 | 90,0 | 94,5 | 113,0 | 123,0 | 119,5 | 104,5 | 86,5 | 76,0 | 86,5 |
| 1957 | 91,5 | 83,0 | 106,0 | 102,5 | 104,5 | 127,0 | 133,0 | 134,0 | 117,5 | 100,5 | 85,0 | 96,0 |
| 1958 | 98,0 | 94,5 | 109,5 | 102,5 | 111,0 | 129,0 | 137,0 | 138,0 | 117,5 | 107,0 | 88,0 | 97,0 |
| 1959 | 108,0 | 99,0 | 121,0 | 116,0 | 126,0 | 135,5 | 141,0 | 142,0 | 132,0 | 122,0 | 109,5 | 119,5 |
| 1960 | 124,0 | 115,0 | 125,0 | 130,5 | 135,5 | 140,0 | 144,0 | 143,0 | 139,0 | 130,5 | 114,0 | 128,0 |
Utilizando o Action para efetuar os cálculos obtemos:
(imagem em falta)
Portanto, sob $ H_0 $ temos $ P(H \ge \chi^2_{11, \alpha}) \approx 0 $ e rejeitamos a hipótese nula de que não existe sazonalidade determinística.
2.4.2 - Teste de Friedman
Considere a série temporal $ Z_t $ tal que podemos interpreta-la na forma do modelo aditivo $ Z_t = T_t + S_t + a_t $.
Para podermos aplicar o teste de Friedman para sazonalidade determinística precisamo considerar a série livre de tendência, ou seja, considerando $ \hat{T_t} $ o estimador para a tendência da série, vamos trabalhar com a série
$$Y_t = Z_t - \hat{T_t}.$$
Dividimos a série em blocos de períodos e calculamos o posto de cada observação em cada bloco, por exemplo, se estivermos analisando uma série temporal com dados mensais durante 20 anos, vamos testar a sazonalidade em cada mês durante os 20 anos, então temos um período de 12 meses e 20 blocos de períodos.
Assim, a estatística do teste pode ser calculada por
$$H = \frac{12}{nk(k+1)}\sum_{j=1}^kR_{.j}^2 - 3n(k+1), \quad \hbox{onde} \ \ R_{,j} = \sum_{i=1}^nR_{ij},$$
onde $ R_{ij} $ é o posto da observação $ Y_{ij} $ dentro do bloco i, n é o número de blocos e k é o tamanho do período. A distribuição de H pode ser aproximada por uma distribuição $ \chi^2 $ com k-1 graus de liberdade.
Exemplo 2.4.1
Consideramos novamente a série temporal AirPassengers do Exemplo 2.3.2 e aplicamos o teste de Friedman.
| Ano/Mês | Jan | Fev | Mar | Abr | Mai | Jun | Jul | Ago | Set | out | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1949 | 112 | 118 | 132 | 129 | 121 | 135 | 148 | 148 | 136 | 119 | 104 | 118 |
| 1950 | 115 | 126 | 141 | 135 | 125 | 149 | 170 | 170 | 158 | 133 | 114 | 140 |
| 1951 | 145 | 150 | 178 | 163 | 172 | 178 | 199 | 199 | 184 | 162 | 146 | 166 |
| 1952 | 171 | 180 | 193 | 181 | 183 | 218 | 230 | 242 | 209 | 191 | 172 | 194 |
| 1953 | 196 | 196 | 236 | 235 | 229 | 243 | 264 | 272 | 237 | 211 | 180 | 201 |
| 1954 | 204 | 188 | 235 | 227 | 234 | 264 | 302 | 293 | 259 | 229 | 203 | 229 |
| 1955 | 242 | 233 | 267 | 269 | 270 | 315 | 364 | 347 | 312 | 274 | 237 | 278 |
| 1956 | 284 | 277 | 317 | 313 | 318 | 374 | 413 | 405 | 355 | 306 | 271 | 306 |
| 1957 | 315 | 301 | 356 | 348 | 355 | 422 | 465 | 467 | 404 | 347 | 305 | 336 |
| 1958 | 340 | 318 | 362 | 348 | 363 | 435 | 491 | 505 | 404 | 359 | 310 | 337 |
| 1959 | 360 | 342 | 406 | 396 | 420 | 472 | 548 | 559 | 463 | 407 | 362 | 405 |
| 1960 | 417 | 391 | 419 | 461 | 472 | 535 | 622 | 606 | 508 | 461 | 390 | 432 |
Então, temos
$$n_j = \hbox{número de meses} = 12, \quad j = 1,2,\dots,12$$
$$N = \sum^{12}_{j=1}n_j = 144$$
Os postos de cada observação, são dados pela tabela abaixo
| Ano/mês | Jan | Fev | Mar | Abr | Mai | Jun | Jul | Ago | Set | Out | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1949 | 2,0 | 5,5 | 12,0 | 11,0 | 8,0 | 14,5 | 21,5 | 21,5 | 16,0 | 7,0 | 1,0 | 5,5 |
| 1950 | 4,0 | 10,0 | 18,0 | 14,5 | 9,0 | 23,0 | 29,5 | 29,5 | 25,0 | 13,0 | 3,0 | 17,0 |
| 1951 | 19,0 | 24,0 | 34,5 | 27,0 | 32,5 | 34,5 | 47,5 | 47,5 | 40,0 | 26,0 | 20,0 | 28,0 |
| 1952 | 31,0 | 36,5 | 43,0 | 38,0 | 39,0 | 54,0 | 59,0 | 67,5 | 52,0 | 42,0 | 32,5 | 44,0 |
| 1953 | 45,5 | 45,5 | 64,0 | 62,5 | 57,0 | 69,0 | 71,5 | 77,0 | 65,5 | 53,0 | 36,5 | 49,0 |
| 1954 | 51,0 | 41,0 | 62,5 | 55,0 | 61,0 | 71,5 | 84,0 | 82,0 | 70,0 | 57,0 | 50,0 | 57,0 |
| 1955 | 67,5 | 60,0 | 73,0 | 74,0 | 75,0 | 91,5 | 112,0 | 100,5 | 89,0 | 78,0 | 65,5 | 80,0 |
| 1956 | 81,0 | 79,0 | 93,0 | 90,0 | 94,5 | 113,0 | 123,0 | 119,5 | 104,5 | 86,5 | 76,0 | 86,5 |
| 1957 | 91,5 | 83,0 | 106,0 | 102,5 | 104,5 | 127,0 | 133,0 | 134,0 | 117,5 | 100,5 | 85,0 | 96,0 |
| 1958 | 98,0 | 94,5 | 109,5 | 102,5 | 111,0 | 129,0 | 137,0 | 138,0 | 117,5 | 107,0 | 88,0 | 97,0 |
| 1959 | 108,0 | 99,0 | 121,0 | 116,0 | 126,0 | 135,5 | 141,0 | 142,0 | 132,0 | 122,0 | 109,5 | 119,5 |
| 1960 | 124,0 | 115,0 | 125,0 | 130,5 | 135,5 | 140,0 | 144,0 | 143,0 | 139,0 | 130,5 | 114,0 | 128,0 |
Utilizando o Action para efetuar os cálculos obtemos:
(imagem em falta)
Portanto, sob $ H_0 $ temos $ P(H \ge \chi^2_{11, \alpha}) \approx 0 $ e rejeitamos a hipótese nula de que não existe sazonalidade determinística.
2.4.3 - Teste F
O teste $ F $ para detectar sazonalidade determinística se trata do mesmo teste de hipóteses utilizado para comparar variâncias em um modelo estatístico.
Considere a série temporal $ Z_t $ tal que podemos interpreta-la na forma do modelo aditivo, neste caso, escrevemos as observações da série temporal sem a componente de tendência no seguinte modelo
$$Y_{ij} = S_j + e_{ij}, \quad i = 1,\dots,n_j; \quad j=1,\dots, k.$$
onde $ n_j $ é o tamanho do período a ser considerado e k o número de blocos de períodos, supondo $ e_{ij} \sim N(0, \sigma^2) $. A estatística do teste $ F $ pode ser escrita como
$$H = \frac{N - k}{k - 1}\frac{\sum_{j=1}^kn_j(\bar{Y_{.j}} - \bar{Y})^2}{\sum_{i=1}^k\sum_{j=1}^{n_j}(Y_{ij} - \bar{Y_{.j}})^2}, \quad \hbox{onde} \quad N = \sum_{j=1}^kn_j.$$
Aproximamos a distribuição de H por uma F de Fisher-Snedcor com (k-1) e (N-k) graus de liberdade, ou seja, $ H \sim F(k-1,N-k) $.
Exemplo 2.4.3
Consideramos novamente a série temporal AirPassengers do Exemplo 2.3.2 e aplicamos o teste F para uma análise de variância.
Os postos de cada observação, são dados pela tabela abaixo
| Ano/mês | Jan | Fev | Mar | Abr | Mai | Jun | Jul | Ago | Set | Out | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1949 | 2,0 | 5,5 | 12,0 | 11,0 | 8,0 | 14,5 | 21,5 | 21,5 | 16,0 | 7,0 | 1,0 | 5,5 |
| 1950 | 4,0 | 10,0 | 18,0 | 14,5 | 9,0 | 23,0 | 29,5 | 29,5 | 25,0 | 13,0 | 3,0 | 17,0 |
| 1951 | 19,0 | 24,0 | 34,5 | 27,0 | 32,5 | 34,5 | 47,5 | 47,5 | 40,0 | 26,0 | 20,0 | 28,0 |
| 1952 | 31,0 | 36,5 | 43,0 | 38,0 | 39,0 | 54,0 | 59,0 | 67,5 | 52,0 | 42,0 | 32,5 | 44,0 |
| 1953 | 45,5 | 45,5 | 64,0 | 62,5 | 57,0 | 69,0 | 71,5 | 77,0 | 65,5 | 53,0 | 36,5 | 49,0 |
| 1954 | 51,0 | 41,0 | 62,5 | 55,0 | 61,0 | 71,5 | 84,0 | 82,0 | 70,0 | 57,0 | 50,0 | 57,0 |
| 1955 | 67,5 | 60,0 | 73,0 | 74,0 | 75,0 | 91,5 | 112,0 | 100,5 | 89,0 | 78,0 | 65,5 | 80,0 |
| 1956 | 81,0 | 79,0 | 93,0 | 90,0 | 94,5 | 113,0 | 123,0 | 119,5 | 104,5 | 86,5 | 76,0 | 86,5 |
| 1957 | 91,5 | 83,0 | 106,0 | 102,5 | 104,5 | 127,0 | 133,0 | 134,0 | 117,5 | 100,5 | 85,0 | 96,0 |
| 1958 | 98,0 | 94,5 | 109,5 | 102,5 | 111,0 | 129,0 | 137,0 | 138,0 | 117,5 | 107,0 | 88,0 | 97,0 |
| 1959 | 108,0 | 99,0 | 121,0 | 116,0 | 126,0 | 135,5 | 141,0 | 142,0 | 132,0 | 122,0 | 109,5 | 119,5 |
| 1960 | 124,0 | 115,0 | 125,0 | 130,5 | 135,5 | 140,0 | 144,0 | 143,0 | 139,0 | 130,5 | 114,0 | 128,0 |
Portanto, temos
$$\sum_{j=1}^{12}12(\bar{Y_{.j}} - \bar{Y})^2 = 211306,90$$
$$\sum_{j=1}^{12}\sum_{i=1}^{12}(Y_{ij} - \bar{Y_{.j}})^2 = 58286,99$$
$$H = \frac{144 - 12}{12 - 1}*\frac{211306,90}{58286,99} = 43,50$$
Utilizando o Action obtemos o mesmo resultado:
(imagem em falta)
Pela tabela da distribuição F para um nível de significância de $ \alpha = 0,05 $, temos $ F_{(11, 132, \alpha=0,05)} = 1,86 $. Portanto, rejeitamos a hipóteses nula de que a série não possui sazonalidade determinística.
3 - Modelos de Suavização Exponencial
Modelos de suavização é uma grande classe de métodos de previsão que se baseiam na ideia de que observações passadas contêm informações sobre o padrão da série temporal. O propósito dos métodos é distinguir um padrão de comportamento de qualquer outro ruído que possa estar contido nas observações da série e então usar esse padrão para prever valores futuros da série.
3.1 - Médias Móveis Simples (MMS)
Considere a série temporal $ Z_1 $, $ Z_2 $, … , $ Z_n $, estacionária e localmente constante, composta de seu nível e mais um ruído aleatório da seguinte forma
$$Z_t = \mu_t + a_t, \quad t=1,\dots,N$$
onde E(at) = 0, Var(at) = $ \sigma_a^2 $ e $ \mu_t $ é um parâmetro desconhecido que varia com o tempo.
A técnica de média móvel consiste em calcular a média aritmética das k observações mais recentes, ou seja
$$M_t = \frac{Z_t + Z_{t-1} + \dots + Z_{t-k+1}}{k} = M_{t-1} + \frac{Z_t - Z_{t-k}}{k}$$
Denotamos por k como sendo o comprimento da média.
Desta forma, $ M_t $ é uma estimativa do nível $ \mu_t $ que não leva em consideração as observações mais antigas. Note que a cada período a observação mais antiga é substituída pela mais recente, calculando-se uma média nova.
Portanto, a previsão dos h valores futuros é dada pela última média móvel calculada, ou seja
$$\hat{Z_t}(h) = M_t,$$
ou ainda
$$\hat{Z_t}(h)= \hat{Z_{t-1}}(h+1) + \frac{Z_t - Z_{t-k}}{k}, \quad \forall h > 0.$$
Podemos perceber que a equação acima corrige a previsão de $ Z_{t+h} $ a cada instante, ou seja, a cada nova observação na série, $ Z_{t+h} $ é atualizado.
Assumindo que $ a_t \sim N(0,\sigma_a^2) $, podemos afirmar que $ \hat{Z_t}(h) \sim N(\mu,\frac{\sigma_a^2}{k}) $ e construir um intervalo de confiança com nível de significância \alpha, dado por
$$\Bigg(\hat{Z_t}(h) - z_{\alpha}\frac{\sigma_a}{\sqrt{k}} ; \hat{Z_t}(h) + z_{\alpha}\frac{\sigma_a}{\sqrt{k}}\Bigg),$$
onde $ z_{\alpha} $ é o quantil de uma distribuição normal padrão, com nível de significância $ \alpha $.
Exemplo 3.1.1
Seja $ Z_t $ uma série temporal referente às médias anuais das temperaturas na cidade de Nova York durante os anos de 1912 e 1971. Vamos ajustar um modelo MMS a está serie temporal e tentar prever a temperatura nos próximos 6 anos.
| Ano | Temperatura | Ano | Temperatura | Ano | Temperatura |
|---|---|---|---|---|---|
| 1912 | 49,9 | 1932 | 51,8 | 1952 | 53,1 |
| 1913 | 52,3 | 1933 | 51,1 | 1953 | 54,6 |
| 1914 | 49,4 | 1934 | 49,8 | 1954 | 52 |
| 1915 | 51,1 | 1935 | 50,2 | 1955 | 52 |
| 1916 | 49,4 | 1936 | 50,4 | 1956 | 50,9 |
| 1917 | 47,9 | 1937 | 51,6 | 1957 | 52,6 |
| 1918 | 49,8 | 1938 | 51,8 | 1958 | 50,2 |
| 1919 | 50,9 | 1939 | 50,9 | 1959 | 52,6 |
| 1920 | 49,3 | 1940 | 48,8 | 1960 | 51,6 |
| 1921 | 51,9 | 1941 | 51,7 | 1961 | 51,9 |
| 1922 | 50,8 | 1942 | 51 | 1962 | 50,5 |
| 1923 | 49,6 | 1943 | 50,6 | 1963 | 50,9 |
| 1924 | 49,3 | 1944 | 51,7 | 1964 | 51,7 |
| 1925 | 50,6 | 1945 | 51,5 | 1965 | 51,4 |
| 1926 | 48,4 | 1946 | 52,1 | 1966 | 51,7 |
| 1927 | 50,7 | 1947 | 51,3 | 1967 | 50,8 |
| 1928 | 50,9 | 1948 | 51 | 1968 | 51,9 |
| 1929 | 50,6 | 1949 | 54 | 1969 | 51,8 |
| 1930 | 51,5 | 1950 | 51,4 | 1970 | 51,9 |
| 1931 | 52,8 | 1951 | 52,7 | 1971 | 53 |
Utilizando o , obtemos os seguintes resultados para um ajuste MMS com comprimento de média k = 3
(há elementos em falta na equação acima)
(imagem em falta)
(imagem em falta)
Desta forma, as previsões com um intervalo de confiança de 95% são dadas por:
(imagem em falta)
3.2 - Suavização Exponencial Simples (SES)
Seja $ Z_1 $,$ Z_2 $, … ,$ Z_n $ uma série temporal estacionária. Podemos descrever uma SES por
$$\bar{Z_t} = \alpha\sum_{j=0}^{t-1}(1- \alpha)^jZ_{t-j} + (1-\alpha)^t\bar{Z}_0, \quad t=1,\dots,N,$$
onde $ \bar{Z_t} $ é denominado valor exponencialmente suavizado e $ \alpha $ é a constante de suavização, tal que $ 0 \le \alpha \le 1 $.
Expandindo a equação acima temos
$$\bar{Z_t} = \alpha Z_t + \alpha(1-\alpha)Z_{t-1} + \alpha(1-\alpha)^2Z_{t-2} + \dots$$
então, podemos concluir que a SES é uma média ponderada que da pesos maiores às observações mais recentes, eliminando uma das desvantagens do método de MMS.
A previsão dos h valores futuros é dada pelo último valor exponencialmente suavizado, ou seja
$$\hat{Z}(h) = \bar{Z_t}, \quad \forall h$$
$$\hat{Z}(h) = \alpha Z_t + (1 - \alpha)\hat{Z_{t-1}}(h+1)$$
Supondo $ a_t \sim N(0,\sigma_a^2) $, podemos construir um intervalo de confiança assintótico para $ Z_{t+h} $, dado por
$$\Bigg(\hat{Z_t}(h) - z_{\gamma}\sigma_a\sqrt{\frac{\alpha}{2 - \alpha}} \ ; \ \hat{Z_t}(h) + z_{\gamma}\sigma_a\sqrt{\frac{\alpha}{2 - \alpha}}\Bigg)$$
onde $ z_{\gamma} $ é o quantil de uma distribuição normal padrão com nível de significância $ \gamma $.
Exemplo 3.2.1
Considere a série temporal AirPassengers que representa o número de passageiros em um aeroporto no decorrer do tempo. Vamos ajustar um modelo de SES para estes dados.
| Ano/Mês | Jan | Fev | Mar | Abr | Mai | Jun | Jul | Ago | Set | out | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1949 | 112 | 118 | 132 | 129 | 121 | 135 | 148 | 148 | 136 | 119 | 104 | 118 |
| 1950 | 115 | 126 | 141 | 135 | 125 | 149 | 170 | 170 | 158 | 133 | 114 | 140 |
| 1951 | 145 | 150 | 178 | 163 | 172 | 178 | 199 | 199 | 184 | 162 | 146 | 166 |
| 1952 | 171 | 180 | 193 | 181 | 183 | 218 | 230 | 242 | 209 | 191 | 172 | 194 |
| 1953 | 196 | 196 | 236 | 235 | 229 | 243 | 264 | 272 | 237 | 211 | 180 | 201 |
| 1954 | 204 | 188 | 235 | 227 | 234 | 264 | 302 | 293 | 259 | 229 | 203 | 229 |
| 1955 | 242 | 233 | 267 | 269 | 270 | 315 | 364 | 347 | 312 | 274 | 237 | 278 |
| 1956 | 284 | 277 | 317 | 313 | 318 | 374 | 413 | 405 | 355 | 306 | 271 | 306 |
| 1957 | 315 | 301 | 356 | 348 | 355 | 422 | 465 | 467 | 404 | 347 | 305 | 336 |
| 1958 | 340 | 318 | 362 | 348 | 363 | 435 | 491 | 505 | 404 | 359 | 310 | 337 |
| 1959 | 360 | 342 | 406 | 396 | 420 | 472 | 548 | 559 | 463 | 407 | 362 | 405 |
| 1960 | 417 | 391 | 419 | 461 | 472 | 535 | 622 | 606 | 508 | 461 | 390 | 432 |
Assim, utilizando o Action para efetuar os cálculos, obtemos os resultados:
(há elementos em falta na equação acima)
(imagem em falta)
(imagem em falta)
(imagem em falta)
A previsão será de 432 pessoas em janeiro de 1961. Note que esse tipo de previsão não é efetiva para mais do que um passo no futuro, pois devido sua formula de previsão o valor é repetido consecutivamente, independente do valor da constante de suavização $ \alpha $.
3.3 - Suavização Exponencial de Holt (SEH)
Esta técnica de suavização é recomendada para séries que apresentam tendência. Considere o caso de uma série temporal que é composta localmente da soma de nível, tendencia e resíduo com média zero e variância constante $ \sigma_a^2 $, isto é
$$Z_t = \mu_t + T_t + a_t, \quad t = 1, \dots , N$$
Esta técnica é similar a uma Suavização Exponencial Simples (SES) com uma constante extra para modelar a componente de tendência. Os valores do nível e da tendência da série serão estimados por
$$\bar{Z_t} = AZ_t + (1-A)(\bar{Z_{t-1}} + \hat{T_{t-1}}), \quad 0< A < 1 \quad e \quad t = 2, \dots , N,$$
$$\hat{T_t} = C(\bar{Z_t} - \bar{Z_{t-1}}) + (1-C)\hat{T_{t-1}}, \quad 0 < C < 1 \quad e \quad t = 2, \dots , N$$
onde A e C são denominados constantes de suavização, tal que $ A \ge C $.
Assim, a previsão do valor $ Z_{t+h} $ com origem em t é dada por
$$\hat{Z_t}(h) = \bar{Z_t} + h\hat{T_t} \quad \forall h > 0$$
Exemplo 3.3.1
Considere a mesma série temporal do exemplo 3.2.1, vamos tentar prever o número de passageiros na linha aérea para os próximos 6 anos.
| Ano/Mês | Jan | Fev | Mar | Abr | Mai | Jun | Jul | Ago | Set | out | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1949 | 112 | 118 | 132 | 129 | 121 | 135 | 148 | 148 | 136 | 119 | 104 | 118 |
| 1950 | 115 | 126 | 141 | 135 | 125 | 149 | 170 | 170 | 158 | 133 | 114 | 140 |
| 1951 | 145 | 150 | 178 | 163 | 172 | 178 | 199 | 199 | 184 | 162 | 146 | 166 |
| 1952 | 171 | 180 | 193 | 181 | 183 | 218 | 230 | 242 | 209 | 191 | 172 | 194 |
| 1953 | 196 | 196 | 236 | 235 | 229 | 243 | 264 | 272 | 237 | 211 | 180 | 201 |
| 1954 | 204 | 188 | 235 | 227 | 234 | 264 | 302 | 293 | 259 | 229 | 203 | 229 |
| 1955 | 242 | 233 | 267 | 269 | 270 | 315 | 364 | 347 | 312 | 274 | 237 | 278 |
| 1956 | 284 | 277 | 317 | 313 | 318 | 374 | 413 | 405 | 355 | 306 | 271 | 306 |
| 1957 | 315 | 301 | 356 | 348 | 355 | 422 | 465 | 467 | 404 | 347 | 305 | 336 |
| 1958 | 340 | 318 | 362 | 348 | 363 | 435 | 491 | 505 | 404 | 359 | 310 | 337 |
| 1959 | 360 | 342 | 406 | 396 | 420 | 472 | 548 | 559 | 463 | 407 | 362 | 405 |
| 1960 | 417 | 391 | 419 | 461 | 472 | 535 | 622 | 606 | 508 | 461 | 390 | 432 |
Assim, utilizando o Action para efetuar os cálculos, obtemos os resultados:
(há elementos em falta na equação acima)
(imagem em falta)
(imagem em falta)
(imagem em falta)
Note que este modelo de suavização é o mais indicado quando o fator predominante na série temporal é a tendência, pois é o diferencial do modelo, utilizar a tendência para diferenciar e aproximar mais as previsões.
3.4 - Suavização Exponencial de Holt - Winters (HW)
No caso de séries que apresentam um comportamento um pouco mais complexo, como sazonalidade, utilizamos outras formas de suavização como o método de Holt - Winters.
Essa técnica envolve três equações com três parâmetros de suavização que são associados a cada componente da série: nível, tendência e sazonalidade.
Portanto, temos dois casos a serem considerados
Série Sazonal Multiplicativa
Considere uma série sazonal com período p. A variante mais usual do método de HW considera o fator sazonal $ S_t $ como sendo multiplicativo, enquanto a tendência continua aditiva, ou seja
$$Z_t = \mu_t S_t + T_t + a_t, \quad t = 1, \dots , N.$$
E assim, calculamos as três equações de suavização por
$$\hat{S_t} = D\Bigg(\frac{Z_t}{\bar{Z_t}}\Bigg) + (1-D)\hat{S}_{t-p}, \quad 0 < D < 1,$$
$$\bar{Z_t} = A\Bigg(\frac{Z_t}{\hat{S_{t-s}}}\Bigg) + (1-A)(\bar{Z_{t-1}} + \hat{T_{t-1}}), \quad 0 < A < 1,$$
$$\hat{T_t} = C(\bar{Z_t} - \bar{Z_{t-1}}) + (1-C)\hat{T_{t-1}}, \quad, 0 < C < 1,$$
que representam estimativas do fator sazonal, do nível e da tendência, respectivamente; onde A, C e D são as constantes de suavização.
Uma previsão de h passos a frente utilizando o modelo Multiplicativo pode ser encontrado através da seguinte fórmula
$$\hat{Z}(h) = (\bar{Z_t} + h\hat{T_t})\hat{S_{t+h-p}}, \quad h= 1, 2, \dots , p,$$
$$\hat{Z}(h) = (\bar{Z_t} + h\hat{T_t})\hat{S_{t+h-2p}}, \quad h= p+1, \dots , 2p,$$
$$\vdots \quad \quad \quad \quad \quad \vdots$$
onde $ \bar{Z_t} $, $ \hat{S_t} $ e $ \hat{T_t} $ são dadas pelas equações acima. Para atualizarmos as previsões quando temos uma nova observação $ Z_{t+1} $ basta fazermos os mesmos procedimentos com a nova observação e voltando um passo na previsão, ou seja
$$\hat{Z_{t+1}}(h-1) = (\bar{Z_{t+1}} + (h-1)\hat{T_{t+1}})\hat{S}_{t+1+h-p}, \quad h= 1, 2, \dots , p+1,$$
$$\hat{Z_{t+1}}(h-1) = (\bar{Z_{t+1}} + (h-1)\hat{T_{t+1}})\hat{S}_{t+1+h-2p}, \quad h= p+2, \dots , 2p+1,$$
Para um valor inicial das equações de recorrência, utilizamos as seguintes fórmulas
$$\hat{S_j} = \frac{Z_j}{(\frac{1}{p})\sum_{k=1}^{p}Z_k}, \quad j = 1,2,\dots , p; \quad \quad \bar{Z}_p = \frac{1}{p}\sum_{k=1}^pZ_k; \quad \quad \hat{T}_p = 0.$$
Série Sazonal Aditiva
Neste caso, a série é composta por
$$Z_t = \mu_t + T_t + S_t + a_t $$
E portanto, podemos calcular as equações de suavização por
$$\hat{S_t} = D(Z_t - \hat{Z_t}) + (1-D)\hat{S_{t-s}} , \quad 0 < D < 1,$$
$$\bar{Z_t} = A(Z_t - \hat{S_{t-s}}) + (1-A)(\bar{Z_{t-1}} + \hat{T_{t-1}}), \quad 0 < A < 1,$$
$$\hat{T_t} = C(\bar{Z_t} - \bar{Z_{t-1}}) + (1-C)\hat{T_{t-1}}, \quad 0 < C < 1.$$
que representam a estimativa do fator sazonal, do nível e da tendência, respectivamente, onde A, C e D são as constantes de suavização.
Uma previsão de h passos a frente pode ser feita através das equações
$$\hat{Z_t}(h) = \bar{Z_t} + h\hat{T_t} + \hat{S_{t+h-p}}, \quad h = 1,2,\dots p,$$
$$\hat{Z_t}(h) = \bar{Z_t} + h\hat{T_t} + \hat{S_{t+h-2p}}, \quad h = p+1,\dots 2p,$$
$$\vdots \quad \quad \quad \quad \quad \vdots$$
Se obtemos uma nova observação $ Z_{t+1} $ podemos atualizar a previsão de $ Z_{t+h} $ recalculando as equações de recorrência para o ponto t+1, ou seja
$$\hat{S_{t+1}} = D(Z_{t+1} - \hat{Z_{t+1}}) + (1-D)\hat{S_{t+1-s}}$$
$$\bar{Z_{t+1}} = A(Z_{t+1} - \hat{S}_{t+1-s}) + (1-A)(\bar{Z}_{t} + \hat{T}_{t}),$$
$$\hat{T_{t+1}} = C(\bar{Z_{t+1}} - \bar{Z}_{t}) + (1-C)\hat{T}_{t}.$$
e assim, a nova previsão para $ Z_{t+h} $ será
$$\hat{Z_{t+1}}(h-1) = \bar{Z_{t+1}} + (h-1)\hat{T_{t+1}} + \hat{S}_{t+1+h-p}, \quad h = 1,2,\dots p+1,$$
$$\hat{Z_{t+1}}(h-1) = \bar{Z_{t+1}} + (h-1)\hat{T_{t+1}} + \hat{S}_{t+1+h-2p}, \quad h = p+2,\dots 2p+1,$$
$$\vdots \quad \quad \quad \quad \quad \vdots$$
Exemplo 3.4.1
Considere a mesma série temporal do exemplo 3.2.1, vamos tentar prever o número de passageiros na linha aérea para os próximos três anos, isso é 36 passos à frente.
| Ano/Mês | Jan | Fev | Mar | Abr | Mai | Jun | Jul | Ago | Set | out | Nov | Dez |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1949 | 112 | 118 | 132 | 129 | 121 | 135 | 148 | 148 | 136 | 119 | 104 | 118 |
| 1950 | 115 | 126 | 141 | 135 | 125 | 149 | 170 | 170 | 158 | 133 | 114 | 140 |
| 1951 | 145 | 150 | 178 | 163 | 172 | 178 | 199 | 199 | 184 | 162 | 146 | 166 |
| 1952 | 171 | 180 | 193 | 181 | 183 | 218 | 230 | 242 | 209 | 191 | 172 | 194 |
| 1953 | 196 | 196 | 236 | 235 | 229 | 243 | 264 | 272 | 237 | 211 | 180 | 201 |
| 1954 | 204 | 188 | 235 | 227 | 234 | 264 | 302 | 293 | 259 | 229 | 203 | 229 |
| 1955 | 242 | 233 | 267 | 269 | 270 | 315 | 364 | 347 | 312 | 274 | 237 | 278 |
| 1956 | 284 | 277 | 317 | 313 | 318 | 374 | 413 | 405 | 355 | 306 | 271 | 306 |
| 1957 | 315 | 301 | 356 | 348 | 355 | 422 | 465 | 467 | 404 | 347 | 305 | 336 |
| 1958 | 340 | 318 | 362 | 348 | 363 | 435 | 491 | 505 | 404 | 359 | 310 | 337 |
| 1959 | 360 | 342 | 406 | 396 | 420 | 472 | 548 | 559 | 463 | 407 | 362 | 405 |
| 1960 | 417 | 391 | 419 | 461 | 472 | 535 | 622 | 606 | 508 | 461 | 390 | 432 |
Assim, utilizando o Action para efetuar os cálculos, obtemos os resultados:
(há elementos em falta na equação acima)
(imagem em falta)
(imagem em falta)
(imagem em falta)
Neste caso, o comprimento sazonal é k = 12. Como esta série tem um comportamento sazonal e tendência bastante evidente, torna-se um caso ótimo para previsão utilizando a suavização de HW.
3.5 - Medidas de Acurácia
As estatísticas MAPE, MAD e MSD são informações importantes para comparmos os modelos de suavização e decidirmos se estes representam um bom ajuste aos nossos dados.
Média Percentual Absoluta do Erro (MAPE - Mean Absolute Percentage Erro)
Expressa a acurácia do erro em percentagem. Por exemplo, se temos um MAPE de 7%, quer dizer que o nosso ajuste esta errado em 7% dos dados.
Para calcular o MAPE utilizamos a seguinte formula:
$$ \frac{\sum_{t=1}^{n} |(y_t - \hat{y_t})/y_t|}{n}\times 100\quad\text{se } y_t \not= 0 $$
onde $ y_t $ são os nossos dados, $ \hat{y_t} $ são os ajustes e $ n $ é o número de observações. Note que se $ y_t = \hat{y_t} $ obtemos MAPE = 0, ou seja, quanto menor o MAPE melhor é o nosso ajuste.
Desvio Padrão Absoluto da Média (MAD - Mean Absolute Deviation)
Representa o desvio padrão do ajuste em relação à média nas mesmas unidades dos dados. Por exemplo, se estamos ajustando uma série temporal de visitas durante o tempo e encontramos um MAD de 72, quer dizer que o nosso ajuste possui um desvio padrão da média de 72 dias.
Para encontrarmos os MAD, realizamos o seguinte calculo:
$$ \frac{\sum_{t=1}^{n} |(y_t - \hat{y_t})|}{n} $$
onde $ y_t $ são os nossos dados, $ \hat{y_t} $ são os ajustes e $ n $ é o número de observações. Note que se $ y_t = \hat{y_t} $ obtemos MAD = 0, ou seja, quanto menor o MAD melhor é o nosso ajuste.
Desvio Padrão Quadrático da Média (MSD - Mean Squared Deviation)
Esta medida de acurácia é bastante comum em ajustes de séries temporais. Quando temos outliers em nosso conjunto de dados, essa medida é mais afetada do que o MAD. Portanto se temos um MAD baixo e um MSD alto podemos imaginar que temos outliers em nosso conjunto de dados.
Para calcularmos o MSD utlizamos a formula:
$$ \frac{\sum_{t=1}^{n} |(y_t - \hat{y_t})|^2}{n} $$
onde $ y_t $ são os nossos dados, $ \hat{y_t} $ são os ajustes e $ n $ é o número de observações. Note que se $ y_t = \hat{y_t} $ obtemos MSD = 0, ou seja, quanto menor o MSD melhor é o nosso ajuste.
4 - Modelos ARIMA
Esta metodologia consiste em ajustar modelos autorregressivos integrados de médias móveis, ARIMA(p,d,q), a um conjunto de dados. Para a construção do modelo seguimos um algorítimo no qual a escolha da estrutura do modelo é baseado nos próprios dados.
Podemos descrever o algorítimo através dos seguintes passos:
- Considera-se uma classe geral de modelos para a análise;
- identifica-se um modelo com base na análise de autocorrelações, autocorrelações parciais e outros critérios;
- estima-se os parâmetros do modelo identificado;
- verificar se o modelo ajustado é adequado aos dados através de uma análise de resíduos.
- Caso o modelo não seja adequado o algoritmo é repetido, voltando à fase de identificação.
Existem vários critérios para identificação de um modelo, por isso, é possível identificar modelos diferentes dependendo do critério que foi escolhido para identificação.
4.1 - Modelos Autorregressivos (AR)
Dizemos que $ {X_t, t \in Z} $ é um processo autorregressivo de ordem p e escrevemos $ X_t \sim AR(p) $ se podemos escrever o processo na seguinte forma
$$X_t = \phi_0 + \phi_1X_{t-1} + \dots + \phi_pX_{t-p} + \varepsilon_t$$
onde $ \phi_0, \phi_1, \dots , \phi_p $ são parâmetros reais e $ \varepsilon_t $ é i.i.d. com $ E(\varepsilon_t) = 0 $ e $ Var(\varepsilon_t) = \sigma^2 $.
Um caso particular simples de grande importância é o processo autorregressivo de ordem p = 1, AR(1)
$$X_t = \phi X_{t-1} + \varepsilon_t$$
Fazendo substituições sucessivas, $ X_{t-1}, X_{t-2} $, etc, na equação acima obtemos
$$X_t = \varepsilon_t + \phi\varepsilon_{t-1} + \phi^2\varepsilon_{t-2} + \dots = \sum_{j=0}^{\infty} \phi^j\varepsilon_{t-j} \hspace{6.0cm} (4.11)$$
onde a convergência é em média quadrática. Logo, a condição $ |\phi| < 1 $ é suficiente para que $ X_t $ seja estácionario.
Podemos calcular a função de autocovariância (f.a.c.v.) multiplicando ambos os lados de (4.11) por $ X_{t-\tau} $ e tomando a esperança
$$E(X_tX_{t-\tau}) = \phi E(X_{t-1}E_{t-\tau}) + \phi^2E(X_{t-2}X_{t-\tau}) + \dots + \phi^pE(X_{t-p}X_{t - \tau}) + E(\varepsilon_tX_{t-\tau})$$
$$\gamma_{\tau} = \phi\gamma_{\tau-1} = \dots = \phi^{\tau}\gamma_0$$
mas, sabemos que
$$\gamma_0 = \sigma^2_X = \sigma^2\sum^{\infty}_{j=0}\phi^{2j} = \frac{\sigma^2}{1 - \phi^2}$$
portanto, segue que
$$\gamma_{\tau} = \frac{\sigma^2}{1 - \phi^2}\phi^{|\tau|} , \quad \tau \in Z$$
Assim, a partir da função de autocovariância podemos calcular também a função de autocorrelação (f.a.c.)
$$\rho_{\tau} = \frac{\gamma_{\tau}}{\gamma_0} = \phi^{|\tau|}, \quad \tau \in Z$$
No caso geral, podemos calcular as funções de autocovariância e autocorrelação por
$$\gamma_j = \phi_1\gamma_{j-1} + \phi_2\gamma_{j-2} + \dots + \phi_p\gamma_{j-p}, \quad j > 0 $$
$$\rho_j = \phi_1\rho_{j-1} + \phi_2\rho_{j-2} + \dots + \phi_p\rho_{j-p}, \quad j > 0, \quad \quad (4.12)$$
respectivamente.
Se fizermos j = 1, 2, … , p, em (4.12) obtemos
$$\rho_1 = \phi_1 + \phi_2\rho_2 + \dots + \phi_p\rho_{p-1}$$
$$\rho_2 = \phi_1\rho_1 + \rho_2 + \dots + \phi_p\rho_{p-2}$$
$$\vdots \quad = \quad \vdots$$
$$\rho_p = \phi_1\rho_{p-1} + \phi_2\rho_{p-2} + \dots + \phi_p$$
que é um método recursivo para calcular as autocorrelações, conhecidas como equações de Yule-Walker.
Exemplo 4.1.1
Considere um modelo AR(1), com $ \phi = 0,7 $. Como $ -1 < \phi < 1 $ temos que o modelo satisfaz as condições de estacionariedade. Calculando a função de autocorrelação temos
$$\rho_j = \phi\rho_{j-1} = \phi^j, \quad j \ge 0.$$
Então, a função de autocorrelação decai exponencialmente, com valores todos positivos. Se $ \phi = 0,7 $, $ \rho_j = (0,7)^j $, $ j \ge 0 $, a função de auto correlação decairia exponencialmente para zero.
Como conhecemos $ \phi $ podemos calcular os $ \rho_j $ exatamente, mas normalmente precisamos estimar os valores de $ \phi $ e obtermos estimativas $ r_j $ para os valores da f.a.c
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $ \rho_j $ | 1,00 | 0,70 | 0,49 | 0,34 | 0,24 | 0,17 | 0,12 | 0,08 | 0,06 | 0,04 | 0,03 |
| $ r_j $ | 1,00 | 0,71 | 0,41 | 0,36 | 0,20 | 0,10 | -0,09 | -0,12 | -0,04 | -0,11 | -0,16 |
(imagem em falta)
4.2 - Modelos de Médias Móveis (MA)
Considere um processo linear $ (X_t, t \in Z) $, dizemos que este processo é de médias móveis de ordem q, denotado por MA(q), se satisfizer a equação de diferenças
$$X_t = a_t - \theta_1 a_{t-1} - \dots - \theta_q a_{t-q}$$
onde $ \mu, \theta_1, \dots , \theta_q $ são constantes reais, $ a_t $ é i.i.d. e $ a_t \sim N(0,\sigma^2) $.
Segue que $ X_t $ é estacionário, de média $ \mu $. Suponha que $ \mu = 0 $, calculando a função de autocovariância(f.a.c.v.) do processo obtemos
$$\gamma_j = E(X_tX_{t-j}) = E\Bigg(\Bigg[a_t - \sum_{k=1}^q \theta_k a_{t-k} \Bigg] \Bigg[ a_{t-j} - \sum_{l=1}^q \theta_l a_{t-l-j} \Bigg[\Bigg)$$
$$\gamma_j = E(a_ta_{t-j}) - \sum_{k=1}^q E(a_{t-j}a_{t-k}) - \sum_{l=1}^q E(a_t a_{t-j-l}) + \sum_{k=1}^q\sum_{l=1}^q \theta_k \theta_l E(a_{t-l}a_{t-j-l})$$
Como os $ a_t $ são não correlacionados, temos
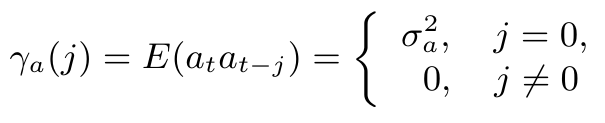
$$\gamma_0 = Var(X_t) = \sigma_X^2 = \sigma^2(1 + \theta_1^2 + \dots + \theta_q^2)$$
Então,
$$ \gamma_j = \gamma_a(j) - \sum_{k=1}^q \gamma_a(k-j) - \sum_{l=1}^q \gamma_a(j+l) + \sum_{k=1}^q\sum_{l=1}^q \theta_k \theta_l E(a_{t-l}a_{t-j-l})\gamma_a(j+l+k) $$

Exemplo 4.2.1
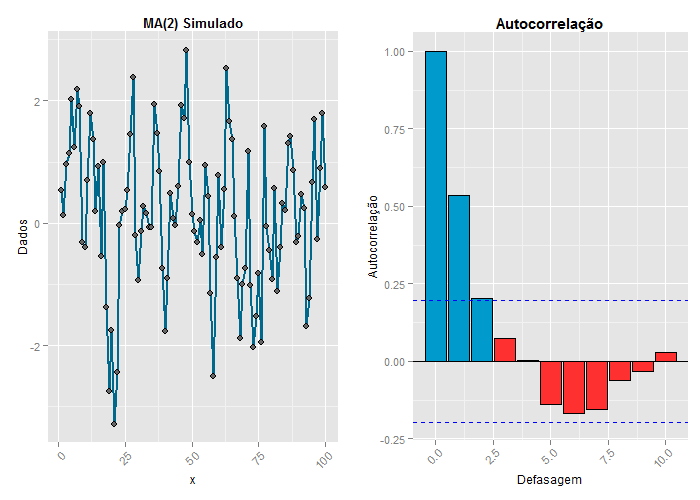
Considere a série simulada com 50 observações, geradas de acordo com um processo MA(2): $ X_t = a_t + 0,63a_{t-1} + 0,2a_{t-2} $ e $ \sigma^2_a = 1 $. Os dados deste exemplo podem ser obtidos clicando aqui.
Podemos calcular as f.a.c.v. e f.a.c. exatas por
$$\gamma_0 = (1 + \theta_1^2 + \theta_2^2)\sigma_a^2 = (1 + (0,63)^2 + (0,2)^2)1 = 1,437$$
$$\rho_1 = \frac{\theta_1(1 +\theta_2)}{1+\theta_1^2 + \theta_2^2} = \frac{0,63(1 - 0,2)}{1+0,63^2 + (0,2)^2} = 0,526;$$
$$\rho_2 = \frac{\theta_2}{1+\theta_1^2 + \theta_2^2} = \frac{0,2}{1+(0,63)^2+(0,2)^2} = 0,139;$$
$$\rho_j = 0, \quad j=3,4,5, \dots$$
| j | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $ \rho_j $ | 1,00 | 0,526 | 0,139 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| $ r_j $ | 1,00 | 0,536 | 0,202 | 0,073 | 0,004 | -0,138 | -0,168 | -0,154 | -0,061 | -0,031 | 0,028 |
4.3 - Modelos Autorregressivos e de Médias Móveis
Modelos autorregressivos e de médias móveis é a junção dos modelos AR e MA. Denotamos por ARMA(p,q) um processo autorregressivo e de médias móveis de ordem (p,q) e pode ser representado por
$$X_t = \phi_1X_{t-1} + \cdots \phi_pX_{t-p} + a_t - \theta_1a_{t-1} - \cdots - \theta_qa_{t-q}$$
Um modelo frequentemente utilizado é o ARMA(1,1), ou seja
$$X_t = \phi X_{t-1} + a_t - \theta a_{t-1}$$
No caso geral, calculamos a f.a.c.v. por
$$\gamma_j = \phi_1 \gamma_{j-1} + \phi_2 \gamma_{j-2} + \cdots + \phi_p \gamma_{j-p} +\gamma_{Xa}(j) - \theta_1\gamma_{Xa}(j-1) - \cdots - \theta_q\gamma_{Xa}(j-q)$$
onde $ \gamma_{Xa}(j) $ é a covariância cruzada entre $ X_t $ e $ a_t $, definida por
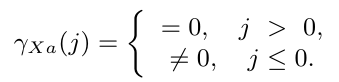
Assim, a f.a.c.v. fica
$$\gamma_j = \phi_1\gamma_{j-1} + \phi_2\gamma_{j-2} + \cdots + \phi_p\gamma_{j-p}, \quad j \ > \ q$$
e a f.a.c. é obtida por
$$\rho_j = \frac{\gamma_j}{\gamma_0} = \phi_1\rho_{j-1} + \phi_2\rho_{j-2} + \cdots + \phi_p\rho_{j-p}, \quad j \ > \ q.$$
Um processo ARMA(p,q) tem f.a.c. infinita, a qual decai de acordo com exponenciais e/ou senoides amortecidas após o “lag” p-q. Essa observação é importante na identificação do modelo aos dados observados.
Exemplo 4.3.1
Considere um modelo ARMA(2,1) simulado com n = 200, dado por $ X_t = 0,26X_{t-1} + 0,37X_{t-2} + 0,81a_{t-1} + a_t. $
Calculando a função de autocorrelação estimada e teórica temos:
| $ \bold{j} $ | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $ \bold{\rho_j} $ | 1,000 | 0,809 | 0,580 | 0,450 | 0,332 | 0,253 | 0,188 | 0,143 | 0,107 | 0,081 | 0,060 |
| $ \bold{r_j} $ | 1,000 | 0,779 | 0,519 | 0,405 | 0,312 | 0,195 | 0,044 | -0,028 | -0,052 | -0,121 | -0,187 |
(imagem em falta)
4.4 - Modelos Autorregressivos, Integrados e de Médias Móveis
Os modelos AR, MA e ARMA, são apropriados para descrever séries temporais estacionárias, isto é, séries que se desenvolvem no tempo ao redor de uma média constante.
Muitas séries encontradas na prática não são estacionárias, mas, como visto anteriormente, quando tomamos a série diferenciada esta se torna estacionária.
Modelos autorregressivos, integrados e de médias móveis (ARIMA) trata-se de representar série diferenciada por um modelo ARMA.
Seja $ Z_t $ uma série temporal não estacionária. Tomamos $ W_t = \Delta Z_t = Z_t - Z_{t-1} $ sendo a série diferenciada uma vez de $ Z_t $, denotamos por $ W_t^d = \Delta^d Z_t $ a série temporal diferenciada d vezes de $ Z_t $.
Podemos representar $ W_t $ por um modelo ARMA, como $ W_t $ é uma diferença de $ Z_t $ então, $ Z_t $ é uma integral de $ W_t $, assim dizemos que $ Z_t $ segue um modelo autorregressivo, integrado e de médias móveis, isto é, um modelo ARIMA de ordem (p,d,q) e escrevemos ARIMA(p,d,q) onde p é a ordem da componente autorregressiva, d é o número de diferenças tomadas na série e q é a ordem da componente de médias móveis.
Portanto, podemos descrever todos os modelos vistos anteriormente utilizando a nomenclatura ARIMA, isto é
i) ARIMA(p,0,0) = AR(p);
ii)ARIMA(0,0,q) = MA(q);
iii)ARIMA(p,0,q) = ARMA(p,q).
e no caso de uma série não estacionária utilizamos o modelo completo, ARIMA(p,d,q) com d diferenças na série original.
4.5 - Identificação de Modelos ARIMA
A identificação particular de um modelo ARIMA a ser ajustado aos dados pode ser considerado uma das fases mais críticas ao se utilizar uma modelagem ARIMA. A escolha do modelo a ser utilizado é feita principalmente com base nas autocorrelações e autocorrelações parciais estimadas, que utilizaremos para comparar com as quantidades teóricas e identificar um possível modelo para os dados.
Lembramos que a f.a.c. $ \rho_j $ é estimada por
$$r_j = \frac{g_j}{g_0}, \quad j = 0, 1, \dots , N-1$$
onde $ g_j $ é a estimativa da f.a.c.v. $ \gamma_j $, dado por
$$g_j = \frac{1}{N}\sum_{t=1}^{N-j} [(X_t - \bar{X})(X_{t+j} - \bar{X})], \quad j = 0,1,\dots , N-1$$
sendo $ \bar{X} = \frac{1}{N}\sum_{j=1}^{N}X_t $ a média amostral. Como as funções de auto correlação são funções pares, temos que $ g_{-j} = g_j $ e $ r_{-j} = r_{j} $.
Os modelos AR(p), MA(q) e ARMA(p,q) apresentam f.a.c. com características especiais:
i) um processo AR(p) tem f.a.c. infinita em extensão que decai de acordo com exponenciais e/ou senoides amortecidas;
ii) um processo MA(q) tem f.a.c. finita, no sentido que ela apresenta um corte após a defasagem q;
iii) um processo ARMA(p,q) tem f.a.c. infinita que decai de acordo com exponencias e/ou senoides amortecidas após a defasagem (q-p).
Assim, a partir das f.a.c. estimadas, tentamos identificar um padrão que se comporte teoricamente com algum modelo. Em particular, a f.a.c. estimada é útil para identificar modelos MA por causa da característica (ii) e não são muito úteis na identificação de modelos ARMA, que possuem f.a.c. complicadas.
Função de Autocorrelação Parcial (f.a.c.p.)
Uma outra ferramenta utilizada no processo de identificação do modelo é a função de autocorrelação parcial(f.a.c.p.). Esta medida corresponde a correlação de $ X_t $ e $ X_{t-k} $ removendo o efeito das observações $ X_{t-1}, X_{t-2}, \dots , X_{t-k+1} $ e é denotada por $ \phi_{kk} $, ou seja
$$\phi_{kk} = Corr(X_t, X_{t-l}/X_{t-1}, X_{t-2},\dots,X_{t-k+1})$$
Um método geral para encontrar a f.a.c.p. para um processo estacionário com f.a.c. $ \rho_k $ é utilizando as equações de Yule-Walker, isto é, para um certo k temos
$$\rho_j = \phi_{k1}\rho_{j-1} + \phi{k2}\rho_1 + \cdots + \phi_{kk}\rho{j-1}, \quad j = 1, 2, \dots , k$$
Desenvolvendo a equação temos
$$\rho_1 = \phi_{k1} + \phi_{k2}\rho_1 + \cdots + \phi_{kk}\rho_{j-1}$$
$$\rho_2 = \phi_{k1}\rho_1 + \phi_{k2} + \cdots + \phi_{kk}\rho_{j-2}$$
$$\quad \vdots \quad = \quad \vdots$$
$$\rho_j = \phi_{k1}\rho_{j-1} + \phi_{k2}\rho_{j-2} + \cdots + \phi_{kk}$$
Resolvendo as equações acima sucessivamente para k = 1, 2, …, obtemos $ \phi_{kk} $ da seguinte maneira
$ \phi_{11} = \rho_1 $
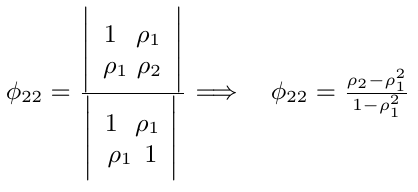
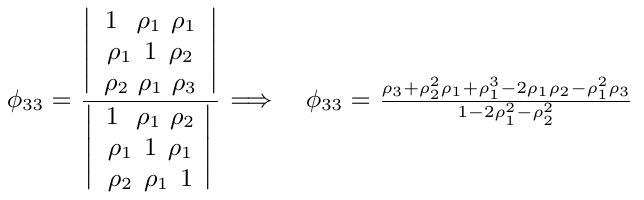
em geral temos
$$\phi_{kk} = \frac{|P^*_k|}{|P_k|}$$
onde $ P_k $ é a matriz de autocorrelação, e $ P^*_k $ é a matriz $ P_k $ com a ultima coluna substituída pelo vetor de autocorrelação.
Nos processos AR, MA e ARMA temos as seguintes f.a.c.p. teóricas:

ii)em um processo MA(q) a f.a.c.p. se comporta de maneira similar à f.a.c. de um processo AR(p), isto é, composta por exponenciais e\ou senoides amortecidas;
iii)um processo ARMA(p,q) tem f.a.c.p. que se comporta como a f.a.c.p. de um processo MA puro.
Devido aos fatores acima, segue que a f.a.c.p. é útil para identificar modelos AR puros, não sendo tão útil para identificar modelos MA e ARMA.
Uma maneira simples de estimar as f.a.c.p. de um processo consistem em substituir nas equações de Yullie-Walker as f.a.c. por sua estimativas
$$r_j = \hat{\phi_{k1}}r_{j-1} + \cdots + \hat{\phi_{kk}}r_{j-k}, \quad j=1,\dots,k,$$
e resolver estas equações para k=1, 2, 3,….
Exemplo 4.5.1
Observe na tabela abaixo uma estimativa das f.a.c.p. dos processos AR(1), MA(1) e ARMA(1,1), de séries temporais simuladas computacionalmente com 100 observações cada.
| j | AR(1) | MA(1) | ARMA(1,1) |
|---|---|---|---|
| 1 | -0,4514 | 0,3828 | -0,0187 |
| 2 | -0,0640 | -0,2738 | -0,0833 |
| 3 | -0,0460 | -0,0710 | -0,1950 |
| 4 | -0,0305 | -0,1540 | 0,1094 |
| 5 | 0,0144 | -0,0599 | -0,0949 |
| 6 | -0,0425 | -0,0412 | 0,0537 |
| 7 | 0,0939 | -0,0412 | 0,0708 |
| 8 | -0,0470 | -0,1616 | -0,1851 |
| 9 | -0,0256 | 0,0528 | 0,1552 |
| 10 | 0,0080 | -0,0296 | 0,0474 |
| 11 | -0,0754 | -0,0305 | -0,1351 |
| 12 | 0,0846 | -0,1096 | -0,0056 |
| 13 | 0,0457 | -0,0883 | 0,0532 |
| 14 | 0,0330 | 0,0115 | -0,0495 |
| 15 | -0,0132 | 0,0761 | 0,0547 |
Representadas graficamente por:
(imagem em falta)
Critérios de informação AIC e BIC
Após selecionarmos possíveis modelos ARIMA para os dados observados, identificamos o melhor modelo possível utilizando os critérios AIC e BIC. Queremos encontrar as ordens k e l que minimizam os critérios AIC e BIC para a determinação das ordens p e q do modelo, isto é, queremos minimizar
$$AIC(k,l) = -2ln(\hat{\sigma}^2_{k,l}) + 2(k+l+2)$$
$$BIC(k,l) = -2ln(\hat{\sigma}^2_{k,l}) + (k+l)\frac{lnN}{N}$$
onde, N é o número de observações e $ \hat{\sigma}_{k,l}^2 $ é o estimador de máxima verossimilhança da variância residual do modelo ARMA(k,l).
Exemplo 4.5.2
Considere os retornos das ações da Petrobras durante o período de 10/01/2008 a 10/02/2008. Construímos uma série temporal utilizando a média dos retornos em cada hora por dia, com um total de 110 observações. Vamos identificar um modelo ARIMA para esta série.
| j | $ X_j $ | j | $ X_j $ | j | $ X_j $ | j | $ X_j $ | j | $ X_j $ |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0,0012 | 23 | 0,0004 | 45 | -0,0011 | 67 | 0,0106 | 89 | -0,0036 |
| 2 | 0,0006 | 24 | -0,0035 | 46 | -0,0149 | 68 | -0,0025 | 90 | 0,0001 |
| 3 | -0,0059 | 25 | 0,0019 | 47 | 0,0003 | 69 | 0,0058 | 91 | -0,0030 |
| 4 | -0,0054 | 26 | -0,0107 | 48 | 0,0012 | 70 | -0,0088 | 92 | -0,0020 |
| 5 | -0,0039 | 27 | 0,0042 | 49 | -0,0148 | 71 | -0,0053 | 93 | -0,0154 |
| 6 | -0,0222 | 28 | 0,0030 | 50 | 0,0006 | 72 | -0,0242 | 94 | 0,0090 |
| 7 | -0,0017 | 29 | -0,0150 | 51 | 0,0136 | 73 | -0,0089 | 95 | 0,0083 |
| 8 | 0,0096 | 30 | -0,0215 | 52 | -0,0152 | 74 | -0,0133 | 96 | 0,0035 |
| 9 | 0,0102 | 31 | -0,0029 | 53 | -0,0113 | 75 | -0,0075 | 97 | -0,0038 |
| 10 | -0,0068 | 32 | -0,0575 | 54 | 0,0037 | 76 | -0,0037 | 98 | -0,0025 |
| 11 | 0,0105 | 33 | 0,0045 | 55 | 0,0282 | 77 | 0,0065 | 99 | 0,0342 |
| 12 | 0,0100 | 34 | -0,0043 | 56 | -0,0008 | 78 | -0,0107 | 100 | -0,0043 |
| 13 | 0,0079 | 35 | -0,0077 | 57 | -0,0192 | 79 | -0,0017 | 101 | 0,0567 |
| 14 | 0,0069 | 36 | 0,0186 | 58 | 0,0060 | 80 | -0,0064 | 102 | 0,0033 |
| 15 | 0,0097 | 37 | 0,0039 | 59 | 0,0077 | 81 | 0,0120 | 103 | 0,0012 |
| 16 | -0,0009 | 38 | 0,0269 | 60 | -0,0092 | 82 | 0,0021 | 104 | 0,0053 |
| 17 | -0,0056 | 39 | -0,0101 | 61 | -0,0010 | 83 | -0,0031 | 105 | 0,0066 |
| 18 | -0,0011 | 40 | -0,0010 | 62 | -0,0003 | 84 | -0,0047 | 106 | -0,0082 |
| 19 | -0,0035 | 41 | 0,0043 | 63 | 0,0048 | 85 | 0,0014 | 107 | 0,0192 |
| 20 | -0,0313 | 42 | 0,0099 | 64 | -0,0017 | 86 | -0,0022 | 108 | 0,0020 |
| 21 | 0,0094 | 43 | 0,0003 | 65 | 0,0008 | 87 | -0,0008 | 109 | 0,0122 |
| 22 | -0,0045 | 44 | 0,0022 | 66 | -0,0023 | 88 | 0,0090 | 110 | 0,0032 |
(imagem em falta)
Visualizando o gráfico da série, podemos identificar alguns pequenos ciclos repetitivos o que torna a série não estacionária e analisando a f.a.c. estimada da série não conseguimos identificar um modelo apropriado para o ajuste, então tomamos uma diferença na série e analisamos novamente as f.a.c. e f.a.c.p estimadas.
(imagem em falta)
A análise das f.a.c. e f.a.c.p. estimadas sugerem um modelo de médias móveis MA(p) na série diferenciada. Calculamos então os critérios de informação AIC e BIC para confirmar um modelo do tipo ARIMA(0,1,p).
| p | AIC | BIC |
|---|---|---|
| 1 | -637,4155 | -632,0145 |
| 2 | -635,4466 | -627,3451 |
| 3 | -633,7607 | -622,9587 |
| 4 | -632,4030 | -618,9006 |
| 5 | -630,6355 | -614,4326 |
| 6 | -628,6938 | -609,7904 |
| 7 | -627,4892 | -605,8854 |
| 8 | -627,2289 | -602,9245 |
| 9 | -627,2354 | -600,2306 |
| 10 | -626,7906 | -597,0853 |
Note que entre as 10 primeiras ordens o menor valor entre os critérios é para ordem p = 1, portanto, concluímos que um modelos ideal para o conjunto de dados é um ARIMA(0,1,1).
4.6 - Estimação de Modelos ARIMA
Identificada a ordem de um modelo ARIMA para uma série temporal precisamos agora estimar os parâmetros deste modelo. Para isso, podemos utilizar método dos momentos, estimadores de mínimos quadrados e estimadores máxima verossimelhança.
Considere um modelo ARIMA(p,d,q) e coloquemos seus p+q+1 parâmetros no vetor $ \xi = (\phi, \theta, \sigma^2_a) $, onde $ \phi = (\phi_1, \phi_2, \dots, \phi_p) $, $ \theta = (\theta_1, \theta_2, \dots, \theta_q) $. Quando d $ > $ 0 supomos $ \mu = 0 $, caso contrário precisamos considerar $ \mu $ como um parâmetro e estima-lo, então teríamos p+q+2 parâmetros a serem estimados.
Dado as N observações, $ X_1, \dots, X_n $, consideramos a função de verossimilhança $ L(\xi | X_1, \dots, X_n) $ como uma função de $ \xi $, então queremos encontrar os valores de $ \xi $ que minimizam $ L $ ou $ l = log(L) $.
Para determinar o EMV trabalharemos com a suposição que o processo $ a_t $ é normal, ou seja, para cada t, temos $ a_t \sim N(0, \sigma_a^2) $, nestas considerações os EMV serão aproximadamente estimadores de mínimos quadrados (EMQ).
Inicialmente, tomamos d diferenças na série para alcançarmos estacionariedade, ficamos com n = N - d observações denotadas por $ W_1, \dots, W_n $, onde $ W_t = \Delta^dZ_t $, resultando em um modelo ARMA(p,q) estacionário e invertível, então escrevemos
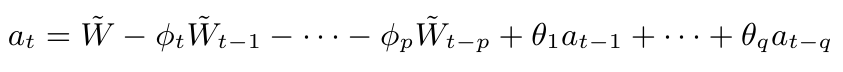
onde $ ~{W_t} = W_t - \mu $.
Para calcular os $ a_t $ é necessário obter valores iniciais para os $ ~{W} $’s e os a’s. Podemos resolver esta questão através de dois métodos: Condicional, que os valores iniciais desconhecidos são substituídos por valores que supomos serem razoáveis; incondicional, em que o valores iniciais são estimados utilizando um precedimento denominado “backforecasting”.
Procedimento Condicional
Supondo a normalidade de $ a_t $, a função densidade conjunta de $ a_1, \dots, a_n $ é dada por
$$f(a_1, \dots, a_n) = (2\pi)^{-n/2}(\sigma_a)^n exp\Bigg(-\sum_{t=1}^n \frac{a_t^2}{2\sigma_a^2}\Bigg).$$
Suponha que são dados p valores $ W_t $ e q valores $ a_t $, denotados por $ W_t^* $ e $ a_t^* $. A função de verossimilhança é dada por
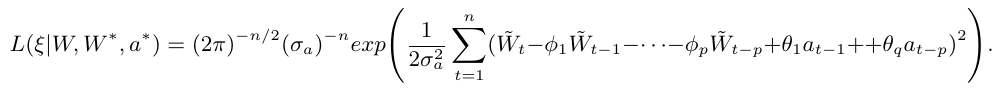
Tomando o logaritmo de L, considere $ \eta = (\phi, \theta) $, temos

Procedimento não Condicional
Pode ser demonstrado que o logaritmo da função de verossimilhança não condicional é dado por
$$l(\xi) \simeq -nlog(\sigma_a) - \frac{S(\eta)}{2\sigma_a^2}$$
em que
$$S(\eta) = S(\phi,\theta) = \sum_{t=-\infty}^n [a_t(\eta,W)]^2$$
é a soma de quadrados não condicional, com $ [a_t(\eta,W)] = E(a_t|\eta,W). $
Portanto, estimadores de mínimos quadrados obtidos minimizando $ S(\eta) $ serão boas aproximações para os estimadores de máxima verossimilhança.
Para calcular a soma de quadrados para um dado $ \eta $, precisamos usar o procedimento chamado “backforecasting” (“previsão para o passado”) para calcular $ [W_{-j}] $ e $ [a_{-j}] $, ou seja, gerando (prevendo) valores antes do inicio da série. Pode-se demonstrar que a chamada forma “backward” do processo fornece uma representação estacionária e invertível na qual $ W_t $ é expressa somente em termos de valores futuros de $ W_t $ e $ e_t $, onde $ e_t $ tem distribuição normal com média zero e mesma variância de $ a_t $.
Desta forma, o valor $ W_{-j} $ tem a mesma relação probabilística com $ W_1, \dots, W_n $ que $ W_{n+j+1} $ tem com $ W_n, W_{n-1}, \dots, W_1 $, ou seja, fazer previsão de antes que a série comece é equivalente a prever a série inversa.
Exemplo 4.6.1
Considere uma série temporal $ Z_1, \dots, Z_n $, na qual identificamos um modelo ARIMA(0,1,1). Seja $ W_t = \Delta Z_t $, então podemos escrever
$$a_t = W_t + \theta a_{t-1}.$$
No caso condicional, suponha $ \theta = 0,7 $ e iniciamos $ a_t $ especificando $ a_0 = 0 $ e $ Z_0 = 200 $, portanto podemos calcular recursivamente os valores de $ a_t $. Utilizando dados hipotéticos para $ Z_t $ temos
| t | $ \bold{Z_t} $ | $ \bold{W_t = \Delta Z_t} $ | $ \bold{a_t} $ |
|---|---|---|---|
| 0 | 200 | 0 | |
| 1 | 197 | -3 | -3,0 |
| 2 | 190 | -7 | -9,1 |
| 3 | 194 | 4 | -2,4 |
| 4 | 189 | -5 | -6,7 |
| 5 | 187 | -2 | -6,7 |
| 6 | 192 | 5 | 0,3 |
| 7 | 197 | 5 | 5,2 |
| 8 | 201 | 4 | 7,7 |
| 9 | 204 | 3 | 8,4 |
| 10 | 202 | -2 | 3,9 |
Desta forma, segue que a soma de quadrados condicional fica
$$S^*(0,7) = \sum_{t=1}^{10} a_t^2(0,7|a_0 = 0) = 357,3.$$
4.7 - Diagnóstico de Modelos ARIMA
Após identificar e estimar o modelo que ajusta as observações para a série temporal, precisamos verificar se ele representa, ou não, adequadamente os dados. A verificação do modelo pode ser feita analisando os resíduos. Suponha que o modelo ajustado seja da seguinte forma
$$\phi (B) W_t = \theta (B) a_t$$
onde $ W_t = \Delta^dX_t $ representando que tomamos d diferenças na séries, $ \phi (B) $ e $ \theta (B) $ são os polinômios utilizando operador de retardo B que garantem que o processo é estacionário e inversível.
Podemos então descrever os resíduos por
$$a_t = \theta^{-1} (B) \phi (B) W_t$$
Se o modelo estiver correto os resíduos exatos $ a_t $ devem ser i.i.d com distrubuição N(0,1).
Um método de verificar esta hipótese é verificar se os resíduos estimados do modelo são não correlacionados.
4.7.1 - Teste de Box - Pierce
Box e Pierce sugeriram um teste para as auto correlações dos resíduos estimados, o qual indica se estes valores estão muito altos.
As hipóteses do teste são

Inicialmente, calculamos uma estimativa para as auto correlações por
$$\hat{r_k} = \frac{\sum^n_{t = k+1} \hat{a_t} \hat{a_{t-k}}}{\sum^n_{t=1} \hat{a_t}^2}$$
é possível mostrar que $ \hat{r}_k \sim N(0, \frac{1}{n}) $.
Se o modelo for apropriado, a estatística do teste
$$Q(k) = n \sum^K_{j=1} \hat{r}^2_j$$

4.7.2 - Teste de Ljung - Box
Ljung e Box propuseram uma pequena alteração no teste de Box - Pierce, na qual torna o teste mais generalizado. Foi observado na literatura que o teste de Ljung - Box apresenta melhores resultados do que o teste de Box - Pierce.
As hipóteses do teste são as mesmas:
$$\text{Os resíduos não são i.i.d..}$$
(há elementos em falta na equação acima)
Calculamos as estimativas de autocorrelações por
$$\hat{r_k} = \frac{\sum^n_{t = k+1} \hat{a_t} \hat{a_{t-k}}}{\sum_{t=1}^n \hat{a_t}^2}.$$
É possível mostrar que $ \hat{r}_k \sim N(0, \frac{1}{n}) $.
Se o modelo for apropriado, a estatística do teste
$$Q(k) = n(n-2) \sum^K_{j=1} \frac{\hat{r}^2_j}{(n-j)}$$

4.8 - Previsão com modelos ARIMA
Um dos maiores interesses no estudo de séries temporais é conseguir fazer previsões das observações no tempo.
A partir do momento que conseguimos identificar e estimar um modelo ARIMA adequado às observações, vamos então estudar métodos que possamos utilizar a modelagem ARIMA para prever os valores das observações h passos a frente.
Vale a pena ressaltar que previsões utilizando modelos ARIMA serão eficazes para um período curto e as melhores previsões serão aquelas que apresentam um erro quadrático médio (EQM) mínimo.
4.8.1 - Introdução
Estamos interessados em prever um valor $ X_{t+h}, h \ge 1 $, supondo que temos todas as observações até o instante t, isto é, $ …,X _{t-2}, X_{t-1}, X_t $, dizemos que t é a origem das previsões.
Denotamos por $ \hat{X_t(h)} $ a previsão de h passos a partir da origem t. Vamos supor um modelo ARIMA(p,d,q), estacionário, invertível e com os parâmetros conhecidos. Nestas situações, temos 3 possíveis formas de previsão:
(i) forma de equação de diferenças
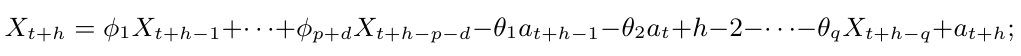
(ii) forma de choques aleatórios
$$X_{t+h} = \sum_{j = -\infty}^{t+h} \psi_{t+h-j}a_j = \sum_{j = 0}^{\infty} \psi_ja_{t+h-j},$$
onde $ \psi_o = 1 $ e os demais pesos são obtidos resolvendo um sistema de operadores de retardos dado por $ \phi(B)\psi(B) = \theta(B) $;
(iii) forma invertida
$$X_{t+h} = \sum_{j=1}^{\infty} \pi_jX_{t+h-j} + a_{t+h},$$
onde os pesos $ \pi_j $ são obtidos resolvendo o sistema de operadores de retardos dado por $ \phi(B) = \theta(B)\pi(B) $.
Previsão do erro quadrático médio (EQM) mínimo

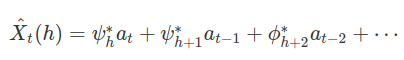
desta forma, queremos encontrar os pesos $ \psi^*_j $ que minimize o EQM de previsão. Calculando o EQM através do erro de previsão $ e_t(h) $ temos
$$E[e_t(h)]^2 = E[X_{t+h} - \hat{X_t(h)}]^2 = E\Bigg[ \sum_{j = 0}^{\infty} \psi_ja_{t+h-j} - \sum_{j=0}^{\infty} \psi_{h+j}^*a_{t-j} \Bigg]^2$$
$$ \Longrightarrow E[e_t(h)]^2 = E\Bigg[ \psi_0a_{t+h} + psi_1a_{t+h+1} + \cdots + \psi_{h=1}a_{t+1} + \sum_{j = 0}^{\infty}(\psi_{h+j} - \psi_{h+j}^*)a_{t-j}\Bigg]^2$$
$$\Longrightarrow E[e_t(h)]^2 = (1 + \psi_1^2 + \cdots + \psi_{h-1}^2)\sigma_a^2 + \sum_{j = 0}^{\infty}(\psi_{h+j} - \psi_{h+j}^*)^2\sigma^2_a,$$
devido ao fato de que os $ a_t $ são não correlacionados. Segue que o EQM será mínimo quando $ \psi_{h+j}^* = \psi_{h+j}, j = 1,2,…,h $ fixo.
Portanto, a previsão com EQM mínimo é dado por
$$X_t(h) = \psi_ha_{t} + \psi_{h+1}a_{t-1} + \cdots = \sum_{j=0}^{\infty} \psi_{h+j}a_{t-j}$$
e o erro de previsão por
$$e_t(h) = a_{t+h} + \psi_{h+1}a_{t+h-1} + \cdots + \psi_{h-1}a_{t+1} = \sum_{j=0}^{h-1} \psi_ja_{t+h-j}.$$
Como consequência dos resultados acima, podemos notar que
$$X_{t+h} = \hat{X_t(h)} + e_t(h), \quad h \ge 1.$$
Para facilitar, vamos utilizar a notação
$$[X_{t+h}] = E[X_{t+h} | X_t, X_{t-1}, …]$$
Utilizando a notação acima, temos as seguintes conclusões:
(i) $ [e_t(h)] = 0 $ e a variância do erro de previsão é $ Var(h) = (1 + \psi_1^2 + \psi_2^2 + \cdots + \psi_{h-1}^2)\sigma_a^2. $
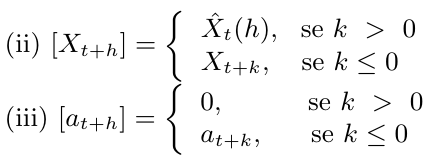
4.8.2 - Equação de Previsão
Supomos um modelo ARIMA(p,d,q) estacionário, inversível e com os parâmetros conhecidos, então a equação de previsão, considerada como uma função de h, com origem t fixa é dada por
$$\hat{X_t(h)} = \sum_{i = 1}^{p+q} \phi_i\hat{X_t(h-1)}, \quad h \ > \ q$$
Temos que para $ h \ > \ q-p-d $, a função $ \hat{X_t(h)} $ consistirá de uma mistura de polinômios, exponenciais e senóides amortecidades, com sua forma exata determinada pelas raízes do operador de retardo $ \phi(B) = 0 $. A solução geral terá a forma
$$\hat{X_t(h)} = c_1^{(t)}f_1(h) + c_2^{(t)}f_2(h) + \cdots + c_{p+q}^{(t)}f_{p+q}(h), \quad h \ > \ q-p-d$$
onde $ f_i(h), h=1,\dots,p+q $, são funções de h e $ c_1^{(t)},\dots,c_{p+q}^{(t)} $ são coeficientes adaptados que dependem da origem da previsão e são determinados por $ \hat{X_t}(1), \hat{X_t}(2),\dots, \hat{X_t}(p+d) $.
Exemplo 4.8.2.1
Supomos um modelo ARIMA(0,1,2) com a presença do intercepto $ \theta_0 $. Escrevendo na forma do operador de retardo temos
$$(1-B)X_t = \theta_0 + (1 - \theta_1B - \theta_2B^2)a_t \ \ \Longleftrightarrow \ \ X_t = \theta_0 + X_{t-1} - a_t - \theta_1a_{t-1} - \theta_2a_{t-2}$$
substituindo t por t+h temos
$$X_{t+h} = \theta_0 + X_{t+h-1} -a_{t+h} - \theta_1a_{t+h-1} - \theta_2a_{t+h-2}$$
assim,
$$\hat{X_t(1)} = [X_{t+1}] = \theta_0 + X_t - \theta_1a_t - \theta_2a_{t-1}$$
$$\hat{X_t(2)} = [X_{t+2}] = \theta_0 + \hat{X_t(1)} - \theta_2a_{t} = 2\theta_0 + X_t - (\theta_1 + \theta_2)a_t - \theta_2a_{t-1}$$
$$\hat{X_t(3)} = [X_{t+3}] = \theta_0 + \hat{X_t(2)} = 3\theta_0 + X_t - (\theta_1 + \theta_2)a_t - \theta_2a_{t-1}$$
em geral,
$$\hat{X_t(h)} = [X_{t+h}] = X_t + h\theta_0 - (\theta_1 + \theta_2)a_t - \theta_2a_{t-1}.$$
4.8.3 - Atualização das Previsões
Considere as previsões de $ X_{t+h+1} $ feitas a partir de duas origens
(i) $t+1: \hat{X_{t+1}}(h) = \psi_ha_{t+1} + \psi_{h+1}a_t + \psi_{h+2}a_{t-1} + \cdots$
(ii) $t: \hat{X_t}(h+1) = \psi_{h+1}a_t + \psi_{h+2}a_{t-1} + \cdots$
Subtraindo (ii) de (i) obtemos
$$\hat{X_{t+1}}(h) = \hat{X_t}(h+1) + \psi_ha_{t+1}$$
Desta forma, a previsão de $ X_{t+h+1} $, feita no instante t, pode ser atualizada quando um novo dado $ X_{t+1} $ for observado. Assim, faremos a previsão de $ X_{t+h+1} $, na origem t+1, adicionando à previsão $ \hat{X}(h+1) $ um múltiplo do erro de previsão $ a_{t+1} = X_{t+1} - \hat{X_t}(1) $. Para melhor compreensão, vamos analisar um exemplo.
Exemplo 4.8.3.1
Seja $ X_t $ um processo AR(2), então
$$X_t = \phi_1X_{t-1} + \phi_2X_{t-2} + a_t$$
no instante (t+h) o valor da série é
$$X_{t+h} = \phi_1X_{t+h-1} + \phi_2X_{t+h-1} + a_{t+h}$$
fazendo a previsão a partir da origem t, temos
$$\hat{X_t(h)} = \phi_1\hat{X_t}(h-1) + \phi_2\hat{X_t}(h-2), \quad h \ > \ 0$$
$$\hat{X_t(h)} = \phi_1^h\hat{X_t}(0) + \phi_2^{h}\hat{X_{t-1}}(0), \quad h \ > \ 0$$
analogamente, fazendo a previsão da origem (t-1), temos
$$\hat{X_{t-1}}(h+1) = \phi_1\hat{X_{t-1}}(h) + \phi_2\hat{X_{t-1}}(h-1), \quad h \ > \ 0$$
$$\hat{X_{t-1}}(h+1) = \phi_1^h\hat{X_{t-1}}(1) + \phi_2^{h}\hat{X_{t-2}}(1), \quad h \ > \ 0$$
subtraindo $ \hat{X_{t-1}}(h+1) $ de $ \hat{X_t(h)} $,
$$\hat{X_t(h)} - \hat{X_{t-1}}(h+1) = \phi_1^h\hat{X_t}(0) + \phi_2^{h}\hat{X_{t-1}}(0) - \phi_1^h\hat{X_{t-1}}(1) - \phi_2^{h}\hat{X_{t-2}}(1)$$
$$\hat{X_t(h)} - \hat{X_{t-1}}(h+1) = \phi_1^h[X_t - \hat{X_{t-1}}(1)] + \phi_2^{h}[X_{t-1} - \hat{X_{t-2}}(1)]$$
mas, sabemos que
$$a_t = X_t - \hat{X_{t-1}}(1)$$
$$a_{t-1} = X_{t-1} - \hat{X_{t-2}}(1)$$
então, substituindo temos que a previsão atualizada será dada por
$$\hat{X_t(h)} - \hat{X_{t-1}}(h+1) = \phi_1^ha_t + \phi_2a_{t-1}^{h}$$
$$\hat{X_t(h)} = \hat{X_{t-1}}(h+1) + \phi_1^ha_t + \phi_2a_{t-1}^{h}.$$
Exemplo 4.8.3.2
Considerem um modelo ARIMA(2,0,0) com n = 105 observações, vamos calcular as 3 primeiras estimativas baseado nas observações já ajustadas da tabela abaixo
| t | $ \bold{X_t} $ | t | $ \bold{X_t} $ | t | $ \bold{X_t} $ | t | $ \bold{X_t} $ | t | $ \bold{X_t} $ |
|---|---|---|---|---|---|---|---|---|---|
| 1 | -0,255 | 21 | -0,289 | 41 | 0,225 | 61 | 0,334 | 81 | 0,167 |
| 2 | -0,409 | 22 | -1,190 | 42 | -0,926 | 62 | -1,282 | 82 | -1,547 |
| 3 | -2,196 | 23 | -2,473 | 43 | -1,670 | 63 | -1,092 | 83 | -1,187 |
| 4 | -1,942 | 24 | -2,306 | 44 | -2,361 | 64 | -2,315 | 84 | -1,201 |
| 5 | -1,284 | 25 | -1,873 | 45 | -1,867 | 65 | -1,372 | 85 | -0,710 |
| 6 | -0,352 | 26 | -0,433 | 46 | 0,194 | 66 | 0,753 | 86 | 1,298 |
| 7 | 1,940 | 27 | 1,774 | 47 | 1,928 | 67 | 2,829 | 87 | 3,250 |
| 8 | 3,062 | 28 | 2,813 | 48 | 4,287 | 68 | 3,148 | 88 | 2,952 |
| 9 | 2,655 | 29 | 2,798 | 49 | 3,465 | 69 | 3,470 | 89 | 3,150 |
| 10 | 2,916 | 30 | 1,955 | 50 | 2,405 | 70 | 2,007 | 90 | 2,530 |
| 11 | 2,551 | 31 | 2,198 | 51 | 2,717 | 71 | 2,370 | 91 | 2,017 |
| 12 | 1,373 | 32 | 0,434 | 52 | 0,988 | 72 | 1,669 | 92 | 2,119 |
| 13 | 2,066 | 33 | 1,875 | 53 | 2,135 | 73 | 1,406 | 93 | 0,365 |
| 14 | 2,225 | 34 | 1,366 | 54 | 0,968 | 74 | 1,106 | 94 | 0,812 |
| 15 | 0,925 | 35 | 1,703 | 55 | 2,107 | 75 | 2,165 | 95 | 2,408 |
| 16 | 1,833 | 36 | 2,486 | 56 | 2,294 | 76 | 1,814 | 96 | 1,995 |
| 17 | 2,765 | 37 | 1,493 | 57 | 1,270 | 77 | 1,106 | 97 | 1,415 |
| 18 | 2,203 | 38 | 1,507 | 58 | 1,660 | 78 | 2,500 | 98 | 2,762 |
| 19 | 1,536 | 39 | 1,754 | 59 | 2,005 | 79 | 2,141 | 99 | 2,183 |
| 20 | 2,905 | 40 | 3,241 | 60 | 3,832 | 80 | 4,490 | 100 | 4,150 |
O ajuste do modelo ARIMA(2,0,0) com intercepto temos:
$$X_t = 1,28 + 0,35X_{t-1} + 0,54X_{t-2} + a_t$$
segue que,
$$X_{t+h} = 1,28 + 0,35X_{t+h-1} + 0,54X_{t+h-2} + a_{t+h}$$
$$\hat{X_t(h)} = 1,28 + 0,35\hat{X_t}(h-1) + 0,54\hat{X_t}(h-2)$$
portanto, as 3 primeiras previsões a partir de t = 100 são dadas por
$$\hat{X_{100}}(1) = 1,28 + 0,35X_{100} + 0,54X_{99} = 5,27$$
$$\hat{X_{100}}(2) = 1,28 + 0,35\hat{X_{100}}(1) + 0,54X_{100} = 3,90$$
$$\hat{X_{100}}(3) = 1,28 + 0,35\hat{X_{100}}(2) + 0,54\hat{X_{100}}(1) = 4,62$$
(imagem em falta)
A partir do momento em que temos o valor $ X_{101} $ podemos atualizar as previsões. Dado que $ X_{101} = 5,41 $ temos
$$a_{101} = X_{101} - \hat{X_{100}}(1) = 5,41 - 5,27 = 0,14.$$
Para a atualização, precisamos calcular os pesos $ \psi_j, j =1,2,…,5 $. Sabemos que devemos ter
$$\phi(B)\psi(B) = \theta(B)$$
ou seja,
$$(1 - 0,35B - 0,54B^2)(1 + \psi_1B + \psi_2B^2 + \cdots) = 1$$
é fácil ver que
$$\psi_1 = 0,35$$
$$\psi_2 = 0,35\psi_1 - 0,54 = -0,4175$$
$$\psi_3 = \psi_1\psi_2 - 0,54\psi_1 = -0,3351$$
desta forma,
$$\hat{X_{101}}(1) = \hat{X_{100}}(2) + \psi_1a_{101} = 3,90 + 0,35 \ast 0,14 = 3,95$$
$$\hat{X_{101}}(2) = \hat{X_{100}}(3) + \psi_2a_{101} = 4,62 - 0,4175 \ast 0,14 = 4,56$$
Exemplo 4.8.3.3
Considere o modelo ARIMA(0,1,2) dado por $ X_t = X_{t-1} - a_t - 0,17a_{t-1} - 0,62a_{t-2} $. Vamos calcular uma previsão para este modelo utilizando os dados da tabela abaixo:
| t | $ \bold{X_t} $ | t | $ \bold{X_t} $ | t | $ \bold{X_t} $ | t | $ \bold{X_t} $ | t | $ \bold{X_t} $ |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 6 | 0,155237 | 11 | 3,024628 | 16 | 3,087684 | 21 | 6,752729 |
| 2 | 7,951044 | 7 | 8,624721 | 12 | 9,738347 | 17 | 8,02558 | 22 | 7,482817 |
| 3 | 6,397658 | 8 | 3,640904 | 13 | 3,101355 | 18 | 2,516373 | 23 | 3,561021 |
| 4 | 4,610894 | 9 | 4,743764 | 14 | 3,223571 | 19 | 3,519417 | 24 | 4,574021 |
| 5 | 4,979417 | 10 | 6,885646 | 15 | 7,654261 | 20 | 8,479282 | 25 | 7,505544 |
Como visto no Exemplo 4.8.2.1, as previsões neste modelo com $ \theta_0 = 0 $, são calculadas por
$$\hat{X_t(h)} = [X_{t+h}] = X_t - (\theta_1 + \theta_2)a_t - \theta_2a_{t-1}$$
$$\hat{X_t(h)} = [X_{t+h}] = X_t - 0,79a_t - 0,62a_{t-1}.$$
após os ajuste, temos os seguintes resíduos
| t | $ \bold{a_t} $ | t | $ \bold{a_t} $ | t | $ \bold{a_t} $ | t | $ \bold{a_t} $ | t | $ \bold{a_t} $ |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 6 | 0,12919554 | 11 | 2,4073518 | 16 | -0,296116 | 21 | 2,2849263 |
| 2 | 1,00483218 | 7 | -0,88764535 | 12 | 0,6177981 | 17 | -1,247726 | 22 | -0,727535 |
| 3 | -0,16309921 | 8 | -2,25773061 | 13 | -0,057221 | 18 | 0,876457 | 23 | 0,9349287 |
| 4 | 0,32909621 | 9 | -0,52464252 | 14 | -1,644572 | 19 | 0,9083047 | 24 | 1,9634528 |
| 5 | -0,50776379 | 10 | 0,72467078 | 15 | 0,975214 | 20 | 0,1950138 | 25 | -1,635194 |
Segue que a previsão de t = 26, a partir da origem t = 25 é dada por
$$\hat{X_{25}}(1) = X_{25} - 0,79a_{25} - 0,62a_{24}$$
$$\hat{X_{25}}(1) = 7,50 - 0,79(-1,63) - 0,62(1,96) = 7,5725$$
4.8.4 - Intervalos de Confiança
Sabemos que uma previsão não se trata de algo exato, por isso é interessante estimarmos um intervalo de confiança para as previsões. Para isso, será necessário uma suposição adicional para os erros de previsões, ou seja, além de supormos que $ E(a_t) = 0 $, $ Var(a_t) = \sigma_a^2 $ para todo t e $ E(a_ta_s) = 0 $, $ t \not= s $, iremos supor que $ a_t \sim N(0,\sigma_a^2) $, para cada t.
Segue que, dado os valores passados e presentes da série, $ X_t, X_{t-1}, \dots $, a distribuição condicional de $ X_{t+h} $ será $ N(\hat{X_t(h)}, Var(h)) $.
Sabemos que
$$Z = \frac{X_{t+h} - \hat{X_t(h)}}{[Var(h)]^{1/2}} \sim N(0,1)$$
fixando o coeficiente de significância $ \alpha $, temos que
$$P(-z_{\alpha} \ < \ Z \ < \ z_{\alpha}) = 1 - \alpha$$
ou seja, um intervalo de confiança com nível de confiança de $ (1 - \alpha) $ é dado por
$$\hat{X_t(h)} - z_{1-\alpha}[Var(h)]^{1/2} \le X_{t+h} \le \hat{X_t(h)} + z_{1-\alpha}[Var(h)]^{1/2}.$$
Mas, temos que em Var(h), o valor de $ \sigma^2_a $ não é conhecido e, portanto, é substituído pela sua estimativa $ \sigma^2_a $. Desta forma, o intervalo de confiança para a previsão de $ X_{t+h} $ será dado por
$$\hat{X_t(h)} - z_{1-\alpha}\hat{\sigma}_a^2\Bigg[1+ \sum^{h-1}_{j=1} \psi_j^2 \Bigg]^{1/2} \le X_{t+h} \le \hat{X_t(h)} + z_{1-\alpha}\hat{\sigma}_a^2\Bigg[1+ \sum^{h-1}_{j=1} \psi_j^2 \Bigg]^{1/2}.$$
Exemplo 4.8.4.1
Vamos determinar um intervalo de confiança para $ X_{t+h} $ no Exemplo 4.8.3.2 para h = 3.
Assim, temos
$$\hat{Var}(3) = (1 + \psi_1^2 + \psi_2^2)\hat{\sigma}^2_a, \text{ onde } \hat{\sigma}^2_a = 0,17$$
Logo,
$$\hat{Var}(3) = (1+ (-0,4175)^2 + (0,3351)^2)0,17 =0,219$$
Para $ \alpha = 5(porcentagem) $ temos $ z_{\alpha} = 1,96 $. Portanto,
$$\hat{X_t}(3) - 1,96[\hat{Var}(3)]^{1/2} \le X_{t+3} \le \hat{X_t}(3) + 1,96[\hat{Var}(3)]^{1/2}$$
Desta forma, um intervalo de confiança para $ X_{103} $ é $ [3,703; 5,536] $.
5 - Séries Temporais Financeiras
No mercado financeiro uma grande ferramenta de auxilio na previsão do mercado é a estimativa de volatilidade dos ativos. Este parâmetro não é diretamente observável e por isso modelos para o cálculo de volatilidade foram estimados utilizando regressão linear.
Neste capítulo, apresentamos algumas metodologias para o cálculo de volatilidade e qual interpretação devemos dar a estes dados.
5.1 - Retornos
A maior parte dos estudos financeiros concentram-se na análise de séries de retornos ao invés do uso da série dos preços dos ativos. A razão de utilizarmos série de retornos tem dois fatores, as informações de retornos atendem aos interesses de investidores e a série de retornos possui propriedades estatísticas mais interessantes do que série dos preços.
Denotamos o preço do ativo no instante $ t $ por $ P_t $, podemos calcular o retorno entre os instantes $ t-1 $e $ t $ é por
$$R_t = \frac{P_t - P_{t-1}}{P_{t-1}} = \frac{P_t}{P_{t-1}} - 1 \quad \Longrightarrow \quad 1 + R_t = \frac{P_t}{P_{t-1}}$$
Na prática, os preços dos ativos entres os instantes $ t $ e $ t - \Delta t $ são bastante próximos e portanto $ R_t \ < < \ 1 $.
Sabemos que neste caso, $ ln(1 + R_t) \approx R_t $ então é aconselhável utilizar o log-retorno
$$r_t = ln(1 + R_t) = ln\Bigg(\frac{P_t}{P_{t-1}}\Bigg) = ln(P_t)- ln(P_{t-1}) \approx R_t$$
Utilizamos log-retorno devido a suas propriedades estatísticas, como estacionariedade e ergodicidade.
Podemos descrever alguns fatos estiliazados que são encontrados na maioria das séries de retornos:
(i) estacionariedade;
(ii) fraca dependência linear e não linear;
(iii) caudas pesadas na distribuição e excesso de curtose;
(iv) comportamento heterocedástico condicional.
O comportamento heterocedástico reúne características como aglomerados de volatilidade e efeitos alavanca, que aponta para o efeito de choque. Choques negativos normalmente afetam a volatilidade condicional em maior magnitude do que choques positivos, ou seja, uma queda no retorno implica uma volatilidade condicional alta.
Exemplo 5.1.1
Considere observações das ações da Petrobras no dia 21/07/2009 a cada minuto, com um total de 401 observações. Calculamos os retornos neste dia.
(imagem em falta)
5.2 - Volatilidade
A volatilidade é um dos parâmetros de maior relevância no apreçamento de ações. É uma variável não observável diretamente. Além disso, a volatilidade em séries financeiras não é constante ao longo do tempo, responsável portanto pelo seu comportamento heterocedástico.
As características da volatilidade podem ser modeladas por processos heterocedásticos condicionais ARCH (Autoregressive Conditional Heterocedasticity) introduzida por Engle(1982) e sua extensão GARCH (Generalized ARCH) proposto por Bollerslev (1986).
5.2.1 - Modelos ARCH
O primeiro modelo desenvolvido para estimação da volatilidade foi proposto por Engle (1982) denominado ARCH (Autoregressive Conditional Heterocedasticity) que utilizando uma função quadrática das observações passadas estima-se a volatilidade no instante t.
Considere $ r_t $ uma série temporal estacionária de retornos, estimamos a sua variância condicional(volatilidade) $ h_t $ no instante $ t $ utilizando um modelo ARCH de ordem q por
$$r_t = \sqrt{h_t} \varepsilon_t,$$
$$h_t = \alpha_0 + \alpha_1r_{t-1}^2 + \cdots + \alpha_qr_{t-q}^2$$
onde $ \alpha_0 \ > \ 0, \alpha_i \ge 0, i=1,2,…,q-1, \alpha_q \ > \ 0 $ são condições que garantem a positividade de $ h_t $, além disso segue que $ \varepsilon_t $ é i.i.d. com média zero, e possui uma distribuição normal ou t-student. As constantes $ \alpha_i, i = 0,1,2,…,q $ são calculadas utilizando Regressão Linear.
Uma condição que garante que um processo ARCH(q) é estacionário
$$ \sum^q_{i = 1} \alpha_i \ < \ 1.$$
Um processo ARCH estacionário, tem as seguintes estatísticas
$$E(r_t) = 0$$
$$Var(r_t) = \alpha_0 / \Bigg (1 - \sum^q_{i=1} \alpha_i \Bigg)$$
$$Cov(r_t,r_{t-k}) = E(r_t,r_{t-k}) = 0, \quad k = 1, 2,…$$
Para melhor compreender um modelo ARCH, consideremos um modelo ARCH(1), em que a sua variância condicional depende apenas do instante anterior.
$$r_t = \sqrt{h_t} \varepsilon_t$$
$$h_t = \alpha_0 + \alpha_1r_{t-1}^2$$
com $ \alpha_0 \ > \ 0 $ e $ \alpha_1 \ge 0 $.
Pode-se demonstrar que o modelo possui as seguintes propriedades:
- A média não condicionada de $ r_t $ é zero;
- A variância não condicionada de $ r_t $ é dada por $ Var(r_t) = \frac{\alpha_0}{1 - \alpha_1}. $
Na construção de modelos ARCH, um primeiro passo é tentar ajustar um modelo ARIMA, para remover a correlação serial na série, se esta existir.
Segue que, quando nos referimos a $ r_t $, estamos supondo que a série de retornos é não correlacionada ou então ela é o resíduo da aplicação de um modelo ARIMA à série original.
Para verificar se a série apresenta heterocedasticidade condicional, podemos aplicar o teste de Ljung - Box na série $ r_t^2 $.
Exemplo 5.2.1.1
Consideramos uma série temporal com as cotações das ações da Petrobras durante o dia 21/07/2009 minuto a minuto. Vamos calcular a série de retornos e ajustar um modelo ARCH para o calculo da volatilidade neste dia.
(imagem em falta)
Aplicando o teste de Ljung - Box para analisar a autocorrelação de $ r_t^2 $ obtemos um p-valor de 0,5049, ou seja, aceitamos que a série não é i.i.d., isto é, existe autocorrelação na série. Precisamos então ajustar um modelo ARIMA na série de retornos.
Utilizando o critério de informação AIC, identificamos um modelo ARIMA(2,0,0) como melhor ajuste à série de retornos.
$$r_t = 0,18r_{t-1} - 0,09r_{t-2} + a_t$$
Desta forma, ajustando um modelo ARIMA(2,0,0)-ARCH(1), temos que a variância condicional(volatilidade) pode ser calculada em cada instante t por
$$r_t = 0,18r_{t-1} - 0,09r_{t-2} + a_t$$
$$a_t = \sqrt{h_t}\varepsilon_t$$
$$h_t = 1.6 \ast 10^{-8} + 0,139a_{t-1}^2$$
Fazendo uma análise nos resíduos do modelo, verificamos normalidade nos resíduos e utilizando o teste de Ljung - Box obtemos um p-valor de 0,95 indicando que o modelo é adequado para modelar dependência linear entre sucessivos retornos.
(imagem em falta)
Exemplo 5.2.1.2
Considere os valores das ações da Petrobras, minuto a minuto, durante o dia 8 de julho de 2010. Vamos modelar as observações através de uma série temporal, calcular os retornos e a volatilidade utilizando o ARCH.
(imagem em falta)
Inicialmente aplicamos o teste de Ljung - Box para autocorrelação nos retornos e com um p-valor = 0,99 rejeitamos a hipótese das observações serem i.i.d.. Portanto, precisamos ajustar um modelo ARIMA aos retornos para podermos utilizar o ARCH para o cálculo da volatilidade.
Através do teste ADF, detectamos que a série de retornos não é estacionária. Calculamos a série de diferenças para alcançar a estacionariedade e identificamos o modelo ARIMA(2,1,3) como melhor modelo para descrever as observações através do critério AIC.
$$r_t = -1,84r_{t-1} - 0,88r_{t-2} + a_t - 0,87a_{t-1} + 0,95a_{t-2} + 0,87a_{t-3}$$
A partir dos resíduos do modelo ARIMA(2,1,3), calculamos 4 modelos ARCH para identificar o melhor através do critério AIC
| Modelo | AIC |
|---|---|
| ARCH(1) | -6244,382 |
| ARCH(2) | -6345,931 |
| ARCH(3) | -6349,556 |
| ARCH(4) | -6339,856 |
Portanto, o melhor modelo via critério AIC é o ARCH(3)
$$r_t = -1,84r_{t-1} - 0,88r_{t-2} + a_t - 0,87a_{t-1} + 0,95a_{t-2} + 0,87a_{t-3}$$
$$a_t = \sqrt{h_t}\varepsilon_t$$
$$h_t = 3,24 \ast 10^{-9} + 0,009a_{t-1}^2 + 0,18a_{t-2} + 3,4 \ast 10^{-15}a_{t-3}$$
(imagem em falta)
5.2.2 - Modelos GARCH
Modelos GARCH(generalized ARCH) se trata de um generalização dos modelos ARCH, proposto por Bollerslev(1986). A diferença entre os modelos é uma componente adicional, referente à varância condicional nos instantes anteriores. A vantagem do modelo GARCH é que ele pode ser utilizado para descrever a volatilidade com menos parâmetros do que um modelo ARCH.
Um modelo GARCH(p,q) é definido por
$$r_t = \sqrt{h_t}\varepsilon_t,$$
$$h_t = \alpha_o + \sum_{i=1}^{p}\alpha_ir_t^2 + \sum^q_{j=1}\beta_jh_{t-j}$$
em que $ \varepsilon_t $ é i.i.d., $ \alpha_0 \ > \ 0, \alpha_i \ge 0, \beta_j \ge 0 $. As constantes do modelo, $ \alpha_i $ e $ \beta_j $ são calculadas utilizando Regressão Linear.
Analogamente ao caso do modelo ARCH, segue que os $ \varepsilon_t $ são normais ou seguem um distribuição t-Student.
A estacionariedade de um modelo GARCH de ordem (p,q) é garantida se
$$\sum_{i=1}^m(\alpha_i + \beta_i) \ < \ 1, \quad \text{em que }m = max(p,q).$$
A identificação da ordem de um modelo GARCH a ser aplicado a uma série temporal real é difícil, recomenda-se que ajuste vários modelos de baixa ordem e depois escolha o melhor se baseando em vários critérios, como AIC ou BIC, valores de assimetria e curtose, da log-verossimilhança ou de alguma função de perda.
Exemplo 5.2.2.1
Considere a série temporal do IBOVESPA, referente ao dia 29/07/2009 com observações geradas minuto a minuto. Vamos calcular a série de retornos e ajustar um modelo GARCH(1,1) para o calculo da volatilidade.
(imagem em falta)
Aplicando o teste de Ljung - Box para analisar a autocorrelação de $ r_t $, aceitamos a hipótese de que os retornos são i.i.d., então, não precisamos utilizar um modelo ARIMA para ajustar os dados.
Ajustamos um modelo GARCH(1,1) diretamente aos retornos e obtemos
$$r_t = \sqrt{h_t}\varepsilon_t$$
$$h_t = 7,617 \ast 10^{-7} + 0,127r_{t-1}^2 + 0,843h_{t-1}^2$$
Fazendo uma análise nos resíduos do modelo, verificamos a normalidade nos resíduos e, utilizando o teste de Ljung - Box no quadrado dos resíduos obtemos um p-valor = 0,806, indicando que o modelo é apropriado para descrever a dependência linear entre os sucessivos retornos.
(imagem em falta)
Exemplo 5.2.2.2
Considere os Índices da Bovespa durante o dia 05 de maio de 2010. Vamos modelar as observações minuto a minuto através de uma série temporal calcular os retornos e as volatilidades utilizando o GARCH.
(imagem em falta)
Inicialmente aplicamos o teste de Ljung - Box para autocorrelação nos retornos e aceitamos a hipótese dos retornos serem i.i.d., portanto, podemos calcular a volatilidade diretamente nos retornos.
Verificamos 4 modelos para identificar o melhor para o calculo da volatilidade através do critério AIC, obtemos
| Modelo | AIC |
|---|---|
| GARCH(1,1) | -6448,39 |
| GARCH(1,2) | -6359,22 |
| GARCH(2,1) | -6354,13 |
| GARCH(2,2) | -6359,84 |
Desta forma, identificamos o GARCH(1,1) o modelo mais adequado para o cálculo da volatilidade.
$$r_t = \sqrt{h_t}\varepsilon_t$$
$$h_t = 2,743 \ast 10^{-7} + 0,25r_{t-1}^2 + 0,58h_{t-1}^2$$
Fazendo uma análise nos resíduos do modelo, verificamos a normalidade nos resíduos e, utilizando o teste de Ljung - Box no quadrado dos resíduos, obtemos um p-valor = 0,466, indicando que o modelo é apropriado para descrever a dependência linear entre os sucessivos retornos.
(imagem em falta)
5.3 - Cointegração em Séries Temporais
Cointegração em séries temporais é de suma importância para quem trabalha com séries econômicas, pois possibilitam estudar e analisar relações estruturais entre as séries envolvidas. Mais precisamente, testes de cointegração permitem determinar se as séries temporais envolvidas possuem ou não uma relação a longo prazo.
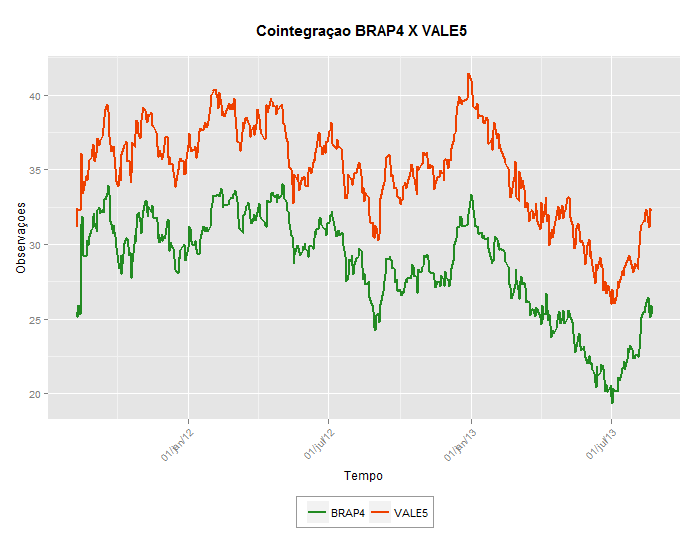
Existe na literatura, vários testes para detectar cointegração em séries temporais. Os mais complexos utilizam uma representação em vetor autoregressivo, proposto pro Johansen, e temos testes que consistem em modelos de regressão, estudando uma combinação linear entre as séries temporais envolvidas.
5.3.1 - Introdução
Para iniciarmos o estudo sobre cointegração precisamos entender alguns conceitos iniciais. Considere um modelo de regressão linear simples para $ y_t $ contendo uma tendência linear fixa, de inclinação $ \beta $.
$$y_t = y_0 + \beta t + u_t, \quad t=1,…,T$$
Então, o termo de erro $ u_t $ é um processo autorregressivo de primeira ordem
$$u_t = \rho u_{t-1} + \varepsilon_t$$
onde $ \varepsilon_t $ é um ruido branco, isto é, é uma sequência de erros aleatórios I.I.D com distribuição $ N(0,\sigma^2_\varepsilon) $.
Reescrevendo a equação acima utilizando operador de retardo temos
$$u_t = \frac{\varepsilon_t}{1 - \rho L}$$
Analisando $ \rho $ percebemos que se $ |\rho| < 1 $ podemos expandir o termo $ 1/(1 - \rho L) $ por $ (1 + \rho L + \rho^2 L^2 + \cdots) $, entao
$$u_t = \varepsilon_t + \rho \varepsilon_{t-1} + \rho^2 \varepsilon_{t-2} + \cdots$$
Neste caso, $ u_t $ será a soma dos ruídos brancos $ \varepsilon_{t-i} $ tal que o efeito de pertubação diminui com o passar do tempo, pois $ |\rho| < 1 $. Dizemos então que o processo $ u_t $ é não integrado, ou ainda, integrado de ordem 0, denotado por $ u_t \sim I(0) $. Utilizando palavras que ja conhecemos, isto quer dizer que o processo $ u_t $ não possui raiz unitária e é estacionário.
Caso $ \rho = 1 $ temos
$$u_t = \varepsilon_t + \varepsilon_{t-1} + \varepsilon_{t-2} + \cdots$$
então, $ u_t $ possuirá uma pertubação persistente que tende ao infinito com o passar do tempo, conhecida como tendência estocástica $ \sum_{i=1}^t \varepsilon_t $. Se analisarmos as raízes do termo $ (1 - \rho L) $ notamos que $ u_t $ possui uma raiz unitária e, portanto, é não estacionário. Dizemos então que $ u_t $ é integrado de ordem 1, denotado por $ u_t \sim I(1) $.
Cointegração
Para determinar se duas ou mais séries temporais são cointegradas precisamos que algumas hipóteses sejam verificadas:
-
As duas séries são não estacionárias de ordem I(1);
-
Existe pelo menos uma combinação linear das séries temporais a qual o resíduo da regressão entre elas é estacionária.
Com essas hipóteses satisfeitas dizemos que existe uma relação de cointegração nas séries temporais envolvidas.
Definição 6.1
Dizemos que duas séries temporais $ X_t $ e $ Y_t $ não estacionárias de ordem I(1) são cointegradas se existe um $ \beta $ tal que
$$Z_t = Y_t - \beta X_t$$
De forma que a série $ Z_t $, conhecida como Spread Residual, é estacionária.
5.3.2 - Teste de Engle - Granger
O teste mais conhecido para detectar cointegração entre séries temporais é o teste de Engle - Granger, que segue basicamente a definição de cointegração. As hipóteses do teste são

Sejam $ X_t $ e $ Y_t $ duas séries temporais. Primeiramente precisamos verificar se $ X_t $ e $ Y_t $ são não estacionárias de ordem I(1), para isso podemos utilizar algum teste de raiz unitária, por exemplo: Teste ADF, teste PP ou teste KPPS.
Após verificado a presença de raiz unitária nas séries temporais $ X_t $ e $ Y_t $, precisamos definir qual o tipo de regressão se adequa melhor aos nossos dados, entre os casos: Com intercepto, com tendência e intercepto ou sem nenhum termo adicional. Em cada caso, os modelos de regressão são dados por
$$Z_t = Y_t - \beta X_t + \alpha $$
$$Z_t = Y_t - \beta X_t + \gamma t + \alpha $$
$$Z_t = Y_t - \beta X_t $$
respectivamente, onde $ \beta $ é o parâmetro de cointegração, $ \alpha $ é o intercepto (constante) e $ \gamma $ é o parâmetro de tendência.
Assim, aplicamos novamente um teste de raiz unitária nos resíduos, respeitando o modelo adotado em $ Z_t $, porém, com valores críticos levemente alterados pois estamos reaplicando o teste em uma aproximação. Neste caso estes valores foram simulados utilizando simulação de Monte Carlo.
Exemplo 5.3.2.1
Sejam $ X_t $ e $ Y_t $ duas séries temporais dos valores de fechamento diário dos ativos ACBC4 e ITUB3 da bolsa de valore de São Paulo, durante o período de 9 de agosto de 2011 a 22 de agosto de 2013. Vamos verificar se existe cointegração entre $ X_t $ e $ Y_t $.
Primeiramente, aplicamos o teste ADF às séries $ X_t $ e $ Y_t $, obtendo p-valores 0,569 e 0,592 respectivamente, portanto aceitamos a hipótese nula das séries serem não estacionárias.
Calculando o parâmetro $ \beta $ obtemos o spread
$$Z_t = Y_t - 0,4671 X_t$$
Aplicando o teste ADF ao resíduo da regressão obtemos um p-valor de 0,031, portanto, rejeitamos a hipótese nula de as séries $ X_t $ e $ Y_t $ não serem cointegradas, isto é, $ X_t $ e $ Y_t $ são cointegradas.
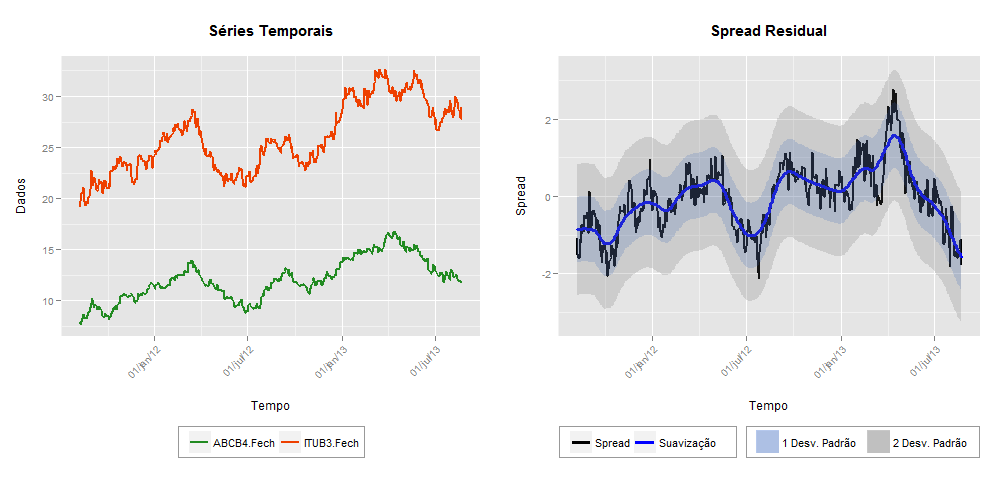
5.3.3 - Teste de Phillips - Ouliaris
Phillips e Ouliaris propuseram dois testes baseados nos resíduos, chamados Taxa de Variância e Traço Multivariado. A Diferença entre eles é que o teste usando a estatística do Traço Multivariado tem a propriedade de ser invariante à normalização, isto é, qual é a variável explicada e qual é a explicativa.
As hipóteses do teste são:

Seja $ x_t $ e $ y_t $ duas séries temporais. Inicialmente verificamos se as séries $ x_t $ e $ y_t $ são não estacionárias de ordem I(1) utilizando algum teste de raiz unitária: Teste ADF, teste PP ou teste KPPS.
Após verificado a presença de raiz unitária em $ x_t $ e $ y_t $ tomamos a partição $ \mu_t = (y_t, x_t \prime) $ calculamos um vetor autorregressivo de primeira ordem, isto é, fazemos uma regressão de $ \mu_t $ em $ \mu_{t-1} $ sem intercepto
$$\mu_t = \alpha \mu_{t-1} + r_t$$
Baseando-se no resíduo da regressão de defasagem, Phillips e Ouliaris propõem duas estatísticas que podem ser utilizadas para detectar cointegração entre as séries temporais:
- Taxa de Variância:
$$P_u = \frac{N^2\hat{\omega_{11.2}}}{\sum^N_{i=1}\hat{r_i}^2}$$
onde
$$\hat{\omega_{11.2}} = \hat{\omega_{11}} - \hat{\omega_{21}}\prime\hat{\Omega_{22}}^{-1} \hat{\omega_{21}}$$
Tal que $ \Omega $ representa matriz de variância e covariância escrita na forma
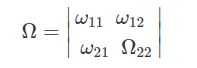
e é estimada por
$$ \hat{\Omega} = N^{-1}\sum_{t=1}^N r_t^2 + N^{-1}\sum_{s=1}^l w_{sl}\sum_{t = s+1}^N (r_t r_{t-s}\prime+r_{t-s}r_t\prime)$$
onde $ r_t $ são os resíduos da regressão de defasagem acima e $ w_{ls} = 1 - s/(l+1) $ para algum número de defasagens $ l $.
- Traço Multivariado:
$$P_z = N tr(\hat{\Omega}M_{zz}^{-1}), \quad \hbox{onde} \quad M_{zz} = N^{-1}\sum_{t=1}^N \mu_t \mu_t\prime$$
em que $ \hat{\Omega} $ igual definida acima.
Exemplo 5.3.3.1
Considere os ativos financeiros da bolsa de valores de São Paulo, ITSU4 e ITUB4. Vamos analisar se os ativos financeiros são cointegrados durante o período de 01/08/2011 à 09/09/2013 com observações a cada 15 minutos em um total de 14531 observações.
Utilizamos o Action para efetuar os cálculos e obtemos os resultados:
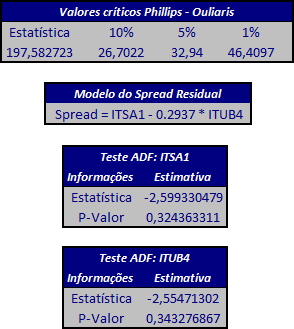
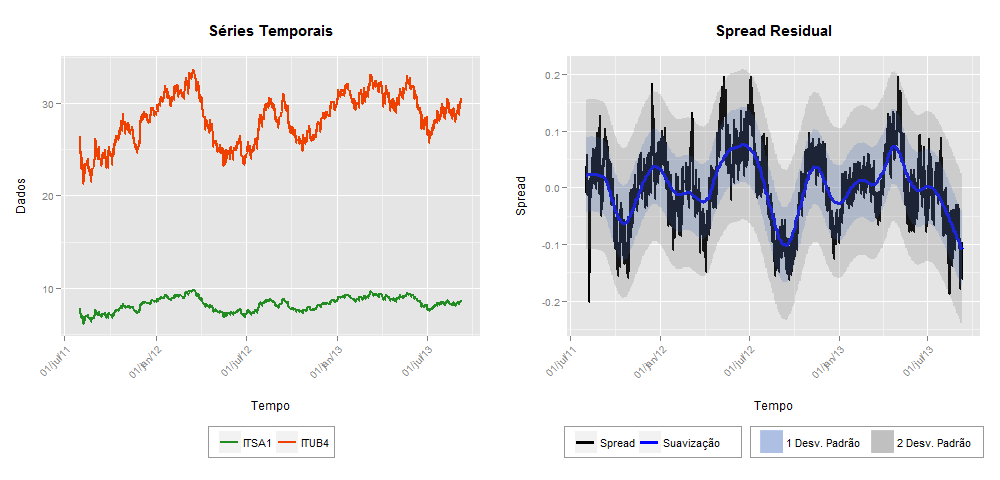
Portanto, recusamos a hipótese nula de que não existe cointegração entre as séries temporais.
5.3.4 - Modelo de Vetores Autorregressivos (VAR)
Esta metodologia é uma extensão de uma regressão univariada para um ambiente multivariado, onde cada equação definida pelo VAR é uma regressão por mínimos quadrados ordinários de determinada variável em variáveis defasadas de si própria e de outras variáveis componentes do modelo.
O modelo VAR pode ser expresso por
$$X_t = A_0 + A_1X_{t-1} + \cdots + A_pX_{t-p} + B_0Z_1 + B_1Z_{t-1} + \cdots + B_pZ_{t-p} + e_t$$
onde:
- $ A_0 $ é o vetor de termos de interceptos;
- $ A_1,..,A_p $ são matrizes $ N \times N $ de coeficientes que relacionam valores defasados das variáveis endógenas.
- $ B_0,…,B_p $ são matrizes $ N \times N $ que relatam valores atuais e defasados de variáveis exógenas;
- $ e_t $ é uma vetor $ N \times 1 $ de erros.
Para selecionar o melhor modelo VAR, usa-se os critérios de informações SC e AIC, os quais são importantes para determinar o número de defasagens a serem incluídas no modelo. Assim, como estes critérios levam em consideração a soma dos quadrados dos resíduos, o número de observações e de estimadores do parâmetro, temos que quanto menor forem os valores, melhor será o modelo.
No estudo de cointegração, uma adaptação do modelo VAR foi proposta, conhecido como modelo de correção de erros (VEC) que pode ser escrito como
$$\Delta Z_t = \Gamma_1 \Delta Z_{t-1} + \cdots + \Gamma_{k-1} \Delta Z_{t-k+1} + \Pi Z_{t-k} + \Phi D_t + u_t$$
onde:
- $ Z_t $ é um vetor com k variáveis;
- $ u_t $ é um vetor de erro aleatório;
- $ D_t $ é um vetor binário para captar a variação sazonal;
- $ \Gamma_i = -(I - A_1 - \cdots - A_i), (i = 1,2,…,k-1) $;
- $ \Pi = -(I - A_1 - \cdots - A_k) $
na qual a matriz $ \Pi $ tem fundamental importância na análise se cointegração, cada linha de $ \Pi $ representa uma relação de cointegração.
5.3.5 - Teste de Johansen
Seja $ Z_t $ uma matrix $ (n \times p) $ de séries temporais sendo que cada coluna representa uma série temporal. Para utilizarmos a metodologia de Johansen é necessário modelar $ Z_t $ como um vetor autorregressivo (VAR) sem restrições envolvendo k defasagens de $ Z_t $. O modelo VAR pode ser escrito da seguinte forma
$$Z_t = A_1 Z_{t-1} + \cdots + A_k Z_{t-k} + \Phi D_t + u_t$$
onde $ u_t \sim IN(0, \sum), Z_t $ é um vetor $ (n \times 1) $ e cada elemento $ A_i $ é uma matriz de parâmetros de ordem $ (n \times n) $ e $ D_t $ representa termos determinísticos, tais como constante, tendência linear e sazonalidade.
No caso da metodologia de Johansen também se torna necessário determinar a ordem da defasagem de $ Z_t $, pois este procedimento tem como base a hipótese de que ao se introduzir um certo número de defasagem, é possível obter os resíduos bem comportados, isto é, estacionários.
Desta forma, a equação acima pode ser modificada em termos de um modelo de correção de erros (VEC) da seguinte forma
$$\Delta Z_t = \Gamma_1 \Delta Z_{t-1} + \cdots + \Gamma_{k-1} \Delta Z_{t-k+1} + \Pi Z_{t-k} + \Phi D_t + u_t$$
onde $ \Gamma_i = -(I - A_1 - \cdots - A_i), (i = 1,2,…,k-1), $ e $ \Pi = -(I - A_1 - \cdots - A_k) $. A principal vantagem em escrever o sistema em termos do modelo de correção de erros é o fato de que, nesse formato, são incorporadas informações de longo e curto prazo.
A metodologia de Johansen apresenta três situações se baseando no posto de $ \Pi $
- $ \Pi $ possui posto completo. Neste caso temos que há $ p = r $ colunas linearmente independentes, então as variáveis em $ Z_t $ são $ L(0) $, isto é, as séries em $ Z_t $ são estacionárias.
- $ \Pi $ possui posto igual a zero, então não existe cointegração nas séries temporais de $ Z_t $
- $ \Pi $ possui posto reduzido. Este é o caso mais importante, quando há $ r \le (p-1) $ séries cointegradas em $ Z_t $, podemos escrever $ \Pi = \alpha \beta $ sendo que $ \alpha $ é uma matriz $ (n \times p) $ que representa a velocidade de ajustamento dos parâmetros da matriz no curto prazo e $ \beta $ é uma matriz $ (n \times p) $ de coeficientes de cointegração de longo prazo. Podemos então, dizer que o termo $ \beta Z_{t-k} $ representa as $ p-1 $ relações de cointegração no modelo multivariado, assegurando assim que $ Z_t $ converge para uma solução a longo prazo.
Para testar a presença de séries cointegradas em $ Z_t $ existe duas estatísticas a serem consideradas
$$J_{trace} = -T \sum_{i = r+1}^n ln(1 - \hat{\lambda}_i)$$
$$J_{max} = -T ln(1 - \hat{\lambda}_{r+1})$$

A estatística $ J_{trace} $ testa as hipóteses
$$H_0: \lambda_i = 0; \quad i=r+1, … , n$$
$$H_1: \lambda_i = 0; \quad i=1,2,…,n$$
Ou seja, a hipótese nula é que somente os $ r $ primeiros autovalores são diferentes de zero, isto é, existe $ r $ séries temporais cointegradas em $ Z_t $.
A estatística $ J_{max} $ testa a hipótese nula de existir $ r $ séries cointegradas contra existir $ r+1 $ séries cointegradas, a qual na prática não é utilizada, uma vez que o teste da estatística $ J_{trace} $ foi mostrado ser mais robusto para simetria e excesso de curtose.
Os valores críticos da estatística $ J_{trace} $ foram calculadas por Johansen em 1995, através de estudos de simulações utilizando Movimento Browniano.
Exemplo 5.3.5.1
Considere $ Z_t $ uma matriz com duas séries temporais referente aos ativos financeiros GGBR4 e GOAU3 da bolsa de valores de São Paulo durante o período de 09/08/2013 a 03/09/2013. Vamos testar a cointegração entre os ativos utilizando o teste de Johansen
Devido ao fato da metodologia de Johansen ser bastante complexa, não é viável gerar os cálculos analiticamente. Portanto, utilizando o Action para efetuar os cálculos obtemos os seguintes resultados:

Então, rejeitamos a hipótese de existir 0 cointegrações e aceitamos a hipótese de existir 1 relação de cointegração em $ Z_t $. Conclusão: Os ativos financeiros GGBR4 e GOAU3 são cointegrados.
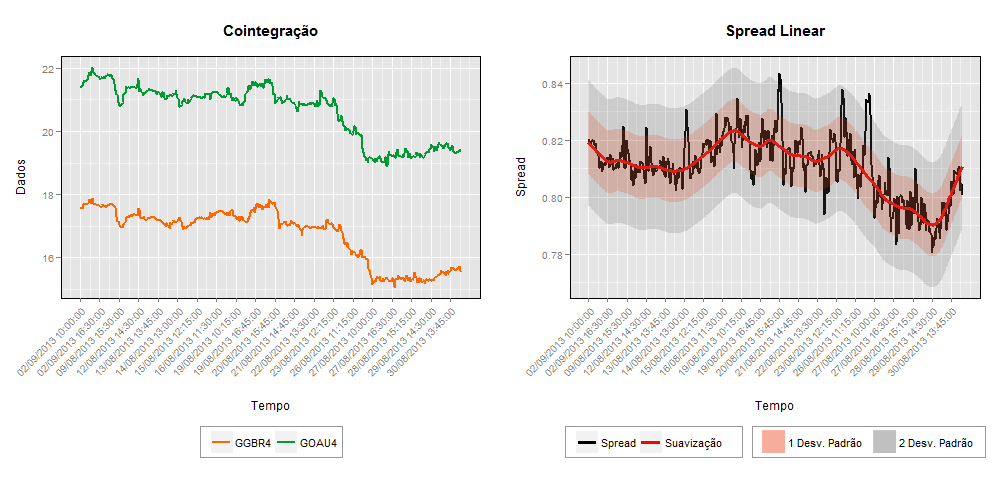
5.4 - Pairs Tradring
5.4.1 - Introdução
Pairs trading é uma estratégia que implica em encontrar ativos financeiros cointegrados e através do estudo sobre o spread pode-se identificar momentos certos a se investir nos ativos financeiros envolvidos.
Podemos dividir a estratégia em duas etapas:
- Encontrar pares de ativos financeiros cointegrados com a característica de reversão de média, através ds dados históricos dos ativos financeiros;
- Realizar testes no spread para identificar com quais parâmetros encontra-se os melhores momentos para investimento.
Para descobrirmos se o par cointegrado possui a propriedade de reversão de média podemos utilizar o teste de Dickley - Fuller para estacionariedade. Considere a taxa logaritima $ y_t = logA_t + logB_t $ onde $ A_t $ e $ B_t $ são os preços dos ativos financeiros $ A $ e $ B $. Então, testamos
$$\Delta y_t = \mu + \gamma y_{t-1} + \varepsilon_t$$
Em outras palavras, estamos testando $ \Delta y_t $ nos valores defasados de $ y_t $. A hipótese nula do teste é que $ \gamma = 0 $, a qual implica que o processo não possui reversão de média. Portanto, se rejeitarmos a hipótese nula com nível de confiança superior a 99% temos que o processo será estacionário e possui a característica de reversão de média.
Estudos dizem que se o nível de confiança do teste não for muito alto os pares não possuem reversão de média suficientemente boa o qual implica em retornos não satisfatórios.
A segunda etapa da estratégia não é exatamente definida e possui vários ajustes diferentes em cada caso que é fundamental para se obter lucro. Podemos considerar que dependendo do número de ativos financeiros avaliados no estudo, encontraremos muitos pares cointegrados que podem ser avaliados para compra e venda, mas alguns pares não são viáveis devido a quesitos práticos, como por exemplo o volume movimentado pelos ativos financeiros.
Portanto, dentre os pares cointegrados encontrados utilizamos algumas medidas para “filtrar” os resultados e utilizar apenas os pares com potenciais.
Referências
[1] Morettin, Pedro A. “Econometria financeira.” Edgard Blücher, (2008).
[2] Morettin, Pedro A., and Clélia Toloi. Análise de séries temporais. Blucher, 2006.
[3 ]Vidyamurthy, Ganapathy. Pairs Trading: quantitative methods and analysis. Vol. 217. John Wiley & Sons, 2004.
[4] Hendry, David F., and Katarina Juselius. “Explaining cointegration analysis: Part 1.” The Energy Journal (2000): 1-42.
[5] Hendry, David F., and Katarina Juselius. “Explaining cointegration analysis: Part II.” The Energy Journal (2001): 75-120.