22. Tabela Cruzada
A tabela cruzada, também conhecida como tabela de contingência, tem como principal objetivo que uma variável não seja influenciada pela outra, entretanto, em muitos casos esta influência ocorre. Este tipo de influência pode ser vista de dois modos.
A primeira é quando variáveis classificatórias causam uma dependência nos grupos ou populações. Para este tipo de influência, podemos citar um grupo de pessoas com doenças psiquiátricas, em que são classificadas como “atividade retardada” e “atividade não retardada” e que cada grupo pode ser classificado em três categorias, “desordem afetiva”, “esquizofrenia” e “neurose”. Para este tipo de aplicação queremos testar se o tipo de atividade sofre alguma influência das categorias de doenças psiquiátricas, ou seja, queremos testar se os grupos têm independência em relação as atividades retardadas ou não.
A segunda é usada quando pretendemos saber se os dados associados às categorias de uma das variáveis se comporta de modo homogêneo ou similar nas diversas classes ou populações definidas pelas categorias da outra variável classificatória. Para este tipo de influência podemos citar a efetividade de um medicamento, para isto selecionamos 100 doentes, dentre eles 50 são medicados e os outros 50 recebem um placebo, neste estudo foram verificados os efeitos secundários presentes ou ausentes. Para estes efeitos podemos fazer uma classificação em diversos modos, como por exemplo, se o indivíduo teve ou não uma melhora na doença, ou ainda se obteve uma reação ao tipo de medicamento. Nesta aplicação, queremos testar se o grupo de indivíduos medicados e o grupo de indivíduos que usaram placebo têm comportamentos similares em relação a esses efeitos secundários, isto é, se as populações são homogêneas.
Em geral, uma tabela cruzada r x c é uma matriz de números naturais dispostos em r linhas e c colunas, dessa forma temos rc células para os números.
Através das tabelas cruzadas é possível classificar os membros de uma população ou grupos dos mais diversos modos, tanto para o teste de homogeneidade, quanto para o teste de independência. Por exemplo, as pessoas podem ser classificadas quanto ao seu sexo, podem ser classificadas em solteiras ou casadas (classificações dicotômicas), classificadas em canhotas, destras ou ambidestras etc. A classificação pode ser feita sobre informações de dados contínuos, basta considerarmos classes de valores desses dados e depois classificarmos relativamente à classe a que pertencem.
De um modo geral, uma tabela cruzada é uma representação dos dados, sejam eles qualitativos ou quantitativos. Quando classificamos de modo bivariado, eles podem ser classificados segundo dois critérios. Caso classificarmos segundo mais de dois critérios estamos no caso multivariado.
1 - Introdução às Tabelas Cruzadas
As tabelas cruzadas, como dito anteriormente, são usadas para avaliar o relacionamento das categorias com respeito aos grupos segundo dois modos, independência ou homogeneidade. Nesta seção, vamos mostrar algumas construções destas tabelas.
A aplicação de tabela cruzada 2x2 é dada quando n elementos selecionados aleatoriamente de uma população são classificados em duas categorias. Depois dos elementos serem classificados um tratamento é aplicado e alguns elementos são examinados novamente e classificados nas duas categorias. O que queremos saber é: O tratamento alterou significativamente a proporção de objetos em cada uma das duas categorias?
Por exemplo, na tabela 1.1 temos uma amostra de 5375 mortes por tuberculose classificadas de acordo com duas variáveis qualitativas, sexo e tipo de tuberculose que provocou a morte.
| Tuberculose do Sistema Respiratório | Outras formas de tuberculose | |
|---|---|---|
| Masculino | 3534 | 270 |
| Feminino | 1319 | 252 |
Tabela 1.1: Mortes por tuberculose.
Esta é uma tabela cruzada 2x2 (os membros da amostra foram classificados segundo dois critérios dicotômicos), ou seja, uma tabela cruzada bidimensional, pois temos dois critérios de classificação. O objetivo deste exemplo é verificar se há dependência ou associação entre as variáveis sexo e tipo de tuberculose que provocou a morte.
Como uma generalização imediata da tabela cruzada 2 x 2, temos uma tabela cruzada com r linhas e c colunas, chamada tabela cruzada r x c. Este tipo de tabela pode ser usado para apresentar dados contidos em várias amostras ou em uma amostra simples, onde cada elemento da amostra pode ser classificado em r diferentes categorias de acordo com um critério ou podem ser classificados em uma ou c categorias diferentes ao mesmo tempo de acordo com um segundo critério.
Para exemplificar tabelas com mais de dois critérios de classificação, temos uma aplicação feita em um hospital, que descrevemos com detalhes na seção Homogeneidade das populações. Neste hospital, avaliamos o nível de compreensão de um prontuário pelos diversos profissionais que o utilizam, ver tabela 1.2, dividimos o nível de compreensão do prontuário nas categorias Totalmente, Parcialmente e Não entendeu, e selecionamos sete populações de profissionais:
- Enfermeiro;
- Fisioterapeuta;
- Fonoaudiólogo;
- Médico;
- Nutricionista;
- Psicólogo;
- Terapeuta Ocupacional.
Nesse exemplo, temos uma tabela cruzada multidimensional.
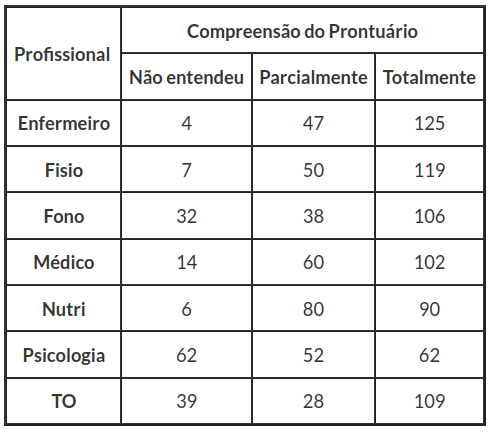
Tabela 1.2: Compreensão do prontuário.
Esta é uma tabela cruzada rxc, ou seja, uma tabela cruzada multidimensional, pois temos mais de dois critérios de classificação, ou seja, temos uma tabela com mais que 4 células. O objetivo deste exemplo é verificar se os dados associados as categorias se comportam de modo similar ou homogêneo nas diversas classes definidas pelas categorias da outra variável.
A forma geral da tabela cruzada, na qual uma amostra de n observações é classificada relativamente a duas variáveis qualitativas, uma com r categorias ou populações no caso de teste de homogeneidade e outra com c categorias. Estas são denominadas tabela cruzada r x c e a frequência observada ou contagem das categorias i da variável linha e das categorias j da variável coluna, é representada por $O_{ij}$. O total de observações na categoria i da variável linha é ni. e o total de observações na categoria j da variável coluna é $n_{.j}$. Estes são chamados totais marginais e em termos das frequências das células, $n_{ij}$, são expressos por:
| Categoria 1 | Categoria 2 | $ \dots $ | Categoria c | Total | |
|---|---|---|---|---|---|
| Categoria 1 | $ O_{11} $ | $ O_{12} $ | $ \dots $ | $ O_{1c} $ | $ n_{1.} $ |
| Categoria 2 | $ O_{21} $ | $ O_{22} $ | $ \dots $ | $ O_{2c} $ | $ n_{2.} $ |
| $ \vdots $ | $ \vdots $ | $ \vdots $ | $ \ddots $ | $ \vdots $ | $ \vdots $ |
| Categoria r | $ O_{r1} $ | $ O_{r2} $ | $ \dots $ | $ O_{rc} $ | $ n_{r.} $ |
| Total | $ n_{.1} $ | $ n_{.2} $ | $ \dots $ | $ n_{.c} $ | $ n $ |
em que,
$$n_{i.} = \sum^{c}_{j=1}O_{ij},~~~~~i=1,\dots,r$$
$$n_{.j} = \sum^{r}_{i=1}O_{ij},~~~~~j=1,\dots,c$$
$$n=\sum_{i=1}^{r}\sum^{c}_{j=1}O_{ij} = \sum_{i=1}^{c}n_{i.} = \sum_{j=1}^{r}n_{.j}$$
A seguir, apresentamos o primeiro teste para tabelas cruzadas, o teste de independência.
2 - Independência dos critérios de classificação
O teste de independência é usado quando estamos interessados em testar o grau de dependência ou de associação entre as variáveis classificatórias, cujas categorias não identificam necessariamente diferentes classes ou subpopulações.
Consideremos duas variáveis R (linha) e C (coluna), sendo que a variável C (coluna) tem c categorias e a variável R (linha) tem r categorias.
Dada uma amostra de n observações de uma população X consideremos o vetor ($O_{11}, O_{12} … , O_{rc}$) de variáveis aleatórias, sendo Oij o número de observações da linha i e coluna j (de entre as n observações da amostra) classificadas na categoria i e na categoria j das variáveis R (linha) e C (coluna), respectivamente, i=1,…, r e j=1,…,c.
Se $p_{ij}$ é a probabilidade de uma observação ser classificada nas classes i e j, das variáveis R (linha) e C (coluna), respectivamente, com i=1,…,r e j=1,…,c, então o vetor aleatório ($O_{11}, O_{12} … , O_{rc}$) tem distribuição multinomial, ou seja:
$$P(O_{11}=o_{11},O_{12}=o_{12},\dots, O_{rc}=o_{rc})=\cfrac{n!}{\displaystyle\prod^r_{i=1}\prod^c_{j=1}o_{ij}!}\displaystyle \prod^r_{i=1}\prod^c_{j=1}p^{o_{ij}}_{ij}\quad {com},\quad\sum^c_{i=1}\sum^r_{j=1}O_{ij}=n$$
A frequência esperada de observações classificadas na categoria i e na categoria j das variáveis R (linha) e C (coluna) será respectivamente:

2.1 - Análise Estatística para o teste de Independência
A independência dos critérios de classificação significa que há independência entre as variáveis R (linha) e C (coluna). Esta independência é expressa probabilisticamente pelo conjunto das seguintes igualdades:
Dois eventos R e C são ditos independentes se:
$$P(R\cup C) = P(R)\times P(C)$$
Usando essa analogia temos que:

Teste Qui-Quadrado para independência
Um dos testes usados para detectar a existência de associação entre as variáveis linha $ R $ e as variáveis coluna $ C $ em uma tabela cruzada é o teste Qui-Quadrado. Primeiramente, descrevemos alguns pressupostos do teste Qui-Quadrado para independência:
- Os dados são selecionados aleatoriamente.
- Todas as frequências esperadas são maiores ou iguais a 1 (isto é, $ E_{ij}> 1 $).
- Não mais de 20% das frequências esperadas são inferiores a 5.
Os estimadores de máxima verossimilhança de $ p_{i.} $ e $ p_{.j} $ são:
$$\hat{p_{i.}}=\cfrac{n_{i.}}{n},~~i=1,\dots,r$$
$$\hat{p_{.j}}=\cfrac{n_{.j}}{n},~~j=1,\dots,c$$
Então, se as hipóteses de independência são válidas, os estimadores de máxima verossimilhança de $ p_{ij} $ são:

Seja válida a hipótese de independência dos critérios de classificação com $ O_{ij}=(O_{11},O_{12},\dots,O_{rc}) $ o vetor de contagens observadas com distribuição multinomial, e $ E_{ij} $ as frequências esperadas, a estatística do teste é dada por:
$$Q^2_{obs}=\sum^r_{i=1}\sum^c_{j=1}\cfrac{(O_{ij}-E_{ij})^2}{E_{ij}}$$
que tem distribuição assintótica Qui-Quadrado com $ (r-1)(c-1) $ graus de liberdade (Ver demonstração em Cramér (1946), páginas 417-419).
Pela estatística $ \chi^2 $ podemos entender qual a região crítica do teste de independência. Quando não ocorre independência é natural que as frequências observadas $ O_{ij} $ sejam substancialmente diferentes das frequências esperadas $ E_{ij}, $ ou seja, esperamos observar quando a independência ocorre. Então devemos rejeitar a hipótese nula $ H_0 $ de independência dos critérios de classificação quando a estatística $ Q^2_{obs} $ é maior que um ponto crítico $ \chi^2_{\alpha} $ usando a Tabela da distribuição Qui-Quadrado (ver Apêndice) ou usando o software Action (ver manual Action módulo Distribuições).
Assim, dado um nível de significância $ \alpha $, o p-valor é determinado por:
$$\text{p-valor}=P[Q^2_{obs}> \chi^2_{\alpha;(r-1)(c-1)}|H_0]$$
(imagem em falta)
Figura 2.2.1: Teste Qui-Quadrado de Pearson
Restrições na aplicação do teste Qui-Quadrado
É clássico afirmar que o valor mínimo de $ E_{ij} $ deve ser superior a 10 em uma tabela cruzada $ 2\times 2 $, e superior a 5 se o grau de liberdade é igual a 2 ou mais, pois nestes tipos de situações, quando utilizamos o teste Qui-quadrado, supomos que o tamanho das amostras sejam “grandes”. Na prática, em tabelas cruzada a estatística $ X^2 $ é aproximada, pois utilizamos tamanhos amostrais “pequenos”. Para resolver este tipo de situação, utilizamos a correção de Yates ou o teste exato de Fisher, que será dito nos módulos seguintes.
Quando $ E_{ij} $ é abaixo de 10 em tabelas $ 2\times 2 $ e 5 e o número de graus de liberdade for 2 ou mais, é habitual fundir uma das classes com outras. Com isso obtemos novas classes com frequências esperadas superior a 10, e trabalhamos com 1 grau de liberdade. Este procedimento é totalmente incorreto, visto que afeta a aleatoriedade da amostra, além de eventualmente, haver perda de informação na fusão de categorias.
Contagem dos graus de liberdade
O número total de células em uma tabela cruzada $ (r\times c) $ é $ rc $. Conhecendo os $ r $ totais das linhas, fica imediatamente conhecido o $ r $ dos $ rc $ valores das células (um de cada linha). Então o número de células independentes passará a $ rc-r $. Se considerarmos os $ c $ totais das colunas, perceberemos que apenas $ c-1 $ deles devem ser considerados, cada um destes com $ c-1 $ totais. Fixamos um valor de célula em cada coluna. Então o número de termos independentes passará a ser $ (rc-r)-(c-1)=(r-1)(c-1). $
2.2 - Aplicações para teste de independência
Exemplo 2.2.1
Consideramos um grupo de 90 doentes psiquiátricos que apresentam os quadros de Atividade Retardada e Atividade Não Retardada. Dentro de cada grupo temos as classificações Desordem Afetiva, Esquizofrenia e Neurose ao nível de significância de $ \alpha=0,05 $ (5%). Os dados estão resumidos na tabela 2.2.1.
| Desordem Afetiva | Esquizofrenia | Neurose | Total | |
|---|---|---|---|---|
| Atividade Retardada | 12 | 13 | 5 | 30 |
| Atividade Não Retardada | 18 | 17 | 25 | 60 |
| Total | 30 | 30 | 30 | 90 |
Tabela 2.2.1: Atividade de doentes psiquiátricos.
(imagem em falta)
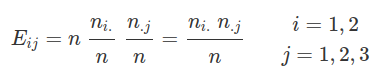
$$E_{11}=\cfrac{30~30}{90}=10$$
$$\vdots$$
$$E_{23}=\cfrac{60~30}{90}=20$$
Assim, montamos uma tabela das frequências esperadas como na tabela (2.3.2)
| VALORES ESPERADOS | |||
|---|---|---|---|
| Desordem Afetiva | Esquizofrenia | Neurose | |
| Atividade Retardada | 10 | 10 | 10 |
| Atividade Não Retardada | 20 | 20 | 20 |
Tabela 2.2.2: Frequências esperadas.
$$Q^2_{11}=\cfrac{(12-10)^2}{10}$$
$$\vdots$$
$$Q^2_{23}=\cfrac{(25-20)^2}{20}$$
Agora, montamos uma tabela com os valores de $ Q^2 $ no ponto $ (i,j) $ como na tabela (2.3.3)
| VALORES PADRONIZADOS | |||
|---|---|---|---|
| Desordem Afetiva | Esquisofrenia | Neurose | |
| Atividade Retardada | 0,4 | 0,9 | 2,5 |
| Atividade Não Retardada | 0,2 | 0,45 | 1,25 |
Tabela 2.2.3: Valores de $ Q^2 $ no ponto $ (i,j) $.
$$Q^2_{obs}=\sum^r_{i=1}\sum^c_{j=1}\cfrac{(O_{ij}-E_{ij})^2}{E_{ij}}=\cfrac{(12-10)^2}{10}+\ldots+\cfrac{(25-20)^2}{20}=5,7$$
$${p-valor}=P[5,7> \chi^2_{(2-1)(3-1)}|H_0]=0,057844$$
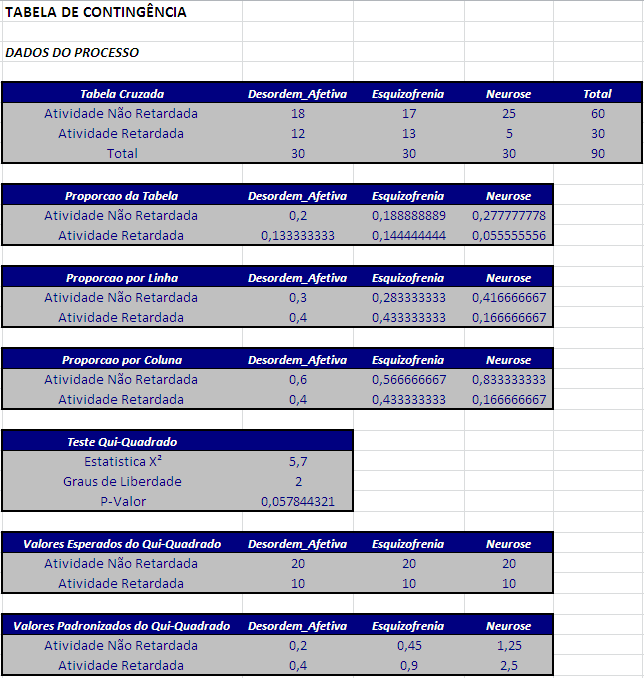
Se quisermos testar se o tipo de atividade não é influenciada pelo tipo de desordem psiquiátrica, então devemos estimar as frequências esperadas e após o cálculo da estatística de teste, obtemos $ Q^2_{obs}=5,7 $ e do p-valor=0,057844, assim não rejeitarmos a hipótese nula. Portanto, concluímos que não existe dependência entre o tipo de atividade e o tipo de desordem psiquiátrica, ao nível de significância de 5%, ou seja, são independentes.
Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.
(imagem em falta)
Exemplo 2.2.2
Um supermercado quer testar se há alguma dependência do período do dia (manhã, tarde e noite) em relação aos modos de pagamento (cartão de débito, cartão de crédito e dinheiro) ao nível de significância de 5%. Os dados estão resumidos na tabela 2.2.2.
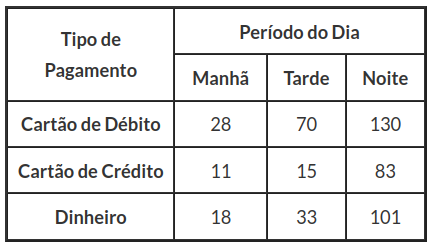
Tabela 2.2.2: Movimentação das compras em cada período do dia.
Assim, obtemos os seguintes resultados.
(imagem em falta)
(imagem em falta)
(imagem em falta)
À partir dos resultados obtidos pelo software Action, obtemos $ Q^2_{obs}=13,98 $ e do p-valor=0,0073, assim rejeitarmos a hipótese nula. Portanto, concluímos que existe dependência entre o período do dia, ao nível de significância de 5%. Pela tabela 2.2.2, observamos que o período da noite é o que tem o maior volume de compras, intuitivamente é plausível, pois é um horário em que as pessoas estão saindo do trabalho e vão ao supermercado para fazer compras.
2.3 - Medidas de Associação
Medidas baseadas em $ Q^2_{obs} $
As medidas de associação são utilizadas com a finalidade de medir o nível de associação entre variáveis qualitativas nominais.
- Coeficiente de contingência quadrático médio: usa o próprio valor da estatística $ Q^2_{obs} $ como medida de associação, mas como $ Q^2_{obs} $ depende de n, implica que a medida é crescente em n. Para se obter uma medida não afetada pela dimensão da amostra, definimos este coeficiente
$$\Phi^2=\cfrac{Q^2_{obs}}{n}$$
Desvantagens: Não é limitado superiormente.
- Coeficiente de contingência proposto por Pearson (1904)
$$P=\sqrt{\cfrac{\frac{Q^2_{obs}}{n}}{1+\frac{Q^2_{obs}}{n}}}=\sqrt{\cfrac{Q^2_{obs}}{n+Q^2_{obs}}}$$
Obtemos valores entre 0 e 1, atingindo o seu valor mínimo se, e somente se $ Q^2_{obs} = 0 $, ou seja, no caso de completa independência. O valor máximo não é, em geral atingido. Mesmo em casos de completa dependência, o valor é modificado com o número de linhas e de colunas da tabela. Para solucionar este problema propomos:
- Coeficiente de Tschuprov
$$T=\sqrt{\cfrac{\frac{Q^2_{obs}}{n}}{\sqrt{(r-1)(c-1)}}}$$
Tem valor 0 no caso de independência e consegue atingir o valor máximo 1, no caso de dependência completa, mas apenas se $ r = c $.
- Coeficiente de Cramér
$$C=\cfrac{\frac{Q^2_{obs}}{n}}{\sqrt{\min(r-1;c-1)}}$$
O valor deste coeficiente fica próximo de 1 em caso de forte dependência e próximo de 0 em caso de independência. O coeficiente de Cramér não é limitado superiormente.
Para quaisquer dos coeficientes apresentados existem expressões para as suas variâncias. A grande desvantagem destes coeficientes é que não permitem interpretações probabilísticas como as que se fazem com o coeficiente de correlação, por exemplo, mas nos dão uma boa ideia do nível de associação entre as variáveis.
Quanto maior o valor do coeficiente, maior o nível de associação entre as variáveis.
Exemplo 2.3.1
Consideremos o exemplo 2.2.1.
| Desordem Afetiva | Esquizofrenia | Neurose | Total | |
|---|---|---|---|---|
| Atividade Retardada | 12 | 13 | 5 | 30 |
| Atividade Não Retardada | 18 | 17 | 25 | 60 |
| Total | 30 | 30 | 30 | 90 |
Tabela 2.3.1: Atividade de doentes psiquiátricos.
- Coeficiente de contingência quadrático médio:
$$\Phi^2=\cfrac{Q^2_{obs}}{n}=\cfrac{5,7}{90}=0,0633$$
- Coeficiente de contingência
$$P=\sqrt{\cfrac{\frac{Q^2_{obs}}{n}}{1+\frac{Q^2_{obs}}{n}}}=\sqrt{\cfrac{Q^2_{obs}}{n+Q^2_{obs}}}=\sqrt{\cfrac{5,7}{90+5,7}}=0,244$$
- Coeficiente de Tschuprov
$$T=\sqrt{\cfrac{\frac{Q^2_{obs}}{n}}{(r-1)(c-1)}}=\sqrt{\cfrac{\frac{5,7}{90}}{(3-1)(2-1)}}=0,178$$
- Coeficiente de Cramer
$$C=\cfrac{\frac{Q^2_{obs}}{n}}{\min(r-1;c-1)}=\cfrac{\frac{5,7}{90}}{\min(3-1,2-1)}=0,0633$$
Pelo coeficiente de contingência (P = 0,24) temos uma associação moderada. Para as demais, temos uma baixa associação.
Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.
(imagem em falta)
Exemplo 2.3.2
Consideremos o exemplo 2.2.2.
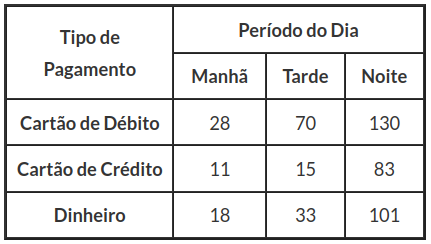
Tabela 2.3.2: Movimentação das compras em cada período do dia.
Pelo coeficiente de contingência (P = 0,16) temos uma associação moderada. Para as demais, temos uma baixa associação.
(imagem em falta)
3 - Homogeneidade de populações
O teste de homogeneidade é usado quando pretendemos testar se os dados associados às categorias de uma das variáveis se comporta de modo homogêneo ou similar nas diversas classes ou populações definidas pelas categorias da outra variável classificatória.
Os dados da tabela cruzada 3.1, foram colhidos de um estudo sobre os efeitos secundários provocados por um medicamento. Para isto, foram selecionados 100 pacientes doentes. Selecionamos 50 doentes para receber medicamentos e outros 50 doentes como grupo de testemunha medicando eles com um placebo, conforme mostrado na tabela (3.1).
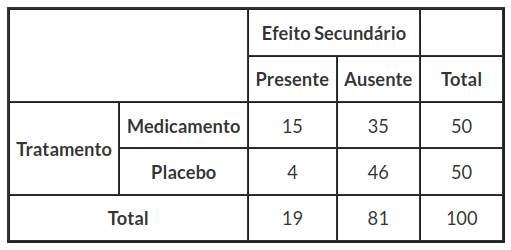
Tabela 3.1: População tratados com medicamento e outra população com placebo.
Esta tabela é radicalmente diferente das anteriores, pois o número de doentes a quem está sendo aplicado o medicamento e o número de doentes para o qual foi aplicado o placebo está fixado, ou seja, a tabela tem uma das margens fixada antes do experimento.
Neste caso, as frequências absolutas que aparecem em cada entrada do interior da tabela (e as correspondentes probabilidades) são condicionais, e não conjuntas como anteriormente.
Outra aplicação para ilustrarmos este tipo de experimento, é referente a análise de prontuários de um hospital, em que avaliamos o nível de compreensão de um prontuário pelos diversos profissionais que o utilizam (ver tabela 3.2). Dividimos o nível de compreensão do prontuário em três categorias, são elas:
- Totalmente, quando o profissional conseguiu entender a letra, abreviaturas e não compreende até duas siglas;
- Parcialmente, quando o profissional não conseguiu entender três siglas (independente do julgamento dele);
- Não entendeu, quando o profissional não conseguiu entender nada do que estava escrito ou não entendeu mais do que três siglas.
Selecionamos sete populações de profissionais, que são:
- Enfermeiro;
- Fisioterapeuta;
- Fonoaudiólogo;
- Médico;
- Nutricionista;
- Psicólogo;
- Terapeuta Ocupacional.
Para este estudo, a amostra foi calculada separadamente para cada profissional de interesse, visando permitir a análise por categoria profissional. Para isso foi levantada a quantidade de pacientes atendidos nas diferentes unidades hospitalares, em um período de 15 dias, separados por tipo de profissional.
Desta forma, o cálculo do tamanho de amostra para cada equipe profissional, representativo ao período citado, foi baseado em uma amostra aleatória estratificada, a um nível de confiança de 95%, em que os estratos foram fixados com os tamanhos amostrais indicados na tabela 3.2. O objetivo principal desse estudo seria verificar a compreensão da evolução lida independente de qual profissional fizesse a leitura e analisar quantitativamente as informações em conformidade com as políticas institucionais de avaliação e de prontuário.
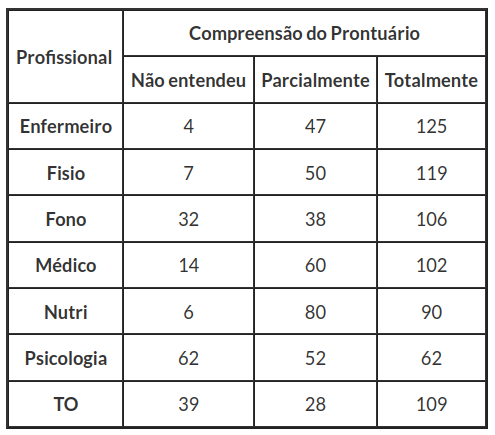
Tabela 3.2: Compreensão do prontuário.
A seguir, vamos apresentar o teste de homogeneidade para tabelas cruzadas.
3.1 - Função de probabilidade das frequências
Consideramos uma tabela cruzada r x c, em que temos r amostras ou populações da variável R (variável linha) e c classes ou categorias da variável C (variável coluna). Logo, temos r variáveis multinomiais (se for a margem correspondente ao critério da linha fixada), uma para cada amostra.
Dada uma amostra de $ n_{i.} $ observações da população i da variável R, com i=1,…,r, Consideramos o vetor $ (O_{i1},O_{i2},…,O_{ic}) $ de variáveis aleatórias, sendo $ O_{ij} $ o total de observações (de entre as $ n_{i.} $ da amostra i) classificadas na categoria j da variável C, com j=1,…,c.
Se $ p_{j|i}=P(\text{uma observação da amostra}~ i~\text{ ser classificada na classe}~ j~\text{ da variável}~C), $ j=1,…,c
então o vetor aleatório $ (N_{i1},…,N_{ic}) $ tem distribuição multinomial, ou seja
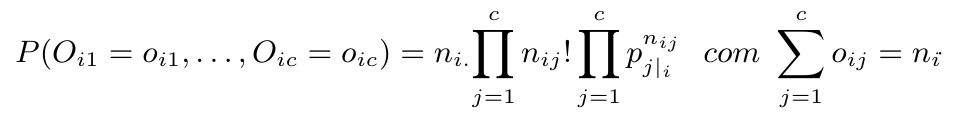
Repetimos esta probabilidade para r amostras independentes das r populações. Com isso, temos r vetores aleatórios independentes com distribuição multinomial, embora eventualmente distintas.
Assim, obtemos a frequência esperada de observações da amostra i, classificadas na população j da variável C (coluna) da seguinte forma:
$$F_{j|_i}=n_{i.}~\hat{p}_{j|_i}~~~~j=1,\dots, c$$
Com isso, os estimadores de máxima verossimilhança de pj|i são:

A seguir, apresentamos a análise estatística para o teste de homogeneidade para tabelas cruzadas.
3.2 - Análise Estatística para o teste de homogeneidade
Temos agora r situações multinomiais independentes (se for a margem correspondente ao critério linha fixada), uma para cada linha da tabela, e queremos saber se aquelas r situações são idênticas, ou seja, queremos saber se as r situações multinomiais são idênticas em termos probabilísticos. A identidade das distribuições multinomiais significa que a homogeneidade em termos probabilísticos da classificação pelas C categorias do critério para todas as r populações. Esta homogeneidade é expressa probabilisticamente pelo conjunto das seguintes igualdades:
$$p_{j|_1}=p_{j|_2}=\dots=p_{j|_r}\quad\quad j=1,\dots,c$$
em que, pj|i é a Probabilidade de uma amostra da população i ser classificada na classe j da variável C, j=1,…, c.
$$p_{j|_i}=\cfrac{p_{ij}}{p_{i.}}~j=1,\dots,c\quad (3.2.1)$$
$$p_{i.}=\sum^c_{j=1}p_{ij}~i=1,\dots,r$$
Em resumo, nosso objetivo é testarmos a hipótese de homogeneidade das r amostras das populações relativamente à classificação nas categorias da variável C (coluna). Assim, as hipóteses são:

Teste Qui-Quadrado para homogeneidade
O teste Qui-Quadrado de independência (que foi discutido na seção 2.2) é um teste sobre uma amostra a partir de uma única população. Cada indivíduo da população é classificada em duas formas (atividade e doença psiquiátrica). Agora, discutimos um segundo tipo de teste Qui-Quadrado, que pode ser usado para comparar as proporções em diferentes populações.
Definição
Em um teste Qui-Quadrado de homogeneidade, podemos testar a afirmação de que diferentes populações têm a mesma proporção de indivíduos com alguma característica.
Voltando a equação (3.2.1), temos que o estimador de máxima verosimilhança de pj|i é dada por:
$$\hat{p_{j|_i}}=\cfrac{O_{ij}}{n_{i.}}~~~j=1,\dots,c$$
Mas, se a hipótese H0 (hipótese de homogeneidade) é válida, sabemos que:
$$p_{j|_1} = p_{j|_2} = \dots =p_{j|_r} = p_j~~~j=1,\dots,c$$
Logo, os estimadores de máxima verosimilhança de pj|i=pj são:
$$\hat{p_{j|_i}}=\hat{p_j}=\cfrac{\displaystyle\sum_{i=1}^rO_{ij}}{n}=\cfrac{O_{.j}}{n}~~~j=1,\dots,c$$
Os estimadores de máxima verosimilhança das frequências esperadas Fj|i ,sob a hipótese nula H0 válida, é dada por:
$$E_{j|_i}=n_{i.}~\hat{p}_{j|_i}=\cfrac{n_{i.}~O_{.j}}{n}~~~j=1,\dots,c$$
Portanto, sendo (Oi1,Oi2,…,Oic) o vetor de frequências da amostra i, e admitindo que é válida a hipótese de homogeneidade no critério de classificação. Temos que a estatística
$$Q^2_{c|i}=\sum^c_{j=1}\cfrac{(O_{ij}-E_{j|i})^2}{E_{j|i}}$$
tem distribuição assintótica com (c-1) graus de liberdade.
Se repetirmos o mesmo raciocínio para as r amostras, vamos somar r variáveis com distribuição Qui-Quadrado, ou seja, a estatística de teste é dada por:
$$Q^2_{obs}=\sum^r_{i=1}Q^2_{c|i}=\sum^r_{i=1}\sum^c_{j=1}\cfrac{(O_{ij}-E_{j|i})^2}{E_{j|i}}$$
tem distribuição assintótica Qui-Quadrado com (r-1)(c-1) graus de liberdade.
Pela expressão da estatística $ Q^2_{obs} $ podemos entender qual a região crítica do teste de homogeneidade. Quando não ocorre homegeneidade é natural que as frequências observadas Oij sejam substancialmente diferentes das frequências que esperamos observar quando a homogeneidade ocorre (Ej|i). Então devemos rejeitar a hipótese H0 de homogeneidade da distribuição de probabilidade das categorias de classificação da variável C (coluna), para todas as amostras, quando a estatística $ Q^2_{obs} $ é maior que um ponto crítico $ \chi^2_{\alpha} $ usando a Tabela da distribuição Qui-Quadrado - Apêndice ou usando o software Action (ver manual Action módulo Distribuições).
Assim, dado um nível de significância $ \alpha $, o p-valor é determinado por
$${p-valor}=P[Q^2_{obs}> \chi^2_{\alpha;(r-1)(c-1)}|H_0]$$
Contagem dos Graus de Liberdade
O número total de frequências numa tabela cruzada r x c é rc. Como é conhecida a quantidade de cada amostra (correspondente ao total de cada linha), a distribuição em cada amostra das frequências de classificação pelas c categorias da variável C (coluna), é feita com uma restrição. Assim em cada uma das r linhas temos livres apenas (c-1) frequências. Conhecendo os c totais das colunas, por exemplo, na última as frequências ficam imediatamente determinadas. Assim nesta última linha os valores não são livres. Consequentemente, temos como independentes as frequências de (r-1) amostras, cada uma como (c-1) frequências independentes. Então o total de graus de liberdade será de (r-1)(c-1).
3.3 - Aplicações para o teste de Homogeneidade
Exemplo 3.3.1
Observemos a tabela de contingência descrita na introdução, no qual os dados foram colhidos de um estudo sobre os efeitos secundários provocados por um medicamento. Neste estudo utilizamos um medicamento em 50 doentes, e aplicamos a outros 50 doentes (grupo de testemunha) um placebo, conforme mostrado na tabela (3.3.1).
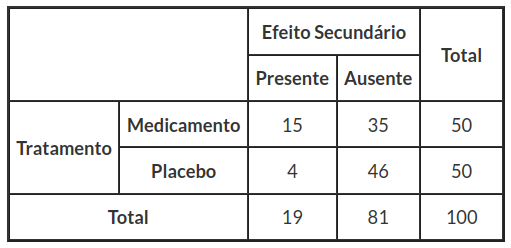
Tabela 3.3.1: População tratados com medicamento e outra população com placebo.
(imagem em falta)
Testemos a homogeneidade do efeito secundário do medicamento, para a população em que ele foi administrado e para a população em que ele não foi administrado (placebo).
$$E_{j|_i}=n_{i.}~\hat{p}_{j|_i}=\cfrac{n_{i.}~N_{.j}}{n}~~~j=1,\dots,c$$
$$E_{1|1}=\cfrac{19~50}{100}=9,5 \ldots E_{2|3}=\cfrac{81~50}{100}=40,5$$
Assim, montamos uma tabela das frequências esperadas como na tabela (3.3.2)
| VALORES ESPERADOS | ||
|---|---|---|
| Presente | Ausente | |
| Medicamento | 9,5 | 40,5 |
| Placebo | 9,5 | 40,5 |
Tabela 3.3.2: Frequências esperadas.
$$Q^2_{11}=\cfrac{(15-9,5)^2}{9,5}\ldots Q^2_{23}=\cfrac{(46-9,5)^2}{9,5}$$
Agora, montamos uma tabela com os valores de $ Q^2 $ no ponto $ (i,j) $ como na tabela (3.3.3)
| VALORES PADRONIZADOS | ||
|---|---|---|
| Presente | Ausente | |
| Medicamento | 3,1842 | 0,746 |
| Placebo | 3,1842 | 0,746 |
Tabela 3.3.3: Valores de $ Q^2 $ no ponto $ (i,j) $.
$$Q^2_{obs}=\sum^r_{i=1}\sum^c_{j=1}\cfrac{(O_{ij}-E_{ij})^2}{E_{ij}}=$$
$$=\cfrac{(15-9,5)^2}{9,5}+\ldots+\cfrac{(46-9,5)^2}{9,5}=$$
$$=7,8662$$
$${p-valor}=P[7,8662> \chi^2_{0,05;(2-1)(2-1)}=3,8415|H_0]=0,005848$$
Após o cálculo da estatística de teste, $ Q^2_{obs}=7,8662 $ e do p-valor=0,005848, rejeitamos a hipotese H0, concluímos que existe uma diferença significativa entre o tipo de efeito provocado pela administração do medicamento e pela administração do placebo, com uma significância de 5%.
Nos resultados obtidos pelo software Action, o valor da estatística $ Q^2_{obs} $ é calculada com a correção de Yates, pois temos uma das células com frequência menor ou igual a 5. Caso queira saber como é feita a correção veja no módulo Correções por continuidade de Yates.
Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.
(imagem em falta)
Exemplo 3.3.2
Afim de analisar o nível de compreensão em relação a prontuários de um hospital descrito na seção homogeneidade de populações. Montamos uma tabela de contingência como a seguir.
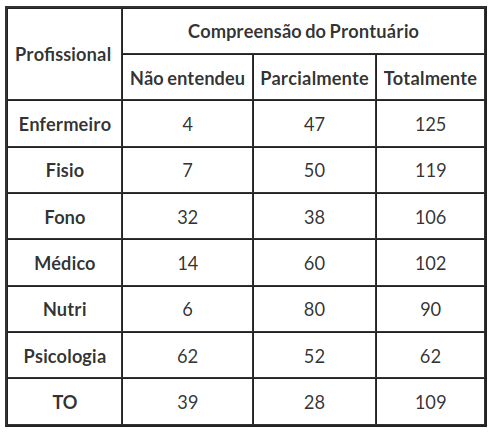
Tabela 3.3.2: Compreensão do prontuário.
Obtemos os seguintes resultados:
(imagem em falta)
(imagem em falta)
(imagem em falta)
(imagem em falta)
À partir dos resultados obtidos pelo software Action, obtemos $ Q^2_{obs}=179,45 $ e do p-valor$ \approx0 $. Assim, rejeitamos a hipótese nula. Portanto, concluímos que existe diferença significativa entre os profissionais em relação ao nível de compreensão dos prontuários, ao nível de significância de 5%.
3.6 - Uso indiscriminado do teste de homogeneidade
Vejamos agora um exemplo de como o teste de homogeneidade em tabelas cruzadas com uma das margens fixa pode ser usado de modo pouco apropriado.
Antes das eleições, um consultor político foi encarregado de uma pesquisa frente a opinião pública e colheu os seguintes dados. De 400 eleitores entrevistados, 200 pretendiam votar a favor do partido que veio a ganhar as eleições, e os outros 200 estavam decididos a votar no partido de oposição. Depois das eleições, o governo instituiu uma legislação trabalhista e um teto salarial, que eventualmente poderiam causar descontentamento entre o eleitorado. O mesmo consultor político entrevistou de novo as mesmas 400 pessoas, e desta vez 182 declararam que eram partidárias do governo, enquanto 218 declararam que, se houvesse eleições naquele momento, votariam contra o governo. Com base nestes dados, o especialista elaborou a tabela cruzada (3.6.1) , no qual determinamos $ Q^2_{obs} =1,448 $ e p-valor$ =0,23 $, e assim não há razão para rejeitar a hipótese de homogeneidade mesmo ao nível de significância, pouco usual, de 0,2. O governo, contentíssimo, mandou publicar esta análise em todos os jornais, provando que continuava a ter o apoio da população.
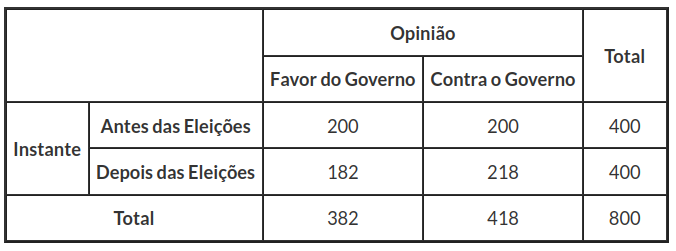
Tabela 3.6.1: Pesquisa de Opinião.
Vamos ver os resultados obtidos pelo software Action:
(imagem em falta)
(imagem em falta)
(imagem em falta)
Claro que em um caso desses, o partido de oposição não teve a menor dificuldade em fazer chacota do governo, pois a análise está totalmente errada. De fato, o analista não tem 800 respostas independentes, o fato de cada pessoa responder duas vezes introduz uma correlação nos resultados que não pode ser ignorada. O que deve ser analisado são os 400 pares de respostas, e não as 800 respostas isoladas. Assim, usamos o coeficiente de correlação proposto por Yule (1900) variando em um intervalo [-1,1]. Porém, primeiramente, definimos o odds ratio (razão de chances) para tabelas cruzadas 2x2. Então temos que o odds ratio é dado pela seguinte fórmula:
$$OR=\frac{O_{11}\times O_{22}}{O_{12}\times O_{21}}$$
Agora, definimos o coeficiente de correlação de Yule da seguinte forma:
$$\psi=\frac{OR-1}{OR+1}$$
Portanto, para nosso exemplo temos:
$$OR=\frac{200\times 218}{200\times 182}=1,197\quad{e}\quad\psi=\frac{1,197-1}{1,197+1}=0,089$$
Assim, o número de eleitores que antes votaram contra e que agora votariam a favor depois das eleições é calculada da seguinte forma:
$$O_{2^\prime 1^\prime}=\psi\times O_{21}=0,089\times 182\approx 16$$
Agora, como o número de eleitores entrevistados foi de 200, então temos que o número de eleitores que foi contra antes das eleições e que continuaram contra depois das eleições é de $ 200-16=184 $ eleitores. Portanto a tabela que deveria ser analisada, é mostrada na tabela (3.6.2)
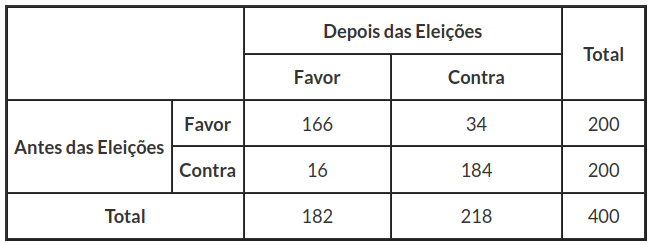
Tabela 3.6.2: Pesquisa de Opinião do Antes e Depois das Eleições.
(imagem em falta)
(imagem em falta)
Observamos pelos resultados obtidos pelo software Action, que $ Q^2_{obs} =223,82 $ e p-valor$ asymp;0 $. Assim rejeitamos a hipótese de homogeneidade ao nível de significância 5%. Pelos resultados, vemos também que cerca de 15% dos eleitores que antes eram a favor do governo, agora são contra.
Nota: Caso pretendamos testar a independência dos critérios de classificação, ou caso pretendamos testar a homogeneidade de populações relativamente a um critério de classificação, a estatística Qui-Quadrado continua a ter a mesma expressão e para amostras grandes terá distribuição limite Qui-Quadrado com 1 grau de liberdade.
4 - Correção por continuidade de Yates
Utilizamos a Correção de Yates como uma aproximação para a análise de tabelas cruzadas 2 x 1 e 2 x 2. Uma tabela cruzada 2 x 2 apresenta as frequências de ocorrência de todas as combinações dos níveis de duas variáveis dicotômicas, em uma amostra de tamanho $ n $. Uma forma esquemática desse quadro é dado pela tabela 4.1.
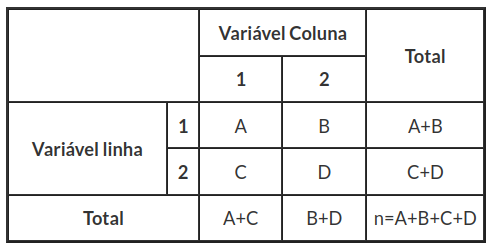
Tabela 4.1: Tabela Cruzada 2 x 2.
Uma investigação de interesse é se as variáveis resumidas em uma tabela cruzada são independentes umas das outras.
Por exemplo, em um estudo aleatorizado com as margens fixas, o julgamento do número de categorias a serem escolhidas aleatoriamente para cada grupo seria especificada e as margens de linha seriam fixas, mas as margens da coluna não. Em um estudo pareado, porém, em que uma amostra pode ter 100 casos (fumantes, por exemplo) e 1000 controles (não-fumantes). Ao testarmos cada um dos 1100 indivíduos na presença ou ausência de alguma exposição que pode ser prevista pela sua própria condição de fumante, que nesse caso seriam as margens de uma coluna que estão fixadas.
Agora, um outro exemplo seria o experimento famoso de Fisher de degustação de chá, em que uma senhora tentava adivinhar a ordem de mistura dos ingredientes de um chá, em outras palavras, a senhora tentava identificar se havia diferença no sabor quando coloca o leite antes do chá ou o chá antes do leite. O experimento foi realizado fazendo a mistura em 8 copos, dois grupos de quatro, tanto a linha e a coluna teriam as margens fixadas pelo experimento.
Quando as margens das linhas e colunas são fixadas, a independência pode ser testada usando teste exato de Fisher. Este teste é baseado na distribuição hipergeométrica e é computacionalmente intensivo, especialmente em grandes amostras. Assim, Fisher defendeu a utilização da estatística de Pearson,
$$X^2=\cfrac{n~(AD-BC)^2}{(A+B)(C+D)(A+C)(B+D)}$$
que sob a hipótese nula temos uma distribuição Qui-Quadrado com um grau de liberdade. Yates argumentou que esta distribuição nos dá apenas valores aproximados.
As estimativas das probabilidades discretas associadas aos dados de frequência e os p-valores com base na estatística $ X^2 $ de Pearson geralmente subestimam os verdadeiros p-valores. Em geral, quando uma estatística toma os valores discretos A < B < C, o p-valor correspondente a B é estimado pela cauda da função contínua definida pelo ponto $ (a+b)/2 $.
Portanto, a cauda da função contínua calculada em B subestima o p-valor. Neste contexto, Yates sugeriu que as estatísticas $ X^2 $ devem ser corrigidas para a continuidade e propôs a estatística de teste corrigido da seguinte forma:
$$\cfrac{n~(|AD-BC|-\frac{1}{2}~n)^2}{(A+B)(C+D)(A+C)(B+D)}$$
Embora a correção de Yates é mais conhecida por seu uso na análise de tabelas cruzadas 2 x 2, também é aplicável à análise de tabelas cruzada 2 x 1. A tabela de cruzada 2 x 1 mostra as frequências de ocorrência de duas categorias em uma amostra aleatória de tamanho n, elaborado à partir de uma população em que a proporção de casos nas duas categorias são p e (1 - p).
A questão pesquisada é normalmente observada se o número de casos x e (n - x) nas duas categorias foram amostrados em uma população com um valor pré-especificado p. Isso pode ser testado usando estatística de Pearson,
$$X^2=\cfrac{(x-np)^2}{n~p(1-p)}$$
que assintoticamente têm uma distribuição ($ \chi^2_1 $) Qui-Quadrado com um grau de liberdade sob a hipótese nula H0.
Yates mostrou que, neste caso, bem como a utilização dos resultados do Qui-Quadrado de Pearson, os valores de p sistematicamente subestimam os verdadeiros p-valores com base na distribuição Binomial. Por isso, ele sugeriu a estatística corrigida:
$$\cfrac{(|x-np|-\frac{1}{2})^2}{n~p(1-p)}~~(4.1)$$
Kendall e Stuart observaram que o procedimento de Yates é um caso especial de um conceito geral de uma correção de continuidade, enquanto que Pearson notou que correção de Yates deriva naturalmente do teorema de Euler-Maclaurin usados para aproximarmos as distribuições binomial e hipergeométrica. Em seguida, o uso da correção de Yates para a estatística Qui-Quadrado de Pearson tem sido amplamente enfatizado para a análise das tabelas cruzadas.
Há, no entanto, vários problemas relacionados com a correção de Yates e vamos discutir algumas destas.
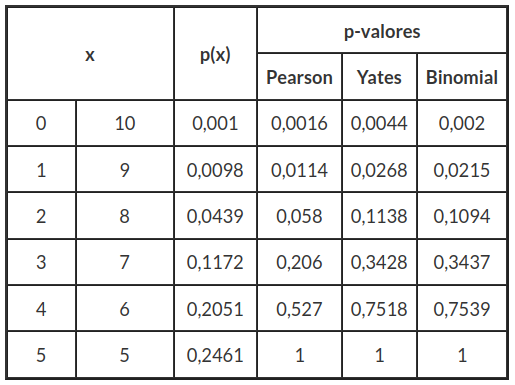
Tabela 4.2: Distribuição Binomial para n=10 e p=0,5, e bilateral para os p-valores (Adaptado de Richardson)
Em primeiro lugar, na análise de tabelas cruzadas 2 x 1, os p-valores associados com a estatística corrigida (equação 4.1) tendem a superestimar os verdadeiros p-valores para as caudas da distribuição e subestimá-los para o centro. Isto é ilustrado na tabela 4.2, que apresenta p-valores de um teste em uma tabela cruzada com n=10 e p=0,5, obtido com $ X^2 $ de Pearson e correção de Yates. Os resultados desta tabela também estão os verdadeiros p-valores da distribuição binomial que são o padrão. É também necessário salientar que os p-valores obtidos com a correção de continuidade são muito menos precisos quando a probabilidade p binomial é substancialmente diferente de 0,5.
Em segundo lugar, correção de Yates é apropriada apenas para testes unilaterais, pois, como é baseado em uma comparação entre a contingência observada e a contingência forte próxima na mesma direção (Haber, Mantel). Para os testes bilaterais, a estatística envolve uma hiper correção. Na mesma linha, pode ser provado analiticamente que a correção de Yates é sistematicamente conservadora quando realizados em testes bilaterais.
Em terceiro lugar, uma questão mais importante relacionada com a correção de Yates e a sua aplicação à análise de tabelas cruzadas, são resultantes da investigação diferentes planejamentos. Muitos pesquisadores têm argumentado que a correção de Yates é baseada em comparações entre as tabelas cruzada com a linha fixa e coluna marginal total.
Particularmente Yates está especialmente preocupado com a aproximação da distribuição hipergeométrica e do teste exato de Fisher. Contudo, o método de Yates também tem sido recomendado para a análise de contingência em tabelas resultantes 2 x 2 e esquemas de amostragem em que um ou ambos conjuntos marginais totais são livres para variar e são, portanto, sujeitos a erros de amostragem.
Devemos notar que tais esquemas de amostragem são mais frequentemente encontrados em contexto da pesquisa atual. Enquanto Yates sustenta ao longo das linhas de raciocínio de Fisher de que a análise de tabelas cruzada 2 x 2 deve ser sempre realizada subordinada à marginais totais observadas, essa abordagem ainda é objeto de debate.
Por outro lado, quando os totais marginais não são fixados, o processo envolve uma subcorreção de Yates adicionais e o teste estatístico passa a ser conservador. Esta tem sido investigada através de simulações Monte Carlo (Grizzle, Richardson), e confirmado analiticamente (Conover, Haber). Em particular, Grizzle observou que, para tabelas cruzadas com marginais totais não fixas, o procedimento de Yates “produz um teste que é tão conservador que é quase inútil”.
Finalmente, para concluirmos esta seção, a correção de Yates originou-se como um dispositivo para eliminar as discrepâncias que emergiram da aproximação da distribuição hipergeométrica para o teste exato de Fisher. A aproximação com $ X^2 $ de Pearson foi necessário “para a simplicidade comparativa dos cálculos” (Fisher, página 99), pois a análise exata das tabelas cruzadas 2 x 2 e com a computação limitada disponível na época, tornava inviável seu uso em muitos casos, não sendo o caso na atual conjectura, pois os recursos computacionais não são mais o problema.
Na verdade, Agresti observa que a correção de Yates não é mais necessário desde que o software atual faça teste exato de Fisher, computacionalmente viável, mesmo quando os tamanhos de amostra são grandes.
4.1 - Aplicações para a Correção de continuidade de Yates
Exemplo 4.1.1
Vejamos a sua aplicação no exemplo 3.3.1, em que os dados foram colhidos de um estudo sobre os efeitos secundários provocados por um medicamento.
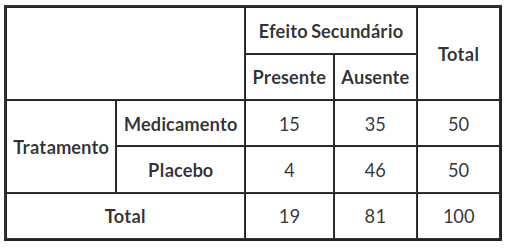
Tabela 4.1.1: População tratados com medicamento e outra população com placebo.
Vamos calcular a correção de Yates:
$$Q^2_{corr}=\cfrac{n~(|AD-BC|-\frac{1}{2}~n)^2}{(A+B)(C+D)(A+C)(B+D)}= \cfrac{100~(|15*46-35*4|-\frac{1}{2}~100)^2}{(15+35)(4+46)(15+4)(35+46)}=6,4977$$
e o p-valor:
$${p-valor}=P[6,4977> \chi^2_{0,05;(2-1)(2-1)}|H_0]=0,0108$$
(imagem em falta)
(imagem em falta)
Observação: O software Action, já faz a correção de Yates automaticamente.
Após o cálculo da estatística de teste, $ Q^2_{obs}=6,4977 $ e do p-valor$ =0,0108 $, concluímos que existe uma diferença das probabilidades do tipo de efeito provocado pela administração do medicamento e pela administração do placebo, com um nível de significância de $ \alpha=0,05 $ (5%). Compare com o resultados da aplicação do módulo teste de homogeneidade obtido e tire as devidas conclusões.
5 - Teste exato de Fisher
Em tabelas cruzadas 2 x 2, os valores esperados menores que 5 e amostras pequenas, podem afetar a aproximação da distribuição Qui-Quadrado da estatística $ Q^2_{obs} $ fazendo com que a mesma não seja suficientemente boa. Neste caso é preferível usar o teste exato de Fisher, que passamos a descrever nesta seção.
No teste exato de Fisher, nos baseamos no cálculo da distribuição de probabilidade das frequências da tabela. Contudo, isso não é possível na situação das tabelas com margens livres ou com uma margem fixa e outra livre porque a probabilidade de uma dada distribuição das frequências é função de parâmetros de valor desconhecido.
Fisher (1934) propôs que a distribuição de probabilidade das frequências de qualquer um destes tipos de tabelas sejam substituídas pela probabilidade da distribuição das mesmas frequências, considerando tabelas com duas margens fixas, ou seja, uma distribuição de probabilidade hipergeométrica para a única frequência de valor livre (independente).
Para a tabela 5.1 (arranjada de modo que $ n_{1.}\leq n_{.1}\leq n_{.2}\leq n_{2.} $), se X for a frequência de valor independente, a frequência da célula (1,1), considerando:
$$P_a=P[X=a]=\cfrac{\displaystyle{a+b \choose a} \displaystyle{c+d \choose c}}{\displaystyle{n \choose a+c}}=\cfrac{(a+b)!(c+d)!(a+c)!(b+d)!}{a!b!c!d!n!}$$
O teste exato de Fisher consiste na determinação desta probabilidade e dos arranjos possíveis que, com os mesmos totais marginais, tenham ainda mais desvios em relação à hipótese nula H0 ,isto é, as probabilidades de tabelas com as mesmas margens e com menores valores na entrada cujo valor, na tabela cruzada em questão, já foram consideradas baixas, neste caso
| $ a-1 $ | $ b+1 $ | $ a+b $ |
|---|---|---|
| $ c+1 $ | $ d-1 $ | $ c+d $ |
| $ a+c $ | $ b+d $ | $ n $ |
| $ a-2 $ | $ b+2 $ | $ a+b $ |
|---|---|---|
| $ c+2 $ | $ d-2 $ | $ c+d $ |
| $ a+c $ | $ b+d $ | $ n $ |
$ \vdots $
| $ 0 $ | $ a+b $ | $ a+b $ |
|---|---|---|
| $ c+a $ | $ d-a $ | $ c+d $ |
| $ a+c $ | $ b+d $ | $ n $ |
Se a soma $ P_a+P_{a-1}+…+P_0 $ for inferior ao nível de significância $ \alpha, $ devemos rejeitar a hipótese de independência ou a hipótese de homogeneidade que estipulamos.
5.1 - Aplicação do Teste Exato de Fisher
Exemplo 5.1.1
De maneira geral, os doentes psiquiátricos podem ser classificados em psicóticos e neuróticos. Um psiquiatra realiza um estudo sobre os sintomas suicidas em duas amostras de 20 doentes de cada grupo. A nossa hipótese é que a proporção de psicóticos com sintomas suicidas é igual a proporção de neuróticos com estes sintomas (em um teste de independência, a hipótese nula seria, a presença ou ausência de sintomas suicidas é independente do tipo de doente envolvido). Assim, temos os dados resumidos na tabela 5.1.1.
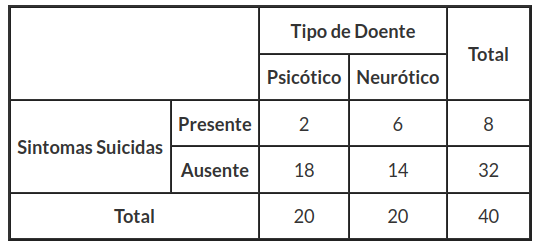
Tabela 5.1.1: Incidência de sintomas suicidas.
As tabelas que evidenciam maior afastamento da hipótese nula seriam
| 1 | 7 | 8 |
|---|---|---|
| 19 | 13 | 32 |
| 20 | 20 | 40 |
| 0 | 8 | 8 |
|---|---|---|
| 20 | 12 | 32 |
| 20 | 20 | 40 |
e portanto a aplicação do teste exato de Fisher, resultaria em:
$$P=P_2+P_1+P_0=0,095760 + 0,020160 + 0,001638 = 0,117558$$
que nos dá a probabilidade de observar que, entre os 8 doentes com sintomas suicidas, 2 ou menos são psicóticos, quando a hipótese de igualdade da proporção de psicóticos e neuróticos com sintomas suicidas é verdadeira. Verificamos que a probabilidade da discrepância maior ou igual a observada ter ocorrido, é de 0,117558, que é consideravelmente elevada. Logo, as proporções de psicóticos e neuróticos são homogêneas no que diz respeito aos sintomas suicidas.
É claro que este teste que realizamos foi um teste unilateral, enquanto que se tivéssemos usado o teste Qui-Quadrado tínhamos realizado um teste bilateral que mediria as diferenças relativamente à igualdade de proporções nos dois sentidos. Mas o teste de Fisher também pode ser realizado bilateralmente. Duas propostas podem ser feitas nesse sentido.
-
Como neste exemplo, as duas amostras têm a mesma dimensão, podemos multiplicar o valor de P por 2, e decidir do mesmo modo por comparação com o valor de $ \alpha $.
-
Caso as amostras sejam muito diferentes (ou os totais de coluna, em um teste de independência), poderíamos ainda calcular a probabilidade de ter a frequência mais discrepante do que a observada. Mas no nosso exemplo, medimos os casos mais extremos em que a proporção de ausência de sintomas suicidas dos neuróticos é muito maior do que a proporção de ausência de sintomas suicidas dos psicóticos. Neste caso, as tabelas seriam:
| 6 | 2 | 8 |
|---|---|---|
| 14 | 18 | 32 |
| 20 | 20 | 40 |
| 7 | 1 | 8 |
|---|---|---|
| 13 | 19 | 32 |
| 20 | 20 | 40 |
| 8 | 0 | 8 |
|---|---|---|
| 12 | 20 | 32 |
| 20 | 20 | 40 |
$$P^{**} = P_2 + P_1 + P_0 + P_6 + P_7 + P_8 = 0,235116,$$
calculando o p-valor, obtemos:
que são as mesmas conclusões caso o cálculo do p-valor seja adotado pela proposta 1, pois
$$P^{*}=2\times P=2\times 0,117558=0,235116.$$
Observação
Experimente aplicar o teste Qui-Quadrado mesmo admitindo frequências esperadas inferiores a 5 e aplicar a correção de Yates.
Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.
(imagem em falta)
(imagem em falta)
6 - Teste de McNemar para frequências correlacionadas
Amostras pareadas são muitas vezes utilizadas para aumentar a precisão de uma comparação. Contudo, duas amostras pareadas não são amostras independentes, mas sim correlacionadas. Consequentemente se forem utilizadas em um estudo de tabelas de contingência, a usual estatística Qui-Quadrado não pode ser utilizada no sentido estrito para averiguar as diferenças entre frequências de duas amostras. O teste apropriado para comparar frequências oriundas de amostras pareadas devemos a McNemar (1955).
Como introdução, consideramos a tabela 6.1, em que pretendemos analisar a presença ou ausência de um atributo A em duas amostras I e II, pareadas.
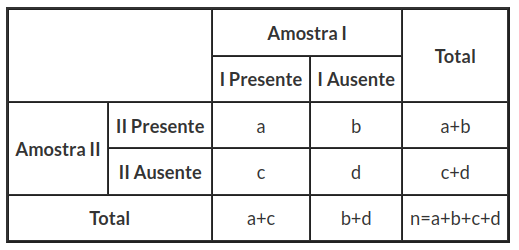
Tabela 6.1: Frequências em amostras pareadas.
Como estamos preocupados com as diferenças entre as duas amostras, as frequências b e c não nos interessam, mas sim as frequências a e d que registam mudança na observação do atributo A. Se a hipótese nula $ H_0 $ que queremos testar é a de que não existem diferenças nas amostras, no que diz respeito a observação do atributo A, então podemos considerar que a é o número de sucessos, porque passa de uma ausência a uma presença de A, e que d é o número de insucessos (fracassos), porque passa de uma presença a uma ausência de A. Se a hipótese nula é verdadeira, então a tem distribuição binomial de parâmetros $ (a + d; 1/2) $ e a frequência esperada das células $ (1, 1) $ e $ (2, 2) $ é de $ (a+d)/2 $.
McNemar propôs que, ao invés de usarmos o teste exato, utilizemos à estatística Qui-Quadrado aplicada as frequências a e d,
$$ Q^2_{obs}=\cfrac{(a-d)^2}{(a+d)}\quad (6.1.1) $$
que, condicional à hipótese nula $ H_0 $ de homogeneidade, tem uma distribuição assintótica Qui-Quadrado com 1 grau de liberdade.
Em alguns casos, podemos usar uma modificação da estatística (6.1.1) (“uma correção de continuidade semelhante à correção de Yates”) como a seguir:
$$ Q^2_{obs}=\cfrac{(|a-d|-1)^2}{a+d} $$
Repare que este teste apresenta uma resposta ao problema colocado no módulo teste de homogeneidade. De fato as amostras são pareadas e podemos agora aplicar o teste de McNemar.
6.1 Aplicação do Teste de McNemar
Exemplo 6.1.1
Voltando ao exemplo 3.3.1. Vimos que as amostras são pareadas e podemos agora aplicar o teste de McNemar.
Para o teste Qui-Quadrado de Pearson obtemos $ X^2 = 7,86 $ e temos $ {p-valor}=P[\chi^2_{0,05;(2-1)(2-1)}> 7,86|H_0]=0,005048 $ o que nos leva a concluir pela rejeição da hipótese de homogeneidade ao nível de 5% de significância.
Aplicando o teste de McNemar obtemos o teste:
$$ Q^2_{obs}=\cfrac{(a-d)^2}{(a+d)}=\cfrac{(35-4)^2}{(35+4)}=24,641 $$
$$ {p-valor}= 6,907\times10^{-7} $$
Se aplicarmos a correção de continuidade, $ Q^2_{obs} =6,4977 $ e $ {p-valor} = P(\chi^2_{0,05;(2-1)(2-1)}> 6,4977|H_0)=0,01080 $ que nos leva a decisão idêntica.
Aplicando o teste de McNemar obtemos o teste:
$$ Q^2_{obs}=\cfrac{|a-d|^2-1}{(a+d)}=\cfrac{|35-4|^2-1}{(35+4)}=24,615 $$
$$ {p-valor}= 7,02\times10^{-7} $$
Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.
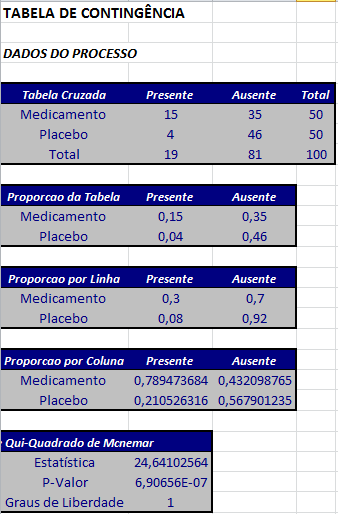
(imagem em falta)
7 - Análise de Resíduos
Outro processo que podemos utilizar na tentativa de identificar as categorias responsáveis por um valor significante da estatística Qui-Quadrado, foi sugerido por Haberman (1973). Este processo envolve a análise dos resíduos normalizados:
$$ r_{ij}=\cfrac{n_{ij}-E_{ij}}{\sqrt{E_{ij}}} $$
Obtemos uma estimativa da variância de $ r_{ij} $:
$$ \hat{v_{ij}}=\left(1-\cfrac{n_{i.}}{n}\right)\left(1-\cfrac{n_{.j}}{n}\right) $$
Então, para cada célula da tabela cruzada, podemos calcular o resíduo padronizado $ d_{ij} $ como a seguir:
$$ d_{ij}=\cfrac{r_{ij}}{\sqrt{v_{ij}}} $$
Quando as variáveis que constituem a tabela cruzada são independentes, os termos que $ d_{ij} $ têm distribuição aproximada Normal reduzida. Comparando os valores absolutos de $ d_{ij} $ com um quantil de probabilidade $ 1-\alpha/2 $ da distribuição normal reduzida.
Exemplo 7.1.1
Voltando ao exemplo 3.6.1
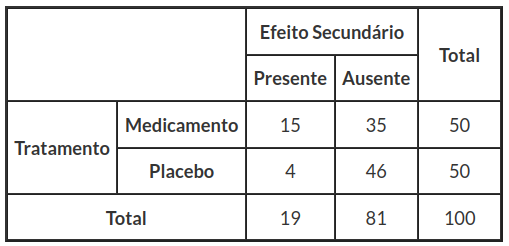
Tabela 7.1.1: População tratados com medicamento e outra população com placebo.
Primeiramente calculamos os resíduos:
$$ r_{ij}=\cfrac{n_{ij}-E_{ij}}{\sqrt{E_{ij}}} $$
$$ r_{11}=\cfrac{n_{11}-E_{11}}{\sqrt{E_{11}}}=1,78 \ldots r_{22}=\cfrac{n_{22}-E_{22}}{\sqrt{E_{22}}}=0,86 $$
e os resultados dos cálculos dos resíduos são encontrados na tabela 7.1.2:
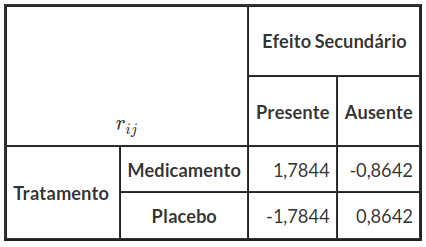
Tabela 7.1.2: Resíduos $ r_{ij} $
Com os resíduos, não temos uma sensibilidade para concluirmos algo, vamos agora calcular os resíduos padronizados e compararmos com a Normal reduzida.
Primeiro vamos encontrar os estimativas das variâncias:
$$ v_{ij}=\left(1-\cfrac{n_{i.}}{n}\right)\left(1-\cfrac{n_{.j}}{n}\right) $$
$$ v_{11}=\left(1-\cfrac{19}{100}\right)\left(1-\cfrac{50}{100}\right) \ldots v_{22}=\left(1-\cfrac{81}{100}\right)\left(1-\cfrac{50}{100}\right) $$
Obtemos as estimativas das variâncias na tabela 7.1.3:
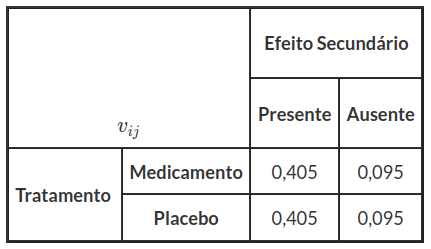
Tabela 7.1.3: Estimativas da variância $ v_{ij} $
Assim, calculamos os resíduos padronizados a seguir:
$$ d_{ij}=\cfrac{r_{ij}}{\sqrt{v_{ij}}} $$
$$ d_{11}=\cfrac{r_{11}}{\sqrt{v_{11}}}=\cfrac{1,7844}{\sqrt{0,405}}=2,8039 $$
$$ \vdots $$
$$ d_{22}=\cfrac{r_{22}}{\sqrt{v_{22}}}=\cfrac{1,7844}{\sqrt{0,405}}=2,8039 $$
obtemos os resíduos padronizados na tabela 7.1.4:
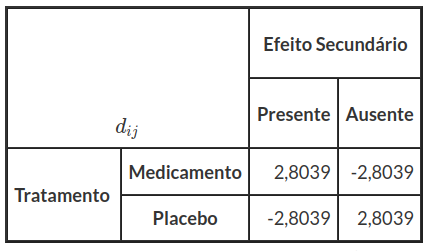
Tabela 7.1.4: Resíduos Padronizados $ d_{ij} $
e comparados os seus valores absolutos com o quantil de probabilidade $ 0,975 $ da Normal Reduzida, ou seja $ 1,96 $, observamos que todas as células apresentam valores significativos.
Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.
(imagem em falta)
(imagem em falta)
8 - Modelos Log Lineares para Tabelas de Contingência
Neste módulo, vamos estudar a aplicação de modelos de regressão de Poisson para a análise das tabelas cruzadas. A distribuição de Poisson é talvez uma das mais populares na aplicação de modelos log-lineares para tabelas cruzadas, pois são baseados na existência de uma estreita relação entre ela e a distribuição multinomial. Consideramos tabelas cruzadas simples, ou seja, tabelas 2 x 2. No entanto, os conceitos a serem introduzidos se aplicam igualmente aos casos mais gerais.
Exemplo 8.1
Para testar o efeito de um medicamento para um certo tipo de doença, foram selecionados 1330 pacientes, em que cruzamos o tipo de tratamento (medicamento ou placebo) e a presença ou ausência de efeitos em relação ao tipo de doença. Há vários esquemas de amostragem que poderíamos ter conduzido estes dados.
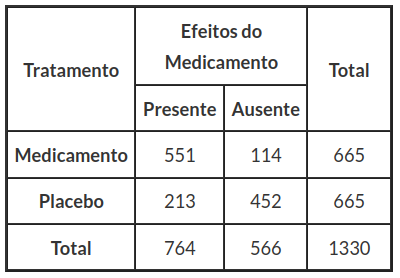
Tabela 8.1: Tabela de Tratamento versus Efeito do Medicamento.
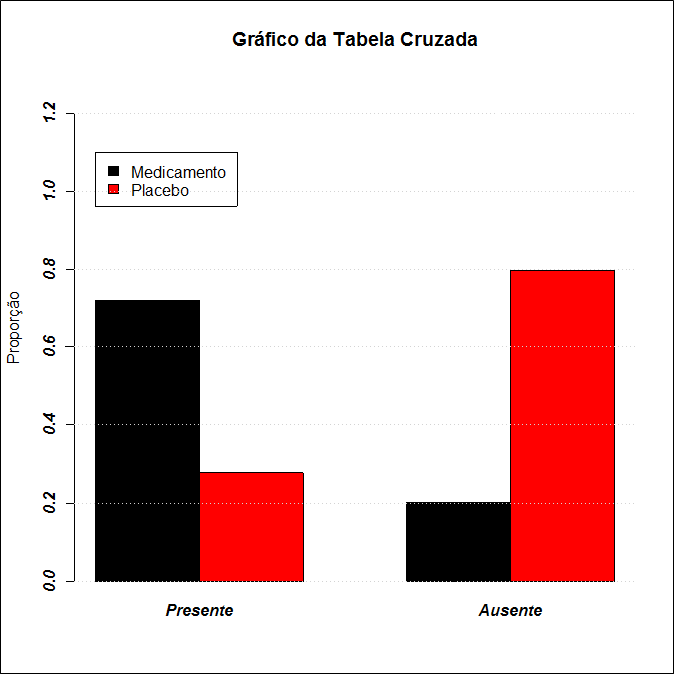
A seguir, vamos apresentar o modelo Poisson para tabelas cruzadas.
Modelo de Poisson
Um modelo alternativo para os dados da Tabela 8.1 é tratarmos as quatro frequências das variáveis aleatórias independentes de Poisson, pois estamos tratando primeiramente de uma tabela 2x2. A física possível do modelo é imaginar que existem quatro grupos de pessoas, um para cada célula da tabela, e que os membros de cada grupo chegam ao acaso em um hospital ou centro médico durante um período de tempo, digamos que para um exame de saúde. Neste modelo o tamanho total da amostra não é fixo e todas as contagens são, portanto, aleatórias.
Partindo do pressuposto de que as observações são independentes, a distribuição conjunta das quatro contagens é um produto de distribuições de Poisson:
$$ P[Y=y]=\displaystyle\prod^r_{i=1}\prod^c_{j=1} \cfrac{\lambda_{ij}^{y_{ij}}\exp{(-\lambda_{ij})}}{y_{ij}!}~~(8.1) $$
tomando log obtemos o log da verossimilhança usual de Poisson.
Em termos da estrutura sistemática do modelo, podemos considerar três modelos log-lineares para as contagens esperadas:
- modelo nulo;
- modelo aditivo;
- modelo saturado.
No modelo nulo supomos que todos os tipos de pacientes (4 tipos de pacientes) chegam ao laboratório na mesma proporção. Já no modelo aditivo supomos que a taxa de chegada depende do tratamento e da presença ou ausência de efeitos sobre a doença, mas não na combinação dos dois. Por fim, no modelo saturado diríamos que cada grupo tem seu próprio ritmo ou número esperado de chegadas.
Neste ponto, você pode tentar ajustar o modelo de Poisson aditivo para as quatro contagens na Tabela 8.1, tratamento e supor o efeito do medicamento como fatores ou preditores discretos.
Se pudermos escrever os valores ajustados, descobriremos que eles são exatamente os mesmos que no modelo multinomial. Esse resultado, evidentemente, não é uma coincidência. Testar a hipótese de independência no modelo multinomial é exatamente equivalente a testar a qualidade do ajuste do modelo de Poisson aditivo. A prova rigorosa desse resultado pode ser vista em (Fienberg,2006), mas podemos fornecer informações suficientes para mostrar que o resultado é intuitivamente razoável de entender quando pode ser usado.
Primeiro, observamos que, se as quatro contagens independentes têm distribuição de Poisson, sua soma tem distribuição Poisson com média igual à soma das médias. Simbolicamente, se $ Y_{ij}\sim P(\lambda_{ij}), $ então o total $ Y_{..}=\displaystyle\sum^r_{i=1}\sum^c_{j=1} Y_{ij} $ tem distribuição de Poisson com média $ \lambda_{..}=\displaystyle\sum^r_{i=1}\sum^c_{j=1} \lambda_{ij} $. Além disso, a distribuição condicional das quatro contagens dado o seu total é multinomial com probabilidades:
$$ \pi_{ij}=\frac{\lambda_{ij}}{n} $$
no qual usamos $ n $ para a observação total $ y_{..}=\displaystyle\sum^r_{i=1}\sum^c_{j=1} y_{ij}. $ Este resultado decorre diretamente do fato de que a distribuição condicional das contagens $ Y $ dado o seu total $ Y_{..} $ pode ser obtida como a relação entre a distribuição conjunta da contagem e do total (que é o mesmo que a distribuição conjunta das contagens, o que implica a total) para a distribuição marginal do total. Dividindo a distribuição conjunta dada na Equação (7.2) por marginais, que é Poisson com média $ \lambda_{..}, $ que nos leva diretamente à distribuição multinomial.
Em segundo lugar, notamos que a estrutura sistemática dos dois modelos é a mesma.
No modelo de independência, a probabilidade conjunta é o produto das marginais:
$$ \pi_{ij}=\pi_{i.}\pi_{j.} $$
Assim tomando o $ \log $ obtemos:
$$ \log\pi_{ij}=\log\pi_{i.}+\log\pi_{.j}, $$
que ainda pode ser escrita em termos das frequências esperadas $ E_{ij} = n\pi_{ij} $ , como:
$$ n\times n\times\pi_{ij}=n\times \pi_{i.}\times n\times\pi_{j.} $$
Aplicando o $ \log $ temos:
$$ \log(n\times \underbrace{n~\pi_{ij}}_{E_{ij}})=\log(\underbrace{n~\pi{i.}}_{E_{i.}})+\log(\underbrace{n~\pi_{.j}}_{E_{.j}}) $$
$$ \log E_{ij}=\log E_{i.}+\log E_{.j}-\log n~~(8.2) $$
Somando em i para a equação 8.2, temos:
$$ \sum^r_{i=1}\log E_{ij}=\sum^r_{i=1}\log E_{i.}+r\log E_{.j}-r\log n $$
Agora somamos em j para a equação 8.2:
$$ \sum^c_{j=1}\log E_{ij}=c\log E_{i.}+\sum^c_{j=1}\log E_{.j}-c\log n $$
que é exatamente a estrutura do modelo de Poisson aditivo:
$$ \log\lambda_{ij}=\eta+\alpha_i+\beta_j $$
Em ambos os casos, o registro da contagem esperada depende da linha e da coluna, mas não a combinação dos dois. Na verdade, é apenas as restrições que diferem entre os dois modelos. O modelo multinomial restringe as probabilidades conjuntas e marginais para adicionar um. O modelo de Poisson utiliza o método de referência das células e conjuntos $ \alpha_1=\beta_1=0. $
Se a estrutura sistemática e aleatória dos dois modelos é a mesma, então não teremos nenhuma surpresa se eles produzirem os mesmos valores ajustados e levar aos mesmos testes de hipóteses. Em (Fienberg,2006) mostra que temos a equivalência das duas distribuições condicionais contidas em $ n $, mas na análise de Poisson o total $ n $ é aleatória e não condicionadas em seu valor. Lembremos, contudo, que o modelo de Poisson, incluindo a constante, reproduz exatamente o total da amostra. Acontece que não necessitamos de condições em n, pois o modelo reproduz o seu valor exato de qualquer maneira.
Uma outra equivalência para o modelo de Poisson está quanto ao uso de outra técnica para o tratamento destes dados, que é a de modelos lineares generalizados, os detalhes destes modelo será tratado em um outro conteúdo estatístico. No software Action este modelo já está implementado, assim usamos esta ferramenta para tratarmos o uso de modelos log lineares para tabelas cruzadas. Portanto, reescrevendo o modelo (8.2) obtemos:
$$ \log E_{ij}=\beta_0+\beta_1~X_1+\beta_2~X_2~~(8.3) $$
A moral desta história é que não precisamos nos preocupar com modelos multinomiais e pode sempre recorrer ao modelo de Poisson equivalentemente. Embora o ganho é trivial no caso de uma tabela $ 2\times 2 $, pode ser muito significativo à medida que avançamos para classificações cruzadas envolvendo três ou mais variáveis, particularmente não temos que nos preocupar com a maximização da probabilidade multinomial sob restrições. O único truque que precisamos aprender é como traduzir as perguntas de independência que surgem no contexto multinomial para os modelos log lineares correspondentes no contexto de Poisson.
Exemplo 8.2
Voltando ao exemplo 8.1
| Tratamento | Efeito | Quantidade |
|---|---|---|
| 1 | 1 | 551 |
| 1 | 2 | 114 |
| 2 | 1 | 213 |
| 2 | 2 | 452 |
em que, para a variável tratamento temos que 1 é o medicamento e 2 é placebo e 1. Já para a variável Efeitos temos que 1 é presente e 2 é ausente. Assim, usando a equação (8.3) temos o seguinte modelo:
$$ \log(E_{ij})=\beta_0+\beta_1*{Tratamento}+\beta_2*{Efeito} $$
Usando o software Action, temos:
(imagem em falta)
Agora, vamos calcular os valores esperados que é o mesmo para o teste Qui-Quadrado para tabelas cruzadas. Então temos:
$$ E_{11}=\exp\left(\beta_0+\beta_1*1+\beta_2*1\right)=\exp(6,24+(-1,32)*1+(-0,29)*1)=382 $$
$$ E_{12}=\exp\left(\beta_0+\beta_1*1+\beta_2*2\right)=\exp(6,24+(-1,32)*1+(-0,29)*2)=283 $$
$$ E_{21}=\exp\left(\beta_0+\beta_1*2+\beta_2*1\right)=\exp(6,24+(-1,32)*2+(-0,29)*1)=382 $$
$$ E_{22}=\exp\left(\beta_0+\beta_1*2+\beta_2*2\right)=\exp(6,24+(-1,32)*2+(-0,29)*2)=283 $$
Agora, mostramos o resultado obtidos pelo software Action para o teste Qui-Quadrado:
(imagem em falta)
Observe que os valores da tabela dos Valores Esperados são os mesmos obtidos pelo preditor linear do modelo Poisson e o p-valor da estatística Qui-Quadrado é bem próximo do p-valor para o coeficiente do efeito, com isso, temos as mesmas conclusões, ou seja, as variáveis são independentes.
9 - Aplicações de Tabela Cruzada
Nesta seção, vamos mostrar algumas aplicações da Tabela Cruzada. Todos os casos apresentados são reais e foram elaborados pelo cliente com a participação da equipe Portal Action.
Teste de independência para estudo da quantidade de erro na distribuição de materiais de uma editora
Uma editora quer realizar um estudo sobre a quantidade de erros que acontecem na distribuição de materiais produzidos por duas empresas. Para isso realizamos um estudo considerando duas variáveis, a empresa que produz o exemplar e o número de exemplares faltantes que deveriam ser recebidos pelo distribuidor, estas variáveis foram divididas da seguinte forma:
(imagem em falta)
Iniciamos montando a tabela cruzada das observações:
| A | B | C | Total | |
|---|---|---|---|---|
| Empresa A | 1093 | 1222 | 770 | 3085 |
| Empresa B | 1472 | 908 | 750 | 3130 |
| Total | 2565 | 2130 | 1520 | 6215 |
Tabela 9.1.1: Tabela cruzada.
(imagem em falta)
Agora calculamos as frequências esperadas:
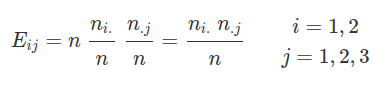
$$E_{11}=\cfrac{3085*2566}{6215}=1273,21$$
$$E_{12}=\cfrac{3085*2130}{6215}=1057,29$$
$$E_{13}=\cfrac{3085*1520}{6215}=754,50$$
$$E_{21}=\cfrac{3130*2565}{6215}=1291,79$$
$$E_{22}=\cfrac{3130*2130}{6215}=1072,71$$
$$E_{23}=\cfrac{3130*1520}{6215}=765,50$$
Dessa forma, montamos uma tabela das frequências esperadas:
| A | B | C | |
|---|---|---|---|
| Empresa A | 1273,21 | 1057,29 | 754,50 |
| Empresa B | 1291,79 | 1072,71 | 765,50 |
Tabela 9.1.2: Frequências esperadas.
Agora calculamos os valores padronizados:
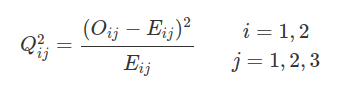
$$Q^2_{11}=\cfrac{(1093-1273,71)^2}{1273,71}=25,51$$
$$Q^2_{12}=\cfrac{(1222-1057,29)^2}{1057,29}=25,66$$
$$Q^2_{13}=\cfrac{(770-754,50)^2}{754,50}=0,32$$
$$Q^2_{21}=\cfrac{(1472-1291,79)^2}{1291,79}=25,14$$
$$Q^2_{22}=\cfrac{(908-1072,71)^2}{1072,71}=25,29$$
$$Q^2_{23}=\cfrac{(750-765,50)^2}{765,50}=0,31$$
Dessa forma, montamos uma tabela com os valores de $ Q^2 $ no ponto $ (i,j) $:
| A | B | C | |
|---|---|---|---|
| Empresa A | 25,51 | 25,66 | 0,32 |
| Empresa B | 25,14 | 25,29 | 0,31 |
Tabela 9.1.3: Valores de $ Q^2 $ no ponto $ (i,j) $.
$$Q^2_{obs}=\sum^r_{i=1}\sum^c_{j=1}\cfrac{(O_{ij}-E_{ij})^2}{E_{ij}}=25,51+25,66+0,32+25,14+25,29+0,31=102,23$$
$${p-valor}=P[102,23> \chi^2_{(2-1)(3-1)}|H_0]=6,31744E^{-23}$$
Como obtemos $ Q^2_{obs}=102,23 $ e do $ p-valor=6,31744E^{-23} $, rejeitarmos a hipótese nula. Portanto, concluímos que existe dependência entre a empresa e a falta de exemplares, ao nível de significância de 5%, ou seja, não são independentes.
Agora calculamos as medidas de associação:
- Coeficiente de contingência quadrático médio:
$$\Phi^2=\cfrac{Q^2_{obs}}{n}=\cfrac{102,23}{6215}=0,016$$
- Coeficiente de contingência
$$P=\sqrt{\cfrac{\frac{Q^2_{obs}}{n}}{1+\frac{Q^2_{obs}}{n}}}=\sqrt{\cfrac{Q^2_{obs}}{n+Q^2_{obs}}}=\sqrt{\cfrac{102,23}{6215+102,23}}=0,127$$
- Coeficiente de Tschuprov
$$T=\sqrt{\cfrac{\frac{Q^2_{obs}}{n}}{(r-1)(c-1)}}=\sqrt{\cfrac{\frac{102,23}{6215}}{(3-1)(2-1)}}=0,091$$
- Coeficiente de Cramer
$$C=\cfrac{\frac{Q^2_{obs}}{n}}{\min(r-1;c-1)}=\cfrac{\frac{102,23}{6215}}{\min(3-1,2-1)}=0,016$$
Notamos que nos 4 casos o valor do coeficiente é muito baixo, o que significa que a associação entre as variáveis é muito pequena.
Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.
(imagem em falta)
Teste de independência para estudo de produtos rejeitados
Uma empresa quer realizar um estudo sobre a quantidade de produtos que foi rejeitado por mês, no primeiro semestre do ano. Para isso realizamos um estudo considerando duas variáveis, ação que refere-se a ação de rejeitar ou não rejeitar o produto e o mês em que a ação foi tomada, estas variáveis foram divididas da seguinte forma:
(imagem em falta)
Iniciamos montando a tabela cruzada das observações:
| Não Rejeitado | Rejeitado | Total | |
|---|---|---|---|
| Janeiro | 357 | 249 | 606 |
| Fevereiro | 383 | 328 | 711 |
| Março | 535 | 295 | 830 |
| Abril | 605 | 354 | 959 |
| Maio | 553 | 554 | 1107 |
| Junho | 425 | 460 | 885 |
| Total | 2858 | 2240 | 5098 |
Tabela 9.2.1: Tabela cruzada.
(imagem em falta)
Agora calculamos as frequências esperadas:
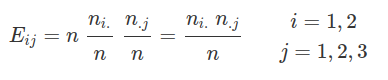
$$E_{11}=\cfrac{606*2858}{5098}=339,73$$
$$\vdots$$
$$E_{62}=\cfrac{885*2240}{5098}=388,86$$
Dessa forma, montamos uma tabela das frequências esperadas:
| Não Rejeitado | Rejeitado | |
|---|---|---|
| Janeiro | 339,73 | 266,27 |
| Fevereiro | 398,6 | 312,4 |
| Março | 465,31 | 364,69 |
| Abril | 537,63 | 421,37 |
| Maio | 620,6 | 486,4 |
| Junho | 496,14 | 388,86 |
Tabela 9.2.2: Frequências esperadas.
Agora calculamos os valores padronizados:
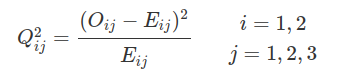
$$Q^2_{11}=\cfrac{(357-339,73)^2}{339,73}=0,88$$
$$\vdots$$
$$Q^2_{62}=\cfrac{(460-388,86)^2}{388,86}=13,02$$
Dessa forma, montamos uma tabela com os valores de $ Q^2 $ no ponto $ (i,j) $:
| Não Rejeitado | Rejeitado | |
|---|---|---|
| Janeiro | 0,88 | 1,12 |
| Fevereiro | 0,61 | 0,78 |
| Março | 10,44 | 13,32 |
| Abril | 8,44 | 10,77 |
| Maio | 7,36 | 9,39 |
| Junho | 10,20 | 13,02 |
Tabela 9.2.3: Valores de $ Q^2 $ no ponto $ (i,j) $.
$$Q^2_{obs}=\sum^r_{i=1}\sum^c_{j=1}\cfrac{(O_{ij}-E_{ij})^2}{E_{ij}}=0,88+1,12+0,61+0,78+10,44+13,32+8,44+10,77+7,36+9,39+10,20+13,02=86,33$$
$${p-valor}=P[86,33> \chi^2_{(6-1)(2-1)}|H_0]=3,95762E^{-17}$$
Como obtemos $ Q^2_{obs}=86,33 $ e do $ p-valor=3,95762E^{-17} $, rejeitarmos a hipótese nula. Portanto, concluímos que existe dependência entre o mês e a ação, ao nível de significância de 5%, ou seja, não são independentes.
Agora calculamos as medidas de associação:
- Coeficiente de contingência quadrático médio:
$$\Phi^2=\cfrac{Q^2_{obs}}{n}=0,02$$
- Coeficiente de contingência
$$P=\sqrt{\cfrac{\frac{Q^2_{obs}}{n}}{1+\frac{Q^2_{obs}}{n}}}=\sqrt{\cfrac{Q^2_{obs}}{n+Q^2_{obs}}}=0,13$$
- Coeficiente de Tschuprov
$$T=\sqrt{\cfrac{\frac{Q^2_{obs}}{n}}{(r-1)(c-1)}}=0,06$$
- Coeficiente de Cramer
$$C=\cfrac{\frac{Q^2_{obs}}{n}}{\min(r-1;c-1)}=0,02$$
Notamos que nos 4 casos o valor do coeficiente é muito baixo, o que significa que a associação entre as variáveis é muito pequena.
Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.
(imagem em falta)
Apêndice
Distribuição Qui-Quadrado
| Graus de Liberdade | 97,50% | 95% | 5% | 2,5% |
|---|---|---|---|---|
| 1 | 0,001 | 0,004 | 3,841 | 5,024 |
| 2 | 0,051 | 0,103 | 5,991 | 7,378 |
| 3 | 0,216 | 0,352 | 7,815 | 9,348 |
| 4 | 0,48 | 0,71 | 9,49 | 11,14 |
| 5 | 0,83 | 1,15 | 11,07 | 12,83 |
| 6 | 1,24 | 1,64 | 12,59 | 14,45 |
| 7 | 1,69 | 2,17 | 14,07 | 16,01 |
| 8 | 2,18 | 2,73 | 15,51 | 17,53 |
| 9 | 2,7 | 3,33 | 16,92 | 19,02 |
| 10 | 3,25 | 3,94 | 18,31 | 20,48 |
| 11 | 3,82 | 4,57 | 19,68 | 21,92 |
| 12 | 4,4 | 5,23 | 21,03 | 23,34 |
| 13 | 5,01 | 5,89 | 22,36 | 24,74 |
| 14 | 5,63 | 6,57 | 22,68 | 26,12 |
| 15 | 6,26 | 7,26 | 25 | 27,49 |
| 16 | 6,91 | 7,96 | 26,3 | 28,85 |
| 17 | 7,56 | 8,67 | 27,59 | 30,19 |
| 18 | 8,23 | 9,39 | 28,87 | 31,53 |
| 19 | 8,91 | 10,12 | 30,14 | 32,85 |
| 20 | 9,59 | 10,85 | 31,41 | 34,17 |
| 21 | 10,28 | 11,59 | 32,67 | 35,48 |
| 22 | 10,98 | 12,34 | 33,92 | 36,78 |
| 23 | 11,69 | 13,09 | 35,17 | 38,08 |
| 24 | 12,4 | 13,85 | 36,42 | 39,36 |
| 25 | 13,12 | 14,61 | 37,65 | 40,65 |
| 26 | 13,84 | 15,38 | 38,89 | 41,92 |
| 27 | 14,57 | 16,15 | 40,11 | 43,19 |
| 28 | 15,31 | 16,93 | 41,34 | 44,46 |
| 29 | 16,05 | 17,71 | 42,56 | 45,72 |
| 30 | 16,79 | 18,49 | 43,77 | 46,98 |
Tabela: valores de $ \nu_C $ tais que $P(\chi^2\geq \nu_C) = p$
Referências Bibliográficas
- Agresti, A. (2002) Categorical Data Analysis. New York: Wiley.
- Berger, V.W. (2000) Pros and cons of permutation tests in clinical trials. Statistics in Medicine, 19, 1319-1328.
- Conover, W.J. (1974) Some reasons for not using the Yates continuity correction on 2 x 2 contingency tables. Journal of the American Statistical Association, 69, 374-376.
- Fisher, R.A. (1934) Statistical Methods for Research Workers. 5th Edition, Edinburgh: Oliver and Boyd.
- Grizzle, J.E. (1967) Continuity correction in the 2 test for 2 x 2 tables. The American Statistician, 21, 28-32.
- Haber, M. (1980) A comparison of some continuity corrections for the chi-squared test on 2 x 2 tables. Journal of the American Statistical Association, 75, 510-515.
- Haber, M. (1982) The continuity correction and statistical testing. International Statistical Review, 50, 135-144.
- Kendall, M.G. and Stuart, A. (1967) The Advanced Theory of Statistics. Vol 2, 2nd Edition, London: Griffin.
- Mantel, N. (1976) The continuity correction. The American Statistician, 30, 103-104.
- Maxwell, E.A. (1976) Analysis of contingency tables and further reasons for not using Yates correction in 2 x 2 tables. Canadian Journal of Statistics, 4, 277-290.
- Pearson, E.S. (1947) The choice of statistical tests illustrated on the interpretation of data classed in a 2 x 2 table. Biometrika, 34, 139-167.
- Plackett, R.L. (1964) The continuity correction in 2 x 2 tables. Biometrika, 51, 327-337.
- Richardson, J.T.E. (1990) Variants of chi-square for 2 x 2 contingency tables. British Journal of Mathematical and Statistical Psychology, 43, 309-326.
- Richardson, J.T.E. (1994) The analysis of 2 x 1 and 2 x 2 contingency tables: an historical review. Statistical Methods in Medical Research, 3, 107-133.
- Salsburg, D. (2002) The Lady Tasting Tea: How Statistics Revolutionized Science in the Twentieth Century. London: Owl Books.
- Siegel, S. and Castellan, N.J. (1988) Nonparametric Statistics for the Behavioural Sciences. 2nd Edition, New York: McGraw-Hill.
- Yates, F. (1934) Contingency tables involving small numbers and the 2 test. Journal of the Royal Statistical Society, Suppl.1, 217-235.
- Yates, F. (1984) Tests of significance for 2 x 2 contingency tables. Journal of the Royal Statistical Society Series A, 147, 426-463.
- S.E. Fienberg. Log-linear Models in Contingency Tables. Wiley Online Library, 2006.