7. TÉCNICAS NÃO PARAMÉTRICAS

Todos os procedimentos básicos de estatística - o teste T, o teste F, a análise de variância (ANOVA), entre outros - dependem fortemente da suposição de que os dados da amostra (ou as estatísticas suficientes) estejam distribuídos de acordo com uma distribuição específica. Mas, para cada teste clássico, existe uma alternativa não-paramétrica com menos hipóteses sobre os dados. Mesmo se as hipóteses a partir de um modelo paramétrico são modestas e pouco restritivas, elas serão, sem dúvida, falsas, no sentido mais puro.

Os testes paramétricos assumem que a distribuição de probabilidade da população no qual retiramos os dados seja conhecida e que somente os valores de certos parâmetros, tais como a média e o desvio padrão, sejam desconhecidos. Se os dados não satisfazem as suposições assumidas pelas técnicas tradicionais, métodos não paramétricos de inferência estatística devem usados. As técnicas não paramétricas assumem pouca ou nenhuma hipótese sobre a distribuição de probabilidade da população no qual retiramos os dados

A partir dos anos de 1940, a ideia de testes de postos (ranks) ganharam força na literatura estatística. Hotelling e Pabst (1936) escreveram um dos primeiros artigos sobre o assunto, as correlações de ordem. Desde então, temos testes não-paramétricos para uma amostra, para comparação de duas ou mais amostras, para amostras pareadas, correlação bivariada e muito mais. A chave para avaliar os dados em uma estrutura não-paramétrica é comparar observações com base em seus postos no interior da amostra. A tabela a seguir mostra as analogias dos testes não-paramétricos para os procedimentos conhecidos paramétricos.

Paramétrico	Não-Paramétrico
Coeficiente de Pearson para Correlação	Coeficiente de Spearman para Correlação
Teste-t 1 Amostra	Teste de Wilcoxon 1 Amostra
Teste-t Pareado	Teste de Wilcoxon Pareado
Teste-t 2 Amostras	Teste de Wilcoxon-Mann-Whitney Amostras Independentes
ANOVA	Teste de Kruskal-Wallis
ANOVA experimento fatorial em blocos	Teste de Friedman

Figura: Frank Wilcoxon (1892-1965). Henry Berthold Mann (1905-2000) e Professor Emeritus Donald Ransom Whitney.

Em geral, os métodos não paramétricos são aplicados em problemas de inferência no qual as distribuições das populações envolvidas não precisam pertencer a uma família específica de distribuições de probabilidade tal como Normal, Uniforme, Exponencial etc. Por isso, os testes não paramétricos são também chamados testes livres de distribuição (“distribution free tests”).

1 - Teste de Wilcoxon - Amostra Única

Consideremos uma população P com distribuição contínua e simétrica no qual retiramos uma amostra aleatória $X_{1}$, $X_{2}$, …, $X_{n}$ . Nosso interesse é estudar o comportamento da mediana populacional com relação a um valor $θ_{0}$ especificado.

O teste de Wilcoxon é baseado nos postos (ranks) dos valores obtidos. Postos são as posições, representados por números, que os valores ocupam quando colocados em ordem crescente. Por exemplo, considere o seguinte conjunto de valores:

12	17	15	19	14	16	11

Colocando em ordem crescente e atribuindo a cada valor seu posto, temos

Valor	11	12	14	15	16	17	19
Posto	1	2	3	4	5	6	7

As seguintes hipóteses são necessárias para o desenvolvimento deste teste de hipóteses:

1. As observações $X_{i}$’s são independentes.

2. Cada observação $X_{i}$ é obtida de uma população que é contínua e simétrica em torno de $θ_{0}$. Desta forma, admitimos que a probabilidade (em teoria) de que dois valores amostrais coincidam é zero.

Para a realização do teste de Wilcoxon estabelecemos uma das seguintes hipóteses:

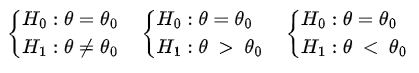
que são equivalentes as hipóteses

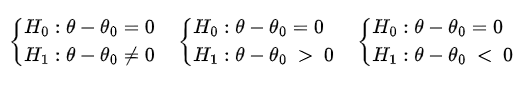
Inicialmente devemos subtrair $θ_{0}$ de cada valor $X_{i}$, i = 1, …, n, da amostra e assim obtemos um novo conjunto de dados, $Z_{1}$, $Z_{2}$, …, $Z_{n}$ onde $Z_{i}$ = $X_i-θ_{0}$.

Ordenamos de forma crescente o novo conjunto de dados {$|Z_{1}|, |Z_{2}|, …, |Z_{n}|$} (observe que ordenamos o conjunto dos valores absolutos, ou seja, não consideramos o sinal do elemento $Z_{i}$) e associamos a cada valor $Z_{i}$ o posto $R_{i}$ correspondente. A seguir, definimos as variáveis indicadoras $ψ_{i}$, i = 1, 2, …, n, dadas por

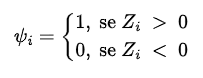
ou seja, se $X_i-θ_{0 }$> 0, então $ψ_{i }$= 1, caso contrário, $ψ_{i}$ = 0.

Obtemos os n produtos $R_1ψ_{1}$, …, $R_nψ_{n}$. Cada produto $R_iψ_{i}$ é chamado posto positivo de $Z_{i}$. Neste caso, se $Z_{i}$ > 0, $R_iψ_{i}$ é igual ao posto $R_{i}$ correspondente e se $Z_{i}$ < 0, $R_iψ_{i}$ é igual a 0.

Definimos a estatística $T^{+}$ como a soma dos postos que têm sinal positivo, ou seja, $$T^+=\sum_i^n R_i\psi_i$$

Exemplo 1.1

Considere a seguinte amostra

126	142	156	228	245	246
370	419	433	454	478	503

Suponha que os dados da amostra são distribuídos simetricamente em torno da mediana $θ_{0}$ = 220.

Subtraindo o valor 220 de cada valor da amostra temos um novo conjunto de dados:

-94	-78	-64	8	25	26	150	199	213	234	258	283

Colocando em ordem crescente os valores absolutos, associamos à cada valor o posto correspondente $(R_{i}$) e as variáveis indicadoras $ψ_{i}$.

Valor	8	25	26	-64	-78	-94	150	199	213	234	258	283
Posto	1	2	3	4	5	6	7	8	9	10	11	12
ψi	1	1	1	0	0	0	1	1	1	1	1	1

Tabela 1.1: Postos combinados para uma amostra única.

Neste caso, a estatística $T^{+}$ é a soma dos postos positivos, isto é $$T^+=\sum_{i=1}^{12} R_i\psi_i = 1 + 2 + 3 + 7 + 8 + 9 + 10 + 11 + 12 = 63.$$

1.1 - Um estimador do parâmetro de posição

Na tentativa de estimar o parâmetro de posição θ, consideraremos as médias ($X_i$+$X_j$)/2 entre as observações $X_i$ e $X_j$ tais que i ≤ j. Neste caso, se temos n observações da população, segue que temos M = n(n+1)/2 médias desse tipo. O estimador de θ associado com a estatística $T^{+}$ do teste de Wilcoxon é

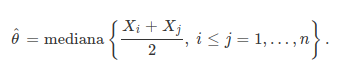
Sejam $W^{(1)}$, $W^{(2)}$, …, $W^{(M)}$ os valores ordenados de $(X_i+X_j)/2$ com i ≤ j. Então, se M é ímpar, ou seja, M = 2k + 1, então k = (M-1)/2 e $$\hat{\theta}=W^{(k+1)},$$

que é o valor que ocupa a posição k + 1 na lista de médias ($X_i+X_j$)/2. Se M é par, ou seja, M = 2k, então k = M/2 e $$\hat{\theta}=\frac{W^{(k)}+W^{(k+1)}}{2}.$$

Isto é, quando M é par, $\hat{\theta}$ é a média dos dois valores ($X_i+X_j$)/2 que ocupam as posições k e k + 1.

Definição 1.1.1

O estimador $\hat{\theta}$ é chamado de pseudo-mediana.

Exemplo 1.1.1

Encontre a pseudo-mediana para o seguinte conjunto de dados

-4	-3	-1	2	5	6

Temos que as médias ($X_i+X_j$)/2 entre as observações $X_i$ e $X_j$ tais que i ≤ j ordenadas são dadas na tabela abaixo

-4	-3,5	-3	-2,5	-2	-1	-1
-0,5	0,5	0,5	1	1	1,5	2
2	2,5	3,5	4	5	5,5	6

Como temos 6 observações, temos 6(6+1)/2 = 21 médias entre as observações $X_i$ e $X_j$ com i ≤ j. Como M = 21 é um número ímpar, então temos que a pseudo-mediana será a observação 11, ou seja $$\hat{\theta}=1.$$

1.2 - Distribuição exata da estatística de Wilcoxon

Para encontrar a distribuição exata de $T^{+}$ sob $H_0$, considere B o número de $Z_i’s$ positivos ($Z_i = X_i - θ_0$) e sejam $r_1$ < … < $r_B$ os ranks (posições) ordenadas dos valores absolutos destes $Z_i’s$ positivos. Podemos obter a distribuição diretamente da representação $T^+=\sum_{i=1}^Br_i$. Sob a hipótese de que as distribuições de cada $Z_i$ são todas contínuas, a probabilidade de que os valores absolutos de $Z_i’s$ sejam iguais ou que algum $Z_i$ seja 0 é zero. Além disso, sob $H_0$ as distribuições de todos os $Z_i’s$ são simétricas em torno de θ = $θ_0$. Portanto, se temos uma amostra de n elementos, temos 2^n possibilidades para a configuração ($r_1, r_2, …, r_B$) e cada uma delas ocorre com probabilidade (1/2)^n. Neste caso, temos que

$$P(T^+=t)=\frac{u(t)}{2^n}$$

onde u(t) é o número de maneiras de atribuir valores para as configurações ($r_1, r_2, …, r_B$) de forma que $$\sum_{i=1}^Br_i=t.$$

Exemplo 1.2.1

Considere o caso em que temos uma amostra de n = 3 elementos.

Neste caso, temos $2^3$ = 8 possíveis configurações para ($r_1, r_2, …, r_B$) e os valores associados de $T^{+}$ são dados na seguinte tabela.

B	(r1, r2, …, rB)	Probability under $H_0$	$ T^+=\sum_{i=1}^Br_i $
0		1/8	0
1	r1 = 1	1/8	1
1	r1 = 2	1/8	2
1	r1 = 3	1/8	3
2	r1 = 1, r2 = 2	1/8	3
2	r1 = 1, r2 = 3	1/8	4
2	r1 = 2, r2 = 3	1/8	5
3	r1 = 1, r2 = 2, r3 = 3	1/8	6

Assim, para este exemplo, a probabilidade de $T^{+}$ ser igual a 3 (P[$T^{+}$ = 3]) é igual a 2/8 já que o evento $T^{+}$ = 3 ocorre quando B = 1 ($r_1 = 3$) ou quando B = 2 ($r_1 = 1, r_2 = 2$) e cada uma dessas ocorrências ocorre com probabilidade 1/8.

$T^{+}$	Probabilidade sob $H_0$
0	1/8
1	1/8
2	1/8
3	2/8
4	1/8
5	1/8
6	1/8

Em um teste de Wilcoxon em que o tamanho amostral n é pequeno (geralmente n < 50) utilizamos a distribuição exata da estatística $T^{+}$ e, a partir desta distribuição, calculamos os valores críticos do teste, o p-valor e o intervalo de confiança.

1. Cálculo dos valores críticos.

Se estamos realizando um teste bilateral, então devemos encontrar os valores críticos $t_1$ e $t_2$ tais que $$P[T^+ \ < \ t_1] = P[T^+ \ > \ t_2]\approx \frac{\alpha}{2}.$$

Se o teste é unilateral à direita, então devemos encontrar o valor crítico t tal que $$P[T^+ \ > \ t] \approx \alpha$$

e se o teste é unilateral à esquerda, então devemos encontrar o valor crítico t tal que $$P[T^+ \ < \ t] \approx \alpha.$$

2. Critério.

Se o teste é bilateral e

$$T^{+}_{obs} < t_1$$

ou $$T^{+}_{obs} > t_2$$

então rejeitamos $H_0$, caso contrário não rejeitamos $H_0$. Ou seja, se $t_1$ ≤ $T^{+}_{obs}$ ≤ $t_2$, não rejeitamos a hipótese nula $H_0$.

No caso do teste unilateral à direita, se $T^{+}$ > t, rejeitamos a hipótese $H_0$, caso contrário não rejeitamos $H_0$. Isto é, se $T^{+}$ ≤ t não rejeitamos a hipótese nula $H_0$.

Se o teste é unilateral à esquerda e $T^{+}$ < t, rejeitamos a hipótese $H_0$, caso contrário não rejeitamos $H_0$. Isto é, se $T^{+}$ ≥ t não rejeitamos a hipótese nula $H_0$.

3. Cálculo do p-valor.

Se o teste é bilateral, o p-valor do teste exato é dado por

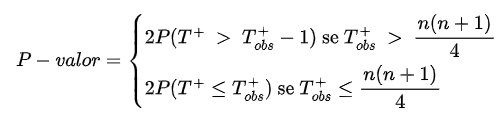
Se o teste é unilateral à direita, o p-valor do teste exato é dado por $$P-valor=P(T^+ \ > \ T^+_{obs}-1)$$

e se o teste é unilateral à esquerda, o p-valor do teste exato é dado por $$P-valor=P(T^+ \leq \ T^+_{obs}).$$

4. Intervalo de Confiança para o parâmetro de posição.

De forma análoga à estimativa do parâmetro de posição, consideramos as médias $(X_i+X_j)/2$ entre as observações $X_i$ e $X_j$ tal que i ≤ j. Neste caso, se temos n observações da população, segue que temos M = n(n+1)/2 médias desse tipo.

Sejam $W^{(1)}, W^{(2)}, …, W^{(M)}$ os valores ordenados desta médias.

Se o teste é bilateral e o nível de significância é α encontramos os valores L e U tais que $$P(T^+ \leq L)\approx \frac{\alpha}{2} \qquad U = \frac{n(n+1)}{2}-L$$

e o intervalo de confiança 100(1-α)% para o parâmetro de posição θ é então dado por $$IC_{1-\alpha}(\theta)=(W^{(L)},W^{(U+1)}).$$

Se o teste é unilateral à direita, encontramos o valor L tal que $$P(T^+ \leq L)\approx \alpha$$

e o intervalo de confiança 100(1-α)% para o parâmetro de posição θ é então dado por $$IC_{1-\alpha}(\theta)=(W^{(L)},\infty).$$

Se o teste é unilateral à esquerda, encontramos os valores L e U tais que $$P(T^+ \leq L)\approx \alpha \qquad U = \frac{n(n+1)}{2}-L$$

e o intervalo de confiança 100(1-α)% para o parâmetro de posição θ é então dado por $$IC_{1-\alpha}(\theta)=(-\infty,W^{(U+1)}).$$

Exemplo 1.2.2

Considere a seguinte amostra

126	142	156	228	245	246
370	419	433	454	478	503

Vamos testar, com um nível de significância α = 0,05, se os dados estão distribuídos simetricamente em torno de $θ_0$ = 220.

1. Estabelecemos as hipóteses

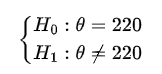
já que queremos testar se os dados estão ou não distribuídos simetricamente em torno $θ_0$ = 220.

Como já vimos no Exemplo 1.1, o valor da estatística $T^{+}$ é dado por $T^{+}$ = 63.

2. Cálculo dos valores críticos.

Como estamos realizando um teste bilateral, devemos encontrar os valores $t_1$ e $t_2$ tais que $$P(T^+ \ < \ t_1) = P(T^+ \ > \ t_2)\approx \frac{\alpha}{2}.$$

Neste caso, temos que os valores $t_1$ e $t_2$ são dados por $t_1$ = 14 e $t_2$ = 64. Como $t_1$ = 14 < $T^{+}_{obs}$ = 63 < $t_2$ = 64, então não rejeitamos a hipótese nula de que os dados estão distribuídos simetricamente em torno de $θ_0$ = 220.

3. Cálculo do p-valor.

Como o teste é bilateral, o p-valor do teste exato é dado por

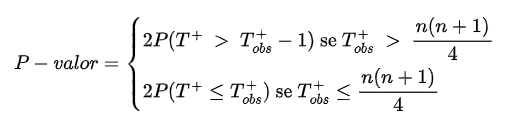
Temos que n(n+1)/4 = 52 e como $T^{+}_{obs}$ = 63 > 52, segue que

$$P-valor = 2P(T^+ \ > \ T^+_{obs}-1) = 2P(T^+ \ > \ 62) = 0,06396484.$$

4. Intervalo de confiança.

Para se calcular o intervalo de confiança, consideramos os valores ordenados das médias $(X_i+X_j)/2$ com i ≤ j. Estes valores estão calculados na tabela abaixo:

Médias ordenadas $(Xi+Xj)/2$:

126	134	141	142	149	156
177	185	185,5	186	192	193,5
194	200,5	201	228	236,5	237
245	245,5	246	248	256	263
272,5	279,5	280,5	287,5	287,5	290
294,5	298	299	302	305	307,5
308	310	314,5	317	322,5	323,5
329,5	330,5	332	332,5	339	339,5
341	349,5	350	353	361,5	362
365,5	370	374	374,5	394,5	401,5
412	419	424	426	433	436,5
436,5	443,5	448,5	454	455,5	461
466	468	478	478,5	490,5	503

Encontramos agora os valores L e U tais que $$P(T^+\leq L)\approx\alpha/2 \qquad U = \frac{n(n+1)}{2}-L.$$

Neste caso, temos que L = 14 e U = 64 e o intervalo de confiança com será dado por $$IC_{1-\alpha}(\theta)=(W^{(14)},W^{(65)})=(200,5;433).$$

5. Estimador para o parâmetro de posição (pseudo-mediana)

A partir da tabela das médias acima, temos que a quantidade total dessas médias é M = 78 = 2k com k = 39. Neste caso, segue que $$\hat{\theta}=\frac{W^{(k)}+W^{(k+1)}}{2}=\frac{314,5+317}{2}=315,75.$$

Utilizando o software Action, os resultados são dados a seguir

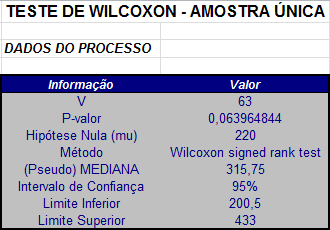
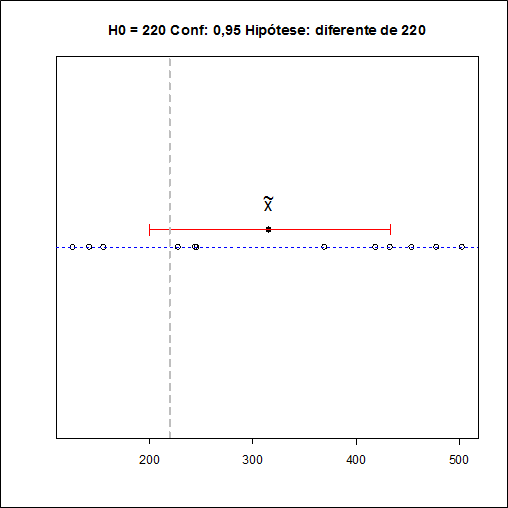
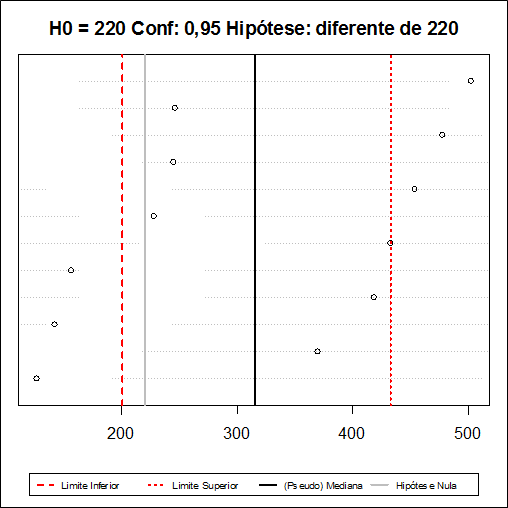
1.3 - Aproximação Normal

Para amostras de tamanho n > 50, utilizamos uma aproximação normal. Consideremos a estatística $T^{+}$ como dada anteriormente, ou seja, $T^{+}$ é a soma de todos os postos positivos.

Teorema 1.3.1

Sob a hipótese nula, ou seja, sob a hipótese de que os valores $X_{i }$estão igualmente distribuídos em torno do valor $θ_{0}$ temos que o valor esperado de $T^{+}$, $E_{0}$($T^{+}$), e a variância de $T^{+}$, $Var_{0}$($T^{+}$), são dados pelas fórmulas abaixo $$E(T^+ \mid \theta=\theta_0)=\frac{n(n+1)}{4} \quad \hbox{e} \quad Var(T^+ \mid \theta=\theta_0)=\frac{n(n+1)(2n+1)}{24}$$

Demonstração

Para cada i, considere a variável aleatória $V_{i}$ dada por

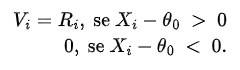
Sob a hipótese $H_{0}$, temos que os valores de $X_{i}$ estão igualmente distribuídos em torno de $θ_{0}$, desta forma as variáveis aleatórias $V_{i}$ são igualmente distribuídas com a seguinte distribuição de probabilidade $$P(V_i=i) =P(V_i=0)=\frac{1}{2}$$

para i = 1, 2, …, n. Desta forma, temos que $$E(T^+ \mid \theta=\theta_0)=E\left[\sum_{i=1}^n V_i \mid \theta=\theta_0\right]=\sum_{i=1}^n E [V_i \mid \theta=\theta_0]= \frac{1}{2} \sum_{i=1}^n i=\frac{1}{2}\left[\frac{n(n+1)}{2}\right]=\frac{n(n+1)}{4}$$

e $$Var(T^+\mid\theta=\theta_0)=\sum_{i=1}^n Var(V_i \mid \theta=\theta_0)=\sum_{i=1}^n E(V_i^2 \mid \theta=\theta_0)-[E(V_i \mid \theta=\theta_0)]^2=$$

$$\sum_{i=1}^n \left(\frac{i^2}{2}-\frac{i^2}{4}\right)=\frac{i^2}{4}$$

ou seja, $$Var(T^+ \mid \theta=\theta_0)=\frac{1}{4}\sum_{i=1}^n i^2= \frac{1}{4}\left[\frac{n(n+1)(2n+1)}{6}\right] = \frac{n(n+1) (2n+1)} {24}$$

como queríamos demonstrar.

Aproximação Normal

Utilizando resultados assintóticos, temos que a estatística Z, dada por $$Z = \frac{T^+-E_0(T^+)}{\sqrt{Var_0(T^+)}}=\frac{T^+-\frac{1}{4}n(n+1)}{\sqrt{[n(n+1) (2n+1)/24]}} \qquad (1.3.1)$$

tem distribuição aproximadamente Normal com média 0 e variância 1. Então o teste fica reduzido para um teste normal padrão.

Os passos para a realização deste teste:

1. Estabelecemos as seguintes hipóteses:

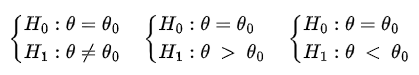
que são equivalentes as hipóteses

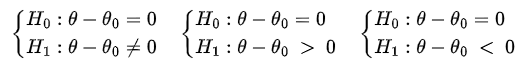
2. Primeiramente devemos subtrair $θ_{0}$ de cada valor $X_{i}$, i = 1, 2, …, n, da amostra e assim obtemos um novo conjunto de dados, $(X_1-θ_{0}$, $X_2-θ_{0}$, …, $X_n-θ_{0}$).

3. Ordenamos de forma crescente de magnitude os valores desse novo conjunto de dados e associamos a cada valor o posto correspondente, tendo cada posto o mesmo sinal do valor que este representa.

4. Calculamos o valor da estatística $T^{+}$.

5. Calculamos o valor de $Z_{obs}$ através da equação (1.3.1) . Em seguida, fixamos o nível de significância α.

6. Encontramos os valores críticos referentes ao nível de significância α fixado.

• Se o teste é bilateral, os valores críticos são $-Z_{\alpha/2}$ e $Z_{\alpha/2}$.

• Se o teste é unilateral à direita, o valor crítico é $Z_{\alpha}$.

• Se o teste é unilateral à esquerda, o valor crítico é $-Z_{\alpha}$.

7. Critério de rejeição:

• Se o teste é bilateral, rejeitamos a hipótese nula se $Z_{obs} \ > \ Z_{\alpha/2}$ ou se $Z_{obs} \ < \ -Z_{\alpha/2}$, caso contrário, não rejeitamos a hipótese nula.

• Se o teste é unilateral à direita, rejeitamos a hipótese nula se $Z_{obs} \ > \ Z_{\alpha}$, caso contrário, não rejeitamos a hipótese nula.

• Se o teste é unilateral à esquerda, rejeitamos a hipótese nula se $Z_{obs} \ < \ -Z_{\alpha}$, caso contrário, não rejeitamos a hipótese nula.

8. Cálculo do p-valor

• Se o teste é bilateral, então o p-valor é dado por $$P-valor = P[|Z| \ > \ |Z_{obs}||H_0] = 2 P[Z \ > |Z_{obs}|].$$

• Se o teste é unilateral à direita, então o p-valor é dado por $$P-valor = P[Z \ > \ Z_{obs}|H_0].$$

• Se o teste é unilateral à esquerda, então o p-valor é dado por $$P-valor = P[Z \ < \ Z_{obs}|H_0].$$

Aproximação normal com correção de continuidade

Como estamos utilizando uma distribuição contínua, é conveniente utilizar uma correção de continuidade, de acordo com o tipo de teste que está sendo realizado.

• Se o teste é bilateral, calculamos A dado por $$A = T^+-\frac{n(n+1)}{4}.$$

Se A ≥ 0, a estatística será dada por $$Z_{cor}=\frac{T^+-\frac{1}{2}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}}$$

e se A < 0, a estatística será dada por $$Z_{cor}=\frac{T^++\frac{1}{2}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}}.$$

• Se o teste é unilateral à direita, a estatística será dada por $$Z_{cor}=\frac{T^+-\frac{1}{2}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}}.$$

• Se o teste é unilateral à esquerda, a estatística será dada por $$Z_{cor}=\frac{T^++\frac{1}{2}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}}.$$

Os passos utilizados são análogos aos anteriores, porém utilizamos $Z_{cor}$ ao invés de $Z_{obs}$.

Exemplo 1.3.1

Considere a seguinte amostra de 60 elementos

221	106	272	136	353	331
242	335	257	248	312	211
81	321	336	318	186	169
328	355	114	184	264	322
363	284	299	323	228	245
365	268	270	131	138	196
259	293	152	202	300	199
260	263	185	311	240	325
124	162	142	346	163	261
343	123	362	95	132	281

Vamos testar se os elementos estão distribuídos simetricamente em torno de $θ_{0}$ = 220.

1. Para realizar este teste, estabelecemos as hipóteses

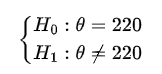
2. Subtraindo $θ_{0}$ = 220 de cada elemento da amostra e colocando todos os valores em ordem crescente de magnitude, obtemos:

1	8	-9	-18	20	-21
22	-24	25	28	-34	-35
-36	37	39	40	41	43
44	48	50	-51	52	-57
-58	61	64	-68	73	-78
79	80	-82	-84	-88	-89
91	92	-96	-97	98	101
102	103	105	-106	108	111
-114	115	116	123	-125	126
133	135	-139	142	143	145

3. Associando os postos correspondentes destes valores, temos que

Postos:

1	2	-3	-4	5	-6
7	-8	9	10	-11	-12
-13	14	15	16	17	18
19	20	21	-22	23	-24
-25	26	27	-28	29	-30
31	32	-33	-34	-35	-36
37	38	-39	-40	41	42
43	44	45	-46	47	48
-49	50	51	52	-53	54
55	56	-57	58	59	60

4. A partir dos valores dos postos acima, calculamos o valor $T^{+}$ que será dado por $$T^+=1222.$$

5. Calculamos o valor da estatística Z dada na equação (1.3.1) $$Z = \frac{T^+-\frac{1}{4}n(n+1)}{\sqrt{[n(n+1)(2n+1)/24]}}=\frac{1222-915}{135,84}=2,260012.$$

Fixamos o nível de significância α = 0,05.

6. Encontramos os valores críticos da distribuição Normal. Neste caso, como o teste é bilateral, os valores são $Z_{α/2}$ = 1,96 e $-Z_{α/2}$ = -1,96.

7. Critério.

Como $Z_{obs }$= 2.260012 > 1,96, rejeitamos a hipótese nula de que os dados estão simetricamente distribuídos em torno de $θ_{0}$ = 220.

8. Cálculo do p-valor

Neste caso, com o teste é bilateral, o p-valor é dado por $$P-valor = 2P(Z \ > \ Z_{obs})=2P(Z \ > \ 2.260012)=0,0238.$$

Utilizando o software Action, temos os seguintes resultados:

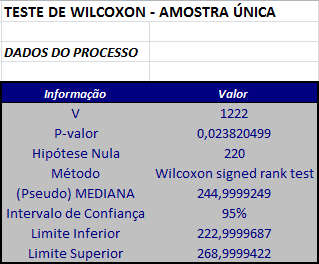
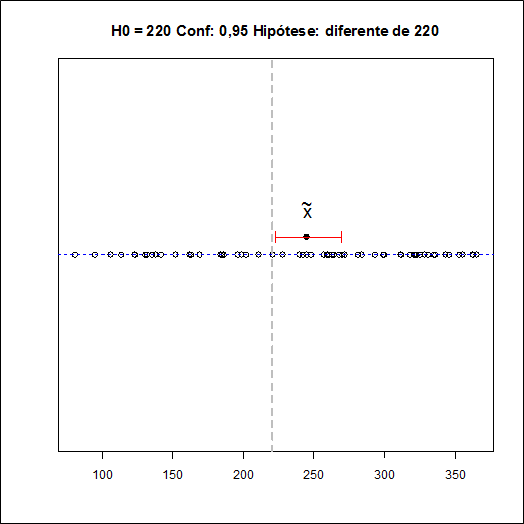
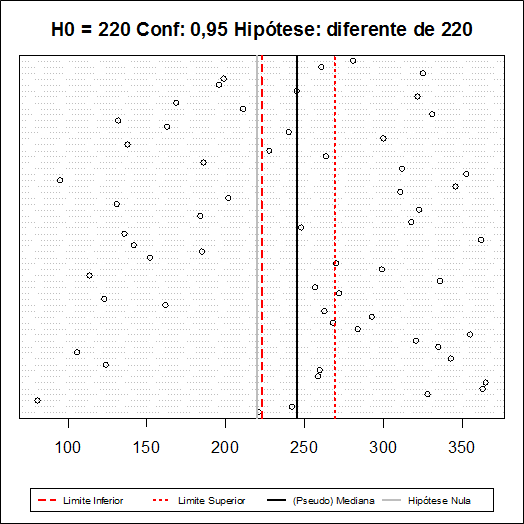
Caso, quiséssemos realizar o teste com correção de continuidade calculamos o valor A dado por $$A = T^+-\frac{n(n+1)}{4}= 1222-915=307.$$

Como A = 307 ≥ 0, a estatística é dada por $$Z_{cor}=\frac{T^+-\frac{1}{2}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)}{24}}}=\frac{306,5}{135,84}=2,256331.$$

E, neste caso, o p-valor é dado por $$P-valor = 2P(Z \ > \ 2.256331)=0,02405.$$

Utilizando o software Action, temos os seguinte resultados:

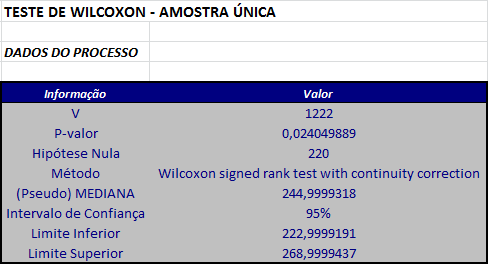
1.4 - Observações Repetidas

Agora veremos o caso em que, ao observarmos uma amostra, encontramos valores repetidos.

Consideremos uma amostra de tamanhos n. Os passos para a realização deste teste são análogos ao do caso anterior. O que mudará neste caso são os postos: quando os módulos dos números se repetem, teremos postos iguais para os números. O posto desses números será a média entre os postos que eles assumiriam no caso comum. Os postos dos números que não se repetem continuam sendo os números associados à posição em que o valor se encontra na listagem.

Para um maior esclarecimento consideremos a seguinte sequência de números:

-8	9	-15	15	16	18	32	32	32	-39

Os postos no caso comum seriam:

Valor	-8	9	-15	15	16	18	32	32	32	-39
Posto	1	2	3	4	5	6	7	8	9	10

Mas observe que nesta sequência o número 15 aparece 2 vezes e o número 32 aparece 3 vezes. Assim, temos repetições. Portanto, o posto dos dois números 15 será a média dos números que correspondem à suas colocações na listagem, ou seja, (3+4)/2 = 3,5. De maneira análoga, o posto dos três números 32 será (7+8+9)/3 = 8. Os valores que não se repetem continuam com os mesmos postos. Então, temos que os valores observados e seus respectivos postos são

Valor	-8	9	-15	15	16	18	32	32	32	-39
Posto	1	2	3,5	3,5	5	6	8	8	8	10

Se tivermos valores 0 na amostra, eliminamos estes valores e realizamos o teste para os valores restantes.

Exemplo 1.4.1

Suponha que em um teste de Wilcoxon temos os seguintes desvios:

0	0	3	-7	9	9	-11	11	11	14	16	17	17	18

Como temos dois valores 0 no conjunto de dados, esses valores são eliminados e ficamos com os dados restantes, isto é,

3	-7	9	-9	-11	11	11	14	16	17	17	18

A seguir, calculamos o módulo de cada elemento do conjunto de dados e atribuímos a ele, seu posto correspondente. Desta forma, os postos serão:

$Z_i$	3	-7	9	-9	-11	11	11	14	16	17	17	18
Posto	1	2	3,5	3,5	6	6	6	8	9	10,5	10,5	12

Observação

Para amostras que possuem valores repetidos ou valores zeros, o p-valor e o intervalo de confiança para um teste de Wilcoxon não são calculados de forma exata e os testes realizados são sempre assintóticos (utilizando aproximação normal).

Observações repetidas

Se existem r conjuntos diferentes de repetições, seja $d_{i}$, i = 1, …, r o número de observações repetidas no conjunto i. Definimos $d_{0}$ como o número de zeros existente na amostra. Neste caso, a estatística Z, dada por

$$Z = \frac{T^{+}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)-d_{0}(d_{0}+1)(2d_{0}+1)}{24} - \frac{\sum_{i=1}^{r}(d_{i}^3-d_{i})}{48}}}.~~~(1.4.1)$$

tem uma distribuição aproximadamente normal, para valores grandes de n.

Vejamos os passos para aplicar o Teste de Wilcoxon para observações repetidas.

1. Estabeleça uma hipóteses:

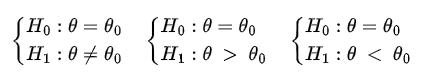
2. Primeiramente, subtraímos $θ_{0}$ de cada valor $X_{i}$, i = 1, …, n da amostra e assim obtemos um novo conjunto de dados, $(X_{1}$ - $θ_{0}$, …, $X_{n }$- $θ_{0}$).

3. Ordenamos de forma crescente os módulos dos valores desse novo conjunto de dados e associamos a cada valor o posto correspondente, sendo esse posto como definido acima.

4. Calculamos o valor da estatística $T^{+}$, que foi definida como sendo a soma dos postos dos elementos que tem sinal positivo.

5. Seja $d_{i}$, i = 1, …, r o número de observações repetidas, se existem r conjuntos de diferentes repetições. Calculamos o valor de Z através da equação (1.4.1). Em seguida, fixamos o nível de significância α.

6. Encontramos na Tabela da distribuição Normal os valores críticos.

• Se o teste é bilateral, encontramos os valores $Z_{α/2}$ e $-Z_{α/2}$.

• Se o teste é unilateral à direita, encontramos o valor crítico $Z_{α}$.

• Se o teste é unilateral à esquerda, encontramos o valor crítico $-Z_{α}$.

7. Critério:

• No caso bilateral, rejeitamos a hipótese nula se $Z_{obs} \ > \ Z_{\alpha/2}$ ou $Z_{obs} \ < \ -Z_{\alpha/2}$, caso contrário, não rejeitamos a hipótese nula.

• No caso unilateral à direita, rejeitamos a hipótese nula se $Z_{obs} \ > \ Z_{\alpha}$, caso contrário, não rejeitamos a hipótese nula.

• No caso unilateral à esquerda, rejeitamos a hipótese nula se $Z_{obs} \ < \ -Z_{\alpha}$, caso contrário, não rejeitamos a hipótese nula.

8. Cálculo do p-valor

• Se o teste é bilateral, o p-valor é calculado da seguinte forma

$$P-valor = P[|Z| \ > \ |Z_{obs}||H_0]=2P[Z \ > \ |Z_{obs}|].$$

• Se o teste é unilateral à direita, então o p-valor é dado por

$$P-valor = P[Z \ > \ Z_{obs}|H_0].$$

• Se o teste é unilateral à esquerda, então o p-valor é dado por

$$P-valor = P[Z \ > \ Z_{obs}|H_0].$$

Correção de Continuidade

• Se o teste é bilateral, então calculamos o valor A dado por

$$A = T^+-\frac{n(n+1)}{4}$$

e, se A ≥ 0 segue que a estatística será dada por

$$Z_{cor}=\frac{T^+-\frac{1}{2}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)-d_0(d_0+1)(2d_0+1)} {24}-\frac{\sum_{i=1}^{r}(d_{i}^3-d_{i})}{48}}}$$

e se A < 0, a estatística será dada por

$$Z_{cor}=\frac{T^++\frac{1}{2}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)-d_0(d_0+1)(2d_0+1)} {24}-\frac{\sum_{i=1}^{r}(d_{i}^3-d_{i})}{48}}}.$$

• Se o teste é unilateral à direita, a estatística será dada por

$$Z_{cor}=\frac{T^+-\frac{1}{2}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)-d_0(d_0+1)(2d_0+1)} {24}-\frac{\sum_{i=1}^{r}(d_{i}^3-d_{i})}{48}}}.$$

• Se o teste é unilateral à esquerda, a estatística será dada por

$$Z_{cor}=\frac{T^++\frac{1}{2}-\frac{n(n+1)}{4}}{\sqrt{\frac{n(n+1)(2n+1)-d_0(d_0+1)(2d_0+1)} {24}-\frac{\sum_{i=1}^{r}(d_{i}^3-d_{i})}{48}}}.$$

Exemplo 1.4.2

Consideremos a amostra:

153	166	181	192	244	248	258	264	296	305	305	312
330	340	356	361	395	427	433	467	544	551	625	783

Use o teste de Wilcoxon para testar as hipóteses

Subtraindo 220 de cada valor da amostra e colocando todos os valores obtidos em ordem crescente de magnitude, obtemos:

24	-28	28	38	-39	44	-54	-67	76	85	85	92
110	120	136	141	175	207	213	247	324	331	405	563

A seguinte tabela nos dá os desvios obtidos acima, seus respectivos postos e os valores $R_iψ_{i}$.

Valor	24	-28	28	38	-39	44	-54	-67	76	85	85	92
Posto	1	-2,5	2,5	4	-5	6	-7	-8	9	10,5	10,5	12
$R_iψ_i$	1	0	2,5	4	0	6	0	0	9	10,5	10,5	12
Valor	110	120	136	141	175	207	213	247	324	331	405	563
Posto	13	14	15	16	17	18	19	20	21	22	23	24
$R_iψ_i$	13	14	15	16	17	18	19	20	21	22	23	24

A partir dos valores $R_iψ_{i}$, calculamos o valor $T^{+}$, dado por

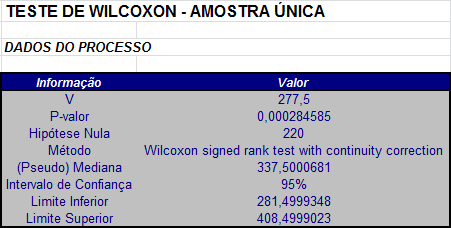
$$T^+=\sum_{i=1}^{24}R_i\Psi_i=277,5.$$

Com temos duas repetições envolvendo duas observações, segue que $d_{1}=d_{2}=2$ e $n=24$.

A estatística Z é dada por

$$Z=\frac{277,5-150}{\sqrt{\frac{24(24+1)(48+1)}{24}-\frac{(6+6)}{48}}}=3,643229.$$

Neste caso, o p-valor é dado por

$$P-valor = P[|Z| \ > \ |Z_{obs}||H_0]=2P[Z \ > \ 3,643229]=0,000269239.$$

Conclusão

Rejeitamos $H_{0}$ se considerarmos qualquer nível de significância maior que 0,0269239%.

Utilizando o software Action temos os seguinte resultados:

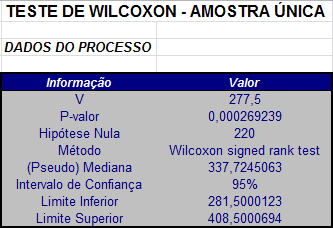
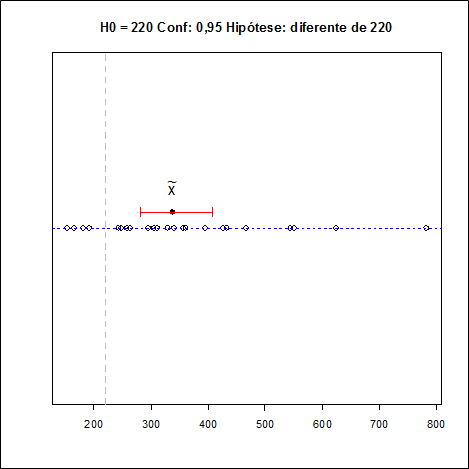
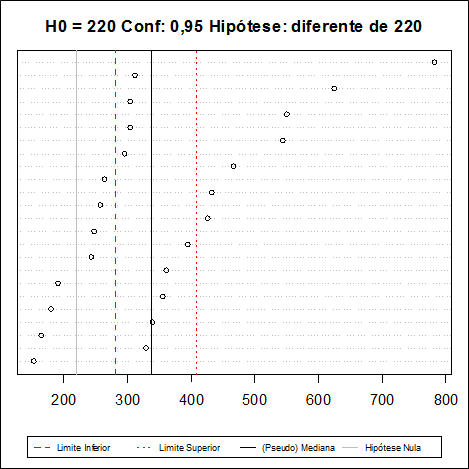
Utilizando a correção de continuidade, como o teste é bilateral, temos que A é dado por

$$A = T^+-\frac{n(n+1)}{4}=277,5-\frac{24\times25}{4}=277,5-150=127,5 \ > \ 0.$$

Então, utilizando a correção de continuidade, a estatística $Z_{cor}$ é calculada da seguinte forma

$$Z_{cor}=\frac{277,5-0,5-150}{\sqrt{\frac{24(24+1)(48+1)}{24}-\frac{(6+6)}{48}}}=3,628942$$

e, neste caso, o p-valor é dado por

$$P-valor = P[|Z| \ > \ |Z_{obs}||H_0]=2P[Z \ > \ 3,628942]=0,000284585$$

Conclusão

Rejeitamos $H_{0}$ se considerarmos qualquer nível de significância maior que 0,0284585%.

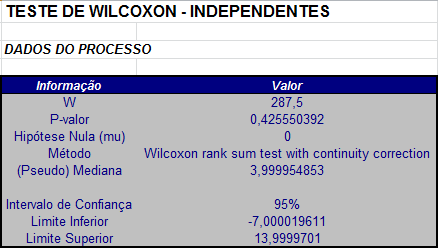
2 - Teste de Wilcoxon-Mann-Whitney - Amostras Independentes

Consideremos duas populações $P_1$ e $P_2$ das quais não temos informações a respeito de suas distribuições, mas as variáveis envolvidas tenham uma escala de medida pelo menos ordinal. Ou seja, podemos abordar o caso de variáveis aleatórias qualitativas ordinais ou quantitativas. Consideremos também duas amostras independentes das duas populações. Queremos testar se as distribuições são iguais em localização, isto é, estaremos interessados em saber se uma população tende a ter valores maiores do que a outra, ou se elas têm a mesma mediana. Este teste é chamado de Teste de Wilcoxon-Mann-Whitney.

O teste de Wilcoxon-Mann-Whitney é baseado nos postos dos valores obtidos combinando-se as duas amostras. Isso é feito ordenando-se esses valores, do menor para o maior, independentemente do fato de qual população cada valor provém.

No caso de termos uma variável aleatória qualitativa ordinal, comumente associamos números às diversas categorias (ou classes, ou atributos), segundo as quais a variável é classificada. Por exemplo, podemos ter 1 para bom, 2 para muito bom e 3 para ótimo. Vemos, então, que esses valores são postos. Neste caso e em outras situações é preferível trabalhar com postos do que com valores arbitrários associados à variável qualitativa.

Sejam $X_1, X_2, …, X_m$ uma amostra aleatória da população $P_1$ e $Y_1, Y_2, …, Y_n$ uma amostra aleatória da população $P_2$ de modo que os $X_i’s$ são independentes e identicamente distribuídos e os $Y_i’s$ são independentes e identicamente distribuídos. Além disso, suponha que os $X_i’s$ e os $Y_i’s$ são mutuamente independentes e tome a amostra Y aquela com o menor tamanho amostral, isto é, n ≤ m.

Para aplicar o teste de Wilcoxon-Mann-Whitney, supomos que F e G sejam as funções de distribuição correspondentes as populações $P_1$ e $P_2$, respectivamente e, neste caso, consideramos como hipótese nula, a hipótese

$$H_0: F(t)=G(t) \ \hbox{para todo} \ t.$$

A hipótese alternativa consiste em considerar que Y tende a ser maior (ou menor) que X. Um modelo útil para descrever esta alternativa é um modelo de translação chamado modelo de mudança de posição. Neste modelo temos que

$$G(t)=F(t-\Delta) \ \hbox{para todo} \ t.$$

Outra maneira de interpretação é considerar que Y tem a mesma distribuição de X+Δ. Neste caso, considerando que a esperança E(X) da população 1 exista e tomando E(Y) como a esperança da população 2, segue que

$$\Delta = E(Y)-E(X)$$

e, desta forma, a hipótese nula $H_0$ se reduz a

$$H_0:\Delta=0.$$

Com isto, estabelecemos uma das seguintes hipóteses em um teste de Wilcoxon-Mann-Whitney:

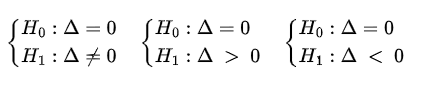
Em seguida, ordenamos todos os valores (das duas amostras) em ordem crescente e colocamos os postos associados. Consideramos $S_m$ e $S_n$ as somas dos postos relacionados aos elementos das amostras X e Y respectivamente. A partir dos valores $S_m$ e $S_n$, calculamos os valores

$$U_{m} = S_{m}-\frac{1}{2}m(m+1)~~~(2.1)$$

e

$$U_{n} = S_{n}-\frac{1}{2}n(n+1).~~~(2.2)$$

Como $S_m + S_n$ é igual a soma de todos os postos (das duas amostras), isto é,

$$S_{m}+S_{n} = \frac{1}{2}(m+n)(m+n+1)~~~(2.3)$$

é fácil ver que os valores $U_m$ e $U_n$ estão relacionados segundo a equação abaixo

$$U_{m} = mn - U_{n}~~~(2.4)$$

por isso, apenas um dos $U_m, U_n$ precisa ser calculado e, através da equação (2.4) encontramos o valor do outro de maneira fácil. No teste de Wilcoxon-Mann-Whitney, a estatística W do teste será dada por $U_n$.

Exemplo 2.1

Duas amostras forneceram os seguintes valores de certa variável.

Amostra 1:

29	39	60	78	82	112	125	170
192	224	263	275	276	286	369	756

Amostra 2:

126	142	156	228	245	246
370	419	433	454	478	503

Temos na Tabela (2.1) todos os valores amostrais em ordem crescente e os postos associados. Para facilitar a identificação, valores e postos da segunda amostra foram sublinhados.

Valor	29	39	60	78	82	112	125	126	142	156
Posto	1	2	3	4	5	6	7	8	9	10
Valor	170	192	224	228	245	246	263	275	276	286
Posto	11	12	13	14	15	16	17	18	19	20
Valor	369	370	419	433	454	478	503	756
Posto	21	22	23	24	25	26	27	28

Tabela 2.1: Postos combinados para as duas amostras independentes.

Aqui m = 16 e n = 12. Então,

$$S_{m} = 1+2+3+4+5+6+7+11+12+13+17+18+19+20+21+28=187$$

e

$$S_n = 8+9+10+14+15+16+22+23+24+25+26+27=219$$

Então,

$$U_{m}=187-(\frac{1}{2}\times 16\times 17)=51$$

e

$$U_{n}=219-(\frac{1}{2}\times 12\times 13)=141.$$

Portanto, a estatística W é dada por

$$W=U_{n}=141.$$

2.1 - Um Estimador para a Diferença entre as Posições

Para estimar a diferença Δ entre as medianas das populações, consideramos todas as m x n diferenças $y_i - x_j$ ordenadas de forma crescente. O estimador $\hat{\Delta}$ associado a estatística de Wilcoxon-Mann-Whitney é definido por

$$\hat{\Delta}= \ \hbox{mediana}{((y_i-x_j), \ i=1,\ldots, n; j=1,\ldots,m)}.$$

Sejam $U^{(1)}, U^{(2)}, …, U^{(mn)}$, os valores ordenados destas diferenças. Se m é um número ímpar, isto é, mn = 2k +1, temos que k = (mn-1)/2 e então tomamos

$$\hat{\Delta}=U^{(k+1)},$$

isto é, a diferença que ocupa a posição k + 1 na lista das diferenças ordenadas. Se mn é um número par, isto é, mn = 2k, então k = mn/2 e então tomamos

$$\hat{\Delta}=\frac{U^{(k)}+U^{(k+1)}}{2},$$

isto é, $\hat{\Delta}$ é a média das diferenças $y_i - x_j$ que ocupam as posições k e k + 1 na lista das diferenças ordenadas.

Obs: O estimador $\hat{\Delta}$ é chamado de pseudo-mediana.

Exemplo 2.1.1

Considere os dados do Exemplo 2.1.

Temos na Tabela 2.1.1 as diferenças entre valores observados.

	126	142	156	228	245	246	370	419	433	454	478	503
29	97	113	127	199	216	217	341	390	404	425	449	474
39	87	103	117	189	206	207	331	380	394	415	439	464
60	66	82	96	168	185	186	310	359	373	394	418	443
78	48	64	78	150	167	168	292	341	355	376	400	425
82	44	60	74	146	163	164	288	337	351	372	396	421
112	14	30	44	116	133	134	258	307	321	342	366	391
125	1	17	31	103	120	121	245	294	308	329	353	378
170	-44	-28	-14	58	75	76	200	249	263	284	308	333
192	-66	-50	-36	36	53	54	178	227	241	262	286	311
224	-98	-82	-68	4	21	22	146	195	209	230	254	279
263	-137	-121	-107	-35	-18	-17	107	156	170	191	215	240
275	-149	-133	-119	-47	-30	-29	95	144	158	179	203	228
276	-150	-134	-120	-48	-31	-30	94	143	157	178	202	227
286	-160	-144	-130	-58	-41	-40	84	133	147	168	192	217
369	-243	-227	-213	-141	-124	-123	1	50	64	85	109	134
736	-610	-594	-580	-508	-491	-490	-366	-317	-303	-282	-258	-233

Tabela 2.1.1: Diferenças

Temos que nm = 12 x 16 = 192 que é um número par, isto é 192 = 2k com k = 96. Deste modo, o estimador da mediana entre as diferenças $y_i - x_j$ é dado por

$$\hat{\Delta}=\frac{U^{(96)}+U^{(97)}}{2}=\frac{133+134}{2}=133,5.$$

2.2 - Distribuição exata da estatística de Wilcoxon-Mann-Whitney

Suponha que sob $H_0$, a distribuição de W é contínua, de modo que a probabilidade de encontrarmos valores repetidos nas amostras de X e Y é zero. Para encontrar a distribuição exata da estatística W sob $H_0$, considere n e m os tamanhos amostrais das populações Y e X, respectivamente. Além disso, considere que N = n + m. Deste modo, temos

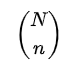
possibilidades para os ranks (posições) dos elementos de Y e cada um deles tem probabilidade

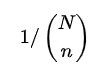
Por exemplo, no caso em que m = 3 e n = 2, existem

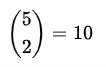
possibilidades para os ranks das duas observações dos elementos de Y e os valores correspondentes da estatística W são dados na seguinte tabela

Ranks	Probabilidade	W
1,2	1/10	3
1,3	1/10	4
1,4	1/10	5
1,5	1/10	6
2,3	1/10	5
2,4	1/10	6
2,5	1/10	7
3,4	1/10	7
3,5	1/10	8
4,5	1/10	9

Assim, sob $H_0$, a probabilidade de que W seja igual a 5 é igual a 2/10, pois W = 5 quando a configuração dos ranks de Y é {1,4} ou {2,3} e cada uma delas ocorre com probabilidade 1/10. Deste modo, temos para a distribuição sob $H_0$ que

Valores de W	Probabilidade
3	0,1
4	0,1
5	0,2
6	0,2
7	0,2
8	0,1
9	0,1

Então, por exemplo, a probabilidade sob $H_0$ de W ser maior ou igual a 7 é dada por

$$P[W\geq 7]=P(W=7)+P(W=8)+P(W=9)=0,2+0,1+0,1=0,4$$

Em um teste de Wilcoxon-Mann-Whitey em que o tamanho amostral n é pequeno (geralmente n < 50) e não temos observações repetidas ou nulas, utilizamos a distribuição exata da estatística W e, a partir desta distribuição, calculamos os valores críticos do teste, o p-valor e o intervalo de confiança.

1. Cálculo dos valores críticos.

Se estamos realizando um teste bilateral, então sob $H_0$, devemos encontrar os valores críticos $t_1$ e $t_2$ tais que

$$P[W \ < \ t_1]=P[W \ > \ t_2]=\approx\frac{\alpha}{2}.$$

Se o teste é unilateral à direita, então devemos encontrar o valor crítico t tal que

$$P[W \ > \ t]\approx\alpha$$

e se o teste é unilateral à esquerda, então devemos encontrar o valor crítico t tal que

$$P[W \ < \ t]\approx\alpha.$$

2. Critério.

Se o teste é bilateral e $W_{obs}$ < $t_{1}$ ou $W_{obs}$ > $t_2$ então rejeitamos $H_0$, caso contrário, não rejeitamos $H_0$, ou seja, se $t_1$ < $W_{obs}$ < $t_2$, não rejeitamos a hipótese nula $H_0$.

No caso do teste unilateral à direita, se $W_{obs}$ > $t$, então rejeitamos $H_0$, caso contrário, não rejeitamos $H_0$, ou seja, se $W_{obs}$ < t, não rejeitamos a hipótese nula $H_0$.

Se o teste é unilateral à esquerda e $W_{obs}$ < t, então rejeitamos $H_0$, caso contrário, não rejeitamos $H_0$, ou seja, se $W_{obs}$ > t, não rejeitamos a hipótese nula $H_0$.

3. Cálculo do p-valor.

Se o teste é bilateal, o p-valor do teste exato é dado por

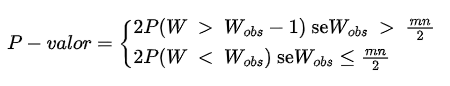
Se o teste é unilateal à direita, o p-valor do teste exato é dado por

$$P-valor = P(W \ > \ W_{obs}-1)$$

e se o teste é unilateral à esquerda, o p-valor do teste exato é dado por

$$P-valor = P(W \ < W_{obs}).$$

4. Intervalo de confiança para a diferença entre os parâmetros de posição das populações Y e X.

De forma análoga a utilizada na estimativa da diferença entre os parâmetros de posição das populações Y e X, consideramos todas as m x n diferenças $y_i$ - $x_j$ ordenadas de forma crescente. Considerando que X tem m elementos e Y tem n elementos e que n ≤ m, então temos m x n diferenças deste tipo.

Sejam $W^{(1)}, W^{(2)}, …, W^{(mn)}$ estas diferenças ordenadas.

Se o teste é bilateral e o nível de significância é α, encontramos os valores L e U tais que

$$P(W \ < \ L)\approx \frac{\alpha}{2} \qquad U = nm-L$$

e o intervalo de confiança 100(1-α)% é dado por

$$IC_{1-\alpha}(\theta)=(W^{(L)},W^{(U+1)}).$$

Se o teste é unilateral à direita, encontramos o valor L tal que

$$P(W \ < \ L)\approx\alpha$$

e o intervalo de confiança 100(1-α)% é dado por

$$IC_{1-\alpha}(\theta)=(W^{(L)},\infty)$$

e se o teste é unilateral à esquerda, encontramos o valor U tal que

$$P(W \ > \ U)\approx\alpha$$

e o intervalo de confiança 100(1-α)% é dado por

$$IC_{1-\alpha}(\theta)=(-\infty,W^{(U+1)}).$$

Exemplo 2.2.1

Considere novamente o Exemplo 2.1 em que duas amostras fornecem valores de determinada variável.

Amostra 1:

29	39	60	78	82	112	125	170
192	224	263	275	276	286	369	756

Amostra 2:

126	142	156	228	245	246
370	419	433	454	478	503

Vamos testar se, a um nível de significância de 5%, existe diferença significativa entre as medidas de posições das duas populações. Neste caso, estabelecemos as hipóteses

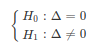
Como já foi visto, a estatística W é dada por

$$W=141.$$

1. Cálculo dos valores críticos.

Como estamos realizando um teste bilateral, devemos encontrar os valores $t_1$ e $t_2$ tais que

$$P[W \ < \ t_1]=P[W \ > \ t_2]\approx 0,025.$$

Neste caso, temos que os valores de $t_1$ e $t_2$ são dados por $t_1$ = 54 e $t_2$ = 138.

2. Critério.

Como $W_{obs}$ = 141 > $t_{2}$ = 138, então rejeitamos a hipótese nula. Neste caso, temos evidência de que as duas populações não possuem medidas de posição iguais.

3. Cálculo do p-valor.

Como $W_{obs}$ 141 > mn/2 = 96, o p-valor é dado por

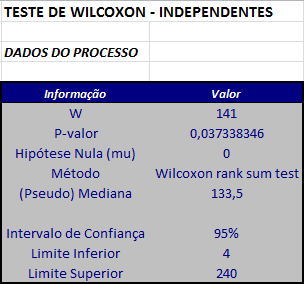
$$P-valor = 2P(W \ > \ W_{obs}-1)=0,03733835.$$

4. Intervalo de Confiança.

Consideramos as m x n diferenças da forma $y_i$ - $x_j$ ordenadas de forma crescente na tabela abaixo

-630	-614	-600	-528	-511	-510	-386	-337	-323	-302	-278	-253
-243	-227	-213	-160	-150	-149	-144	-141	-137	-134	-133	-130
-124	-123	-121	-120	-119	-107	-98	-82	-68	-66	-58	-50
-48	-47	-44	-41	-40	-36	-35	-31	-30	-30	-29	-28
-18	-17	-14	1	1	4	12	17	21	22	30	31
36	44	44	48	50	53	54	58	60	64	64	66
74	75	76	78	82	84	85	87	94	95	96	97
103	103	107	109	113	116	117	120	121	127	133	133
134	134	143	144	146	146	147	150	156	157	158	163
164	167	168	168	168	170	178	178	179	185	186	189
191	192	195	199	200	202	203	206	207	209	215	216
217	217	227	227	228	230	240	241	245	249	254	258
262	263	279	284	286	288	292	294	307	308	308	310
311	321	329	331	333	337	341	341	342	351	353	355
359	366	372	373	376	378	380	390	391	394	394	396
400	404	415	418	421	425	425	439	443	449	464	474

Os valores de L e U para o cálculo do intervalo de confiança são dados por

$$L = 54 \ \hbox{e} \ U = 138.$$

Desta forma, segue que o intervalo com 95% de confiança é dado por

$$IC_{0,95}(\theta)=(W^{(L)},W^{(U+1)})=(4,230).$$

5. Para o cálculo da pseudo mediana da diferença entre a população Y e a população X, utilizamos a tabela acima. Como mn = 192 e 192 = 2 x 96 é um número par, a pseudo mediana é dada por

$$\hat{\Delta}=\frac{W^{(96)}+W^{(97)}}{2}=\frac{133+134}{2}=133,5.$$

Utilizando o software Action, obtemos os seguintes resultados:

2.3 - Aproximação Normal

Para valores m e n grandes, geralmente maiores que 50, uma aproximação normal, como veremos a seguir, é utilizada. Consideremos a estatística W como definida anteriormente, isto é, W = $U_{n}$.

Teorema 2.3.1

Sob a hipótese nula, ou seja, sob a hipótese de que a diferença entre as posições é Δ = 0, temos que o valor esperado de W, $E_{0}$(W) e a variância de W, $Var_{0}$(W) são dados pelas fórmulas abaixo

$$E_0(W)=\frac{mn}{2} \ \hbox{e} \ Var_0(W)=\frac{mn(m+n+1)}{12}$$

Aproximação Normal

Utilizando resultados assintóticos, temos a estatística Z dada por

$$Z = \frac{W-\frac{1}{2}mn}{\sqrt{\frac{mn(m+n+1)}{12}}}~~~(2.3.1)$$

tem distribuição aproximadamente Normal com média 0 e variância 1. Então o teste fica reduzido a um teste normal padrão.

Vejamos com realizar este teste:

1. Estabelecemos uma das seguintes hipóteses:

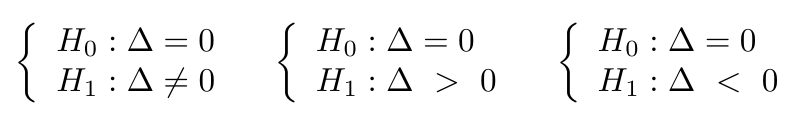
2. Ordenamos todos os valores (das duas amostras) em ordem crescente e colocamos os postos associados.

3. Em seguida, calculamos o valor de $S_{n}$ (a soma dos postos associados aos elementos da amostra y).

4. Obtemos o valor W = $U_{n}$. Em seguida, fixamos o nível de significância α.

5. Calculamos o valor

$$Z_{obs}= \frac{W-\frac{1}{2}mn}{\sqrt{\frac{mn(m+n+1)}{12}}}.$$

6. Encontramos os valores críticos da distribuição Normal padrão segundo o tipo de teste.

• Se o teste é bilateral, encontramos os valores críticos $Z_{\alpha/2}$ e $-Z_{\alpha/2}$ tais que $P[Z \ > \ Z_{\alpha/2}]=P[Z \ < \ -Z_{\alpha/2}]=\alpha/2.$

• Se o teste é unilateral à direita, encontramos o valor crítico $Z_{\alpha}$ tal que $P[Z \ > \ Z_{\alpha}]=\alpha$.

• Se o teste é unilateral à esquerda, encontramos o valor crítico $-Z_{\alpha}$ tal que $P[Z \ < \ -Z_{\alpha}]=\alpha$.

7. Critério:

• Se o teste é bilateral, rejeitamos a hipótese nula $H_{0}$ se o valor observado $Z_{obs} \ > \ Z_{\alpha/2}$ ou se $Z_{obs} \ < \ -Z_{\alpha/2}$, caso contrário não rejeitamos a hipótese nula.

• Se o teste é unilateral à direita, rejeitamos a hipótese nula $H_{0}$ se o valor observado $Z_{obs} \ > \ Z_{\alpha}$, caso contrário, não rejeitamos a hipótese nula.

• Se o teste é unilateral à esquerda, rejeitamos a hipótese nula $H_{0 }$se o valor observado $Z_{obs} \ < \ -Z_{\alpha}$, caso contrário, não rejeitamos a hipótese nula.

8. Cálculo do p-valor:

Se o teste é bilateral, o p-valor é dado por

$$P-valor = P(|Z| \ > \ |Z_{obs}||H_0) = 2P(Z \ > \ |Z_{obs}||H_0).$$

Se o teste é unilateral à direita, o p-valor é dado por

$$P-valor = P(Z \ > \ Z_{obs}|H_0)$$

e se o teste é unilateral à esquerda, o p-valor é dado por

$$P-valor = P(Z \ < \ Z_{obs}|H_0).$$

onde Z ~ N(0,1).

Aproximação Normal com correção de continuidade

Como estamos utilizando uma distribuição contínua, é conveniente utilizar uma correção de continuidade. Assim como foi visto anteriormente, a correção é feita de acordo com o tipo de teste efetuado.

• Se o teste é bilateral, calculamos A dado por

$$A = W -\frac{1}{2}nm.$$

Se A ≥ 0, então

$$Z_{cor}= \frac{W - \frac{1}{2}-\frac{1}{2}nm}{\sqrt{\frac{mn(m+n+1)}{12}}}.$$

Se A < 0, então

$$Z_{cor}= \frac{W+\frac{1}{2}-\frac{1}{2}nm}{\sqrt{\frac{mn(m+n+1)}{12}}}.$$

• Se o teste é unilateral à direita, a estatística é dada por

$$Z_{cor}=\frac{W-\frac{1}{2}-\frac{1}{2}nm}{\sqrt{\frac{mn(m+n+1)}{12}}}.$$

• Se o teste é unilateral à esquerda, a estatística é dada por

$$Z_{cor}=\frac{W+\frac{1}{2}-\frac{1}{2}nm}{\sqrt{\frac{mn(m+n+1)}{12}}}.$$

Exemplo 2.3.1

Considere as duas amostras dadas abaixo. A primeira de tamanho m = 60 e a segunda de tamanho n = 50 e vamos testar se existe diferença significativa entre suas medidas de posição.

Amostra 1:

0,020783	1,190577	0,254776	0,326478	0,166423	-0,60854
-1,09347	-0,87468	-0,68062	-0,44368	1,107722	0,835386
-0,4732	0,614336	-0,14765	-0,73586	1,103766	0,304864
0,487065	1,437288	-0,01432	-0,39427	-0,0318	-0,55498
-0,92408	-0,09976	0,730077	0,698887	-1,62009	-0,61324
-1,31087	-2,12763	0,445035	0,321711	1,583911	-0,10288
-0,90719	0,390517	-0,95791	-0,13997	1,192579	0,78557
-0,70691	-0,36727	-0,36615	-0,12643	-1,55418	-1,74463
0,102534	0,29614	1,496525	0,037918	1,334108	-2,17951
-1,23783	0,43527	-0,70575	1,53077	0,773895	-0,80207

Amostra 2:

0,849954	-0,06994	0,459771	-1,39136	-0,36113
0,130024	-0,57095	0,1313	1,494435	2,012758
0,357575	0,881379	0,343893	2,295901	-0,04778
0,2508	0,767977	0,622242	-0,00538	0,823678
0,310109	-0,45953	-0,26607	-1,60654	-1,49409
-1,05302	-1,62618	0,833893	-1,75903	-0,32571
1,770791	-0,0034	-0,13192	1,438544	-0,30188
-0,00674	0,392139	1,307978	0,065984	-1,32595
-0,85192	0,653739	0,838055	0,406276	-1,11364
0,267735	0,412184	0,10388	-0,71385	-0,3809

Neste caso, temos que m = 60 e n = 50.

Como queremos testar se existe diferença significativa entre suas medidas de posição, estabelecemos as seguintes hipóteses

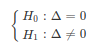
Ordenando os valores das duas amostras e calculando a soma dos postos associados aos elementos da amostra de tamanho n = 50, temos que $S_{n}$ = 2931. Deste modo, a estatística W é dada por

$$W = U_n = S_n-\frac{n(n+1)}{2}=2931-\frac{50\times 51}{2}= 1656.$$

A seguir calculamos o valor da estatística Z dada por

$$Z=\frac{W-1/2mn}{\sqrt{[mn(m+n+1)/12]}}=\frac{1656-(0,5\times60\times50)}{\sqrt{(60\times50\times111)/12}}=0,9364684.$$

Fixando o nível de significância α = 0,05 temos que os valores críticos são $Z_{\alpha/2} = 1,96$ e $-Z_{\alpha/2} = -1,96$, uma vez que o teste é bilateral. Como o valor observado foi $Z_{obs}$ = 0,9364684, não rejeitamos a hipótese nula, isto é, concluímos que não existe diferença significativa entre as medidas de posição das duas amostras.

Calculamos o p-valor da seguinte forma:

$$P-valor = P[|Z| \ > \ |Z_{obs}||H_0]= 2P[Z \ > \ |Z_{obs}||H_0]=2P[Z \ > \ 0,9364684]= 0,3490321.$$

Utilizando o software Action temos os seguintes resultados:

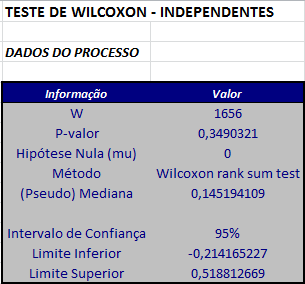
Caso quiséssemos realizar o teste com correção de continuidade, calculamos o valor de A dado por

$$A = W - \frac{mn}{2}=1656=\frac{3000}{2}=156.$$

Como A ≥ 0, temos que

$$Z_{cor}=\frac{W - \frac{1}{2}-\frac{1}{2}nm}{\sqrt{\frac{mn(m+n+1)}{12}}}=\frac{155,5}{166,5833}=0,9334669.$$

Como -1,96 = $-Z_{α/2}$ < $Z_{cor}$ = 0,9334669 < $Z_{α/2}$ = 1,96, então a um nível de significância de 5% não rejeitamos a hipótese de que os dados tem mesma medida de posição.

E, neste caso, o p-valor é dado por

$$P-valor = 2P(Z \ > \ 0,9334669 = 0,350579.$$

Utilizando o software Action, temos os seguintes resultados:

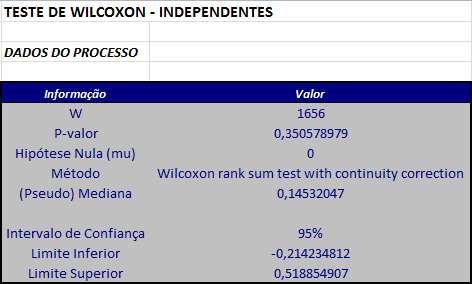
2.4 - Observações Repetidas

Agora vamos ver o caso em que ao observarmos duas amostras encontramos valores repetidos ou valores nulos. De forma análoga a realizada no caso de uma única amostra, quando os módulos dos números se repetem, teremos postos iguais para os números e o posto destes números será a média aritmética que os números assumiriam no caso comum.

Observação

Se as amostras possuem valores repetidos ou nulos, o p-valor e os intervalos de confiança não são calculados de forma exata e os testes realizados são sempre assintóticos (utilizando aproximação normal)

Consideremos duas amostras X e Y de duas populações $P_{1}$ e $P_{2}$, com tamanhos m e n respectivamente de modo que existam valores repetidos e/ou nulos no conjunto das duas amostras. Neste caso, a estatística será modificada para

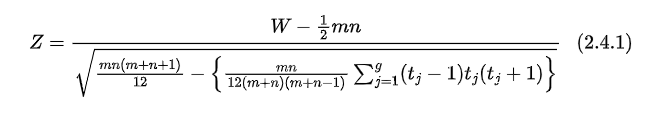
em que $t_{j}$ é o tamanho do grupo de elementos repetidos j e g é o número total de grupos. Uma observação que não se repete é considerada como um grupo de tamanho 1.

Vejamos os passos para realizar este teste:

1. Estabelecemos uma das hipóteses:

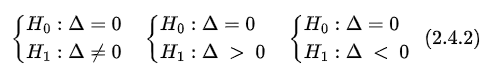
2. Ordenamos os valores da duas amostras em ordem crescente.

3. Consideramos $S_{m}$ e $S_{n}$ como anteriormente (soma dos postos correspondentes aos valores das amostras de tamanhos m e n respectivamente). Seja

$$W=U_n=S_n-\frac{n(n+1)}{2}.$$

4. Calculamos o valor de $Z$ utilizando a equação (2.4.1), isto é

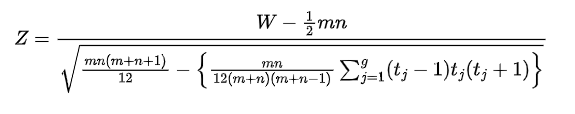
5. Fixamos o nível de significância α.

6. Encontramos o valor crítico utilizando a distribuição Normal Padrão.

• Se o teste é bilateral, encontramos os valores críticos $Z_{α/2}$ e $-Z_{α/2}$ tais que P[Z > $Z_{α/2}$] = P[Z < $-Z_{α/2}$] = α/2.

• Se o teste é unilateral à direita, encontramos o valor crítico $Z_{α}$ tal que P[Z > $Z_{α}$] = α.

• Se o teste é unilateral à esquerda, encontramos o valor crítico $-Z_{α}$ tal que P[Z < $-Z_{α}$] = α.

7. Critério:

• Se o teste é bilateral e $Z_{obs}$ > $Z_{α/2}$ ou $Z_{obs}$ < $-Z_{α/2}$ rejeitamos a hipótese nula $H_{0}$, caso contrário, não rejeitamos a hipótese nula.

• Se o teste é unilateral à direita e $Z_{obs}$ > $Z_{α}$ rejeitamos a hipótese nula $H_{0}$, caso contrário não rejeitamos a hipótese nula.

• Se o teste é unilateral à esquerda e $Z_{obs}$ < $-Z_{α}$ rejeitamos a hipótese nula $H_{0}$, caso contrário não rejeitamos a hipótese nula.

8. Cálculo do p-valor.

• Se o teste é bilateral o p-valor é dado por

$$P-valor = P[|Z| \ > \ |Z_{obs}||H_0]=2P[Z \ > \ |Z_{obs}||H_0].$$

• Se o teste é unilateral à direita, o p-valor é dado por

$$P-valor = P[Z \ > \ Z_{obs}|H_0].$$

• Se o teste é unilateral à esquerda, o p-valor é dado por

$$P-valor = P[Z \ < \ Z_{obs}|H_0].$$

onde Z ~ N(0,1).

Aproximação Normal com correção de continuidade

Aqui também é conveniente utilizar uma correção de continuidade. Assim como visto anteriormente, a correção é feita de acordo com o tipo de teste utilizado.

• Se o teste é bilateral, calculamos A dado por

$$A = W -\frac{1}{2}nm.$$

Se A ≥ 0, então

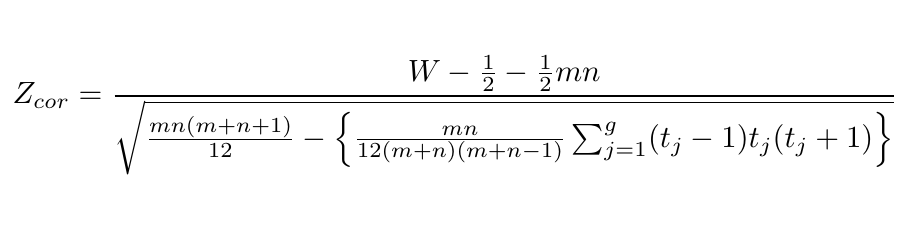
Se A < 0, então

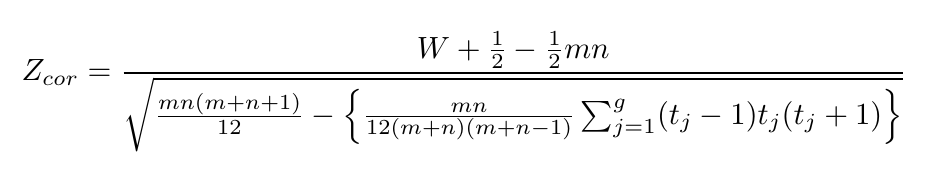
• Se o teste é unilateral à direita, a estatística é dada por

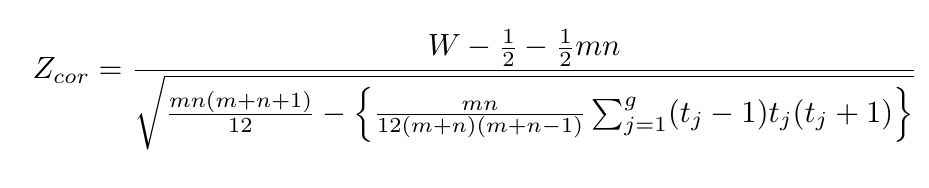
• Se o teste é unilateral à esquerda, a estatística é dada por

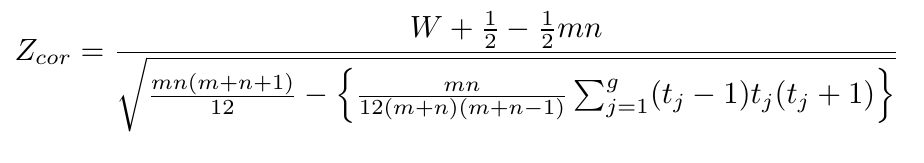
Exemplo 2.4.1

Consideremos duas amostras:

Amostra 1:

0	19	22	30	31	37	55	56	66	66	67	67
68	71	73	75	75	78	79	82	83	83	88	96

Amostra 2:

13	13	22	26	33	33	59	72	72	72	77	78
78	80	81	82	85	85	85	86	88

Usamos o teste da aproximação normal para amostras grandes para testar a hipótese de que estes dados podem ser considerados como amostras para populações idênticas contra a hipótese de que as populações diferem em localização.

Como os tamanhos das amostras são m = 24 e n = 21, respectivamente, a aproximação para amostras grandes será suficiente.

Na Tabela 2.3.1 temos os valores das amostras 1 e 2 colocados em ordem crescente com seus respectivos postos. Os postos dos valores repetidos são as médias entre os valores que os postos assumiriam normalmente. Veja a tabela:

Valor	0	13	13	19	22	22	26	30	31	33	33	37
Posto	1	2,5	2,5	4	5,5	5,5	7	8	9	10,5	10,5	12
Valor	55	56	59	66	66	67	67	68	71	72	72	72
Posto	13	14	15	16,5	16,5	18,5	18,5	20	21	23	23	23
Valor	73	75	75	77	78	78	78	79	80	81	82	82
Posto	25	26,5	26,5	28	30	30	30	32	33	34	35,5	35,5
Valor	83	83	85	85	85	86	88	88	96

Tabela 2.4.1: Postos combinados para as duas amostras independentes com valores repetidos.

Assim, temos que

$$S_n=518,5.$$

Pela equação(2.4) temos que

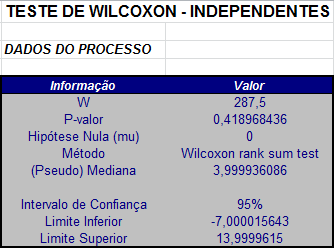
$$W= U_n = S_n-\frac{n(n+1)}{2}=518,5-\frac{21\times 22}{2}= 287,5.$$

Neste caso, temos 19 grupos e o número de elementos de cada grupo pode ser visto na tabela abaixo

0	13	19	22	26	30	31	33	37	55	56	59	66	67	68	71	72	73	75	77	78	79	80	81	82	83	85	86	88	96
1	2	1	2	1	1	1	2	1	1	1	1	2	2	1	1	3	1	2	1	3	1	1	1	2	2	3	1	2	1

e então, segue que

$$\sum_{j=1}^{19}(t_j-1)t_j(t_j+1)=126$$

Usando a equação(2.4.1) temos que

$$Z = (287,5 - 252)/\sqrt{1929,327}= 35,5/43,9241=0,8082123.$$

Ao nível de significância de 5%, temos que $Z_{0,025}$ = 1,96 e como -1,96 < 0,8082123 < 1,96, não rejeitamos a hipótese de que as populações são idênticas.

O p-valor, neste caso é dado por

$$P-valor = 2P[Z \ > \ |Z_{obs}||H_0]=2P[Z \ > \ 0,8082123|H_0]=0,4189684.$$

Se tivéssemos utilizado a correção de continuidade, teríamos

$$A = W-\frac{1}{2}nm=287,5-252 = 35,5 \ > \ 0$$

e então,

$$Z_{cor}=\frac{287,5-0,5-252}{\sqrt{1929,443}}=\frac{35}{43,9241}=0,796829.$$

Deste modo, também não rejeitamos a hipótese de que as populações são idênticas, porém, neste caso, o p-valor é dado por

$$P-valor = 2P[Z \ > \ |Z_{cor}||H_0]=2P[Z \ > \ 0.796829]=0,4255504.$$

3 - Teste de Wilcoxon Pareado

O teste de Wilcoxon pareado é utilizado para comparar se as medidas de posição de duas amostras são iguais no caso em que as amostras são dependentes.

Para isto, consideramos duas amostras dependentes de tamanho n vindas de duas populações $P_{1}$ e $P_{2}$, isto é, $X_{1}$, …, $X_{n}$ e $Y_{1}$, …, $Y_{n}$. Como neste caso as amostras são dependentes não podemos aplicar o Teste de Wilcoxon-Mann-Whitney.

Neste caso vamos considerar observações pareadas, isto é, podemos considerar que temos na realidade uma amostra de pares:

$${(X_1, Y_1),\ldots , (X_n, Y_n)}.$$

Vamos definir $D_{i}$ = $X_{i}$ - $Y_{i}$, para i = 1, 2, …, n. Assim, obtemos a amostra $D_{1}$, $D_{2}$, …, $D_{n}$, resultante das diferenças entre os valores de cada par.

Para realizar o Teste de Wilcoxon Pareado devemos primeiramente estabelecer as hipóteses:

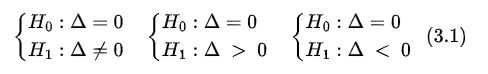
Ou seja, estaremos testando se as populações diferem em localização ou não utilizando a seguinte idéia: se aceitarmos a hipótese nula, temos que a mediana da diferença é nula, ou seja, as populações não diferem em localização. Já, se a hipótese nula for rejeitada, ou seja, se a mediana da diferença não for nula, temos que as populações diferem em localização.

Dessa forma, o nosso teste se tornou um Teste de Wilcoxon para uma única amostra - a amostra $D_{1}$, …, $D_{n}$ onde $θ_{0}$ = 0.

A partir daí, devemos seguir os passos do Teste de Wilcoxon para uma única amostra.

Observação

No Teste de Wilcoxon o conjunto de dados analisado é o conjunto obtido subtraindo-se $θ_{0}$ de cada valor da amostra. Como neste caso $θ_{0}$ = 0, o conjunto que analisaremos é o próprio conjunto $D_{1}$, …, $D_{n}$.

Exemplo 3.1

Consideremos duas amostras dependentes cujos dados estão na Tabela abaixo. Existem evidências de diferença entre as duas amostras?

Amostra 1	564	521	495	564	560	481	545	478	580	484	539	467
Amostra 2	557	505	465	562	545	448	531	458	562	485	520	445
Diferença	7	16	30	2	15	33	14	20	18	-1	19	22

Denotamos as observações da amostra 1 por $X_{i}$, i = 1, …, 12, e da amostra 2 por $Y_{i}$, i = 1, …, 12. Podemos escrever os pares de observações $(X_1,Y_{1}$), $(X_2,Y_{2}$), …, $(X_{12},Y_{12}$). Analisamos a diferença $D_{i}$= $Y_{i}$$-X_{i}$. $D_{1}$, …, $D_{12}$ é uma amostra de 12 observações independentes e igualmente distribuídas.

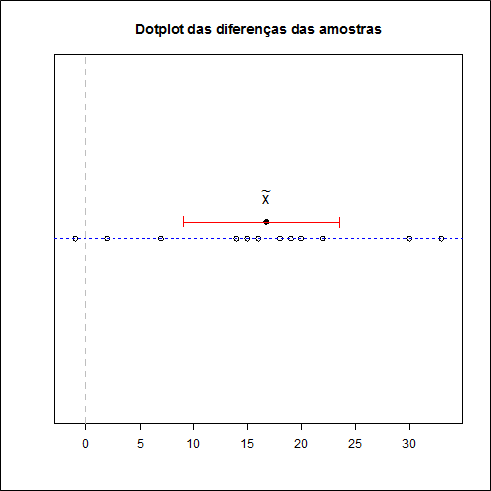
A Tabela abaixo nos da as diferenças da Tabela 3.1 ordenadas de forma crescente (a partir dos valores absolutos das diferenças) e seus respectivos postos.

Diferença	-1	2	7	14	15	16	18	19	20	22	30	33
Postos	1	2	3	4	5	6	7	8	9	10	11	12

Assim, nosso teste agora se resume em um Teste de Wilcoxon para uma única amostra.

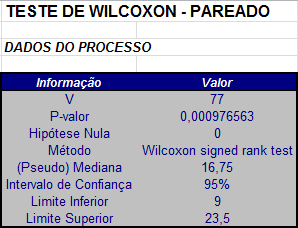
Temos que a estatística $T^{+}$ que é soma dos postos positivos é dada por

$$T^+=2+3+4+5+6+7+8+9+10+11+12 = 77.$$

Utilizando a distribuição exata da estatística de Wilcoxon para uma única amostra, temos que, para α = 5%, os valores críticos são $t_{1}$ = 14 e $t_{2}$ = 64.

Conclusão

Como o valor crítico $T_{obs}^{+}$ = 77 > $t_{2}$ = 64, rejeitamos a hipótese nula. Portanto, há evidências de diferenças entre as duas amostras.

4 - Teste de Kruskal Wallis

O teste de Kruskal-Wallis (KW) é uma extensão do teste de Wilcoxon-Mann-Whitney. É um teste não paramétrico utilizado para comparar três ou mais populações. Ele é usado para testar a hipótese nula de que todas as populações possuem funções de distribuição iguais contra a hipótese alternativa de que ao menos duas das populações possuem funções de distribuição diferentes.

Figura 4.1: William Henry Kruskal (1919 - 2005); Wilson Allen Wallis (1912-1998).

O teste de Kruskal-Wallis é o análogo ao teste F utilizado na ANOVA 1 fator. Enquanto a análise de variância dos testes dependem da hipótese de que todas as populações em confronto são independentes e normalmente distribuídas, o teste de Kruskal-Wallis não coloca nenhuma restrição sobre a comparação. Suponha que os dados provenham de k amostras aleatórias independentes com tamanhos amostrais $n_{1}$, $n_{2}$, …, $n_{k}$ sendo N = $n_{1 }$+ $n_{2 }$+ … + $n_{k}$ o número total de elementos considerados em todas as amostras.

Amostra 1	$ X_{11} $	$ X_{12} $	……	$ X_{1,n_1} $
Amostra 2	$ X_{21} $	$ X_{22} $	……	$ X_{2,n_2} $
⋮⋮	⋮⋮	⋮⋮	⋮⋮	⋮⋮
Amostra k-1	$ X_{k-1,1} $	$ X_{k-1,2} $	……	$ X_{k-1,n_{k-1}} $
Amostra k	$ X_{k,1} $	$ X_{k,2} $	……	$ X_{k,n_k} $

Hipóteses

1) As N variáveis aleatórias ${X_{j1}, X_{j2}, \ldots, X_{j,n_j}}$ com $j=1,2,\ldots, k$ são mutuamente independentes.

2) Para cada $j\in {1,\ldots,k}$ as $n_{j}$ variáveis aleatórias ${X_{j1},X_{j2},\ldots,X_{j,n_j}}$ são uma amostra aleatória de uma distribuição contínua com função de distribuição $F_{j}$.

3) As funções de distribuição $F_{1}$, $F_{2}$, …, $F_{k}$ se relacionam através da relação

$$F_j(t)=F(t-\tau_j),\quad -\infty < t < \infty,$$

para j = 1, 2, …, k, em que F é uma função de distribuição para uma distribuição contínua com mediana desconhecida e $τ_{j}$ é o efeito do tratamento (desconhecido) para a população j.

Neste caso, a hipótese nula $H_{0}$ de interesse é a de que não há diferença entre os efeitos $\tau_1, \cdots , \tau_k$, isto é

$$H_0: \tau_1=\tau_2=\ldots=\tau_k.$$

Esta hipótese nula garante que cada função de distribuição $F_{1}$, $F_{2}$, …, $F_{k}$ é igual, ou seja, $F_1_{ }$= $F_{2}$ = … = $F_{k}$.

Para aplicar o método de Kruskal-Wallis, primeiramente ordenamos todas as N observações das k amostras da menor para a maior observação e consideramos $r_{ij}$ como sendo o posto de $X_{ij}$. Tomamos

$$R_i=\sum_{j=1}^{n_i}r_{ij} \quad \hbox{e} \quad R_{i\cdot}=\frac{R_i}{n_i}, \quad i = 1,\ldots, k.$$

Deste modo, temos por exemplo, que $R_{1}$ é a soma dos postos dos elementos da amostra 1 e $R_{i.}$ é o posto médio destas mesmas observações. A estatística de Kruskal-Wallis H, será dada por

$$H=\frac{\frac{12}{N(N+1)}\sum_{i=1}^kn_i\left(R_{i\cdot}-\frac{N+1}{2}\right)^2}{1-\frac{ \sum_{j=1}^g t_j^3-t_j}{N^3-N}}=\frac{\left(\frac{12}{N(N+1)}\sum_{i=1}^k \frac{R_i^2}{n_i} \right)-3(N+1)}{1-\frac{\sum_{j=1}^g t_j^3-t_j}{N^3-N}}$$

em que $t_{j}$ é o tamanho do grupo de elementos repetidos j e g é o número de grupos. Uma observação que não se repete é considerada como um grupo de tamanho 1. Esta estatística tem, aproximadamente, uma distribuição qui-quadrado com k-1 graus de liberdade.

Os passos para realização deste teste são dados a seguir:

1. Estabelecemos as hipótese

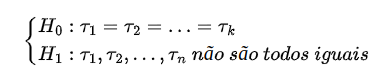
2. Ordenamos de forma crescente de magnitude os valores deste novo conjunto de dados e associamos a cada valor seu posto correspondente, tendo cada posto o mesmo sinal do valor que este representa.

3. Calculamos o valor da estatística H. Em seguida, fixamos o nível de significância α.

4. Encontramos os valores críticos referentes ao nível de significância fixado. Neste caso, calculamos os valores $Q_{α}$ de modo que P[H > $Q_{α }$] = α (sob $H_0$).

5. Se $H_{obs}$ > $Q_{α}$ rejeitamos a hipótese nula de que as amostras provém de populações igualmente distribuídas.

6. O p-valor é calculado da seguinte forma

$$P-valor = P[\chi^2_{k-1} \geq H|H_0]$$

Exemplo 4.1

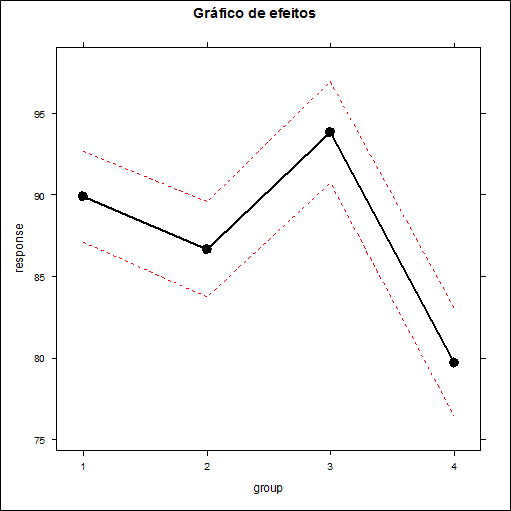
Os dados a seguir são de uma experiência clássica agrícola para avaliar o rendimento de culturas divididas em quatro grupos diferentes. Para manter a simplicidade, identificamos os tratamentos usando os números inteiros {1,2,3,4}. Queremos avaliar se os dados provém de distribuições igualmente distribuídas.

Grupos	Resposta
1	83
1	91
1	94
1	89
1	89
1	96
1	91
1	92
1	90
1	84
2	91
2	90
2	81
2	83
2	84
2	83
2	88
2	91
2	89
3	101
3	100
3	91
3	93
3	96
3	95
3	94
3	81
4	78
4	82
4	81
4	77
4	79
4	81
4	80

1. Estabelecemos as hipóteses:

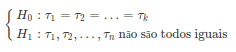
2. A partir dos dados temos a seguinte tabela, relacionando os postos de cada elemento, os tamanhos amostrais de cada grupo e os valores $R_{i}$ para cada grupo:

$j$	$r_{1j}$	$r_{2j}$	$r_{3j}$	$r_{4j}$
1	11	23	34	2
2	23	19,5	33	9
3	28,5	6,5	23	6,5
4	17	11	27	1
5	17	13,5	31,5	3
6	31,5	11	30	6,5
7	23	15	28,5	4
8	26	23	6,5
9	19,5	17
10	13,5
$R_i$	210	139,5	213,5	32
$N$	34	34	34	34
$ni$	10	9	8	7

3. Cálculo da estatística H.

$$H=\frac{\left(\frac{12}{N(N+1)}\sum_{i=1}^k \frac{R_i^2}{n_i} \right)-3(N+1)}{1-\frac{\displaystyle\sum_{j=1}^g t_j^3-t_j}{N^3-N}}=$$

$$=\frac{0,010084034*(122,5+36+675,28125+1170,035714)}{1-0,006417112}=$$

$$=20,337.$$

4. Cálculo dos valores críticos.

Fixando o nível de significância α = 0,05 e sabendo que k = 4, temos que o valor crítico corresponde ao ponto $Q_{0,95}$ = 7,815.

5. Critério de rejeição.

Como $H_{obs}$ = 20,337 > $Q_{0,95}$ = 7,815, rejeitamos a hipótese nula.

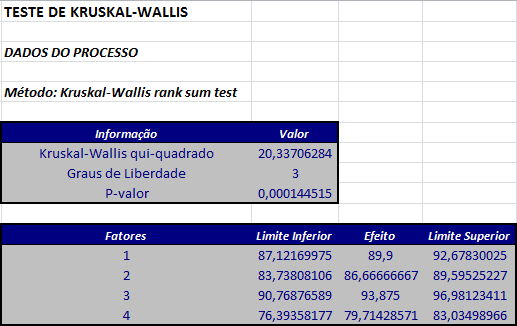
6. Neste caso, o p-valor é dado por

$$P-valor = P[\chi^2_{k-1}\geq H_{obs}]=P[\chi^2_{3}\geq 20,337]=0,0001445.$$

Comparações Múltiplas

Ao compararmos vários tratamentos, por exemplo na área médica, o números de tratamentos geralmente é bastante pequeno. Porém, ao compararmos a evasão dos alunos de graduação de alguma universidade, por exemplo, obtemos maior números de tratamentos. Quando rejeitamos a hipótese nula $H_0$ no teste de Kruskal-Wallis, indica que ao menos um dos grupos é diferente dos demais. Porém, não temos a informação de quais são diferentes. Neste sentido, procedimento de comparações múltiplas nos permite determinar quais grupos são diferentes. Existe um procedimento simples para determinar quais os pares de grupos são diferentes.

Começamos testando as diferenças para todos os pares de grupos. Quando o tamanho da amostra é grande, estas diferenças tem distribuição assintótica normal padrão. No entanto, quando temos um grande número de diferenças e se essas diferenças não forem independentes, o procedimento de comparação múltipla deve ser ajustada de forma apropriada. Suponha que a hipótese de não haver diferença entre os $k$ grupos foi testada e rejeitada ao nível de significância $\alpha.$ Uma alternativa descrita em Siegel e Castellan é testar a significância dos pares de diferenças através da seguinte desigualdade,

$$|R_{i.}-R_{j.}|\geq Z_{\left(\frac{\alpha}{k(k-1)}\right)}\sqrt{\frac{N(N+1)}{12}\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}~~~(4.1)$$

em que

• $n_i$ e $n_j$ são os tamanhos da amostra dos grupos $i$ e $j$ respectivamente;
• $N=n_1+n_2+\dots+n_k$ o número total de elementos considerados em todas as amostras;
• $R_{i.}$ e $R_{j.}$ é o efeito dos postos (ranks) dos grupos $i$ e $j$ respectivamente;
• $|R_{i.}-R_{j.}|$ é a diferença observada;
• $Z_{\left(\frac{\alpha}{k(k-1)}\right)}\sqrt{\frac{N(N+1)}{12}\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}$ é a diferença crítica.

Assim, se (4.1) ocorre podemos rejeitar a hipótese $H_0:\tau_i=\tau_j$ e concluir que $H_1:\tau_i\neq\tau_j.$ Vale lembrar que neste teste de comparações múltiplas, se temos $k$ grupos, então o número de comparações é de $\frac{k(k-1)}{2}.$ Agora, vamos aplicar os conceitos no seguinte exemplo.

Exemplo 4.2

Voltando ao exemplo 4.1

1. Calcular as diferenças observadas.

$j$	$r_{1j}$	$r_{2j}$	$r_{3j}$	$r_{4j}$
1	11	23	34	2
2	23	19,5	33	9
3	28,5	6,5	23	6,5
4	17	11	27	1
5	17	13,5	31,5	3
6	31,5	11	30	6,5
7	23	15	28,5	4
8	26	23	6,5
9	19,5	17
10	13,5
$\overline{R}_{i.}$	21	15,5	26,68	4,57

Tabela 4.1: Postos para cada grupo.

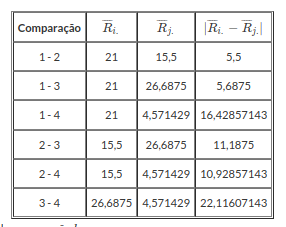
Tabela 4.2: Diferença observada para cada comparação $k$.

2. Consultar na tabela da normal padrão o valor de Z:

$$Z_{\left(\frac{\alpha}{k(k-1)}\right)}=Z_{\left(\frac{0,05}{4(4-1)}\right)}=2,638257$$

3. Calcular as diferenças críticas:

Comparação	$Z_{(\frac{\alpha}{k(k-1)})}$	$\sqrt{\frac{N(N+1)}{12}\left(\frac{1}{n_i}+\frac{1}{n_j}\right)}$	Diferença Crítica
1 - 2	2,638257	4,575498	12,07134
1 - 3	2,638257	4,723611	12,4621
1 - 4	2,638257	4,907477	12,94719
2 - 3	2,638257	4,838838	12,7661
2 - 4	2,638257	5,018484	13,24005
3 - 4	2,638257	5,153882	13,59727

Tabela 4.3: Diferenças Críticas.

Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.

(imagem em falta)

5 - Teste de Friedman

O teste de Friedman é uma alternativa não paramétrica para o teste de experimentos em blocos ao acaso (RBD - Randon Blocks Design) na ANOVA regular. Ele substitui o RBD quando os pressupostos de normalidade não estão assegurados, ou quando as variações são possivelmente diferentes de população para população. Este teste utiliza os ranks dos dados ao invés de seus valores brutos para o cálculo da estatística de teste. Como o teste de Friedman não faz suposições sobre a distribuição, ele não é tão poderoso quanto o teste padrão se as populações forem realmente normais.

Milton Friedman publicou os primeiros resultados para este tipo teste. Ele recebeu o Prêmio Nobel de Economia em 1976 e uma das publicações sobre sua descoberta foi o artigo “O Uso de Ranks para evitar a suposição de normalidade implícitos na análise de variância “, publicado em 1937.

Figura 5.1: Milton Friedman (1912-2006).

Lembremos que o projeto RBD exige medidas repetidas para cada bloco em cada nível de tratamento. Suponha que $X_{ij}$, representa o resultado experimental do fator (ou “bloco”) i com o tratamento j, onde i = 1, …, b e j = 1, …, k.

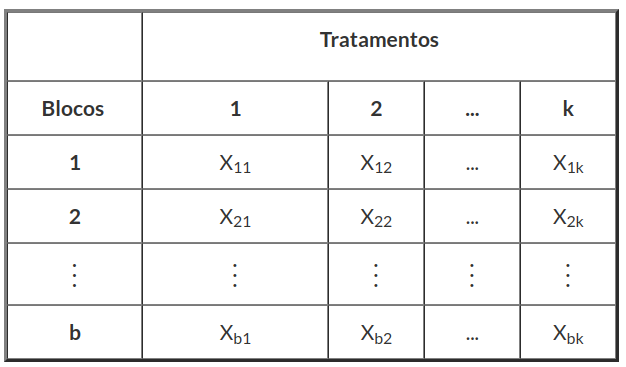
Tabela 5.1: Tabela Cruzada dos Dados.

Para calcular a estatística de teste de Friedman, ordenamos as k observações da menor para a maior de forma separada em cada um dos b blocos e atribuímos os ranks {1, 2, …, k} para cada bloco da tabela de observações. Assim, a posição esperada de qualquer observação sob $H_{0}$ é (k + 1)/2. Sendo $r(X_{ij}$) o rank da observação $X_{ij}$ definimos a soma de todos os ranks da coluna j (ou seja, de cada tratamento) por

$$R_j=\sum^b_{i=1}r(X_{ij}), \quad 1\leq j\leq k.\quad (5.1)$$

Se $H_{0}$ é verdadeira, o valor esperado de $R_{j}$ é $E(R_{j}$)=b(k+1)/2. Desta forma, a estatística

$$\sum^k_{j=1}\left(R_j-\frac{b(k+1)}{2}\right)^2$$

é uma forma intuitiva para revelar as diferenças entre os tratamentos.

A estatística do teste de Friedman será dada por

$$S=\frac{12b}{k(k+1)}\sum_{j=1}^k\left(\frac{R_j}{b}-\frac{k+1}{2}\right)^2=\left[\frac{12} {bk(k+1)}\displaystyle\sum_{j=1}^k R_j^2\right]-3b(k+1)$$

Se $F_{j}$(t) = $F(t+τ_{j}$) é a função de distribuição do tratamento j, com j = 1, 2, …, k, no teste de Friedman estamos interessados em testar a hipótese $H_{0}$: $τ_{1}$ = $τ_{2}$ = … = $τ_{k}$ contra a hipótese alternativa de que $τ_{1}$, $τ_{2}$, …, $τ_{k}$ não são todos iguais. Neste caso, ao nível de significância α, rejeitamos a hipótese $H_{0}$ se S ≥ $s_{α}$, caso contrário não rejeitamos a hipótese nula, em que a constante $s_{α}$ é escolhida de modo que a probabilidade de erro do tipo I seja igual a α.

Aproximação para amostras grandes

Sob $H_{0}$, a estatística S tem, quando n tende ao infinito, uma distribuição qui-quadrado $\chi^2$ com k-1 graus de liberdade. Neste caso, utilizando a aproximação qui-quadrado, rejeitamos $H_{0}$ se $S\geq \chi_{k-1,\alpha}^2$, caso contrário não rejeitamos $H_{0}$, onde $\chi_{k-1,\alpha}^2$ é tal que $P[\chi^2_{k-1}\geq \chi^2_{k-1,\alpha}]=\alpha$.

Observações repetidas

Se existem observações repetidas entre as k observações de um mesmo bloco, uma modificação para a estatística S é necessária. Neste caso substituímos S por

$$S^{\prime}=\frac{12\displaystyle\sum_{j=1}^k R_j^2-3b^2k(k+1)^2}{bk(k+1)-[\frac{1}{k-1}]\displaystyle\sum_{i=1}^n ({(\displaystyle\sum_{j=1}^{g_1}t_{i,j}^3)-k})},$$

no qual $g_{i}$ denota o número de grupos de observações repetidas no i-ésimo bloco e $t_{i,j}$ é o tamanho do j-ésimo grupo de observações repetidas no i-ésimo bloco. Em particular, se não há observações repetidas entre as observações no i-ésimo bloco, então $g_{i}$ = k e $t_{i,j}$ = 1 para cada j = 1, …, k. Se em todos os blocos não existem observações repetidas, então S' se reduz a S.

O p-valor é calculado da seguinte forma

$$P-valor = P[\chi^2_{k-1}\geq S^{\prime}|H_0].$$

Exemplo 5.1

Em uma avaliação de desempenho de veículos, seis motoristas avaliaram três carros (A, B e C) em um estudo aleatório. O objetivo do estudo é estudar o desempenho dos veículos e supostamente, na análise dos motoristas, a marca do veículo não influencia na avaliação. Na tabela abaixo, temos as classificações de cada carro, segundo cada motorista, em uma escala de 1 a 10.

Carro	Motorista	Resposta
A	1	7
A	2	6
A	3	6
A	4	7
A	5	7
A	6	8
B	1	8
B	2	10
B	3	8
B	4	9
B	5	10
B	6	8
C	1	9
C	2	7
C	3	8
C	4	8
C	5	9
C	6	9

Inicialmente, montamos a tabela dos Ranks

Bloco	A	B	C
1	1	2	3
2	1	3	2
3	1	2,5	2,5
4	1	3	2
5	1	3	2
6	1,5	1,5	3
Total	6,5	15	14,5

Neste caso, temos que os números de grupos de observações repetidas em cada bloco são $g_{1 }$= 3, $g_{2 }$= 3, $g_{3 }$= 2, $g_{4 }$= 3, $g_{5 }$= 3 e $g_{6 }$= 2. Além disso, os tamanhos de cada grupo são dados por $t_{1,1 }$= $t_{1,2 }$= $t_{1,3 }$= $t_{2,1 }$= $t_{2,2 }$= $t_{2,3 }$= $t_{4,1 }$= $t_{4,2 }$= $t_{4,3 }$= $t_{5,1 }$= $t_{5,2 }$= $t_{5,3 }$= 1 e, além disso, $t_{3,1 }$= 1, $t_{3,2 }$= 2, $t_{6,1 }$= 2 e $t_{6,2 }$= 1.

Neste caso, temos que a estatística S' é dada por

$$S^{\prime}=\frac{12(42,25+225+210,25)-3\times 36\times3(3+1)^2}{6\times 3(3+1)-\frac{1}{2}\left(6+6\right)}=8,272728$$

Neste caso o p-valor é

$$P-valor = P[\chi^2_2\geq 8,272728]=0,01598085.$$

Comparações Múltiplas

No teste de Friedman, assim como no teste de Kruskal-Wallis, podemos realizar comparações múltiplas no teste de Friedman. Quando a hipótese nula $H_0$ é rejeitada, temos que, ao menos um dos grupos é diferente dos demais. Porém, não temos a informação de quais grupos são diferentes. Neste sentido, o procedimento de comparações múltiplas nos permite determinar quais grupos são diferentes. Utilizamos um procedimento simples para determinar quais os pares de grupos são diferentes.

Testamos a significância dos pares de diferenças entre os grupos i e j a partir da seguinte desigualdade.

$$|R_{i}-R_{j}|\geq Z_{\left(\frac{\alpha}{k(k-1)}\right)}\sqrt{\frac{N\times k(k+1)}{6}}~~~(5.2)$$

em que

• $ k $ é o número de grupos;

• $ N $ é o número de blocos;

• $R_{i} $ e $ R_{j} $ é o soma dos postos (ranks) dos grupos $ i $ e $ j $ respectivamente, definidos na equação (5.1);

• $|R_{i}-R_{j}| $ é a diferença observada;

• $ Z_{\left(\frac{\alpha}{k(k-1)}\right)}\sqrt{\frac{N\times k(k+1)}{6}} $ é a diferença crítica.

Assim, se (5.2) ocorre podemos rejeitar a hipótese $H_0:\tau_i=\tau_j$ e concluir que $ H_1:\tau_i\neq\tau_j. $ Vale lembrar que, neste teste de comparações múltiplas, se temos $ k $ grupos, então o número de comparações é de $ \frac{k(k-1)}{2}.$ Aplicamos os conceitos no seguinte exemplo.

Exemplo 5.2

Voltando ao exemplo 5.1. Temos o seguinte conjunto de dados.

Carro	Motorista	Resposta
A	1	7
A	2	6
A	3	6
A	4	7
A	5	7
A	6	8
B	1	8
B	2	10
B	3	8
B	4	9
B	5	10
B	6	8
C	1	9
C	2	7
C	3	8
C	4	8
C	5	9
C	6	9

No procedimento de comparações múltiplas, vamos seguir os seguintes passos:

1. Montamos a tabela de Ranks.

Bloco	A	B	C
1	1	2	3
2	1	3	2
3	1	2,5	2,5
4	1	3	2
5	1	3	2
6	1,5	1,5	3
Total	6,5	15	14,5

2. Calculamos as diferenças observadas:

Comparação	$ R_i $	$ R_j $	$ |R_i-R_j| $
A - B	6,5	15	8,5
A - C	6,5	14,5	8
B - C	15	14,5	0,5

3. Consultar na tabela da normal padrão o valor de Z:

$Z_{\left(\frac{\alpha}{k(k-1)}\right)}=Z_{\left(\frac{0,05}{3(3-1)}\right)}=2,3939$

4. Calcular a diferença crítica:

$ Z_{\left(\frac{\alpha}{k(k-1)}\right)}\sqrt{\frac{N\times k(k+1)}{6}}=2,3939\times \sqrt{\frac{6\times 3(3+1)}{6}}=8,29299$

Veja a seguir os resultados obtidos pelo software Action para o mesmo exemplo.

(imagem em falta)

6 - Teste de Aderência

Nesta seção vamos descrever algumas técnicas para realização de testes de aderência. Os testes de aderência consistem em verificar a adequabilidade de um modelo probabilístico a um conjunto de dados.

6.1 - Teste de Anderson-Darling

O problema que vamos considerar aqui é o de testar a hipótese de que uma dada amostra tenha sido retirada de uma dada população com função de distribuição acumulada contínua $F(x)$, isto é, seja $x_1,x_2,\ldots,x_n$ uma amostra aleatória e suponha que um provável candidato para a FDA dos dados seja $F(x)$, então, o teste de hipóteses para verificar a adequabilidade da distribuição é:

Anderson e Darling (1952, 1954) propuseram a seguinte estatística para este teste $$\displaystyle A^2=n\int_{-\infty}^{\infty}\frac{[F_n(x)-F(x)]}{F(x)(1-F(x))}dF(x)$$

onde $F_n(x)$ é a função de distribuição acumulada empírica definida como

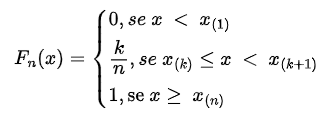
e $x_{(1)}\leq x_{(2)}\leq\ldots\leq x_{(n)}$, são as estatísticas de ordem da amostra aleatória.

A estatística $A^2$ pode ser colocada numa forma equivalente: $$A^2=-n-\frac{1}{n}\sum_{i=1}^n[(2i-1)\ln(F(x_{(i)}))+(2(n-i)+1)\ln(1-F(x_{(i)}))]$$

A transformação $F(x_{(i)})$ leva $x_{(i)}$ em $U_{(i)}$ de uma amostra de tamanho n com distribuição uniforme em $(0,1)$. Logo, $$A^2=-n-\frac{1}{n}D\qquad(\star)$$

em que $D$ é dado por $$D=\sum_{i=1}^n[(2i-1)\ln(U_{(i)})+(2(n-i)+1)\ln(1-U_{(i)})]$$

Para calcular o valor da estatística $A^2$ procedemos da seguinte forma:

• Ordenamos os valores da amostra: $x_{(1)}\leq x_{(2)}\leq \ldots\leq x_{(n)}$;
• Quando necessário, estime os parâmetros da distribuição de interesse;
• Calcule $U_i = F(x_{(i)})$ e calcule o valor da estatística de Anderson Darling $$\displaystyle A^2=-n-\frac{1}{n}\sum_{i=1}^n[(2i-1)(\ln(U_{(i)})+(2(n-i)+1)\ln(1-U_{(i)})]$$
• Para cada uma das distribuições calcule, se for o caso, o valor da estatística modificada de acordo com as tabelas dadas para cada uma delas.

Para uma distribuição com parâmetros conhecidos temos os valores da função de distribuição acumulada da estatística $A^2$ tabulados em Peter and Lewis (1960). O problema surge quando um ou dois dos parâmetros da distribuição precisam ser estimados. Para contornar esse problema Stephens (1974, 1976, 1977) utilizou métodos assintóticos para tabular os valores dessas probabilidades quando os parâmetros das distribuições são desconhecidos.

Nas próximas seções apresentamos o teste de Anderson-Darling para algumas distribuições contínuas.

6.1.1 - Distribuição Log Normal

Para a distribuição Log-Normal com função densidade de probabilidade dada por:

$$f(x) = \dfrac{1}{\sqrt{2 \pi}, , x \sigma} , \exp \left[-\dfrac{1}{2} \left(\dfrac{\log (x) - \mu}{\sigma} \right)^2\right] ,\qquad x~>~0, -\infty~<~\mu~<~\infty \ \text{e} \ \sigma~>~0$$

Temos que a distribuição Log-normal surge quando se toma o exponencial da distribuição Normal, desta forma os dados podem ser analisados segundo uma distribuição Normal caso se trabalhe com o logaritmo dos dados ao invés dos valores originais. A seguinte tabela fornece alguns valores de quantis e a estatística de Anderson Darling modificada, dada por $$A^2_m=\left(1+\frac{0,75}{n}+\frac{2,25}{n^2}\right)A^2$$

Caso 0: O parâmetro $\theta (\mu,\sigma^2)$ é totalmente conhecido.

Caso 1: $\mu$ é conhecido e $\sigma^2$^ é estimado por $s^2$.

Caso 2: $\sigma^2$ é conhecido e $\mu$ é estimado por $\overline{X}$.

Caso 3: Nenhum dos componentes de $\theta = (\mu,\sigma^2)$ é conhecido e são estimados por ($\overline{X},s^2$)

Caso	Modificação	15,0	10,0	5,0	2,5	1,0
Caso 0	-	1,610	1,933	2,492	3,070	3,857
Caso 1	-	0,784	0,897	1,088	1,281	1,541
Caso 2	-	1,443	1,761	2,315	2,890	3,682
Caso 3	$A^2(1+(0,75/n)+(2,25/n^2))$	0,560	0,632	0,751	0,870	1,029

Em relação ao cálculo do p-valor, temos que este depende do valor da estatística de Anderson-Darling modificada $A_{m}^{2}$. A partir do valor desta é utilizada uma interpolação que aproxima uma função exponencial. Apresentamos na tabela a seguir o cálculo do p-valor.

$ A_{m}^{2} $	P-valor
$ A_{m}^{2} < 0,200 $	$ p-valor = 1 - exp(-13,436 + 101,14 * A_{m}^{2} - 223,73 * (A_{m}^{2})^{2}) $
$ 0,200 < A_{m}^{2} < 0,340 $	$ p-valor = 1 - exp(-8,318 + 42,796 * A_{m}^{2} - 59,938 * (A_{m}^{2})^{2}) $
$ 0,340 < A_{m}^{2} < 0,600 $	$ p-valor = exp(0,9177 - 4,279 * A_{m}^{2} - 1,38 * (A_{m}^{2})^{2}) $
$ A_{m}^{2} > 0,600 $	$ p-valor = exp(1,2937 - 5,709 * A_{m}^{2} + 0,0186 * (A_{m}^{2})^{2}) $

Observação: Como trabalhamos com o logaritmo dos dados e por consequência com a distribuição normal, temos que a estatística modificada $A^2$, os casos citados dos parâmetros e a tabela são iguais, tanto para a distribuição Normal quanto para a Log-normal, para mais detalhes Teste de Anderson-Darling para a distribuição Normal.

Exemplo 6.1.1:

A seguir, apresentamos os dados ordenados e os valores utilizados para os cálculos da estatística de Anderson-Darling:

$ i $	$ x_i $	$ log(x_i) $	$ F_x $	$ D_i $
1	0,1366026	-1,9906790	0,0177512	-5,804454
2	0,1670097	-1,7897036	0,0297473	-13,474327
3	0,1692331	-1,7764784	0,1027915	-26,012798
$ \vdots $	$ \vdots $	$ \vdots $	$ \vdots $	$ \vdots $
50	6,6128613	1,8890164	0,9824390	-5,796058

Vamos testar:

Para calcular a estatística de Anderson-Darling, devemos tomar o logaritmo dos dados, $log(x_i)$, como dado na tabela acima. Após isto, devemos estimar os parâmetros da distribuição, visto que estes não são conhecidos. As estimativas dos parâmetros são dadas por:

$$ \overline{X}=\frac{X_1+\ldots+X_n}{n} = \frac{-1,9906790 + … + 1,8890164}{50} = -0,05284422 $$

$$ \displaystyle s^2=\sum_{i=1}^n\frac{(X_i-\overline{X})^2}{n-1} = \sum_{i=1}^{50}\frac{(-1,9906790 - 0,01)^2 + … + (1,8890164- 0,01)^2}{50-1} = 0,9216453 $$

Utilizando a fórmula $(\star)$, temos que $$D = -2524,497.$$

$$A^2=-n-\frac{D}{n}=-50+\frac{-2524,497}{50}=0,4899346.$$

A estatística de Anderson Darling modificada para este caso (Caso 3, com μ e σ desconhecidos) é dada por: $$A_m^2=A^2\left(1+\frac{0,75}{n}+\frac{2,25}{n^2}\right)=0,4977246.$$

Calculando o p-valor temos:

$$p-valor = exp(0,9177 - 4,279 * A_{m}^{2} + 1,38 * (A_{m}^{2})^{2})=exp(0,9177 - 4,279 * 0,4977246 + 1,38 * (0,4977246)^{2})=0,2114153$$

Adotando o nível de significância de $5(porcentagem)%$, temos que existe forte evidência de que os dados provém de uma distribuição Log-normal.

6.1.2 - Distribuição Exponencial

Para a distribuição Exponencial com função densidade de probabilidade dada por:

$$f(x) = \frac{1}{\beta} exp ( { - \frac{(x - \alpha)}{\beta} ) } \ (x > \alpha), $$

a seguinte tabela fornece alguns valores de quantis com estatística de Anderson Darling modificada, que é dada por:

$$A^2_m = A^2\left( 1 + \frac{0,6}{n} \right) $$

Vale ressaltar que, em nosso caso, temos que $\alpha$ = 0.

Caso 1: O parâmetro $\alpha$ é desconhecido e $\beta$ é conhecido.

Caso 2: O parâmetro $\alpha$ é conhecido e $\beta$ é desconhecido.

Caso 3: Ambos os parâmetros $(\alpha, \beta)$ são desconhecidos.

Caso	Modificação	15,0	10,0	5,0	2,5	1,0
Caso 1	-	1,610	1,933	2,492	3,070	3,880
Caso 2	$ A^2_m = A^2(1 + (0,6/n)) $	0,916	1,062	1,321	1,591	1,959
Caso 3	-	0,916	1,062	1,321	1,591	1,959

Observação: Para o Caso 1 os valores são válidos quando $n \geq 5$.

Em relação ao cálculo do p-valor, temos que este depende do valor da estatística de Anderson-Darling modificada $A_{m}^{2}$. A partir do valor desta é utilizada uma interpolação que aproxima uma função exponencial. Apresentamos na tabela a seguir o cálculo do p-valor.

$ A_{m}^{2} $	P-valor
$ A_{m}^{2} < 0,260 $	$ p-valor = 1 - exp(-12,2204 + 67,459 \times A_{m}^{2} - 110,3 \times (A_{m}^{2})^{2}) $
$ 0,260 < A_{m}^{2} < 0,510 $	$ p-valor = 1 - exp(-6,1327 + 20,218 \times A_{m}^{2} - 18,663 \times (A_{m}^{2})^{2}) $
$ 0,510 < A_{m}^{2} < 0,950 $	$ p-valor = exp(0,9209 - 3,353 \times A_{m}^{2} + 0,3 \times (A_{m}^{2})^{2}) $
$ A_{m}^{2} > 0,950 $	$ p-valor = exp(0,731 - 3,009 \times A_{m}^{2} + 0,15 \times (A_{m}^{2})^{2}) $

Exemplo 6.1.2:

A seguir, apresentamos os dados ordenados e os valores utilizados para os cálculos da estatística de Anderson-Darling:

$ i $	$ x_i $	$ F_x $	$ D_i $
1	0,0037143	0,0070976	-5,653167
2	0,0162376	0,0306586	-13,474952
3	0,0307592	0,0572802	-19,902688
$ \vdots $	$ \vdots $	$ \vdots $	$ \vdots $
50	1,8187078	0,9694286	-6,561485

Vamos testar:

Temos que o parâmetro $\alpha$ é conhecido e igual a zero, contudo o parâmetro $\beta$ é desconhecido, logo devemos estimá-lo. A estimativa do parâmetro é dada por:

$$ \frac{1}{\overline{X}}=\frac{1}{\frac{X_1+\ldots+X_n}{n} = \frac{0,0037143 + … + 1,8187078}{50}} = \frac{1}{0,52146462} = 1,917676$$

Utilizando a fórmula $(\star)$, temos que $$D = -2510,124.$$

$$A^2=-n-\frac{D}{n}=-50+\frac{-2510,124}{50} = \ 0,2024727.$$

A estatística de Anderson Darling modificada para este caso (Caso 2, com $\alpha$ conhecido e $\beta$ desconhecido) é dada por: $$A^2_m = A^2\left(1+\frac{0,6}{n}\right)=0,2049024$$

Através da tabela dos valores críticos concluímos que o p-valor deve ser superior a 15%. Então, existe forte evidência de que os dados provém de uma distribuição Exponencial. Para o cálculo do p-valor é utilizada a seguinte expressão:

$$ \text{p-valor} = 1 - \exp(-12,2204 - 67,459A^2_m - 110,30A^2_m) = 0,951628$$

Assim temos um p-valor igual a 0,951628, logo temos forte evidência de que os dados provém de uma distribuição Exponencial.

6.1.3 - Distribuição Logística

Para a distribuição Logística com função densidade de probabilidade dada por:

$$f(x)=\frac{\exp({\frac{x-\mu}{s})}}{s((1+\exp({\frac{x-\mu}{s})}))^2},\quad x,\mu\in \mathbb{R},~~\sigma> 0.$$

a seguinte tabela fornece alguns valores de quantis com estatística de Anderson Darling modificada, que é dada por:

$$A^2_m = A^2(( 1 + \frac{0,25}{n} )) $$

Caso 1: O parâmetro $\mu$ é desconhecido e $s$ é conhecido.

Caso 2: O parâmetro $\mu$ é conhecido e $s$ é desconhecido.

Caso 3: Ambos os parâmetros $(\mu, s)$ são desconhecidos.

Caso	Modificação	25,0	10,0	5,0	2,5	1,0
Caso 1	-	0,615	0,857	1,046	1,241	1,505
Caso 2	-	1,043	1,725	2,290	2,880	3,685
Caso 3	$ A^2(1+ (0,25/n)) $	0,428	0,563	0,660	0,769	0,906

Exemplo 6.1.3:

A seguir, apresentamos os dados e os valores utilizados para os cálculos da estatística de Anderson-Darling:

$ i $	$ x_i $	$ F_x $	$ D_i $
1	94,85255	0,0012447	-6,812172
2	97,12315	0,0236866	-13,553785
3	97,68437	0,0481041	-19,855401
$ \vdots $	$ \vdots $	$ \vdots $	$ \vdots $
50	103,05806	0,9827216	-5,783810

Vamos testar:

As equações dadas acima podem ser resolvidas via métodos iterativos e, por meio destes obtivemos:

$$ \hat{\mu} = 99,96753 \ \text{e}\ \hat{s}=0,76489$$

Utilizando a fórmula $(\star)$, temos que $$D=-2518,056.$$

$$A^2=-n-\frac{D}{n}=-50+\frac{-2518,056}{50}=0,361104.$$

A estatística de Anderson Darling modificada para este caso (Caso 3, com $\mu$ e $s$ desconhecidos) é dada por: $$ A^2_m = A^2(( 1 + \frac{0,25}{n} )) = 0,3629095$$

Através da tabela dos valores críticos concluímos que o p-valor deve ser superior a 25%. Então, existe forte evidência de que os dados provém de uma distribuição Logística.

6.1.4 - Distribuição Gama

Para a distribuição Gama com função densidade de probabilidade dada por:

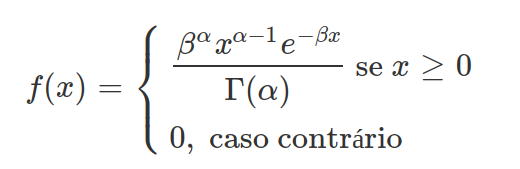
a seguinte tabela fornece alguns valores de quantis com estatística de Anderson Darling modificada, que é dada por:

$$A^2_m = A^2(( 1 + \frac{0,25}{n} )) $$

Caso 1: O parâmetro $\alpha$ é conhecido e $\beta$ é desconhecido.

Caso 2: O parâmetro $\beta$ é conhecido e $\alpha$ é desconhecido.

Caso 3: Ambos os parâmetros $(\alpha, \beta)$ são desconhecidos.

$ \alpha $	25,0	10,0	5,0	2,5	1,0
1	0,486	0,657	0,786	0,917	1,092
2	0,477	0,643	0,768	0,894	1,062
3	0,475	0,639	0,762	0,886	1,052
4	0,473	0,637	0,759	0,883	1,048
5	0,472	0,635	0,758	0,881	1,045
6	0,472	0,635	0,757	0,880	1,043
8	0,471	0,634	0,755	0,878	1,041
10	0,471	0,633	0,754	0,877	1,040
12	0,471	0,633	0,754	0,876	1,039
15	0,470	0,632	0,753	0,876	1,038
20	0,470	0,632	0,752	0,875	1,037
$ \infty $	0,470	0,631	0,786	0,873	1,035

Exemplo 6.1.4:

A seguir, apresentamos os dados e os valores utilizados para os cálculos da estatística de Anderson-Darling:

$ i $	$ x_i $	$ F_x $	$ D_i $
1	0,0101666	0,0274852	-6,353236
2	0,0117768	0,0317676	-13,479390
3	0,0118973	0,0320875	-20,294737
$ \vdots $	$ \vdots $	$ \vdots $	$ \vdots $
50	2,046896	0,9963288	-5,971350

em que $ \psi(\alpha) $ e a função digama. Temos que o parâmetro $\beta$ pode ser estimado por:

$$ \hat{\beta} = \frac{\overline{X}}{\hat{\alpha}}$$

Por meio de métodos iterativos obtivemos:

$$ \hat{\alpha}=0,9998007 \ \text{e}\ \hat{\beta}=2,739132 $$

Utilizando a fórmula $(\star)$, temos que $$D=-2509,936.$$

$$A^2=-n-\frac{D}{n}=-50+\frac{-2509,936}{50}=0,1987166.$$

Comparando com a tabela de valores críticos da distribuição Gama temos que $\hat{\alpha} \approx 1 $ e a estatística $A^2$ é inferior ao valor tabelado, isto é, 0,1987166 é menor que 0,486. Logo temos que o p-valor deve ser superior a 0,25. Então, existe forte evidência de que os dados provém de uma distribuição Gama.

6.1.5 - Distribuição Weibull

Para a distribuição Weibull com função densidade de probabilidade dada por:

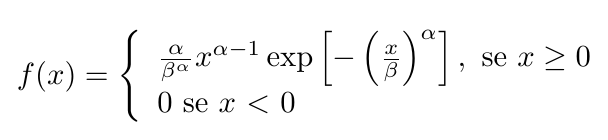
a seguinte tabela fornece alguns valores de quantis com estatística de Anderson Darling modificada, que é dada por:

$$A^2_m = A^2(( 1 + \frac{0,2}{\sqrt{n}} )) $$

Caso 1: O parâmetro $\alpha$ é conhecido e $\beta$ é desconhecido.

Caso 2: O parâmetro $\beta$ é conhecido e $\alpha$ é desconhecido.

Caso 3: Ambos os parâmetros $(\alpha, \beta)$ são desconhecidos.

Caso	Modificação	25,0	10,0	5,0	2,5	1,0
Caso 1	-	0,736	1,062	1,321	1,591	1,959
Caso 2	-	1,060	1,725	2,277	2,854	3,640
Caso 3	$ A^2(1+(0,75/\sqrt{n})) $	0,474	0,637	0,757	0,877	1,038

Exemplo 6.1.5:

A seguir, apresentamos os dados e os valores utilizados para os cálculos da estatística de Anderson-Darling:

$ i $	$ x_i $	$ F_x $	$ D_i $
1	0,8358289	0,0231670	-6,085545
2	0,9263182	0,0362156	-13,532898
3	0,9324390	0,0372630	-20,056397
$ \vdots $	$ \vdots $	$ \vdots $	$ \vdots $
50	2,6410101	0,9764851	-6,105903

Vamos testar:

Logo:

$$ \hat{\alpha} = 4,411486 \ \text{e}\ \hat{\beta} = 1,957228$$

Utilizando a fórmula $(\star)$, temos que $$D=-2515,786.$$

$$A^2=-n-\frac{D}{n}=-50+\frac{-2515,786}{50}=0,3158042.$$

A estatística de Anderson Darling modificada para este caso (Caso 3, com $\alpha$ e $\beta$ desconhecidos) é dada por: $$ A^2_m = A^2(( 1 + \frac{0,2}{\sqrt{n}} )) = 0,3170674$$

Através da tabela dos valores críticos concluímos que o p-valor deve ser superior a 25%. Então, existe forte evidência de que os dados provém de uma distribuição Weibull.

6.1.6 - Distribuição Gumbel

Para a distribuição Gumbel com função densidade de probabilidade dada por:

$$f(x)=\frac{1}{\sigma}\exp([\frac{x-\mu}{\sigma}-\exp((\frac{x-\mu}{\sigma})))]\qquad x\in (-\infty,\infty)$$

a seguinte tabela fornece alguns valores de quantis com estatística de Anderson Darling modificada, que é dada por:

$$A^2_m = A^2(( 1 + \frac{0,2}{\sqrt{n}} )) $$

Note que a estatística de Anderson Darling modificada é igual para as distribuições Weibull e Gumbel. Vale ressaltar que a distribuição Gumbel surge quando se toma o logaritmo de uma variável com a distribuição Weibull.

Caso 1: O parâmetro $\mu$ é conhecido e $\sigma$ é desconhecido.

Caso 2: O parâmetro $\sigma$ é conhecido e $\mu$ é desconhecido.

Caso 3: Ambos os parâmetros $(\sigma, \mu)$ são desconhecidos.

Logo, a tabela de valores críticos para a distribuição Wiebull também fornece alguns valores críticos para a estatística de Anderson Darling quando testamos a distriuição Gumbel.

Exemplo 6.1.6:

A seguir, apresentamos os dados e os valores utilizados para os cálculos da estatística de Anderson-Darling:

$ i $	$ x_i $	$ F_x $	$ D_i $
1	987,9316	0,0410970	-7,346391
2	988,6517	0,0520598	-14,052082
3	989,3635	0,0646470	-20,043039
$ \vdots $	$ \vdots $	$ \vdots $	$ \vdots $
50	1046,4969	0,9939219	-5,706632

Logo:

$$ \hat{\sigma} = 998,7901 \ \text{e}\ \hat{\mu} = 9,35564$$

Utilizando a fórmula $(\star)$, temos que $$D=-2537,886.$$

$$A^2=-n-\frac{D}{n}=-50+\frac{-2537,886}{50}=0,7577566.$$

A estatística de Anderson Darling modificada para este caso (Caso 3, com $\sigma$ e $\mu$ desconhecidos) é dada por: $$A^2_m = A^2(( 1 + \frac{0,2}{\sqrt{n}} ))=0,7791892$$

Através da tabela dos valores críticos concluímos que a estatística $A^2_m$ está entre 0,757 e 0,877. Logo, por meio de interpolação linear, temos que

$$\frac{0,877-0,757}{0,025 - 0,05} = \frac{0,7791892 - 0,757}{x - 0,05}$$

Assim, temos

$$x = 0,04537725$$

Como o $p-valor=0,04537725$, adotando o nível de significância de 5%, temos que existe evidência de que os dados não provém de uma distribuição Gumbel.

7 - Modelo de Intensidade

Dados discretos surgem em diversas situações comuns em confiabilidade, economia, manutenção, ciências sociais entre outros. Um típico exemplo de dados discretos em economia do trabalho está relacionado à duração do desemprego medidos em meses completos de desemprego que é um exemplo em que a resposta é um valor inteiro. Uma ampla discussão sobre as consequências de modelos discretos para dados usados em economia com distribuição de probabilidade contínua é apresentada por Grimshaw et al (2005). Outra aplicação para dados discretos, podemos citar os índices de “evasão da Universidade”, em que o tempo para concluir o curso é medida em “semestres”. Em aplicações industriais, alguns equipamentos operam sob demanda ou em ciclos, e nestes casos, contamos o número de operações ou ciclos até a falha. Assim, embora tenhamos uma abundância de estudos na literatura para dados relativos a tempo de sobrevivência contínuos, ver Aalen (1978), Fleming e Harrington (1990), Andersen et al. (1993) e Aalen et al (2009), há uma escassez de estudos na literatura aplicados à dados relativos a tempo de sobrevivência discreto, ver Gupta et al (1997), Grimshaw et al (2005), Karlis e Patilea (2007) e Yu (2007), tendo em vista isto, vamos apresentar o modelo de intensidade para variáveis aleatórias discretas na presença de censura baseados nos trabalhos de Leão e Ohashi.

7.1 - Introdução

A motivação para os modelos de intensidade para dados discretos, pode ser descrito através da seguinte aplicação descrita em Klein e Moeschberger (1997) no qual comparamos duas funções de sobrevivência na presença de cruzamento das estimativas de Kaplan-Meier. O Grupo de Estudo de Tumores Gastrointestinais (1982) reportou os resultados do estudo comparando a quimioterapia versus quimioterapia combinada com a radioterapia no tratamento de um câncer gástrico. O tempo de sobrevivência reportado em dias, para os 45 pacientes em cada tratamento são os seguintes:

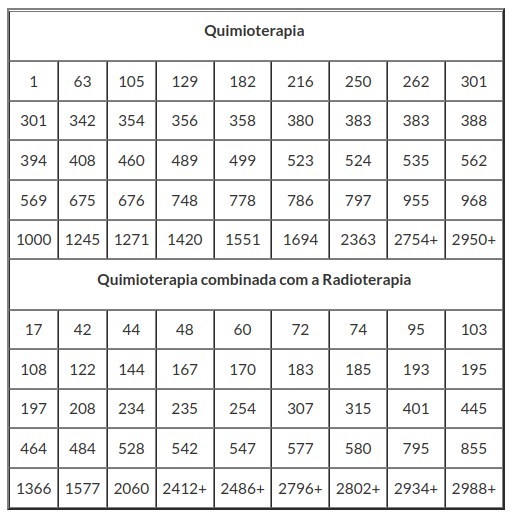
Tabela 1: Conjunto de dados do estudo de tumores gastrointestinais. O símbolo + significa que o dado está censurado.

A principal motivação destes dados é o cruzamento das funções de intensidades empíricas. Nesta situação, a maioria dos testes têm baixo poder (ver Klein e Moeschberger (1997)), fato que é um dos principais problemas em testes de hipóteses para a homogeneidade de curvas de sobrevivência. A figura (1) ilustra o cruzamento entre as estimativas de Kaplan-Meier.

(imagem em falta)

Figura 1: Produto limite estimado da distribuição da sobrevivência.

7.2 - Modelo de Intensidade para V.A discretas na presença de censura

Nesta seção, vamos abordar as idéias principais sobre o modelo de intensidade para as variáveis aleatórias discretas. Inicialmente, um processo estocástico é uma família de variáveis aleatórias $M={M(n):\in \mathbb{N}}$ definidas sobre o espaço de probabilidade $(\Omega,\mathcal{F},P),$ no qual $\Omega$ é o espaço de Cantor (ver conteúdo de probabilidades). Assim, consideramos $(\Omega, \mathcal{F}, P)$ um espaço de probabilidade e seja $\mathcal{K}={1,\dots, k}\subseteq \mathbb{N}$ finito ou infinito enumerável. O espaço amostral $\Omega$ usado neste modelo está descrito no conteudo de probabilidade na seção $\sigma$-álgebra e construção da v.a. Seja $Y$ uma variável aleatória com valores em $\mathcal{K}$ sendo $\pi_i=P[Y=i]$ a probabilidade da variável resposta ($Y$) assumir a $i$-ésima categoria. Assumindo que as categorias são mutuamente exclusivas, temos que $\pi_1+\pi_2+\dots+\pi_k=1.$ Neste caso, dizemos que $Y$ é uma variável aleatória discreta. Para mais detalhes das definições e as propriedades Martingale consulte o conteúdo de Processos Estocáticos.

Consideramos $W$ e $C$ duas variáveis aleatórias independentes discretas com valores em $\mathcal{K}$. A variável aleatória discreta $W$ descreve o evento de interesse, enquanto a variável aleatória discreta $C$ denota a variável de censura. Seja $X$ a variável aleatória assumindo valores em $\mathcal{K}$ como em (2.1.1) definida por $$X=\min(W,C)$$

Baseados em $X$ definimos os processos de contagem (para mais detalhes ver conteúdo de Processos de Contagem)

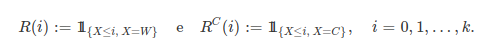
O processo de contagem $R$ $(R^C)$ determina a categoria para o qual o evento de interesse (censura) ocorre. Tomamos $(\Omega,\mathcal{F},\mathbf{A}, P)$ a base estocástica com filtragem gerada por $R$ e $R^C,$ como a seguir $$\mathcal{A}_0:={\Omega,\emptyset},~~~~\mathcal{A}_i:=\sigma{\Delta R(\ell),\Delta R^C(\ell):1\leq \ell \leq i},~~~i\in \mathcal{K},$$

no qual, $\mathbf{A}={\mathcal{A}_i;i=0,1,\dots,k}.$ Obtemos que $R$ é um processo $\mathbf{A}$-adaptado, não decrescente e consequentemente, obtemos da decomposição de Doob-Meyer que $R = Y +A,$ no qual $Y$ é um martingale e $A$ é um processo previsível não decrescente satisfazendo

$$Y(i)=\sum^i_{\ell=1}(R(\ell)-E[R(\ell)|\mathcal{A}_{\ell-1}]) ~~~~{e}~~~A(i)=\sum^i_{\ell=1}(E[R(\ell)|\mathcal{A}_{\ell-1}]-R(\ell-1)),$$

com $A(0)=0, Y(0)=0.$ Calculando os processos estocásticos relacionados com a decomposição.

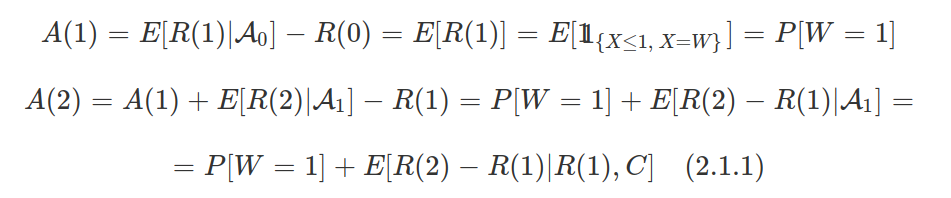
Notamos que, se $R(1)=1,$ então

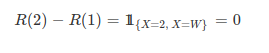
Disto, obtemos $$E[R(2)-R(1)|R(1),C]=0,\quad \text{se}~R(1)=0~\text{e}~C=1$$

$$E[R(2)-R(1)|R(1),C]\neq0,\quad \text{se}~R(1)=0~\text{e}~C\geq 2$$

Com, $W$ e $C$ independentes obtemos

De forma geral, obtemos

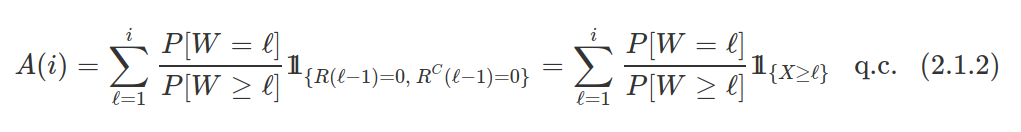
para qualquer $i\geq 1.$

Portanto, a função de intensidade $h:{0,1, \cdots , k} )→[0,1]$ associado ao processo de contagem $R$ é dada por $$h(i):=\frac{P[W=i]}{P[W\geq i]},\quad(2.1.3.1)$$

com $h(0)=0,~0~<~ h(i)~<~1,$ para qualquer $i=1,\dots,k$ e $h(k)=1$ (caso $k$ seja finito). Com isso, obtemos que $h$ descreve unicamente a distribuição de probabilidade da variável aleatória $W$ (que descreve o evento de interesse). Além disso, temos que $$P[W=i]=h(i)\prod^{i-1}_{\ell=1}[1-h(\ell)].$$

De fato, $$P[W\geq i-1]=\prod^{i-2}_{\ell=1}(1-h(\ell)), \quad \text{hipótese de indução}~~~~(2.1.3)$$

Por indução sobre $i$, obtemos que

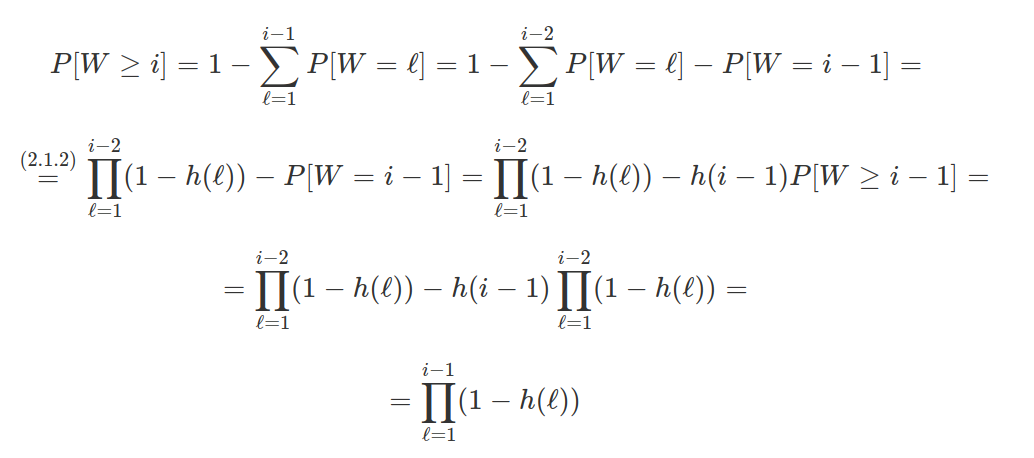
Portanto $$P[W=i]=h(i)\prod^{i-1}_{\ell=1}(1-h(\ell))$$

Assim, concluímos que a relação apresentada na equação (2.1.3) é válida. Agora, vamos exemplificar algumas funções de intensidade para dados discretos à partir de distribuições de probabilidade conhecidas.

Exemplo 2.1: (Distribuição Geométrica)

$P[W=i]=(1-p)^i p$ com parâmetro $p,~ 0 ~< p~<~ 1.$ Assim, obtemos pela definição a função de intensidade para a distribuição Geométrica da seguinte forma $$h(i):=\frac{P[W=i]}{P[W\geq i]}=\frac{(1-p)^i p}{1-p\underbrace{\displaystyle\sum^i_{\ell=0}(1-p)^\ell}_{\frac{(1-p)^i-1}{(1-p)-1}}}=\frac{(1-p)^i p}{(1-p)^i}=p$$

que é uma taxa de falha constante.

Exemplo 2.2: (Distribuição Poisson)

$P[W=i]=\displaystyle\frac{e^{-\lambda}\lambda^i}{i!},~i=1,2,\dots,~~\lambda> 0.$ Assim, obtemos pela definição a função de intensidade para a distribuição Poisson da seguinte forma

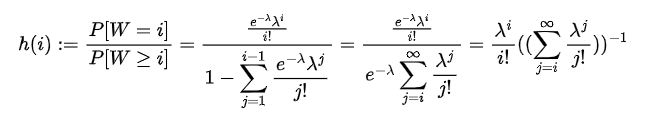
Exemplo 3: (Distribuição Binomial)

$P[W=i]=\displaystyle{n \choose k}p^i(1-p)^{n-i},~~i=0,1,2,\dots,n.$ Assim, obtemos pela definição a função de intensidade para a distribuição Binomial da seguinte forma $$h(i):=\frac{P[W=i]}{P[W\geq i]}=\frac{\displaystyle{n \choose i}p^i(1-p)^{n-i}}{\displaystyle\sum^n_{j=i}{n \choose j}p^j(1-p)^{n-j}}=\displaystyle{n \choose i}((\displaystyle\sum^n_{j=i}{n \choose j}((\frac{p}{1-p}))^{j-i}))^{-1}$$

Exemplo 2.3: (Distribuição Binomial Negativa)

$P[W=i]=\displaystyle{k+i-1 \choose i}p^k(1-p)^{i},~~~~0<~p<~1,~n> 0,~i=0,1,2,\dots,n.$ Assim, obtemos pela definição a função de intensidade para a distribuição Binomial Negativa da seguinte forma $$h(i):=\frac{P[W =i]}{P[W\geq i]}=\frac{\displaystyle{k+i-1 \choose i}p^k(1-p)^{i}}{\displaystyle\sum^n_{j=i}{k+j-1 \choose j}p^k(1-p)^{j}}=\displaystyle{k+i-1 \choose i}((\displaystyle\sum^n_{j=i}{k+j-1 \choose j}(1-p)^{j-i}))^{-1}$$

Exemplo 2.4: (Distribuição Série Logarítmica)

$P[W=i]=\displaystyle-\frac{\theta^i}{i~\log(1-\theta)},~~0<\theta< 1,~i=1,2,\dots. $ Assim, obtemos pela definição a função de intensidade para a distribuição Série Logarítmica da seguinte forma

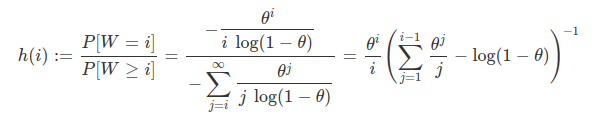
Assim, temos que $$R(i)=Y(i)+A(i)=$$

$$=\sum^i_{\ell=1}(R(\ell)-E[R(\ell)|\mathcal{A}_{\ell-1}])+\sum^i_{\ell=1}V(\ell)\Delta H(i)=$$

$$=\sum^i_{\ell=1}(R(\ell)-E[R(\ell)|\mathcal{A}_{\ell-1}])+(V.H)(i),~~~~~i=0,1,\dots,k,$$

Além disso, temos que a representação $A(i)$ é um processo previsível representado na forma multiplicativa, no qual $\Delta H(\ell)=H(\ell)-H(\ell-1)=h(\ell).$ Como $V$ é previsível, o processo $A$ é determinado pela função intensidade $h$ (ou, pela função intensidade acumulada $H$). Desta forma, temos uma relação um-a-um entre a função intensidade $h$ e a variável aleatória $W$ via relação (2.1.3). Portanto, para compararmos distribuições discretas vamos avaliar as funções intensidade envolvidas.

O processo (2.1.4) é denominado modelo de intensidade multiplicativo (ver Aalen (1978)) para variáveis aleatórias discretas. A seguir, apresentamos a inferência para o modelo discreto na presença de censura.

A seguir, apresentamos dois resultados, que são importantes na demonstração da consistência dos testes sob certas hipóteses alternativas.

Hipótese 2.1: (Proporcionalidade do tamanho da amostra)

Todos os resultados assintóticos, tem como hipótese o fato de que existe o limite $\displaystyle b_p=\lim_{n^\star)→ \infty}\frac{n_p}{n}$ e $X^p$ é integrável para todo $p \in \mathcal{J}.$ Isto que dizer que as amostras aumentam de tamanho de forma proporcional.

Proposição 2.1

O número de ítens sob risco na categoria $\ell,$ denotado por $V^{n_p}(\ell)$ tem distribuição binomial com parâmetros $n_p$ e $\theta^p_\ell,$ em que $\theta^p_\ell=P[X^p\geq \ell]$ para cada $\ell\geq 1.$

Agora, apresentamos dois resultados, fixamos $p$ e para $\ell=1,\dots,k$ temos que $$\mathbf{E}([\frac{V^{n_p}(\ell)}{n_p})]\overset{\text{Proposição}(2.1)}{=} \theta^p_\ell~~~(2.1.5)$$

Já para o segundo resultado, temos que para $\ell=1,\dots,k$ e $p=1,\dots,J$ obtemos $$\frac{V^{n^\star}(\ell)}{n_p}=\frac{([V^{n_1}(\ell)+V^{n_2}(\ell)+\cdots+V^{n_J}(\ell))]}{n_p}=$$

$$=\frac{n_1}{n_p}\frac{V^{n_1}(\ell)}{n_1}+\frac{n_2}{n_p}\frac{V^{n_2}(\ell)}{n_2}+\cdots+\frac{n_J}{n_p}\frac{V^{n_J}(\ell)}{n_J}~~~~(2.1.6)$$

Logo, usando (2.1.5) e (2.1.6) temos o seguinte resultado $$\mathbf{E}([\frac{V^{n^\star}(\ell)}{n_p})]=\frac{n_1}{n_p}\mathbf{E}([\frac{V^{n_1}(\ell)}{n_1})]+\frac{n_2}{n_p}\mathbf{E}([\frac{V^{n_2}(\ell)}{n_2})]+\cdots+\frac{n_J}{n_p}\mathbf{E}([\frac{V^{n_J}(\ell)}{n_J})]$$

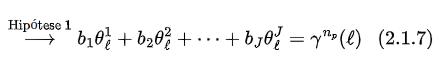
Nosso interesse consiste em testar a hipótese de homogeneidade das $J$ populações discretas sujeitas a censura aleatória. Neste caso, queremos testar a hipótese $H_0:\pi^1_\ell=\dots=\pi^J_\ell~~~\forall\ell=1,\dots, k-1$. Como a função intensidade caracteriza a variável aleatória discreta, a hipótese de homogeneidade é equivalente a $H_0: h^1(\ell)=\dots=h^J(\ell) ~~~\forall\ell=1,\dots, k-1$, no qual $k$ pode ser finito ou não. No próximo capítulo, vamos descrever os testes não paramétricos usados.

7.2.1 - A estatística de Log-rank Ponderado

O teste de Log-rank foi proposto por Mantel-Haennszel (1959) para comparar duas populações. Este teste foi estendido por Aalen (1978) e Gill (1980) para comparar duas curvas de sobrevivência sujeitas a dados censurados. O caso de $J$ populações com diversas estruturas de censura foi desenvolvido por Andersen et al (1982).

Esse teste não paramétrico é baseado na diferença entre as taxas de falha (ou funções intensidade) de cada curva de sobrevivência. Apesar do teste de Log-rank ser o teste não paramétrico mais utilizado para se comparar duas ou mais populações sujeitas a dados censurados, este teste apresentada duas restrições. Primeiro, toda a teoria assintótica envolvida com o teste de Log-rank, tem como hipótese o fato das populações envolvidas terem distribuições contínuas ou no máximo mistas. Segundo, o teste de Log-rank não apresenta bom comportamento quando as funções intensidade cruzam.

Os teoremas gerais propostos por Gill (1980) e Andersen et al (1982) não são aplicáveis ao caso discreto. O caso puramente discreto foi recentemente tratado por Leão e Ohashi (2011). Segundo Leão e Ohashi, o teste de Log-rank é consistente apenas para o caso em que não ocorrem cruzamentos entre as funções intensidade. Klein e Moeschberger (1997) mostraram que o teste de Log-rank tem baixo poder em situações no qual as funções intensidade cruzam. A principal causa do baixo poder neste tipo de situação, é que as diferenças iniciais em favor de uma população (antes do cruzamento) são canceladas após o cruzamento pelas diferenças em favor da outra população.

No caso de duas populações, diversas soluções foram avaliadas em Klein e Moeschberger (1997), entre elas, citamos a classe de testes do tipo Renyi, proposta por Gill (1980). Entretanto, estes testes são aplicados apenas no caso de duas populações e para populações com distribuições contínuas. Baseado no clássico teste de Cramér von-Mises, Leão e Ohashi (2011) propuseram modificações no teste de Log-rank de tal forma que este é consistente para qualquer hipótese alternativa.

Nesta seção, vamos estender as estatísticas de Log-rank Ponderadas proposta por Fleming e Harrington (1990) para comparar $J$ populações discretas na presença de censura arbitrária. Lembramos que $R^{n^\star}(i)=R^{n_1}(i)+\dots+R^{n_J}(i)$ é o número total de eventos de interesse da categoria $i$ e que $V^{n^\star}(i)=V^{n_1}(i)+\dots+V^{n_J}(i)$ é o número total de ítens sob Risco na categoria $i$, para qualquer $i=1,2,\dots,k$. Além disso, denotamos por $n^{\star} = (n_1, n_2 , \cdots , n_J)$ o vetor de números naturais correspondente ao tamanho da amostra retirado de cada população e $n=n_1 + n_2 + \cdots n_J$ o total de elementos nas amostras. Também dizemos que $n^\star )→ \infty$ se $n_p )→ \infty$ para todo $p=1 \cdots , J$. Vamos derivar uma classe de estatísticas de teste para a hipótese $H_0:h^1(\ell)=h^2(\ell)=\dots=h^J(\ell)$, para todo $\ell=1,\dots,i$, no qual $i$ pode ser finito ou não. A seguir, denotamos a sequência de $\mathbb{F}$ tempos de parada $$d^u=\sup ((\ell:\min_{q \in \mathcal{J}}\theta^q (\ell)>0 )),$$

em que $\theta^q(\ell):=P[X^q\geq\ell],\quad q\in(1,\dots,J),~\ell\geq0~~\text{e}$ $$d^u_{n^\star}=\sup (( \ell: \min_{q \in \mathcal{J} } V^{n_q}( \ell )> 0 )),~n^\star\in \mathbb{N}^J.$$

Podemos verificar que $d_{n^\star}^u\rightarrow d^u$ em probabilidade quando $n^\star → \infty,$ em que $1\leq d^u\leq\infty$ e $d^u_{n^\star}<\infty$ para todo $n^\star\in\mathbb{N}^J$ (propriedades $S_1$ e $S_2$ do artigo de Leão e Ohashi). É importante ressaltar que todos os resultados assintóticos deste trabalho são obtidos com a hipótese de proporcionalidade do tamanho da amostra (2.1). Considerando o problema de duas populações $(J=2),$ Fleming e Harrington (1990) propuseram as seguintes estatísticas de Log-rank Ponderada,

$$LR(n^\star,d_{n^\star})^u=\sum^i_{\ell=1}U^{n_1}_{n_2}(n^\star,\ell)[\hat{h}^{n_2}(\ell)-\hat{h}^{n_1}(\ell)],$$

com função de ponderação dada por

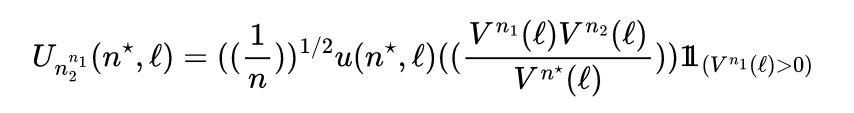
em que $u$ é um processo previsível, limitado, que converge em probabilidade para uma função limitada $w: (0,1,2, \cdots , k ) )→ \Bbb{R}$ e $n=n_1 + n_2$. Uma das principais ponderações é a classe de Tarone-Ware (1977), $$u(n^\star,\ell)=((\frac{V^{n^\star}(\ell)}{n}))^{\gamma},\quad\text{em que}~n=\sum^J_{i=1}n_i,~\gamma>0,$$

e as classes introduzidas por Harrington e Fleming (1982),

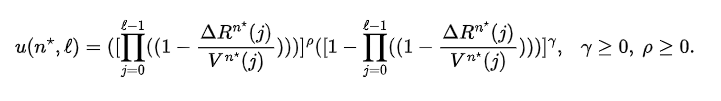
Se tomarmos $u(n^\star,\ell) = 1$ para todo $\ell$, obtemos a clássica estatística de Log-rank. Na tabela (2.1) temos as funções de ponderação mais utilizadas (ver Klein e Moeschberger página 210).

Peso	$ u(n^\star,\ell) $
Log-rank	1
Gehan	$ \displaystyle\frac{V^{n^\star}(\ell)}{n} $
Tarone e Ware $ \gamma>0 $	$ \displaystyle\left(\frac{V^{n^\star}(\ell)}{n}\right)^\gamma $
Peto e Peto	$ \displaystyle\prod^{\ell-1}_{j=1}\left(1-\left(\frac{\Delta R^{n^\star}(j)}{1+V^{n^\star}(j)}\right)\right) $
Peto e Peto Modificado	$ \displaystyle\prod^{\ell-1}_{j=1}\left(1-\left(\frac{\Delta R^{n^\star}(j)}{1+V^{n^\star}(j)}\right)\right)~\left[\frac{\left(V^{n^\star}(j)\right)}{1+\left(V^{n^\star}(j)\right)}\right] $
Fleming e Harrington $ \gamma>0,\rho\geq0 $	$ \displaystyle\left[\prod_{j=0}^{\ell-1}\left(1-\cfrac{\Delta R^{n^\star}(j)}{V^{n^\star}(j)}\right)\right]^{\rho}\left[1-\prod^{\ell-1}_{j=0}\left(1-\cfrac{\Delta R^{n^\star}(j)}{V^{n^\star}(j)}\right)\right]^{\gamma} $

Tabela 2.1: Funções de ponderação.

A escolha do processo de ponderação $u(n^\star,\ell)$ determina a função poder da estatística do teste contra diferentes hipóteses alternativas. A estatística escolhida será mais sensível com relação às diferenças entre as funções intensidades nas categorias em que $u(n^\star,\cdot)$ é grande e menos sensível nas categorias em que $u(n^\star,\cdot)$ é pequena. Para os processos de ponderação do tipo Fleming e Harrington com $\rho>0, \gamma=0,$ intuitivamente, têm um bom poder para detectar precocemente diferenças (entre as funções intensidades) que desaparecem ao longo do tempo. Por outro lado, com o mesmo processo mas $\rho=0, \gamma>0$ será mais poderosa contra as alternativas com funções intensidade não proporcionais. O processo de ponderação do tipo log-rank, tem desempenho satisfatório para alternativas com funções de intensidade constantes ou proporcionais.

Agora, vamos tratar para o problema de $J$ populações. Para testarmos a hipótese nula $H_0: h^1=\dots=h^J$, derivamos uma generalização da estatística de Log-rank ponderada proposta por Fleming e Harrington (2005) que pode ser encontrada em Andersen et al.. Usando a função de ponderação

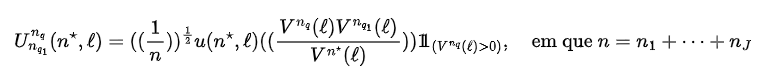
obtemos $$LR_{q}({n^{\star}}, j)=\sum_{q_1\neq q}\sum_{\ell=1}^{j}U^{n_q}_{n_{q_1}} (n^{\star}, \ell ) ([ \hat{h}^{n_q} (\ell)-\hat{h}^{n_{q_1}} (\ell))]$$

$$=\sum_{\ell=1}^{j}(( \frac{1}{n} ))^{1/2} u (n^{\star}, \ell) ([ \Delta R^{n_q} (\ell) - V^{n_q} (\ell)\frac{\Delta R^{n^{\star}} (\ell)}{V^{n^{\star}} (\ell)} )]$$

$$=\sum_{\ell=1}^{j} (( \frac{1}{n} ))^{1/2} u (n^{\star}, \ell) V^{n_q} (\ell) ([ \frac{\Delta R^{n_q} (\ell)}{V^{n_q} (\ell)} - \frac{\Delta R^{n^{\star}} (\ell)}{V^{n^{\star}} (\ell)} )], ~n^\star\in \mathbb{N}^J,~j\ge 1.$$

Agora, segue do Teorema (3.1) (Leão e Ohashi (2012)) e Proposição (2.1), que sob $H_0$ o vetor aleatório $$LR({n^{\star}}, d^u_{n^{\star}}) :=(LR_1({n^{\star}},d^u_{n^{\star}}), \ldots , LR_{J}({n^{\star}},d^u_{n^{\star}}))^T$$

converge em distribuição para $N(0,\displaystyle\Gamma(d^u))$ quando $n^{\star})→ \infty$, em que $\Gamma(d^u)$ admite um estimador consistente $\hat{\Gamma}(n^\star,d^u_{n^\star}),$ na forma $\hat{\Gamma}(n^\star,i):=\displaystyle\sum^i_{\ell=1} \hat{Q}(\ell),~i\geq 1$ com $$\hat{Q}(\ell)_{i,j}=\langle\hat{Q}(\ell)a_i,a_j\rangle$$

para todo $a\in \mathbb{R}^J$ e $\langle \cdot , \cdot \rangle_{\mathbb{R}^J}$ o produto interno no $\mathbb{R}^J$. A forma matricial é dada por

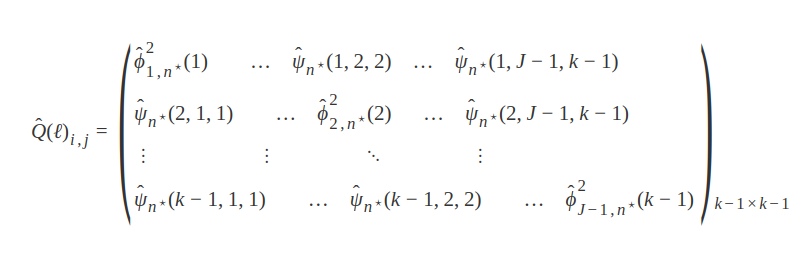
em que

$$\hat{\phi}^2_{q,n^\star}(\ell):=\sum_{q_1\neq q}([\frac{|U^{n_q}_{n_{q_1}}(n^\star,\ell)|^2}{V^{n_{q_1}}(\ell)}\hat{h}^{n_{q_1}}(\ell)[1-\hat{h}^{n_{q_1}}(\ell)]+\frac{|U^{n_q}_{n_{q_1}}(n^\star,\ell)|^2}{V^{n_{q}}}\hat{h}^{n_{q}}(\ell)[1-\hat{h}^{n_{q}}(\ell)])]+$$

$$+2\sum_{q_1,q_2\in A_q}\frac{U^{n_q}_{n_{q_1}}(n^\star,\ell)U^{n_q}_{n_{q_2}}(n^\star,\ell)}{V^{n_{q}}(\ell)}\hat{h}^{n_{q}}(\ell)[1-\hat{h}^{n_{q}}(\ell)],~~~\ell\geq 1$$

no qual, $A_q=((x,y)\in \mathcal{J}\times \mathcal{J}; x\neq y, x\neq q, y\neq q, 1\leq x < y \leq J )$ e $\mathcal{J}=(1,\dots,J).$

Além disso,

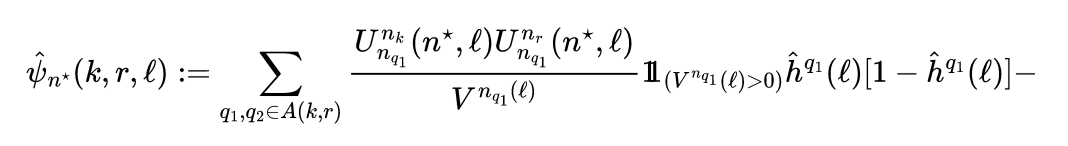
$$-\sum_{q_1\neq k}\cfrac{U^{n_k}_{n_{q_1}}(n^\star,\ell)U^{n_r}_{n_{k}}(n^\star,\ell)}{V^{n_{k}(\ell)}}1!!1_{(V^{n_{k}}(\ell)>0)}\hat{h}^{k}(\ell)[1-\hat{h}^{k}(\ell)]-$$

$$-\sum_{q_2\neq r}\cfrac{U^{n_r}_{n_{q_2}}(n^\star,\ell)U^{n_k}_{n_{r}}(n^\star,\ell)}{V^{n_{r}(\ell)}}1!!1_{(V^{n_{r}}(\ell)>0)}\hat{h}^{r}(\ell)[1-\hat{h}^{r}(\ell)],~~~~\ell\geq 1$$

em que, $$A(k,r)= ((q_1,q_2)\in \mathcal{J}\times \mathcal{J}; q_1\neq k,q_2\neq r, q_1=q_2)~e~\mathcal{J}=(1,\dots,J).$$

No entanto, como uma consequência da definição da estatística $LR_q(n^\star,d^u_{n^\star})$, temos que $\displaystyle \sum^J_{q=1}LR_q(n^\star,d^u_{n^\star}) = 0.$ Assim, o vetor aleatório das estatísticas de Log-rank Ponderado é linearmente dependente e a matriz de covariância assintótica $\Gamma(n^\star,d^u_{n^\star})$ tem posto não superior a $J-1.$ Sob condições gerais sobre $h^p$ $(p=1,\dots,J),$ tal como a existência para qualquer $q, p=1,\dots,J$ de pelo menos um índice $\ell\leq i$ tal que $h^p(\ell)>0$ e $h^q(\ell)>0,$ pode ser provado que o posto de $\Gamma(i)$ é $J-1,$ para qualquer $i\geq 1$ (ver, Gill (1986), Apêndice 1). Da mesma forma, o estimador da covariância $$\hat{\Gamma}(n^\star,i):=\sum^i_{\ell=1}\hat{Q}(n^\star,\ell),~~~~i\geq 1$$

tem posto $J-1.$ Além disso, para qualquer $q, p = 1,\dots,J$, existe pelo menos um índice $\ell\leq i$ tal que $\Delta R^{n_p}(\ell)$ e $\Delta R^{n_q}(\ell)$ são positivos. Além disso, como $\hat{\Gamma}(n^\star,i)$ é um estimador consistente de $\Gamma(i),$ obtemos que a probabilidade de $\hat{\Gamma}(n^\star,i)$ converge para $1$ quando $n^\star$ tende ao infinito. Assim, sob $H_0,$ a estatística $$X^2(n^\star,d^u_{n^\star})=LR(n^\star,d^u_{n^\star})^T\hat{\Gamma}(n^\star,d^u_{n^\star})^{-1}LR(n^\star,d^u_{n^\star})$$

tem distribuição assintótica Qui-Quadrado com $J- 1$ graus de liberdade, no qual $\hat{\Gamma}^{-1}(n^\star,d^u_{n^\star})$ é uma inversa generalizada. Portanto, se excluirmos a última linha e última coluna de $\hat{\Gamma}(n^\star,d^u_{n^\star}),$ resultando em $\hat{\Gamma}_0(n^\star,d^u_{n^\star})=\displaystyle\sum^j_{\ell=1}\hat{Q}_0(n^\star,\ell),j\geq1,$ obtemos por consistência de $\hat{\Gamma}(n^\star,d^u_{n^\star})$ que o posto é $J-1,$ ou seja, a probabilidade de $\hat{\Gamma}$ ter posto $J-1$ cresce para 1 quando $n^\star)→\infty.$ Assim, tomando o vetor aleatório $$ LR_0(n^\star,d^u_{n^\star})=(LR_1(n^\star,d^u_{n^\star}),\dots,LR_{J-1}(n^\star,d^u_{n^\star}))^T,$$

concluímos que $$X^2(n^\star,d^u_{n^\star})=LR_0(n^\star,d^u_{n^\star})^T\hat{\Gamma}_0(n^\star,d^u_{n^\star})^{-1}LR_0(n^\star,d^u_{n^\star})$$

tem distribuição assintótica Qui-Quadrado com $J-1$ graus de liberdade, no qual $\hat{\Gamma_0}(n^\star,d^u_{n^\star})^{-1}$ é a inversa clássica.

Para investigarmos o poder do teste, removemos o pressuposto de $H_0$. Neste caso, temos que $$LR_{q}( {n^{\star}}, i)=\sum_{\ell=1}^{i} \sum_{q_1\neq q}U^{n_q}_{n_{q_1}} (n^{\star}, \ell ) ([ \hat{h}^{n_q} (\ell) -\hat{h}^{n_{q_1}} (\ell))] =$$

$$=\sum_{\ell=1}^{i} \sum_{q_1\neq q}U^{n_q}_{n_{q_1}} (n^{\star}, \ell ) ([ \frac{ \Delta Y^{n_q}(\ell)1!!1_{(V^{n_q}(\ell)>0)}}{V^{n_q}(\ell)}-\frac{\Delta Y^{n_{q_1}}(\ell) 1!!1_{(V^{n_{q_1}}(\ell)>0 )}}{V^{n_{q_1}}(\ell)} )] +$$

$$+\sum_{\ell=1}^{i}\sum_{q_1\neq q}U^{n_q}_{n_{q_1}}(n^{\star},\ell)([ h^{q}(\ell)-h^{q_1}(\ell))], ~ i \in \mathcal{K}.$$

Seja $(Q_n : n \in \mathbb{N})$ uma sequência de testes estatísticos e $(R_n : n \in \mathbb{N})$ as respectivas regiões de rejeição associadas a um nível de significância fixado. Dizemos que uma sequência de estatísticas de teste $Q_n$ é consistente com uma hipótese alternativa $H_1$ se $\lim_n P(Q_n \in R_n \mid H_1)=1$, veja Fleming e Harrington (1991) para mais detalhes. A classe de hipóteses alternativas $H_1: h^1(\ell)> h^q(\ell)$, para qualquer $\ell =1, \cdots , k-1$ e $q=2,\cdots,J$ é chamado de hipóteses alternativas de intensidades ordenadas.

Lema 2.1.1

Sob hipóteses alternativas de intensidades ordenadas, o teste de Log-rank Ponderado $X^2(k-1)$ é consistente, para $k$ finito ou não.

Demonstração

ver Watanabe A.H.

Exemplo 2.1.1

Voltando ao exemplo citado na seção de introdução.

Pelos gráficos da função de sobrevivência e das funções de intensidade, notamos um cruzamento severo (aproximadamente em 1000 dias) e pode causar uma dificuldade em detectar diferenças significativas entre $W_1$ e $W_2.$

(imagem em falta)

(imagem em falta)

(imagem em falta)

(imagem em falta)

O teste de Log-rank Ponderado não detecta diferença significativa ao nível de significância $\alpha=0,05,$ para o peso log-rank $u(n^\star,\ell)=1,$ Nas demais seção estatística de Cramér-von Mises, vamos apresentar uma estatística que detecta diferenças quando temos cruzamento das funções de intensidade.

7.2.2 - A estatística de Log-rank Modificado

O teste de Log-rank Ponderado pode não ter um bom comportamento quando há cruzamento das funções de intensidade. Para resolver este problema, propomos uma modificação nas estatísticas de Log-rank Ponderado para tratarmos espaços amostrais finitos $(\ell=1, \cdots , k~({Finito})).$ Primeiramente definimos

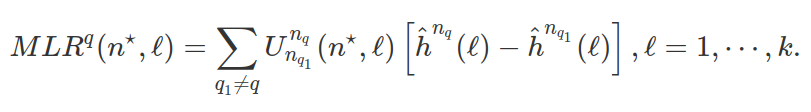
Decorre do Teorema (3.1) (Leão e Ohashi) que, sob $H_0$, $MLR^{q} ({n^{\star}}, \ell )$ tem distribuição assintótica normal com média zero e matriz de covariância $Q(\ell)$, cujo estimador $\hat{Q}(\ell)$ está definido na seção 2.1. Além disso, o martingale $MLR^{q} ({n^{\star}}, \cdot )$ tem incrementos assintóticamente independentes. Nesse caso, se denotarmos $$MLR_0({n^{\star}},\ell)=(MLR^1({n^{\star}}, \ell),MLR^2({n^{\star}}, \ell), \dots , MLR^{J-1}({n^{\star}}, \ell))^T,$$

obtemos a estatística de Log-rank Modificado

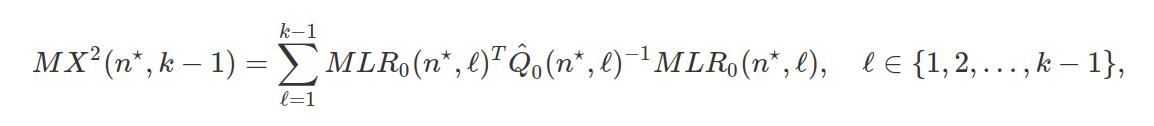
que tem distribuição assintótica Qui-Quadrado com $(J-1)\times (k-1)$ graus de liberdade, no qual $\hat{Q}_{0}(n^{\star}, \ell)$ é o operador de covariância $\hat{Q} (n^{\star},\ell)$ sem a última linha e a última coluna, assim como argumentado na seção anterior, e denotamos $\hat{Q_0}(n^{\star}, \ell)^{-1}$ como a inversa.

Com esse tipo de modificação em relação ao Log-rank Ponderado proposto por Fleming e Harrington (1990) para duas populações (J=2) e estendido por Leão e Ohashi para J populações discretas, resolvemos o problema das diferenças iniciais canceladas em favor da outra população, como dita na seção introdução. Portanto, resolvemos o problema do cruzamento das funções de intensidade para espaços amostrais finitos. Para o caso de espaços amostrais infinitos enumeráveis, usamos a estatística de Cramér-von Mises proposta por Leão e Ohashi.

Ao retirarmos a hipótese $H_0$, chegamos a seguinte equação $$MLR^{q}({n^{\star}},\ell)=\sum_{q_1\neq q}U^{n_q}_{n_{q_1}} (n^{\star}, \ell ) ([ \hat{h}^{n_q} (\ell) -\hat{h}^{n_{q_1}} (\ell))] =$$

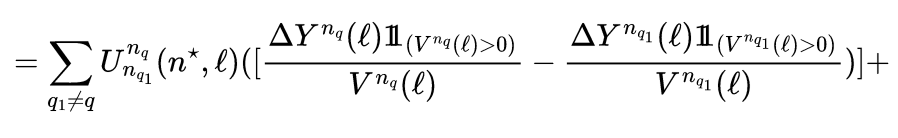
$$+\sum_{q_1\neq q} U^{n_q}_{n_{q_1}}(n^{\star}, \ell ) ([ h^{q}(\ell) - h^{q_1}(\ell))], ~ \ell \in \mathcal{K}.$$

Assim como na seção Estatística de Log-rank Ponderado, definimos $(Q_n : n \in \mathbb{N})$ uma sequência de testes estatísticos e $(R_n : n \in \mathbb{N})$ as respectivas regiões de rejeição associadas a um nível de significância fixado. Dizemos que uma sequência de estatísticas de teste $Q_n$ é consistente com uma hipótese alternativa $H_1$ se $\displaystyle\lim_n P(Q_n \in R_n \mid H_1)=1.$ Assim, a classe de hipóteses alternativas é definida como

Definição 2.2.1 (Hipótese alternativa de intensidades)

Existe pelo menos um par de índices $q,q_1=1,\cdots, J$ com $q\neq q_1$ para os quais $H_1:h^q(\ell) \neq h^{q_1}(\ell)$, para algum $\ell =1, \cdots , k-1.$

Exemplo 2.2.1 (Teste de Homogeneidade em tabelas $2\times2$)

Suponhamos que $n_1 + n_2$ observações de dados estão resumidos em uma tabela $2\times 2,$

	Categoria 1	Categoria 2	Total
Pop1	$ \Delta R^{n_1}(1) $	$ \Delta R^{n_1}(2) $	$ n_1=V^{n_1}(1) $
Pop2	$ \Delta R^{n_2}(1) $	$ \Delta R^{n_2}(2) $	$ n_2=V^{n_2}(2) $
Total	$ \Delta R^{n^\star}(1) $	$ \Delta R^{n^\star}(2) $	$ n_1+n_2=V^{n^\star} $

Vamos admitir que cada amostra é uma amostra aleatória, sendo elas independentes entre si e cada observação pode ser classificada na categoria $1$ ou na categoria $2$, mas não em ambas. Seja $\pi^1_1$ a probabilidade de que um elemento da população 1 seja classificado na categoria $1$ e $\pi^2_1$ o correspondente da população 2. Neste exemplo, queremos testar a hipótese $H_0:\pi^1_1=\pi^2_1,$ ou equivalentemente, $H_0:h^1(1)=h^2(1).$ Então, temos a seguinte estatística de Log-rank $(u(n^\star,1)=1)$ $$MLR(n^\star,1)=((\frac{1}{n_1+n_2}))^{1/2}((\frac{V^{n_1}(1)V^{n_2}(1)}{V^{n^\star}}))([\hat{h}^{n_2}(1)-\hat{h}^{n_1}(1))]=$$

$$=((\frac{1}{n_1+n_2}))^{1/2}((\frac{V^{n_1}(1)V^{n_2}(1)}{V^{n^\star}}))([\frac{\Delta R^{n_2}(1)}{V^{n_2}(1)}-\frac{\Delta R^{n_1}(1)}{V^{n_1}(1)})]\overset{\Delta R^{n_2}=\Delta R^{n^\star}-\Delta R^{n_1}}{=}$$

$$=((\frac{1}{n_1+n_2}))^{1/2}((\Delta R^{n_1}(1)-\frac{V^{n_1}(1)}{V^{n^\star}}\Delta R^{n^\star}(1))),~~~~(1.1)$$

que corresponde ao conhecido teste exato de Fisher. Foi provado em (Leão e Ohashi) que $\frac{MLR(1)}{\sqrt{\hat{\phi}^2_{n^\star}(1)}}$ converge em distribuição para $N(0,1)$ quando $n^\star)\rightarrow \infty,$ no qual $$\hat{\phi}^2_{n^\star}(1):=\frac{V^{n_2}(1)}{V^{n^\star}(1)}\hat{h}^{n_1}(1)([1-\hat{h}^{n_1}(1))]+\frac{V^{n_1}(1)}{V^{n^\star}(1)}\hat{h}^{n_2}(1)([1-\hat{h}^{n_2}(1))]$$

Às vezes é necessário combinar resultados de diversas tabelas de contingência $2\times 2$ em uma análise geral. Esta situação ocorre quando um experimento geral consiste em vários experimentos menores conduzidos em várias situações. Neste caso, os dados são resumidos em diversas tabelas de contingência $2\times 2$ obtidas à partir de experimentos independentes. Seja $k$ o número de tabelas e $\pi^1_{\ell}$ a probabilidade de uma observação na linha 1 ser classificada na coluna 1, na $\ell$-ésima tabela de contingência, e $\pi^2_{\ell}$ a probabilidade correspondente da linha 2. Consideramos a hipótese nula $H_0: \pi^1_{\ell}=\pi^2_{\ell},$ para todo $\ell =1,\dots,k-1.$ Denotamos $MLR(\ell)$ o vetor de Log-rank Modificado para a $\ell$-ésima tabela e $\hat{\phi}^{2,\ell}_{n^\star}(\ell)$ a variância associada. Assim, chegamos à estatística de Mantel-Haenszel para tabelas de contingência $2\times2$ da seguinte forma $$MH(1)=\frac{MLR(n^\star,1)}{\sqrt{\displaystyle\hat{\phi}^{2}(n^\star,1)}}$$

Agora, a estatística de Log-rank Modificada é dada por $$MX^2(n^\star,1)=\frac{(MLR(n^\star,1))^2}{\hat{\phi}^{2}(n^\star,1)}$$

Exemplo 2.2.2: (Teste de Homogeneidade em tabelas $J\times k$)

Esta tabela pode ser utilizada para apresentar dados contidos em várias amostras. Temos $J$ amostras, e em vez de cada amostra fornecer duas categorias, consideramos $k$ categorias. No entanto, estamos sob o modelo de estrutura com censura, no qual os dados observados são dadas por $(\Delta R^p_m,\Delta R^{C,p}_m(\ell)).$ Para cada categoria podemos associar a tabela (2.2.1).

	Categoria 1	……	Categoria 2	Total
Número de Eventos	$ \Delta R^{n_1}(\ell) $	……	$ \Delta R^{n_J}(\ell) $	$ \Delta R^{n^\star}(\ell) $
Número de Eventos sob Risco	$ V^{n_1}(\ell) $	……	$ V^{n_J}(\ell) $	$ V^{n^\star}(\ell) $

Tabela 2.2.1: Resumo das observações para a $\ell$-ésima categoria.

Agora, vamos generalizar o exemplo (2.2.1) para tabelas de contingência $J\times k.$ temos a equação

Segue de (1) e tomando o peso log-rank, ou seja, $u(n^\star,\ell)=1$ que $$MLR^{q}({n^{\star}}, \ell):=\sum_{q_1\neq q}((\frac{1}{n}))^{1/2}((\frac{V^{n_q}(\ell)V^{n_{q_1}}(\ell)}{V^{n^\star}(\ell)}))[\underbrace{\hat{h}^{n_{q_1}}(\ell)}_{\frac{\Delta R^{n_{q_1}}(\ell)}{V{n_{q_1}}}(\ell)}-\underbrace{\hat{h}^{n_q}(\ell)}_{\frac{\Delta R^{n_{q}}(\ell)}{V{n_{q}}(\ell)}}]=$$

$$=((\frac{1}{n}))^{1/2}([\Delta R^{n_{q}}(\ell)-\frac{V^{n_{q}}(\ell)\Delta R^{n^\star}(\ell)}{V^{n^\star}(\ell)})]~~~(2.2.1)$$

Assim, obtemos a estatística de Log-rank Modificado $$MX^2({n^{\star}}, k-1)=\sum_{\ell=1}^{k-1} MLR_0({n^{\star}}, \ell)^T \hat{Q}_{0}(n^{\star}, \ell)^{-1} MLR_0({n^{\star}}, \ell),$$

Seja $\pi^p_\ell$ a probabilidade de um elemento selecionado aleatoriamente à partir da variável aleatória de interesse $W^p$ ser classificada na $\ell$-ésima categoria, para $p=1,\dots,J$ e $\ell=1,\dots,k.$ A hipótese $H_0:\pi^1_\ell=\dots=\pi^J_\ell$ para todo $\ell$, afirma que a probabilidade de estar na categoria $\ell$ é o mesmo para todas as variáveis aleatórias de interesse $W^p,$ que é equivalente a hipótese $H_0:h^1(\ell)=\dots=h^J(\ell)$ para todo $\ell=1, \cdots , k-1$. Neste caso, podemos aplicar a estatística de Log-rank Ponderada $X^2(n^{\star},k-1)$ e a estatística de Log-rank Modificada $MX^2(n^{\star},k-1)$ para testarmos a hipótese nula $H_0.$

7.2.3 - A estatística de Cramér-von Mises

Nesta seção, enunciamos a estatística de Cramér-von Mises proposta por Leão e Ohashi para populações discretas na presença de censura. A seguir, definimos a primeira categoria observada nas amostras por $$d^l_{n^{\star}} = \inf ( \ell : \Delta R^{n^{\star}} (\ell ) > 0 )~~~(2.3.1)$$

e assumimos que todos os processos ponderados tem a forma (2.3.1). Assim, $d^l_{n^{\star}}\rightarrow d^l$ em probabilidade quando $n^\star\rightarrow \infty$ em que, $$d^l:= \inf ( \ell : b_1 h^1(\ell) + \cdots +b_J h^J (\ell)>0)$$

para $b_p=\displaystyle\lim_{n^\star)\rightarrow\infty}\frac{n_p}{n},~p\in\mathcal{J}$ (ver Leão e Ohashi pág.19).

Para testarmos a homogeneidade das populações discretas na presença de censura arbitrária com infinitas categorias, enunciamos uma versão da estatística de Cramér-von Mises proposto no trabalho de Leão e Ohashi (os detalhes matemáticos podem ser vistos neste trabalho).

Primeiramente, consideramos $LR(n^\star,r)$ com $n^\star\in \mathbb{N}^J$ e $r\geq 1$ ponderado pela sequência $\hat{\phi_{n^\star}}=(\hat{\phi}_{1,n^\star}(r),\dots,\hat{\phi}_{J,n^\star}(r) : r =1,2,3, \cdots)$ no espaço de Hilbert $\ell^2(\mathbb{N})$, obtendo

$$GLR_q(n^\star, \hat{\phi_{n^\star}} ,r)=\hat{\phi}_{q, n^\star}(r)LR_{q}(n^\star,r);\quad q=1,\ldots,J-1~~~(2.3.2)$$

Assim, temos que $$GLR(n^\star, \hat{\phi_{n^\star}} ,r)=((\hat{\phi}_{1, n^\star}(r)LR_{1}(n^\star,r), \dots, \hat{\phi}_{J-1, n^\star}(r)LR_{J-1}(n^\star,r)))^T$$

$$\overset{(2.3.2)}{=}((GLR_1(n^\star, \hat{\phi_{n^\star}} ,r), \dots, GLR_{J-1}(n^\star, \hat{\phi_{n^\star}} ,r)))^T~~~~(2.3.3)$$

para $r\geq1$ e $n^\star \in \mathbb{N}^J.$

Construímos agora $M_0(\ell):=\text{diag}(\phi_1(\ell),\ldots,\phi_{J-1}(\ell))$ e o operador de covariância, porém, usamos a notação $\Gamma_0$ em vez de $\Gamma$ na forma quadrática. Denotamos o operador linear $\mathcal{Y}_0(d^l,d^u):\ell^2)\rightarrow\ell^2$ de modo que $(J-1)k(d^l,i)$-ésima coordenada de $\mathcal{Y}_0(d^l,d^u)a\doteq Y_0(d^l,i)(a_1,\ldots,a_{(J-1)k(d^l,i)})$ para $a\in \ell^2$ e $k(d^l,i)=i-d^l+1; i\geq d^l$. Assim, introduzimos o conjunto $L(d^l_{n^\star},d^u_{n^\star})=( d^l_{n^\star}\leq\ell\leq d^u_{n^\star}: \Delta R^{n^\star} (\ell) > 0)$ das categorias observáveis e $L(n^\star)$ a cardinalidade. Para um determinado $n^\star\in\mathbb{N}^J$ e $a\in \ell^2$, definimos $$\hat{\mathcal{{Y}}}_0(d^l_{n^\star}, d^u_{n^\star})a$$

uma sequência real em que a $(J-1)L(n^{\star})$-ésima coordenada é obtida por $$\hat{Y_0}(d^l_{n^\star}, d^u_{n^\star})(a_1\ldots, a_{(J-1)L(n^{\star})});$$

e $\hat{Y_0}(d_{n^\star}^l,d_{n^\star}^u)$ é o operador aleatório auto-adjunto definido pela seguinte forma quadrática no espaço $\mathbb{R}^{(J-1)L(n^{\star})}.$ Assim, obtemos o seguinte produto interno $$\langle \hat{\mathcal{Y}}_0(d^l_{n^{\star}},d^u_{n^\star})a,a\rangle=\sum_{j \in L(d^l_{n^\star},d^u_{n^\star})} \langle \hat{M}_0(j)\hat{\Gamma}_0(j) \hat{M}_0(j)a_j,a_j\rangle_{\mathbb{R}^{J-1}} +$$

$$+\sum_{( \ell< j : \ell, j \in L(d^l_{n^\star},d^u_{n^\star}))} \langle \hat{M}_0(\ell) \hat{\Gamma}_0(\ell) \hat{M}_0(j)a_{\ell},a_j\rangle_{\mathbb{R}^{J-1}} +$$

$$+\sum_{ ( j < \ell : \ell, j \in L(d^l_{n^\star},d^u_{n^\star}) )} \langle \hat{M}_0(\ell) \hat{\Gamma}_0(j) \hat{M}_0(j)a_{\ell},a_j\rangle_{\mathbb{R}^{J-1}}$$

Portanto, $\mathcal{\hat{Y_0}}(d^l_{n^\star}, d^u_{n^\star}):\ell^2)\rightarrow \ell^2$ é uma sequência bem definida de operadores aleatórios auto-adjuntos de posto finito.

Por fim, definimos a estatística de Cramér-von Mises associadas aos modelos discretos na presença de censura da seguinte forma $$CVM (n^\star,d^l_{n^{\star}} , d^u_{n^{\star}}) := |GLR(n^\star, \hat{\phi_{n^\star}}, d^l_{n^{\star}},d^u_{n^{\star}})|^2_{\ell^2}; n^\star\in \mathbb{N}^{J-1}.$$

Vamos enunciar dois teoremas do artigo de Leão e Ohashi, que são resultados fundamentais para a estatística de Cramér-von Mises.

Teorema 2.3.1

Suponha que os pressupostos (M1, M2, M3', M4') e (H1') (Leão e Ohashi ) são satisfeitos e seja $1\leq d^l\leq d^u<\infty$ e que as propriedades (S1-S2) também são satisfeitas. Então o limite $\lim_{n^\star)\rightarrow\infty}GLR(n^\star, \hat{\phi_{n^\star}}, d^l_{n^{\star}},d^u_{n^{\star}})$ é uma medida de Gauss com média zero em $\ell^2$ com o operador covariância $\mathcal{\hat{Y}}(d^l_{n^\star}, d^u_{n^\star})$ em $\ell^2$. Em particular, $$|GLR(n^\star, \hat{\phi_{n^\star}}, d^l_{n^{\star}},d^u_{n^{\star}})|^2_{\ell^2})\rightarrow \sum_{s=1}^{\infty} \sum_{q=1}^{J-1} \lambda_{sq}\chi^2_{sq}~~~~~\text{em distribuição quando}~n^\star)\rightarrow \infty$$

em que $(\lambda_{sq} ; s\geq 1, q=1, \ldots , J-1)$ são os auto-valores do operador de covariância $\mathcal{Y}_0(d^l,d^u)$ e $(\chi^2_{sq},~~s\geq 1,q=1,\dots,J)$ é um subconjunto de variáveis aleatórias i.i.d. Qui-Quadrado com um grau de liberdade

Assim, como consequência do teorema (2.3.1) e da proposição (2.1), obtemos o seguinte resultado.

Teorema 2.3.2

Assumimos que $U$ pertence a classe $\mathcal{K}$ e satisfaz a condição de proporcionalidade do tamanho da amostra da proposição (2.1) e seja $(d^l,d^u, d^l_{n^\star},d^l_{n^\star})$ as categorias dos tempos de parada. Então, sob $H_0$ $$CVM (n^\star,d^l_{n^{\star}} , d^u_{n^{\star}}))\rightarrow \sum_{s=1}^{\infty} \sum_{q=1}^{J-1} \lambda_{sq}\chi^2_{sq}~~~~~\text{em distribuição quando}~n^\star\rightarrow \infty$$

em que $(\lambda_{sq} ; s\geq 1, q=1, \ldots , J-1)$ são os auto-valores do operador de covariância $\mathcal{Y}_0(d^l,d^u).$ Em particular, se $X^q$ é quadrado integrável para todo $q\in \mathcal{J}$ então

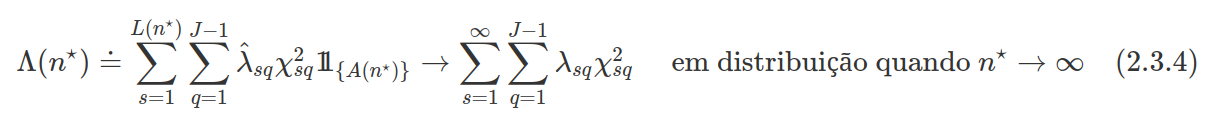
em que $(\hat{\lambda}_{sq} ; 1\leq s\leq L(n^\star), q=1, \ldots , J-1)$ são os auto-valores aleatórios do estimador do operador de covariância $\hat{\mathcal{Y}}_0(d^l,d^u),$ e $A(n^\star)\doteq(\hat{\mathcal{Y}}_0(d^l,d^u),~~\text{é não negativo}),$ desde que $P[A(n^\star)])\rightarrow1$ quando $n^\star)\rightarrow \infty.$

Notamos que à partir de (2.3.4), o p-valor para o teste de hipótese sob $H_0$ é dada por $$P [\Lambda(n^\star)> CVM (n^\star,d^l_{n^{\star}} , d^u_{n^{\star}}) | H_0],$$

com $\Lambda(n^\star)$ soma ponderada de variáveis aleatórias Qui-Quadrado independentes. Para calcularmos o p-valor usamos um dos algoritmos descritos na literatura, como por exemplo (Robert B. Davies [4]).

Exemplo 2.3.1

Voltando ao exemplo citado na seção de introdução.

Pelos gráficos da função de sobrevivência e das funções de intensidade, notamos um cruzamento severo (aproximadamente em 1000 dias) e pode causar uma dificuldade em detectar diferenças significativas entre $W_1$ e $W_2.$

(imagem em falta)

(imagem em falta)

(imagem em falta)

(imagem em falta)

O teste de Cramér-von Mises ao contrário do teste de Log-rank Ponderado detecta diferença significativa ao nível de significância $\alpha=0,05,$ para o peso log-rank $u(n^\star,\ell)=1.$ Logo, a estatística de Cramér-von Mises têm um bom desempenho quando temos cruzamento severo das funções de intensidade.

7.3 - Referências Bibliográficas

[1] O. Aalen. Nonparametric inference for a family of counting processes. The Annals of Statistics, 6:701–726, 1978.

[2] O.O. Aalen, P.K. Andersen, Ø. Borgan, R.D. Gill, and N. Keiding. History of applications of martingales in survival analysis. Electronic Journal for History of Probability and Statistics, 5(1), 2009.

[3] P. K. Andersen, Ø. Borgan, R. D. Gill, and N. Keiding. Statistical models based on counting processes. Springer Verlag (New York), 1993.

[4] R.B. Davies. Algorithm as 155: The distribution of a linear combination of 2 random variables. Journal of the Royal Statistical Society. Series C (Applied Statistics), 29(3):323–333, 1980.

[5] T.R. Fleming and D.P. Harrington. Counting processes and survival analysis, volume 8. Wiley New York, 1991.

[6] X. Gao, M. Alvo, J. Chen, and G. Li. Nonparametric multiple comparison procedures for unbalanced one-way factorial designs. Journal of Statistical Planning and Inference, 138(8):2574–2591, 2009.

[7] RD Gill. Censoring and Stochastic Integrals, Mathematical Centre Tracts 124. Amsterdam: Mathematisch Centrum, 1980.

[8] S.D. Grimshaw, J. McDonald, G.R. McQueen, and S. Thorley. Estimating hazard functions for discrete lifetimes. Communications in Statistics-Simulation and Computation, 34(2):451–463, 2005.

[9] P.L. Gupta, R.C. Gupta, and R.C. Tripathi. On the monotonic properties of discrete failure rates. Journal of Statistical Planning and Inference, 65(2):255–268, 1997.

[10] D.P. Harrington and T.R. Fleming. A class of rank test procedures for censored survival data. Biometrika, 69(3):553, 1982.

[11] Y. Hochberg. A sharper Bonferroni procedure for multiple tests of significance. Biometrika, 75(4):800, 1988.

[12] WATANABE, Alexandre Hiroshi. Comparações de populações discretas. 2013. Dissertação (Mestrado em Ciências de Computação e Matemática Computacional) - Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, São Carlos, 2013.

8 - Referências Bibliográficas

[1] Gibbons, J. D. and Chakraborti, S. (2003) - Nonparametric Statistical Inference, Marcel Dekker Inc.

[2] Hájek, J. Sidák, Z. and Sen, P. K. (1999) - Theory of Rank Tests, Academic Press.

[3] Hollander, M. and Wolfe, D. (1999) - Nonparametric Statistical Methods, John Wiley and Sons.

[4] Sprent, P. (1989) - Applied Nonparametric Statistical Methods, 1 edição, Chapman and Hall

[5] Sidney Siegel and N John Castellan. Nonparametric statistics for the behavioral sciences. 1988.

[6] Conover, William Jay, and W. J. Conover. “Practical nonparametric statistics.” (1980).

[7] D’Agostino, Ralph B. Goodness-of-fit-techniques. CRC press, 1986.