23.3 Precisão
Nesta seção, vamos avaliar a precisão. A precisão deve ser expressa por meio da repetitividade, da precisão intermediária e da reprodutibilidade. Além disso, nos ensaios quantitativos, a precisão deve ser demonstrada por meio da dispersão dos resultados, calculando o desvio padrão relativo (DPR) da série de medições, também conhecido como coeficiente de variação, conforme a fórmula $DPR= \dfrac{DP}{CMD} \times 100$, em que DP é o desvio padrão e CMD, a concentração média determinada. A seguir , apresentamos o trecho da RDC 166.
A determinação da repetitividade deve obedecer aos seguintes critérios:
I - avaliar as amostras sob as mesmas condições de operação, mesmo analista e mesma instrumentação, em uma única corrida analítica.
II - utilizar, no mínimo, 9 (nove) determinações, contemplando o intervalo linear do método analítico, ou seja, 3 (três) concentrações: baixa, média e alta, com 3 (três) réplicas em cada nível ou 6 (seis) réplicas a 100% (cem por cento) da concentração do teste individualmente preparadas.
A reprodutibilidade deve ser obtida por meio da proximidade dos resultados obtidos em laboratórios diferentes.
§1° A reprodutibilidade é aplicável em estudos colaborativos ou na padronização de métodos analíticos para inclusão desses em compêndios oficiais, mediante testes estatísticos adequados.
A determinação da precisão intermediária deve obedecer aos seguintes critérios:
I - expressar a proximidade entre os resultados obtidos da análise de uma mesma amostra, no mesmo laboratório, em pelo menos dois dias diferentes, realizada por operadores distintos; e
II - contemplar as mesmas concentrações e o mesmo número de determinações descritas na avaliação da repetibilidade.
| Analito, % | Fração Mássica (C) | Unidade | DPR, % |
|---|---|---|---|
| 100 | 1 | 100% | 1,3 |
| 10 | 10 $^{-1}$ | 10% | 1,9 |
| 1 | 10 $^{-2}$ | 1% | 2,7 |
| 0,1 | 10 $^{-3}$ | 0,1% | 3,7 |
| 0,01 | 10 $^{-4}$ | 100 ppm (mg\kg) | 5,3 |
| 0,001 | 10 $^{-5}$ | 10 ppm (mg\kg) | 7,3 |
| 0,0001 | 10 $^{-6}$ | 1 ppm (mg\kg) | 11 |
| 0,00001 | 10 $^{-7}$ | 100 ppb (μg\kg) | 15 |
| 0,000001 | 10 $^{-8}$ | 10 ppb (μg\kg) | 21 |
| 0,0000001 | 10 $^{-9}$ | 1 ppb (μg\kg) | 30 |
Tabela 23.3.1: Critério para avaliação da repetibilidade. Fonte: AOAC, 2016
| Analito, % | Fração Mássica (C) | Unidade | DPR predito, % |
|---|---|---|---|
| 100 | 1 | 100% | 2 |
| 10 | 10 $^{-1}$ | 10% | 3 |
| 1 | 10 $^{-2}$ | 1% | 4 |
| 0,1 | 10 $^{-3}$ | 0,1% | 6 |
| 0,01 | 10 $^{-4}$ | 100 ppm (mg\kg) | 8 |
| 0,001 | 10 $^{-5}$ | 10 ppm (mg\kg) | 11 |
| 0,0001 | 10 $^{-6}$ | 1 ppm (mg\kg) | 16 |
| 0,00001 | 10 $^{-7}$ | 100 ppb (μg\kg) | 22 |
| 0,000001 | 10 $^{-8}$ | 10 ppb (μg\kg) | 32 |
| 0,0000001 | 10 $^{-9}$ | 1 ppb (μg\kg) | 45 |
Tabela 23.3.2: Critério para avaliação da reprodutibilidade. Fonte: AOAC, 2016
Uma forma adequada de realizar o estudo de precisão intermediária, é considerar uma única amostra matriz e uma gama de concentrações de analito. Mais especificamente, dentre as concentrações, é aconselhável que tenhamos pelo menos três níveis de concentração (baixo, médio e alto), abrangendo o intervalo de trabalho, com um número de n réplicas para cada concentração. Segundo Gustavo González, o documento ICH Q2B recomenda três réplicas e o documento da FDA em validação bioanalítica considera cinco réplicas, de modo que 3-5 repetições são aconselháveis.
Os critérios de aceitação devem ser definidos e justificados de acordo com os seguintes aspectos:
- Objetivo do método;
- variabilidade intrínseca do método;
- concentração de trabalho;
- concentração do analito na amostra.
Exemplo 1.4.1
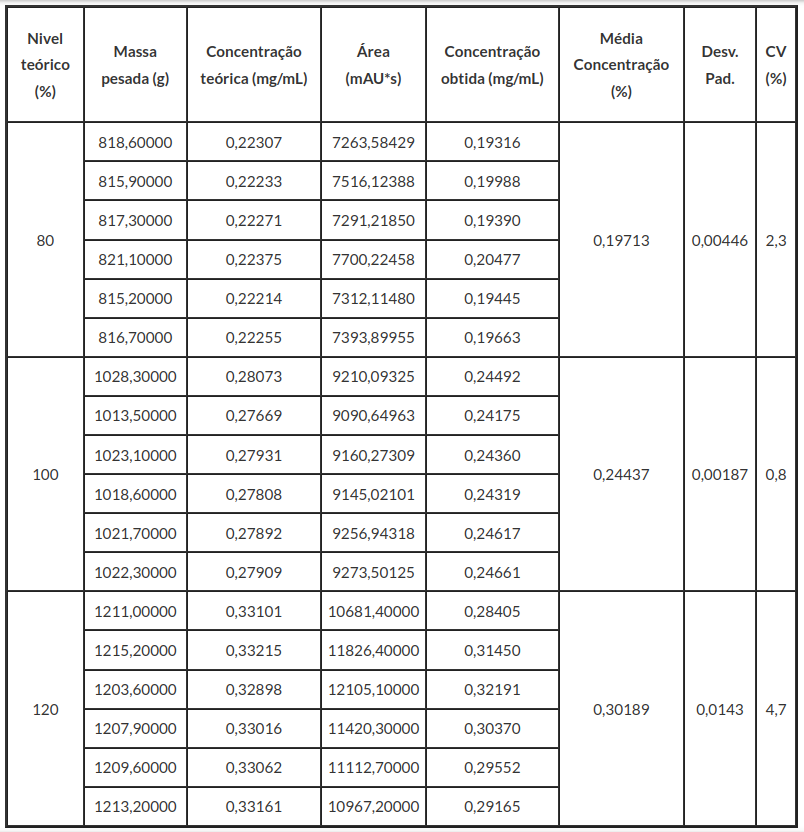
A seguir, apresentamos os dados coletados para repetibilidade.
| Nível teórico (%) | Massa pesada (g) | Concentração teórica (mg/mL) | Área (mAU*s) | Concentração obtida (mg/mL) | Média Concentração (%) | Desv. Pad. | CV (%) |
|---|---|---|---|---|---|---|---|
| 80 | 818,60000 | 0,22307 | 7263,58429 | 0,19316 | 0,19713 | 0,00446 | 2,3 |
| 815,90000 | 0,22333 | 7516,12388 | 0,19988 | ||||
| 817,30000 | 0,22271 | 7291,21850 | 0,19390 | ||||
| 821,10000 | 0,22375 | 7700,22458 | 0,20477 | ||||
| 815,20000 | 0,22214 | 7312,11480 | 0,19445 | ||||
| 816,70000 | 0,22255 | 7393,89955 | 0,19663 | ||||
| 100 | 1028,30000 | 0,28073 | 9210,09325 | 0,24492 | 0,24437 | 0,00187 | 0,8 |
| 1013,50000 | 0,27669 | 9090,64963 | 0,24175 | ||||
| 1023,10000 | 0,27931 | 9160,27309 | 0,24360 | ||||
| 1018,60000 | 0,27808 | 9145,02101 | 0,24319 | ||||
| 1021,70000 | 0,27892 | 9256,94318 | 0,24617 | ||||
| 1022,30000 | 0,27909 | 9273,50125 | 0,24661 | ||||
| 120 | 1211,00000 | 0,33101 | 10681,40000 | 0,28405 | 0,30189 | 0,0143 | 4,7 |
| 1215,20000 | 0,33215 | 11826,40000 | 0,31450 | ||||
| 1203,60000 | 0,32898 | 12105,10000 | 0,32191 | ||||
| 1207,90000 | 0,33016 | 11420,30000 | 0,30370 | ||||
| 1209,60000 | 0,33062 | 11112,70000 | 0,29552 | ||||
| 1213,20000 | 0,33161 | 10967,20000 | 0,29165 |
A seguir, avaliamos a repetibilidade através do software Action Stat e obtemos os seguintes resultados:
- Primeiramente apresentamos a função de Repetibilidade no Action Stat. Para acessá-la vamos no menu Action Stat ->Validação Analítica -> Precisão -> Repetibilidade
(imagem em falta)
- O próximo passo é preencher a janela do resumo descritivo
(imagem em falta)
A seguir apresentamos a saída obtida pelo Action Stat.
(imagem em falta)
Para os níveis teóricos de 80%, 100% e 120% temos coeficientes de variação de 2,264%, 0,7638% e 4,7% respectivamente.
Precisão Intermediaria
A forma adequada de realizar o estudo de precisão intermediária, é expressar a proximidade entre os resultados obtidos da análise de uma mesma amostra, no mesmo laboratório, em pelo menos dois dias diferentes, realizada por operadores distintos contemplando as mesmas concentrações e o mesmo número de determinações descritas na avaliação da repetibilidade.
Desta forma, temos três possíveis cenários para a Análise de Precisão Intermediaria:
- Com dois fatores e interação: Dia, Analista e Interação entre Dia e Analista:
- Com dois fatores sem interação: Dia e Analista
- Com um fator: Dia e Analista.
Em todos os casos utilizamos o método de Analise de Variância (ANOVA) com a variação dos fatores conforme cada caso.
Análise de variância (ANOVA) Método Cruzado
O experimento cruzado de dois fatores com interação é o modelo que utilizaremos a primeira situação. Tipicamente, os dois fatores são referidos como “Dia” e “Analista”. Aqui consideramos a tabela da ANOVA, em que modelamos o experimento com dados balanceados e ambos fatores são aleatórios.
O modelo com dois fatores balanceados e com efeitos cruzados com interação é dado por:
$$Y_{ijk}=\mu+\alpha_i+\gamma_{j}+\tau_{ij}+\varepsilon_{ijk} \quad \begin{cases}i=1,\dots, p \cr j=1,\dots,o \cr k=1,\dots,r \end{cases} \tag{1.4.1}$$
Para este modelo $ \mu $ é um parâmetro comum a todos os tratamentos e representa a média geral dos dados, $ \alpha_{i} $ e $ \gamma_j $ é o efeito devido ao i-ésimo e ao j-ésimo nível do fator D (dia) e A (analista) e são variáveis aleatórias independentes com média zero e variâncias $ \sigma^2_D $ e $ \sigma^2_A $ respectivamente e $ \tau_{ij} $ é a interação entre os fatores D e A, que também tem distribuição normal com média zero e variância $ \sigma^2_I. $ A variável aleatória $ \varepsilon_{ijk} $ corresponde ao erro aleatório experimental, isto é, a variabilidade não explicada pelo modelo devido a variações presentes em diversas fontes não consideradas no estudo. Este tem distribuição normal com média zero e variância $ \sigma^2. $ Resumindo,
- $ \mu $ é a média geral dos dados;
- $ \alpha_{i} $ é o efeito do nível $i$ do fator dia;
- $ \gamma_{j} $ é efeito do nível $j$ do fator analista;
- $ \tau_{ij} $ é efeito do nível $ij$ da interação entre dia e analista;
- $ \varepsilon_{ijk} $ é a componente aleatória do erro.
Agora, vamos desenvolver a análise de variância para o modelo de efeitos aleatórios. A partir de considerações dos dados, temos:
$ Y_{i..}=\displaystyle \sum_{j=1}^{o}\sum^r_{k=1} Y_{ijk} $: soma das observações do nível $i$ do fator dia;
$ \overline{Y_{i..}}=\displaystyle\frac{Y_{i..}}{pr} $: média das observações do nível $i$ do fator dia;
$ Y_{.j.}=\displaystyle \sum_{i=1}^{p}\sum^r_{k=1} Y_{ijk} $: soma das observações do nível $j$ do fator analista;
$ \overline{Y_{.j.}}=\displaystyle\frac{Y_{.j.}}{or} $: média das observações do nível $j$ do fator analista;
$ Y_{ij.}=\displaystyle \sum^r_{k=1} Y_{ijk} $: soma das observações dos níveis $i$ e $j$ dos fatores dia e analista;
$ \overline{Y_{ij.}}=\displaystyle\frac{Y_{.j.}}{or} $: média das observações dos níveis $i$ e $j$ dos fatores dia e analista;
$ Y_{…}=\displaystyle\sum^p_{i=1} \sum^{o}_{j=1}\sum^r_{k=1} Y_{ijk} $: soma de todas as observações;
$ \overline{Y_{…}}=\displaystyle\frac{Y_{…}}{por} $: média geral das observações.
Além disso, assumimos que o erro tem distribuição Normal com média zero e variância $ \sigma^{2}_{\varepsilon} $ e que os erros são mutuamente independentes. Com isso, temos que
$$\varepsilon_{ij}\sim~N(0,\sigma^{2}_{\varepsilon}).$$
Agora, para o efeito $ \alpha_i $, assumimos que tem distribuição Normal com média zero e variância $ \sigma^2_{D}. $ Assumimos também que os efeitos são mutuamente independentes. Assim,
$$\alpha_{i}\sim~N(0,\sigma^{2}_{D}).$$
Para o efeito $ \gamma_j $, assumimos que tem distribuição Normal com média zero e variância $ \sigma^2_{A}. $ Assumimos também que os efeitos são mutuamente independentes. Assim,
$$\gamma_{j}\sim~N(0,\sigma^{2}_{A}).$$
Por fim temos que para o efeito $ \tau_{ij} $, assumimos que tem distribuição Normal com média zero e variância $ \sigma^2_{I}. $ Assumimos também que os efeitos são mutuamente independentes. Assim,
$$\tau_{ij}\sim~N(0,\sigma^{2}_{I}).$$
A análise de variância para o modelo (1.4.1) é obtida pela decomposição da variação total $ Y_{ijk}-\overline{Y_{…}} $ como segue
$$SQT=\sum_{i=1}^{p}\sum_{j=1}^{o}\sum_{k=1}^{r}(Y_{ijk}-\overline{Y_{…}})^2=o~r\sum_{i=1}^{p}(\overline{Y_{i..}}-\overline{Y_{…}})^2 +p~r\sum_{j=1}^{o}(\overline{Y_{.j.}}-\overline{Y_{…}})^2 +r~ \sum_{i=1}^{p}\sum_{j=1}^{o}(\overline{Y_{ij.}}-\overline{y_{i..}}-\overline{Y_{.j.}}+ \overline{Y_{…}})^2+\sum_{i=1}^{p}\sum_{j=1}^{o}\sum_{k=1}^{r}(Y_{ijk}-\overline{Y_{ij.}})^2$$
$$=SQD+SQA+SQI+SQE$$
em que
$$SQT=\sum_{i=1}^{p}\sum_{j=1}^{o}\sum_{k=1}^{r}(Y_{ijk}-\overline{Y_{…}})^2$$
$$SQD=o~r\sum_{i=1}^{p}(\overline{Y_{i..}}-\overline{Y_{…}})^2$$
$$SQA=p~r\sum_{j=1}^{o}(\overline{Y_{.j.}}-\overline{Y_{…}})^2$$
$$SQI=r~\sum_{i=1}^{p}\sum_{j=1}^{o}(\overline{Y_{ij.}}-\overline{Y_{i..}}-\overline{Y_{.j.}}+\overline{Y_{…}})^2$$
$$SQE=\sum_{i=1}^{p}\sum_{j=1}^{o}\sum_{k=1}^{r}(Y_{ijk}-\overline{Y_{ij.}})^2$$
Assim, obtemos a tabela da ANOVA da seguinte forma
| Fator | Graus de Liberdade | Soma de Quadrados | Quadrados Médios | F | P-Valor |
|---|---|---|---|---|---|
| Fator D | $ p -1 $ | $ SQD $ | $ QMD $ | $ F_{D}=\frac{QMD}{QMI} $ | $ P(F> F_D) $ |
| Fator A | $ o -1 $ | $ SQA $ | $ QMA $ | $ F_{A}=\frac{QMA}{QMI} $ | $ P(F> F_A) $ |
| Interação ($ D\times A $) | $ (p -1)(o -1) $ | $ SQI $ | $ QMI $ | $ F_{I}=\frac{QMI}{QME} $ | $ P(F> F_{I}) $ |
| Erro | $ p~o~(r -1) $ | $ SQE $ | $ QME $ | ||
| Total | $ p~o~r - 1 $ | $ SQT $ |
Tabela 23.3.3: Tabela da ANOVA
A seguir, apresentamos os testes de hipóteses:
- Teste do efeito do fator Dia:
$$ \begin{cases} H_0: \sigma^{2}_{D} = 0 \cr H_1: \sigma^{2}_{D} > 0 \end{cases}$$
e a estatística de teste é dada por $ F_D=\dfrac{QMD}{QMI} $
se $ \mathbb{P} \left[F_{(o-1,(o-1)*(p-1))}> F_D|H_0 \right] > 0,05 $ rejeitamos a hipótese de que o efeito do fator Dia é significativo;
se $ \mathbb{P} \left[F_{(o-1,(o-1)*(p-1))}> F_D|H_0 \right] \leq 0,05 $ não rejeitamos a hipótese de que o efeito do fator Dia é significativo.
- Teste do efeito do fator Analista:
$$ \begin{cases} H_0: \sigma^{2}_{A} = 0 \cr H_1: \sigma^{2}_{A} > 0 \end{cases}$$
e a estatística de teste é dada por $ F_A=\dfrac{QMA}{QMI} $
se $ \mathbb{P} \left[F_{(o-1,(o-1)*(p-1))}> F_A|H_0\right]> 0,05 $ rejeitamos a hipótese de que o efeito do fator Analista é significativo;
se $ \mathbb{P} \left[F_{(o-1,(o-1)*(p-1))}> F_A|H_0\right]\leq 0,05 $ não rejeitamos a hipótese de que o efeito do fator Analista é significativo.
- Teste do efeito da interação entre Dia e Analista:
$$ \begin{cases} H_0: \sigma^{2}_{I} = 0 \cr H_1: \sigma^{2}_{I} > 0 \end{cases}$$
e a estatística de teste é dada por $ F_I=\dfrac{QMI}{QME} $
se $ \mathbb{P} \left[F_{((o-1)*(p-1),po(r-1))}> F_I|H_0\right]> 0,05 $ rejeitamos a hipótese de que o efeito da interação entre Dia e Analista é significativo;
se $ \mathbb{P} \left[F_{((o-1)*(p-1),po(r-1))}> F_I|H_0\right]\leq 0,05 $ não rejeitamos a hipótese de que o efeito da interação entre Dia e Analista é significativo.
Análise de variância (ANOVA) Sem Interação
No caso em que rejeitamos a significância da interação entre os fatores Dia e Analista, fazemos o estudo da precisão intermediária desconsiderando a interação. De forma idêntica ao método cruzado com algumas pequenas alterçãoes.
Nesse caso somente não temos a interação no modelo:
$$Y_{ijk}=\mu+\alpha_i+\gamma_{j}+\varepsilon_{ijk}\quad \begin{cases} i=1,\dots, p\cr j=1,\dots,o\cr k=1,\dots,r \end{cases} \tag{1.4.2}$$
A tabela ANOVA e a estatística do deste sofre uma alteração:
| Fator | Graus de Liberdade | Soma de Quadrados | Quadrados Médios | F | P-Valor |
|---|---|---|---|---|---|
| Fator D | $ p -1 $ | $ SQD $ | $ QMD $ | $ F_{D}=\frac{QMD}{QME} $ | $ P(F> F_D) $ |
| Fator A | $ o -1 $ | $ SQA $ | $ QMA $ | $ F_{A}=\frac{QMA}{QME} $ | $ P(F> F_A) $ |
| Erro | $ por - p -o +1 $ | $ SQE $ | $ QME $ | ||
| Total | $ p~o~r - 1 $ | $ SQT $ |
Tabela 23.3.4: Tabela da ANOVA sem interação
Então, os testes de hipóteses ficam:
- Teste do efeito do fator Dia:
$$ \begin{cases} H_0: \sigma^{2}_{D} = 0 \cr H_1: \sigma^{2}_{D} > 0 \end{cases}$$
e a estatística de teste é dada por $ F_D=\dfrac{QMD}{QME} $
se $ \mathbb{P} \left[F_{(p-1,por-p-o+1)}> F_D|H_0 \right]> 0,05 $ rejeitamos a hipótese de que o efeito do fator Dia é significativo;
se $ \mathbb{P} \left[F_{(p-1,por-p-o+1)}> F_D|H_0 \right] \leq 0,05 $ não rejeitamos a hipótese de que o efeito do fator Dia é significativo.
Teste do efeito do fator Analista:
$$ \begin{cases} H_0: \sigma^{2}_{A} = 0 \cr H_1: \sigma^{2}_{A} > 0 \end{cases}$$
e a estatística de teste é dada por $ F_A=\dfrac{QMA}{QME} $
se $ \mathbb{P} \left[F_{(o-1,por-p-o+1)}> F_A|H_0\right]> 0,05 $ rejeitamos a hipótese de que o efeito do fator Analista é significativo;
se $ \mathbb{P} \left[F_{(o-1,por-p-o+1)}> F_A|H_0\right] \leq 0,05 $ não rejeitamos a hipótese de que efeito do fator Dia é significativo.
Análise de Variância (ANOVA) com Dia e Analista confundidos
No caso em que temos Dia e Analista confundidos, Situação 1 = (Dia 1, Analista 1) e situação 2 = (Dia 2, Analista 2), fazemos o estudo de precisão intermediária com um único fator, de forma idêntica ao caso sem interação do modelo ANOVA um fator.
Nesse caso temos o modelo:
$$Y_{ijk}=\mu+\alpha_i+\varepsilon_{ik}\quad \begin{cases} i=1,\dots, p \cr k=1,\dots,r \end{cases} $$
A tabela ANOVA e a estatística do deste sofre uma alteração:
| Fator | Graus de Liberdade | Soma de Quadrados | Quadrados Médios | F | P-Valor |
|---|---|---|---|---|---|
| Fator S | $ p -1 $ | $ SQS $ | $ QMS $ | $ F_{S}=\frac{QMS}{QME} $ | $ P(F> F_S) $ |
| Erro | $ pr - p $ | $ SQE $ | $ QME $ | ||
| Total | $ pr - 1 $ | $ SQT $ |
Tabela 23.3.5: Tabela da ANOVA com um fator Situação
Então, os testes de hipóteses ficam:
- Teste do efeito do fator Situação:
$$ \begin{cases} H_0: \mu_1 = \mu_2 = \cdots = \mu_p \cr H_1: \ \hbox{Pelo menos uma média é diferente} \end{cases}$$
e a estatística de teste é dada por $ F_{S}=\frac{QMS}{QME} $
se $ \mathbb{P} \left[F_{(p-1,pr-p)}> F_S|H_0 \right]> 0,05 $ rejeitamos a hipótese de que o efeito do fator Situação é significativo;
se $ \mathbb{P} \left[F_{(p-1,pr-p)}> F_S|H_0 \right] \leq 0,05 $ não rejeitamos a hipótese de que o efeito do fator Situação é significativo.
Exemplo 1.4.2
Agora, avaliamos a precisão intermediária e a reprodutibilidade, para isto, observe os resultados obtidos pelo Action Stat.
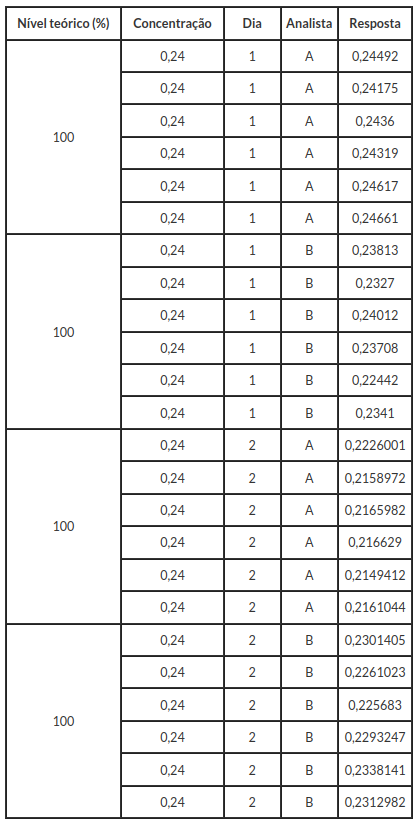
- Para isso, acessamo o menu Action Stat -> Validação Análitica -> Precisão -> Intermediária
(imagem em falta)
- A segui preenchemos selecionamos os dados e clicamos no botão Ler. Selecionamos as variáveis e para realizar o intervalo de confiança. Clicamos em Ok e obtemos os resultados.
(imagem em falta)
- Por fim, obtemos os seguintes resultados:
(imagem em falta)
Observamos que interação entre dia e analista é significativa ao nível de significância de 5%. Porém não encontramos diferenças significativas entre os Dias (p-valor de 0,38), nem mesmo entre os Analistas (p-valor de 0,93).
Exemplo 1.4.3
Agora, avaliamos a precisão intermediária e a reprodutibilidade, para isto, observe os resultados obtidos pelo Action Stat.
| Situação | Concentração |
|---|---|
| A | 93,97385 |
| A | 95,14364 |
| A | 95,41374 |
| A | 95,63412 |
| A | 96,60754 |
| A | 96,89411 |
| B | 94,73515 |
| B | 94,06646 |
| B | 93,39936 |
| B | 93.87990 |
| B | 93,95359 |
| B | 95,85671 |
Temos que A = (Dia 1, Analista 1) e B = (Dia 2, Analista 2).
- Para isso, acessamo o menu Action Stat -> Validação Análitica -> Precisão -> Intermediária
(imagem em falta)
- A segui preenchemos selecionamos os dados e clicamos no botão Ler. Selecionamos as variáveis e para realizar o intervalo de confiança. Clicamos em Ok e obtemos os resultados.
(imagem em falta)
- Por fim, obtemos os seguintes resultados:
(imagem em falta)
Observando a Tabela ANOVA, temos que a Situação apresenta um p-valor menor que 0,05. Logo a Situação é significativa ao nível de significância de 5%, isto é, a situação impacta na concentração. Contudo vale ressaltar que a Situação A possui valores de concentração superiores a Situação B, o que pode impactar na análise. Por outro lado temos que o coeficiente de variação da precisão intermediária encontra-se abaixo de 2%.
(imagem em falta)
(imagem em falta)
Observando o gráfico de efeitos principais, notamos que a concentração diminui quando passamos da situação A (Dia 1, Analista 1) para a situação B (Dia 2, Analista 2). Não podemos concluir apenas utilizando o gráfico, assim é necessário é fazermos uma análise estatística para verificarmos se cada fator é significante e se a interação realmente não é significante.