23.4 Exatidão
Nesta seção, vamos avaliar a exatidão para isto utilizamos a seção VI da RDC Nº166. No artigo 44 a exatidão de um método analítico está definida como grau de concordância entre os resultados individuais, obtidos pelo método em estudo, em relação a um valor de referência aceito como verdadeiro. Os critérios de preparação do ensaio está descrito na RDC Nº166 seção VI.
| Analito, % | Fração Mássica (C) | Unidade | Recuperação média, % |
|---|---|---|---|
| 100 | 1 | 100% | 98-102 |
| 10 | 10 $^{-1}$ | 10% | 98-102 |
| 1 | 10 $^{-2}$ | 1% | 97-103 |
| 0,1 | 10 $^{-3}$ | 0,1% | 95-105 |
| 0,01 | 10 $^{-4}$ | 100 ppm (mg\kg) | 90-107 |
| 0,001 | 10 $^{-5}$ | 10 ppm (mg\kg) | 80-110 |
| 0,0001 | 10 $^{-6}$ | 1 ppm (mg\kg) | 80-110 |
| 0,00001 | 10 $^{-7}$ | 100 ppb (μg\kg) | 80-110 |
| 0,000001 | 10 $^{-8}$ | 10 ppb (μg\kg) | 60-115 |
| 0,0000001 | 10 $^{-9}$ | 1 ppb (μg\kg) | 40-120 |
Tabela 23.4.1: Critério para avaliação da exatidão.Fonte: AOAC, 2016
A equação de medição da recuperação é dada por:
$$\text{Rec}=\frac{C_o}{C_t}\times 100$$
em que
- Rec: é a recuperação, em ($ \char37 $);
- é a concentração obtida em $ mg/mL; $
(há elementos em falta na equação acima)
- é a concentração teórica em $ mg/mL; $
(há elementos em falta na equação acima)
Consideremos uma amostra aleatória simples $ \text{Rec}_1,\text{Rec}_2,\ldots,\text{Rec}_n $, obtida de uma população com distribuição normal, com média $ \mu=100 $ e variância $ \sigma^2 $ desconhecidas. Como neste caso a variância é desconhecida, utilizaremos a variância amostral $ s^2 $ no lugar de $ \sigma^2 $. Assim, temos que
$$T=\frac{|\overline{\text{Rec}}-100|}{s/\sqrt{n}}\sim t_{(n-1)}\quad ~(1)$$
ou seja, a variável $ T $ tem distribuição t de Student com $ n-1 $ graus de liberdade.
Então, ao fixarmos o nível de significância $ \alpha $, obtemos da Tabela da distribuição t de Student com $ n-1 $ graus de liberdade, o valor $ t_{((n-1),\alpha/2)} $, que satisfaz
$$\mathbb{P}\left(-t_{((n-1),\alpha/2)}\leq T\leq t_{((n-1),\alpha/2)}\right)=1-\alpha$$
Analogamente ao caso anterior, obtemos que
$$\mathbb{P}\left(-t_{((n-1),\alpha/2)}\leq \frac{\overline{\text{Rec}}-100}{s/\sqrt{n}}\leq t_{((n-1),\alpha/2)}\right)=1-\alpha$$
ou seja,
$$\mathbb{P}\left(\overline{\text{Rec}}-t_{((n-1),\alpha/2)}\frac{s}{\sqrt{n}}\leq100\leq \overline{\text{Rec}}+t_{((n-1),\alpha/2)}\frac{s}{\sqrt{n}}\right)=1-\alpha.$$
Logo, o intervalo com $ 100(1-\alpha)\char37 $ de confiança para $ \mu=100 $, com variância desconhecida, será dado por
$$IC(\mu=100,1-\alpha)=\left(\overline{\text{Rec}}-t_{\alpha/2}\frac{s}{\sqrt{n}};\overline{\text{Rec}}+t_{\alpha/2}\frac{s}{\sqrt{n}}\right).$$
Para facilitar a execução do teste, podemos seguir os passos:
- Estabelecer as hipóteses:
Fixamos $\mu=\mu_0=100 $.
(há elementos em falta na equação acima)
$\mu\neq\mu_0 \quad \text{(teste bilateral)} $;
(há elementos em falta na equação acima)
-
Fixar o nível de significância $ \alpha $.
-
Determinar a região crítica.
Como o teste é bilateral, determinamos os pontos críticos $ -t_{\alpha/2} $ e $ t_{\alpha/2} $ tais que $ \mathbb{P}[T \ > \ t_{\alpha/2}]=\mathbb{P}[T \ < -t_{\alpha/2}]=\alpha/2 $ a partir da distribuição t de Student com $ n-1 $ graus de liberdade.
- Calcular, sob a hipótese nula, o valor:
$$T_{\text{obs}}=\frac{|\overline{\text{Rec}}-100|}{\frac{s}{\sqrt{n}}}$$
em que
- $ \overline{\text{Rec}} $: valor da média da recuperação.
- $ s $: valor do desvio padrão amostral.
- $ n $: tamanho da amostra.
- Critério:
Teste bilateral: se $ T_{\text{obs}} \ > \ t_{\alpha/2} $ ou se $ T_{\text{obs}} \ < \ -t_{-\alpha/2} $, rejeitamos $ H_0 $. Caso contrário, não rejeitamos $ H_0 $.
- O p-valor no teste bilateral é dado por
$$\text{p-valor} = \mathbb{P}[|t| \ > \ |T_{\text{obs}}||H_0]=2\mathbb{P}[T \ > \ |T_{\text{obs}}| | H_0].$$
(imagem em falta)
- Como vimos anteriormente o intervalo de confiança é dado por
$$IC(\mu,1-\alpha)=\left(\overline{\text{Rec}}-t_{\alpha/2}\frac{s}{\sqrt{n}};\overline{\text{Rec}}+t_{\alpha/2}\frac{s}{\sqrt{n}}\right)$$
Segundo Gustavo González [2], a estatística do teste (equação 1) por ser escrita como:
$$T=\frac{\overline{\text{Rec}}-100}{u(\text{Rec})}$$
em que
$$u(\text{Rec})=\sqrt{\left(\frac{\partial \text{Rec}}{\partial C_o}\right)^2u^2(C_o)+\left(\frac{\partial \text{Rec}}{\partial C_t}\right)^2u^2(C_t)+u^2(\varepsilon)}$$
no qual
- Rec: é a recuperação, em (%);
- é a concentração obtida em $ mg/mL. $ A incerteza é dada pela preparação da amostra (para mais detalhes consulte cálculo de incerteza devido às soluções)
(imagem em falta)
- é a concentração teórica em $ mg/mL; $ A incerteza é dada pelo certificado da solução de referência (ISO GUIDE);
(imagem em falta)
- é o desvio padrão da média dada por $ s/\sqrt{n}. $
(imagem em falta)
Além disso, temos que:
$$\frac{\partial \text{Rec}}{\partial C_o}=\frac{1}{C_t}$$
$$\frac{\partial \text{Rec}}{\partial C_t}=-\frac{C_o}{C^2_t}$$
De acordo com o protocolo LGC/VAM descrito no artigo de Gustavo González [2], se o graus de liberdade associados a incerteza da recuperação são conhecidas, T é comparado com o bicaudal valor tabelado $ t_{(\nu,1-\alpha)} $ para o número de graus de liberdade $ \nu $ com $ (1-\alpha)\char37 $ de confiança. E se$ T\leq t_{tab}, $ a recuperação de consenso não é significativamente diferente de 1. Em alternativa, ao invés do $ t_{tab}, $ podemos utilizar o fator de abrangência $ k $ para a comparação. Os valores típicos são $ k=2 $ ou 3 para 95% ou 99% de confiança, respectivamente. Assim
Se $ \frac{|\overline{\text{Rec}}-100|}{u(\text{Rec})}\leq k $, a recuperação não é significativamente diferente de 100;
Se $ \frac{|\overline{\text{Rec}}-100|}{u(\text{Rec})}> k $, a recuperação é significativamente diferente de 100 e o resultado analítico tem de ser corrigido por $ \overline{\text{Rec}}. $
Outra forma de avaliação descrita em Gustavo González [2] é avaliarmos os limites aceitáveis dadas pelos órgãos reguladores.
Exemplo 1.5.1
Nesta seção, foi calculada a incerteza expandida relativa, que corresponde a 0,29%. A seguir, apresentamos os dados coletados.
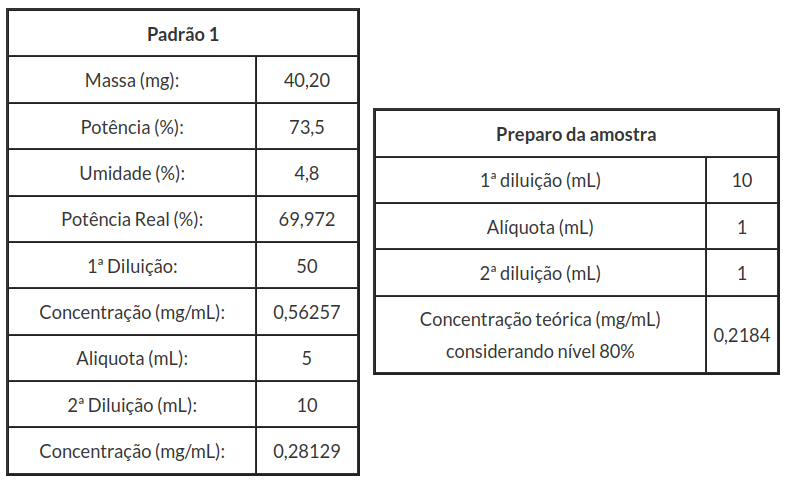
Para especificidade normal obtemos as seguintes medições:
| Concentração |
|---|
| 0,182856676 |
| 0,201313318 |
| 0,190572332 |
| 0,181481821 |
| 0,181340121 |
| 0,189112134 |
| 0,190115447 |
| 0,176140016 |
| 0,19486329 |
| 0,183852917 |
| Amostra | Massa (mg) | Vol. Pd (mL) | Concentração teórica (mg/mL) | Área (mAU*s) | Concentração obtida (mg/mL) | Recuperação (%) |
|---|---|---|---|---|---|---|
| 1 | 728,68 | 0,00 | 0,1912 | 7447,27975 | 0,18716 | 97,88 |
Para especificidade normal temos:
$$\text{Rec}=\frac{C_o}{C_t}\times100=\frac{0,18716}{0,1912}\times100=97,88\char37\pm 3,9\char37$$
A seguir, testamos a exatidão através do software Action Stat e obtemos os seguintes resultados:
- Primeiramente apresentamos a função Exatidão no Action Stat.
(imagem em falta)
- O próximo passo é preencher a janela da Exatidão
(imagem em falta)
- Por fim, obtemos os seguintes resultados:
(imagem em falta)
(imagem em falta)
(imagem em falta)
Logo, a recuperação está dentro do critério de aceitação.