23.7 Robustez

Nesta seção, vamos analisar a robustez, segundo critérios da RDC Nº166. Nela a robustez é definida como indicação da capacidade de um método analítico em resistir a pequenas e deliberadas variações dos parâmetros analíticos. Para a determinação da robustez do método devem ser avaliados, no mínimo, os parâmetros descritos na Tabela 1 do anexo III.

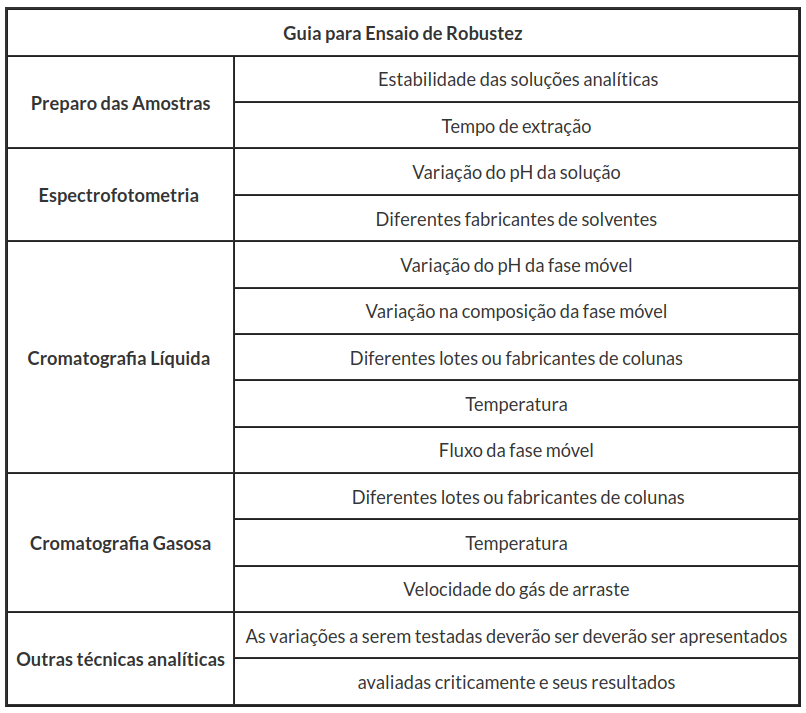
Tabela 1: Parâmetros para a avaliação da robustez do método.

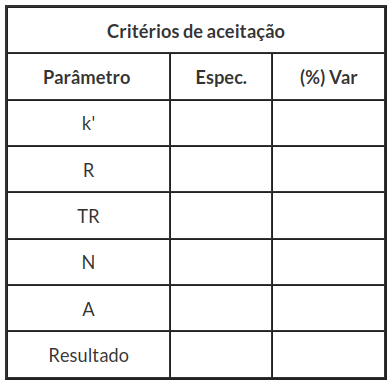
Tabela 2: Preencimento do critério de aceitação.

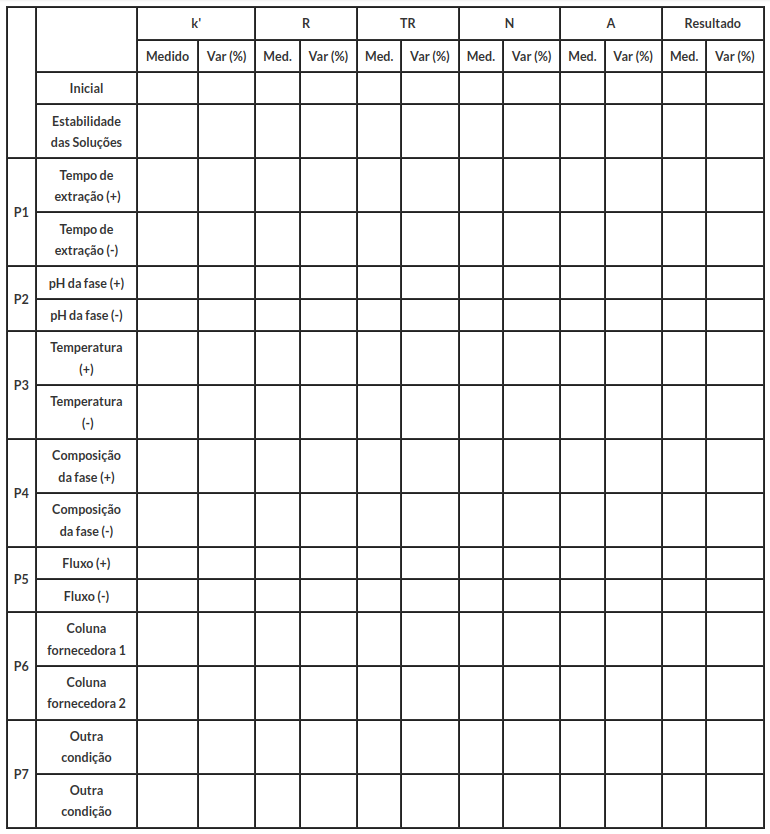
Tabela 3: Dados para Robustez.

Em algumas situações o número de combinações dos fatores do experimento é grande. Nestes casos, recursos podem estar disponíveis apenas para uma única execução do projeto, ou seja, o experimento não possuirá réplicas. Existem alguns métodos para tratarem estes experimento, dentre eles citamos os métodos de Daniel e Lenth que são métodos objetivos para decidir quais efeitos são significativos na análise de experimentos sem réplicas, nas situações em que o modelo está saturado e assim, não há graus de liberdade para estimar a variância do erro.

O teste de Youden permite avaliar se modificações no método causam diferenças significativas. Outro ponto que pode ser avaliado neste método, é que podemos ordenar se uma combinação de influências podem causar diferenças significativas nos resultados finais.

Neste método são realizados oito ensaios separadamente, visando determinar quais efeitos das diferentes etapas no procedimento analítico afetam o resultado. A tabela de planejamento pelo método de Youden é dado por:

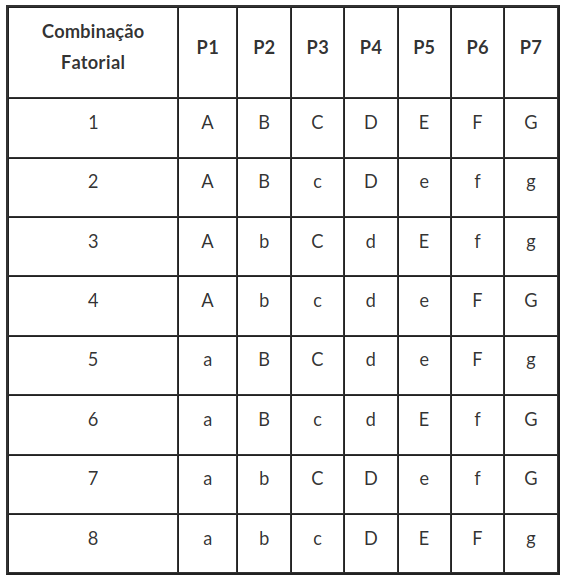
Em cada parâmetro analítico da tabela, definimos o nível alto (letra maiúscula) como (+) e o nível baixo (letra minúscula) como (-). Assim, obtemos a tabela a seguir:

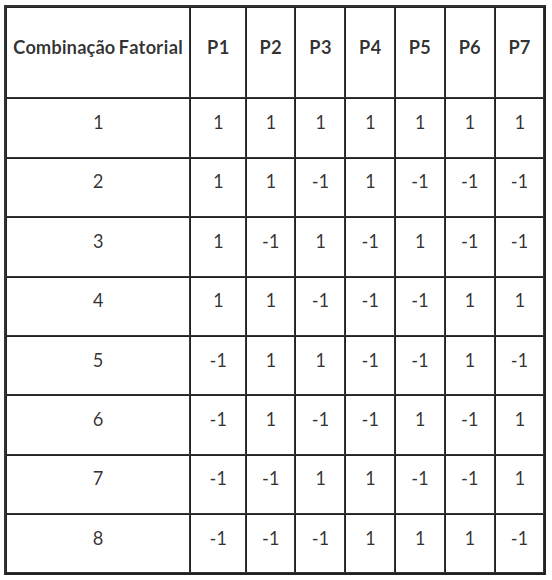
Para análisar o Experimento de Youden seguimos os seguintes passos:

• Calculamos os efeitos apara cada parâmetro analítico;

• Utilizamos o método de Lenth e o gráfico de Daniel para avaliar se os efeitos ativos são significativos.

Gráfico de Daniel

No estudo de experimento fatoriais sem réplicas Cuthbert Daniel (1959) propôs um método que avalia estes efeitos ativos.

A ideia de Daniel é bastante utilizada até os dias atuais por ser simples e conseguir apontar a direção correta dos efeitos em grande parte dos experimentos. Segundo Daniel, esperamos que apenas uma pequena fração dos contrastes sejam ativos dentre todos aqueles envolvidos no estudo. Nestes gráficos, os efeitos cujos pontos estiverem claramente afastados de uma reta imaginária, formada pela nuvem de pontos, serão julgados ativos.

A aplicação eficaz desses gráficos depende do fato das estimativas dos efeitos terem a mesma variância, e os pontos em que temos “efeitos esparsos” são detectados pelo método.

Definição 1.8.1

$$\left(\hat{c}_{(i)}, \Phi^{-1}\left(\frac{(i-0,5)}{n}\right)\right)$$

em que $ \Phi^{-1} $ representa a função da distribuição acumulada normal padrão.

Alguns autores preferem utilizar o gráfico half-normal cujas coordenadas são dadas por:

$$\left(|\hat{c}_{(i)}|, \Phi^{-1}\left(0,5+\frac{(i-0,5)}{n}\right)\right)$$

Uma das vantagens em utilizar o half-normal é o fat ode que os efeitos possivelmente ativos vão se apresentar no canto superior direito do gráfico.

Método de Lenth

O método de Lenth tem sido considerado como um método muito eficiênte, quando trabalhamos com análise de experimentos fatoriais sem réplicas. Um ponto para análise destes experimentos, é o estudo de um número grande de contrastes e que as estimativas destes contrastes tenham a mesma variabilidade.

O método de Lenth, assim como Daniel, parte do princípio de que tenhamos apenas poucos “efeitos esparsos'' (efeitos dispersos), que o autor trata como efeitos ativos (diferente de zero), ou seja, efeitos significativamente não nulos do ponto de vista estatístico.

Definição 1.8.2

Considere um experimento fatorial com dois níveis e suponha que existam $ m $$ k_1,k_2,\dots,k_m $ contrastes $ c_1,c_2,\dots,c_m $ ou efeitos estimados independentes e que eles têm a mesma variância, denotada por $ \tau^2 $ com distribuição Normal $ N(k_i,\sigma^2). $ Sendo $ N $ o número de observações, por exemplo, temos que $ m=N-1 $ no caso de modelo saturado. Desta forma, temos que cada contraste ou efeito estimado é dado por

$$c=\overline{y_{+}}-\overline{y_{-}},$$

sendo que $ \overline{y_{+}} $ é a média das $ N/2 $ observações no nível “alto'' do fator em questão e $ \overline{y_{-}} $ é a média das $ N/2 $ observações no nível “baixo''. Como já mencionado, cada contraste tem a mesma variância $ \tau^2=4 \sigma^2/N $, em que $ \sigma^2 $ é a variância do erro.

Sejam $ c_{1}, c_{2}, …, c_{m} $ os contrastes ou efeitos estimados, com $ m=N-1 $. Inicialmente, calculamos a quantidade

$$s_{0}=1,5 \times \text{mediana} (|c_{j}|)\quad j=1,\dots,m.$$

Então, calculamos o pseudo erro padrão (PSE) como sendo

$$|c_{j}|\leq2,5 s_{0})\quad j=1,\dots,m,$$

(há elementos em falta na equação acima)

sendo que o termo PSE é um estimador para $ \tau^2. $ Notamos que $ s_0 $ e $ PSE $ são bastante similares, com uma pequena diferença na mediana do $ PSE, $ que é mais restrita. Esta restrição é devido aos pontos ativos e é descrita no artigo Russel Lenth (1989), que é feita para obtermos estimativas consistentes para $ \tau. $

Em relação ao critério de decisão de quais efeitos são significativos, definimos uma margem de erro dos contrastes $ c_{i} $, denotada por ME. O valor da margem de erro é dada por

$$ME = t_{(1-\frac{\alpha}{2};d)} \times PSE,$$

sendo que $ t_{(1-\frac{\alpha}{2};d)} $ é o quantil $ (1-\frac{\alpha}{2}) $ da distribuição t-student com $ d $ graus de liberdade e $ \alpha $ é o nível de significância adotado. (Geralmente, utilizamos $ d=m/3 $ e $ \alpha=0,05 $). Assim, temos que ME é uma margem de erro para $ c_i $ com confiança aproximada de $ 95(porcentagem) $. Contrastes que excedem o valor de ME em valor absoluto são considerados significativos com nível de significância de $ 95(porcentagem) $, por exemplo.

Entretanto, quando há um grande número de contrastes $ m $, esperamos que uma ou duas estimativas de contrastes não significativos excedam o valor de ME, conduzindo a uma falsa conclusão. Desta forma, a fim de tratar estes casos, é definida uma margem de erro simultânea, que será denotada por SME. Esta medida é calculada multiplicando o pseudo erro padrão PSE por um fator $ t_{\gamma;d} $. De fato,

$$SME = t_{\gamma;d} \times PSE,$$

em que

$$\gamma=(1+0,95^{1/m})/2.$$

A constante $ \gamma $ vem do fato de que as estimativas dos contrastes são independentes. É usual construir um gráfico para exibir as informações aqui calculadas. Para isto, construímos um gráfico de barra mostrando os valores absolutos das estimativas dos contrastes ou efeitos estimados e adicionamos linhas de referências com os valores de ME e SME. Os contrastes cujas barras estendem a linha SME são considerados ativos. Já aqueles cujas barras não estendem a linha de referência ME são considerados inativos. Os contrastes cujas barras estão entre as linhas de referências ME e SME requerem um cuidado maior na decisão. A região entre as linhas ME e SME é dita região de incerteza e é necessário um bom argumento para decidir se o(s) contraste(s) é(são) significativo(s) ou não.

Critérios para avaliar os efeitos

• Intervalo de Confiança:

O efeito é aceitável ao nível de significância $ \alpha $ se o efeito pertencer ao intervalo de confiança $ (1-\alpha )\times $ 100% com limites:

• $ LI=\hat{c}_j-ME,\quad \text{Limite Inferior} $
• $ LS=\hat{c}_j+ME,\quad \text{Limite Superior}\quad j=1,\dots,m $
• Teste de Hipóteses:

Outro modo de avaliarmos os efeitos, é através do teste de hipóteses:

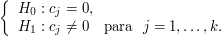
Para isto, calculamos a estatística de Lenth, dada por:

$$T_{L_j}=\frac{|\hat{c}_j|}{PSE}\sim t_{(d)},\quad j=1,\dots,k$$

sendo $ PSE $ o pseudo erro padrão, $ d $ o número de contrastes dividido por 3 e $ t_{(d)} $ a distribuição t-Student com $ d $ graus de liberdade. Portanto, obtemos a seguinte regra de decisão para um nível de significância $ \alpha. $

• Se $ |T_{L_j}| > t_{(d;1-\alpha/2)} $ rejeitamos $ H_0, $ ou seja, o efeito é significativo do ponto de vista estatístico;
• Se $ |T_{L_j}| \leq t_{(d;1-\alpha/2)} $ não rejeitamos $ H_0, $ ou seja, efeito não é significativo do ponto de vista estatístico.
• P-valor:

representa o menor nível de significância para o qual rejeitamos $ H_0 $. Logo, para um nível de significância = 0,05 adotado, rejeitamos $ H_0 $ se o P-valor obtido for menor que 0,05, enquanto que não rejeitamos $ H_0 $ se o P-valor for maior que 0,05. Para o teste t, o P-valor é calculado na forma

$$\text{p-valor}=2\times P[t_d>|T_{L_j}|~|~H_0]$$

Com isso, rejeitamos $ H_0 $ quando o p-valor for menor que o nível de significância $ \alpha $ proposto (usualmente 0,05), caso contrário (p-valor > $ \alpha $) não rejeitamos $ H_0. $

Exemplo 1.8.1

A seguir, apresentamos os dados coletados. Sete parâmetros analíticos foram selecionados e pequenas variações foram induzidas nos valores nominais do método.

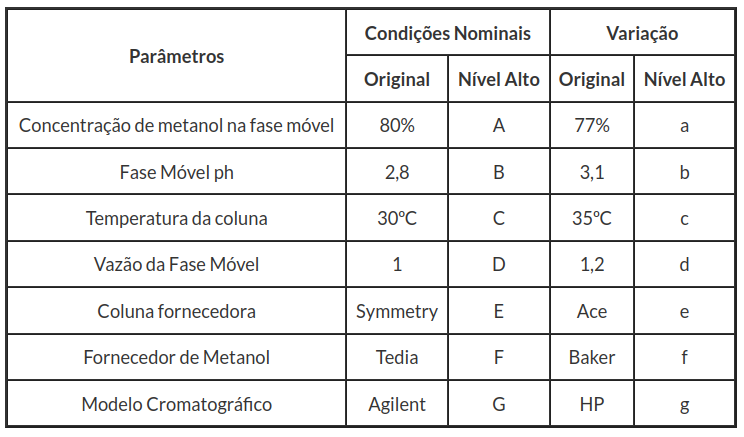
Tabela 3.3.3: Parâmetros analíticos.

Utilizando o experimento de Youden obtemos a seguinte tabela:

P1	P2	P3	P4	P5	P6	P7	Resposta
1	1	1	1	1	1	1	99,63
1	1	-1	1	-1	-1	-1	99,8
1	-1	1	-1	1	-1	-1	99,85
1	-1	-1	-1	-1	1	1	99,63
-1	1	1	-1	-1	1	-1	99,48
-1	1	-1	-1	1	-1	1	99,64
-1	-1	1	1	-1	-1	1	99,6
-1	-1	-1	1	1	1	-1	99,51

Tabela 3.3.4: Conjunto de dados.

A seguir, calculamos o limite de detecção através do software Action Stat e obtemos os seguintes resultados:

1. Primeiramente acessamos a Análise de Robustes no Action Stat através do menu: Action Stat -> Validação de Metodologia -> Robustez -> Análise

(imagem em falta)

2. O próximo passo é preencher a janela da análise de robustez. Selecionamos os dados e clicamos no botão Ler. Depois basta indicar qual é a coluna com a variável resposta e montar a formula completa. Clicamos em Ok e obtemos os resultados.

(imagem em falta)

A seguir, apresentamos os resultados obtidos pelo software Action Stat.

(imagem em falta)

Tabela 1: Resultados do experimento fatorial sem réplicas.

(imagem em falta)

Tabela 2: Valores dos efeitos em módulo versus escores da distribuição Half-Normal,

(imagem em falta)

Figura 1: Lenth Plot para robustez.

(imagem em falta)

Figura 2: Daniel plot para robustez.

Das figuras 1 e 2 , temos indícios que os parâmetros P1 e P6 interferem no método. Agora, testamos as hipóteses:

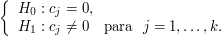
Da tabela 1 obtemos que os parâmetros P1 e P6 interferem no método ao nível de signficância de 5%. Portanto, a menos dos parâmetros P1 e P6, o método é robusto.